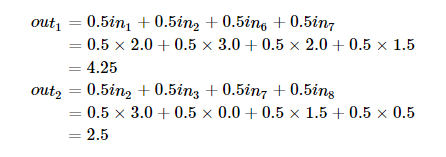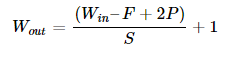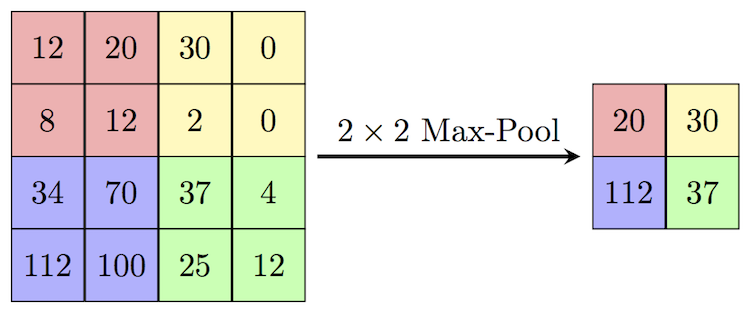В предыдущем вводном туториале по нейронным сетям была создана трехслойная архитектура для классификации рукописных символов датасета MNIST. В конце туториала была показана точность приблизительно 86%. Для простого датасета, как MNIST, это плохое качество. Дальнейшая оптимизация смогла улучшить результат плотно соединенной сети до 97-98% точности. Это уже намного лучше, но всё еще не достаточно для MNIST. Требуется более современный метод, который может действительно называться глубоким обучением. В данном туториале представлен такой метод — сверточная нейронная сеть (Convolutional Neural Network, CNN), который достигает высоких результатов в задачах классификации картинок. В частности, будет рассмотрена и теория, и практика реализации CNN при помощи PyTorch.
PyTorch — набирающий популярность мощный фреймворк глубокого машинного обучения. Его особенность — он чувствует себя как дома в Python, а прототипирование осуществляется очень быстро. Туториал не предполагает больших знаний PyTorch. Весь код для сверточной нейронной сети, рассмотренной здесь, находится в этом репозитории. Давайте приступим.
Особенности CNN
Полностью соединенная нейросеть с несколькими слоями может много, но чтобы показать действительно выдающиеся результаты в задачах классификации, необходимо идти глубже. Другими словами, требуется использовать намного больше слоев в сети. Однако, добавление многих новых слоев влечет проблемы. Во-первых, сталкиваемся с проблемой забывания градиента, хотя это и можно решить при помощи чувствительной функции активации — семейства ReLU функций. Другая проблема с глубокими полностью соединенными сетями — количество весов для тренировки быстро растет. Это означает, что процесс тренировки замедляется или становится практически невыполнимым, а модель может переобучаться. Тем не менее, решение есть.
Сверточные нейронные сети пытаются решить вторую проблему, используя корреляции между смежными входами в картинках или временных рядах. Например, на картинке с котиком и собачкой пиксели, близкие к глазам котика, более вероятно будут коррелировать с расположенными рядом пикселями на его носу, чем с пикселями носа собаки на другой стороне картинки. Это означает, что нет необходимости соединять каждый узел с каждым в следующем слое. Такой прием уменьшает количество весовых параметров для тренировки модели. CNN также имеют и другие особенности, улучшающие процесс тренировки, которые будут рассмотрены в других главах.
Принцип работы CNN
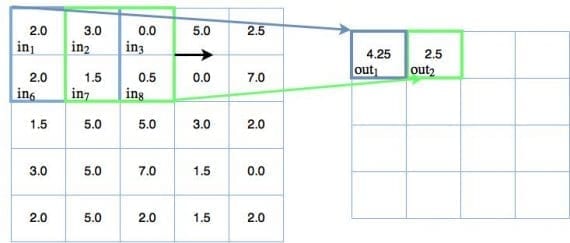
Свертка — фактически главное, что необходимо понять о сверточных нейронных сетях. Этот замысловатый математический термин нужен для движущегося окна или фильтра по исследуемому изображению. Перемещающееся окно применяется к определенному участку узлов, как показано ниже. Где примененный фильтр — ( 0.5 * значение в узле):
На диаграмме показаны только два выходных значения, каждое из которых отображает входной квадрат размера 2×2. Вес отображения для каждого входного квадрата, как ранее упоминалось, равен 0.5 для всех четырех входов (inputs). Поэтому выход может быть посчитан так:
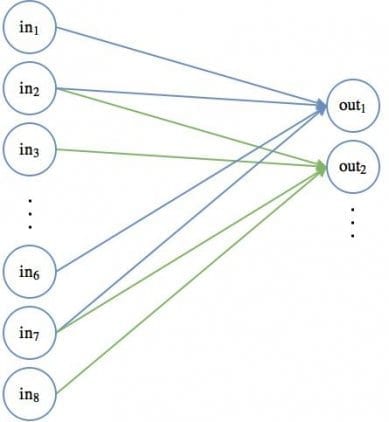
В сверточной части нейронной сети можно представить, что такой движущийся 2 х 2 фильтр скользит по всем доступным узлам или пикселям входного изображения. Такая операция может быть проиллюстрирована с использованием стандартных диаграмм узлов нейронных сетей:
Первое положение связей движущегося фильтра показано синей линией, второе — зеленой. Веса для каждых таких соединений равны 0.5.
Вот несколько вещей в сверточном шаге, которые ускоряют процесс тренировки, сокращая количество параметров, весов:
- Редкие связи — не каждый узел в первом (входном) слое соединен с каждым узлом во втором слое. Этим отличается архитектура CNN от полностью связанной нейронной сети, где каждый узел соединен со всем другими в следующем слое.
- Постоянные параметры фильтра. Другими словами, при движении фильтра по изображению одинаковые веса применяются для каждого 2 х 2 набора узлов. Каждый фильтр может быть обучен для выполнения специфичных трансформаций входного пространства. Следовательно, каждый фильтр имеет определенный набор весов, которые применяются для каждой операции свертки. Этот процесс уменьшает количество параметров. Нельзя говорить, что любой вес постоянен внутри отдельного фильтра. В примере выше веса были [0.5, 0.5, 0.5, 0.5], но ничего не мешало им быть и [0.25, 0.1, 0.8, 0.001]. Выбор конкретных значений зависит от обучения каждого фильтра.
Эти два свойства сверточных нейронный сетей существено уменьшают количество параметров для тренировки, по сравнению с полносвязными сетями.
Следующий шаг в структуре CNN — прохождение выхода операции свертки через нелинейную активационную функцию. Речь идет о некотором подвиде ReLU, который обеспечивает известное нелинейное поведение этой нейронной сети.
Процесс, использующийся в сверточном блоке, называется признаковым отображением (feature mapping). Название основано на идее, что каждый сверточный фильтр может быть обучен для поиска различных признаков в изображении, которые затем могут быть использованы в классификации. Перед разговором о следующем свойстве CNN, называемом объединением (pooling), рассмотрим идею признакового отображения и каналов.
Отображение признаков и мультиканальность
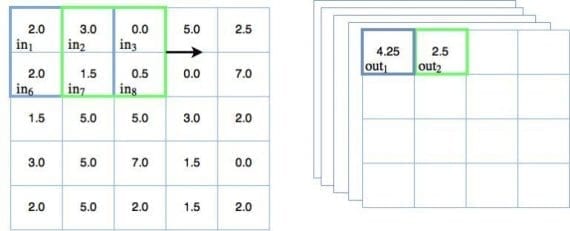
Поскольку веса отдельных фильтров остаются постоянными, будучи примененными на входных узлах, они могут обучаться выбирать определенные признаки из входных данных. В случае изображений, архитектура способна учиться различать общие геометрические объекты — линии, грани и другие формы исследуемого объекта. Вот откуда взялось определение признакового отображения. Из-за этого любой сверточный слой нуждается в множестве фильтров, которые тренируются детектировать различные признаки. Следовательно, необходимо дополнить предыдущую диаграмму движущегося фильтра следующим образом:
Теперь в правой части рисунка можно видеть несколько сложенных (stacked) выходов операции свертки. Их несколько, потому что существует несколько обучаемых фильтров, каждый из которых производит собственный 2D выход (в случае 2D изображения). Такое множество фильтров часто в глубоком обучении часто называют каналами. Каждый канал должен обучаться для выделения на изображении определенного ключевого признака. Выход сверточного слоя для черно-белого изображения, как в датасете MNIST, имеет 3 измерения — 2D для каждого из каналов и еще одно для их числа.
Если входной объект мультиканальный, то в случае цветного RGB изображения (один канал для каждого цвета) выход будет четырехмерным. К счастью, любая библиотека глубокого обучения, включая PyTorch, легко справляется с отображением. Наконец, не стоит забывать, что операция свертки проходит через активационную функцию в каждом узле.
Следующая важная часть сверточных нейронных сетей — концепция, называемая пулингом.
Объединение (Pooling)
Основными преимуществами для пулинга в сверточной нейронной сети являются:
- Уменьшение количества параметров в вашей модели благодаря процессу даунсемплинга (down-sampling).
- Детектирование признаков становится более правильным при изменении ориентации или размера объекта.
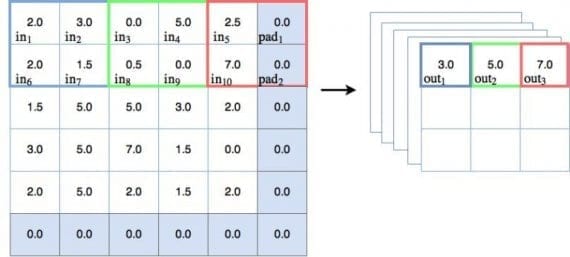
Пулинг — другой тип техники скользящего окна, где вместо применения обучаемых весов используется статистическая функция некоторого типа по содержимому этого окна. Наиболее частый тип пулинга — max pooling, который применяет функцию max(). Есть и другие варианты — mean pooling (который применяет функцию усреднения по содержимому окна), которые применяются в особых случаях. В этом туториале мы будем концентрироваться на max pooling. На рисунке ниже показано, как работает операция max pooling:
Давайте пройдемся по некоторым пунктам, связанным с диаграммой:
Основы
На диаграмме можно наблюдать действие max pooling. Для первого окна голубого цвета max pooling выдает значение 3.0, которое является максимальным значением узла в 2х2 окне. Таким же образом зеленое окно выводит максимальное значение, равно 5.0, а для красного окна максимальное значение — 7.0. Здесь всё просто и понятно.
Шаги и даунсемплинг
На диаграмме сверху можно заметить, что пулинговое окно каждый раз перемещается на 2 места. Можем говорить, что шаг равен 2. На диаграмме показаны шаги только вдоль оси x, но для задачи предотвращения перекрытия окна, шаг должен быть также равен 2 и в направлении y. Другими словами, шаг обозначается как [2,2]. Следует упомянуть, если во время пулинга шаг больше 1, тогда размер выхода будет уменьшен. Как можно видеть на диаграмме, входной объект размера 5×5 уменьшается до 3х3 на выходе. И это хорошо — такое явление называется даунсемплингом и уменьшает количество обучаемых параметров в модели.
Padding
Важно отметить также, что в пулинговой диаграмме есть дополнительный столбец и строка, добавленные к входу размера 5х5, делающие эффективный размер пулингового пространства равным 6х6. Это делается для того, чтобы пулинговое окно размером 2х2 корректно работало с шагом [2,2]. Такой прием называется padding. Padding-узлы зачастую фиктивные, так как значения на них равны 0, и операция max pooling их не видит. Этот факт нужно будет учитывать при создании нашей сверточной сети на PyTorch.
Теперь мы разобрались в механизме работы пулинга в CNN, выяснили его полезность в осуществлении даунсемплинга. Рассмотрим еще его некоторые функции и ответим на вопрос, почему max pooling используется так часто.
Использование пулинга в сверточных нейронных сетях
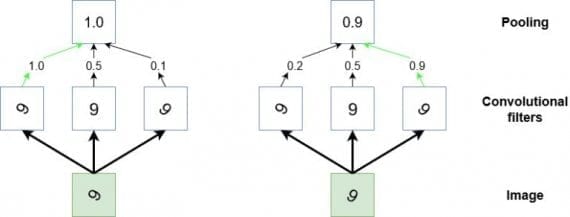
В дополнении к функции даунсемплинга пулинг используется в CNN, чтобы детектировать определенные признаки, инвариантные к изменениям размера или ориентации. Другой способ представить действие пулинга — он обобщает низкоуровневую, сложно структурированную информацию. Представим случай, когда у нас есть сверточный фильтр, который во время тренировки обучается распознавать знак «9» в различных положениях на входном изображении. Чтобы сверточная сеть научилась корректно классифицировать появление «9» на картинке, требуется каким-то образом активировать сеть каждый раз, когда эта цифра появляется на изображении независимо от размера и ориентации (кроме случая, когда «9» напоминает «9»). Пулинг может помочь в такой задаче выбора высокоуровневых, обобщенных признаков. Этот процесс иллюстрирован ниже:
Диаграмма — стилизованное представление операции пулинга. Если мы считаем, что маленький участок входного изображения содержит цифру 9 (зеленый квадрат), и предполагаем, что пытаемся детектировать эту цифру на изображении. В таком случае несколько сверточных фильтров обучаются активироваться с помощью ReLU функции каждый раз, когда они видят «9» на картинке. Однако, они будут активироваться более или менее сильно в зависимости от того, как она расположена. Мы хотим научить сеть обнаруживать цифру на изображении независимо от ее ориентации. Здесь наступает черед пулинга. Он«смотрит» на выходы трех фильтров и берет настолько высокое значение, насколько высокий порог функций активации этих фильтров.
Следовательно, пулинг выступает в качестве механизма обобщения низкоуровневых данных и позволяет нейросети переходить от данных с высоким разрешением до информации с более низким разрешением. Другими словами, пулинг в паре со сверточными фильтрами делают возможным детектирование объекта на изображении.
Общий взгляд
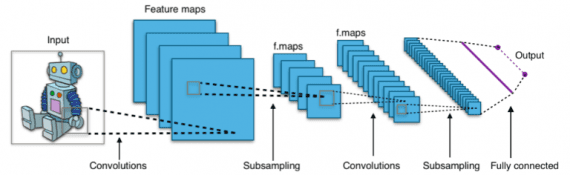
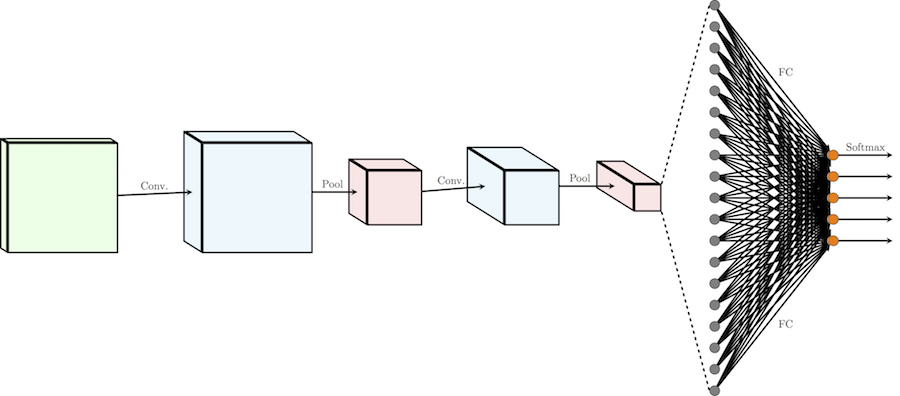
Ниже представлено изображение из Википедии, которое показывает структуру полностью разработанной сверточной нейронной сети:
Если смотреть на рисунок сверху слева направо, сначала мы видим изображение робота. Далее серия сверточных фильтров сканирует входное изображение для отображения признаков. Из выходов этих фильтров операции пулинга выбирают подвыборку. После этого идет следующий набор сверток и пулинга на выходе из первого набора операций пулинга и свертки. Наконец, на выходе нейросети находится прикрепленный полносвязный слой, смысл которого нуждается в объяснении.
Полносвязный слой
Ранее обсуждалось, сверточная нейронная сеть берет данные высокого разрешения и эффективно трансформирует их в представления объектов. Полносвязный слой может рассматриваться как стандартный классификатор над богатым информацией выходом нейросети для интерпретации и финального предсказания результата классификации. Для прикрепления полносвязного слоя к сети измерения выхода CNN необходимо «расплющить».
Рассматривая предыдущую диаграмму, на выходе имеем несколько каналов x x y тензоров/матриц. Эти каналы необходимо привести к одному (N x 1) тензору. Возьмем пример: имеем 100 каналов с 2х2 матрицами, отображающими выход последней пулинг операции в сети. В PyTorch можно легко осуществить преобразование в 2х2х100 = 400 строк, как будет показано ниже.
Теперь, когда основы сверточных нейронных сетей заложены, настало время реализовать CNN с помощью PyTorch.
Реализация CNN на PyTorch
Любой достойный фреймворк глубокого обучения может с легкостью справиться с операциями сверточной нейросети. PyTorch является таким фреймворком. В данном разделе будет показано, как создавать CNN с помощью PyTorch шаг за шагом. В идеале вы должны обладать некоторым представлением о PyTorch, но это не обязательно. Мы хотим разработать нейронную сеть для классификации символов в датасете MNIST. Полный код к этому туториалу находится в этом репозитории на GitHub.
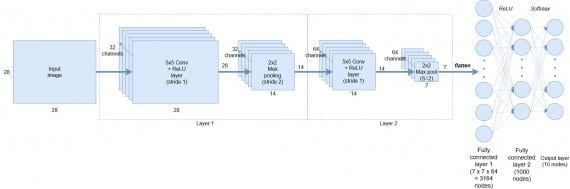
Мы собираемся реализовать следующую архитектуру сверточной сети:
В самом начале на вход подаются черно-белые представления символов размером 28х28 пикселей каждое. Первый слой состоит из 32 каналов сверточных фильтров размера 5х5 + активационная функция ReLU, затем идет 2х2 max pooling с даунсемплингом с шагом 2 (этот слой выводит данные размером 14х14). На следующий слой подается выход с первого слоя размера 14х14, который сканируется снова 5х5 сверточными фильтрами с 64 каналов, затем следует 2х2 max pooling с даунсемплингом для генерирования выхода размером 7х7.
После сверточной части сети следует:
- операция выравнивания, которая создает 7х7х64=3164 узлов
- средний слой из 1000 полносвязных улов
- операция softmax над крайними 10 узлами для генерирования вероятностей классов.
Эти слои представлены в выходном классификаторе.
Загрузка датасета
В PyTorch уже интегрирован датасет MNIST, который мы можем использовать при помощи функции DataLoader. В этом подразделе выясним, как установить загрузчик данных для датасета MNIST. Но для начала нужно определить предварительные переменные:
num_epochs = 5 num_classes = 10 batch_size = 100 learning_rate = 0.001 DATA_PATH = 'C:UsersAndyPycharmProjectsMNISTData' MODEL_STORE_PATH = 'C:UsersAndyPycharmProjectspytorch_models'
Прежде всего, устанавливаем тренировочные гиперпараметры. Далее идет спецификация пути папки для хранения датасета MNIST (PyTorch автоматически загрузит датасет в эту папку) и локации для тренировочных параметров модели после того, как обучение будет завершено.
Далее задаем преобразование для применения к MNIST и переменные для данных:
trans = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) train_dataset = torchvision.datasets.MNIST(root=DATA_PATH, train=True, transform=trans, download=True) test_dataset = torchvision.datasets.MNIST(root=DATA_PATH, train=False, transform=trans)
Первое, на что необходимо обратить внимание в коде сверху, это функция transform.Compose(). Функция находится в пакете torchvision. Она позволяет разработчику делать различные манипуляции с указанным датасетом. Численные трансформации могут быть соединены вместе в список при использовании функции Compose(). В этом случае сначала устанавливается преобразование, которое конвертирует входной датасет в PyTorch тензор. PyTorch тензор — особый тип данных, используемый в библиотеке для всех различных операций с данными и весами внутри нейросети. По сути, такой тензор — простая многомерная матрица. Но в любом случае, PyTorch требует преобразования датасета в тензор таким образом, что его можно использовать для тренировки и тестирования сети.
Следующий аргумент в списке Compose() — нормализация. Нейронная сеть обучается лучше, когда входные данные нормализованы так, что их значения находятся в диапазоне от -1 до 1 или от 0 до 1. Чтобы это сделать с помощью нормализации PyTorch, необходимо указать среднее и стандартное отклонение MNIST датасета, которые в этом случае равны 0.1307 и 0.3081 соответственно. Отметим, среднее значение и стандартное отклонение должны быть установлены для каждого входного канала. У MNIST есть только один канал, но уже для датасета CIFAR c 3 каналами (по одному на каждый цвет из RGB спектра) надо указывать среднее и стандартное отклонение для каждого.
Далее необходимо создать объекты train_dataset и test_dataset, которые будут последовательно проходить через загрузчик данных. Чтобы создать такие датасеты из данных MNIST, требуется задать несколько аргументов. Первый — путь до папки, где хранится файл с данными для тренировки и тестирования. Логический аргумент train показывает, какой файл из train.pt или test.pt стоит брать в качестве тренировочного сета. Следующий аргумент — transform, в котором мы указываем ранее созданный объект trans, который осуществляет преобразования. Наконец, аргумент загрузки просит функцию датасета MNIST загрузить при необходимости данные из онлайн источника.
Теперь когда тренировочный и тестовый датасеты созданы, настало время загрузить их в загрузчик данных:
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size,shuffle=True) test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)
Объект загрузчик данных в PyTorch обеспечивает несколько полезных функций при использовании тренировочных данных:
- Возможность легко перемешивать данные.
- Возможность группировать данные в партии.
- Более эффективное использование данных с помощью параллельной загрузки, используя многопроцессорную обработку.
Как можно видеть, требуется задать три простых аргумента. Первый — данные, которые вы хотите загрузить; второй — желаемый размер партии; третий — перемешивать ли случайным образом датасет. Загрузчик может использоваться в качестве итератора. Поэтому для извлечения данных мы можем просто воспользоваться стандартным итератором Python, например, перечислением. Такая возможность будет позже продемонстрирована на практике в туториале.
Создание модели
На этом шаге необходимо задать класс nn.Module, определяющий сверточную нейронную сеть, которую мы хотим обучить:
class ConvNet(nn.Module): def __init__(self): super(ConvNet, self).__init__() self.layer1 = nn.Sequential( nn.Conv2d(1, 32, kernel_size=5, stride=1, padding=2), nn.ReLU(), nn.MaxPool2d(kernel_size=2, stride=2)) self.layer2 = nn.Sequential( nn.Conv2d(32, 64, kernel_size=5, stride=1, padding=2), nn.ReLU(), nn.MaxPool2d(kernel_size=2, stride=2)) self.drop_out = nn.Dropout() self.fc1 = nn.Linear(7 * 7 * 64, 1000) self.fc2 = nn.Linear(1000, 10)
Это то место, где определяется модель. Наиболее простой способ создания структуры нейронной сети в PyTorch — создание наследственного класса от материнского nn.Module. Класс nn.Module очень полезен в PyTorch, он содержит всё необходимое для конструирования типичной глубокой нейронной сети. Кроме этого, класс имеет удобные функции: способы перемещения переменных и операций на GPU или обратно на CPU, применение рекурсивных функций через все свойства в классе (например, перенастройка всех весовых переменных), создание оптимизированных интерфейсов для тренировки и тому подобное. Все доступные методы можно посмотреть здесь.
Первый шаг — создание нескольких объектов последовательного слоя с помощью функции class _init_. Сначала создаем слой 1 (self.layer1) через создание объекта nn.Sequential. Этот метод позволяет создавать упорядоченные слои в сети и является удобным способом создания последовательности свертка + ReLu + пулинг. Как можно видеть, первый элемент в определении этой последовательности — метод Conv2d, который создает набор сверточных фильтров. В этом методе первый аргумент — количество входных каналов; в нашем случае изображения MNIST черно-белые и количество каналов равно 1. Второй аргумент в Conv2d — количество выходных каналов; как показано на диаграмме архитектуры модели, первый слой сверточных фильтров состоит из 32 каналов, поэтому значение второго аргумента равно 32.
Аргумент kernel_size отвечает за размер сверточного фильтра, в нашем случае мы хотим фильтр размеров 5х5, поэтому аргумент равен 5. Если бы мы хотели фильтры с разными размерными формами по оси х и y, необходимо было указать параметры в виде python tuple (размер по х, размер по y). Наконец, мы хотим установить padding, что делается несколько сложнее. Размер измерения на выходе от операции сверточной фильтрации или пулинга может быть посчитан с помощью уравнения:
Где W(in) — ширина выхода, F — размер фильтра, P — паддинг, S — шаг. Такая же формула применима для расчета высоты. В нашем случае изображение и фильтрация симметричны, поэтому формула применима и к ширине и к высоте. Если хотим оставить входные и выходные измерения без изменений с размером фильтра 5 и шагом 1, то исходя из верхней формулы паддинг нужно задать равным 2. Таким образом, аргумент для паддинга в Conv2d равен 2.
Следующий аргумент в последовательности — простая ReLU функция активации. Последний элемент в последовательном определении для self.layer1 — операция max pooling. Первый аргумент — размер объединения, который равен 2х2; следовательно, аргумент равен 2. Во втором аргументе мы хотим взять подвыборку из данных через уменьшение эффективного размера изображения с факторов 2. Чтобы это сделать используя формулу выше, устанавливаем шаг равным 2 и паддинг равным 0. Следовательно, шаговый аргумент равен 2. Паддинг аргумент по умолчанию равен 0, если не указано другое значение, что сделано в коде сверху. Из этих вычислений теперь понятно, что выход слоя self.layer1 имеет 32 канала и “изображения” размером 14х14.
Второй слой, self.layer2, определяется таким же образом, как и первый. Единственное отличие здесь — вход в функцию Conv2d теперь 32 канальный, а выход — 64 канальный. Следуя такой же логике и учитывая пулинг и даунсемплинг, выход из self.layer2 представляет из себя 64 канала изображения размера 7х7.
Далее определяем отсеивающий слой для предотвращения переобучения модели. В конце создаем два полносвязных слоя. Первый слой имеет размер 7х7х64 узла и соединяется со вторым слоем с 1000 узлами. Чтобы создать полносвязный слой в PyTorch, используем метод nn.Linear. Первый аргумент метода — число узлов в данном слое, второй аргумент — число узлов в следующем слое.
Определение слоев создано при помощи _init_. Следующий шаг — определить потоки данных через слои при прямом прохождении через сеть:
def forward(self, x): out = self.layer1(x) out = self.layer2(out) out = out.reshape(out.size(0), -1) out = self.drop_out(out) out = self.fc1(out) out = self.fc2(out) return out
Здесь важно назвать функцию “forward”, так как она будет использовать базовую функцию прямого распространения в nn.Module и позволит всему функционалу nn.Module работать корректно. Как можно видеть, функция принимает на вход аргумент х, представляющий собой данные, которые должны проходить через модель (например, партия данных). Направляем эти данные в первый слой (self.layer1) и возвращаем выходные данные как out. Эти выходные данные поступают на следующий слой и так далее. Отметим, после self.layer2 применяем функцию преобразования формы к out, которая разглаживает размеры данных с 7х7х64 до 3164х1. После двух полносвязных слоев применяется dropout-слой и из функции возвращается финальное предсказание.
Мы определили, что такое сверточная нейронная сеть, и как она работает. Настало время обучить нашу модель.
Обучение модели
Перед тренировкой модели мы должны сначала создать экземпляр (instance) нашего класса ConvNet(), определить функцию потерь и оптимизатор:
model = ConvNet() criterion = nn.CrossEntropyLoss() optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
Экземпляр класса ConvNet() создается под названием model. Далее определяем операцию над потерями, которая будет использоваться для подсчета потерь. В нашем случае используем доступную в PyTorch функцию CrossEntropyLoss(). Вы уже могли заметить, что мы еще не задали активационную функцию SoftMax для последнего слоя, выполняющего классификацию. Это сделано потому, что функция CrossEntropyLoss() объединяет и SoftMax и кросс-энтропийную функцию потерь в единую функцию. Далее определяем оптимизатор Adam. Первым аргументом функции являются параметры, которые мы хотим обучить оптимизатором. Это легко сделать с помощью класса nn.Module, из которого вы получается ConvNet. Всё что нужно сделать — снабдить функцию аргументом model.parameters() и PyTorch будет отслеживать все параметры нашей модели, которые необходимо обучить. Последним определяется скорость обучения.
Тренировочный цикл выглядит следующим образом:
total_step = len(train_loader) loss_list = [] acc_list = [] for epoch in range(num_epochs): for i, (images, labels) in enumerate(train_loader): # Прямой запуск outputs = model(images) loss = criterion(outputs, labels) loss_list.append(loss.item()) # Обратное распространение и оптимизатор optimizer.zero_grad() loss.backward() optimizer.step() # Отслеживание точности total = labels.size(0) _, predicted = torch.max(outputs.data, 1) correct = (predicted == labels).sum().item() acc_list.append(correct / total) if (i + 1) % 100 == 0: print('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}, Accuracy: {:.2f}%' .format(epoch + 1, num_epochs, i + 1, total_step, loss.item(), (correct / total) * 100))
Самыми важными частями для начала являются два цикла. Первый цикл проходит по количеству эпох, в нём итерации проходят по train_loader используя перечисление. Во внутреннем цикле сначала считаются выходы прямого прохождения изображений (которые представляют собой партии нормализованных MNIST изображений из train_loader). Отметим, нам не требуется вызывать model.forward(images), так как nn.Module знает, что нужно вызывать forward при выполнении model(images).
Следующий шаг — отправление выходов модели и настоящих меток в функцию CrossEntropyLoss, определенную как criterion. Потери добавляются в список, который будет использован позже для отслеживания прогресса обучения. Затем — выполнение обратного распространения ошибки и оптимизированного шага тренировки. Сначала градиенты должны быть обнулены, что легко делается вызовом zero_grad() на оптимизаторе. Далее вызываем функцию .backward() на переменной loss для выполнения обратного распространения. Теперь, когда градиенты посчитаны при обратном распространении, просто вызываем optimizer.step() для выполнения шага обучения оптимизатора Adam. PyTorch делает процесс обучения модели очень легким и интуитивным.
Следующий набор строк отвечает за отслеживание точности на тренировочном сете. Предсказания модели могут быть определены с помощью функции torch.max(), которая возвращает индекс максимального значения в тензоре. Первый аргумент этой функции — тензор, который мы хотим исследовать; второй — ось, по которой определяется максимум. Выходящий из модели тензор должен иметь размер (batch_size,10). Чтобы определить предсказание модели, необходимо для каждого примера в партии найти максимальные значения из 10 выходных узлов. Каждый из этих узлов будет соответствовать одному рукописному символу (например, выход 2 равен символу «2» и так далее). Выходной узел с наибольшим значением и будет предсказанием модели. Следовательно, надо задать второй аргумент в функции torch.max() равным 1, что указывает функции максимума проверить ось выходного узла (axis = 0 соответствует размерности batch_size).
На этом шаге возвращается список целочисленных предсказаний модели, а следующая строка сравнивает эти предсказания с настоящими метками (predicted == labels) и суммирует правильные предсказания. Отметим, что на этом шаге выход функции sum() всё еще тензор, поэтому для оценки его значений требуется вызвать .item(). Делим количество правильных предсказаний на размер партии batch_size (эквивалентно labels.size(0)) для подсчета точности. Наконец, во время тренировки после каждых 100 итераций внутреннего цикла выводим прогресс.
Результаты тренировки будут выглядеть следующим образом:
Epoch [1/6], Step [100/600], Loss: 0.2183, Accuracy: 95.00%
Epoch [1/6], Step [200/600], Loss: 0.1637, Accuracy: 95.00%
Epoch [1/6], Step [300/600], Loss: 0.0848, Accuracy: 98.00%
Epoch [1/6], Step [400/600], Loss: 0.1241, Accuracy: 97.00%
Epoch [1/6], Step [500/600], Loss: 0.2433, Accuracy: 95.00%
Epoch [1/6], Step [600/600], Loss: 0.0473, Accuracy: 98.00%
Epoch [2/6], Step [100/600], Loss: 0.1195, Accuracy: 97.00%
Теперь напишем код для определения точности на тестовом наборе.
Тестирование
Для тестирования модели используем следующий код:
model.eval() with torch.no_grad(): correct = 0 total = 0 for images, labels in test_loader: outputs = model(images) _, predicted = torch.max(outputs.data, 1) total += labels.size(0) correct += (predicted == labels).sum().item() print('Test Accuracy of the model on the 10000 test images: {} %'.format((correct / total) * 100)) # Сохраняем модель и строим график torch.save(model.state_dict(), MODEL_STORE_PATH + 'conv_net_model.ckpt')
В первой строке устанавливаем режим оценки используя model.eval(). Это удобная функция запрещает любые исключения или слои нормализации партии в модели, которые будут мешать объективной оценке. Конструкция torch.no_grad() выключает функцию автоградиента в модели, так как она не нужна при тестировании/оценке модели и замедляет вычисления. Остальная часть кода совпадает с вычислением точности во время тренировки, за исключением того, что в этом случае итерации проходят по test_loader.
Наконец, результат выводится в консоль, а модель сохраняется при помощи функции torch.save().
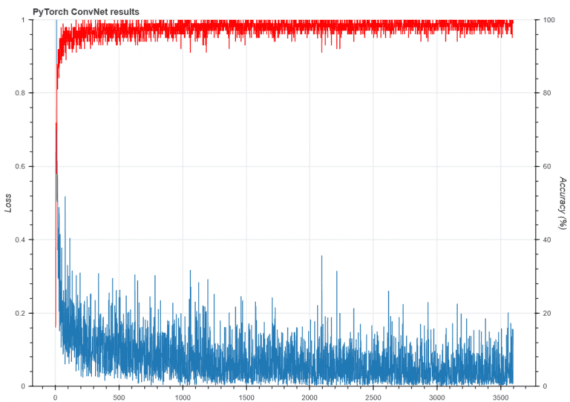
В последней части кода в этом репозитории на GitHub дополнительно построен график отслеживания точности и потерь, используя библиотеку для рисования Bokeh. Финальный результат выглядит так:
Точность на тестовой выборке на 10000 картинках составляет 99.03%
Можно видеть, сеть достаточно быстро достигает высокого уровня точности на тренировочном сете. На тестовом наборе после 6 эпох модель показывает точность 99%, что очень хорошо. Этот результат определенно лучше точности базовой полносвязной нейронной сети.
Как итог: в туториале были показаны все преимущества и структура сверточной нейронной сети, механизм её работы. Вы также научились реализовывать CNN в библиотеке глубокого обучения PyTorch, которая имеет большое будущее.
Интересные статьи:
- Как создать чат-бота с нуля на Python: подробная инструкция
- Как создать собственную нейронную сеть с нуля на языке Python
- Как создать собственный датасет из картинок Google
This tutorial demonstrates training a simple Convolutional Neural Network (CNN) to classify CIFAR images. Because this tutorial uses the Keras Sequential API, creating and training your model will take just a few lines of code.
Import TensorFlow
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
import matplotlib.pyplot as plt
2022-12-14 02:35:18.952623: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer.so.7'; dlerror: libnvinfer.so.7: cannot open shared object file: No such file or directory 2022-12-14 02:35:18.952732: W tensorflow/compiler/xla/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libnvinfer_plugin.so.7'; dlerror: libnvinfer_plugin.so.7: cannot open shared object file: No such file or directory 2022-12-14 02:35:18.952748: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Cannot dlopen some TensorRT libraries. If you would like to use Nvidia GPU with TensorRT, please make sure the missing libraries mentioned above are installed properly.
Download and prepare the CIFAR10 dataset
The CIFAR10 dataset contains 60,000 color images in 10 classes, with 6,000 images in each class. The dataset is divided into 50,000 training images and 10,000 testing images. The classes are mutually exclusive and there is no overlap between them.
(train_images, train_labels), (test_images, test_labels) = datasets.cifar10.load_data()
# Normalize pixel values to be between 0 and 1
train_images, test_images = train_images / 255.0, test_images / 255.0
Downloading data from https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz 170498071/170498071 [==============================] - 3s 0us/step
Verify the data
To verify that the dataset looks correct, let’s plot the first 25 images from the training set and display the class name below each image:
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i])
# The CIFAR labels happen to be arrays,
# which is why you need the extra index
plt.xlabel(class_names[train_labels[i][0]])
plt.show()
Create the convolutional base
The 6 lines of code below define the convolutional base using a common pattern: a stack of Conv2D and MaxPooling2D layers.
As input, a CNN takes tensors of shape (image_height, image_width, color_channels), ignoring the batch size. If you are new to these dimensions, color_channels refers to (R,G,B). In this example, you will configure your CNN to process inputs of shape (32, 32, 3), which is the format of CIFAR images. You can do this by passing the argument input_shape to your first layer.
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
Let’s display the architecture of your model so far:
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 30, 30, 32) 896
max_pooling2d (MaxPooling2D (None, 15, 15, 32) 0
)
conv2d_1 (Conv2D) (None, 13, 13, 64) 18496
max_pooling2d_1 (MaxPooling (None, 6, 6, 64) 0
2D)
conv2d_2 (Conv2D) (None, 4, 4, 64) 36928
=================================================================
Total params: 56,320
Trainable params: 56,320
Non-trainable params: 0
_________________________________________________________________
Above, you can see that the output of every Conv2D and MaxPooling2D layer is a 3D tensor of shape (height, width, channels). The width and height dimensions tend to shrink as you go deeper in the network. The number of output channels for each Conv2D layer is controlled by the first argument (e.g., 32 or 64). Typically, as the width and height shrink, you can afford (computationally) to add more output channels in each Conv2D layer.
Add Dense layers on top
To complete the model, you will feed the last output tensor from the convolutional base (of shape (4, 4, 64)) into one or more Dense layers to perform classification. Dense layers take vectors as input (which are 1D), while the current output is a 3D tensor. First, you will flatten (or unroll) the 3D output to 1D, then add one or more Dense layers on top. CIFAR has 10 output classes, so you use a final Dense layer with 10 outputs.
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10))
Here’s the complete architecture of your model:
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 30, 30, 32) 896
max_pooling2d (MaxPooling2D (None, 15, 15, 32) 0
)
conv2d_1 (Conv2D) (None, 13, 13, 64) 18496
max_pooling2d_1 (MaxPooling (None, 6, 6, 64) 0
2D)
conv2d_2 (Conv2D) (None, 4, 4, 64) 36928
flatten (Flatten) (None, 1024) 0
dense (Dense) (None, 64) 65600
dense_1 (Dense) (None, 10) 650
=================================================================
Total params: 122,570
Trainable params: 122,570
Non-trainable params: 0
_________________________________________________________________
The network summary shows that (4, 4, 64) outputs were flattened into vectors of shape (1024) before going through two Dense layers.
Compile and train the model
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
history = model.fit(train_images, train_labels, epochs=10,
validation_data=(test_images, test_labels))
Epoch 1/10 1563/1563 [==============================] - 10s 4ms/step - loss: 1.5316 - accuracy: 0.4406 - val_loss: 1.2891 - val_accuracy: 0.5438 Epoch 2/10 1563/1563 [==============================] - 6s 4ms/step - loss: 1.1786 - accuracy: 0.5810 - val_loss: 1.1129 - val_accuracy: 0.6107 Epoch 3/10 1563/1563 [==============================] - 6s 4ms/step - loss: 1.0249 - accuracy: 0.6390 - val_loss: 1.0288 - val_accuracy: 0.6382 Epoch 4/10 1563/1563 [==============================] - 6s 4ms/step - loss: 0.9256 - accuracy: 0.6734 - val_loss: 0.9192 - val_accuracy: 0.6806 Epoch 5/10 1563/1563 [==============================] - 6s 4ms/step - loss: 0.8491 - accuracy: 0.7019 - val_loss: 0.8938 - val_accuracy: 0.6849 Epoch 6/10 1563/1563 [==============================] - 7s 4ms/step - loss: 0.7900 - accuracy: 0.7233 - val_loss: 0.9419 - val_accuracy: 0.6702 Epoch 7/10 1563/1563 [==============================] - 6s 4ms/step - loss: 0.7399 - accuracy: 0.7398 - val_loss: 0.8676 - val_accuracy: 0.7004 Epoch 8/10 1563/1563 [==============================] - 6s 4ms/step - loss: 0.6971 - accuracy: 0.7558 - val_loss: 0.8899 - val_accuracy: 0.6975 Epoch 9/10 1563/1563 [==============================] - 6s 4ms/step - loss: 0.6560 - accuracy: 0.7680 - val_loss: 0.9169 - val_accuracy: 0.6899 Epoch 10/10 1563/1563 [==============================] - 6s 4ms/step - loss: 0.6225 - accuracy: 0.7801 - val_loss: 0.8744 - val_accuracy: 0.7137
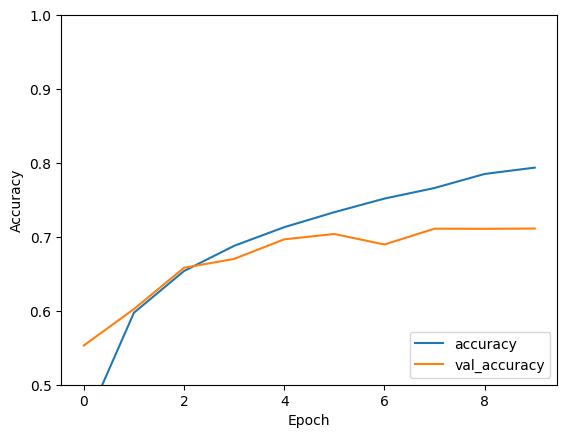
Evaluate the model
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
313/313 - 1s - loss: 0.8744 - accuracy: 0.7137 - 652ms/epoch - 2ms/step
print(test_acc)
0.713699996471405
Your simple CNN has achieved a test accuracy of over 70%. Not bad for a few lines of code! For another CNN style, check out the TensorFlow 2 quickstart for experts example that uses the Keras subclassing API and tf.GradientTape.
Комплексное руководство по сверточным нейронным сетям для чайников
В сфере Искусственного интеллекта наблюдается стремительный рывок в устранении разрыва между возможностями человека и машин. И ученые, и любители, работая над многочисленными проблемами в этой области, делают удивительные вещи. Одним из многих таких направлений является Computer Vision (компьютерное зрение).
Повестка дня в этой области состоит в том, чтобы дать возможность машинам видеть мир так, как это делают люди, воспринимать его схожим образом и даже использовать знания для множества задач, таких как Распознавание Изображений и Видео, Анализ и Классификация Изображений, Восстановление Медиа, Системы Рекомендаций, Обработка Естественного языка и т.д. Достижения в области Computer Vision и Deep Learning были разрабатывались и совершенствовались с течением времени, главным образом благодаря совершенно конкретному алгоритму — Сверточной нейронной сети (Convolutional Neural Network).
Введение

Сверточная нейронная сеть (Convolutional Neural Network — ConvNet/CNN) — это Deep Learning-алгоритм, который может принимать входное изображение, присваивать важность (усваиваемые веса и смещения) различным областям/объектам в изображении и может отличать одно от другого. Предварительной обработки в ConvNet требуется значительно меньше по сравнению с другими алгоритмами классификации. В то время как в примитивных методах фильтры сконструированы вручную, ConvNets при достаточном обучении способны изучать эти фильтры/характеристики.
Архитектура ConvNet схожа с архитектурой связности нейронов в человеческом мозге и была вдохновлена организацией зрительной коры. Отдельные нейроны реагируют на раздражители только в ограниченной зоне поля зрения, известной как рецептивное поле. Совокупность таких полей накладывается, чтобы покрыть всю зону поля зрения.
ConvNets или Feed-Forward Neural Nets (FF, FFNN — Нейронные сети прямого распространения)?

На изображении не что иное, как матрица пиксельных значений, верно? Так почему бы просто не сгладить изображение (например, матрицу изображения 3×3 по вектору 9×1) и передать его в многослойный персептрон для классификации? Ну… Все не так просто.
В случае очень простых двоичных изображений этот метод может показывать среднюю оценку точности при прогнозировании классов, но когда речь идет о сложных изображениях, имеющих повсеместную зависимость от пикселей, ни о какой точности не может идти и речи.
ConvNet хорошо умеет захватывать пространственно-временные зависимости в изображении с помощью соответствующих фильтров. Архитектура обеспечивает лучшее совпадение с набором данных изображения благодаря уменьшению количества задействованных параметров и возможности повторного использования весов. Другими словами, сеть можно научить лучше понимать сложность изображения.
Входное изображение

На рисунке у нас есть RGB-изображение, разделенное по трем цветовым плоскостям — красной, зеленой и синей. Существует несколько таких цветовых пространств, в которых существуют изображения: Grayscale (оттенки серого), RGB, HSV, CMYK и т.д.
Можете представить, что станет с вычислительными ресурсами, когда изображения достигнут размеров, скажем, 8K (7680 × 4320). ConvNet нужен, чтобы преобразовать изображения в ту форму, которую легче обрабатывать без потери характеристик, которые имеют решающую роль для получения хорошего прогноза. Это важно, когда мы хотим разработать архитектуру, которая будет не просто хороша в обучении, но еще и масштабируема для массивных наборов данных.
Сверточный слой — Кернел (the kernel)

Размеры изображения = 5 (высота) x 5 (ширина) x 1 (количество каналов, например, RGB)
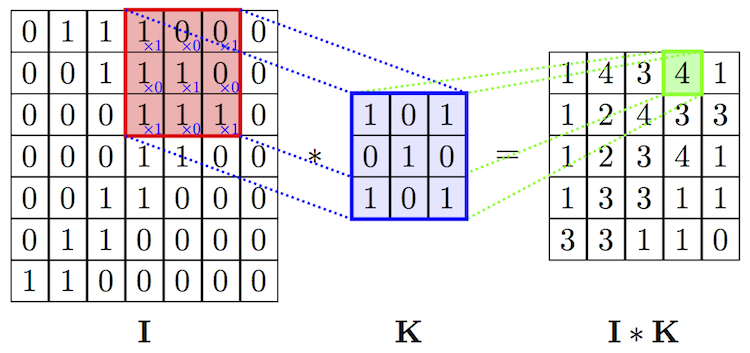
На гифке выше видно, что зеленая часть напоминает наше входное изображение 5x5x1, I. Элемент, участвующий в выполнении операции свертки в первой части сверточного слоя, называется кернелом/фильтром, K, показан желтым цветом. Мы выбрали K в качестве матрицы 3x3x1.
Кернел/Фильтр, К =1 0 10 1 01 0 1
Кернел смещается 9 раз, так как длина страйда (Stride) = 1, каждый раз выполняя операцию умножения матриц между K и частью P изображения, над которым кернел зависает.

Фильтр двигается вправо с определенным значением страйда до тех пор, пока он не проанализирует всю ширину. Двигаясь дальше, он переходит к началу (слева) изображения с тем же значением шага и повторяет процесс до тех пор, пока не будет пройдено все изображение.

В случае, когда у изображения несколько каналов (например, RGB), кернел имеет ту же глубину, что и входное изображение. Матричное умножение выполняется между стэками Kn и In ([K1, I1]; [K2, I2]; [K3, I3]), и все результаты суммируются со смещением, чтобы выдать нам сжатый выходной сигнал одной глубины.

Цель операции свертки — извлечь из входного изображения высокоуровневые признаки, например, линии, края. ConvNets вовсе не обязательно должны быть ограничены только одним сверточным слоем. Традиционно, первый ConvLayer отвечает за захват низкоуровневых признаков, таких как края, цвет, градиентная ориентация и т.д. Благодаря добавленным слоям архитектура адаптируется также к высокоуровневым признакам, выдавая нам сеть, которая имеет столь же здравое понимание изображений в наборе данных, что и мы.
Эта операция может давать два типа результатов: один, в котором свернутый признак имеет меньшую размерность по сравнению с входным, в другом же размерность либо увеличивается, либо остается неизменной. Это делается путем применения паддинга без дополнения (Valid Padding) в случае первого или паддинга с дополнением нулями (Same Padding) в случае последнего.

Когда мы преобразуем изображение 5x5x1 в изображение 6x6x1, а затем применяем к нему кернел размерностью 3x3x1, мы обнаруживаем, что размер свернутой матрицы — 5x5x1. Отсюда и название — Same-паддинг.
В то же время если мы выполним ту же операцию без паддинга, мы получим матрицу, которая имеет размеры самого кернела (3x3x1) — Valid-паддинг.
В данном репозитории хранится множество таких GIF-файлов, которые помогут вам лучше понять, как взаимодействуют паддинг и длина страйда для достижения результатов, соответствующих нашим потребностям.
Пулинговый слой (Pooling Layer)

Подобно сверточному слою, пулинговый слой необходим для уменьшения размера свернутого элемента в пространстве. Это помогает уменьшить вычислительную мощность, необходимую для обработки данных, за счет уменьшения размерности. Кроме того, это важно и для извлечения доминирующих признаков, инвариантных вращения и позиционирования, таким образом поддерживая процесс эффективного обучения модели.
Существует два типа пулинга: максимальный (Max Pooling) и средний (Average Pooling). Максимальный пулинг возвращает максимальное значение из части изображения, покрываемой кернелом. А Средний пулинг возвращает среднее всех значений из части изображения, покрываемой кернелом.
Максимальный пулинг также выступает в роли шумоподавителя (Noise Suppressant). Он полностью исключает шумовые сигналы, а также совмещает подавление шума с уменьшением размерности. Средний же пулинг просто использует уменьшение размерности как способ подавления шума. То есть можно сказать, что Max Pooling работает намного лучше, чем Average Pooling.

Сверточный слой и пулинговый слой вместе образуют i-й слой сверточной нейронной сети. В зависимости от сложности изображений количество таких слоев может быть увеличено с целью еще более точного захвата деталей низкого уровня, но ценой большей вычислительной мощности.
Выполнение описанного выше процесса позволяет модели успешно изучить признаки. Далее мы сглаживаем окончательный результат и передаем его в обычную нейронную сеть в целях классификации.
Классификация — Полностью Связанный Слой (Fully Connected Layer, FC Layer)
Добавление FC Layer — это (обычно) дешевый способ изучить нелинейные комбинации высокоуровневых признаков, представленных выходными данными сверточного слоя. FC Layer изучает возможную нелинейную функцию в этом пространстве.
Теперь, когда мы преобразовали наше входное изображение в подходящий формат для нашего многослойного персептрона, мы сведем изображение в вектор-столбец. Сглаженный вывод подается в нейронную сеть с прямой связью, и затем к каждой итерации обучения применяется обратное распространение. После серии эпох (epochs) модель способна различать доминирующие и некоторые низкоуровневые признаки изображений и классифицировать их с помощью техники Softmax.
Существуют множество архитектур доступных CNN, которые сыграли ключевую роль в построении алгоритмов, которые обеспечивают сейчас и будут обеспечивать работу Искусственного интеллекта как такового в ближайщем будущем. Некоторые из них перечисляю ниже:
- LeNet
- AlexNet
- VGGNet
- GoogLeNet
- RESNET
- ZFNet
GitHub Notebook — Распознавание рукописных цифр с использованием набора данных MNIST с TensorFlow
Источник
Глубокое обучение для новичков: распознаем изображения с помощью сверточных сетей
Время на прочтение
27 мин
Количество просмотров 94K
Введение
Представляем вторую статью в серии, задуманной, чтобы помочь быстро разобраться в технологии глубокого обучения; мы будем двигаться от базовых принципов к нетривиальным особенностям с целью получить достойную производительность на двух наборах данных: MNIST (классификация рукописных цифр) и CIFAR-10 (классификация небольших изображений по десяти классам: самолет, автомобиль, птица, кошка, олень, собака, лягушка, лошадь, корабль и грузовик).
На прошлом уроке мы ввели базовые понятия глубокого обучения и показали, как можно быстро смоделировать модели нейронных сетей с помощью фреймворка Keras. Напоследок многослойный перцептрон (MLP), содержащий два слоя, применили к MNIST, достигнув уровня точности 98.2%, причем это значение достаточно просто улучшить. Но все же полносвязный перцептрон обычно не выбирают для задач, связанных с распознаванием изображений — в этом случае намного чаще пользуются преимуществами сверточных нейронных сетей (Convolutional Neural Networks, CNN). Пройдя этот курс, вы будете понимать принцип работы и научитесь строить CNN в Keras, достигая хорошего уровня точности на CIFAR-10.
Эта статья предполагает знакомство с предыдущей статьей цикла.
Обработка изображений
Упомянутый выше многослойный перцептрон представляет собой самую мощную и возможных нейронных сетей прямого распространения. Он состоит из нескольких слоем, где каждый слой организован таким образом, что каждый нейрон в одном слое получает свою копию всех выходных данных предыдущего слоя. Эта модель идеально подходит для определенных типов задач, например, обучение на ограниченном количество более или менее неструктурированных параметров.
Тем не менее, посмотрим, что происходит с количеством параметров (весов) в такой модели, когда ей на вход поступают необработанные данные. Например, CIFAR-10 содержит 32 x 32 x 3 цветных изображений, и если мы будем считать каждый канал каждого пикселя независимым входным параметром для MLP, каждый нейрон в первом скрытом слое добавляет к модели около 3000 новых параметров! И с ростом размера изображений ситуация быстро выходит из-под контроля, причем происходит это намного раньше, чем изображения достигают того размера, с которыми обычно работают пользователи реальных приложений.
Одно из популярных решений — понижать разрешение изображений до той степени, когда MLP становится применим. Тем не менее, когда мы просто понижаем разрешение, мы рискуем потерять большое количество информации, и было бы здорово, если бы можно было осуществлять полезную первичную обработку информации еще до применения понижения качества, не вызывая при этом взрывного роста количества параметров модели.
Свертка функций
Оказывается, существует весьма эффективный способ решения этой задачи, который обращает в нашу пользу саму структуру изображения: предполагается, что пиксели, находящиеся близко друг к другу, теснее “взаимодействуют” при формировании интересующего нас признака, чем пиксели, расположенные в противоположных углах. Кроме того, если в процессе классификации изображения небольшая черта считается очень важной, не будет иметь значения, на каком участке изображения эта черта обнаружена.
Введем понятие оператора свертки. Имея двумерное изображение I и небольшую матрицу K размерности (так называемое ядро свертки), построенная таким образом, что графически кодирует какой-либо признак, мы вычисляем свернутое изображение I * K, накладывая ядро на изображение всеми возможными способами и записывая сумму произведений элементов исходного изображения и ядра:
На самом деле, точное определение предполагает, что матрица ядра будет транспонирована, но для задач машинного обучения не важно, выполнялась эта операция или нет.
На рисунках ниже схематически изображена вышеуказанная формула, а также представлен результат применения операции свертки (с двумя разными ядрами) к изображению с целью выделить контуры объекта.
Сверточные и субдискретизирующие слои
Оператор свертки составляет основу сверточного слоя (convolutional layer) в CNN. Слой состоит из определенного количества ядер (с аддитивными составляющими смещения
для каждого ядра) и вычисляет свертку выходного изображения предыдущего слоя с помощью каждого из ядер, каждый раз прибавляя составляющую смещения. В конце концов ко всему выходному изображению может быть применена функция активации
. Обычно входной поток для сверточного слоя состоит из d каналов, например, red/green/blue для входного слоя, и в этом случае ядра тоже расширяют таким образом, чтобы они также состояли из d каналов; получается следующая формула для одного канала выходного изображения сверточного слоя, где K — ядро, а b — составляющая смещения:
Обратите внимание, что так как все, что мы здесь делаем — это сложение и масштабирование входных пикселей, ядра можно получить из имеющейся обучающей выборки методом градиентного спуска, аналогично вычислению весов в многослойном перцептроне (MLP). На самом деле MLP мог бы в совершенстве справиться с функциями сверточного слоя, но времени на обучение (как и обучающих данных) потребовалось бы намного больше.
Заметим также, что оператор свертки вовсе не ограничен двухмерными данными: большинство фреймворков глубокого обучения (включая Keras) предоставляют слои для одномерной или трехмерной свертки прямо “из коробки”.
Стоит также отметить, что хотя сверточный слой сокращает количество параметров по сравнению с полносвязным слоем, он использует больше гиперпараметров — параметров, выбираемых до начала обучения.
В частности, выбираются следующие гиперпараметры:
- Глубина (depth) — сколько ядер и коэффициентов смещения будет задействовано в одном слое;
- Высота (height) и ширина (width) каждого ядра;
- Шаг (stride) — на сколько смещается ядро на каждом шаге при вычислении следующего пикселя результирующего изображения. Обычно его принимают равным 1, и чем больше его значение, тем меньше размер выходного изображения;
- Отступ (padding): заметим, что свертка любым ядром размерности более, чем 1х1 уменьшит размер выходного изображения. Так как в общем случае желательно сохранять размер исходного изображения, рисунок дополняется нулями по краям.
Как читатель уже догадался, операции свертки — не единственные операции в CNN (хотя существуют многообещающие исследования на тему “чисто-сверхточных” сетей); они чаще применяются для выделения наиболее полезных признаков перед субдискретизацией (downsampling) и последующей обработкой с помощью MLP.
Популярный способ субдискретизации изображения — слой подвыборки (также называемый слоем субдискретизации, по-английски downsampling или pooling layer), который получает на вход маленькие отдельные фрагменты изображения (обычно 2х2) и объединяет каждый фрагмент в одно значение. Существует несколько возможных способов агрегации, наиболее часто из четырех пикселей выбирается максимальный. Этот способ схематически изображен ниже.
Итого: обычная CNN
Теперь, когда у нас есть все строительные блоки, давайте рассмотрим, как выглядит обычная CNN целиком!
Обычную архитектуру CNN для распределения изображений по k классам можно разделить на две части: цепочка чередующихся слоев свертки/подвыборки (иногда с несколькими слоями свертки подряд) и несколько полносвязных слоев (принимающих каждый пиксель как независимое значение) с слоем softmax в качестве завершающего. Я не говорю здесь о функциях активации, чтобы наша схема стала проще, но не забывайте, что обычно после каждого сверточного или полносвязного слоя ко всем выходным значениям применяется функция активации, например, ReLU.
Один проход влияет на изображение следующим образом: он сокращает длину и ширину определенного канала, но увеличивает его значение (глубину).
Softmax и перекрестная энтропия более подробно рассмотрены на предыдущем уроке. Напомним, что функция softmax превращает вектор действительных чисел в вектор вероятностей (неотрицательные действительные числа, не превышающие 1). В нашем контексте выходные значения являются вероятностями попадания изображения в определённый класс. Минимизация потерь перекрестной энтропии обеспечивает уверенность в определении принадлежности изображения определенному классу, не принимая во внимание вероятность остальных классов, таким образом, для вероятностных задач softmax предпочтительней, чем, например, метод квадратичной ошибки.
Отступление: переобучение, регуляризация и dropout
Впервые (и, надеюсь, только однажды) я обращу ваше внимание на тему, на первый взгляд, не относящуюся к предмету. Она касается очень важного подводного камня глубокого обучения — проблемы переобучения (overfitting). Хотя эта тема будет основной в следующей статье цикла, отрицательный эффект переобучения заметно проявляется на сетях, подобных той, что мы собираемся построить, а значит, необходимо найти способ защититься от этого явления прежде, чем мы пойдем дальше. К счастью, существует очень простой метод, который мы и применим.
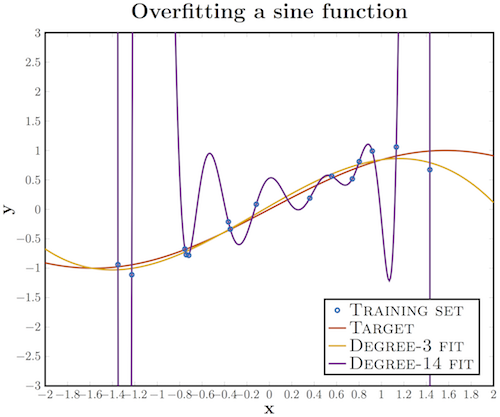
Переобучение — это излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению. Другими словами, наша модель могла выучить обучающее множество (вместе с шумом, который в нем присутствует), но она не смогла распознать скрытые процессы, которые это множество породили. В качестве примера рассмотрим задачу аппроксимации синусоиды с аддитивным шумом.
У нас есть обучающее множество (синие кружки), полученное из исходной кривой синуса, с некоторым количеством шума. Если мы приложим к этим данным график многочлена третьей степени, мы получим хорошую аппроксимацию исходной кривой. Кто-то возразит, что многочлен 14-й степени подошел бы лучше; действительно, так как у нас есть 15 точек, такая аппроксимация идеально описала бы обучающую выборку. Тем не менее, в этом случае введение дополнительных параметров в модель приводит к катастрофическим результатам: из-за того, что наша аппроксимация учитывает шумы, она не совпадает с исходной кривой нигде, кроме обучающих точек.
У глубоких сверточных нейронных сетей масса разнообразных параметров, особенно это касается полносвязных слоев. Переобучение может проявить себя в следующей форме: если у нас недостаточно обучающих примеров, маленькая группа нейронов может стать ответственной за большинство вычислений, а остальные нейроны станут избыточны; или наоборот, некоторые нейроны могут нанести ущерб производительности, при этом другие нейроны из их слоя не будут заниматься ничем, кроме исправления их ошибок.
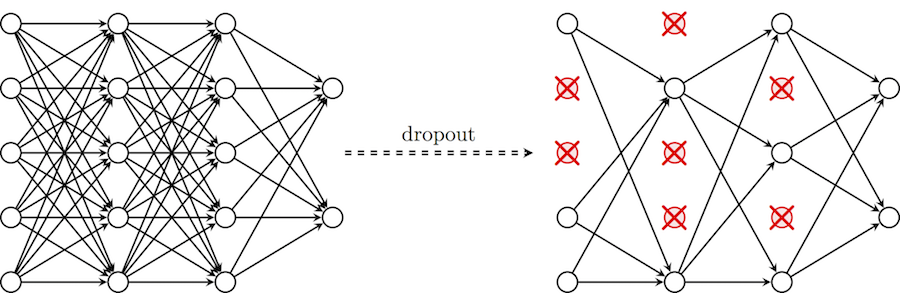
Чтобы помочь нашей сети не утратить способности к обобщению в этих обстоятельствах, мы вводим приемы регуляризации: вместо сокращения количества параметров, мы накладываем ограничения на параметры модели во время обучения, не позволяя нейронам изучать шум обучающих данных. Здесь я опишу прием dropout, который сначала может показаться “черной магией”, но на деле помогает исключить ситуации, описанные выше. В частности, dropout с параметром p за одну итерацию обучения проходит по всем нейронам определенного слоя и с вероятностью p полностью исключает их из сети на время итерации. Это заставит сеть обрабатывать ошибки и не полагаться на существование определенного нейрона (или группы нейронов), а полагаться на “единое мнение” (consensus) нейронов внутри одного слоя. Это довольно простой метод, который эффективно борется с проблемой переобучения сам, без необходимости вводить другие регуляризаторы. Схема ниже иллюстрирует данный метод.
Применение глубокой CNN к CIFAR-10
В качестве практической части построим глубокую сверточную нейронную сеть и применим ее к классификации изображений из набора CIFAR-10.
Импорты те же, что и в прошлый раз, за исключением того что мы используем большее разнообразие слоев:
from keras.datasets import cifar10 # subroutines for fetching the CIFAR-10 dataset
from keras.models import Model # basic class for specifying and training a neural network
from keras.layers import Input, Convolution2D, MaxPooling2D, Dense, Dropout, Flatten
from keras.utils import np_utils # utilities for one-hot encoding of ground truth values
import numpy as npUsing Theano backend.Как уже говорилось, обычно CNN использует больше гиперпараметров, чем MLP. В этом руководстве мы все еще будем использовать заранее известные “хорошие” значения, но не будем забывать, что в последующей лекции я расскажу, как их правильно выбирать.
Зададим следующие гиперпараметры:
- batch_size — количество обучающих образцов, обрабатываемых одновременно за одну итерацию алгоритма градиентного спуска;
- num_epochs — количество итераций обучающего алгоритма по всему обучающему множеству;
- kernel_size — размер ядра в сверточных слоях;
- pool_size — размер подвыборки в слоях подвыборки;
- сonv_depth — количество ядер в сверточных слоях;
- drop_prob (dropout probability) — мы будем применять dropout после каждого слоя подвыборки, а также после полносвязного слоя;
- hidden_size — количество нейронов в полносвязном слое MLP.
NB: я задал 200 итераций, что может занять слишком много времени, если в вашем распоряжении нет графического процессора (в этом случае узким местом будут сверточные слои). Если вы собираетесь обучать сеть на CPU, стоит сократить количество итераций и/или ядер.
batch_size = 32 # in each iteration, we consider 32 training examples at once
num_epochs = 200 # we iterate 200 times over the entire training set
kernel_size = 3 # we will use 3x3 kernels throughout
pool_size = 2 # we will use 2x2 pooling throughout
conv_depth_1 = 32 # we will initially have 32 kernels per conv. layer...
conv_depth_2 = 64 # ...switching to 64 after the first pooling layer
drop_prob_1 = 0.25 # dropout after pooling with probability 0.25
drop_prob_2 = 0.5 # dropout in the FC layer with probability 0.5
hidden_size = 512 # the FC layer will have 512 neuronsЗагрузка и первичная обработка CIFAR-10 осуществляется ровно так же, как и загрузка и обработка MNIST, где Keras выполняет все автоматически. Единственное отличие состоит в том, что теперь мы не рассматриваем каждый пиксель как независимое входное значение, и поэтому мы не переносим изображение в одномерное пространство. Мы снова преобразуем интенсивность пикселей так, чтобы она попадала в отрезок [0,1] и используем прямое кодирование для выходных значений.
Тем не менее, в этот раз этот этап будет выполнен для более общего случая, что позволит проще приспосабливаться к новым наборам данных: размер будет не жестко задан, а вычислен из размера набора данных, количество классов будет определено по количеству уникальных меток в обучающем множестве, а нормализация будет выполнена путем деления всех элементов на максимальное значение обучающего множества.
NB: мы также разделим тестовое множество на максимальное значение обучающего множества, потому что нашим алгоритмам не позволено видеть тестовые данные до того как завершится процесс обучения, и поэтому мы не можем вычислять на их основе никакие статистические метрики кроме как применения тех же трансформаций, что происходили с обучающим множеством.
(X_train, y_train), (X_test, y_test) = cifar10.load_data() # fetch CIFAR-10 data
num_train, depth, height, width = X_train.shape # there are 50000 training examples in CIFAR-10
num_test = X_test.shape[0] # there are 10000 test examples in CIFAR-10
num_classes = np.unique(y_train).shape[0] # there are 10 image classes
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= np.max(X_train) # Normalise data to [0, 1] range
X_test /= np.max(X_train) # Normalise data to [0, 1] range
Y_train = np_utils.to_categorical(y_train, num_classes) # One-hot encode the labels
Y_test = np_utils.to_categorical(y_test, num_classes) # One-hot encode the labels
Настало время моделирования! Наша сеть будет состоять из четырех слоев Convolution_2D и слоев MaxPooling2D после второй и четвертой сверток. После первого слоя подвыборки мы удваиваем количество ядер (вместе с описанным выше принципом принесения высоты и ширины в жертву глубине). После этого выходное изображение слоя подвыборки трансформируется в одномерный вектор (слоем Flatten) и проходит два полносвязных слоя (Dense). На всех слоях, кроме выходного полносвязного слоя, используется функция активации ReLU, последний же слой использует softmax.
Для регуляризации нашей модели после каждого слоя подвыборки и первого полносвязного слоя применяется слой Dropout. Здесь Keras также выделяется на фоне остальных фреймворков: в нем есть внутренний флаг, который автоматически включает и выключает dropout, в зависимости от того, находится модель в фазе обучения или тестирования.
В остальном спецификация нашей модели совпадает с нашими предыдущими настройками для MNIST:
- Мы используем перекрестную энтропию в качестве функции потерь;
- Мы используем оптимизатор Адама для градиентного спуска;
- Мы измеряем точность модели (так как исходные данные распределены по классам равномерно)*;
- Мы оставляем 10% данных для последующей валидации.
* Чтобы понять, почему точность не подойдет для случаев, когда распределение данных по классам неравномерно, рассмотрим предельный случай, когда 90% тестовых данных принадлежит классу x (например, в задаче диагностики у пациентов редкого заболевания). В этом случае классификатор, который просто выводит x, достигает значительной точности 90%, хотя на деле не выполняет ни обучения, ни обобщения.
inp = Input(shape=(depth, height, width)) # N.B. depth goes first in Keras!
# Conv [32] -> Conv [32] -> Pool (with dropout on the pooling layer)
conv_1 = Convolution2D(conv_depth_1, kernel_size, kernel_size, border_mode='same', activation='relu')(inp)
conv_2 = Convolution2D(conv_depth_1, kernel_size, kernel_size, border_mode='same', activation='relu')(conv_1)
pool_1 = MaxPooling2D(pool_size=(pool_size, pool_size))(conv_2)
drop_1 = Dropout(drop_prob_1)(pool_1)
# Conv [64] -> Conv [64] -> Pool (with dropout on the pooling layer)
conv_3 = Convolution2D(conv_depth_2, kernel_size, kernel_size, border_mode='same', activation='relu')(drop_1)
conv_4 = Convolution2D(conv_depth_2, kernel_size, kernel_size, border_mode='same', activation='relu')(conv_3)
pool_2 = MaxPooling2D(pool_size=(pool_size, pool_size))(conv_4)
drop_2 = Dropout(drop_prob_1)(pool_2)
# Now flatten to 1D, apply FC -> ReLU (with dropout) -> softmax
flat = Flatten()(drop_2)
hidden = Dense(hidden_size, activation='relu')(flat)
drop_3 = Dropout(drop_prob_2)(hidden)
out = Dense(num_classes, activation='softmax')(drop_3)
model = Model(input=inp, output=out) # To define a model, just specify its input and output layers
model.compile(loss='categorical_crossentropy', # using the cross-entropy loss function
optimizer='adam', # using the Adam optimiser
metrics=['accuracy']) # reporting the accuracy
model.fit(X_train, Y_train, # Train the model using the training set...
batch_size=batch_size, nb_epoch=num_epochs,
verbose=1, validation_split=0.1) # ...holding out 10% of the data for validation
model.evaluate(X_test, Y_test, verbose=1) # Evaluate the trained model on the test set!Посмотреть листинг обучения
Train on 45000 samples, validate on 5000 samples
Epoch 1/200
45000/45000 [==============================] - 9s - loss: 1.5435 - acc: 0.4359 - val_loss: 1.2057 - val_acc: 0.5672
Epoch 2/200
45000/45000 [==============================] - 9s - loss: 1.1544 - acc: 0.5886 - val_loss: 0.9679 - val_acc: 0.6566
Epoch 3/200
45000/45000 [==============================] - 8s - loss: 1.0114 - acc: 0.6418 - val_loss: 0.8807 - val_acc: 0.6870
Epoch 4/200
45000/45000 [==============================] - 8s - loss: 0.9183 - acc: 0.6766 - val_loss: 0.7945 - val_acc: 0.7224
Epoch 5/200
45000/45000 [==============================] - 9s - loss: 0.8507 - acc: 0.6994 - val_loss: 0.7531 - val_acc: 0.7400
Epoch 6/200
45000/45000 [==============================] - 9s - loss: 0.8064 - acc: 0.7161 - val_loss: 0.7174 - val_acc: 0.7496
Epoch 7/200
45000/45000 [==============================] - 9s - loss: 0.7561 - acc: 0.7331 - val_loss: 0.7116 - val_acc: 0.7622
Epoch 8/200
45000/45000 [==============================] - 9s - loss: 0.7156 - acc: 0.7476 - val_loss: 0.6773 - val_acc: 0.7670
Epoch 9/200
45000/45000 [==============================] - 9s - loss: 0.6833 - acc: 0.7594 - val_loss: 0.6855 - val_acc: 0.7644
Epoch 10/200
45000/45000 [==============================] - 9s - loss: 0.6580 - acc: 0.7656 - val_loss: 0.6608 - val_acc: 0.7748
Epoch 11/200
45000/45000 [==============================] - 9s - loss: 0.6308 - acc: 0.7750 - val_loss: 0.6854 - val_acc: 0.7730
Epoch 12/200
45000/45000 [==============================] - 9s - loss: 0.6035 - acc: 0.7832 - val_loss: 0.6853 - val_acc: 0.7744
Epoch 13/200
45000/45000 [==============================] - 9s - loss: 0.5871 - acc: 0.7914 - val_loss: 0.6762 - val_acc: 0.7748
Epoch 14/200
45000/45000 [==============================] - 8s - loss: 0.5693 - acc: 0.8000 - val_loss: 0.6868 - val_acc: 0.7740
Epoch 15/200
45000/45000 [==============================] - 9s - loss: 0.5555 - acc: 0.8036 - val_loss: 0.6835 - val_acc: 0.7792
Epoch 16/200
45000/45000 [==============================] - 9s - loss: 0.5370 - acc: 0.8126 - val_loss: 0.6885 - val_acc: 0.7774
Epoch 17/200
45000/45000 [==============================] - 9s - loss: 0.5270 - acc: 0.8134 - val_loss: 0.6604 - val_acc: 0.7866
Epoch 18/200
45000/45000 [==============================] - 9s - loss: 0.5090 - acc: 0.8194 - val_loss: 0.6652 - val_acc: 0.7860
Epoch 19/200
45000/45000 [==============================] - 9s - loss: 0.5066 - acc: 0.8193 - val_loss: 0.6632 - val_acc: 0.7858
Epoch 20/200
45000/45000 [==============================] - 9s - loss: 0.4938 - acc: 0.8248 - val_loss: 0.6844 - val_acc: 0.7872
Epoch 21/200
45000/45000 [==============================] - 9s - loss: 0.4684 - acc: 0.8361 - val_loss: 0.6861 - val_acc: 0.7904
Epoch 22/200
45000/45000 [==============================] - 9s - loss: 0.4696 - acc: 0.8365 - val_loss: 0.6349 - val_acc: 0.7980
Epoch 23/200
45000/45000 [==============================] - 9s - loss: 0.4584 - acc: 0.8387 - val_loss: 0.6592 - val_acc: 0.7926
Epoch 24/200
45000/45000 [==============================] - 9s - loss: 0.4410 - acc: 0.8443 - val_loss: 0.6822 - val_acc: 0.7876
Epoch 25/200
45000/45000 [==============================] - 8s - loss: 0.4404 - acc: 0.8454 - val_loss: 0.7103 - val_acc: 0.7784
Epoch 26/200
45000/45000 [==============================] - 8s - loss: 0.4276 - acc: 0.8512 - val_loss: 0.6783 - val_acc: 0.7858
Epoch 27/200
45000/45000 [==============================] - 8s - loss: 0.4152 - acc: 0.8542 - val_loss: 0.6657 - val_acc: 0.7944
Epoch 28/200
45000/45000 [==============================] - 9s - loss: 0.4107 - acc: 0.8549 - val_loss: 0.6861 - val_acc: 0.7888
Epoch 29/200
45000/45000 [==============================] - 9s - loss: 0.4115 - acc: 0.8548 - val_loss: 0.6634 - val_acc: 0.7996
Epoch 30/200
45000/45000 [==============================] - 9s - loss: 0.4057 - acc: 0.8586 - val_loss: 0.7166 - val_acc: 0.7896
Epoch 31/200
45000/45000 [==============================] - 9s - loss: 0.3992 - acc: 0.8605 - val_loss: 0.6734 - val_acc: 0.7998
Epoch 32/200
45000/45000 [==============================] - 9s - loss: 0.3863 - acc: 0.8637 - val_loss: 0.7263 - val_acc: 0.7844
Epoch 33/200
45000/45000 [==============================] - 9s - loss: 0.3933 - acc: 0.8644 - val_loss: 0.6953 - val_acc: 0.7860
Epoch 34/200
45000/45000 [==============================] - 9s - loss: 0.3838 - acc: 0.8663 - val_loss: 0.7040 - val_acc: 0.7916
Epoch 35/200
45000/45000 [==============================] - 9s - loss: 0.3800 - acc: 0.8674 - val_loss: 0.7233 - val_acc: 0.7970
Epoch 36/200
45000/45000 [==============================] - 9s - loss: 0.3775 - acc: 0.8697 - val_loss: 0.7234 - val_acc: 0.7922
Epoch 37/200
45000/45000 [==============================] - 9s - loss: 0.3681 - acc: 0.8746 - val_loss: 0.6751 - val_acc: 0.7958
Epoch 38/200
45000/45000 [==============================] - 9s - loss: 0.3679 - acc: 0.8732 - val_loss: 0.7014 - val_acc: 0.7976
Epoch 39/200
45000/45000 [==============================] - 9s - loss: 0.3540 - acc: 0.8769 - val_loss: 0.6768 - val_acc: 0.8022
Epoch 40/200
45000/45000 [==============================] - 9s - loss: 0.3531 - acc: 0.8783 - val_loss: 0.7171 - val_acc: 0.7986
Epoch 41/200
45000/45000 [==============================] - 9s - loss: 0.3545 - acc: 0.8786 - val_loss: 0.7164 - val_acc: 0.7930
Epoch 42/200
45000/45000 [==============================] - 9s - loss: 0.3453 - acc: 0.8799 - val_loss: 0.7078 - val_acc: 0.7994
Epoch 43/200
45000/45000 [==============================] - 8s - loss: 0.3488 - acc: 0.8798 - val_loss: 0.7272 - val_acc: 0.7958
Epoch 44/200
45000/45000 [==============================] - 9s - loss: 0.3471 - acc: 0.8797 - val_loss: 0.7110 - val_acc: 0.7916
Epoch 45/200
45000/45000 [==============================] - 9s - loss: 0.3443 - acc: 0.8810 - val_loss: 0.7391 - val_acc: 0.7952
Epoch 46/200
45000/45000 [==============================] - 9s - loss: 0.3342 - acc: 0.8841 - val_loss: 0.7351 - val_acc: 0.7970
Epoch 47/200
45000/45000 [==============================] - 9s - loss: 0.3311 - acc: 0.8842 - val_loss: 0.7302 - val_acc: 0.8008
Epoch 48/200
45000/45000 [==============================] - 9s - loss: 0.3320 - acc: 0.8868 - val_loss: 0.7145 - val_acc: 0.8002
Epoch 49/200
45000/45000 [==============================] - 9s - loss: 0.3264 - acc: 0.8883 - val_loss: 0.7640 - val_acc: 0.7942
Epoch 50/200
45000/45000 [==============================] - 9s - loss: 0.3247 - acc: 0.8880 - val_loss: 0.7289 - val_acc: 0.7948
Epoch 51/200
45000/45000 [==============================] - 9s - loss: 0.3279 - acc: 0.8886 - val_loss: 0.7340 - val_acc: 0.7910
Epoch 52/200
45000/45000 [==============================] - 9s - loss: 0.3224 - acc: 0.8901 - val_loss: 0.7454 - val_acc: 0.7914
Epoch 53/200
45000/45000 [==============================] - 9s - loss: 0.3219 - acc: 0.8916 - val_loss: 0.7328 - val_acc: 0.8016
Epoch 54/200
45000/45000 [==============================] - 9s - loss: 0.3163 - acc: 0.8919 - val_loss: 0.7442 - val_acc: 0.7996
Epoch 55/200
45000/45000 [==============================] - 9s - loss: 0.3071 - acc: 0.8962 - val_loss: 0.7427 - val_acc: 0.7898
Epoch 56/200
45000/45000 [==============================] - 9s - loss: 0.3158 - acc: 0.8944 - val_loss: 0.7685 - val_acc: 0.7920
Epoch 57/200
45000/45000 [==============================] - 8s - loss: 0.3126 - acc: 0.8942 - val_loss: 0.7717 - val_acc: 0.8062
Epoch 58/200
45000/45000 [==============================] - 9s - loss: 0.3156 - acc: 0.8919 - val_loss: 0.6993 - val_acc: 0.7984
Epoch 59/200
45000/45000 [==============================] - 9s - loss: 0.3030 - acc: 0.8970 - val_loss: 0.7359 - val_acc: 0.8016
Epoch 60/200
45000/45000 [==============================] - 9s - loss: 0.3022 - acc: 0.8969 - val_loss: 0.7427 - val_acc: 0.7954
Epoch 61/200
45000/45000 [==============================] - 9s - loss: 0.3072 - acc: 0.8950 - val_loss: 0.7829 - val_acc: 0.7996
Epoch 62/200
45000/45000 [==============================] - 9s - loss: 0.2977 - acc: 0.8996 - val_loss: 0.8096 - val_acc: 0.7958
Epoch 63/200
45000/45000 [==============================] - 9s - loss: 0.3033 - acc: 0.8983 - val_loss: 0.7424 - val_acc: 0.7972
Epoch 64/200
45000/45000 [==============================] - 9s - loss: 0.2985 - acc: 0.9003 - val_loss: 0.7779 - val_acc: 0.7930
Epoch 65/200
45000/45000 [==============================] - 8s - loss: 0.2931 - acc: 0.9004 - val_loss: 0.7302 - val_acc: 0.8010
Epoch 66/200
45000/45000 [==============================] - 8s - loss: 0.2948 - acc: 0.8994 - val_loss: 0.7861 - val_acc: 0.7900
Epoch 67/200
45000/45000 [==============================] - 9s - loss: 0.2911 - acc: 0.9026 - val_loss: 0.7502 - val_acc: 0.7918
Epoch 68/200
45000/45000 [==============================] - 9s - loss: 0.2951 - acc: 0.9001 - val_loss: 0.7911 - val_acc: 0.7820
Epoch 69/200
45000/45000 [==============================] - 9s - loss: 0.2869 - acc: 0.9026 - val_loss: 0.8025 - val_acc: 0.8024
Epoch 70/200
45000/45000 [==============================] - 8s - loss: 0.2933 - acc: 0.9013 - val_loss: 0.7703 - val_acc: 0.7978
Epoch 71/200
45000/45000 [==============================] - 8s - loss: 0.2902 - acc: 0.9007 - val_loss: 0.7685 - val_acc: 0.7962
Epoch 72/200
45000/45000 [==============================] - 9s - loss: 0.2920 - acc: 0.9025 - val_loss: 0.7412 - val_acc: 0.7956
Epoch 73/200
45000/45000 [==============================] - 8s - loss: 0.2861 - acc: 0.9038 - val_loss: 0.7957 - val_acc: 0.8026
Epoch 74/200
45000/45000 [==============================] - 8s - loss: 0.2785 - acc: 0.9069 - val_loss: 0.7522 - val_acc: 0.8002
Epoch 75/200
45000/45000 [==============================] - 9s - loss: 0.2811 - acc: 0.9064 - val_loss: 0.8181 - val_acc: 0.7902
Epoch 76/200
45000/45000 [==============================] - 9s - loss: 0.2841 - acc: 0.9053 - val_loss: 0.7695 - val_acc: 0.7990
Epoch 77/200
45000/45000 [==============================] - 9s - loss: 0.2853 - acc: 0.9061 - val_loss: 0.7608 - val_acc: 0.7972
Epoch 78/200
45000/45000 [==============================] - 9s - loss: 0.2714 - acc: 0.9080 - val_loss: 0.7534 - val_acc: 0.8034
Epoch 79/200
45000/45000 [==============================] - 9s - loss: 0.2797 - acc: 0.9072 - val_loss: 0.7188 - val_acc: 0.7988
Epoch 80/200
45000/45000 [==============================] - 9s - loss: 0.2682 - acc: 0.9110 - val_loss: 0.7751 - val_acc: 0.7954
Epoch 81/200
45000/45000 [==============================] - 9s - loss: 0.2885 - acc: 0.9038 - val_loss: 0.7711 - val_acc: 0.8010
Epoch 82/200
45000/45000 [==============================] - 9s - loss: 0.2705 - acc: 0.9094 - val_loss: 0.7613 - val_acc: 0.8000
Epoch 83/200
45000/45000 [==============================] - 9s - loss: 0.2738 - acc: 0.9095 - val_loss: 0.8300 - val_acc: 0.7944
Epoch 84/200
45000/45000 [==============================] - 9s - loss: 0.2795 - acc: 0.9066 - val_loss: 0.8001 - val_acc: 0.7912
Epoch 85/200
45000/45000 [==============================] - 9s - loss: 0.2721 - acc: 0.9086 - val_loss: 0.7862 - val_acc: 0.8092
Epoch 86/200
45000/45000 [==============================] - 9s - loss: 0.2752 - acc: 0.9087 - val_loss: 0.7331 - val_acc: 0.7942
Epoch 87/200
45000/45000 [==============================] - 9s - loss: 0.2725 - acc: 0.9089 - val_loss: 0.7999 - val_acc: 0.7914
Epoch 88/200
45000/45000 [==============================] - 9s - loss: 0.2644 - acc: 0.9108 - val_loss: 0.7944 - val_acc: 0.7990
Epoch 89/200
45000/45000 [==============================] - 9s - loss: 0.2725 - acc: 0.9106 - val_loss: 0.7622 - val_acc: 0.8006
Epoch 90/200
45000/45000 [==============================] - 9s - loss: 0.2622 - acc: 0.9129 - val_loss: 0.8172 - val_acc: 0.7988
Epoch 91/200
45000/45000 [==============================] - 9s - loss: 0.2772 - acc: 0.9085 - val_loss: 0.8243 - val_acc: 0.8004
Epoch 92/200
45000/45000 [==============================] - 9s - loss: 0.2609 - acc: 0.9136 - val_loss: 0.7723 - val_acc: 0.7992
Epoch 93/200
45000/45000 [==============================] - 9s - loss: 0.2666 - acc: 0.9129 - val_loss: 0.8366 - val_acc: 0.7932
Epoch 94/200
45000/45000 [==============================] - 9s - loss: 0.2593 - acc: 0.9135 - val_loss: 0.8666 - val_acc: 0.7956
Epoch 95/200
45000/45000 [==============================] - 9s - loss: 0.2692 - acc: 0.9100 - val_loss: 0.8901 - val_acc: 0.7954
Epoch 96/200
45000/45000 [==============================] - 8s - loss: 0.2569 - acc: 0.9160 - val_loss: 0.8515 - val_acc: 0.8006
Epoch 97/200
45000/45000 [==============================] - 8s - loss: 0.2636 - acc: 0.9146 - val_loss: 0.8639 - val_acc: 0.7960
Epoch 98/200
45000/45000 [==============================] - 9s - loss: 0.2693 - acc: 0.9113 - val_loss: 0.7891 - val_acc: 0.7916
Epoch 99/200
45000/45000 [==============================] - 9s - loss: 0.2611 - acc: 0.9144 - val_loss: 0.8650 - val_acc: 0.7928
Epoch 100/200
45000/45000 [==============================] - 9s - loss: 0.2589 - acc: 0.9121 - val_loss: 0.8683 - val_acc: 0.7990
Epoch 101/200
45000/45000 [==============================] - 9s - loss: 0.2601 - acc: 0.9142 - val_loss: 0.9116 - val_acc: 0.8030
Epoch 102/200
45000/45000 [==============================] - 9s - loss: 0.2616 - acc: 0.9138 - val_loss: 0.8229 - val_acc: 0.7928
Epoch 103/200
45000/45000 [==============================] - 9s - loss: 0.2603 - acc: 0.9140 - val_loss: 0.8847 - val_acc: 0.7994
Epoch 104/200
45000/45000 [==============================] - 9s - loss: 0.2579 - acc: 0.9150 - val_loss: 0.9079 - val_acc: 0.8004
Epoch 105/200
45000/45000 [==============================] - 8s - loss: 0.2696 - acc: 0.9127 - val_loss: 0.7450 - val_acc: 0.8002
Epoch 106/200
45000/45000 [==============================] - 9s - loss: 0.2555 - acc: 0.9161 - val_loss: 0.8186 - val_acc: 0.7992
Epoch 107/200
45000/45000 [==============================] - 9s - loss: 0.2631 - acc: 0.9160 - val_loss: 0.8686 - val_acc: 0.7920
Epoch 108/200
45000/45000 [==============================] - 9s - loss: 0.2524 - acc: 0.9178 - val_loss: 0.9136 - val_acc: 0.7956
Epoch 109/200
45000/45000 [==============================] - 9s - loss: 0.2569 - acc: 0.9151 - val_loss: 0.8148 - val_acc: 0.7994
Epoch 110/200
45000/45000 [==============================] - 9s - loss: 0.2586 - acc: 0.9150 - val_loss: 0.8826 - val_acc: 0.7984
Epoch 111/200
45000/45000 [==============================] - 9s - loss: 0.2520 - acc: 0.9155 - val_loss: 0.8621 - val_acc: 0.7980
Epoch 112/200
45000/45000 [==============================] - 9s - loss: 0.2586 - acc: 0.9157 - val_loss: 0.8149 - val_acc: 0.8038
Epoch 113/200
45000/45000 [==============================] - 9s - loss: 0.2623 - acc: 0.9151 - val_loss: 0.8361 - val_acc: 0.7972
Epoch 114/200
45000/45000 [==============================] - 9s - loss: 0.2535 - acc: 0.9177 - val_loss: 0.8618 - val_acc: 0.7970
Epoch 115/200
45000/45000 [==============================] - 8s - loss: 0.2570 - acc: 0.9164 - val_loss: 0.7687 - val_acc: 0.8044
Epoch 116/200
45000/45000 [==============================] - 9s - loss: 0.2501 - acc: 0.9183 - val_loss: 0.8270 - val_acc: 0.7934
Epoch 117/200
45000/45000 [==============================] - 8s - loss: 0.2535 - acc: 0.9182 - val_loss: 0.7861 - val_acc: 0.7986
Epoch 118/200
45000/45000 [==============================] - 9s - loss: 0.2507 - acc: 0.9184 - val_loss: 0.8203 - val_acc: 0.7996
Epoch 119/200
45000/45000 [==============================] - 9s - loss: 0.2530 - acc: 0.9173 - val_loss: 0.8294 - val_acc: 0.7904
Epoch 120/200
45000/45000 [==============================] - 9s - loss: 0.2599 - acc: 0.9160 - val_loss: 0.8458 - val_acc: 0.7902
Epoch 121/200
45000/45000 [==============================] - 9s - loss: 0.2483 - acc: 0.9164 - val_loss: 0.7573 - val_acc: 0.7976
Epoch 122/200
45000/45000 [==============================] - 8s - loss: 0.2492 - acc: 0.9190 - val_loss: 0.8435 - val_acc: 0.8012
Epoch 123/200
45000/45000 [==============================] - 9s - loss: 0.2528 - acc: 0.9179 - val_loss: 0.8594 - val_acc: 0.7964
Epoch 124/200
45000/45000 [==============================] - 9s - loss: 0.2581 - acc: 0.9173 - val_loss: 0.9037 - val_acc: 0.7944
Epoch 125/200
45000/45000 [==============================] - 8s - loss: 0.2404 - acc: 0.9212 - val_loss: 0.7893 - val_acc: 0.7976
Epoch 126/200
45000/45000 [==============================] - 8s - loss: 0.2492 - acc: 0.9177 - val_loss: 0.8679 - val_acc: 0.7982
Epoch 127/200
45000/45000 [==============================] - 8s - loss: 0.2483 - acc: 0.9196 - val_loss: 0.8894 - val_acc: 0.7956
Epoch 128/200
45000/45000 [==============================] - 9s - loss: 0.2539 - acc: 0.9176 - val_loss: 0.8413 - val_acc: 0.8006
Epoch 129/200
45000/45000 [==============================] - 8s - loss: 0.2477 - acc: 0.9184 - val_loss: 0.8151 - val_acc: 0.7982
Epoch 130/200
45000/45000 [==============================] - 9s - loss: 0.2586 - acc: 0.9188 - val_loss: 0.8173 - val_acc: 0.7954
Epoch 131/200
45000/45000 [==============================] - 9s - loss: 0.2498 - acc: 0.9189 - val_loss: 0.8539 - val_acc: 0.7996
Epoch 132/200
45000/45000 [==============================] - 9s - loss: 0.2426 - acc: 0.9190 - val_loss: 0.8543 - val_acc: 0.7952
Epoch 133/200
45000/45000 [==============================] - 9s - loss: 0.2460 - acc: 0.9185 - val_loss: 0.8665 - val_acc: 0.8008
Epoch 134/200
45000/45000 [==============================] - 9s - loss: 0.2436 - acc: 0.9216 - val_loss: 0.8933 - val_acc: 0.7950
Epoch 135/200
45000/45000 [==============================] - 8s - loss: 0.2468 - acc: 0.9203 - val_loss: 0.8270 - val_acc: 0.7940
Epoch 136/200
45000/45000 [==============================] - 9s - loss: 0.2479 - acc: 0.9194 - val_loss: 0.8365 - val_acc: 0.8052
Epoch 137/200
45000/45000 [==============================] - 9s - loss: 0.2449 - acc: 0.9206 - val_loss: 0.7964 - val_acc: 0.8018
Epoch 138/200
45000/45000 [==============================] - 9s - loss: 0.2440 - acc: 0.9220 - val_loss: 0.8784 - val_acc: 0.7914
Epoch 139/200
45000/45000 [==============================] - 9s - loss: 0.2485 - acc: 0.9198 - val_loss: 0.8259 - val_acc: 0.7852
Epoch 140/200
45000/45000 [==============================] - 9s - loss: 0.2482 - acc: 0.9204 - val_loss: 0.8954 - val_acc: 0.7960
Epoch 141/200
45000/45000 [==============================] - 9s - loss: 0.2344 - acc: 0.9249 - val_loss: 0.8708 - val_acc: 0.7874
Epoch 142/200
45000/45000 [==============================] - 9s - loss: 0.2476 - acc: 0.9204 - val_loss: 0.9190 - val_acc: 0.7954
Epoch 143/200
45000/45000 [==============================] - 9s - loss: 0.2415 - acc: 0.9223 - val_loss: 0.9607 - val_acc: 0.7960
Epoch 144/200
45000/45000 [==============================] - 9s - loss: 0.2377 - acc: 0.9232 - val_loss: 0.8987 - val_acc: 0.7970
Epoch 145/200
45000/45000 [==============================] - 9s - loss: 0.2481 - acc: 0.9201 - val_loss: 0.8611 - val_acc: 0.8048
Epoch 146/200
45000/45000 [==============================] - 9s - loss: 0.2504 - acc: 0.9197 - val_loss: 0.8411 - val_acc: 0.7938
Epoch 147/200
45000/45000 [==============================] - 9s - loss: 0.2450 - acc: 0.9216 - val_loss: 0.7839 - val_acc: 0.8028
Epoch 148/200
45000/45000 [==============================] - 9s - loss: 0.2327 - acc: 0.9250 - val_loss: 0.8910 - val_acc: 0.8054
Epoch 149/200
45000/45000 [==============================] - 9s - loss: 0.2432 - acc: 0.9219 - val_loss: 0.8568 - val_acc: 0.8000
Epoch 150/200
45000/45000 [==============================] - 9s - loss: 0.2436 - acc: 0.9236 - val_loss: 0.9061 - val_acc: 0.7938
Epoch 151/200
45000/45000 [==============================] - 9s - loss: 0.2434 - acc: 0.9222 - val_loss: 0.8439 - val_acc: 0.7986
Epoch 152/200
45000/45000 [==============================] - 9s - loss: 0.2439 - acc: 0.9225 - val_loss: 0.9002 - val_acc: 0.7994
Epoch 153/200
45000/45000 [==============================] - 8s - loss: 0.2373 - acc: 0.9237 - val_loss: 0.8756 - val_acc: 0.7880
Epoch 154/200
45000/45000 [==============================] - 8s - loss: 0.2359 - acc: 0.9238 - val_loss: 0.8514 - val_acc: 0.7936
Epoch 155/200
45000/45000 [==============================] - 9s - loss: 0.2435 - acc: 0.9222 - val_loss: 0.8377 - val_acc: 0.8080
Epoch 156/200
45000/45000 [==============================] - 9s - loss: 0.2478 - acc: 0.9204 - val_loss: 0.8831 - val_acc: 0.7992
Epoch 157/200
45000/45000 [==============================] - 9s - loss: 0.2337 - acc: 0.9253 - val_loss: 0.8453 - val_acc: 0.7994
Epoch 158/200
45000/45000 [==============================] - 9s - loss: 0.2336 - acc: 0.9257 - val_loss: 0.9027 - val_acc: 0.7882
Epoch 159/200
45000/45000 [==============================] - 9s - loss: 0.2384 - acc: 0.9230 - val_loss: 0.9121 - val_acc: 0.8016
Epoch 160/200
45000/45000 [==============================] - 9s - loss: 0.2481 - acc: 0.9217 - val_loss: 0.9495 - val_acc: 0.7974
Epoch 161/200
45000/45000 [==============================] - 9s - loss: 0.2450 - acc: 0.9224 - val_loss: 0.8510 - val_acc: 0.7884
Epoch 162/200
45000/45000 [==============================] - 9s - loss: 0.2433 - acc: 0.9220 - val_loss: 0.8979 - val_acc: 0.7948
Epoch 163/200
45000/45000 [==============================] - 9s - loss: 0.2339 - acc: 0.9262 - val_loss: 0.8979 - val_acc: 0.7978
Epoch 164/200
45000/45000 [==============================] - 9s - loss: 0.2298 - acc: 0.9257 - val_loss: 0.9036 - val_acc: 0.7990
Epoch 165/200
45000/45000 [==============================] - 9s - loss: 0.2404 - acc: 0.9236 - val_loss: 0.8341 - val_acc: 0.8052
Epoch 166/200
45000/45000 [==============================] - 9s - loss: 0.2402 - acc: 0.9227 - val_loss: 0.8731 - val_acc: 0.7996
Epoch 167/200
45000/45000 [==============================] - 9s - loss: 0.2367 - acc: 0.9250 - val_loss: 0.9218 - val_acc: 0.7992
Epoch 168/200
45000/45000 [==============================] - 9s - loss: 0.2267 - acc: 0.9262 - val_loss: 0.8767 - val_acc: 0.7922
Epoch 169/200
45000/45000 [==============================] - 9s - loss: 0.2336 - acc: 0.9254 - val_loss: 0.8418 - val_acc: 0.8038
Epoch 170/200
45000/45000 [==============================] - 9s - loss: 0.2434 - acc: 0.9232 - val_loss: 0.8362 - val_acc: 0.7920
Epoch 171/200
45000/45000 [==============================] - 9s - loss: 0.2328 - acc: 0.9265 - val_loss: 0.8712 - val_acc: 0.7950
Epoch 172/200
45000/45000 [==============================] - 9s - loss: 0.2346 - acc: 0.9262 - val_loss: 0.9256 - val_acc: 0.7976
Epoch 173/200
45000/45000 [==============================] - 8s - loss: 0.2382 - acc: 0.9242 - val_loss: 0.8875 - val_acc: 0.7982
Epoch 174/200
45000/45000 [==============================] - 9s - loss: 0.2400 - acc: 0.9239 - val_loss: 0.8264 - val_acc: 0.7864
Epoch 175/200
45000/45000 [==============================] - 9s - loss: 0.2334 - acc: 0.9261 - val_loss: 0.9178 - val_acc: 0.8014
Epoch 176/200
45000/45000 [==============================] - 9s - loss: 0.2427 - acc: 0.9219 - val_loss: 0.8458 - val_acc: 0.7920
Epoch 177/200
45000/45000 [==============================] - 9s - loss: 0.2310 - acc: 0.9257 - val_loss: 0.9171 - val_acc: 0.8062
Epoch 178/200
45000/45000 [==============================] - 9s - loss: 0.2310 - acc: 0.9265 - val_loss: 0.8544 - val_acc: 0.7990
Epoch 179/200
45000/45000 [==============================] - 9s - loss: 0.2378 - acc: 0.9240 - val_loss: 0.9259 - val_acc: 0.8000
Epoch 180/200
45000/45000 [==============================] - 9s - loss: 0.2381 - acc: 0.9242 - val_loss: 0.8573 - val_acc: 0.8056
Epoch 181/200
45000/45000 [==============================] - 9s - loss: 0.2231 - acc: 0.9297 - val_loss: 0.8935 - val_acc: 0.8002
Epoch 182/200
45000/45000 [==============================] - 9s - loss: 0.2419 - acc: 0.9248 - val_loss: 1.0145 - val_acc: 0.7900
Epoch 183/200
45000/45000 [==============================] - 9s - loss: 0.2336 - acc: 0.9266 - val_loss: 0.8838 - val_acc: 0.8006
Epoch 184/200
45000/45000 [==============================] - 9s - loss: 0.2429 - acc: 0.9242 - val_loss: 0.8685 - val_acc: 0.7918
Epoch 185/200
45000/45000 [==============================] - 9s - loss: 0.2317 - acc: 0.9260 - val_loss: 0.8297 - val_acc: 0.7942
Epoch 186/200
45000/45000 [==============================] - 9s - loss: 0.2330 - acc: 0.9264 - val_loss: 0.8831 - val_acc: 0.8026
Epoch 187/200
45000/45000 [==============================] - 9s - loss: 0.2353 - acc: 0.9254 - val_loss: 0.8934 - val_acc: 0.7956
Epoch 188/200
45000/45000 [==============================] - 9s - loss: 0.2312 - acc: 0.9247 - val_loss: 0.9275 - val_acc: 0.8042
Epoch 189/200
45000/45000 [==============================] - 9s - loss: 0.2239 - acc: 0.9282 - val_loss: 0.9246 - val_acc: 0.7934
Epoch 190/200
45000/45000 [==============================] - 9s - loss: 0.2349 - acc: 0.9253 - val_loss: 0.8628 - val_acc: 0.8000
Epoch 191/200
45000/45000 [==============================] - 9s - loss: 0.2313 - acc: 0.9266 - val_loss: 0.9020 - val_acc: 0.7978
Epoch 192/200
45000/45000 [==============================] - 9s - loss: 0.2358 - acc: 0.9254 - val_loss: 0.9481 - val_acc: 0.7966
Epoch 193/200
45000/45000 [==============================] - 9s - loss: 0.2298 - acc: 0.9276 - val_loss: 0.8791 - val_acc: 0.8010
Epoch 194/200
45000/45000 [==============================] - 9s - loss: 0.2279 - acc: 0.9265 - val_loss: 0.8890 - val_acc: 0.7976
Epoch 195/200
45000/45000 [==============================] - 9s - loss: 0.2330 - acc: 0.9273 - val_loss: 0.8893 - val_acc: 0.7890
Epoch 196/200
45000/45000 [==============================] - 9s - loss: 0.2416 - acc: 0.9243 - val_loss: 0.9002 - val_acc: 0.7922
Epoch 197/200
45000/45000 [==============================] - 9s - loss: 0.2309 - acc: 0.9273 - val_loss: 0.9232 - val_acc: 0.7990
Epoch 198/200
45000/45000 [==============================] - 9s - loss: 0.2247 - acc: 0.9278 - val_loss: 0.9474 - val_acc: 0.7980
Epoch 199/200
45000/45000 [==============================] - 9s - loss: 0.2335 - acc: 0.9256 - val_loss: 0.9177 - val_acc: 0.8000
Epoch 200/200
45000/45000 [==============================] - 9s - loss: 0.2378 - acc: 0.9254 - val_loss: 0.9205 - val_acc: 0.7966
9984/10000 [============================>.] - ETA: 0s
[0.97292723369598388, 0.7853]
Наша модель достигает точности около 76.6% на тестовом множестве; для такой сложной задачи, где даже человеческий взгляд показывает точность всего около 90%, а также учитывая относительную простоту модели, это вполне достойный результат. Тем не менее, более сложные модели в последних исследованиях достигали точности 96.53%.
Полагаю, что тонкая настройка модели, если в вашем распоряжении нет графического процессора, будет крайне затруднительна. Тем не менее, советую вам попробовать применить эту модель к набору MNIST с прошлого урока; на CNN с dropout’ом у вас почти без усилий должно получиться достигнуть точности 99.3%.
Заключение
Сегодня мы изучили базовые понятия сверточных нейронных сетей, рассмотрели проблему переобучения и выяснили в общих чертах, как ее решают с помощью регуляризации (в частности, методом dropout), а также успешно построили четырехслойную глубокую CNN в Keras, протестировав ее на CIFAR-10 и уложившись в 50 строк кода.
В следующий раз мы рассмотрим сразу несколько тем, изучим приемы и хитрости, связанные с тонкой настройкой моделей, достижения максимальной производительности и контролем за переобучением.
In this tutorial, you will receive a gentle introduction to training your first Convolutional Neural Network (CNN) using the PyTorch deep learning library. This network will be able to recognize handwritten Hiragana characters.

Today’s tutorial is part three in our five part series on PyTorch fundamentals:
- What is PyTorch?
- Intro to PyTorch: Training your first neural network using PyTorch
- PyTorch: Training your first Convolutional Neural Network (today’s tutorial)
- PyTorch image classification with pre-trained networks (next week’s tutorial)
- PyTorch object detection with pre-trained networks
Last week you learned how to train a very basic feedforward neural network using the PyTorch library. That tutorial focused on simple numerical data.
Today, we will take the next step and learn how to train a CNN to recognize handwritten Hiragana characters using the Kuzushiji-MNIST (KMNIST) dataset.
As you’ll see, training a CNN on an image dataset isn’t all that different from training a basic multi-layer perceptron (MLP) on numerical data. We still need to:
- Define our model architecture
- Load our dataset from disk
- Loop over our epochs and batches
- Make predictions and compute our loss
- Properly zero our gradient, perform backpropagation, and update our model parameters
Furthermore, this post will also give you some experience with PyTorch’s DataLoader implementation which makes it super easy to work with datasets — becoming proficient with PyTorch’s DataLoader is a critical skill you’ll want to develop as a deep learning practitioner (and it’s a topic that I’ve dedicated an entire course to inside PyImageSearch University).
To learn how to train your first CNN with PyTorch, just keep reading.
CNNs are a type of deep learning algorithm that can analyze and extract features from images, making them highly effective for image classification and object detection tasks. In this tutorial, we will go through the steps of implementing a CNN in PyTorch
Looking for the source code to this post?
Jump Right To The Downloads Section
Throughout the remainder of this tutorial, you will learn how to train your first CNN using the PyTorch framework.
We’ll start by configuring our development environment to install both torch and torchvision, followed by reviewing our project directory structure.
I’ll then show you the KMNIST dataset (a drop-in replacement for the MNIST digits dataset) that contains Hiragana characters. Later in this tutorial, you’ll learn how to train a CNN to recognize each of the Hiragana characters in the KMNIST dataset.
We’ll then implement three Python scripts with PyTorch, including our CNN architecture, training script, and a final script used to make predictions on input images.
By the end of this tutorial, you’ll be comfortable with the steps required to train a CNN with PyTorch.
Updates:
This blog post was last updated in January 2023 with additional explanations of CNNs and PyTorch background information.
Let’s get started!
Configuring your development environment
To follow this guide, you need to have PyTorch, OpenCV, and scikit-learn installed on your system.
Luckily, all three are extremely easy to install using pip:
$ pip install torch torchvision $ pip install opencv-contrib-python $ pip install scikit-learn
If you need help configuring your development environment for PyTorch, I highly recommend that you read the PyTorch documentation — PyTorch’s documentation is comprehensive and will have you up and running quickly.
And if you need help installing OpenCV, be sure to refer to my pip install OpenCV tutorial.
Having problems configuring your development environment?
All that said, are you:
- Short on time?
- Learning on your employer’s administratively locked system?
- Wanting to skip the hassle of fighting with the command line, package managers, and virtual environments?
- Ready to run the code right now on your Windows, macOS, or Linux system?
Then join PyImageSearch University today!
Gain access to Jupyter Notebooks for this tutorial and other PyImageSearch guides that are pre-configured to run on Google Colab’s ecosystem right in your web browser! No installation required.
And best of all, these Jupyter Notebooks will run on Windows, macOS, and Linux!
The KMNIST dataset

The dataset we are using today is the Kuzushiji-MNIST dataset, or KMNIST, for short. This dataset is meant to be a drop-in replacement for the standard MNIST digits recognition dataset.
The KMNIST dataset consists of 70,000 images and their corresponding labels (60,000 for training and 10,000 for testing).
There are a total of 10 classes (meaning 10 Hiragana characters) in the KMNIST dataset, each equally distributed and represented. Our goal is to train a CNN that can accurately classify each of these 10 characters.
And lucky for us, the KMNIST dataset is built into PyTorch, making it super easy for us to work with!
Project structure
Before we start implementing any PyTorch code, let’s first review our project directory structure.
Start by accessing the “Downloads” section of this tutorial to retrieve the source code and pre-trained model.
You’ll then be presented with the following directory structure:
$ tree . --dirsfirst . ├── output │ ├── model.pth │ └── plot.png ├── pyimagesearch │ ├── __init__.py │ └── lenet.py ├── predict.py └── train.py 2 directories, 6 files
We have three Python scripts to review today:
lenet.py: Our PyTorch implementation of the famous LeNet architecturetrain.py: Trains LeNet on the KMNIST dataset using PyTorch, then serializes the trained model to disk (i.e.,model.pth)predict.py: Loads our trained model from disk, makes predictions on testing images, and displays the results on our screen
The output directory will be populated with plot.png (a plot of our training/validation loss and accuracy) and model.pth (our trained model file) once we run train.py.
With our project directory structure reviewed, we can move on to implementing our CNN with PyTorch.
Implementing a Convolutional Neural Network (CNN) with PyTorch
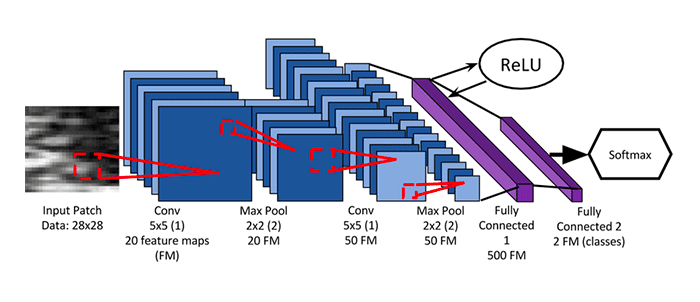
The Convolutional Neural Network (CNN) we are implementing here with PyTorch is the seminal LeNet architecture, first proposed by one of the grandfathers of deep learning, Yann LeCunn.
By today’s standards, LeNet is a very shallow neural network, consisting of the following layers:
(CONV => RELU => POOL) * 2 => FC => RELU => FC => SOFTMAX
As you’ll see, we’ll be able to implement LeNet with PyTorch in only 60 lines of code (including comments).
The best way to learn about CNNs with PyTorch is to implement one, so with that said, open the lenet.py file in the pyimagesearch module, and let’s get to work:
# import the necessary packages from torch.nn import Module from torch.nn import Conv2d from torch.nn import Linear from torch.nn import MaxPool2d from torch.nn import ReLU from torch.nn import LogSoftmax from torch import flatten
Lines 2-8 import our required packages. Let’s break each of them down:
Module: Rather than using theSequentialPyTorch class to implement LeNet, we’ll instead subclass theModuleobject so you can see how PyTorch implements neural networks using classesConv2d: PyTorch’s implementation of convolutional layersLinear: Fully connected layersMaxPool2d: Applies 2D max-pooling to reduce the spatial dimensions of the input volumeReLU: Our ReLU activation functionLogSoftmax: Used when building our softmax classifier to return the predicted probabilities of each classflatten: Flattens the output of a multi-dimensional volume (e.g., a CONV or POOL layer) such that we can apply fully connected layers to it
With our imports taken care of, we can implement our LeNet class using PyTorch:
class LeNet(Module): def __init__(self, numChannels, classes): # call the parent constructor super(LeNet, self).__init__() # initialize first set of CONV => RELU => POOL layers self.conv1 = Conv2d(in_channels=numChannels, out_channels=20, kernel_size=(5, 5)) self.relu1 = ReLU() self.maxpool1 = MaxPool2d(kernel_size=(2, 2), stride=(2, 2)) # initialize second set of CONV => RELU => POOL layers self.conv2 = Conv2d(in_channels=20, out_channels=50, kernel_size=(5, 5)) self.relu2 = ReLU() self.maxpool2 = MaxPool2d(kernel_size=(2, 2), stride=(2, 2)) # initialize first (and only) set of FC => RELU layers self.fc1 = Linear(in_features=800, out_features=500) self.relu3 = ReLU() # initialize our softmax classifier self.fc2 = Linear(in_features=500, out_features=classes) self.logSoftmax = LogSoftmax(dim=1)
Line 10 defines the LeNet class. Notice how we are subclassing the Module object — by building our model as a class we can easily:
- Reuse variables
- Implement custom functions to generate subnetworks/components (used very often when implementing more complex networks, such as ResNet, Inception, etc.)
- Define our own
forwardpass function
Best of all, when defined correctly, PyTorch can automatically apply its autograd module to perform automatic differentiation — backpropagation is taken care of for us by virtue of the PyTorch library!
The constructor to LeNet accepts two variables:
numChannels: The number of channels in the input images (1for grayscale or3for RGB)classes: Total number of unique class labels in our dataset
Line 13 calls the parent constructor (i.e., Module) which performs a number of PyTorch-specific operations.
From there, we start defining the actual LeNet architecture.
Lines 16-19 initialize our first set of CONV => RELU => POOL layers. Our first CONV layer learns a total of 20 filters, each of which are 5×5. A ReLU activation function is then applied, followed by a 2×2 max-pooling layer with a 2×2 stride to reduce the spatial dimensions of our input image.
We then have a second set of CONV => RELU => POOL layers on Lines 22-25. We increase the number of filters learned in the CONV layer to 50, but maintain the 5×5 kernel size. Again, a ReLU activation is applied, followed by max-pooling.
Next comes our first and only set of fully connected layers (Lines 28 and 29). We define the number of inputs to the layer (800) along with our desired number of output nodes (500). A ReLu activation follows the FC layer.
FInally, we apply our softmax classifier (Lines 32 and 33). The number of in_features is set to 500, which is the output dimensionality from the previous layer. We then apply LogSoftmax such that we can obtain predicted probabilities during evaluation.
It’s important to understand that at this point all we have done is initialized variables. These variables are essentially placeholders. PyTorch has absolutely no idea what the network architecture is, just that some variables exist inside the LeNet class definition.
To build the network architecture itself (i.e., what layer is input to some other layer), we need to override the forward method of the Module class.
The forward function serves a number of purposes:
- It connects layers/subnetworks together from variables defined in the constructor (i.e.,
__init__) of the class - It defines the network architecture itself
- It allows the forward pass of the model to be performed, resulting in our output predictions
- And, thanks to PyTorch’s autograd module, it allows us to perform automatic differentiation and update our model weights
Let’s inspect the forward function now:
def forward(self, x): # pass the input through our first set of CONV => RELU => # POOL layers x = self.conv1(x) x = self.relu1(x) x = self.maxpool1(x) # pass the output from the previous layer through the second # set of CONV => RELU => POOL layers x = self.conv2(x) x = self.relu2(x) x = self.maxpool2(x) # flatten the output from the previous layer and pass it # through our only set of FC => RELU layers x = flatten(x, 1) x = self.fc1(x) x = self.relu3(x) # pass the output to our softmax classifier to get our output # predictions x = self.fc2(x) output = self.logSoftmax(x) # return the output predictions return output
The forward method accepts a single parameter, x, which is the batch of input data to the network.
We then connect our conv1, relu1, and maxpool1 layers together to form the first CONV => RELU => POOL layer of the network (Lines 38-40).
A similar operation is performed on Lines 44-46, this time building the second set of CONV => RELU => POOL layers.
At this point, the variable x is a multi-dimensional tensor; however, in order to create our fully connected layers, we need to “flatten” this tensor into what essentially amounts to a 1D list of values — the flatten function on Line 50 takes care of this operation for us.
From there, we connect the fc1 and relu3 layers to the network architecture (Lines 51 and 52), followed by attaching the final fc2 and logSoftmax (Lines 56 and 57).
The output of the network is then returned to the calling function.
Again, I want to reiterate the importance of initializing variables in the constructor versus building the network itself in the forward function:
- The constructor to your
Moduleonly initializes your layer types. PyTorch keeps track of these variables, but it has no idea how the layers connect to each other. - For PyTorch to understand the network architecture you’re building, you define the
forwardfunction. - Inside the
forwardfunction you take the variables initialized in your constructor and connect them. - PyTorch can then make predictions using your network and perform automatic backpropagation, thanks to the autograd module
Congrats on implementing your first CNN with PyTorch!
Creating our CNN training script with PyTorch
With our CNN architecture implemented, we can move on to creating our training script with PyTorch.
Open the train.py file in your project directory structure, and let’s get to work:
# set the matplotlib backend so figures can be saved in the background
import matplotlib
matplotlib.use("Agg")
# import the necessary packages
from pyimagesearch.lenet import LeNet
from sklearn.metrics import classification_report
from torch.utils.data import random_split
from torch.utils.data import DataLoader
from torchvision.transforms import ToTensor
from torchvision.datasets import KMNIST
from torch.optim import Adam
from torch import nn
import matplotlib.pyplot as plt
import numpy as np
import argparse
import torch
import time
Lines 2 and 3 import matplotlib and set the appropriate background engine.
From there, we import a number of notable packages:
LeNet: Our PyTorch implementation of the LeNet CNN from the previous sectionclassification_report: Used to display a detailed classification report on our testing setrandom_split: Constructs a random training/testing split from an input set of dataDataLoader: PyTorch’s awesome data loading utility that allows us to effortlessly build data pipelines to train our CNNToTensor: A preprocessing function that converts input data into a PyTorch tensor for us automaticallyKMNIST: The Kuzushiji-MNIST dataset loader built into the PyTorch libraryAdam: The optimizer we’ll use to train our neural networknn: PyTorch’s neural network implementations
Let’s now parse our command line arguments:
# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-m", "--model", type=str, required=True,
help="path to output trained model")
ap.add_argument("-p", "--plot", type=str, required=True,
help="path to output loss/accuracy plot")
args = vars(ap.parse_args())
We have two command line arguments that need parsing:
--model: The path to our output serialized model after training (we save this model to disk so we can use it to make predictions in ourpredict.pyscript)--plot: The path to our output training history plot
Moving on, we now have some important initializations to take care of:
# define training hyperparameters
INIT_LR = 1e-3
BATCH_SIZE = 64
EPOCHS = 10
# define the train and val splits
TRAIN_SPLIT = 0.75
VAL_SPLIT = 1 - TRAIN_SPLIT
# set the device we will be using to train the model
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
Lines 29-31 set our initial learning rate, batch size, and number of epochs to train for, while Lines 34 and 35 define our training and validation split size (75% of training, 25% for validation).
Line 38 then determines our device (i.e., whether we’ll be using our CPU or GPU).
Let’s start preparing our dataset:
# load the KMNIST dataset
print("[INFO] loading the KMNIST dataset...")
trainData = KMNIST(root="data", train=True, download=True,
transform=ToTensor())
testData = KMNIST(root="data", train=False, download=True,
transform=ToTensor())
# calculate the train/validation split
print("[INFO] generating the train/validation split...")
numTrainSamples = int(len(trainData) * TRAIN_SPLIT)
numValSamples = int(len(trainData) * VAL_SPLIT)
(trainData, valData) = random_split(trainData,
[numTrainSamples, numValSamples],
generator=torch.Generator().manual_seed(42))
Lines 42-45 load the KMNIST dataset using PyTorch’s build in KMNIST class.
For our trainData, we set train=True while our testData is loaded with train=False. These Booleans come in handy when working with datasets built into the PyTorch library.
The download=True flag indicates that PyTorch will automatically download and cache the KMNIST dataset to disk for us if we had not previously downloaded it.
Also take note of the transform parameter — here we can apply a number of data transformations (outside the scope of this tutorial but will be covered soon). The only transform we need is to convert the NumPy array loaded by PyTorch into a tensor data type.
With our training and testing set loaded, we drive our training and validation set on Lines 49-53. Using PyTorch’s random_split function, we can easily split our data.
We now have three sets of data:
- Training
- Validation
- Testing
The next step is to create a DataLoader for each one:
# initialize the train, validation, and test data loaders trainDataLoader = DataLoader(trainData, shuffle=True, batch_size=BATCH_SIZE) valDataLoader = DataLoader(valData, batch_size=BATCH_SIZE) testDataLoader = DataLoader(testData, batch_size=BATCH_SIZE) # calculate steps per epoch for training and validation set trainSteps = len(trainDataLoader.dataset) // BATCH_SIZE valSteps = len(valDataLoader.dataset) // BATCH_SIZE
Building the DataLoader objects is accomplished on Lines 56-59. We set shuffle=True only for our trainDataLoader since our validation and testing sets do not require shuffling.
We also derive the number of training steps and validation steps per epoch (Lines 62 and 63).
At this point our data is ready for training; however, we don’t have a model to train yet!
Let’s initialize LeNet now:
# initialize the LeNet model
print("[INFO] initializing the LeNet model...")
model = LeNet(
numChannels=1,
classes=len(trainData.dataset.classes)).to(device)
# initialize our optimizer and loss function
opt = Adam(model.parameters(), lr=INIT_LR)
lossFn = nn.NLLLoss()
# initialize a dictionary to store training history
H = {
"train_loss": [],
"train_acc": [],
"val_loss": [],
"val_acc": []
}
# measure how long training is going to take
print("[INFO] training the network...")
startTime = time.time()
Lines 67-69 initialize our model. Since the KMNIST dataset is grayscale, we set numChannels=1. We can easily set the number of classes by calling dataset.classes of our trainData.
We also call to(device) to move the model to either our CPU or GPU.
Lines 72 and 73 initialize our optimizer and loss function. We’ll use the Adam optimizer for training and the negative log-likelihood for our loss function.
When we combine the nn.NLLoss class with LogSoftmax in our model definition, we arrive at categorical cross-entropy loss (which is the equivalent to training a model with an output Linear layer and an nn.CrossEntropyLoss loss). Basically, PyTorch allows you to implement categorical cross-entropy in two separate ways.
Get used to seeing both methods as some deep learning practitioners (almost arbitrarily) prefer one over the other.
We then initialize H, our training history dictionary (Lines 76-81). After every epoch we’ll update this dictionary with our training loss, training accuracy, testing loss, and testing accuracy for the given epoch.
Finally, we start a timer to measure how long training takes (Line 85).
At this point, all of our initializations are complete, so it’s time to train our model.
Note: Be sure you’ve read the previous tutorial in this series, Intro to PyTorch: Training your first neural network using PyTorch, as we’ll be building on concepts learned in that guide.
Below follows our training loop:
# loop over our epochs for e in range(0, EPOCHS): # set the model in training mode model.train() # initialize the total training and validation loss totalTrainLoss = 0 totalValLoss = 0 # initialize the number of correct predictions in the training # and validation step trainCorrect = 0 valCorrect = 0 # loop over the training set for (x, y) in trainDataLoader: # send the input to the device (x, y) = (x.to(device), y.to(device)) # perform a forward pass and calculate the training loss pred = model(x) loss = lossFn(pred, y) # zero out the gradients, perform the backpropagation step, # and update the weights opt.zero_grad() loss.backward() opt.step() # add the loss to the total training loss so far and # calculate the number of correct predictions totalTrainLoss += loss trainCorrect += (pred.argmax(1) == y).type( torch.float).sum().item()
On Line 88, we loop over our desired number of epochs.
We then proceed to:
- Put the model in
train()mode - Initialize our training loss and validation loss for the current epoch
- Initialize our number of correct training and validation predictions for the current epoch
Line 102 shows the benefit of using PyTorch’s DataLoader class — all we have to do is start a for loop over the DataLoader object. PyTorch automatically yields a batch of training data. Under the hood, the DataLoader is also shuffling our training data (and if we were doing any additional preprocessing or data augmentation, it would happen here as well).
For each batch of data (Line 104) we perform a forward pass, obtain our predictions, and compute the loss (Lines 107 and 108).
Next comes the all important step of:
- Zeroing our gradient
- Performing backpropagation
- Updating the weights of our model
Seriously, don’t forget this step! Failure to do those three steps in that exact order will lead to erroneous training results. Whenever you write a training loop with PyTorch, I highly recommend you insert those three lines of code before you do anything else so that you are reminded to ensure they are in the proper place.
We wrap up the code block by updating our totalTrainLoss and trainCorrect bookkeeping variables.
At this point, we’ve looped over all batches of data in our training set for the current epoch — now we can evaluate our model on the validation set:
# switch off autograd for evaluation with torch.no_grad(): # set the model in evaluation mode model.eval() # loop over the validation set for (x, y) in valDataLoader: # send the input to the device (x, y) = (x.to(device), y.to(device)) # make the predictions and calculate the validation loss pred = model(x) totalValLoss += lossFn(pred, y) # calculate the number of correct predictions valCorrect += (pred.argmax(1) == y).type( torch.float).sum().item()
When evaluating a PyTorch model on a validation or testing set, you need to first:
- Use the
torch.no_grad()context to turn off gradient tracking and computation - Put the model in
eval()mode
From there, you loop over all validation DataLoader (Line 128), move the data to the correct device (Line 130), and use the data to make predictions (Line 133) and compute your loss (Line 134).
You can then derive your total number of correct predictions (Lines 137 and 138).
We round out our training loop by computing a number of statistics:
# calculate the average training and validation loss
avgTrainLoss = totalTrainLoss / trainSteps
avgValLoss = totalValLoss / valSteps
# calculate the training and validation accuracy
trainCorrect = trainCorrect / len(trainDataLoader.dataset)
valCorrect = valCorrect / len(valDataLoader.dataset)
# update our training history
H["train_loss"].append(avgTrainLoss.cpu().detach().numpy())
H["train_acc"].append(trainCorrect)
H["val_loss"].append(avgValLoss.cpu().detach().numpy())
H["val_acc"].append(valCorrect)
# print the model training and validation information
print("[INFO] EPOCH: {}/{}".format(e + 1, EPOCHS))
print("Train loss: {:.6f}, Train accuracy: {:.4f}".format(
avgTrainLoss, trainCorrect))
print("Val loss: {:.6f}, Val accuracy: {:.4f}n".format(
avgValLoss, valCorrect))
Lines 141 and 142 compute our average training and validation loss. Lines 146 and 146 do the same thing, but for our training and validation accuracy.
We then take these values and update our training history dictionary (Lines 149-152).
Finally, we display the training loss, training accuracy, validation loss, and validation accuracy on our terminal (Lines 149-152).
We’re almost there!
Now that training is complete, we need to evaluate our model on the testing set (previously we’ve only used the training and validation sets):
# finish measuring how long training took
endTime = time.time()
print("[INFO] total time taken to train the model: {:.2f}s".format(
endTime - startTime))
# we can now evaluate the network on the test set
print("[INFO] evaluating network...")
# turn off autograd for testing evaluation
with torch.no_grad():
# set the model in evaluation mode
model.eval()
# initialize a list to store our predictions
preds = []
# loop over the test set
for (x, y) in testDataLoader:
# send the input to the device
x = x.to(device)
# make the predictions and add them to the list
pred = model(x)
preds.extend(pred.argmax(axis=1).cpu().numpy())
# generate a classification report
print(classification_report(testData.targets.cpu().numpy(),
np.array(preds), target_names=testData.classes))
Lines 162-164 stop our training timer and show how long training took.
We then set up another torch.no_grad() context and put our model in eval() mode (Lines 170 and 172).
Evaluation is performed by:
- Initializing a list to store our predictions (Line 175)
- Looping over our
testDataLoader(Line 178) - Sending the current batch of data to the appropriate device (Line 180)
- Making predictions on the current batch of data (Line 183)
- Updating our
predslist with the top predictions from the model (Line 184)
Finally, we display a detailed classification_report.
The last step we’ll do here is plot our training and validation history, followed by serializing our model weights to disk:
# plot the training loss and accuracy
plt.style.use("ggplot")
plt.figure()
plt.plot(H["train_loss"], label="train_loss")
plt.plot(H["val_loss"], label="val_loss")
plt.plot(H["train_acc"], label="train_acc")
plt.plot(H["val_acc"], label="val_acc")
plt.title("Training Loss and Accuracy on Dataset")
plt.xlabel("Epoch #")
plt.ylabel("Loss/Accuracy")
plt.legend(loc="lower left")
plt.savefig(args["plot"])
# serialize the model to disk
torch.save(model, args["model"])
Lines 191-201 generate a matplotlib figure for our training history.
We then call torch.save to save our PyTorch model weights to disk so that we can load them from disk and make predictions from a separate Python script.
As a whole, reviewing this script shows you how much more control PyTorch gives you over the training loop — this is both a good and a bad thing:
- It’s good if you want full control over the training loop and need to implement custom procedures
- It’s bad when your training loop is simple and a Keras/TensorFlow equivalent to
model.fitwould suffice
As I mentioned in part one of this series, What is PyTorch, neither PyTorch nor Keras/TensorFlow is better than the other, there are just different caveats and use cases for each library.
Training our CNN with PyTorch
We are now ready to train our CNN using PyTorch.
Be sure to access the “Downloads” section of this tutorial to retrieve the source code to this guide.
From there, you can train your PyTorch CNN by executing the following command:
$ python train.py --model output/model.pth --plot output/plot.png
[INFO] loading the KMNIST dataset...
[INFO] generating the train-val split...
[INFO] initializing the LeNet model...
[INFO] training the network...
[INFO] EPOCH: 1/10
Train loss: 0.362849, Train accuracy: 0.8874
Val loss: 0.135508, Val accuracy: 0.9605
[INFO] EPOCH: 2/10
Train loss: 0.095483, Train accuracy: 0.9707
Val loss: 0.091975, Val accuracy: 0.9733
[INFO] EPOCH: 3/10
Train loss: 0.055557, Train accuracy: 0.9827
Val loss: 0.087181, Val accuracy: 0.9755
[INFO] EPOCH: 4/10
Train loss: 0.037384, Train accuracy: 0.9882
Val loss: 0.070911, Val accuracy: 0.9806
[INFO] EPOCH: 5/10
Train loss: 0.023890, Train accuracy: 0.9930
Val loss: 0.068049, Val accuracy: 0.9812
[INFO] EPOCH: 6/10
Train loss: 0.022484, Train accuracy: 0.9930
Val loss: 0.075622, Val accuracy: 0.9816
[INFO] EPOCH: 7/10
Train loss: 0.013171, Train accuracy: 0.9960
Val loss: 0.077187, Val accuracy: 0.9822
[INFO] EPOCH: 8/10
Train loss: 0.010805, Train accuracy: 0.9966
Val loss: 0.107378, Val accuracy: 0.9764
[INFO] EPOCH: 9/10
Train loss: 0.011510, Train accuracy: 0.9960
Val loss: 0.076585, Val accuracy: 0.9829
[INFO] EPOCH: 10/10
Train loss: 0.009648, Train accuracy: 0.9967
Val loss: 0.082116, Val accuracy: 0.9823
[INFO] total time taken to train the model: 159.99s
[INFO] evaluating network...
precision recall f1-score support
o 0.93 0.98 0.95 1000
ki 0.96 0.95 0.96 1000
su 0.96 0.90 0.93 1000
tsu 0.95 0.97 0.96 1000
na 0.94 0.94 0.94 1000
ha 0.97 0.95 0.96 1000
ma 0.94 0.96 0.95 1000
ya 0.98 0.95 0.97 1000
re 0.95 0.97 0.96 1000
wo 0.97 0.96 0.97 1000
accuracy 0.95 10000
macro avg 0.95 0.95 0.95 10000
weighted avg 0.95 0.95 0.95 10000
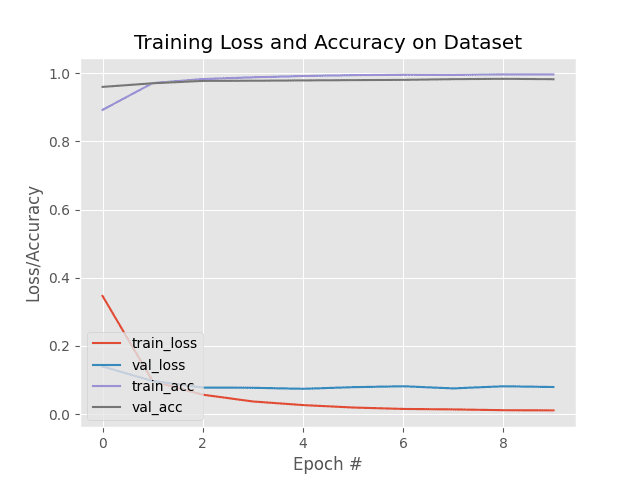
Training our CNN took ≈160 seconds on my CPU. Using my GPU training time drops to ≈82 seconds.
At the end of the final epoch we have obtained 99.67% training accuracy and 98.23% validation accuracy.
When we evaluate on our testing set we reach ≈95% accuracy, which is quite good given the complexity of the Hiragana characters and the simplicity of our shallow network architecture (using a deeper network such as a VGG-inspired model or ResNet-like would allow us to obtain even higher accuracy, but those models are more complex for an introduction to CNNs with PyTorch).
Furthermore, as Figure 4 shows, our training history plot is smooth, demonstrating there is little/no overfitting happening.
Before moving to the next section, take a look at your output directory:
$ ls output/ model.pth plot.png
Note the model.pth file — this is our trained PyTorch model saved to disk. We will load this model from disk and use it to make predictions in the following section.
Implementing our PyTorch prediction script
The final script we are reviewing here will show you how to make predictions with a PyTorch model that has been saved to disk.
Open the predict.py file in your project directory structure, and we’ll get started:
# set the numpy seed for better reproducibility import numpy as np np.random.seed(42) # import the necessary packages from torch.utils.data import DataLoader from torch.utils.data import Subset from torchvision.transforms import ToTensor from torchvision.datasets import KMNIST import argparse import imutils import torch import cv2
Lines 2-13 import our required Python packages. We set the NumPy random seed at the top of the script for better reproducibility across machines.
We then import:
DataLoader: Used to load our KMNIST testing dataSubset: Builds a subset of the testing dataToTensor: Converts our input data to a PyTorch tensor data typeKMNIST: The Kuzushiji-MNIST dataset loader built into the PyTorch librarycv2: Our OpenCV bindings which we’ll use for basic drawing and displaying output images on our screen
Next comes our command line arguments:
# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-m", "--model", type=str, required=True,
help="path to the trained PyTorch model")
args = vars(ap.parse_args())
We only need a single argument here, --model, the path to our trained PyTorch model saved to disk. Presumably, this switch will point to output/model.pth.
Moving on, let’s set our device:
# set the device we will be using to test the model
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# load the KMNIST dataset and randomly grab 10 data points
print("[INFO] loading the KMNIST test dataset...")
testData = KMNIST(root="data", train=False, download=True,
transform=ToTensor())
idxs = np.random.choice(range(0, len(testData)), size=(10,))
testData = Subset(testData, idxs)
# initialize the test data loader
testDataLoader = DataLoader(testData, batch_size=1)
# load the model and set it to evaluation mode
model = torch.load(args["model"]).to(device)
model.eval()
Line 22 determines if we will be performing inference on our CPU or GPU.
We then load the testing data from the KMNIST dataset on Lines 26 and 27. We randomly sample a total of 10 images from this dataset on Lines 28 and 29 using the Subset class (which creates a smaller “view” of the full testing data).
A DataLoader is created to pass our subset of testing data through the model on Line 32.
We then load our serialized PyTorch model from disk on Line 35, passing it to the appropriate device.
Finally, the model is placed into evaluation mode (Line 36).
Let’s now make predictions on a sample of our testing set:
# switch off autograd with torch.no_grad(): # loop over the test set for (image, label) in testDataLoader: # grab the original image and ground truth label origImage = image.numpy().squeeze(axis=(0, 1)) gtLabel = testData.dataset.classes[label.numpy()[0]] # send the input to the device and make predictions on it image = image.to(device) pred = model(image) # find the class label index with the largest corresponding # probability idx = pred.argmax(axis=1).cpu().numpy()[0] predLabel = testData.dataset.classes[idx]
Line 39 turns off gradient tracking, while Line 41 loops over all images in our subset of the test set.
For each image, we:
- Grab the current image and turn it into a NumPy array (so we can draw on it later with OpenCV)
- Extracts the ground-truth class label
- Sends the
imageto the appropriatedevice - Uses our trained LeNet model to make predictions on the current
image - Extracts the class label with the top predicted probability
All that’s left is a bit of visualization:
# convert the image from grayscale to RGB (so we can draw on
# it) and resize it (so we can more easily see it on our
# screen)
origImage = np.dstack([origImage] * 3)
origImage = imutils.resize(origImage, width=128)
# draw the predicted class label on it
color = (0, 255, 0) if gtLabel == predLabel else (0, 0, 255)
cv2.putText(origImage, gtLabel, (2, 25),
cv2.FONT_HERSHEY_SIMPLEX, 0.95, color, 2)
# display the result in terminal and show the input image
print("[INFO] ground truth label: {}, predicted label: {}".format(
gtLabel, predLabel))
cv2.imshow("image", origImage)
cv2.waitKey(0)
Each image in the KMNIST dataset is a single channel grayscale image; however, we want to use OpenCV’s cv2.putText function to draw the predicted class label and ground-truth label on the image.
To draw RGB colors on a grayscale image, we first need to create an RGB representation of the grayscale image by stacking the grayscale image depth-wise a total of three times (Line 58).
Additionally, we resize the origImage so that we can more easily see it on our screen (by default, KMNIST images are only 28×28 pixels, which can be hard to see, especially on a high resolution monitor).
From there, we determine the text color and draw the label on the output image.
We wrap up the script by displaying the output origImage on our screen.
Making predictions with our trained PyTorch model
We are now ready to make predictions using our trained PyTorch model!
Be sure to access the “Downloads” section of this tutorial to retrieve the source code and pre-trained PyTorch model.
From there, you can execute the predict.py script:
$ python predict.py --model output/model.pth [INFO] loading the KMNIST test dataset... [INFO] Ground truth label: ki, Predicted label: ki [INFO] Ground truth label: ki, Predicted label: ki [INFO] Ground truth label: ki, Predicted label: ki [INFO] Ground truth label: ha, Predicted label: ha [INFO] Ground truth label: tsu, Predicted label: tsu [INFO] Ground truth label: ya, Predicted label: ya [INFO] Ground truth label: tsu, Predicted label: tsu [INFO] Ground truth label: na, Predicted label: na [INFO] Ground truth label: ki, Predicted label: ki [INFO] Ground truth label: tsu, Predicted label: tsu

As our output demonstrates, we have been able to successfully recognize each of the Hiragana characters using our PyTorch model.
What’s next? I recommend PyImageSearch University.
Course information:
76 total classes • 90 hours of on-demand code walkthrough videos • Last updated: May 2023
★★★★★ 4.84 (128 Ratings) • 16,000+ Students Enrolled
I strongly believe that if you had the right teacher you could master computer vision and deep learning.
Do you think learning computer vision and deep learning has to be time-consuming, overwhelming, and complicated? Or has to involve complex mathematics and equations? Or requires a degree in computer science?
That’s not the case.
All you need to master computer vision and deep learning is for someone to explain things to you in simple, intuitive terms. And that’s exactly what I do. My mission is to change education and how complex Artificial Intelligence topics are taught.
If you’re serious about learning computer vision, your next stop should be PyImageSearch University, the most comprehensive computer vision, deep learning, and OpenCV course online today. Here you’ll learn how to successfully and confidently apply computer vision to your work, research, and projects. Join me in computer vision mastery.
Inside PyImageSearch University you’ll find:
- ✓ 76 courses on essential computer vision, deep learning, and OpenCV topics
- ✓ 76 Certificates of Completion
- ✓ 90 hours of on-demand video
- ✓ Brand new courses released regularly, ensuring you can keep up with state-of-the-art techniques
- ✓ Pre-configured Jupyter Notebooks in Google Colab
- ✓ Run all code examples in your web browser — works on Windows, macOS, and Linux (no dev environment configuration required!)
- ✓ Access to centralized code repos for all 500+ tutorials on PyImageSearch
- ✓ Easy one-click downloads for code, datasets, pre-trained models, etc.
- ✓ Access on mobile, laptop, desktop, etc.
Click here to join PyImageSearch University
Summary
In this tutorial, you learned how to train your first Convolutional Neural Network (CNN) using the PyTorch deep learning library.
You also learned how to:
- Save our trained PyTorch model to disk
- Load it from disk in a separate Python script
- Use the PyTorch model to make predictions on images
This sequence of saving a model after training, and then loading it and using the model to make predictions, is a process you should become comfortable with — you’ll be doing it often as a PyTorch deep learning practitioner.
Speaking of loading saved PyTorch models from disk, next week you will learn how to use pre-trained PyTorch to recognize 1,000 image classes that you often encounter in everyday life. These models can save you a bunch of time and hassle — they are highly accurate and don’t require you to manually train them.
To download the source code to this post (and be notified when future tutorials are published here on PyImageSearch), simply enter your email address in the form below!
Download the Source Code and FREE 17-page Resource Guide
Enter your email address below to get a .zip of the code and a FREE 17-page Resource Guide on Computer Vision, OpenCV, and Deep Learning. Inside you’ll find my hand-picked tutorials, books, courses, and libraries to help you master CV and DL!