Элементарное руководство по теории детерминантов - RukovodstvoRus.ru

Главная / Произведения Кэрролла / Математические труды

Живая математика от Льюиса Кэрролла

Льюис Кэрролл оставил после себя не только сказочные истории, но и серьезные математические труды. Он писал большие книги и небольшие брошюры, а также часто публиковал статьи в различных журналах.

Мы рассмотрим лишь наиболее известные и крупные работы Льюиса Кэрролла.

• В 1858 году он написал «Алгебраический разбор V книги Эвклида». Главным трудом древнегреческого математика Эвклида было сочинение «Начало», состоящее из 13 книг. Его пятая книга, которую и рассматривал Льюис Кэрролл в своей работе, была посвящена общей теории пропорций.

• В 1867 году мир увидела книга «Элементарное руководство по теории детерминантов» — элементарный трактат о детерминантах с их применением для линейных и алгебраических уравнений.

• В 1879 году Льюис Кэрролл окончил математический труд, посвященный древнегреческом математику: «Эвклид и его современные соперники». В книге Кэрролл защищал подход древнегреческого математика Эвклида к преподаванию геометрии. Несмотря на то, что это научная работа, повествование ведется в форме причудливых диалогов между математиком по имени Минос и «адвокатом дьявола» профессором Никто, который воплощает в себе «современных соперников Эвклида».

Цитата из предисловия к этой книге нанесена на первый логотип «Википедии»:

Использованная цитата полностью (серым — части, которые не видны на логотипе, черным — те, что видны):

In one respect this book is an experiment, and may chance to prove a failure: I mean that I have not thought it necessary to maintain throughout the gravity of style which scientific writers usually affect, and which has somehow come to be regarded as an ‘inseparable accident’ of scientific teaching. I never could quite see the reasonableness of this immemorial law: subjects there are, no doubt, which are in their essence too serious to admit of any lightness of treatment – but I cannot recognise Geometry as one of them. Nevertheless it will, I trust, be found that I have permitted myself a glimpse of the comic side of things only at fitting seasons, when the tired reader might well crave a moment’s breathing-space, and not on any occasion where it could endanger the continuity of the line of argument.

• В том же году Кэрролл издал «Дублеты, словесные загадки» — книгу, на страницах которой описал новую игру со словами.

• В 1888 году писатель издал «Математические курьезы» (часть I), а через пять лет в 1893 году — вторую часть под названием «Полуночные задачи». В сборник «Полуночные задачи» вошли 72 задачи по тригонометрии, алгебре и планиметрии. Эти задачи Льюис Кэрролл придумывал ночами, когда его мучила бессонница, и сам же их решал во тьме. Но «Полуночные задачи», по словам писателя, не средство от бессонницы, а способ избавиться от навязчивых мыслей, которые часто одолевают свободные от занятий умы.

• В 1890 году Кэрролл издал брошюру «Круглый бильярд», в которой описал собственное изобретение — круглый стол для бильярда.

Математические книги для детей

Писатель любил занимать детские умы математическими задачками и головоломками.

В 1878 году он написал сборник загадок и игр для детей «История с узелками». Сборник оформлен как рассказ с действующими персонажами и любопытными математическими задачками, понятными и интересными маленьким читателям.

Через 9 лет в 1887 году Льюис Кэрролл выпустил книгу «Логическая игра», в которой автор знакомит юных читателей с оригинальным графическим методом решения соритов и силлогизмов. В приложении Кэрролл описывает несколько игр, фокусов и головоломок для учеников 8–10-х классов.

Льюис Кэрролл попытался создать учебник для школы. Его «Символическая логика» (часть I), опубликованная в 1890 году, должна была стать серьезным школьным учебником.

В отличие от сухих учебников тех времен, «Символическая логика» полна примерами, а также головоломками, которые можно решить играя. Вторая часть «Символической логики» издана уже после смерти автора, в 1977 году.

Источник

…Во-первых, было два основоположника литературы абсурда — Эдвард Лир, издавший несколько «Книг нонсенса», и Льюис Кэрролл, издавший сперва «Алису в стране чудес», потом «Алису в Зазеркалье», а потом (в марте 1876 года) «Охоту на Снарка».

Во-вторых, Льюис Кэрролл тридцать лет преподавал математику в Колледже Церкви Христа, что в городе Оксфорде, написал за свою жизнь много ученых книг и чуть ли не сто тысяч писем разным людям — взрослым и детям, немножко заикался и замечательно фотографировал.

Именно математика открыла юному Кэрроллу дорогу в «большую» жизнь: мальчик был зачислен в престижный колледж Оксфордского университета, выиграл стипендию и удостоился отличия первого класса, а юношей был назначен лектором по математике Оксфорда.

Доктор Доджсон поселился в небольшом доме с башенками и сам скоро стал одной из достопримечательностей Оксфорда. Во внешности его было что-то странное: легкая асимметрия лица — один глаз несколько выше другого, уголки рта подвернуты — один вниз, другой вверх. Говорили, что он левша и только усилием воли заставляет себя писать правой рукой. Он был глух на одно ухо и сильно заикался. Лекции читал отрывистым, ровным, безжизненным тоном. Знакомств избегал, часами бродил по окрестностям. У него было несколько любимых занятий, которым он посвящал все свободное время.

Много времени Кэрролл уделял исследовательской работе по математике: он издал «Аналитический разбор пятой книги Евклида», «Конспекты по алгебраической планиметрии», «Элементарное руководство по теории детерминантов», «Евклид и его современные соперники», а также «Математические кузьезы» и «Символическую логику».

Многие достижения Льюиса в области математической логики намного опередили свое время. Кэрролл разработал графический метод решения логических задач – более удобный, чем пресловутый способ Эйлера или Венна. С искусством сравнивали способность Кэрролла решать так называемые сориты (сорит по-гречески «куча») – логические задачи, представленные цепочкой силлогизмов, у которых заключение одного силлогизма служит посылкой другого.

«А что такое математика?» — спросила Алиса. Одной из основных задач изучения математики является развитие интереса к предмету, умение видеть математические задачи в повседневной жизни.

Алиса прыгнула в кроличью нору и попала из мира традиционной математики в мир математики современной, в которой развивается топология, изучается множество иррациональных чисел, звучат идеи о многомерности пространства.

Во фрагменте с Гусеницей Алиса подвергается странным метаморфозам, то увеличиваясь, то уменьшаясь в размерах.(слово «алгебра» происходит от арабской фразы «альджебр аль мукабала», что означает уменьшение). Пытаясь восстановить себя до первоначального размера, она добивалась обратного эффекта.

Гусеница советует Алисе оставаться пропорциональной, даже если она не сможет «держаться в едином размере хоть 10 минут!». Пропорциональность, а не абсолютный размер — вот что имело значение в наземном мире Евклидовой геометрии.

В этом же эпизоде обращается внимание на особенности строения круга – отсутствие у него углов, сторон и вершин.

«– Откусишь с одной стороны – подрастешь, с другой – уменьшишься! -сказала Гусеница

– С одной стороны чего? – подумала Алиса. – С другой стороны чего?

С минуту Алиса задумчиво смотрела на гриб, пытаясь определить, где у него одна сторона, а где – другая; гриб был круглый, и это совсем сбило ее с толку.»

Также понятие круга используется в отрывке, где Додо предлагает героям, которые промокли в луже слез, обсохнуть, бегая по кругу. После того как Додо сказал: «Бег закончен!» все спросили, кто победил. Но он не смог сразу ответить на этот вопрос.

С математической точки зрения его замешательство можно объяснить тем, что все стояли в хаотичном порядке и начали бег в разное время, а закончили по команде одновременно. Но потом Додо сказал, что победили все, потому что цель достигнута – все обсохли.

В начале произведения мы сталкиваемся с понятием «центральная симметрия». Пока Алиса летела вниз по кроличьей норе, она думала:

« Я, верно, приближаюсь к центру земли. А не пролечу ли я всю землю насквозь? Вот будет смешно! Вылезаю – а люди вниз головой!».

Центр земли – это центр симметрии. Центральная симметрия – это симметрия относительно точки.

В главе «Свинья и перец», когда Алиса выносит ребёнка Герцогини из дома, и он становится поросёнком, автор пародирует принцип преемственности, который был введён в середине 19 века во Франции.

Этот принцип (сейчас – важный аспект топологии) предполагает, что одну фигуру можно согнуть или растянуть в другую, сохраняя при этом основные свойства – круг, эллипс и параболу можно трансформировать друг в друга.

Доджсон заставил Шляпника, Кролика и Соню ходить вокруг да около чайного столика, чтобы продемонстрировать кватернионы — численную систему, основанную на четырёхмерном Евклидовом пространстве.

В сказке Люиса Кэрролла можно найти и другие математические модели.

Источник

Графическая логическая игра Льюиса Кэрролла

Время на прочтение
6 мин

Количество просмотров 12K

Льюис Кэрролл известен миру прежде всего как автор «Алисы в Стране чудес» с необычными волшебными персонажами — Чеширским Котом, Мартовским Зайцем, Птицей Додо, Белым Кроликом и, конечно, загадочным Шалтаем-Болтаем. Однако Льюис Кэрролл кроме популярных детских книжек также написал серьёзные трактаты по аналитической геометрии и линейной алгебре. В юные годы он был зачислен в престижный колледж Оксфордского университета, получил стипендию и должность профессора математики. Достижения Льюиса Кэрролла в области математической логики намного опередили свою эпоху. Он посвящал много времени исследовательской работе, были изданы: «Аналитический разбор пятой книги Евклида», «Конспекты по алгебраической планиметрии», «Элементарное руководство по теории детерминантов», «Евклид и его современные соперники», «Математические курьёзы» и «Символическая логика». Также он увлекался математическими головоломками и интересными задачками.

В одном из выпусков библиотеки журнала «Квант» я обнаружил перевод книги Льюиса Кэрролла «Логическая игра» (The Game of Logic). В этой книге автор рассказывает об оригинальном графическом способе визуализации логических суждений с помощью размеченного особым образом квадратного поля и фишек двух цветов. Этот способ помогает легко оперировать логическими множествами и на основе некоторых предпосылок формулировать новые утверждения. Давайте попробуем разобраться, как это работает.

Немного теории

С помощью метода Льюиса Кэрролла можно оперировать тремя свойствами объекта. Для иллюстрации двух свойств автор предлагает нарисовать квадрат, разделённый на четыре маленьких квадратика. Эти квадратики будут соответствовать наличию или отсутствию у объекта одного из двух свойств — такая маленькая логическая таблица истинности:

верхний левый квадрат: оба свойства есть;
верхний правый квадрат: свойство 1 — есть, свойство 2 — отсутствует;
нижний левый квадрат: свойство 1 — отсутствует, свойство 2 — есть;
нижний правый квадрат: оба свойства отсутствуют.

Чтобы добавить ещё одно свойство, немного расширим наш исходный квадрат так, чтобы каждый из четырёх маленьких квадратиков имел две области:

внутреннюю — свойство 3 есть;
внешнюю — свойство 3 отсутствует.

У нас получилась диаграмма, состоящая из 8 областей, которые соответствуют всем возможным комбинациям наличия или отсутствия у объекта каждого из трёх свойств.

Булочки как объект исследования

Давайте рассмотрим пример. Возьмём какой-нибудь аппетитный объект, например, булочки. Допустим, булочки могут обладать следующими свойствами: свежесть, вкусность и полезность. Тогда для каждого свойства у нас будут пары наличия этого свойства у булочки и его отсутствия:

свежие — несвежие;
вкусные — невкусные;
полезные — вредные.

Пусть внутренний жёлтый квадрат соответствует первым двум свойствам, а внешний — третьему свойству.

Множества у нас есть, теперь нужно описать с помощью этой системы определённые суждения. Для этого будем использовать фишки двух цветов:

Красная фишка будет означать «некоторые».
Чёрная фишка будет означать «ни одна».

С помощью размещения фишек на поле мы можем не только иллюстрировать различные глубокомысленные суждения о булочках, но и на основе исходных данных выводить новые суждения — узнавать о булочках что-то новое и поразительное.

Булочки вкусные и свежие

Для начала давайте попробуем проиллюстрировать некоторые суждения, используя только два первых свойства — вкусность и свежесть. Пока мы не будем выходить за пределы внутреннего жёлтого квадрата. Установим логические связи между двумя свойствами булочек. По правилам игры мы можем размещать фишки как в середине маленьких квадратиков, так и на границах между ними.

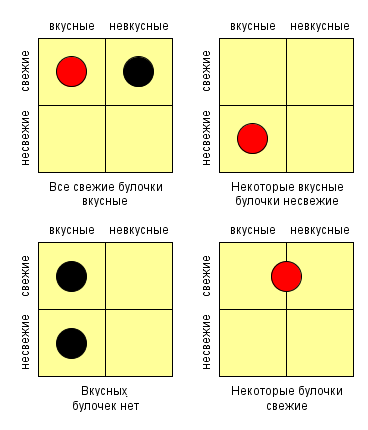
В первой диаграмме мы расположили фишку чёрного цвета на квадратике «свежие и невкусные». Это означает, что таких булочек не существует, ведь чёрная фишка означает «ни одна». А в квадратике «свежие и вкусные» у нас расположена красная фишка. Это означает, что некоторые булочки свежие и вкусные. И, действительно, могут же существовать ещё и несвежие булочки — нижние квадратики. Но для нас важно, что в верхних квадратиках больше нет места. Получается, что установив таким образом фишки, мы однозначно высказались по поводу свежих булочек: они бывают только вкусными!

Во второй диаграмме всё попроще — есть одна красная фишка, которая стоит в нижнем левом квадратике и означает простое утверждение: «Некоторые вкусные булочки несвежие».

На третьей диаграмме в левых квадратиках стоят чёрные фишки. Однозначно и категорично это означает, что вкусных булочек нет. Это специальная диетическая диаграмма.

На четвёртой диаграмме красная фишка установлена на границе между двумя верхними квадратиками. Это значит, что фишка относится ко всей верхней части диаграммы, соответствующей свежести булочек. А вот про вкусность мы ничего определённого сказать не можем. Также мы ничего не знаем о несвежих булочках. Может, они есть, а может их не существует. Получается, что по этой диаграмме мы определённо знаем, что некоторые булочки свежие.

Булочки ещё и полезные

Теперь, чтобы высказать своё авторитетное мнение о полезности булочек, добавим внешний бежевый квадрат.

На первой диаграмме есть две чёрные фишки и одна красная. Если бы у нас был только внутренний жёлтый квадрат, что чёрные фишки нам сообщили бы о том, что невкусных булочек не существует. Но теперь у нас есть ещё и третье свойство — полезность булочек. На нашей диаграмме жёлтый квадрат — это полезные булочки, а бежевый — вредные. Таким образом, мы можем сделать вывод, что невкусных полезных булочек не бывает. Но существуют ли вредные невкусные булочки? На этот вопрос нам даёт ответ красная фишка. Она нам сообщает, что некоторые вредные булочки ещё и невкусные. Объединив всё это вместе, мы можем сказать, что все невкусные булочки вредные. Великолепно!

Вторая диаграмма сообщает нам следующую информацию:

Нет вредных несвежих булочек.
Все вкусные несвежие булочки полезны.

Попробуйте самостоятельно разобраться в расположении фишек на этой диаграмме.

От булочек к предикатам

Льюис Кэрролл не просто показывает, как оперировать логическими утверждениями. Книга «Логическая игра» по сути является оригинальным и необычным учебником логики, в которой рассказывается об основных понятиях и законах этой науки. Вот, например, как в книге определено понятие суждения:

Суждение — это предложение, утверждающее, что некоторые или все предметы, принадлежащие определённому классу, называемому субъектом, одновременно являются предметами, принадлежащими другому классу, называемому предикатом (или что ни один предмет, принадлежащий классу «субъект», не является предметом, принадлежащим классу «предикат»).

Автор книги не даст вам заскучать:

Эти девять слов — суждение, признак, термин, суждения, субъект, предикат, частное и общее суждение — окажутся необычайно полезными, если кому-нибудь из ваших приятелей придёт в голову поинтересоваться, не приходилось ли вам когда-нибудь изучать логику. Не забудьте употребить в своём ответе все девять слов, и ваш приятель удалится совершенно потрясённым, «став не только мудрее, но и печальнее».

В суждении «Некоторые свежие булочки суть вкусные булочки» субъект — это «некоторые булочки», а предикат — «вкусные булочки».

Булочный силлогизм

Давайте вернёмся к нашим диаграммам. С помощью несложного правила можно переходить от большой диаграммы к малой — избавляться от третьего свойства в утверждениях. На диаграмме это правило выглядит на удивление просто — если во внешнем квадрате стоит красный кружок, то его можно перенести во внутренний квадрат.

Попробуем разобраться. На первой диаграмме показано, что:

Ни одна вкусная булочка не вредная.
Некоторые свежие булочки вредные.

Переносим красный кружок во внутренний квадрат и получаем новое утверждение: некоторые свежие булочки невкусные.

Посмотрим внимательно на верхний правый квадратик второй диаграммы. На первой диаграмме к ней примыкает красная фишка. Она нам сообщает, что в принципе в природе существуют свежие невкусные булочки — в рамках второй диаграммы нам не важно, полезные они или вредные. Значит, мы с полным правом можем поставить красную фишку на этот квадратик во второй диаграмме. Про три другие клетки мы ничего определённого сказать не можем, эти клетки на второй диаграмме остаются пустыми.

То, что мы только что проделали, называется силлогизмом — на основе заданных посылок мы сделали заключение. Это только один небольшой пример логических преобразований, которые можно выполнить с помощью диаграмм Льюиса Кэрролла. Чтобы узнать о других возможностях логической игры, предлагаю вам изучить на досуге эту занимательную книгу. Кстати, нашей игре посвящён только первый раздел, а там есть ещё шесть разделов. И, конечно, не забудьте запастись вкусными, свежими и полезными булочками — так читать будет даже интереснее.

Логическая игра (русский перевод в библиотеке журнала «Квант»).
The Game of Logic (PDF).

Статья была впервые опубликована на другом ресурсе 1 апреля 2021.

Источник

Лью́ис Кэ́рролл (англ. Lewis Carroll, настоящее имя Чарльз Лю́твидж До́джсон, Charles Lutwidge Dodgson; 1832—1898) — английский писатель, математик, логик, философ и фотограф. Наиболее известные работы — «Алиса в стране чудес» и «Алиса в Зазеркалье», а также юмористическая поэма «Охота на Снарка».

Биография

Родился 27 января 1832 в доме приходского священника в деревне Дарсбери, графство Чешир. Всего в семье было 7 девочек и 4 мальчика. Учиться начал дома, показал себя умным и сообразительным. Был левшой; по непроверенным данным, ему запрещали писать левой рукой, чем травмировали молодую психику. В двенадцать лет поступил в небольшую частную школу недалеко от Ричмонда. Ему там понравилось. Но в 1845 году ему пришлось поступить в Rugby School, где ему нравилось значительно меньше.

В начале 1851 года переехал в Оксфорд, где поступил в Christ Church, один из наиболее аристократических колледжей при Оксфордском университете. Учился не очень хорошо, но благодаря выдающимся математическим способностям после получения степени бакалавра выиграл конкурс на чтение математических лекций в Christ Church. Он читал эти лекции в течение следующих 26 лет, они давали неплохой заработок, хотя и были ему скучны.

Писательскую карьеру начал во время обучения в колледже. Писал стихотворения и короткие рассказы, отсылая их в различные журналы под псевдонимом Льюис Кэрролл. Постепенно приобрел известность. С 1854 года его работы стали появляться в серьезных английских изданиях: The Comic Times, The Train.

В 1856 году в колледже появился новый декан — Генри Лидл (Henry Liddell), вместе с которым приехали его жена и пять детей, среди которых была и 4-летняя Алиса.

В 1864 году написал знаменитое произведение «Алиса в стране чудес».

Публиковал также много научных трудов по математике под собственным именем. Одним из его увлечений была фотография.

Умер 14 января 1898 в Гилфорде, графство Суррей.

Дружба с девочками

Льюис Кэрролл был холостяком. В прошлом считалось, что он не дружил с особами противоположного пола, делая исключение для актрисы Эллен Терри.

Мартин Гарднер замечает[1]:

Наибольшую радость доставляла Кэрроллу дружба с маленькими девочками. «Я люблю детей (только не мальчиков)», — записал он однажды.

…Девочки (в отличие от мальчиков) казались ему удивительно красивыми без одежды. Порой он рисовал или фотографировал их обнаженными — конечно, с разрешения матерей.

Сам Кэрролл считал свою дружбу с девочками совершенно невинной; нет оснований сомневаться в том, что так оно и было. К тому же в многочисленных воспоминаниях, которые позже оставили о нем его маленькие подружки, нет ни намека на какие-либо нарушения приличий.

«Миф Кэррола»

Информация, а также цитаты, размещенные ниже, взяты из статьи А. Борисенко и Н. Демуровой «Льюис Кэрролл: мифы и метаморфозы», которая, в свою очередь основана на работах Hugues Lebailly и Karoline Leach.

В последние десятилетия выяснилось, что большинство его «маленьких» подруг было старше 14, многие 16-18 лет и старше. Подруги Кэрролла в воспоминаниях часто занижали свой возраст. Так, например, актриса Иза Боумен пишет в своих мемуарах [1]

В детстве я часто развлекалась тем, что рисовала карикатуры, и однажды, когда он писал письма, я принялась делать с него набросок на обороте конверта. Сейчас уж не помню, как выглядел рисунок, — наверняка это был гадкий шарж, — но внезапно он обернулся и увидел, чем я занимаюсь. Он вскочил с места и ужасно покраснел, чем очень меня испугал. Потом схватил мой злосчастный набросок и, разорвав его в клочья, молча швырнул в огонь. (…) Мне было тогда не более десяти-одиннадцати лет, но и теперь этот эпизод стоит у меня перед глазами, как будто все это было вчера…

В действительности ей было не менее 13 лет.

Другая «юная подружка» Кэрролла, Рут Гэмлен, в своих мемуарах сообщает, как в 1892 году родители пригласили на обед Кэрролла с гостившей у него в то время Изой. Там Иза описана как «застенчивый ребенок лет двенадцати», в действительности в 1892 году ей было 18 лет.

Сам Кэрролл также называл словом «ребёнок» (child) не только маленьких девочек, но и женщин 20-30 лет. Так, в 1894 году он писал:

Одна из главных радостей моей — на удивление счастливой — жизни проистекает из привязанности моих маленьких друзей. Двадцать или тридцать лет тому назад я бы сказал, что десять — идеальный возраст; теперь же возраст двадцати — двадцати пяти лет кажется мне предпочтительней. Некоторым из моих дорогих девочек тридцать и более: я думаю, что пожилой человек шестидесяти двух лет имеет право все еще считать их детьми.

Как показали исследования, больше половины «девочек», с которыми он переписывался, старше 14 лет; из 870 комментариев, сделанных им по поводу актерской игры, 720 относятся ко взрослым актерам и только 150 — к детям.

В викторианской Англии конца XIX века девочки до 14 лет считались асексуальными. Дружба Кэрролла с ними была, с точки зрения тогдашней морали, совершенно невинной причудой. С другой стороны, слишком близкое общение с молодой женщиной (особенно наедине) строго осуждалось. Это и могло заставить Кэрролла своих знакомых женщин и девушек объявлять «маленькими девочками», а их самих — занижать свой возраст.

Библиография

* «Полезная и назидательная поэзия» (1845)

* «Алгебраический разбор Пятой книги Эвклида» (1858)

* «Алиса в стране чудес» (1865)

* «Сведения из теории детерминантов» (1866)

* «Элементарное руководство по теории детерминантов» (1867)

* «Месть Бруно» (основное ядро романа «Сильви и Бруно») (1867)

* «Сквозь Зеркало и Что там увидела Алиса» (1871)

* «Охота на Снарка» (1876)

* «История с узелками» (1878?) — сборник загадок и игр

* Математический труд «Эвклид и его современные соперники»; «Дублеты, словесные загадки» (1879)

* Первый русский перевод «Страны чудес» (1879)

* «Эвклид» (I и II книги) (1881)

* Сборник «Стихи? Смысл?» (1883)

* «Логическая игра» (1887)

* «Математические курьёзы» (часть I) (1888)

* «Сильви и Бруно» (часть I) (1889)

* «Алиса для детей» и «Круглый бильярд»; «Восемь или девять мудрых слов о том, как писать письма» (1890)

* «Символическая логика» (часть I) (1890)

* «Заключение „Сильви и Бруно“» (1893)

* Вторая часть «Математических курьёзов» («Полуночные задачи») (1893)

Экранизации

* Алиса в стране чудес (мультфильм, 1951)

* Алиса в стране чудес (фильм, 1972)

* Алиса в стране чудес (мультфильм, 1981)

* Алиса в Зазеркалье (мультфильм, 1982)

* Алиса в стране чудес (фильм, 1986)

* Алиса в стране чудес (фильм, 1999)

* По мотивам «Алисы в Стране Чудес» снято множество фильмов и мультфильмов. Последним, на сегодняшний день, является фильм Тима Бартона «Алиса в Стране Чудес»

[1] Мартин Гарднер Аннотированная «Алиса» = The Annotated «Alice». Alice’s Adventures in Wonderland and Through the Looking-Glass by Lewis Carroll. Illustrated by John Tenniel. With an Introduction and Notes by Martin Gardner. NY, 1960. — 2-е стереотипное издание. — М.: Наука, 1991.

Материал из Википедии — свободной энциклопедии

Иллюстрации к «Алисе» разных авторов.

Источник

Льюис Кэрролл более всего известен как автор «Алисы в Стране чудес» с ее волшебным чеширским котом, чудесным эликсиром и очаровательным Шалтаем-Болтаем. Кроме этого, Льюис Кэрролл прославился как математик и логик.

Интересно, что свои труды в области математики автор подписывал настоящим именем «Чарльз Доджсон», а вот литературные пробы – псевдонимом. Как мы помним, наиболее известным произведением Кэрролла является его «Алиса в Стране чудес», но мало кто знает, что и многие свои математические изыскания автор посвящал детям. Так, в сборнике для детей «Логическая игра» автор разработал стратегию игры в «Пятнашки», а также представил огромное количество логических задач, например: в данный треугольник вписать такой шестиугольник, чтобы его противоположные стороны были равны и параллельны, три из них лежали на сторонах треугольника, а диагонали пересекались в заданной точке внутри треугольника. Много головоломок составлены Кэрроллом на тему «Последовательности и ряды»: 4, 3, 3, 5, 4, 4, 3, 5… Попробуйте отгадать следующее число последовательности!

Долгое время считалось, что математическое наследие Кэрролла несущественно, т.к. основывалось лишь на нескольких учебниках; но в последнее время к математическим находках автора, ранее невостребованным, обращается все больше внимания.

Любовь к литературе была у Кэрролла с детства: он любил играть в шумные игры, придумывать для своих братьев и сестер (а их было 10) рассказы и стишки, создавать волшебные персонажи. У Льюиса всегда было много друзей, а некоторые из них стали полноправными героями его произведений, как малышка Элис (Алиса), превратившаяся в героиню, путешествующую по Стране чудес. Книга «Приключения Алисы в стране чудес» увидела свет в июле 1863 г.

Художественный мир «Алисы…» наполнен снами, воспоминаниями, волшебными символами (чудесное зеркало и Зазеркалье), шахматными партиями и играми в крокет и карты, а также замысловатой словесной игрой и незабываемыми образами (Кролика, Шляпника, Королевы, Чеширского Кота и др.).

Книга Льюиса, написанная для детей, отличается непосредственностью, простотой и искренностью; вспомните некоторые цитаты: «Алиса не знала, что ей делать, пожать руку одному, а потом другому? А вдруг второй обидится? Тут ее осенило, она протянула им обе руки сразу» или «Я знаю, кем я была сегодня утром, когда проснулась, но с тех пор я уже несколько раз менялась». Мир Зазеркалья полностью отражает детское мировосприятие с его фантастикой, приключениями и альтернативными мирами. Но, признают многие ученые, книга Кэрролла не настолько проста: многие считают ее серьезным экзистенциальным произведением, порождающим сотни интерпретаций (вспомним недавний фильм Т. Бертона).

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Источник