Каталог статей
- Введение в EViews
- EViews скачать
Введение в EViews
EViews — это всемирно известный эконометрический инструмент. Друзья могут позаимствовать этот эконометрический инструмент EViews для обработки данных или использовать его для построения графиков, анализа моделирования, программирования и т. Д. Можно сказать, что EViews представляет собой лучшую интеграцию передовых функций и современных программных технологий.Программное обеспечение представляет собой наиболее совершенную программу, которая обеспечивает беспрецедентные функции в гибком объектно-ориентированном интерфейсе.
EViews скачать
Ссылка для скачивания
Ссылка: https://pan.baidu.com/s/1V92dI0a-ogmr_0b7TF0r7w
Код извлечения:5xbp
После копирования этого содержимого откройте мобильное приложение Baidu Netdisk, что удобнее.
После успешной загрузки разархивируйте и запустите программу формата .EXE из пакета.
После недолгого ожидания следующий
договор об установке после следующего
Нажмите «Обзор», чтобы изменить путь установки (если он вам не нужен, можете пропустить его), затем
Мой путь установки следующий (необходимо создать новую папку и нажать кнопку «Обзор»)
Откройте exe-файл по пути в каталоге загрузки
Проверить что заполнять серийник и имя
Вернитесь к интерфейсу установки и заполните следующий
Просто следующий
next
No… , next
Подождите
Нажмите Да в обоих появившихся окнах.
finish
Найдите … patch.exe, который вы только что использовали, и скопируйте его.
Вставьте его в каталог установки EViews
Каталог, установленный ранее, не обязательно такой же, как у меня
Дважды щелкните скопированный файл и щелкните патч
Появится следующий интерфейс, затем успех
Откройте интерфейс следующим образом
Eviews (далее пакет) установлен в директорий Program Files/Eviews3. Запуск осуществляется выбором соответствующего значка в панели Пуск/Программы/Eviews3/Eviews 3.1 (файл C:Program FilesEViews3EViews3.exe) (см. рис. 1) или щелчком (двойным щелчком – в зависимости от установок) по соответствующей пиктограмме на рабочем столе.
Рис. 1.
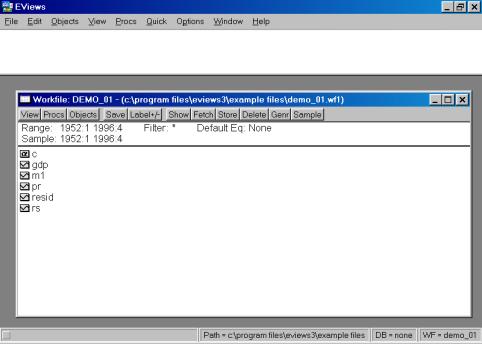
Если Вы все сделали правильно, появится стартовое окно пакета (рис.2).
Рис. 2.
Если в настоящий момент окно, содержащее пакет, является активным, то первая строка экрана (Title Bar) будет темнее остальных. При переключении в другое окно цветовая окраска данной строки изменит цвет на более приглушенный (серый).
Ниже следует строка основного меню (Main Menu). Принцип его построения прост – при нажатии на соответствующие клавиши появляется раскрывающееся меню (drop-down menu). Доступные в настоящий момент опции являются затемненными (darkened menu items). Те пункты, с которыми в настоящий момент работа невозможна, приглушены (grayed menu items).
Далее располагается командная строка (окно) (command window). В нем происходит непосредственный набор команд, которые выполняются после нажатия клавиши Enter (Ввод). Для исполнения многих команд отсутствует необходимость их набора – просто надо выбрать нужный пункт в основном меню.
Большая часть экрана пакета отведена под рабочую область (work area). В ней размещаются рабочие объекты. Переключение между ними осуществляется нажатием клавиши F6.
Последняя область экрана показывает текущее состояние (status line) пакета (рабочий каталог, текущий файл и др.).
Завершение работы с пакетом осуществляется путем выбора в командной строке опции File/Exit. Система предложит сохранить/не сохранить имеющиеся данные. Если имя файла не было задано ранее, автоматически будет предложено имя UNTITLED. Его можно изменить на любое другое. Пакет имеет обширнуюсправочную систему (пункт основного меню Help).
Знакомство с пакетом начнем с файла, содержащего данные о совокупном спросе на деньги (M1) – (aggregate money demand) (M1) – зависимая переменная;независимые: доход (ВВП) — income (GDP); уровень цен (PR) — price level (PR); краткосрочная процентная ставка (RS) — short term interest rate (RS).
Проведем некоторые преобразования и расчеты.
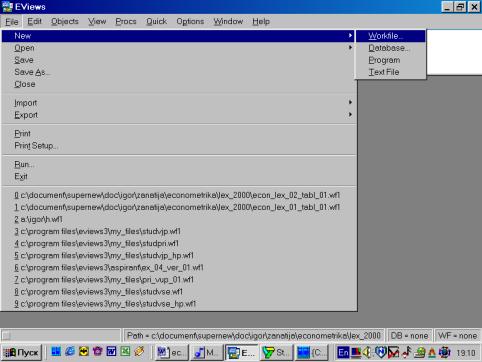
Первым шагом создадим новый рабочий файл (workfile). Его имя должно иметь следующий вид и состоять только из латинских букв: Номер_группы_demo_01.wf1 (расширение wf1 присваивается автоматически). Например: 451_demo_01.wf1. Расположить его следует в директории, относящемся к Вашему факультету (внимательно ознакомьтесь с памяткой в компьютерном классе). Исходные данные находятся в файле Excel. Они должны быть импортированы в пакет. Создание рабочего файла начнем с того, что выберем File/New/Workfile в основном меню (см. рис. 3).
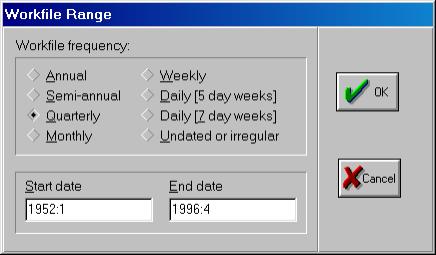
После нажатия на кнопке со словом Workfile откроется диалоговое окно, с помощь которого можно задать тип вводимых Вами данных (см. рис. 4).
Рис. 3.
Рис. 4.
Важным является указание начальной (start) и конечной (end) даты/наблюдения (date/observation).
В нашем примере начальным периодом является первый квартал 1952 г. (1952:1), конечным – четвертый квартал 1996 г. (1996:4).
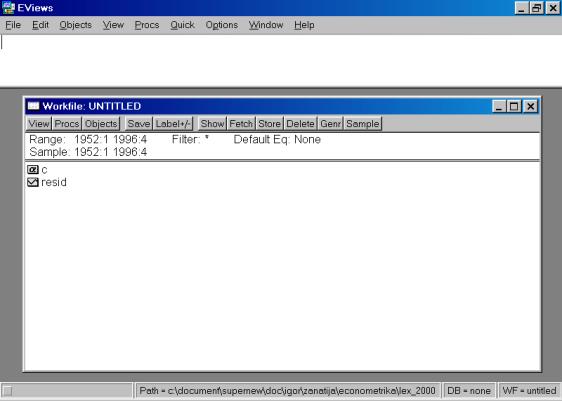
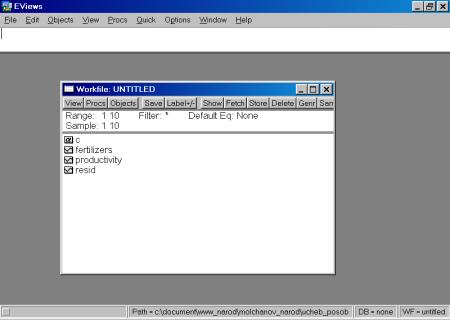
Закончив ввод временных периодов, надо нажать клавишу OK. Пакет создаст рабочий файл без имени, и на дисплее в рабочей области появится окно (см. рис. 5). Все рабочие файлы пакета всегда содержат вектор коэффициентов C и серию RESID.
Рис. 5.
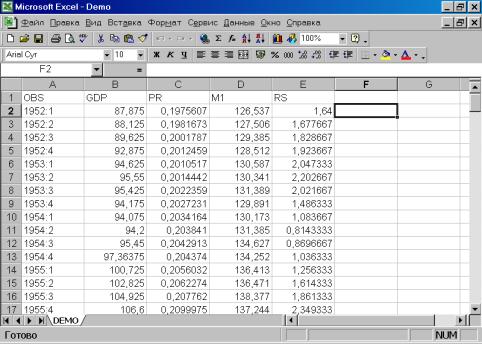
Следующим шагом является просмотр исходных данных, содержащихся в исходном файле по адресу Program Files/Eviews3/Example files/demo.xls (формат Exсelверсии 5.0 и младше). Важное замечание: имеющаяся версия пакета позволяет импортировать файлы Excel не старше версии 5.0. В противном случае будет выдано сообщение об ошибке. Всегда сохраняйте свои файлы как файлы Microsoft Excel 5.0/95. Для визуализации данных необходимо запустить табличный процессор Excel (действия аналогичны запуску Eviews). Результат представлен на рис. 6. Ознакомившись с данными, файл, подлежащий экспортированию,необходимо закрыть.
Рис. 6.
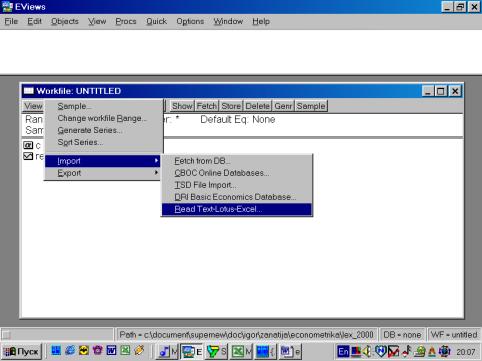
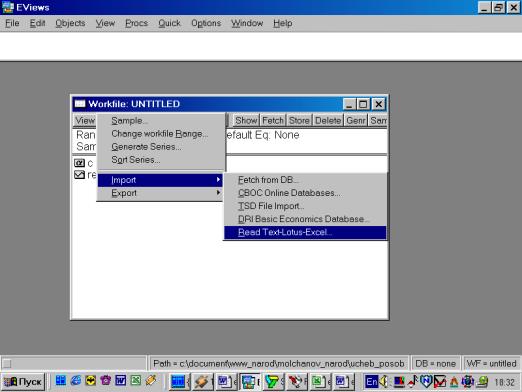
Для чтения данных, созданных в других программах, надо выбрать в рабочем файле опцию Procs/Import/Read Text-Lotus-Excel… (см. рис. 7). Появится диалог, представленный на рис. 8.
Рис. 7.
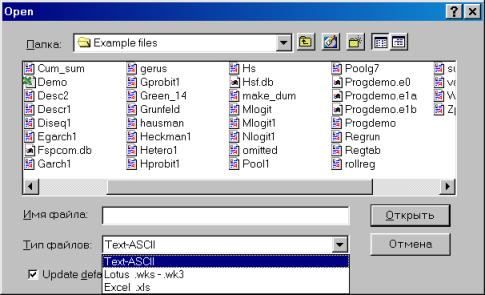
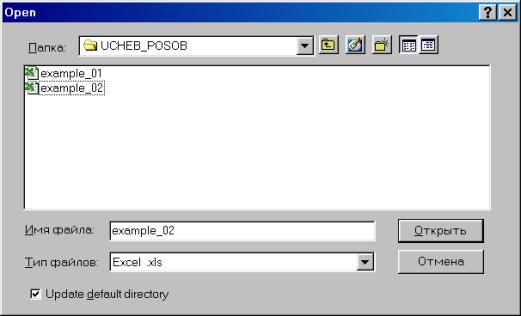
Перейдем к папке, содержащей искомый файл (для упрощения поиска в опции Тип файлов (Files of type) можно выбрать Excel.xls (см. рис.8). Для того, чтобы пакет «помнил» Ваши перемещения по папкам компьютера, можно поставить флажок в опции Update default directory (см. рис. 8).
Рис. 8.
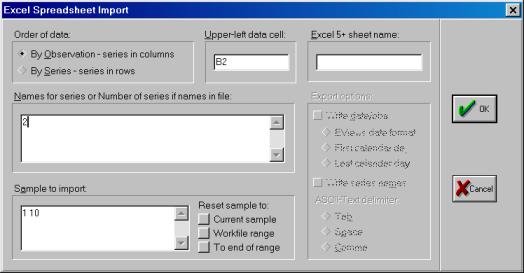
Наведем курсор на файл demo.xls и нажмем кнопку Открыть (см. рис. 8). Появится диалог открытия электронных таблиц формата Excel (см. рис. 9).
Рис. 9.
Рис. 10.
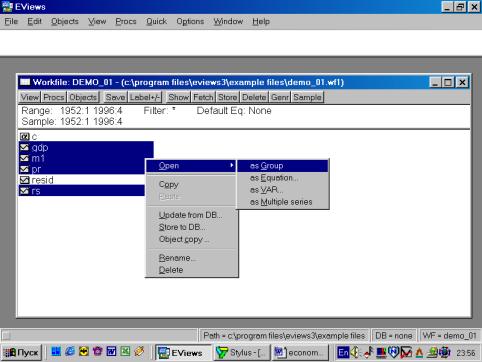
После того, как исходные данные перенесены Вами в рабочую область пакета (появились имена переменных), надо провести их верификацию (проверку правильности). Вам необходимо создать новую группу, содержащую все импортированные серии (переменные). Это делается следующим образом: необходимокликнуть мышкой по имени первой переменной (например, GNP), затем, удерживая клавишу CTRL кликнуть по переменным M1, PR и RS. Все серии на экране будут зачернены. Затем необходимо подвести курсор мыши на зачерненную область экрана и кликнуть правой кнопкой. Далее необходимо выбрать опцию Open. Пакет откроет диалоговое окно со следующими опциями (см. рис. 11).
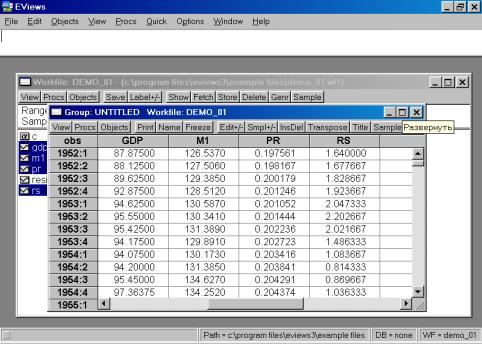
Выберем Open Group (открыть в одной группе). Пакет создаст группу с именем UNTITLED, в которую войдут все переменные (серии). По умолчанию, данные будут представлены в виде электронной таблицы (возможны другие варианты представления) – см. рис. 12.
Рис. 11.
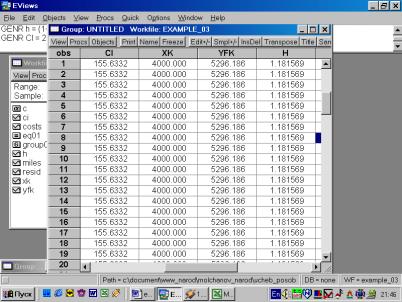
Рис. 12.
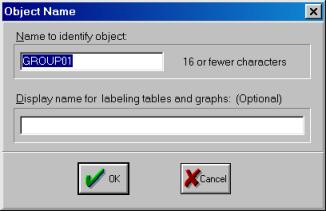
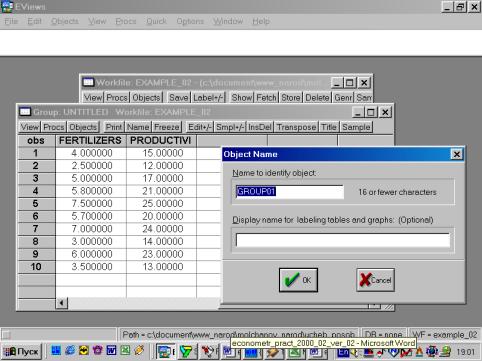
Проведите визуальную проверку корректности данных. Сравните, как разместились переменные из исходного файла, обратите внимание на столбец слева от первой переменной (он серого цвета). В нем отображены годы и порядковые номера кварталов. Полученной новой группе данных можно дать имя. Для этого необходимо нажать кнопку Name в текущем окне (см. рис. 12). Появится диалоговое окно (рис. 13.). Автоматически будет предложено имя – GROUP01. Его можно принять, нажав кнопку OK. В рабочем файле сразу добавится одна переменная с введенным Вами именем. Теперь к ней всегда можно перейти простым нажатием клавиши мыши.
Рис. 13.
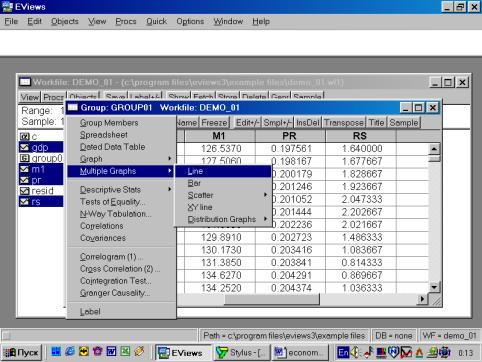
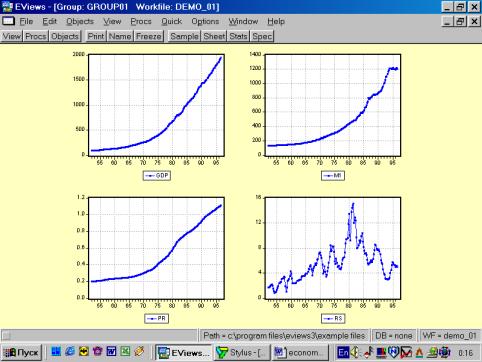
Образованную Вами группу можно просматривать не только в виде электронной таблицы. Если, находясь внутри GROUP01, выбрать последовательность командView/Multiple Graphs/Line (см. рис. 14), то данные предстанут не в виде таблицы, а как линейные графики по каждой серии (переменной) – см. рис. 15.
Рис. 14.
Для того, чтобы вернуться к прежней форме представления данных (например, электронной таблице), надо выбрать View/Spreadsheet.
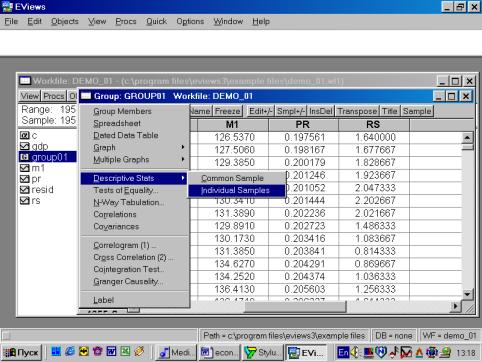
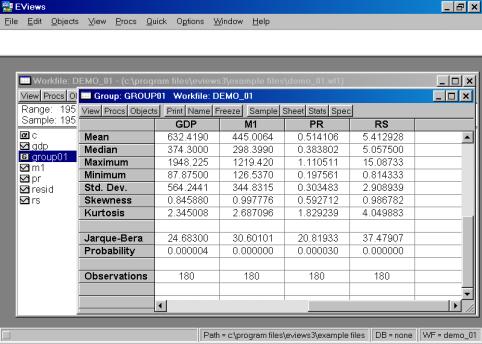
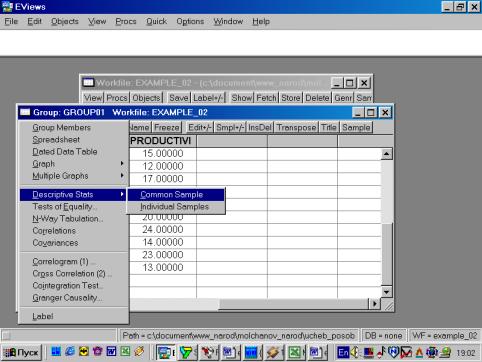
Для просмотра числовых характеристик (описательных статистик) отмеченных переменных необходимо выбрать в рабочем файле View/Descriptive Stats/Individual Samples (см. рис. 16).
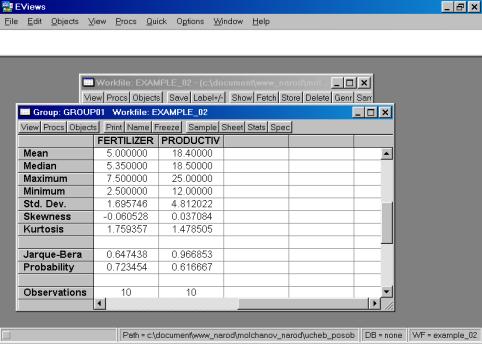
В результате появится окно, представленное на рис. 17. В нем содержатся:
Mean – Среднее арифметическое значение;
Median – Медиана;
Maximum – Максимальное значение;
Minimum – Минимальное значение;
Std. Dev. – Стандартное отклонение (среднее квадратическое отклонение);
Skewness – Коэффициент асимметрии;
Kurtosis – Эксцесс;
Probability – Вероятность;
Observations – Количество наблюдений.
Рис. 15.
Рис. 16.
Рис. 17.
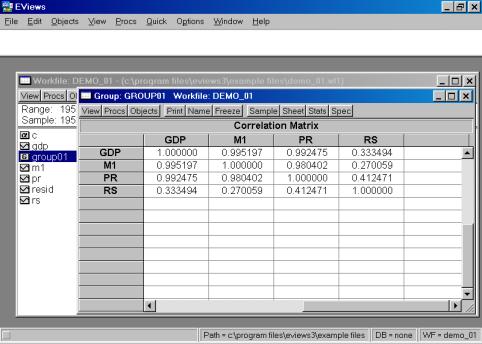
Если возникает необходимость проанализировать матрицу коэффициентов корреляции, то необходимо выбрать View/Correlations. Результат представлен на рис. 18.
Рис. 18.
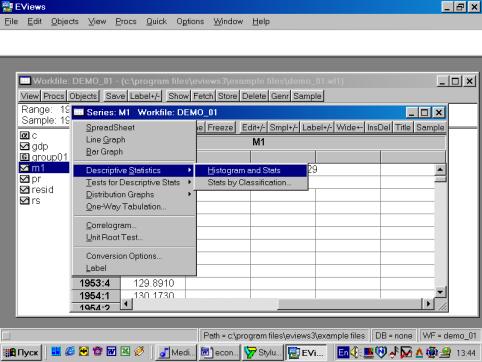
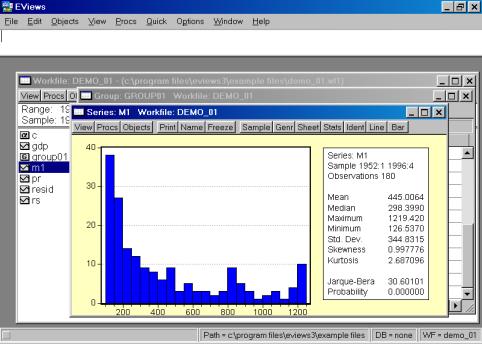
Вы также можете исследовать характеристики для отдельных серий (переменных), совместив вывод диаграммы и числовых характеристик. Дважды кликните на имени серии (например, на переменной М1) и выберете в рабочем файле пункт меню View/Descriptive Stats/Histogram and Stats (см. рис. 19). Результат наглядно виден на рис. 20.
Рис. 19.
Рис. 20.
С другими возможностями пакета Вы познакомитесь на последующих занятиях.
Для индивидуальной работы по предложенной выше схеме предназначены нижеследующие данные. Подумайте, все ли данные необходимо заносить в электронную таблицу или импортировать из неё.
Пример 1. Стоимость однокомнатных квартир в Москве [6].
Данные из газеты «Из рук в руки» за период с декабря 1996 г. по сентябрь 1997г.
Была выбрана Юго-Западная часть города, в которой высок спрос на жилые площади (всего 69 наблюдений). Файл example_01.xls.
Найдите среднее арифметическое, выборочное стандартное отклонение и другие статистики параметров. Найдите коэффициенты корреляции параметров с ценой квартиры. Соответствуют ли полученные значения экономической интуиции?
Практическое занятие № 2.
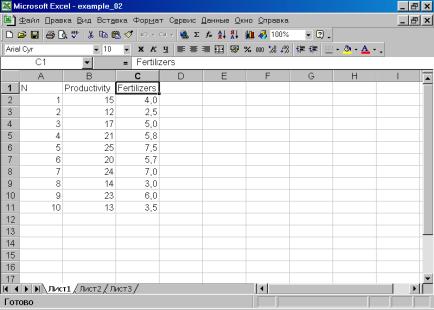
Пример 2. Имеются следующие данные по 10 фермерским хозяйствам области:
|
№ пп |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Урожайность зерновых цга |
15 |
12 |
17 |
21 |
25 |
20 |
24 |
14 |
23 |
13 |
|
Внесено удобрений на 1 га посевов, кг |
4,0 |
2,5 |
5,0 |
5,8 |
7,5 |
5,7 |
7,0 |
3,0 |
6,0 |
3,5 |
Порядок выполнения задания
Рис. 27.
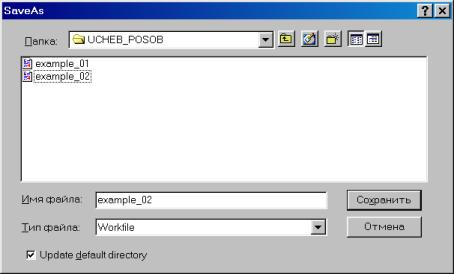
Рис. 28.
Сохраним рабочий файл (рис. 28).
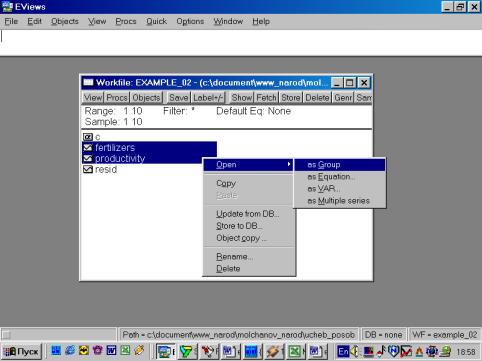
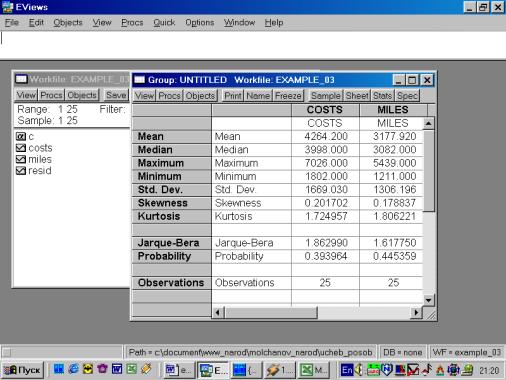
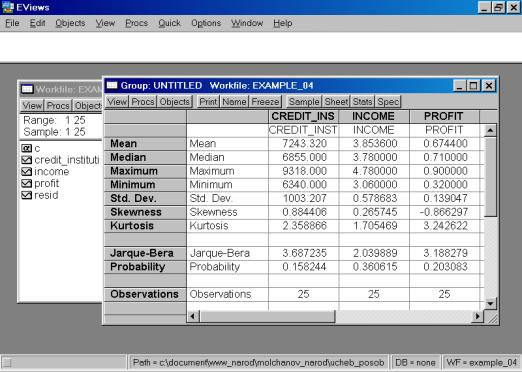
4. Значения описательных статистик находим следующим образом: в окне workfile выделяем переменные, щелкаем мышкой по выделенной части и далее выбираем: Open/As Group/ (рис. 29). Открывается окно с исходными данными. Новую группу можно сохранить, выбрав опцию Name (рис. 30). Для просмотра описательных статистик View/Descriptive Stats/Common Sample (рис 31). Результат представлен на рис. 32.
Рис. 29.
Рис. 30.
Рис. 31.
Рис. 32.
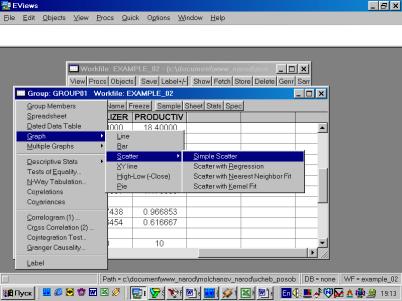
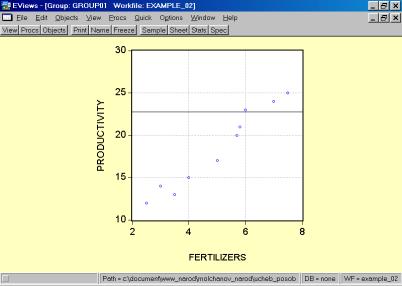
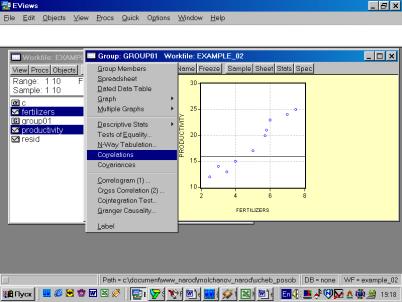
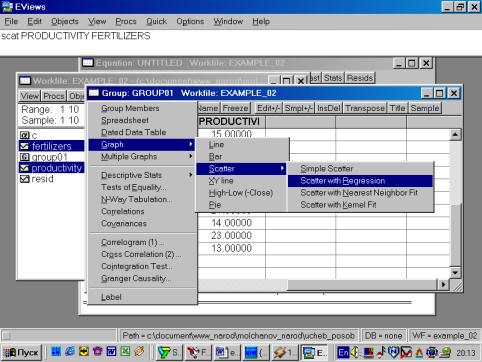
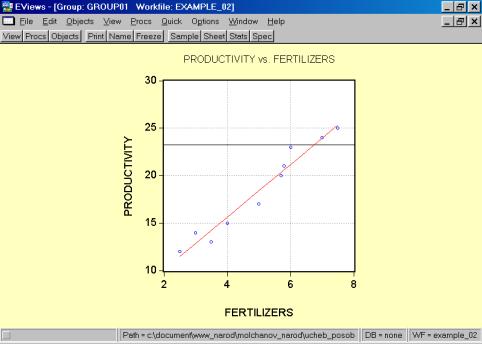
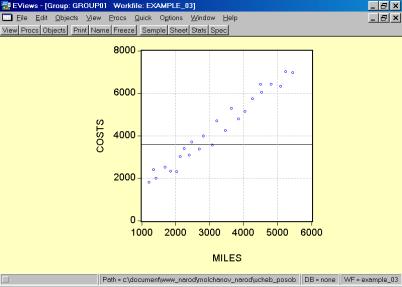
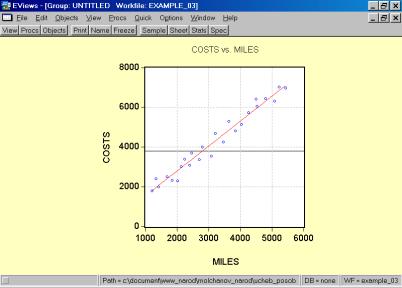
5. В окне workfile (рис. 32) для построения поля корреляции необходимо выбрать следующие пункты меню: VIEW/GRAPH/SCATTER/SIMPLE SCATTER/(рис. 33). Полученный в результате график представляет собой поле корреляции результативного и факторного признаков (рис. 34).
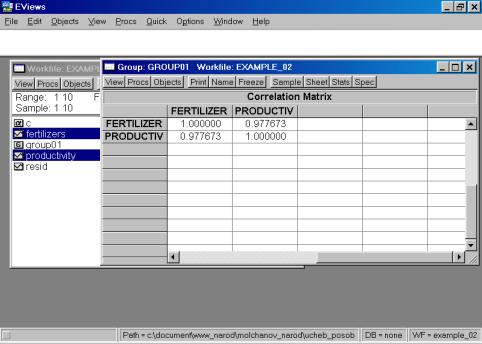
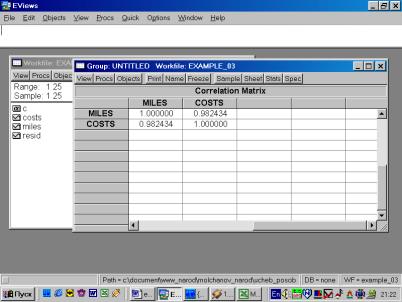
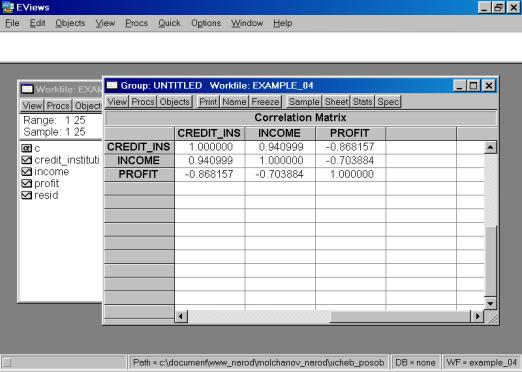
6. В окне Workfile (используя созданную группу из двух переменных) выбрать: /VIEW/CORRELATION/ (рис. 35). Полученная таблица — корреляционная матрица, в которой отражено значение коэффициента парной корреляции результативного и факторного признаков (рис. 36).
Рис. 33.
Рис. 34.
Рис. 35.
Рис. 36.
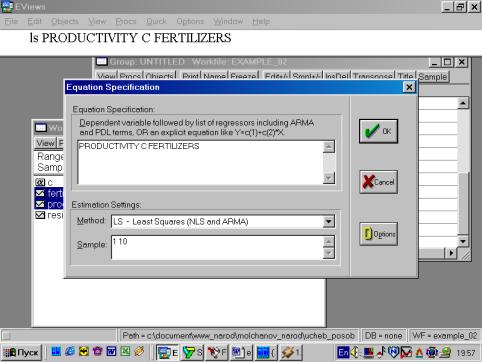
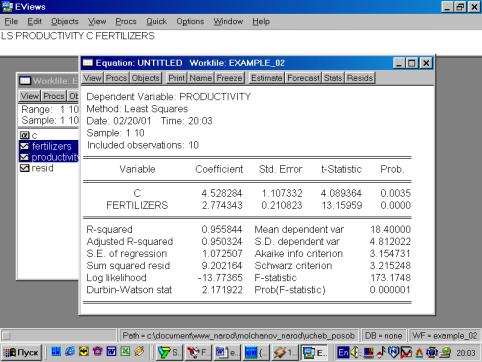
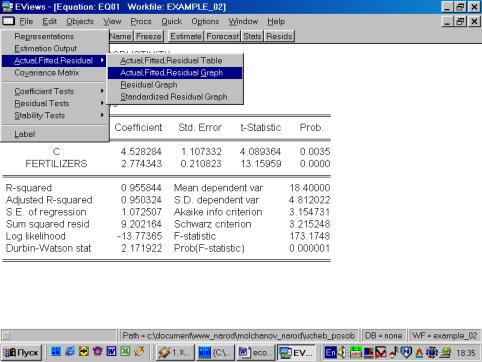
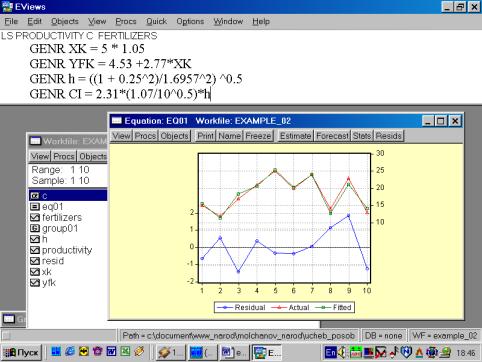
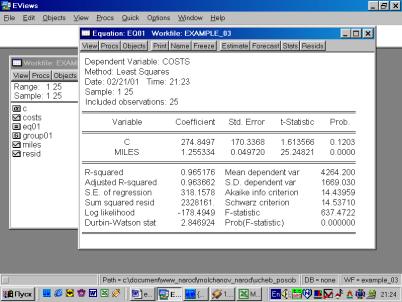
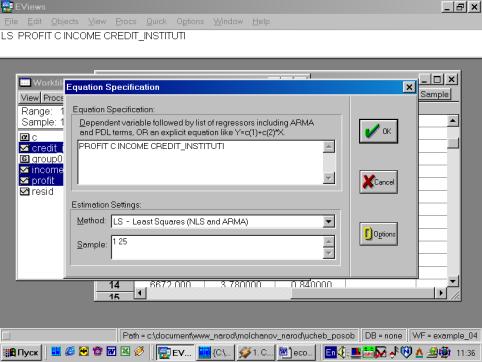
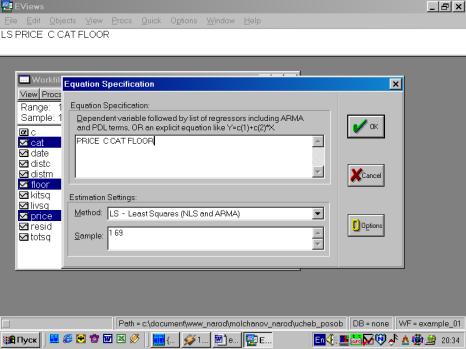
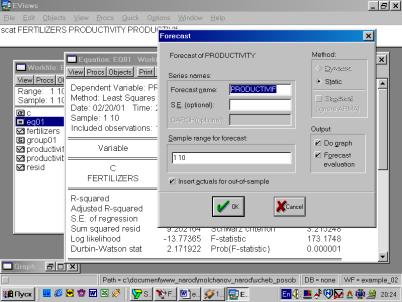
7. В диалоговом окне описать в общем виде искомое уравнение: LS PRODUCTIVITY C FERTILIZERS <Enter> (метод наименьших квадратов (LS) эндогенная переменная, константа, экзогенная переменная), или выбрать в строке главного меню EVIEWS: QUICK/ESTIMATE EQUATION/ PRODUCTIVITY C FERTILIZERS (рис. 37). В открывшемся окне (рис. 38) должны быть переменные: зависимая переменная, применяемый метод, число наблюдений, параметры уравнения регрессии, стандартные ошибки, значения t – статистик и соответствующие им вероятности, значение и ряд других показателей.
Рис. 37.
Рис. 38.
8. и 9. Результаты выполнения п.7 позволяют оценить статистическую значимость параметров уравнения регрессии и объяснить полученное значение R .
Рис. 43.
Рис. 44.
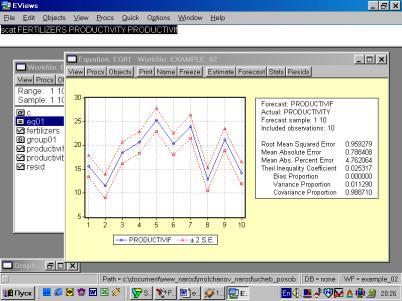
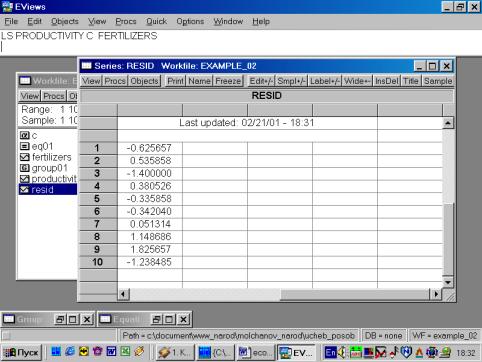
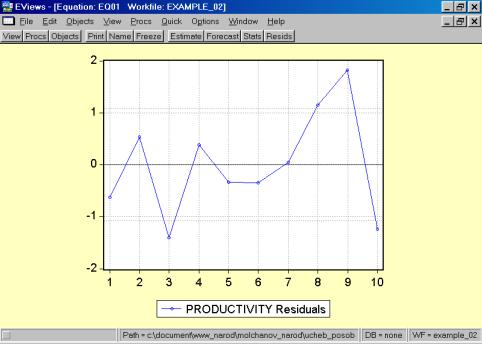
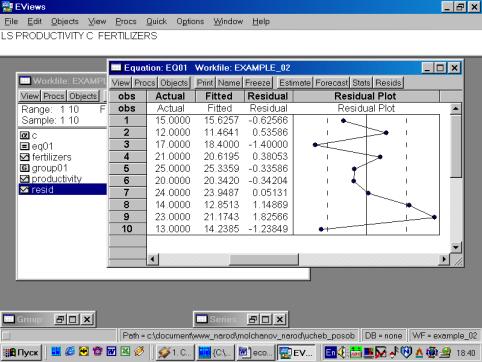
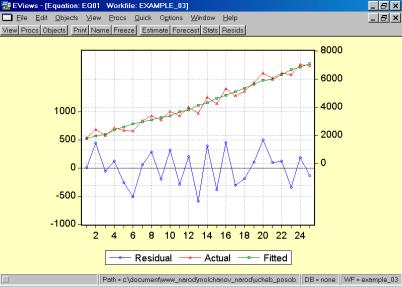
11. Данная операция возможна только в том случае, если ей предшествует построение регрессионного уравнения. В окне Workfile можно дважды щелкнуть на переменной Resid (рис. 45). Далее, выбрать: VIEW/LINE GRAPH/, или, открыв окно с параметрами уравнения регрессии, выбрать: VIEW /ACTUAL,FITTED…/ACTUAL, FITTED…TABLE/ (рис. 46). Результат представлен на рис. 47. Другой вариант вывода (фактические, предсказанные значения переменных, остатки, график остатков) – рис. 48.
Рис. 45.
Рис. 46.
Рис. 47.
Рис. 48.
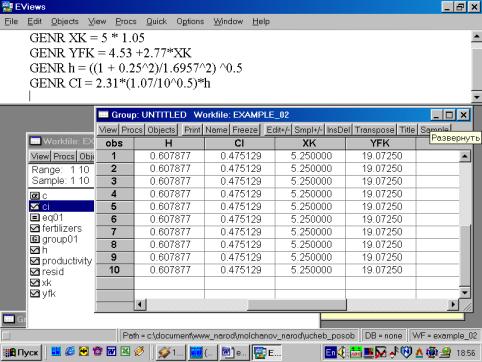
12. Для нахождения границ доверительного интервала в командной строке необходимо указать (рис. 49):
GENR XK = 5 * 1.05
GENR YFK = 4.53 +2.77*XK
GENR h = ((1 + 0.25^2)/1.6957^2) ^0.5
GENR CI = 2.31*(1.07/10^0.5)*h
В результате искомые границы определяются следующим образом:
YFKCI , т.е. от YFK+CI до YFK-CI (см. рис. 50).
Рис. 49.
Рис. 50.
13. Оформить отчет по занятию.
Отчет должен содержать: подробные пояснения расчетов, ссылки на используемые формулы, результаты работы Eviews в виде экранных копий, другую, необходимую на Ваш взгляд, информацию.
Практическое занятие № 3.
«Применение Eviews при построении и анализе линейной однофакторной модели регрессии»
Выполняется самостоятельно.
|
№ пп |
Miles (Х) |
Costs (У) |
|
1 |
1211 |
1802 |
|
2 |
1345 |
2405 |
|
3 |
1422 |
2005 |
|
4 |
1687 |
2511 |
|
5 |
1849 |
2332 |
|
6 |
2026 |
2305 |
|
7 |
2133 |
3016 |
|
8 |
2253 |
3385 |
|
9 |
2400 |
3090 |
|
10 |
2468 |
3694 |
|
11 |
2699 |
3371 |
|
12 |
2806 |
3998 |
|
13 |
3082 |
3555 |
|
14 |
3209 |
4692 |
|
15 |
3466 |
4244 |
|
16 |
3643 |
5298 |
|
17 |
3852 |
4801 |
|
18 |
4033 |
5147 |
|
19 |
4267 |
5738 |
|
20 |
4498 |
6420 |
|
21 |
4533 |
6059 |
|
22 |
4804 |
6426 |
|
23 |
5090 |
6321 |
|
24 |
5233 |
7026 |
|
25 |
5439 |
6964 |
Результаты расчетов:
Рис. 51.
Рис. 52.
Рис. 53.
Рис. 54.
Рис. 55.
Рис. 56.
Рис. 57.
Практическое занятие № 4.
«Применение Eviews при построении и анализе многофакторной модели регрессии. Выявление мультиколлинеарности и гетероскедастичности в модели. Проверка спецификации модели»
Введем следующие обозначения:
– прибыль кредитных организаций, %;
— чистый доход на 1$ депозита;
– число кредитных учреждений.
|
Год |
|
|
|
|
1 |
3,92 |
7298 |
0,75 |
|
2 |
3,61 |
6855 |
0,71 |
|
3 |
3,32 |
6636 |
0,66 |
|
4 |
3,07 |
6506 |
0,61 |
|
5 |
3,06 |
6450 |
0,7 |
|
6 |
3,11 |
6402 |
0,72 |
|
7 |
3,21 |
6368 |
0,77 |
|
8 |
3,26 |
6340 |
0,74 |
|
9 |
3,42 |
6349 |
0,9 |
|
10 |
3,42 |
6352 |
0,82 |
|
11 |
3,45 |
6361 |
0,75 |
|
12 |
3,58 |
6369 |
0,77 |
|
13 |
3,66 |
6546 |
0,78 |
|
14 |
3,78 |
6672 |
0,84 |
|
15 |
3,82 |
6890 |
0,79 |
|
16 |
3,97 |
7115 |
0,7 |
|
17 |
4,07 |
7327 |
0,68 |
|
18 |
4,25 |
7546 |
0,72 |
|
19 |
4,41 |
7931 |
0,55 |
|
20 |
4,49 |
8097 |
0,63 |
|
21 |
4,7 |
8468 |
0,56 |
|
22 |
4,58 |
8717 |
0,41 |
|
23 |
4,69 |
8991 |
0,51 |
|
24 |
4,71 |
9179 |
0,47 |
|
25 |
4,78 |
9318 |
0,32 |
Рис. 58.
5. Построить корреляционную матрицу для всех переменных, включенных в модель (рис. 59).
Рис. 59.
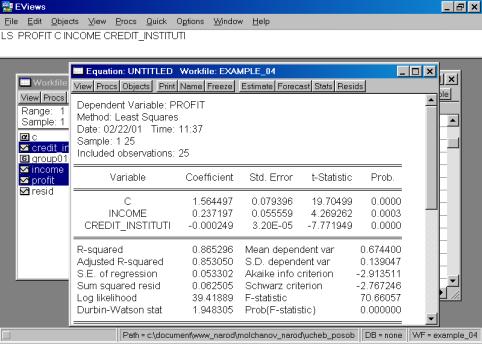
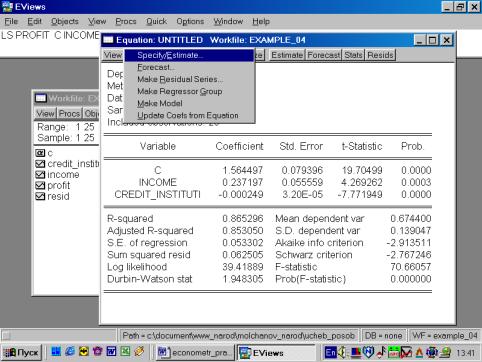
6. Построить регрессионное уравнение МНК, в котором зависимая переменная – прибыль кредитных организаций, а независимые – чистый доход на 1$ депозита и число кредитных учреждений (рис. 60, 61).
Рис. 60.
Рис. 61.
Уравнение примет следующий вид:
.
Подставим полученные оценки из итоговой формы вывода:
.
7. Оценить статистическую значимость параметров полученного уравнения и всей модели в целом.
8. Проверить наличие мультиколлинеарности в модели. Сделать вывод.
Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии.
Для проверки появления мультиколлинеарности применяются два метода, доступные во всех статистических пакета.
Ø Вычисление матрицы коэффициентов корреляции для всех объясняющих переменных. Если коэффициенты корреляции между отдельными объясняющими переменными очень велики, то, следовательно, они коллинеарны. Однако, при этом не существует единого правила, в соответствии с которым есть некоторое пороговое значение коэффициента корреляции, после которого высокая корреляция может вызвать отрицательный эффект и повлиять на качество регрессии.
Ø Для измерения эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»:
ü 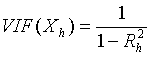
— значение коэффициента множественной корреляции, полученное для регрессора
как зависимой переменной и остальных переменных
. При этом степень мультиколлинеарности, представляемая в регрессии переменной
, когда переменные
включены в регрессию, есть функция множественной корреляции между
и другими переменными
.
ü Если , то объясняющие переменные, коррелирующие между собой, считаются мультиколлинеарными.
Существует еще ряд способов, позволяющих обнаружить эффект мультиколлинеарности:
Ø Стандартная ошибка регрессионных коэффициентов близка к нулю.
Ø Мощность коэффициента регрессии отличается от ожидаемого значения.
Ø Знаки коэффициентов регрессии противоположны ожидаемым.
Ø Добавление или удаление наблюдений из модели сильно изменяют значения оценок.
Ø Значение F-критерия существенно, а t-критерия – нет.
Для устранения мультиколлинеарности может быть принято несколько мер:
Ø Увеличивают объем выборки по принципу, что больше данных означает меньшие дисперсии оценок МНК. Проблема реализации этого варианта решения состоит в трудности нахождения дополнительных данных.
Ø Исключают те переменные, которые высококоррелированны с остальными. Проблема здесь заключается в том, что возможно переменные были включены на теоретической основе, и будет неправомочным их исключение только лишь для того, чтобы сделать статистические результаты «лучше».
Ø Объединяют данные кросс-секций и временных рядов. При этом методе берут коэффициент из, скажем, кросс-секционной регрессии и заменяют его на коэффициент из эквивалентных данных временного ряда.
Проделанные манипуляции позволяют предположить, что мультиколлинеарность может присутствовать (оценки любой регрессии будут страдать от нее в определенной степени, если только все независимые переменные не окажутся абсолютно некоррелированными), однако в данном примере это не влияет на результаты оценки регрессии. Следовательно, выделять «лишние» переменные не стоит, так как это отражается на содержательном смысле модели.
9. Проверить спецификацию модели. Объяснить полученные результаты.
Подробно теоретические вопросы, связанные с проблемами спецификации эконометрических моделей, были рассмотрены в лекционном курсе.
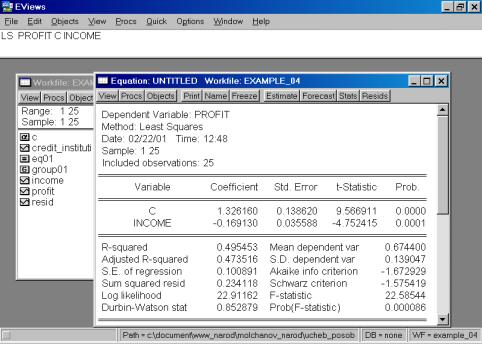
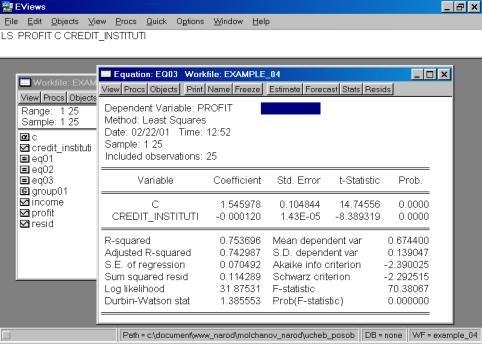
В нашем случае мы ограничимся тем, что попробуем исключить поочередно независимые переменные. Первой исключаем переменную CREDIT_INSTITUTI(рис. 62). Коэффициент при переменной INCOME изменил знак на противоположный.
Рис. 62.
Рис. 63.
В случае исключения из первоначальной модели переменной INCOME, знак регрессионного коэффициента при переменой CREDIT_INSTITUTI остался без изменения (рис. 63). Представляется разумным разделять эффект двух независимых переменных на зависимую переменную в модели с совместным их влиянием в регрессионном уравнении. Данный пример иллюстрирует важность использования множественной регрессии вместо парной в случае, когда изучаемое явление существенно детерминирует несколько независимых переменных.
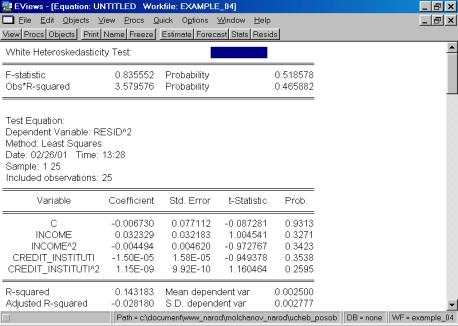
10. Проверить наличие гетероскедастичности в модели. Объяснить полученные результаты.
Проверкой на гетероскедастичность служит тест Голдфелда-Кванта. Он требует, чтобы остатки были разделены на две группы из наблюдений, одна группа с низкими, а другая – с высокими значениями. Обычно срединная одна шестая часть наблюдений удаляется после ранжирования в возрастающем порядке, чтобы улучшить разграничение между двумя группами. Отсюда число остатков в каждой группе составляет
, где
представляет одну шестую часть наблюдений.
Критерий Голдфелда-Кванта – это отношение суммы квадратов отклонений (СКО) высоких остатков к СКО низких остатков:
.
Этот критерий имеет распределение с
степенями свободы.
Следовательно, дисперсия коэффициентов запишется:
.
Отсюда если , мы трансформируем регрессионную модель к виду:
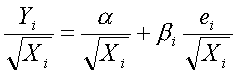
Если , т.е. дисперсия увеличивается в пропорции к квадрату рассматриваемой переменной
, трансформация приобретает вид:
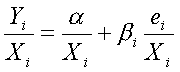
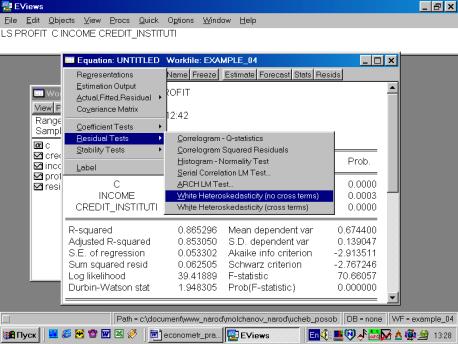
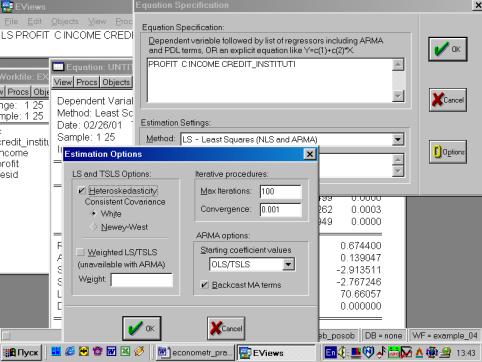
Используя Eviews, можно провести проверку и устранение гетероскедастичности следующим образом:
Ø Запустить стандартную регрессию.
Ø Вычислить остатки.
Ø Запустить регрессию с использованием квадрата остатков как зависимой переменной и оценить зависимую переменную как независимую переменную (тестWhite).
Ø Оценить nR2, где n – объем выборки, R2 – коэффициент детерминации.
Ø Использовать статистику с одной степенью свободы (в EVIEWS – используется F – статистика) для проверки существенности отличия nR2 от нуля.
Ø Основным способом устранения гетероскедастичности является применение взвешенного метода наименьших квадратов.
Выбираем тест White (см. рис. 64).
Рис. 64.
Итог формы вывода представлен на рис. 65.
Рис. 65.
Как следует из приведенной распечатки, вероятность ошибки первого рода равна 51,86%. Следовательно, нулевую гипотезу (об отсутствии гетероскедастичности) нельзя отклонить.
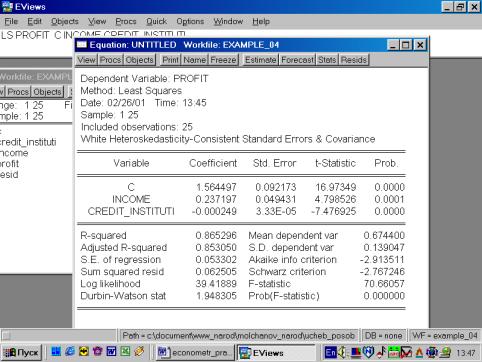
Рис. 66.
Рис. 67.
Появилось новое, переоцененное уравнение (рис. 68). Полученное уравнение можно вновь проверить по тесту White.
Рис. 68.
Практическое занятие № 5.
«Фиктивные переменные»
Иногда необходимо включение в регрессионную модель одной или более качественных переменных (например, разделение по полу: мужской и женский; по уровню образования: общее и профессиональное и т.д.).
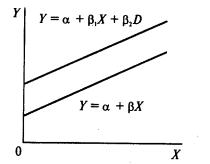
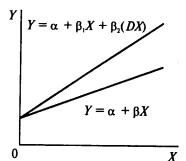
Фиктивные переменные бывают двух типов — сдвига и наклона. Фиктивная переменная сдвига — это переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной (рис. 69). Фиктивная переменная наклона — это та переменная, которая изменяет наклон линии регрессии в случае использования качественной переменной (рис. 70). Оба типа фиктивных переменных будут иметь значение или
, когда наблюдения данных совпадают с уместной количественной переменной, но будут иметь нулевое значение при совпадении с наблюдениями, где эта качественная переменная отсутствует.
|
|
|
|
Рис. 69. |
Рис. 70. |
Пример 5. По данным примера 1 (файл example_01.xls.) дать интерпретацию бинарным, «фиктивным» переменным, принимающим значения 0 или 1: floor – принимает значение 0, если квартира расположена на первом или последнем этаже, cat –принимает значение 1, если квартира находится в кирпичном доме.
.
Рис. 71.
Рис. 72.
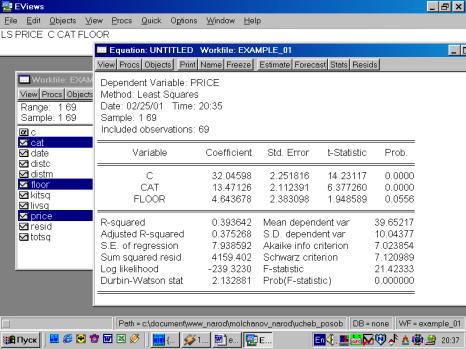
Используя результаты оценивания уравнения, содержащиеся в форме вывода (рис. 72), можно записать такое уравнение:
.
Как же можно интерпретировать полученные результаты? Полученный коэффициент при CAT означает, что квартиры в кирпичных домах стоят в среднем на $13471 дороже аналогичных квартир в панельных домах. Коэффициент при FLOOR может быть интерпретирован так: квартиры на не первом/последнем этажах стоят в среднем на $4644 дороже аналогичных, расположенных на первом/последнем этажах.
Источник: http://molchanov.narod.ru/ucheb_posob/econometr_pract_2000.html
Как построить уравнение регрессии в eviews
Библиографическая ссылка на статью:
Эм А.А., Баженов Р.И. Разработка в среде Eviews регрессионной модели реализации продукции компании по производству резинометаллических изделий // Экономика и менеджмент инновационных технологий. 2015. № 4. Ч. 2 [Электронный ресурс]. URL: https://ekonomika.snauka.ru/2015/04/8673 (дата обращения: 24.01.2022).
Для большого предприятия или же для своего бизнеса очень важно следить за всеми финансовыми операциями. Практически любое экономическое явление в реальной действительности связано со многими другими. Оптимальным вариантом, который облегчает расчеты, является применение регрессионного анализа, который достаточно широко используется в расчетах и экономических исследованиях.
Проблемы и методы построения различных регрессионных моделей изучаются многими российскими и зарубежными учеными. Так, вопрос использования программы при анализе векторных моделей авторегрессии и коррекции регрессионных остатков в Eviews описал В.А.Банников [1]. Эконометрический анализ рынка подержанных автомобилей в Eviews показал А.Л.Богданов [2]. Модель предсказания курса доллара и эффективные методы прогнозирования в Excel и Eviews представил В.Г.Брюков [3]. В.М. Матюшок и др. рассмотрели основы эконометрического моделирования с использованием EVIEWS [4]. Литовченко И.С. провел анализ количества малых предприятий в 1999 – 2010 годах в Eviews [5]. Возможности для применения интеллектуального анализа исследовали Р.И.Баженов и др. 11. Зарубежные ученые применяют регрессионный анализ [21,22].
Объектом исследования является рассмотрение основных возможностей работы среды Eviews на примере расчета значений описательных статистик, полей корреляции результативного и факторного признаков, эмпирической линии регрессии. Для примера были взяты данные для фирмы по производству резинометаллических изделий из полиуретана: затраты на производство (руб./мес.); заработанные деньги на реализации продукции (руб./мес.) (Табл.1).
Таблица 1 – Данные
Перенесем данные в Microsoft Excel и переименуем обозначения переменных: Месяц – N; Затраты на производство – spend; Реализация – earned (Рис. 1).
Сохраняем таблицу.
Запускаем Eviews (Рис. 2).
Создаем новый рабочий файл — File → New → Workfile (Рис.3).
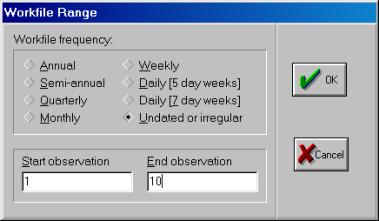
Выбираем подходящий тип структуры нашего рабочего файла: unstructured or irregular -неструктурированная/без даты (Рис. 4).
В поле Observation вводим количество месяцев, в данном случае 24 и нажимаем ОК (Рис. 5).
Импортируем таблицы из Microsoft Excel в рабочий документ: Procs → Import → ReadText-Lotus-Excel (Рис. 6).
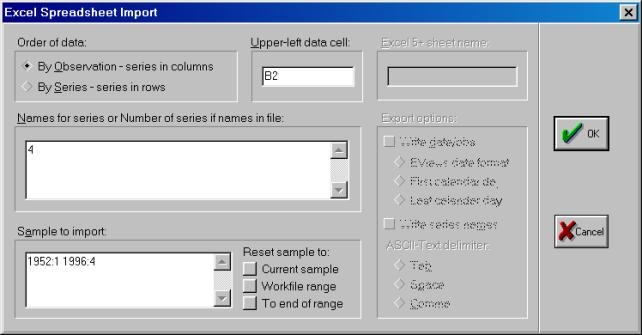
В появившемся окне в поле Upper – left data cell , вводим адрес ячейки в которой записаны данные первой переменной, в нашем случае B2 , а в поле Names for series or Number if named in file , вводим количество переменных, в нашем случае 2 (Рис. 7).
В появившемся окне появились переменные (spend и earned), константа (с) и остатки (resid) (Рис. 8).
Вычислим значения описательных статистик : Выделяем переменные (spend и earned) →правой кнопкой мыши открываем контекстное меню→ Open → AsGroup (Рис. 9, 10).
Построим поле корреляции: View → Graph → в поле General выбираем Basic graph → в поле Specific выбираем Scatter (Рис. 11, 12).
Полученный график является полем корреляции результативного и факторного признаков (Рис. 13).
Для того чтобы увидеть значения описательных статистик нужно выбрать вкладку Stats (Рисунок 14).
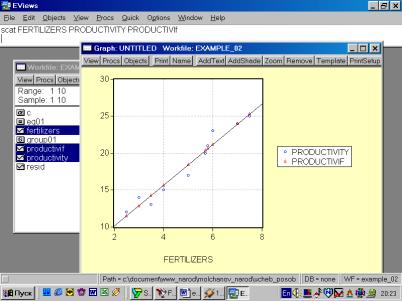
Построим эмпирическую линию регрессии: View → Graph → в поле General выбираем Basic graph → в поле Specific выбираем Scatter → в поле Fit lines выбираем Regression Line (Рис.15, Рис. 16).
Полученный график является эмпирической линией регрессии (Рисунок.17).
Найдем уравнение регрессии: Proc → MakeEquation (Рисунок 18, Рисунок 19).
Из работы следует, что уравнение регрессии представляется как
EARNED = 1,807085 * SPEND – 442,1016.
R 2 (коэффициент детерминации) = 0,945024
В следующем месяце мы планируем затратить 60000 рублей.
EARNED = 1,807085 * 60.000 – 442,1016
EARNED = 107982,99
Прогнозируемый приблизительный заработок в следующем месяце составляет 107983 рублей.
В процессе решения задачи были изучены основные функции для решения эконометрических задач с помощью программы Eviews. На рис. 17 видно, что полученные точки корреляционного поля расположены в форме эллипса, и его главная диагональ имеет положительный угол наклона (/), это означает, что корреляция положительная. Построена эмпирическая линия регрессии EARNED = 1,807085 * SPEND – 442,1016, она отображает зависимость между затраченными финансовыми средствами на производство продукции и заработанными деньгами на их реализации фирмы по производству резинометаллических изделий из полиуретана и спрогнозирован примерный доход в следующем месяце.
Библиографический список
- Банников В.А. Векторные модели авторегрессии и коррекции регрессионных остатков (Eviews) // Прикладная эконометрика. 2006. №3. С. 96-129.
- Богданов А.Л. Эконометрический анализ рынка подержанных автомобилей // Вестник Томского государственного университета. 2006. № 290. С. 104-107.
- Брюков В.Г. Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и Eviews. М.:КНОРУС, 2011. 272 с.
- Матюшок В.М. Основы эконометрического моделирования с использованием EVIEWS: учебное пособие / В. М. Матюшок, С. А. Балашова, И. В. Лазанюк. Москва, 2010.
- Литовченко И.С. Анализ количества малых предприятий в 1999 – 2010 годах // Вестник Северо-Кавказского федерального университета. 2012. № 3 (32). С. 236-239.
- Муллинов Д.О., Баженов Р.И. Разработка в среде Eviews регрессионной модели рынка гаражных помещений г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 43.
- Пронина О.Ю., Баженов Р.И. Исследование методов регрессионного анализа программной среды Eviews // Nauka-Rastudent.ru. 2015. № 1 (13). С. 45.
- Векслер В.А., Баженов Р.И. Определение взаимосвязи номенклатурных позиций средствами 1С:Предприятие 8.3 // Современные научные исследования и инновации. 2014. № 7 (39). С. 45-49.
- Лагунова А.А., Баженов Р.И. Разработка в среде GRETL регрессионной модели рынка вторичного жилья г. Биробиджана // Nauka-Rastudent.ru. 2015. № 1 (13). С. 40.
- Остроушко А.А., Баженов Р.И. Анализ ассортимента электротоваров с использованием ABC-анализа // Экономика и менеджмент инновационных технологий. 2014. № 10 (37). С. 73-81.
- Бронштейн К.С., Наумов А.А., Баженов Р.И. Применение классического ABC-анализа для анализа ассортимента блюд кафе // Экономика и менеджмент инновационных технологий. 2014. № 11 (38). С. 100-110.
- Резниченко Н.В., Наумов А.А., Баженов Р.И. Совершенствование ассортимента блюд кафе и системы закупок компонентов на основе ABC-XYZ-анализа // Экономика и менеджмент инновационных технологий. 2014. № 12 (39). С. 14-24.
- Жилкин С.А., Баженов Р.И. Совершенствование ассортимента товаров медицинского назначения на основе ABC-анализа // Экономика и менеджмент инновационных технологий. 2014. № 12 (39). С. 103-110.
- Якимов А.С., Баженов Р.И. Сегментация клиентов с помощью RFM-анализа // Экономика и менеджмент инновационных технологий. 2015. № 1 (40). С. 55-61.
- Наумов А.А., Наумова А.А., Баженов Р.И. О некоторых моделях и модификациях классического ABC-анализа // Современные научные исследования и инновации. 2014. № 12-2 (44). С. 138-146.
- Татаринова Е.Д., Наумов А.А., Баженов Р.И. Совершенствование ассортимента продажи товаров на основе ABC-XYZ-анализа // Экономика и менеджмент инновационных технологий. 2015. № 2 [Электронный ресурс]. URL: http://ekonomika.snauka.ru/2015/02/7393 (дата обращения: 19.02.2015).
- Перминова Н.А., Баженов Р.И. Совершенствование ассортимента обуви магазина «Велес» на основе АВС-XYZ-анализа // Экономика и менеджмент инновационных технологий. 2015. № 3 [Электронный ресурс]. URL: http://ekonomika.snauka.ru/2015/03/7782 (дата обращения: 27.03.2015).
- Черемисина И.А., Баженов Р.И., Совершенствование ассортимента товаров продовольственного магазина на основе классического ABC-анализа // Современные научные исследования и инновации. 2015. № 3 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2015/03/50776 (дата обращения: 28.03.2015).
- Дубовик А.В., Баженов Р.И. RFM-анализ базы данных заказчиков фотографа // Nauka-Rastudent.ru. 2015. № 3 (15). С. 4.
- Пивенко К.А., Баженов Р.И. Построение регрессионной модели в среде Gretl на примере рынка поддержанных автомобилей г. Биробиджана и г. Хабаровска // Экономика и менеджмент инновационных технологий. 2015. № 4 [Электронный ресурс]. URL: http://ekonomika.snauka.ru/2015/04/8362 (дата обращения: 09.04.2015).
- Tsani S. On the relationship between resource funds, governance and institutions: Evidence from quantile regression analysis // Resources Policy. 2015.Т. 44. С. 94-111
- Benos N., Zotou S. Education and Economic Growth: A Meta-Regression Analysis // World Development. 2014. Т.64. С. 669-689.
Количество просмотров публикации: Please wait
Связь с автором (комментарии/рецензии к статье)
Оставить комментарий
Вы должны авторизоваться, чтобы оставить комментарий.
Эконометрика: прогноз EURUSD на один шаг вперед
Введение
В статье рассматривается прогноз пары EURUSD на один шаг вперед с помощью пакета EViews с последующей оценкой результатов прогнозирования с помощью программы на EViews и советника на MQL 4. Данная статья является продолжением статьи «Анализ статистических характеристик индикаторов», положения которой будут использоваться без дополнительных разъяснений.
1. Построение модели
Предыдущая статья заканчивалась анализом следующего уравнения регрессии:
EURUSD = C(1)*EURUSD_HP(1) + C(2)*D(EURUSD_HP(1)) + C(3)*D(EURUSD_HP(2))
Это уравнение было получено в результате реализации идеи постепенной декомпозиции исходных котировок цен Close. В основе идеи лежит выделение из исходной котировки детерминированной составляющей с последующим анализом полученного остатка.
Начнем построение модели для символа EURUSD часового таймфрейма на барах за одну неделю: с 12.09.2011 по 17.09.2011.
1.1. Анализ исходной котировки EURUSD
С самого начала проанализируем исходный ряд EURUSD с целью составления плана на следующий шаг.
Для начала сформируем файл котировок для последующего анализа в EViews . Для этого я использую индикатор, который вешается на соответствующий график и формирует необходимый файл котировок.
Текст индикатора приведен ниже и, по-моему мнению, в комментариях не нуждается.
Задав указанные выше даты, я получил файл котировок, состоящий из 119 строк, последняя из которой имеет вид «Прогноз,0» – это место для будущего прогноза. Замечу, что работаю я с ценами Open . Также обращаю внимание, что порядок котировок в файле противоположный тому, который принят в MQL 4, т.е. как в языках программирования.
Индикатор, естественно, формирует файл kotir.txt в папке терминала expertfiles. Рассмотренный ниже советник в режиме DEMO или REAL торгов будет брать файл котировок из этой папки, но в режиме тестера этот файл необходим в папке testerfiles, поэтому я вручную перемещаю файл kotir.txt в папку testerfiles терминала.
Рис. 1. График котировок EURUSD, таймфрейм Н1
Визуально наблюдаем то ли один, то ли много трендов, но наша цель состоит в прогнозе будущей стабильности торговой системы. Поэтому проведем анализ на стационарность исходных котировок EURUSD_H1.
Вычислим описательные статистики:
Рис. 2. Описательные статистики
Из описательной статистики следует, что:
- Имеется скос вправо (должен быть ноль, а имеем 0.244950);
- Вероятность нормального распределения нашей исходной котировки 9.64%.
Конечно, визуально гистограмма не имеет никакого отношения к нормальному распределению, но вероятность в 9.64% порождает определенные иллюзии.
Давайте наглядно сравним с теорией:
Рис. 3. Сравнение гистограммы EURUSD с теоретической кривой нормального распределения
Визуально мы находим подтверждение, что котировка EURUSD _Н1 крайне далека о нормального распределения.
Однако делать выводы пока рано, так как визуально мы видим тренд, что говорит о наличии в котировках детерминированной составляющей, а наличие такой составляющей может полностью исказить статистические характеристики случайной величины (котировок).
Вычислим автокорреляцию котировок.
Она имеет следующий вид:
Рис. 4. Автокорреляционная функция котировок EURUSD_H1
При построении графика была получена вероятность отсутствия зависимостей межу лагами — для первых 16 лагов она не равна нулю. По графику и вероятности можно смело утверждать, что в EURUSD_H1 имеются зависимости между лагами, т.е. в котировке имеется детерминированная составляющая.
Какими статистическими характеристиками будет обладать этот остаток, если из исходной котировки вычесть детерминированную составляющую?
Для это проведем тест на единичный корень, который должен показать нам, будет ли более перспективной работа с первой разностью (остатком) исходной котировки.
Таблица 1. Тест на единичный корень
Проведенный тест показывает, что:
- Вероятность, что исходная котировка имеет единичный корень (первая разность имеет нормальное распределение), равна 41%;
- Статистика DW (Durbin-Watson) чуть больше 2.2, что также говорит о нормальном распределении первой разности.
По аналогии с предыдущей статьей для выделения детерминированной составляющей котировки EURUSD будем использовать сглаживание Ходрика-Прескотта (Hodrick-Prescott filter).
Цифра «10» в именах рядов означает параметр «лямбда» в сглаживании Ходрика-Прескотта. Из теории этого сглаживания известно, что величина лямбды имеет большое значение для результата, который имеет следующий вид:
Рис. 5. Результат сглаживания ряда фильтром Ходрика-Прескотта
Из предыдущей статьи будем использовать уравнение, которое в обозначениях EViews выглядит следующим образом:
kotir = C(1) * HP(-1) + C(2) * D(HP(-1)) + C(3)*D(HP(-2))
т.е в данном уравнении мы учитываем детерминированную составляющую и шум, под которым мы понимаем разность между исходной котировкой и ее детерминированной составляющей.
При анализе данной модели исходной котировки получаем следующие показатели уравнения регрессии:
Таблица 2. Оценка уравнения регрессии
Конечно, крайне неприятным является вероятность в 39% того, что коэффициент при НР1_D(-1) равен нулю. Оставляем все как есть, так как строим демонстрационный пример.
Получив оценку уравнения регрессии (оценку коэффициентов уравнения) можно сделать прогноз на один шаг вперед.
Результат выглядит следующим образом:
Рис. 6. Прогноз EURUSD на один шаг вперед (на 0 часов понедельника)
1.3. Оценка остатков от уравнения регрессии
Проведем ограниченный анализ остатка от уравнения регрессии. Этот остаток получен путем вычитания из исходных котировок EURUSD значений, вычисленных по уравнению регрессии.
Напомню, что по характеристикам этого остатка можно будет судить о будущей устойчивости торговой системы.
Первый тестом будет тест на анализ зависимостей между лагами в остатке:
Рис. 7. Автокорреляционная функция остатка
К сожалению, зависимости между лагами остались, а наличие зависимостей ставит под сомнение статистический анализ.
Следующий тест, который проведем — это тест на нормальность распределения остатка.
Результат имеет следующий вид:
Рис. 8. Гистограмма остатка от уравнения регрессии
Вероятность того, что остаток распределен по нормальному закону, равна 25.57%, это достаточно большая величина.
Проведем тесты на наличие гетероскедастичности в остатке.
Получаем следующие результаты:
- Вероятность отсутствия гетероскедастичности типа GARCH = 16.08%
- Вероятность отсутствия общей гетероскедастичности типа White = 0.0066%
Так как я ставлю перед собой цель демонстрации построения торговой системы на основе прогноза, то продолжу расчеты с целью получения интересующих трейдеров характеристик – прибыли или убытка.
2. Оценка результатов прогнозирования
При торговле нас интересует прибыль, а не ошибка прогноза, которую следует воспринимать как вспомогательное средство анализа для сравнения разных моделей, и не более того.
Для оценки прогноза была написана программа на языке EViews . В программе сравниваются приращения фактических движений котировок EURUSD с прогнозируемыми. Если эти приращения совпадают, то имеем прибыль, если не совпадают, то получаем убыток. Далее подсчитывается прибыль, которая равна сумме всех приращений, совпавших с приращениями прогноза, и соответствующий убыток.
Отношение прибыли к убытку обозначено как профит-фактор. Подсчитывается отношение прибыльных и убыточных приращений (отношение прибыльных и убыточных сделок). Также подсчитываем количество подряд убыточных сделок и отношение убытка в подряд убыточных сделках к прибыли (фактор восстановления).
Программа на языке EViews для оценки результатов моделирования в терминах торговой системы состоит из основной программы и двух подпрограмм.
Основная программа (головная) имеет следующий вид:
Предполагается, что основных программ столько, сколько подпрограмм, содержащих модели (см. ниже), это сделано для упрощения работы.
С изменением модели в основной программе надо менять две строчки, связанные с изменением имени подпрограммы для модели.
Подпрограмма, в которую вынесена модель (уравнение регрессии):
Этих подпрограмм должно быть равно количеству моделей.
Для другой модели следует изменить имя подпрограммы и, соответственно, имена в основной программе.
Подпрограмма, которая вычисляет показатели прибыли/убытка по модели:
Результат приведенных выше простых программ на EViews для нашего уравнения следующий:
Таблица 3. Результат оценки прибыльности в EViews
До сих пор в статье котировки EURUSD_H1 анализировались средствами программы EViews.
Однако очень заманчивым является использование результатов прогноза в советнике терминала МetaТrader 4 для торговли.
Далее рассмотрим обмен данными между программами EViews и МetaТrader 4, а затем с помощью советника в МetaТrader 4 еще раз проанализируем результаты.
3. Обмен данными между EViews и МetaТrader 4
В данной статье используется обмен данными между EViews и МetaТrader 4 при помощи файлов типа .txt.
Алгоритм обмена выглядит следующим образом:
Советник в МetaТrader 4:
- Формирует файл котировок;
- Запускает EViews.
- Запускается по команде из советника;
- Выполняет программу вычисления прогноза для полученной из советника котировки kotir.txt ;
- Записывает в файл EViewsForecast.txt результаты прогноза.
Советник в МetaТrader 4:
- Дождавшись окончания формирования результатов в EViews , читает файл с прогнозом;
- Принимает решение о входе в позицию или выходе из позиции.
Несколько слов по поводу размещения файлов.
Файлы терминала МetaТrader 4 размещаются в своих обычных каталогах: советник в папке expert, а индикатор (который не нужен для тестирования) в папке expertindicators. Все это находится в папке терминала. Советник устанавливается вместе с другими советниками.
Файлы, которыми обменивается советник с EViews , при работе советника находятся в expert files , при тестировании советника — в папке testerfiles.
Файл, который советник отправляется для EViews , имеет имя kotir . txt , которое не зависит от выбранного символа и таймфрейма. Поэтому советник можно прикреплять к любому символу, а размер шага прогноза указывается в параметрах советника при его запуске.
EViews возвращает файл с именем EVIEWSFORECAST.txt. В каталог терминала помещается рабочий файл EViews под именем worf.wf1.
В программах EViews, которые прилагаются к статье, указаны каталоги, которые скорее всего не будут совпадать с каталогами, установленными на вашем компьютере. У меня эти программы установлены в корневую папку диска. В EViews придется разобраться с каталогом по умолчанию или указать ваши каталоги (каталоги по умолчанию, которые использует сам EViews, я не использовал).
4. Советник на MQL4
Алгоритм работы советника упрощен по максимуму:
- Советник прикрепляется к таймфрейму М1 любого символа;
- Шаг прогноза указывается в минутах в параметрах советника. По умолчанию – шаг прогноза 60 минут (Н1). Прикрепление советника к М1 дает наглядность при рассмотрении результатов тестирования, так как можно сжать график тестирования, переходя к любому старшему таймфрейму;
- Для прогнозирования в EViews советник формирует файл kotir .txt с количеством баров (наблюдений), указанных в параметрах советника;
- Если прогноз больше текущей цены, то открывается long ;
- Если прогноз меньше текущей цены, то открывается short ;
- Советник открывает не более одной позиции (работает без долива позиции);
- Вне зависимости от прогноза предыдущая позиция закрывается, а новая открывается. Этот алгоритм открытия позиций совпадает с алгоритмом подсчета прибыльности/убыточности в программе на EViews;
- Объем открываемой позиции равен 0.1 лота;
- Стоп лоссы и тэйк профиты не используются (указаны равными в 100 пипсов, хотя в советнике имеется код для установки стопов на расстоянии ошибки прогноза);
- Рисуется график с указанием величины прогноза и двух линий на расстоянии одной стандартной ошибки прогноза. При просмотре графика из тестера на более мелких таймфреймах, чем тот на котором был прикреплен советник, следует иметь ввиду, что линия прогноза смещена назад, т.е. рисуется прогноз, к которому текущая цена должна прийти в конце периода.
Советник прикрепляем к таймфрейму М1, график из тестера удобнее просматривать на таймфрейме М5.
Исходный код советника на MQL4 для торговли по паре EURUSD в статье не привожу из-за его объемности (около 600 строк). Текст можно посмотреть в файле EvewsMT4.mq4 в архиве EViews_MetaTrader_4.zip, прикрепленном к статье.
5. Результаты тестирования советника
Запустим советник в тестере на таймфрейме М1.
Входные параметры показаны ниже.
Рис. 9. Входные параметры советника
Фрагмент графика тестирования приведен ниже:
Рис. 10. Тестирование советника в режиме визуализации
Результаты тестирования советника, который использует прогнозы на один час (шаг) вперед, показаны ниже.
Strategy Tester Report
EURUSD (Euro vs US Dollar)
1 Минута (M1) 2011.09.12 00:00 — 2011.09.16 21:59 (2011.09.12 — 2011.09.17)
Все тики (наиболее точный метод на основе всех наименьших доступных таймфреймов)
StepForecast=60; NumberBars=101; MultSE=2;
Баров в истории
Ошибки рассогласования графиков
Короткие позиции (% выигравших)
Длинные позиции (% выигравших)
Прибыльные сделки (% от всех)
Убыточные сделки (% от всех)
непрерывных выигрышей (прибыль)
непрерывных проигрышей (убыток)
непрерывная прибыль (число выигрышей)
непрерывный убыток (число проигрышей)
Рис. 11. Результаты тестирования советника
Результаты лучше, чем полученные в EViews.
Отмечу, что вычисление результата в EViews и тестере различаются исходными данными. В EViews берется 118 баров и вычисляется прогноз, начиная с 3 бара слева, и постепенно прогноз на один шаг вперед движется к концу временного периода, увеличивая количество баров, на который производится оценка уравнения регрессии.
Советник сдвигает окно в 118 баров и вычисляется прогноз на 119 бар, т.е. оценка уравнения регрессии всегда производится на 118 барах, поскольку EViews расширяет окно в пределах выборки, а советник двигает окно фиксированной ширины.
С помощью советника мы получили расширенную таблицу оценки модели. Если выше она состояла из одной строчки, то теперь в ней 117 строк – для каждой даты, на которую был получен прогноз.
Таблица имеет следующий вид:
| Начало выборки |
Конец выборки |
Факт на конец |
Прогноз на 1 шаг |
Ошибка прогноза |
Прибыль выборки |
Убыток выборки |
Maксимум просадки |
Кол-во убытков |
P/F в пипсах |
P/F в наблюд. | Фактор восстан. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 12.09.2011 0:00 | 16.09.2011 21:00 | 1,3791 | 1,3788 | 0,0019 | 0,0581 | 0,1531 | 0,0245 | 7 | 0,38 | 0,67 | 2,37 |
| 12.09.2011 0:00 | 16.09.2011 21:00 | 1,3791 | 1,3788 | 0,0019 | 0,0581 | 0,1531 | 0,0245 | 7 | 0,38 | 0,67 | 2,37 |
| 09.09.2011 21:00 | 16.09.2011 20:00 | 1,3784 | 1,3793 | 0,0019 | 0,0569 | 0,1619 | 0,0245 | 7 | 0,35 | 0,64 | 2,32 |
| 09.09.2011 20:00 | 16.09.2011 19:00 | 1,3794 | 1,3796 | 0,002 | 0,0596 | 0,1609 | 0,0245 | 7 | 0,37 | 0,67 | 2,43 |
| 09.09.2011 19:00 | 16.09.2011 18:00 | 1,3783 | 1,3782 | 0,0021 | 0,0642 | 0,1554 | 0,0245 | 7 | 0,41 | 0,69 | 2,62 |
| 09.09.2011 18:00 | 16.09.2011 17:00 | 1,3783 | 1,3806 | 0,002 | 0,0616 | 0,1606 | 0,0245 | 7 | 0,38 | 0,68 | 2,51 |
| 09.09.2011 17:00 | 16.09.2011 16:00 | 1,3829 | 1,3806 | 0,002 | 0,0642 | 0,1586 | 0,0245 | 7 | 0,4 | 0,71 | 2,62 |
| 09.09.2011 16:00 | 16.09.2011 15:00 | 1,3788 | 1,3793 | 0,002 | 0,0626 | 0,1565 | 0,0245 | 7 | 0,4 | 0,71 | 2,56 |
| 09.09.2011 15:00 | 16.09.2011 14:00 | 1,3798 | 1,38 | 0,0021 | 0,063 | 0,1633 | 0,0245 | 7 | 0,39 | 0,73 | 2,57 |
| 09.09.2011 14:00 | 16.09.2011 13:00 | 1,3808 | 1,381 | 0,0022 | 0,062 | 0,1656 | 0,0318 | 9 | 0,37 | 0,71 | 1,95 |
| 09.09.2011 13:00 | 16.09.2011 12:00 | 1,3809 | 1,3813 | 0,0021 | 0,0602 | 0,1679 | 0,0318 | 9 | 0,36 | 0,66 | 1,89 |
| 09.09.2011 12:00 | 16.09.2011 11:00 | 1,3792 | 1,3808 | 0,0021 | 0,0666 | 0,1613 | 0,0245 | 7 | 0,41 | 0,73 | 2,72 |
| 09.09.2011 11:00 | 16.09.2011 10:00 | 1,3795 | 1,3826 | 0,0021 | 0,0666 | 0,167 | 0,0245 | 7 | 0,4 | 0,73 | 2,72 |
| 09.09.2011 10:00 | 16.09.2011 9:00 | 1,3838 | 1,3847 | 0,0022 | 0,0652 | 0,1668 | 0,0318 | 9 | 0,39 | 0,71 | 2,05 |
| 09.09.2011 9:00 | 16.09.2011 8:00 | 1,3856 | 1,3854 | 0,0022 | 0,0675 | 0,165 | 0,0318 | 9 | 0,41 | 0,73 | 2,12 |
| 09.09.2011 8:00 | 16.09.2011 7:00 | 1,386 | 1,3856 | 0,0022 | 0,0671 | 0,1652 | 0,0318 | 9 | 0,41 | 0,71 | 2,11 |
| 09.09.2011 7:00 | 16.09.2011 6:00 | 1,3861 | 1,3857 | 0,0022 | 0,067 | 0,1663 | 0,0318 | 9 | 0,4 | 0,68 | 2,11 |
| 09.09.2011 6:00 | 16.09.2011 5:00 | 1,3852 | 1,3855 | 0,0022 | 0,0655 | 0,1681 | 0,0318 | 9 | 0,39 | 0,63 | 2,06 |
| 09.09.2011 5:00 | 16.09.2011 4:00 | 1,3844 | 1,3851 | 0,0022 | 0,0662 | 0,1674 | 0,0318 | 9 | 0,4 | 0,66 | 2,08 |
| 09.09.2011 4:00 | 16.09.2011 3:00 | 1,3848 | 1,3869 | 0,0022 | 0,0654 | 0,1683 | 0,0318 | 9 | 0,39 | 0,68 | 2,06 |
| 09.09.2011 3:00 | 16.09.2011 2:00 | 1,3879 | 1,3875 | 0,0022 | 0,0694 | 0,1624 | 0,0318 | 9 | 0,43 | 0,73 | 2,18 |
| 09.09.2011 2:00 | 16.09.2011 1:00 | 1,3865 | 1,3879 | 0,0022 | 0,0698 | 0,1634 | 0,0318 | 9 | 0,43 | 0,71 | 2,19 |
| 09.09.2011 1:00 | 16.09.2011 0:00 | 1,3881 | 1,3883 | 0,0022 | 0,0726 | 0,1604 | 0,0245 | 7 | 0,45 | 0,76 | 2,96 |
| 09.09.2011 0:00 | 15.09.2011 23:00 | 1,3876 | 1,3882 | 0,0022 | 0,0721 | 0,162 | 0,0245 | 7 | 0,45 | 0,73 | 2,94 |
| 08.09.2011 23:00 | 15.09.2011 22:00 | 1,3885 | 1,3884 | 0,0022 | 0,0718 | 0,1614 | 0,0245 | 7 | 0,44 | 0,72 | 2,93 |
| 08.09.2011 22:00 | 15.09.2011 21:00 | 1,3888 | 1,3883 | 0,0022 | 0,0737 | 0,1597 | 0,0245 | 7 | 0,46 | 0,77 | 3,01 |
| 08.09.2011 21:00 | 15.09.2011 20:00 | 1,3885 | 1,3874 | 0,0022 | 0,0729 | 0,1604 | 0,0318 | 9 | 0,45 | 0,74 | 2,29 |
| 08.09.2011 20:00 | 15.09.2011 19:00 | 1,3867 | 1,386 | 0,0022 | 0,0721 | 0,1604 | 0,0318 | 9 | 0,45 | 0,74 | 2,27 |
| 08.09.2011 19:00 | 15.09.2011 18:00 | 1,3856 | 1,3834 | 0,0022 | 0,0721 | 0,1628 | 0,0318 | 9 | 0,44 | 0,72 | 2,27 |
| 08.09.2011 18:00 | 15.09.2011 17:00 | 1,385 | 1,3861 | 0,0023 | 0,0702 | 0,1651 | 0,0318 | 9 | 0,43 | 0,72 | 2,21 |
| 08.09.2011 17:00 | 15.09.2011 16:00 | 1,3885 | 1,3824 | 0,0023 | 0,0739 | 0,1638 | 0,0245 | 7 | 0,45 | 0,72 | 3,02 |
| 08.09.2011 16:00 | 15.09.2011 15:00 | 1,3773 | 1,3784 | 0,0021 | 0,0719 | 0,1556 | 0,0318 | 9 | 0,46 | 0,72 | 2,26 |
| 08.09.2011 15:00 | 15.09.2011 14:00 | 1,3795 | 1,3794 | 0,0021 | 0,0726 | 0,1537 | 0,0318 | 9 | 0,47 | 0,72 | 2,28 |
| 08.09.2011 14:00 | 15.09.2011 13:00 | 1,3814 | 1,3792 | 0,0021 | 0,0736 | 0,1564 | 0,0318 | 9 | 0,47 | 0,74 | 2,31 |
| 08.09.2011 13:00 | 15.09.2011 12:00 | 1,3802 | 1,3764 | 0,0021 | 0,0712 | 0,159 | 0,0318 | 9 | 0,45 | 0,74 | 2,24 |
| 08.09.2011 12:00 | 15.09.2011 11:00 | 1,3769 | 1,3753 | 0,0021 | 0,0719 | 0,1568 | 0,0318 | 9 | 0,46 | 0,72 | 2,26 |
| 08.09.2011 11:00 | 15.09.2011 10:00 | 1,3765 | 1,3732 | 0,0021 | 0,0721 | 0,1564 | 0,0318 | 9 | 0,46 | 0,74 | 2,27 |
| 08.09.2011 10:00 | 15.09.2011 9:00 | 1,3722 | 1,3718 | 0,0021 | 0,0716 | 0,1538 | 0,0318 | 9 | 0,47 | 0,72 | 2,25 |
| 08.09.2011 8:00 | 15.09.2011 7:00 | 1,371 | 1,3716 | 0,0021 | 0,0729 | 0,1542 | 0,0318 | 9 | 0,47 | 0,74 | 2,29 |
| 08.09.2011 8:00 | 15.09.2011 7:00 | 1,371 | 1,3716 | 0,0021 | 0,0729 | 0,1542 | 0,0318 | 9 | 0,47 | 0,74 | 2,29 |
| 08.09.2011 7:00 | 15.09.2011 6:00 | 1,3723 | 1,3727 | 0,0021 | 0,0716 | 0,1547 | 0,0318 | 9 | 0,46 | 0,72 | 2,25 |
| 08.09.2011 6:00 | 15.09.2011 5:00 | 1,3726 | 1,3725 | 0,0021 | 0,0711 | 0,1564 | 0,0318 | 9 | 0,45 | 0,69 | 2,24 |
| 08.09.2011 5:00 | 15.09.2011 4:00 | 1,3719 | 1,3731 | 0,0021 | 0,0711 | 0,1563 | 0,0318 | 9 | 0,45 | 0,69 | 2,24 |
| 08.09.2011 4:00 | 15.09.2011 3:00 | 1,374 | 1,3744 | 0,0021 | 0,0713 | 0,1547 | 0,0318 | 9 | 0,46 | 0,69 | 2,24 |
| 08.09.2011 3:00 | 15.09.2011 2:00 | 1,3748 | 1,3747 | 0,0021 | 0,0705 | 0,1547 | 0,0318 | 9 | 0,46 | 0,68 | 2,22 |
| 08.09.2011 2:00 | 15.09.2011 1:00 | 1,3743 | 1,3742 | 0,0021 | 0,0715 | 0,1544 | 0,0318 | 9 | 0,46 | 0,7 | 2,25 |
| 08.09.2011 1:00 | 15.09.2011 0:00 | 1,3738 | 1,3743 | 0,0021 | 0,0714 | 0,1544 | 0,0318 | 9 | 0,46 | 0,7 | 2,25 |
| 08.09.2011 0:00 | 14.09.2011 23:00 | 1,375 | 1,3743 | 0,0021 | 0,0724 | 0,1532 | 0,0318 | 9 | 0,47 | 0,73 | 2,28 |
| 07.09.2011 23:00 | 14.09.2011 22:00 | 1,375 | 1,3736 | 0,0021 | 0,0727 | 0,1532 | 0,0318 | 9 | 0,47 | 0,74 | 2,29 |
| 07.09.2011 22:00 | 14.09.2011 21:00 | 1,3751 | 1,3735 | 0,0021 | 0,0734 | 0,1532 | 0,0318 | 9 | 0,48 | 0,74 | 2,31 |
| 07.09.2011 21:00 | 14.09.2011 20:00 | 1,3748 | 1,3716 | 0,0021 | 0,0722 | 0,1555 | 0,0318 | 9 | 0,46 | 0,72 | 2,27 |
| 07.09.2011 20:00 | 14.09.2011 19:00 | 1,3714 | 1,3712 | 0,0021 | 0,0812 | 0,145 | 0,0189 | 6 | 0,56 | 0,74 | 4,3 |
| 07.09.2011 19:00 | 14.09.2011 18:00 | 1,371 | 1,3697 | 0,0021 | 0,0692 | 0,1577 | 0,0318 | 9 | 0,44 | 0,69 | 2,18 |
| 07.09.2011 18:00 | 14.09.2011 17:00 | 1,3673 | 1,369 | 0,0021 | 0,0695 | 0,154 | 0,0318 | 9 | 0,45 | 0,72 | 2,19 |
| 07.09.2011 17:00 | 14.09.2011 16:00 | 1,3687 | 1,3693 | 0,0021 | 0,0695 | 0,1548 | 0,0318 | 9 | 0,45 | 0,72 | 2,19 |
| 07.09.2011 16:00 | 14.09.2011 15:00 | 1,3704 | 1,3704 | 0,0021 | 0,066 | 0,1591 | 0,0318 | 11 | 0,41 | 0,69 | 2,08 |
| 07.09.2011 15:00 | 14.09.2011 14:00 | 1,373 | 1,37 | 0,002 | 0,066 | 0,1577 | 0,0318 | 10 | 0,42 | 0,69 | 2,08 |
| 07.09.2011 14:00 | 14.09.2011 13:00 | 1,3712 | 1,3681 | 0,002 | 0,066 | 0,1562 | 0,0318 | 9 | 0,42 | 0,69 | 2,08 |
| 07.09.2011 13:00 | 14.09.2011 12:00 | 1,3685 | 1,3653 | 0,002 | 0,0665 | 0,1534 | 0,0318 | 9 | 0,43 | 0,74 | 2,09 |
| 07.09.2011 12:00 | 14.09.2011 11:00 | 1,3655 | 1,3646 | 0,002 | 0,0673 | 0,1504 | 0,0318 | 9 | 0,45 | 0,77 | 2,12 |
| 07.09.2011 11:00 | 14.09.2011 10:00 | 1,3656 | 1,3634 | 0,002 | 0,0709 | 0,15 | 0,0318 | 9 | 0,47 | 0,77 | 2,23 |
| 07.09.2011 10:00 | 14.09.2011 9:00 | 1,3625 | 1,3625 | 0,002 | 0,0725 | 0,1461 | 0,0318 | 9 | 0,5 | 0,83 | 2,28 |
| 07.09.2011 9:00 | 14.09.2011 8:00 | 1,3631 | 1,3638 | 0,002 | 0,0719 | 0,1465 | 0,0318 | 9 | 0,49 | 0,8 | 2,26 |
| 07.09.2011 8:00 | 14.09.2011 7:00 | 1,3641 | 1,3643 | 0,002 | 0,0707 | 0,1481 | 0,0318 | 9 | 0,48 | 0,77 | 2,22 |
| 07.09.2011 7:00 | 14.09.2011 6:00 | 1,3635 | 1,3648 | 0,002 | 0,0724 | 0,1481 | 0,0318 | 9 | 0,49 | 0,8 | 2,28 |
| 07.09.2011 6:00 | 14.09.2011 5:00 | 1,3647 | 1,3656 | 0,002 | 0,0724 | 0,1476 | 0,0318 | 9 | 0,49 | 0,8 | 2,28 |
| 07.09.2011 5:00 | 14.09.2011 4:00 | 1,3665 | 1,3676 | 0,002 | 0,0667 | 0,1536 | 0,0318 | 9 | 0,43 | 0,72 | 2,1 |
| 07.09.2011 4:00 | 14.09.2011 3:00 | 1,3694 | 1,3683 | 0,002 | 0,0675 | 0,1504 | 0,0318 | 9 | 0,45 | 0,74 | 2,12 |
| 07.09.2011 3:00 | 14.09.2011 2:00 | 1,3682 | 1,3682 | 0,002 | 0,0672 | 0,1498 | 0,0318 | 9 | 0,45 | 0,74 | 2,11 |
| 07.09.2011 2:00 | 14.09.2011 1:00 | 1,3684 | 1,3686 | 0,002 | 0,067 | 0,1512 | 0,0318 | 9 | 0,44 | 0,72 | 2,11 |
| 07.09.2011 1:00 | 14.09.2011 0:00 | 1,3679 | 1,3686 | 0,002 | 0,067 | 0,1514 | 0,0318 | 9 | 0,44 | 0,72 | 2,11 |
| 07.09.2011 0:00 | 13.09.2011 23:00 | 1,3678 | 1,3691 | 0,002 | 0,0679 | 0,1507 | 0,0318 | 9 | 0,45 | 0,74 | 2,14 |
| 06.09.2011 23:00 | 13.09.2011 22:00 | 1,3692 | 1,3698 | 0,002 | 0,066 | 0,1517 | 0,0318 | 9 | 0,44 | 0,69 | 2,08 |
| 06.09.2011 22:00 | 13.09.2011 21:00 | 1,3708 | 1,3705 | 0,002 | 0,0652 | 0,1512 | 0,0318 | 9 | 0,43 | 0,69 | 2,05 |
| 06.09.2011 21:00 | 13.09.2011 20:00 | 1,3719 | 1,3709 | 0,002 | 0,0652 | 0,1512 | 0,0318 | 9 | 0,43 | 0,69 | 2,05 |
| 06.09.2011 20:00 | 13.09.2011 19:00 | 1,371 | 1,3691 | 0,002 | 0,0652 | 0,1517 | 0,0318 | 9 | 0,43 | 0,69 | 2,05 |
| 06.09.2011 19:00 | 13.09.2011 18:00 | 1,3677 | 1,3669 | 0,002 | 0,0666 | 0,1485 | 0,0318 | 9 | 0,45 | 0,72 | 2,09 |
| 06.09.2011 18:00 | 13.09.2011 17:00 | 1,3678 | 1,3677 | 0,002 | 0,0666 | 0,149 | 0,0318 | 9 | 0,45 | 0,72 | 2,09 |
| 06.09.2011 17:00 | 13.09.2011 16:00 | 1,3698 | 1,3659 | 0,002 | 0,0625 | 0,1555 | 0,0318 | 9 | 0,4 | 0,64 | 1,97 |
| 06.09.2011 16:00 | 13.09.2011 15:00 | 1,3658 | 1,3643 | 0,002 | 0,065 | 0,1513 | 0,0318 | 9 | 0,43 | 0,72 | 2,04 |
| 06.09.2011 15:00 | 13.09.2011 14:00 | 1,3665 | 1,3636 | 0,002 | 0,0643 | 0,1527 | 0,0318 | 9 | 0,42 | 0,69 | 2,02 |
| 06.09.2011 14:00 | 13.09.2011 13:00 | 1,3639 | 1,3619 | 0,002 | 0,0659 | 0,1552 | 0,0318 | 9 | 0,42 | 0,74 | 2,07 |
| 06.09.2011 13:00 | 13.09.2011 12:00 | 1,3617 | 1,3628 | 0,0021 | 0,0824 | 0,1432 | 0,0189 | 6 | 0,58 | 0,8 | 4,36 |
| 06.09.2011 12:00 | 13.09.2011 11:00 | 1,3616 | 1,361 | 0,0021 | 0,0824 | 0,1435 | 0,0189 | 6 | 0,57 | 0,8 | 4,36 |
| 06.09.2011 11:00 | 13.09.2011 10:00 | 1,3582 | 1,3631 | 0,002 | 0,0795 | 0,1435 | 0,0189 | 6 | 0,55 | 0,8 | 4,21 |
| 06.09.2011 10:00 | 13.09.2011 9:00 | 1,3654 | 1,3656 | 0,002 | 0,077 | 0,146 | 0,0189 | 6 | 0,53 | 0,74 | 4,07 |
| 06.09.2011 9:00 | 13.09.2011 8:00 | 1,3655 | 1,3664 | 0,0021 | 0,0813 | 0,1442 | 0,0189 | 6 | 0,56 | 0,77 | 4,3 |
| 06.09.2011 8:00 | 13.09.2011 7:00 | 1,3679 | 1,3673 | 0,0022 | 0,0834 | 0,1435 | 0,0189 | 6 | 0,58 | 0,77 | 4,41 |
| 06.09.2011 7:00 | 13.09.2011 6:00 | 1,3685 | 1,3668 | 0,0022 | 0,0828 | 0,1448 | 0,0189 | 6 | 0,57 | 0,74 | 4,38 |
| 06.09.2011 6:00 | 13.09.2011 5:00 | 1,3676 | 1,3669 | 0,0022 | 0,0879 | 0,1406 | 0,0189 | 6 | 0,63 | 0,85 | 4,65 |
| 06.09.2011 5:00 | 13.09.2011 4:00 | 1,3669 | 1,3653 | 0,0022 | 0,0821 | 0,1458 | 0,0189 | 6 | 0,56 | 0,8 | 4,34 |
| 06.09.2011 4:00 | 13.09.2011 3:00 | 1,3635 | 1,3639 | 0,0022 | 0,0821 | 0,1428 | 0,0189 | 6 | 0,57 | 0,8 | 4,34 |
| 06.09.2011 3:00 | 13.09.2011 2:00 | 1,3637 | 1,3646 | 0,0022 | 0,0821 | 0,1428 | 0,0189 | 6 | 0,57 | 0,8 | 4,34 |
| 06.09.2011 2:00 | 13.09.2011 1:00 | 1,3657 | 1,364 | 0,0022 | 0,0825 | 0,1407 | 0,0189 | 6 | 0,59 | 0,8 | 4,37 |
| 06.09.2011 1:00 | 13.09.2011 0:00 | 1,366 | 1,3639 | 0,0022 | 0,085 | 0,1384 | 0,0141 | 6 | 0,61 | 0,83 | 6,03 |
| 06.09.2011 0:00 | 12.09.2011 23:00 | 1,3678 | 1,3655 | 0,0022 | 0,083 | 0,1416 | 0,0141 | 6 | 0,59 | 0,8 | 5,89 |
| 05.09.2011 23:00 | 12.09.2011 22:00 | 1,366 | 1,3613 | 0,0022 | 0,0806 | 0,1424 | 0,0123 | 6 | 0,57 | 0,8 | 6,55 |
| 05.09.2011 22:00 | 12.09.2011 21:00 | 1,3572 | 1,3585 | 0,002 | 0,0731 | 0,1414 | 0,0152 | 6 | 0,52 | 0,77 | 4,81 |
| 05.09.2011 21:00 | 12.09.2011 20:00 | 1,3576 | 1,3601 | 0,002 | 0,0714 | 0,1432 | 0,0152 | 6 | 0,5 | 0,74 | 4,7 |
| 05.09.2011 20:00 | 12.09.2011 19:00 | 1,3607 | 1,3637 | 0,0021 | 0,0712 | 0,1406 | 0,0129 | 6 | 0,51 | 0,74 | 5,52 |
| 05.09.2011 19:00 | 12.09.2011 18:00 | 1,3632 | 1,3619 | 0,0021 | 0,0712 | 0,1405 | 0,0129 | 6 | 0,51 | 0,74 | 5,52 |
| 05.09.2011 18:00 | 12.09.2011 17:00 | 1,3609 | 1,3641 | 0,0021 | 0,073 | 0,1378 | 0,0129 | 6 | 0,53 | 0,77 | 5,66 |
| 05.09.2011 17:00 | 12.09.2011 16:00 | 1,3684 | 1,3659 | 0,002 | 0,0713 | 0,1334 | 0,0083 | 6 | 0,53 | 0,74 | 8,59 |
| 05.09.2011 16:00 | 12.09.2011 15:00 | 1,3665 | 1,3636 | 0,002 | 0,0727 | 0,1343 | 0,0083 | 6 | 0,54 | 0,77 | 8,76 |
| 05.09.2011 15:00 | 12.09.2011 14:00 | 1,363 | 1,3601 | 0,002 | 0,072 | 0,1348 | 0,0083 | 6 | 0,53 | 0,77 | 8,67 |
| 05.09.2011 14:00 | 12.09.2011 13:00 | 1,3603 | 1,3594 | 0,002 | 0,0752 | 0,1304 | 0,0083 | 6 | 0,58 | 0,83 | 9,06 |
| 05.09.2011 13:00 | 12.09.2011 12:00 | 1,3623 | 1,3589 | 0,002 | 0,0742 | 0,1304 | 0,0083 | 6 | 0,57 | 0,83 | 8,94 |
| 05.09.2011 12:00 | 12.09.2011 11:00 | 1,3597 | 1,3561 | 0,0019 | 0,0737 | 0,1291 | 0,0083 | 6 | 0,57 | 0,8 | 8,88 |
| 05.09.2011 11:00 | 12.09.2011 10:00 | 1,3561 | 1,3551 | 0,0019 | 0,0729 | 0,1275 | 0,0083 | 6 | 0,57 | 0,8 | 8,78 |
| 05.09.2011 10:00 | 12.09.2011 9:00 | 1,3556 | 1,3552 | 0,002 | 0,072 | 0,1283 | 0,0083 | 6 | 0,56 | 0,77 | 8,67 |
| 05.09.2011 9:00 | 12.09.2011 8:00 | 1,3536 | 1,3532 | 0,002 | 0,072 | 0,1271 | 0,0083 | 6 | 0,57 | 0,77 | 8,67 |
| 05.09.2011 8:00 | 12.09.2011 7:00 | 1,3519 | 1,3554 | 0,0019 | 0,0703 | 0,1288 | 0,0083 | 6 | 0,55 | 0,74 | 8,47 |
| 05.09.2011 7:00 | 12.09.2011 6:00 | 1,3583 | 1,3579 | 0,0019 | 0,072 | 0,1224 | 0,0083 | 6 | 0,59 | 0,77 | 8,67 |
| 05.09.2011 6:00 | 12.09.2011 5:00 | 1,3591 | 1,3582 | 0,0019 | 0,0715 | 0,1224 | 0,0083 | 6 | 0,58 | 0,77 | 8,61 |
| 05.09.2011 5:00 | 12.09.2011 4:00 | 1,3593 | 1,3589 | 0,0019 | 0,0713 | 0,1224 | 0,0083 | 6 | 0,58 | 0,75 | 8,59 |
| 05.09.2011 3:00 | 12.09.2011 2:00 | 1,3583 | 1,361 | 0,0019 | 0,0746 | 0,1192 | 0,0083 | 6 | 0,63 | 0,78 | 8,99 |
Таблица 4. Результаты тестирования в EViews
Из таблицы видно, что наша модель (столь примитивная и недоделанная) практически безнадежна. Необходимо ее дорабатывать.
Построим график двух колонок: P/F в пипсах и P/F в наблюдениях.
Рис. 12. Графики прибыльности модели на выборке в 118 баров
Этот график представляет собой зависимость профит-факторов от количества баров в анализе. Очевиден растущий тренд.
Проверим на выборке в 238 баров. Получаем следующий график:
Рис. 13. Графики прибыльности модели на выборке в 236 баров
http://www.mql5.com/ru/articles/1345
Молчанов
И.Н., Герасимова И.А.
Практикум
Ростов-на-Дону
2001
УДК [330.43](076.5)
М 75
1Л4
Молчанов И.Н., Герасимова И.А. Компьютерный практикум по
начальному курсу эконометрики (реализация на Eviews): Практикум /Ростовский
государственный экономический университет. — Ростов-н/Д., — 2001. – 58 с. — ISBN
5-7972-0377-4.
Практикум представляет собой попытку создания учебного
пособия, ориентированного на специфику преподавания эконометрики в экономическом
вузе с использованием специализированного эконометрического пакета Eviews. Практикум ориентирован на начальный курс
эконометрики.
Для студентов и аспирантов вузов, обучающихся по
экономическим специальностям.
Замечания и предложения просим направлять по адресу:
344007, г.Ростов-на-Дону, ул.
Большая Садовая, 69, к. 404, каф. СМиП.
|
E—mail: |
IGORM@APPLECLUB.DONPAC.RU |
|
Интернет: |
http://molchanov.narod.ru/econometrics.html |
Рецензенты:
Л.И.Ниворожкина, доктор экономических наук,
профессор, зав. кафедрой СМиП РГЭУ «РИНХ».
В.С.Князевский, доктор экономических наук,
профессор, Заслуженный деятель науки Российской Федерации, РГЭУ «РИНХ».
Утверждено
в качестве практикума редакционно-издательским советом РГЭУ
ISBN 5-7972-0377-4
|
Ó Ростовский государственный экономический |
|
|
Ó Молчанов И.Н., Герасимова И.А., 2001 |
Предисловие
Эконометрический
пакет Eviews обеспечивает особо
сложный и тонкий инструментарий обработки данных, позволяет выполнять регрессионный
анализ, строить прогнозы в Windows-ориентированной компьютерной среде. С помощью этого программного
средства можно очень быстро выявить наличие статистической зависимости в
анализируемых данных и затем, используя полученные взаимосвязи, сделать прогноз
изучаемых показателей.
Целесообразно
выделить следующие сферы применения Eviews:
Ø анализ научной информации и оценивание;
Ø финансовый анализ;
Ø макроэкономическое прогнозирование;
Ø моделирование;
Ø прогнозирование состояния рынков.
Особо широкие возможности открывает Eviews при анализе данных, представленных в виде
временных рядов.
Подробную информацию
об условиях приобретения и распространения пакета можно получить на сайте
производителя: http://www.eviews.com . Пакет занимает после инсталляции около 12
Мб на жестком диске.
Все используемые в
практикуме задания (примеры) доступны в виде файлов в формате Excel и Eviews по адресу: http://molchanov.narod.ru/econometrics.html .
При выполнении предлагаемых заданий могут оказаться
полезными следующие учебники и пособия:
1.
Айвазян С.А., Мхитарян В.С. Прикладная
статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1022 с. ISBN
5-238-00013-8.
2.
Доугерти К. Введение в эконометрику. — М.:
ИНФРА-М, 1997. – XIV,
402 с.: ил. — (Университетский учебник) Библиография: с.384-386. ISBN
5-86225-458-7; 0-19-50346-4.
3.
Елисеева И.И. Эконометрика: Учебник
/И.И.Елисеева и др. – М.: Финансы и статистика, 2001. – ISBN 5-279-01955-0.
4.
Князевский В.С., Житников И.В. Анализ временных
рядов и прогнозирование: Учеб. пособие. – Ростов-на-Дону: РГЭА, 1998. – 161 с.
5. Князевский
В.С., Молчанов И.Н.
Статистические расчеты на компьютере с использованием ППП Microstat. —
Ростов-на-Дону: РГЭА, 1996. — 86 с.
6. Магнус
Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.:
Дело, 2000. – 400 с. ISBN 5-7749-0055-X.
7. Практикум
по эконометрике: Учеб. пособие /И.И.Елисеева и др. – М.: Финансы и статистика,
2001. – 192 с. ISBN
5-279-02313-2.
8.
Greene,
W.H. Econometric
analysis, Prentice Hall, 4th Edition, 2000. – 1004 p.
9.
Verbeek,
M. A Guide to
Modern Econometrics,
Wiley, 2000. – 400 p.
Практическое занятие № 1.
«Знакомство с эконометрическим пакетом Eviews»
Eviews
(далее пакет) установлен в директорий Program Files/Eviews3. Запуск
осуществляется выбором соответствующего значка в панели Пуск/Программы/Eviews3/Eviews 3.1 (файл
C:Program FilesEViews3EViews3.exe) (см. рис. 1) или щелчком (двойным щелчком
– в зависимости от установок) по соответствующей пиктограмме на рабочем столе.
Рис. 1.
Если Вы все сделали правильно,
появится стартовое окно пакета (рис.2).
Рис. 2.
Если в настоящий момент окно,
содержащее пакет, является активным, то первая строка экрана (Title Bar) будет темнее
остальных. При переключении в другое окно цветовая окраска данной строки
изменит цвет на более приглушенный (серый).
Ниже следует строка основного
меню (Main Menu).
Принцип его построения прост – при нажатии на соответствующие клавиши появляется
раскрывающееся меню (drop-down menu). Доступные
в настоящий момент опции являются затемненными (darkened menu items). Те
пункты, с которыми в настоящий момент работа невозможна, приглушены (grayed menu items).
Далее располагается командная
строка (окно) (command window). В нем происходит непосредственный набор
команд, которые выполняются после нажатия клавиши Enter (Ввод). Для исполнения многих команд
отсутствует необходимость их набора – просто надо выбрать нужный пункт в основном
меню.
Большая часть экрана пакета отведена под рабочую область (work area). В ней размещаются рабочие объекты.
Переключение между ними осуществляется нажатием клавиши F6.
Последняя область экрана показывает текущее состояние (status line) пакета (рабочий каталог,
текущий файл и др.).
Завершение работы с пакетом осуществляется путем выбора в командной строке
опции File/Exit. Система предложит сохранить/не
сохранить имеющиеся данные. Если имя файла не было задано ранее, автоматически
будет предложено имя UNTITLED. Его можно изменить на любое другое. Пакет
имеет обширную справочную систему (пункт основного меню Help).
Знакомство с пакетом начнем с
файла, содержащего данные о совокупном спросе на деньги (M1) – (aggregate money demand) (M1) – зависимая переменная; независимые:
доход (ВВП) — income (GDP); уровень цен (PR) — price
level (PR); краткосрочная процентная ставка (RS) — short
term interest rate (RS).
Проведем некоторые преобразования и расчеты.
Первым шагом создадим новый рабочий
файл (workfile). Его имя должно иметь следующий вид и состоять только
из латинских букв: Номер_группы_demo_01.wf1 (расширение wf1
присваивается автоматически). Например: 451_demo_01.wf1. Расположить его следует в
директории, относящемся к Вашему факультету (внимательно ознакомьтесь с
памяткой в компьютерном классе). Исходные данные находятся в файле Excel. Они должны быть
импортированы в пакет. Создание рабочего файла начнем с того, что выберем File/New/Workfile в основном меню (см. рис.
3).
После нажатия на кнопке со словом Workfile откроется диалоговое
окно, с помощь которого можно задать тип вводимых Вами данных (см. рис. 4).
Рис. 3.
Рис. 4.
Рис. 5.
Рис. 6.
Для чтения данных, созданных в
других программах, надо выбрать в рабочем файле опцию Procs/Import/Read Text-Lotus-Excel… (см.
рис. 7). Появится диалог, представленный на рис. 8.
Рис. 7.
Перейдем к папке, содержащей искомый файл (для упрощения
поиска в опции Тип файлов (Files of type) можно выбрать Excel.xls (см. рис.8). Для того, чтобы
пакет «помнил» Ваши перемещения по папкам компьютера, можно поставить флажок в
опции Update default
directory (см. рис. 8).
Рис. 8.
Рис. 9.
Рис. 10.
После того, как исходные данные перенесены Вами в рабочую
область пакета (появились имена переменных), надо провести их верификацию (проверку
правильности). Вам необходимо создать новую группу, содержащую все
импортированные серии (переменные). Это делается следующим образом: необходимо кликнуть
мышкой по имени первой переменной (например, GNP), затем, удерживая
клавишу CTRL кликнуть по переменным M1, PR и RS. Все серии на экране будут зачернены. Затем необходимо
подвести курсор мыши на зачерненную область экрана и кликнуть правой кнопкой.
Далее необходимо выбрать опцию Open. Пакет откроет диалоговое окно со следующими опциями
(см. рис. 11).
Выберем Open
Group (открыть в одной группе). Пакет создаст группу с именем UNTITLED, в которую войдут все
переменные (серии). По умолчанию, данные будут представлены в виде электронной
таблицы (возможны другие варианты представления) – см. рис. 12.
Рис. 11.
Рис. 12.
Проведите визуальную проверку корректности данных. Сравните,
как разместились переменные из исходного файла, обратите внимание на столбец
слева от первой переменной (он серого цвета). В нем отображены годы и порядковые
номера кварталов. Полученной новой группе данных можно дать имя. Для этого
необходимо нажать кнопку Name
в текущем окне (см. рис. 12). Появится диалоговое окно (рис. 13.).
Автоматически будет предложено имя – GROUP01. Его можно принять, нажав кнопку OK. В рабочем файле сразу добавится одна переменная с
введенным Вами именем. Теперь к ней всегда можно перейти простым нажатием
клавиши мыши.
Рис. 13.
Рис. 14.
Для того, чтобы вернуться к прежней форме представления
данных (например, электронной таблице), надо выбрать View/Spreadsheet.
Для просмотра числовых характеристик (описательных
статистик) отмеченных переменных необходимо выбрать в рабочем файле View/Descriptive Stats/Individual Samples (см.
рис. 16).
В результате появится окно, представленное на рис. 17. В нем
содержатся:
Mean
– Среднее арифметическое значение;
Median
– Медиана;
Maximum –
Максимальное значение;
Std.
Dev. –
Стандартное отклонение (среднее квадратическое отклонение);
Skewness
– Коэффициент асимметрии;
Kurtosis
– Эксцесс;
Probability
– Вероятность;
Observations – Количество
наблюдений.
Рис. 15.
Рис. 16.
Рис. 17.
Если возникает необходимость проанализировать матрицу
коэффициентов корреляции, то необходимо выбрать View/Correlations. Результат представлен
на рис. 18.
Рис. 18.
Вы также можете исследовать характеристики для отдельных
серий (переменных), совместив вывод диаграммы и числовых характеристик. Дважды
кликните на имени серии (например, на переменной М1) и выберете в рабочем файле пункт меню View/Descriptive Stats/Histogram and Stats (см. рис. 19). Результат наглядно виден на рис. 20.
Рис. 19.
Рис. 20.
С другими возможностями пакета Вы познакомитесь на
последующих занятиях.
Для индивидуальной работы по предложенной выше схеме
предназначены нижеследующие данные. Подумайте, все ли данные необходимо
заносить в электронную таблицу или импортировать из неё.
Пример 1. Стоимость
однокомнатных квартир в Москве [6].
Данные из газеты «Из рук в руки» за период с декабря 1996 г.
по сентябрь 1997г.
Была выбрана Юго-Западная часть города, в которой высок
спрос на жилые площади (всего 69 наблюдений). Файл example_01.xls.
Переменные:
N — Номер по порядку.
distc Удаленность. от центра, км.
distm Удаленность от метро, мин.
totsq Общая площадь квартиры, кв.м.
kitsq Площадь кухни, кв.м.
livsq Площадь комнаты, кв.м.
floor Этаж.
0-первый/последний, 1-нет.
cat Категория дома. 1-кирпичный, 0-нет.
price Цена квартиры, тыс. USD.
Найдите среднее арифметическое, выборочное стандартное
отклонение и другие статистики параметров. Найдите коэффициенты корреляции параметров
с ценой квартиры. Соответствуют ли полученные значения экономической интуиции?
|
N |
region |
distc |
distm |
totsq |
kitsq |
livsq |
floor |
cat |
price |
|
1 |
Фрунзенская |
4 |
10 |
34,00 |
7,50 |
19,00 |
1 |
1 |
54 |
|
2 |
Ленинский |
5,7 |
7 |
36,00 |
10,00 |
20,00 |
0 |
0 |
35 |
|
3 |
Ленинский |
5,7 |
12 |
45,00 |
13,00 |
20,00 |
1 |
1 |
59 |
|
4 |
Академическая |
7,6 |
10 |
35,30 |
10,00 |
20,00 |
1 |
0 |
35 |
|
5 |
Университет |
8,7 |
6 |
33,00 |
5,50 |
22,00 |
1 |
0 |
33 |
|
6 |
Нов.Черемуш. |
10,3 |
3 |
33,00 |
8,50 |
18,00 |
1 |
1 |
57 |
|
7 |
Юго-Западная |
13,3 |
10 |
37,00 |
10,00 |
19,00 |
1 |
0 |
43 |
|
8 |
Коньково |
14,8 |
2 |
38,00 |
8,50 |
19,10 |
1 |
0 |
39 |
|
9 |
Фрунзенская |
4 |
15 |
54,00 |
9,20 |
27,20 |
1 |
1 |
70 |
|
10 |
Университет |
8,7 |
15 |
35,00 |
6,00 |
20,00 |
0 |
1 |
43 |
|
11 |
Пр.Вернадск. |
11,4 |
10 |
31,40 |
5,20 |
21,30 |
1 |
0 |
33 |
|
12 |
Ленинский |
5,7 |
7 |
32,00 |
6,00 |
21,00 |
1 |
0 |
37 |
|
13 |
Нов.Черемуш |
10,3 |
7 |
38,00 |
8,00 |
19,00 |
0 |
0 |
33 |
|
14 |
Университет |
8,7 |
10 |
31,60 |
8,80 |
14,00 |
0 |
0 |
31 |
|
15 |
Юго-Запад |
13,3 |
5 |
32,00 |
8,00 |
17,00 |
1 |
0 |
37 |
|
16 |
Юго-Запад |
13,3 |
10 |
37,00 |
10,00 |
19,00 |
1 |
0 |
43 |
|
17 |
Ленинский |
5,7 |
5 |
32,00 |
8,00 |
17,00 |
1 |
1 |
38 |
|
18 |
Академическая |
7,6 |
10 |
37,00 |
8,00 |
19,00 |
1 |
1 |
51 |
|
19 |
Академическая |
7,6 |
15 |
32,20 |
6,50 |
17,00 |
0 |
1 |
30 |
|
20 |
Коньково |
14,8 |
3 |
33,00 |
8,00 |
19,00 |
1 |
0 |
30 |
|
21 |
Коньково |
14,8 |
5 |
37,50 |
9,60 |
19,80 |
1 |
0 |
36 |
|
22 |
Коньково |
14,8 |
10 |
33,00 |
7,00 |
19,00 |
1 |
0 |
33 |
|
23 |
Университет |
8,7 |
15 |
32,00 |
6,00 |
21,50 |
1 |
0 |
35 |
|
24 |
Пр.Вернадск. |
11,4 |
5 |
29,70 |
6,00 |
16,10 |
0 |
0 |
28 |
|
25 |
Пр.Вернадск. |
11,4 |
15 |
36,00 |
8,60 |
18,00 |
0 |
0 |
40 |
|
26 |
Юго-Запад |
13,3 |
15 |
36,00 |
10,00 |
19,00 |
0 |
0 |
33 |
|
27 |
Ленинский |
5,7 |
2 |
31,60 |
6,00 |
21,60 |
1 |
1 |
35 |
|
28 |
Ленинский |
5,7 |
5 |
52,00 |
12,00 |
34,00 |
1 |
1 |
75 |
|
N |
region |
distc |
distm |
totsq |
kitsq |
livsq |
floor |
cat |
price |
|
29 |
Коньково |
14,8 |
3 |
36,00 |
10,00 |
19,00 |
1 |
0 |
40 |
|
30 |
Коньково |
14,8 |
5 |
33,00 |
8,00 |
18,00 |
1 |
0 |
30 |
|
31 |
Университет |
8,7 |
5 |
32,00 |
5,50 |
20,10 |
1 |
0 |
31 |
|
32 |
Академическая |
7,6 |
15 |
35,00 |
9,80 |
20,00 |
1 |
0 |
37 |
|
33 |
Нов.Черемуш |
10,3 |
15 |
38,00 |
10,00 |
19,50 |
1 |
0 |
40 |
|
34 |
Коньково |
14,8 |
1 |
39,00 |
8,50 |
19,00 |
1 |
0 |
40 |
|
35 |
Фрунзенская |
4 |
5 |
34,00 |
8,00 |
19,00 |
1 |
1 |
58 |
|
36 |
Фрунзенская |
4 |
10 |
38,00 |
6,50 |
18,00 |
0 |
1 |
48 |
|
37 |
пр.Вернадск. |
11,4 |
3 |
35,00 |
10,00 |
20,00 |
1 |
0 |
40 |
|
38 |
Юго-запад |
13,3 |
7 |
36,00 |
9,00 |
19,50 |
1 |
0 |
42 |
|
39 |
Нов.Черемуш. |
10,3 |
7 |
34,00 |
8,00 |
18,00 |
1 |
1 |
51 |
|
40 |
Коньково |
14,8 |
5 |
38,00 |
8,50 |
19,00 |
1 |
0 |
43 |
|
41 |
Коньково |
14,8 |
7 |
33,00 |
6,00 |
19,00 |
1 |
0 |
30 |
|
42 |
Коньково |
14,8 |
10 |
32,00 |
8,00 |
17,00 |
1 |
0 |
40 |
|
43 |
Коньково |
14,8 |
10 |
38,00 |
8,50 |
19,10 |
1 |
0 |
43 |
|
44 |
Академическая |
7,6 |
5 |
43,00 |
8,50 |
25,00 |
0 |
1 |
53 |
|
45 |
Академическая |
7,6 |
10 |
30,00 |
6,00 |
18,30 |
1 |
1 |
28 |
|
46 |
Коньково |
14,8 |
7 |
34,80 |
7,80 |
17,80 |
0 |
0 |
29 |
|
47 |
Коньково |
14,8 |
15 |
35,00 |
10,00 |
19,60 |
1 |
0 |
37 |
|
48 |
Коньково |
14,8 |
3 |
32,80 |
6,50 |
18,50 |
1 |
0 |
30 |
|
49 |
НовЧеремуш. |
10,3 |
10 |
39,00 |
9,00 |
19,00 |
1 |
0 |
45 |
|
50 |
Университет |
8,7 |
15 |
49,00 |
9,00 |
20,50 |
0 |
1 |
52 |
|
51 |
Фрунзенская |
4 |
3 |
32,00 |
6,20 |
19,00 |
1 |
1 |
53 |
|
52 |
Пр.Вернадск. |
11,4 |
10 |
33,00 |
6,50 |
19,00 |
1 |
0 |
32 |
|
53 |
Пр.Вернадск. |
11,4 |
15 |
32,30 |
6,00 |
21,90 |
0 |
0 |
28 |
|
54 |
Юго-Запад |
13,3 |
10 |
30,00 |
7,00 |
19,80 |
1 |
0 |
34 |
|
55 |
Юго-Запад |
13,3 |
10 |
34,00 |
9,00 |
19,00 |
1 |
0 |
42 |
|
56 |
Юго-Запад |
13,3 |
7 |
33,00 |
7,00 |
19,00 |
0 |
0 |
33 |
|
57 |
Академическая |
7,6 |
10 |
30,00 |
6,00 |
18,30 |
1 |
1 |
28 |
|
58 |
Академическая |
7,6 |
15 |
32,00 |
6,00 |
18,00 |
1 |
0 |
30 |
|
59 |
Коньково |
14,8 |
5 |
33,10 |
7,50 |
18,00 |
1 |
0 |
32 |
|
60 |
Коньково |
14,8 |
2 |
38,00 |
7,50 |
19,00 |
1 |
0 |
41 |
|
61 |
Коньково |
14,8 |
7 |
38,00 |
8,60 |
19,00 |
1 |
0 |
43 |
|
62 |
Коньково |
14,8 |
5 |
37,30 |
6,50 |
19,00 |
1 |
0 |
31 |
|
63 |
Ленинский |
5,7 |
8 |
31,40 |
5,60 |
21,00 |
1 |
0 |
33 |
|
64 |
Ленинский |
5,7 |
7 |
52,00 |
10,00 |
34,00 |
1 |
1 |
60 |
|
65 |
Нов.Черемуш |
10,3 |
15 |
30,00 |
6,00 |
17,00 |
1 |
1 |
37 |
|
66 |
Нов.Черемуш |
10,3 |
5 |
36,00 |
11,00 |
20,00 |
1 |
0 |
41 |
|
67 |
Пр.Вернадск. |
11,4 |
5 |
28,00 |
6,70 |
14,40 |
1 |
0 |
35 |
|
68 |
Пр.Вернадск. |
11,4 |
10 |
31,40 |
5,20 |
21,30 |
1 |
0 |
33 |
|
69 |
Юго-Запад |
13,3 |
5 |
32,00 |
8,00 |
17,00 |
1 |
0 |
37 |
Практическое занятие № 2.
«Применение Eviews при построении и анализе линейной однофакторной модели
регрессии»
Пример 2. Имеются следующие
данные по 10 фермерским хозяйствам области:
|
№ пп |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Урожайность зерновых цга |
15 |
12 |
17 |
21 |
25 |
20 |
24 |
14 |
23 |
13 |
|
Внесено удобрений на |
4,0 |
2,5 |
5,0 |
5,8 |
7,5 |
5,7 |
7,0 |
3,0 |
6,0 |
3,5 |
Необходимо:
1. Создать
файл с исходными данными в среде Excel (файл example_02.xls).
2. Осуществить
импорт исходных данных в Eviews.
3. Создать
workfile (рабочий
файл).
4. Найти
значения описательных статистик по каждой переменной и объяснить их.
5. Построить
поле корреляции моделируемого (результативного) и факторного признаков.
Объяснить полученные результаты.
6. Найти
значение линейного коэффициента корреляции и пояснить его смысл.
7. Определить
параметры уравнения парной регрессии и интерпретировать их. Объяснить смысл
полученного уравнения регрессии.
8. Оценить
статистическую значимость коэффициента регрессии и уравнения в целом.
Сделать выводы.
9. Объяснить
полученное значение .
10. Построить эмпирическую и
теоретическую линию регрессии и объяснить их.
11. Построить и
проанализировать график остатков.
12. С вероятностью 0,95
построить доверительный интервал для ожидаемого значения урожайности по точечному значению
.
13. Оформить отчет по
занятию.
Порядок выполнения задания
1. В
Excel исходные данные
должны быть организованы таким образом, чтобы в каждой колонке были представлены
данные по соответствующей переменной (рис. 21). Имена переменных набираются
латинскими буквами. Файл необходимо сохранить в формате Excel 5.0/95 (рис. 22). Введем
обозначения: урожайность зерновых – переменная Productivity (зависимая, Y); внесено удобрений на 1 га посевов – Fertilizers (независимая, X).
Рис. 21.
Рис. 22.
2.
Создаем рабочий файл для импортирования исходных данных из Excel в Eviews, работая с диалоговым окном File/New/Workfile (рис. 23), далее выбираем: Procs/Import/Read Text—Lotus—Excel (рис. 24).
Рис. 23.
Рис. 24.
3.
Далее в открывшемся окне находим и выбираем файл Excel с исходными данными
(файл не должен в этот момент использоваться любыми
программами), осуществляя автоматический импорт исходных данных в workfile (рис. 25). В
следующем открывшемся диалоговом окне нужно указать адрес ячейки, в которой
записаны данные первого по счету наблюдения и число переменных в рассматриваемом примере (рис. 26).. Если
все выполнено правильно, то в открывшемся окне workfile должны появиться имена переменных, а также константа (с)
и остатки (resid)
(рис. 27).
Рис. 25.
Рис. 26.
Рис.
27.
Рис. 28.
Сохраним рабочий файл (рис. 28).
4.
Значения описательных статистик находим следующим образом: в окне workfile выделяем переменные, щелкаем мышкой по выделенной
части и далее выбираем: Open/As Group/ (рис. 29).
Открывается окно с исходными данными. Новую группу можно сохранить, выбрав опцию
Name (рис. 30).
Для просмотра описательных статистик View/Descriptive
Stats/Common
Sample (рис 31). Результат представлен на
рис. 32.
Рис. 29.
Рис. 30.
Рис. 31.
Рис. 32.
5. В
окне workfile (рис. 32)
для построения поля корреляции необходимо выбрать следующие пункты меню: VIEW/GRAPH/SCATTER/SIMPLE SCATTER/ (рис. 33).
Полученный в результате график представляет собой поле корреляции результативного
и факторного признаков (рис. 34).
6. В
окне Workfile
(используя созданную группу из двух переменных) выбрать: /VIEW/CORRELATION/ (рис. 35). Полученная
таблица — корреляционная матрица, в которой отражено значение коэффициента
парной корреляции результативного и факторного признаков (рис. 36).
Рис. 33.
Рис. 34.
Рис. 35.
Рис. 36.
7.
В диалоговом окне описать в общем виде искомое уравнение: LS PRODUCTIVITY C FERTILIZERS
<Enter> (метод
наименьших квадратов (LS)
эндогенная переменная, константа, экзогенная переменная), или выбрать в
строке главного меню EVIEWS: QUICK/ESTIMATE
EQUATION/ PRODUCTIVITY C FERTILIZERS (рис. 37). В открывшемся окне (рис. 38)
должны быть переменные: зависимая переменная, применяемый метод, число
наблюдений, параметры уравнения регрессии, стандартные ошибки, значения t – статистик и соответствующие им
вероятности, значение и ряд других
показателей.
Рис. 37.
Рис. 38.
8. и 9. Результаты
выполнения п.7 позволяют оценить статистическую значимость параметров уравнения
регрессии и объяснить полученное значение R .
Рис. 39.
10.
Для построения эмпирической линии регрессии в окне workfile выделить группу
переменных и выбрать: VIEW/GRAPH/SCATTER/SCATTER WITH REGRESSION/ (рис.
39). В промежуточном окне (рис. 40) необходимо нажать <Ok>. Полученный график (рис. 41)
– эмпирическая линия регрессии. Чтобы построить теоретическую (подогнанную)
линию регрессии, необходимо найти теоретические (вычисленные с помощью уравнения регрессии) значения
результативного признака. Для этого открыть окно с параметрами уравнения
регрессии, далее выбрать Forecast
(рис. 42). Появится окно (рис. 43), в котором к исходным добавилась
новая переменная PRODUCTIVIf (прогнозное, (теоретическое, выровненное) значение переменной PRODUCTIVITY).
Затем, выделив все переменные (включая теоретическое значение
результативного признака), в командной строке записать SCAT FERTILIZERS
PRODUCTIVITY PRODUCTIVIf. Полученный график (рис. 44) –
теоретическая (подогнанная) линия регрессии.
Рис. 40.
Рис. 41.
Рис. 42.
Рис. 43.
Рис. 44.
11.
Данная операция возможна только в том случае, если ей
предшествует построение регрессионного уравнения. В окне Workfile можно дважды щелкнуть на
переменной Resid (рис.
45). Далее, выбрать: VIEW/LINE GRAPH/, или, открыв
окно с параметрами уравнения регрессии, выбрать: VIEW /ACTUAL, FITTED…/ACTUAL, FITTED…TABLE/ (рис. 46). Результат
представлен на рис. 47. Другой вариант вывода (фактические, предсказанные
значения переменных, остатки, график остатков) – рис. 48.
Рис. 45.
Рис. 46.
Рис. 47.
Рис. 48.
12. Для нахождения границ
доверительного интервала в командной строке необходимо указать (рис. 49):
GENR XK = 5 * 1.05
GENR YFK = 4.53 +2.77*XK
GENR h = ((1 + 0.25^2)/1.6957^2) ^0.5
GENR CI = 2.31*(1.07/10^0.5)*h
В результате
искомые границы определяются следующим образом:
YFKCI , т.е. от YFK+CI до YFK—CI (см. рис. 50).
Рис.
49.
Рис.
50.
13. Оформить отчет по
занятию.
Отчет должен
содержать: подробные пояснения расчетов, ссылки на используемые формулы,
результаты работы Eviews
в виде экранных копий, другую, необходимую на Ваш взгляд, информацию.
Практическое занятие № 3.
«Применение Eviews при построении и анализе
линейной однофакторной модели регрессии»
Выполняется
самостоятельно.
Пример 3. Компания American Express Company в течение долгого времени полагала, что
владельцы ее кредитных карточек имеют тенденцию путешествовать более интенсивно, как по делам бизнеса, так и для
развлечений. Как часть объемного исследования, проведенного Нью-Йоркской
компанией рыночных исследований по заказу American Express Company, было осуществлено определение
взаимосвязи между путешествиями и расходами владельцев кредитных карточек.
Исследовательская фирма случайным образом выбрала 25 владельцев карточек из
компьютерного файла American
Express Company и записала суммы их общих расходов за определенный
период времени. Для выбранных владельцев карточек фирма так же подготовила и
разослала по почте вопросы о числе миль, которые провел в путешествиях владелец
карточки за изучаемый период. Данные, полученные из опроса, составляют исходную
информацию анализа (Х – число миль, проведенных в пути; У – расходы путешественников
(усл. ден ед.)[1].
|
№ пп |
Miles |
Costs (У) |
|
1 |
1211 |
1802 |
|
2 |
1345 |
2405 |
|
3 |
1422 |
2005 |
|
4 |
1687 |
2511 |
|
5 |
1849 |
2332 |
|
6 |
2026 |
2305 |
|
7 |
2133 |
3016 |
|
8 |
2253 |
3385 |
|
9 |
2400 |
3090 |
|
10 |
2468 |
3694 |
|
11 |
2699 |
3371 |
|
12 |
2806 |
3998 |
|
13 |
3082 |
3555 |
|
14 |
3209 |
4692 |
|
15 |
3466 |
4244 |
|
16 |
3643 |
5298 |
|
17 |
3852 |
4801 |
|
18 |
4033 |
5147 |
|
19 |
4267 |
5738 |
|
20 |
4498 |
6420 |
|
21 |
4533 |
6059 |
|
22 |
4804 |
6426 |
|
23 |
5090 |
6321 |
|
24 |
5233 |
7026 |
|
25 |
5439 |
6964 |
1. Создать
файл с исходными данными в среде Excel (файл example_03.xls).
2. Осуществить
импорт исходных данных в Eviews.
3. Создать
рабочий файл (workfile).
4. Найти
значения описательных статистик по каждой переменной и объяснить их (рис. 51).
5. Построить
поле корреляции моделируемого (результативного) и факторного признаков (рис.
52). Объяснить полученные результаты.
6. Найти
значение линейного коэффициента корреляции и пояснить его смысл (рис. 53).
7. Определить
параметры уравнения парной регрессии и интерпретировать их. Объяснить смысл
полученного уравнения регрессии (рис. 54).
8. Оценить
статистическую значимость коэффициента регрессии и уравнения в целом.
Сделать выводы.
9. Объяснить
полученное значение .
10. Построить эмпирическую и
теоретическую линию регрессии и объяснить их (рис. 55).
11. Построить и
проанализировать график остатков (рис. 56).
12. С вероятностью 0,95
построить доверительный интервал для оценки ожидаемого значения средних
расходов владельцев карточек, дальность путешествий которых составила 4000 миль
(рис. 57).
13. Оформить отчет по
занятию.
Результаты расчетов:
Рис. 51.
Рис. 52.
Рис. 53.
Рис. 54.
Рис. 55.
Рис. 56.
Рис. 57.
Практическое занятие № 4.
«Применение Eviews при построении и
анализе многофакторной
модели регрессии. Выявление мультиколлинеарности и гетероскедастичности
в модели. Проверка спецификации модели»
Пример 4. Имеются данные о вариации дохода кредитных организаций США за период 25 лет в зависимости от
изменений годовой ставки по сберегательным депозитам и числа кредитных
учреждений[2].
Введем следующие обозначения:
– прибыль кредитных организаций, %;
— чистый доход на
1$ депозита;
– число кредитных
учреждений.
|
Год |
|
|
|
|
1 |
3,92 |
7298 |
0,75 |
|
2 |
3,61 |
6855 |
0,71 |
|
3 |
3,32 |
6636 |
0,66 |
|
4 |
3,07 |
6506 |
0,61 |
|
5 |
3,06 |
6450 |
0,7 |
|
6 |
3,11 |
6402 |
0,72 |
|
7 |
3,21 |
6368 |
0,77 |
|
8 |
3,26 |
6340 |
0,74 |
|
9 |
3,42 |
6349 |
0,9 |
|
10 |
3,42 |
6352 |
0,82 |
|
11 |
3,45 |
6361 |
0,75 |
|
12 |
3,58 |
6369 |
0,77 |
|
13 |
3,66 |
6546 |
0,78 |
|
14 |
3,78 |
6672 |
0,84 |
|
15 |
3,82 |
6890 |
0,79 |
|
16 |
3,97 |
7115 |
0,7 |
|
17 |
4,07 |
7327 |
0,68 |
|
18 |
4,25 |
7546 |
0,72 |
|
19 |
4,41 |
7931 |
0,55 |
|
20 |
4,49 |
8097 |
0,63 |
|
21 |
4,7 |
8468 |
0,56 |
|
22 |
4,58 |
8717 |
0,41 |
|
23 |
4,69 |
8991 |
0,51 |
|
24 |
4,71 |
9179 |
0,47 |
|
25 |
4,78 |
9318 |
0,32 |
1.
Создать файл с исходными данными в среде Excel (файл example_04.xls).
2. Осуществить
импорт исходных данных в Eviews.
3. Создать
workfile.
4.
Найти значения описательных статистик по каждой
переменной и объяснить их (рис. 58).
Рис. 58.
5.
Построить корреляционную матрицу для всех переменных,
включенных в модель (рис. 59).
Рис. 59.
6. Построить
регрессионное уравнение МНК, в котором зависимая переменная – прибыль
кредитных организаций, а независимые – чистый доход на 1$ депозита и число
кредитных учреждений (рис. 60, 61).
Рис. 60.
Рис. 61.
Уравнение примет следующий вид:
.
Подставим полученные оценки из итоговой формы вывода:
.
7. Оценить
статистическую значимость параметров полученного уравнения и всей модели в
целом.
8. Проверить
наличие мультиколлинеарности в модели. Сделать вывод.
Мультиколлинеарность – это коррелированность двух или
нескольких объясняющих переменных в
уравнении регрессии. В результате высококоррелированные объясняющие переменные
действуют в одном направлении и имеют недостаточно независимое колебание, чтобы
дать возможность модели изолировать влияние каждой переменной. Проблема
мультиколлинеарности возникает только в случае множественной регрессии.
Мультиколлинеарность особенно часто имеет место при анализе макроэкономических
данных (например, доходы, производство). Получаемые оценки оказываются нестабильными
как в отношении статистической значимости, так и по величине и знаку (например,
коэффициенты корреляции). Следовательно, они ненадежны. Значения коэффициентов R2 могут быть высокими, но
стандартные ошибки тоже высоки, и отсюда
t- критерии малы, отражая недостаток значимости.
Для проверки появления мультиколлинеарности применяются два метода, доступные во всех
статистических пакетах[3]:
Ø
Вычисление матрицы коэффициентов корреляции для всех
объясняющих переменных. Если коэффициенты корреляции между отдельными
объясняющими переменными очень велики,
то, следовательно, они коллинеарны. Однако, при этом не существует единого
правила, в соответствии с которым есть некоторое пороговое значение коэффициента
корреляции, после которого высокая корреляция может вызвать отрицательный
эффект и повлиять на качество регрессии.
Ø
Для измерения эффекта мультиколлинеарности используется
показатель VIF –
«фактор инфляции вариации»:
ü
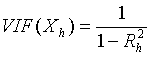
— значение коэффициента множественной корреляции, полученное
для регрессора как зависимой
переменной и остальных переменных . При этом степень мультиколлинеарности, представляемая в
регрессии переменной , когда переменные
включены в регрессию,
есть функция множественной корреляции между и другими переменными
.
ü Если
, то объясняющие переменные, коррелирующие между собой, считаются мультиколлинеарными.
Существует еще ряд способов, позволяющих обнаружить эффект
мультиколлинеарности:
Ø
Стандартная ошибка регрессионных коэффициентов близка к
нулю.
Ø
Мощность коэффициента регрессии отличается от ожидаемого
значения.
Ø
Знаки коэффициентов регрессии противоположны ожидаемым.
Ø
Добавление или удаление наблюдений из модели сильно
изменяют значения оценок.
Ø
Значение F-критерия существенно, а t-критерия – нет.
Для устранения мультиколлинеарности может быть принято
несколько мер:
Ø Увеличивают объем выборки по принципу, что
больше данных означает меньшие дисперсии оценок МНК. Проблема реализации этого
варианта решения состоит в трудности нахождения дополнительных данных.
Ø Исключают те переменные, которые высококоррелированны
с остальными. Проблема здесь заключается в том, что возможно переменные были
включены на теоретической основе, и будет неправомочным их исключение только
лишь для того, чтобы сделать статистические результаты «лучше».
Ø
Объединяют
данные кросс-секций и временных рядов. При этом методе берут коэффициент из,
скажем, кросс-секционной регрессии и заменяют его на коэффициент из
эквивалентных данных временного ряда.
Проделанные манипуляции позволяют предположить, что
мультиколлинеарность может присутствовать (оценки любой регрессии будут страдать от нее в определенной степени,
если только все независимые переменные не окажутся абсолютно
некоррелированными), однако в данном примере это не влияет на результаты оценки
регрессии. Следовательно, выделять «лишние» переменные не стоит, так как это
отражается на содержательном смысле модели.
9. Проверить
спецификацию модели. Объяснить полученные результаты.
Подробно
теоретические вопросы, связанные с проблемами спецификации эконометрических
моделей, были рассмотрены в лекционном курсе.
В нашем случае мы ограничимся тем, что попробуем исключить поочередно
независимые переменные. Первой исключаем переменную CREDIT_INSTITUTI
(рис. 62). Коэффициент при переменной INCOME изменил знак на
противоположный.
Рис. 62.
Рис. 63.
В случае
исключения из первоначальной модели переменной INCOME, знак
регрессионного коэффициента при переменой CREDIT_INSTITUTI остался без
изменения (рис. 63). Представляется разумным разделять эффект двух независимых
переменных на зависимую переменную в модели с совместным их влиянием в
регрессионном уравнении. Данный пример иллюстрирует важность использования
множественной регрессии вместо парной в случае, когда изучаемое явление
существенно детерминирует несколько независимых переменных.
10. Проверить наличие
гетероскедастичности в модели. Объяснить полученные результаты.
Если остатки имеют постоянную дисперсию, они называются гомоскедастичными,
но если они непостоянны, то гетероскедастичными. Гетероскедастичность
приводит к тому, что коэффициенты регрессии больше не представляют собой
лучшие оценки или не являются оценками с минимальной дисперсией, следовательно,
они больше не являются наиболее эффективными коэффициентами.
Воздействие гетероскедастичности на оценку интервала
прогнозирования и проверку гипотезы заключается в том, что хотя коэффициенты не
смещены, дисперсии и, следовательно, стандартные ошибки этих коэффициентов
будут смещены. Если смещение отрицательно, то оценочные стандартные ошибки будут
меньше, чем они должны быть, а критерий проверки будет больше, чем в
реальности. Таким образом, мы можем сделать вывод, что коэффициент значим,
когда он таковым не является. И наоборот, если смещение положительно, то
оценочные ошибки будут больше, чем они должны быть, а критерии проверки – меньше.
Значит, мы можем принять нулевую гипотезу, в то время как она должна быть
отвергнута.
Проверкой на гетероскедастичность служит тест
Голдфелда-Кванта. Он требует, чтобы остатки были разделены на две группы из наблюдений, одна
группа с низкими, а другая – с высокими значениями. Обычно срединная одна
шестая часть наблюдений удаляется после ранжирования в возрастающем порядке,
чтобы улучшить разграничение между двумя группами. Отсюда число остатков в
каждой группе составляет , где
представляет одну
шестую часть наблюдений.
Критерий Голдфелда-Кванта – это отношение суммы квадратов
отклонений (СКО) высоких остатков к СКО низких остатков:
.
Этот критерий имеет распределение с
степенями свободы.
Чтобы решить проблему гетероскедастичности, нужно исследовать
взаимосвязь между значениями ошибки и переменными и трансформировать регрессионную
модель так, чтобы она отражала эту взаимосвязь. Это может быть достигнуто
посредством регрессии значений ошибок по различным формам функций переменной,
которая приводит к гетероскедастичности, например,
,
где — независимая переменная (или какая-либо функция независимой
переменной), которая предположительно является причиной гетероскедастичности, а
отражает степень
взаимосвязи между ошибками и данной переменной, например, или
и т. д.
Следовательно, дисперсия коэффициентов запишется:
.
Отсюда если , мы трансформируем регрессионную модель к виду:
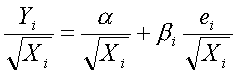
Если , т.е. дисперсия увеличивается в пропорции к квадрату рассматриваемой
переменной , трансформация приобретает вид:
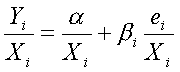
Используя Eviews, можно провести проверку и устранение гетероскедастичности следующим образом:
Ø Запустить стандартную регрессию.
Ø Вычислить остатки.
Ø Запустить регрессию с использованием квадрата
остатков как зависимой переменной и оценить зависимую переменную как независимую
переменную (тест White).
Ø Оценить nR2, где n –
объем выборки, R2 – коэффициент детерминации.
Ø Использовать статистику с одной степенью свободы (в EVIEWS – используется F – статистика) для проверки существенности
отличия nR2 от нуля.
Ø Основным способом устранения
гетероскедастичности является применение взвешенного метода наименьших
квадратов.
Выбираем тест
White (см. рис. 64).
Рис. 64.
Итог формы вывода представлен на рис. 65.
Рис. 65.
Как следует из приведенной
распечатки, вероятность ошибки первого рода равна 51,86%. Следовательно,
нулевую гипотезу (об отсутствии гетероскедастичности) нельзя отклонить.
Для случая, когда
гетероскедастичность присутствует, проблему гетероскедастичности можно решать
следующим образом:
Выбираем в пунктах меню текущего
окна опцию Proc/Specify/Estimate… (рис. 66). Появляется окно
оценки регрессии, где необходимо нажать клавишу Options и в появившимся окне
отметить Heteroskedasticity (рис. 67).
Рис. 66.
Рис. 67.
Появилось новое, переоцененное уравнение (рис. 68).
Полученное уравнение можно вновь проверить по тесту White.
Рис. 68.
11. Оформить отчет.
Практическое занятие № 5.
«Фиктивные переменные»
Иногда необходимо включение в регрессионную модель одной или
более качественных переменных (например, разделение по полу: мужской и женский;
по уровню образования: общее и профессиональное и т.д.). Альтернативно может
понадобиться сделать качественное различие между наблюдениями одних и тех же
данных. Так, если проверяется взаимосвязь между размером компании и месячными
доходами по акциям, может быть желательным включение качественной переменной,
представляющей месяц январь, по причине хорошо известного «январского эффекта»
во временных рядах доходов по ценным бумагам. Данный «январский эффект» — это
феномен, заключающийся в том, что средние доходы по акциям, особенно небольших
компаний, в среднем выше в январе, чем в другие месяцы. Таким образом, если мы рассматриваем январские наблюдения как
качественно отличные от других наблюдений, фиктивная переменная позволит произвести
подобное качественное различие.
Фиктивные переменные бывают двух
типов — сдвига и наклона. Фиктивная переменная сдвига — это переменная,
которая меняет точку пересечения линии регрессии с осью ординат в случае
применения качественной переменной (рис. 69). Фиктивная переменная наклона —
это та переменная, которая изменяет наклон линии регрессии в случае
использования качественной переменной (рис. 70). Оба типа фиктивных переменных
будут иметь значение или
, когда наблюдения данных совпадают с уместной количественной
переменной, но будут иметь нулевое значение при совпадении с наблюдениями, где
эта качественная переменная отсутствует.
|
|
|
|
Рис. 69. |
|
Рис. 70. |
Пример 5. По данным примера 1
(файл example_01.xls.)
дать интерпретацию бинарным, «фиктивным» переменным, принимающим значения 0 или
1: floor – принимает значение 0, если квартира расположена на
первом или последнем этаже, cat –принимает значение 1,
если квартира находится в кирпичном доме.
Построим регрессионное уравнение вида LS PRICE C CAT FLOOR (рис
71). Тем самым мы предполагаем (хотя в действительности это может быть и не
так), что на цену квартиры оказывают влияние только две, указанные выше,
составляющие. В результате получится уравнение следующего вида (рис 72):
.
Рис. 71.
Рис. 72.
СОДЕРЖАНИЕ |
||
|
1. |
Предисловие |
3 |
|
2. |
Практическое занятие № 1. «Знакомство |
4 |
|
3. |
Практическое занятие № 2. «Применение Eviews при |
18 |
|
4. |
Практическое занятие № 3. «Применение Eviews при построении и анализе линейной |
32 |
|
5. |
Практическое занятие № 4. «Применение Eviews при построении и анализе |
36 |
|
6. |
Практическое занятие № 5. «Фиктивные переменные» |
46 |
|
7. |
Практическое занятие № 6. «Однофакторные стохастические модели |
48 |
КОМПЬЮТЕРНЫЙ ПРАКТИКУМ ПО
НАЧАЛЬНОМУ КУРСУ ЭКОНОМЕТРИКИ (РЕАЛИЗАЦИЯ НА EVIEWS)
Практикум
Молчанов Игорь Николаевич
Герасимова Ирина Алексеевна
Ответственная за
выпуск
Начальник РИО РГЭУ
В.Е. Смейле
Редактирование и
корректура авторов
Оригинал-макет
И.Н.Молчанов
Лицензия ЛР N
020276 от 18.02.97
Государственного Комитета Российской Федерации по печати
|
Изд. |
Подписано к печати |
28.02.2001. |
||||||||
|
Бумага офсетная. |
Печать офсетная. |
Формат 60·84/16 |
||||||||
|
Объем 4,0 уч.-изд.л. |
Тираж 100 экз. |
Заказ № |
«C» 65 |
|||||||
344007, Ростов-на-Дону, ул. Большая Садовая,
69, РГЭУ «РИНХ», Издательство
Отпечатано в копировально-множительном
центре.
Ростов-на-Дону, ул. Большая Садовая, 79.
ПБОЮЛ Зайчиков О.Б.
-
Log in
-
Join
Watch in our app
Open in app
Материалы будут выкладываться по мере прохождения материала.
В файле представлена информация о типах временных рядов в Eviews, а также о видах графиков.
Тема 1_Временные ряды_начало.pdf
Adobe Acrobat Document
384.6 KB
Изучение временного ряда в Eviews
Информация о временном ряде, которую можно получить с помощью описательных статистик ряда.
Описательные статистики.pdf
Adobe Acrobat Document
390.4 KB
Диагностика временного ряда в Eviews
Метод, который может быть полезен для проверки ряда на стационарность, условий Гаусса-Маркова для остатков модели, а также идентификации модели.
Коррелограмма временного ряда.pdf
Adobe Acrobat Document
493.6 KB
Примеры задания ARMA-моделей в EViews
Описаны разные виды моделей, а также объяснен переход от AR модели в Eviews к обычной записи модели
ARMA.pdf
Adobe Acrobat Document
949.8 KB
Дано описание теста Чоу на удачу предсказания. Объясняется построение статического и динамического прогнозов и их различие. Приведены показатели качества прогноза.
Прогноз и его качество.pdf
Adobe Acrobat Document
678.5 KB
Примеры
В материале приведено много примеров коррелограмм и моделей, построенных по результатам анализа. Этот файл является дополнительным к материалу о Коррелограмме временного ряда
Диагностика модели временного ряда по ко
Adobe Acrobat Document
1.4 MB
Прогноз и его качество
В материале рассмотрены тесты на стабильность, а также имеется информация по построению прогнозов в программе Eviews, а также сводная таблица показателей, используемых при оценке качества прогноза.
Прогноз и его качество.pdf
Adobe Acrobat Document
682.9 KB
Здесь можно посмотреть образцы введений в самостоятельное исследование.