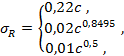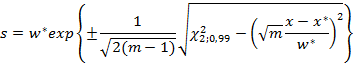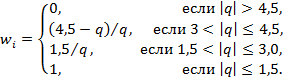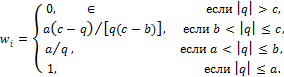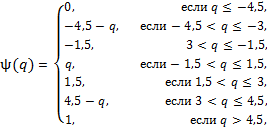ГОСТ Р ИСО 21748-2021
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ ОЦЕНОК ПОВТОРЯЕМОСТИ, ВОСПРОИЗВОДИМОСТИ И ПРАВИЛЬНОСТИ ПРИ ОЦЕНКЕ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ
Statistical methods. Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty evaluation
ОКС 03.120.30;
17.020
Дата введения 2022-01-01
Предисловие
1 ПОДГОТОВЛЕН Закрытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ЗАО «НИЦ КД») на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Применение статистических методов»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 28 сентября 2021 г. N 1018-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 21748:2017* «Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений» (ISO 21748:2017 «Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty evaluation», IDT).
Международный стандарт разработан Техническим комитетом ISO/TC 69.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5)
5 ВЗАМЕН ГОСТ Р ИСО 21748-2012
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ «О стандартизации в Российской Федерации«. Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.ru)
Введение
Знание неопределенности результатов измерений крайне важно для интерпретации результатов. Без количественных оценок неопределенности невозможно принять решение о превышении наблюдаемых отклонений результатов измерений заданной характеристики изменчивости и соответствии объектов испытаний установленным требованиям. При отсутствии информации о неопределенности результатов измерений велика вероятность ошибочного принятия решений, которые могут привести к непредусмотренным расходам в процессе производства, неправильным судебным выводам, неблагоприятным последствиям для здоровья человека или неблагоприятным социальным последствиям.
Лаборатории, аккредитованные в соответствии с ИСО/МЭК 17025, обязаны оценивать неопределенность результатов измерений и испытаний и указывать ее в соответствующем отчете. В Руководстве ИСО/МЭК 98-3 установлен стандартный подход к оценке неопределенности результатов измерений. Приведенный в этом документе подход относится к ситуации, когда известна модель процесса измерений. Широкий диапазон стандартных методов испытаний может быть подвергнут совместному исследованию в соответствии с ИСО 5725-2. Настоящий стандарт устанавливает методы оценки неопределенности результатов измерений и испытаний, основанные на анализе данных, полученных при межлабораторном исследовании, и в полной мере соответствует принципам GUM.
Общий подход, используемый в настоящем стандарте, требует, чтобы:
— оценки повторяемости, воспроизводимости и правильности метода, полученные при межлабораторном исследовании в соответствии с ИСО 5725-2, могли быть получены из опубликованной информации об использовании метода испытаний. Эти оценки позволяют получать внутрилабораторные и межлабораторные составляющие дисперсии, а также оценку неопределенности результатов, связанную с правильностью метода;
— лаборатория подтвердила на основе проверок присущих ей смещения и прецизионности, что выполнение лабораторией метода испытаний соответствует установленным характеристикам метода испытаний. Это подтверждает, что опубликованные данные применимы к результатам, полученным лабораторией;
— все воздействия на результаты измерений, не охваченные межлабораторными исследованиями, были идентифицированы, а дисперсия, связанная с результатами, вызванными этими воздействиями, определена количественно.
Оценку неопределенности определяют путем объединения соответствующих оценок дисперсии в порядке, установленном в Руководстве по выражению неопределенности измерений (GUM). Эта оценка вместе с другими составляющими неопределенности может быть использована при оценке суммарной неопределенности или, при их отсутствии, может быть окончательной, установленной оценкой неопределенности.
Общий принцип применения данных воспроизводимости при оценке неопределенности иногда называют «нисходящим» подходом.
Для контроля полного понимания метода разброс результатов, полученных в межлабораторном исследовании, полезно сравнивать с оценками неопределенности измерений, полученными с использованием процедур GUM. Такие сравнения будут более эффективны при использовании последовательных оценок одного и того же параметра, полученных на основе данных совместных исследований.
1 Область применения
В настоящем стандарте приведено руководство для:
— оценки неопределенности результатов измерений на основе данных, полученных в результате исследований, проводимых в соответствии с ИСО 5725-2;
— сравнения результатов, полученных в межлабораторном исследовании, с оценками неопределенности измерений исследуемого параметра, полученными с использованием принципов распространения неопределенности (см. раздел 14).
В ИСО 5725-3 установлены дополнительные модели для анализа промежуточной прецизионности. Однако, хотя к использованию таких моделей может быть применен тот же общий подход, оценка неопределенности с использованием этих моделей не включена в настоящий стандарт.
Настоящий стандарт применим во всех областях измерений и испытаний, когда должна быть определена неопределенность результатов.
В настоящем стандарте не рассмотрено применение данных повторяемости в отсутствие данных воспроизводимости.
В настоящем стандарте использовано предположение, что признанные значимыми систематические воздействия устранены либо путем численной корректировки результатов, включенной в метод измерений, либо путем анализа и устранения причины воздействий.
В настоящем стандарте приведено общее руководство. Представленный подход к оценке неопределенности применим во многих случаях, однако возможно применение и других методов.
В общем случае информация, приведенная в настоящем стандарте, относительно результатов, методов и процессов измерений относится также к результатам, методам и процессам испытаний.
2 Нормативные ссылки
В настоящем стандарте нормативные ссылки отсутствуют.
3 Термины и определения
В настоящем стандарте применены термины по ИСО 5725-3, а также следующие термины с соответствующими определениями.
Терминологические базы данных ИСО и МЭК доступны по следующим интернет-адресам:
— электронная база МЭК Electropedia по адресу: http://www.electropedia.org/;
— электронная платформа ИСО с функцией онлайн-просмотра терминов по адресу: http://www.iso.org/obp.
3.1 смещение (bias): Разность между математическим ожиданием результатов измерений или испытаний и истинным значением.
Примечание 1 — Смещение представляет собой общую систематическую ошибку
в противоположность случайной ошибке. Могут существовать одна или несколько составляющих систематической ошибки. Большее систематическое отклонение от истинного значения соответствует большему значению смещения.
_________________
Применительно к измерениям под ошибкой следует понимать «погрешность».
Примечание 2 — Смещение средств измерений определяют в виде среднего арифметического ошибок его показаний по соответствующему количеству повторных измерений. Ошибка показания — «показания измерительного прибора минус истинное значение соответствующей величины».
Примечание 3 — На практике вместо истинного значения применяют принятое опорное значение.
[ИСО 3534-2:2006, 3.3.2]
3.2 суммарная стандартная неопределенность (combined standard uncertainty): Стандартная неопределенность результата измерения, полученного из значений ряда других величин, равная положительному квадратному корню взвешенной суммы дисперсий или ковариаций этих величин, весовые коэффициенты при которых определяются зависимостью изменения результата измерения от изменения этих величин.
[Руководство ИСО/МЭК 98-3:2008, 2.3.4]
3.3 коэффициент охвата (coverage factor): Коэффициент, на который умножают суммарную стандартную неопределенность для получения расширенной неопределенности.
Примечание — Коэффициент охвата
обычно принимает значения от 2 до 3.
[Руководство ИСО/МЭК 98-3:2008, 2.3.6]
3.4 расширенная неопределенность (expanded uncertainty): Величина, определяющая интервал вокруг математического ожидания результата измерения, который содержит большую часть распределения значений, которые с достаточным основанием могут быть приписаны измеряемой величине.
Примечание 1 — Долю распределения, охватываемую интервалом, можно рассматривать как вероятность охвата или уровень доверия для данного интервала.
Примечание 2 — Чтобы сопоставить интервалу, рассчитанному через расширенную неопределенность, некоторые значения уровня доверия, необходимо сделать в явном или неявном виде предположение о форме распределения вероятностей результатов измерений и их суммарной стандартной неопределенности (3.2). Уровень доверия, поставленный в соответствие этому интервалу, может соответствовать действительности только в той мере, в которой оправдано сделанное предположение о форме распределения.
Примечание 3 — В рекомендациях [20] расширенная неопределенность названа общей неопределенностью.
[Руководство ИСО/МЭК 98-3:2008, 2.3.5]
3.5 прецизионность (precision): Близость независимых результатов испытаний/измерений, полученных в конкретных регламентированных условиях.
Примечание 1 — Прецизионность зависит от распределения случайных ошибок и не связана ни с истинным, ни с установленным значениями.
Примечание 2 — Меру прецизионности обычно выражают в терминах неточности и вычисляют как стандартное отклонение результатов испытаний/измерений. Меньшая прецизионность соответствует большему стандартному отклонению.
Примечание 3 — Количественные значения меры прецизионности существенно зависят от принятых условий. Условия повторяемости (3.7) и условия воспроизводимости (3.10) являются примерами крайних вариантов принятых условий.
[ИСО 3534-2:2006, 3.3.4]
3.6 повторяемость (repeatability): Прецизионность (3.5) в условиях повторяемости (3.7).
Примечание — Повторяемость может быть выражена количественно в виде характеристики разброса результатов наблюдений.
[ИСО 3534-2:2006, 3.3.5]
3.7 условия повторяемости (repeatability conditions): Условия наблюдений, при которых независимые результаты испытаний/измерений получают одним и тем же методом на идентичных объектах испытаний/измерений, в одной и той же лаборатории, с применением одних и тех же средств испытаний/измерений, одним и тем же оператором, с использованием одного и того же оборудования в течение короткого периода времени.
Примечание — Условия повторяемости предполагают использование одних и тех же:
— процедур измерений или испытаний;
— операторов;
— измерительного и испытательного оборудования, используемого в одних и тех же условиях;
— расположений оборудования;
— повторений в течение короткого периода времени.
[ИСО 3534-2:2006, 3.3.6]
3.8 стандартное отклонение повторяемости (repeatability standard deviation): Стандартное отклонение результатов испытаний/измерений, полученных в условиях повторяемости (3.7).
Примечание 1 — Стандартное отклонение повторяемости является мерой рассеяния результатов испытаний или измерений в условиях повторяемости.
Примечание 2 — Аналогично могут быть введены и использованы в качестве меры рассеяния результатов испытаний или измерений в условиях повторяемости «дисперсия повторяемости» и «коэффициент вариации повторяемости».
[ИСО 3534-2:2006, 3.3.7]
3.9 воспроизводимость (reproducibility): Прецизионность (3.5) в условиях воспроизводимости (3.10).
Примечание 1 — Воспроизводимость может быть выражена количественно в виде характеристик разброса результатов.
Примечание 2 — Под результатами обычно понимают исправленные (скорректированные) результаты.
[ИСО 3534-2:2006, 3.3.10]
3.10 условия воспроизводимости (reproducibility conditions): Условия, при которых независимые результаты испытаний/измерений получены одним и тем же методом, на идентичных объектах испытаний/измерений, в разных лабораториях с применением различных средств испытаний/измерений, разными операторами с использованием различного оборудования.
[ИСО 3534-2:2006, 3.3.11]
3.11 стандартное отклонение воспроизводимости (reproducibility standard deviation): Стандартное отклонение результатов испытаний или измерений, полученных в условиях воспроизводимости (3.10).
Примечание 1 — Стандартное отклонение воспроизводимости является мерой рассеяния результатов испытаний или измерений в условиях воспроизводимости.
Примечание 2 — Аналогично могут быть введены и использованы в качестве меры рассеяния результатов испытаний или измерений в условиях воспроизводимости «дисперсия воспроизводимости» и «коэффициент вариации воспроизводимости».
[ИСО 3534-2:2006, 3.3.12]
3.12 стандартная неопределенность (standard uncertainty): Неопределенность (3.14) результата измерения, выраженная в виде стандартного отклонения.
[Руководство ИСО/МЭК 98-3:2008, 2.3.1].
3.13 правильность (trueness): Близость математического ожидания результатов испытаний или измерений к истинному значению.
Примечание 1 — В качестве меры правильности обычно используют смещение (3.1).
Примечание 2 — Правильность иногда трактуют как «точность среднего». Применение такого термина не рекомендуется.
Примечание 3 — На практике в качестве истинного значения обычно используют принятое опорное значение.
[ИСО 3534-2:2006, 3.3.3]
3.14 неопределенность (измерения) (uncertainty): Параметр, относящийся к результату измерения и характеризующий разброс значений, которые могли быть обоснованно приписаны измеряемой величине.
Примечание 1 — Параметром может быть, например, стандартное отклонение (или величина, пропорциональная стандартному отклонению) или полуширина интервала, которому соответствует заданный уровень доверия.
Примечание 2 — Неопределенность измерения, как правило, включает в себя много составляющих. Некоторые из них могут быть оценены из статистического распределения результатов ряда измерений и описаны выборочными стандартными отклонениями. Другие составляющие, которые также могут быть описаны стандартными отклонениями, оценивают, исходя из основных предположений или иной информации о виде закона распределения
Примечание 3 — Предполагается, что результат измерения является лучшей оценкой измеряемой величины, а все составляющие неопределенности, включая обусловленные систематическими воздействиями (разного рода поправками, используемыми эталоном сравнения), вносят свой вклад в разброс значений измеряемой величины.
[Руководство ИСО/МЭК 98-3:2008, 2.2.3]
3.15 бюджет неопределенности (uncertainty budget): Перечень источников неопределенности (3.14) с соответствующими им стандартными неопределенностями, составленный для определения оценки суммарной стандартной неопределенности (3.2) результата измерений.
Примечание — Перечень обычно включает в себя дополнительную информацию, такую как коэффициент чувствительности (изменчивость результатов в зависимости от изменчивости воздействия на результат), число степеней свободы, соответствующее каждой стандартной неопределенности, и идентификацию методов оценки каждой стандартной неопределенности в терминах оценок типа А или типа В (см. Руководство ИСО/МЭК 98-3).
4 Обозначения
В настоящем стандарте использованы следующие обозначения:
|
|
— |
свободный член эмпирической функции , указывающий отрезок, отсекаемый этой прямой на оси ординат; |
|
|
— |
лабораторная составляющая смещения; |
|
|
— |
угловой коэффициент эмпирической функции ; |
|
|
— |
коэффициент эмпирической функции ; |
|
|
— |
коэффициент чувствительности ; |
|
|
— |
показатель степени эмпирической функции ; |
|
|
— |
случайная погрешность результата измерений в условиях повторяемости; |
|
|
— |
числовой коэффициент, на который умножают суммарную стандартную неопределенность при определении расширенной неопределенности (коэффициент охвата); |
|
|
— |
номер лаборатории; |
|
|
— |
математическое ожидание (среднее) измеряемой величины; |
|
|
— |
количество составляющих, используемых при вычислении суммарной неопределенности; |
|
|
— |
количество объединяемых составляющих при вычислении суммарной неопределенности в дополнение к совместно исследуемым данным; |
|
|
— |
количество повторений, выполняемых лабораторией при исследовании сертифицированного образца сравнения; |
|
|
— |
количество повторений измерения; |
|
|
— |
количество лабораторий; |
|
|
— |
количество объектов испытаний из большей (по количеству) партии; |
|
|
— |
количество назначенных величин в соответствии с принятым соглашением в процессе совместных исследований; |
|
|
— |
коэффициент корреляции и ; |
|
|
— |
стандартное отклонение межгрупповой составляющей дисперсии; |
|
|
— |
оценочное или экспериментальное стандартное отклонение результатов наблюдений, полученных повторными измерениями на образце сравнения, используемом при контроле смещения; |
|
|
— |
стандартное отклонение, обусловленное неоднородностью образца; |
|
|
— |
оценка стандартного отклонения повторяемости с степенями свободы для -й лаборатории при верификации повторяемости; |
|
|
— |
экспериментальное или оцененное внутрилабораторное стандартное отклонение; |
|
|
— |
скорректированная оценка стандартного отклонения типа , когда зависит от переменной отклика; |
|
|
— |
оценка внутрилабораторного стандартного отклонения; оценка стандартного отклонения для ; |
|
|
— |
скорректированная оценка внутрилабораторного стандартного отклонения, когда вклад зависит от переменной отклика; |
|
|
— |
оценка стандартного отклонения воспроизводимости; |
|
|
— |
оценка стандартного отклонения воспроизводимости, скорректированная для лабораторной оценки стандартного отклонения повторяемости; |
|
|
— |
скорректированная оценка стандартного отклонения воспроизводимости, вычисленная по эмпирической модели, когда вклады зависят от переменной отклика; |
|
|
— |
оценка внутрилабораторного стандартного отклонения, полученная на основе повторных измерений или других исследований повторяемости; |
|
|
— |
оценка стандартного отклонения оценки смещения , полученная при межлабораторных исследованиях; |
|
|
— |
лабораторное стандартное отклонение разностей, определяемых при сравнении обычного для лаборатории метода с заданным методом или с величинами, назначенными в соответствии с принятым соглашением; |
|
|
— |
неопределенность, соответствующая , вызванная неопределенностью оценки , по измерениям эталона или образца сравнения с паспортным значением ; |
|
|
— |
неопределенность, соответствующая паспортному значению ; |
|
|
— |
неопределенность, соответствующая входному значению , а также неопределенность, соответствующая , где и отличаются только константой; |
|
|
— |
суммарная стандартная неопределенность, соответствующая ; |
|
|
— |
вклад в суммарную неопределенность , соответствующий значению ; |
|
|
— |
суммарная стандартная неопределенность результата или назначенного значения ; |
|
|
— |
суммарная неопределенность результата ; |
|
|
— |
неопределенность, соответствующая неоднородности выборки; |
|
|
— |
расширенная неопределенность, равная стандартной неопределенности , умноженной на ; |
|
|
— |
расширенная неопределенность ; |
|
|
— |
значение -й входной величины при определении результата; |
|
|
— |
отклонение -й входной величины от номинального значения ; |
|
|
— |
объединенный результат, представляющий собой функцию других результатов ; |
|
|
— |
результат испытаний -го объекта заданным методом при сравнении методов или назначенного значения со значениями, установленными в соответствии с принятым соглашением; |
|
|
— |
результат испытаний -го объекта обычным методом при сравнении методов; |
|
|
— |
лабораторное смещение; |
|
|
— |
оценка смещения -й лаборатории, равная среднему лаборатории минус паспортное значение ; |
|
|
— |
среднее смещение лаборатории при сравнении обычного метода с заданным методом или со значениями, назначенными в соответствии с принятым соглашением; |
|
|
— |
смещение, присущее используемому методу измерений; |
|
|
— |
оценка смещения метода измерений; |
|
|
— |
неизвестное математическое ожидание идеального результата; |
|
|
— |
паспортное значение образца сравнения; |
|
|
— |
стандартное отклонение для проверки квалификации; |
|
|
— |
истинное значение стандартного отклонения результатов наблюдений, полученных на основе повторных измерений на образце сравнения, используемом при контроле смещения; |
|
|
— |
межлабораторное стандартное отклонение; стандартное отклонение типа ; |
|
|
— |
внутрилабораторное стандартное отклонение, стандартное отклонение ; |
|
|
— |
стандартное отклонение в пределах группы; |
|
|
— |
стандартное отклонение, необходимое для адекватной работы (см. Руководство ИСО 33); |
|
|
— |
число эффективных степеней свободы для стандартного отклонения или неопределенности, соответствующей результату ; |
|
|
— |
число степеней свободы, соответствующее -му вкладу в неопределенность; |
|
|
— |
число степеней свободы, соответствующее оценке стандартного отклонения для лаборатории при верификации повторяемости. |
5 Принципы
5.1 Отдельные результаты и свойства процесса измерений
5.1.1 Неопределенность измерений относят к отдельным результатам измерений. Повторяемость, воспроизводимость и правильность относят к выполнению процесса измерений или испытаний. При проведении анализа неопределенности в соответствии с ИСО 5725 (все части) процесс измерений или испытаний должен быть единым методом измерений, используемым всеми лабораториями, принимающими участие в исследовании. Следует заметить, что в настоящем стандарте под методом измерений понимают единственную полностью детализованную процедуру (как определено в Руководстве ИСО/МЭК 99:2007, 2.6). В настоящем стандарте предполагается, что графики показателей функционирования процесса, полученные при исследовании выполнения метода, соответствуют всем отдельным результатам измерений, полученным с использованием данного процесса. Это предположение требует подтверждающих доказательств в виде соответствующих данных контроля и обеспечения качества выполнения процесса измерений (раздел 7).
5.1.2 В некоторых случаях может потребоваться учитывать различия между отдельными объектами испытаний. Однако в этом случае нет необходимости в проведении специальных детальных исследований неопределенности для каждого объекта испытаний при наличии устойчивого процесса измерений с известными характеристиками.
5.2 Применение данных воспроизводимости
Применение настоящего стандарта основано на двух принципах:
— стандартное отклонение воспроизводимости, полученное при совместных исследованиях, является основой для оценки неопределенности измерений (см. А.2.1);
— воздействия, не наблюдаемые в процессе совместных исследований, должны быть незначительными или должны быть учтены. Данный принцип является расширением основной модели, используемой для совместных исследований (см. А.2.3).
5.3 Основные уравнения статистической модели
5.3.1 Статистическая модель, на которой основаны изложенные в настоящем стандарте методы оценки неопределенности, может быть записана в виде уравнения
, (1)
где
— результат измерений, относительно которого предполагается, что он может быть вычислен по соответствующей функции;
— (неизвестное) математическое ожидание идеальных результатов;
— смещение, присущее методу измерений;
— лабораторная составляющая смещения;
— отклонение от номинального значения
;
— коэффициент чувствительности, равный
;
— случайная погрешность в условиях повторяемости.
Предполагается, что
и
подчиняются нормальному распределению с нулевым средним и дисперсиями
и
соответственно. Эти предположения формируют модель, используемую в ИСО 5725-2 для совместного анализа данных.
Так как наблюдаемые стандартные отклонения смещения метода
, лабораторного смещения
и случайных ошибок
полностью описывают разброс в условиях совместного исследования, сумма
учитывает воздействия, которые вызывают отклонения, не включенные в
,
или
, и, таким образом, эта сумма позволяет учесть влияние действий, которые не выполнялись в ходе совместных исследований.
Примерами таких действий являются:
a) подготовка объекта испытаний, выполняемая для каждого испытываемого объекта, выполненная до проведения совместных исследований;
b) формирование подвыборки в случае, когда объекты, подвергнутые совместному исследованию, были гармонизированы до проведения совместного исследования. Предполагается, что
подчиняются нормальному распределению с нулевым математическим ожиданием и дисперсией
.
Пояснения к этой модели приведены в приложении А.
Примечание — Погрешность обычно определяют как разность между установленным значением и результатом измерений. В GUM [16] «погрешность» (значение) отличают от «неопределенности» (разброса значений). При оценке неопределенности, однако, важно характеризовать разброс значений, вызванный случайными воздействиями, и включить его в модель. Для этого в уравнение (1) включают член с нулевым математическим ожиданием, характеризующий «погрешность».
Учитывая модель, описываемую уравнением (1), стандартную неопределенность
можно оценить, применяя уравнение
, (2)
где
— оценка дисперсии
;
— оценка дисперсии
;
— стандартная неопределенность, вызванная неопределенностью оценки
, полученной на основе измерений эталона или образца сравнения с паспортным значением
;
— стандартная неопределенность, соответствующая
.
Учитывая, что стандартное отклонение воспроизводимости
, задаваемое равенством
,
, можно заменить на
, уравнение (2) можно привести к уравнению
. (3)
5.4 Данные повторяемости
Данные повторяемости использованы в настоящем стандарте, прежде всего для проверки прецизионности, которая вместе с другими проверками подтверждает, что конкретная лаборатория может применять данные воспроизводимости и правильности при оценке неопределенности. Данные повторяемости используют также при вычислении составляющей воспроизводимости в неопределенности (см. 7.3 и раздел 11).
6 Оценка неопределенности с использованием оценок повторяемости, воспроизводимости и правильности
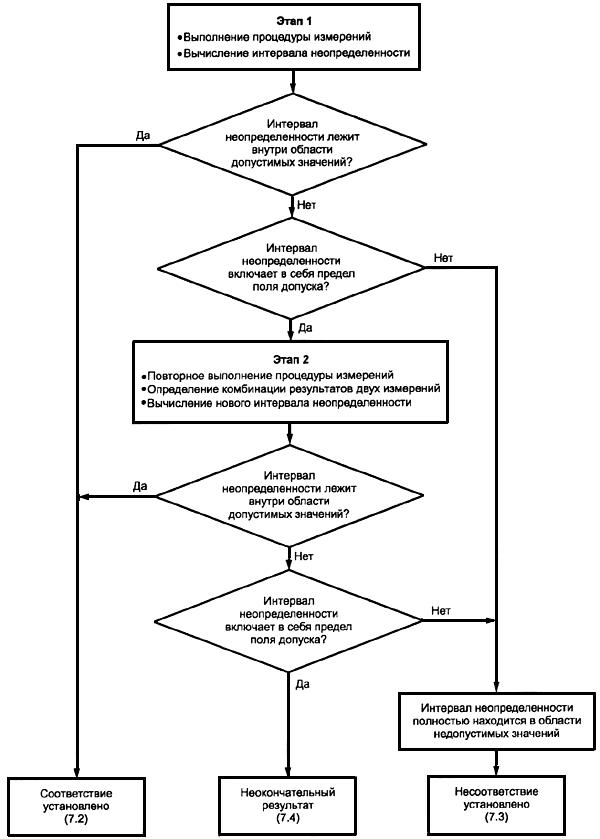
6.1 Процедура оценки неопределенности измерений
Принципы, на которых основан настоящий стандарт (см. 5.1), приводят к следующей процедуре оценки неопределенности измерений:
a) определение оценок повторяемости, воспроизводимости и правильности метода на основе опубликованной информации о методе;
b) проверка непревышения лабораторным смещением, рассчитанным по измерениям, ожидаемого смещения, определенного на основе данных, полученных в соответствии с перечислением a);
c) проверка непревышения прецизионностью, полученной по текущим измерениям, ожидаемой прецизионности, полученной на основе оценок повторяемости и воспроизводимости, определенных в соответствии с перечислением a);
d) идентификация любых воздействий на измерение, которые не были учтены в процессе исследований в соответствии с перечислением a), и определение количественной оценки отклонений, которые могут вызывать эти воздействия, учитывая коэффициент чувствительности и неопределенность каждого из воздействий;
e) объединение оценки воспроизводимости (см. перечисление a)) с неопределенностью, соответствующей правильности (см. перечисления a) и b)) и результатами дополнительных воздействий (см. перечисление d)) для формирования оценки суммарной неопределенности, когда смещение и прецизионность находятся под контролем в соответствии с перечислениями b) и c).
Этапы этой процедуры описаны более подробно в разделах 7-11.
Примечание — В настоящем стандарте предполагается, что в случае, когда смещение является неконтролируемым, выполняют корректирующие действия для приведения процесса в устойчивое состояние
6.2 Различия между фактической прецизионностью и ее ожидаемым значением
Если фактическая прецизионность отличается от ожидаемого значения прецизионности, полученного на основе исследований в соответствии с перечислением 6.1 a), должны быть учтены соответствующие вклады в неопределенность. В 8.5 описаны корректировки оценок воспроизводимости для общего случая, когда прецизионность приближенно пропорциональна уровню переменной отклика.
7 Установление соответствия данных выполнения метода результатам измерений для конкретного процесса измерений
7.1 Общие положения
По результатам совместных исследований определяют значения
,
и в некоторых случаях оценку смещения метода, на основе которых формируют спецификацию рабочих характеристик метода. При применении метода для установленных целей ожидается, что лаборатория продемонстрирует выполнение этих требований. В большинстве случаев для этого проводят исследования, направленные на подтверждение выполнения требований к повторяемости (см. 7.3) и лабораторной составляющей смещения (см. 7.2), а также регулярно проводят проверки правильности выполнения метода (контроль и обеспечение качества исполнения метода (см. 7.4)).
7.2 Демонстрация контролируемости лабораторной составляющей смещения
7.2.1 Общие требования
7.2.1.1 Лаборатория должна продемонстрировать, что соответствующее ей смещение при выполнении метода является контролируемым, т.е. лабораторная составляющая смещения не выходит за пределы смещения, полученного при совместных исследованиях. Далее предполагается, что контроль смещения выполнен на образцах материалов, значения характеристик которых близки к объектам исследования при обычных испытаниях. В тех случаях, когда материалы, используемые для проверки смещения, имеют значения характеристик, значительно отличающиеся от материалов, исследуемых при обычных испытаниях, итоговые вклады смещения в неопределенность должны быть скорректированы в соответствии с 8.4 и 8.5.
7.2.1.2 В общем случае проверка лабораторной составляющей смещения сводится к сравнению результатов, полученных в лаборатории, с некоторыми эталонными значениями и представляет собой оценку
. Уравнение (2) показывает, что неопределенность, связанная с изменениями
, характеризуется
, непосредственно входящей в
. Однако проверке смещения соответствует своя неопределенность, поэтому неопределенность сравнения в общем случае увеличивает неопределенность результатов, которые могут быть получены при применении метода. По этой причине важно гарантировать, что неопределенность, связанная с проверкой смещения, мала по сравнению с
(в идеале меньше, чем
) и, следовательно, соответствующее увеличение неопределенности является незначительным. В этом случае, если свидетельства чрезмерной лабораторной составляющей смещения не обнаружены, уравнение (3) применяют без изменений. Если неопределенность, соответствующая проверке смещения, является большой, целесообразно увеличивать неопределенность, оцененную на основе уравнения (3), например, путем включения в суммарную неопределенность дополнительных членов (см. 3.15).
В тех случаях, когда из совместных исследований правильности известно, что смещение метода не является пренебрежимо малым, известное смещение метода следует учитывать при оценке лабораторного смещения, например, путем корректировки результатов на известное смещение метода.
7.2.2 Методы демонстрации контролируемости лабораторной составляющей смещения
7.2.2.1 Общие положения
Контролируемость смещения может быть продемонстрирована одним из методов, приведенных в 7.2.2.2-7.2.2.4. При всех проверках смещения, приведенных в настоящем стандарте, последовательно используют одни и те же общие критерии. Допускается применение более строгих методов проверки.
7.2.2.2 Исследование образца сравнения или эталона
Лаборатория
должна выполнить
повторных измерений на эталоне сравнения в условиях повторяемости, чтобы получить оценку смещения на нем
(равную среднему лаборатории
минус паспортное значение
). При этом
следует выбирать так, чтобы неопределенность удовлетворяла неравенству
. Следует заметить, что эталон сравнения в общем случае не является тем же эталоном, который использовали при оценке правильности метода. Кроме того,
, как правило, не равно
. Следуя Руководству ИСО 33 (с соответствующим изменением обозначений), процесс измерений выполняется адекватно, если
. (4)
Для оценки
из неравенства (4) используют оценку
, заданную уравнением (5)
:
_________________
См. 4.3 ГОСТ Р ИСО 5725-2-2002 и 4.2.3 ГОСТ Р ИСО 5725-6-2002.
, (5)
где
— количество повторений лаборатории
;
— внутрилабораторное стандартное отклонение, полученное на основе
повторений или других исследований повторяемости;
— межлабораторное стандартное отклонение, полученное при совместных исследованиях.
Выполнение неравенства (4) является подтверждением того, что лабораторная составляющая смещения
находится в интервале значений, установленном при совместных исследованиях. Следует обратить внимание на то, что стандартный образец или эталон сравнения используют здесь для независимой проверки или в качестве контрольного материала, а не для калибровки.
Примечание 1 — Лаборатория может применять более строгий критерий, чем неравенство (4), используя коэффициент охвата менее 2 или выполняя более чувствительный метод на выявление смещения.
Примечание 2 — Эти процедуры предполагают, что неопределенность, соответствующая эталонному значению, мала по сравнению с
.
7.2.2.3 Сравнение с заданным методом испытаний, обладающим известной неопределенностью
Лаборатории
необходимо провести испытания
объектов испытаний, применяя как заданный метод испытаний, так и метод испытаний, используемый лабораторией, получив, таким образом,
пар
(
— результат применения заданного метода к
-му объекту, а
— значение, полученное применением обычного для лаборатории метода испытаний для
-го объекта). Затем лаборатория должна вычислить соответствующее среднее смещение
, используя уравнение (6) и стандартное отклонение разностей
(см. (7)):
, (6)
, (7)
где
.
На практике значение
должно быть выбрано так, чтобы выполнялось неравенство
. По аналогии с неравенством (4) и уравнением (5) процесс измерений удовлетворяет требованиям, если
, где
. В этом случае (3) используют без изменений.
Примечание 1 — Лаборатория может выбирать более строгий критерий, чем неравенство (4), используя коэффициент охвата менее 2 или применяя более чувствительный метод выявления смещения.
Примечание 2 — Эти процедуры предполагают, что стандартная неопределенность, соответствующая эталонному методу, мала по сравнению с
и отклонения
принадлежат к совокупности с постоянной дисперсией.
7.2.2.4 Использование метода при сравнении с другими лабораториями
Если
-я лаборатория участвует в дополнительных совместных исследованиях (например, при проверке квалификации в соответствии с ИСО/МЭК 17043), для которых она может оценивать смещение, данные этих исследований можно использовать для контроля смещения. Применяют два возможных варианта.
a) При выполнении испытаний используют эталон или стандартный образец с независимо приписанным значением и неопределенностью. Затем применяют процедуру 7.22.2 без изменений.
b) Проводят последовательную проверку соответствия
(
1) заданных значений
,
, …,
. Лаборатория по результатам
,
, …,
должна рассчитать среднее смещение
в соответствии с уравнением (8) и стандартное отклонение
(см. уравнение (9)):
, (8)
, (9)
где
.
Процесс измерений удовлетворяет требованиям, если
, где
. В этом случае (3) используют без изменений.
Примечание 1 — Эта процедура предполагает, что заданные значения основаны на количестве результатов, превышающем
, и обладают незначительной неопределенностью, а отклонения
принадлежат совокупности с постоянной дисперсией.
В некоторых программах проверки квалификации все значения
преобразуют в
-значения
, вычитая из
приписанное значение
и деля разность на стандартное отклонение
(см. ИСО/МЭК 17043)
. В этом случае для проверки квалификации стандартное отклонение меньше или равное
для метода и среднее
-значений в пределах
для
приписанных значений обеспечивают достаточное свидетельство контролируемости смещения. Это удобно для вычислений и обеспечивает меньшую чувствительность к предположению о постоянстве дисперсии (см. примечание 1). Однако это обычно более строгий критерий, чем описанный в 7.2.2.4. Лаборатория может использовать более строгий критерий (см. примечание 2), но вычисления, установленные в 7.2.2.4, необходимы для проверки эквивалентности.
_________________
См. также ГОСТ Р ИСО 13528-2011.
Примечание 2 — Лаборатория может использовать более строгий критерий, чем описанный в 7.2.2.4.
7.2.3 Выявление существенной лабораторной составляющей смещения
Как отмечено в разделе 1, настоящий стандарт применим только в тех случаях, когда лабораторная составляющая смещения находится под контролем. Если обнаружено чрезмерное смещение, предполагается, что должны быть предприняты необходимые действия для приведения смещения в границы требуемого диапазона до продолжения выполнения измерений. Такие действия обычно требуют проведения исследований и устранения причины, вызывающей смещение.
7.3 Верификация повторяемости
7.3.1 Испытательная лаборатория
должна продемонстрировать, что ее повторяемость согласуется со стандартным отклонением повторяемости, полученным при совместных исследованиях. Для демонстрации этого выполняют повторные испытания одного или нескольких соответствующих испытуемых образцов и получают (объединяя результаты при необходимости) стандартное отклонение повторяемости
с
степенями свободы. Значение
необходимо сравнить со стандартным отклонением повторяемости
, полученным при совместных исследованиях, используя F-критерий с уровнем доверия 95%. На практике следует выполнить такое количество повторений, чтобы получить
15.
7.3.2 Если
значительно больше
, лаборатория должна или идентифицировать и устранить соответствующие причины, либо использовать
вместо
во всех оценках неопределенности, рассчитанных с использованием настоящего стандарта. Следует обратить внимание, что это вызывает увеличение оценки стандартного отклонения повторяемости
, так как
должно быть заменено на
(
является скорректированной оценкой стандартного отклонения воспроизводимости). Если
значительно меньше
, лаборатория может также использовать
вместо
, получая меньшую оценку неопределенности.
Во всех исследованиях прецизионности важно подтверждать, что данные свободны от неизвестных смещений, и проверять постоянство стандартного отклонения
для различных объектов испытаний. Если стандартное отклонение
не постоянно, может быть полезно оценивать прецизионность отдельно для каждого класса объектов или построить общую модель (см. 8.5) этой зависимости.
Примечание — Если требуется сравнение с заданным значением прецизионности, в Руководстве ИСО 33 более детально описан соответствующий тест, основанный на
, в котором
соответствует требуемому значению прецизионности.
7.4 Продолжение верификации выполнения метода
Кроме предварительной оценки смещения и прецизионности лаборатория должна принимать необходимые меры для обеспечения статистической управляемости процедуры измерений. Для этого проводят:
— соответствующий контроль качества выполнения метода измерений, включая регулярные проверки смещения и прецизионности. Для этих проверок в качестве объектов испытаний могут быть использованы любые уместные стабильные однородные объекты или материалы. Настоятельно рекомендуется использование контрольных карт (см. ИСО 5725-5 и ИСО 5725-6);
— мероприятия по обеспечению качества выполнения метода измерений, включая привлечение обученного и квалифицированного персонала, предусмотренные системой менеджмента качества.
При использовании контрольных карт стандартное отклонение наблюдений за рассматриваемый период времени должно быть меньше
, вычисленного в соответствии с 7.3.2, если прецизионность и смещение находятся под контролем.
8 Учет особенностей объекта испытаний
8.1 Общие положения
В совместных исследованиях или при оценке промежуточных показателей прецизионности в соответствии с ИСО 5725-2 и ИСО 5725-3 обычно проводят измерения на ограниченном количестве типов однородных материалов или образцов. Это является обычной практикой для разделения подготовленных для измерений материалов. Однако объекты испытаний могут иметь широкий диапазон возможных изменений, что может требовать дополнительной их обработки до испытаний. Например, образцы для экологических испытаний часто поставляют высушенными и гомогенизированными. Обычные образцы, как правило, являются влажными, неоднородными и грубо разделенными. Соответственно необходимо исследовать образцы и, если необходимо, учитывать различия в их состоянии.
8.2 Отбор выборки
8.2.1 Процесс отбора выборки
Совместные исследования редко включают этап отбора выборки (образцов). Если метод, используемый внутри лаборатории, включает формирование подвыборки, а также при регулярном применении процедуры оценки свойств большого объема материала по выборке малого объема, влияние процедуры отбора выборки необходимо исследовать. При этом полезно использовать документацию по отбору выборки, например ИСО 11648-1 или другие стандарты.
8.2.2 Неоднородность (негомогенность)
Неоднородность обычно исследуют экспериментально с применением дисперсионного анализа (ANOVA)
к нескольким объектам испытаний, для которых составляющая дисперсии
, описывающая разброс между объектами, характеризует неоднородность. Если после всех установленных действий по гомогенизации испытуемые материалы признаны существенно неоднородными, эту оценку дисперсии следует преобразовать непосредственно в стандартную неопределенность (т.е.
). В некоторых обстоятельствах, особенно когда стандартное отклонение негомогенности найдено по выборке из
объектов, отобранных из партии, а средний результат предполагается применять к другим объектам партии, вклад неопределенности оценивают на основе предикционного интервала (т.е.
). Влияние негомогенности можно также оценить теоретически, используя знание процесса отбора выборки и предположения о распределении, соответствующем выборке.
_________________
Принятая в международной практике аббревиатура для обозначения дисперсионного анализа (Analysis of Variance).
8.3 Подготовка и предварительная обработка
В большинстве исследований образцы являются гомогенными и дополнительно могут быть подвергнуты стабилизации до распределения по лабораториям. Могут потребоваться исследования, позволяющие учитывать воздействия специфических процедур предварительной обработки внутри лаборатории. Как правило, такие исследования устанавливают воздействие этой процедуры на результаты измерений на исследуемых материалах с приблизительно или точно установленными свойствами. Результатом воздействия может быть изменение разброса или появление систематических воздействий. Существенные изменения разброса следует устранять прибавлением соответствующей составляющей к бюджету неопределенности (предполагая, что воздействия увеличивают разброс). Если выявлены существенные систематические воздействия, наиболее удобно устанавливать соответствующий верхний предел. Следуя рекомендациям GUM, этот предел можно рассматривать как границу прямоугольного или другого ограниченного симметричного распределения, а оценку стандартной неопределенности можно задавать в виде половины длины области изменений функции распределения, деленной на соответствующий коэффициент.
8.4 Изменение типа объекта испытаний
При необходимости следует исследовать неопределенность, являющуюся результатом изменения типа или состава объекта испытаний по сравнению с используемыми в совместных исследованиях. Как правило, подобные воздействия должны быть предсказаны на основе установленных воздействий, объемных свойств материала (которые дают оценку неопределенности, полученную в соответствии с GUM) или исследованы введением систематических или случайных изменений типа или состава объекта испытаний (см. приложение В).
8.5 Изменение неопределенности в зависимости от уровня переменной отклика
8.5.1 Корректировка
Как правило, некоторые или большая часть составляющих неопределенности измерений зависят от измеренного значения. В ИСО 5725-2 рассмотрено три простых случая, когда стандартное отклонение воспроизводимости для положительной величины
может быть приближенно описано одной из следующих моделей:
; (10)
; (11)
, (12)
где
— скорректированная оценка стандартного отклонения воспроизводимости, рассчитанная по приближенной модели;
,
,
и
— эмпирические коэффициенты, полученные на основе пяти или большего количества различных объектов испытаний с различными средними откликов
(
,
и
являются положительными).
При использовании формул (10)-(12) оценка неопределенности должна быть основана на оценке воспроизводимости, рассчитанной с использованием соответствующей модели.
В условиях 7.3 оценка
должна учитывать измененный вклад члена
, отражающего вклад повторимости. В большинстве случаев имеет место простое пропорциональное изменение
:
, (13)
где
имеет то же самое значение, как и в 7.3.
8.5.2 Изменение других вкладов в неопределенность
В общем случае если любой вклад в неопределенность изменяется в соответствии с измеренным значением переменной отклика предсказуемым способом, соответствующая стандартная неопределенность
должна быть откорректирована.
Примечание — Если вклады в неопределенность прямо пропорциональны
, часто бывает удобно выражать все существенные воздействия в терминах мультипликативных воздействий на
, а всю неопределенность — в форме относительных стандартных отклонений.
9 Дополнительные факторы
В разделе 8 рассмотрены основные факторы, различающиеся в совместных исследованиях и обычных испытаниях. Возможно, что в специфических случаях могут проявляться другие воздействия. Это может быть вызвано тем, что контролируемые переменные случайно или преднамеренно рассматривались как постоянные в процессе совместного исследования, или тем, что при совместных исследованиях не был выполнен полный диапазон условий, достижимых в обычной практике.
Воздействия факторов, которые считаются постоянными или которые недостаточно изменяются при совместных исследованиях, следует оценивать отдельно либо в процессе экспериментального изменения, либо в соответствии с прогнозом на основе теоретических моделей. В тех случаях, когда воздействия являются существенными, неопределенность, связанную с соответствующими факторами, необходимо оценить, зарегистрировать и объединить с другими вкладами обычным способом (т.е. суммировать в соответствии с уравнением (3)).
10 Общее выражение для суммарной стандартной неопределенности
При оценке суммарной стандартной неопределенности
, соответствующей результату
и необходимости использовать скорректированную оценку
вместо
, для учета факторов, рассматриваемых в разделе 8, уравнение (3) принимает вид
. (14)
Значение
подсчитывают в соответствии с уравнением (15) (см. также (А.8)):
, (15)
где
— количество лабораторий;
— количество повторений в каждой лаборатории;
— неопределенность, соответствующая паспортному значению
, используемому для оценки смещения в лабораторных исследованиях.
Переменная
не использована в уравнении (14), потому что неопределенность
, соответствующая
, уже включена в
. Индекс
охватывает воздействия, идентифицированные в разделах 7 и 8 (индексы изменяются от 1 до
). Очевидно, что если воздействия и соответствующие им неопределенности малы по сравнению с
, то ими можно пренебречь для большинства практических целей. Например, неопределенность менее
ведет к изменению менее чем на
оценки полной неопределенности.
Примечание 1 — Если все составляющие неопределенности выражены в форме относительных стандартных отклонений или процентов, как предложено в примечании к 8.5.2, формулы (14) и (15) могут быть применены непосредственно к относительным значениям, и полученная неопределенность
будет иметь форму относительного стандартного отклонения или процента.
Примечание 2 — Если смещение метода измерений рассматривают как пренебрежимо малое и при выполнении измерений на испытуемом образце используют ту же процедуру, что и при межлабораторном совместном исследовании, суммарная стандартная неопределенность принимает вид
.
11 Бюджет неопределенности, основанный на данных совместных исследований
Настоящий стандарт использует только одну, приведенную в уравнении (3), модель для описания результатов измерений или испытаний. Информация, подтверждающая справедливость модели, может быть получена из различных источников, но если неопределенность, соответствующая испытаниям, остается незначительной, используют уравнение (3). Однако существует несколько различных ситуаций, для которых уравнение (3) принимает несколько иной вид, например, в случае, когда параметры воспроизводимости или повторяемости зависят от переменной отклика. В таблице 1 приведен бюджет неопределенности в случае, когда неопределенность не зависит от переменной отклика в исследуемом диапазоне, в таблице 2 приведен бюджет неопределенности в случае, когда неопределенность зависит от переменной отклика.
Таблица 1 — Составляющие неопределенности, не зависящие от переменной отклика
|
Источник воздействия |
Стандартная неопределенность , соответствующая |
Примечание |
|
|
|
Используют только в случае, если при совместных исследованиях установлена поправка на смещение и неопределенность является значимой |
|
|
|
См. таблицу 2 |
|
|
|
Если среднее, полученное по полных повторений метода , применяют к объекту испытаний, неопределенность, соответствующая , принимает вид: |
|
|
|
См. раздел 8 и приложение В |
|
Стандартную неопределенность выражают в тех же единицах, что и . При необходимости она может быть выражена в относительных величинах (см. примечание к разделу 10). Метод может устанавливать количество повторений всего метода, включая все предусмотренные стадии метода. |
Таблица 2 — Составляющие неопределенности, зависящие от переменной отклика
|
Источник воздей- ствия |
Стандартная неопреде- ленность , соответст- вующая |
Примечание |
|
|
|
Используют только в случае, когда выявленное при совместном исследовании смещение устранено, а неопределенность является существенной. (Производную используют, чтобы охватить случаи, когда устранение смещения не сводится к простому сложению или вычитанию) |
|
|
|
и — коэффициенты предполагаемой линейной зависимости между и средним (математическим ожиданием) отклика , аналогично (11). Данная форма применима только в случае, когда установлена зависимость от . В противном случае используют комбинированную оценку, соответствующую и из таблицы 1 |
|
|
|
и — коэффициенты предполагаемой линейной зависимости между и средним (математическим ожиданием) отклика , аналогично (9). Если среднее, полученное по полных повторений метода, применяют к объекту испытаний, неопределенность, соответствующая , принимает вид: . Эта форма применима только в случае, когда установлена зависимость от . В противном случае используют объединенную оценку, соответствующую и из таблицы 1 |
|
, |
|
и — коэффициенты линейных соотношений между и средним переменной отклика , как определено в (10), (11) и (12). Эту объединенную оценку следует использовать вместо отдельных оценок и (см. таблицу 1), когда отдельные зависимости и от не установлены |
|
|
|
См. раздел 8 и приложение В |
|
Стандартную неопределенность выражают в тех же единицах, что и . При необходимости она может быть выражена в относительных величинах (см. примечание к разделу 10). Предполагается простая линейная зависимость, соответствующая уравнению (11). Метод может включать повторений всего метода, включая все предусмотренные повторения. |
12 Оценка неопределенности суммарного результата
12.1 Суммарный результат
формируют из совокупности результатов
различных испытаний, каждый из которых охарактеризован совместными исследованиями. Например, анализ состава мяса обычно включает определение содержания в мясе белка (рассчитанного путем определения содержания в мясе азота), жира и воды. При этом содержание каждой составляющей определяют соответствующим стандартным методом.
12.2 Стандартная неопределенность
для каждого результата
может быть получена на основе принципов, установленных в настоящем стандарте или непосредственно при использовании уравнения (А.1) или (А.2) соответственно. Если величины
независимы, суммарную стандартную неопределенность
для результата
вычисляют по формуле
. (16)
Если
не являются независимыми, должны быть сделаны предположения относительно корреляции в соответствии с GUM (также использующим уравнение (А.2)).
13 Представление информации о неопределенности
13.1 Общие положения
Неопределенность может быть представлена в виде суммарной стандартной неопределенности
или расширенной неопределенности
(
— коэффициент охвата) (см. 13.2 и GUM). В некоторых случаях удобно представить неопределенность в относительных величинах в виде коэффициента вариации или расширенной неопределенности в процентах от зарегистрированных значений результатов.
13.2 Выбор коэффициента охвата
13.2.1 Общие положения
При оценке расширенной неопределенности выполняют следующие действия для выбора коэффициента охвата
.
13.2.2 Уровень доверия
Для практических целей должно быть указано значение расширенной неопределенности, соответствующее уровню доверия 95%, Однако выбор уровня доверия зависит от диапазона факторов, таких как критичность и последствия применения неправильных результатов. Эти факторы вместе со всеми рекомендациями или юридическими требованиями, касающимися применения, должны быть рассмотрены при выборе
.
13.2.3 Число степеней свободы, соответствующих оценке
13.2.3.1 Для большинства практических целей, когда требуется уровень доверия 95% и число степеней свободы в доминирующих составляющих неопределенности превышает 10 (>10), выбор
2 обеспечивает достаточно надежный охват вероятного диапазона значений. Однако есть обстоятельства, в которых это приводит к существенно заниженной оценке, особенно когда один или более значимых членов уравнения (14) имеют число степеней свободы менее 7.
13.2.3.2 Если один такой член
с
степенями свободы доминирует (признаком является выполнение неравенства
), обычно достаточно выбрать
в качестве эффективного числа степеней свободы
, соответствующего
.
13.2.3.3 Если несколько значимых членов имеют приблизительно равную величину и число степени свободы, удовлетворяющее условию
10, для получения эффективных значений числа степеней свободы
следует применять уравнение Велча-Саттервейта (см. уравнение (17)):
. (17)
Значение
в этом случае выбирают на основе
, используя значение квантиля двустороннего распределения Стьюдента
для требуемого уровня доверия и
степеней свободы. Это наиболее безопасно при округлении нецелых значений
до ближайшего меньшего целого числа.
Примечание — Во многих областях измерений и испытаний для нормального распределения частота статистических выбросов является достаточно высокой, поэтому применение высоких уровней доверия (>95%) без хорошего знания распределения не рекомендуется.
14 Сравнение данных выполнения метода и неопределенности
14.1 Основные предположения
Оценка неопределенности измерений в соответствии с настоящим стандартом обеспечивает суммарную стандартную неопределенность, которая, хотя и основывается прежде всего на оценках воспроизводимости или промежуточной прецизионности, отдает должное факторам, которые не изменяются в процессе исследований, в которых эти оценки прецизионности получены. В идеале итоговая суммарная стандартная неопределенность
должна быть идентична неопределенности, полученной на основе детальной математической модели процесса измерений. Сравнение этих двух оценок, если это возможно, обеспечивает полезную проверку качества оценки. Рекомендованная процедура описана в 14.2.
Процедура основана на двух важных предположениях:
— во-первых, оценку суммарной стандартной неопределенности
с
степенями свободы обычно определяют в предположении о нормальном распределении наблюдений (это означает, что
подчиняется
распределению с
степенями свободы). Это предположение позволяет использовать F-критерий. Однако, поскольку суммарная стандартная неопределенность может включать неопределенность, связанную с величинами, описываемыми распределениями различной формы с различными дисперсиями, результаты испытаний необходимо рассматривать как индикатор, а уровень доверия следует выбирать с необходимой осторожностью;
— во-вторых, обычно предполагают, что две сопоставляемые оценки суммарной стандартной неопределенности полностью независимы. Это также маловероятно на практике, так как некоторые факторы могут быть общими для обеих оценок. Более тонкие воздействия являются предметом исследований для выявления влияния составляющей неопределенности, соответствующей выполнению работ в разных лабораториях. Предполагается, что приняты необходимые меры предосторожности, чтобы избежать этого воздействия. Если значимые факторы являются общими для обеих оценок суммарной стандартной неопределенности, очевидно, что сопоставление оценок будет значительно чаще выявлять их аналогию. В этом случае, если последовательные испытания не позволяют выявлять существенных различий, результаты не следует трактовать как свидетельство адекватности модели измерений.
14.2 Процедура сравнения
Для сравнения двух оценок
и
, (
) с эффективными числами степеней свободы
и
, соответственно, и уровнем доверия
(например, для уровня доверия 95%
0,05) необходимо выполнить следующие действия:
a) Вычислить
.
b) Найти по таблицам или получить с помощью программного обеспечения одностороннее верхнее критическое значение
. Если даны верхнее и нижнее значения, выбирают верхнее значение, которое всегда больше 1;
c) Если
, то
следует считать значительно больше
.
14.3 Причины различий
Существует много причин для существенного различия оценок суммарной стандартной неопределенности. Они включают:
— наличие различий в работе лабораторий;
— использование модели, не учитывающей влияния всех существенных воздействий на измерения;
— неверное определение оценки значимости вклада в суммарную стандартную неопределенность.
Приложение А
(справочное)
Подходы к оценке неопределенности
А.1 Подход GUM
В руководстве по выражению неопределенности измерений (GUM) установлена методология оценки неопределенности измерений результата
в соответствии с моделью процесса измерений. Методология GUM основана на рекомендациях Международной палаты мер и весов (BIPM) [20], в соответствии с которыми составляющие неопределенности оценивают либо на основе статистического анализа серии наблюдений (оценка типа А), либо другими способами (оценка типа В), например используя данные публикаций о неопределенности стандартных образцов, эталонов, измерений или, при необходимости, о мнениях специалистов. Отдельные составляющие выражают в виде стандартных отклонений и, при необходимости, затем объединяют.
Выполнение рекомендаций BIPM в GUM начинают с построения модели измерений в виде функции
, связывающей результат измерений
с входными величинами
. Тогда в случае независимых входных величин GUM дает неопределенность
в виде
, (А.1)
где
— коэффициент чувствительности
(частная производная
по
);
и
— стандартные неопределенности (неопределенности измерений в виде стандартных отклонений)
и
соответственно.
Если входные величины не являются независимыми, выражение для неопределенности является более сложным:
, (А.2)
где
— ковариация между
и
;
и
— коэффициенты чувствительности, соответствующие (А.1).
На практике часто ковариацию выражают через коэффициент корреляции
, (А.3)
где
.
В случаях, учитывающих нелинейность модели измерений, в (А.1) включают члены более высокого порядка. Эта ситуация более подробно описана в GUM.
После вычисления суммарной стандартной неопределенности с использованием (А.1)-(А.3) расширенную неопределенность определяют, умножая
на коэффициент охвата
, который выбирают на основе числа степеней свободы для
. Более подробно это описано в разделе 13.
В подходе GUM существует неявное предположение, что входные данные измерены или назначены. Если существуют воздействия (например, воздействие оператора), которые могут быть не определены через измеримые величины, удобно сформировать дополнительную стандартную неопределенность
, которая учитывает такие воздействия, или ввести дополнительные переменные в
.
Из-за ориентации на входные величины этот подход иногда называют восходящим подходом оценки неопределенности.
Физическая интерпретация
не является однозначной. Поскольку при оценке неопределенности могут быть использованы экспертные оценки, то
можно рассматривать как функцию, характеризующую «степень доверия». Можно получить более четкую физическую интерпретацию, заметив, что вычисления, выполненные для определения
, приводят к значению стандартного отклонения, которое было бы получено, если бы все входные переменные изменялись случайным образом в соответствии с принятыми для них распределениями.
А.2 Принцип совместных исследований
А.2.1 Основная модель
Планирование эксперимента при совместных исследованиях, их организация и статистическая обработка подробно описаны в ИСО 5725-1-ИСО 5725-6. Самая простая модель, лежащая в основе статистической обработки данных совместных исследований, задана уравнением (обозначения по ИСО 5725)
, (А.4)
где
— математическое ожидание
;
— лабораторная составляющая смещения в условиях повторяемости и предположения о нормальном распределении со средним 0 и стандартным отклонением
;
— случайная погрешность в условиях повторяемости и предположения о нормальном распределении со средним 0 и стандартным отклонением
.
Кроме того, предполагается, что
и
некоррелированы.
Применение (А.1) к простой модели дает (А.5) для единственного результата
:
. (А.5)
Поскольку
и
являются дисперсиями, соответствующими
и
, и их оценивают с помощью дисперсии между лабораториями
и дисперсии повторяемости
, полученными в процессе межлабораторных исследований, так, что
и
, возможно получить выражение (А.6) для суммарной стандартной неопределенности результата
:
. (А.6)
По сравнению с ИСО 5725-2 уравнение (А.6) представляет собой лишь оценку стандартного отклонения воспроизводимости
.
Так как этот подход ориентируется на полное выполнение метода, его называют иногда нисходящим подходом.
Следует учитывать, что каждая лаборатория вычисляет свою оценку по уравнению
, полагая ее наилучшей оценкой измеряемой величины
y
для лаборатории. Тогда, если
— общая модель, используемая для описания поведения измерительной системы, то, следовательно, при вычислении
m
предполагается, что дисперсии, характеризующиеся оценками
и
, являются результатом изменения величин
, …,
. Если предполагается, что условия воспроизводимости обеспечиваются для случайной величины при всех существенных воздействиях и применяется физическая интерпретация
, приведенная выше, то из этого следует, что
в уравнении (А.6) является оценкой
, описанной (А.1) или (А.2).
Стандартное отклонение воспроизводимости, полученное в совместном исследовании, является основой для оценки неопределенности измерений (первый принцип, на котором основан настоящий стандарт).
А.2.2 Включение данных правильности
Правильность в общем случае характеризуют смещением относительно принятого опорного значения. В некоторых совместных исследованиях правильность метода в конкретной системе измерений (обычно СИ) исследуют путем анализа аттестованного стандартного образца (CRM
) или эталона единицы физической величины с паспортным значением
, выраженным в единицах этой системы (ИСО 5725-4). Итоговая статистическая модель имеет вид
________________
CRM — certified reference material.
где
— паспортное значение;
— смещение метода.
Совместное исследование может дать оценку смещения
со стандартным отклонением
, рассчитанным по формуле
, (А.8)
где
— количество лабораторий;
— количество повторений в каждой лаборатории.
Неопределенность
, соответствующая этому смещению, задается уравнением
, (А.9)
где
— неопределенность, соответствующая паспортному значению
, используемому для оценки правильности при совместном исследовании.
Если смещение, оцененное в процессе испытаний, используют при вычислении результатов в лабораториях, соответствующую ему неопределенность (если она является значительной) следует включать в бюджет неопределенности.
А.2.3 Другие воздействия. Объединенная модель
На практике
и
не обязательно включают все изменения, влияющие на результаты измерений. Отсутствие некоторых важных факторов вызвано характером совместных исследований; некоторые факторы могут отсутствовать или не оцениваться случайно или в соответствии с планом эксперимента. Второй принцип, на котором основан настоящий стандарт, состоит в том, что воздействия, не наблюдаемые в процессе совместного исследования, или являются незначительными, или должны быть учтены.
Проще всего учесть эти воздействия, рассматривая воздействия отклонений
от номинальных значений
, необходимых для определения оценки
, предполагая приближенную линейность этих воздействий. Объединенная модель может быть описана уравнением
. (А.10)
Суммирование ведется по всем воздействиям, кроме представленных
,
и
.
Примеры таких воздействий могут включать воздействия отбора выборки, подготовки пробы и изменения состава или типа отдельных испытываемых образцов. В строгом смысле это линеаризованная форма самой общей модели. При необходимости можно включать в нее члены более высокого порядка или члены, учитывающие корреляцию, как описано в GUM.
Очевидно, что центрирование
не оказывает влияния на
, так как
, из чего следует, что для оценки неопределенности, соответствующей
, можно использовать уравнение (А.10) и следующее уравнение:
. (А.11)
Суммирование ведется по воздействиям, не учтенным в других членах уравнения.
Следует отметить, что при оценке выполнения метода условия промежуточной прецизионности также могут быть описаны уравнением (А.10), хотя число членов суммы соответственно будет больше, поскольку по сравнению с условиями воспроизводимости в промежуточных условиях меньшее количество переменных меняется случайным образом. В общем случае уравнение (А.10) можно применять к любым условиям прецизионности, учитывая, что воздействия суммируются. В случае, когда
и
равны нулю, а неопределенность общего смещения не определена, уравнение (А.11) становится идентичным уравнению (А.1).
Из этого следуют два вывода:
— во-первых, необходимо продемонстрировать, что количественные данные, полученные из совместного исследования, согласуются с рассматриваемыми результатами испытаний;
— во-вторых, даже при согласованности данных совместного исследования для определения реальной оценки неопределенности с учетом дополнительных воздействий (
в уравнении (А.10)) могут быть необходимы дополнительные исследования и предположения. При учете дополнительных воздействий предполагается применение уравнения (А.1).
И, наконец, в настоящем стандарте для утверждения, что надежную оценку неопределенности измерений можно получить на основе анализа данных повторяемости, воспроизводимости и правильности, полученных в соответствии с ИСО 5725-1-ИСО 5725-6, использованы те же предположения, что и в перечисленных стандартах.
a) Если используются данные воспроизводимости, предполагается, что все лаборатории подобны по выполнению работ. В частности, их прецизионность повторяемости для данного объекта испытаний одинакова, а лабораторная составляющая смещения
в уравнении (А.10) соответствует тому же распределению, что и при совместных исследованиях.
b) Испытуемые материалы, используемые в исследовании, являются гомогенными и стабильными.
А.3 Сопоставление подходов
Приведенные рассуждения описывают два различных подхода к оценке неопределенности. Подход GUM описывает неопределенность в виде дисперсии, полученной на основе дисперсий входных данных, соответствующих математической модели. Другой подход использует тот факт, что, если одни и те же воздействия заметно изменяются в процессе исследования воспроизводимости, наблюдаемая дисперсия является оценкой исследуемой неопределенности. На практике значения неопределенности, полученные на основе различных подходов, различны для разных условий, включая:
a) неполные математические модели (т.е. при наличии неизвестных воздействий);
b) неполное или несущественное изменение всех воздействующих факторов в процессе оценки воспроизводимости.
Сравнение двух различных оценок поэтому полезно для оценки полноты модели измерений. Однако следует обратить внимание, что наблюдаемую повторяемость или другую оценку прецизионности очень часто рассматривают как отдельную составляющую неопределенности даже в подходе GUM. Точно так же индивидуальные воздействия обычно проверяют на их значимость или оценивают количественно до оценки воспроизводимости. На практике для оценки неопределенности часто используют некоторые элементы обоих подходов.
Когда оценка неопределенности для интерпретации сопровождается результатами, важно, чтобы пробелы в каждом подходе были заполнены. Возможности неполных моделей на практике обычно дополняют гарантированными оценками, расширяющими неопределенность модели. В настоящих рекомендациях для устранения неадекватных изменений входных воздействий рекомендуется определять оценки дополнительных воздействий. Это является гибридным подходом, объединяющим элементы и нисходящего и восходящего подходов.
Приложение В
(справочное)
Экспериментальная оценка неопределенности
В.1 Процедура оценки коэффициента чувствительности
Если входные величины
могут изменяться непрерывно по всему диапазону значений, рекомендуется исследовать воздействие таких изменений. Простая процедура, предполагающая приблизительно линейную зависимость результатов от
, следующая:
a) выбирают диапазон изменения переменной
, который должен быть ориентирован на лучшую оценку (или на значение, характерное для указанного метода);
b) выполняют всю процедуру измерений (или ту часть, которая касается
) в каждом из пяти или более уровней
с повторением, при необходимости;
c) рассчитывают и изображают линейную модель в соответствии с результатами, используя
в качестве абсциссы, а результат измерений — в качестве ординаты;
d) используют коэффициент чувствительности, равный угловому коэффициенту
, в уравнениях (А.1) или (14).
Этот подход может дать различные коэффициенты чувствительности для различных объектов испытаний. Это может быть преимуществом во всесторонних исследованиях конкретного объекта или класса объектов. При этом, если коэффициент чувствительности должен быть применен к большому диапазону различных ситуаций, важно убедиться, что различные объекты ведут себя аналогично.
В.2 Простая процедура оценки неопределенности, вызванной случайным воздействием
Если входные величины
являются дискретными и/или неконтролируемыми, соответствующую неопределенность можно определить на основе анализа экспериментов, в которых переменная изменяется случайным образом. Например, состав почвы в экологических исследованиях может иметь непредсказуемое воздействие на результаты анализа. Если случайные ошибки не зависят от уровня исследуемой величины, можно исследовать дисперсию ошибки, являющейся результатом таких изменений, используя серию объектов, для которых заданное значение или доступно, или, если изменение известно, может быть получено теоретически.
Общая процедура включает в себя следующее:
a) выполнение полного измерения на представительном наборе объектов испытаний в условиях повторяемости, используя равное количество повторений для каждого объекта;
b) вычисление разности с заданным значением для каждого наблюдения;
c) проведение анализа результатов (ранжированных по величине) в соответствии с ANOVA с использованием суммы квадратов для формирования оценок составляющей дисперсии
внутри группы и составляющей дисперсии
между группами. Стандартная неопределенность
, являющаяся результатом изменения
, равна
.
Примечание — Если различные объекты или классы объектов по-разному реагируют на исследуемую величину (т.е. существует взаимосвязь величины и класса исследуемых объектов), взаимодействие увеличивает значение
. Детальное исследование этой ситуации в настоящем стандарте не приводится.
Приложение С
(справочное)
Примеры расчета неопределенности
С.1 Измерение содержания монооксида углерода (СО) в выхлопных газах автомобиля
С.1.1 Общие положения
До поставки на рынок легковые автомобили должны проходить испытания типа транспортного средства для проверки выполнения обязательных требований относительно количества угарного газа в выхлопных газах. (Верхний допустимый предел составляет 2,2 г/км.) Метод испытаний описан в [21], где введены следующие требования:
— цикл двигателя задан как функция скорости (км/ч), времени (с) и числа оборотов двигателя. Исследуемый автомобиль помещают на специальный стенд для выполнения заданного количества циклов;
— измерительное оборудование — газоанализатор СО;
— контроль окружающей среды проводят с использованием специальной камеры мониторинга загрязнений;
— персонал должен иметь специальную подготовку.
Такие испытания на соответствие установленным требованиям можно выполнять в испытательной лаборатории организации, занимающейся производством автомобилей или в независимой испытательной лаборатории.
С.1.2 Данные совместных исследований
Перед принятием и использованием такого метода испытаний необходимо оценить факторы или источники, влияющие на результаты испытаний (и, следовательно, на неопределенность результатов испытаний). Такая оценка выполнялась по данным экспериментов, проводимых в различных лабораториях. Для контроля метода испытаний межлабораторный эксперимент проводился в соответствии с ИСО 5725-2. Цель межлабораторного эксперимента состоит в оценке прецизионности метода испытаний при применении его в заданной совокупности испытательных лабораторий. Оценка прецизионности получена на основе данных, собранных в межлабораторном эксперименте со статистическим анализом в соответствии с ИСО 5725-2. Исследования проведены так, чтобы каждый участник выполнял все необходимые процессы измерений и учитывал воздействующие факторы.
Было установлено, что повторяемость в лабораториях значимо не различается, а оценка стандартного отклонения повторяемости метода испытаний равна 0,22 г/км. Оценка стандартного отклонения воспроизводимости метода испытаний равна 0,28 г/км.
С.1.3 Контроль смещения
Оценка правильности (контроль смещения по отношению к эталону) включает методологические и технические вопросы. Не существует «эталонного автомобиля» как образца сравнения. Правильность следует контролировать при калибровке оборудования системы испытаний. Например, калибровку анализатора СО можно выполнять с помощью эталонного газа, а калибровку испытательного стенда можно выполнять для таких величин, как время, расстояние, скорость и ускорение. Знание норм выбросов выхлопных газов для различных скоростей и наличие другой аналогичной информации подтверждает, что неопределенность, связанная с этими калибровками, не дает существенных вкладов в неопределенность, связанную с результатами измерений (т.е. вся расчетная неопределенность много меньше, чем стандартное отклонение воспроизводимости). Таким образом, смещение находится под контролем.
С.1.4 Прецизионность
Повторные испытательные прогоны в лаборатории показали, что разброс содержания СО в выхлопных газах (повторяемость) не превышает 0,20 г/км и находится в пределах диапазона повторяемости, найденного при межлабораторном исследовании. Таким образом, прецизионность находится под контролем.
С.1.5 Соответствие объектов испытаний
Метод признают подходящим для всех транспортных средств, относящихся к легковым автомобилям. Поскольку неопределенность имеет тенденцию уменьшаться для более низких уровней выхлопных газов, неопределенность наиболее важна на уровнях, близких к установленной границе. Поэтому было решено использовать оценку неопределенности, равную установленной границе, как корректную и несколько консервативную (гарантированную) оценку неопределенности для более низких уровней выхлопа СО. Необходимо заметить, если испытания транспортного средства показывают выхлоп существенно больше установленной границы, может оказаться необходимым проведение дополнительных исследований неопределенности, если сравнения являются критичными. На практике, однако, такое транспортное средство нельзя предлагать для продажи без его модернизации.
С.1.6 Оценка неопределенности
Поскольку предшествующие исследования установили хорошую контролируемость смещения и прецизионности в пределах испытательной лаборатории, а также отсутствие воздействующих факторов, не учтенных при совместных исследованиях, стандартное отклонение воспроизводимости, используемое для оценки стандартного отклонения неопределенности, дает расширенную неопределенность
0,56 г/км (
2) с уровнем доверия 95%.
Примечание — Интерпретация неопределенности результатов в области проверки соответствия рассмотрена в ИСО 10576-1
.
_________________
См. также 4.2.2 (примечание 2) ГОСТ Р ИСО 5725-6-2002.
С.2 Определение состава мяса
С.2.1 Общие положения
Для продукции из мяса необходимо гарантировать, что состав мяса соответствует заявленному. Состав мяса определяют как комбинацию содержания азота (преобразованного к общему белку) и жира. Представленный пример показывает принцип объединения различных составляющих неопределенности, каждую из которых непосредственно определяют на основе оценок воспроизводимости, как описано в разделе 12.
Примеры приведены в соответствии с [23], [24], [25] и [26].
С.2.2 Основные уравнения
Полный состав мяса
определяют в соответствии с уравнением
, (С.1)
где
— общий белок в мясе, выраженный в виде процента массы;
— общее содержание жира, выраженное в виде процента массы.
Белок в мясе
вычисляют по формуле
, (С.2)
где
— коэффициент содержания азота, соответствующий исследуемому материалу;
— полное содержание азота в мясе.
В этом случае
идентично общему содержанию азота
, определяемому в соответствии с анализом Кьельдаля.
С.2.3 Этапы эксперимента по определению состава мяса
При определении состава мяса выполняют следующие действия:
a) определяют содержание жира
;
b) определяют содержание азота
по Кьельдалю (среднее дублированных измерений);
c) вычисляют содержание обезжиренного мяса
и
(уравнение (С.2));
d) вычисляют общий состав мяса
(уравнение (С. 1)).
С.2.4 Составляющие неопределенности
Составляющие неопределенности соответствуют каждой из величин, перечисленных в С.2.3. Наиболее существенным является
, составляющий приближенно 90% массы мяса
. Наибольшая неопределенность, соответствующая
, является результатом:
a) неопределенности коэффициента
, вызванной неполным знанием исследуемого материала;
b) отклонений метода в условиях воспроизводимости при повторении метода и при точном выполнении метода в течение длительного времени;
c) неопределенности, вызванной смещением метода;
c) неопределенности, соответствующей содержанию жира
.
Примечание — Неопределенности, указанные в перечислениях a), b) и c), относятся к образцу, лаборатории и методу соответственно. Часто бывает полезно грубо рассмотреть каждую из этих трех составляющих при идентификации неопределенности, а также неопределенность, соответствующую отдельным этапам процедуры.
С.2.5 Оценка составляющих неопределенности
С.2.5.1 Неопределенность, соответствующая
Неопределенность, соответствующая
, может быть оценена по приведенным в публикациях значениям. В [22] приведены результаты исследований содержания азота в говядине, которые показывают четкие различия между данными, полученными при исследовании образцов мяса от различных поставщиков и кусков мяса. В [22] также даны рекомендации по вычислению наблюдаемого стандартного отклонения для
0,052 и относительного стандартного отклонения 0,014 для большого диапазона типов выборок.
Примечание — Непосредственно применены данные содержания азота, определенные в [22], полученные с использованием метода Кьельдаля.
С.2.5.2 Неопределенность, соответствующая
Информация о двух совместных испытаниях [22], [23] позволяет определить оценку неопределенности, вызванной низкой воспроизводимостью или ошибками выполнения метода. Тщательная проверка условий испытаний показывает, во-первых, что каждое исследование проводят по широкому диапазону типов выборки и с хорошим репрезентативным набором компетентных лабораторий, а во-вторых, что стандартное отклонение воспроизводимости
хорошо коррелирует с уровнем азота. Для обоих испытаний наиболее подходящей является линейная функция
. Кроме того исследование показывает, что стандартное отклонение повторяемости пропорционально
с
0,018,
и
.
Метод таков, что каждое измерение повторяют и определяют выборочное среднее. Член, характеризующий повторяемость и представляющий собой оценку повторяемости единственного результата, должен быть соответствующим образом откорректирован для учета влияния среднего арифметического двух результатов в лаборатории (см. комментарий, относящийся к
в таблице 1). Неопределенность
, соответствующая содержанию азота, имеет вид
. (С.3)
Выражение (С.3) дает лучшую оценку неопределенности с
, соответствующей разумным изменениям при выполнении метода.
Воспроизводимость также используют в качестве критерия оценки прецизионности отдельной лаборатории. Метод устанавливает, что результаты должны быть отброшены, если данные попадают вне 95%-ного доверительного интервала (с границами, приблизительно равными
). Эта проверка гарантирует, что внутрилабораторная прецизионность соответствует прецизионности совместного исследования.
Примечание — Если эта проверка показывает отрицательный результат чаще, чем в 5% случаев, вероятно, что контролируемость прецизионности недостаточна и необходимы действия по корректировке процедуры.
Необходимо также рассмотреть неопределенность, соответствующую
и являющуюся результатом воздействия неизвестного смещения метода. В отсутствие надежных стандартных образцов сравнение с альтернативными методами, использующими другие принципы, является установленным средством оценки смещения. Сравнение метода Кьельдаля с методом анализа при сжигании образца для определения полного азота и различных типов выборки установило различие
. Это удовлетворяет критерию
(см. Руководство ИСО 33, уравнение (4)), подтверждающему, что неопределенность, вызванная смещением, адекватно подсчитана для данных воспроизводимости.
С.2.5.3 Неопределенность, соответствующая
Дополнительные данные совместных испытаний для анализа жира [25] дают оценку стандартного отклонения воспроизводимости
. Анализ снова выполняют дважды, а результаты принимают только в случае, если разность находится в соответствующих пределах повторяемости, гарантируя, что лабораторная прецизионность находится под контролем. В результате верификации работ по определению жира на соответствующем стандартном образце установлено, что неопределенность, связанная со смещением, адекватна значениям воспроизводимости.
С.2.6 Суммарная стандартная неопределенность
В таблице С.1 приведены величины и неопределенность, подсчитанная с использованием этих величин
Таблица С.1 — Составляющие бюджета неопределенности для определения состава мяса
|
Наименование |
Значение показателя |
||
|
показателя |
(% массы) |
|
|
|
Содержание жира |
5,50 |
0,110 |
0,020 |
|
Содержание азота |
3,29 |
0,056 |
0,017 |
|
Коэффициент |
3,65 |
0,052 |
0,014 |
|
Белок |
90,1 |
90,1 0,022=1,98 |
|
|
Общий состав мяса |
95,6 |
|
0,021 |
При определении расширенной неопределенности с уровнем доверия 95% суммарную стандартную неопределенность умножают на коэффициент охвата
, равный 2. При округлении до двух знаков после запятой получают расширенную неопределенность на состав мяса
4,0%; т.е.
(95,6±4,0)%.
Примечание — В соответствии с приведенными расчетами в некоторых случаях значение
может превышать 100%.
С.3 Неопределенность измерений, полученных методом АОАС 990.12 (с применением пластин для подсчета аэробных бактерий)
С.3.1 Общие положения
Метод представляет собой метод микробиологического анализа деятельности микроорганизмов в пищевых продуктах [27]. Метод использует пластины для бактериальной культуры в виде сухой среды и растворимого в воде геля. Пробы наносят на пластины в количестве 1,0 мл на пластину и распределяют по площади приблизительно на 20 см
. После инкубации подсчитывают количество колоний. Измеряемой величиной является количество сформировавшихся колоний. Для получения значений, отличных от нуля, в качестве результатов использован логарифм с основанием 10 (lg) от количества сформировавшихся колоний (CFU
). Оценка неопределенности необходима для трех видов пищевых продуктов: креветок, муки и овощей.
_________________
CFU — colony-forming units.
Пример основан на данных руководства A2LA [28]. Также см. [27].
С.3.2 Данные совместных исследований
Метод валидирован на основе совместных исследований двенадцатью лабораториями шести образцов продуктов с различными уровнями загрязнения, по две пробы на образце продукта и два повторения на пробу. Проведение анализа данных в соответствии с требованиями ИСО 5725-2 и валидационное исследование включало все этапы проверки за исключением этапа определения точного объема подвыборки (измеренные пробы были получены в совместном исследовании). В таблице С.2 приведены зафиксированные оценки стандартных отклонений для повторяемости и воспроизводимости, соответствующие этим трем видам продуктов, в процентах.
Таблица С.2 — Данные совместных исследований аэробных бактерий
|
Вид продукта |
Стандартное отклонение воспроизводимости, % |
Стандартное отклонение повторяемости, % |
|
Креветки |
11,1 |
9,8 |
|
Овощи |
9,2 |
6,3 |
|
Мука |
5,8 |
5,3 |
Данные повторяемости и воспроизводимости представлены в виде стандартных отклонений относительно среднего наблюдаемого значения для десятичного логарифма (lg) от количества колоний. Это удобно для данного метода, у которого разброс значений приблизительно пропорционален наблюдаемым значениям и относительное стандартное отклонение является приблизительно устойчивым.
С.3.3 Контроль смещения
Чтобы установить, находится ли лабораторное смещение в ожидаемых пределах, лаборатория выполняет сравнение своих результатов с результатами эталонной лаборатории. Результаты для овощей и креветок всегда находятся в пределах ±10% (
,
— среднее соответствующих наблюдений). Сравнение результатов для муки показывает результат ±5% (
). Эти отклонения совместимы со стандартным отклонением воспроизводимости, поэтому смещение является приемлемым.
С.3.4 Контроль прецизионности
Чтобы установить, находится ли прецизионность в пределах ожидаемых границ, в лаборатории определяют оценки стандартного отклонения повторяемости по сериям из 10 повторений. Стандартное отклонение повторяемости для всех видов продукции составляет не более 5% (
). Поэтому принято решение, что повторяемость является не только приемлемой, но также может быть рассчитана более низкая скорректированная оценка воспроизводимости, как описано в 7.3.2. Стандартные отклонения воспроизводимости приведены в таблице С.3.
Таблица С.3 — Скорректированные стандартные отклонения воспроизводимости
|
Вид продукта |
Стандартное отклонение воспроизводимости, % |
Относительное стандартное отклонение между лабораториями, % |
Относительное стандартное отклонение повторяемости, % |
Скорректированное стандартное отклонение воспроизводимости, % |
|
Креветки |
11,1 |
5,2 |
5,0 |
7,2 |
|
Овощи |
9,2 |
6,7 |
5,0 |
8,4 |
|
Мука |
5,8 |
2,4 |
5,0 |
5,5 |
С.3.5 Обоснование выбора объекта испытаний
С.3.5.1 Подготовка образцов и предварительная обработка
Совместное исследование исключило стадию отбора выборки. Рассмотрение этапа отбора выборки показало, что подготовка образцов (отбор подвыборки, взвешивание) вносит дополнительно 3,0% в суммарную стандартную неопределенность (на основе мнений экспертов). Этот вклад приведен в таблице С.4.
С.3.5.2 Изменение неопределенности в зависимости от уровня переменной отклика
Воспроизводимость, повторяемость и вклад дополнительных этапов подготовки образцов приблизительно пропорциональны количеству колоний аэробных бактерий на пластине. Поэтому основная модель может иметь форму уравнения (10), в котором коэффициент
равен скорректированному относительному стандартному отклонению воспроизводимости, а дополнительный вклад отбора выборки включен как пропорциональный вклад. Это эквивалентно простому подходу (использованному выше), когда все вклады в неопределенность представлены в относительном виде.
С.3.6 Суммарная стандартная неопределенность
Суммарная стандартная неопределенность (в виде относительного стандартного отклонения) для каждого вида продуктов приведена в таблице С.4.
Таблица С.4 — Относительное стандартное отклонение воспроизводимости
|
Вид продукта |
Межлабораторное относительное стандартное отклонение, % |
Относительное стандартное отклонение повторяемости, % |
Вклад подготовки образцов в стандартную неопределенность, % |
Суммарная стандартная неопределенность (в виде относительного стандартного отклонения), % |
|
Креветки |
5,2 |
5,0 |
3,0 |
7,8 |
|
Овощи |
6,7 |
5,0 |
3,0 |
8,9 |
|
Мука |
2,4 |
5,0 |
3,0 |
6,4 |
С.3.7 Расширенная неопределенность
Расширенную неопределенность вычисляют, используя коэффициент охвата 2, который соответствует уровню доверия приблизительно 95%. Расширенная неопределенность составила 15,6%, 17,8% и 12,8% (как процент от lg (количество колоний) для креветок, овощей и муки соответственно).
С.3.8 Дополнительный анализ
Результаты метода традиционно получают в виде десятичного логарифма от количества колоний аэробных бактерий. Однако для единственного объекта испытаний часто более полезно определить расширенный интервал неопределенности (в тех же единицах). Для значений с неопределенностью в области значений lg это лучше всего сделать, вычисляя расширенную неопределенность в области значений lg (см. С.3.7) и преобразуя значение CFU впоследствии. Это можно проиллюстрировать вычислением расширенных интервалов неопределенности для исследуемых материалов со значением CFU 150. Соответствующие вычисления приведены в таблице С.5.
Таблица С.5 — Скорректированное стандартное отклонение воспроизводимости
|
Вид продукта |
Стандартная неопреде- ленность (как стандартное отклонение) |
Расширенная неопреде- ленность (как процент значений CFU) |
lg от 150 CFU |
Расширенная неопреде- ленность в единицах десятичного логарифма |
Интервал неопреде- ленности для lg (CFU) |
Итоговый интервал неопреде- ленности CFU |
|
Креветки |
7,8 |
15,6 |
2,1761 |
0,3395 |
1,8366-2,5156 |
68-328 |
|
Овощи |
8,9 |
17,8 |
2,1761 |
0,3873 |
1,7888-2,5634 |
61-366 |
|
Мука |
6,4 |
12,8 |
2,1761 |
0,2785 |
1,8976-2,4546 |
79-285 |
С.4 Неопределенность при определении количества грубых волокон
С.4.1 Общие положения
Метод используют при определении количества грубых волокон в кормах для животных. Под грубыми волокнами понимают количество обезжиренных органических веществ, не растворимых в кислых и щелочных средах Содержание волокон в кормах для животных обычно изменяется в интервале от 2% до 12% от массы корма.
С.4.2 Вычисление концентрации волокон
Содержание волокон
, как процент от массы пробы (т.е. массовую долю в процентах) вычисляют по формуле
, (С.4)
где
— масса пробы (для анализа взята проба массой 1 г), в граммах;
— масса тигля и пробы после высушивания постоянной массы, в граммах;
— масса тигля и пробы после озоления, в граммах;
— масса тигля и пустой пробы после высушивания до постоянной массы, в граммах;
— масса тигля и пустой пробы после озоления, в граммах.
Примечание — Пустая проба предполагает использование пустого тигля на всех стадиях метода.
Блок-схема, иллюстрирующая основные этапы метода, представлена на рисунке С.1.
С.4.3 Данные совместных исследований
Метод был объектом совместных исследований в соответствии с ИСО 5725-2. В процессе испытаний было исследовано пять различных видов корма для животных, представляющих типичные концентрации грубых волокон и жира. Участники испытаний выполнили все этапы метода, включая размол проб. Полученные оценки повторяемости и воспроизводимости приведены в таблице С.6.
Таблица С.6 — Данные совместных исследований содержания грубых волокон
|
Объект испытаний |
Среднее содержание волокон, % |
Стандартное отклонение воспроизводимости , % |
Относительное стандартное отклонение воспроизводимости |
Стандартное отклонение повторяемости , % |
|
A |
2,3 |
0,293 |
0,127 |
0,198 |
|
B |
12,1 |
0,563 |
0,046 5 |
0,358 |
|
C |
5,4 |
0,390 |
0,072 2 |
0,264 |
|
D |
3,4 |
0,347 |
0,102 |
0,232 |
|
E |
10,1 |
0,575 |
0,056 9 |
0,391 |
С.4.4 Контроль смещения
Чтобы установить, находится ли лабораторное смещение в ожидаемых пределах, лаборатория выполняет сопоставление с образцом сравнения, сертифицированным рассматриваемым методом (это существенно, поскольку измеряемая величина определена заданным методом анализа). Паспортное значение составляет (93±14) г/кг (9,3%). Лаборатория получила значение 9,16%, соответствующее лабораторному смещению
-0,14%. Оно находится в пределах ожидаемого интервала исходя из стандартного отклонения воспроизводимости на уровне 9%. Стандартная неопределенность паспортного значения составляет приближенно 7 г/кг (массовая доля 0,7%). Она невелика по сравнению со стандартным отклонением воспроизводимости для аналогичных уровней содержания грубых волокон в таблице С.6. Поэтому смещение является приемлемым.
С.4.5 Контроль прецизионности
Как часть верификации метода в лаборатории были выполнены эксперименты для оценки повторяемости (в пределах партии) кормов, концентрация грубых волокон в которых аналогична концентрации в некоторых пробах, проанализированных в совместных исследованиях. Результаты приведены в таблице С.7. Сравнение с таблицей С.6 показывает, что лаборатория получает прецизионность, очень близкую к найденной в совместных исследованиях.
Таблица С.7 — Данные повторяемости для оценки концентрации грубых волокон
|
Объект испытаний |
Среднее содержание волокон, % |
Стандартное отклонение повторяемости , % |
|
F |
3,0 |
0,198 |
|
G |
5,5 |
0,264 |
|
H |
12,0 |
0,358 |
С.4.6 Изменение неопределенности в зависимости от переменной отклика
Стандартные отклонения повторяемости и воспроизводимости, приведенные в таблице С.6, увеличиваются с увеличением концентрации грубых волокон. Однако очевидно несоответствие относительного стандартного отклонения воспроизводимости простой пропорциональной модели. Поэтому лаборатория при определении неопределенности на различных наблюдаемых уровнях концентрации волокон использует воспроизводимость, найденную на аналогичных уровнях в совместных исследованиях; например, для уровней концентрации волокон не выше 2,5% (массовая доля) стандартное отклонение воспроизводимости 0,29% (массовая доля) выбрано из таблицы С.6.
С.4.7 Дополнительные факторы
Лаборатория провела экспериментальные и другие исследования влияния различных величин на результаты для типичных объектов испытаний. Полученные оценки неопределенности приведены в таблице С.8. Ни один из вкладов не является существенным, кроме влияния высушивания до постоянной массы. Неопределенность, соответствующая этому этапу процесса, получена исходя из требования постоянной массы, установленного лабораторией; «постоянная масса» не определена в стандартном методе, и лаборатория приняла решение использовать метод высушивания, приводящий к массе в пределах 0,002 г массы. Деление этого максимального отклонения на
дает оценку неопределенности 0,115% (массовая доля) содержания волокон, если для анализа взят 1 г пробы.
Таблица С.8 — Влияние различных величин на определение содержания грубых волокон
|
Источник неопределенности |
Значение |
Стандартная неопреде- ленность |
Соответствующая неопределенность в виде стандартного отклонения повторяемости |
Источник информации |
|
Масса пробы |
1,0 г |
0,00020 г |
0,00020 |
Свидетельство о калибровке |
|
Концентрация кислоты |
— |
— |
0,00030 |
Опубликованные данные об изменении содержания волокна в зависимости от концентрации кислоты |
|
Концентрация щелочи |
— |
— |
0,00048 |
Опубликованные данные об изменении содержания волокна в зависимости от концентрации щелочи |
|
Время разрушения в кислой среде |
— |
— |
0,0090 |
Опубликованные данные об изменении содержания волокна в зависимости от времени вываривания |
|
Время разрушения в щелочной среде |
— |
— |
0,0072 |
Опубликованные данные об изменении содержания волокна в зависимости от времени вываривания |
|
Высушивание до постоянной массы |
— |
0,00115 г |
— |
Лабораторные требования постоянной массы |
|
Температура и время озоления |
— |
Незначитель- ная |
— |
Опубликованные данные об отсутствии существенных изменений содержания волокон в зависимости от изменения температуры и времени озоления |
|
Потеря массы после озоления для холостой пробы |
— |
Незначитель- ная |
— |
Экспериментальные исследования |
С.4.8 Суммарная стандартная неопределенность
Поскольку неопределенность, соответствующая высушиванию до постоянной массы, не пропорциональна уровню грубых волокон, невозможно принять простую пропорциональную модель для оценки неопределенности. Вместо этого удобно оценивать неопределенность, соответствующую типичным уровням грубых волокон. Оценки неопределенности приведены в таблице С.9.
Таблица С.9 — Скорректированное стандартное отклонение воспроизводимости
|
Содержание волокон, % |
Стандартное отклонение воспроизводимости , % |
Дополнительный вклад высушивания, % |
Суммарная стандартная неопределенность , % |
|
2,5 |
0,293 |
0,115 |
0,31 |
|
2,5 к 5 |
0,390 |
0,115 |
0,41 |
|
5 к 10 |
0,575 |
0,115 |
0,59 |
С.4.9 Расширенная неопределенность
Расширенная неопределенность вычислена с коэффициентом охвата 2, который соответствует уровню доверия, приблизительно равному 95%, дает расширенную неопределенность 0,6%, 0,8% и 1,2% соответственно для различных диапазонов содержания волокон в таблице С.9.
|
|
Рисунок С.1 — Действия по оценке содержания грубых волокон
Библиография
|
[1] |
ISO 3534-1, |
Statistics — Vocabulary and symbols — Part 1: General statistical terms and terms used in probability |
|
[2] |
ISO 3534-2, |
Statistics — Vocabulary and symbols — Part 2: Applied statistics |
|
[3] |
ISO 3534-3, |
Statistics — Vocabulary and symbols — Part 3: Design of experiments |
|
[4] |
ISO 5725-1, |
Accuracy (trueness and precision) of measurement methods and results — Part 1: General principles and definitions |
|
[5] |
ISO 5725-2, |
Accuracy (trueness and precision) of measurement methods and results — Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method |
|
[6] |
ISO 5725-3, |
Accuracy (trueness and precision) of measurement methods and results — Part 3: Intermediate measures of the precision of a standard measurement method |
|
[7] |
ISO 5725-4, |
Accuracy (trueness and precision) of measurement methods and results — Part 4: Basic methods for the determination of the trueness of a standard measurement method |
|
[8] |
ISO 5725-5, |
Accuracy (trueness and precision) of measurement methods and results — Part 5: Alternative methods for the determination of the precision of a standard measurement method |
|
[9] |
ISO 5725-6, |
Accuracy (trueness and precision) of measurement methods and results — Part 6: Use in practice of accuracy values |
|
[10] |
ISO 7870-4, |
Control charts — Part 4: Cumulative sum charts |
|
[11] |
ISO 7870-2, |
Control charts — Part 2: Shewhart control charts |
|
[12] |
ISO 10576-1, |
Statistical methods — Guidelines for the evaluation of conformity with specified requirements — Part 1: General principles |
|
[13] |
ISO 11648 (all parts), |
Statistical aspects of sampling from bulk materials |
|
[14] |
ISO Guide 33, |
Reference materials — Good practice in using reference materials |
|
[15] |
ISO/IEC 17025, |
General requirements for the competence of testing and calibration laboratories |
|
[16] |
ISO/IEC Guide 98-3, |
Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM: 1995) |
|
[17] |
ISO/IEC Guide 99:2007, |
International vocabulary of metrology — Basic and general concepts and associated terms (VIM) |
|
[18] |
ISO/IEC 17043, |
Conformity assessment — General requirements for proficiency testing |
|
[19] |
AFNOR FD X07-021, (October 1999) |
Normes fondamentales — et applications de la statistique — Aide la pour I’estimation et I’utilisation de I’incertitude des mesures et des d’essais |
|
[20] |
Recommendation INC-1 (1980), BIPM |
|
|
[21] |
European Directive 70/220, Measures to be taken against air pollution by emissions from motor vehicles |
|
|
[22] |
Kaarls R. -verbaux du International des Poids et Mesures, 49, BIPM, 1981, pp.A.1-A.12 |
|
|
[23] |
Analytical Methods Committee. Analyst (Lond.). 1993, 118 p.1217 |
|
|
[24] |
Shure B., Corrao P.A., Glover A., Malinowski A. J.J. AOAC Int. 1982, 65 p.1339 |
|
|
[25] |
King-Brink M., & Sebranek J.G.J. AOAC Int. 1993, 76 p.787 |
|
|
[26] |
Breese Jones D. US Department of Agriculture Circular No. 183 (August 1931) |
|
|
[27] |
Official Methods of Analysis. AOAC Int. Gaithersburg, MD, Twentieth Edition, 2016 |
|
|
[28] |
A2LA Guidance Document G108 — Guidelines for Estimating Uncertainty for Microbiological Counting Methods American Association for Laboratory Accreditation, 2014 |
|
УДК 58.562.012.7:65.012.122:006.354 |
ОКС |
03.120.30; |
|
17.020 |
||
|
Ключевые слова: оценки неопределенности, повторяемости, воспроизводимости, правильности, математическое ожидание, прецизионность, стандартное отклонение, дисперсия, смещение, суммарная неопределенность, расширенная неопределенность |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р |
Статистические методы
ПРИМЕНЕНИЕ
ПРИ ПРОВЕРКЕ КВАЛИФИКАЦИИ
ПОСРЕДСТВОМ
МЕЖЛАБОРАТОРНЫХ ИСПЫТАНИЙ
(ISO 13528:2015,
Statistical methods for use in proficiency testing
by interlaboratory comparison, MOD)
|
|
Москва |
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом
«Научно-исследовательский центр контроля и диагностики технических систем» (АО
«НИЦ КД») на основе собственного перевода на русский язык англоязычной версии
стандарта, указанного в пункте 4, при участии Федерального государственного
унитарного предприятия «Уральский научно-исследовательский институт метрологии»
(ФГУП «УНИИМ»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125
«Применение статистических методов»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального
агентства по техническому регулированию и метрологии от 12 сентября 2017 г. №
1061-ст
4 Настоящий стандарт является
модифицированным по отношению к международному стандарту ИСО 13528:2015
«Статистические методы для применения при проверке квалификации посредством
межлабораторных испытаний» (ISO 13528:2015 «Statistical methods for use in proficiency testing by
interlaboratory comparison», MOD) путем внесения
отклонений, объяснение которых приведено во введении к настоящему стандарту.
Международный стандарт разработан техническим комитетом ТС
56 «Dependability» международной электротехнической
комиссии (IEC).
Наименование настоящего стандарта изменено относительно
наименования указанного международного стандарта для приведения в соответствие
с ГОСТ
Р 1.5-2012 (пункт 3.5).
Сведения о соответствии
ссылочных национальных и межгосударственных стандартов международным
стандартам, использованным в качестве ссылочных в примененном международном
стандарте, приведены в дополнительном приложении ДА
5 ВЗАМЕН ГОСТ
Р ИСО 13528-2010
Правила применения настоящего стандарта установлены в
статье 26 Федерального
закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской
Федерации». Информация об изменениях к настоящему стандарту публикуется в
ежегодном (по состоянию на 1 января текущего года) информационном указателе
«Национальные стандарты», а официальный текст изменений и поправок — в
ежемесячном информационном указателе «Национальные стандарты». В случае
пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление
будет опубликовано в ближайшем выпуске ежемесячного информационного указателя
«Национальные стандарты». Соответствующая информация, уведомление и тексты
размещаются также в информационной системе общего пользования — на
официальном сайте Федерального агентства по техническому регулированию и
метрологии в сети Интернет (www.gost.ru)
Содержание
Введение
0.1 Цели проверки квалификации
Проверка квалификации посредством межлабораторных
сравнительных испытаний предназначена для определения способности участников
(которыми могут быть лаборатории, контролирующие органы или физические лица)
проводить испытания или измерения, а также для проверки их работы. Во введении
к ГОСТ
ISO/IEC 17043-2013
приведены основные задачи проверки квалификации лабораторий, например:
— определение оценок характеристик функционирования
лабораторий;
— выявление проблем в лабораториях;
— установление результативности и сопоставление методов
испытаний или измерений;
— обеспечение дополнительного доверия заказчиков
лаборатории;
— подтверждение заявленной неопределенности;
— обучение участвующих лабораторий.
Применяемые статистические и аналитические методы должны
быть приемлемыми для указанных целей.
0.2 Обоснование для выбора критериев проверки квалификации
Для проверки квалификации используют различные стратегии.
Несмотря на то что детали расчетов разные, в большинстве схем проверки
квалификации отклонение результатов измерений участника от приписанного
значения сравнивают с критерием для того, чтобы определить, является ли
отклонение поводом для беспокойства. Поэтому стратегии, используемые для выбора
приписанного значения и критерия оценки отклонений, очень значимы. В частности,
важно определить, следует ли выбирать приписанное значение и критерий
независимо от результатов измерений участников или их следует определять на
основе результатов измерений, представленных участниками. В настоящем стандарте
рассмотрены обе стратегии. В разделах 7 и 8
рассмотрены преимущества и недостатки выбора приписанных значений и критериев
оценки отклонений независимо от результатов измерений участников. В целом выбор
приписанных значений и критериев независимо от результатов измерений участников
является предпочтительным. Это, в частности, касается критериев, используемых
для оценки отклонения от приписанного значения, таких как стандартное
отклонение оценки квалификации или допуск на погрешность измерений, для которых
выбор, основанный на пригодности использования для конечного пользователя,
особенно важен.
0.3 Настоящий стандарт и ГОСТ
ISO/IEC 17043
Настоящий стандарт дополняет ГОСТ
ISO/IEC 17043 в части
требований к статистическим методам валидации образцов для проверки
квалификации, анализа результатов, общей статистической отчетности. В
приложении В ГОСТ
ISO/IEC 17043-2013
кратко описаны общие статистические методы, используемые в программах проверки
квалификации. Настоящий стандарт предназначен в качестве дополнения к ГОСТ
ISO/IEC 17043 и содержит рекомендации по применению статистических
методов для проверки квалификации.
Определение проверки квалификации, приведенное в ГОСТ
ISO/IEC 17043, совпадает с представленными в настоящем стандарте
замечаниями, которые описывают различные типы проверки квалификации и набор
планов эксперимента, которые могут быть использованы. Настоящий стандарт не
охватывает все цели, планы эксперимента, матрицы и измеряемые величины. Методы,
представленные в настоящем стандарте, предназначены для широкого применения,
особенно для вновь создаваемых программ проверки квалификации. Предполагается,
что статистические методы, используемые в конкретных программах проверки
квалификации, будут совершенствоваться с изменением программ, планов
эксперимента, критериев оценки, а графические методы — уточняться для учета
потребностей целевой группы участников, органов аккредитации и регулирующих
органов.
В настоящем стандарте приведено руководство по проверке
квалификации химических аналитических лабораторий [1], а также дополнительно представлен набор
процедур, позволяющих использовать валидированные методы измерений и работы с
данными. Настоящий стандарт представляет статистические методы и содержит
указания по их применению, расширенные, по мере необходимости, в соответствии с
упомянутыми документами и ГОСТ
ISO/IEC 17043. В ГОСТ
ISO/IEC 17043 приведены требования относительно проверки квалификации
для отдельных лиц и проверяющих органов; в приложении B — сведения,
относящиеся к качеству результатов.
В настоящем стандарте приведены статистические методы,
согласующиеся со статистическими методами других международных стандартов,
особенно разработанных комитетом ИСО/ТС 69/ SC6, в
частности с методами, представленными в серии стандартов ГОСТ Р ИСО 5725.
Методы, приведенные в настоящем стандарте, согласованы с ГОСТ
Р 54500-3/Руководство ИСО/МЭК 98-3 (GUM).
0.4 Статистическая экспертиза
В соответствии с требованиями ГОСТ
ISO/IEC 17043-2013 провайдер проверки квалификации должен быть
компетентным в области проведения межлабораторных сличений, наделен
полномочиями по осуществлению статистической экспертизы, привлечению персонала
для выполнения статистического анализа. Однако ни в ГОСТ
ISO/IEC 17043, ни в настоящем стандарте не установлены требования к
необходимости проведения проверки. В некоторых случаях обозначено наличие
специального образования у провайдера, но, как правило, требования к проверке
могут быть выполнены и техническими специалистами, знакомыми с основными
статистическими понятиями и имеющими опыт работы или обученными общим методам
анализа данных, применяемым в программе проверки квалификации. Если физическое
лицо привлекают к статистической обработке или анализу данных, то даже при
наличии специального образования в области статистики очень важно, чтобы этот
специалист имел опыт в области межлабораторных сравнительных испытаний. Обычное
обучение статистическим методам не включает в себя методы, применяемые при
межлабораторных сравнительных испытаниях, и описание причин возникновения
ошибок измерений, которые происходят при проверке квалификации и часто остаются
невыясненными. В настоящем стандарте не могут быть представлены весь спектр
возникающих проблем и опыт, накопленный при работе, связанной с
межлабораторными сравнительными испытаниями.
0.5 Программное обеспечение
Компьютерное программное обеспечение, которое необходимо для
статистического анализа данных проверки квалификации, весьма разнообразно — от
электронных таблиц для выполнения арифметических операций, используемых в
случае известных опорных значений, до сложного программного обеспечения,
применяемого для итерационных расчетов или других современных численных
методов. Для большинства методов, перечисленных в настоящем стандарте,
достаточно использования электронных таблиц с настройкой для работы с
конкретными программами или для проведения анализа; некоторые методы требуют
применения компьютерных приложений, которые находятся в свободном доступе. Во
всех случаях пользователи должны проверять точность своих расчетов, особенно
при использовании специальных программ. Тем не менее даже тогда, когда методы,
приведенные в настоящем стандарте, являются надлежащими и правильно
реализованными соответствующими компьютерными приложениями, их не следует
применять без тщательной технической и статистической экспертизы, достаточной
для выявления и изучения отклонений, которые могут произойти на любом этапе
проверки квалификации.
0.6 Отклонения от ИСО 13528:2015
Из раздела 2
исключены стандарты, которые нецелесообразно применять в соответствии с
требованиями национальной системы стандартизации.
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРИМЕНЕНИЕ ПРИ ПРОВЕРКЕ КВАЛИФИКАЦИИ
ПОСРЕДСТВОМ МЕЖЛАБОРАТОРНЫХ ИСПЫТАНИЙ
Statistical methods. Use in
proficiency testing by interlaboratory comparison
Дата введения —
2018-12-01
1 Область применения
В настоящем стандарте приведены статистические методы,
используемые провайдерами проверки квалификации лабораторий для разработки
программ проверки квалификации и анализа полученных данных при выполнении этих
программ. В настоящем стандарте приведены рекомендации по интерпретации данных
проверки квалификации, и он предназначен для использования участниками данных
программ и органами по аккредитации.
Процедуры, приведенные в настоящем стандарте, предназначены
для демонстрации того, что полученные результаты измерений лабораторий
(проверяющих органов, физических лиц) подтверждают (или не подтверждают)
качество их работы. Настоящий стандарт применим к проверке квалификации,
результатами которой являются количественные или качественные результаты
наблюдений, выполняемые на образцах.
Примечание — Процедуры, установленные в настоящем стандарте,
могут быть применены к экспертным оценкам, когда мнения или заключения экспертов
представлены в форме, допускающей объективное сопоставление с некоторой
независимой эталонной величиной или согласованной статистикой: например, при
классификации образцов для проверки квалификации на несколько категорий с
помощью контроля или при определении во время контроля принадлежности (или нет)
образцов для проверки квалификации одному источнику и объективного
сопоставления результатов классификации. В этом случае могут быть применены
положения настоящего стандарта, относящиеся к номинальным (качественным)
свойствам.
2
Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на
следующие документы:
ГОСТ
ISO/IEC 17043-2013 Оценка соответствия. Основные требования к проведению
проверки квалификации
ГОСТ
ISO Guide 35-2015 Стандартные образцы. Общие и
статистические принципы сертификации (аттестации)
ГОСТ
ИСО/МЭК 17025-2009 Общие требования к компетентности испытательных и
калибровочных лабораторий
ГОСТ
Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и
результатов измерений. Часть 1. Основные положения и определения
ГОСТ
Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и
результатов измерений. Часть 2. Основной метод определения повторяемости и
воспроизводимости стандартного метода измерений
ГОСТ
Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и
результатов измерений. Часть 5. Альтернативные методы определения
прецизионности стандартного метода измерений
ГОСТ
Р ИСО 16269-4-2017 Статистические методы. Статистическое представление
данных. Часть 4. Выявление и обработка выбросов
ГОСТ
Р 54500.3—2011/Руководство ИСО/МЭК
98-3:2008 Неопределенность измерения. Часть 3. Руководство по выражению
неопределенности измерения
ГОСТ
Р ИСО 7870-2-2015 Статистические методы. Контрольные карты. Часть 2.
Контрольные карты Шухарта
Примечание — При пользовании настоящим стандартом целесообразно
проверить действие ссылочных стандартов в информационной системе общего
пользования — на официальном сайте Федерального агентства по техническому
регулированию и метрологии в сети Интернет или по ежегодному информационному
указателю «Национальные стандарты», который опубликован по состоянию на 1
января текущего года, и по выпускам ежемесячного информационного указателя
«Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на
который дана недатированная ссылка, то рекомендуется использовать действующую
версию этого стандарта с учетом всех внесенных в данную версию изменений. Если
заменен ссылочный стандарт, на который дана датированная ссылка, то
рекомендуется использовать версию этого стандарта с указанным выше годом
утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный
стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее
положение, на которое дана ссылка, то это положение рекомендуется применять без
учета данного изменения. Если ссылочный стандарт отменен без замены, то
положение, в котором дана ссылка на него, рекомендуется применять в части, не
затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими
определениями:
3.1 межлабораторные сравнительные испытания1)
(interlaboratory comparison): Организация,
выполнение и оценка результатов измерений или испытаний одного и того же или
нескольких подобных образцов двумя или более лабораториями в соответствии с
заранее установленными условиями.
__________
1) Синонимами являются
термины «межлабораторные сличительные испытания», «межлабораторные сличения».
3.2 проверка квалификации (proficiency
testing): Оценка характеристики функционирования участника по заранее
установленным критериям посредством межлабораторных сравнительных испытаний.
Примечание — В
настоящем стандарте термин «проверка квалификации» употребляется в широком
понимании и включает следующее (перечень может быть дополнен):
— количественную программу,
когда целью является определение количественной оценки одной или нескольких
измеряемых величин каждого образца для проверки квалификации;
— качественную программу
испытаний, когда целью является идентификация или описание одной или нескольких
качественных характеристик образца для проверки квалификации;
— последовательную программу,
когда один или несколько образцов для проверки квалификации последовательно
распределяют для испытаний или измерений и возвращают провайдеру проверки
квалификации через определенные интервалы;
— параллельную программу,
когда образцы для проверки квалификации распределяют для выполнения
одновременных испытаний или измерений в течение определенного периода времени;
— единоразовое задание, когда
образцы проверки квалификации возможно предоставить только один раз;
— непрерывную программу,
когда образцы для проверки квалификации предоставляют через регулярные
интервалы времени;
— выборочный контроль, когда
выборки отбирают для последующего анализа, а цели программы проверки
квалификации включают оценку выполнения выборочного контроля;
—
интерпретацию данных, когда предоставляют наборы данных и обрабатывают другую
информацию для обеспечения их интерпретации (или получения иного результата).
3.3 приписанное значение (assigned
value): Значение, приписываемое конкретному свойству образца для
проверки квалификации.
3.4 стандартное отклонение для оценки квалификации (standard deviation for proficiency assessment): Мера
рассеяния, используемая при оценке результатов проверки квалификации.
Примечание 1 — Стандартное отклонение может быть
интерпретировано как стандартное отклонение результатов, полученных некоторой
гипотетической совокупностью лабораторий, работающих в точном соответствии с
установленными требованиями.
Примечание 2 — Стандартное отклонение для оценки квалификации
применяют только к результатам, полученным по шкале отношений или шкале
разности.
Примечание 3 — Не
во всех программах проверки квалификации оценка квалификации основана на
анализе рассеяния результатов.
[ГОСТ
ISO/IЕС 17043-2013]
3.5 погрешность измерений (measurement
error): Разность между результатом и опорным значением величины.
3.6 максимально допустимая погрешность (maximum permissible error): Максимальное значение погрешности
измерений по отношению к известному опорному значению величины, разрешенное
процедурами спецификации или нормативными документами для данного метода
(методики) измерений, средства измерений или измерительной системы.
3.7 z-индекс (z-score): Стандартизованная мера
характеристики функционирования, вычисленная с использованием результата
измерений участника, приписанного значения и стандартного отклонения для оценки
квалификации.
Примечание — Общая вариация z-индекса
(иногда обозначается z’ и произносится z-штрих)
формируется путем объединения неопределенности приписанного значения со
стандартным отклонением для оценки квалификации до вычисления z-индекса.
3.8 Дзета-индекс (Zeta score):
Стандартная мера характеристики функционирования, вычисленная с использованием
результата измерений участника, приписанного значения и суммарной стандартной
неопределенности результата и приписанного значения.
3.9 доля допустимого предельного индекса (proportion of allowed limit score): Стандартизованная мера
характеристики функционирования, вычисленная с использованием результатов
участника, приписанного значения и критерия для погрешности измерений при
проверке квалификации.
Примечание — Для единичных результатов характеристика
функционирования выражена в виде отклонения от приписанного значения (D или D %).
3.10 сигнал к действиям (action
signal): Признак, указывающий на то, что по результатам проверки
квалификации необходимо выполнить какие-либо действия.
Пример
— Значение z-индекса более двух
подразумевает необходимость проведения анализа возможных причин происходящего, а
значение индекса равное трем — выполнения корректирующих
действий.
3.11 согласованная величина (consensus
value): Величина, полученная на основе набора результатов при
межлабораторных сравнительных испытаниях.
Примечание — Термин «согласованная величина» обычно используют
для описания оценок параметров положения и разброса, полученных по результатам
участников раунда в межлабораторных сравнительных испытаниях, но может быть
также использован для значений, полученных по результатам установленного
подмножества таких результатов или, например, ряда экспертных лабораторий.
3.12 выброс (outlier):
Наблюдение в совокупности, которое признано несовместимым с остальными членами
совокупности.
Примечание 1 — Выброс может появиться за счет случайности из
рассматриваемой совокупности, принадлежать другой совокупности, быть
результатом некорректной записи или грубой ошибки.
Примечание 2 — Во
многих программах проверки квалификации термин «выброс» используют для
обозначения сигнала к действиям. Но это не всегда так. Сигнал к действиям может
появиться и при отсутствии выбросов.
[ГОСТ
Р ИСО 5725-1:2002, добавлено
примечание]
3.13 участник (participant):
Лаборатория, организация или физическое лицо, которые получают образцы для
проверки квалификации и представляют результаты на рассмотрение провайдеру
проверки квалификации.
3.14 образец для проверки квалификации (proficiency test item): Проба, продукт, искусственный объект
(артефакт), стандартный образец, часть оборудования, эталон, набор данных или
другая информация, используемые для проверки квалификации.
Примечание — В большинстве случаев термин «образец для проверки
квалификации» соответствует определению термина «стандартный образец».
3.15 провайдер проверки квалификации1) (proficiency testing provider): Организация, которая несет
ответственность за все задачи по разработке и выполнению программы проверки
квалификации.
__________
1) Синонимом является
термин «провайдер межлабораторных сличительных испытаний».
3.16 программа проверки квалификации (proficiency testing scheme): Процедура проверки квалификации,
разработанная и реализованная за один или несколько раундов в определенной
области испытаний, измерений, калибровки или контроля.
Примечание — Программа проверки квалификации может охватывать
конкретный вид испытаний, калибровки, контроля или ряд испытаний, калибровок
или контрольных операций на образцах для проверки квалификации.
3.17 стандартный образец; RM
(reference material, RM):
Материал (вещество), достаточно однородный и стабильный по отношению к одному
или нескольким определенным свойствам для того, чтобы использовать его в
соответствии с назначением в измерительном процессе.
Примечание 1 — Стандартный образец — общее понятие.
Примечание 2 — Свойства могут быть охарактеризованы количественными
или качественными величинами (например, идентичность веществ или категорий).
Примечание 3 — Использование может включать калибровку
(градуировку) измерительной системы, определение пригодности методики
измерений, приписывание значений свойств другим материалам и контроль качества.
3.18 сертифицированный стандартный образец1);
CRM (certified
reference material, CRM): Стандартный образец,
одно или несколько определенных свойств которого установлены метрологически
обоснованной процедурой, сопровождаемый паспортом, в котором приведено значение
этого свойства, связанной с ним неопределенности и утверждение о
метрологической прослеживаемости.
__________
1) Синонимом является
термин «аттестованный стандартный образец».
Примечание — Термин «значения» охватывает как количественные,
так и качественные характеристики, такие как идентичность или
последовательность. Неопределенность такой характеристики может быть выражена с
помощью вероятности или уровня доверия.
4 Основные принципы
4.1 Основные требования к статистическим методам
4.1.1 Используемые статистические методы должны
соответствовать целям и быть статистически обоснованными. Все статистические
предположения, на которых основаны методы или планы проверки, должны быть
указаны в программе проверки квалификации, и их применение должно быть
обосновано.
Примечание — Статистически обоснованный метод имеет прочную
теоретическую основу, известные свойства в ожидаемых условиях использования, и
опирается на предположения или условия, при которых данные могут быть применены
для целей обработки.
4.1.2 Статистические методы планирования эксперимента и
анализа данных должны соответствовать целям программы проверки квалификации.
4.1.3 Провайдер проверки квалификации должен предоставить
участникам описание используемых методов расчета, объяснение общей
интерпретации результатов, а также обоснование всех ограничений, касающихся
интерпретации результатов. Эта информация должна быть представлена в каждом
отчете для каждого раунда программы проверки квалификации или в отдельных
процедурах и должна быть доступной для участников.
4.1.4 Провайдер проверки квалификации должен гарантировать,
что все программное обеспечение является адекватным.
4.2 Базовая модель
4.2.1 Если в программах проверки
квалификации для заданного образца результатом проверки квалификации является
единственный результат, представляющий собой количественную величину, то
базовая модель имеет вид:
|
|
(1) |
где —
результат проверки квалификации i-го участника;
— истинное значение измеряемой
величины;
—
погрешность измерений i-го участника,
подчиняющаяся распределению в соответствии с моделью.
Примечание 1 — Общие модели для ε включают: нормальное
распределение со средним,
равным 0, и дисперсией, одинаковой или различной для каждой лаборатории; более
общие модели включают «загрязненное (с выбросом)» нормальное распределение,
представляющее собой сочетание нормального распределения с распределением,
представляющим собой совокупность ошибочных результатов.
Примечание 2 — Основой модели сравнительной оценки с
использованием z-индексов и является
предположение о том, что в «идеальной» генеральной совокупности квалифицируемых
лабораторий межлабораторное стандартное отклонение должно быть или меньше.
Примечание 3 — Данная модель отличается от базовой модели,
установленной в стандартах серии ГОСТ Р ИСО 5725, так как она не
использует термин «лабораторное смещение» . Это происходит потому, что термины «лабораторное
смещение» и «остаточная погрешность» не могут быть применены в случае
единственного наблюдения. Однако если рассматривают результаты участников в
нескольких раундах или при проверке используют несколько образцов, может быть
полезно включение лабораторного смещения.
4.2.2 Для порядковых или качественных результатов могут быть
использованы другие модели или вообще отсутствовать необходимые статистические
модели.
4.3 Общие подходы к сравнительной оценке результатов
4.3.1 Существуют три различных общих
подхода к оценке показателей в программе проверки квалификации. Применение того
или иного подхода зависит от целей программы проверки квалификации. Ниже
перечислены эти подходы, как то оценка показателя на основе сопоставления:
a) с независимо выведенным
критерием;
b) показателями других участников;
c) заявленной
неопределенностью результатов измерений.
4.3.2 Для определения приписанного значения и определения
критерия сравнительной оценки общие подходы могут быть использованы по-разному.
Например, если приписанное значение является робастным средним участника и
сравнительную оценку выполняют на основе или
и ,
где —
заранее определенная допустимая погрешность измерений и .
Аналогично, в некоторых случаях приписанное значение может быть опорным
значением, a —
робастным стандартным отклонением результатов участника. В подходе с) 4.3.1, использующем неопределенность измерений,
приписанное значение обычно соответствует опорному значению.
5 Руководство по
планированию эксперимента для программ проверки квалификации
5.1 Введение
Проверка квалификации связана с оценкой показателей
участников и по существу не связана со смещением или прецизионностью (хотя и
они могут быть оценены в некоторых конкретных случаях). Показатели участников
оценивают с помощью статистической сравнительной оценки их результатов на
основе измерений или интерпретаций, которые они выполняют на образцах при
проверке квалификации. Показатель часто выражают в виде индексов, которые дают
возможность единой интерпретации результатов измерений, позволяя тем самым
сопоставлять различные результаты измерений с единой базой. Индекс обычно
определяют на основе сопоставления разности полученного результата участника,
зафиксированного в отчете, и приписанного значения со стандартным отклонением
или с оценкой неопределенности результатов измерений. Анализ индексов за
несколько раундов программы проверки квалификации может дать информацию,
свидетельствующую о наличии систематических ошибок (смещений) или низкой
долговременной прецизионности в лабораториях.
В разделах 5
— 10 приведены
рекомендации по разработке программ проверки квалификации и статистической
обработке результатов для количественных величин, включая вычисление и
интерпретацию различных индексов. В разделе 11 приведены
рекомендации для качественных программ проверки квалификации, включая программы
с порядковыми данными для количественных величин.
5.2 Основы статистического планирования эксперимента
5.2.1 В соответствии с 4.4.4.1 ГОСТ
ISO/IEC 17043-2013 «следует разработать методы статистического
планирования эксперимента, отвечающие целям программы проверки квалификации,
учитывающие тип данных (качественные или количественные, включая порядковые и
категоризированные данные), статистические предположения, особенности ошибок и
ожидаемое количество результатов». Следовательно, в программах проверки
квалификации с различными целями и источниками ошибок следует применять
различные планы эксперимента.
Ниже приведены планы эксперимента для общих целей. Но другие
цели также возможны.
Пример 1
— Для программы проверки квалификации, в которой сопоставляют результаты
участников с предварительно определенным опорным значением в пределах границ,
которые устанавливают до начала раунда, для планирования эксперимента требуются
метод получения внешне определенного опорного значения, методы установления
границ и расчета индексов.
Пример 2
— Для программы проверки квалификации, в которой сопоставляют результаты
участников с комбинированными результатами группы в одном и том же раунде и
границами, которые устанавливают до начала раунда, для планирования
эксперимента необходимо предусмотреть определение приписанного значения по
комбинированным результатам, а также метод установления границ и метод
индексов.
Пример 3
— Для программы проверки квалификации, в которой сопоставляют результаты
участников с комбинированными результатами группы в одном и том же раунде и
границами, определенными на основе изменчивости результатов участников,
необходимо рассмотреть расчеты приписанного значения и соответствующей меры разброса,
а также метод определения индекса.
Пример 4
— Для программы проверки квалификации, в которой сопоставляют результаты
участников с приписанным значением, полученным на основе их собственной
неопределенности, при планировании эксперимента, необходимо рассмотреть способ
получения приписанного значения и его неопределенности и использование
неопределенности измерений участников при получении индекса.
Пример 5
— Для программы проверки квалификации с целью сопоставления различных
методов измерений при планировании эксперимента, необходимо рассмотреть
соответствующие обобщенные статистики и процедуры их вычисления.
5.2.2 При проверке квалификации
используют различные типы данных, включая количественные, номинальные
(категоризированные) и порядковые. Для количественных переменных некоторые
результаты могут быть определены по интервальной или относительной шкале либо
шкале отношений. В некоторых случаях при измерении количественных величин могут
быть получены только дискретные или прерывистые наборы данных (например, при
последовательном разбавлении), однако во многих случаях эти данные могут быть
обработаны с помощью методов, применяемых к непрерывным данным.
Примечание 1 — Интервальная шкала для количественных величин
представляет собой шкалу, на которой можно определить интервалы (разности)
значений, но нельзя определить отношения величин, например, шкала Цельсия. Для
шкалы отношений значимыми являются как интервалы, так и отношения величин,
например, шкала Кельвина или наиболее общие единицы измерения длины.
Примечание 2 — Для качественных величин применяют классификацию
по категориям, при этом упорядочивание значений не имеет смысла, например,
упорядочивание наименований видов бактерий. Для порядковой шкалы порядок
расположения величин имеет значение, но разности между ними не могут быть
определены, например, такие понятия, как «большая, средняя, маленькая
величины», могут быть упорядочены, но разность между величинами не может быть
определена, кроме как в виде промежуточных значений.
5.2.3 Кроме того, программы проверки квалификации могут быть
использованы для других целей (см. 0.1 ГОСТ
ISO/IEC 17043-2013). Для всех установленных целей конкретной программы
проверки квалификации должен быть определен подходящий план эксперимента.
5.3 Анализ статистического распределения результатов
5.3.1 В соответствии с 4.4.4.2 ГОСТ
ISO/IEC 17043-2013 методы статистического анализа данных должны быть
согласованы со статистическими предположениями относительно данных. Большая
часть методов общего статистического анализа данных, используемых при проверке
квалификации, предполагает, что набор результатов участников подчиняется
приблизительно нормальному распределению или, по крайней мере, унимодальному и
достаточно симметричному либо результаты могут быть преобразованы к таким
данным. Общее дополнительное предположение состоит в том, что распределение
результатов измерений представляет собой смесь, включающую результаты из
совокупности ошибочных измерений, являющихся выбросами. Обычно интерпретация в
баллах основана на предположении о нормальности распределения, но только для
основного предполагаемого распределения для компетентных участников.
5.3.1.1 Как правило, нет необходимости в проверке того, что
результаты принадлежат нормальному распределению, но очень важно проверить
(хотя бы визуально) симметричность распределения. Если нельзя проверить
симметричность плотности распределения, то провайдеру проверки квалификации
следует использовать методы, которые устойчивы к асимметрии плотности распределения
(см. приложение C).
5.3.1.2 Если ожидаемое распределение для программы проверки
квалификации не является достаточно симметричным (с учетом загрязнения
выбросами), провайдер программы квалификации должен выбрать методы анализа
данных, которые учитывают ожидаемую асимметрию и устойчивы к выбросам, и методы
расчета индексов, учитывающие особенности ожидаемого распределения результатов
участников.
Такие методы могут включать:
— преобразование, обеспечивающее переход к приближенно
симметричному распределению;
— методы оценки, устойчивые к асимметрии распределения;
— методы оценки, учитывающие предположения о распределении
(например, метод максимального правдоподобия, подходящий для предполагаемого
распределения, при необходимости — исключение выбросов).
Пример 1
— Результаты, полученные на основе разбавления растворов, например при
расчетах в микробиологических исследованиях или в методах анализа
иммунологического статуса, часто имеют логарифмически нормальное распределение,
и первым этапом анализа данных может быть их логарифмическое преобразование.
Пример 2
— Результаты подсчета небольшого количества частиц могут быть
распределены в соответствии с распределением Пуассона, и поэтому критерии
оценки могут быть определены по таблицам вероятностей Пуассона, на основе
расчета среднего для группы участников.
5.3.1.3 В некоторых случаях калибровки результаты участников
могут иметь распределение, описанное в процедуре выполнения измерений
(например, экспоненциальное, прямоугольное, треугольное или другое
распределение); это распределение следует указывать во всех протоколах оценки.
5.3.2 В соответствии с 4.4.4.2 ГОСТ
ISO/IEC 17043-2013 провайдер проверки квалификации должен обосновать
все используемые статистические предположения. Эти доказательства могут быть
основаны, например, на данных наблюдений, результатах предыдущих раундов
программы проверки квалификации или технической литературе.
Примечание — Обоснование предположений о виде распределения
является менее строгим, чем доказательство справедливости этого предположения.
5.4 Исследования для небольшого количества участников
5.4.1 План эксперимента для программы проверки квалификации
должен устанавливать минимальное количество участников, необходимых для
достижения поставленных целей, а также альтернативные подходы в том случае,
если количество участников будет недостаточным [см. 4.4.4.3, перечисление b) ГОСТ
ISO/IEC 17043-2013]. Статистические методы, которые подходят для
большого количества участников, не следует применять при недостаточном
количестве участников. Опасность состоит в том, что результаты, определяемые
при небольшом количестве участников, могут быть недостаточно достоверными, а
оценка участника может быть сопоставлена с группой, неподходящей для сравнения.
Примечание — В [2]
приведены полезные рекомендации для программ проверки квалификации с небольшим
количеством участников. Приписанное значение рекомендуется устанавливать на
основе независимых достоверных измерений: например, на основе использования
сертифицированных стандартных образцов, независимо от назначенного посредством
калибровки национальным метрологическим институтом, или с помощью
гравиметрической подготовки образцов. Кроме того, стандартное отклонение для
оценки квалификации не может быть определено на основе наблюдаемого разброса
результатов участников одного раунда программы проверки квалификации.
5.4.2 Минимальное количество участников, необходимое для
выполнения различных статистических методов, зависит от различных ситуаций, в
частности:
— используемых статистических методов, например, робастных
методов или выбранной стратегии удаления выбросов;
— опыта участников конкретной программы проверки
квалификации;
— опыта работы провайдера проверки квалификации с матрицами,
измеряемыми величинами, методами или группой участников;
— определения приписанного значения и стандартного
отклонения или того и другого.
Дальнейшие рекомендации по методам обработки результатов при
небольшом количестве участников приведены в D.1 приложения
D.
5.5 Рекомендации по выбору формы отчета
5.5.1 В соответствии с 4.6.1.2 ГОСТ
ISO/IEC 17043-2013, провайдеры проверки квалификации должны
предоставить участникам подробные инструкции по выполнению измерений и
оформлению отчета о результатах проверки квалификации так же, как для
большинства повседневно выполняемых измерений, за исключением особых случаев.
Это требование в некоторых ситуациях может затруднить
получение точной оценки прецизионности и правильности измерений участников или
квалификации при выполнении процедуры измерений. Провайдер проверки
квалификации должен установить форму отчета для программы проверки
квалификации, но, по возможности, использовать единицы измерений, знакомые
большинству участников, и выбрать форму отчета, минимизирующую ошибки при
переписывании данных и другие ошибки. Может быть установлено автоматическое
предупреждение об использовании ненадлежащих единиц измерения.
Примечание 1 — Целью некоторых программ проверки квалификации
является оценка способности участника выполнять стандартный метод, использующий
определенную единицу измерений или конкретное количество значащих цифр.
Примечание 2 — Количество ошибок переписывания при сборе данных
можно существенно уменьшить или совсем устранить за счет использования
электронных систем отчетности, которые позволяют участникам вводить свои данные
самостоятельно.
5.5.2 Если программа проверки квалификации требует выполнения
репликаций измерений на образцах, используемых при проверке квалификации,
участник обязан внести в отчет все результаты репликаций измерений. Это может
потребоваться в том случае, когда надо оценить прецизионность измерений
участника на репликациях измерений известных образцов для проверки квалификации
или когда для процедуры измерений необходимо выделить отчет о многократных
наблюдениях. В таких ситуациях провайдер проверки квалификации также может
попросить участника сообщить выборочное среднее своих результатов (или другую
оценку параметра положения) и неопределенность измерений для анализа данных.
5.5.3 Если результаты в отчете записывают в виде «больше»
или «меньше» ограничения (например, уровень калибровки или ограничение
количественной величины) или если числовые результаты необходимы для оценки в
виде индексов, провайдер должен определить, каким образом результаты должны
быть обработаны.
5.5.3.1 Для цензурированных данных (см. E.1
приложения E)
провайдер должен либо принять утвержденные процедуры обработки данных и
определения индексов, либо требовать от участников результаты измерений вместо
или в дополнение к обычно фиксируемым в отчете значениям.
Примечание 1 — Процедуры обработки индексов могут не учитывать
такие данные.
Примечание 2 — Требования участников о фиксировании в отчете
числовых значений вне диапазона обычно указываемых значений (например, ниже
границы числовых значений) позволят использовать статистические методы, но
могут приводить к определению индексов, которые не отражают уровень
обслуживания участником потребителей.
5.5.3.2 Если при использовании согласованных статистик
цензурированных значений достаточно много, может оказаться невозможно выполнить
оценку, так как эти данные влияют на робастность метода. В тех случаях, когда
количество цензурированных результатов достаточно велико и влияет на
робастность метода, результаты должны быть оценены с использованием статистических
методов, которые позволяют получить несмещенную оценку при наличии
цензурированных данных [3], или
результаты не должны быть оценены. В случае сомнений относительно выбранной процедуры
провайдеру проверки квалификации необходимо рассчитать суммарные статистики и
оценки показателей в соответствии с каждой альтернативной статистической
процедурой, потенциально применимой в данной ситуации, и исследовать значимость
различий полученных оценок.
5.5.3.3 Если ожидаются или
наблюдаются цензурированные результаты, такие как «меньше заявленного
значения», в план эксперимента программы проверки квалификации следует включать
положения для определения индексов и/или производить другие действия с
цензурированными данными, сообщаемыми участниками, а участники должны быть
уведомлены об этих положениях.
Примечание — В E.1 приложения E приведен пример некоторых подходов к анализу цензурированных данных. В
этом примере показаны робастные согласованные статистики с тремя различными
подходами: с удалением цензурированных данных, с заменой цензурированных данных
на максимальные значения (указываемые после знака «<») и с заменой
цензурированных данных на половину максимальных значений.
5.5.4 Как правило, количество значащих цифр, указанных в
отчете, определяют при разработке плана эксперимента программы проверки
квалификации.
5.5.4.1 При определении количества значащих цифр,
указываемых в отчете, необходимо обеспечить, чтобы ошибка округления была
пренебрежимо малой по сравнению с ожидаемыми вариациями результатов участников.
Примечание — В некоторых ситуациях корректный отчет является
частью определения квалификации участника, а количество значащих цифр и знаков
после запятой может быть различным.
5.5.4.2 Если количество значащих цифр, указанное участником
в отчете о результатах измерений в обычных условиях, затрудняет обработку
данных провайдером (например, когда в соответствии с процедурой измерений
необходимо фиксировать небольшое количество значащих цифр), провайдер проверки
квалификации может сообщить участнику количество значащих цифр, которые
требуется указать.
Пример
— В процедуре измерений установлено, что результаты измерений можно
указывать с точностью до 0,1 ,
что приводит к появлению большого количества (> 50 %) одинаковых результатов
измерений и таким образом к неправильному расчету робастных средних и
стандартных отклонений. Поэтому провайдер проверки квалификации может
потребовать от участников указывать в отчете результаты измерений с точностью
до 2-го или 3-го знака после запятой для получения достаточно достоверных
оценок параметров положения и разброса.
5.5.4.3 Если допускается, что различные участники фиксируют
в отчете результаты измерений с указанием различного количества значащих цифр,
провайдеру проверки квалификации следует принять это во внимание при
определении согласованных статистик (таких как приписанное значение и стандартное
отклонение для оценки квалификации).
6 Предварительный анализ образцов и результатов при
проверке квалификации
6.1 Однородность и стабильность
образцов при проверке квалификации
6.1.1 Провайдер проверки квалификации
должен гарантировать, что партии образцов для проверки квалификации являются
достаточно однородными, стабильными и пригодными для целей программы проверки
квалификации. Провайдер должен оценить однородность и стабильность образцов с
использованием критериев, позволяющих гарантировать, что неоднородность и
нестабильность образцов не оказывают отрицательного влияния на оценку работы
участника. При оценке однородности и стабильности следует использовать один или
несколько из следующих подходов:
a)
экспериментальные исследования, описанные в приложении B, или альтернативные
экспериментальные методы, которые обеспечивают равную им или большую
уверенность в однородности и стабильности образцов;
b) использование аналогичных
образцов в предыдущих раундах программы проверки квалификации, подтверждающие
приемлемость образцов для текущего раунда;
c) оценка
данных участников в текущем раунде программы проверки квалификации для
доказательства согласованности с предыдущими раундами, то есть для доказательства
возможных изменений после подготовки отчета или в порядке производства и всех
неожиданных отклонений, характерных для неоднородности или нестабильности.
Примечание 1 — Эти подходы могут быть применены с использованием
соответствующих статистических методов и технического обоснования для каждого
подхода. В течение срока действия программы проверки квалификации подход может
быть применен многократно, накопленный опыт со временем снижает первоначальную
потребность в экспериментальных исследованиях.
Примечание 2 —
Эксперимент [см. перечисления а) — с)] является разумной основой до тех
пор, пока выполняются следующие требования:
1 В процессе изготовления
партий образцов для проверки квалификации не возникают изменения, которые могут
повлиять на однородность образцов.
2 Материалы, используемые в
производстве образцов для проверки квалификации, не изменяются таким образом,
что могут повлиять на однородность образцов.
3 Не появляются нарушения
однородности, выявленные с помощью проверки на однородность или по реакции
участников.
4
Требования к однородности материала регулярно анализируют с учетом
предполагаемого использования материала при проведении анализа, чтобы
гарантировать, что однородность, достигнутая за счет производственного
процесса, остается пригодной для целей проверки квалификации.
Пример
— Если в предыдущих раундах программы проверки квалификации использованы
проверенные образцы, которые были в наличии, и продемонстрировано, что их
однородность и стабильность являются достаточными, и участники проверки не
изменились в новом раунде, то, если межлабораторное стандартное отклонение в
текущем раунде не превышает стандартного отклонения в предыдущих раундах, это
является доказательством достаточной однородности и стабильности образцов в
текущем раунде.
6.1.2 Для программ проверки квалификации при калибровке,
когда один и тот же артефакт используют несколько участников, провайдер
проверки квалификации должен гарантировать его стабильность в течение всего
раунда или иметь процедуры идентификации и оценки его нестабильности в процессе
выполнения раунда программы проверки квалификации. Необходимо также исследовать
тенденции изменения отдельных образцов и измеряемых величин, такие как дрейф.
По возможности для уверенности в стабильности следует учитывать влияние
использования одинаковых артефактов из различных партий.
6.1.3 Все результаты измерений величин
(или свойств) должны быть проверены на однородность и стабильность. Однако если
показано, что некоторое подмножество свойств может обеспечить хорошую индикацию
однородности и стабильности для всех наблюдаемых свойств в этом раунде,
программы проверки квалификации оценки, описанные в 6.1.1, могут быть ограничены этим подмножеством
свойств. Проверяемые измеряемые величины должны быть чувствительными к
источникам неоднородности и нестабильности в процессе работы с образцами для
проверки квалификации. Некоторые важные случаи:
a) если результатом измерений
является доля, характерная особенность которой ее небольшое значение, эта
величина может быть трудно управляемой и более чувствительной к изменениям
однородности;
b) если испытуемый образец
нагревается во время работы с ним, то в качестве измеряемой величины следует
выбрать величину, чувствительную к неравномерному нагреву;
c) если измеряемая величина
характеризует свойство, зависящее от отстаивания, выпадения осадка и других
явлений, зависящих от времени подготовки образца, то это свойство следует
проверять косвенным способом.
Пример
— В программе проверки квалификации при определении содержания токсичных
металлов в почве результат зависит от влажности образца почвы. Последовательная
проверка содержания влаги в почве может быть признана достаточной для
обеспечения адекватной стабильности содержания токсичных металлов.
Примечание — Пример проверки на однородность и стабильность с
использованием статистических методов, рекомендованных в приложении B, приведен в E.2 приложения E.
6.2 Анализ различных методов
измерений
6.2.1 Если все участники проверки должны сообщать значение
одной и той же измеряемой величины, приписанное значение обычно должно быть
одинаковым для всех участников. Но если участникам предоставлен выбор
собственного метода измерений, то возможно, что единственное приписанное
значение для каждого исследуемого вещества или свойства не будет подходить для
всех участников. Однако существует вероятность того, что при использовании
различных методов измерений результаты будут несопоставимыми. В этом случае
провайдер проверки квалификации может использовать для каждого метода измерений
свое приписанное значение.
Примеры
a) Медицинские исследования, в
которых при установлении диагноза для одного и того же исследуемого материала
различные методы измерений дают различные результаты и имеют различные
диапазоны нормальных значений.
b)
Оперативно определяемые измеряемые величины, такие как выщелачиваемые токсичные
металлы в почвах, для которых доступны различные стандартные методы измерений и
прямое сравнение величин не предполагается, по программе проверки квалификации
устанавливают без ссылки на установленный метод испытаний.
6.2.2 При разработке программы проверки квалификации следует
рассматривать необходимость использования различных приписанных значений
(например, сделать заготовки для отчетов по конкретным методам), а также при
анализе данных по каждому раунду.
6.3 Удаление грубых ошибок
6.3.1 В B.2.5 ГОСТ
ISO/IEC 17043-2013 и согласованом протоколе IUPAC рекомендуют
удалять очевидные грубые ошибки из набора данных на ранней стадии анализа данных
перед использованием любой робастной процедуры или любого теста по выявлению
статистических выбросов. Как правило, эти результаты следует рассматривать
отдельно (например, по согласованию с участником). Некоторые грубые ошибки
можно исправить, но это должно быть сделано только в соответствии с
утвержденной политикой и процедурами.
Примечание — Очевидные грубые ошибки, такие как результаты,
указанные в отчете в неправильных единицах измерений, спутанные результаты
различных образцов, возникают в большинстве раундов проверки квалификации, и
эти результаты только ухудшают применение последующих статистических методов.
6.3.2 При наличии подозрений в том, что результат является
грубой ошибкой, он должен быть сохранен в наборе данных и подвергнут последующей
обработке в соответствии с 6.4 — 6.6.
6.4 Визуальный анализ данных
6.4.1 В качестве первого этапа анализа данных провайдер
должен организовать визуальный анализ данных, проводимый человеком, имеющим
адекватные технические и статистические знания и опыт. Этот анализ необходим
для подтверждения ожидаемого распределения результатов, а также для выявления
аномалий или непредвиденных источников изменчивости. Например, бимодальное
распределение может быть свидетельством того, что данные представляют собой
смесь результатов из различных совокупностей, полученных различными методами,
или использования загрязненных проб, или применения плохо сформулированных
инструкций. Эта ситуация должна быть разрешена до выполнения анализа или
оценки.
Примечание 1 — Наиболее полезным и широко доступным способом
определения вида распределения является гистограмма. Она позволяет определить
унимодальность и симметричность распределения, а также выявить необычные
выбросы (см. 10.2). Однако
интервалы, используемые для составления гистограммы, и количество результатов в
интервале влияют на качество гистограммы, при небольшом количестве точек
гистограммы ее может быть трудно построить. Более полезным для выявления
возможной бимодальности или отсутствия симметрии является график плотности (см.
подраздел 10.3).
Примечание 2 — Также могут быть полезны и другие методы,
например, график кумулятивной функции распределения или диаграмма «стебель с
листьями». Некоторые графические методы анализа данных приведены в E.3 и E.4 приложения E.
6.4.2 Если проведение визуального анализа всех наборов
данных невозможно, должна быть предусмотрена процедура предупреждения появления
неожиданной вариации в наборе данных, например с помощью сравнительного анализа
неопределенности приписанного значения и ее сопоставления с критериями или с
предыдущими раундами программы проверки квалификации.
6.5 Робастные статистические методы
6.5.1 Робастные статистические методы
могут быть использованы для описания центральной части нормального
распределения набора результатов без идентификации выбросов и исключения их из
последующего анализа. На 1-м этапе большинство используемых робастных методов в
качестве параметров применяют оценки медианы и размаха для центральных 50 %
результатов — это показатели положения центра и разброса данных, аналогичные
среднему и стандартному отклонению. В общем случае при проведении анализа надо
отдавать предпочтение робастным методам, а не тем, для которых перед
использованием требуется удаление выбросов.
Примечание — Стратегии, которые используют классические
статистики, такие как стандартное отклонение, после удаления выбросов, как
правило, приводят к заниженной оценке дисперсии для приблизительно нормальных
данных; робастные статистики, как правило, дают несмещенные оценки дисперсии.
6.5.2 В качестве простых оценок применимы медиана,
масштабированная медиана абсолютного отклонения MAD и нормированный межквартильный размах nlQR.
Алгоритм А преобразует исходные данные с помощью процесса, называемого
винсоризацией, для получения альтернативных оценок среднего и стандартного
отклонения для данных, не подчиняющихся нормальному распределению, и является
наиболее полезным, когда ожидаемая доля выбросов составляет менее 20 %. Методы и
для оценки стандартного отклонения (см. приложение C)
особенно полезны в той ситуации, когда в большинстве случаев (> 20 %)
результаты являются несоответствующими или когда специалисты не могут
достоверно проанализировать данные. Другие методы, описанные в приложении C, также
достаточно эффективны, если ожидаемая доля экстремальных значений составляет
более 20 % (см. приложение D).
Примечание — Медиана, среднее абсолютное отклонение,
межквартильный размах и масштабированная медиана абсолютного отклонения имеют
большую изменчивость, чем среднее и стандартное отклонения при применении к
данным, подчиняющимся распределению близкому к нормальному. Более сложные
робастные оценки дают более высокую эффективность для данных с распределением
близким к нормальному, обеспечивая при этом большую устойчивость при
использовании выбросов за счет использования медианы и межквартильного размаха.
6.5.3 Выбор статистических методов является обязанностью
провайдера проверки квалификации. Робастные среднее и стандартное отклонения
могут быть использованы для различных целей, оценка работы участников — лишь
одна из них. Робастные средние и стандартные отклонения могут быть также
использованы в качестве общих статистик для различных групп участников или для
конкретных методов.
Примечание — Более подробно робастные процедуры описаны в
приложении C. В E.3 и E.4 приложения E приведены примеры, иллюстрирующие использование
робастных статистических методов, приведенных в приложении C.
6.6 Методы работы с выбросами для
индивидуальных результатов
6.6.1 Проверка на выбросы может быть использована при
визуальном анализе аномальных значений или в случае исключения выброса для
обеспечения устойчивости к экстремальным значениям при вычислении общих
статистик. При использовании методов выявления выбросов следует подтвердить
выполнение предположений, лежащих в их основе, чтобы обеспечить пригодность
этих методов для целей программы проверки квалификации, в частности многие
критерии используют предположение о нормальности распределения данных.
Примечание — В ГОСТ
Р ИСО 16269-4 и ГОСТ
Р ИСО 5725-2 приведено несколько процедур идентификации выбросов,
применимых к межлабораторным данным.
6.6.2 Если робастные методы не применяют (см. 6.5.1), то допускается использование
стратегии отклонения выбросов, которая основана на исключении из обработки
выбросов, обнаруженных с помощью соответствующих критериев с высоким уровнем
доверия, и дальнейшем применении простых статистик, таких как среднее и
стандартное отклонения. При использовании стратегий исключения выбросов
провайдер проверки квалификации должен:
a) документировать критерии и
уровень доверия, применяемые для выявления исключаемого выброса;
b) устанавливать ограничения на долю
исключенных данных при применении тестов выявления выбросов в случае их
использования;
c) демонстрировать, что полученные
оценки параметров положения и (при необходимости) масштаба обладают
достаточными свойствами (включая эффективность и смещение) для целей программы
проверки квалификации.
Примечание — В ГОСТ
Р ИСО 5725-2 приведены рекомендации по выбору уровня доверия,
подходящего для отклонения выбросов в межлабораторных исследованиях по
определению прецизионности методов испытаний. В частности, в соответствии с ГОСТ
Р ИСО 5725-2 рекомендуется исключать данные только в том случае, когда
при выявлении выброса был использован уровень доверия 99 %, если нет другого
основания отказаться от конкретного результата.
6.6.3 В тех случаях, когда исключение выброса является
частью процедуры обработки данных и результат удаляют как выброс, работу
участника тем не менее следует оценивать в соответствии с критериями,
используемыми для всех участников программы проверки квалификации.
Примечание 1 — Выбросы среди зарегистрированных значений часто
идентифицируют с помощью критерия Граббса для выявления выбросов в соответствии
с ГОСТ
Р ИСО 5725-2. Оценку в этой процедуре определяют с использованием
стандартного отклонения всех участников, включая возможные выбросы. Поэтому
данную процедуру необходимо применять, когда показатели работы участников
соответствуют ожиданиям, основанным на результатах предыдущих раундов, а
количество выбросов невелико (один или два выброса с каждой стороны среднего).
Обычные таблицы для критерия Граббса предполагают одно применение для
возможного выброса или два — для установленного параметра положения, но допустимо
последовательное применение этого критерия. Если таблицы Граббса применяют
последовательно, вероятности ошибки I рода для испытаний можно не применять.
Примечание 2 — Если результаты репликаций совпадают или если в
раунде программы проверки квалификации использованы идентичные образцы, это
является основанием для использования критерия Кохрена для повторяющихся
выбросов в соответствии с ГОСТ
Р ИСО 5725-2.
Примечание 3 — Выбросы также могут быть идентифицированы с
помощью робастных или непараметрических методов: например, если вычислены
робастное среднее и стандартное отклонение значения, отклоняющиеся от
вычисленного среднего более чем на три робастных стандартных отклонения, могут
быть идентифицированы как выбросы.
7
Определение приписанного значения и его стандартной неопределенности
7.1 Выбор метода определения приписанного значения
7.1.1 В 7.3 — 7.7 приведены пять методов определения
приписанного значения. За выбор метода отвечает провайдер проверки
квалификации.
Примечание — Подразделы 7.3
— 7.6 аналогичны подходам,
используемым для определения характеристик свойств сертифицированных
стандартных образцов, описанных в ГОСТ
ISO Guide 35.
7.1.2 Альтернативные методы определения приписанного
значения и его неопределенности могут быть использованы при условии, что они
имеют строгое статистическое обоснование, а используемый метод описан в
документированном плане для программы проверки квалификации, и это описание
полностью известно участникам. Независимо от метода, используемого для
определения приписанного значения, всегда целесообразно проверить
обоснованность выбора приписанного значения для конкретного раунда программы
проверки квалификации. Более подробное обсуждение этого положения приведено в 7.8.
7.1.3 Подходы к определению приписанных значений для
качественных данных рассмотрены в 11.3.
7.1.4 Метод определения приписанного значения и соответствующей
ему неопределенности должен быть указан в каждом отчете для участников или
четко описан в протоколе программы проверки квалификации, доступном всем
участникам.
7.2 Определение неопределенности приписанного значения
7.2.1 В руководстве по выражению неопределенности измерения ГОСТ
Р 54500.3 приведены рекомендации по оценке неопределенности. В ГОСТ
ISO Guide 35 представлены рекомендации по определению неопределенности
приписанного значения для аттестованных значений показателей свойств, которые
могут быть использованы при разработке многих программ проверки квалификации.
7.2.2 Общая модель приписанного значения и его
неопределенности описывается уравнениями (2)
и (3).
Модель приписанного значения
может быть рассчитана следующим образом:
|
|
(2) |
где —
приписанное значение;
—
показатель свойства, полученный при характеризации (определении приписанного
значения);
—
погрешность, вызванная различиями образцов для проверки квалификации;
—
погрешность, вызванная нестабильностью условий транспортирования;
—
погрешность, вызванная нестабильностью процесса проведения проверки
квалификации.
Соответствующая модель
неопределенности приписанного значения имеет вид:
|
|
(3) |
где —
стандартная неопределенность приписанного значения;
—
стандартная неопределенность, соответствующая характеризации;
—
стандартная неопределенность, связанная с различиями между образцами;
—
стандартная неопределенность, соответствующая нестабильности условий
транспортирования образцов;
—
стандартная неопределенность, соответствующая нестабильности процесса
проведения проверки квалификации.
Примечание 1 — Ковариация источников неопределенности или даже незначительных
источников неопределенности может привести к другой модели в конкретных
случаях. В некоторых ситуациях все компоненты неопределенности могут быть равны
нулю или ничтожно малы.
Примечание 2 — При расчете стандартного отклонения результатов
участников составляющие неопределенности, обусловленные неоднородностью,
условиями транспортирования и нестабильностью процесса проверки, в значительной
степени отражаются в изменчивости результатов участников. В этом случае
достаточно учитывать неопределенность характеризации в соответствии с 7.3 — 7.7.
Примечание 3 — Обычно предполагают, что провайдер проверки
квалификации гарантирует, что изменения,
связанные с нестабильностью процесса или условиями транспортирования образцов,
пренебрежимо малы по сравнению со стандартным отклонением для оценки
квалификации; то есть гарантируют, что и
пренебрежимо малы. Если это требование удовлетворено,
и
можно считать равными нулю.
7.2.3 Приписанное значение может иметь смещение, которое не
учтено в выражении (2). Это следует по возможности
учитывать при разработке программы проверки квалификации. Если проведена
корректировка смещения приписанного значения, то неопределенность,
соответствующая такой корректировке, должна быть включена в оценку
неопределенности приписанного значения.
7.3 Состав образцов
7.3.1 Образец для проверки квалификации может быть
подготовлен путем смешивания материалов с различными известными уровнями
содержания вещества в установленных пропорциях или добавления установленного
количества вещества к основному материалу.
7.3.1.1 Приписанное значение получают
путем расчета на основе содержания веществ в используемых материалах. Такой
подход особенно важен, когда отдельные образцы для проверки квалификации
подготовлены описанным способом и пропорции используемых материалов известны.
7.3.1.2 Следует предпринять необходимые действия для того,
чтобы обеспечить следующее:
a) основной материал должен быть
практически свободен от дополнительных компонентов, или их доли должны быть
точно известны;
b) компоненты должны быть смешаны до
однородности (если это необходимо);
c) все существенные источники ошибок
должны быть идентифицированы (например, не всем известно, что стекло поглощает
соединения ртути, так что концентрация соединения ртути в водном растворе может
измениться, если раствор находится в стеклянном контейнере);
d) не существует неблагоприятного
взаимодействия между компонентами и основным веществом;
e) свойства образцов для
квалификационных испытаний, содержащих дополнительный материал, должны быть
аналогичны свойствам образцов, обычно используемых заказчиком. Например, чистые
материалы, добавляемые к природной основе, часто извлечь легче из такой же
субстанции природного происхождения. Если существует возможность возникновения
такой ситуации, провайдер должен обеспечить пригодность образцов для
используемых методов проверки квалификации.
7.3.1.3 Если в образцах для проверки квалификации добавки
более слабо связаны, чем в обычно проверяемых образцах, или находятся в другой
форме, предпочтительнее использовать другой подход для подготовки образцов.
7.3.1.4 Определение приписанного значения по составу
материала образцов является одним из случаев общего подхода к характеризации
сертифицированных стандартных образцов, описанного в ISO
Guide 35, когда единственная лаборатория определяет приписанное
значение с использованием основного метода измерения. Существуют и другие
способы определения приписанного значения единственной лабораторией с помощью
основного метода (см. 7.5)
7.3.2 Если приписанное значение рассчитывают на основе
состава материала образцов для проверки квалификации, оценки стандартной
неопределенности определяют
с помощью сочетания неопределенностей, используемых в соответствующей модели. Например,
при проверке квалификации лабораторий, выполняющих химические измерения,
основными являются неопределенности, связанные с гравиметрическими измерениями,
измерениями объема и чистотой всех материалов, используемых при составлении
образца. Стандартную неопределенность приписанного значения рассчитывают
по уравнению (3).
7.4 Сертифицированный стандартный образец
7.4.1 Если образец для проверки
квалификации является сертифицированным стандартным образцом CRM, его сертифицированное значение используется
в качестве приписанного значения .
Ограничения такого подхода вызваны следующим:
— обеспечить каждого участника сертифицированным стандартным
образцом потребует больших средств;
— обеспечить долговременную стабильность образца часто очень
сложно, что может приводить к нецелесообразности замены образца;
— сертифицированные стандартные образцы могут быть известны
участникам, и поэтому важно скрыть их истинные характеристики.
7.4.2 При использовании CRM в качестве образца для проверки квалификации стандартную
неопределенность приписанного значения выводят из информации о
неопределенности, указанной в сертификате. Сертификат должен включать в себя
информацию о компонентах из уравнения (3) и
информацию о предполагаемом использовании образца для целей программы проверки
квалификации.
7.5 Результаты одной лаборатории
7.5.1 Приписанное значение может быть определено
единственной лабораторией с использованием эталонного метода, например,
основного метода. Используемый эталонный метод должен быть полностью описан и
понятен с утверждением полной неопределенности и документированной
метрологической прослеживаемостью, подходящей для целей программы проверки
квалификации. Эталонный метод должен быть совместим со всеми методами
измерений, используемыми участниками.
7.5.1.1 Приписанное значение рассчитывают как среднее
арифметическое, определяемое для двух или большего количества образцов или
условий измерений и при достаточном количестве репликаций измерений.
7.5.1.2 Неопределенность характеризации представляет собой
соответствующую оценку неопределенности для эталонного метода и условий
исследования в соответствии с планом эксперимента.
7.5.2 Приписанное значение образца
для проверки квалификации может быть получено с помощью единственной
лаборатории и посредством использования подходящего метода измерений по данным
калибровки на соответствие опорному значению, соответствующему
сертифицированному стандартному образцу.
Такой подход предполагает, что CRM совместим со всеми методами измерений, используемыми
участниками.
7.5.2.1 Это определение требует проведения серии испытаний,
проводимых в одной лаборатории, на образцах для проверки квалификации и CRM с использованием одного и
того же метода и в условиях повторяемости.
Если —
приписанное значение для CRM;
—
приписанное значение образца для проверки квалификации;
di — разность
между средним арифметическим результатов для образца проверки квалификации и CRM для i-го
образца;
— среднее арифметическое разностей di
тогда
|
|
(4) |
Примечание — и
независимы,
за исключением того редкого случая, когда CRM
получен экспертной лабораторией.
7.5.2.2 Стандартную
неопределенность характеризации выводят на основе неопределенности измерений,
используемых для определения приписанного значения. Такой подход позволяет
установить приписанное значение таким образом, чтобы была обеспечена
метрологическая прослеживаемость с сертифицированным значением CRM и стандартной
неопределенностью, полученной в соответствии с уравнением (5):
|
|
(5) |
Пример, приведенный в E.5 приложения E, показывает, как требуемая неопределенность
может быть вычислена в простом случае, когда приписанное значение образца для
проверки квалификации устанавливают прямым сопоставлением с единственным CRM.
7.5.3 Если опорное значение присваивают до начала раунда
последовательной программы проверки квалификации, а затем опорное значение
проверяют, используя туже измерительную систему, то разность полученных
значений должна быть меньше, чем удвоенная неопределенность этой разности (то
есть результаты должны быть метрологически совместимыми). В таких случаях
провайдер проверки квалификации может принять решение об использовании в
качестве приписанного значения среднего арифметического результатов измерений с
соответствующей неопределенностью. Если результаты не являются метрологически
совместимыми, провайдер должен исследовать причину различий и принять
соответствующие меры, включая использование альтернативных методов определения
приписанного значения и его неопределенности или прекращения раунда.
7.6 Согласованное значение по
данным экспертных лабораторий
7.6.1 Приписанное значение может быть определено с
применением межлабораторных сравнительных испытаний с привлечением экспертных
лабораторий в соответствии с ISO Guide 35 для
использования межлабораторного сравнения для характеризации CRM. Сначала подготавливают образцы для проверки
квалификации и распределяют их между участниками. Некоторые из этих образцов
отбирают случайным образом, и затем их анализирует группа экспертов с
использованием протокола, в котором устанавливают количество образцов и
репликаций и все другие соответствующие условия. Каждая эталонная лаборатория
должна обеспечить стандартную неопределенность своих результатов.
7.6.2 Если экспертные лаборатории
сообщают единственный результат и в соответствии с протоколом не требуется
обеспечить достаточную информацию о неопределенности результатов или при
наличии свидетельств либо предположении о недостаточной достоверности
полученной неопределенности, согласованная величина должна быть получена в
соответствии с методами, приведенными в 7.7,
применяемыми к набору результатов экспертных лабораторий. Если каждая из
экспертных лабораторий получает более одного результата (например, включая
репликации), провайдер в программе проверки квалификации должен установить
альтернативный метод определения приписанного значения, его неопределенности, и
допускать наличие выбросов или других отклонений от ожидаемого распределения
результатов, который должен быть статистически обоснованным.
(Поправка).
7.6.3 Если экспертные лаборатории вместе с результатами
измерений указывают их неопределенности, оценка приписанного значения путем
согласования результатов является сложной проблемой, и для ее решения
существует много подходов, включая, например, применение взвешенного среднего
арифметического, невзвешенного среднего арифметического, процедур, допускающих
большой разброс данных, и процедур, допускающих наличие выбросов или ошибочных
результатов и оценок неопределенности [4].
Провайдер проверки квалификации должен соответствующим образом установить
процедуру оценки, которая должна:
a) включать проверку достоверности
указанных оценок неопределенности, например, проверку соответствия в полной
мере указанной неопределенности наблюдаемому разбросу результатов;
b) использовать взвешенные процедуры
с весами, соответствующими степени достоверности и размеру указанной
неопределенности, например, равные веса в случае близких неопределенностей,
либо низкой или неизвестной достоверности (см. 7.6.2);
c) допускать возможность того, что
указанные неопределенности могут не в полной мере соответствовать наблюдаемому
(полному) разбросу, например, путем включения дополнительного члена;
d) допускать возможность появления
неожиданных удаленных значений в указанных результатах или неопределенностях;
e) иметь обоснованную теоретическую
основу;
f) иметь продемонстрированные
свойства (например, на данных испытаний или на моделях), необходимые для целей
программы проверки квалификации.
7.7 Приписанное значение на
основе согласованного значения результатов участников
7.7.1 При таком подходе приписанным значением для
образца, используемого в раунде программы проверки квалификации, является
оценка параметра положения (например, робастное среднее, медиана или среднее
арифметическое), сформированная на основе результатов, представленных
участниками раунда, и рассчитанная с использованием процедуры в соответствии с
планом эксперимента, приведенным в приложении C. Методы, описанные в 6.2 — 6.6, следует использовать до объединения результатов
для обеспечения достаточной согласованности результатов.
7.7.1.1 В некоторых случаях провайдер проверки квалификации
использует только группу участников, которые определены как надежные по
некоторым критериям, например, на основе статуса аккредитации или
предварительной работы. Методы настоящего подраздела применимы к таким
ситуациям, в том числе и к определению размера группы.
7.7.1.2 Вместо методов, приведенных в приложении C, могут
быть использованы и другие методы при условии, что они имеют статистическое обоснование
и указаны в отчете.
7.7.1.3 Преимущества такого подхода заключаются в том:
a) что для получения приписанного
значения никаких дополнительных измерений не требуется;
b) подход может быть особенно
полезен для стандартизованной, оперативно определяемой измеряемой величины, так
как часто нет более надежного способа получения равноценных результатов.
7.7.1.4 Недостатками данного подхода являются следующие:
a) между участниками могут
отсутствовать необходимые соглашения;
b) согласованное значение может
включать неизвестное смещение, вызванное общим использованием ошибочного
метода, и это смещение не будет учтено в стандартной неопределенности
приписанного значения;
c) согласованное значение может
иметь смещение вследствие применения методов, дающих смещение при определении
приписанного значения;
d) трудно определить метрологическую
прослеживаемость согласованного значения. Поскольку результат всегда связан с
результатами отдельных лабораторий, четкое установление прослеживаемости за их
пределами может быть обеспечено только тогда, когда провайдер проверки
квалификации имеет полную информацию об используемых калибровочных стандартах и
контролирует условия других соответствующих методов, применяемых всеми
участниками, участвующими в определении согласованного значения.
7.7.2 Стандартная неопределенность
приписанного значения зависит от используемой процедуры. Если требуется самый
общий подход, провайдер проверки квалификации должен рассмотреть вопрос об
использовании бутстреп-метода для оценки стандартной погрешности приписанного
значения. Подробное описание бутстреп-метода приведено в [5], [6].
Примечание — Пример использования бутстреп-метода приведен в E.6 приложения E.
7.7.3 Если
приписанное значение определяют на основе робастного среднего, вычисляемого с использованием
процедур, приведенных в C.2, C.3
или C.5 приложения C, оценку стандартной
неопределенности приписанного значения и ()
можно определить по формуле
|
|
(6) |
где —
робастное стандартное отклонение результатов. (Здесь «результатом» является
среднее арифметическое всех результатов измерений, выделенных на образце для
проверки квалификации.)
Примечание 1 — В данной модели, когда приписанное значение и
робастное стандартное отклонение определяют по результатам участников,
предполагается, что неопределенность приписанного значения включает влияние
неопределенностей, соответствующих неоднородности, условиям транспортирования и
нестабильности.
Примечание 2 — Значение коэффициента 1,25 выбрано на основе
стандартного отклонения медианы или эффективности медианы как оценки среднего в
большом наборе результатов, описываемых нормальным распределением. Следует
понимать, что эффективность более сложных робастных методов может быть намного
больше, чем методов, использующих медиану с поправочным коэффициентом менее
1,25. Тем не менее рекомендуется применять этот коэффициент, поскольку
результаты проверки квалификации, как правило, не подчиняются строго
нормальному распределению и содержат неизвестные доли результатов из различных
распределений («загрязненные результаты»). Коэффициент 1,25 обеспечивает
получение гарантированной (завышенной) оценки с учетом возможного загрязнения.
Провайдер проверки квалификации может обосновать использование меньшего
значения коэффициента или другого уравнения в зависимости от опыта и
используемой робастной процедуры.
Примечание 3 — Пример получения робастного среднего по
результатам участников приведен в E.3 приложения E.
7.8 Сопоставление приписанного
значения с независимым опорным значением
7.8.1 Если для установления приписанного значения используют
методы, приведенные в 7.7, при
наличии независимой оценки ,
например, из сведений о подготовке образцов или об опорном значении,
согласованное значение следует сопоставлять с .
Если для установления приписанного значения используют
методы, приведенные в 7.3 — 7.6, робастное среднее арифметическое полученное
по результатам раунда, следует сопоставлять с приписанным значением после
каждого раунда программы проверки квалификации.
Стандартную неопределенность
разности или
определяют
в следующем виде:
|
|
(7) |
где —
неопределенность опорного значения для сопоставления;
—
неопределенность приписанного значения.
Примечание — Пример сопоставления опорного значения с
согласованным значением включен в E.7 приложения E.
7.8.3 Если разность больше удвоенной соответствующей ей
неопределенности, следует исследовать возможные причины этого явления.
Возможными причинами могут быть:
— наличие смещения соответствующего метода измерений;
— общего смещения результатов участников;
— ошибки в понимании ограничений метода измерений при
использовании метода, приведенного в 7.3;
— смещения в результатах экспертных лабораторий при
использовании подходов, приведенных в 7.5
или 7.6;
— опорное значение и приписанное значение не связаны с одним
и тем же метрологическим эталоном.
7.8.3 В зависимости от выявленной причины провайдер проверки
квалификации должен решить, следует ли оценивать результаты раунда или нет, а
также (для непрерывных программ проверки квалификации) нужно ли изменить план
эксперимента для последующих программ проверки квалификации. Если разность
достаточно велика и может повлиять на оценку функционирования лаборатории или
можно предположить наличие существенного смещения у методов измерений,
используемых участниками, разность следует указать в отчете. В таких случаях
эту разность следует учитывать при разработке будущих программ проверки квалификации.
8
Определение критериев оценки работы лабораторий
8.1 Подходы к определению критериев оценки
8.1.1 Основным подходом во всех случаях является
сопоставление результатов измерений, выполненных на образце , с
приписанным значением . Для
оценки работы разность сравнивают с допустимой погрешностью измерений. Это
сравнение обычно выполняют для стандартизованной статистики (например, z, z‘, ζ, ) в
соответствии с 9.4 — 9.7. Также эту разность можно сравнивать с
определенным критерием (D или
D % сравнивают с ) в
соответствии с 9.3. Альтернативным
подходом является сопоставление разности с неопределенностью результатов,
заявленной участниками, объединенной с неопределенностью приписанного значения и ζ.
8.1.2 Если обязательные требования или соответствие цели
заданы в виде стандартного отклонения, то оно может быть использовано
непосредственно как .
Если обязательные требования или цели заданы в виде максимально допустимой
погрешности измерений, то для получения критерий
может быть поделен на значение границы зоны действия. Установленная максимально
допустимая погрешность может быть использована непосредственно в качестве для использования с D или D %.
Преимущества такого подхода для непрерывных программ состоят в следующем:
а) оценки функционирования лабораторий имеют
последовательную интерпретацию с точки зрения соответствия конкретной цели в
каждом раунде;
b) оценки функционирования зависят
от ожидаемой вариации при оценке разброса по фиксированным результатам.
Пример
— Если критерием оценки работы является максимально допустимая
погрешность и 3,0 — граница зоны действия при оценке
с z-индексом, то для определения значение
установленного критерия делят на 3,0.
8.1.3 Если критерий оценки работы основан на согласованных
статистиках из текущего или предыдущего раундов программы проверки квалификации,
то предпочтительной статистикой является робастная оценка стандартного
отклонения результатов участников. При использовании такого подхода, как
правило, удобнее всего использовать при оценке работы z-индекс
и установить в качестве стандартного отклонения для оценки квалификации выборочное
стандартное отклонение.
8.2 Чувствительность экспертов
8.2.1 Значение максимально допустимой погрешности или
стандартного отклонения для оценки квалификации может быть установлено как
значение, которое соответствует такому уровню работы, который, по мнению органа
по аккредитации или технических экспертов провайдера, является приемлемым для
участников.
8.2.2 Установленная максимальная допустимая погрешность
может быть преобразована в стандартное отклонение для оценки квалификации путем
деления ее предельного значения на число кратное ,
которое используют для определения границ зоны действия (или неприемлемого
результата). Аналогично установленное значение может
быть преобразовано в .
8.3 Оценка на основе данных
предыдущих раундов проверки квалификации
8.3.1 Стандартное отклонение для оценки квалификации и
максимально допустимая погрешность могут быть определены на основе данных предыдущих раундов
проверки квалификации для одной и той же измеряемой величины со сопоставимыми
значениями показателей, если участники используют согласованные процедуры
измерений. Это полезный подход, если нет согласия между экспертами относительно
соответствия установленным целям. Преимущества данного подхода:
— оценки основаны на разумных ожиданиях качества работы
участников;
— критерии оценки не изменяют во всех раундах из-за
случайных вариаций или изменений в составе участников;
— критерии оценки не меняют для различных провайдеров, если
для испытаний или калибровки утверждены два или более провайдеров.
8.3.2 Анализ предыдущих раундов программы проверки
квалификации должен включать рассмотрение показателей компетентных участников и
не затронутых влиянием новых участников или не затронутых случайными изменениями,
например, сокращением группы или других факторов, присущих конкретному раунду.
Заключения могут быть сделаны субъективно, на основе изучения данных предыдущих
раундов, объективно — в соответствии среднему или регрессионной модели,
установленной для измеряемой величины. Линия регрессии может быть прямой или
кривой [7]. Стандартные отклонения и
относительные стандартные отклонения следует рассматривать с учетом значений,
более подходящих области значений измеряемых величин. Соответствующая
максимально допустимая погрешность может быть рассчитана таким же способом.
8.3.3 Если критерии для оценки показателя функционирования
основаны на согласованных статистиках предыдущих раундов программы проверки
квалификации, следует использовать робастную оценку стандартного отклонения.
Примечание 1 — Алгоритм S (см. C.4 приложения C) обеспечивает определение робастного общего
стандартного отклонения и применим в том случае, когда все рассматриваемые
предыдущие раунды программы проверки квалификации имеют одинаковое среднее
стандартное отклонение или (если для оценки использованы относительные
отклонения) то же относительное стандартное отклонение.
Примечание 2 — Пример вывода значения по данным предыдущих
раундов программы проверки квалификации приведен в E.8 приложения E.
8.4 Использование общей модели
8.4.1 Значение стандартного отклонения для оценки
квалификации может быть получено из общей модели воспроизводимости метода
измерений. Преимуществами этого метода являются объективность и согласованность
измеряемых величин, а также его эмпирическая основа. В зависимости от
используемой модели такой подход можно рассматривать как частный случай
соответствия целевому критерию.
8.4.2 Все средние стандартные отклонения, выбранные с
помощью общей модели, должны быть обоснованы. Если результаты очень большой или
очень маленькой доли участников попали в зону сигнала к действиям и сигнала
предупреждения, провайдер проверки квалификации должен гарантировать, что это
согласуется с целью программы проверки квалификации.
8.4.3 Конкретная оценка, учитывающая особенности проблемы
измерений, как правило, предпочтительнее подхода на основе общей модели.
Следовательно, перед использованием общей модели следует изучить возможность
применения подходов, приведенных в 8.2,
8.3 и 8.5.
Пример
— Кривая Хорвица.
Общая модель для применения при
проведении химических исследований описана Хорвицем [8] и модифицирована Томпсоном [7]. Такой подход дает общую модель
воспроизводимости аналитических методов, которая может быть использована для
вывода выражения для стандартного отклонения воспроизводимости:
|
|
если с < 1,2 · 10-7, если 1,2 · 10-7≤ с если с > 0,138, |
(8) |
где с —
массовая доля химических соединений, которые необходимо определить, 0 ≤ с
≤ 1.
Примечание 1 — Модель Хорвица является эмпирической, основанной
на наблюдениях в течение длительного периода времени в совместных испытаниях с
большим количеством параметров. Значения являются средними верхними границами межлабораторной
изменчивости в совместных испытаниях в тех случаях, когда совместные испытания
не имеют значимых проблем. Следовательно, значение не может быть походящим критерием при определении
квалификации в программе проверки квалификации.
Примечание 2 — Пример определения значения на основе
модифицированной модели Хорвица приведен в E.9 приложения E.
8.5 Использование стандартного
отклонения повторяемости и воспроизводимости на основе данных предварительных
совместных исследований прецизионности метода измерений
8.5.1 Если метод измерений,
используемый в программе проверки квалификации, стандартизован, и информация о
стандартном отклонении повторяемости и
стандартном отклонении воспроизводимости метода
доступна, стандартное отклонение для оценки квалификации может
быть вычислено с использованием следующего выражения:
|
|
(9) |
где m — количество репликаций
измерений, которые каждый участник должен выполнить в раунде программы проверки
квалификации.
Примечание — Данное выражение получено из основной модели
случайных воздействий в соответствии с ГОСТ
Р ИСО 5725-2.
8.5.2 Если стандартные отклонения повторяемости и
воспроизводимости зависят от среднего арифметического результатов испытаний,
функциональные зависимости должны быть получены с помощью методов, приведенных
в ГОСТ
Р ИСО 5725-2. Эти зависимости должны быть использованы для расчета
значений стандартных отклонений повторяемости и воспроизводимости
соответствующего приписанного значения, используемого в программе проверки
квалификации.
8.5.3 Для валидации вышеуказанных методов должно быть
проведено совместное исследование в соответствии с требованиями ГОСТ
Р ИСО 5725-2 или аналогичного документа.
Примечание — Пример представлен в E.10 приложения E.
8.6 Использование данных, полученных в том же раунде
программы проверки квалификации
8.6.1 В данном подходе стандартное отклонение для оценки
квалификации вычисляют
по результатам участников, полученных в одном и том же раунде программы
проверки квалификации.
При использовании такого подхода, как правило, удобнее всего
использовать индексы, характеризующие работу лаборатории, такие как z-индексы. Как правило, для расчета используют
робастную оценку стандартного отклонения результатов, представленных всеми
участниками, которая получена с использованием методов, перечисленных в
приложении C.
В общем случае оценки с D или
D % и использующие не
подходят в таких ситуациях, однако PA может быть применима в качестве стандартизованного индекса
для сопоставления со всеми измеряемыми величинами (см. 9.3.6).
8.6.2 Использование результатов участников может приводить к
определению неподходящих критериев оценки функционирования лаборатории.
Провайдер проверки квалификации должен обеспечивать, чтобы ,
используемое для оценки работы лаборатории, соответствовало целям проверки
квалификации.
8.6.2.1 Провайдер проверки квалификации должен установить
ограничение на наименьшее значение для
случая, когда робастное стандартное отклонение очень мало. Это ограничение
должно быть выбрано таким образом, чтобы, когда погрешность измерений является
удовлетворительной в подавляющем количестве случаев, z-индекс
имел значение менее 3,0.
Пример
— В программе проверки квалификации лаборатория определяет плотность
ткани, измеряемой величиной является количество нитей на 1 см ткани. Робастное
стандартное отклонение в некоторых раундах может быть небольшим (менее 1 см ткани),
а погрешность менее четырех нитей на сантиметр считают незначительной.
Провайдер определяет, что робастное стандартное отклонение используют как в
этом случае менее
1,3 нити на 1 см, поэтому =
1,3.
8.6.2.2 Провайдер проверки квалификации должен установить
ограничение на наибольшее используемое значение или
на результаты измерений, которые следует оценивать как приемлемые (нет
сигнала), в том случае, когда значение робастного стандартного отклонения очень
большое. Это ограничение должно быть выбрано таким образом, чтобы результаты,
которые не соответствуют целям, воспринимались как сигнал к действиям.
8.6.2.3 Иногда провайдер проверки квалификации может
устанавливать верхнюю и нижнюю границы на результаты, которые могут быть
оценены как приемлемые (нет сигнала предупреждения или сигнала к действиям),
когда симметричные интервалы включают результаты, не соответствующие
установленным целям.
Пример
— При определении качества не питьевой (технической) воды в схеме
проверки квалификации лабораторий установлено, что результаты должны находиться
в пределах ± 3 от
робастного среднего результатов участников. Однако поскольку в некоторых
случаях размах приемлемых результатов может включать 0 м/дм3,
все результаты менее 10 % установленного значения должны вызывать сигнал к
действиям (являются неприемлемыми). Образец для проверки квалификации
составляет 4,0 м/дм3
регламентированного вещества. Робастное среднее участников составляет 3,2 м/дм3
и =1,1
м/дм3.
Следовательно, возможно представление участником результата 0,0 м/дм3,
который находится в пределах ± 3 но
все результаты менее 0,4 м/дм3
будут признаны как неприемлемые.
(Поправка).
8.6.3 Основными преимуществами такого подхода являются
простота и успешное применение во многих ситуациях. Иногда он может быть
единственно возможным.
8.6.4 Существует несколько недостатков данного подхода:
a) значение может
существенно меняться при переходе от раунда к раунду программы проверки
квалификации, что затрудняет участникам использование значения z-индекса для выявления трендов, которые сохраняются в
течение нескольких раундов;
b) стандартные отклонения могут быть
недостоверными, когда количество участников программы проверки квалификации
мало или когда объединяют результаты различных методов измерений. Например,
если p = 20, стандартное отклонение для данных
из нормального распределения может изменяться на ± 30 % от его истинного
значения от одного раунда программы проверки квалификации к другому;
c) использование мер рассеяния,
полученных на основе данных, может приводить к приблизительно постоянной
пропорции приемлемых индексов. Очевидно, что в этом случае плохое
функционирование лаборатории может быть не обнаружено с помощью индексов, а в
целом хорошие показатели могут стать причиной того, что хороший участник
получит плохую оценку;
d) отсутствие полезных интерпретаций
относительно соответствия конечному использованию результатов.
Примечание — Примеры использования данных участников приведены в
комплексном примере (см. E.3 приложения E).
8.7 Мониторинг межлабораторных соглашений
8.7.1 Для проверки работы участников, а также оценки
преимуществ программы проверки квалификации для участников, провайдеру проверки
квалификации следует применять процедуру мониторинга межлабораторных
соглашений, чтобы отслеживать изменения в работе лабораторий и обеспечивать
обоснованность применения статистических процедур.
8.7.2 Результаты, полученные в каждом раунде программы
проверки квалификации, необходимо использовать для расчета оценок стандартных
отклонений воспроизводимости метода измерений (и повторяемости, при
необходимости), используя робастные методы, описанные в приложении C. Эти
оценки необходимо наносить на график последовательно или в виде временных рядов
вместе со значениями стандартного отклонения повторяемости и воспроизводимости,
полученными при исследовании прецизионности в соответствии с ГОСТ
Р ИСО 5725-2 (при наличии) и/или ,
если использованы методы, приведенные в 8.2
— 8.4.
8.7.3 Полученные графики должны быть исследованы провайдером
проверки квалификации. Если графики показывают, что прецизионность значений,
полученных в конкретном раунде проверки квалификации, в два или более раз
больше значений, ожидаемых на основе ранее полученных данных или из опыта, то
провайдер проверки квалификации должен исследовать причину того, что
согласование в данном раунде хуже, чем в предыдущем. Аналогично тенденция к улучшению
или ухудшению значения прецизионности становится основанием для анализа
наиболее вероятных причин этого явления.
9
Вычисления статистик функционирования лабораторий
9.1 Общие положения при определении качества работы
лабораторий
9.1.1 Статистики, используемые при определении качества
работы лабораторий, должны соответствовать цели(ям) программы проверки
квалификации.
Примечание — Статистики функционирования более полезны, если
участники и заинтересованные стороны понимают их структуру и вывод.
9.1.2 Индексы функционирования должны быть легко
анализируемыми для всех уровней измеряемой величины и различных раундов
программы проверки квалификации.
9.1.3 Результаты участников должны быть определены и
проанализированы относительно выполнения предположений, используемых при
разработке программы проверки квалификации, чтобы обеспечить значимость
статистики функционирования. Например, проверить, не существует ли каких-либо
доказательств ухудшения образца для проверки квалификации, или не смешаны ли
группы участников, или нет ли серьезных нарушений статистических предположений
о свойствах данных.
9.1.4 В общем случае нецелесообразно использовать методы
оценки, которые намеренно устанавливают фиксированную долю результатов для
получения сигнала к действиям.
9.2 Ограничения неопределенности приписанного значения
9.2.1 Если стандартная неопределенность
приписанного
значения велика по сравнению с критерием оценки функционирования лаборатории, то
существует риск того, что некоторые участники получат сигнал к действиям и
сигнал предупреждения из-за неточностей в определении приписанного значения, а
не по причине плохой работы участника. Поэтому стандартная неопределенность
приписанного значения должна быть определена заранее и сообщена всем участникам
(см. 4.4.5 и 4.8.2 ГОСТ
ISO/IEC 17043-2013).
Если соблюдены приведенные ниже
критерии, то неопределенность приписанного значения можно считать пренебрежимо
малой и ее можно не учитывать при интерпретации результатов раунда проверки
квалификации
|
|
(10) |
Примечание — если
— зона сигнала к действиям.
9.2.2 Если этот критерий не выполняется, то провайдер
проверки квалификации должен выполнить перечисленные ниже действия, гарантируя
при этом, что любые предпринятые действия по-прежнему соответствуют
согласованной политике в области оценки функционирования лаборатории в
программе проверки квалификации:
a) следует
выбрать метод определения приписанного значения таким образом, чтобы неопределенность
приписанного значения удовлетворяла неравенствам (10);
b) необходимо использовать
неопределенность приписанного значения при анализе результатов программы
проверки квалификации (см. 9.5 для z-индексов, 9.6 для
ζ-индексов или 9.7 для -индексов);
(Поправка).
c) если приписанное значение
получено по результатам участников и из-за различий между подгруппами
участников неопределенность приписанного значения слишком велика, следует
использовать значения неопределенности для каждой подгруппы участников
(например, сгруппировать участников по видам используемых методов измерений).
Примечание — В гармонизированном протоколе IUPAC [1] описана конкретная процедура
обнаружения бимодальности, основанная на проверке графика плотности ядра с
установленной «шириной полосы пропусканий»;
d) должны
информировать участников о том, что неопределенность приписанного значения не
является незначительной и это может повлиять на оценку их работы.
Если неприменимо ни одно из перечислений а) — d), то
участники должны быть проинформированы, что приписанное значение и индексы
функционирования не могут быть определены достоверно.
Примечание — Методы, представленные в данном разделе, приведены
в E.3 и E.4 приложения E.
9.3 Оценка отклонения
(погрешности измерений)
9.3.1 Пусть представляет
результат измерений характеристики свойства образца для проверки квалификации
(или среднее арифметическое репликаций измерений), указанных в отчете i-го участника в одном из раундов программы проверки
квалификации. Тогда простая мера качества работы участника может быть вычислена
как разность между результатом и
приписанным значением
|
|
(11) |
можно
интерпретировать как погрешность измерений результатов в той степени, в которой
приписанное значение можно рассматривать как обычное или опорное значение
количественной величины.
Разность может
быть выражена в тех же единицах, что и приписанное значение, или в процентах,
вычисленных по формуле
|
|
(12) |
9.3.2 Разность D или D %,
как правило, сопоставляют с критерием ,
основанным на соответствии цели или данных предыдущих раундов программы
проверки квалификации; критерий, обозначаемый здесь как ,
представляет собой припуск к погрешности измерений. Если , то
работу лаборатории можно считать приемлемой (сигнал отсутствует). (Тот же
критерий применяют для D %
в зависимости от выражения для .)
(Поправка).
9.3.3 Значение тесно
связано с используемым
для расчета z-индексов (9.4), если определено
на основе соответствия цели или ожидания от предыдущих раундов. Соотношение
определяется критерием оценки для z-индексов. Например,
если z ≥ 3 определяют как границу сигнала к
действиям, то = 3
или
эквивалентно =
/3.
Различные выражения для являются
обычными при проверке квалификации в области медицины или в функциональных
требованиях к методам измерений и продукции.
9.3.4 Преимущества D как статистики и как
критерия функционирования состоят в том, что у участников существует
интуитивное понимание этих статистик, так как они непосредственно связаны с
погрешностью измерений и являются общими в качестве критериев соответствия
цели. Преимущество статистики D
% состоит в том, что она является интуитивно понятной, стандартизирована
для уровня измеряемой величины и связана с общими причинами погрешности
(например, некорректная калибровка или смещение при разбавлении растворов).
9.3.5 Недостатками этой статистики может быть то, что она не
является общепринятой при проверке квалификации во многих странах и областях
измерений, а также и то, что D не
стандартизована, и это не дает возможности простого просмотра отчетов для
определения сигналов к действиям в программах проверки квалификации с
несколькими аналитами, или в том случае, где критерии соответствия цели могут
изменяться в зависимости от уровня измеряемой величины.
Примечание — Использование D
и D
% обычно предполагает симметричность
функции распределения результатов участников в том смысле, что областью
приемлемых значений является диапазон — < D <
.
9.3.6 Для
сравнения различных уровней измеряемой величины в том случае, когда критерий
соответствия цели может изменяться, или для объединения раундов или измеряемых
величин D и D % могут быть преобразованы в
стандартизованный индекс функционирования, который показывает разности с
критерием для измеряемых величин. Для этого следует вычислить «процент
допустимого отклонения» PA для
каждого результата:
|
|
(13) |
Следовательно, РА
≥ 100 % или PA ≤ -100 % указывает на сигнал к действиям
(неприемлемости функционирования).
Примечание 1 — Можно сопоставлять значения PA для различных
уровней измеряемых величин и различных раундов программы проверки квалификации
или отображать их на графиках. Эти оценки функционирования аналогичны по
использованию и интерпретации z-индексам, которые имеют общий критерий оценки, такой
как z ≤ -3 или z ≥ 3 для сигналов к действиям.
Примечание 2 — Часто используют вариации этой статистики,
особенно в медицине, где проверку квалификации проводят более часто с
использованием большого количества аналитов.
Примечание 3 — Иногда целесообразно использовать абсолютное
значение PA для того, чтобы отразить приемлемость (или
неприемлемость) результатов относительно приписанного значения.
9.4 z-индексы
9.4.1 z-индекс
для результата проверки квалификации вычисляют
по следующей формуле
|
|
(14) |
где —
приписанное значение;
—
стандартное отклонение для оценки квалификации.
9.4.2 Общепринятая интерпретация z-индекса
состоит в следующем (см. B.4.1.1 приложения В ГОСТ
ISO/IEC 17043-2013):
— результат считают приемлемым, если ;
— результат находится в зоне предупреждения (сигнал
предупреждения), если ;
— результат считают неприемлемым (сигнал к действиям), если .
Участникам необходимо проверить процедуры измерений при
появлении предупреждающего сигнала, так как он служит признаком появившейся или
повторяющейся проблемы.
Примечание 1 — В некоторых случаях в качестве границы зоны
сигнала к действиям провайдеры используют z-индекс, равный
2.
Примечание 2 — Выбор в качестве критерия допускает вышеуказанную интерпретацию. Этот критерий
широко используют для оценки квалификации, и такая интерпретация очень похожа
на границы контрольных карт.
Примечание 3 — Обоснование для использования границ 2,0 и 3,0
для z-индексов состоит в следующем. Правильно выполненные измерения
предполагают получение результатов, которые могут быть описаны (после
преобразования при необходимости) распределением со средним и стандартным отклонением
. Тогда z-индексы
тоже подчиняются нормальному распределению со средним 0 и стандартным
отклонением 1. В этом случае в среднем только около 0,3 % результатов выйдут за
пределы интервала -3,0 ≤ z ≤ 3,0 и
только около 5 % результатов выйдут за пределы интервала -2,0 ≤ z ≤ 2,0. Так как вероятность выхода за границы ± 3,0
очень мала, то вероятность случайного появления сигнала к действиям очень
низка, и такой выход означает появление реальных аномалий.
Примечание 4 — Предположения, на которых основана эта
интерпретация, относятся только к гипотетическому распределению квалифицируемых
лабораторий, но не к распределению наблюдаемых результатов. Не требуется
предположений о самих наблюдаемых результатах.
Примечание 5 — Если истинная межлабораторная изменчивость менее , то вероятность
ошибок сокращается.
Примечание 6 — Если стандартное отклонение для оценки
квалификации устанавливают в соответствии с 8.2 или 8.4,
оно может существенно отличаться от (робастного) стандартного отклонения
результатов и доли результатов, выходящих за границы ± 2,0 и 3,0, также могут
существенно отличаться от 5 и 0,3 % соответственно.
9.4.3 Провайдер проверки квалификации определяет правила
округления для полученных z-индексов на основе
количества значащих цифр для результатов приписанного значения и стандартного
отклонения для проверки квалификации. Эта информация должна быть доступна всем
участникам.
Примечание — Обычно редко используют более двух знаков после
запятой.
9.4.4 Если в качестве стандартного отклонения результатов
участников используют и
количество участников проверки слишком велико, провайдер проверки квалификации
может проверить нормальность распределения, используя реальные результаты или z-индексы. С другой стороны, если количество участников слишком
мало, сигнал к действиям может вообще не появиться. В этом случае более
полезными являются графические методы, которые дают возможность проследить за
индексами функционирования в течение нескольких раундов, что может обеспечить
более полезные данные о квалификации участников, чем результаты отдельных
раундов.
9.5 z’-индексы
9.5.1 Если появляются опасения
по поводу неопределенности приписанного значения ,
например если ,
то эта неопределенность может быть учтена путем добавления ее в знаменатель при
расчете z-индекса, который в этом случае называют z’-индексом и вычисляют (в обозначениях 9.4) следующим образом:
|
|
(15) |
Примечание — Если и/или
вычисляют по результатам участников, то индексы
функционирования коррелируют с результатами отдельных участников, потому что
эти результаты влияют на робастные среднее и стандартное отклонения. Корреляция
для отдельного участника зависит от весового коэффициента, назначенного этому
участнику в объединенной статистике. По этой причине индекс функционирования,
включающий неопределенность приписанного значения без учета корреляции, дает заниженный
индекс и заниженные результаты по сравнению с ситуацией, когда ковариацию
учитывают. Например, если то снижение оценки z’-индекса
составляет около 10. Таким образом, формулу (15) следует использовать, если и/или
определяют по результатам участников.
9.5.2 Индексы D и D % также могут быть модифицированы для учета неопределенности
приписанного значения с помощью следующей формулы, обеспечивающей получение :
|
|
(16) |
где — расширенная
неопределенность приписанного значения вычисленная
с коэффициентом охвата k = 2.
9.5.3 z’-индекс можно
интерпретировать тем же способом, что и z-индекс (см. 9.4), и использовать те же критические
значения 2,0 и 3,0 в зависимости от программы проверки квалификации. Аналогично
D и D % следует затем сравнивать с (см.
9.3).
9.5.4 Сравнение формул для
расчета индексов z и z’ в
соответствии с 9.4 и 9.5 для раунда программы проверки квалификации
показывает, что z’-индекс всегда меньше z-индекса. Отношение z’-индекса к z-индексу составляет
|
|
В случае введения ограничений на неопределенность приписанного
значения в соответствии с 9.2.1 это
значение находится в интервале:
|
|
В этом случае z’-индекс
почти совпадает с z-индексом, и можно сделать вывод,
что при оценке функционирования неопределенностью приписанного значения можно
пренебречь.
Если требования 9.2.1
на неопределенность приписанного значения не выполнены, то разность значений z’-индекс и z-индекс может быть столь
существенной, что когда z-индекс достигает значений 2
или 3, что соответствует «сигналу предупреждения» и «сигналу к действиям», z’-индекс не достигает таких критических значений и,
следовательно, не дает никаких сигналов.
В общем случае для ситуаций, когда приписанное значение
и/или не
определяют по результатам участников, использование z’-индекса
может быть предпочтительнее, поскольку когда критерий в соответствии с 9.2.1 выполнен, разность между z’-индексом и z-индексом пренебрежимо
мала.
9.6 Дзета-индекс
9.6.1 Применение дзета-индекса полезно, если целью программы
проверки квалификации является оценка способности участника получать
результаты, близкие к приписанному значению в пределах указанной участником
неопределенности.
С учетом обозначений,
использованных в 9.4, ζ-индекс
вычисляют по следующей формуле
где —
собственная оценка лабораторией стандартной неопределенности ее результата ;
—
стандартная неопределенность приписанного значения .
Примечание 1 — Если приписанное значение рассчитывают на основе согласованного значения
результатов участников, то коррелирует с результатами участников. Корреляция для
отдельного участника зависит от весового коэффициента этого участника в
приписанном значении и в меньшей степени от неопределенности приписанного
значения. По этой причине оценки функционирования, включая неопределенность
приписанного значения, но не включая припуск на корреляцию, являются
заниженными оценками, то есть оценками при отсутствии корреляции. Занижение
оценки несущественное, если неопределенность приписанного значения мала; при
использовании робастных методов для большинства внешних участников опасность
получения неблагоприятных значений индекса функционирования очень мала.
Следовательно, формула (17) может быть
использована с согласованными статистиками без учета корреляции.
Примечание 2 — Дзета-индекс отличается от -индекса (см. 9.7)
использованием стандартных неопределенностей и
, а не
расширенных неопределенностей и
. Значение ζ-индекса
выше 2 или ниже -2 может быть вызвано систематическим смещением метода или
плохой оценкой неопределенности результатов измерений участником.
Следовательно, ζ-индекс обеспечивает строгую оценку полного
результата, предоставленного участником.
9.6.2 Использование дзета-индексов позволяет осуществлять
прямую оценку способности лаборатории обеспечить корректные результаты, то есть
результаты, согласованные с , в пределах
неопределенности их результатов измерений. Дзета-индексы могут быть
интерпретированы с использованием тех же значений 2,0 и 3,0, как и z-индексы, или с умножением на коэффициент охвата,
используемым при оценке расширенной неопределенности. Однако неблагоприятный
дзета-индекс может указывать либо на большое отклонение от
либо
на недооценку неопределенности участником, или на то и другое одновременно.
Примечание — Для провайдера полезно получить дополнительную
информацию о достоверности зафиксированных в отчете неопределенностей. Полезные
указания по такой оценке приведены в 9.8.
9.6.3 Дзета-индексы могут быть использованы в сочетании z-индексами как дополнительное средство для улучшения работы
участников. Если участник получает z-индекс,
многократно превышающий критическое значение 3,0, необходимо проанализировать
методику исследований шаг за шагом и получить для нее оценку неопределенности.
Оценка неопределенности позволит идентифицировать те шаги в процессе измерений,
в которых появляется большая неопределенность, и участники могут увидеть, где
необходимо затратить усилия, чтобы добиться улучшений. Если дзета-индексы
участника также повторно превышают критическое значение 3,0, это означает, что
оценка неопределенности участника не включает в себя все существенные источники
неопределенности (то есть пропущено что-то важное). И наоборот, если участник
повторно получает дзета-индекс более или равный трем, а дзета-индекс — менее
двух, это указывает на то, что участник точно оценивает неопределенность своих
результатов, но его результаты не соответствуют ожидаемому уровню работы для
программы проверки квалификации. Это может быть в случае, например, если
участник использует метод скрининга в процессе измерений, а другие участники
применяют количественные методы. Если участник считает, что неопределенность
его результатов обоснована, то никаких действий проводить не требуется.
Примечание — Если дзета-индекс использован самостоятельно, он
может быть интерпретирован только для проверки соответствия неопределенности
результатов участника конкретному наблюдаемому отклонению и не может быть
использован как признак соответствия результатов конкретного участника целям
испытаний.
Определение соответствия целям может быть сделано отдельно
(например, участником или органом по аккредитации) с помощью проверки
отклонений разности или
объединенных стандартных неопределенностей по сравнению с целевой
неопределенностью.
9.7 -индексы
9.7.1 -индексы
могут быть использованы в том случае, если целью программы проверки
квалификации является оценка способности участников получать результаты,
близкие к приписанному значению в пределах заявленной ими расширенной
неопределенности. Эта статистика является обычной для проверки квалификации при
калибровке, но может быть использована и для других видов проверки
квалификации. Эту статистику вычисляют по формуле
|
|
(18) |
где —
приписанное значение, определенное в эталонной лаборатории;
—
расширенная неопределенность результатов участника ;
—
расширенная неопределенность приписанного значения .
Примечание — Непосредственное объединение расширенных
неопределенностей не соответствует требованиям [6] и не эквивалентно расчету объединенной
расширенной неопределенности, за исключением случая, когда коэффициент охвата и
число эффективных степеней свободы одинаковы для и
.
9.7.2 -индекс
следует интерпретировать с осторожностью, поскольку он является отношением двух
отдельных (независимых) показателей функционирования. Числитель представляет
собой отклонение результата от приписанного значения (рассмотрение
интерпретации этого показателя приведено в 9.3).
Если участник правильно определил и
провайдер проверки квалификации правильно определил ,
знаменатель представляет собой объединенную расширенную неопределенность,
которая не должна быть больше отклонений числителя. Таким образом, значения или
могут
указывать на необходимость анализа оценок неопределенности или на необходимость
коррекции выполнения измерений; аналогично следует
рассматривать как признак успешной работы только в том случае, если
неопределенности валидированы и отклонение меньше,
чем необходимо заказчику участника.
Примечание — Несмотря на то что интерпретация -индексов может быть достаточно сложной, это не
препятствует их использованию. Включение информации о неопределенности в
интерпретацию результатов проверки квалификации может играть важную роль в
улучшении понимания участниками неопределенности измерений и ее оценки.
9.8 Оценки неопределенности
результатов участников
9.8.1 Применение ГОСТ
ИСО/МЭК 17025 обеспечивает более глубокое понимание неопределенности
измерений. Использование оценок неопределенности при оценке функционирования
лабораторий распространено в программах проверки квалификации в различных
областях калибровки (так же как -индексов,
но при проверке квалификации испытательных лабораторий не применялось). ζ-индексы,
описанные в 9.6, и -индексы,
описанные в 9.7, представляют собой
варианты оценки результатов по отношению к заявленной неопределенности.
9.8.2 Некоторые провайдеры проверки квалификации признали,
что указание лабораториями в отчете неопределенности результатов при проверке
квалификации является полезным. Это может быть полезно даже тогда, когда
неопределенности не используют в расчетах. Существуют несколько целей сбора
такой информации:
a) органы по аккредитации могут
гарантировать, что участники укажут неопределенности, которые соответствуют их
области аккредитации;
b) участники могут проанализировать
свою неопределенность по отношению к другим участникам и получить возможность
определить, учтены ли в их оценке неопределенности все возможные составляющие
неопределенности и не завышена ли неопределенность некоторых составляющих;
c) проверка квалификации может быть
использована для подтверждения заявленной неопределенности, и это легче
сделать, когда неопределенность указана вместе с результатом.
Примечание — Пример анализа данных, когда неопределенности
указаны, приведен в E.3 приложения E.
9.8.3 Если определено
в соответствии с процедурами, установленными в 7.3 — 7.6,
и соответствует
критерию 9.2.1, то маловероятно, что
результат участника будет иметь меньшую стандартную неопределенность, тогда может
быть использована в качестве нижнего предела при скрининге, то есть как .
Если приписанное значение определяют по результатам участников (см. 7.7), то провайдер проверки квалификации
должен определить границы реального скрининга для .
Примечание — Если включает
изменчивость вследствие неоднородности или нестабильности, участников может быть меньше
.
9.8.4 Маловероятно также, что все участники указали
стандартную неопределенность, более чем в 1,5 раза превышающую робастное стандартное
отклонение участников 1,5 это
значение может быть использовано как реальная верхняя граница для скрининга
зафиксированных неопределенностей, называемая .
Примечание — Коэффициент 1,5 является верхним пределом
изменчивости стандартных отклонений, который можно ожидать для согласованного
стандартного отклонения десяти или более результатов на основе квадратного
корня процентили F-распределения. Провайдер проверки квалификации может
использовать и другое значение этого коэффициента.
9.8.5 Если для определения отклоняющих неопределенностей
используют .
или или
другие критерии, провайдер проверки квалификации должен объяснить участникам,
что указанная ими неопределенность должна
быть валидирована, даже если она менее или
более .
Если это происходит, участники и все заинтересованные стороны должны проверить
результат или оценку неопределенности. Аналогично, если указанная
неопределенность больше и
меньше ,
это не обеспечивает ее валидацию. Это всего лишь индикатор.
9.8.6 Провайдеры проверки квалификации могут также обратить
внимание на необычно высокие или низкие значения неопределенности на основе:
— установленных квантилей, соответствующих указанным
неопределенностям (например, ниже 5-й процентили и выше 95-й процентили для
указанных стандартных или расширенных неопределенностей);
— границ, построенных на предполагаемом распределении, со
шкалой, созданной на разбросе указанных неопределенностей;
— требуемой неопределенности результатов измерений.
Примечание — Поскольку маловероятно, что неопределенности
подчиняются нормальному распределению, будет необходимо выполнение
преобразования при использовании границ, полученных на основе приближенно
нормального или нормального распределения, например, границы на диаграмме «ящик
с усами» основаны на межквартильном размахе и имеют вероятностную интерпретацию
только тогда, когда распределение является приближенно нормальным.
9.9 Комбинированные индексы функционирования
9.9.1 Обычно в пределах одного раунда программы проверки
квалификации должны быть получены результаты для нескольких образцов или
нескольких измеряемых величин. В этом случае результаты для каждого образца
проверки квалификации и каждой измеряемой величины необходимо интерпретировать
в соответствии с 9.3 — 9.7; то есть результаты для каждого образца и каждой
измеряемой величины следует рассматривать отдельно.
9.9.2 Существуют случаи, когда в программу проверки
квалификации включены два или более образцов со специально разработанными
уровнями для измерения других аспектов работы лаборатории, например, для
исследования повторяемости, систематической погрешности или линейности модели.
Например, два аналогичных образца могут быть использованы в программе проверки
квалификации с применением графика Юдена (см. 10.5). В такой ситуации провайдер проверки
квалификации должен предоставить участникам полное описание плана эксперимента
и используемых процедур.
9.9.3 Рекомендуется использовать графические методы,
описанные в 10, если
результаты получены по нескольким исследуемым образцам или нескольким
измеряемым величинам, при условии, что они тесно связаны между собой и/или
получены одним тем же методом. Значения показателей объединяют подобного рода
способами, которые не скрывают информацию о высоких значениях отдельных
показателей. Таким образом, может быть получена дополнительная информация о
работе лабораторий, например, как корреляция между результатами для различных
измеряемых величин, не очевидная по данным таблиц для отдельных показателей.
9.9.4 В схемах проверки квалификации, в которых использовано
большое количество измеряемых величин для оценки качества работы, могут быть
применены подсчет или соотношение количества сигналов к действиям и
предупреждения.
9.9.5 Комбинированные индексы функционирования либо
поощрительные или штрафные индексы следует использовать с осторожностью, так
как может быть трудно описать лежащие в основе статистические предположения. В
то же время комбинированные индексы функционирования в случае использования
нескольких образцов и единственной измеряемой величины могут иметь ожидаемые
распределения и быть полезны для выявления постоянного смещения, усреднение или
суммирование индексов для нескольких измеряемых величин и одних и тех же или
разных образцов может замаскировать смещение результатов для измеряемой
величины. Таким образом, метод расчета, интерпретации и ограничений всех
комбинированных или штрафных индексов должен быть понятен участникам.
10
Графические методы описания индексов функционирования
10.1 Применение графических методов
Для подготовки графиков в соответствии с 10.2 и 10.3
провайдер обычно использует индексы, полученные в каждом раунде программы
проверки квалификации. Использование индексов функционирования PA, z, z’, ξ, и в
таких графиках дает преимущество использования стандартизованных осей, что
позволяет упростить их представление и интерпретацию. Графики должны быть
доступны участникам, предоставляя каждому возможность видеть расположение
собственных результатов по отношению к результатам других участников. При этом
могут быть использованы буквенные и числовые коды так, чтобы каждый участник
имел возможность идентифицировать свои результаты, но не мог идентифицировать
результаты других участников. Графики могут быть использованы провайдером или
органом по аккредитации для того, чтобы делать выводы об общей эффективности
программы проверки квалификации и определения необходимости анализа критерия
оценки квалификации.
10.2 Гистограммы результатов или
индексов функционирования
10.2.1 Гистограмма представляет собой общий статистический
прием, полезный при проведении анализа результатов проверки квалификации с двух
точек зрения. Во-первых, график полезен на предварительном этапе анализа для
проверки обоснованности статистических предположений или при наличии
отклонений, которые невозможно предвидеть, таких как бимодальное распределение,
значительная доля выбросов или необычная асимметрия.
Использование гистограмм в отчетах участников полезно для
программ проверки квалификации с небольшим или средним количеством участников
(менее 100), что дает участникам возможность сопоставить свою работу с
результатами других участников: например, с помощью выделения блока данных в
вертикальных столбцах, представляющих результаты участников, или (при небольшой
группе участников) используя индивидуальные характеристики для каждого
участника.
10.2.2 При построении гистограмм могут быть использованы
результаты участников или индексы функционирования. Использование результатов
участников имеет преимущество, состоящее в том, что они непосредственно связаны
с представленными данными и могут быть оценены без дальнейших вычислений и
преобразований индекса функционирования в погрешность измерений. Преимущество
гистограмм, основанных на индексах функционирования, состоит в том, что они
связаны с оценкой функционирования: их можно сравнивать по измеряемым величинам
и раундам программы проверки квалификации.
Размах и размеры интервалов, используемых для диаграммы,
должны быть определены для каждого набора данных на основе изменчивости и
количества результатов. Это можно сделать и на основе данных предыдущих
проверок квалификации, но в большинстве случаев после первичного анализа
разбиение на интервалы необходимо корректировать. Если при построении
гистограммы используют индексы функционирования, полезно применить шкалу на
основе стандартного отклонения для оценки квалификации и выделить точки
сигналов предупреждения и сигналов к действиям.
10.2.3 Масштаб и интервалы на графике следует выбирать таким
образом, чтобы бимодальность (если она присутствует) могла быть обнаружена, не
создавая ситуаций появления ложных сигналов тревоги, связанных с разрешающей
способностью средств измерений или небольшим количеством результатов.
Примечание 1 — Форма гистограммы зависит от выбранной ширины
интервалов и положения их границ (при постоянной ширине интервалов эти
положения зависят от начальной точки). Если ширина интервалов слишком мала, то
гистограмма будет включать много невысоких столбиков (использование слишком
больших интервалов), не обеспечивая существенного различия столбиков по высоте
вблизи среднего. Изменение ширины интервалов сразу приводит к изменению их
высоты, особенно там, где набор данных мал и/или имеется некоторая группировка
данных.
Примечание 2 — Примеры гистограмм приведены в E.3 приложения E.
10.3 График ядерной плотности
10.3.1 График ядерной плотности представляет сглаженную
кривую, описывающую общую форму плотности распределения набора данных. Для
определения ядерной плотности каждую точку данных заменяют заданным
распределением (как правило, нормальным) с центром в этой точке и стандартным
отклонением ;
обычно
называют «шириной полосы». Все распределения объединяют и результирующее
распределение масштабируют таким образом, чтобы площадь под кривой плотности
была равна 1, это позволяет получить оценку плотности, которая представляет
собой гладкую кривую.
10.3.2 Для подготовки графика ядерной плотности необходимо
выполнить следующие этапы. Предположим, что набор данных X
состоит из p значений x1,
x2, …, xp,
используемых для построения графика. Обычно это результаты участников, но могут
быть индексы функционирования, полученные на основе этих результатов.
i) Выбирают подходящую «ширину
полосы» .
Для этого используют два подходящих способа:
a) для общего контроля устанавливают
,
где —
робастное стандартное отклонение величин x1,
…, xp, вычисленное с использованием
процедур, приведенных в C.2 или C.3
приложения C;
b) при проверке набора данных с
большими модами, которые имеют важное значение для сопоставления с критериями
оценки работы, устанавливают при
использовании z-индекса или ζ-индекса или при
использовании D и D %.
Примечание 1 — Вариант a) предложен Сильверманом [9], который рекомендует выбирать на основе нормализованного межквартильного интервала nlQR. Другие правила выбора
«ширины столбца» (длины интервала для диаграммы), которые обеспечивают
аналогичные результаты, предложенные Скоттом [10], сведены к замене множителя 0,9 на 1,06. В [10] описан близкий к оптимальному, но
гораздо более сложный метод выбора ширины столбца. На практике визуальные
различия незначительны, и выбор зависит от наличия необходимого программного
обеспечения.
Примечание 2 — Вариант b) предложен в руководстве IUPAC [1].
ii) Устанавливают на графике
значения и
так,
что , а
.
iii) Выбирают количество точек nk для построения кривой, обычно nk = 200 достаточно, если нет выбросов в
пределах заданного диапазона (,
).
iv) Вычисляют положение на графике
значений от
до
|
|
(19) |
v) Вычисляют nk
значений от
до
|
|
(20) |
где (.) — плотность стандартного
нормального распределения.
vi) На график наносят пары значений и
Примечание 1 — Иногда полезно указать на графике отдельные точки
данных. Обычно эти точки наносят под кривой плотности в виде вертикальных
черточек («коврика»), но можно наносить их прямо на кривую плотности.
Примечание 2 — График плотности лучше всего формировать с
помощью программного обеспечения. Приведенные этапы вычислений могут быть
выполнены посредством электронных таблиц, если объемы данных невелики.
Имеющееся в собственности и в свободном доступе программное обеспечение часто
включает построение графиков плотности на основе материалов одинаковой ширины
по умолчанию. В более современном программном обеспечении для построения
графиков плотности могут быть использованы приведенный алгоритм или вычисления,
основанные на методах свертки.
Примечание 3 — Примеры графиков ядерной плотности приведены в E.3, E.4 и E.6 приложения E.
10.3.3 Форма кривой указывает на распределение, которому
принадлежат данные. Моды выглядят в виде пиков, выбросы тоже имеют вид пиков,
но удаленных от основного массива данных.
Примечание 1 — График плотности чувствителен к выбранному
значению . Если это
значение слишком мало, график покажет много небольших возвышений, что может
сделать неясным положение истинной моды.
Примечание 2 — Как и в случае гистограмм при составлении графика
плотности лучше использовать массивы среднего или большого объема, так как
наборы данных небольшого объема (десять и менее) могут включать небольшие
выбросы или очевидные моды, в частности, если в качестве основы для выбора
ширины столбца использовано робастное стандартное отклонение.
10.4 Штриховые графики для
стандартизованных индексов функционирования
10.4.1 Штриховые графики подходят для представления индексов
функционирования большого количества аналогичных характеристик на одном
графике. Эти графики применяют в тех ситуациях, когда существуют общие свойства
индексов участника: например, если участник имеет несколько высоких значений z-индекса, указывающих на недостаточное качество работы, то
есть участник имеет положительное смещение.
10.4.2 Для подготовки штрихового графика собирают значения
стандартизованных индексов функционирования и отражают их на графике, как
показано на рисунке E.10
приложения E,
для каждого участника индексы объединяют в одну группу. Другие
стандартизованные индексы функционирования, такие как D % и PA, могут быть
нанесены на график для тех же целей.
10.4.3 Если в раунде программы проверки квалификации выполняют
репликации измерений, результаты могут быть использованы для расчета и
составления графика меры прецизионности, например k-статистики
в соответствии с ГОСТ
Р ИСО 5725-2 или с масштабированной мерой стандартного отклонения
робастного среднего, так как это определено в алгоритме S (см.
C.4 приложения C).
Примечание — Пример штрихового графика для z-индексов
приведен в E.11 приложения E.
10.5 График Юдена
10.5.1 Если в раунде проверки квалификации были проверены
два аналогичных образца, то график Юдена обеспечивает очень информативный
графический метод исследования результатов. Этот график может быть полезен для
демонстрации коррелированности (или независимости) результатов на различных
образцах исследования причин появления сигналов к действиям.
10.5.2 На график наносят результаты участника или z-индексы, полученные на одном образце проверки квалификации,
вместе с результатами, или z-индексы, полученные на
другом образце. Для облегчения интерпретации на график наносят вертикальную и
горизонтальную линии, которые делят плоскость на четыре квадранта. Линии
проходят через приписанные значения или медианы для двух распределений
результатов, или через 0 при использовании z-индексов.
Примечание — Для правильной интерпретации графика Юдена важно,
чтобы два используемых в проверке образца имели аналогичные (или идентичные)
уровни измеряемой величины; это объясняется тем, что природа систематической
погрешности измерений одна и та же в интервале измерений. Графики Юдена могут
быть полезны для различных уровней измеряемой величины при наличии последовательной
систематической погрешности, но могут ввести в заблуждение, если ошибка
калибровки не является последовательно положительной или отрицательной по всей
области уровней измеряемой величины.
10.5.3 После построения графика Юдена проводят его анализ.
Для этого проверяют график:
a) на наличие точек, которые
отличаются от остальных данных. Если участник некорректно использует метод
испытаний, то его результаты имеют систематическую погрешность, и точки
находятся далеко от остальных, в нижнем левом или верхнем правом квадранте.
Точки, отстоящие далеко от остальных и находящиеся в верхнем левом и нижнем
правом квадрантах, представляют участников, у которых повторяемость выше, чем у
большинства участников; методы измерений показывают различную чувствительность
к компонентам образцов или то (иногда), что участники случайно перепутали
образцы;
b) предмет выявления признаков
взаимосвязи между результатами образцов для проверки квалификации (например,
все точки находятся приблизительно вокруг наклонной линии). Если признаки
взаимосвязи существуют, это означает, что у участников существуют смещения, на
которые одинаково воздействуют образцы. Если же никакой зависимости между
результатами не наблюдается (все точки расположены внутри окружности, обычно с
более высокой плотностью в центре), то погрешности измерений для двух образцов
в значительной степени независимы. Если визуального анализа недостаточно,
зависимость можно проверить с помощью статистики ранговой корреляции;
c) участников точек, расположенных
по диагонали или другим упорядоченным способом, для закрытых групп. Наличие
таких точек указывает на различия в методах.
Примечание 1 — Если в исследованиях все участники используют
один и тот же метод или графики результатов получены по единственному методу, а
результаты лежат вдоль прямой линии, это означает, что метод измерений не был
установлен должным образом. Исследование метода испытаний может позволить
улучшить общую воспроизводимость метода.
Примечание 2 — Пример графика Юдена приведен в E.12 приложения E.
10.6 Графики стандартных
отклонений повторяемости
10.6.1 Если участниками раунда программы проверки квалификации
выполнены репликации измерений, результаты могут быть использованы для
построения графика идентификации всех участников, у которых выборочное среднее
и стандартное отклонения существенно отличаются от остальных.
10.6.2 На графике изображают внутрилабораторное стандартное
отклонение для
каждого участника в зависимости от соответствующего выборочного среднего участника.
В качестве альтернативы вместо стандартного отклонения может быть использован
размах репликаций.
Пусть
—
робастное среднее значений x1, x2, …, xр,
вычисленное в соответствии с алгоритмом А;
—
робастное объединенное значение величин s1, s2, …, sp,
вычисленное в соответствии с алгоритмом S.
Предположим, что данные
подчиняются нормальному распределению. Для нулевой гипотезы (результаты
лабораторий относятся к одной генеральной совокупности, или не существует
различий между лабораториями по внутрилабораторным средним или стандартным
отклонениям) статистика
|
|
(21) |
имеет распределение, близкое к χ2-распределению
с двумя степенями свободы. Следовательно, критическую область с уровнем
значимости приблизительно 1 % можно изобразить на графике, откладывая
|
|
(22) |
по оси стандартного отклонения в точках на оси
среднего x из интервала
|
от |
(23) |
Примечание — Данная процедура основана на методике, предложенной
Нуландом в [11]. Для распределения
стандартного отклонения в методе Нуланда использовано обычное нормальное
распределение, что может образовать критическую область, содержащую
отрицательные стандартные отклонения. Приведенный метод использует приближение
для распределения стандартного отклонения, которое исключает эту возможность,
но критическая область уже не является эллипсом, как в оригинале. Кроме того,
для центральной точки использованы робастные значения вместо простых выборочных
средних, как в оригинале.
10.6.3 График может выявить участников, в результатах
которых смещение в условиях повторяемости слишком велико. Если количество
репликаций достаточно велико, этот метод может также
идентифицировать участников, у которых повторяемость очень
мала. Однако поскольку количество репликаций, как правило, невелико,
интерпретация подобных случаев затруднена.
Примечание — Пример графика стандартных отклонений повторяемости
приведен в E.13 приложения E.
10.7 Разделенные пробы
10.7.1 Разделенные пробы используют при необходимости для
выполнения детального сравнения двух участников или в том случае, когда
проверка квалификации невозможна и требуется внешняя верификация. Получают
пробы нескольких материалов, представляющих широкую амплитуду исследуемых
свойств. Каждую пробу разбивают на две части, и каждая лаборатория выполняет
несколько (не менее двух) репликаций измерений на каждой пробе.
В том случае, если количество участников более двух, одну из
лабораторий следует рассматривать как экспертную, а другие лаборатории
сопоставляют свои результаты с ее результатами описанным ниже методом.
Примечание 1 — Этот метод исследования является общим, иногда
его называют по-другому — «метод парных сравнений» или «метод двусторонних
сравнений».
Примечание 2 — План эксперимента разделенных проб не следует
путать с планом эксперимента с разделенным уровнем, описанным в стандартах
серии ГОСТ Р ИСО 5725, когда участникам поставляют два образца, немного
отличающихся по уровням.
10.7.2 Данные эксперимента с разделенной пробой следует
использовать для построения графиков, отображающих различия между репликациями
измерений, для каждого из двух участников и средними результатами участников для
каждой пробы. Двумерные графики с использованием полного диапазона концентраций
могут иметь такую шкалу, которая затруднит идентификацию важных различий между
участниками, в этом случае более полезными могут быть графики различий или
процентов различий между результатами двух участников. Дальнейший анализ
зависит от сделанных выводов.
10.8 Графические методы
объединения индексов после нескольких раундов программы проверки квалификации
10.8.1 При необходимости объединения стандартизованных
индексов функционирования по результатам нескольких раундов программы проверки
квалификации провайдер проверки квалификации может рассмотреть подготовку
графиков в соответствии с 10.8.2
или 10.8.3. Использование графиков,
в которых индексы функционирования для нескольких раундов программы проверки
квалификации объединены, может допускать наличие трендов и других особенностей
результатов, которые необходимо идентифицировать и которые не могут быть
выявлены при исследовании индексов в каждом раунде отдельно.
Примечание — При использовании «текущих индексов» или
«накопленных индексов», в которых объединены индексы функционирования, полученные
участником в нескольких раундах программы проверки квалификации, индексы
следует отобразить на графике. Участник может иметь несоответствие, которое
обнаруживается при работе с образцом для проверки квалификации в одном раунде,
но не обнаруживается в других раундах; «бегущий индекс» может скрыть это
несоответствие. Тем не менее в некоторых случаях (например, при частом
повторении раундов) «сглаживание» случайных выбросов индексов может быть
полезным для более наглядной демонстрации основных показателей.
10.8.2 Контрольная карта Шухарта
является эффективным методом идентификации проблем, вызывающих большие
отклонения значений z-индекса. Рекомендации по
построению карт Шухарта и правила построения границ действия приведены в ГОСТ
Р ИСО 7870-2.
10.8.2.1 Для подготовки карты Шухарта стандартизованные
индексы, такие как z-индексы или PA-индексы,
для участника наносят на карту в виде отдельных точек вместе с границами зон
предупреждения и действия в соответствии с программой проверки квалификации.
Если в каждом раунде измеряют несколько характеристик, индексы для различных
характеристик могут быть представлены на одном графике, но точки для различных
характеристик должны быть нанесены с использованием различных символов и/или
различных цветов. Если в один раунд проверки включено несколько образцов
проверки квалификации, индексы функционирования могут быть нанесены в виде
нескольких точек в каждый момент времени. В этом случае на график можно
добавить линию, соединяющую средние индексы в каждый момент времени.
10.8.2.2 Обычно правило интерпретации контрольной карты
Шухарта состоит в том, что наблюдаемое значение считают выходящим за
установленные границы зоны сигнала к действиям, если:
a) единственная точка выходит за
пределы зоны сигнала к действиям (± 3,0 для z-индексов
или 100 % для PA);
b) две из трех последовательных
точек лежат вне зоны сигнала предупреждения (± 2,0 для z-индексов
или 70 % для PA);
c) шесть последовательных
результатов либо все положительны, либо все отрицательны.
10.8.2.3 Если контрольная карта Шухарта показывает, что наблюдаемая
характеристика выходит за установленные границы, участник должен исследовать
возможные причины этого явления.
Примечание — Стандартное отклонение для оценки квалификации не обязательно является стандартным отклонением
разностей , так что уровни вероятностей, которые обычно
соответствуют границам зон предупреждения и действия карт Шухарта, не могут
быть применены.
10.8.3 Если уровень характеристики
свойства изменяется от одного раунда программы проверки квалификации к другому,
графики стандартизованных индексов функционирования, таких как z-индексы или PA-индексы,
в зависимости от приписанного значения будут это отражать, если смещение
результатов участника изменяется вместе с уровнем. Если более чем один образец
включается в один и тот же раунд, индексы функционирования могут быть
представлены на графике независимо.
Примечание 1 — Может быть полезным отмечать на карте результаты
текущего раунда другим символом или цветом, чтобы их отличать от предыдущих
раундов.
Примечание 2 — Пример такой карты с использованием PA-индекса приведен в E.14 приложения E. Такую карту
легко использовать и для z-индекса. Только изменения надо наносить по
вертикальной шкале.
11
Планирование эксперимента и анализ программ проверки квалификации для
качественных показателей (включая номинальные и порядковые свойства)
11.1 Вид качественных данных
Довольно часто при проверке квалификации используют свойства,
которые идентифицируют по качественной шкале. Среди видов качественных данных
различают программы проверки квалификации, в которых:
— результаты фиксируют по категориальной шкале (иногда
называемой «номинальной шкалой»), где характеристика свойства не имеет
числового значения (например, тип вещества или организма);
— фиксируют наличие или отсутствие свойства, определяемого
по субъективным критериям или значению сигнала при выполнении процедуры
измерений. Эту ситуацию можно рассматривать как частный случай категориальной
или порядковой шкалы с двумя значениями (также называемой «дихотомической» или
«бинарной»);
— результаты фиксируют по порядковой шкале, эти результаты
могут быть упорядочены, но для них арифметические соотношения неприменимы.
Например, порядковая шкала может иметь значения «высокий», «средний», «низкий».
Такие программы проверки квалификации требуют особого
внимания на этапах планирования эксперимента, выбора приписанного значения и
оценки показателей функционирования (индексов), так как:
— приписанные значения очень часто основаны на мнении
экспертов;
— статистическая обработка, предназначенная для непрерывных
значений и количественных данных, не применима к качественным данным. Например,
при определении результатов по порядковой шкале не имеет смысла применять
средние и стандартные отклонения, даже если результаты могут быть ранжированы.
В следующих подразделах приведены рекомендации по
планированию, выбору приписанного значения и оценке функционирования для схем
проверки квалификации с использованием качественных характеристик.
Примечание — Рекомендации для порядковых данных не применяют к
результатам измерений, которые основаны на количественной шкале с дискретными
показателями (см. 5.2.2).
11.2 Статистическое планирование эксперимента
11.2.1 Для программ проверки квалификации, в которых мнение
экспертов используют при определении приписанного значения или оценке отчетов
участников, необходимо собрать комиссию из квалифицированных экспертов и дать
ей время для обсуждения и выработки согласованного мнения. Там, где есть
необходимость полагаться на мнение отдельных экспертов при выборе индексов или
назначении величин, провайдер проверки квалификации должен дополнительно
обеспечить оценку и проверку согласованности мнений различных экспертов.
Пример
— В программе проверки квалификации в клинике, где для диагностики
используют микроскоп, для оценки предметных стекол, предоставляемых участникам,
используют экспертное заключение, которое обеспечивает соответствующий
клинический диагноз для образцов проверки квалификации. Провайдер проверки
квалификации может выбрать и раздать членам экспертной комиссии образцы вслепую
(без указания участника) для обеспечения согласованности диагноза или проводить
периодические совещания для получения согласованной оценки всех членов
экспертной комиссии.
11.2.2 Для программ проверки квалификации, в которых
участники фиксируют простые, однозначные, категоризированные или порядковые
результаты, провайдеру проверки квалификации следует рассмотреть возможность:
— обеспечения двух или более образцов проверки квалификации
в раунде;
— запроса результатов репликаций измерений для каждого
образца проверки квалификации в соответствии с количеством установленных заранее
репликаций измерений.
Любая из этих стратегий позволяет подсчитывать результат для
каждого участника, который может быть использован либо в анализе данных, либо
для расчета индексов. Использование двух или более образцов обеспечивает
дополнительную информацию об особенностях ошибок, а также позволяет определить
более сложные индексы при оценке квалификации.
Пример 1
— В программе проверки квалификации фиксируют наличие или отсутствие
загрязняющего вещества, предоставленные образцы содержат некоторый диапазон
уровней загрязняющего вещества на каждом уровне его содержания как функцию
уровня содержания загрязняющего вещества. Это может быть использовано,
например, для предоставления информации участникам о возможности обнаружения
выбранным методом испытаний загрязняющего вещества или для получения средней
вероятности обнаружения и последующего определения индексов функционирования,
которые в свою очередь могут быть распределены среди участников на основе
оценок вероятностей конкретных моделей отклика.
Пример 2
— Проверка квалификации для судебно-медицинских исследований часто
требует сопоставления образцов на предмет того, получены они из одного и того
же источника или из различных источников (например, отпечатки пальцев, ДНК,
гильзы от пули, следы и т.д.). В большинстве случаев возможен ответ «не
определено». Программа проверки квалификации может включать в себя несколько
образцов из различных источников, и участников просят для каждой пары образцов
установить, принадлежат ли они одному и тому же источнику, различным источникам
или их источник не может быть определен. Это позволяет дать объективные оценки
в виде числа (или %) правильных или неправильных заключений или количества
правильных решений о соответствии или отклонении. Затем могут быть установлены
критерии их функционирования по степени пригодности использования или сложности
задачи.
11.2.3 Однородность должна быть подтверждена анализом
соответствующей выборки из образцов, каждый из которых должен
продемонстрировать ожидаемое свойство. Для некоторых качественных показателей,
например наличие или отсутствие чего-либо, может быть возможна проверка
однородности с помощью измерений количественных показателей, таких как
микробиологический подсчет объектов или спектр поглощения выше заданного
порога. В таких ситуациях могут быть целесообразны испытания на однородность
или демонстрация всех результатов выше или ниже заданного значения.
11.3 Приписанное значение для
качественных показателей
11.3.1 Приписанные значения для
образцов могут быть установлены на основе:
a) экспертной оценки;
b) использования стандартных
образцов в качестве образцов для проверки квалификации;
c) сведений о происхождении или
подготовке образца(ов);
d) использования моды или медианы
результатов участника (медиана подходит только для порядковых значений).
Для получения достоверных результатов может быть использован
также любой другой способ выбора приписанного значения. Ниже рассмотрена каждая
из перечисленных выше стратегий.
Примечание — Эти способы обычно не подходят для обеспечения количественной
информации о неопределенности приписанного значения в программах проверки
квалификации, использующих качественные показатели. Тем не менее в соответствии
с 11.3.2 — 11.3.5 необходима такая базовая информация о
достоверности приписанного значения, чтобы участники могли взвешенно оценить,
может ли полученный плохой результат быть связан с ошибкой при установлении
приписанного значения.
11.3.2 Значения, присвоенные на
основании заключения экспертов, обычно должны базироваться на согласованном
мнении всех квалифицированных экспертов. Любое значимое расхождение между
членами комиссии должно быть записано в отчете по результатам раунда. Если
комиссия не может достичь соглашения в отношении конкретного образца, провайдер
может рассмотреть альтернативный способ присвоения приписанного значения из
перечисленных в 11.3.1. Если этот
способ не подходит, образец не должен быть использован для оценки работы
участников.
Примечание — В некоторых случаях приписанное значение может
определить единственный эксперт.
11.3.3 Если в качестве образца для проверки квалификации
участникам предоставляют стандартный образец в качестве приписанного значения
для данного раунда, следует использовать соответствующее опорное значение или
сертифицированное значение. Информация, представленная вместе со стандартным
образцом, относящаяся к обоснованию правильности установления приписанного значения,
должна быть доступна для участников следующих раундов.
Примечание — Ограничения данного подхода приведены в 7.4.1.
11.3.4 Если образцы получены из известного источника,
приписанное значение может быть определено на основании информации об источнике
получения материала. Провайдер должен сохранять записи о происхождении,
транспортировании и обработке используемых материалов. В связи с этим следует
соблюдать осторожность для подтверждения загрязнения образцов, которое может
привести к неверным результатам участников. Сведения об источнике и/или детали
подготовки образцов должны быть доступны участникам после завершения раунда или
по запросу, или в качестве части отчета о раунде по проверке квалификации.
Пример
— Образцы вина, представленные участникам программы проверки квалификации
для проверки его подлинности, могут быть закуплены непосредственно у
изготовителя в указанном регионе или через коммерческого поставщика, способного
обеспечить свидетельства подлинности.
11.3.4.1 По возможности рекомендуется проводить
подтверждающие испытания или измерения, особенно если использование образца
может привести к его загрязнению. Например, образец, идентифицированный как
экземпляр одного вида микроорганизмов, растений или животных, как правило,
должен быть проверен на наличие отклика для других соответствующих видов. Такие
испытания должны быть по возможности максимально чувствительными, чтобы
гарантировать либо отсутствие загрязняющих видов, либо количественное определение
уровня загрязнения.
11.3.4.2 Провайдер должен предоставить информацию о
каких-либо обнаруженных загрязнениях или сомнениях о происхождении образца,
которые могут поставить под угрозу его использование.
Примечание — Более подробное описание таких образцов выходит за
рамки области применения настоящего стандарта.
11.3.5 В качестве приписанного
значения для результатов по категориальной или порядковой шкале может быть
использована мода (наиболее частое наблюдение), для результатов на порядковой
шкале в качестве приписанного значения также может быть использована медиана.
При использовании этих статистик в отчет о раунде проверки квалификации следует
включать указание доли результатов, использованных при выборе приписанного
значения. Нецелесообразно рассчитывать средние значения или стандартные
отклонения для результатов проверки квалификации для качественных показателей,
в том числе для порядковых значений, поскольку для этих величин неприменимы
арифметические операции.
11.3.6 Если приписанные значения определяют на основе
измеримых величин (например, наличие или отсутствие), то приписанное значение
обычно может быть определено достаточно точно, то есть с низкой
неопределенностью. Статистические расчеты при определении неопределенности
могут быть применены для уровней измеряемой величины как «неопределенный» или
«сомнительный».
11.4 Оценка функционирования и определения индексов для
качественных показателей
11.4.1 Оценка работы участников в программе проверки
квалификации, использующей качественные показатели, частично зависит от
характера требуемого отчета. В некоторых программах проверки квалификации, где
требуется значимое количество оценок участников и выводы должны быть тщательно
проанализированы и точно сформулированы, отчеты участников могут быть переданы
экспертам для общей оценки и направлены для общего учета. С другой стороны, для
оценки работы участника иногда достаточно выяснить, насколько точно его
результаты совпадают с приписанным значением для соответствующего образца
проверки квалификации. Ниже приведены рекомендации относительно оценки
функционирования и определения индексов для целого ряда обстоятельств.
11.4.2 Для экспертной оценки отчетов участников требуется
один или несколько экспертов для анализа каждого отчета участника для каждого
образца и назначения оценки или индекса функционирования. В такой программе
проверки квалификации провайдер должен гарантировать:
— что конкретный участник эксперту неизвестен, в частности
отчет не должен включать информацию, по которой эксперт может идентифицировать
участника;
— анализ, маркировка и оценка функционирования соответствуют
ранее установленным критериям и по возможности соответствующим целям:
— положения 11.3.2
в отношении согласованности между экспертами выполнены;
— при необходимости для участника предусмотрена возможность
обжалования мнения конкретного эксперта и/или проведения повторного анализа
заключений вблизи важных границ функционирования.
11.4.3 При наличии единственного зафиксированного результата
качественного показателя на основе приписанного значения могут быть
использованы две системы определения индекса:
i) каждый результат считают
приемлемым (или успешным), если он точно совпадает с приписанным значением, и
неприемлемым, имеющим неблагоприятный индекс функционирования, в противном
случае.
Пример
— В программе проверки квалификации при определении наличия или
отсутствия загрязняющего вещества правильному результату присваивают единицу, а
неверному — нуль;
ii) результаты, точно совпадающие с
приписанным значением, считают приемлемыми, и им присваивают соответствующий
индекс, результатам, не точно совпадающим с приписанным значением, присваивают
индекс, который зависит от особенностей несоответствия. Такая система должна
присваивать более низкие индексы более хорошей работе для согласования такой
системы с другими типами индексов (например, z-индексы,
PA-индексы, ξ, и ).
Пример 1
— В программе проверки квалификации при оценке клинической патологии провайдер
присваивает оценку 0 для абсолютно точной идентификации микробиологического
вида, оценку 1 для неверного результата с правильным лечением (например, при
идентификации другого микробиологического вида с правильным и аналогичным
лечением) и оценку 3 для неверной идентификации, приводящей к неправильному
лечению пациента. Эта система оценок, как правило, требует экспертной оценки
характера несоответствий, по возможности полученной до присвоения оценки.
Пример 2
— В программе проверки квалификации, в которой возможны шесть
ранжированных ответов, соответствующему присваивают индекс 0, и индекс
увеличивается на 2 для каждого следующего значения из возможных шести (так,
ближайший результат к приписанному значению имеет индекс 2).
Участникам должны быть предоставлены их индивидуальные
индексы функционирования для каждого образца. При репликациях наблюдений могут
быть представлены суммарные индексы для каждого результата.
11.4.4 Если для каждого образца зафиксировано несколько
результатов репликаций или если каждому участнику предоставлено несколько
образцов, провайдер может рассчитать и использовать комбинированные индексы
функционирования или суммарный индекс. Комбинированные или суммарные индексы
функционирования могут быть вычислены, например, в виде:
— суммы всех индексов для всех образцов;
— суммы для
каждого назначенного уровня функционирования;
— доли правильных
результатов;
— метрического
расстояния, определенного на основе разностей результатов и приписанных
значений.
Пример
— В качестве метрического расстояния иногда используют такую статистику
для качественных данных, как коэффициент Гауэра [12]. Она позволяет объединить количественные и
качественные данные на основе объединения аналогичных индексов. Для
категоризированных или бинарных данных индекс равен 1 в случае точного
соответствия категории и 0 в противоположном случае; для порядковых данных
индекс равен 1 минус разность рангов, деленная на количество имеющихся рангов;
для интервальной шкалы или шкалы отношений индекс равен 1 минус абсолютная
величина разности, деленная на наблюдаемый размах всех значений. Эти индексы
находятся в интервале от О до 1, их суммируют и используют сумму, деленную на
количество используемых переменных. Также может быть применен вариант с
использованием весовых коэффициентов.
Комбинированные индексы функционирования можно рассматривать
как общую оценку функционирования лаборатории. Например, работу можно считать
приемлемой при наличии установленной доли (как правило, высокой) правильных
результатов, если это соответствует целям программы проверки квалификации.
11.4.5 Для предоставления участникам информации об их работе
могут быть использованы графические методы или представлены общие данные в
отчете по раунду.
Примечание — Пример анализа порядковых данных приведен в E.15 приложения E.
Приложение A
(обязательное)
Обозначения
d — разность измеряемой
величины для образца, используемого в испытаниях при проверке квалификации и
приписанного значения для CRM;
— выборочное среднее разности измеренных величин и
приписанного значения для CRM;
D — разность результата
участника и приписанного значения ;
D % —
отношение разности результата участника и приписанного значения к приписанному
значению, %;
—
критерий максимально допустимой погрешности для разностей;
—
погрешность, связанная с различиями между образцами для проверки квалификации;
—
погрешность, связанная с нестабильностью в процессе испытаний;
—
погрешность, связанная с нестабильностью условий транспортирования;
— индекс
стандартизованной погрешности, который включает неопределенности результатов
участников и приписанного значения;
—
количество образцов, используемых при проверке однородности;
т — количество повторных измерений, выполняемых на
образце;
р — количество участников раунда программы проверки
квалификации;
PA — доля
допустимой погрешности D/ (может
быть выражена в процентах);
sr — оценка стандартного отклонения повторяемости;
sR — оценка стандартного отклонения воспроизводимости;
ss — оценка стандартного отклонения изменчивости между
образцами;
—
робастная оценка стандартного отклонения участника;
— стандартное отклонение выборочных средних арифметических;
sw — выборочное или лабораторное стандартное отклонение;
—
стандартное отклонение ширины полосы, используемое для построения графиков
ядерной плотности распределения;
—
межлабораторное (между участниками) стандартное отклонение;
—
стандартное отклонение для оценки квалификации;
—
стандартное отклонение повторяемости;
—
стандартное отклонение воспроизводимости;
—
стандартная неопределенность, соответствующая различиям между образцами,
используемыми при проверке квалификации;
—
стандартная неопределенность, соответствующая нестабильности условий проведения
проверки квалификации;
—
стандартная неопределенность, соответствующая нестабильности условий
транспортирования;
—
стандартная неопределенность результата i-го
участника;
—
стандартная неопределенность приписанного значения;
—
стандартная неопределенность опорного значения;
—
расширенная неопределенность зафиксированных результатов i-го
участника;
—
расширенная неопределенность приписанного значения;
—
расширенная неопределенность опорного значения;
wt — размах результатов измерений на различных экземплярах
одного образца;
—
робастная оценка повторяемости участника;
x —
результат измерений (в общем случае);
— значение характеристики, полученное в соответствии с
определением приписанного значения;
— приписанное значение для показателя CRM;
— результат измерений i-го
участника;
— приписанное значение;
— опорное значение для установленной цели;
—
робастная оценка среднего участника;
—
среднее арифметическое набора результатов;
z — индекс, используемый для оценки
квалификации;
z’ — модифицированный z-индекс, включающий неопределенность приписанного значения;
ζ — дзета-индекс, модифицированный z-индекс,
включающий неопределенность результата участника и приписанного значения.
Приложение B
(обязательное)
Однородность и стабильность образцов для проверки квалификации
B.1 Общая процедура проверки однородности
B.1.1 Для проверки однородности при
подготовке образцов следует выполнять приведенную ниже процедуру.
Выбирают свойство (или свойства) или измеряемую(ые)
величину(ны) для проверки однородности.
Для проверки однородности выбирают лабораторию и используемый
метод измерений. Метод измерений должен иметь достаточно малое стандартное
отклонение повторяемости sr чтобы любая значительная неоднородность могла быть
обнаружена. Отношение стандартного отклонения повторяемости метода измерений к
стандартному отклонению для оценки квалификации должно составлять менее 0,5 в
соответствии с рекомендациями гармонизированного протокола IUPAC
(или 1/6 ).
Так как это не всегда возможно, то провайдер должен использовать большее
количество репликаций измерений.
Подготавливают и упаковывают достаточное количество образцов
для проверки квалификации для раунда программы проверки квалификации и для
проверки их однородности.
Из готовых упакованных образцов случайным образом отбирают образцов,
≥ 10. Количество образцов для проверки
однородности может быть уменьшено при наличии соответствующих данных предыдущих
проверок однородности для образцов, подготовленных с применением тех же самых
процедур.
Подготавливают т ≥ 2 исследуемых порций
для каждого образца, используя приемы, соответствующие исследуемому образцу,
чтобы минимизировать различия между исследуемыми порциями.
Случайным образом отбирают · m исследуемых
порций и определяют результаты измерений на каждой порции, получая серию
результатов измерений в условиях повторяемости.
Вычисляют общее выборочное среднее ,
стандартное отклонение sw и стандартное отклонение ss в соответствии с B.3.
B.1.2 Если нет возможности
выполнения репликаций измерений, например в случае разрушающих испытаний, в
качестве ss можно
использовать стандартное отклонение результатов. В такой ситуации важно иметь
метод, обладающий достаточно низким стандартным отклонением повторяемости sr
B.2 Критерий проверки однородности
B.2.1 Следует использовать следующие
три проверки, чтобы обеспечить валидацию данных испытаний на однородность:
a) проверяют результаты измерений
для каждой исследуемой порции для выявления тренда или дрейфа; если выявлен
тренд, необходимо предпринять соответствующие корректирующие действия по
отношению к методу измерений или соблюдать осторожность в интерпретации
результатов;
b) проверяют результаты для
выборочных средних образцов для проверки квалификации в порядке получения, если
существует явный тренд, который может привести к тому, что образец превысит
критерий, установленный в B.2.2, или
возникнут обстоятельства, препятствующие использованию образца, то (i) устанавливают индивидуальные значения для каждого образца
или (ii) исключают поврежденные образцы и повторно
проверяют оставшиеся образцы на однородность; или (iii)
поступают в соответствии с положениями B.2.4, если
тренд охватывает все образцы;
c) сопоставляют разности результатов
репликаций (или размах при выполнении более двух репликаций) и при
необходимости используют критерий Кохрена для проверки наличия статистически
значимых различий между результатами репликаций измерений (см. ГОСТ
Р ИСО 5725-2). Если разность результатов репликаций велика, для всех
пар следует найти техническое обоснование этого явления и при необходимости
исключить отличающуюся группу из анализа или удалить одну точку, если т >
2 и высокая дисперсия обусловлена единственным выбросом.
Примечание — Если т > 2 и исключено одно
наблюдение, то при дальнейших расчетах необходимо учесть дисбаланс между sw и ss.
B.2.2 Сопоставляют стандартное отклонение ss со стандартным
отклонением для оценки квалификации .
Образцы для проверки квалификации можно считать однородными если:
|
|
(B.1) |
Примечание 1 — Коэффициент 0,3 означает, что при выполнении
критерия выборочного стандартного отклонения в изменчивость оценка
функционирования не превышает 10 %, поэтому эти оценки вряд ли влияют на
оценку.
Примечание 2 — Аналогично ss можно сравнить
с :
|
|
(B.2) |
B.2.3 Для учета
фактической выборочной погрешности и повторяемости при проверке однородности
может быть полезно расширить критерий. В этих случаях необходимо выполнить
следующие действия:
a) вычислить ;
b) ,
где sw — выборочное
стандартное отклонение, вычисляемое в соответствии с B.3.
Значения F1 и F2
определяют по таблице B.1 для выбранного количества образцов для проверки
квалификации и с каждым образцом, исследуемым два раза [13].
Таблица
B.1 — Коэффициенты F1
и F2 для использования при проверке
однородности
|
|
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
|
F1 |
1,59 |
1,60 |
1,62 |
1,64 |
1,67 |
1,69 |
1,72 |
1,75 |
1,79 |
1,83 |
1,88 |
1,94 |
2,01 |
2,10 |
|
F2 |
0,57 |
0,59 |
0,62 |
0,64 |
0,68 |
0,71 |
0,75 |
0,80 |
0,86 |
0,93 |
1,01 |
1,11 |
1,25 |
1,43 |
Если т > 2, F2 в перечислении b)
B.2.3 и таблице B.1 необходимо заменить на F2m = , где
—
расширенное значение, соответствующее вероятности 0,05 для случайной величины,
подчиняющейся F-распределению с ( —
1) и (т — 1) степенями
свободы.
Примечание — Значения F1 и F2 в
таблице B.1 получены из стандартных статистических таблиц следующим образом:
, где
— значение, которое случайная величина, подчиняющаяся
-распределению с (
— 1) степенями свободы, превышает с вероятностью 0,05.
, где
—
значение, которое случайная величина, подчиняющаяся F-распределению
с ( — 1) и
степенями
свободы, превышает с вероятностью 0,05;
c) если ,
это является свидетельством того, что партия образцов для испытаний
недостаточно однородная.
B.2.4 Если
значение неизвестно
заранее, например, когда является
робастным стандартным отклонением результатов участников, провайдеру проверки
квалификации следует выбрать другие критерии для определения наличия
достаточной однородности. Соответствующие процедуры могут включать в себя:
a) проверку наличия статистически
значимых различий между образцами, например, с помощью критерия Фишера и
дисперсионного анализа для α = 0,05;
b) использование информации из
предыдущих раундов проверки квалификации для оценки ;
c) использование данных эксперимента
на прецизионность (таких как стандартное отклонение воспроизводимости по ГОСТ
Р ИСО 5725-2);
d) принятие риска наличия неоднородных
образцов и проверку критерия после вычисления согласованного значения .
B.2.5 Если критерий достаточной
однородности не выполнен, провайдер должен принять решение о выполнении одного
из следующих действий:
a) включение стандартного отклонения образца в
стандартное отклонение для оценки квалификации путем вычисления в
соответствии с (B.3). Важно, чтобы эта информация была доведена до
участников
b)
включение ss в
неопределенность приписанного значения и использование z’
или ‘
для получения оценки функционирования участника (см. 9.5);
c) если робастное
стандартное отклонение результатов участников, то неоднородность между
образцами включают в .
Таким образом критерий приемлемой однородности становится более слабым и должен
быть использован с осторожностью.
Если ни одно из действий, приведенных в перечислении a)
— c), не может быть
применено, следует отказаться от применения образца и повторить подготовку
после устранения причины неоднородности.
B.3 Формулы
для проверки однородности
Оценки стандартных отклонений sw и ss могут быть вычислены с использованием дисперсионного
анализа, как показано ниже. Метод применяют для выбранного количества образцов с
репликациями т измерений каждого.
Данные проверки однородности представлены значениями
переменной xt,k
где t — соответствует образцу (t = 1, 2, …, );
k —
соответствует исследуемой порции (k = 1, 2, …, т).
Вычисляют выборочное среднее и выборочную дисперсию для
образца:
|
|
(B.4) |
а также оценку дисперсии между исследуемыми порциями:
|
|
(B.5) |
Вычисляют общее выборочное среднее:
|
|
(B.6) |
оценку дисперсии выборочных средних:
|
|
(B.7) |
а также оценку выборочной дисперсии:
|
|
(B.8) |
Определяют оценку объединенной дисперсии ss и sw:
|
|
(B.9) |
Определяют оценку:
|
|
(B.10) |
Примечание — В том случае если < 0, то лучше использовать ss = 0.
В общем случае, если т = 2, следует использовать
приведенные ниже вычисления.
Определяют выборочные средние по
порциям:
|
|
(B.11) |
и размах между исследуемыми порциями как
|
|
(B.12) |
Вычисляют общее выборочное среднее:
Вычисляют оценку стандартного отклонения оценок
и выборочное стандартное отклонение по всем
образцам:
Суммирование в формулах (B.13),
(B.14)
и (B.15)
ведется по образцам (t =
1, 2, …, ).
Вычисляют оценку стандартного
отклонения между образцами:
|
|
(B.16) |
Примечание 1 — Если sx меньше sw то разность будет
отрицательной. Это возможно при высокой однородности. В этом случае принимают ss= 0.
Примечание 2 — Вместо размахов можно использовать оценки
стандартных отклонений исследуемых порций
|
|
Примечание 3 — Пример приведен в E.2 приложения E.
B.4 Процедуры проверки стабильности
B.4.1 Общие положения
Ниже приведены общие рекомендации по проверке выполнения требований
к стабильности, установленные в 6.1.
Положения, установленные в 6.1.3 в
отношении исследуемых свойств, применимы к любой экспериментальной проверке на
стабильность в течение раунда проверки квалификации и стабильности в процессе
транспортирования.
B.4.1.1 Если предыдущие
экспериментальные исследования, опыт или знания позволяют быть уверенными в
том, что нестабильность маловероятна, экспериментальную проверку стабильности
можно проводить только в случае появления значительных изменений в процессе
раунда проверки квалификации и после раунда. Если такой уверенности нет,
исследования влияния транспортирования на стабильность и стабильности типового
раунда проверки квалификации могут иметь форму планируемых исследований,
проводимых до распространения образцов проверки квалификации, либо для каждого
раунда, либо на ранних стадиях планирования и определения возможности
согласованных условий транспортирования и хранения. Провайдеры проверки
квалификации могут также проводить проверку на наличие нестабильности путем
анализа приведенных в отчете результатов измерений на наличие тренда с
результатами измерений.
B.4.1.2 При проверке стабильности
могут быть выполнены следующие действия:
— все показатели, используемые в программе проверки
квалификации, должны быть проверены на стабильность (или их стабильность должна
быть подтверждена другим способом). Это может быть сделано на основе опыта
работы и технических заключений на основе знаний матрицы (или артефакта) и
измеряемой величины;
— при проверке следует использовать не менее двух образцов,
если изменчивость между образцами является достаточно большой; большее
количество образцов или репликаций следует использовать при наличии сомнений
относительно повторяемости (например, если sw или sr > 0,5 ).
Примечание — В ISO
Guide 35 приведены стратегии минимизации влияния на
исследования стабильности долгосрочных изменений процесса измерений, в том
числе изохронные исследования или использование стабильных стандартных
образцов.
B.4.2 Процедура проверки
стабильности при проведении раунда проверки квалификации
B.4.2.1
Удобным способом проверки стабильности при проведении раунда проверки
квалификации являются испытания небольшого количества образцов для проверки
квалификации после окончания раунда и сравнение их с образцами до проведения
раунда, чтобы гарантировать, что никаких изменений образцов за время проведения
раунда не произошло. Проверка может также включать проверку влияния на образцы
условий транспортирования с помощью сохранения образцов для исследования
влияния продолжительности условий транспортирования. Для исследования влияния
только условий транспортирования сравнивают образцы, поставленные для раунда
испытаний, с образцами, сохраняемыми в контролируемых условиях.
Примечание 1 — Провайдер может использовать результаты проверки
однородности до проведения раунда проверки квалификации вместо выбора и
измерения конкретного набора образцов.
Примечание 2 — Данный способ в равной степени относится к
программам проверки квалификации при испытаниях и калибровке.
B.4.2.2 Если провайдер включает в
процедуру оценки стабильности поставленные образцы в соответствии с B.4.2.1,
то влияние условий транспортирования таким образом будет учтено при оценке
стабильности. Если влияние условий транспортирования проверяют отдельно, то
следует использовать процедуру, установленную в B.6.
B.4.2.3
Процедура по проверке базовой стабильности, использующая измерения до и после
раунда проверки квалификации, включает следующие действия:
a) случайным
образом отбирают 2 образцов для раунда, где
≥
2;
b) выбирают единственную
лабораторию, использующую единственный метод измерений с хорошей промежуточной
прецизионностью;
c) выполняют измерения на образцах до
плановой даты представления образцов участникам. Репликации измерений должны
быть выполнены случайным образом;
d) оставшиеся образцов
сохраняют в условиях, аналогичных предполагаемым условиям хранения у
участников;
e) в максимально сжатые сроки после
даты возвращения результатов участников выполняют измерения на оставшихся образцах в той же
лаборатории, используя тот же метод измерений и то же количество репликаций
измерений как в перечислении а), все репликации
измерений проводят случайным образом;
f) вычисляют средние арифметические и
результатов
для двух групп (до и после раунда) соответственно.
B.4.2.4 В процедуре, установленной в
B.4.2.3,
могут быть сделаны следующие изменения:
a) 1-я группа из образцов может быть
исключена, если имеются другие результаты измерений набора образцов,
выполненные в той же лаборатории и с тем же методом измерений, например, можно
использовать данные проверки однородности;
b) для обеспечения большей
уверенности в стабильности могут быть использованы условия, обеспечивающие
ускоренные изменения образцов;
c) 2-я группа образцов может быть
дополнительно помещена в условия, ожидаемые при транспортировании, для проверки
их воздействия на образцы;
d) могут быть использованы все
другие планы и условия, которые вместе с выбранными критериями проверки
стабильности обеспечивают большую или равную стабильность.
B.5 Критерий проверки стабильности
B.5.1 Сравнивают общее среднее арифметическое результатов
измерений, полученных до проверки однородности, с общим средним арифметическим
результатов, полученных при проверке стабильности. Образцы можно считать
стабильными, если:
B.5.2
Если существует возможность, что промежуточная прецизионность метода измерений
(или неопределенность результатов измерений образца) вносит свой вклад в
несоответствие критерию, то следует выполнить одно из следующих действий:
a) использовать исследование
изохронной стабильности (см. ISO Guide 35);
b) увеличить неопределенность
приписанного значения для учета возможной нестабильности;
c)
расширить критерий приемки путем добавления неопределенности разности к в соответствии со следующей формулой
Примечание — Коэффициент 2 в формуле (B.18) является коэффициентом охвата расширенной
неопределенности разности, обеспечивающим уровень доверия около 95 %, при
вычислении комбинированной неопределенности предполагается, что и
являются независимыми.
B.5.3 Если неравенства, приведенные
в формулах (B.17) и (B.18), не выполнены,
необходимо осуществить следующие действия:
— количественно оценить влияние нестабильности и учесть его
при определении оценок (например, используя z’-индексы);
— проверить процедуры подготовки и хранения образцов для
выявления возможности их улучшений;
— не определять оценки функционирования участников.
B.5.4 Критерии, приведенные в B.5.1
или B.5.2, могут быть заменены подходящим статистическим
критерием, позволяющим установить различия двух наборов данных, при условии,
что этот критерий учитывает повторяемость измерений и обеспечивает
идентификацию стабильности по крайней мере не менее, чем в формуле (B.18).
Примечание — Обычно t-критерий, выявляющий
существенные различия наборов данных с уровнем достоверности 95 %, использующий
средние для каждого образца, обеспечивает такое же или более высокое выявление
нестабильности, чем в формуле (B.18), при условии, что количество используемых образцов
более или равно 3.
B.6
Стабильность в условиях транспортирования
B.6.1 Провайдер должен проверить
воздействие условий транспортирования на образцы по крайней мере на ранних
стадиях программы проверки квалификации. При такой проверке необходимо (при
возможности) сопоставить образцы, сохраняемые в помещении провайдера, с
образцами, поставляемыми и возвращаемыми участниками. Также могут быть проведены
исследования на основе выдерживания образцов в разумных пределах в условиях
транспортирования.
B.6.2 При определении оценки
функционирования участника необходимо исследовать воздействие на образцы всех
известных условий транспортирования. Значимое увеличение неопределенности,
связанной с транспортированием образцов, следует включить в неопределенность
приписанного значения.
B.6.3 В том случае, если проверка
стабильности условий транспортирования включает сравнение результатов для двух
групп образцов, одну группу подвергают воздействию условий транспортирования, а
другую — нет, критерием достаточной стабильности при транспортировании является
критерий, установленный в B.5.1 или B.5.2.
Примечание 1 — Если приписанное значение и стандартное
отклонение оценки квалификации определяют по результатам участников (например,
с помощью робастных методов), то среднее арифметическое и стандартное отклонения
для оценок квалификации отражают любое смещение и увеличение изменчивости
(соответственно), вызванные условиями транспортирования образцов.
Примечание 2 — Пример проверки стабильности приведен в E.2 приложения E.
Приложение C
(обязательное)
Робастный анализ
C.1 Введение
Межлабораторные сравнительные испытания представляют собой
особый анализ данных. В то время как большинство межлабораторных сравнительных
испытаний представляют данные, подчиняющиеся унимодальному и приблизительно
симметричному распределению в задачах проверки квалификации, большая часть
наборов данных включает часть результатов, неожиданно далеко отстоящих от
основного набора данных. Причины появления таких данных могут быть различными:
например, появление новых, менее опытных участников проверки, появление новых
и, возможно, менее точных методов измерений, непонимание некоторыми участниками
инструкции или неправильная обработка образцов. Такие отличающиеся результаты
(выбросы) могут быть весьма изменчивы, в этом случае применение традиционных
статистических методов, в том числе вычисление среднего арифметического и
стандартного отклонений, может дать недостоверные результаты.
Провайдерам рекомендуется (см. 6.5.1) использовать статистические методы, устойчивые к
выбросам. Большинство таких методов предложено в книгах по математической
статистике, и многие из них успешно использованы в задачах проверки
квалификации. Обычно робастные методы обеспечивают дополнительную устойчивость
при обработке данных из асимметричных распределений с выбросами.
В данном приложении описано несколько простых в применении
методов, используемых в задачах проверки квалификации и имеющих различные
возможности в отношении определения устойчивости оценок при наличии данных из
загрязненных совокупностей (например, эффективности и пороговой точки). Методы
представлены в порядке возрастания сложности (первый — самый простой, последний
— самый сложный), и в порядке убывания эффективности, поэтому наиболее сложные
оценки требуют доработки для повышения их эффективности.
Примечание 1 — В приложении D приведена дополнительная информация об эффективности,
пороговых точках и чувствительности к небольшим модам — трем важным показателям
различных робастных методов определения оценки функционирования.
Примечание 2 — Робастность является свойством алгоритма
определения оценки, а не свойством полученных оценок, поэтому не совсем
корректно называть средние значения и стандартные отклонения, рассчитанные с
помощью такого алгоритма, робастными. Однако, чтобы избежать использования
чрезмерно громоздких терминов, в настоящем стандарте применены термины
«робастное среднее» и «робастное стандартное отклонение». Следует учитывать,
что это означает оценки среднего или стандартного отклонения, полученные в
соответствии с робастным алгоритмом.
C.2 Простые
устойчивые к выбросам оценки для среднего и стандартного отклонений
совокупности
C.2.1
Медиана
Медиана является наиболее простой, высоко устойчивой к
выбросам оценкой среднего для симметричного распределения. Обозначим медиану med(x). Для определения med(x) по совокупности из р
данных необходимо:
i) расположить р данных в
порядке неубывания:
|
|
ii) вычислить
|
|
(C.1) |
C.2.2
Абсолютное отклонение от медианы MADe
Абсолютное отклонение от медианы MADe(x) обеспечивает определение оценки стандартного
отклонения генеральной совокупности для данных из нормального распределения и
является высоко устойчивым при наличии выбросов. Для определения MADe(x) вычисляют:
i) абсолютные
значения разностей di(i = 1, …, р)
|
|
(C.2) |
ii) MADe(x)
|
|
(C.3) |
Если у половины или большего
количества участников результаты совпадают, то MADe(x) = 0, и следует использовать оценку nlQR в соответствии с C.2.3, стандартное отклонение, полученное после
исключения выбросов, или процедуру, описанную в C.5.2.
C.2.3 Нормированный
межквартильный размах nlQR
Данный метод определения
робастной оценки стандартного отклонения аналогичен методу определения MADe(x). Эту оценку
получить немного проще, поэтому ее часто используют в программах проверки
квалификации. Данную оценку определяют как разность 75-го процентиля (или 3-го
квартиля) и 25-го процентиля (или 1-го квартиля) результатов участника. Данную
статистику называют нормированным межквартильным размахом nlQR
и вычисляют по формуле
|
|
(C.4) |
где —
25-й процентиль выборки (i = 1, 2, …, р);
—
75-й процентиль выборки (i = 1, 2, …, р).
Если 75-й и 25-й процентили совпадают, то nlQR = 0 [как и MADe(x)], а для
вычисления робастного стандартного отклонения следует использовать
альтернативную процедуру, такую как арифметическое стандартное отклонение
(после исключения выбросов), или процедуру, описанную в C.5.2.
Примечание 1 — Для расчета nlQR
требуется сортировка данных только один
раз в отличие от вычисления MADe, но nlQR имеет пороговую
точку в 25 % (см. приложение D), в то время как у MADe пороговая
точка 50 %. Поэтому MADe устойчива
при значительно более высокой доле содержания выбросов, чем nlQR.
Примечание 2 — При р < 30 обе оценки обладают заметным
отрицательным смещением, неблагоприятно влияющим на оценки участников при
проверке квалификации.
Примечание 3 — Различные пакеты статистических программ
используют различные алгоритмы расчета квартилей и, следовательно, могут давать
оценки nlQR с
некоторыми различиями.
Примечание 4 — Пример использования робастных оценок приведен в E.3 приложения E.
C.3 Алгоритм
А
C.3.1
Алгоритм А с итеративной шкалой
Данный алгоритм дает робастные оценки среднего и стандартного
отклонения на основе используемых данных.
Для выполнения алгоритма А р
данные располагают в порядке неубывания
|
|
Полученные по этим данным робастное
среднее и робастное стандартное отклонения обозначают и
.
Вычисляют начальные значения для и
по
формулам:
|
|
(C.5) |
|
|
(C.6) |
Примечание 1 — Алгоритмы А и S, приведенные в
настоящем приложении, соответствуют ГОСТ
Р ИСО 5725-5 с добавлением критерия остановки: при совпадении до 3-го
знака после запятой среднего и стандартного отклонения вычисления прекращают.
Примечание 2 — В некоторых случаях более половины результатов будут идентичны (например, количество нитей в
образцах ткани или количество электролитов в образцах сыворотки крови). В этом
случае начальное значение = 0 и робастная процедура будут некорректными. Если
начальное значение = 0, допустимо
заменить выборочное стандартное отклонение после проверки всех очевидных
выбросов, которые могут сделать стандартное отклонение неоправданно большим.
Такую замену проводят только для начального значения и после этого итеративный алгоритм применяют в
соответствии с описанием.
Вычисляют новые значения и
.
Для этого вычисляют
Для каждого (i = 1, 2, …, р) вычисляют
|
|
(C.8) |
Вычисляют новые значения и
|
|
(C.9) |
где суммирование
производят по i.
Робастные оценки и
получают
на основе итеративных, то есть повторных вычислений и
в
соответствии с (C.7) — (C.10) до тех пор, пока
процесс не начнет сходиться, то есть разности предыдущих и последующих значений
и
не
станут пренебрежимо малы. Обычно итеративные вычисления прекращают при
совпадении в предыдущих и последующих значениях трех знаков после запятой.
Альтернативные критерии сходимости могут быть определены в
соответствии с требованиями к плану эксперимента и к отчету по результатам
проверки квалификации.
Примечание — Примеры использования алгоритма А приведены
в E.3 и E.4 приложения E.
C.3.2 Варианты алгоритма А
Итеративный алгоритм А, приведенный в C.3.1, имеет скромную разбивку (примерно 25 % для
больших наборов данных [14]) и
начальную точку для и
предложенную
в C.3.1, для наборов данных, где MADe(x) = 0 может серьезно ухудшить устойчивость при наличии
нескольких выбросов в наборе данных. Если в наборе данных ожидаемая доля
выбросов составляет более 20 % или если начальное значение подвержено
неблагоприятному влиянию экстремальных выбросов, то следует рассмотреть
следующие варианты:
i) замена MADe на при
MADe = 0 либо использование альтернативной
оценки в соответствии с C.5.1 или
арифметического стандартного отклонения (после исключения выбросов);
ii) если при
оценке робастное стандартное отклонение не используют, следует применять MADe [исправленное в соответствии
с i)], и не изменяют во
время итерации. Если при оценке используют робастное стандартное отклонение,
заменяют в
соответствии с C.5 оценкой и не изменяют
во
время итерации.
Примечание — Вариант, приведенный в перечислении ii), улучшает пороговую точку алгоритма А до 50 %
[14], что позволяет применять
алгоритм при наличии высокой доли выбросов.
C.4 Алгоритм
S
Данный алгоритм применяют к стандартным отклонениям (или
размахам), которые вычисляют, если участники представляют результаты т
репликаций измерений измеряемой величины образца или в исследовании используют т
идентичных образцов. Алгоритм позволяет получить робастное объединенное
значение стандартных отклонений или размахов.
Имеющиеся р стандартных
отклонений или размахов располагают в порядке неубывания
|
|
Обозначим робастное объединенное
значение a v — число степеней свободы, соответствующее каждому wi (Если wi — размах, то v =
1. Если wi — стандартное отклонение
для т результатов испытаний, то v = т
— 1.) Значения , и η определяют в
соответствии с алгоритмом, приведенным в таблице C.1.
Вычисляют начальное значение :
|
|
(C.11) |
Примечание — Если более половины wi имеют
значения, равные нулю, то начальное значение равно нулю, а робастный метод является некорректным.
Если начальное значение равно нулю, то
после устранения выбросов, которые могут повлиять на выборочное среднее,
заменяют стандартное отклонение объединенного среднего арифметического (или
размах средних арифметических). Эту замену выполняют только для начального
значения после чего процедуру продолжают согласно описанию.
Значение вычисляют
следующим образом:
|
|
(C.12) |
Для каждого значения wi
(i =1, 2, …, р) вычисляют
|
|
(C.13) |
Вычисляют новое значение
|
|
(C.14) |
Робастную оценку получают
итеративным методом, вычисляя значение несколько
раз, пока процесс не начнет сходиться. Сходимость считают достигнутой, если
значения в
последовательных итерациях совпадают в трех знаках после запятой.
Примечание — Алгоритм S обеспечивает оценку
стандартного отклонения генеральной совокупности, если оно получено по
стандартным отклонениям из того же нормального распределения (и, следовательно,
обеспечивает оценку стандартного отклонения повторяемости при выполнении
предположений в соответствии с ГОСТ
Р ИСО 5725-2).
Таблица C.1 — Коэффициенты,
необходимые для проведения робастного анализа: алгоритм S
|
Число степеней свободы v |
Лимитирующий коэффициент η |
Поправочный коэффициент |
|
1 |
1,645 |
1,097 |
|
2 |
1,517 |
1,054 |
|
3 |
1,444 |
1,039 |
|
4 |
1,395 |
1,032 |
|
5 |
1,359 |
1,027 |
|
6 |
1,332 |
1,024 |
|
7 |
1,310 |
1,021 |
|
8 |
1,292 |
1,019 |
|
9 |
1,277 |
1,018 |
|
10 |
1,264 |
1,017 |
|
Примечание — Значения |
C.5 Сложные
для вычислений робастные оценки: -метод
и оценка Хампеля
C.5.1
Обоснование оценок
Робастные оценки среднего и стандартного отклонения
генеральной совокупности, описанные в C.2 и C.3,
используют в тех случаях, когда вычислительные ресурсы ограничены или когда
требуется краткое обоснование статистических процедур. Эти процедуры оказались
полезными в самых разных ситуациях, в том числе в программах проверки
квалификации в новых областях исследований или при калибровке и в тех областях
экономики, где проверка квалификации раньше не была доступна. Однако эти методы
являются недостоверными в тех случаях, когда количество выбросов в результатах
превышает 20 %, или в случае бимодального (или мультимодального) распределения
данных, и некоторые из них могут стать неприемлемо изменчивыми для небольшого
количества участников. Кроме того, ни один из этих методов не может работать с
данными репликаций измерений участников. В соответствии с ГОСТ
ISO/IEC 17043 необходимо, чтобы эти ситуации были предусмотрены до
проведения расчетов или выполнены в процессе анализа до проведения оценки
функционирования участника, однако это не всегда возможно.
Кроме того, некоторые робастные методы, описанные в C.2
и C.3, имеют низкую статистическую эффективность. Если
количество участников менее 50, а робастное среднее и/или стандартное
отклонение используют для определения индексов, то существует значимый риск
неверной классификации участников при применении неэффективных статистических
методов.
Робастные методы, объединяющие высокую эффективность (то
есть сравнительно низкую изменчивость) с возможностью работы с высокой долей
выбросов в данных, обычно являются достаточно сложными и требуют серьезных
вычислительных ресурсов, но эти методы представлены в литературе и
международных стандартах. Некоторые из них обеспечивают получение
дополнительных преимуществ, когда основное распределение данных является
асимметричным или определенные результаты находятся ниже предела их
обнаружения.
Ниже приведены некоторые высокоэффективные методы
определения оценок стандартного отклонения и параметра положения (среднего),
которые показывают более низкую изменчивость, чем простые оценки, и полезны при
использовании для данных с большой долей выбросов. Одну из описанных оценок
можно применять для оценки стандартного отклонения воспроизводимости, если
участники сообщают о большом количестве наблюдений.
C.5.2
Определение робастного стандартного отклонения с использованием -метода
и -метода
C.5.2.1 Оценка [15] является
высокоэффективной оценкой стандартного отклонения генеральной совокупности с
разбивкой, которая становится несмещенной для данных нормального распределения
(при условии отсутствия выбросов).
-метод
учитывает единственный результат для каждого участника (включающий среднее или
медиану репликаций измерений). Расчет основан на использовании попарных
различий в наборе данных и поэтому не зависит от оценки среднего или медианы.
Выполнение этого метода включает корректировки, позволяющие
обеспечить несмещенность оценки для всех фактических объемов наборов данных.
При вычислении для набора данных (x1,
x2, …, xp)
с p результатами:
i)
вычисляют р(р — 1)/2 абсолютных разностей
|
|
(C.15) |
ii) для разностей используют
обозначения
|
|
(C.16) |
iii) вычисляют
|
|
(C.17) |
где k — количество различных пар,
выбранных из h объектов,
где
|
|
(C.18) |
iv) вычисляют
|
|
(C.19) |
где определяют
по таблице C.2
для конкретного количества данных, если р > 12, вычисляют
по формуле
|
|
(C.20) |
где
Примечание 1 — Коэффициент 2,2219 является поправочным,
обеспечивающим несмещенность оценки стандартного отклонения для больших р.
Поправочные коэффициенты для
небольших значений р определяют по таблице C.2, а при р > 12 эти
коэффициенты устанавливают в соответствии с [15], используя экстенсивное моделирование и
последующее применение регрессионного анализа.
Примечание 2 — Простой алгоритм, описанный выше, для больших
наборов данных, например, при р > 1000, требует значительных
вычислительных ресурсов. Для быстрой обработки опубликованы программы (см. [15]) для использования с более
крупными наборами данных (на момент публикации приведена обработка данных с
объемом выше 8000 за приемлемое время).
Таблица
C.2 — Поправочный коэффициент для
2 ≤ р ≤ 12
|
р |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
0,9937 |
0,9937 |
0,5132 |
0,8440 |
0,6122 |
0,8588 |
0,6699 |
0,8734 |
0,7201 |
0,8891 |
0,7574 |
C.5.2.2 -метод позволяет
получить высокоэффективную оценку стандартного отклонения результатов проверки
квалификации, представленных различными лабораториями, с разбивкой. -метод не является
устойчивым не только при наличии выбросов, но и в той ситуации, когда большая
часть результатов испытаний равны между собой, например, когда результаты
представляют собой дискретные числа или при округлении данных. В такой ситуации
другие подобные методы не следует применять, поскольку многие разности равны
нулю.
-метод можно использовать для проверки
квалификации как в случае предоставления участником единственного результата (в
виде среднего и медианы репликаций измерений), так и результатов репликаций.
Прямое использование репликаций измерений в вычислениях повышает эффективность
метода.
Расчет основан на использовании разностей пар в наборе
данных, и таким образом оценка не зависит от оценки среднего или медианы
данных. Метод называют -методом, или методом Хампеля, если его
используют вместе с алгоритмом конечных шагов для определения оценки Хампеля,
описанной в C.5.3.3.
Обозначим результаты измерений
участников, сгруппированные по лабораториям
Кумулятивная функция распределения абсолютных значений разностей
результатов участников имеет следующий вид:
где – индикаторная функция.
Обозначим точки разрыва функции :
|
|
Значения функции в точках
|
|
(C.23) |
Пусть =
0.
Значения функции для
х вне интервала [0, хr]
вычисляют с помощью линейной интерполяции между точками разрыва 0 < x1 < x2
< … <xr
Робастное стандартное отклонение
результатов испытаний для различных лабораторий имеет вид:
|
|
(C.24) |
где вычисляют
аналогично формуле (C.22) и = 0
в случае точного совпадения данных, и (q) — квантиль стандартного нормального распределения
уровня q.
Примечание 1 — Этот алгоритм не зависит от среднего, он может
быть использован либо вместе со значением, полученным по объединенным
результатам участников, или в соответствии с установленным опорным значением.
Примечание 2 — Другие варианты -метода, позволяющие получить робастную оценку
стандартных отклонений воспроизводимости и повторяемости, приведены в [14], [15].
Примечание 3 — Теоретические основы -метода, включая его асимптотическую эффективность и
разбивку на конечное число выборок, описаны в [16] и [15].
Примечание 4 — Если исходные данные участников представлены
единственным результатом измерений, полученным с помощью одного установленного
метода измерений, робастное стандартное отклонение является оценкой
стандартного отклонения воспроизводимости, как и в (C.21).
Примечание 5 — Стандартное отклонение воспроизводимости не
обязательно является наиболее подходящим стандартным отклонением для
использования в проверке квалификации, так как это, как правило, оценка
разброса единственных результатов, а не оценка разброса средних или медиан
результатов репликаций каждого участника. Однако разброс средних или медиан
результатов репликаций лишь немного менее разброса единственных результатов
различных лабораторий, если отношение стандартного отклонения воспроизводимости
к стандартному отклонению повторяемости более двух. Если это отношение менее
двух, для определения оценок при проверке квалификации может быть использована
замена стандартного отклонения воспроизводимости sR скорректированным
значением
|
|
где т — количество репликации;
— дисперсия повторяемости, вычисленная в соответствии
с [17], или можно использовать
среднее значение репликаций измерений участника -метода.
Примечание 6 — Примечание 5 применяют только в том случае, если
индексы определяют на основе средних или медиан результатов репликаций. Если
репликации проводят вслепую, индексы следует рассчитывать для каждой
репликации. В этом случае стандартное отклонение воспроизводимости является
наиболее подходящим стандартным отклонением.
Примечание 7 — Пример применения -метода приведен в E.3 приложения E.
C.5.3 Определение робастного
среднего, используемого в оценке Хампеля
C.5.3.1 Оценка Хампеля является
высокоустойчивой высокоэффективной оценкой общего среднего всех результатов
различных лабораторий. Поскольку формулы вычисления оценки Хампеля не
существует, ниже приведены два алгоритма получения этой оценки. Первый из них
является более простым, но может привести к отклонениям результатов при
выполнении. Второй алгоритм обеспечивает получение однозначных результатов,
зависящих только от базового стандартного отклонения.
C.5.3.2 Далее
приведены вычисления, обеспечивающие получение итеративной взвешенной оценки
Хампеля, для параметра положения.
i) Пусть x1,
x2, …, xp — данные.
ii) Пусть —
медиана med(x)
(см. C.2.1).
iii) Пусть —
соответствующая робастная оценка стандартного отклонения, например, MADe, или
в
соответствии с -методом.
iv) Для каждой точки xi вычисляют qi
|
|
v) Вычисляют вес wi
|
|
vi) Пересчитывают
|
|
vii)
Повторяют действия в соответствии с перечислениями iv)
— vi) до тех
пор, пока значения не
начнут сходиться. Сходимость считают достаточной, если разность в
двух последних итерациях станет менее ,
что соответствует приблизительно 1 % стандартной погрешности .
Могут быть использованы и другие более точные критерии сходимости.
Данный алгоритм получения оценки Хампеля не гарантирует
получение единственной и наилучшей оценки, так как неудачный выбор начального
значения и/или
может привести к исключению важной части набора данных.
Провайдеру следует предпринять соответствующие меры для проверки возможности
получения неудачного результата или обеспечить однозначные правила выбора
параметра положения. Наиболее общим правилом является выбор параметра
положения, максимально близкого к медиане. Анализ результатов для подтверждения
того, что большая часть данных не выходит за пределы области >
4,5, может также помочь в принятии правильного решения.
Примечание 1 — Определение оценки Хампеля для данных из
нормального распределения обладает эффективностью, приблизительно равной 96 %.
Примечание 2 — Примеры выполнения этого алгоритма приведены в E.3 приложения E.
Примечание 3 — Эффективность и устойчивость к выбросам оценки
Хампеля могут быть повышены с помощью изменения весовой функции. Общая форма
весовой функции имеет вид:
|
|
где а, b и с —
регулируемые параметры. Для приведенного алгоритма а = 1,5, b = 3,0 и с
= 4,5. Более высокая эффективность достигается за счет увеличения области
изменений q. Повышения устойчивости к выбросам или изменениям
режимов достигают за счет уменьшения области изменений q.
C.5.3.3 Ниже
приведен алгоритм конечных шагов, позволяющий получить оценку Хампеля для
параметра положения [14].
Вычисляют средние арифметические .
Вычисляют робастное среднее как корень уравнения
где
|
|
(C.26) |
—
робастное стандартное отклонение, полученное -методом.
Точное решение может быть получено за конечное число шагов,
без итерации, используя свойство, при котором как функция
является
частично линейной, имея в виду точки интерполяции в левой стороне уравнения (C.25).
Вычисляют все точки интерполяции:
— для 1-го значения :
— для 2-го значения :
— и так далее для всех .
Располагают в порядке неубывания
.
Затем для каждого т = 1,
…, (6 · p — 1)
вычисляют
|
|
и проверяют, являются ли следующие
условия:
(i) если =
0, то — решение уравнения (C.25);
(ii) если =
0, то, — решение уравнения (C.25);
(iii)
если <
0, то — решение уравнения (C.25).
Пусть S — множество всех решений уравнения (C.25).
Решением является
ближайшая медиана, используемая в качестве параметра положения то
есть
|
|
Могут существовать несколько
решений. Если существуют два решения, наиболее близких к медиане, или если не
существует никакого решения вообще, то в качестве параметра положения используют
медиану.
Примечание 1 — Эта оценка Хампеля для данных из нормального
распределения обладает эффективностью, приблизительно равной 96 %.
Примечание 2 — При использовании этого метода результаты
лабораторий, отличающиеся от среднего более чем на 4,5 стандартных отклонений
воспроизводимости, не оказывают никакого влияния на результат, то есть их
рассматривают как выбросы.
C.5.4 Метод /Хампеля
Метод /Хампеля использует
-метод, описанный в C.5.3.2, для вычисления робастного стандартного
отклонения и
алгоритм конечных шагов для оценки Хампеля, описанный в C.5.3.3,
для вычисления параметра положения .
Если участники сообщают много наблюдений для вычисления
робастного стандартного отклонения воспроизводимости sR,
используют -метод, описанный в C.5.3.2.
Для вычисления робастного стандартного отклонения повторяемости sr применяют 2-й
алгоритм, использующий парные разности в пределах лаборатории.
Примечание — Веб-приложения для метода /Хампеля приведены в [18].
C.6 Другие робастные методы
Методы, описанные в настоящем приложении, не представляют
собой целостную совокупность всех подходов. Ни один из них не является
гарантированно оптимальным во всех ситуациях. По усмотрению провайдера могут
быть использованы другие робастные методы при условии анализа их эффективности
и всех остальных свойств, соответствующих определенным требованиям программы
проверки квалификации.
Приложение D
(справочное)
Дополнительное руководство к статистическим процедурам
D.1
Процедуры в случае небольшого количества участников
D.1.1 Общие положения
В программах проверки квалификации обычно принимает участие
небольшое количество лабораторий, или при наличии большого общего количества
участников выполняют сопоставление групп с небольшим количеством участников.
Это происходит, когда участников группируют и подсчитывают оценки с помощью
единого метода, как, например, это бывает в медицинских лабораториях.
В том случае, если количество участников невелико,
приписанное значение в идеале должно быть определено с использованием
валидированной метрологической процедуры независимо от участников, например,
путем расчета или по данным эталонной лаборатории.
Критерий оценки функционирования лаборатории также должен
быть основан на внешних критериях, таких как выборы экспертов или соответствие
целям. В идеальной ситуации, когда качество функционирования оценивают с
использованием предварительно определенного приписанного значения и критерия
функционирования, проверка квалификации может быть проведена при наличии одного
участника. Такой тип межлабораторных сравнительных испытаний можно назвать
билатеральным, или аудитом измерений, он может быть очень полезным во многих
ситуациях, например, при калибровке.
Если эти идеальные условия не могут быть выполнены,
приписанное значение или дисперсия, или то и другое должны быть получены по
результатам участников. Если количество участников слишком мало для выполнения
конкретной процедуры, то оценка функционирования лаборатории может стать
недостоверной, поэтому важно рассмотреть вопрос об установлении минимального
количества участников оценки функционирования.
Далее приведено руководство по получению критерия оценки
качества работы при небольшом количестве участников, когда для получения
критерия функционирования используют результаты участников.
D.1.2 Процедуры идентификации выбросов
Хотя для загрязненных выбросами генеральных совокупностей
настоятельно рекомендуется использование робастных статистик, для очень
небольших наборов данных их все же не рекомендуют (исключения приведены ниже).
Проверка на наличие выбросов для очень маленьких наборов данных, однако,
возможна. В случае очень маленьких программ или групп предпочтительным является
отклонение выброса с последующим вычислением среднего или стандартного
отклонения.
Различные критерии выявления выбросов применимы к различным размерам
наборам данных. В ГОСТ
Р ИСО 5725-2 приведены таблицы теста Граббса для выявления единичного
выброса и для двух одновременных выбросов в одном и том же направлении. В
критерии Граббса и ряде других критериев необходимо установить заранее
количество возможных выбросов, а при большом количестве выбросов эти критерии
не выполняются, лучше всего они работают при р > 10 (в зависимости от
возможной доли выбросов).
Примечание 1 — После исключения выбросов следует соблюдать
осторожность при оценке дисперсии, так как оценка может быть смещена в меньшую
сторону. Смещение обычно не очень большое, если исключают выбросы, выявляют с
уровнем доверия 99 % и выше.
Примечание 2 — Большинство одномерных робастных оценок
параметров положения и разброса приемлемы при р ≥ 12.
D.1.3 Процедуры оценки параметра
положения
D.1.3.1 Приписанные значения,
полученные из небольших наборов данных участников, должны по возможности
удовлетворять критерию неопределенности приписанного значения, приведенному в 9.2.1. В ситуации с использованием в
качестве приписанного значения среднего и в качестве стандартного отклонения
оценки стандартного отклонения результатов этот критерий не может быть
использован для нормального распределения с р ≤ 12 после
удаления выбросов. При использовании медианы в качестве приписанного значения
(с эффективностью 0,64) критерий не может быть использован для р ≤
18. Другие робастные оценки, такие как в алгоритме А (C.3),
имеют промежуточную эффективность и могут соответствовать критерию при р
> 12, если учтены положения примечания 2 к 7.7.3.
D.1.3.2 Существуют ограничения на
объем набора данных, применяемых для определения некоторых оценок параметра
положения. Рекомендуются несколько численных робастных оценок среднего набора
данных небольшого объема. Нижний предел, как правило, составляет р ≤
15, хотя провайдеры могут иметь возможность продемонстрировать приемлемую
работу с учетом установленных предположений для меньших наборов данных. Медиана
применима для меньших объемов данных вплоть до р = 2 (если она равна
среднему), но при 3 ≤ р ≤ 5 медиана обладает
небольшим преимуществом по сравнению со средним, за исключением тех случаев,
когда существует необычно высокий риск получения плохих результатов.
D.1.4 Процедуры оценки дисперсии
D.1.4.1 Не рекомендуется
использовать критерии функционирования, основанные на разбросе результатов
участников для набора данных небольшого объема из-за очень высокой изменчивости
всех оценок разброса. Например, при р = 30 оценки стандартного отклонения для
данных из нормального распределения в среднем отклоняются от истинного значения
не более чем на 25 % (с уровнем доверия 95 %). Для данных из нормального
распределения не существует лучших оценок.
D.1.4.2 Если оценки разброса необходимы
для других целей (например, как суммарные статистики или оценка разброса данных
для робастной оценки параметра положения) или если программа проверки
квалификации устойчива к высокой изменчивости оценок разброса данных, для
небольших наборов данных следует выбирать оценки разброса с самой высокой
доступной эффективностью.
Примечание 1 — Под высокой доступностью следует понимать наличие
программного обеспечения и соответствующего опыта.
Примечание 2 — Оценка стандартного
отклонения, описанная в C.5, является значительно более эффективной, чем MADe или nlQR из C.1.
Примечание 3 — При
очень небольших наборах данных для робастных оценок разброса данных необходимо
использовать следующие рекомендации [2]:
— для р = 2 необходимо
использовать ;
— р = 3, если параметр положения и шкала неизвестны,
необходимо использовать MADe для защиты
от чрезмерно высоких оценок стандартного отклонения или среднего абсолютного
значения отклонения, для защиты от слишком маленьких оценок стандартного
отклонения, например, если из-за ошибок округления могут быть получены два
одинаковых значения;
—
р ≥ 4 необходимо использовать
установленную М-оценку стандартного отклонения, полученную на основе
логарифмически взвешенной функции, рекомендуемой в [19], а также близкий эквивалент алгоритма А без
итерации при определении параметра положения с использованием медианы в
качестве оценки параметра положения.
Примечание 4 — Для получения оценки стандартного отклонения на
основе абсолютного значения разности и медианы используют следующую формулу:
|
|
(D.1) |
D.2 Эффективность и пороговые точки
робастных процедур
D.2.1 Различные статистические
оценки (робастные методы) можно сопоставлять по трем показателям:
— пороговая точка — доля значений в наборе данных, которые
можно заменить сколь угодно большими значениями, без того чтобы оценка также
стала сколь угодно большой;
— эффективность оценки — отношение дисперсии оценки к
дисперсии минимальной оценки дисперсии для рассматриваемого распределения;
— устойчивость к противоречивым результатам — способность
оценки быть устойчивой к небольшому количеству противоречивых результатов (как
правило, менее 20 % набора данных).
Эти показатели в значительной степени зависят от
распределения результатов участников и особенностей результатов, полученных
некомпетентными участниками (участниками, которые не следуют инструкциям или
методике измерений). Загрязнение данных может проявиться в виде наличия
выбросов, результатов с большой дисперсией или результатов с различными
средними (бимодальное распределение).
Пороговые точки и эффективность оценок различны для
различных ситуаций, их тщательный анализ выходит за рамки настоящего стандарта.
Однако в предположении о нормальном распределении данных могут быть сделаны
простые сопоставления результатов лабораторий со средним, равным , и
стандартным отклонением, равным .
D.2.2 Пороговая точка
Пороговая точка — доля выбросов в наборе данных, которая не
влияет на оценку неблагоприятным образом. Пороговая точка — это мера
устойчивости к выбросам, высокое значение этой точки говорит об устойчивости к
наличию большой доли выбросов. Пороговые точки и устойчивость к противоречивым
результатам оценок, приведенных в приложении C, представлены в таблице
D.1.
Следует отметить, что для процедуры, приведенной в 6.3 и 6.4,
необходимо проводить предварительный анализ данных и не использовать данные с
большим количеством выбросов. Однако существуют ситуации, в которых визуальный
анализ нецелесообразен.
Таблица
D.1 — Пороговая точка для оценки среднего и
стандартного отклонений (доля выбросов, которая может привести к несостоятельности
оценки)
|
Статистическая оценка |
Оцениваемый параметр совокупности |
Пороговая точка, % |
Устойчивость к противоречивым результатам |
|
Выборочное среднее |
Среднее |
0 |
Плохая |
|
Выборочное стандартное отклонение |
Стандартное отклонение |
0 |
Плохая |
|
Выборочная медиана |
Среднее |
50 |
Хорошая |
|
nlQR |
Стандартное отклонение |
25 |
Умеренная |
|
MADe |
Стандартное отклонение |
50 |
Умеренно хорошая |
|
Алгоритм А |
Среднее и стандартное отклонения |
25 |
Умеренная |
|
Оценки |
Среднее и стандартное отклонения |
50 |
Умеренная (очень хорошая для точки устойчивости, |
Примечание — Определение пороговой точки, используемое здесь,
сводится к определению доли большого набора данных из нормального распределения,
которая может изменяться до бесконечности, без того чтобы оценка также
двигалась к бесконечности. Например, если менее 50 % данных набора заменить на
бесконечность, медиана останется конечной величиной.
Таким образом, выборочные среднее и стандартное отклонения
могут дать недостоверную оценку при наличии единственного выброса. Робастные
методы, использующие медиану MADe и /Хампеля, могут выдержать очень большую
долю выбросов. Алгоритм А с итеративным стандартным отклонением и nlQR имеют пороговую точку 25 %.
Надо помнить, что в любой ситуации при большой доле выбросов (> 20 %) как
традиционные, так и робастные оценки могут дать смещенные оценки параметров
положения и разброса, и это следует учитывать при интерпретации таких оценок.
D.2.3 Относительная эффективность
Все оценки имеют выборочную дисперсию, то есть оценки могут
отличаться от раунда к раунду программы проверки квалификации, даже если все участники
квалифицированные и нет выбросов или подгрупп участников с различными средними
или дисперсиями. Робастные оценки видоизменяют представленные результаты,
которые находятся слишком далеко от середины распределения, на основании
теоретических предположений, и поэтому эти оценки имеют большую дисперсию, чем
оценки с минимальной дисперсией, в том случае, когда набор данных фактически
подчиняется нормальному распределению.
Выборочное среднее и стандартное отклонения являются
оценками среднего и стандартного отклонений с минимальной дисперсией, и поэтому
они имеют эффективность 100 %. Оценки с более низкой эффективностью имеют
большую изменчивость, то есть они могут изменяться от раунда к раунду, даже
если нет выбросов или различных подгрупп участников. В таблице D.2
приведена относительная эффективность оценок, представленных в приложении C.
Таблица
D.2 — Относительная эффективность робастных оценок
среднего и стандартного отклонений генеральной совокупности для нормально
распределенного набора данных с n от 50 до 500
участников
В процентах
|
Статистическая оценка |
Среднее п = 50 |
Среднее п = 500 |
SD п |
SD п |
|
Выборочное среднее и стандартное отклонения |
100 % |
100 % |
100 % |
100 % |
|
Медиана и nlQR |
66 % |
65 % |
38 % |
37 % |
|
Медиана и MADe |
66 % |
65 % |
37 % |
37 % |
|
Алгоритм А |
97 % |
97 % |
74 % |
73 % |
|
|
96 % |
96 % |
73 % |
81 % |
Согласно таблице D.2 становится
очевидным, что не существует статистического метода, идеально подходящего во
всех ситуациях. Выборочные среднее и стандартное отклонения являются
оптимальными оценками в случае нормального распределения данных, но неудачны в
случае выбросов. Простые робастные методы, такие как медиана, MADe или nlQR,
являются не очень хорошими для данных из нормального распределения, но могут
быть эффективными при наличии выбросов или небольшом объеме данных.
D.3 Использование данных проверки
квалификации для оценки воспроизводимости и повторяемости метода измерений
D.3.1 Во введении ГОСТ
ISO/IEC 17043-2013 установлено, что оценка свойств
метода измерений, как правило, не является целью проверки квалификации. Тем не
менее результаты программы проверки квалификации можно использовать для
проверки и, возможно, установления повторяемости и воспроизводимости метода
измерений [20], если программа
проверки квалификации удовлетворяет следующим условиям:
a) образцы для проверки квалификации
однородны и стабильны;
b) участники способны дать
последовательные удовлетворительные результаты;
c) квалификация участников (или
подгруппы участников) продемонстрирована до начала раунда проверки
квалификации, и результаты проверки квалификации не ставят эту квалификацию под
сомнение.
D.3.2 Для того чтобы обеспечить
достаточное количество данных для оценки повторяемости и воспроизводимости
метода испытаний в программе проверки квалификации, должны быть выполнены
следующие условия:
a) при проведении исследований
имеется достаточное количество участников, продемонстрировавших свою
квалификацию в части выполнения метода измерений на предыдущих раундах
программы проверки квалификации, которые приняли обязательства следовать методу
измерений без изменений;
b) при оценке повторяемости в каждом
раунде проверки квалификации должно быть использовано не менее двух образцов
для проверки квалификации или выполнены репликации наблюдений;
c) по возможности участники должны
быть обеспечены отдельно идентифицированными репликациями «вслепую», что
является более предпочтительным, чем выполнение репликаций на одном и том же
образце;
d) образцы, используемые в одном или
нескольких раундах программы проверки квалификации, должны охватывать весь
диапазон уровней и типов обычных образцов, для которых предназначен метод
измерений;
e) процедуры анализа данных,
применяемые для оценки повторяемости и воспроизводимости, должны
соответствовать стандартам серии ГОСТ Р ИСО 5725 или используемому
совместному протоколу исследования.
Приложение E
(справочное)
Иллюстративные примеры
В данном приложении приведены примеры, иллюстрирующие
процедуры, установленные в настоящем стандарте, и позволяющие пользователям
настоящего стандарта проверить правильность своих вычислений. Приведенные примеры
не следует рассматривать как рекомендации для использования в конкретных
программах проверки квалификации.
E.1 Влияние
цензурированных данных (см. 5.5.3.3)
В таблице E.1 приведены 23 результата раунда программы проверки
квалификации, из которых пять результатов представлены в виде «менее некоторого
числа». Робастные среднее и
стандартное отклонение в
соответствии с алгоритмом А вычисляют тремя различными способами:
1) знак «<» игнорируют, а данные анализируют как обычные
количественные данные;
2) данные со знаком «<» удаляют;
3) данные со знаками «<» и «>» заменяют половиной их
значений, а результаты используют для определения оценки как количественные
результаты.
В каждом варианте результаты, выпадающие за допустимые
границы, помечены знаком «#». Это означает, что в результате будет получена
неприемлемая оценка (сигнал к действиям) для любых результатов, количественное
значение которых находится вне пределов (* ±
3).
Провайдер может использовать альтернативные правила для действий с результатами
со знаками «<» или «>».
Таблица
E.1 — Пример набора данных с цензурированными
(<) результатами и три способа работы с такими результатами
|
Участник |
Результат |
Набор данных с прогнозированным знаком «<» |
Набор данных после исключения данных со знаком |
Набор данных после результатов со знаком «>» и |
|
А |
< 10 |
10 |
— |
5 |
|
В |
< 10 |
10 |
— |
5 |
|
С |
12 |
12 |
12 |
12 |
|
D |
19 |
19 |
19 |
19 |
|
Е |
< 20 |
20 |
— |
10 |
|
F |
20 |
20 |
20 |
20 |
|
G |
23 |
23 |
23 |
23 |
|
Н |
23 |
23 |
23 |
23 |
|
J |
25 |
25 |
25 |
25 |
|
К |
25 |
25 |
25 |
25 |
|
L |
26 |
26 |
26 |
26 |
|
М |
28 |
28 |
28 |
28 |
|
N |
28 |
28 |
28 |
28 |
|
Р |
< 30 |
30 |
— |
15 |
|
Q |
28 |
28 |
28 |
28 |
|
R |
29 |
29 |
29 |
29 |
|
S |
30 |
30 |
30 |
30 |
|
T |
30 |
30 |
30 |
30 |
|
U |
31 |
31 |
31 |
31 |
|
V |
32 |
32 |
32 |
32 |
|
W |
32 |
32 |
32 |
32 |
|
Y |
45 |
45 |
45# |
45 |
|
Z |
< 50 |
50# |
— |
25 |
|
Итого |
||||
|
Количество результатов |
23 |
23 |
18 |
23 |
|
|
26,01 |
26,81 |
23,95 |
|
|
|
7,23 |
5,29 |
8,60 |
Выбор способа обработки данных со
знаком «<» оказывает существенное влияние на робастное среднее и стандартное
отклонения, а также на оценку функционирования. Провайдер проверки квалификации
должен определить соответствующий метод.
E.2 Тест на
однородность и стабильность. Содержание мышьяка As в
шоколаде (см. 6.1)
Образцы для проверки квалификации подготавливают для
использования при международной проверке квалификации и затем используют как
стандартный образец. Изготовлено 1000 флаконов.
Проверка однородности: выбирают 10 образцов, используя
стратифицированный случайный отбор образцов из различных порций
производственного процесса. Две исследуемые порции извлекают из каждой бутылки
и проверяют в случайном порядке Данные приведены в таблице E.2. Итоговые статистики
получены в соответствии с процедурой, описанной в B.3
приложения B.
Целевое значение для
As в шоколаде составляет 15 %, таким образом, оценку
выборочной изменчивости сопоставляют при проверке с 0,3 .
Таблица E.2
— Данные для проверки однородности данных при контроле содержания мышьяка в
шоколаде
|
Номер бутылки |
Проба 1 |
Проба 2 |
|
3 |
0,185 |
0,194 |
|
111 |
0,187 |
0,189 |
|
201 |
0,182 |
0,186 |
|
330 |
0,188 |
0,196 |
|
405 |
0,191 |
0,181 |
|
481 |
0,188 |
0,180 |
|
599 |
0,187 |
0,196 |
|
704 |
0,177 |
0,186 |
|
766 |
0,179 |
0,187 |
|
858 |
0,188 |
0,196 |
Общее среднее: 0,18715.
SD среднего
арифметического: 0,00398.
sw:
0,00556.
:
0,00060.
: 0,18715 · 0,15 = 0,02807.
Проверочное значение: 0,3 =
0,00842.
Значение ss менее проверочного значения, следовательно, однородность
является достаточной.
Проверка стабильности: два образца для проверки квалификации
отбирают случайным образом и хранят при повышенной температуре (60 °С) в
течение всего раунда программы проверки квалификации (6 нед.). Образцы
протестированы в двух экземплярах (см. таблицу E.3), и четыре результата
проверены на однородность значений.
Таблица
E.3 — Данные для проверки стабильности образцов на
содержание мышьяка в шоколада
|
Выбранный образец |
Проба 1 |
Проба 2 |
|
164 |
0,191 |
0,198 |
|
732 |
0,190 |
0,196 |
Общее среднее: 0,19375.
Разность со средним при проверке однородности: 0,19375 —
0,18715 = 0,00660.
Проверочное значение: 0,3 =
0,00842.
Разность средних меньше проверочного значения,
следовательно, стабильность является достаточной.
E.3
Содержание атразина в питьевой воде
В программе проверки квалификации по определению содержания
гербицида (атразина) в питьевой воде участвуют 34 участника. В таблице E.4
представлены исходные данные, упорядоченные по возрастанию, а также значения робастных
среднего и стандартного отклонений, рассчитанных в соответствии с алгоритмом А
в процессе шести итераций, то есть до тех пор пока в робастных среднем и
стандартном отклонениях перестают изменяться три значащих цифры после запятой.
На рисунках E.1,
E.2
и E.3
представлены соответственно график упорядоченных данных, гистограмма и
график плотности вероятностей.
В таблице E.5 приведены оценки параметра положения среднего и
стандартного отклонений, полученные с использованием классических и робастных
методов. Неопределенность оценки параметра положения также приведена.
Статистики для бутстреп-метода получены в соответствии с процедурами,
описанными в [9], [10], а также с применением пакета программного
обеспечения R. На рисунке E.4 показаны
различные оценки параметра положения и оценки расширенной неопределенности .
(Поправка).
Таблица
E.4 — Вычисление робастных среднего и
стандартного отклонений для содержания атразина в питьевой воде
|
|
1-я итерация |
2-я итерация |
3-я итерация |
4-я итерация |
5-я итерация |
6-я итерация |
|
|
|
0,204163 0,319837 |
0,199732 0,315969 |
0,198466 0,315871 |
0,198037 0,316065 |
0,197865 0,316185 |
0,197790 0,316243 |
|
|
1 |
0,0400 |
0,2042 |
0,1997 |
0,1985 |
0,1980 |
0,1979 |
0,1978 |
|
2 |
0,0550 |
0,2042 |
0,1997 |
0,1985 |
0,1980 |
0,1979 |
0,1978 |
|
3 |
0,1780 |
0,2042 |
0,1997 |
0,1985 |
0,1980 |
0,1979 |
0,1978 |
|
4 |
0,2020 |
0,2042 |
0,2020 |
0,2020 |
0,2020 |
0,2020 |
0,2020 |
|
5 |
0,2060 |
0,2060 |
0,2060 |
0,2060 |
0,2060 |
0,2060 |
0,2060 |
|
6 |
0,2270 |
0,2270 |
0,2270 |
0,2270 |
0,2270 |
0,2270 |
0,2270 |
|
7 |
0,2280 |
0,2280 |
0,2280 |
0,2280 |
0,2280 |
0,2280 |
0,2280 |
|
8 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
|
9 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
0,2300 |
|
10 |
0,2350 |
0,2350 |
0,2350 |
0,2350 |
0,2350 |
0,2350 |
0,2350 |
|
11 |
0,2360 |
0,2360 |
0,2360 |
0,2360 |
0,2360 |
0,2360 |
0,2360 |
|
12 |
0,2370 |
0,2370 |
0,2370 |
0,2370 |
0,2370 |
0,2370 |
0,2370 |
|
13 |
0,2430 |
0,2430 |
0,2430 |
0,2430 |
0,2430 |
0,2430 |
0,2430 |
|
14 |
0,2440 |
0,2440 |
0,2440 |
0,2440 |
0,2440 |
0,2440 |
0,2440 |
|
15 |
0,2450 |
0,2450 |
0,2450 |
0,2450 |
0,2450 |
0,2450 |
0,2450 |
|
16 |
0,2555 |
0,2555 |
0,2555 |
0,2555 |
0,2555 |
0,2555 |
0,2555 |
|
17 |
0,2600 |
0,2600 |
0,2600 |
0,2600 |
0,2600 |
0,2600 |
0,2600 |
|
18 |
0,2640 |
0,2640 |
0,2640 |
0,2640 |
0,2640 |
0,2640 |
0,2640 |
|
19 |
0,2670 |
0,2670 |
0,2670 |
0,2670 |
0,2670 |
0,2670 |
0,2670 |
|
20 |
0,2700 |
0,2700 |
0,2700 |
0,2700 |
0,2700 |
0,2700 |
0,2700 |
|
21 |
0,2730 |
0,2730 |
0,2730 |
0,2730 |
0,2730 |
0,2730 |
0,2730 |
|
22 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
|
23 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
0,2740 |
|
24 |
0,2780 |
0,2780 |
0,2780 |
0,2780 |
0,2780 |
0,2780 |
0,2780 |
|
25 |
0,2811 |
0,2811 |
0,2811 |
0,2811 |
0,2811 |
0,2811 |
0,2811 |
|
26 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
|
27 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
0,2870 |
|
28 |
0,2880 |
0,2880 |
0,2880 |
0,2880 |
0,2880 |
0,2880 |
0,2880 |
|
29 |
0,2890 |
0,2890 |
0,2890 |
0,2890 |
0,2890 |
0,2890 |
0,2890 |
|
30 |
0,2950 |
0,2950 |
0,2950 |
0,2950 |
0,2950 |
0,2950 |
0,2950 |
|
31 |
0,2960 |
0,2960 |
0,2960 |
0,2960 |
0,2960 |
0,2960 |
0,2960 |
|
32 |
0,3110 |
0,3110 |
0,3110 |
0,3110 |
0,3110 |
0,3110 |
0,3110 |
|
33 |
0,3310 |
0,3198 |
0,3160 |
0,3159 |
0,3161 |
0,3162 |
0,3162 |
|
34 |
0,4246 |
0,3198 |
0,3160 |
0,3159 |
0,3161 |
0,3162 |
0,3162 |
|
Среднее арифметическое |
0,2512 |
0,2579 |
0,2572 |
0,2571 |
0,2570 |
0,2570 |
0,2570 |
|
SD |
0,0672 |
0,0342 |
0,0345 |
0,0347 |
0,0348 |
0,0348 |
0,0348 |
|
|
0,0578 |
0,0581 |
0,0587 |
0,0590 |
0,0592 |
0,0592 |
|
|
Новое |
0,2620 |
0,2579 |
0,2572 |
0,2571 |
0,2570 |
0,2570 |
0,2570 |
|
Новое |
0,0386 |
0,0387 |
0,0391 |
0,0393 |
0,0394 |
0,0395 |
0,0395 |
Таблица
E.5 — Итоговые статистики для примера E.3
|
Процедура определения оценки |
Параметр положения (среднее) |
Стандартное отклонение |
|
|
Определение |
0,2620 |
0,0402 (0,0386) |
0,0086 |
|
Определение |
0,2570 |
0,0395 |
0,0085 |
|
Определение |
0,2600 |
0,0426 |
0,0091 |
|
Бутстреп |
0,2503 |
0,0667 |
0,0113 |
|
Вычислительная |
0,2588 |
0,0337 |
0,0061 |
|
Вычислительная |
0,2512 |
0,0672 |
0,0115 |
Примечание — Различные коммерческие пакеты программ используют
различные процедуры расчета квартилей, что может привести к заметным различиям
в значениях nlQR.
Незначительные отклонения от приведенных выше значений могут быть вызваны этими
различиями или различиями при округлении.
|
|
|
Рисунок E.1 — Упорядоченные значения содержания атразина |
|
|
|
Рисунок E.2 — Гистограмма результатов участников |
|
|
|
Рисунок E.3 — График плотности по результатам участников |
|
|
|
Рисунок E.4 — Итоговые робастные статистики по данным таблицы E.5 |
E.4
Содержание ртути в корме для животных
В раунде программы проверки квалификации участников просили
фиксировать свои результаты так, как они это обычно делают, а также расширенную
неопределенность и
коэффициент охвата . Затем провайдер вычислял стандартную
неопределенность в виде
.
Флажки присваивали полученным неопределенностям в соответствии с критериями 9.8. Данные, приведенные в таблицах E.6
и E.7,
показывают общее содержание ртути в корме. Приведенная в таблице E.6
стандартная неопределенность получена на основе, указанной участниками расширенной
неопределенности в
виде и приведена с округлением. Для расчета статистик,
приведенных в таблице E.7, использованы неокругленные значения .
Участник с кодом Е23 не сообщил коэффициент охвата, поэтому использовано значение
1,732 (корень квадратный из 3, округленный).
Индексы работы вычислены с
использованием методов, описанных в разделе 9. Для всех расчетов в качестве использовалось опорное значение, а в качестве
— значение функции пригодности назначению, определенное на
основе предыдущего опыта. Неопределенность приписанного значения определена в
виде суммы общей стандартной неопределенности опорного значения и
неопределенности вследствие неоднородности (различия от бутылки к бутылке):
.
На графике плотности (см. рисунок E.6)
показано бимодальное распределение, связанное с применением различных методов.
Однако это не влияет на оценку функционирования, поскольку в качестве использовано опорное значение, а в качестве
значение функции пригодности назначению. При выполнении
этого анализа результаты со знаком «<» удалены.
Таблица
E.6 — Результаты проверки квалификации для 24
участников при исследовании IMEP 111
|
Код лаборатории |
Значение |
|
|
|
Критерий |
Метод |
|
L04 |
0,013 |
0,003 |
2 |
0,002 |
b |
АМА |
|
L05 |
0,013 |
0,007 |
2 |
0,004 |
а |
АМА |
|
L23 |
0,0135 |
0,00108 |
1,732 |
0,00062 |
b |
АМА |
|
L02 |
0,014 |
0,004 |
2 |
0,002 |
b |
АМА |
|
L15 |
0,014 |
0,0005 |
2 |
0,0003 |
b |
АМА |
|
L17 |
< 0,015 |
— |
— |
— |
— |
CV-ICP-AES |
|
L06 |
0,016 |
0,003 |
2 |
0,002 |
b |
АМА |
|
L09 |
0,017 |
0,008 |
2 |
0,004 |
а |
АМА |
|
L26 |
0,019 |
0,003 |
2 |
0,002 |
b |
AAS |
|
L12 |
0,0239 |
0,0036 |
2 |
0,0018 |
b |
АМА |
|
L13 |
< 0,034 |
— |
— |
— |
— |
TDA-AAS |
|
L03 |
0,037 |
0,013 |
2 |
0,007 |
а |
CV-AAS |
|
L29 |
0,039 |
0,007 |
2 |
0,004 |
а |
CV-AAS |
|
L07 |
0,04 |
0,008 |
2 |
0,004 |
а |
ICP-MS |
|
L21 |
0,04 |
0,03 |
2 |
0,02 |
с |
HG-AAS |
|
L25 |
0,040 |
0,010 |
2 |
0,005 |
а |
CV-AAS |
|
L16 |
0,0424 |
0,008 |
2 |
0,004 |
а |
CV-AAS |
|
L08 |
0,044 |
0,007 |
2 |
0,004 |
а |
CV-AAS |
|
L10 |
0,045 |
0,007 |
2 |
0,004 |
а |
ICP-MS |
|
L24 |
0,045 |
0,005 |
2 |
0,003 |
а |
HG-AAS |
|
L18 |
0,046 |
0,007 |
2 |
0,004 |
а |
CV-AAS |
|
L28 |
0,049 |
0,0072 |
2 |
0,0036 |
а |
CV-AAS |
|
L01 |
0,053 |
0,007 |
2 |
0,004 |
а |
CV-AAS |
|
L14 |
< 0,1 |
— |
— |
— |
— |
ICP-MS |
|
|
|
Рисунок E.5 — Результаты участников и соответствующие |
Линии с крупным пунктиром показывают
границы со значениями ±
, а
линии с мелким пунктиром — границы со значениями ( ± 2
).
Вертикальные линии,
заканчивающиеся открытым кружком, показывают значения со знаком «<».
|
|
|
Рисунок E.6 — График плотности распределения результатов |
Таблица
E.7 — Статистики функционирования для различных
методов
|
Код лаборатории |
D, % |
Ра |
z |
z’ |
|
|
|
L04 |
-70,5 % |
-156,6 % |
-4,70 |
-3,99 |
-7,10 |
-3,55 |
|
L05 |
-70,5 % |
-156,6 % |
-4,70 |
-3,99 |
-5,75 |
-2,88 |
|
L23 |
-69,3 % |
-154,0 % |
-4,62 |
-3,93 |
-7,35 |
-3,69 |
|
L02 |
-68,2 % |
-151,5 % |
-4,55 |
-3,86 |
-6,58 |
-3,29 |
|
L15 |
-68,2 % |
-151,5 % |
-4,55 |
-3,86 |
-7,30 |
-3,65 |
|
L17 |
— |
— |
— |
— |
— |
— |
|
L06 |
-63,6 % |
-141,4 % |
-4,24 |
-3,60 |
-6,41 |
-3,21 |
|
L09 |
-61,4 % |
-136,4 % |
-4,09 |
-3,47 |
-4,71 |
-2,36 |
|
L26 |
-56,8 % |
-126,3 % |
-3,79 |
-3,22 |
-5,73 |
-2,86 |
|
L12 |
-45,7 % |
-101,5 % |
-3,05 |
-2,59 |
-4,49 |
-2,24 |
|
L13 |
— |
— |
— |
— |
— |
— |
|
L03 |
-15,9 % |
-35,4 % |
-1,06 |
-0,90 |
-0,91 |
-0,46 |
|
L29 |
-11,4 % |
-25,3 % |
-0,76 |
-0,64 |
-0,93 |
-0,46 |
|
L07 |
-9,1 % |
-20,2 % |
-0,61 |
-0,51 |
-0,70 |
-0,35 |
|
L21 |
-9,1 % |
-20,2 % |
-0,61 |
-0,51 |
-0,26 |
-0,13 |
|
L25 |
-9,1 % |
-20,2 % |
-0,61 |
-0,51 |
-0,62 |
-0,31 |
|
L16 |
-3,6 % |
-8,1 % |
-0,24 |
-0,21 |
-0,28 |
-0,14 |
|
L08 |
0,0 % |
0,0 % |
0,00 |
0,00 |
0,00 |
0,00 |
|
L10 |
2,3 % |
5,1 % |
0,15 |
0,13 |
0,19 |
0,09 |
|
L24 |
2,3 % |
5,1 % |
0,15 |
0,13 |
0,21 |
0,10 |
|
L18 |
4,5 % |
10,1 % |
0,30 |
0,26 |
0,37 |
0,19 |
|
L28 |
11,4 % |
25,3 % |
0,76 |
0,64 |
0,92 |
0,46 |
|
L01 |
20,5 % |
45,5 % |
1,36 |
1,16 |
1,67 |
0,83 |
|
L14 |
— |
— |
— |
— |
— |
— |
Данный пример предоставлен Институтом
эталонных материалов и измерений Объединенного исследовательского центра
Европейской комиссии из Международной программы по оценке измерений (IMEP®), исследование 111.
E.5 Опорное
значение по данным единственной лаборатории: испытания по методу Лос-Анджелеса
(см. 7.5)
В таблице E.8 приведен пример данных,
полученных в серии испытаний образцов для проверки квалификации и аналогичного
сертифицированного стандартного образца CRM,
который имеет сертифицированное значение показателя 21,62 единиц LA и соответствующую неопределенность 0,26 единиц LA. В примере показано, как опорное значение и
неопределенность могут быть получены для образца проверки квалификации. Следует
помнить, что неопределенность значения CRM включает в себя неопределенность, связанную с
неоднородностью, транспортированием и долгосрочной стабильностью:
|
|
|
|
|
где 0,26 —
стандартная неопределенность значения CRM, а
0,24 — стандартная неопределенность .
Таблица
E.8 — Вычисление разности средних арифметических,
соответствующих CRM и
образцам проверки квалификации, и стандартного отклонения этой разности
|
Выборка |
Образец проверки квалификации |
CRM |
Разность средних испытуемого объекта и CRM, единицы LA |
||
|
Испытание 1, единицы LA |
Испытание 2, единицы LA |
Испытание 1, единицы LA |
Испытание 2, единицы LA |
||
|
1 |
20,5 |
20,5 |
19,0 |
18,0 |
2,00 |
|
2 |
21,1 |
20,7 |
19,8 |
19,9 |
1,05 |
|
3 |
21,5 |
21,5 |
21,0 |
21,0 |
0,50 |
|
4 |
22,3 |
21,7 |
21,0 |
20,8 |
1,10 |
|
5 |
22,7 |
22,3 |
20,5 |
21,0 |
1,75 |
|
6 |
23,6 |
22,4 |
20,3 |
20,3 |
2,70 |
|
7 |
20,9 |
21,2 |
21,5 |
21,8 |
-0,60 |
|
8 |
21,4 |
21,5 |
21,9 |
21,7 |
-0,35 |
|
9 |
23,5 |
23,5 |
21,0 |
21,0 |
2,50 |
|
10 |
22,3 |
22,9 |
22,0 |
21,3 |
0,95 |
|
11 |
23,5 |
24,1 |
20,8 |
20,6 |
3,10 |
|
12 |
22,5 |
23,5 |
21,0 |
22,0 |
1,50 |
|
13 |
22,5 |
23,5 |
21,0 |
21,0 |
2,00 |
|
14 |
23,4 |
22,7 |
22,0 |
22,0 |
1,05 |
|
15 |
24,0 |
24,2 |
22,1 |
21,5 |
2,30 |
|
16 |
24,5 |
24,4 |
22,3 |
22,5 |
2,05 |
|
17 |
24,8 |
24,7 |
22,0 |
21,9 |
2,80 |
|
18 |
24,7 |
25,1 |
21,9 |
21,9 |
3,00 |
|
19 |
24,9 |
24,4 |
22,4 |
22,6 |
2,15 |
|
20 |
27,2 |
27,0 |
24,5 |
23,7 |
3,0 |
|
Разность |
1,73 |
||||
|
Стандартное |
1,07 |
||||
|
Стандартная |
0,24 |
||||
|
Примечание — Данные представляют собой результат измерений |
E.6 Пример
бутстреп-метода для содержания бактерий группы кишечной палочки Coliform в образце пищи
(см. 7.7.2)
В программе проверки
квалификации на наличие бактерий группы кишечной палочки в пробе молока
участвовали 35 лабораторий, которые выполняли по 5 репликаций измерений каждая.
Среднее логарифмов CFU данных каждого участника было
использовано для оценки приписанного значения и его неопределенности. Значение
пригодности цели, равное 0,25 ,
установлено в качестве , в
то время как стандартное отклонение функции ядерной плотности задано 0,75 .
График ядерной плотности (см. рисунок E.7) имеет вид
ассиметричного распределения. Бутстреп-метод (1000 репликаций) применен для
определения оценки моды и соответствующей стандартной погрешности функции
ядерной плотности распределения данных, обозначенных и
,
соответственно получены следующие значения:
|
|
Примечание — Поскольку > 0,3
оценка функционирования лаборатории определена с
помощью z’-индекса.
|
|
|
Рисунок E.7 — Плотность распределения результатов участников |
Ниже приведена программа обработки приведенных данных на языке
R.
E.7
Сопоставление опорного значения с согласованным средним (см. 7.8)
Для пояснения процедуры, приведенной в 7.8, сравнивают опорное значение с робастным средним
по полученным результатам участников на основе примера E.4
и данных таблицы E.6.
В этом раунде программы проверки
квалификации робастное среднее =
0,03161 и робастное стандартное отклонение =
0,0164 получены с помощью алгоритма А, после удаления трех результатов
со знаком «<» (п = 24). Затем определена неопределенность робастного
среднего
|
|
|
|
|
В соответствии с 7.8
неопределенность разности между и
имеет
следующий вид:
Таким образом, разность в два раза
больше ее неопределенности.
Никаких действий не рекомендуется, так как в некоторых
методах присутствует смещение.
E.8
Определение критериев оценки на основании опыта предыдущих раундов: содержание
токсафена в питьевой воде (см. 8.3)
Два провайдера организации программы проверки квалификации
лаборатории проверяют содержание пестицида токсафена в питьевой воде.
В течение пяти лет проведено 20 раундов проверки
квалификации, в которых каждый раз принимали участие 20 или более лабораторий,
уровень токсафена в исследуемых пробах питьевой воды колебался от 3 до 20 мг/л.
В таблице E.9
представлены результаты 20 раундов проверки квалификации, упорядоченные
в порядке убывания приписанных значений. На рисунках E.8 и E.9
приведены точечные диаграммы для относительного робастного стандартного
отклонения RSD, %, и робастного стандартного
отклонения SD для
каждого раунда программы проверки квалификации по отношению к приписанному
значению (рассчитанному по формуле). На каждом рисунке обозначена линия
регрессии, полученная по методу наименьших квадратов. Линию регрессии по методу
наименьших квадратов можно определить с помощью общедоступного программного
обеспечения. (Полиномиальная модель 2-го порядка также проверена в качестве
функции взаимосвязи стандартного отклонения и приписанного значения, но
квадратичный член не признан статистически значимым, что указывает на отсутствие
существенной кривизны линии регрессии для этой модели, следовательно, линейная
модель более подходящая.)
Очевидно, что RSD является достаточно постоянным и составляет около 19 % для
всех уровней, линия регрессии для стандартного отклонения достаточно
достоверная (R2 = 0,82). Регулирующий
орган может потребовать, чтобы стандартное отклонение оценки составляло 19 % от
приписанного значения (или, возможно, 20 %), или осуществить вычисления
среднего стандартного отклонения на основе уравнения линии регрессии для
стандартного отклонения.
Таблица E.9
— Данные содержания токсафена в питьевой воде для р ≥ 20
результатов
|
Код провайдера |
Приписанное значение |
Робастное среднее отклонение |
Стандартное отклонение |
Выполнение требований, % |
RSD, % |
p |
|
Р004 |
3,96 |
3,98 |
0,639 |
100,5 |
16,1 |
25 |
|
Р001 |
4,56 |
5,18 |
0,638 |
113,6 |
14,0 |
23 |
|
Р001 |
5,99 |
5,98 |
0,995 |
99,8 |
16,6 |
22 |
|
Р004 |
6,08 |
5,80 |
1,48 |
95,4 |
24,3 |
20 |
|
Р001 |
6,20 |
6,66 |
0,97 |
107,4 |
15,7 |
23 |
|
Р001 |
6,72 |
7,13 |
1,43 |
106,1 |
21,3 |
22 |
|
Р004 |
8,10 |
7,09 |
2,23 |
87,5 |
27,5 |
21 |
|
Р001 |
8,73 |
8,15 |
1,80 |
93,4 |
20,6 |
22 |
|
Р001 |
9,57 |
8,60 |
1,45 |
89,9 |
15,2 |
23 |
|
Р001 |
12,1 |
12,4 |
1,44 |
102,5 |
11,9 |
23 |
|
Р001 |
12,5 |
13,8 |
2,25 |
110,4 |
18,0 |
24 |
|
Р004 |
13,1 |
12,0 |
2,41 |
91,6 |
18,4 |
20 |
|
Р004 |
15,6 |
13,3 |
3,57 |
85,3 |
22,9 |
27 |
|
Р004 |
15,9 |
13,6 |
2,44 |
85,5 |
15,3 |
28 |
|
Р004 |
16,3 |
13,5 |
3,60 |
82,8 |
22,1 |
31 |
|
Р004 |
16,3 |
14,2 |
3,09 |
87,1 |
19,0 |
40 |
|
Р004 |
17,0 |
15,6 |
2,63 |
91,8 |
15,5 |
24 |
|
Р004 |
17,4 |
16,0 |
2,85 |
92,0 |
16,4 |
23 |
|
Р004 |
17,4 |
16,0 |
3,36 |
92,0 |
19,3 |
23 |
|
Р004 |
19,0 |
16,4 |
3,20 |
86,3 |
16,8 |
27 |
|
|
|
Рисунок E.8 — Относительное стандартное отклонение результатов |
|
|
|
Рисунок E.9 — Стандартное отклонение участников (мг/л) и |
E.9 Общая
модель: уравнение Хорвица (см. 8.4)
Одна из общих моделей,
применяемых в химии, описана Хорвицем [8],
[7]. Этот подход дает общую модель
воспроизводимости аналитических методов, которая может быть использована для
получения следующего выражения для стандартного отклонения воспроизводимости:
|
|
где с —
содержание химических компонентов, определенное в массовых долях.
Например, в программе проверки
квалификации по определению содержания меламина в сухом молоке использованы два
образца с опорными уровнями А = 1,195 мг/кг и В = 2,565 мг/кг
(0,000 001 195 и 0,000 002 565). Тогда среднее стандартное отклонение
воспроизводимости имеет следующий вид для образца:
|
А (1,195 |
|
|
В (2,565 |
E.10
Определение характеристик в экспериментах на прецизионность: определение
содержания цемента в твердом бетоне.
Содержание цемента в бетоне обычно измеряют в единицах
массы, кг/м3. На практике бетон производят в соответствии с сортами,
которые отличаются по содержанию цемента на 25 кг/м3 друг от друга,
и необходимо, чтобы участники имели возможность правильно определить сорт. По
этой причине желательно, чтобы выбранное значение составляло не более половины от 25 кг/м3 (
< 12,5 кг/м3).
В эксперименте на прецизионность получены следующие
результаты для бетона со средним содержанием цемента 260 кг/м3: = 23,2 кг/м3 и
= 14,3 кг/м3. Предположим, что сделано т
= 2 репликаций измерений.
Тогда в соответствии с формулой
(9):
|
|
Таким образом, цель < 25/2 кг/м3 = 12,5 кг/м3 является
неосуществимой на практике.
Примечание — В ГОСТ
Р ИСО 5725-2 ,где
—
составляющая, характеризующая межлабораторную дисперсию.
В данном примере может быть вычислена следующим образом:
|
|
E.11
Штриховые графики для нормированного смещения: концентрация антител (см. 10.4)
Значения z-индексов для раунда
проверки квалификации с тремя связанными измеряемыми величинами (антителами)
приведены на рисунке E.10 на штриховом графике. Данные для двух из трех
аллергенов приведены в таблице E.10.
Из этого графика видно, что, например, лабораториям В
и Z следует искать
причину, которая влияет на все три уровня и дает примерно одинаковую величину
смещения, в то время как для лабораторий K и P z-индекс зависит от типа антител.
E.12 График
Юдена: концентрация антител (см. 10.5)
В таблице E.10 приведены данные,
полученные с помощью исследования двух аналогичных образцов проверки квалификации
при определении концентрации антител. Показанные на рисунке E.11 индексы
функционирования z основаны на робастных среднем и
стандартном отклонениях, полученных в соответствии с алгоритмом А.
Из рисунка E.11 видно,
что значения двух участников (5 и 23) находятся в правом верхнем квадрате и,
следовательно, могут иметь устойчивое положительное смещение. Лаборатория 26
имеет высокое значение z-индекса на образце аллергена В
и отрицательное значение z-индекса (-0,055) на образце
аллергена А и поэтому может иметь низкую воспроизводимость.
|
|
|
Рисунок E.10 — Штриховой график z-индексов (от |
Результаты участников 5, 23 и 26 попадают в область сигнала
«предупреждения». Эти участники должны проверить, в какую зону попадают их
результаты в следующем раунде программы. Визуальный анализ и коэффициент
корреляции указывают на тенденцию к последовательному изменению z-индекса (положительному или отрицательному), так что может
существовать возможность улучшения метода измерений с более подробными
инструкциями.
|
|
|
Рисунок E.11 — График Юдена для z-индексов |
Таблица
E.10 — Данные и вычисления по определению
концентрации антител для двух аналогичных образцов аллергенов
|
Лаборатория |
Данные |
z-индексы |
||
|
i |
Аллерген А |
Аллерген В |
Аллерген А |
Аллерген В |
|
1 |
12,95 |
9,15 |
0,427 |
0,515 |
|
2 |
6,47 |
6,42 |
-1,540 |
-0,428 |
|
3 |
11,40 |
6,60 |
-0,043 |
-0,366 |
|
4 |
8,32 |
4,93 |
-0,978 |
-0,942 |
|
5 |
18,88 |
13,52 |
2,228 |
2,023 |
|
6 |
15,14 |
8,22 |
1,092 |
0,194 |
|
7 |
10,12 |
7,26 |
-0,432 |
-0,138 |
|
8 |
17,94 |
9,89 |
1,942 |
0,770 |
|
9 |
11,68 |
4,17 |
0,042 |
-1,204 |
|
10 |
12,44 |
7,39 |
0,272 |
-0,093 |
|
11 |
6,93 |
7,78 |
-1,400 |
0,042 |
|
12 |
9,57 |
5,80 |
-0,599 |
-0,642 |
|
13 |
11,73 |
5,77 |
0,057 |
-0,652 |
|
14 |
12,29 |
6,97 |
0,227 |
-0,238 |
|
15 |
10,95 |
6,23 |
-0,180 |
-0,493 |
|
16 |
10,95 |
5,90 |
-0,180 |
-0,607 |
|
17 |
11,17 |
7,74 |
-0,113 |
0,028 |
|
18 |
11,20 |
8,63 |
-0,104 |
0,335 |
|
19 |
7,64 |
3,74 |
-1,185 |
-1,353 |
|
20 |
12,17 |
7,33 |
0,190 |
-0,114 |
|
21 |
10,71 |
5,70 |
-0,253 |
-0,676 |
|
22 |
7,84 |
6,07 |
-1,124 |
-0,549 |
|
23 |
20,47 |
15,66 |
2,710 |
2,762 |
|
24 |
12,60 |
11,76 |
0,321 |
1,415 |
|
25 |
11,37 |
4,91 |
-0,052 |
-0,949 |
|
26 |
11,36 |
13,51 |
-0,055 |
2,019 |
|
27 |
10,75 |
5,48 |
-0,241 |
-0,752 |
|
28 |
12,21 |
9,77 |
0,203 |
0,729 |
|
29 |
7,49 |
5,82 |
-1,230 |
-0,635 |
|
Среднее арифметическое |
11,54 |
7,66 |
0,00 |
0,00 |
|
Стандартное отклонение |
3,29 |
2,90 |
1,00 |
1,00 |
|
Коэффициент корреляции |
0,706 |
0,706 |
||
|
Примечание 1 — Данные выражаются в тысячах, к, единиц, U, Примечание 2 — z-индексы в этой таблице вычислены с использованием |
E.13 График
стандартных отклонений повторяемости: концентрации антител (см. 10.6)
В таблице E.11 приведены результаты определения концентрации
определенных антител в образце сыворотки крови. Каждый участник выполнил четыре
репликации определения в условиях повторяемости. Для построения графика,
представленного на рисунке E.12, использована формула, приведенная выше. Согласно
графику результаты некоторых лабораторий попадают в зону действия или
предупреждения.
Таблица E.11
— Концентрация антител в образце сыворотки крови (четыре репликации определения
на каждом образце, выполненные каждым участником)
|
Номер лаборатории |
Среднее арифметическое, kU/L |
Стандартное отклонение, kU/L |
|
1 |
2,15 |
0,13 |
|
2 |
1,85 |
0,21 |
|
3 |
1,80 |
0,08 |
|
4 |
1,80 |
0,24 |
|
5 |
1,90 |
0,36 |
|
6 |
1,90 |
0,32 |
|
7 |
1,90 |
0,14 |
|
8 |
2,05 |
0,26 |
|
9 |
2,35 |
0,39 |
|
10 |
2,03 |
0,53 |
|
11 |
2,08 |
0,25 |
|
12 |
1,25 |
0,24 |
|
13 |
1,13 |
0,72 |
|
14 |
1,00 |
0,26 |
|
15 |
1,08 |
0,17 |
|
16 |
1,20 |
0,32 |
|
17 |
1,35 |
0,4 |
|
18 |
1,23 |
0,36 |
|
19 |
1,23 |
0,33 |
|
20 |
0,90 |
0,43 |
|
21 |
1,48 |
0,40 |
|
22 |
1,20 |
0,55 |
|
23 |
1,73 |
0,39 |
|
24 |
1,43 |
0,30 |
|
25 |
1,28 |
0,22 |
|
Робастное среднее |
1,57 |
|
|
Робастное стандартное |
0,34 |
|
|
Примечание — Данные представлены в тысячах единиц, kU, |
|
|
|
Рисунок |
E.14 Графические
методы отслеживания функционирования во времени (см. 10.8)
Участникам полезно отслеживать свою оценку работы с течением
времени или иметь данные, подготовленные провайдером проверки квалификации. Самым
простым методом контроля для этого является контрольная карта, или карта
Шухарта. В связи с чем необходимо иметь стандартизованные индексы
функционирования, такие как z-индекс или PA-индекс, и участвовать в нескольких раундах.
Данный пример относится к программе проверки квалификации медицинских
лабораторий, в процессе которой участники определяют содержание калия в
сыворотке крови.
Для приемки провайдер использовал фиксированный интервал ± 5
% с округлением значений до 0,1 ммоль/л, но не менее ± 0,2 ммоль/л приписанного
значения. Провайдер использовал оценки PA-индексов,
а не z-индекс (см. таблицу E.12).
Таблица
E.12 — Значения PA-индексов
за пять раундов программы проверки квалификации с тремя образцами сыворотки
крови каждый
|
Код раунда |
Образец для проверки квалификации |
Результат |
Приписанное значение |
PA-индекс |
Среднее арифметическое значений PA |
|
101 |
А |
6,4 |
6,2 |
75 |
42 |
|
101 |
В |
4,2 |
4,1 |
50 |
— |
|
101 |
С |
4,1 |
4,1 |
0 |
— |
|
102 |
А |
6,0 |
5,9 |
25 |
8 |
|
102 |
В |
4,3 |
4,4 |
-33 |
|
|
102 |
С |
5,5 |
5,4 |
33 |
|
|
103 |
А |
4,1 |
4,2 |
-33 |
-28 |
|
103 |
В |
3,6 |
3,7 |
-50 |
— |
|
103 |
С |
4,2 |
4,2 |
0 |
— |
|
104 |
А |
5,7 |
5,8 |
-25 |
11 |
|
104 |
В |
3,9 |
4,0 |
-50 |
— |
|
104 |
С |
6,3 |
5,9 |
110 |
— |
|
105 |
А |
3,6 |
3,7 |
-50 |
-19 |
|
105 |
В |
4,5 |
4,6 |
-33 |
— |
|
105 |
С |
5,3 |
5,2 |
25 |
— |
Полученные результаты могут быть
представлены на графике. Для визуального анализа рекомендуется использовать два
вида графиков:
— контрольная карта для стандартизованного индекса
функционирования для каждого раунда, показывающая результаты на нескольких
образцах в одном и том же раунде проверки квалификации. Это позволяет показать
характеристику функционирования во времени, в том числе выявить тенденции ее
изменения (см. рисунок E.13);
— точечная диаграмма
стандартизированных индексов функционирования в зависимости от приписанных значений
для анализа зависимости характеристики функционирования от уровня концентрации
и выявления тенденций, связанных с уровнем измеряемой величины (см. рисунок E.14).
|
|
|
Рисунок |
|
|
|
Рисунок |
E.15
Качественный анализ данных: реакция кожи на косметическое средство (см. 11)
Программа проверки квалификации включает анализ реакции на
продукцию, предназначенную для ухода за кожей, при ее применении к стандартному
животному. Любую воспалительную реакцию оценивают по следующей шкале:
— 1 — отсутствие реакции;
— 2 — умеренное покраснение;
— 3 — значительное раздражение или отек;
— 4 — тяжелая реакция, в том числе нагноение или
кровотечение.
Участникам представлены два образца, состоящие из двух
различных продуктов, обозначенных как продукт А и продукт В.
Каждый продукт исследуют 50 участников. Результаты участников приведены в
таблице E.13 и
графически показаны на рисунке E.15. Мода и медиана
указаны по результатам участников для каждого образца проверки квалификации.
Таблица E.13
— Результаты для двух образцов: раздражение кожи
|
Реакция |
Продукт А |
Продукт В |
|
1 |
20 (40 %) # |
8 (16 %) |
|
2 |
18 (36 %) @ |
12 (24 %) |
|
3 |
10 (20 %) |
20 (40 %) # @ |
|
4 |
2 (4 %) |
10 (20 %) |
|
# — |
||
|
@ — |
|
|
|
Рисунок |
Следует учитывать, что медиана или
мода могут быть использованы в качестве общей статистики для этих образцов, они
указывают, что уровень реакции на продукт В является более тяжелым, чем
реакция на продукт А. Провайдер может определить, что сигнал к действиям
будет появляться для любого результата, который отстоит от медианы более чем на
одну единицу измерения, в этом случае для продукта А — два результата
«4» (4 %) попадают в зону сигнала к действиям, а для продукта В — восемь
результатов «1» (16 %).
Приложение ДА
(справочное)
Сведения о соответствии ссылочных национальных и межгосударственных стандартов
международным стандартам, использованным в качестве ссылочных в примененном
международном стандарте
Таблица
ДА.1
|
Обозначение ссылочного национального и |
Степень соответствия |
Обозначение и наименование соответствующего |
|
ГОСТ |
IDT |
ISO/IEC 17043:2010 |
|
ГОСТ |
IDT |
ISO Guide 35:2006 «Стандартные образцы. Общие и статистические принципы |
|
ГОСТ |
IDT |
ISO/IEC 17025:2005 |
|
ГОСТ |
IDT |
ISO 5725-1:1994 |
|
ГОСТ |
IDT |
ISO 5725-2:1994 |
|
ГОСТ |
IDT |
ISO 5725-5:1998 |
|
ГОСТ |
IDT |
ISO 16269-4:2010 |
|
ГОСТ |
IDT |
ISO/IEC Guide 98-3:2008 «Неопределенность измерения. Часть 3. Руководство по |
|
ГОСТ |
IDT |
ISO 7870-2:2013 |
|
Примечание — В — |
Библиография
|
[1] |
Thompson М., Ellison S.L.R., |
|
[2] |
Kuselman I., Fajgelj A. IUPAC/CITAC |
|
[3] |
Helsel D.R. Nondetects and data analysis: |
|
[4] |
CCQM Guidance note: Estimation of a |
|
[5] |
Davison A.C., Hinkley D.V. Bootstrap |
|
[6] |
Efron B., Tibshirani R. An Introduction |
|
[7] |
Thompson M. Analyst (Lond.). 2000, 125 |
|
[8] |
Horwitz W. Evaluation of analytical |
|
[9] |
Silverman B.W. Density Estimation. |
|
[10] |
Sheather S.J., Jones M.C. A reliable |
|
[11] |
van Nuland Y. ISO 9002 and the circle |
|
[12] |
Gower J.C. Ageneral coefficient of |
|
[13] |
Thompson M., Willetts P, Anderson S., |
|
[14] |
Maronna R.A., Martin R.D., Yohai V.J. |
|
[15] |
Uhlig S. Robust estimation of variance |
|
[16] |
Muller C.H., Uhlig S. Estimation of |
|
[17] |
Uhlig S. Robust estimation of between and |
|
[18] |
http://quodata.de/en/web-services/QHampel.html |
|
[19] |
Rousseeuw P.J., Verboven S. Comput. Stat. |
|
[20] |
Analytical Method Committee. Royal |
Ключевые слова:
межлабораторные сравнительные испытания, проверка квалификации, приписанное
значение, z-индекс, дзета-индекс, согласованная
величина, выброс, образец для проверки квалификации, провайдер проверки
квалификации, программа проверки квалификации, образец сравнения,
сертифицированный образец сравнения CRM
Снять ограничение
ГОСТ Р ИСО 22514-1-2015
ГОСТ Р ИСО 22514-1-2015
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
УПРАВЛЕНИЕ ПРОЦЕССАМИ
Часть 1
Общие принципы
Statistical methods. Process management. Part 1. General principles
Дата введения 2016-07-01
Предисловие
4 Настоящий стандарт идентичен международному стандарту ИСО 22514-1:2014* «Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 1. Основные принципы» (ISO 22514-1:2014 «Statistical methods in process management — Capability and performance — Part 1: General principles and concepts», IDT).
________________
Введение
1 Область применения
2 Нормативные ссылки
3 Термины и определения
,
,
.
,
.
.
,
,
.
,
,
,
.
.
.
,
.
.
,
.
4 Обозначения
В настоящем стандарте применены следующие обозначения.
|
|
— индекс воспроизводимости процесса измерений;
|
|
|
— индекс воспроизводимости измерительной системы;
|
|
|
— индексы воспроизводимости;
|
|
|
— индексы пригодности машины;
|
|
|
— индексы воспроизводимости процесса;
|
|
|
— индексы пригодности процесса;
|
|
|
— целевой индекс воспроизводимости процесса;
|
|
L |
— нижняя граница поля допуска;
|
|
|
— стандартное отклонение генеральной совокупности исследуемой характеристики;
|
|
|
— оценка стандартного отклонения по наблюдениям исследуемой характеристики;
|
|
U |
— верхняя граница поля допуска;
|
|
|
— математическое ожидание генеральной совокупности исследуемой характеристики;
|
|
|
— квантиль распределения уровня 99,865%;
|
|
|
— квантиль распределения уровня 50%;
|
|
|
— квантиль распределения уровня 0,135%;
|
|
|
— квантиль стандартного нормального распределения уровня (1-
|
|
|
— функция распределения стандартного нормального распределения.
|
5 Предварительные условия применения
6 Сбор данных
7 Анализ пригодности и воспроизводимости процесса
|
|
Рисунок 1 — Гистограмма
|
|
Рисунок 2 — Распределение
Этап 3. Идентифицируют границы поля допуска для выбранной характеристики (рисунок 3).
|
|
Рисунок 3 — Границы поля допуска
|
|
Рисунок 4 — Сопоставление в соответствии с этапом 4
|
|
|
|
Рисунок 6 — Нестабильный процесс и его пригодность
|
|
Рисунок 7 — Зона позиционного допуска
, (1)
. (2)
8 Результаты применения
9 Преимущества использования
10 Ограничения и недостатки
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
|
Обозначение ссылочного международного стандарта |
Степень соответствия |
Обозначение и наименование соответствующего национального стандарта |
|
ISO 1101 |
MOD |
ГОСТ Р 53442-2015 (ИСО 1101:2012) «Основные нормы взаимозаменяемости. Характеристики изделий геометрические. Установление геометрических допусков. Допуски формы, ориентации, месторасположения и биения» |
|
ISO 22514-7 |
IDT |
ГОСТ Р ИСО 22514-7-2014 «Статистические методы. Управление процессами. Часть 7. Воспроизводимость процессов измерений» |
|
Примечание — В настоящей таблице использованы следующие условные обозначения степени соответствия стандартов:
— MOD — модифицированный стандарт;
— IDT — идентичный стандарт.
|
Приложение ДБ
(справочное)
Сведения о соответствии ссылочных международных стандартов, указанных в библиографии настоящего стандарта, национальным стандартам
Таблица ДБ.1
|
Обозначение ссылочного международного стандарта |
Степень соответствия |
Обозначение и наименование соответствующего национального стандарта |
|
ISO 3534-1 |
IDT |
ГОСТ Р ИСО 3534-1-2019 «Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей» |
|
ISO 3534-2 |
IDT |
ГОСТ Р ИСО 3534-2-2019 «Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика» |
|
ISO 5725-1 |
IDT |
ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения» |
|
ISO 5725-2 |
IDT |
ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений» |
|
ISO 5725-3 |
IDT |
ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений» |
|
ISO 5725-4 |
IDT |
ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений» |
|
ISO 5725-5 |
IDT |
ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений» |
|
ISO 5725-6 |
IDT |
ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике» |
|
ISO 9000 |
IDT |
ГОСТ Р ISO 9000-2011** «Системы менеджмента качества. Основные положения и словарь» |
|
________________ ** Вероятно, ошибка оригинала. Следует читать: ГОСТ ISO 9000-2011. — Примечание изготовителя базы данных. |
||
|
ISO 14253-2 |
— |
* |
|
ISO 22514-2 |
IDT |
ГОСТ Р ИСО 22514-2-2015 «Статистические методы. Управление процессами. Часть 2. Оценка пригодности и воспроизводимости процесса на основе модели его изменения во времени» |
|
ISO 22514-3 |
IDT |
ГОСТ Р ИСО 22514-3-2015 «Статистические методы. Управление процессами. Часть 3. Анализ пригодности машин на основе данных измерений единиц продукции» |
|
ISO/TR 22514-4 |
IDT |
ГОСТ Р 50779.46-2012/ISO/TR 22514-4:2007 «Статистические методы. Управление процессами. Часть 4. Оценка показателей воспроизводимости и пригодности процесса» |
|
Руководство ISO/IEC 98-3 |
IDT |
ГОСТ Р 54500.3-2011/Руководство ИСО/МЭК 98-3:2008 «Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения» |
|
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта.
Примечание — В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов:
— IDT — идентичные стандарты.
|
Библиография
|
[1] |
ISO 3534-1
|
Statistics — Vocabulary and symbols — Part 1: General statistical terms and terms used in probability
|
|
[2] |
ISO 3534-2
|
Statistics — Vocabulary and symbols — Part 2: Applied statistics
|
|
[3] |
ISO 5725 (all parts)
|
Accuracy (trueness and precision) of measurement methods and results
|
|
[4] |
ISO 9000
|
Quality management systems — Fundamentals and vocabulary
|
|
[5] |
ISO 14253-2
|
Geometrical Product Specifications (GPS) — Inspection by measurement of workpieces and measuring equipment — Guide to the estimation of uncertainty in GPS measurement, in calibration of measuring equipment and in product verification
|
|
[6] |
ISO 22514-2
|
Statistical methods in process management — Capability and performance — Part 2: Process capability and performance of time-dependent process models
|
|
[7] |
ISO 22514-3
|
Statistical methods in process management — Capability and performance — Part 3: Machine performance studies for measured data on discrete parts
|
|
[8] |
ISO 22514-8
|
Statistical methods in process management — Capability and performance — Part 8: Machine performance of a multi-state production process
|
|
[9] |
ISO/TR 22514-4
|
Statistical methods in process management — Capability and performance — Part 4: Process capability estimates and performance measures
|
|
[10] |
ISO/IEC Guide 98-3
|
Uncertainty of measurement — Part 3: Guide to the expression of uncertainty in measurement (GUM:1995)
|
|
[11] |
AIAG, Measurement Systems Analysis — Reference Manual (June 2010, 4th Edition)
|
|
|
[12] |
AIAG, Statistical Process Control — Reference Manual (July 2005, 2nd Edition)
|
|
УДК 658.562.012.7:65.012.122:006.354 |
ОКС 03.120.30 |
|
Ключевые слова: спецификация, верхняя граница поля допуска, нижняя граница поля допуска, интервал требований, целевое значение, распределение характеристики продукции, границы опорного интервала характеристики продукции, опорный интервал характеристики продукции, условия воспроизводимости процесса, условия пригодности процесса, индекс воспроизводимости процесса, индекс пригодности процесса
|


Для продолжения необходимо войти в систему
ГОСТ Р ИСО 10576-1-2006
Группа Т59
ОКС 03.120.30
Дата введения 2007-01-01
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») и Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 17 октября 2006 г. N 229-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 10576-1:2003 «Руководство по оценке соответствия установленным требованиям. Часть 1. Общие принципы» (ISO 10576-1:2003 «Guidelines for the evaluation of conformity with specified requirements — Part 1: General principles»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении С
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
ВНЕСЕНА поправка, опубликованная в ИУС N 7, 2011 год
Поправка внесена изготовителем базы данных
Введение
Цель оценки соответствия состоит в подтверждении соответствия установленным требованиям в форме декларации поставщика или свидетельства третьего лица (ИСО/МЭК Руководство 2:2004 «Стандартизация и смежные виды деятельности. Общий словарь»). Обычно в требованиях указывают для измеряемой характеристики единственное предельное значение LV или два предельных значения (верхнее и нижнее). Если требования имеют отношение к характеристикам, связанным со здоровьем, предельные значения иногда называют предельно допустимыми значениями TLV или предельно допустимыми воздействиями PEL.
Когда оценка соответствия связана с оценкой неопределенности измерений, обычно применяют элементы теории статистической проверки гипотез. Зная процедуры измерений и соответствующую неопределенность, можно оценить и минимизировать риск принятия ошибочных решений о соответствии или несоответствии установленным требованиям. На практике обычно понимают, что если объект объявлен соответствующим требованиям, его статус не должен изменяться в результате последующих измерений на объекте, даже при использовании более точных методов или технологий измерений. С позиций анализа риска это означает, что риск ошибочного решения о несоответствии объекта требованиям должен быть небольшим. Следовательно, необходимо допустить (большой) риск, что объект, характеристики которого несколько лучше требований, не будет признан соответствующим. Применение двухэтапной процедуры вместо одноэтапной процедуры в общем случае приводит к уменьшению риска.
Аналогичные соображения справедливы и в том случае, если испытания проводят для оценки несоответствия.
Настоящий стандарт задачу оценки соответствия рассматривает применительно к разработке требований и проверке продукции или услуг на соответствие или несоответствие установленным требованиям.
Из-за очевидной аналогии с процедурами приемочного выборочного контроля иногда планы приемочного выборочного контроля используют при оценке соответствия. Приемочный выборочный контроль и оценка соответствия используют элементы проверки гипотез (например, ИСО 2854:1976 «Статистическое представление данных. Методы оценки и проверки гипотез о средних и дисперсиях»). Однако важно понимать, что цели этих процедур существенно различны, в частности они подразумевают различные подходы к оценке риска ошибочного решения (см. ИСО 2854).
1 Область применения
Настоящий стандарт является руководством в следующих ситуациях:
a) при разработке требований к объекту оценки, которые могут быть сформулированы в виде предельных значений для количественных параметров объекта;
b) при оценке соответствия упомянутым требованиям, когда результаты измерений или испытаний указаны вместе с неопределенностью.
Стандарт применим в случаях, когда неопределенность может быть оценена количественно в соответствии с принципами, изложенными в GUM [1]. Термин [1] «неопределенность» используют для описания всех элементов изменчивости результатов измерений, включая неопределенность, связанную с отбором выборки.
В настоящем стандарте не приведены правила для ситуации, когда получен неокончательный результат оценки соответствия.
Примечание — Стандарт не содержит ограничений на объект и требований к измеряемой характеристике. Примеры объектов и измеряемых характеристик приведены в таблице А.1 (приложение А).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 2602:1980 Статистическое представление результатов испытаний. Оценка среднего. Доверительный интервал
ИСО 2854:1976 Статистическое представление данных. Методы оценки и проверки гипотез о средних и дисперсиях
ИСО 3534-1:1993 Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основные статистические термины
ИСО 3534-2:1993 Статистика. Словарь и условные обозначения. Часть 2. Статистическое управление качеством
ИСО 5725-1:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ИСО 5725-2:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ИСО 5725-3:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ИСО 5725-4:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
ИСО 5725-5:1998 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
ИСО 5725-6:1994 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
ИСО/ТУ 14253-2:1999 Спецификации на геометрические размеры продукции (GPS). Контроль измерений заготовок и измерительного оборудования. Часть 2. Руководство по оценке неопределенности измерений GPS при калибровке измерительного оборудования и верификации продукции
3 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-1 и ИСО 3534-2, а также следующие термины с соответствующими определениями:
3.1 предельные значения, пределы поля допуска (limiting values, specification limits) : Установленные значения параметра, представляющие собой верхнюю и/или нижнюю границы допустимых значений.
[ИСО 3534-2, пункт 1.4.3]
3.2 нижняя граница поля допуска (lower specification limit) : Нижняя граница допустимых значений параметра.
3.3 верхняя граница поля допуска (upper specification limit) : Верхняя граница допустимых значений параметра.
3.4 оценка соответствия (conformity test): Систематическая оценка соответствия продукции, процесса или услуги установленным требованиям посредством испытаний.
3.5 область допустимых значений (region of permissible values): Интервал или интервалы всех допустимых значений параметра.
Примечание — Если иначе не установлено, предельные значения считают принадлежащими области допустимых значений.
3.6 область недопустимых значений (region of non-permissible values): Интервал или интервалы всех недопустимых значений параметра.
Примечание — На рисунке 1 показаны возможные ситуации разделения области возможных значений параметра на область допустимых и недопустимых значений.
Рисунок 1 — Разделение области значений параметра
Обозначения:
— область допустимых значений;
— область недопустимых значений;
,
,
,
и
— пределы поля допуска
Рисунок 1 — Разделение области значений параметра
3.7 интервал неопределенности (uncertainty interval): Интервал, получаемый на основе измерений параметра и оценки его неопределенности, накрывающий область возможных значений, которые обоснованно могут быть приписаны измеряемому параметру.
Примечания
1 Интервал неопределенности может быть симметричным интервалом с центром в точке значения результата измерений, как определено в пункте 6.2.1 GUM [1].
2. В случае, когда неопределенность получают путем оценки типа А для компонентов неопределенности, интервалом неопределенности может быть доверительный интервал для параметра (см. например, пункт 2.57 ИСО 3534-1 и пункт G.3 GUM [1]).
1 Границы и
доверительного интервала — это статистики (ИСО 3534-1, пункт 2.45), которые в общих предположениях принимают различные значения от выборки к выборке.
2 В длинном ряду выборок относительная частота случаев, когда доверительный интервал накрывает истинное значение параметра совокупности , больше или равна (
).
[ИСО 3534-1, пункт 2.5
3.9 доверительная вероятность, уровень доверия (confidence coefficient, confidence level): Величина () — вероятность, связанная с доверительным интервалом или со статистически накрывающим интервалом.
Примечание — Величину () часто выражают в процентах.
[ИСО 3534-1, пункт 2.59]
4 Требования
4.1 Общие требования при установлении предельных значений
4.1.1 Объект должен быть четко и однозначно определен.
4.1.2 Количественный параметр объекта должен быть четко и однозначно определен. Процедуры измерений или испытаний, выполняемые для определения значения параметра, должны позволять получать оценку неопределенности измерений.
4.1.3 Процедура измерений или испытаний должна быть стандартизованной процедурой*.
________________
* Стандартизованная процедура — это процедура, соответствующая требованиям Государственной системы обеспечения единства измерений и стандартов на методы измерений и испытаний.
4.1.4 Устанавливаемые предельные значения не должны включать в себя (в явном или неявном виде) неопределенность измерений.
4.2 Особенности предельных значений
Предельные значения должны быть установлены при выполнении требований 4.1.1 и 4.1.2. Область допустимых значений количественного параметра может быть ограничена только с одной стороны или с двух сторон. Границы области поэтому бывают двух видов: двусторонние, состоящие из верхней и нижней границ, и односторонние, состоящие из верхней или нижней границы.
Примеры
1 Двусторонние границы
Для единственной единицы продукции — барреля моторного масла (объект) требования к кинематической вязкости масла (параметр) могут быть заданы в следующем виде:
— кинематическая вязкость должна быть не менее 0,5·10 мм
/с и не более 1,0·10
мм
/с.
2 Двусторонние границы
Для одной партии бутылок растительного масла (объект) требования к средней температуре кипения при атмосферном давлении 101,6 кПа для масла в бутылках (параметр) могут быть заданы в следующем виде:
— средняя температура кипения должна находиться внутри интервала от 105,0 °С до 115,0 °С.
3 Односторонняя верхняя граница
Для отгрузки сырой нефти (объект) требования к массовой доле серы (параметр) могут быть заданы в следующем виде:
— массовая доля серы должна быть не более 2%.
4 Односторонняя граница
Дли индивидуума (объект) требования к молярной концентрации свинца в крови (параметр) могут быть заданы в следующем виде:
— молярная концентрация свинца в крови должна быть не более 0,96 мкмоль/л.
5 Односторонняя нижняя граница
Для партии битума (объект) требования к растворимости битума в керосине при 20 °С (параметр) могут быть заданы в следующем виде:
— растворимость битума в керосине при 20 °С должна быть не менее 99% массы.
6 Односторонняя верхняя граница
Для отгрузки яблок (объект) требования к доле яблок, зараженных вредителями (параметр), могут быть заданы в следующем виде:
— доля яблок, зараженных вредителями, должна быть менее 0,2%.
Из-за различий в массе отдельных яблок доля зараженных яблок по массе будет отличаться от доли зараженных яблок по количеству.
Примечание — Во многих случаях (например, в экологии) дополнительный подразумеваемый предел, такой как 0%, 0,0 кг/л и 100%, может быть не указан вследствие его очевидности. В этом случае может быть установлено единственное предельное значение.
5 Неопределенность результатов
5.1 Общие положения
При сравнении результатов измерений или испытаний с предельными значениями необходимо учитывать неопределенность результатов измерений. Неопределенность должна быть оценена в соответствии с [1]. Для идентификации некоторых составляющих неопределенности могут быть использованы ИСО 5725-1 — ИСО 5725-6.
Примечание — Должны быть учтены вклады в неопределенность всех стадий процедуры измерений, а также неопределенности, связанной с отбором выборки.
5.2 Регистрация неопределенности результатов измерений
Результаты измерений параметра и неопределенность измерений должны быть зарегистрированы. Неопределенность измерений следует представлять в виде интервала неопределенности. Если этот интервал является доверительным интервалом, необходимо указывать доверительную вероятность (), соответствующую интервалу (см. пункты 2.57 и 2.59 ИСО 3534-1). В противном случае следует указывать коэффициент охвата интервала неопределенности (см. [1], пункт 6.2.1).
6 Оценка соответствия требованиям
6.1 Общие положения
Оценка соответствия — это систематическая экспертиза (посредством измерений) соответствия объекта установленным требованиям. Цель оценки соответствия — обеспечить уверенность в том, что объект соответствует установленным требованиям. Настоящий стандарт рекомендует выполнять оценку соответствия как двухэтапную процедуру. В случаях, когда двухэтапная процедура не может быть выполнена или по каким-то причинам не должна быть выполнена, необходимо выполнять одноэтапную процедуру. При выполнении двухэтапной процедуры должна быть применена соответствующая процедура оценки результатов измерений.
Примечание — Преимущество двухэтапной процедуры по сравнению с одноэтапной процедурой состоит в том, что двухэтапной процедуре присуща значительно более высокая вероятность соответствия для объектов с допустимыми значениями количественного параметра, близкими к предельному значению. Недостаток двухэтапной процедуры состоит в том, что для нее характерна несколько более высокая вероятность решения о соответствии объекта с недопустимыми значениями контролируемого параметра, близкими к предельному значению. Если эта вероятность решения о соответствии несоответствующих объектов не может быть принята, должна быть применена одноэтапная процедура.
6.2 Двухэтапная процедура оценки соответствия
6.2.1 Этап 1
Проводят измерения и рассчитывают неопределенность результатов измерений.
Решение о соответствии требованиям может быть принято тогда и только тогда, когда интервал неопределенности, построенный по результатам измерений, находится внутри области допустимых значений. Второй этап должен быть выполнен тогда и только тогда, когда границы интервала неопределенности, рассчитанные после первого этапа, выходят за пределы поля допуска.
6.2.2 Этап 2
Проводят измерения еще раз и получают соответствующую комбинацию результатов измерений двух этапов, чтобы определить окончательный результат измерений и вычислить его неопределенность.
Решение о соответствии требованиям может быть принято только в том случае, если интервал неопределенности окончательного результата измерений находится внутри области допустимых значений.
Если после первого или после второго этапа принимают решение о соответствии, его формулируют согласно 7.2.
Примечание — Если интервал неопределенности находится внутри области допустимых значений и одна из границ интервала неопределенности совпадает с предельным значением, считают, что интервал неопределенности находится в области допустимых значений.
Если интервал неопределенности результатов измерений полностью лежит в области недопустимых значений, после первого или после второго этапа принимают решение о несоответствии требованиям, которое формулируют согласно 7.3.
Примечание — Если интервал неопределенности находится в области недопустимых значений и одна из границ интервала неопределенности совпадает с границей поля допуска, считают, что интервал неопределенности находится в области недопустимых значений.
Если интервал неопределенности, рассчитанный после этапа 2, включает в себя границу поля допуска, результат оценки соответствия является неокончательным. Решение формулируют согласно 7.4.
Примечание — Процедуры измерений, используемые на этих двух этапах, могут быть неидентичны. Соответствующая комбинация результатов первого и второго этапов, отнесенная к этапу 2, включает в себя также ситуацию, когда, например, только результат этапа 2 используют как окончательный результат измерений.
Схема двухэтапной процедуры оценки соответствия приведена на рисунке 2.
Рисунок 2 — Схема двухэтапной процедуры оценки соответствия
Рисунок 2 — Схема двухэтапной процедуры оценки соответствия
6.3 Одноэтапная процедура оценки соответствия
Проводят измерения и вычисляют неопределенность результатов измерений.
Решение о соответствии требованиям может быть принято в том случае, если интервал неопределенности результатов измерений находится внутри области допустимых значений.
Примечание — Если интервал неопределенности находится в области допустимых значений и одна из границ интервала неопределенности совпадает с пределом поля допуска, считают, что интервал неопределенности находится в области допустимых значений.
Если интервал неопределенности результатов измерений целиком лежит в области недопустимых значений, то может быть принято решение о несоответствии требованиям. Решение формулируют согласно 7.3.
Примечание — Если интервал неопределенности находится в области недопустимых значений и одна из границ интервала неопределенности совпадает с пределом поля допуска, считают, что интервал неопределенности находится в области недопустимых значений.
Если интервал неопределенности включает в себя границу поля допуска, оценка соответствия является неокончательной. Решение формулируют согласно 7.4.
6.4 Интервал неопределенности, заданный в форме доверительного интервала
В настоящем подразделе рассмотрена ситуация, когда интервал неопределенности задан в форме доверительного интервала с доверительной вероятностью () (см. 5.2). Если в требованиях указана единственная граница поля допуска [случай а) или b) на рисунке 1], то вероятность ошибочного решения о соответствии составляет не более
для одноэтапной процедуры и не более (
) для двухэтапной процедуры. В случае с двумя пределами поля допуска [случай с) или d) на рисунке 1] вероятность ошибочного решения о соответствии зависит от математического ожидания длины доверительного интервала. Однако если средняя длина доверительного интервала составляет часть разности между пределами поля допуска, то вышеупомянутое выражение для вероятности ошибочного решения о соответствии все же можно использовать.
Если можно предположить, что неопределенность измерений известна (т.е. неопределенность не рассчитана по наблюдениям), вероятность решения о соответствии требованиям и вероятность получения неокончательного решения при оценке соответствия могут быть рассчитаны.
6.5 Неокончательный результат оценки соответствия
Если значение параметра находится в окрестности предела поля допуска, существует большая вероятность того, что результат оценки соответствия будет неокончательным. Это ситуация в принципе неудовлетворительная, но она неизбежна, если декларация о соответствии требованиям должна содержать доказательство утверждения, приведенного в 7.2.
7 Составление отчета о результатах оценки соответствия
7.1 Общие положения
Поскольку результаты измерений являются случайными величинами, основанное на них утверждение может быть неверным. Программа измерений и испытаний должна предусматривать это в расчетах, результаты которых приведены в отчете об оценке соответствия.
В отчете о результатах оценки соответствия утверждения для соответствия, несоответствия или неокончательной оценки, приведенные в 7.2, 7.3 и 7.4, должны быть дополнены всеми свидетельствами, которые удостоверяют использованное утверждение.
7.2 Решение о соответствии
Если интервал неопределенности результатов измерений находится внутри области допустимых значений (см. 6.1 и 6.2), принимают решение о соответствии. Решение о соответствии должно быть сформулировано следующим образом: оценка соответствия продемонстрировала, что значение контролируемого параметра соответствует требованиям.
7.3 Решение о несоответствии
Если интервал неопределенности результатов измерений находится внутри области недопустимых значений (см. 6.1 и 6.2), то принимают решение о несоответствии.
Решение о несоответствии должно быть сформулировано следующим образом: оценка соответствия продемонстрировала, что значение контролируемого параметра не соответствует требованиям.
7.4 Неокончательный результат
Если в соответствии с 6.1 или 6.2 не может быть принято решение ни о соответствии, ни о несоответствии требованиям, результат оценки соответствия является неокончательным. Результат неокончательной оценки должен иметь следующую формулировку: оценка соответствия не способна продемонстрировать, что значение контролируемого параметра соответствует или не соответствует требованиям.
Приложение А (справочное). Примеры объектов и количественных параметров
Приложение А
(справочное)
Таблица А.1 — Примеры объектов с соответствующими количественными параметрами
|
Объект |
Количественный параметр объекта |
|||
|
Параметр единицы продукции |
Среднее |
Параметр гомогенности |
Относительная частота |
|
|
Различимая единица продукции или отдельный ее представитель |
х |
— |
— |
— |
|
{гиря для весов} |
{масса} |
— |
— |
— |
|
Группа различимых единиц продукции (партия или совокупность) |
— |
х |
х |
х |
|
{партия мешков сахара} |
— |
{средняя масса мешка} |
{стандартное отклонение массы мешка} |
{процент мешков |
|
Процесс |
— |
х |
х |
х |
|
{продукция в бутылках} |
— |
{средний объем продукции |
{стандартное отклонение объема продукции в бутылке} |
{процент бутылок |
|
Партия нештучной продукции (сыпучий, жидкий или газообразный материал) |
— |
х |
х |
х |
|
{партия доломита} |
— |
{доля массы асбестовых волокон} |
{стандартное отклонение массовой доли асбестовых волокон по отобранным образцам} |
{массовая доля асбестовых волокон соответствующей длины} |
|
Услуги |
— |
х |
х |
х |
|
{лечение конкретной болезни} |
— |
{среднее время |
{стандартное отклонение времени от появления болезни до начала ее лечения} |
{процент времени |
|
Примечание — Символ «х» означает то, что параметр может соответствовать указанному объекту. Конкретные примеры приведены в фигурных скобках. Приведенные в таблице виды объектов и перечень параметров не являются исчерпывающими. |
Приложение В (справочное). Примеры
Приложение В
(справочное)
В.1 Общие положения
Следующие примеры охватывают только некоторые из комбинаций объектов и количественных параметров, указанных в таблице А.1*.
_____________
* В примерах использована различная разрядность результатов вычисления. Обычно в промежуточных вычислениях сохраняют на две значащие цифры больше, чем в исходных данных. Это позволяет гарантировать, что в числовом значении результата вычислений ошибка округления может повлиять лишь на последнюю значащую цифру, если окончательный результат вычислений и исходные данные приводятся с одинаковым количеством значащих цифр.
В.2 Пример 1
Для ряда чисто выточенных стальных стержней, имеющих номинальные размеры 25 мм х 150 мм, пределы поля допуска для диаметра
24,9 мм и
25,0 мм. Таким образом, объектом является стержень, а параметром — диаметр стержня.
Измерения выполнены с использованием аналогового внешнего микрометра, имеющего диапазон измерений от 0 до 25 мм с ценой деления верньерной шкалы 10 мм. Стандартная неопределенность измерений
3,79·10
мм рассчитана с учетом нескольких источников неопределенности (см. пункт А.2 ИСО/ТУ 14253-2). По экономическим причинам была выполнена одноэтапная проверка для каждого стержня ряда. Интервалы неопределенности были рассчитаны в соответствии с пунктом 6.2.1 GUM [1] для коэффициента охвата
2. Интервалы неопределенности для размеров трех стержней: (24,857±0,0076) мм; (24,907±0,0076) мм и (24,962±0,0076) мм. В соответствии с 6.3 первый стержень является несоответствующим, а третий стержень соответствует требованиям. Оценка соответствия второго стержня дает неокончательный результат.
,*
где — квантиль уровня (
) стандартного нормального распределения (ИСО 2602).
_____________
* Здесь (так же, как и в примере В.4) неявно предполагается, что систематическими погрешностями, связанными с действиями лаборанта, средством измерений и пр., можно пренебречь. Справедливость такого предположения требует проверки в каждой конкретной задаче.
Измерена концентрация свинца в крови конкретного человека, для которого источником свинца являются ежедневный рацион питания и выхлопные газы автомашин. Оценка концентрации свинца по измерениям первой пробы крови (1) составила
0,60 мкмоль/л. Интервал неопределенности, заданный в форме доверительного интервала (с доверительной вероятностью 0,95), включает в себя значения от 0,504 до 0,693 мкмоль/л. Так как этот интервал полностью попадает в допустимую область, согласно 6.3 принято решение о соответствии установленным требованиям.
Измерена концентрация свинца в крови другого человека, который подвергается дополнительному воздействию свинца по дороге на работу. Измерение первой пробы (1) дает
1,06 мкмоль/л, а соответствующий доверительный интервал для концентрации свинца включает в себя значения от 0,96 до 1,15 мкмоль/л. Так как этот интервал содержит предельное значение, измерена вторая проба (
1). Результат измерений составил 1,00 мкмоль/л. Измерения двух этапов объединены:
(1,06+1,00)/2 мкмоль/л=1,03 мкмоль/л. Доверительный интервал для среднего арифметического двух оценок концентрации свинца, рассчитанный для
2, включает в себя значения от 0,96 до 1,10 мкмоль/л. Предельное значение находится в этом интервале. Таким образом, решение о том, что концентрация свинца соответствует требованиям, не может быть принято. Также не может быть принято решение о том, что концентрация свинца не соответствует требованиям. Согласно 6.3 результат двух этапов оценки соответствия является неокончательным*.
_____________
* Необходимо подчеркнуть, что приведенная процедура оценки соответствия концентрации свинца в крови человека не эквивалентна обычно используемой процедуре.
В.4 Пример 3
Определено, что полная масса кадмия в сбрасываемой воде электростанции не должна превышать ежедневную массу 5 г в более чем 20% дней за период измерений. Таким образом, объектом является процесс ежедневного сброса воды электростанцией. Параметром является 80%-й процентиль (т.е. квантиль уровня 0,8) распределения ежедневного сброса кадмия. Верхним пределом допуска для процентиля является 5 г. Измерение ежедневного количества кадмия в сбрасываемой воде показало, что оно может быть описано логнормальным распределением. Верхняя доверительная граница , соответствующая доверительной вероятности (
) для
-квантиля логнормального распределения, основанная на выборке из
независимых измерений, имеет вид
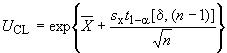
где — среднее арифметическое
логарифмов наблюдений;
— соответствующее выборочное стандартное отклонение;
— квантиль уровня (
) нецентрального t-распределения с (
) степенями свободы и параметром нецентральности
.
Если означает квантиль уровня
стандартного нормального распределения, то для
справедлива формула
.
Одноэтапная оценка соответствия была выполнена на 10 образцах сбрасываемой воды. Образцы выбирали последовательно с интервалом в 14 дней. Измеряли содержание кадмия в каждом образце и оценивали ежедневный выход кадмия. Предполагалась однородность содержания кадмия в сбрасываемой воде. Неопределенность отдельных результатов измерений (т.е. ежедневного выхода кадмия) незначительна по сравнению с отклонениями в выходе кадмия по дням. Ежедневные наблюдения содержания кадмия (в граммах) в сбрасываемой воде составили:
0,3486; 0,1408; 0,0890; 1,1417; 0,7524; 0,6262; 3,7560; 0,5520; 0,2304; 1,7226.
Среднее арифметическое и стандартное отклонение натурального логарифма наблюдений составили:
-0,624837 и
1,14379.
Поскольку 0,80, то
0,841621 и, таким образом,
-2,66144. Для 95%-го доверительного интервала (т.е.
0,05) для 80%-го процентиля
.
Верхний предел одностороннего 95%-го доверительного интервала для 80%-го процентиля распределения ежедневного количества кадмия в сбрасываемой воде
.
Так как 5, можно подтвердить соответствие требованиям.
В.5 Пример 4
Скандинавский доломит обычно содержит незначительную долю волокон асбеста, которые могут нанести вред здоровью людей, работающих с доломитом. Поэтому был определен верхний предел доли асбеста в массе скандинавского доломита, используемого в промышленности. Пределами допуска являются массовые доли 0,001% и 0,1%. Перед обработкой партий доломита проводят оценку их соответствия этим требованиям. Таким образом, объектом является партия доломита, а исследуемым параметром — массовая доля волокон асбеста в партии. Измерения проводят для проверки требования
0,1%.
Для оценки исследуемого параметра из партии отбирают несколько первичных образцов. Из каждого образца формируют заданное количество лабораторных проб и используют их для анализа. Для каждого образца подсчитывают выборочное среднее массовой доли по соответствующим лабораторным пробам. Известно, что, если количество лабораторных проб является большим, распределение (по первичным образцам) выборочных средних хорошо описывается нормальным распределением со средним
и дисперсией
. Дисперсия
включает в себя вклад отклонений между первичными образцами, вклад отклонений в пределах первичных образцов и неопределенность измерений, связанную с анализом лабораторных проб. Если проанализировано
первичных проб и из каждого первичного образца сформировано одинаковое количество лабораторных проб, массовую долю волокон асбеста в партии оценивают с помощью среднего арифметического
по результатам измерений первичных образцов, т.е.
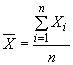
Предполагая, что наблюдения являются независимыми с одинаковой дисперсией, оценку дисперсии можно получить по формуле
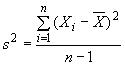
Доверительный интервал для среднего с доверительной вероятностью () имеет вид
,
где — квантиль t-распределения уровня (
) с (
) степенями свободы в соответствии с ИСО 2602.
Партия скандинавского доломита была представлена для оценки соответствия требованиям к содержанию асбеста. Так как процедура измерений требует очень много времени, было принято решение выполнять оценку соответствия как двухэтапную процедуру с пятью образцами на первом этапе и четырьмя образцами на втором этапе. Было сформировано для анализа 10 лабораторных проб от каждого образца.
На первом этапе были получены следующие результаты в массовых долях асбеста: 0,152%; 0,0704%; 0,0772%; 0,0731%; 0,0551%.
На основе наблюдений первого этапа для 0,05 был получен следующий доверительный интервал для
:
0,0856%±(2,776·0,0381%)/(0,038%; 0,133%).
Так как граница поля допуска 0,1% лежит в этом интервале, было принято решение о переходе ко второму этапу оценки соответствия и анализу 10 лабораторных проб от каждого из четырех образцов. Были получены следующие результаты:
0,0828%; 0,0671%; 0,0743%; 0,0561%.
С использованием приведенных выше процедур получен следующий доверительный интервал:
0,0787%+2,306·0,0290/%=(0,056%; 0,101%).
Поскольку этот интервал также содержит границу поля допуска, принимают решение о несоответствии установленным требованиям.
Приложение С (справочное). Сведения о соответствии национальных стандартов Российской Федерации ссылочным международным стандартам
Приложение С
(справочное)
Таблица С.1
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего национального стандарта |
|
ИСО 2602:1980 |
ГОСТ Р 50779.22-2005 (ИСО 2602:1980) Статистические методы. Статистическое представление данных. Точечная оценка и доверительный интервал для среднего |
|
ИСО 2854:1976 |
ГОСТ Р 50779.21-2004 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение |
|
ИСО 3534-1:1993 |
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения |
|
ИСО 3534-2:1993 |
ГОСТ Р 50779.11-2000 (ИСО 3534-2-93) Статистические методы. Статистическое управление качеством. Термины и определения |
|
ИСО 5725-1:1994 |
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения |
|
ИСО 5725-2:1994 |
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений |
|
ИСО 5725-3:1994 |
ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений |
|
ИСО 5725-4:1994 |
ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений |
|
ИСО 5725-5:1998 |
ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений |
|
ИСО 5725-6:1994 |
ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике |
|
ИСО/ТУ 14253-2:1999 |
* |
|
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. |
Библиография
[1] Guide to the expression of uncertainty in measurement (GUM) 1995
[2] Christensen, J.M., Poulsen, O.M. and Anglov, Т., Protocol for the design and interpretation of method evaluation in ASS analysis. Application to the determination of lead and manganese in blood. Journal of Analytical Atomic Spectroscopy, 1992, vol. 7, p.329-334
[3] Christensen, J.M., Human Exposure to Toxic Metals. Factors influencing Interpretation of Biomonitoring Results, Science of the Total Environment, 1995, vol. 166, p.89-135
[4] Kristiansen, J., Christensen, J.M. and Nielsen, J.L., Uncertainty of atomic absorption spectrometry: Applications to the determination of lead in blood. Mikrochimica Acta, 1996, vol. 123, p.241-249
[5] Kristiansen, J. and Christensen, J.M., Traceability and uncertainty in analytical measurements. Annals of Clinical Biochemistry, 1998, vol. 35, p.371-379