Готовые задачи к руководство к решению задач - RukovodstvoRus.ru - инструкции пользования и руководства

Высшая математика: решебники, руководства к решению задач

Руководства к решению задач по ВМ

Решебники по высшей математике

Интересные ссылки

Готовые решения из задачника Кузнецова

Готовые типовые расчёты

Сайты с решениями

Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения»

Кафедра «Строительная механика»

В.А. Бобрин Л.П. Миронов

РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ

ЧАСТЬ 1

Рекомендовано Дальневосточным региональным учебно-методическим центром (ДВ РУМЦ)

в качестве учебного пособия для студентов специальностей 270102 «Промышленное и гражданское строительство», 270201 «Мосты и транспортные тоннели», 270204 «Строительство железных дорог, путь и путевое хозяйство», 190205 «Подъемно-транспортные, строительные,

дорожные машины и оборудование» вузов региона

Хабаровск Издательство ДВГУПС

2006

УДК 624.04 (075.8)

ББК Н112я73

Б 724

Рецензенты:

Кафедра «Механика деформируемого твердого тела» Хабаровского государственного технического университета (заведующий кафедрой кандидат технических наук, доцент

А.А. Вайсфельд)

Заведующий кафедрой «Механика деформируемого твердого тела» Дальневосточного государственного технического университета

доктор технических наук, профессор

К.П. Горбачев

Бобрин, В.А.

Б 724 Руководство к решению задач по строительной механике : учеб. пособие. В 3 ч. Ч. 1 / В.А. Бобрин, Л.П. Миронов; под ред. Л.П. Миронова. – Хабаровск : Изд-во ДВГУПС, 2006. – 141 с.

Учебное пособие соответствует дисциплине «Строительная механика» по ГОС ВПО направления 271100 «Строительство» специальности 270102 «Промышленное и гражданское строительство», направления 270200 «Транспортное строительство» специальностей 270204 «Строительство железных дорог, путь и путевое хозяйство» и 270201 «Мосты и транспортные тоннели», направления 190200 «Транспортные машины и транспортнотехнологические комплексы» специальности 190205 «Подъемно-транспорт- ные, строительные, дорожные машины и оборудование».

Пособие состоит из 3 частей. В части 1 рассмотрены методы кинематического анализа и построения линий влияния усилий в статически определимых балках, арках, рамах и фермах. Подробно разобраны примеры решения типовых задач, приведены 360 вариантов задач для самостоятельного решения и ответы к ним.

Предназначено студентам всех форм обучения.

УДК 624.04 (075.8)

ББК Н112я73

ãГОУ ВПО «Дальневосточный государственный университет путей сообщения» (ДВГУПС), 2006

ВВЕДЕНИЕ

Настоящее пособие посвящено методам построения линий влияния усилий в плоских статически определимых стержневых системах и их использованию при расчете сооружений на действие неподвижных и подвижных нагрузок. Пособие начинается с изложения кратких сведений из теоретической механики и математики, позволяющих студентам преодолеть трудности, возникающие при использовании аппарата этих дисциплин. В пособии излагаются основные положения теории, методические указания и подробные решения типовых задач по кинематическому анализу расчетных схем сооружений, статическому и кинематическому методам построения линий влияния и расчеты по ним.

Приведены более 190 задач с 360 вариантами исходных данных для самостоятельного решения. Тематика и набор задач отражают многолетний опыт кафедры по преподаванию строительной механики. Ко всем задачам приведены ответы в числовой или графической форме.

Всовременной доступной учебной литературе отсутствуют примеры

инаборы задач для использования в аудитории с целью организации самостоятельной индивидуальной работы студентов или тестирования их знаний по разделам курса строительной механики. Настоящее пособие восполняет этот пробел.

Наличие ответов стимулирует самостоятельный поиск студентом правильных решений, которые представляются им в письменном виде. Совпадение полученного решения с ответом благотворно влияет на возникновение у студента чувства уверенности в овладении учебным материалом.

Особое значение пособие имеет для студентов заочной формы обучения, основная масса которых живет и работает в отдаленных районах, где доступ к подобной учебной литературе затруднен.

Впособии принята тройная нумерация задач и ответов к ним. Первая цифра указывает раздел, вторая – её подраздел , третья – порядковый номер задачи.

Пособие написали В.А. Бобрин: разд. 1, подразд. 3.1, 3.2, 4.2–4.6, 5.2–5.6; Л.П. Миронов: разд. 2, подразд. 3.3–3.5, 4.1, 4.7, 5.1, 5.7.

Все замечания и рекомендации по улучшению данного пособия будут с благодарностью приняты авторами.

1.ЭЛЕМЕНТЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ И МАТЕМАТИКИ

1.1.Проекции плоской системы сил на оси прямоугольной системы координат. Моменты сил

В строительной механике широко используется аппарат теоретической механики и математики. Ниже напоминаются некоторые необходимые при расчетах стержневых систем элементы указанных дисциплин. Общепринято считать проекции сил, совпадающие (несовпадающие) с положительным направлением координатных осей, со знаком плюс (минус). Положительное направление вращения в строительной механике допустимо принимать как по ходу, так и против хода часовой стрелки, сообразуясь с удобством вычислений. Пусть имеется плоская система сил в составе сосредоточенных сил Fi, сплошных распределенных нагрузок интенсивностью qi, и сосредоточенных моментов (пар сил) mi (рис. 1.1).

Силовая плоскость

= —R sinβ

Центр

Линия действия F1

qi=q(ξ)

тяжести

F3y= —F3sinα3

F1y= F1sinα1

90°

Плечо r1

α1

F2y= —F2

Плечо r3=0

Rq-равнодействующая

Идентичные

m1 изображения

Плечо r2

K Плечо rq

пар сил

90°

α2=90°

90°

α3

= F cosα

F3z= F3cosα3

=–R cosβ

Моментная точка

Рис. 1.1. Проекции сил (изображены светлыми стрелками) на координатные оси. Моменты сил относительно произвольной точки

Тогда алгебраическая сумма проекций всех нагрузок на ось Z составит:

∑ FZ = F1сosα1 + F3сosα3 – Rqсosβ, а сумма проекций этих же нагрузок на ось Y будет равна: ∑ FY = F1sinα1 – F2 – F3sinα3 – Rqsinβ,

где Rq = ò q(ξ)dξ – равнодейcтвующая		Rq= qa	q= const.
0

распределенной нагрузки, приложенная в

центре тяжести её полосы загружения.

Если q(ξ) = q = const, то Rq = qa и		a/2

приложена посередине полосы (рис. 1.2).			a

Пары сил mi не имеют проекций на

координатные оси.	Рис. 1.2. Равнодействующая
Алгебраическая сумма моментов сил
равномерно распределенной
относительно моментной точки К в данном	нагрузки

случае будет :

∑MK = –F1r1 + F2r2 + F30 – Rqrq – m1 + m2 или при обратном правиле знаков

∑MK = F1r1 – F2r2 + F30 + Rqrq + m1 – m2.

Единицы измерения нагрузок таковы: Fi, Rqi – [кН], qi – [кН/м], mi – [кНּм].

1.2. Уравнения равновесия (статики) на плоскости

а) Если сосредоточенные силы Fi и равнодействующие Rqi распределенных нагрузок сходятся в одной точке (рис 1.3), то независимых уравнений равновесия здесь два: ∑FZ = 0, ∑FY = 0.

б) Для произвольной плоской системы сил (рис. 1.4) используют три эквивалентных варианта уравнений статики:

1)∑FZ = 0; ∑FY = 0; ∑MK = 0;

2)∑Mk1 = 0; ∑Mk2 = 0; ∑FY = 0 (или ∑FZ =0);

3)∑Mk1 = 0; ∑Mk2 = 0; ∑Mk3 = 0,

где моментные точки К1, К2, К3 не должны совпадать и в последнем случае не должны лежать на одной прямой.

	y
Rq3	F2	F3	y	F1		F3
			K3

F1		Rq1 z	m1		k1		Rq

			F2		K2
	Rq2			m2

	Рис. 1.3. Система сходящихся сил	Рис. 1.4. Произвольная
	система сил

F2 z

Рис. 1.5. Нагрузки, лежащие на одной прямой

в) Если линии действия всех сил лежат на одной прямой, то рассматривают одно условие статики

(рис. 1.5): ∑FZ = 0.

1.3. Построение графиков (эпюр) элементарных функций

Многие расчеты в строительной механике сопровождаются построением различного вида графиков (эпюр). Напомним, как это делается для алгебраических функций одной независимой переменной. Например, построение эпюр внутренних усилий начинается с разбивки расчетной схемы конструкции на участки, на каждом из которых указывают пределы изменения независимой переменной. Такой участок в математике называется областью определения функции, в пределах которой и строят эпюру с указанием характерных значений (величины и знака) искомых ординат. В зависимости от выбранного начала отсчета независимой переменной (аргумента функции) указывают пределы её изменения на данном участке либо как а ≤ z ≤ b, либо как 0 ≤ z ≤ b. В последнем случае начало отсчета совмещают с началом участка, что удобнее.

Рассмотрим примеры. Пусть:

а) составлена функция ƒ1(z) = 4 с областью определения 0 ≤ z < 4,2. Её эпюра представлена на рис. 1.6, а. Очевидно, что если в выражение функции переменная z не входит, её значение на данном участке постоянно;

б) составлена функция ƒ2(z) = –3z+8 с областью определения 0 ≤ z ≤ 4. Так как функция содержит переменную z в первой степени, её эпюра есть прямая (линейная функция). Вычисляем концевые ординаты:

ƒ2(0) = 8; ƒ2(4) = –3·4 + 8 = –4. Эпюра ƒ2(z) представлена на рис. 1.6, б.

Абсцисса нулевой ординаты определяется из условия ƒ2(z0)= –3z0+8 = 0,

откуда z0 = 8/3 = 2,666;

в) составлена функция ƒ3(z) = –1,2 · z2 + 9,2 z – 4 с областью определения 0 ≤ z ≤ 6. Так как старшая степень переменной z равна 2, эта функция – парабола.

Эпюру ƒ3(z) строим по характерным точкам кривой, ординаты которых вычисляем так: в начале участка при z = 0, ƒ3(0) = –4; посередине участка при zср = 3 получаем ƒср = –1,2 · 32 + 9,2 · 3 – 4 = 12,8. Экстремальное

значение находим из условия равенства нулю первой	производной от
ƒ3(z), что дает	∂f3( z )	= −2,4zextr + 9,2 = 0, откуда zextr	=	9,2/2,4 = 3,833.
∂z
Подставляя zextr	в уравнение функции, получаем
6

ƒ3max(3,833) = –1,2 · 3,8332 + 9,2 · 3,833 – 4 = 13,333. Концевая ордината при z = 6: ƒ3(6) = -1,2 · 62 + 9,2 · 6 – 4 = 8.

Положение нулевой ординаты находим из условия ƒ3(z0) = –1,2 z02 + 9,2 z0 – 4 = 0, откуда:

1 é

-9,2 ± 8,09

-9,2

9,2

— 4 (-1,2) (-4)ú

-2, 4

(-1,2) ë

		z0(1) = − 9,2 + 8,09	= 0,462	и		z0(2) =	− 9,2 − 8,09	= 7,204 .
										— 2,4										— 2,4
																					ƒ3(z)				Эпюраƒ3(z)
																	в	14			maxƒ =13,333
																						ƒср=12,8

																		12
																				ƒк=9,6	K
ƒ1(z)															10

Эпюраƒ1(z)					8
																										8
																		6
																				φк


																	z	4


																									Касательная
1		2		3		4			2

ƒ2(z)	Эпюраƒ2(z)					0																		z

												1	2	3			4	5	6
											ƒ2(z0)=0	z	2



										3	4	4					Z0=0,462


1		2

Z0=2,666										4						Zк =2
																								Zср	=3

																							Zmax =3,833

Рис. 1.6. Эпюры функций ƒi(z)

Первое значение z0(1) = 0,462 принадлежит участку, а второе z0(2)

выводит за пределы участка и должно быть отброшено. Эпюра ƒ3(z) показана на рис. 1.6, в. В заключение определим тригонометрические функции угла φК наклона касательной к кривой в точке К с абсциссой zК = 2 (рис. 1.6, в). Как известно, первая производная функции в декартовых

координатах равна тангенсу угла ϕК . Поэтому при zК = 2 имеем

tgjК =	df3 (z)	= -2,4 zК	+ 9,2 = -2, 4×2 + 9,2 = 4,40.
dz
		1				1
Тогда cos jK	=			=		= 0,2216	, а sinjK = tgjK × cos jK =

1+ tgϕ2		1+ 4,42
			K

= 0,2216 · 4,4 = 0,9752,			а	sin2 ϕK + cos2 ϕK	= 0,97522 + 0,22162 = 1.

1.4. Некоторые соотношения для плоских фигур

Прямоугольник (рис. 1.7). Площадь ω = hλ; если это полоса загружения равномерно распределенной (погонной) нагрузкой интенсивностью q0 = сonst, то на некоторых стадиях расчета сооружений ее представляют равнодействующей Rq = q0λ [кH], приложенной в центре С тяжести прямоугольника (zc = λ/2).

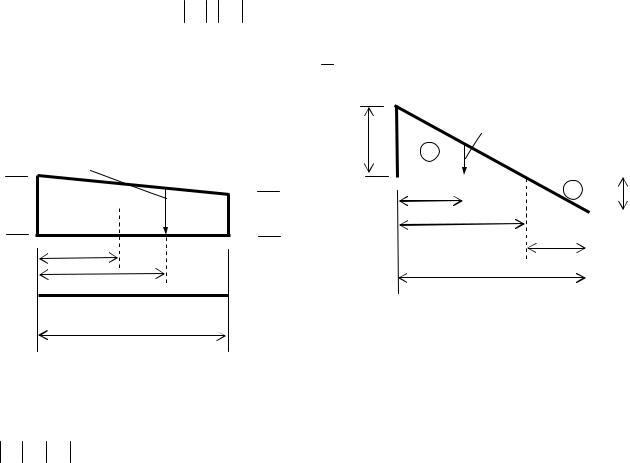
Прямоугольный треугольник (рис. 1.8). Площадь ω = 1/2 hλ; если это полоса загружения распределенной нагрузкой переменной интенсивности qz , то её равнодействующая Rq = q0 λ/2 и приложена в центре С тяжести с координатой zc = λ/3; tgα=h/λ.

)				q0=const

0	c
h(q		Rq




	zc=λ/2
			λ
Рис. 1.7. Прямоугольник

h(q0)

qz = q0 (λ − z )

Рис. 1.8. Прямоугольный треугольник

Трапеция (рис. 1.9). Площадь w =

(h1 + h2)

l ; если это полоса распре-

(l — z)

деленной нагрузки переменной интенсивности q

= q

+ (q

— q

)

(q1 + q2)

то ее равнодействующая Rq =

l и приложена в центре С тяжести

с координатой zc =

(h1 + 2h2 ) λ

(q1 + 2q2 )λ

3(h1 + h2 )

3(q1

+ q2 )

Двузначная трапеция (рис. 1.10). Площадь w =	(h1 + h2)	l , где h2 < 0;
2

; здесь

Текущая ордината yz

qz = q2 + (q1

h1 , h2 принимать по абсолютной величине.

= h1 — (h1 + h2 ) lz .

— q2 )×	(λ − z)	1	yz
h


l

h1(q1)

h2(q2)


z		h
		2
	z0


	a
	λ

Рис. 1.10. Двузначная трапеция

Рис. 1.9. Трапеция

Полезно иметь в виду, что площади двузначных фигур в алгебраическом смысле могут быть равны нулю (например, здесь при h1 = h2 ). Но если бы определялась площадь ω фигуры для ее окраски,

1.5. О некоторых правилах приближенных вычислений

Реальные конструкции обычно несколько отличаются от их расчетных схем как величиной нагрузок, характеристиками материалов, так и размерами элементов. Поэтому так называемый «точный» расчет на самом деле таковым не является. В связи с этим выполняемые расчеты всегда более или менее приближенные, и стремление получать числовые результаты с большим количеством разрядов не оправдано. Не имеет смысла во всех случаях переписывать все, что появляется на индикаторе калькулятора. Сложились выработанные практикой некоторые правила обеспечения точности вычислений в разумных рамках.

Нужно сохранять в результатах лишь только верные значащие цифры. Нули, с которых начинаются числа, значащими не считаются. Но нули, стоящие в середине или в конце числа, удостоверяющие

отсутствие в числе единиц соответствующего разряда – цифры значащие. Например, в числе 0,003080 подчеркнутые нули слева значащими не считаются, остальные нули – значащие. Если значение какой-либо величины содержит лишние или недостоверные цифры, то его округляют. При этом правила округления таковы:

1)если первая отбрасываемая цифра больше 4, то последняя сохраняемая цифра увеличивается на единицу. Например, округляя число 51,5762 до сотых (здесь первая отбрасываемая цифра 6 > 4), принимаем 51,58;

2)если первая отбрасываемая цифра меньше или равна 4, то последняя сохраняемая цифра не изменяется. Если округляем до сотых число 51,5732, где первая отбрасываемая цифра не больше 4 (здесь 3 < 4), то принимаем 51,57;

3)если отбрасываемая часть числа состоит из одной цифры 5, то число округляют так, чтобы последняя сохраняемая цифра была четной. Например, округляя число 8,4375 до тысячных, принимаем 8,438, а если округляем число 8,345 до сотых, то принимаем 8,34;

4)при сложении и вычитании в результатах сохраняют столько десятичных знаков, сколько их имеет число с наименьшим количеством десятичных знаков;

5)при умножении и делении в результатах оставляют столько значащих цифр, сколько их имело приближенное число с наименьшим количеством значащих цифр;

6)расчет значений функций xn , nx, lg x приближенного числа x должен

содержать столько значащих цифр, сколько их содержит само число x. При вычислении промежуточных результатов сохраняют на одну

цифру больше (запасную цифру), которая в окончательном результате отбрасывается.

2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ СИСТЕМ

2.1. Виды систем

Расчетная схема сооружения получается из отдельных элементов, соединенных между собой и прикрепленных к земле. Совокупность всех элементов, связей между ними и связей элементов с землей будем называть системой. Различают три вида систем.

1. Геометрические неизменяемые системы – это такие системы, в

которых перемещения отдельных точек возможны только при деформировании некоторых элементов. Например, в системе, показанной на рис. 2.1, а, узел А может перемещаться только в том случае, если прикрепляющие его к земле стержни АВ и АС будут деформироваться.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Не справляетесь с задачами? Нужно больше примеров и объяснений по какой-то теме высшей математики (от действия с векторами до решения систем дифференциальных уравнений в матричном виде)?

Вам помогут так называемые решебники по высшей математике. Чаще всего, это именно подробные руководства, содержащие и краткую теорию, и множество разобранных задач по математике самой разной сложности, изучив которые вы наверняка сможете сделать и свои задания.

Помимо лучших книг-руководств, которые учат решать задачи, мы приведем также ссылки на решебники к популярным задачникам (Кузнецов, Рябушко, Чудесенко, Ермаков, Минорский, Шипачев, Лунгу, Данко и т.п.).

Правильно и подробно выполним задачи в Word

Ниже вы найдете ссылки на популярные, понятные, подробные руководства по решению задач и сборники задач, снабженные решенными примерами по высшей математике.

Данко П., Попов А., Кожевникова Т. «Высшая математика в упражнениях и задачах», том 1, 1986. Скачать (11.5 Мб, pdf)

Содержание I части охватывает следующие разделы программы: аналитическую геометрию, основы линейной алгебры, дифференциальное исчисление функций одной и нескольких переменных, интегральное исчисление функций одной независимой переменной, элементы линейного программирования.
В каждом параграфе приводятся необходимые теоретические сведения. Типовые задачи даются с подробными решениями. Имеется большое количество задач для самостоятельной работы.
Данко П., Попов А., Кожевникова Т. «Высшая математика в упражнениях и задачах», том 2, 1999. Скачать (4.0 Мб, Djvu).

Содержание II части охватывает следующие разделы программы: кратные и криволинейные интегралы, ряды, дифференциальные уравнения, теорию вероятностей, теорию функций комплексного переменного, операционное исчисление, методы вычислений, основы вариационного исчисления.
Запорожец Г. И. «Руководство к решению задач по математическому анализу». М., 1966, 464 c. Скачать (7.5 Мб, Djvu).

«Руководство» предназначено для студентов высших технических учебных заведении и особенно для тех, кто самостоятельно, без повседневной квалифицированной помощи преподавателя, изучает математический анализ и желает приобрести необходимые навыки в решении задач.
В начале каждого раздела помещены определения, теоремы, формулы и другие краткие сведения по теории и методические указания, необходимые для решения последующих задач; затем приводятся подробные примерные решения типичных задач.
Зимина О.В., Кириллов А.И., Сальникова Т.А. «Высшая математика. Решебник». 2005, 368 c. Скачать (21.8 Мб, Djvu).
Книга содержит примеры решения почти всех типовых задач по высшей математике. Каждой задаче отведен отдельный раздел, содержащий общую постановку задачи, план ее решения с необходимыми теоретическими пояснениями и решение конкретного примера. Кроме того, в каждый раздел включены десять задач для самостоятельного решения и ответы к ним.
Афанасьев В.И., Зимина О.В. и др. (под ред. Кириллова А.И.) «Решебник. Высшая математика. Специальные разделы». 2003, 400 c. Скачать (2.2 Мб, Djvu).

Книга содержит примеры решения типовых задач по теории функций комплексной переменной, операционному исчислению, рядам Фурье, преобразованию Фурье, уравнениям математической физики, теории вероятностей и математической статистике. Каждой задаче отведен отдельный раздел, содержащий общую постановку задачи, план ее решения с необходимыми теоретическими пояснениями и решение конкретного примера.
Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. «Математический анализ: введение в анализ, производная, интеграл» (АнтиДемидович 1). М., 2001, 360 c. Скачать (7.6 Мб, Djvu).

В том 1 включен материал по следующим разделам курса математического анализа: введение в анализ, дифференциальное исчисление функций одной переменной, неопределенный и определенный интегралы.
Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. «Математический анализ: ряды, функции векторного аргумента» (АнтиДемидович 2). М., 2003, 224 c. Скачать (2.4 Мб, Djvu).

Том 2 по содержанию соответствует первой половине второго тома «Справочного пособия по математическому анализу» и включает в себя теорию рядов и дифференциальное исчисление функций векторного аргумента.
Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. «Математический анализ: кратные и криволинейные интегралы» (АнтиДемидович 3). М., 2001, 224 c. Скачать (2.6 Мб, Djvu).

Том 3 по содержанию соответствует второй половине второго тома «Справочного пособия по математическому анализу». В нем рассматриваются интегралы, зависящие от параметра, кратные и криволинейные интегралы, а также элементы векторного анализа.
Боярчук А.К. «Функции комплексного переменного: теория и практика» (АнтиДемидович 4). М., 2001, 352 c. Скачать (4.7 Мб, Djvu).

Том 4 является логическим продолжением трех предыдущих ориентированных на практику томов и содержит более четырехсот подробно решенных задач, но при этом отличается более детальным изложением теоретических вопросов и может служить самостоятельным замкнутым курсом теории функций комплексного переменного. Помимо вопросов, обычно включаемых в курсы такого рода, в книге излагается ряд нестандартных — таких, как интеграл Ньютона—Лейбница и производная Ферма—Лагранжа.
Лунгу К.Н., Макаров Е.В. «Высшая математика. Руководство к решению задач. Часть 1», 2005, 216 c. Скачать (2.12 Мб, Djvu).

Учебник следует рассматривать как некоторое методическое руководство по решению наиболее типичных математических задач. Большое внимание уделяется построению и исследованию графиков функций, вычислению пределов последовательностей и пределов функций. Авторы предлагают разные способы решения задач и используют этот прием для ознакомления читателя с большим количеством действий и выбором простейшего.
Лунгу К.Н., Макаров Е.В. «Высшая математика. Руководство к решению задач. Часть 2», 2007, 216 c. Скачать (2.25 Мб, Djvu).

Руководство является продолжением одноименного учебного пособия и содержит указания по решению задач основного курса, начиная с неопределенного интеграла и кончая дифференциальными уравнениями, а также задач по теории вероятностей и математической статистике. Наряду с большим числом решенных задач приводятся упражнения для самостоятельного решения, в каждой из восьми глав даны контрольные задания.
Марон И.А. «Дифференциальное и интегральное исчисление в примерах и задачах (Функции одной переменной)» М., 1970, 400 c.
Скачать (11.0 Мб, Djvu).

Большинство параграфов книги содержит краткие теоретические введения, решения типовых примеров и задачи для самостоятельного решения. Кроме задач алгоритмически-вычислительного характера, в ней содержится много задач, иллюстрирующих теорию и способствующих более глубокому ее усвоению, развивающих самостоятельное математическое мышление учащихся. Цель книги — научить студентов самостоятельно решать задачи по курсу математического анализа (изучение теории должно производиться по какому-либо из существующих учебников).

Понравилось? Добавьте в закладки

Помимо лучших книг-руководств, которые учат решать задачи, мы приведем также ссылки на решебники задач к популярным задачникам. Сами задачники (Кузнецов, Рябушко, Чудесенко, Ермаков, Минорский, Шипачев, Лунгу, и т.п.) вы найдете на странице Учебники по высшей математике.

Учитывайте, что большинство решений на нижеприведенных сайтах присланы и выложены студентами, за их правильность никто не ручается. Проверяйте решение, сверяйте ответы, будьте готовы к ошибочным решениям.

Если риск не для вас — закажите подробное решение в МатБюро.

Образцы решений некоторых задач из Минорского Не все задачи решены. Доступ бесплатный.
Решебник Филлипова задач по дифференциальным уравнениям: задачи хорошо оформлены, очень много. Доступ бесплатный.
Решенные РГР из учебника Чудесенко: разные ИДЗ, разные варианты, сканированные решения. Есть ТФКП и ТВ. Доступ бесплатный.

Нет времени копаться в учебниках? Мы поможем с решением!

Более 670 решенных задач
Как решать задачи по ВМ онлайн

Более 170 готовых контрольных
Высшая математика для чайников

Источник

Главная » Математика » Практическое руководство к решению задач по высшей математике. В 3 частях — Соловьев И.А., Шевелев В.В. и др.

Часть 1. Учебное пособие посвящено практическому освоению теоретического материала по следующим разделам высшей математики: векторная алгебра, аналитическая геометрия, элементы линейной алгебры, введение в математический анализ, дифференциальное исчисление функции одной переменной. Предлагается последовательное изучение методов решения основных задач по каждому разделу. Имеется большое количество задач для самостоятельного решения, которые снабжены ответами. Пособие содержит расчетно-графические задания по всем рассмотренным темам. В пособии излагаются основы высшей математики, поэтому оно может быть полезным для студентов инженерных специальностей университетов, академий, технических, экономических, финансовых, экологических и сельскохозяйственных ВУЗов как очной, так и заочной или дистанционной форм обучения. Расчетно-графические задания могут использоваться преподавателями в качестве заданий для самостоятельной внеаудиторной работы. Предполагается выпуск дальнейших частей учебного

Рубрика: Математика / Студентам Математика Студентам Математика
Автор: Соловьев И.А., Шевелев В.В. и др.
Год: 2007
Язык учебника: Русский
Формат: PDF
Страниц: Ч1 — 320c., Ч2 — 288c., Ч3 — 448c.

Источник

Лунгу К. Н., Макаров Е. В. Высшая математика. Руководство к решению задач. Часть 2

Лунгу К. Н., Макаров Е. В. Высшая математика. Руководство к решению задач. Ч. 2 — М., 2007 — 384 с.
Настоящее пособие написано на основе многолетнего опыта чтения лекций и проведения практических занятий по высшей математике в Московском государственном открытом университете на различных факультетах Оно является продолжением одноименного учебного пособия и содержит указания по решению задач основного курса, начиная с неопределенного интеграла и кончая дифференциальными уравнениями, а также задач по теории вероятностей и математической статистике Наряду с большим числом решенных задач приводятся упражнения для самостоятельного решения, в каждой из восьми глав даны контрольные задания.
Пособие рассчитано на студентов очной, заочной и вечерней форм обучения факультетов, где математика не является профилирующей дисциплиной.
ОГЛАВЛЕНИЕ
Предисловие….6
Раздел А. Основной курс
Глава I Неопределенный интеграл ….8
§ 1 Первообразная и неопределенный интеграл……..8
§ 2 Простейшие методы интегрирования……..19
§ 3 Интегрирование по частям……..28
§ 4 Интегрирование рациональных функции ….35
§ 5 Интегрирование тригонометрических функций……..40
§ 6 Интегрирование гиперболических функций……..45
§ 7 Интегрирование иррациональных функций…….47
Контрольные задания……..55
Глава II Определенный интеграл и его применения …..58
§ 1 Определение, свойства, вычисление и применения определенного интеграла…..58
§2 Применения определенного интеграла к вычислению геометрических величин…..67
§ 3 Применения определенного интеграла к вычислению физических величин…..78
§ 4 Несобственные интегралы….86
Контрольные задания…..91
Глава III Кратные, криволинейные и поверхностные интегралы….94
§ 1 Двойной интеграл, его свойства и вычисление…..94
§ 2 Замена переменных в двойном интеграле…..104
§ 3 Применения двойного интеграла…..109
§ 4 Тройной интеграл и его свойства…..115
§ 5 Криволинейные интегралы….125
§ 6 Поверхностные интегралы…..138
Контрольные задания…..147
Глава IV Дифференциальные уравнения…..151
§ 1 Дифференциальные уравнения первого порядка Геометрический смысл дифференциального уравнения и его решения…..151
§ 2 Уравнения с разделенными и с разделяющимися переменными…..157
§ 3 Однородные уравнения первого порядка……161
§ 4 Линейные дифференциальные уравнения первого порядка и уравнения Бернулли……164
§ 5 Уравнения в полных дифференциалах……167
§ 6 Дифференциальные уравнения первого порядка, не разрешенные относительно производной……170
§ 7 Дифференциальные уравнения порядка выше первого Уравнения, допускающие понижение порядка…..179
§ 8 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами……186
§ 9 Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами……191
§ 10 Линейные дифференциальные уравнения с постоянными коэффициентами порядка выше второго……197
§ 11 Системы дифференциальных уравнений…..202
Контрольные задания…..215
Глава V Ряды…..218
§ 1 Числовой ряд и его сходимость…..218
§ 2 Сходимость знакопеременных рядов…..226
§ 3 Функциональные ряды Степенные ряды…..228
§ 4 Применение рядов в приближенных вычислениях Разложение функций в степенной ряд…..234
§ 5 Ряды Фурье …..41
Контрольные задания……250
Раздел Б. Основы теории вероятностей и математической статистики
Глава VI Случайные события. Вероятность …..252
§ 1 Элементы комбинаторики…..252
§ 2 Основные понятия теории вероятностей…..257
§ 3 Теорема сложения вероятностей несовместных событий….265
§ 4 Теорема умножения вероятностей…..267
§ 5 Теорема сложения вероятностей совместных событий…..273
§ 6 Формула полной вероятности Формула Байеса…..275
§ 7 Повторные испытания Формула Бернулли……280
§ 8 Формула Пуассона Поток событий…..283
§ 9 Формула Лапласа….285
§ 10 Вероятность отклонения относительной частоты от постоянной вероятности события…..288
Контрольные задания…..290
Глава VII Случайные величины….297
§ 1 Дискретные случайные величины Основные законы распределения ….297
§ 2 Числовые характеристики дискретных случайных величин…..302
§ 3 Непрерывные случайные величины…..309
§4 Числовые характеристики непрерывных случайных величин…..312
§ 5 Основные законы распределения непрерывных случайных величин …..319
§ 6 Закон больших чисел 324 Контрольные задания…..326
Глава VIII Элементы математической статистики ….33
§ 1 Статистический материал и его обработка….333
§ 2 Числовые характеристики законов распределения эмпирических величин….337
§ 3 Построение теоретического закона распределения и его согласование с эмпирическими данными…..347
§ 4 Проверка гипотезы о нормальном распределении генеральной совокупности…..348
§ 5 Проверка гипотезы о распределении генеральной совокупности по биномиальному закону…..355
§ 6 Проверка гипотезы о распределении генеральной совокупности по закону Пуассона…..357
§ 7 Проверка гипотезы о распределении генеральной совокупности по показательному закону….358
§ 8 Линейная корреляция случайных величин…..360
§ 9 Однофакторный дисперсионный анализ….364
Контрольные задания….370
Приложение….377
Список литературы….382

Источник

Здесь представлены готовые решения по задачнику Кузнецова Л.А. по высшей математике. Сам задачник можно посмотреть здесь.

Также можно купить отдельные задачи:

Линейная алгебра
Уравнения математической физики

то ее следовало бы вычислять арифметически w =

^* В ячейках таблицы указано количество найденных материалов.

Показать быстрые кнопки

Полное описание файла

Содержание архива

Быстрый редактор названия

Быстрый редактор типа

Быстрый редактор тегов

Быстрый редактор цен

Сбросить настройки

Наполняется папка «учёба»? Заработай на ней!

Заработать

Свежие статьи

Популярно сейчас

Источник

Руководство к решению задач по прикладной механике, Чиченев Н.А., Свистунов Е.А., 1979.

ПРЕДИСЛОВИЕ.

Цель пособия — помочь студентам овладеть методами решения типовых задач, составляющих домашние расчетно-графические работы, и приобрести необходимые навыки расчета и проектирования элементов механических систем. Опыт преподавания курса «Прикладная механика» (как и других дисциплин механического цикла) показывает, что наибольшие затруднения для студентов обычно связаны с решением задач и выполнением домашних расчетно-графических работ. В то же время именно эта часть курса способствует приобретению навыков, необходимых для сознательного выбора расчетных схем, составления алгоритма вычислений и технически грамотного оформления полученных результатов.

Задача 2. ПЛАНЫ СКОРОСТЕЙ И УСКОРЕНИЙ.

Для заданного положения механизма, представленного на рис. 1, найти способом построения планов скоростей и ускорений линейные скорости и ускорения точек А, В, С, D, К, а также угловые скорости и ускорения всех звеньев (исходные данные см. задачу 1).

ОГЛАВЛЕНИЕ.

Предисловие.
Задача 1. Мгновенные центры скоростей.
Задача 2. Планы скоростей и ускорений.
Задача 3. Опорные реакции в двухопорной балке.
Задача 4. Реакции в опорах вала редуктора.
Задача 5. Определение усилий в стержнях фермы.
Задача 6. Эпюры продольных сил и нормальных напряжений при растяжении-сжатии.
Задача 7. Эпюры крутящих моментов.
Задача 8. Эпюры поперечных сил и изгибающих моментов для балки на двух опорах.
Задача 9. Эпюры поперечных и продольных сил, изгибающих и крутящих моментов для вала редуктора.
Задача 10. Главные центральные осевые моменты инерции плоской фигуры, составленной из стандартных профилей.
Задача 11. Расчет на прочность при изгибе.
Задача 12. Внецентренное сжатие.
Задача 13. Косой изгиб.
Задача 14. Растяжение с кручением.
Задача 15. Изгиб с кручением.
Задача 16. Эпюры крутящих моментов, касательных напряжений и углов закручивания.
Задача 17. Эпюры прогибов и углов поворота.
Задача 18. Эпюры поперечных сил, изгибающих моментов, прогибов и углов поворота статически неопределимой балки.
Задача 19. Расчет на устойчивость.
Задача 20. Кинематический расчет привода конвейера.
Задача 21. Расчет косозубой цилиндрической передачи.
Задача 22. Расчет вала редуктора.
Задача 23. Расчет подшипников качения.
Задача 24. Выбор и расчет муфты.
Список литературы.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Руководство к решению задач по прикладной механике, Чиченев Н.А., Свистунов Е.А., 1979 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать
— djvu — Яндекс.Диск.

Дата публикации: 09.08.2019 09:47 UTC

Теги:

Чиченев :: Свистунов :: 1979 :: механика

Следующие учебники и книги:

Физика, теория и методы решения конкурсных задач, часть II, Колесников В.А., 1999
Разностный метод решения уравнений Максвелла, Головашкин Д.Л., Казанский Н.Л., 2007
Численные методы решения задач строительной механики, Сахаров А.С., 1978
Численное решение динамических задач упругопластического деформирования твердых тел, Иванов Г.В., Волчков Ю.М., Вогульский И.О., 2002

Предыдущие статьи:

ФИЗИКА, задачи с ответами и решениями, Черноуцан А.И., 2011
Методы решения задач по физике, механика, кинематика, прямолинейное равномерное движение, Бершадский М.Е., Бершадская Б.А., 2001
1001 задача по физике с ответами, указаниями, решениями, Гельфгат И.М., Генденштейн Л.Э., Кирик Л.А., 1999
Общая теория радиолокации и радионавигации, распространение радиоволн, Фомин А.Н., Копылов В.А., Филонов А.А., Андронов А.В., Фомина А.Н., 2017

Источник