Инструкцию можно записать только для решения логической задачи

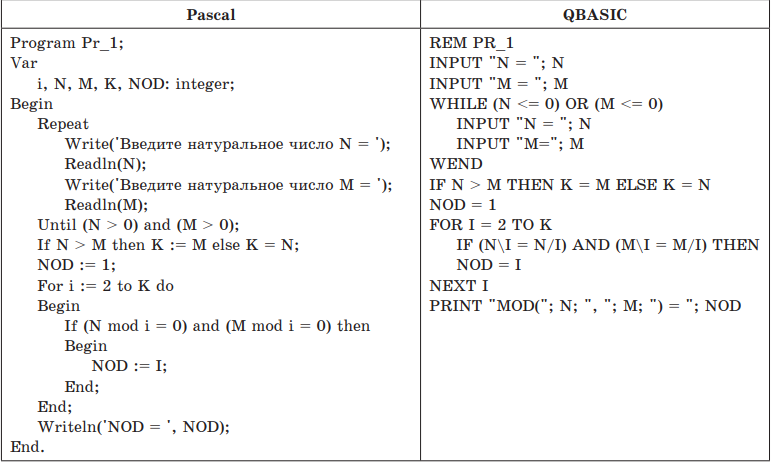
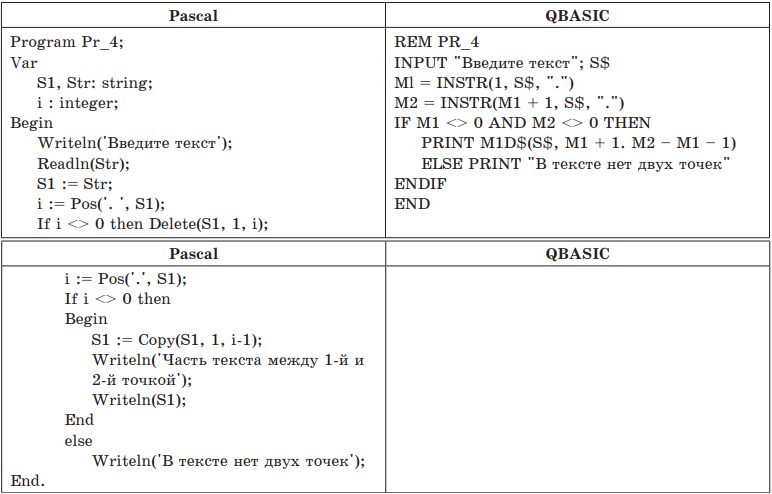
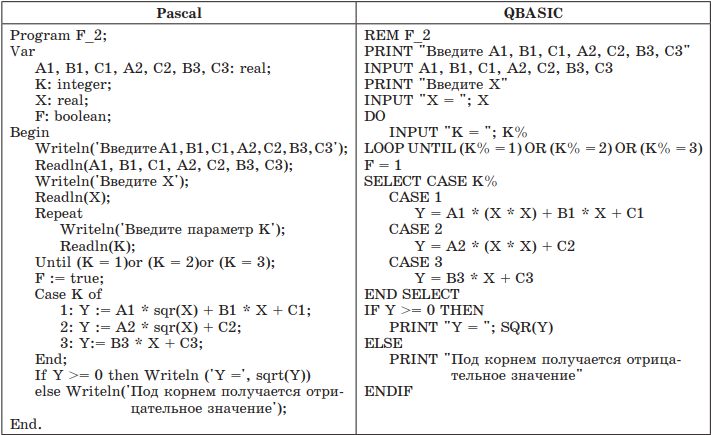
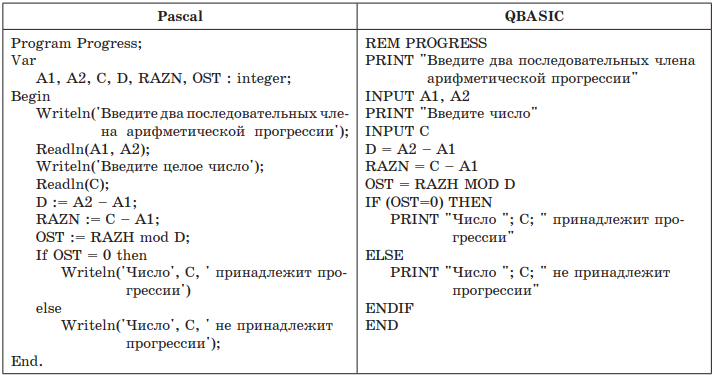
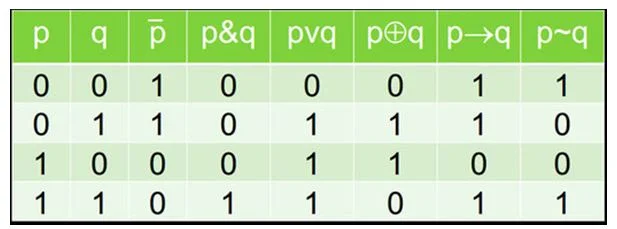
Рейтинг:   / 78

Подробности

Создано 23.04.2018 08:03

Просмотров: 6405

[an error occurred while processing the directive]

[an error occurred while processing the directive]
[an error occurred while processing the directive]
[an error occurred while processing the directive]
[an error occurred while processing the directive][an error occurred while processing the directive][an error occurred while processing the directive]

[an error occurred while processing the directive]

.

Что такое алгоритм.

Критерий сложности основан на подсчете количества специальных (инструментальных) средств, которые предполагается использовать в проекте:
(*ответ*) да
 нет
Методы математического доказательства правильности программ обычно относят к теоретической информатике, а методы тестирования — к технологии программирования:
(*ответ*) да
 нет
Модели данных прошли эволюционный путь развития от иерархических и сетевых к реляционным:
(*ответ*) да
 нет
Модель процесса — порядок проведения типового проекта по разработке программного обеспечения:
(*ответ*) да
 нет
Оценка риска — список различных факторов и обстоятельств, которые могут отрицательно повлиять на выполнение проекта:
(*ответ*) да
 нет
Периодическая отчетность — процедура, обеспечивающая обратную связь в контуре управления порядком прохождения проектов:
(*ответ*) да
 нет
При работе над проектом используется управляемая вехами, ориентированная на заказчика, итеративная, последовательная, модель процесса:
(*ответ*) нет
 да
Процесс конструирования программного обеспечения состоит из последовательности шагов, использующих методы, утилиты и процедуры:
(*ответ*) да
 нет
Сверхлегкий проект характеризуется тем, что присутствует технический риск допущения грубых ошибок на фазах анализа и проектирования:
(*ответ*) нет
 да
Технологический процесс — последовательность технологических операций, необходимых для выполнения определенного вида работ:
(*ответ*) да
 нет
Фаза внедрения включается в процесс разработки и не рассматривается в MSF как отдельный процесс:
(*ответ*) нет
 да
Цель тестирования устойчивости — проверка того, что для допустимых (правильных) входных данных получаются допустимые (правильные, корректные, удовлетворительные, соответствующие спецификациям) результаты:
(*ответ*) нет
 да
COM-объект, умеющий создавать другой объект, называется
(*ответ*) моникером
OLE сервера и клиенты взаимодействуют с системными библиотеками при помощи таблиц виртуальных
(*ответ*) функций
В основе спиральной модели жизненного цикла лежит применение RAD-технологии — технологии быстрой разработки
(*ответ*) приложений
В основе структурного программирования лежит теорема: алгоритм для решения любой логической задачи можно составить только из структур
(*ответ*) следование
(*ответ*) ветвление
(*ответ*) цикл
 итерация
В тех случаях, когда тело цикла непременно потребуется выполнить хотя бы один раз, следует применять цикл
(*ответ*) repeat
 for
 while
В функциональных языках программирования цикл обычно реализуется в виде
(*ответ*) рекурсии
Величины, используемые только в подпрограмме, следует описывать внутри нее как _ переменные
(*ответ*) локальные
 глобальные
 виртуальные

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Верно ли утверждение, что решение любой задачи можно описать как последовательность действий (шагов)?

Вопрос пользователя

Верно ли утверждение, что решение любой задачи можно описать как последовательность действий (шагов)?

Ответ эксперта

да, это верно

Тема: «Программирование ветвлений. Условный оператор».

Класс: 9 А.

Продолжительность: 40 минут.

Тип урока: формирование ЗУН.

Форма урока: комбинированный.

Формы работы: фронтальная, индивидуальная, групповая.

Методы обучения: информационно-репродуктивный (объяснительно-иллюстративный), инструктивно-практический; эвристический (частично-поисковый).

Цель урока: сформировать у учащихся представление об условном операторе в языке Pascal и возможностях его применения при решении практических задач.

УУД

• Личностные УУД

— Стимулировать учащихся к саморазвитию;

— развивать готовность и способность к самостоятельности;

— развивать умение ориентироваться в межличностных отношениях.

• Регулятивные УУД

— Самостоятельно формулировать тему урока;

— составлять план и последовательность действий;

— Осуществлять итоговый и пошаговый контроль.

• Познавательные УУД

— Применять правила;

— ориентироваться в разнообразии способов решения задач;

— контролировать и оценивать процесс и результат деятельности;

— самостоятельно составлять алгоритмы при решении задач разного характера.

• Коммуникативные УУД

— составлять вопросы;

— обращаться за помощью;

— формулировать свои затруднения;

— предлагать помощь и сотрудничество.

Планируемые результаты: Знать; структуру оператора ветвления в Паскале, с применением знаний о разветвляющемся алгоритме;

Уметь: решать практические задачи с составление программ на языке Паскаль, содержащие оператор ветвления.

Материально-техническое оснащение:

• Учебник;

• Тетрадь;

• Компьютер;

• Мультимедийный проектор и экран;

• Раздаточный материал;

• Доска.

План урока.

1. Организационный момент (1 минута).

2. Актуализация внимания и знаний(3 минуты).

3. Проверка домашнего задания (5 минут).

4. Объяснение нового материала (10 минут).

5. Физкультминутка (2 минуты).

6. Закрепление изученного материала (10 минут).

7. Домашнее задание (1 минута)

8. Контроль усвоения ЗУН (3 минуты)

9. Рефлексия (2 минуты).

10. Итоги урока (2 минуты).

11. Окончание урока (1 минута).

Ход урока.

1. Организационный момент (1 минута).

Приветствие класса и учителя, класса и гостей. Проверка готовности класса к урока (наличие необходимых школьных принадлежностей). Проверка отсутствующих на уроке.

1. Актуализация внимания и знаний(3 минуты).

Романтические 1960-е годы положили начало дружбе голландца Эдсгера Дейкстры, англичанина Энтони Хоара и швейцарца Никлауса Вирта.

1 ученик. «… Помнятся года, когда мне надо было сделать выбор – либо прекратить программировать и стать настоящим респектабельным теоретическим физиком, либо как-то формально завершить моё обучение теоретической физике с минимальными усилиями и стать… Кем же? Программистом? Но разве это респектабельная профессия? В конце- концов, что такое программирование? В чём должен был состоять тот солидный объём знаний, который позволил бы считать программирование научной дисциплиной?».

2 ученик. «Ваши опасения, Эдсгер, были очевидны, ведь когда компьютеров ещё не было, то программирование не составляло никакой проблемы. Когда у нас появилось несколько маломощных компьютеров, то программирование стало проблемой средней сложности. Теперь же, когда мы располагаем гигантскими компьютерами, то и программирование превращается в гигантскую проблему. Как Вы считаете, Никлаус?».

3 ученик «Да-да, я совершенно с вами согласен. Сейчас мы живём в сложном мире и стараемся решать сложные по своей сути проблемы, которые зачастую для своего решения требуют сложных устройств. Однако, это не значит, что мы не должны найти элегантные решения, убеждающие своей ясностью и эффективностью. Простые элегантные решения более эффективны, но найти их труднее, чем сложные, и для этого требуется больше времени».

И они нашли простое элегантное решение став патриархами структурного программирования и лауреатами премии Тьюринга, приравниваемой в компьютерных науках к Нобелевской премии.

Структурное программирование – подход, при котором для передачи управления в программе используется только 3 инструкции, допускающих последовательную, условную и циклическую передачу данных.

Скажите, какую Структуру передачи данных из этих 3 мы с вами уже изучили? (последовательную.).

Сегодня мы с вами продолжим изучать основы структурного программирования. А для того, чтобы понять какую именно, вам надо разгадать ребус. (Формулирование учениками при помощи учителя темы урока).

Да, мы с вами сегодня изучим структуру «ветвление» на языке Паскаль, который , как вам уже известно, был разработан в конце 60-х годов Н. Виртом. (Дети записываю число и тему урока).

Цели нашего сегодняшнего урока

— Познакомиться с понятием «Условный оператор»;

— Научиться составлять программы на языке Паскаль с использование условного оператора;

— Научиться решать практические задачи, содержащие структуру «ветвление» на ЭВМ в среде программирования PASCAL ABC.

1. Проверка домашнего задания (5 минут).

Но прежде чем мы приступим к изучению новой темы, я предлагаю вспомнить прошлый материал. Откройте свои тетради и выполняем 1- задание.

Задание 1.

Произведите сортировку данных свойств в соответствии с их отношением к свойствам информации или к свойствам алгоритма.

Свойства

алгоритмов

Свойства

информации

Понятность, полезность, массовость, актуальность, полнота, дискретность, результативность, детерминированность, конечность, достоверность.

Сверяем с доской. У кого всё совпало ставит себе 5 баллов, у кого 1 ошибка – ставит 4 балла, 2 ошибки – 3 балла, 3 ошибки – 2 балла, 4 ошибки – 1 балл, более 4 ошибок – 0 баллов.

Переходим к заданию 2.

Заполняется с учителем.

Задание 3.

Составьте четыре правильные по смыслу фразы, соединив их стрелками.

7. Словесный, графический и на алгоритмическом языке

1. Исполнителем алгоритма может быть

6. Для решения целого класса задач

1. Четкое предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи

2. Называется программой

7. Называется системой команд исполнителя

8. Можно составить разные алгоритмы

8. Линейный, разветвляющийся или циклический

5.Называется алгоритмом

4. Основные алгоритмические структуры:

3. Набор действий, которые может выполнить исполнитель

2. Один и тот же алгоритм может быть использован

3. Для решения одной задачи

9. Можно записать только одним способом

4. Любой объект живой природы или автоматическое устройство

9. Называется программой

10. Каждый алгоритм

10. Для решения только одной задачи

5. Алгоритм записанный на языке программирования

11. Можно записать разными способами

6. Только человек

11. Словесный, графический и на алгоритмическом языке

После выполнения задания, учащиеся обмениваются тетрадями и сверяют с доской.4 совпадения – 4 балла, 3 совпадения – з балла, 2 совпадения – 2 балла, 1 совпадение – 1 балл. Если совпадений нет – 0 баллов.

1. Объяснение нового материала (10 минут).

Перед объяснением нового материала выполняется упражнение на стимуляцию слуха.

Это упражнение улучшает слух, кроме того, после него начинает отчетливей восприниматься собственный голос. В некоторых случаях подобный массаж ушей даже вызывает из памяти информацию, которую мы перед этим напрасно пытались вспомнить. Это упражнение должно повторяться как можно чаще.
• Возьмите обеими руками внешнюю часть уха, и потяните туда-сюда очень бережно.
• Массируйте край уха и немного выверните его наружу, начните с верха уха, а потом, медленно массируя, перемещайтесь вниз. Теперь сложите средним указательным пальцем обеих рук букву V. Приложите оба пальца к голове, так ухо оказалось в середине. Начните двигать пальцами вверх-вниз, крепко прижимая их к голове. А затем сделайте из пальцев другой руки полушарие и прикройте им ухо. Потом кончиками пальцев другой руки пару раз постучите по этому куполу. Почувствуйте хлопки в костях черепа, таким образом, вы возбуждаете не только нервы уха, но и мозг.
• Повторите то же самое с другим ухом

Ребята, эпиграф нашего урока «Хочешь быть альпинистом – иди в горы. Хочешь быть образованным – учись мыслить и думать.» Я прошу вас во время объяснения нового материала не только слушать меня, но обдумывать сказанное мною, анализировать.

Алгоритмическая структура «ветвление» в отличие от линейных алгоритмов, в которых команды выполняются одна за другой, входит условие, в зависимости от выполнения или не выполнения которого реализуется та или иная последовательность команд (серия).

Возникает вопрос. Что же такое условие?

Условие – это логическое выражение, которое может быть записано в операторе явно или вычислено в программе.

Виды условия.

последовательные

вложенные

Сложные

(составные)

Простые

Сложные условия – логические выражения, записанные с помощью логических операций not – инверсия (отрицание), and – конъюнкция (умножение), or – дизъюнкция (сложение).

Любой алгоритм можно записать 3-мя способами – словесный, графический, программный.

Словесный – естественная устная или письменная речь,

Графический (блок-схема) – изображение алгоритма при помощи геометрических фигур (дети записывают название и зарисовывают).

Программный – использование операторов языков программирования.

Условному оператору отвечают 2 структуры, выбор которых зависит от формы ветвления

Формы ветвления.

сокращённая

полная

Начнём с полной формы условного оператора. Если , то , иначе. Заменяем слова ЕСЛИ, ТО, ИНАЧЕ на зарезервированные в Паскале слова, получим оператор полного ветвления.

If then else .

Рассмотреть пример.

Сокращённая форма условного оператора Если , то . Условие задачи не предполагает выполнение каких-либо действий при невыполнении условия. Заменяем слова ЕСЛИ, ТО на зарезервированные в Паскале слова, получим оператор сокращённого ветвления

If then .

Рассмотреть пример.

В случае, если у нас не один оператор, а серия операторов, то используются операторные скобки begin … end., заключающие в себя эту последовательность операторов.

1. Физкультминутка (2 минуты).

2. Закрепление изученного материала (10 минут).

Выполнение задания 4 — 6.

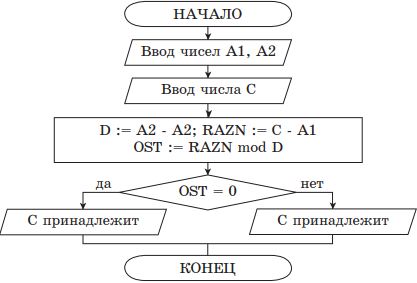
Задание 4.

Определить значение переменной А в результате выполнения фрагмента алгоритма, представленного блок-схемой.

1. Если А = 25, В = 5

Ответ____________ .

1. Если А = 25, В = 4

Ответ____________ .

Два правильных ответа – 2 балла, один правильный ответ – 1 балл.

Задание 5.

Построить график, описываемый алгоритмом. Если (X -2) и (XY:= X*X, иначе Y:=4.

Если справились полностью 2 балла.

Перед выполнением упражнения 6, выполнить упражнение на расслабление глаз.

Это упражнение ослабляет напряжение, расслабляет глазные нервы, а в некоторой степени успокаивает ум.
• Разогреваем руки, потерев одну ладонь о другую. Делаем это до тех пор, пока руки не станут теплыми. Теперь нужно облокотиться на стол перед собой, сложить пальцы обеих рук в два полушария и мягко прикрыть ими глаза. Почувствуйте, как приятны для глаз тепло и темнота. Можно усилить это чувство, сделав при этом пару глубоких вдохов. Представьте себе, что при вдохе наполняются не только легкие, но и глаза свежим кислородом, что делает их более свежими и сильными.

ГРУППА 1. Ввести с клавиатуры 2 числа. Вывести на экран их разность, вычитая из большего числа меньшее число.

Задание 6.

Работа в группе. Решение практических задач на языке программирования Pascal.

ГРУППА 2. Ввести с клавиатуры 2 числа. Вывести на экран их частное или сообщение «На ноль делить нельзя!»

Математическая модель + блок схема + программа = 3 балла. (каждому из группы).

1. Домашнее задание (1 минута)

2. Контроль усвоения ЗУН (3 минуты)

Перед выполнением итогового контроля, когда силы обучающихся уже истощены выполняются упражнения, которые позволяют поплнить энергию.

Источник энергии

Это классическое упражнение. Оно расслабляет затылочную и плечевую мускулатуру и улучшает дыхание. В головной мозг поступает много кислорода, за счет чего улучшается еще и слух и зрение.
• Положите руки на стол перед собой. Выдохните и позвольте своей голове медленно опуститься вниз. Почувствуйте, мускулы вашего затылка растянулись, полностью расслабьте плечи. Теперь снова медленно поднимите голову и при этом сделайте вдох. Дайте голове полностью откинуться назад, пока вам не покажется, что ваша грудная клетка распахнулась и наполнилась воздухом. Когда вы снова будете выдыхать, делайте это медленно и снова опустите голову вниз, пока подбородок вновь не ляжет на грудь. Подарите себе три таких особенных освежающих вдоха

Итоговый контроль усвоения знаний.

1. Алгоритм, в котором его выполнение определяется проверкой каких-либо условий, называется…

A. разветвляющимся

B. циклическим

C. следования

D. линейным

E. процедурным

2. Служебное слово IF в условном операторе переводится как…

A. если

B. то

C. иначе

D. ввод

E. условие

3. Служебное слово THEN в условном операторе переводится как…

A. если

B. то

C. иначе

D. ввод

E. условие

4. Служебное слово ELSE в условном операторе переводится как…

A. если

B. то

C. иначе

D. ввод

E. условие

5. Укажите правильный вариант использования условного оператора.

A. IF THEN begin end ELSE begin end;

B. IF THEN ; ELSE ;

C. THEN begin end IF ELSE begin end;

D. THEN ELSE IF ;

E. IF THEN

6. Укажите правильный вариант использования неполного ветвления.

A. IF THEN begin end;

B. THEN ; ELSE ;

C. IF ELSE begin end;

D. ELSE IF ;

E. THEN IF

Проверяется учителем. Результат на следующий урок.

1. Рефлексия (2 минуты).

2. Итоги урока (2 минуты).

3. Окончание урока (1 минута).

В течение всего урока, по окончании каждого этапа при помощи методики цветописи Лутошкина учащиеся оценивают свой эмоциональный настрой.

Этапы								трудно сказать
Орг. момент
Актуализация внимания и знаний
Проверка домашнего задания
Изучение нового материала.
Закрепление
Домашнее задание
Контроль усвоения ЗУН
Рефлексия
Итоги урока

Оценка – количественный показатель эмоциональной атмосферы.

Алгоритмизация и программирование

Алгоритмы, виды алгоритмов, описание алгоритмов. Формальное исполнение алгоритмов

Термин «алгоритм», впервые употребленный в современном значении. Лейбницем (1646–1716), является латинизированной формой имени великого персидского математика Мухаммеда бен Муссы аль-Хорезми (ок. 783 – ок. 850). Его книга «Об индийском счете» в XII в. была переведена на латинский язык и пользовалась широкой популярностью не одно столетие. Имя автора европейцы произносили как Алгоритми (Algorithmi), и со временем так стали называть в Европе всю систему десятичной арифметики.

Научное определение алгоритма дал А. Чёрч в 1930 году. В наше время понятие алгоритма является одним из основополагающих понятий вычислительной математики и информатики.

Алгоритм — это точное и полное описание последовательности действий над заданными объектами, позволяющее получить конечный результат.

Можно сказать, что алгоритм решения какой-либо задачи — это последовательность шагов реализации (или нахождения) этого решения, а процесс построения алгоритма (алгоритмизация) — разложение задачи на элементарные действия или операции.

Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи, области применения различных алгоритмов, а также созданию новых алгоритмов. Теория алгоритмов находит широкое применение в различных областях деятельности человека — в технике, производстве, медицине, образовании и т. д. Появление компьютера позволило решать чрезвычайно сложные, трудоемкие задачи.

Определение алгоритма для применения в области информатики нуждается в некотором уточнении. Во-первых, решение задач в информатике всегда связано с преобразованием информации, а значит, исходными данными и результатом работы алгоритма должна быть информация. Это может быть представлено в виде схемы.

Во-вторых, алгоритмы в информатике предназначены для реализации в виде компьютерных программ или для создания некоторой компьютерной технологии. Для выполнения алгоритма требуется конечный объем оперативной памяти и конечное время.

Основные требования, предъявляемые к алгоритмам:

Дискретность (прерывность): алгоритм должен представлять решение задачи в виде последовательности простых (или ранее определенных) этапов (шагов). Каждый шаг алгоритма формулируется в виде инструкций (команд).

Определенность (детерминированность; лат. determinate — определенность, точность): шаги (операции) алгоритма должны допускать однозначную трактовку и быть понятными для исполнителя алгоритма. Это свойство указывает на то, что любое действие в алгоритме должно быть строго определено и описано для каждого случая.

Массовость: алгоритм должен давать решение не только для конкретного набора значений, а для целого класса задач, который определяется диапазоном возможных исходных данных (область применимости алгоритма). Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.

Результативность: алгоритм должен давать конкретный результат, т. е. должны быть рассмотрены все возможные ситуации и для каждой из них получен результат. Под результатом может пониматься и сообщение о том, что задача решения не имеет.

Конечность: количество шагов алгоритма должно быть конечным.

Эффективность: количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.

Для оценки и сравнения алгоритмов существует много критериев. Чаще всего анализ алгоритма (или, как говорят, анализ сложности алгоритма) состоит в оценке временных затрат на решение задачи в зависимости от объема исходных данных. Используются также термины «временная сложность», «трудоемкость» алгоритма. Фактически эта оценка сводится к подсчету количества основных операций в алгоритме, поскольку каждая из них выполняется за заранее известное конечное время. Кроме временной сложности, должна оцениваться также емкостная сложность, т. е. увеличение затрат памяти в зависимости от размера исходных данных. Оценка сложности дает количественный критерий для сравнения алгоритмов, предназначенных для решения одной и той же задачи. Оптимальным (наилучшим) считается алгоритм, который невозможно значительно улучшить в плане временных и емкостных затрат.

Анализом сложности алгоритмов, исследованием классов задач, решаемых с помощью алгоритмов той или иной сложности, и многими другими теоретическими вопросами занимается специальная область информатики.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов.

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур:

1. следование — образуется из последовательности действий, следующих одно за другим;
2. ветвление (развилка) — обеспечивает в зависимости от результатов проверки условия (ДА или НЕТ) выбор одного из альтернативных путей алгоритма;
3. цикл — обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

Для описания алгоритмов наиболее распространены следующие методы (языки):

Обычный язык. Изложение алгоритма ведется на обычном языке с разделением на последовательные шаги.

Блок-схемы. Графическое изображение алгоритма с помощью специальных значков-блоков.

Формальные алгоритмические языки (языки программирования). При записи алгоритмов используют строго определенный набор символов и составленных из них специальных зарезервированных слов. Имеют строгие правила построения языковых конструкций.

Псевдокод. Синтез алгоритмического и обычного языков. Элементы некоторого базового алгоритмического языка используются для строгой записи базовых структур алгоритма.

Словесный способ (запись на обычном языке) не имеет широкого распространения, т. к. таких описаний есть ряд недостатков:

• строго не формализуемы;
• достаточно многословны;
• могут допускать неоднозначность толкования отдельных предписаний;
• сложные задачи с анализом условий, с повторяющимися действиями трудно представляются в словесной или словесно-формульной форме.

Графический способ представления информации является более наглядным и компактным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление алгоритма называется блок-схемой. Определенному типу действия (ввод/вывод данных, проверка условия, вычисление выражения, начало и конец алгоритма и т. п.) соответствует определенная геометрическая фигура — блочный символ. Блоки соединяются между собой линиями переходов, которые определяют очередность выполнения действий.

Название символа	Графическое изображение	Комментарии
Пуск/Останов (блоки начала и конца алгоритма)		Указание на начало или конец алгоритма
Ввод/Вывод данных (блоки ввода, вывода		Организация ввода/вывода в общем виде
Процесс (операторные блоки)		Выполнение вычислительного действия или последовательности действий (можно объединять в один блок), которые изменяют значение, форму представления или размещение данных
Условие (условный блок)		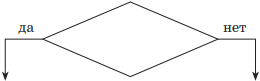Выбор направления выполнения алгоритма. Если условие, записанное внутри ромба, выполняется, то управление передается по стрелке «да», в противном случае — по стрелке «нет». Таким образом, реализуется процесс изменения последовательности вычислений в зависимости от выполнения условия
Начало цикла с параметром		Используется для организации циклических конструкций с известным количеством итераций (повторений) и известным шагом изменения параметра цикла. Внутри блока для параметра цикла указываются через запятую его начальное значение, конечное значение и шаг изменения. Цикл, для которого неизвестно количество повторений, записывается с помощью условного и операторных блоков
Предопределенный процесс		Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращения к библиотечным подпрограммам
Печать сообщений (документ)		Вывод результатов на печать

При составлении блок-схемы необходимо проверять выполнение следующих условий:

1. из каждого прямоугольника и параллелограмма (кроме конца алгоритма) должна выходить только одна стрелка;
2. в каждый прямоугольник и параллелограмм (кроме начала алгоритма) должна входить хотя бы одна стрелка;
3. в каждый ромб должна входить хотя бы одна стрелка, а выходить из него — две стрелки, помеченные словами «ДА» и «НЕТ».

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. В псевдокоде не приняты строгие синтаксические правила для записи команд, что отличает формальные языки программирования. Однако в псевдокоде есть некоторые конструкции, которые присущи формальным языкам, что облегчает переход от записи алгоритма на псевдокоде к записи алгоритма на языке программирования. Псевдокоды бывают разные. Рассмотрим учебный (школьный) алгоритмический язык АЯ.

Алфавит учебного алгоритмического языка является открытым. В него могут быть введены любые понятные всем символы: русские и латинские буквы, знаки математических операций, знаки отношений, специальные знаки и т. д. Кроме алфавита, в алгоритмической нотации определяются служебные слова, которые являются неделимыми. Служебные слова обычно выделяются жирным шрифтом или подчеркиванием. К служебным словам относятся:

алг — заголовок алгоритма	нц — начало цикла	знач
нач — начало алгоритма	кц — конец цикла	и
кон — конец алгоритма	дано	или
арг — аргумент	надо	не
рез — результат	если	да
цел — целый	то	нет
сим — символьный	иначе	при
лит — литерный	всё	выбор
лог — логический	пока	утв
вещ — вещественный	для	ввод
таб — таблица	от	вывод
длин — длина	до

Общий вид записи алгоритма на псевдокоде:

алг — название алгоритма (аргументы и результаты)

дано — условие применимости алгоритма

надо — цель выполнения алгоритма

нач — описание промежуточных величин

последовательность команд (тело алгоритма)

кон

Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон, — телом алгоритма (исполняемой частью алгоритма).

В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное именем массива и граничными парами по каждому индексу элементов массива.

Команды учебного языка:

1. Оператор присваивания, который обозначается «:=» и служит для вычисления выражений, стоящих справа, и присваивания их значений переменным, указанным в левой части. Например, если переменная а имела значение 5, то после выполнения оператора присваивания а := а + 1, значение переменной а изменится на 6.

2. Операторы ввода/вывода:

ввод (список имен переменных)

вывод (список вывода)

Список вывода может содержать комментарии, которые заключаются в кавычки.

3. Оператор ветвления (с использованием команды если…то… иначе…всё; выбор);

4. Операторы цикла (с использованием команд для, пока, до).

Запись алгоритма на псевдокоде:

Здесь в предложениях дано и надо после знака «|» записаны комментарии. Комментарии можно помещать в конце любой строки, они существенно облегчают понимание алгоритма.

При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается произвольное изображение команд. Вместе с тем такая запись позволяет понять человеку суть дела и исполнить алгоритм. Однако алгоритм, предназначенный для исполнения на компьютере, должен быть записан на строго формализованном языке. Такой язык называется языком программирования, а запись алгоритма на этом языке — компьютерной программой.

Для решения одной и той же задачи можно предложить несколько алгоритмов. Алгоритмы составляются с ориентацией на определенного исполнителя алгоритма. У каждого исполнителя имеется свой конечный набор команд, которые для него понятны и исполняемы. Этот набор называется системой команд исполнителя. Пользуясь системой команд, исполнитель может выполнить алгоритм формально, не вникая в содержание поставленной задачи. От исполнителя требуется только строгое выполнение последовательности действий, предусмотренной алгоритмом. Таким образом, в общем случае алгоритм претерпевает изменения по стадиям:

• первая стадия — алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает;
• вторая стадия — алгоритм должен быть представлен в форме, понятной исполнителю алгоритма (вторая стадия может отсутствовать, если исполнять алгоритм будет сам разработчик).

Примеры решения задач

Пример 1. Исполнитель Утроитель может выполнить только две команды, которым присвоены номера:

1 — вычти 1;

3 — умножь на 3.

Первая команда уменьшает число на 1, вторая — увеличивает его втрое.

Написать набор команд (не более пяти) получения из числа 3 числа 16. В ответе указать только номера команд.

Решение.

1 (3 – 1 = 2)

3 (2 * 3 = 6)

3 (6 * 3 = 18)

1 (18 – 1 = 17)

1 (17 – 1 = 16)

Ответ: 13311

Пример 2. Имеется Исполнитель алгоритма, который может передвигаться по числовой оси.

Система команд Исполнителя алгоритма:

1. «Вперед N» (Исполнитель алгоритма делает шаг вперед на N единиц).

2. «Назад M» (Исполнитель алгоритма делает шаг назад на M единиц).

Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?

Решение.

1. Найдем, сколько было команд «Вперед», а сколько «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение: x + (x + 12) = 50, где x — количество команд «Вперед». Тогда общее количество команд «Вперед»: x = 19, а количество команд «Назад»: 19 + 12 = 31.

2. Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед 3», Исполнитель алгоритма оказался бы на отметке числовой оси 57 (19 * 3 = 57). После выполнения 31 раз команды «Назад 2» (31 * 2 = 62) он оказался бы на отметке –5 (57 – 62 = –5).

3. Все эти команды можно заменить одной — «Назад 5».

Ответ: команда«Назад 5».

Пример 3. Черепашка является исполнителем для создания графических объектов на рабочем поле. При движении Черепашка оставляет след в виде линии. Черепашка может исполнять следующие команды:

Название команды	Параметр	Действия исполнителя
вп	Число шагов	Продвигается в направлении головы на указанное число шагов
нд	Число шагов	Продвигается в направлении, противоположном направлению головы на указанное число шагов
пр	Число градусов	Поворачивается направо относительно направления, заданного головой черепашки
лв	Число градусов	Поворачивается налево относительно направления, заданного головой черепашки

Для записи повторяющихся действий (цикла) используется команда Повтори. В этой команде два параметра: первый задает количество повторений (итераций), а второй — список команд которые должны повторяться (тело цикла); список заключается в квадратные скобки.

Записать для исполнителя Черепашка алгоритмы:

а) построения квадрата со стороной 100;

б) построения правильного шестиугольника со стороной 50.

в) построения изображения цифры 4, если голова Черепашки смотрит на север.

Ответ: а) Повтори 4 [вп 100 пр 90]; б) Повтори 6 [вп 50 пр 360/6]; в) вп 100; повтори [лв 135 вп 50].

Пример 4. Два игрока играют в следующую игру (это вариант восточной игры). Перед ними лежат три кучки камней, в первой из которых 2, во второй — 3, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в одной из кучек, или добавляет по два камня в каждую из них. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в трех кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ следует обосновать.

Решение. Удобнее всего составить таблицу возможных ходов обоих игроков. Заметим, что в каждом случае возможны всего четыре варианта хода. В таблице курсивом выделены случаи, которые сразу же приносят поражение игроку, делающему этот ход (например, когда камней в какой-либо кучке становится больше или равно 8, другой игрок непременно выигрывает следующим ходом, удваивая количество камней в этой кучке). Из таблицы видно, что при безошибочной игре обоих игроков первый всегда выиграет, если первым ходом сделает 4, 5, 6. У второго игрока в этом случае все ходы проигрышные.

	1-й ход	2-й ход
Начало	1-й игрок	2-й игрок	1-й игрок	2-й игрок
2,3,4	4,3,4	8,3,4	выигрыш
4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
4,3,8	выигрыш
6,5,6	12,5,6	выигрыш
6,10,6	выигрыш
6,5,12	выигрыш
8,7,8	выигрыш
	2,6,4	4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
2,12,4	выигрыш
2,6,8	выигрыш
4,8,6	выигрыш
2,3,8	выигрыш
4,5,6	8,5,6	выигрыш
4,10,6	выигрыш
4,5,12	выигрыш
6,7,8	выигрыш

Пример 5. Записано 7 строк, каждая из которых имеет свой номер. В нулевой строке после номера записана цифра 001. Каждая последующая строка содержит два повторения предыдущей строки и добавленной в конец большой буквы латинского алфавита (первая строка — A, вторая строка — B и т. д.). Ниже приведены первые три строкиєтой записи (в скобках указан номер строки):

(0) 001

(1) 001001A

(2) 001001A001001AB

Какой символ находится в последней строке на 250-м месте (считая слева направо)?

Примечание. Первые семь букв латинского алфавита: A, B, C, D, E, F, G.

Решение. Найдем длину каждой строки. Длина каждой следующей строки в два раза больше длины предыдущей плюс один символ, длина строк составит:

(0) 3 символа;

(1) 3*2+1=7;

(2) 7*2+1=15;

(3) 15*2+1=31;

(4) 31*2+1=63;

(5) 63*2+1=127;

(6) 127*2+1=255 символов.

Так как задано 7 строк, а нумерация начинается с нулевой строки, последняя строка имеет номер 6 и содержит 255 символов. Последний символ в строке — F. Предпоследний элемент — E, далее идут символы D, C, B, A, 1 (по правилу формирования строк). Таким образом, 250-й символ — это 1.

Ответ: 1.

Пример 6. Имеется фрагмент алгоритма, записанный на учебном алгоритмическом языке:

n := Длина(а)

k = 2

b := Извлечь(а, k)

нц для i от 7 до n – 1

с := Извлечь(а, i)

b := Склеить(b, с)

кц

Здесь переменные а, b, с — строкового типа; переменные n, i — целые.

В алгоритме используются следующие функции:

Длина(х) — возвращает количество символов в строке х. Имеет тип «целое».

Извлечь(х, i) — возвращает i-й символ слева в строке х. Имеет строковый тип.

Склеить(х, у) — возвращает строку, в которой находятся все символы строки х, а затем все символы строки у. Имеет строковый тип.

Какое значение примет переменная b после выполнения этого фрагмента алгоритма, если переменная а имела значение «ВОСКРЕСЕНЬЕ»?

Решение. Находим общее число символов в строке а, получим, что n = 11.

Выполняя команду b := Извлечь(а, k) при k = 2, получим, что b примет значение «О«.

В цикле последовательно, начиная с 7-го символа строки а и заканчивая предпоследним (n – 1), извлекаем символ из строки а и присоединяем к строке b.

В результате получим слово «ОСЕНЬ» (символы с номерами 2 + 7 + 8 + 9 + 10).

Ответ: «ОСЕНЬ«

Пример 7. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который называется его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака», написанной в 1202 году. Он выглядит так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…

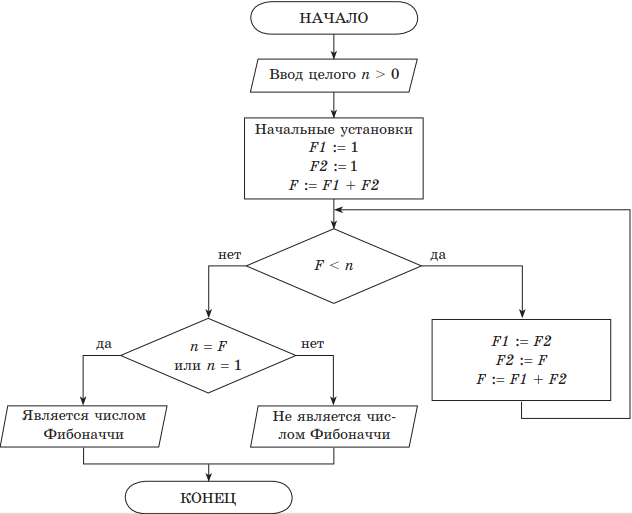
В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составить словесный алгоритм и блок-схему проверки принадлежности введенного числа n ряду Фибоначчи.

Решение. Словесный алгоритм:

1. Ввести число n.
2. Установить значение первых трех чисел Фибоначчи: 1, 1, 2 (сумма двух предыдущих чисел).
3. Пока введенное число n больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи.
4. Если число Фибоначчи равно введенному n или было введено число n = 1, значит, что было введено число Фибоначчи, в противном случае — введенное число не является числом Фибоначчи.

Приведенный словесный алгоритм в пункте 1, 2 содержит начальные установки, в пункте 3 — цикл с условием, а пункт 4 — это вывод результата работы алгоритма.

Блок-схема алгоритма:

Обозначения:

F — текущее число ряда Фибоначчи;

F1 и F2 — два предыдущих числа ряда Фибоначчи для числа F;

n — число, для которого требуется определить, является ли оно числом из ряда Фибоначчи.

Использование основных алгоритмических конструкций: следование, ветвление, цикл

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

Базовая структура СЛЕДОВАНИЕ указывает на то, что управление передается последовательно от одного действия к другому.

Учебный алгоритмический язык	Язык блок-схем
действие 1 действие 2 … действие n

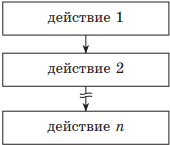Использование исключительно этой структуры возможно лишь для достаточно простых задач, ход решения которых не меняется в зависимости от конкретных исходных данных и состоит в последовательном выполнении определенных операций.

В качестве примера рассмотрим решение простой задачи.

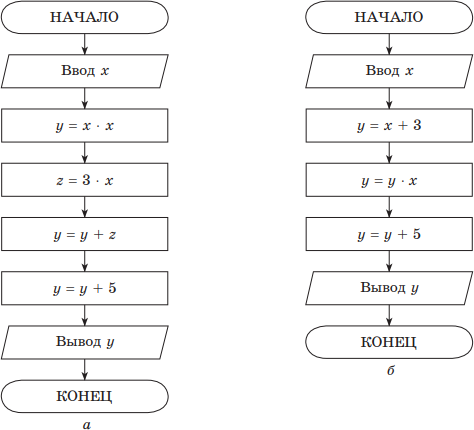
Пример. Найти y(x) = x2 + 3x + 5, используя только операции умножения и сложения.

Решение. На рис. приводятся два алгоритма, реализующие решение поставленной задачи.

Порядок вычисления y(x) в первом случае — обычный, а во втором — (x + 3) x + 5. Обе формулы эквивалентны, но в первом случае для вычисления необходимо 2 умножения, 2 сложения и 3 переменных (x, y, z), а во втором используются 1 умножение, 2 сложения и 2 переменные (x, y).

Приведенный пример показывает, что даже простые задачи могут решаться с помощью различных вариантов алгоритмов.

Обратите внимание, как в блоке следования используется оператор присваивания.

Операция присваивания — важнейшая операция во всех языках программирования. С помощью присваивания переменные получают новые значения: в левой части инструкции ставится идентификатор величины, а в правой части — выражение, значение которого можно определить.

В операторах присваивания используется либо привычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных правой части уже определены.

Базовая структура ВЕТВЛЕНИЕ (РАЗВИЛКА) используется в случае, когда выполнение программы может измениться в зависимости от результата проверки условия и пойти двумя разными (альтернативными) путями. Другими словами, условие является некоторым высказыванием (предикатом) и может быть истинным или ложным (принимать значение TRUE или FALSE). Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

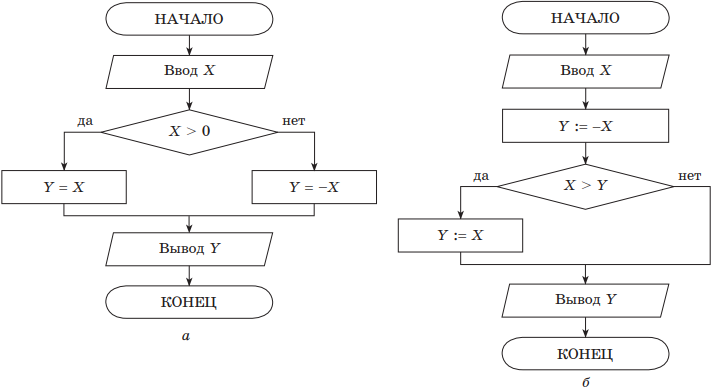
Различают две структуры этого типа — полную и неполную. В случае полной структуры, если условие выполняется (является истинным), вслед за ним выполняется действие 1, иначе — действие 2. В случае неполной структуры, если условие выполняется (является истинным), то вслед за ним выполняется действие 1, иначе ничего не происходит.

Важную роль в операторах ветвления играют содержащиеся в них условия. В простейшем случае условиями служат отношения между величинами. Условия с одним отношением называют простыми условными выражениями, или простыми условиями. В некоторых задачах необходимы более сложные условия, состоящие из нескольких простых, например условие А < X < С, т. е. Х < А и (Х > C) (возможна запись (Х < А) and (Х > C)). Объединение нескольких простых условий в одно образует составное условное выражение, или составное условие. Составные условия образуются с помощью логических операторов not (отрицание), and (логическое И), or (логическое ИЛИ), хоr (исключающее ИЛИ).

Структура ВЕТВЛЕНИЕ существует в четырех основных вариантах:

если — то (неполная структура);

если — то — иначе (полная структура);

выбор (неполный);

выбор — иначе (полный).

Учебный алгоритмический язык	Язык блок-схем
1) если — то
если условие то действие 1 всё
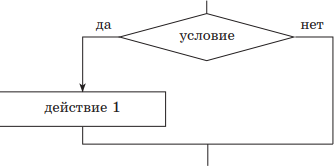2) если — то — иначе
если условие то действие 1 иначедействие 2 всё
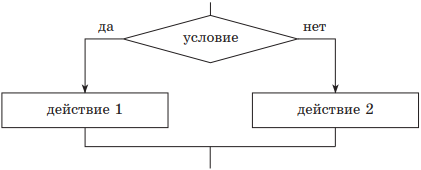3) выбор
выбор при условие 1: действие 1 при условии 2: действие 2 … при условие N: действие N всё
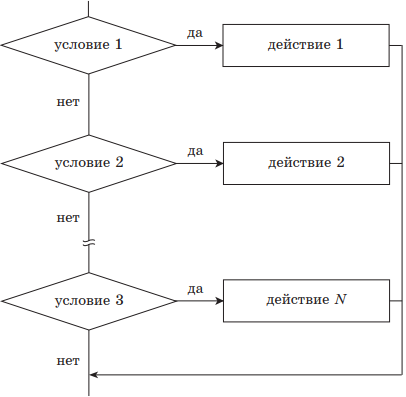4) выбор — иначе
выбор при условие 1: действие 1 при условие 2: действие 2 … при условие N: действие N + 1 иначе действия N + 1 всё

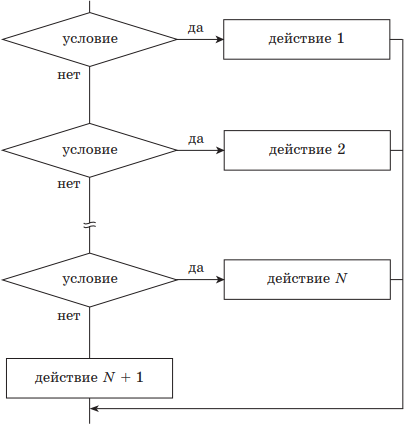В качестве простого примера рассмотрим нахождение модуля числа y(x) = |x|. Решение приведено на рис. для случаев полной (а) и неполной (б) структур ветвления.

Базовая структура ЦИКЛ служит для записи алгоритмов, в которых некоторая часть алгоритма (тело цикла) должна повторяться несколько раз. Количество повторений цикла может определяться разными способами, в зависимости от которых различают три вида циклов.

1. Цикл с предусловием, или цикл «пока». При реализации этого цикла сначала проверяется условие его выполнения. Пока оно выполняется, будут происходить повторения тела цикла. Отсюда и другое его название — цикл «пока». Если условие не выполняется при первой проверке, то тело цикла не будет выполняться вообще. После выхода из цикла управление передается следующей структуре. Для того чтобы избежать зацикливания, т. е. бесконечного цикла, в теле цикла обязательно должны изменяться параметры, записанные в условии.

Учебный алгоритмический язык	Язык блок-схем
нц пока условие тело цикла (последовательность действий) кц

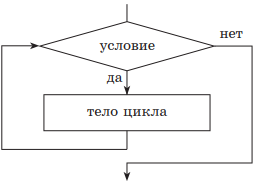2. Цикл с параметром. Этот вид цикла удобно использовать в тех случаях, когда заранее извесно количество повторений цикла. Вводится понятие счетчика цикла, который по умолчанию считается равным либо 1, либо –1. В некоторых случаях изменение счетчика цикла (приращение) указывают явно. Для организации цикла необходимо задать верхнюю и нижнюю границы изменения счетчика цикла. В зависимости от значения верхней и нижней границы определяется шаг цикла (1 или −1), т. е. значение счетчика цикла.

Учебный алгоритмический язык	Язык блок-схем
нц для i от i1 до i2 тело цикла (последовательность действий) кц

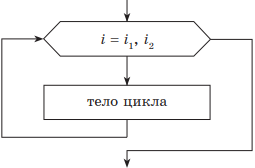3. Цикл с постусловием, или цикл «до». При реализации этого цикла условие завершение цикла проверяется после тела цикла. В этом случае тело цикла всегда выполняется хотя бы один раз. Цикл будет выполняться до выполнения условия, отсюда и другое название — цикл «до». А пока условие не выполнено, будет повторяться тело цикла (выполнение условия, таким образом, является условием окончания цикла). В этом случае, как и в цикле «пока», необходимо предусмотреть в теле цикла изменение параметров условия цикла.

Учебный алгоритмический язык	Язык блок-схем
нц тело цикла (последовательность действий) до условие кц

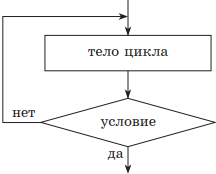Для всех видов цикла предусмотрена возможность досрочного выхода, т. е. прерывание работы цикла.

Помимо трех рассмотренных видов цикла существует и так называемый интерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия. На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата. Классический пример — вычисление суммы ряда с заданной точностью.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное условие выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т. е. не будет выполняться основное свойство алгоритма — результативность.

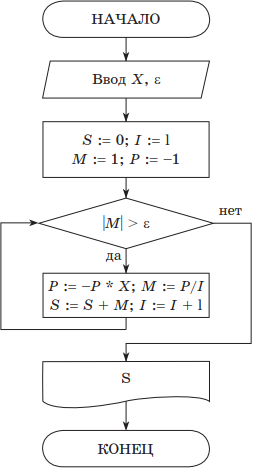
Пример. Вычислить сумму знакопеременного ряда $S=x-{x^2}/{2}+{x^3}/{3}-{x^4}/{4}+…$ с заданной точностью $ε$.

Для данной знакочередующейся бесконечной суммы требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше $ε$.

Решение. Запишем блок-схему алгоритма, где будем использовать следующие обозначения:

$S$ — частичная сумма ряда (стартовое значение равно 0);

$ε$ — точность вычисления;

$i$ — номер очередного слагаемого;

$m$ — значение очередного слагаемого;

$p$ — числитель очередного слагаемого.

На псевдокоде алгоритм можно записать следующим образом:

Примечание. Следует отметить, что ряд будет сходящимся только при выполнении условия 0 < х < 1.

Возможны случаи, когда внутри тела цикла необходимо повторить некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле, или вложенного цикла. Глубина вложения циклов (количество вложенных друг в друга циклов) может быть различной.

При использовании такой структуры для экономии времени выполнения необходимо выносить из внутреннего цикла во внешний все действия, результаты которых не зависят от параметра внутреннего цикла.

Пример. Вычислить сумму элементов для заданной матрицы (таблицы из 5 строк и 3 столбцов) А(5,3).

Решение. Алгоритм решения задачи на псевдокоде:

Основная часть блок-схемы нахождения суммы элементов матрицы будет иметь следующий вид:

Здесь порядок выполнения вложенных циклов следующий: счетчик внутреннего цикла изменяется быстрее, т. е. для i = 1(внешний цикл), j пробегает значения 1, 2, 3 (внутренний цикл); далее i = 2, j опять пробегает значения 1, 2, 3 и т. д.

Примеры решения задач

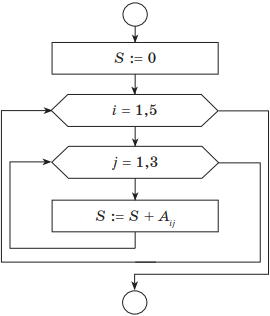
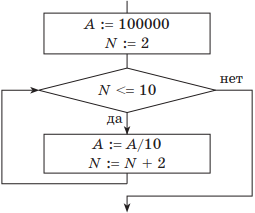
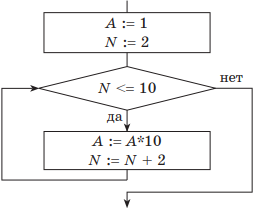
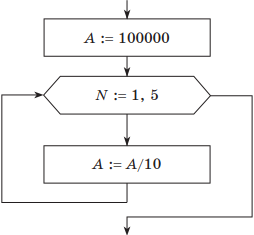
Пример 1. Дан фрагмент блок-схемы некоторого алгоритма.

Определить значение переменной А после выполнения фрагмента алгоритма.

Какие исправления нужно внести, чтобы изменение значения переменной А происходило в обратном порядке?

Как записать исходный алгоритм с помощью двух других видов цикла?

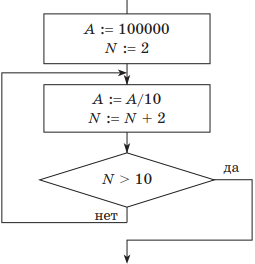
Решение. Если представить пошаговое выполнение алгоритма в виде таблицы, получим:

Начальные установки:	A = 100000; N = 2
1-я итерация	A = 10000; N = 4
2-я итерация	A = 1000; N = 6
3-я итерация	A = 100; N = 8
4-я итерация	A = 10; N = 10
5-я итерация, выполнилось условие выхода: N > 10	Ответ: А = 1; N = 12

Таблица обратного хода изменения значения А будет иметь такой вид:

Начальные установки:	A = 1; N = 2
1-я итерация	A = 10; N = 4
2-я итерация	A = 100; N = 6
3-я итерация	A = 1000; N = 8
4-я итерация	A = 10000; N = 10
5-я итерация, выполнилось условие выхода: N > 10	А = 100000; N = 12

Блок-схема алгоритма примет такой вид:

В алгоритме нужно изменить начальное значение А и операцию деления заменить операцией умножения. Счетчик N в данном случае изменять не нужно.

В приведенной в условии блок-схеме используется цикл с предусловием. Для цикла с параметром блок-схема алгоритма будет иметь такой вид:

Понятно, что цикл должен выполниться пять раз. В заголовке цикла необходимо указать начальное и конечное значение счетчика цикла N (приращение по умолчанию равно 1).

Для цикла с постусловием блок-схема исходного алгоритма имеет такой вид:

В данной схеме условие завершения цикла находится после тела цикла. Цикл, в отличие от цикла с предусловием, выполняется, пока значение условия ложно.

Пример 2. Сколько раз выполнится тело цикла в программе?

Q := 27; P := 36

нц пока (div(Q, 5) = div(P, 7))

Q := Q + 2

P := P + 3

кц

Примечание. Результат функции div(X, Y) — целая часть от деления X на Y.

Решение. Рассмотрим пошаговое выполнение алгоритма, оформив его в виде таблицы.

Начальные установки	Q := 27; P := 36
Проверка выполнения условия	div(27, 5) = 5; div(36, 7) = 5; 5 = 5
1-я итерация; выполнение тела цикла	Q := 29; P := 39
Проверка выполнения условия	div(29, 5) = 5; div(39, 7) = 5; 5 = 5
2-я итерация; выполнение тела цикла	Q := 31; P := 42
Проверка выполнения условия	div(31, 5) = 6; div(42, 7) = 6; 6 = 6
3-я итерация; выполнение тела цикла	Q := 33; P := 45
Проверка выполнения условия	div(33, 5) = 6; div(45, 7) = 6 6 = 6
4-я итерация; выполнение тела цикла	Q := 35; P := 48
Проверка выполнения условия. Условие не выполняется, цикл завершает работу	div(35, 5) = 7; div(48, 7) = 6; 7 ≠ 6

Ответ: цикл выполнится 4 раза.

Использование переменных. Объявление переменной (тип, имя, значение).
Локальные и глобальные переменные

Величины служат для описания объектов и процессов в материальном мире. Каждая величина имеет некоторые характеристики. В программировании понятие величины несколько отличается от понятия величины в естественных науках — оно является более формальным. Величиной называют объект — переменную, с которым связывается определенное множество значений. Такому объекту присваивается имя — идентификатор. Понятие переменной в программировании сходно с понятием переменной в математике. Например, в алгебраическом равенстве C = F + 2B – 5 значение переменной С зависит от значений переменных F и B, указанных в правой части равенства. Например, при F = 2 и B = 6, С = 9. Такое же равенство можно записать в программе, например на языке программирования Бейсик: C = F + 2*B – 5. В терминах языка программирования C, F и B — это идентификаторы (имена) переменных.

Переменная — это объект программы, имеющий имя и изменяемое значение. Для хранения переменной в памяти компьютера выделено определенное место.

Переменные величины в отличие от постоянных величин (констант) могут со временем менять свое значение. Константой называется величина, которая в ходе выполнения программы не меняет своего значения.

Назначение программы состоит в обработке информации, при этом, конечно, основную роль играют переменные.

Переменная характеризуется:

• идентификатором;
• типом;
• значением.

Каждая переменная имеет свой идентификатор, т. е. свое уникальное имя. Имя переменной показывает, в каком месте памяти компьютера она хранится, значение переменной считывается из указанного ее именем места в памяти. Двух переменных с одним именем в одном программном модуле (блоке) быть не должно. Примерами идентификаторов величин могут быть, например, следующие последовательности символов: a1, SUMMA, X_1, Y_1, My_program.

Во многих языках программирования существуют некоторые ограничения на задания имен переменных. Имена составляются из букв и цифр; первой литерой должна быть буква. Знак подчеркивания «_» считается буквой, его удобно использовать, чтобы улучшить восприятие длинных имен переменных. Разумно давать переменным логически осмысленные имена, в соответствии с их назначением. Нельзя использовать в качестве имен зарезервированные (служебные) слова языка программирования.

Тип переменной — это диапазон (набор) всех значений, которые может принимать данная переменная. Тип переменной определяет, какие операции для нее допустимы. Другими словами, тип переменной — это характеристика, которая для величины определяет:

• необходимый размер памяти;
• диапазон значений, которые может принимать величина;
• возможные операции над величиной (подразумеваются действия относительно использования величин в выражениях);
• формы представления величин (или формат представления величин).

Стандартные типы — это числовые, литерные и логические типы.

Числовой тип, к которому относятся целые и вещественные величины, позволяет оперировать с числами. Целые числа, которые в учебном алгоритмическом языке составляют тип цел, сверху ограничены положительным числом N_max, а снизу — отрицательным числом N_min. Значения N_max и N_min определяются объемом ячеек памяти, в которые записываются целые числа. Обычно для целых чисел выделяется два байта памяти, соответственно границы диапазона равны [N_min = –32768 и N_max = 32767]. Считается, что все операции с величинами типа цел выполняются по обычным правилам арифметики, за одним исключением: возможны две операции деления div и mod.

Операция div обозначает целочисленное деление. При делении с точностью до целых чисел получается два результата — частное и остаток. Знак результата берется по обычным правилам, а полученный остаток игнорируется. Например:

23 div 5 = 4;

2 div 6 = 0;

(–13) div 5 = –2;

(–13) div (–5) = 2.

Операция mod определяет остаток при делении двух целых чисел.

Например:

23 mod 5 = 3;

2 mod 6 = 2;

(–13) mod 5 = –3;

(–13) mod (–5) = 3;

8 mod 2 = 0.

Целые числа чаще всего используются в простых арифметических выражениях и выступают в программах в качестве различных счетчиков и значений индексов.

К другому числовому типу относятся вещественные (вещ) величины. Значения вещественных величин могут изображаться в форме с фиксированной запятой (например, 0,3333; 2,0; –4,567 и т. д.) и с плавающей запятой (например, 7,0*10², 5,173*10^–3 и т. д.).

В отличие от целых чисел, действия с вещественными числами могут быть неточными — это связано с ошибками округлений. Объем памяти, который предоставляется для хранения значений вещественной переменной, — от 4 до 10 байтов (в зависимости от выбранного формата числа). Над числовыми величинами можно выполнять как арифметические операции, так и операции сравнения (>, <, >=, <=, =, ).

Литерный тип, включающий символы и строки, дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов: букв, цифр, знаков препинания, пробела и других специальных знаков (возможными символами могут быть символы таблицы ASCII). Литерные величины обычно заключаются в кавычки: «а», «В», «СТРОКА», «1_2_3». В учебном алгоритмическом языке литерные величины обозначаются как лит. В других языках программирования (например, в Паскале) различают символьный (char) и строковый (string) типы. Величины символьного типа состоят из одного символа и занимают в памяти всего 1 байт. Величины строкового типа представляют собой различные последовательности символов, которые предусмотрены кодовой страницей, установленной в компьютере. Длина строки может составлять от 0 до 255 символов. Над всеми литерными величинами возможны операции сравнения. С помощью отношений типа «a» < «b», «b» < «c», «c» < «d»,… выполняется упорядочение литерных величин (сортировка по возрастанию или убыванию).

Еще одной операцией, характерной для символьных и строковых величин, является операция конкатенации (слияния): «a» + «b» = «ab».

Логический тип позволяет определять логические переменные, которые могут принимать только два значения: истина (true) или ложь (false). Для представления логической величины достаточно одного бита, однако, поскольку место в памяти выделяется по байтам, логической величине отводится минимальная «порция» памяти — один байт. Над логическими величинами можно выполнять все стандартные логические операции.

Значение — это непосредственно то, чему равна переменная в конкретный момент времени. Это может быть число, символ, текст и т. д. Значение переменной в программе можно задать двумя способами: присваиванием и с помощью процедуры ввода.

Оператор присваивания

Во всех языках программирования оператор присваивания является одним из важнейших. С помощью присваивания переменные получают новые значения, например:

Д := 13;

D1 := C;

Х := Х + 1.

В операторах присваивания используется либо обычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных в правой части уже определены и выполняется соответствие типов для правой и левой части оператора присваивания. Например, С := А > B выполнится только в том случае, если для переменной С определен булевский (логический) тип. Операция присваивания может быть применена к большинству типов величин. Однако для каждого из типов предусмотрен свой набор операций.

Локальные, глобальные и общие переменные

Каждая переменная характеризуется областью действия или областью видимости. По зоне видимости в языках программирования различают локальные и глобальные переменные. Первые доступны только конкретному подалгоритму (вспомогательному алгоритму, подпрограмме, модулю), вторые — всему алгоритму (программе). С распространением модульного и объектного программирования появились еще и общие переменные, доступные для определенных уровней иерархии подпрограмм.

Ограничение зоны видимости придумали как для возможности использовать одинаковые имена переменных, так и для защиты от ошибок, связанных с неправомерным использованием переменных.

Имена локальных и глобальных переменных могут совпадать. При этом действует правило: локальные переменные на время работы подпрограмм, в которых они объявлены, экранируют, т. е. перекрывают глобальные переменные. Например, если в основной программе переменная с именем с определена как логическая, а в подпрограмме идентификатор с используется для задания вещественной переменной, то только на время работы подпрограммы с можно использовать как число — в остальных случаях идентификатор с определяет логическую переменную.

Примеры решения задач

Пример 1. Значения заданных переменных А, В перераспределить таким образом, чтобы А и В поменялись значениями.

Решение. Возможны два варианта решения:

С использованием промежуточной переменной С	Без использования дополнительной переменной
C := A; A := B; B := C	A := A + B; B := A – B; A := A – B

Пример 2. Определить значение переменной A после выполнения фрагмента алгоритма:

Решение. Оформим решение в виде таблицы.

A	B	D	Условие
2	–2	10	да
–4	–2	12	да
8	–2	14	да
–16	–2	16	да
32	–2	18	да
–64	–2	20	да
128	–2	22	нет — окончание цикла

Ответ: А = 128.

Пример 3. Определить значение переменной S:

A := –1; B := 1

нц пока A + B < 10

A := A + 1; B := B + A

кц

S := A * B

Решение. Оформим решение в виде таблицы.

A	B	A + B	S
–1	1	0
0	1	1
1	2	3
2	4	6
3	7	10 — условие выхода из цикла	21

Ответ: S = 21.

Пример 4. Записать последовательность операций присваивания (:=), которая позволит определить номера подъезда и этажа по номеру N квартиры девятиэтажного дома, считая, что на каждом этаже по 4 квартиры, а нумерация квартир начинается с первого подъезда.

Решение.

4 * 9 = 36 {количество квартир в подъезде}

Х := (N – 1) div 36 + 1 {номер подъезда}

N := N – (X – 1) * 36 { N ∊[1, 36] }

Y := (N – 1) div 4 + 1 {номер этажа}

Например, для квартиры с номером 150 получим:

Х = (150 – 1) div 36 + 1 = 4 + 1 = 5;

N = 150 – (5 – 1) * 36 = 6;

Y = (6 – 1) div 4 + 1 = 2.

Ответ: квартира с номером 150 находится в пятом подъезде, на втором этаже.

Работа с массивами (заполнение, считывание, поиск, сортировка, массовые операции и др.)

Величины числового, литерного, логического типов представляются одним значением и относятся к простым типам данных. Характерной особенностью простых типов является атомарность, т. е. они не могут вмещать элементы других типов. Типы данных, которые не удовлетворяют данному условию, называются структурированными, или составными. Например, массивы, записи, строки, множества, файлы. Структурированный тип характеризуется множеством элементов, из которых складываются данные этого типа. Элементы структурированного типа называются компонентами. В свою очередь компонента структурированного типа может принадлежать также к структурированному типу. Из простых данных сложные структуры могут получаться двумя способами:

1. объединением однородных элементов данных;
2. объединением разнородных элементов данных.

В первом случае примером могут служить массивы, а во втором — записи.

Информацию удобно представлять в виде таблиц. Наиболее привычными являются прямоугольные таблицы, т. е. таблицы, состоящие из строк и столбцов. В том числе таблицы, состоящие из единственной строки или единственного столбца, — линейные таблицы, имеющие одно «измерение».

Табличные величины относятся к составным величинам, т. к. включают в себя другие величины. В учебном алгоритмическом языке табличный тип обозначается как таб. Таблицы в программировании принято называть массивами. В математике прототипом массивов являются матрицы и векторы.

Массив

Массив — это упорядоченный набор данных, имеющий одно имя и состоящий из фиксированного числа однотипных элементов.

Каждый элемент массива снабжен индексом. Индекс — это порядковый номер элемента, определяющий его положение в массиве. Таким образом, элементы массива идентифицируются с помощью имени массива и с помощью своих индексов.

Количество элементов массива называется размерностью массива.

Итак, массив характеризуется:

• размерностью;
• базовым типом элементов;
• типом индекса (может быть только порядковым типом);
• множеством значений для индекса.

Массив может быть одномерным (вектор) и многомерным (матрица).

Одномерный массив содержит одно измерение; каждый элемент массива обозначается идентификатором (именем) массива с индексом. Многомерный массив содержит n-е количество измерений; каждый элемент массива обозначается идентификатором массива для n индексов.

Существует несколько способов заполнения массива данными:

1. непосредственное присваивание значений элементам;
2. заполнение массива произвольными элементами, случайными числами;
3. ввод значений элементов с клавиатуры или чтение из файла.

Необходимо заметить, что заполнение массива происходит поэлементно. Для этого используют оператор цикла. Вывод массива также осуществляется поэлементно с помощью оператора цикла.

Примечание. Строковый тип данных напоминает одномерный массив, в котором элементами являются символы. К примеру, строку «МАМА КУПИЛА ХЛЕБ» можно рассматривать как одномерный массив из 16 символов (включая пробелы). Эту строку можно обозначить идентификатором (например, Novost) и пронумеровать все символы, считая их элементами массива: Novost (l)  = «М», … Novost (16) = «Б».

Однако для работы с символьной информацией более гибким инструментом является не одномерный массив, а строка (string). Это связано с тем, что количество символов в строке, в отличие от массива, не фиксировано. Благодаря этому к строке можно без ограничений применять стандартные операции и функции, предназначенные для работы с текстом.

Задачи, связанные с обработкой массивов, как и все задачи вообще, условно можно разделить на два вида:

1. стандартные задачи;
2. задачи, решение которых требует знания вспомогательных алгоритмов, специальных методов и приемов.

Очевидно, что без умения решать задачи первых двух видов невозможно решать нестандартные задачи.

Стандартные задачи обработки массивов

Пример 1. В массиве А каждый элемент равен 0 или 1. Заменить все нули единицами и наоборот.

Решение. Достаточно одного оператора присваивания в теле цикла:

A[i] := 1 – A[i].

Пример 2. В массиве каждый элемент равен 0, 1 или 2. Переставить элементы массива так, чтобы сначала располагались все 0, затем все 1 и, наконец, все 2. Дополнительный массив не использовать.

Решение. Можно не переставлять элементы массива, а подсчитать количество 0, 1, 2 и заново заполнить массив требуемым образом.

Пример 3. Даны два n-элементных массива Х и Y одного типа. Поменять местами все X_i и Y_i, (i = 1…n), не используя промежуточные величины.

Решение. Обмен можно выполнить в цикле для всех i от 1 до n с помощью серии из трех операторов присваивания:

X[i] := X[i] + Y[i]

Y[i] := X[i] – Y[i]

X[i] := X[i] – Y[i].

Пример 4. Записать алгоритм нахождения максимального элемента массива А(n) и его номера.

Решение. На псевдокоде требуемый алгоритм запишется следующим образом:

Примечание. Если таких элементов несколько, будет найден номер последнего.

Пример 5. Найти сумму элементов одномерного массива А(n).

Решение. На псевдокоде алгоритм нахождения суммы запишется следующим образом:

Примечание. Для нахождения суммы положительных элементов массива вместо оператора

S := S + A[i] необходимо записать:

если A[i] > 0

то S := S + A[i]

всё

Пример 6. Записать алгоритм вычисления произведения элементов столбцов заданной вещественной двумерной матрицы A(n, m).

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 7. Подсчитать количество элементов для заданной целочисленной матрицы A(n, m), равных ее максимальному элементу.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 8. Запиcать алгоритм обмена элементами строк с номерами P и Q в заданной вещественной матрице A(n, m).

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 9. Включить заданное число D в одномерный упорядоченный по возрастанию массив F(n) с сохранением упорядоченности.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 10. Сформировать новый массив B из элементов целочисленного массива A(n), для которых выполняется условие D < A_i < C.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 11. Найти в заданном целочисленном массиве А(m) хотя бы одну пару элементов, совпадающих по значению.

Решение. На псевдокоде алгоритм запишется следующим образом:

Поиск — одна из важных невычислительных задач. Проведение поиска в упорядоченном и неупорядоченном массивах отличается. В неупорядоченном массиве, если нет никакой дополнительной информации об элементе поиска, его выполняют с помощью последовательного просмотра всего массива. Такой поиск называют линейным. В любом случае существуют два условия окончания поиска:

1. элемент найден;
2. весь массив просмотрен — элемент не найден.

В упорядоченном массиве поиск можно значительно ускорить, применяя метод половинного деления, или бинарный поиск. Его идея заключается в следующем. Пусть фиксированный массив упорядочен по неубыванию (a_i ≤ a_{i + 1}). Случайно выбранный элемент am (обычно берут средний элемент) сравнивают с элементом поиска х. Если он меньше х, то искомый элемент может быть среди элементов a_{m + i}, …, а_n, т. е. в правой половине массива. Если он больше х — то среди элементов левой части массива. Если же он равен х, то поиск успешно заканчивается.

К стандартным задачам относятся задачи сортировки массива. Сортировка массива — это перерасположение элементов массива в заданном порядке. Основная цель сортировки — облегчить последующий поиск. Методы условно разделяют по главной идее алгоритма, а реализуются они целым семейством алгоритмов.

К простым методам сортировки относят:

• сортировку с помощью обмена (метод пузырька);
• сортировку с помощью прямого включения;
• сортировку с помощью выбора.

Сортировка с помощью обмена. При использовании этого метода сортировки соседние элементы массива сравниваются и при необходимости меняются местами до тех пор, пока массив не будет полностью упорядочен. Повторные проходы массива каждый раз сдвигают наименьший (наибольший) элемент оставшейся части массива к левому его концу. Метод широко известен под названием «пузырьковая сортировка», т. к. большие (меньшие) элементы массива, подобно пузырькам, «всплывают» на соответствующую позицию. Основной фрагмент программы содержит два вложенных цикла, причем внутренний цикл удобнее выбрать с убывающим шагом.

Алгоритм сортировки массива A(n) по возрастанию на псевдокоде:

Сортировка с помощью прямого включения (вставки). На каждом шаге этого метода массив разделен на две части: левую, уже отсортированную, и правую, еще не отсортированную. Первый элемент правой части вставляется в левую часть массива так, чтобы левая часть осталась отсортированной. В результате отсортированная часть увеличивается на один элемент, а неотсортированная — на один элемент уменьшается. Таким образом, на каждом шаге алгоритма сортировки вставками приходится выполнять две операции: поиск позиции для вставки элемента и собственно его вставку с последующим сдвигом на одну позицию вправо от элементов отсортированной части. Этот сдвиг «стирает» первый элемент неотсортированной части. Сначала отсортированным подмассивом считаем первый элемент, а остальная часть массива относится к неотсортированной части. Поскольку операции сравнения и перемещения чередуются друг с другом, этот способ сортировки часто называют просеиванием или погружением.

Сортировка с помощью прямого выбора. При сортировке этим методом сначала выбирается наименьший (наибольший) элемент массива и меняется местами с первым. Затем выбирается наименьший (наибольший) среди оставшихся (n – 1) элементов и меняется местами со вторым и т. д. до тех пор, пока не останется один наибольший (наименьший) элемент. Сортировка осуществляется с помощью двух вложенных циклов.

Приведенные алгоритмы сортировки не требуют дополнительной оперативной памяти. Время выполнения алгоритмов сортировки пропорционально количеству операций сравнения и перестановки элементов. Сортировка массива из $n$ элементов методом выбора главного элемента требует выполнения ${n^2}/{2}$ операций сравнения и n операций обмена элементами. Метод сортировки вставками требует ${n^2}/{4}$ операций сравнения и столько же операций обмена, а метод пузырьковой сортировки — ${n^2}/{2}$ операций сравнения и столько же операций обмена. Таким образом, из трех рассмотренных методов сортировки массива методы вставки и выбора приблизительно эквивалентны, а обменная сортировка — медленнее. Кроме того, что в методе вставки исходные элементы могут поступать последовательно, а в методе выбора они должны быть в наличии до начала сортировки.

Примеры решения задач

Пример 1. Одномерный массив, содержащий десять элементов, заполняется по следующему закону: A[1] = 1; A[2] = X; A[i] = 2 * X * A[i – 1] – A[i – 2], где i = 3, 4, …, 10. Каким будет значение A[5] при X = 1?

Решение. Представим значения первых пяти элементов массива А, полученные по заданному закону при Х = 1:

A[1] = 1; A[2] = Х = 1;

A[3] = 2 * Х * A[2] – A[1] = 2 * 1 * 1 – 1 = 1;

A[4] = 2 * Х * A[3] – A[2] = 2 * 1 * 1 – 1 = 1;

A[5] = 2 * Х * A[4] – A[3] = 2 * 1 * 1 – 1 = 1.

Таким образом, значение A[5] при Х = 1 будет равно 1.

Ответ: 1.

Пример 2. Задан двумерный массив А(n, n). Определить, что вычисляет приведенный фрагмент алгоритма:

Решение. В данном алгоритме переменной S присваивается значение 0. Затем в структуре циклов по переменным i и j каждый из элементов массива А_ij сравнивается с нулем (А[i, j] > 0) и если элементы А_ij положительны, то квадраты А[i, j]^2 положительных элементов А_ij увеличивают значение суммы S (S := S + A[i, j]^2).

Ответ: фрагмент алгоритма вычисляет сумму квадратов положительных элементов массива.

Пример 3. Задан фрагмент алгоритма, использующий двумерный массив (таблицу) М(n, n), два одномерных массива A(n), B(n) и переменную X. Определить назначение массивов А и В и переменной.

Решение. Представим фрагмент алгоритма словесно.

1. Переменной X присвоить значение 0.
2. Переменной i присвоить значение 1.
3. Если i ≤ n, то перейти к следующему пункту; в противном случае — конец фрагмента алгоритма.
4. Элементу одномерного массива А с индексом i присвоить значение элемента двумерного массива М, находящегося в i-й строке и первом столбце.
5. Элементу одномерного массива В с индексом i присвоить значение 1.
6. Переменной j присвоить значение 1.
7. Если j ≤ n, то перейти к следующему пункту; в противном случае — к п. 13.
8. Если М[i, j] < A[i], то перейти к следующему пункту; иначе — к п. 11.
9. Элементу A[i] присвоить значение элемента массива М, находящегося в i-й строке и j-м столбце.
10. Элементу В[i] присвоить значение переменной j.
11. Переменной Х присвоить значение суммы X + M[i, j].
12. Переменной j присвоить значение суммы j + 1 и вернуться к п. 7.
13. Переменной i присвоить значение суммы i + 1 и вернуться к п. 3.

Таким образом, анализ алгоритма показывает, что переменная X накапливала сумму всех элементов массива М; массив А — минимальные элементы соответствующих строк массива М; массив В — индексы (порядковые номера столбцов) минимальных элементов в соответствующих строках массива М.

Пример 4. Составить алгоритм определения наличия среди элементов главной диагонали заданной целочисленной матрицы A(n, m) хотя бы одного положительного нечетного элемента.

Решение. Для всех элементов А_ij главной диагонали выполняется условие i = j. Определение наличия нечетных элементов выполняется с помощью операции mod (остаток от целочисленного деления), при этом, если результат mod равен 1, — число нечетное.

Алгоритм:

Структурирование задачи при ее решении для использования вспомогательного
алгоритма. Вспомогательные алгоритмы: процедуры и функции

Разработка алгоритмов решения задач на компьютере требует определенных навыков. При построении алгоритма нужно стремиться к тому, чтобы запись алгоритма была понятной и наглядной. Кроме того, внося изменения в алгоритм, желательно не перестраивать его полностью. Эти требования можно удовлетворить, если придерживаться структурного подхода.

Самым важным преимуществом структурного подхода является возможность нисходящего программирования, благодаря которой можно двигаться от крупных задач к более мелким. Крупная задача будет разбиваться на менее крупные блоки, те в свою очередь — на меньшие блоки и т. д. Каждый блок алгоритма должен быть максимально самостоятельным и логически завершенным.

Разбиение на блоки должно определяться внутренней логикой задач. Процесс разбиения завершается, когда решение исходной задачи сводится к решению ряда простых задач, для которых легко построить алгоритм. На каждом шаге этого процесса происходит детализация, т. е. переход от общих задач к частным, которые в свою очередь детализируются в виде конкретных подзадач. Такой метод называется методом пошаговой детализации. Таким образом, при структурном подходе можно комбинировать не только базовые структуры (следование, ветвление, цикл), но и подключать алгоритмы, написанные ранее. Алгоритмы, которые целиком используются в составе других алгоритмов, называются вспомогательными, или подалгоритмами.

Если вспомогательный алгоритм в процессе работы программы выполняется многократно, отличаясь только параметрами, то обычно прибегают к оформлению вспомогательного алгоритма в виде подпрограммы — алгоритма-процедуры, или алгоритма-функции.

Подпрограмма — это именованный, логически законченный алгоритм, который оформляется специальным образом и может многократно использоваться при решении более общей задачи.

Описание подпрограмм можно сравнить с записываемой в математике формулой «в общем виде», в которую при расчетах подставляются конкретные значения. Далеко не каждую задачу можно свести к единственной формуле, но всегда можно записать алгоритм ее решения, а значит, подпрограмма — это инструкция по решению некоторой задачи. Как и формулу, подпрограмму можно использовать для обработки различных данных, передаваемых из главной программы или других подпрограмм.

В языках программирования подпрограмма является частью основной программы, ее описание располагается в описательной части программы. Структура подпрограммы такая же, как и основной программы; различие заключается лишь в оформлении заголовка подпрограммы. Заголовок подпрограммы состоит из служебного слова — идентификатора подпрограммы (имени подалгоритма) — и списка формальных параметров (список параметров не обязателен, допускаются подпрограммы без параметров). При вызове процедуры из текста программы вместо формальных параметров подставляются фактические параметры, при этом соблюдаются следующие правила:

• количество формальных и фактических параметров должно совпадать, причем соответствие между параметрами команды вызова и формальными параметрами процедуры устанавливается по порядку следования: первый фактический параметр соответствует первой переменной, записанной в заголовке подпрограммы, второй фактический параметр — второй переменной и т. д.;
• типы соответствующих параметров команды вызова и заголовка подпрограммы должны совпадать.

Команда вызова подпрограммы выполняется в три этапа:

1. вычисление фактических аргументов;
2. исполнение алгоритма подпрограммы;
3. присвоение полученных значений результатов алгоритма-подпрограммы соответствующим фактическим переменным.

Программа может содержать более одной подпрограммы; допускается использование вложенных подпрограмм, которые, в свою очередь, могут содержать свои вложенные подпрограммы.

Различают два вида подпрограмм — процедуры и функции. Имея один и тот же смысл и аналогичную структуру, процедуры и функции различаются назначением и способом их использования. Основное отличие функций от процедур заключается в том, что результатом выполнения функции является некоторое единственное значение. Функция — это алгоритмически вычисляемое выражение, которое присваивается идентификатору функции.

Подпрограммы бывают двух видов: стандартные и пользовательские. Стандартные, или встроенные, подпрограммы входят в состав языка программирования. Эти подпрограммы определенным образом организованы в специальные библиотеки. С помощью встроенных процедур и функций выполняются операции ввода/вывода, работа с файлами, обработка символьной информации, вычисление различных математических функций и т. п.

Подпрограммы, которые написаны пользователем, называются пользовательскими.

Технология программирования

Чтение короткой (30±50 строк) простой программы на алгоритмическом языке (языке программирования)

Запись алгоритма в словесной форме, в виде блок-схемы или на псевдокоде должна быть точна настолько, чтобы позволить исполнителю правильно выполнить алгоритм, при этом изображение команд произвольное. При решении любой задачи на компьютере предполагается, что некоторая информация подвергается обработке по предварительно составленной инструкции, называемой программой. Язык, на котором записывается алгоритм для исполнения компьютером, называется языком программирования. Языки программирования принадлежат к формальным языкам. При записи алгоритма на языке программирования все правила языка должны строго выполняться. Программа — это алгоритм, записанный на языке программирования.

Для записи программ используется конечный набор символов, составляющих алфавит языка программирования. В отличие от привычных алфавитов (например, русского) алфавит языка программирования включает в себя, кроме букв, цифры, знаки препинания, знаки арифметических действий и некоторые другие дополнительные символы. Программа записывается в виде последовательности символов из алфавита своего языка программирования. Естественно, что не любой текст, составленный из символов алфавита, будет правильной программой. Как и в естественных языках, правильность построения программы из символов алфавита можно проверить, используя синтаксис языка программирования.

Синтаксис языка программирования — это набор правил, которые определяют способы построения правильных программ из символов алфавита. Зная синтаксис языка, можно построить алгоритм, который определяет, является ли данный текст правильной программой или нет. Этот алгоритм позволяет компьютеру проверять синтаксическую правильность вводимых в него программ.

Должна быть определена и семантика языка программирования. Семантика языка программирования — это набор правил, по которым исполнитель выполняет программы на этом языке. Пользуясь семантикой языка, можно однозначно определить результат выполнения программы с заданными входными данными.

При чтении программы необходимо сначала определить, к какому виду она относится. Условно программы можно разделить на два вида: простая программа без использования подпрограмм (кроме стандартных процедур вводавывода) и программа, использующая подпрограммы (подалгоритмы). Такая программа может включать в свою структуру как стандартные подпрограммы, так и подпрограммы, написанные пользователем.

Для чтения простой программы необходимо выяснить:

• что является входными данными и как они вводятся в программу;
• какие действия последовательно выполняются с помощью каждого функционального узла программы (операторов), т. е. рассмотреть пошаговое выполнение операторов, при этом обратить внимание на роль вспомогательных переменных, массивов и т.д.;
• что является результаты работы программы;
• каковы ограничения по работе алгоритма.

При чтении программы, использующей подпрограммы, необходимо сначала проанализировать, что и как выполняют подпрограммы, каковы их входные и выходные параметры. Затем в основной программе вызовы каждой из подпрограмм рассматривать уже как результат работы соответствующего подалгоритма.

Существенно облегчает чтение программ наличие комментариев — поясняющего текста. Комментарии можно добавлять в любое место программы. Наличие комментариев — обязательное условие хорошо и грамотно написанной программы.

Примеры чтения программ на языках Pascal, QBASIC

Примечание. В приведенных примерах программа приводится для двух языков программирования. В зависимости от того, какой язык программирования изучается, и следует рассматривать ее вариант записи и соответствующие пояснения.

Пример 1. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы и описываются переменные;
2. вводятся натуральные числа М и N, причем проверяется условие корректности ввода: числа должны быть положительные. Если введенные значения не удовлетворяют условию, то ввод повторяют, пока условие не будет выполнено;
3. выбирается наименьшее значение из М и N, результат записывается в K;
4. NOD присваивается значение 1;
5. в цикле от двух до K генерируется число I;
6. тело цикла — в условном операторе проверяется, является ли значение переменной I одновременно делителем М и N. Если условие выполняется, то текущее значение I сохраняется в переменной NOD; если условие не выполняется, NOD не изменит своего значения;
7. после перебора всех значений I в NOD или запишется наибольший делитель двух чисел М и N, или останется значение 1;
8. последний оператор программы служит для вывода результата работы программы — значения переменной NOD.

Переменные, используемые в программе:

N, М — исследуемые числа;

I — переменная цикла;

NOD — наибольший общий делитель;

К — наименьшее из М и N.

Ответ: данная программа позволяет определить для двух чисел М и N их наибольший общий делитель NOD.

Примечание. Эту же задачу можно решить, используя алгоритм Евклида.

Пример 2. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы, описываются переменные и одномерный массив MAS целого типа (для Pascal целый массив длиной 100);
2. вводится фактическая длина массива N с проверкой на положительное значение N;
3. вводится значение первого элемента массива MAS;
4. устанавливается начальное значение МАХ по первому элементу массива;
5. переменной К присваивается значение 1;
6. последовательно, в цикле, просматриваются вводимые элементы массива, и если очередной элемент MAS(I) больше или равен МАХ, то переписывается значение MAS(I) в МАХ и в переменной К запоминается I;
7. выводятся результаты: МАХ — значение максимального элемента массива и К — номер максимального элемента в исходном массиве (если таких элементов несколько, выведется номер самого правого максимума).

Переменные, используемые в программе:

MAS — массив чисел;

N — размер массива;

I — переменная цикла;

МАХ — значение наибольшего элемента;

К — номер наибольшего элемента.

Ответ: программа написана для поиска значения максимального элемента массива и его номера (если таких элементов несколько, то будет найден номер самого правого максимума).

Пример 3. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы и описываются переменные;
2. вводится строка символов S;
3. определяется длина строки, значение которой заносится в переменную L;
4. в цикле осуществляется замена ‘!’ на ‘.’ в исходной строке;
5. выводится преобразованная строка.

Переменные, используемые в программе:

I — переменная цикла;

L — длина строки;

S — строка текста.

В программе на языке Pascal используется встроенная функция языка:

Length(STR) — она определяет фактическую длину строки STR (длина строки не более 256 символов).

В программе на языке QBASIC используются встроенные функции:

Len(X) — определяет фактическую длину строки X (длина строки не более 256 символов);

M1D$(X$, N, M) — выделяет M символов, начиная с N-го символа в символьном выражении X$ (M можно опустить).

Ответ: данная программа позволяет заменить во введенной строке символов все восклицательные знаки на точки.

Пример 4. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем текст программы на языке Pascal:

1. формируется тело программы и описываются переменные;
2. вводится строка STR и дублируется во вспомогательной переменной S1;
3. определяется местоположение первой точки в тексте; если точка есть, то из S1 вырезается текст до нее;
4. ищется вторая точка; если она есть, то из S1 вырезается текст после нее;
5. в зависимости от присутствия точек результат выводится на экран.

Используемые переменные:

I — номер позиции, которая соответствует точке;

STR — строка текста;

S1 — вспомогательная переменная.

В данной программе используются встроенные функции языка Pascal:

Pos(S1, S2) — поиск подстроки S1 в строке S2 ;

Delete(S, N, M) — удаление из строки S M символов, начиная с позиции N;

Copy(S, N, M) — выделение подстроки из M символов, которые располагаются в строке S начиная с позиции N.

Проанализируем текст программы на языке QBASIC:

1. формируется тело программы, и описываются переменные;
2. вводится строка символов S;
3. определяется местоположение первой точки в тексте — М1;
4. ищется вторая точка в строке (поиск начинается с символа М1 + 1); если в строке есть две точки, то на экран выводится текст, находящийся между двумя точками, если нет — сообщение «В тексте нет двух точек».

Используемые переменные:

S — строка текста;

Ml, M2 — номера позиций двух точек; если точек нет, то значения Ml и М2 равны нулю.

В данной программе используются встроенные функции языка:

INSTR(N, X$, Y$) — поиск подстроки Y в строке X, начиная с N-го символа (N можно опустить);

MID$(X$, N, M) — выделение M символов, начиная с N-го символа в символьном выражении X$ (M можно опустить).

Ответ: данная программа из заданной строки символов выделяет подстроку между первой и второй точкой.

Пример 5. Проанализировать тексты программы.

Решение.

1. Формируется тело программы и описываются переменные и двумерный массив MАS;
2. вводится фактический размер массива MAS и значения его элементов;
3. просматриваются строки массива справа налево, находиться минимальный элемент в строке и запоминаются значения индексов (номер столбца) этого элемента;
4. для каждой строки выводится значение и местоположение самого правого минимального элемента.

Используемые переменные:

MAS — двумерный массив;

N, M — количество строк и столбцов массива;

I, J — переменные цикла;

JM — столбец минимального элемента для данной строки;

MIN — текущий минимум.

Ответ: программа решает задачу поиска в каждой строке двумерной матрицы минимального элемента и его координат. Если таких элементов в строке несколько, то выводится значение и координаты самого правого элемента.

Поиск и исправление ошибок в небольшом фрагменте программы (10±20 строк)

Существует три аспекта проверки программы:

1. на правильность;
2. на эффективность реализации;
3. на вычислительную сложность.

Эти проверки, вместе взятые, направлены на получение экспериментального ответа на вопросы: работает ли алгоритм и насколько хорошо он работает? Предполагается, что проверка правильности удостоверяет, что программа делает в точности то, для чего она была предназначена. Проверка эффективности реализации направлена на поиск способов «заставить» правильную программу работать быстрее или расходовать меньше памяти. Чтобы улучшить программу, пересматриваются результаты этапа реализации в процессе построения алгоритма.

Проверка вычислительной сложности сводится к экспериментальному анализу сложности алгоритма или к экспериментальному сравнению двух или более алгоритмов, решающих одну и ту же задачу.

Наличие ошибок в только что разработанной программе — вполне нормальное, закономерное явление. Составить реальную (достаточно сложную) программу без ошибок практически невозможно. Нельзя делать вывод, что программа правильна, лишь на том основании, что она считает и выдает результаты.

Текст программы можно проконтролировать за столом с помощью просмотра, проверки и прокрутки.

Просмотр. Текст программы просматривается на предмет обнаружения явных ошибок и расхождений с алгоритмом. Нужно просмотреть организацию всех циклов, чтобы убедиться в правильности операторов, задающих кратности циклов. Полезно просмотреть еще раз условия в условных операторах, аргументы в обращениях к подпрограммам и т. п.

Проверка. При проверке программы программист по тексту программы мысленно старается восстановить тот вычислительный процесс, который определяет программа, после чего сверяет его с требуемым алгоритмом.

Прокрутка. Основой прокрутки является имитация программистом за столом выполнения программы на машине. Для выполнения прокрутки приходится задаваться какими-то исходными данными и производить над ними необходимые вычисления.

Прокрутка — трудоемкий процесс, поэтому ее следует применять только для контроля логически сложных участков программы.

После просмотра программы вручную ее необходимо отладить и протестировать на компьютере.

Отладка — это процесс поиска и устранения ошибок в программе, производимый по результатам ее прогона на компьютере.

Тестирование — это испытание, проверка правильности работы программы в целом или ее составных частей.

Отладка и тестирование — два разных этапа:

• при отладке происходит локализация и устранение синтаксических ошибок и явных ошибок кодирования;
• в процессе тестирования проверяется работоспособность программы, не содержащей явных ошибок. Тестирование устанавливает факт наличия ошибок, а отладка выясняет их причину.

Как бы тщательно ни была отлажена программа, решающим этапом, устанавливающим ее пригодность для работы, является контроль программы по результатам ее выполнения на системе тестов. Программу условно можно считать правильной, если ее запуск для выбранной системы тестовых исходных данных во всех случаях дает правильные результаты.

Тестовые данные должны обеспечить проверку всех возможных условий возникновения ошибок. Процесс тестирования можно разделить на три этапа:

1. Проверка в нормальных условиях. Предполагает тестирование на основе данных, которые характерны для реальных условий функционирования программы.
2. Проверка в экстремальных условиях. Тестовые данные включают граничные значения области изменения входных переменных, которые должны восприниматься программой как правильные данные. Типичными примерами таких значений являются очень маленькие или очень большие числа и отсутствие данных. Еще один тип экстремальных условий — граничные объемы данных. Например, когда массивы состоят из слишком малого или слишком большого количества элементов.
3. Проверка в исключительных ситуациях. Проводится с использованием данных, значения которых лежат за пределами допустимой области изменений.

Ошибки могут быть допущены на всех этапах решения задачи. Разновидности характерных ошибок:

• Неправильная постановка задачи — верное решение неверно сформулированной задачи.
• Неверный алгоритм — выбор алгоритма, приводящего к неточному, неэффективному решению задачи.
• Ошибки анализа — неполный учет ситуаций, которые могут возникнуть; логические ошибки.
• Семантические ошибки — неправильный порядок выполнения операций.
• Синтаксические ошибки — нарушение правил, определяемых языком программирования.
• Ошибки при выполнении операций — слишком большое число (переполнение), деление на нуль, извлечение квадратного корня из отрицательного числа и т. п.
• Ошибки в данных — неправильное определение возможного диапазона изменения данных.
• Опечатки — перепутаны близкие по написанию символы, например цифра 1 и буква I.
• Ошибки ввода/вывода — неверное считывание входных данных, неверное задание форматов, отсутствие некоторых данных.

В качестве примера рассмотрим программу, в которой вычисляется значение функции по приведенным формулам в зависимости от значения параметра K, который является номером режима.

$y(x)={table√{a_1x^2+b_1x+c_1}, text»если» K=1; √{a_2x^2+c_2}, text»если» K=2; √{b_3x+c_3}, text»если» K=3;$

Программа имеет вид

Ошибки, допущенные при написании программы:

1. Пропущен ввод исходных данных А1, B1, C1, A2, C2, B3, C3; пропущено описание переменной Y (для языка Pascal).
2. В приведенной программе не предусмотрена обработка ситуации, когда под корнем получается отрицательное значение. Необходимо использовать условный оператор для определения положительности подкоренного выражения.
3. Отсутствует анализ ситуации, когда вместо цифр 1, 2, 3 для переменной К считана другая цифра. В этом случае, можно выдавать, например, сообщение: «Номер режима неверен». Для выдачи такого сообщения в программе в саsе-операторе после строки с меткой 3 нужно добавить строку вида else <Печать сообщения> (вариант 1). Можно также организовать ввод параметра K с проверкой введенного значения, и при ошибочном вводе требовать повторения ввода значения для переменной K (вариант 2).

Пример откорректированной программы (вариант 1).

Пример откорректированной программы (вариант 2).

Создание собственной программы (30±50 строк) для решения простых задач

Процесс создания компьютерной модели можно представить как путь от постановки задачи до реализации модели на компьютере. При разработке компьютерной модели очень важен выбор программного обеспечения (ПО), с помощью которого будет реализована модель. Возможны два основных варианта выбора — это, во-первых, прикладное ПО и, во-вторых, среда программирования. Если в качестве ПО была выбрана среда программирования, то построение компьютерной модели завершается созданием программы.

При написании программы прежде всего следует четко уяснить задачу, которую должна решать программа. Затем предварительно разработанный алгоритм решения задачи записывается в виде упорядоченной последовательности команд (инструкций), т. е. составляется программа, ориентированная на определенную среду программирования.

При написании программы обязательно следует проверять, насколько она соответствует намеченной цели, т. е. делает ли программа для всех наборов данных то, что от нее требуется, не выполняет ли она каких-либо лишних действий. Основное внимание следует сосредоточить на предотвращении логических ошибок. Для этого рекомендуется перед написанием программы построить блок-схему алгоритма решения или словесный алгоритм, что позволит абстрагироваться от конкретного языка программирования и сосредоточиться на анализе алгоритма.

Примеры разработки программ

Пример 1. Составить словесный алгоритм, разработать блок-схему и написать программу проверки принадлежности введенного числа данной арифметической прогрессии. Прогрессия задается двумя последовательными членами.

Решение. Словесный алгоритм.

Начало алгоритма

1. Ввести два последовательных члена арифметической прогрессии: A1, A2.
2. Ввести произвольное целое число C.
3. Найти разность (D) арифметической прогрессии.
4. Найти разность между введенным числом C и членом арифметической прогрессии, например A1.
5. Найти остаток от деления нацело найденной разности на D.
6. Если остаток от деления равен 0, то это значит, что число C принадлежит рассматриваемой арифметической прогрессии»; иначе получаем, что число C не принадлежит рассматриваемой арифметической прогрессии.

Конец алгоритма.

Блок-схема алгоритма:

Программа:

Примечание. Mod — операция, результатом которой является остаток от целочисленного деления.

Пример 2. Составить словесный алгоритм, алгоритм в виде блок-схемы и написать программу поиска в строковом массиве, содержащем фамилии 10 учеников, заданной фамилии, обеспечить запоминание ее порядкового номера (массив фамилий может быть неупорядочен).

Решение.

Словесный алгоритм

Начало алгоритма

1. Ввести все десять фамилий (строковый массив из 10 элементов).
2. Ввести фамилию, которую нужно найти.
3. Сравнивать ее с очередным элементом строкового массива, пока не будет найдена такая же фамилия или пока не закончится список (массив).
4. Если фамилия найдена, вывести ее номер в списке (массиве), если нет — сообщить о том, что фамилия не найдена.

Конец алгоритма.

Блок-схема алгоритма

Программа:

План урока:

Способы решению задач по логике

Табличный способ – этапы, особенности

Сравнение методов решения

Построение таблиц истинности для различных типов задач

Построение электрических схем, реализующих логические операции

Способы решения задач по логике

Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:

• рассуждая над условием;
• решая логические операции;
• используя таблицы истинности.

Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.

Этапы решения логических задач:

• Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
• Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
• Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
• Проверить, соответствует ли полученный результат условию задачи.

Табличный способ – этапы, особенности

Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.

Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.

Метод таблиц

Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.

Существует общий алгоритм построения таблиц:

• Определить число логических значений/переменных (n) в примере.
• Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
• Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
• Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
• Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2ⁿ+ 1 (шапка).
• Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
• Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
• Сделать выводы на основании полученных результатов.

Если необходимо перебрать все значения простых выражений, то для задач:

• с 2-мя переменными может быть только 4 набора логических переменных;

Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.

 Обязательно учитывают приоритет операций:

• Указанные в скобках.
• Отрицание.
• Логическая конъюнкция чисел.
• Дизъюнкция.
• Строгая дизъюнкция.
• Импликация.
• Эквивалентность.

Обозначение логических операций:

Сравнение методов решения

Метод рассуждений

Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.

Пример №1.

Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.

Известно, что:

• дом плотника правее егеря;
• стоматолог проживает левее егеря;
• дом гитариста с самого краю;
• стоматолог живет рядом с гитаристом;
• Владимир не гитарист, и его дом не соседствует с гитаристом;
• дома Дмитрия и егеря соседние;
• здание, в котором прописан Андрей, правее стоматолога;
• между домами Андрея и Дмитрия один дом.

Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:

Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:

Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.

Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.

Такой подход лучше не использовать, если условие сложное или много данных.

Табличный метод

Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).

Чтобы построить таблицу истинности логических выражений, следует:

• Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
• Записать условие задачи, как составное выражение из символов логических операций.
• Нарисовать таблицу истинности для полученных данных.
• Выбрать такой вариант, при котором полученные значения подходят под условие.
• Проверить соответствие выбранного варианта и условия задачи.

Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:

Рассмотрим тот же пример.

Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:

Метод компактнее, для некоторых задач нагляднее.

Построение таблиц истинности для различных типов задач

Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.

Пример 2.

Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.

Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:

А — «Первый студент летал в Англию»;

В — «Второй студент летал в Англию»;

С — «Третий студент летал в Англию».

Запишем выясненные данные при помощи логических операций:

Пример 3.

Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:

• Если А получит максимальный бал, то максимальный бал получат Ви С.
• А и С получат или не получат максимальный бал одновременно.
• Необходимым условием получения высшего бала С класса является получение высшего бала В классом.

По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.

Выясним, какие же классы добились высшего бала.

Разбиваем условие задачи на элементарные высказывания:

А – «А добьется высшего бала»;

В – «В добьется высшего бала»;

С – «С добьется высшего бала».

Запишем логические операции, описанные в примере:

Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.

Пример 4.

Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:

• последняя – гласная (Х1);
• или первая буква согласная (Х2)
• вторая – согласная (Х3).

¬(Х1→Х2)VХ3

Предложенные имена: Арина, Артур, Кэтрин, София.

Решим задачу, используя таблицу.

Сначала решим пошагово, выполняя операции по приоритету:

Указанному условию соответствует первое имя.

Пример 5.

Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.

Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.

Маша Марина: «Саша заняла второе место, а Света – первое».

Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».

Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».

Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».

Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».

Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.

Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.

 Построение электронных схем, реализующих логические операции

Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.

Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.

Электросхема с конъюнктором

 Рассмотрим все варианты:

• Все контакты включены, тогда источник света горит.
• Первый контакт в положении «выключено» – свет не горит.
• Второй контакт выключен – лампа не светит.
• Все контакты отключены – свет не горит.

Заключение – эта электрическая цепь реализует операцию «И».

Дизъюнктор, схема электропитания

Рассмотрим этот вид электрической цепочки:

• Все контакты включены – лампа горит.
• Первый контакт включен, второй выключен – свет горит.
• Обратная ситуация – выключен первый, включен второй – лампа светится.
• Все контакты выключены – света нет.

Заключение – такой вид электросхем соответствует логической операции «ИЛИ».

Инвертор в электросхемах

В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.

Заключение: схема соответствует логической операции «НЕ».

Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.

Обозначение логических элементов

Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.