Оригами-тетраэдр из бумаги – эффектный и многофункциональный декоративный элемент. В зависимости от модели, он может служить интерьерной подвеской, ёлочным украшением и частью модного настенного панно в скандинавском стиле. Тетраэдр – четырёхгранная пирамида, в основании которой лежит треугольник. Чаще всего для декора используют несколько таких фигур, объединённых в композицию.
Традиционный вариант
Объёмный тетраэдр-оригами можно сделать из классического квадрата или листа бумаги формата А4. Схема во втором варианте – сложнее, однако для долговечного декора лучше выбирать именно её. Модель получается многослойной, а потому меньше изнашивается в процессе эксплуатации.
Пошаговая инструкция:
Нам понадобится 2 альбомных листа. Складываем их поочерёдно по одному и тому же алгоритму.
- Располагаем лист короткой стороной к себе. Намечаем вертикальную ось симметрии.
- Правый нижний угол поднимаем к центральной линии из шага 1.
- Переворачиваем заготовку.
- Левый верхний угол опускаем, делая сгиб по линии, намеченной в шаге 2.
- Вот что должно получиться.
- Раскрываем изделие.
- Повторяем шаги 2-5 с другой стороны.
- Срезаем верхнюю часть по выделенной на схеме линии.
- Складываем левый верхний угол по пунктиру. Его вершину совмещаем с точкой, указанной стрелкой.
- Повторяем то же действие для правого нижнего угла.
- Вот такая полоска-«конверт» должна получиться.
- Повторяем шаги 1-10 для другого листа А4, но зеркально.
- Кладём один модуль поверх другого, как показано на схеме.
- Нижний элемент складываем в тетраэдр.
- Оборачиваем верхнюю часть вокруг получившейся фигуры.
- Вставляем оставшийся клапан в зазор, чтобы тетраэдр-оригами не распадался.
Эта модель великолепно смотрится в настенных панно:
Или мобильных подвесках:
Есть и немного другая схема сборки тетраэдра – из одного листа А4. Она представлена в видео-уроке:
Модель от Томоко Касахары
Японский оригамист предлагает сделать модель тетраэдра из квадратного листа. Схема сборки от Касахары настолько подробная, что изготовить по ней фигурку сможет даже начинающий. Для удобства рекомендуется использовать бумагу со сторонами разного цвета – это поможет следить за процессом складывания. Опытные мастера могут брать однотонные листы, что улучшит эстетические качества модели.
Пошаговая инструкция:
- Начинаем с изнанки листа. Делим квадрат пополам путём складывания. Намечаем «засечку» и раскрываем сгиб. Правую половину тоже складываем вдвое. Наносим отметку примерно на полпути вверх. Разворачиваем лист до исходного состояния.
- Делаем сгиб по пунктиру, ориентируясь на «засечки» из шага 1.
- Повторяем аналогичное действие с противоположной стороны.
- Опускаем верхний край на 1 см.
- Подгибаем уголки по стрелкам.
- Раскрываем все складки, кроме последних. Делим новый квадрат пополам по горизонтали.
- Намечаем диагональные сладки в местах, указанных пунктиром.
- Делаем короткие боковые сгибы по стрелкам. Важно каждый раз совмещать нижний край клапана с меткой по центру.
- Предварительные сгибы нанесены, теперь можно переходить к складыванию объёмной фигуры. Нижний левый угол сгибаем по пунктирной линии до пересечения, указанного стрелкой.
- Далее совмещаем его с вершиной треугольника.
- Точку 1 опускаем до конца стрелки, а затем откидываем клапан 2, чтобы зафиксировать последний сгиб.
- Получившаяся фигура напоминает перевёрнутый рожок для мороженого. Нажимаем на складки в правой части модели, поднимаем точку 1 вверх, как показано на схеме, и «заправляем» под клапан. Тетраэдр-оригами почти готов, но у него остаётся одна лишняя грань. Чтобы завершить сборку, точку 2 перемещаем по стрелке и фиксируем клапаном.
Освоив схему сборки тетраэдра Касахары, можно также изготавливать из бумаги своими руками эффектные подарки – разнообразные панно и картины:


Очень простая двухцветная модель
Необычно и эффектно смотрится тетраэдр из двух половинок. Каждую можно сложить из бумаги другого цвета, что сделает геометрический декор ещё интереснее. Если предыдущие модели адресованы, скорее, опытным мастерам, эта – как раз по плечу начинающим.
Пошаговая инструкция:
- Сгибаем квадрат по диагонали «горой». Делим пополам, складывая слева направо и сверху вниз. Делаем складки и раскрываем.
- Намечаем сгиб слева по пунктирной линии. Соединяем вершину угла с ближней засечкой.
- Аналогичные сгибы делаем ещё с трёх сторон.
- Все четыре края складываем по пунктирным линиям. Центральные треугольники выступают вверх, образуя так называемые «заячьи уши». Раскрываем их изнутри и сплющиваем.
- Сгибаем фигуру пополам «долиной».
Аналогичным образом собираем вторую часть. Остаётся склеить двухцветный тетраэдр из бумаги и придумать ему применение.
Декор из картона
Рассматривая варианты оригами-тетраэдра, нельзя обойти вниманием фигуры, изготовленные другим способом, но не менее популярные. Речь идёт о картонных моделях, которые складываются из развёртки, как упаковочные коробочки. Скачиваем трафарет правильного тетраэдра:
Остаётся распечатать его на цветной картон и вырезать заготовки, а затем склеить:
Звёздчатый многогранник
Самая красивая модель получается из нескольких тетраэдров, соединённых между собой. Этот так называемый звёздчатый многогранник, легко сделать своими руками из картона. Тетраэдры собирают из отдельных граней – узких полосок, сложенных «уголком». Именно поэтому нужна не бумага, а плотный картон, иначе ажурная конструкция быстро сомнётся под собственным весом.
Число выступов декоративного кристалла может быть разным. Максимум можно использовать 5 взаимно пересекающихся тетраэдров. Их размер для схемы не важен, но соотношение сторон исходного листа должно составлять 1:3.
Пошаговая инструкция:
Для начала запасаемся листами тонкого дизайнерского картона. Для звезды диаметром 16,5 см нам понадобится 30 прямоугольников размером 5х15 см. Можно выбрать другие параметры, главное, сохранить указанные пропорции. Чтобы не запутаться, рекомендуем делать полосы партиями по 6 штук разного цвета.
- Первую полосу сгибаем вдвое по высоте. Раскрываем складку.
- Оба края сводим к середине.
- Делаем складку-засечку «долиной».
- Левый угол сгибаем, чтобы красная точка коснулась отметки из шага 3. Раскрываем.
- С помощью обратной складки заводим левый угол внутрь.
- Раскрываем правую сторону. «Прячем» выступающий уголок. И вновь закрываем правую половину.
- Намечаем складку «долиной» с другой стороны.
- Повторяем шаги 3-7 на противоположном конце полосы.
Таких заготовок понадобится 30 штук. На лицевой стороне делаем складку «долиной», а на обороте – «горой».
Начинаем сборку пирамидок. Для первой используем 6 красных элементов. Верхний угол намечаем небольшой бумажной полоской, чтобы в дальнейшем упростить себе работу.
Остальные грани собираем и склеиваем по 3 штуки. Тщательно проходим стыки, тогда конструкция получится прочной и долговечной.
К первому красному тетраэдру добавляем полуготовую фигуру из 3-х граней. Ориентируемся на фото-образец. Теперь фиксируем второй – жёлтый тетраэдр, приклеивая ещё 3 недостающие грани.
Аналогичным образом вставляем следующую заготовку, например, голубого цвета и закрепляем её.
Поворачиваем тетраэдр-звезду другой стороной и продолжаем работу.
Следим, чтобы каждая добавленная фигура располагалась под тем же углом, что и остальные.
Последний, фиолетовый, многоугольник крепим с особой тщательностью.
Прежде чем приклеить 3 завершающие грани, несколько раз осматриваем звезду под разными углами. Желательно добиться идеальной симметрии.
Казалось бы, сложная конструкция, на деле требует только аккуратности, внимания и терпения, как и остальные модульные многогранники.
Тетраэдр из картона послужит отличным украшением праздничного интерьера или, например, магазинной витрины.
А эксцентричные невесты вполне могут заменить им свадебный букет.
Звёздчатый многогранник – единственный способ сложить оригами-тетраэдр из модулей. Есть и не менее интересные варианты:
Интересные факты
Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.
Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.
В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.
Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.
Мы этого не замечаем, но вокруг нас существует огромное количество объемных геометрических фигур. Практически все технические устройства, дома, мебель и автомобили созданы с их применением. Именно поэтому знакомство с многогранниками начинается еще в школе. Представление тел в 3D — измерении лишь только кажется сложным и скучным. Рассмотрим доступные инструкции, как сделать из бумаги объемные фигуры геометрической формы, а также интересные примеры поделок из них.
Содержание
- 1. Как правильно сделать объемные фигуры из бумаги и картона
- 2. Развертки простых объемных геометрических фигур
- 2.1. Шаблон для склеивания параллелепипеда
- 2.2. Правильная четырехгранная пирамида
- 2.3. Правильна многогранная пирамида
- 2.4. Непростая развертка усеченной пирамиды
- 2.5. Развертка шестигранной призмы
- 2.6. Как правильно сделать круглый конус
- 2.7. Развертка цилиндра
- 3. Шаблоны и схемы правильных выпуклых многогранников
- 3.1. Тетраэдр или фигура из четырех равносторонних треугольников
- 3.2. Куб или гексаэдр, то есть фигура из шести квадратов
- 3.3. Фигура октаэдра состоит из 8 равносторонних треугольников
- 3.4. Додекаэдр, то есть фигура из 12 правильных пятиугольников
- 3.5. Икосаэдр, то есть фигура из 20 равносторонних треугольников
- 4. Забавные приключения объемных геометрических фигур: модели, фигурки животных, декор
- 5. Комментарии посетителей по теме статьи
Как правильно сделать объемные фигуры из бумаги и картона
Удобнее всего выполнить задание, используя плотную бумагу или картон. Разумеется, необходимо знать, как выглядит требуемая фигура в 3D – формате. Кроме того, необходимо начертить или распечатать схему развертки многогранника. Чаще всего макет склеивают, и для этого чертеж должен иметь соответствующие припуски материала. Впрочем, многие геометрические фигуры дети могут сделать своими руками в технике оригами из нескольких листов бумаги, то есть без клея.
Имея навыки черчения, схему несложно начертить на бумаге самостоятельно. Грани фигур состоят из треугольника, квадрата, ромба, круга, трапеции или другого многоугольника. При этом ребра многогранников должны иметь точный одинаковый размер, иначе фигуру не получится собрать. В случае одинаковых граней можно подготовить шаблон одной из них, а затем его обвести, формируя полный чертеж развертки.
Чтобы грани были аккуратными, ровными, рекомендуется подготовить линии изгибов, прочертив их тупой стороной иглы по металлической линейке. Таким образом, в общей сложности для работы потребуются:
- тонкий картон или плотная бумага;
- карандаш и линейка;
- клей для бумаги и канцелярские ножницы.
Из цветного материала получится веселая и привлекательная фигурка. Лучший вариант клея – ПВА.
Развертки простых объемных геометрических фигур
Грани объемных фигур вовсе не обязаны быть одинаковыми. Получается большое разнообразие возможных вариантов, и мы рассмотрим основные из них.
Шаблон для склеивания параллелепипеда
Тривиальный параллелепипед встречается повсюду. Фигура имеет шесть граней в виде параллелограммов. Если его грани прямоугольные, значит и параллелепипед – прямоугольный.
При вычерчивании шаблона для изготовления фигуры необходимо обеспечить углы 90°, а прямоугольники должны быть попарно одинаковые. В следующем примере грани фигуры образуют ромбы, а не параллелограммы. Удобно изготовить шаблон одного из них, а затем обвести 6 раз.
Это видео поможет изготовить параллелепипед из бумаги или картона.
Правильная четырехгранная пирамида
Такая пирамида называется правильной не потому, что хорошо себя ведет, а потому, что в ее основании — равносторонняя геометрическая фигура. В данном случае это квадрат. Чертеж выполнить очень просто: сначала изображаем квадрат, а к нему пристыковываем 4 одинаковых треугольника. К ним добавляем 4 припуска на склейку.
Можно распечатать шаблон с формулами расчета параметров фигуры. Очень поможет на уроке!
Это видео поможет изготовить пирамиду из бумаги.
Кстати, из правильной четырехгранной пирамиды получается оригинальная коробочка для подарка. Ее лучше изготовить из плотной цветной бумаги. Другой вариант – сделать упаковку из картона и оклеить бумагой с рисунком. В верхней части треугольников нужно пробить отверстия дыроколом и пропустить через низ красивый шнурок с бантом.
Правильна многогранная пирамида
Непростая развертка усеченной пирамиды
Шаблон усеченной пирамиды — не самый простой. Его чертеж достаточно точно можно выполнить с помощью циркуля и линейки.
Для склейки фигуры следует оставить припуски в соответствии с рисунком.
Чертеж шаблона с конкретными размерам представлен на следующем фото.
Это видео поможет изготовить четырехгранную усеченную пирамиду своими руками.
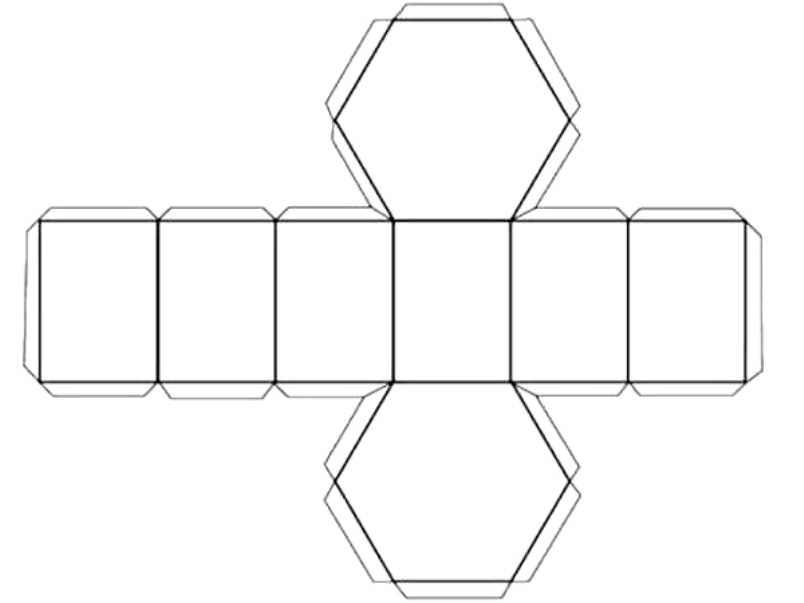
Развертка шестигранной призмы
Это видео поможет изготовить четырехгранную призму своими руками.
Как правильно сделать круглый конус
Проще всего шаблон для изготовления круглого конуса распечатать на принтере.
Припуски на склейку можно предусмотреть либо на круглом основании, либо на боковой поверхности конуса.
Это видео поможет правильно вырезать шаблон и склеить конус.
Развертка цилиндра
Добавляем припуски на склейку и получаем полноценный шаблон для изготовления цилиндра. Следующее видео поможет правильно вырезать шаблон и склеить цилиндр.
Шаблоны и схемы правильных выпуклых многогранников
Тетраэдр или фигура из четырех равносторонних треугольников
Другой вариант разметки шаблона – разделить пополам две противоположные стороны параллелограмма.
Грани тетраэдра можно раскрасить в разные цвета. Фигура станет веселее и поможет ребенку запомнить названия цветов.
Еще один вариант оформления тетраэдра – наклеить на его грани веселые детские картинки.
Грани тетраэдра можно отметить цифрами, чтобы упростить ребенку их запоминание.
Это видео поможет правильно вырезать и склеить тетраэдр.
Это видео поможет собрать 3D — фигуру в технике оригами, то есть без клея.
Куб или гексаэдр, то есть фигура из шести квадратов
Его развертку можно построить из квадратов, добавим припуски на склейку.
Грани гексаэдра можно отметить цифрами, чтобы упростить ребенку их запоминание.
Куб небольших размеров превращается в игральный кубик, если на его грани нанести маркером соответствующее количество точек.
Это видео поможет правильно вырезать и склеить куб.
Фигура октаэдра состоит из 8 равносторонних треугольников
Составляем параллелограмм из 3-х ромбов с углами 60° и добавляем короткие диагонали. Достраиваем снизу и сверху по треугольнику, а также добавляем припуски на склейку. Получаем шаблон для вырезания октаэдра.
Грани поделки можно оклеить веселыми картинками для детей.
Еще один вариант оформления – распечатать шаблон с формулами расчета параметров фигуры. Это поможет на уроке!
Далее видео изготовления звездчатого октаэдра.
Додекаэдр, то есть фигура из 12 правильных пятиугольников
Развертка додекаэдра состоит из 2-х одинаковых групп пятиугольников.
Грани фигуры можно украсить занимательными детскими картинками.
Это видео поможет собрать 3D — фигуру додекаэдра в технике оригами, то есть без клея.
Икосаэдр, то есть фигура из 20 равносторонних треугольников
Составляем параллелограмм из 5-ти ромбов с углами 60° и проводим короткие диагонали. Достраиваем снизу и сверху по 5 треугольников, а также добавляем припуски на склейку. Получаем шаблон для вырезания икосаэдра.
Есть еще один вариант шаблона, который удобен для вырезания из квадратного листа бумаги.
Возможно, такая схема шаблона покажется более понятной.
Это видео поможет правильно вырезать шаблон и склеить икосаэдр.
Если по заданию учителя изготовить не один, а два икосаэдра, можно собрать композицию снеговика и гарантированно рассчитывать на 5 баллов!
Один икосаэдр должен быть чуть больше другого. Склеиваем их вместе и подрисовываем фломастерами глаза, щеки и пуговички у снеговика. Нос – маленькая пятигранная пирамида, которую нужно сделать из красной бумаги.
Забавные приключения объемных геометрических фигур: модели, фигурки животных, декор
Освоив изготовление объемных геометрических фигур по заданию учителя, самое время сделать теперь что-то повеселее. Используя полученные навыки, можно создать своими руками 3Д — фигурки животных и героев мультфильмов, коробочки для подарков, сами праздничные подарки, элементы украшения комнаты и прочие поделки для детей. Рассмотрим наиболее интересные пошаговые инструкции для учащихся и дошкольников.
Так, шестигранная призма превращается в карандаш, если ее увенчать шестигранной же пирамидой. Шаблон следует раскрасить в соответствии с фото, и тогда получится полная аналогия.
Дети очень любят фигурки животных. Используя приведенную выкройку, можно изготовить очаровательную таксу.
С помощью такого шаблона можно изготовить игрушечный домик. В следующем видео Вы найдете еще один вариант домика из бумаги.
Таким образом из объемных геометрических фигурок можно построить целый город.
Как известно, из цветной бумаги делают самые разные цветы. При этом, даже если бутоны представляют из себя объемные геометрические фигуры, из них можно сформировать очаровательный букет.
Один из вариантов сборки красочных бутонов представлен в следующем мастер-классе. Шаблон представляет из себя восьмиконечную звезду.
В итоге получаются вот такие фигуры. Их собирают с помощью клея ПВА.
Объемные геометрические фигуры, изготовленные из цветной бумаги и картона, удивительным образом подходят для оформления интерьера.
Достаточно подвесить их на нитях к потолку, и необычное оформление комнаты к празднику обеспечено.
Впрочем, и на столе они произведут неизгладимое впечатление. Подобные украшения легко изготовить к празднику, так же просто и выбросить их после окончания торжества.
Как Вам такая вазочка с набором желаний, которые размещены внутри уже знакомых фигур? Просто и со вкусом.
Собирайте своими руками объемные геометрические фигуры и радуйтесь их прямой и правильной красоте!
Тетраэдр, сделанный из бумаги или картона можно использовать в качестве модели, объясняя школьнику особенности этой фигуры в геометрии. Ещё самодельные объёмные фигуры можно использовать для декора комнаты или рабочего стола. Чтобы научиться делать тетраэдр своими руками, нужно прочесть несколько поэтапных инструкций по изготовления фигур из разных материалов.
Особенности фигуры, сколько граней и углов у тетраэдра
Тетраэдр – это объёмная геометрическая фигура треугольной формы. Она выглядит как пирамида. У тетраэдра 6 ребер, 4 вершины и 4 грани. Размеры и формы граней зависят от вида геометрической фигуры.
Какими бывают тетраэдры:
| Равногранный | Грани равны между собой. |
| Ортоцентрический | Высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке. |
| Прямоугольный | Ребра, прилежащие к 1 из вершин, перпендикулярны между собой. |
| Инцентрический | Отрезки фигуры соединяют вершины с центральными точками окружностей, вписанных в противоположные грани и пересекающихся в 1 точке. |
Самый простой вид фигуры называется «правильный тетраэдр». Его грани – это односторонние треугольники. Собрать правильный тетраэдр из бумаги или картона намного проще, чем другие виды этой фигуры. Далее в статье можно рассмотреть примеры построения развёрток, а также прочесть инструкцию по склеиванию объёмной фигуры.
Что понадобиться, чтобы сделать тетраэдр своими руками
Перечень материалов и инструментов, необходимых для создания бумажного, либо картонного тетраэдра:
- тонкий картон;
- бумага или жесткий картон;
- простой карандаш;
- линейка;
- транспортир;
- ножницы, канцелярский нож;
- клей карандаш или клей «Момент».
Желательно, чтобы бумага, на которой будет построен чертеж, была плотной. Подойдут листы для черчения, акварельная бумага или листы из альбома. Можно использовать бумагу для принтера, плотностью не менее 80 г/кв. м. Более тонкий материал будет плохо держать форму, а также рваться и мяться в процессе склеивания фигуры.
Как сделать из бумаги А4
Изготовление тетраэдра проходит в 5 этапов:
- расчет размера;
- подготовка шаблона из тонкого картона;
- составление чертежа;
- вырезание детали;
- склеивание фигуры.
Для склеивания бумажных конструкций можно использовать обыкновенный канцелярский клей или ПВА. Для фигур, сделанных из более плотных материалов, желательно использовать клей «Момент» или качественный двухсторонний скотч без мягкой прослойки между клеевыми лентами.
Расчет размера
Размер будущей фигуры зависит вида развертки. Грани можно расположить по кругу. В таком случае фигура получиться небольшой. Высота такого тетраэдра будет около 6 см. Если начертить горизонтальную развёртку, где грани будут расположены в таком порядке, что образуют фигуру в виде параллелограмма. В таком случае, можно получить более крупную фигуру.
Оптимальная длина ребра тетраэдра, начерченного в горизонтальной развертке на листе формата А4 – 10 см.
В итоге получится параллелограмм с диагональю равной 26,6 см. Размер листа формата А4 равен 21×29,7 см. Диагональ листа равна 36,4 см. Поэтому развертка с диагональю 26,6 см идеально поместиться на бумаге А4, и еще останется свободнее место, чтобы начертить полосы для склеивания фигуры.
Подготовка шаблона из картона
Из картона можно сделать шаблон 1 грани тетраэдра, чтобы потом было проще построить развертку.
Как сделать заготовку поэтапно:
- На тонком картоне, с помощью линейки и простого карандаша, провести горизонтальную линию, равную длине ребра фигуры.
- Приложить к левому концу линии транспортир. Поставить отметку на 60 градусах.
- Приложить транспортир к правому углу линии, также отметить 60 градусов.
- Через отметки провести 2 линии.
- Измерить длину линий до места их пересечения. Все 3 стороны фигуры должны быть равны.
Ножницами аккуратно вырезать шаблон.
Построение развертки, чертежи
Как начертить круговую развертку тетраэдра с помощью картонного шаблона:
- Разместить треугольник в центре листа, расположив острым углом вниз. Обвести шаблон по контуру, без нажима на карандаш.
- Приложить плоскую сторону шаблона к верхней части уже обведенного треугольника. Основание шаблона и начерченной фигуры должны совпасть. Обвести картонную заготовку.
- Переместить заготовку к левому краю первого треугольника. Их стороны также должны совпасть. Обвести шаблон.
- Переместить заготовку к правой стороне центрального треугольника. Снова обвести шаблон по контуру.
- Убрать картонную заготовку.
- С помощью линейки четко прочертить все линии. Ластиком исправить неточности. Измерить стороны треугольников. Они должны быть одинаковыми.
- С помощью линейки, отмерить 1,5 см от левой стороны верхнего треугольника. Начертить линию, параллельную этой стороне. Соединить края линий таким образом, чтобы образовались скошенные углы. То есть, длину новой линии нужно сократить на 10 мм (по 5 с каждого конца).
- По аналогии, начертить ещё 2 «ушка» для склеивания фигуры. 1 должно расположиться на нижней части треугольника, расположенного внизу, с лева. Другое «ушко» начертить на боковой стороне нижнего правого треугольника.
Ластиком удалить лишние линии.
Как начертить горизонтальную развертку тетраэдра, не используя картонный шаблон:
- Лист бумаги формата А4 расположить на столе горизонтально.
- От нижнего левого угла листа отступить вверх 2 см. Поставить точку и обозначить её буквой «А».
- От точки «А» отложить вправо отрезок равный 20 см. Конец линии отметить буквой «С».
- Разделить линию пополам, поставить точку «В».
- Приложить к точке «А2 транспортир и поставить отметку на 60 градусах.
- Приложить транспортир к отметке «В», отметить 60 градусов.
- Через точки провести 2 линии, до их пересечения.
- От вершины получившегося треугольника отложить вправо 10 см. Провести линию. Конец отрезка назвать «D».
- Приложить транспортир к точке «D», отметить 60 градусов вниз. Провести линию до точки «В».
- Соединить точки «С» и «D» линией.
- От точки «D» отложить вправо 10 см. Соединить конец этой линии с точкой «С» новой чертой.
- В итоге получится параллелограмм, разделённый на 4 равных треугольника. Треугольники нужно пронумеровать слева направо.
- На верхней части треугольника №2 начертить «ушко» для склеивания фигуры. Такие же «ушки» нужно сделать на нижней части треугольника № 3, и на боковой стороне треугольника № 4.
Когда чертеж будет готов, его нужно вырезать по контуру. Можно использовать ножницы или канцелярский нож.
Работа с готовой формой, склеивание
Склеить фигуру по вырезанной развертке несложно.
Порядок действий:
- Продавить все линии сгиба тупым предметом. Можно использовать линейку или высохший стержень от шариковой ручки.
- Сложить фигуру таким образом, чтобы чертеж расположился внутри.
- Проверить, совпадают ли размеры, нет ли больших просветов и других неточностей.
- Развернуть заготовку.
- Поочередно смазывая «ушки» для крепления клеем, собрать фигуру.
Располагать «ушки» для крепления нужно изнутри. Чтобы детали хорошо склеились, необходимо придерживать пальцами места соединений в течение 10-15 сек.
Большой тетраэдр из картона
Тетраэдр из картона (сделать поэтапно можно по инструкции, представленной далее в статье) получится крепким и будет хорошо держать форму. Размер объёмной фигуры зависит от вида картона.
Какой картон можно использовать для работы:
- Цветной (для детского творчества). Подойдет для создания тетраэдров высотой до 25 см. Этот картон довольно тонкий, поэтому крупная фигура, сделанная из него, будет неустойчивой. Грани могут прогнуться и деформироваться. Зато из цветного картона можно сделать разноцветный тетраэдр, если использовать для каждой грани лист другого цвета. В таком случае развёртка будет отличаться от стандартного варианта. Все грани потребуется начертить отдельно и добавить к ним «ушки» для крепления.
- Полиграфический. Этот картон более плотный. Его используют для создания твердого переплета книг и блокнотов, а также для упаковки мелкого товара. Из такого картона можно собрать тетраэдр высотой от 25 до 45 см.
- Упаковочный. Самый прочный тип картона. Он имеет гофрированную текстуру и состоит из нескольких слоев. Работать с таким материалом сложно, но из него получаются крепкие фигуры. Размер тетраэдров может быть более 45 см в высоту. Такие фигуры можно использовать для домашнего декора.
Не цветной картон после сборки тетраэдра можно покрасить или обклеить бумагой с узорами. Если на грани небольшой фигуры наклеить календарные листы или фотографии, можно получить необычное украшение для рабочего стола.
Особенности работы с жестким картоном
Тетраэдр из картона (сделать поэтапно развертку можно, не используя шаблоны) изготавливают следуя этим правилам:
- Для построения чертежа удобнее использовать длинную линейку (около 30 см). Составляя развёртку с короткой линейкой можно легко ошибиться. Из развёртки с погрешностями очень сложно собрать ровную фигуру.
- Вырезать заготовку нужно канцелярским ножом, прикладывая к линиям линейку. Использовать ножницы можно только для тонкого картона. На плотном материале не получится ровных срезов. В некоторых местах будут образовываться заломы.
- Чтобы согнуть упаковочный картон, его нужно продавить. Для этой цели не желательно использовать линейку или стержень от ручки. Эти инструменты могут повредить несколько слоев картона, а при сильном давлении, вовсе порвать его. Лучше воспользоваться тупым концом ручки или десертной ложки. Тогда линии получаться толще, но картон не порвётся.
- Когда деталь будет вырезана, необходимо осмотреть её со всех сторон и срезать мелкие заусенцы.
- Фиксировать «ушки» для склеивания нужно по очереди. Прежде, чем смазать клеем новое «ушко», нужно дождаться полного высыхания клея на предыдущем.
Удобнее всего работать с двухслойным гофрированным картоном. Его можно вырезать из большой коробки, в которой перевозят бытовую технику. С картоном, сложенным в 3 и более слоя, работать будет намного сложнее. Такой материал плохо гнется и тяжело склеивается.
Подготовка и вырезание шаблона
Тетраэдр из картона (сделать поэтапно можно за 1 ч) можно изготовить, используя любой вид развертки. В этом мастер-классе описан процесс составления круговой развертки, без использования шаблона.
Порядок действий:
- В центре картонного листа начертить горизонтальную линию, длина которой будет равна размеру ребра фигуры.
- К левому концу линии приложить транспортир. Отметить 60 градусов.
- Приложить транспортир к правому концу линии. Отметить 60 градусов.
- Через отметки провести 2 линии до их пересечения. Должен получиться равносторонний треугольник.
- От вершины треугольника, отложить 60 градусов с левой стороны. Начертить новый треугольник сбоку. 1 его сторона станет общей с уже начерченной фигурой.
- Приложить транспортир к основе 1 фигуры. Отметить 60 градусов с обоих концов. Провести линии. Получилась 3 грань тетраэдра.
- Последнюю грань начертить по аналогии, приложив транспортир к правой стороне нижнего треугольника.
В итоге должна получиться развертка из 4 треугольных граней. Остается добавить «ушки» для крепления. Чем шире будут «ушки», тем надежнее будет соединение. Минимальная ширина этих полосок – 5 см.
Где должны располагаться «ушки»:
- на нижней стороне треугольника слева;
- на левой стороне верхнего треугольника;
- На правой стороне треугольника, расположенного справа.
Вырезать развертку канцелярским ножом.
Соединение граней
Как соединить грани фигуры:
- Продавать все линии сгиба.
- Согнуть детали по намеченным линиям.
- Придерживая грани 2 руками (можно попросить кого-нибудь о помощи), рассмотреть фигуру. Все стыки должны быть ровными, без заусенцев и просветов.
- Развернуть заготовку.
- Смазать 1 из «ушек» клеем. Желательно использовать клей «Момент», чтобы не приходилось долго ждать.
- Прижать ушко к внутренней стороне 1 из граней. Придавить пальцами.
- Приклеить еще 1 «ушко», по аналогии.
- Последнее место соединения нужно хорошо смазать клеем, и аккуратно вставить внутрь фигуры, слегка отодвинув пальцами стенку.
Дождаться полного высыхания клея. Если остались излишки (застывшие капли или паутинки), их можно аккуратно срезать канцлерским ножом.
Научиться делать тетраэдр из бумаги или картона помогут инструкции, где все действия расписаны поэтапно. Главное, составить точный чертеж, а затем аккуратно вырезать развертку, используя подходящие инструменты.
Видео о создании тетраэдра из картона
Как сделать треугольную пирамиду:
Оригами-тетраэдр из бумаги – эффектный и многофункциональный декоративный элемент. В зависимости от модели, он может служить интерьерной подвеской, ёлочным украшением и частью модного настенного панно в скандинавском стиле. Тетраэдр – четырёхгранная пирамида, в основании которой лежит треугольник. Чаще всего для декора используют несколько таких фигур, объединённых в композицию.
Декор из картона
Рассматривая варианты оригами-тетраэдра, нельзя обойти вниманием фигуры, изготовленные другим способом, но не менее популярные. Речь идёт о картонных моделях, которые складываются из развёртки, как упаковочные коробочки. Скачиваем трафарет правильного тетраэдра:
Остаётся распечатать его на цветной картон и вырезать заготовки, а затем склеить:
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Сложных фигур
3d
Октаэдра
Тетраэдра
Икосаэдра
Додекаэдра
Гексаэдра
Фигурок из треугольников
Звёздчатый многогранник
Самая красивая модель получается из нескольких тетраэдров, соединённых между собой. Этот так называемый звёздчатый многогранник, легко сделать своими руками из картона. Тетраэдры собирают из отдельных граней – узких полосок, сложенных «уголком». Именно поэтому нужна не бумага, а плотный картон, иначе ажурная конструкция быстро сомнётся под собственным весом.
Число выступов декоративного кристалла может быть разным. Максимум можно использовать 5 взаимно пересекающихся тетраэдров. Их размер для схемы не важен, но соотношение сторон исходного листа должно составлять 1:3.
Пошаговая инструкция:
Для начала запасаемся листами тонкого дизайнерского картона. Для звезды диаметром 16,5 см нам понадобится 30 прямоугольников размером 5х15 см. Можно выбрать другие параметры, главное, сохранить указанные пропорции. Чтобы не запутаться, рекомендуем делать полосы партиями по 6 штук разного цвета.
- Первую полосу сгибаем вдвое по высоте. Раскрываем складку.
- Оба края сводим к середине.
- Делаем складку-засечку «долиной».
- Левый угол сгибаем, чтобы красная точка коснулась отметки из шага 3. Раскрываем.
- С помощью обратной складки заводим левый угол внутрь.
- Раскрываем правую сторону. «Прячем» выступающий уголок. И вновь закрываем правую половину.
- Намечаем складку «долиной» с другой стороны.
- Повторяем шаги 3-7 на противоположном конце полосы.
Таких заготовок понадобится 30 штук. На лицевой стороне делаем складку «долиной», а на обороте – «горой».
Начинаем сборку пирамидок. Для первой используем 6 красных элементов. Верхний угол намечаем небольшой бумажной полоской, чтобы в дальнейшем упростить себе работу.
Остальные грани собираем и склеиваем по 3 штуки. Тщательно проходим стыки, тогда конструкция получится прочной и долговечной.
К первому красному тетраэдру добавляем полуготовую фигуру из 3-х граней. Ориентируемся на фото-образец. Теперь фиксируем второй – жёлтый тетраэдр, приклеивая ещё 3 недостающие грани.
Аналогичным образом вставляем следующую заготовку, например, голубого цвета и закрепляем её.
Поворачиваем тетраэдр-звезду другой стороной и продолжаем работу.
Следим, чтобы каждая добавленная фигура располагалась под тем же углом, что и остальные.
Последний, фиолетовый, многоугольник крепим с особой тщательностью.
Прежде чем приклеить 3 завершающие грани, несколько раз осматриваем звезду под разными углами. Желательно добиться идеальной симметрии.
Казалось бы, сложная конструкция, на деле требует только аккуратности, внимания и терпения, как и остальные модульные многогранники.
Тетраэдр из картона послужит отличным украшением праздничного интерьера или, например, магазинной витрины.
А эксцентричные невесты вполне могут заменить им свадебный букет.
Звёздчатый многогранник – единственный способ сложить оригами-тетраэдр из модулей. Есть и не менее интересные варианты:
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Конуса
Пирамиды
Шестигранника
Макета с припусками
Параллелепипеда
Трапеции
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Многогранника
Параллелограмма
Интересные факты
Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.
Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.
В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.
Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.
Необычная головоломка
Хотите порадовать любимых деток необычной головоломкой или сделать незабываемый фотоальбом? Тогда вам пригодится небольшой мастер-класс по созданию куба-трансформера. На каждой грани такого кубика можно расположить картинку или фотографию, а внутри еще целых шесть картинок.
Для изготовления такого кубика вам понадобится:
- 12 картинок или фотографий;
- Клей;
- 8 кубиков с гранями по 4 см;
- Скотч.
Кубики можно взять самые обычные детские или склеить самому по такой развертке:
Для начала посмотрите места крепления кубиков:
Важно понимать! Весь секрет трансформаций такой головоломки состоит в правильном склеивании пар кубиков.
Чтобы было более понятно, рассмотрим этот процесс пошагово. Сначала склейте две пары кубиков так, как показано желтыми полосками на схеме:
Расположите эти четыре кубика рядом и склейте в местах, указанных синим цветом:
Поставьте кубики так, как показано на схеме. При этом желтая склейка окажется со стороны противоположной красной. Склейте по красным линиям:
Статья по теме: Воротник вязаный крючком: масте-класс со схемами и видео
Фото нужно расположить на четверке кубиков. Размер фотографий 8 на 8 см.
Важно приклеить фото аккуратно, особенно, если вы будете делать это при помощи клея. Иначе можно ненароком склеить те грани, которые отвечают за правильную трансформацию головоломки. Так что лучше воспользоваться горячим клеем или двусторонним скотчем.
Необычный фотоальбом из кубика-трансформера готов! Как его можно раскладывать и просматривать картинки, вы можете увидеть на фото:
Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Статья по теме: Закладка «Обезьянка» крючком с описанием и схемами
Японское изобретение
Настоящей головоломкой может стать не только сам куб, изобретенный японским ученым Наоки Йошимото в 1971 году, но и сборка этого необычного изделия. По данной схеме нужно собрать 48 пирамидок.
Как правильно собрать эту чудесную поделку и о ее трансформациях, вы можете наглядно посмотреть в данном видеоуроке:
На скорую руку
Сделать самостоятельно кубик можно путем применения простой техники – это всего 5 действий, которые под силу выполнить даже ребенку. Заготовка представляется на картинке.
Заготовка для куба
Последовательность действий представляется следующим образом:
1Для начала следует начертить представленную заготовку. Длина ребра куба может быть различным – в соответствии с требованиями. На рисунке приведен пример, как требуется чертить заготовку-развертку. Пунктирные линии указывают на прибавку, с помощью которой будут приклеиваться стороны будущего объемного куба.
2Заготовку можно просто распечатать и вырезать по пунктирным линиям.
3Далее требуется разрезать части в углах пунктирной прибавки – это позволит соединить и склеить куб. Дополнительно сгибают части по линии, собрав заготовку в кубик.
4Согнуть прибавки по линии, чтобы в последующем приклеить их к граням куба.
5Канцелярским клеем смазать стороны прибавки и приклеить их к сторонам куба, сформировав фигуру.
Это самый простой способ формирования куба, развертку которого можно сделать любых размеров. Во время сборки заготовку рекомендуется украсить – цифрами, фигурами, смайликами и прочими рисунками, которые задействуются в игре. Рисовать на сторонах во время заготовки проще, нежели потом отображать детали на готовом объемном кубе.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
к оглавлению ^
Из бумаги
Из картона
Развертки куба
к оглавлению ^
Треугольника
к оглавлению ^
Прямоугольника
к оглавлению ^
Цилиндра
Ромба
Призмы
к оглавлению ^
Задание 2 (построение прямоугольного треугольника)
Постройте на нелинованной бумаге треугольник , чтобы угол был прямым, длина стороны равнялась 15 см, а длина сторогы – 20 см.
Построим точку (Рис. 18).
Рис. 18. Точка
Проведем через точку прямую (Рис. 19).
Рис. 19. Прямая, проведенная через точку
Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон совпала с лучом, как показано на рис. 20.
Рис. 20. Построение прямого угла
Проведем по второй стороне прямого угла треугольника луч из точки и получим прямой угол (Рис. 21).
Рис. 21. Полученный прямой угол
Выполним построение сторон треугольника. Построим отрезок , который равен 15 см (Рис. 22).
Рис. 22. Отрезок
Построим отрезок , который равен 20 см (Рис. 23).
Рис. 23. Отрезок
Соединим полученные точки отрезком . Мы получили прямоугольный треугольник (Рис. 24) с прямым углом и сторонами см и см.
Рис. 24. Треугольник
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
к оглавлению ^
Конуса
к оглавлению ^
Пирамиды
к оглавлению ^
Шестигранника
к оглавлению ^
Макета с припусками
Параллелепипеда
к оглавлению ^
Трапеции
к оглавлению ^
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
к оглавлению ^
Многогранника
к оглавлению ^
Параллелограмма
Задание 1 (определение вида треугольников)
Назовите номера тупоугольных, остроугольных и прямоугольных треугольников на рисунке 16.
Рис. 16. Иллюстрация к заданию 1
Треугольник номер 1 – остроугольный, у него все углы острые. Треугольники номер 3 и 4 – тупоугольные, каждый из них имеет один тупой угол. Фигура номер 2 – прямоугольный треугольник. Проверим, действительно ли эта фигура имеет прямой угол, с помощью прямоугольного треугольника (Рис. 17).
Рис. 17. Проверка треугольника номер 2
Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
к оглавлению ^
Сложных фигур
3d
Октаэдра
к оглавлению ^
Тетраэдра
к оглавлению ^
Икосаэдра
к оглавлению ^
Додекаэдра
к оглавлению ^
Гексаэдра
Фигурок из треугольников
Виды углов
Развернутый угол. (Рис. 4)
Угол называется развернутым, если его стороны лежат на одной прямой.
Рис. 4. Виды углов: развернутый
Прямой угол (Рис. 5)
Прямой угол составляет половину развернутого.
Рис. 5. Виды углов: прямой угол
Прямой угол можно получить путем складывания бумаги. Сложив лист дважды, мы получим модель прямого угла, его составляют линии сгиба.
Приложим модель угла к углу на чертеже (Рис. 5) таким образом, чтобы углы и стороны совпали (Рис. 6).
| Рис. 5. Модель угла и угол на чертеже | Рис. 6. Модель угла, приложенная к углу на чертеже |
Мы убедились, что на чертеже действительно изображен прямой угол.
Для удобства определения, прямой угол или нет, используют особый инструмент – прямоугольный треугольник (Рис. 7).
Рис. 7. Прямоугольный треугольник
Непрямые углы делятся на острые (Рис. 
| Рис. 8. Виды углов: острый угол Острый угол меньше прямого (Рис. 10). Рис. 10. Сравнение острого и прямого угла |
Рис. 11. Виды углов: тупой угол
Тупой угол больше прямого (Рис. 12). Рис. 12. Сравнение тупого и прямого угла |
Макеты из бумаги
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
к оглавлению ^
Оригами
Дом
к оглавлению ^
Животные
Корабль
Применяется множество вариантов, как сделать кораблик из бумаги.
Простая схема.
Полигональные чертежи
Игрушки из фигур
Геометрические маски
к оглавлению ^
Карандаш
( 1 оценка, среднее 5 из 5 )