Загрузить PDF
Загрузить PDF
Человеку, не знакомому с использованием логарифмической линейки, она покажется работой Пикассо. Она имеет как минимум три различных шкалы, почти на каждой из которых цифры расположены даже не на одинаковом расстоянии друг от друга. Но разобравшись, что к чему, вы поймете, почему логарифмическая линейка была такой удобной во времена до изобретения карманных калькуляторов. Правильно расположив нужные цифры на шкале, вы сможете выполнить умножение двух любых чисел гораздо быстрее, чем выполняя расчеты на бумаге.
-
1
Обратите внимание на промежутки между цифрами. В отличие от обычной линейки, расстояние между ними не одинаковое. Наоборот, оно определяется по особой «логарифмической» формуле, меньше с одной стороны и больше с другой. Благодаря этому вы можете совместить две шкалы нужным образом и получить ответ на задачу по умножению, как описано ниже.
-
2
Метки на шкале. Каждая шкала логарифмической линейки имеет буквенное или символьное обозначение с левой или правой стороны. Ниже описаны общепринятые обозначения на логарифмических линейках:[1]
- Шкалы C и D похожи на одноразрядную вытянутую линейку, метки на которой расположены слева направо. Такая шкала называется «одноразрядной десятичной» шкалой.
- Шкалы A и B — «двухразрядные десятичные» шкалы. Каждая состоит из двух небольших вытянутых линеек, расположенных впритык.
- K — это трехразрядная десятичная шкала или три вытянутые линейки, расположенные впритык. Такая шкала имеется не на всех логарифмических линейках.
- Шкалы C| и D| аналогичны C и D, но читаются справа налево. Часто они имеют красную окраску. Они присутствуют не на всех логарифмических линейках.
- Логарифмические линейки бывают разные, поэтому и обозначение шкал может быть другим. На некоторых линейках шкалы для умножения могут быть помечены как A и B и находиться сверху. Независимо от буквенных обозначений, на многих линейках рядом со шкалами есть символ π, отмеченный в подходящем месте; в большинстве своем шкалы находятся напротив друг друга, либо в верхнем, либо в нижнем промежутке. Рекомендуем решить несколько простых задач на умножение, чтобы вы могли понять, правильно ли вы используете шкалы. Если произведение 2 и 4 не равняется 8, попробуйте использовать шкалы на другой стороне линейки.
-
3
Научитесь понимать деления шкалы. Посмотрите на вертикальные линии на шкале C или D и ознакомьтесь с тем, как они читаются:
- Основные цифры на шкале начинаются с 1 от левого края и продолжаются до 9, а затем завершаются еще одной 1 справа. Обычно все они нанесены на линейку.
- Вторичные деления, обозначенные чуть меньшими вертикальными линиями, разделяют каждую основную цифру на 0,1. Вас не должно сбивать с толку, если они обозначены как «1, 2, 3»; все равно они соответствуют «1,1; 1,2; 1,3» и так далее.
- Также могут присутствовать меньшие деления, которые обычно соответствуют шагу 0,02. Следите за ними внимательно, так как они могут исчезать в верхней части шкалы, где цифры находятся ближе друг к другу.
-
4
Не ожидайте получить точные ответы. При чтении шкалы вам часто придется приходить к «наиболее вероятному предположению», когда ответ не будет попадать тютелька в тютельку. Логарифмическая линейка используется для быстрых подсчетов, а не для максимальной точности.
- Например, если ответ находится между отметками 6,51 и 6,52, запишите то значение, которое вам кажется ближе. Если совсем непонятно, то запишите ответ как 6,515.
Реклама
-
1
Запишите числа, которые вы будете умножать. Запишите числа, которые подлежат умножению.
- В примере 1 этого раздела мы подсчитаем, сколько будет 260 x 0,3.
- В примере 2 мы подсчитаем, сколько будет 410 x 9. Это немного сложнее, чем пример 1, поэтому сначала рассмотрим более простую задачу.
-
2
Переместите десятичные точки для каждого числа. Логарифмическая линейка имеет цифры от 1 до 10. Переместите десятичную точку каждого умножаемого числа, чтобы они соответствовали своим значениям. После решения задачи мы переместим десятичную точку в ответе в нужное положение, что будет описано в конце раздела.
- Пример 1: чтобы подсчитать 260 x 0.3, начинайте вместо этого с 2,6 x 3.
- Пример 2: чтобы подсчитать 410 x 9, начинайте вместо этого с 4,1 x 9.
-
3
Найдите меньшие цифры на шкале D, затем передвиньте к ней шкалу C. Найдите меньшую цифру на шкале D. Сдвиньте шкалу C таким образом, чтобы «1» слева (левый индекс) располагалась на одной линии с этой цифрой.
- Пример 1: сдвиньте шкалу C таким образом, чтобы левый индекс совпал с 2,6 на шкале D.
- Пример 2: сдвиньте шкалу C таким образом, чтобы левый индекс совпал с 4,1 на шкале D.
-
4
Переместите металлический указатель ко второй цифре на шкале C. Указатель — это металлический предмет, который перемещается по всей линейке. Совместите указатель со второй цифрой вашей задачи на шкале C. Указатель будет указывать ответ к задаче на шкале D. Если он не перемещается так далеко, переходите к следующему шагу.
- Пример 1: переместите указатель к цифре 3 на шкале C. В этом положении он также будет указывать на 7,8 на шкале D или около того. Переходите к шагу 6.
- Пример 2: постарайтесь переместить указатель так, чтобы он указывал на 9 на шкале C. Это будет невозможно на большинстве линеек или указатель будет указывать на пустое место в конце шкалы D. Решение проблемы описано в следующем шаге.
-
5
Если указатель не перемещается к ответу, используйте правый индекс. Если указатель блокируется перегородкой в центре линейки или ответ расположен за пределами шкалы, то используйте немного иной подход.[2]
Сдвиньте шкалу C таким образом, чтобы правый индекс или 1 справа располагались над большим коэффициентом вашей задачи. Переместите указатель к другому коэффициенту по шкале C и прочтите ответ на шкале D.- Пример 2: переместите шкалу C таким образом, чтобы 1 справа совпала с 9 по шкале D. Переместите указатель к 4,1 по шкале C. Указатель показывает на шкалу D в точке между 3,68 и 3,7, поэтому наиболее вероятный ответ будет 3,69.
-
6
Прикидывайте правильную десятичную точку. Независимо от производимого умножения, ваш ответ всегда будет считываться по шкале D, которая содержит лишь цифры от одного до десяти. Вам не обойтись без предположения и умственного подсчета, чтобы определить местонахождение десятичной точки в фактическом ответе.
- Пример 1: нашей первоначальной задачей было 260 x 0,3, а линейка дала ответ 7,8. Округлите первоначальную задачу до удобных чисел и решите ее в голове: 250 x 0,5 = 125. Такой ответ гораздо ближе к 78, чем к 780 или 7,8, поэтому правильный ответ будет 78.
- Пример 2: нашей первоначальной задачей было 410 x 9, а линейка дала ответ 3,69. Прикиньте первоначальную задачу как 400 x 10 = 4000. Ближайшим числом будет 3690, которое и станет фактическим ответом.
Реклама
-
1
Возведение в квадрат по шкалам D и A. Эти две шкалы обычно неподвижны. Просто переместите металлический указатель к значению по шкале D, а значение по шкале A будет соответствовать второй степени числа.[3]
Как и в случае с умножением, положение десятичной точки придется определять самостоятельно.- Например, чтобы решить 6,12, переместите указатель к 6,1 по шкале D. Соответствующее значение по шкале A будет 3,75.
- Прикиньте 6,12 как 6 x 6 = 36. Расположите десятичную точку так, чтобы получить ответ, который примерно соответствует данному значению: 37,5.
- Обратите внимание, что точный ответ будет 37,21. Ответ на линейке дает погрешность в 1 %, чего вполне достаточно для практических задач.
-
2
Возведение в куб по шкалам D и K. Только что мы увидели как шкала A, которая соответствует шкале D, уменьшенной на 1/2, позволяет возвести число в квадрат. Аналогичным образом шкала K, которая соответствует шкале D, уменьшенной на 1/3, позволяет возвести число в куб. Просто переместите указатель к значению по шкале D и прочитайте результат на шкале K. Прикиньте расположение десятичной точки.
- Например, чтобы решить 1303, переместите указатель к 1,3 по шкале D. Соответствующее значение по шкале K будет 2,2. Так как 1003 = 1 x 106, и 2003 = 8 x 106, мы понимаем, что ответ будет где-то посредине. Ответ должен быть 2,2 x 106, или 2 200 000.
Реклама
-
1
Запишите число в экспоненциальном представлении для извлечения квадратного корня. Как и всегда, на линейке есть только значения от 1 до 10, поэтому для извлечения квадратного корня вам потребуется записать число в экспоненциальном представлении.
- Пример 3: для решения √(390) запишите задачу как √(3,9 x 102).
- Пример 4: для решения √(7100) запишите задачу как √(7,1 x 103).
-
2
Определите, какую сторону шкалы A необходимо использовать. Чтобы извлечь квадратный корень числа, для начала переместите указатель к этому числу по шкале A. Но так как шкала A нанесена дважды, необходимо решить, какую использовать.[4]
В этом помогут следующие правила:- Если экспонента вашего числа четная (как 2 в примере 3), используйте левую сторону шкалы A («первый десятичный разряд»).
- Если экспонента вашего числа нечетная (как 3 в примере 4), используйте правую сторону шкалы A («второй десятичный разряд»).
-
3
Переместите указатель по шкале A. Пока опустите экспоненту десяти и переместите металлический указатель по шкале A к необходимому значению.
- Пример 3: для решения √(3,9 x 102) переместите указатель к 3,9 слева по шкале A (используем левую шкалу, так как экспонента четная).
- Пример 4: для решения √(7,1 x 103) переместите указатель к 7,1 справа по шкале A (используем правую шкалу, так как экспонента нечетная).
-
4
Находим ответ по шкале D. Прочитайте значение по шкале D, на которое наведен указатель. Прибавьте к нему «x10n«. Для подсчета n возьмите исходную степень 10, округлите в меньшую сторону до ближайшего четного числа и разделите на 2.
- Пример 3: соответствующее значение шкалы D при A=3,9 будет 1,975. Изначальная цифра в экспоненциальном представлении имела 102. 2 уже четная, поэтому просто разделите на 2, чтобы получить 1. Окончательный ответ будет 1,975 x 101 = 19,75.
- Пример 4: соответствующее значение шкалы D при A=7,1 будет 8,45. Изначальная цифра в экспоненциальном представлении имела 103, поэтому округлите 3 до ближайшего четного числа, 2, а затем разделите на 2, чтобы получить 1. Окончательный ответ будет 8,45 x 101 = 84,5.
-
5
Аналогичным способом извлекайте кубические корни по шкале K. Процесс извлечения кубического корня очень схож. Самое главное — определить, какую из трех шкал K следует использовать. Для этого разделите количество цифр вашего числа на три и узнайте остаток. Если остаток 1, используйте первую шкалу. Если 2, используйте вторую шкалу. Если 3, используйте третью шкалу (еще один способ — многократно считать от первой шкалы до третьей, пока не достигнете количества цифр в вашем ответе).[5]
- Пример 5: для извлечения кубического корня из 74 000 необходимо подсчитать количество цифр (5), разделить его на 3 и узнать остаток (1, остаток 2). Так как остаток 2, используем вторую шкалу (также можно выполнить счет по шкалам пять раз: 1–2–3–1–2).
- Переместите курсор к 7,4 по второй шкале K. Соответствующее значение по шкале D будет примерно 4,2.
- Так как 103 меньше 74 000, но 1003 больше 74 000, ответ должен быть в рамках от 10 до 100. Переместите десятичную точку, чтобы получить 42.
Реклама
Советы
- Логарифмическая линейка позволяет также выполнять расчет других функций, особенно если на ней имеется шкала логарифмов, шкала тригонометрических расчетов или другие специализированные шкалы. Попробуйте разобраться в них самостоятельно или почитайте информацию в интернете.
- Можно использовать метод умножения для преобразования между двумя единицами измерения. Например, поскольку 1 дюйм = 2,54 сантиметра, задачу «преобразовать 5 дюймов в сантиметры» можно трактовать как пример умножения 5 x 2,54.
- Точность логарифмической линейки зависит от количества различимых масштабных отметок. Чем больше длина линейки, тем выше ее точность.
Реклама
Предупреждения
- Не допускайте воздействия на логарифмическую линейку тепла и влаги. Коробление и усыхание конструкции приведет к снижению точности линейки.[6]
Реклама
Об этой статье
Эту страницу просматривали 142 098 раз.
Была ли эта статья полезной?
Уверены, что умеете пользоваться логарифмической линейкой: проверьте себя
Не стоит забывать, что именно с помощью логарифмической линейки человек впервые ступил на Луну.
Unsplash
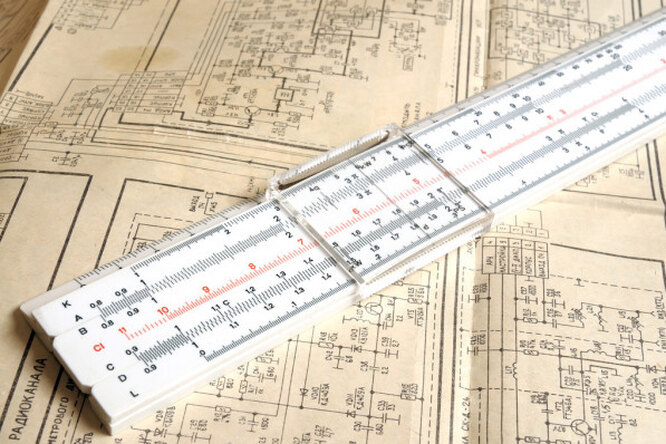
Логарифмическая линейка — это универсальный счетный прибор, который применялся для умножения, деления, возведения в квадрат и куб, вычисления квадратных и кубических корней, синусов, тангенсов и других значений. До появления калькуляторов, компьютеров и смартфонов инженеры носили логарифмические линейки на поясе, а линейка «Pickett» даже полетела на Луну вместе с космонавтами.
Уильям Отред — изобретатель логарифмической линейки
Уильям Отред, выпускник Итонской школы и Кембриджского королевского колледжа, пастор церкви в Олсбери в графстве Суррей, был страстным математиком и с удовольствием преподавал любимый предмет многочисленным ученикам, с которых не брал никакой платы. «Маленького роста, черноволосый и черноглазый, с проницательным взглядом, он постоянно что-то обдумывал, чертил какие-то линии и диаграммы в пыли, — так описывал Отреда один из биографов. — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.
История изобретения
В 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Форстер был восхищен и позднее писал: «Это превосходило любой из инструментов, которые были мне известны. Я удивлялся, почему он скрывал это полезнейшее изобретение многие годы…» Сам Отред говорил, что он «просто изогнул и свернул шкалу Гюнтера в кольцо», и к тому же был уверен, что «настоящее искусство [математики] не нуждается в инструментах…», их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Споры об авторстве
Авторство этого изобретения оспаривал другой его ученик — Ричард Деламэйн, опубликовавший в 1630 году книгу «Граммелогия, или Математическое кольцо». Некоторые утверждают, что он просто украл изобретение счетной линейки у учителя, но возможно, он пришел к похожему решению независимо. Еще один претендент на авторство - лондонский математик Эдмунд Уингейт, предложивший в 1626 году использовать две линейки Гюнтера, скользящие друг относительно друга. До современного состояния инструмент довели Роберт Биссакер, сделавший линейку прямой (1654), Джон Робертсон, снабдивший ее бегунком (1775), и Амеде Маннгейм, оптимизировавший расположение шкал и бегунка.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Логарифмическая линейка значительно облегчила сложные вычисления для инженеров и ученых. В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.
Как пользоваться логарифмической линейкой
Рассмотрим, как проводить базовые математические операции с помощью логарифмической линейки. Принцип ее действия основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.
Сложение
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Представим, что нам нужно найти сумму двух и четырех. На одной линейке (нижней) откладываем два деления (на рисунке отрезок а), вторую линейку (верхнюю) сдвигаем вправо на эти же два деления, после чего откладываем на ней еще четыре деления (отрезок b на рисунке). Смотрим на нижней линейке, над каким числом находится точка, в которую мы пришли — это шесть.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Умножение
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Для начала введем переменные: a ∙ b = с при a = 2, b = 3. Затем возведем в логарифм обе части равенства и получим Lg(a) + lg(b )= lg(с). Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3.
На основной шкале корпуса линейки (вторая снизу) выбираем первый сомножитель и на него устанавливаем начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса).
Затем на основной шкале движка волосок бегунка устанавливается на втором сомножителе. На основной шкале корпуса линейки под волоском смотрим ответ. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Деление
Пусть a/b = с при a = 8, b = 4. Возведем в логарифм обе части равенства и тогда получим: Lg(a) – lg(b) = lg(с). Разность логарифмов делимого и делителя дает логарифм частного, в нашем случае — 2.
На основной шкале корпуса линейки выбирается делимое, на которое устанавливается волосок бегунка. Под волосок подводится делитель, найденный на основной шкале движка. Результат определяется на основной шкале корпуса напротив начала или конца движка.
Читайте также:
Зачем нужен безель в наручных часах?
Невероятные механические головоломки от инженера-энтузиаста: мир шестеренок
Загрузка статьи…
Download Article
Download Article
To someone who doesn’t know how to use it, a slide rule looks like a ruler designed by Picasso. There are at least three different scales, and on most of them the numbers aren’t even spaced evenly apart. But after you learn about it, you can see why the slide rule was so useful in the centuries before pocket calculators. Line up the right numbers on the scale, and you can multiply any two numbers together, with much less math than you would use with pencil and paper.
-
1
Notice the gaps between numbers. Unlike an ordinary ruler, the numbers on a slide rule scale aren’t spaced on an even, linear scale. Instead, the numbers are spaced using a special «logarithmic» formula, closer together on one side than the other. This lets you line up the scales to get the answer to multiplication problems, as described below.
-
2
Look for scale labels. Each scale on the slide rule should have a letter or symbol identifying it, printed to the left or right. This guide will assume your slide rule uses the most common notation:[1]
- The C and D scales each look like a single stretched out ruler, reading from left to right. These are called «single decade» scales.
- The A and B scales are «double decade» scales. Each one has two smaller stretched rulers stacked end-to-end.
- The K scale is a triple decade scale, or three stretched rulers stacked end-to-end. Not all models have this.
- The C| and D| scales are the same as the C and D scales, but read right to left. These are often printed in red. Not all models have these.
- Note that slide rules vary, so the scales marked «C» and «D» on your slide rule may not be the same as those described here. One some slide rules the scales used for multiplication are marked «A» and «B» and are on the top. Whatever the designating letter, these scales often have the Pi symbol marked at the suitable place and are almost always the two scales opposing each other on the slides, either the upper or lower gap. It is suggested you try a few simple multiplication problems to verify that you are using the correct scale as described in the article. If «2×4» doesn’t come to «8», try the scales on the other side of the slide rule instead.
Advertisement
-
3
Interpret the divisions of the scale. Take a look at the vertical lines of the C or D scale, and get used to reading them:
- The primary numbers on the scale begin with 1 on the extreme left edge, extend up to 9, then end with another 1 on the far right edge. These are usually all labeled.
- The secondary divisions, marked by the second-tallest vertical lines, divide each primary number by 0.1. Don’t be confused if these are labeled «1, 2, 3;» remember they actually represent «1.1, 1.2, 1.3» and so on.
- There are usually smaller divisions, typically representing increments of 0.02. Pay close attention, since these may disappear on the high end of the scale, where numbers get closer together.
-
4
Don’t expect exact answers. You’ll often have to make a «best guess» when reading a scale, when the answer doesn’t fall exactly on a line. Slide rules are used for quick calculations, not for purposes that require extreme precision.
- For instance, if the answer falls between the 6.51 and 6.52 marks, write down whichever value it’s closer to. If you can’t tell, write 6.515.
Advertisement
-
1
Write down the numbers you are multiplying. Write down the two numbers you plan to multiply together.
- In Example 1 throughout this section, we’ll calculate 260 x 0.3.
- In Example 2, we’ll calculate 410 x 9. This ends up being a little more complicated than Example 1, so you might want to follow Example 1 first.
-
2
Move the decimal points for each number. The slide rule is only labeled with numbers between 1 and 10. Move the decimal point in each number you are multiplying, so they fall between these values. After the problem is complete, we’ll move the decimal point in the answer back to the right place, as described at the end of this section.[2]
- Example 1: to calculate 260 x 0.3 on a slide rule, start with 2.6 x 3 instead.
- Example 2: to calculate 410 x 9, start with 4.1 x 9 instead.
-
3
Find the smaller number on the D scale, then slide the C scale onto it. Find the smaller number on the D scale. Slide the C scale so the «1» on the far left (called the left index) is directly in line with that number.[3]
- Example 1: slide the C scale so the left index is in line with the 2.6 on the D scale.
- Example 2: slide the C scale so the left index is in line with the 4.1 on the D scale.
-
4
Slide the metal cursor to the second number on the C scale. The cursor is the metal object that slides over the entire slide rule. Line the cursor up with the second number in your multiplication problem, on the C scale. The cursor will point to the answer to your problem on the D scale.[4]
If it can’t slide that far, go to the next step.- Example 1: slide the cursor so it points to 3 on the C scale. At this position it should also point to 7.8 on the D scale, or extremely close to it. Skip ahead to the estimation step.
- Example 2: try to slide the cursor so it points to the 9 on the C scale. On most slide rules, this will not be possible, or the cursor will be pointing to empty air off the end of the D scale. See the next step for how to fix this.
-
5
Use the right index instead if the cursor won’t slide to the answer. If the cursor is blocked by a «bridge» in the center of the slide rule, or if the answer is «off the scale,» take a slightly different approach instead.[5]
Slide the C scale so the right index, or the 1 on the extreme right end, is located over the larger factor in the multiplication problem. Slide the cursor to the location of the other factor on the C scale, and read the answer on the D scale.- Example 2: slide the C scale so the 1 on the far right lines up with the 9 on the D scale. Slide the cursor to 4.1 on the C scale. The cursor is pointing to the D scale in between 3.68 and 3.7, so the answer must be about 3.69.
-
6
Use estimation to find the correct decimal point. No matter what multiplication you try, your answer will always be read off the D scale, which only displays numbers from one to ten. You’ll need to use some estimation and mental math to determine where to put the decimal point in your actual answer.
- Example 1: Our original problem was 260 x 0.3, and the slide rule gave us an answer of 7.8. Round the original problem to convenient numbers and solve it in your head: 250 x 0.5 = 125. This is much closer to 78 than it is to 780 or 7.8, so the answer is 78.
- Example 2: Our original problem was 410 x 9, and we read an answer of 3.69 on the slide rule. Estimate the original problem as 400 x 10 = 4,000. The closest we can get to that by moving the decimal point is 3,690, so that must be the actual answer.
Advertisement
-
1
Use the D and A scales to find squares. These two scales are typically fixed in place. Simply slide the metal cursor to a value on the D scale, and the A value will be its square.[6]
Just like a multiplication problem, you’ll need to determine the position of the decimal point yourself.- For example, to solve 6.12, slide the cursor to 6.1 on the D scale. The corresponding A value is about 3.75.
- Estimate 6.12 to 6 x 6 = 36. Position the decimal point to get an answer near this value: 37.5.
- Note that the exact answer is 37.21. The slide rule answer is off by less than 1%, easily accurate enough for most real-world circumstances.
-
2
Use the D and K scales to find cubes. You’ve just seen how the A scale, which is a D scale shrunk to 1/2 scale, lets you find the square of numbers. Similarly, the K scale, which is a D scale shrunk to 1/3 scale, lets you find the cubes. Simply slide the cursor to a D value and read the result on the K scale. Use estimation to place the decimal.[7]
- For example, to solve 1303, slide the cursor to 1.3 on the D value. The corresponding K value is 2.2. Since 1003 = 1 x 106, and 2003 = 8 x 106, we know the answer must be somewhere between them. The answer must be 2.2 x 106, or 2,200,000.
Advertisement
-
1
Convert the number to scientific notation before finding a square root. As always, the slide rule only has values from 1 to 10, so you’ll need to write the number in scientific notation before you can find its square root.[8]
- Example 3: to solve √(390), write it as √(3.9 x 102).
- Example 4: to solve √(7100), write it as √(7.1 x 103).
-
2
Determine which side of the A scale to use. To find the square root of a number, the first step is sliding the cursor to that number on the A scale. However, since the A scale is printed twice, you’ll have to decide which one to use first.[9]
To do so, follow these rules:- If the exponent in your scientific notation is even (such as 2 in Example 3), use the left side of the A scale (the «first decade»).
- If the exponent in your scientific notation is odd, (such as 3 in Example 4), use the right side of the A scale (the «second decade»).
-
3
Slide the cursor on the A scale. Ignoring the exponent of ten for now, slide the metal cursor along the A scale to the number you’ve ended up with.[10]
- Example 3: To find √(3.9 x 102), slide the cursor to 3.9 on the left A scale. (Use the left scale because the exponent is even, as described above.)
- Example 4: To find √(7.1 x 103), slide the cursor to 7.1 on the right A scale. (Use the right scale because the exponent is odd.)
-
4
Determine the answer from the D scale. Read the D value where the cursor is pointing. Add «x10n» to this value. To calculate n, take the original power of 10, round down to the nearest even number, and divide by 2.[11]
- Example 3: The corresponding D value at A=3.9 is about 1.975. The original number in scientific notation had 102. 2 is already even, so just divide by 2 to get 1. The final answer is 1.975 x 101 = 19.75.
- Example 4: The corresponding D value at A=7.1 is about 8.45. The original number in scientific notation had 103, so round the 3 down to the nearest even number, 2, then divide by 2 to get 1. The final answer is 8.45 x 101 = 84.5.
-
5
Use a similar process on the K scale to find cube roots. The process for finding cube roots is very similar. The most important step is determining which of the three K scales to use. To do this, divide the number of digits in your number by three and find the remainder. If the remainder is 1, use the first scale. If 2, use the second scale. If 3, use the third scale. (Another way to accomplish this is to repeatedly count from the first scale to the third, until you reach the number of digits in your answer.)[12]
- Example 5: To find the cube root of 74,000, first count the number of digits (5), divide by 3 and find the remainder (1 remainder 2). Since the remainder is 2, use the second scale. (Alternatively, count the scales five times: 1–2–3–1–2.)
- Slide the cursor to 7.4 on the second K scale. The corresponding D value is approximately 4.2.
- Since 103 is smaller than 74,000, but 1003 is larger than 74,000, the answer must be in between 10 and 100. Move the decimal point to make 42.
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
There are other functions you can calculate on your slide rule, especially if it contains «log-log» scales, scales for trigonometric calculations, or other specialized scales. Play around with these yourself, or look up the letter next to the scale online for more information.
-
You can use the multiplication method to convert between two units of measurement. For example, since 1 inch = 2.54 centimeters, the problem «convert 5 inches to centimeters» can be treated as a multiplication problem 5 x 2.54.
-
The precision of a slide rule depends on how many distinguishable calibrations marks you can make on it. The longer a slide rule is, the more precise you can be.
Thanks for submitting a tip for review!
Advertisement
-
Keep your slide rule away away from heat and damp. Warping and shrinking can make the slide rule inaccurate.[13]
Advertisement
References
About This Article
Article SummaryX
To use a slide rule to multiply 2 numbers together, move the decimal points for each number you are multiplying so they fall between the values of 1 and 10. Next, find the smaller number on the D scale and slide the C scale so the «1» on the far left lines up with the smaller number. Then, line the metal cursor up with the second number on the C scale. The cursor will point to the answer to your problem on the D scale. For tips on using a slide rule to find squares and cubes, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 97,457 times.
Did this article help you?
Логарифмическая линейка (фото см. ниже) была придумана как прибор для экономии умственных затрат и времени, связанных с математическими расчетами. Особое распространение она получила в практике инженеров в институтах, ориентированных на научно-исследовательскую деятельность, и в статистических бюро до момента внедрения электронной вычислительной техники.
Линейка логарифмическая: история
Прообразом счетного устройства была шкала для вычислений английского математика Э. Гантера. Он придумал ее в 1623 г., вскоре после открытия логарифмов, для упрощения работы с ними. Шкала использовалась в сочетании с циркулем. Им отмеривались необходимые градуированные отрезки, которые потом складывались или вычитались. Операции с числами заменялись действиями с логарифмами. Используя их основные свойства, умножить, делить, возводить в степень или вычислять корень числа оказалось намного проще.
В 1623 году линейка логарифмическая была усовершенствована У. Отредом. Он добавил вторую подвижную шкалу. Она перемещалась вдоль основной линейки. Отмерять отрезки и считывать результаты исчислений стало легче. Для повышения точности устройства в 1650 году была реализована попытка увеличения длины шкалы за счет ее расположения по спирали на вращающемся цилиндре.
Добавление в конструкцию бегунка (1850 г.) сделало процесс исчисления еще более удобными. Дальнейшее усовершенствование механизма и способа нанесения логарифмических шкал на стандартную линейку не добавили точности прибору.
Устройство
Линейка логарифмическая (стандартная) изготавливалась из плотной древесины, стойкой к истиранию. Для этого в промышленных масштабах использовалось грушевое дерево. Из него изготавливался корпус и движок – планка меньшего размера, монтируемая во внутреннем пазе. Ее можно перемещать параллельно основанию. Бегунок изготавливался из алюминия или стали со смотровым окошком из стекла или пластика. На него нанесена тонкая вертикальная линия (визир). Бегунок двигается по боковым направляющим и подпружинивается стальной пластинкой. Корпус и движок облицованы светлым целлулоидом, на котором тиснением нанесены шкалы. Их деления заполнены типографской краской.
На лицевой стороне линейки располагаются семь шкал: четыре- на корпусе и три — на движке. На боковых гранях нанесена простая измерительная разметка (25 см) с делениями 1 мм. Шкалы (C) на движке внизу и (D) на корпусе сразу под ней считаются главными. На основании сверху располагается кубическая разметка (K), под ней – квадратичная (A). Ниже (сверху на движке) есть точно такая же симметричная вспомогательная шкала (B). Внизу на корпусе еще есть разметка для значений логарифмов (L). В самом центре лицевой части линейки между разметками (B) и (C) нанесена обратная шкала чисел (R). С другой стороны движка (планку можно вынуть из пазов и перевернуть) присутствуют еще три шкалы для расчета тригонометрических функций. Верхняя (Sin) – предназначена для синусов, нижняя (Tg) – тангенсов, средняя (Sin и Tg) – общая.
Разновидности
Стандартная линейка логарифмическая имеет длину измерительной шкалы 25 см. Выпускался еще карманный вариант длиной 12,5 см и устройство повышенной точности 50 см. Существовало деление линеек на первый и второй сорта в зависимости от качества исполнения. Внимание уделялось четкости наносимых штрихов, обозначений и вспомогательных линий. Движок и корпус должны были быть ровными и идеально подогнаны друг к другу. Изделия второго сорта могли иметь незначительные царапины и точки на целлулоиде, но они не искажали обозначений. Также мог присутствовать незначительный люфт в пазах и прогиб.
Существовали и другие карманные (похожие на часы диаметром 5 см) варианты устройства – логарифмическая дисковая (типа «Спутник») и круговая (КЛ-1) линейки. Они отличались и конструкцией, и меньшей точностью измерений. В первом случае для установки чисел на замкнутых круговых логарифмических шкалах использовалась прозрачная крышка с линией-визиром. Во втором – механизм управления (две вращающиеся ручки) был смонтирован на корпусе: одной управлялся дисковый движок, другая управляла стрелкой-визиром.
Возможности
Логарифмической линейкой общего назначения можно было осуществлять деление и умножение чисел, возведить их в квадрат и куб, извлекать корень, решать уравнения. Кроме этого, по шкалам производились тригонометрические вычисления (синус и тангенс) по заданным углам, определялись мантиссы логарифмов и обратные действия – находились числа по их значениям.
Правильность вычислений во многом зависела от качества линейки (длинны ее шкал). В идеале можно было надеяться на точность до третьего знака после запятой. Такие показатели были вполне достаточными для технических расчетов в XIX веке.
Возникает вопрос: как пользоваться логарифмической линейкой? Одного знания назначения шкал и способов нахождения на них чисел еще не достаточно для произведения расчетов. Чтобы использовать все возможности линейки, нужно понимать, что такое логарифм, знать его характеристики и свойства, а также принципы построения и зависимости шкал.
Как считать на логарифмической линейке
Для уверенной работы с устройством требовались определенные навыки. Сравнительно простые вычисления с одним бегунком. Для удобства движок (чтобы не отвлекал) можно удалять. Установив черту на значения любого числа на основной (D) шкале можно сразу же по визиру получить результат возведения его в квадрат на шкале выше (A) и в куб – на самой верхней (K). Внизу (L) будет значение его логарифма.
Деление и умножение чисел производится с помощью движка. Применяются свойства логарифмов. Согласно им, итог умножения двух чисел равен результату сложения их логарифмов (аналогично: деление и разница). Зная это, можно достаточно быстро производить расчеты, используя графические шкалы.
Чем сложна логарифмическая линейка? Инструкция по ее правильному использованию шла в комплекте с каждым экземпляром. Кроме знания свойств и характеристик логарифмов, нужно было уметь правильно находить исходные числа на шкалах и уметь в нужном месте считывать результаты, в том числе самостоятельно определять точное место расположения запятой.
Актуальность
Как пользоваться логарифмической линейкой, в наше время знают и помнят немногие, и с уверенностью можно утверждать, что число таких людей будет снижаться.
Логарифмическая линейка из разряда карманных счетных приспособлений давно стала раритетом. Для уверенной работы с ней нужна постоянная практика. Методика расчетов с примерами и разъяснениями тянет на брошюру в 50 листов.
Для среднестатистического человека, далекого от высшей математики, логарифмическая линейка может представлять какую-то ценность разве что справочными материалами, размещенными на обратной стороне корпуса (плотность некоторых веществ, температура плавления и пр.). Преподаватели даже не утруждаются вводить запрет на ее наличие при сдаче экзаменов и зачетов, понимая, что разобраться с тонкостями ее использования современному студенту очень сложно.
35
21
17,4
32,2
[Принцип работы
логарифмической линейки]
Логарифмическая линейка позволяет Вам
решать [проблемы умножения или
деления] с помощью [сложения или
вычитания], используя закон, что log (A +
B) = log (A) + (B) (где log является
логарифмом с 10 в качестве основы).
Соответственно число “10” является
основой логарифмической линейки и
принимается за “индексную единицу”.
В нашей вращающейся логарифмической
линейке мы применили шкалу от 10 — 99
без какого-нибудь дополнительного
масштабирования (2-значные целые
числа, 1 цифра после десятичной точки)
Таким образом, вычисленные значения и
результаты должны конвертироваться в
значения в соответствии со шкалой.
Так как логарифмическая линейка
основана на логарифме “log”, упомянутом
выше, то конвертация выполняется
кратно 10 (… 1/100, 1/10, 1,00 …)
Использование вращающейся логарифмической
линейки
[Наименования каждой части]
1. Умножение и деление
(Обращайтесь к рис. 1)
С помощью вращения логарифмической
линейки, Вы можете легко выполнять при
частом использовании [умножение] и
[деление].
В таком случае основой становится
вышеупомянутое число “10” в качестве
индексной единицы фиксированной
шкалы.
<Пример>
Найти значение “25 × 14″
Поверните “14” на движущейся шкале на
индексную единицу “10”.
При такой установке “35” на движущейся
шкале поравняется с “25” на
фиксированной шкале. Так как
произведение “25 × 14” должно состоять
из трех цифр, то ответ будет “350”, т.е. 10
раз по 35.
2. Конвертация валюты
(Обращайтесь к рис. 2)
Путем применения 1. становится
возможно также выполнять конвертацию
валюты.
<Пример>
Найдите значение $20, 00 США в
японских иенах при курсе обмена валют
$1, 00 США = ¥105 японских иен.
Поверните “10,5” на движущей шкале
(разделите на 10, так как на шкале нет
значения для 105) на индексную единицу
“10” на фиксированной шкале. При такой
установке “21” на движущейся шкале
поравняется с “20” на фиксированной
шкале.
Так как $20,00 США составят 4 цифры
при конвертации в японские иены, то
ответ будет 100 раз по 21, что составит
“¥2.100”.
3. Преобразование расстояния
(Обращайтесь к рис. 3)
Вы можете легко конвертировать единицы
расстояния, такие как статутная миля,
морская миля и километр.
Как показано на фиксированной шкале
“NAUT” означает морскую милю, “STAT”
означает статутную милю, а “KM”
означает километр.
<Пример>
Преобразуйте 20 статутных милей в
километры и в морские мили.
Поверните “20” на движущейся шкале на
треугольную индексную отметку
положения “STAT” на фиксированной
шкале.
При такой установке “32,2” на
движущейся совпадет с треугольной
индексной меткой положения “КM” на
фиксированной шкале.
Также “17,4” на движущейся шкале
совпадет с треугольной индексной меткой
положения “NAUT” на фиксированной
шкале.
Таким образом, Вы найдете, что 20
статутных миль соответствуют “32,2
километрам” и “17,4 морским милям”.
Рис. 1 3
Рис. 2
Рис. 1
РУССКИЙ
[Километр]
[Статутная миля]
[Морская миля]
[Фиксированная шкала]
[Движущаяся шкала]
[Индексная единица]
KM
NA
UT
STAT
SUN
Логарифмическая линейка — заслуженный патриарх всех современных вычислительных устройств.

Wikipedia
Логарифмическая линейка — это универсальный счетный прибор, который применялся для умножения, деления, возведения в квадрат и куб, вычисления квадратных и кубических корней, синусов, тангенсов и других значений. До появления калькуляторов, компьютеров и смартфонов инженеры носили логарифмические линейки на поясе, а линейка «Pickett» даже полетела на Луну вместе с космонавтами.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Уильям Отред — изобретатель логарифмической линейки
Уильям Отред, выпускник Итонской школы и Кембриджского королевского колледжа, пастор церкви в Олсбери в графстве Суррей, был страстным математиком и с удовольствием преподавал любимый предмет многочисленным ученикам, с которых не брал никакой платы. «Маленького роста, черноволосый и черноглазый, с проницательным взглядом, он постоянно что-то обдумывал, чертил какие-то линии и диаграммы в пыли, — так описывал Отреда один из биографов. — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.
История изобретения
В 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Форстер был восхищен и позднее писал: «Это превосходило любой из инструментов, которые были мне известны. Я удивлялся, почему он скрывал это полезнейшее изобретение многие годы…» Сам Отред говорил, что он «просто изогнул и свернул шкалу Гюнтера в кольцо», и к тому же был уверен, что «настоящее искусство [математики] не нуждается в инструментах…», их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Споры об авторстве
Авторство этого изобретения оспаривал другой его ученик — Ричард Деламэйн, опубликовавший в 1630 году книгу «Граммелогия, или Математическое кольцо». Некоторые утверждают, что он просто украл изобретение счетной линейки у учителя, но возможно, он пришел к похожему решению независимо. Еще один претендент на авторство - лондонский математик Эдмунд Уингейт, предложивший в 1626 году использовать две линейки Гюнтера, скользящие друг относительно друга. До современного состояния инструмент довели Роберт Биссакер, сделавший линейку прямой (1654), Джон Робертсон, снабдивший ее бегунком (1775), и Амеде Маннгейм, оптимизировавший расположение шкал и бегунка.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Логарифмическая линейка значительно облегчила сложные вычисления для инженеров и ученых. В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.
Как пользоваться логарифмической линейкой
Рассмотрим, как проводить базовые математические операции с помощью логарифмической линейки. Принцип ее действия основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.
1. Сложение
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Представим, что нам нужно найти сумму двух и четырех. На одной линейке (нижней) откладываем два деления (на рисунке отрезок а), вторую линейку (верхнюю) сдвигаем вправо на эти же два деления, после чего откладываем на ней еще четыре деления (отрезок b на рисунке). Смотрим на нижней линейке, над каким числом находится точка, в которую мы пришли — это шесть.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
2. Умножение
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Для начала введем переменные: a ∙ b = с при a = 2, b = 3. Затем возведем в логарифм обе части равенства и получим Lg (a) + lg (b)= lg (с). Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3. На основной шкале корпуса линейки (вторая снизу) выбираем первый сомножитель и на него устанавливаем начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса). Затем на основной шкале движка волосок бегунка устанавливается на втором сомножителе. На основной шкале корпуса линейки под волоском смотрим ответ. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
3. Деление
Пусть a/b = с при a = 8, b = 4. Возведем в логарифм обе части равенства и тогда получим: Lg (a) — lg (b) = lg (с). Разность логарифмов делимого и делителя дает логарифм частного, в нашем случае — 2. На основной шкале корпуса линейки выбирается делимое, на которое устанавливается волосок бегунка. Под волосок подводится делитель, найденный на основной шкале движка. Результат определяется на основной шкале корпуса напротив начала или конца движка.
Загрузка статьи…








































