Как пользоваться логарифмической линейкой ссср инструкция - RukovodstvoRus.ru

Загрузить PDF

Человеку, не знакомому с использованием логарифмической линейки, она покажется работой Пикассо. Она имеет как минимум три различных шкалы, почти на каждой из которых цифры расположены даже не на одинаковом расстоянии друг от друга. Но разобравшись, что к чему, вы поймете, почему логарифмическая линейка была такой удобной во времена до изобретения карманных калькуляторов. Правильно расположив нужные цифры на шкале, вы сможете выполнить умножение двух любых чисел гораздо быстрее, чем выполняя расчеты на бумаге.

1

Обратите внимание на промежутки между цифрами. В отличие от обычной линейки, расстояние между ними не одинаковое. Наоборот, оно определяется по особой «логарифмической» формуле, меньше с одной стороны и больше с другой. Благодаря этому вы можете совместить две шкалы нужным образом и получить ответ на задачу по умножению, как описано ниже.
2
Метки на шкале. Каждая шкала логарифмической линейки имеет буквенное или символьное обозначение с левой или правой стороны. Ниже описаны общепринятые обозначения на логарифмических линейках:^[1]
- Шкалы C и D похожи на одноразрядную вытянутую линейку, метки на которой расположены слева направо. Такая шкала называется «одноразрядной десятичной» шкалой.
- Шкалы A и B — «двухразрядные десятичные» шкалы. Каждая состоит из двух небольших вытянутых линеек, расположенных впритык.
- K — это трехразрядная десятичная шкала или три вытянутые линейки, расположенные впритык. Такая шкала имеется не на всех логарифмических линейках.
- Шкалы C| и D| аналогичны C и D, но читаются справа налево. Часто они имеют красную окраску. Они присутствуют не на всех логарифмических линейках.
- Логарифмические линейки бывают разные, поэтому и обозначение шкал может быть другим. На некоторых линейках шкалы для умножения могут быть помечены как A и B и находиться сверху. Независимо от буквенных обозначений, на многих линейках рядом со шкалами есть символ π, отмеченный в подходящем месте; в большинстве своем шкалы находятся напротив друг друга, либо в верхнем, либо в нижнем промежутке. Рекомендуем решить несколько простых задач на умножение, чтобы вы могли понять, правильно ли вы используете шкалы. Если произведение 2 и 4 не равняется 8, попробуйте использовать шкалы на другой стороне линейки.
3
Научитесь понимать деления шкалы. Посмотрите на вертикальные линии на шкале C или D и ознакомьтесь с тем, как они читаются:
- Основные цифры на шкале начинаются с 1 от левого края и продолжаются до 9, а затем завершаются еще одной 1 справа. Обычно все они нанесены на линейку.
- Вторичные деления, обозначенные чуть меньшими вертикальными линиями, разделяют каждую основную цифру на 0,1. Вас не должно сбивать с толку, если они обозначены как «1, 2, 3»; все равно они соответствуют «1,1; 1,2; 1,3» и так далее.
- Также могут присутствовать меньшие деления, которые обычно соответствуют шагу 0,02. Следите за ними внимательно, так как они могут исчезать в верхней части шкалы, где цифры находятся ближе друг к другу.
4
Не ожидайте получить точные ответы. При чтении шкалы вам часто придется приходить к «наиболее вероятному предположению», когда ответ не будет попадать тютелька в тютельку. Логарифмическая линейка используется для быстрых подсчетов, а не для максимальной точности.
- Например, если ответ находится между отметками 6,51 и 6,52, запишите то значение, которое вам кажется ближе. Если совсем непонятно, то запишите ответ как 6,515.
Реклама

1
Запишите числа, которые вы будете умножать. Запишите числа, которые подлежат умножению.
- В примере 1 этого раздела мы подсчитаем, сколько будет 260 x 0,3.
- В примере 2 мы подсчитаем, сколько будет 410 x 9. Это немного сложнее, чем пример 1, поэтому сначала рассмотрим более простую задачу.
2
Переместите десятичные точки для каждого числа. Логарифмическая линейка имеет цифры от 1 до 10. Переместите десятичную точку каждого умножаемого числа, чтобы они соответствовали своим значениям. После решения задачи мы переместим десятичную точку в ответе в нужное положение, что будет описано в конце раздела.
- Пример 1: чтобы подсчитать 260 x 0.3, начинайте вместо этого с 2,6 x 3.
- Пример 2: чтобы подсчитать 410 x 9, начинайте вместо этого с 4,1 x 9.
3
Найдите меньшие цифры на шкале D, затем передвиньте к ней шкалу C. Найдите меньшую цифру на шкале D. Сдвиньте шкалу C таким образом, чтобы «1» слева (левый индекс) располагалась на одной линии с этой цифрой.
- Пример 1: сдвиньте шкалу C таким образом, чтобы левый индекс совпал с 2,6 на шкале D.
- Пример 2: сдвиньте шкалу C таким образом, чтобы левый индекс совпал с 4,1 на шкале D.
4
Переместите металлический указатель ко второй цифре на шкале C. Указатель — это металлический предмет, который перемещается по всей линейке. Совместите указатель со второй цифрой вашей задачи на шкале C. Указатель будет указывать ответ к задаче на шкале D. Если он не перемещается так далеко, переходите к следующему шагу.
- Пример 1: переместите указатель к цифре 3 на шкале C. В этом положении он также будет указывать на 7,8 на шкале D или около того. Переходите к шагу 6.
- Пример 2: постарайтесь переместить указатель так, чтобы он указывал на 9 на шкале C. Это будет невозможно на большинстве линеек или указатель будет указывать на пустое место в конце шкалы D. Решение проблемы описано в следующем шаге.
5
Если указатель не перемещается к ответу, используйте правый индекс. Если указатель блокируется перегородкой в центре линейки или ответ расположен за пределами шкалы, то используйте немного иной подход.^[2] Сдвиньте шкалу C таким образом, чтобы правый индекс или 1 справа располагались над большим коэффициентом вашей задачи. Переместите указатель к другому коэффициенту по шкале C и прочтите ответ на шкале D.
- Пример 2: переместите шкалу C таким образом, чтобы 1 справа совпала с 9 по шкале D. Переместите указатель к 4,1 по шкале C. Указатель показывает на шкалу D в точке между 3,68 и 3,7, поэтому наиболее вероятный ответ будет 3,69.
6
Прикидывайте правильную десятичную точку. Независимо от производимого умножения, ваш ответ всегда будет считываться по шкале D, которая содержит лишь цифры от одного до десяти. Вам не обойтись без предположения и умственного подсчета, чтобы определить местонахождение десятичной точки в фактическом ответе.
- Пример 1: нашей первоначальной задачей было 260 x 0,3, а линейка дала ответ 7,8. Округлите первоначальную задачу до удобных чисел и решите ее в голове: 250 x 0,5 = 125. Такой ответ гораздо ближе к 78, чем к 780 или 7,8, поэтому правильный ответ будет 78.
- Пример 2: нашей первоначальной задачей было 410 x 9, а линейка дала ответ 3,69. Прикиньте первоначальную задачу как 400 x 10 = 4000. Ближайшим числом будет 3690, которое и станет фактическим ответом.
Реклама

1
Возведение в квадрат по шкалам D и A. Эти две шкалы обычно неподвижны. Просто переместите металлический указатель к значению по шкале D, а значение по шкале A будет соответствовать второй степени числа.^[3] Как и в случае с умножением, положение десятичной точки придется определять самостоятельно.
- Например, чтобы решить 6,1², переместите указатель к 6,1 по шкале D. Соответствующее значение по шкале A будет 3,75.
- Прикиньте 6,1² как 6 x 6 = 36. Расположите десятичную точку так, чтобы получить ответ, который примерно соответствует данному значению: 37,5.
- Обратите внимание, что точный ответ будет 37,21. Ответ на линейке дает погрешность в 1 %, чего вполне достаточно для практических задач.
2
Возведение в куб по шкалам D и K. Только что мы увидели как шкала A, которая соответствует шкале D, уменьшенной на 1/2, позволяет возвести число в квадрат. Аналогичным образом шкала K, которая соответствует шкале D, уменьшенной на 1/3, позволяет возвести число в куб. Просто переместите указатель к значению по шкале D и прочитайте результат на шкале K. Прикиньте расположение десятичной точки.
- Например, чтобы решить 130³, переместите указатель к 1,3 по шкале D. Соответствующее значение по шкале K будет 2,2. Так как 100³ = 1 x 10⁶, и 200³ = 8 x 10⁶, мы понимаем, что ответ будет где-то посредине. Ответ должен быть 2,2 x 10⁶, или 2 200 000.
Реклама

1
Запишите число в экспоненциальном представлении для извлечения квадратного корня. Как и всегда, на линейке есть только значения от 1 до 10, поэтому для извлечения квадратного корня вам потребуется записать число в экспоненциальном представлении.
- Пример 3: для решения √(390) запишите задачу как √(3,9 x 10²).
- Пример 4: для решения √(7100) запишите задачу как √(7,1 x 10³).
2
Определите, какую сторону шкалы A необходимо использовать. Чтобы извлечь квадратный корень числа, для начала переместите указатель к этому числу по шкале A. Но так как шкала A нанесена дважды, необходимо решить, какую использовать.^[4] В этом помогут следующие правила:
- Если экспонента вашего числа четная (как ² в примере 3), используйте левую сторону шкалы A («первый десятичный разряд»).
- Если экспонента вашего числа нечетная (как ³ в примере 4), используйте правую сторону шкалы A («второй десятичный разряд»).
3
Переместите указатель по шкале A. Пока опустите экспоненту десяти и переместите металлический указатель по шкале A к необходимому значению.
- Пример 3: для решения √(3,9 x 10²) переместите указатель к 3,9 слева по шкале A (используем левую шкалу, так как экспонента четная).
- Пример 4: для решения √(7,1 x 10³) переместите указатель к 7,1 справа по шкале A (используем правую шкалу, так как экспонента нечетная).
4
Находим ответ по шкале D. Прочитайте значение по шкале D, на которое наведен указатель. Прибавьте к нему «x10ⁿ«. Для подсчета n возьмите исходную степень 10, округлите в меньшую сторону до ближайшего четного числа и разделите на 2.
- Пример 3: соответствующее значение шкалы D при A=3,9 будет 1,975. Изначальная цифра в экспоненциальном представлении имела 10². 2 уже четная, поэтому просто разделите на 2, чтобы получить 1. Окончательный ответ будет 1,975 x 10¹ = 19,75.
- Пример 4: соответствующее значение шкалы D при A=7,1 будет 8,45. Изначальная цифра в экспоненциальном представлении имела 10³, поэтому округлите 3 до ближайшего четного числа, 2, а затем разделите на 2, чтобы получить 1. Окончательный ответ будет 8,45 x 10¹ = 84,5.
5
Аналогичным способом извлекайте кубические корни по шкале K. Процесс извлечения кубического корня очень схож. Самое главное — определить, какую из трех шкал K следует использовать. Для этого разделите количество цифр вашего числа на три и узнайте остаток. Если остаток 1, используйте первую шкалу. Если 2, используйте вторую шкалу. Если 3, используйте третью шкалу (еще один способ — многократно считать от первой шкалы до третьей, пока не достигнете количества цифр в вашем ответе).^[5]
- Пример 5: для извлечения кубического корня из 74 000 необходимо подсчитать количество цифр (5), разделить его на 3 и узнать остаток (1, остаток 2). Так как остаток 2, используем вторую шкалу (также можно выполнить счет по шкалам пять раз: 1–2–3–1–2).
- Переместите курсор к 7,4 по второй шкале K. Соответствующее значение по шкале D будет примерно 4,2.
- Так как 10³ меньше 74 000, но 100³ больше 74 000, ответ должен быть в рамках от 10 до 100. Переместите десятичную точку, чтобы получить 42.
Реклама

Советы

Логарифмическая линейка позволяет также выполнять расчет других функций, особенно если на ней имеется шкала логарифмов, шкала тригонометрических расчетов или другие специализированные шкалы. Попробуйте разобраться в них самостоятельно или почитайте информацию в интернете.
Можно использовать метод умножения для преобразования между двумя единицами измерения. Например, поскольку 1 дюйм = 2,54 сантиметра, задачу «преобразовать 5 дюймов в сантиметры» можно трактовать как пример умножения 5 x 2,54.
Точность логарифмической линейки зависит от количества различимых масштабных отметок. Чем больше длина линейки, тем выше ее точность.

Предупреждения

Не допускайте воздействия на логарифмическую линейку тепла и влаги. Коробление и усыхание конструкции приведет к снижению точности линейки.^[6]

Об этой статье

Эту страницу просматривали 142 098 раз.

Была ли эта статья полезной?

Источник

Уверены, что умеете пользоваться логарифмической линейкой: проверьте себя

Не стоит забывать, что именно с помощью логарифмической линейки человек впервые ступил на Луну.

Unsplash

Логарифмическая линейка — это универсальный счетный прибор, который применялся для умножения, деления, возведения в квадрат и куб, вычисления квадратных и кубических корней, синусов, тангенсов и других значений. До появления калькуляторов, компьютеров и смартфонов инженеры носили логарифмические линейки на поясе, а линейка «Pickett» даже полетела на Луну вместе с космонавтами.

Уильям Отред — изобретатель логарифмической линейки

Уильям Отред, выпускник Итонской школы и Кембриджского королевского колледжа, пастор церкви в Олсбери в графстве Суррей, был страстным математиком и с удовольствием преподавал любимый предмет многочисленным ученикам, с которых не брал никакой платы. «Маленького роста, черноволосый и черноглазый, с проницательным взглядом, он постоянно что-то обдумывал, чертил какие-то линии и диаграммы в пыли, — так описывал Отреда один из биографов.  — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.

История изобретения

В 1631 году Отред опубликовал главный труд своей жизни — учебник Clavis Mathematicae («Ключ математики»), выдержавший несколько переизданий на протяжении почти двух веков. Однажды, обсуждая «механические вычисления» с помощью линейки Гюнтера со своим учеником Уильямом Форстером, Отред отметил несовершенство этого метода. Между делом учитель продемонстрировал свое изобретение — несколько концентрических колец с нанесенными на них логарифмическими шкалами и двумя стрелками.

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Форстер был восхищен и позднее писал: «Это превосходило любой из инструментов, которые были мне известны. Я удивлялся, почему он скрывал это полезнейшее изобретение многие годы…» Сам Отред говорил, что он «просто изогнул и свернул шкалу Гюнтера в кольцо», и к тому же был уверен, что «настоящее искусство [математики] не нуждается в инструментах…», их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Споры об авторстве

Авторство этого изобретения оспаривал другой его ученик — Ричард Деламэйн, опубликовавший в 1630  году книгу «Граммелогия, или Математическое кольцо». Некоторые утверждают, что он просто украл изобретение счетной линейки у учителя, но возможно, он пришел к похожему решению независимо. Еще один претендент на авторство  - лондонский математик Эдмунд Уингейт, предложивший в 1626 году использовать две линейки Гюнтера, скользящие друг относительно друга. До современного состояния инструмент довели Роберт Биссакер, сделавший линейку прямой (1654), Джон Робертсон, снабдивший ее бегунком (1775), и Амеде Маннгейм, оптимизировавший расположение шкал и бегунка.

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Логарифмическая линейка значительно облегчила сложные вычисления для инженеров и ученых. В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.

Как пользоваться логарифмической линейкой

Рассмотрим, как проводить базовые математические операции с помощью логарифмической линейки. Принцип ее действия основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.

Сложение

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Представим, что нам нужно найти сумму двух и четырех. На одной линейке (нижней) откладываем два деления (на рисунке отрезок а), вторую линейку (верхнюю) сдвигаем вправо на эти же два деления, после чего откладываем на ней еще четыре деления (отрезок b на рисунке). Смотрим на нижней линейке, над каким числом находится точка, в которую мы пришли — это шесть.

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Умножение

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Для начала введем переменные: a ∙ b = с при a = 2, b = 3. Затем возведем в логарифм обе части равенства и получим Lg(a) + lg(b )= lg(с). Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3.

На основной шкале корпуса линейки (вторая снизу) выбираем первый сомножитель и на него устанавливаем начало основной, нижней, шкалы движка (она на лицевой стороне последнего и точно такая же, как основная шкала корпуса).

Затем на основной шкале движка волосок бегунка устанавливается на втором сомножителе. На основной шкале корпуса линейки под волоском смотрим ответ. Если при этом волосок выходит за пределы шкалы, то на первый сомножитель устанавливают не начало, а конец движка (с числом 10).

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Деление

Пусть a/b = с при a = 8, b = 4. Возведем в логарифм обе части равенства и тогда получим: Lg(a) – lg(b) = lg(с). Разность логарифмов делимого и делителя дает логарифм частного, в нашем случае — 2.

На основной шкале корпуса линейки выбирается делимое, на которое устанавливается волосок бегунка. Под волосок подводится делитель, найденный на основной шкале движка. Результат определяется на основной шкале корпуса напротив начала или конца движка.

Быстрые вычисления

Прилагаемая (ниже) инструкция предлагает умножать и делить в три движения: вращением подвижной шкалы на указатель, вращением стрелки до нужного значения, и вращением циферблата до другого значения. Однако гораздо интереснее использовать оба циферблата, подвижный и неподвижный с обратной стороны линейки, и делать вычисления в два движения. При этом возможно получать сразу весь спектр значений, просто вращая циферблат, и тут же считывая значения.

Для этого на неподвижном циферблате нужно стрелкой выставить либо множитель (в случае умножения), либо делимое (в случае деления), и, перевернув линейку, вращением подвижного циферблата выставить второй множитель на стрелку, либо делитель на указатель, и сразу прочитать результат. Продолжая вращать циферблат, тут же считываем другие значения функции. Обычный калькулятор такое не умеет делать.

Дюймы в сантиметры

К примеру, нам нужно преобразовать сантиметры в дюймы, либо наоборот. Для этого вращением головки с красной точкой выставляем на неподвижном циферблате стрелкой значение 2,54. После этого будем смотреть, сколько в нашем 24" мониторе сантиметров — вращением головки с чёрной точкой подвижного циферблата выставляем на стрелке значение 24, и считываем с неподвижного указателя значение 61 см (2.54*24=60.96). При этом можно легко узнать и обратные значения, например узнаем сколько дюймов в нашем 81 см телевизоре, для этого вращением головки с чёрной точкой подвижного циферблата устанавливаем на неподвижном указателе значение 81, и считываем на стрелке значение 32" (81/2.54=31.8898).

Градусы Фарингейта в градусы Цельсия

На неподвижном циферблате выставляем значение 1.8, из градусов по Фаренгейту вычитаем в уме 32 и устанавливаем полученное значение напротив неподвижного указателя, считываем на стрелке градусы по Цельсию. Для обратного вычисления устанавливаем значение на стрелке, и к значению на указателе прибавляем в уме 32.

20*1.8+32 = 36+32 = 68

(100-32)/1.8 = 68/1.8 = 37.8 (37.7778)

Мили в километры

Выставляем на неподвижной шкале значение 1.6, вращением подвижной шкалы получаем мили в километрах или километры в милях.

Посчитаем скорость разгона машины времени в фильме «Назад в будущее»: 88*1.6=141км/ч (140.8)

Время и расстояние от скорости

Чтобы узнать за сколько времени проедем 400 километров при скорости 60 км/ч, выставляем на неподвижном циферблате значение 6, и крутим подвижный циферблат до значения 4, получаем 6.66 часов (6 часов 40 минут).

Инструкция к линейке

У имеющейся у меня линейки инструкция очень потрёпана, ведь она аж 1966 года выпуска. Поэтому я решил оцифровать её для сохранности в электронном виде.

Полная инструкция к логарифмической линейке «КЛ-1»:

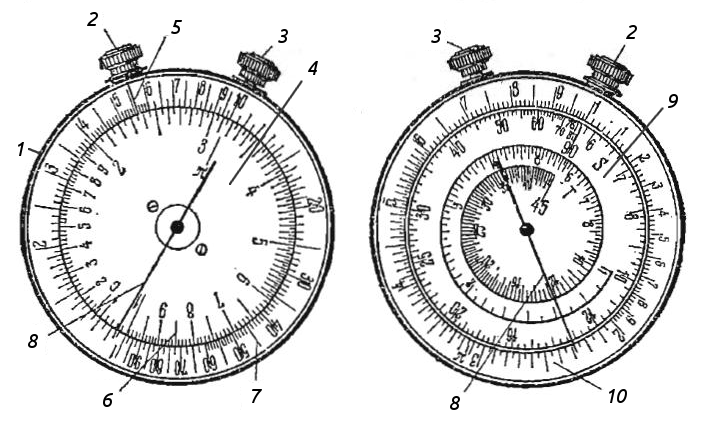
Круговая логарифмическая линейка «КЛ-1»

Корпус.
Головка с черной точкой.
Головка с красной точкой.
Подвижный циферблат.
Неподвижный указатель.
Основная шкала (счетная).
Шкала квадратов числа.
Стрелка.
Неподвижный циферблат.
Счетная шкала.

ВНИМАНИЕ!
Вытаскивание головок из корпуса не допускается.

Круговая логарифмическая линейка «КЛ-1» предназначена для выполнения наиболее часто встречающихся в практике математических операций: умножения, деления, комбинированных действий, возведения в кладрат, извлечения квадратного корня, нахождения тригонометрических функций синуса и тангенса, а также соответствующих обратных тригонометрических функций, вычисления площади круга.

Логарифмическая линейка состоит из корпуса с двумя головками, 2-х циферблатов, один из которых вращается при помощи головки с черной точкой и 2-х стрелок, которые вращаются при помощи головки с красной точкой. Против головки с черной точкой над подвижным циферблатом имеется неподвижный указатель.

На подвижном циферблате нанесены 2 шкалы: внутренняя — основная — счетная и наружная — шкала квадратов чисел.

На неподвижном циферблате нанесены 3 шкалы: наружная шкала — счетная, аналоичная внутренней шкале на подвижном циферблате, средняя цшкала «S»-значений углов для отсчета их синусов и внутренняя шкала «T»-значений углов для отсчета их тангенсов.

Выполнение математических операций на линейке «КЛ-1» производится следующим образом:

I. Умножение

Вращением головки с черной точкой повернуть подвижный циферблат до совмещения первого сомножителя по счетной шкале с указателем.
Вращением головки с красной точкой совместить стрелку с отметкой «1».
Вращением головки с черной точкой повернуть подвижный циферблат до совмещения второго сомножителя по счетной шкале со стрелкой.
Против указателя по счетной шкале отсчитать искомое значение произведения.

II. Деление

Вращением головки с черной точкой повернуть подвижный циферблат до совмещения делимого по счетной шкале с указателем.
Вращением головки с красной точкой совместить стрелку с делителем по счетной шкале.
Вращением головки с черной точкой повернуть подвижный циферблат до совмещения отметки «1» со стрелкой.
Против указателя по счетной шкале отсчитать искомое значение частного.

III. Комбинированные действия

Вращением головки с черной точкой повернуть подвижный циферблат до совмещения первого сомножителя по счетной шкале с указателем.
Вращением головки с красной точкой совместить стрелку с делителем по счетной шкале.
Вращением головки с черной точкой повернуть подвижный циферблат до совмещения второго сомножителя по счетной шкале со стрелкой.
Против указателя по счетной шкале отсчитать окончательный результат.

Пример: (2×12)/6=4

IV. Возведение в квадрат

Вращением головки с черной точкой повернуть подвижный циферблат до совмещения значения числа, возводимого в квадрат, по счетной шкале с указателем.
Против того же указателя по шкале квадратов прочитать искомое значение квадрата этого числа.

V. Извлечение квадратного корня

Вращением головки с черной точкой повернуть подвижный циферблат до совмещения значения подкоренного числа по шкале квадратов с указателем.
Против того же указателя по внутренеей (счетной) шкале прочитать искомое значение квадратного корня.

VI. Нахождение тригонометрических функций угла

Вращением головки с красной точкой совместить стрелку над неподвижным циферблатом со значением заданного угла по шкале синусов (шкала «S») или по шкале тангенсов (шкала «T»).
Против той же стрелки на том же циферблате по наружной (счетной) шкале прочитать соответствующее значение синуса или тангенса этого угла.

VII. Нахождение обратных тригонометрических функций

Вращением головки с красной точкой совместить стрелку над неподвижным циферблатом по наружной (счетной) шкале с заданным значением тригонометрической функции.
Против той же стрелки по шкале синусов или тангенсов прочитать значение соответстующей обратной тригонометрической функции.

VIII. Вычисление площади круга

Вращением головки с черной точкой повернуть подвижный циферблат до совмещения значения диаметра круга по счетной шкале с указателем.
Вращением головки с красной точкой совместить стрелку с отметкой «C».
Вращением головки с черной точкой повернуть подвижный циферблат до совмещения отметки «1» со стрелкой.
Против указателя по шкале квадратов отсчитать искомое значение площади круга.

Техническо-сбытовая организация «Рассвет» г. Москва, А-57, ул. Острякова, дом №8.
СТУ 36-16-64-64
Артикул В-46
Штамп ОТК <1>
Цена 3 руб. 10 коп.

Штамп с датой выпуска: 20 июня 1966

Размер линейки:

Сейчас логарифмические линейки выпускаются только в наручных часах. Человечество что-то потеряло, полностью перейдя от аналоговых вычислителей на чисто цифровые.

П.С.: фотографии не мои, взяты в интернете. На последнем снимке на циферблате маркировка завода МЛТЗКП, если кто знает что означает эта аббревиатура, прошу сообщить мне. Я смог расшифровать лишь её часть: «Московский Л? Т? Завод Контрольных Приборов», выпускал эту линейку «Московский опытный завод контрольных приборов «Контрольприбор»».

12 апреля 2013

Источник

Логарифмическая линейка (фото см. ниже) была придумана как прибор для экономии умственных затрат и времени, связанных с математическими расчетами. Особое распространение она получила в практике инженеров в институтах, ориентированных на научно-исследовательскую деятельность, и в статистических бюро до момента внедрения электронной вычислительной техники.

Линейка логарифмическая: история

Прообразом счетного устройства была шкала для вычислений английского математика Э. Гантера. Он придумал ее в 1623 г., вскоре после открытия логарифмов, для упрощения работы с ними. Шкала использовалась в сочетании с циркулем. Им отмеривались необходимые градуированные отрезки, которые потом складывались или вычитались. Операции с числами заменялись действиями с логарифмами. Используя их основные свойства, умножить, делить, возводить в степень или вычислять корень числа оказалось намного проще.

В 1623 году линейка логарифмическая была усовершенствована У. Отредом. Он добавил вторую подвижную шкалу. Она перемещалась вдоль основной линейки. Отмерять отрезки и считывать результаты исчислений стало легче. Для повышения точности устройства в 1650 году была реализована попытка увеличения длины шкалы за счет ее расположения по спирали на вращающемся цилиндре.

Добавление в конструкцию бегунка (1850 г.) сделало процесс исчисления еще более удобными. Дальнейшее усовершенствование механизма и способа нанесения логарифмических шкал на стандартную линейку не добавили точности прибору.

Устройство

Линейка логарифмическая (стандартная) изготавливалась из плотной древесины, стойкой к истиранию. Для этого в промышленных масштабах использовалось грушевое дерево. Из него изготавливался корпус и движок – планка меньшего размера, монтируемая во внутреннем пазе. Ее можно перемещать параллельно основанию. Бегунок изготавливался из алюминия или стали со смотровым окошком из стекла или пластика. На него нанесена тонкая вертикальная линия (визир). Бегунок двигается по боковым направляющим и подпружинивается стальной пластинкой. Корпус и движок облицованы светлым целлулоидом, на котором тиснением нанесены шкалы. Их деления заполнены типографской краской.

На лицевой стороне линейки располагаются семь шкал: четыре- на корпусе и три — на движке. На боковых гранях нанесена простая измерительная разметка (25 см) с делениями 1 мм. Шкалы (C) на движке внизу и (D) на корпусе сразу под ней считаются главными. На основании сверху располагается кубическая разметка (K), под ней – квадратичная (A). Ниже (сверху на движке) есть точно такая же симметричная вспомогательная шкала (B). Внизу на корпусе еще есть разметка для значений логарифмов (L). В самом центре лицевой части линейки между разметками (B) и (C) нанесена обратная шкала чисел (R). С другой стороны движка (планку можно вынуть из пазов и перевернуть) присутствуют еще три шкалы для расчета тригонометрических функций. Верхняя (Sin) – предназначена для синусов, нижняя (Tg) – тангенсов, средняя (Sin и Tg) – общая.

Разновидности

Стандартная линейка логарифмическая имеет длину измерительной шкалы 25 см. Выпускался еще карманный вариант длиной 12,5 см и устройство повышенной точности 50 см. Существовало деление линеек на первый и второй сорта в зависимости от качества исполнения. Внимание уделялось четкости наносимых штрихов, обозначений и вспомогательных линий. Движок и корпус должны были быть ровными и идеально подогнаны друг к другу. Изделия второго сорта могли иметь незначительные царапины и точки на целлулоиде, но они не искажали обозначений. Также мог присутствовать незначительный люфт в пазах и прогиб.

Существовали и другие карманные (похожие на часы диаметром 5 см) варианты устройства – логарифмическая дисковая (типа «Спутник») и круговая (КЛ-1) линейки. Они отличались и конструкцией, и меньшей точностью измерений. В первом случае для установки чисел на замкнутых круговых логарифмических шкалах использовалась прозрачная крышка с линией-визиром. Во втором – механизм управления (две вращающиеся ручки) был смонтирован на корпусе: одной управлялся дисковый движок, другая управляла стрелкой-визиром.

Возможности

Логарифмической линейкой общего назначения можно было осуществлять деление и умножение чисел, возведить их в квадрат и куб, извлекать корень, решать уравнения. Кроме этого, по шкалам производились тригонометрические вычисления (синус и тангенс) по заданным углам, определялись мантиссы логарифмов и обратные действия – находились числа по их значениям.

Правильность вычислений во многом зависела от качества линейки (длинны ее шкал). В идеале можно было надеяться на точность до третьего знака после запятой. Такие показатели были вполне достаточными для технических расчетов в XIX веке.

Возникает вопрос: как пользоваться логарифмической линейкой? Одного знания назначения шкал и способов нахождения на них чисел еще не достаточно для произведения расчетов. Чтобы использовать все возможности линейки, нужно понимать, что такое логарифм, знать его характеристики и свойства, а также принципы построения и зависимости шкал.

Как считать на логарифмической линейке

Для уверенной работы с устройством требовались определенные навыки. Сравнительно простые вычисления с одним бегунком. Для удобства движок (чтобы не отвлекал) можно удалять. Установив черту на значения любого числа на основной (D) шкале можно сразу же по визиру получить результат возведения его в квадрат на шкале выше (A) и в куб – на самой верхней (K). Внизу (L) будет значение его логарифма.

Деление и умножение чисел производится с помощью движка. Применяются свойства логарифмов. Согласно им, итог умножения двух чисел равен результату сложения их логарифмов (аналогично: деление и разница). Зная это, можно достаточно быстро производить расчеты, используя графические шкалы.

Чем сложна логарифмическая линейка? Инструкция по ее правильному использованию шла в комплекте с каждым экземпляром. Кроме знания свойств и характеристик логарифмов, нужно было уметь правильно находить исходные числа на шкалах и уметь в нужном месте считывать результаты, в том числе самостоятельно определять точное место расположения запятой.

Актуальность

Как пользоваться логарифмической линейкой, в наше время знают и помнят немногие, и с уверенностью можно утверждать, что число таких людей будет снижаться.

Логарифмическая линейка из разряда карманных счетных приспособлений давно стала раритетом. Для уверенной работы с ней нужна постоянная практика. Методика расчетов с примерами и разъяснениями тянет на брошюру в 50 листов.

Для среднестатистического человека, далекого от высшей математики, логарифмическая линейка может представлять какую-то ценность разве что справочными материалами, размещенными на обратной стороне корпуса (плотность некоторых веществ, температура плавления и пр.). Преподаватели даже не утруждаются вводить запрет на ее наличие при сдаче экзаменов и зачетов, понимая, что разобраться с тонкостями ее использования современному студенту очень сложно.

Источник

: April 12 2009, 16:39

Category:

Транспорт
Cancel

Круглая логарифмическая линейка

Я еще не рассказывал вам про круглую логарифмическую линейку. Ее разработали в те времена, когда карманные калькуляторы были еще в области фантастики.
Вот она:

Пять сантиметров в диаметре, она имеет две стороны со стрелками и шкалами. Первая сторона видна выше, а вторая — под катом.

Круговая линейка умеет: умножать, делить, возводить в квадрат, извлекать корни и вычислять синусы и тангенсы. Складывать и вычитать, впрочем, как и обычные логарифмические линейки, она не умеет.
Сверху вы видите две ручки. Одна синхронно поворачивает стрелки с двух сторон, а вторая — вращает поверхность со шкалами, но только с одной стороны. Под второй ручкой обратите внимание на маленький указатель. Он нам пригодится.

На первой стороне цифрой 1 помечена основная шкала со значениями от 1 до 10 для умножения и деления, или от 0.1 до 1 для вычисления синусов/тангенсов. Вторая шкала — шкала синусов от 6 до 90 градусов. А третья — шкала тангенсов от 1 до 45 градусов. Вычислять синусы и тангенсы очень просто — двигаем стрелку для значения градусов и в шкале 1 сразу читаем ответ. На фото стрелка стоит около 11.5 градусов. Получаем ответ: sin 11.5^o = 0.2
Вторая сторона имеет две шкалы — шкала чисел и шкала квадратов чисел. Стрелка стоит около числа 3, а сразу над ней — цифра 9.

Самое сложное в этой линейке — умножение и деление. Сложное — потому, что если линейкой долго не пользоваться, то все время забываешь, какие шкалы для чего нужны. А если разобраться, то становится очень просто.
Сначала одной ручкой устанавливается множимое на основной шкале, где синусы и тангенсы. После этого линейка переворачивается, и другой ручкой крутится поверхность так, чтобы поверхность повернулась к стрелке значением множителя. И как только нужная цифра встанет под стрелкой, маленький указатель сразу покажет ответ.
На фото показан пример умножения 2 * 3 = 6.

На счет практического применения в те времена — не знаю. Пользоваться ей, в отличие от обычной логарифмической линейки немного неудобно, точность меньше. Зато ее можно легко носить в кармане; в трамвае, если что, можно быстро извлечь корень, а то и взять тангенс.

Источник