Содержание
- Расскажем о том, как собрать бумажный октаэдр
- Начинаем собирать фигуру
- Особенности монтажа граней
- Нужные навыки
- Полезные геометрические сувениры
- Обучение и хобби
- Развёртка геометрической фигуры — октаэдр
- КОММЕНТАРИИ
- Октаэдр
- Поэтому на вопрос — «что такое октаэдр?», можно дать следующее определение: » Октаэдр это геометрическое тело из восьми граней, каждая их которых — правильный треугольник «.
- Математические характеристики октаэдра
- Вариант развертки
- Видео. Октаэдр из набора «Волшебные грани»
- Видео. Вращение правильных многогранников
- Рассмотрим, как сделать октаэдр из бумаги
- Подготовим материалы
- Эскиз – верный помощник
- Все своими руками
- Уроки стереометрии
- Замысловатые тайны геометрии
Расскажем о том, как собрать бумажный октаэдр
В данной статье мы рассмотрим, как собрать бумажный октаэдр, что эта фигура собой представляет и чем она может быть полезна для каждого из нас. Возможно, кто-то найдет себя в подобном виде творчества или же наконец-то получит вариант самодельного подарка близкому человеку. Инструкция по изготовлению этой стереометрической фигуры проста, и с ней справится даже ребенок дошкольного возраста, поэтому поехали.
Начинаем собирать фигуру
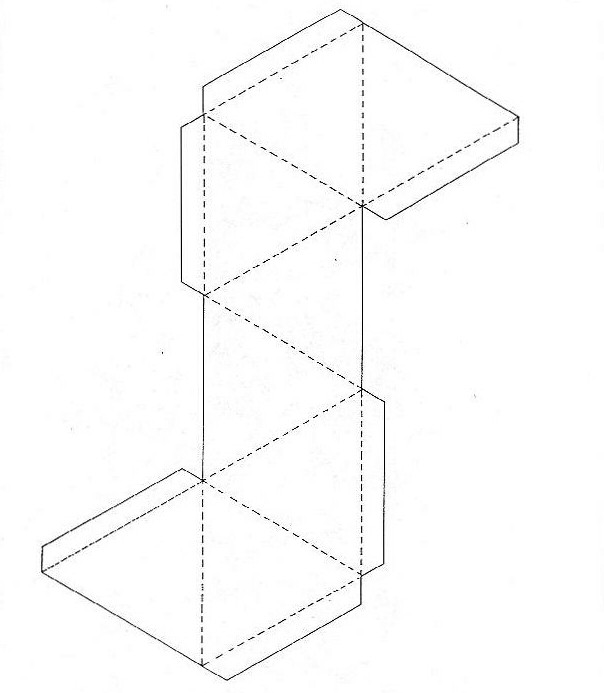
Многие, глядя на октаэдр в развертке, недоумевают, как правильно соединить между собой все его грани и стороны, чтобы фигура приобрела правильный внешний вид. Попробуем раскрыть эту геометрическую тайну и понять, как собрать бумажный октаэдр. Для начала нам понадобится сама фигура в развертке. Ее можно переснять из книги или же распечатать изображение, которое приложено к статье. Можно сказать, что это есть готовая схема. Как сделать октаэдр самостоятельно? Это также несложно. За основу возьмите любую величину, которая вам потребуется. Это будет длина каждой грани фигуры. Затем прорисуйте шесть равносторонних треугольников так, как вы их видите на рисунке, а к ним дорисуйте еще два.
Особенности монтажа граней
Многие даже после того, как построят развертку фигуры, не понимают, как собрать бумажный октаэдр так, чтобы он получился правильным. Для этого нужно, вырезая фигуру, оставить припуски для склеивания. Они имеют скошенные края, и на одном из рисунков они изображены. Теперь наносим на эти припуски клей и собираем стереометрическую фигуру по линиям сгиба. Важно, чтобы вы предварительно проделали четкие сгибы в месте пересечения всех граней фигуры. Так ваша поделка будет иметь более красивый и точный, с геометрической точки зрения, внешний вид.
Нужные навыки
Когда вы знаете, как собрать бумажный октаэдр, вам проще работать с более сложными геометрическими фигурами. Некоторым людям это необходимо для работы, другие просто пополняют свой багаж знаний и расширяют творческий диапазон таким образом. Стоит отметить, что собирать эту поделку можно из обыкновенной тонкой бумаги, если вы тренируетесь. Когда октаэдр нужен для каких-либо других целей, желательно использовать ватман или плотный картон.
Полезные геометрические сувениры
Интересным фатом является то, что октаэдр из бумаги может стать отличной идеей для подарка близкому человеку. Если вы намереваетесь преподнести в качестве презента лишь милую безделушку, то непосредственно перед склеиванием на каждую грань октаэдра нужно нанести рисунок. Его можно сделать в виде аппликации или же нарисовать, если вы владеете навыками художника. Более «серьезной» затеей будет календарь-октаэдр. Вместо рисунков на каждую грань, кроме двух, наносим разметку дней. В каждом треугольничке должно поместиться два месяца.
Обучение и хобби
Во многих дошкольных заведениях детей учат тому, как рисовать стереометрические фигуры в развертке, а после этого собирать их и склеивать. Если вы видите, что у вашего ребенка подобных навыков нет, обучите его всему этому на дому. Также если в данной области пробелы имеются у вас, вы всегда можете наверстать упущенное и, распечатав приложенную схему, собрать бумажный октаэдр с помощью обычного канцелярского набора.
Источник
Развёртка геометрической фигуры — октаэдр
Октаэдр — один из пяти выпуклых правильных многогранников.
Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Википедия расскажет вам о вычислении площади октаэдра и других Платоновых телах.
Или сохраните развёртки октаэдра в jpg-формате:
КОММЕНТАРИИ
у меня получилось, спс большое,только было бы лучше если можно было бы распичатать по честям
ничего не получилась!! не октаэдр,а какой-то прямоугольник у которого одна часть больше другой.
У меня получился довольно таки симпотяшный октаэдр и довольно просто его было сделать спс большое. Александр если руки и одного сета и мозгов нету то тогда тебе не одна инструкция и формула не поможет.
Отличный получился октаэдр 🙂 Спасибо большое!
Классный октаэдр, всё довольно легко и быстро) Спасибо огромное;))
Все получилось , спасибо за чертеж , а у которых не получается значит руки кривые .
Развертка норм, но потратил часа полтора
Спасибо огромное! Всё делал сам, чертил, вырезал и клеил!) Отличный получился октаэдр! Такой же, как на картинке! Сделал за 25 минут.
Отстой,углы вообще не сходятся.
Я ищу я делаю А вы как там
вы народ сколько там сантиметров пожалеть Подскажите
Спасибо большое. Скачивать не стала, стало интересно начертить самостоятельно . Все получилось идеально!
Источник
Октаэдр
Древние греки дали многограннику имя по числу граней. «Окто» означает восемь, «хедра» — означает грань (октаэдр – восьмигранник).
Поэтому на вопрос — «что такое октаэдр?», можно дать следующее определение: » Октаэдр это геометрическое тело из восьми граней, каждая их которых — правильный треугольник «.
Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .
- Тип грани – правильный треугольник;
- Число сторон у грани – 3;
- Общее число граней – 8;
- Число рёбер, примыкающих к вершине – 4;
- Общее число вершин – 6;
- Общее число рёбер – 12;
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.
Октаэдр имеет центр симметрии — центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Математические характеристики октаэдра
Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы октаэдра определяется по формуле:
Сфера может быть вписана внутрь октаэдра.
Радиус вписанной сферы октаэдра определяется по формуле:
Площадь поверхности октаэдра
Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8. Либо воспользоваться формулой:
Объем октаэдра определяется по следующей формуле:
Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.
Вариант развертки
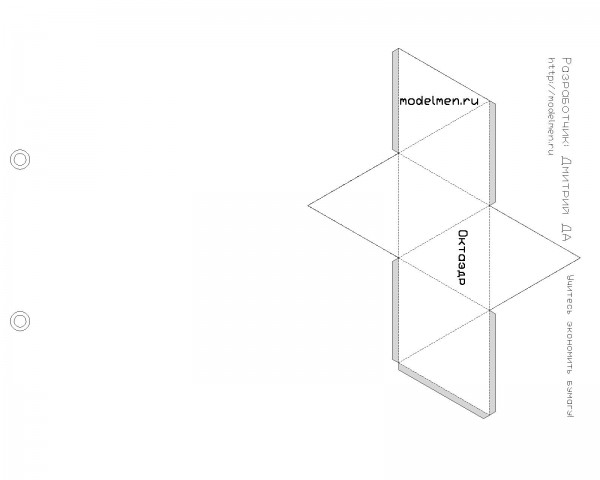
Октаэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.
Древнегреческий философ Платон ассоциировал октаэдр с «земным» элементом воздух, поэтому для построения модели этого правильного многогранника мы выбрали серый цвет.
Заметим, что это не единственный вариант развертки.
Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
— если Вы предполагаете распечатать на цветном принтере — цветная развертка
— если Вы предполагаете использовать для сборки цветной картон — развертка
Классический вариант раскраски предполагает окраску октаэдра четырьмя различными цветами, причем таким образом, что каждая грань имеет свой цвет отличный от соседней и только противоположные не соприкасающиеся друг с другом грани окрашиваются в одинаковые цвета.
Вариант окраски представлен на рисунке. Вы можете скачать развертку с соответствующей раскраской граней.
Видео. Октаэдр из набора «Волшебные грани»
Вы можете изготовить модель октаэдра воспользовавшись деталями для сборки из набора «Волшебные грани».
Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
вращение готового многогранника:
Видео. Вращение правильных многогранников
Источник
Рассмотрим, как сделать октаэдр из бумаги
Среди всех существующих геометрических фигур, которые появились еще во времена античности, одной из самых интересных считается октаэдр. Эта фигура является одной из пяти тел, именуемых платоновыми. Она правильная, симметричная и многогранная, а также имеет сакральное значение с точки зрения стереометрии, практикуемой в Древней Греции. Сегодня данное геометрическое тело изучается детьми в школе, и для того, чтобы понять его структуру лучше, мы рассмотрим, как сделать октаэдр из бумаги.
Подготовим материалы
Все, что понадобится в ходе данного процесса – это ножницы, клей, карандаш, линейка, и сама бумага, которая ляжет в основу будущей поделки. Считается, что самостоятельное производство подобных стереометрических фигур улучшает абстрактное мышление, позволяет лучше сориентироваться в пространстве. Поэтому вы можете с помощью нашего краткого урока наверстать упущенные в школе геометрические навыки или же предложить своему чаду слепить нечто подобное, если у него наблюдаются проблемы с восприятием геометрических пространств и фигур.
Эскиз – верный помощник
Первый вариант того, как сделать октаэдр из бумаги – это уже готовый эскиз. В статье предложена картинка, на которой изображена данная фигура в развертке, и все, что вам остается – это распечатать ее и склеить по намеченным линиям. Так ваша поделка будет иметь наиболее точные параметры. Не забудьте только предварительно наклеить бумагу на картон, чтобы октаэдр был более прочным и прослужил дольше. Особенно важно это в том случае, если он предназначается для ребенка.
Все своими руками
Другой вариант того, как сделать октаэдр из бумаги, основывается на несложных формулах и черчении. Данная геометрическая фигура состоит из 8-ми граней, 6-ти вершин и 12-ти ребер, каждые 4 из которых сходятся у одной вершины. Если сложить в единое число все углы октаэдра, то сумма будет равна 240 градусам. Стоит также отметить, что эта мифическая стереофигура имеет треугольное основание и полностью симметрична, поэтому ее нередко называют антипризмой.
Уроки стереометрии
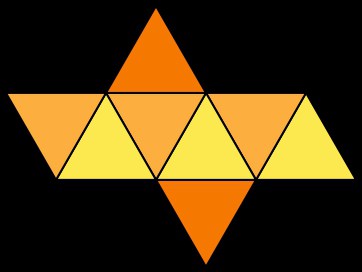
Развертка октаэдра представляет определенный набор полностью равных между собой треугольников. Шесть из них выстроены в единый ряд по принципу «валета», а два остальных своими основаниями примыкают к двум средним фигурам с различных сторон. Поэтому ответ на вопрос о том, как сделать октаэдр из бумаги без макетов, прост. Вам нужно лишь выбрать единую величину грани, и положить ее в основу восьми равносторонних треугольников. Не забудьте только оставить припуски на линии сгиба, по которым вы склеите будущую поделку.
Замысловатые тайны геометрии
Существуют различные разновидности подобной стереофигуры. Среди таковых стоит назвать кубооктаэдр. Развертка представляет из себя 6 квадратов и 8 правильных треугольников, которые собраны в объемное тело согласно правилам симметрии. Фигура эта полуправильная, и, стоит отметить, достаточно молодая. Открыта она была творцом Леонардо да Винчи, а называлась тогда «звездчатый октаэдр». Сделать его вы также можете по предложенной в статье схеме.
Источник
Дата публикации: 12 апреля 2017.
То, что сейчас является обязательным к изучению на уроках геометрии, в древние времена считалось опасной ересью. Раньше геометрия считалась священным знанием. О геометрических фигурах, таких как: тетраэдр, икосаэдр, куб было опасно говорить, за это можно было поплатиться жизнью, эти тела считались кирпичиками Вселенной.
Октаэдр одна из геометрических фигур, которую относится к сакральной геометрии, алхимии и изучается в стереометрии. Эта фигура называется платоновым телом и является одним из пяти священных фигур, одним из пяти правильных многогранников. Его соотносят со стихией воздуха, эфиром, с энергетическим телом человека. Слово октаэдр состоит из двух слов: восемь и грань, другими словами октаэдр – это восьмигранник, ограниченный восемью треугольниками, обладающий симметрией. Эта геометрическая фигура состоит из 8 граней, 6 вершин (в каждой из которых, сходится 4 ребра) и 12 ребер. Сумма углов октаэдра составляет 240°. Октаэдр считается антипризмой, имеющей треугольное основание.
Виды октаэдров
Октаэдр Брикара. В 1897 французский математик Брикар году доказал, что существуют изгибаемые октаэдры, эти фигуры не имеют самопересечений и являются не выпуклыми.
Октаэдр Брикара
Существует еще один октаэдр, который был открыт Леонардо да Винчи, и называется он – звездчатый октаэдр. Его можно рассматривать, как соединение двух тетраэдров. Сто лет спустя звездчатый октаэдр был заново открыт Иоганном Кеплером, который назвал его звезда восьмиугольная.
Где можно встретить октаэдр? Чаще всего эту фигуру можно встретить в природе, она – великий творец такие фигур и форм. Алмазы часто имеют вид октаэдра. Уже в XIV веке стали делать огранку, которая повторяет эту геометрическую фигуру. Самый знаменитый алмаз «Шах» сохранил свой естественный вид – форму кристалла октаэдра, его масса составляет 88,7 карата.
Алмаз «Шах»
Другие минералы тоже имеют форму октаэдра, например, куприт (красная медная руда). Также октаэдр можно найти среди других руд: самородная медь, малахит, лимонит. Такие минералы, как хлорид натрия (поваренная соль), оливин, перовскит, шпинель, флюорит тоже имеют форму этой геометрической фигуры. Различные металлы, например никель, магний, титан, лантан имеют структуру пор и пустот похожую на октаэдр. Формула октаэдра применяется при выделки кожи, протравливания тканей. Игрушка головоломка «Октаэдр» называется умным подарком и напоминает всем известный кубик Рубика. При изготовлении алюминия используют алюминиево-калиевые кварцы имеющие форму этой геометрической фигуры. В играх основанных на правилах Dungeons & Dragons, игральные кости иногда имеют форму октаэдра.
Совсем недавно была представлена интересная находка из Марокко – графитовые кристаллы, имеющие форму октаэдра. Это удивительно, потому что никогда раньше не встречался графит такой конфигурации. Природа продолжает творить божественные фигуры, преподнося нам изумительное открытия и необычные геометрические подарки.
Сколько всего познавательного и удивительного можно узнать о том, что в школе нам казалось неинтересным и не нужным. Великие мыслители с почтением относились к геометрическим фигурам и считали их священными. Художники используют их в своих творениях, писатели рассказывают о них в фантастических произведениях. Интересные факты о геометрических фигурах вызывают у детей живой интерес и желание изучать геометрию, создавать эти замечательные фигуры на уроках в школе или дома.
Развертка октаэдра из бумаги или из картона
Ниже вы найдете схемы, позволяющие сделать октаэдр из бумаги или картона своими руками. При сборке октаэдра можно применить фантазию, поместив на его гранях различные рисунки. Для этого необходимо подобрать картинки в интернете или лучше нарисовать самим и поместить их на грани вашей фигуры в каком либо графическом редакторе, например Photoshop или даже Paint. Такой оригинальный октаэдр с картинками можно преподнести как замечательный сувенир или подарок. Друзьям или родителям обязательно понравятся эти поделки из бумаги, сделанные с любовью и большой выдумкой.
Развёртка геометрической фигуры — октаэдр
Написать комментарий
КОММЕНТАРИИ
-
Очень хорошая книга по работе с бумагой!
Дмитрий ДА
16.11.2009 -
Пробником можно проверить лампочки, реле, концевые выключатели автомобиля, предохранители и просто напряжения на клеммах, а тонкий гибкий щуп проникает в любые автомобильные колодки.
Илья И
11.03.2016 -
Представляю вам пошаговый обзор, как можно сделать кленовый лист оригами самым простым способом. Не страшно, что он состоит из множества деталей, все равно процесс не сложен, в отличие от тех вариантов, где листик создают из одного листа бумаги.
Александра
11.10.2021
Страница сгенерирована за 0,016107797622681 сек.
SQL-запросов: 6
Памяти использовано: 489 kB.
Развёртка октаэдра для склеивания
Кажется, что сделать октаэдр из бумаги сложно. На самом деле, если есть шаблон развертки для вырезания — все предельно просто.
Вам потребуются:
- бумага (картон)
- клей
- ножницы
- возможно карандаш и линейка.
Скачайте, распечатайте, вырежьте по контуру нужный шаблон с разверткой октаэдра и склейте по специально сделанным для этого припускам.
Скачать развертки октаэдра в формате pdf
Новые трафареты и шаблоны
Диплом об окончании начальной школы
Диплом выпускника детского сада
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
к оглавлению ^
Из бумаги
Из картона
Развертки куба
к оглавлению ^
Треугольника
к оглавлению ^
Прямоугольника
к оглавлению ^
Цилиндра
Ромба
Призмы
к оглавлению ^
Задание 2 (построение прямоугольного треугольника)
Постройте на нелинованной бумаге треугольник , чтобы угол был прямым, длина стороны равнялась 15 см, а длина сторогы – 20 см.
Построим точку (Рис. 18).
Рис. 18. Точка
Проведем через точку прямую (Рис. 19).
Рис. 19. Прямая, проведенная через точку
Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон совпала с лучом, как показано на рис. 20.
Рис. 20. Построение прямого угла
Проведем по второй стороне прямого угла треугольника луч из точки и получим прямой угол (Рис. 21).
Рис. 21. Полученный прямой угол
Выполним построение сторон треугольника. Построим отрезок , который равен 15 см (Рис. 22).
Рис. 22. Отрезок
Построим отрезок , который равен 20 см (Рис. 23).
Рис. 23. Отрезок
Соединим полученные точки отрезком . Мы получили прямоугольный треугольник (Рис. 24) с прямым углом и сторонами см и см.
Рис. 24. Треугольник
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
к оглавлению ^
Конуса
к оглавлению ^
Пирамиды
к оглавлению ^
Шестигранника
к оглавлению ^
Макета с припусками
Параллелепипеда
к оглавлению ^
Трапеции
к оглавлению ^
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
к оглавлению ^
Многогранника
к оглавлению ^
Параллелограмма
Задание 1 (определение вида треугольников)
Назовите номера тупоугольных, остроугольных и прямоугольных треугольников на рисунке 16.
Рис. 16. Иллюстрация к заданию 1
Треугольник номер 1 – остроугольный, у него все углы острые. Треугольники номер 3 и 4 – тупоугольные, каждый из них имеет один тупой угол. Фигура номер 2 – прямоугольный треугольник. Проверим, действительно ли эта фигура имеет прямой угол, с помощью прямоугольного треугольника (Рис. 17).
Рис. 17. Проверка треугольника номер 2
Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
к оглавлению ^
Сложных фигур
3d
Октаэдра
к оглавлению ^
Тетраэдра
к оглавлению ^
Икосаэдра
к оглавлению ^
Додекаэдра
к оглавлению ^
Гексаэдра
Фигурок из треугольников
Виды углов
Развернутый угол. (Рис. 4)
Угол называется развернутым, если его стороны лежат на одной прямой.
Рис. 4. Виды углов: развернутый
Прямой угол (Рис. 5)
Прямой угол составляет половину развернутого.
Рис. 5. Виды углов: прямой угол
Прямой угол можно получить путем складывания бумаги. Сложив лист дважды, мы получим модель прямого угла, его составляют линии сгиба.
Приложим модель угла к углу на чертеже (Рис. 5) таким образом, чтобы углы и стороны совпали (Рис. 6).
| Рис. 5. Модель угла и угол на чертеже | Рис. 6. Модель угла, приложенная к углу на чертеже |
Мы убедились, что на чертеже действительно изображен прямой угол.
Для удобства определения, прямой угол или нет, используют особый инструмент – прямоугольный треугольник (Рис. 7).
Рис. 7. Прямоугольный треугольник
Непрямые углы делятся на острые (Рис. 
| Рис. 8. Виды углов: острый угол Острый угол меньше прямого (Рис. 10). Рис. 10. Сравнение острого и прямого угла |
Рис. 11. Виды углов: тупой угол
Тупой угол больше прямого (Рис. 12). Рис. 12. Сравнение тупого и прямого угла |
Макеты из бумаги
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
к оглавлению ^
Оригами
Дом
к оглавлению ^
Животные
Корабль
Применяется множество вариантов, как сделать кораблик из бумаги.
Простая схема.
Полигональные чертежи
Игрушки из фигур
Геометрические маски
к оглавлению ^
Карандаш
( 1 оценка, среднее 5 из 5 )