Как собрать кубик рубика алгоритм бога пошаговая инструкция

Несмотря на то, что кубику Рубика уже много десятков лет, эта головоломка продолжает оставаться популярной. Ставятся рекорды — как людьми, так и роботами, совершенствуется алгоритм решения головоломки. Причем сейчас компьютеры уже могут научить собирать Кубик человека с любым уровнем опыта (речь здесь идет о приложениях обучающих, коих немало). Правильно собрать все грани после пары дней обучения при помощи компьютера смогут даже те, кто взял игрушку в руки в первый раз.

К слову, чемпион мира по сборке кубика Рубика (да, есть и такие чемпионы) решает головоломку всего за 4,9 секунды. Чемпиона зовут Лукас Эттер, это подросток из США. Аналогичный рекорд для роботизированной системы составляет уже 0,887 секунды (правда, этот результат еще не подтвержден). Но как научиться быстро собирать кубик Рубика самостоятельно? Можно тренироваться (на это могут уйти многие годы). А можно воспользоваться специальной программой, которая поможет собрать кубик в минимальное число ходов (так называемый алгоритм бога). Здесь никакие тренировки не нужны, приложение делает все само.

Вот так собирает кубик чемпион-человек:

А так — чемпион-компьютер:

Вообще говоря, существует множество алгоритмов для сборки головоломки. Для обычного человека среднее число ходов составляет около 40. Немногие чемпионы умеют собирать кубик по алгоритму бога. Если кратко, то так называют алгоритм, который требует для сборки любой начальной конфигурации минимальное количество ходов. Для кубика Рубика это число равно 20.

А теперь вернемся к дополненной реальности. Разработчик по имени Martin Španěl создал приложение Mistr Kostky, которое помогает собирать кубик Рубика человеку. Причем число ходов как раз то самое — ровно 20. Приложение может определять состояние 2-3 граней кубика одновременно, а для распознавания получаемых изображений используется библиотека OpenCV.

В дополненной реальности показывается, как нужно вращать грани головоломки, чтобы достичь оптимального количества ходов. Разработчик создал свою программу в рамках научной работы — он является студентом Карлова университета (Прага).

Работает программа в два этапа. На первом происходит распознавание состояния каждой грани. После того, как система завершает первый этап, начинается второй — приложение показывает пользователю, куда и как нужно вращать грани кубика для решения головоломки (иногда получается это сделать менее, чем за 20 ходов).

Интересно, что если владелец головоломки ошибается, то приложение приходится перезапускать — оно не в состоянии перестроиться «на лету». Отмечу, что приложения для решения кубика рубика появились не сейчас. Это одно из лучших, да, но еще в 2009 году в каталог приложений Apple была добавлена программа Cube Cheater. Она помогала пользователю найти решение по фотографии граней.

Изначально автор создавал свое приложение под Android, но обещал выпустить и версию под другие платформы. Вот ветка обсуждения Mistr Kostky на Reddit.

Есть ли у вас кубик Рубика?

Проголосовали 846 пользователей.

Воздержались 103 пользователя.

Теория алгоритма бога

В основу теории Алгоритма Бога было заложено утверждение, что собрать Кубик Рубика необходимо не более 20 ходов.

Еще десять лет назад было доказано, что наименьшее число ходов для сбора кубика 23.Однако сейчас число ходов сократилось до 20, благодаря компании Google, которая потратила 35 лет компьютерных вычислений, чтобы доказать, что алгоритм бога Кубика Рубика 3х3 существует. Именно так его окрестили ученые, работавшие над поиском формулы по сбору кубика за 20 ходов. Для создания универсального решения было придумано множество алгоритмов, каждый из которых решал свою задачу по сбору той или другой грани Кубика Рубика.

Один алгоритм вычислял оптимальное решение для сбора фронтальной поверхности. Другой — верхних и нижних граней. Формул для сбора Кубика Рубика существует множество, отличающихся друг от друга по количеству ходов и степени сложности. Среднестатистический любитель этой головоломки умеет собирать кубик за 40 и более ходов. Поэтому алгоритм, который решает задачу по сбору Кубика Рубика за наименьшее число ходов, назвали «Алгоритм Бога».

Спустя 15 лет после того, как Эрне Рубик создал свою головоломку любители кубика доказали, что 20 шагов достаточно, чтобы собрать любой, перемешанный произвольным образом, кубик.

Формула Бога для Кубика Рубика 3х3

Не смотря на то, что учеными было доказано, что любую позицию можно собрать за 20 ходов, универсальной формулы для сборки Кубика Рубика пока не придумали. Но была выведена обобщенная формула бога для Кубика Рубика 3х3 которая решает 95% всех вариантов сборки.

B2 D2 FI R2 F U2 R2 FI R2 U2 F R U L B D RI D L2 UI

Для удобства сборки головоломки лучше всего за основу брать светлую грань белую или желтую.

Расшифровка формулы Бога (Этапы сборки)

• Этап №1

  B2 (back) — поворот задней стороны кубика по часовой стрелке 2 раза
  

• Этап №2

  D2 (down) — поворот нижней стороны кубика по часовой стрелке 2 раза
  

• Этап №3

  FI(front) — поворот фронтальной (передней) части кубика против часовой стрелки 1 раз
  

• Этап №4

  R2 (right) — поворот правой стороны кубика по часовой стрелке 2 раза
  

• Этап №5

  F (front) — поворот фронтальной (передней) части кубика по часовой стрелке 1 раз
  

• Этап №6

  U2 (up) — поворот верхней стороны кубика по часовой стрелке 2 раза
  

• Этап №7

  R2 (right) — поворот правой стороны кубика по часовой стрелке 2 раза
  

• Этап №8

  FI (front) — поворот фронтальной (передней) части кубика против часовой стрелки 1 раз
  

• Этап №9

  R2 (right) — поворот правой стороны кубика по часовой стрелке 2 раза
  

• Этап №10

  U2 (up) — поворот верхней стороны кубика по часовой стрелке 2 раза
  

• Этап №11

  F (front) — поворот фронтальной (передней) части кубика по часовой стрелке 1 раз
  

• Этап №12

  R (right) — поворот правой стороны кубика по часовой стрелке 1 раз
  

• Этап №13

  U (up) — поворот верхней стороны кубика по часовой стрелке 1 раз
  

• Этап №14

  L (left) — поворот левой стороны кубика по часовой стрелке 1 раз
  

• Этап №15

  B (back) — поворот задней стороны кубика по часовой стрелке 1 раз
  

• Этап №16

  D (down) — поворот нижней стороны кубика по часовой стрелке 1 раз
  

• Этап №17

  RI (right) — поворот правой стороны кубика против часовой стрелки 1 раз
  

• Этап №18

  D (down) — поворот нижней стороны кубика по часовой стрелке 1 раз
  

• Этап №19

  L2 (left) — поворот левой стороны кубика по часовой стрелке 2 раза
  

• Этап №20

  UI (up) — поворот верхней стороны кубика против часовой стрелки 1 раз
  

ВАЖНО!!! В процессе сборки кубика нужно быть внимательным относительно вращения граней по часовой стрелки и против часовой стрелки. Многие во время сборки путают направления вращения и потом говорят, что алгоритм бога Кубика Рубика не работает.

Напоминаем что данный способ подходит только для 95% ситуаций. Поэтому если у вас не получается большое количество раз собрать Кубик Рубика, нужно еще раз хорошенько его перемешать и повторить сборку по формуле Бога.

Научно исследовательская работа на тему: Математика волшебного кубика.

МБОУ СОШ № 19 Им. Б. И. Северинова

Всероссийская научно-практическая конференция школьников, студентов, аспирантов и молодых ученых «Исследования молодых – регионами»

Тема: » Математика волшебного кубика «

Выполнил(а): Федосеев Юрий Сергеевич

8 «А» класс СОШ № 19

Научный Руководитель: Рыбакова Е.И –

учитель математики СОШ № 19

Уфа 2012

Введение:

Любопытство подтолкнуло меня на изучение «Математики волшебного кубика». Все началось вот с чего. Как-то раз, шагая по улице, я увидел, что ребята собирают тот самый «Волшебный кубик»- кубик Рубика. При этом они собирали его очень быстро, будто у них пальцы в узел завязывались. Придя домой, я заглянул в интернет, чтобы научиться сборке. Выучив за сутки необходимую теорию, я отправился по магазинам в поисках хорошего кубика. Купив кубик, сборку отработал за два дня.

Основная часть:

Когда я начал изучать теорию таинственного кубика, я обнаружил такую историю…

Лучшая головоломка ХХ века, придуманная 13 лет назад венгерским преподавателем дизайна Эрнё Рубиком, упорно сопротивляется попыткам разгадать все ее тайны. Сразу после изобретения кубика Рубика начался поиск самого короткого пути к ее решению. Первые разработанные алгоритмы требовали 200-300 ходов (поворотов граней) для того, чтобы вернуть кубик в исходное состояние. Постепенно длина алгоритмов (т. е. минимальное число ходов, гарантирующее решение) сокращалась. Это происходило за счет изменения последовательности сборки разных частей головоломки (улучшения стратегии) и применения более коротких операций для перестановки и правильной ориентации маленьких кубиков (улучшения тактики). Ставший самым популярным послойный алгоритм кубика Рубика осуществляет сборку не более чем за 108 ходов. Совершенствуя его, удается уменьшить это число до 86 ходов. Дальнейшие улучшения требуют резкого увеличения количества формул, которые необходимо держать в голове или на бумаге в процессе сборки. В период всеобщего увлечения кубиком (1981-1988 гг.) редакция ‹Кванта› получила не менее десятка объемистых разработок, авторы которых, проделав гигантскую работу по поиску новых операций, получили алгоритмы, позволяющие решать «головоломку века» в среднем за 50-60 ходов. Наиболее основательную работу проделал московский инженер А. Карасев, разработавший таблицы для сборки кубика из 5412 операций, разбитых на 22 группы по 246 формул в каждой группе! Одновременно с любителями решать головоломку, держа ее в руках, неприступный кубик штурмовали и программисты. Сначала успеха добились «менее безумные» из них — те, кто взялись за Малый кубик размером 2X2X2 кубичка. Задачу они решали с конца.

В дальнейшем этот алгоритм удалось несколько улучшить — сначала этого добился сам англичанин, а пару лет назад Х. Клоостерман из Голландии довел длину алгоритма до 42 ходов. Важно отметить, что эта граница обоснована строго (а не эмпирически), т. е. доказано, что из любого состояния кубика Рубика можно вернуться в правильное не более чем за 42 хода, причем данный рекордный алгоритм не может гарантировать лучшего результата. (Это не означает, что другой алгоритм не может оказаться короче.) Конечно, это доказательство существенно использует компьютер (как, например, и относительно недавнее решение знаменитой «проблемы четырех красок»): для каждого из этапов сборки был осуществлен полный перебор вариантов, число ходов, понадобившееся в худшем случае, и принимается за «длину» данного этапа. Совсем недавно нового достижения добился немецкий математик Герберт Коцемба. Он был среди тех «менее безумных», кто 10 лет назад победили Малый кубик, но затем примкнул к «самым самым» и, возможно, уже остался единственным, кто до наших дней продолжал штурм головоломки века. Теперь к нему пришел заслуженный успех. Он разработал алгоритм и написал программу, которая решает головоломку Рубина менее чем за 21 ход! Сразу скажем, что эта оценка длины, в отличие от предыдущей, эмпирическая: все состояния кубика, которые предлагались программе Коцембы, были упорядочены не более чем за 21 ход. В частности, программа нашла более короткие решения для многих задач на составление узоров на кубика (или пасьянсов), весьма популярных в «золотую эру» кубика. Нет никакой гарантии, однако, что состояний, требующих больше 21 поворота по программе Коцембы, не существует вовсе. Более того, такую гарантию мог бы дать только полный перебор вариантов для каждого этапа программы (их два), а он пока не под силу даже программе Коцембы и его более мощному, чем у предшественников, компьютеру.

Идея алгоритма Герберта Коцембы

Собственно говоря, то, что придумал Коцемба, не является «алгоритмом сборки кубика» в том смысле, как его обычно понимают в «кубологии». Обычные алгоритмы сборки представляют собой наборы правил, позволяющих для любого заданного состояния кубика поставить некую ближайшую цель и достичь ее, выполнив последовательность поворотов граней, предписываемую правилами в данной ситуации. Тем самым кубик переводится в новое состояние, более близкое к правильному (по крайней мере, с точки зрения данного алгоритма). Например, цель может состоять в том, чтобы найти неправильно стоящий угловой кубичек и переместить его в свой угол, не трогая остальные угловые кубички. И таких маленьких шажков приходится делать очень много. В алгоритме Коцембы ставится только одна промежуточная цель — кубик надо перевести в одно из состояний, которые так и названы — промежуточными. Они характеризуются тем, что любое промежуточное состояние можно получить из правильного (а значит, и наоборот — превратить его в правильное)‚ поворачивая четыре боковые грани только а 180°‚ а верхнюю и нижнюю- а произвольный угол (естественно, кратный 90°). Первая цель (задача первого этапа) алгоритма Коцембы — восстановить такую раскраску из хаотического исходного состояния. При этом, конечно, можно пользоваться любыми поворотами. На втором этапе применяются только повороты, перечисленные выше. Легко понять, что они автоматически сохраняют нашу вспомогательную раскраску. По существу, на втором этапе происходит только установка каждого кубичка на его место. А благодаря сохранению вспомогательной раскраски правильная ориентация кубичков на своих местах будет обеспечена автоматически. Таким образом, число промежуточных состояний равно числу допустимых перестановок кубичков (т. е. перестановок получаемых из правильной поворотам граней), при которых реберные кубички среднего слоя остаются в этом слое. Отметим, что метод Коцембы также восходит к алгоритму Тистлетуэйта. Однако в последнем используются не один, а три вложенных друг в друга класса промежуточных состояний, отвечающих поэтапному сужению набора разрешенных поворотов; второй из этих трех классов и составляют промежуточные состояния Коцембы. Понятно, что если вам нужно добраться из пункта А (исходное состояние) в пункт В (правильное состояние) и по дороге обязательно посетить пункт С (промежуточное состояние). то такой путь АСВ может оказаться длиннее прямого пути АВ, даже если его отрезки АС и СВ проходятся оптимально. А если еще и на пути из А в С надо завернуть в D, а из С в В — в дополнительное промежуточное состояние Е. то получится еще более длинный путь АВСЕВ. Зато каждый из отрезков этого пути уже настолько сокращается, что полный перебор случаев становится возможным. Так и появились рекордные результаты Тистлетузйта и Клоостермана.

Как работает программа Коцембы

Грубо говоря, Коцемба заставляет машину просматривать всевозможные цепочки поворотов, разрешенных на соответствующем этапе, и ловить момент, когда цель этого этапа будет достигнута. Однако при таком лобовом подходе объем просматриваемых вариантов был бы слишком велик. Так, первый ход можно сделать 6х3=18 способами (любую из шести граней можно повернуть на один из трех углов — 180°; +90°), на втором и каждом из следующих ходов число способов равно 15, так как нет смысла дважды подряд поворачивать одну грань. Таким образом, возникает «дерево вариантов», от каждой ветви которого отходят пять следующих ветвей. Из-за сращивания ветвей дерева вариантов число 18 можно еще увеличить. (В свое время промелькнуло сообщение о том, что доказано существование состояний, не решаемых быстрее, чем за 21 ход; впрочем, оно могло быть не вполне достоверным.) Как видим, результаты, показываемые программой Коцембы, близки к наилучшим. Сокращения перебора Герберт Коцемба добился с помощью специальной фильтрующей программы. Она хранит определенную информацию о всех цепочках из, скажем, не более чем 8 ходов, и позволяет отсеивать состояния, которые заведомо не упорядочиваются (в смысле 1-го или 2-го этапов алгоритма) такими цепочками. Начав «сборку а, компьютер настраивается выполнить первый этап за 10 ходов. Он порождает первые два хода и включает фильтр на 8 ходов; если возникшее состояние не отсеется, производится третий ход и включается фильтр на 7 ходов, и т. д. Если на каком-то шагу произойдет отсев, надо поменять предыдущий сделанный ход. Пока что для всех позиций, предлагавшихся программе, удавалось осуществить первый этап не более чем за 10, а второй — не более чем за 14 ходов.

Заключение:

И в заключение я хотел бы сказать, что математика применяется не только для вычисления разных формул и решения задач, но и для решения различных головоломок. Ведь именно математика помогла человеку найти секрет сборки «Волшебного кубика Рубика». 300 ходов человек сократил в 15 РАЗ и теперь кубик загадку можно собрать за 20 ходов. Вот он прогресс математики.

Так же я понял, что нельзя останавливаться на достигнутом мной результате . На данном моменте я выучил только послойную сборку и сейчас изучаю скоростную (по методу Джессики Фридрих). С помощью нее можно собирать кубик довольно быстро. Мировой рекорд сейчас составляет 5,66 секунд, и я хочу его побить!

Список литературы:

1. М. Мыльников Всем кубикам кубик // Юный техник. -1982. — № 7.
2. В. Дубровский, А. Калинин Новости кубологии // Квант. — 1992. — № 11. — С. 52-56.
3. К. Кноп «Кубик Рубика: штурм твердыни, и снова о кубике». Компьютера.
4. Membrana.Ru: «Рубик и его кубик: раскрутка, сказочное везение, возвращение»
5. Публикации из журналов «Наука и жизнь», «Квант», «Юный техник»: алгоритмы, пасьянсы на кубике, каталог вращений кубика.
6. Кубик Рубика и проблема Хигмана. Материалы 20-й летней конференции международного математического Турнира городов.

Любая позиция Кубика Рубика может быть решена не более, чем за 20 шагов.

Несколько лет назад было доказано, что для Кубика Рубика есть решение за 23 хода. Теперь это число сократилось до 20. Чтобы это сделать, потребовалось 35 (тридцать пять) лет компьютерного времени, пожертвованного Гуглом.

Каждый блок решения использовал свой алгоритм — последовательность шагов для достижения нужной конфигурации. Например, один алгоритм предназначался для решения верхней грани, а другой — для позиционирования средних краев. Есть множество различных алгоритмов, различающихся по степени сложности и количеству требуемых шагов, но те, которые может запомнить человек, обычно требуют больше 40 шагов.

Разумно полагать, что Бог может использовать более эффективный алгоритм, который решает задачу за наикратчайшее число шагов. Этот алгоритм известен как “алгоритм Бога”. Число шагов в худшем случае называется числом Бога. В конце концов, было показано, что это число — 20.

После изобретения Кубика Рубика пятнадцать лет ушло на поиск позиции, которая наверняка решается за 20 шагов. Через 15 лет после этого мы доказали, что 20 шагов достаточно для любой позиции.

Кажется, что Кубик Рубика существовал всегда. Однако его изобрел в 1975 году венгерский скульптор Эрнё Рубик, а головоломке понадобилось меньше 50 лет, чтобы завоевать мир.

Шутка ли: по всему миру продано 450 миллионов копий головоломки, как официальных, так и поддельных (оригинал запатентован, поэтому выпускается определенными тиражами).

Такой популярности не добивались не то что спиннеры. Вероятно, кубик Рубика может поспорить с шахматами и другими древнейшими играми-головоломками-таймкиллерами.

Почему кубик Рубика стал таким популярным?

Секрет популярности прост: кубик Рубика является детской игрушкой только на первый взгляд. На деле это серьезная математическая задача по комбинаторике, воплощенная в форме.

Что такое кубик Рубика известно всем. Что такое собрать его? Это означает привести его в исходное состояние, когда каждая грань заполнена одним цветом. Для этого необходимо менять местами раскрашенные квадраты до полного успеха.

Каждый отдельный случай — одно из 43 252 003 274 489 856 000 состояний кубика Рубика. Ещё раз, округленно: 43,3¹⁸, или чуть больше 43 квинтиллионов различных вариантов. Каждый может участвовать в конкретном решении.

С учетом центральных элементов, число возможных вариантов текущего состояния кубика Рубика равно 88,5*10²¹. Архив интернета на март 2019 года составляет 45*10¹⁵ байт, или 45 петабайт.

По этой причине у кубика нет однозначного решения: оно требует слишком объемных расчетов, и подчиняется только комбинаторике как подразделу математической статистики. Впрочем, вероятность той или иной конфигурации можно оценить.

Поскольку элементы повторяемы, и для сбора головоломки достаточно собрать по цвету все грани, возможно создать алгоритм, который приведет к правильному решению.

Огромное число возможных решений привело к тому, что все существующие алгоритмы срабатывают только для бОльшей части (80-98%) начальных состояний. Иногда их приходится комбинировать.

Тем не менее, существуют наиболее распространенные, простые и понятные без серьезных математических выкладок (хотя совсем без них не обойдется): именно они позволяют собирать затейливую головоломку чаще всего.

Как умные люди собирают кубик Рубика?

Для сборки или приведения кубика к виду с гранями одного цвета существует несколько официально разработанных методик:

• официальный способ Рубика
• авторская методика Karalov Brothers
• алгоритм Бога (сборка за 20 шагов)
• традиционная «советская» методика из журнала «Наука и жизнь»
• метод крестов и ребер

Последний гарантирует, что кубик рано или поздно будет собран и достаточно прост в освоении. Поэтому его сегодня и рассмотрим, оставив прочие варианты для фанатов.

Важно: если кубик упал и рассыпался, то неправильный «ремонт» приведет к невозможности собрать головоломку.

Для ускорения процесса можно воспользоваться Решателем кубика Рубика. Помогает, хотя в некоторых случаях предложенные компьютером варианты не приведут к положительному итогу.

Из чего состоит кубик Рубика. Важно знать, прежде чем собирать

Внутри кубика Рубика прячется крестовидный каркас, на котором закреплены подвижные и статичные элементы головоломки.

• Центры — 6 шт. Один цвет, всегда остаются на своем месте.
• Ребра — 12 шт. Крайние элементы с двумя цветами.
• Углы — 8 шт. Угловые элементы с тремя цветами.
• Грань — совокупность 9 элементов, которые можно вращать одновременно.

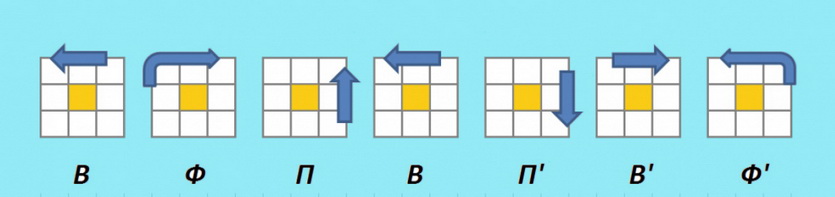
Для записи алгоритмов используют упрощенные наименования базовых элементов, которые определяются наблюдателем (человеком, который проводит сборку) относительно самого себя:

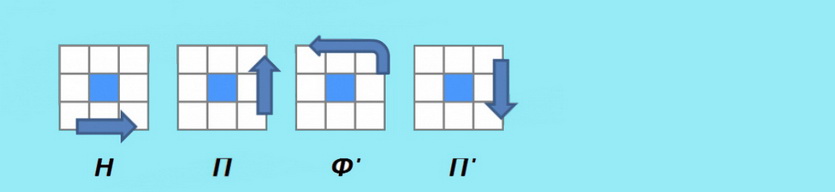
• Ф — фасад
• Т — тыл
• П — правая грань
• Л — левая грань
• В — верх
• Н — низ
• С — средний слой

В формуле каждый символ соответствует повороту указанного элемента на 90° по часовой стрелке: Ф, Т, П, Л, В, Н. Поворот против часовой определяет штрих: Ф’, Т’, П’, Л’, В’, Н’. Цифра после буквы обозначает количество повторов операции.

Пример: формула НП’Ф’В2

1. Повернуть нижнюю грань на 90° по часовой (вправо).

2. Повернуть правую грань на 90° против часовой (на себя).

3. Повернуть фасадную грань на 90° против часовой.

4. Повернуть правую грань на 90° по часовой (на себя) дважды, или один раз на 180°.

Все формулы (повороты) выполняются до тех пор, пока не будет получен удовлетворяющий (показанный на рисунке) результат.

Поехали, начинаем собирать кубик Рубика. Инструкция далее.

1. Начинаем. Объемный крест

На первом этапе сборки необходимо определить основной цвет, цвет верхней грани, он же цвет центрального выбранного элемента.

Важно: от выбора цвета дальнейшее решение не зависит.

Далее необходимо поднять элементы того же цвета, чтобы получить так называемый «крест верхней грани»:

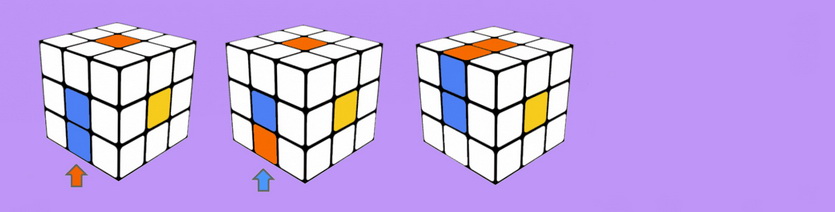
1.1 НПФ’П’ — если угловой кубик на нижней грани (поворот боковой грани и несколько поворотов нижней)

1.2 ФФ — если угловой кубик на боковой грани (поворот нижней грани).

Сборка первой части дает понимание процесса и в целом не зависит от формул — эта часть решается без применения комбинаторики простыми вращениями.

2. Продолжаем. Сторона

Для сборки верхней грани нужно поставить 4 угловых кубика выбранного цвета на свои места. В этом случае возможно несколько «фасадов», так как угловой кубик может быть развернут 3 способами относительно граней.

Возможно 3 ситуации, для каждой из которых применяется собственный алгоритм:

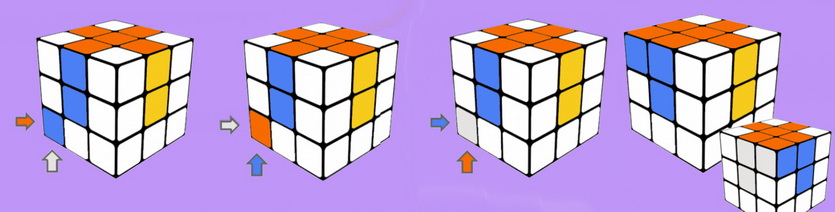
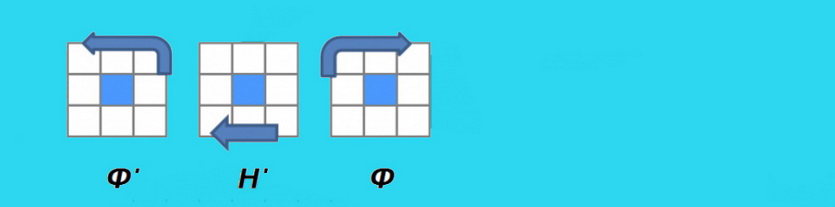
2.1 ЛН’Л’ – если кубик выбранного цвета на боковой грани

2.2 Ф’Н’Ф — если кубик выбранного цвета на фронтальной грани

2.3 (Ф’П’)Н2(ПФ) — если кубик выбранного цвета на нижней грани

3. Следующее. Пояс

Этап предполагает 2 возможных раскладки и 2 формулы, с помощью которых необходимо собрать второй от верхней грани слой (пояс).

После последней операции кубик для перестановки в этой находится под центральным элементом фасадной грани. Его нужно вывести на фасад так, чтобы цвет центрального и углового элементов совпадали.

Используется 2 основных алгоритма:

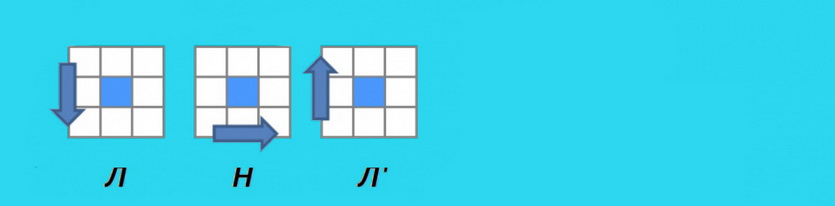
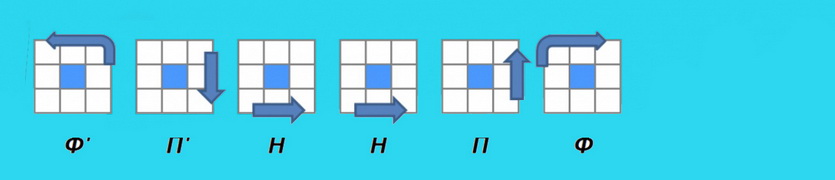
3.1 (НЛН’Л’)(Н’Ф’НФ) — если элемент идет на левую грань

3.2 (Н’П’НП)(НФН’Ф’) — если элемент идет на правую грань

Если нужный кубик находится в среднем слое, необходимо применить любой алгоритм до тех пор, пока кубик не окажется на нижней грани.

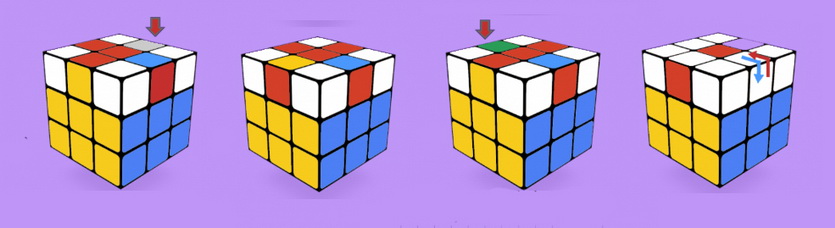
4. Теперь – выставка рёбер

Важно: данный этап требует перевернуть кубик на 180° от себя, так, чтобы нижняя грань оказалась вверху, а прочие остались на своих местах.

На данном этапе необходимо правильно выставить с помощью единственной формулы рёберные кубики, за счет чего на нижней грани окажется 2 кубика верного цвета.

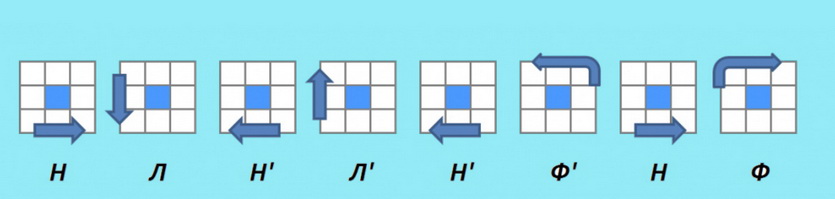
4.1 (ВФП)В(П’В’Ф’)

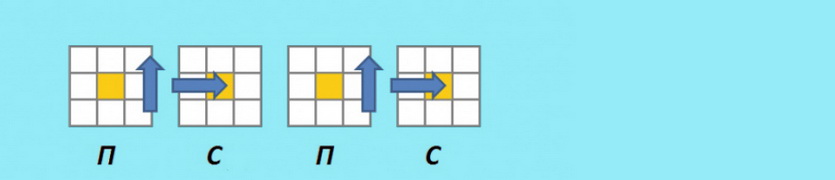
5. Делаем согласованный крест

После этапа 3 возможны 3 базовых начальных позиции, применив к которым формулы этапа, получится необходимая сборка. Если текущая ситуация не подходит ни под один из вариантов, необходимо выполнить алгоритм 5.3 дважды.

Для каждой базовой ситуации имеется свой алгоритм решения? который сводится к повторению одной комбинации:

5.1 (ПС)4 В (ПС)4 В’

5.2 (ПС)4 В’ (ПС)4 В

5.3 (ПС)4 В2 (ПС)4 В2

Внимание: поворот средней грани «С» осуществляется с нижней стороны.

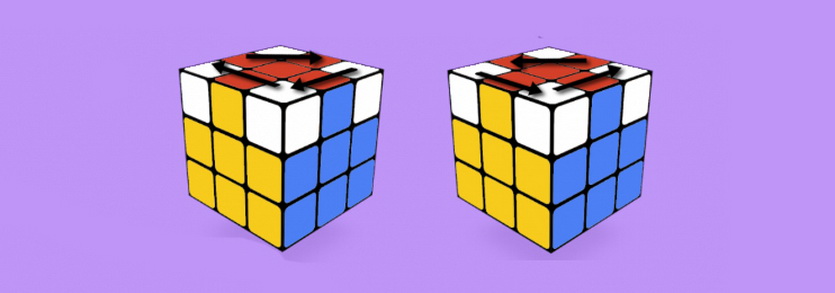
6. Затем – расстановка углов

На этом этапе снова нужно перевернуть, переориентировать кубик таким образом, чтобы в левом дальнем углу верхней грани оказался подходящий по цвету угловой кубик.

Выбор алгоритма зависит от конкретной ситуации и остаётся за «игроком»:

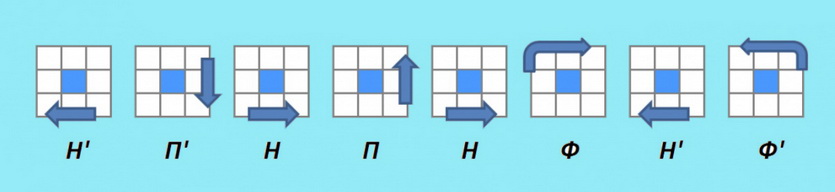
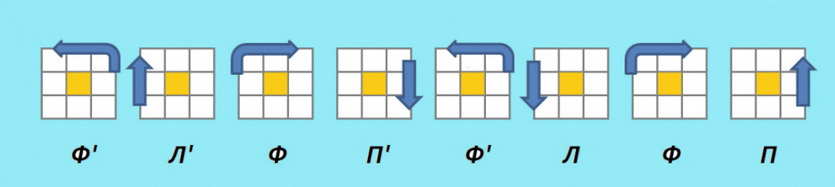
6.1 (П’Ф’Л’Ф)(ПФ’ЛФ) — прямой алгоритм

6.2 (Ф’Л’ФП’)(Ф’ЛФП) — обратный алгоритм

7. Теперь разворот углов

Заключительный этап сборки самый ответственный, поскольку неправильная сборка (выполнение алгоритма) приведет к нарушению конструкции и откату на несколько шагов назад.

В зависимости от сложившейся комбинации, необходимо применить один из алгоритмов, которые сводятся к одному:

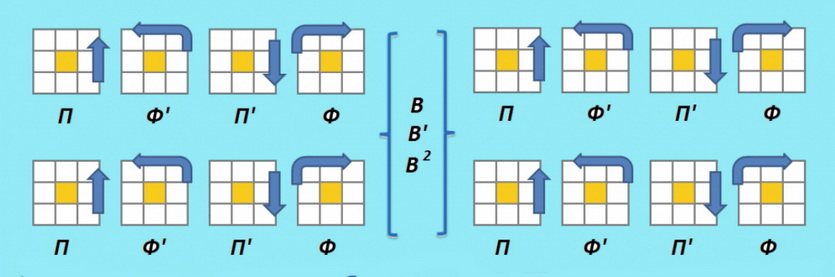
7.1 (ПФ’П’Ф)2 В (ПФ’П’Ф)2

7.2 (ПФ’П’Ф)2 В’ (ПФ’П’Ф)2

7.3 (ПФ’П’Ф)2 В2 (ПФ’П’Ф)2

Каждый выполняется в 2 этапа: первая половина до правильной ориентации углового кубика, вторая половина (после поворота) до возвращения порядка в нижних слоях.

Ура, почти всё. Завершение сборки

Завершается сборка единственным поворотом последней собранной грани на 90° по/против часовой в зависимости от текущей ситуации.

Кубик Рубика собран!

А есть способы проще?

Нет, если вы не гений-рекордсмен. Вначале надо научиться собирать правильно.

Каждый из этапов сборки осуществляется строго из базового положения. Причем, в некоторых случаях кубик необходимо привести к базовому положению самостоятельно, переориентировав его либо повторно выполнив текущий (предыдущий) алгоритм.

Важен не только алгоритм конкретной операции, но и общая последовательность сборки. В противном случае нарушается строй решения задачи и возможен непредсказуемый вариант.

Остаётся ответить самому себе на вопрос: зачем собирать кубик Рубика?

Для основной массы населения планеты ответ очевиден. В отличие от спиннеров и других простых способов занять руки кубик Рубика позволяет тренировать не только руки, но и ум.

Решение (сборка) кубика вслепую невозможны. Вероятность этого события намного меньше, чем появление разумных инопланетян на Земле, начало Звездных войн или самостоятельное возрождение динозавров.

Так что руки в ноги — и за кубиком!

(172 голосов, общий рейтинг: 4.56 из 5)