«Начала» (греч. Στοιχεῖα, лат. Elementa) — главный труд Евклида, написанный около 300 г. до н. э. и посвящённый систематическому построению геометрии. Считается вершиной античной геометрии и античной математики вообще, итогом её трёхсотлетнего развития и основой для последующих исследований. «Начала», наряду с двумя трудами Автолика из Питаны — древнейшее из дошедших до современности античных математических сочинений; все труды предшественников Евклида известны только по упоминаниям и цитатам позднейших комментаторов.
Прокл сообщает (ссылаясь на Евдема), что подобные сочинения создавались и до Евклида: «Начала» были написаны Гиппократом Хиосским, а также платониками Леонтом и Февдием. Но эти сочинения, по-видимому, были утрачены ещё в античности.
Текст «Начал» на протяжении веков были предметом дискуссий, к ним написаны многочисленные комментарии. Из античных комментариев сохранился текст Прокла, являющийся важнейшим источником по истории и методологии греческой математики. В нём Прокл даёт краткое изложение истории греческой математики (так называемый «Евдемов каталог геометров»), обсуждает взаимосвязь метода Евклида и логики Аристотеля, роль воображения в доказательствах. Среди древних комментаторов — Папп Александрийский; основные комментаторы эпохи Возрождения — Пьер де ла Рамэ, Федериго Коммандино, Христоф Шлюссель (Клавиуса) и Генри Савиль.
«Начала» оказали огромное влияние на развитие математики вплоть до Новейшего времени, высокий интеллектуальный уровень произведения и его фундаментальная значимость для науки в целом отмечается ключевыми учёными современности. Книга переведена на множество языков мира, по количеству переизданий «Начала» не имеют себе равных среди светских книг.
В «Началах» излагаются планиметрия, стереометрия, арифметика, отношения по Евдоксу. В классической реконструкции Гейберга весь труд состоит из 13 книг. К ним традиционно присоединяют две книги о пяти правильных многогранниках, приписываемые Гипсиклу Александрийскому и школе Исидора Милетского.
Изложение в «Началах» ведётся строго дедуктивно. Каждая книга начинается с определений. В первой книге за определениями идут аксиомы и постулаты. Затем следуют предложения, которые делятся на задачи (в которых нужно что-то построить) и теоремы (в которых нужно что-то доказать). Определения, аксиомы, постулаты и предложения пронумерованы, например, ссылка «I, Определения, 2» — второе определение первой книги.
Первая книга
Первая книга начинается определениями, из которых первые семь (I, Определения, 1—7) гласят:
- Точка есть то, что не имеет частей. (Σημεῖόν ἐστιν, οὗ μέρος οὐθέν— букв. «Точка есть то, часть чего ничто»)
- Линия — длина без ширины.
- Края же линии — точки.
- Прямая линия есть та, которая равно лежит на всех своих точках. (Εὐθεῖα γραμμή ἐστιν, ἥτις ἐξ ἴσου τοῖς ἐφ’ ἑαυτῆς σημείοις κεῖται)
- Поверхность есть то, что имеет только длину и ширину.
- Края же поверхности — линии.
- Плоская поверхность есть та, которая равно лежит на всех своих линиях.
Комментаторы эпохи Возрождения предпочитали говорить, что точка есть место без протяжения. Современные авторы, напротив, признают невозможность определения основных понятий, в частности, таков подход в «Основаниях геометрии» Гильберта.
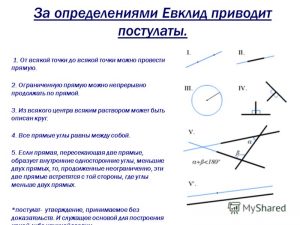
Постулаты Евклида
Наиболее интересен в аксиоматике Евклида последний, знаменитый пятый постулат. Среди других, интуитивно очевидных постулатов, он нарочито чужероден, его громоздкая формулировка закономерно вызывает некоторое чувство протеста и желание отыскать для него доказательство. Такие доказательства уже в древности пытались построить Птолемей и Прокл; а в Новое время из этих попыток развилась неевклидова геометрия. Следует отметить, что первые 28 теорем I книги относятся к абсолютной геометрии, то есть не опираются на V постулат.
Прокл (V в. н. э.)
За постулатами следуют аксиомы (I, Аксиомы, 1—9), которые имеют характер общих утверждений, относящихся в равной мере как к числам, так и к непрерывным величинам:
- Равные одному и тому же равны и между собой.
- И если к равным прибавляются равные, то и целые будут равны.
- И если от равных отнимаются равные, то остатки будут равны.
- (И если к неравным прибавляются равные, то целые будут не равны.)
- (И удвоенные одного и того же равны между собой.)
- (И половины одного и того же равны между собой.)
- И совмещающиеся друг с другом равны между собой.
- И целое больше части.
- (И две прямые не содержат пространства.)
В скобки взяты аксиомы, принадлежность которых Евклиду Гейберг, автор классической реконструкции текста «Начал», счёл сомнительной. Постулаты 4—5 (I, Постулаты, 4—5) в ряде списков выступают как аксиомы (I, Аксиомы, 10—11).
За аксиомами следуют три теоремы, представляющие собой задачи на построение, давно вызывающие споры. Так, вторая из них (I, Предложения, 2) предлагается «от данной точки отложить прямую, равную данной прямой». Нетривиальность этой задачи состоит в том, что Евклид не переносит отрезок на прямую соответствующим раствором циркуля, полагая такую операцию недозволенной, и использует третий постулат (I, Постулаты, 3) в неожиданно узком смысле.
При доказательстве четвёртой теоремы (I, Предложения, 4), выражающей признак равенства треугольников, Евклид использует метод наложения, никак не описанный в постулатах и аксиомах.
Затем рассматриваются различные случаи равенства и неравенства треугольников; теоремы о параллельных прямых и параллелограммах; так называемые «местные» теоремы о равенстве площадей треугольников и параллелограммов на одном основании и под одной высотой. Заканчивается I книга теоремой Пифагора.
Книги II—XIII
II книга — теоремы так называемой «геометрической алгебры».
III книга — предложения об окружностях, их касательных и хордах, центральных и вписанных углах.
IV книга — предложения о вписанных и описанных многоугольниках, о построении правильных многоугольников.
V книга — общая теория отношений, разработанная Евдоксом Книдским.
VI книга — учение о подобии геометрических фигур. Эта книга завершает евклидову планиметрию.
VII, VIII и IX книги посвящены теоретической арифметике. Евклид в качестве чисел рассматривает исключительно натуральные числа; для него «Число есть совокупность единиц». Здесь излагаются теория делимости и пропорций, доказывается бесконечность множества простых чисел, приводится алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, строятся чётные совершенные числа. Евклид доказывает также формулу для суммы геометрической прогрессии.
X книга — классификация несоизмеримых величин. Это самая объёмная из книг «Начал».
XI книга — начала стереометрии: теоремы о взаимном расположении прямых и плоскостей; теоремы о телесных углах, объём параллелепипеда и призмы, теоремы о равенстве и подобии параллелепипедов.
XII книга — теоремы о пирамидах и конусах, доказываемые с помощью метода исчерпывания. Здесь доказывается, например, теорема о том, что объём конуса составляет одну треть от объёма цилиндра с теми же основанием и высотой.
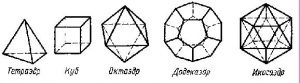
XIII книга — построение правильных многогранников; доказательство того, что существует ровно пять правильных многогранников.
Евклид нигде в книге не ссылается на других греческих математиков, хотя несомненно опирается на их результаты. Историки науки показали, что прототипом для труда Евклида послужили более ранние сочинения античных математиков:
- Книги I—IV и XI — «Начала» Гиппократа Хиосского.
- Книги V—VI и XII — труды Евдокса Книдского.
- Книги VII—IX — сочинения Архита Тарентского и других пифагорейцев. По мнению Ван дер Вардена, это самая древняя по содержанию часть «Начал», восходящая к V веку до н. э.
- Книги X и XIII — труды Теэтета Афинского.
Вопрос о том, содержат ли «Начала» какие-либо результаты самого Евклида или автор занимался только систематизацией и унификацией накопленных знаний, является предметом дискуссий. Есть предположение, что алгоритм построения правильного 15-угольника разработан Евклидом; вероятно, он же произвёл отбор и окончательную формулировку аксиом и постулатов.
В целом содержание «Начал» покрывает значительную часть античной теоретической математики. Однако некоторая часть известного древнегреческим математикам материала осталась вне этого труда — например, конические сечения (Евклид посвятил им отдельный труд, который не сохранился), длина окружности, теория приближённых вычислений.
Манускрипты и издания
Греческий текст «Начал»
При раскопках античных городов найдено несколько папирусов, содержащих небольшие фрагменты «Начал» Евклида. Самый известный был найден в «городе папирусов» Оксиринхе в 1896—1897 и содержит формулировку одного из утверждений второй книги с рисунком (II, Предложения, 5).
Папирус из Оксиринха
Греческий текст «Начал» Евклида известен по византийским манускриптам, два самых известных из них хранятся Бодлианской библиотеке и Ватиканской апостольской библиотеке (двухтомный Ватиканский манускрипт).
На их основе, а также с учётом арабских переводов «Начал» (датируемых IX веком и позднее) оригинальный текст был реконструирован датским историком науки Гейбергом в конце XIX века, его методы подробно описаны Хизом (англ. Thomas Little Heath)). Гейберг использовал в своей реконструкции 8 греческих манускриптов, датируемых современными исследователями IX—XI веками. Из этих манускриптов семь в своем заглавии имеют пометку «из издания Теона» или «из лекций Теона» и поэтому называются Теоновскими. Ватиканский манускрипт такой пометки не имеет и считается неподверженным редакции Теона. Теоновские манускрипты разнятся между собой, и общих признаков, отличающих их от ватиканского манускрипта, немного (наиболее существенный — концовка IV книги). На полях манускриптов имеются многочисленные комментарии, взятые частично из комментариев Прокла, которые вписывают «Начала» в контекст греческой культуры, например, сообщается о том, что Пифагор, открыв свою теорему, принёс в жертву быков.
История обретения византийских манускриптов темна. Вероятно, они попали в Европу ещё в XVI веке, но не были опубликованы. В первом издание греческого текста, осуществленном Йоханом Хервагеном (Johann Herwagen) между 1533 и 1558 годами под редакцией Симона Гринера (Simon Gryner, он же Grynaeus, профессор греческого языка в базельском университете), использованы манускрипты, которые, по мнению Гейберга, представляют собой весьма плохие копии XVI века. Лишь в 1808 году Пейрар (фр. François Peyrard) во время наполеоновских экспроприаций нашёл три манускрипта в Риме и среди них важнейший — двухтомный ватиканский манускрипт.
Латинский текст «Начал»
Манускрипт из Люнебурга, ок. 1200 года, передающий геометрию Боэция
В Европе «Начала» Евклида на латинском языке были хорошо известны и в Средние века, и в эпоху Возрождения, однако далеко не в привычном теперь виде. Средневековые латинские трактаты, содержащие фрагменты «Начал» Евклида, каталогизированы мюнхенским учёным Фолькертсом (нем. Menso Folkerts), разделившим манускрипты на следующие группы:
- Так называемая «Геометрия Боэция» (в действительности трактат Боэцию не принадлежит). Трактаты этой группы начинаются словами «Incipit Geometriae Boetii», имеют ряд общих признаков, хотя их тексты значительно расходятся. Текст занимает пять-шесть рукописных листов. Доказательства предложений отсутствуют, однако имеются иллюстрации с дополнительными построениями. Иногда доказательствами снабжаются только первые три теоремы. Первым определением предшествует утверждение о том, что основа геометрии в измерении длин, высот и ширин, после этого евклидовы определения приобретают другой смысл, например, линия — объект, длину которого измеряют, а ширину нет и т. д. Язык не испытал влияния арабского, поэтому считается, что геометрия Боэция — прямой перевод с греческого на латинский. Опубликован манускрипт из Люнибурга.
- «Геометрия» Аделарда составляет большой класс манускриптов, написанных разными авторами в разное время. Наибольшая подгруппа, названная как «Adelard II», содержит все 15 книг «Начал» Евклида, впрочем, сохранность манускриптов такова, что говорить об этом нужно с осторожностью. Характерная черта — наличие доказательств, причём в лучших манускриптах доказательства предшествуют изложению (enucatio); некоторые доказательства даны подробно, другие лишь намечены. Некоторые изложения (enunciatio) в Adelard II буквально воспроизводят Боэция, другие имеют иную формулировку часто с арабскими эквивалентами вместо латинских терминов. Текст значительно разнится от манускрипта к манускрипту (в книгах VII—IX и XI—XIII доказательства особенно разнятся), так, что в средние века не было канонического текста для Adelard II, который все время дополнялся и улучшался. Стоит подчеркнуть, что доказательства отличаются способом выражения, но не математической сутью. В течение всего XII века шла работа по улучшению доказательств.
- «Геометрия» Кампануса— комплекс рукописей XIII—XV веков. В этой версии «Начала» весьма схожи с византийскими манускриптами и вполне могут рассматриваться как довольно точный перевод, в котором, однако присутствуют арабские термины (например, параллелепипед назван «belmaui»).
Это издание представляет собой 15 книг, формулировки предложений близки к Adelard II, но доказательства следует за изложением. В заглавии манускриптов обычно отождествлены Евклид, автор «Начал», и ученик Сократа философ Евклид Мегарский. Печатные издания «Начал» Евклида каталогизированы Томасом-Стэнфордом (англ. Charles Thomas—Stanford). Первое печатное издание «Начал» было осуществлено Эрхардом Ратдольтом в Венеции в 1482 году и воспроизводило «Начала» в обработке Кампано. Следующее издание не копировало первое, было осуществлено Бартоломео Дзамберти в 1505 году. Из предисловия известно, что Дзамберти переводил греческий манускрипт, передающий «Начала» в обработке Теона, однако, Гейбергу не удалось его идентифицировать.
В XVI веке считалось, что Евклиду принадлежат лишь формулировки теорем, доказательства же были придуманы позже; были распространены издания «Начал» без доказательств и издания, сравнивающие доказательства Кампана и Дзамберти. Этот взгляд имел вполне твёрдую основу: в начале XVI века была издана геометрия Боэция, которая тоже являлась переводом «Начал» Евклида, но доказательств в этом издании не содержалось. Считалось также, что использование в доказательствах буквенных обозначений подразумевает знакомство с буквенной алгеброй. Это мнение было отвергнуто в XVII веке.
Русские переводы
Первое издание «Начал» на русском языке издано в 1739 году; книга вышла в Петербурге под названием «Евклидовы элементы из двенадцати нефтоновых книг выбранныя и в осмь книг через профессора мафематики Андрея Фархварсона сокращенныя, с латинского на российский язык хирургусом Иваном Сатаровым преложенныя». Перевод выполнил Иван Сатаров под руководством шотландского математика Генри Фарварсона. Имя Ньютона («Нефтона») в названии упомянуто, возможно, в рекламных целях, к содержанию книги он никакого отношения не имеет. Перевод был сделан с сокращённого французского издания «Начал» Такэ (фр. André Tacquet). Немного позднее вышли ещё 2 перевода, также сокращённые до 8 книг:
- 1769 год: перевод Курганова «Евклидовы Елементы Геометрии, то есть первыя основания науки о измерении протяжения»;
- 1784 год: перевод Прохора Суворова и Василия Никитина «Евклидовых стихий осьмь книг, а именно: первая, вторая, третья, четвёртая, пятая, шестая, одиннадцатая и двенадцатая; к сим прилагаются книги тринадцатая и четырнадцатая. Переведены с греческого и поправлены. В Санкт-Петербурге, в типографии Морского шляхетного Кадетского Корпуса» (переизданы в 1789 году).
Практически полностью (кроме X книги) «Начала» на русском языке вышли в переводе Фомы Петрушевского: книги 1—6 и 11—13 в 1819 году, книги 7—9 в 1835 году. В 1880 году вышел перевод Ващенко-Захарченко. Ещё один сокращённый перевод был издан в Кременчуге (1877 год) под названием «Восемь книг геометрии Эвклида»; перевод под руководством А. А. Соковича (1840—1886), директора местного реального училища, выполнили два воспитанника этого училища.
Последнее по времени полное академическое издание было опубликовано в 1949—1951 годах, перевод с греческого и комментарии — Дмитрия Мордухай-Болтовско́го.
Всемирное распространение
На китайском языке первые 6 книг «Начал» издал Маттео Риччи во время своей миссии в Китае (1583‑1610 годы). Полный перевод, выполненный британским миссионером Уайли (англ. Alexander Wylie), вышел с хвалебным предисловием Цзэн Гофаня, написанным в 1865 году.
Муниципальное бюджетное образовательное учреждение
«Новоаганская общеобразовательная средняя школа № 2»
Евклид и его книга «Начала»
Работу выполняла:
Екатерина Полякова, учащаяся 6б класса
руководитель:
Чекина Ольга Александровна,
учитель математики.
пгт. Новоаганск
2014
План
- Ведение.
- Цели и задачи.
II. Основная часть.
- Кто такой Евклид?
- Главная работа Евклида – «Начала».
- О чем его книга?
- Что сделал Евклид?
III. Заключение.
IV. Использованная литература.
Введение
Цель моей работы:
Расширить свои знания по выбранной теме. Узнать больше о жизни Эвклида, о его работе, о знаменитой книге «Начала».
Подготовиться к выступлению на ученической конференции.
Задачи:
1) Найти информацию по теме «Эвклид и его книга «Начала».
2) Познакомиться с его книгой «Начала».
3) Оформить доклад.
4) Выполнить презентацию.
5) Выступить на конференции.
Кто такой Евклид?
Евклид (иначе Эвклид) – древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения об Евклиде крайне скудны. Известно лишь, что учителями Евклида в Афинах были ученики Платона, а в правление Птолемея I (306-283 до н.э.) он преподавал в Александрийской академии. Евклид – первый математик александрийской школы.
О жизни этого ученого почти ничего не известно. До нас дошли только отдельные легенды о нем. Первый комментатор «Начал» Прокл (V век нашей эры) не мог указать, где и когда родился и умер Евклид. По Проклу, «этот ученый муж» жил в эпоху царствования Птолемея I. Некоторые биографические данные сохранились на страницах арабской рукописи XII века: «Евклид, сын Наукрата, известный под именем «Геометра», ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира».
Большую часть жизни Эвклид провел в Александрии — городе, заложенном Александром Македонским на берегу Средиземного моря, у устья Нила. Царь Птолемей I сделал Александрию столицей Египта; чтобы возвеличить свое государство, он привлекал в страну ученых и поэтов, создав для них Мусейон— храм муз.
Его работа?
Так как знания по математике нужно было как-то записывать, то Евклид написал книгу под названием «Начала», в которой было все, что люди тогда знали о геометрии и даже сейчас эти знания используются. Правда, потом древние книги безжалостно уничтожали, потому что они не нравились христианам и мусульманам. Но в некоторых переводах все же книга «Начала» выжила.
Важнейший математический труд гениального Евклида его книга
«Начала» имеет весьма почтенный возраст — свыше двух тысячелетий.
Главная работа Евклида – содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел (например, алгоритм Евклида);
состоит из 13-ти книг, к которым присоединяют две книги о пяти правильных многогранниках, до сих пор неизвестно кто их автор? Их приписывают Гипсиклу Александрийскому.
В «Началах» Евклид подвёл итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики.
Из других математических сочинений Евклида надо отметить «О делении фигур», сохранившееся в арабском переводе, четыре книги «Конические сечения», материал которых вошёл в одноимённое произведение Аполлония Пергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Паппа Александрийского.
О чем его книга?
Евклидова книга «Начала» представляет собой изложение той геометрии, которая известна и поныне под названием евклидовой. Она описывает метрические свойства пространства, которое современная наука называет евклидовым. Евклидово пространство является ареной физических явлений классической физики, основы которой были заложены Галилеем и Ньютоном. Это пространство пустое, безграничное, изотропное, имеющее три измерения. Евклид придал математическую определенность атомистической идее пустого пространства, в котором движутся атомы. Простейшим геометрическим объектом у Евклида является точка, которую он определяет как то, что не имеет частей. Другими словами, точка — это неделимый атом пространства.
Сочинение Евклида состоит из 15 книг.
В 1-й книге формулируются исходные положения геометрии, а также содержатся основополагающие теоремы планиметрии, среди которых теорема о сумме углов треугольника и теорема Пифагора.
Во 2-й книге излагаются основы геометрической алгебры.
3-я книга посвящена свойствам круга, его касательных и хорд.
В 4-й книге рассматриваются правильные многоугольники.
Книга 5-я и 6-я посвящены теории отношений и ее применению к решению алгебраических задач.
Книга 7-я, 8-я и 9-я посвящены теории целых и рациональных чисел.
В книге 10-й рассматриваются квадратичные иррациональности.
В книге 11-й рассматриваются основы стереометрии.
В 12-й книге доказываются теоремы, относящиеся к площади круга и объему шара, выводятся отношения объемов пирамид, конусов, призм и цилиндров.
В основу 13-й книги легли результаты, полученные в области правильных многогранников.
Книги 14-я и 15-я не принадлежат Евклиду, они были написаны позднее: 14-я — во II в. до н. э., а 15-я — в VI в.
У Евклида мы встречаем также описание монохорда — однострунного прибора для определения высоты тона струны и ее частей. Полагают, что монохорд придумал Пифагор, а Евклид только описал его («Деление канона», III век до нашей эры).
Изобретение монохорда имело значение для развития музыки. Постепенно вместо одной струны стали использоваться две или три. Так было положено начало созданию клавишных инструментов, сначала клавесина, потом пианино, А первопричиной появления этих музыкальных инструментов стала математика.
Что сделал Евклид?
Евклид — это древний мыслитель, который открыл науку геометрию. Можно сказать, что именно Евклид навел порядок в математике того времени.
Евклид – автор ряда работ по астрономии, оптике, музыке и др. Арабские авторы приписывают Евклиду и различные трактаты по механике, в том числе сочинения о весах и об определении удельного веса.
Шли века, менялись народы, исчезали с лица земли одни государства и возникали другие, рушились города, горели в пламени пожаров книги и библиотеки. А «Начала», написанные впервые на хрупком папирусе, прошли сквозь время.
Созданные в III в. до н. э. «Начала» не потеряли своего значения и сейчас. Они занимают особое место в истории математики.
Эвклид, один из величайших геометров, решил найти законы, которым подчиняются все линии и тела в природе, и расположить эти законы в строгой системе…
Конечно все особенности евклидова пространства были открыты не сразу, а в результате многовековой работы научной мысли, но отправным пунктом этой работы послужили «Начала» Евклида.
Знание основ евклидовой геометрии является ныне необходимым элементом общего образования во всем мире.
Заключение
В результате проделанной работы я познакомилась с жизнедеятельностью Евклида. Изучила историю возникновения книги «Начала», её содержание.
Оформила доклад, выполнила презентацию.
Презентация может послужить дополнительным материалом на уроках математики.
Источники информации
В предыдущей статье описан алгоритм
нахождения наибольшего общего делителя (НОД)
двух неотрицательных целых чисел, разработанный
древнегреческим математиком Евклидом. Кто же
этот ученый? К сожалению, о его жизни почти ничего
не известно. До нас дошли только отдельные
легенды о нем. По Проклу, “этот ученый муж” жил в
эпоху царствования Птолемея I (306–283 гг. до н.э.).
Некоторые биографические данные сохранились на
страницах арабской рукописи XII века: “Евклид, сын
Наукрата, известный под именем “Геометра”,
ученый старого времени, по своему происхождению
грек, по местожительству сириец, родом из Тира”.
Одна из легенд рассказывает, что царь Птолемей
решил изучить геометрию. Но оказалось, что
сделать это не так-то просто. Тогда он призвал
Евклида и попросил указать ему легкий путь к
математике. “К геометрии нет царской дороги”, —
ответил ему ученый. Так в виде легенды дошло до
нас это ставшее крылатым выражение.
Расцвет деятельности Евклида — около
300 г. до н.э. Царь Птолемей I, чтобы возвеличить
свое государство, привлекал в страну ученых и
поэтов, создав для них храм муз — Мусейон. Здесь
были залы для занятий, ботанический и
зоологический сады, астрономический кабинет,
астрономическая башня, комнаты для уединенной
работы и главное — великолепная библиотека. В
числе приглашенных ученых оказался и Евклид,
который основал в Александрии — столице Египта
— математическую школу и написал для ее учеников
свой фундаментальный труд, объединенный под
общим названием “Начала” (по-гречески “Elementa” — “Elementa”) — главный
труд своей жизни. Сочинения под названием
“Начала” появлялись еще до Евклида. Так, мы
знаем о существовании “Начал” Гиппократа
Хиосского (около 430–400 гг. до н.э.) и некоторых
других авторов, но “Начала” Евклида превзошли
сочинения его предшественников и на протяжении
более двух тысячелетий оставались основным
трудом по элементарной математике. В 13 частях,
или книгах, “Начал” содержится бо?льшая часть
знаний по геометрии и арифметике эпохи Евклида.
Его личный вклад сводился к такому расположению
материала, при котором каждая теорема логически
следовала бы из предыдущих. Книга I начинается с
определений, недоказываемых постулатов и “общих
понятий”, а заканчивается теоремой Пифагора и
обратной ей теоремой. Со времен античности и до XIX
века неоднократно предпринимались попытки
доказать так называемый “пятый постулат”
(“Постулат параллельности”). Лишь в XIX веке было
окончательно признано, что Евклид был прав,
полагая, что этот постулат невозможно вывести из
четырех других постулатов. Отрицание пятого
постулата лежит в основе так называемых
“неевклидовых геометрий” — эллиптической и
гиперболической (в первой из них отрицается не
только пятый, но и второй постулат). Книга II
содержит геометрические теоремы, эквивалентные
некоторым алгебраическим формулам, в том числе и
построение корней квадратных уравнений. Книги III
и IV посвящены окружности (при работе над ними
Евклид мог воспользоваться сочинением
Гиппократа). В книгах V и VI излагается теория
пропорций Эвдокса и ее приложения, в книгах VII, VIII
и IX — теория чисел, в т.ч. формула для
“совершенных” чисел, алгоритм Евклида
нахождения наибольшего общего делителя и
доказательство несуществования наибольшего
простого числа (см. ниже). По мнению многих, книга X
— наиболее красивая часть “Начал”. Она
посвящена несоизмеримым величинам (парам
величин одинаковой размерности, не представимых
в виде отношения целых чисел). Последние три
книги “Начал” посвящены стереометрии и
завершаются доказательством того, что
существуют пять и только пять правильных
многогранников.
Текст “Начал” сохранился в шести
греческих рукописях, датируемых IX–XII вв. Имеются
и арабские рукописи того же периода, но они столь
же фрагментарны, как и более древние греческие
рукописи. Две из ранних греческих рукописей
содержат также менее крупные сочинения Евклида
— “Оптику” (геометрические теоремы о
прямолинейном распространении света) и
“Феномены” (об астрономии и сферической
геометрии). Сохранились еще два сочинения
Евклида, одно на древнегреческом, другое только в
арабском переводе. В первом из них (“Данные”)
рассматривается вопрос о том, что необходимо
знать, чтобы задать фигуру, во втором (“О делении
фигур”) решается задача о разбиении данной
фигуры на другие с требуемыми свойствами формы и
площади.
Пять дошедших до нас сочинений Евклида
составляют лишь малую часть его наследия.
Названия многих его утерянных сочинений
известны со слов древнегреческих комментаторов:
“Псевдария” (о логических ошибках), “Поризмы”
(об условиях, определяющих кривые), “Конические
сечения”, “Геометрические места на
поверхностях” (по-видимому, о конусах, сферах и
цилиндрах или о кривых на этих поверхностях),
“Начала музыки” (возможно, с изложением
пифагорейской теории гармонии) и “Катоптрика”
(о свойствах зеркал). Арабские авторы приписывают
Евклиду и различные трактаты по механике, в том
числе сочинения о весах и об определении
удельного веса.
Вот такой человек жил более двух тысяч
лет назад…
Литература
1. Осипенко И.Н. “Начала”
Евклида. М., 1994.
2. Глебкин В.В. Наука в контексте
культуры. М., 1994.
3. http://www.krugosvet.ru/articles/27/1002759/1002759a1.htm
Доказательство Евклидом
несуществования наибольшего простого числа
Суть доказательства состоит в
следующем. Предположим, что мы нашли самое
большое простое число. Перемножим все известные
простые числа и прибавим к произведению 1.
Полученное число будет простым, так как при
делении на любое число результат не будет целым,
в остатке всегда будет 1. Это означает, что
получено простое число, большее того, которое мы
считали самым большим. Если применить те же
рассуждения к полученному числу, можно получить
еще большее новое простое число и т.д. Не правда
ли — изящно?
« Основные свойства геометрических фигур»
1. Как называют науку о свойствах геометрических фигур?
а)Алгебра; б)Геометрия; в)Физика.
2. Кто создал руководство по математике под названием «Начала»?
а)Птолемей; б) Евклид; в)Ньютон.
3.Основными геометрическими фигурами являются:
а)Отрезок и точка; б) Прямая и луч; в)Точка и прямая.
4. Допиши основное свойство принадлежности точек и прямых:
Через любые две точки можно провести…………
а)Прямую и только одну; б)Две прямых: в)Два отрезка.
5.Что называется отрезком ?
а) часть прямой, которая состоит из всех точек этой прямой; б) Часть луча; в) прямая .
6 Дополни основное свойство расположения точек на прямой.:
Из трёх точек на прямой……….
а)одна и только одна лежит между двумя другими;
б) Две точки лежат между двумя другими;
в) Все три точки не лежат на этой прямой.
7.Дополни основное свойство измерения отрезков:
Каждый отрезок……..
а)Не имеет длины; б)имеет определённую длину; в) Имеет длину , большую нуля.
8.Три точки А,В,С лежат на одной прямой. Известно , что
А B C
АС=17 см, ВС =7,9 см, Найдите длину отрезка АВ?
Какое свойство лежит в основе решения этой задачи ?
9. Полупрямой или лучом называется :
а) Часть прямой, которая состоит из всех точек этой прямой, лежащих от данной точки;
б) Часть луча ;
в) Часть отрезка с данными точками.
« Основные свойства геометрических фигур»
1. Как называют науку о свойствах геометрических фигур?
а)Алгебра; б)Геометрия; в)Физика.
2. Кто создал руководство по математике под названием «Начала»?
а)Птолемей; б) Евклид; в)Ньютон.
3.Основными геометрическими фигурами являются:
а)Отрезок и точка; б)Прямая и луч; в)Точка и прямая.
4. Допиши основное свойство принадлежности точек и прямых:
Через любые две точки можно провести…………
а)Прямую и только одну; б)Две прямых: в)Два отрезка.
5.Что называется отрезком ?
а) часть прямой, которая состоит из всех точек этой прямой; б) Часть луча; в) прямая .
6 Дополни основное свойство расположения точек на прямой.:
Из трёх точек на прямой……….
а)одна и только одна лежит между двумя другими;
б) Две точки лежат между двумя другими;
в) Все три точки не лежат на этой прямой.
7.Дополни основное свойство измерения отрезков:
Каждый отрезок……..
а)Не имеет длины; б)имеет определённую длину; в) Имеет длину , большую нуля.
8.Три точки А,В,С лежат на одной прямой. Известно , что
А B C
АС=17 см, ВС =7,9 см, Найдите длину отрезка АВ?
Какое свойство лежит в основе решения этой задачи ?
9. Полупрямой или лучом называется :
а) Часть прямой, которая состоит из всех точек этой прямой, лежащих от данной точки;
б) Часть луча ;
в) Часть отрезка с данными точками.
1
2
МБОУ СОШ с Широкий Уступ Кривошеева А.И гг
3
Категории Создал руководство по математике под названием «Начала» Автор первого русского учебника математики Доказал теорему о свойствах корней квадратного уравнения Его имя носит теорема о сторонах прямоугольного треугольника Его именем названа не изучаемая в школе геометрия Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Н.И. Лобачевский Евклид Л.Ф. Магницкий Франсуа Виет Фалес Пифагор
4
Создал руководство по математике под названием «Начала» Н.И. Лобачевский Евклид Л.ф. Магницкий Франсуа Виет Фалес Пифагор
5
Создал руководство по математике под названием «Начала» Лобачевский Николай Иванович ( ), русский математик Увы.. Лобачевский Н.И. не является создателем руководства по математике под названием «Начала ». Вы проиграли. «Начала» – это 15 книг, которые содержат изложение планиметрии, стереометрии, алгебры и методов определения площадей и объёмов. Способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков описан в геометрической форме впервые автором в этом труде.
6
Создал руководство по математике под названием «Начала» Пифагор Самосский (VI в. до н. э.), древнегреческий математик Увы.. Пифагор не является создателем руководства по математике под названием «Начала ». Вы проиграли. «Начала» – это 15 книг, которые содержат изложение планиметрии, стереометрии, алгебры и методов определения площадей и объёмов. Способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков описан в геометрической форме впервые автором в этом труде.
7
Создал руководство по математике под названием «Начала» Виет Франсуа ( ), французский математик Увы.. Виет не является создателем руководства по математике под названием «Начала ». Вы проиграли. «Начала» – это 15 книг, которые содержат изложение планиметрии, стереометрии, алгебры и методов определения площадей и объёмов. Способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков описан в геометрической форме впервые автором в этом труде.
8
Создал руководство по математике под названием «Начала» Фалес Милетский (ок до н. э.)– древнегреческий математик Увы.. Фалес не является создателем руководства по математике под названием «Начала ». Вы проиграли. «Начала» – это 15 книг, которые содержат изложение планиметрии, стереометрии, алгебры и методов определения площадей и объёмов. Способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков описан в геометрической форме впервые автором в этом труде.
9
Создал руководство по математике под названием «Начала» Магницкий Леонтий Филиппович. ( ) -русский математик-педагог.. Увы.. Магницкий Л.Ф. не является создателем руководства по математике под названием «Начала ». Вы проиграли. «Начала» – это 15 книг, которые содержат изложение планиметрии, стереометрии, алгебры и методов определения площадей и объёмов. Способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков описан в геометрической форме впервые автором в этом труде.
10
Создал руководство по математике под названием «Начала» Евклид (около около 300 г.г. до н. э.) — древнегреческий математик Вы правы. Именно Евклид является создателем этого трактата по математике под названием «Начала ». «Начала» – это 15 книг, которые содержат изложение планиметрии, стереометрии, алгебры и методов определения площадей и объёмов. Способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков описан в геометрической форме впервые автором в этом труде. На протяжении двух тысячелетий геометрия изучалась в том объёме, порядке и стиле, как она была изложена в «Началах» Наши современные учебники имеют много общих черт с «Началами». Ни одна научная книга не пользовалась таким успехом, как «Начала»
11
Автор первого русского учебника математики Н.И. Лобачевский Евклид Л.ф. Магницкий Франсуа Виет Фалес Пифагор
12
Автор первого русского учебника математики Лобачевский Николай Иванович ( ), русский математик Увы.. Лобачевский Н.И. не является автором первого русского учебника математики. Вы проиграли. Первый российский учебник по математике, изданный в 1703 году, назывался «Арифметика, сиречь наука числителная». По этому учебнику два столетия учились российские отроки. «Арифметика» оказалась наиболее известной из всех учебников математики в России.
13
Автор первого русского учебника математики Пифагор Самосский (VI в. до н. э.), древнегреческий математик Увы.. Пифагор не является автором первого русского учебника математики. Вы проиграли. Первый российский учебник по математике, изданный в 1703 году, назывался «Арифметика, сиречь наука числителная». По этому учебнику два столетия учились российские отроки. «Арифметика» оказалась наиболее известной из всех учебников математики в России
14
Автор первого русского учебника математики Виет Франсуа ( ), французский математик Увы.. Виет не является автором первого русского учебника математики. Вы проиграли. Первый российский учебник по математике, изданный в 1703 году, назывался «Арифметика, сиречь наука числителная». По этому учебнику два столетия учились российские отроки. «Арифметика» оказалась наиболее известной из всех учебников математики в России.
15
Автор первого русского учебника математики Фалес Милетский (ок до н. э.)– древнегреческий математик Увы.. Фалес не является автором первого русского учебника математики. Вы проиграли. Первый российский учебник по математике, изданный в 1703 году, назывался «Арифметика, сиречь наука числителная». По этому учебнику два столетия учились российские отроки. «Арифметика» оказалась наиболее известной из всех учебников математики в России.
16
Автор первого русского учебника математики Евклид (около около 300 г.г. до н. э.) — древнегреческий математик Увы.. Евклид не является автором первого русского учебника математики. Вы проиграли. Первый российский учебник по математике, изданный в 1703 году, назывался «Арифметика, сиречь наука числителная». По этому учебнику два столетия учились российские отроки. «Арифметика» оказалась наиболее известной из всех учебников математики в России.
17
Автор первого русского учебника математики Магницкий Леонтий Филиппович. ( ) -русский математик-педагог.. Ну, конечно же, автором первого русского учебника по математики является учитель Школы математических и навигацких наук в Москве, лучший в то время математик Москвы, Магницкий Л.Ф. Первый российский учебник по математике, изданный в 1703 году, назывался «Арифметика, сиречь наука числителная». По этому учебнику два столетия учились российские отроки. «Арифметика» оказалась наиболее известной из всех учебников математики в России.
18
Доказал теорему о свойствах корней квадратного уравнения Н.И. Лобачевский Евклид Л.ф. Магницкий Франсуа Виет Фалес Пифагор
19
Доказал теорему о свойствах корней квадратного уравнения Лобачевский Николай Иванович ( ), русский математик К сожалению, эта теорема не называется теоремой Лобачевского. Она носит имя другого математика. Вы проиграли. Теорема: Сумма корней приведенного квадратного трехчлена x 2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q, т. е. x 1 + x 2 = – p и x 1 x 2 = q Эта теорема позволяет угадывать целые корни квадратного трехчлена
20
Доказал теорему о свойствах корней квадратного уравнения ки Пифагор Самосский (VI в. до н. э.), древнегреческий математик К сожалению, это не теорема Пифагора. Она носит имя другого математика. Вы проиграли. Теорема: Сумма корней приведенного квадратного трехчлена x 2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q, т. е. x 1 + x 2 = – p и x 1 x 2 = q Эта теорема позволяет угадывать целые корни квадратного трехчлена
21
Доказал теорему о свойствах корней квадратного уравнения Фалес Милетский (ок до н. э.)– древнегреческий математик К сожалению, эта теорема не называется теоремой Фалеса. Она носит имя другого математика. Вы проиграли. Теорема: Сумма корней приведенного квадратного трехчлена x 2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q, т. е. x 1 + x 2 = – p и x 1 x 2 = q Эта теорема позволяет угадывать целые корни квадратного трехчлена
22
Доказал теорему о свойствах корней квадратного уравнения Евклид (около около 300 г.г. до н. э.) — древнегреческий математик К сожалению, эта теорема не называется теоремой Евклида. Она носит имя другого математика. Вы проиграли. Теорема: Сумма корней приведенного квадратного трехчлена x 2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q, т. е. x 1 + x 2 = – p и x 1 x 2 = q Эта теорема позволяет угадывать целые корни квадратного трехчлена
23
Доказал теорему о свойствах корней квадратного уравнения Магницкий Леонтий Филиппович. ( ) -русский математик-педагог.. Теорема: Сумма корней приведенного квадратного трехчлена x 2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q, т. е. x 1 + x 2 = – p и x 1 x 2 = q Эта теорема позволяет угадывать целые корни квадратного трехчлена К сожалению, эта теорема не называется теоремой Магницкого. Она носит имя другого математика. Вы проиграли.
24
Доказал теорему о свойствах корней квадратного уравнения Виет Франсуа ( ), французский математик Теорема Виета. Конечно же так называется эта теорема. Вы угадали. Теорема: Сумма корней приведенного квадратного трехчлена x 2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q, т. е. x 1 + x 2 = – p и x 1 x 2 = q Эта теорема позволяет угадывать целые корни квадратного трехчлена
25
Его имя носит теорема о сторонах прямоугольного треугольника Н.И. Лобачевский Евклид Л.ф. Магницкий Франсуа Виет Фалес Пифагор
26
Его имя носит теорема о сторонах прямоугольного треугольника Лобачевский Николай Иванович ( ), русский математик К сожалению, эта теорема не называется теоремой Лобачевского. Она носит имя другого математика. Вы проиграли. На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, эта теорема является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
27
Его имя носит теорема о сторонах прямоугольного треугольника Фалес Милетский (ок до н. э.)– древнегреческий математик К сожалению, это не теорема Фалеса. Она носит имя другого математика. Вы проиграли. На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, эта теорема является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
28
Его имя носит теорема о сторонах прямоугольного треугольника Евклид (около около 300 г.г. до н. э.) — древнегреческий математик К сожалению, эта теорема не называется теоремой Евклида. Она носит имя другого математика. Вы проиграли. На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, эта теорема является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
29
Его имя носит теорема о сторонах прямоугольного треугольника Магницкий Леонтий Филиппович. ( ) -русский математик-педагог.. К сожалению, эта теорема не называется теоремой Магницкого. Она носит имя другого математика. Вы проиграли. На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, эта теорема является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
30
Его имя носит теорема о сторонах прямоугольного треугольника Виет Франсуа ( ), французский математик На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, эта теорема является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. К сожалению, это не теорема Виета. Она носит имя другого математика. Вы проиграли.
31
Его имя носит теорема о сторонах прямоугольного треугольника ия ки Пифагор Самосский (VI в. до н. э.), древнегреческий математик Несмотря на то, что ещё в XII в. до н. э. китайцы знали свойства египетского треугольника, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадется На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, эта теорема является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Квадрат гипотенузы равен сумме квадратов катетов. Трудно найти человека, у которого имя этого учёного не ассоциировалось бы с данной теоремой. Открытие этой теоремы окружено ореолом красивых легенд. Прокл, комментируя последнее предложение первой книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принес в жертву быка».
32
Его именем названа не изучаемая в школе геометрия Н.И. Лобачевский Евклид Л.ф. Магницкий Франсуа Виет Фалес Пифагор
33
Его именем названа не изучаемая в школе геометрия Фалес Милетский (ок до н. э.)– древнегреческий математик Понятно, что создателем этой геометрии не мог быть Фалес, так как он жил ещё до нашей эры. Вы проиграли. День 23 февраля 1826 года стал днём рождения неевклидовой геометрии. На собрании физико- математического факультета была изложена математическая работа»Сокращённое изложение начал геометрии». В основе новой геометрии лежала аксиома параллельных прямых, невозможность её доказательства.
34
Его именем названа не изучаемая в школе геометрия Евклид (около около 300 г.г. до н. э.) — древнегреческий математик Понятно, что создателем этой геометрии не мог быть Евклид, так как он жил ещё до нашей эры. Вы проиграли. День 23 февраля 1826 года стал днём рождения неевклидовой геометрии. На собрании физико- математического факультета была изложена математическая работа»Сокращённое изложение начал геометрии». В основе новой геометрии лежала аксиома параллельных прямых, невозможность её доказательства
35
Понятно, что создателем этой геометрии не мог быть Л.Ф. Магницкий, так как он жил не в том веке. Вы проиграли. Его именем названа не изучаемая в школе геометрия Магницкий Леонтий Филиппович. ( ) -русский математик-педагог.. День 23 февраля 1826 года стал днём рождения неевклидовой геометрии. На собрании физико- математического факультета была изложена математическая работа»Сокращённое изложение начал геометрии». В основе новой геометрии лежала аксиома параллельных прямых, невозможность её доказательства
36
Его именем названа не изучаемая в школе геометрия Виет Франсуа ( ), французский математик День 23 февраля 1826 года стал днём рождения неевклидовой геометрии. На собрании физико- математического факультета была изложена математическая работа»Сокращённое изложение начал геометрии». В основе новой геометрии лежала аксиома параллельных прямых, невозможность её доказательства Понятно, что создателем этой геометрии не мог быть Виет, так как он жил не в том веке. Вы проиграли.
37
Его именем названа не изучаемая в школе геометрия Пифагор Самосский (VI в. до н. э.), древнегреческий математик Понятно, что создателем этой геометрии не мог быть Пифагор, так как он жил не в том веке. Вы проиграли День 23 февраля 1826 года стал днём рождения неевклидовой геометрии. На собрании физико- математического факультета была изложена математическая работа»Сокращённое изложение начал геометрии». В основе новой геометрии лежала аксиома параллельных прямых, невозможность её доказательства
38
Его именем названа не изучаемая в школе геометрия Лобачевский Николай Иванович ( ), русский математик Геометрия Лобачевского была первой из нескольких, построенных его последователями. И Вы, конечно же, правы! День 23 февраля 1826 года стал днём рождения неевклидовой геометрии. На собрании физико- математического факультета была изложена математическая работа»Сокращённое изложение начал геометрии». В основе новой геометрии лежала аксиома параллельных прямых, невозможность её доказательства Созданием неевклидовой геометрии было основано на гипотезе острого угла, в которой имеется не одна прямая, параллельная данной прямой и проходящая через данную точку, а две. Ни одна из этих двух параллельных прямых не пересекается с прямой, которой они обе параллельны, так же как и любая прямая, лежащая внутри угла, образованного двумя указанными параллельными прямыми, и проходящая через фиксированную точку.
39
Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Н.И. Лобачевский Евклид Л.ф. Магницкий Франсуа Виет Фалес Пифагор
40
Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Евклид (около около 300 г.г. до н. э.) — древнегреческий математик Вы ошиблись – это не Евклид. Он был первым, кто придал геометрии логический характер науки и ввел в нее понятие доказательства. Он выполнял задачи на построение с помощью циркуля и линейки, доказал равенство вертикальных углов и углов при основании равнобедренного треугольника. Он доказал теорему о вписанном угле, который опирается на диаметр, и признак равенства треугольников по стороне и двум прилежащим углам. Но чаще всего его имя вспоминают в связи с теоремой о пропорциональности отрезков, которые отсекаются параллельными прямыми на сторонах угла.
41
Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Магницкий Леонтий Филиппович. ( ) -русский математик-педагог.. Он был первым, кто придал геометрии логический характер науки и ввел в нее понятие доказательства. Он выполнял задачи на построение с помощью циркуля и линейки, доказал равенство вертикальных углов и углов при основании равнобедренного треугольника. Он доказал теорему о вписанном угле, который опирается на диаметр, и признак равенства треугольников по стороне и двум прилежащим углам. Но чаще всего его имя вспоминают в связи с теоремой о пропорциональности отрезков, которые отсекаются параллельными прямыми на сторонах угла. Вы ошиблись – это не Магницкий Л.Ф.
42
Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Виет Франсуа ( ), французский математик Он был первым, кто придал геометрии логический характер науки и ввел в нее понятие доказательства. Он выполнял задачи на построение с помощью циркуля и линейки, доказал равенство вертикальных углов и углов при основании равнобедренного треугольника. Он доказал теорему о вписанном угле, который опирается на диаметр, и признак равенства треугольников по стороне и двум прилежащим углам. Но чаще всего его имя вспоминают в связи с теоремой о пропорциональности отрезков, которые отсекаются параллельными прямыми на сторонах угла. Вы ошиблись – это не Виет.
43
Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Пифагор Самосский (VI в. до н. э.), древнегреческий математик Он был первым, кто придал геометрии логический характер науки и ввел в нее понятие доказательства. Он выполнял задачи на построение с помощью циркуля и линейки, доказал равенство вертикальных углов и углов при основании равнобедренного треугольника. Он доказал теорему о вписанном угле, который опирается на диаметр, и признак равенства треугольников по стороне и двум прилежащим углам. Но чаще всего его имя вспоминают в связи с теоремой о пропорциональности отрезков, которые отсекаются параллельными прямыми на сторонах угла. Вы ошиблись – это не Пифагор.
44
Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Фалес Милетский (ок до н. э.)– древнегреческий математик Он был первым, кто придал геометрии логический характер науки и ввел в нее понятие доказательства. Он выполнял задачи на построение с помощью циркуля и линейки, доказал равенство вертикальных углов и углов при основании равнобедренного треугольника. Он доказал теорему о вписанном угле, который опирается на диаметр, и признак равенства треугольников по стороне и двум прилежащим углам. Но чаще всего его имя вспоминают в связи с теоремой о пропорциональности отрезков, которые отсекаются параллельными прямыми на сторонах угла. Вы не ошиблись – это выдающийся древнегреческий математик Фалес.
45
Доказал теорему о равенстве отрезков, отсекаемых на сторонах угла параллельными прямыми Лобачевский Николай Иванович ( ), русский математик Он был первым, кто придал геометрии логический характер науки и ввел в нее понятие доказательства. Он выполнял задачи на построение с помощью циркуля и линейки, доказал равенство вертикальных углов и углов при основании равнобедренного треугольника. Он доказал теорему о вписанном угле, который опирается на диаметр, и признак равенства треугольников по стороне и двум прилежащим углам. Но чаще всего его имя вспоминают в связи с теоремой о пропорциональности отрезков, которые отсекаются параллельными прямыми на сторонах угла. Вы ошиблись – это не Лобачевский Н.И.
46
Источники:
евклид
• древнегреческий математик, автор «Начала»
• папа, родоначальник геометрии
• древнегреческий математик, астроном
• с именем этого математика связывают появление геометрической алгебры как науки
• каждое математическое рассуждение этого математика заканчивается фразой: «Что и требовалось доказать!»
• его «Начала» уместились всего лишь в 15 томиков
• древнегреческий математик, астроном, философ
• «отец» геометрии
• великий геометр
• математик из Древней Греции
• родоначальник геометрии
• отец-основатель геометрии
• древнегреческий математик
• отец-основатель всей геометрии
• далекий родитель всей геометрии
• древнегреческий геометр
• «отец» геометрии в рифму к Гераклиду
• математик античных времен
• придумал алгоритм нахождения НОД
• Древнегреческий математик (3 в. до н. э., »Начала»)
Буквы:
1
2
3
4
5
6
Муниципальное казенное
общеобразовательное учреждение средняя общеобразовательная школа № 9 сельского
поселения «Поселок Софийск» Верхнебуреинского муниципального района
Хабаровского края
Заседание клуба «Знатоки математики»
для
учащихся 8-11 классов
Составил
учитель математики Т.А. Токарева
2013
г.
Ведущий (учитель
математики): Несколько лет назад была объявлена
премия за сочинение на тему «Как человек без математики жил». Премия так и
осталась не выданной, т. к., по-видимому, не нашлось сочинителя, который сумел
бы описать жизнь человека, лишенного математических представлений. И
действительно с математикой мы встречаемся ежедневно, с утра до вечера.
Просыпаясь, мы смотрим на часы, чтобы узнать, который час; в транспорте
рассчитываем время в пути, в магазине опять занимаемся расчетами. Если бы не
математика, люди никогда не смогли осуществить полёты в космос. Без математики
нельзя изучить ни физику, ни химию, ни географию, ни черчение и даже в
рисовании без неё не обойтись! Вот такая она важная
математика!
Сегодня встречаются две команды,
команда «Треугольник» и команда «Квадрат», чтобы соревноваться в своих
математических знаниях. Итак, давайте их поприветствуем! Под музыку и
аплодисменты выходят команды на сцену. Судить их будет уважаемое жюри
(называются имена и фамилии). Займите, пожалуйста, свои места.
Итак, начинаем!
Разминка. «Конкурс на внимательность»
Для решения большинства задач
недостаточно одних знаний. Необходима ещё и внимательность. С чего начинается
решение задачи? Конечно, с условия. Но условие можно читать по-разному:
прочтёшь невнимательно – вот и утеряна главная ниточка. Проверим, умеют ли
команды быстро улавливать условие задачи. Кто быстрее решит задачи?
- На березе 16 сучков, на каждом
сучке по 10 веток, на каждой ветке по 4 яблока. Сколько всего яблок?
(Нисколько) - На руках 10 пальцев. Сколько
пальцев на 10 руках? (50) - Из одной точки вылетели 3
ласточки. Когда они будут в одной плоскости? (Всегда) - Величина угла 300. Чему она
будет равна, если рассматривать угол в лупу с 2-кратным увеличением? (300)
- Электропоезд идет с востока на
запад со скоростью 60 км/ч. В том же направлении – с востока на запад –
дует ветер, но со скоростью 50
км/ч, в какую сторону отклоняется дым поезда? (Электропоезд бездымен) - Как называется отрезок,
образующий прямой угол с данной прямой? (Перпендикуляр)
I
гейм «Гонка за лидером»
Участники команд по очереди выбирают
вопросы из трех представленных категорий и отвечают на них, получая за каждый
верный ответ балл.
Вопросы к гейму см. приложение № 1
|
Категории |
|
Из |
|
Ну – ка, |
|
Ученые |
Приложение № 1
I
гейм «Гонка за лидером» Из истории математики
- Где
возникло градусное измерение углов? (В древнем Вавилоне)
- Ещё
Клавдий Птолемей (II
в.) использовал в своих трудах единицы измерения углов: градус, минута,
секунда. Как он их обозначал? (0, /, //)
- В
1873 появилась новая единица измерения углов. Где это произошло и как
называлась эта единица? (Англия, радиан)
- Что
означает в переводе с латинского слово sinus
– синус? (Изгиб, извилина)
- На
каком здании была надпись: «Незнающий геометрии, да не войдет сюда»? (На
здании академии греческого философа-идеалиста Платона) - Индийцы
называли его «сунья», арабские математики «сифр». Как мы называем его
сейчас? (Нуль) - Какая
теорема в старину называлась: «теоремой невесты»? (Теорема Пифагора) - При
царе Иване IV
были выпущены монеты, на которых изображен всадник с копьем в руке. Как
назывались эти монеты? (Копейка) - При
каком царе впервые русские меры (верста, сажень, вершок, дюйм, фут, пуд,
фунт, золотник) были приведены в определенную систему? (При Петре I) - Её
знакомство с математикой произошло в 8 лет, так как стены её комнаты были
оклеены листами с записями лекций по математике профессора Островского.
Кто она? (С. В. Ковалевская)
I гейм «Гонка за
лидером» Ну-ка, смекни!
- Есть
ли разница между числом и цифрой? (Да) - Что
больше: произведение или сумма десяти цифр 0,1,2,3,4,5,6,7,8,9? (Сумма) - Горело
семь свечей, две погасло. Сколько свечей осталось? (7) - Сколько
граней у шестигранного карандаша? (8) - На
березе 16 сучков, на каждом сучке по 10 веток, на каждой ветке по четыре
яблока. Сколько яблок всего? (0) - Сколько
горошин входит в пустой стакан? (Нисколько, горошины не ходят) - На
руках 10 пальцев. Сколько пальцев на 10 руках? (50) - Произведение
каких трех чисел равно их сумме? (1, 2, 3) - У
Марины было целое яблоко, две половины и четыре четвертинки. Сколько
яблок неё было? (3) - Один
мальчик говорит другому: «Если ты дашь мне половину своих денег, я смогу
купить карандаш». Сколько денег было у второго мальчика? (Установить
невозможно)
I гейм «Гонка за
лидером» Учёные
- По
профессии пивовар, он был прекрасным экспериментатором, исследовал законы
выделения теплоты электрическим током, внес большой вклад в кинетическую
теорию газов. (Джоуль) - В
честь какой женщины-математика назван цветок? (Именем известной
вычислительницы француженки Гартензии (Лекот 1723-1788) назван цветок
ГОРТЕНЗИЯ, привезенный ею из Индии) - Он
открыл один из важнейших количественный закон цепи электрического тока. Он
установил постоянство силы тока в различных участках цепи, показал, что
сила тока убывает с увеличением длины провода и с уменьшением площади его
поперечного сечения. Он нашел ряд из многих веществ по возрастанию
сопротивления. (Георг Ом) - Какой
великий русский математик не получил диплома, хотя дважды успешно выдержал
выпускные экзамены в университете? (М.В.
Остроградский (1801-1873), он не согласился слушать лекции по богословию) - Назовите
фамилию ученого, который написал самый первый учебник по геометрии. Он
однофамилец известного греческого медика. (Гиппократ) - Кому
принадлежат слова: «Теперь я знаю, как выглядит атом?» (Эти слова
принадлежат английскому физику Резерфорду, сказаны они в 1911
г.) - Назовите
фамилию ученого, который в 1831 г. установил, что индукционный ток в
контуре всегда возникает такого направления, при котором его магнитное
поле противодействует изменению магнитного потока, пронизывающего этот
контур. (Э. Х. Ленц) - Какой
ученый создал руководство по математике под названием «Начала»? (Евклид) - Кто
изобрел электрическую лампочку накаливания? (Русский изобретатель –
Александр Николаевич Лодыгин. Американский изобретатель Эдисон получил
несколько лампочек Лодыгина. Их привез в Америку один русский офицер. В
конце 1879 г. Эдисон создал свою лампочку с винтовым цоколем и патроном,
называемым эдисоновским. Все выданные Эдисону патенты были сформулированы
лишь как предложения об усовершенствовании ранее запатентованной лампы
Лодыгина.) - На
могиле этого великого математика был установлен памятник с изображением
шара и описанного около него цилиндра. Спустя почти 200 лет по этому
чертежу нашли его могилу. Кто этот математик? (Архимед)
I I
гейм «Спешите видеть»
ЗАДАНИЕ №1
Каждый
знает, даже дошкольник
Что такое
треугольник
А уж вам-то как не
знать,
Но совсем другое
дело-
Быстро, точно и
умело
Треугольники
считать.
Например, в фигуре
этой
Сколько разных?
Рассмотри!
Всё внимательно
исследуй
И по краю и
внутри!
Ответ: (20)
Балл зарабатывает
та команда, чей ответ был наиболее близок к правильному.
I I I
гейм «Ты – мне, я — тебе»
Каждая команда
задаёт по три вопроса соперникам.
I V
гейм «Тёмная лошадка»
Ведущий. Каменева
Татьяна Ивановна учитель технологии, черчения: Уважаемые эрудиты математики!
На уроках геометрии при решении задач, связанных с окружностью, обычно
указывают, чему равен радиус окружности. А вот на технических чертежах и
эскизах обязательно наносят диаметры окружности, а не радиусы. Можете ли вы,
объяснить причину этого?
Правильный ответ. При вычерчивании
окружности надо знать её радиус, но в готовой детали проще замерять диаметр
сверла, а не радиус.
Ведущий. Карепова Анастасия Сергеевна – учитель физики. Уважаемые, знатоки! В
начале 40-х годах нашего века авиастроители всего мира столкнулись со страшным
и непонятным явлением. Во время скоростного полета самолета на некоторой, так
называемой критической скорости, возникла стремительно нарастающая вибрация
конструкции. Она внезапно охватила самолет, и иногда достаточно было нескольких
секунд, чтобы машина развалилась на куски. С земли казалось, что самолеты
взрываются. Многочисленные исследования, проведенные в США, Англии, Германии не
принесли успеха. Полностью разобраться в этой запутанной проблеме удалось лишь
известному советскому математику. Были найдены простые и эффективные методы
предупреждения вибрации. Угроза самолета и экипажу были полностью
ликвидирована. За выдающийся вклад в решении труднейшей проблемы этот математик
в 1942 году удостоен государственной премии СССР. Мои вопросы к вам, уважаемые
знатоки, таковы.
- Какое название получило в технике
описанное явление? - Какова фамилия советского
математика, о котором я рассказал?
Ответ. Явление получило название
«флаттер». Математик, решивший задачу, Мстислав Всеволодович Келдыш, академик,
трижды герой Социалистического труда, выдающийся советский учёный, много лет,
проработавший на посту Президента АН СССР.
Ведущий. Вопрос Виктории
Юрьевны учитель русского языка и литературы. Перефразируя одного великого
русского писателя, можно сказать, что человек подобен дроби, числитель – это
хорошее, что о нём говорят и думают люди, а знаменатель – это то, что о себе он
сам. Известное правило – чем больше числитель, тем больше дробь, верно не
только в математике, но и в жизни. Назовите этого русского писателя.
Ответ. Лев Толстой.
Ведущий. Ольги Ивановны учитель
математики. Уважаемые игроки! У меня в руках игральная карта – бубновый король.
Посмотрите внимательно, на карте вы видите изображение ромба. У меня к вам
такой вопрос. Почему на картах бубновой масти изображен именно ромб, а не
что-нибудь другое?
Правильный ответ. Слово «ромб»
происходит от греческого слова « ромбос», означающего «бубен». Мы привыкли к
тому, что бубен имеет круглую форму, а раньше бубны имели форму квадрата или ромба.
Ведущий. Внимание!
(Звучит музыка) Черный ящик!
Внести, чёрный ящик!
То, что лежит в чёрном ящике,
изобрёл очень талантливый юноша. Под теплом Помпеи археологи обнаружили много
таких предметов, изготовленных из бронзы. В нашей стране это было обнаружено
при раскопках в Нижнем Новгороде. В Древней Греции умение пользоваться этим
предметом считалось верхом совершенства, а уж умение решать задачи с его
помощью – признаком высокого положения в обществе и большого ума. Этот предмет
незаменим в архитектуре и строительстве. За многие сотни лет конструкция этого
предмета не изменилась. В настоящее время им умеет пользоваться любой
старшеклассник. Вопрос. Что лежит в черном ящике?
Ведущий: А теперь моя пора задать вам вопрос, уважаемые знатоки. Кто из
величайших математиков древности провозгласил, что числа правят миром? Он
понимал природу, умел слушать шум ветра, разговаривать с рекой. Кто он?
V
гейм «Дальше, дальше, дальше…»
Командам необходимо ответить на ответить
на 16 вопросов. (см. приложение № 2)
Приложение
№ 2
8-9 класс. Команда «Треугольник»
- Часть прямой, соединяющая две
точки? (Отрезок). - Имеет ли прямая линия концы?
(Нет) - Очень плохая оценка знаний?
(Двойка) - Уравнение второй степени?
(Квадратное) - Есть ли разница между числом и
цифрой? (Да) - Сумма углов треугольника равна
… (180°) - Автор учебника «Алгебра»? (Мордкович)
- Наименьшее натуральное число?
(1) - Сумма длин сторон
многоугольника? (Периметр) - Площадь квадрата со стороной
а? (а2) - Луч, делящий угол пополам?
(Биссектриса) - Существует ли треугольник с
двумя прямыми углами? (Нет) - Сколько медиан можно провести
в треугольнике? (Три) - Число разрядов в классе? (Три)
- Вертикальные углы … (Равны)
- Сотая часть числа? (Процент)
- 202= … (400)
10-11 классы.
Команда «Квадрат»
- Сколько можно провести высот в
треугольнике? (Три) - Автор учебника «Геометрия»? (Атанасян)
- Формула пути? (S=v*t)
- Направленный отрезок? (Вектор)
- Какие числа используются при
счете? (Натуральные) 
=…
(11)- Катет прямоугольного
треугольника, лежащий против угла в 30° равен … (Половине гипотенузы) - Радиус равен 3. Чему равна S
круга? (9пи) - Сумма углов четырехугольника?
(360°) - Очень хорошая оценка знаний …
(«5») - Есть ли края у плоскости?
(Нет) - Знак корня? (Радикал)
- sin30°=… (
) - Площадь прямоугольника?(S= a*
b) - Название функции y=logax?
(Логарифметическая) - В прямоугольном треугольнике
отношение прилежащего катета к гипотенузе называется … (Koсинусом) - Объем 1кг воды? (1литр)
)V I
гейм «Супер-гейм» «Отгадывание
кроссворда»
Первая русская женщина-математик (Ковалевская)
- Плоская геометрическая фигура.
- Замкнутая кривая.
- Вид параллелограмма.
- Вид четырехугольника.
- Часть прямой.
- Вид прямой.
- Замкнутая, выпуклая плоская
кривая. - Прямая, пересекающая другие
линии. - Правильный многогранник.
- Основное геометрическое
понятие.
ОТВЕТЫ: 1. Круг. 2. Окружность. 3. Квадрат. 4. Параллелограмм.
5. Луч. 6. Перпендикуляр. 7. Овал. 8. Секущая. 9. Куб. 10. Трапеция. 11.
Прямая.
Ответ: КОВАЛЕВСКАЯ (по вертикали).
Подведение итогов. Слово жюри. Награждение победителей.
8-9 класс. Команда «Треугольник»
1. Часть
прямой, соединяющая две точки?
2. Имеет ли
прямая линия концы?
3. Очень
плохая оценка знаний?
4. Уравнение
второй степени?
5. Есть ли
разница между числом и цифрой?
6. Сумма
углов треугольника равна …
7. Автор
учебника «Алгебра»?
8. Наименьшее
натуральное число?
9. Сумма длин
сторон многоугольника?
10. Площадь квадрата
со стороной а?
11. Луч, делящий угол
пополам?
12. Существует ли
треугольник с двумя прямыми углами?
13. Сколько медиан
можно провести в треугольнике?
14. Число разрядов в
классе?
15. Вертикальные углы
…
16. Сотая часть
числа?
17. 202= …
10-11 классы. Команда «Квадрат»
1. Сколько
можно провести высот в треугольнике?
2. Автор
учебника «Геометрия»?
3. Формула
пути?
4. Направленный
отрезок?
5. Какие
числа используются при счете?
6. 
=…
7. Катет
прямоугольного треугольника, лежащий против угла в 30° равен
8. Радиус
равен 3. Чему равна S круга?
9. Сумма
углов четырехугольника?
10. Очень хорошая
оценка знаний …
11. Есть ли края у
плоскости?
12. Знак корня?
13. sin30°=…
14. Площадь
прямоугольника?
15. Название функции
y=logax
16. В прямоугольном
треугольнике отношение прилежащего катета к гипотенузе называется …
17. Объем 1кг воды