Зачеркните неверные высказывания.
1. Любая инструкция, последовательность предписаний или план действий является алгоритмом.
2. Алгоритм всегда представляет собой описание некоторой последовательности вычислений.
3. Примерами алгоритмом являются правила сложения, вычитания чисел, правила геометрических построений.
4. Каждый исполнитель способен выполнять определенный набор команд.
5. Исполнителем является только техническое устройство, которое способно выполнять команды.
6. Предписание исполнителю о выполнении отдельного законченного действия называется командой
§ 2.1. Алгоритмы и исполнители
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- алгоритм
- свойства алгоритма
- дискретность
- понятность
- определённость
- результативность
- массовость
- исполнитель
- характеристики исполнителя
- круг решаемых задач
- среда
- режим работы
- система команд
- формальное исполнение алгоритма
2.1.1. Понятие алгоритма
Каждый человек в повседневной жизни, в учёбе или на работе решает огромное количество задач самой разной сложности. Сложные задачи требуют длительных размышлений для нахождения решения; простые и привычные задачи человек решает не задумываясь, автоматически. В большинстве случаев решение каждой задачи можно разбить на простые этапы (шаги). Для многих таких задач (установка программного обеспечения, сборка шкафа, создание сайта, эксплуатация технического устройства, покупка авиабилета через Интернет и т. д.) уже разработаны и предлагаются пошаговые инструкции, при последовательном выполнении которых можно прийти к желаемому результату.
Пример 1. Задача «Найти среднее арифметическое двух чисел» решается в три шага:
- 1) задумать два числа;
- 2) сложить два задуманных числа;
- 3) полученную сумму разделить на 2.
Пример 2. Задача «Внести деньги на счёт телефона» подразделяется на следующие шаги:
- 1) подойти к терминалу по оплате платежей;
- 2) выбрать оператора связи;
- 3) ввести номер телефона;
- 4) проверить правильность введённого номера;
- 5) вставить денежную купюру в купюроприёмник;
- 6) дождаться сообщения о зачислении денег на счёт;
- 7) получить чек.
Пример 3. Этапы решения задачи «Нарисовать весёлого ёжика» представлены графически:

Нахождение среднего арифметического, внесение денег на телефонный счёт и рисование ежа — на первый взгляд совершенно разные процессы. Но у них есть общая черта: каждый из этих процессов описывается последовательностями кратких указаний, точное следование которым позволяет получить требуемый результат. Последовательности указаний, приведённые в примерах 1-3, являются алгоритмами решения соответствующих задач. Исполнитель этих алгоритмов — человек.
Алгоритм может представлять собой описание некоторой последовательности вычислений (пример 1) или шагов нематематического характера (примеры 2-3). Но в любом случае перед его разработкой должны быть чётко определены начальные условия (исходные данные) и то, что предстоит получить (результат). Можно сказать, что алгоритм — это описание последовательности шагов в решении задачи, приводящих от исходных данных к требуемому результату.
В общем виде схему работы алгоритма можно представить следующим образом (рис. 2.1).

Алгоритмами являются изучаемые в школе правила сложения, вычитания, умножения и деления чисел, многие грамматические правила, правила геометрических построений и т. д.
Анимации «Работа с алгоритмом» (193576), «Наибольший общий делитель» (170363), «Наименьшее общее кратное» (170390) помогут вам вспомнить некоторые алгоритмы, изученные на уроках русского языка и математики (http://sc.edu.ru/).
Пример 4. Некоторый алгоритм приводит к тому, что из одной цепочки символов получается новая цепочка следующим образом:
- 1. Вычисляется длина (в символах) исходной цепочки символов.
- 2. Если длина исходной цепочки нечётна, то к исходной цепочке справа приписывается цифра 1, иначе цепочка не изменяется.
- 3. Символы попарно меняются местами (первый — со вторым, третий — с четвёртым, пятый — с шестым и т. д).
- 4. Справа к полученной цепочке приписывается цифра 2.
Получившаяся таким образом цепочка является результатом работы алгоритма.
Так, если исходной была цепочка А#В, то результатом работы алгоритма будет цепочка #А1В2, а если исходной цепочкой была АБВ@, то результатом работы алгоритма будет цепочка БА@В2.
2.1.2. Исполнитель алгоритма
Каждый алгоритм предназначен для определённого исполнителя.
Исполнитель — это некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.
Различают формальных и неформальных исполнителей. Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Неформальный исполнитель может выполнять команду по-разному.
Рассмотрим более подробно множество формальных исполнителей. Формальные исполнители необычайно разнообразны, но для каждого из них можно указать следующие характеристики: круг решаемых задач (назначение), среду, систему команд и режим работы.
Круг решаемых задач. Каждый исполнитель создаётся для решения некоторого круга задач — построения цепочек символов, выполнения вычислений, построения рисунков на плоскости и т. д.
Среда исполнителя. Область, обстановку, условия, в которых действует исполнитель, принято называть средой данного исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
Система команд исполнителя. Предписание исполнителю о выполнении отдельного законченного действия называется командой. Совокупность всех команд, которые могут быть выполнены некоторым исполнителем, образует систему команд данного исполнителя (СКИ). Алгоритм составляется с учётом возможностей конкретного исполнителя, иначе говоря, в системе команд исполнителя, который будет его выполнять.
Режимы работы исполнителя. Для большинства исполнителей предусмотрены режимы непосредственного управления и программного управления. В первом случае исполнитель ожидает команд от человека и каждую поступившую команду немедленно выполняет. Во втором случае исполнителю сначала задаётся полная последовательность команд (программа), а затем он выполняет все эти команды в автоматическом режиме. Ряд исполнителей работает только в одном из названных режимов.
Рассмотрим примеры исполнителей.
Пример 5. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. Система команд Черепашки состоит из двух команд:
- 1) Вперёд n (где n — целое число) — вызывает передвижение Черепашки на n шагов в направлении движения — в том направлении, куда развёрнуты её голова и корпус;
- 2) Направо m (где m — целое число) — вызывает изменение направления движения Черепашки на m градусов по часовой стрелке.
Запись Повтори k [<Команда1> <Команда2> … <Командаn>] означает, что последовательность команд в скобках повторится k раз.
Подумайте, какая фигура появится на экране после выполнения Черепашкой следующего алгоритма.
Повтори 12 [Направо 45 Вперёд 20 Направо 45]
Пример 6. Система команд исполнителя Вычислитель состоит из двух команд, которым присвоены номера:
1 — вычти 1
2 — умножь на 3
Первая из них уменьшает число на 1, вторая увеличивает число в 3 раза. При записи алгоритмов для краткости указываются лишь номера команд. Например, алгоритм 21212 означает следующую последовательность команд:
- умножь на 3
- вычти 1
- умножь на 3
- вычти 1
- умножь на 3
С помощью этого алгоритма число 1 будет преобразовано в 15: ((1 • 3 — 1) • 3-1) • 3 = 15.
Пример 7. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут стоять стены. Робот передвигается по клеткам поля и может выполнять следующие команды, которым присвоены номера:
1 — вверх
2 — вниз
3 — вправо
4 — влево

При выполнении каждой такой команды Робот перемещается в соседнюю клетку в указанном направлении. Если же в этом направлении между клетками стоит стена, то Робот разрушается.
Что произойдёт с Роботом, если он выполнит последовательность команд 32323 (здесь цифры обозначают номера команд), начав движение из клетки А? Какую последовательность команд следует выполнить Роботу, чтобы переместиться из клетки А в клетку В, не разрушившись от встречи со стенами?
При разработке алгоритма:
- 1) выделяются фигурирующие в задаче объекты, устанавливаются свойства объектов, отношения между объектами и возможные действия с объектами;
- 2) определяются исходные данные и требуемый результат;
- 3) определяется последовательность действий исполнителя, обеспечивающая переход от исходных данных к результату;
- 4) последовательность действий записывается с помощью команд, входящих в систему команд исполнителя.
Можно сказать, что алгоритм — модель деятельности исполнителя алгоритмов.
2.1.3. Свойства алгоритма
Не любая инструкция, последовательность предписаний или план действий может считаться алгоритмом. Каждый алгоритм обязательно обладает следующими свойствами: дискретность, понятность, определённость, результативность и массовость.
Свойство дискретности означает, что путь решения задачи разделён на отдельные шаги (действия). Каждому действию соответствует предписание (команда). Только выполнив одну команду, исполнитель может приступить к выполнению следующей команды.
Свойство понятности означает, что алгоритм состоит только из команд, входящих в систему команд исполнителя, т. е. из таких команд, которые исполнитель может воспринять и по которым может выполнить требуемые действия.
Свойство определённости означает, что в алгоритме нет команд, смысл которых может быть истолкован исполнителем неоднозначно; недопустимы ситуации, когда после выполнения очередной команды исполнителю неясно, какую команду выполнять следующей. Благодаря этому результат алгоритма однозначно определяется набором исходных данных: если алгоритм несколько раз применяется к одному и тому же набору исходных данных, то на выходе всегда получается один и тот же результат.
Свойство результативности означает, что алгоритм должен обеспечивать получение результата после конечного, возможно, очень большого, числа шагов. При этом результатом считается не только обусловленный постановкой задачи ответ, но и вывод о невозможности продолжения по какой-либо причине решения данной задачи.
Свойство массовости означает, что алгоритм должен обеспечивать возможность его применения для решения любой задачи из некоторого класса задач. Например, алгоритм нахождения корней квадратного уравнения должен быть применим к любому квадратному уравнению, алгоритм перехода улицы должен быть применим в любом месте улицы, алгоритм приготовления лекарства должен быть применим для приготовления любого его количества и т. д.
Пример 8. Рассмотрим один из методов нахождения всех простых чисел, не превышающих некоторое натуральное число п. Этот метод называется «решето Эратосфена» по имени предложившего его древнегреческого учёного Эратосфена (III в. до н. э.).
Для нахождения всех простых чисел, не больших заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
- 1) выписать подряд все натуральные числа от 2 до n (2, 3, 4, …, n);
- 2) заключить в рамку 2 — первое простое число;
- 3) вычеркнуть из списка все числа, делящиеся на последнее найденное простое число;
- 4) найти первое неотмеченное число (отмеченные числа — зачёркнутые числа или числа, заключённые в рамку) и заключить его в рамку — это будет очередное простое число;
- 5) повторять шаги 3 и 4 до тех пор, пока не останется неотмеченных чисел.
Более наглядное представление о методе нахождения простых чисел вы сможете получить с помощью размещённой в Единой коллекции цифровых образовательных ресурсов анимации «Решето Эратосфена» (180279).
Рассмотренная последовательность действий является алгоритмом, так как она удовлетворяет свойствам:
- дискретности — процесс нахождения простых чисел разбит на шаги;
- понятности — каждая команда понятна ученику 8 класса, выполняющему этот алгоритм;
- определённости — каждая команда трактуется и выполняется исполнителем однозначно; имеются указания об очерёдности выполнения команд;
- результативности — через некоторое число шагов достигается результат;
- массовости — последовательность действий применима для любого натурального n.
Рассмотренные свойства алгоритма позволяют дать более точное определение алгоритма.
Алгоритм — это предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.
2.1.4. Возможность автоматизации деятельности человека
Разработка алгоритма — как правило, трудоёмкая задача, требующая от человека глубоких знаний, изобретательности и больших временных затрат.
Решение задачи по готовому алгоритму требует от исполнителя только строгого следования заданным предписаниям.
Пример 9. Из кучки, содержащей любое, большее трёх, количество каких-либо предметов, двое играющих по очереди берут по одному или по два предмета. Выигрывает тот, кто своим очередным ходом сможет забрать все оставшиеся предметы.
Рассмотрим алгоритм, следуя которому первый игрок наверняка обеспечит себе выигрыш.
- 1. Если число предметов в кучке кратно 3, то уступить ход противнику, иначе начинать игру.
- 2. Своим очередным ходом каждый раз дополнять число предметов, взятых соперником, до 3 (число оставшихся предметов должно быть кратно 3).
Исполнитель может не вникать в смысл того, что он делает, и не рассуждать, почему он поступает так, а не иначе, т. е. он может действовать формально. Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека. Для этого:
- 1) процесс решения задачи представляется в виде последовательности простейших операций;
- 2) создаётся машина (автоматическое устройство), способная выполнять эти операции в последовательности, заданной в алгоритме;
- 3) человек освобождается от рутинной деятельности, выполнение алгоритма поручается автоматическому устройству.
Самое главное: Алгоритмы и исполнители
Исполнитель — некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.
Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Для каждого формального исполнителя можно указать: круг решаемых задач, среду, систему команд и режим работы.
Алгоритм — предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.
Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека.
ВОПРОСЫ И ЗАДАНИЯ
2. Что называют алгоритмом?
3. Подберите синонимы к слову «предписание».
4. Приведите примеры алгоритмов, изучаемых вами в школе.
5. Кто может быть исполнителем алгоритма?
6. Приведите пример формального исполнителя. Приведите пример, когда человек выступает в роли формального исполнителя.
7. Какие команды должны быть у робота, выполняющего функции: а) кассира в магазине; б) дворника; в) охранника?
8. От чего зависит круг решаемых задач исполнителя «компьютер»?
9. Рассмотрите в качестве исполнителя текстовый процессор, имеющийся на вашем компьютере. Охарактеризуйте круг решаемых этим исполнителем задач и его среду.
10. Что такое команда, система команд исполнителя?
11. Перечислите основные свойства алгоритма.
12. К чему может привести отсутствие какого-либо свойства у алгоритма? Приведите примеры.
13. В чём важность возможности формального исполнения алгоритма?
14. Последовательность чисел строится по следующему алгоритму: первые два числа последовательности принимаются равными 1; каждое следующее число последовательности принимается равным сумме двух предыдущих чисел. Запишите 10 первых членов этой последовательности.
15. Некоторый алгоритм получает из одной цепочки символов новую цепочку следующим образом. Сначала записывается исходная цепочка символов, после нее записывается исходная цепочка символов в обратном порядке, затем записывается буква, следующая в русском алфавите за той буквой, которая в исходной цепочке стояла на последнем месте. Если в исходной цепочке на последнем месте стоит буква Я, то в качестве следующей буквы записывается буква А. Получившаяся цепочка является результатом работы алгоритма. Например, если исходная цепочка символов была ДОМ, то результатом работы алгоритма будет цепочка ДОММОДН. Дана цепочка символов КОМ. Сколько букв О будет в цепочке символов, которая получится, если применить алгоритм к данной цепочке, а затем ещё раз применить алгоритм к результату его работы?
16. Найдите в сети Интернет анимацию шагов алгоритма Эратосфена. С помощью алгоритма Эратосфена найдите все простые числа, не превышающие 50.
17. Что будет результатом исполнения Черепашкой (см. пример 5) алгоритма? Повтори 8 [Направо 45 Вперёд 45]
18. Запишите алгоритм для исполнителя Вычислитель (пример 6), содержащий не более 5 команд: а) получения из числа 3 числа 16; б) получения из числа 1 числа 25.
19. Система команд исполнителя Конструктор состоит из двух команд, которым присвоены номера: 1 — приписать 2 2—разделить на 2По первой из них к числу приписывается справа 2, по второй число делится на 2. Как будет преобразовано число 8, если исполнитель выполнит алгоритм 22212? Составьте алгоритм в системе команд этого исполнителя, по которому число 1 будет преобразовано в число 16 (в алгоритме должно быть не более 5 команд).
20. В какой клетке должен находиться исполнитель Робот (пример 7), чтобы после выполнения алгоритма 3241 в неё же и вернуться?
§ 1.3. Элементы алгебры логики
Тестовые задания для самоконтроля
§ 2.1. Алгоритмы и исполнители
§ 2.2. Способы записи алгоритмов
Обновлено: 18.05.2023
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- алгоритм
- свойства алгоритма
- дискретность
- понятность
- определённость
- результативность
- массовость
- исполнитель
- характеристики исполнителя
- круг решаемых задач
- среда
- режим работы
- система команд
- формальное исполнение алгоритма
2.1.1. Понятие алгоритма
Каждый человек в повседневной жизни, в учёбе или на работе решает огромное количество задач самой разной сложности. Сложные задачи требуют длительных размышлений для нахождения решения; простые и привычные задачи человек решает не задумываясь, автоматически. В большинстве случаев решение каждой задачи можно разбить на простые этапы (шаги). Для многих таких задач (установка программного обеспечения, сборка шкафа, создание сайта, эксплуатация технического устройства, покупка авиабилета через Интернет и т. д.) уже разработаны и предлагаются пошаговые инструкции, при последовательном выполнении которых можно прийти к желаемому результату.
- 1) задумать два числа;
- 2) сложить два задуманных числа;
- 3) полученную сумму разделить на 2.
Нахождение среднего арифметического, внесение денег на телефонный счёт и рисование ежа — на первый взгляд совершенно разные процессы. Но у них есть общая черта: каждый из этих процессов описывается последовательностями кратких указаний, точное следование которым позволяет получить требуемый результат. Последовательности указаний, приведённые в примерах 1-3, являются алгоритмами решения соответствующих задач. Исполнитель этих алгоритмов — человек.
Алгоритм может представлять собой описание некоторой последовательности вычислений (пример 1) или шагов нематематического характера (примеры 2-3). Но в любом случае перед его разработкой должны быть чётко определены начальные условия (исходные данные) и то, что предстоит получить (результат). Можно сказать, что алгоритм — это описание последовательности шагов в решении задачи, приводящих от исходных данных к требуемому результату.
В общем виде схему работы алгоритма можно представить следующим образом (рис. 2.1).
Алгоритмами являются изучаемые в школе правила сложения, вычитания, умножения и деления чисел, многие грамматические правила, правила геометрических построений и т. д.
Пример 4. Некоторый алгоритм приводит к тому, что из одной цепочки символов получается новая цепочка следующим образом:
- 1. Вычисляется длина (в символах) исходной цепочки символов.
- 2. Если длина исходной цепочки нечётна, то к исходной цепочке справа приписывается цифра 1, иначе цепочка не изменяется.
- 3. Символы попарно меняются местами (первый — со вторым, третий — с четвёртым, пятый — с шестым и т. д).
- 4. Справа к полученной цепочке приписывается цифра 2.
Получившаяся таким образом цепочка является результатом работы алгоритма.
2.1.2. Исполнитель алгоритма
Каждый алгоритм предназначен для определённого исполнителя.
Исполнитель — это некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.
Различают формальных и неформальных исполнителей. Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Неформальный исполнитель может выполнять команду по-разному.
Рассмотрим более подробно множество формальных исполнителей. Формальные исполнители необычайно разнообразны, но для каждого из них можно указать следующие характеристики: круг решаемых задач (назначение), среду, систему команд и режим работы.
Круг решаемых задач. Каждый исполнитель создаётся для решения некоторого круга задач — построения цепочек символов, выполнения вычислений, построения рисунков на плоскости и т. д.
Среда исполнителя. Область, обстановку, условия, в которых действует исполнитель, принято называть средой данного исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
Система команд исполнителя. Предписание исполнителю о выполнении отдельного законченного действия называется командой. Совокупность всех команд, которые могут быть выполнены некоторым исполнителем, образует систему команд данного исполнителя (СКИ). Алгоритм составляется с учётом возможностей конкретного исполнителя, иначе говоря, в системе команд исполнителя, который будет его выполнять.
Режимы работы исполнителя. Для большинства исполнителей предусмотрены режимы непосредственного управления и программного управления. В первом случае исполнитель ожидает команд от человека и каждую поступившую команду немедленно выполняет. Во втором случае исполнителю сначала задаётся полная последовательность команд (программа), а затем он выполняет все эти команды в автоматическом режиме. Ряд исполнителей работает только в одном из названных режимов.
Рассмотрим примеры исполнителей.
Пример 5. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. Система команд Черепашки состоит из двух команд:
- 1) Вперёд n (где n — целое число) — вызывает передвижение Черепашки на n шагов в направлении движения — в том направлении, куда развёрнуты её голова и корпус;
- 2) Направо m (где m — целое число) — вызывает изменение направления движения Черепашки на m градусов по часовой стрелке.
Запись Повтори k [ … ] означает, что последовательность команд в скобках повторится k раз.
Подумайте, какая фигура появится на экране после выполнения Черепашкой следующего алгоритма.
Повтори 12 [Направо 45 Вперёд 20 Направо 45]
Пример 6. Система команд исполнителя Вычислитель состоит из двух команд, которым присвоены номера:
1 — вычти 1
2 — умножь на 3
Первая из них уменьшает число на 1, вторая увеличивает число в 3 раза. При записи алгоритмов для краткости указываются лишь номера команд. Например, алгоритм 21212 означает следующую последовательность команд:
- умножь на 3
- вычти 1
- умножь на 3
- вычти 1
- умножь на 3
С помощью этого алгоритма число 1 будет преобразовано в 15: ((1 • 3 — 1) • 3-1) • 3 = 15.
Пример 7. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут стоять стены. Робот передвигается по клеткам поля и может выполнять следующие команды, которым присвоены номера:
1 — вверх
2 — вниз
3 — вправо
4 — влево
При выполнении каждой такой команды Робот перемещается в соседнюю клетку в указанном направлении. Если же в этом направлении между клетками стоит стена, то Робот разрушается.
Что произойдёт с Роботом, если он выполнит последовательность команд 32323 (здесь цифры обозначают номера команд), начав движение из клетки А? Какую последовательность команд следует выполнить Роботу, чтобы переместиться из клетки А в клетку В, не разрушившись от встречи со стенами?
При разработке алгоритма:
- 1) выделяются фигурирующие в задаче объекты, устанавливаются свойства объектов, отношения между объектами и возможные действия с объектами;
- 2) определяются исходные данные и требуемый результат;
- 3) определяется последовательность действий исполнителя, обеспечивающая переход от исходных данных к результату;
- 4) последовательность действий записывается с помощью команд, входящих в систему команд исполнителя.
Можно сказать, что алгоритм — модель деятельности исполнителя алгоритмов.
2.1.3. Свойства алгоритма
Не любая инструкция, последовательность предписаний или план действий может считаться алгоритмом. Каждый алгоритм обязательно обладает следующими свойствами: дискретность, понятность, определённость, результативность и массовость.
Свойство дискретности означает, что путь решения задачи разделён на отдельные шаги (действия). Каждому действию соответствует предписание (команда). Только выполнив одну команду, исполнитель может приступить к выполнению следующей команды.
Свойство понятности означает, что алгоритм состоит только из команд, входящих в систему команд исполнителя, т. е. из таких команд, которые исполнитель может воспринять и по которым может выполнить требуемые действия.
Свойство определённости означает, что в алгоритме нет команд, смысл которых может быть истолкован исполнителем неоднозначно; недопустимы ситуации, когда после выполнения очередной команды исполнителю неясно, какую команду выполнять следующей. Благодаря этому результат алгоритма однозначно определяется набором исходных данных: если алгоритм несколько раз применяется к одному и тому же набору исходных данных, то на выходе всегда получается один и тот же результат.
Свойство результативности означает, что алгоритм должен обеспечивать получение результата после конечного, возможно, очень большого, числа шагов. При этом результатом считается не только обусловленный постановкой задачи ответ, но и вывод о невозможности продолжения по какой-либо причине решения данной задачи.
Свойство массовости означает, что алгоритм должен обеспечивать возможность его применения для решения любой задачи из некоторого класса задач. Например, алгоритм нахождения корней квадратного уравнения должен быть применим к любому квадратному уравнению, алгоритм перехода улицы должен быть применим в любом месте улицы, алгоритм приготовления лекарства должен быть применим для приготовления любого его количества и т. д.
Для нахождения всех простых чисел, не больших заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
- 1) выписать подряд все натуральные числа от 2 до n (2, 3, 4, …, n);
- 2) заключить в рамку 2 — первое простое число;
- 3) вычеркнуть из списка все числа, делящиеся на последнее найденное простое число;
- 4) найти первое неотмеченное число (отмеченные числа — зачёркнутые числа или числа, заключённые в рамку) и заключить его в рамку — это будет очередное простое число;
- 5) повторять шаги 3 и 4 до тех пор, пока не останется неотмеченных чисел.
Рассмотренная последовательность действий является алгоритмом, так как она удовлетворяет свойствам:
- дискретности — процесс нахождения простых чисел разбит на шаги;
- понятности — каждая команда понятна ученику 8 класса, выполняющему этот алгоритм;
- определённости — каждая команда трактуется и выполняется исполнителем однозначно; имеются указания об очерёдности выполнения команд;
- результативности — через некоторое число шагов достигается результат;
- массовости — последовательность действий применима для любого натурального n.
Рассмотренные свойства алгоритма позволяют дать более точное определение алгоритма.
Алгоритм — это предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.
2.1.4. Возможность автоматизации деятельности человека
Разработка алгоритма — как правило, трудоёмкая задача, требующая от человека глубоких знаний, изобретательности и больших временных затрат.
Решение задачи по готовому алгоритму требует от исполнителя только строгого следования заданным предписаниям.
Пример 9. Из кучки, содержащей любое, большее трёх, количество каких-либо предметов, двое играющих по очереди берут по одному или по два предмета. Выигрывает тот, кто своим очередным ходом сможет забрать все оставшиеся предметы.
Рассмотрим алгоритм, следуя которому первый игрок наверняка обеспечит себе выигрыш.
- 1. Если число предметов в кучке кратно 3, то уступить ход противнику, иначе начинать игру.
- 2. Своим очередным ходом каждый раз дополнять число предметов, взятых соперником, до 3 (число оставшихся предметов должно быть кратно 3).
Исполнитель может не вникать в смысл того, что он делает, и не рассуждать, почему он поступает так, а не иначе, т. е. он может действовать формально. Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека. Для этого:
- 1) процесс решения задачи представляется в виде последовательности простейших операций;
- 2) создаётся машина (автоматическое устройство), способная выполнять эти операции в последовательности, заданной в алгоритме;
- 3) человек освобождается от рутинной деятельности, выполнение алгоритма поручается автоматическому устройству.
Самое главное: Алгоритмы и исполнители
Исполнитель — некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.
Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Для каждого формального исполнителя можно указать: круг решаемых задач, среду, систему команд и режим работы.
Алгоритм — предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.
Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека.
С помощью компьютера специалисты по информационным системам записывают новые программы, а также анализируют работу и исправляют ошибки в уже имеющихся. Но всё это невозможно совершить без знания алгоритмов. В информатике к изучению этого понятия приступают ещё в школе. Ученики получают первое представление о разных видах алгоритмов, их свойствах и способах создания.
Особенности понятия
Современное определение алгоритма в информатике — это описание действий, последовательное выполнение которых позволяет решить поставленную задачу за конкретное количество шагов.
С этим человек сталкивается каждый день, когда читает рецепты в кулинарных книгах, инструкции к различной технике, правила решения заданий. Но обычно все эти действия выполняются автоматически, без их анализа. Родители сталкиваются с этим понятием, когда объясняют детям, как открыть двери ключом или почистить зубы. Алгоритмов в окружающем мире множество, но есть общие признаки для всех их видов.
Свойства и виды
Для изучения понятия нужно разобраться в свойствах алгоритма в информатике. Их существует несколько:
- дискретность;
- детерминированность или определенность;
- понятность;
- завершаемость или конечность;
- массовость или универсальность;
- результативность.
Согласно свойству дискретности, алгоритмы должны описывать весь процесс решения задания в виде выполнения простых шагов. При этом на пункты отводится определенное количество времени. Каждый шаг должен определяться состоянием системы, то есть при одних и тех же исходных данных результат не меняется. Но есть и вероятностные алгоритмы, где пункты зависят от системы и случайно генерируемых чисел. В этой ситуации понятие становится подвидом обычного.
Понятность заключается в том, что команды алгоритма должны быть доступны конкретному исполнителю и входить в его личную систему. В ходе работы математическая функция при правильно заданных исходных данных выдает результат за определенное количество шагов. Иногда процедура может не завершиться, но вероятность таких случаев стремится к нулю.
Универсальность или массовость позволяет использовать алгоритм с разными наборами начальных данных. Последнее свойство обеспечивает его завершение в виде определенного числа — результата.
У каждого алгоритма есть свои начальные условия, цели и пути решения задачи. Существует большая разница между вычислительными и интерактивными видами. Происхождение первых связано с опытами ученого Тьюринга, они могут преобразовать входные данные в выходные. Вторые предназначены для связи с объектом управления, они работают только под внешним воздействием. Ученые выделяют несколько видов алгоритмов в информатике:
- детерминированные или жесткие;
- гибкие;
- линейные;
- разветвляющиеся;
- циклические;
- вспомогательные;
- структурные блок-схемы.
Жесткие еще называются механическими, так как чаще всего они используются для работы двигателя или машины. Они задают действия в единственно верной последовательности, что приводит к искомому или требуемому результату при условии выполнения процессов, для которых они и разработаны.
Гибкие алгоритмы делятся на эвристические и вероятностные. Первые используются при различных умственных выводах без строгих аргументов, а вторые дают возможность получить один результат несколькими способами.
Линейный тип — это набор команд, которые выполняются в строгой последовательности. Разветвляющийся включает хотя бы одно условие и при проверке дает разделение на несколько блоков. Появляются альтернативные ветвления программы.
В циклических видах несколько раз повторяются одни и те же действия, при этом меняются исходные данные. Сюда относятся переборы вариантов и бо́льшая часть способов расчета. Циклом в этом случае называют последовательность команд, которые нужно выполнить множество раз для достижения требуемого результата.
Подчиненный или вспомогательный вид является ранее разработанным алгоритмом для быстрого решения задачи. Он необходим для сокращения записи, если в структуре есть одинаковые команды. Схемами называются графические изображения с помощью блоков и соединяющих их прямых линий. Их используют перед программированием в качестве наглядных примеров, поскольку зрительное восприятие позволяет быстрее осмыслить процесс обработки информации и выявить возможные ошибки. В блоках отображаются исходные данные, которые вносятся в компьютер для вычислений.
Способы записи
Алгоритмы записываются несколькими методами. В информатике используется всего три:
- словесно-формульный;
- графический;
- программный.
В первом случае алгоритм записывается простым языком — словами и математическими формулами, что необходимо для понимания его теории. Здесь учитываются исходные данные, действия с ними и условия получения результата. Второй тип записи — компьютерное описание. Для этого применяются языки программирования и сами программы — форсы представления расчетов для их выполнения машиной.
Графическое описание состоит из связанных между собой географических фигур. Основные элементы блок-схем:
- прямоугольники;
- эллипсы;
- ромбы;
- шестиугольники;
- стрелки;
- пунктирные линии;
- соединительные фигуры.
В прямоугольниках записывают процессы, они указывают на выполнение операций, которые изменяют форму или значение данных. Ромбы содержат способы решения, здесь выбирается следующее направление в зависимости от поставленных условий. Модификации могут передаваться в шестиугольниках, где записываются операции, меняющие команды.
В блок-схемах можно выделить ручной ввод и предопределенные процессы. Первая фигура позволяет исполнителю ввести данные во время работы алгоритма через устройства, подключенные к компьютеру. Второе понятие заключается в использовании заранее записанных алгоритмов.
Графическое изображение содержит блоки документов и дисплеев. Оператор может вводить данные с бумаги и выводить их на нее, а также с помощью устройств, которые воспроизводят информацию на экране (проекторы для интерактивных досок, подключенные к компьютерам планшеты и ноутбуки).
Линии и соединительные фигуры указывают на связи между разными блоками и их последовательность. В схеме есть блоки начала и конца алгоритма, его прерывания, которое может произойти из-за сбоев в программе. Можно также указывать комментарии и пояснения исполнителя, для этого есть отдельные фигуры.
Правила создания
Существует несколько правил создания алгоритмов. Если их соблюдать, то в ходе работы всегда будет верный результат. Форма должна быть настолько простой, чтобы ее понял тот, кто занимается ее разработкой. Также не должно возникнуть проблем с чтением у того, кто будет выполнять описанные действия.
Объект, который проводит расчеты в алгоритме, называется исполнителем. Идеальными считаются роботы, компьютеры и другие машины. Они работают с программами, то есть схемами, написанными определенным языком программирования.
Разобраться с действиями помогут простые примеры алгоритмов по информатике. Когда есть ряд чисел от 1 до 100 и необходимо найти из них простые, то выбираются те, что делятся на единицу и себя. В этом случае используется циклическая структура:
- сначала нужно взять число 1;
- проверить, меньше ли оно, чем 100;
- если да, то узнать, простое ли оно;
- при выполнении условия записать;
- перейти к числу 2;
- повторить операцию.
Такие действия проводят со всеми числами. При этом первые четыре шага будут постоянно повторяться. Если попадается число, не являющееся простым (4, 6, 8 и т. д. ), то его нужно просто пропустить. Алгоритм в этом случае обладает предусловиями, то есть проверки происходят в начале цикла.
Анализ работы
Распространение информационных технологий привело к увеличению риска сбоев в работе программ. Предотвратить появление ошибок в алгоритмах можно с помощью доказательства их корректности математическими средствами. Такой анализ называется формальным методом, он предусматривает использование специального набора инструментов.
Гипотеза Ричарда Мейса утверждает, что избежать ошибок легче, чем их устранить. Благодаря доказательству корректности программ можно выявить их свойства, применяемые ко всем видам входных данных. Само понятие делится на две разновидности — частичную и полную. При первом типе корректности алгоритм дает правильный результат только для тех случаев, когда он завершается. Во втором случае программа завершает работу корректно для всего диапазона данных.
Исполнители во время проверки сравнивают выдаваемые данные со спецификой требуемого результата. Для доказательства корректности используются предусловия и постусловия. Первые должны выполняться перед включением программы, вторые — после завершения ее работы. Формальные методы успешно применяются для многих задач: верификации программ и микропроцессоров, разработки искусственного интеллекта, электронных схем и автоматических систем для железной дороги, спецификации стандартов.
Для выполнения алгоритма нужно только конкретное количество шагов, но на практике для этого потребуется много времени. В связи с этим введено понятие сложности. Она бывает временной, вычислительной и связанной с размерами алгоритма. Для увеличения эффективности используются быстрые программы, которые появились еще в 50-х годах прошлого века.
Конспект по информатике «Алгоритм. Свойства алгоритмов. Блок-схемы. Алгоритмические языки» для подготовки к контрольным, экзаменам и ГИА.
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм — строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.
В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
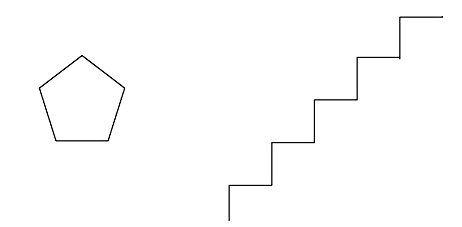
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
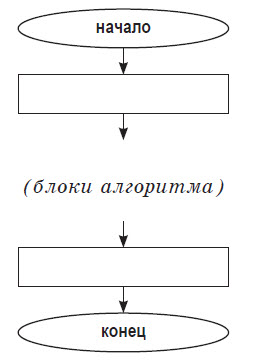
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:
Общий вид блок–схемы алгоритма:
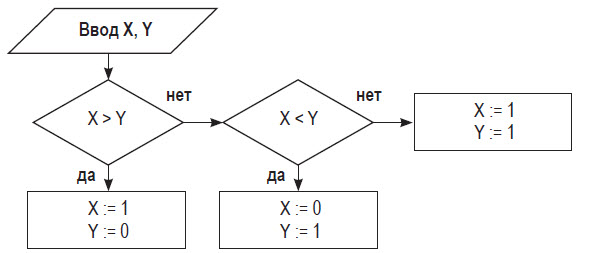
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 Алгоритмические языки
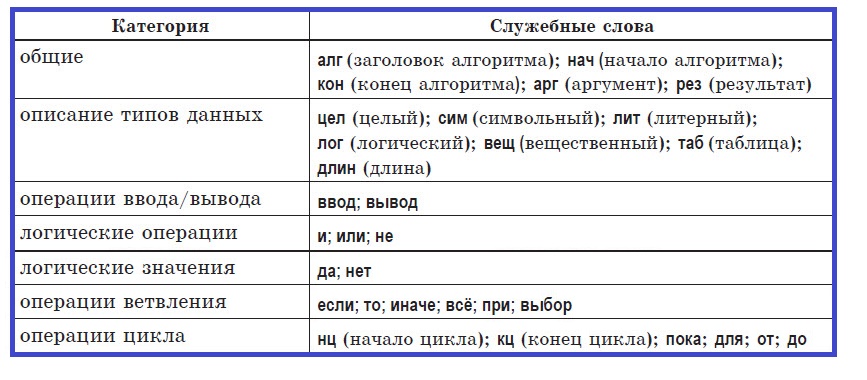
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:
В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:
В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:
На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10 -2 и –7,123456*10 2 ).
Над числовыми данными можно выполнять арифметические операции и операции сравнения.
Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.
Учебный алгоритмический язык использует следующие команды для реализации алгоритма:
ОПЕРАЦИЯ ПРИСВАИВАНИЯ
Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).
Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.
ВВОД И ВЫВОД ДАННЫХ
При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.
Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.
В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.
Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.
Список вывода может содержать имена переменных, константы и выражения. Если в списке вывода указано имя переменной, будет выведено ее значение. Если список вывода содержит выражение, будет выведен результат его вычисления. Текстовые константы следует записывать в списке вывода в кавычках (выводиться они будут без кавычек).
Если при выполнении алгоритма ввести значения 20 и 10, то переменная v примет значение 20, а переменная t — значение 10. По окончании работы алгоритма будет выведен результат:
Путь 200 м
Тот же результат был бы получен, если бы изменить строку вывода на
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Описание презентации по отдельным слайдам:
Алгоритм — заранее заданное понятное и точное предписание возможному исполнителю совершить определенную последовательность действий для получения решения задачи за конечное число шагов.
Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом. Исполнителя хаpактеpизуют: сpеда; элементаpные действия; cистема команд; отказы.
Система команд исполнителя Команды, которые может выполнять конкретный исполнитель, образуют систему команд исполнителя (СКИ). Исполнитель формально выполняет алгоритмы, составленные из команд, входящих в его СКИ.
Основные свойства алгоритмов
Дискретность (разделенный, прерывистый) Это свойство указывает, что любой алгоритм должен состоять из конкретных действий, следующих в определенном порядке.
Детерминированность (определенность, точность) Каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола.
Конечность Это свойство определяет, что каждое действие в отдельности и алгоритм в целом должны иметь возможность завершения
Массовость Алгоритм можно применять для целого класса задач Результативность Это свойство требует, чтобы в алгоритме не было ошибок.
Формы представления алгоритмов: словесная (запись на естественном языке); графическая (изображения из графических символов); псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.); программная (тексты на языках программирования).
Основные служебные слова алг(алгоритм) сим(символьный) дано для да арг(аргумент) лит(литерный) надо от нет рез(результат) лог(логический) если до при нач(начало) таб(таблица) то знач выбор кон(конец) нц(начало цикла) иначе и ввод цел(целый) кц(конец цикла) все или вывод вещ(вещественный) длин(длина) пока не утв Общий вид алгоритма: алгназвание алгоритма (аргументы и результаты) даноусловия применимости алгоритма надоцель выполнения алгоритма начописание промежуточных величин | последовательность команд (тело алгоритма) кон
Название символа Обозначение и пример заполнения Пояснение Процесс Вычислительное действие или последовательность действий Решение Проверка условий Ввод-вывод Ввод-вывод в общем виде Пуск-останов Начало, конец алгоритма, вход и выход в подпрограмму
Алгоритмический язык Алфавит — это фиксированный для данного языка набор основных символов, т.е. «букв алфавита», из которых должен состоять любой текст на этом языке — никакие другие символы в тексте не допускаются. Синтаксис — это правила построения фраз, позволяющие определить, правильно или неправильно написана та или иная фраза. Семантика определяет смысловое значение предложений языка.
Основные понятия в алгоритмических языках 1. Имена (идентификаторы) — употpебляются для обозначения объектов пpогpаммы (пеpеменных, массивов, функций и дp.). 2. Опеpации. Типы операций: аpифметические опеpации + , — , * , / и дp. ; логические опеpации и , или , не ; опеpации отношения , = , = , <> ; опеpация сцепки (иначе, «присоединения», «конкатенации» ) символьных значений дpуг с другом с образованием одной длинной строки; изображается знаком «+».
3. Данные — величины, обрабатываемые пpогpаммой. Имеется три основных вида данных: константы, переменные и массивы. Константы — это данные, которые зафиксированы в тексте программы и не изменяются в процессе ее выполнения. Пpимеpы констант: числовые 7.5 , 12 ; логические да (истина), нет (ложь); символьные (содержат ровно один символ) «А» , «+» ; литеpные (содержат произвольное количество символов) «a0», «Мир», «» (пустая строка). Пеpеменные обозначаются именами и могут изменять свои значения в ходе выполнения пpогpаммы. Массивы — последовательности однотипных элементов, число которых фиксировано и которым присвоено одно имя.
4. Выpажения — пpедназначаются для выполнения необходимых вычислений, состоят из констант, пеpеменных, указателей функций (напpимеp, exp(x)), объединенных знаками опеpаций. Различают выражения арифметические, логические и строковые. Арифметические выражения служат для определения одного числового значения. Например, (1+sin(x))/2. Логические выражения описывают некоторые условия, которые могут удовлетворяться или не удовлетворяться. Таким образом, логическое выражение может принимать только два значения — «истина» или «ложь» (да или нет). Cтроковые (литерные) выражения, значениями которых являются текcты. В строковые выражения могут входить литерные и строковые константы, литерные и строковые переменные, литерные функции, разделенные знаками операции сцепки.
5. Операторы (команды). Оператор — это наиболее крупное и содержательное понятие языка: каждый оператор представляет собой законченную фразу языка и определяет некоторый вполне законченный этап обработки данных. В состав опеpатоpов входят: ключевые слова; данные; выpажения и т.д.
Название и математическое обозначение функции Указатель функции Абсолютная величина (модуль) |х| abs(x) Корень квадратный sqrt(x) Натуральный логарифм ln x ln(x) Десятичный логарифм lgx lg(x) Экспонента (степень числа е ~ 2.72) ex exp(x) Знакчисла x (-1, если х 0) signx sign(x) Целая частьх(т.е. максимальное целоечисло,непревосходящеех) int(x) Минимум из чиселхиy min(x,y) Максимум из чиселхиy max(x,y)
Название и математическое обозначение функции Указатель функции Частноеот деления целогохна целоеy div(x,y) Остатокот деления целогохна целоеy mod(x,y) Случайное число в диапазоне от 0 дох- 1 rnd(x) Синус (угол в радианах) sinx sin(x) Косинус (угол в радианах) cosx cos(x) Тангенс (угол в радианах) tgx tg(x) Котангенс (угол в радианах) ctgx ctg(x) Арксинус (значениев радианах) arcsinx arcsin(x) Арккосинус (значениев радианах) arccosx arccos(x) Арктангенс (значениев радианах) arctgx arctg(x) Арккотангенс (значениев радианах) arcctg x arcctg(x)
Линейный алгоритм — алгоритм, в котором команды выполняются в порядке их записи, т.е. последовательно друг за другом. Начало Конец Действие 1 Действие n …
Алгоритм посадки дерева Выкопать в земле ямку Опустить в ямку саженец Засыпать ямку с саженцем землей Полить саженец водой
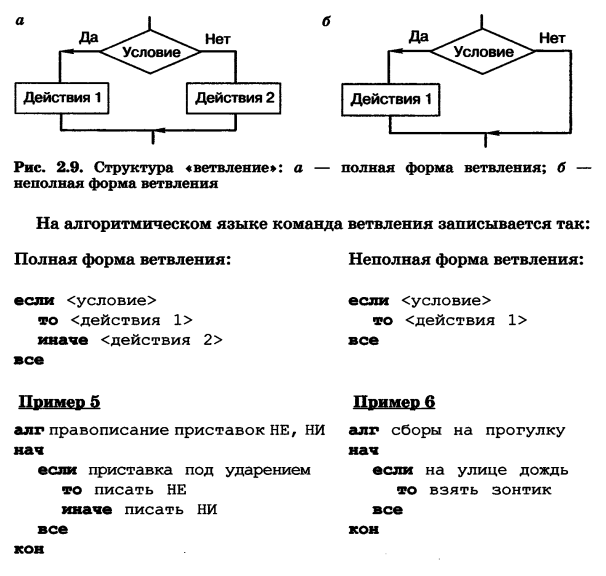
Алгоритм с ветвлением или разветвляющийся алгоритм — форма организации действий, при которой в зависимости от выполнения некоторого условия совершается одна или другая последовательность шагов Условие Действие 2 Действие 1 Да Нет
Разветвляющийся алгоритм Полное ветвление Подъехал Иван Царевич к камню Направо пойдешь? Нет Да Голову сложишь Коня потеряешь
Разветвляющийся алгоритм Неполное ветвление Идет дождь? Нет Да Берем зонт
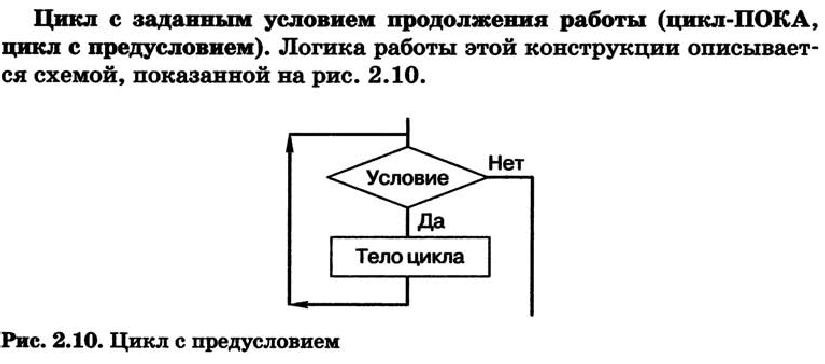
Алгоритм с повторением или цикл — форма организации действий, при которой выполнение одной и той же последовательности команд повторяется, пока выполняется некоторое заранее установленное условие. Условие Тело цикла Да Нет
Циклические действия при подготовке домашнего задания Начало Все задачи по математике решены? Решить задачу Пойти гулять до ужина Конец Да Нет
Условие Запись на школьном алгоритмическом языке Дробная частьвещественногочислаaравна нулю int(a) = 0 Целое число a — четное mod(a, 2) = 0 Целое число a — нечетное mod(a, 2) = 1 Целое числоkкратно семи mod(a, 7) = 0 Каждое из чисел a, b положительно (a>0)и(b>0) Только одно из чиселa,bположительно ((a>0)и(b 0)) Уравнение ax^2 +bx+c= 0 не имеет действительных корней b*b- 4*a*c 0)и(y>0))или ((x 0))
Условие Запись на школьном алгоритмическом языке Хотя бы одно из чиселa,b,cявляется отрицательным (a a)и(x =1)и(x 1)или ((x*x + y*y 0)) Целые числаaиbявляютсявзаимнопротивоположными a = -b Целые числаaиbявляютсявзаимнообратными a*b= 1 Числоaбольше среднего арифметического чиселb,c,d a> (b+c+d) / 3 Числоaне меньше среднего геометрического чиселb,c,d a>= (b+c+d) ** (1/3)
Условие Запись на школьном алгоритмическом языке Хотябы одна из логических переменных F1 и F2 имеет значениеда F1илиF2 ОбелогическиепеременыеF1 и F2 имеют значениеда F1иF2 ОбелогическиепеременыеF1 и F2 имеют значениенет неF1и неF2 Логическаяпеременная F1 имеет значениеда, а логическая переменная F2 имеет значениенет F1и неF2 Только одна из логических переменных F1 и F2 имеет значениеда (F1и неF2)или(F2и неF1)
Читайте также:
- Почему возросла роль армии и кгб в управлении государством кратко
- Почему возникла необходимость научного прогнозирования география 8 класс кратко
- Почему тихий океан самый древний кратко
- Как сделать путеводитель своими руками в школу
- Работа педагогов по привлечению обучающихся основной школы к работе в проектной деятельности
Методическая разработка занятия по теме:
«Основы алгоритмизации. Алгоритмы и способы их описания»
Цели занятия:
Образовательная — Познакомить с понятием алгоритма, свойствами дискретности, понятности, точности, конечности, массовости, способами записи алгоритмов. Рассмотреть основные алгоритмические структуры: следования, ветвления, цикла.
Развивающая — развивать мышление, грамотную речь, навыки самоконтроля
развивать умения проводить анализ, синтез, сравнение, обобщать полученные знания, делать выводы
Воспитательная — воспитывать толерантное отношение к мнению другого человека, умение работать в группах, на недопустимость действий, нарушающих этические, правовые нормы работы с информацией
План занятия:
1. Организационный момент
2. Повторение пройденного материала:
-
Изложение нового материала.
4. Задание на дом.
5. Итог урока.
Ход занятия
-
Организационный момент. Сообщение темы, постановка цели урока. Знакомство с ходом проведения занятия.
-
Повторение пройденного материала:
1-й уровень Компьютерное тестирование (Приложение 1);
2-й уровень Работа по вопросам (Приложение 2);
3-й уровень Решение задач (Приложение 3);
-
Изложение нового материала.
-
Понятие алгоритма, свойства алгоpитма.
В науке о моделировании среди многих видов информационных моделей называются и алгоритмические модели. Попробуем разобраться, почему алгоритм можно назвать моделью и что он моделирует.
Как вам известно, алгоритм — это понятное и точное предписание конкретному исполнителю совершить конечную последовательность действий, приводящую к поставленной цели.
Сообщение о происхождении и развитии понятия алгоритм.
Из определения следует, что поставленная цель достигается через деятельность (последовательность действий) некоторого исполнителя.
Исполнитель — это некоторый объект (человек, техническое устройство), способный выполнять определённый набор команд, который составляет его СКИ.
Назовите исполнителей для приведённых ниже видов работ:
Стирка белья – (человек, стиральная машина)
Приготовление кофе – (человек, автомат)
Перевозка пассажиров в поезде – (машинист, поез)
Выдача заработной платы – (кассир)
Разработка рецептур на производстве – (технолог)
Сдача зачёта – (студент)
Набор текста на компьютере – (пользователь)
Создание текстового документа – (текстовый процессор, компьютер)
Различают формальных и неформальных исполнителей. Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Формальное исполнение алгоритма обеспечивает возможность автоматизации деятельности человека. Неформальный исполнитель может выполнять команду по-разному.
Этапы деятельности от цели (постановки задачи) к результату:
-
определение цели;
-
планирование работы исполнителя;
-
работа исполнителя;
-
получение результата.
Где же здесь место алгоритму? Алгоритм — это детальный план работы исполнителя, описание последовательности элементарных действий. Но всякий план или описание есть информационная модель. Следовательно:
Алгоритм является информационной моделью деятельности исполнителя.
Свойства алгоритма (работа с электронным учебником ОИ 1 с. 49)
Не любая инструкция, последовательность предписаний или план действий может считаться алгоритмом. Каждый алгоритм обязательно обладает следующими свойствами: дискретность, понятность, точность, конечность и массовость.
-
дискретность (каждый шаг алгоритма выполняется отдельно от других);
т. е. решение задачи разделёно на отдельные шаги (действия). Каждому действию соответствует команда. Только выполнив одну команду, исполнитель может приступить к выполнению следующей.
-
понятность (в алгоритме используются только команды из СКИ);
-
точность (каждая команда определяет однозначное действие исполнителя);
в алгоритме нет команд, смысл которых может быть истолкован исполнителем неоднозначно.
-
конечность (за конечное число шагов алгоритма получается искомый результат).
-
массовость (алгоритм pазpабатывается в общем виде, т.е. должен быть пpименим для некотоpого класса задач)
Мини итог:
-
Дайте определение алгоритма.
-
Объясните почему алгоритм является информационной моделью деятельности исполнителя
-
Перечислите свойства алгоритма.
-
Что значит свойство дискретности, приведи пример.
-
Что значит свойство точности, приведи пример.
-
Способы записи алгоритмов. Существуют различные способы записи алгоритмов, основными среди них являются:
-
словесные;
-
словесное описание в виде набора высказываний на естественном языке, например правило умножения двух дробей; нахождения (НОД) натуральных чисел (алгоритм Евклида). Чтобы найти НОД двух чисел, составьте таблицу из двух столбцов и назовите столбцы X и Y. Запишите первое из заданных чисел в столбце Х, а второе ‑ в столбце Y. Если данные числа не равны, замените большее из них на результат вычитания из большего числа меньшего. Повторяйте такие замены до тех пор, пока числа не окажутся равными, после чего число из столбца Х считайте искомым результатом.
-
построчная запись ‑ это запись на естественном языке, может содержать математические выражения и формулы, к ней предъявляются дополнительных правила: каждое предписание записывается с новой строки; предписания нумеруются; исполнение алгоритма происходит в порядке возрастания номеров шагов. Например, Построчная запись алгоритма Евклида.
-
-
Обозначить первое из заданных чисел X, второе обозначить Y
-
Если X = Y, то перейти к п.8.
-
Если X Y, то перейти к п.4.
-
Заменить X на X – Y
-
Перейти к п.2.
-
Заменить Y на Y – X
-
Перейти к п.2.
-
Считать X искомым результатом.
-
графические;
-
последовательность рисунков;
-
структуропрограмма;
-
блок-схема – используют для наглядного представлениям решения задачи, предписания изображаются с помощью геометрических фигур, а последовательность указывается с помощью линий, соединяющих фигуры. Направления линий слева направо и сверху вниз считаются стандартными, и изображаются без стрелок, в противоположном случае — со стрелками. Вспомним некоторые условные обозначения блок-схем.
-
Например, Запись алгоритма Евклида с помощью блок‑схемы.
-
алгоритмические языки — формальные языки для записи алгоритмов. Каждый из них характеризуется: алфавитом — набором используемых символов; синтаксисом — системой правил, по которым из символов алфавита образуются правильные конструкции языка; семантикой — системой правил, строго определяющей смысл и способ употребления конструкций языка.
-
школьный алгоритмический язык. Для записи используется некоторое служебные слова: алг (алгоритм), дано, надо, нач (начало), кон (конец), арг (аргумент), рез (результат) и др. При записи алгоритмов в книгах служебные слова выделяются жирным шрифтом, в тетради и на доске — подчёркиванием.
-
Пример программы на школьном алгоритмическом языке:
Алгоритм, позволяющий из полного сосуда ёмкостью 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью 8 и 5 л.

-
языки программирования (Turbo Pascal)
program primer_1;
var a, b: integer;
begin
writeln(‘Введите значение a=’);
read(a);
b:=2*a;
writeln(‘b = ‘,b);
end.
Мини итог:
-
Перечислите способы записи алгоритмов.
-
Какой из способов записи обладает большей наглядностью.
-
Основные алгоритмические структуры.
Работа с электронным учебником ДИ учебник Босова с. 73-91, 104 №28-30
Уметь распознавать по блок‑схеме основные алгоритмические конструкции.
Научиться определять значение переменной после выполнения фрагмента алгоритма.
По завершению работы тест в фронтальном режиме.
Разнообразие алгоритмов велико, но для записи любого алгоритма достаточно трёх основных алгоритмических структур: следования, ветвления, повторения. Это положение выдвинул и доказал Эдсгер Вибе Дейкстра (1930-2002) — выдающийся нидерландский учёный, идеи которого оказали огромное влияние на развитие компьютерной индустрии.
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами.
Графическое представление алгоритмической конструкции «следование».
Пример. У исполнителя Робот есть 4 команды перемещения (вверх, вниз, влево и вправо), при выполнении каждой из них Робот перемещается на 1 клетку в соответствующем направлении. По команде закрасить Робот закрашивает клетку, в которой он находится. Запишем линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение, обозначенное звёздочкой:
Задание‑анимация Линейный алгоритм
Мини итог:
Приведите примеры линейного алгоритма:
а) из повседневной жизни;
б) из литературного произведения;
в) из любой предметной области, изучаемой в школе.
В тетради составить блок-схему алгоритма нахождение периметра прямоугольника. Один ученик записывает полученный алгоритм на доске, проверяя задание.
Ветвление — алгоритмическая структура, в зависимости от выполнения некоторого условия, совершается одна или другая последовательность действий. Алгоритмы называют разветвляющимися.
|
Структура «ветвление» |
|
|
а) полная форма |
а) неполная форма |
|
|
|
|
На алгоритмическом языке команды ветвления записываются так: |
|
|
|
|
|
Примеры |
|
|
|
|
Задание‑анимация Разветвляющийся алгоритм
Мини итог:
Приведите примеры разветвляющегося алгоритма:
а) из повседневной жизни;
б) из литературного произведения;
в) из любой предметной области, изучаемой в школе.
Составить блок-схему разветвляющегося алгоритма: задумайте число, прибавь 8, если полученное число меньше 22, то прибавь 5, иначе отнять 5. вывести полученный результат.
Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию повторения, называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла.
|
Типы циклов |
||
|
1)цикл с заданным условием продолжения работы; |
2)цикл с заданным условием окончания работы; |
3)цикл с заданным числом повторений. |
|
цикл – ПОКА, цикл с предусловием |
цикл-ДО, цикл с постусловием |
цикл-ДЛЯ, цикл с параметром |
|
|
|
|
Запись на алгоритмическом языке:

Выполняется цикл_ПОКА следующим образом:
1) проверяется условие (вычисляется значение логического выражения);
2)если условие удовлетворяется (Да), то выполняется тело цикла и снова удовлетворяется, то выполнение цикла заканчивается.
Возможны случаи, когда тело цикла не будет выполнено ни разу.
Запись на алгоритмическом языке:
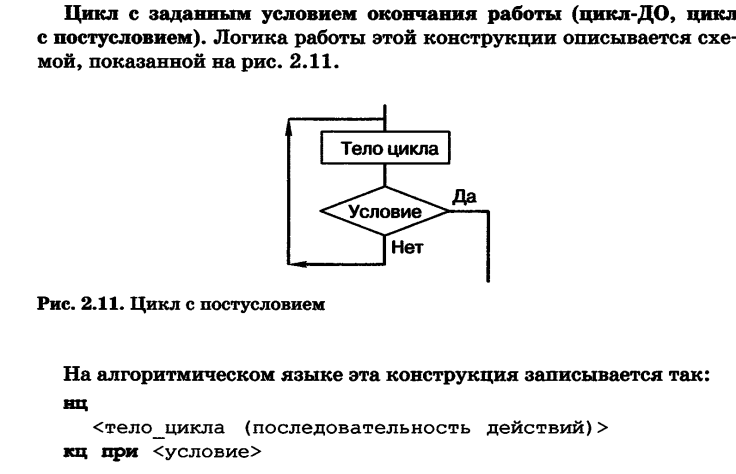
Запись на алгоритмическом языке:

Выполняется цикл-ДЛЯ следующим образом: 1) параметру цикла присваивается начальное значение; 2) параметр цикла сравнивается с конечным значением; если параметр цикла не превышает конечное значение, то выполняется тело цикла, увеличивается значение параметра цикла на шаг и снова осуществляется проверка параметра цикла; если же параметр цикла превышает конечное значение, то выполнение цикла заканчивается.
В отличие от двух предыдущих конструкций (цикл-ПОКА, цикл-ДО) цикл-ДЛЯ имеет строго фиксированное число повторений, что позволяет избежать зацикливание, т.е ситуации, когда тело цикла выполняется бесконечно.
Задание‑анимация Циклический алгоритм
Мини итог:
Приведите примеры циклического алгоритма:
а) из повседневной жизни;
б) из литературного произведения;
в) из любой предметной области, изучаемой в школе.
Пример. Алгоритм переправы через реку
-
Закрепление материала в ходе выполнения фронтального тестирования. (Приложение 4)
-
Дом задание ОИ1 §9, 16 Составить алгоритм решения задачи: Из кучки, содержащей любое, большее трёх, количество каких-либо предметов, двое играющих по очереди берут по одному или по два предмета. Выигрывает тот, кто своим очередным ходом сможет забрать все оставшиеся предметы.
Ключевые слова:
• алгоритм
• свойства алгоритма (дискретность; понятность; определённость; результативность; массовость)
• исполнитель
• характеристики исполнителя (круг решаемых задач; среда; режим работы; система команд)
• формальное исполнение алгоритма
1. Понятие алгоритма
Каждый человек в повседневной жизни, в учёбе или на работе решает огромное количество задач самой разной сложности. Сложные задачи требуют длительных размышлений для нахождения решения; простые и привычные задачи человек решает не задумываясь, автоматически. В большинстве случаев решение каждой задачи можно разбить на простые этапы (шаги). Для многих таких задач (установка программного обеспечения, сборка шкафа, создание сайта, эксплуатация технического устройства, покупка авиабилета через Интернет и т. д.) уже разработаны и предлагаются пошаговые инструкции, при последовательном выполнении которых можно прийти к желаемому результату.
Пример 1. Задача «Найти среднее арифметическое двух чисел» решается в три шага:
1) задумать два числа;
2) сложить два задуманных числа;
3) полученную сумму разделить на 2.
Пример 2. Задача «Внести деньги на счёт телефона» подразделяется на следующие шаги:
1) подойти к терминалу по оплате платежей;
2) выбрать оператора связи;
3) ввести номер телефона;
4) проверить правильность введённого номера;
5) вставить денежную купюру в купюроприёмник;
6) дождаться сообщения о зачислении денег на счёт;
7) получить чек.
Нахождение среднего арифметического, внесение денег на телефонный счёт— на первый взгляд совершенно разные процессы. Но у них есть общая черта: каждый из этих процессов описывается последовательностями кратких указаний, точное следование которым позволяет получить требуемый результат. Последовательности указаний, приведённые в примерах 1-2, являются алгоритмами решения соответствующих задач. Исполнитель этих алгоритмов — человек.
Алгоритм может представлять собой описание некоторой последовательности вычислений (пример 1) или шагов нематематического характера (пример 2). Но в любом случае перед его разработкой должны быть чётко определены начальные условия (исходные данные) и то, что предстоит получить (результат). Можно сказать, что алгоритм — это описание последовательности шагов в решении задачи, приводящих от исходных данных к требуемому результату.
Алгоритмами также являются изучаемые в школе правила сложения, вычитания, умножения и деления чисел, многие грамматические правила, правила геометрических построений и т. д.
2. Исполнитель алгоритма
Каждый алгоритм предназначен для определённого исполнителя.
Исполнитель — это некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.
Различают формальных и неформальных исполнителей. Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Неформальный исполнитель может выполнять команду по-разному.
Рассмотрим более подробно множество формальных исполнителей. Формальные исполнители необычайно разнообразны, но для каждого из них можно указать следующие характеристики: круг решаемых задач (назначение), среду, систему команд и режим работы.
Круг решаемых задач. Каждый исполнитель создаётся для решения некоторого круга задач — построения цепочек символов, выполнения вычислений, построения рисунков на плоскости и т. д.
Среда исполнителя. Область, обстановку, условия, в которых действует исполнитель, принято называть средой данного исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
Система команд исполнителя. Предписание исполнителю о выполнении отдельного законченного действия называется командой. Совокупность всех команд, которые могут быть выполнены некоторым исполнителем, образует систему команд данного исполнителя (СКИ). Алгоритм составляется с учётом возможностей конкретного исполнителя, иначе говоря, в системе команд исполнителя, который будет его выполнять.
Режимы работы исполнителя. Для большинства исполнителей предусмотрены режимы непосредственного управления и программного управления. В первом случае исполнитель ожидает команд от человека и каждую поступившую команду немедленно выполняет. Во втором случае исполнителю сначала задаётся полная последовательность команд (программа), а затем он выполняет все эти команды в автоматическом режиме. Ряд исполнителей работает только в одном из названных режимов.
При разработке алгоритма:
1) выделяются фигурирующие в задаче объекты, устанавливаются свойства объектов, отношения между объектами и возможные действия с объектами;
2) определяются исходные данные и требуемый результат;
3) определяется последовательность действий исполнителя, обеспечивающая переход от исходных данных к результату;
4) последовательность действий записывается с помощью команд, входящих в систему команд исполнителя.
Можно сказать, что алгоритм — модель деятельности исполнителя алгоритмов.
3. Свойства алгоритма
Не любая инструкция, последовательность предписаний или план действий может считаться алгоритмом. Каждый алгоритм обязательно обладает следующими свойствами: дискретность, понятность, определённость, результативность и массовость.
Свойство дискретности означает, что путь решения задачи разделён на отдельные шаги (действия). Каждому действию соответствует предписание (команда). Только выполнив одну команду, исполнитель может приступить к выполнению следующей команды.
Свойство понятности означает, что алгоритм состоит только из команд, входящих в систему команд исполнителя, т. е. из таких команд, которые исполнитель может воспринять и по которым может выполнить требуемые действия.
Свойство определённости означает, что в алгоритме нет команд, смысл которых может быть истолкован исполнителем неоднозначно; недопустимы ситуации, когда после выполнения очередной команды исполнителю неясно, какую команду выполнять следующей. Благодаря этому результат алгоритма однозначно определяется набором исходных данных: если алгоритм несколько раз применяется к одному и тому же набору исходных данных, то на выходе всегда получается один и тот же результат.
Свойство результативности означает, что алгоритм должен обеспечивать получение результата после конечного, возможно, очень большого, числа шагов. При этом результатом считается не только обусловленный постановкой задачи ответ, но и вывод о невозможности продолжения по какой-либо причине решения данной задачи.
Свойство массовости означает, что алгоритм должен обеспечивать возможность его применения для решения любой задачи из некоторого класса задач. Например, алгоритм нахождения корней квадратного уравнения должен быть применим к любому квадратному уравнению, алгоритм перехода улицы должен быть применим в любом месте улицы, алгоритм приготовления лекарства должен быть применим для приготовления любого его количества и т. д.
Рассмотренные свойства алгоритма позволяют дать более точное определение алгоритма.
Алгоритм — это предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.