Предисловие
Автор данной книги, как и многие почитатели компьютерных вычислений, прошел долгий путь их реализации: от программируемых микрокалькуляторов до работы на малых и персональных ЭВМ, использующих универсальные языки программирования высокого уровня. Это нашло отражение в его ранних книгах [1-3]. Совсем недавно пользователь ЭВМ, решая даже простые численные задачи, был вынужден осваивать основы программирования и готовить кустарные программы, вряд ли нужные кому-либо еще, кроме их создателя. Между тем возможности компьютеров постоянно росли. Сейчас персональный компьютер (ПК) с микропроцессором класса Pentium II, III или 4 намного превосходит по своим возможностям первые ЭВМ, занимавшие целые комнаты и залы. А скорость вычислений нынешних ПК в сотни раз превосходит скорость вычислений легендарных IBM PC XT и AT (первых ПК) и вплотную приближается к скорости вычислений суперЭВМ недавнего прошлого.
В связи с этим стал меняться взгляд на назначение компьютера. На первое место вышло применение их для работы с текстовыми процессорами (например, Microsoft Word) и прикладными программными системами для автоматизации офисной деятельности. Увы, при этом многие пользователи стали забывать о том, что ЭВМ изначально создавались для вычислений, а вовсе не для замены ими популярной, но ставшей неудобной пишущей машинки. Развитие мультимедиа привело к бурному применению компьютеров в роли игровых автоматов. В результате главный стимул развития «электронного помощника» создается отнюдь не высокоинтеллектуальными задачами.
Однако времена меняются и вечные ценности, к коим принадлежат разум и образование, вновь возвращаются. В последние годы во всем мире существенно возрос интерес к серьезному применению ПК, в том числе в области математических расчетов. Этому в большой степени способствовала разработка специальных компьютерных математических программных систем, резко снизивших потребность в написании собственных программ при решении математических задач. Первое поколение таких систем [4-10] было ориентировано на операционную систему MS-DOS и появилось, казалось бы, совсем недавно — в начале 90-х гг. Так или иначе, но компьютерный мир вновь заговорил об «искусственном интеллекте», понимая под этим способность электронной машины выдавать нетривиальные решения и обучаться решению новых задач. Интерес к компьютерному моделированию в самых широких областях заметно возрос после шахматных баталий между суперкомпьютером фирмы IBM и бывшим чемпионом мира по шахматам Гарри Каспаровым. Как известно, они завершились триумфальной победой машины — или, точнее говоря, коллективного разума тех, кто создал ее и ее программное обеспечение.
В последние годы показателем интеллектуальной мощи компьютеров, в том числе и персональных, стали уже не программы для игры в шахматы, а новейшие программные системы символьной математики или компьютерной алгебры [17-38]. Созданные для проведения символьных преобразований математических выражений, эти системы были доведены до уровня, позволяющего резко облегчить, а подчас и заменить, труд самой почитаемой научной элиты мира — математиков: теоретиков и аналитиков. Уже появились открытия, сделанные с помощью таких систем — но не ими самими! Вряд ли есть хоть один действительно серьезный научный проект, связанный с математикой, где они не применялись бы в деле.
Системы символьной математики долгое время были ориентированы на большие компьютеры, С появлением ПК класса IBM PC и Macintosh и с ростом их возможностей эти системы были переработаны под них и доведены до уровня массовых серийных программных систем. Сейчас системы символьной математики (или компьютерной алгебры) выпускаются самого разного «калибра» — от рассчитанной «на всех» системы Mathcad [11-21], поразительно компактной, быстрой и удобной для простых символьных вычислений системы Derive [22-24] и до компьютерных монстров Mathematica [26-28], MATLAB [29-31] и Maple [32-38], имеющих тысячи встроенных и библиотечных функций и изумительные возможности графической визуализации вычислений:
Все эти системы работают на персональных компьютерах, оснащенных популярными операционными системами класса Windows 95/98/NT/2000. Но не только на них — есть версии под операционные системы Linux, Unix, Mac и др. Они давно знакомы пользователям больших компьютеров и даже суперкомпьютеров.
К среднему уровню таких систем относятся интенсивно развиваемые системы класса Mathcad,» имеющие (в дополнение к прекрасным средствам числовых вычислений) приобретенное по лицензии у фирмы Waterloo Maple Inc. (создателя систем Maple) ядро символьных вычислений. Ядро системы Maple используется и в другой маститой системе — MATLAB, придавая ей необычные для нее возможности символьной математики.
В данной книге впервые дается достаточно полное описание одной из самых мощных и интеллектуальных систем компьютерной алгебры — Maple под Windows, ее последней реализации — Maple 7. Эта система была создана группой ученых, занимающихся символьными вычислениями (The Symbolic Group), организованной Кейтом Геддом (Keith Geddes) и Гастоном Гонэ (Gaston Gonnet) в 1980 году в университете Waterloo, Канада. Вначале она была реализована на больших компьютерах и прошла долгий путь апробации, вобрав в свое ядро и библиотеки большую часть математических функций и правил их преобразований, выработанных математикой за столетия развития. Есть реализации программы на платформах ПК Macintosh, Unix, Sun и др.
Системам класса Maple посвящены сотни книг. Отметим лишь некоторые из них [39-56], изданные за рубежом. Достаточно полный список (около 400 наименований) книг по системам Maple можно найти на сайте разработчика этой системы — компании Waterloo Maple Software (www.maplesoft.com). Однако книг по системе Maple 7 (за исключением фирменных руководств по ней) на момент сдачи рукописи данной книги в этом списке не было.
Вряд ли эта мощная математическая система, разделяющая претензии на мировое лидерство с системами Mathematica фирмы Wolfram Research Inc., нужна секретарше или даже директору небольшой коммерческой фирмы. Но, несомненно, любая серьезная научная лаборатория или кафедра вуза должны располагать подобной системой, если они всерьез заинтересованы в автоматизации выполнения математических расчетов любой степени сложности. Несмотря на свою направленность на серьезные математические вычисления, системы класса Maple необходимы довольно широкой категории пользователей: студентам и преподавателям вузов, инженерам, аспирантам, научным работникам и даже учащимся математических классов общеобразовательных и специальных школ. Все они найдут в Maple многочисленные достойные возможности для применения.
По мнению автора данной книги, сравнение системы Maple 7 с лидером среди систем компьютерной математики — системой Mathematica 4.1 — непродуктивно. У каждой программы есть свои достоинства и недостатки. А главное — у них есть свои приверженцы, которых бесполезно убеждать, что иная система в чем-то лучше. Это все равно, что сравнивать великих исполнителей джазовой и рок-музыки Луи Амстронга и Би Би Кинга. Все, кто всерьез применяют системы компьютерной математики, должны работать с несколькими системами, ибо только это гарантирует высокий уровень надежности сложных вычислений.
И все же надо отметить, что интерфейс Maple 7 более интуитивно понятен, чем у строгой Mathematica 4.1. Maple 7 на первый взгляд имеет несколько менее мощную графику, но простота управления параметрами и легкость подготовки графических процедур часто позволяет визуализировать решения математических задач с меньшими усилиями, чем при использовании системы Mathematica 4.1. Обе системы в последних реализациях сделали качественный скачок в направлении эффективности решения задач в численном виде, в частности за счет повышения скорости выполнения матричных операций.
Особенно эффективно использование Maple при обучении математике. Высочайший «интеллект» этой системы символьной математики объединяется в ней с прекрасными средствами математического численного моделирования и просто потрясающими возможностями графической визуализации решений. Применение таких систем, как Maple, возможно при преподавании и самообразовании от самых основ до вершин математики.
Практика (да и личный опыт автора) показывает, что самым трудным является первый этап освоения системы. Первое знакомство с программой многих пользователей просто подавляет — убедившись в невероятном множестве возможностей системы и не имея ее систематизированного описания (а оно поставляется в виде трех книг приличного размера, включая книги учебного характера [39, 40]), многие пользователи помещают систему в архив, где она «пылится» без дела.
Эта книга впервые основательно знакомит читателя с новейшей версией системы Maple — Maple 7 в форме подробного учебного курса. Книга написана на основе ранее изданного учебного курса по системе Maple 6 [37], существенно переработанного и дополненного. Среди новых материалов, появившихся в книге, следует отметить:
- полное описание инсталляции системы Maple 7;
- улучшенное описание интерфейса;
- обновление материала по информационной поддержке системы, в том числе через Интернет;
- адаптация примеров и рисунков к новой версии Maple 7;
- устранение замеченных в предыдущем издании [37] неточностей и опечаток;
- впервые представленное описание целого ряда новых встроенных математических пакетов системы (CurveFitting, LinearFunctionalSystems, PolynomialTools, OrthogonalSeries, RandomTools и др.);
- описание расширенной поддержки Интернета и встроенного пакета XMLTools, который ее обеспечивает;
- впервые приведенное описание новейших средств поддержки стандарта MathML и пакета MathML;
- описание многочисленных новинок системы Maple 7 в области реализации вычислений и их графической визуализации;
- десятки новых примеров применения Maple 7.
Основное внимание в книге уделено обучению основам и приемам эффективной работы с системой Maple 7. На роль всеобъемлющего справочного руководства книга не претендует, хотя во многих случаях способна выполнять роль справочника или руководства пользователя Maple 7. Хотя эта книга одна из самых обширных среди русскоязычных книг, посвященных системе Maple, автор был вынужден ограничить описание ряда важных возможностей программы. Основной акцент в книге сделан на описание возможностей системы в области математических расчетов и интерфейса пользователя. Менее подробно, а порой просто не описаны средства расширения системы и пакеты узкоспециального назначения (электронная база данных по системе Maple 7 дает полное представление о всех свыше 3000 операторов и функций этой системы, большинство из которых используется крайне редко).
Хотя книга посвящена версии Maple 7, большинство материала может использоваться и пользователями предшествующей версии Maple 6. В частности, это достигнуто выделением новых возможностей Maple 7 в отдельные разделы книги. Остальные разделы книги без каких-либо ограничений могут быть отнесены к наиболее распространенной версии Maple — Maple 6.
Структура книги
Книга содержит 17 уроков и составлена так, что эти уроки постепенно знакомят читателя с возможностями системы. Уже после прохождения урока 1 вы сможете начать осмысленно и плодотворно работать с системой. Этот урок является как бы ознакомительным курсом по работе с системой Maple 7. Он может быть полезен как для быстрого самостоятельного освоения системы не слишком требовательным пользователем, так и как основа вводного курса по системе в вузах и школах, где для основательного изучения Maple 7 не предусмотрено достаточного количества учебных часов. Кроме того, этот урок знакомит читателя с основами интерфейса пользователя и правилами работы с панелями инструментов и форматирования выражений. По сравнению с учебным курсом по системе Maple 6 [37] этот урок существенно переработан и дополнен. В частности, подробно описана инсталляция системы Maple 7 и аппаратные требования для работы с ней. Последующие уроки расширяют заведенное знакомство и постепенно готовят читателя к серьезной самостоятельной работе практически без применения какой-либо иной документации, кроме встроенной в систему справочной базы данных. Урок 2 посвящен знакомству с мощной справочной базой данных системы Maple 7 и информационной поддержкой этой системы в Интернете. Данные разделы намеренно вынесены в начало книги, поскольку успех освоения системы Maple 7 до профессионального уровня требует обучения работе со справочной базой данных. В уроке 3 описаны основные приемы работы с файлами документов, которые готовятся в Maple 7. Урок 4 дает систематизированное описание интерфейса, хотя и без многих подробностей, известных всем пользователям операционных систем класса Windows 95/98/NT/2000.
Остальные уроки посвящены базовым математическим возможностям системы Maple 7 и основам практической работы в ней. В уроке 5 описаны основные типы данных системы, а в уроке 6 — основные виды встроенных операторов и функций. Урок 7 посвящен основам программирования в среде Maple 7. Читатель должен понимать, что все описанные и в других главах команды системы Maple 7 являются одновременно и командами ее языка программирования. Именно это позволяет считать язык программирования Maple 7 языком программирования сверхвысокого уровня, проблемно ориентированным на математические расчеты. Урок 8 является одним из наиболее важных. Он посвящен решению типовых задач математического анализа, таких как вычисление сумм и произведений последовательностей, производных и интегралов, разложений функций в ряд и т. д. При этом особое внимание уделяется технике аналитических вычислений, где возможности системы Maple 7 вызывают особый интерес. Но и техника численных расчетов рассмотрена достаточно детально, в частности арифметика высокой точности. Работа с функциями и степенными многочленами (полиномами) описана в уроке 9. Урок 10 посвящен изучению главной «козырной карты» системы Maple 7 — ее возможностям в области символьной математики. Здесь описано много тонкостей работы с математическими выражениями и другими объектами системы, позволяющими выполнять множество математических преобразований и подстановок.
Два больших урока — уроки 11 и 12 — посвящены графическим возможностям системы. При этом урок 11 описывает обычные графические средства, а в уроке 12 дается описание расширенных средств, позволяющих эффективно решать задачи визуализации решений математических проблем — вплоть до подготовки графиков с элементами анимации.
Учитывая огромную роль дифференциальных уравнений в решении ряда математических, физических и технических задач, работе с ними посвящен отдельный урок 13. Наряду с решением одиночных дифференциальных уравнений первого и второго порядка рассматривается решение систем линейных и нелинейных дифференциальных уравнений как аналитическими, так и численными методами. Большое внимание уделено графической визуализации решений и построению наглядных фазовых портретов решения. В уроке отражены новые возможности Maple 7 в решении дифференциальных уравнений.
В уроке 14 рассмотрены важнейшие пакеты системы Maple 7 математической направленности. Эти пакеты поставляются вместе с системой, и применение функций из них столь же важно, как и применение средств ядра системы. Описанные в уроке 14 пакеты рассмотрены достаточно полно.
В отдельный урок 15 вынесены широко используемые на практике средства решения задач линейной алгебры. Это операции с векторами и матрицами, различные их преобразования и техника решения систем линейных уравнений. Здесь описаны такие важные пакеты, как linalg (стандартные средства линейной алгебры) и LinearAlgebra. В последний пакет входят новые средства линейной алгебры повышенной эффективности на основе алгоритмов, заимстованных из знакомого математикам пакета программ NAG (Numbering Algorithms Group). Впервые описан новый пакет анализа линейных функциональных систем LinearFunctionalSystems, появившийся в версии Maple 7.
Остальные пакеты, относящиеся к сравнительно узким областям математики и п-редставляющие ограниченный интерес для большинства читателей, рассмотрены обзорно или в виде аннотации в уроке 16. К сожалению, материал по всем пакетам расширения Maple 7 настолько обширен, что его невозможно отразить в одной книге (тем более в форме учебного курса). Тем не менее в отличие от учебного курса по системе Maple 6 [37] этот урок существенно расширен и в нем впервые описан ряд новых пакетов системы Maple, в частности пакеты PolymomialTools, OrthogonalSeries, RandomTools, MathML и XMLTools.
Последний урок 17 описывает законченное решение ряда конкретных и интересных задач из области математики, физики и радиоэлектроники. Таким образом, читатель получает возможность познакомиться с широким спектром применения системы Maple 7 — от примеров простых расчетов и вычислений (таких в книге тысячи) до решения конкретных научных и технических проблем. Материал книги иллюстрируется многими сотнями копий экрана как в виде отдельных рисунков, так и фрагментов вычислений и программных процедур в тексте книги. Они дают наглядное представление о реальном диалоге с системой и о форматах ввода и вывода.
Большинство примеров в книге оригинальны и отражают взгляд автора на методологию изучения системы Maple. В то же время в книге использованы и лучшие (и наиболее поучительные) примеры, которые приведены в обширной библиотеке процедур, составленных пользователями систем Maple разных реализаций со всего мира, и примеры из ряда учебников по системе — в том числе новейших электронных (таких; как Power Tools), размещенных в Интернете. Все заимствованные примеры также специально адаптированы применительно к новейшей версии системе Maple 7, описанной в книге.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
140
Добавлен:
24.03.2015
Размер:
2.27 Mб
Скачать
С. Е. Савотченко,
Т.Г. Кузьмичева
Методы решения математических задач в
Maple
Рекомендовано Редакционно-издательским советом Белгородского государственного университета в качестве учебного пособия для студентов социально-психологического и естественно-географического факультетов Белгородского государственного университета
Белгород
2001

Методы решения математических задач в Maple
ББК 22.11
С 13
Рецензенты: Чеканов Н.А. д.ф.-м.н., профессор БелГУ; Сурков Э.П. к.ф.-м.н., профессор БГСХА.
Савотченко С.Е., Кузьмичева Т.Г.
С13 Методы решения математических задач в Maple: Учебное пособие – Белгород: Изд. Белаудит, 2001. – 116 с.
ISBN 5-7414-0046-9
Данная книга является учебным пособием по дисциплинам
«Математика и информатика», «Информационные технологии».
Пособие представляет собой практическое руководство по изучению возможностей пакета аналитических вычислений Maple. Подробные теоретические сведения чередуются с практическими заданиями. Последовательное изучение тем и выполнение заданий позволит шаг за шагом освоить основные приемы работы в математической системе
Maple.
Учебное пособие предназначено для студентов 1 и 2 курсов социально-психологического и естественно-географического факультетов университета, а также для аспирантов и научных работников, использующих математические методы и модели в естественнонаучных исследованиях.
ББК 22.11
|
ISBN 5-7414-0046-9 |
© Савотченко С.Е., Кузьмичева Т.Г., |
|
2001 |
2

Методы решения математических задач в Maple
Предисловие
Данное пособие представляет собой практическое руководство по изучению возможностей пакета аналитических вычислений Maple.
Следует отметить, что эта книга ни в коей мере не может считаться описанием программного продукта Maple. Она предназначена в первую очередь для обучения студентов решению математических задач на персональном компьютере при помощи Maple. Задачи и упражнения, приведенные в качестве примеров и практических заданий, соответствуют программам по курсу общей математики для студентов естественнонаучных и социальнопсихологических специальностей вузов.
Структура пособия: пособие состоит из семи тем. В каждой теме содержатся:
теоретическая часть – в ней приведено описание изучаемых команд Maple;
практические задания – подробное пошаговое описание действия команд Maple на конкретных примерах по математике; эти задания предназначены для выполнения студентами под руководством преподавателя;
контрольные задания – задачи и упражнения для самостоятельного выполнения студентами;
контрольные вопросы – предназначены для закрепления теоретического материала.
Практические задания можно выполнять на лабораторных работах по одной теме на каждую лабораторную работу.
Выполнение заданий по темам №1 и 2 расчитано на 2-х часовые занятия, выполнение заданий по остальным темам предполагает 4-х часовые аудиторные занятия, включая выполнение контрольных заданий.
Материал, содержащийся в темах №1-5, соответствует программам по математике для студентов 1 курса, а материал, содержащийся в темах №6-7, рассчитан для студентов 2 курса специальностей с более углубленными программами по математики, например, «химия».
Авторы выражают благодарность Воронову В.П., благодаря которому была начата работа над данной книгой.
3

Методы решения математических задач в Maple
I. Структура окна Maple. Арифметические операции, числа, константы и стандартные функции.
Элементарные преобразования математических выражений
1.Структура окна Maple.
2.Арифметические операции, целые и рациональные числа и константы Maple.
3.Синтаксис команд. Стандартные функции.
4.Преобразования математических выражений.
§1. Структура окна Maple
Maple − это пакет для аналитических вычислений на компьютере, содержащий более двух тысяч команд, которые позволяют решать задачи алгебры, геометрии, математического анализа, дифференциальных уравнений, статистики, математической физики.
Для того, чтобы запустить Maple, необходимо в Главном меню Windows выбрать в группе Программы название данного приложения:
Maple.
Maple представляет собой типичное окно Windows, которое состоит из Строки названия, Основного меню, Панели инструментов, Рабочего поля и Строки состояния, а также Линейки и Полос прокрутки.
Вид фрагмента окна Maple 6, содержащего Строку названия,
Основное меню, Панель инструментов:
Пункты Основного меню:
File (Файл) − содержит стандартный набор команд для работы с файлами, например: сохранить файл, открыть файл, создать новый файл и т.д.
Edit (Правка) − содержит стандартный набор команд для редактирования текста, например: копирование, удаление выделенного текста в буфер обмена, отмена команды и т.д.
View (Вид) – содержит стандартный набор команд, управляющих структурой окна Maple.
4

Методы решения математических задач в Maple
Insert (Вставка) – служит для вставки полей разных типов: математических текстовых строк, графических двух и трехмерных изображений.
Format (Формат) – содержит команды оформления документа, например: установка типа, размера и стиля шрифта.
Options (Параметры) – служит для установки различных параметров ввода и вывода информации на экран, принтер, например, таких как качество печати.
Windows (Окно) – служит для перехода из одного рабочего листа в другой.
Help (Справка) – содержит подробную справочную информацию о Maple.
Работа в Maple проходит в режиме сессии – пользователь вводит предложения (команды, выражения, процедуры), которые воспринимаются условно и обрабатываются Maple. Рабочее поле разделяется на три части:
1)область ввода — состоит из командных строк. Каждая командная строка начинается с символа >;
2)область вывода — содержит результаты обработки введенных команд в виде аналитических выражений, графических объектов или сообщений об ошибке;
3)область текстовых комментариев — содержит любую текстовую информацию, которая может пояснить выполняемые процедуры. Текстовые строки не воспринимаются Maple и никак не обрабатываются.
Для того, чтобы переключить командную строку в текстовую,
следует на Панели инструментов нажать мышью на кнопку Обратное переключение текстовой строки в командную осуществляется нажатием на Панели инструментов на кнопку
Задание 1.
1.Запустите Maple.
2.После запуска Maple первая строка оказывается командной. Переведите ее в текстовую. Наберите в этой строке: «Лабораторная работа №1» и название темы. Перейдите на следующую строку, нажав Enter.
3.В новой строке наберите «Выполнил студент » и свою фамилию. Нажмите Enter.
4.На следующей строке наберите «Задание №1».
5

Методы решения математических задач в Maple
5.Сохраните свой файл на дискете. Для этого в меню Fail выберите пункт Save и наберите имя вашего файла в виде: Фамилия_1, где указывается ваша фамилия и 1 – номер лабораторной работы.
6.После этого в следующей строке наберите текст: «Файл с заданиями лабораторной работы №1 сохранен под именем: Фамилия_N».
Вдальнейшем выполнение каждой лабораторной работы должно оформляться таким способом. В начале каждой лабораторной работы следует набирать текст: «Лабораторная работа N», N – номер темы. Выполнение каждого задания следует начинать с текстового комментария: «Задание N». Для правильности вычислений перед выполнением каждого пункта задания следует выполнять команду restart. Перед выполнением контрольных заданий следует набирать
в текстовом режиме «Контрольные задания». После окончания выполнения работы необходимо сохранить файл со всеми выполненными заданиями на диск. Имя вашего файла набирается в виде: Фамилия_N, где указывается ваша фамилия и N – номер темы.
§2. Арифметические операции.
Целые и рациональные числа, константы в Maple
Математические константы и арифметические операции.
Основные математические константы:
Pi – число π; I – мнимая единица i; infinity – бесконечность; Gamma – константа Эйлера; true, false – логические константы, обозначающие истинность и ложность высказывания.
Знаки арифметических операций: + — сложение; – — вычитание;
|
* — умножение; |
/ — деление; |
|
|
^ — возведение в степень; |
! – факториал. |
Знаки сравнения: <, >, >=,<=, <>, =.
Комплексные, целые и рациональные числа.
Числа в Maple бывают действительные (real) и комплексные (compleх). Комплексное число записывается в алгебраической форме z=x+iy, и в командной строке такая запись должна выглядеть так:
> z:=x+I*y;
Вещественные числа разделяются на целые и рациональные. Целые числа (integer) выражаются цифрами в десятичной записи. Рациональные числа могут быть представлены в 3-х видах:
6

Методы решения математических задач в Maple
1)рациональной дроби с использованием оператора деления, например: 28/70;
2)с плавающей запятой (float), например: 2.3;
3)в показательной форме, например: 1,602*10^(-19) означает
1,602 10-19.
Для того, чтобы получить рациональное число не в точной форме, а в виде приближенного значения (числа с плавающей запятой), следует дописывать к целой части числа .0. Пример:
> 75/4;
75
4
> 75/4.0;
18.75000000
В Maple можно записать буквы греческого алфавита в полиграфическом виде. Для этого в командной строке набирается название греческой буквы. Например, буква α получится, если
|
набрать alpha. |
||||
|
Таблица строчных греческих букв и их названий: |
||||
|
α — alpha |
η — eta |
μ — mu |
φ — phi |
|
|
β — beta |
θ — theta |
ξ -xi |
χ — chi |
|
|
γ — gamma |
ι — ita |
π — pi |
ψ — psi |
|
|
δ — delta |
κ — kappa |
ρ — rho |
ω -omega |
|
|
λ — lambda |
||||
|
ε — epsilon |
σ — sigma |
|||
|
ς — zeta |
ν — nu |
υ — upsilon |
Заглавные греческие буквы можно записать, если набирать
название греческой буквы с заглавной, например, чтобы получить Ω, следует набрать Omega. Греческие буквы также можно набирать с помощью специального меню.
Задание 2.
1.Перейдите в текстовый режим и наберите «Задание №2». После не забудьте перейти в режим командной строки.
|
2. Вычислите значение |
6 + 2 5 − 6 − 2 5 . Для этого в |

командной строке наберите:
> (sqrt(6+2*sqrt(5))-sqrt(6-2*sqrt(5)))/sqrt(3);
7
Методы решения математических задач в Maple
|
и нажмите Enter. В результате получится точное значение |
2 |
3 . |
|
3 |
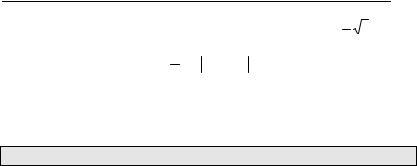
3.Наберите формулы ω = θt и f (x) − δ < ε . Для этого в командной
строке наберите:
> omega=theta/t; abs(f(x)-delta)<epsilon;
нажмите Enter.
§3. Синтаксис команд. Стандартные функции
Синтаксис команд.
Стандартная команда Maple состоит из имени команды и ее параметров, указанных в круглых скобках: command(p1, p2, …). В конце каждой команды должен быть знак (;) или (:). Разделитель (;) означает, что в области вывода после выполнения этой команды будет сразу виден результат. Разделитель (:) используется для отмены вывода, то есть когда команда выполняется, но ее результат на экран не выводится.
Символ процента (%) служит для вызова предыдущей команды. Этот символ играет роль краткосрочной замены предыдущей команды
сцелью сокращения записи. Пример использования (%):
>a+b;
a+b
> %+c;
a+b+c.
Для присвоения переменной заданного значения используется знак присвоить (:=).
Когда программа Maple запускается, она не имеет ни одной команды, полностью загруженной в память. Большая часть команд имеют указатели их нахождения, и при вызове они загружаются автоматически. Другие команды находятся в стандартной библиотеке и перед выполнением обязательно должны быть вызваны командой readlib(command), где command – имя вызываемой команды.
Остальная часть процедур Maple содержится в специальных библиотеках подпрограмм, называемых пакетами. Пакеты необходимо подгружать при каждом запуске файла с командами из этих библиотек. Имеется два способа вызова команды из пакета:
1)можно загрузить весь пакет командой with(package) где package – имя пакета;
8

Методы решения математических задач в Maple
2)вызов какой-нибудь одной команды command из любого пакета package можно осуществить, если набрать команду в специальном формате:
> package[command](options);
где вначале записывается название пакета package, из которого надо вызвать команду, а затем в квадратных скобках набирается имя самой команды command, и после чего в круглых скобках следуют параметры options данной команды.
К библиотекам подпрограмм Maple относятся, например, следующие пакеты: linalg – содержит операции линейной алгебры; geometry – решение задач планиметрии; geom3d – решение задач стереометрии; student – содержит команды, позволяющие провести поэтапное решение задачи в аналитическом виде с промежуточными вычислениями.
Стандартные функции.
Стандартные функции Maple
|
Математическая запись |
Запись в Maple |
|||
|
ex |
exp(x) |
|||
|
ln x |
ln(x) |
|||
|
lg x |
log10(x) |
|||
|
loga x |
log[a](x) |
|||
|
x |
sqrt(x) |
|||
|
x |
abs(x) |
|||
|
sin x |
sin(x) |
|||
|
cos x |
cos(x) |
|||
|
tgx |
tan(x) |
|||
|
ctgx |
cot(x) |
|||
|
sec x |
sec(x) |
|||
|
cosecx |
csc(x) |
|||
|
arcsin x |
arcsin(x) |
|||
|
arccos x |
arccos(x) |
|||
|
arctgx |
arctan(x) |
|||
|
arcctgx |
arccot(x) |
|||
|
shx |
sinh(x) |
|||
|
chx |
cosh(x) |
9

Методы решения математических задач в Maple
|
thx |
tanh(x) |
|
cthx |
coth(x) |
|
δ(x) — функция Дирака |
Dirac(x) |
|
θ(x) — функция |
Нeaviside(х) |
|
Хевиссайда |
Maple содержит огромное количество специальных функций, таких, как Бесселевы функции, Эйлеровы бета- и гамма – функции, интеграл ошибок, эллиптические интегралы, различные ортогональные полиномы.
С помощью функции exp(x) определяется число е=2.718281828… посредством записи exp(1).
Задание 3.
1.Перейдите в текстовый режим и наберите «Задание №3». После не забудьте перейти в режим командной строки.
2.Вычислите cos π3 + tg 143π Для этого наберите в командной строке:
> cot(Pi/3)+tan(14*Pi/3);
Нажмите Enter. В результате в области вывода должно появиться
|
число: − |
2 |
3 . |
||||||||||
|
3 |
π |
3π |
5π |
7π |
||||||||
|
3. Вычислите |
sin4 |
+ cos4 |
+ sin4 |
+ cos4 |
. Для этого |
|||||||
|
8 |
8 |
8 |
8 |
наберите в командной строке:
> combine((sin(Pi/8))^4+(cos(3*Pi/8))^4+ (sin(5*Pi/8))^4+ (cos(7*Pi/8))^4);
Нажмите Enter. (значение команды combine – преобразовывать выражения, например, со степенями). В результате в области вывода
должно появиться число: 23 .
§4. Преобразование математических выражений
Maple обладает широкими возможностями для проведения аналитических преобразований математических формул. К ним относятся такие операции, как приведение подобных, разложение на
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more

