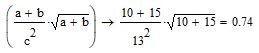Mathcad 15 руководство пользователя русифицированное

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

                    Евгений Макаров
ИНЖЕНЕРНЫЕ
РАСЧЕТЫ В
УЧЕБНЫЙ КУРС k
е. Макаров инженерные расчеты в Mathcad 15^
Евгений Макаров
ИНЖЕНЕРНЫЕ
РАСЧЕТЫ В
D Id
УЧЕБНЫЙ КУРС
Kt
ПИТЕР'
Москва  Санкт-Петербург • Нижний Новгород  Воронеж
Ростов-на-Дону  Екатеринбург  Самара  Новосибирск
Киев  Харьков  Минск
2011
ББК 004.42(075)
УДК 32.973.23-018.2я7
М15
Макаров Е.
М15 Инженерные расчеты в Mathcad 15: Учебный курс. — СПб.: Питер, 2011. —
400 с.: ил.
ISBN 978-5-459-00357-4
Книга предназначена для самостоятельного освоения работы в 15-й версии популярного матема-
тического пакета Mathcad. Издание имеет формат учебного курса и состоит из четырех частей.
В первой части содержатся сведения, необходимые для начала работы в Mathcad и решения боль-
шинства практических задач. Вторая часть посвящена вычислительным возможностям программы,
здесь на конкретных примерах рассматриваются Особенности использования встроенных функ-
ций, основные приемы и способы вычислений. В третьей части рассматриваются возможности
подготовки документов Mathcad, а четвертая содержит перечень примеров решения инженерных
задач в Mathcad.
Важнейшее приложение книги размещено на интернет-сайте издательства — это электронная
книга, встраиваемая в оболочку Mathcad. Она содержит примеры использования всех встроенных
функций, программы решения 56 примеров, приведенных в четвертой части книги, и пояснения
к ним. Электронная книга — это инструмент быстрого создания программ любой сложности.
Книга предназначена для всех пользователей Mathcad, как начинающих, так и опытных, и будет
полезна студентам, инженерам и научным работникам.
ББК 004.42(075)
УДК 32.973.23-018.2я7
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было фор-
ме без письменного разрешения владельцев авторских прав.
Информация, содержащаяся в данной книге, получена из источников, рассматриваемых издательством как
надежные. Тем не менее, имея в виду возможные человеческие или технические ошибки, издательство не
может гарантировать абсолютную точность и полноту приводимых сведений и не несет ответственности за
возможные ошибки, связанные с использованием книги.
ISBN 978-5-459-00357-4
© ООО Издательство «Питер», 2011
Краткое оглавление
Предисловие.....................................................11
Электронная книга...........,...................................17
Часть I. Начало работы с Mathcad................................23
Глава 1. Построение выражений и графиков в Mathcad...........24
Глава	2.	Некоторые возможности Mathcad......................47
Часть II. Вычисления в Mathcad..................................85
Глава	3.	Решение уравнений..................................86
Глава 4. Работа с векторами и матрицами.....................105
Глава	5.	Символьные вычисления.............................128
Глава 6. Решение дифференциальных уравнений.................159
Глава 7. Обработка экспериментальных данных.................192
Глава 8. Математическая статистика..........................217
Часть ill. Дополнительные возможности Mathcad.................225
Глава 9. Программирование..................................226
Глава 10. Анимация.........................................255
Глава 11. Учет размерностей................................261
Глава 12. Дополнительные встроенные функции Mathcad........275
Глава 13. Работа с Mathcad-документами.....................300
Глава 14. Работа с текстом.................................316
Глава 15. Работа с графиками...............................323
Глава 16. Справочная информация в Mathcad..................345
Глава 17. Создание электронных книг........................354
Глава 18. Работа с электронной книгой......................365
Часть IV. Примеры инженерных расчетов в Mathcad...............373
Оглавление
Предисловие.............................................................11
Mathcad и его возможности............................................11
Новое в Mathcad 15...................................................13
Рекомендации по работе с книгой......................................15
От издательства......................................................16
Электронная книга.......................................................17
ReadMe...............................................................17
Сведения об электронной книге........................................19
Назначение электронной книги.........................................21
Часть I. Начало работы с Mathcad........................................23
Глава 1 - Построение выражений и графиков в Mathcad..................24
1.1.	Интерфейс Mathcad...............................................24
1.1.1.	Рабочее окно Mathcad......................................24
1.1.2.	Главное меню.............................................. 25
1.1.3.	Панели инструментов.......................................26
1.2.	Построение выражений и их вычисление............................30
1.3.	«Цепкие» операторы..............................................31
1.4.	Редактирование объектов Mathcad.................................32
1.5.	Стандартные функции.............................................33
1.6.	Числовые константы. Ввод греческих букв.........................34
1.7.	Ввод текста.....................................................35
1.8.	Функции пользователя............................................36
1.9.	Дискретные переменные. Построение таблиц........................37
1.10.	Форматирование чисел...........................................38
1.11.	Построение плоского графика функции............................39
1.12.	Построение трехмерных графиков.................................44
Глава 2. Некоторые возможности Mathcad...............................47
2.1.	Ступенчатые и разрывные функции и выражения. Условие в Mathcad..47
2.2.	Глобальное присвоение значений..................................49
2.3.	Символьные вычисления...........................................50
2.4.	Решение уравнений...............................................52
2.4.1.	Символьное решение........................................52
2.4.2.	Численное решение (функция root)..........................52
2.5.	Решение систем уравнений (функция find).........................54
2.6.	Приближенное решение систем уравнений (функция minerr)..........56
2.7.	Исследование функции на экстремум...............................57
2.8.	Работа с матрицами..............................................58
2.8.1.	Создание матриц...........................................58
2.8.2.	Основные действия с матрицами.............................59
2.8.3.	Решение матричных уравнений...............................60
2.9.	Оператор векторизации...........................................61
2.10.	Решение дифференциальных уравнений.............................63
2.11.	Анализ экспериментальных данных................................67
2.11.1.	Интерполяция.............................................68
2.11.2.	Регрессия................................................68
Оглавление
5
2.12.	Элементы математической статистики.............................73
2.13.	Обмен данными с другими программами............................74
2.14.	Учет размерностей в Mathcad....................................75
2.15.	Преобразование функции в матрицу и	матрицы в функцию...........79
2.16.	Строковые функции..............................................80
2.17.	Программирование...............................................80
2.18.	Анимация.......................................................81
2.19.	Отладка Mathcad-документов.....................................81
2.20.	«Горячие» клавиши..............................................82
Часть II. Вычисления в Mathcad..........................................85
Глава 3. Решение уравнений.......................................... 86
3.1.	Функция root....................................................86
3.2.	Решение уравнения с переменными параметрами.....................89
3.3.	Нахождение корней полинома. Функция polyroots ..................91
3.4.	Решение систем уравнений........................................93
3.5.	Трудности при решении уравнений.................................98
3.6.	Приближенное решение уравнений и систем уравнений...............98
3.7.	Исследование функции на экстремум..............................100
3.8.	Рекурсивные вычисления.........................................102
Глава 4. Работа с векторами и матрицами.............................105
4.1.	Создание матрицы...............................................105
4.2.	Нумерация элементов матрицы.....<.............................107
4.3.	Встроенная переменная ORIGIN...................................107
4.4.	Определение параметров матрицы.................................108
4.5.	Образование новых матриц из уже существующих...................109
4.6.	Ввод больших массивов..........................................110
4.7.	Сортировка векторов и матриц...................................111
4.8.	Матричные операторы............................................111
4.8.1.	Транспонирование матрицы.................................111
4.8.2.	Вычисление определителя матрицы..........................112
4.8.3.	Нахождение матрицы, обратной заданной.....................ИЗ
4.8.4.	Сложение, вычитание и умножение матриц...................113
4.8.5.	Оператор векторизации....................................115
4.8.6.	Последовательное и параллельное вычисление элементов массива . . . 116
4.9.	Собственные числа и собственные векторы матриц.................116
4.10.	Норма квадратной матрицы....................................:	. 119
4.11.	Число обусловленности квадратной матрицы......................120
4.12.	Матричные разложения..........................................120
4.12.1.	Разложение Холесского...................................121
4.12.2.	QR-разложение...........................................121
4.12.3.	LU-разложение...........................................121
4.12.4.	Сингулярное разложение..................................122
4.13.	Вывод векторов и матриц.......................................122
4.14.	Составные массивы............................................ 124
4.15.	Работа с комплексными числами.................................125
Глава 5. Символьные вычисления......................................128
5.1.	Оптимизация численных вычислений...........................  .	. 128
5.2.	Использование меню символьных вычислений Symbolics.............129
5.2.1.	Символьная оценка выражения..............................130
Оглавление
5.2.2.	Упрощение выражений.....................................131
5.2.3.	Раскрытие выражений.....................................132
5.2.4.	Разложение на множители.................................133
5.2.5.	Приведение подобных слагаемых...........................133
5.2.6.	Коэффициенты полинома...................................134
5.2.7.	Вычисление пределов.....................................134
5.2.8.	Замена переменной.......................................135
5.2.9.	Вычисление производной или интеграла....................135
5.2.10.	Символьное решение уравнений и неравенств..............137
5.2.11.	Разложение в ряд Тейлора...............................137
5.2.12.	Разложение на простейшие дроби.........................138
5.2.13.	Символьные операции с матрицами.............:..........138
5.2.14.	Вычисление интегральных преобразований.................140
5.3.	Использование символьной панели инструментов..................143
5.3.1.	Символьные операции без использования ключевых слов.....144
5.3.2.	Символьные операции с использованием ключевых слов......144
5.3.3.	Символьное решение уравнений............................148
5.3.4.	Использование нескольких команд одновременно............148
5.3.5.	Символьные операции с матрицами.........................150
5.4.	Новые возможности символьных вычислений в Mathcad 13-15.......151
5.4.1.	Новые ключевые слова....................................151
5.4.2.	Новые слова-модификаторы................................153
5.4.3.	Символьная векторизация выражений.......................155
5.4.4.	Новые функции символьных вычислений.....................155
5.5.	Встроенные функции и переменные...............................156
5.6.	Особенности символьной обработки..............................156
Глава 6. Решение дифференциальных уравнений........................159
6.1.	Вычислительный блок Given-Odesolve............................159
6.1.1.	Решение ОДУ с начальными и граничными условиями.........160
6.1.2.	Объединение ОДУ с помощью операторов условия............160
6.1.3.	Решение ОДУ, заданных неявно............................162
6.1.4.	Решение систем ОДУ..............>.......................162
6.1.5.	Работа блока Given-Odesolve.............................163
6.1.6.	Новые функции решения ОДУ в Mathcad 14..................165
6.1.7.	Решение ОДУ с переменными параметрами...................167
6.2.	Использование функций rkfixed, Rkadapt, Bulstoer..............167
6.2.1.	Решение дифференциального уравнения первого порядка.....169
6.2.2.	Дифференциальные уравнения более высокого порядка.......170
6.2.3.	Системы дифференциальных уравнений......................172
6.3.	Жесткие системы дифференциальных уравнений....................173
6.3.1.	Функция Radau в Mathcad 14..............................177
<6.4. Нахождение решения только в конечной точке...................178
6.5.	Двухточечные краевые задачи...................................179
6.6.	Решение дифференциальных уравнений в частных производных......184
6.6.1.	Функции решения параболических и гиперболических уравнений . . . 184
6.6.2.	Решение эллиптических уравнений (Лапласа и Пуассона)....188
Глава?. Обработка экспериментальных данных.........................192
7.1.	Интерполяция..............................................«...	192
7.1.1.	Линейная интерполяция...................................192
7.1.2.	Кубическая сплайн-интерполяция..........................193
Оглавление
7
7.1.3.	В-сплайн-интерполяция.....................................194
7.1.4.	Линейное предсказание.....................................196
7.1.5.	Интерполяция функции двух переменных......................197
7.2.	Функции регрессии...............................................200
7.2.1.	Одномерная регрессия......................................201
7.2.2.	Двухмерная регрессия......................................203
7.2.3.	Обобщенная регрессия......................................204
7.3.	Функции сглаживания...........................................  208
7.4.	Дискретные преобразования.......................................210
7.4.1.	Преобразование Фурье......................................210
7.4.2.	Двухмерное преобразование Фурье...........................213
7.4.3.	Волновое преобразование...................................215
Глава 8. Математическая статистика...................................217
8.1.	Характеристики выборки данных и связи двух массивов.............217
8.2.	Функции распределения вероятностей..............................219
8.3.	Генераторы случайных чисел......................................221
8.4.	Построение гистограмм....................................,.	. . . 222
8.5.	Расчет доверительного интервала.................................224
Часть III. Дополнительные возможности Mathcad...........................225
Глава 9. Программирование............................................226
9.1.	Создание программ...............................................226
9.1.1.	Ввод строк в программу ...................................226
9.1.2.	Локальное присвоение значений.............................227
9.2.	Условный оператор if............................................229
9.3.	Операторы цикла.................................................231
9.3.1.	Оператор while............................................231
9.3.2.	Оператор for..............................................232
9.3.3.	Операторы break, continue, return.........................234
9.4.	Вывод результатов расчета из программы..........................235
9.5.	Подпрограммы-функции........................................... 237
9.6.	Интегрирование функции методом трапеций.........................238
9.7.	Решение уравнений и систем уравнений в программе................239
9.8.	Нахождение экстремума функции в программе.......................240
9.9.	Учет размерностей в программе.................................  242
9.10.	Решение дифференциальных уравнений внутри программы............244
9.11.	Отладка программ...............................................247
9.12.	Возможности ускорения работы Mathcad...........................252
Глава 10. Анимация...................................................255
10.1.	Создание анимации..............................................255
10.2.	Галерея анимационных клипов....................................259
Глава 11. Учет размерностей........................................  261
11.1.	Выбор системы единиц измерения.................................261
11.2.	Ввод пользовательских единиц измерения.........................263
11.3.	Изменение масштаба результатов расчета.........................264
11.4.	Учет внесистемных размерностей.................................267
» 11.5. Размерность элементов массива.................................267
11.6.	Учет размерностей в цикле......................................269
3
Оглавление
11.7.	Построение графиков с учетом размерностей......................269
11.8.	Учет размерностей в программе..................................270
11.9.	Ограничения на проведение расчетов с учетом размерностей.......270
11.10.	Статическая проверка размерностей.............................271
11.11.	Квазиразмерности..............................................272
Глава 12. Дополнительные встроенные функции Mathcad..................275
12.1.	Функции для работы с комплексными числами......................275
12.2.	Тип выражения..................................................276
12.3.	Доступ к файлам................................................277
12.4.	Функции поиска значений матрицы................................280
12.5.	Преобразование функций и матриц................................282
12.5.1.	Преобразование функции в матрицу.........................282
12.5.2.	Преобразование матрицы в функцию.........................283
12.6.	Функции преобразования координат...............................286
12.7.	Функции условия................................................290
12.8.	Функции округления чисел.......................................294
12.9.	Функции комбинаторики и теории чисел...........................294
12.10.	Функции тригонометрические, гиперболические, логарифмические
и экспоненциальные...................................................294
12.11.	Специальные функции...........................................295
12.11.1.	Функции Бесселя.........................................295
12.1J.2.	Другие специальные функции............................. 297
12.11.3.	Дополнительные неактивные функции.......................297
12.12.	Строковые функции.............................................298
Глава 13. Работа с Mathcad-документами...............................300
13.1.	Построение математических выражений............................300
13.1.1.	Стили записи выражений...................................300
13.2.	Аннотация файлов и областей файлов.............................305
13.3.	Защита информации в Mathcad....................................307
13.4.	Закрытые зоны в Mathcad........................................309
13.5.	Создание вычислительных комплексов.............................310
13.5.1.	Использование ссылок на другие файлы.....................311
13.5.2.	Использование гиперссылок................................312
13.6.	Новые служебные функции Mathcad 13.............................314
13.6.1.	Уменьшение размера файлов................................314
13.6.2.	Переключатель версий Mathcad.............................315
13.6.3.	Автосохранение...........................................315
Глава 14. Работа с текстом...........................................316
14.1.	Изменение стиля текстовых областей.............................316
14.1.1.	Установка свойств абзаца.................................316
14.1.2.	Изменение стиля отдельной текстовой области..............318
14.1.3.	Списки и таблицы в тексте................................319
14.2.	Использование гиперссылок......................................320
14.2.1.	Переход на метку.........................................320
14.2.2.	Всплывающий документ.....................................322
Глава 15. Работа с графиками.........................................323
15.1.	Построение двухмерного плоского графика........................323
15.2.	Построение полярных графиков...................................327
Оглавление
9
15.3.	Построение трехмерных графиков.......................................328
15.3.1.	Построение графика по массиву значений функции.................328
15.3.2.	Быстрое построение графика.....................................329
15.3.3.	Создание массива значений функции..............................332
15.3.4.	Поверхности тел вращения.......................................334
15.3.5.	Построение сложных фигур.......................................336
15.3.6.	Построение многогранников......................................338
15.3.7.	Быстрое изменение типа графика........................... . 339
15.3.8.	График векторного поля.........................................340
15.4.	Особенности форматирования графиков в	новых версиях Mathcad....340
15.4.1.	Редактирование двухмерных графиков.............................340
15.4.2.	Форматирование двухмерных графиков.............................342
15.4.3.	Функции logspace и logpts......................................343
Глава 16. Справочная информация в Mathcad..................................345
16.1.	Меню Help (Помощь)...................................................345
16.2.	Перевод справочной системы Mathcad...................................347
16.3.	Электронная книга qscheet............................................348
16.3.1.	Обзор и учебник................................................350
16.3.2.	Примеры и справочные таблицы...................................350
16.4.	Mathcad и Интернет...................................................352
16.4.1.	Техническая поддержка Mathcad..................................353
Глава 17. Создание электронных книг........................................354
17.1.	Создание Mathcad-файлов для электронной книги........................355
17.2.	Подготовка содержания электронной книги..............................356
17.3.	Создание системы ссылок между файлами................................357
17.4.	Создание НВК-файла...................................................357
17.5.	Вложенные папки......................................................359
17.6.	Проверка электронной книги...........................................360
17.7.	Создание поисковых индексов..........................................361
Глава 18. Работа с электронной книгой......................................365
18.1.	Обработка экспериментальных данных...................................365
18.2.	Обработка цифрового сигнала..........................................368
18.3.	Оптимизация нагрузки на балку........................................369
Часть IV. Примеры инженерных расчетов в Mathcad...............................373
Пример 1. Проверка статистических гипотез..................................375
Пример 2. Расчет электрической цепи переменного тока.......................375
Пример 3. Переходные процессы при замыкании-размыкании электрической
цепи.................................................................376
Пример 4. Кинематический анализ кулачкового механизма......................376
Пример 5. Движение двух машин по мосту.....................................377
Пример 6. Расчет моментов инерции сечения, заданного аналитически..........378
Пример 7. Расчет моментов инерции сечения, заданного набором точек
на контуре...........................................................378
Пример 8. Расчет геометрических характеристик составного сечения....378
Пример 9. Определение внутренних усилий при растяжении стержня......379
Пример 10. Определение внутренних усилий при кручении стержня.......379
Пример И. Определение внутренних усилий при изгибе консольной балки	.	.	.	380
Пример 12. Определение внутренних усилий при изгибе балки на двух опорах	.	380
10
Оглавление
Пример 13.	Растяжение статически-определимого стержня.................381
Пример 14.	Растяжение статически-неопределимого стержня...............382
Пример 15.	Растяжение-сжатие статически неопределимой
шарнирно-стержневой системы................................382
Пример 16. Расчет простейших соединений...................'...........382
Пример 17. Расчет статически определимого стержня на кручение.........382
Пример 18.	Расчет	статически неопределимого стержня	на кручение......383
Пример 19.	Расчет	на изгиб консольной балки..........................383
Пример 20.	Расчет	на изгиб балки на двух опорах......................384
Пример 21.	Расчет	на изгиб балок на упругом основании................384
Пример 22.	Учет пластических деформаций при растяжении-сжатии........385
Пример 23.	Учет упругопластических деформаций при изгибе.............385
Пример 24.	Учет пластических деформаций при кручении.................385
Пример 25.	Расчет прямого стержня на сложное сопротивление...........385
Пример 26.	Расчет пространственного стержня на сложное сопротивление. . . . 386
Пример 27.	Определение перемещений систем из нескольких элементов....387
Пример 28.	Раскрытие статической неопределимости плоской рамы........387
Пример 29.	Расчет	один раз статически неопределимой системы..........388
Пример 30.	Расчет	пространственной статически неопределимой рамы.....388
Пример 31.	Расчет	многопролетной балки с одной заделкой на изгиб.....389
Пример 32.	Расчет	многопролетной балки на изгиб......................389
Пример 33.	Расчет	на устойчивость сжатого стержня....................389
Пример 34. Определение критических нагрузок на сжатый стержень
энергетическим методом................................................390
Пример 35.	Продольно-поперечный изгиб балок..........................390
Пример 36.	Расчет консольной балки на удар и колебания...............391
Пример 37.	Расчет балки на двух опорах на удар и колебания...........391
Пример 38.	Расчет сложной системы на удар и устойчивость.............391
Пример 39.	Статистическая обработка результатов эксперимента.........392
Пример 40.	Расчет болта на усталостную прочность.....................392
Пример 41.	Расчет долговечности детали при нестационарном нагружении . . . 392
Пример 42.	Расчет долговечности полосы с трещиной....................393
Пример 43.	Построение диаграммы истинных напряжений..................393
Пример 44.	Расчет тонкостенной оболочки..............................394
Пример 45.	Оптимизация расчета кронштейна............................395
Пример 46.	Оптимальный расчет сферической крышки.....................395
Пример 47.	Подбор нагрузок по перемещениям балки.....................396
Пример 48. Подбор нагрузок на балку, удовлетворяющих граничным
условиям..............................................................396
Пример 49.	Поиск оптимальных размеров сечения балки..................396
Пример 50.	Динамический расчет балки матричным методом перемещений . . . 396
Пример 51. Динамический расчет плоской рамы методом конечных
элементов.............................................................397
Пример 52. Расчет пространственной стержневой системы.................397
Пример 53. Расчет кольца методом конечных элементов...................397
Пример 54. Решение уравнения Пуассона при кручении стержня............398
Пример 55. Решение плоской упругопластической задачи методом конечных
элементов.............................................................398
Пример 56. Использование прямоугольного квадратичного элемента в методе
конечных элементов....................................................399
Предисловие
Основное назначение этой книги — помочь пользователям быстро создавать
свои расчетные программы любой сложности. Для удобства читателей книга
разбита на 4 части.
Часть I предназначена для тех, кто впервые сталкивается с Mathcad. Здесь со-
держатся основные сведения, необходимые и достаточные для решения боль-
шинства задач.
В части II содержатся подробные сведения обо всех возможностях Mathcad, на
конкретных примерах рассматриваются особенности использования встроенных
функций, основные приемы и способы вычислений.
В части III рассматриваются возможности подготовки документов Mathcad.
Часть IV книги содержит 56 примеров решения инженерных задач в Mathcad.
ВНИМАНИЕ --------------------------------------------------------
Неотъемлемой частью книги является электронная книга, встраиваемая в оболочку Math-
cad, которую можно скачать с сайта издательства www.piter.com или с сайта автора книги
www.emakarov.nsknet.ru. В электронной книге вы найдете Mathcad-программы использо-
вания всех встроенных функций и всех описанных в книге примеров.
При написании книги я отошел от традиционного описания меню и панелей.
Интерфейс Mathcad ничем не отличается от традиционных Windows-прило-
жений. Знакомство с меню происходит непосредственно во время работы. По-
яснения к отдельным пунктам меню появляются в тексте по мере необходи-
мости.
Mathcad и его возможности
Mathcad создан разработчиками как инструмент работы расчетчиков-инжене-
ров. Он не предназначен для профессиональных математиков — для них есть
другие системы, действующие в областях символьной математики и математиче-
ской статистики.
Время от времени выходят новые версии Mathcad, но они почти не добавляют
новых функций, новых расчетных возможностей. Зато добавляют новые ограни-
чения, новые сложности в использовании Mathcad.
На мой взгляд, лучшей версией был Mathcad И. Последующие программы
в связи с переходом на Net-технологии стали гораздо более медленными, и до-
полнились множеством ограничений. Последние версии Mathcad, 14 и 15, по
своим вычислительным возможностям абсолютно одинаковы. Особенно прият-
но, что они «русифицированы» — вы увидите меню на русском языке. В Math-
cad 15 даже включено руководство пользователя на русском языке, но все статьи
в разделе Help (Помощь) по-прежнему написаны на английском языке.
12
Предисловие
На одном компьютере одновременно могут работать две версии программы:
Mathcad Ии Mathcad 14 (или 15), Mathcad 13 и Mathcad 15. Но обратите вни-
мание на то, что версии Mathcad 14 и Mathcad 15 не будут работать вместе.
ВНИМАНИЕ ----------------------------------------------------------
При установке двух версий на компьютер вначале ставится более старая версия, например
Mathcad И, а затем новая. В противном случае со сбоями будут работать обе версии.
Mathcad в современном виде не предназначен и для программирования сложных
задач — для этого есть система Mathlab, языки программирования Fortran и C++.
Он создавался как мощный микрокалькулятор, позволяющий легко справляться
с рутинными задачами инженерной практики, ежедневно встречающимися в ра-
боте: решение алгебраических или дифференциальных уравнений с постоянны-
ми и переменными параметрами; анализ функций, поиск их экстремумов; чис-
ленное и аналитическое дифференцирование и интегрирование; вывод таблиц
и графиков при анализе найденных решений.
Главными достоинствами Mathcad и его колоссальным преимуществом перед
другими расчетными средствами являются легкость и наглядность программи-
рования задачи, отображение сложных математических выражений в том виде,
в каком они обычно записываются на листе бумаги, то есть отсутствие специаль-
ного языка программирования, простота использования, возможность создания
средствами Mathcad высококачественных технических отчетов с таблицами, гра-
фиками и текстом.
Mathcad завоевал популярность во всем мире. Им пользуются в работе свыше
0,5 млн человек. Уже в первых версиях Mathcad появилась дискретная перемен-
ная, позволяющая одновременно находить значения функций для целого ряда
значений переменной и на основе полученных результатов строить таблицы
и графики без применения операторов программирования. При построении гра-
фиков поверхностей можно создавать почти произведения искусства. Доведена
до логического завершения великолепная функция решения дифференциальных
уравнений Odesolve.
На это^1 фоне в полном забвении находится раздел программирования в Math-
cad. По-видимому, этот раздел изначально был задуман для создания несложных
программных модулей, необходимых для многократного вычисления небольших
расчетных блоков из нескольких операторов.
На основании личного опыта я хочу в этой книге показать, что даже в таком
в общем-то зачаточном состоянии программирования Mathcad позволяет решать
задачи абсолютно любой сложности.
Кроме мелких недоработок в Mathcad есть два существенных недостатка, огра-
ничивающих его применение в качестве средства программирования:
1. Отсутствие встроенных средств отладки программ, которые есть в других
языках программирования.
2. Недостаточная скорость расчетов.
Новое в Mathcad 15
13
ПРИМЕЧАНИЕ --------------------------------------------------------
В Mathcad 13 появились средства отладки программ: панель Debug, функции trace
и pause, — но реальной помощи в отладке программ они не оказывают.
Некоторые рекомендации по ускорению расчетов в Mathcad приведены в главе 9.
На протяжении ряда лет я использую Mathcad для проведения сложных инже-
нерных расчетов. Я преподаю студентам ряд дисциплин механики с решением
всех задач в Mathcad. В математически сложных курсах, таких как теория пла-
стичности, численное решение любой, даже самой простой, задачи можно полу-
чить, только решив ее на компьютере. Удобнее всего это делать в Mathcad.
Главные достоинства Mathcad — простота и удобство использования — практи-
чески исчезают при составлении сравнительно сложных программ. Сплошь и ря-
дом возникают ситуации, когда Mathcad оказывается не в состоянии решить эле-
ментарные примеры. Вроде все просто и записано верно, а расчет не получается.
После длительных размышлений ошибка всегда обнаруживается и чаще всего
оказывается примитивной, но на отладку документа затрачивается масса вре-
мени.
Пользователи Mathcad — студенты и инженеры — не могут позволить себе не-
сколько дней корпеть над отладкой программ. Выходом из положения становится
сборка собственных программ из готовых и отлаженных фрагментов. В этом
вам поможет электронная книга (скачайте ее с сайта издательства www.piter.com).
Система вложенных оглавлений со ссылками позволяет практически мгновенно
найти нужный фрагмент, скопировать его в буфер обмена и вставить в свой ра-
бочий документ. Остается подправить вставленные фрагменты в соответствии со
своими исходными данными и обозначениями, связать их между собой по смыс-
лу — и документ готов. Такой метод «электронных кубиков» позволяет много-
кратно уменьшить затраты времени на создание и отладку расчетных программ,
возвращая Mathcad простоту и удобство использования.
Новое в Mathcad 15
После того как в 2006 году фирма РТС приобрела фирму Mathsoft, изменилось
стратегическое направление развития Mathcad.
Mathcad не является главным продуктом фирмы РТС. Основные продукты
фирмы — пакеты Pro/ENGINEER, Windchill и Arbortext, предназначенные для
автоматического проектирования конструкций и сопровождения проектов, соз-
дания технической документации, обмена информацией и объединения различ-
ных проектов.
Фирма РТС сразу занялась интеграцией своих продуктов с Mathcad, оставив без
внимания математическое развитие пакета Mathcad, и решила создать принци-
пиально новый пакет Mathcad Prime, сильно отличающийся от традиционного
прежде всего необычным интерфейсом и набором функций. Первый выпуск
Mathcad Prime вызвал резко отрицательный отклик пользователей. Тогда РТС
решила на время вернуться к старому варианту Mathcad, выпустив в 2010 году
14
Предисловие
Mathcad 15, не добавив в него практически ничего нового по сравнению с Math-
cad 14.
Вот что сказано о Mathcad 15 в рекламном проспекте фирмы РТС:
Описание: Mathcad® 15.0 включает в себя 25 функциональных обновлений, улучшенные
расчетные библиотеки и расширенную интеграцию с решениями сторонних производите-
лей, например с последней версией Microsoft Excel. Традиционно Mathcad® 15.0 превос-
ходно поддерживает работу систем автоматизированного проектирования, например Pro/
ENGINEER®, а также программное решение для управления данными от РТС — Windchill®
для крупных компаний и такое же решение для сектора среднего и малого бизнеса —
Windchill Product Point®. Что позволяет пользователям лучше управлять критически
важными инженерными данными, упрощает возможность взаимодействия команды разра-
ботчиков и повторного использования информации об изделии.
Новый Mathcad 15 — это
О функции для расчетов по планированию экспериментов (design of experiments (DoE)) —
добавлено 25 новых функций, помогающих сократить время, затраченное на натурные
эксперименты, за счет понимания общей тенденции при испытаниях. Приложения
DoE помогают найти критические факторы и оптимальные условия при испытаниях
сложных процессов. Содержатся шаблоны для проведения нескольких экспериментов,
при наличии нескольких уровней эксперимента (режимов тестирования) и различных
условий;
О углубленная интеграция с базой данных KnovelMath — быстрый доступ к базе по ин-
женерным и техническим стандартам сокращает время проведения сложных расчетов;
О интеграция с программным обеспечением Kornucopia, выпускаемым компанией Bodie
Technology, предназначенным для сокращения времени и усилий, затрачиваемых на
проведение анализа. Предоставляя шаблоны для расчетов в Mathcad, этот модуль по-
зволяет использовать наработанные процессы для всеобъемлющей оценки данных на-
турных экспериментов и результатов расчетов;
О первая интеграция с базой данных Truenumbers — Truenumbers от True Engineering
Technology предоставляет разработчикам доступ к различным справочным мате-
риалам и данным. Результаты из Mathcad просто передаются в различные форматы
документов, что значительно облегчает передачу данных по ключевой цепочке со-
трудников;
О поддержка операционной системы Microsoft Windows 7;
О поддержка Microsoft Excel 2007.
С точки зрения инженерных расчетов новые функции планирования экспери-
мента нужны лишь узким специалистам и не представляют интереса для боль-
шинства пользователей Mathcad. Чтобы ознакомиться с новыми функциями,
в стандартном меню Mathcad выберите Вставка функций ► План эксперимента
(рис. 0.1).
Интеграция с базами данных, анонсированная в рекламном проекте, представля-
ет собой выход на сайты, содержащие эти базы данных. Выйти на них можно
просто из оболочки Mathcad (рис. 0.2), выбрав в стандартном меню Mathcad
Инструменты ► Knovel, Kornucopia или Truenumbers.
Рекомендации по работе с книгой
15
Вставка функции
категория функции	ИМя функции
®	!	ОК	Вставка Отмена
Рис. 0.1. Функции планирования эксперимента в Mathcad 15
Mathcad - [Безымянный: 1 ]
Я Файл Правка Вид Вставка Формат
Инструменты
Символьные операции Окно Справка Проверка правописания
D т Й й в й	®	Анимация
[Normal vj Arial- Защитить документ...
Сравнить документы...
Поиск в Knovel Math
Поиск в технических библиотеках Kornucopia®
Truenumbers®
Вычислить
Оптимизировать
Отладка
Knovel®
Э X
100%
В
&
[*]
XS
<?
33
- П X
Рис. 0.2. Интеграция с новыми базами данных в Mathcad 15
Других новшеств в Mathcad 15 нет, к тому же сам Mathcad 15 идентифицирует
себя как Mathcad 14.
Рекомендации по работе с книгой
Изучать Mathcad, только читая книгу, бесполезно. Осваивать Mathcad надо,
сидя за компьютером. Рекомендую следующий стиль работы.
16
Предисловие
Прочитайте первую часть книги, затем садитесь за компьютер и шаг за шагом ос-
ваивайте основные приемы работы в Mathcad. Сведений, содержащихся в пер-
вой части, достаточно для выполнения подавляющего большинства расчетов.
Внимательно изучите их и приступайте к изучению Mathcad.
Остальные главы пока полистайте, чтобы иметь общее представление, о чем там
идет речь. При решении конкретных задач, когда сведений, приведенных в двух
главах первой части, становится недостаточно, обращайтесь к последующим гла-
вам или поищите похожую задачу (или кусок задачи) в электронной книге.
Нужный вам фрагмент программы скопируйте из электронной книги, вставьте
в свой расчет и подправьте в соответствии с вашими потребностями.
В Mathcad все операции можно выполнить, нажав соответствующую кнопку на
математической панели или клавишу на клавиатуре. Рекомендуется запомнить
наиболее часто употребляемые клавиши («горячие» клавиши), чтобы не обра-
щаться постоянно к математической панели. Это сэкономит вам много времени
при наборе программы. Сочетание клавиш для выполнения какой-либо опера-
ции появляется на экране рядом с курсором при наведении курсора на значок
данной операции в математическом меню.
Отзывы о данной книге прошу оставлять на сайте автора www.emakarov.nsknet.ru
или присылать по электронной почте emakarov@inbox.ru.
От издательства
Ваши замечания, предложения и вопросы отправляйте по адресу электронной
почты comp@piter.com (издательство «Питер», компьютерная редакция). Мы бу-
дем рады узнать ваше мнение! Подробную информацию о наших книгах вы най-
дете на веб-сайте издательства www.piter.com.
Электронная книга
Электронная книга, которую можно скачать с сайта издательства www.piter.com
или с сайта автора книги www.emakarov.nsknet.ru, является важнейшим дополне-
нием книги печатной.
Скачав папку «Электронная книга», прежде всего прочитайте файл Read Me.
Здесь вы найдете сведения об установке электронной книги. Ввиду важности
этой процедуры продублируем файл Read Me полностью.
ReadMe
В данной папке находятся:
1.	Файл ReadMe — сведения об установке электронной книги в оболочку Math-
cad.
2.	Электронная книга Расчеты в Mathcad, встраиваемая в оболочку Mathcad, ко-
торая содержит свыше ста Mathcad-файлов. В электронной книге приведены
все примеры, упоминаемые на страницах печатного издания, и 56 программ
решения задач в Mathcad,
3.	Примеры инженерных расчетов в Mathcad — подробные пояснения (в формате
pdf) ко всем 56 примерам, приведенным в электронной книге.
4.	Сведения об авторе книги (в формате pdf).
В папке находятся две одинаковые электронные книги, сохраненные в разных
версиях Mathcad.
1)	Mathcad 11Primer — файлы с расширением med, сохранены в формате версии
Mathcad 2000 и работают во всех версиях, включая Mathcad 15.
2)	Mathcad 14Primer-xmcd — файлы с расширением xmed, сохранены в формате
версии Mathcad 14 и могут быть открыты в Mathcad 14 или 15.
В Mathcad 13 или 14 при открытии файлов с расширением med у некоторых
пользователей не отображается русский шрифт (эта проблема связана не с де-
фектом электронной книги, а с операционной системой Windows). При запуске
файлов с расширением xmed русский текст отображается нормально.
Резюме: Для работы в Mathcad 14 или 15 установите электронную книгу Primer-
xmed. Для работы в старых версиях Mathcad, включая Mathcad 13, установите
электронную книгу Primer с расширением файлов tped.
Установка электронной книги
□	Для установки электронной книги надо скопировать папку primer и файл
primer.hbk в подкаталог установки
Mathcad_XXXHandbook (XXX — номер версии Mathcad).
В Mathcad 12 и 13 подкаталог Handbook отсутствует. Создайте его сами.
В ранних версиях Mathcad скопируйте каталог primer и файл primert.hbk
в корневой каталог Mathcad.
18
Электронная книга
□	После копирования указанных файлов при запуске Mathcad электронная
книга появляется в стандартном меню.
□	Для открытия электронной книги:
О в стандартной версии Mathcad выберите меню Help ► E-books ► Расчеты
в Mathcad;
О в ранних версиях Mathcad выберите меню Help ► E-books ► Open book и ука-
жите путь к файлу primer.hbk.
В Mathcad 12 не работают большинство программ, созданных в предыдущих
версиях.
В Mathcad 13-15 практически все программы работают правильно, за исключе-
нием нескольких операторов.
В Mathcad 11 все программы работают идеально.
В более ранних версиях проблем не возникает, если в программе не используют-
ся функции, добавленные в более поздних версиях.
Для работы с русским текстом в Mathcad 11 и более ранних версиях скопируйте
файл Normal.met в каталог Mathcad/Template, заменив стоящий там файл.
В Mathcad 12-15 скопируйте файл Normal.xmct в указанный выше каталок
После этого при запуске Mathcad будет открываться русифицированный шаб-
лон документа.	1
Если в электронной книге вместо русского текста напечатана абракадабра, за-
пустите файл RUSFONTS.exe из папки Русский шрифт и перезагрузитесь.
НЖрнерные расчеты в Mathcad; Г Program FilesMathsoftMa.
| File Edit View Insert Format Tools Symbolics gook Help
a di ffl й e ©
Данная электронная книга содержит:
Разработанные автором примеры
использования операторов и
встроенных функций Mathcad
Примеры использования Mathcad в
инженерных расчетах.
Инженерные расчеты в Mathcad
Qi
Автор электронной книги Е.Г.Макаров,
доцент БГТУ-Военмех, Санкт-Петербург.
для просмотра содержания книги щелкните мышью на слове
СОДЕРЖАНИЕ
При создании собственных Mathcad-документов пользователь
ж ______________________________________________
&
Press Fl for help.
AUTO
Рис. К.1. Титульная страница электронной книги
Сведения об электронной книге
19
Сведения об электронной книге
При выборе в стандартном меню Mathcad Help /Е-books/ Расчеты в Mathcad на эк-
ране монитора появляется титульная страница электронной книги Расчеты в Math-
cad, показанная на рис. К.1.
В электронной книге можно найти все примеры, представленные на страницах
печатного издания. Основное оглавление электронной книги содержит названия
глав (рис. К.2). Щелчок левой кнопкой мыши на названии главы вызывает от-
крытие Mathcad-файла данной главы.
Глава 19. Новое в Mathcad 13	Темы Рисунки
Нетрадиционные решения задач
Примеры инженерных расчетов в Mathcad
Press Fl for help.	AUTO
Рис. К.2. Основное оглавление электронной книги (начало и конец)
Рядом с названием главы расположены две кнопки, Темы и Рисунки. Выбор од-
ной из них вызывает появление вложенного оглавления с перечнем тем, рас-
смотренных в этой главе (рис. К.З), или списка рисунков этой главы. Каждый за-
головок связан ссылкой с соответствующим фрагментом Mathcad-документа.
В нижней части рис. К.2 показаны последние строки основного оглавления элек-
тронной книги. Обратите внимание на два важных раздела:
□	Нетрадиционные решения задач;
□	Примеры инженерных расчетов.
20
Электронная книга
№
Инженерные расуетыв Mmhcad:
File Edit View Insert Format Tools Symbolics Book Help
fl f Ф * 'О Qi й 1 @
Инженерные расчеты в Mathcad
Ра здел: Содержание справочника
Глава 3. Решение уравнений Темы
3.1.	Функция ГООТ
3.2.	Решение уравнения с переменными параметрами
3.3.	Нахождение корней полинома функция polyroots
3.4.	Решение систем уравнений
Решение системы уравнении с переменным параметром
Решение матричных уравнений
Путем обращения матрицы
С помощью функции Isolve (Mathcad 13)
3.6.	Приближенное решение уравнении и систем уравнении
3.7.	Исследование функции на экстремум
равенство нулю производной
U-a. .	______________В
[Press Fl for help.	AUTO
Рис. К.З. Оглавление Темы для главы 3
^,^нжсй₽рнне расчеты в Mathcad
File Edit View Insert Format Tools Symbolics Book Help
~ @ Di й О Э
Нетрадиционные решения задач
Ускоренное интегрирование функции методом трапеций
Поиск максимума функции путем перебора значений аргумента
без учета размерностей
с учетом размерностей
Использование вычислительного блока
Given-Find в программах
Использования преобразования координат
для изображения деформированного тела
Решение системы линейных алгебраических уравнений с
ленточной матрицей коэффициентов методом Холесского МСНВ
Решение дифференциального уравнения функции с разрывами
Двумерная интерполяция на неквадратнои поверхности
Фильтрация сигнала путем разложения в ряд Фурье
Использование составного массива для вывода
ряда скаляров и матриц из программного модуля
Учет размерностей в программных модулях	еще
Использование анимации для многократного
решения вычислительного блока Given-Find и др.
be____________________
Press Fl for help.	AUTO
Рис. К.4. Авторские «изюминки» в электронной кнйге
Назначение электронной книги
21
Раздел Примеры инженерных расчетов содержит ссылки на 56 примеров, разме-
щенных в электронной книге.
Раздел Нетрадиционные решения задач представляет собой перечень оригиналь-
ных авторских решений (со ссылками на Mathcad-файлы), позволяющих упро-.
стать и ускорить решение особо сложных задач (рис. К.4).
Система вложенных оглавлений позволяет быстро найти интересующий вас
фрагмент электронной книги, скопировать его в буфер обмена и вставить в свой
рабочий документ.
Подробные пояснения ко всем 56 примерам инженерных расчетов, приведенным
в электронной книге, можно найти в файле Примеры-все.рсН (Примеры инженер-
ных расчетов в Mathcad). Для его открытия на компьютере пользователя должна
быть установлена программа Acrobat Reader, FoxitReader или STDUViewer. Одна из
страниц этого файла показана на рис. К.5. В левой части окна программы выбе-
рите пункт Закладки (Bookmarks), чтобы увидеть перечень всех примеров. Щел-
чок левой кнопкой мыши на названии любого примера вызывает появление со-
ответствующей страницы документа на экране компьютера.
Рис. К.5. Примеры инженерных расчетов
Назначение электронной книги
Основное назначение электронной книги — дать возможность пользователю со-
бирать собственные программы из готовых фрагментов.
Написать программу расчета в Mathcad сравнительно просто, но на отладку про-
граммы уходит значительно больше времени, чем на ее написание, что лишает
22
Электронная книга
Mathcad его основного преимущества перед другими вычислительными систе-
мами.
Когда пользователь создает свою программу «с нуля», ему приходится выиски-
.вать в книгах примеры использования необходимых функций Mathcad, а затем
отлаживать написанную программу. Все это требует огромных усилий и боль-
ших затрат времени. Иной раз на то, чтобы исправить одну ошибку, уходит не-
сколько дней.
Ни один нормальный человек не в состоянии запомнить правила использования
встроенных функций и операторов Mathcad, да это и не требуется. В созданной
электронной книге подробно и с большим количеством примеров описываются
все возможности Mathcad. Описание почти каждой встроенной функции сопро-
вождается электронными ссылками на примеры инженерных расчетов.
Еще одно затруднение, с которым сталкиваются пользователи Mathcad, — это то,
что вся официальная документация Mathcad (файлы помощи и примеры) напи-
сана на английском языке. Но далеко не все пользователи в совершенстве владе-
ют иностранным языком и могут разобраться во всех тонкостях представленных
материалов. Недаром российские сайты по Mathcad буквально заполнены прось-
бами помочь отыскать русскоязычный Help к Mathcad. Предлагаемая электрон-
ная книга является практически первым русскоязычным полным электронным
справочником по пакету Mathcad.
Разработку программы надо начинать с создания алгоритма решения задачи
в виде последовательности связанных друг с другом формул, проще всего сде-
лать этот шаг на бумаге. Затем с помощью системы активных ссылок отыщите
в электронной книге подходящие примеры инженерных расчетов и примеры ис-
пользования встроенных функций. Нужные фрагменты электронной книги сле-
дует скопировать в свой рабочий документ, объединить их в единую программу
и ввести свои исходные данные. Документ готов.
Составление программы методом «электронных кубиков» позволяет многократ-
но сократить время, затраченное на изготовление программы, обеспечивает вы-
сокий уровень программирования. Mathcad действительно становится простым
и удобным средством решения инженерных расчетных задач.
Часть I
Начало работы с Mathcad
В этой части книги приводятся основные сведения, необходимые
для работы с Mathcad. Используя их, можно решить примерно
95 % всех задач. Внимательно изучите их и приступайте к работе
с Mathcad.
Глава 1
Построение выражений и графиков
в Mathcad
Перед началом работы в Mathcad ознакомимся с рабочим окном и содержанием
панелей управления. Далее описываются панели и окна Mathcad 14. В других
версиях Mathcad внешний вид и содержание панелей и окон немного отличают-
ся от описываемых ниже.
1.1. Интерфейс Mathcad
Интерфейс Mathcad по своей структуре аналогичен интерфейсу других Windows-
приложений.
1.1.1. Рабочее окно Mathcad
При открытии файла Mathcad.exe на экране появляется рабочее окно Mathcad
с главным меню и пятью панелями: Standard (Стандартная); Formatting (Форма-
тирование), Math (Математическая), Controls (Контроль) и Resources (Докумен-
тация) (рис. 1.1).
Рис. 1.1. Вид рабочего окна Mathcad после загрузки
1.1. Интерфейс Mathcad
25
Автоматически загружается файл Untitled 1 (Безымянный 1), представляющий
собой шаблон Normal (Обычный) рабочего документа Mathcad, называемого
Worksheet (Рабочий лист). Кроме того, автоматически загружаются окна Tip
of the day (Совет дня) и Mathcad Resource (Документация Mathcad). Перед нача-
лом работы их надо закрыть. В окне Tip of the day следует снять флажок Show tip
at startup (Показывать совет при загрузке) и щелкнуть на кнопке Close.
1.1.2. Главное меню
Главное меню Mathcad занимает верхнюю строку рабочего окна. Оно не зря на-
зывается главным. Все необходимые действия можно выполнить, следуя пунктам
этого меню и последовательно открывающихся окон. Вид главного меню пока-
зан на рис. 1.2, вверху. Щелчок мышью на любом пункте меню открывает подме-
ню с перечнем команд:
Рис. 1.2. Главное меню и панели Mathcad
1.	Управление рабочим окном Mathcad.
2.	File (Файл) — команды, связанные с созданием, открытием, сохранением, пе-
ресылкой по электронной почте и печатью на принтере файлов с документами.
3.	Edit (Правка) — команды, относящиеся к правке текста (копирование, встав-
ка, удаление фрагментов и т. д.).
26
Глава 1. Построение выражений и графиков в Mathcad
4.	View (Вид) — команды, управляющие внешним видом документа в рабочем
окне Mathcad, а также команды создания файлов анимации.
5.	Insert (Вставка) — команды вставки различных объектов в документ.
6.	Format (Формат) — команды форматирования текста, формул и графиков.
7.	Tools (Инструменты) — команды управления вычислительным процессом.
8.	Symbolics (Символьные вычисления) — команды символьных вычислений.
9.	Window (Окно) — команды, позволяющие управлять расположением окон
с различными документами на экране.
10.	Help (Помощь) — команды вызова справочной информации.
Щелчок мышью на пункте подменю вызывает появление соответствующего
диалогового окна.
Выбрав в главном меню (рис. 1.3) Tools ► Preference (Инструменты ► Пред-
почтения), можно сделать работу в Mathcad более удобной.
Рис. 1.3. Окно Preferences в Mathcad 15
1.1.3.	Панели инструментов
Панели инструментов служат для быстрого выполнения наиболее часто приме-
няемых команд. Вид панелей показан на рис. 1.2:
□	Главное меню Mathcad (на рисунке вверху) осуществляет полное управление
всеми процессами, кроме того, позволяет выполнить все команды, объединен-
ные в остальные меню.
□	Standard (Стандартная) служит для выполнения действий с файлами, редак-
тирования документов, вставки объектов и т. д.
1.1. Интерфейс Mathcad
27
□	Formatting (Форматирование) предназначена для форматирования текста
и формул.
□	Math (Математика) служит для вставки математических символов и операто-
ров в документы.
□	Recources (Дополнительные ресурсы) содержит список электронных книг,
включенных в оболочку Mathcad.
□	Controls (Контроль) содержит кнопки для дополнительного контроля работы
Mathcad-документа.
□	Debug (Отладка) появилась в Mathcad 13, служит для трассировки выполне-
ния программ.
При наведении указателя мыши (курсора) на любую из кнопок рядом с ней по-
является всплывающая подсказка — короткий текст, поясняющий назначение
кнопки.
Содержание панелей (кроме главного меню) можно корректировать. При наве-
дении курсора на панель и нажатии правой кнопки мыши появляется контекст-
ное меню с двумя пунктами, Hide (Скрыть панель) и Customize (Выбрать нужные
кнопки). Выбрав Customize, можно удалить старые и добавить на панель новые
кнопки из предлагаемого списка.
Кратко рассмотрим типичное содержание панелей, показанных на рис. 1.2.
Стандартная панель
Стандартная панель Mathcad содержит перечисленные далее пункты:
1.	Создание документа на основе шаблона Normal (Обычный).
2.	Перечень предлагаемых шаблонов документов.
3.	Открытие файла.
4.	Сохранение файла.
5.	Печать файла.
6.	Просмотр печати (вид готового документа).
7.	Проверка орфографии (только англоязычного текста).
8.	Вырезание объекта.
9.	Копирование объекта.
10.	Вставка объекта.
И. Отмена предыдущего действия (только при вводе текста или формул).
12.	Повтор отмененного действия.
13.	Выравнивание выделенной группы объектов по горизонтали.
14.	Выравнивание выделенной группы объектов по вертикали.
15.	Список встроенных функций и их вставка.
16.	Список размерностей и их вставка.
17.	Пересчет документа.
28
Глава 1. Построение выражений и графиков в Mathcad
18.	Вставка гиперссылки.
19.	Component Wizard (Вставка компонентов) — вставка в рабочий документ окна
другого приложения.
20.	Масштаб и его изменение.
21.	Открытие окна Mathcad Help (Справочная система Mathcad).
Ряд кнопок стандартного меню, показанного на рис. 1.2, мною уже удален. Это
кнопки вызова конкретных компонентов других программ, о которых в данной
книге не говорится.
Панель форматирования
Панель форматирования Mathcad содержит следующие пункты:
1.	Стиль набора текста и формул.
2.	Шрифт, применяемый для набора текста и формул.
3.	Размер шрифта.
4.	Полужирный шрифт.
5.	Курсив.
6.	Подчеркнутый шрифт.
7.	Выравнивание текста по левому краю.
8.	Выравнивание текста по центру.
9.	Выравнивание текста по правому краю.
10.	Маркированный список.
И. Нумерованный список.
Математическая панель
Математическая панель со всеми подчиненными панелями инструментов пока-
зана на рис. 1.4. Щелчок мышью на любом из значков вызывает вставку на место
курсора в рабочем документе соответствующего этому значку символа или шаб-
лона выполнения математической операции.
Рассмотрим панели инструментов подробнее:
1.	Calculator (Калькулятор) — вставка шаблонов основных математических опе-
раций, цифр, знаков арифметических операций.
2.	Graph (График) — вставка шаблонов графиков.
3.	Matrix (Матрица) — вставка шаблонов матриц и матричных операций.
4.	Evaluation (Оценка) — операторы присвоения значений и вывода результатов
расчета.
5.	Calculus (Вычисления) — вставка шаблонов дифференцирования, интегриро-
вания, суммирования.
6.	Boolean (Булевы операторы) — вставка логических (булевых) операторов.
7.	Programming (Программирование) — операторы, необходимые для создания
программных модулей.
8.	Greek (Греческие буквы).
1.1. Интерфейс Mathcad
29
9.	Symbolics (Символика) — вставка операторов символьных вычислений.
Панель ресурсов
В выпадающем меню панели Resources (см. рис. 1.2) содержится список элек-
тронных книг, включенных в пакет Mathcad:
Рис. 1.4. Математическая панель
□	Tutorials — обучение работе с Mathcad.
□	QuickSheets — примеры использования Mathcad.
□	Reference Tables — справочные таблицы.
□	Data Analysis Extension Pack — пакет для работы с наборами данных.
□	Images Processing — обработка изображений в Mathcad.
□	Signal Processing — обработка цифровых сигналов в Mathcad.
□	Wavelets Extension Pack — волновые преобразования массивов данных в Mathcad.
□	Расчеты в Mathcad — электронная книга.
При нажатии кнопки Go открывается окно справочной информации Mathcad.
Панель контроля
Панель Controls содержит кнопки для дополнительного контроля над работой
Mathcad-документа. Эти кнопки предназначены для украшения документа, ис-
пользуются в качестве средства диалога с пользователем, для управления рабо-
той подключенных к документу других файлов. Их использование, как правило,
требует написания пользовательских DDL-файлов. При разработке Mathcad-
30
Глава 1. Построение выражений и графиков в Mathcad
документов нет необходимости использовать такие средства контроля. В данной
книге они не рассматриваются. Подробные сведения о них содержатся в меню
Help (Помощь), раздел Developer’s Reference (Руководство для разработчиков).
Панель Debug (Отладка)
Панель Debug, появившаяся в Mathcad 13, содержит кнопки вызова на экран
окна отладки программ и включения (остановки) процесса трассировки (вывода
промежуточных результатов расчета на экран) (см. рис. 9.27).
При наведении курсора на кнопку панели инструментов появляется всплываю-
щая подсказка с названием операции и сочетанием клавиш, нажатие которых эк-
вивалентно щелчку на данной кнопке.
1.2.	Построение выражений и их вычисление
Перед началом работы курсор на экране имеет вид крестика. В момент ввода вы-
ражения курсор приобретает вид синего уголка, обрамляющего вводимое выра-
жение. В рабочем документе введите какие-либо буквенные выражения и при-
свойте им численные значения. Имя выражения (все, что стоит слева от оператора
присваивания) может состоять из латинских, русских, греческих и других букв
и цифр, знаков подчеркивания (_), штриха ('), символа процента (%), знака бес-
конечности, вводимых с клавиатуры.
Имена переменных и функций не могут начинаться с цифры, знака подчеркива-
ния, штриха, символа процента, не могут включать в себя пробелы. Символ бес-
конечности может быть только первым символом в имени.
ВНИМАНИЕ ----------------------:---------------------------------
Mathcad воспринимает прописные и строчные буквы как различные идентификаторы,
то же касается букв, изображенных различными шрифтами, — это разные имена.
Mathcad не делает различий между именами переменных и функций. Если вна-
чале определить функцию /(х), а затем — переменную /, окажется невозможно
использовать f(x) в расчетах где-либо после определения /.
ПРИМЕЧАНИЕ -----------------------------------------------------------
Mathcad 12 не допускает переопределения значений функций. Mathcad 13-15 его разре-
шают, но предупреждают о нем появлением волнистой линии под именем функции.
В окне Preference (Параметры) (см. рис. 1.3), выбрав вкладку Warnings (Предупреждения),
можно такие предупреждения отключить.
Некоторые имена уже используются Mathcad для встроенных констант, единиц
измерения и функций. Имена можно переопределить, но следует учитывать, что
это уничтожит их встроенные значения и этими константами и функциями поль-
зоваться будет нельзя.
Оператор присваивания (:=) в первый раз выберите на математической панели
Calculator (Калькулятор). Познакомьтесь с содержанием панели. При наведении
стрелки указателя мыши на какую-либо кнопку появляется всплывающая под-
сказка с названием оператора, вызываемого при щелчке на этой кнопке, и указа-
1.3. «Цепкие» операторы
31
нием клавиши или сочетания клавиш, нажатие которых вызывает то же дейст-
вие, что и щелчок на кнопке. В дальнейшем оператор присваивания вы будете
набирать с клавиатуры, нажав клавишу «двоеточие» (:). Запоминайте «горячие»
клавиши!
Все операции в Mathcad продублированы. Их можно ввести:
□	выбрав соответствующий пункт меню;
□	нажав соответствующую клавишу (сочетание клавиш) на клавиатуре.
Набрав вычисляемое выражение, нажмите клавишу (=) — появится численный
результат (рис. 1.5).
Попробуйте набрать Х - - — у вас получится х + —. Для правильной записи
4	4
надо нажать клавишу пробела так, чтобы уголок курсора охватывал нужную часть
выражения (в нашем случае х + у). Другой способ — взять выражение в скобки
(% + у). В некоторых случаях это просто необходимо.
х = 5	у:=3	а:=10	(5 + 3)10 = 80 (х+у)а = 80
J*a
3.	1П3	d 3 ..
х dx = 2 .5 х 10	—х = 75
о	<**
Рис. 1.5. Примеры построения математических выражений
1.3. «Цепкие» операторы
С первым захватом «цепкого» оператора вы уже познакомились на примере дро-
би. «Цепкие» операторы — это возведение в степень, извлечение корня, знамена-
тель дроби (рис. 1.6). Чтобы «вырваться из объятий» «цепкого» оператора, надо
выделить клавишей пробела или клавишей —> (стрелка вправо) нужную часть
выражения, тогда следующая операция будет относиться ко всему выделенному
выражению.
надо записать так
2х + а = 42
2	0.3
х + V
-----i----а + 2= 116.612
1п(а)
7(х + у) - - 8 - -7.434
забыл нажимать пробелы
~х+а _ _ 1 п4
2	= 3.277 х 10
о.з
2+у*‘>‘+а
X 7
= 127.696
х + у——— = 2.828
а-8
Рис. 1.6. Примеры построения выражений с «цепкими» операторами
На первых порах «цепкие» операторы раздражают. Вы начинаете печатать быст-
рее и не всегда вспоминаете о выделении нужной части выражения. В результате
вместо, например, х2 + у на экране появляется х2 + у. Поупражняйтесь во введе-
нии выражений и получении их результатов (рис. 1.7).
Для возведения числа в степень используйте клавишу А.
32
Глава 1. Построение выражений и графиков в Mathcad
вычислить самостоятельно Л
а := 3 b := 5 с := 2
2
24 + б012 Ьа <а+.^<а-Ь!) + 2-———
а<С-Ь> • с3 + 2
'"С
32 0.12	1	£
J12 +-------- ,	,
v ________	2	а b «	d b
^26 - 3	е a da —а
Jo
Рис. 1.7. Самостоятельная работа. Построение выражений и их вычисление
1.4.	Редактирование объектов Mathcad
Редактирование введенных выражений производится обычным для всех Windows-
приложений способом:
□	Уголок курсора перемещается по экрану клавишами со стрелками или щелч-
ком левой кнопки мыши в нужном месте экрана.
□	Для выделения уголком курсора одного символа надо установить синий уго-
лок курсора так, чтобы он охватывал нужный символ слева или справа.
□	Для расширения выделения на часть выражения или на все выражение цели-
ком следует использовать клавиши со стрелками или клавишу пробела. Для
выхода из «цепкого» оператора предпочтительно пользоваться клавишей про-
бела. Уголок курсора должен охватывать все выражение или всю его часть,
над которой надо выполнить какие-либо действия.
□	Для выделения части выражения или всего выражения надо щелкнуть мы-
шью в начале или в конце выделяемой части выражения и переместить кур-
сор до другого края, не отпуская левую кнопку мыши. Можно использовать
комбинацию клавиш Shift+<— или Shift+—>. Выделенная часть выражения име-
ет черный фон. Выделение в Mathcad используется для вырезания или копи-
рования части выражения, изменения шрифта, а также для выполнения сим-
вольных вычислений с частями выражений.
□	Для выделения объекта или группы объектов (любых — математических,
текстовых или графических) надо щелкнуть мышью на свободном месте ра-
бочего документа и растянуть пунктирный прямоугольник выделения так,
чтобы он охватил нужные вам объекты. Один объект при этом будет выде-
лен синим уголком курсора, а группа объектов — обведена пунктирной рам-
кой.
Все три вида выделения выражений показаны на рис. 1.8.
Если надо удалить, вырезать или скопировать в буфер обмена выделенную часть
выражения, выделенный объект целиком или группу выделенных объектов, вы-
полните следующие действия:
□	для удаления (безвозвратного) нажмите клавишу Delete или Backspace;
□	для вырезания в буфер обмена нажмите кнопку Cut (Вырезать) с изображе-
нием ножниц на стандартной панели Mathcad. При начатии кнопки Cut
объект исчезает из рабочего документа, но переносится в буфер;
1.5. Стандартные функции
33
□	для копирования в буфер обмена нажмите кнопку Сору (Копировать) с изо-
бражением двух страниц на стандартной панели Mathcad. При нажатии кноп-
ки Сору объект остается в рабочем документе и копируется в буфер;
□	для вставки объекта из буфера обмена установите крестообразный курсор
в то место, куда вы хотите вставить содержимое буфера обмена, и нажмите
кнопку Paste (Вставить) на стандартной панели Mathcad.
Поскольку вырезать, копировать, вставлять объекты приходится часто, полезно
запомнить сочетания клавиш, нажатие которых вызывает эти действия:
□	Cut (Вырезать) — Ctrl+x;
□	Сору (Копировать) — Ctrl+c;
□	Paste (Вставить) — Ctrl+v;
□	Undo (Отмена предыдущего действия) — Ctrl+z.
Эти действия выполняются сочетаниями клавиш, расположенных по соседству,
и поэтому легко запоминаются. Как и во всех Windows-приложениях, выделен-
ный объект или выделенную группу объектов можно перетащить или скопиро-
вать с помощью мыши. Для этого следует:
□	подвести мышь к выделенному объекту или группе объектов, чтобы появи-
лась черная ладошка;
□	при нажатой левой кнопке мыши перетащить курсор в то место, куда надо пе-
реместить объекты;
□	если нужно скопировать выделенные объекты, после появления черной ла-
дошки нужно нажать левую кнопку мыши, затем клавишу Ctrl и, удерживая
их нажатыми, перетащить курсор в нужное место.
СОВЕТ -----------------------------------------------------------------
При работе с Mathcad постоянно пользуйтесь правой кнопкой мыши. В возникающем при
этом контекстном меню появляются, как правило, самые нужные в данный момент пунк-
ты, в частности, почти всегда присутствуют пункты Cut (Вырезать), Сору (Копировать),
Paste (Вставить).
1.5.	Стандартные функции
Mathcad содержит свыше 200 встроенных функций. На стандартной панели на-
жмите кнопку f(x). Вы увидите список всех встроенных функций. Просмотрите
группы функций (левый список). Щелкнув мышью на любой из групп функций,
вы увидите справа перечень функций, входящих в эту группу. В этой части кни-
ги мы рассмотрим не все функции, а только те, которые используются в приве-
денных примерах. Познакомиться с остальными функциями можно в части II
книги, а также нажав кнопку f(х) на стандартной панели.
Начнем с двух групп: Log and Exponential (Логарифмические и экспоненциаль-
ные) и Trigonometric (Тригонометрические). Присмотритесь к написанию этих
функций (см. рис. 1.8), которое не всегда совпадает с привычной математиче-
ской записью. Названия функций можно вводить со стандартной панели из
34
Глава 1. Построение выражений и графиков в Mathcad
раскрытого окна функций f(х), выделив название функции и нажав кнопку Insert
(Вставить), или набрав имя функции на клавиатуре в точности так, как оно за-
писано в окне функций.
Наберите и вычислите несколько разных функций.
Числовые константы] е = 2.718 л = 3.142 оо
[стандартные функций) х := 5 а := 10
In! = 2 log(x) = 0.699 expf-^ = 24.121
= -0.4621
tan(a) = 0.648 cot(a) = 1.542 atan(a) = 1.471
Рис. 1.8. Примеры использования встроенных констант и функций
1.6.	Числовые константы. Ввод греческих букв
Введенная с клавиатуры латинская буква е внутри математического выражения
означает основание натурального логарифма (см. рис. 1.8) е = 2,718. Это значение
можно отменить и присвоить е другое значение, использовав знак локального
присваивания :=, например: е:=2.
Знак бесконечности оо можно вставить с математической панели Calculs (со зна-
ком интеграла).
Часто используемое в выражениях число tv можно набрать с математической па-
нели Calculator (Калькулятор), где есть кнопка tv, или нажать аналогичную кноп-
ку панели греческих букв.
СОВЕТ -------------------------------------------------------------
Есть и более простой способ ввода греческих букв. Надо с клавиатуры набрать латинский
аналог греческой буквы, как правило, первую букву в латинском названии греческой бук-
вы. Введя аналог греческой буквы, следует нажать комбинацию клавиш Ctrl+G. На экране
появится греческая буква — прописная или строчная в зависимости от того, в верхнем или
в нижнем регистре был набран ее латинский аналог.
Греческие буквы:	
Их аналоги:	a bcdehg Imnwfpyr s tqxz
Наберите несколько выражений с греческими буквами, например: 6:= 2, Д:= 2,
sin(a)n т. д.
ВНИМАНИЕ -----------------------------------
Mathcad вычисляет выражения слева направо и сверху вниз.
1.7. Ввод текста
35
Если какой-либо константе или переменной не присвоено никакого значения ле-
вее и выше ее положения на экране, то она окрашена в красный цвет, что свиде-
тельствует об ошибке.
1.7.	Ввод текста
Для ввода текста в документ можно в главном меню выбрать команду Insert ► Text
Region (Вставить ► Текстовую область), но лучше ввести с клавиатуры символ "
(кавычка). При этом на экране появляется текстовая область, в которой можно пе-
чатать текст.
СОВЕТ --------------------------------------------------------------
Еще лучше, сменив латинский шрифт на русский, печатать текст прямо в математической
области. Когда напечатано первое слово, при нажатии клавиши пробела область с напеча-
танным словом автоматически из математической превращается в текстовую.
В текстовую область можно вставлять математическую область. Для этого в глав-
ном меню Mathcad следует выбрать команду Insert ► Math. Region (Вставить ►
Математическую область). Вставленная математическая область участвует в вы-
числениях наравне с другими математическими выражениями.
ПРИМЕЧАНИЕ ---------------------------------------------------------
Начиная с Mathcad 13 при наборе текстовой области в контекстном меню (при нажатии правой
кнопки мыши) присутствует пункт Insert Math.Region (Вставить математическую область).
При желании вставленную математическую область можно отключить (рис. 1.9).
Для этого щелкните правой кнопкой мыши на вставленном выражении и в от-
крывшемся контекстном меню выберите команду Disable Evaluation (Отключить
вычисление). После этого вставленное математическое выражение будет играть
роль иллюстрации.
вычислить самостоятельно f (z) :=
sm* х |-21	----------------------------------
Примечание для выбранного фрагмента...
Отображать умножение как
X Вырезать
§=> Копировать
| ® Вставить
Й* Свойства...
Отключить вычисление
Оптимизировать
Рис. 1.9. Математическая область, вставленная в текст
Текстовой области в Mathcad присвоен стиль Normal. Чтобы настроить его, про-
делайте следующее:
1. В главном меню выберите команду Style ► Normal ► Modify ► Font (Стиль ► Обыч-
ный ► Изменить ► Шрифт).
36
Глава 1. Построение выражений и графиков в Mathcad
2. В появившемся диалоговом окне выберите нужные вам шрифт (Font), форму
шрифта (Style Font) и размер (Size).
Шрифты Mathcad плохо воспринимают кириллицу. В частности, привычный по
работе в Word шрифт Times New Roman кириллицу не принимает. С кирилли-
цей работают шрифты System и Ms Sans Serif.
СОВЕТ ------------------------------------------------------------------
В электронной книге содержатся файлы Normal.met и Normal.xmed с установленными
шрифтами, работающими с кириллицей. Для Mathcad 12, 13, 14 файл Normal.xmcd надо
скопировать в каталог Template папки, в которой установлен Mathcad. Если Mathcad само-
стоятельно выбирал путь для своей установки, то это C:Program Files MathsoftMathcad
14Template. Новый шаблон из электронной книги заменит старый, и впредь при каждом
открытии Mathcad на экране будет появляться установленный вами приспособленный
для работы с кириллицей шаблон документа. Для более ранних версий в каталог Template
надо скопировать файл Normal.met.
В Mathcad можно вводить и редактировать текст почти как в Word, но все-таки
это не так удобно. О вводе текста речь пойдет в части III книги.
1.8.	Функции пользователя
Удобство и эффективность расчетов в Mathcad определяется прежде всего воз-
можностью и легкостью создания функций пользователя. При многократном ис-
пользовании одного и того же выражения без функций пользователя просто не
обойтись.
Вид функции пользователя (рис. 1.10):
слева название функции (с параметрами в скобках),
справа, после оператора присваивания :=, вычисляемое выражение.
Переменные величины, входящие в правую часть, должны быть записаны в па-
раметры после имени функции. Все величины из правой части, не входящие
в параметры левой части, должны быть заданы численно левее и выше функции
пользователя. В противном случае Mathcad указывает на ошибку, окрашивая не
заданную величину в красный цвет. При выделении функции щелчком мыши
появляется текст сообщения об ошибке This variable is not definited above (Эта пе-
ременная не определена ранее).
х := 3 а := 0.4 f(z) := sinx z / fl(z) := I f(z) dz
d	d3	°
f2(z) := ±f(z)	f3(z) > * f(z)
dz	dz
Здесь x и a - константы.
Рис. 1.10. Функции пользователя
Функция пользователя не вычисляется Mathcad, а принимается к сведению. Для
вычисления функции надо задать численные значения всех параметров в имени
1.9. Дискретные переменные. Построение таблиц
37
функции, набрать имя функции и нажать клавишу = или щелкнуть мышью на
кнопке = на стандартной панели Mathcad либо в математическом меню на пане-
ли Calculator Toolbar (Калькулятор).
1.9.	Дискретные переменные. Построение таблиц
Одно из лучших творений создателей Mathcad — это дискретная переменная, вы-
полняющая роль оператора цикла. В ряде книг по Mathcad ее называют ранжиро-
ванной переменной. Однако это не лучший перевод выражения «range variable».
Выражение «дискретная переменная», использовавшееся в ранних книгах, более
точно отражает суть понятия — диапазон изменения переменной: вместо непре-
рывной переменной используется ряд чисел, выстроенных в порядке возрастания
или убывания. Простота использования этого оператора восхищает. Без использо-
вания дискретной переменной было бы очень сложно построить графики, вывести
таблицы результатов расчета. Если в функцию пользователя подставить числен-
ное значение переменной, результатом расчета будет число. Дискретная перемен-
ная задает ряд значений переменной, для которых вычисляется функция пользо-
вателя. Этот ряд значений функции можно вывести в виде графика или таблицы.
Определение дискретной переменной имеет вид х := 0..5, что означает задание
ряда значений х = 0, 1, 2, 3, 4, 5. Пример:
/(х}= sin(x)cos(x), х:= 0..5, /(х) = ответ.
Ответ выводится в виде вектора — столбца чисел (рис. 1.11) — или графика
(рис. 1.12).
а:=10Ь:=5 п:=5 поменяйте а ,Ь,п
z:=O..J z =		5 zi : z) -	= 0,0.2.. zl =		1	z2 := e fl(zl) =	b - i,a + — r z2 =		 a L	.. b zj (2(z2) =	J:=b,b- = s3 =			b - a 	.. a n f3(z3) =
0		0		0		0		10		0.094		5		-0.106
1		0.141		0.2		0.171		9		0.189		6		-0.064
2		0.729		0.4		0.362		8		0.283				-0.034
3		0.998		0.6		0.514		7		0.362		T		-0.014
4		0.872		0.8		0.617		6		0.406		T		-5.754-1 O’4
5		0.542		1		0.669		5		0.384		10		7.867-10-3
измените формат чисел
Рис. 1.11. Дискретные переменные. Числовые результаты выведены
для функций, приведенных на рис. 1.10
Дискретная переменная может задавать как целые, так и дробные значения пере-
менной, но обязательно равноотстоящие друг от друга, например:
□	х — 0..5 — ряд целых чисел от 0 до 5;
□	х:= 1, 1,1..5 — ряд дробных чисел, где 1 — первое число, 1,1 — второе число,
5 — последнее число. Интервал между числами 1,1 - 1 =0,1;
38
Глава 1. Построение выражений и графиков в Mathcad
□	х:= А, А------..В — ряд чисел, где А — первое, А-----— второе, В — по-
п	п
следнее число (А и В должны быть заданы заранее), п — число интервалов, на
которые разбит отрезок от А до В. Такая форма записи удобна, когда рассмат-
риваются разные варианты одного расчета и изменение констант Ап В позво-
ляет мгновенно пересчитать результаты и перестроить графики.
ВНИМАНИЕ ----------------------------------------------------------:----
Двоеточие — знак диапазона нельзя набирать с клавиатуры, нажимая два раза клавишу
«точка». Надо на клавиатуре нажать клавишу ; (точка с запятой) или в математической
панели выбрать Matrix (значок матрицы) ► т..п.
Если константы, входящие в правую часть функции пользователя, не задаются
непосредственно перед использованием функции, Mathcad берет их значения, ис-
пользовавшиеся в последний раз перед данным расчетом. Проверьте, устраивают
ли вас эти значения. Наберите имя параметра и нажмите клавишу =.
Самостоятельно сделайте такой же график и отформатируйте его до такого вида
Рис. 1.12. Графики функций, приведенных на рис. 1.10
1.10.	Форматирование чисел
В Mathcad на результат расчета повлиять нельзя, но можно изменить формат
вывода чисел. Mathcad вычисляет все выражения с точностью 20 знаков, но вы-
водит на экран не все значащие цифры.
Установив указатель мыши на нужном численном результате расчета, сделайте
двойной щелчок левой кнопкой мыши. Откроется окно форматирования чисел
Result Format (Формат результата), открытое на пункте Number Format (Формат
чисел). В этом окне можно выбрать следующие форматы:
□	General (Общий) — принят по умолчанию. Числа отображаются с порядком.
Количество знаков перед запятой определяется в пункте Exponential threshold
(Порог экспоненты).
□	Scientific (Научный) — числа отображаются только с порядком: 1,22 • 105.
1.11. Построение плоского графика функции
39
□	Decimal (Десятичный) — десятичное представление чисел с плавающей запя-
той: 12,2564.
□	Engeneering (Инженерный) — числа отображаются только с порядком, крат-
ным 3: 1,22 • 106.
5	2
□	Fraction (Дробь) — в виде правильной или неправильной дроби: — или 1 -.
3	3
В дробном формате можно выбрать уровень точности (Level of accuracy) и сме-
шанные числа (Use fixed number).
Кроме вида формата можно изменять количество знаков после запятой (Number
of decimal pieces) и порог порядка (Exponential threshold). При превышении по-
рога число отображается с порядком. Примеры вывода чисел в различных фор-
матах приведены на рис. 1.13. Mathcad автоматически округляет числа до нуля,
если они меньше установленного порога.
форматы чисел| для выражения а := е10
4
General (по умолчани1о) а = 2.203 х 10
Scientific	а - 2.203 х 104 а = 2.203 х 104
Decimal	а « 22026.5
3
Engineering а = 22.026 х 10 а = 22.026Е-Ю03
с Г	11053739568	ппап. 233754 Fraction	а =	 а = 22026	 501839	501839 Вывод значений функций с использованием дискретной переменной Формат чисел z := 1.. 5 десятичный научный	инженерный z =	f(z) =	fl(z) =	f2(z) =								
	1		0.14112		6.692-10-1		-1.188-10°	
	2		-0.72905		3.201-10 -1		-541.892-10-3	
	3		-0.99838		-5.858-10-1		-35.271-10-3	
	4		-0.8723		-1.545-10°		255.407-Ю-з	
	5		-0.5415		-2.263-10°		384.096-Ю-з	
Рис. 1.13. Примеры форматирования результата численного расчета
Выбранные установки могут быть применены только к выделенному числу (вы-
берите пункт ОК) или по умолчанию ко всем числам данного документа (выбе-
рите пункт Set as default (Применить по умолчанию)).
1.11.	Построение плоского графика функции
Для построения плоского графика функции следует:
□	установить крестообразный курсор в то место, где надо построить график;
□	на математической панели щелкнуть мышью на кнопке Graph Toolbar ► X-Y Plot
(Плоский график);
40
Глава 1. Построение выражений и графиков в Mathcad
□	в появившемся на месте курсора шаблоне плоского графика ввести на оси
абсцисс имя аргумента, на оси ординат — имя функции;
□	щелкнуть мышью вне шаблона графика. График построен для заданного диа-
пазона изменения аргумента.
Если диапазон значений аргумента не задан, по умолчанию график будет постро-
ен в диапазоне значений аргумента от -10 до 10.
Чтобы на одном шаблоне разместить несколько графиков, надо, набрав на оси
ординат имя первой функции, нажать клавишу запятой (уголок курсора при этом
обязательно должен находиться в конце имени функции). В появившемся месте
ввода (черном квадратике) впишите имя второй функции и т. д.
Если две функции имеют разные аргументы, например, /t(x) и /2(#)> т0 на оси
ординат нужно ввести (через запятую) имена обеих функций, а на оси абсцисс
(также через запятую) — имена обоих аргументов, х и у. Тогда первый график
будет построен для первой функции по первому аргументу, а второй график —
для второй функции по второму аргументу.
Если функций введено несколько, а аргументов — 2, то график первой функции
строится по первому аргументу, а графики остальных функций — по второму.
Если ввести на осях ординат и абсцисс имена двух функций одного аргумента,
то будет построен параметрический график функции (рис. 1.14).
acos(a)
Рис. 1.14. Параметрический график функции
Чтобы отформатировать график, сделайте двойной щелчок мышью в поле графи-
ка — откроется окно форматирования графика (рис. 1.15). «Погуляйте» по окну.
Выбирайте различные пункты меню (щелкнув на них мышью, а затем на кнопке
Применить или ОК) и посмотрите, как изменится при этом вид графика.
В открывшемся окне (см. рис. 1.15) видны заголовки пяти вкладок:
1.	X-Y Axes (Оси X-Y) — отформатировать оси координат: нанести сетку линий,
проставить численные значения; ось абсцисс провести через ноль ординаты
(Crossed — по центру) или по нижнему краю графика (Boxed — по краям),
1.11. Построение плоского графика функции
41
Рис. 1.15. Окно форматирования плоского графика
нанести метки на графике. Щелкните мышью на нужных пунктах подменю
(отметьте их флажком):
О Log Scale — представить численные значения на осях в логарифмиче-
ской шкале. По умолчанию численные значения наносятся в равномерной
шкале;
О Grid Lines — нанести сетку линий;
О Numbered — нанести численные значения для каждой линии сетки;
О Auto Scale автоматически выбирает предельные численные значения на
осях, бблыпие максимальных вычисленных значений. Если этот пункт не
отмечен, предельными будут максимальные вычисленные значения;
О Autogrid — количество линий сетки выбирается автоматически. Если пункт
не отмечен, надо задать количество линий Number of Grids;
О Show Markers — нанести метки на графике. На каждой оси появляются два
места ввода, в которые можно ввести численные значения (можно не вво-
дить ничего или ввести одно число или буквенные обозначения констант).
На графике появятся горизонтальные или вертикальные пунктирные ли-
нии, соответствующие указанному значению на оси. В конце этой линии
появляется само число (см. рис. 1.14).
Имеется возможность нанести численные значения как слева, так и справа от
графика. Если это вам надо, поставьте флажок на пункте Enable Secondery Y-axis
(Включить дополнительную ось Y). С правой стороны графика появится Placeholder
(Место ввода), куда надо вписать имя функции, выводимой на график.
42
Глава 1. Построение выражений и графиков в Mathcad
.4
Рис. 1.16. Окно Trace (Трассировка) двухмерного графика в Mathcad
Цвет
Тип
ОсьУ
ЛИН
ЛИН.
рин.
ЛИН.
2.	Trace (Трассировка) — отформатировать графики функций (рис. 1.16). Для
каждого графика в отдельности задаются:
О Symbol Frequency (Частота символов) — на графике можно отмечать не все
расчетные точки, а через одну, через 2 и т. д.;
О Symbol (Символ) — обозначение расчетных точек на графике (выбрать
кружок, крестик, прямоугольник, ромб);
О Symbol Weight (Ширина символа) — размер значка, которым обозначается
расчетная точка;
О Line (Линия) — вид линии: Solid — сплошная, Dot — пунктир, Dash — длин-
ный пунктир, Dadot — штрих-пунктир;
О Line Weight (Толщина линии) — толщина линии;
О Color (Цвет) — цвет линии;
О Туре (Тип) — тип графика: Lines — линия, Points — точки, Ваг или Solid-
bar — столбики, Step — ступенчатый график и др.;
О Y-Axis (Ось Y) — в этой колонке Mathcad сам проставляет Y или Y2 в зави-
симости от того, слева или справа будут выведены численные значения
функции.
3.	Number Format (Формат чисел) — формат чисел, выводимых на графике.
4.	Labels (Заголовки) — вписать в область графика заголовок. В окне Title (Заго-
ловок) нужно записать текст заголовка, выбрать его положение — вверху или
внизу графика. Указать, если надо, названия осей (Axis Label).
1.11. Построение плоского графика функции
43
5.	Defaults (По умолчанию) — вернуться к виду графика, принятому по умолча-
нию (Change to default), либо использовать по умолчанию для всех графиков
данного документа (Use for default) выполненные вами изменения.
Выполните самостоятельную работу (рис. 1.17) и поработайте с графиками при-
веденных в примерах функций.
вычислить самостоятельно
и построить графики функций с ” ’
f(x) := sin(x)cos(x)	f(x) := е С Х „+ b sin(c x)
J-b	2
f(x) dx f2(x) := — f(x) f3(x) X,f(x)
c	*	dx
Рис. 1.17. Самостоятельная работа с графиками
Чтобы изменить размеры графика, нужно:
□	щелкнуть мышью в поле графика;
□	подвести указатель мыши к одному из черных квадратиков на краю графика;
□	при появлении двунаправленной стрелки нажать левую кнопку мыши и, удер-
живая ее, переместить край графика в нужное место.
Чтобы переместить график, нужно:
□	щелкнуть мышью в поле графика;
□	подвести указатель мыши к краю графика;
□	при появлении черной ладошки нажать левую кнопку мыши и, удерживая ее,
переместить график в нужное место.
ПРИМЕЧАНИЕ ------------------------------------------------------------
Точно так же можно переместить любой объект документа: выражение, текст, график.
Описанный способ перемещения объектов — традиционный для Windows. Однако
для больших документов он не всегда удобен, например, если надо перетащить
выделенную группу объектов на другую страницу. В этом случае удобнее другой
способ:
□	Нажать левую кнопку мыши и, удерживая ее, двигать мышь, заключая в по-
являющуюся при этом пунктирную рамку объекты, которые надо переместить.
□	На стандартной панели Mathcad щелкнуть мышью на кнопке Cut (Вырезать).
При этом выделенная группа объектов будет удалена из документа и помеще-
на в буфер обмена. Если нажать кнопку Сору (Копировать), выделенные объ-
екты будут скопированы в буфер, оставаясь на своем месте.
□	Подвести указатель мыши к месту, куда надо вставить вырезанные объекты,
и щелкнуть левой кнопкой мыши. Появится крестообразный курсор.
□	На стандартной панели Mathcad щелкнуть мышью на кнопке Paste (Вставить).
Готово, выделенные объекты перемещены в заданное место.
44
Глава 1. Построение выражений и графиков в Mathcad
СОВЕТ ---------------------------------------------------------------------
На первых порах не торопитесь вырезать объекты. В описанной процедуре перемещения,
вместо того чтобы вырезать объект в буфер, лучше скопировать его, а затем вставить из бу-
фера в нужное место. Убедившись, что все вышло, как задумано, можно вернуться в исход-
ную позицию и удалить теперь уже лишние объекты, то есть снова выделить их рамкой и
нажать на клавиатуре клавишу Delete (удалить безвозвратно) либо вырезать в буфер.
Если объекты (выражения, графики) перекрывают друг друга, в контекстном ме-
ню появляются пункты Bring to Front (Выдвинуть на передний план) и Send to
Back (Убрать на задний план). Использование этих пунктов позволяет эконо-
мить место в документе, специально накладывая края объектов один на другой.
Если вам надо раздвинуть наложившиеся друг на друга объекты, выделите их,
перечеркнув мышью при нажатой левой кнопке. Все выделенные объекты будут
обведены пунктирной рамкой. В главном меню Mathcad выберите Format ►
Separate Region (Разделить области). При этом будут раздвинуты только выде-
ленные области.
Если надо раздвинуть два объекта, подведите к одному из них курсор. При появ-
лении черной ладошки нажмите левую кнопку мыши и, двигая мышь, перемес-
тите объект в нужное место.
ВНИМАНИЕ -----------------------------------------------------------
Постарайтесь не нажимать кнопку Separate Region, не выделив предварительно объекты,
так как Mathcad при этой команде раздвигает области сразу во всем документе. Для эконо-
мии места в документе объекты обычно располагают как можно ближе друг к другу.
Mathcad раздвигает документы сверху вниз и при этом может нарушить нужную вам по-
следовательность вычислений.
1.12.	Построение трехмерных графиков
Для построения трехмерного графика
□	наберите имя функции двух переменных, знак присвоения значения := и вы-
ражение функции;
□	установите курсор в то место, где вы хотите построить график;
□	в математической панели щелкните мышью на кнопке Graph Toolbar (Панель
графиков), изображающей график, затем на Surface Plot (График поверхности).
На месте курсора появится шаблон трехмерного графика;
□	в единственном поле ввода шаблона графика введите имя функции;
□	щелкните мышью вне области шаблона. График построен (рис. 1.18, слева).
Кроме описанного способа ускоренного построения графика поверхности по функ-
ции двух переменных существует и часто применяется другой способ создания
графика поверхности — с использованием массива численных значений функ-
ции. Результат такого построения показан на рис. 1.18, справа. Для построения
BD-графика нужно:
1.12. Построение трехмерных графиков
45
□	с помощью дискретных переменных ввести значения обоих аргументов задан-
ной функции;
□	ввести массив, элементами которого являются значения функции, вычислен-
ные при заданных значениях аргументов;
□	установить курсор в то место, где вы хотите построить график;
□	в математической панели щелкнуть мышью на кнопке, изображающей гра-
фик, и выбрать трехмерный график. На месте курсора появится шаблон трех-
мерного графика;
□	в единственном поле ввода шаблона графика ввести имя функции;
□	щелкнуть мышью вне области шаблона. График построен.
Построение графика поверхности
путем создания массива данных
Построение графика поверхности
ускоренным путем (заданием функции)
Рис. 1.18. Построение трехмерных графиков
п := 5 m := 7 i := 0.. n j := 0.. m
X. > 0.5 i ¥. > 0.2 j Z. . := sinfX.Y.|
i	j J i,j  i
Z
График получился черно-белый, некрасивый, Mathcad позволяет сделать из него
почти произведение искусства. Подробно о возможностях форматирования по-
говорим в главе 15, а пока выполните следующие действия:
□	Сделайте двойной щелчок мышью в поле графика — появится окно формати-
рования графика (рис. 1.19).
□	Выберите пункт Appearance ► Fill surface ► Colormap (Оформление ► Поверх-
ность с заливкой ► Карта цветов). Щелкните мышью на кнопке Применить.
График стал цветным.
□	Выберите в окне форматирования пункт Lighting ► Enable Lighting ► On (Под-
светка ► Необходима подсветка ► Включить подсветку). Выберите схему осве-
щения (Lighting schema). В выпадающем меню находится 6 различных схем.
Выберите любую и нажмите кнопку Применить или ОК. Полюбуйтесь на эф-
фект освещения.
46
Глава 1. Построение выражений и графиков в Mathcad
□	Щелкните правой кнопкой мыши на графике — откроется контекстное меню,
дающее дополнительные возможности улучшения графика. Выбирайте раз-
личные пункты и смотрите, как они влияют на график.
В окне форматирования на вкладке General (Общие) внизу перечислены 6 типов
графиков (см. рис. 1.19):
□	Surface plot — график поверхности;
□	Contour plot — график линий уровня;
□	Date points — на графике только расчетные точки;
□	Vector Field plot — график векторного поля;
□	Bar plot — график трехмерной гистограммы;
□	Patch plot — площадки расчетных значений.
Щелкните мышью на каком-либо типе графика, а затем на кнопке Применить.
Посмотрите все типы графиков, кроме векторной диаграммы. Ее построение рас-
сматривается в главе 15.
Рис. 1.19. Панель форматирования ЗО-графиков
Дополнительные возможности работы с графиком:
□	Вращение графика. Поместите курсор в область графика. Двигайте курсор при
нажатой левой кнопке мыши.
□	Масштабирование графика. Действия те же при нажатой клавише Ctrl.
□	Анимация графика. Действия те же при нажатой клавише Shift. Для останов-
ки вращения щелкните левой кнопкой мыши внутри поля графика.
Панель форматирования трехмерных графиков, приведенная на рис. 1.19, со-
держит 9 вкладок, обеспечивающих огромные возможности форматирования
графиков.
Подробнее о построении и форматировании ЗО-графиков рассказано в главе 15.
Глава 2
Некоторые возможности Mathcad
Научившись строить математические выражения, функции пользователя и гра-
фики, познакомимся с основными возможностями Mathcad, наиболее часто ис-
пользуемыми функциями и приемами работы.
2.1.	Ступенчатые и разрывные функции и выражения.
Условие в Mathcad
Используемые в расчетах функции не всегда бывают непрерывными. Часто при
разных значениях аргумента функция описывается различными выражениями.
Бывают функции ступенчатые или с разрывами. При вычислении производных
или интегралов от таких функций приходится их брать по частям. Условный
оператор позволяет записать такие функции в виде одного выражения, что упро-
щает расчеты и украшает Mathcad-документ.
В Mathcad существует три различных способа ввода условий:
□	с помощью функции условия if;
□	с помощью оператора if с панели программирования;
□	с использованием булевых операторов.
Рассмотрим пример вычисления перемещения балки при изгибе с помощью ин-
теграла Мора (рис. 2.1). На балке есть два участка, на которых изгибающий мо-
мент описывается различными функциями, Мх (х) и М2(х
Для использования функции условия if нужно:
□	записать имя выражения и оператор присваивания (:=);
□	на стандартной панели нажать кнопку f(x) и в списке встроенных функций
выбрать if, после чего нажать кнопку Insert (Вставить). Появится шаблон
функции if с тремя местами ввода;
□	заполнить места ввода.
Обращение к функции:
if(cond,x, у),
где cond — условие типа х < £t, х и у — значения, возвращаемые функцией. Если
условие выполняется, то выражению присваивается значение х, если не выпол-
няется, то значение у.
Чтобы записать условный оператор с панели программирования, следует:
□	записать имя выражения и оператор присваивания (:=);
□	вызвать панель программирования Programming Toolbar нажатием соответст-
вующей кнопки математической панели и щелкнуть мышью на кнопке Add
lines (Добавить линию);
48
Глава 2. Некоторые возможности Mathcad
Изгибающие моменты от внешних сил
/ ы
М1(х) :=Fx- q —	М2(х) :=F x- q-LlIx- — I + МО
Изгибающий момент от единичной силы MM(x) := х
Условный оператор
программирования if
М(х) := |М1(х) if х<Ы
|М2(х) otherwise
Функция условия if
М(х) > if(x < L1 ,М1(х) ,М2(х))
если то иначе
Применение булевых операторов М(х) := М1(х) (х < LI) + М2(х) (х > L1)
Все 3 выражения М(х) эквивалентны
F, q, МО, L1, L- заданы глобально около графика
И	-8
поперечная сила прогиб балки Е:=2Ю J := 2000 10
fL
d	х	М(х)	ММ(х) х	х
Q(x) := — М(х)	А :=	——------— dx	А	= 0.013
dx	EJ
J0
Рис. 2.1. Определение перемещения балки
□	в верхнем поле ввода (черный квадратик) ввести выражение для изгибающе-
го момента на первом участке;
□	щелкнуть мышью на кнопке if на панели программирования (выражение для
изгибающего момента при этом должно быть полностью выделено синим
уголком или взято в скобки); появится место ввода, куда надо вписать усло-
вие, например, х < Lx или 0 < х < Lx;
□	в нижнем поле ввода (у вертикальной черты) ввести изгибающий момент
для второго участка и выделить его целиком синим уголком (клавишей про-
бела);
□	щелкнуть мышью на кнопке Otherwise (Иначе) на панели программирования
или выбрать if и вписать условие х >	. Функция М(х) готова.
Использование логических (булевых) операторов состоит в умножении слагае-
мых заданного выражения на соответствующий логический оператор. Логиче-
ские операторы вводятся с панели булевых операторов (кнопка Boolean Toolbar).
Булевы операторы могут возвращать только 0 или 1. Если условие справедливо,
то значением оператора является 1, если несправедливо, то 0. В математическом
выражении умножение на логический оператор обращает соответствующее сла-
гаемое в ноль или не меняет его значения. Пример применения всех трех форм
записи условия показан на рис. 2.1.
2.2. Глобальное присвоение значений
49
Схемы грузового и единичного состояния балки, изображенные на рис. 2.1, вы-
полнены автором в Corel Draw. Для вставки любого объекта, подготовленного
в другом приложении, в Mathcad надо выбрать пункт меню Insert ► Object (Встав-
ка ► Объект). Появится стандартное диалоговое окно Windows Вставка объекта.
В этом окне надо выбрать команду Создать из файла ► Обзор, затем выбрать имя
файла, в котором сохранен рисунок. Чтобы в дальнейшем можно было редакти-
ровать рисунок, не выходя из оболочки Mathcad, рекомендуется установить фла-
жок Связь в диалоговом окне Вставка объекта. Рисунок появился в документе.
Подробнее об использовании условия в Mathcad говорится в главе 12 (раз-
дел 12.7).
2.2.	Глобальное присвоение значений
Посмотрите на функцию М(х) (рис. 2.2), она содержит константы — нагрузки
и длины, Р, q, MQ и До сих пор эти константы не были заданы. Но строгий
Mathcad тем не менее не указывает на ошибку. Дело в том, что константы заданы
глобально около графика.
Глобальное присвоение
значений. Поменяйте числа
и наблюдайте за графиками
МО 5 3000
F s 4000
q г 2000
Lls3
Ls6
ще 100
самостоятельно построить эпюры М и Q
F := 100 q := 20
дня х<2 М(х):=Рх
для 2 < х < 5 М(х) := F х - **
Рис. 2.2. Эпюры внутренних усилий для балки, изображенной на рис. 2.1
Чтобы присвоить некоторой константе глобальное значение, нужно:
□	набрать с клавиатуры имя константы;
□	в математической панели щелкнуть мышью на кнопке х=;
□	щелкнуть на кнопке = в открывшейся панели Evaluation (Вычисление) или на-
жать комбинацию клавиш Shift-*-—.
Обратите внимание: если локальный оператор присваивания (:=) действует
вправо и вниз от места ввода, то глобальный оператор присваивания (=) действу-
ет по всему документу, и вверх, и вниз. При открытии документа интерпретатор
50
Глава 2. Некоторые возможности Mathcad
Mathcad вначале просматривает весь документ сверху вниз, отыскивая глобаль-
ные операторы присваивания, затем при втором проходе выполняет локальные
присваивания.
СОВЕТ --------------------------------------------------------------------
Следует избегать присвоения одному и тому же имени константы и глобального, и локаль-
ного значений, так как при этом глобальное значение отменяется локальным.
Глобальные операторы присваивания значений константам удобно размещать
вблизи таблиц’или графиков, чтобы, изменяя присваиваемое значение, сразу ви-
деть изменение результатов расчета.
В рассматриваемом примере поменяйте значения нагрузок Р, q, MQ, длин L
и число интервалов разбиения длины балки п. Самостоятельно постройте и от-
форматируйте графики для функции, заданной на рис. 2.2.
2.3.	Символьные вычисления
Наряду с числовыми расчетами Mathcad может производить вычисления в сим-
вольном виде. Существует два способа символьных вычислений:
1.	С использованием меню Symbolics (Символьные вычисления) из главного
меню Mathcad.
2.	С использованием панели Symbolic из математической панели.
Оба способа будут подробно рассмотрены в главе 5. Пример использования
меню Symbolics приведен в следующем разделе (рис. 2.4), а пока ограничимся
наиболее простым и часто используемым методом — применением символьного
знака равенства (->). В качестве примера рассмотрим вычисление неопределен-
ного интеграла (рис. 2.3). Далее описан порядок символьных вычислений:
□	В математической панели щелкнуть мышью на кнопке Calculs Toolbar (Па-
нель вычислений) со значком интеграла.
□	В открывшейся панели Calculus (Вычисления) выбрать, щелкнув мышью,
шаблон неопределенного интеграла.
□	Заполнить места ввода — вписать интегрируемое выражение или имя интег-
рируемой функции, а также имя переменной в шаблоне дифференциала.
□	Ввести символьный знак равенства (—>). Это можно сделать с помощью двух
панелей, вызываемых из математической: Symbolic Toolbar и Evaluation Toolbar.
Можно ввести этот оператор и с клавиатуры, нажав комбинацию клавиш
Ctrl+. (точка). На экране появится результат символьного вычисления.
Аналогично можно выполнить все операции, предусмотренные на панели
Calculus, а именно: вычисление производной любого заданного порядка, опреде-
2.3. Символьные вычисления
51
р := 2
f(z) := sin(g z) cos^—
вместо р1 поставьте р,
оно будет заменено числом
р := р отмена
предыдущего
численного
значения р
— (sin(v) • cos (v)) -> cos (v) - sin(v)
dv
(gp 4- 1	(gp- 1
cos --->—z cos----------z
I p.............I ?-.-2
2 gp + 1	2 gp- 1
2
г	sin(3t)
hm -------—-------->0
2
t-»co h(l + 2 t)
самостоятельно проинтегрируйте и
продифференцируйте функции
2	2	3-t t
tan(t)	(tan(t) 4- cot(t))	e 3
вычислите сумму и произведение членов 2 n + 1
ряда при п, стремящемся к бесконечности	2
п (п+ 1)
вычислить пределы функций при t, sin(t) - atan(t)
стремящемся к нулю	з
t
Рис. 2.3. Символьное вычисление производной, интеграла, сумм, произведений,
пределов
ленного и неопределенного интегралов, суммы или произведения ряда, предела
выражения. Решите самостоятельно приведенные на рис. 2.3 примеры.
Недостаток использования символьного знака равенства заключается в том, что
величины, которым были ранее присвоены численные значения, сохраняют их
и при символьном вычислении, то есть вместо символьного вычисления получа-
ется численное.
СОВЕТ --------------------------------------------------------------------
Чтобы получить символьное вычисление вместо численного, необходимо отменить пре-
дыдущие численные значения всех параметров, присвоив каждому параметру значение са-
мого себя, например: х := х (см. рис. 2.3).
Достоинство использования символьного знака равенства в том, что найденное
решение пересчитывается автоматически при изменении выражения или входя-
щих в него величин и участвует в последующих расчетах.
52
Глава 2. Некоторые возможности Mathcad
2.4.	Решение уравнений
Mathcad позволяет решить любое алгебраическое, а также многие дифференци-
альные и интегральные уравнения. Произвольно, «с потолка» взятые дифферен-
циальные и интегральные уравнения и системы уравнений вообще могут не
иметь решений, и Mathcad не в силах сотворить чудо.
Для примера возьмем квадратное уравнение и найдем его решение вначале сим-
вольным, затем численным способом.
2.4.1.	Символьное решение
Для символьного решения уравнения нужно:
□	набрать решаемое уравнение и синим уголком курсора выделить переменную,
относительно которой нужно решить уравнение;
□	в главном меню выбрать команду Symbolics ► Variable ► Solve (Символьные
вычисления ► Переменная ► Решить). Появится ответ (рис. 2.4).
Решить уравнение
символьно
о
2h +h-bbaO
С помощью меню . A . ~ .
Symbolic	msgMapleSolve
Символьная оценка функции Root
-1	1	2
- + -(l+8bb/
4	4
-1	1	2
---•(l+8bb/
4	4
rootb-h^ + h - bb,h)
1
-1	1	2
- + -(l+8bb/
4	4
-1	1	2
---<l+8bb/
4	4
Рис. 2.4. Символьное решение уравнения
Недостаток использования меню Symbolics заключается в том, что найденное ре-
шение не пересчитывается автоматически при изменении выражения или входя-
щих в него величин и не участвует в последующих расчетах.
Достоинством использования меню Symbolics является то, что ранее принятые
численные значения величин не учитываются в символьных расчетах.
Если выделенное выражение не имеет символьного решения (а большинство
уравнений не имеет символьного решения), то Mathcad сообщает об ошибке:
«No solution was found» («Решение не найдено»).
В Mathcad есть и другие возможности символьного решения уравнений, напри-
мер, с использованием функции root (см. рис. 2.4, внизу). О прочих возможно-
стях символьных вычислений говорится в главе 5.
2.4.2.	Численное решение (функция root)
Рассмотрим одну из ряда функций, позволяющих решать алгебраические урав-
нения, — функцию root.
2.4. Решение уравнений
53
Обращение к функции:
root(/(x), х),
где /(х) = 0. Возвращает значение х, при котором функция /(х) = 0.
Функция root решает уравнения итерационным методом секущих и поэтому тре-
бует задания перед собой начальных значений. Кроме того, функция root, выпол-
няя вычисления методом спуска, находит и выводит только один корень, бли-
жайший к начальному приближению.
Прежде чем решать уравнение, желательно построить график функции /(х)
(рис. 2.5). На графике видно, пересекает ли кривая /(х) ось абсцисс, то есть име-
ет ли действительные корни. Если точки пересечения кривой с осью есть, нужно вы-
бирать начальное приближение поближе к значению корня. Если корней несколько,
для нахождения каждого корня надо задавать свое начальное приближение.
Если же точек пересечения нет, то корни уравнения могут быть только мнимыми
числами. Для их нахождения нужно задавать начальное приближение в ком-
плексной форме. В результате расчета корни уравнения появляются в комплекс-
ном виде.
ВНИМАНИЕ ---------------------------------------------------------
Для ввода мнимой единицы надо на клавиатуре набрать 1г или 1 j. При выходе из области
мнимого числа единица исчезает, и мы видим комплексное число в обычном виде.
С помощью функции root можно найти и экстремум функции, приравняв произ-
водную к нулю (см. рис. 2.5). Функции
root
должно предшествовать начальное приближение (по умолчанию
#(*) _ ГН
dx
54
Глава 2. Некоторые возможности Mathcad
Для нахождения экстремума функции следует:
□	задать начальное приближение поближе к экстремуму;
□	записать выражение с функцией root, включив в качестве функции, которая
должна быть равна нулю, производную по заданной переменной;
□	вычислить ч значение заданной функции от найденного корня уравнения
df(x}
= 0. Экстремум найден (см. рис. 2.5).
ах
Функция root в старых версиях (до Mathcad 12) позволяет решить уравнение
и в символьном виде. При этом задавать начальное приближение не требуется,
нужно лишь ввести выражение, содержащее функцию root, и выбрать символь-
ный знак равенства, нажав комбинацию клавиш Ctrl+. (точка). Если символьное
решение существует, появится ответ, содержащий сразу все корни уравнения,
а не один, как при численном решении уравнения (см. рис. 2.4).
2.5.	Решение систем уравнений (функция find)
В Mathcad системы уравнений решаются с помощью вычислительного блока
Given-find. Так как системы уравнений решаются итерационным методом, пе-
ред решением необходимо задать начальные приближения для всех неизвест-
ных.
Чтобы решить систему алгебраических уравнений, нужно:
□	задать начальные приближения для всех неизвестных, входящих в сис-
тему;
□	напечатать ключевое слово Given (Дано). Убедитесь, что при печати вы не на-
ходитесь в текстовой области. Если нажать клавишу пробела, то математиче-
ское выражение становится текстовой областью и слово Given перестает вос-
приниматься как ключевое;
□	ввести уравнения и неравенства, входящие в систему, правее и ниже ключе-
вого слова Given. Между левой и правой частями уравнения должен стоять
знак равенства. Это не знак присвоения значения, а знак логического равен-
ства. Для его ввода используйте комбинацию клавиш Ctrl+= или выберите
его на панели Boolean (Булевы операторы);
□	введите любое выражение, содержащее функцию find. При печати слов Given
и find можно использовать любой шрифт, прописные и строчные буквы.
Обращение к функции:
find(x, г/, z...),
где x,y,z — неизвестные. Количество неизвестных должно быть равно количеству
уравнений. Возвращает значения неизвестных х, г/, z, обращающих уравнения
в тождества.
Функция find может решать и одно уравнение с одним неизвестным как частный
случай системы уравнений. Для системы из нескольких уравнений функция find
выводит решение в виде вектора.
2.5. Решение систем уравнений (функция find)
55
Пример решения системы уравнений приведен на рис. 2.6. Заданная система
уравнений состоит из уравнения окружности и уравнения прямой. Если прямая
и окружность пересекаются (рис. 2.8), то для нахождения двух точек пересече-
ния нужно задавать два разных начальных приближения. Если окружность
и прямая не пересекаются, действительных корней нет. Для нахождения мнимых
корней следует задавать начальное приближение в виде комплексного числа.
окружность и прямая пересекаются - действительные решения есть
х := 1 у := 0 начальное приближение
Given
2	2
х +у =36	х+у=2	F := Find(х,у)	F =
Для вывода второго корня надо задаться
другим начальным приближением х=-1 у=0
5.123 j
-3.123 J
Если окружность и прямая не пересекаются - действительных решений нет
х := 1
Given
х := 1
Given
у := 1 начальное приближение
F := Find(x|,y)
| Эта переменная не определена"!
у := 0 начальное приближение
комплексное число (введите х := 1 i)
2	2	(5-2.6461 А
х+у=36 х + у=10 F := Find(x,y) F =
5 + 2.646i /
Рис. 2.6. Решение системы уравнений
Функция find, так же как и функция root, позволяет решать системы уравнений
и в численном, и в символьном виде (рис. 2.7).
ПРИМЕЧАНИЕ ----------------------------------------------------------
В Mathcad 13-15 функция root требует другой формы оращения с 4 параметрами (раздел 5.3.4).
Given - начало ввода системы уравнений
2	2
х + у = аа
Find(x,y) ->
2
l.bb_ l.(-bb2 + 2 aa)
2	2
1
2
-bb + -(-bb2 + 2aa)
2	2
2
-bb + -(-bb2 + 2aa)
2	2
2
-bb - -(-bb2 + 2-a J
2	2
Рис. 2.7. Символьное решение системы уравнений
Если система уравнений не имеет точного решения, для приближенного реше-
ния в Mathcad существует функция minerr.
56
Глава 2. Некоторые возможности Mathcad
2.6.	Приближенное решение систем уравнений
(функция minerr)
Для приближенного решения систем уравнений используется вычислительный
блок Given-minerr. Обращение к нему аналогично обращению к блоку Given-
find.
На рис. 2.8 представлена геометрическая интерпретация системы уравнений
в виде окружности и прямой линии. Если прямая пересекает окружность, корни
системы уравнений действительные, если не пересекает — мнимые.
Если решение системы уравнений существует, х + у = 2 (см. рис. 2.6 и пунктир-
ная линия на рис. 2.8), функция minerr дает тот же ответ, что и функция find.
Если решение системы уравнений не существует, функция minerr возвращает
минимум невязки решения (см. рис. 2.8, сплошная линия). В случае х + у = 10
функция minerr возвращает значения координат точки, при которых расстояние
между кривыми минимально.
х := 1 у := 1
2	2
Given х + у =36
Приближенное решение
(
х + у = 10 F := Minen(x,y) F = I
Проверим решение системы уравнений с помощью графика
п:=50	ф := 0,2- —..2-я	х1 := -5,-5 + —.. 8
п	п
параметрическое уравнение окружности	у(ф) := 6-э!п(ф)
х(ф) := б соб(ф)
уравнение прямой yl(xl) := 10 - xl у2(х1) := 2 - х1
у(Ф)
yl(xl)
у2(х1)
х(ф) ,Х1
Рис. 2.8. Приближенное решение системы уравнений, если прямая
не пересекается с окружностью
Функцию minerr удобно использовать для поиска экстремума негладких функ-
ций с переломами на графике.
2.7. Исследование функции на экстремум
57
2.7.	Исследование функции на экстремум
Отметим четыре пути поиска экстремума:
1.	Для непрерывной функции используем равенство нулю производной от за-
данной функции. В этой процедуре используют функцию root.
2.	Для функции с переломами используем функцию minerr. Для этого по графи-
ку выбираем число заведомо большее (или меньшее) экстремального значе-
ния функции и записываем его в качестве ограничения в блоке Given-minerr.
Функция minerr возвращает значение аргумента, при котором расхождение
между заданным числом и значением функции минимально. Возвращаемый
результат зависит от выбора начального приближения.
3.	Для непрерывных функций удобно использовать функции maximize и mini-
mize (они вводятся аналогично функции find). Ключевое слово Given обычно
можно опускать — оно необходимо лишь при наличии ограничений.
4.	Для ступенчатых функций целесообразно использовать функцию автора Fmax,
реализующую простой метод перебора значений функции (функция Fmax опи-
сана в разделе 9.8). Другого средства определения максимума ступенчатой
функции в Mathcad нет.
СОВЕТ -------------------------------------------------------------
При анализе конкретного уравнения рекомендуется внимательно изучить график функ-
ции, на котором хорошо видны области нахождения экстремумов.
Все четыре способа определения экстремумов функции имеют свои плюсы и ми-
нусы. Творческий подход к их выбору почти всегда позволяет правильно найти
экстремумы функции.
На рис. 2.9 в качестве функции рассмотрена кубическая парабола и показан ее
график с двумя экстремумами (максимумом и минимумом). На рис. 2.10-2.12
показано определение этих экстремумов разными способами. Результаты расче-
та, естественно, совпадают.
з
у(х) := 2-х - 16 х + j
х > -33,-3.25.. 3
Рис. 2.9. Заданная функция и ее график
58
Глава 2. Некоторые возможности Mathcad
х : -3 начальное значение х^дх : rooti — у(х) ,х I
^dx J
xmax = -1-633 y(xmax) = 22.419 максимум
х :• 3 другое начальное приближение х^ > root! — у(х) ,х
Idx .
xKlin= 1.633 y(xmm) =-12.419 минимум
Рис. 2.10. Нахождение экстремума функции путем приравнивания к нулю
ее первой производной
х:» -3 начальное приближение
Given у(х) а 30 Хщ^ := Minen(x)
*max “ -1633 ytxnuJ « 22.419 максимум
х := 3 начальное приближение
Given у(х) а -20 х^ := Minen(x)
xmm “ 1 633 ytxnun) » -12.419 минимум
Рис. 2.11. Нахождение экстремума функции с использованием функции minerr
ключевое слово given необходимо
только в случае наличия ограничений
х > -3 начальное значение Хкшх > Махйшхе(у,х)
xmax = -1633 ytemaJ = 22.419 максимум
х := 3 Given х > 0	:= Minimize(y,x)
= 1 633 yjxmm) = -12.419 минимум
Рис. 2.12. Нахождение экстремума функции с помощью функций minimize и maximize
Подробнее о нахождении экстремума функции говорится в разделе 3.7.
2.8.	Работа с матрицами
Преимущества Mathcad особенно явно видны при работе с матрицами. Опера-
ции с матрицами трудоемки и, как правило, требуют компьютерного программи-
рования. В системе Mathcad мы видим традиционную запись матричных выра-
жений, как на листе бумаги, но уже с готовым численным или символьным
ответом.
2.8.1.	Создание матриц
Чтобы определить вектор или матрицу, следует:
□	записать имя матрицы, ввести оператор присваивания (:=);
□	в математическом меню выбрать кнопку с изображением матрицы. Откроется
панель Matrix (Матрица), на которой нужно вновь выбрать кнопку с изобра-
жением матрицы. На этот раз откроется диалоговое окно, в котором надо вве-
2.8. Работа с матрицами
59
сти число строк и число столбцов матрицы и нажать кнопку ОК. На экране
появится шаблон матрицы. То же действие вызывается нажатием комбина-
ции клавиш Ctrl+m;
□	каждое место ввода в шаблоне заполнить числами или буквенными выраже-
ниями. Матрица готова.
С помощью шаблона можно ввести матрицу, содержащую не более 100 элемен-
тов. Как ввести матрицы больших размеров, рассказано в главе 4 (раздел 4.1).
Вектор — это матрица, состоящая из одного столбца.
Доступ к любому элементу матрицы можно получить, задав имя матрицы с дву-
мя индексами. Первый индекс обозначает номер строки, второй — номер столб-
ца. Произвольный элемент вектора задается одним индексом.
Для набора нижнего индекса можно открыть панель Vector and Matrix Toolbar
(Матрицы) нажатием соответствующей кнопки на математической панели, по-
сле чего щелкнуть на кнопке Хн (Subscript), но лучше использовать клавишу [
(открывающая квадратная скобка), так как при работе с матрицами ставить ниж-
ний индекс приходится очень часто.
Нумерация элементов массива
Нумерация элементов массива (вектора или матрицы) может начинаться с 0, 1
или с любого другого числа (положительного или отрицательного). Порядком
нумерации элементов массива управляет встроенная переменная ORIGIN. По
умолчанию ORIGIN = 0. Это означает, что первый элемент массива имеет но-
мер 0.
Чтобы нумерация членов векторов и матриц начиналась, как обычно принимает-
ся в математике, с 1, нужно перед вводом матрицы, а лучше в начале документа,
напечатать ORIGIN:=1 (все буквы прописные).
На рис. 2.13, вверху показано создание элементов матрицы D по формуле с ис-
пользованием нижних индексов. По умолчанию ORIGIN = 0, поэтому Лоо = 10.
После ввода ORIGIN:=1 элемент Е>00 не имеет смысла, a i = 10.
2.8.2.	Основные действия с матрицами
Mathcad позволяет выполнять с матрицами основные арифметические действия:
сложение, вычитание, умножение, а также операции транспонирования, обраще-
ния, вычисления определителя матрицы, нахождения собственных чисел и соб-
ственных векторов и т. д. Примеры численного и символьного выполнения этих
операций приведены на рис. 2.13-2.15.
СОВЕТ -------------------------------------------------------------
Во время работы с матрицами внимательно следите за размерами матриц. При появлении
сообщения о несоответствии размеров матриц (см. рис. 2.13) напишите в сторонке имя
матрицы и нажмите клавишу =. Если размер матрицы отличается от того, что вы вводили,
обнулите матрицу перед очередным оператором присваивания, написав, например, А:=0.
60
Глава 2. Некоторые возможности Mathcad
ORIGIN = О z	ч а
(по умолчанию)	i = Q..2
j := 0..4
Формирование
матрицы
Dij := 10-i-j
г10 9 8 7 6^
транспонирование
9 8 7 65	матрицы
< 8 7 6 5 4?
(10 9 8А
Влияние ORIGIN на нумерацию элементов матрицы
ORIGIN =0 Do,о = Ю
ORIGIN := 1
г3 4 5х
4 5 1
Do,о =  Dij = 10
| Индекс массива является недопустимым для этого массива. |
В := 5 12
перемножение
матриц
| Размерности массива не совпадают. |
BD|= и
умножение матриц
9 8 7
8 7 6
7 6 5
6 5 4,
1 2 3
<2 3 4,
Рис. 2.13. Арифметические действия с матрицами
^12^	(144	132	120	108	96
И	132	121	110	99	88	(Ц	р 2 3^
10	VVT= 120	110	100	90	80	2 (1 2 3) = 2 4 6
9	108	99	90	81	72	UJ	(з 6 9,
<8;	1<96	88	80	72	64,
столбец х строку = Матрица
VTV = (510)
(1 2 3)- 2 =(14)
<3>
строка х столбец = число
Рис. 2.14. Произведение векторов
2.8.3.	Решение матричных уравнений
Матричные уравнения представляют собой, как правило, систему линейных ал-
гебраических уравнений А • X = В и решаются путем обращения матрицы коэф-
фициентов X = Л-1 • В (рис. 2.16).
2.9. Оператор векторизации
61
Транспонирование матрицы
г5 3^	л6 8 2У
D:= 7 1	С:= 3 5 1
<4 2.1	Ь 3 7,
г6 3 2>
8 5 3
<2 1 7;
Определитель квадратной матрицы с| = 38
D - неквадратная матрица |d| = |i 
Обращение матрицы
• 0.842 -1.316
С'1 = -0*5	1
<-0.026 -0.053
-0.053 *
0
0.158
Единичная матрица
| Эта матрица должна быть квадратной. |
1 1.166x10" 15
Проверка С С =0	1
Е := identity(5) Е
ко 0
^1	0	0	0	0А
0	10	0	0
0	0	10	0
0	0	0	1	0
<00001;
Рис. 2.15. Операции с матрицами
<1 2 З"1
А := 3 2 1
<2 1 3,
Х:-А 1В
Рис. 2.16. Решение системы алгебраических линейных уравнений путем обращения
матрицы коэффициентов
Символьные операции с матрицами можно выполнять с помощью меню Symbolics
(Символьные операции), а также символьного знака равенства. В примерах, приве-
денных на рис. 2.17, используется только символьный знак равенства —Подробно о
символьных операциях с матрицами рассказывается в главе 5, разделы 5.2.13 и 5.3.
При выполнении символьных операций с матрицами необходимо помнить, что
если какому-либо символу ранее присвоено численное значение, то при исполь-
зовании символьного знака равенства этот символ участвует в символьных рас-
четах как число. Если символу ранее присвоено значение вектора или матрицы,
то символьные вычисления с его участием становятся невозможными. В этом
случае нужно использовать для символьных вычислений меню Symbolics.
2.9.	Оператор векторизации
Mathcad допускает вводить в качестве аргумента функции не только числа, но
и векторы. При этом вычисляется значение функции для всех элементов вектора.
62
Глава 2. Некоторые возможности Mathcad
т (ees ee t
ВХ1 -»
Iff s fft
произведение векторов и матриц
транспонирование
обратная матрица
(as + bt
АХ-»
les + dt
BT X-> ees + fft
(ad- be)
—c
(a d - be)
-b
(a d - be)
a
(a d - b e)
определитель
|A| -» a d- be
собственные
числа
eigenvals(A)
1	1	1 f 2	2
-a+ — d + -la -2ad+ d +4bcJ
2	2	2
£
- a+ -d- - (a2-2 a d+ <? + 4-b c)
2	2	2
Рис. 2.17. Символьные операции с матрицами
Если аргумент функции — матрица, то, чтобы вычислить значения функции для
всех элементов матрицы, надо использовать оператор векторизации (рис. 2.18).
Для использования оператора векторизации нужно:
□	ввести выражение или функцию;
□	выделить синим уголком необходимую часть выражения (чаще всего выраже-
ние целиком);
□	на математической панели щелкнуть на кнопке Vector and Matrix Toolbar
(Матри- цы), а в открывшейся панели — на кнопке Vectorize (Векто-
ризация). Над выделенной частью выражения появится стрелка — символ
операции векторизации;
□	нажать клавишу =,
Оператор векторизации изменяет смысл векторной или матричной операции.
Векторизация означает выполнение однотипной операции, предписанной выра-
жением, со всеми элементами массива. Например, 4а — операция невозможная,
если А — вектор или матрица. Как уже сказано, аргумент функции может быть
вектором, и функция, как и в случае использования дискретной переменной, вы-
числяется для всех элементов вектора. Если аргумент функции — матрица, необ-
ходимо применение оператора векторизации, чтобы выполнить то же самое дей-
ствие, то есть вычислить функцию для всех элементов матрицы. В нашем случае
это нахождение корня квадратного из каждого элемента матрицы А, Перемноже-
ние матриц А . В — это матричное произведение, а А • В — это попарное произве-
2.10. Решение дифференциальных уравнений
63
дение элементов матриц А и В с одинаковыми индексами. Все массивы под зна-
ком векторизации должны быть одного размера, так как операция над всеми мас-
сивами производится поэлементно. Примеры использования векторов или мат-
риц в качестве аргументов функции приведены на рис. 2.18.
^0.5^
В := 0.3
<0.8;
<1 4>
ВВ := 2 5
<3 6;
sin (В) = 0.296
<0.717;
(0.841 -0 757Л
------>
sin(BB) = 0.909 -0.959
<0.141 -0.279;
f 0.479 4
sin(BB) = ji
Значение должно быть вектором.
--------->	403.429	2.981 х Ю3
ехр(А + В) =
1<2.203x 10 1.628x 10 J
---> I 5
<лв)-|21
12
32 /
А ( 0.2 0.333 
В " ‘ 0.429 0.5 ’
Если аргумент число - или вектор, векторизация не нужна
Если аргумент - матрица, векторизация нжна
Рис. 2.18. Операция векторизации
2.10. Решение дифференциальных уравнений
Математически решение дифференциальных уравнений — очень сложная про-
блема. Mathcad не в состоянии решить без дополнительных упрощений многие
дифференциальные уравнения и их системы. Все, что Mathcad может сделать
с ними, подробно описано в главе 6. Здесь же рассмотрим использование лишь
функции Odesolve.
Имя функции Odesolve можно писать и с прописной, и со строчной буквы. Алго-
ритм функции Odesolve использует большинство имеющихся в Mathcad функ-
ций решения дифференциальных уравнений, фактически заменяя их. Odesolve
может решать и системы дифференциальных уравнений. В контекстном меню
есть возможность выбора метода решения дифференциальных уравнений.
Функция Odesolve позволяет записывать уравнение в блоке решения в привыч-
ном виде, как обычно записывают уравнение на листе бумаги.
Обращение к функции Odesolve требует записи вычислительного блока, кото-
рый содержит три части.
1.	Ключевое слово Given.
2.	Дифференциальное уравнение и начальные или граничные условия для него
или система дифференциальных уравнений и ее условия.
3.	Функция Odesolve(x, xk, и), где х — имя переменной, относительно которой
решается уравнение; xk — конец интервала интегрирования. Начало интер-
вала интегрирования указано ранее, в начальных условиях; п — необязатель-
ный внутренний параметр, определяющий число шагов интегрирования,
64
Глава 2. Некоторые возможности Mathcad
используемый при интерполяции решения, то есть при переходе от матрицы
численных значений к функции. Параметр п не является обязательным. Его
можно удалить, предоставив Mathcad возможность самому выбирать число
шагов интегрирования. По умолчанию Mathcad использует п = 1000.
ВНИМАНИЕ ------------------------------------------------------------
Появление других математических выражений в вычислительном блоке между словами
Given и Odesolve недопустимо. Текстовую область внутри вычислительного блока разме-
щать можно. Граничные условия можно задавать лишь в двух точках, одна из которых —
начало интервала интегрирования.
Примеры использования функции Odesolve приведены на рис. 2.19-2.22.
(исходное уравнение)
з
-^Цу(х) +х2—у(х) + ху(х) = eXcos(x)
dx
Дифференциальное уравнение с начальными условиями
2	х
Given у"'(х) + х у'(х) + ху(х) = е cos(x)
у(0) = -8	у'(0) = 3 у”(0) = 3
у := Odesolve(x,5) х := 0,0.1.. 5
Рис. 2.19. Решение дифференциального уравнения с начальными условиями
2.10. Решение дифференциальных уравнений
65
дано уравнение 4-“ <t) + <t) = t
dt
граничные условия х(С) = A <D) = В
А := 4 В := 10 С > -3 D > б
Поменяйте граничные условия A.B.C.D
решение уравнения
Рис. 2.20. Решение дифференциального уравнения с граничными условиями
ПРИМЕЧАНИЕ --------------------------------------------------------
Исходное уравнение можно записывать с использованием как оператора дифференциро-
вания, так и штриха (рис. 2.21). Граничные условия следует записывать только со штри-
хом. Для набора штриха используйте комбинацию клавиш Ctrl+F7.
Функция Odesolve возвращает решение дифференциального уравнения в виде
функции, а не в виде массива, как все остальные функции, описанные в главе 6,
поэтому найденное решение можно интегрировать и дифференцировать (см.
рис. 2.19-2.21), а также использовать в последующих расчетах как функцию
пользователя.
Функция Odesolve решает дифференциальные уравнения как с начальными ус-
ловиями, когда все условия заданы в начале интервала интегрирования, так
и с граничными условиями, заданными в двух точках. Из этих двух точек одна
обязательно является началом интервала интегрирования, другая произвольная,
но ее аргумент больше, чем в начальной точке. Решение уравнения с начальны-
ми условиями показано на рис. 2.19, уравнения с граничными условиями — на
рис. 2.20. Решение дифференциального уравнения высокого порядка (4-го) про-
демонстрировано на рис. 2.21.
Глава 2. Некоторые возможности Mathcad
2	4
к := 3	у*н,(х) - 2 к у*’(х) + к у(х) = О
Given d4 , s _ ,2 s . ,4 n
—дУ(х) - 2 k —jy(x) + к y(x) = 0
dx	dx
у(3) я О У(3) = 0	y“((J) я 3
Y := Odesolve(x,l(T)
Рис. 2.21. Решение дифференциального уравнения 4-го порядка
Given
2х1(С> + 1X*) УФ -+ ХО  0 XQ)  ° Текстовая область^
4 yXt) + y(t) я + z(t) уХО) я -1 между словами
given и odesolve
—Xt) - ХО в ХО + УС) ОД а -1 Допустима
Рис. 2.22. Решение системы дифференциальных уравнений с начальными условиями
2.11. Анализ экспериментальных данных
67
Решение системы дифференциальных уравнений приведено на рис. 2.22. При
этом обращение к функции Odesolve изменилось. Для решения одного уравне-
ния:
odesolve(x, xk, п),
для решения системы дифференциальных уравнений:
odesolve((BeKTop имен неизвестных), х, xk, п).
В примере, приведенном на рис. 2.22, при решении системы трех уравнений век-
тор имен неизвестных содержит три имени.
Потренируйтесь в использовании функции Odesolve (рис. 2.23).
Решить самостоятельно
100-	+ 10-<t) + 101 <t) = 50-cosf i-tl
dt2 *	H J
<0) = 0 ВД a 1
У* =----------- yffl) = 0
ln(y)cos(x)
ГСх- 1) - / = 0 У® = 2	y*(2) a 1	у“(2) a 1
у**' - 2-y*1 + у* а о поменяйте граничные условия
Решить систему ОДУ u’(t) - lu(t) + 5-v(t) = 0
- 5-u(0 я lv(t)
при u(0) a -1 еда!
Рис. 2.23. Примеры для самостоятельной работы
2.11. Анализ экспериментальных данных
При проведении различных экспериментов обычно требуется массив экспери-
ментальных данных представить в виде функции, которую можно использовать
в дальнейших расчетах. Если кривая, описываемая этой функцией, должна про-
ходить через все экспериментальные точки, операция получения промежуточ-
ных точек и расчетной функции называется интерполяцией.
Если кривая, описываемая этой функцией, не должна проходить через все экспе-
риментальные точки и является аппроксимацией (усреднением) исходных дан-
ных, операция получения промежуточных точек и расчетной функции называет-
ся регрессией.
Если необходимо уменьшить разброс данных или исключить некоторую систе-
матическую погрешность, например, в виде наложенных колебаний, используют
сглаживание данных или фильтрацию спектра колебаний данных.
Подробно о работе с массивами опытных данных рассказано в главе 7. Здесь же
поговорим только о наиболее удобных способах интерполяции и регрессии.
68
Глава 2. Некоторые возможности Mathcad
2.11.1. Интерполяция
В Mathcad имеется несколько функций интерполяции, различающихся способом
«соединения» точек данных (прямой линией или различными кривыми). В этой
главе поговорим только о кубической сплайн-интерполяции, при которой экспе-
риментальные точки соединяются отрезками кубических полиномов. В про-
цессе интерполяции одновременно используются две функции, interp и cspline.
Обращение к функциям:
interp(s, х, г/, 0; cspline(x, г/),
где х — вектор значений аргумента, элементы которого расположены в порядке
возрастания; у — вектор значений функции того же размера; 5 — вектор вторых
производных, создаваемый функцией cspline, которая обеспечивает равенство
вторых производных на границах стыковки полиномов, то есть в эксперимен-
тальных точках; t — значение аргумента, при котором вычисляется интерполи-
рующая функция.
Координаты экспериментальных точек не могут быть комплексными числами.
Примеры интерполяции приведены на рис. 2.24.
¥>(38 15 5.5 23 51 79 105 126 144 156 164 166 162 152 137 117 93 66)
Т	я
¥>¥	n>17	i>0..n Ф1 := i— число замеров п+1 = 18
YY(x) > interp (с spline(ф, y) ,ф,¥,х) YY(x) - функция, ее можно интегрировать
.	2 л. пп - новое число точек, задано глобально
j.- ..пп Ф^ .= — j около графиков. Поменяйте его
¥1 > interp (с spline (ф, ¥) ,ф,¥,ф1)	Y1 - массив -интегрировать нельзя
Рис. 2.24. Интерполяция исходных данных
При записи функции интерполяции удобно две функции объединять в одну за-
пись:
YY(t) := interp(cspline(X, У), X, У, t).
В результате интерполяции можно получить функцию или массив данных с лю-
бым количеством точек интерполяции (см. рис. 2.24). Если результатом являет-
ся функция, ее можно интегрировать, дифференцировать, использовать в функ-
циях пользователя.
На рис. 2.25 число точек пп массива после интерполяции задано глобально. Для
удобства наблюдения за изменением результатов расчета пп = 5 помещено около
графика. Поменяйте пп.
2.11.2. Регрессия
Смысл регрессии состоит в подборе функции, аппроксимирующей эксперимен-
тальные данные. Регрессия сводится к подбору коэффициентов в той или иной
аналитической зависимости.
2.11. Анализ экспериментальных данных
69
интеграл и производная от интерполированного выражения
В Mathcad имеется несколько встроенных функций регрессии двух типов:
□	позволяющих увидеть аналитическую зависимость, то есть возвращающих
набор аппроксимирующих коэффициентов;
□	не позволяющих увидеть аналитическую зависимость.
Рассмотрим две функции, которые не выводят коэффициентов и аппроксимиру-
ют массив данных одним степенным полиномом или отрезками нескольких по-
линомов.
В Mathcad регрессия с использованием одного полинома реализуется комбина-
цией встроенных функций регрессии и интерполяции
interp(s, х, г/, 0; regress(x, г/, /г),
где х — вектор значений аргумента, элементы которого расположены в порядке
возрастания; у — вектор значений функции того же размера; s — вектор коэффи-
циентов для построения аппроксимирующего полинома, создаваемый функцией
regress; t — значение аргумента, при котором* вычисляется интерполирующая
функция; п — степень аппроксимирующего полинома.
Степень аппроксимирующего полинома может быть любой. Практика показывает,
что полинома 5-й степени достаточно для аппроксимации почти любой кривой.
Обращение к указанным функциям:
s:=regress(X, У, и),
yy(0:=interp(s, X, У, 0
или
yy(0:=interp(regress(X, У, п), X, У, 0.
70
Глава 2. Некоторые возможности Mathcad
Регрессия с использованием нескольких отрезков полинома реализуется комби-
нацией встроенных функций регрессии и интерполяции interp(s, х, у, t) и loess
(х, у, span), где s:=loess(X, У, span) — вектор коэффициентов для построения ап-
проксимирующего полинома 2-й степени, требуемый функцией interp; span > 0 —
параметр, определяющий размер отрезков полиномов.
Параметр span задает степень сглаженности данных. На практике 0,2 < span < 2.
При span = 2 результат аппроксимации тот же, что и при аппроксимации одной
параболой. При span = 0,2 аппроксимирующая кривая почти точно описывает
любой набор данных.
Примеры использования полиномиальной регрессии приведены на рис. 2.26.
регрессия полиномом степениПт] |п> 3|
Yieg(x) * interp(regress(|,Y,n) ,ф,¥,х)
где ф иУ-массивы экспериментальных точек.
п -степень полинома (поменяйте степень полинома)
регрессия отрезками полинома второй степени!
Чем больше span .тем больше
длина отрезков (поменяйте span)
span:« 0.4 vsl :« loessfo, Y, span) Y]oess(x) : interp(vsl ,ф, Y ,x)
та же запись, но короче Y]oess(x) : interp (loess (♦,Y,span),+,Y,x)
Yi
• ••
YY(x)
Yne(x)
 •  
Y]ot«(x)
Рис. 2.26. Регрессия исходных данных (см. рис. 2.24) без получения
аналитической зависимости
В Mathcad имеется восемь встроенных функций для получения аналитического
выражения аппроксимирующей функции. Однако при их использовании необ-
ходимо знать форму аналитического выражения. Функции, использующие лю-
бой произвольный вид аппроксимирующей функции, будут рассмотрены в гла-
ве 7. Здесь же рассмотрим только наиболее простые в применении функции,
каждая из которых строит аппроксимирующую функцию лишь определенного
вида.
2.11. Анализ экспериментальных данных
71
Используйте соответствующий вид регрессии, если хорошо представляете себе,
какой зависимостью описывается ваш массив данных. Когда вид регрессии пло-
хо соответствует набору данных, ее результат часто оказывается неудовлетвори-
тельным и зависит от выбора начальных приближений.
Из восьми встроенных функций пять требуют предварительного задания век-
тора начальных приближений:
□	expfit(X, У, g) — регрессия экспонентой f(t) = а • ebt + с;
□	sinfit(X, У, g) — регрессия синусоидой f (t) = а• sin(£ + b) + с
□	pwrfit(X, У, g) — регрессия степенной зависимостью f(t) = a -tb + с;
□	Igsfit(X, У, g) — регрессия логистической функцией а(е) — а/(1 + b • e~ct);
□	logfit(X, У, g) — регрессия логарифмической функцией f(t) = я - 1п(£+ &)+ с.
В этих функциях х — вектор значений аргумента, элементы которого расположе-
ны в порядке возрастания; у — вектор значений функции того же размера; g —
вектор начальных приближений коэффициентов а, b и с; t — значение аргумента,
при котором вычисляется интерполирующая функция.
Примеры использования этих функций приведены на рис. 2.27 и 2.28.
Эти функции требуют начальных приближений
expfit -- у = аеЬх + с
¥1(х) :- С0-еС1'Х + Cj
С :« ехрШ.(ф, Y, с)
согг(У1(ф) ,Y) -0.60716588
sinfit -- у = asib(x + b) + с
Y2(x) ^Сд вЦх+С^ + C2
pwrfit - Y = a x + c
Y3«:-C0xC1 + C2
< 10 >
c20.1
<10,
logfit- y= »Xi+b) + c cl _ 1Q
Y4(x) CQln(x + Cj + C2 l Ю,
Igsfit --y=-----------
1 . к ~cx
1 + be
<io>
c3:= 1
< 1 >
Y5(x) :=
co
Iе
C:» sinfit(<t>,Y,c)
CO и(У2(ф) ,Y) » 0.98538802
Cpwifit(|,Y,c2)
corr(У3(ф),у) -0.68961301
Clogfit(|,Y,cl)
сои(У4(ф) ,Y) --0.61951307
C := lgsfit(|,Y,c3)
CO п(У5(ф) ,Y) - 0.88153268
Рис. 2.27. Регрессия исходных данных (см. рис. 2.24) с выводом аналитической зависимости
72
Глава 2. Некоторые возможности Mathcad
УВД
У2(х)
уад
У4>)
У5(х)
к- -х-х
Рис. 2.28. Результаты регрессии исходных данных (см. рис. 2.24) функциями,
приведенными на рис. 2.27
Функции, не требующие начальных приближений:
□	line(X, У) — регрессия прямой линией, использующая минимизацию суммы
квадратов ошибок f(t) = а + b-t*,
□	medfit(X, У) — регрессия прямой линией, использующая медиан-медианную
линейную регрессию f(t) = а + b t. Функции line и medfit дают близкие ре-
зультаты, слегка различающиеся наклоном прямых линий;
□	lnfit(X, У) — регрессия логарифмической функцией f(t) = л • 1п(£) + b.
Примеры использования этих функций приведены на рис. 2.29 и 2.30.
Эти функции не требуют начальных приближений
/3414б
medfit а+Ь*х С := medfitfo,У) С = I I Y5(x) := CQ + С^х
согг(У5(ф) ,У) = 0.62220544
line a+b*x С := Бпе(ф,У) С = Г44968^ уб(х) = со + С1Х
118538 J
coir(Уб(ф),У) =0.62220544
Infit a*ln(x)+b С := 1ЫН(ф,у) С =	=	+ С1
coir(¥7(ф) ,¥) = 0.60503411
Рис. 2.29. Регрессия исходных данных (см. рис. 2.24) с выводом аналитической зависимости
Во всех примерах, приведенных на рис. 2.27-2.30, использованы одни и те же
массивы данных, характер распределения которых, естественно, не соответству-
ет использованным видам регрессии. Для оценки связи между массивом данных
и значениями аппроксимирующей функции подсчитан коэффициент корреля-
ции согг. Опытные данные неплохо аппроксимируются синусоидой (коэффици-
2.12. Элементы математической статистики
73
ент корреляции 0,98). В остальных случаях связь между величинами плохая (ко-
эффициент корреляции примерно 0,6).
AY := READPRN("Data.pm") Чтение из файла Data.prn
Рис. 2.30. Результаты регрессии исходных данных (см. рис. 2.24) функциями,
приведенными на рис. 2.29
2.12.	Элементы математической статистики
В Mathcad встроено много функций для решения задач математической стати-
стики. Подробно они рассматриваются в главе 8. Здесь же остановимся лишь на
функциях оценки параметров выборки данных. Все перечисленные далее функ-
ции можно применять и для векторов, и для прямоугольных матриц. Примеры
вычисления средних арифметических и средних геометрических значений, ме-
дианы, средних квадратических отклонений и дисперсий показаны на рис. 2.31.
WRITEPRN("primer") := АТ
APPENDPRN("primer.pm") > ВТ
А 2 3 4 5
К:= READPRN("primer.pm")
2 ,3 4 5 1
3 4 5 1 2
4 5 12 3
^5 1 5 3 4)
Рис. 2.31. Оценка параметров выборки данных AY
ВНИМАНИЕ -----------------------------------------------------
Функции, начинающиеся с прописной и со строчной буквы, — это разные функции.
74
Глава 2. Некоторые возможности Mathcad
2.13.	Обмен данными с другими программами
В нижней части рис. 2.30 продемонстрирована еще одна очень важная возмож-
ность Mathcad — запись числовых данных в файл и считывание их из файла. По-
является вбзможность передачи данных из одной программы в другую и даже
создания вычислительных комплексов из нескольких программ, исполняемых
в различных компьютерных системах. Например, данные из Excel передаются
в Fortran, из Fortran — в Mathcad и, если нужно, обратно в Fortran.
В Mathcad существует три функции, позволяющие считать числовые данные из
других файлов или записать числовые данные в другой файл:
□	APPENDPRN("file") — добавляет числовые данные в существующий файл.
Здесь file — имя файла или путь к файлу, если он находится в другом каталоге;
□	READPRN("file") — считывает числовые данные из файла;
□	WRITEPRN(”file") — записывает числовые данные в файл.
Все три функции работают только с файлами, в которых числа образуют прямо-
угольную матрицу (вектор чисел — частный случай прямоугольной матрицы).
Пример обмена данными показан на рис. 2.32. Функция WRITEPRN записывает
массив А в файл primer, который сама же и создает с расширением .ргп. Функция
APPENDPRN добавляет в этот же файл массив В. Функция READPRN считывает
данные из файла primer.
К := READPRN("primer.pm")
WRITEPRN( - primer") = АТ
APPENDPRN("primer.pm") = ВТ
Рис. 2.32. Запись данных в файл и чтение из файла
Для записи прямоугольной матрицы или вектора в отдельный файл необходимо
выполнить следующие действия:
□	В стандартном меню выбрать кнопку f(x). Появится окно Insert function (Вста-
вить функцию).
□	Выбрать группу функций File Access (Доступ к файлам).
□	Выбрать имя функции WRITEPRN.
□	В появившийся шаблон вписать имя файла, затем оператор присваивания :=
й имя числового массива. Массив будет записан в файл с указанным вами
именем и расширением .ргп и помещен в тот же каталог, в котором находится
и рабочий файл.
ВНИМАНИЕ -------------------------------------------------------------
Перед тем как вписать имя файла, не забудьте ввести символ " (кавычки).
2.14. Учет размерностей в Mathcad
75
Для передачи в Mathcad данных из какого-либо файла, содержащего прямо-
угольную матрицу числовых данных, выполните следующие действия:
□	Наберите имя, которое присваиваете массиву, считываемому из файла, и знак
присвоения значения :=.
□	В стандартном меню выберите кнопку f(x). Появится окно Insert function.
□	Выберите группу функций File Access.
□	Выберите имя функции READPRN.
□	В появившийся шаблон впишите имя файла с расширением, если оно есть, не
забывая перед этим ввести символ " (кавычки).
Подробнее об обмене данными говорится в разделе 12.3.
ПРИМЕЧАНИЕ ----------------------------------------------------------
В Mathcad 13 появилась функция Readfile, позволяющая считывать данные из любых
файлов. Подробно о ней написано в разделе 12.3.
2.14.	Учет размерностей в Mathcad
Mathcad позволяет вести расчеты с учетом размерностей. Для этого при вводе
исходных данных достаточно умножить число на стандартную размерность. Те-
перь любые действия с введенными таким образом величинами выполняются
с учетом размерностей.
Перед началом работы с размерными величинами надо установить систему еди-
ниц, в которой вы будете работать:
Рис. 2.33. Установка системы единиц
76
Глава 2. Некоторые возможности Mathcad
□	В главном меню Mathcad выберите Tools ► Worksheet Options ► Unit System
(Параметры документа ► Система единиц измерения ► Встроенные перемен-
ные), как показано на рис. 2.33.
□	В открывшемся диалоговом окне выберите при помощи переключателя сис-
тему единиц, например SI (International). Щелкните на кнопке ОК. Если в диа-
логовом окне выбрать None (Нет), то никакие размерности в расчете не учи-
тываются.
В дальнейшем в начале документа при вводе исходных данных для расчета их
надо записывать, умножая число на стандартное обозначение размерности (мож-
но ввести его с клавиатуры либо выбрать в стандартном меню Mathcad кнопку
Insert (Вставить) (рис. 2.34), щелкнув мышью на соответствующем обозначе-
нии).
Рис. 2.34. Окно выбора стандартных размерностей
В принципе можно придумать и использовать свои, абсолютно любые размер-
ности. Тогда в начале Mathcad-документа надо ввести свои производные раз-
мерности, например размерности на русском языке, присвоив их значениям раз-
мерностей, указанных в стандартном меню Mathcad (рис. 2.35).
При выводе результатов расчета после нажатия клавиши = появляется число
и рядом с ним — место ввода единицы размерности. Если число уже имеет раз-
мерность, то рядом с размерностью появляется еще одно место ввода. Сюда мож-
но поместить любую переменную, константу или выражение.
ВНИМАНИЕ ------------------------------------------------------------
Не забывайте, что всякий раз, когда что-нибудь находится в месте ввода единицы измере-
ния, Mathcad изменяет полученный результат так, чтобы произведение числа и выраже-
ния, стоящего на месте размерности, давало правильное значение.
2.14. Учет размерностей в Mathcad
77
Рис. 2.35. Окно установки своих размерностей
Можно использовать место ввода, чтобы, например, выразить, значение угла
в долях числа tv или вывести числовой коэффициент при каком-то буквенном
выражении.
Размерность элементов массива вводится так же, как и размерность чисел, путем
умножения выражения на стандартную размерность на английском языке или
производную размерность, введенную ранее.
Дискретная переменная может быть размерной. Для этого в ней необходимо ум-
ножить числа на соответствующую размерность.
Графики всегда строятся в стандартных размерностях, приведенных в List of
built-in-units (Список встроенных функций). Ввести пользовательские размерно-
сти на графиках нельзя. Для изменения масштаба графика разделите на нем йа-
звания аргумента и функции на размерность (рис. 2.36).
Ограничения на проведение расчетов с учетом размерностей:
□	При расчетах с матрицами все элементы используемых в расчетах матриц
должны иметь одинаковую размерность.
□	Ряд встроенных функций не может работать с размерными величинами. Это
функции регрессии, сглаживания, функция Odesolve (решение дифференци-
альных уравнений), вычисления логарифма числа (функции In и log). Для
того чтобы преодолеть это ограничение, нужно сделать безразмерными аргу-
менты функций, разделив размерную величину на ее размерность.
78
Глава 2. Некоторые возможности Mathcad
□	В сложных расчетах при использовании многих функций и нескольких дис-
кретных переменных учет размерностей может оказаться сложным. В таких
случаях размерность (для справки) можно указать рядом с результатом рас-
чета в виде текстового комментария.
Подробные сведения об учете размерностей в расчетах можно найти в главе И.
ПРИМЕЧАНИЕ -----------------------------------------------------------
В Mathcad 13 введена статическая проверка размерностей, накладывающая гораздо больше
ограничений на учет размерностей. Из-за этого ряд программ, работающих в предыдущих
версиях, не действует в этой версии. Подробнее о статической проверке размерностей напи-
сано в разделе 11.10.
Квазиразмерности
По сути дела процесс присвоения числу размерности состоит в умножении чис-
ла на некоторый числовой коэффициент. Буквенному обозначению размерности
достаточно присвоить численное значение, не умножая его на стандартную раз-
мерность.
Ввод производных размерностей
метр := m сек := s мин:= 60-сек час := ЗбОО-s град - deg
Размерные массивы Ф:=(10 55 200 340 400 420)Ттрад угол поворота
Т := (0 3 7 10 15 17)Тмин время
Размерная функция Ф1(г) := interp(lspline(T ,ф) ,Т ,Ф ,t) Ф2ф :«
Размерная дискретная переменная t := 1-сек,2-мин.. 20-мин
t Т
мин ’ мин
Рис. 2.36. Различные действия с размерными величинами
Ф2(1) =
2.15. Преобразование функции в матрицу и матрицы в функцию
79
ПРИМЕЧАНИЕ -------------------------------------------------------------
Стандартный ввод размерности — производной размерности присваивается число, умно-
женное на стандартную размерность.
Ввод квазиразмерности — производной размерности присваивается число.
Использование квазиразмерностей позволяет избежать всех ограничений, также
позволяет использовать размерности в программах, в матричных расчетах. При-
мер использования квазиразмерностей показан на рис. 11.19.
При использовании квазиразмерностей Mathcad уже не следит за правильно-
стью использования размерностей и вся ответственность за результаты расчета
ложится на расчетчика, который сам должен следить за логикой расчета и впи-
сывать в поле ввода ответа правильную размерность.
2.15.	Преобразование функции в матрицу
и матрицы в функцию
Преобразование функции в матрицу и матрицы в функцию необходимо в связи
с особенностями встроенных функций Mathcad. Это делается, например, если
одни функции возвращают матрицу, а вам надо иметь функцию для последую-
щего интегрирования или дифференцирования, или, наоборот, Mathcad выводит
функцию, а вам нужна матрица для последующих матричных преобразований.
Заданы векторы аргумента X и функции V
Х:=(-3 15 6 9 10)Т	¥ := (2 5 -3 4 9 2)Т
Finteip(x) := inteip(cspline(X,Y),X,Y,x) интерполяция
Fregress(x) > inteip(regress(X,Y,4) ,X,Y,x) регрессия полиномом
4-й степени
Рис. 2.37. Преобразование вектора данных в функцию
80
Глава 2. Некоторые возможности Mathcad
Для преобразования массива данных в функцию используют интерполяцию или
регрессию. На рис. 2.37 показано преобразование вектора в функцию. Там же по-
казана возможность дифференцирования полученной функции.
Для получения массива данных с помощью заданной функции надо задать век-
торы значений аргументов функции и, подставив в функцию значения аргумен-
тов, получить массив (рис. 2.38).
ORIGIN > 1
х:=(3 5 9)Т у:= (2 -20 7 15)Т
i : 1.. rows(x) j1.. rows(y)
M. •>
bJ
xi + yj
<0.513	-0.354	0.406	0.303 >
M=	0.481	-0.403	0.359	0.276
<0.404	-0.561	0.304	0.238;
Рис. 2.38. Получение массива значений с помощью заданной функции
2.16.	Строковые функции
Строковые функции в Mathcad позволяют выполнять действия с фрагментами
текста, формировать из них необходимую реплику (рис. 2.39). На том же рисун-
ке показана функция CWD, позволяющая узнать путь к рабочему файлу. Эта
функция полезна, когда на диске находится несколько копий файла и важно не
перепутать, с какой из них идет работа.
путь к открытому файлу CWD = "О:Быстрыи стартХ"
п = 6 m := 4 С := "должно быть равно "
А := "Число строк" В "Число столбцов "
DI := num2sti(n) D2 := num2str(m)
Z := concat(A,C,Dl) if n>m
concat(A,C,D2) if m>n
1 otherwise
Z = "Число строк должно быть равно 6"
Рис. 2.39. Формирование реплики с помощью строковых функций
Подробнее о строковых функциях читайте в разделе 12.12.
2.17.	Программирование
Раздел «Программирование» занимает особое место в Mathcad. При начальном
обучении этот раздел совершенно не нужен. Огромные возможности Mathcad
2.19. Отладка Mathcad-документов
81
позволяют решать подавляющее число задач без использования программирова-
ния, да к тому же, как правило, несколькими способами.
Но есть класс задач, которые невозможно решить без программирования. Это за-
дачи, в которых часть документа из нескольких или многих операторов надо вы-
полнить многократно. В таких случаях документ должен состоять из отдельных
подпрограмм, объединенных в единую «головную» программу.
Использование раздела «Программирование» позволяет написать в Mathcad
программы любой сложности. Подробные сведения о создании программ содер-
жатся в главе 9.
2.18.	Анимация
Mathcad предусматривает возможность анимации графиков и результатов вы-
числений путем создания AVI-файлов и вставки их в Mathcad-документ. Вос-
производятся AVI-файлы встроенными в Windows средствами. Анимация не уп-
рощает и не Улучшает расчеты, а лишь украшает их презентацию. Поэтому на
первых шагах обучения Mathcad обращаться к ней не следует. Подробные сведе-
ния о создании анимации к расчетам содержатся в главе 10.
2.19.	Отладка Mathcad-документов
Mathcad-документ — «то набор исходных данных для расчета, расчетных фор-
мул, выведенных на экран результатов расчета в виде чисел, таблиц и графиков.
Каждый из перечисленных объектов занимает одну математическую область
(Math Region). Между ними в произвольном порядке располагаются текстовые
области (Text Region). Все математические объекты взаимодействуют друг с дру-
гом. Напомним, что Mathcad вычисляет выражения сверху вниз и слева направо
последовательно друг за другом и не переходит к вычислению следующего объ-
екта, не закончив работу с предыдущим. Текстовые области никак не влияют на
математические области.
Если в каком-либо выражении есть ошибка, величина, содержащая ошибку, ото-
бражается красным цветом. Щелкните мышью на объекте с ошибкой. Под объек-
том появляется сообщение об ошибке. При нажатии клавиши F1 на экране появ-
ляется часть раздела справки (на английском языке) (рис. 2.40).
Щелчок мышью на любом из сообщений открывает расшифровку ошибки ана-
логично нажатию клавиши F1.
В Mathcad есть функция Trace Errors (Трассировка ошибок), позволяющая про-
следить всю цепочку ошибочных вычислений, то есть найти место, где была до-
пущена ошибка. Щелкните правой кнопкой мыши на выражении с ошибкой.
Если ошибка возникла не в этом выражении, то в контекстном меню появляется
82
Глава 2. Некоторые возможности Mathcad
Рис. 2.40. Описание возможных ошибок в меню Help Mathcad 15
пункт Trace Errors (Трассировка ошибок). Выберите этот пункт и, следуя указа-
ниям, найдите выражение, из которого исходит ошибка. На практике эта функ-
ция не слишком полезна, так как в простых случаях и без нее понятно, откуда
взялась ошибка, а в сложных программах Mathcad сам этого не понимает. В та-
ких случаях в диалоговом окне все кнопки, кроме Close (Закрыть), заблокирова-
ны (затемнены).
Многие ошибки устраняются легко. Прочитайте сообщение об ошибке, и станет
ясно, что делать. Но встречаются ошибки, на устранение которых уходит несколь-
ко дней глубоких раздумий. В таких случаях надо просмотреть численные значе-
ния всех входящих в ошибочное выражение величин. Возможно, заданные вами
значения где-то были заменены другими.
СОВЕТ -----------------------------------------------------------------
Если правильно записанное выражение выводит неправильный числовой ответ, попро-
буйте «обнулить» имя выражения и значения ряда параметров перед их последним вычис-
лением, так как возможно наложение значений друг на друга.
2.20.	«Горячие» клавиши
В Mathcad есть операции, многократно повторяющиеся при наборе программы.
Для экономии времени работы желательно запомнить сочетания клавиш, нажа-
тие которых вызывает выполнение таких операций. Ниже приводится таблица
2.20. «Горячие» клавиши
83
таких сочетаний клавиш («Горячие» клавиши). Полезно распечатать такую таб-
лицу и держать ее на столе перед компьютером в первое время работы с Math-
cad. Для удобства распечатки эта таблица включена в папку Интернет-файлов
в виде файла гор-клав.doc.
Клавиша	Результат нажатия клавиши (или их сочетания)
Ctrl+R	Освежение экрана (уборка мусора с экрана)
Enter	Вставка чистой строки
Delete	Удаление чистой строки
♦, /, +, -	Умножение, деление, сложение, вычитание
	Возведение в степень
	Извлечение квадратного корня
1	|Af| — модуль числа, длина вектора, определитель матрицы, если М — число, вектор или матрица
[	Нижний индекс у элемента вектора или матрицы. Для ввода нижнего индекса-комментария надо ввести имя переменной, нажать клавишу . (точка), набрать комментарий: Мх или МглаВное
Латинский эквива- лент гре- ческой бу- квы, далее Ctrl+G	Ввод греческих букв. Греческие буквы/Латинские эквиваленты: a/а p/b х/с 8/d е/е ц/h y/g Х/1 ц/m v/n co/w <p/f л/р у/у p/r т/t 0/q Vx C/z
е	Основание натурального логарифма
Ctrl-*-Enter	Сложение с переносом строки (перенос части длинной строки)
: (двоето- чие)	а:=Ь — присвоение значения (локальное), действует направо и вниз От места присвоения (отменяет глобальное присвоение (а=Ь)
	а=Ь — присвоение значения (глобальное), действует по всему документу (обычно помещают вблизи графика или таблицы)
Ctrl+=	а=Ь — жирный знак равенства, (логическое равенство, а не знак присвоения), используется после слова Given
;(точка с запятой)	х:=1..п или х:=1,1.1..п — диапазон чисел дискретной переменной х , где 1 — первое значение, 1.1 — второе значение, п — последнее значение. Разность первого и второго значений определяет шаг выбираемых значений х. Нельзя набирать две точки с клавиатуры!
Ctrl+m	Вставить матрицу
=	Вывод результата численного расчета
Ctrl-*-. (точ- ка)	—> вывод результата символьного расчета
	<- в программах — локальное присвоение
]	Вертикальная черта— add line — добавка строки в программу
Пробел+ или —>	Выделение выражения или его части
84
Глава 2. Некоторые возможности Mathcad
Mathcad вычисляет выражения слева направо и сверху вниз.
Для выделения объекта его надо перечеркнуть курсором при нажатой левой
кнопке мыши. Далее выделенный объект можно
□	переместить при нажатой левой кнопке мыши;
□	удалить, нажав клавишу Del;
□	переместить в буфер, выбрав «ножницы» на панели инструментов, клавиши
Ctrl+x;
□	скопировать в буфер, выбрав Сору на панели инструментов, клавиши Ctrl+c;
□	вставить из буфера, выбрав Paste на панели инструментов (портфель), клави-
ши Ctrl+v.
Те же действия можно выполнить, нажав правую кнопку мыши и выбрав в кон-
текстном меню команды Cut, Сору или Paste соответственно.
Часть II
Вычисления в Mathcad
В этой части книги содержатся подробные сведения обо всех воз-
можностях Mathcad, на конкретных примерах рассматриваются
особенности использования встроенных функций, основные прие-
мы и способы вычислений.
Глава 3
Решение уравнений
Встроенные функции Mathcad в состоянии решить любое алгебраическое урав-
нение. Для решения одного уравнения с одним неизвестным можно использо-
вать функции root, polyroot или find. Mathcad решает уравнения или системы ите-
рационным методом, поэтому перед решением необходимо задать начальное
приближение для всех корней.
3.1.	Функция root
Функция root используется для решения одного уравнения с одним неизвест-
ным.
Обращение к функции:
root(/(x)), где /(х) — выражение, равное нулю; х — аргумент, варьируя который,
система ищет значение, обращающее функцию в нуль (рис. 3.1).
з
Уравнение х -5х-1 = О
начальное приближение х := О
решение root!, х3 - 5 х - 1, х * = -0 202
з
ИЛИ f(x) =х -5х-1 х .= 0 root(f(x) ,х) = -0 202
другие корни X = 10 хО •= root(f(x) ,х) хО = 2 33
х .= -5 хО = root(f(x) ,х) хО = -2 128
х:=-3,-2 9 3
х
Задан интервал поиска корней
root(f(x),x,-5,-l) = -2.128	root(f (х) ,х, 11) = -0.202
root(f (х), х, -3,1) = j i	root(f (х), х, 1,5) = 2.33
| Значения функции в конечных точках должны иметь противоположные знаки. |
Рис. 3.1. Использование функции root
Функция /(х) и аргумент х должны быть скалярами, то есть результат вычисле-
ния функции — число, а не вектор или матрица. Функция root использует итера-
ционный метод секущих. Корень уравнения — ближайшее к начальному прибли-
жению значение х, обращающее функцию /(х) в нуль. Если корней несколько,
3.1. Функция root
87
для отыскания каждого корня необходимо задавать свое начальное приближе-
ние.
СОВЕТ --------------------------------------------------------------
Перед началом решения желательно построить график функции, чтобы проверить, есть ли
корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего вы-
брать по графику поближе к значению корня. Итерационные методы весьма чувствитель-
ны к выбору начального приближения.
Mathcad позволяет вместо начального приближения задавать диапазон значений
аргумента, в котором лежит значение искомого корня (см. рис. 3.1). В этом слу-
чае обращение к функции root должно иметь 4 параметра:
root (/(x),x,a,Z>),
где а и b — границы интервала, в котором лежит корень уравнения. Внутри ин-
тервала не должно быть больше одного корня, так как Mathcad выводит на экран
лишь один корень, лежащий внутри интервала.
ВНИМАНИЕ ----------------------------------------------------------------
Значения функции на границах интервала должны быть разного знака, иначе, возможно,
корень не будет найден (см. последнюю строчку на рис. 3.1).
Если уравнение не имеет действительных корней, то есть функция /(х) нигде не
равна пулю, то Mathcad выводит комплексное число. В старых версиях при от-
сутствии действительного корня надо было вводить начальное приближение
в комплексной форме (рис. 3.2).
Если функция имеет мнимый корень,
начальное приближение задается комплексным числом
9 2
ад := х - 15 х - 20	Ц-1) = -5.809 + 0.5881 х -3.. 6
Рис. 3.2. Решение уравнения с комплексными корнями в Mathcad 11
88
Глава 3. Решение уравнений
ПРИМЕЧАНИЕ ------------------------------;-----
Для ввода мнимой единицы надо ввести с клавиатуры 1i или 1j.
Подробнее об использовании комплексных чисел написано в конце главы 4 (раз-
дел 4.15). Если уравнение имеет несколько корней, то для их нахождения можно
использовать разложение функции /(х) на простые множители:
f(x) = (х - xt )(х - х2 )• • -(х - х„ >
где хр х2, ..., хп — корни уравнения. Начальное приближение можно задать толь-
ко для первого корня. В качестве функции f(x) нужно взять
Л(х): = Л(х)1_1 / (х — xi),
где Л(х)0 = /(х> h(x = h(x)0 / (х - xt ) и т. д. (рис. 3.3).
з
f(x) := х - 20 х + 5 У этой функции 3 корня
х := -5,-4.9.. 5 диапазон значений х для вывода графика
х := 1	х1 :»root(f(x) ,х)	х1 »0.2507995
hl(x) :«	х2 > root(hl(x) ,х)	х2 = 4.341
X - х1
h2(x) -5^- хЗ := root(h2(x) ,х) хЗ = -4.593
х - х2
Рис. 3.3. Определение трех корней уравнения
Если функция /(х) имеет малый наклон вблизи искомого корня, то функция
root(/(x)^x) может сходиться к значению, довольно далеко отстоящему от корня.
В таком случае для уточнения корня необходимо уменьшить значение погреш-
ности вычислений, задаваемое встроенной переменной TOL. Для этого
□	в стандартном меню Mathcad выберите команду Tools ► Worksheet Options ►
Built-In Variables (Инструменты ► Параметры документов ► Встроенные пере-
менные);
□	в открывшемся окне поменяйте значение Convergence Tolerance (TOL) (По-
грешность сходимости).
Чем меньше константа TOL, тем ближе к нулю будет значение функции при най-
денном корне уравнения, но тем больше будет время вычисления корня.
3.1. Функция root
89
Для повышения точности расчета корня можно заменить /(х) на
g(x) = f(x)/	77 
ах
Корень можно найти и по графику, увеличив масштаб (рис. 3.4). Для этого необ-
ходимо:
□	выделить график, щелкнув левой кнопкой мыши внутри графика;
□	в главном меню Mathcad выбрать команду Format ► Graph ► Zoom (Формат ►
График ► Масштаб);
□	при нажатой левой кнопке мыши обвести пунктирной линией область графи-
ка вблизи искомого корня, которую надо увеличить;
□	в открытом окне X-Y Zoom (Масштаб по осям X-Y) нажать кнопку Zoom.
Прямо с графика можно передать в буфер обмена численное значение корня.
Для этого выполните следующие действия:
□	Выделите график, щелкнув левой кнопкой мыши внутри графика.
□	В главном меню Mathcad выберите команду Format ► Graph ► Trace (Фор-
мат ► График ► Трассировка).
□	Щелкните левой кнопкой мыши внутри графика — появится перекрестье осей.
□	Двигая мышь при нажатой левой кнопке, установите перекрестье на пересе-
чение графика с осью абсцисс. При этом численные значения координат пе-
рекрестья появляются в открытом окне X-Y Trace (Трассировка X и Y).
□	Правильно выбрав положение перекрестья, нажмите кнопки Copy X и Сору
Y — численные значения будут помещены в буфер (см. рис. 3.4).
□	Вне поля графика запишите имя, которое хотите дать корню, и оператор при-
сваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad
или в контекстном меню, открывающемся при нажатии правой кнопки мыши.
X Y Zoom	X
xl := root(f(x) ,х) х1 = 0.2507887
OK Cancel
Рис. 3.4. Определение корня уравнения по графику
90
Глава 3. Решение уравнений
СОВЕТ ------------------------------------------------------------------------
При работе с Mathcad постоянно пользуйтесь цравой кнопкой мыши (в контекстном меню
каждый раз появляются новые, наиболее нужные в данный момент функции). Щелкните пра-
вой кнопкой мыши на графике: в открывшемся контекстном меню есть пункты Zoom (Мас-
штаб) и Trace (Трассировка).
В окне X-Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если
установить этот флажок, при перемещении мыши пунктирное перекрестье на
графике будет перемещаться скачками, отмечая расчетные значения функции.
Если флажок снять, движение перекрестья становится плавным.
3.2.	Решение уравнения с переменными
параметрами
Если нужно многократно решать уравнение при изменении одного или не-
скольких его параметров, то необходимо создать собственную функцию, вклю-
чающую функции root. Такая функция принимается Mathcad «к сведению».
Для ее вычисления надо задать значения (диапазоны значений) параметров, ука-
занных в названии функции. Например, в функции f(a,x) — ах- tg(ar), варьи-
руя параметр а, находим соответствующий каждому значению а корень уравне-
ния х (обращающий f(a,x) в нуль). Результаты расчета можно вывести в виде
вектора решений xQ или графика х0(а) (рис. 3.5). Начальное приближение при
этом задается лишь один раз. Результат предыдущего вычисления является на-
чальным приближением для последующего.
один переменный параметр Ца,х) := ах - tan(ax)
а := 0,0.2.. 4
корни уравнения при различных а
х := 1	х0(а) := root(f(a,x) ,х)
с:=0..5
хО(с) =
1
0.024
0.013
-0.009
-0.007
-0.005
Рис. 3.5. Решение уравнения с одним переменным параметром
Решение уравнения f(b,c,x) — х1 + Ьх — с = 0, приведенное на рис. 3.6, зависит
от численных значений параметров бис. Задавая значение одного из параметров
в виде константы, а другого — в виде дискретной переменной, с помощью функ-
ции root можно найти ряд решений уравнения, соответствующих заданным зна-
3.3. Нахождение корней полинома. Функция polyroots
91
чениям параметров b и с. В таблице на рис. 3.6 выведены значения корня уравне-
ния х0 при с = 4 и b — ряде значений, определяемых дискретной переменной 6.
На графике b — ряды значений. Так как функция root выводит значение одного
корня, а квадратное уравнение имеет два корня, поменяйте значение начального
приближения для вывода таблицы и графика, соответствующих второму корню.
х:« 1 поменяйте знак начального приближения
(ведь у квадратного уравнения два корня),
зсО(Ь,с) root(f(b,c,x) ,х) xq _ решение уравнения
Вывод результатов расчета
b =
~0
4
—6
8
для с=4
хО(Ъ,ф =
2
1.236
0.829
0.606
0.472
0.385
Рис. 3.6. Решение уравнения с двумя переменными параметрами
При построении графика поверхности х0(6,с) значения параметров b = 0 - 10
и с = 0 - 5 заданы с помощью меню 3-D Plot Format ► Quick Plot Data (Формат 3D-
графика ► Данные быстрого графика), открывающегося после двойного щелчка
мышью в поле графика.
3.3.	Нахождение корней полинома. Функция polyroots
Для нахождения корней полинома можно использовать функцию polyroots(K),
которая определяет все корни полинома одновременно. Здесь К — вектор коэф-
фициентов полинома, начиная со свободного члена (рис. 3.7). Нулевые коэффи-
циенты опускать нельзя. Если полином имеет N корней (с учетом кратности), то
вектор К включает в себя N + 1 коэффициент. Начальное приближение вводить
не надо.
СОВЕТ ------------------------------------------------------------
Если исходный полином записан не в развернутом виде, а, например, как произведение
полиномов, в этом случае коэффициенты можно определить, использовав меню Symbolics
(Символьные операции), как показано в главе 5 и на рис. 3.8.
92
Глава 3. Решение уравнений
з
у(х) = 2 х - 16 х + 5
f 5
-16
к =
О
К 2 >
Г-2 973Л
хО = 0 316
ч 2 657 ,
Рис. 3.7. Нахождение корней полинома с помощью функции polyroots
У(х)
О
yl(x) := (х2 - 2х + з) ix2 - б) исходное выражение
для определения коэффициентов используем меню
•	выделите х в выражении
•	в меню Symbolic нажмите Polynomial Coefficient
х0 := polyroots(k)
х0 =
^-2.449^
1 -2i
1 +2i
< 2.449 >
Рис. 3.8. Нахождение корней полинома при неявном задании коэффициентов
Для функции polyroots можно выбрать один из двух численных методов: метод
полиномов Лагерра (он установлен по умолчанию) или метод сопровождающей
матрицы (см. рис. 3.7).
3.4. Решение систем уравнений
93
Для смены метода проделайте описанные далее операции:
1.	Щелкните правой кнопкой мыши на слове polyroots, вызвав контекстное
меню.
2.	В открывшемся меню выберите LaGerre (Метод Лагерра) или Companion
Matrix (Сопровождающая матрица).
3.	Щелкните мышью вне поля функции — произойдет пересчет корней в соот-
ветствии с выбранным методом.
Чтобы оставить выбор за Mathcad, в контекстном меню установите флажок
AutoSelect (Автоматический выбор).
Графики функций, изображенные на рис. 3.7 и 3.8, построены для проверки пра-
вильности определения корней.
3.4.	Решение систем уравнений
Для решения систем уравнений нужно использовать вычислительный блок сле-
дующего вида:
1.	Начальные приближения для всех переменных.
2.	Ключевое слово Given (Дано).
3.	Система уравнений (при записи уравнений надо использовать жирный знак
равенства (клавиши Ctrl+=), так как это не знак присвоения значения, а опе-
ратор отношения).
4.	Ограничения на поиск решения в виде неравенств, если они есть.
5.	Выражение, содержащее функцию find, с неизвестными в качестве парамет-
ров.
Результат расчета — вектор решения системы. Вычислительный блок позволяет
решать системы, содержащие от 1 до 200 уравнений.
Mathcad допускает использование двухсторонних неравенств типа а < х < Ь.
Операторы < и > выбираются на математической панели.
Решение, выданное функцией find, желательно проверить, подставив в уравне-
ния найденные корни, так как в зависимости от начального приближения Math-
cad может вывести корни, не имеющие физического смысла.
На рис. 3.9 показана проверка решения системы трех уравнений путем подста-
новки корней в уравнения и путем построения графиков уравнений и определе-
ния корней как точек пересечения поверхностей. На графике видна точка Z пере-
сечения трех поверхностей, координаты которой являются решением системы,
обращающим все уравнения в тождества.
При обычном ускоренном построении графика поверхности значения аргумен-
тов выбираются Mathcad автоматически в диапазоне от -5 до 5, что в нашем
примере приводит к делению на нуль и невозможности построения графика.
Пределы значений координат можно изменить (см. главу 15). Для этого дважды
щелкните мышью в поле графика и в открывшемся окне выберите страницу
Quick Plot Data (Данные быстрого графика), на которой введите необходимые
пределы изменения переменных.
94
Глава 3. Решение уравнений
х := 1 у := 1 z := 1 начальное приближение
Given х2 yz2  144 х2 у2 z  48 х у2 z2 • 36
<х0>
уО
<z0>
х0> (4>
уО = 1
.zoj кЗ>
/д
4 точка
1 пересечения
ч3J поверхностей
проверка x02 y0 z02 = 144 т£? уО2 zO = 48 ХО усЛгО2 - 36
Рис. 3.9. Решение системы уравнений с помощью функции find
Функция find реализует градиентные численные методы и предлагает на вы-
бор три метода. Щелкните правой кнопкой мыши на названии функции find. В от-
крывшемся контекстном меню и его подменю выберите нужный метод (рис. 3.10):
□	Linear (Линейный метод) — метод касательной;
□	Nonlinear (Нелинейный метод).
z:« 1 начальное приближение
ЮуО^
L 4	... L L	_
х у z =144 х у z = 48
Автовыбор
проверка
Fl(x.y)
36
точка
пересечения
поверхностей
X Вырезать
Копировать
2 Л
г*1'
Квази-Ньютон
Й? Свойства..
Отключить вычисление
Оптимизировать
Дополнительные параметры
ткенык
Рис. 3.10. Выбор метода решения системы уравнений
Нелинейных методов три:
□	Conjugate Gradient (Метод сопряженных градиентов);
□	Quasi-Newton (Квази-ньютоновский метод);
□	Levenberg-Marquart (Метод Левенберга).
3.4. Решение систем уравнений
95
Кроме выбора самого метода, нажав кнопку Advanced Options (Дополнительные
параметры), можно выбрать:
□	оценку производной конечными разностями (Derivative Estimation):
О Forward (Вперед) — правая двухточечная схема;
О Central (Центральная) — трехточечная симметричная схема;
□	оценку переменной (Variable Estimation):
О Tangent (Касательная) — касательная — прямая линия,
О Quadratic (Квадратичная) — касательная — парабола;
□	проверку линейности:
О Yes (Да);
О No (Нет).
Если вы уверены, что нелинейности всех функций, входящих в уравнения, мало
влияют на значения их частных производных, выберите при проверке нелиней-
ности пункт No. В этом случае производные будут приняты постоянными и не
будут вычисляться на каждом шаге, что уменьшит время расчета.
К выбору метода расчета стоит обращаться, если вы хорошо разбираетесь в чис-
ленных методах и тогда, когда Mathcad не может найти решение. В болыпйнстве
же случаев лучше доверить выбор метода Mathcad, отметив пункт AutoSelect
(Автоматический выбор).
3	{Ь А
fl(a,b,x,y) > х -cosl — yj - ab
3
f2(a,b,x,y) := у
х ;= 1 у :я 1 начальные приближения
Given fl(a,b,x,y) я 0	f2(a,b,x,y) = О
Я^а,Ь) •= Find(x,y) хО(а,Ь) •= ^a,b)g yO(a,b) > ^a,b)j
один из параметров делаем
константой, другой варьируем
b := 3
а:=0..4 для таблицы
хО(а,Ь) я уО(а,Ъ) =
0		0	хО(а,Ь)
2.115		1.248	уО(а,Ь)    
3.138		1.375	
2.693		1.092	
2.344		0.37	
это корни х и у системы уравнений
для заданных значений а и b
Рис. 3.11. Решение системы уравнений с переменными параметрами
96
Глава 3. Решение уравнений
Градиентные методы, реализованные функцией find, требуют многократного вы-
числения производных. При работе с достаточно гладкими функциями они обес-
печивают быстрый и надежный поиск корня.
Как и функция root, функция find может использоваться в функциях пользовате-
ля для нахождения корней системы уравнений при переменных значениях пара-
метров, перечисленных в названии функции пользователя (рис. 3.11 и 3.12). Для
системы уравнений решение выводится в виде массива, каждый столбец которо-
го соответствует вектору решения для одной переменной.
Меняем оба параметра, а и b
Диапазон изменения
координат а и b задан
на странице Quick Plot Data
окна форматирования
хО,уО
Рис. 3.12. Поверхность решений системы уравнений (см. рис. 3.11)
Решение системы алгебраических линейных уравнений
А*Х=В путем обращения матрицы А
<1 2 3^
А > 3 2 1
<2 1 3,
Х>А
< 10.833 >
Х = -9.167
< 5.833 ,
Блок решения Given-find /цА
начальное приближение Х:= 10
<10,
<10.833 Л
Given АХ=В X:=Find(X)
root(A Х-В,Х) = ।
Х= -9.167
<5.833 ,
Функция root с матрицами работать не может
Рис. 3.13. Решение системы уравнений в матричном виде
3.4. Решение систем уравнений
97
Mathcad позволяет решать системы линейных алгебраических уравнений (СЛАУ)
не только в скалярной, но и в матричной форме, при этом начальные условия
и ограничения задаются в виде векторов (рис. 3.13).
Для решения СЛАУ предназначена также функция Isolve. Она использует более
быстрый алгоритм и может работать с неквадратными матрицами, то есть ре-
шать недоопределенные и переопределенные системы уравнений с действитель-
ными и комплексными числами в матрицах (рис. 3.14).
Обращение к этой функции:
Isolve(A.B), где А —прямоугольная матрица числовых коэффициентов уравне-
ний (действительных или комплексных), В — вектор (или матрица) правых
частей уравнений (свободных членов), имеющий то же число строк, что и мат-
рица А.
<2.3 9.8
А := 24 1
<6 12,
В := 2
<3,
х := lsolve(A ,Е)
|< 0.08
1<0.159 J
	г23	6.7	9.8 >		< 0.272 >
А :=	24	42	1	В := 2	х := lsolve(A,B)	х= -0.111
		0	12 >		<0.114 ,
	г2.3	6.7	2.8	9.8 >		
А :=	24	42	7	1	В:=	2
	<6	0	8	12 2		<з>
х > lsolve(A ,Е)
	<2.3 6.7	2.8	9.8''		< 1-П	
А :=	24 42	7i	1	В :=	2	х := lsolve(A,E)
	<6i 0	8	12 >		<-3i>	
+
< 0.156 >
-0.069
0.155
<0.068 ,
<-0.361 - 0.1651 >
0.194 + 0.1051
-0.091 - 0.3641
<-0.022 + 0.1731,
Рис. 3.14. Применение функции Isolve
ПРИМЕЧАНИЕ -----------------------------------------------------
Решение систем уравнений в символьном виде возможно с помощью функции find
(см. главу 5).
ВНИМАНИЕ ------------------------------------------------------------
Блоки решения уравнений не могут быть вложены друг в друга. Каждый блок может
иметь только одно ключевое слово Given и одно имя функции find. Внутри блока решения
нельзя использовать оператор присваивания вида х:=1, а нужно использовать знак логиче-
ского равенства = (жирный знак равенства).
98
Глава 3. Решение уравнений
3.5.	Трудности при решении уравнений
Не допускается присутствие между словами Given и find
□	других вычисляемых выражений;
□	дискретных переменных (х:=0..20);
□	знака «не равно».
Если Mathcad не может найти решение, то следует:
□	признать, что решения не существует;
□	уяснить, что корни — мнимые числа, и ввести начальные значения в мнимой
форме;
□	поискать другое начальное приближение;
□	увеличить или уменьшить точность расчетов. Для этого в главном меню
Mathcad выберите команду Math ► Options ► Built-In Variables (Математика ►
Параметры документа ► Встроенные переменные). Уменьшите допустимую
погрешность вычислений (Convergence Tolerance) TOL. По умолчанию TOL —
= 0,001;
□	изменить ограничения в блоке Given-find;
□	вместо функции find использовать minerr;
□	внимательно изучить график функции (возможно попадание в локальный
максимум или минимум функции), поискать другое приближение или доба-
вить ограничения на поиск решения;
□	посмотреть, не достигнута ли точка, из которой не может быть получено бо-
лее точное решение, например, когда график функции только касается оси ар-
гументов, не пересекая ее.
3.6.	Приближенное решение уравнений
и систем уравнений
Если уравнение не имеет точного решения, например, график функции не пере-
секается с осью аргументов (нет вещественных корней), можно найти значение
аргумента, при котором невязка будет минимальной (для случая двух уравне-
ний — минимальное расхождение между двумя кривыми). Для этого использует-
ся функция minerr.
Обращение к minerr аналогично обращению к функции find. Функция find дает
точное решение, a minerr — приближенное. Функция minerr использует тот же
вычислительный алгоритм, что и функция find. При нажатии правой кнопки
мыши открывается контекстное меню, позволяющее выбрать метод вычислений.
Используется функция minerr аналогично функции root. Замена в вычислитель-
ном блоке Given-find функции find на minerr дает то же решение, если оно сущест-
вует. Если решения нет, то функция root указывает на ошибку, a minerr находит
3.6. Приближенное решение уравнений и систем уравнений
99
минимум невязки, то есть возвращает значение аргумента, соответствующее ми-
нимальному расхождению между заданным значением у и функцией у(х).
На рис. 3.15 показано определение координат точек пересечения прямой линии
с эллипсом. Точек пересечения две. Одна точка найдена на рисунке. Найдите
вторую точку пересечения, взяв другое начальное приближение.
Сравнение функций find и minerr	Л Л.
________ х « 0,0110
ЭЛЛИПС f(x) : ^25-yj Прямые yl«>17-х у2(х>20-х
х * 50 начальное приближение ао
кривые пересекаются - решение есть
Gwen — -h—= 25	у+х=17	15
Решение той же системы уравнений у2(х)
с помощью функции Minerr	....
5
2	2
Gwta —«25	у + х» 17
4	9
найдите вторую точку пересечения кривых, поменяв начальные приближения
Рис. 3.15. Приближенное решение системы уравнений
При использовании уравнения прямой х + у = 17, которая пересекается с эллип-
сом, обе функции, find и minerr, дают одинаковые результаты.
При использовании уравнения прямой х + у = 20, которая не пересекается с эл-
липсом, функция find выдает ошибку. Функция minerr выдает координаты точки
эллипса, наиболее близкой к прямой линии (рис. 3.16).
Функцию minerr удобно использовать для нахождения экстремумов функции.
кривые не пересекаются - find не может найти решения
2	2
~ Х У ос
Given-------1----= 25
4	9
2	2
х	у
Given — + — = 25
4	9
у + х = 20
у + х = 20
I Эта переменная не определена. I
ХСП-----с-------—-----proq----1—5.616
:= Minerr (х, у)	=
уО /	VyOj у 12.635
Рис. 3.16. Приближенное решение системы уравнений (продолжение)
100
Глава 3. Решение уравнений
При использовании функции minerr для решения системы уравнений необходи-
мо проверять полученные результаты. Нередко решение оказывается ошибоч-
ным, так как система уравнений имеет несколько корней и Mathcad может пред-
ложить корень, не имеющий физического смысла или просто бесполезный. Же-
лательно как можно точнее указывать начальные приближения к решению.
3.7.	Исследование функции на экстремум
Поиск экстремума функции включает в себя задачи нахождения локального
и глобального экстремумов. Mathcad с помощью встроенных функций решает
задачу нахождения только локального экстремума. Для поиска глобального экс-
тремума необходимо вычислить все локальные экстремумы и выбрать из них
наибольший (наименьший).
Отметим три пути поиска экстремума:
□	Для непрерывной функции используем равенство нулю производной от функ-
ции (рис. 3.17).
з
исходная функция у(х) := 2 х - 16 х + 5 х:« -33,-3.25.. 3
х
х := -3 начальное значение	Xmax > root — у(х) ,х
dx )
xmax = ”1- <533	y(xm^ = 22.419 максимум
х := 3 другое начальное приближение х^:« root! —у(х) ,х
dx )
xmin = 1-633 y(xmin) = -12.419 минимум
Рис. 3.17. Нахождение экстремумов функции путем приравнивания
производной к нулю
□	Для функции с переломами используем функцию minerr (рис. 3.18). Для это-
го по графику выбираем число, заведомо большее (или меньшее) экстремаль-
ного значения функции, и записываем его в качестве ограничения в блоке
Given. Функция minerr возвращает значение аргумента, при котором расхож-
дение между заданным числом и значением функции минимально, на том
участке, где выбрано начальное приближение.
3.7. Исследование функции на экстремум
101
поиск экстремума с помощью функции Minerr
2
у(х) := (х - 1) (х < 4) + (6 - х) (х > 4)
х> 0,0.1 ..10
начальное приближение х :* 3
( свое для каждого экстремума )
Given у(х) = 10 Хщ^ := MinEn(x)
*ni« = 4	- 9 максимум
функции
х := 3 начальное приближение
Given у(х) в -10 х^ : MinEn(x)
v • 1	 - л МИНИМУМ
xmm-l	функции
Рис. 3.18. Поиск экстремума ступенчатой функции
ПРИМЕЧАНИЕ --------------------------------------------------------
Для определения максимума ступенчатой функции удобно использовать программу
Fmax, приведенную в разделе 9.7 (рис. 9.14-9.17).
□	Для непрерывных функций удобно использовать функции maximize и mini-
mize (они вводятся аналогично функции find) (рис. 3.19). Ключевое слово
Given можно опустить — оно необходимо лишь при наличии ограничений.
3
у(х) 2 х - 16 х + 5 начальное значение х:» -2
Хтах := Maxknize(y ,х) Xj^ = -1.633 yfamax) = 22.419
х := -5 Given х > 0 Хд^ := Minimize(y,x) х^д = 1.633 y(xmin) = -12.419
Рис. 3.19. Использование функций maximize и minimize
2	2
f(x,y) := 2 + 2 х + 2 у - х - (Зу)
f(x,y) := (у3 " х2) " (1 " *)3
поменяйте
функции
местами
поиск минимума (максимума) функции двух переменных
Результат зависит от начального приближения,
Поменяйте условия на х := -2 у := 0.5
х := 2 у := 2 Given — f(x,y) в 0	— f(x,y) в 0
dx	dy
'х')	fx4) <2.215^
:= MinEn(x,y) = L nn J	f(x,y) = -3.113
<У/	У/	003 J
то же самое с функциями Maximize и Minimize
Р := Maximize^,х,у)
Q := Minimize(f ,х,у)
f(P0'Pl) " -0-369
f(Qo-Qi)"-3113
f
Рис. 3.20. Нахождение экстремума функции двух переменных
102
Глава 3. Решение уравнений
Нахождение экстремумов функции нескольких переменных аналогично иссле-
дованию функции одной переменной. На примере функции двух переменных
рассмотрим влияние ограничений на поиск экстремумов (рис. 3.20 и 3.21).
Функции minimize и maximize способны вычислить, соответственно, минимум
и максимум как с ограничениями, так и без них. Результаты решения в значи-
тельной степени зависят от выбранных начальных приближений и далеко не
всегда соответствуют истине.
область ограничений в виде квадрата
с ограничениями Given -2 < х < 2 -2 < у < 2
QMinimize(f ,х,у) Q - I I ffQg.Qj) - -3
область ограничений в виде прямой линии
х:» 4 у:» 4 Given х - у я 1
(0 566 I г
R > Maximize^,х,у) R = I q | f(RQ ,Rj - -0.484
Рис. 3.21. Нахождение экстремума функции двух переменных с ограничениями
СОВЕТ ------------------------------------------------------------------
При анализе конкретного уравнения рекомендуется внимательно изучить поверхностный
график функции и график линий уровня, на котором хорошо видны области нахождения
экстремумов.
Все три способа определения экстремумов функции имеют свои плюсы и мину-
сы. Творческий подход к их выбору почти всегда позволяет правильно найти
экстремумы функции.
3.8.	Рекурсивные вычисления
Mathcad допускает внутри тела функции обращение функции к самой себе, по-
зволяя создавать рекурсивные функции, использующие значения, известные на
момент вычислений. Примером такой функции является вычисление факториа-
ла (рис. 3.22).
На этом же рисунке приведен пример рекурсивного вычисления корня квадрат-
ного числа, где последовательность приближений записана в виде вектора. Но-
мер попытки — индекс элемента вектора. В рекурсивном вычислении сначала
вычисляется первый элемент массива, затем — последовательные элементы, ис-
пользующие значения предыдущих элементов.
Для отметки точного вычисления корня на график нанесена метка VA. Для нане-
сения метки двойным щелчком мыши на графике откройте окно форматирова-
3.8. Рекурсивные вычисления
103
ния графика и на вкладке X-Y Axes установите флажок Show Markers (Показы-
вать маркеры). В одном из появившихся мест ввода впишите 4а, а второе
оставьте пустым.
Вычисление факториала
fact(ri) := if(n  0,1 ,nfact(n - 1))
fact(l) - 1 fact(ip) » 3628800
Вычисление квадратного корня числа А
А > 17348	131711811	i>0..5
Рис. 3.22. Рекурсивное вычисление корня квадратного числа А
итерационные вычисления
модель развития эпидемии
i:=0.. 15 дней

vo
Ч)
Ы
<	50 >
22000
0
<	0 >
vl+l
LH-1
Zd. .
h-17
0.0001 V.In.
V. - 0.0001 V. In.
L. + 0.55In.
In - инфекция
V - восприимчивость
L - смертность
Zd - выздоровление
Zd. + 0.45In.
Рис. 3.23. Рекурсивные вычисления в модели распространения инфекции
104
Глава 3. Решение уравнений
Можно выполнить многократные рекурсивные вычисления нескольких вектор-
ных переменных одновременно. Такая разновидность рекурсивных вычислений
используется для решения систем уравнений в методе конечных разностей.
На рис. 3.23 описана модель развития инфекции среди животных. Четыре урав-
нения связывают друг с другом четыре переменные: число восприимчивых, ин-
фицированных, умерших и выздоровевших животных.
ПРИМЕЧАНИЕ -----------------------------------------------------------
Mathcad вычисляет все выражения справа перед присваиванием значений величинам сле-
ва. Ничто справа не может зависеть ни от чего слева.
ПРИМЕЧАНИЕ -----------------------------------------------------------
В Mathcad 12 запрещено определять функцию пользователя посредством рекуррентных
выражений, например,/(х) :=/(х) + 1. При попытке вычисления /(х) вместо ее нового (ре-
куррентного) присваивания, как происходило в предыдущих версиях, будет организован
бесконечный цикл. Для организации рекуррентных вычислений используйте новое имя
функции, например /i(x) := /(х) + 1, либо именной оператор (namespace operator).
В Mathcad 13 и 14 переопределение функций разрешено.
Глава 4
Работа с векторами и матрицами
Преимущество работы с Mathcad особенно ощутимо при работе с массивами
(векторами и матрицами). Как правило, эта работа состоит в многократном по-
вторении однотипных расчетов со всеми элементами матрицы.
Одиночное число будем называть скаляром, столбец чисел — вектором, а прямо-
угольную таблицу чисел — матрицей. Фактически вектор — это матрица, состоя-
щая из одного столбца чисел.
4.1.	Создание матрицы
Есть три способа создания массива чисел:
1	. Заполнение шаблона матрицы, содержащего пустые места ввода чисел, что
подходит для ввода небольших массивов (не более 100 элементов).
2	. Использование дискретной переменной. Этот метод подходит, когда есть яв-
ная формула для вычисления элементов массива.
3	. Считывание данных из файлов. Этот метод рассматривался в главе 2 (раз-
дел 2.13).
Рассмотрим подробно первый, наиболее простой метод создания матрицы:
□	Установите курсор в то место, где надо создать матрицу.
□	Щелкните на кнопке математической панели Vector and Matrix Toolbar (Векто-
ры и матрицы), а в появившейся панели инструментов щелкните на кнопке
Matrix or Vector (Матрица или вектор), как показано на рис. 4.1. Можно в глав-
ном меню Mathcad выбрать команду Insert ► Matrix (Вставка ► Матрица) или
нажать комбинацию клавиш Ctrl+m.
□	В появившемся диалоговом окне впишите число строк (Rows) и число столб-
цов (Columns), а затем щелкните на кнопке ОК. На месте курсора появится
шаблон матрицы.
□	В каждое место ввода впишите число, буквенную константу или функцию.
Переход от одного места ввода к другому осуществляется клавишами со
стрелками. Можно также щелкнуть мышью на нужном месте ввода, но это не
так удобно, как перемещение с помощью клавиш.
ПРИМЕЧАНИЕ -----------------------------------------------------
Диалоговое окно Insert Matrix в Mathcad 13-15 позволяет создавать матрицу из одного чис-
ла размерностью 1x1.
Примеры набора матриц показаны на рис. 4.2.
106
Глава 4. Работа с векторами и матрицами
Рис. 4.1. Панели для работы с матрицами
|ORIGIN : 1| нумерация элементов в матрицах
начинается с 1 (по умолчанию ORIGIN=0)
элемент
массива
А1,2" 2
v3-10
выделение
столбца массива
Самостоятельно наберите вектор 3 х 1 и матрицу 3 х 2 из любых чисел
и с ними проделайте все последующие операции
Рис. 4.2. Примеры набора массивов и вывода их элементов
Можно изменять размер матрицы, вставляя и удаляя строки и столбцы
(рис. 4.3):
□	Щелкните мышью на крайнем элементе матрицы. Синий уголок курсора дол-
жен находиться справа от выделенного элемента.
□	Выберите значок матрицы в математическом меню или нажмите комбинацию
клавиш Ctrl+m. В появившемся окне впишите число строк и столбцов, кото-
рые надо вставить или удалить.
□	Щелкните на кнопке Insert (Вставить) или Delete (Удалить), затем на ОК.
Если вы хотите вставить или удалить одну строку, то надо вписать количест-
во строк — 1, количество столбцов — 0 и выбрать пункт Insert или Delete.
ПРИМЕЧАНИЕ ----------------------------------------------------------
Mathcad вставляет строки или столбцы вправо и вниз от выделенного элемента матрицы,
удаляет строки и столбцы вправо и вниз, включая выделенный элемент.
Чтобы удалить всю матрицу, выделите ее черным цветом и нажмите клавишу
Delete (для безвозвратного удаления) или выберите Cut на стандартной панели
Mathcad (чтобы вырезать в буфер). Можно также выбрать команду Cut в контек-
стном меню, появляющемся при щелчке на выделенной матрице правой кнопкой
мыши.
4.3. Встроенная переменная ORIGIN
107
результат удаления
двух первых строк
результат добавления
двух последних строк
Рис. 4.3. Изменение размеров матрицы
СОВЕТ --------------------------------------------------------------------
При работе с Mathcad почаще нажимайте правую кнопку мыши, проверяя, что можно сде-
лать с помощью контекстного меню. Как правило, в нем появляются самые необходимые
в данный момент пункты.
4.2.	Нумерация элементов матрицы
Элементы матрицы определяются двумя нижними индексами, элементы векто-
ра — одним.	*
Для ввода нижнего индекса можно щелкнуть в математической панели на кноп-
ке Subscript (Нижний индекс) (см. рис. 4.1), но лучше использовать клавишу
[ (открывающая квадратная скобка), так как во время работы с матрицами вво-
дить нижний индекс приходится очень часто.
Чтобы из матрицы выделить вектор (один из столбцов матрицы), используется
верхний индекс. Эта операция применяется не очень часто, поэтому для ее вы-
полнения лучше использовать математическую панель инструментов:
□	Введите имя матрицы и выделите его синим уголком курсора.
□	В математическом меню щелкните на кнопке Matrix and Vectors Toolbar (Па-
нель векторов и матриц) и щелкните на кнопке М< > Matrix Column (Столбец
матрицы).
□	В появившемся месте ввода впишите номер столбца.
4.3.	Встроенная переменная ORIGIN
Начало нумерации элементов в векторах и матрицах определяется встроенной
переменной ORIGIN.
По умолчанию ORIGIN = 0, то есть первый элемент вектора, первая строка и пер-
вый столбец матрицы имеют индекс нуль.
Чтобы изменить нумерацию индексов в первой строке документа, наберите
(прописными буквами) ORIGIN:=1. Можно переопределить встроенную перемен-
ную ORIGIN другим способом. Выберите в главном меню команду Tools ►Work-
sheet Options (Инструменты ► Параметры документа), в открывшемся окне
108
Глава 4. Работа с векторами и матрицами
перейдите на вкладку Built-In Variables (Встроенные переменные) и в поле Array
Origin (ORIGIN) введите индекс первого элемента массива (рис. 4.4). Переменной
ORIGIN можно присваивать разные значения, в том числе отрицательные.
Рис. 4.4. Встроенные переменные Mathcad
В Mathcad есть встроенные функции, в алгоритм которых по умолчанию вклю-
чены величины с нулевым индексом, например, mean (вычисление среднего зна-
чения) или fft (разложение в ряд Фурье). Если ORIGIN:=1 введено с клавиатуры,
неизбежна ошибка в расчетах. Измените значение встроенной переменной ORI-
GIN в главном меню Mathcad, и ошибки в расчетах не будет.
ПРИМЕЧАНИЕ -------------------------------------------------------
Исключение составляет функция Matrix. При любом значении ORIGIN она возвращает мат-
рицу, нумерация элементов в которой начинается с нуля.
ВНИМАНИЕ ---------------------------------------------------------
Во всех примерах этой главы установлено значение ORIGIN = 1.
4.4.	Определение параметров матрицы
В Mathcad есть встроенные функции для определения параметров матрицы
(рис. 4.5):
□	rows(Af) — число строк в массиве или векторе;
□	cols(Af) — число столбцов в массиве;
□	last(Af) — индекс последнего элемента в векторе;
□	тах(Л/) и min(Af) — максимальное и минимальное значения элементов в массиве;
4.5. Образование новых матриц из уже существующих
109
□	сумма элементов вектора вычисляется нажатием кнопки V на панели Matrix;
□	tr(Af) — сумма диагональных элементов квадратной матрицы, называемая
следом матрицы, где М — имя матрицы.
[функции для работы с матрицами |
число столбцов в массиве cols(A) = 2 cols(B) = 3
индекс последнего элемента в векторе iast(V) = 5
max и min элементы в массиве
тах(А) = 5	tnin(A) = 1
max(V) = 12	= 8
Рис. 4.5. Функции определения параметров массивов
4.5.	Образование новых матриц
из уже существующих
Рассмотрим встроенные функции для образования новых матриц из уже сущест-
вующих (рис. 4.6):
□	augment^, В) объединяет матрицы А и В бок о бок. Матрицы А и В должны
иметь одинаковое число строк.
С := augment(A ,В) Cl := submathx(C, 1,2,1,3)
С2 := submatrix(C,3,5,3,5) поменяйте номера
строк и столбцов
<1 2 3 4 5>
2 3 4 5 1
С= 34512
4 5 12 3
<5 1 2 3 4;
А 2 3^
<5 1 2>
С2= 12 3
<2 3 4;
2 3 4
D > stacfc(Cl ,С2)
5 1 2
1 2 3
2 3 4J
Рис. 4.6. Функции объединения и вырезания матриц
110
Глава 4. Работа с векторами и матрицами
□	stacked, В) объединяет матрицы друг над другом. Матрицы А и В должйы
иметь одинаковое число столбцов.
□	submatrixfA, irows, jrows, icols, jcols) создает матрицу, вырезанную из матри-
цы А. Новая матрица содержит элементы матрицы А, вырезаемые от ряда
irows до ряда jrows, от столбца icols до столбца jcols.
Для ввода указанных функций выполните следующие действия:
□	Наберите имя новой матрицы и оператор присваивания.
□	На стандартной панели выберите кнопку f(x).
□	В открывшемся списке функций найдите нужную и щелкните мышью на
кнопке Insert (Вставить). Имя функции можно набирать и с клавиатуры,
главное — не сделать в нем ошибки.
□	В места ввода впишите нужные имена массивов.
4.6.	Ввод больших массивов
В Mathcad есть ограничения на размер вводимых массивов. При использовании
шаблона матрицы можно создать массив, состоящий не более чем из 100 элемен-
тов. Если надо ввести массив больших размеров, используются встроенные функ-
ции augment и stack.
Можно ввести массив практически неограниченных размеров с использованием
дискретной переменной по какой-либо расчетной формуле либо считать его из
внешнего файла функцией READPRN (рис. 4.7).
создание массива с помощью дискретной переменной
п:«4 m:=5	i:=l..n	п и m могут быть любыми числами
	г0.02 0.04	0.04 0.08	0.06 0.12	0.08 0.159	0.1 0.199
Xp-O.l i у.0 2 j f.^.sinlx^yj f-	0.06	0.12	0.179	0.238	0.296
поменяйте вид функции и значения пит	<0.08	0.159	0.238	0.315	0.389 )
считывание массива из файла с именем "Mio" с помощью функции Readprn
F READPRN(“Miu") FT -		1	2	3	4	5	6	7	8
	1	1	2	3	4	5	6	7	8
	2	26	4	6	6	30	8	10	10
	3	' 24	26	26	28	28	30	30	32
	4	2	2	4	26	6	6	8	30
Рис. 4.7. Способы создания больших массивов
ПРИМЕЧАНИЕ ------------------------------------------------------
О дополнительных возможностях преобразования функции в матрицу читайте в разде-
ле 12.5.
4.8. Матричные операторы
111
4.7.	Сортировка векторов и матриц
В Mathcad имеется несколько встроенных функций для сортировки элементов
массива в порядке возрастания или убывания:
□	sort(a) — сортировка элементов вектора в порядке возрастания;
□	reverse(a) — перестановка элементов вектора в обратном порядке;
□	csort(Af, г) — перестановка строк матрицы М в порядке возрастания элемен-
тов i-го столбца;
□	rsort(M, Г) — перестановка столбцов матрицы М в порядке возрастания эле-
ментов г-й строки.
ПРИМЕЧАНИЕ ----------------------------------------------------------
Если элементы вектора или матрицы — комплексные числа, то сортировка выполняется
по действительной части, а мнимая часть игнорируется.
Примеры сортировки элементов массивов приведены на рис. 4.8.
функции сортировки]
reverse(sort(V))
<12^
10
9
8
i 5 j
В :=
4
5
1
<2
1
2
3
4>
rsort(B,5) =
<3 4
4 5 1
42 3 4)
4
5
1
2
3
5 1 2
1 2 3
Рис. 4.8. Примеры сортировки элементов массивов
4.8.	Матричные операторы
Рассмотрим лишь наиболее часто употребляемые операторы.
4.8.1.	Транспонирование матрицы
Транспонированием называется операция, в результате которой столбцы исход-
ной матрицы становятся строками, а строки — столбцами.
Для реализации этой и последующих операций выполните следующие действия:
□	Наберите имя матрицы.
□	Щелкните на кнопке со значком матрицы на математической панели.
□	На панели Matrix (Матрицы) щелкните мышью на значке соответствующей
операции, в данном случае Мт.
При вводе больших векторов из соображений экономии места удобно вводить их
в виде строки с последующим транспонированием (рис. 4.9).
112
Глава 4. Работа с векторами и матрицами
Транспонирование матрицы
Определитель квадратной матрицы
2 3 4 5 1
1 2 3
<2 3 4;
Г1 2 5 1 2^
2 3 12 3
С .= 3 4 5 1 2
4 5 12 3
<5 1 2 3 4,
|С| = 1 875 х 103
<12А
Ввод столбца в виде строки
W .= (12 11 10 9 8)Т W= 10
D - неквадратная матрица
| Эта матрица должна быть квадратной.-]
Вывод столбца в виде строки
WT= (12 И .10 9 8)
X = -5	|х| = 5 модуль вещественного числа
X .= 2 - 3 i |х| = 3.606 модуль комплексного числа
Рис. 4.9. Транспонирование матрицы и вычисление ее определителя
Все матричные операторы и матричные функции работают только с векторами
(в виде столбца), но не со строками, поэтому строки вначале приходится транс-
понировать в столбец, а после выполнения нужной операции вновь транспони-
ровать в строку.
ПРИМЕЧАНИЕ ---------------------------------------------------------
В Mathcad 12 при преобразовании строки в столбец имена строки и столбца должны быть
разными.
4.8.2.	Вычисление определителя матрицы
Для нахождения определителя заданной матрицы на панели Matrix выберите зна-
чок |Х|, имеющий тройное значение:
□	вычисление определителя матрицы, если X — матрица;
□	модуль числа, если X — вещественное или комплексное число (см. рис. 4.9);
□	длина вектора, если X — вектор.
В Mathcad вычисление определителя матрицы и вывод модуля числа (его поло-
жительного значения) производится одним и тем же оператором М. В Math-
cad 11 действие этого оператора определялось здравым смыслом: для квадратной
матрицы вычислялся определитель, ддя числа или вектора чисел, а также как ре-
зультат действия дискретной переменной выводилась абсолютная величина чи-
сел или длина вектора.
В Mathcad 13-15 требуется в контекстном меню выбрать необходимое действие
(рис. 4.10). Неприятный момент состоит в том, что этот выбор не сохраняется
при сохранении файла. При открытии файла с таким оператором расчет останав-
ливается на этом операторе, указывая на ошибку. Требуется вмешательство рас-
4.8. Матричные операторы
113
X := -5
Х:= 2-3i
|х| = 5 модуль вещественного числа
ПХДПи.Д^>ЬДСТП<^и4Г.АДАСА..1.|1иСГкЭ. ,,,
Примечание для выбранного фрагмента...
р Абсолютное значение
Определитель квадратной матрицы
X вырезать
Ч=| Копировать
S1 Вставить
Й? Свойства...
Отключить вычисление
Рис. 4.10. Вычисление модуля числа
четчика, чтобы вручную ввести нужное действие. При сохранении файла в фор-
мате xmed подобной ошибки нет..
4.8.3.	Нахождение матрицы, обратной заданной
Для нахождения матрицы, обратной заданной, выберите значок X-1 на панели
Matrix.
Произведение прямой матрицы на обратную есть единичная матрица (рис. 4.11).
Иногда единичная матрица необходима для решения матричных уравнений. Для
создания единичной матрицы в Mathcad есть встроенная функция identity(n), где
п — размер квадратной матрицы.
Обращение матрицы
	<-0.187 0.013 0.013 0.013 0.213 >		<1 0 0 0 0^
	0.013 0.013 0.013 0.213 -0.187		0 10 0 0
1 =	0.013 0.013 0.213 -0.187 0.013	Проверка С С 1 =	0 0 10 0
	0.013 0.213 -0.187 0.013 0.013		0 0 0 1 0
	< 0.213 -0.187 0.013 0.013 0.013 ;		<00001,
<1 О О О (Р
0 10 0 0
Единичная матрица Е := identity(5)
0 0 10 0
0 0 0 1 0
<0 0 0 0 17
Рис. 4.11. Вычисление матрицы, обратной заданной
4.8.4.	Сложение, вычитание и умножение матриц
Сложение и вычитание матриц выполняется с помощью традиционных операто-
ров сложения и вычитания «плюс» и «минус» (рис. 4.12).
114
Глава 4. Работа с векторами и матрицами
Сложение, вычитание,умножение матриц
не удовлетворяет правилу перемножения матриц
| Размерности массива не совпадают. |
Рис. 4.12. Арифметические действия с матрицами
Для умножения матриц используется традиционный знак умножения (клавиша
со звездочкой). Знак умножения в Mathcad-документе по умолчанию обознача-
ется точкой.
Вид значка в документе можно поменять. Для этого щелкните правой кнопкой
мыши на выражении, в котором есть знак умножения. В открывшемся контекст-
ном меню найдите пункт View Multiplication as (Вид знака умножения). Щелкните
мышью на одном из предлагаемых семи пунктов — значок изменится.
Точно так же можно изменить вид знака присвоения значения, но делать этого
не рекомендуется, чтобы не перепутать знак присвоения значения и знак логиче-
ского равенства.
По правилу перемножения матриц, число столбцов первой матрицы должно
быть равно числу строк второй матрицы, Л(тх п) • В(п xk) = С(тх k) (в скобках
указаны размеры перемножаемых матриц).
ПРИМЕЧАНИЕ -------------------------------------------------------------
Полезно запомнить, что произведение строки на столбец дает число, а произведение
столбца на строку дает полностью заполненную квадратную матрицу (рис. 4.13).
Скалярное произведение векторов дает число, равное сумме попарных произве-
п
дений элементов этих векторов, UV =	где п — число элементов каждого
вектора, или UV =|t7|| V|-cos(0} где 0 — угол между векторами.
4.8. Матричные операторы
115
<144 132 120 108 96
132 121 110
VVT = 120 110 100
99 88
90 80
108 99 90 81 72
<96 88 80 72 64;
столбец х строку = матрица
VTV = (510)
(1 2 3)- 2 =(14)
строка х столбец = число
Рис. 4.13. Умножение векторов
Для вычисления скалярного произведения векторов используется обычный знак
умножения (клавиша *) или значок XY на панели Matrix (рис. 4.14).
V = 2 U = 4
ч 3 J	к 5 У
скалярное
произведение
VU = 53
векторное
произведение
' -2 '
VxU= -41
к 34 ,
попарное
произведение
Г 30)
(VU) = 8
VI = (2 5 1 7)т U1 - (-2 4 8 3)Т VI U1 = 45
VlxUl = ji
| Значение должно быть вектором с тремя элементами?)
Рис. 4.14. Умножение векторов (продолжение)
Векторное произведение двух векторов, X и У, с углом между ними 0 равно век-
тору с модулем | U | У|• sin(0)> направленному перпендикулярно плоскости, опреде-
ляемой векторами U и V. Оператор векторного произведения можно ввести толь-
ко с панели Matrix при помощи значка Хх Y,
Векторное произведение можно вычислить только для векторов с тремя элемен-
тами (см. рис. 4.14).
4.8.5.	Оператор векторизации
В Mathcad существует несколько необычный оператор, называемый оператором
векторизации и предназначенный для работы с массивами. Он позволяет выпол-
нить однотипную операцию со всеми элементами массива (рис. 4.15), например,
вычислить cos(ot), где а — матрица углов. Для этого
□	выделите клавишей пробела все выражение;
116
Глава 4. Работа с векторами и матрицами
если аргумент вектор, оператор векторизации не нужен
U= 4 cos(U) = -0.654
<5j I 0.284 >
и3 =
64
< 20.086 >
54.598
< 148.413 >
V125J
U
е
если аргумент матрица, оператор векторизации нужен
Л
А3
2>
3
-0.416
cos(A) =
8
27
64
<125
27
64
125
-0.99
-0.654
< 0.284
' 2.718
7.389
20.086
54.598
<148.413
-0.416
-0.99
-0.654
0.284
0.54 J
7.389 >
20 086
54.598
148.413
2.718 ;
А =
2
3
4
4
5
8
1 )
А
Рис. 4.15. Использование оператора векторизации
□	на панели матриц щелкните на кнопке f(M). Над выделенным выражением
появится знак векторизации;
□	нажмите клавишу =.
Mathcad допускает использование вектора в качестве аргумента функции, и в этом
случае знак векторизации не требуется. Например, если V— вектор, cos(V) = ответ —
без знака векторизации.
4.8.6.	Последовательное и параллельное вычисление
элементов массива
В Mathcad 13-15 матричные операции, такие как вычисление определителя мат-
рицы, перемножение матриц, обращение матрицы, вычисление собственных чи-
сел матриц и их собственных векторов, выполняются более быстрым алгорит-
мом благодаря одновременному (параллельному) вычислению нескольких
элементов массива.
В Mathcad 11 значения массива чисел вычисляются последовательно, а в Math-
cad 13-15 — одновременно, что может дать различные ответы (рис. 4.16).
Показанное на рис. 4.17, слева последовательное вычисление значений векторов
работает в Mathcad И. В Mathcad 13 для подобных вычислений необходимо ис-
пользовать программный оператор (рис. 4.17, справа).
4.9.	Собственные числа и собственные
векторы матриц
В технических расчетах весьма актуальна задача определения собственных чисел
и собственных векторов квадратных матриц. В Mathcad имеется несколько встро-
енных функций для решения стандартной и нестандартной задач.
4.9. Собственные числа и собственные векторы матриц
117
Рис. 4.16. Параллельное в Mathcad 13 и последовательное в Mathcad 11
вычисление элементов массива
работает в Mathcad 11
i := 1.. 4 8g := 2 bg := 3 f V-
I bl J '
| This array index is invalid for this array. |
в mathcad 13
*0
for i e 1.. 4
- .6 b.
al
+ 0.2-a.
bl
3.2
4.016
4.35
<4.162 J
3.64
4.443
5.313
<6.1467
Рис. 4.17. Рекурсия в Mathcad 11 и 13
Рассмотрим стандартную задачу на собственные числа А • L = X • L или
(	Л - X Е) • L = 0, где Е — единичная матрица, А — квадратная матрица, X — век-
тор собственных чисел, L — спектр собственных векторов (рис. 4.18).
Для решения стандартной задачи используются следующие функции:
□	eigenvals(X) вычисляет вектор собственных чисел матрицы Л, превращающий
ее в диагональную матрицу;
□	eigenvecs(X) вычисляет спектр собственных векторов матрицы А. Результат
расчета — матрица, каждый столбец которой А<1> представляет собой норми-
рованный собственный вектор для одного из собственных чисел Х2.
Пример стандартной задачи: по заданному тензору напряжений найти 3 главных
напряжения (собственные числа) и соответствующие им направляющие косину-
сы для нормалей к трем главным площадкам (собственные векторы).
Нестандартная задача на собственные числа имеет вид А • L — X • В • L или
(Л - X • В) • L = 0, где А и В — квадратные матрицы (неединичные), X — вектор
собственных чисел, L — спектр собственных векторов (рис. 4.19).
118
Глава 4. Работа с векторами и матрицами
Стандартная задача на собственные числа
<1 2 3 4 5Л
2 3 4 5 1
3 4 5 1 2
4 5 12 3
ALsXL
или (A-1E)l = 0
где Е-единичная матрица
5 1 2 3 47
собственные числа
собственные векторы
1:« eigenvals(A)
<-4.25 А
-2.63
L :> eigenvecs(A)
'-0.56 -0.62 -0.1	0.29 0.45 >
-0.45 0.45	0.45 -0.45 0.45
2.63
4.25
L- 0.29 -0.1 -0.62 -0.56 0.45
V 15 J
0.62 -0.29 0.56	0.1	0.45
< 0.1	0.56 -029 0.62 0.45;
Создание диагональной матрицы из собственных чисел
(-425 0	0	0 0 Л
Ахшав diag(x)
-2.63	0	0	0
0	2.63	0	0
О	0	4.25	О
О	0	0	15;
Рис. 4.18. Определение собственных чисел квадратной матрицы
Нестандартная задача на собственные числа
ALaJLBL или (a-1B)L«0	/2 3 4 А	(3 1 4>
где А и В симметричные матрицы А > 3 -2 -5	В1 5 2
1^4 —5 1 ;	<4 2 6;
собственные числа	собственные векторы
''-9.614А	С 0.814 -0526 0.685 >
genvals(A,B)  0.752	genvecs(A,B)  -0.044 0.06	0.421
<2.612 J	V-0.578 -0.373 -0.595,
Рис. 4.19. Обобщенные собственные числа матрицы
Пример нестандартной задачи: определение собственных частот колебаний уп-
ругих систем. В этой задаче собственное число Х = ш2 — квадрат собственной
частоты колебаний, собственный вектор 1<г> — форма колебания для собствен-
ной частоты ш  (см. главу 4, примеры 26 и 27 электронной книги).
Для решения нестандартной задачи используются следующие функции:
□	genvals0, В) вычисляет вектор обобщенных собственных чисел X;
□	genvecs0, В) вычисляет спектр собственных векторов. Результат расчета —
матрица, каждый столбец которой L<1> соответствует собственному чис-
лу Xf.
4.10. Норма квадратной матрицы
119
ПРИМЕЧАНИЕ ----------------------------------------------------------
Функции Genvals и Genvecs принимают к расчету и комплексные матрицы.
Результаты расчета собственных чисел и собственных векторов выводятся в отсортиро-
ванном виде.
Вектор собственных чисел можно преобразовать в диагональную матрицу с по-
мощью функции diag(X). Результат ее действия — диагональная матрица, на
главной диагонали, которЬй расположены элементы вектора X.
В старых версиях Mathcad функция diag принимала вектор чисел, а возвращала
квадратную матрицу с элементами вектора на диагонали. В Mathcad 13 функция
diag выполняет уже два действия:
1) если принимает вектор, то возвращает диагональную матрицу с элементами
вектора на главной диагонали;
2) если принимает диагональную матрицу, то возвращает вектор чисел, стоящих
на главной диагонали (рис. 4.20).
i:=0..2 v. := 2 i i	r0 0 o'*	
Md := diag(v) Md =	0 2 0	diag(M(f) = 2
	<0 0 4;	4>
Рис. 4.20. Два действия, выполняемые функцией diag
4.10.	Норма квадратной матрицы
Норма квадратной матрицы характеризует порядок величины элементов мат-
рицы.
В Mathcad есть 4 функции для оценки нормы (рис. 4.21):
□	norm 1 (Л) — норма в пространстве
□	погт2(Л) — норма в пространстве Z2;
□	погте(Л) — евклидова норма;
□	поптн(Л) — max-норма, или оо-норма.
<1 2 3 4 5^
2 3 4 5 1
C:=	3 4 5 1 2	norml (C) = 15
	4 5 12 3	norme(C) = 16.583
V 1 2 3 4) СС := 100 С
norml(CC) - 1500
norme(CC) = 1658
norm2(C) = 15
normi(C) = 15
norm2(CC) = 1500
normi(CC) = 1500
Рис. 4.21. Функции вычисления нормы матрицы
120
Глава 4. Работа с векторами и матрицами
Евклидова норма эквивалентна длине многомерного вектора ногте = А? •
Как видно из рис. 4.21, величина нормы мало зависит от способа ее вычисления.
При увеличении всех элементов матрицы в 100 раз все нормы также увеличива-
ются в 100 раз.
4.11.	Число обусловленности квадратной матрицы
Число обусловленности является мерой чувствительности системы линейных
алгебраических уравнений АХ = В, определяемой матрицей коэффициентов А,
к погрешностям вектора В правых частей уравнений. Чем больше число обуслов-
ленности, тем более неустойчив процесс решения системы. В примере, приведен-
ном на рис. 4.22, матрица А хорошо обусловленная, а матрица ЛА, в которой вто-
рая строка почти пропорциональна первой, плохо обусловленная.
Х:=А
condl(A) = 44 cond2(A) = 34471
conde(A) - 34.5 cond^A) = 44 МаТрИЦа A' Х°Р°Ш° °6У“енная
2 5
2 5.001
XX := АА-1ВВ
( 20005
XX =
1-8000
condl(AA) = 35009 cond2(AA) = 29005
. лч	or™ Матрица АА- плохо обусловленная
conde(AA) = 29005 condi(AA) = 35009	J
Рис. 4.22. Функции вычисления обусловленности квадратной матрицы
4.12.	Матричные разложения
Большинство матричных методов решения систем линейных алгебраических
уравнений основано на представлении матрицы коэффициентов уравнения в виде
произведения матриц специального вида, полученных путем разложения исход-
ной матрицы.
13 7 4
А = 7 9 -3
<4-39;
'20 3 4
АА = 3 2-5
<4-59;
L = cholesky(A|A.)
| Матрица должна быть положительно определенной. |
Рис. 4.23. Разложение матрицы по методу Холесского
4.12. Матричные разложения
121
В Mathcad имеется несколько функций, реализующих алгоритмы наиболее по-
пулярных матричных разложений.
4.12.1.	Разложение Холесского
Разложением матрицы по методу Холесского является представление ее в виде
А = L Г, где L — нижняя треугольная матрица (то есть матрица, в которой
сверху от диагонали находятся нули). Выполняется это разложение функци-
ей cholesky(A), где А — симметричная, положительно-определенная матрица
(рис. 4.23).
4.12.2.	QR-разложение
QR-разложение представляет исходную матрицу в виде А = Q • R, где Q — орто-
нормированная матрица, то есть состоящая из ортогональных друг другу векто-
ров единичной длины, a R — верхняя треугольная матрица (нули под главной
диагональю).
Выполняется это разложение функцией qr(A). Результатом действия функции
является матрица Z, полученная из двух матриц, Q и R, составленных бок о бок.
Чтобы выделить каждую матрицу отдельно, используем функцию submatrix
(рис. 4.24).
< 0.97	-0.145	0.194	20.616	2.231	4.899 >
L1 =	0.146	-0.292	-0.945	0	-5.746	9.385
<0.194	0.945	-0.262	0	0	3.149;
Q := submatxixf LI, 1 ,rows(Ll), 1,
< 0.97 -0.145 0.194
Q= 0.146 -0.292 -0.945
<0.194 0.945 -0.262;
(	cols(Ll)
R := submatrixl LI, 1 ,rows(Ll),-------—- + 1, cols(Ll)
<20.616 2.231 4.899
R= 0	-5.746	9.385
< 0	0	3.149;
Рис. 4.24. QR-разложение квадратной матрицы
4.12.3.	LU-разложение
LU-разложением матрицы А, или треугольным разложением, является матрич-
ное разложение типа РА = LU, где U и L — верхняя и нижняя треугольные мат-
рицы. Р, A, L, U — квадратные матрицы одного размера.
LU-разложение квадратной матрицы А выполняется функцией lu(A).
Фактически треугольное разложение матрицы выполняется при решении систе-
мы линейных алгебраических уравнений методом Гаусса.
Функция lu(A), как и функция qr(A), выводит составную матрицу, содержащую
матрицы Р, Z, Z7, составленные бок о бок (рис. 4.25).
122
Глава 4. Работа с векторами и матрицами
LU - разложение
<20 3 -4^
А := -2 2 -2
<4-5 9;
LI := 1и(А)
<0	1	0	1	0	0	-2	2	-2
Ll=	1	0	0	-10	1	0	0	23	-24
<0	0	1	-2	-0.043	1	0	0	3.957;
{	cols(Ll)
Р := submatrixl LI, 1 ,rows(Ll), 1,---
<0 1 (Р
Р= 1 О О
<0 0 1;
т к х  Гн 1 zt cols(Ll) 1 cols(Ll)-2>|
L := submatnxl LI, 1 ,rows(Ll),---------+ 1,------------ I
<1	О	(Р
L= -10	1	О
<-2 -0.043 1;
{	cols(LlY2
U := submatnxl LI, 1 ,rows(Ll),--
<-2 2	-2	>
U- 0 23 -24
< 0 0 3.957 >
<-2 2 -2>
Проверка P A = 20 3 -4
U -5 9 J
<-2 2 -З''
LU = 20 3 -4
<4 -5 9>
Рис. 4.25. LU-разложение квадратной матрицы
4.12.4. Сингулярное разложение
Сингулярным разложением матрицы А размером MxN, где M>N, является раз-
ложение вида А = Bxsx С7, где В и С — ортогональные матрицы размером MxN
и NxM соответственно, 5 — диагональная матрица с сингулярными числами мат-
рицы А на главной диагонали, svds(71) — вектор, состоящий из сингулярных чи-
сел, svd(71) — сингулярное разложение матрицы А.
Примеры поиска сингулярных чисел невырожденной матрицы А и сингулярной
матрицы At приведены на рис. 4.26.
Начиная с Mathcad 13 сингулярное разложение выполняется одной функцией
svd2, заменяющей две функции, svd и svds. Новая функция svd2 для сингулярно-
го разложения матриц работает и с комплексными числами. Кроме того, она сде-
лана более удобной в использовании.
Функция svd2 возвращает составной массив, состоящий из трех вложенных мас-
сивов, входящих в выражение А = Bxsx (7. На рис. 4.27 показано использование
функции svd2.
4.13. Вывод векторов и матриц
В Mathcad существует два способа отображения массивов: в виде матрицы
и в виде таблицы (рис. 4.28).
4.13. Вывод векторов и матриц
Сингулярное разложение
<20 3 4
3 2-5
4-5 9
V? -3 -2J
АА := svd(A)
	< -0.92	0.142	-0.347 >
	-0.084	0.516	0.167
	-0.258	-0.832	0.203
АА =	-0.281	0.147	0.9
	-0.974	0.185	0.135
	-0.036	0.459	-0.888
	<-0.226	-0.869	-0.441;
Вырежем матрицы В и С из матрицы АА
(л л «	.«г rows(AA) А 4	« лч
АА, 1, с eill-----1,1, cols(AA)
В»
< -0.92	0.142	-0.347 >
-0.084	0.516	0.167
-0.258	-0.832	0.203
<-0.281	0.147	0.9 ;
1 ,rows(AA), 1, cols(AA)
	22.251	0	0 >		<-0.974	0.185	0.135 >
s : diag(svds(A)) s =	0	11.272	0	Cn	-0.036	0.459	-0.888
	< 0	0	4.984;		<-0.226	-0.869	-0.441;
<20 3 4 >
B -s CT -
Проверка
3 2-5
4-5 9
<7 -3 -2}
Рис. 4.26. Сингулярное разложение матрицы
49.419
2.192
В Mathcad 13
r2.3 24 >		<{2,1}''	
6.7 42	svd2(A) =	{3,2}	svd2(A) =
<2.8 7;		Ы	
Свернутый и развернутый
массив вывода
<0.487	-0.58 >
0.861	0.192
<0.148	0.792 ;
'0.148	0.989 '
l 0.989	-0.148 >
r s 1
В := svd2(A)
< 49.419
s -
I 2.192
В =
<0.487 -0.58
0.861 0.192
<0.148 0.792;
<0.148 0.989
С =
<0.989 -0.148
<2.3
Проверка В Ла@О) СТ - 6.7
г2.3 24>
А- 6.7 42
<2.8 7/	<2.8 7 )
Рис. 4.27. Применение функции svd2
124
Глава 4. Работа с векторами и матрицами
Рис. 4.28. Изменение стиля отображения массива
Для изменения стиля отображения массива выберите в главном меню Format ►
Result (Формат ► Результаты), перейдите на вкладку Display Options (Параметры
отображения). В поле Matrix display style (Стиль отображения матриц) выберите
Matrix (Матрица), Table (Таблица) или Automatic (Автоматический выбор).
Как правило, Mathcad выбирает Matrix для маленьких массивов и Table для боль-
ших.
Более простой путь форматирования выведенного массива — дважды щелкнуть
левой кнопкой мыши в поле массива, который надо отформатировать. При этом
появляется диалоговое окно Result Format (Формат результата), открытое на
вкладке Number Format (Формат чисел). Остается только перейти на нужную
вкладку (Display Options).
Если число элементов в строке или столбце больше 10, то в стиле Table для эко-
номии места в документе Mathcad выводит только 10 чисел, а сбоку и вверху —
полосы прокрутки для просмотра остальных элементов массива.
Стиль отображения Table допускает различное выравнивание выведенного мас-
сива относительно его имени. Для установки выравнивания надо, поместив кур-
сор в область массива, щелкнуть правой кнопкой мыши и в открывшемся кон-
текстном меню выбрать Alignment (Выравнивание), где на выбор предлагается
5 мест расположения названия массива: Тор (Верх), Center (Центр), Bottom
(Низ), Above (Выше), Below (Ниже) (рис. 4.29). Пункт Properties (Свойства) это-
го же контекстного меню позволяет установить или убрать нумерацию строк
и столбцов.
В окне Display Options (Параметры отображения) есть пункт Expand nested arrays
(Разворачивать вложенные массивы). Установите там флажок, если хотите уви-
деть все массивы, вложенные в составной массив.
4.14. Составные массивы
Для удобства вычислений иногда формируют массив из различных по смыслу
и по размерности элементов. Такой массив называется составным. Необходи-
4.15. Работа с комплексными числами
125
мость в составных массивах возникает при составлении больших программ.
В программе одно место вывода, а вывести надо несколько различных величин
(чисел, векторов, матриц). Примеры составных массивов приведены в главе 9
и в примерах 6, 20, 30 и 31 электронной книги.
Рис. 4.29. Контекстное меню для матрицы в стиле Table
4.15. Работа с комплексными числами
Mathcad с одинаковым успехом вычисляет выражения с действительными
и с комплексными числами.
Комплексные числа можно записывать в любой принятой в математике форме:
□	обычной (в виде суммы действительной и мнимой частей числа) — с = а 4- Ы,
□	в тригонометрической форме — с = А • (cos(cp) + i • sin(cp));
□	в экспоненциальной форме — с = Ае' *.
Для ввода мнимой единицы надо набрать с клавиатуры 1i или 1j и ввести число.
При выведении курсора из области числа символ 1 исчезает, остается комплекс-
ное число в привычном виде (рис. 4.30).
В качестве примера рассмотрим расчет токов и напряжений в цепи переменного
тока по законам Кирхгофа. В этом случае ЭДС Е в цепи, напряжения U, тока J,
сопротивления Z — комплексные числа. ЭДС Е задана в экспоненциальной фор-
ме, но при нажатии клавиши = выводится в обычном виде. После ввода кон-
стант в комплексной форме все формулы записываются так же, как и для дейст-
вительных чисел. При расчете вектора напряжений на различных участках цепи
126
Глава 4. Работа с векторами и матрицами
по закону Ома использован оператор векторизации для расчета попарных произ-
ведений Ui = JiZi (рис. 4.31).
Ввод мнимой единицы 1 i или 1j или i := л/ч
С = а + bi = А- 81п(ф) + icos (ф)»Ае*Ф
например
С := 2 - 3 i
D := 2 + 3 j
С = 2 — 31
СС = 1.5 + 2.5981
DD Зе" 21 DD - -1248 - 2.7281
Переменный ток.
Em:- 179	* 20	Е:- —Лф Е-51.652 + 115.5531
Расчет токов в цепи по уравнениям Кирхгофа ORIGIN:« 1
< j 10
30
-150
< i-60 >
<1-11 о о >
00-11 1
2|	0	0	0
0 Zj Zj	0
<0 0 ° ”z4 Z5>
ММ

;>	40
о
Е
Е
Рис. 4.30. Ввод комплексных чисел
( 2.826 + 2.9961
1> А"1^
2.72 + 2.911
1= -0.106 - 0.0861
-0.634 - 0.5151
< 0.528 + 0.4291 >
Расчет напряжений и := Iz U = -4.035 + 175.5021
по закону Ома
J	без оператора векторизации выведено скалярное произведение векторов
	<-29.956. + 28.259? 81.608 + 87.2951		<-29.956 - 28.2591^ 81.608 - 87.2951
и > (Iz) и =	-4.225 - 3.4311 -25.731 + 31.691 < -25.731 + 31.691 >	и =	-4.225 + 3.4311 -25.731 - 31.691 < -25.731 - 31.691 >
это не аргумент функции-без
оператора векторизации не обойтись
вывод комплексно-сопряженных чисел
Рис. 4.31. Расчеты с векторами комплексных чисел
В Mathcad есть оператор преобразования комплексного числа в комплексно-со-
пряженное. Он не представлен на математической панели, а вызывается с помо-
щью символа кавычки (") (см. рис. 4.31).
4.15. Работа с комплексными числами
127
Модуль комплексного числа А = у Re2 -F Im2 вычисляется оператором 11, вводи-
мым с панели Calculator (Калькулятор) или Matrix (Матрица). Тот же оператор
позволяет вычислить модуль вектора или определитель матрицы.
Аргумент комплексного числа вычисляется встроенной функцией arg(A), кото-
рая выдает угол поворота вектора в системе координат Re-Im (рис. 4.32).
модуль комплексного числа. Необходим оператор векторизации
	<4.118>		<41.182>	
	3.983		1195	11,1-4.118
Й1-	0.136	|и|-	5.443	
	0.816		40.82	
	< 0.68 >		< 40.82 ;	
аргумент комплексного числа
( 0.815 Л
0.819
arg^I j) = 0.815

-2.46
♦ >
-2.46
^0.682 7
♦
<0.815> 0.819		f 4661 > 46.928
-2.46 -2.46		-140.925 -140.925
<0.682 ;		< 39.075 ;
deg
в радианах
угол в градусах
угол
Рис. 4.32. Вычисление модуля и аргумента комплексных чисел
Глава 5
Символьные вычисления
Основой символьных вычислений в Mathcad являются формулы и правила их
преобразования, заимствованные из системы символьной математики Maple 5,
предназначенной для математиков высшей квалификации. Из более чем 300
символьных функций Maple 5 в Mathcad включено около 20, но и этого доста-
точно для инженерно-технических работников, для которых и предназначен
Mathcad.
Большинство пользователей Mathcad в своей работе используют в основном
численные расчеты и графики для анализа результатов расчетов. Лишь изредка
возникает необходимость в символьных вычислениях. Некоторые встроенные
функции Mathcad требуют предварительных символьных вычислений для сво-
его успешного применения:
□	При нахождении корней полинома функцией polyroot символьным путем же-
лательно найти коэффициенты полинома для ввода их в качестве параметров
функции polyroot.
□	При использовании функции общей регрессии^депШ надо создать вектор, со-
держащий в символьном виде саму аппроксимирующую функцию и ее пер-
вую и вторую производные.
□	При решении дифференциальных уравнений необходимо задание высшей
производной в явном виде. Иногда это можно сделать, использовав символь-
ное решение уравнения относительно производной высшего порядка.
5.1. Оптимизация численных вычислений
В Mathcad есть возможность оптимизации решений. Если выбрать пункт меню
Tools ► Optimize ► Worksheet (или Equation) (Инструменты ► Оптимизировать ►
Документ (или Выражение)), то перед вычислением каждого выражения сим-
вольный процессор Mathcad будет пытаться упростить все выражения (или одно
выражение) для ускорения и уточнения вычислений.
В Mathcad есть два самостоятельных процессора: численный и символьный, ко-
торые обычно не имеют связи друг с другом. При включении оптимизации они
работают совместно.
Можно включить оптимизацию для вычисления одного конкретного выражения
более просто. Для этого щелкните правой кнопкой мыши на интересующем вас
выражении и в открывшемся контекстном меню выберите пункт Optimize (Опти-
мизировать). Около выражения, для которого Mathcad будет искать символьное
решение, появится красная звездочка (рис. 5.1).
ВНИМАНИЕ ----------------------------------------------------------
Оптимизация возможна только для выражений, содержащих оператор присваивания ( :=).
5.2. Использование меню символьных вычислений Symbolics
129
Оптимизация расчетов
Г1 Г2 Г3 2 3 . . .
g =	х у zdxdydz
Jo ^0
g= 18
нет оптимизации
*1 /*2 рЗ
I х^ y^ zdxdy dz = 18
0 ^0 ^0
Рис. 5.1. Оптимизация вычислений
В некоторых случаях, например, при вычислении интегралов по поверхности
или объему (двойной или тройной интеграл), удается найти символьное реше-
ние интеграла (см. рис. 5.1), что резко ускоряет расчет, ведь вычисление интегра-
лов — самая медленная операция в Mathcad. В Mathcad есть два способа сим-
вольных вычислений:
1. С помощью меню Symbolics (Символьные вычисления) из главного меню
Mathcad.
2. С помощью панели Symbolic Keyword Toolbar (Символьная панель инструмен-
тов), вызываемой соответствующим значком математической панели.
5.2. Использование меню символьных вычислений
Symbolics
Этот способ предоставляет меньше возможностей, чем символьная панель инст-
рументов. Однако он прост и тем удобен. В ряде случаев лучше обращаться
к меню Symbolics, чем к символьной панели инструментов.
В главном меню Mathcad выберите пункт Symbolics, откроется подменю, содер-
жащее ряд команд (рис. 5.2). Для выполнения любой из этих команд необходимо
сначала выделить объект вычислений:
Рис. 5.2. Вид меню Symbolics
130
Глава 5. Символьные вычисления
□	Щелкните мышью на выражении, если надо произвести символьную опера-
цию над всем выражением.
□	Если надо произвести действия над частью выражения, выделите эту часть
черным цветом, то есть подведите указатель мыши к началу нужной части
выражения, нажмите левую кнопку мыши и переместите курсор до конца
этой части при нажатой левой кнопке мыши.
□	Щелкните мышью на переменной, относительно которой надо произвести
символьные действия.
ПРИМЕЧАНИЕ -----------------------------------------------------------
Выделение черным цветом используется в Mathcad, когда какие-либо действия нужно вы-
полнить над частью выражения: вырезать в буфер, скопировать, удалить, изменить размер
или стиль шрифта и т. д.
Выполняя символьные операции, следует помнить, что не всякое выражение
поддается символьным преобразованиям, что поставленная задача часто не име-
ет символьного решения (в отличие от численного).
Рассмотрение символьных операций начнем с последнего пункта меню Symbolics ►
Evaluation Style (Стиль вычислений). Этот пункт позволяет выбрать стиль выво-
димого символьного решения: горизонтально — рядом с исходным выражением,
вертикально — под ним, с комментариями и без них (рис. 5.3). На рис. 5.4-5.Э
выбрано горизонтальное расположение ответов с комментариями.
Рис. 5.3. Меню выбора стиля вывода символьного результата
ВНИМАНИЕ -----------------------------------------------------------
Перед выполнением символьных операций убедитесь, что включен (помечен флажком)
пункт Automatic Calculation (Автоматический режим вычислений) в меню Math (Математика).
5.2.1.	Символьная оценка выражения
Для выполнения символьной оценки:
□	выделите выражение или его часть;
□	в главном меню выберите команду Symbolics ► Evaluate (Символьные вычисле-
ния ► Вычислить).
5.2. Использование меню символьных вычислений Symbolics
131
Этот пункт предлагает на выбор три варианта вычисления выражения: Symbo-
lically (Символьное), Floating Point (С плавающей точкой), Complex (В комплекс-
ной форме).
Символьный процессор по-разному обрабатывает числа с десятичной точкой
и без нее. Сформулируем общие правила:
Mathcad - [Glava05-Symboi-(|)]
Файл Правка Вид Вставка Формат Инструменты
Символьные операции
Окно Справка
Вычислить
предварительно выделить
все выражение
21п(а) в результате
упростить
Развернуть
Факторизовать
Сборка
Полиномиальные коэффициенты
<Г
0^
в результате
ю
к=2
n (n+ 1) (2 п + 1)
Переменная
Матрица
Преобразование
в результате
80926932541
99532800000
Формат вычислений.
□ ’ о?н еа? х

4*
2
6
80926932541 в результате расчета с плавающей точкой 0.813067979
99532800000
у[з в результате расчета с плавающей точкой	1.73205081
выбрано 9 знаков
7=3 в результате расчета на комплексной плоскости о + y/3 i
оценить самостоятельно
Рис. 5.4. Примеры символьной оценки выражений
□	Если символьный процессор получает числа, содержащие десятичную точку,
то любые возвращаемые численные результаты будут десятичными прибли-
жениями точного решения.
□	Если символьный процессор получает числа без десятичных точек, то любые
возвращаемые численные результаты будут выражены без десятичных точек,
когда это возможно.
□	Если символьная операция дает ответ в виде десятичной дроби, то этот ответ
всегда отображается с 20 значащими цифрами. На это отображение не дейст-
вуют ни локальный, ни глобальный числовой формат.
Примеры использования команды Evaluate приведены на рис. 5.4.
5.2.2.	Упрощение выражений
Команда Simplify (Упростить) служит для основных алгебраических и тригоно-
метрических упрощений выбранного выражения. Она выполняет арифметиче-
ские преобразования, сокращает общие множители, использует основные тожде-
ства для тригонометрических и обратных функций, упрощает степени. Можно
132
Глава 5. Символьные вычисления
упрощать как все выражение целиком, так и его части. Если преобразование все-
го выражения не дает желаемого результата, попытайтесь выделить и упро-
стить часть выражения. Примеры использования команды Simplify приведены
на рис. 5.5.
Siplify - упростить
1	„	। I
-------if а# 1л а < 1
а- 1
оо if 1 а
упрощение до
3! к лз-к
kl 3 - к!
упрощение до х +
упрощение до
1+2х-5
sin(2 х) + cos(3 х) упрощение ДО sin(2 х) + cos(3x)
3 + <7 упрощение ДО о 66327108092812676853
19 0	93
Рис. 5.5. Примеры упрощения выражений
5.2.3.	Раскрытие выражений
Операция символьного разложения по смыслу противоположна операции упро-
щения. В ходе разложения раскрываются все суммы и произведения, а сложные
тригонометрические выражения разлагаются с помощью тригонометрических
тождеств. Если выражение — дробь, числитель будет разложен и выражение бу-
дет представлено как сумма дробей. Примеры использования команды Expand
(Раскрытие) приведены на рис. 5.6.
Expand - разложить
, расширение до 4 з 2
(х + 4)	х + 16 х + 96 х + 256х+256
tan(3 х) + cos(2 х) расширение до	_ з
cos(x) - sin(x)--------------
3 tan(x)2 - 1
(х + 1) (х - 1) расширение до 2 ,
х — 1
cos(5 х) расширение до	5 1П , чз , ч2 _
cos(x) - 10 cos(x) sin(x) + 5 cos(x) sin(x)
разложить самостоятельно
tan(3x) (x+3)(2x+4)
Рис. 5.6. Примеры разворачивания выражений
5.2. Использование меню символьных вычислений Symbolics
133
5.2.4.	Разложение на множители
Команда Factor (Разложить на множители) позволяет разложить полиномы на
произведение более простых полиномов, а целые числа — на простые сомножи-
тели. Команда будет объединять сумму дробей в одну дробь и упрощать много-
этажную дробь с несколькими дробными чертами. Примеры использования ко-
манды Factor приведены на рис. 5.7.
ВНИМАНИЕ ------------------------------------------------------
Mathcad разлагает на множители только то, что выделено.
разложить самостоятельно
tan(3 х) (х 4- 3) (2x4- 4)
Factor - разложить на множители
19125 в результате факторизации 32 53
а-Ь 4- а с в результате факторизации а (Ь 4- с)
х3 4- у3 в Результате факторизации (х + у) I, х2 _ х у + у21
2х3-Зх+1 в результате факторизации (х	2 х r
х3 + 2х2-9х-18	(х-3).(х+3)(х+2)
разложить самостоятельно
.25 к 5	3	2 3
2а у 4-aby - aby - 2а у
3_____1
х4- 1	х4- 3
3	1
1-х 3-х
Рис. 5.7. Примеры разложения выражений на множители
5.2.5.	Приведение подобных слагаемых
Команда Collect (Привести подобные слагаемые) объединяет члены, содержащие
одинаковые степени выделенной курсором переменной. Примеры использова-
ния команды Collect приведены на рис. 5.8.
Collect - приведение подобных слагаемых
2	2
х 4-2 х — 3 у 4-4 у 4-х у — 2 х у-Зху
по переменной х в результате приведения подобных членов
по переменной у в результате приведения подобных членов
самостоятельно приведите
подобные слагаемые 2	2	2
ПО ХИ ПО у	х - а у х 4-2-у х-х
О 2 I I 2	2 I	1
-2 ух 4- -3 у 4- у 4- 3 х 4- у
-3 X у^ 4- * -2 х^ 4- X 4- 1) у 4- 3 X
Рис. 5.8. Примеры приведения подобных слагаемых
134
Глава 5. Символьные вычисления
5.2.6.	Коэффициенты полинома
Многие выражения или части выражения могут быть представлены в виде поли-
номов от выделенной переменной. Коэффициенты полинома могут быть найде-
ны символьным процессором. При этом коэффициенты могут быть сложными
функциями других переменных. Примеры использования команды Polynomial
Coefficients (Коэффициенты полинома) приведены на рис. 5.9.
Нахождение коэффициентов полинома Polynomial Coefficients
34 Л 2, s3 2 имеются коэффициенты
За х у+2х (а + ху) -аху
найденные коэффициенты полинома, разложенного
по степеням х
имеются
коэффициенты
по степеням
3 4.32
а х + 6 х а
4
о х а- а х
по степеням а
/.53	)
2 х у
г 4 2	2
ох у -ху
с 3
О X у
„4 о 2
ч Зх у + 2 х у
самостоятельно разложить по степеням а, Ь. с
la3-b-c2,3(bc-3a)2
Рис. 5.9. Примеры нахождения коэффициентов полинома
5.2.7.	Вычисление пределов
Для вычисления пределов в Mathcad выполните следующие действия:
□	На математической панели выберите кнопку со знаком интеграла, откроется
панель Calculus (Исчисление), на которой внизу есть три оператора вычисле-
ния пределов. Выберите один из них.
□	Введите выражение в поле ввода справа от Нт.
□	В поле ввода под словом lim введите имя переменной, по которой надо вы-
числить предел, и ее предельное значение.
□	Выделите уголком или черным цветом все выражение целиком.
□	В главном меню Mathcad выберите Symbolics ► Evaluate ► Symbolically (Сим-
вольные вычисления ► Вычислить ► Символьно). Mathcad возвращает значе-
ние предела, если оно существует. Примеры вычисления пределов приведены
на рис. 5.10.
Вычислить предел выражения можно только символьно.
5.2. Использование меню символьных вычислений Symbolics
135
Variable Limits - пределы
предварительно выделить
все выражение
/~2	1
lim	в результате	з
х-^З-х+6
lim	—в результате	1
х-> о х
lim tan(x) _	„„
' в результате
hm tan(x) в результате
Самостоятельно вычислить пределы функций
при х—>0	f—— 1	прип->0
х	.	n+2j
Рис. 5.10. Примеры вычисления пределов функций
5.2.8.	Замена переменной
Команда Substitute (Подстановка) заменяет выделенным и скопированным в бу-
фер выражением заданную переменную. Чтобы использовать эту команду, нуж-
но:
□	выделить выражение, которое будет заменять переменную;
□	скопировать его в буфер обмена;
□	выделить переменную, которую надо заменить;
□	в главном меню выбрать Symbolics ► Variable ► Substitute (Символьные вычи-
сления ► Переменная ► Подстановка), как показано на рис. 5.11.
Mathcad подставит выражение из буфера обмена вместо выделенной перемен-
ной?
Примеры подстановки переменной показаны на рис. 5.12.
5.2.9.	Вычисление производной или интеграла
С помощью меню Symbolics производную или интеграл можно вычислить двумя
способами:
1.	В нужном выражении, записанном без знаков производной или интеграла,
выделите переменную, по которой надо вычислить производную или взять
интеграл. В главном меню выберите команду Symbolics ► Variable ► Differentiate
(Символьные вычисления ► Переменная ► Вычислить производную) или
136
Глава 5. Символьные вычисления
Рис. 5.11. Меню Symbolics ► Variable
Variable Substitute - подставить в выражение
подставить f(sin(x)) вместо у
f (sin(x))	скопировать в буфер
cos (у) 4- У1 4- у2
постановки cos(f(sin(x))) + 7f(sin(x))2
Вместо х подставить вектор
скопировать в буфер
cos(x) sin(x)
-sin(x) cos(x)
в результате
подстановки
Рис. 5.12. Примеры замены переменных
Symbolics ► Variable ► Integrate (Символьные вычисления ► Переменная ► Вы-
числить интеграл).
2.	На панели Calculus (Вычисления) выберите знак интеграла или производной
и запишите с его помощью нужное выражение. В главном меню выберите ко-
манду Symbolics ► Evaluate ► Symbolically (Символьные вычисления ► Вычи-
слить ► Символьно).
Примеры вычисления производной и интеграла приведены на рис. 5.13.
5.2. Использование меню символьных вычислений Symbolics
137
Variable
Differentiate Integrate - дифференцировать интегрировать
2 х	в результате
х е	дифференцирования
2 х	в результате
х е	дифференцирования
2
2 х ехр(х) 4- х ехр(х)
х2-ехр(х) - 2 х ехр(х) 4- 2 ехр(х)
—ж (z atan(z))
dz
в результате
дифференцирования
1	1
-х	в результате
е	дифференцирования	2.к2
о	2
Самостоятельно вычислить производную
и интеграл от следующих выражений
х2-2х-10	-Уа2-х2
х2 + Ь	*
о sm« klW2
Рис. 5.13. Примеры символьного дифференцирования и интегрирования
выражений
5.2.10.	Символьное решение уравнений и неравенств
Решить уравнение символьно труднее, чем численно. Может оказаться, что ре-
шения в символьном виде не существует. Чтобы решить уравнение символьно,
следует:
□	напечатать уравнение, использовав жирный знак равенства (знак логического
равенства, а не знак присвоения значения). Если в выражении отсутствует
знак равенства, Mathcad полагает, что выражение равно нулю;
□	выделить переменную, относительно которой надо решить уравнение;
□	в главном меню выбрать команду Symbolics ► Variable ► Solve (Символьные
вычисления ► Переменная ► Решить).
Если решений несколько, Mathcad выводит вектор решений.
Примеры символьного решения уравнений приведены на рис. 5.14.
5.2.11.	Разложение в ряд Тейлора
Чтобы разложить выражение в ряд Тейлора с остаточным членом в форме Пиа-
но, выполните следующие действия:
□	выделите переменную в выражении, которое надо разложить в ряд;
□	в главном меню выберите команду Symbolics ► Variable ► Expand to Series (Сим-
вольные вычисления ► Переменная ► Разложить в ряд);
□	в появившемся диалоговом окне укажите порядок остаточного члена.
138
Глава 5. Символьные вычисления
Variable Solve - решить уравнение или неравенство
1 А
3	2
х -10-х +9 имеются
решения
3	2
X -5х -4х+20> 0
3 V13 9
2 + 2
имеются Г (-2 < х) (х < 2)
9 з уТз
<2	2
( 1
решения
Самостоятельно решить уравнение и неравенство
2	2
х +х+3=0 х +Зх-7<0
Рис. 5.14. Символьное решение уравнений и неравенств
В полученном ответе остаточный член обозначен О(л^), то есть отброшены чле-
ны ряда, содержащие х6 и выше. Прежде чем использовать разложение для даль-
нейших вычислений, остаточный член надо удалить.
Ряд Тейлора для функции обычно сходится только в малой окрестности выбран-
ной точки. В качестве точки разложения Mathcad принимает нуль. Для разложе-
ния функции в точке, отличной от нуля, необходима замена переменной. Напри-
мер, для разложения в ряд функции ln(x) в окрестности точки х = 1 надо
разложить в ряд функцию ln(x + 1), а затем переменную х заменить разностью
х - 1. Этот и другие примеры разложения в ряд приведены на рис. 5.15.
5.2.12.	Разложение на простейшие дроби
Сложное выражение можно преобразовать в сумму простейших дробей:
□	Выделите переменную в заданном выражении.
□	В главном меню выберите команду Symbolics ► Variable ► Convert to Partial
Fraction (Символьные вычисления ► Переменная ► Разложить на простейшие
дроби).
Символьный процессор будет пытаться разложить знаменатель выражения на
множители. Mathcad не станет разлагать выражение, которое содержит десятич-
ные точки. Примеры разложения выражения на простейшие дроби приведены на
рис. 5.16.
5.2.13.	Символьные операции с матрицами
Mathcad позволяет выполнить с матрицами ряд символьных операций. Для
этого
□	создайте матрицу с цифровыми или буквенными элементами;
□	выделите ее любым способом;
□	в главном меню выберите пункт Symbolics ► Matrix (Символьные вычисления ►
Матрица).
5.2. Использование меню символьных вычислений Symbolics
139
cos(x) преобразование в серию 2	4
ч 1 2	1 4	_/ 6j	1	2 + 24
1---х + — х + О'х j	z
2	24
разбиение на 2 строки
длинного ответа
cos(x) преобразование в серию
L 1 2	1 4	1 б 18	1	10
2	24	720	40320	3628800'
1	12	1	14	16 j
ч 479001600	87178291200	J
2х2 - Зх+ 1
3	2
х + 2х - 9 x4- 18
преобразование в серию
1	5
------х
18 36
Разложить в ряд функцию 1п(х)
ln(x+ 1) преобразование в серию
замена переменной
х- 1
23 2	13 3 _/ 4
------х 4------х 4- О' х ‘
648	432
выбрано 4 члена ряда
.	1 2	1 3	4'|
1-х---х 4- - х 4- О'х ’
2	3
в результате подстановки
х_ 1 _ l.(x_ I)2 + 2 (х- 1)3 + о[(х- I)4]
Самостоятельно разложить в ряд
tan(x)
х2 - 6х + 3
sin(x)
X2
е
Рис. 5.15. Примеры разложения функций в ряд Тейлора
Разложить на элементарные дроби Convert to Partial fractions
2
2x - 3x4- 1
3	2
x + 2x -9x- 18
расширение элементарных дробей до
1	14	3
З-(х-З) + 3(х+3) х+2
расширение элементарных дробей до
е 1	16	81
х — 6 4--------------1-------
2 (х + 1) х+2	2(х+3)
Самостоятельно разложить на элементарные дроби
4
3 о 2 . ? a	ах+х-2
х-2х+3х-6	>	-------
-------;----	"	, ч 2 .
Гх-213	а=1 <а + х)
Рис. 5.16. Примеры разложения выражений на простейшие дроби
Откроется подменю из трех пунктов: Transpose (Транспонировать), Invert (Найти
обратную) и Determinant (Вычислить определитель). Выбрав один из этих
пунктов, можно найти результат вычисления. На рис. 5.17 указанные операции
выполнены на примере матрицы направляющих косинусов для плоской задачи.
140
Глава 5. Символьные вычисления
Попутно эти примеры доказывают свойство ортогональности матрицы на-
правляющих косинусов, то есть то, что обратная матрица равна транспониро-
ванной.
Чтобы выполнить арифметические действия над несколькими (чаще всего дву-
мя) матрицами, надо выделить целиком все матричное выражение и в главном
меню выбрать команду Symbolics ► Evaluate ► Symbolically (Символьные вычисле-
ния ► Вычислить ► Символьно). На рис. 5.17 показано символьное решение сис-
темы линейных алгебраических уравнений, записанных в матричном виде.
Символьные операции с матрицами
' cos(x)	sin(x)	O’1
-sin(x)	cos(x)	0
ч 0	0	1J
< cos(x)	sin(x)	o'
-sin(x)	cos(x)	0
ч 0	0	b
f cos(x)	sin(x)	(P
-sin(x)	cos(x)	0
< o	0	b
в результате
обращения матрицы
Решение СЛАУ
в результате
транспонирования матрицы
cos(x) -sin(x) (cos(x) -sin(x) О4'
sin(x) cos(x) sin(x)	cos(x) 0
ч 0	0^0	0	1/
^cos(x)
_________1_________sin(x)
2	2
cos(x) + sin(x)
4	0
-sin(x)
cos(x)
0
0	'
0
, .2	, 4 2
cos(x) + Sin(x) 7
2	2
имеется определитель cos(x) + sm(x)
f x^	7al bl * f cl
J  a2 b2 J c2
Вычислить аналитически
в результате
( Ь2 , bl 
-----------cl------------с2
al Ь2 - bl а2 al Ь2-Ь1а2
-а2	.	al
---------cl +---------- с2
alb2-bla2 alb2-bla2 J
Рис. 5.17. Примеры символьных операций с матрицами
5.2.14.	Вычисление интегральных преобразований
Mathcad позволяет вычислить символьно три интегральных преобразования:
Фурье, Лапласа и z-преобразование.
Прямое преобразование Фурье возвращает функцию от и, определяемую форму-
лой
Г7(*К^
J -оо
— выражение, которое надо преобразовать.
Обратное преобразование Фурье возвращает функцию от t, задаваемую выраже-
нием
5.2. Использование меню символьных вычислений Symbolics
141
где F(w) — выражение, которое надо преобразовать.
Прямое преобразование Лапласа возвращает функцию от s, определяемую фор-
мулой
где f(t) — выражение, которое надо преобразовать.
Обратное преобразование Лапласа возвращает функцию от t, задаваемую выра-
жением
1 г» а-Ное	. „
— Г F(s)e ds,
2тгг ** CT-io°
где F(s) — выражение, которое надо преобразовать, и все его особенности нахо-
дятся слева от линии Re(s) = о.
Прямое z-преобразование возвращает функцию от 5, определяемую формулой
+оо
£У(п)г’я,
и=0
где f(ri) — выражение, которое нужно преобразовать.
Обратное z-преобразование возвращает функцию от п, задаваемую контурным
интегралом вокруг начала координат
^-$F(z)z"-ldz,
где F(z) — выражение, которое нужно преобразовать; С — контур, включающий
в себя все особенности подынтегрального выражения.
Для выполнения любого из шести указанных преобразований выполните сле-
дующее:
□	введите нужное выражение;
□	выделите переменную курсором;
□	в главном меню выберите Symbolics ► Transform ► Fourier (Символьные опе-
рации ► Преобразование ► Фурье) или укажите другую нужную команду:
Inverse Fourier, Laplace, Inverse Laplace, Z, Inverse Z (Обратное Фурье, Лапласа,
Обратное Лапласа...).
Примеры указанных преобразований приведены на рис. 5.18. В выводимых отве-
тах Mathcad использует специальные функции (рис. 5.19). Так, в преобразовани-
ях Фурье используется функция Dirac (Дельта-функция Дирака). Об этой
и других специальных функциях можно прочитать в Mathcad Help (Справка
Mathcad).
142
Глава 5. Символьные вычисления
Интегральные преобразования
имеется	1 А z	А z ч 1
cos(x)2 преобразование Фурье 2 Д 2 + п А	тг А (и + 2)
имеется обратное 1	.	1 1
преобразование Фурье 4 exp(2it) + 2 + 4 ехР( 21 м
2
2	s + 2
cos (х) имеется преобразование Лапласе----
s +4s
имеется обратное - cos (21) + -
преобразование Лапласа 2	2
(х 4- а)2 имеется Z-преобразование zla2 Z2- 2 a2 z+ а2 + 2 az- 2 a + z + 1)
(z-1)3
имеется обратное Z-преобразование n2 + 2 • an + а2
Рис. 5.18. Примеры интегральных преобразований функций
Рис. 5.19. Поиск специальных функций в Mathcad Help
5.3. Использование символьной панели инструментов
143
5.3.	Использование символьной
панели инструментов
Символьная панель инструментов вызывается из математической панели щелч-
ком на значке Symbolic Keyword Toolbar (значок с изображением шапочки акаде-
мика). Содержание панели показано на рис. 5.20.
Символьные
Мате... х
В * [:Н]
»• <?
float
solve
factor
collect
fourier
invfourier
mt ->
explicit
rewrite
rectangular
simpllty
expand
series
laplace
invlaplace
n'1 -»
combine
Modifiers
assume
substitute
coeffs
parfrac
ztrans
invztrans
|n| ->
confrac
Рис. 5.20. Символьная панель инструментов
В Mathcad существует символьный знак равенства — он вводится с клавиату-
ры сочетанием клавиш Ctrl+.(точка) или с панелей Symbolic Keyword Toolbar
(Символьная панель инструментов) и Evaluation Toolbar (Панель вычислений).
В отличие от обычного знака равенства, символьный знак равенства возвращает
не число, а выражение.
По умолчанию символьный знак равенства упрощает выражение слева от знака
аналогично команде Evaluate Symbolically (Вычислить символьно) из меню Sym-
bolics. Для всестороннего контроля выполнения символьных вычислений нужно
использовать символьную панель инструментов.
ПРИМЕЧАНИЕ -----------------------------------------------------------------
Как уже говорилось, при использовании меню Symbolics Mathcad игнорирует предыдущие
определения всех величин, входящих в рассматриваемое выражение, и не учитывает
функции пользователя.
При использовании символьного знака равенства и панели инструментов Symbolic Math-
cad учитывает все предыдущие определения и при пересчете всей программы пересчиты-
вает и результат символьных вычислений и работает с функциями пользователя.
Чтобы отменить предыдущее присвоение значения переменной, например, х, введите вы-
ражение х:=х.
На символьной панели инструментов (см. рис. 5.20) есть два символьных знака
равенства: с одним местом ввода и с двумя местами ввода. Одно место ввода
предназначено для ввода выражения или функции (встроенной или пользовате-
ля), второе — для ввода ключевого слова, означающего выполняемое действие.
144
Глава 5. Символьные вычисления
Символьный знак равенства с двумя местами ввода позволяет создавать про-
граммы символьных вычислений, включающих в себя несколько последователь-
ных действий.
5.3.1.	Символьные операции без использования
ключевых слов
Одноместный символьный знак равенства используется для символьного вычис-
ления интегралов, производных, сумм и произведений (рис. 5.21) и эквивален-
тен выполнению команды Simplify (Упростить).
Очистка использованного ранее значения переменной х = х
X
-X- п	-
Ух	2
п=0 2 *1'
Символьное интегрирование и дифференцирование
А2	7
—=tan(z) -> 2 tan(z) * tan(z) + 1)
dz
4	2
-^-3tan(z) -> 16 tan(z) - I tan(z)^ + 11 + 8 tan(z)^ (tan(z)^ + 11
dz
tan(z) dz—> -ln(cos(z))
fb fc	ta2-b2Hb2-c2'
xydxdy ‘
4
Рис. 5.21. Символьные вычисления с одноместным знаком равенства
При выполнении большинства символьных операций удобно использовать
функции пользователя (рис. 5.22). Это облегчает понимание смысла выполняе-
мых действий и делает документ менее громоздким.
5.3.2.	Символьные операции с использованием
ключевых слов
На символьной панели инструментов находится 26 кнопок с названиями сим-
вольных операций. Почти все эти операции есть и в меню Symbolics. При нажа-
тии одной из кнопок на экране появляется шаблон символьной операции с ука-
занием ключевого слова (двухместный символьный знак равенства). В шаблоне
надо заполнить места ввода, а если остаются или появляются лишние места вво-
да, их надо удалить (выделить место ввода курсором и нажать клавишу Delete).
ПРИМЕЧАНИЕ ---------------------------------------------------------
Символьную операцию можно ввести и с клавиатуры. Для этого вначале надо нажать
Ctrl+Shift+. (точка). Появится шаблон с двумя местами ввода. В левое место ввода ввести
математическое выражение, а в правое — ввести ключевое слово для данной операции.
5.3. Использование символьной панели инструментов
145
использование функций пользователя
f(x) .= х2-б х+2 х-12	— f(x)-»2 x-4
dx
Гь	3	J
f(x) dx-> 2 а - — + 12 а+— - 2 b - 12 b
J.	3	3
Решение уравнений и неравенств
f(xa) = 0 solve,ха
-2
6
f(xa) > 0 solve,ха —> ха < -2 V 6 < ха
ха - 5 ха - 4 ха+ 20 > 0 solve,ха —> 5 < ха V -2 < ха < 2
Рис. 5.22. Использование функций пользователя в символьных вычислениях
Команды, их шаблоны и действия команд приведены в табл. 5.1. В ней жирные
точки обозначают места ввода выражений (слева) и ключевых слов (справа).
Таблица. 5.1. Действия, выполняемые с помощью ключевых слов
Команда	Шаблон	Действие команды
float	• float, • ->	Вычисления с плавающей точкой
rectangular	• rectangular ->	Возвращает комплексное число
expand	• expand, • ->	Раскрытие степеней и произведений, сумм не- скольких переменных
solve	• solve, • ->	Решение уравнений и систем уравнений для ука- занной после запятой переменной
simplify	• simplify ->	Упрощение выражений
substitute	• substitute, • = • ->	Вычисление выражений с подстановкой опреде- ленных значений или с заменой переменной
collect	• collect, • ->	Упрощение выражений представлением их сум- мой простых полиномов
series	• series, • = • ->	Разложение выражения в степенной ряд. Число членов вводится в правое поле ввода
assume	• assume, • ->	Вычисления с присвоением определенных значе- ний переменных (действительное, мнимое, целое, >0, <0)
parfrac	• parfrac ->	Разложение выражения на простые дроби
coeffs	• coeffs, • ->	Определение вектора коэффициентов полинома
factor	• factor. • ->	Разложение выражения на произведения
fourier	• fourier, • ->	Прямое преобразование Фурье	Л 	 продолжение &
146
Глава 5. Символьные вычисления
Таблица. 5.1 (продолжение)		
Команда	Шаблон	Действие команды
laplace	• laplace, • ->	Прямое преобразование Лапласа
ztrans	• ztrans, • ->	Прямое ^-преобразование
invfourier	• invfourier, • ->	Обратное преобразование Фурье
invlaplace	• invlaplace, • ->	Обратное преобразование Лапласа
invztrans	• invztrance, • ->	Обратное ^-преобразование
MT—>	• —>	Транспонирование матрицы
M"1 ->	• -1 ->	Обращение матрицы
|m|->	lel ->	Вычисление определителя матрицы
explicit	• explicit ->	Подстановка числовых значений и размерностей в формулу
combine	Употребляются в со-	Упрощает выражение с ехр или In
confrac	четании с другими словами	Разложение непрерывной дроби на фракции
rewrite		Переписывает выражение с указанными элемен- тарными функциями
Modifiers		Вывод панели Modifier
Подробно о предназначении и использовании каждого ключевого слова можно
узнать, выбрав Mathcad Help ► Symbolics and Keywords ► Using keywords for sym-
bolic operations (Mathcad Помощь ► Символы и ключевые слова ► Использование
ключевых слов для символьных операций), а также посмотрев в начале главы
разделы 5.2.1-5.2.9. Примеры использования ключевых слов с одноместным
символьным знаком равенства приведены на рис. 5.23.
Некоторые команды, имеющие в своих шаблонах места ввода, стоящие после за-
пятой, могут иногда использоваться и без указания там аргумента. Так применя-
ются команды expand, factor, collect, solve, coeff, если в выражении есть только
один аргумент (рис. 5.23 и 5.24).
Далее приведем некоторые пояснения к отдельным ключевым словам.
При использовании команды substitute (Заменить) необходимо задать вариант
подстановки. Если нужно заменить не одну переменную, а несколько, то второй
и последующие варианты подстановки вводятся через запятую и набираются
с клавиатуры (см. рис. 5.24).
Ключевое слово assume позволяет ввести ограничения на значения переменных,
что бывает необходимо, если, например, функция имеет разрыв в некоторой точ-
ке (см. рис. 5.23). Ключевое слово assume — должно появляться после ключевого
слова, обозначающего действие, на которое вы хотите ввести ограничения.
Ключевое слово coeff выводит коэффициенты полинома, начиная с наименьшей
степени. Если полином содержит более одной переменной, необходимо после
ключевого слова coeff поставить запятую и ввести имя переменной, относительно
которой нужно вывести коэффициенты. В Mathcad 14 появилась возможность,
5.3. Использование символьной панели инструментов
147
хх у - у очистка переменных х и
assume assume Должно появляться после ключевого слова обозначающего
a»uin<7 действие на которое вы хотите ввести ограничения
lx3 - 1 X2 - 21  0 solve ->
/2
-д/2
2	2
1х3- 1Кх2-2) - О
solve
assume, х -
solve	f 1
assume, x  RealRange( 0,2) L/j
U 2 7
coeff работает только в Mathcad 14
solve
-»1
assume,x - integer
4	2
х + 3-х + 7-х- 3 coeffs ->
3	2-2	-1
х у + х у - 3-х-у - 12-у + 5 coeffs,у,degree ->
expand
factor
float
series
-2
-3 х
Рис. 5.23. Применение ключевых слов в символьных вычислениях
-Zt	’	-
е dtass___ х ~2 _2
100 fector -» 2 -5
tt float —> 3 1415926535897932385
3	3	2	2	3
(х + у) expand -»х +3 х -у + 3-х-у +у
2	2
cos(2-x) expand ->cos(x) -sin(x)
3	3	f 2	2i
x - у fector -> (x - у) Л x + x-y + у
л float,7 -» 3.141593	7 - указано число знаков после запятой	4
работает только в Mathcad 14 и 15
2	3	4	5	х2
еХ series ->1 + х + — + — + — + еХ series ,3 -» 1 + х + ^- здесь 3 - число
2	б	24	120	2	членов ряда
х	-
е senes ,х  2
е2 + е2 (х- 2) + Л(Х- 2)2 + е2<Х-2)3 + ? (Х- 2)4 +	2)5
4	'	2	6	24	120
24
7
3
О
2
х
5
О
О
Simplify (х + З)3 + 2-х — б simplify -»(х+ 1)-(х2 + 8х + 21)
2	2
sin(x) + cos(x) simplify -» 1
substitute c 2 . x и*** u n	*
5-x + 3-x-6 substitute,x  b - 2 -»5-b - 17-b + 8
3	2
a x -b-x + c substitute,x  -
z
3 nu 2 o
c-z -2-b-z + 8-a
Рис. 5.24. Применение ключевых слов в символьных вычислениях
148
Глава 5. Символьные вычисления
введя два слова, coeff, degree, вывести два столбца: значения коэффициентов
и показатель степени данного члена полинома (см. рис. 5.23).
При разложении в ряд Тейлора (команда series) необходимо указать координаты
точки, в окрестности которой производится разложение, и число членов ряда.
Если не указать это число, то Mathcad по умолчанию выводит результат с ше-
стью членами ряда Тейлора (см. рис. 5.24).
5.3.3.	Символьное решение уравнений
Для символьного решения уравнений и неравенств на символьной панели ин-
струментов нужно выбрать команду solve (Решить). При этом на экране появ-
ляется символьный знак равенства с местом ввода, где надо указать перемен-
ную, относительно которой решается уравнение или неравенство (см. рис. 5.22,
5.25).
solve sm(x) = cos(x) solve —» — sm(x) = cos(x) solve, fully —>
4
— + тг _n if _n € Z
4
'	3	3
s:sm(4 z) expand -» 4 cos(z) sm(z) - 4 cos(z) sm(z) if k € S
I 4
2	I
(x + 1) (x - 1) expand —» x - 1	| undefined otherwise
undefined otherwise
f(a) = (3a-7)x = 1 solve,x,fully —»
z J 2	2i „	„23^2	3
(a - x) ' a - a x + x I collect,x -» 2 ax - x + -2 a x + a
3 ~ 2 < . о <2 . 3 _	.	«3
a + 3 a b + 3 a b + b factor -» (a + b)
r+ s s
----+------- 2
s r — s----r
------------- simplify —> —
—	s
r-s
az+1 -а Л ,
---------e =0 solve,z —»
z- b
* 2 + - - e a solve,b -> z - e& (a z+ 1)
z-b
/ П complex -» cos(0 n) + sm(0 n) i
Рис. 5.25. Символьное решение уравнения с использованием ключевого слова solve
Для символьного решения уравнений можно использовать также функцию
root и вычислительный блок Given-find (рис. 5.26). При этом для вывода резуль-
тата используется одноместный символьный знак равенства -> (клавиши Ctrl+.).
В Mathcad 13-15 функция root для символьного решения уравнения требует
указать диапазон поиска корней (см. рис. 5-26).
5.3.4.	Использование нескольких команд одновременно
Использование нескольких команд одновременно — довольно сложный процесс,
так как надо знать, может ли быть преобразован промежуточный символьный
результат. Чтобы убедиться в этом, его надо увидеть, то есть вывести каждый
результат отдельно. Одновременное действие нескольких команд показано на
рис. 5.27.
Символьные вычисления начинают с ввода исходного выражения, подлежащего
преобразованию:
5.3. Использование символьной панели инструментов
149
Не работает в
Mathcad 13
Надо указать диапазон изменения переме Функции 'Yoof с 2 аргументами является численной.
Для аналитических расчетов используйте форму с 4 аргументами или t
Работает в
Mathcad 13
b е а+ 1
- а
а- е
sm(z) = - tan(z) solve, z —>
решение системы уравнений
Given
х+2у-тг=а 4x+y=b
Fmd(x,y) ->
' а-2 к b Л
” 8тг- 1
b - 4 а
< 8тт- 1 ?
поменять местами
find и minerr
Mmerr(x,y)->
Рис. 5.26. Использование функций root, find и minerr для символьных вычислений
2	5	2	5
х +у substitute,хв z + 1,у в z-2 -»(z+l) + (z-2)
использование нескольких команд одновременно
substitute ,х  (у + I)2	(у2 + 2у + J
«Pand	f 4 . 3 , 2 . Л
1у + 4у + бу + 4 у + 1/
substitute ,xsz+l,yxz-2 n	« д о
-> -79 z + 82 z - 31 + z - 10 z + 40 z
factor
2
2z +6z+9
f-3 3 Л
— + — i
complex	2	2
solve, z~* -3	3
-------i
U 2 )
2
2z +6-Z+9.0
complex /-1.5000000000000000000 - 1.50000000000000000001
solve,z^ 1-1.5000000000000000000 + 1.5000000000000000000 i
число 9 с десятичной точкой
Рис. 5.27. Использование двухместного знака символьного равенства
□ Для выполнения команды simplify и для вычисления интегралов, производ-
ных, сумм и произведений выберите на символьной панели инструментов од-
номестный знак символьного равенства (или введите его с клавиатуры соче-
танием клавиш Ctrl+.).
2	5
X + у
150
Глава 5. Символьные вычисления
□	Для выполнения других символьных операций после ввода выражения на-
жмите на символьной панели инструментов кнопку с названием необходимой
операции. В появившемся на экране шаблоне заполните нужные места ввода
и удалите ненужные.
□	Для одновременного выполнения нескольких символьных операций выбери-
те на панели двухместный знак символьного равенства. В появившемся шаб-
лоне заполните нужные места ввода и удалите ненужные.
□	Для вывода результатов символьных вычислений выведите курсор за преде-
лы выражения и нажмите левую кнопку мыши.
ВНИМАНИЕ -------------------------------------------------------------
При использовании двухместного символьного знака равенства после ввода каждого клю-
чевого слова с названием символьной операции автоматически появляется свободное ме-
сто для ввода следующей символьной операции. После ввода всех символьных операций
надо удалить лишние места ввода и автоматически появляющиеся лишние скобки.
5.3.5.	Символьные операции с матрицами
Одноместный символьный знак равенства позволяет выполнять различные опе-
рации с массивами. Кроме трех функций (транспонирования, обращения и вы-
числения определителя матрицы), находящихся на символьной панели инстру-
ментов, можно выполнять операции сложения, вычитания и перемножения
матриц (рис. 5.28), а также использовать встроенные функции для работы с мат-
рицами, например, для нахождения собственных чисел (eigenvals) и собственных
векторов (eigenvecs) (рис. 5.29).
т (кр kq
ВС1 ->
mp mq
В С -> к р + m q
( ак + ЬяЛ
АВ -> |
ск + dm J
Т
В С кр + m-q
Решение матричного
уравнения А*Х=С
Х:-А * С
d	Ъ
	р	q
(ad-be)------------(ad-be)
-c	a
	p +----------q
(a d-b-------------e)	(ad-be)
Рис. 5.28. Символьные операции с массивами
5.4. Новые возможности символьных вычислений в Mathcad 13-15
151
eigenvals(A) ->
9+ - d + - (з24-3б4+ d2 + 4bc)
2	2
9+ - d- - (324-36 d+ d2 + 4 b c)
2	2
eigenvecs(A)-> 1 отключено, большое выражение
Рис. 5.29. Символьное определение собственных чисел и собственных векторов матрицы
Возможность получения символьного решения почти любого матричного выра-
жения является большим достоинством Mathcad.
5.4.	Новые возможности символьных вычислений
в Mathcad 13-15
В Mathcad 14 применен совершенно новый символьный процессор MuPad. В ре-
зультате теперь выполняется ряд новых операций и расширены возможности су-
ществовавших ранее.
5.4.1.	Новые ключевые слова
На символьной панели появились новые ключевые слова:
□ Combine (Комбинировать) позволяет упростить выражения в случае экспо-
ненциальной или логарифмической функции. Обратите внимание на то, что
ключевое слово Expand (Разложить) отменяет действие слова Combine. Набе-
рите запятую после ключевого слова Combine, а за ней — модификатор, опре-
деляющий элементарную функцию, например ехр или In (рис. 5.30).
m n . m+n
х х combine —>х
х 2у ,	х+2 у
е е combine, ехр —» е
h(x) + h(2) + 3h^^ combine,h —»-j—
m n ,. m+n
x x combine —>x
(m+n)	, m n
x expand -»x x
Рис. 5.30. Использование ключевого слова Combine
XI .	-xi.
е i е	i
sm(x) rewrite, ехр —> —— + —-—
fl). (-i)x ixTflYl _
I - I i e -e 11 - J rewrite, smcos —> sm(x)
Рис. 5.31. Использование ключевого слова Rewrite
152
Глава 5. Символьные вычисления
□	Rewrite (Переписать) позволяет переписать выражения с использованием не-
которых элементарных функций, например exp, sincos (рис. 5.31).
□	Confrac — разложение непрерывной дроби на фракции. По умолчанию Math-
cad возвращает такое количество фракций, чтобы точность вычислений со-
ставляла 10 значащих цифр. Изменить точность вычислений можно, введя
через запятую число выводимых фракций. Чтобы увидеть полные фракции,
введите через запятую Confrac, fraction (рис. 5.32).
□	Explicit (Явная подстановка) означает подстановку числовых значений и раз-
мерностей в формулу. Примеры использования explicit приведены на рис.
5.33.
1
7
24
8
<24;
'
1
Н/З - Л 1
—-— confrac,4 —> 1
7
7
<24,
—х— с onfrac.fr action
7
cos (a) confrac —»
cos (а) confrac, fraction —> 1 +
(-6 О J
Рис. 5.32. Использование ключевого слова Confrac
Записав математическое выражение, надо ввести ключевое слово explicit, выбрав
его на математической панели. Далее через запятую нужно ввести имена пара-
метров, чьи численные значения надо подставить, и знак символьного вычисле-
ния Чтобы получить окончательный результат вычислений, следует после
символьного результата нажать клавишу = (равно) и, если нужно, ввести в поле
ввода производную размерность.
ПРИМЕЧАНИЕ ----------------------------------------------------------
В Mathcad 13 появилась возможность использовать в одной строке два знака равенства:
символьный —> и численный =. Попытка третий раз ввести знак присвоения значения ре-
зультата не имеет (см. рис. 5.33). Приходится вновь записывать (копировать) имя выраже-
ния, чтобы ввести знак численного равенства.
5.4. Новые возможности символьных вычислений в Mathcad 13-15
153
М := 200 b := 2 h := 5
сгизг .= ------- explicit, М, b ,h —>-------
bh2	2-52
б	б
<тюг=24 |	УДОБНО |
M + Fq Lo + FiLi З-Fo-Lq 3 Fl Li
ror “	. , 2	25 + 25 + исходные данные
—	в векторной форме
6	НЕУДОБНО
M + FqLo + FiLi	200 + Fq Lo + Fi I4
МизГ =----------------explicit, M,b,h,F,L —>------------------
bh2	252
б	6
„ M 200	M	200
Д1 :=---------> —»---- М2 :=----------------------- explicit,M,b,h —>----
W(b,h) W(2,5)	W(b,h)	W(2,5)
Рис. 5.33. Ключевое слово explicit в символьных вычислениях
В случае если символьные вычисления производятся с элементами матриц, ре-
зультат получается несимпатичным, что называется, «не смотрится».
В сложных выражениях, содержащих внутри себя имена других функций, Math-
cad так и переписывает имена этих функций, поставив в скобках численные зна-
чения их аргументов.
5.4.2.	Новые слова-модификаторы
В Mathcad 14 введено несколько новых модификаторов, позволяющих изменить
смысл ключевых слов:
□	АН применяет записанное далее условие ко всем переменным в выражении.
□	Degree используется при вычислении коэффициентов полинома. Выводит
вторую колонку чисел — степень того члена полинома, для которого выведен
коэффициент.
□	Domain используется с ключевым словом factor или parfrac, чтобы определить
область чисел, в которой должно быть выполнено разложение на множители
или на простые дроби.
□	Ехр используется со словом Combine или Rewrite, чтобы записать выражение
с использованием экспоненты (рис. 5.34).
□	Ln используется со словом Combine, чтобы представить выражение в виде ло-
гарифмов.
□	Sincos используется со словом Rewrite, чтобы записать результат вычислений
в терминах sin и cos.
154
Глава 5. Символьные вычисления
р := 5	q := 3	г := -1
2	2
р +3q	r . 4ТТ	5+3-3
------------------ explicit,ALL —>	
5 + r----------------------5 + -1
r-4 .O'1
3	2	0 1
3z + 5z -4 coeffs, degree
5 2
J 3,
x3-2
factor, domain = complex
->(x- 1.26) (x + 0 63 - 1.09i)-(x+ 0.63 + 1.09i)
float, 3
— if a # 0
a
a-zs'l solve, z, fully —>
. , 1
az = 1 solve,z -» -
a
undefined if a = 0
cos(z) = 0 solve,fully —>
— + 7r n if n € Z
2
undefined otherwise
cos(z) = 0 solve,fully —>
— + 7r _n if _n € Z
substitute, %n = к —>
— + 7rnif n € Z
2
undefined otherwise
undefined otherwise
Рис. 5.34. Использование модификаторов All, degree, domain
□	Fully возвращает полное подробное решение уравнения. Для уравнений,
имеющих периодическое решение, использование слова fully после слова solve
возвращает результат, содержащий произвольную постоянную %п, которую
можно заменить, использовав подстановку со словом substitute или using. Math-
cad использует символ %, чтобы избежать конфликта с другими переменны-
ми в данном Mathcad-документе (рис. 5.35).
□	Using используется для замены произвольной постоянной %п при решении
уравнения, имеющего периодическое решение.
az= 1 solve, z,fully —>
. . 1
a-z = 1 solve,z —> —
a
undefined if a = 0
cos(z) = 0 solve,fully -»
— + 7T - n if n € Z
2
undefined otherwise
cos(z) = 0 solve,fully —>
— + K _n if _й € Z substitute,%n = k -»
— + 7r _n if _n € Z
undefined otherwise
undefined otherwise
Рис. 5.35. Использование модификаторов fully и using
5.4. Новые возможности символьных вычислений в Mathcad 13-15
155
□	Raw фактически отменяет действие ранее записанного ключевого слова, воз-
вращая исходное выражение.
5.4.3.	Символьная векторизация выражений
В Mathcad 14 допускается символьное вычисление с использованием оператора
векторизации (рис. 5.36). В более ранних версиях Mathcad этот оператор ис-
пользовался лишь в процессе численных вычислений.
'03 02 0.5^
V = 040607
ч0 9 1 07,
численная векторизация
г 17 458 11 537	30
23 578 3|6 87 44 427 deg
 64 158	90	44 427/
символьная векторизация
asm(V) ->
1 12
0 201 0 524"
0 644 0 775
-	0 775
2 J
f 0 305
Рис. 5.36. Символьная векторизация выражений
5.4.4.	Новые функции символьных вычислений
В Mathcad 14 появились три новые функции, используемые при символьных
вычислениях.
□	Numer, Denom возвращают числитель или знаменатель дроби (рис. 5.37).
f а + b +
numer
—> а + b + d
. fa + Ь + (Р
denom --------
I 2	2
 х +у ;
IsPrime(8) —> 0
IsPrime(7) -> 1
IsPnme(2 5|)—»
Дробь
[integer expected)
Рис. 5.37. Использование новых функций
Numer, Denom и IsPrime
156
Глава 5. Символьные вычисления
□	IsPrime возвращает 1, если целое число простое, и 0 — в противном случае.
Попытка оценить дробное число или матрицу приводит к ошибке.
При использовании символьного знака равенства Mathcad учитывает все преды-
дущие присвоения значений константам и переменным и подставляет их в ре-
зультат символьных вычислений. Если значение не задано, Mathcad окрашивает
данный символ красным цветом, но символьное выражение вычисляет правиль-
но. Поэтому лучше использовать величины, которым не присвоены численные
значения. Если это нежелательно, надо использовать меню Symbolics, которое иг-
норирует все ранее присвоенные численные значения.
5.5.	Встроенные функции и переменные
Символьный и численный процессоры используют несовпадающие списки
встроенных функций. Эти списки частично пересекаются. Часть встроенных
функций, имеющих общепринятое математическое значение, подобно sin или
log, участвует в символьных преобразованиях. Другие функции, подобно interp
или rnd, не имеющие общепризнанного математического значения, не преобразу-
ются символьным процессором. В то же время символьный процессор использу-
ет ряд функций, не вычисляемых численным процессором. Список таких функ-
ций можно найти, обратившись за помощью к Mathcad.
Список встроенных функций, используемых в символьных вычислениях, вклю-
чает в себя тригонометрические и гиперболические функции и обратные им, ло-
гарифмические и показательные функции, функции Re и Im вещественной
и мнимой частей комплексного числа, функцию ошибок erf, гамма-функцию Г,
функцию вычисления остатка от деления mod, ступенчатую функцию Хэвисайда
Ф, функции max и min, матричные функции identity и eigenvals. В целом эти
функции трактуются одинаково символьным и численным процессорами.
Встроенные константы, имеющие общепринятое математическое значение, трак-
туются одинаково символьным и численным процессорами. Символьный процес-
сор распознает v и оо. Они сохраняют свой смысл в символьных вычислениях.
Встроенные константы, не имеющие общепринятого математического значения,
не распознаются символьным процессором. Например, TOL или ORIGIN будут об-
рабатываться подобно любой неопределенной переменной.
ВНИМАНИЕ ---------------------------------------------------------
Функции и переменные, задаваемые пользователем самостоятельно, распознаются сим-
вольным процессором при использовании символьного знака равенства и не распознаются
при использовании меню Symbolics.
5.6.	Особенности символьной обработки
При работе с символьным процессором необходимо помнить следующее:
□	Многие вычисления могут быть выполнены только численно.
□	Еще больше вычислений возвращают такие длинные ответы, что их неудобно
использовать, поэтому удобнее выполнять эти вычисления численно.
5.6. Особенности символьной обработки
157
Для компьютера символьные вычисления намного труднее, чем соответствую-
щие численные операции. Так, большинство уравнений не могут быть решены
символьно. Большинство интегралов, порой выглядящих просто, не имеют сим-
вольного решения, выраженного через элементарные функции.
Символьные вычисления могут производить настолько длинные ответы, что они
не помещаются в рабочем окне. Если ответ состоит из слагаемых, его можно раз-
делить «плюсами» на несколько строк (рис. 5.38). Для этого нужно:
□	выделить весь ответ. Вновь установить указатель курсора на черном выраже-
нии и, нажав правую кнопку мыши, переместить ответ на свободное место.
Появится копия ответа;
□	уголком курсора выделить всю часть выражения перед знаком «плюс», после
которого надо сделать перенос;
□	нажать комбинацию клавиш Ctrl+Enter;
□	удалить лишний знак «плюс»;
□	повторить перенос строки столько раз, сколько строк вы хотите получить.
Иногда символьный ответ получается настолько длинным, что его не удается
удобно разместить в рабочем документе. На рис. 5.38 при решении уравнения
Перенос длинной строки
х+у	nn^i	1 2	12131212	13
е * senes,х 0,у 0,4 ->1+х+у+-х + ух+-у + -х + -ух +-ух+-у
2	2	6	2	2	6
Скопировать ответ. Перед знаком плюс нажать Ctrl+Enter
Удалить лишнее место ввода
12	1	2^
-х + ух+ - у
2	2	,
_ -	2 12	1 ।
•х + -ух + -у х+-у
2	2	6
I.--3 • 1
6 "	2
/1	1 1	OU 1
I - + — I = а + ЗЬ solve,х —>
V У/
Здесь нет ответа
используем меню
Symbolic - Variable - Solve
MATR IX([ [ (1 /2*у/(-1 +а*уА3+3*Ь*уА3)*(4*а+12*b+4*aA2*yA3+24*a*yA3*b+36*bA2*-
ул3-4*((а +3*Ь)А2)А(1 /2)+4*((а+3*Ь)А2)А(1 /2)*а*уА3+12*((а +3*Ь)А2)Л(1 /2)*Ь*улЗ)л(1 -
/3)+2*yA2*(a+3*b)/(-1+a*yA3+3*b*yA3)/(4*a+12*b+4*aA2*yA3+24*a*yA3*b+36*bA-
2*уА3-4*((а+3*Ь)А2)л(1 /2) +4*((а +3*Ь)А2)Л(1 /2)*а*уА3+12*((а +3*Ь)А2)Л(1 /2)*Ь*уА3)-
А(1/3)+1/(-1 +а*уА3+3*Ь*уА3))*у], это лишь часть ответа
Рис. 5.38. Обработка длинных ответов
158
Глава 5. Символьные вычисления
с использованием символьного знака равенства процессор сообщил о длинном
ответе, но не предложил его вывести. При использовании меню Symbolics ►
Variable ► Solve (Символьные вычисления ► Переменная ► Решить) Mathcad
спрашивает, не следует ли ответ поместить в буфер обмена. Если вы нажали
кнопку OK, Mathcad поместит строку в буфер обмена. Выбрав команду Paste
(Вставить), вы увидите на экране ответ на языке, похожем на Fortran. О том, как
разобраться в таком ответе, рассказано в Resource Center (Центре документа-
ции) Mathcad.
Подводя итоги изучения символьных вычислений, следует отметить, что в Math-
cad символьные вычисления имеют вспомогательное значение:
□	В инженерных расчетах к символьным операциям приходится прибегать до-
вольно редко.
□	Часто вообще не существует символьного результата вычислений.
□	Ряд символьных операций проще выполнить вручную, чем обращаться
к Mathcad.
□	В разделах справки (Help) и в Центре документации сведений о символьных
операциях очень мало, мало также примеров символьных вычислений.
□	Выполнение некоторых, даже очевидных, символьных операций вызывает не-
понятное затруднение у символьного процессора Mathcad.
□	Mathcad — это инструмент расчетчика. Инструмент должен быть удобным.
Если выполнение некоторых операций сложно, неудобно и сравнительно бы-
строе получение результатов расчета невозможно, то вряд ли есть смысл
в этих случаях обращаться к Mathcad.
Профессиональные математики и ученые, которым часто приходится прибегать
к символьным вычислениям, вряд ли обратятся за этим к Mathcad. Для них су-
ществуют более мощные пакеты, например Maple и Mathematica.
Глава 6
Решение дифференциальных уравнений
Дифференциальное уравнение называется обыкновенным (ОДУ), если в него
входят производные только по одной переменной. В противном случае говорят
об уравнении в частных производных. Mathcad предоставляет большие возмож-
ности для решения ОДУ и очень ограниченные — для решения уравнений в ча-
стных производных.
Поскольку решение дифференциальных уравнений состоит в интегрировании,
чтобы обеспечить однозначность решения, необходимо задавать дополнитель-
ные условия для определения постоянных интегрирования.
Mathcad решает ОДУ двух типов:
□	задачи Коши — ОДУ с начальными условиями, в которых задаются значения
функции и ее производных в начальной точке интервала интегрирования;
□	краевые задачи — ОДУ с граничными условиями, где задаются значения
функции и ее производных в начале и в конце интервала интегрирования.
ВНИМАНИЕ --------------------------------------------------
Mathcad в состоянии решить только ОДУ, которые можно записать в стандартном виде, то
есть решить алгебраически относительно производной высшего порядка и записать в виде
«/'(*)=/(*)•
Для численного интегрирования одного ОДУ (равно как и системы ОДУ) мож-
но использовать вычислительный блок Given-Odesolve (рис. 6.1) или применить
встроенные функции, унаследованные от ранних версий Mathcad. Рассмотрим
оба варианта решения ОДУ.
6.1.	Вычислительный блок Given-Odesolve
Простота и удобство использования блока Given-Odesolve позволили описать
его применение уже в главе 2. Напомним кратко, как использовать его для реше-
ния одного дифференциального уравнения.
Применение функции Odesolve требует записи вычислительного блока, состоя-
щего из трех частей:
□	ключевого слова Given (Дано);
□	дифференциального уравнения и начальных или граничных условий к нему;
□	функции Odesolve(x, xk, п) (решение ОДУ), где х — имя переменной, относи-
тельно которой решается уравнение; xk — конец интервала интегрирования
(начало интервала интегрирования указано ранее, в начальных условиях);
п — необязательный внутренний параметр, определяющий число интервалов,
используемых для интерполяции функции решения уравнения.
Примеры использования функции Odesolve приведены в главе 2 на рис. 2.19-
2.22 и далее на рис. 6.1-6.5.
160
Глава 6. Решение дифференциальных уравнений
6.1.1.	Решение ОДУ с начальными и граничными
условиями
Число условий в вычислительном блоке Given-Odesolve должно быть равно по-
рядку ОДУ. Если все условия задаются в точке начала интервала интегрирова-
ния, такие условия называются начальными. Пример решения ОДУ с начальны-
ми условиями приведен на рис. 6.1.
Если часть условий задана в одной точке, а часть — в другой точке, то это гра-
ничные условия. Независимо от порядка ОДУ Mathcad принимает граничные
условия только в двух точках. Пример решения ОДУ с граничными условиями
приведен на рис. 6.2.
Одна точка обязательно должна быть началом интервала интегрирования, дру-
гая точка — любая. Однако решение оказывается достаточно точным, только
если обе точки являются границами интервала интегрирования.
у'"(х) - 2 Х у'(х) = x sin(x)
Given
-^Цу(х) - 2 * — у(х) = x sin(x)
dx
исходное
уравнение
у(0) = 1 у'(0) = 1 у"(0) = -0 5 начальные условия
у = Odesolve(x,2) х = 0,0 1 .2
Рис. 6.1. Использование функции Odesolve
6.1.2.	Объединение ОДУ с помощью операторов условия
Если вид дифференциального уравнения изменяется с изменением аргумента,
например, уравнение содержит ступенчатую разрывную функцию, то такое урав-
нение можно записать с использованием условия, то есть записать несколько
уравнений в виде одного уравнения (рис. 6.3).
Mathcad позволяет записать условие несколькими способами:
□	с использованием булевых операторов:
яг/"(х)+ 6г/(х)г2(х < 0)+ г/(х)(1- х)(х > 0) = с,
6.1. Вычислительный блок Given-Odesolve
161
2	( V
x(t)2l,x(t)+ lx(t) =t
dt	/
поменяйте местами
выражения
Given , . 2 „, .	., . 3
x(t) x (t) + x (t) = t
x(0) = 3	x(6) = 2 x = Odesolve(t,9) t = 0,0.2 9
граничные условия можно задавать лишь в двух точках-
в начале и в конце интервала интегрирования
Рис- 6-2. Решение уравнения с граничными условиями
поменяйте местами
выражения
у"(х) + у'(х) 1г[х < 1 ,х^, I 3 - х^ )] = if(х < 2,sin(x),5)
с функцией if
_.	....	2 ,	0.21 . .	. .. .	с булевыми
Gwen у (х) + х (х < 1) + у(х) !.3-х ) (х £ 1) = sin(x) (х < 2) + 5 (х £ 2) операторами
Рис. 6.3. Объединение двух дифференциальных уравнений в одно
□	с использованием функции if:
еи/"(х) + if[x <0, by(x)x2, у(х)(1- х)]== с.
В данном случае невозможно записать условие с использованием условного опе-
ратора программирования if, так как вертикальной черте (обязательному призна-
ку программирования) должен предшествовать оператор присваивания :=, тогда
как в нашем случае использован знак + или знак логического равенства =.
162
Глава 6. Решение дифференциальных уравнений
6.1.3.	Решение ОДУ, заданных неявно
В Mathcad все встроенные функции для решения дифференциальных уравнений
требуют записи производной высшего порядка в явном виде. Однако, как пока-
зано на рис. 6.2, присутствие коэффициента (постоянного или переменного) пе-
ред производной высшего порядка не помеха при решении ОДУ. Если уравнение
есть сложная функция от высшей производной, предварительно надо решить это
уравнение алгебраически относительно высшей производной. На рис. 6.4 исход-
ное уравнение решено символьно относительно г/'(х). Для выполнения этой опе-
рации надо выделить переменную, затем в главном меню выбрать команду Sym-
bolics ► Variable ► Solve (Символьные вычисления ► Переменная ► Решить).
Найденный результат подставлен в дифференциальное уравнение, которое ре-
шено с помощью функции Odesolve.
Дано уравнение у(1 - у*(х)2) = у*(х)
решим уравнение символьно относительно у*(х)
у (1 a2) s a so*ut’on(s)
уравнение в стандартном виде
подставим в блок Given - Odesolve
Два корня уравнения дают
два решения ОДУ
1
Given
у*(х) = —-— -1 +
2y(x)L
(1 + 4уф2)
у(0.1)«5
Рис. 6.4. Приведение дифференциального уравнения к стандартному виду и его решение
6.1.4.	Решение систем ОДУ
Функция Odesolve может решать и системы дифференциальных уравнений. При
этом несколько изменяется обращение к функции.
Обращение к функции для решения одного уравнения выглядит так:
Odesolve(x, xk, п).
6.1. Вычислительный блок Given-Odesolve
163
Для решения системы дифференциальных уравнений —
Odesolve((BeKTop имен неизвестных), х, xk, п).
На рис. 6.5 приведено решение системы из трех дифференциальных уравнений
первого порядка. Соответственно, вектор имен неизвестных содержит имена
трех неизвестных, х, у и z. Граничные условия заданы в точке t = -1. Конечная
точка интервала интегрирования t = 3. Следовательно, интервал интегрирова-
ния — от -1 до 3. Конечное значение всегда должно быть больше начального.
Если график строится для значений, выходящих за пределы интервала интегри-
рования, Mathcad экстраполирует значения функции за пределы интервала ин-
тегрирования, получая чаще всего неправдоподобные результаты.
ВНИМАНИЕ ------------------------------------------------------------
Если в Mathcad 11 функция Odesolve решает системы уравнений только с начальными
параметрами, то начиная с Mathcad 12 — и с начальными, и с граничными условиями.
Given
Поменяйте
вид уравнений и
граничные условия
О 6x"(t) + y'(t) = О х(1) = °
y'(t)-z(t) = O ^ = -10
0.5 z'(t) - 2x'(t) = 0 Z'(	= 10
y'(-l) = -5
Рис. 6.5. Решение системы ОДУ функцией Odesolve
Функция Odesolve может принимать в качестве ограничений алгебраические
уравнения (рис. 6.6 и 6.7), но только в задачах с начальными условиями.
6.1.5.	Работа блока Given-Odesolve
Рассмотрим механизм работы блока Given-Odesolve. Фактически блок решения
ОДУ Odesolve включает в себя все лучшее, что было создано для решения ОДУ
в предыдущих версиях Mathcad. Блок Odesolve преобразует заданные дифферен-
циальные уравнения к стандартному виду, используемому функциями rkfixed и
164
Глава 6. Решение дифференциальных уравнений
Rkadapt, применение которых описано далее. С помощью указанных функций он
решает систему ОДУ (или одно ОДУ) с начальными условиями. В результате
расчета получают массив значений функции и ее производные.
Given
x"'(t) 4- y(t) = 0 дифференциальные
уравнения
О 3 z(t) - x(t) = О
алгебраическое
уравнение
алгебраическое уравнение
должно удовлетворять
граничным условиям
требуется
6 начальных
условий
х(-1) = о х’(—1) = -Ю х”(-1) = 1
у(-1) = -10	у’(-1) = 0	z’(-l) = 0
Рис. 6.6. Решение системы ОДУ с алгебраическими
ограничениями функцией Odesolve
y"(t)-z(t) = О
Далее используются функции интерполяции Ispline и interp, преобразующие мас-
сив решений системы ОДУ в функцию, которую затем можно дифференциро-
вать или интегрировать. Кстати, необязательный параметр steps в обращении
к функции Odesolve как раз и задает число точек интерполяции. Чем больше
steps, тем выше точность интерполяции, но тем больше время решения задачи.
Для решения системы жестких ОДУ используется функция Radau. Ее описание
приводится далее в данной главе (раздел 6.3.1).
Если граничные условия заданы в двух точках, в начале решения функция
Odesolve преобразует задачу с граничными условиями к задаче с начальными ус-
ловиями, используя для этого функции sbval и bvalfit, описанные далее. Затем ре-
шается задача с начальными условиями с помощью функций rkfixed, Rkadapt или
Radau в зависимости от выбранного пользователем метода решения — Fixed,
Adaptive или Stiff.
Таким образом, функция Odesolve объединила все лучшие функции решения
ОДУ, существующие в данный момент, в единый блок.
6.1. Вычислительный блок Given-Odesolve
165
При решении системы ОДУ с помощью функции Odesolve есть возможность вы-
брать метод решения. Для этого надо установить курсор на слове Odesolve и на-
жать правую кнопку мыши. В открывшемся контекстном меню выбрать Fixed
(Решение с фиксированным шагом функцией rkfixed), Adaptive (Решение с пере-
менным шагом функцией Rkadapt) или Stiff (Решение жесткой системы ОДУ
функцией Radau), как показано на рис. 6.7.
Given	—=u(x) +—u(x) = 1
dx
алгебраическое , , , , „
уравнение u<x>+ 3v<x> = "6
v(0) = -3
u(0) = 3
u'(0) = О
Рис. 6.7. Выбор метода решения дифференциальных уравнений
6.1.6.	Новые функции решения ОДУ в Mathcad 14
В Mathcad 14 добавлены три новых функции решения ОДУ:
□	Adams, которая базируется на методе Адамса и предназначена для решения
нежестких систем.
Обращение к этой функции: Adams(z/, Х, Хч, т, D, [tol]).
□	BDF, которая использует формулы обратного дифференцирования и предна-
значена для решения жестких систем.
Обращение к этой функции: BDF(z/, хц Х2, т, D, [J], [tol]).
□	AdamsBDF — гибридная функция, которая сама определяет, является система
жесткой или нежесткой, и вызывает функции Adams или BDF соответственно.
Обращение к этой функции: AdamsBDFQ/, xi, Х2, т, D, [J], [tol]).
Аргументы всех трех функций те же, что у функции rkfixed (раздел 6.2): у — век-
тор начальных условий размерности п. Здесь п — порядок дифференциального
уравнения или число уравнений в системе (если решается система дифференци-
альных уравнений); xt и х2 — начало и конец интервала интегрирования, на кото-
ром ищется решение дифференциального уравнения. Начальные условия, задан-
ные в векторе г/, — это значения решения в точке xt; т — число точек (не считая
166
Глава 6. Решение дифференциальных уравнений
начальной точки), в которых ищется приближенное решение. При помощи этого
аргумента определяется число строк (1 + т) в матрице, возвращаемой указанны-
ми функциями; [tol] — необязательный параметр, определяющий точность расче-
та каждой переменной. Вводится как число или вектор чисел. Можно использо-
вать параметр [tol], чтобы изменить используемую по умолчанию точность 10-5;
[J] ~ матрица Якоби (матрица частных производных системы ОДУ по всем пе-
ременным). Необязательный параметр. Используется только в функциях BDF
или AdamsBDF. Ввод его может повысить точность решения.
Эти три новые функции включены в алгоритм функции Odesolve. В контекстном
меню, появляющемся при наведении стрелки мыши на слово «Odesolve», пред-
лагается выбор способа решения ОДУ (см. рис. 6.7):
□	Adams (Метод Адамса);
□	Fixed (С постоянным шагом);
□	Adaptive (Адаптивный метод);
□	Radau (Метод Radaus).
Рис. 6.8. Пояснения к выбору метода решения ОДУ в разделе Помощь Mathcad
Подробно о методах решения ОДУ функцией Odesolve читайте в разделе По-
мощь Mathcad (рис. 6.8).
Обратите внимание на то, что если Mathcad-документ был создан в более ранней вер-
сии, то в Mathcad 14 он будет открываться с использованием пункта Adams.
6.1. Вычислительный блок Given-Odesolve
167
6.1.7.	Решение ОДУ с переменными параметрами
В Mathcad 12 и 13 функция Odesolve может решать дифференциальные уравне-
ния с переменными параметрами. Появилась возможность записать функцию
пользователя с использованием встроенной функции Odesolve (рис. 6.9). Число
параметров функции пользователя может быть любым. Для вывода результатов
расчета эти параметры можно задать числом или в виде дискретной переменной.
Результаты расчета можно вывести в виде таблицы, графика или семейства кривых.
Given ax"(t) + cx'(t) = t° x(tO) = 5 x(tfc) = 0 D(a,b,c) := Odesolve! t,tfc I
b = l c=l F(a,t) = D(a,b,c,t)
a = 0..3	b = 0. 3
Семейства кривых при переменных значениях параметров
Рис. 6.9. Решение ОДУ с переменными параметрами
Вывод решения при двух переменных
и двух постоянных параметрах
(поменяйте параметры)
F(a,b) = D(a,b,2,4)
F
Отключен длительный расчет
Чтобы ускорить расчет на
вкладке Quick Plot Data
задайте малое число
точек (# of Grids)
например, по 6 точек
Рис. 6.10. Вывод решения ОДУ с двумя переменными
параметрами
168
Глава 6. Решение дифференциальных уравнений
При двух переменных параметрах можно вывести график поверхности, но в этом
случае возрастет время расчета (рис. 6.10).
В Mathcad 13 появилась возможность использовать функцию Odesolve в про-
граммных модулях. Примеры использования этой функции в программах приве-
дены в главе 9.
6.2.	Использование функций rkfixed, Rkadapt,
Bulstoer
Рассмотрим три функции, предназначенные для решения дифференциальных
уравнений и их систем: rkfixed, Rkadapt и Bulstoer.
Обращение к этим трем функциям одинаково:
rkfixed(z/, xlf х2, т, D),
где у — вектор начальных условий размерности п. Здесь п — порядок дифферен-
циального уравнения или число уравнений в системе (если решается система
дифференциальных уравнений); xt и х2 — начало и конец интервала интегриро-
вания, на котором ищется решение дифференциального уравнения. Начальные
условия, заданные в векторе г/, — это значения решения в точке хх; т — число то-
чек (не считая начальной точки), в которых ищется приближенное решение. При
помощи этого аргумента определяется число строк (1 + т) в матрице, возвра-
щаемой указанными функциями.
Функции rkfixed и Rkadapt реализуют метод Рунге—Кутта четвертого порядка.
Этот метод не является самым быстродействующим, но почти всегда приводит
к искомому результату.
ВНИМАНИЕ -----------------------------------------------------------
Все три функции решают ОДУ и их системы только с начальными, но не с граничными ус-
ловиями, в отличие от функции Odesolve, которая решает дифференциальное уравнение
любого порядка как с начальными, так и с граничными условиями.
Функция rkfixed ищет решение с постоянным шагом. Функция Rkadapt проверя-
ет, как быстро изменяется приближенное решение, и, соответственно, адаптиру-
ет шаг решения. Адаптивный контроль величины шага дает возможность функ-
ции Rkadapt вычислять значения приближенного решения на более мелкой сетке
в тех местах, где оно меняется быстро, и на более крупной — там, где оно меняет-
ся медленно. Это позволяет и повысить точность, и сократить время решения за-
дачи.
Хотя функция Rkadapt при решении дифференциального уравнения использует
во внутренних расчетах переменный шаг, возвращает она приближенное реше-
ние на равномерной сетке (в равноотстоящих точках).
Когда известно, что решение является гладкой функцией, лучше применить
функцию Bulstoer, которая использует метод Булирша—Штера вместо метода
6.2. Использование функций rkfixed, Rkadapt, Bulstoer
169
Рунге—Кутта, как в функциях rkfixed и Rkadapt. Найденное функцией Bulstoer
решение будет немного более точным, чем при использовании других функций.
Для решения дифференциального уравнения или системы уравнений необходимо
задать:
□	начальные условия;
□	число точек, в которых надо найти решение;
□	само дифференциальное уравнение, записанное в некотором специальном
виде, который будет описан далее.
6.2.1.	Решение дифференциального уравнения
первого порядка
При интегрировании дифференциального уравнения первого порядка появляет-
ся одна произвольная постоянная, поэтому надо задать одно начальное условие
z/0, если ORIGIN = 0, или если ORIGIN = 1 (Mathcad ожидает начальные условия
в виде вектора).
Далее нужно ввести функцию двух переменных Щх,у), которая содержит вектор
первых производных от неизвестных функций. Для ОДУ первого порядка функ-
ция D(x,y) содержит одну первую производную у' (х
|ОДУ первого порядка!	+
y + 3j/ = 0 исходное уравнение
п := 50 уд := 4 начальное приближение у(0)=4
О(Х>У)*= -Зу0 первая производная в явном виде
Z := rkfixed(y,0,4,n,D) решение с фиксированным шагом
Рис. 6.11. Решение дифференциального уравнения первого порядка
В примерах на рис. 6.11 и 6.12 было просто решить уравнение относительно пер-
вой производной и определить функцию D(x,y). В случае нелинейного диффе-
ренциального уравнения необходимо решить это уравнение алгебраически от-
носительно высшей производной (в данном случае первой производной). Это
можно сделать в символьном виде и подставить решение в функцию 1х,уУ Да-
лее вызывается функция rkfixed (или Rkadapt, или Bulstoer), которая возвращает
170
Глава 6. Решение дифференциальных уравнений
решение уравнения. В результате решения получается матрица, содержащая два
столбца:
□	первый столбец содержит координаты х точек, в которых найдено решение;
□	второй столбец содержит значения найденного решения в указанных точках.
Найденное решение можно вывести в виде таблиц или графиков.
У+у2 х = 0 Нелинейное уравнение
у0 :« 1 начальное приближение у(0)=1
n>50 D(x,y) >-(у0)2 х
Z := Rkadapt(y,0,3,n,D) решение с переменным шагом
Рис. 6.12. Решение дифференциального уравнения с переменным шагом
ВНИМАНИЕ ---------------------------------------------------------
Функции rkfixed, Rkadapt, Bulstoer возвращают матрицы, а не функции, поэтому интегриро-
вание и дифференцирование найденного решения стандартными методами Mathcad не-
возможно. Необходимо использовать функции интерполяции для перехода от матрицы
к функции.
6.2.2.	Дифференциальные уравнения более высокого
порядка
Для решения уравнений высокого порядка используются функции rkfixed,
Rkadapt, Bulstoer. Для решения дифференциального уравнения порядка п нужно:
□ задать вектор начальных условий, который состоит из п элементов, опреде-
ляющих начальные условия для искомой функции и ее производных у. у1, у",
у'", -,у(п~'
□	ввести функцию D(x, у), которая теперь является вектором, содержащим п
элементов:
у"(х)
D(x,y) =
[У(п)(х)
6.2..Использование функций rkfixed, Rkadapt, Bulstoer
171
□	ввести выражение, содержащее функцию rkfixed, Rkadapt или Bulstoer.
В результате решения получается матрица, содержащая п+1 столбец: первый —
для значений аргумента х, оставшиеся столбцы содержат искомую функцию у
и ее производные у(х} у'(х), у"(х),..., у(п~1)(х).
Пример решения ОДУ четвертого порядка показан на рис. 6.13 и 6.14.
Исходное уравнение
—}У(х) " 2 х-^у(х) + sin(x)y(x) = О
dx	dx
xl >10 х2 := 11 п:= 20 первые производные
в явном виде
граничные условия			' У1 '	yj-y1
		зКФ-о	ъ	у2яу“
	1	у'(О) > 1 D(x,y)		
у:=	2	уКГО-з	Уз	у3 » у“
		у-СФ-З	2 х у2 - sin(x) y0>	Уд
z>:	Rkadapt(y,xl ,x2,n,D)		i:= 0..n	
где у -вектор начальных условий
L1 -начало интервала интегрирования
L2 -конец интервала интегрирования
п -число точек для вычислений
D -вектор первых производных в явном виде
Поменяйте Rkadapt на rkfixed или Bulstoer
Рис. 6.13. Решение дифференциального уравнения четвертого порядка
Рис. 6.14. Результаты решения уравнения, приведенного на рис 6.13
172
Глава 6. Решение дифференциальных уравнений
6.2.3.	Системы дифференциальных уравнений
Методика решения систем дифференциальных уравнений такая же, как и мето-
дика решения одного дифференциального уравнения высокого порядка.
Любое дифференциальное уравнение порядка п
У<п> =f(x,y(n~ly{n~2).у', у)
путем замены
У1<х) = у(х);
у2(х) = у'(х);
Уп(х) = У<п~')(х)
может быть представлено в виде системы дифференциальных уравнений:
У1(Х) = У2<ХУ
У2<х) = Уз<,хУ>
у'„(х) = f{x,y{n-ly(n~2} ,...,у',у).
Заметим, что в приведенных уравнениях содержатся производные только перво-
го порядка. Преобразовав подобным образом каждое из уравнений, входящих
в исходную систему, получим систему уравнений с большим количеством неиз-
вестных функций, но с производными только первого порядка.
Исходная система уравнений
— -y + t — = х+е? при х(0)=1 и у(0)=0
dt	dt
Рис. 6.15. Решение системы ОДУ первого порядка
6.3. Жесткие системы дифференциальных уравнений
173
В результате решения получается матрица, содержащая п+1 столбец: первый —
для значений аргумента х в точках, где найдены решения, оставшиеся столбцы
содержат искомые функции и их производныеу(х), yf(x), у"(х),..., y(n~i}(x).
Примеры решения систем ОДУ первого и второго порядка показаны на рис. 6.15
и 6.16.
Фактически так и решалось дифференциальное уравнение высокого порядка
(см. рис. 6.13), где функция D(x,y) представляла собой систему уравнений пер-
вого порядка.
Система ОДУ второго порядка
u'-2v	v'-4v-2u
начальные условия вектор первых и вторых производных
л 5 Vй
1.5 и'(°)
':=	1	v((J)
< 1 J *'Р)
F:=rkfixed(y,O,l,n,D)
Рис. 6.16. Решение системы ОДУ второго порядка
Примеры для самостоятельного решения дифференциальных уравнений и их
систем приведены на рис. 6.17.
6.3.	Жесткие системы дифференциальных уравнений
Система дифференциальных уравнений, записанная в матричном виде,
Y = А х X, считается жесткой, если матрица коэффициентов почти вырожденная.
В этом случае решение, возвращаемое функцией rkfixed, может быть неустойчи-
вым. При решении жесткой системы необходимо использовать одну из трех
функций, специально разработанных для решения жестких систем дифференци-
альных уравнений. К ранее существовавшим функциям Stiffb и Stiff г, реализующим
174
Глава 6. Решение дифференциальных уравнений
Решить самостоятельно с помощью функций rkfixed
или Rkadapt, с начальными условиями
У(0)=0
у* =------------
ln(y)cos($
y*H‘(x - 1) - у" S 0	у(2) = 2
у**1 - 2 у“ + у* я 0 варьируйте граничные условия
У*(2) = 1 у"(2) = 1
Системы ОДУ
d
—х1 = х- - х.
dt 1
d
-*9 = х<
dt1	1
d
— X = --------
dt З-х + 2-у
‘y.-z—
dt 2-x + 3-y
Рис. 6.17. Примеры для самостоятельной работы
с ОДУ и их системами
методы Булирша—Штера или Розенброка соответственно, в Mathcad 200li доба-
вилась функция Radau, реализующая метод RADAU5. Рассмотрим вначале бо-
лее ранние функции Stiff b и Stiff г.
Вид матрицы, возвращаемой этими функциями, совпадает с возвращаемым функ-
цией rkfixed. Однако функции Stiff г и Stiff b требуют дополнительно задания яко-
биана системы уравнений.
Обращение к этим функциям:
Stiffb(z/, Xi, х2, n,
Stiffr(z/, xlf x2, n, D,J).
Здесь у — вектор начальных условий размерности т, где т — порядок ОДУ или
число уравнений в системе ОДУ; xt и х2 — начало и конец интервала интегриро-
вания, на котором ищется решение системы ОДУ; начальные условия, заданные
вектором у, — это значение решения в точке xt; п — число точек (не считая на-
чальной), в которых ищется решение; D(x,y) — m-мерный вектор, который со-
держит первые производные неизвестных функций; J(x,y) — функция, которая
возвращает матрицу размером т х (т + 1). Первый столбец ее содержит произ-
водные F(t,у) по у. Остальные столбцы представляют собой матрицу Якоби сис-
темы ОДУ.
Пример решения жесткой системы ОДУ приведен на рис. 6.18.
Следует заметить, что увеличение числа шагов в 1000 раз позволяет решить при-
веденную систему с помощью функции rkfixed (рис. 6.19), но это оттого, что за-
данная система не слишком жесткая. Если увеличить разницу в коэффициентах
уравнений, то функция rkfixed потребует гигантского числа шагов и в принципе
не сможет решить систему.
6.3. Жесткие системы дифференциальных уравнений
175
Жесткие ОДУ
F(t,y):- 01
уО:-
-0.1у0 + 100 У1 у2
Уо - 100 У2 " 1И» У}
1000у|
100у2	100-У1
-100 у2 - 1000 -100 у1
1000	0	>
D := Stiffb(y0,0,50,50,F,J)
D(0>
Рис. 6.18. Пример решения жесткой системы ОДУ
у0:= 0
<0,
(	-0.1 у0+ 100У1у2
F(t,y) := 0.1 yQ - 100 yt y2 - 1000 у(
1000У1
D := risfixed(y0,0,50,20000,F)
Рис. 6.19. Решение жесткой системы ОДУ функцией rkfixed
176
Глава 6. Решение дифференциальных уравнений
Новая функция Radau имеет такой же список аргументов, как и функции Rkadapt
и Bulstoer, а именно: Radau(z/, xv х2, D).
Функция Radau предназначена для решения систем жестких ОДУ, как и функ-
ции Stiff г и Stiff b. Преимуществом функции Radau перед Stiff г и Stiff b является то,
что она не требует указания якобиана в качестве параметра функции.
Сравнение результатов расчета жесткой системы ОДУ с помощью функций
Radau и Stiff г приведено на рис. 6.20. Численные результаты, естественно, совпа-
дают, но использование функции Radau проще.
з
-2
х! := 0
х2 := 3
асе := 10
D(x,Y) :=
-4
npts := 3 kmax := 50 step := 10
( 22YQ + 42 Yj
0 22 42
-21Уп-41 У.
и .
0 -21 -41

J(x,Y) :=
A := stiffi(y,xl,x2,acc,D,J,kmax,step)
В :- radau(y,xl ,x2,acc,D, kmax, step)
C:« Stiffi(y,xl ,x2,npts,D,J)
	0	1	2
0	0	3	-2
1	0.008	2.876	-1.868
2	0.015	2.775	-1.761
3	0.022	2.689	-1.667
4	0.029	2.615	-1.585
5	0.037	2.552	-1.515
<0	3	-2
D := Radau(y,xl ,x2,npts,D)
	0	1	2
0	0	3	-2
1	0.001	2.99	-1.989
2	0.005	2.92	-1.915
3	0.024	2.663	-1.638
4	0.044	2.503	-1.458
5	0.064	2.41	-1.344
Таблицы
из 50 точек
5.437
14.78
-2.718
-7.39
^3 40.182 -20.0917
(0	3	-2	>
1 5.438 -2.719
2 14.778 -7.389
<3 40.172 -20.086;
Таблицы
из 3 точек
Рис. 6.20. Решение жесткой системы уравнений функциями Radau и Stiff г
Given x'(t) = 22 x(t) + 42 y(t) x(0) = 3
y*(t) ж-21x(t) - 41y(t)	y(0) =-2
t:=0..3
t =
J)
1
"7
x(t) =
______3
5.43
14.777
40.172
y(t) =
______-2
-2.715
-7.389
-20.086
Рис. 6.21. Решение жесткой системы уравнений функцией Odesolve
6.3. Жесткие системы дифференциальных уравнений
177
На рис. 6.21 показано решение той же системы ОДУ с использованием функции
Odesolve (в контекстном меню выбран способ решения Stiff).
6.3.1.	Функция Radau в Mathcad 14
В Mathcad 14 в обращении к функции Radau появилось три новых необязатель-
ных аргумента:
□	J — матрица Якоби;
□	М — матрица связи переменных в форме	&У>
□	[tol] — число или вектор чисел, указывающих точность расчета по каждой пе-
ременной.
Обращение к функции Radau:
Radau(i/, xlf х2, т, D, [J], [М], [tol]).
В приведенном на рис. 6.22 примере решается система из двух дифференциаль-
ных и одного алгебраического уравнения.
—х = -0.4 х+ 104 y z
dt
—у = 0.04-х- 104yz- 3-10?у2
dt
x + y+z-l = 0
Для справки
-у) = f(t,y)
I dt J
f(t,y) •=
У1
<У2,
d
dt
d
dt
Матрица связи
'1 0 (P
M:= 0 10
k0 0 0;
Матрица Якоби
4
- O4 yo+ 10 УГУ2
4	7,2
.04-yo- 10 У1У2- 310 •(yi |
У0 + У1 + У2 “ 1
4	4	
10 y2 10 yi
4	7	4
-10 У2-6 10 yi -10 yi
1 1 >
Рис. 6.22. Подготовка системы ОДУ к решению
В матрице связи М нуль внизу на главной диагонали означает, что правая часть
третьего уравнения равна нулю.
Для повышения точности расчетов в обращение к функции Radau включена мат-
рица Якоби. Однако для данного примера якобиан можно удалить. Результаты
расчета приведены на рис. 6.23.
178
Глава 6. Решение дифференциальных уравнений
Начальные условия Диапазон интегрирования
УО ;= 1 У1 := о У2 := 0	:= 0	:= 4104
Z := Radau(y,tH,tK, 1000,f,М)
.	„<0>	„<1>	7<2>	7<3>
t .= L х .= L у .= L z .= L
Рис. 6.23. Результат решения системы уравнений с помощью функции Radau
6.4.	Нахождение решения только в конечной точке
Функции для численного решения дифференциальных уравнений, описанные
ранее, искали решение z/(x) в равноотстоящих точках на отрезке от xt до х2. Од-
нако часто возникает задача, когда необходимо найти решение только в конечной
точке интервала у(х2) Функции, описанные ранее, будут давать такое решение,
однако при этом делать много ненужной работы. Если нужно только значение
функции в конце интервала у(х2), можно использовать функции, описанные
в дальнейшем. Каждая из них соответствует одной из функций, перечисленных
ранее, и обладает аналогичными свойствами. Имена таких функций начинаются
со строчной буквы.
Обращение к этим функциям:
bulstoer(z/, xlf х2, асе, Z>, kmax, save);
rkadapt(z/, xif x2, acc, D, kmax, save);
radau(z/, xp x2, acc, D, kmax, save);
stiffb(z/, xp x2, acc, D,J, kmax, save)*
stiffr(z/, xt, x2, acc, D,J, kmax, save),
где у — вектор начальных условий размерности п (п — порядок ОДУ или число
уравнений в системе ОДУ); х{ и х2 — граничные точки интервала, на котором
ищется решение системы ОДУ; начальные условия, заданные вектором у, — это
значение решения в точке xt; асе — параметр, контролирующий качество решения.
6.5. Двухточечные краевые задачи
179
Малое значение асе вынуждает алгоритм брать меньшие шаги вдоль траектории,
что увеличивает точность решения, значения асе, близкие к 0,001, приводят
к хорошей точности решения; D(x,y ) — n-мерный вектор, который содержит пер-
вые производные неизвестных функций; — функция, которая возвращает
матрицу размером п х (п + 1), первый столбец ее содержит производные F(t,y)
по у, остальные столбцы представляют собой матрицу Якоби системы ОДУ;
&тах ~ максимальное число промежуточных точек, в которых ищется решение,
ограничивает число строк матрицы, возвращаемой этими функциями; save — ми-
нимально допустимый интервал между точками, в которых ищется приближен-
ное решение. Он определяет минимальное различие между любыми двумя чис-
лами в первом столбце матрицы, возвращаемой функцией.
Следует отметить, что экономия времени при использовании таких функций не-
велика, и поэтому применение их вряд ли целесообразно.
Примеры использования таких функций приведены на рис. 6.20 и 6.24.
Исходное уравнение = 2Х~У^ при у(0)=5
-5	-3
х1 := -3 х2 := 3 асе := 10 kmax := 10 save := 10
х-Уо
y0:=5 D(x,y) := 2 У0
Z = rkfixed(y,-3,3,20,D) Обычное решение в 20 точках
Z1 := bulstoe<y,xl,х2,асе,D,kmax,save) DrtlАП„^„ПП11П11П
’	7 Решения, справедливые
Z2 := rkadapt(y,xl ,х2, асе ,D ,kmax, save)	лишь в конечной точке
Рис. 6.24. Нахождение решения ОДУ только в конечной точке
При использовании этих функций точный результат получается только в конеч-
ной точке. Вывод промежуточных точек бесполезен (см. рис. 6.24).
6.5.	Двухточечные краевые задачи
При решении дифференциального уравнения первого порядка задается одно
граничное условие, и оно обязательно должно быть задано в начале интервала
интегрирования. При решении одного дифференциального уравнения выше пер-
вого порядка число граничных условий должно быть равно порядку уравнения.
Эти условия могут быть заданы в одной точке, в которой обязательно должно
180
Глава 6. Решение дифференциальных уравнений
быть начало интервала интегрирования, или в двух точках, одна из которых обя-
зательно должна быть началом интервала интегрирования. Вторая точка может
быть любой в Mathcad 13 и 14. В старых версиях — обязательно правее начала
интервала.
Для решения дифференциальных уравнений любого порядка с граничными ус-
ловиями лучше всего использовать функцию Odesolve. Однако можно использо-
вать и все остальные рассмотренные функции, например rkfixed, Rkadapt, Bulstoer
и др. Можно, но сложно. Гораздо сложнее, чем Odesolve.
Допустим следующее:
□	дана система дифференциальных уравнений или одно дифференциальное
уравнение порядка п;
□	в начальной точке х интервала, на котором ищется решение, задана часть
граничных условий;
□	внутри или в конце интервала в точке х2 заданы недостающие граничные ус-
ловия;
□	общее количество граничных условий равно п.
В этом случае необходимо использовать функцию sbval, чтобы найти недостаю-
щие граничные условия в точке хх. После этого можно будет решать обычную за-
дачу с начальными условиями (задачу Коши). Для решения задачи Коши можно
использовать любую из описанных ранее в этой главе функций.
ВНИМАНИЕ ------------------------------------------------------------
Функция sbval не решает дифференциальное уравнение — она только вычисляет недос-
тающие начальные условия.
Для того чтобы найденные функцией sbval недостающие начальные условия
были согласованы с граничными условиями во второй точке интервала, исполь-
зуется алгоритм стрельбы. Суть метода стрельбы заключается в пробном зада-
нии недостающих начальных условий и решении затем задачи Коши известны-
ми методами.
Обращение к функции sbval выглядит следующим образом:
sbval(z, xif х2, Z, load, score),
где z — вектор начальных приближений для недостающих начальных условий
в точке xt; xt и х2 — точки интервала, в которых заданы граничные условия;
1х,у) — функция, содержащая в виде вектора из п элементов первые производ-
ные неизвестных функций; load(xt, у} — векторная функция, содержащая значе-
ния начальных условий в точке xt. Вектор состоит из п элементов, которые соот-
ветствуют вектору начальных условий в точке xt. Некоторые из этих условий
будут константами, определяемыми начальными условиями. Другие элементы
неизвестные и в дальнейшем будут определены функцией sbval; score(x2, у) —
векторная функция, возвращающая вектор, количество элементов которого равно
порядку уравнения п. Каждый элемент вектора содержит разность между на-
чальным условием, заданным в точке х2, и значением искомого решения уравнения
6.5. Двухточечные краевые задачи
181
в этой точке. Вектор score показывает, насколько значения найденного решения
в точке х2 близки к значениям, заданным в точке х2. Значение 0 для любого эле-
мента указывает на полное совпадение начального условия и того значения, ко-
торое возвращается функцией sbval.
В качестве примера решения двухточечной краевой задачи на рис. 6.25 показано
решение дифференциального уравнения упругой линии балки с двумя консоля-
ми (определение прогиба балки). И что же? Mathcad не справился с поставлен-
ной задачей. Все встроенные функции для решения дифференциальных уравне-
ний, включая и функцию Odesolve, требуют обязательно задания одного из двух
граничных условий на левом конце балки. Поэтому прогиб балки на левой кон-
соли определить не удается (рис. 6.26). Mathcad определяет прогиб балки во
всех точках, начиная с левой опоры балки (точка Л), х = а.
а:-0.5 b:=1.5 L:=2 Р := 1 Е:=210П J:=410‘
М(х) := -Рх + Р (х - а)(х > а) + Р (х - Ь)(х > Ь)
х. := 1 начальное приближение для у*(а)
• и / „ 
D(x,y)
У1
М(х)
/ 0 А известное у (а)
load(x,z) .- II неизвестное
разница между вычисленными
и заданными значениями у
S sbval(z, a,b,D,load, score)
S = (з.12б X 10- 5) первая производная
score(b,y) := уд
yyl := rkfixed
. q ' при х=а_
« ,a,L,10,D
ЧП
score1
решение точное
Рис. 6.25. Расчет прогиба балки функциями sbval и rkfixed
На балке три участка, поэтому уравнение изгибающего момента М(х) записано
с использованием булевых операторов (возможна запись М(х) с использованием
функции условия if или условного оператора if с панели программирования).
Для сравнения на рис. 6.26 показано решение той же задачи с помощью функции
Odesolve.
182
Глава 6. Решение дифференциальных уравнений
Для сравнения то же решение с помощью функции odesolve
Given EJy"(x) = М(х) у(а) = 0 у(Ь) = О
ПСФ =  	УУ(0.5) = 0	уу(1) = 7.812 х 10‘
| Argument outside of solution interval. |
Рис. 6.26. Определение прогиба балки (см. рис. 6.25) функцией Odesolve
В некоторых случаях бывает, что кроме граничных условий в двух точках задано
условие и в некоторой третьей точке внутри интервала интегрирования. В этом
случае необходимо использовать функцию bvalfit, которая, как и sbval, вычисляет
недостающие начальные условия для последующего решения задачи Коши.
Обращение к функции bvalfit:
bvalfit(zt, z2, xt, x2, Xf, D, loadl, Ioad2, score),
где — вектор, содержащий начальное приближение для начальных условий, не
заданных в точке xt; z2 — то же самое для граничных условий, не заданных в точ-
ке х2; xt и х2 — точки интервала, где заданы граничные условия; Xf — некоторая
точка между хх и х2. В этой точке решения, начинающиеся в точках xt и х2, долж-
ны быть равны; D(x,y) — функция, содержащая в виде вектора первые производ-
ные неизвестных функций; loadl(хр zt) — векторная функция, возвращающая
значения начальных условий в точке xt. Вектор состоит из п элементов, которые
соответствуют вектору начальных условий в точке Некоторые из этих усло-
вий будут константами, определяемыми начальными условиями. Другие элемен-
ты неизвестны и в дальнейшем будут определены функцией bvalfit; Ioad2(x2, z2) —
функция, аналогичная loadt, но для значений в точке х2; score(jty, у) — векторная
функция, возвращающая вектор из п элементов. Он определяет, насколько зна-
чения решений, начинающихся из точек xt и х2, соответствуют друг другу в точ-
ке х^ Если необходимо, чтобы решения совпали, определите score(xy, у) = у.
Этот метод нужно использовать, когда производные имеют разрыв где-либо на
интервале поиска решения.
Пример использования функции bvalfit приведен на рис. 6.27, результаты расче-
та — на рис. 6.28. Для дифференциального уравнения второго порядка с разрыв-
ной правой частью d в точке лу = 0 с помощью функции bvalfit найдены недостаю-
щие граничные условия в точках xt и х2. Далее с помощью функции rkfixed
решено уравнение для х < 0.
6.5. Двухточечные краевые задачи
183
Решение этого уравнения в точке Xj использовано в качестве начальных условий
для решения этого же уравнения при х > 0.
Дифференциальное уравнение с разрывной правой частью
при х<0
при х>0
У1
у0 (х<0) -у0 (х>0)
краевые условия
у(1)ж2
xf := 0 точка стыковки двух
кусков решения
zig := 1	стартовые значения у*(1)
„	4	для поиска величин
й0:=1	у*(-1)
( 1	у(-1)
loadl(xl ,zl) = I I стартовое значение y*(-l)
Ioad2(x2,z2)
У(1)
стартовое значение y*(l)
score(xf,y) •= у условие, приводящее к стыковке
решений в точке x=xf
S := bvalfit(zl ,22,-1,1,0,D,loadl ,load2, score)
S = (0 092 -0.678) содержит y*(-l) и y*(l)
Рис. 6.27. Краевая задача с граничным условием в промежуточной точке
Решаем 2 дифференциальных уравнения
с известными начальными условиями
Y1 = rkfixed
1
,-1,0,10,D
So,о/
Y2 = rkfixed
,0,l,10,D
LY110,2 )
Для сравнения то же решение с помощью функции odesolve
У“(Х) = £(х < 0,у(х) ,-у(х)) Поменяйте местами
Given у"(х) = у(х) (х < 0) - у(х) (х £ 0) эти 2 уравнения
у(-1) = 1	у(1) = 2 у = Odesolve(x, 1) х = -1 ,-0 9.. 1
Решение уравнения с использованием функций
odesolve	bvalfit и rkfixed
Рис. 6.28. Решение уравнения (см. рис. 6.27) функцией Odesolve
184
Глава 6. Решение дифференциальных уравнений
Теперь посмотрите, как это же уравнение решает функция Odesolve с использо-
ванием булевых операторов для записи правой части уравнения или функции
условия if (см. рис 6.28). Условный оператор программирования if в данном слу-
чае применить нельзя, так как перед вертикальной чертой, указывающей на ввод
программы, должен стоять оператор присвоения значения :=, а не логический
знак равенства =.
На рис. 6.28 также выведены графики решения дифференциального уравнения
с помощью функции Odesolve и функций bvalfit и rkfixed. Оба графика полностью
совпадают. Функция Odesolve возвратила функцию, а функция rkfixed — массив.
6.6.	Решение дифференциальных уравнений
в частных производных
Дифференциальные уравнения в частных производных требуют нахождения
функции не одной, а нескольких переменных. Mathcad имеет очень ограничен-
ные возможности для решения таких уравнений, ведь для решения каждого вида
уравнений в частных производных требуется свой метод решения.
Уравнения в частных производных можно разделить на три типа:
□	параболические, содержащие первую производную по одной переменной
и вторую — по другой, причем все производные входят в уравнение с одина-
ковым знаком:
□	гиперболические, содержащие первую производную по одной переменной
и вторую — по другой, входящие в уравнение с разными знаками;
□	эллиптические, содержащие только вторые производные, причем одного
знака.
6.6.1. Функции решения параболических
и гиперболических уравнений
Mathcad включает в себя две функции для решения параболических и гипербо-
лических уравнений, pdesolve и numol.
Функция pdesolve используется в составе вычислительного блока Given-pdesolve
для решения гиперболических или параболических уравнений (или систем урав-
нений) в частных производных, имеющих в качестве аргументов, как правило,
время t и пространственную координату х.
Обращение к этой функции:
pdesolve(w, х, xrange, t, Grange, [xpts], [£pts])
возвращает скалярную (для одного уравнения) или векторную (для системы
уравнений) функцию, являющуюся решением уравнения (или системы уравне-
ний). Здесь и — явно заданный вектор имен функций (без указания имен аргу-
ментов), подлежащих вычислению. Эти функции, а также граничные условия
должны быть определены внутри вычислительного блока Given-pdesolve; х —
пространственная координата; xrange — вектор значений аргумента х для гра-
ничных условий. Он должен состоять из двух чисел, представляющих две границы
6.6. Решение дифференциальных уравнений в частных производных
185
расчетного интервала; t — время (имя второго аргумента неизвестной функции);
Grange — вектор значений аргумента t для граничных условий, состоящий из
двух чисел, представляющих две границы расчетного интервала; xpts — количе-
ство пространственных точек дискретизации (может не указываться); £pts — ко-
личество временных слоев (также может не указываться).
Пример использования функции pdesolve приведен на рис. 6.29. Запись вычис-
лительного блока с функцией pdesolve аналогична записи блока с функцией
Odesolve. Результаты расчета показаны на рис. 6.30.
Решение одномерного
волнового уравнения
d , Л 2d, ,ч
—xw(x,t) = а —»w(x,t)
dt	dx
Здесь w- перемещение, v- скорость перемещения
где	—w(x,t) = v(x,t) тогда — v(x,t) = а^ w(x,t)
dt	dt
Представим первое уравнение как
систему двух уравнений первого порядка
Given t s 2	. ч
vt(x,t) = a w„(x,t)
wt(x,t) = v(x,t)
граничные условия
w(0,t) = о
Глобальное
L « 2 присвоение
параметров
Тж2л
Рис. 6.29. Пример использования функции pdesolve
Сетка решений волнового уравнения
на временном и пространственном интервалах
М:= CreateMeshCw,0,L,0,T)
М
Рис. 6.30. Результаты решения волнового уравнения
186
Глава 6. Решение дифференциальных уравнений
Обратите внимание на то, что уравнения внутри вычислительного блока должны
записываться с аргументами. Для идентификации частных производных следует
использовать нижний индекс, например, ип (х, t) — вторая производная функции
и по пространственной координате х.
Недостатком функции pdesolve (как и функции Odesolve) является невозмож-
ность ее использования в составе выражения — программы для многократного
решения дифференциального уравнения. При необходимости многократного ре-
шения обыкновенных дифференциальных уравнений в состав программного мо-
дуля можно включать старые функции Rkadapt и Bulstoer
При необходимости многократного решения дифференциальных уравнений
в частных производных в состав программного модуля можно включать функ-
цию numol, которая, как и pdesolve, появилась в Mathcad 11.
Функция numol предназначена для решения тех же уравнений, что и функция pdesolve.
Обращение к этой функции:
numol(xrange, xpts, Grange, £pts, Mpde, Mae, rhs, init, be)
возвращает матрицу решения дифференциального уравнения в частных произ-
водных в каждой точке по пространственной (по строкам) и временной (по
столбцам) координате. Если решается не одно уравнение, а система уравнений,
то результатом решения является составная матрица, образованная путем слия-
ния (слева направо) со значениями каждой искомой сеточной функции. Здесь
xrange — вектор значений аргумента х для граничных условий. Он должен состо-
ять из двух чисел, представляющих две границы расчетного интервала; Grange —
вектор значений аргумента t для граничных условий, состоящий из двух чисел,
представляющих две границы расчетного интервала; xpts — количество простран-
ственных точек дискретизации (может не указываться); £pts — количество времен-
ных слоев (также может не указываться); Mpde — количество дифференциальных
уравнений в частных производных в системе; Мае — количество дополнительных
алгебраических уравнений, входящих в систему; rhs — вектор правых частей урав-
нений; init — векторная функция, определяющая начальные условия для каждой
неизвестной функции; Ьс — функциональная матрица граничных условцй.
Вектор граничных условий может иметь значения трех типов:
□	rhs содержит вторые пространственные производные: граничные условия
(или Дирихле «D», или Неймана «N») требуются по одному с каждой сторо-
ны интервала интегрирования;
□	rhs содержит первые пространственные производные: граничные условия Ди-
рихле на левой или правой границе интервала, на другой стороне NA;
□	нет пространственных производных — граничные условия не требуются.
Функциональная матрица Ьс содержит три столбца, имеющие следующий вид:
□	(init_left(0 init_right(£) «D») — для граничных условий Дирихле;
□	(initJeft(0 init_right(£) «N») — для граничных условий Неймана.
Пользоваться функцией numol намного сложнее, чем функцией pdesolve (рисун-
ки 6.31 и 6.32).
6.6. Решение дифференциальных уравнений в частных производных
187
исходно© уравнение то же.	а2	2 а2
что и при решении функцией pdesolve	= *
-	2
заменено системой д , ч ч	д , ч 2 а , ч
уравнений	-w(x,») = v(x,t)	-’(«.О = а —2w(x,t)
л	dt	а«
Npde = 2 Дифференциальных уравнений	алгебраических
в частных производных 2 Nae " 0 уравнений нет
вектор правых частей уравнений
здесь, и*] = v и Ug = w.
Вектор начальных условий
Г раничные условия
в начале и в конце
выбранных интервалов х и t
Решение уравнения
rhslx.t.UjUx.Uxxl
(шЛ(О)о imt(L)o "D"
bc_func(t) .=
I "NA" "NA" "D"
пх = 30 nt.= 20
В этом примере 20 точек по времени на каждую функцию
Итого получаем матрицу из 40 колонн.
sol = numol
, nt, Npde, Nae, rhs, inrt, bcjunc
Рис. 6.31. Решение волнового уравнения с помощью функции numol
rows (sol) « 30	cok(sol) - 40
Матрица sol содержит два решения: первое для u0=w и второе для u^v
(посмотрите их. Для этого на трехмерном графике замените SOL на sol)
Исключим второе решение u1 SOL stibmatrix(sol,0 ,nx - 1,0 ,nt)
i.-О..ЗО L-2	x.:-^ t0:-0
1 ЗП
Сравним решение уравнения функциями numol и pdesolve
при t0=0 - поменяйте значение to.
Сравним сетку решений в пространстве и времени
Рис. 6.32. Сравнение решения волнового уравнения функциями numol и pdesolve
188
Глава 6. Решение дифференциальных уравнений
ПРИМЕЧАНИЕ -------------------------------------------------------
Граничное условие называется условием Дирихле, если задано значение функции, или
Неймана, если задана первая производная функции.
Процесс изменения решения во времени удобно наблюдать с использованием
анимации результатов расчета (рис. 6.33). Подробно об анимации графиков рас-
сказано в главе 10.
Аниммация плоского графика tt = FRAME — 2
nt
Рис. 6.33. Анимация решения волнового уравнения
6.6.2. Решение эллиптических уравнений
(Лапласа и Пуассона)
С помощью двух встроенных функций, multigrid и relax, можно решить простей-
шие случаи уравнения Пуассона: Это уравнение очень часто используется в тех-
нике, например, для описания полей напряжений и деформаций в плоской задаче
теории упругости, в задачах теплопроводности, гидроаэродинамики, электроста-
тики.
В Mathcad для численного решения уравнения Пуассона используется метод
конечных разностей.
Уравнение Пуассона имеет вид
ох	оу
Если правая часть уравнения равна нулю, такое уравнение называется уравнени-
ем Лапласа
d2F(x,y) а2Е(х,у)
дх2 ду2
На квадратной области уравнение Пуассона представляется в виде
аим j 4- bu^ j + cuij+i + dUi j_x + ещj = r
Численное решение ищется в Mathcad только на квадратной области, состоящей
из (п + 1) х (п + 1) точек. Поэтому граничные условия должны быть определены
пользователем для всех четырех сторон квадрата. Самый простой (и наиболее
6.6. Решение дифференциальных уравнений в частных производных
189
часто используемый) вариант — это нулевые граничные условия (уравнение Ла-
пласа). В таком случае можно использовать функцию multigrid.
Обращение к функции:
multigrid(M, Afcycle),
где М — квадратная матрица размером 1 х 2и, которая содержит значения правой
части уравнения Пуассона в соответствующей точке квадратной области;
Afcycle — число циклов на каждом уровне итерации функции multigrid. Значение
Ncycle = 2 обычно дает хорошую аппроксимацию решения.
Пример использования функции multigrid приведен на рис. 6.34.
М = о обнуление предыдущих значений М
п = 32 Мп,п = 0 Обнуление матрицы правых частей уравнения
[i = 1 |j = 1 ,n^ [Mtj = -2^ Включите выражения в рамке |
Мл д .= —200 М?п 1? = 200	9S := —200 т
Три точечных источника
Значения правой части уравнения
F - multjgnd(M, 2)	Пуассона постоянны во всех точках
F
Рис. 6.34. Решение уравнения Лапласа с помощью функции multigrid
Если граничные условия по сторонам квадрата ненулевые, необходимо исполь-
зовать функцию relax.
Обращение к функции:
relax(a, b, с, d, е, f, и, rjac),
где a, b, c,d,e — квадратные матрицы одинакового размера, содержащие коэффи-
циенты аппроксимирующего уравнения; f — квадратная матрица, содержащая
значения правой части уравнения в каждой точке области, где ищется решение;
и — квадратная матрица, содержащая граничные значения решения на границах
квадратной области и начальное приближение для решения внутри области;
rjac — спектральный радиус итераций Якоби. Это число между 0 и 1, которое
управляет сходимостью процесса релаксации.
190
Глава 6. Решение дифференциальных уравнений
Использование этой функции требует глубокого знания метода конечных разно-
стей для составления указанных матриц. Пример использования функции relax
приведен на рис. 6.35 и 6.36.
Определим размеры сетки
п := 32 1 = 0.. n j := 0 . п
aq j ,= 1 Ь = а
a d = а
Определим положение и интенсивность источника тепла
Пусть во всех узлах интенсивность постоянная
Sij := 0.05
Г раничные условия
на верхней границе f0 j := о
на нижней границе	fn d := 2 cos
по бокам	, Л 1
fi,o = 2-
п
Спектральный радиус Якоби г
Решение уравнения Пуассона
Поменяйте
условия
j л	Включите
Ьк—	выражения
в рамке
fi.n = 2 -
п
= 1 - — г = О 804
п
F := relax(a,b,c,d,e,S,f,r)
|Sj,j = 0.01^1
^7^1
^7^1
|f.,o = 20^
|fj,n = 20^
Рис. 6.35. Решение уравнения Пуассона с помощью функции relax
В части IV книги приводится пример решения уравнения Пуассона при кру-
чении стержней произвольного поперечного сечения с помощью значительно
более мощного метода конечных элементов (пример 54 электронной книги).
Этот пример может быть полезен и при других приложениях уравнения Пуас-
сона.
-F
Рис. 6.36. Результаты решения уравнения Пуассона с помощью функции relax
6.6. Решение дифференциальных уравнений в частных производных
191
Завершая рассмотрение возможностей решения дифференциальных уравнений,
отметим, что созданная универсальная функция Odesolve, включившая в свой
механизм решения ОДУ все созданные ранее функции плюс функции интерпо-
ляции, одна может справиться с любой из рассмотренных в этой главе задач.
Простота использования этой функции в сочетании с огромными возможностя-
ми восхищает. Тем не менее Mathcad пока не в силах решать некоторые диффе-
ренциальные уравнения.
Глава 7
Обработка экспериментальных данных
При обработке экспериментальных данных, как правило, возникает задача ап-
проксимации результатов эксперимента аналитической зависимостью у = f(x),
которую можно использовать в последующих расчетах.
Существует три возможности аппроксимации опытных данных.
1.	Аппроксимирующая функция /(х) должна проходить через все опытные точ-
ки. Такой способ аппроксимации называется интерполяцией.
2.	Выбрать аппроксимирующую функцию таким образом, чтобы она сглажива-
ла, усредняла опытные данные. Такой способ аппроксимации называется рег-
рессией, или сглаживанием.
3.	Подобрать аппроксимирующую функцию, отбросив систематическую по-
грешность, так называемые шумы, наложившиеся на экспериментальные дан-
ные. Такой способ называется сглаживанием с фильтрацией данных.
В Mathcad имеется много встроенных функций для обработки массивов данных.
Рассмотрим последовательно все три способа обработки данных.
7.1.	Интерполяция
Встроенные функции Mathcad позволяют при интерполяции проводить через
экспериментальные точки кривые разной степени гладкости.
7.1.1.	Линейная интерполяция
При линейной интерполяции аппроксимирующая функция соединяет опытные
точки отрезками прямых линий. Для линейной интерполяции используется встро-
енная функция linterp.
Обращение к функции:
linterp(x, у, t),
где х — вектор опытных значений аргумента; у — вектор опытных значений
функции; t — значение аргумента, при котором вычисляется интерполирующее
значение функции.
Иногда надо знать одно интерполирующее значение функции, но чаще опреде-
ляется ряд значений функции, тогда t — вектор значений, а результат расчета —
массив интерполирующих значений. Еще чаще t — просто переменная (аргумент
интерполирующей функции), тогда результат расчета — функция, которую мож-
но далее интегрировать, дифференцировать и т. д. Примеры линейной интерпо-
ляции показаны на рис. 7.1. Исходный массив данных Y на этом рисунке создан
генератором случайных чисел rnd, о котором рассказано в следующей главе. Ко-
ординаты X в этом примере взяты равноотстоящими друг от друга, но это не обя-
зательно.
7.1. Интерполяция
193
массив экспериментальных данных (X.Y)
Х:= (0 1 3 4 6 7 10 11 13 14 15)Т
Y:»(3 7 9 5 5 2 7 9 6 2 2)Т
YI := linterp(X,Y,5) Y1 = 5
интерполирующее значение
в одной точке Х=5
XI := (-1 2 8 9 12 18)Т
Y2lintetp(X,Y,Xl)
Y2 - массив интерполирующих значений массива Y в точках,
заданных вектором Х1
t := 0,0.2..ma<X) Y^t) := linteip(X,Y,t) непрерывная интерполирующая
функция
Крайние точки на графике - экстраполяция за пределы массива X
Рис. 7.1. Линейная интерполяция экспериментальных данных
ВНИМАНИЕ -------------------------------------------------------------
В этой главе для всех встроенных функций в массиве опытных данных элементы вектора х
должны быть расположены обязательно в порядке возрастания.
7.1.2.	Кубическая сплайн-интерполяция
В большинстве случаев желательно соединять экспериментальные точки не ло-
маной линией, а гладкой кривой. Для этих целей используется сплайн-интерпо-
ляция. Кубическая сплайн-интерполяция позволяет провести кривую через на-
бор точек таким образом, что первые и вторые производные кривой непрерывны
в каждой точке. Эта кривая образуется путем создания ряда кубических полино-
мов, проходящих через наборы из трех соседних точек. Кубические полиномы
затем состыковываются друг с другом так, чтобы образовать единую кривую.
Для кубической сплайн-интерполяции используется встроенная функция interp.
Обращение к функции:
interp(as, X, У, 0,
где vs — вектор вторых производных, созданный одной из трех функций, lspline(X, У),
pspline(X, У), cspline(X, У); X — вектор опытных значений аргумента, расположен-
194
Глава 7. Обработка экспериментальных данных
ных в порядке возрастания; Y — вектор опытных значений функции; t — значе-
ние аргумента, при котором вычисляется интерполирующее значение функции.
Сплайн-интерполяция организована в Mathcad несколько сложнее, чем линей-
ная. Перед применением функции interp необходимо определить первый из ее
аргументов — вектор vs. Делается это при помощи одной из трех встроенных
функций тех же аргументов (х, у):
□	lspline(X, У) создает вектор коэффициентов кривой, которая приближается
к прямой линии в граничных точках;
□	pspline(X, У) создает вектор коэффициентов кривой, которая приближается
к квадратичной параболе в граничных точках;
□	cspline(X, У) создает вектор коэффициентов кривой, которая приближается
к кубической параболе в граничных точках.
Выбор конкретной функции сплайн-коэффициентов влияет на интерполяцию
вблизи конечных точек интервала. Использование двух функций для интерпо-
ляции можно совместить, записав, например, interp(cspline(X, У), X, У, t). Приме-
ры кубической сплайн-интерполяции показаны на рис. 7.2.
Y]sp(t) := interp(lspline(X,Y),X,Y,t)
Ypsp(t) := intetp(pspline(X,Y) ,X,Y,t)
YCSp(t) := interp(cspline(X,Y),X,Y,t)
Рис. 7.2. Кубическая сплайн-интерполяция массива Y, приведенного на рис. 7.1
7.1.3.	В-сплайн-интерполяция
В-сплайн-интерполяция отличается от обычной сплайн-интерполяции тем,
что сшивка отдельных отрезков (сплайнов) производится не в точках Xit
а в точках, координаты которых задаются пользователем. Применяется интер-
поляция В-сплайнами так же, как и обычная сплайн-интерполяция, но для опре-
деления сплайн-коэффициентов применяется функция bspline.
7.1. Интерполяция
195
Обращение к функции:
bspline(X, У, XX, п),
где X — вектор опытных значений аргумента, расположенных в порядке возрас-
тания; Y — вектор опытных значений функции; XX — вектор значений аргумен-
та, при которых вычисляются интерполирующие значения функции; п — поря-
док полиномов сплайн-интерполяции (1, 2 или 3).
Размерность вектора XX должна быть на (п - 1) меньше, чем размерность векто-
ра X. Первый элемент вектора XX должен быть меньше первого элемента векто-
ра X или равен ему. Последний элемент вектора XX должен быть больше послед-
него элемента X или равен ему.
Наложенные на вектор XX ограничения делают крайне неудобным использова-
ние В-сплайн-интерполяции, так как пользователь лишен возможности свобод-
ного выбора точек сшивки полиномов. К тому же по непонятным причинам
функция bspline отказывается интерполировать некоторые наборы данных.
В центре документации Mathcad примеры использования этой функции отсутст-
вуют. Пример использования функции bspline приведен на рис. 7.3.
пп > 2 поменяйте порядок полиномов пп=1,2 или 3
Х:=(0 1 2 3 4 5 6)Т массивы
исходных
У > (4 2 3 4 3 5 6)Т	данных
ХХ =Г-1 1 3 4 5 7ЧТ	аргументы точек соединения
'	полиномов интерполяции
xminXjnax := max(XX) х := х^^^ +---------——-.. Хд^
Рис. 7.3. В-сплайн-интерполяция массива У, приведенного на рис. 7.1
196
Глава 7. Обработка экспериментальных данных
ПРИМЕЧАНИЕ --------------------------------------------------------
Если два соседних значения аргумента близки, все функции интерполяции, кроме linterp,
дают всплеск на графике в этом месте (рис. 7.4). Чтобы убрать всплеск, раздвиньте близле-
жащие точки. В этих случаях желательно использовать функции регрессии вместо функ-
ций интерполяции.
Х:=(-3 -1 0 2 3 4 5 б 7 8)Т
¥:=(3 4 2 1 2 3 5 2 1 2)Т
xmin:=	xmax := max(X) х := xmjLn,xmjLn +	—	—.. х^ах
30
пусть а 4 приблизим к ней соседнюю точку Х^ :« 4.02
Две точки близки - на графиках всплеск	сдвиньте вверх
увеличьте расстояние между точками	это выражение
Рис. 7.4. Влияние близких точек на результат интерполяции. Массив Y приведен на рис. 7.1
7.1.4.	Линейное предсказание
Кроме интерполяции в промежуточных точках иногда нужно оценить значения
функции за пределами области заданных точек. Все рассмотренные ранее функ-
ции интерполяции выполняют экстраполяцию данных за пределами интервала
заданных точек с помощью соответствующей зависимости, основанной на анали-
зе расположения нескольких исходных точек на границе интервала данных. Но
в Mathcad имеется и специальная функция предсказания predict.
Обращение к функции:
predict(Y, т, п),
где Y — вектор заданных значений функции, обязательно взятых через равные
интервалы аргумента; т — число последовательных значений У, на основании
которых функция predict возвращает п предсказанных значений У.
Значений аргумента для данных не требуется, поскольку по определению
функция действует на данные, следующие друг за другом с одинаковым шагом.
7.1. Интерполяция
197
Обратите внимание на то, что результат функции predict надо вставлять
«в хвост» исходных данных.
Функция predict использует линейный алгоритм предсказания, который являет-
ся полезным, когда экстраполируется функция гладкая и осциллирующая, хотя
необязательно периодическая. Эта функция использует последние т исходных
значений данных, чтобы вычислить коэффициенты предсказания. Как только
это сделано, она использует последние т точек, чтобы предсказать координаты
(т + 1)-й точки, фактически создавая скользящее окно шириной т точек.
Как видно из рис. 7.5, функция предсказания может быть полезной при экстра-
поляции данных на небольшие расстояния. Вдали от исходных данных резуль-
тат чаще всего оказывается неудовлетворительным. Если исходных данных мало,
то результат также окажется бесполезным.
задан массив из пп точек
пп := 50 i := 0.. пп у.:« 10- е *sin(0.2 i)
предсказать значения еще п точек .
m := 30 п:« 100 ур := predict(y,m,n) k:=0..n
-10 -------------1------------1------------
0	50	100	150
i,k+im+l
Рис. 7.5. Функция предсказания в Mathcad
7.1.5.	Интерполяция функции двух переменных
Mathcad выполняет интерполяцию кубическими сплайнами функции двух пере-
менных таким же образом, как и при одномерной интерполяции, рассмотренной
ранее. Mathcad проводит через сетку узлов поверхность, составленную из куби-
ческих полиномов от х и г/, так, что первые и вторые частные производные явля-
ются непрерывными в каждом узле сетки.
Первый шаг в двухмерной сплайн-интерполяции (как и в одномерной) — опре-
деление узлов, через которые поверхность должна пройти:
□	Создайте матрицу XY размерностью п х 2, элементы которой определяют ко-
ординаты х и у диагонали прямоугольной сетки. Таким образом, число узлов
по осям координат х и у обязательно должно быть одинаковым, что резко ог-
раничивает возможности двухмерной интерполяции или заставляет прибе-
гать к специальным приемам, чтобы привести неквадратную область к квад-
ратной.
198
Глава 7. Обработка экспериментальных данных
□	Введите матрицу Z размерностью п х и, каждый элемент которой — заданное
значение функции в соответствующем узле.
□	Вычислите вектор вторых производных cspline(Xy, Z) функции Z в узлах.
□	Чтобы найти интерполируемое значение функции Z в произвольной точке,
скажем, в точке с координатами xq и у$, используйте функцию interp:
Zo:= interp cspline (ХУ, Z), ХУ, Z,
x0
Уо[
На практике приходится вычислять интерполируемые значения функции сразу
во всех узлах сетки. Для этого записываем Z как функцию от х и у и с помощью
функции CreateMech создаем массив точек для графика поверхности:
ZZ(x,z/):= interp cspline(Xy,Z), ХУ, Z,
[У
Zt: = CreateMech (ZZ, xt, x2, yx, у 2, nx, ny).
В обращении к функции CreateMech обязательным является только параметр ZZ,
остальные можно опустить. Здесь xlf х2, ylf у2 — нижний и верхний пределы аргу-
ментов х и у (по умолчанию от -5 до 5); пх и пу — число точек сетки по перемен-
ным х и у (по умолчанию 20). Примеры двухмерной интерполяции приведены
на рис. 7.6 и 7.7. О применении функции CreateMech написано в главе 15 (раздел
15.3.3).
Массив значений функции Z задан на квадратной области
в точках с координатами X и Y
Х:=(0 1 2 3 4 5)Т
¥>(0 1 2 3 4 5)Т
Координаты точек перестраиваем в двухмерный массив XY
и вводим в параметры функции interp
Х¥<0> := X Х¥(1> > ¥
<0
fo 0	0	0	0 0^
Х¥ =
0	0.345	0.559	0.559	0.345	0
0	0.559	0.905	0.905	0.559	0
0	0.559	0.905	0.905	0.559	0
0	0.345	0.559	0.559	0.345	0
<0	0	0	0	0	0;
ZZ(x,y) := interp cspline(X¥,25,X¥,Z,
Рис. 7.6. Двухмерная интерполяция массива данных
7.1. Интерполяция
199
поверхность массива ZZ
поверхность исходного массива Z (значения, аргументов
по умолчанию от -5 до 5)
Z
поверхность массива ZZ
(значения аргументов введены
с помотаю меню Quick Plot Data)
Рис. 7.7. Графики поверхности исходных точек Z
и поверхности интерполирующей функции
ZZ
поверхность массива ZZ, построенная
с помешаю функции CreateMech
Zl := CreateMtri(zZ,0,5,0,5,30,30)
Z1
При построении графика поверхности можно обойтись без явного использова-
ния функции CreateMech. На математической панели выбрать значок графика
Graph Toolbar ► Surface Plot (Панель графиков ► График поверхности). В поле
ввода ввести имя функции двух переменных (без параметров). Появится график
поверхности функции. По умолчанию берутся пределы изменения переменных
от -5 до +5. Чтобы их изменить, сделайте двойной щелчок в поле графика и в от-
крывшемся окне форматирования графика выберите вкладку Quick Plot Data
(Данные быстрого графика), на которой впишите необходимые пределы измене-
ния переменных (rangel и range2) (рис. 7.8). При таком построении графика
внутренний алгоритм Mathcad самостоятельно использует функцию CreateMech.
Для двухмерной интерполяции векторы значений координат по осям х и у долж-
ны иметь одинаковый размер, то есть интерполяция выполняется только на
квадратной поверхности. Однако это требование можно обойти.
Перед вычислением значений функции на неквадратной плоскости нужно обну-
лить массив значений функции на квадратной поверхности, большей, чем задан-
ная неквадратная. После этого вычислить значения функции на заданной по-
верхности (рис. 7.9) и построить график поверхности (рис. 7.10). В результате
поверхность появится лишь над частью квадратной плоскости.
200
Глава 7. Обработка экспериментальных данных
Рис. 7.8. Установка пределов значений координат
Х:=(0 1 2 3 4 5)Т	Y:-(0 1 2 3 4 5)Т массивы данных
п:= 10
i:=0..n j := 0.. n Z. . := О
J	bJ
Обнуление функции на
квадратной поверхности
ХГ0:=1 XYbl:=j
т (0 123456789 10
XY1 =
10 123456789 10
il := 0.. 3 jl := 0.. 4 индексы элементов массива данных Z1
Z1 :=
<0.345 0.559 0.559 0.345 0.345^
0.559 0.905 0.505 0.559 0.559
0.559 0.305 0.905 0.559 0.559
^0.345 0.559 0.559 0.345 0.345 J
Неквадратный массив Z1
можно поместить в любое
место квадратной области Z
(поменяйте индексы массива Z)
7	= 71
11+5J1+3 • il,jl
Рис. 7.9. Двухмерная интерполяция на неквадратной области
На рис. 7.10 поверхность Zt (справа) — это график массива, созданного функцией
CreateMech, после двухмерной интерполяции массива Z (см. рис. 7.9). Поверх-
ность ZZ построена непосредственно после интерполяции с использованием
вкладки Quick Plot Data. Работая'с этим рисунком, поменяйте размеры неквадрат-
ной области.
7.2.	Функции регрессии
Mathcad включает ряд функций для вычисления регрессии. Эти функции созда-
ют кривые или поверхности определенного типа с минимальным отклонением от
имеющегося набора данных. Функции различаются прежде всего типом кривой
или поверхности, которую они используют, чтобы аппроксимировать данные.
В отличие от функций интерполяции, эти функции не требуют, чтобы аппрокси-
мирующая кривая или поверхность проходила через точки данных.
7.2. Функции регрессии
201
<0 0 0	о
ООО	о
ООО	о
л л л	л
ООО	о
ООО
ООО
ООО
л л л
ООО
Z- О О 0 0.35 0.56 0.56 0.35
ООО	0.56	0.91	0.51	0.56
ООО	0.56	0.31	0.91	0.56
ООО	0.35	0.56	0.56	0.35
0 0 0	0	О	О	О
О
О
О
Л
О
0.35
0.56
0.56
0.35
О
О
О
О
О
Л
О
О
О
О
О
о
о
Z2CreiteMeshCZZ.O.n.O.n)
^0 0 0 0 О О О
csplin^XY.Z^XV.Z,
77	Z2
Рис. 7.10. Результаты интерполяции на неквадратной поверхности
7.2.1.	Одномерная регрессия
Mathcad допускает регрессию одномерных и многомерных массивов. Вначале
рассмотрим регрессию одномерных массивов.
Ряд функций регрессии возвращают коэффициенты аналитической функции
и позволяют записать аппроксимирующую функцию в явном виде. Эти функции
описаны в главе 2 (раздел 2.11.2), и здесь не рассматриваются.
Ряд функций регрессии не позволяют получить аппроксимирующую функцию
в явном виде. Они возвращают лишь численные результаты в виде таблиц или
графиков. Две из них — regress и loess — также рассмотрены в разделе 2.11.2.
Эти две функции не выводят коэффициенты и аппроксимируют массив данных
одним степенным полиномом (regress) или отрезками нескольких полиномов
(loess).
В Mathcad регрессия с использованием одного полинома реализуется комбина-
цией встроенных функций регрессии regress и интерполяции interp.
Обращение к указанным функциям:
s:=regress(X, У, п); yy(£):=interp(s, X, У, t)
или
yy(0:=interp(regress(X, У, п), X, Y, 0,
202
Глава 7. Обработка экспериментальных данных
где X — вектор значений аргумента, элементы которого расположены в порядке
возрастания; Y — вектор значений функции того же размера; s — вектор коэффи-
циентов для построения аппроксимирующего полинома, создаваемый функцией
regress; t — значение аргумента, при котором вычисляется интерполирующая
функция; п — степень аппроксимирующего полинома.
Степень аппроксимирующего полинома может быть любой.
Регрессия с использованием нескольких отрезков полинома также реализуется
комбинацией встроенных функций регрессии и интерполяции
interp(s, х, у, t) и loess(x, у, span),
где s:=loess(X, У, span) — вектор коэффициентов для построения аппроксими-
рующего полинома второй степени, требуемый функцией interp; span > 0 — па-
раметр, определяющий размер отрезков полиномов.
Параметр span задает степень сглаженности данных. Аргумент span определяет
размер отрезков полиномов, из которых «сшивается» аппроксимирующая кри-
вая. На практике 0,2 < span < 2. При span = 2 результат аппроксимации тот же,
что и при аппроксимации одной параболой. При span = 0,2 аппроксимирующая
кривая почти точно описывает любой набор данных.
Примеры использования функций regress и loess приведены в главе 2 на рис.
2.26 и на рис. 7.11.
Y = (3 0 -5 -4 -1 2 5 6 4 1)Т массив значений функции
X -(-2 0 1 3 5 6 9 11 12 15 J массив значений ар^мента
и 1 э э о у 11 и; в возрастающем порядке
поменяйте параметры 1<N<20 и 0.2<L<2
N = 4 степень полинома
L = 0.5 характеристика длины отрезков полиномов
Xregress (х) •= interp (regress (X, Y, N), X, Y, х)
YioeSS(x) = interp (loess (X, Y,L) ,X. Y
Рис. 7.11. Функции регрессии, не дающие аналитического выражения
7.2. Функции регрессии
203
7.2.2.	Двухмерная регрессия
Функции regress и loess допускают и многомерную регрессию. Пример двухмер-
ной регрессии приведен на рис. 7.12 и 7.13. В этом случае массив XY координат
точек х становится двухмерным массивом, состоящим из двух столбцов: первый
столбец — это координаты по оси х, второй — координаты по оси у.
/0 0 о о'А
ZA
О 0.84 0.91 0
0 0.91 0.84 0
Исходный массив точек
. координаты точек
х и у даны для
построения
массива XY
1,0 о о о J
ZA
Рис. 7.12. Исходные массивы и их перестройка для двухмерной регрессии
ВНИМАНИЕ -------------------------------------------------------------
При двухмерной интерполяции массив координат точек XY состоит из координат точек
диагонали квадратной области. Например, для массива точек 4x4 вводятся координаты
лишь 4 точек. Координаты остальных точек определяются автоматически. При двухмер-
ной регрессии массив координат точек XY состоит из координат всех точек прямоуголь-
ной области (не обязательно квадратной), записанных по столбцам. Например, для
массива точек 4x5 вводятся координаты всех 20 точек.
Массив значений функции Z во всех точках прямоугольной области вводится по
столбцам. Число строк вектора Z равно числу строк массива XY.
Двухмерная интерполяция производится как функцией regress(XK, Z, N), так
и функцией loess(XK, Z, span). Здесь N — порядок аппроксимирующего полино-
ма, span определяет размер отрезков полиномов, как и при одномерной рег-
рессии.
Mathcad допускает многомерную регрессию. Можно увеличивать число незави-
симых переменных, просто добавляя столбцы в массив XY, а затем добавляя со-
ответствующее число строк к вектору Z, которые передаются функции interp.
204
Глава 7. Обработка экспериментальных данных
Функция regress может иметь любое число независимых переменных, но она бу-
дет работать слишком медленно и требовать много памяти. Функция loess до-
пускает максимум 4 независимые переменные.
Перестройка двухмерных массивов функции и ее аргументов в одномерные (по столбцам)
массив координат х и у
<0 0 0 0 0 1 1 1 1 12222233333 V
XY:=
ко 10 20 30 35 0 10 20 30 35 0 10 20 30 35 0 10 20 30 35>
Z:- (0 0 0 0 0 0 0.84 0.91 0.61 0 0 051 0.84 0.77 0 0 0 0 0 0)Т
ZMgresj(x,y) := inteip regress (XY,Z, 4) >XY,Z
Zbess(x,y) := inteip loess(XY,Z,0.6) ,XY,Z
значения аргументов к=О..З и у^0..35 установлены при
форматировании графика в меню QuickPlot Data
loess
^regress
Рис. 7.13. Результаты двухмерной интерполяции массива, приведенного на рис. 7.10
Для функции regress число значений данных т должно удовлетворять соотно-
шению
n+k-\n+k
k п
где п — число независимых переменных (число столбцов ХУ); k — желаемая сте-
пень полинома; т — число значений данных (число строк в массиве XY). Напри-
мер, если имеется 5 независимых переменных и ищется приближение полино-
мом 4-й степени, потребуется более 126 наблюдений.
7.2.3.	Обобщенная регрессия
Бывают случаи, когда закон изменения функции известен и требуется подобрать
лишь ее коэффициенты, однако сама аппроксимирующая функция такова, что
использовать функции специальной регрессии невозможно. В этом случае
Mathcad предлагает использовать две функции регрессии общего вида — Unfit
и genfit.
7.2. Функции регрессии
205
Если предполагаемая зависимость представляет собой линейную комбинацию
некоторых функций
У = ао/о(х) + Oi/iUH-+an/n(^)
и надо лишь подобрать коэффициенты этих функций, то используется функция
Unfit, например:
/(х) = ах sin(2r)+ а2 cos(3r),
linfit(x, у, F) возвращает вектор, содержащий набор коэффициентов при функци-
ях у(х) — вектор заданных значений функции при значениях аргумента,
содержащихся в векторе х, F — вектор функций, входящих в линейную комбина-
цию у(х).
Для произвольной функции с неизвестными коэффициентами надо использо-
вать функцию genfit, например:
/(x) = 2sin(a1x)+ 3cos(a2x),
genfit(x, у, С, F) возвращает вектор, содержащий п параметров, наилучшим обра-
зом аппроксимирующих данные из векторов хи //заданной функцией f(x). Здесь
F(x) — функция, которая возвращает (п + 1)-мерный вектор, содержащий функ-
цию f(x) и ее частные производные относительно неизвестных параметров; С —
n-мерный вектор начальных значений для п неизвестных параметров.
Примеры применения функций Unfit и genfit приведены на рис. 7.14-7.19.
Y = (06 2 28 35 4.2 46 4 32 2 4)Т массив значений функции
X = (0 1 2 3 5 6 9 11 12 15)т
массив значений аргумента
в возрастающем порядке
х2 А набор функций, входящих в линейную комбинацию
F(x) =
cos(x) поменяйте функции в векторе F(x)
. х у f-0 059
S = linfit(X,Y,F) S= -0 363
найденные коэффициенты
при функциях
1 024 J
f(x) = F(x) S линейная комбинация функций
2
ff (х) = -0 059 х - 0 365 sm(x) + 1 024 х
эта формула - всего лишь иллюстрация к f(x).
В документе она не нужна
.	Xmax-Xmm
Xmm = тш(Х) х^ = тах(Х) х = хтт,хтт+-------—---- х^
206
Глава 7. Обработка экспериментальных данных
массив значений аргумента в возрастающем порядке
X := (0 123456789 10)Т
массив значений функции
Y := (О 0.7 0.9 0.3 0 -0.2 -0.4 -04 -04 -0.3 -0.2)Т
3
f(x,a,b,c) := а х cos(c x) предлагаемая функция
4
х +ь	поменяйте функцию
символьное вычисление производных
з
d г/ . ч к XX cos(ccxx)
—f(xx,a,b,cc) —>-------------
da	4 . i.
4
dr, к ч axx sin(cc-xx)
—i(xx,a,b,cc) —>------------------
^cc	xx^ 4- b
—f(xx,a,b,cc)
db
( 2 Л a
k:= 2 b
a xx cos(cc xx)
начальные
приближения
Рис. 7.15. Нелинейная регрессия данных функцией genfit в Mathcad 11
и более старых версиях
с
3
kg---------cosl'k2 xi
4 ,
х +kj
предлагаемая функция
FF(x,k) :=
3
—------cos(k2 х)
4
х +kj
3
х
kg---------- • cos (к2 х I
(x4+ktj
ее производная по а
ее производная по b
4
X
ко—--------sin(k2X,l
x4 + ki
ее производная по с
( 2.56 А
К = genfit(X,Y,k,FF) К= 1.877
<0414,
вектор найденных
параметров функции
’ F(x) .= FF(x,K)o искомая функция с найденными параметрами
з	эта формула - всего лишь
ff(x) - Л*?:*—cos(0.406 x)	иллюстрация к F(x). В
х4 + j 855	документе она не н^жна
Рис. 7.16. Нелинейная регрессия данных функцией genfit в Mathcad 11 (окончание)
1.2- Функции регрессии
207
До появления Mathcad 13 использование функции genfit было весьма сложным
в связи с необходимостью вычисления частных производных искомой функции
по всем неизвестным параметрам. Символьное вычисление таких производных
и их использование показано на рис. 7.15 и 7.16.
Рис. 7.17. Результаты нелинейной регрессии данных функцией genfit
В Mathcad 13 использование функции genfit значительно упростилось. Функция
genfit теперь допускает задание параметров в явном виде (рис. 7.18). Однако ча-
стные производные от аппроксимирующей функции по ее параметрам в этом
случае надо определять самому пользователю.
X := (0.5 1 1 5 2 2 5 3 3.5 4 4.5)Т
Y := (16 12 20 23 19 24 46 69 120)Т
f(x,A,4) := А е^’х аппроксимирующая функция
(1
к :=
начальные приближения параметров А и у
Р(х,А,ч)
rf(x,A,4)
еТХ
функция И
ее производные
по Аиу
La x ^ XJ К := genfit(X, Y,k,F)
FF(x) .= f(x,K0,Kl)
Рис. 7.18. Ввод явных параметров в функцию genfit в Mathcad 13
208
Глава 7. Обработка экспериментальных данных
В Mathcad 13 функция genfit не требует обязательного вычисления производных
по всем расчетным параметрам. Если в обращение к функции вписано имя ис-
ходной функции, то необходимые производные вычисляются численно внутрен-
ним алгоритмом Mathcad. Правда, все параметры, которые надо определить,
должны быть элементами вектора. Для этого вектора и задаются начальные при-
ближения (рис. 7.19).
В контекстном меню функции genfit предлагается 2 метода Levenberg-Maquardt
(Левенберга—Маккарта) и Optimized Levenberg-Maquardt (Оптимизированный
метод Левенберга—Маккарта). Если используемый по умолчанию метод Leven-
berg-Maquardt не дает решения, то выберите в контекстном меню метод Opti-
mized Levenberg-Maquardt. Так пришлось поступить в примере на рис. 7.19. При
таком вводе несколько уменьшается точность расчета.
массив значений аргумента в возрастающем порядке
Х = (0 123456789 10)Т
массив значений функции
Y = (О 0 7 0 9 0 3 0 -0 2 -0 4 -0 4 -0 4 -0 3 -0 2)Т
Хямп - пип(Х) Хщах - max(X) х - х^мп,х^мп +
3
„ .ч ах , ч
i(x,a,b,c) .=--------cos(c х)
х4 + Ь
3
ffl(x,k) = kg-------- cosl k2 х)
4
х +ki
предлагаемая
функция В контекстном меню выберите метод
z 2 A Optimized Levenberg Marquardt
k= 2 К = genfit(X, Y,k,ffl)
<04j Fl(x) = ffl(x,K)
Здесь kg - это a, k| - это b. k2 - это c
Рис. 7.19. Применение функции genfit без вычисления производных в Mathcad 13
7.3.	Функции сглаживания
В процессе сглаживания из исходного набора данных получается новый набор
данных, более гладкий, чем исходный.
СОВЕТ ------------------------------------------------------------------
Убедитесь, что каждый элемент в векторе исходных данных определен. Mathcad присваи-
вает значение 0 любым элементам, значения которых не определены.
7.3. Функции сглаживания
209
Mathcad предлагает три встроенные функции сглаживания (рис. 7.20):
□	medsmoothQ/, п) возвращает m-мерный вектор, созданный сглаживанием с по-
мощью скользящей медианы. Здесь у — ти-мерный вектор вещественных чи-
сел; п — ширина окна, по которому происходит сглаживание, п должно быть
нечетным числом, меньшим или равным числу элементов вектора у.
□	ksmooth(x, г/, Ь) возвращает гг-мерный вектор. Здесь хи у — гг-мерные векторы,
вектор у создан сглаживанием при помощи гауссова ядра данных из у b — па-
раметр, управляющий окном сглаживания. Он должен быть в несколько раз
больше величины интервала между точками х. Чем больше Ь, тем больше
окно, используемое при сглаживании.
□	supsmooth(x, у) возвращает n-мерный вектор, созданный локальным исполь-
зованием симметричной линейной процедуры сглаживания методом наимень-
ших квадратов по правилу k ближайших соседей, в которой k выбирается
адаптивно. Здесь х и у — n-мерные векторы исходных данных. Элементы х
должны быть расположены в порядке возрастания.
4)Т массив значений функции
массив значений аргумента
в возрастающем порядке
¥:=(0.6 2 2.8 3.5 4.2 4.6 4 3.2 2
X := (0 1 2 3 5 6 9 И 12 15)Т
Рис. 7.20. Сглаживание данных с созданием массива значений
Функция medsmooth наиболее устойчивая из всех трех встроенных функций, так
как в меньшей степени подвержена влиянию зашумленных данных.
Функция ksmooth использует гауссово ядро, чтобы вычислить локально взве-
шенные средние значения исходного вектора у. Такое сглаживание наиболее по-
лезно, когда интервалы между точками данных примерно одинаковой величины.
Функция supsmooth полезна, если длина интервалов существенно изменяется.
Эта функция адаптивно выбирает различную ширину полосы сглаживания для
различных частей вектора данных.
В отличие от регрессии и интерполяции, функции сглаживания возвращают
массив, а не функцию. Для получения функции после сглаживания необходимо
использовать интерполяцию или регрессию (рис. 7.21).
210
Глава 7. Обработка экспериментальных данных
Функции сглаживания возвращают массив, а не функцию.
Чтобы получить функцию, добавьте интерполяцию
YmterpCO > intexp(cspline(X,Y) ,X,Y,x) интерполяция без сглаживания
интерполяция
co сглаживанием
x := 0,0.1.. max(X)
Yinterp.sup(x) > interp(cspline(X, sup), X,sup ,х)
YmterpinedCO > inteip(cspline(X,me$ ,X,med,x)
Ymterp.ksm(x) > interp(cspline(X,ksm) ,X,ksm,x)
YjnuapjaM!d(x)
m  MB 
^тЬефкш1(х)
Рис. 7.21. Сглаживание данных с созданием функции
7.4.	Дискретные преобразования
Mathcad содержит функции для быстрого дискретного преобразования Фурье
(БПФ) и его обращения, а также для одномерного волнового преобразования
и его обращения. Все эти функции имеют векторные аргументы.
7.4.1.	Преобразование Фурье
В Mathcad входят два типа функций для дискретного преобразования Фурье: fft
и ifft, cfft и icfft. Эти функции дискретны: они берут в качестве аргументов и возвра-
щают векторы и матрицы. Они не могут быть использованы с другими функциями.
Используйте функции fft и ifft, если выполнены следующие два условия:
□	аргументы вещественные;
□	вектор данных имеет 2т элементов.
Используйте функции cfft и icfft во всех прочих случаях.
Соблюдать первое условие необходимо, потому что функции fft и ifft используют
тот факт, что для вещественных данных вторая половина преобразования Фурье
является комплексно-сопряженной с первой. Mathcad отбрасывает вторую поло-
вину вектора результата, что сохраняет время и память при вычислениях.
Функции cfft и icfft не используют симметрию в преобразовании и могут исполь-
зоваться для вещественных и комплексных чисел.
7.4. Дискретные преобразования
211
Второе условие требуется, потому что пара функций, fft и ifft, использует высоко-
эффективный алгоритм быстрого преобразования Фурье. Для этого вектор аргу-
мента, используемого функцией fft, должен иметь 2т элементов. Алгоритм функ-
ций cfft и icfft допускает в качестве аргументов векторы и матрицы произвольного
размера. Для двухмерного преобразования Фурье используются только эти
функции.
Существуют различные формулировки определения преобразования Фурье, ис-
пользующие различные нормировочные коэффициенты и соглашения о знаке
перед мнимой единицей в показателе экспоненты прямого и обратного преобра-
зований. Функции fft, ifft, cfft, icfft используют нормировочный коэффициент
1 / 4п и положительный показатель степени в прямом преобразовании. Функ-
ции FFT, IFFT, CFFT, ICFFT используют нормировочный коэффициент 1 / п и отри-
цательный показатель степени в прямом преобразовании.
ВНИМАНИЕ -------------------------------------------------------------
Аргумент х не входит в параметры встроенных функций, так как по умолчанию х берется
через равные интервалы в возрастающем порядке.
Перечислим функции дискретного преобразования Фурье:
□	fft(i/) возвращает коэффициенты ряда Фурье вектора у, содержащего 2т эле-
ментов. Результат — комплекснозначный вектор размерности 1+ 2т-1. Эле-
менты вектора коэффициентов, возвращаемого fft, вычисляются по формуле
е, =4=ё^г’,ш’“.
у/п k=0
В этой формуле п — число элементов вектора у; i — мнимая единица. Если
частота измерения исходного сигнала /5, то частота, соответствующая ck,
□	ifft(c) возвращает обратное дискретное преобразование Фурье. Результат —
вещественный. Вектор с должен иметь 1 + 2т элементов, где т — целое.
Функция возвращает вектор d, чьи элементы вычисляются по формуле
dj
Vw k=o
где w — вектор, комплексно-сопряженный у. Это та же самая формула, что и для
fft, за исключением знака «минус» в показателе степени. Функции fft и ifft — точ-
ные обращения. Для всех вещественных у справедливо ifft(fft(i/)) = у.
□	cfft(z/) возвращает коэффициенты ряда Фурье вектора или массива, содержа-
щих как вещественные, так и комплексные числа. Число элементов вектора у
может быть любым. Возвращаемый массив имеет тот же размер, что и массив,
используемый как аргумент.
□	icfft(c) возвращает обратное преобразование Фурье вектора или матрицы
данных.
Функции cfft и icfft — обратные друг к другу. То есть icfft(cfft(i/)) = у.
212
Глава 7. Обработка экспериментальных данных
Рассмотренные преобразования Фурье не являются единственно возможными.
Широко распространен следующий вид формул преобразования Фурье:
j п-1	п-1
CJ = -ty^(j/n)k^j =^wke2^J/n)k,
Пk=Q	k=Q
Эти формулы используются функциями FFT и IFFT.
Функции FFT, IFFT, CFFT и ICFFT используются аналогично функциям fft, ifft, cfft, icfft.
В рассмотренном на рис. 7.22 примере экспериментальная функция создана пу-
тем наложения на произвольную аналитическую функцию (sin + cos) случайных
чисел, созданных функцией rnd(n), возвращающей случайное число, лежащее
между 0 и и. Функция cfft возвращает коэффициенты ряда Фурье для созданно-
го массива чисел. Из набора найденных коэффициентов можно выбрать ряд ко-
эффициентов, удовлетворяющих заданному условию < [/t ] < k2.
Зададим сигнал п = 100	i:= 0,.п
qi := sm — 16 7г + cos — 19 к I Поменяйте аргументы sin и cos
О00	/	<100 J и число точек n
Добавим помехи si :=	md(2) - 1
Рис. 7.22. Формирование массива зашумленных данных для последующей очистки
Далее с помощью функции icfft находим функцию, представляющую собой сум-
му синусоид с коэффициентами, выбранными согласно заданному условию. Ме-
няя условие (величины и k2), можно включать в создаваемую функцию толь-
ко необходимые гармоники (рис. 7.23). Поработайте с интересным примером.
7А. Дискретные преобразования
213
прямое преобразование f = cfiEt(s)
построить ряд Фурье, значения коэффициентов которого
выбор коэффициентов обратное преобразование
gj = iffkl < |fj| < k2,fj,0)	h = icfft(g)
Поменяйте cfft и icfft на CFFT и ICFFT
2
1
hi 0
-1
-2
0	20	40	60	80	100

Рис. 7.23. Фильтрация данных с использованием разложения в ряд Фурье
Поменяйте саму функцию, условие, число точек. Функция cfft позволяет рабо-
тать с массивом из любого числа точек.
Разложение функции в ряд Фурье использовано в примере 4 электронной книги
для определения параметров движения кулачкового механизма.
7.4.2.	Двухмерное преобразование Фурье
В Mathcad имеется возможность применения встроенных функций комплексно-
го преобразования Фурье не только к одномерным, но и к двухмерным масси-
вам.
На рис. 7.24 приведена ступенчатая функция У(х, у) и показана ее поверхность.
Обратите внимание на запись условия при создании ступенчатой функции. Ус-
ловие С(х, у) записано в виде произведения булевых операторов. С(х, у) = 1,
если условие выполняется, и С(х, у) = 0, если условие не выполняется. По функ-
ции У(х, у) сформирован массив данных УУ. Работая с примером, поменяйте ис-
ходные данные.
С помощью генератора случайных чисел rnd на массив УУ наложены помехи.
214
Глава 7. Обработка экспериментальных данных
Сформируем массив значений сигнала YY
на области значений аргументов а, р
А3 амплитуда сигнала п > 30
i:=0..n j:=O..n ou >7 — р; := 7 -2- область аргументов
30 J 30
а := 2 b 4 с : 3 d:« 5 границы области сигнала
с(х,у)(а £ х < b) (c £ у £ d) область сигнала
у(х,у):- |А if с(х,у) ™ .„. .Исходный
|о otherwise м	сигнал
Добавить помехи УР£ j YY. j + md(l) - 0.5
YY	YP
Рис. 7.24. Наложение помех на двухмерный массив
На рис. 7.25 показано дискретное преобразование Фурье функции YP с помеха-
ми. Слева показан массив коэффициентов, справа — результат обратного преоб-
разования Фурье.
Выбираем ряд значений коэффициентов ряда Фурье между к1 и к2
К cffi(YP) kl1 И15 поменяйте И и к2 Поменяйте cfflна CFFT
jif (kl £ |K£ j| S k2 j ,0) YA icffi(^	и icffi на ICFFT
К	YA
Рис. 7.25. Двухмерное преобразование Фурье массива данных с помехами (см. рис. 7.24)
7.4. Дискретные преобразования
215
Для обратного преобразования использованы только гармоники, у которых ко-
эффициенты лежат внутри выбранного диапазона значений g.
7.4.3.	Волновое преобразование
Волновое (вейвлетное) преобразование в ряде случаев оказывается более эф-
фективным, чем преобразование Фурье. Преобразование Фурье раскладывает
заданную функцию на ряд гармоник (бесконечно осциллирующих синусоид).
При волновом преобразовании базовые функции локализованы в некоторой ог-
раниченной области значений аргумента, а вдали от нее — малы или равны
нулю.
Mathcad имеет одну встроенную функцию для волновых преобразований, ис-
пользующую функцию Даубечи:
□	wave(z/) — вектор прямого волнового преобразования;
□	iwave(r) — вектор обратного волнового преобразования.
Здесь у — вектор данных, взятых через равные промежутки значений аргумента;
v — вектор данных вейвлет-спектра (коэффициентов волнового преобразова-
ния).
и
А := 2.5 В := 5 N := 32 число, равное 2
Y(t) := if(2 < t < 4,А,0)	t:=0,0.01..B i:=0.. N-l
Y(t)
lKi|
YYj :=	K := wwe(YY)
поменяйте пределы
шт	выбираемых коэффициентов
YK := iwave(KK)
YKi
Рис. 7.26. Пример волнового преобразования данных
216
Глава 7. Обработка экспериментальных данных
Вектор у должен содержать 2” элементов (п — целое число). Результатом функ-
ции wave является вектор, содержащий несколько коэффициентов двухпара-
метрического вейвлет-спектра. Пример волнового преобразования приве-
ден на рис. 7.26. Выполняемые действия, включая фильтрацию коэффици-
ентов, аналогичны действиям по преобразованию Фурье, показанному на
рис. 7.22-7.25.
ПРИМЕЧАНИЕ -----------------------------------------------------------
В Mathcad 11 и более поздние версии включена электронная книга, посвященная волно-
вым преобразованиям. Она содержит дополнительные функции обработки сигналов
и много примеров волновых преобразований. Правда, воспользоваться сразу этими функ-
циями нельзя — необходимо приобрести полный пакет на сайте фирмы Mathsoft.
Глава 8
Математическая статистика
Mathcad имеет большой набор функций математической статистики, позволяю-
щих вычислять характеристики выборки данных: средние величины, дисперсию,
коэффициенты корреляции и другие коэффициенты, вычислять плотности веро-
ятности, функции вероятности, квантили вероятности для 17 различных видов
распределения случайных величин. Кроме того, в нем есть генераторы случай-
ных чисел, соответствующие всем 17 видам распределения, позволяющие эф-
фективно выполнять моделирование методом Монте-Карло.
8.1.	Характеристики выборки данных и связи двух
массивов
Mathcad содержит 16 различных функций для оценки параметров выборки дан-
ных. Перечислим основные из них:
□	mean(A) возвращает среднее значение элементов массива Л;
□	hmean(x) возвращает среднее гармоническое значение элементов массива Л;
□	gmean(A) возвращает среднее геометрическое значение элементов массива А;
□	var(A) возвращает дисперсию элементов массива Л;
□	Var(A) возвращает несмещенную дисперсию элементов массива А;
□	stdev(A) возвращает среднее квадратическое отклонение элементов масси-
ва А;
□	Stdev(A) возвращает несмещенное среднее квадратическое отклонение эле-
ментов массива А;
□	median(A) возвращает медиану массива А, которая делит гистограмму плот-
ности вероятностей на две равные части;
□	mode(A) возвращает моду массива А (наиболее часто встречающееся значе-
ние выборки данных);
□	skew(A) возвращает асимметрию массива А (степень асимметричности гисто-
граммы плотности вероятности относительно оси, проходящей через ее центр
тяжести);
□	kurt(x) возвращает эксцесс массива А (степень сглаженности плотности веро-
ятности в окрестности главного максимума);
□	stderr(A, В) возвращает стандартную ошибку при линейной регрессии масси-
вов А и В;
□	cvar(A, В) возвращает ковариацию элементов двух массивов, А и В;
□	согг(А, В) возвращает коэффициент корреляции двух массивов, А и В;
□	hist(int, у) — функция построения гистограммы массива А;
□	histogram(n, у) — функция построения гистограммы массива А.
Формулы для расчета указанных характеристик приведены на рис. 8.1 и 8.2.
218
Глава 8. Математическая статистика
ORIGIN > 1
Векторы наблюдений К := (25 33 33 30 34 37) К:« КТ n := rows(K)
среднее арифметическое mean(K) = 32
m := mean(K)
среднее геометрическое gmean(K) = 31.766
среднее гармоническое hmean(K) = 31.516
32
31.516
Рис. 8.1. Оценка параметров выборки данных
дисперсия
смещенная оценка var(K) = 14
; S (Ki-m)2=14
п
несмещенная оценка Var(K) = 16.8
п- 1
среднее квадратическое отклонение
смещенная оценка
stdev(K) = 3.742
несмещенная оценка
медиана
Stdev(K) = 4 099
median(K) = 33
Vvar(K) = 3 742
VVar(K) = 4.099
мода
mode (К) = 33
Эксцесс
асимметрия
kurt(K) = 1 339
skew(K) = -0 941
Рис. 8.2. Оценка параметров выборки данных (продолжение)
Все приведенные статистические функции могут использоваться для работы как
с векторами, так и с матрицами. При этом статистические характеристики рас-
считываются для совокупности значений всех элементов матрицы, без разделе-
ния ее на строки и столбцы. Так, для матрицы размерностью т х п объем выбор-
ки равен т *п.
Массивы наблюдений К:-(25 33 33 30 34 37) К:-КТ А:=(10 15 13 20 22 27)	M :=	г1б 31 <24	22y 9 17>
mean(K,A,M) = 23.222	mean(M,A,K) median(K,A,M) = 23	stdev(A,M,K)	= 23.222 = 8.417		
Рис. 8.3. Оценка параметров нескольких массивов данных
8.2. Функции распределения вероятностей
219
В качестве аргументов функций можно указать любое количество векторов, мат-
риц и скаляров. Пример вычисления статистических характеристик для не-
скольких массивов приведен на рис. 8.3. Порядок указания массивов не имеет
значения.
В Mathcad имеется три функции для оценки связи двух векторов или матриц:
□	stderr^, В) возвращает стандартную ошибку при линейной регрессии масси-
вов А и В;
□	суаг(Л, В) возвращает ковариацию элементов массивов А и В;
□	согг(Л, В) возвращает коэффициент корреляции массивов А и В.
Коэффициент корреляции и ковариация различаются лишь нормировкой.
Ковариация определяется по формуле
C = ^±(Ai-Acp)(Bi-Bcp),
И i=l
коэффициент корреляции — по формуле
Я = —,
аАаВ
где ол и ов — средние квадратические отклонения массивов А и В.
Чаще на практике используется коэффициент корреляции, дающий относитель-
ную, а не абсолютную (как ковариация) оценку связи двух массивов. Чем ближе
к единице коэффициент корреляции, тем теснее связь. Призер расчета парамет-
ров связи массивов приведен на рис. 8.4.
К >(25 33 33 30 34 37) К>КТ
Векторы наблюдений А	™	* ХТ
г	А >(10 15 13 20 22 27) А>А
Оценка связи двух массивов
ковариация	cva<K,A) = 16.167
коэффициент корреляции сон(К,А) в 0.751
стандартная ошибка stderr(K,A) « 4.659
Рис. 8.4. Оценка связи векторов А и К
8.2.	Функции распределения вероятностей
В Mathcad имеются встроенные функции для оценки 17 видов распределения
случайных величин. Эти функции рассчитывают плотность вероятности, функ-
цию распределения, квантиль вероятности, генерируют вектор случайных чисел,
распределенных по любому из 17 видов распределения.
Функции различаются написанием первой буквы, а другая часть имени функции
указывает выбранный вид распределения (в списке функций эта часть обозначе-
на звездочкой):
220
Глава 8. Математическая статистика
□	d*(x, par) — плотность вероятности;
□	р*(х, par) — функция распределения;
□	q*(P, par) — квантиль распределения;
□	r*(M, par) — вектор из М независимых чисел, распределенных по выбранному
закону.
Здесь х — значение случайной величины; Р — значение вероятности; par — спи-
сок параметров распределения.	ч
Чтобы получить функции, относящиеся, например, к нормальному распределе-
нию, надо вместо звездочки поставить norm. Список параметров для нормально-
го распределения содержит две величины: ц — математическое ожидание и а —
среднее квадратическое отклонение. Указанные функции приобретают следую-
щий вид: dnorm(x,|i,a), pnorm(x,p,a), qnorm(P,|ji,o), rnorm(M,p,a).
Перечислим все типы распределения, использованные в Mathcad, вместе с их па-
раметрами, обозначив звездочкой первую букву встроенных функций:
□	*Р(х,5!,52) — бета-распределение (х — значение случайной величины
О < х < 1, Sj, s2 > 0 — параметры);
□	* binom (k,n,p) — биномиальное распределение (п — целый параметр,
0<k<n,0<p<l — вероятность успеха единичного испытания);
□	* cauchy (x,/,s) — распределение Коши (/ — параметр разложения, 5 > 0 — па-
раметр масштаба);
□	* chisq (x,d) — у2 («хи-квадрат»)-распределение (d > 0 — число степеней сво-
боды);
□	* ехр (х, г) — экспоненциальное распределение (г > 0 — показатель экспоненты);
□	* F (х, dt, d2) — распределение Фишера (rfi, б?2 > 0 — числа степеней свободы);
□	~ гамма-распределение (5 > 0 — параметр формы);
□	* geom (k,p) — геометрическое распределение (0 < р < 1 — параметр, равный
вероятности успеха единичного испытания, k > 0 — целое число);
□	* hypergeom (k,a,b,ri)— гипергеометрическое распределение (а, Ь,п — целые
числа);
□	* Inort (х,ц,а) — логарифмически нормальное распределение (ц — натураль-
ный логарифм математического ожидания, о > 0 — натуральный логарифм
среднего квадратического отклонения);
□	* logis (x,/,s) — логистическое распределение (/ — математическое ожидание,
5 > 0 — параметр масштаба);
□	* nbinom (k,п,р) — отрицательное биномиальное распределение (п > 0 — целое
число, 0 < р < 1);
□	* norm (х,ц,а) — нормальное распределение (ц — математическое ожидание,
а > 0 — среднее квадратическое отклонение);
□	* pois (k, X) — распределение Пуассона (X > 0 — параметр);
□	* t (х, d) — распределение Стьюдента (d > 0 — число степеней свободы);
8.3. Генераторы случайных чисел
221
□	* unit (х, а, Ь) — равномерное распределение (а < b — границы интервала);
□	* weibull (х, s) — распределение Вейбулла (5 > 0 — параметр).
Примеры определения плотности вероятности, функции распределения и кван-
тилей распределения приведены на рис. 8.5 и 8.6.
[Функции распределения случайных чисел|
плотность
вероятности
х.= -5,-4.95..5
р(х) := dnorm(x,0,l)
р(х) := dt(x,10(T)
р(х) := dunif(x,-2,2)
р(х) := dlnorm(x,0,l)
р(х) := dlogis(x,0,l)
функция
распределения
W(x) := pnorm(x,0,l)
W(x) := pt(x,10Q)
W(x) := punif(x,-2,2)
W(x) := plnorm(x,0,1)
W(x) := plogis(x,0,l)
сдвигая график W и p вниз, посмотрите
различные распределения вероятностей
W(x)
р(х)
Рис. 8.5. Плотность вероятности р и функция распределения вероятностей W
Обращение функций распределения (квантиль вероятности)
q(p) := qnorm(p ,0,1) q(p) := qpois(p, 1)
q(p) ••= qt(p,qt(p,l^) q(p) > qlnonn(p,0,l)
p := 0,0.05.. 1 Сдвиньте вниз одно из выражений q(p)
q(p)
Р
Рис. 8.6. График определения квантиля вероятности q
8.3.	Генераторы случайных чисел
Для каждого закона распределения в Mathcad имеется функция — генератор слу-
чайных чисел, что позволяет выполнять моделирование методами Монте-Карло.
Простейшая из них, функция rnd(N), возвращает одно случайное число, лежащее
в интервале от 0 до N. Все другие функции — генераторы случайных чисел создают
вектор чисел, распределенных по выбранному закону. Например, runif(M, а, Ь)
создает вектор из М чисел, равномерно распределенных в интервале от а до Ь.
Примеры работы генератора случайных чисел приведены на рис. 8.7. и 8.8.
222
Глава 8. Математическая статистика
создать одно случайное число.равномерно распределенное между 0 и х
(сотрите знак равенства и введите его вновь-число поменяется) md(x)
~ з
md(2) = 2 537 х 10 ОДНО ЧИСЛО i = 1..4 Vi:=md(10) вектор
V := morm(5,10,2) V = rchisq(5,10) V := rexp(5,0.3) V .= rgeom(5,0.2)
Опустите вниз одно из выражений V
V := sort(V) V := reverse(V) сортировка вектора по росту и обратно
		среднее арифметическое	mean(V) = 3.6
	7	дисперсия	var(V) = 11.44
(V) =	3	среднее квадратическое	stdev(V) = 3 382
	0	отклонение	
	<0,	медиана	median(V) = 3
Рис. 8.7. Работа генератора случайных чисел
Формирование массива случайных чисел
Для всех функций, кроме rnd N : 4 а:=1	b:=4 k:=l.. N
<к> е := runif(3,»,b)	Z1.79 3.17 3.04 1.36
поменяйте генератор чисел в = 2.84 3.45 1.85 2.96
<1.08 3.75 1.98 3.77;
Для функции rnd n:=3 m:=4	i:=l..n	j:=l..m
r0.213 1.877 2.44 3.016
Ajj > md(5) A= 0.142 2.236 2.86 0.38
<3.063 3.484 4.398 3.256;
Рис. 8.8.' Работа генератора случайных чисел (продолжение)
8.4.	Построение гистограмм
Гистограммой называется график, аппроксимирующий по случайным данным
плотность их распределения. При построении гистограммы область значений
случайной величины разбивается на заданное число сегментов, а затем подсчи-
тывается число попаданий в каждый сегмент.
В Mathcad встроено две функции построения гистограмм:
□	histogram(n, data). Здесь п — число интервалов, на которые разбивается весь
диапазон исходных данных data. Эта функция возвращает 2 столбца. В пер-
вом содержатся средние точки каждого из п интервалов, во втором — частоты
попадания случайных чисел вектора data в каждый из п интервалов. Пример
построения гистограммы приведен на рис. 8.9. Массивы исходных данных V
из 1000 чисел на этом рисунке создаются генераторами случайных чисел,
соответствующих выбранному закону распределения. Число интервалов пп
выбрано 21.
□	hist(int, data). Здесь int имеет двоякий смысл: либо это вектор середин интер-
валов (можно задать интервалы разной ширины), либо число интервалов,
data — вектор случайных чисел. Пример использования функции hist приве-
ден на рис. 8.10.
8.4. Построение гистограмм
223
нормальное распределение
распределение Стьюдента
равномерное распределение
логарифмически нормальное
логистическое распределение
построение гистограммы
Vmoxm(1000,10,l)
VIrtGOOO ,100)
V2runif(1000,-2,2)
V3 rlnoxm(1000,0,1)
V4:-rlogis(1000,0,l)
nn : 21 hh := histogram(nn,V)
mthh<^ вектор средних точек интервалов
<2>
h :« hh частота попадания чисел в интервал
(в функции histogram поменяйте имя массива данных V )
V:« rpois(1000,10) или V :® morm(1000,10,l)
int > 0 сброс предыдущих значений int п := 15 i := 1.. п
max - mm
maxmax(V) minmin(V) int :=------------i + min
1 n
Для закрашивания гистограммы надо дважды щелкнуть мышью на графике и
в открывшемся окне форматирования графика (рис. 8.11) выбрать Traces ►
Туре ► Solidbar (Трассировка ► Тип ► Сплошные столбики) или Traces ► Туре ►
Ваг (Трассров-ка ► Тип ► Выбрать тип столбиков).
224
Глава 8. Математическая статистика
Форматирование выбранного графика X-Y
Отмена [	| Справка
Рис. 8.11. Выбор внешнего вида графиков
8.5.	Расчет доверительного интервала
В качестве примера статистических расчетов рассмотрим расчет доверительного
интервала математического ожидания для малой выборки К из 6 чисел
(рис. 8.12). Для расчета использовано распределение Стьюдента. Квантиль рас-
пределения определяет ширину доверительного интервала. Он показывает,
сколько значений среднего квадратического отклонения надо отложить влево
и вправо от среднего арифметического значения. Доверительный интервал опре-
делен для вероятности попадания числа внутрь интервала 99 %.
В технике существует понятие «расчет на три девятки». Смысл его в том, что
при расчете с вероятностью неразрушения 99,9 % надо отложить от средней дол-
говечности в сторону ее уменьшения «три сигма» (три средних квадратических
отклонения), потому что квантиль нормального распределения примерно равен
3 при вероятности 99,9 %.
Расчет доверительного интервала
К:=(25 33 33 30 34 36) К:=КТ := mean(K) 1^ = 31.833
по Стыоденту квантиль t:= qt(0.99,n) t= 2.602
отклонение от среднего арифметического di := tstdev(K) di« 9.191
Доверительный интервал Kcp-di<KK<Kcp+di
31.833 - 9.191 < КК< 31.833 + 9.191
Рис. 8.12. Оценка доверительного интервала для малой выборки данных
Часть III
Дополнительные возможности
Mathcad
В этой части книги рассматриваются дополнительные возможно-
сти Mathcad: программирование, анимация, учет размерностей, под-
готовка документов.
Глава 9
Программирование
Раздел «Программирование» занимает особое место в Mathcad. При начальном
обучении этот раздел совершенно не нужен. Огромные возможности Mathcad
позволяют решать подавляющее число задач без использования программирова-
ния, да к тому же, как правило, несколькими способами. Но есть класс задач, ко-
торые невозможно решить без программирования. Это задачи, в которых часть
документа из нескольких или многих операторов надо выполнить многократно.
В таких случаях документ должен состоять из отдельных подпрограмм, объеди-
ненных в единую «головную» программу. И в этом случае программирования
можно было бы избежать, если бы создатели Mathcad предусмотрели оператор
перехода к метке, который есть (был) во многих языках программирования, в ча-
стности в Fortran. Серьезные программисты считают дурным тоном использова-
ние перехода к метке, полагая, что в любой программе можно обойтись без ме-
ток. Это верно, но зачастую требует больших усилий. Система Mathcad предна-
значена для простых инженеров, не всегда являющихся специалистами в про-
граммировании, и поэтому должна быть простой в использовании.
Использование раздела «Программирование» позволяет записать в Mathcad
программы любой сложности. Образцом такой программы является решение
плоской упруго-пластической задачи методом конечных элементов, приведен-
ной в примере 55 электронной книги.
Программирование в Mathcad чрезвычайно наглядно и понятно, так как про-
грамма представляет собой последовательность формул. Далее программами бу-
дем называть не все обычные Mathcad-документы, а только те из них, которые
написаны с использованием панели программирования.
Основные операторы программирования расположены на панели Programming
Toolbar (Панель программирования), вызываемой соответствующей кнопкой ма-
тематической панели.. Прибегать к помощи панели программирования прихо-
дится в основном при неоднократном повторении каких-либо частей документа.
9.1.	Создание программ
Программа Mathcad есть частный случай выражения Mathcad. Подобно любому
выражению, программа возвращает значение, если за ней следует знак равенства.
Обычное выражение Mathcad состоит из одной строки. Выражение-программа
содержит много строк. Фактически это составное выражение.
Выражение-программа состоит из названия выражения, следующего за ним зна-
ка присвоения значения и необходимых выражений в правой части, записанных
в столбик и объединенных слева вертикальной чертой.
9.1.1.	Ввод строк в программу
Для создания программы надо:
□	ввести имя выражения-программы;
□	ввести оператор присваивания (:=);
9.1. Создание программ
227
□	щелкнуть на кнопке панели программирования Add Line (Добавить строку)
столько раз, сколько строк должна содержать программа;
□	в появившиеся места ввода ввести нужные операторы, лишние места ввода
удалить.
Чтобы создать недостающие места ввода, надо поставить синий уголок курсора
в конец строки, после которой ввести новую строку. Клавишей пробела следует
выделить полностью всю строку и нажать кнопку Add Line. При этом возможны
два варианта:
□	Если синий уголок курсора находится в начале строки, то после нажатия Add
Line место ввода появится выше этой строки.
□	Если синий уголок курсора находится в конце строки, то после нажатия Add
Line место ввода появится ниже этой строки (рис. 9.1).
положение курсора
результат действия Add Line
Рис. 9.1. Ввод строки в программу
Программиро...®	
Add Line	
If	otherwise
for	while
break	continue
return	on error
В некоторых случаях, например, при необходимости вставить строку между дву-
мя вложенными циклами, что при создании программы встречается очень часто,
указанный прием не работает. В этом случае необходимо:
□	выделить черным цветом весь внутренний цикл;
□	вырезать его в буфер кнопкой Cut (Вырезать);
□	нажать кнопку Add Line;
□	вставить из буфера вырезанный фрагмент на прежнее место;
□	заполнить появившееся дополнительное место ввода.
При определенном навыке этот прием удобно использовать во всех случаях
вставки дополнительных строк.
9.1.2.	Локальное присвоение значений
Программа Mathcad — это обособленный модуль внутри Mathcad-документа со
своими именами переменных и их значениями, которые не видны из других мест
Mathcad-документа.
Присваивание значений переменным и константам в программах производится
с помощью программного оператора присваивания который вводится с панели
228
Глава 9. Программирование
программирования нажатием кнопки . При создании программы, когда этот
знак приходится использовать часто, полезно пользоваться клавишей {.
Локальные значения переменных нельзя использовать вне программы. Если это
все же необходимо, их надо вывести из программы специальным образом
(см. раздел 9.4, «Вывод результатов расчета из программы»).
ВНИМАНИЕ -----------------------------------------------------------
Ни оператор присвоения значения (.—), ни оператор вывода (=) в пределах программ не
применяются.
Из основного документа в программу передаются в виде констант все значения
величин, имеющих одинаковые имена в основном документе и в программном
модуле. Эти значения сохраняются неизменными при любых действиях с ними
внутри программы.
Для того чтобы любые величины стали переменными, им надо присвоить значе-
ния внутри программы с помощью программного оператора присваивания. На
рис. 9.7 первый оператор в программе А А замените на АА А или удалите
его. Результат изменится.
В большой программе, например, при решении упруго-пластической задачи ме-
тодом конечных элементов (МКЭ) (пример 55, часть IV), где в головную про-
грамму ZZ надо передать много переменных величин, всем им в начале програм-
мы надо присвоить значения. Обратите внимание на то, что имена передаваемых
и принимаемых величин чаще всего совпадают, чтобы программу было легче по-
нять. В указанном примере передается 6 величин, и каждая занимает одну стро-
ку в программе, что увеличивает длину программы.
Передать нужные величины в программу можно и другим способом, создав про-
грамму-функцию, где передаваемые величины записаны в параметры функции.
Так в рассмотренном примере оформлены все подпрограммы, используемые за-
тем в головной программе. При этом программа занимает меньше места в длину,
но больше — в ширину.
Для экономии места в документе можно использовать наложение объектов друг
на друга. Щелкните правой кнопкой мыши и выберите в контекстном меню Bring
to Front (Выдвинуть на передний план) или Send to Back (Убрать на задний
план). Документ получается более компактным. Именно так скомпонованы все
программы в этой книге.
ПРИМЕЧАНИЕ -----------------------------------------------------------
Оператор программирования в Mathcad 13 не допускает наличия одинаковых имен в ле-
вой и правой частях оператора локального присвоения . Например, массиву нельзя при-
своить имя функции.
Любая программа представляет собой сочетание обычных математических выра-
жений с операторами условия и цикла. Разберем последовательно действие этих
операторов.
9.2. Условный оператор if
229
9.2.	Условный оператор if
Действие условного оператора состоит из двух частей. Сначала проверяется ус-
ловие, записанное справа от оператора if. Если оно верно, выполняется выраже-
ние, стоящее слева от if, если не верно, происходит переход к следующей строке
программы.
Чтобы вставить условный оператор в программу, нужно:
□	в создаваемой программе установить курсор на свободное место ввода, где
должен появиться условный оператор;
□	на панели программирования (Programming Toolbar) щелкнуть на кнопке if.
В программе появится шаблон оператора с двумя местами ввода;
□	в правое место ввода ввести условие. Пользуйтесь при этом логическими опе-
раторами, вводя их с панели Boolean (Булевы операторы);
□	слева от оператора if ввести выражение, которое должно выполняться, если
условие верно;
□	если при выполнении условия должно выполняться сразу несколько выраже-
ний, надо иметь несколько мест ввода. Установите курсор на место ввода сле-
ва от if и нажмите Add Line столько раз, сколько строк надо ввести. Обратите
внимание на то, что при этом изменяется вид условного оператора. Столбик
мест ввода появляется не слева, а под оператором if (рис. 9.2).
использование оператора
программирования if
а = 8 поменяйте а
у = if а < 3
использование булевых операторов
yl := [ta(-/aL(a < 3) + 2 (3 < а < 5) + [(а4- 1)^ - а] (а > 5)]
использование функции if
у2 .= if[a < 3,1п(-/а) ,1^3 < а < 5,2,(а4- 1)^ - aj
у = 73 yl = 73 у2 = 73
2 if 3 < а < 5
otherwise
с <- а+ 1
2
с - а
Рис. 9.2. Три способа записи условия в Mathcad
Если условие не верно, происходит переход к следующей строке программы.
Она может содержать новое условие или быть обычным выражением.
Часто встречается условие с двумя вариантами действия: если ..., то ..., иначе ....
Для слова «иначе» на панели Programming имеется оператор otherwise (Иначе),
который вводится так же, как if.
На практике лучше вводить условие в несколько ином порядке:
□	На свободное место ввода в программе вводят выражение, выполняемое, если
условие верно.
230
Глава 9. Программирование
□	Выделяют курсором выражение так, чтобы уголок курсора был в конце выра-
жения, и на панели программирования нажимают if.
□	Справа от оператора if вводят условие.
□	На следующем свободном месте ввода (на следующей строке) пишут выраже-
ние, выполняемое «иначе», если условие не выполняется.
□	Выделяют курсором выражение так, чтобы уголок курсора был в конце выра-
жения, и на панели программирования нажимают otherwise.
На рис. 9.3 приведен пример использования условного оператора if. В качестве
примера выбрано построение эпюр изгибающих моментов и поперечных сил
в балке (рис. 9.4). Применение условного оператора особенно удобно при выпол-
нении операции со ступенчатыми функциями. Участков на балке может быть не-
сколько, но функция изгибающих моментов одна.
^пользование оператора if для описания ступенчатых
функций (построение эпюр Q и М при изгибе балки)
q := 20 Pl := 20 Р2 := 30 МО := 30 а := 3 b := 2
Q(x) := I Pl - qx if x< a
|(Pl + P2 - q a) otherwise	x := °’01" 5
MP(x) :=
Pl-x - q a- x-----
I 2
Рис. 9.3. Использование условного оператора if
+ P2-(x - 2) + M0
otherwise
Рис. 9.4. Эпюры поперечной силы и изгибающего момента
при изгибе балки (см. рис. 9.3)
9.3. Операторы цикла
231
Напомним, что в Mathcad есть три способа записи условия:
□	с помощью оператора программирования if;
□	с помощью булевых операторов;
□	с помощью функции if.
Применение всех трех способов записи условия показано на рис. 9.2.
9.3.	Операторы цикла
Важнейшим элементом программирования, помимо условного оператора, явля-
ется оператор цикла. В обычном Mathcad-документе использование дискретной
переменной фактически аналогично применению оператора цикла, используемого
для вычисления одного выражения. Mathcad вычисляет выражения сверху вниз и
переходит к следующему выражению, лишь завершив все вычисления предыдущего
выражения, поскольку вернуться к нему уже не сможет. Если же в каждом цикле
должно быть вычислено несколько выражений, необходимо составлять программу.
ВНИМАНИЕ -------1--------------------------------------------------
Использование дискретных переменных внутри программ невозможно.
Панель программирования Mathcad содержит два оператора цикла, for и while:
□ Если число выполнений цикла заранее известно, используется оператор for.
□ Если цикл должен завершиться по выполнении некоторого условия и момент
выполнения этого условия неизвестен, используется оператор while.
Рассмотрим каждый из них.
9.3.1.	Оператор while
Цикл while выполняется до тех пор, пока остается истинным условие цикла, по-
этому нет необходимости знать число вычислений заранее. Важно только, чтобы
где-либо внутри цикла или в другом выполняемом участке программы присутст-
вовал оператор, делающий условие цикла ложным. В противном случае цикл бу-
дет выполняться бесконечно.
Если выполняемая программа зациклилась, ее можно остановить, нажав клави-
шу Esc.
Чтобы записать цикл while, выполните следующие действия:
□	Установите курсор на свободное место ввода в программе (справа от верти-
кальной черты).
□	На панели программирования нажмите кнопку while. Появится шаблон с дву-
мя местами ввода.
□	Справа от слова «while» введите условие выполнения цикла. Обычно это ло-
гическое выражение.
□	В оставшееся поле ввода (внизу под словом «while») введите выражение, ко-
торое вычисляется в цикле.
□	Если в цикле надо вычислять несколько выражений, то вначале установите
курсор на место ввода и нажмите кнопку Add Line (или клавишу ]) столько
232
Глава 9. Программирование
раз, сколько строк будет содержать цикл. Затем заполните все места ввода,
введя нужные выражения. Удалите лишние места ввода.
Обнаружив заголовок цикла while, Mathcad проверяет условие цикла. Если оно
истинно, то Mathcad выполняет тело цикла и снова проверяет условие. Если оно
ложно, Mathcad заканчивает выполнение цикла.
Пример использования цикла while приведен на рис. 9.5.
Нахождение первого элемента вектора, большего заданного значения К:« 1.6
3j-------------------
j > 1.. 7 v. > ТРТ	ORIGIN > 1
	1	2	3	4	5	6	7
1	0	1	1.26	1.442	1.587	1.71	1.817
j - номер элемента
Рис. 9.5. Применение оператора цикла while
9.3.2.	Оператор for
В цикле for число повторений цикла определяется переменной, задаваемой в на-
чале цикла. Рассмотрим создание такого цикла:
□	Установите курсор на свободное место ввода в программе (справа от верти-
кальной черты).
□	На панели программирования нажмите кнопку for Loop (Цикл for). Появится
шаблон с тремя местами ввода.
□	Справа от слова «for» введите имя переменной цикла. После знака е введите
диапазон изменения переменной цикла так же, как это делается с помощью
дискретной переменной. Переменной цикла может быть ряд чисел, или век-
тор, или список скаляров, диапазонов, векторов, разделенных запятой (рис. 9.6).
переменная цикла - 2 вектора
переменная цикла по типу
дискретной переменной
Z :=	m <	H 1		<1.414>
	for s € 1,1.2.. 2			1.483
		x m ’	Z =	1.549 1.612
		m <- m + 1		1.673
	X			<1.732;
Z1 :=	m <	H 1	<13>
	for S € А,В		15
		X <— s	71 - m	~	17
		m <— m + 1	1
	X		<3;
Рис. 9.6. Применение оператора цикла for
9.3. Операторы цикла
233
□	В оставшееся поле ввода (внизу, под словом «for») введите выражение, кото-
рое вычисляется в цикле.
□	Если в цикле надо вычислять несколько выражений, то вначале установите
курсор на место ввода и нажмите кнопку Add Line (или клавишу ]) столько
раз, сколько строк будет содержать цикл. Затем заполните все места ввода,
введя нужные выражения. Удалите лишние места ввода.
Mathcad легко справляется со сложными математическими проблемами и легко
решает сложные уравнения. А вот простые для любого человека логические за-
дачи решаются с большим трудом. На рис. 9.7 - 9.9 показаны примеры использо-
вания программирования для решения логических задач выборки нужных зна-
чений вектора или матрицы. В этих примерах показаны различные приемы
записи условия в операторе if: в виде обычных булевых операторов (рис. 9.9) или
в виде логической функции (рис. 9.8). Здесь демонстрируются также приемы
формирования массивов выходных данных. При работе с массивами удобно ис-
пользовать привычную нумерацию элементов массива, начиная с 1, поэтому
в примерах на программирование далее используется ORIGIN = 1.
Вставка массива В в массив А
(3 2 1
А := identity(5) В I
А ряд г := 3
место вставки стРолбец с;=2
С := А <- А
ORIGIN := 1
fl
О О О О'1
10 0 0
0 10 0
0 0 10
0 0 0 1;
"Передача массива А в программу"
for i е 1.. rows(B)
for j € 1.. cols(B)
Ar+i-l ,c+j-1 Bi, j
A
fl 0 0 0 0^
0 10 0 0
0 3 2 1 0
0 12 3 0
<00001;
Рис. 9.7. Вставка массива в массив
Извлечение элементов вектора D,
удовлетворяющих условию с(х) := 2 < х < 4
ORIGIN = 1
D-mont<8,3,2) DT - (4.116 2.51 3.179 5.524 1.589 3.004 5215 4.785)
Извлечение :=
i<— 1
for j € 1.. rows(D)
tfc(Dj)-l
U^Dj
A^j
i<- i+ 1
A
W<2> U
W
логическая функция c(D)
принимает значения
1 - верно,0 - неверно
c^Dj) « 1 эквивалентно
условию 2 < Dj < 4
Е := Извлечение
<2 2.51 >
Е= 3 3.179
<6 3.004;
А - номер элемента
U - значение элемента,
удовлетворяющего условию
Рис. 9.8. Извлечение нужных элементов вектора
234
Глава 9. Программирование
Извлечение1 элементов массива М,
удовлетворяющих условию 3 < х < 5
ORIGIN := 1
i > 1.. 4
1..3 М. .
создание массива
md^ случайных чисел
М =
г8.76
4.621
9.968
<8.401
9.559
8.622
6.115
3.759
5.393 >
7.797
2.662
6.772 ;
for m € 1.. rows(M)
for n € 1.. cols(M)
if 3 < M <5
Элементы := Z(M)
Элементы =
1
<4.621
2
3.759 >
строка
столбец
число
Рис. 9.9. Извлечение нужных элементов матрицы
В примере на рис. 9.7 показан ввод комментария в программу.
Для ввода комментария в программу нужно установить курсор на свободное ме-
сто ввода в программе и ввести символ ” (кавычки). Появится символ введения
строковой переменной: две пары кавычек с местом ввода между ними. Введите
туда текст комментария.
Mathcad вычисляет выражения слева направо, сверху вниз. Результаты действия
программы можно вывести правее и ниже места присвоения значения.
Для экономии места в документе используется наложение одной области на дру-
гую, ведь программа занимает прямоугольную область, большая часть которой
пустует. Для этого переместите любое выражение в область программы и при
выделенном выражении, нажав правую кнопку мыши, в контекстном меню вы-
берите Bring to Front (На передний план). Можно также, выделив программу, вы-
брать в контекстном меню Send to Back (На задний план).Таким образом, ском-
понованы все примеры в части IV книги.
9.3.3.	Операторы break, continue, return
Эти операторы используются для управления работой циклов и всей программы
в целом:
□	continue возвращает расчет к началу цикла;
□	break обеспечивает выход из цикла и продолжение работы программы;
□	return обеспечивает выход из программы.
Работа этих операторов показана на рис. 9.10. Оператор continue в этом примере
создает список нечетных чисел (вектор V), осуществляя возврат в начало цикла,
если остаток от деления числа п на 2 (mod(n, 2)) равен 0. Оператор break осуще-
ствляет выход из цикла и продолжение работы программы, если п < 0. Оператор
9.4. Вывод результатов расчета из программы
235
return осуществляет выход из программы, если п — —10, с записью введенного
комментария (выход из программы).
f(n) .=
for ke 1.. n
a<— a+ 1
Vae-k
break if n < 0
continue if mod(k,2) = 0
return " выход из программы"
f(—10) = " выход из программы"
"Конец цикла"
s S 1000
Рис. 9.10. Применение операторов continue, break, return
ВНИМАНИЕ ------------------------------------------------------------
Для вставки в программу операторов continue, break, return, как и других операторов про-
граммирования, можно пользоваться только панелью программирования. Их нельзя наби-
рать с клавиатуры.
9.4.	Вывод результатов расчета из программы
Итогом действия программы является результат выполнения последнего опера-
тора программы. Если последним оператором является математическое выраже-
ние, то результат его вычисления и будет результатом действия программы.
Если Надо выводить данные, это делается путем формирования внутри програм-
мы массивов и составных массивов.
На рис. 9.5 из программы надо вывести 2 числа: номер первого элемента, боль-
шего К, и численное значение этого элемента. Как уже сказано, выражение-про-
грамма принимает значение последнего оператора программы.
Чтобы вывести результаты расчета, выполните следующие действия:
□	Установите курсор на пустое место ввода последнего оператора.
□	Для вывода одного числа введите имя соответствующей переменной (любой,
которой присвоено какое-либо значение в программе или в основном доку-
менте).
236
Глава 9. Программирование
□	Для вывода вектора или матрицы введите их имя, но каждый элемент масси-
ва должен быть определен либо в программе, либо в основном документе.
Элементы вектора или матрицы можно ввести их именами (см. рис. 9.5). Для
этого, установив курсор на место ввода последнего оператора, комбинацией кла-
виш Ctrl+m надо вызвать шаблон матрицы, ввести число строк и столбцов (в на-
шем случае 2 строки, 1 столбец), ввести имена элементов, которым присвоены
значения.
При разработке серьезных больших программ стоит задача вывода результатов
расчета. Одновременно надо вывести и скаляры, и векторы, и матрицы. Но ведь
место вывода только одно!
Напомним, что Mathcad присваивает выражению с именем программы значение
последнего оператора программы.
Выход из трудного положения дает составной массив, который имеет структуру
обычного массива, но его элементы могут быть одновременно числами, вектора-
ми или матрицами, совершенно не связанными друг с другом.
Массив Z на рис. 9.11 — это матрица-столбец (вектор), для уменьшения размера
программы записанный в транспонированном виде. Он содержит 3 элемента:
Zt — 4 массива различной размерности, Z2 — 4 вектора, расположенных бок о
бок, Z3 — скаляр (число итераций). На этом рисунке показано, как, используя
верхние и нижние индексы, вывести любое расчетное значение. Поупражняйтесь
самостоятельно в выводе расчетных значений. Убедитесь в неограниченных воз-
можностях вывода любых расчетных данных.
z =
а«— 1
while а < 5
for ie 1 а
Vjа +1
for j е 1 а
Mjj <— а +1 + j
MMq <— М
w<a><-v
а«— а+ 1
(ММ W а)т
			
z =	{4,4}		Z1
	. 5 ;		Z2
Z1 =	ЧмГ (2,2) (3,3) <(4,4) , г2 3	4 5'	Z3
0 4 5 6
0 0 6 7
<0 0 0 87
- 4 массива различной
размерности
- 4 вектора бок о бок
- число итерациий
	Л6 7	7 8	8 9	9 ' 10
'Zl.'4 =	8	9	10	И
	<9	10 ъ	11 /	12 у Зч
(Z2)<2> =
4
0
константе можно присвоить значение элемента массива
(4 5 1
Z3 = 5 A=(Z1L А=	B=riZill
2 Is 6J L
т’
Замените матрицу-столбец вывода (мм w а)
В = 9
fMM
на матрицу
а потом на матрицу-строку (ММ W а) и самостоятельно выведите
W
1
результаты расчета ,
Рис. 9.11. Вывод результатов работы программы с помощью составного массива
9.5. Подпрограммы-функции
237
Составные массивы не имеют физического и математического смысла, поэтому
операции матричного исчисления, за исключением операции транспонирования,
к ним применять нельзя.
9.5.	Подпрограммы-функции
Любая программа является выражением, состоящим из ряда выражений (объе-
диненных вертикальной чертой), каждое из которых, в свою очередь, может быть
программой. Например, если часть программы, состоящая из нескольких опера-
торов, должна выполняться несколько раз внутри программы, ее целесообразно
записать в виде подпрограммы-функции и вызывать, меняя внутренние парамет-
ры, каждый раз, когда это нужно. Формально подпрограммой, состоящей из од-
ного оператора, является любая функция пользователя, входящая в состав дру-
гой программы.
На рис. 9.12 головная программа Z содержит внутри себя две подпрограммы,
f1(x) и f2(x), которые многократно вызываются внутри цикла for. В конце про-
граммы с помощью составного массива выводятся необходимые результаты рас-
чета.
fl(X) :=
sin(x) if х < О
cos(2x) otherwise
f2(x) := root(fl(x) ,x)
Функции
пользователя
(подпрограммы)
k := (3 7 12 15 17) список значений аргумента
Головная программа
Z := п<— 1
for iek
а<—fl(i)
bn«—f2(a) if |a| <0.8
bn <— 0 otherwise
cn«~i
"нумерация элементов 11
n<— n+ 1
(b c)
b := zP с :=
-15.708
0.785
0.785
Рис. 9.12. Вложенные подпрограммы
Как правило, подпрограмма-функция располагается где-то выше головной про-
граммы, в которой она используется. Результаты расчета можно вывести в лю-
бой позиции правее и ниже имени выражения-программы. Примеры сложных
238
Глава 9. Программирование
программ с использованием многих подпрограмм находятся в части IV книги
(примеры 55 и 56).
9.6.	Интегрирование функции методом трапеций
Операция интегрирования самая медленная в Mathcad. Особенно длительным
является вычисление интегральной функции с использованием дискретной пе-
ременной при* построении графика. Смена метода интегрирования, предостав-
ляемая Mathcad при вызове контекстного меню, не прйводит к ускорению рас-
чета.
Для ускорения операции интегрирования предлагаю простую программу интег-
рирования функции методом трапеций, самым простым из всех возможных ме-
тодов интегрирования. Это программа lnt(F, Z2> показанная на рис. 9.13.
Здесь F — имя функции, Lr и L2 — верхний и нижний пределы интегрирования,
N — число промежуточных точек интегрирования. Сама программа очень проста
и не требует комментариев.
Для примера выбрана функция, полученная интерполяцией экспериментального
массива данных. Формирование этой функции показано на рис. 9.13, вверху.
Сравнение результатов интегрирования с помощью функции Int и стандартным
оператором интегрирования Mathcad показано на рис. 9.14. Функция Int позво-
ляет в несколько раз сократить время операции. Совпадение графиков показы-
вает, что функция Int обеспечивает достаточную точность расчета даже при ма-
лом количестве точек интегрирования.
массив экспериментальных данных (X.Y)
Х:=(0 1 3 4 6 7 10 11 13 14 20)Т
Y:=(3 7 9 5 5 2 7 9 6 2 2)Т
Преобразуем массив в функцию путем интерполяции или регрессии
F(t) =mterp(lspline(X,Y),X,Y,t)
приближение к прямой линии
в граничных точках
Функция интегрирования методом трапеций
Int(F,Ll ,L2,N) •=
L2-L1
F - имя интегрируемой функции
(без параметров)
for 1 е 0 N
fl <- F(L1)
L1 и L2 - верхний и нижний
пределы интегрирования
N - число точек
интегрирования
f2 «— F (х)
fl+f2 ЛТ
-----AL
2
Рис. 9.13. Программа интегрирования функции методом трапеций
N
LI <—х
9.7. Решение уравнений и систем уравнений в программе
239
Рис. 9.14. Сравнение результатов интегрирования, выполненного с помощью функции Int
и стандартным оператором интегрирования Mathcad
9.7.	Решение уравнений и систем уравнений
в программе
В главе 3 (раздел 3.2) описано использование функции пользователя для нахож-
дения корней уравнения при переменных значениях параметров Ь, перечислен-
ных в названии функции пользователя (см. рис. 3.5 и 3.6). То же самое для сис-
тем уравнений описано в разделе 3.4 (см. рис. 3.11, 3.12).
В старых версиях Mathcad функцию root можно было использовать в программ-
ных модулях, как показано на рис. 9.15. Решаемое уравнение записывалось
в виде функции f(a, b, z), равной нулю . Далее внутри двух вложенных циклов
for задавались переменные параметры i и с. Корень уравнения для каждого зна-
чения а и 6, определяемый функцией root, записывался в массив Z. Это было
очень удобно для расчетов. К сожалению, в новых версиях Mathcad использова-
ние функции root в программных модулях невозможно.
Довольно сложным моментом является решение системы уравнений в про-
граммном модуле. Вычислительный блок Given-find, оформленный как функция
пользователя, вместе с начальными приближениями для каждой переменной
размещается выше программы. Решение системы уравнений в этом случае выво-
дится в виде массива, каждый столбец которого соответствует вектору решения
для одной переменной.
ПРИМЕЧАНИЕ ---------------------------------------------------------
Существенным недостатком использования вычислительного блока со словом «given»
(Given-find, Given-minerr, Given-maximize, Given-Odesolve) является то, что начальные при-
ближения задаются вне программного модуля и не могут быть изменены внутри него.
В ряде случаев (для ступенчатых функций) это приводит к невозможности решения задачи.
В примере на рис. 9.15 внутри двух вложенных циклов for на каждом шаге вызы-
вается функция пользователя w(a, b), где значения а и b заданы как переменные
цикла, хотя их можно задать и массивом значений и вычислять по какой-либо
формуле. Результаты вычисления значений х и у записываются в массив К при
240
Глава 9. Программирование
ГИ уравнение, решаемое
Ца,ь,z) -az- asmhl - I в программе функцией root
2	2	/ v
fl(x,y) = х cos (О 3 у) £2(х,у) = 10 j--------
Jsm(0 2x)2
х = 1 у = 1 начальные приближения
Given а = fl(x,y) b = f2(x,y) система уравнений
w(a,b) = Fmd(x,y) функция. передаваемая в программу
Z =
for ае 1 .25
for b е 1 25
za f Ь root(f(a, b, х), х)
"решение системы уравнений"
Ка,ь<— w(a,b)
xa,b <Ka,b
Уа,Ь (Ka,b *2
(x у z)T
root в программах
наработает в
Mathcad 13 и выше
(поставьте za>b<- 0)
X = Z1 у = Z2 z = Z3
Г рафики зависимости
корней уравнения f и
системы уравнений fl и 12
от параметров а и b
z(a,b)
х(а,Ь)
У(а,Ь)
Рис. 9.15. Решение уравнений и систем уравнений в программе
каждом значении переменных а и Ь. При этом сама функция w(a, b) на каждом
шаге вызывается один раз, а не два, чтобы найти значения хи у. Такой прием по-
зволяет вдвое сократить время выполнения программы, которое при большем
количестве уравнений может быть значительным, ведь основное время в про-
грамме тратится на вычисление функции w(a, b). С помощью составного масси-
ва (последний оператор программы) расчетные значения х, у и z выводятся из
программы и представлены в виде графика поверхностей х(а, Ь), у(а, Ь) и z(a, b).
9.8.	Нахождение экстремума функции в программе
Средства нахождения экстремума функции в Mathcad (функции minerr и maxi-
mize) имеют серьезные ограничения. Они не могут определить экстремум функ-
ций со скачками и разрывами. Приходится выбирать свои начальное приближе-
ние и ограничения для каждого участка ломаной кривой графика функции,
а также выбирать из нескольких локальных экстремумов один главный. Это оз-
начает, что расчет не проходит автоматически и требует ручного вмешательства
пользователя, для того чтобы корректировать начальные условия и ограничения.
Организовать автоматическое прохождение всех участков внутри программного
модуля тоже не удается. При использовании вычислительного блока Given-(find,
minerr, maximize или minimize) внутри программы вызывается только функция, но
не меняется начальное приближение. К тому же не срабатывают ограничения на
диапазон поиска экстремума. Функции maximize и minimize в принципе не допус-
9.8. Нахождение экстремума функции в программе
241
кают присутствия переменных параметров. В результате эти функции внутри
программного модуля часто дают неверные результаты.
В большинстве практических задач можно использовать простейший перебор
значений заданной функции в заданном диапазоне значений аргумента и вы-
брать из них экстремальное. На рис. 9.16 и 9.17 показан поиск максимального по
абсолютной величине значения ступенчатой функции М(х) без учета размерно-
стей. На графике значения функции взяты по модулю. Поиск максимума функ-
ции выполняется с помощью программы-функции Fmax(F, ZH, ZK, N). Ее парамет-
ры: F — имя функции, для которой ищется максимум; ZH — начало интервала
поиска; ZK — конец интервала поиска; W — число точек внутри интервала поиска,
в которых определяется значение функции.
Рис. 9.16. Безразмерная функция, максимум которой найден на рис. 9.17
Поиск максимума функции
путем перебора ее значений
Поменяйте параметры поиска
Ьд = о Lk=l N = юоо
Fmax* F,Lh,Lk,N) =
L<- Ьд
Al<- |F(L)|
while L < Lr
T T Lx-Lh
L <— L 4-----
N
A2<- |F(L)|
if A2 > Al
A14-A2
Ll«-L
(Al L1)T
Вывод результатов поиска
Mmax = Fmax( M,LH,LK,N(i
Xmax = Fmaxl MjLhjLrjNI
Mmax = 800
Xmax = 2
Рис. 9.17. Поиск максимума безразмерной функции со скачками (см. рис. 9.16)
242
Глава 9. Программирование
Внутри программы вначале определяются значение аргумента L и значение
функции F(L) в начале поиска. Затем внутри цикла (while L < LK) для W значений
аргумента определяются значения функции F(L). Каждое значение функции
сравнивается с предыдущим и, если оно больше предыдущего, записывается как
максимальное At. Как Lt записывается значение ее аргумента. По окончании рас-
чета (закрытии цикла while) последние значения At и Lt выводятся из програм-
мы с помощью составного массива. Для расчета максимума заданной функции
надо в параметры функции вписать истинное имя функции (без параметров)
и числовые значения LH, LK, N.
С учетом размерностей
Н = N кН = 1000 N м = m см = 0 01 м Нм = Н м кНм .= кН м
Поменяйте
М := (200 400 500)ТНм F = (50 400)” Н L = 2-м исходные х = о,— L
данные	100
Рис. 9.18. Размерная функция, максимум которой найден на рис. 9.19
Lji = 0 м Lk := L N = 1000 Поменяйте параметры поиска
В составном массиве вывода результатов расчета
сделать все размерности одинаковыми
F^iF^I^N)^
L <— Гн	= FmaxfMjLHjLj-.N) *
А1<“ |F(L)|	Возвращение
while L < Lk	К ИСХОДНОЙ раЗМерНОСТИ
А2 <- |F(L) I	= 800 Нм
if A2 > Al	Xmax = 2m
Al A2 чтобы избежать сложностей с
L2 <- L размерностями в программах,
т используйте квазиразмерности
Рис. 9.19. Поиск максимума размерной функции со скачками (см. рис. 9.18)
9.9. Учет размерностей в программе
243
Эта программа простая, не использует градиентных методов поиска, но работает
хорошо и полезна для практических расчетов.
В случае выполнения расчетов с учетом размерности в начале расчета вводятся
производные размерности (на русском языке). Далее вводятся исходные данные,
умноженные на производную размерность, и заданная функция (в данном слу-
чае М(х)). Исходные данные и график заданной функции показаны на рис. 9.18.
Поиск максимального значения функции в заданном интервале значений аргу-
мента х показан на рис. 9.19.
Программа поиска максимума та же, что и для расчета безразмерной функции,
но есть нюансы ее использования. Они описаны в следующем разделе.
9.9.	Учет размерностей в программе
Размерности в программном модуле можно учесть, если все выводимые из моду-
ля данные имеют одинаковую размерность.
Производные размерности надо задавать в начале документа. Во внутренних
операторах программы могут использоваться величины любой размерности. Из
программы выводится значение последнего оператора. Если это составной мас-
сив, то все элементы составного массива должны иметь одинаковую размер-
ность. На рис. 9.20 все элементы составного массива имеют размерность длины,
поэтому проблем нет. Программе в этом случае безразлично, учитывается раз-
мерность или нет.
м:= 100 cm csk:=s xr:=kg Н := N производные
размерности
а := 4--- At := 1 • сек	m := Зкг
2
сек
Все результаты расчета одной размерности
Z := for 1 € 1.. 4
Г 4 >
t<- At i
2
SL a t
2
S2	. <- 0.5 a (t- 1сек)
S3	SI + S2
<{4.1}
Z = {4,1} m
k{4.1}>
64j
(Z3)4 = 82m

(SI S2 S3)T
Рис. 9.20. Все выводимые величины одной размерности
На рис. 9.21 из программы выводятся время t, скорость v и путь 5, имеющие, ес-
тественно, разную размерность. В этом случае надо выровнять размерности, сде-
лать их одинаковыми. Для этого элементы составного массива умножаются на
выравнивающую производную размерность, по смыслу каждый раз разную. При
выводе результатов расчета выражение надо умножить на размерность, обрат-
ную выравнивающей. Теперь ответы выводятся в правильной размерности.
244
Глава 9. Программирование
Надо сделать одинаковыми размерности выходного массива.
Затем вернуться к исходной размерности
Z :=
for i € 1.. 4
t Ati
V. <н a t
i
S.f-V.t
i i
Т.<н t
i
V-сек
S
„ M
T----
 сек/
Z = {4,1} m
Рис. 9.21. Выводимые величины имеют разную размерность
Аналогичное выравнивание размерностей проведено в программе Fmax на рис. 9.19.
Так как в последнем операторе (составном массиве величина А1 имеет размер-
ность момента (Нм), то и второй элемент этого массива, L2, должен иметь раз-
мерность момента силы, а не длины (м), поэтому он умножается на размерность
Н — ньютон. Для возвращения к правильной размерности результат расчета хтах
разделен на размерность Н ~ ньютон.
С использованием размерностей в программе выполнен пример 5 части IV книги.
9.10.	Решение дифференциальных уравнений внутри
программы
Возможности решать дифференциальные уравнения в теле программного моду-
ля в Mathcad крайне ограничены. Каждый оператор внутри программного моду-
ля должен возвращать число. Функция Odesolve возвращает функцию и по этой
причине не может использоваться в программах старых версий Mathcad. Остает-
ся использовать в программах старые функции решения дифференциальных
уравнений. На рис. 9.22 показано использование функции rkfixed. В программе
можно варьировать лишь два параметра: границы интервала интегрирования
и число точек, в которых выводится решение.
ПРИМЕЧАНИЕ ----------------------------------------------------
В старых версиях Mathcad нельзя изменять параметры самого дифференциального урав-
нения, что как раз и необходимо в практических задачах.
В Mathcad 13 уже разрешено изменение параметров функции Odesolve внутри программ-
ного модуля (рис. 9.23 и 9.24).
Использование функций, дающих решение в двух точках, возможно. Оно анало-
гично примеру, приведенному на рис. Й.22, и столь же бесполезно.
В Mathcad 13 появилась возможность использовать функцию Odesolve в про-
граммных модулях. На рис. 9.23 приведено решение дифференциального урав-
9.10. Решение дифференциальных уравнений внутри программы
245
71 < 7^
z	bb = 2
Z2<'1'>«—zi	1з,
(bb Z2)T	р 0.2491
ZT = 5 0.012
,5 0 001 J
у = 0 обнуление предыдущего массива у
у' + 3 • у = 0	исходное уравнение
У1 = 5 начальное приближение у(0)=5
D(x,y) = -3 I yi j	первая производная в явном виде
Вариируемые параметры
а = о ь = 3 границы интервала интегрирования
п = 1 число точек, в которых выводится решение
ZZ = for i е 1 . b	,,	_
bb := ZZi Z := ZZ2
Z <— Rkadapt(y, а, i, n, D)
правая граница
интервала
интегрирования
решение уравнения в
начале и в конце
интервала
интегрирования
Рис. 9.22. Решение дифференциального уравнения внутри программы
нения свободных затухающих колебаний с переменными параметрами, оформ-
ленное в виде функции пользователя D(m, /г, k).
Далее поставлена задача найти значения коэффициентов дифференциального
уравнения, при которых решение ОДУ наилучшим образом соответствует экспе-
риментальным данным. Решение ОДУ (функция х <— D(m, /г, k)) введено в под-
программу локально (см. рис. 9.24).
В предыдущих версиях каждый оператор в программном модуле должен был
быть числом. В Mathcad 13 такой оператор может быть просто функцией, ко-
торой в дальнейшем надо присвоить численное значение. Так, на рис. 9.24
первый оператор в подпрограмме Err х <— D(m, /г, k) является функцией и как
бы принят к сведению. Второй оператор, x(tt)> является уже числом и участву-
ет в расчете.
Вектор отклонения решения ОДУ от экспериментальных данных рассчитывает-
ся в подпрограмме Err. Оператор (x(tt)-xx) благодаря векторизации одновре-
менно вычисляет весь вектор отклонений аналогично оператору цикла.
Для нахождения параметров, обеспечивающих минимальное расхождение рас-
четных и опытных данных, использована функция minerr, в вычислительном
блоке которой в итерационном процессе многократно вызывается подпрограмма
Err. В процессе выполнения подпрограммы minerr многократно вызывается
функция Odesolve, отчего время выполнения оператора велико. Сопоставление
опытных данных с рассчитанными по оптимальным параметрам приведено на
рис. 9.25.
246
Глава 9. Программирование
Экспериментальные данные (перемещение хх от времени tt)
tt := (О 0 6 1 2 1.8 2 4 3 3.6 4.2 4 8 5.4 6)Т
хх:=(1 0.902 0.655 0.337 0.023 -0.228 -0.382 -0432 -0.419 -0 382 -0 245)Т
Подобрать коэффициенты m, h, к дифференциального
уравнения свободных затухающих колебаний системы,
наиболее удовлетворяющие опытным данным
Ю = 0 tk := 6	начало и конец интервала Поменяйте	. _ п
интегрирования	условия	"
А = 1 В .= 1 граничные условия задачи
d2	d
Given	m —,x(t) + 2-h-m-—x(t) + kx(t) = 0
dt	<fc
x(t0) = А x*(t0) = В
D(m,h,k) := Odesolve! t,^)
Рис. 9.23. Функция пользователя с использованием Odesolve
Найдем вектор ошибки Err, используя Mathcad-программу
Функцию х определяем в программе локально
En(tn,h,k) := х <— D(m,h,k)
(<tt) - хх)
Для отыскания минимальной ошибки
используем функцию Minerr
mjh := 0.2 k := 1000 начальные приближения параметров
Given En(ni,h,k) s 0
h := Minerr(m,h,k)
Решение m-0.99
h - 0.205 k - 1017.037
у := D(m,h,k)
Рис. 9.24. Использование функции Odesolve в программе
9.10. Решение дифференциальных уравнений внутри программы
247
Рис. 9.25. Результаты решения ОДУ (см. рис. 9.23)
Решение ОДУ с переменными параметрами, но без программирования
to .= О tk = 6 начало и конец интервала
интегрирования
А = 1 В .= 1 граничные условия
а2
Given	m —-y(t) + k y(t) = 0
dt
y(tO) = O y'(tO) = 1 t= 0,0 02 1
Z(m,k) = Odesolve (t,tfc)	m = 1 k = 500
0	0 2	0 4	0.6	0.8	1
t
Решение предыдущего ОДУ с переменными параметрами
тик при t = 1 с использованием программирования
Zl(m) =
for	 ie	1 .5		r-0.019>
	к«-	- 1000 i		0 003
	m<-	-1+021	Zl(m) =	-0 015
	х<-	-Z(m,k,l)		-0
				
		— X		<-0 005>
Н
Рис. 9.26. Решение ОДУ с переменными параметрами
248
Глава 9. Программирование
Простой пример создания функции пользователя для решения ОДУ с перемен-
ными параметрами приведен на рис. 9.26. Такая функция может использоваться
как внутри программного модуля, так и самостоятельно. Обратите внимание на
то, что функция пользователя 7(щ&):= Odesolve(£, tk) содержит два параметра, т
и k, хотя является функцией трех переменных, т, k, t. При выводе результатов
(на графике и в программе) необходимо писать эту функцию с тремя параметра-
ми
9.11.	Отладка программ
Mathcad — перспективное средство программирования. Создать расчетную про-
грамму в Mathcad можно во много раз быстрее и значительно проще, чем на дру-
гих языках программирования. Кроме того, программа Mathcad — это фактиче-
ски записанный в виде последовательности формул алгоритм решения задачи.
Она абсолютно понятна каждому, знающему суть задачи. В отличие от нее про-
граммы на других языках представляют собой очень трудный для понимания
длинный список операторов.
Приведенная в примере 55 части IV программа решения упруго-пластической
задачи методом конечных элементов — это 3 страницы, на которых в виде фор-
мул записаны операторы, подпрограммы и головная программа. Та же програм-
ма на языке Fortran представляет собой 15 страниц сложных для понимания
операторов.
Складывается впечатление, что создатели Mathcad (фирма Mathsoft) не рассчи-
тывали на применение Mathcad в качестве средства создания серьезных боль-
ших программ. Раздел программирования в Mathcad проработан явно слабее ос-
тальных разделов.
В Mathcad 13 наконец-то появились две функции, Trace и Debug, предназначен-
ные для отладки программ. Увы, эти средства работают лишь в отлаженных про-
граммах и не работают в неотлаженных, где они, собственно, и нужны.
В Mathcad 13 разработчики предусмотрели специальную область окна Mathcad,
называемую Trace Window (Окно отладки), а также дополнительную панель инст-
рументов Debug (Отладка) и встроенные функции trace и pause. Функция trace
осуществляет вывод наблюдаемых переменных в окно отладки; функция pause
приостанавливает вычисления, позволяя анализировать выведенные в окне дан-
ные промежуточных вычислений.
Обращение к этим функциям:
tracef'format string”, х, у, z...);
pausef'format string", х, у, z...),
где format string — строка, содержащая текст (на английском языке), предшест-
вующий выводимому числу; х, у, z... — список аргументов, значения которых вы-
водятся на экран.
9.11. Отладка программ
249
ВНИМАНИЕ ---------------------------------------------------------
Для включения этих функций в работу нужно в меню View выбрать Toolbars ► Debug и
в появившейся на экране панели включить обе кнопки, Touggle Debugging и Trace Window
(рис. 9.27).
Pause/Stop
Step —j- ► 
Toggle debug mode
—View Trace Window
Рис. 9.27. Панель Debug
Строка текста, взятая в кавычки, должна заканчиваться знаком = и порядковым
номером метки в фигурных скобках, которая отмечает оператор, чей результат
действия выводится в окне Trace Window (рис. 9.28).
Нахождение первого элемента вектора,
большего заданного значения К := 1.6
ORIGIN := 1
j := 1.. 7 vj :=	- 1 j - номер элемента
	1	2	3	4	5	6	7
1	0	1	1.26	1.442	1.587	1.71	1.817
tl
J<-1
while |vj| К
zz<— К
tracei -K=(0) j=(l),yj=(2)’ ,K,J ,vj I
J<~J+ 1
tl =	6
V1.71J
ом
K=l. 6, j=3,vj=l. 2599210498 9487
K=l.6,j=4,vj=l.44224957030741
K=l.6,j=5,vj=l.5874010519682
j=l, vj=0
j=2,vj=l
j=3,vj=l.25992104989487
j=4, vj=l.44224957030741
j=5,vj=l.5874010519682
The value = vector{1} [0]
Рис. 9.28. Результат действия функции trace
250
Глава 9. Программирование
ПРИМЕЧАНИЕ ----------------------------------------------------:---
Для вывода результата действия функции trace выделить все выражение с этой функцией
и нажать клавишу = (равно) или написать имя выражения-программы с функцией trace
и оценить выражение, нажав клавишу = (равно).
Функция pause отказывается принимать конкретные числовые значения либо
указанный элемент массива. Примеры, приведенные в файлах помощи Mathcad,
зависают и останавливаются после нескольких операций. Сложность использо-
вания функции pause делает ее бесполезной без доработки в последующих вер-
сиях Mathcad.
Функция Debug работает только в работающей программе. Между тем требуется
вывести сообщение о том, в каком месте происходит сбой программы, то есть
требуется вывод пошаговых значений. В таком виде, в котором она существует,
функция Debug оказывается бесполезной.
Рекомендации, описанные далее, составлены на основании моего личного опыта
программирования.
При разработке программы начните со следующих действий:
□	Составьте формульный алгоритм программы.
□	Выделите и запишите в виде подпрограмм-функций повторяющиеся несколь-
ко раз или просто загромождающие программу части.
□	Составьте головную программу. Она должна быть сравнительно краткой и вклю-
чать в себя обращения к подпрограммам.
Далее начинается отладка программы. Вначале отлаживается каждая подпро-
грамма.
Просмотрите список величин, используемых в данной подпрограмме.
Константы, не изменяющиеся внутри программы, должны быть заданы в основ-
ном Mathcad-документе где-либо выше места использования подпрограммы.
Можно присвоить им значения и в самой подпрограмме, но нежелательно без
нужды увеличивать размер подпрограммы.
ВНИМАНИЕ -------------------------------------------------------------
Переменным величинам, изменяющимся внутри подпрограммы, должны быть присвоены
значения обязательно внутри подпрограммы, или эти величины должны быть записаны
в число параметров в названии подпрограммы-функции. В противном случае величины
будут иметь значения, присвоенные им в основном документе, и не смогут изменяться
в процессе расчета в подпрограмме.
В конце подпрограммы создайте место вывода результатов расчета в виде со-
ставного массива, включив в него как можно больше величин промежуточных
расчетов, выполняемых в подпрограмме. Посмотрите на результаты расчета. Как
правило, программа с первого раза не работает и результатов не дает.
9.11. Отладка программ
251
Щелкните мышью внутри подпрограммы. Посмотрите, есть ли сообщение об
ошибках. Если сообщение об ошибках есть, постарайтесь исправить их, учтя со-
общение.
Чаще всего появляется сообщение «This variable or function is not defined above»
(«Эта переменная или функция еще не определена»). В этом случае проследите
по документу, где этой величине должно быть присвоено значение (внутри про-
граммы, в подпрограмме, в основное документе). Если оно должно быть при-
своено внутри программы, присвойте правильное значение, если в основном до-
кументе — проверьте значение, написав имя переменной и нажав клавишу =.
Если же значение должно быть присвоено в подпрограмме, щелкните на ней.
Если сообщений нет, нужно проанализировать подпрограмму, как описано да-
лее.
Часто встречается сообщение «Value of subscript or superscript is too big (or too
small) for this array» («Значение верхнего или нижнего индекса слишком велико
или слишком мало для этого массива»). В этом случае, если массив вводился
в основном документе, проверьте его значения. Если массив бблыпих размеров,
чем вы задали, значит, надо обнулить массив перед вводом значений. Если мас-
сив вводился внутри программы или подпрограммы, проверьте диапазоны пере-
менных циклов, их соответствие значению ORIGIN. Если ORIGIN = 1, переменные
цикла не должны иметь значение 0.
Демонтаж подпрограммы
PP(P.g.Ag) :=
п <- rows(g)
for i е 1.. n
for j € 1.. 2 NU
куски программы
;for’j”e I’iNU,
! । *
K. Agj if g. s j
(P.-К. •As’j
I J /
otherwise [
Kj,aA® Vi
fP. - K. AgA otherwise
I J /
Монтаж проверочной
программы
AA :=
for i e 1.. n
АА :=
for i е 1.. n
for je 1..2 NU
K. Agi if g.s j
otherwise
(к p Ag)
Рис. 9.29. Изготовление проверочной программы
Если сообщений об ошибках нет, предстоит разделить программу на части для
проверки:
252
Глава 9. Программирование
□	Выделите чёрным цветом проверяемый кусок программы и вырежьте его
в буфер, нажав кнопку Cut (Вырезать).
□	Щелкните мышью вне программы и вставьте в это место из буфера вырезан-
ный фрагмент, нажав кнопку Paste (Вставить).
□	Используемый в программировании знак присвоения <— замените обычным
оператором присвоения значения (:=).
□	Задайте численные значения величин, входящих в вырезанное (и вставлен-
ное) выражение, и посмотрите результат расчета, нажав клавишу =. Добей-
тесь правильного ответа. Оператор цикла или условия вырезается по частям
(рис. 9.29).
□	В любом месте вне программы напишите имя будущей проверочной програм-
мы, оператор присваивания (:=) и, щелкнув на кнопке Add line, создайте не-
сколько мест ввода (про запас).
□	Выделите тело цикла или условия и вырежьте его в буфер.
□	Встайьте вырезанный фрагмент в любое место вне программы.
□	Выделите и вырежьте в буфер заголовок цикла или условия.
□	Вставьте заголовок цикла или условия в нужное место ввода проверочной
программы.
□	Выделите перечеркиванием мышью при нажатой левой кнопке вырезанное
ранее тело цикла или условия и скопируйте его в буфер.
□	В место ввода в проверочной программе вставьте из буфера тело цикла или
условия.
□	Закончите составление проверочной программы, не забыв вставить составной
массив вывода результатов расчета. Проверьте результаты расчета.
Если при выполнении программы не появилось сообщений об ошибке, но и чис-
ленные результаты не выводятся, предстоит полная разборка программы, как
описано ранее. Отлаживайте каждый кусок программы отдельно, а затем встав-
ляйте в основную программу. Важно получить хоть какие-нибудь результаты.
Если наконец вы получили результат, но он неверен, добавьте строки в состав-
ной массив вывода результатов. Выведите для просмотра большинство расчет-
ных величин. Постепенно возвращайте на место вырезанные куски программы
после их отладки.
Конечно, эти способы отладки очень примитивны, но других разработчики
Mathcad пока нам не предоставили. Тем не менее повторяю, что составление
программ в Mathcad более удобно и просто, чем при использовании других язы-
ков программирования, а отладка не труднее, чем, скажем, на языке Fortran. Вре-
мя составления и отладки программы в Mathcad в несколько раз меньше, чем
требуется для выполнения той же работы на языке Fortran.
9.12. Возможности ускорения работы Mathcad
Решение задачи в Mathcad обычно продолжается дольше, чем решение анало-
гичной задачи, полученное при использовании любого из компилируемых язы-
9.12. Возможности ускорения работы Mathcad
253
ков программирования. Это не имеет значения при однократном вычислении
выражения. Однако в больших программах при выполнении многократных рас-
четов (итерационных процедур, расчетов, где переменной является время или
температура) время расчета становится недопустимо большим.
Эта задержка связана с тем, что язык программирования в Mathcad является не
компилируемым, а интерпретируемым, то есть Mathcad перед выполнением каж-
дого оператора выполняет некие подготовительные операции. В компилируемых
же языках программирования подготовительные операции выполняются один
раз, до решения задачи, а после редактирования и компиляции программы соз-
дается объектный модуль (ехе-файл).
Рассмотрим некоторые случаи, когда ускорение решения задачи в Mathcad все-
таки возможно.
Больше всего времени в Mathcad занимает операция интегрирования; Если кур-
сор установлен на знаке интеграла, при нажатии правой кнопки мыши открыва-
ется контекстное меню, предлагающее четыре способа вычисления интеграла.
По умолчанию Mathcad автоматически выбирает адаптивный метод, наиболее
точный, но и наиболее длительный. Выберите другой метод интегрирования.
Для этого щелкните правой кнопкой мыши на значке интеграла. В открывшемся
контекстном меню выберите один из предлагаемых методов интегрирования.
Уменьшите стандартную постоянную ТОС из меню Tools ► Worksheet Option. Воз-
можно, скорость вычисления интеграла возрастет. Проверьте это на примере вы-
числения интеграла Дюамеля, приведенного в примере 36 части IV. В приме-
рах 51 и 52 матрицу масс элемента можно вычислить, как интеграл
dx,
но это очень долго. Счет идет во много раз быстрее, если введены стандартные
матрицы с элементами-формулами.
При интегрировании функции одной переменной расчет многократно ускоряет-
ся, если вместо стандартного оператора интегрирования использовать функцию
Int, описанную в разделе 9.6.
В ряде случаев вместо функции можно использовать матрицы. Если каждый
элемент матрицы является функцией от других матриц, то при вычислении каж-
дого элемента матрицы программа вычисляет всю матрицу, а затем берет из нее
лишь одно значение. В программах в методе конечных элементов при формиро-
вании матрицы жесткости можно записать два вида выражений:
KE(k):=A(k)T CA(k)Fkt;
KEk:= А-С• Ak • Fk t.
При большом числе элементов первое из этих выражений «висит», второе — «ле-
тит». Скорость вычисления второго выражения в сотни раз больше, чем первого.
При работе с большими матрицами, когда используется обращение матрицы (ре-
шение системы уравнений), оператор Д:= К~{Р, хорошо работающий в приме-
254
Глава 9. Программирование
pax 50-54, требует много времени (по методу Гаусса идет пересчет всех элемен-
тов матрицы, включая нули). В методе конечных элементов при работе с лен-
точными матрицами рекомендуется использовать метод Холесского, реализо-
ванный в программе МСНВ. Такая программа включена в пример 55.
Существует немало других возможностей ускорения работы Mathcad и облегче-
ния отладки программ. Главное — сохранить основные преимущества Mathcad:
наглядность, простоту, удобство работы.
Глава 10
Анимация
Mathcad предусматривает возможность анимации графиков и результатов вы-
числений путем создания AVI-файлов и вставки их в Mathcad-документ. Вос-
производятся созданные AVI-файлы встроенными в Windows средствами.
10.1.	Создание анимации
Mathcad имеет встроенную переменную FRAME, предназначенную только для соз-
дания анимационных клипов. FRAME принимает целочисленные значения от 0 до п
и должна быть включена в расчетные выражения так, чтобы с изменением FRAME
изменялся вид соответствующего графика. Фактически FRAME — это номер кадра.
Переменной FRAME нельзя присваивать какое-либо значение в Mathcad-докумен-
те. Диапазон значений FRAME задается в диалоговом окне главного меню коман-
дой Tools ► Animation ► Record (Инструменты ► Анимация ► Запись). Перед созда-
нием анимационного клипа убедитесь, что в главном меню Mathcad в окне Tools
включен режим автоматических вычислений.
Рассмотрим процесс создания анимации:
□	Введите переменную FRAME в математическое выражение, определяющее вид
графика (рис. 10.1).
□	Выберите пункт меню Tools ► Animation ► Record (Инструменты ► Анимация ►
Запись). В разных версиях Mathcad пункт Animation находится в разных мес-
тах главного меню, а в Mathcad 14 и 15 присутствует в стандартном меню.
□	После открытия диалогового окна анимации (рис. 10.1) курсором выделите
нужный фрагмент изображения.
□	В диалоговом окне задайте общее число кадров и частоту их воспроизведе-
ния. Установленное по умолчанию число 10 — слишком большая скорость
воспроизведения кадров. Лучше установить 2-3 кадра в секунду, иначе «кино»
длится 1 секунду.
□	Щелкните на кнопке Animate (Анимировать) и наблюдайте за созданием кад-
ров. Затем появится окно проигрывателя видеофайлов. В этом окне можно ус-
тановить размер кадра и скорость воспроизведения (рис. 10.1, справа), В поя-
вившемся окне Playback можно выбрать Вид (Половинный размер, Обычный
размер — в масштабе 1:1, Двойной размер) и скорость воспроизведения кад-
ров. Если вы оставили в окне анимации 10 кадров в секунду, то движком надо
уменьшить скорость примерно до 30 %. Если в окне анимации вы уже поста-
вили 3 кадра в секунду, то регулятор скорости лучше не трогать, а то скорость
движения станет совсем маленькой и эффекта кино не получится. Размеры
окна можно изменить и обычным способом, то есть растянув его за угол мы-
шью. Однако при этом пропорции окна могут измениться.
□	Созданный клип сохраните с помощью команды Save As (Сохранить как). Со-
храненный файл можно использовать и вне Mathcad-документа.
256
Глава 10. Анимация
□	Сохраненный как AVI-файл клип нужно вставить в Mathcad-документ. Для
этого в главном меню Mathcad выберите команду Insert ► Object (Вставка ►
Объект). Откроется окно Вставка объекта. Выберите в этом окне Создать из
файла. Выберите нужный файл, щелкнув в диалоговом окне на кнопке Обзор
(рис. 10.2).
Желательно нажать кнопку Связь в том же окне. Это позволит редактировать
AVI-файл непосредственно из Mathcad-документа.
Если в том же окне установить флажок В виде значка и нажать ОК, то на месте
курсора в Mathcad-документе появится значок AVI-файла. Двойной щелчок мы-
шью на этом значке вызовет появление проигрывателя видеофайлов и исполне-
ние анимации.
Если флажок В виде значка не устанавливать, то после нажатия кнопки ОК на
месте курсора в Mathcad-документе появится картинка с первым кадром AVI-
файла. Двойной щелчок мышью на этом значке вызовет появление проигрывате-
ля видеофайлов и исполнение анимации.
х:= 0,0.1.. 30	r(x)=x+FRAME
Рис. 10.1. Пример подготовки анимации графика
Вид
Скорость
Открыть...
Закрыть
Копировать
Настройка... Ctrl+D
Команда...
Вставленный в документ AVI-файл можно отредактировать. Для этого щелкните
на объекте (значке или картинке) правой кнопкой мыши. В появившемся кон-
текстном меню выберите Связанный объект: Видеозапись ► Правка, как показано
на рис. 10.3.
В открывшемся окне редактирования (рис. 10.4) выберите пункт Правка ►
Параметры. Желательно установить флажок Автоповтор, тогда «кино» бу-
дет длиться бесконечно долго, до тех пор, пока вы не щелкнете мышью вне
объекта.
10.1. Создание анимации
257
Рис. 10.2. Диалоговое окно вставки Объекта
Properties...
сь
Рис. 10.3. Начало редактирования AVI-файла
Файлы анимации (AVI-файлы) обычно занимают много места на диске. Mathcad
позволяет сохранять их в сжатом формате. Перед созданием анимации можно
выбрать, какие методы сжатия использовать и сжимать ли файл вообще. Для
этого в диалоговом окне Animate (см. рис. 10.1) нужно выбрать Options (Свойст-
ва), а в окне Compressor Options (Параметры сжатия) — программу сжатия или ко-
манду Полные кадры (без сжатия), рис. 10.5.
ВНИМАНИЕ--------------------------------------------------------------
При создании анимационных клипов рекомендуется отключить автоматическое масшта-
бирование графика, так как возможны скачки изображения при изменении масштаба. Вве-
дите числовые значения на осях графика вручную.
258
Глава 10. Анимация
55 qq1.avi - Видеозапись в Client Document
Файл Правка Устройство Шкала Справка
6,00 6,10 6,20 6,30 6,40 6,50 pen 670 ляп ляп i лл
i(x)-===j
____ 180 j
210
150
180
qql.a
210
Рис. 10.4. Установка параметров редактирования AVI-файла
For FRAME
From:	|o
Io:	[9
At:	|1O
Frames/Stjc
FRAME®
Select ап area of your worksheet whose contents are based on
the FRAME variable, enter starting and ending FRAME values,
and choos e Animate.
Compressor Options
Программа сжатия:
Полные <.адры (без сжатия)
I nt el I nde з® Video R3.2
Microsoft Video 1
Microsoft RLE
Видео Indeo® 5.04
VD 0 net VDO Wave_________
Полные |.адры I бе;. слатияГ
Рис. 10.5. Выбор метода сжатия AVI-файла
Рекомендую вставить анимационный клип в Mathcad-документ не в виде значка,
а в виде картинки. После этого график, на основе которого сделан клип, можно
удалить. Двойной щелчок мышью в поле объекта приведет к воспроизведенцю
клипа.
10.2. Галерея анимационных клипов
259
10.2.	Галерея анимационных клипов
Рисунки 10.6-10.11 иллюстрируют некоторые возможности анимации. Исполь-
зуются различные типы графиков и числовая анимация. Для наглядности на ри-
сунках использовано значение FRAME = 13, то есть изображен 13-й кадр анима-
ции. Самостоятельно изготовьте анимационные клипы. Перед анимацией необхо-
димо отключить оператор FRAME:=13.
Много интересных примеров анимации объектов (графиков и числовых дан-
ных) приведено в файлах помощи Mathcad и в электронной книге (примеры 6
и 26).
х:= 0,0.1 ..30
<х) := х + FRAME
Рис. 10.6. Движение спирали
n := FRAME0.2
Рис. 10.7. Американские горки
n := FRAME-0.2
F(y,x) : sin(nx)-cos(ny)
F
Рис. 10.8. Рост леса синусоид
i:=0..20	j:=0..20	L:=11..2O
Af .:«i-FRAME-0.06
AT .:« (20 - L)-FRAME-0.03
Рис. 10.9. Строительство сарая
260
Глава 10. Анимация
0.. FRAME + 1
g^icosG)
(g.h.k)
к. =
1
о
10
~20
"10
—40
~50
”60
То
80
То
Too
ТГо
"ПО

0	0
0.54	0.841
-0.832	1.819
-2.97	0.423
-2.615	-3.027
1.418	-4.795
5.761	-1.676
5.277	4.599
-1.164	7.915
-8.2	3.709
-8.391	-5.44
0.049	-11
10.126	-6.439
Рис. 10.10. Смерч
a:=2FRAME i:=0..40 j:=0..40
F
Рис. 10.11. Анимация кбнтурной карты. Установите FRAME =18
Глава 11
Учет размерностей
В Mathcad возможны вычисления с учетом размерностей используемых вели-
чин. Единицы измерения, хотя они и не требуются в выражениях Mathcad, могут
помочь упростить ввод данных, обнаружить ошибки и улучшить отображение
результатов вычислений.
Присвоение числу размерности эквивалентно его умножению на размерность.
Внутренний алгоритм Mathcad умножает число на переводной коэффициент, со-
ответствующий вписанной размерности, и все вычисления выполняет с безраз-
мерными числами, соответствующими СИ (Система интернациональная).
11.1.	Выбор системы единиц измерения
В Mathcad встроено большое количество единиц измерения. С ними можно об-
ращаться как со встроенными переменными. Чтобы связать единицу измерения
с числом, достаточно умножить число на ее наименование.
Перед началом работы с размерными величинами надо установить систему еди-
ниц, в которой вы будете работать:
□	В главном меню Mathcad выберите Tools ► Worksheet Options ► Unit System
(Инструменты ► Параметры документа ► Система единиц), как показано на
рис. 41.1.
□	В открывшемся диалоговом окне выберите систему единиц, например SI
(International). Щелкните на кнопке ОК. Если в диалоговом окне выбрать None
(Нет), то никакие размерности в расчете не учитываются.
Рис. 1Т.1. Выбор системы единиц
262
Глава 11. Учет размерностей
После этого просмотрите встроенные единицы измерения в выбранной системе.
Для этого на стандартной панели Mathcad щелкните на кнопке Insert Unit (Вста-
вить единицу) с изображением мерной кружки. Вначале ничего вставлять не
надо, просто познакомьтесь со списком единиц, которые можно использовать
в расчетах по умолчанию. В дальнейшем в начале документа при вводе исходных
данных для расчета их надо записывать, умножая число на стандартное обозна-
чение размерности, которое можно ввести с клавиатуры либо выбрать в окне
Insert Units (Вставить единицы измерения), щелкнув мышью на соответствую-
щем обозначении (рис. 11.2).
Подробные сведения по использованию размерностей в Mathcad можно найти
в файлах помощи Mathcad (рис. 11.3).
Рис. 11.2. Окно вставки встроенных единиц измерения
Рис. 11.3. Получение справки по единицам измерения в Mathcad Help
11.2. Ввод пользовательских единиц измерения
263
В Mathcad 13 появилась возможность устанавливать смешанную систему раз-
мерностей. Для этого нужно в меню Tools ► Worksheet Options ► Units System уста-
новить флажок на пункте Custom. Затем выбрать систему, на которой будет ба-
зироваться новая система размерностей, например SI или MKS, нажать кнопку
Change и выбрать что-нибудь из предложенных размерностей (рис. 11.4). С точ-
ки зрения российских пользователей, это бесполезное нововведение, так как
предлагается выбрать лишь из размерностей, употребляемых в западном мире,
например, добавить фунты, дюймы, галлоны и т. д. Ввести наши производные
размерности, тем более на русском языке, невозможно.
Рис. 11.4. Установка смешанной системы размерностей
11.2.	Ввод пользовательских единиц измерения
Обозначать размерности нам привычнее русскими буквами, а это уже нестан-
дартное обозначение размерностей.
Для ввода пользовательских обозначений размерностей нужно:
□	выбрать пункт главного меню Mathcad Tools ► Worksheets Options (Инстру-
менты ► Параметры документа) и перейти на вкладку Dimensions (Размерно-
сти), показанную на рис. 11.5;
□	установить флажок Display dimensions (Показывать размерности). Удалить
старые размерности и ввести с клавиатуры свои размерности, абсолютно лю-
бые;
□	в начале Mathcad-документа ввести производные от исходных размерностей
(рис. 11.6). Далее можно вводить исходные данные, умноженные на размер-
ности стандартные (на английском языке) или производные от стандартных.
После вычисления результаты расчета будут появляться на экране уже с вве-
денными вами размерностями.
264
Глава 11. Учет размерностей
Рис. 11.5. Ввод пользовательских размерностей
Ввод размерностей, производных от базовых
метр := m кг := kg сек := s Н := N т := 1000 • кг
кН := 1000 • N Р := 3 • кН мин := 60 • сек час := 3600 • s
можно и так мм := mm мин := min час := hr км := km
Ввод величин со стандартными размерностями
a:=2 m М := 5000 kg t:= 120 s Р := 3000 • N
Ввод величин с производными размерностями
а := 2 • метр М := 5 • т t := 2 • мин Р := 3 • кН
Вывод на экран, если в меню Math Option:
Своих размерностей нет
а = 2m М = 5000kg t = 120sec Р = 3000kgmsec
Введены свои размерности масса-кг, длина-метр, время-сек
-2
а = 2 метр М = 5000 кг t = 120 сек Р = 3000 кг метр сек
В поле ввода вписаны производные размерности
а = 2000мм М = 5т t = 120сек Р = ЗкН
Рис. 11.6. Пример ввода размерностей в исходных данных к расчету
11.3.	Изменение масштаба результатов расчета
Часто бывает нужно вывести результаты расчета в размерностях, кратных исход-
ным, например, вместо килограммов использовать тонны, вместо метров — кило-
11.3. Изменение масштаба результатов расчета
265
метры, вместо секунд — часы или минуты. Производные размерности вводят как
обычные константы, с использованием оператора присваивания := (рис. 11.6).
ПРИМЕЧАНИЕ ----------------------------------------------------------
Производную размерность нельзя определить, умножив число на пользовательскую раз-
мерность, вписанную на вкладке Tools ► Options ► Dimensions (Инструменты ► Параметры
документа ► Размерности). Умножать число надо на стандартную размерность, записан-
ную на английском языке, или на другую производную размерность, которой ранее в доку-
менте присвоено какое-либо значение.
При выводе результатов расчета после нажатия клавиши (=) появляется число
и рядом с ним — место ввода единицы размерности. Если число уже имеет раз-
мерность, то рядом с размерностью появляется еще одно место ввода. Сюда мож-
но поместить любую переменную, константу или выражение.
ВНИМАНИЕ -------------------------------------------------------------
Не забудьте, что всякий раз, когда что-нибудь находится в месте ввода единицы измере-
ния, Mathcad изменяет полученный результат так, чтобы произведение числа и выраже-
ния, стоящего на месте размерности, давало правильное значение.
Можно использовать место ввода, чтобы выразить, например, значение угла
в долях числа тг или вывести числовой коэффициент при каком-то буквенном
выражении. На рис. 11.7 рассчитанная величина А выведена двумя способами:
1. Естественным для Mathcad — в единицах, введенных в окне Worksheet Options
(Параметры документа).
Ра
2. Выведен числовой коэффициент при — .
Р = 3 кН t := 120 • s а := 2 m А :=
5 а
Pt
---dx
2
х
А = 144000 кг-сек'^
Ответ в размерностях меню Dimension ,
В поле ввода размерности введено —-	А = 0.8Р - -
а	а
Рис. 11.7. Ввод какого-либо выражения на место ввода размерности
Для расчета тригонометрических функций Mathcad требует ввода угловых зна-
чений в радианах. При выводе результатов в радианах иногда желательно пред-
ставить их в градусах. Для этого в поле ввода надо вписать deg (градус). Появит-
ся ответ в градусах (рис. 11.8).
Если исходные данные для расчета введены с размерностями, то выводимый ре-
зультат расчета всегда будет содержать размерность в стандартном обозначении,
если вы не вводили пользовательскую размерность, или пользовательскую, если
вы ее вводили.
266
Глава 11. Учет размерностей
град = deg
asm(0.5) = 0.524
asin(0.5) = 0.524 rad
asin(0 5) = 30 deg
180
asin(0.5)-----= 30
7T
atan(l) = 0 785
atan(l) = 0 25 tt
atan(l) = 45 град
atan(l) = 45
180
Рис. 11.8. Вывод значения угла в радианах и в градусах
Если где-либо введены производные размерности, например, как на рис. 11.6,
и вы хотите видеть результат в этой размерности, то сделайте следующее:
□	установите курсор в поле ввода справа от выведенной размерности и введите
производную размерность. При этом исчезнет не только старая размерность,
но и сам числовой результат расчета;
□	щелкните мышью вне выражения. Появится новое число, соответствующее
введенной вами размерности, и сама размерность (рис. 11.9).
В поле вывода числа в черный квадратик вписать
свою введенную размерность-результат изменится.
t := 2 мин Р > 3 кН
v:=gt Мгог:=Ра
v = 1177.2 метр сек
у =1177^
а > 50 см g := 9.81
метр
2
сек
2
кгметр
Мюг= 1500---
сек
2
Мюг= 1500^_
сек
размерность,
введенная в меню
размерность
форматирована
v = 4237.92 — Мизг « 1.5 кН • m вписана своя размерность
час
дробная размерность
7 _ 1ПЛ 74?1ггР
Z. = 1ио./4окг метр сек
Рис. 11.9. Вывод результатов расчета в различных размерностях
11.5. Размерность элементов массива
267
В зависимости от вычисляемого выражения размерность может быть как в сте-
пени, обозначенной целым числом, так и в дробной степени.
Можно включить автоматический перевод единиц измерения в более простые
формы:
□	Дважды щелкните мышью на результате вычислений — откроется диалоговое
окно Result Format (Формат результата).
□	Выберите в нем команду Unit Display (Отображение единиц измерения).
□	Установите оба флажка, Format Units (Формат размерностей) и Symplify units
when possible (Упрощать размерности, если возможно).
□	Если вы щелкнете на кнопке ОК, то к выделенному выражению будет приме-
нено упрощение размерностей. При выборе Set as default (Установить по
умолчанию) упрощение размерностей будет применено ко всему документу.
11.4.	Учет внесистемных размерностей
Иногда бывает удобно вести расчеты в своих собственных единицах измерения,
которых нет в системе СИ, например, подсчитать количество мешков, людей, ма-
шин и т. д. Такие размерности назовем внесистемными. Их можно обозначить
как константы.
м := m человек := 1 квартира := 60 • м дом := 200 • квартира
в городе проживает М := 10б  человек
в городе N := 2000 • дом
В среднем по городу	2
жилплощадь на 1 человека s := —	S = 24———
М	человек
_	м М	человек
Проживает людей m := — в одной квартире m = 2.5-----------
N	квартира
в одном доме m = 500-------
дом
Рис. 11.10. Учет внесистемных размерностей
На рис. 11.10 приведен пример расчета плотности населения в городе. В качестве
единиц измерения взяты человек, квартира, дом. Если квартира измеряется
в квадратных метрах, то человек — внесистемная размерность. Размерность
плотности заселения города т вписана в черный квадратик ввода рядом с числом.
11.5.	Размерность элементов массива
Размерность элементов массива вводится так же, как и размерность чисел, умно-
жением выражения на стандартную размерность на английском языке или про-
изводную размерность, введенную ранее. Действия с размерными массивами по-
казаны на рис. 11.11.
268
Глава 11. Учет размерностей
<1 2 3^
А := 2 3 4 кН
<3 4 5,
<1000
А= 2000
<3000
2000 3000 >
кгметр
3000 4000 --------
2
4000 5000 J сек
<0.02^
V = 0.04 метр
V = 4 см
10.06 У
<280^
А • V = 400 кгметр'
<520,
2	-2
) сек
A-V =
<280^
400
<520 J сек
2
кгметр
2~
/0.28^
AV= 0.4 метр кН
<0.52 J
Рис. 11.11. Работа с размерными массивами
Массив А введен в килоньютонах, массив V — в миллиметрах. При выводе резуль-
тата Mathcad использует размерности, вписанные на вкладке Dimensions (Размерно-
сти), — кг м2 с2. После установки флажка Format units (Формат размерностей)
кг • м2 „
размерность на экране меняет вид на---—. Для ввода производной размерности
с
«кН» надо в дополнительное место ввода вписать «кН», при этом численный резуль-
тат исчезает. Щелчок мышью вне выражения — и результат пересчитан в метр • кН.
ВНИМАНИЕ----------------------------------------------------------------
Размерности всех элементов массива должны быть одинаковыми.
t-О..З w>0.12 V(t)=wt- —
hr
V(t) =
размерность
стандартная
V(t) =
____о
0.12
0^7
0.36
км
час
метр сек
0.033
0.067
——-	введенная
Рис. 11.12. Ввод и вывод размерной функции
11.7. Построение графиков с учетом размерностей
269
11.6.	Учет размерностей в цикле
Дискретная переменная может быть размерной. При использовании ее размер-
ность можно учесть, поместив дискретную переменную выше определения функ-
ции и введя размерность в определение функции (рис. 11.12) или записав дис-
кретную переменную с помощью размерных величин. Можно также в дискрет-
ной переменной умножить числа на соответствующую размерность. •
При выводе результата расчета появляется размерность, введенная пользователем
на вкладке Dimensions (Размерности) (на русском языке). Для ввода производной
размерности надо вписать ее в место ввода справа от выведенной размерности.
11.7.	Построение графиков с учетом размерностей
Графики строятся в стандартных размерностях, приведенных в списке встроен-
ных функций. Ввести пользовательские размерности на графиках нельзя. Для
изменения масштаба графика разделите на графике названия аргумента и функ-
ции на размерность (рис. 11.13).
Выполните самостоятельно упражнения с размерностями, приведенные на рис. 11.14.
График построен (по умолчанию) Скорость в км/час
в m и s. т.е. в метр и сек	Время в мин
Рис. 11.13. Учет размерности при построении графика
Дано:
а := 50 • см
b := 20 • мм
h := 40 • мм Р := 3 • кН
_ кН
q := 10 —
м
М := 20  кН м Е := 2 105 МПа
самостоятельно поиграйте с размерностями
М > Р • а
з
Р _ М „Ра
арест агог:=- f> —
Рис. 11.14. Упражнения для самостоятельной работы с размерностями
270
Глава 11. Учет размерностей
11.8.	Учет размерностей в программе
Размерности в программном модуле можно учесть, если все выводимые из моду-
ля данные имеют одинаковую размерность. Примеры использования размерных
величин в программах приведены в разделе 9.9 и в примерах 5 и 19 электронной
книги.
При составлении сложных программ, когда из программного модуля нужно вы-
вести несколько величин (скаляров или массивов) различной размерности, сле-
дует выполнять расчет без учета размерностей. В этом случае программный мо-
дуль получается компактным, сравнительно простым и понятным. При учете
размерностей придется составлять несколько программных модулей и из каждо-
го модуля выводить величины одной размерности. Расчет получается значитель-
но более сложным.
При составлении простых программ, где выводится только одна величина, ис-
пользование размерностей допустимо и только украшает программу.
11.9.	Ограничения на проведение расчетов
с учетом размерностей
□	При расчетах с матрицами все элементы используемых в расчетах матриц
должны иметь одинаковую размерность.
□	Ряд встроенных функций не могут работать с размерностями. Это функ-
ции:
6 н
Н = N м = m МПа = 10 • — цикл := 1
м
сталь ДОХ ств := 1000 • МПа Зк := 2 • ств стсим := 0.5 • ств Nq := 3 • 10^ • цикл
Построение усталостной кривой
в логарифмических координатах
lgo(x) := lintetp(X,Y,x)
ДО :=0..1og(N0)
( logCD
Ijog(No) J
1 I I
log --
ДМПа7
I СТСИМ I
log --
V ДМПа^
]gp(]gN)
• ••
Рис. 11.15. Вычисление логарифма размерного числа
11.10. Статическая проверка размерностей
271
О интерполяции, регрессии, сглаживания;
О Odesolve (решение дифференциальных уравнений);
О In, log (вычисление логарифма числа).
В таких случаях нужно вводить безразмерные аргументы функции, разделив
размерную величину на ее размерность (рис. 11.15).
Примеры инженерных расчетов с учетом размерностей приведены в части IV
(примеры 5, 9-20, 47, 49, 53).
11.10.	Статическая проверка размерностей
В *Mathcad 12, 13 и 14 ужесточен контроль правильности использования размер-
ностей. Применена техника статической проверки размерностей, запрещающая
расчет функций, которые в зависимости от значения аргумента могут возвра-
щать результат различной размерности. Например,/(0) = 1/п2, а/(1) = 1/п3.
В Mathcad 13 встроены функции статической проверки размерностей. До вычис-
лений Mathcad проверяет размерности всех введенных величин слева направо
и при наличии ошибок (реальных или кажущихся) выводит сообщение о том,
какими размерности должны быть (рис. 11.16).
а = 2 м Ъ = 3 м
D = ^ + Ь2
Значение имеет единицы измерения: длинаЛ2,
а должно иметь единицы измерения: длина.
Рис. 11.16. Результат статической проверки размерностей
Другой способ анализа размерностей состоит в том, чтобы записать имя функ-
ции без указания параметров. В Mathcad Ив этом случае выводилось слово
«function». В Mathcad 13 при написании имени функции без параметров выво-
дится перечень размерностей, использованных в функции (рис. 11.17). На этом
рисунке апу1, апу2 и апуЗ обозначают размерность первого, второго и третьего
параметров, указанных в имени функции. Индекс соответствует степени этой ве-
личины в правой части выражения. Если параметром функции является другая
функция, то в перечне параметров появляется /(список параметров) (рис. 11.17,
выражение для Д1).
После знака равенства появляется ожидаемая размерность результата расчета
выражения. Для величин, входящих в правую часть выражения, указывается
конкретный класс размерности (давление, масса, длина, время). Кроме указан-
ных видов записи в сообщениях встречаются слова unitless — безразмерный
и [апу1] — размерный массив.
Для практических расчетов статическая проверка размерностей — вещь не только
бесполезная, но и вредная. В ряде примеров инженерных расчетов, приведенных
272
Глава 11. Учет размерностей
6FL	4FL f ч 4FL
cr(b,h,F) :=---- A(b,h) :=------- Al(b,h,o) :=----------o(b,h,F)
bh2	Ebh3	Eb-h3
ст = f(anyl, any2, апуЗ) => апу1Л-1 • апу2Л-2  апуЗ • Length
A = ffanyl • апу2Л3 • Pressure^!, апу2Л-1) => апу1Л-1 • Mass • Length'M  TimeA-2
Al = f(anyl, any2, ffanyl, any2, Force) =>4any3) => anylA-l • апу2Л-3 • апуЗ • Lengths
Рис-11.17. Статическая проверка размерностей функции без параметров
К(у,ф) =
/	7 о	X
Дг(р,го,6,у) 10	+ г(у)
поверхность цилиндрической
оболочки после деформации
S = CreateMesh(K,0,L,0,2-7v,fmap)
ЧуР
К1(у,ф) = ф
поверхность цилиндрической
оболочки до деформации
S 1| .= CreateMesh(K 1,0, L, 0,2 тг,ftnap)
Значение имеет форму: (длина, длина, длина, Unitless),
а должно иметь форму: Unn~up4 длина.______________
Рис. 11.18. Фрагмент примера 44 из электронной книги
в электронной книге, функции, в том числе встроенные, хорошо работающие
в Mathcad И, не работают в Mathcad 13 (рис. 11.18). Если в ранних версиях
Mathcad ряд функций (regress, Odesolve, CreateMech и др.) допускали использо-
вание размерных величин, когда размерность совпадала с базовой в системе СИ,
то сейчас с этим строго: в Mathcad 13 никакие размерные величины в таких
функциях уже не допускаются.
Подводя итоги этой главы, следует заметить, что учет размерностей несложен
для простых задач, где синими и так все ясно. В сложных расчетах при использо-
вании многих функций и нескольких дискретных переменных учет размерно-
стей может оказаться сложным, а в ряде случаев вообще невозможным. В таких
случаях размерность можно указать рядом с результатом расчета в виде тексто-
вого комментария (для справки).
11.11.	Квазиразмерности
Как следует из предыдущих разделов этой главы, учет размерностей очень прост
в простых примерах и очень сложен в сложных примерах. Многочисленные об-
ращения к фирме Mathsoft с предложениями об уменьшении числа ограничений
на использование размерностей в расчетах остались без ответа. Мне пришла
в голову идея, как упростить использование размерностей в расчетах. По сути
11.11. Квазиразмерности
273
дела процесс присвоения числу размерности состоит в умножении числа на не-
который числовой коэффициент. Буквенному обозначению размерности доста-
точно присвоить численное значение, не умножая его на стандартную размер-
ность.
На рис. 11.19 показан пример учета квазиразмерностей в расчетах. Вначале про-
изводится присвоение квазиразмерностям численного значения. Далее записаны
исходные данные, умноженные на квазиразмерности. Затем введены расчетные
формулы и выведены результаты расчета:
□	без учета размерностей, то есть в системе СИ (в ньютонах и в метрах);
□	с учетом размерностей, для этого в черный квадратик ввода размерностей
(справа от числа) вписана размерность.
На графиках, которые в Mathcad по определению не работают с размерностями
и выводят результаты в системе СИ, имена переменной и функции делятся на
размерность, как обычно.
Квазиразмерность - это просто числовой коэффициент
при стандартной размерности в системе СИ
м = 1 см = 0.01 мм = 0.001 кН s 1000 кНм s 1000 МПа s 10б
Исходные данные, умноженные на квазиразмерности
F = 3 кН L = 2 м d := 12 см Е := 2 105 МПа q .= 2 —
м
Расчетные формулы
4	3	7 М	F • L
J = 0 05 d W = 0.1 d М = q L ст := — Д .=---------
W 3 EJ
Результаты расчета без учета размерностей, то есть в системе СИ
-5	-4
J = 1.037 х 10 W = 1.728 х 10 М = 8000 ст = 46296296 Д = 0.004
Д = 3 858 • мм
Результаты расчета с учетом квазиразмерностей
4	3
J= 1036.8 см W= 172.8 см М = 8 кНм ст = 46-МПа
см
Рис. 11.19. Учет квазиразмерностей в расчетах
кНм
274
Глава 11. Учет размерностей
ПРИМЕЧАНИЕ ------------------------------------------------------------
Стандартный ввод размерности — производной размерности присваивается число, умно-
женное на стандартную размерность.
Ввод квазиразмерности — производной размерности присваивается число.
Использование квазиразмерностей позволяет избежать всех ограничений, пере-
численных в разделе 11.9, а также использовать размерности в программах
и матричных расчетах.
При использовании квазиразмерностей Mathcad уже не следит за правильно-
стью использования размерностей и вся ответственность за результаты расчета
ложится на расчетчика, который сам должен следить за логикой расчета и впи-
сывать в поле ввода ответа правильную размерность.
Большинство примеров в этой книге разрабатывались постепенно в течение ряда
лет. Все они могут быть легко перестроены с использованием квазиразмерно-
стей. Необходимости в этом нет, но в дальнейшем я постараюсь использовать
в расчетах именно квазиразмерности.
Глава 12
Дополнительные встроенные
функции Mathcad
В предыдущих главах рассказывалось о наиболее часто используемых в работе
встроенных функциях. В этой главе речь пойдет о функциях, сравнительно ред-
ко используемых, поэтому описание функций дано в краткой форме с некоторы-
ми примерами. Дополнительные сведения о работе с этими функциями можно
найти в разделе Help (Помощь) главного меню Mathcad. Проще всего найти опи-
сание нужной функции, нажав на стандартной панели инструментов Mathcad
кнопку Insert Function (Вставить функцию) со значком f(x). Найдите в открыв-
шемся списке нужную функцию и щелкните на ней мышью. Прочитайте внизу
описание функции. Для получения дополнительных сведений нажмите кнопку ?
(знак вопроса) — откроется раздел справки, посвященный этой функции. В кон-
це каждого раздела есть ссылки на сопутствующие разделы и на примеры ис-
пользования функций. Совершим обзор встроенных функций. Откроем в стан-
дартном меню Mathcad пункт Insert Function и рассмотрим основные группы
функций. Полагаем, что х — вещественное безразмерное число, х > 0.
ПРИМЕЧАНИЕ -----------------------------------------------
Для удобства работы с матрицами во всех примерах этой главы ORIGIN = 1.
12.1.	Функции для работы с комплексными числами
Комплексные числа в Mathcad можно ввести тремя способами:
□	в виде суммы вещественной и мнимой частей, С,— а + Ы;
□	в тригонометрической форме, С:= >l(cos(ip)+ ci -sin(ip));
□	в экспоненциальной форме, С:= Ае1С,
Ввод мнимой единицы 1 i или 1j или i = -J-i
Способ ввода комплексного числа
С = а + b i = А (соз(ф) + с 1зш(ф)) = А е С
Примеры ввода комплексных чисел
а = 3 b •= -5	с = 12 А = 120	ф = 20 deg
С = a + bi	С = 3-51
С = Ае1С	С = 101 3-64 41
С = А[соз(ф) + с (151п(ф))] С = 112 8 + 492 51
|с| = 505.3 модуль комплексного числа
arg(C) = 1 3 arg(C) = 77.1 deg аргумент комплексного числа
Рис. 12.1. Ввод комплексных чисел
276
Глава 12. Дополнительные встроенные функции Mathcad
Чаще всего комплексное число возникает в расчетах как результат вычисления ка-
кого-либо выражения. Примеры ввода комплексных чисел приведены на рис. 12.1.
ВНИМАНИЕ------------------------------------------------------------
Напомним, для ввода мнимой единицы надо ввести 1i или 1 j. После вывода курсора из об-
ласти числа единица исчезает и Mathcad воспринимает число как комплексное.
Mathcad содержит несколько функций для работы с комплексными числами:
□	Re(z) — действительная часть комплексного числа z;
□	lm(z) — мнимая часть комплексного числа z;
□	arg(z) — аргумент комплексного числа z, —tv < arg(z) < %
□	csgn(z) — функция комплексного знака числа (возвращает либо 0, если z = 0;
либо 1, если Re(z) > 0 или Re(z) = 0 и lm(z) > 0; либо -1 — в остальных слу-
чаях);
□	signum(z) — возвращает 1, если z = 0, и z/|z| — в остальных случаях.
Здесь z — вещественное, мнимое или комплексное число.
Примеры использования указанных функций приведены на рис. 12.2.
z := 20 - 5-х Re(z) = 20 Im(z) = -5 arg(z) = -0.245
csgn(z) = 1 signum(z) = 0.97 - 0.2431 arg(z) = -14.036 deg
“gO -1 !
| This must be either a scalar or a vector. |
signutn(zl) =
( 0.894 - 0.4471
-0.894+0.4471
< -1
f-0.464^
arg(zl) = 2.678
<3.142;
Рис. 12.2. Функции для работы с комплексными числами
Функции Re и Im могут работать со скалярами, векторами и матрицами. Осталь-
ные функции с матрицами работать не могут.
Все функции, содержащиеся в двух последующих разделах меню Insert Functi-
on, — Curve Fitting (Функции регрессии) и Differential Equation Solving (Функции
решения дифференциальных уравнений) — были подробно рассмотрены в гла-
вах 2, 6 и 7, поэтому переходим сразу к разделу Expression Туре (Тип выражения).
12.2.	Тип выражения
Изначально в этом разделе было четыре функции:
□	lsArray(x) — возвращает 1, если х — матрица или вектор, иначе возвращает 0;
12.3. Доступ к файлам
277
□	IsScalar(x) возвращает 1, если х — вещественный или комплексный скаляр,
иначе возвращает 0;
□	IsString(x) возвращает 1, если х — строка, иначе возвращает 0;
□	SiUnitsOf(x) возвращает размерность х, введенную в меню Dimension. Если х —
безразмерная величина, то возвращает 1.
В Mathcad 14 к этим функциям добавились еще 2:
□	IsNaN возвращает 1, если выражение не число, иначе возвращает 0. Может ис-
пользоваться только при символьных вычислениях;
□	IsPrime возвращает 1, если число простое, иначе возвращает 0. Может исполь-
зоваться только при символьных вычислениях.
Смысл этих функций понятен из их описания.
12.3.	Доступ к файлам
В разделе File Access (Доступ к файлам) 27 функций. Четыре из них являются чрез-
вычайно важными при разработке сложных программ. Это функции READPRN,
WRITEPRN, APPENDPRN и READFILE — функции передачи данных в Mathcad из
других файлов и из Mathcad в другие файлы:
□	APPENDPRN(’’file”) добавляет числовые данные в существующий файл.
Здесь "file" — имя файла или путь к файлу, если он находится в другом ката-
логе;
□	READPRN("file") считывает числовые данные из файла;
□	WRITEPRN("file") записывает числовые данные в файл;
□	READFILE("file", "type", [colwidths], [rows], [cols], [emptyfill]) считывает данные из
других файлов.
Остальные функции предназначены для обработки графических и музыкальных
файлов. Эти функции здесь не рассматриваются. С их описанием и применени-
ем можно познакомиться в Mathcad Help и в Resource Center.
Хотя в меню Insert Function отсутствуют старые функции APPEND("file"), READ
("file") и WRITE("file"), но Mathcad понимает и допускает их использование.
Если функции APPENDPRN, READPRN и WRITEPRN добавляют, считывают и запи-
сывают в файл прямоугольную матрицу (число — частный случай матрицы раз-
мерностью 1 х 1), то функции APPEND, READ и WRITE добавляют, считывают и за-
писывают одно число.
Функции APPENDPRN, READPRN, WRITEPRN и READFILE позволяют обмениваться
данными с другими программами, создавая вычислительные комплексы из не-
скольких различных программ. Примеры использования этих функций приведе-
ны в главе 2 и на рис. 12.3. Создание вычислительного комплекса показано в чет-
вертой части книги, в примере 55.
278
Глава 12. Дополнительные встроенные функции Mathcad
ПРИМЕЧАНИЕ -------------------------------------------------------
При считывании матрицы функцией READPRN текст (чаще всего заголовки таблиц) игно-
рируется, принимаются только числа.
ВНИМАНИЕ----------------------------------------------------------
При вводе в название функции имени файла не забывайте ставить кавычки. Имя файла
вводите с расширением, так, как оно записано в каталоге. Расширение может быть любым,
а не только .ргп, или отсутствовать вообще.
На рис. 12.3 показаны запись матрицы Ат в файл primer.prn, добавление к нему
матрицы Вт, считывание данных из этого файла в матрицу К (заголовок таблицы
при этом пропущен) и присвоение разным элементам матрицы К разных имен.
Такая процедура позволяет записывать в один файл и считывать из одного фай-
ла много различных данных.
WRITEPRN("primer") := АТ
APPENDPRN("primer.pm") > ВТ
К := READPRNC primer.prn")
Заголовок файла primer вписан от
Заголовок файла primer игнорируется при чтении
fl 2 3 4 5^
Cl := submatrix(K,4,5,3,5)
К-
2 3 4 5 1
3 4 5 12
4 5 12 3
Cl =
С2С1(1>
С2 =
1 2
5 3
3
4
5 1 5 3 4/
СЗ := ICj 4 СЗ = 1
Рис. 12.3. Обмен данными между файлами
Для чтения данных из других файлов в Mathcad 13 появилась новая универсаль-
ная функция READFILE. Эта функция объединяет в себе почти все другие сущест-
вовавшие ранее способы чтения файлов.
Обращение к этой функции:
READFILE(”file”, ’’type”, [colwidths], [rows], [cols], [emptyfill]).
12.3. Доступ к файлам
279
Параметры функции:
□	file — имя файла, из которого считываются данные (файл должен быть поме-
щен в тот же каталог, в котором находится и считывающий файл);
□	type — тип файла. В кавычках, как и имя файла, надо вписать одно из следую-
щих ключевых слов:
О delimited — колонки данных с любым разделителем между ними. Это фай-
лы с расширениями :csv, .txt, .prn;
О Fixed — таблицы с фиксированной шириной колонок;
О Excel — файлы формата Excel.
Первые два параметра функции READFILE являются обязательными, остальные
можно пропустить.
□	Colwidths — ширина колонок для таблиц с фиксированной шириной колонок.
Задается в виде числа считываемых позиций в колонке, если ширина всех ко-
лонок одинакова, или в виде вектора чисел, если ширина колонок разная.
□	Rows — задается одним числом, указывающим, начиная с какого ряда надо
считать данные, или вектором из двух чисел, указывающих, с какого по какой
ряд данные надо считать. Если rows не задан, считываются все ряды.
□	Cols — то же, что для rows, но для колонок таблицы данных.
□	Emptyfill — указывает Mathcad, какой текст вывести при отсутствии данных
в одной из ячеек таблицы. По умолчанию (при отсутствии параметра emptyfill)
вводится NAN (НеЧисло).
Примеры использования функции READFILE с необязательными параметрами
и без них приведены на рис. 12.4.
В прежних версиях Mathcad для выполнения тех же операций с файлами дан-
ных требовалось в главном меню выбрать Insert ► Data ► Data Import Wizard
(Вставить ► Данные ► Мастер импорта данных) и далее следовать указаниям
мастера.
Для сравнения на рис. 12.5 показано считывание данных с использованием Data
Import Wizard.
А
archivaapeca-2005. csv
А1 :=
Мои документыИРАКнига1 ,xls
Выбраны ряды 6 - 8 адресной книги
Документ Excel целиком
"Mathcad"
"Maths oft"
< "Svetlana Ilyicheva"
" c ollab admin@maths oft. c om"
" help@maths oft. с о .uk"
"Svetlanal@softline.ru" >
Рис. 12.4. Импорт данных с помощью функции READFILE
280
Глава 12. Дополнительные встроенные функции Mathcad
ZZ1 := READFILE("адреса-2005.csv" /'delimited")
ZZ2 := READFILE "адреса-2005.csv" /'delimited" ,
ZZ3 := READFILE("GU.PRN" /'delimited")
ZZ4:= READFILE "GU.PRN" /’delimited" ,
AA := READFILE("Книга! xls" /'Excel")
вся книга целиком
строки с 6 по 8
весь файл целиком
строки с 2 по 3 и столбцы с 2 по 3
Документ Excel целиком
* М athc ad"	" с ollab admin@maths oft. с от"
" help@maths oft. с о .uk"
"Svetlanal@softline.ru" ;
Рис. 12.5. Импорт данных с помощью Data Import Wizard
ZZ2 = "Mathsoft"
< "Svetlana Ilyicheva"
	1	2	3
1	1	4	0.514
2	1	6	0.539
3	1	8	0.643
4	1	9	0.727
5	1	10	0.724
12.4.	Функции поиска значений матрицы
В Mathcad имеется четыре функции поиска значений матрицы:
□	lookup(z, Л, В) в векторе или матрице А ищет заданную величину z и возвра-
щает величины, стоящие в матрице В в той же позиции, что и z в матрице А.
Если найдено несколько значений z, то возвращается вектор значений вели-
чин в строгом порядке по рядам слева направо (рис. 12.6);
□	hlookup(z, Л, г) в первом ряду матрицы А ищет заданную величину z и возвра-
щает величины в той же колонке в ряду г. Если найдено несколько значений
z, то возвращается вектор значений величин (рис. 12.7);
□	vlookup(z, Л, с) в первой колонке матрицы А ищет заданную величину z и воз-
вращает величины в том же ряду в колонке с. Если найдено несколько значе-
ний z, то возвращается вектор значений величин (рис. 12.8);
□	match(z, А) в векторе или матрице А ищет заданную величину z и возвращает
индексы, то есть номер строки и номер столбца. Если найдено несколько зна-
чений z, то возвращается вектор найденных позиций величин в строгом по-
рядке по рядам слева направо (рис. 12.9).
В названиях функций z — действительное или комплексное число или строка; А
и В — матрица или вектор; г и с — целые числа, номер строки и номер столбца.
Функции hlookup и vlookup возвращают одно число. С помощью дискретной пе-
ременной в приведенных примерах организован поиск по всей матрице.
12.4. Функции поиска значений матрицы
281
lookup выводит элементы матрицы D в той же позиции, что и
число z в матрице В. По рядам, начиная с первой колонки.
	<35 4 7 ^		<3 4 5>	z:= 5	Г 5>
	4 15 1		4 5 1		
					15
D>	5 13 50	В :=	5 1 5	lookup(z,B,D) =	у
	11 22 33		1 2’3		
					<50;
	<2 31 4;		<2 3 4>		
Рис. 12.6. Пример использования функции lookup
hlookup ищет число z в первом ряду матрицы В и выводит число,
стоящее в той же колонке, что и число z, в ряду номер m
<3 4 5^
4 5 1
В := 5 15
z> 5
m := 1.. rows(B)
(5)
(1)
hlookup(z,B,m) = (5)
1 2 3
<2 3 4;
(3)
Рис. 12.7. Пример использования функции hlookup
vlookup ищет число z в первой колонке матрицы В и выводит число,
стоящее в том же ряду .что и число z, в колонке номер п
В :=
4
5
1
<2
4
5
1
2
3
1
5
3
4;
z:= 5
п : 1.. cols(B)
(О
vlookup(z,B,n) = (1)
L(OJ
Рис. 12.8. Пример использования функции vlookup
match определяет место числа z в матрице В
В :=
<3 4 5>к
<2 3 4>
z := max(E) z = 5
Z:= match(z,B)
i := 1.. rows(25
номер
строки
(ZJ -
(	1/1
2
1
номер
столбца
1
координаты
числа z
32,1) >
Z= {2,1}
U2,l) J
4 5 1
5 1 О
1 2 3
2
7
Рис. 12.9. Пример использования функции match
282
Глава 12. Дополнительные встроенные функции Mathcad
Функция match для каждой найденной позиции числа z выводит две координаты
(номер строки и номер столбца) в виде составного массива. Чтобы раскрыть со-
ставной массив, нужно:
□	написать имя выражения и нажать клавишу =. Появится ответ в виде состав-
ного массива, где указаны только размерности вложенных массивов;
□	дважды щелкнуть мышью на составном массиве. Появится меню Result For-
mat;
□	в этом меню открыть страницу Display Options (Параметры изображения)
и на ней установить флажок Expand nested arrays (Развертывать вложенные
массивы).
На рис. 12.9 показано, как с помощью дискретной переменной вывести отдельно
два вектора координат (по строкам и по столбцам).
12.5.	Преобразование функций и матриц
Преобразование функции в матрицу или матрицы в функцию необходимо по
причине особенностей встроенных функций Mathcad. Это делается, например,
если одни функции возвращают матрицу, а вам надо иметь функцию для после-
дующего интегрирования или дифференцирования. Или, наоборот, Mathcad вы-
водит функцию, а вам нужна матрица для последующих матричных преобразо-
ваний.
12.5.1.	Преобразование функции в матрицу
В Mathcad есть встроенная функция matrix, которая преобразует функцию в мат-
рицу. Пример ее использования приведен на рис. 12.10.
Обращение к функции:
matrix(?n, и, F)
возвращает матрицу размерностью т х и, элементы которой — значения функ-
ции F(i, J), где i := 0..т - 1 и; := 0,.п - 1.
Функция matrix по умолчанию использует ORIGIN = 0. Обычно же расчетчики
используют ORIGIN = 1. Первая строка и первый столбец матрицы обозначаются
номером 1. matrix значение ORIGIN = 1 не принимает, поэтому приходится выре-
зать нулевые значения с помощью функции submatrix. Получается громоздко
и сложно. Кроме того, значения х = i и у = j — только целочисленные. Конечно,
дробные значения аргументов организовать можно, записав х и у как некоторое
выражение от i nj, но и в этом случае наложено ограничение: значения аргумен-
тов равноотстоят друг от друга.
На рис. 12.10 показано, как получить массив из функции, не используя довольно
неудобную функцию matrix. С помощью дискретных переменных получается
массив значений, равноотстоящих друг от друга. Указывая произвольные векто-
ры х и г/, получаем массив значений заданной функции для абсолютно произ-
вольных аргументов, в том числе дробных.
12.5. Преобразование функций и матриц
283
fo О О о
F(x,y) := sin(x у) М :« matrix(4,4,F)
О 0.841 0.909 0.141
О 0.909 -0.757 -0.279
кО 0.141 -0.279 0.412 7
М := submatrix(M,2,4,2,4)
^0.841 0.909 0.141
М= 0.909 -0.757 -0.279
<0.141 -0.279 0.412 >
аналог функции matrix
<0.841 0.909 0.141 А
п := 3 i := 1.. n j := 1.. п
luL j := sin(i j) М= 0.909 -0.757
' лучше, чем функция matrix
/ ч (25 S
<15
2.7
<<0.141 -0.279
-0.279
0.412 ;
Ц2.05,
X 5 /
1.. rows(x) j:« 1.. rows(y)
<-0.913 0.334 -0.614 -0388''i

M= 0.347 0.905 -0.84 -0.644
<-0.336 0.9 0.785 -0.531 >
Рис. 12.10. Преобразование функции в матрицу
В Mathcad 13 функция Matrix может создавать матрицы, содержащие не только
действительные и мнимые числа, как в прежних версиях, но и строки, используя
строчные функции, например, Format (рис. 12.11).
<0 0	0
F(x,y) := sinfxy)М := matrix(2,3,F) М =
1о 0.841 0.909
<0.841 0.909 0.141
matrix[2,3 Дх,у) <- sin[(x + 1) (у + 1)]] =
к 0.909 -0.757 -0.279
Г (О (О (О 1
matrix(2,3,f(i,j) <- identity^ + 1)) =
matrix(2,2 <H foimat("{0}, {1}"
< ”0,0”
V’1,0”
”0,1”
”1,1”
Рис. 12.11. Функция Matrix использует и строчные функции
12.5.2.	Преобразование матрицы в функцию
Преобразование матрицы в функцию выполняется с использованием встроен-
ных функций интерполяции или регрессии, которые, обрабатывая массивы то-
чек, возвращают функцию.
284
Глава 12. Дополнительные встроенные функции Mathcad
На рис. 12.12 показано преобразование вектора в функцию. Здесь X — вектор
значений аргумента, элементы которого обязательно располагаются в возрастаю-
щем порядке, Y — вектор значений функции. В примере использована кубиче-
ская сплайн-интерполяция Ispline со стыковкой сплайнов по прямой линии и ин-
терполяция с регрессией функцией regress. Приведенный на этом рисунке график
показывает совпадение значений вектора со значениями найденной функции
и возможность ее интегрирования и дифференцирования. Там же показано об-
ратное преобразование функции в матрицу.
t = 0,05 10 для графика
V(t) = mt«p(lspline(X,Y),X,Y,t)
V(t) .= interp (regress (X, Y,3) ,X, Y,t)
Выключите или поднимите вверх это выражение
Рис. 12.12. Преобразование вектора в функцию
Преобразование матрицы в функцию двух переменных осуществляется с помо-
щью двухмерной интерполяции (рис. 12.13), выполнение которой объяснялось
в главе 7. Вверху на рис. 12.13 приведены исходные данные массива данных. В ка-
ждой конкретной задаче он уже создан, и предстоит лишь его интерполяция. По-
лученную интерполяцией функцию ZZ(x, у) можно интегрировать и дифферен-
цировать. Можно выводить отдельные численные значения найденной функции.
При быстром построении графика поверхности достаточно в шаблон графика
вписать имя функции — и график построен (рис. 12.14). Но при этом пределы
изменения аргументов берутся по умолчанию, и график получается несопоста-
вимым с графиком исходных значений массива. Чтобы изменить масштаб гра-
фика, надо, дважды щелкнув мышью на графике, открыть окно форматирования
графика и выбрать вкладку Quick Plot Data (Данные быстрого графика), а затем
ввести пределы изменения координат х и у (наибольшее и наименьшее значения
элементов векторов X и У). Обратите внимание: на левом графике значения ко-
ординат — это индексы i nj. На правом графике значения координат — это коор-
динаты х и у.
12.5. Преобразование функций и матриц
285
Исходные данные: массив значений функции М
при значениях аргументов X и Y
	гп				'О.З 0.9 -0.5 0.6 >		
	3		8		0.1 -0.9 -0.9 0.8		3
Х:=		Y :=		М:=		Y •=	
	7		12		0.6 -0.5 0.7 -0.9		7
					<0.9 0.9 0.9 0.5 ;		
Только интерполяция
XY^ := X XY^ Y Двухмерный массив координат точек
ZZ(x,y) interp cspline(XY,M),XY,M,
Интерполяция с регрессией
Перестройка двухмерных массивов функции и ее аргументов
в одномерные (по столбцам)
fill 1 333 3777 7888 8 V1
XY1:-
U 8 12 15 1 8 12 15 1 8 12 15 1 8 12 15)
Z>(0.8 0.1 0.6 0.9 0.9 -0.9 -0.5 OP -0.5 -0.9 0.7 0.9 0.6 0.8 -0.9 0.5)Т
zregress(x»y) ;= “top regress(XYl ,Z ,4), XY1 ,Z, I	I
Z]oess(x>y) interp|oess(XYl ,Z,0.8) ,XY1 ,Z,
Рис. 12.13. Преобразование матрицы в функцию
Действия с функцией
<x,y)>lzZ(x,y)
dx
b(x,y) ^-2regrcss(x,y)
dy
<1,2) - -0.542
b(l,2) --0.151
^regress
Рис. 12.14. Результаты преобразования матрицы М (см. рис. 12.13) в функцию
286
ГЛава 12. Дополнительные встроенные функции Mathcad
В практических задачах встречаются случаи, когда требуется изменить число
элементов вектора чисел или определить элементы вектора при других (задан-
ных) значениях аргумента. Для этого требуется вначале превратить вектор
в функцию с помощью встроенной функции interp, затем ввести вектор новых
значений аргумента и вычислить вектор значений функции для нового вектора
аргумента (рис. 12.15).
ММС«Ы* F - (0 5 5 6.625 7 25 7 5 675)ТкН
данных	AL«(0 1 1 5 3 5 б 8)ТММ
•Хора оЛХю F1(z)”1“P(csPbne(AL.F) .al.f-.z)
Для построения графика функции	_
п > 50 z0 = min(AL) zk.= max(AL) z=z0,z0 +----,.zk
n
Равномерная разбивка функции на m (много точек)
zl = 0 обнуление ранее использованного значения z1
m = 10 1=1. m zlj =z0+i-------F2j « F1 (zip
m
Неравномерная разбивка функции на небольшое
число точек, заданных вектором чисел
Т
z2 (0 1 2 4 5 7 3) мм i1. rows(z2) F3tFlfz2p
исходный
массив
F - б.б кН
7.3
75
результат
расчета
F3= 5 3 кН
7.2
J.4

Рис. 12.15. Изменение числа элементов вектора
12.6.	Функции преобразования координат
В Mathcad имеется несколько функций преобразования координат:
□	xy2pol(x, у) — прербразование прямоугольных координат в полярные;
□	ро!2ху(г, 0?) — преобразование полярных координат в Прямоугольные;
□	xyz2cyl(x, у, z) — преобразование прямоугольных координат в цилиндриче-
ские;
□	cyl2xyz(r, 0, z) — преобразование цилиндрических координат в прямоуголь-
ные;
12.6. Функции преобразования координат
287
□	xyz2sph(x, у, г) — преобразование прямоугольных координат в сферические;
□ sph2xyz(x, 0, ср?) — преобразование сферических координат в прямоугольные.
Эти функции используются иногда для упрощения расчетов, но чаще для по-
строения графиков. Ряд примеров построения графиков с использованием дан-
ных функций приведен в главе 15.
ВНИМАНИЕ --------------------------------------------------------------
Функции преобразования координат не могут работать с размерными величинами, но по-
зволяют вводить угловые координаты как в радианах, так и в градусах. Для ввода углов
в градусах надо умножить число на deg. Для вывода углов в градусах надо вписать deg
в поле ввода справа от числа.
Примеры преобразования координат приведены на рис. 12.16-12.21.
Z := 0 Обнуление ранее использованого массива Z
<10 >
2 Y
-3 /
i := 1.. rows(X)
Z. := xy2polJX.,Yj для одновременной
Х:=
декартовы
координаты
точек
Использование индексов
обработки всего массива
Полярные координаты точек
в радианах в градусах
R. =
i
i?
8.2
.17
____О
1.3
17
04 =
О
76
121
deg
8

Рис. 12.16. Преобразование декартовых координат в полярные
Функции преобразования координат выводят составной массив, содержащий
преобразованные координаты точек. Напомним: для раскрытия составного мас-
сива надо дважды щелкнуть на нем мышью и в открывшемся меню Result Format
(Формат результата) выбрать команду Display Options ► Expand nested arrays (Пара-
метры отображения ► Развертывать вложенные массивы). На рис. 12.16-12.21
показаны две различные формы работы используемых функций с векторами. По
умолчанию эти функции работают только со скалярами. Для одновременного
преобразования массива координат используется либо индексная форма (см.
рис. 12.16 и 12.17), либо оператор векторизации (см. рис. 12.18-12.21). Исполь-
зование оператора векторизации предпочтительно — так проще и элегантнее.
288
Глава 12. Дополнительные встроенные функции Mathcad
декартовы координаты
полярные
координаты
полярных координат в декартовы
( ° 1
¥ - 0.8
<-13;
<0 5^
Z - 1
J5;
i  1 rows(X)
Использование оператора
векторизации для одновременной
обработки всего массива
Z1 •- xyz2cyl(X,Y,Z)
цилиндрические координаты
Рис. 12.18. Преобразование
декартовых координат
в цилиндрические
’ <05" '
0
<05,
<09"
21
< 1 /
<1.5 >
-21
к 15 ;.
декартовы координаты
цилиндрические координаты
<05^
г- 1
( ° )
8 *= 20 deg
<-45;
ZZ = cyl2xyz(r ,0 ,z)	i  1 rows(r)
декартовы координаты
yr(ZZJ2 z^ZZ^
v у-
0 51	01	0,5
0 9	0.3	1
1 1	-1 1 Тб
n := rows(X)
Z2 := xyi2sph(X,Y,Z) i .= 1 . n
сферические координаты
^ “(Z2i)2	*>(Z2i)3
ri “ pj =	7i»
‘ <07> '
0
<08j
p4>|
21
< 2 A
-21
<07
Рис. 12.19. Преобразование
цилиндрических координат в декартовы
Рис. 12.20. Преобразование
декартовых координат в сферические
сферические координаты
Z .= sph2xyz(r,p
декартовы координаты
удИ, vlaJ3
о
ч0.7,
<-0.7 5
-0.2
<1.2;
f-2^
0.7
ч0 ;
Рис. 12.21. Преобразование сферических координат в декартовы
12.6. Функции преобразования координат
289
Функции преобразования координат используются внутренним алгоритмом Math-
cad при построении трехмерных графиков поверхности. Исходная функция двух
переменных вводится как параметр функции CreateMech. В качестве еще одного
из параметров этой функции, fmap, используются функции преобразования ко-
ординат, рассмотренные ранее. Они преобразуют полярные, цилиндрические
или сферические координаты в декартовы, затем по массиву декартовых коорди-
нат строится график поверхности.
сферические координаты
радиус й М ’
меридиональный угол о(г,ф) :=
тангенциальный угол
цилиндрические координаты

радиус
угол по окружности,
перпендикулярной оси z
осевая координата
преобразование
цилиндрических
или сферических
координат в
прямоугольные
переключите выражения для fmap, оставляя
включенным лишь одно выражение
30:»0 zl>- фО:«0 ф! > 1я поменяйте
2	значения
М = CreateMesh(G,zO,zl ,ф0 ,ф! ,50,50,fmap)
Ml = CreateMesh(G,zO,zl ,фО,ф1,50,50,fmapl)
Рис. 12.22. Пример построения графика поверхности по функциям координат
♦
На рис. 12.22 показан пример построения графика поверхности в цилиндриче-
ских и сферических координатах. Работая с примером, сделайте радиус г посто-
янным — получите цилиндр и шар. Тот же результат гораздо проще получить
с использованием окна форматирования графика поверхности:
□	На математической панели выберите Graph ► Surface Plot (Графика ► График
поверхности).
□	В появившемся шаблоне графика поверхности впишите внизу имя функции
G (без параметров).
□	Дважды щелкните мышью на графике и в окне форматирования 3-D Plot
Format (Формат 3D графика) выберите вкладку QuickPlot Data (Данные быст-
рого графика).
290
Глава 12. Дополнительные встроенные функции Mathcad
□	На этой вкладке выберите систему координат Spherical (Сферическая) или
Cylindrical (Цилиндрическая). По умолчанию устанавливается Cartesian (Де-
картова система координат).
□	Впишите пределы изменения для первой (Rangel — область дискретных
значений) и второй (Range2) переменных. Установите число линий, образую-
щих сетку (# of Grids).
□	Раскрасьте график с помощью вкладки Appearance (Внешний вид).
Как видно из рис.* 12.22, оба способа построения графиков дают абсолютно оди-
наковый результат. Этого и следовало ожидать, ведь внутренний алгоритм Math-
cad использует для построения графика поверхности функцию CreateMech. Вы-
бирая на вкладке QuickPlot Data (Данные быстрого графика) систему координат,
мы фактически вызываем одну из описанных в этом разделе функций преобра-
зования координат.
12.7.	Функции условия
В Mathcad есть несколько способов записи условия. Наиболее популярные из
них были рассмотрены в главах 2 и 9. Повторим еще раз три основных способа
записи условия в Mathcad:
□	с помощью функции условия if;
□	с помощью оператора if с панели программирования;
□	с использованием булевых операторов.
Для использования функции условия if нужно:
□	записать имя выражения и оператор присваивания (:=);
□	на стандартной панели нажать кнопку f(x) и в списке встроенных функций
выбрать if, после чего нажать кнопку Insert (Вставить). Появится шаблон
функции if с тремя местами ввода;
□	заполнить места ввода.
Обращение к функции:
if(cond, х, г/),
где cond — условие типа х <	, х и у — значения, возвращаемые функцией. Если
условие выполняется, то выражению присваивается значение х, если не выпол-
няется, то — значение у.
Чтобы записать условный оператор с панели программирования, следует:
□	записать имя выражения и оператор присваивания (:=);
□	вызвать панель программирования Programming Toolbar нажатием соответст-
вующей кнопки математической панели и щелкнуть мышью на кнопке Add
line (Добавить линию);
□	в верхнем поле ввода ввести выражение для рассматриваемой функции на
первом участке диапазона переменной;
□	щелкнуть мышью на кнопке if на панели программирования (выражение для
изгибающего момента при этом должно быть полностью выделено синим
12.7. Функции условия
291
уголком или взято в скобки); появится место ввода, куда надо вписать усло-
вие, например, х < или 0 < х < ;
□	в нижнем поле ввода (у вертикальной черты), ввести выражение функции для
второго участка и выделить его целиком синим уголком (клавишей пробела);
□	щелкнуть мышью на кнопке Otherwise (Иначе) на панели программирования
или выбрать if и вписать условие х > Zt.
Использование логических (булевых) операторов состоит в умножении слагае-
мых заданного выражения на соответствующий логический оператор. Логиче-
ские операторы вводятся с панели булевых операторов (кнопка Boolean Toolbar).
Булевы операторы могут возвращать только 0 или 1. Если условие справедливо,
то значением оператора является 1, если несправедливо, то 0. В математическом
выражении умножение на логический оператор обращает соответствующее сла-
гаемое в нуль или не меняет его значения.
СОВЕТ ----------------------------------------------------------------
Логические операторы <, >, = (меньше, больше, равно) можно набирать с клавиатуры.
Другие операторы, например NOT, AND, OR, XOR (нет, и , или), надо вводить с панели
Boolean Toolbar во избежание возможных математических ошибок.
Пример применения всех трех форм записи условия показан на рис. 12.23.
Функция if допускает использование нескольких условий в одном выражении
путем вложения условий одно в другое. На рис. 12.23 функция М(х) содержит
одно условие, а функция Мх(х) — четыре вложенных друг в друга условия. На
практике функция if используется редко, так как два других способа записи ус-
ловия проще и нагляднее.
Для ввода с панели программирования функции Aft(x), включающей в себя 4 ус-
ловия, необходимо сразу ввести 4 места ввода (4 раза нажать Add Line).
При использовании булевых операторов вместо четырех условий введено только
три. Четвертое условие, Мх(х) = 0 при х < 1, выполняется автоматически, так как
Mathcad по умолчанию присваивает нулевое значение всем незаданным величинам.
Добавим к ним еще три функции, используемые реже. Это функция Хевисай-
да — Ф, символ Кронекера — 6 и функция знака — sign:
□	Ф(х) — функция Хевисайда, возвращает 0, если х < 0, иначе — 1. Функция
Хевисайда включает или выключает слагаемые в выражении в зависимости
от значения аргумента.
□	6(i,j) — символ Кронекера, возвращает 1, если i =j, иначе — 0. Символ Кроне-
кера 6(i, j) используется в операциях с матрицами, включает, выключает или
просто изменяет диагональные члены матрицы.
□	sign(x) возвращает 0, если х = 0, возвращает 1, если х > 0, и -1 — во всех ос-
тальных случаях. Функцию sign(x) удобно использовать для перемены знака
выражения.
292
Глава 12. Дополнительные встроенные функции Mathcad
Использование функции if
М(х) = if(x < 1,3,5-х)
Функция if с четырьмя вложенными условиями
М1(х) = if(x < l,0,if(l < X < 2,2 x,if(2 < X < 4,2 х4-6- З х,2 х4-6- З х-2)))
Использование панели программирования
М1(х) = 0 if х< 1	Все три выражения М1(х)
2 х if 1 < х < 2	эквивалентны друг другу
2-х + 6- 3х if 2 < х < 4
(2 x4-6 - З х-2) otherwise х:=0,02..5
Использование булевых операторов
М1(х) = 2 х (х > 1) 4- (6 - 3-х)-(х > 2) - 2 (х > 4)
Рис. 12.23. Три способа записи условия в Mathcad
Примеры использования указанных функций приведены на рис. 12.24-12.26.
Использование функции Хевисайда почти аналогично использованию буле-
вых операторов (сравните рис. 12.23 и 12.24). Умножение соответствующего
слагаемого на функцию Хевисайда включает или выключает слагаемое в вы-
ражении.
Так как функция Хевисайда возвращает 0, то, если аргумент функции равен О
или меньше 0, записав в качестве аргумента соответствующее выражение, можно
наложить на выражение любое ограничение.
На рис. .12.25 показана возможность перемены знака выражения с помощыЬ
функции sign, что иногда требуется, если аргумент возводится в четную сте-
пень.
На рис. 12.26 показано применение символа Кронекера при использовании в вы-
числениях тензорной записи. В качестве примера приведен расчет девиатора за-
данного тензора напряжений
P.bRJ-R’o],
здесь [DCT ] — девиатор тензора напряжений [Та ]; [Го ] — шаровой тензор напряже-
ний.
12.7. Функции условия
293
Функция Хевисайда включает слагаемое,
если выражение в скобках > 0.
Ф(х)=0, если х<0. Ф(х)=1, если х > О
М(х) .= 2 х Ф(х - 1) + (б - Зх) Ф(х - 2) - 2 Ф(х - 4)
Функцию sign(x) удобно использовать .
для перемены знака выражения
sign(x}=0, если х=0, sigii(x)=l, если х>0, sigii(x)=-l, если х<0
2	2
А1(х) > (х - 3)	А2(х) := (х - 3) • sign(x - 3)
Рис. 12.24. Пример использования
функции Хевисайда
х
Рис. 12.25. Пример использования функции
перемены знака
Символ Кронекерa 5(i, j) используется в операциях с матрицами,
включая, выключая или просто изменяя диагональные члены матрицы.
6j j =1, если i=j, иначе 6^ =0.
Определение девиатора напряжений
тензор напряжении
1.. 3 j := 1.. 3
< 15 -25 10 >
q:= -25 -10 5
^ 10 5 20 7
среднее
1 3 напряжение
ci,i сто = 8.3
i = l
	( 6.7	-25	10 >
Da =	-23 -	-18.3	5
	<10	5	11.7;
(8.3 0		0	
то =	0 8.3	0	
	0 0	8.3,	
тензорная запись
Dor. . •= cri,j -	*0
шаровой тензор
o0i := Q[To := diag(oO)
матричная запись		( 6.7	-25	10
Da := q - Tq	Da =	-25	-18.3	5
		<10	5	11.7;
Рис. 12.26. Пример использования символа Кронекера
В тензорной записи
Daij =Tai . -6((,ст0,
где <т 0 — среднее напряжение; 6f. — символ Кронекера.
Как видно из примера, тензорная запись короче и проще, чем матричная.
294
Глава 12. Дополнительные встроенные функции Mathcad
12.8.	Функции округления чисел
Mathcad содержит четыре функции округления чисел:
□	ceil(x) возвращает ближайшее целое число, большее х («потолок»);
□	floor(x) возвращает ближайшее целое число, меньшее х («пол»);
□	trunc(x) возвращает целую часть числа;
□	round(x, п) возвращает округленное значение числа х с точностью до п знаков
после запятой.
Примеры использования этих функций приведены на рис. 12.27.
Функции округления чисел
ceil(19.3) = 20
floo<19.3) = 19
round(19.577,2) = 19 6
round(19.577) = 20
tiunc(19.377) = 19
Функции комбинаторики
V:=(12 16 24 36 8)T
combin(6,2) = 15
gcd(45,81,18,63) = 9 gcd(V) = 4
lctn(15,25,45,75) = 225 lctn(V) = 144
mod(225,-50) = 25
__	z <4	n!
permut(o,2) = 30 permut(n,k) =-------
(n-k)!
Рис. 12.27. Функции округления и комбинаций чисел
12.9.	Функции комбинаторики и теории чисел
В этом разделе функций Mathcad содержится пять функций:
□	combin(n, k) возвращает число сочетаний из п целых чисел по k, где п > k;
□	permut(n, k) возвращает число размещений из п целых чисел по k, где п > k;
□ lcm(A, В, С...) возвращает наименьшее общее кратное для чисел Л, В, С...;
□ gcd(A, В, С...) возвращает наибольший общий делитель для чисел А,
В, С...;
□	mod(x, у) возвращает остаток от деления на у, записанный со знаком чис-
ла х.
В функциях Icm и gcd аргументом может быть как строка чисел, указанных через
запятую, так и вектор. Примеры использования этих функций приведены на
рис. 12.27.
12.10.	Функции тригонометрические,
гиперболические, логарифмические
и экспоненциальные
Встроенные в Mathcad тригонометрические, гиперболические, логарифмические
и экспоненциальные функции приведены на рис. 12.28. Их применение понятно
и без пояснений. Обратите внимание на написание некоторых функций, не сов-
падающее с общепринятым в математике.
12.11. Специальные функции
295
В функции log(z, b) второй параметр b является необязательным. Если он отсут-
ствует, вычисляется десятичный логарифм. Если присутствует, вычисляется ло-
гарифм по основанию Ь.
Обратите внимание на функции angle(x, у) и atan(x, у) (угол и арктангенс). Обе
они, в принципе, определяют одно и то же: угол между осью абсцисс и радиус-
вектором точки с координатами х и у. Но если функция angle вычисляет угол
в пределах от 0 до 2тс, то функция atan вычисляет угол от —тс до тс. По умолчанию
эти функции вычисляют углы в радианах. Чтобы вывести углы в градусах, надо
в месте ввода размерности (справа от числового результата) ввести deg (градус).
тригонометрические функции
прямые
sin(2) = 0.9
cos(2) = -0.4
tan(2) = -2.2
cot(2) = -0.5
sec(2) = -2.4
csc(2) = 1.1
обратные
asin(2) = 1.6-1.31
acos(2) = 1.31
atan(2) = 1.1
acot(2) = 0.5
asec(2) = 1
acsc(2) = 0.5
гиперболические функции
прямые
sinh(2) = 3.6
cosh(2) = 3.8
tanh(2) = 1
coth(2) = 1
sech(2) = 0.3
csch(2) = 0.3
обратные
asinh(2) = 1.4
acosh(2) = 1.3
atanh(2) = 0.5 - 1.61
acoth(2) =0.5
asech(2) = 1
acsch(2) =0.5
atan2(l,3) =71.6 deg
atan2(-l,-3) = -108.4 deg
от -я до +я
angle(l ,3) = 71.6 deg
angle(-l ,-3) = 251.6 deg
от 0 до 2я
Логарифмы и экспонента
ехр(2) = 7.4 1п(2) = 0.7 log(2) = 0.3	log(2,3)=0.6
Рис. 12.28. Элементарные математические функции
12.11.	Специальные функции
В этом разделе рассмотрим некоторые редко используемые функции. Среди них
есть функции активные — вычисляемые и неактивные — невычисляемые, они
используются во внутренних алгоритмах Mathcad.
12.11.1.	Функции Бесселя
Функции Бесселя по определению являются решениями различных краевых за-
дач для некоторых обыкновенных дифференциальных уравнений. Функции Бес-
селя первого и второго рода часто возникают как решения волнового уравнения
с цилиндрическими граничными условиями.
Mathcad содержит 40 встроенных функций Бесселя. Перечислим некоторые из
таких функций.
Обычные функции Бесселя:
□	J0(x) — функция Бесселя первого рода нулевого порядка;
□	Л(х) — функция Бесселя первого рода первого порядка;
□	Jn(ra, х) — функция Бесселя первого рода m-го порядка;
□	У0(х) — функция Бесселя второго рода нулевого порядка, х > 0;
296
Глава 12. Дополнительные встроенные функции Mathcad
□	Y1 (х) — функция Бесселя второго рода первого порядка, х > 0;
□	Yn(m, х) — функция Бесселя второго рода m-го порядка, х > 0.
Здесь х — вещественное безразмерное число; т — порядок, целое число, 0 < т < 100.
Модифицированные функции Бесселя:
□	10(х) — модифицированная функция Бесселя первого рода нулевого порядка;
□	11(х) — модифицированная функция Бесселя первого рода первого порядка;
□	ln(m, х) — модифицированная функция Бесселя первого рода m-го порядка;
□	К0(х) — модифицированная функция Бесселя второго рода нулевого поряд-
ка, х > 0;
□	К1(х) — модифицированная функция Бесселя второго рода первого порядка,
х > 0;
□	Kn(m, х) — модифицированная функция Бесселя второго рода m-го порядка,
х > 0.
Здесь х — вещественное безразмерное число; т — порядок, целое число, 0 < т < 100.
Примеры графического представления некоторых функций Бесселя показацы
на рис. 12.29 и 12.30.
Рис. 12.29. Функции Бесселя первого рода: а —модифицированные; б — обычные
б)
Рис. 12.30. Функции Бесселя: а — второго рода; б — сферические
12.11. Специальные функции
297
Функции Эйри являются независимыми решениями ОДУ:
□	Ai(x) — функция Эйри первого рода;
□	Bi(x) — функция Эйри второго рода.
Здесь х — вещественное безразмерное число.
Комплексная комбинация функций Бесселя — Кельвина является решением со-
ответствующего ОДУ, зависящего от параметра п:
□	bei(n, х) — мнимая часть функции Бесселя — Кельвина порядка и;
□	ber(n, х) — действительная часть функции Бесселя — Кельвина порядка п.
Сферические функции Бесселя:
□	js(n, х) — сферическая функция Бесселя первого рода порядка и, х > 0;
□	ys(n, х) — сферическая функция Бесселя второго рода порядка и, х > 0.
Здесь п — порядок (целое число).
12.11.2.	Другие специальные функции
В Mathcad введено много различных специальных функций. Кроме функций
Бесселя, это гамма-функция, гипергеометрические функции, ортогональные по-
линомы и т. д. Описание этих функций, математические формулы и примеры ис-
пользования имеются в справочной системе Mathcad. На рис. 12.31 также при-
ведено несколько примеров использования этих функций.
Полиномы порядка п
Эрмита	F(n,x)	:=	Не<п,х)
Ла герра	F(n,x)	:=	Lag(n,x)
Лежандра	F(n,x)	:=	Leg(n,x)
Якоби	F(n,x)	:=	Jac(n,2,l ,x)
Чебышева F(n,x) := Tcheb(n,x)
первого рода
Чебышева F(n,x) := Ucheb(n,x)
второго рода
Гамма-функция F(n,x) := Г(п,х)
х:= -2,-1.9..2
сдвигая график вниз,
посмотрите все функции
Рис. 12.31. Примеры использования ортогональных полиномов
12.11.3.	Дополнительные неактивные функции
При загрузке символьного процессора Mathcad распознает ряд дополнительных
специальных функций: интегралы Френеля, интегральные синус, косинус, пока-
зательную функцию, дилогарифм, функцию Дирака. Статус этих функций не-
обычен — они могут фигурировать в результатах символьных операций, но не-
доступны для обычных численных вычислений. Эти функции, по существу,
являются текстовыми записями. Выражения с неактивными функциями Math-
cad помещает в буфер обмена, и их можно извлечь оттуда для просмотра. Описа-
ние этих функций есть в справочной системе Mathcad.
298
Глава 12. Дополнительные встроенные функции Mathcad
12.12.	Строковые функции
Строковые функции (Strings) используются для вывода стандартных сообще-
ний, возникающих в результате вычислений. Такие функции выполняют дейст-
вия со строковыми переменными. Строка представляет собой цепочку символов,
заключенных в кавычки. В Mathcad имеются следующие функции для работы со
строками:
□	concat(A В, С...) — строковая переменная, полученная объединением строко-
вых переменных или констант Л, В, С;
□	num2str(z) — представление числа z;
□	str2num(5) — преобразование строкового представления числа 5 в веществен-
ное число;
□	str2vec(5) — преобразование в вектор строки 5, содержащей записи вещест-
венных чисел в строковом формате;
А := “Этавеличина11 В := “должна быть ” С := “скаляром “ D := "вектором"
S := concat(A,B,C)	объединение строк
S = "Эта величина должна быть скаляром"
strlen(S) = 34	число символов в строке
search(S,С,0) = 25	число позиций с начала строки S до подстроки С
substr(S,12,8) = " должна11 выделяет подстроку из 7 символов,
начиная с позиции 11
Vstr2vec(B) VT •= (228 238 235 230 237 224 32 225 251 242 252 32)
преобразование строки символов в вектор ASCII-кодов
vec2str(V) = "должна быть "
преобразование вектора ASCII-кодов в строку символов
num2str(2.35 10 ) = 2350000 преобразование числа
str2num("2350000") = 2350000 в строку и обратно
CWD = "САКнига 3ПитерГлава 12-доп-функции"
полный путь к данному документу
Рис. 12.32. Примеры применения строковых функций
□	str1en(5) — количество знаков в строке 5;
□	vec2str(V) — строковое представление вектора V;
□	lstring(5) возвращает 1, если 5 — строка;
□	search(5i, Sub5, т) возвращает стартовую позицию подстроки Sub5 в строке
51, начиная с позиции т. Возвращает 1, если подстрока не найдена;
□	еггог(5) при появлении ошибки возвращает строку 5;
□	CWD возвращает полный путь к папке, где хранится открытый документ.
12.12. Строковые функции
299
Примеры действий со строками приведены на рис. 12.32.
При работе со строками первая позиция считается нулевой.
ВНИМАНИЕ ------------------------------------------------------------
Для того чтобы в строке можно было писать русские буквы, для констант должен быть вы-
бран шрифт, работающий с кириллицей. Если он не был установлен ранее, надо устано-
вить уголок курсора на любой численный результат. На панели форматирования появится
название стиля Constants (Константы). Нужно открыть список шрифтов и выбрать шрифт,
работающий с кириллицей, например Times New Roman Cyr.
Глава 13
Работа с Mathcad-документами
Данная книга рассчитана на людей, знакомых с работой в Windows. Интерфейс
Mathcad типичен для Windows-приложений, поэтому не ставится целью описать
содержание всех панелей Mathcad. В процессе работы с Mathcad пользователь
поневоле вынужден ознакомиться с интерфейсом Mathcad. В данной главе сооб-
щим лишь сведения, необходимые для инженерных расчетов в Mathcad и позво-
ляющие избежать определенные трудности в работе.
13.1.	Построение математических выражений
Построение математических выражений было описано в главе 1. Тем не менее
один важный абзац из первой главы повторим и здесь.
Имя выражения (все, что стоит слева от знака присвоения значения) может со-
стоять из латинских, русских, греческих и других букв и цифр, знаков подчерки-
вания (_), штриха ( 4 ), символа процента (%), знака бесконечности (оо), вводи-
мых с клавиатуры.
Имена переменных и функций не могут начинаться с цифры, знака подчеркива-
ния, штриха, символа процента (%), не могут включать в себя пробелы. Символ
бесконечности оо может быть только первым символом в имени.
ВНИМАНИЕ-------------------------------------------------
Mathcad воспринимает прописные и строчные буквы как различные идентификаторы, так
же как одна и та же буква, изображенная различными шрифтами, — это разные имена.
В Mathcad 13 в меню View ► Toolbars появился пункт Custom Characters (рис.
13.1), выбрав который, можно быстро вставить некоторые символы, встречаю-
щиеся в Mathcad-документах, такие как °F, °C, ±, «, 11.
Имена переменных и констант в Mathcad могут иметь нижний индекс-коммен-
тарий. Для ввода его нужно, выделив имя уголком, нажать клавишу (точка)
и ввести с клавиатуры любой комментарий, например, оглавное.
Отличить нижний индекс-комментарий от индекса элемента вектора или матри-
цы в Mathcad 13 позволяет точка около индекса-комментария (сравните Vk
и Vk), которая видна при выделении выражения.
Построенные математические выражения нельзя форматировать произвольно.
Для отдельно взятого выражения нельзя выбрать свой формат.
13.1.1.	Стили записи выражений
Математические выражения могут содержать лишь переменные и константы.
Соответственно, в Mathcad предусмотрены определения стиля переменных
и констант (Variables, Constants).
13.1. Построение математических выражений
301
Normal
Toolbars
Stancard
Formatting
Math
Controls
Resources
Debug
Ruler
v* Status Bar
|^| Trace Window
r ti!. File Edit
□ ’ & I
Insert Format Tools Symbolizs Window Help
tP •
Header and Footer...
Regions
Annotations
Refresh
Zoom...
Ctrl+R
Calculator
Graph
Matrix
Evaluation
Calculus
Boolean
Programming
Greek
Symbolic
Modifier
Icustoh Characters


Рис. 13.1. Выбор дополнительных символов в Mathcad 13
ВНИМАНИЕ-----------------------------------------------------------------
Если вы, установив курсор на одном из выражений (или выделив это выражение целиком
или частично), с помощью панели форматирования измените наименование шрифта или
его размер, то это изменение автоматически будет применено ко всем выражениям, отно-
сящимся, соответственно, к переменным или константам.
Такое же изменение формата переменных или констант можно выполнить из
главной панели Mathcad, выбрав Format ► Equation. Откроется диалоговое окно
Equation Format (для переменных) (рис. 13.2). Выберите Variables (Переменные)
или Constants (Константы) ► Modify (Изменить). В новом окне выберите
Шрифт, Начертание, размер ► ОК. Последнее окно относится к интерфейсу
Windows, и даже в англоязычной версии пункты меню написаны на русском
языке (рис. 13.3).
Итак, Mathcad не разрешает изменять стиль одного отдельно взятого математи-
ческого выражения. Но «если нельзя, но очень хочется, то ... можно». Для этого
надо создать новый стиль и применить его к выбранному выражению.
302
Глава 13. Работа с Mathcad-документами
Рис. 13.2. Меню форматирования переменных и констант
Для создания своего стиля надо в главном меню Mathcad выбрать Format ►
Equation (Формат ► Уравнение). В появившемся окне Equation Format (Формат
уравнений) выбрать один из стилей Users (при желании переименовать его) ►
Modify (Изменить) ► Font (Шрифт) ► выбрать шрифт, начертание, размер ► ОК
(рис. 13.3). Аналогично можно создать свой шрифт для работы с текстом
(рис. 13.4). Только в меню Format вместо Equation выбрать Style.
А вот стиль вывода результатов расчета для одного-единственного числа соз-
дать не удается. Стили Users в этом случае не принимаются, а любое изменение
формата числа приводит к аналогичному изменению формата всех чисел в до-
кументе.
Обратите внимание на то, что при использовании окна Equation Format (Формат
уравнений) в наборе шрифтов присутствуют шрифты, работающие с кирилли-
цей (см. рис. 13.3).
*i	--............................._______________________________	--1*1 *
□ - & q e a v e	w d = с» poo* j де t
[Мой!	jl] | Arial Суr	3F2	3 B I U £ £ ;E {=
Начертание:
Размер:
Полужирный Курсив
16
18
Атрибуты
Г" Подчеркнутый
Образец
АаВМаОо
Обычный
Курсив
Полужирный
Полужирный Курсив
12
io~2
11 i
12
14 -J
Шрифт TrueType. Он
печати.
НЕ||
Math Style
Style Name
I. 0K.....I
Отмена [
Набор символов:
I Кириллица
Цвет_______
|Hi Черный
Рис. 13.3. Создание своего стиля для работы с переменными
Шрифт:_________
Arial
Arial Ж
Tf Arial Black
Arial Narrow
ЧГ BookAntiqua
Bookman Old Style
Calisto MT
Ф Century Gothic
Q
41
XB
<?
£
чг
13.1. Построение математических выражений
303
Рис. 13.4. Создание нового текстового стиля
Пример использования нового стиля приведен на рис. 13.5.
стандартные функции	ftУМКЫНУ
а- 10 atan(a) - 1 471 ateHfa) * 1 471 atan(^ - 11
Sterna) - । aian(g) - 1373_________________
| Эта переменная не определена. |
Рис. 13.5. Применение вновь созданных стилей
Первое выражение в верхней строке рис. 13.5 создано текстовым стилем Normal,
второе — вновь созданным стилем Nov 1.
Во второй и третьей строках для переменных варьируются стиль Variable и вновь
созданный Users 1. Для вывода результатов применен единый стиль Constants.
Обратите внимание на то, что переменная а, введенная стилем Variable, становит-
ся неопределенной для Mathcad при введении ее другим стилем.
Сделанные изменения переменных и констант не касаются результатов расче-
тов. Для них существует свой способ форматирования.
Если в меню Format (Формат) выбрать Results (Результаты), то откроется окно
форматирования результатов расчетов, где можно выбрать Number Format (Фор-
мат чисел), Display options (Вид на экране), Units Display (Изображение размерно-
стей), Tolerance (Погрешность) (рис. 13.6).
304
Глава 13. Работа с Mathcad-документами
Рис. 13.6. Окно форматирования результатов расчета
Вкладка Number Format (Формат числа) предназначена для форматирования чи-
сел — это подробно описано в главе 1.
Вкладка Display options (Параметры отображения) предназначена для выбора
вида на экране (эти действия описаны в главе 4, посвященной работе с матрица-
ми, поскольку именно вид матриц предлагается изменять в этом пункте меню).
Здесь же можно задать вид мнимой единицы на экране: либо г, либо j.
На вкладке Units Display (Отображение единиц измерения) можно выбрать вид
размерностей на экране (описано в главе 11). Нажатие кнопки Format Units
(Формат размерностей) изображает отрицательные степени размерностей в виде
дроби. Пункт Simplify units as possible (Упрощать размерности, если можно), как
правило, ничего не меняет.
На вкладке Tolerance (Погрешность) можно выбрать порог отображения ком-
плексного числа (Complex threshold), по умолчанию равный 10. Это означает, что при
——— > 1О10 число будет изображено как действительное (без мнимой части). При
Im(Z)
Im(Z) > iqio число будет изображено как чисто мнимое (без действительной части).
Re(Z)
Кроме того, на этой вкладке устанавливается порог равенства числа нулю (Zero
threshold). По умолчанию этот порог равен 15, то есть число, меньшее 10“15, будет
изображено как нуль.
Если необходимо выделить цветом или размером букв одно или несколько выра-
жений, используйте пункт Property (Свойства), содержащийся в контекстном
меню, открывающемся при нажатии правой кнопки мыши на нужном выраже-
нии. Предварительно нужно выделить нужный объект или группу объектов
(рис. 13.7), перечеркнув их курсором.
ПРИМЕЧАНИЕ --------------------------------------------------------
Напоминаем, что содержание контекстного меню зависит от выделенного объекта. В нем
каждый раз появляются наиболее нужные в данный момент пункты.
13.2. Аннотация файлов и областей файлов
305
:arg(C)'= 13: iarg(C) = 77Л de^ ардаёнт комплексного числа;
Рис. 13.7. Выбор свойств выделенной группы объектов
Цвет	I ? ;IXi
Дополнительные цвета:
ГГГГГГГГ
гггггггг
На рис. 13.7 предлагается выделить объекты цветом и рамкой.
Вкладка Protect (Защитить) позволяет запретить редактирование выделенных
объектов, но только в том случае, если включена защита всего документа в це-
лом.
13.2.	Аннотация файлов и областей файлов
В Mathcad 12 и 13 есть возможность добавления комментариев в свойства опера-
торов и файлов. Рекомендуется в шаблон документа добавить имя создателя
файлов и организации, тогда эти сведения будут присутствовать в каждом соз-
данном документе.
В главном меню Mathcad выберите File ► Properties и в открывшемся окне впи-
шите сведения о создаваемом файле (рис. 13.8). Если необходимые сведения
ввести для чистой страницы и сохранить ее как шаблон документа, эти сведения
будут присутствовать в каждом создаваемом вами на основе этого шаблона фай-
ле. Правда, эти сведения можно прочитать только в оболочке Mathcad. Они не
видны из файловых менеджеров, например, Мой компьютер, Проводник (в Win-
dows), Windows Commander.
Чтобы добавить комментарии к отдельным математическим выражениям, в стан-
дартном меню Mathcad выберите View и отметьте флажком пункт Annotation.
Если к каким-либо объектам уже добавлены комментарии, то эти пункты будут
выделены цветными скобками. Цвет этих скобок можно определить, выбрав
в стандартном меню Format ► Color ► Annotation. Для ввода аннотации щелкните
правой кнопкой мыши на том объекте, где надо ввести аннотацию, в контекстном
306
Глава 13. Работа с Mathcad-документами
меню выберите пункт Annotate Selection и в появившемся окне введите текст
комментария. После этого такой объект на экране будет виден в круглых скобках
выбранного цвета. Чтобы увидеть комментарий к объекту, щелкните на нем пра-
вой кнопкой мыши и в контекстном меню выберите пункт View/Edit Annotation.
На экране появится окно с комментарием (рис. 13.9).
arg(C) = 1.:
Рис. 13.8. Ввод комментария к документу
Рис. 13.9. Просмотр комментария к массиву А
13.3. Защита информации в Mathcad
307
13.3.	Защита информации в Mathcad
Чтобы включить защиту всего документа в целом, надо в главном меню Mathcad
выбрать Format ► Protect Worksheet (Защитить документ). В появившемся окне
предлагается три уровня защиты документа (рис. 13.10):
1.	File (Файл) не накладывает никаких ограничений на редактирование и копи-
рование любых регионов файла, то есть защита отключена.
2.	Content (Содержание) — существующие регионы защищены от редактирова-
ния. Новые регионы могут быть созданы. Защищенные регионы можно копи-
ровать.
3.	Editing (Редактирование) — созданные регионы не могут редактироваться или
копироваться. Новые регионы не могут быть созданы. При нажатии правой
кнопки мыши контекстное меню не действует.
Выбор пункта Password (Пароль) наиболее эффективно защищает документ. Не-
обходимо ввести пароль два раза и нажать ОК.
Рис. 13.10. Защита документа от редактирования или копирования
Для снятия защиты надо в главном меню Mathcad выбрать Format ► Unprotect
Worksheet (Снять защиту с документа). Если был введен пароль, появится сооб-
щение с предложением ввести паррль для снятия защиты.
В Mathcad имеется возможность защищать от редактирования только часть ре-
гионов. Для этого щелкните правой кнопкой мыши на любом объекте. В открыв-
шемся контекстном меню выберите Properties ► Protect (рис. 13.11).
По умолчанию пункт Protect region from editing (Защитить регион от редактиро-
вания) включен у всех выражений. Снимите поставленный флажок, чтобы
в дальнейшем при включении защиты в меню Tools ► Protect Worksheet (Инстру-
менты ► Защита документа)объект остался незащищенным и мог быть отредак-
тирован.
Не забудьте сохранить файл, чтобы защита оставалась включенной при откры-
тии файла.
В Mathcad можно использовать установку уровня защиты по умолчанию для
всех открываемых документов. Для этого в главном меню Mathcad выберите
Tools ► Preference ► Script Security (Инструменты ► Параметры ► Безопасность скрип-
тов). Откроется окно, показанное на рис. 13.12.
308
Глава 13. Работа с Mathcad-документами
Рис. 13.11. Включение возможности защиты документа
Рис. 13.12. Установка уровня защиты открываемых документов
В открывшемся окне предлагается выбрать уровень безопасности, чтобы опреде-
лить действия, совершаемые при открытии документов, содержащих защищен-
ные объекты. Отметьте щелчком мыши один из трех уровней защиты:
13.4. Закрытые зоны в Mathcad
309
1.	Low Security (Низкий уровень безопасности) — документ открывается без уче-
та уровня защиты документа.
2.	Medium Security (Средний уровень безопасности) — при открытии документа,
содержащего защищенные регионы, на экран выводится предупреждение.
3.	High Security (Высокий уровень безопасности) — защищенные регионы авто-
матически отключены при открытии документа.
Использование этого меню необязательно при включении защиты документа.
13.4.	Закрытые зоны в Mathcad
Закрытая зона — это часть Mathcad-документа, которая присутствует в докумен-
те, участвует в расчетах, но не видна на экране. Необходимость в создании такой
зоны возникает в двух случаях: для уменьшения размера документа и для сокры-
тия информации от посторонних глаз.
Чтобы создать закрытую зону, сделайте следующее:
□	В главном меню Mathcad выберите Insert ► Area (Вставка ► Область). На экра-
не появятся две горизонтальные линии с указателями слева. Перетащите их
мышью в начало и в конец области, которую надо закрыть.
□	Щелкните правой кнопкой мыши в выделенной линиями области. В открыв-
шемся контекстном меню выберите Collapse (Свернуть). Выделенная область
исчезнет. Останется лишь одна горизонтальная линия с указателем.
Выражения, скрытые в закрытой области, продолжают работать в документе, хотя
и не видны на экране. Чтобы открыть закрытую область, нужно сделать двойной
щелчок левой кнопкой мыши на линии с указателем. Скрытая область становится
открытой и появляется на экране в обрамлении двух линий с указателями.
Чтобы удалить закрытую область, щелкните мышью на одной из линий с указа-
телем, выделив ее, и нажмите клавишу Del (Удалить).
Чтобы запретить доступ к закрытой зоне, вначале закройте ее, выбрав Collapse
(Свернуть). Затем, щелкнув на линии с указателем правой кнопкой мыши,
в контекстном меню выберите Lock (Блокировать). Появится запрос ввести па-
роль, причем два раза, для надежности (рис. 13.13). После ввода пароля на ли-
нии рядом с указателем появятся замок и дата закрытия зоны.
Блокировка области
Пароль (необязательно):
Повторение:
OK j
И ^вернуть область]
г 1 Разрешить развертывание и свертывание области во
время блокировки
0 Показывать время блокировки
Отмена |
Рис. 13.13. Ввод пароля при запирании и отпирании зоны
310
Глава 13. Работа с Mathcad-документами
Для открытия запертой зоны щелкните правой кнопкой мыши на линии с указа-
телем и в контекстном меню выберите Unlock (Развернуть). Появится запрос на
ввод пароля. После ввода пароля зона открыта, замки на линии с указателями
исчезнут.
Различные варианты зоны показаны на рис. 13.14.
В Mathcad 13 расширены возможности оформления закрытой зоны. Щелкнув
правой кнопкой мыши на скрытой зоне, выберите в контекстном меню вклад-
ку Area (рис. 13.15). На этой вкладке можно вписать заголовок закрытой
зоны, отметить выделение ее линиями и значком, сделать эту зону совсем не-
видимой.
Рис. 13.14. Сжатие и запирание зоны
13.5.	Создание вычислительных комплексов
Использовав панель программирования, с помощью Mathcad можно составить
программу абсолютно любой сложности. Но переводить на Mathcad программы,
написанные на других алгоритмических языках, было бы безумием. Mathcad по-
зволяет создавать вычислительные комплексы, объединяющие различные про-
граммы. В этом случае нужно лишь дописать к готовым программам недостаю-
щие фрагменты на Mathcad.
Есть несколько способов объединения различных программ в один вычисли-
тельный комплекс. Рассмотрим два таких способа: с использованием ссылок
и гиперссылок.
13.5. Создание вычислительных комплексов
311
Здесь скрыта программа интегрирования уравнения движения методом Ньюмарка
Двойной щелчок мышью на этой линии открывает закрытую зону
Двойной щелчок мышью на этой линии закрывает открытую зону
Рис. 13.15. Оформление закрытой зоны
13.5.1.	Использование ссылок на другие файлы
В примере 53 электронной книги продемонстрирована возможность объедине-
ния нескольких Mathcad-документов в один с помощью ссылки на них. Для это-
го в основном документе делается ссылка на другой документ. В результате оба
документа объединяются в один и работают совместно, хотя второго документа
и не видно на экране.
Для создания ссылки надо в главном меню Mathcad выбрать Insert ► Reference
(Вставить ► Ссылка). В открывшемся окне, выбрав Browse (Поиск), укажите
путь к документу, который хотите включить в расчет. Нажмите ОК. В основном
документе появится строка с именем подключенного документа.
Рекомендуется при создании ссылки использовать относительный путь. Указав
путь к документу, пометьте флажком пункт Use relative pass for reference (Ис-
пользовать относительный путь для ссылки). При этом в строке документа, ука-
зывающей на ссылку, появится буква (R). В этом случае ссылка останется дейст-
вующей, даже если вы переместите основной документ в другую папку. Важно
лишь, чтобы оба документа находились на одном диске.
312
Глава 13. Работа с Mathcad-документами
На рис. 13.16 показано меню вставки ссылки. Сразу под меню показан результат
ссылки: строка со ссылкой и начало расчета с использованием ссылки в примере 53.
число узлов	NTJ = 	число узлов в ряду nr = 11
число элементов	NE = 	число рядов в столбце пф = 5
Рис. 13.16. Вставка ссылки на другой файл
При каких-либо изменениях в том или ином документе автоматический пере-
счет происходит только после сохранения изменений в обоих документах. Ино-
гда для успешной работы комплекса программ после сохранения приходится за-
крыть и вновь открыть файл.
13.5.2.	Использование гиперссылок
В примере 53 для ввода данных и их корректировки использовалось включение
программы Matr-ind в основной документ с помощью ссылки (Reference). В при-
мере 55 для корректировки данных используется гиперссылка (Hyperlink).
Гиперссылка позволяет открывать файл, с которым создана связь, в той оболоч-
ке, в которой он создан. Для создания гиперссылки нужно:
□	выделить слово, с которым будет связан интересующий вас файл, желательно
черным цветом. Тогда после установления связи это слово будет выделено
жирным шрифтом;
□	в главном меню Mathcad выбрать Insert ► Hyperlinc ► Browse ► указать путь
к файлу, с которым надо связать выделенное слово ► ОК;
□	в окне Edit Hyperlink установить флажок на пункте Use relative path for hyperlink.
В этом случае связь будет работать даже тогда, когда вы переместили каталог
со связанными файлами в другое место.
Если вы хотите вызвать на экран не начало, а определенное место выбранного
файла, его необходимо задать. Этот процесс описан в разделе 14.2.1.
Двойной щелчок мышью на выделенном слове открывает файл, с которым уста-
новлена связь. Теперь этот файл можно отредактировать и сохранить. Для пере-
дачи данных в Mathcad-документ надо внутри связанного файла записать их
в другой внешний файл, откуда затем считать функцией READPRN.
13.5. Создание вычислительных комплексов
313
На рис 13.17 показано создание гиперссылки на файл Dan.dat, где находятся ис-
ходные данные для расчета на Fortran из примера 55. После создания гипер-
ссылки при подведении курсора к слову, с которым связана гиперссылка, курсор
приобретает вид указательного пальца. Двойной щелчок на этом слове вызывает
открытие связанного, с ним файла в его оболочке, в данном случае Блокнот
(рис. 13.18). Теперь можно проверить исходные данные, изменить их для новой
задачи, сохранить. Однако в расчеты Mathcad-документа измененные данные
еще не попадут.
Документы, присоединенные гиперссылкой, не работают автоматически в Math-
cad-документе. Их надо вызвать двойным щелчком мыши на связанном с ними
слове и запустить.
Matj-ind' coord Miuf gu ссылки
Рис. 13.17. Вставка гиперссылки в примере 55
Matr-ind
Рис. 13.18. Открытие файла Coord.ргп
314
Глава 13. Работа с Mathcad-документами
Двойной щелчок на слове «Matr.ind» вызывает запуск и пересчет программы
расчета матрицы индексов. Двойной щелчок на слове «Coord» открывает табли-
цу координат узлов, записанную в этом файле.
Если расчеты в Mathcad должны быть переданы в другую программу для про-
должения расчетов или оформления вывода результатов, то в Mathcad-докумен-
те нужные результаты расчетов должны быть записаны в отдельный файл функ-
цией WRITEPRN, откуда их «заберет» другая программа.
Подведем итог: ссылка (Reference) работает в Mathcad-документе автоматиче-
ски, гиперссылка (Hyperlink) требует запуска каждой подключенной программы
отдельно двойным щелчком мыши.
Основное предназначение гиперссылок — создание электронных книг. Об этом
речь пойдет в главе 17.
13.6.	Новые служебные функции Mathcad 13
В Mathcad 13 появилось несколько интересных возможностей работы с доку-
ментами.
13.6.1.	Уменьшение размера файлов
При сохранении файла в текстовом формате XML для уменьшения размера фай-
ла Mathcad 13 позволяет выбрать формат XMCD — текстовый или XMCDZ —
zip-архив файда (автоматически- раскрывается в Mathcad). Размер файла 53-
кольцо (из электронной книги) при сохранении в формате Mathcad 200li (MCD)
Рис. 13.19. Переключатель версий Mathcad
13.6. Новые служебные функции Mathcad 13
315
составил 723 Кбайт, в формате XMCD — 321 Кбайт, в формате XMCDZ —
123 Кбайт.
13.6.2.	Переключатель версий Mathcad
В Mathcad 13 в меню Tools ► Worksheet Options ► Compatibility имеется переключа-
тель совместимости с предыдущими версиями (рис. 13.19). При открытии
в Mathcad 13 документа, созданного в Mathcad И или в более старых версиях,
переключатель автоматически устанавливается на Mathcad И (МС11).
Такой переключатель есть и в версии Mathcad 14. Фирма Mathsoft дает пользо-
вателям время для постепенного перевода своих файлов к формату Mathcad 13.
13.6.3.	Автосохранение
В Mathcad 13 появилась возможность автосохранения файлов в процессе работы
с ними. В главном меню выберите Options ► Preferences. На вкладке Save можно
установить промежуток времени, после которого Mathcad автоматически сохра-
няет файл в формате XML или XMLZ (в сжатом виде) (рис. 13.20).
Рис. 13.20. Настройка сохранения файлов
Глава 14
Работа с текстом
Основные положения работы с текстом приведены в главе 1. Здесь же повто-
рим главное из сказанного там. Для ввода текста на русском языке лучше все-
го, сменив латинский шрифт на русский, набирать текст прямо в математи-
ческой области. Когда набрано первое слово, при нажатии клавиши пробела
область со словом автоматически из математической превращается в тексто-
вую.
В отличие от Word, устанавливающего строгие правила размещения текста на
странице, в Mathcad текст можно набирать в любом месте страницы. Размеры
текстовой области можно менять обычным для Mathcad способом: щелкнуть мы-
шью на нужной области, подвести курсор к черному прямоугольнику на рамке,
окружающей выделенный объект, чтобы появилась стрелка, двигать мышь при
нажатой левой кнопке.
Изменение стиля текстовой области не влияет на результаты расчета математи-
ческих выражений, поэтому можно изменить стиль как всего текста, так и от-
дельного слова или буквы.
14.1.	Изменение стиля текстовых областей
Для изменения стиля всех текстовых областей в документе надо в главном меню
Mathcad выбрать команду Format ► Style ► Normal ► Modify (Формат ► Стиль ►
Обычный ► Изменить). В открывшемся окне Define Style (Определение стиля)
нажмите кнопку Font (Шрифт). Откроется окно Text Format (Формат текста), где
надо задать Font, Font style (Вид шрифта) и Size (Размер шрифта).
Открывающиеся при изменении стиля текста окна показаны на рис. 14.1 и 14.2.
Рис. 14.1. Изменение стиля текста
14.1.1.	Установка свойств абзаца
В окне Define Style (Определение стиля) есть кнопка Paragraph (Абзац), позво-
ляющая создавать текстовые области, редактируемые средствами, похожими на
14.1. Изменение стиля текстовых областей
317
Рис. 14.2. Изменение стиля текста (окончание}
используемые в Word. Средств этих немного, но с их помощью можно создавать
хорошие технические отчеты и электронные книги.
Главное назначение окна Paragraph Format (Формат абзаца) — создание электрон-
ных книг, сочетающих в себе текст, работающие формулы, которые можно изме-
нять и анализировать, результаты расчета, а также ссылки на другие области до-
кумента или другие файлы, легко открывающиеся щелчком мыши на них.
Окно Paragraph Format (Формат абзаца) показано на рис. 14.3.
Рис. 14.3. Панель установки параметров абзаца
Слева вверху окна задается отступ (Indent) текста в дюймах (inches) или санти-
метрах (centimeters) с левой (left) и с правой (right) стороны.
Справа вверху окна пункт Special (Специальный) задает положение первой стро-
ки абзаца:
□	None — нет сдвига первой строки;
318
Глава 14. Работа с текстом
□	First Line (Красная строка) — сдвиг первой строки вправо по отношению к ос-
тальному тексту;
□	Hanging (Висячая строка) — сдвиг первой строки влево по отношению к ос-
тальному тексту.
На рис. 14.4 показан образец применения стиля Paragraph (Формат абзаца).
Здесь верхняя часть текста записана с использованием пункта First Line (Первая
строка). Последний абзац оформлен с применением пункта Hanging (Висячая
строка).
Г F0 I
Истинные деформации определяются по формуле еи = In —
X F /
Применение этой формулы требует замера диаметра образца в
процессе испытаний, что обычно не делается, поэтому она применена лишь
дня определения деформации в момент разрыва образца.
•	Д о о бр аз ов ания шейки в о бр азце используется другая ф ормула
8И S 1п(1 + в), не требующая замера диаметра.
I
Ей
•	Истинные напряжения определяются по формуле сти := сте г
также не требующей замера диаметра.
1.	Результаты расчета деформаций и напряжений приведены на
рисунке 4Р.4, а вид диаграмм условных и истинных напряжений
на рис.4Р.б (слева). Истинные деформации и напряжения в
момент разрыва в несколько раз больше условных.
Рис. 14.4. Образцы применения стиля Paragraph (Формат абзаца)
14.1.2.	Изменение стиля отдельной текстовой области
Стиль может быть единым для всего текста, если он установлен в начале ввода
текста и в дальнейшем не менялся. Можно задать собственный стиль для одного
или нескольких абзацев, если, установив курсор на одном из абзацев, правой кноп-
кой мыши вызвать контекстное меню (рис. 14.5, слева), в котором есть пункты
Font, Paragraph, Style, выбор которых открывает рассмотренные ранее окна Text
Format, Paragraph Format и Text Style. Выберите нужный пункт и поменяйте уста-
новки для выбранного объекта.
Если в контекстном меню выбрать пункт Properties (Свойства), как показано на
рис. 14.5, справа, то, открыв страницу Text (Текст), можно установить парамет-
ры:
□	Occupy Page Width (Занять всю ширину страницы);
□	Push Regions Down As You Type (Сдвигать области вниз, когда вы печа-
таете).
Кроме того, изменить размер текстовой области можно традиционным способом.
Если щелкнуть мышью внутри области, появится рамка с черными квадратика-
ми для изменения размеров. Установите курсор на такой квадратик, подождите
до появления стрелки, нажмите левую кнопку мыши и, двигая мышь, растяните
или сожмите область.
14.1. Изменение стиля текстовых областей
319
Иг
Пр:
процессе мс
для определ!
еи  ln(
, также н
L Резуль
X Вырезать
^Копировать
е Вставить
Выделить все
Е§* Свойства...
Вставить регион формул
А Шрифт...
П Абзац...
Стиль...
Подстрочный
Надстрочный
& Гиперссылка
Рис. 14.5. Использование контекстного меню для изменения свойств текста
14.1.3.	Списки и таблицы в тексте
В окне Paragraph (Формат абзаца) (см. рис. 14.3) слева внизу есть пункт Bullets
(Маркированный список), содержащий три пункта:
□	None — нет маркировки;
□	Bullets — маркированный список (с точкой слева);
□	Numbers — нумерованный список (с номером слева).
На рис. 14.4 в середине текста два абзаца оформлены стилем Bullets, в нижней
части один абзац выполнен в стиле Numbers.
Для ввода таблиц в окне Paragraph (Формат абзаца) (см. рис. 14.3) предназначе-
на кнопка Tabs (Табуляция) (рис. 14.6). Щелчок мышью на ней открывает окно
Tabs, в котором надо установить позиции каждого столбца в дюймах. Результат
установки позиций показан на рисунке внизу.
Рис. 14.6. Установка параметров ввода таблицы и результат их действия
320
Глава 14. Работа с текстом
14.2. Использование гиперссылок
Одним из достоинств электронных документов является возможность быстрого
открытия других файлов с помощью гиперссылок. Гиперссылка (Hyperlink) мо-
жет не только вывести на экран нужный файл, но и показать нужное место от-
крытого документа либо соответствующий сайт в Интернете. Гиперссылки
особенно эффективны в больших документах, в обучающих и презентацион-
ных программах, в электронных книгах.
На рис. 14.4 в последнем абзаце с выражецием «Результаты расчета» связана ги-
перссылка на пример 13 («Построение диаграммы истинных напряжений»). При
двойном щелчке мышью на выделенных словах открывается файл примера 4
в том месте, где находятся результаты расчета истинных напряжений и дефор-
маций.
Процедура создания гиперссылки описана в главе 13 (раздел 13.4.2). Напомним:
для создания гиперссылки нужно в меню Insert выбрать пункт Hyperlink (Гипер-
ссылка), нажать кнопку Browse (Обзор) для выбора пути к нужному файлу, за-
тем Use relative path for hyperlink (Использовать относительный путь для гипер-
ссылки) и кнопку ОК.
При двойном щелчке мышью на слове, с которым связана ссылка, откроется вы-
бранный файл, причем на экране видно начало файла.
14.2.1.	Переход на метку
Если вы хотите вызвать на экран не начало, а определенное место выбранного
файла, его необходимо задать. Для этого
Ис
Пр:
процессе ис
для определи
еи=Ч
.также н
1, Резуль
Ж Вырезать
4=) Копировать
в Вставить
Выделить все
Свойства...
Вставить регион формул
А Шрифт...
Абзац...
Стиль...
Подстрочный
Надстрочный
Гиперссылка
Рис. 14.7. Установка метки на место, с которого откроется файл
14.2. Использование гиперссылок
321
□	откройте файл, на который будет создана ссылка;
□	установите курсор на объект (слово, выражение или график), который при
вызове файла будет находиться на экране вверху;
□	щелкните на нем правой кнопкой мыши и в открывшемся контекстном меню
выберите Properties (Свойства);
□	в окне Тад (Метка) впишите имя метки (в нашем случае — 111), как показано
на рис. 14.7. Нажмите кнопку ОК.
После создания метки следует создать гиперссылку. Вводя путь к файлу, укажи-
те и имя метки, записав в конце адреса #111 (рис. 14.8). Теперь при двойном
щелчке мышью на слове, с которым связана гиперссылка, указанный в адресе
файл откроется с того места, на которое установлена метка.
Истинные деформацю
I Вставка гиперссылки
Применение этой фор»
процессе испытаний, что обычг
для определения деформации в :
•	До образования ше
еи  1п(1 + е), не требующе!
•	Истинные напряже
.также не требующей заме;
L Результаты расчета де<|
рисунке 4Р4, а вид
на рис 4Р.6 (слева),
момент разрыва в 1
Ссылка на файл или
43-dag.xmcd#lll
| Обзор...
Введите или укажите путь к документу, на который нужно создать ссылку. Это
может быть адрес в Интернете (URL-адрес), документ, находящийся на жестком
диске компьютера, или документ в локальной сети организации.
0 Использовать относительный nyi □ Показывать как всплывающий документ
Сообщение в строке состояния при наведении указателя на гиперссылку:
ОК ] [ Отмена
Рис. 14.8. Создание гиперссылки на файл с указанием метки #111
Истинные деформации определяются по формуле ви = In
Рис. 14.9. Открытие гиперссылки на всплывающий документ
322
Глава 14. Работа с текстом
14.2.2.	Всплывающий документ
Если при создании гиперссылки флажком отметить пункт Display as pop-up
document (Показывать как всплывающий документ), то выбранный файл откро-
ется в отдельном окне (рис. 14.9), при этом метка игнорируется. На этом рисун-
ке гиперссылка связана с выражением «Истинные деформации». Размеры окна
можно изменять обычным способом, потянув мышью за угол или за середину
стороны окна. Файл, открытый как всплывающий документ, вычисляется, но не
редактируется.
Глава 15
Работа с графиками
О построении плоских и пространственных графиков говорилось в главе 1. По-
вторим общие правила построения графиков, а затем остановимся на особенно-
стях их построения.
15.1.	Построение двухмерного плоского графика
Рассмотрим построение графика функции:
□	Установите крестообразный курсор в то место, где надо построить график.
□	На математической панели щелкните на кнопке Graph Toolbar (Панель графи-
ков), а на открывшейся панели — на кнопке с изображением плоского гра-
фика.
□	В появившемся на месте курсора шаблоне плоского графика введите на оси
абсцисс имя аргумента, на оси ординат — имя функции.
□	Щелкните мышью вне шаблона графика. График построен для заданного диа-
пазона изменения аргумента.
Если диапазон значений аргумента не задан, по умолчанию график будет постро-
ен в диапазоне значений аргумента от -10 до 10.
Чтобы в одном шаблоне разместить несколько графиков, надо, набрав на оси ор-
динат имя первой функции, нажать клавишу «запятая» (уголок курсора при этом
обязательно должен находиться в конце имени функции). В появившемся месте
ввода (черном квадратике) впишите имя второй функции и т. д.
ORIGIN := 1
XI > rlogis(10,20,10) Yl := tunif(10,5,20)
Рис. 15.1. Различные типы изображения точек на графике
Функцию можно задать аналитически или массивами значений аргумента и функ-
ции. Для построения плоского графика массивы обязательно должны быть век-
торами одинаковой размерности.
324
Глава 15. Работа с графиками
При задании функции массивами в местах ввода на осях графика надо вписать
имена массивов с указанием индексов или без них. На рис. 15.1 массивы чисел
созданы генераторами случайных чисел (Х^ и Yt — в произвольном порядке, X
и Y — отсортированные в порядке возрастания массивы). На этом рисунке пока-
заны различные типы изображения вычисленных значений на графике.
Напомним, что при двойном щелчке мышью в поле графика открывается окно
форматирования графика (см. рис. 1.9).
ПРИМЕЧАНИЕ --------------------------------------------------------
Это окно (рис. 15.2) для версий Mathcad И и более ранних. Окно для версий Mathcad 13
и 14 показано на рис. 1.16. Пункты меню в обоих окнах почти одни и те же. Старое меню,
на мой взгляд, было более удобным.
При выборе вкладки Traces (Линии) (рис. 15.2 в Mathcad Ии рис. 1.16
в Mathcad 15) предоставляется возможность выбрать следующие параметры:
□	Line (Вид линии) — solid (сплошная), dot (мелкий пунктир), dadot (штрих-
пунктир), dash (крупный пунктир);
□	Color (Цвет линии);
□	Weight (Толщина линии);
□	Туре (Тип линии) — line (линия), point (точка), bar (столбик, гистограмма),
solidbar (закрашенный столбик), step (ступенька, лестница), stem (палочка
с кружочком), draw (рисованная линия), error (позволяет отложить на графи-
ке заранее вычисленную ошибку);
□	Symbol (Значок, отмечающий вычисленную точку) — попе (знак отсутствует),
x’s (крестик), +’s (плюс), box (прямоугольник), dmnd (ромб), o’s (кружок).
Рис. 15.2. Окно выбора типа линии в Mathcad 11
Чтобы построить график с отложенной ошибкой вычислений (рис. 15.3), нужно
наряду с основной функцией вычислить функции ее верхней и нижней ошибки,
15.1. Построение двухмерного плоского графика
325
присвоив названию функции тип error. График на рис. 15.3 построен по резуль-
татам испытаний стальных образцов на усталость, приведенным в главе 8
(см. рис. 8.12 и 8.13). Вычисленные верхнее (yt) и нижнее (у2) отклонения пред-
ставляют собой доверительный интервал, соответствующий вероятности разру-
шения 99 %.
х
Г рафик доверительного
интервала при выборе в
меню форматирования
графиков типа линии errors
Рис. 15.3. График с отложенной ошибкой вычислений (сравните с рис. П2.3)
Этот тип кривой представляется совершенно бесполезным. Как видно из рис. 8.13,
тип кривой line лучше отображает вид интервала вероятности, чем тип error.
На рис. 15.4 приведены примеры построения плоских графиков — обычный гра-
фик зависимости функции от аргумента и параметрический график. Обратите
внимание на наличие маркеров на левом графике (см. также рис. 2.16).
х := 0,0.1.. 15 f(x) := x cos(x)	fl(x) > x sin(x)
A := 3 C := 8 D := -8 маркеры
Рис. 15.4. Примеры построения плоских графиков
326
Глава 15. Работа с графиками
Для создания маркеров (пунктирных горизонтальных линий на графике) нужно
□	дважды щелкнуть мышью на графике и в открывшемся окне форматирова-
ния графиков отметить птичкой Show Markers (Показывать метки) по оси X
и(или) У;
□	щелкнуть мышью вне графика. Окно исчезнет. Около выбранной оси появят- .
ся два черных квадратика, в которые можно ввести либо числа, либо имя кон-
станты. Имя писать удобнее, так как при перемене значения константы авто-
матически смещается и метка.
На рис. 15.5 показано увеличение масштаба графика:
□	Поместите курсор в поле графика и нажмите правую кнопку мыши. В от-
крывшемся контекстном меню выберите Zoom (Масштаб).
□	Обведите пунктирной линией при нажатой левой кнопке мыши область гра-
фика, которую хотите увеличить.
□	В открытом окне X-Y Zoom (Масштаб по осям Х-Y) нажмите кнопку Zoom
(Масштабировать). Выделенная область увеличится до размеров всей рамки
графика.
□	Если вы хотите вернуться к исходному виду графика, нажмите Unzoom (От-
менить масштабирование) или Full View (Вид полностью). Если надо оставить
увеличенное изображение, нажмите кнопку ОК.
х= -1,-0.997., 1
Увеличенная центральная
Х-коорд!. 0.128
I______________И--V
У-коорди 0.12789
Трассировка графика X-Y
0 Отслеживать точки данных
Рис. 15.5. Увеличение масштаба и трассировка графика в Mathcad 15
| Копировать Y2 [
Закрыть
X
В контекстном меню, открывающемся при нажатии правой кнопки мыши, есть
пункт Trace (Трассировка). Выбор этого пункта вызывает появление окна трасси-
ровки X-Y Trace (рис. 15.5, справа).
15.2. Построение полярных графиков
327
Щелкните левой кнопкой мыши на графике. На острие курсора появится пере-
крестье пунктирных линий, перемещающееся при движении курсора при нажатой
левой кнопке мыши. Одновременно в окне X-Y Trace бегут цифры, указывающие
координаты перекрестья. Установив перекрестье на нужную точку графика, мож-
но скопировать его координаты в буфер обмена и затем вставить в документ для
использования в расчетах.
Если поставлен флажок Track Data Points (Отслеживать точки данных), то пере-
крестье скачет от точки к точке. Если снять этот флажок, движение перекре-
стья будет плавным.
15.2.	Построение полярных графиков
Чтобы построить график функции в полярных координатах, следует:
□	в панели графиков Graph Toolbar щелкнуть на кнопке, изображающей поляр-
ный график;
□	в местах ввода ввести: внизу — угловой аргумент функции, слева — имя функ-
ции для построения обычного графика. Для построения параметрического гра-
фика нужно ввести в обоих местах ввода имена функций углового аргумента
(рис. 15.6).
Форматирование полярных графиков аналогично форматированию плоских гра-
фиков. Полярные графики, как и плоские, можно строить в обычных и в лога-
рифмических координатах.
Для построения графика в логарифмических координатах в окне форматирова-
ния графика надо отметить флажком пункт Log Scale (Логарифмический мас-
штаб). Пример использования логарифмических координат для плоского графи-
ка приведен на рис. 8.13, для полярного графика — на рис. 15.6.
На полярном графике маркеры можно ставить только для радиальной координаты,
выбрав в окне форматирования графика пункт Show Markers (Показать метки).
Рис. 15.6. Примеры графиков в полярных координатах
В полярных координатах можно, как и в плоских графиках, использовать измене-
ние масштаба и трассировку, выбрав в контекстном меню пункт Zoom (Масштаб)
328
Глава 15. Работа с графиками
или Trace (Трассировка). Заметим, что в логарифмических координатах можно
использовать пункт Trace и нельзя использовать пункт Zoom.
15.3.	Построение трехмерных графиков
Правила построения трехмерных графиков были описаны в главе 1.
Существует несколько возможностей построения трехмерных графиков:
□	с помощью кнопки графиков Graph с математической панели;
□	с помощью мастера построения графиков, вызываемого из главного меню
Mathcad.
Можно построить трехмерный график, создав матрицу значений функции двух
переменных, а также использовать ускоренный метод построения ЗВ-графиков
без создания матрицы значений функции или специальные функции CreateMech
и CreateSpace для создания массива значений функции и построения графика.
15.3.1.	Построение графика по массиву значений
функции
На рис. 15.7 показано построение графика функции двух переменных, заданных
массивом значений. При этом два аргумента являются независимыми перемен-
ными, а функция — зависимой переменной.
построение пирамиды
Р. . := ceil - min
2
п := 20 i :=1.. n j := 1.. п
z(x,y) := cos(xy) х. := 0.2-i - 2
yj:-0.2j-2
м
Рис. 15.7. Построение трехмерного графика по заданному массиву значений функции
4n- i
j
<4n-jj;
□	Создайте вектор значений функции, предварительно задав векторы значений
аргументов функции.
15.3. Построение трехмерных графиков
329
□	Установив курсор на то место, где нужно построить график, откройте панель
Graph Toolbar (Панель графиков), щелкнув на соответствующем значке мате-
матической панели, затем щелкните на кнопке Surface plot (График поверхно-
сти). На экране появится шаблон графика.
□	В единственном месте ввода введите имя функции (без аргументов). График
построен.
Появившийся график больше похож на скелет из отдельных линий. Чтобы сде-
лать из него почти произведение искусства, надо дважды щелкнуть мышью в по-
ле графика. Откроется окно форматирования графика. О содержании этого окна
рассказано в главе 1. Чуть позднее Мы вернемся к форматированию графиков,
а пока продолжим разговор о способах создания графиков.
15.3.2.	Быстрое построение графика
На рис. 15.8 показан самый простой и удобный способ построения графика:
□	Запишите функцию двух переменных.
□	Установив курсор на то место, где нужно построить график, откройте панель
графиков Graph Toolbar, затем щелкните на кнопке графика поверхности
Surface plot. На экране появится шаблон графика.
□	В единственном месте ввода введите имя функции (без аргументов). График
построен.
В Mathcad есть возможность построения нескольких графиков на одном шабло-
не. Для этого в единственном месте ввода нужно вписать через запятую назва-
ния всех функций (рис. 15.8, справа).
G
(5 + 2cos(a))cos(b)
G(a,b) >
(5 + 2cos(a))sin(b)
2sin(a)
Рис. 15.8. Пример быстрого построения графиков
2 поверхности на одном рисунке
2	2
Z(x,y) := х + у - 30
Z,G
При быстром построении графиков Mathcad по умолчанию выбирает значения
обоих аргументов в пределах от -5 до +5 и число контурных линий 20. Для изме-
нения этих значений дважды щелкните мышью на графике и в открывшемся окне
форматирования выберите вкладку Quick Plot Data (Данные быстрого графика).
Измените пределы значений переменных и нажмите кнопку ОК.
330
Глава 15. Работа с графиками
На рис. 15.9 показан тот же график, что и на рис. 15.8, но после установки новых
пределов изменения аргументов. Для этого предназначены области окна Ran-
ge 1 — для первого аргумента и Range 2 — для второго аргумента. Введите свои
численные значения аргументов: start — начальное значение, end — конечное зна-
чение, # of Grids — число линий сетки, покрывающей поверхность. В принципе все
линии с поверхности можно удалить. Для этого на вкладке Appearance (Внешний
вид) выберите в группе Line options (Параметры линии) переключатель No Lines
(Без линий).
После ввода новых пределов значений бочонок оказался разрезанным двумя се-
чениями.
Рис. 15.9. Тот же график, что и на рис. 15.8, после изменения
пределов значений аргументов
На той же вкладке Quick Plot Data (см. рис. 15.9) пункт Coordinate System (Система
координат) позволяет быстро построить график в декартовой (Cartesian), сфери-
ческой (Spherical) или цилиндрической (Cylindrical) системе координат. Для быст-
рого перестроения графика в другой системе координат надо выбрать переключа-
тель, соответствующий одной из трех систем, и щелкнуть на кнопке ОК. График
перестроен.
На рис. 15.10 показан пример построения графика функции в двух проекциях.
В поле ввода имя функции указано два раза. Двойным щелчком мыши открываем
окно форматирования графика. На вкладке General (Общие) внизу (см. рис. 1.12)
есть раздел Display as (Показать как), в котором для каждой функции можно вы-
брать тип графика.
В нашем примере выбраны: для первой функции — Surface plot (График по-
верхности), для второй функции — Contour plot (График контуров). Каждый
график форматируется отдельно. Для контурного графика (рис. 15.11) в окне
форматирования на вкладке Special (Специальная) можно указать, нужны ли
линии уровня. Если линии нужны, то следует указать вид этих линий, их чис-
ло, проставлять ли цифровые значения на графике. Установите флажки Fill (За-
ливка поля графика цветом), Draw Lines (Рисовать линии), Auto Contour (Автома-
15.3. Построение трехмерных графиков
331
тический контур), Numbered (С указанием чисел). Можно снять флажок Auto
Contour и задать число линий контура (Number).
f(x,y) := sin(x) cos(y)
Рис. 15.10. Еще один пример быстрого построения графиков
Рис. 15.11. Пример форматирования контурного графика
В списке Line Style можно выбрать вид линий: solid (сплошные), dotted (мелкий
пунктир), dashed (крупный пунктир), da-dot (штрих-пунктир).
Вернемся к рис. 15.10. На этом рисунке линии уровня не показаны. Все флажки,
кроме Fill, сняты. Проекция на горизонтальную плоскость выглядит просто как
тень предмета в полдень. На этом же рисунке справа показана смена системы ко-
ординат для вывода графика. На вкладке Quick Plot Data (Данные быстрого гра-
фика) (см. рис. 15.9) выбрана сферическая система координат (Spherical). Это
означает, что Mathcad принимает исходную функцию /(х, у) как заданную в сфе-
рических координатах и для построения графика поверхности их надо преобра-
зовать в прямоугольные.
332
Глава 15. Работа с графиками
15.3.3.	Создание массива значений функции
Для. быстрого построения графика функции двух переменных Mathcad использу-
ет встроенную функцию CreateMech. Эту функцию может использовать и поль-
зователь Mathcad для создания массива значений функции.
CreateMech принимает выражения для исходной функции, заданной в виде одной
функции двух переменных или функции-вектора из трех элементов или трех
отдельных функций, параметрически задающих функцию двух переменных,
поверхность которой надо построить.
CreateMech возвращает массив координат х, у, z параметрически заданной функ-
ции. По этим значениям и строится график поверхности.
Обращение к функции:
CreateMech(G (или F, или /ьА/з), %	sgrid, £grid, fmap),
где G, F (Jp /2, /з) — исходная функция двух переменных, возможный вид кото-
рых показан на рис. 15.12; s0, tQ, tx — пределы изменения переменных, по умол-
чанию от -5 до 5; sgrid, /grid — число расчетных точек по интервалу изменения
переменных s и t (число линий в сетке, покрывающей график). По умолчанию
sgrid = 20, £grid = 20; fmap — трехэлементная векторная функция (или три функ-
ции), осуществляющая пересчет исходных координат (полярных, цилиндриче-
ских или сферических) в декартовы. По умолчанию (если параметр fmap отсут-
ствует) исходные координаты — декартовы.
Если вас устраивают значения, принимаемые по умолчанию, в параметрах функ-
ции CreateMech можно указать только имя функции (см. рис. 15.12).
Рис. 15.12. Оформление графика поверхности
ПРИМЕЧАНИЕ ---------------------------------------------------------
Включать функцию CreateMech в документы нерационально. Внутренний алгоритм
Mathcad использует эту функцию по умолчанию. Фактически вкладка Quick Plot Data
(Данные быстрого графика) служит для установки параметров функции CreateMech.
15.3. Построение трехмерных графиков
333
Пришло время рассмотреть раскраску графика. Когда вы вписали в шаблон трех-
мерного графика имя функции и щелкнули мышью вне поля графика, на экране
появился черно-белый график функции. Чтобы раскрасить его, двойным щелч-
ком мыши в поле графика откройте окно форматирования графика и выберите
вкладку Appearance (Оформление) (см. рис. 15.12).
В разделе Fill Options (Параметры заливки графика) по умолчанию отмечен
пункт No Fill (Без заливки). Установите переключатель Fill Surface (Поверхность
с заливкой), а в разделе Color Options (Параметры цвета) установите флажок
Colormap (Карта цветов). Если хотите нанести на график расчетные точки, уста-
новите в разделе Point Options (Параметры точек) флажок Draw Points (Нарисо-
вать точки).
В разделе Line Options (Параметры линий) установите переключатель Wireframe
(Каркас). В этом же разделе можно выбрать толщину линий (Weight) и цвет ли-
ний (Color Options). Остальные пункты этого меню, как и всех других, опробуйте
в процессе работы с графиками.
На рис. 15.13 приведен еще один пример использования функции CreateMech.
Этот график изображен в двух проекциях. В окне форматирования на вкладке
General (Общие) установлено Show Box (Показать рамку), на вкладке Axes Style
(Вид осей) — Corner (В углу) и Equal Scales (Равные шкалы по осям).
Каждый из двух графиков форматируется отдельно. Перейдите на вкладку вни-
зу Plot 2 (График 2). Там (в данном примере) отражаются те же установки, что
и для графика 1.
В разделе View (Вид) можно выбрать углы поворота изображенной поверхности
вокруг всех трех осей:
□	Rotation (Поворот) — вращение вокруг оси Z. Значения углов от -360°
до 360°;
□	Tilt (Наклон) — вращение вокруг оси X после вращения вокруг оси Z. Углы
могут принимать значения от 0° до 180°;
□	Twist (Изгиб) — вращение вокруг оси Z после вращений вокруг Z и X. Углы
могут принимать значения от -360° до 360°.
Поменяйте углы и посмотрите на вид графика.
Этот способ вращения хорош, если надо поточнее развернуть поверхность. Од-
нако обычно используют более простой способ, описанный в главе 1. Следует ус-
тановить курсор в поле графика, а затем выполнить следующие действия:
□	двигать мышь при нажатой левой кнопке. График поворачивается;
□	двигать мышь при нажатой левой кнопке и нажатой клавише Ctrl. График при-
ближается или удаляется;
□	двигать мышь при нажатой левой кнопке и нажатой клавише Shift. Начинает-
ся вращение графика (анимированное). Для остановки вращения надо щелк-
нуть мышью в поле графика.
334
Глава 15. Работа с графиками
Рис. 15.13. Вкладка General (Общие) окна форматирования трехмерных графиков
15.3.4.	Поверхности тел вращения
Аналитически тела вращения, как правило, описываются в сферических или ци-
линдрических координатах. Mathcad строит трехмерные графики в декартовых
координатах. В таких случаях необходимо преобразовать исходные координа-
ты в декартовы. Для таких преобразований можно использовать аналитические
формулы или встроенные функции cyl2xyz и sph2xyz.
На рис. 15.14 показано построение поверхности шара с использованием аналити-
ческого преобразования сферических координат в прямоугольные без примене-
ния функции CreateMech.
<	. .	.л
п := 40	1 := 1.. n	j := 1.. п 04 := 1- —
п
Pj := j 2 Zb XiJ " cos(Pj)
Yi,j:= s*n(ai) s*n(Pj) zi j '= cos(aj)
(X,Y,Z)
Рис. 15.14. Построение шара с использованием
аналитического преобразования координат
15.3. Построение трехмерных графиков
335
О(0,ф)
поменяйте местами fmap
finap(v) = cyl2xyzi vj, V2 ,V3!
Snap(v) = sph2xyzl vi, V2, V31
cos (а)л
fmap(r,a,z) = r sin(a)
GO = 0 01 = it ф0 := 17T ф! := 1.5 лпоменяйте значения углов е и <f>
М := CreateMesh(G,00,01 ,ф0,ф1,50,50,fmap) Ml = CreateMesh(G,fmap)
Рис. 15.15. Построение поверхности тела вращения с вырезом
Ml
На рис. 15.15 показано построение поверхности шара с применением функции
CreateMech. В качестве функции преобразования координат fmap прилагаются
аналитическое преобразование цилиндрических координат в декартовы функци-
ей cyl2xyz и преобразование сферических координат в декартовы функцией sph2xyz.
Поменяйте эти выражения местами.
яр(ф) sin(|) уравнение образующей fmap(v) > cyl2xyz(v1,v2,v3)
Тад] |ьт Поменяйте пределы а и Ь
♦
K(z,|) >
S := CreateMesh(K.,0,a,0,b,ftnap) z := 0,0.1.. а
Рис. 15.16. Поверхность вращения плоской кривой
336
Глава 15. Работа с графиками
В этом примере функция CreateMech применена с параметрами и без парамет-
ров. Если использована функция без параметров, получается замкнутая фигура,
а если с параметрами — есть возможность, меняя пределы изменения углов, мо-
дифицировать размеры выреза.
На рис. 15.16 показана возможность построения поверхности вращения по урав-
нению ее образующей. На рис. 15.17 подобное построение гораздо проще выпол-
нено с помощью вкладки Quick Plot Data (Данные быстрого графика).
S(u,v) := f(u)cos(v)
то же самое гораздо проще выполнить
с помощью вкладки Quick Plot Data f(x) := x sin(x)2
Рис. 15.17. График поверхности, построенный с помощью вкладки
Quick Plot Data (Данные быстрого графика)
Vf(u) sin(v) J
x:= -3.14,-3.. 2 л
график образующей

СОВЕТ -----------------------------------------------------------------
Не используйте в расчетах функцию CreateMech. Те же параметры можно и нужно вводить
с помощью вкладки Quick Plot Data.
15.3.5.	Построение сложных фигур
Построение пространственной кривой с применением
функции CreateSpace
Встроенная функция CreateSpace принимает трехэлементную векторную функ-
цию одной переменной и возвращает декартовы координаты пространственной
кривой.
Обращение к функции:
CreateSpace(F, tQ, tif £grid, fmap),
где F — трехэлементная векторная функция одной переменной; t0 и tx — пределы
изменения переменной, по умолчанию от -5 до 5; fgrid — число точек кривой, по
умолчанию 20; fmap — функция преобразования координат. Параметр fmap не-
обязателен. При его отсутствии входная функция по умолчанию считается
заданной в декартовых координатах.
Применение функции CreateSpace показано на рис. 15.18.
15.3. Построение трехмерных графиков
337
F(z) >
H(t) :=
finap(v) := cy!2xyz^V| ,У2»Уз)
С := CreateSpace(F,tO,tl ,200,ftnap)
Поменяйте местами выражения С
^/t- sin(t)
< t ;
tO := 0 tl := 16
C := CreateSpace(H,tO,tl ,200)
Рис. 15.18. Построение пространственной кривой
Пересекающиеся фигуры
На рис. 15.19 и 15.20 показаны возможности создания в Mathcad сложных пере-
секающихся фигур. Обе фигуры получены путем формирования массивов коор-
динат точек фигур по формулам. На этих фигурах поупражняйтесь в формати-
ровании рисунков.
Пересечение цилиндров
п.= 40 i := 1.. n j := 1.. п
Рис. 15.19. Пересечение трех цилиндров
ORIGIN := 0 N := 60 i:=0..N
♦i:=i-2— j:=O..N o^jl-
N	J N
x. . := (5 + 2-cos(<|>i)) cos(a,j)
yi,j:= + 2 C0SW) sm(aj) zij := 2 sin(*i)
Рис. 15.20. Два связанных кольца
338
Глава 15. Работа с графиками
15.3.6.	Построение многогранников
В Mathcad имеется возможность быстрого построения поверхностей многогран-
ников. Всего можно построить 80 многогранников. Описание многогранни-
ков, которые Mathcad может вывести на экран, можно найти в Центре докумен-
тации: Resource Center ► QuickSheets and Reference Tables ► Reference Tables ►
Geometry Formulas ► Polyhedra (Центр ресурсов ► Таблица справок ► Геометри-
ческие формулы ► Многогранники).
Polyhedron("#40")
Рис. 15.21. Построение поверхностей полиэдров
Для построения полиэдра выведите на экран шаблон ЗВ-графика и в поле ввода
напишите Polyhedron (”#«номер от 1 до 80»”). Примеры построения многогранни-
ков приведены на рис. 15.21 и 15.22.
Polyhedron("#80")
Рис. 15.22. Примеры построения поверхностей многогранников
Polyhedron(#j
15.3.^Построение трехмерных графиков
339
15.3.7.	Быстрое изменение типа графика
В заключение главы рассмотрим некоторые типы графиков, довольно редко ис-
пользуемых на практике, но тем не менее имеющихся в арсенале Mathcad.
F	F
Рис. 15.23. Примеры построения точечного (слева) и столбчатого (справа) графиков
В окне форматирования BD-графиков на вкладке General внизу (см. рис. 15.13)
имеются шесть кнопок перестроения графиков:
□	Surface Plot — график поверхности;
□	Contour Plot — линии уровня;
□	Data Points — точки данных, расположение расчетных точек в пространстве
(рис. 15.23, слева);
□	Vector Field Plot — векторное поле (рис. 15.25);
□	Bar Plot — столбчатая диаграмма (рис. 15.23, справа);
□	Patch Plot — лоскутный график, похожий на точечный график, каждая точка
в нем имеет вид лоскутка (рис. 15.24).
Рис. 15.24. График поверхности из лоскутков (Patch Plot)
Построив один из графиков, можно легко перестроить его в другой, отметив
флажком соответствующий тип графика на вкладке General, за исключением
Vector Field Plot.
340
Глава 15. Работа с графиками
15.3.8.	График векторного поля
Векторное представление функции создается построением коротких стрелочек —
векторов. Стрелочка направлена в сторону возрастания высоты поверхности (уве-
личения значений функции). Плотность стрелок зависит от скорости изменения
функции, то есть от ее градиента. Длина стрелочки пропорциональна модулю
вектора. Такого вида графики удобно приводить при расчете различных полей:
электромагнитных, тепловых, гравитационных и т. д.
у := 0 обнуление прежнего значения массива у
Fl(x,y) := sin(xy) F2(x,y) := cos(xy) n := 10 m .= 10
я .	я . '
y^-.j
И1. j := Fl(xi>yj) H2. . := F2(Wj) G. j := Hl. j +
Поменяйте фунцию F и число точек пит
(Hl ,Н2) Вместо (Н1 ,Н2) поставьте G
Рис. 15.25. Векторное поле функции, проекции которой — Н, и Н2
При построении векторного поля требуется задать двухмерный массив значений
функции в заданных точках. На рис. 15.25 показано векторное поле — поток
функции G, у которой проекции на осях X и Y — это и Н2 соответственно. Ино-
гда удобно представить функцию как матрицу комплексных чисел, где одна из
проекций вектора — его вещественная часть, другая проекция — мнимая часть.
Работая с примером, поменяйте функцию и количество точек.
15.4. Особенности форматирования графиков
в новых версиях Mathcad
15.4.1.	Редактирование двухмерных графиков
Двойной щелчок мышью в поле двухмерного графика вызывает появление окна
форматирования графика. В Mathcad 13 в этом окне изменилась вкладка Traces
(Трассировка). На рис. 15.26 показана вкладка Traces. Поскольку окно резко
15.4. Особенности форматирования графиков в новых версиях Mathcad
341
увеличилось в размерах, не помещающаяся в окне часть вкладки «подклеена»
к рис. 15.26. Столбцы в окне прежних версий стали строками в Mathcad 13. От-
метим новый столбец Symbol Frequency (Частота символов), который позволяет
показывать на графике не все расчетные точки, а каждую вторую, третью и т. д.
Форматирование выбранного графика X-Y
Оси X, Y Трассировка формат числа Подписи По умолчанию
П Скрыть аргументы;	[^Скрыть легенду
ОК	Отмена	[ Справка
Рис. 15.26. Окно форматирования двухмерного графика в Mathcad 15
Рис. 15.27. Ввод комментария к графику
342
Глава 15. Работа с графиками
Появилась ‘возможность выбора местоположения комментария к графику (рис.
15.27). Комментарий вводится на вкладке Trace (Трассировка). Вместо слов
«кривая №» можно вписать свой текст. В нижней левой части вкладки можно
выбрать его положение (внизу, вверху, слева, справа).
В Mathcad 12 появилась возможность указывать на графике численные значе-
ния на двух вертикальных осях Y (слева и справа от графика). На рис. 15.28 по-
казана вкладка X-Y Axes окна форматирования графика. Для введения второй
шкалы Y справа от графика вначале нужно отметить флажком пункт Ena-
ble secondary Y axis (Включить дополнительную ось Y), затем закрыть окно
форматирования. Затем в шаблоне графика в появившемся справа месте
ввода вписать имя функции, снова открыть окно форматирования на вклад-
ке Trace (Трассировка) и установить нужные параметры графика.
Рис. 15.28. Две шкалы по оси Yна плоском графике
15.4.2.	Форматирование двухмерных графиков
В Mathcad 14 в окне форматирования двухмерных графиков появилась новая
вкладка, позволяющая изменять формат чисел (рис. 15.29).
На рис. 15.30 приведен пример форматирования чисел, выводимых на графике.
Для начала график был укрупнен путем вписывания нужных пределов чисел на
оси X. Затем двойным щелчком мышью вызвано окно форматирования, в кото-
ром выбрана вкладка Number Format. Для наглядности выбран совсем уж экзоти-
ческий вариант — представление чисел в виде дробей. Не самое нужное нововве-
дение, но оно есть.
15.4. Особенности форматирования графиков в новых версиях Mathcad
343
Рис. 15.29. Вкладка форматирования чисел в окне форматирования плоских графиков

Форматирование выбранного графика X-Y
ОК | [ Отмена | [ Применить ) [ Справка |
Рис. 15.30. Экзотика. Изменение формата чисел на осях графика
15.4.3.	Функции logspace и logpts
В Mathcad 13 появились две функции для работы с графиками с использовани-
ем логарифмической шкалы.
344
Глава 15. Работа с графиками
Обращение к ним:
logspace(min, max, npts);
logpts(minexp, dec, dnpts),
где min и max — минимальное и максимальное значения диапазона чисел; dec —чис-
ло декад (значащих цифр между ними); npts и dnpts — общее число точек и число
точек в каждой декаде.
Функция logspace создает вектор чисел, распределенных по логарифмическому
закону между min и max.
Функция log pts создает вектор чисел, распределенных по линейному закону
внутри каждой декады числового ряда. Общее число точек равно произведению
dec х dnpts. Пример создания таких массивов показан на рис. 15.31.
ORIGIN > 1
YY := logspace(l ,8000,8)
XX := logpts(2,2,4)
i:= 1.10
f 1 1
3.611
13.037
47.071
169.956
613.651
2215.673
< 8000 ;
< 100 >
325
550
775
1000
3250
5500
<7750;
номер точки
Рис. 15.31. Сравнение векторов чисел, созданных функциями logspace и logpts
номер точки
Глава 16
Справочная информация в Mathcad
В меню Help Mathcad есть три источника справочной информации:
□	собственно Help Mathcad (Справка), вызываемый клавишей F1 или непосред-
ственно из меню Help;
□	электронная книга qscheet, содержащая несколько разделов (в разных верси-
ях они разные);
□	Интернет.
Рассмотрим кратко эти источники информации.
16.1.	Меню Help (Помощь)
При выборе пункта Help в главном меню Mathcad открывается подменю с не-
сколькими пунктами (рис. 16.1):
□	Mathcad Help (Справка по Mathcad) — система справок по всем вопросам ра-
боты в Mathcad;
□	Developer’s Reference (Руководство для разработчиков) — дополнительные
справки для разработчиков приложений Mathcad;
□	Author’s Reference (Руководство для авторов) — дополнительные главы справ-
ки для авторов электронных книг;
Рис. 16.1. Вызов справки в Mathcad
346
Глава 16. Справочная информация в Mathcad
□	Tutorials (Руководства и учебники) — сборник статей, обучающих работе
в Mathcad;
□	QuickSheets (Шпаргалки) — сборник примеров расчетов в Mathcad;
□	Reference Tables (Справочные таблицы) — таблицы справочных данных;
□	E-books (Электронные книги) — перечень электронных книг, включенных
в оболочку Mathcad, в том числе две электронные книги;
□	перечень интернет-адресов для связи с фирмой Mathsoft.
Во всех ранних версиях Mathcad (до Mathcad И) все перечисленные пункты,
кроме Mathcad Help, были объединены в один пункт Recource Centre (Центр до-
кументации).
Если в какой-либо момент работы в Mathcad вам понадобится помощь, выберите
в главном меню команду Help ► Mathcad Help, либо щелкните на кнопке со знаком
вопроса (?) на стандартной панели Mathcad, либо воспользуйтесь клавишей F1. От-
кроется окно справочной системы Mathcad (рис. 16.2).
Mathcad Help
Файл [Травка Вид Вставка Формат Инструменты Символьные операции Книга Справка
T] Welcome to Mathcad
Getting Started
О Vectors and Matrices
О Operators
Functions
ф Solving
Programming
< Units
G 2D and 3D Plots
ф Symbolics and Keywords
О External Files and Applicatic
О Other Resources
Mathcad
Welcome to Mathcad!
Welcome to Mathcad 15 - The standard for
Engineering Calculation and Communication!
You can use Mathcad to perform, document,
and share all your calculations and design
work. Mathcad's visual format and scratchpad
interface integrate standard mathematical
notation, text, and graphs in a single
worksheet - making Mathcad ideal for
knowledge capture, calculation reuse, and
engineering collaboration. Mathcad allows you
to design and document your engineering work
with unit-aware calculations.
Mathcad's open application architecture
combined with its support of .NET and its
native XML format make it easy to integrate
Mathcad into other engineering applications.
Mathcad is the only enterprise-wide solution
for managing engineering design and
attributes. The files you produce are readily
publishable into a variety of formats: XML,
HTML, PDF, and RTF, and with the use of the
Mathcad Calculation Server, you can publish
Г отово
АВТО
Рис. 16.2. Окно справки Mathcad
16.2. Перевод справочной системы Mathcad
347
Справка в Mathcad является контекстно-зависимой, то есть ее содержание зависит
от того, из какого места документа Mathcad она вызвана. Например, при установке
курсора на имени функции polyroots и нажатии клавиши F1 на экране появляется
окно Mathcad Help, открытое на месте описания функции polyroots (см. рис. 16.2).
Окно справочной системы Mathcad построено в характерном для Windows стиле
и состоит из двух частей. Слева отображаются названия статей, справа — их текст.
Справочная система насыщена гиперссылками, находящимися в тексте статей
и обеспечивающими переход от одной статьи к другой. Для перехода от одной
статьи к другой установлены кнопки навигации Back (Назад), Forward (Вперед),
Ноте (Домой).
В тексте статей часто встречаются кнопки QuickSheet Example, вызывающие при-
мер расчета, связанный с содержанием справочной статьи.
Статей гораздо больше, чем заголовков в содержании. Для вывода большинства
из них на экран потребуется один-два перехода по гиперссылкам.
В конце почти каждой статьи есть кнопка Related Topics (Статьи, близкие
по смыслу). Щелчок мышью на этой кнопке открывает перечень статей на сход-
ные темы, связанных гиперссылками с данными статьями.
16.2.	Перевод справочной системы Mathcad
Все статьи справочной системы Mathcad написаны на английском языке. Если
английский текст вам непонятен, воспользуйтесь какой-либо системой-пере-
водчиком, например Prompt.
Выделите черным цветом фрагмент текста, который хотите перевести, или в глав-
ном меню Mathcad выберите команду Edit ► Select all (Редактировать ► Выделить
все). Затем скопируйте выделенный текст в буфер (рис. 16.3). В меню Prompt вы-
берите пункт Перевод Clipboard (Перевод содержимого буфера обмена). В поя-
вившемся окне выберите направление перевода: Англо-русский перевод — и на-
жмите кнопку ОК. Машинный перевод, конечно, примитивный, но зато быстрый,
и, в общем, становится понятно, о чем идет речь (рис. 16.4).
Рис. 16.3. Выделение текста для перевода
348
Глава 16. Справочная информация в Mathcad
IV Clipboard: Англо-Русский перевод	RFI
«Мй I I ни I ? I
__________[ Заменить [ Направление] Справка |
Сообщения об ошибках в Численных расчетах
Любые ошибки в рабочем листе отмечены с сообщением об ошибках и
названием(именем) оскорбления, или оператор высвечен в различном цвете
(обычно красный).
Рабочий лист не может обрабатывать выражение, содержащее ошибку. Для
выражения, чтобы обработать, Вы должны установить ошибку.
Для информации относительно специфического сообщения об ошибках, нажмите —
на это в списке ниже:
"НаходящийсяТгоказаться") или "Minerr" нужно предшествовать "Данным"
Чтобы получить подсказку, нажмите F1
Рис. 16.4. Перевод текста, выделенного на рис. 16.3
В Mathcad Help все статьи подготовлены в текстовом редакторе, и поэтому элек-
тронный переводчик обрабатывает их без проблем.
Сложнее обстоит дело со статьями из электронных книг. Они подготовлены как
часть электронной книги в Mathcad и не могут быть переведены текстовым элек-
тронным переводчиком. Эти статьи вначале надо перенести в текстовый редактор.
Выделите текст статьи электронной книги. Скопируйте его в буфер обмена
и вставьте в пустой документ Mathcad. Поскольку электронная книга создана
в Mathcad, то только в Mathcad ее можно преобразовать в текстовый файл.
В меню File (Файл) выберите команду Save as (Сохранить как), в открывшемся
окне впишите какое-либо имя и выберите тип файла Rich Text Format File (*.rtf),
затем нажмите кнопку Сохранить. Созданный документ стал текстовым файлом,
и теперь он открывается в Word.
Из документа Word текст скопируйте в буфер обмена, затем вызовите электрон-
ный переводчик и выберите команду Перевод Clipboard ► Англо-русский перевод.
Примеры перевода текста из электронной книги Resource Center приведены на
рис. 16.6-16.9.
ПРИМЕЧАНИЕ -------------------------------------------------------
Электронный переводчик Promt 7 переводит тексты, созданные в различных Windows-
приложениях, включая Mathcad, после копирования их в буфер обмена и не требует пре-
образования в текстовый файл.
16.3.	Электронная книга qscheet
Электронная книга qscheet представляет собой сборник статей и примеров, по-
ясняющих работу операторов и встроенных функций Mathcad, а также примеров
решения различных математических, физических, инженерных задач с помощью
Mathcad.
16.3. Электронная книга qscheet
349
Чтобы вызвать эту электронную книгу на экран, следует в меню Help выбрать
нужный раздел (см. рис. 16.1). На экране появится титульный лист этой элек-
тронной книги (рис. 16.5).
Рис. 16.5. Заглавная страница электронной книги qscheet
На титульном листе все заголовки являются гиперссылками. Щелчок мышью на
них открывает соответствующий раздел книги. Всего разделов три:
□	Tutorial (Учебник) — информация о возможностях системы и основные прие-
мы работы с Mathcad;
□	QuickSheets — сборник примеров;
□	Reference Tables — справочные таблицы.
Передвигаться по разделам электронной книги очень легко. В начале каждого
раздела и подразделов приводится оглавление, выполненное в виде гиперссы-
лок. При наведении на гиперссылку курсор приобретает вид руки с вытянутым
указательным пальцем. При щелчке мышью на соответствующей гиперссылке
пользователь переходит в нужный раздел электронной книги.
350
Глава 16. Справочная информация в Mathcad
Особенностью электронных книг в Mathcad является выполнение расчетов пря-
мо на страницах книги, причем пользователь может изменять любые параметры
и наблюдать изменение результатов расчета. Правда, сохранить результаты пере-
счета прямо в электронной книге нельзя, поскольку в ней включена защита от
записи. Зато нужные фрагменты книги можно скопировать в свой документ.
Чтобы скопировать фрагмент книги, надо выделить его пунктирной рамкой, об-
ведя курсором при нажатой левой кнопке мыши, а затем скопировать в буфер
обмена и оттуда вставить в нужное место своего документа.
Есть и более простой способ копирования, типичный для всех Windows-прило-
жений. Можно выделенный фрагмент перетащить по экрану в свой документ
при нажатой левой кнопке мыши.
16.3.1.	Обзор и учебник
В разделе Tutorial (Учебник) пользователь найдет основные сведения по данной
версии Mathcad на английском языке. В Mathcad 15 включен раздел Users Guide
на русском языке. Чтобы открыть его, выберите пункты Справка ► Руководства
и учебники ► Users Guide. На рис. 16.6 показано оглавление этого раздела.
Начало учебника (рис. 16.7) посвящено обучению основам работы в Mathcad
и похоже на главу 1 данной книги. В последующих разделах идет углубленное
изучение Mathcad и приведено большое количество примеров, как правило, очень
простых.
Рис. 16.6. Первая страница учебника и оглавление User Guide на русском языке
Содержание
16.3.2.	Примеры и справочные таблицы
В разделе Quickschets электронной книги сосредоточено большое количество
примеров, в основном из математики и физики, с использованием большинства
встроенных функций и различных возможностей Mathcad.
16.3. Электронная книга qscheet
351
Mathcad Resouices QuickSheets Content*
Fie fcdrt View Iroert Fwmat Tools Symbols fiook Help
a* > < s ® в» ей й a ©
Pre» F1 for help	AUTO
Рис. 16.7. Оглавление раздела Getting Started Tutorial с переводом
Рис. 16.8. Первая страница раздела Reference Tables
352
Глава 16. Справочная информация в Mathcad
Раздел Reference Tables (Справочные таблицы) содержит простейшие математи-
ческие формулы, сведения о свойствах различных материалов и т. п. (рис. 16.8).
Сведения эти бессистемные и в общем мало кому нужные. Правда, в разделе
Geometry Formulas (Геометрические формулы) есть хоть и не очень нужный, но
весьма любопытный раздел Polyhedra (Многогранники), содержащий графики
поверхностей 80 многогранников (правильных). Об использовании этого разде-
ла шла речь в главе 15 (см. рис. 15.20 и 15.21).
16.4.	Mathcad и Интернет
Для работы в Интернете Mathcad имеет встроенный браузер, позволяющий поль-
зоваться услугами Интернета, не выходя из программы. Кнопки доступа в Ин-
тернет из среды Mathcad находятся в выпадающем меню кнопки Help стандарт-
ного меню Mathcad (см. рис. 16.1):
□	User Forums — форумы пользователей Mathcad;
□	Mathcad.com — открытие начальной страницы фирмы Mathsoft;
□	Consulting & Training — обучение Mathcad.
Встроенный в Mathcad браузер обладает рядом недостатков, поэтому для работы
с сайтом PTC Mathcad лучше пользоваться другими браузерами (например,
Internet Explorer). Запустите браузер и наберите в его окне поиска ключевую
triunity Community: Mathcad
Вставка Формат Инструменты Символьные операции Книга Справка
Di Ы & (3
planetPTC
COMMUNITY	д community for PTC customers and everyone dedicated to product development excellence
Д Welcorr? Evgenie Makarov <Log out	Go to PTC com О share
PlanetPTC Community Mathcad	Browse	‘leedhteip7
Mathcad
Overview
SUB-COMMUNITIES
Mathcad Usage
О Algebra & Geometry
О Aerospace Engineering
О Biology
О Calculus & Des
О Chemical Engineering
О См! Engineering
D Electrical Engineering
Geology
О Math Homework Help
 Discussions (99)
Documents; If Blog Videos Set as default Ub
HERO OF THE MONTH
Щ Valery Ochkov
Our first Hero of the Month has
been a passionate Mathcad user
for over 20 years!
> Learn why Valery is a Hero
TOP PARTICIPANTS
ALL RECENT MATHCAD CONTENT
Mike Armstrong
Рис. 16.9. Страница сайта форума Mathcad, открытая в браузере Mathcad
16.4. Mathcad и Интернет
353
фразу PTC Mathcad, и вы получите большой список тематических ссылок. Мож-
но самостоятельно ввести следующие адреса:
□	http://www.ptc.com/ — начальная страница фирмы РТС, которая в 2003 году
купила фирму Mathsoft и в настоящее время продолжает работу по совер-
шенствованию системы Mathcad.
□	http://www.ptc.com/appserver/mkt/products/home.jsp?k=3901 — помимо кратких
описаний программных продуктов, выпускаемых фирмой РТС, здесь можно
найти полезные утилиты (как платные, так и бесплатные) и сотни файлов
с примерами их использования, последние новости и другую полезную ин-
формацию.
□	http://communities.ptc.com/community/mathcad — сайт, на котором пользовате-
ли из разных стран обсуждают вопросы, связанные с работой в Mathcad
(рис. 16.9).
16.4.1. Техническая поддержка Mathcad
На сайте PTC Mathcad работает служба технической поддержки (ссылка Support
на главной странице сайта). Зарегистрированные пользователи имеют полный
доступ к документации по системе Mathcad и другой полезной информации,
возможности незарегистрированных пользователей ограничены.
В целом Mathcad неплохо интегрирован с Интернетом. Фирма Mathsoft много
работает именно в этом направлении. Большинство изменений, появившихся
в последних версиях Mathcad, в первую очередь касаются работы в Интернете.
Глава 17
Создание электронных книг
Создание электронных книг — своего рода высший пилотаж в среде Mathcad.
Электронная книга сочетает в себе текст и примеры вычислений в Mathcad.
Большое количество ссылок обеспечивает быстрое и удобное перемещение по
книге, поиск нужного фрагмента. Все приведенные примеры работают, допуска-
ют изменение параметров расчета с мгновенным пересчетом примера. Измене-
ния в электронной книге нельзя сохранить в ней, но любой фрагмент книги мож-
но скопировать в другой файл Mathcad и сохранить там.
В Mathcad 15 включено пять электронных книг:
□	Quick Sheets — примеры использования операторов и встроенных функций
Mathcad. Эта книга содержит три раздела:
О Tutorials — обучение работе в Mathcad;
О Quick Sheets — примеры расчетов в Mathcad;
О Reference Tables — справочные таблицы;
□	Data Analysis Extension Pack — анализ наборов данных;
□	Image Processing — цифровая обработка изображений в Mathcad;
□	Signal Processing — обработка сигналов в Mathcad;
□	Wavelets Extension Pack — волновые преобразования массивов данных.
Перечисленные электронные книги можно вызвать на экран из главного меню
Mathcad, выбрав пункт Справка ► Электронные книги (рис. 17.1). В оболочку
Mathcad я добавил и три свои электронные книги:
□	«Инженерные расчеты в Mathcad» — она содержит все, что вы видите на
страницах этой книги;
□	«Справочник по инженерным расчетам в Mathcad» — электронный конструк-
тор для сборки собственных программ из готовых фрагментов. Этот справоч-
ник выпущен фирмой «Новый диск» на компакт-диске под названием «Math-
cad — конструктор программ»;
□	«Сопротивление материалов» — подготовка нового компакт-диска с примера-
ми решения прочностных задач.
Наличие на компьютере встроенной в оболочку Mathcad нужной электронной
книги очень полезно и удобно. Благодаря системе вложенных друг в друга ог-
лавлений и системе ссылок можно практически мгновенно найти нужный мате-
риал, скопировать необходимый фрагмент в буфер обмена и вставить его в соб-
ственную программу.
Создание электронных книг предусматривает следующие действия:
1.	Создание необходимых Mathcad-файлов.
2.	Подготовку содержания электронной книги.
17.1. Создание Mathcad-файлов для электронной книги
355
3.	Добавление электронных ссылок из содержания на соответствующие файлы.
4.	Создание НВК-файла, определяющего порядок следования файлов в элек-
тронной книге.
5.	Создание индексов для поиска нужного фрагмента книги.
6.	Проверку правильности индексов, НВК-файла и Mathcad-файлов, включен-
ных в электронную книгу.
Mathcad - [Безымянный: 1]	Г
Справка
Файл Правка Вид Вставка Формат Инструменты Символьные операции
"	- & х
□ - ® Справка Matbead	Fl	/W V =	□ 100% - (х)
^тЛ7агоэтотаюе? Sttft+F1	в 1 и :=|=
Руководство для разработчиков
Руководство для авторов
Руководства и учебники
Шпаргалки
Справочные таблицы
2лектр«оннь1е книги
Форумы пользователей
Веб-узел Matbead
Обучение Matbead
О программе Matbead...
Рис. 17.1. Окно выбора электронных книг
17.1.	Создание Mathcad-файлов
для электронной книги
Все файлы, включаемые в электронную книгу, должны быть помещены в одну
папку, имеющую то же название, что и электронная книга. Наличие вложенных
папок допускается, но не рекомендуется, так как при этом некоторые функции
электронной книги станут недоступными. Если в тексте предполагается появле-
ние всплывающих окон со вспомогательным материалом, то содержание этих
окон как раз и надо размещать во вложенной папке под именем Popups.
Полезно перед началом подготовки электронной книги создать свои пользова-
тельские стили, отличающиеся от стандартных цветом, шрифтом и т. д. Это
удобно для придания единообразия всем создаваемым документам.
На экране компьютера люди читают текст значительно медленнее, чем на листах
обычной книги, поэтому для облегчения чтения примите к сведению несколько
советов:
□	Текст на экране должен быть сравнительно крупный и четкий, черный на бе-
лом фоне. Ключевые слова лучше выделить другим шрифтом или цветом.
356
Глава 17. Создание электронных книг
Обычный текст лучше печатать полужирным шрифтом размером 12 пунктов.
Жирный текст читать тяжелее, поэтому его используйте для отдельных клю-
чевых слов. Ссылки желательно подчеркнуть и выделить цветом.
□	Математические области в документе должны быть упорядочены, выровне-
ны, снабжены краткими текстовыми комментариями. Желательно, чтобы на
экране можно было видеть одновременно весь законченный по смыслу фраг-
мент вычислений. Основные уравнения, а также исходные данные, которые
можно менять, желательно выделить цветом.
□	Включайте в текст больше заголовков, разделяя ими разные по смыслу фраг-
менты вычислений.
□	При вводе текста в Mathcad-документ избегайте использования клавиши
Enter для перехода на другую строку. Набирайте текст подряд, а затем, под-
ведя курсор к краю рамки, установите нужный размер текстовой области.
В этом случае достигается наилучшая видимость на мониторах различных
размеров.
17.2.	Подготовка содержания электронной книги
Закончив работу с Mathcad-файлами, подготовьте оглавление электронной кни-
ги. Поместите его в файл под названием TOC.mcd. Оглавление должно быть как
можно более подробным. Рекомендуется делать вложенные оглавления, тогда
основное оглавление не будет чрезмерно большим. Почти каждому крупному
пункту основного оглавления будет соответствовать связанное с ним ссылкой
вложенное оглавление. Пример основного и вложенного оглавлений показан на
рис. 17.2.
Рис. 17.2. Основное и одно из вложенных оглавлений электронной книги
17.4. Создание НВК-файла
357
17.3.	Создание системы ссылок между файлами
Для быстрого просмотра содержания электронной книги надо установить ссыл-
ки между файлами. В главе 13 (раздел 13.4) описывается порядок создания ги-
перссылок (Hyperlink) между файлами. Напомним его.
Гиперссылка позволяет открывать файл, с которым создана связь, в той оболоч-
ке, в которой он создан. Для создания гиперссылки нужно:
□	выделить слово или фрагмент текста, с которым будет связан интересующий
вас файл, желательно, черным цветом. Тогда после установления связи выде-
ленное слово будет выделено жирным шрифтом и подчеркнуто;
□	в главном меню Mathcad выбрать Insert ► Hyperlinc ► Browse (Вставка ► Гипер-
ссылка ► Обзор) ► указать путь к файлу, с которым надо связать выделенное
слово ► ОК;
□	в окне Edit Hyperlink (редактировать гиперссылку) установить флажок на
пункте Use relative path for hyperlink (Использовать относительный путь для
гиперссылки). В этом случае связь будет работать даже в том случае, если вы
переместили каталог с электронной книгой в другое место;
□	двойной щелчок мышью на выделенном слове открывает файл, с которым ус-
тановлена связь.
Если вы хотите вызвать на экран не начало, а определенное место выбранного
файла, то его необходимо задать (этот процесс описан в разделе 14.2.1):
□	откройте файл, на который будет создана ссылка;
□	установите курсор на объект (слово, выражение или график), который при
вызове файла будет находиться вверху на экране;
□	щелкните на нем правой кнопкой мыши и в открывшемся контекстном меню
выберите Properties (Свойства);
□	в окне Тад (Метка) впишите имя метки (в нашем случае — 931), как показано
на рис. 17.3. Нажмите кнопку ОК.
После создания метки следует создать гиперссылку, как указано ранее. Вводя
путь к файлу, укажите и имя метки, записав в конце адреса, например, #931
(рис. 17.4). Теперь при двойном щелчке мышью на слове, с которым связана ги-
перссылка, указанный в адресе файл откроется с того места, на которое установ-
лена метка.
Чем больше установлено гиперссылок, тем быстрее пользователь сможет найти
нужный материал в электронной книге.
17.4.	Создание НВК-файла
НВК-файл играет ту же роль, что и переплет в обычной книге. Он устанавливает
порядок следования файлов в электронной книге.
358
Глава 17. Создание электронных книг
Ис
Пр
процессе мс
для определи
еж«1п(
,также н
L Резут
& Вырезать
^Копировать
е Вставить
Выделить все
Й? Свойства...
Вставить регион формул
А Щэифт...
Абзац...
Стиль...
□одстрочньй
Надстрочный
Свойства
OK j [ Отмена j [ Справка j
Ob Гиперссылка
Рис. 17.3. Установка метки на место, с которого откроется файл
Рис. 17.4. Установка гиперссылки между файлами
НВК-файл — это простой текстовый файл, который обеспечивает:
□	порядок обзора или последовательность Mathcad-файлов в вашей книге;
□	Mathcad-файлы, соответствующие оглавлению, индексу и открытой странице;
□	текст, появляющийся в области заголовка окна электронной книги при от-
крытии любого раздела;
□	заголовок книги, как замечено в области заголовка и меню Help ► Open Book;
□	сообщения, которые появляются, когда читатель нажимает гиперссылку.
Для создания НВК-файла можно использовать любой текстовый редактор, на-
пример Блокнот Windows или Microsoft Word.
17.5. Вложенные папки
359
В начале НВК-файла должны присутствовать четыре ключевых слова:
□	Version;
□	Title;
□	Splash;
□	TOC (должно быть набрано прописными буквами).
Пример НВК-файла показан на рис. 17.5.
;электронная книга Mathcad
;copyright 2005 Макаров All rights reserved.
.version 2000
.title инженерные расчеты в Mathcad
.path электронная книга2
splash splash.med
TOC TOC.med	: содержание справочника
GlavaOl-Nachalo GlavaOl-Nachalo.mcd : построение выражений и графиков в Mathcad
Glava02-vozmojnosti	Glava02-vozmojnosti.med	:	основные возможности Mathcad
Glava03-uravnenie	Glava03-uravnenie.mcd	:	Решение уравнений
Glava04-Matrix Glava04-Matrix.mcd	:	Работа с матрицами
GlavaO5-Symbol Glava05-Symbol.med	:	символьные вычисления
Glava06-odesolve	Giava06-odesolve.mcd	:	Решение дифференциальных уравнений
GlavaO6-CTapwe GlavaO6-cTapbie.mcd	:	Решение дифференциальных	уравнении
GlavaO6-4acTHbie GlavaO6-4acTHbie.mcd	:	Решение дифференциальных	уравнений
с1ауа07-эксперимент	Glava07-3KcnepnMeHT.mcd	:	обработка экспериментальных данных
Glava08-statistica	Glava08-statistica.mcd	:	математическая статистика
Glava09-Program Glava09-Program.mcd	:	программирование
GlavalO-Animation	GlavalO-Animation.mcd	:	Аниммация
Glavall-Razmernost	Glavall-Razmernost.med	:	Учет размерностей
Glaval2-specfunction	Glaval2-specfunction.mcd	: встроенные функции
Glaval5-Graphic Glaval5-Graphic.mcd : построение графиков
Рис. 17.5. Пример НВК-файла
Строки НВК-файла, начинающиеся с точки с запятой, игнорируются Mathcad
и могут использоваться как комментарии.
Каждый Mathcad-файл внутри НВК-файла записывается в три столбца:
'□ в первом столбце пишется имя файла без расширения;
□	во втором столбце — имя файла с расширением .med;
□	в третьем столбце пишется двоеточие (:), пробел (лучше несколько пробелов)
и заголовок файла, который должен появиться в области заголовка при про-
смотре электронной книги.
Для перехода между столбцами используйте клавишу табуляции (Tab).
При сохранении НВК-файлу присваивается имя, совпадающее с названием пап-
ки, в которой хранятся все Mathcad-файлы. После него нужно вписать расшире-
ние .hbk. Например, все файлы нашей электронной книги хранятся в папке с на-
званием Primer, и HBK-файл имеет имя Primer.hbk.
17.5.	Вложенные папки
Если в электронной книге очень много файлов, то можно использовать вложен-
ные папки. В этом случае в верхней части НВК-файла нужно указать путь к каж-
дой папке ниже заголовка и версии.
360
Глава 17. Создание электронных книг
К папкам, содержащим всплывающие окна (Popups), указывать путь не надо, так
как эти файлы не включаются в НВК-файл.
в а
Ч Инженерные расчеты в Mathcad. Содержание справочм!
Fie Edit View Insert Format Tods Symbolics Book Help
а е о
 .. [makarov] 2»
Имя
П [инж-расчеты]
С](Часп»1|
О|часть2]
О [частьЗ]
р.) Splash, med
р] TOC med
;электронная книга Mathcad
;Copyright 2005 Макаров All
.version 11
.title инженерные расчеты
.pathan-KH
.path3n-KH4acTb3
.path3n-KH4acTbl
.ра1Ьэл-кнчасть2
.patЬэл-книнж-расчеты
splash splash.med
toc TOC.mcd	:
;часть1
GlavaOl-Nachalo GlavaOl-Nac
G1ava02-vozmojnosti
;часть2
Glava03-uravnenie _________
Glava04-Matrix Glava04-Mat
; частьЗ
GlavaOO-Program Glava09-Prc
GlavalO-Animation	Gia
Glavall-Razmernost	Gia
Gia
G1 с
д'
;инж-расчеты
Ol-Geom-кривые Ol-Geom-кри
02-Geom-MaccHB 02-Geom-Mac
03-внутр-изгиб 03-внутр-ин
F3 Просмотр
For Help. press F1

Инженерные расчеты в Mathcad
Раздел: Содержание справочника
Часть 1
Темы
Глава 1. Построение выражений
и графиков в Mathcad
Глава 2. Основные возможности Mathcad Темы
Часть 2
Глава 3. Решение уравнении	Темы
Глава 4. Работа с векторами и матрицами Темы
Часть 3
Темы
Темы
Глава 9. Программирование
Глава 10. Аннммация
Глава 11. Учет размерностей
Инженерные расчеты
01 Расчет геометрических характеристик сечении,
___заданных математическими выражениями
02 Расчет геометрических характеристик сечении.
“ Press F1 for help.
WCT
Темы
EJ^Wind. .	|w| 2 Micro ^||^2 Mat .. * эл-кн-Б.. | R(j g « <
Рисуню
Рисуню
Рисуню
Рисуню
Рисуню
Рисуню
Рисуню
дито
Раде 1
И
Рис. 17.6. Вложенные папки в электронной книге
Если все Mathcad-файлы содержатся в одной папке, указывать путь к папке не
обязательно. На рис. 17.6 показан вариант НВК-файла для электронной книги
с вложенными папками.
ВНИМАНИЕ --------------------------------------------------------
При наличии вложенных папок становится невозможной навигация по электронной книге
с помощью стрелок <— и но все ссылки работают нормально.
17.6.	Проверка электронной книги
Для проверки НВК-файла необходимо перезагрузить Mathcad в режиме НВК.
Для этого в окне Windows нажмите кнопки Пуск ► Выполнить. В появившемся
окне Запуск программы выберите Обзор и укажите путь к файлу mathcad.exe. Да-
лее через пробел введите /hbkmode (рис. 17.7, слева), затем OK. Mathcad будет за-
гружен в режиме НВК. На экране появится окно, изображенное на рис. 17.7,
справа. Выберите Check Handbook, укажите путь к проверяемому НВК-файлу, на-
жмите ОК. Результаты проверки автоматически записываются в файл ErrorLog.txt
в тот же каталог, где находится НВК-файл. Вид этого файла показан на рис. 17.8.
17.7. Создание поисковых индексов
361
1 Пуж|
AUTO
н 2Wind... 2 Micro... *-| ^2 Math... -J Microsoft
Рис. 17.7. Запуск программы проверки электронной книги
RU б «
Рис. 17.8. Файл результатов проверки электронной книги
Файл ErrorLog сообщает о следующих ошибках:
□	файлах в папках электронной книги, которые не перечислены в НВК-файле;
□	файлах, перечисленных в НВК-файле, которых нет в папках электронной книги;
□	неправильно установленных гиперсвязях;
□	вычислительных ошибках в каждом Mathcad-документе электронной книги.
После проверки и исправления отмеченных ошибок надо снова запустить Math-
cad в режиме НВ К, добиваясь безошибочной работы электронной книги.
17.7.	Создание поисковых индексов
Для поиска нужного фрагмента текста, содержащего ключевое слово или фразу,
можно создать систему поисковых индексов. Работа эта кропотливая и длительная.
В каждом из множества файлов надо отыскать все характерные слова и отметить
их индексом в свойствах объекта, тогда в электронной книге открывается систе-
ма поиска фрагментов по ключевым словам (рис. 17.9).
362
Глава 17. Создание электронных книг
-flSETTING STARTED PRIMERS
Рис. 17.9. Система поиска в электронной книге
Для создания системы поисковых индексов надо запустить Mathcad в авторском
режиме (Authoring mode). Для этого в стартовом окне Windows нажмите кнопки
Пуск ► Выполнить. В появившемся окне Запуск программы (см. рис. 17.7, слева)
выберите Обзор и укажите путь к файлу mathcad.exe. Далее через пробел введи-
те /а, затем нажмите OK. Mathcad будет загружен в авторском режиме. На экра-
не появится окно, изображенное на рис. 17.7, справа. Выберите Generate Index,
нажмите ОК.
После запуска Mathcad откройте нужный файл, выберите объект, который вы
хотите пометить индексом (любой — текстовый или математический). Нажав на
Оператор ци^ша ton
Рис. 17.10. Ввод индекса в Mathcad-файл
17.7. Создание поисковых индексов
363
него правой кнопкой мыши, выберите в контекстном меню Properties (Свойства).
В окне свойств (рис. 17.10) появится новый раздел Указатель (Index). Впишите
фразу, при выборе которой в электронной книге данный файл будет открывать-
ся на этом объекте. Можно вписать несколько различных фраз. Они должны раз-
деляться вертикальной чертой (без пробела).
Г index.txt Блокнот
Файл Ставка Формат Вид Справка
Loess|418|Glava02-vozmojnosti.med
regressI414|Glava02-vozmojnosti.med
root|64|Glava02-vozmojnost1.med
аналитический!4|07-Geom.mcd
векторизации!286|Glava02-vozmojnost1.med
выбор нагрузок на балку!5I15-оптимиз-балка.med
выражения|2|G1avaOl-Nachalо.med
динамический расчет балки|4|25-колеб-балки.med
дискретные переменные!63|G1avaOl-Nachalо.med
дифференциальных!304|Glava02-vozmojnosti.med
знак равенства|48|Glava02-vozmojnost1.med
изгиб балок на упругом основании|4|17-ynp-ocH.mcd
изгиб продольно-поперечный|4|22-прод-попер-изгиб.med
изопараметрический конечный элемент!4|31-изопарам-эл-т.med
интерполяция!389|Glava02-vozmojnosti.med
комплексные числа!4I03-Кирхгоф.med
к оэффициенты1104|G1ava03-uravneni е.med
матрицы!207|Glava02-Vozmojnosti.med
матричных!262|Glava02-Vozmojnost1-med
Метод конечных элементов 4 27-мкэ-стерж-сист.med
метод конечных элементов 4 29-MK3-nyaccoH.mcd
метод конечных элементов “ '2 "'7
метод конечных элементов 4 31-изопарам-эл-т.med
обмен данными|480|Glava02-vozmo1nosti.med
оператор!286|Glava02-vozmojnosti.med
оптимизацияI 5115-оптимиз-балк а.med
оптимизация|4|16-оптимиз-поиск.med
переходные процессы в электрической цепи14104-эл-переход.med
пласт-из гиб 14114-из гиб-пласт.med
..... стерж-CMCT.mcd
30-МЮ-пласт. med
5
Рис. 17.11. Ввод индексов в электронную книгу
После того как будут созданы все индексные входы, можно приступить к автома-
тической генерации индексов. Запустите Mathcad в режиме НВК. В диалоговом
окне (см. рис. 17.7), появившемся на экране, выберите Generate Index и нажмите
ОК. В результате работы Mathcad в той же папке, где находится и ваш НВК-
файл, появится файл Index.txt (рис. 17.11). Откройте его в Word для сортировки.
Выделите весь файл. В меню Таблица выберите Преобразовать в таблицу. В поя-
вившемся диалоговом окне задайте число столбцов — 3, разделитель — другой
и укажите в качестве него вертикальную черту.
Теперь надо отсортировать индексы. В меню Таблица выберите Сортировка.
В появившемся окне укажите Сортировать — столбец 1, тип — текст, затем —
столбец 3, тип — текст, затем — столбец 2, тип — число. Нажмите ОК.
Далее таблицу нужно вновь преобразовать в текст, выбрав разделитель — верти-
кальную черту. Сохранить файл как Только текст.
Заключительная часть — обработка индексов. В главной папке Mathcad найдите
файл Newdict.exe и скопируйте его в ту же папку, где находятся НВК-файл
и файл Index.txt. В MS-DOS в командной строке напечатайте последовательно
364
Глава 17. Создание электронных книг
имена трех файлов, например, Newdict,exe lndex.txt Primer.hbk. Нажмите Enter.
В результате действия программы в том же каталоге появятся два файла, out.dct
и out.rfs.
Если в файле lndex.txt есть ошибки, то Newdict.exe, останавливает выполнение
программы и указывает номер строки, где находится ошибка. Выполняйте про-
грамму Newdict.exe до тех пор, пока все ошибки не будут устранены.
После этого переименуйте файлы out.dct и out.rfs. Вместо out напишите имя ва-
шей электронной книги, например, Primer.dct и Primer.rfs. Переместите DCT-
и RFS-файлы в тот же каталог, где находится и ваш НВК-файл.
ПРИМЕЧАНИЕ ---------------------------------------------------------------
При любых изменениях в одном из файлов электронной книги или в НВК-файле необхо-
димо повторить процедуру создания индексов.
Ошибки часто возникают при наличии пустых линий или пробелов в индексе или в НВК-
файле, а также из-за несоответствия имен файлов в индексном файле и в НВК-файле или
отсутствия нужных имен.
Для устранения индексных ошибок приходится многократно возвращаться к редактиро-
ванию индексных входов в файлах электронной книги.
Процедура создания системы поисковых индексов настолько сложная и дли-
тельная, что встает вопрос: а зачем все это надо?
Навигация по электронной книге и система ссылок прекрасно работают и без по-
исковых индексов. Единственно, что отсутствует, — это поиск фрагмента по за-
данному слову (или фразе). Для успешного поиска пользователь электронной
книги должен ввести ключевое слово (или фразу) точно так, как вы ее вписали
в индекс. Если он ошибся хоть в одной букве, поиск не удастся.
На мой взгляд, овчинка выделки не стоит. Электронная книга прекрасно работа-
ет и без системы поисковых индексов.
Глава 18
Работа с электронной книгой
Электронная книга «Расчеты в Mathcad» — это не просто справочник и интерак-
тивные иллюстрации к основной книге. Это мощный инструмент создания соб-
ственных программ пользователя.
Для создания собственной программы надо вначале составить формульный ал-
горитм решения поставленной задачи, то есть последовательный список формул
и этапов расчета. Затем, пользуясь системой вложенных оглавлений, отыскать
в электронной книге нужные фрагменты Mathcad-файлов, решающих подобные
задачи, и вставить их в свой рабочий документ. Нужно подправить вставленные
фрагменты в соответствии с условиями своей задачи, связать их между собой по
смыслу, ввести свои исходные данные и оценить результаты расчета.
Далее приводится ряд примеров подготовки программ пользователя с примене-
нием электронной книги.
18.1.	Обработка экспериментальных данных
В результате какого-то эксперимента получены два массива данных: массив зна-
чений аргумента X и массив значений функции У. Для последующих расчетов
требуется получить функцию у(х). Физический смысл этих массивов может
быть любым.
Пусть измерена зависимость перемещения х автомобиля от времени t. Надо най-
ти скорость перемещения, то есть производную dx/dt, и работу, затраченную на
движение автомобиля. Введите в Mathcad-документ свои исходные данные (мас-
сивы экспериментальных замеров).
Массивы опытных данных надо превратить в функцию перемещения от време-
ни. Для этого можно использовать интерполяцию или регрессию. Начнем с ин-
терполяции. В электронной книге откройте раздел Глава 7. Обработка экспери-
ментальных данных ► Темы ► кубическая интерполяция. Вам понадобится всего од-
на строчка оттуда, но я рекомендую скопировать в свой документ большой фраг-
мент раздела Интерполяция вместе с исходными данными для того, чтобы, поду-
мав и проверив в работе, выбрать нужный вариант (в данном случае вариант
интерполяции).
Интерполяция отрезками прямых линий в данном случае не годится, так как
уравнение прямой линии не имеет второй производной и не позволяет найти ус-
корение тела, хотя позволяет искать интеграл функции. Кубическая сплайн-ин-
терполяция позволяет выполнить все необходимые расчеты. Копируем в область
своих расчетов строчку с функцией Ispline, в которой сшивка сплайнов (отрез-
ков) в граничных точках происходит по прямой линии (рис. 18.1).
366
Глава 18. Работа с электронной книгой
Обработка результатов эксперимента
массивы экспериментальных данных (Т.Х) i := 0 .20
время т. > i масса m :« 1
положение
точки
Х>(0 1 5 22 30 111 111 132 177 321 512 833 958 958 ЮС
остановка	остановка
u(t) interp(cspline(T,X) ,T,X,t) функция интерполяции
скорость
0 if - u(t) < 0
dt
otherwise
ускорение
J
a(t) :« *u(t)
dt
t:-0,1..20
сила инерции
> m I Kt) I
Импульс силы

Здесь офыта функция Int (интегрирование методом трапеций)
Метод трапеций
A(t) > Int(AA,0,t,5(T)
Стандартный интеграл Mathcad
Г1
A(t)> F^tXQdt
J0
отключено
(очень долго считает)
Рис. 18.1. Преобразование массивов в функцию и ввод расчетных формул
Вписываем в документ свои расчетные формулы для скорости, ускорения, силы
инерции. Для скорости используем в расчетах только положительные значения,
так как на торможение не затрачивается энергия двигателя.
Работу силы
L	t
инерции А — J Fm du = J FHHvdt
о	о
можно подсчитать с помощью стан-
дартного оператора интегрирования Mathcad. Если нужно вычислить интеграл
для фиксированных пределов, Mathcad справляется с работой хорошо, но если
надо вычислить серию интегралов для построения интегральной кривой (с ис-
пользованием дискретной переменной), то время вычислений очень велико
и лучше воспользоваться простой программой вычисления интеграла методом
трапеций из раздела программирования. В электронной книге выберите Глава 9.
Программирование ► Темы ► Интегрирование функций методом трапеций. Скопи-
руйте эту программу-функцию в свой документ. На рис. 18.1 эта программа
вставлена в документ и скрыта в закрытой зоне. Оставлен лишь оператор вызова
этой функции.
Результаты расчета показаны на рис. 18.2. Кстати, шаблон графика тоже удобно
копировать из электронной книги, где он уже отредактирован и расцвечен.
Функции интерполяции проводят расчетную кривую точно через все экспери-
ментальные точки, не исправляя случайные погрешности эксперимента.
18.1. Обработка экспериментальных данных
367
Можно использовать сочетание функций сглаживания и интерполяции. Для
этого выберите в электронной книге раздел Глава 7. Обработка эксперименталь-
ных данных ► Темы ► 7.3. Функции сглаживания. Однако в нашем случае отклоне-
ние от расчетных точек при сглаживании получается неправдоподобно большим.
Тем не менее в ряде других случаев сглаживание оказывается полезным.
Если экспериментальные данные не набор случайных точек, а предположи-
тельно плавная кривая, то лучше использовать функции регрессии для преоб-
разования массива в функцию. На рис. 18.3 набор данных преобразуется в поли-
ном 5-й степени с помощью функции regress (скопируйте из электронной книги
Регрессия N := 5 u(t) : interp(regress(T,X,N),T,X,t)
скорость
ускорение
«2
Kt) “ u(t)
dt
сила инерции
F^:-m | КО |
Импульс силы
0 if -u(t) < О
dt
I — u(t) I otherwise
Idt )
Рис. 18.3. Результаты расчета с использованием функции регрессии

368
Глава 18. Работа с электронной книгой
нужный фрагмент из раздела Глава 7. Обработка экспериментальных данных ► Те-
мы ► 7.2.1. Одномерная регрессия). Расчетные формулы надо скопировать ниже
функции регрессии, иначе не произойдет пересчета формул после регрессии.
Функцию регрессии loess использовать в расчетах не удается, так как нельзя вы-
числить интеграл от найденной функции.
Результаты расчета озадачивают. Неправдоподобно гладко выглядят графики
скорости и ускорения, а ведь автомобиль движется рывками и с остановками.
Соответственно, и затраченная энергия двигателя на разгоны и торможения A(t)
оказалась в 15 раз меньше, чем при использовании интерполяции. Все логично,
но будьте бдительны, Mathcad ведь не вникает в суть проблемы — он всего лишь
математический инструмент.
18.2.	Обработка цифрового сигнала
Предположим, вы имеете файл с записью цифрового сигнала. Надо очистить
сигнал от случайных помех. Для этого воспользуемся разложением в ряд Фурье.
В новый Mathcad-документ введите свой массив цифрового сигнала, прочитав
его из файла с помощью функции Readprn. В электронной книге выберите Глава
7. Обработка экспериментальных данных ► Темы ► 7.4.1. Преобразование Фурье.
Скопируйте открывшийся пример в свой документ.
Посмотрите график своего сигнала (рис. 18.4), введя в поле ввода графика имя,
присвоенное массиву данных. Введите это имя в функции прямого преобразова-
ния Фурье cfft. Посмотрите на графике (рис. 18.5) значения коэффициентов
ряда Фурье. Введите свои значения диапазона выбираемых коэффициентов k{
и k2. После обратного преобразования Фурье с учетом выбранного ряда коэффи-
циентов вы увидите (рис. 18.6) график очищенного сигнала. Варьируй значения
kx и k2, подберите нужный вам вид очищенного сигнала. Графика исходного сиг-
нала вы не увидите, так как у вас его просто нет.
Обработка цифрового сигнала
Здесь скрыто формирование массива опытных данных
И----------------------------------------
S := READPRN(”18-2.pm”)
Рис. 18.4. График сигнала, требующего очистки от помех
18.3. Оптимизация нагрузки на балку
369
прямое преобразование f =
построить ряд Фурье, значения коэффициентов которого лежат между к1 и к2
выбор коэффициентов
^=^к1<|г|<к2,Г,0)
обратное преобразование h:= icfft(g)
Рис. 18.5. Процедура очистки сигнала от помех
Исходный сигнал до наложения помех
х
Рис. 18.6. Сравнение очищенного сигнала с исходным
18.3.	Оптимизация нагрузки на балку
Балка на двух опорах нагружена тремя силами, две из которых приложены
к концам балки. Определить положение третьей силы (силы F2), ПРИ котором
максимальный прогиб балки будет наименьшим. Исходные данные для расчета
показаны на рис. 18.7.
Похожая задача решается в примере 5 (Движение двух машин на мосту) в элек-
тронной книге. Посмотрите этот пример. Он весьма сложный, связан с програм-
мированием и решением системы уравнений с переменными параметрами. Пой-
дем простейшим путем, чтобы не демонстрировать «высший пилотаж» в Mathcad,
а показать простоту составления программ пользователя.
370
Глава 18. Работа с электронной книгой
Расчет на прочность 1 раз статически
неопределимой плоской рамы	origin := 1
Заданная рама
Каноническое уравнение метода сил Xl &i i + Л1 р s О
Уравнение одно, в программе везде заменить
вектор Х( на число X (измененные блоки голубого цвета)
Рис. 18.7. Схема балки и исходные данные для расчета
Рассчитаем максимальный прогиб балки при заданном положении силы F2. Рас-
чет выполним с учетом размерностей, поэтому из любого примера, приведенного
в электронной книге, скопируем в свой документ производные размерности. Да-
лее введем исходные данные.
Расчет начнем с определения реакций опор и построения эпюры изгибающих
моментов. Откроем в электронной книге пример 12. Определение внутренних уси-
лий при изгибе балки. Скопируем оттуда определение поперечной силы Q и изги-
бающего момента Л/, а также определение опорных реакций. Копируем оттуда же
определение прогиба балки методом начальных параметров. Поскольку в нашем
случае отсутствует распределенная нагрузка, то слагаемые, учитывающие ее,
удаляем. После отладки программы (а она состоит в возможной корректировке
некоторых обозначений) для достижения краткости и элегантности программы
отдельные фрагменты можно спрятать в закрытых зонах (рис. 18.8).
Получив функцию прогиба f от положения выбранного сечения х, найдем мак-
симальный прогиб балки (по абсолютной величине). Для его определения вос-
пользуемся функцией Fmax из электронной книги Глава 9. Программирование ►
Темы ► 9.8. Нахождение экстремума функции в программе. Поскольку надо найти
максимальный по абсолютной величине прогиб, то вначале находим модуль /t
от функции прогиба /, затем в обращение к функции записываем имя /t
(см. рис. 18.8).
Задаем величину 12 и выводим результаты расчета на график (рис. 18.9).
Далее требуется определить, при каком значении Ь2 максимальный прогиб будет
минимальным. Как отмечено в начале этого примера, для Mathcad это очень
сложная проблема.
18.3. Оптимизация нагрузки на балку
371
Здесь скрыто определение опорных реакций и внутренних усилий Q и М
0------------------------------------------------------------
Здесь скрыто определение прогиба балки методом начальных параметров
а-----------------------------------------------------------------
здесь скрыта программа Fmax для определения тахМ и max прогиба М(х) = |MeI Ra,Rb,L2,xi|
0------------------------------------------------------------------------------------------1-
MMX.= Fme(M,LB,L1[,N) fl(x) = |f(x)| Дт« =Fme'fl.LH,Lx,N>
Рис. 18.8. Расчетная часть документа со скрытыми зонами
Выполним почти цирковой трюк. Анимируем этот график при движении силы F2
вдоль балки. В область анимации включаем заданное значение Ь2 и расчетное
значение максимального прогиба Атах. В таком случае от кадра к кадру будут из-
меняться и график, и выводимые числовые значения.
Уменьшим скорость проигрывания клипа, выбрав в меню Record Animation ско-
рость 1 кадр в секунду. Наблюдая за клипом, запоминаем значение Ь2, при кото-
ром значение Атах минимально. Выключите значение Frame (см. рис. 18.7), вве-
дите нужное значение Ь2 и внимательнее рассмотрите результаты оптимального
расчета.
372
Глава 18. Работа с электронной книгой
К такому примитивному трюку приходится прибегать вследствие несовершенст-
ва системы Mathcad, которая крайне неуклюже работает с вычислительными
блоками Given-find (minerr, Odesolve, maximize, minimize), не допуская свободной
вариации параметров функций и использования вычислительного блока в про-
граммных модулях.
Часть IV
Примеры инженерных расчетов
в Mathcad
Содержит примеры решения инженерных задач в Mathcad, кото-
рые иллюстрируют различные приемы работы в Mathcad.
Скачайте с сайта издательства www.piter.com или с сайта автора www.emakarov.
nsknet.ru архив электронной книги Эл-книга-zip. В этом архиве находится элек-
тронная книга «Расчеты в Mathcad» с программами для 56 примеров слож-
ных инженерных расчетов. Подробное описание этих примеров и пояснения
к ним находятся в этом же архиве. Они записаны в формате pdf, для про-
смотра файлов необходимо установить на компьютере Acrobat Reader любой
версии, а еще лучше FoxitReader, который работает значительно быстрее, чем
AcrobatReader.
Распакуйте архив и откройте файл Примеры-Bce.pdf (рис. П.1). Выберите в ле-
вом верхнем углу окна пункт Закладки — откроется список всех 56 примеров.
Щелкните мышью на любом примере и читайте пояснения к нему.
Рис. П.1. Выбор примера в окне Acrobat Reader
Mathcad-программы всех примеров находятся в электронной книге «Расчеты
в Mathcad». Порядок установки электронной книги описан в файле ReadMe, на-
ходящемся в папке Эл-книга. После ее установки откройте Mathcad и в главном
меню Mathcad выберите Справка ► Электронные книги ► Расчеты в Mathcad (Help ►
E-books ► Расчеты в Mathcad). В открывшейся электронной книге выберите При-
меры инженерных расчетов в Mathcad и далее название интересующего вас приме-
ра (рис. П.2).
Работать с примером можно и внутри электронной книги, однако, чтобы сохра-
нить произведенные изменения, надо выделить все (клавиши Ctrl+A), скопиро-
вать в буфер обмена (клавиши Ctrl+C), вставить в новый Mathcad-документ
(клавиши Ctrl+V), сохранить файл (клавиши Ctrl+S). В диалоговом окне сохране-
ния файла ввести имя файла и выбрать версию Mathcad, в которой вы хотите со-
хранить файл.
Пример 2. Расчет электрической цепи переменного тока
375
Рис. П.2. Выбор нужного примера в электронной книге
Далее приведем основные сведения (схемы и условия задачи) для всех 56 при-
меров, находящихся в электронной книге.
Пример 1. Проверка статистических гипотез
Для заданной выборки данных требуется подобрать закон распределения и опре-
делить его параметры.
Выдвигаются три гипотезы закона распределения и определяются функции ве-
роятности для них.
Предполагается, что выборка данных подчиняется:
□	нормальному распределению (функция вероятности pnorm);
□	логистическому распределению (plogis);
□	равномерному распределению (punif).
Оценка трех гипотез производится с помощью коэффициентов корреляции,
взвешенных квадратов отклонений, методом Пирсона и Романовского, методом
максимального правдоподобия.
Пример 2. Расчет электрической цепи переменного тока
В цепи (рис. П.З) действует источник синусоидальной ЭДС. Требуется опреде-
лить токи и напряжения, действующие на всех участках цепи; проверить баланс
мощностей и найти показания приборов.
376
Примеры инженерных расчетов в Mathcad
Расчет ведется двумя методами: по уравнениям Кирхгофа и методом эквива-
лентных преобразований.
Рис. П.З. Схема электрической цепи переменного тока
Пример 3. Переходные процессы при замыкании-
размыкании электрической цепи
В примере рассматривается цепь, содержащая источник тока Е, катушку индук-
тивности L, два сопротивления, R1 и R2, конденсатор С и рубильник (рис. П.4).
Определить распределение токов и напряжений в ветвях электрической цепи во
времени.
В программе рассматриваются: решение дифференциального уравнения второго
порядка и решение системы дифференциальных уравнений первого порядка.
Рис. П.4. Схема электрической цепи
Пример 4. Кинематический анализ кулачкового
механизма
Заданы массивы углов поворота кулачка и соответствующих им углов поворота
коромысла. Для определения динамических нагрузок на конструкцию требуется
определить скорость и ускорение коромысла.
В программе расчета массивы преобразуются в функции, которые затем диффе-
ренцируются. Для сглаживания экспериментальных замеров используется раз-
ложение в ряд Фурье.
Пример 5. Движение двух машин ло мосту
377
Пример 5. Движение двух машин по мосту
Две машины массой т и m2 въезжают на мост с разных сторон со скоростями
VI и V2. Определить прогиб моста под нагрузкой и наибольшие напряжения
в балках моста в зависимости от положения машин на мосту (рис. П.5).
В программе определяются нагрузки на мост, максимальные напряжения и про-
гиб балок моста в зависимости от времени. Рассмотрены три варианта расчета:
использование программирования с подпрограммами без учета и с учетом раз-
мерностей, а также расчет без использования программирования. Для демонст-
рации результатов расчета используется анимация.
Рис. П.5. Схема движения двух машин по мосту
Фигура задана 4 кривыми
Рис. П.6. Сечение, заданное аналитически
378
Примеры инженерных расчетов в Mathcad
Пример 6. Расчет моментов инерции сечения,
заданного аналитически
Задано сечение, ограниченное четырьмя кривыми. Найти главные центральные
моменты инерции фигуры (рис. П.6), образованной этими кривыми, и положе-
ние главных осей инерции.
Расчет ведется по формулам сопротивления материалов путем непосредственно-
го интегрирования.
Пример 7. Расчет моментов инерции сечения,
заданного набором точек на контуре
Сечение задано десятью точками (5 точек — верхний контур, 5 точек — нижний
контур). Найти главные центральные моменты инерции, образованной всеми
точками фигуры, и положение главных осей инерции.
Массив точек на контуре сечения преобразуется в функцию. Далее выполняется
интегрирование, как и в призере 6.
Пример 8. Расчет геометрических характеристик
составного сечения
Рассматривается сечение из 7 элементов (рис. П.7). Для каждого элемента вво-
дится ширина 6, высота h, площадь Л, координаты центра тяжести У и Z в виде
элементов вектора для выполнения последующих однотипных операций. Вво-
дится код элемента К и признак наличия выреза К1.
Рис. П.7. Сечение из семи элементов
Пример 10. Определение внутренних усилий при кручении стержня
379
Пример 9. Определение внутренних усилий
при растяжении стержня
Для стержня, нагруженного тремя сосредоточенными и двумя распределенны-
ми нагрузками, построить эпюру продольных усилий. Чтобы не загромождать
рис. П.8, на нем показаны только две нагрузки вместо пяти.
Пример 10. Определение внутренних усилий
при кручении стержня
Для стержня, закручиваемого двумя парами сил и двумя распределенными мо-
ментами, построить эпюру крутящих моментов. Чтобы не загромождать рис. П.9,
на нем показаны только две нагрузки из четырех.
Рис. П.9. Условная схема кручения стержня
380
Примеры инженерных расчетов в Mathcad
Пример 11. Определение внутренних усилий
при изгибе консольной балки
Для консольной балки, нагруженной тремя силами, двумя парами сил и двумя
распределенными нагрузками, построить эпюры поперечных сил и изгибающих
моментов. Чтобы не загромождать рис. П.10, на нем показаны только три нагруз-
ки из семи. Средствами Mathcad опрёделяются максимальные значения внут-
ренних усилий.
Рис. П.10. Условная схема нагружения консольной балки
Пример 12. Определение внутренних усилий
при изгибе балки на двух опорах
Для балки на двух опорах, нагруженной тремя силами, двумя парами сил и дву-
мя распределенными нагрузками, построить эпюры поперечных сил и изгибаю-
Рис. П.11. Условная схема нагружения балки на двух опорах
Пример 13. Растяжение статически-определимого стержня
381
щих моментов. Чтобы не загромождать рис. П.11, на нем показаны только три
нагрузки из семи.
Пример 13. Растяжение статически-определимого
стержня
Для стержня переменного сечения (рис. П.12), нагруженного тремя силами
и двумя распределенными нагрузками, требуется найти распределение напряже-
ний и перемещений по длине стержня.
Рис. П.12. Условная схема растяжения стержня
Рис. П.13. Растяжение статически-неопределимого стержня
382
Примеры инженерных расчетов в Mathcad
Пример 14. Растяжение статически-неопределимого
стержня
Для статически-неопределимого стержня переменного сечения (рис. ПЛЗ), на-
груженного тремя силами и двумя распределенными нагрузками, требуется най-
ти распределение напряжений и перемещений по длине стержня. Учесть измене-
ние температуры Д£ и монтажную погрешность Дмонт.
Пример 15. Растяжение-сжатие статически
неопределимой шарнирно-стержневой системы
Для статически-неопределимой шарнирно-стержневой системы (рис. П.14), на-
груженной тремя силами и двумя распределенными нагрузками, требуется най-
ти напряжения в стержнях и удлинение стержней. Учесть изменение температу-
ры At и монтажную погрешность Д монт.
Рис. П.14. Растяжение шарнирно-стержневой системы
Пример 16. Расчет простейших соединений
Из условия прочности определить прочные размеры тяги, штифта и сварного со-
единения (рис. П.15).
Рис. П.15. Схемы для расчета тяги, штифта и сварного соединения
Пример 17. Расчет статически определимого стержня
на кручение
Для заданного ступенчатого стержня (рис. П.16), нагруженного пятью различ-
ными нагрузками, определить распределение максимальных касательных напря-
жений и угла закручивания по длине стержня.
Пример 19. Расчет на изгиб консольной балки
383
Рис. П.16. Условная схема нагружения ступенчатого стержня
Пример 18. Расчет статически неопределимого стержня
на кручение
Из условий прочности и жесткости на кручение определить диаметр статически-
неопределимой трубы (рис. П.17).
Рис. П.17. Кручение статически-неопределимого стержня
Пример 19. Расчет на изгиб консольной балки
Для заданной балки коробчатого поперечного сечения (рис. П.18) определить
максимальные напряжения и построить упругую линию балки.
384
Примеры инженерных расчетов в Mathcad
В процессе расчета строятся эпюры нормальных и касательных напряжений
в опасном сечении балки. Перемещения балки при изгибе определяются тремя
способами: путем непосредственного интегрирования уравнения упругой линии,
методом начальных параметров и с помощью интеграла Мора.
Рис. П.18. Схема нагружения консольной балки
Пример 20. Расчет на изгиб балки на двух опорах
Для заданной балки на двух опорах коробчатого поперечного сечения (рис. П.19)
определить максимальные напряжения и построить упругую линию балки.
Рис. П. 19. Расчетная схема балки на двух опорах
Пример 21. Расчет на изгиб балок на упругом основании
В примере приведен расчет трех балок на упругом основании (рис. П.20): балки
с одной силой посередине и сплошным упругим основанием, балки с тремя сила-
ми на сплошном упругом основании, балки с тремя силами и двумя участками
упругого основания.
В программе функцией Odesolve решается дифференциальное уравнение 4-го
порядка. Сосредоточенные силы заменяются нагрузками, распределенными на
малом участке балки.
Рис. П.20. Схемы балок на упругом основании
Пример 25. Расчет прямого стержня на сложное сопротивление
385
Пример 22. Учет пластических деформаций
при растяжении-сжатии
Для заданной статически-неопределимой шарнирно-стержневой системы (рис. П.21)
найти зависимость предельной нагрузки F от перемещения точки приложения
силы.
В расчетах используются три вида аппроксимации диаграммы деформирования:
диаграмма Прандтля, диаграммы с линейным и степенным упрочнением.
Рис. П.21. Схема шарнирно-стержневой системы
Пример 23. Учет упругопластических деформаций
при изгибе
В примере определяется распределение деформаций и напряжений в попереч-
ном сечении балки при изгибе, а также остаточных напряжений при упругопла-
стических деформациях. В расчетах используются три вида аппроксимации диа-
граммы деформирования: диаграмма Прандтля, диаграммы с линейным и степен-
ным упрочнением.
Пример 24. Учет пластических деформаций при кручении
В примере определяется распределение деформаций и напряжений в попереч-
ном сечении стержня при кручении, а также остаточных напряжений при упру-
гопластических деформациях. Для проведения расчетов диаграмма деформиро-
вания материала балки при растяжении о — е перестраивается в диаграмму
сдвига т — ч- В расчетах используются три вида аппроксимации диаграммы де-
формирования: диаграмма Прандтля, диаграммы с линейным и степенным уп-
рочнением.
Пример 25. Расчет прямого стержня на сложное
сопротивление
Для заданного прямого стержня переменного поперечного сечения (рис. П.22),
нагруженного 23 нагрузками, определяется максимальное эквивалентное напря-
жение и строятся графики перемещений по шести направлениям (трем линей-
ным и трем угловым).
386
Примеры инженерных расчетов в Mathcad
Это большая сложная программа, включающая в себя фрагменты приме-
ров 9-12.
Рис. П.22. Стержень переменного сечения (вверху) и условная схема
его нагружения (внизу)
Пример 26. Расчет пространственного стержня
на сложное сопротивление
Для заданного пространственного стержня (рис. П.23) подобрать прочные раз-
меры поперечных сечений и горизонтальное перемещение конца стержня.
Пример 28. Раскрытие статической неопределимости плоской рамы
387
Рис. П.23. Схема нагружения пространственного стержня
Пример 27. Определение перемещений систем
из нескольких элементов
Для заданной системы, состоящей из двух балок, связанных пружиной и стерж-
нем (рис. П.24), определить вертикальное перемещение под силой и угол пово-
рота сечения на опоре D.
Перемещения определяются с помощью интеграла Мора.
Рис. П.24. Схема нагружения сложной системы
Пример 28. Раскрытие статической неопределимости
плоской рамы
В примере методом сил раскрывается статическая неопределимость плоской
рамы (рис. П.25), определяется одно из перемещений и выполняется проверка
правильности решения.
388
Примеры инженерных расчетов в Mathcad
Эквивалентная система
Заданная система
Рис- П.25. К расчету плоской рамы
Пример 29. Расчет один раз статически неопределимой
системы
Расчет такой системы (рис. П.26) почти аналогичен примеру 28, но потребовалась
новая система индексов. В конце примера произведен расчет рамы на прочность.
Эквивалентная система
Заданная рама
Пример 30. Расчет пространственной статически
неопределимой рамы
Для заданной, пять раз статически неопределимой пространственной рамы (рис. П.27)
требуется раскрыть статическую неопределимость и сделать проверку правиль-
ности решения, выбрать опасное сечение и определить диаметр стержней рамы
из условия прочности.
Л
*
Рис. П.27. Схема пространственной рамы
Пример 33. Расчет на устойчивость сжатого стержня
389
Пример 31. Расчет многопролетной балки с одной
заделкой на изгиб
Расчет ведется методом сил. Количество опор, как и количество нагрузок, дейст-
вующих на балку, может быть любым (рис. П.28).
Рис. П.28. Схема многопролетной балки с заделкой
Пример 32. Расчет многопролетной балки на изгиб
Программа расчета такой балки (рис. П.29) близка к программе, приведенной
в примере 31. Но в предыдущем примере основная система (балка с заделкой) не
требует определения опорных реакций, в этом примере основная система (балка
на двух опорах) требует многократного определения опорных реакций.
Рис. П.29. Схема многопролетной балки
Пример 33. Расчет на устойчивость сжатого стержня
Для стержня круглого сечения, нагруженного сжимающей осевой силой (рис. П.30),
определить диаметр стержня из расчета на устойчивость.
Расчет ведется методом последовательных приближений с использованием про-
граммирования.
390
Примеры инженерных расчетов в Mathcad
d
Рис. П.30. Схема сжатого стержня
Пример 34. Определение критических нагрузок на сжатый
стержень энергетическим методом
Определить нагрузку, соответствующую потере устойчивости для ступенчатого
стального стержня с двумя заделками и промежуточной шарнирной опорой, на-
груженного двумя силами (рис. П.31).
Расчет ведется по формуле Рэлея, в которой уравнение упругой линии аппрок-
симируется полиномом степени т.
Рис. П.31. К расчету ступенчатого сжатого стержня на устойчивость
Пример 35. Продольно-поперечный изгиб балок
Для двух балок, нагруженных продольной и поперечной нагрузками (рис. П.32),
определить прогиб балок и максимальные напряжения.
Расчет ведется двумя способами с решением дифференциальных уравнений вто-
рого и четвертого порядка.
Рис. П.32. Расчетные схемы нагружения балок
Пример 38. Расчет сложной системы на удар и устойчивость
391
Пример 36. Расчет консольной балки на удар и колебания
Для консольной балки массой т0 (рис. П.ЗЗ) определить:
□	максимальные динамические напряжения при падении на балку груза массой
т в точку с координатой хт,
□	собственную частоту колебаний с учетом массы балки и сосредоточенной
массы т в точке хт,
□	перемещение u(t) точки хт балки под действием возмущающей силы F(£),
приложенной к этой точке.
Рис. П.ЗЗ. Консольная балка под действием ударной нагрузки
Пример 37. Расчет балки на двух опорах на удар и колебания
Для балки на двух опорах массой mQ (рис. П.34) определить те же величины, что
и в примере 36.
Расчет почти такой же, как в примере 36, но требующий определения опорных
реакций для всех видов нагружения.
Рис. П.34. Балка на двух опорах под действием ударной нагрузки
Пример 38. Расчет сложной системы на удар
и устойчивость
Для заданной системы, состоящей из двух балок, связанных пружиной и стерж-
нем (рис. П.35), определить вертикальное перемещение под силой и угол пово-
рота сечения на опоре D,
392
Примеры инженерных расчетов в Mathcad
Фактически этот пример является продолжением примера 27, но в данной зада-
че определяются не статические, а динамические напряжения и перемещения.
Рис. П.35. Схема ударного нагружения сложной системы
Пример 39. Статистическая обработка результатов
эксперимента
В программе приведены результаты испытаний на усталость серии из 10 сталь-
ных образцов. Требуется построить усталостную кривую и определить довери-
тельный интервал для вероятности неразрушения образцов р = 99 %.
Пример 40. Расчет болта на усталостную прочность
Определить диаметр болта (рис. П.36), испытывающего нагружение асиммет-
ричным циклом растяжения из расчета: на статическую прочность, по пределу
выносливости, на долговечность N = 105циклов.

Рис. П.36. Схема болтового соединения и характеристики цикла нагружения
Пример 41. Расчет долговечности детали
при нестационарном нагружении
Определить срок службы автомобильной оси из стали 18ХНМА (рис. П.37). Об-
работка циклограммы нагружения позволила свести процесс нагружения оси
Пример 43. Построение диаграммы истинных напряжений
393
к повторению блока нагружения. Определить, сколько блоков нагружения вы-
держит ось до разрушения.
Расчетная схема Циклограмма нагружения
Обработка циклограммы
за 1 час работы
Рис. П.37. Нестационарное нагружение автомобильной оси
Пример 42. Расчет долговечности полосы с трещиной
В полосе из стали 20Х (рис. П.38) обнаружена боковая трещина длиной L = 2 мм.
Полоса испытывает пульсирующий цикл нагружения. Как характеристика мате-
риала приводится экспериментально найденная зависимость
— = 1,5 10-13(ДК)3.
dN
Определить число циклов N подрастания трещины до критической длины ZKp.
Пульсирующий цикл
нагружения полосы
О
Ртп = 600Ш
Полоса с трещиной
я)
250
Рис. П.38. Схема полосы с трещиной и цикл ее нагружения
Пример 43. Построение диаграммы истинных напряжений
Указанная диаграмма строится по результатам испытаний стандартного образца
на растяжение. По замерам образца до и после испытаний в расчет вводятся на-
чальные длина Zo и диаметр образца б/0, а также диаметр образца в шейке после
разрыва dK
С нарисованной испытательной машиной диаграммы в координатах нагрузка —
перемещение снимаются координаты нескольких характерных точек. Далее рас-
считываются условные и истинные напряжения и деформации, определяется за-
висимость напряжений от деформаций при линейной и степенной аппроксима-
ции диаграммы деформирования.
394
Примеры инженерных расчетов в Mathcad
Пример 44. Расчет тонкостенной оболочки
Для оболочки, состоящей из трех частей: конической, цилиндрической и сфери-
ческой (рис. П.39), при заданных габаритных размерах и внутреннем давлении
найти толщину стенки.
Рис. П.39. Схема цилиндрической оболочки
Рис. П.40. Схема нагружения кронштейна
Пример 46. Оптимальный расчет сферической крышки
395
Пример 45. Оптимизация расчета кронштейна
Для кронштейна из двух шарнирно соединенных стержней (рис. П.40) требуется
определить:
□	площади сечений, стержней из условия прочности,
□	углы наклона стержней 1 и 2 из условия равенства напряжений в стержнях,
□	углы 2 и 2 из условия минимального веса кронштейна.
Пример 46. Оптимальный расчет сферической крышки
Сосуд высокого давления герметично закрыт сферической крышкой (рис. П.41).
Давление в сосуде р, диаметр сосуда 2г0, толщина крышки d неизвестна, но
должна удовлетворять условию прочности. Требуется определить радиус кри-
визны крышки /?, при котором масса крышки m(R) будет минимальной.
Рис. П.41. Сферическая крышка под внутренним давлением
Рис. П.42. Перемещения консольной балки и нагрузки, которые надо определить
396
Примеры инженерных расчетов в Mathcad
Пример 47. Подбор нагрузок по перемещениям балки
Для консольной балки прямоугольного сечения (рис. П.42) заданы перемещения
в трех точках после деформации. Требуется подобрать нагрузки, действие кото-
рых на балку вызовет появление заданных перемещений.
Пример 48. Подбор нагрузок на балку, удовлетворяющих
граничным условиям
В этой задаче заданы равенство нулю прогиба и угла поворота в заделке = О,
прогиб = 0,5 см, изгибающий момент М = 10 кг см в сечении L2 = 50 см и попе-
речная сила Q = 50 кг на свободном конце балки Z3 = 100 см (рис. ПЛЗ). В прин-
ципе можно задать любые граничные условия. Определяются нагрузки, удовле-
творяющие заданным условиям.
Рис. (1.43. Балка, граничные условия и нагрузки на балку
Пример 49. Поиск оптимальных размеров сечения балки
Консольная балка прямоугольного сечения нагружена одной силой на свобод-
ном конце. Требуется подобрать размеры прямоугольного сечения балки из ус-
ловий, что максимальное напряжение отах = [сгдоп ], перемещение конца балки
Д < [Д] = 2 мм. На размеры сечения тоже наложены ограничения 2 • см < b < 6 • см
и 1 • см < h < 10 • см.
Пример 50. Динамический расчет балки матричным
методом перемещений
Для тонкой линейки из оргстекла, защемленной одним концом (рис. П.44), опреде-
лить: 1) собственные частоты, 2) отклик балки на воздействие вынуждающих сил.
Статический и динамический расчет ведется методом конечных элементов с раз-
бивкой на семь плоских стержневых элементов.
Рис. П.44. Разбивка балки на конечные элементы и нумерация перемещений в ней
h
ь
Пример 53. Расчет кольца методом конечных элементов
397
Пример 51- Динамический расчет плоской рамы методом
конечных элементов
Расчет аналогичен предыдущему. Отличается только ориентацией стержней-
элементов (рис. П.45).
Рис. П.45. Разбивка плоской рамы на конечные элементы и нумерация перемещений в ней
Пример 52. Расчет пространственной стержневой системы
Расчет аналогичен предыдущему. Отличается только ориентацией стержней-
элементов в пространстве (рис. П.46).
Рис. П.46. Разбивка пространственной рамы на конечные элементы и нумерация
перемещений в ней
Пример 53. Расчет кольца методом конечных элементов
В данном примере решается плоская задача теории упругости. Кольцо, нагру-
женное двумя силами, имеет две оси симметрии, поэтому для повышения точности
398
Примеры инженерных расчетов в Mathcad
расчета рассматривается одна четвертая часть кольца (рис. П.47). Четверть коль-
ца разбиваем на треугольные конечные элементы с шестью степенями свободы.
О 5 10 15 20 25 30
Рис. П.47. Расчетная схема кольца под нагрузкой и выбранные для расчета узлы
Пример 54. Решение уравнения Пуассона при кручении
стержня
Для стержня заданного сечения (рис. П.48) определить: момент инерции и мо-
мент сопротивления при кручении, распределение касательных напряжений
в сечении.
В данном примере рассматривается решение уравнения Пуассона методом ко-
нечных элементов для областей произвольной формы и произвольной разбивки
на элементы. Распределение касательных напряжений при кручении стержня
произвольного сечения подчиняется уравнению Пуассона.
10 см
сечение стержня
10 см
положение узлов в сечении
0,1 [---•--—р---------------
•	• •	•
•	• о •	•
0,05 ---•-------------------
о •	•
ol------------1—------------
0	0,05	0,1
Рис. П.48. Поперечное сечение стержня и выбранные для расчета узлы
Пример 55. Решение плоской упругопластической задачи
методом конечных элементов
Данный пример иллюстрирует возможность и удобство программирования на
Mathcad любой сколь угодно сложной задачи.
Пример 56. Использование прямоугольного квадратичного элемента
399
Для кольца под нагрузкой (см. рис. П.47) рассчитывается распределение напря-
жений и деформаций. Влияние пластических деформаций учитывается методом
переменных параметров упругости.
Пример 56. Использование прямоугольного
квадратичного элемента в методе конечных элементов
Для длинной толстой трубы под давлением 700 атмосфер найти распределение
напряжений в поперечном сечении.
Для расчета используется прямоугольный квадратичный элемент с восемью уз-
лами, что позволяет достичь требуемой точности расчета даже при использова-
нии одного конечного элемента (рис. П.49).

4
о
20
3
Y
Рис. П.49. Прямоугольный квадратичный элемент с восемью узлами
и девятью точками интегрирования
Евгений Макаров
Инженерные расчеты в Mathcad 15. Учебный курс
Заведующий редакцией
Руководитель проекта
Ведущий редактор
Художественный редактор
Корректор
Верстка
А. Кривцов
А. Юрченко
Ю. Сергиенко
Л. Адуевская
И. Тимофеева
Л. Харитонов
ООО «Мир книг», 198206, Санкт-Петербург, Петергофское шоссе, 73, лит. А29.
Налоговая льгота — общероссийский классификатор продукции ОК 005-93, том 2; 95 3005 — литература учебная.
Подписано в печать 26.01.11. Формат 70x100/16. Усл. п. л. 32,250. Тираж 2000. Заказ 25117.
Отпечатано по технологии CtP в ОАО «Печатный двор» им. А. М. Горького.
197110, Санкт-Петербург, Чкаловский пр., 15.
сплд
САНкт-петеРБУРгекяя
АНТИВИРУСНАЯ
ЛАБОРАТОРИЯ
ДАНИЛОВА
www.SRLD.rij
8 (812) 336-3739
Антивирусные
програттные продукты
Евгений Георгиевич Макаров — доцент Балтийского государственного
технического университета. Опытный преподаватель,
много лет использует Mathcad в учебном процессе и в научной работе;
автор нескольких книг о Mathcad, создатель ряда обучающих
компакт-дисков с Mathcad-программами. Награжден почетным
знаком «Отличник высшей школы».
Книга предназначена для самостоятельного освоения работы в 15-й версии популярного математического
пакета Mathcad. Издание имеет формат учебного курса и состоит из четырех частей. В первой части
содержатся сведения, необходимые для начала работы в Mathcad и решения большинства практических
задач. Вторая часть посвящена вычислительным возможностям программы, здесь на конкретных примерах
рассматриваются особенности использования встроенных функций, основные приемы и способы
вычислений. В третьей части рассматриваются возможности подготовки документов Mathcad,
а четвертая содержит перечень примеров решения инженерных задач в Mathcad. Важнейшее приложение
книги размещено на интернет-сайте издательства — это электронная книга, встраиваемая в оболочку
Mathcad. Она содержит примеры использования всех встроенных функций, программы решения
56 примеров, приведенных в четвертой части книги, и пояснения к ним. Электронная книга —
это инструмент быстрого создания программ любой сложности. Книга предназначена для всех пользователей
Mathcad, как начинающих, так и опытных, и будет полезна студентам, инженерам и научным работникам.
Тема: Математические пакеты. Mathcad
Уровень пользователя: начинающий
ПИТЕР
Заказ книг:
197198, Санкт-Петербург, а/я 127
тел.: (812) 703-73-74, postbook@piter.com
61093, Харьков-93, а/я 9130
тел.: (057) 758-41-45, 751-10-02, piter@kharkov.piter.com
www.piter.com — вся информация о книгах и веб-магазин
                

Курсы повышения квалификации

Подготовка детей дошкольного возраста к обучению в школе

Продолжительность 72 часа

В статье приведены базовые рекомендации по оформлению расчетных работ для студентов и специалистов. Приведены полезные фунции mathcad 15

• Базовые рокомендации по оформлению
• Функция interp()
• Функция explicit
• Импорт данных из внешнего файла

Базовые рекомендации по оформлению расчетов

Расчет, выполненный вами под определенный проект или задачу, может быть хорошим подспорьем для будующих проектов. Кроме того, ваши наработки могут быть использованы другими специалистами. Поэтому, если у вас большой проект с формулами и константами, то рекомендуется во время работы писать комментарии, указывая: для чего нужна та или иная формула, откуда она была взята (ссылку на страницу учебника или книги), границы использования формулы, константы и переменные входящие в ее состав и т.д.

Если в расчете приводится график, то он должен быть удобен для восприятия. Обязательно подписывайте оси координат. Обязательно включайте сетку, чтобы график было удобнее читать. Если на графике изображается более одной кривой, то нужно их выделять разными цветами и добавлять легенду, из которой ясно, какая кривая что описывает. Если вы используете дополнительную ось ординат, то добейтесь того, что бы цены делений обеих осей совпадали, тогда сетка построится корректно и чтение графика будет проще. Пример оформления графиков рассматривался в раделе графики

Если ваш расчет в последствии должен распечатываться на принтере и подшиваться вместе с другими документами, то в этом случае необходимо настроить параметры страницы в mathcad. Это можно сделать, перейдя в меню по следующему пути: File -> Page setup… Вы увидите окно настройки полей и формата вашего листа. Как правило, левое поле листа оставляют более широким, поскольку в этом месте страницы скрепляются либо зажимаются в канцелярских папках. На рисунке 1 можно посмотреть пример настройки листа

Рис. 1. Оформление листа для печати

Если вы решаете инженерную задачу, где присутствуют физические величины, то необходимо всегда указывать единицы измерения. Единицы измерения можно ввести руками в виде обычного текста либо автоматически. Таким образом, можно контролировать правильность конечного результата и избежать множества ошибок в процессе решения задачи. Для автоматического ввода единиц измерения переменных нужно просто напечатать на клавиатуре их название сразу после значения. Результат автоматически выведется уже с получившейся единицей измерения. На рисунке 2 приведен пример синтаксиса.

Рис. 2. Ввод единиц измерения в Mathcad

Функция для интерполяции данных interp()

В инженерной среде иногда приходится иметь дело с массивами экспериментальных данных. Чаще всего приходится строить, анализировать и оформлять графики. В mathcad 15 есть возможность провести интерполяцию точек графика с помощью функции interp()

Введем две матрицы-столбца: столбец X и столбец Y. Заполним их данными и отобразим на графике. Как построить график по точкам и оформить его можно посмотреть в разделе графики

Рис. 3. График по точкам

Функция interp() имеет следующий синтаксис: y(x):=interp(cspline(X,Y), X, Y, x). Cspline — тип кривой (кубический сплайн), которой интерполируются точки. В качестве входных параметров используются данные матриц-столбцов X и Y. Тип кривой может быть выбран и другой (см. help mathcad), но как показывает личная практика cspline корректно работает в большинстве инженерных расчетов. Помимо cspline в функцию interp() требуется ввести данные матриц-столбцов и указать имя аргумента — в нашем случае это переменная x

Вся функция interp() присваивается функции y(x), с которой далее очень удобно работать. Теперь подставляя любые значения x в функцию y(x) можно получать значения функции y

Рис. 4. Интерполяция графика по точкам в mathcad 15

Подстановка значений переменных в формулу в mathcad 15

Иногда в расчетах присутствует огромное количество разных переменных и констант и не всегда сразу понятно, какое значение какой переменной работает в формуле. При оформлении расчетных работ часто бывает полезно подставить значения переменных в формулу

Чтобы увидеть какие значения переменных учавствуют формулах mathcad 15 существует функция explicit. Введем ряд переменных и присвоим им числовые значения. Затем введем формулу и найдем значение выражения. Пример приведен ниже на рисунке 5.

Рис. 5. Значение выражения по умолчанию

Теперь щелкните левой кнопкой мыши по формуле и установите курсор, как показано на рисунке 6. Для этого используйте клавиши: стрелка влево, стрелка вправо и пробел

Рис. 6. Ввод функции explicit

На панели Symbolic найдите кнопку explicit и нажмите ее. Возле формулы появится фраза explicit. Далее, после этой фразы поставте запятую и введите все переменные, значения которых вы бы хотели видеть. Синтаксис приведен на рисунке 7.

Рис. 7. Работа функции explicit для постановки значений в формулу

Можно скрыть название функции и переменные после команды explicit. Так документ станет легче воспринимать стороннему человеку. Для этого щелкните правой кнопкой мыши по выражению и в выпадающем меню нажмите «Hide keywords». Уберите выделение с выражения и вы увидите, что оно отображается без служебных фраз

Рис. 8. Скрытие функции explicit

Импорт данных из внешнего файла блокнот.txt и excel.xlsx

Не редко приходится работать с массивами данных, которые сохранены в txt файлах либо в таблицах excel. В mathcad 15 есть возможность импорта данных из внешнего файла для обработки и анализа

Для импорта числовых данных из txt файла в основном меню выполните следующие действия: Insert -> Data -> File input…

Рис. 9. Импорт данных в Mathcad 15

В появивщемся окне нажмите Browse… и выберете файл с данными. Для примера используется заранее созданный файл as1.txt, в котором записаны числовые значения. Далее нажмите Next и затем Finish

Рис. 10. Импорт данных в Mathcad 15

Вы увидите свободный маркер, которому присвоен «файл»

Рис. 11. Импорт данных в Mathcad 15

Введите имя переменной на месте маркера. Теперь данные файла сохранены в переменной и с ними можно работать

Рис. 12. Импорт данных в Mathcad 15 из блокнота

Обратите внимание, что если данные в файле постоянно обновляются и вам нужно иметь актуальные расчеты в mathcad, то необходимо обновлять страницу. Это можно сделать с помощью сочетания клавиш Ctrl + F9, либо перейдя в основном меню по следующему пути: Tools > Calculate > Calculate Worksheet. Таким образом, все операции в вашем расчете пересчитаются, а импортированные данные обновятся

Рис. 13. Импорт данных в Mathcad 15 из блокнота. Обновление данных

Из текстового файла возможно импортировать прямоугольную матрицу. Для этого между числами в файле должен быть разделитель — пробел. См. пример на рисунке 14

Рис. 14. Импорт матрицы из блокнота в mathcad 15

Чтобы импортировать числовые данные из файла ecxel в основном меню выполните переход: Insert > Data > File input… Затем в File format выберете пункт Microsoft Excel и нажмите кнопку Browse…

Рис. 15. Импорт данных из файла ecxel в mathcad 15

В появившемся окне выберете ваш файл и нажмите кнопку Open.

Рис. 16. Импорт данных из файла ecxel в mathcad 15

Нажмите кнопку Next и вы попадете в меню настройки импорта. Вы можете оставить все ячейки без изменений и тогда mathcad импортирует все содержимое файла excel. Нажмите кнопку Finish и в рабочем поле mathcad вы увидете, что появился свободный маркер, котоорму присвоена иконка вашего файла

Рис. 17. Импорт данных из файла ecxel в mathcad 15

В место маркера введите какую либо переменную, например N, и выведете ее значение, используюя операцию равенства. На рисунке 18 видно, что переменная N содержит массив (матрицу) значений импортированных из файла excel

Рис. 18. Импорт данных из файла ecxel в mathcad 15

Если есть необходимость импортировать только часть данных из файла excel, то после выбора файла на диске нужно указать соответсвующий диапазон ячеек. В этом случае импортируются данные из указанного диапазона

Рис. 19. Импорт диапазона данных из файла ecxel в mathcad 15

После нажатия кнопки Finish вы снова увидите, что появился свободный маркер, которому присвоена иконка вашего файла. Введем новую переменную, например N2, и сразу же выведем ее значение, с помощью комады равенства. На рис. 20 видно, что переменная содержит матрицу значений, которые импортировались из определенного диапазона ячеек файла excel

Рис. 20. Импорт диапазона данных из файла ecxel в mathcad 15

При импортировании чисел с десятичными дробями из txt файлов обратите внимание на то, чтобы разделителем была запятая. Иначе mathcad не распознаст дробное число

Обратите внимание, что числовые данные с десятичными дробями в excel должны иметь разделитель, который корректно прочитается в mathcad. В противном случае число не импортируется корректно