Графическое представление физического процесса делает его более наглядным, а значит облегчает понимание рассматриваемого явления и, довольно часто, позволяет значительно упростить расчеты. На практике графики широко используются для решения различных задач. Следовательно, умение читать их сегодня является обязательным для многих специалистов. Представленные варианты графических задач позволяют охватить материал всего раздела «Механики» на примере одного графика. Рекомендуется для проведения контроля по отдельным темам раздела «Механика» и итогового контроля.
Методические приёмы, которые можно использовать в процессе обучения решению задач в начальной школе:
I. Методический приём сравнения используется для приобретения опыта математического анализа текстов учебных заданий. Сравнение важный способ перехода от созерцания к абстрактному мышлению. В процессе формирования понятия и обобщённых способов действий этот переход осуществляется путём установления соотношений между предметными, вербальными, графическими и символическими моделями. Приём сравнения лежит в основе обобщения и систематизации знаний; установления более глубоких связей ранее изученного материала с новым; поиска общих признаков при формировании понятий; поиска закономерностей. Умение выделять признаки и, ориентируясь на них, сравнивать предметы, ученики переносят на математические объекты. По внешним признакам, доступным для восприятия, учащиеся устанавливают сходство и различие между ними и осмысливают эти признаки с точки зрения различных понятий.
Формирование умения пользоваться этим приёмом следует осуществлять поэтапно, в тесной связи с изучением конкретного содержания. Работу по формированию у учащихся приёма сравнения лучше всего начать с первых уроков математики в начальной школе, а затем продолжить в основной школе, где дети самостоятельно используют этот приём, без указания: «сравни…», «в чём сходство и различие…».
II. Методический приём выбора используется для формирования у учащихся умения обосновывать свои суждения, используя для этого математическое содержание задания. Этот приём позволяет осознать сущность формируемых понятий, общих способов действий и содержательную зависимость между ними. Процесс выполнения любого задания должен всегда представлять цепочку суждений, для обоснования, истинности которых учащиеся используют различные способы.
Покажем это на примерах.
1. Выбор ответа к данной задаче.
Задача. 8 кг муки разложили поровну в 4 пакета. Сколько граммов муки в каждом пакете? Выбери и подчеркни верный ответ. 1) 2000 г 2) 200 г 3) 20 000 г
Использование данного приёма стимулирует учащихся к анализу текста, к установлению зависимости между данными и искомым, переводу одних единиц измерения в другие. Решив задачу, ученик подчёркивает верный ответ. Подобные задачи помогают готовиться к итоговому тестированию.
2. Выбор решения задачи.
Задача. На велогонках стартовали 70 спортсменов. На первом этапе с трассы сошли 4 велосипедиста, на втором – 6. Сколько спортсменов пришли к финишу? Выбери выражение, которое является решением задачи:
В данном случае приём выбора помогает учащимся обосновывать каждое выражение с использованием условия и вопроса задачи, тем самым способствует развитию умения анализировать, понимать условие задачи, соотносить текст с решением.
3. Выбор данных к условию задачи из её решения.
Задача. Лесник посадил … дубков, а елей – на … … . Сколько всего деревьев посадил лесник? Вставь пропущенные в тексте числа и слова, используя решение задачи: 1) 30 + 12 = 42 (д.) 2) 42 + 30 = 72 (д.)
Здесь приём выбора способствует не только усвоению структуры задач, но ставит учащихся перед необходимостью анализировать связи между решением и условием, формирует умение устанавливать нужную связь, позволяющую правильно выбрать числа для условия задачи.
4. Выбор схемы к задаче.
Задача. В портфеле 14 тетрадей. Из них 9 в клетку, остальные в линейку. Сколько тетрадей в линейку лежит в портфеле? Выбери схему, которая поможет ре» шить задачу.
В процессе выбора схемы, соответствующей тексту задачи, ученик анализирует каждую из них, соотносит числовые данные со схемой.
У учащихся в процессе выполнения этого задания формируется умение переводить словесную (текстовую) модель в схематическую.
5. Выбор вопроса, соответствующего условию.
Задача. В одной коробке 10 карандашей, а в другой – на 3 карандаша больше.
Выбери вопрос, который можно по» ставить к данному условию, чтобы получилась задача. 1) Сколько карандашей в первой коробке? 2) Сколько карандашей во второй коробке? 3) На сколько карандашей в первой коробке меньше, чем во второй? 4) Сколько карандашей в двух короб» ках?
Использование приёма выбора стимулирует учащихся к анализу текста, высказыванию суждений, их обоснованию. Например, прочитав первый вопрос, учащиеся отмечают, что в нём спрашивается о том, что из условия задачи известно, – значит, этот вопрос не подходит. Рассматривая четвёртый вопрос, ученики делают вывод, что в вопросе спрашивается о том, что неизвестно. Неизвестное можно найти, пользуясь данными числами; значит, этот вопрос можно поставить к данному условию. Таким образом, учащиеся не только усваивают структуру задачи, но встают перед необходимостью анализировать связи между данными и искомым, вырабатывают умение устанавливать нужную связь, позволяющую ответить на вопрос задачи.
6. Выбор выражения, которое является решением задачи.
Задача. На первой полке было 9 книг, на второй – 8 книг, 7 книг взяли. Сколько книг осталось на двух полках?
9 + 7 + 8; (9 + 
Учащиеся анализируют каждое выражение, обосновывают, какие из них имеют смысл, доказывают выбор правильного выражения и называют его: (9 + 
III. Методический приём преобразования лежит в основе осознания причинно-следственных связей между изучаемыми понятиями и обобщёнными способами действий, способствует формированию умения выполнять различные видоизменения числового и буквенного материала. Действия учеников в ходе выполнения соответствующих заданий направляются в основном указанием: «измени …», «представь …», «замени …» и др.
Приведём примеры заданий.
1. Приём преобразования вопроса.
Задача. В одной коробке 20 конфет, а в другой на 3 конфеты меньше. Сколько конфет в двух коробках? Измени вопрос так, чтобы задача решалась в одно действие.
2. Приём преобразования отношений в соответствии с математической записью.
Подумай, что можно изменить в тексте задачи, чтобы выражение 19 – 6 было её решением.
Задача. В коллекции у Серёжи 19 жуков, а пауков на 6 больше. Сколько жуков и пауков в коллекции у Серёжи?
В процессе анализа учащиеся приходят к выводу, что задача решается в два действия. Им необходимо изменить условие и вопрос таким образом, чтобы задача решалась в одно действие. Для этого следует внести изменения в условие задачи и сформулировать вопрос.
3. Преобразование решённой задачи.
Измени вопрос задачи, используя её решение.
Задача. Два парохода отошли одновременно от двух пристаней и идут навстречу друг другу. Встретились они через 2 часа. Один пароход шёл со скоростью 20 км в час, другой – 30 км в час. Найди расстояние между пристанями. Решение: 1) 20 + 30 = 50 (км) 2) 50 . 2 = 100 (км)
При составлении задачи необходимо обратить внимание учащихся на то, что неверно включать в условие результаты промежуточных действий. В условие задачи необходимо включить её ответ, т.е. результат последнего действия. Поэтому может быть составлена следующая задача: Два парохода вышли одновременно навстречу друг другу от двух пристаней и встретились через 2 часа. Расстояние между пристанями 100 км. Один пароход шёл со скоростью 20 км в час. Определи скорость второго парохода.
Эту задачу желательно решить двумя способами. После решения полезно сравнить условия обеих задач, а также способы их решения, обсудить, какие числа входят в условия обеих задач.
IV. Методический приём конструирования способствует формированию умения самостоятельно устанавливать соответствия между предметными, графическими и символическими моделями, преобразовывать их в математические; переносить усвоенные знания, умение и навыки на область новых знаний. Конструирование заданий включает учащихся в поисковую деятельность и тем самым создаёт условия для развития их мышления. Это помогает школьникам структурировать данные (ситуацию, проблему и т.п.), выяснять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать её, что обеспечивает условия для формирования математической компетентности учащегося, которая даёт возможность адекватного применения математики для решения возникающих в повседневной жизни проблем. Действия учеников в ходе выполнения подобных заданий направляются в основном указанием «поставь …», «составь …», «подумай …», «подбери …» и др.
Приведём примеры заданий.
1. Поиск и выделение необходимой информации.
Задача. У Коли 9 конфет, а у Пети – 6. Закончи рисунок, если каждая конфета обозначена кругом.
Закрась красным цветом столько конфет у Коли, сколько их было у Пети.
2. Составление вопроса задачи.
Придумай вопросы к задачам, чтобы они решались: одним действием; двумя действиями.
Задача. У Миши 13 белых голубей, а серых – на 9 меньше.
3. Дополнение условия задачи.
Выбери данные, которыми можно дополнить условие задачи, чтобы ответить на поставленный вопрос.
Задача. В гараже было 36 машин. Сколько машин осталось? Данные, которыми можно дополнить условие задачи. а) Утром приехало 9 машин, а вечером уехала 21 машина. б) Уехало на 12 машин больше, чем было. в) Уехало сначала 9 машин, а потом 21 машина.
Дети учатся доказывать свою точку зрения, мыслить и рассуждать при анализе условия задачи. В данном случае они приходят к мнению, что из предложенных данных можно дополнить условие пунктами а) и в), пункт б) не удовлетворяет условию и вопросу задачи, так как не могло уехать больше машин, чем было в гараже.
Итак, мы постарались доказать, что в процессе обучения решению задач в начальной школе необходимо использовать специальные задания, включающие сочетания различных методических приёмов.
Подходы
к решению текстовых задач
Основные цели решения текстовых задач в школьном курсе математики:
—
научить переводить реальные предметные ситуации в математические модели;
—
обеспечить действенное усвоение обучающимися основных методов и приёмов решения
учебных математических задач.
Этапы решения текстовых задач.
1.
Анализ содержания задачи.
2.
Поиск пути решения задачи.
3.
Составление плана решения задачи.
4.
Осуществление плана решения задачи.
5.
Проверка решения задачи.
Приёмы, используемые на
этапе «Анализ задачи»
1.
Представление той ситуации, которая
описана в задаче. Цель такого воспроизведения – выявление основных
количественных и качественных характеристик ситуации, представленных в задаче.
2.
Постановка специальных вопросов и поиск
ответов на них. Включает стандартный набор вопросов, ответы на которые
позволяют детально разобраться с условием и содержанием задачи: о чём говорится
в задаче? что об этом говорится? что известно в задаче? что требуется найти в
задаче? что неизвестно в задаче? и другие.
3.
Переформулировка текста задачи.
Состоит в замене данного в задаче описания некоторой ситуации другим описанием,
сохраняющим все отношения, связи, условия, но более явно их выражающим. При
необходимости строится вспомогательная модель задачи: краткая запись условия,
таблица, рисунок, чертёж, схема и т.д.
4.
Моделирование ситуации, описанной в
задаче, с помощью реальных предметов, предметных моделей или графических
моделей.
Приёмы, используемые на
этапе «Поиск пути решения задачи и составление плана её решения».
1 Анализ задачи по тексту или её
вспомогательной модели.
2 Рассуждения от вопроса задачи к данным
(аналитический путь) или от данных к вопросу (синтетический путь).
3
Комбинированный путь (анализ и синтез).
4
Разбиение задачи на составные части.
Введение
новых (подходящих) обозначений в том случае, когда данные (или искомые) в
задаче не обозначены.
Рекомендуемый алгоритм решения
задач.
Обозначим
неизвестную величину через х.
1.
Выразим через неё другие величины.
2.
Из условия задачи найдём зависимость между
ними и составим уравнение.
3.
Решим уравнение.
4.
Найдём ответ на вопрос задачи.
5.
Проверим правильность решения задачи.
6.
Запишем ответ.
|
Сложности |
Пути их решения |
|
Составление математической модели |
Тщательно изучить и правильно содержание задачи, выразив величины через известные введенные переменные. Не периодичности маршрута при окружности, а мыслить только время, путь, |
|
Составление |
Важно |
|
Нахождение |
Держать в |
|
Решение |
Решение |
Для
того, чтобы научиться решать задачи, надо приобрести опыт их решения путем
многократного повторения операций, действий, составляющих предмет изучения. Редкие
ученики самостоятельно приобретают такой опыт. Долг учителя — помочь обучающимся
приобрести опыт решения задач, научить их решать задачи. Помощь учителя не
должна быть чрезмерной, но и не быть слишком малой. Навыки решения текстовых
задач формируются на основе осмысленных знаний и умений. Для формирования
навыков нужна тщательно продуманная система упражнений и задач «от простого к
сложному». Знания учащихся по математике должны совершенствоваться с решением
каждой новой задачи. Следует добиваться, чтобы осознанные умения и навыки
ученики получали при наименьших затратах времени. Следует учитывать
индивидуальные особенности и возможности обучающихся.
Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения»
Кафедра «Строительная механика»
В.А. Бобрин Л.П. Миронов
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ
ЧАСТЬ 1
Рекомендовано Дальневосточным региональным учебно-методическим центром (ДВ РУМЦ)
в качестве учебного пособия для студентов специальностей 270102 «Промышленное и гражданское строительство», 270201 «Мосты и транспортные тоннели», 270204 «Строительство железных дорог, путь и путевое хозяйство», 190205 «Подъемно-транспортные, строительные,
дорожные машины и оборудование» вузов региона
Хабаровск Издательство ДВГУПС
2006
УДК 624.04 (075.8)
ББК Н112я73
Б 724
Рецензенты:
Кафедра «Механика деформируемого твердого тела» Хабаровского государственного технического университета (заведующий кафедрой кандидат технических наук, доцент
А.А. Вайсфельд)
Заведующий кафедрой «Механика деформируемого твердого тела» Дальневосточного государственного технического университета
доктор технических наук, профессор
К.П. Горбачев
Бобрин, В.А.
Б 724 Руководство к решению задач по строительной механике : учеб. пособие. В 3 ч. Ч. 1 / В.А. Бобрин, Л.П. Миронов; под ред. Л.П. Миронова. – Хабаровск : Изд-во ДВГУПС, 2006. – 141 с.
Учебное пособие соответствует дисциплине «Строительная механика» по ГОС ВПО направления 271100 «Строительство» специальности 270102 «Промышленное и гражданское строительство», направления 270200 «Транспортное строительство» специальностей 270204 «Строительство железных дорог, путь и путевое хозяйство» и 270201 «Мосты и транспортные тоннели», направления 190200 «Транспортные машины и транспортнотехнологические комплексы» специальности 190205 «Подъемно-транспорт- ные, строительные, дорожные машины и оборудование».
Пособие состоит из 3 частей. В части 1 рассмотрены методы кинематического анализа и построения линий влияния усилий в статически определимых балках, арках, рамах и фермах. Подробно разобраны примеры решения типовых задач, приведены 360 вариантов задач для самостоятельного решения и ответы к ним.
Предназначено студентам всех форм обучения.
УДК 624.04 (075.8)
ББК Н112я73
ãГОУ ВПО «Дальневосточный государственный университет путей сообщения» (ДВГУПС), 2006
2
ВВЕДЕНИЕ
Настоящее пособие посвящено методам построения линий влияния усилий в плоских статически определимых стержневых системах и их использованию при расчете сооружений на действие неподвижных и подвижных нагрузок. Пособие начинается с изложения кратких сведений из теоретической механики и математики, позволяющих студентам преодолеть трудности, возникающие при использовании аппарата этих дисциплин. В пособии излагаются основные положения теории, методические указания и подробные решения типовых задач по кинематическому анализу расчетных схем сооружений, статическому и кинематическому методам построения линий влияния и расчеты по ним.
Приведены более 190 задач с 360 вариантами исходных данных для самостоятельного решения. Тематика и набор задач отражают многолетний опыт кафедры по преподаванию строительной механики. Ко всем задачам приведены ответы в числовой или графической форме.
Всовременной доступной учебной литературе отсутствуют примеры
инаборы задач для использования в аудитории с целью организации самостоятельной индивидуальной работы студентов или тестирования их знаний по разделам курса строительной механики. Настоящее пособие восполняет этот пробел.
Наличие ответов стимулирует самостоятельный поиск студентом правильных решений, которые представляются им в письменном виде. Совпадение полученного решения с ответом благотворно влияет на возникновение у студента чувства уверенности в овладении учебным материалом.
Особое значение пособие имеет для студентов заочной формы обучения, основная масса которых живет и работает в отдаленных районах, где доступ к подобной учебной литературе затруднен.
Впособии принята тройная нумерация задач и ответов к ним. Первая цифра указывает раздел, вторая – её подраздел , третья – порядковый номер задачи.
Пособие написали В.А. Бобрин: разд. 1, подразд. 3.1, 3.2, 4.2–4.6, 5.2–5.6; Л.П. Миронов: разд. 2, подразд. 3.3–3.5, 4.1, 4.7, 5.1, 5.7.
Все замечания и рекомендации по улучшению данного пособия будут с благодарностью приняты авторами.
3

1.ЭЛЕМЕНТЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ И МАТЕМАТИКИ
1.1.Проекции плоской системы сил на оси прямоугольной системы координат. Моменты сил
В строительной механике широко используется аппарат теоретической механики и математики. Ниже напоминаются некоторые необходимые при расчетах стержневых систем элементы указанных дисциплин. Общепринято считать проекции сил, совпадающие (несовпадающие) с положительным направлением координатных осей, со знаком плюс (минус). Положительное направление вращения в строительной механике допустимо принимать как по ходу, так и против хода часовой стрелки, сообразуясь с удобством вычислений. Пусть имеется плоская система сил в составе сосредоточенных сил Fi, сплошных распределенных нагрузок интенсивностью qi, и сосредоточенных моментов (пар сил) mi (рис. 1.1).
|
Y |
||||||||||||
|
Силовая плоскость |
= —R sinβ |
Центр |
||||||||||
|
Линия действия F1 |
R |
qi=q(ξ) |
||||||||||
|
тяжести |
||||||||||||
|
F3y= —F3sinα3 |
qy |
q |
||||||||||
|
F1y= F1sinα1 |
||||||||||||
|
F1 |
90° |
F3 |
a |
|||||||||
|
Плечо r1 |
ξ |
|||||||||||
|
α1 |
F2y= —F2 |
Плечо r3=0 |
Rq-равнодействующая |
|||||||||
|
Идентичные |
||||||||||||
|
m1 изображения |
||||||||||||
|
Плечо r2 |
K Плечо rq |
пар сил |
||||||||||
|
90° |
||||||||||||
|
α2=90° |
F2 |
90° |
m2 |
|||||||||
|
α3 |
β |
Z |
||||||||||
|
0 |
F |
1z |
= F cosα |
F3z= F3cosα3 |
R |
=–R cosβ |
||||||
|
1 |
1 |
Моментная точка |
qz |
q |
||||||||
Рис. 1.1. Проекции сил (изображены светлыми стрелками) на координатные оси. Моменты сил относительно произвольной точки
Тогда алгебраическая сумма проекций всех нагрузок на ось Z составит:
4

∑ FZ = F1сosα1 + F3сosα3 – Rqсosβ, а сумма проекций этих же нагрузок на ось Y будет равна: ∑ FY = F1sinα1 – F2 – F3sinα3 – Rqsinβ,
а
|
где Rq = ò q(ξ)dξ – равнодейcтвующая |
Rq= qa |
q= const. |
||||
|
0 |
||||||
|
распределенной нагрузки, приложенная в |
||||||
|
центре тяжести её полосы загружения. |
||||||
|
Если q(ξ) = q = const, то Rq = qa и |
a/2 |
|||||
|
приложена посередине полосы (рис. 1.2). |
a |
|||||
|
Пары сил mi не имеют проекций на |
||||||
|
координатные оси. |
Рис. 1.2. Равнодействующая |
|||||
|
Алгебраическая сумма моментов сил |
||||||
|
равномерно распределенной |
||||||
|
относительно моментной точки К в данном |
нагрузки |
случае будет :
∑MK = –F1r1 + F2r2 + F30 – Rqrq – m1 + m2 или при обратном правиле знаков
∑MK = F1r1 – F2r2 + F30 + Rqrq + m1 – m2.
Единицы измерения нагрузок таковы: Fi, Rqi – [кН], qi – [кН/м], mi – [кНּм].
1.2. Уравнения равновесия (статики) на плоскости
а) Если сосредоточенные силы Fi и равнодействующие Rqi распределенных нагрузок сходятся в одной точке (рис 1.3), то независимых уравнений равновесия здесь два: ∑FZ = 0, ∑FY = 0.
б) Для произвольной плоской системы сил (рис. 1.4) используют три эквивалентных варианта уравнений статики:
1)∑FZ = 0; ∑FY = 0; ∑MK = 0;
2)∑Mk1 = 0; ∑Mk2 = 0; ∑FY = 0 (или ∑FZ =0);
3)∑Mk1 = 0; ∑Mk2 = 0; ∑Mk3 = 0,
где моментные точки К1, К2, К3 не должны совпадать и в последнем случае не должны лежать на одной прямой.
|
y |
|||||||
|
Rq3 |
F2 |
F3 |
y |
F1 |
F3 |
||
|
K3 |
|||||||
|
F1 |
Rq1 z |
m1 |
k1 |
Rq |
|||
|
F2 |
K2 |
||||||
|
Rq2 |
m2 |
||||||
|
Рис. 1.3. Система сходящихся сил |
Рис. 1.4. Произвольная |
|
|
система сил |
||
5

q

F1
Рис. 1.5. Нагрузки, лежащие на одной прямой
в) Если линии действия всех сил лежат на одной прямой, то рассматривают одно условие статики
(рис. 1.5): ∑FZ = 0.
1.3. Построение графиков (эпюр) элементарных функций
Многие расчеты в строительной механике сопровождаются построением различного вида графиков (эпюр). Напомним, как это делается для алгебраических функций одной независимой переменной. Например, построение эпюр внутренних усилий начинается с разбивки расчетной схемы конструкции на участки, на каждом из которых указывают пределы изменения независимой переменной. Такой участок в математике называется областью определения функции, в пределах которой и строят эпюру с указанием характерных значений (величины и знака) искомых ординат. В зависимости от выбранного начала отсчета независимой переменной (аргумента функции) указывают пределы её изменения на данном участке либо как а ≤ z ≤ b, либо как 0 ≤ z ≤ b. В последнем случае начало отсчета совмещают с началом участка, что удобнее.
Рассмотрим примеры. Пусть:
а) составлена функция ƒ1(z) = 4 с областью определения 0 ≤ z < 4,2. Её эпюра представлена на рис. 1.6, а. Очевидно, что если в выражение функции переменная z не входит, её значение на данном участке постоянно;
б) составлена функция ƒ2(z) = –3z+8 с областью определения 0 ≤ z ≤ 4. Так как функция содержит переменную z в первой степени, её эпюра есть прямая (линейная функция). Вычисляем концевые ординаты:
ƒ2(0) = 8; ƒ2(4) = –3·4 + 8 = –4. Эпюра ƒ2(z) представлена на рис. 1.6, б.
Абсцисса нулевой ординаты определяется из условия ƒ2(z0)= –3z0+8 = 0,
откуда z0 = 8/3 = 2,666;
в) составлена функция ƒ3(z) = –1,2 · z2 + 9,2 z – 4 с областью определения 0 ≤ z ≤ 6. Так как старшая степень переменной z равна 2, эта функция – парабола.
Эпюру ƒ3(z) строим по характерным точкам кривой, ординаты которых вычисляем так: в начале участка при z = 0, ƒ3(0) = –4; посередине участка при zср = 3 получаем ƒср = –1,2 · 32 + 9,2 · 3 – 4 = 12,8. Экстремальное
|
значение находим из условия равенства нулю первой |
производной от |
|||
|
ƒ3(z), что дает |
∂f3( z ) |
= −2,4zextr + 9,2 = 0, откуда zextr |
= |
9,2/2,4 = 3,833. |
|
∂z |
||||
|
Подставляя zextr |
в уравнение функции, получаем |
|||
|
6 |

ƒ3max(3,833) = –1,2 · 3,8332 + 9,2 · 3,833 – 4 = 13,333. Концевая ордината при z = 6: ƒ3(6) = -1,2 · 62 + 9,2 · 6 – 4 = 8.
Положение нулевой ординаты находим из условия ƒ3(z0) = –1,2 z02 + 9,2 z0 – 4 = 0, откуда:
|
1 é |
ù |
-9,2 ± 8,09 |
||||||||||
|
2 |
||||||||||||
|
z0 |
= |
ê |
-9,2 |
± |
9,2 |
— 4 (-1,2) (-4)ú |
= |
-2, 4 |
, |
|||
|
2 |
||||||||||||
|
(-1,2) ë |
û |
|
z0(1) = − 9,2 + 8,09 |
= 0,462 |
и |
z0(2) = |
− 9,2 − 8,09 |
= 7,204 . |
|||||||||||||||||||||||||||||||||||
|
— 2,4 |
— 2,4 |
|||||||||||||||||||||||||||||||||||||||
|
ƒ3(z) |
Эпюраƒ3(z) |
|||||||||||||||||||||||||||||||||||||||
|
в |
14 |
maxƒ =13,333 |
||||||||||||||||||||||||||||||||||||||
|
ƒср=12,8 |
||||||||||||||||||||||||||||||||||||||||
|
12 |
||||||||||||||||||||||||||||||||||||||||
|
ƒк=9,6 |
K |
|||||||||||||||||||||||||||||||||||||||
|
ƒ1(z) |
10 |
|||||||||||||||||||||||||||||||||||||||
|
Эпюраƒ1(z) |
8 |
|||||||||||||||||||||||||||||||||||||||
|
8 |
||||||||||||||||||||||||||||||||||||||||
|
6 |
||||||||||||||||||||||||||||||||||||||||
|
φк |
||||||||||||||||||||||||||||||||||||||||
|
z |
4 |
|||||||||||||||||||||||||||||||||||||||
|
Касательная |
||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
2 |
||||||||||||||||||||||||||||||||||||
|
ƒ2(z) |
Эпюраƒ2(z) |
0 |
z |
|||||||||||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|||||||||||||||||||||||||||||||||||
|
ƒ2(z0)=0 |
z |
2 |
||||||||||||||||||||||||||||||||||||||
|
3 |
4 |
4 |
Z0=0,462 |
|||||||||||||||||||||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||||||||||||||||
|
Z0=2,666 |
4 |
Zк =2 |
||||||||||||||||||||||||||||||||||||||
|
Zср |
=3 |
|||||||||||||||||||||||||||||||||||||||
|
Zmax =3,833 |
Рис. 1.6. Эпюры функций ƒi(z)
Первое значение z0(1) = 0,462 принадлежит участку, а второе z0(2)
выводит за пределы участка и должно быть отброшено. Эпюра ƒ3(z) показана на рис. 1.6, в. В заключение определим тригонометрические функции угла φК наклона касательной к кривой в точке К с абсциссой zК = 2 (рис. 1.6, в). Как известно, первая производная функции в декартовых
координатах равна тангенсу угла ϕК . Поэтому при zК = 2 имеем
7

|
tgjК = |
df3 (z) |
= -2,4 zК |
+ 9,2 = -2, 4×2 + 9,2 = 4,40. |
|||||||
|
dz |
||||||||||
|
1 |
1 |
|||||||||
|
Тогда cos jK |
= |
= |
= 0,2216 |
, а sinjK = tgjK × cos jK = |
||||||
|
1+ tgϕ2 |
1+ 4,42 |
|||||||||
|
K |
||||||||||
|
= 0,2216 · 4,4 = 0,9752, |
а |
sin2 ϕK + cos2 ϕK |
= 0,97522 + 0,22162 = 1. |
1.4. Некоторые соотношения для плоских фигур
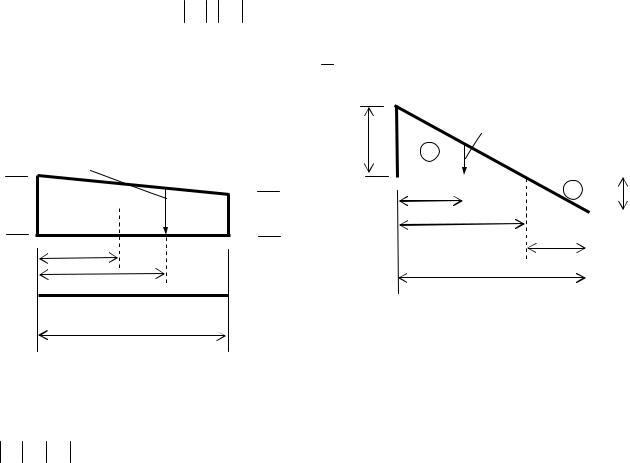
Прямоугольник (рис. 1.7). Площадь ω = hλ; если это полоса загружения равномерно распределенной (погонной) нагрузкой интенсивностью q0 = сonst, то на некоторых стадиях расчета сооружений ее представляют равнодействующей Rq = q0λ [кH], приложенной в центре С тяжести прямоугольника (zc = λ/2).
Прямоугольный треугольник (рис. 1.8). Площадь ω = 1/2 hλ; если это полоса загружения распределенной нагрузкой переменной интенсивности qz , то её равнодействующая Rq = q0 λ/2 и приложена в центре С тяжести с координатой zc = λ/3; tgα=h/λ.
|
) |
q0=const |
||||||
|
0 |
c |
||||||
|
h(q |
Rq |
||||||
|
zc=λ/2 |
|||||||
|
λ |
|||||||
|
Рис. 1.7. Прямоугольник |
h(q0)
qz = q0 (λ − z )
c
λ
α
Rq
λ
z
|
Рис. 1.8. Прямоугольный треугольник |
||||||||||||||||||
|
Трапеция (рис. 1.9). Площадь w = |
(h1 + h2) |
l ; если это полоса распре- |
||||||||||||||||
|
2 |
(l — z) |
|||||||||||||||||
|
деленной нагрузки переменной интенсивности q |
z |
= q |
2 |
+ (q |
— q |
2 |
) |
, |
||||||||||
|
1 |
l |
|||||||||||||||||
|
(q1 + q2) |
||||||||||||||||||
|
то ее равнодействующая Rq = |
l и приложена в центре С тяжести |
|||||||||||||||||
|
2 |
||||||||||||||||||
|
с координатой zc = |
(h1 + 2h2 ) λ |
º |
(q1 + 2q2 )λ |
. |
||||||||||||||
|
3(h1 + h2 ) |
3(q1 |
+ q2 ) |
||||||||||||||||
8
|
Двузначная трапеция (рис. 1.10). Площадь w = |
(h1 + h2) |
l , где h2 < 0; |
|
|
2 |
|||
|
z0 |
= |
h1 |
l |
; здесь |
||||||||
|
h1 |
+ |
h2 |
||||||||||
Текущая ордината yz
qz = q2 + (q1
h1 , h2 принимать по абсолютной величине.
= h1 — (h1 + h2 ) lz .
|
— q2 )× |
(λ − z) |
1 |
yz |
||
|
h |
|||||
|
l |
|||||
h1(q1)
c
zc
z

λ
h2(q2)
|
z |
h |
|||||
|
2 |
||||||
|
z0 |
||||||
|
a |
||||||
|
λ |
||||||
Рис. 1.10. Двузначная трапеция
Рис. 1.9. Трапеция
Полезно иметь в виду, что площади двузначных фигур в алгебраическом смысле могут быть равны нулю (например, здесь при h1 = h2 ). Но если бы определялась площадь ω фигуры для ее окраски,
|
то ее следовало бы вычислять арифметически w = |
h1 |
z0 |
+ |
h2 |
a |
. |
|
2 |
2 |
|||||
1.5. О некоторых правилах приближенных вычислений
Реальные конструкции обычно несколько отличаются от их расчетных схем как величиной нагрузок, характеристиками материалов, так и размерами элементов. Поэтому так называемый «точный» расчет на самом деле таковым не является. В связи с этим выполняемые расчеты всегда более или менее приближенные, и стремление получать числовые результаты с большим количеством разрядов не оправдано. Не имеет смысла во всех случаях переписывать все, что появляется на индикаторе калькулятора. Сложились выработанные практикой некоторые правила обеспечения точности вычислений в разумных рамках.
Нужно сохранять в результатах лишь только верные значащие цифры. Нули, с которых начинаются числа, значащими не считаются. Но нули, стоящие в середине или в конце числа, удостоверяющие
9

отсутствие в числе единиц соответствующего разряда – цифры значащие. Например, в числе 0,003080 подчеркнутые нули слева значащими не считаются, остальные нули – значащие. Если значение какой-либо величины содержит лишние или недостоверные цифры, то его округляют. При этом правила округления таковы:
1)если первая отбрасываемая цифра больше 4, то последняя сохраняемая цифра увеличивается на единицу. Например, округляя число 51,5762 до сотых (здесь первая отбрасываемая цифра 6 > 4), принимаем 51,58;
2)если первая отбрасываемая цифра меньше или равна 4, то последняя сохраняемая цифра не изменяется. Если округляем до сотых число 51,5732, где первая отбрасываемая цифра не больше 4 (здесь 3 < 4), то принимаем 51,57;
3)если отбрасываемая часть числа состоит из одной цифры 5, то число округляют так, чтобы последняя сохраняемая цифра была четной. Например, округляя число 8,4375 до тысячных, принимаем 8,438, а если округляем число 8,345 до сотых, то принимаем 8,34;
4)при сложении и вычитании в результатах сохраняют столько десятичных знаков, сколько их имеет число с наименьшим количеством десятичных знаков;
5)при умножении и делении в результатах оставляют столько значащих цифр, сколько их имело приближенное число с наименьшим количеством значащих цифр;
6)расчет значений функций xn , n
содержать столько значащих цифр, сколько их содержит само число x. При вычислении промежуточных результатов сохраняют на одну
цифру больше (запасную цифру), которая в окончательном результате отбрасывается.
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ СИСТЕМ
2.1. Виды систем
Расчетная схема сооружения получается из отдельных элементов, соединенных между собой и прикрепленных к земле. Совокупность всех элементов, связей между ними и связей элементов с землей будем называть системой. Различают три вида систем.
1. Геометрические неизменяемые системы – это такие системы, в
которых перемещения отдельных точек возможны только при деформировании некоторых элементов. Например, в системе, показанной на рис. 2.1, а, узел А может перемещаться только в том случае, если прикрепляющие его к земле стержни АВ и АС будут деформироваться.
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5