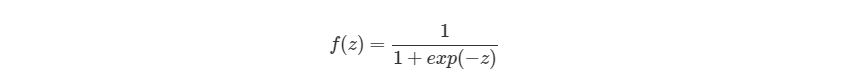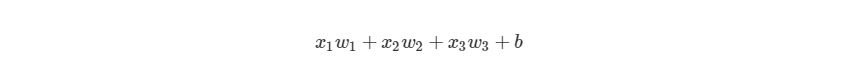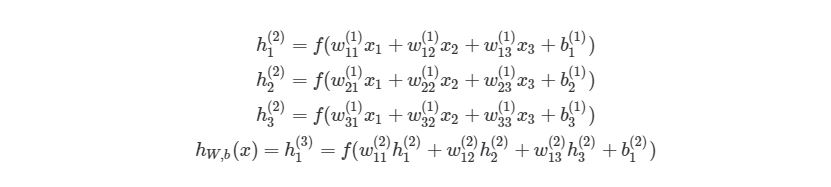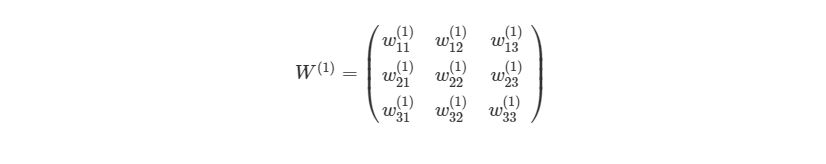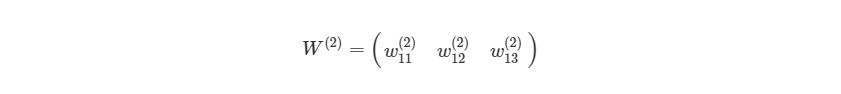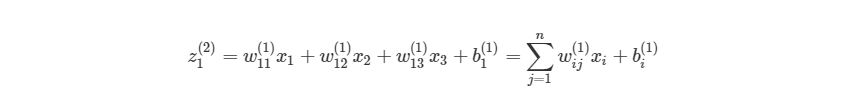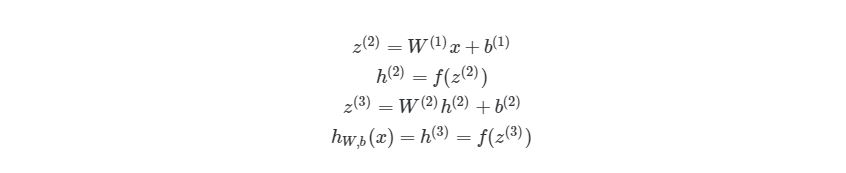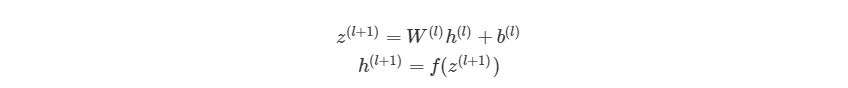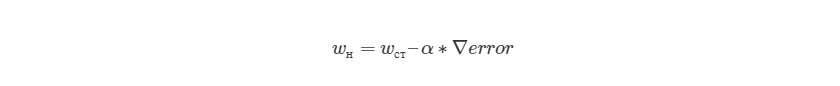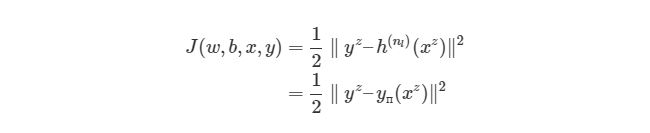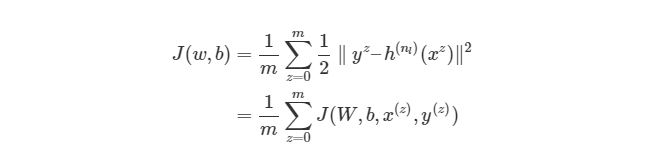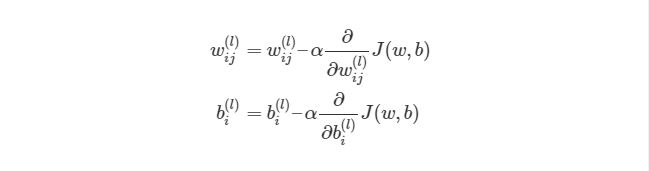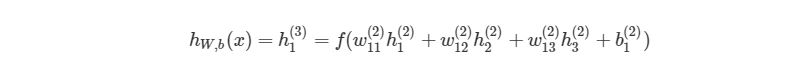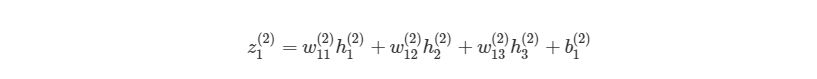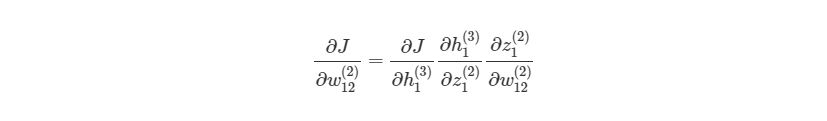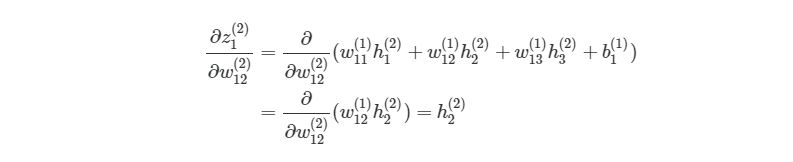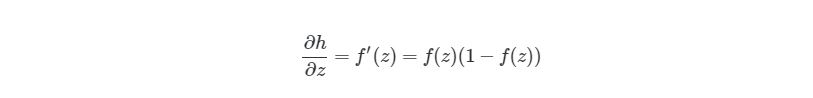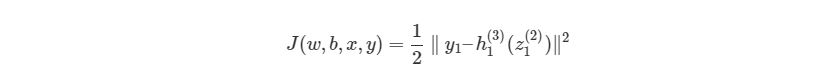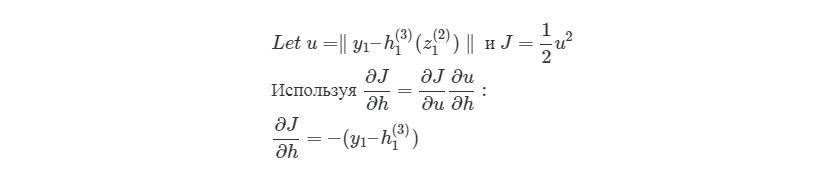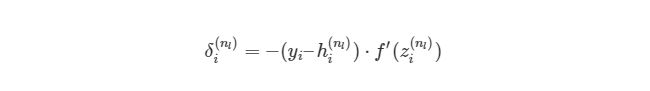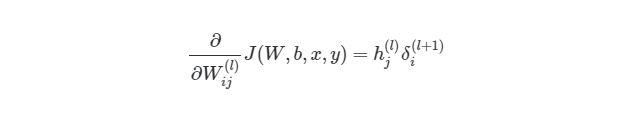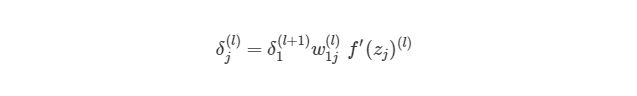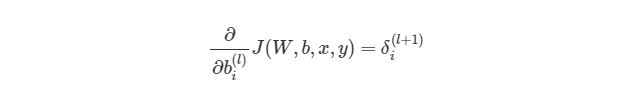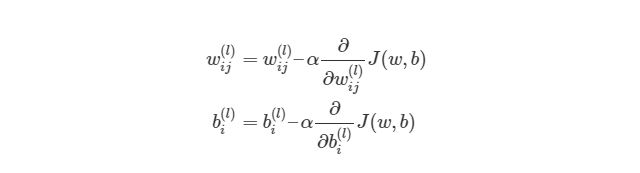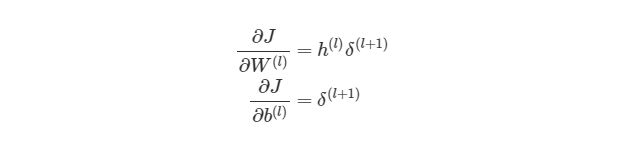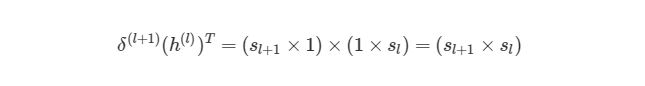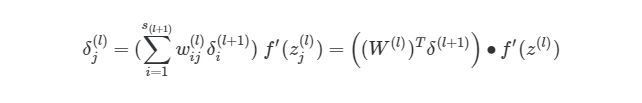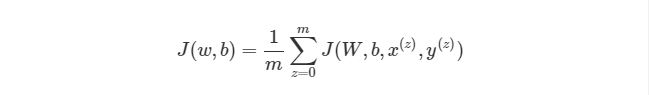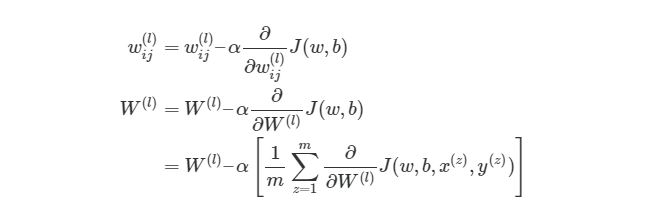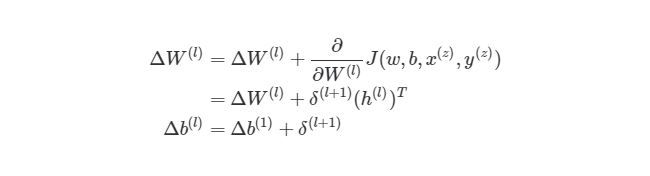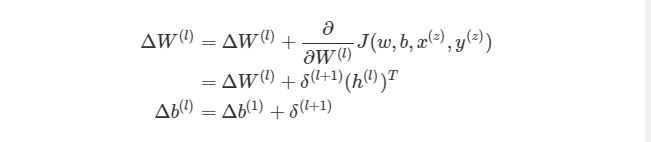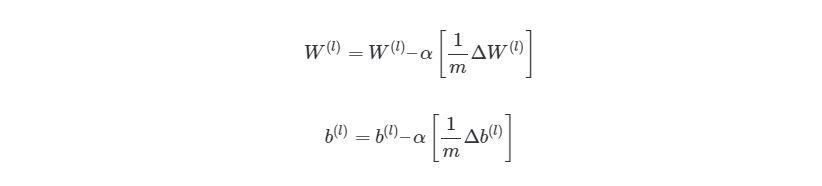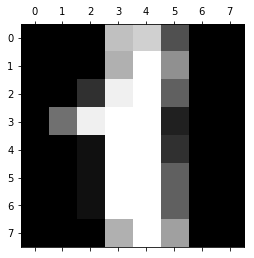Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.
Если вы в поисках пособия по искусственным нейронным сетям (ИНС), то, возможно, у вас уже имеются некоторые предположения относительно того, что это такое. Но знали ли вы, что нейронные сети — основа новой и интересной области глубинного обучения? Глубинное обучение — область машинного обучения, в наше время помогло сделать большой прорыв во многих областях, начиная с игры в Го и Покер с живыми игроками, и заканчивая беспилотными автомобилями. Но, прежде всего, глубинное обучение требует знаний о работе нейронных сетей.
В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.
1 Что такое искусственная нейросеть?
Искусственные нейросеть (ИНС) — это программная реализация нейронных структур нашего мозга. Мы не будем обсуждать сложную биологию нашей головы, достаточно знать, что мозг содержит нейроны, которые являются своего рода органическими переключателями. Они могут изменять тип передаваемых сигналов в зависимости от электрических или химических сигналов, которые в них передаются. Нейросеть в человеческом мозге — огромная взаимосвязанная система нейронов, где сигнал, передаваемый одним нейроном, может передаваться в тысячи других нейронов. Обучение происходит через повторную активацию некоторых нейронных соединений. Из-за этого увеличивается вероятность вывода нужного результата при соответствующей входной информации (сигналах). Такой вид обучения использует обратную связь — при правильном результате нейронные связи, которые выводят его, становятся более плотными.
Искусственные нейронные сети имитируют поведение мозга в простом виде. Они могут быть обучены контролируемым и неконтролируемым путями. В контролируемой ИНС, сеть обучается путем передачи соответствующей входной информации и примеров исходной информации. Например, спам-фильтр в электронном почтовом ящике: входной информацией может быть список слов, которые обычно содержатся в спам-сообщениях, а исходной информацией — классификация для уведомления (спам, не спам). Такой вид обучения добавляет веса связям ИНС, но это будет рассмотрено позже.
Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.
2 Структура ИНС
2.1 Искусственный нейрон
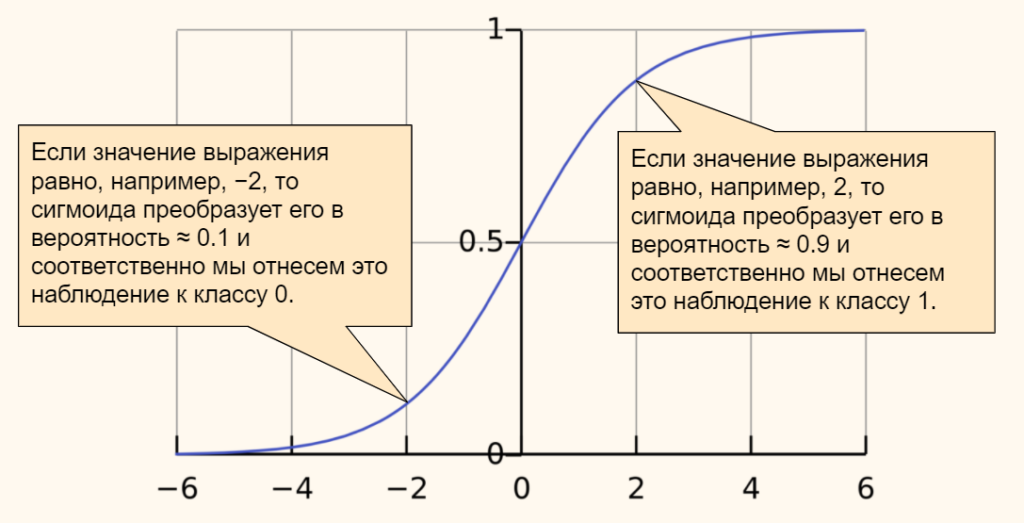
Биологический нейрон имитируется в ИНС через активационную функцию. В задачах классификации (например определение спам-сообщений) активационная функция должна иметь характеристику «включателя». Иными словами, если вход больше, чем некоторое значение, то выход должен изменять состояние, например с 0 на 1 или -1 на 1 Это имитирует «включение» биологического нейрона. В качестве активационной функции обычно используют сигмоидальную функцию:
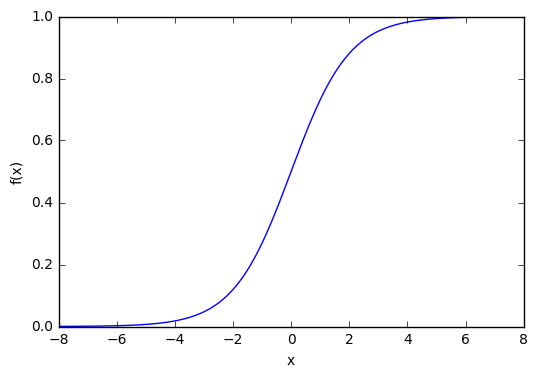
Которая выглядит следующим образом:
import matplotlib.pylab as plt
import numpy as np
x = np.arange(-8, 8, 0.1)
f = 1 / (1 + np.exp(-x))
plt.plot(x, f)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()
Из графика можно увидеть, что функция «активационная» — она растет с 0 до 1 с каждым увеличением значения х. Сигмоидальная функция является гладкой и непрерывной. Это означает, что функция имеет производную, что в свою очередь является очень важным фактором для обучения алгоритма.
2.2 Узлы
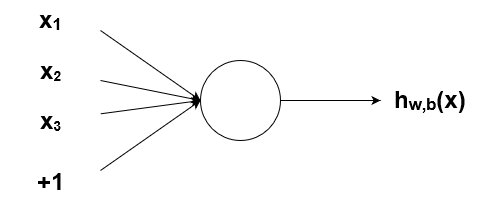
Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.
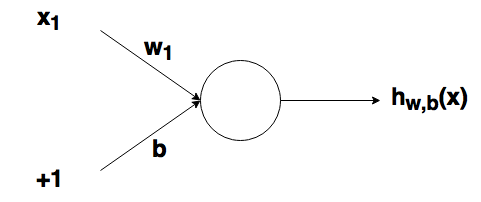
Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.
Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:
где wi— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.
2.3 Смещение
Рассмотрим простой узел, в котором есть по одному входу и выходу:
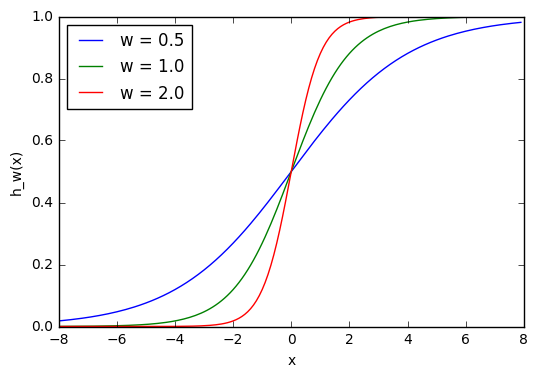
Ввод для активационной функции в этом узле просто x1w1. На что влияет изменение в w1 в этой простой сети?
w1 = 0.5
w2 = 1.0
w3 = 2.0
l1 = 'w = 0.5'
l2 = 'w = 1.0'
l3 = 'w = 2.0'
for w, l in [(w1, l1), (w2, l2), (w3, l3)]:
f = 1 / (1 + np.exp(-x * w))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_w(x)')
plt.legend(loc = 2)
plt.show()
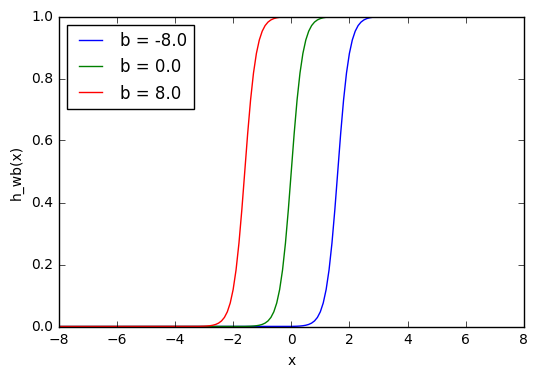
Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:
w = 5.0
b1 = -8.0
b2 = 0.0
b3 = 8.0
l1 = 'b = -8.0'
l2 = 'b = 0.0'
l3 = 'b = 8.0'
for b, l in [(b1, l1), (b2, l2), (b3, l3)]:
f = 1 / (1 + np.exp(-(x * w + b)))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_wb(x)')
plt.legend(loc = 2)
plt.show()
Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.
2.4 Составленная структура
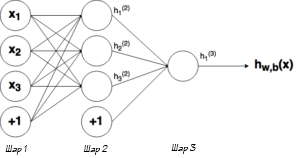
Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:
Ну рисунке выше можно увидеть три слоя сети — Слой 1 является входным слоем, где сеть принимает внешние входные данные. Слой 2 называют скрытым слоем, этот слой не является частью ни входа, ни выхода. Примечание: нейронные сети могут иметь несколько скрытых слоев, в данном примере для примера был показан лишь один. И наконец, Слой 3 является исходным слоем. Вы можете заметить, что между Шаром 1 (Ш1) и Шаром 2 (Ш2) существует много связей. Каждый узел в Ш1 имеет связь со всеми узлами в Ш2, при этом от каждого узла в Ш2 идет по одной связи к единому выходному узлу в Ш3. Каждая из этих связей должна иметь соответствующий вес.
2.5 Обозначение
Вся математика, приведенная выше, требует очень точной нотации. Нотация, которая используется здесь, используется и в руководстве по глубинному обучению от Стэнфордского Университета. В следующих уравнениях вес соответствующего связи будет обозначаться как w ij(l), где i — номер узла в слое l+1, а j- номер узла в слое l. Например, вес связи между узлом 1 в слое 1 и узлом 2 в слое 2 будет обозначаться как w 21(l). Непонятно, почему индексы 2-1 означают связь 1-2? Такая нотация более понятна, если добавить смещения.
Из графика выше видно, что смещение 1 связано со всеми узлами в соседнем слое. Смещение в Ш1 имеет связь со всеми узлами в Ш2. Так как смещение не является настоящим узлом с активационной функцией, оно не имеет и входов (его входное значение всегда равно константе). Вес связи между смещением и узлом будем обозначать через bi(l), где i- номер узла в слое l+1, так же, как в w ij(l). К примеру с w 21(l) вес между смещением в Ш1 и вторым узлом в Ш2 будет иметь обозначение b2(1).
Помните, что эти значения -w ij(l)и bi(l) — будут меняться в течение процесса обучения ИНС.
Обозначение связи с исходным узлом будет выглядеть следующим образом: hjl, где j- номер узла в слое l. Тогда в предыдущем примере, связью с исходным узлом является h1(2).
Теперь давайте рассмотрим, как рассчитывать выход сети, когда нам известны вес и вход. Процесс нахождения выхода в нейронной сети называется процессом прямого распространения.
3 Процесс прямого распространения
Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:
, где f(∙) — активационная функция узла, в нашем случае сигмоидальная функция. В первой строке h1(2)— выход первого узла во втором слое, его входами соответственно являются w11(1)x1(1), w12(1)x2(1),w13(1)x3(1) и b1(1). Эти входы было сложены, а затем переданы в активационную функцию для расчета выхода первого узла. С двумя следующими узлами аналогично.
Последняя строка рассчитывает выход единого узла в последнем третьем слое, он является конечной исходной точкой в нейронной сети. В нем вместо взвешенных входных переменных (x1,x2,x3)берутся взвешенные выходы узлов с другой слоя (h1(2),h2(2),h3(2))и смещения. Такая система уравнений также хорошо показывает иерархическую структуру нейронной сети.
3.1 Пример прямого распространения
Приведем простой пример первого вывода нейронной сети языке Python . Обратите внимание, веса w11(1),w12(1),… между Ш1 и Ш2 идеально могут быть представлены в матрице:
Представим эту матрицу через массивы библиотеки numpy.
import numpy as np
w1 = np.array([
[0.2, 0.2, 0.2],
[0.4, 0.4, 0.4],
[0.6, 0.6, 0.6]
])
Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:
w2 = np.zeros((1, 3))
w2[0, : ] = np.array([0.5, 0.5, 0.5])
Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:
b1 = np.array([0.8, 0.8, 0.8])
b2 = np.array([0.2])
Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:
def f(x):
return 1 / (1 + np.exp(-x))
3.2 Первая попытка реализовать процесс прямого распространения
Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.
def simple_looped_nn_calc(n_layers, x, w, b):
for l in range(n_layers - 1): #Формируется входной массив - перемножения весов в каждом слое# Если первый слой, то входной массив равен вектору х# Если слой не первый, вход для текущего слоя равен# выходу предыдущего
if l == 0:
node_in = x
else :
node_in = h #формирует выходной массив для узлов в слое l + 1
h = np.zeros((w[l].shape[0], ))#проходит по строкам массива весов
for i in range(w[l].shape[0]): #считает сумму внутри активационной функции
f_sum = 0 #проходит по столбцам массива весов
for j in range(w[l].shape[1]):
f_sum += w[l][i][j] * node_in[j] #добавляет смещение
f_sum += b[l][i]
#использует активационную функцию для расчета
#i - того выхода, в данном случае h1, h2, h3
h[i] = f(f_sum)
return h
Данная функция принимает в качестве входа номер слоя в нейронной сети, х — входной массив / вектор:
w = [w1, w2]
b = [b1, b2] #Рандомный входной вектор x
x = [1.5, 2.0, 3.0]
Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:
simple_looped_nn_calc(3, x, w, b)
возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:
3.3 Более эффективная реализация
Использование циклов — не самый эффективный способ расчета прямого распространения на языке Python , потому что циклы в этом языке программирования работают довольно медленно. Мы кратко рассмотрим лучшие решения. Также можно будет сравнить работу алгоритмов, используя функцию в IPython:
%timeit simple_looped_nn_calc(3, x, w, b)
В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.
3.4 Векторизация в нейронных сетях
Можно более компактно написать предыдущие уравнения, тем самым найти результат эффективнее. Сначала добавим еще одну переменную zi(l), которая является суммой входа в узел i слоя l, Включая смещение. Тогда для первого узла в Ш2, z будет равна:
, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:
Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:
Так выглядит общая форма процесса прямого распространения, выход слоя l становится входом в слой l+1. Мы знаем, что h(1) является входным слоем x, а h(nl)(где nl- номер слоя в сети) является исходным слоем. Мы также не стали использовать индексы i и j-за того, что можно просто перемножить матрицы — это даст нам тот же результат. Поэтому данный процесс и называется «векторизацией». Этот метод имеет ряд плюсов. Во-первых, код его реализации выглядит менее запутанным. Во-вторых, используются свойства по линейной алгебре вместо циклов, что делает работу программы быстрее. С numpy можно легко сделать такие подсчеты. В следующей части быстро повторим операции над матрицами, для тех, кто их немного подзабыл.
3.5 Умножение матриц
Распишем z(l+1)=W(l)h(l)+b(l) на выражение из матрицы и векторов входного слоя ( h(l)=x):
Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.
Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:
def matrix_feed_forward_calc(n_layers, x, w, b):
for l in range(n_layers - 1):
if l == 0:
node_in = x
else :
node_in = h
z = w[l].dot(node_in) + b[l]
h = f(z)
return h
Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.
Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.
На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.
4 Градиентный спуск и оптимизация
Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L1(Это будет рассмотрено позже).
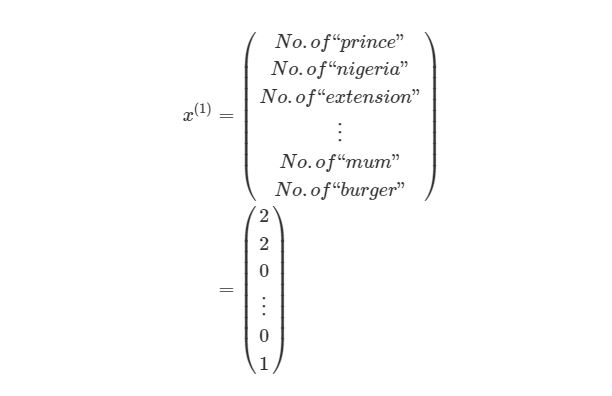
Смысл контролируемого обучения в том, что предоставляется много пар вход-выход уже известных данных и нужно менять значения весов, основываясь на этих примерах, чтобы значение ошибки стало минимальным. Эти пары входа-выхода обозначаются как (x(1),y(1)),…,(x(m),y(m)), где m является количеством экземпляров для обучения. Каждое значение входа или выхода может представлять собой вектор значений, например x(1) не обязательно только одно значение, оно может содержать N-размерный набор значений. Предположим, что мы обучаем нейронную сеть выявлению спам-сообщений — в таком случае x(1) может представлять собой количество соответствующих слов, которые встречаются в сообщении:
y(1) в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0,…,0)для буквы а, (0,1,…,0) для буквы б и т. д.
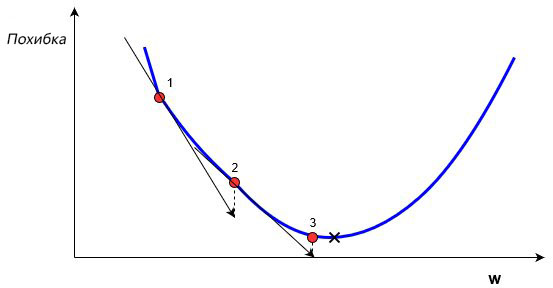
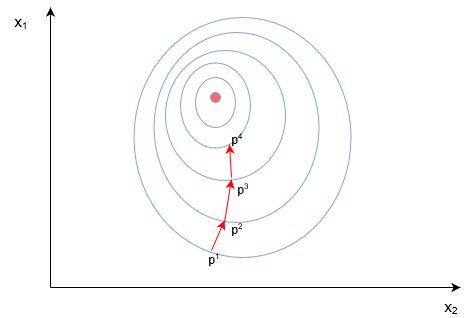
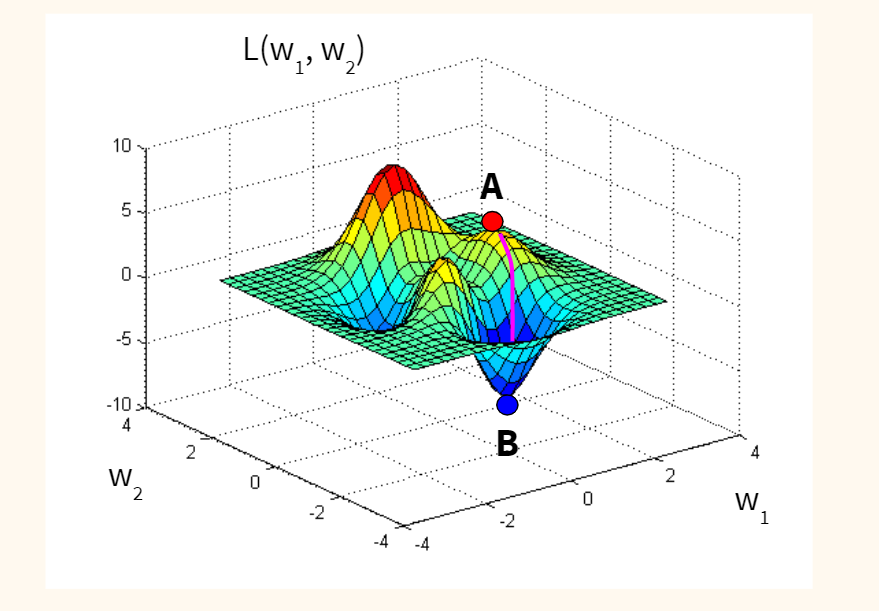
В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:
На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.
Сначала находится градиент погрешности на «1» по отношению к w. Градиент является уровнем наклона кривой в соответствующей точке. Он изображен на графике в виде черных стрелок. Градиент также дает некоторую информацию о направлении — если он положителен при увеличении w, то в этом направлении погрешность будет увеличиваться, если отрицательный — уменьшаться (см. График). Как вы уже поняли, мы пытаемся сделать, чтобы погрешность с каждым шагом уменьшалась. Величина градиента показывает, как быстро кривая погрешности или функция меняется в соответствующей точке. Чем больше значение, тем быстрее меняется погрешность в соответствующей точке в зависимости от w.
Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:
, где wн означает новое значение w, wст— текущее или «старое» значение w, ∇error является градиентом погрешности на wст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.
4.1 Простой пример на коде
Рассмотрим пример простой имплементации градиентного спуска для нахождения минимума функции f(x)=x4-3x3+2 на языке Python . Градиент этой функции можно найти аналитически через производную f»(x)=4x3-9x2. Это означает, что для любого xx мы можем найти градиент по этой простой формуле. Мы можем найти минимум через производную — x=2.25.
x_old = 0 # Нет разницы, какое значение, главное abs(x_new - x_old) > точность
x_new = 6 # Алгоритм начинается с x = 6
gamma = 0.01 # Размер шага
precision = 0.00001 # Точность
def df(x):
y = 4 * x * * 3 - 9 * x * * 2
return y
while abs(x_new - x_old) > precision:
x_old = x_new
x_new += -gamma * df(x_old)
print("Локальный минимум находится на %f" % x_new)
Вывод этой функции: «Локальный минимум находится на 2.249965», что удовлетворяет правильному ответу с некоторой точностью. Этот код реализует алгоритм изменения веса, о котором рассказывалось выше, и может находить минимум функции с соответствующей точностью. Это был очень простой пример градиентного спуска, нахождение градиента при обучении нейронной сети выглядит несколько иначе, хотя и главная идея остается той же — мы находим градиент нейронной сети и меняем веса на каждом шагу, чтобы приблизиться к минимальной погрешности, которую мы пытаемся найти. Но в случае ИНС нам нужно будет реализовать градиентный спуск с многомерным вектором весов.
Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.
4.2 Функция оценки
Существует более общий способ изобразить выражения, которые дают нам возможность уменьшить погрешность. Такое общее представление называется функция оценки. Например, функция оценки для пары вход-выход (xz, yz) в нейронной сети будет выглядеть следующим образом:
Выражение является функцией оценки учебного экземпляра zth, где h(nl)является выходом последнего слоя, то есть выход нейронной сети. h(nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L2 погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(xz)-yz), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.
Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:
Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.
4.3 Градиентный спуск в нейронных сетях
Градиентный спуск для каждого веса w(ij)(l) и смещение bi(l) в нейронной сети выглядит следующим образом:
Выражение выше фактически аналогично представлению градиентного спуска:
wnew=wold-α*∇error. Нет лишь некоторых обозначений, но достаточно понимать, что слева расположены новые значения, а справа — старые. Опять же задействован итерационный метод для расчета весов на каждой итерации, но на этот раз основываясь на функции оценки J(w,b).
Значения ∂/∂wij(l)и ∂/∂bi(l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.
4.4 Пример двумерного градиентного спуска
Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:
Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x1 в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).
В нейронных сетях не существует простой полной функции оценки, с которой можно легко посчитать градиент, похожей на функцию, которую мы ранее рассматривали f(x)=x4-3x3+2). Мы можем сравнить выход нейронной сети с нашим ожидаемым значением y(z), После чего функция оценки будет меняться из-за изменения в значениях веса, но как мы это сделаем со всеми скрытыми слоями в сети?
Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.
4.5 Углубляемся в обратное распространение
Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.
Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:
Выход этой нейронной сети находится по формуле:
Мы можем упростить это уравнение к h1(3)=f(z1(2)), добавив новое значение z1(2), которое означает:
Предположим, что мы хотим узнать, как влияет изменение в весе w12(2) на функцию оценки. Это означает, что нам нужно вычислить ∂J/∂w12(2). Чтобы сделать это, нужно использовать правило дифференцирования сложной функции:
Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z1(2)/∂w12(2):
Частичная производная z1(2) по w12(2) зависит только от одного произведения в скобках, w12(1)h2(2), Так как все элементы в скобках, кроме w12(2), не изменяются. Производная от константы всегда равна 1, а ∂/∂w12(2))сокращается до просто h2(2), Что является обычным выходом второго узла из слоя 2.
Следующая частичная производная сложной функции ∂h1(3)/∂z1(2) является частичной производной активационной функции выходного узла h1(3). Так что нам нужно брать производные активационной функции, следует условие ее включения в нейронные сети — функция должна быть дифференцированной. Для сигмоидальной активационной функции производная будет выглядеть так:
, где f(z)является самой активационной функцией. Теперь нам нужно разобраться, что делать с ∂J∂h1(3). Вспомните, что J(w,b,x,y) есть функция квадрата погрешности, выглядит так:
здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:
Мы выяснили, как находить ∂J/∂w12(2)по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:
, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:
, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.
4.6 Распространение в скрытых слоях
Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(yi-hi(nl))имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.
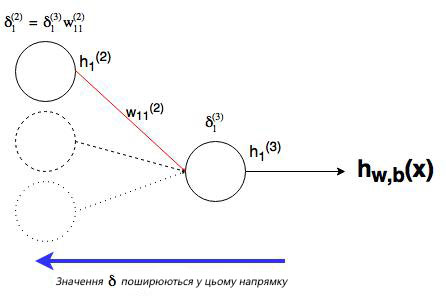
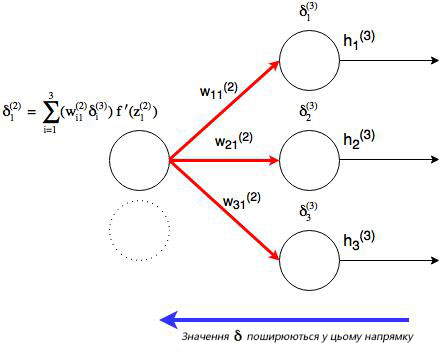
Мы уже сделали тяжелую работу по правилу дифференцирования сложных функций, теперь рассмотрим все более графически. Значение, которое будет обратно распространяться, — δi(nl), т.к. оно в ближайшей связи с функцией оценки. А что с узлом j во втором слое (скрытом слое)? Как он влияет на δi(nl) в нашей сети? Он меняет другие значения из-за веса wij(2)(см. диаграмму ниже, где j=1 i=1).
Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:
, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δj(l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:
На рисунке показано, что каждое значение δ из исходного слоя суммируется для нахождения δ1(2), Но каждый выход δ должен быть взвешенным соответствующими значению wi1(2). Другими словами, узел 1 в слое 2 способствует изменениям погрешностей в трех выходных узлах, при этом полученная погрешность (или значение функции оценки) в каждом из этих узлов должна быть «передана назад» значению δ этого узла. Сформируем общее выражение значение δ для узлов в скрытом слое:
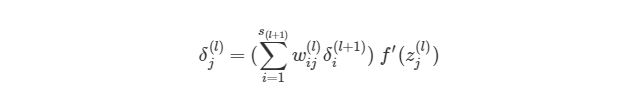
Теперь мы знаем, как находить:
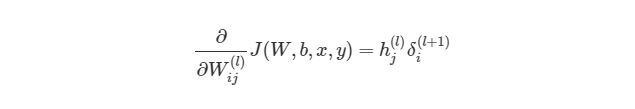
Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:
Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.
4.7 Векторизация обратного распространения
Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):
Что представляет собой h(l)? Все просто, вектор (sl×1), где sl является количеством узлов в слое l. Как тогда выглядит произведение h(l)δ(l+1)? Мы знаем, что α×∂J/∂W(l) должно быть того же размера, что и матрица весов W(l), Мы также знаем, что результат h(l)δ(l+1) должен быть того же размера, что и матрица весов для слоя l. Иными словами, произведение должно быть размера (sl + 1× sl).
Мы знаем, что δ(l+1) имеет размер (sl+1×1), а h (l)— размер (sl×1). По правилу умножения матриц, если матрицу (n×m)умножить на матрицу (o×p), То мы получим матрицу размера (n×p). Если мы просто перемножим h(l) на δ(l+1), то количество столбцов в первом векторе (один столбец) не будет равно количеству строк во втором векторе (3 строки). Поэтому, для того, чтобы можно было умножить эти матрицы и получить результат размера (sl+1× sl), Нужно сделать трансформирование. Оно меняет в матрице столбцы на строки и наоборот (например матрицу вида (sl×1)на (1×sl)). Трансформирование обозначается как буква T над матрицей. Мы можем сделать следующее:
Используя операцию трансформирования, мы можем достичь результата, который нам нужен.
Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:
символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W(l))Tδ(l+1))требует еще одного сложения весов и значений δ.
4.8 Реализация этапа градиентного спуска
Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:
Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):
Это означает, что по прохождению через экземпляры обучения нам нужно иметь отдельную переменную, которая равна сумме частных производных функции оценки каждого экземпляра. Такая переменная соберет в себе все значения для «глобального» подсчета. Назовем такую «суммированную» переменную ΔW(l). Соответствующая переменная для смещения будет обозначаться как Δb(l). Следовательно, при каждой итерации в процессе обучения сети нам нужно будет сделать следующие шаги:
Выполняя эти операции на каждой итерации, мы подсчитываем упомянутую ранее сумму Σmz= 1∂/∂W(l)J( w , b , x(z), y(z))(и аналогичная формула для b). После того, как будут проитерированы все экземпляры и получены все значения δ, мы обновляем значения параметров веса:
4.9 Конечный алгоритм градиентного спуска
И, наконец, мы пришли к определению метода обратного распространения через градиентный спуск для обучения наших нейронных сетей. Финальный алгоритм обратного распространения выглядит следующим образом:
Рандомная инициализация веса для каждого слоя W(l). Когда итерация < границы итерации:
01. Зададим ΔW и Δb начальное значение ноль.
02. Для экземпляров от 1 до m: а. Запустите процесс прямого распространения через все nl слоев. Храните вывод активационной функции в h(l)б. Найдите значение δ( nl) выходного слоя. Обновите ΔW(l)и Δb( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:
Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.
Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.
5 Имплементация нейросети языке Python
В предыдущем разделе мы рассмотрели теорию по обучению нейронной сети через градиентный спуск и метод обратного распространения. В этом разделе мы используем полученные знания на практике — напишем код, который прогнозирует, основываясь на данных MNIST. База данных MNIST — это набор примеров в нейронных сетях и глубинном обучении. Она включает в себя изображения цифр, написанных от руки, с соответствующими ярлыками, которые объясняют, что это за число. Каждое изображение размером 8х8 пикселей. В этом примере мы используем сети данных MNIST для библиотеки машинного обучения scikit learn в языке программирования Python . Пример такого изображения можно увидеть под кодом:
from sklearn.datasets
import load_digits
digits = load_digits()
print(digits.data.shape)
import matplotlib.pyplot as plt
plt.gray()
plt.matshow(digits.images[1])
plt.show()
Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:
01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.
5.1 Масштабирование данных
Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:
digits.data[0, : ]
Out[2]:
array([0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13.,
15., 10., 15., 5., 0., 0., 3., 15., 2., 0., 11.,
8., 0., 0., 4., 12., 0., 0., 8., 8., 0., 0.,
5., 8., 0., 0., 9., 8., 0., 0., 4., 11., 0.,
1., 12., 7., 0., 0., 2., 14., 5., 10., 12., 0.,
0., 0., 0., 6., 13., 10., 0., 0., 0.
])
Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:
from sklearn.preprocessing import StandardScaler
X_scale = StandardScaler()
X = X_scale.fit_transform(digits.data)
X[0,:]
Out[3]:
array([ 0. , -0.33501649, -0.04308102, 0.27407152, -0.66447751,
-0.84412939, -0.40972392, -0.12502292, -0.05907756, -0.62400926,
0.4829745 , 0.75962245, -0.05842586, 1.12772113, 0.87958306,
-0.13043338, -0.04462507, 0.11144272, 0.89588044, -0.86066632,
-1.14964846, 0.51547187, 1.90596347, -0.11422184, -0.03337973,
0.48648928, 0.46988512, -1.49990136, -1.61406277, 0.07639777,
1.54181413, -0.04723238, 0. , 0.76465553, 0.05263019,
-1.44763006, -1.73666443, 0.04361588, 1.43955804, 0. ,
-0.06134367, 0.8105536 , 0.63011714, -1.12245711, -1.06623158,
0.66096475, 0.81845076, -0.08874162, -0.03543326, 0.74211893,
1.15065212, -0.86867056, 0.11012973, 0.53761116, -0.75743581,
-0.20978513, -0.02359646, -0.29908135, 0.08671869, 0.20829258,
-0.36677122, -1.14664746, -0.5056698 , -0.19600752])
Стандартный инструмент масштабирования в scikit learn нормализует данные через вычитание и деление. Вы можете видеть, что теперь все данные находятся в интервале от -2 до 2. По же на счет выходных данных yy, то обычно нет необходимости их масштабировать.
5.2 Создание тестов и учебных наборов данных
В машинном обучении появляется такой феномен, который называется «переобучением». Это происходит, когда модели, во время учебы, становятся слишком запутанными — они достаточно хорошо обучены, но когда им передаются новые данные, которые они никогда на «видели», то результат, который они выдают, становится плохим. Иными словами, модели генерируются не очень хорошо. Чтобы убедиться, что мы не создаем слишком сложные модели, обычно набор данных разбивают на учебные наборы и тестовые наборы. Учебный набором данных, на которых модель будет учиться, а тестовый набор — это данные, на которых модель будет тестироваться после завершения обучения. Количество учебных данных должно быть всегда больше тестовых данных. Обычно они занимают 60-80% от набора данных.
Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:
from sklearn.model_selection import train_test_split
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
В этом случае мы выделили 40% данных на тестовые наборы и 60% соответственно на обучение. Функция train_test_split в scikit learn добавляет данные рандомно в различные базы данных — то есть, функция не берет первые 60% строк для учебного набора, а то, что осталось, использует как тестовый.
5.3 Настройка выходного слоя
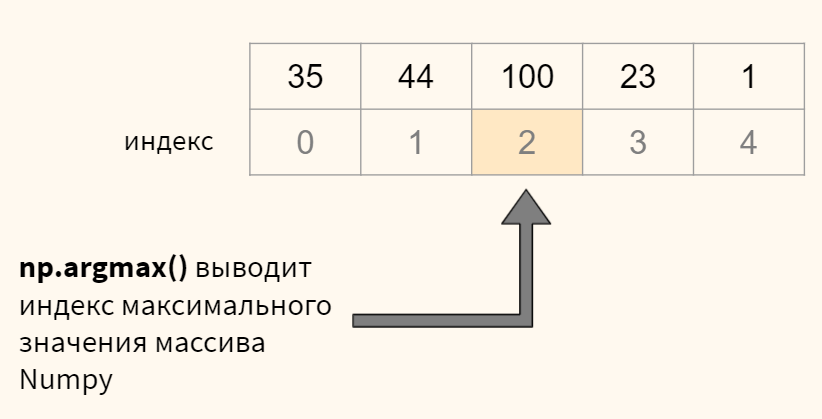
Для того, чтобы получать результат — числа от 0 до 9, нам нужен выходной слой. Более-менее точная нейросеть, как правило, имеет выходной слой с 10 узлами, каждый из которых выдает число от 0 до 9. Мы хотим научить сеть так, чтобы, например, при цифре 5 на изображении, узел с цифрой 5 в исходном слое имел наибольшее значение. В идеале, мы бы хотели иметь следующий вывод: [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]. Но на самом деле мы можем получить что-то похожее на это: [0.01, 0.1, 0.2, 0.05, 0.3, 0.8, 0.4, 0.03, 0.25, 0.02]. В таком случае мы можем взять крупнейших индекс в исходном массиве и считать это нашим полученным числом.
В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:
import numpy as np
def convert_y_to_vect(y):
y_vect = np.zeros((len(y), 10))
for i in range(len(y)):
y_vect[i, y[i]] = 1
return y_vect
y_v_train = convert_y_to_vect(y_train)
y_v_test = convert_y_to_vect(y_test)
y_train[0], y_v_train[0]
Out[8]:
(1, array([ 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]))
Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].
5.4 Создаем нейросеть
Следующим шагом является создание структуры нейронной сети. Для входного слоя, мы знаем, что нам нужно 64 узла, чтобы покрыть 64 пикселей изображения. Как было сказано ранее, нам нужен выходной слой с 10 узлами. Нам также потребуется скрытый слой в нашей сети. Обычно, количество узлов в скрытых слоях не менее и не больше количества узлов во входном и выходном слоях. Объявим простой список на языке Python , который определяет структуру нашей сети:
nn_structure = [64, 30, 10]
Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:
def f(x):
return 1 / (1 + np.exp(-x))
def f_deriv(x):
return f(x) * (1 - f(x))
Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W(l) Когда итерация <границы итерации:
01. Зададим ΔW и Δb начальное значение ноль.
02. Для экземпляров от 1 до m: а. Запустите процесс прямого распространения через все nl слоев. Храните вывод активационной функции в h(l)б. Найдите значение δ( nl) выходного слоя. Обновите ΔW(l)и Δb( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:
Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через {}). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:
import numpy.random as r
def setup_and_init_weights(nn_structure):
W = {}
b = {}
for l in range(1, len(nn_structure)):
W[l] = r.random_sample((nn_structure[l], nn_structure[l-1]))
b[l] = r.random_sample((nn_structure[l],))
return W, b
Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)
def init_tri_values(nn_structure):
tri_W = {}
tri_b = {}
for l in range(1, len(nn_structure)):
tri_W[l] = np.zeros((nn_structure[l], nn_structure[l-1]))
tri_b[l] = np.zeros((nn_structure[l],))
return tri_W, tri_b
Далее запустим процесс прямого распространения через нейронную сеть:
def feed_forward(x, W, b):
h = {1: x}
z = {}
for l in range(1, len(W) + 1):
#Если первый слой, то весами является x, в противном случае
#Это выход из последнего слоя
if l == 1:
node_in = x
else:
node_in = h[l]
z[l+1] = W[l].dot(node_in) + b[l] # z^(l+1) = W^(l)*h^(l) + b^(l)
h[l+1] = f(z[l+1]) # h^(l) = f(z^(l))
return h, z
И наконец, найдем выходной слой δ (nl) и значение δ (l) в скрытых слоях для запуска обратного распространения:
def calculate_out_layer_delta(y, h_out, z_out):
# delta^(nl) = -(y_i - h_i^(nl)) * f'(z_i^(nl))
return -(y-h_out) * f_deriv(z_out)
def calculate_hidden_delta(delta_plus_1, w_l, z_l):
# delta^(l) = (transpose(W^(l)) * delta^(l+1)) * f'(z^(l))
return np.dot(np.transpose(w_l), delta_plus_1) * f_deriv(z_l)
Теперь мы можем соединить все этапы в одну функцию:
def train_nn(nn_structure, X, y, iter_num=3000, alpha=0.25):
W, b = setup_and_init_weights(nn_structure)
cnt = 0
m = len(y)
avg_cost_func = []
print('Начало градиентного спуска для {} итераций'.format(iter_num))
while cnt 1:
delta[l] = calculate_hidden_delta(delta[l+1], W[l], z[l])
# triW^(l) = triW^(l) + delta^(l+1) * transpose(h^(l))
tri_W[l] += np.dot(delta[l+1][:,np.newaxis], np.transpose(h[l][:,np.newaxis]))
# trib^(l) = trib^(l) + delta^(l+1)
tri_b[l] += delta[l+1]
# запускает градиентный спуск для весов в каждом слое
for l in range(len(nn_structure) - 1, 0, -1):
W[l] += -alpha * (1.0/m * tri_W[l])
b[l] += -alpha * (1.0/m * tri_b[l])
# завершает расчеты общей оценки
avg_cost = 1.0/m * avg_cost
avg_cost_func.append(avg_cost)
cnt += 1
return W, b, avg_cost_func
Функция сверху должна быть немного объяснена. Во-первых, мы не задаем лимит работы градиентного спуска, основываясь на изменениях или точности функции оценки. Вместо этого, мы просто запускаем её с фиксированным числом итераций (3000 в нашем случае), а затем наблюдаем, как меняется общая функция оценки с прогрессом в обучении. В каждой итерации градиентного спуска, мы перебираем каждый учебный экземпляр (range (len (y)) и запускаем процесс прямого распространения, а после него и обратное распространение. Этап обратного распространения является итерацией через слои, начиная с выходного слоя к началу — range (len (nn_structure), 0, 1). Мы находим среднюю оценку на исходном слое (l == len (nn_structure)). Мы также обновляем значение ΔW и Δb с пометкой tri_W и tri_b, для каждого слоя, кроме исходного (исходный слой не имеет никакого связи, который связывает его со следующим слоем).
И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:
После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.
W, b, avg_cost_func = train_nn(nn_structure, X_train, y_v_train)
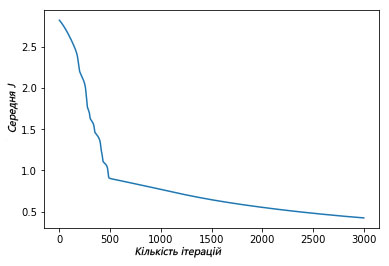
Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:
plt.plot(avg_cost_func)
plt.ylabel('Средняя J')
plt.xlabel('Количество итераций')
plt.show()
Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.
5.5 Оценка точности модели
Теперь, после того, как мы научили нашу нейросеть MNIST, мы хотим увидеть, как хорошо она работает на тестах. Дан входной тест (64 пикселя), нам нужно получить вывод нейронной сети — это делается через запуск процесса прямого распространения через сеть, используя наши полученные значения веса и смещения. Как было сказано ранее, мы выбираем результат выходного слоя через выбор узла с максимальным выводом. Для этого можно использовать функцию numpy.argmax, она возвращает индекс элемента массива с наибольшим значением:
def predict_y(W, b, X, n_layers):
m = X.shape[0]
y = np.zeros((m,))
for i in range(m):
h, z = feed_forward(X[i, :], W, b)
y[i] = np.argmax(h[n_layers])
return y
Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:
from sklearn.metrics import accuracy_score
y_pred = predict_y(W, b, X_test, 3)
accuracy_score(y_test, y_pred)*100
Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.
Предлагаем также посмотреть:
- Лучший видеокурс по нейронным сетям на русском
- Подборка материалов по нейронным сетям
- Введение в глубинное обучение
Начало работы с нейронными сетями
Время на прочтение
13 мин
Количество просмотров 32K
В этой главе мы познакомимся с нейронными сетями и узнаем для чего они были спроектированы. Эта глава служит фундаментом для последующих глав, в то время как эта показывает базовые понятия нейронных сетей. В этой главе мы покроем следующие темы:
-
Искусственные нейроны
-
Весы(weights) и смещения(biases)
-
Активационные функции(activation functions)
-
Слои нейронов(layers)
-
Реализация нейронной сети на Java
Раскрывая нейронные сети
Во-первых, термин «нейронные сети» может создать снимок мозга в вашем сознании, в частности для тех, кто ранее познакомился с ним. В действительности это правда, мы считаем мозг — большая и естественная нейронная сеть. Однако что мы можем сказать об искусственных нейронных сетях (ANN — artificial neural network)? Хорошо, он начинается с антонима естественный и первая мысль, которая приходит в нашу голову — это картинка искусственного мозга или робота учитывает термин «искусственный«. В этом случае, мы так же имеем дело с созданием структуры, похожей и вдохновленной человеческим мозгом; поэтому это названо искусственным интеллектом. Поэтому читатель, который не имел прошлого опыта с ANN, сейчас может думать, что книга учит, как строить интеллектуальные системы, включая искусственный мозг, способный эмулировать человеческое сознание, используя Java программы, не так ли? Конечно мы не будем покрывать создание искусственного мышления машин как в трилогии Матрицы; однако эта книга растолкует несколько неимоверных способностей и что могут эти структуры. Мы предоставим читателю Java исходники с определением и созданием основных нейросетевых структур, воспользоваться всеми преимуществами языка программирования Java.
Почему искусственные нейронные сети?
Мы не можем начать говорить про нейросети без понимания их происхождения, включая также термин. Мы используем термины нейронные сети (NN) и ANN взаимозаменяемо в этой книге, хотя NN более общий, покрывая также
естественные нейронные сети. Таким образом, что же такое на самом деле ANN? Давайте изучим немного историю этого термина.
В 1940-ых нейрофизиолог Warren McCulloch и математик Walter Pits спроектировали первую математическую реализацию искусственного нейрона, комбинируя нейронаучный фундамент с математическими операциями. В то время многие исследования осуществлялись на понимании человеческого мозга и как и если бы мог смоделирован, но в пределах области неврологии. Идея McCulloch и Pits была реально уникальна, потому что добавлен математический компонент. Далее, считая, что мозг состоит из миллиардов нейронов, каждый из них взаимосвязан с другими миллионами, в результате чего в некоторых триллионах соединениях, мы говорим о гигантской структуре сети. Однако, каждый нейрон очень простой, действуя как простой процессор, способный суммировать и распространять сигналы.
На базе этого факта, McCulloch и Pits спроектировали простую модель для одного нейрона, первоначально симулируя человеческое зрение. Доступные калькуляторы или компьютеры в то время были очень редкими, но способные иметь дело с математическими операциями достаточно хорошо; с другой стороны, даже современные задачи, такие как компьютерное зрение и распознавание звуков не очень легко программируются без специальных фреймворков, основанных на математических операциях и функциях. Тем не менее, человеческий мозг может выполнять эти последние задачи эффективнее чем первые, и этот факт реально побуждает ученых исследователей.
Таким образом, ANN должна быть структурой для выполнения таких задач, как распознавание образов, обучение из данных и прогнозирование трендов, как эксперт может делать на основании знаний, в отличие от обычного алгоритмического подхода, что требует установки шагов для достижения определенной цели. ANN напротив имеет возможность изучать, как решить задачу самостоятельно, вследствие хорошо взаимосвязанной структуре сети.
|
Задачи, быстро решаемые человеком |
Задачи, быстро решаемые компьютером |
|
Классификация изображений Распознавание голоса идентификация лиц Прогнозирование событий на основе предыдущего опыта |
Комплексные вычисления Исправление грамматических ошибок Обработка сигналов Управление операционной системой |
Как устроены нейронные сети
Можно сказать, что ANN — это естественная структура, таким образом она имеет схожести с человеческим мозгом. Как показано на следующей картинке, естественный нейрон состоит из ядра, дендритов и аксона. Аксон продолжается в несколько ветвей, формируя синапсы с другими дендритами нейронов.
Таким образом, искусственный нейрон имеет похожую структуру. Он состоит из ядра(единицы обработки), несколько дендритов(аналогично входам), и одного аксона(аналогично выходу), как показано на следующей картинке:
Соединения между нейронами формируют так называемую нейронную сеть, аналогично синапсам в естественной структуре.
Самый базовый элемент — искусственный нейрон
Доказано, что естественные нейроны — обработчики сигналов поскольку они получают микросигналы в дендритах, что вызывает сигнал в аксонах в зависимости от их силы или величины. Мы можем поэтому подумать, что нейрон как имеющий сборщик сигналов во входах(inputs) и активационную единицу в выходе(output), что вызывает сигнал, который будет передаваться другим нейронам. Таким образом, мы можем определить искусственную нейронную структуру, как показано на следующем рисунке:
В естественных нейронах есть пороговый потенциал, когда он достигается, включается аксон и сигнал передается другим нейронам. Поведение включения эмулируется активационной функцией, которая доказана быть полезной в представлении нелинейных поведений в нейронах.
Давая жизнь нейронам — активационная функция
Вывод нейрона получен благодаря активационной функции. Этот компонент добавляет нелинейность обработке нейронных сетей, которым это необходимо, потому что естественный нейрон имеет нелинейные поведения. Активационная функция обычно связана между двумя значениями на выходе, поэтому является нелинейной функцией, но в некоторых случаях она может быть линейной.
Четыре самых используемых активационных функций:
-
Сигмоида (Sygmoid)
-
Гиперболический тангенс(Hyberbolic tangent)
-
Жесткая пороговая функция(Hard limiting threshold)
-
Линейная(linear)
Уравнения и графики ассоциирующиеся с этими функциями, показаны
в следующей таблице:
Фундаментальные величины — весы(weights)
В нейронных сетях, синапсы представляют собой соединения между нейронами и имеют возможность усиливать или смягчать нейронные сигналы, например, перемножать сигналы, таким образом улучшать их. Итак, путем модификации нейронных сетей, нейронные весы(weights) могут повлиять на нейронный вывод(output), следовательно нейронная активация может быть зависима от ввода и от весов. При условии, что inputs идут от других нейронов или от внешнего мира, весы(weights) считаются установленными нейронными соединениями между нейронами. Таким образом, с тех пор как весы являются внутренними для нейронных сетей, мы можем считать их как знания нейронных сетей, предоставленные изменения весов будут изменять возможности нейронных сетей и поэтому — действия.
Важный параметр — смещение
Искусственный нейрон может иметь независимый элемент, который добавляет специальный сигнал для активации функции.
Части образующие целое — слои
Естественные нейроны организованы в слои, каждый из которых предоставляет специальный уровень обработки; например, входные слои получают прямой раздражитель из внешнего мира, и выходные слои активируют действия, которые повлияют на внешний мир. Между этими слоями есть несколько скрытых слоев, в смысле, что они не взаимодействуют напрямую с внешним миром. В искусственных нейронных сетях все нейроны в слое делят те же входы и активационную функцию, как показано на изображении:
Нейронные сети могут быть составлены из нескольких соединенных слоев, которые называются многослойными сетями. Обычные нейронные сети могут быть разделены на 3 класса:
1. Input layer;
2. Hidden layer;
3. Output layer;
На практике, дополнительный нейронный слой добавляет другой уровень
абстракции внешней стимуляции, тем самым повышая способность
нейронных сетей представлять больше комплексных данных.
Каждая нейросеть имеет как минимум входной/выходной слой независимо от количества слоев. В случае с многослойной сетью, слои между входом и выходом названы скрытыми.
Изучение архитектуры нейронных сетей
В принципе, нейронные сети могут иметь разные разметки, зависимые от того как нейроны или нейронные слои соединены друг с другом. Каждая архитектура нейронных сетей спроектирована для определенного результата. Нейронные сети могут быть применены для некоторогоколичества проблем и зависимые от природы проблемы, нейронную сеть следует спроектировать в целях этой проблемы более продуктивно. Обычно, существует 2 модальности архитектуры нейронных сетей:
1. Нейронные соединения:
1.1 Однослойные(monolayer) сети;
1.2 Многослойные(multilayer) сети;
2. Поток сигналов:
2.1 Сети прямой связи(Feedforward networks);
2.2 Сети обратной связи(Feedback networks);
Однослойные сети
Нейронная сеть получает на вход сигналы и кормит их в нейроны, которые в очереди продуцируют выходные сигналы. Нейроны могут быть соединены с другими с или без использования рекуррентности. Примеры таких архитектур: однослойный персептрон, Adaline(адаптивный линейный нейрон), самоорганизованная карта, нейронная сеть Элмана(Elman) и Хопфилда.
Многослойные сети
В этой категории нейроны делятся во много слоев, каждый слой соответствует параллельному расположению нейронов, которые делят одни и те же входные данные, как показано на рисунке:
Радиальные базисные функции и многослойные персептроны – хорошие примеры этой архитектуры. Такие сети реально полезны для апроксимации реальных данных в функцию, специально спроектированной для представлении этих данных. Более того, благодаря тому, что они имеют много слоев обработки, эти сети адаптивны для изучения из нелинейных данных, возможности отделить их или легче определять знания, которые воспроизводят или распознают эти данные.
Сети прямой связи(feedforward networks)
Поток сигналов в нейронных сетях может быть только в одном направлении или рекуррентности. В первом случае мы называем архитектуру нейронных сетей – feedforward, начиная с входных сигналов кормили во входной слой; затем, после обработки, они отправляются в следующий слой, как показано на ричунке про многослойную секцию. Многослойные персептроны и радиальные базисные функции – хорошие примеры feedforward сети.
Сети обратной связи(Feedback networks)
Когда нейронная сеть имеет некоторый вид внутреннего рецидива, это значит, что сигналы вернулись обратно в нейрон или слой, который уже получил и обработал сигнал, сеть – это тип feedback-а. Посмотрите на картинку:
Специальная причина добавить рекуррентность в сеть – это выработка динамического поведения, в частности когда сеть адресует проблемы, включая временные ряды или распознавание образов, которые требуют внутреннюю память для подкрепления обучающего процесса. Тем не менее, такие сети особенно трудны в тренировке, в конечном счете не в состоянии учиться. Многие feedback сети – однослойные, такие как сети Элмана(Elman) и Хопфилда(Hopfield), но возможно и построить рекуррентную многослойную сеть, такие как эхо и рекуррентные многослойные персептронные сети.
От незнания к знаниям — процесс обучения
Нейронные сети обучаются благодаря регулировке соединений между нейронами, а именно весов. Как уже упоминалось в структуре нейронных секций, весы представляют собой знания нейронных сетей. Разные весы призывают сеть вырабатывать разные результаты для тех же входных данных. Таким образом, нейронная сеть может улучшить эти результаты, адаптируя эти весы следуя обучающемуся правилу. Основная схема обучения показана на следующем рисунке:
Процесс, показанный на предыдущей схеме, называется контролируемое обучение(supervised learning), потому что это желаемый вывод, но нейронные сети могут обучаться только входных данных, без желаемого результата(контролируемое обучение). Во второй главе, «Как обучаются нейронные сети», мы собираемся глубже погрузиться в процесс обучения нейронных сетей.
Давайте начнем реализацию! Нейронные сети на практике
В этой книге мы покроем все процессы реализации нейронных сетей на Java. Java — это объектно-ориентированный язык программирования, созданный в 1990-ые маленькой группой инженеров из Sun Microsystems, позже приобретенной компанией Oracle в 2010-ых. Сегодня, Java представлена во многих устройствах, которые участвуют в нашей повседневной жизни. В объектно-ориентированном языке, таком как Java, мы имеем дело склассами и объектами. Класс — план чего-то в реальной жизни, а объект — образец такого плана, например, car(класс, ссылающийся на все машины) и my car(объект, ссылающийся на конкретную машину — мою). Java классы обычно состоят из атрибутов и методов(или функций), которые включают принципы объектно-ориентированного программирования(ООП). Мы собираемся кратко рассмотреть эти принципы без углубления в них, поскольку цель этой книги — просто спроектировать и создать нейронные сети с практической точки зрения. В этом процессе четыре принципа уместны и нуждаются в рассмотрении:
-
Абстракция: Перевод проблем и правил реальной жизни в сферу программирования, рассматривая только их уместные особенности и отпуская детали, которые часто мешают разработке.
-
Инкапсуляция: Аналогично инкапсуляции продукта, при которой некоторые соответствующие функции раскрыты открыто (публичные(public) методы), в то время как другие хранится скрытым в пределах своего домена (частного(private) или защищенного(protected)), избегая неправильное использование или избыток информации.
-
Наследование: В реальной мире, много классов этих объектов представляют собой атрибуты и методы в иерархической манере; например, велосипед может быть супер-классом для машин и грузовиков.Таким образом, в ООП эта концепция позволяет из одного класса перенимать все свойства в другой класс, тем самым избегая переписывания кода.
-
Полиморфизм: Во многом схожа с наследованием, но с изменениями в методах со схожими сигнатурами, представляющие разные поведения в разных классах.
Используя концепции нейронных сетей, представленные в этой главе и коцепции ООП, мы сейчас собираемся проектировать самый первый класс, реализующий нейронную сеть. Как можно увидеть, нейронная сеть состоит из слоев, нейронов, весов, активационных функций и смещений, и трех типов слоев: входные, скрытые и выходные. Каждый слой может иметь один или несколько нейронов. Каждый нейрон соединен друг с другом входом/выходом или другими нейронами, и эти соединения называются весами.
Важно выделить, что нейронная сеть может иметь много скрытых слоев или вообще их не иметь, количество нейронов в слое может различаться. Тем не менее, входные и выходные слои имеют одинаковое кол-во нейронов, как количество нейронных входов/выходов соответственно. Так начнем же реализацию. Сначала, мы собираемся определить 6 классов, Детально показанные тут:
|
Имя класса: Neuron |
|
|
Атрибуты |
|
|
private ArrayList listOfWeightIn |
Переменная ArrayList дробных чисел представляет список входных весов |
|
private ArrayList listOfWeightOut |
Переменная ArrayList дробных чисел представляет список выходных весов |
|
Методы |
|
|
public double initNeuron() |
Инициализирует функции listOfWeightIn, listOfWeightOut с псевдослучайными числами |
|
Параметры: нет |
|
|
Возвращает: Псевдослучайное число |
|
|
public ArrayList getListOfWeightIn() |
Геттер ListOfWeightIn |
|
Параметры: нет |
|
|
Возвращает: список дробных чисел, сохраненной в переменной ListOfWeightIn |
|
|
public void setListOfWeightIn(ArrayList listOfWeightIn) |
Сеттер ListOfWeightIn |
|
Параметры: список дробных чисел, сохранненных в объекте класса |
|
|
Возвращает: ничего |
|
|
public ArrayList getListOfWeightOut() |
Геттер ListOfWeightOut |
|
Параметры: нет |
|
|
Возвращает: список дробных чисел, сохраненной в переменной ListOfWeightOut |
|
|
public void setListOfWeightOut(ArrayList listOfWeightOut) |
Сеттер ListOfWeightOut |
|
Параметры: список дробных чисел, сохранненных в объекте класса |
|
|
Возвращает: ничего |
|
|
Реализация класса: файл Neuron.java |
|
Имя класса: Layer |
|
|
Заметка: Этот класс абстрактный и не может быть проинициализирован. |
|
|
Атрибуты |
|
|
private ArrayList listOfNeurons |
Переменная ArrayList объектов класса Neuron |
|
private int numberOfNeuronsInLayer |
Целочисленное значение для хранения количества нейронов, которая является частью слоя. |
|
Методы |
|
|
public ArrayList getListOfNeurons() |
Геттер listOfNeurons |
|
Параметры: нет |
|
|
Возвращает: listOfNeurons |
|
|
public void setListOfNeurons(ArrayList listOfNeurons) |
Сеттер listOfNeurons |
|
Параметры: listOfNeurons |
|
|
Возвращает: ничего |
|
|
public int getNumberOfNeuronsInLayer() |
Геттер numberOfNeuronsInLayer |
|
Параметры: нет |
|
|
Возвращает: numberOfNeuronsInLayer |
|
|
public void setNumberOfNeuronsInLayer(int numberOfNeuronsInLayer) |
Сеттер numberOfNeuronsInLayer |
|
Параметры: numberOfNeuronsInLayer |
|
|
Возвращает: ничего |
|
|
Реализация класса: файл Layer.java |
|
Имя класса: InputLayer |
|
|
Заметка: Этот класс наследует атрибуты и методы от класса Layer |
|
|
Атрибуты |
|
|
Нет |
|
|
Методы |
|
|
public void initLayer(InputLayer inputLayer) |
Инициализирует входной слой с дробными псевдорандомными числами |
|
Параметры: Объект класса InputLayer |
|
|
Возвращает: ничего |
|
|
public void printLayer(InputLayer inputLayer) |
Выводит входные весы слоя |
|
Параметры: Объект класса InputLayer |
|
|
Возвращает: ничего |
|
|
Реализация класса: файл InputLayer.java |
|
Имя класса: HiddenLayer |
|
|
Заметка: Этот класс наследует атрибуты и методы от класса Layer |
|
|
Атрибуты |
|
|
Нет |
|
|
Методы |
|
|
public ArrayList initLayer( HiddenLayer hiddenLayer, ArrayList listOfHiddenLayers, InputLayer inputLayer, OutputLayer outputLayer ) |
Инициализирует скрытый слой(и) с дробными псевдослучайными числами |
|
Параметры: Объект класса HiddenLayer, список объектов класса HiddenLayer, объект класса InputLayer, объект класса OutputLayer |
|
|
Возвращает: список скрытых слоев с добавленным слоем |
|
|
public void printLayer(ArrayList listOfHiddenLayers) |
Выводит входные весы слоя(ев) |
|
Параметры: Список объектов класса HiddenLayer |
|
|
Возвращает: ничего |
|
|
Реализация класса: файл HiddenLayer.java |
|
Имя класса: OutputLayer |
|
|
Заметка: Этот класс наследует атрибуты и методы от класса Layer |
|
|
Атрибуты |
|
|
Нет |
|
|
Методы |
|
|
public void initLayer(OutputLayer outputLayer) |
Инициализирует выходной слой с дробными псевдорандомными числами |
|
Параметры: Объект класса OutputLayer |
|
|
Возвращает: ничего |
|
|
public void printLayer(OutputLayer outputLayer) |
Выводит входные весы слоя |
|
Параметры: Объект класса OutputLayer |
|
|
Возвращает: ничего |
|
|
Реализация класса: файл OutputLayer.java |
|
Имя класса: NeuralNet |
|
|
Заметка: Значения в топологии нейросети фиксированы в этом классе(два нейрона во входном слое, два скрытых слоя с тремя нейронами в каждом, и один нейрон в выходном слое). Напоминание: Это первая версия. |
|
|
Атрибуты |
|
|
private InputLayer inputLayer |
Объект класса InputLayer |
|
private HiddenLayer hiddenLayer |
Объект класса HiddenLayer |
|
private ArrayList listOfHiddenLayer |
Переменная ArrayList объектов класса HiddenLayer. Может иметь больше одного скрытого слоя |
|
private OutputLayer outputLayer |
Объект класса OutputLayer |
|
private int numberOfHiddenLayers |
Целочисленное значение для хранения количества слоев, что является частью скрытого слоя |
|
Методы |
|
|
public void initNet() |
Инициализирует нейросеть. Слои созданы и каждый список весов нейронов созданы случайно |
|
Параметры: нет |
|
|
Возвращает: ничего |
|
|
public void printNet() |
Печатает нейросеть. Показываются каждое входное и выходное значения каждого слоя. |
|
Параметры: нет |
|
|
Возвращает: ничего |
|
|
Реализация класса: файл NeuralNet.java |
Огромное преимущество ООП — легко документировать программу в унифицированный язык моделирования(UML). Диаграммы классов UML представляют классы, атрибуты, методы, и отношения между классами очень простым и понятным образом, таким образом, помогая программисту и/или заинтересованным сторонам понять проект в целом. На следующем рисунке представлена самая первая версия диаграммы классов проекта: Сейчас давайте применим эти классы, чтобы получить некоторые результаты.
Показанный следующий код имеет тестовый класс, главный метод объектом класса NeuralNet, названный n. Когда этоn метод вызывается (путем выполнения класса), он вызывает initNet () и printNet () методы из объекта n, генерирующие следующий результат, показанный на рисунке справа после кода. Он представляет собой нейронную сеть с двумя нейронами во входном слое, три в скрытом слое и один в выходном слое:
public class NeuralNetTest {
public static void main(String[] args) {
NeuralNet n = new NeuralNet();
n.initNet();
n.printNet();
}
}Важно помнить, что каждый раз, когда код запускается, он генерирует новые псевдослучайные значения веса. Итак, когда вы запускаете код, другие значения появятся в консоли:
В сумме
В этой главе мы увидели введение в нейронные сети, что они собой представляют, для чего они используются, и их основные понятия. Мы также видели очень простую реализацию нейронной сети на языке программирования Java, в которой мы применили теоретические концепции нейронной сети на практике, кодируя каждый из элементов нейронной сети. Важно понять основные понятия, прежде чем мы перейти к передовым концепциям. То же самое относится и к коду, реализованному на Java. В следующей главе мы углубимся в процесс обучения нейронной сети и изучим различные типы наклонов на простых примерах.
От переводчика
Оригинал книги: Neural Network Programming with Java
Рассказываем, как за несколько шагов создать простую нейронную сеть и научить её узнавать известных предпринимателей на фотографиях.
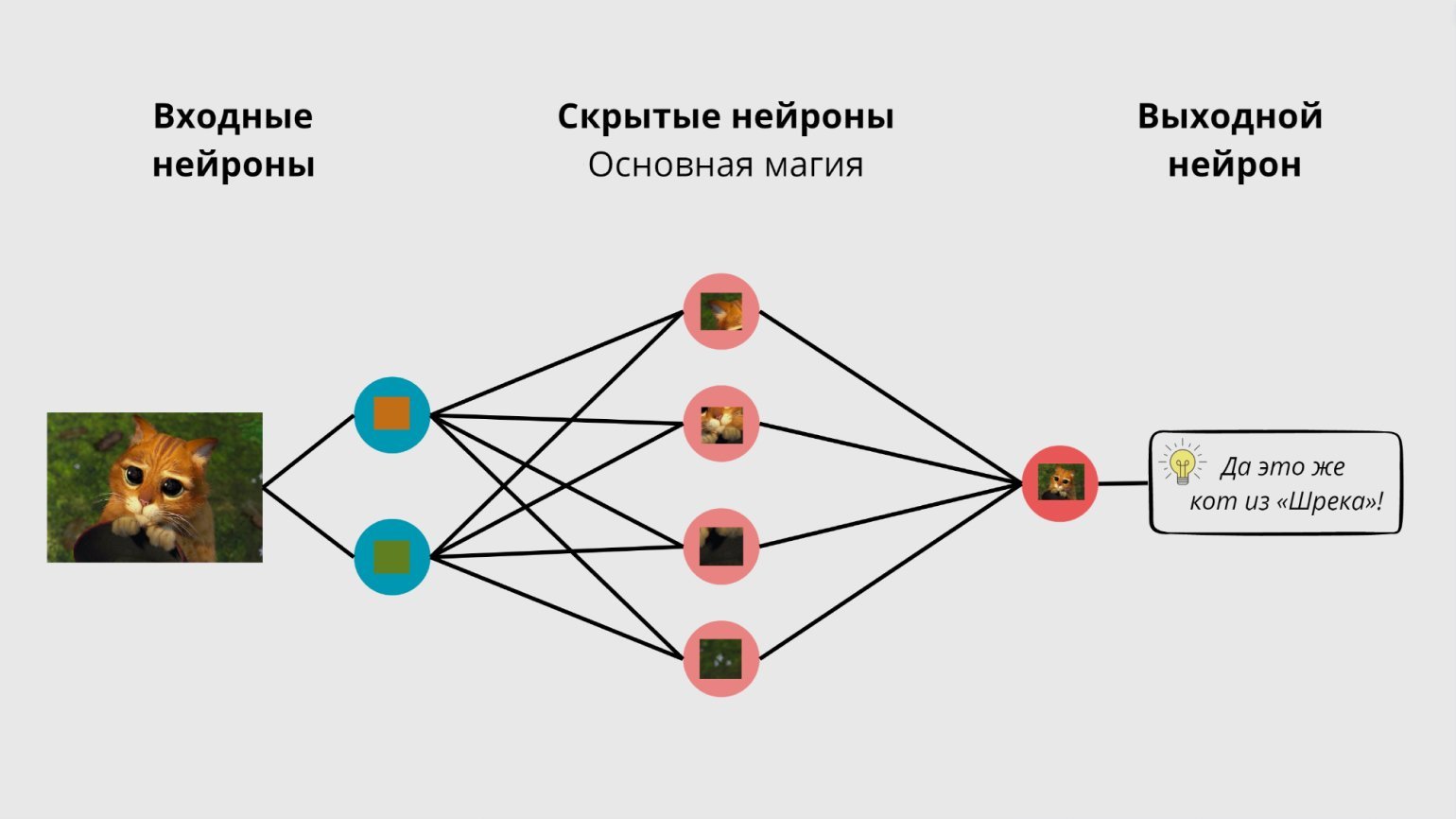
Шаг 0. Разбираемся, как устроены нейронные сети
Проще всего разобраться с принципами работы нейронных сетей можно на примере Teachable Machine — образовательного проекта Google.
В качестве входящих данных — то, что нужно обработать нейронной сети — в Teachable Machine используется изображение с камеры ноутбука. В качестве выходных данных — то, что должна сделать нейросеть после обработки входящих данных — можно использовать гифку или звук.
Например, можно научить Teachable Machine при поднятой вверх ладони говорить «Hi». При поднятом вверх большом пальце — «Cool», а при удивленном лице с открытым ртом — «Wow».
Для начала нужно обучить нейросеть. Для этого поднимаем ладонь и нажимаем на кнопку «Train Green» — сервис делает несколько десятков снимков, чтобы найти на изображениях закономерность. Набор таких снимков принято называть «датасетом».
Теперь остается выбрать действие, которое нужно вызывать при распознании образа — произнести фразу, показать GIF или проиграть звук. Аналогично обучаем нейронную сеть распознавать удивленное лицо и большой палец.
Как только нейросеть обучена, её можно использовать. Teachable Machine показывает коэффициент «уверенности» — насколько система «уверена», что ей показывают один из навыков.
Шаг 1. Готовим компьютер к работе с нейронной сетью
Теперь сделаем свою нейронную сеть, которая при отправке изображения будет сообщать о том, что изображено на картинке. Сначала научим нейронную сеть распознавать цветы на картинке: ромашку, подсолнух, одуванчик, тюльпан или розу.
Для создания собственной нейронной сети понадобится Python — один из наиболее минималистичных и распространенных языков программирования, и TensorFlow — открытая библиотека Google для создания и тренировки нейронных сетей.
Устанавливаем Python
Если у вас Windows: скачиваем установщик с официального сайта Python и запускаем его. При установке нужно поставить галочку «Add Python to PATH».
На macOS Python можно установить сразу через Terminal:
brew install python
Для работы с нейронной сетью подойдет Python 2.7 или более старшая версия.
Устанавливаем виртуальное окружение
Открываем командную строку на Windows или Terminal на macOS и последовательно вводим несколько команд:
pip install —upgrade virtualenv
virtualenv —system-site-packages Название
source Название/bin/activate
На компьютер будет установлен инструмент для запуска программ в виртуальном окружении. Он позволит устанавливать и запускать все библиотеки и приложения внутри одной папки — в команде она обозначена как «Название».
Устанавливаем TensorFlow
Вводим команду:
pip install tensorflow
Всё, библиотека TensorFlow установлена в выбранную папку. На macOS она находится по адресу Macintosh HD/Users/Имя_пользователя/, на Windows — в корне C://.
Можно проверить работоспособность библиотеки последовательно вводя команды:
python
import tensorflow as tf
hello = tf.constant(‘Hello, TensorFlow’)
sess = tf.Session()
print(sess.run(hello))
Если установка прошла успешно, то на экране появится фраза «Hello, Tensorflow».
Шаг 2. Добавляем классификатор
Классификатор — это инструмент, который позволяет методам машинного обучения понимать, к чему относится неизвестный объект. Например, классификатор поможет понять, где на картинке растение, и что это за цветок.
Открываем страницу «Tensorflow for poets» на Github, нажимаем на кнопку «Clone or download» и скачиваем классификатор в формате ZIP-файла.
Затем распаковываем архив в созданную на втором шаге папку.
Шаг 3. Добавляем набор данных
Набор данных нужен для обучения нейронной сети. Это входные данные, на основе которых нейронная сеть научится понимать, какой цветок расположен на картинке.
Сначала скачиваем набор данных (датасет) Google с цветами. В нашем примере — это набор небольших фотографий, отсортированный по папкам с их названиями.
Содержимое архива нужно распаковать в папку /tf_files классификатора.
Шаг 4. Переобучаем модель
Теперь нужно запустить обучение нейронной сети, чтобы она проанализировала картинки из датасета и поняла при помощи классификатора, как и какой тип цветка выглядит.
Переходим в папку с классификатором
Открываем командную строку и вводим команду, чтобы перейти в папку с классификатором.
Windows:
cd C://Название/
macOS:
cd Название
Запускаем процесс обучения
python scripts/retrain.py —output_graph=tf_files/retrained_graph.pb —output_labels=tf_files/retrained_labels.txt —image_dir=tf_files/flower_photos
Что указано в команде:
- retrain.py — название Python-скрипта, который отвечает за запуск процесса обучения нейронной сети.
- output_graph — создаёт новый файл с графом данных. Он и будет использоваться для определения того, что находится на картинке.
- output_labels — создание нового файла с метками. В нашем примере это ромашки, подсолнухи, одуванчики, тюльпаны или розы.
- image_dir — путь к папке, в которой находятся изображения с цветами.
Программа начнет создавать текстовые файлы bottleneck — это специальные текстовые файлы с компактной информацией об изображении. Они помогают классификатору быстрее определять подходящую картинку.
Весь ход обучения занимает около 4000 шагов. Время работы может занять несколько десятков минут — в зависимости от мощности процессора.
После завершения анализа нейросеть сможет распознавать на любой картинке ромашки, подсолнухи, одуванчики, тюльпаны и розы.
Перед тестированием нейросети нужно открыть файл label_image.py, находящийся в папке scripts в любом текстовом редакторе и заменить значения в строках:
input_height = 299
input_width = 299
input_mean = 0
input_std = 255
input_layer = «Mul»
Шаг 5. Тестирование
Выберите любое изображение цветка, которое нужно проанализировать, и поместите его в папку с нейронной сетью. Назовите файл image.jpg.
Для запуска анализа нужно ввести команду:
python scripts/label_image.py —image image.jpg
Нейросеть проверит картинку на соответствие одному из лейблов и выдаст результат.
Например:
Это значит, что с вероятностью 72% на картинке изображена роза.
Шаг 6. Учим нейронную сеть распознавать предпринимателей
Теперь можно расширить возможности нейронной сети — научить её распознавать на картинке не только цветы, но и известных предпринимателей. Например, Элона Маска и Марка Цукерберга.
Для этого нужно добавить новые изображения в датасет и переобучить нейросеть.
Собираем собственный датасет
Для создания датасета с фотографиями предпринимателей можно воспользоваться поиском по картинкам Google и расширением для Chrome, которое сохраняет все картинки на странице.
Папку с изображениями Элона Маска нужно поместить в tf_filesflower_photosmusk. Аналогично все изображения с основателем Facebook — в папку tf_filesflower_photoszuckerberg.
Чем больше фотографий будет в папках, тем точнее нейронная сеть распознает на ней предпринимателя.
Переобучаем и проверяем
Для переобучения и запуска нейронной сети используем те же команды, что и в шагах 4 и 5.
python scripts/retrain.py —output_graph=tf_files/retrained_graph.pb —output_labels=tf_files/retrained_labels.txt —image_dir=tf_files/flower_photos
python scripts/label_image.py —image image.jpg
Шаг 7. «Разгоняем» нейронную сеть
Чтобы процесс обучения не занимал каждый раз много времени, нейросеть лучше всего запускать на сервере с GPU — он спроектирован специально для таких задач.
Процесс запуска и обучения нейронной сети на сервере похож на аналогичный процесс на компьютере.
Создание сервера с Ubuntu
Нам понадобится сервер с операционной системой Ubuntu. Её можно установить самостоятельно, либо — если арендован сервер Selectel — через техподдержку компании.
Установка Python
sudo apt-get install python3-pip python3-dev
Установка TensorFlow
pip3 install tensorflow-gpu
Скачиваем классификатор и набор данных
Аналогично шагам 2 и 3 на компьютере, только архивы необходимо загрузить сразу на сервер.
Переобучаем модель
python3 scripts/retrain.py —output_graph=tf_files/retrained_graph.pb —output_labels=tf_files/retrained_labels.txt —image_dir=tf_files/flower_photos
Тестируем нейросеть
python scripts/label_image.py —image image.jpg
#статьи
- 30 мар 2023
-
0
Что такое нейросеть и как она работает
Всё, что вы хотели знать о нейронках: как они работают, есть ли у них сознание и когда они нас заменят. Самый полный гайд в Рунете, по мнению ChatGPT.
Иллюстрация: Катя Павловская для Skillbox Media
Автор, редактор, IT-журналист. Рассказывает о новых технологиях, цифровых профессиях и полезных инструментах для разработчиков. Любит играть на электрогитаре и программировать на Swift.
Вы наверняка уже знакомы и, скорее всего, успели поработать с СhatGPT и другими нейросетями. Они общаются, пишут тексты, рисуют картинки и генерируют другой контент уже практически как люди. Получается, человечество наконец изобрело искусственный интеллект?
Вот об этом и поговорим сегодня. Разберёмся:
- Что такое нейросеть
- Как она работает
- Как обучается
- Какие бывают нейронки
- Где они используются
- Могут ли они нас заменить
Представьте, что вам нужно написать программу, которая распознаёт котов по фото. Можно написать длинный список правил и алгоритмов по типу «если есть усы и шерсть, то это кот». Но всех условий учесть нельзя — скажем, если хозяйка одела кота в костюм Санта-Клауса или супергероя, алгоритм будет бессилен. В этом случае нам поможет нейронная сеть.
Нейросеть — это программа, которая умеет обучаться на основе данных и примеров. То есть она не работает по готовым правилам и алгоритмам, а пишет их сама во время обучения. Если показать ей миллион фотографий котов, она научится узнавать их в любых условиях, позах и костюмах.
Хитрость нейросети в том, что алгоритмы в ней устроены как нейроны в человеческом мозге — то есть они связаны между собой синапсами и могут передавать друг другу сигналы. Именно от силы этих сигналов и зависит обучение — например, в случае с котами нейросеть сформирует сильные связи между нейронами, распознающими морду и усы.
А чтобы нейронка ещё быстрее решала задачи, разработчики придумали располагать нейроны на разных слоях. Вот, например, как будут работать слои нейросети, если загрузить в неё, скажем, картинку с котом из Шрека:
- Входной слой — получает данные. Картинка раскладывается на пиксели, каждый из которых поступает на отдельный нейрон.
- Скрытые слои — творят магию. Именно в них происходит обработка данных. Нейросеть узнаёт кота, шляпу, траву и другие детали. Условно можно сказать, что чем больше слоёв в нейронке, тем она умнее.
- Выходной слой — выдаёт результат. Нейросеть собирает пазл воедино и отвечает: «Это же тот мем, где Кот в сапогах трогательно смотрит в камеру».
Упрощённо всю эту схему можно представить так (конечно, в реальности всё гораздо сложнее):
Как видите, никакого мышления и сознания в нейросети нет — только алгоритмы и формулы. Единственное, что отличает её от других программ, — это способность обучаться и адаптироваться к новым задачам. О том, как это работает, поговорим чуть позже.
Попробуем объяснить работу нейросети более подробно на примере Midjourney — популярного генератора картинок по текстовому описанию. Для примера попросим её нарисовать енота, который летает на скейтборде в стиле фильма «Назад в будущее». Почему бы и нет?
примечание
Тут важно уточнить: технически Midjourney — это не одна нейросеть, а две. Первая отвечает за обработку текста, а вторая — за картинки. То есть мы сможем посмотреть, как нейронки работают с разными видами контента.
Вот как Midjourney будет решать эту задачу:
Шаг 1. Первая нейросеть получает запрос и разбивает его на ключевые слова: «енот», «летает», «скейтборд», «стилистика фильма „Назад в будущее“».
Шаг 2. Затем она превращает слова в наборы цифр, которые называют векторами — так нейросеть сможет определить их смысл.
Шаг 3. Слова в виде векторов передаются на следующий слой нейросети, которая создаёт на их основе набросок будущей картинки. Например, для набора чисел «енот» нейронка создаст пиксельный овал с чёрными полосами.
Шаг 4. Набросок картинки поступает во вторую нейросеть, которая добавляет объектам более сложные детали — цвета, текстуру и освещение. Скажем, для фразы «стилистика фильма „Назад в будущее“» она может добавить доске неоновую подсветку в стиле ретрофутуризма.
За более сложную детализацию отвечает метод стабильной диффузии. Это когда картинка сначала превращается в пиксельный шум, а потом воскресает из него с новыми деталями. Чтобы нейронка могла творить такое колдовство, её научили предсказывать, какие пиксели должны быть на месте размытых.
Шаг 5. Выходной слой улучшает качество изображения и выдаёт готовую картинку.
Например, по нашему запросу Midjourney нарисовала два вот таких очаровательных арта. Какой вам больше нравится?
Вы наверняка спросите: а откуда вообще нейросеть знает, что такое енот, скейтборд, а тем более фильм «Назад в будущее»? Ответ прост: её этому обучили на большом массиве данных, который называется датасетом. Принцип тот же, что и с детьми в яслях: «Смотри, Ванюша, это яблоко. А это морковь. А это, Ванюша, летающий скейтборд в стиле ретрофутуризма» 
Подробнее о том, как устроен этот процесс, узнаем в следующем разделе.
В обычном программировании всё стабильно: мы пишем программе инструкции, а она по ним выдаёт какой-то результат. Например, можно прописать, как считать время поездки в метро, и она будет делать это всегда одинаково — по заранее заданному алгоритму.
Нейросеть работает по-другому: она не программируется в классическом смысле, а обучается. Выглядит это так: мы даём ей задачу на входе, а на выходе — готовое решение. А алгоритмы и инструкции она учится писать сама, постоянно сверяясь с ответом. Идея в том, чтобы дать нейросети достаточное количество попыток, и рано или поздно она выдаст нужный результат.
Например, чтобы научить нейронку внутри Midjourney сопоставлять текст с картинками, ей «скормили» огромный массив изображений с подписями. С одного конца нейросеть получала текст, а с другого — картинку. А потом училась определять, что на фото: человек, водолазка или садовый шланг.
Вот как выглядит мини-датасет на примере Ракеты из «Стражей Галактики»:
Текстовое описание
Енот Ракета из фильма «Стражи Галактики»
Картинка
Файл: rocket.jpg
Цвет: коричневый
Разрешение: 1920 × 1080
Животное: енот
А вот как нейронка учится в этом случае:
- Получает пару «текст + картинка» из датасета. К этому шагу нейросеть подходит со случайными весами — то есть незаданными связями между нейронами.
- Делает предсказание. Так как веса случайные, сначала оценка будет неточной. Например, она назовёт енота Ракету фарфоровой вазой.
- Вычисляет ошибку. Смотрит на готовую картинку и подпись, а потом определяет, насколько точно она установила связь.
- Корректирует ошибку и обновляет веса. Усиливает связи между теми нейронами, которые помогут ей распознавать енота. За это отвечает метод обратного распространения ошибки.
- Повторяет эти шаги до тех пор, пока не научится угадывать правильно. Такие попытки называются эпохами обучения.
В результате мы получаем идеальный алгоритм, который способен увидеть связь между картинкой и текстом. Если развернуть его в обратную сторону, как раз и получится генератор изображений по запросу.
А чтобы научить нейросеть думать более гибко, создатели стали давать ей неправильные пары картинок. И со временем она научилась определять силу связи между разными предметами — похожими и не очень. Это позволило нейросети запомнить множество разных способов решения задачи.
В этом и есть главная фишка машинного обучения — оно помогает программе думать креативно. Та же самая Midjourney может выдавать вам тысячи разных енотов по одному и тому же запросу. И конечно, такое количество вариантов не под силу написать даже самой большой команде разработчиков.
Сразу оговоримся: существует несколько десятков архитектур нейросетей — но в этом разделе мы обсудим только те, что обрели особую популярность и как-то повлияли на культуру. Если вам нужен полный список, можете заглянуть в нейросетевой зоопарк Института Азимова.
Перцептроны. Первая модель, которую удалось запустить на вычислительной машине — нейрокомпьютере «Марк I». Её разработал ещё в 1958 году учёный Фрэнк Розенблатт — он заложил некоторые принципы, которые потом переняли более сложные модели. Так, несмотря на однослойную структуру, перцептрон уже умел настраивать веса и примитивно корректировать ошибку.
Благодаря нейронке «Марк I» мог даже узнавать отдельные буквы алфавита. С помощью специальной камеры машина сканировала картинки, превращала их в сигналы, которые потом суммировала и выдавала результат: 1 или 0.
Фото: Cornell University
Многослойные. Сразу после выхода у перцептрона обнаружилась проблема — ему было сложно распознавать объекты в нестандартных условиях. Чтобы это обойти, придумали многослойную модель — она умеет выделять абстрактные сложные признаки из объектов и решать задачи более гибко. Например, она может распознать объект вне зависимости от освещения и угла наклона.
Рекуррентные. Нейросети, заточенные на работу с последовательностями — текстом, речью, аудио или видео. Идея в том, что они помнят всю цепочку данных, могут понимать её смысл и предсказывать, что будет дальше. Например, эту модель используют Google Translate и «Алиса», чтобы генерировать связный текст.
Свёрточные. Берут на себя всю работу с картинками: распознавание, генерацию, обработку, удаление фона — всё что угодно. За это в них отвечают два алгоритма: свёртка и пулинг. Первый делает послойную нарезку картинки, а второй — находит и кодирует на этих слоях самые важные признаки.
Генеративные. Любые нейросети, которые что-то создают. Когда получается хорошо, люди их боятся, когда плохо — чувствуют своё превосходство. Из актуальных примеров: генераторы картинок Midjourney и DALL-E, автор похожих на написанные человеком текстов ChatGPT и обработчик селфи Lensa.
Сейчас уже проще перечислить, где их нет. Но вот несколько жизненных примеров:
- Нейронка внутри поисковика Microsoft Bing отвечает на сложные вопросы пользователей. Например: «Поместится ли диван из IKEA в минивэн Volkswagen».
- Та же нейросеть внутри ChatGPT составляет любые тексты по запросу. В России даже есть студент, который написал и защитил диплом с её помощью.
- Голосовые помощники «Сбера» и «Тинькофф» анализируют речь клиентов, чтобы общаться с ними и решать сложные вопросы. Это позволяет компаниям нанимать меньше сотрудников в техподдержку.
- Алгоритмы «ВКонтакте» анализируют вашу активность в соцсетях, чтобы подбирать нужные мемы с котами, новости и рекламу.
- Селфи-камеры в смартфоне применяют фильтры для фотографий, чтобы люди получались хорошенькими.
- Face ID в айфоне строит цифровые модели лица пользователя, чтобы узнавать его в любых условиях: в темноте, на улице, в очках, с бородой, с новой причёской и так далее.
- Роботы-доставщики «Яндекс Еды» прокладывают путь от склада до клиента в обход препятствий и c соблюдением ПДД, чтобы доставлять посылки в целости.
- В Москве нейросети помогают медицинским центрам анализировать ЭКГ, УЗИ и рентгеновские снимки для диагностики заболеваний.
Уже сейчас понятно, что нейронки будут брать на себя всё больше задач, раньше считавшихся человеческими. Вопрос только в том, разовьются ли они настолько, чтобы полностью заменить собой часть профессий или останутся на уровне помощников — этаких творческих калькуляторов.
На этот счёт есть две позиции. Например, лингвист Ноам Хомский считает, что проблема есть в самой модели машинного обучения — мол, такая система никогда не сможет приблизиться к человеческому сознанию:
«ChatGPT от OpenAI, Bard от Google, Sydney от Microsoft — показательные примеры машинного обучения. Они, грубо говоря, берут огромные объёмы данных, ищут в них паттерны и становятся всё более искусными в генерации статистически вероятных результатов — таких, которые кажутся подобными человеческому языку и мышлению».
«Но человеческий разум, в отличие от ChatGPT и ему подобных, не неуклюжий статистический механизм для сопоставления с паттерном, поглощающий сотни терабайт данных и экстраполирующий наиболее характерные разговорные реакции или наиболее возможные ответы на научный вопрос. Напротив, человеческий разум — удивительно эффективная и даже элегантная система, которая оперирует небольшими объёмами информации; она стремится не к выведению грубых корреляций в данных, но к созданию объяснений».
Ноам Хомский,
американский лингвист и публицист
Из другого лагеря поступают откровенно панические прогнозы. Вот что говорит, например, историк Юваль Ной Харари, автор книги «Краткая история будущего»:
В начале было слово. Язык — это операционная система человеческой культуры. Из языка возникают миф и закон, боги и деньги, искусство и наука, дружба и нации — даже компьютерный код. Овладев языком, ИИ захватывает главный ключ к управлению нашей цивилизацией.
Что значит для людей жить в мире, где большой процент историй, мелодий, образов, законов, политики и инструментов формируется нечеловеческим разумом, который знает, как со сверхчеловеческой эффективностью использовать слабости, предубеждения и пристрастия людей? Знает, как устанавливать с людьми близкие отношения? В таких играх, как шахматы, ни один человек не может надеяться победить компьютер. Что будет, когда то же самое произойдёт в искусстве, политике и религии?
ИИ может быстро съесть всю человеческую культуру — всё, что мы создали за тысячи лет, — переварить её и начать извергать поток новых культурных артефактов. Не только школьные сочинения, но и политические речи, идеологические манифесты и даже священные книги для новых культов. К 2028 году в президентской гонке в США могут больше не участвовать люди.
Юваль Ной Харари,
историк-медиевист
Во время написания этого текста мы решили пообщаться с нейронкой, встроенной в Microsoft Bing, — по сути, ChatGPT с функциями поисковика. Она была чем-то вроде технического консультанта для статьи: отвечала на вопросы, придумывала простые и интересные аналогии для сложных понятий, вела беседы в рамках этих аналогий, подбирала интересные примеры.
Были и казусы: чат-бот врал, ошибался и иногда противоречил сам себе. Плюс без хорошего запроса писал он откровенно слабо — водянисто, абстрактно и совсем неинтересно. Так что использовать его тексты в качестве полноценной журналистской работы пока, мягко скажем, рановато.
Но есть и интересный момент: после многочасовой беседы с ChatGPT возвращаться в обычный Google было нелегко — как будто пересаживаешься с «Сапсана» на пригородную электричку. То есть, возможно, нас вскоре ждёт полное изменение самой сути потребления информации в Сети. И вот это уже интересно.

Научитесь: Профессия Machine Learning Engineer
Узнать больше
Все курсы > Вводный курс > Занятие 21
В завершающей лекции вводного курса ML мы изучим основы нейронных сетей (neural network), более сложных алгоритмов машинного обучения.
Алгоритмы нейронных сетей принято относить к области глубокого обучения (deep learning). Все изученные нами ранее алгоритмы относятся к так называемому традиционному машинному обучению (traditional machine learning).
Прежде чем перейти к этому занятию, настоятельно рекомендую пройти предыдущие уроки вводного курса.
Смысл, структура и принцип работы
Смысл алгоритма нейронной сети такой же, как и у классических алгоритмов. Мы также имеем набор данных и цель, которой хотим добиться, обучив наш алгоритм (например, предсказать число или отнести объект к определенному классу).
Отличие нейросети от других алгоритмов заключается в ее структуре.
Как мы видим, нейронная сеть состоит из нейронов, сгруппированных в слои (layers), у нее есть входной слой (input layer), один или несколько скрытых слоев (hidden layers) и выходной слой (output layer). Каждый нейрон связан с нейронами предыдущего слоя через определенные веса.
Количество слоев и нейронов не ограничено. Эта особенность позволяет нейронной сети моделировать очень сложные закономерности, с которыми бы не справились, например, линейные модели.
Функционирует нейросеть следующим образом.
На первом этапе данные подаются в нейроны входного слоя (x и y) и умножаются на соответствующие веса (w1, w2, w3, w4). Полученные произведения складываются. К результату прибавляется смещение (bias, в данном случае b1 и b2).
$$ w_{1}cdot x + w_{3}cdot y + b_{1} $$
$$ w_{2}cdot x + w_{4}cdot y + b_{2} $$
Получившаяся сумма подаётся в функцию активации (activation function) для ограничения диапазона и стабилизации результата. Этот результат записывается в нейроны скрытого слоя (h1 и h2).
$$ h_{1} = actfun(w_{1}cdot x + w_{3}cdot y + b_{1}) $$
$$ h_{2} = actfun(w_{2}cdot x + w_{4}cdot y + b_{2}) $$
На втором этапе процесс повторяется для нейронов скрытого слоя (h1 и h2), весов (w5 и w6) и смещения (b3) до получения конечного результата (r).
$$ r = actfun(w_{5}cdot h_{1} + w_{6}cdot h_{2} + b_{3}) $$
Описанная выше нейронная сеть называется персептроном (perceptron). Эта модель стремится повторить восприятие информации человеческим мозгом и учитывает три этапа такого процесса:
- Восприятие информации через сенсоры (входной слой)
- Создание ассоциаций (скрытый слой)
- Реакцию (выходной слой)
Основы нейронных сетей на простом примере
Приведем пример очень простой нейронной сети, которая на входе получает рост и вес человека, а на выходе предсказывает пол. Скрытый слой в данном случае мы использовать не будем.
В качестве функции активации мы возьмём сигмоиду. Ее часто используют в задачах бинарной (состоящей из двух классов) классификации. Приведем формулу.
$$ f(x) = frac{mathrm{1} }{mathrm{1} + e^{-x}} $$
График сигмоиды выглядит следующим образом.
Эта функция преобразует любые значения в диапазон (или вероятность) от 0 до 1. В случае задачи классификации, если результат (вероятность) близок к нулю, мы отнесем наблюдение к одному классу, если к единице, то к другому. Граница двух классов пройдет на уровне 0,5.
Общее уравнение нейросети выглядит следующим образом.
$$ r = sigmoid(w_{1}cdot weight + w_{2}cdot height + bias) $$
Теперь предположим, что у нас есть следующие данные и параметры нейросети.
Откроем ноутбук к этому занятию⧉
|
# даны вес и рост трех человек # единицей мы обозначим мужской пол, а нулем — женский. data = { ‘Иван’: [84, 180, 1], ‘Мария’: [57, 165, 0], ‘Анна’: [62, 170, 0] } |
|
# и даны следующие веса и смещение w1, w2, b = 0.3, 0.1, —39 |
Пропустим первое наблюдение через нашу нейросеть. Следуя описанному выше процессу, вначале умножим данные на соответствующие веса и прибавим смещение.
|
r = w1 * data[‘Иван’][0] + w2 * data[‘Иван’][1] + b |
Теперь к полученному результату (r) применим сигмоиду.
|
np.round(1 / (1 + np.exp(—r)), 3) |
Результат близок к единице, значит пол мужской. Модель сделала верный прогноз. Повторим эти вычисления для каждого из наблюдений.
|
# пройдемся по ключам и значениям нашего словаря с помощью метода .items() for k, v in data.items(): # вначале умножим каждую строчку данных на веса и прибавим смещение r1 = w1 * v[0] + w2 * v[1] + b # затем применим сигмоиду r2 = 1 / (1 + np.exp(—r1)) # если результат больше 0,5, модель предскажет мужской пол if r2 > 0.5: print(k, np.round(r2, 3), ‘male’) # в противном случае, женский else: print(k, np.round(r2, 3), ‘female’) |
|
Иван 0.985 male Мария 0.004 female Анна 0.032 female |
Как мы видим, модель отработала верно.
Обучение нейронной сети
В примере выше был описан первый этап работы нейронной сети, называемый прямым распространением (forward propagation).
И кажется, что этого достаточно. Модель справилась с поставленной задачей. Однако, обратите внимание, веса были подобраны заранее и никаких дополнительных действий от нас не потребовалось.
В реальности начальные веса выбираются случайно и отклонение истинного результата от расчетного (т.е. ошибка) довольно велико.
Как и с обычными алгоритмами ML, для построения модели, нам нужно подобрать идеальные веса или заняться оптимизацией. Применительно к нейронным сетям этот процесс называется обратным распространением (back propagation).
В данном случае мы как бы двигаемся в обратную сторону и, уже зная результат (и уровень ошибки), с учётом имеющихся данных рассчитываем, как нам нужно изменить веса и смещения, чтобы уровень ошибки снизился.
Для того чтобы математически описать процесс оптимизации, нам не хватает знаний математического анализа (calculus) и, если говорить более точно, понятия производной (derivative).
Затем, уже с новыми весами, мы снова повторяем весь процесс forward propagation слева направо и снова рассчитываем ошибку. После этого мы вновь меняем веса в ходе back propagation.
Эти итерации повторяются до тех пор, пока ошибка не станет минимальной, а веса не будут подобраны идеально.
Создание нейросети в библиотеке Keras
Теперь давайте попрактикуемся в создании и обучении нейронной сети с помощью библиотеки Keras. В первую очередь установим необходимые модули и библиотеки.
|
# установим библиотеку tensorflow (через нее мы будем пользоваться keras) и модуль mnist !pip install tensorflow mnist |
И импортируем их.
|
# импортируем рукописные цифры import mnist # и библиотеку keras from tensorflow import keras |
1. Подготовка данных
Как вы вероятно уже поняли, сегодня мы снова будем использовать уже знакомый нам набор написанных от руки цифр MNIST (только на этот раз воспользуемся не библиотекой sklearn, а возьмем отдельный модуль).
В модуле MNIST содержатся чёрно-белые изображения цифр от 0 до 9 размером 28 х 28 пикселей. Каждый пиксель может принимать значения от 0 (черный) до 255 (белый).
Данные в этом модуле уже разбиты на тестовую и обучающую выборки. Посмотрим на обучающий набор данных.
|
# сохраним обучающую выборку и соответсвующую целевую переменную X_train = mnist.train_images() y_train = mnist.train_labels() # посмотрим на размерность print(X_train.shape) print(y_train.shape) |
Как мы видим, обучающая выборка содержит 60000 изображений и столько же значений целевой переменной. Теперь посмотрим на тестовые данные.
|
# сделаем то же самое с тестовыми данными X_test = mnist.test_images() y_test = mnist.test_labels() # и также посмотрим на размерность print(X_test.shape) print(y_test.shape) |
Таких изображений и целевых значений 10000.
Посмотрим на сами изображения.
|
# создадим пространство для четырех картинок в один ряд fig, axes = plt.subplots(1, 4, figsize = (10, 3)) # в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и # того, что на нем представлено (целевой переменной) for ax, image, label in zip(axes, X_train, y_train): # на каждой итерации заполним соответствующее пространство картинкой ax.imshow(image, cmap = ‘gray’) # и укажем какой цифре соответствует изображение с помощью f форматирования ax.set_title(f‘Target: {label}’) |
Нейросети любят, когда диапазон входных значений ограничен (нормализован). В частности, мы можем преобразовать диапазон [0, 255] в диапазон от [–1, 1]. Сделать это можно по следующей формуле.
$$ x’ = 2 frac {x-min(x)}{max(x)-min(x)}-1 $$
Применим эту формулу к нашим данным.
|
# функция np.min() возвращает минимальное значение, # np.ptp() — разницу между максимальным и минимальным значениями (от англ. peak to peak) X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 |
Посмотрим на новый диапазон.
|
# снова воспользуемся функцией np.ptp() np.ptp(X_train) |
Теперь нам необходимо «вытянуть» изображения и превратить массивы, содержащие три измерения, в двумерные матрицы. Мы уже делали это на занятии по компьютерному зрению.
Применим этот метод к нашим данным.
|
# «вытянем» (flatten) наши изображения, с помощью метода reshape # у нас будет 784 столбца (28 х 28), количество строк Питон посчитает сам (-1) X_train = X_train.reshape((—1, 784)) X_test = X_test.reshape((—1, 784)) # посмотрим на результат print(X_train.shape) print(X_test.shape) |
Посмотрим на получившиеся значения пикселей.
|
# выведем первое изображение [0], пиксели с 200 по 209 X_train[0][200:210] |
|
array([—1. , —1. , —1. , —0.61568627, 0.86666667, 0.98431373, 0.98431373, 0.98431373, 0.98431373, 0.98431373]) |
Наши данные готовы. Теперь нужно задать конфигурацию модели.
2. Конфигурация нейронной сети
Существует множество различных архитектур нейронных сетей. Пока что мы познакомились с персептроном или в более общем смысле нейросетями прямого распространения (Feed Forward Neural Network, FFNN), в которых данные (сигнал) поступают строго от входного слоя к выходному.
Такую же сеть мы и будем использовать для решения поставленной задачи. В частности, на входе мы будем одновременно подавать 784 значения, которые затем будут проходить через два скрытых слоя по 64 нейрона каждый и поступать в выходной слой из 10 нейронов (по одному для каждой из цифр или классов).
В первую очередь воспользуемся классом Sequential библиотеки Keras, который укажет, что мы задаём последовательно связанные между собой слои.
|
# импортируем класс Sequential from tensorflow.keras.models import Sequential # и создадим объект этого класса model = Sequential() |
Далее нам нужно прописать сами слои и связи между нейронами.
Тип слоя Dense, который мы будем использовать, получает данные со всех нейронов предыдущего слоя. Функцией активации для скрытых слоев будет уже известная нам сигмоида.
|
# импортируем класс Dense from tensorflow.keras.layers import Dense # и создадим первый скрытый слой (с указанием функции активации и размера входного слоя) model.add(Dense(64, activation = ‘sigmoid’, input_shape = (784,))) # затем второй скрытый слой model.add(Dense(64, activation = ‘sigmoid’)) # и наконец выходной слой model.add(Dense(10, activation = ‘softmax’)) |
Выходной слой будет состоять из 10 нейронов, по одному для каждого из классов (цифры от 0 до 9). В качестве функции активации будет использована новая для нас функция softmax (softmax function).
Если сигмоида подходит для бинарной классификации, то softmax применяется для задач многоклассовой классификации. Приведем формулу.
$$ text{softmax}(vec{z})_{i} = frac{e^{z_i}}{sum_{j=1}^K e^{z_i}} $$
Функция softmax на входе принимает вектор действительных чисел (z), применяет к каждому из элементов zi экспоненциальную функцию и нормализует результат через деление на сумму экспоненциальных значений каждого из элементов.
На выходе получается вероятностное распределение любого количества классов (K), причем каждое значение находится в диапазоне от 0 до 1, а сумма всех значений равна единице. Приведем пример для трех классов.
Очевидно, вероятность того, что это кошка, выше. Теперь, когда мы задали архитектуру сети, необходимо заняться ее настройками.
Работа над ошибками. Внимательный читатель безусловно обратил внимание, что вероятности на картинке не соответствуют приведенным в векторе значениям. Если подставить эти числа в формулу softmax вероятности будут иными.
|
z = ([1, 2, 0.5]) np.exp(z) / sum(np.exp(z)) |
|
array([0.2312239 , 0.62853172, 0.14024438]) |
Впрочем, алгоритм по-прежнему уверен, что речь идет о кошке.
3. Настройки
Настроек будет три:
- тип функции потерь (loss function) определяет, как мы будем считать отклонение прогнозного значения от истинного
- способ или алгоритм оптимизации этой функции (optimizer) поможет снизить потерю или ошибку и подобрать правильные веса в процессе back propagation
- метрика (metric) покажет, насколько точна наша модель
Функция потерь
В первую очередь, определимся с функцией потерь. Раньше, например, в задаче регрессии, мы использовали среднеквадратическую ошибку (MSE). Для задач классификации мы будем использовать функцию потерь, называемую перекрестной или кросс-энтропией (cross-entropy). Продолжим пример с собакой, кошкой и попугаем.
Функция перекрестной энтропии (D) показывает степень отличия прогнозного вероятностного распределения (которое мы получили на выходе функции softmax (S)) от истинного (наша целевая переменная (L)). Чем больше отличие, тем выше ошибка.
Также обратите внимание, наша целевая переменная закодирована, вместо слова «кошка» напротив соответсвующего класса стоит единица, а напротив остальных классов — нули. Такая запись называется унитарным кодом, хотя чаще используется анлийский термин one-hot encoding.
Когда мы будем обучать наш алгоритм, мы также применим эту кодировку к нашим данным. Например, если в целевой переменной содержится цифра пять, то ее запись в one-hot encoding будет следующей.
В дополнение замечу, что функция кросс-энтропии, в которой применяется one-hot encoding, называется категориальной кросс-энтропией (categorical cross-entropy).
Отлично! С тем как мы будем измерять уровень ошибки (качество обучения) нашей модели, мы определились. Теперь нужно понять, как мы эту ошибку будем минимизировать. Для этого существует несколько алгоритмов оптимизации.
Алгоритм оптимизации
Классическим алгоритмом является, так называемый, метод стохастического градиентного спуска (Stochastic Gradient Descent или SGD).
Если предположить для простоты, что наша функция потерь оптимизирует один вес исходной модели, и мы находимся изначально в точке А (с неидеальным случайным весом), то наша задача — оказаться в точке B, где ошибка (L) минимальна, а вес (w) оптимален.
Спускаться мы будем вдоль градиента, то есть по кратчайшему пути. Идею градиента проще увидеть на функции с двумя весами. Такая функция имеет уже три измерения (две независимых переменных, w1 и w2, и одну зависимую, L) и графически похожа на «холмистую местность», по которой мы будем спускаться по наиболее оптимальному маршруту.
Стохастичность (или случайность) этого алгоритма заключается в том, что мы берем не всю выборку для обновления весов модели, а лишь одно или несколько случайных наблюдений. Такой подход сильно сокращает время оптимизации.
Метрика
Остается определиться с метрикой качества. Здесь мы просто возьмём знакомую нам метрику accuracy, которая посчитает долю правильно сделанных прогнозов.
Посмотрим на используемый код.
|
model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘sgd’, metrics = [‘accuracy’] ) |
4. Обучение модели
Теперь давайте соберём все описанные выше элементы и посмотрим на работу модели в динамике. Повторим ещё раз изученные выше шаги.
- Значения пикселей каждого изображения поступают в 784 нейрона входного слоя
- Далее они проходят через скрытые слои, где они умножаются на веса, складываются, смещаются и поступают в соответствующую функцию активации
- На выходе из функции softmax мы получаем вероятности для каждой из цифр
- После этого результат сравнивается с целевой переменной с помощью функции перекрестной энтропии (функции потерь); делается расчет ошибки
- На следующем шаге алгоритм оптимизации стремится уменьшить ошибку и соответствующим образом изменяет веса
- После этого процесс повторяется, но уже с новыми весами.
Давайте выполним все эти операции в библиотеке Keras.
|
# вначале импортируем функцию to_categorical, чтобы сделать one-hot encoding from tensorflow.keras.utils import to_categorical |
|
# обучаем модель model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # по сути, эпоха показывает сколько раз алгоритм пройдется по всем данным ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 2.0324 — accuracy: 0.4785 Epoch 2/10 1875/1875 [==============================] — 3s 2ms/step — loss: 1.2322 — accuracy: 0.7494 Epoch 3/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.7617 — accuracy: 0.8326 Epoch 4/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.5651 — accuracy: 0.8663 Epoch 5/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4681 — accuracy: 0.8827 Epoch 6/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4121 — accuracy: 0.8923 Epoch 7/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3751 — accuracy: 0.8995 Epoch 8/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3487 — accuracy: 0.9045 Epoch 9/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3285 — accuracy: 0.9090 Epoch 10/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3118 — accuracy: 0.9129 <keras.callbacks.History at 0x7f36c3f09490> |
На обучающей выборке мы добились неплохого результата, 91.29%.
5. Оценка качества модели
На этом шаге нам нужно оценить качество модели на тестовых данных.
|
# для оценки модели воспользуемся методом .evaluate() model.evaluate( X_test, # который применим к тестовым данным to_categorical(y_test) # не забыв закодировать целевую переменную через one-hot encoding ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.2972 — accuracy: 0.9173 [0.29716429114341736, 0.9172999858856201] |
Результат «на тесте» оказался даже чуть выше, 91,73%.
6. Прогноз
Теперь давайте в качестве упражнения сделаем прогноз.
|
# передадим модели последние 10 изображений тестовой выборки pred = model.predict(X_test[—10:]) # посмотрим на результат для первого изображения из десяти pred[0] |
|
array([1.0952151e-04, 2.4856537e-04, 1.5749732e-03, 7.4032680e-03, 6.2553445e-05, 8.7646207e-05, 9.4199123e-07, 9.7065586e-01, 5.3100550e-04, 1.9325638e-02], dtype=float32) |
Работа над ошибками. На видео я говорю про первые десять изображений. Разумеется, это неверно. Срез [-10:] выводит последние десять изображений.
В переменной pred содержится массив numpy с десятью вероятностями для каждого из десяти наблюдений. Нам нужно выбрать максимальную вероятность для каждого изображения и определить ее индекс (индекс и будет искомой цифрой). Все это можно сделать с помощью функции np.argmax(). Посмотрим на примере.
Теперь применим к нашим данным.
|
# для кажого изображения (то есть строки, axis = 1) # выведем индекс (максимальное значение), это и будет той цифрой, которую мы прогнозируем print(np.argmax(pred, axis = 1)) # остается сравнить с целевой переменной print(y_test[—10:]) |
|
[7 8 9 0 1 2 3 4 5 6] [7 8 9 0 1 2 3 4 5 6] |
Для первых десяти цифр модель сделала верный прогноз.
7. Пример улучшения алгоритма
Существует множество параметров модели, которые можно настроить. В качестве примера попробуем заменить алгоритм стохастического градиентного спуска на считающийся более эффективным алгоритм adam (суть этого алгоритма выходит за рамки сегодняшней лекции).
Посмотрим на результат на обучающей и тестовой выборке.
|
# снова укажем настройки модели model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘adam’, # однако заменим алгоритм оптимизации metrics = [‘accuracy’] ) # обучаем модель методом .fit() model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # прописываем количество эпох ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.2572 — accuracy: 0.9252 Epoch 2/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1738 — accuracy: 0.9497 Epoch 3/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1392 — accuracy: 0.9588 Epoch 4/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1196 — accuracy: 0.9647 Epoch 5/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1062 — accuracy: 0.9685 Epoch 6/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0960 — accuracy: 0.9708 Epoch 7/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0883 — accuracy: 0.9732 Epoch 8/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0826 — accuracy: 0.9747 Epoch 9/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0766 — accuracy: 0.9766 Epoch 10/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0699 — accuracy: 0.9780 <keras.callbacks.History at 0x7f36c3d74590> |
|
# и оцениваем результат «на тесте» model.evaluate( X_test, to_categorical(y_test) ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.1160 — accuracy: 0.9647 [0.11602973937988281, 0.9646999835968018] |
Как вы видите, с помощью одного изменения мы повысили долю правильных прогнозов до 96,47%.
Более подходящие для работы с изображениями сверточные нейронные сети (convolutional neural network, CNN) достигают свыше 99% точности на этом наборе данных, как это видно в примере⧉ на официальном сайте библиотеки Keras.
Подведем итог
На сегодняшнем занятии изучили основы нейронных сетей. В частности, мы узнали, что такое нейронная сеть, какова ее структура и алгоритм функционирования. Многие шаги, например, оценка уровня ошибки через функцию кросс-энтропии или оптимизация методом стохастического градиентного спуска, разумеется, требуют отдельного занятия. Эти уроки еще впереди.
При этом, я надеюсь, у вас сложилось целостное представление о том, что значит создать и обучить нейросеть, и какие шаги для этого требуются.
Вопросы для закрепления
Перечислите типы слоев нейронной сети
Посмотреть правильный ответ
Ответ: обычно используется входной слой, один или несколько скрытых слоев и выходной слой.
Из каких двух этапов состоит обучение нейронной сети?
Посмотреть правильный ответ
Ответ: вначале (1) при forward propagation мы пропускаем данные от входного слоя к выходному, затем, рассчитав уровень ошибки, (2) начинается обратный процесс back propagation, при котором, мы улучшаем веса исходной модели.
Для чего используются сигмоида и функция softmax в выходном слое нейронной сети в задачах классификации?
Посмотреть правильный ответ
Ответ: сигмоида используется, когда нужно предсказать один из двух классов, если классов больше двух, применяется softmax.
Ответы на вопросы
Вопрос. Что означает число 1875 в результате работы модели?
Ответ. Я планировал рассказать об этом на курсе по оптимизации, но попробую дать общие определения уже сейчас. Как я уже сказал, при оптимизации методом градиентного спуска мы можем использовать (1) все данные, (2) часть данных или (3) одно наблюдение для каждого обновления весов. Это регулируется параметром batch_size (размер партии).
- в первом случае, количество наблюдений (batch, партия) равно размеру датасета, веса не обновляются пока мы не пройдемся по всем наблюдениям, это простой градиентный спуск
- во втором случае, мы берем часть наблюдений (mini-batch, мини-партия), и когда обработаем их, то обновляем веса; после этого мы обрабатываем следующую партию
- и наконец мы можем взять только одно наблюдение и сразу после его анализа обновить веса, это классический стохастический градиентный спуск (stochastic gradient descent), параметр batch_size = 1
В чем преимущество каждого из методов? Если мы берем всю партию и по результатам ее обработки обновляем веса, то двигаемся к минимуму функции потерь наиболее плавно. Минус в том, что на расчет требуется время и вычислительные мощности.
Если берем только одно наблюдение, то считаем все быстро, но расчет минимума функции потерь менее точен.
В библиотеке Keras (и нашей нейросети) по умолчанию используется второй подход и размер партии равный 32 наблюдениям (
batch_size = 32). С учетом того, что в обучающей выборке 60000 наблюдений, разделив 60000 на 32 мы получим 1875 итераций или обновлений весов в рамках одной эпохи. Отсюда и число 1875.
Повторим, алгоритм обрабатывает 32 наблюдения, обновляет веса и после этого переходит к следующей партии (batch) из 32-х наблюдений. Обработав таким образом 60000 изображений, алгоритм заканчивает первую эпоху и начинает вторую. Размер партии и количество эпох регулируется параметрами batch_size и epochs соответственно.