Оригами многогранники из бумаги пошаговая инструкция фото

Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности. Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка. Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.

Ажурная модель

Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.

Пошаговая инструкция:

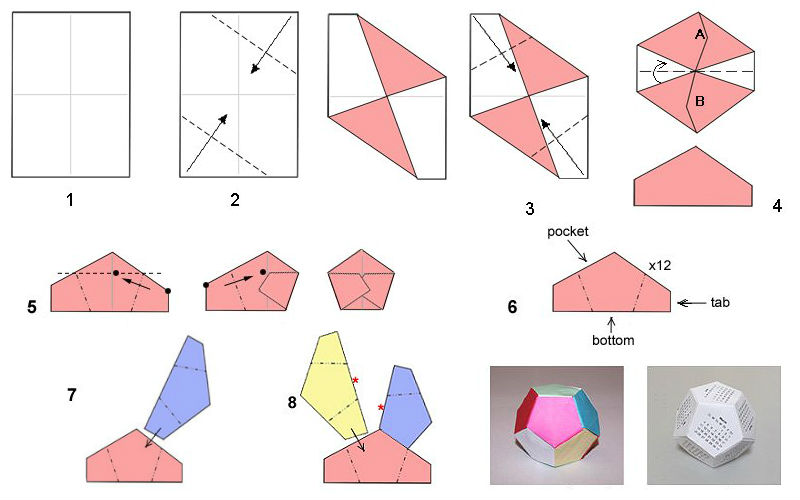
1. Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
2. Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
3. Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
4. Складываем фигуру по диагонали, как показано на рис 4.
5. Модули для додекаэдра-кусудамы готовы.

Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.

Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.

Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.

За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.

Подробная сборка ажурного додекаэдра представлена и в видео-МК:

Кусудама из правильных пятиугольников

Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.

Пошаговая инструкция:

1. Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
2. Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
3. Аналогично складываем противоположные углы.
4. Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
5. Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
6. Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
7. Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
8. Продолжаем сборку, пока не используем все 12 модулей.

Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.

Додекаэдр-звезда

Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.

Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.

Интересные факты о додекаэдре

Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.

Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.

Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.

Игрушки древних римлян

На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.

Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.

В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.

Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.

Сделать из бумаги многогранник — Икосаэдр очень просто в технике оригами из модулей Mitsunobu Sonobe.

Такая интересная поделка кусудама станет интересным украшением или подарком, способным удивить друзей. Бумажный шар кусудама станет к тому же интересной елочной игрушкой на Новый год и отлично украсит новогоднюю елку на праздник.

Сделать икосаэдр не сложно и собирается он из 30 простых модулей, которые изготавливаются из квадратного листа бумаги, мы использовали бумагу размером 7*7 см.

Как сделать модель тетраэдра из бумаги и картона

Оригами-тетраэдр из бумаги – эффектный и многофункциональный декоративный элемент. В зависимости от модели, он может служить интерьерной подвеской, ёлочным украшением и частью модного настенного панно в скандинавском стиле. Тетраэдр – четырёхгранная пирамида, в основании которой лежит треугольник. Чаще всего для декора используют несколько таких фигур, объединённых в композицию.

Традиционный вариант

Объёмный тетраэдр-оригами можно сделать из классического квадрата или листа бумаги формата А4. Схема во втором варианте – сложнее, однако для долговечного декора лучше выбирать именно её. Модель получается многослойной, а потому меньше изнашивается в процессе эксплуатации.

Пошаговая инструкция:

Нам понадобится 2 альбомных листа. Складываем их поочерёдно по одному и тому же алгоритму.

1. Располагаем лист короткой стороной к себе. Намечаем вертикальную ось симметрии.
2. Правый нижний угол поднимаем к центральной линии из шага 1.
3. Переворачиваем заготовку.
4. Левый верхний угол опускаем, делая сгиб по линии, намеченной в шаге 2.
5. Вот что должно получиться.
6. Раскрываем изделие.
7. Повторяем шаги 2-5 с другой стороны.
8. Срезаем верхнюю часть по выделенной на схеме линии.

1. Складываем левый верхний угол по пунктиру. Его вершину совмещаем с точкой, указанной стрелкой.
2. Повторяем то же действие для правого нижнего угла.
3. Вот такая полоска-«конверт» должна получиться.
4. Повторяем шаги 1-10 для другого листа А4, но зеркально.
5. Кладём один модуль поверх другого, как показано на схеме.
6. Нижний элемент складываем в тетраэдр.
7. Оборачиваем верхнюю часть вокруг получившейся фигуры.
8. Вставляем оставшийся клапан в зазор, чтобы тетраэдр-оригами не распадался.

Эта модель великолепно смотрится в настенных панно:

Есть и немного другая схема сборки тетраэдра – из одного листа А4. Она представлена в видео-уроке:

Модель от Томоко Касахары

Японский оригамист предлагает сделать модель тетраэдра из квадратного листа. Схема сборки от Касахары настолько подробная, что изготовить по ней фигурку сможет даже начинающий. Для удобства рекомендуется использовать бумагу со сторонами разного цвета – это поможет следить за процессом складывания. Опытные мастера могут брать однотонные листы, что улучшит эстетические качества модели.

Пошаговая инструкция:

1. Начинаем с изнанки листа. Делим квадрат пополам путём складывания. Намечаем «засечку» и раскрываем сгиб. Правую половину тоже складываем вдвое. Наносим отметку примерно на полпути вверх. Разворачиваем лист до исходного состояния.
2. Делаем сгиб по пунктиру, ориентируясь на «засечки» из шага 1.
3. Повторяем аналогичное действие с противоположной стороны.
4. Опускаем верхний край на 1 см.
5. Подгибаем уголки по стрелкам.
6. Раскрываем все складки, кроме последних. Делим новый квадрат пополам по горизонтали.

1. Намечаем диагональные сладки в местах, указанных пунктиром.
2. Делаем короткие боковые сгибы по стрелкам. Важно каждый раз совмещать нижний край клапана с меткой по центру.
3. Предварительные сгибы нанесены, теперь можно переходить к складыванию объёмной фигуры. Нижний левый угол сгибаем по пунктирной линии до пересечения, указанного стрелкой.
4. Далее совмещаем его с вершиной треугольника.
5. Точку 1 опускаем до конца стрелки, а затем откидываем клапан 2, чтобы зафиксировать последний сгиб.
6. Получившаяся фигура напоминает перевёрнутый рожок для мороженого. Нажимаем на складки в правой части модели, поднимаем точку 1 вверх, как показано на схеме, и «заправляем» под клапан. Тетраэдр-оригами почти готов, но у него остаётся одна лишняя грань. Чтобы завершить сборку, точку 2 перемещаем по стрелке и фиксируем клапаном.

Освоив схему сборки тетраэдра Касахары, можно также изготавливать из бумаги своими руками эффектные подарки – разнообразные панно и картины:

Альтернативный вариант сборки из квадрата:

Очень простая двухцветная модель

Необычно и эффектно смотрится тетраэдр из двух половинок. Каждую можно сложить из бумаги другого цвета, что сделает геометрический декор ещё интереснее. Если предыдущие модели адресованы, скорее, опытным мастерам, эта – как раз по плечу начинающим.

Пошаговая инструкция:

1. Сгибаем квадрат по диагонали «горой». Делим пополам, складывая слева направо и сверху вниз. Делаем складки и раскрываем.
2. Намечаем сгиб слева по пунктирной линии. Соединяем вершину угла с ближней засечкой.
3. Аналогичные сгибы делаем ещё с трёх сторон.
4. Все четыре края складываем по пунктирным линиям. Центральные треугольники выступают вверх, образуя так называемые «заячьи уши». Раскрываем их изнутри и сплющиваем.
5. Сгибаем фигуру пополам «долиной».

Аналогичным образом собираем вторую часть. Остаётся склеить двухцветный тетраэдр из бумаги и придумать ему применение.

Декор из картона

Рассматривая варианты оригами-тетраэдра, нельзя обойти вниманием фигуры, изготовленные другим способом, но не менее популярные. Речь идёт о картонных моделях, которые складываются из развёртки, как упаковочные коробочки. Скачиваем трафарет правильного тетраэдра:

Остаётся распечатать его на цветной картон и вырезать заготовки, а затем склеить:

Звёздчатый многогранник

Самая красивая модель получается из нескольких тетраэдров, соединённых между собой. Этот так называемый звёздчатый многогранник, легко сделать своими руками из картона. Тетраэдры собирают из отдельных граней – узких полосок, сложенных «уголком». Именно поэтому нужна не бумага, а плотный картон, иначе ажурная конструкция быстро сомнётся под собственным весом.

Число выступов декоративного кристалла может быть разным. Максимум можно использовать 5 взаимно пересекающихся тетраэдров. Их размер для схемы не важен, но соотношение сторон исходного листа должно составлять 1:3.

Пошаговая инструкция:

Для начала запасаемся листами тонкого дизайнерского картона. Для звезды диаметром 16,5 см нам понадобится 30 прямоугольников размером 5х15 см. Можно выбрать другие параметры, главное, сохранить указанные пропорции. Чтобы не запутаться, рекомендуем делать полосы партиями по 6 штук разного цвета.

1. Первую полосу сгибаем вдвое по высоте. Раскрываем складку.
2. Оба края сводим к середине.
3. Делаем складку-засечку «долиной».
4. Левый угол сгибаем, чтобы красная точка коснулась отметки из шага 3. Раскрываем.
5. С помощью обратной складки заводим левый угол внутрь.
6. Раскрываем правую сторону. «Прячем» выступающий уголок. И вновь закрываем правую половину.
7. Намечаем складку «долиной» с другой стороны.
8. Повторяем шаги 3-7 на противоположном конце полосы.

Таких заготовок понадобится 30 штук. На лицевой стороне делаем складку «долиной», а на обороте – «горой».

Начинаем сборку пирамидок. Для первой используем 6 красных элементов. Верхний угол намечаем небольшой бумажной полоской, чтобы в дальнейшем упростить себе работу.

Остальные грани собираем и склеиваем по 3 штуки. Тщательно проходим стыки, тогда конструкция получится прочной и долговечной.

К первому красному тетраэдру добавляем полуготовую фигуру из 3-х граней. Ориентируемся на фото-образец. Теперь фиксируем второй – жёлтый тетраэдр, приклеивая ещё 3 недостающие грани.

Аналогичным образом вставляем следующую заготовку, например, голубого цвета и закрепляем её.

Поворачиваем тетраэдр-звезду другой стороной и продолжаем работу.

Следим, чтобы каждая добавленная фигура располагалась под тем же углом, что и остальные.

Последний, фиолетовый, многоугольник крепим с особой тщательностью.

Прежде чем приклеить 3 завершающие грани, несколько раз осматриваем звезду под разными углами. Желательно добиться идеальной симметрии.

Казалось бы, сложная конструкция, на деле требует только аккуратности, внимания и терпения, как и остальные модульные многогранники.

Тетраэдр из картона послужит отличным украшением праздничного интерьера или, например, магазинной витрины.

А эксцентричные невесты вполне могут заменить им свадебный букет.

Звёздчатый многогранник – единственный способ сложить оригами-тетраэдр из модулей. Есть и не менее интересные варианты:

Интересные факты

Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.

Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.

В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.

Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.

Источник

Как сделать многогранник из бумаги

Когда-то разноцветные многогранники из бумаги и картона служили одновременно и наглядным пособием, и украшением школьных кабинетов математики и черчения. Изготовление этих фигур способствовало развитию пространственного мышления, знакомило с многообразием форм в их трехмерном проявлении. Изготовление таких многогранников из цветной бумаги — увлекательнейшее занятие, не лишенное интеллектуальной составляющей, удивительная возможность математикой выразить красоту окружающего мира.

Многогранник — понятие очень обширное, и зачастую новички, увлеченные изготовлением этих выпуклых и звездчатых фигур, поначалу путаются в их названиях, что, в общем-то, неудивительно. Многогранники можно разделить на две категории: так называемые Платоновы тела и Архимедовы тела.

К первым относятся правильные многогранники: тетраэдр, октаэдр, куб (гексаэдр), икосаэдр, додекаэдр. Ко вторым — полуправильные многогранники: усеченные версии Платоновых тел, кубооктаэдр, «курносый» куб и др. Не старайтесь сразу запомнить все эти сложные названия, мастерить их гораздо интереснее, чем заучивать термины 🙂

Для работы понадобится цветной или белый картон, который можно при необходимости раскрасить; линейка и угольники; хороший клей, который не коробит бумагу; ножницы; пинцет. Для изготовления заготовок многогранника удобно пользоваться картонными трафаретами: чертеж заготовки накладывают на плотный картон, шилом или иголкой делают проколы по вершинам детали, после чего по линейке соединяют эти точки.

Тетраэдр

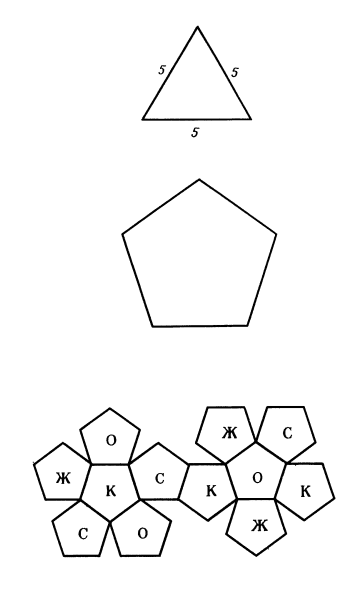
Одним из простейших многогранников, которые проще всего сделать из бумаги (картона), является тетраэдр («Пирамида»). Четыре грани этой фигуры представлены равносторонними треугольниками. Если хочется сделать одноцветный тетраэдр, то можно воспользоваться одной разверткой (см. схему ниже).

Если же тетраэдр нужен разноцветный, то придется сделать четыре цветные заготовки в виде равносторонних прямоугольников. Из картона изготавливают четыре треугольника разного цвета (например, Ж, С, О, К — желтый, синий, оранжевый, красный), обязательно делая небольшие «припуски» для склеивания деталей.

При соединении отдельных заготовок сначала склеивают все четыре детали в положение, изображенное на рисунке ниже, затем приступают к соединению боковых граней. Сначала склеивают между собой только две из них, затем — оставшиеся детали.

Октаэдр

Вторую половину проще клеить таким образом: сначала четыре оставшихся треугольника приклеивают к соответствующим сторонам квадратного основания, затем соединяют соседние грани.

Икосаэдр

На третьем месте по простоте исполнения идет икосаэдр, гранями которого тоже являются равносторонние треугольники. Наиболее эффектно смотрятся разноцветные многогранники, у которых возможно варьирование распределения цветов. Например, можно сделать фигуру, у которой в каждой вершине будут сходиться все используемые цвета, или же у противоположных граней будут одинаковые расцветки, а у вершин будет повторяться один цвет.

Модель собирают из пяти треугольников, соединенных по схеме, указанной на рисунке ниже. В результате получится невысокая пятиугольная пирамида без основания. К сторонам основания приклеивают остальные пять треугольников, руководствуясь любой понравившейся цветовой схемой.

Додекаэдр

И, пожалуй, к несложным, но самым эффектным по своему внешнему виду многогранникам можно отнести додекаэдр. Наиболее красиво выглядят разноцветные додекаэдры: четырех- или шестицветные.

Построение модели начинают со приклеивания пяти разноцветных пятиугольников к центральному пятиугольнику — например, белого цвета. Затем цветные заготовки склеивают между собой — получается половина додекаэдра. Затем остальные грани заготовок подклеивают к уже готовой половине фигуры таким образом, чтобы выдержать задуманную цветовую схему и эффектный многогранник из бумаги будет готов.

Если вам, уважаемые читатели, интересна тема изготовления многогранников из бумаги, и хотелось бы видеть больше схем, пишите об этом в комментариях, публикации будут продолжены. Впереди нас ждут усеченные, «курносые» и красивейшие звездчатые формы многогранников.

Источник

В эту подборку мы собрали три способа с пошаговыми инструкциями, показывающие, как сделать куб из бумаги. Первым, обычным способом вы можете сделать кубик практически любого размера.
Два остальных способа — вариации техники оригами, один — более простой, второй — посложнее.

А если вы хотите научиться делать бабочку в технике оригами, читайте эту подборку.

1. Как сделать кубик из бумаги

Это самый простой и, как правило, известный всем способ. В этом мастер-классе расскажем, как сделать куб из бумаги А4. Для этого вам понадобится принтер, чтобы распечатать шаблон, но вы можете начертить на листе схему самостоятельно.

Вам потребуется:

• плотная бумага формата А4 или тонкий картон такого же формата;
• принтер или карандаш и линейка;
• ножницы для бумаги;
• клей для бумаги.

Шаг 1

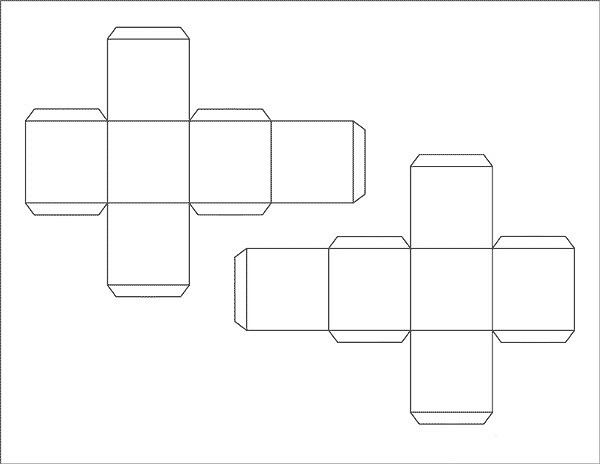
Перечертите этот шаблон на бумаге (шаблон состоит из шести квадратов и клапанов) или картоне или распечатайте его (шаблоны вы можете найти тут).

Шаг 2

Вырежьте фигуру.

Шаг 3

Сложите заготовку по всем линиям, направляя все сгибы в сторону центра.

Шаг 4

На этом этапе вы можете раскрасить стороны кубика, что-то нарисовать на них или написать (например, если вы делаете кубик для какой-то игры).

Шаг 5

Теперь нужно приступить к склеиванию поделки. Нанесите клей на один клапан.

Приклейте клапан к стороне куба. Повторите со всеми другими клапанами и склейте кубик.

Готово!

2. Как сделать разборный оригами-куб

Этот кубик хорош тем, что он, во‑первых, разбирается и легко собирается снова, потому что состоит из отдельных модулей. Во‑вторых, взяв бумажные листы разных цветов, вы получите куб с разноцветными гранями. Для такой поделки лучше подойдёт двусторонняя цветная бумага.

Вам потребуется:

• 6 одинаковых квадратных листочков двусторонней цветной бумаги.

Шаг 1

Возьмите один из квадратных листков и сложите его пополам.

Шаг 2

Раскройте сделанный сгиб. Теперь параллельные сгибу края листа сложите так, чтобы они встретились на линии сгиба. Загладьте новые линии сгиба.

Шаг 3

Согните заготовку пополам поперёк, но не заглаживайте сгиб, а сделайте небольшую отметку. К этой отметке согните края заготовки. У вас должен получиться модуль, как на картинке выше.

Шаг 4

Повторите предыдущие шаги с остальными пятью листками. Теперь у вас есть шесть модулей, из которых можно собрать куб.

Шаг 5

Складывайте заготовки, как это показано на картинке выше.

Готово!

Вы можете сделать несколько таких кубиков.

Если вы не хотите их разбирать, обклейте их прозрачным скотчем, чтобы модули держались прочно.

3. Более сложный оригами-кубик из бумаги

Этот оригами-куб сделать несколько сложнее, чем предыдущие два, зато он получается самым красивым! Для него тоже можно использовать бумагу разных цветов, и за счёт переплетения деталей разноцветных модулей у кубика получаются грани с узором. Для этой поделки тоже лучше взять бумагу, цветную с обеих сторон.

Вам потребуется:

• 6 квадратных листов двусторонней цветной бумаги одинакового размера, но разных цветов.

Шаг 1

Если у вас бумага большого размера, подготовьте квадраты, расчертив их и вырезав из листов. Здесь используются квадраты 15х15 см. Если взять квадраты побольше, кубик будет больше, если меньше — соответственно, меньше. Можно сделать такой куб и из бумаги одного цвета, но начинать лучше с цветных модулей: так будет проще работать, особенно — детям.

Шаг 2

Возьмите один квадрат и сложите его пополам.

Шаг 3

Разверните сгиб, сделанный в шаге выше. Боковые края квадрата, параллельные этому сгибу, сложите к сгибу. Загладьте сделанные сгибы.

Шаг 4

Левый верхний угол заготовки согните вниз по диагонали, так чтобы внизу края совпали. Загладьте сгиб.

Шаг 5

Нижний правый угол заготовки точно так же загните вверх по диагонали. Загладьте сгиб.

Шаг 6

Разверните только что сделанные складки.

Согните правый верхний уголок по диагонали вниз и к центру.

Теперь разогните нижнюю складку, загните левый нижний уголок по диагонали вверх и к центру.

Загните эти уголки внутрь.

Шаг 7

Отогните нижнюю часть работы.

Верхний левый угол работы загните по диагонали вниз, как это показано на фото выше.

Верните нижнюю складку на место.

Точно так же загните вверх правый нижний угол.

Спрячьте клапаны внутрь, чтобы укрепить модуль.

Шаг 8

Переверните модуль. С другой стороны он будет выглядеть, как на картинке выше.

Поверните его вертикально.
Верхний угол сложите вниз.

А нижний — вверх. Один модуль готов.

Шаг 9

Теперь нужно повторить все предыдущие шаги для остальных пяти квадратов, чтобы сделать ещё 5 модулей. Внимательно следите за тем, чтобы все сгибы выполнять в том же направлении, в каком вы действовали, делая первый модуль. Все модули должны получиться совершенно одинаковыми, иначе кубик не получится собрать.

Шаг 10

Теперь нужно собрать куб из модулей. Для этого продевайте клапаны под сгибы, как показано на фото выше.

Это довольно сложный способ, и если вы чего-то не поняли, посмотрите видео:

Фото и источник: onecrazymom.com, teachstarter.com, firstpalette.com, kidslovewhat.com, frugalfun4boys.com