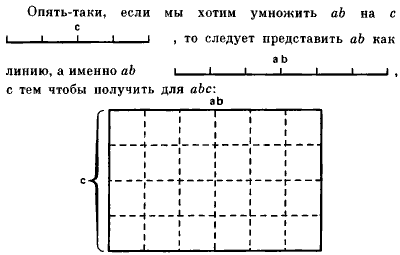
Как видно уже из самого названия трактата,
цель его — двойная. Во-первых, он
предназначен для «руководства ума»
в направлении его усовершенствования
с тем, чтобы обладатель ума, достигнув
определенной степени совершенства,
искусства, смог открыть, «изобрести»,
обрести из самого способа усовершенствования
ума путь познания Истины. Это, следовательно,
правила в классическом средневековом
смысле, правила в смысле приемов,
нормативов времени. Но в то же время они
являются правилами методологическими,
характерными для Нового времени, истина
не дана заранее, ее только следует
открыть, открыть с помощью метода,
орудия, которым может воспользоваться
«всякий … как бы ни был посредственен
его ум», для успешного решения задачи
— ввести ключевое, принципиально новое
разделение на «нас, способных
познавать», и на независимый от нас
объективный мир «самих вещей, которые
могут быть познаны».
Отмеченная выше историческая необходимость
вычленения метода в форме метода
математического предстает в «Правилах…»
как картина внутри логических
закономерностей теоретического развития
Декарта — в исходном, отправном пункте
этого развития, в своем «замысле «.
По замыслу трактат должен был состоять
из трех частей, каждая из которых должна
была включать 12 «Правил». В первой
части предстояло изложить собственно
принципы метода; во второй — показать,
как сделать эмпирию объектом теоретического
исследования: построить математическую
модель физической задачи; в третьей
части предполагалось показать, как
такую задачу решать. Но трактат в том
виде, в каком он нам известен, состоит
из полных восемнадцати «Правил»;
следующие три «Правила» обозначены
лишь заголовками, и после обозначенного
таким образом «Правила ХХ1» Декарт
ставит «Конец».
Прежде чем рассуждать
дальше, рассмотрим, что же представляют
собой эти знаменитые правила.
ПРАВИЛО I
Целью научных знаний должно быть
направление ума таким образом, чтобы
он выносил прочные и истинные суждения
о всех встречающихся предметах.
ПРАВИЛО II
Нужно заниматься только такими предметами,
о которых ваш ум кажется способным
достичь достоверных и несомненных
познаний.
ПРАВИЛО III
В предметах нашего исследования надлежит
отыскивать не то, что
о них думают другие или что мы предполагаем
о них самих, но то, что мы ясно и очевидно
можем усмотреть или надежно дедуцировать,
ибо знание не может быть достигнуто
иначе.
ПРАВИЛО IV
Метод необходим для отыскания истины.
ПРАВИЛО V
Весь метод состоит в порядке и размещении
того, на что должно быть направлено
острие ума в целях открытия какой-либо
истины. Мы строго соблюдем его, если
будем постепенно сводить темные и
смутные положения к более простым и
затем пытаться, исходя из интуиции
простейших, восходить по тем же ступеням
к познанию всех остальных.
ПРАВИЛО VI
Для того, чтобы отделять наиболее простые
вещи от трудных и придерживаться при
этом порядка, необходимо во всяком ряде
вещей, в котором мы непосредственно
выводим какие-либо истины из других
истин, следить, какие из них являются
самыми простыми и как отстоят от них
другие: дальше, ближе или одинаково.
ПРАВИЛО VII
Для завершения знания надлежит все,
относящееся к нашей задаче, вместе и
порознь обозреть последовательным и
непрерывным движением мысли и охватить
достаточной и методической энумерацией.
ПРАВИЛО VIII
Если в ряде исследуемых вещей встретится
какая-либо одна, которую наш ум не может
достаточно хорошо понять, то нужно на
ней остановиться и не исследовать
других, идущих за ней, воздерживаясь от
лишнего труда.
ПРАВИЛО IX
Нужно обращать острие ума на самые
незначительные и простые вещи и долго
останавливаться на них, пока не привыкнем
отчетливо и ясно прозревать в них истину.
ПРАВИЛО Х
Для того чтобы сделать ум проницательным,
необходимо упражнять его в исследовании
вещей, уже найденных другими, и методически
изучать все, даже самые незначительные,
искусства, но в особенности те, которые
объясняют или предполагают порядок.
ПРАВИЛО ХI
После того, как мы усвоим несколько
простых положений и выведем из них
какое-либо иное, полезно обозреть их
путем последовательного и непрерывного
движения мысли, обдумать их взаимоотношения
и отчетливо представить одновременно
наибольшее их количество; благодаря
этому наше знание сделается более
достоверным и наш ум приобретет больший
кругозор.
ПРАВИЛО ХII
Наконец, нужно использовать все
вспомогательные средства интеллекта,
воображения, чувств и памяти как для
отчетливой интуиции простых положений
и для верного сравнения искомого с
известным, чтобы таким путем открыть
его, так еще и для того, чтобы находить
те положения, которые должны быть
сравнимы между собой, словом, не нужно
пренебрегать ни одним из средств,
находящихся в распоряжении человека.
ПРАВИЛО ХIII
Когда мы хорошо понимаем вопрос, нужно
освободить его от всех излишних
представлений, свести его к простейшим
элементам и разбить его на такое же
количество возможных частей посредством
энумерации.
ПРАВИЛО ХIV
Сказанное следует отнести и к реальному
протяжению тел; это протяжение нужно
всецело представлять в виде простых
фигур : таким образом оно сделается
более понятным для интеллекта.
ПРАВИЛО ХV
Большей частью полезно чертить эти
фигуры и преподносить их внешним
чувствам, для того чтобы таким образом
нам было легче сосредоточивать внимание
нашего ума.
ПРАВИЛО ХVI
Что же касается измерений, не требующих
в данный момент внимания нашего ума,
хотя и необходимых для заключения, то
лучше изображать их в виде сокращенных
знаков, чем полных фигур. Таким образом,
именно память не будет нам изменять и
вместе с тем мысль не будет разбрасываться,
чтобы удержать в себе эти измерения, в
то время как она занята выведением
других.
ПРАВИЛО ХVII
Встретившуюся трудность надо просматривать
прямо, не обращая внимания на то, что
некоторые из ее терминов известны, а
некоторые неизвестны, и интуитивно
следовать правильным путем по их взаимной
зависимости.
ПРАВИЛО ХVIII
Для этой цели необходимы только четыре
действия: сложение, вычитание, умножение
и деление. Двумя последними из них часто
здесь даже нет надобности пользоваться
как во избежание ненужных усложнений,
так и потому, что в дальнейшем они могут
быть более легко выполнимы.
ПРАВИЛО ХIХ
Путем такого метода вычислений нужно
отыскивать столько величин, выраженными
двумя различными способами, сколько
неизвестных терминов мы предполагаем
известными, для того чтобы исследовать
трудность прямым путем. Именно таким
образом мы получим столько же сравнений
между двумя равными величинами.
ПРАВИЛО ХХ
Составив уравнения, мы должны совершить
ранее отложенные нами действия, никогда
не пользуясь умножением, если уместно
деление.
ПРАВИЛО ХХI
Если имеется много таких уравнений, то
нужно их привести все к одному, а именно
к тому, термины которого займут наименьшее
количество ступеней в ряде последовательно
пропорциональных величин, где они и
должны быть восставлены в соответствующем
порядке.
Придя к выводу, что «метод необходим
для отыскания истины», Декарт вплотную
приступает к его разработке. «Главный
секрет метода» состоит, по его словам,
в том, что рассматривается не та или
иная вещь сама по себе «нужно… их не
рассматривать изолированно одну от
другой»), а ряд вещей, в котором мы
непосредственно выводим какие-либо
истины из других истин». Для этого
вначале надо определить, «какие из
них являются самыми простыми», а затем
остается лишь «следить…как отстоят
от них другие: дальше, ближе или одинаково
«.
Благодаря тому, что наряду с вещами
рассматриваются и их связи, методическое
движение представляет собой непрерывный
процесс. Так, например, находя «посредством
различных действий отношение сначала
между величинами А и В, затем между В и
С, между С и D и, наконец, между D и E «для
того, чтобы уловить их общую связь и в
дальнейшем учитывать ее, необходимо
обозревать их путем последовательного
движения представления так, чтобы оно
представляло одно из них и в то же время
переходило бы к другому».
Декарт выделяет два основных средства
познания: интуицию и дедукцию. В дальнейшем
к ним присоединяется еще и полная
энумерация, или индукция.
Интуиция — центральное положение
картезианского рационалистического
метода, требующего ясности и отчетливости
как высшего и решающего критерия
истинности. Поэтому учение Декарта об
интуиции совпадает с учением об
естественном свете разума».
Под интуицией имеется в виду «понятие
ясного и внимательного ума, настолько
простое и отчетливое, что оно не оставляет
никакого сомнения в том, что мы мыслим,
или, что одно и то же, прочное понятие
ясного и внимательного ума, порождаемое
лишь естественным светом разума».
Интуиция выступает элементарным актом
познания и его «точкой роста», а
само познание понимается как
последовательность, упорядоченная
цепочка интуиций. Следует подчеркнуть,
что картезианская интуиция не только
не имеет ничего общего с иррациональной,
мистической интуицией средневековых
схоластов, но составляет ее прямую
противоположность.
Интуиция находится в теснейшей связи
с дедукцией. Посредством дедукции мы
познаем все, что необходимо выводится
из чего-либо достоверно известного.
Дедукция необходима в силу того, что»
есть много вещей, которые хотя и не
являются самоочевидными, но доступны
достоверному познанию, если только они
выводятся из верных и понятных принципов
путем последовательного и нигде не
прерывающегося движения мысли при
зоркой интуиции каждого отдельного
положения». То есть под дедукцией
подразумевается «именно движение
или последовательность, чего нет в
интуиции «.
Полная математическая энумерация
завершает обретенное таким образом
знание. «Для завершения знания
необходима энумерация, так как если все
другие предписания и содействуют
разрешению многих вопросов, то только
посредством энумерации мы можем создать
всегда прочное и достоверное суждение
о вещах, с которыми мы имеем дело.
Благодаря ей ничто совершенно не
ускользает от нас и мы оказываемся
осведомленными понемногу обо всем «.
Но она одновременно и продолжает его,
и вновь «начинает», то есть
обеспечивает непрерывное воспроизведение
процесса. Действительно, то, что охвачено
индукцией, становится единой частью
знания, освоенной интуицией; но тогда
мы вновь имеем дело с исходным образом,
посылкой, «схватываемой одним
интуитивным актом.
Развивающаяся таким образом система
на каждом шаге обращается к своим
основаниям. Сомнение — «сомневающаяся»
способность мышления – единственный
достоверный источник всей системы
знания, и сомнение — единственный способ
развития знания. Сомнение, бывшее до
сих пор фактором моральным, становится
сомнением методологическим, методическим.
Усомнившись во всем, Декарт очищается
от схоластических догм и может строить
свою систему на немногих, но прочных
основаниях.
По мнению Декарта, метод является орудием
человека, и схема взаимодействия человек
— метод в процессе работы очень проста
и сводится к следующему : метод
совершенствует определенные способности
человека, доводя само совершенство до
крайних границ. Происходит это в ходе
анализа способностей, состоящего в
сведении их к элементарнейшим, далее
не расчленяемым, простейшим действиям.
Но в таком виде они теряют всякую
конкретную связь с той или иной конкретной
способностью конкретного индивида и
становятся в силу этого элементами
метода, в терминологии Декарта — обретают
статус простейших положений, аксиом,
на которых базируется метод.
Это орудийный аспект использования
метода, то есть отношение субъект
деятельности — орудие деятельности. Но
важнейшей чертой метода Декарта является
его обращенность на объект деятельности
— материальный мир в целом. Но рассмотрение
отношения субъект — объект приводит нас
к основному вопросу философии, а именно
его гносеологическому аспекту. Декарту,
как и любому философу, приходится решить
для себя этот вопрос. Его теория познания
вкратце изложена в правиле ХП. Вот ее
основные положения.
1. Нужно уяснить себе то, что все внешние
чувства, поскольку они составляют части
тела, хотя мы и применяем их к объектам
посредством действия, то есть местного
движения, ощущают собственно лишь
пассивно, подобно тому как воск принимает
фигуру печати.
2. Нужно уяснить себе, что после того как
внешнее чувство приведено объектом в
движение, воспринятая фигура моментально
сообщается другой части тела, называемой
общим чувствилищем, и притом так, что
никакое естество не переходит реально
с одного места на другое.
3. Нужно себе уяснить, что общее чувствилище
действует на фантазию, или воображение,
так же, как печать на воск, запечатлевая
фигуры или идеи, которые приходят к нам
от внешних чувств чистыми и бестелесными.
4. Нужно себе уяснить, что движущая сила,
или сами нервы, имеют свое начало в
мозгу, где находится воображение,
возбуждающими их разными способами,
подобно тому, как внешнее чувство
возбуждает общее чувствилище.
5. Нужно себе уяснить, что сила, посредством
которой мы собственно познаем вещи,
является чисто духовной, отличающейся
от всего телесного не менее, чем кровь
от костей или рука от глаза, единственной
в своем роде, хотя она вместе с фантазией
то воспринимает фигуры, исходящие от
общего чувствилища, то оперирует
фигурами, сохраняющимися в памяти, то
создает новые.
Декартов метод задает способ сведения
(регресса) к «простейшим» аксиомам
исходным геометрическим образам), и
этим регрессом является доказательство.
Выведение из «простейших» является
обращением доказательства и протекает
параллельно последнему. Оно, по выражению
Декарта, возвращается по тем же «ступеням».
Происходит это по правилам вывода,
обретенным в конечной точке регресса,
в пункте «возврата», и позволяет
осознать само доказательство. Вот почему
вывод и тождествен («по тем же
ступеням»), и не тождествен («осознание»)
доказательству.
Схема решения задач, предлагаемая
Декартом в практически неизменном виде,
действует и сейчас. Она заключается в
следующем: сначала сформулировать
задачу в том виде, в каком она дана, затем
построить математическую модель, то
есть выписать уравнения, описывающие
задачу, потом следует решать лишь
математическую задачу, отвлекаясь от
ее конкретного содержания. Когда решение
получено, его надо проинтерпретировать
для конкретного приложения.
Если первые правила описывают собственно
метод, то есть как найти задачу, как
свести ее к более простой и т.д., то
заключительные правила показывают, как
решать математическую задачу. Декарт
видит всеобщее здание науки в виде
«Универсальной математики», поэтому
неудивительно, что он уделяет математике
много места в своих исследованиях. Здесь
ему принадлежат многие значительные
достижения. Введение переменной величины
было поворотным пунктом в математике.
Система координат, носящая имя Декарта,
позволила характеризовать точки числами
(координатами) и породила концепцию
математики, согласно которой алгебра
является способом понимания геометрии.
Декарт ввел множество удобных обозначений.
Создал теорию пропорциональных отношений
и многое другое.
«Правила для руководства ума» имеют
огромное философское, методологическое
и математическое значение. Каждый раз,
когда современный логик или математик
обращает внимание на то, как совершаются
открытия или изобретения, он неизменно
обращается к «Правилам…» Декарта.
Подводя итог всему выше сказанному,
хотелось бы отметить, что развивая свое
учение о методе, Декарт стал основателем
рационализма, то есть направления в
теории познания согласно которому
всеобщий и необходимый характер истин
математики и точного естествознания
имеет источник не в опыте а в разуме.
Критерием достоверности он провозгласил
логические принципы рационального
познания – ясность и отчетливость.
УЧЕНИЕ Р. ДЕКАРТА О ЧЕТЫРЕХ ПРАВИЛАХ
МЕТОДА (ПО РАБОТЕ «РАССУЖДЕНИЕ О МЕТОДЕ»)
Правило I
Целью научных занятий должно быть направление ума таким образом, чтобы он мог выносить твердые и истинные суждения обо всех тех вещах, которые ему встречаются.
Таково обыкновение людей, что всякий раз, когда они замечают какое-либо сходство между двумя вещами, они в своих суждениях приписывают обеим даже в том, чем эти вещи различаются, то, что, как они узнали, является истинным для одной из них. Так, неудачно сравнивая науки, которые целиком заключаются в познании, присущем духу, с искусствами, которые требуют некоторого телесного упражнения и расположения, и видя, что один человек не в состоянии разом обучиться всем искусствам, но легче становится лучшим мастером тот, кто упражняется лишь в одном из них (ведь одни и те же руки не могут приспособиться к возделыванию земли и игре на кифаре или ко многим различным занятиям подобного рода столь же легко, как к одному из них), они думали то же самое и о науках и, отличая их друг от друга сообразно различию их предметов, полагали, что надо изучать каждую науку в отдельности, отбросив все прочие. В этом они безусловно обманывались. Ведь, поскольку все науки являются не чем иным, как человеческой мудростью, которая всегда пребывает одной и той же, на какие бы различные предметы она ни была направлена, и поскольку она перенимает от них различие не большее, чем свет солнца — от разнообразия вещей, которые он освещает, не нужно полагать умам какие-либо границы1, ибо познание одной истины не удаляет нас от открытия другой, как это делает упражнение в одном искусстве, но, скорее, тому способствует. И право, мне кажется удивительным, что многие люди дотошнейшим образом исследуют свойства растений, движения звезд, превращения металлов и предметы дисциплин, подобных этим, но при всем том почти никто не думает о здравом смысле или об этой всеобщей мудрости, тогда как все другие вещи в конце концов следует ценить не столько ради них самих, сколько потому, что они что-то прибавляют к этой мудрости. И оттого не без основания мы выставляем это правило первым среди всех, ибо ничто так не отклоняет нас от прямого пути разыскания истины, как если мы направляем наши занятия не к этой общей цели, а к каким-либо частным. Я говорю не о дурных и достойных осуждения целях, каковыми являются пустая слава или бесчестная нажива: ведь очевидно, что приукрашенные доводы и обманы, приноровленные к способностям толпы, открывают к этим целям путь гораздо более короткий, чем тот, который может потребоваться для прочного познания истинного. Но я разумею именно благородные и достойные похвалы цели, так как они часто вводят нас в заблуждение более изощренно, как, например, когда мы изучаем науки, полезные для житейских удобств или доставляющие то наслаждение, которое находят в созерцании истинного и которое является почти единственным в этой жизни полным и не омраченным никакими печалями счастьем. Конечно, мы можем ожидать от наук этих законных плодов, но, если мы во время занятий помышляем о них, они часто становятся причиной того, что многие вещи, которые необходимы для познания других вещей, мы упускаем или потому, что они на первый взгляд кажутся малополезными, или потому, что они кажутся малоинтересными. И надо поверить в то, что все науки связаны между собой настолько, что гораздо легче изучать их все сразу, чем отделяя одну от других. Итак, если кто-либо всерьез хочет исследовать истину вещей, он не должен выбирать какую-то отдельную науку: ведь все они связаны между собой и друг от друга зависимы; но пусть он думает только о приумножении естественного света разума, не для того, чтобы разрешить то или иное школьное затруднение, но для того, чтобы в любых случаях жизни разум (intellectus) предписывал воле, что следует избрать, и вскоре он удивится, что сделал успехи гораздо большие, чем те, кто занимался частными науками, и не только достиг всего того, к чему другие стремятся, но и превзошел то, на что они могут надеяться.
Правило II
Нужно заниматься только теми предметами, о которых наши умы очевидно способны достичь достоверного и несомненного знания.
Всякая наука есть достоверное и очевидное познание, и тот, кто сомневается во многих вещах, не более сведущ, чем тот, кто о них никогда не думал, но при этом первый кажется более несведущим, чем последний, если о некоторых вещах он составил ложное мнение; поэтому лучше не заниматься вовсе, чем заниматься предметами настолько трудными, что, будучи не в состоянии отличить в них истинное от ложного, мы вынуждены допускать сомнительное в качестве достоверного, ибо в этих случаях надежда на приумножение знания не так велика, как риск его убавления. И таким образом, этим положением мы отвергаем все те познания, которые являются лишь правдоподобными, и считаем, что следует доверять познаниям только совершенно выверенным, в которых невозможно усомниться. И как бы ни убеждали себя ученые в том, что существует крайне мало таких познаний, ибо они вследствие некоего порока, обычного для человеческого рода, отказывались размышлять о таких познаниях как слишком легких и доступных каждому, я, однако, напоминаю, что их гораздо больше, чем они полагают, и что их достаточно для достоверного доказательства бесчисленных положений, о которых до этого времени они могли рассуждать только предположительно; и поскольку они считали недостойным ученого человека признаться в своем незнании чего-либо, они настолько привыкли приукрашивать свои ложные доводы, что впоследствии мало-помалу убедили самих себя и, таким образом, стали выдавать их за истинные.
Но если мы будем строго соблюдать это правило, окажется очень немного вещей, изучением которых можно было бы заняться. Ибо вряд ли в науках найдется какой-либо вопрос, по которому остроумные мужи зачастую не расходились бы между собой во мнениях. А всякий раз, когда суждения двух людей об одной и той же вещи оказываются противоположными, ясно, что по крайней мере один из них заблуждается или даже ни один из них, по-видимому, не обладает знанием: ведь если бы доказательство одного было достоверным и очевидным, он мог бы так изложить его другому, что в конце концов убедил бы и его разум. Следовательно, обо всех вещах, о которых существуют правдоподобные мнения такого рода, мы, по-видимому, не в состоянии приобрести совершенное знание, поскольку было бы дерзостью ожидать от нас самих большего, чем дано другим; так что, если мы правильно рассчитали, из уже открытых наук остаются только арифметика и геометрия, к которым нас приводит соблюдение этого правила.
Мы, однако, не осуждаем ввиду этого тот способ философствования, который дотоле изобрели другие, и орудия правдоподобных силлогизмов, чрезвычайно пригодные для школьных баталий, ибо они упражняют умы юношей и развивают их посредством некоего состязания, и гораздо лучше образовывать их мнениями такого рода, даже если те очевидно являются недостоверными, поскольку служат предметом спора между учеными, чем предоставлять их, незанятых, самим себе. Ведь, может быть, без руководителя они устремились бы к пропасти, но, пока они идут по следам наставников, пусть и отступая иногда от истинного, они наверняка избрали путь во всяком случае более безопасный по той причине, что он уже был изведан более опытными людьми. И мы сами рады, что некогда точно так же были обучены в школах, но поскольку мы уже освободились от клятвы, привязывавшей нас к словам учителя, и наконец в возрасте достаточно зрелом убрали руку из-под его ферулы, если мы всерьез хотим сами установить себе правила, с помощью которых мы поднялись бы на вершину человеческого познания, то среди первых, конечно, следует признать это правило, предостерегающее, чтобы мы не злоупотребляли досугом, как делают многие, пренебрегая всем легким и занимаясь только трудными вещами, о которых они искусно строят поистине изощреннейшие предположения и весьма правдоподобные рассуждения, но после многих трудов наконец слишком поздно замечают, что лишь увеличили множество сомнений, но не изучили никакой науки.
Теперь же, так как мы несколько ранее сказали, что из других известных дисциплин только арифметика и геометрия остаются не тронутыми никаким пороком лжи и недостоверности, то, чтобы более основательно выяснить причину, почему это так, надо заметить, что мы приходим к познанию вещей двумя путями, а именно посредством опыта или дедукции. Вдобавок следует заметить, что опытные данные о вещах часто бывают обманчивыми, дедукция же, или чистый вывод одного из другого, хотя и может быть оставлена без внимания, если она неочевидна, но никогда не может быть неверно произведена разумом, даже крайне малорассудительным. И мне кажутся малополезными для данного случая те узы диалектиков, с помощью которых они рассчитывают управлять человеческим рассудком, хотя я не отрицаю, что эти же средства весьма пригодны для других нужд. Действительно, любое заблуждение, в которое могут впасть люди (я говорю о них, а не о животных), никогда не проистекает из неверного вывода, но только из того, что они полагаются на некоторые малопонятные данные опыта или выносят суждения опрометчиво и безосновательно.
Из этого очевидным образом выводится, почему арифметика и геометрия пребывают гораздо более достоверными, чем другие дисциплины, а именно поскольку лишь они одни занимаются предметом столь чистым и простым, что не предполагают совершенно ничего из того, что опыт привнес бы недостоверного, но целиком состоят в разумно выводимых заключениях. Итак, они являются наиболее легкими и очевидными из всех наук и имеют предмет, который нам нужен, поскольку человек, если он внимателен, кажется, вряд ли может в них ошибиться. Но потому не должно быть удивительным, если умы многих людей сами собой скорее предаются другим искусствам или философии: ведь это случается, поскольку каждый смелее дает себе свободу делать догадки о вещи темной, чем об очевидной, и гораздо легче предполагать что-либо в каком угодно вопросе, нежели достигать самой истины в одном, каким бы легким он ни был.
Теперь из всего этого следует заключить не то, что надо изучать лишь арифметику и геометрию, но только то, что ищущие прямой путь к истине не должны заниматься никаким предметом, относительно которого они не могут обладать достоверностью, равной достоверности арифметических и геометрических доказательств.
Правило III
Касательно обсуждаемых предметов следует отыскивать не то, что думают о них другие или что предполагаем мы сами, но то, что мы можем ясно и очевидно усмотреть или достоверным образом вывести, ибо знание не приобретается иначе.
Следует читать книги древних, поскольку огромным благодеянием является то, что мы можем воспользоваться трудами столь многих людей как для того, чтобы узнать о тех вещах, которые уже некогда были удачно открыты, так и для того, чтобы напомнить себе о тех остающихся во всех дисциплинах вещах, которые еще надлежит придумать. Но при всем том есть большая опасность, как бы те пятна заблуждений, которые возникают из-за слишком внимательного чтения этих книг, случайно не пристали к нам, сколь бы мы тому ни противились и сколь бы осмотрительными мы ни были. Ведь писатели обычно бывают такого склада ума. что всякий раз, когда они по безрассудному легковерию склоняются к выбору какого-либо спорного мнения, они всегда пытаются изощреннейшими доводами склонить нас к тому же; напротив, всякий раз, когда они по счастливой случайности открывают нечто достоверное и очевидное, они никогда не представляют его иначе как окутанным различными двусмысленностями, либо, надо думать, опасаясь, как бы не умалить достоинства открытия простотой доказательства, либо потому, что они ревниво оберегают от нас неприкрытую истину.
Так вот, хотя бы все они были искренними и откровенными и никогда не навязывали нам ничего сомнительного в качестве истинного, но всё излагали по чистой совести, однако, поскольку вряд ли одним человеком было сказано что-нибудь такое, противоположное чему не было бы выдвинуто кем-либо другим, мы всегда пребывали бы в нерешительности, кому из них следует поверить. И совершенно бесполезно подсчитывать голоса, чтобы следовать тому мнению, которого придерживается большинство авторов, так как, если дело касается трудного вопроса, более вероятно, что истина в нем могла быть обнаружена скорее немногими, чем многими. Но хотя бы даже все они соглашались между собой, их учение все же не было бы для нас достаточным: ведь, к слову сказать, мы никогда не сделались бы математиками, пусть даже храня в памяти все доказательства других, если бы еще по складу ума не были способны к разрешению каких бы то ни было проблем, или философами, если бы мы собрали все доводы Платона и Аристотеля, а об излагаемых ими вещах не могли бы вынести твердого суждения: ведь тогда мы казались бы изучающими не науки, а истории.
Кроме того, напомним, что никогда не следует смешивать вообще никакие предположения с нашими суждениями об истине вещей. Это замечание имеет немаловажное значение: ведь нет более веской причины, почему в общепринятой философии еще не найдено ничего столь очевидного и достоверного, что не могло бы привести к спору, чем та, что ученые, не довольствуясь познанием вещей ясных и достоверных, сперва осмелились высказаться и о вещах темных и неведомых, которых они коснулись посредством только правдоподобных предположений; затем они сами мало-помалу прониклись полным доверием к ним и, без разбора смешивая их с вещами истинными и очевидными, в конце концов не смогли заключить ничего, что не казалось бы зависимым от какого-либо положения такого рода и потому не было бы недостоверным.
Но чтобы далее нам не впасть в то же самое заблуждение, рассмотрим здесь все действия нашего разума, посредством которых мы можем прийти к познанию вещей без всякой боязни обмана, и допустим только два, а именно интуицию и дедукцию2.
Под интуицией я подразумеваю не зыбкое свидетельство чувств и не обманчивое суждение неправильно слагающего воображения, а понимание (conceptum) ясного и внимательного ума, настолько легкое и отчетливое, что не остается совершенно никакого сомнения относительно того, что мы разумеем, или, что то же самое, несомненное понимание ясного и внимательного ума, которое порождается одним лишь светом разума и является более простым, а значит, и более достоверным, чем сама дедукция, хотя она и не может быть произведена человеком неправильно, как мы отмечали ранее3. Таким образом каждый может усмотреть умом, что он существует, что он мыслит, что треугольник ограничен только тремя линиями, а шар — единственной поверхностью и тому подобные вещи, которые гораздо более многочисленны, чем замечает большинство людей, так как они считают недостойным обращать ум на столь легкие вещи.
Впрочем, чтобы ненароком не смутить кого-либо новым употреблением слова «интуиция» и других слов, в использовании которых я в дальнейшем вынужден подобным же образом отдаляться от их общепринятого значения4, я здесь вообще предупреждаю, что я совсем не думаю о том, каким образом все эти слова употреблялись в последнее время в школах, поскольку было бы очень трудно пользоваться теми же названиями, а подразумевать совершенно другое; я обращаю внимание только на то, что означает по-латыни каждое такое слово, чтобы всякий раз, когда не хватает подходящих выражений, я мог вложить нужный мне смысл в те слова, которые кажутся мне наиболее пригодными для этого.
Однако же эта очевидность и достоверность интуиции требуется не только для высказываний, но также и для каких угодно рассуждений. Взять, к примеру, такой вывод: 2 и 2 составляют то же, что 3 и 1; тут следует усмотреть не только то, что 2 и 2 составляют 4 и что 3 и 1 также составляют 4, но вдобавок и то, что из этих двух положений с необходимостью выводится и это третье.
Впрочем, может возникнуть сомнение, почему к интуиции мы добавили здесь другой способ познания, заключающийся в дедукции, посредством которой мы постигаем все то, что с необходимостью выводится из некоторых других достоверно известных вещей. Но это нужно было сделать именно так, поскольку очень многие вещи, хотя сами по себе они не являются очевидными, познаются достоверно, если только они выводятся из истинных и известных принципов посредством постоянного и нигде не прерывающегося движения мысли, ясно усматривающей каждую отдельную вещь; точно так же мы узнаем, что последнее звено какой-либо длинной цепи соединено с первым, хотя мы и не можем обозреть одним взором глаз всех промежуточных звеньев, от которых зависит это соединение, — узнаем, если только мы просмотрели их последовательно и помнили, что каждое из них, от первого до последнего, соединено с соседним. Итак, мы отличаем здесь интуицию ума от достоверной дедукции потому, что в последней обнаруживается движение, или некая последовательность, чего нет в первой, и, далее, потому, что для дедукции не требуется наличной очевидности, как для интуиции, но она, скорее, некоторым образом заимствует свою достоверность у памяти. Вследствие этого можно сказать, что именно те положения, которые непосредственно выводятся из первых принципов, познаются в зависимости от различного их рассмотрения то посредством интуиции, то посредством дедукции, сами же первые принципы — только посредством интуиции, и, напротив, отдаленные следствия — только посредством дедукции5.
Эти два пути являются самыми верными путями к знанию, и ум не должен допускать их больше — все другие надо отвергать, как подозрительные и ведущие к заблуждениям; однако это не мешает нам поверить, что те вещи, которые были открыты по наитию, более достоверны, чем любое познание, поскольку вера в них, как и всякая вера в загадочные вещи, является действием не ума, а воли, и, если бы она имела основания в разуме, их прежде всего можно и нужно было бы отыскивать тем или другим из уже названных путей, как мы, быть может, когда-нибудь покажем более обстоятельно.
Правило IV
Для разыскания истины вещей необходим метод.
Смертными владеет любопытство настолько слепое, что часто они ведут свои умы по неизведанным путям без всякого основания для надежды, но только для того, чтобы проверить, не лежит ли там то, чего они ищут; как если бы кто загорелся настолько безрассудным желанием найти сокровище, что беспрерывно бродил бы по дорогам, высматривая, не найдет ли он случайно какое-нибудь сокровище, потерянное путником. Точно так же упражняются почти все химики, большинство геометров и немало философов; я, правда, не отрицаю, что они иногда блуждают до такой степени удачно, что находят нечто истинное, однако я признаю по этой причине не то, что они более усердны, а лишь то, что они более удачливы. Но гораздо лучше никогда не думать об отыскании истины какой бы то ни было вещи, чем делать это без метода: ведь совершенно несомненно, что вследствие беспорядочных занятий такого рода и неясных размышлений рассеивается естественный свет и ослепляются умы; и у всех тех, кто привык таким образом бродить во мраке, настолько ослабляется острота зрения, что впоследствии они не могут переносить яркого света; это подтверждается и на опыте, так как очень часто мы видим, что те, кто никогда не утруждал себя науками, судят о встречающихся вещах гораздо более основательно и ясно, чем те, кто все свое время проводил в школах. Под методом же я разумею достоверные и легкие правила, строго соблюдая которые человек никогда не примет ничего ложного за истинное и, не затрачивая напрасно никакого усилия ума, но постоянно шаг за шагом приумножая знание, придет к истинному познанию всего того, что он будет способен познать.
Здесь же следует отметить два пункта: не принимать безусловно ничего ложного за истинное и достигать познания всех вещей, ибо если мы не знаем какую-либо вещь из тех, которые мы можем знать, то лишь потому, что мы никогда не замечали никакого пути, который вел бы нас к такому познанию, или потому, что мы впали в противоположное заблуждение. Но если метод правильно объясняет, каким образом следует пользоваться интуицией ума, чтобы не впасть в заблуждение, противное истине, и каким образом следует отыскивать дедуктивные выводы, чтобы прийти к познанию всех вещей, то, мне кажется, для того чтобы он был совершенным, не нужно ничего другого, поскольку невозможно приобрести никакого знания, кроме как посредством интуиции ума или дедукции, как уже было сказано раньше. Ведь он не может простираться и до того, чтобы указывать, каким образом следует совершать эти действия, ибо они являются первичными и самыми простыми из всех, так что, если бы наш разум не мог пользоваться ими уже раньше, он не воспринял бы никаких предписаний самого метода, сколь бы легки они ни были. Другие же действия ума, которыми диалектика силится управлять с помощью этих двух первых, здесь бесполезны, или, скорее, их нужно отнести к числу препятствий, так как невозможно прибавить к чистому свету разума ничего, что бы некоторым образом его не помрачило.
Поскольку же польза от этого метода столь велика, что предаваться без него наукам, кажется, скорее вредно, чем полезно, я легко убеждаюсь в том, что он был некоторым образом постигнут уже прежде более сильными умами, хотя бы под руководством одной лишь природы. Ведь человеческий ум заключает в себе нечто божественное, в чем были посеяны первые семена полезных мыслей, так что часто, как бы они ни были попираемы и стесняемы противными им занятиями, они все-таки производят плод, вызревающий сам собой. Это мы замечаем в самых легких из наук — арифметике и геометрии; в самом деле, для нас достаточно ясно, что древние геометры применяли некий анализ, который они распространяли на решение всевозможных проблем, хотя и ревниво утаили его от потомков. И теперь процветает некий род арифметики, называемый алгеброй, который осуществляет в отношении чисел то, что древние делали в отношении фигур. Однако эти две науки являются не чем иным, как появившимися сами собой плодами, вызревшими из врожденных начал данного метода, и я не удивляюсь, что применительно к простейшим предметам этих наук они до сих пор развивались более успешно, чем в остальных науках, где их обычно стесняют большие препятствия, но все-таки и там, если их пестовать с величайшей заботливостью, они, без сомнения, смогут достичь полной зрелости.
Это я главным образом и задумал сделать в данном трактате: ведь я не ценил бы высоко эти правила, если бы они были достаточны только для разрешения тех пустых проблем, которыми привыкли развлекаться досужие счетчики или геометры, ибо я в этом случае полагал бы, что я выделился не чем иным, как тем, что забавлялся пустяками, быть может, более искусно, нежели другие. И хотя здесь я буду много говорить о фигурах и числах, поскольку ни из каких других дисциплин не могут быть почерпнуты примеры столь же очевидные и столь же достоверные, тем не менее всякий, кто будет внимательно следить за моей мыслью, легко заметит, что ни о чем я не думаю здесь так мало, как об общепринятой математике, но излагаю некую другую дисциплину, такую, что упомянутые науки являются скорее ее покровом, нежели частями. Ведь эта наука должна содержать в себе первые начала человеческого рассудка и достигать того, чтобы извлекать истины из какого угодно предмета; и, если говорить откровенно, я убежден, что она превосходит любое другое знание, переданное нам людьми, так как она служит источником всех других знаний. О покрове же я сказал не потому, что хотел бы укрыть и укутать эту науку, чтобы уберечь ее от толпы, но скорее потому, что хотел бы принарядить и украсить ее так, чтобы она могла быть более приемлемой для человеческого ума.
Когда я впервые направил ум на математические дисциплины, я сразу же перечитал большую часть из того, что обычно передается от авторитетов в этих науках; в особенности я чтил арифметику и геометрию, поскольку, как было сказано, это простейшие из наук, являющиеся как бы путями к остальным. Но ни в той, ни в другой мне тогда, пожалуй, не попались в руки авторы, которые бы меня вполне удовлетворили. Конечно же очень многое из того, что я прочитал у этих авторов касательно чисел, было истинным, как я, проведя расчеты, убедился на опыте; касательно же фигур многое они определенным образом представляли моим глазам и выводили на основании некоторых заключений, но почему это обстояло именно так и каким образом было обнаружено, сами они, по-видимому, не показывали уму достаточно хорошо. Поэтому я не был удивлен, что даже многие из даровитых и образованных людей, испробовав эти науки, или быстро бросали их, как ребяческие и пустые, или, напротив, у самого порога отвращались от изучения тех же самых наук, как крайне трудных и запутанных. И действительно, нет ничего более бессмысленного, чем заниматься голыми числами и воображаемыми фигурами, так что может показаться, будто мы желаем найти успокоение в познании подобных пустяков, и потом настолько предаться тем поверхностным доказательствам, которые обнаруживаются чаще благодаря случаю, чем искусству, и относятся больше к зрению и воображению, чем к разуму, что мы некоторым образом отучимся пользоваться самим рассудком. В то же время нет ничего более сбивающего с толку, нежели посредством такого способа доказательства освобождаться от новых трудностей, скрытых в путанице чисел. Когда же потом я подумал, откуда же повелось, что некогда первые создатели философии не хотели допускать к изучению мудрости кого-либо несведущего в математике, как будто эта дисциплина казалась им самой легкой из всех и совершенно необходимой для того, чтобы просветить и подготовить умы к освоению других, более возвышенных наук, я вполне утвердился в подозрении, что они знали некую математику, весьма отличную от общепринятой математики нашего времени. Не то чтобы я считал, что они знали эту самую науку в совершенстве, ведь их безумные ликования и жертвы, приносимые в благодарность за незначительные открытия, ясно показывают, насколько они были безыскусны. И меня не заставят отказаться от моего мнения некоторые их механизмы, которые восхваляются у историков, ибо, хотя эти механизмы, вероятно, были весьма просты, их легко можно было превозносить, вплоть до признания их чудесами, невежественной и склонной к изумлению толпе. Но я убежден, что какие-то первые семена истин, которые присущи человеческим умам от природы и которые мы в себе заглушаем, ежедневно читая и слыша о стольких различных заблуждениях, обладали в той безыскусной и незатейливой древности такою силой, что благодаря тому самому свету ума, при посредстве которого люди видели, что следует предпочитать добродетель удовольствию, а честное — полезному, даже если они а не знали, почему это обстояло именно так, они также познали истинные идеи философии и математики, хотя и не могли еще овладеть в совершенстве самими науками. И мне по крайней мере кажется, что какие-то следы этой истинной математики обнаруживаются еще у Паппа и Диофанта, которые жили пусть и не в самую раннюю эпоху, но все же за много веков до нашего времени6. Я поверил бы тому, что ее впоследствии утаили с неким опасным коварством сами авторы; ведь подобно тому, что многие мастера делали, как стало известно, со своими изобретениями, авторы, возможно, опасались, что эта наука, поскольку она была самой легкой и простой, обесценилась бы, став общедоступной, и вместо нее предпочли показать нам как результаты своей науки, чтобы удивить нас, кое-какие бесплодные истины, остроумно доказанные на основании умозаключений, вместо того чтобы учить самой науке, которая не оставила бы никаких поводов для удивления. Наконец, было несколько даровитейших мужей, которые в наше время попытались воскресить эту самую математику, ибо ничем другим, кажется, не является та наука, которую называют чужеземным именем «алгебра», если бы только она могла быть освобождена от множества чисел и от необъяснимых фигур, которыми она загромождена, таким образом, что не испытывала бы больше недостатка в той высшей ясности и легкости, какая должна быть, как мы предполагаем, в истинной математике. Когда эти мысли обратили меня от частных занятий арифметикой и геометрией к некоему общему исследованию математики, я прежде всего задался вопросом, что же именно подразумевают все под этим названием и почему не только уже упомянутые науки, но также астрономия, музыка, оптика, механика и многие другие называются частями математики. В данном случае, конечно, недостаточно рассмотреть происхождение названия, ибо, если бы слово «математика» означало лишь то же самое, что и «дисциплина», (все прочие) дисциплины назывались бы математическими с не меньшим правом, чем сама геометрия. Но мы видим, что нет почти ни одного человека, который, если он успел хотя бы ступить на пороги школ, не сумел бы легко различить среди встречающихся ему вещей, что же относится к математике, а что — к другим дисциплинам. Рассматривающему это более внимательно стало бы в конце концов ясно, что к математике относятся лишь все те вещи, в которых исследуются какой-либо порядок или мера, и неважно, в числах ли, или фигурах, или звездах, или звуках, в любом ли другом предмете придется отыскивать такую меру; а потому должна существовать некая общая наука, которая, не будучи зависимой ни от какого частного предмета, объясняла бы все то, что может быть обнаружено в связи с порядком и мерой, и эта самая наука должна называться не заимствованным именем, а уже сделавшимся старым, но вновь вошедшим в употребление именем всеобщей математики, ибо в ней содержится все то, благодаря чему другие науки и называются частями математики7. Насколько же она превосходит в полезности и легкости другие, подчиненные ей науки, видно из того, что она распространяется на все те вещи, на которые распространяются и они, и, сверх того, на многие другие, и, если она заключает в себе какие-то трудности, точно такие же обнаруживаются и в этих науках, которым вдобавок присущи и другие трудности, вытекающие из их частных предметов и ей не свойственные. Отчего же теперь, когда все узнали ее название и понимают, даже не уделяя ей внимания, чем она занимается, происходит так, что многие усердно постигают другие дисциплины, которые от нее зависят, но саму ее никто не старается изучить? Я, конечно, удивился бы этому, если бы не знал, что все считают ее слишком легкой, и если бы не заметил уже давно, что человеческие умы, пренебрегая тем, что, как они полагают, можно легко (обнаружить), всегда спешат прямо к новым и более внушительным предметам.
Но, сознавая свою слабость, я решил в поисках знания о вещах твердо придерживаться такого порядка, чтобы, всегда начиная с самых простых и легких вещей, никогда не переходить к другим до тех пор, пока мне не покажется, что в самих этих вещах не осталось более ничего из того, к чему следует стремиться. Вот почему, насколько было в моих силах, я до сих пор разрабатывал эту всеобщую математику так, чтобы потом я мог считать себя способным изучать несколько более возвышенные науки с усердием, отнюдь не преждевременным. Однако, прежде чем отойти от этого, я попытаюсь собрать воедино и расположить по порядку все то, что я нашел весьма достойным внимания в предшествующих занятиях, как для того, чтобы впредь, когда с возрастом ослабеет память, я без труда мог, если потребует необходимость, восстановить это по своей книжке, так и для того, чтобы отныне, освободив память от этих вещей, я мог обратить более свободный ум к другому.
Правило V
Весь метод состоит в порядке и расположении тех вещей, на которые надо обратить взор ума, чтобы найти какую-либо истину. Мы будем строго придерживаться его, если шаг за шагом сведем запутанные и темные положения к более простым, а затем попытаемся, исходя из усмотрения самых простых, подняться по тем же ступеням к познанию всех прочих.
В одном этом заключается итог всего человеческого усердия, и для желающего приступить к познанию вещей следование данному правилу не менее необходимо, чем нить для Тесея, желающего проникнуть в лабиринт. Однако многие или не размышляют над тем, что оно предписывает, или вовсе не знают его, или предполагают, что в нем нет нужды, и часто исследуют труднейшие вопросы настолько беспорядочно, что кажутся мне поступающими точно так же, как если бы они попытались одним прыжком преодолеть расстояние от самой нижней части до верха какого-то здания, пренебрегая ступенями лестницы, предназначенными для этой цели, или не замечая их. Так поступают все астрологи, которые, не зная природы небес и даже не понаблюдав как следует за их движениями, надеются, что они смогут определить их воздействия. Так ведет себя большинство тех людей, которые изучают механику отдельно от физики и наугад изготовляют новые орудия, приводящие в движение. Таким же образом поступают и те философы, которые, пренебрегая опытами, думают, что истина выйдет из их собственного мозга, словно Минерва из головы Юпитера.
И все они очевидно грешат против этого правила. Но так как зачастую порядок, который здесь требуется, является настолько темным и запутанным, что не все будут в состоянии узнать, каков же он, то вряд ли кто-либо сможет достаточно хорошо оградить себя от заблуждения, если он не будет тщательно соблюдать то, что излагается в следующем правиле.
Правило VI
Для того чтобы отделять самые простые вещи от запутанных и исследовать их по порядку, необходимо в каждом ряде вещей, в котором мы прямо вывели некоторые истины из других, усматривать, что в нем является наиболее простым и насколько удалено от этого все остальное — более, или менее, или одинаково.
Хотя и кажется, что это положение не научает ничему особо новому, оно тем не менее содержит главный секрет искусства, и во всем данном трактате нет положения более полезного: ведь оно указывает, что все вещи могут быть выстроены в некие ряды, хотя и не постольку, поскольку они относятся к какому-либо роду сущего, подобно тому как философы распределили их по своим категориям, но поскольку одни из них могут быть познаны на основании других так, что всякий раз, когда возникнет какое-либо затруднение, мы сможем тотчас узнать, не будет ли полезным сначала обозреть некоторые другие вещи, и какие именно, и в каком порядке.
Для того же, чтобы это могло быть сделано правильно, необходимо отметить, во-первых, что все вещи в том смысле, в каком они могут быть полезными для нашего замысла, согласно которому мы не рассматриваем их природы как обособленные, но сравниваем их друг с другом, чтобы познать одни на основании других, можно назвать или абсолютными, или относительными.
Абсолютным я называю все, что заключает в себе искомую чистую и простую природу, например все то, что рассматривается как независимое, причина, простое, всеобщее, единое, равное, подобное, прямое и другое в том же роде. Я называю абсолютное также самым простым и самым легким для того, чтобы пользоваться им для разрешения вопросов.
Относительным же является то, что причастно той же самой природе или по крайней мере чему-либо производному от нее, в соответствии с чем оно может быть соотнесено с абсолютным и выведено из него посредством некоего ряда, но вдобавок оно привносит в свое понятие нечто другое, что я именую отношениями; таковым (т. е. относительным) является все то, что называют зависимым, действием, сложным, частным, множественным, неравным, несходным, непрямым и т. д. Эти относительные вещи отдалены от абсолютных тем больше, чем больше они содержат подобных отношений, подчиненных друг другу; и мы предупреждаем в данном правиле, что необходимо различать все эти отношения и следить за их взаимной связью и их естественным порядком, так чтобы, начав с последнего из них, мы смогли, пройдя через все другие, достичь того, что является наиболее абсолютным.
И секрет всего искусства состоит в том, чтобы среди всех вещей мы старательно подмечали наиболее абсолютное. Ведь некоторые вещи с одной точки зрения более абсолютны, чем другие, но, будучи рассмотрены иначе, оказываются более относительными; так, всеобщее, конечно, более абсолютно, нежели частное, потому что оно обладает более простой природой, но оно же может быть названо и более относительным, нежели частное, так как в своем существовании зависит от единичных вещей и т. д. Подобным же образом некоторые вещи иногда действительно более абсолютны, чем другие, но тем не менее они еще не являются наиболее абсолютными из всех; так, если мы рассматриваем единичные вещи, вид представляет собой нечто абсолютное, если же рассматриваем род, вид есть нечто относительное; среди измеримых вещей протяжение есть нечто абсолютное, но среди протяжений таковым является длина и т. д. И наконец, для того чтобы было более понятно, что мы рассматриваем здесь ряды вещей, подлежащих познанию, а не природу каждой из них, мы намеренно перечислили причину и равное среди абсолютных вещей, хотя их природа в действительности относительна: ведь причина и действие у философов являются соотносительными; однако, если мы здесь отыскиваем, каково действие, сначала надлежит познать причину, а не наоборот. Равные вещи также соответствуют друг другу, но те, которые являются неравными, мы узнаём лишь путем сопоставления с равными, а не наоборот и т. д.
Следует отметить, во-вторых, что существует хотя бы несколько чистых и простых природ, которые можно усмотреть прежде всего и сами по себе, независимо от каких-то других, либо в самих опытах, либо с помощью некоего присущего нам света; и мы говорим, что необходимо старательно подмечать их, ибо они являются теми же самыми природами, которые мы называем наиболее простыми в каждом ряде. Все же прочие могут быть постигнуты не иначе, как если будут выведены из них, и это осуществимо либо непосредственно и ближайшим путем, либо только через посредство двух, или трех, или более того различных заключений, число которых также необходимо заметить, чтобы узнать, на большее или на меньшее число ступеней отдалены они от первого и наиболее простого положения. Таковой является повсюду связь следствий, из коей возникают те ряды искомых вещей, к которым необходимо свести любой вопрос, чтобы он мог быть исследован при помощи верного метода. Но так как нелегко обозреть их все и, кроме того, так как их нужно не столько удерживать в памяти, сколько различать благодаря некоей остроте ума, следует отыскать нечто способное настроить умы таким образом, чтобы всякий раз, когда понадобится, они тотчас замечали их; для этого, конечно, нет, как испытал я сам, ничего более подходящего, чем приучиться с известной проницательностью размышлять обо всем самом малом из того, что мы уже восприняли ранее.
Наконец, в-третьих, следует отметить, что не нужно начинать занятия с исследования трудных вещей, но, прежде чем приступить к разрешению каких-либо определенных вопросов, сначала надлежит без всякого разбора собрать обнаруживающиеся сами собой истины и затем постепенно рассмотреть, можно ли вывести из них какие-либо другие, а из последних — опять-таки другие, и далее в той же последовательности. Потом, сделав это, необходимо внимательно поразмыслить над открытыми истинами и тщательно обдумать, почему мы смогли отыскать одни из них скорее и легче, чем другие, и каковы они, чтобы, исходя из этого, мы также могли, когда займемся каким-либо определенным вопросом, решить, к отысканию каких других истин полезно приступить прежде всего.
Например, если бы мне представилось, что число 6 есть удвоенное 3, я искал бы затем удвоенное 6, а именно 12, и снова искал бы, если угодно, удвоенное 12, а именно 24, и удвоенное 24, а именно 48, и т. д.; и отсюда я, как это нетрудно сделать, вывел бы, что между 3 и 6 существует та же самая пропорция, которая существует между 6 и 12, а также между 12 и 24 и т. д., и ввиду этого числа 3, 6, 12, 24, 48 и т. д. являются непрерывно пропорциональными. Потому-то, хотя бы все это было настолько очевидным, что показалось бы чуть ли не ребяческим, я, внимательно поразмыслив, конечно, понимаю, каким образом запутываются все вопросы, которые могут быть поставлены касательно пропорций или отношений вещей, и в каком порядке они должны быть исследованы; в одном этом заключается свод всей чисто математической науки.
Действительно, я замечаю, во-первых, что удвоенное б найти было не труднее, чем удвоенное 3, и равным образом во всех случаях, когда найдена пропорция между двумя какими бы то ни было величинами, можно допустить бесчисленное множество других величин, между которыми была бы та же самая пропорция, и что природа затруднения не изменилась бы, если бы отыскивались три, или четыре, или большее число величин подобного рода, так как, разумеется, следует искать каждую из них в отдельности, не принимая в расчет прочие. Затем я замечаю, что, хотя для данных величин 3 и 6 я легко нашел бы третью в непрерывной пропорции, а именно 12, тем не менее для двух данных крайних величин, а именно 3 и 12, не так легко можно найти среднюю, а именно 6; для рассматривающего причину этого очевидно, что здесь налицо иной род затруднения, совершенно отличный от предшествующего, так как для того, чтобы найти среднее пропорциональное, следует одновременно обращать внимание на две крайние величины и на пропорцию, которая существует между этими двумя, с тем чтобы путем ее деления получить некую новую величину; это действие весьма отлично от того, которое, если даны две величины, требуется для нахождения третьей в непрерывной пропорции. Я иду еще дальше и исследую, одинаково ли легко для данных величин 3 и 24 можно было бы найти одну из двух средних пропорциональных, а именно 6 и 12; и здесь встречается еще один род затруднения, более запутанный, чем предыдущие, ибо здесь следует одновременно обращать внимание не только на один или на два, а на три различных члена, чтобы найти четвертый. Можно пойти еще дальше и рассмотреть, было ли бы еще труднее, если даны только 3 и 48, найти одно из трех средних пропорциональных, т. е. 6, 12 и 24; на первый взгляд кажется, что это именно так. Но потом сразу же оказывается, что это затруднение можно расчленить и уменьшить, а именно если сначала отыскивать лишь одно среднее пропорциональное — между 3 и 48, т. е. 12, а потом отыскивать другое среднее пропорциональное — между 3 и 12, а именно 6, и другое — между 12 и 48, а именно 24, и, таким образом, это затруднение можно свести ко второму, ранее описанному роду затруднения.
Из всего этого мне вдобавок видно, как можно достичь познания одной и той же вещи различными путями, один из которых гораздо труднее и темнее другого. Так, найти эти четыре непрерывно пропорциональных числа 3, 6, 12, 24, если из них допускаются два следующих друг за другом, а именно 3 и 6, или 6 и 12, или 12 и 24, с тем чтобы на основании этих двух найти остальные, будет действием чрезвычайно легким для выполнения; и тогда мы говорим, что искомая пропорция исследуется прямо. Если же допускаются два числа, чередующиеся через одно, а именно 3 и 12 или 6 и 24, с тем чтобы потом найти остальные, тогда мы говорим, что затруднение исследуется косвенно первым способом. Равным образом, когда допускаются два крайних числа, а именно 3 и 24, с тем чтобы на основании их отыскать промежуточные 6 и 12, тогда пропорция будет исследоваться косвенно вторым способом. Точно так же я мог бы продолжать и далее и вывести из одного этого примера многие другие следствия, но и упомянутых достаточно для того, чтобы читатель понял, что я хотел сказать, когда называл какое-либо положение выводимым прямо или косвенно, и чтобы он признал, что на основе знания о некоторых наиболее легких и первичных вещах многое и в других дисциплинах может быть открыто внимательно размышляющими и тщательно исследующими людьми.
Правило VII
Чтобы придать науке полноту, надлежит все, что служит нашей цели, вместе и по отдельности обозреть в последовательном и нигде не прерывающемся движении мысли и охватить достаточной и упорядоченной энумерацией.
Соблюдение того, что здесь предлагается, необходимо, чтобы отнести к числу достоверных те истины, которые, как мы сказали выше, непосредственно невыводимы из первых и самоочевидных принципов. Ведь это иногда делается при помощи столь длинного ряда выводов, что, когда мы достигаем данных истин, нам нелегко припомнить весь путь, который привел нас к этому; потому мы и говорим, что слабость памяти нужно возместить неким последовательным движением мысли. Так, если, например, посредством различных действий я узнал прежде всего, каковым является отношение между величинами А и В, потом между В и С, затем между С и D и, наконец, между D и Е, я не вижу еще, каково отношение между А и Е, и не могу вполне понять его на основании уже известных отношений, если не вспомню их все. Вот почему я несколько раз пробегаю их неким последовательным движением мысли, созерцающей каждое отношение в отдельности и одновременно переходящей к другим, пока не научусь переходить от первого к последнему настолько быстро, что, не допуская почти никакого участия памяти, смогу, по-видимому, созерцать всё сразу: ведь таким образом не только оказывается помощь памяти, но еще и преодолевается медлительность ума, и в некотором отношении расширяются его способности.
Однако мы добавляем, что это движение нигде не должно прерываться, так как те, кто пытается слишком быстро вывести что-либо из отдаленных принципов, часто не просматривают всю цепь промежуточных заключений настолько тщательно, чтобы не проскочить ненароком многих из них. Но конечно, как только пропускается нечто даже самое малое, тотчас разрывается цепь и рушится вся достоверность заключения.
Кроме того, мы говорим здесь, что энумерация требуется для придания науке полноты, ибо, хотя другие предписания способствуют разрешению очень многих вопросов, но только благодаря энумерации, каким бы вопросом мы ни занимали ум, мы всегда вынесем истинное и достоверное суждение о нем, и потому от нас совершенно ничего не ускользнет, а мы, по-видимому, будем знать что-либо обо всем.
Итак, здесь энумерация, или индукция, — это исследование всего того, что относится к какому-либо предложенному вопросу, настолько тщательное и точное, что на основании его мы можем с достоверностью и очевидностью заключить, что нами ничего не было пропущено по недосмотру8; так что, если искомая вещь и останется скрытой от нас после того, как мы применили эту энумерацию, мы по крайней мере станем более сведущими в том отношении, что твердо уясним: эта вещь не могла быть найдена никаким известным нам путем; и если, как часто бывает, мы случайно сумели бы обозреть все пути, которые открыты к ней людям, то можно было бы смело утверждать, что познание ее превосходит все способности человеческого ума.
Кроме того, следует отметить, что под достаточной энумерацией, или индукцией, мы разумеем только ту, благодаря которой истина выводится достовернее, чем посредством любого другого рода доказательства, за исключением простой интуиции, и всякий раз, когда какое-либо познание нельзя свести к индукции, для нас, если сброшены все узы силлогизмов, остается этот единственный путь, к которому мы должны проявлять полное доверие. Ибо, какие бы положения мы непосредственно ни выводили одни из других, они, если бы вывод был очевиден, оказывались бы уже сведенными к подлинной интуиции. Однако, если мы выводим нечто одно из многочисленных и разрозненных положений, способности нашего разума зачастую бывают недостаточными для того, чтобы он сумел охватить их все единым взором; в таком случае разуму следует довольствоваться достоверностью этого действия. Точно так же мы не можем одним взором глаз различить все звенья какой-либо очень длинной цепи, но тем не менее, если бы мы увидели соединение каждого звена в отдельности с соседним, этого было бы достаточно, чтобы сказать, что мы также усмотрели, каким образом последнее звено соединяется с первым.
Я сказал, что это действие должно быть достаточным, потому что часто оно может быть неполноценным и, следовательно, ведущим к заблуждению. Ведь иногда, хотя бы мы и обозрели посредством энумерации многие весьма очевидные положения, тем не менее если мы упустим нечто даже самое малое, цепь разрывается и рушится вся достоверность заключения. Иногда же мы наверное охватываем энумерацией все положения, но не различаем каждое из них в отдельности, так что все они познаются нами только смутно.
Далее, эта энумерация иногда должна быть полной, иногда — раздельной, а порой от нее не требуется ни того, ни другого, потому-то и было сказано только, что она должна быть достаточной. Действительно, если бы я захотел посредством энумерации доказать, сколько родов сущностей являются телесными и каким-либо образом доступными чувствам, я не стал бы утверждать, что их существует столько-то, и не более, если бы прежде не узнал с достоверностью, что посредством энумерации все они были охвачены мною и каждый из них был отделен от других. Однако, если я захочу тем же путем показать, что разумная душа не является телесной, нет необходимости в том, чтобы энумерация была полной, но будет достаточно, если я разом распределю все тела по нескольким группам таким образом, что докажу: разумная душа не может быть отнесена ни к одной из них. Если, наконец, я захочу показать посредством энумерации, что площадь круга больше всех площадей других фигур равного периметра, то не нужно просматривать все фигуры, но достаточно доказать это для некоторых фигур в частности, чтобы посредством индукции вывести то же самое и для всех других.
Я добавил также, что энумерация должна быть упорядоченной, как потому, что против уже перечисленных недостатков нет никакого более действенного средства, чем исследовать все по порядку, так и потому, что, если бы, как часто случается, каждую из вещей, относящихся к обсуждаемому предмету, потребовалось рассмотреть в отдельности, не хватило бы никакой человеческой жизни, либо оттого, что эти вещи чрезвычайно многочисленны, либо оттого, что одни и те же вещи слишком часто оказывались бы подлежащими повторению. Но если мы расположим их все в наилучшем порядке, так что большинство их окажется сведенным в определенные классы, будет достаточно либо рассмотреть тщательно один из этих классов, или что-нибудь одно из каждого класса, или некоторые из них прежде, чем прочие, либо по крайней мере никогда ничего не просматривать без пользы дважды. Это полезно настолько, что зачастую благодаря правильно установленному порядку за короткое время и без особого труда доводится до конца многое, казавшееся на первый взгляд необъятным.
Однако этот порядок вещей, подлежащих энумерации, в большинстве случаев может быть различным и зависит от выбора каждого, и потому, чтобы удачно придумать его, стоит вспомнить, что было сказано в пятом правиле. Даже в самых незамысловатых человеческих искусствах есть весьма много вещей, весь метод обнаружения которых заключается в установлении этого порядка: так, если бы вы захотели составить наилучшую анаграмму посредством перестановки букв какого-либо имени, не нужно ни переходить от более легкого к более трудному, ни отличать абсолютное от относительного, ведь этим действиям здесь нет места, но вам будет достаточно установить такой порядок исследования перестановок букв, при котором одни и те же перестановки никогда не просматривались бы дважды и совокупность их, например, была бы подразделена на определенные классы таким образом, чтобы тотчас становилось ясно, в каком именно классе больше надежды обнаружить то, что отыскивается, ведь тогда работа часто будет не долгой, а лишь ребяческой. Впрочем, не нужно разделять эти три последних правила, потому что в большинстве случаев о них следует думать одновременно и все они одинаково содействуют совершенствованию метода; и нет большой разницы, какое из них было преподано первым, но мы вкратце объяснили их здесь, потому что в оставшейся части трактата не понадобится почти ничего другого, как только изложить в частности то, что мы охватили здесь в общем.
Правило VIII
Если в ряде вещей, подлежащих изучению, встретится какая-либо вещь, которую наш разум не в состоянии достаточно хорошо рассмотреть, тут необходимо остановиться и не изучать другие вещи, следующие за ней, а воздержаться от ненужного труда.
Три предшествующих правила предписывают порядок и объясняют его, настоящее же указывает, когда именно он совершенно необходим и когда — только полезен. Разумеется, все, что составляет целую ступень в этом ряде, посредством которого следует переходить от относительного к чему-то абсолютному или обратно, с необходимостью нужно исследовать прежде всего дальнейшего. Но если, как часто бывает, многие вещи относятся к одной и той же ступени, всегда полезно при этом обозреть их все по порядку. Однако мы не обязаны соблюдать это требование столь точно и строго, и в большинстве случаев, хотя мы познаём с очевидностью не все, но лишь немногие вещи или даже какую-либо одну, все же можно продвигаться дальше.
Это правило с необходимостью следует из доводов, приведенных для обоснования второго правила, однако не следует считать, что оно не содержит ничего нового для того, чтобы сделать нас более учеными, хотя и кажется лишь удерживающим нас от исследования некоторых вещей и не выявляющим никакой истины: несомненно, что оно по крайней мере не учит новичков ничему другому, как только тому, чтобы они не трудились понапрасну, почти на том же основании, что и второе правило. Но тем, кто вполне усвоил семь предыдущих правил, оно указывает, каким образом они смогут удовлетворить самих себя в какой угодно науке настолько, что не пожелают больше ничего; ибо всякий, кто точно соблюдал бы предыдущие правила для разрешения какого-либо затруднения и кому тем не менее будет предписано этим правилом где-либо остановиться, узнает тогда с достоверностью, что он не сможет найти искомое знание никакими стараниями, и не по причине ущербности ума, но потому, что этому препятствует природа самого затруднения или человеческий удел. Данное познание есть наука в не меньшей мере, чем то, которое выявляет природу самой вещи, и, по-видимому, не был бы в здравом уме тот, кто простирал бы свою любознательность дальше.
Все это следует пояснить одним или двумя примерами. Если, например, кто-либо занимавшийся одной лишь математикой отыскивает ту линию, которую в диоптрике называют анакластической, т. е. ту, на которой параллельные лучи преломляются таким образом, что после преломления все они пересекутся в одной точке, он, конечно, легко заметит, что в соответствии с правилами пятым и шестым определение этой линии зависит от отношения углов преломления к углам падения; но так как он не будет способен к этому исследованию, поскольку оно относится не к математике, а к физике, тут он будет вынужден остановиться на пороге и не делать ничего, если бы даже он захотел почерпнуть это знание у философов или заимствовать его из опыта: ведь он погрешил бы против третьего правила. И кроме того, это положение еще является составным и относительным, однако можно обладать достоверным опытом только в отношении вещей совершенно простых и абсолютных, как будет сказано в своем месте. Тщетно будет он также предполагать между такими углами некое соотношение, которое, по его допущению, будет самым истинным из всех, ведь тогда он скорее отыскивал бы не анакластическую линию, но лишь такую, которая бы соответствовала смыслу его предположения.
Если же какой-либо человек, который не только изучает математику, но и желает, в соответствии с первым правилом, отыскать истину во всех встречающихся вещах, натолкнется на то же самое затруднение, он обнаружит далее, что названное соотношение между углами падения и преломления зависит от изменения этих углов вследствие различия сред, что это изменение опять-таки зависит от способа, каким луч проникает сквозь прозрачное тело, и что познание этого способа проникновения требует, чтобы природа действия света также была известна, что, наконец, для понимания действия света необходимо знать, что такое естественная сила вообще, и понимать, что последняя является наиболее абсолютным во всем данном ряде. Итак, после того как он ясно постигнет это посредством интуиции ума, он вернется по тем же ступеням, согласно пятому правилу, и если на второй ступени он не сможет тотчас же познать природу действия света, он перечислит, по правилу седьмому, все другие естественные силы, так что на основе познания чего-либо другого, по крайней мере посредством сравнения, о котором мы скажем позднее, он уразумеет также и эту природу; сделав это, он отыщет, каким образом луч проникает сквозь прозрачное тело, и так будет просматривать по порядку остальное, пока не дойдет до самой анакластической линии. Хотя до сих пор ее тщетно отыскивали многие, тем не менее я не вижу ничего, что могло бы препятствовать ее очевидному познанию кем-либо в полной мере использовавшим наш метод.
Но приведем самый замечательный пример. Если кто-то поставит своей задачей исследовать все истины, для познания которых достаточно человеческого разумения, — а это, мне кажется, надлежит сделать хотя бы раз в жизни всем, кто серьезно доискивается здравого смысла, — он наверняка обнаружит с помощью данных правил, что ничего невозможно познать прежде, чем разум, так как от него зависит познание всего остального, а не наоборот; затем, постигнув все то, что непосредственно следует за познанием чистого разума, он среди прочего перечислит все другие орудия познания, какими мы обладаем, кроме разума; их окажется только два, а именно фантазия и чувство. Итак, он приложит все старание, чтобы различить и исследовать три этих способа познания, и, увидя, что истина и ложь в собственном смысле могут существовать не иначе как лишь в разуме, но зачастую они ведут свое происхождение только от двух других способов, он постарается обратить внимание на все те вещи, которыми он может быть введен в заблуждение, с тем чтобы остерегаться их, и точно перечислит все пути, которые открыты людям к истине, с тем чтобы следовать верным путем: ведь они не настолько многочисленны, чтобы нельзя было легко найти их все посредством достаточной энумерации.
Неопытным это покажется удивительным и невероятным, как только в отношении каждого предмета он отличит те познания, которые лишь наполняют или украшают память, от тех, благодаря которым кто-либо должен быть назван поистине более просвещенным, что достигается так же легко… Он вполне осознает, что больше не пребывает в неведении относительно чего-либо по недостатку ума или умения и что другим человеком вообще не может быть познано что-нибудь, чего и он не был бы также способен познать, стоит ему как подобает направить ум на то же самое. И хотя зачастую могут предвидеться многие затруднения, исследование которых будет ему запрещено настоящим правилом, но, поскольку он ясно поймет, что эти затруднения превышают все способности человеческого ума, он не будет вследствие этого считать себя более несведущим, но само знание о том, что искомая вещь не может быть познана никем, с избытком удовлетворит его любознательность, если он благоразумен.
Но чтобы нам не быть всегда неуверенными в том, что же может познать ум, и чтобы не усердствовать неосмотрительно и понапрасну, прежде чем мы приступим к познанию вещей в частности, надлежит хотя бы раз в жизни тщательно исследовать, к каким же познаниям способен человеческий разум. Чтобы лучше осуществить это, всегда необходимо из вещей, одинаково легких, сначала исследовать те, которые являются более полезными.
Ведь этот метод подобен тем из механических ремесел, которые не нуждаются в посторонней помощи, но сами наставляют, каким образом надо изготовлять инструменты для них. Действительно, если кто-либо пожелал бы заняться одним из этих ремесел, например кузнечным, но оказался бы лишенным всех инструментов, он вначале, конечно, был бы вынужден использовать твердый камень или какую-нибудь необработанную глыбу железа вместо наковальни, взять булыжник вместо молота, приладить деревянные палки наподобие щипцов и по мере необходимости подбирать другие орудия такого же рода; затем, приготовив это, он не принялся бы тотчас же выковывать для нужд других людей мечи, или шлемы, или еще какую-нибудь вещь из тех, которые делаются из железа, но прежде всего изготовил бы молоты, наковальню, щипцы и прочие полезные для него самого инструменты. Данный пример убеждает нас в том, что, поскольку в этих начинаниях мы сможем обнаружить только некоторые безыскусные предписания, которые кажутся скорее врожденными нашим умам, чем приобретенными при посредстве искусства, не следует тотчас пытаться с их помощью уладить споры философов или распутать хитросплетения математиков; но сначала их следует использовать для того, чтобы с величайшим усердием разыскивать все другое, являющееся более необходимым для исследования истины, в особенности потому, что нет никакой причины, по которой покажется более трудным раскрыть это, чем какие-либо вопросы из тех, что обычно ставятся в геометрии, или физике, или других дисциплинах.
Но здесь поистине не может быть ничего полезнее, чем изучать, что такое человеческое познание и как далеко оно простирается. Потому ныне мы и охватываем это одним-единственным вопросом, который, как мы полагаем, необходимо исследовать первым из всех при помощи правил, уже изложенных ранее, а это хотя бы раз в жизни должно быть сделано каждым из тех, кто мало-мальски любит истину, потому что в исследовании данного вопроса заключены верные средства познания и весь метод. Напротив, ничто не кажется мне более нелепым, чем, как делают многие, смело спорить о тайнах природы, о влиянии небес на эти низшие области, о предсказании грядущих событий и о подобных вещах, никогда, однако, даже не задавшись вопросом о том, достаточно ли человеческого разумения, чтобы это раскрыть. И не должно казаться утомительным или трудным делом определение границ того ума, который мы осознаем в нас самих, раз мы зачастую не колеблемся выносить суждение даже о тех вещах, которые находятся вне нас и совершенно чужды нам. И не является непомерной задачей, если мы хотим объять мыслью все вещи, содержащиеся в нашей вселенной, с тем чтобы узнать, каким образом каждая из них подлежит исследованию нашего ума: ведь не может быть ничего столь многочисленного или разрозненного, что его нельзя было бы посредством той энумерации, о которой мы говорили, заключить в известные границы и распределить по нескольким разделам. Для того же, чтобы опробовать это на предложенном вопросе, мы сначала разделяем на две части все, что его касается, так как он должен быть отнесен или к нам, способным к познанию, или к самим вещам, которые могут быть познаны; два этих пункта мы обсуждаем по отдельности.
И мы, конечно, замечаем в самих себе, что только разум способен к науке, но ему могут содействовать или препятствовать три другие способности, а именно воображение, чувство и память. Следовательно, нужно рассмотреть по порядку, для того чтобы остеречься, в чем каждая из этих способностей может мешать или, чтобы воспользоваться всеми их возможностями, в чем может быть полезной. И таким образом, эта первая часть будет исследована посредством достаточной энумерации, как будет показано в следующем правиле.
Затем нужно перейти к самим вещам, которые должны рассматриваться лишь постольку, поскольку они затрагиваются разумом; в этом смысле мы разделяем их на природы наиболее простые и сложные, или составные. Простые могут быть только духовными, или телесными, или относящимися и к тому и к другому роду; наконец, из составных одни разум сознает пребывающими именно таковыми до того, как он вынесет о них определенное суждение, другие же составляет он сам. Все это будет подробнее изложено в двенадцатом правиле, где будет доказано, что ложь не может иметь места нигде, кроме как в этих последних, которые составляются разумом; потому мы разделяем их еще на те, которые выводятся из простейших и самоочевидных природ и о которых мы будем рассуждать во всей следующей книге, и те, которые предполагают также другие (являющиеся, как мы убеждаемся на опыте, составными в действительности) и для описания которых мы предназначаем целиком третью книгу.
И во всем трактате мы, конечно, будем пытаться все пути, которые открыты людям к познанию истины, проследить столь тщательно и представить столь легкими, что всякий, кто в совершенстве изучит весь этот метод, каким бы посредственным умом он ни обладал, увидит тем не менее, что нет никаких путей, закрытых для него в большей степени, чем для других людей, и что он не останется больше в неведении о чем-либо по недостатку ума или умения. Но всякий раз, как он направит ум на познание какой-либо вещи, он или полностью обретет это познание, или доподлинно узнает, что оно зависит от какого-нибудь опыта, который не в его власти, и потому не станет обвинять свой ум, хотя и будет вынужден на этом остановиться, или, наконец, докажет, что искомая вещь превышает все способности человеческого ума, и, таким образом, он не будет вследствие этого считать себя более несведущим, так как знание этого является знанием в не меньшей степени, чем знание чего бы то ни было другого.
Правило IX
Следует целиком обратить взор ума на самые незначительные и наиболее легкие вещи и дольше задерживаться на них, пока мы не приучимся отчетливо и ясно усматривать истину.
Описав два действия нашего разума — интуицию и дедукцию, которыми, как мы сказали, только и надо пользоваться при изучении наук, продолжим в этом и следующем правилах разъяснение того, какими стараниями мы можем стать более способными к осуществлению этих действий и одновременно усовершенствовать две главные способности ума, а именно проницательность в отчетливом усмотрении каждой из вещей и находчивость в искусном выведении одних из других.
При этом, как нужно пользоваться интуицией ума, мы узнаем хотя бы из сравнения ее со зрением: ведь тот, кто хочет сразу обозреть одним взором много предметов, не увидит отчетливо ни одного из них; и равным образом тот, кто имеет обыкновение в одном акте мышления обращать внимание сразу на многие предметы, обладает путаным умом. Однако те мастера, которые занимаются тонкой работой и привыкли со вниманием устремлять взор на отдельные точки, благодаря упражнению приобретают способность в совершенстве различать сколь угодно малые и тонкие вещи; точно так же те, кто никогда не разбрасывается мыслью сразу на различные предметы, а всегда всецело сосредоточивается на рассмотрении самых простых и легких вещей, становятся проницательными.
Тем не менее порок, общий для смертных, заключается в том, что трудное кажется им более прекрасным; и многие полагают, что они ничего не узнают, когда усматривают весьма ясную и простую причину какой-либо вещи, а между тем они восхищаются некоторыми напыщенными и выспренними рассуждениями философов, хотя они большей частью покоятся на основаниях, никем никогда не изученных в достаточной степени: поистине безрассудны те, кто считает потемки более яркими, чем свет. Напротив, следует отметить, что те, кто действительно знает, с одинаковой легкостью распознают истину независимо от того, вывели они ее из простого предмета или из запутанного: ведь они постигают любую истину посредством сходного, единого и определенного акта, с тех пор как они однажды достигли ее; но вся разница заключается в пути, который, конечно, должен быть длиннее, если он ведет к истине, более удаленной от первых и в высшей степени безусловных начал.
Итак, всем следует привыкнуть сразу охватывать мыслью столь немногое и столь простое, что они никогда не сочтут себя знающими то, что не усматривается ими так же отчетливо, как то, что они познают отчетливее всего. Правда, некоторые рождаются гораздо более способными к этому, чем другие, однако при посредстве искусства, а также упражнения умы могут стать гораздо более способными к этому; есть один пункт, на который, как мне кажется, здесь следует указать прежде всего, а именно: чтобы каждый твердо убедил себя в том, что не из внушительных и темных вещей, а лишь из легких и более доступных должны выводиться сколь угодно сокровенные знания.
Ведь если я, например, захочу исследовать, может ли какая-либо естественная сила в одно мгновение перенестись в отдаленное место через все промежуточное расстояние, я не обращу ум тотчас же ни к магнитной силе, ни к влиянию звезд, ни даже к скорости света, чтобы выяснить, не происходят ли, возможно, такие действия мгновенно: ведь это может быть доказано мною с большим трудом, чем то, что требуется; но я лучше поразмышляю над пространственными перемещениями тел, так как во всем этом роде не может быть ничего более ощутимого. И я замечу, что камень действительно не может мгновенно передвинуться из одного места в другое, так как он является телом; сила же, подобная той, которая движет камнем, передается только мгновенно, если она в чистом виде переходит от одного носителя к другому. Например, если я приведу в движение один конец сколь угодно длинной палки, я легко пойму, что сила, благодаря которой движется эта часть палки, в то же самое мгновение с необходимостью приводит в движение также и все другие ее части, ибо в этом случае сила передается в чистом виде и не находится в каком-либо теле, как, например, в камне, посредством которого она переносится.
Таким же образом, если я захочу узнать, как из одной и той же простой причины могут одновременно проистекать противоположные действия, я не буду заимствовать у врачей лекарства, которые изгоняют одни жидкости и удерживают другие, и не буду нести вздор о Луне, будто она согревает посредством света и охлаждает посредством скрытого качества; но лучше я рассмотрю весы, на которых один и тот же груз в одно и то же мгновение поднимает одну чашу и вместе с тем опускает другую, и т. п.
Правило X
Чтобы стать находчивым, ум должен упражняться в разыскании тех вещей, которые уже были открыты другими, и при помощи метода обозревать даже самые незамысловатые изобретения людей, но в особенности те, которые объясняют или предполагают порядок.
Признаюсь, я родился с таким умом, что всегда находил величайшее удовольствие от занятий не в том, чтобы выслушивать доводы других, а в том, чтобы находить их собственными стараниями; это — единственное, что привлекало меня к изучению наук, когда я был еще молодым, и всякий раз, когда какая-либо книга сулила в заглавии новое открытие, я пробовал, прежде чем читать дальше, узнать, не достиг ли бы и я, возможно, чего-либо подобного благодаря некоей врожденной находчивости, и тщательно остерегался, как бы не лишить себя этого невинного удовольствия поспешным чтением. Это удавалось столь часто, что я наконец заметил, что я успешнее достигал истины вещей не так, как обыкновенно делают другие, т. е. не посредством путаных и проводимых вслепую изысканий и скорее благодаря случаю, нежели искусству, — на основе длительного опыта я выявил верные правила, которые немало способствуют этому и которыми я воспользовался впоследствии для установления многих других правил. И тщательно разработав таким образом весь этот метод, я убедился в том, что с самого начала следовал наиболее полезному из всех способов изучения.
Однако, так как от природы не у всех людей умы настолько склонны к исследованию вещей собственными силами, это правило указывает, что нам не надо сразу же заниматься более трудными и возвышенными вещами, но прежде следует изучить всякие легчайшие и простейшие искусства, и в особенности те, где царит больший порядок, каковыми являются искусство мастеров, которые ткут ткани и ковры, или женщин, которые вышивают либо переплетают нити, меняя узор ткани бесчисленными способами; такого же рода все игры с числами, все, что относится к арифметике, и т. п.: все эти искусства удивительно хорошо упражняют ум, если только мы обязаны их открытием не другим, а самим себе. Ведь поскольку в них не остается ничего скрытого и они всецело соответствуют способности человеческого познания, они отчетливейшим образом представляют нам бесчисленные порядки, совершенно различные между собой и тем не менее правильные, — порядки, в надлежащем соблюдении которых заключается почти вся человеческая находчивость.
И потому мы уведомили, что это нужно отыскивать при помощи метода, который в названных более легких искусствах обычно является не чем иным, как постоянным соблюдением порядка, либо существующего в самой вещи, либо искусно придуманного: так, если мы хотим прочесть писание, запечатленное в неизвестных письменах, мы, хотя тут не видно никакого порядка, все же представляем себе какой-то — как для исследования всех предположений, которые могут быть выдвинуты относительно отдельных знаков, или слов, или фраз, так и для расположения их таким образом, чтобы посредством энумерации мы узнали все, что из них может быть выведено. И более всего надо остерегаться, как бы не потерять попусту время, угадывая подобные вещи случайно и без помощи искусства: ведь, хотя они зачастую могут быть найдены без помощи искусства, а счастливчиками иногда, возможно, быстрее, чем другими при посредстве метода, они, однако, ослабляли бы свет ума и приучали бы к ребяческому и суетному настолько, что впоследствии ум всегда оставался бы на поверхности вещей и не мог бы проникнуть глубже. Но все же, чтобы не впасть в заблуждение тех, кто занимает мысль только важными и весьма возвышенными вещами (о каковых они после многих трудов приобретают лишь смутное знание, тогда как они стремятся к знанию глубокому), нам, стало быть, надлежит сначала упражняться в этих более легких вещах, но с помощью метода, так чтобы приучиться открытыми и знакомыми путями, будто играючи, всегда проникать в сокровенную истину вещей: ведь таким образом впоследствии мы постепенно и в короткое, сверх всякого ожидания, время почувствуем, что мы с одинаковой легкостью способны выводить из очевидных начал многие положения, которые кажутся очень трудными и запутанными.
Но некоторые, возможно, удивятся, что в этом месте, где мы исследуем, каким образом мы можем стать более способными к выведению одних истин из других, мы умалчиваем обо всех предписаниях диалектиков, при посредстве которых они рассчитывают управлять человеческим рассудком, предписывая ему некие формы рассуждения, которые приводят к заключению с такой необходимостью, что, положившись на них, рассудок, даже если он некоторым образом отлынивает от ясного и внимательного рассмотрения самого вывода, сможет тем не менее вывести что-либо достоверное лишь на основании формы. Мы же заметим, что истина часто ускользает из этих уз, а те, кто ими пользуется, сами оказываются запутанными в них. С другими же это случается не так часто, и мы знаем из опыта, что всякого рода остроумнейшие софизмы почти никогда не вводили в заблуждение кого-либо, пользовавшегося лишь чистым рассудком, но обычно вводили в заблуждение самих софистов.
Поэтому, особенно остерегаясь здесь того, чтобы наш рассудок не был праздным в то время, как мы исследуем истину какой-либо вещи, отбросим эти формы, как препятствующие нашему намерению, и лучше отыщем все вспомогательные средства, благодаря которым наша мысль остается внимательной, как будет показано в дальнейшем. Но для того чтобы еще очевиднее обнаружилось, что упомянутое искусство рассуждения совершенно ничего не привносит в познание истины, следует заметить, что диалектики не могли бы составить при посредстве этого искусства ни одного силлогизма, приводящего к истинному заключению, если бы прежде они не располагали материалом для него, т. е. если бы они не знали уже раньше ту самую истину, которая выводится в этом силлогизме. Отсюда явствует, что они сами не узнают ничего нового при помощи такой формы, и потому общепринятая диалектика является совершенно бесполезной для стремящихся исследовать истину вещей, но только иногда может быть полезной для более легкого разъяснения другим уже известных доводов, ввиду чего ее нужно перенести из философии в риторику.
Правило XI
После того как мы усмотрели несколько простых положений, полезно, если мы выводим из них нечто иное, обозреть их в последовательном и нигде не прерывающемся движении мысли, поразмышлять над их взаимными отношениями и отчетливо представить сразу столь многие из них, сколь это возможно: ведь таким образом и наше познание становится гораздо более достоверным, и чрезвычайно расширяются способности ума.
Здесь представляется случай яснее изложить то, что было сказано нами об интуиции ума ранее, в третьем и седьмом правилах, так как в одном месте мы противопоставили ее дедукции, в другом же — только энумерации, которая, как мы определили, является заключением, выведенным из многих разрозненных вещей, простая же дедукция одной вещи из другой, как мы сказали там же, осуществляется при посредстве интуиции.
Это нужно было сделать именно так, потому что для интуиции ума нам необходимы два условия, а именно чтобы положение понималось ясно и отчетливо и затем чтобы оно понималось все сразу, а не в последовательности. Дедукция же, если мы думаем произвести ее так, как в третьем правиле, очевидно не может быть осуществлена вся сразу — она включает в себя некое движение нашего ума, выводящего одно из другого, и потому мы там по праву отличали ее от интуиции. Если же мы обращаемся к ней как к уже завершенной, тогда, как было сказано в седьмом правиле, она больше не означает никакого движения, но является пределом движения, и потому мы полагаем, что она обозревается посредством интуиции тогда, когда она проста и очевидна, но не тогда, когда она сложна и темна; в последнем случае мы дали ей название энумерации, или индукции, так как тогда она не может быть охвачена разумом вся сразу, но ее достоверность некоторым образом зависит от памяти, в которой должны удерживаться суждения о каждой из частей, подлежащих энумерации, с тем чтобы из них всех было выведено что-то одно.
Для разъяснения настоящего правила необходимо было провести все эти различия: ведь, после того как в девятом правиле говорилось только об интуиции ума, а в десятом — об одной лишь энумерации, настоящее правило объясняет, каким образом эти два действия настолько способствуют друг другу и являются настолько взаимодополняющими, что кажутся слившимися в одно действие благодаря некоему движению мысли, внимательно созерцающей каждую из вещей и одновременно переходящей к другим.
Мы отмечаем двоякую пользу этого, а именно: это позволяет достовернее познать заключение, о котором мы раздумываем, и делает ум более способным к тому, чтобы находить другие заключения. Ведь когда память, от которой, как было сказано, зависит достоверность заключений, охватывающих больше, чем мы можем постичь в одном акте интуиции, оказывается неустойчивой и слабой, она должна быть восстановлена и укреплена посредством этого непрерывного и повторяющегося движения мысли: так, если посредством многих действий я узнал сначала, каково отношение между первой и второй величинами, затем — между второй и третьей, потом — между третьей и четвертой и, наконец, между четвертой и пятой, то я не вижу при этом, каково отношение между первой и пятой величинами, и не могу вывести его из уже известных отношений, если не вспоминаю их все; вот почему мне необходимо снова и снова обозревать их мыслью, пока я не буду переходить от первого к последнему столь быстро, что, не оставляя памяти почти никаких частей, я, буду, по-видимому, созерцать всё сразу.
Притом нет никого, кто не увидел бы, что этим способом преодолевается медлительность ума, а также расширяются его способности. Но кроме того, следует заметить, что наибольшая польза настоящего правила заключается в том, что, размышляя над взаимной зависимостью простых положений, мы приобретаем навык мгновенно различать, что является более или менее относительным и через какие ступени оно сводимо к абсолютному. Например, если я обозреваю несколько непрерывно пропорциональных величин, я буду размышлять над всем названным ниже, а именно посредством одинакового акта понимания, не более и не менее легкого, я узнаю отношение между первой и второй, второй и третьей, третьей и четвертой величинами и т. д.; но я не могу так же легко понять, какова зависимость второй величины от первой и третьей одновременно, и мне гораздо труднее понять зависимость второй от первой и четвертой и т. д. На основании этого я затем узнаю, в чем причина того, что, если даны только первая и вторая величины, я легко смогу найти третью и четвертую и т. д., а именно в том, что это осуществляется посредством отдельных и обособленных представлений. Если же даны только первая и третья величины, я не так легко узнаю среднюю величину, потому что это не может произойти иначе как посредством представления, которое одновременно включает два предшествующих представления. Если даны лишь первая и четвертая величины, мне будет еще труднее усмотреть две средние величины, потому что здесь сочетаются сразу три представления, так что вследствие этого показалось бы еще труднее найти на основании первой и пятой величин три средние величины. Но есть другая причина, в силу которой случается иначе, а именно та, что, хотя здесь соединены сразу четыре представления, они тем не менее могут быть разделены, поскольку четыре делится на другое число, так что я был бы в состоянии отыскать только третью величину на основании первой и пятой, а затем вторую — на основании первой и третьей и т. д. Тот, кто привык размышлять над этими и подобными вещами, всякий раз, когда он исследует новый вопрос, тотчас же узнает, что в этом вопросе порождает затруднение и каков простейший из всех способов (его разрешения); это служит величайшим подспорьем в познании истины.
Правило XII
Наконец, следует воспользоваться всеми вспомогательными средствами разума, воображения, чувства и памяти как для отчетливого усмотрения простых положений и для надлежащего сравнения искомых вещей с известными с целью познания первых, так и для отыскания тех вещей, которые должны сравниваться между собой таким образом, чтобы не осталась без внимания никакая Сторона человеческого усердия.
Это правило заключает все, что было сказано выше, и показывает в общем то, что нужно будет разъяснить в частности, следующим образом.
Для познания вещей нужно учитывать лишь два условия, а именно нас, познающих, и сами подлежащие познанию вещи. В нас имеется только четыре способности, которыми мы для этого можем воспользоваться, а именно разум, воображение, чувство и память. Конечно, один лишь разум способен к постижению истины, однако он должен прибегать к помощи воображения, чувства и памяти, с тем чтобы мы случайно не оставили без внимания нечто находящееся в нашем распоряжении. Что же касается вещей, достаточно исследовать три пункта, а именно: сначала то, что очевидно само по себе, затем как познается нечто одно на основании другого и, наконец, что из чего выводится. И эта энумерация кажется мне полной и не упускающей совершенно ничего из того, на что может простираться человеческое усердие.
Поэтому, обращаясь к первому пункту, я хотел бы изложить в этом разделе, что такое человеческий ум, что такое тело, как оно оформляется умом, каковы во всем составном существе способности, служащие познанию вещей, и как действует каждая из них, если бы данный раздел не казался мне слишком тесным для того, чтобы вместить все то, что должно быть предпослано, прежде чем в этих вещах истина сможет стать очевидной для всех. Ведь я всегда стремлюсь писать так, чтобы не утверждать ничего из того, что обычно побуждает к спору, кроме как предпосылая те самые доводы, которые привели меня к данному заключению и которыми, как я полагаю, можно убедить и других.
Но так как сейчас это невозможно, мне достаточно объяснить настолько кратко, насколько я смогу, какой способ постижения всего, что служит в нас познанию вещей, в наибольшей мере соответствует моему намерению. Не верьте, если вам угодно, что дело обстоит именно так, но что помешает вам следовать тем же самым предположениям, если выяснится, что они ничего не отнимают от истины вещей, но только делают все гораздо более ясным? Именно так в геометрии вы выдвигаете некоторые предположения о количестве, которыми никоим образом не ослабляется сила доказательств, хотя зачастую в физике вы думаете о его природе иначе.
Итак, во-первых, следует понять, что все внешние чувства, поскольку они являются частями тела, хотя мы и направляем их на объекты посредством деятельности, а именно посредством пространственного движения, все же, строго говоря, ощущают лишь посредством претерпевания, тем же самым способом, каким воск воспринимает фигуру от печати. И не надо думать, что это сказано ради аналогии, но следует понять, что внешняя фигура ощущающего тела реально изменяется объектом совершенно таким же способом, как фигура, которую образует поверхность воска, изменяется печатью. Это следует допустить не только тогда, когда мы осязаем какое-либо тело как обладающее фигурой, или твердое, или шероховатое и т. д., но и тогда, когда посредством осязания мы воспринимаем тепло или холод и т. п. Точно так же и в других чувствах, а именно: передняя непрозрачная часть глаза воспринимает таким образом фигуру, напечатленную под воздействием света, составленного из различных цветов, и наружная оболочка ушей, ноздрей и языка, непроницаемая для объекта, таким образом заимствует и новую фигуру у звука, запаха и вкуса.
Весьма полезно представить себе все это таким образом, так как ничто не воспринимается чувствами легче, чем фигура, ведь она осязается и созерцается. А то, что из этого предположения не следует ничего ложного скорее, чем из какого угодно другого, доказывается на основании того, что представление о фигуре является настолько общим и простым, что им охватывается любая чувственно воспринимаемая вещь. Например, ты можешь предположить, что цвет является всем, чем угодно, однако ты не будешь отрицать, что он является протяженным и, следовательно, обладающим фигурой. Что же окажется неприемлемым, если, остерегаясь, как бы нам не допустить бесполезно какое-либо новое сущее и опрометчиво не измыслить его, мы при этом не будем отрицать все, что думали о цвете другие, а лишь отвлечемся от всего иного, кроме того, что обладает природой фигуры, и воспримем различие, которое существует между белым, голубым, красным и т. д., как различие, которое существует между этими или подобными им фигурами?
И то же самое может быть сказано обо всем, так как верно, что бесконечного множества фигур достаточно для описания всех различий между чувственно воспринимаемыми вещами.
Во-вторых, следует понять, что в то время, как внешнее чувство возбуждается объектом, фигура, какую оно воспринимает, передается некоей другой части тела, которая называется общим чувством9, в то же самое мгновение и без реального перехода какого-либо сущего из одного места в другое: совершенно таким же способом, каким теперь, когда я пишу, я разумею, что в то же самое мгновение, когда на бумаге вычерчивается каждая из букв, в движении находится не только нижняя часть пера — в ней не может быть никакого, даже малейшего, движения, так чтобы одновременно оно не сообщалось и всему перу; и все эти различия движений обозначены в воздухе и верхней частью пера, хотя я не представляю себе ничего реального, переносимого с одного конца на другой. Кто же подумает, что между частями человеческого тела существует более слабая связь, чем между частями пера, и что проще можно придумать для описания этого?
В-третьих, следует понять, что общее чувство выполняет также роль печати, запечатлевая в фантазии, или воображении, как в воске, эти фигуры или идеи, приходящие от внешних чувств чистыми и бестелесными; эта фантазия является настоящей частью тела, причем такой величины, что разные ее части могут облекаться во множество фигур, отличных друг от друга, и обычно удерживать их довольно долго10; и тогда налицо именно то, что называется памятью.
В-четвертых, следует понять, что двигательная сила или сами нервы берут свое начало в мозгу, где находится фантазия, которой они различным образом приводятся в действие, подобно тому как общее чувство приводится в действие внешним чувством или как перо в целом движимо своей нижней частью. Этот пример также показывает, как фантазия может быть причиной многих движений в нервах; отчетливых образов этих движений она тем не менее не содержит в себе, но она обладает некоторыми другими образами, из которых могут проистекать эти движения, ведь и перо в целом движется не так, как его нижняя часть, более того, в своей большей части оно очевидно движется совершенно иначе и в обратном направлении. На основании этого нетрудно уразуметь, каким образом могут производиться все движения другими живыми существами, хотя в них и не допускается совершенно никакого познания вещей, но допускается лишь чисто телесная фантазия, и, кроме того, каким образом производятся в нас самих все те действия, которые мы совершаем без какого-либо содействия рассудка.
Наконец, в-пятых, следует понять, что та сила, посредством которой мы, собственно, и познаем вещи, является чисто духовной и отличается от тела в целом не менее, чем кровь от кости или рука от глаза; она является единственной в своем роде и либо вместе с фантазией воспринимает фигуры от общего чувства, либо прилагается к тем, какие сохраняются в памяти, либо создает новые фигуры, которые занимают воображение настолько, что часто оно бывает не в состоянии сразу воспринять идеи от общего чувства или претворить их в двигательную силу соответственно чисто телесной предрасположенности. Во всех названных случаях эта познающая сила иногда является пассивной, иногда деятельной и уподобляется то печати, то воску, что, однако, следует принимать здесь лишь за аналогию, ведь в телесных вещах не обнаруживается чего-либо совершенно подобного этой силе. И она является одной и той же силой, которая, когда она вместе с воображением направлена на общее чувство, обозначается словами «видеть», «осязать» и т. д.; когда она направлена на одно лишь воображение, как облекаемое в различные фигуры, она обозначается словом «вспоминать»; когда она направлена на воображение, как измышляющее новые фигуры, — словами «воображать» или «представлять»; когда, наконец, она действует одна — словом «понимать»; как совершается последнее действие, я изложу подробнее в своем месте. И потому же сообразно этим различным функциям эта самая сила называется либо чистым разумом, либо воображением, либо памятью, либо чувством, но, строго говоря, она именуется умом, когда она то создает в фантазии новые идеи, то имеет дело с уже созданными; мы рассматриваем ее как способную к этим различным действиям, и различие между упомянутыми названиями нужно будет иметь в виду в дальнейшем. Поняв же все это таким образом, внимательный читатель легко заключит, на какую помощь от каждой способности следует рассчитывать и как далеко может простираться человеческое усердие, чтобы возместить недостатки ума.
Ведь если разум может приводиться в действие воображением или, наоборот, воздействовать на последнее; если воображение также может воздействовать на чувства посредством двигательной силы, направляя их на объекты, или, наоборот, чувства могут воздействовать на воображение, в котором они и запечатлевают образы тел, а память, по крайней мере та, которая телесна и подобна воспоминанию животных, ничем не отличается от воображения, то из этого, несомненно, следует, что, когда разум имеет дело с теми вещами, в которых нет ничего телесного или подобного телесному, он не может опираться на эти способности. Напротив, чтобы они не мешали ему, необходимо отстранить чувства и освободить воображение от всякого отчетливого впечатления, насколько это возможно. Однако если разум предпринимает исследование какой-либо вещи, могущей быть отнесенной к телу, ее как можно более отчетливая идея должна создаваться в воображении; для того чтобы удобнее было осуществить это, необходимо предъявить внешним чувствам саму вещь, которую данная идея будет представлять. Но много вещей не могут содействовать разуму в отчетливом усмотрении каждой из них. Для того же, чтобы вывести из многого, собранного вместе, что-либо одно, а это часто приходится делать, нужно отсечь от идей о вещах все, что не требует наличного внимания, с тем чтобы остальное легче было удержать в памяти; и таким образом, тогда нужно будет предъявлять внешним чувствам не сами вещи, a скорее их некие упрощенные изображения, которые, если только их достаточно для предотвращения ошибок памяти, оказываются тем более удобными, чем они проще. И всякий, кто будет соблюдать все это, не упустит, как мне кажется, совершенно ничего из того, что относится к этой части вопроса.
Для того чтобы перейти еще и ко второй его части и чтобы строго отличить понятия простых вещей от понятий тех вещей, которые из них составляются, и усмотреть в вещах обоих видов, где может быть ложь, с тем чтобы остеречься ее, и какие вещи могут быть достоверно познаны, с тем чтобы заниматься только ими, в этом разделе, как и в предшествующих, следует допустить некоторые положения, которые, возможно, не у всех получат признание. Однако даже если иные считают, что они являются не более истинными, чем те воображаемые орбиты, посредством которых астрономы описывают свои явления, это не важно, лишь бы с их помощью различали, какое познание о какой угодно вещи может оказаться истинным или ложным.
Итак, мы говорим, во-первых, что единичные вещи по отношению к нашему познанию следует рассматривать иначе, нежели высказываясь о них в зависимости от того, как они существуют в действительности. Ведь, если, например, мы рассмотрим какое-либо протяженное и обладающее фигурой тело, мы признаем при этом, что оно в порядке вещей является чем-то единым и простым, ибо в этом смысле оно не могло бы быть названо составленным из телесной природы, протяжения и фигуры, потому что эти части никогда не существовали отдельно друг от друга. Но по отношению к нашему разуму мы называем данное тело чем-то составленным из этих трех природ, так как мы уразумели каждую из них в отдельности, прежде чем смогли судить, что три эти природы одновременно обнаруживаются в одном и том же предмете. Вот почему, говоря здесь о вещах лишь постольку, поскольку они воспринимаются разумом, мы называем простыми только те, познание которых является столь ясным и отчетливым, что они не могут быть разделены умом на большее число познаваемых более отчетливо частей; таковы фигура, протяжение, движение и т. д.; все же остальные вещи мы представляем себе некоторым образом составленными из этих простых. Это следует понимать в столь общем смысле, чтобы не были исключены даже те вещи, которые мы иногда отвлекаем от самих простых вещей; это бывает, когда мы говорим, что фигура есть предел протяженной вещи, понимая под пределом нечто более общее, чем под фигурой, так как, разумеется, можно говорить также о пределе длительности, пределе движения и т. д. Ведь тогда, хотя обозначение предела отвлечено от фигуры, вследствие этого оно не должно, однако, казаться более простым, чем фигура; но скорее, поскольку понятие предела прилагают и к другим вещам, таким, как предел длительности или движения и т. д., которые отличаются, как вещи совершенно иного рода, от фигуры, оно должно было быть отвлеченным также и от этих вещей, и потому оно является чем-то составленным из многих совершенно различных природ, к которым оно приложимо только неоднозначно.
Во-вторых, мы говорим, что те вещи, которые по отношению к нашему разуму называются простыми, являются или чисто интеллектуальными, или чисто материальными, или общими. Чисто интеллектуальными являются те вещи, которые познаются разумом при посредстве некоего врожденного света и без помощи какого-либо телесного образа. Ибо несомненно, что существуют некоторые вещи такого рода и невозможно измыслить какую-либо телесную идею, которая дала бы нам представление о том, что такое познание, сомнение, незнание, а также что такое действие воли, которое позволительно назвать волением, и тому подобное; тем не менее мы действительно познаем все это, и столь легко, что для этого нам достаточно лишь быть наделенными рассудком. Чисто материальными являются те вещи, которые познаются существующими только в телах: такие, как фигура, протяжение, движение и т. д. Наконец, общими следует называть те, которые без различия приписываются то телесным вещам, то духовным, как, например, существование, единство, длительность и тому подобное. Сюда следует отнести также те общие понятия, которые служат как бы некими узами для соединения других простых природ и на очевидности которых основывается все, что мы выводим в рассуждении. Именно таковы положения: «Две величины, равные какой-либо третьей, равны между собой»; «Две вещи, которые не могут быть отнесены к одной и той же, третьей, одинаковым образом, имеют какое-то различие и между собой» и т. д. И именно эти общие понятия могут быть познаны или чистым разумом, или разумом, созерцающим образы материальных вещей.
Впрочем, к числу этих простых природ позволительно отнести также лишенность и отрицание их, поскольку они разумеются нами, так как познание, посредством которого я усматриваю, что такое ничто, или мгновение, или покой, не менее истинно, чем то, посредством которого я разумею, что такое существование, или длительность, или движение. И данный способ понимания будет содействовать тому, чтобы мы впоследствии получили возможность сказать, что все остальные вещи, которые мы познаем, составлены из этих простых природ: так, если я вынесу суждение о том, что какая-либо фигура не находится в движении, я скажу, что моя мысль является некоторым образом составленной из фигуры и покоя, и так же о прочем.
В-третьих, мы говорим, что все эти простые природы известны сами по себе и никогда не заключают в себе никакой лжи. Это легко будет показано, если мы отличим ту способность разума, посредством которой он созерцает и познает вещь, от той, посредством которой он выносит суждение, утверждая или отрицая; ведь может случиться, что мы сочтем неизвестными нам те вещи, которые мы в действительности познаем (а именно если мы предположим, что в них кроме того, что мы созерцаем, или того, что мы достигаем в мышлении, есть нечто иное, скрытое от нас), и что эта наша мысль окажется ложной. По этой причине очевидно, что мы ошибемся, если решим, что нами никогда не будет полностью познана какая-либо из этих простых природ: ведь если мы достигаем умом хотя бы чего-то наименьшего в ней, что, конечно, необходимо, поскольку мы предполагаем вынести некоторое суждение о ней, из одного этого следует заключить, что мы познаем ее полностью; ибо иначе она не могла бы быть названа простой, а была бы составлена из того, что мы постигаем в ней, и того, что мы считаем нам неизвестным.
В-четвертых, мы говорим, что соединение этих простых вещей между собой является или необходимым, или случайным. Оно необходимо, когда одна вещь настолько подразумевается неким неявным способом в представлении о другой, что мы не сможем отчетливо представить себе ни ту, ни другую, если будем считать, что они отделены друг от друга: таким образом фигура связана с протяжением, движение — с длительностью, или временем, и т. д., потому что невозможно представить себе ни фигуру, лишенную всякого протяжения, ни движение, лишенное всякой длительности. Точно так же, если я говорю: «4 и 3 составляют 7», это составление является необходимым; ибо мы не представляем себе отчетливо число семь, если неким неявным способом не включаем в него чисел три и четыре. Таким же образом и все, что доказывается относительно фигур или чисел, необходимо соединено с тем, о чем это утверждается. И названная необходимость обнаруживается не только в чувственно воспринимаемых вещах, но также, например, если Сократ говорит, что он сомневается во всем, отсюда с необходимостью следует: значит, он понимает по крайней мере то, что он сомневается, и, значит, он познает, что нечто может быть истинным или ложным, и т. д.: ведь эти следствия необходимо связаны с природой сомнения11. Случайным же является сочетание этих вещей, при котором они не соединяются никакой неразрывной связью, как, например, когда мы говорим: тело одушевлено, человек одет и т. д. Существует также много вещей, зачастую с необходимостью связанных между собой, которые причисляются к случайным большинством людей, не замечающих связи между ними; таково положение: «Я существую, следовательно, Бог существует», а также «Я понимаю, следовательно, обладаю умом, отличным от тела» и т. д. Наконец, следует отметить, что случайны и высказывания, обратные очень многим высказываниям, являющимся необходимыми: так, хотя из того, что я существую, я достоверно вывожу, что Бог существует, однако на основании того, что Бог существует, невозможно утверждать, что я также существую.
В-пятых, мы говорим, что мы никогда не сможем уразуметь ничего, кроме этих простых природ и некоторого их смешения, или соединения, между собой; причем зачастую легче сразу заметить многие природы, связанные между собой, чем отделить одну из них от других, ведь я, например, могу познавать треугольник, хотя бы я никогда и не думал о том, что в познании его содержится также познание угла, линии, числа три, фигуры, протяжения и т. д. Это, однако, не мешает нам говорить, что природа треугольника составлена из всех этих природ и что они являются более известными, чем треугольник, поскольку они есть то самое, что в нем разумеется; кроме того, в этом же треугольнике скрыто, возможно, и многое другое, чего мы не замечаем, как, например, величина углов, которые равны двум прямым, и бесчисленные отношения, какие существуют между сторонами и углами, и вместимость площади и т. д.
В-шестых, мы говорим, что те природы, которые мы называем составными, познаются нами или потому, что мы узнаем на опыте, каковы они есть, или потому, что мы составляем их сами. Мы испытываем все, что воспринимаем чувством, все, что слышим от других, и вообще все, что приходит к нашему разуму или извне, или вследствие созерцания, обращенного им на самого себя. Здесь следует заметить, что разум никогда не может быть введен в заблуждение никаким опытом, если он усматривает исключительно лишь ту вещь, которая является его объектом, поскольку он располагает ею или в самом себе, или в образе, и если вдобавок он не признаёт ни того, что воображение верно воспроизводит объекты чувств, ни того, что чувства воспринимают действительные фигуры вещей, ни того, наконец, что внешние вещи всегда таковы, какими они кажутся. Мы подвержены заблуждению во всех следующих случаях: если кто-либо рассказал нам небылицу и мы верим, что речь шла о происшедшем событии; если страдающий желтушной болезнью считает, что все вокруг желтое, так как его глаз окрашен в желтый цвет; если, наконец, когда расстроено воображение, как это случается с меланхоликами, мы полагаем, что его беспорядочные призраки представляют действительные вещи. Однако это не введет в заблуждение разум мудреца, так как все, что он воспримет от воображения, он, конечно, будет считать действительно запечатленным в последнем, однако он никогда не признает, что одна и та же вещь переходит в целости и без какого-либо изменения от внешних вещей к чувствам и от чувств к фантазии, если прежде он не узнал об этом каким-то другим способом. Но мы сами составляем вещи, которые разумеем, всякий раз, когда мы верим, что в них содержится нечто непосредственно не воспринимаемое нашим умом ни в каком опыте: так, когда больной желтухой убеждается в том, что видимые им вещи желтые, эта его мысль будет составлена из того, что представляет ему его фантазия, и того, что он добавляет от себя, а именно: цвет кажется ему желтым не вследствие изъяна глаза, а потому что видимые им вещи действительно желтые. Отсюда следует, что мы можем обманываться только тогда, когда вещи, в которые мы верим, некоторым образом составляются нами самими.
В-седьмых, мы говорим, что это составление может быть осуществлено тремя способами, а именно: посредством внушения, посредством предположения или посредством дедукции. По внушению составляют свои суждения о вещах те, кто располагает свой ум к вере во что-либо, склоняясь к ней не на каком-то разумном основании, а только будучи побуждаем либо некоей вышней силой, либо собственной свободой, либо склонностью фантазии: первая никогда не вводит в заблуждение, вторая — редко, третья — почти всегда; но первая не имеет отношения к данному разделу, так как она не подпадает под правила искусства. Посредством предположения мы составляем суждения, как, например, когда на основании того, что вода, более удаленная от центра мира, чем земля, составляет и более тонкую субстанцию, а также того, что воздух, находящийся выше воды, является и более разреженным, чем она, мы допускаем, что выше воздуха находится нечто эфирное, наичистейшее и гораздо более тонкое, чем сам воздух, и т. д.
Но все, что мы составляем таким способом, хотя и не вводит нас в заблуждение (если мы считаем это только вероятным и никогда не утверждаем, что оно истинно), но и не делает нас более сведущими.
Итак, остается одна лишь дедукция, посредством которой мы сможем составлять вещи так, что будем уверены в их истине; однако и в ней может быть много недостатков: например, если из того, что в данном пространстве, наполненном воздухом, мы ничего не воспринимаем ни посредством зрения, ни посредством осязания, ни посредством какого-либо другого чувства, мы заключаем, что это пространство является пустым, неправильно соединяя природу пустоты с природой этого пространства; и так происходит всякий раз, когда мы считаем, что из отдельной или случайной вещи может быть выведено нечто общее и необходимое. Но в нашей власти избежать этой ошибки, а именно если мы никогда не будем соединять никакие предметы, не усмотрев, что соединение одного с другим является совершенно необходимым, как, например, если мы выводим, что никакая вещь, не будучи протяженной, не может обладать фигурой, из того, что фигура необходимо связана с протяжением, и т. д.
Из всего этого следует, во-первых, что мы четко и, как я думаю, посредством достаточной энумерации разъяснили то, что сначала смогли показать, лишь беспорядочно и грубо [используя оружие, врученное нам] Минервой, а именно: людям не открыто никаких других путей к достоверному познанию истины, кроме очевидной интуиции и необходимой дедукции, а также разъяснили и то, что представляют собой те простые природы, о которых говорилось в восьмом правиле. И ясно, что интуиция ума распространяется как на познание всех этих природ, а также необходимых связей между ними, так, наконец, и на все остальное, что разум прямо испытывает как находящееся или в нем самом, или в фантазии. О дедукции же больше будет сказано в дальнейшем.
Во-вторых, отсюда следует, что не нужно вкладывать никакого труда в познание этих простых природ, так как они достаточно известны сами по себе, но нужно только отделять их друг от друга и созерцать каждую в отдельности, устремляя на нее взор ума. Ведь нет настолько тупоумного человека, который не заметил бы, что, когда он сидит, он некоторым образом отличается от самого себя, стоящего на ногах; однако не все так же четко отделяют природу положения от остального, что содержится в этой мысли, и не могут утверждать, что в данном случае не меняется ничего, кроме положения. Мы не зря предупреждаем здесь об этом, так как зачастую ученые бывают настолько остроумными, что найдут способ стать слепыми даже в том, что является самоочевидным и что всегда знают даже крестьяне; это случается с ними всякий раз, когда они пытаются объяснить эти известные сами по себе вещи при посредстве чего-либо более очевидного: ведь они или разъясняют другое, или не разъясняют совершенно ничего. Действительно, кто не замечает всего того, каким бы оно ни было, по отношению к чему происходит изменение, когда мы меняем место, но кто представит себе то же самое, когда ему будет сказано: место есть поверхность окружающего тела12? В то время как эта поверхность может изменяться, я остаюсь неподвижным и не меняющим места; или, наоборот, она может двигаться со мной так, что, хотя меня будет окружать та же самая поверхность, тем не менее я более не буду находиться в одном и том же месте. Но не кажется ли, что ученые произносят магические слова, которые имеют таинственный смысл и превосходят способности человеческого ума, когда они говорят, что движение — вещь, известнейшая каждому, — есть акт сущего в потенции, поскольку оно находится в потенции13? Ведь кто поймет эти слова? Кто не знает, что такое движение? И кто не признает, что они искали узлы в тростнике? Итак, следует сказать, что никогда не нужно пользоваться для объяснения вещей никакими определениями такого рода, чтобы мы не постигали составные вещи вместо простых; но каждому нужно внимательно созерцать лишь вещи, отделенные от всех других, сообразно свету своего ума.
В-третьих, из сказанного следует, что все человеческое знание заключается только в том, чтобы мы отчетливо усматривали, каким же образом эти простые природы сходятся воедино для составления других вещей. Это весьма полезно отметить, так как всякий раз, когда предполагают исследовать какое-либо затруднение, почти все останавливаются на пороге, пребывая в сомнении относительно того, какими мыслями они должны занять ум, и решив, что необходимо отыскать какой-нибудь новый род сущего, ранее им неизвестный; например, если их спрашивают, какова природа магнита, они, предчувствуя, что это вещь непростая и трудная, тотчас же отвлекают ум от всего того, что очевидно, обращают его ко всему наитруднейшему и, скитаясь, ждут, не найдут ли они случайно, блуждая в пустом пространстве многочисленных причин, чего-либо нового. Но тот, кто думает, что в магните не может быть познано ничего, что не состояло бы из некоторых простых природ, известных сами по себе, и не сомневается в том, что надлежит сделать, сначала тщательно собирает все те опыты с этим камнем, какими он может располагать, затем пытается вывести из них, каково сочетание простых природ, необходимое для того, чтобы произвести все те действия, которые были опытным путем обнаружены им в магните; однажды раскрыв это, он может смело утверждать, что постиг подлинную природу магнита, насколько она могла быть раскрыта человеком на основании данных опытов.
Наконец, в-четвертых, из сказанного следует, что никакие познания вещей не нужно считать более темными, чем другие, поскольку все они одной и той же природы и заключаются лишь в составлении вещей, известных сами по себе. Почти никто этого не замечает, но, отдавая предпочтение противоположному мнению, более самонадеянные даже позволяют себе объявлять свои предположения как бы подлинными доказательствами, и в вещах, которых они совершенно не знают, они предсказывают, что словно сквозь облако узрят истины, зачастую темные; их они не боятся выставлять напоказ, облекая свои представления в те или иные слова, с помощью которых они обыкновенно много рассуждают и последовательно говорят, но которых на самом деле не понимают ни они сами, ни их слушатели. Более же скромные часто воздерживаются от исследования многих вещей, хотя и легких и весьма необходимых для жизни, только потому, что считают себя неспособными их исследовать; и так как они полагают, что эти вещи могут быть постигнуты другими, наделенными большим умом, они присоединяются к мнениям тех, чьему авторитету они больше доверяют.
В-восьмых, мы говорим, что можно только вывести либо вещи из слов, либо причину из действия, либо действие из причины, либо подобное из подобного, либо части или само целое из частей…
Впрочем, для того чтобы кто-либо случайно не упустил из виду ряд наших предписаний, мы разделяем все, что может быть познано, на простые положения и вопросы. Для простых положений мы не выдвигаем иных предписаний, кроме тех, которые подготовляют познавательную способность к более отчетливому созерцанию и более проницательному исследованию каких угодно объектов, так как эти положения должны возникать сами собой и не могут быть искомыми; это мы очертили в первых двенадцати правилах, в которых, как мы полагаем, мы представили все то, что, по нашему мнению, может каким-либо образом сделать более легким использование рассудка. Из вопросов же одни совершенно понятны, если даже неизвестно их решение, — мы будем говорить только о них в двенадцати правилах, непосредственно следующих за настоящим; наконец, другие не разумеются в совершенстве — их мы откладываем до последних двенадцати правил. Такое разделение мы придумали не без умысла: как для того, чтобы не быть принужденными говорить о вещах, которые предполагают познание последующего, так же и для того, чтобы с самого начала усвоить те вещи, которыми, как мы полагаем, и следует прежде всего заниматься с целью усовершенствования умов. Надо заметить, что к числу совершенно понятных вопросов мы относим только те, в которых четко различаем три вещи, а именно: по каким признакам может быть распознано то, что является искомым, когда оно встретится; что именно представляет собой то, из чего мы должны его вывести; и как должно быть доказано, что они зависят друг от друга до такой степени, что одно ни в коем случае не может измениться, если другое остается неизменным. Поскольку мы будем располагать всеми посылками, останется объяснить не что иное, как то, каким образом находят заключение хотя и не посредством выведения из одной простой вещи чего-то одного (ведь, как уже было сказано, это может быть произведено и без предписаний), но посредством выделения чего-то одного зависимого от многих соединенных вместе вещей, — выделения настолько искусного, что для него нигде не потребуется большей способности ума, чем требуется для того, чтобы сделать простейший вывод. Вопросы подобного рода, так как они в большинстве своем являются отвлеченными и встречаются почти исключительно в арифметике или геометрии, неискушенным покажутся малополезными, однако я напоминаю, что в изучении этого искусства должны дольше усердствовать и упражняться те, кто желает в совершенстве овладеть следующей частью данного метода, в которой мы рассуждаем обо всех других вопросах.
Правило XIII
Если мы вполне понимаем вопрос, его надо освободить от любого излишнего представления, свести к простейшему вопросу и посредством энумерации разделить на возможно меньшие части.
Мы подражаем диалектикам лишь в том, что, как они для обучения формам силлогизмов предполагают термины, или содержание последних, известными, так и мы здесь заранее требуем, чтобы вопрос был вполне понят. Однако мы не различаем, как они, два крайних и средний термины, а рассматриваем весь этот предмет таким образом: во-первых, во всяком вопросе с необходимостью должно быть нечто неизвестное, ибо иначе не стоило бы и задаваться им; во-вторых, само это неизвестное должно быть каким-либо способом обозначено, ибо иначе мы не были бы побуждаемы отыскивать именно его скорее, чем что-либо другое; в-третьих, оно может быть обозначено так только через посредство чего-то другого, являющегося известным. Все это есть и в несовершенных вопросах: так, если нас спрашивают, какова природа магнита, то, что, по нашему разумению, обозначается при помощи этих двух слов — «магнит» и «природа», является известным, что и побуждает нас отыскивать именно это скорее, чем другое, и т. д. Но, вдобавок, для того чтобы вопрос был совершенным, мы хотим, чтобы он был во всех отношениях определен настолько, что не отыскивалось бы ничего более, кроме того, что может быть выведено из данного: например, если кто-либо спросит у меня, какой вывод о природе магнита должен быть сделан исключительно на основании тех опытов, проведение которых приписывает себе Гильберт14, будь они верными или неверными; а также, если меня спросят, что я думаю о природе звука исключительно лишь на основании того, что три струны А, В, С издают одинаковый звук и из них струна В по предположению вдвое толще, чем А, но не длиннее ее и натянута грузом в два раза более тяжелым, а струна С хотя и не толще, чем А, но только вдвое длиннее и вместе с тем натянута грузом в четыре раза более тяжелым, и т. д. Из этого легко понять, каким образом все несовершенные вопросы могут быть сведены к совершенным, что подробнее будет изложено в своем месте; а также видно, каким образом может быть соблюдено данное правило, чтобы освободить хорошо понятое затруднение от всякого излишнего представления и довести его до того, чтобы мы больше не помышляли заниматься тем или иным предметом, а в общем сравнивали бы друг с другом некоторые величины. Ибо после того, например, как мы решили рассмотреть лишь те или иные опыты с магнитом, для нашего мышления не будет представлять никакого затруднения отвлечься от всех других опытов.
Кроме того, стоит добавить, что затруднение надо сводить к простейшему, а именно согласно пятому и шестому правилам, и разделять согласно седьмому правилу: например, если я исследую магнит на основании многих опытов, я буду обозревать их по отдельности один за другим; таким же образом, если я исследую звук, то, как было сказано, я буду по отдельности сравнивать друг с другом струны А и В, потом A и С и т. д., чтобы впоследствии охватить их все вместе достаточной энумерацией. И здесь на ум приходят лишь три этих предписания, которые должны соблюдаться чистым разумом по отношению к терминам какого-либо положения, прежде чем мы дойдем до его окончательного разъяснения, если потребуется применить следующие одиннадцать правил; каким образом это надлежит сделать, станет яснее из третьей части данного трактата. Под вопросами же мы разумеем все то, в чем отыскивается истинное или ложное; их различные роды следует перечислить для того, чтобы определить, что мы в состоянии предпринять по отношению к каждому из вопросов.
Мы уже сказали, что только в интуиции вещей, либо простых, либо составных, не может быть лжи; и в этом смысле они еще не называются вопросами, но они получают такое название, как только мы решаем вынести о них какое-то определенное суждение. Ведь мы относим к числу вопросов не только те, которые исходят от других людей, но стоял вопрос также о самом незнании, или, вернее, сомнении Сократа, когда, впервые обратившись к нему, Сократ начал исследовать, не было ли истинным то, что он во всем сомневается, и убедился, что это так.
Отыскиваем же мы либо вещи на основании слов, либо причины на основании действий, либо действия на основании причин, либо целое или другие части на основании частей, либо, наконец, сразу многое из этого.
Мы говорим, что вещи отыскиваются на основании слов, всякий раз когда затруднение заключается в неясности речи; сюда относятся не только все загадки, каковой была загадка Сфинкса о живом существе, которое сначала является четвероногим, затем двуногим и потом наконец становится трехногим, а также загадка рыбаков, которые, стоя на берегу с удилищами и крючками для рыбной ловли, говорили, что у них больше нет того, что они поймали, но, наоборот, у них есть то, чего они еще не смогли поймать, и т. д. — также и большая часть того, о чем спорят ученые, почти всегда относится к вопросу о названии. И не следует столь плохо думать о великих умах, полагая, что они плохо представляют себе сами вещи, всякий раз когда они объясняют их при помощи не вполне подходящих слов: например, когда они называют местом поверхность окружающего тела, они не представляют себе ничего действительно ложного, а лишь неверно употребляют слово «место», обозначающее сообразно общепринятому употреблению ту простую и известную саму по себе природу, в силу которой говорится, что нечто находится здесь или там, и которая целиком заключается в некотором отношении вещи, о коей говорится, что она находится в определенном месте, к частям внешнего пространства, — природу, которую иные, видя, что название «место» укрепилось за окружающей поверхностью, неудачно назвали внутренним «где»15; то же происходит и в других случаях. И эти вопросы о названии встречаются так часто, что если бы среди философов навсегда установилось согласие относительно значения слов, то почти все их споры были бы прекращены.
Причины отыскиваются на основании действий, всякий раз когда мы исследуем относительно какой-либо вещи, существует ли она, или какова она…
Впрочем, поскольку, в то время как нам предлагается разрешить какой-либо вопрос, мы зачастую не узнаем тотчас же, к какому роду он относится, и то ли надо отыскивать вещи на основании слов, то ли причины на основании действий и т. д., мне ввиду этого кажется излишним много говорить об этих предметах в отдельности. В самом деле, будет быстрее и удобнее, если мы сразу проследим по порядку все, что надлежит сделать для разрешения любого затруднения; и потому в каждом данном вопросе прежде всего надо постараться отчетливо уразуметь, что в нем отыскивается.
Ведь иные часто так торопятся в исследовании положений, что направляют на их разъяснение блуждающий ум, прежде чем узнают, по каким признакам они смогут различить искомую вещь, если та случайно встретится; они не менее глупы, чем тот мальчик, который, будучи куда-то послан хозяином, так стремился услужить, что бросился бежать, еще не получив приказаний и не зная, куда же было велено пойти.
Но безусловно, хотя во всяком вопросе и должно быть нечто неизвестное, ибо иначе не стоило бы задаваться им, все же необходимо, чтобы оно было так обозначено посредством определенных условий, что мы всецело были бы вынуждены исследовать что-то одно скорее, чем другое. И таковыми являются условия, о которых мы говорим, что их изучением следует заняться с самого начала: это произойдет, если мы направим взор ума так, чтобы отчетливо усмотреть каждое из них, тщательно исследуя, насколько то неизвестное, которое мы отыскиваем, определяется каждым из них; ведь при этом человеческие умы обыкновенно впадают в заблуждение двояким образом, а именно или допуская нечто большее, чем то, что дано для определения вопроса, или, наоборот, нечто упуская.
Следует остерегаться, как бы не предположить большего и более точного, чем то, что дано, особенно в загадках и других вопросах, искусно придуманных для того, чтобы обводить умы, но подчас и в прочих вопросах, когда для их разрешения, по-видимому, допускается в качестве достоверного нечто, в чем нас убеждает не какой-то верный довод, а укоренившееся мнение. Например, в загадке Сфинкса не нужно думать, что названием «нога» обозначаются только настоящие ноги живых существ, но нужно еще рассмотреть, не может ли оно относиться к чему-то другому, как оно и есть, а именно к рукам ребенка и к палке старца, поскольку и тем и другим пользуются, как ногами, для передвижения. Таким же образом в загадке рыбаков нужно остерегаться, чтобы мысль о рыбах не овладела нашим умом настолько, что отвлекла бы его от представления о тех животных, которых бедняки помимо желания зачастую носят с собой и, поймав, выбрасывают. Таков же и случай, когда отыскивается, каким образом была устроена некогда виденная нами чаша, в центре которой возвышалась колонна, на коей была водружена статуя Тантала, как бы намеревающегося напиться: хотя налитая вода прекрасно держалась в этой чаше, пока не поднималась настолько высоко, что могла бы попасть в рот Тантала, однако лишь только она достигала губ несчастного, вся она тотчас же вытекала. На первый взгляд кажется, что вся хитрость заключалась в устройстве этой статуи Тантала; однако на самом деле оно никоим образом не определяет вопрос, а лишь сопутствует ему, ибо все затруднение состоит только в том, чтобы отыскать, каким образом должна быть устроена чаша, чтобы вся вода вытекала из нее, как только она достигнет определенной высоты, но никак не раньше. Точно так же, наконец, когда на основании всех тех наблюдений за звездами, которыми мы располагаем, отыскивается, что мы можем с достоверностью утверждать об их движениях, не нужно безосновательно допускать, что Земля неподвижна и помещена в центре мира, как делали древние, потому что так казалось нам с детства, но как раз это и должно быть подвергнуто сомнению, с тем чтобы впоследствии мы изучили, какое достоверное суждение можно вынести на этот счет; и так же в остальных случаях.
Пропусками же мы грешим всякий раз, когда не размышляем над каким-либо условием, требующимся для определения вопроса, выражено ли оно в самом вопросе или должно быть понято каким-то иным образом: например, когда отыскивается вечное движение, но не естественное, каковым является движение звезд или ключевых вод, а произведенное человеческим усердием, кто-то (коль скоро некоторые люди верили в то, что это может быть осуществлено, полагая, что Земля беспрерывно вращается вокруг своей оси, а магнит сохраняет все качества Земли) может подумать, что он откроет вечное движение, если приладит этот камень так, чтобы тот двигался по кругу или по крайней мере сообщал железу свое движение вместе с другими своими свойствами. Даже если бы это и произошло, он, однако, не произвел бы при помощи искусства вечного движения, а лишь воспользовался бы тем движением, которое является естественным, точно так, как если бы он в речном потоке расположил колесо таким образом, чтобы оно всегда находилось в движении; а значит, он упустил бы условие, требующееся для определения вопроса, и т. д.
Достаточно поняв вопрос, нужно ясно усмотреть, в чем заключается составляющее его затруднение, чтобы легче разрешить его, освободив от всего остального.
Не всегда достаточно понять вопрос для того, чтобы узнать, в чем заключено составляющее его затруднение; но вдобавок надо поразмыслить над каждой из вещей, которые являются в нем искомыми, с тем чтобы, если нам встретятся легко обнаруживаемые вещи, мы опустили их и, устранив их из обсуждаемого положения, оставили лишь то, что нам неизвестно. Так, в вопросе о чаше, описанном немногим ранее, хотя мы и легко замечаем, как должна быть сделана чаша — в ее центре должна быть воздвигнута колонна, на чаше должна быть изображена птица и т. д., — остается, когда мы отбросим все это как не относящееся к делу, затруднение в чистом виде, заключающееся в том, что вода, содержащаяся в чаше, достигнув определенной высоты, вся вытекает; нужно отыскать, отчего это происходит.
Итак, мы говорим здесь, что только и стоит по порядку обозреть все данное в некотором положении, отбрасывая то, что с очевидностью покажется нам не относящимся к делу, удерживая необходимое и откладывая сомнительное для более тщательного исследования.
Правило XIV
То же самое следует отнести к реальному протяжению тел, и протяжение в целом должно предстать воображению через посредство простых фигур, ибо таким образом оно гораздо отчетливее представляется разумом.
Для того же, чтобы воспользоваться также и помощью воображения, следует отметить, что всякий раз, когда выводится нечто неизвестное из чего-либо другого, уже заранее известного, вследствие этого не открывается какой-то новый род сущего, но все это знание лишь расширяется до такой степени, что мы представляем себе искомую вещь тем или иным способом приобщенной к природе того, что дано в положении. Например, если кто-то слеп от рождения, не надо надеяться на то, что при помощи каких-либо доводов мы когда-нибудь сделаем так, что он представит себе верные идеи цветов, какими мы обладаем, получая их от чувств; однако, если кто-то хотя бы когда-нибудь видел основные цвета, а промежуточных и смешанных не видел никогда, может быть так, что при посредстве некоей дедукции он представит образы и тех цветов, которых он не видел, на основании их сходства с другими цветами. Точно так же, если в магните обнаружится какой-либо род сущего, подобного которому дотоле не постигал наш разум, не надо надеяться на то, что мы когда-нибудь познаем его посредством рассуждения, — для этого мы должны были бы быть наделенными либо каким-то новым чувством, либо божественным умом; но мы поверим, что достигнем всего, что в этом деле может быть осуществлено человеческим умом, если мы весьма отчетливо представим себе то сочетание уже известных сущностей, или природ, которое производит те же самые действия, какие выявляются в магните.
Конечно, все эти уже известные сущности, каковыми являются протяжение, фигура, движение и им подобные, которые здесь неуместно перечислять, познаются посредством одной и той же идеи в различных предметах, и мы не представляем себе по-равному фигуру венца, будь он серебряный или золотой; эта общая идея переносится с одного предмета на другой не иначе как посредством простого сравнения, благодаря которому мы утверждаем, что искомое является в том или ином отношении подобным, либо тождественным, либо равным чему-то данному, так что во всяком рассуждении мы точно познаем истину только посредством сравнения. Например, так: всякое А есть В, всякое В есть С, следовательно, всякое А есть С; сравниваются друг с другом искомое и данное, а именно А и С, соответственно тому, что и то и другое есть В, и т. д. Но, поскольку, как мы уже много раз предупреждали, формы силлогизмов никоим образом не способствуют постижению истины вещей, читателю будет полезно, полностью отбросив их, понять, что вообще все познание, которое не приобретается посредством простой и чистой интуиции какой-либо единичной вещи, приобретается посредством сравнения двух или многих вещей. И конечно, почти все усердие человеческого рассудка состоит в том, чтобы подготовлять это действие, ибо, когда оно очевидно и просто, не требуется никакой помощи искусства, а нужен только естественный свет для того, чтобы усмотреть истину, которая обретается благодаря этому сравнению. Следует отметить, что сравнения называются простыми и очевидными лишь тогда, когда искомая и данная вещи одинаковым образом приобщаются к некоторой природе; все же остальные сравнения нуждаются в подготовке не по какой другой причине, кроме как потому, что эта общая природа находится в обеих вещах не одинаковым образом, а соответственно каким-то другим отношениям или пропорциям, в которые она облекается; и особая роль человеческого усердия состоит не в чем ином, как в сведении этих пропорций к тому, чтобы стало ясно видно равенство между искомым и тем, что известно.
Далее следует отметить, что к такому равенству не может быть сведено ничего, кроме допускающего большее и меньшее, и что все это охватывается названием «величина», так что, после того как в соответствии с предшествующим правилом термины затруднения были отвлечены от любого предмета, мы понимаем, что отныне будем заниматься только величинами вообще.
Но для того чтобы и тогда воображать нечто и пользоваться не чистым разумом, а разумом, прибегающим к помощи образов, рисуемых в фантазии, следует, наконец, отметить, что о величинах вообще нельзя сказать чего-либо, что не могло бы быть отнесено и к каждой из них в отдельности.
Из этого легко заключить, что будет весьма полезно, если мы перенесем то, что, по нашему разумению, можно сказать о величинах вообще, на тот вид величины, который и легче и отчетливее всего рисуется в нашем воображении; а таким является реальное протяжение тел, отвлеченное от всего иного, кроме того, что оно обладает фигурой; это следует из сказанного в двенадцатом правиле, где мы представляли себе саму фантазию вместе с содержащимися в ней идеями не чем иным, как подлинно реальным, протяженным и обладающим фигурой телом. Это также очевидно само по себе, так как ни в каком другом предмете не проявляются более четко все различия пропорций; ведь, хотя одна вещь может быть названа более или менее белой, чем другая, а равно и один звук — более или менее высоким, чем другой, и т. д., мы все же не можем точно определить, состоит ли такое превышение в двойной или тройной пропорции и т. д., кроме как посредством некоторой аналогии с протяжением тела, обладающего фигурой. Следовательно, остается незыблемым и неизменным положение о том, что вполне определенные вопросы едва ли содержат в себе какое-либо затруднение, кроме того, которое заключается в выведении равенств из пропорций; и все то, в чем обнаруживается именно такое затруднение, может и должно быть с легкостью отделено от всякого другого предмета и затем сведено к протяжению и фигурам, о которых мы поэтому, оставив любую другую мысль, только и будем рассуждать далее вплоть до двадцать пятого правила.
Здесь нам хотелось бы найти читателя, склонного к занятиям арифметикой и геометрией, хотя я предпочел бы, чтобы он еще не занимался названными науками, нежели был обучен им по общему обыкновению: ведь применение излагаемых мною здесь правил в изучении этих наук, для которого оно вполне достаточно, является гораздо более легким, чем применение их в вопросах любого другого рода; и польза от этого для достижения более возвышенной мудрости столь велика, что я не побоюсь сказать, что данная часть нашего метода была открыта не благодаря математическим проблемам — скорее сами они должны изучаться почти исключительно ради совершенствования этого метода. И я не предполагаю в упомянутых дисциплинах ничего, кроме, быть может, некоторых вещей, кои известны сами по себе и доступны каждому; однако их познание, каким обычно обладают иные люди, даже если оно не искажено какими-либо явными ошибками, тем не менее затемняется многочисленными двусмысленными и неправильно понятыми принципами, что мы попытаемся в разных местах исправить в дальнейшем.
Под протяжением мы разумеем все то, что обладает длиной, шириной и глубиной, не рассматривая, реальное ли это тело или только пространство; и, кажется, нет нужды в более обстоятельном объяснении, ибо нет ничего, что легче представлялось бы нашим воображением. Так как, однако, ученые часто пользуются столь тонкими различениями, что рассеивают естественный свет и находят неясности даже в тех вещах, которые всегда известны и крестьянам, то их надо предупредить, что словом «протяжение» здесь не обозначается нечто отдельное и обособленное от самого предмета и что вообще мы не признаем таких философских сущностей, которые действительно были бы недоступны воображению. Ведь, хотя кто-нибудь и сумеет убедить себя, например, в том, что, если все, являющееся протяженным в природе вещей, обратится в ничто, это, однако, не окажется противоречащим тому, что будет существовать одно лишь протяжение само по себе, он тем не менее воспользуется для этого представления не телесной идеей, а только разумом, выносящим неправильное суждение. Он сам признает это, если внимательно поразмыслит над тем самым образом протяжения, который он тогда же попытается создать в своей фантазии: действительно, он заметит, что он не воспринимает его лишенным всякого предмета, а представляет себе его совершенно иначе, нежели судит о нем; так что эти отвлеченные сущности (что бы разум ни думал об истине вещей) все-таки никогда не создаются в фантазии отделенными от их предметов.
Но, так как отныне мы не будем ничего предпринимать без помощи воображения, стоит потрудиться над тем, чтобы строго различить, посредством каких идей должно быть сообщено нашему разуму каждое из значений слов. Вот почему мы предлагаем рассмотреть три следующие формы выражения: протяжение занимает место, тело обладает протяжением, и протяжение не есть тело.
Первая из них показывает, каким образом протяжение принимается за то, что является протяженным; действительно, я разумею совершенно одно и то же и когда говорю: протяжение занимает место, и когда говорю: протяженное занимает место. Из этого, однако, не следует, что во избежание двусмысленности лучше пользоваться словом протяженное, ибо оно не обозначало бы столь четко то, что мы разумеем, а именно то, что какой-либо предмет занимает место, так как он является протяженным; и кто-нибудь мог бы истолковать выражение: протяженное есть предмет, занимающий место, — только так, как если бы я сказал: одушевленное занимает место. Это рассуждение объясняет, почему мы сказали, что будем здесь вести речь скорее о протяжении, чем о протяженном, хотя мы и считаем, что протяжение не должно пониматься иначе, чем протяженное.
Перейдем теперь к следующим словам: тело обладает протяжением, — где мы, хотя и понимаем, что протяжение обозначает нечто иное, чем тело, тем не менее не создаем в нашей фантазии двух различных идей: одну — тела, другую — протяжения, а создаем только одну идею протяженного тела; в действительности это не что иное, как если бы я сказал: тело является протяженным, или, вернее, протяженное является протяженным. Это свойственно тем сущностям, которые пребывают только в другом и никогда не могут быть поняты без их предмета; иначе обстоит дело с теми сущностями, которые реально отличаются от их предметов, ибо если бы я, например, сказал: Петр обладает богатствами, — то идея Петра была бы совершенно отлична от идеи богатств; таким же образом, если бы я сказал: Павел богат, — я вообразил бы нечто совершенно иное, чем если бы я сказал: богатый есть богатый. Не распознавая этого различия, многие неверно полагают, что протяжение содержит в себе нечто отличное от того, что является протяженным, подобно тому как богатства Павла есть нечто иное, чем сам Павел.
Наконец, когда говорится: протяжение не есть тело, — тогда слово «протяжение» понимается совсем иначе, чем выше; и в данном значении ему не соответствует в фантазии никакая особая идея, а все это высказывание исходит от чистого разума, который один обладает способностью обособлять отвлеченные сущности такого рода. Это становится причиной заблуждения, свойственного многим людям, которые, не замечая, что протяжение, взятое в таком смысле, не может быть воспринято воображением, представляют его себе посредством верной идеи; поскольку же эта идея необходимо включает в себя понятие тела, то, когда они говорят, что протяжение, понимаемое таким образом, не есть тело, они неразумно противоречат себе самим, приходя к тому, что одна и та же вещь одновременно является и телом и не телом. И весьма важно различать высказывания, в которых такие названия, как протяжение, фигура, число, поверхность, линия, точка, единица и т. д., обладают настолько узким значением, что исключают и то, от чего они на самом деле не отличаются, как тогда, когда говорится: протяжение или фигура не есть тело; число не есть счисляемая вещь; поверхность есть предел тела, линия — поверхности, точка — линии; единица не есть количество и т. д. Все эти и подобные им положения должны быть совершенно отделены от воображения, как бы верны они ни были; вот почему мы не будем вести о них речь в дальнейшем.
Нужно особо отметить, что во всех других положениях, где эти названия, хотя они и сохраняют то же самое значение и признаются тем же самым способом отвлеченными от их предметов, все-таки не исключают или не отрицают что-либо, от чего они реально не отличаются, мы можем и должны воспользоваться помощью воображения, ибо тогда, хотя разум замечает исключительно лишь то, что обозначается словом, воображение все же должно создать верную идею вещи, для того чтобы, когда потребует необходимость, сам разум мог обращаться к другим ее свойствам, не выраженным в названии, и никогда не полагал опрометчиво, что они были исключены. Так, если стоит вопрос о числе, мы воображаем какой-то предмет, измеряемый посредством многих единиц, и, хотя разум в это время размышляет только о множественности данного предмета, мы тем не менее будем остерегаться, чтобы впоследствии он не пришел на основании этого к какому-либо заключению, где предполагалось бы, что счисляемая вещь была исключена из нашего представления; так делают те люди, которые приписывают числам и удивительные тайны, и сущие пустяки, в кои они, конечно, не уверовали бы до такой степени, если бы не представляли себе число отличным от счисляемых вещей. Таким же образом, если мы имеем дело с фигурой, мы будем считать, что говорим о протяженном предмете, понимаемом только в том смысле, что он обладает фигурой; если — с телом, то мы будем считать, что говорим о том же самом предмете как обладающем длиной, шириной и глубиной; если — с поверхностью, то мы представим себе его как обладающий длиной и шириной, опуская, но не отрицая глубину; если — с линией, то представим себе его только как обладающий длиной; если — с точкой, то представим себе его, опуская все иное, кроме того, что он есть сущее.
Хотя я здесь подробно обосновываю все эти выводы, умы смертных все же настолько полны предубеждений, что я еще опасаюсь, что в данной части трактата очень немногие будут достаточно надежно ограждены от всякого риска заблуждения и что в этом длинном рассуждении они найдут объяснение моего мнения слишком кратким; действительно, сами науки — арифметика и геометрия, хотя они и являются наиболее достоверными из всех, тем не менее здесь вводят нас в заблуждение. Ибо какой счетчик не думает, что его числа должны быть не только отвлечены разумом от всякого предмета, но и действительно отделены от него воображением? Какой геометр не затемняет очевидность своего объекта противоречивыми принципами, когда он утверждает, что линии не имеют ширины, а поверхности — глубины, и тем не менее потом образовывает одни из других, не замечая, что та линия, в результате движения которой, по его представлению, возникает поверхность, есть настоящее тело, а та линия, которая не имеет ширины, есть только модус тела, и т. д.? Но, чтобы не задерживаться слишком долго на перечислении этих ошибок, изложим покороче, каким образом, по нашему предположению, должен пониматься наш объект, чтобы мы как можно легче доказали все истинное, что утверждается о нем в арифметике и геометрии.
Итак, мы занимаемся здесь протяженным объектом, не рассматривая в нем совершенно ничего иного, кроме самого протяжения, и умышленно воздерживаясь от употребления слова «количество», ибо некоторые философы настолько изощренны, что они отличили также количество от протяжения16; но мы предполагаем, что все вопросы приведены к такому виду, что не требуется ничего иного, кроме как познать некое протяжение на основании сравнения его с каким-то другим протяжением, уже известным. Действительно, поскольку мы не ожидаем здесь познания какого-нибудь нового сущего, а только хотим привести пропорции, сколь бы запутанными они ни были, к тому, чтобы неизвестное было найдено равным чему-то известному, то, несомненно, все те различия пропорций, которые существуют в других предметах, могут быть обнаружены также и между двумя или многими протяжениями. И потому для нашей цели достаточно рассмотреть в самом протяжении все те свойства, которые могут способствовать выявлению различий пропорций, и таковых оказывается только три, а именно измерение, единица и фигура.
Под измерением мы разумеем не что иное, как способ и основание, в соответствии с которыми какой-либо предмет рассматривается как измеримый, так что не только длина, ширина и глубина суть измерения тела, но и тяжесть есть измерение, в соответствии с которым предметы взвешиваются, скорость есть измерение движения, и других таких примеров бесконечное множество. Ведь само деление на многие равные части, будь оно реальным или только мысленным, есть собственно измерение, в соответствии с которым мы исчисляем вещи; и тот способ, каким образуется число, собственно, и называется видом измерения, хотя есть некоторая разница в значениях этого слова. Действительно, когда мы рассматриваем части по отношению к целому, тогда мы говорим, что исчисляем; когда, наоборот, рассматриваем целое как разделенное на части, мы измеряем его: например, мы измеряем века годами, днями, часами и мгновениями; если же мы будем считать мгновения, часы, дни и годы, мы в конце концов дойдем и до веков.
Из этого явствует, что в одном и том же предмете может быть бесконечное множество различных измерений и что они совершенно ничего не добавляют к измеряемым вещам, но понимаются одинаковым образом, независимо от того, имеют ли они реальное основание в самих предметах или были придуманы по произволу нашего ума. Действительно, чем-то реальным является тяжесть тела, или скорость движения, или разделение века на годы и дни, но не таково разделение дня на часы и мгновения и т. д. Тем не менее все это признается одинаковым, если рассматривается только в отношении измерения, как это следует делать здесь и в математических дисциплинах, ибо исследование того, является ли основание упомянутых измерений реальным, больше касается физиков.
Рассмотрение этого обстоятельства проливает много света на геометрию, так как почти все плохо представляют в ней три вида величины: линию, поверхность и тело. В самом деле, как было отмечено ранее, линия и поверхность непредставимы как действительно отличные от тела или друг от друга, но, когда они рассматриваются просто как отвлеченные разумом, тогда они суть различные виды величины не в большей степени, чем одушевленное и живое в человеке суть различные виды субстанции. И следует заметить мимоходом, что три измерения тел — длина, ширина и глубина — отличаются друг от друга только названием, ибо ничто не мешает в каком-то данном теле избрать какое угодно протяжение в качестве длины, а другое — в качестве ширины и т. д. И хотя только эти три измерения имеют реальное основание во всякой протяженной вещи как просто протяженной, все-таки здесь мы принимаем их во внимание не более, чем бесконечное множество других измерений, которые или создаются разумом, или имеют другие основания в вещах: так, в треугольнике, если мы хотим точно его измерить, необходимо в действительности знать три величины, а именно: либо три стороны, либо две стороны и один угол, либо два угла и площадь и т. д.; точно так же в трапеции необходимо знать пять, а в тетраэдре — шесть величин и т. д., которые все могут быть названы измерениями. Для того же, чтобы избрать здесь те из них, которые в наибольшей степени содействуют нашему воображению, мы никогда не будем одновременно обращать внимание больше, чем на одно или два измерения, рисуемых в нашей фантазии, даже если мы понимаем, что в положении, которым мы будем заниматься, содержится сколько угодно других. Ведь задача искусства — различать возможно большее число их так, чтобы мы замечали только очень немногие из них одновременно, но вместе с тем все — в последовательности.
Единица есть та общая природа, к которой, как мы сказали выше, должны быть одинаково приобщены все те вещи, какие сравниваются между собой. И если в вопросе нет какой-либо уже определенной единицы, мы можем взять вместо нее или одну из уже данных величин, или любую другую, которая и будет общей мерой для всех остальных; и мы поймем, что в ней заключено столько же измерений, сколько и в тех крайних членах, которые должны будут сравниваться между собой, и представим ее себе либо просто как нечто протяженное, отвлекаясь от всего иного (тогда она будет тем же самым, что и точка у геометров, когда они посредством ее движения образуют линию), либо как некоторую линию, либо как квадрат.
Что касается фигур, то выше уже было показано, как посредством их одних могут быть образованы идеи всех вещей; в данном случае нам остается уведомить, что из бесчисленного количества их различных видов мы будем использовать здесь только те, которыми наиболее легко выражаются все различия отношений или пропорций. Существует же только два рода вещей, которые сравниваются между собой: множества и величины; и для того, чтобы сделать их доступными нашему представлению, мы располагаем также и двумя родами фигур. Например, точки, которыми обозначается треугольное число, или древо, которое раскрывает чью-нибудь родословную, и т. д. являются фигурами, представляющими множество; те же фигуры, которые непрерывны и неделимы, такие, как треугольник, квадрат и т. д., представляют величины.
Для того же, чтобы теперь изложить, какими из всех этих фигур мы будем здесь пользоваться, необходимо знать, что все отношения, какие только могут быть между сущностями одного и того же рода, должны быть сведены к двум главным, а именно к порядку или к мере.
Кроме того, надо знать, что для нахождения порядка требуется немало усердия, как это везде можно видеть в настоящем методе, который не научает почти ничему другому; в познании же порядка, после того как он был найден, не заключается совершенно никакой трудности, но мы можем легко обозреть умом, в соответствии с седьмым правилом, каждую из упорядоченных частей, именно потому что в этом роде отношений одни части соотносятся с другими сами по себе, а не через посредство чего-то третьего, как это бывает с мерами, о развертывании которых мы здесь поэтому только и будем рассуждать. Действительно, я узнаю, каков порядок, связывающий А и В, не рассматривая ничего иного, кроме обоих крайних членов; но я не узнаю, каково соотношение по величине между двумя и тремя, если не рассмотрю нечто третье, а именно единицу, которая является общей мерой обоих чисел.
Надо также знать, что непрерывные величины с помощью принятой единицы иногда целиком могут быть сведены к множеству и всегда — по крайней мере частично, а множество единиц может быть затем расположено в таком порядке, что затруднение, которое касается познания меры, будет в конце концов зависеть лишь от рассмотрения порядка, и успеху этого искусство содействует в наибольшей степени.
Надо, наконец, знать, что из измерений непрерывной величины нет ни одного, которое представлялось бы более отчетливо, чем длина и ширина, и что не следует одновременно обращать внимание на большее число измерений в одной и той же фигуре, если мы будем сравнивать друг с другом два различных измерения, ибо требуется искусство для того, чтобы, располагая больше чем двумя различными измерениями, подлежащими сравнению друг с другом, мы последовательно обозревали их, но одновременно обращали внимание только на два из них.
Заметив это, легко заключить, что положения здесь должны быть отвлечены от тех самых фигур, о которых рассуждают геометры, когда вопрос стоит о них, — отвлечены не менее, чем от любой другой материи. Для этой цели не следует оставлять ничего, кроме прямолинейных и прямоугольных поверхностей или прямых линий, которые мы также называем фигурами, потому что через их посредство мы воображаем действительно протяженный предмет в не меньшей степени, нежели через посредство поверхностей, как было сказано выше. Наконец, через посредство тех же самых фигур следует представлять то непрерывные величины, то множество или число; и для того, чтобы выявить все различия отношений, человеческим усердием не может быть изобретено ничего более простого.
Правило XV
В большинстве случаев полезно также чертить эти фигуры и представлять их внешним чувствам для того, чтобы таким способом легче удерживать нашу мысль сосредоточенной.
А то, как следует изображать эти фигуры, чтобы, когда они находятся перед глазами, их образы отчетливее запечатлевались в нашем воображении, является самоочевидным: так, вначале мы изобразим единицу тремя способами, а именно: в виде квадрата , если мы сосредоточим внимание на ней как на обладающей длиной и шириной, либо в виде линии
, если мы будем рассматривать ее только как обладающую длиной, либо, наконец, в виде точки , если мы не заметим в ней ничего иного, кроме того, что благодаря ей составляется множество; но, как бы она ни изображалась и ни понималась, мы всегда будем подразумевать, что она является предметом, вполне протяженным и вмещающим бесконечное множество измерений. Точно так же и термины положения, когда нужно одновременно сосредоточить внимание на двух их различных величинах, следует представлять в виде прямоугольника, две стороны которого будут двумя названными величинами, таким образом:
, когда они несоизмеримы с единицей, либо так:
или так:
, когда они соизмеримы с ней; и не требуется ничего более, если только не ставится вопрос о множестве единиц. Если, наконец, мы сосредоточиваем внимание только на одной из этих величин, мы начертим линию либо в виде прямоугольника, одна сторона которого будет названной величиной, а другая — единицей, таким образом:
— это бывает всякий раз, когда одну и ту же линию необходимо сравнить с какой-то поверхностью; либо в виде одной лишь длины, таким образом:
, если она рассматривается только как несоизмеримая длина; либо таким образом:, если она является множеством.
Правило XVI
Что же касается вещей, которые не требуют наличного внимания ума, хотя и необходимы для заключения, то их лучше обозначать посредством наиболее сокращенных знаков, чем посредством полных фигур, ибо тогда память не сможет ошибаться, а вместе с тем и мысль не будет отвлекаться на то, чтобы удержать их, в то время как она занята выведением других.
Впрочем, поскольку мы сказали, что из бесчисленных измерений, которые могут быть изображены в нашей фантазии, нужно созерцать одним взором глаз или ума не более двух различных измерений, то важно удерживать в памяти все остальные таким образом, чтобы они легко представлялись всякий раз, когда потребует необходимость; по-видимому, с этой целью память и была создана природой. Но так как память зачастую подвержена ошибкам, то для того, чтобы мы не были вынуждены уделять некоторую часть нашего внимания ее восстановлению, в то время когда мы заняты другими мыслями, искусство весьма кстати открыло возможность применения письменности. Полагаясь на ее помощь, мы здесь совершенно ничего не вверяем памяти, но, предоставив свободной фантазии в целом наличные идеи, изображаем на бумаге все, что должно быть сохранено, и делаем это посредством наиболее сокращенных знаков, чтобы, после того как в соответствии с девятым правилом мы рассмотрели каждый из них в отдельности, мы смогли в соответствии с одиннадцатым правилом обозреть их все в наибыстрейшем движении мысли и одновременно охватить взором наибольшее их число.
Итак, все, что для разрешения затруднения надлежит рассматривать как нечто единое, мы будем обозначать одним знаком, который может быть изображен как угодно. Но ради удобства мы воспользуемся буквами а, b, с и т. д. для выражения уже известных величин и А, В, С и т. д. для выражения неизвестных. Мы часто будем ставить перед ними цифры 2, 3, 4, и т. д. для того, чтобы обозначить количество этих величин; вместе с тем мы будем располагать цифры и позади них, для того чтобы обозначать число отношений, которые надлежит в них уразуметь: так, если я напишу 2а3, это будет то же самое, как если бы я сказал: удвоение величины, обозначаемой буквой а и содержащей три отношения. И благодаря этому приему мы не только произведем сокращение многих выражений, но и, что особенно важно, представим термины затруднения в столь чистом и подлинном виде, что, не упуская ничего полезного, мы вместе с тем никогда не найдем в них ничего излишнего и того, что напрасно отвлечет способности ума, в то время как нужно будет одновременно охватить умом многие вещи.
Для того чтобы яснее уразуметь все это, нужно прежде всего заметить, что счетчики имели обыкновение обозначать каждую из величин посредством многих единиц или посредством какого-либо числа, мы же в данном случае отвлекаемся от самих чисел не меньше, чем несколько ранее от геометрических фигур или от любой другой вещи. Мы делаем это как для того, чтобы избежать пресыщения долгим и ненужным вычислением, так и в особенности для того, чтобы части предмета, которые имеют отношение к природе затруднения, всегда оставались раздельными и не скрывались за бесполезными числами: например, если отыскивается основание прямоугольного треугольника, данные стороны которого равняются 9 и 12, счетчик скажет, что оно равно √225, или 15; мы же вместо 9 и 12 поставим а и b и найдем, что основание равно √(а2 + b2), при этом те два члена а2 и b2, которые в числе являются слитыми, останутся раздельными.
Нужно также заметить, что под числом отношений надлежит понимать следующие в непрерывном порядке пропорции, которые в общепринятой алгебре иные пытаются выразить посредством многих измерений и фигур; первую из них они называют корнем, вторую — квадратом, третью — кубом, четвертую — биквадратом и т. д. Признаюсь, что эти названия долгое время вводили меня самого в заблуждение, ибо мне казалось, что после линии и квадрата моему воображению ничто не может представиться яснее, чем куб и другие фигуры, созданные по их подобию; и действительно, с помощью этих фигур я разрешил немало затруднений. Однако в конце концов после многих опытов я убедился в том, что никогда не находил благодаря этому способу понимания ничего такого, чего я не сумел бы познать гораздо легче и отчетливее и без него, а также в том, что нужно полностью отбросить такие названия, чтобы не извратить ими наше представление, ибо одна и та же величина, хотя она и называется кубом или биквадратом, тем не менее, согласно предшествующему правилу, никогда не должна представляться воображению иначе как в виде линии или поверхности. Поэтому нужно особо отметить, что корень, квадрат, куб и т. д. являются не чем иным, как непрерывно пропорциональными величинами, которым, как предполагается, всегда предпослана та принятая единица, о коей мы уже говорили выше. Первая пропорциональная величина связана с этой единицей непосредственно и одним лишь отношением, вторая же связана с ней через посредство первой и потому — двумя отношениями, третья — через посредство первой и второй и тремя отношениями и т. д. Итак, отныне мы будем называть первой пропорциональной ту величину, которая в алгебре именуется корнем, второй пропорциональной — ту, которая именуется квадратом, и т. д.
Наконец, нужно заметить, что, хотя мы отвлекаем здесь термины затруднения от некоторых чисел для того, чтобы исследовать его природу, тем не менее часто бывает так, что оно может быть разрешено более простым способом с помощью данных чисел, чем если бы оно было отвлечено от них: это происходит благодаря двойному применению чисел (которого мы уже коснулись ранее), а именно потому, что одни и те же числа раскрывают то порядок, то меру. И стало быть, после того как мы исследовали это затруднение, выраженное в общих терминах, нужно свести его к данным числам, чтобы увидеть, не наведут ли они нас тогда, быть может, на какое-то более простое решение: например, после того как мы увидели, что основание прямоугольного треугольника со сторонами а и b равно √(a2 + b2) и что вместо а2 надо поставить 81, а вместо b2 — 144, т. е. числа, дающие в сумме число 225, корень которого, или средняя пропорциональная между единицей и 225, равен 15, мы из этого узнаем, что основание 15 соизмеримо со сторонами 9 и 12, но не потому, что оно вообще является основанием прямоугольного треугольника, одна сторона которого относится к другой, как 3 к 4. Все это различаем мы, стараясь обрести очевидное и отчетливое познание вещей, а не счетчики, которые, когда им попадается искомая сумма, бывают удовлетворены, даже если они не замечают, каким образом она зависит от данных чисел; однако только в этом, собственно, и заключается наука.
Вообще же следует заметить, что никогда не нужно вверять памяти какую-либо из тех вещей, которые не требуют постоянного внимания, если мы можем изложить их на бумаге, а именно для того, чтобы бесполезным воспоминанием не отвлекать какую-то часть нашего ума от познания наличного объекта. И надо составить таблицу, в которую мы запишем термины вопроса в том виде, в каком они будут изначально представлены, а затем то, каким образом они отвлекаются и посредством каких знаков выражаются, чтобы, после того как решение будет найдено в этих самых знаках, мы легко и без всякой помощи памяти применили его к частному предмету, о котором будет стоять вопрос; действительно, никогда нельзя отвлекать что-либо, кроме как от чего-то менее общего. Итак, я пишу следующим образом: в прямоугольном треугольнике ABC отыскивается основание АС, — и представляю затруднение в отвлеченном виде, чтобы вообще отыскивалась величина основания по величинам сторон; затем вместо стороны АВ, которая равна 9, я ставлю а, вместо стороны ВС, которая равна 12, я ставлю b, и т. д.
Необходимо отметить, что мы еще воспользуемся этими четырьмя правилами в третьей части настоящего трактата и будем понимать их несколько шире, чем они были истолкованы здесь, так, как будет сказано в своем месте.
Правило XVII
Нужно прямо обогреть предложенное затруднение, отвлекаясь от того, что какие-то его термины являются известными, а какие-то — неизвестными, и усматривая благодаря правильным рассуждениям взаимную зависимость каждого из них от других.
Четыре предшествующих правила указали, каким образом определенные и вполне понятые затруднения должны быть отвлечены от каждого из их предметов и приведены к такому виду, чтобы затем не требовалось ничего другого, кроме как познать некоторые величины на основании того, что они связаны тем или иным отношением с некоторыми данными. Теперь же в этих пяти следующих правилах мы изложим, каким способом те же самые затруднения должны быть преобразованы так, что, сколько бы неизвестных величин ни было в одном положении, все они будут подчинены друг другу и как первая из них будет соотноситься с единицей, точно так же и вторая будет соотноситься с первой, третья — со второй, четвертая — с третьей; таким образом, в последовательности эти величины, если они достаточно многочисленны, составят сумму, равную какой-то известной величине. И это обеспечивается методом настолько надежным, что мы таким образом твердо убеждаемся в том, что указанные величины никакими стараниями не могли быть сведены к более простым терминам.
Что же касается настоящего правила, то следует отметить, что во всяком вопросе, подлежащем разрешению посредством дедукции, есть один ровный и прямой путь, которым мы можем легче всего переходить от одних терминов к другим, все же прочие являются более трудными и окольными. Чтобы это понять, нужно вспомнить сказанное в одиннадцатом правиле, где мы разъяснили, что связь положений такова, что, сравнивая каждое из них с соседними, мы легко замечаем, каким образом соотносятся друг с другом также первое и последнее из них, даже если мы не выводим столь же легко промежуточные положения из крайних. Следовательно, если теперь в не нарушаемом нигде порядке мы рассматриваем зависимость отдельных положений друг от друга, с тем чтобы отсюда вывести, каким образом последнее зависит от первого, то мы обозреваем затруднение прямо; напротив, если мы узнаем, что первое и последнее положения определенным образом связаны между собой, и вследствие этого пожелаем вывести, каковы промежуточные положения, которые их соединяют, то мы будем руководствоваться безусловно косвенным и обратным порядком. Поскольку же мы занимаемся здесь лишь темными вопросами, а именно теми, в которых на основании известных крайних терминов надо в обратном порядке познать некоторые промежуточные, то вся хитрость тут заключается в том, чтобы, допуская неизвестное в качестве известного, мы смогли в сколь угодно запутанных затруднениях представить себе легкий и прямой путь их исследования. И ничто не мешает тому, чтобы так было всегда, ибо, как мы предположили с самого начала этой части, мы знаем, что зависимость тех терминов, которые в вопросе неизвестны, от известных такова, что первые полностью обусловлены последними. Так что если мы поразмыслим над теми самыми терминами, которые поначалу встретятся нам, когда мы признаем такую обусловленность, то, хотя мы и будем причислять эти неизвестные к известным, с тем чтобы постепенно посредством правильных рассуждений вывести из них и все остальные известные, как если бы они были неизвестными, мы выполним все то, что предписывает настоящее правило; примеры, поясняющие это и многое из того, что мы будем говорить в дальнейшем, мы откладываем до двадцать четвертого правила, так как удобнее изложить их там.
Правило XVIII
Для этого требуются только четыре действия: сложение, вычитание, умножение и деление; два последних здесь зачастую не следует производить, как для того, чтобы невзначай не запутать чего-нибудь, так и потому, что впоследствии они могут быть выполнены более легко.
Многочисленность правил часто проистекает из неопытности учителя, и то, что могло бы быть сведено к единому общему предписанию, становится менее очевидным, если разделяется на многие частности. Вот почему все действия, которыми нужно пользоваться при рассмотрении вопросов, т. е. при выведении каких-то величин из других, мы сводим здесь лишь к четырем главным; то, каким образом они оказываются достаточными, познается из их объяснения.
А именно, если мы приходим к познанию одной величины благодаря тому, что мы знаем части, из которых она составлена, это делается посредством сложения; если мы узнаём часть благодаря тому, что знаем целое и превышение целого над той же самой частью, это делается посредством вычитания; и какая-либо величина не может быть большим числом способов выведена из других, взятых в абсолютном смысле, величин, в которых она определенным образом содержится. Если же какая-либо величина должна быть найдена на основании других, от которых она совершенно отлична и в которых она никоим образом не содержится, необходимо соотнести ее с ними каким-нибудь способом; и когда это отношение, или соответствие, нужно обозреть прямо, тогда следует пользоваться умножением, когда косвенно — делением.
Чтобы ясно описать два последних действия, надо знать, что единица, о которой мы уже говорили, является здесь основанием и фундаментом всех отношений и в ряде непрерывно пропорциональных величин она занимает первую ступень, данные же величины содержатся на второй ступени, а искомые — на третьей, четвертой и остальных, если соотношение прямое, если же оно косвенное, искомая величина содержится на второй и других промежуточных ступенях, а данная — на последней.
Действительно, когда говорится, что, как единица относится к а, или к данному числу 5, так b, или данное число 7, относится к искомому, которое равно ab, или 35, тогда а и Ь находятся на второй ступени, и ab, являющееся их произведением, — на третьей. Равным образом, когда добавляют, что, как единица относится к с, или 9, так ab, или 35, относится к искомому аbс, или 315, тогда abc находится на четвертой ступени и получается посредством двух действий умножения ab на с, т. е. величин, находящихся на второй ступени, и т. д. Равным образом, как единица относится к а, (или) 5, так а, (или) 5, относится к а2, или 25; и опять-таки как единица относится к (а, или) 5, так а2, (или) 25, относится к а3, (или) 125; и, наконец, как единица относится к а, (или) 5, так а3, (или) 125, относится к а4, т. е. к 625, и т. д.: ведь когда одна и та же величина умножается на саму себя, умножение производится так же, как и тогда, когда она умножается на другую, совершенно отличную от нее величину.
Когда же теперь говорится, что, как единица относится к а, или 5, данному делителю, так В, или искомое число 7, относится к ab, или 35, данному делимому, тогда порядок является обратным и косвенным, вследствие чего искомое В не может быть получено иначе, кроме как посредством деления данного ab на а, также данное. Равным образом, когда говорится, что, как единица относится к А, или искомому числу 5, так А, или 5, искомое, относится к а2, или 25, данному; или же как единица относится к А, (или) 5, искомому, так А2, или 25, искомое, относится к а3, или 125, данному, и т. д. Все это мы охватываем названием «деление», хотя следует отметить, что последние из примеров такого вида заключают в себе большее затруднение, чем первые, ибо в них чаще встречается искомая величина, которая поэтому предполагает многие отношения. Ведь смысл этих примеров тот же самый, как если бы было сказано, что надо извлечь квадратный корень из а, или <из> 25, либо кубический из а3, или из 125, и т. д.; такой способ выражения употребителен у счетчиков. Или, если объяснить их также в терминах геометров, это то же самое, как если бы было сказано, что надо найти среднюю пропорциональную между той принятой величиной, которую мы называем единицей, и той, которая обозначается а2, либо две средние пропорциональные между единицей и а3, и т. д.
Из этого легко сделать вывод о том, каким образом двух названных действий достаточно для отыскания любых величин, которые должны быть выведены из других величин благодаря какому-либо отношению. После того как мы поняли это, нам следует изложить, каким образом эти действия должны быть рассмотрены воображением и каким образом они должны также предстать перед глазами, для того чтобы затем мы наконец объяснили их использование, или применение.
Если нужно произвести сложение или вычитание, мы представляем себе предмет в виде линии или в виде протяженной величины, в которой должна быть рассмотрена только длина: действительно, если нужно прибавить линию
мы прикладываем одну линию к другой под прямым углом таким образом:
и получается прямоугольник
Наконец, при делении, в котором дан делитель, мы воображаем, что делимая величина представляет собой прямоугольник, одна сторона которого является делителем, а другая — частным; так, если прямоугольник ab нужно разделить на а,
из него убирают ширину а, и остается b в качестве частного: . Или, наоборот, если тот же прямоугольник делят на b, то убирают высоту b, и а будет частным:
.
Что же касается тех делений, в которых делитель не дан, а только обозначен через посредство какого-либо отношения, как, например, когда говорится, что нужно извлечь квадратный или кубический корень и т. д., то следует отметить, что в этих случаях и подлежащий делению, и все другие термины нужно всегда представлять себе как линии, расположенные в ряде непрерывно пропорциональных величин, первой из которых является единица, а последней — делимая величина. О том, каким образом между этой величиной и единицей должно быть найдено сколько угодно средних пропорциональных, будет сказано в своем месте. Теперь же достаточно уведомить, что здесь, как мы предполагаем, подобные действия еще не были доведены до совершенства, так как они должны производиться при посредстве непрямых и обратных актов воображения, а сейчас мы говорим только о вопросах, которые следует обозревать прямо.
Что касается других действий, то они, конечно, весьма легко могут быть осуществлены тем способом, которым, как мы сказали, их надлежит понимать. Вместе с тем остается изложить, каким образом должны быть подготовлены используемые в них термины; ибо, хотя, впервые занимаясь каким-либо затруднением, мы вольны представлять себе его термины как линии или как прямоугольники и никогда не приписывать этим терминам других фигур, как было сказано в четырнадцатом правиле, тем не менее в рассуждении часто бывает, что прямоугольник, после того как он был образован умножением двух линий, затем следует представлять себе в виде линии, для того чтобы выполнить другое действие, либо тот же самый прямоугольник или линию, полученную в результате какого-то сложения или вычитания, затем следует представлять себе как некоторый другой прямоугольник, построенный на обозначенной линии, которой он должен быть разделен.
Итак, здесь стоит изложить, каким образом всякий прямоугольник можно преобразовать в линию и в свою очередь линию или даже прямоугольник — в другой прямоугольник, сторона которого обозначена. Это весьма легко сделать геометрам, если только они заметят, что в виде линий, всякий раз когда мы, как здесь, сравниваем их с каким-либо прямоугольником, мы неизменно представляем себе прямоугольники, одна сторона которых является той длиной, какую мы приняли за единицу. Ведь тогда вся эта задача сводится к положению такого вида: по данному прямоугольнику построить другой, равный ему, на данной стороне.
Хотя это действие известно даже новичкам в геометрии, тем не менее мне хочется объяснить его, чтобы не показалось, будто я что-либо упустил.
Правило XIX
Посредством этого метода рассуждения нужно отыскивать столько величин, выраженных двумя различными способами, сколько неизвестных терминов мы допускаем в качестве известных, для того чтобы прямо обозреть затруднение; ибо таким образом мы будем иметь столько же сравнений между двумя равными терминами.
Правило XX
Отыскав уравнения, нужно произвести опущенные нами действия, ни в коем случае не пользуясь умножением тогда, когда будет уместно деление.
Правило XXI
Если имеется много таких уравнений, их все необходимо свести к одному, а именно к тому, члены которого займут меньшее число ступеней в ряде непрерывно пропорциональных величин, соответственно каковому они и должны быть расположены по порядку.
Конец
Правила для руководства ума
Перевод В.И. Пикова
Декарт жил в эпоху революции, происходящей в умах и в науке. Отказ от старых представлений, основанных на авторитете и общепризнанных умопостигаемых истинах, угрожал потерей опоры в поиске надежного знания. Для Декарта жизненно важно было убедиться, что его стремление к познанию не сводится к пустой игре ума и поэтому любое научное знание можно обосновать на очевидных для ума истинных предпосылках. Но для этого был необходим метод, который позволил бы распутать любой клубок запутанных вопросов, опираясь на фундамент твердых и очевидных истин.
С этой целью Декарт пишет методологический трактат «Правила для руководства ума», в котором методы познания сводятся к исходным простым правилам. Время начала работы над трактатом точно неизвестно, а сам трактат так и остался незавершенным, но главную свою мысль Декарт в нем выразил. В 1628 году или в самом начале 1629 года трактат приобретает тот окончательный вид, в котором он известен сейчас.
Впрочем, эта работа еще не дает представление о философской системе Декарта в целом. Для ее понимания лучше обратиться к трактату «Первоначала философии» (1644 г.), в котором он обобщает основные идеи метафизики, к его книге «Размышления о первой философии» (1640 г.) и к программному труду «Мир» (1634 г.). Однако принципы мышления и познания он излагает в «Правилах…», которые могут служить методологическим введением в философию Декарта.
Правило I
Целью научных занятий должно быть направление ума таким образом, чтобы он выносил прочные и истинные суждения о всех встречающихся предметах
Декарт считает, что обыденное мышление запутывает и усложняет понимание, а научное мышление, напротив, приводит к простоте понимания на основе твердых и истинных суждений. Поэтому нужно отказаться от ошибок обыденного мышления. Например, если две вещи чем-то похожи, то люди склонны переносить свойства одной из них на другую. Исходя из этого, специалисты в какой-либо одной узкой области начинают судить обо всем многообразии мира со своей узкоспециальной точки зрения. Не понимая многообразия, они не только не постигают всеобщей мудрости, но и не задумываются о здравом смысле.
Заметив какое-нибудь сходство между двумя вещами, люди имеют обыкновение приписывать им обеим, даже в том, чем эти вещи между собою различаются, свойства, которые они нашли истинными для одной из них. Так, они ошибочно сравнивают науки, всецело заключающиеся в познании духа, с искусствами, требующими лишь некоторого телесного упражнения и расположения, и видя, что один человек не может научиться одновременно всем искусствам, но легче становится хорошим мастером тот, кто занимается лишь одним из них, — ибо приучиться одними и теми же руками возделывать землю и играть на цитре или одновременно выполнять множество других различных действий не так легко, как делать что-нибудь одно, — они придерживаются такого же мнения и о науках. Отличая одну науку от другой на основании различия их предметов, они полагают, что и изучать их нужно отдельно, оставив все прочие. В этом они глубоко ошибаются, ибо если все знания в целом являются не чем иным, как человеческой мудростью, остающейся всегда одинаковой, как бы ни были разнообразны те предметы, к которым она применяется, и если это разнообразие имеет для нее не более значения, нежели для солнца разнообразие освещаемых им тел, то не нужно полагать человеческому уму какие бы то ни было границы. Изучение одной науки не препятствует нам, как это имеет место при упражнении в одном искусстве, преуспевать в другой, но скорее даже способствует. И, право, мне кажется удивительным нрав большинства людей: они весьма старательно изучают свойства растений, движение звезд, превращение металлов и предметы подобных наук, но почти никто и не помышляет о хорошем уме (bona mens) или об этой всеобъемлющей Мудрости, между тем как все другие занятия ценны не столько сами по себе, сколько потому, что они оказывают ей некоторые услуги. Поэтому не без основания мы ставим настоящее правило во главе всех других, ибо ничто не отклоняет нас от прямого пути к искомой истине более, нежели направление наших занятий не к этой общей цели, а к тем или иным целям частного порядка. Я не говорю здесь о дурных и предосудительных целях, которые преследуются, например, из тщеславия или позорного корыстолюбия, ибо ясно, что лживые расчеты и низкие уловки грубых натур открывают к ним пути гораздо более короткие, нежели тот, который доступен действительному познанию истины. Я разумею здесь честные и похвальные намерения, ибо и они, часто незаметно, вводят нас в заблуждение, как, например, когда мы стремимся к приобретению полезных знаний ради житейских удобств либо ради удовольствия созерцания истины, доставляющего почти единственное в этой жизни не омрачимое никакими печалями блаженство. Это законные плоды, которые мы бесспорно в праве ожидать от занятия науками. Но если мы во время наших занятий будем слишком много о них думать, то может случиться, что мы упустим многое из того, что необходимо нам для познания других вещей, ибо с первого взгляда они покажутся нам либо мало полезными, либо мало занимательными. Нужно думать, что все науки настолько связаны между собой, что легче изучать их все сразу, нежели какую-либо одну из них в отдельности от всех прочих. Следовательно, тот, кто серьезно стремится к познанию истины, не должен избирать какую-нибудь одну науку, — ибо все они находятся во взаимной связи и зависимости одна от другой, — а должен заботиться лишь об увеличении естественного света разума и не для разрешения тех или иных школьных трудностей, а для того, чтобы его ум мог указывать воле выбор действий в житейских случайностях. Вскоре он удивится тому, что продвинулся гораздо далее, нежели те люди, которые занимаются частными науками, и достиг не только тех результатов, которых они хотели бы добиться, но и других, более ценных, о которых те не смеют и мечтать.
Декарт делает вывод, что все науки связаны и в основе многообразия знания лежит всеобщая мудрость, постичь которую значительно легче изучая все науки сразу, а не по отдельности. Здесь следует выделить важный момент, который раскрывает культурный смысл позиции этого философа. В Средневековье объяснить явление означало соотнести его с высшей истиной, то есть с такой идеальной определенностью, которая подтверждается авторитетами, традицией или религиозным откровением. Однако Декарт является человеком новой эпохи, поэтому истину ищет в критическом переосмыслении познавательных способностей. В дальнейшем, в соответствии с логикой развития науки, этот путь приведет к разрыву между научным знанием и простотой человеческой интуиции, представляющей мир на простых самоочевидных истинах. Но этого Декарт не мог знать, а если бы узнал, то вряд ли смог бы с этим смириться. Поэтому он уверен, что может найти за разнообразием научного знания всеобщую мудрость, то есть ту же определенную истину, но которая теперь была бы удостоверена не авторитетами и традицией, а критическим мышлением.
Правило II
Нужно заниматься только такими предметами, о которых наш ум кажется способным достичь достоверных и несомненных познаний
Познание должно вести к простоте истины, поэтому важно правильно выбрать его путь. Неопределенное и запутанное знание, в котором трудно разграничить истину и ложь, лишь отдаляет нас от цели. Путь познания должен быть прямым, поэтому исходить следует из тех наук, которые дают максимально определенное знание, исключающее ложное толкование.
Всякая наука заключается в достоверном и очевидном познании, и тот, кто сомневается во многих вещах, не более сведущ, чем тот, кто о них никогда не размышлял. Но я считаю первого даже менее сведущим, если он составил относительно некоторых вещей ложное мнение. Поэтому лучше не заниматься совсем, нежели заниматься исследованием настолько трудных вещей, что, будучи не в силах отличить в них истинное от ложного, мы вынуждены допускать в качестве достоверного сомнительное, ибо при таких занятиях приходится не столько надеяться увеличить свои знания, сколько опасаться их уменьшить. Поэтому мы отвергаем настоящим правилом все познания, являющиеся только вероятными, и полагаем, что можно доверять только совершенно достоверным и не допускающим никакого сомнения. Быть может, ученые убеждены в том, что такие знания чрезвычайно редки, ибо вследствие известного недостатка, свойственного человеческому уму, они не считают их заслуживающими внимания как слишком легкие и доступные всем; я, однако, заявляю, что число их несравненно больше, нежели они предполагают, и что их достаточно для достоверного доказательства множества таких вещей, о которых они доныне могли высказывать лишь предположения. Считая недостойным своей учености признаться себе в незнании чего-либо, они до того привыкли разукрашивать свои ложные доводы, что мало-помалу убедили ими самих себя и начали выдавать их за истинные.
Впрочем, если мы будем строго соблюдать это правило, то для нас останется весьма немного вещей, изучению которых мы могли бы себя посвятить, ибо вряд ли в науках найдется какой-либо вопрос, по которому ученые не расходились бы в своих мнениях. А всякий раз, когда два человека придерживаются противоположных мнений об одном и том же, несомненно, что по крайней мере один из них ошибается или даже ни один из них не владеет истиной; ведь если бы доводы одного были достоверны и очевидны, то он мог бы изложить их другому так, что наконец убедил бы его. Следовательно, обо всем том, что нам дает основание лишь для предположений, мы, по-видимому, не в состоянии достигнуть совершенного познания, ибо мы не можем без излишнего самомнения считать себя вправе надеяться на большее, чем другие. Поэтому, если наш расчет верен, из всех наук остаются лишь арифметика и геометрия, к изучению которых и приводит нас соблюдение этого правила.
Неразрешимые споры в науке указывают на то, что ученые обращаются не к твердым истинам, а лишь к правдоподобным мнениям. Возможно, что занятие науками о сложных вещах, позволяющих получать только правдоподобное мнение, полезно для тренировки ума или обучения, но в поиске истины следует исходить из таких дисциплин, которые дают надежную неоспоримую истину. Такими дисциплинами являются арифметика и геометрия.
По этой причине мы, однако, не осуждаем ни те приемы философствования, которые применялись до нашего времени другими, ни употребление вероятных силлогизмов, являющихся превосходным оружием в школьных турнирах, ибо они упражняют и в соревновании двигают вперед умы молодых людей, а лучше уж образовывать их умы на таких мнениях, которые очевидно не являются достоверными, поскольку служат предметом ученых споров, чем предоставлять их самим себе. Быть может, без руководителя они низвергнулись бы в пропасть; покамест же они следуют по стопам учителя, пусть даже иногда и уклоняясь от истины, они, конечно, идут более верным путем, по крайней мере потому, что этот путь был уже изведан людьми более опытными. Мы сами счастливы тем, что получили такое воспитание в школах. Но освободившись теперь от уз, которые связывали нас со словами учителя, и сделавшись, наконец, достаточно зрелыми для того, чтобы убрать руки из-под его ферулы, если мы серьезно желаем установить себе правила, с помощью которых мы могли бы подняться на вершины человеческих знаний, то нам бесспорно надлежит поставить на первый план это правило, удерживающее нас от злоупотребления нашим досугом, как это делают многие люди, которые всячески пренебрегают легкими занятиями и занимаются только трудными вещами. Правда, относительно последних они искусно строят остроумнейшие догадки и весьма правдоподобные суждения, но после многих трудов они поздно убеждаются в том, что, не получив никаких знаний, только увеличили свои сомнения.
Но если, как мы уже говорили несколько выше, из всех прочих известных нам наук только арифметика и геометрия чисты от всего ложного или недостоверного, то заметим теперь, чтобы доказать более подробно справедливость сказанного, что мы приходим к познанию вещей двумя путями, а именно: путем опыта и дедукции. Кроме того, заметим, что опыт часто вводит нас в заблуждение, тогда как дедукция, или чистое умозаключение об одной вещи через посредство другой, если и может быть упущено, когда его нельзя усмотреть, то никогда не может быть плохо построено, даже и у умов, весьма мало привычных к мышлению. Мне кажется, что те пути, с помощью которых диалектикирассчитывают управлять человеческим разумом, не могут принести большой пользы, хотя я и не отрицаю их пригодности в другом применении. Действительно, все заблуждения, в которые впадают люди — я не говорю о животных, — никогда не проистекают из плохо построенного вывода, но всегда имеют своей причиной то, что люди исходят именно из плохо понятых фактов или из поспешных и необоснованных суждений.
Декарт исходит из того, что наше познание опирается либо на дедукцию, либо на эмпирический опыт, то есть опыт, который дают органы ощущения.
Арифметика и геометрия позволяют с помощью дедукции получать неоспоримое знание. Дедукция — это вид умозаключения, с помощью которого из общего выводится частное. Поскольку общее уже содержит в себе частное, такой вывод должен быть абсолютно достоверен. В отличие от дедукции эмпирический опыт может быть обманчивым, поскольку органы ощущений дают нам знание лишь об отдельных вещах.
Из этого ясно, почему арифметика и геометрия гораздо более достоверны, чем все другие науки, а именно — предмет их столь ясен и прост, что они совсем не нуждаются ни в каких предположениях, которые опыт может подвергнуть сомнению, но всецело состоят в последовательном выведении путем рассуждения. Итак, они являются наиболее легкими и ясными из всех наук и имеют своим предметом то, что нам желательно, ибо если не быть невнимательным, то вряд ли возможно допустить в них какую-либо ошибку. Однако же вследствие этого не нужно удивляться, что многие умы охотнее посвящают себя другим занятиям или философии: это обусловливается именно тем, что всякий смелее пользуется свободой разгадывать темные вещи, нежели очевидные, и что гораздо легче строить догадки по тому или иному вопросу, нежели постичь истину, как бы она ни была проста.
Из всего сказанного нужно, однако, заключить не то, что следует изучать только арифметику и геометрию, но лишь то, что ищущие верного пути к истине не должны заниматься исследованием таких вещей, о которых они не могут иметь знаний, по достоверности равных арифметическим и геометрическим доказательствам.
Здесь Декарт закладывает фундамент традиции рационализма. Достоверно лишь умственное познание, а познание органами ощущений ненадежно и поэтому должно проверяться и обосновываться на умственном. Образцом такого познания служат арифметика и геометрия, всякий иной способ должен соответствовать этому образцу.
Правило III
В предметах нашего исследования надлежит отыскивать не то, что о них думают другие или что мы предполагаем о них сами, но то, что мы ясно и очевидно можем усмотреть или надежно дедуцировать, ибо знание не может быть достигнуто иначе
Конечно, следует обращаться к знаниям, которые накоплены предшественниками, но при этом надо отличать знания от мнений. Знания — это то, что усматривается как очевидность либо достоверным образом выводится из очевидных истин. Мнения предполагают случайные и непроверенные представления. Они могут быть разными, всякое их обсуждение приводит к неразрешимым спорам. Лишь опираясь на надежное знание на собственном пути познания, мы можем прийти к согласию с другими людьми.
Необходимо читать книги древних писателей, ибо нам доставляет огромную выгоду использование трудов столь многих людей как потому, что мы узнаем от них о полезных открытиях, которые были некогда совершены, так и потому, что они напоминают нам, что еще осталось открыть во всех науках. Однако есть большая опасность, как бы слишком старательное чтение этих книг не ввело нас в некоторые заблуждения вопреки нашему желанию и без нашего ведома, ибо все писатели, по неосмотрительному легковерию придерживающиеся спорных мнений, имеют обыкновение пускать в ход самые хитроумные доводы для того, чтобы нас убедить, а всякий раз, когда им посчастливится найти что-нибудь достоверное и очевидное, они стараются изложить это нам не иначе, как с различными двусмысленностями, разумеется, боясь того, что простота их приемов умалит достоинства их открытия, либо не желая говорить об открытой истине.
Но если даже они будут прямыми и откровенными, никогда не будут навязывать нам ничего сомнительного под видом истинного и чистосердечно изложат все, что они узнали, то, поскольку вряд ли было что-нибудь высказано одним автором, не вызвав противоположного заявления со стороны кого-либо другого, мы всегда будем в нерешимости, кому из них следует отдать предпочтение. Совершенно бесполезно в этом случае подсчитывать голоса, чтобы следовать тому мнению, которого придерживается большинство авторов, ибо если дело касается трудного вопроса, то более вероятно, что истина находится на стороне меньшинства, а не большинства. Даже и при всеобщем согласии нам будет недостаточно только знать их учение. Мы никогда, например, не сделаемся математиками, даже зная наизусть все чужие доказательства, если наш ум неспособен самостоятельно разрешать какие бы то ни было проблемы, или философами, прочтя все сочинения (argumenta) Платона и Аристотеля, но не будучи в состоянии вынести твердого суждения о данных вещах, ибо в этих случаях мы увеличим только свои исторические сведения, но не знания.
Данное высказывание Декарта о Платоне и Аристотеле чрезвычайно важно для понимания сути его философии. Философ не может заимствовать знание предшественников в готовом виде. Следует переосмыслить это знание на основе собственного пути познания. В противном случае мы перекроем развитие философии, подменив его историей этой науки. При этом Декарт полагает, что достоверный путь познания определен простыми и ясными законами мышления и потому обязательно приведет к столь же ясной и определенной истине. Заблуждения, которые привели к неразрешимым спорам между философами, связаны не с отсутствием достоверного пути, а с отклонением от него, когда неведомые вещи исследуются сомнительными методами.
Кроме того, напомним, что не следует смешивать никаких допускаемых нами предположений с суждениями об истине вещей. Это замечание имеет довольно серьезное значение, ибо немаловажная причина, в силу которой в обычной (vulgaris) философии нет ничего настолько очевидного и достоверного, что не могло бы вызывать споров, заключается в том, что ученые, изначала не удовлетворяющиеся познанием ясных и достоверных вещей, отваживаются также на темные и непонятные утверждения, к которым они приходят лишь путем правдоподобных предположений, а затем сами постепенно подкрепляют их полной верой, без разбора смешивают их с истинными и очевидными и в конце концов оказываются совершенно не в состоянии сделать ни одного вывода, не зависимого от этих предположений, который поэтому не был бы недостоверным.
Для того чтобы в дальнейшем не подвергать себя подобному заблуждению, мы рассмотрим здесь все те действия нашего интеллекта, посредством которых мы можем прийти к познанию вещей, не боясь никаких ошибок. Возможны только два таких действия, а именно: интуиция и дедукция.
Под интуицией я разумею не веру в шаткое свидетельство чувств и не обманчивое суждение беспорядочного воображения, но понятие ясного и внимательного ума, настолько простое и отчетливое, что оно не оставляет никакого сомнения в том, что мы мыслим, или, что одно и то же, прочное понятие ясного и внимательного ума, порождаемое лишь естественным светом разума и благодаря своей простоте более достоверное, чем сама дедукция, хотя последняя и не может быть плохо построена человеком, как я уже говорил выше. Так, например, всякий может интуитивно постичь умом, что он существует, что он мыслит, что треугольник ограничивается только тремя линиями, что шар имеет только одну поверхность и подобные этим истины, гораздо более многочисленные, чем это замечает большинство людей вследствие того, что не считает достойными внимания такие простые вещи.
Достоверное знание, как считает Декарт, дает дедукция, потому что именно здесь частное суждение с необходимостью следует из более общего. В свою очередь интуиция удостоверяет самые общие суждения, которые нельзя вывести дедуктивно.
В естественном языке слово «интуиция» означает непосредственное усмотрение без какого-либо предварительного рассуждения. Мы можем различать житейскую, научную, религиозную, мистическую интуицию. Однако Декарт говорит об особой интуиции — интеллектуальной, которая удостоверяет истины, самоочевидные для ума.
Может показаться, что эта идея не нова. К этому вел Сократ[1] в своих философских дискуссиях с афинянами. Это подразумевали другие античные мыслители, усматривая разумную упорядоченность мира в соответствии с мировым логосом или миром идей. Однако они исходили из онтологической предпосылки, суть которой в том, что мир устроен разумно, поэтому человек как его часть обладает разумом, удостоверяющим истину. Однако Декарт приходит к пониманию достоверности интеллектуальной интуиции не на основе онтологического убеждения, а на основе гносеологического анализа собственных познавательных способностей.
Впрочем, чтобы не смутить кого-либо новым употреблением слова интуиция, а также и других слов, которые я вынужден в дальнейшем употреблять тоже в отличном от общепринятого смысле, я здесь вообще предупреждаю, что совсем не думаю о значении, придаваемом в последнее время этим словам в школах, так как было бы очень трудно пользоваться одними и теми же словами для обозначения совершенно различных понятий; я обращаю внимание на значение каждого такого слова только на латинском языке, чтобы всякий раз, когда у меня недостает собственных выражений, взять те слова, которые мне кажутся наиболее пригодными для выражения моей мысли.
Эти же очевидность и достоверность интуиции должны иметь место не только в отдельных утверждениях, но также и во всякого рода рассуждениях. Так, например, в последовательности 2 и 2 составляют то же, что 3 и 1; нужно интуитивно постигать не только то, что 2 и 2 составляют 4 и что 3 и 1 составляют также 4, но еще и то, что из первых двух положений необходимо вытекает это третье.
Может возникнуть сомнение, для чего мы добавляем к интуиции еще и этот другой способ познания, заключающийся в дедукции, посредством которой мы познаем все, что необходимо выводится из чего-либо достоверно известного. Это нужно было сделать потому, что есть много вещей, которые хотя и не являются самоочевидными, но доступны достоверному познанию, если только они выводятся из верных и понятных принципов путем последовательного и нигде не прерывающегося движения мысли при зоркой интуиции каждого отдельного положения. Подобно этому мы узнаем, что последнее кольцо длинной цепи соединено с первым, хотя мы и не можем охватить одним взглядом все находящиеся между ними кольца, которые обусловливают это соединение, лишь бы мы последовательно проследили их и вспомнили, что каждое из них, от первого до последнего, соединено с соседним. Итак, мы отличаем здесь интуицию ума (mentis intuitus) от правильной дедукции в том отношении, что под дедукцией подразумевается именно движение или последовательность, чего нет в интуиции; кроме того, дедукция не нуждается в наличной очевидности, как интуиция, но скорее как бы заимствует свою достоверность у памяти. Отсюда следует, что положения, непосредственно вытекающие из первого принципа, можно сказать, познаются как интуитивным, так и дедуктивным путем, в зависимости от способа их рассмотрения, сами же принципы — только интуитивным, как и, наоборот, отдельные их следствия — только дедуктивным путем.
И именно это — два наиболее верных пути, ведущих к знанию, сверх которых ум не должен допускать ничего. Все остальные, напротив, должны быть отброшены как подозрительные и подверженные заблуждениям. Тем не менее это не мешает нам считать откровения Божии достовернейшими из всех наших знаний, поскольку вера в них, как и во все скрытые вещи, является делом не ума, а воли, но если бы она имела основания в нашем интеллекте, все эти вещи можно и нужно было бы исследовать именно одним из двух уже указанных способов, что мы объясним, быть может, когда-нибудь более подробно.
Декарт делает вывод: интуиция и дедукция — это два метода, необходимых и достаточных для того, чтобы обрести достоверное знание. Интеллектуальная интуиция не имеет ничего общего с верой в загадочные вещи, поскольку последняя является действием не ума, а воли. Если интуиция указывает на достоверное знание непосредственно, то дедукция предполагает последовательность выводов и поэтому уступает интуиции в ясности и самоочевидности. Чтобы провести дедукцию правильно, нужны усилия и внимательность, а прежде всего — правильный метод.
Правило IV
Метод необходим для отыскания истины
Под методом Декарт понимает набор ясных и простых правил ума, которые позволяют получать и упорядочивать новое знание, избегая заблуждений. Неупорядоченное знание, даже если оно не является ложным, отдаляет от понимания истины. Это знает всякий человек, который брался за большое научное исследование. Без ясного метода, отсекающего блуждания мысли в стороне от прямой дороги познания, возникает ворох разрозненных фактов и представлений, который невозможно удерживать в уме.
Смертными настолько владеет слепое любопытство, что они направляют свой ум на неизведанные пути без всякого основания для надежды, просто лишь для того, чтобы испытать, не подвернется ли им под руку то, что они ищут, подобно тому, кто, обуреваемый безрассудным желанием найти драгоценность, вечно блуждает по дорогам в надежде на то, что ее может обронить какой-нибудь прохожий. Так трудятся почти все химики, многие геометры и немалое число философов. Я не отрицаю, что во время их блужданий им иногда удавалось находить кой-какие истины, но, по моему мнению, этим они обязаны не умению, а счастию. Уже лучше совсем не помышлять об отыскании каких бы то ни было истин, чем делать эго без всякого метода, ибо совершенно несомненно то, что подобные беспорядочные занятия и темные мудрствования помрачают естественный свет и ослепляют ум. Всякий, привыкший таким образом блуждать во мраке, настолько ослабляет остроту своего зрения, что не может больше переносить яркий свет. Подтверждение этого мы видим на опыте, весьма часто встречая людей, никогда не усердствовавших над учеными трудами, но рассуждающих более основательно и здраво о любой вещи, чем те, которые всю жизнь провели в школах. Под методом же я разумею точные и простые правила, строгое соблюдение которых всегда препятствует принятию ложного за истинное и, без излишней траты умственных сил, но постепенно и непрерывно увеличивая знания, способствует тому, что ум достигает истинного познания всего, что ему доступно.
Декарт уверен, что метод, основанный на интуиции и дедукции, позволит отличить истинное от ложного и достичь познания всех вещей. Здесь просматривается убежденность Декарта в том, что мир можно понять рационально и ничего непостижимого в нем быть не должно. Если мы сталкиваемся с непостижимым, то это следствие неправильного способа познания.
Здесь надлежит заметить два следующих пункта: никогда не принимать за истинное то, что ложно, и добиваться познания всего. Ведь если мы не знаем чего-нибудь из того, что мы можем знать, то это объясняется только тем, что мы либо совсем не нашли никакой дороги, которая могла бы нас к нему привести, либо подверглись заблуждению. Но если метод правильно показывает, как нужно пользоваться интуицией ума, чтобы не впасть в заблуждение, противное истине, и как должны быть построены дедукции для достижения познания всего, то, мне кажется, он не требует более ничего для того, чтобы быть совершенным, ибо невозможно достигнуть никакого знания иначе, как путем интуиции ума и дедукции, о чем уже говорилось выше. Ведь он не простирается также до того, чтобы учить, как производятся эти действия, ибо они являются простейшими и первичными, и именно, если наш разум не умел пользоваться ими раньше, он не в состоянии будет понять и никаких предписаний нашего метода, как бы они ни были просты. Что же касается других действий ума, которыми диалектика старается управлять с помощью этих двух первых, то они здесь бесполезны или, скорее, их можно считать даже помехой, ибо нельзя привнести в чистый свет разума ничего, что его не ослабило бы так или иначе.
Для Декарта жизненно важным было убеждение в том, что вся действительность может быть понята в соответствии с простым и ясным методом. Он был достаточно образованным и умным человеком, чтобы понять, как легко поставить под сомнение любое знание. Поэтому он ищет надежную основу, желая убедиться: дело его жизни — философия и наука — не какая-то игра досужего ума, а действительно познание мира. Далее в тексте он делает отсылку к тому, что ум заключает в себе нечто божественное и потому обладает врожденными способностями приводить к правильному пониманию мира. Но он не удовлетворится констатацией и попытается обосновать эту врожденную способность ума на основе самопознания.
Так как польза этого метода настолько велика, что приступать без него к научным занятиям скорее вредно, чем полезно, я легко склоняюсь к убеждению, что уже давно люди постигали его в той или иной степени благодаря своим исключительным дарованиям или указаниям одной только природы. Ведь человеческий ум содержит в себе нечто божественное, в чем посажены первые семена полезных мыслей так, что часто, как бы они ни были заглушаемы и оттесняемы посторонними занятиями, они вопреки всему приносят самопроизвольно плоды. Доказательством этого для нас могут служить самые простые науки: арифметика и геометрия. Действительно, достаточно хорошо замечено, что уже древние геометры для разрешения всевозможных проблем применяли известный анализ, хотя и не пожелали передать его потомству. И в настоящее время процветает особого рода арифметика, именуемая алгеброй, заключающаяся в действиях над числами, подобных тем, которые древние производили над фигурами. Итак, обе эти науки являются не чем иным, как самопроизвольными плодами, возникшими из врожденных начал этого метода, и я не удивляюсь тому, что в применении к таким простым предметам упомянутых наук они получили к настоящему времени более пышное развитие, чем в других науках, где их обыкновенно стесняют большие препятствия, но где они несомненно могут тоже достичь полной зрелости, если их заботливо выращивать.
По мнению Декарта именно математика наиболее совершенно демонстрирует метод познания на основе интуиции и дедукции. Более того, именно она содержит первые начала человеческого рассудка. В связи с этим он очень пространно рассуждает о том, как он приходит к математике, углубляется в ее историю и оценивает вклад в науку других математиков, порой подвергая их критике за отсутствие системы. В этих рассуждениях можно увидеть, как у Декарта зарождается идея нового системного построения «всеобщей математики».
Это я и ставлю главной задачей настоящего трактата, и, конечно, я не придавал бы такого большого значения этим правилам, если бы они служили только для решения пустых головоломок, которыми счетчики и геометры развлекаются во время досуга; в подобном случае я считал бы себя, может быть, только более искусным в безделицах, чем другие. И хотя в настоящем трактате мне часто придется говорить о фигурах и числах, поскольку нет никакой другой области знаний, из которой можно было бы извлечь примеры, столь же очевидные и достоверные, тем не менее всякий, кто будет внимательно следить за моей мыслью, без труда заметит, что здесь я менее всего разумею обыкновенную математику, но что я излагаю некую другую науку, для которой упомянутые науки являются скорее покровом, нежели частью. Ведь эта наука должна содержать в себе первые начала человеческого разума и простирать свои задачи на извлечение истин относительно любой вещи. И если говорить откровенно, я убежден, что ее нужно предпочесть всем другим знаниям, которые предоставлены нам, людям, ибо она является их источником. Говоря же о покрывале, я не высказывал этим желания укутать и скрыть ее, для того чтобы оградить ее от толпы, наоборот, я хотел так одеть и украсить ее, чтобы она сделалась более привлекательной для человеческого ума.
Когда я впервые отдался душой математическим наукам, я сразу перечитал большую часть трудов, которые доставляют нам в этой области авторы. Наиболее охотно я занимался арифметикой и геометрией, потому что они считались тогда самыми простыми из всех наук и как бы дверью для всех остальных. Но ни в той ни в другой мне не посчастливилось найти такого автора, который бы меня вполне удовлетворил, а именно: большую часть того, что я прочел у них о числах, по проверке принципов я нашел верной; что же касается фигур, то наглядно они до известной степени вскрывали многое и выводили сообразно той или иной последовательности доводов, но почему это делалось так, а не иначе и каким путем достигались подобные открытия, они не могли объяснить моему уму удовлетворительно. Поэтому меня не удивляло то, что большинство способных и сведущих людей, испробовав эти науки, тотчас же начинали относиться к ним как к детским и праздным занятиям или, наоборот, устрашенные тем, что они слишком трудны и запутаны для дальнейшего изучения, останавливались на пороге. Ведь действительно нет ничего более бессмысленного, нежели трудиться над пустыми числами и вымышленными фигурами, как бы желая успокоиться на познании подобных пустяков, и до того увлекаться их поверхностными доказательствами, достигнутыми благодаря скорее случайности, чем искусству, относящимися скорее к зрению и воображению, чем к интеллекту, что ум как бы остывает от работы. Точно так же нет ничего более тягостного, нежели разрешать с помощью этого рода доказательств новые трудности, скрывающиеся в путанице чисел. Однако, когда я затем подумал, почему основоположники философии не хотели допускать к изучению мудрости людей, не сведущих в математике, словно эта наука казалась им самой легкой из всех и более всего необходимой для того, чтобы просветить и приготовить ум для постижения других, более высоких, я сразу догадался, что они разумели под ней науку, весьма отличную от обыкновенной математики нашего времени. Я отнюдь не думаю, что они постигли ее в совершенстве. Безумные ликования и жертвы, приносимые ими по поводу каких-нибудь незначительных открытий, ясно свидетельствуют о том, насколько они были еще неразвиты. Мое мнение не поколеблют и хвалы историков по поводу машин, изобретенных ими, ибо эти машины были, вероятно, чрезвычайно просты, но их прославила как чудо невежественная и легковерная толпа. Но я убежден, что посаженные природой в человеческих умах первые семена истины, которые мы заглушаем, ежедневно читая и слушая о стольких заблуждениях, имели такую мощь в этой наивной и простой древности, что с помощью того же света ума, который дал им возможность узреть необходимость предпочтения добродетели — удовольствию, чести — пользе, хотя они и не сознавали оснований этого предпочтения, они достигли истинных идей в философии и математике, даже если еще и не могли постичь эти науки в совершенстве. И мне кажется, что некоторые следы этой истинной математики можно заметить еще у Паппа и Диофанта, которые, хотя и не относятся к ранним векам, все же жили задолго до нашего времени. Но я склоняюсь к убеждению, что писатели из пагубной хитрости сами потом утаили ее, ибо подобно тому, что известно об обращении художников с их произведениями, они, боясь, как бы легкость и простота их открытия не умалили его ценность, сделав его общедоступным, и чтобы заставлять восхищаться собой, предпочли взамен его показывать как произведения их искусства кой-какие бесплодные, хотя и остроумно выведенные истины, вместо того чтобы обучать самому искусству, которое, будучи понятным, не вызывало бы более никакого удивления. Наконец, несколько гениальнейших людей нашего времени пытаются воскресить это искусство, ибо не чем иным, как искусством, представляется им наука, обозначаемая иностранным названием «алгебра», если ее освободить лишь от множества загромождающих ее знаков и непонятных фигур настолько, чтобы у нее не было недостатка в той высшей ясности и простоте, которую мы предполагаем необходимой для истинной математики. Такие размышления, отвлекшие меня от занятий только арифметикой и геометрией к общему исследованию математических наук, сначала натолкнули меня на вопрос, что разумеется именно под этим последним названием и почему не только вышеупомянутые науки, но также астрономия, музыка, оптика, механика и многие другие считаются как бы частями математики. В данном случае недостаточно рассмотреть лишь происхождение слова, ибо если слово «математика» означает только «наука», то науки, которые я здесь перечисляю, имеют не меньшее право называться математическими, чем геометрия. Впрочем, нет такого человека, который, коснувшись лишь порога школы, не сумел бы легко распознать, какие из данных предметов относятся к ведению математических, какие — к ведению других наук. Всякий, кто внимательно обдумает это, поймет наконец, что к области математики относятся только те науки, в которых рассматривается либо порядок, либо мера, и совершенно несущественно, будут ли это числа, фигуры, звезды, звуки или что-нибудь другое, в чем отыскивается эта мера; таким образом, должна существовать некая общая наука, объясняющая все, относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем всеобщей математики, ибо она содержит в себе все то, благодаря чему другие науки называются частями математики. Насколько она превосходит своей легкостью и доступностью все эти подчиненные ей науки, видно из того, что она простирается на предметы всех этих наук, так же как и многих других, и если она заключает в себе некоторые трудности, то такие же трудности содержатся и в последних, имеющих еще сверх того и другие, которые проистекают из частных объектов их и для нее не существуют. Чем же объясняется то, что теперь, когда всем известно название этой науки и все, даже не занимавшиеся ею, знают, в чем состоит ее предмет, большинство, не жалея сил, ищет знаний в других науках, зависящих от нее, и никто не пытается обратиться к ней самой? Я удивлялся бы этому наверное, если бы не знал, что все считают ее слишком легкой, и если бы я давно не заметил, что человеческий ум всегда отстраняет то, что ему кажется легко выполнимым, и прямо стремится к познанию самого нового и важного.
Конец ознакомительного фрагмента.
- Книги
- Учебная литература
- Рене Декарт
📚 Правила для руководства ума читать книгу
Правила для руководства ума
Читайте только на ЛитРес!
Как читать книгу после покупки
- Чтение только в Литрес «Читай!»
По вашей ссылке друзья получат скидку 10% на эту книгу, а вы будете получать 10% от стоимости их покупок на свой счет ЛитРес. Подробнее
Стоимость книги: 249 ₽
Ваш доход с одной покупки друга: 24,90 ₽
Чтобы посоветовать книгу друзьям, необходимо войти или зарегистрироваться
- Объем: 98 стр.
- Жанр: книги по философии, учебная литератураРедактировать
Эта и ещё 2 книги за 399 ₽
По абонементу вы каждый месяц можете взять из каталога одну книгу до 700 ₽ и две книги из специальной подборки. Узнать больше
Оплачивая абонемент, я принимаю условия оплаты и её автоматического продления, указанные в оферте
Описание книги
В издании представлена одна из самых ранних работ Декарта. «Правила» являются историко-философским документом, по которому можно судить о процессе выработки Декартом своей философской системы и дают важный материал для понимания, развития философского метода Декарта. Для студентов, аспирантов и преподавателей философских факультетов вузов, а также для всех интересующихся философской общегуманитарной проблематикой.
Подробная информация
- Возрастное ограничение:
- 0+
- Дата выхода на ЛитРес:
- 02 июня 2019
- Дата написания:
- 2019
- Объем:
- 98 стр.
- ISBN:
- 9785534071535
- Общий размер:
- 0 MB
- Общее кол-во страниц:
- 98
- Размер страницы:
- 140 x 210 мм
- Правообладатель:
- ЮРАЙТ
«Правила для руководства ума» — читать онлайн бесплатно фрагмент книги. Оставляйте комментарии и отзывы, голосуйте за понравившиеся.
Оставьте отзыв
Другие книги автора
На что хотите пожаловаться?
Сообщение отправлено
Мы получили Ваше сообщение.
Наши модераторы проверят книгу
в ближайшее время.
Спасибо, что помогаете нам.
Сообщение уже отправлено
Мы уже получили Ваше сообщение.
Наши модераторы проверят книгу
в ближайшее время.
Спасибо, что помогаете нам.
Поделиться отзывом на книгу
Рене Декарт, Василий Иванович Пиков, ещё 0 авторов
Правила для руководства умаPDF
Мы используем куки-файлы, чтобы вы могли быстрее и удобнее пользоваться сайтом. Подробнее
Правила для руководства ума
Рене Декарт
1628
ПРЕДИСЛОВИЕ
Здесь необходимо упомянуть о самоотверженных людях которые раскидывают знания выдающихся предшественников по миру, осознавая всю ценность необходимости просвещения человечества.
Перевод данного трактата с латинского – В.И.Пикова.
Из открытых источников:
ПИКОВ ВАСИЛИЙ ИВАНОВИЧ
1906, д. Жмолиха Кировской обл.
Кандидат философских наук. Работал старшим научным сотрудником Института философии АН СССР в 1934–1936 гг., был учеником И.К. Луппола. Под его руководством В.И. Пиков перевёл «Правила для руководства ума» Декарта и «Кимвал мира» Бонавентюра (Бонавантюра) Деперье (М.: Academia, 1936), философские сочинения Дидро (статьи для Энциклопедии). В 1933 опубликовал книгу о Пьере Бейле, вышедшую с предисловием И.К. Луппола. Во время Великой отечественной войны служил в 131-й стрелковой дивизии на Сталинградском фронте и пропал без вести в 1942 г.
Содержание
Правило I
Правило II
Правило III
Правило IV
Правило V
Правило VI
Правило VII
Правило VIII
Правило IX
Правило X
Правило XI
Правило XII
Правило XIII
Правило XIV
Правило XV
Правило XVI
Правило XVII
Правило XVIII
Правило XIX
Правило XX
Правило XXI
Cogito, ergo sum — лат. «я мыслю, следовательно, я существую».) — Декарт Рене
ПРАВИЛА ДЛЯ РУКОВОДСТВА УМА.
(примерно 1628г)
ПРАВИЛО I
Целью научных занятий должно быть направление ума таким образом, чтобы он выносил прочные и истинные суждения о всех встречающихся предметах.
Заметив какое-нибудь сходство между двумя вещами, люди имеют обыкновение приписывать им обеим, даже в том, чем эти вещи между собой различаются, свойства, которые они нашли истинными для одной из них. Так, они ошибочно сравнивают науки, всецело заключающиеся в познании духа, с искусствами, требующими лишь некоторого телесного упражнения и расположения, и видя, что один человек не может научиться одновременно всем искусствам, но легче становится хорошим мастером тот, кто занимается лишь одним из них, — ибо приучиться одними и теми же руками возделывать землю и играть на цитре или одновременно выполнять множество других различных действий не так легко, как делать что-нибудь одно, — они придерживаются такого же мнения и о науках. Отличая одну науку от другой на основании различия их предметов, они полагают, что и изучать их нужно каждую отдельно, оставив все прочие. В этом они глубоко ошибаются, ибо если всезнания в целом являются не чем иным, как человеческой мудростью, остающейся всегда одинаковой, как бы ни были разнообразны те предметы, к которым она применяется, и если это разнообразие имеет для неё не более значения, нежели для солнца разнообразие освещаемых им тел, то не нужно полагать человеческому уму какие бы то ни было границы. Изучение одной науки не препятствует нам, как это имеет место при упражнении в одном искусстве, преуспевать в другой, но скорее даже способствует. И право, мне кажется удивительным нрав большинства людей — они весьма старательно изучают свойства растений, движение звёзд, превращение металлов и предметы подобных наук, но почти никто и не помышляет о хорошем уме или об этой всеобъемлющей мудрости, между тем как все другие занятия ценны не столько сами по себе, сколько потому, что они оказывают ей некоторые услуги. Поэтому не без основания мы ставим настоящее правило во главе всех других, ибо ничто не отклоняет нас от прямого пути к искомой истине более, нежели направление наших занятий не к этой общей цели, a к тем или иным целям частного порядка. Я не говорю здесь о дурных и предосудительных целях, которые преследуются например из тщеславия или позорного корыстолюбия, ибо ясно, что лживые расчёты и низкие уловки грубых натур открывают к ним пути гораздо более короткие, нежели тот, который доступен действительному познанию истины. Я подразумеваю здесь честные и похвальные намерения, ибо и они, часто незаметно, вводят нас в заблуждение, как например когда мы стремимся к приобретению полезных знаний ради житейских удобств либо ради удовольствия созерцания истины, доставляющего почти единственное в этой жизни не омрачаемое никакими печалями блаженство. Это — законные плоды, которые мы бесспорно в праве ожидать от занятия науками. Но если мы во время наших занятий будем слишком много о них думать, то может случиться, что мы упустим многое из того, что необходимо нам для познания других вещей, ибо с первого взгляда они покажутся нам либо мало полезными, либо мало занимательными. Нужно думать, что все науки настолько связаны между собой, что легче изучать их все сразу, нежели какую-либо одну из них в отдельности от всех прочих. Следовательно тот, кто серьёзно стремится к познанию истины, не должен избирать какую-нибудь одну науку, ибо все они находятся во взаимной связи и зависимости одна от другой, a должен заботиться лишь об увеличении естественного света разума, и не для разрешения тех или иных школьных трудностей, a для того, чтобы его ум мог указывать воле выбор действий в житейских случайностях. Вскоре он удивится тому, что продвинулся гораздо далее, нежели те люди, которые занимаются частными науками, и достиг не только тех результатов, которых они хотели бы добиться, но и других, более ценных, о которых те не смеют и мечтать.
ПРАВИЛО II
Нужно заниматься только такими предметами, о которых наш ум кажется способным достичь достоверных и несомненных познаний.
Всякая наука заключается в достоверном и очевидном познании, и тот, кто сомневается во многих вещах, не более сведущ, чем тот, кто о них никогда не размышлял. Но я считаю первого даже менее сведущим, если он составил относительно некоторых вещей ложное мнение. Поэтому лучше не заниматься совсем, нежели заниматься исследованием настолько трудных вещей, что, будучи не в силах отличить в них истинное от ложного, мы вынуждены допускать в качестве достоверного сомнительное, ибо при таких занятиях приходится не столько надеяться увеличить свои знания, сколько опасаться их уменьшить. Поэтому мы отвергаем настоящим правилом все познания, являющиеся только вероятными, и полагаем, что можно доверять только совершенно достоверным и не допускающим никакого сомнения. Быть может учёные убеждены в том, что такие знания чрезвычайно редки, ибо вследствие известного недостатка, свойственного человеческому уму, они не считают их заслуживающими внимания как слишком лёгкие и доступные всем; я однако заявляю, что число их несравненно больше, нежели они предполагают, и что их достаточно для достоверного доказательства множества таких вещей, о которых они доныне могли высказывать лишь предположения. Считая недостойным своей учёности признаться себе в незнании чего-либо, они до того привыкли разукрашивать свои ложные доводы, что мало-помалу убедили ими самих себя и начали выдавать их за истинные.
Впрочем, если мы будем строго соблюдать это правило, то для нас останется весьма немного вещей, изучению которых мы могли бы себя посвятить, ибо вряд ли в науках найдётся какой-либо вопрос, по которому учёные не расходились бы в своих мнениях. A всякий раз, когда два человека придерживаются противоположных мнений об одном и том же, несомненно, что по крайней мере один из них ошибается или даже ни один из них не владеет истиной; ведь если бы доводы одного были достоверны и очевидны, то он мог бы изложить их другому так, что наконец убедил бы его. Следовательно обо всём том, что нам даёт основание лишь для предположений, мы по-видимому не в состоянии достигнуть совершенного познания, ибо мы не можем без излишнего самомнения считать себя в праве надеяться на большее, чем другие. Поэтому, если наш расчёт верен, из всех наук остаются лишь арифметика и геометрия, к изучению которых и приводит нас соблюдение этого правила.
По этой причине мы однако не осуждаем ни те приёмы философствования, которые применялись до нашего времени другими, ни употребление вероятных силлогизмов, являющихся превосходным оружием в школьных турнирах, ибо они упражняют и в соревновании двигают вперёд умы молодых людей, a лучше уж образовывать их умы на таких мнениях, которые очевидно не являются достоверными, поскольку служат предметом учёных споров, чем предоставлять их самим себе. Быть может без руководителя они низвергнулись бы в пропасть, покамест же они следуют по стопам учителя, пусть даже иногда и уклоняясь от истины, они конечно идут более верным путём, по крайней мере потому, что этот путь был уже изведан людьми более опытными. Мы сами счастливы тем, что получили такое воспитание в школах. Но освободившись теперь от уз, которые связывали нас со словами учителя, и сделавшись наконец достаточно зрелыми, для того чтобы убрать руки из-под его ферулы, если мы серьёзно желаем установить себе правила, с помощью которых мы могли бы подняться на вершины человеческих знаний, то нам бесспорно надлежит поставить на первый план это правило, удерживающее нас от злоупотребления нашим досугом, как это делают многие люди, которые всячески пренебрегают лёгкими занятиями и занимаются только трудными вещами. Правда, относительно последних они искусно строят остроумнейшие догадки и весьма правдоподобные суждения, но после многих трудов они поздно убеждаются в том, что, не получив никаких знаний, только увеличили свои сомнения.
Но если, как мы уже говорили несколько выше, из всех прочих известных нам наук только арифметика и геометрия чисты от всего ложного или недостоверного, то заметим теперь, чтобы доказать более подробно справедливость сказанного, что мы приходим к познанию вещей двумя путями, a именно: путём опыта и дедукции. Кроме того заметим, что опыт часто вводит нас в заблуждение, тогда как дедукция, или чистое умозаключение об одной вещи через посредство другой если и может быть упущено, когда его нельзя усмотреть, то никогда не может быть плохо построено, даже и y умов, весьма мало привычных к мышлению. Мне кажется, что те пути, с помощью которых диалектики рассчитывают управлять человеческим разумом, не могут принести большой пользы, хотя я и не отрицаю их пригодности в другом применении. Действительно, все заблуждения, в которые впадают люди, я не говорю о животных, никогда не проистекают из плохо построенного вывода, но всегда имеют своей причиной то, что люди исходят именно из плохо понятых фактов или из поспешных и необоснованных суждений.
Из этого ясно, почему арифметика и геометрия гораздо более достоверны, чем все другие науки, a именно — предмет их столь ясен и прост, что они совсем не нуждаются ни в каких предположениях, которые опыт может подвергнуть сомнению, но всецело состоят в последовательном выведении путём рассуждения. Итак, они являются наиболее лёгкими и ясными из всех наук и имеют своим предметом то, что нам желательно, ибо если не быть невнимательным, то вряд ли возможно допустить в них какую-либо ошибку. Однако же вследствие этого не нужно удивляться, что многие умы охотнее посвящают себя другим занятиям или философии: это обусловливается именно тем, что всякий смелее пользуется свободой разгадывать тёмные вещи, нежели очевидные, и что гораздо легче строить догадки по тому или иному вопросу, нежели постичь истину, как бы она ни была проста.
Из всего сказанного нужно однако заключить не то, что следует изучать только арифметику и геометрию, но лишь то, что ищущие верного пути к истине не должны заниматься исследованием таких вещей, o которых они не могут иметь знаний, по достоверности равных арифметическим и геометрическим доказательствам.
ПРАВИЛО III
В предметах нашего исследования надлежит отыскивать не то, что о них думают другие или что мы предполагаем о них сами, но то, что мы ясно и очевидно можем усмотреть или надёжно дедуцировать, ибо знание не может быть достигнуто иначе.
Необходимо читать книги древних писателей, ибо нам доставляет огромную выгоду использование трудов столь многих людей как потому, что мы узнаем от них о полезных открытиях, которые были некогда совершены, так и потому, что они напоминают нам, что ещё осталось открыть во всех науках. Однако есть большая опасность, как бы слишком старательное чтение этих книг не ввело нас в некоторые заблуждения вопреки нашему желанию и без нашего ведома, ибо все писатели, по неосмотрительному легковерию придерживающиеся спорных мнений, имеют обыкновение пускать в ход самые хитроумные доводы, для того чтобы нас убедить, a всякий раз, когда им посчастливится найти что-нибудь достоверное и очевидное, они стараются изложить это нам не иначе, как с различными двусмысленностями, разумеется, боясь того, что простота их приёмов умалит достоинства их открытия, либо не желая говорить об открытой истине.
Ho если даже они будут прямыми и откровенными, никогда не будут навязывать нам ничего сомнительного под видом истинного и чистосердечно изложат всё, что они узнали, то, поскольку вряд ли было что-нибудь высказано одним автором, не вызвав противоположного заявления со стороны кого-либо другого мы всегда будем в нерешимости, кому из них следует отдать предпочтение. Совершенно бесполезно в этом случае подсчитывать голоса, чтобы следовать тому мнению, которого придерживается большинство авторов, ибо если дело касается трудного вопроса, то более вероятно, что истина находится на стороне меньшинства, a не большинства. Даже и при всеобщем согласии нам будет недостаточно только знать их учение. Мы никогда например не сделаемся математиками, даже зная наизусть все чужие доказательства, если наш ум неспособен самостоятельно разрешать какие бы то ни было проблемы, или философами, прочтя все сочинения Платона и Аристотеля, но не будучи в состоянии вынести твёрдого суждения о данных вещах, ибо в этих случаях мы увеличим только свои исторические сведения, но не знания.
Кроме того напомним, что не следует смешивать никаких допускаемых нами предположений с суждениями об истине вещей. Это замечание имеет довольно серьёзное значение, ибо немаловажная причина, в силу которой в обычной философии нет ничего настолько очевидного и достоверного, что не могло бы вызывать споров, заключается в том, что учёные, изначала не удовлетворяющиеся познанием ясных и достоверных вещей, отваживаются также на тёмные и непонятные утверждения, к которым они приходят лишь путём правдоподобных предположений, a затем сами постепенно подкрепляют их полной верой, без разбора смешивают их с истинными и очевидными и в конце концов оказываются совершенно не в состоянии сделать ни одного вывода, независимого от этих предположений, который поэтому не был бы недостоверным.
Для того чтобы в дальнейшем не подвергать себя подобному заблуждению, мы рассмотрим здесь все те действия нашего интеллекта, посредством которых мы можем достичь познание вещей, не боясь обмануться хотя и рискуя. Возможны только два таких действия, a именно: интуиция и дедукция[1].
Под интуицией я подразумеваю не веру в шаткое свидетельство чувств и не обманчивое суждение беспорядочного воображения, а понятие ясного и внимательного ума, настолько простое и отчётливое, что оно не оставляет никакого сомнения в том, что мы мыслим, или, что одно и то же, прочное понятие ясного и внимательного ума, порождаемое лишь естественным светом разума и благодаря своей простоте более достоверное, чем сама дедукция, хотя последняя и не может быть плохо построена человеком, как я уже говорил выше. Так например всякий может интуитивно постичь умом, что он существует, что он мыслит, что треугольник ограничивается только тремя линиями, что шар имеет только одну поверхность, и подобные этим истины, гораздо более многочисленные, чем это замечает большинство людей вследствие того, что не считает достойными внимания такие простые вещи.
Впрочем, чтобы не смутить кого-либо новым употреблением слова интуиция, a также и других слов, которые я вынужден в дальнейшем употреблять тоже в отличном от общепринятого смысле, я здесь вообще предупреждаю, что я совсем не думаю о значении, придаваемом в последнее время этим словам в школах, так как было бы очень трудно пользоваться одними и теми же словами для обозначения совершенно различных понятий; я обращаю внимание на значение каждого такого слова только на латинском языке, чтобы всякий раз, когда y меня недостаёт собственных выражений, взять те слова, которые мне кажутся наиболее пригодными для выражения моей мысли.
Эти же очевидность и достоверность интуиции должны иметь место не только в отдельных утверждениях, но также и во всякого рода рассуждениях. Так например в последовательности 2 и 2 составляют то же, что 3 и 1, нужно интуитивно постигать не только то, что 2 и 2 составляют 4 и что 3 и 1 составляют также 4, но ещё и то, что из первых двух положений необходимо вытекает это третье.
Может возникнуть сомнение, для чего мы добавляем к интуиции ещё и этот другой способ познания, заключающийся в дедукции, посредством которой мы познаём всё, что необходимо выводится из чего-либо достоверно известного. Это нужно было сделать потому, что есть много вещей, которые хотя и не являются самоочевидными, но доступны достоверному познанию, если только они выводятся из верных и понятных принципов путём последовательного и нигде не прерывающегося движения мысли при зоркой интуиции каждого отдельного положения. Подобно этому мы узнаем, что последнее кольцо длинной цепи соединено с первым, хотя мы и не можем охватить одним взглядом все находящиеся между ними кольца, которые обусловливают это соединение, лишь бы мы последовательно проследили их и вспомнили, что каждое из них, от первого до последнего, соединено с соседним. Итак, мы различаем здесь интуицию ума от правильной дедукции в том отношении, что под дедукцией подразумевается именно движение или последовательность, чего нет в интуиции; кроме того дедукция не нуждается в наличной очевидности, как интуиция, но скорее как бы заимствует свою достоверность y памяти. Отсюда следует, что положения, непосредственно вытекающие из первого принципа, можно сказать, познаются как интуитивным, так и дедуктивным путём, в зависимости от способа их рассмотрения, сами же принципы — только интуитивным, как и, наоборот, отдалённые их следствия – только дедуктивным путём.
И именно это – два наиболее верных пути, ведущих к знанию, сверх которых ум не должен допускать ничего. Все остальные, напротив, должны быть отброшены как подозрительные и подверженные заблуждениям. Тем не менее это не мешает нам считать откровения божьи достовернейшими из всех наших знаний, поскольку вера в них, как и во все скрытые вещи, является делом не ума, не действием личности, а воли, но если бы она имела основания в нашем интеллекте, все эти вещи можно и нужно было бы исследовать именно одним из двух уже указанных способов, что мы объясним быть может когда-нибудь более подробно.
ПРАВИЛО IV
Метод необходим для отыскания истины.
Смертными настолько владеет слепое любопытство, что они направляют свой ум на неизведанные пути без всякого основания для надежды, просто лишь для того, чтобы испытать, не подвернётся ли им под руку то, что они ищут, подобно тому, кто, обуреваемый безрассудным желанием найти драгоценность, вечно блуждает по дорогам в надежде на то, что её может обронить какой-нибудь прохожий. Так трудятся почти все химики, многие геометры и немалое число философов. Я не отрицаю, что во время их блужданий им иногда удавалось находить кой-какие истины, но по моему мнению, этим они обязаны не умению, а счастью. Уже лучше совсем не помышлять об отыскании каких бы то ни было истин, чем делать это без всякого метода, ибо совершенно несомненно то, что подобные беспорядочные занятия и тёмные мудрствования помрачают естественный свет и ослепляют ум. Всякий, привыкший таким образом блуждать во мраке, настолько ослабляет остроту своего зрения, что не может больше переносить яркий свет. Подтверждение этого мы видим на опыте, весьма часто встречая людей, никогда не усердствовавших над учёными трудами, но рассуждающих более основательно и здраво о любой вещи, чем те, которые всю жизнь провели в школах. Под методом же я подразумеваю точные и простые правила, строгое соблюдение которых всегда препятствует принятию ложного за истинное и, без излишней траты умственных сил, но постепенно и непрерывно увеличивая знания, способствует тому, что ум достигает истинного познания всего, что ему доступно.
Здесь надлежит заметить два следующих пункта: никогда не принимать за истинное то, что ложно, и добиваться познания всего. Ведь если мы не знаем чего-нибудь из того, что мы можем знать, то это объясняется только тем, что мы либо совсем не нашли никакой дороги, которая могла бы нас к нему привести, либо подверглись заблуждению. Но если метод правильно показывает, как нужно пользоваться интуицией ума, чтобы не впасть в заблуждение, противное истине, и как должны быть построены дедукции для достижения познания всего, то, мне кажется, он не требует более ничего, для того чтобы быть совершенным, ибо невозможно достигнуть никакого знания иначе, как путём интуиции ума и дедукции, о чём уже говорилось выше. Ведь он не простирается даже для того чтобы учить, как производятся эти действия, ибо они являются простейшими и первичными, и именно, если наш разум не умел пользоваться ими раньше, он не в состоянии будет понять и никаких предписаний нашего метода, как бы они ни были просты. Что же касается иных видов или правил умственной деятельности, которые направляют мысль во главе с диалектикой[2], то они здесь бесполезны, или, скорее, их можно считать даже помехой, ибо нельзя привнести в чистый свет разума ничего, что его не ослабило бы так или иначе.
Так как польза этого метода настолько велика, что приступать без него к научным занятиям скорее вредно, чем полезно, я легко склоняюсь к убеждению, что уже давно люди постигали его в той или иной степени благодаря своим исключительным дарованиям или указаниям одной только природы. Ведь человеческий ум содержит в себе нечто божественное, в чём посажены первые семена полезных мыслей так, что часто, как бы они ни были заглушаемы и оттесняемы посторонними занятиями, они вопреки всему приносят самопроизвольно плоды. Доказательством этого для нас могут служить самые простые науки: арифметика и геометрия. Действительно, достаточно хорошо замечено, что уже древние геометры для разрешения всевозможных проблем применяли известный анализ, хотя и не пожелали передать его потомству. И в настоящее время процветает особого рода арифметика, именуемая алгеброй, заключающаяся в действиях над числами, подобных тем, которые древние производили над фигурами. Итак, обе эти науки являются не чем иным, как самопроизвольными плодами, возникшими из врождённых начал этого метода, и я не удивляюсь тому, что в применении к таким простым предметам упомянутых наук они получили к настоящему времени более пышное развитие, чем в других науках, где их обыкновенно стесняют большие препятствия, но где они несомненно могут тоже достичь полной зрелости, если их заботливо выращивать.
Это я и ставлю главной задачей настоящего трактата, и конечно я не придавал бы такого большого значения этим правилам, если бы они служили только для решения пустых головоломок, которыми счетчики и геометры развлекаются во время досуга; в подобном случае я считал бы себя может быть только более искусным в безделицах, чем другие. И хотя в настоящем трактате мне часто придётся говорить о фигурах и числах, поскольку нет никакой другой области знаний, из которой было бы можно извлечь примеры, столь же очевидные и достоверные, тем не менее всякий, кто будет внимательно следить за моей мыслью, без труда заметит, что здесь я менее всего подразумеваю обыкновенную математику, но что я излагаю некую другую науку, для которой упомянутые науки являются скорее покровом, нежели частью. Ведь эта наука должна содержать в себе первые начала человеческого разума и простирать свои задачи на извлечение истин относительно любой вещи. И если говорить откровенно, я убеждён, что её нужно предпочесть всем другим знаниям, которые предоставлены нам, людям, ибо она является их источником. Говоря же о покрывале, я не высказывал этим желания укутать и скрыть её, для того чтобы оградить ее от толпы, наоборот, я хотел так одеть и украсить её, чтобы она сделалась более привлекательной для человеческого ума[3].
Далее учёный пишет о понятии «всеобщая математика», как он пришёл к общему исследованию математических наук, что существует отличная от обыкновенной математики наука – освобождённая от множества загромождающих её знаков и непонятных фигур настолько, чтобы у неё не было недостатка в той высшей ясности и простоте – истинная математика. Что не только алгебра, арифметика, геометрия, но также астрономия, музыка, оптика, механика и многие др. считаются как бы частями этой математики. Что к области последней относятся только те науки, в которых рассматривается либо порядок либо мера, и совершенно несущественно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера; таким образом должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов — «всеобщая математика», ибо она содержит в себе всё то, благодаря чему другие науки называются частями математики.[4]
Когда я впервые отдался душой математическим наукам, я сразу перечитал большую часть трудов, которые доставляют нам в той области авторы. Наиболее охотно я занимался арифметикой и геометрией, потому что они считались тогда самыми простыми из всех наук и как бы дверью для всех остальных. Но ни в той, ни в другой мне не посчастливилось найти такого автора, который бы меня вполне удовлетворил, a именно: большую часть того, что я прочёл y них о числах, по проверке принципов я нашёл верной; что же касается фигур, то наглядно они до известной степени вскрывали многое и выводили сообразно той или иной последовательности доводов, но почему это делалось так, a не иначе, и каким путём достигались подобные открытия, они не могли объяснить моему уму удовлетворительно. Поэтому меня не удивляло то, что большинство способных и сведущих людей, испробовав эти науки, тотчас же начинало относиться к ним как к детским и праздным занятиям или, наоборот, устрашённые тем, что они слишком трудны и запутаны для дальнейшего изучения, останавливалось на пороге. Ведь действительно нет ничего более бессмысленного, нежели трудиться над пустыми числами и вымышленными фигурами, как бы желая успокоиться на познании подобных пустяков, и до того увлекаться их поверхностными доказательствами, достигнутыми скорее благодаря случайности, чем искусству, относящимися скорее к зрению и воображению, чем к интеллекту, что ум как бы остывает от работы. Точно так же нет ничего более тягостного, нежели разрешать с помощью этого рода доказательств новые трудности, скрывающиеся в путанице чисел. Однако, когда я затем подумал, почему основоположники философии не хотели допускать к изучению мудрости людей несведущих в математике, словно эта наука казалась им самой лёгкой из всех и более всего необходимой, для того чтобы просветить и приготовить ум для постижения других, более высоких, я сразу догадался, что они подразумевали под ней науку, весьма отличную от обыкновенной математики нашего времени. Я отнюдь не думаю, что они постигли её в совершенстве. Безумные ликования и жертвы, приносимые ими по поводу каких-нибудь незначительных открытий, ясно свидетельствуют о том, насколько они были ещё неразвиты. Моё мнение не поколеблют и хвалы историков по поводу машин, изобретённых ими, ибо эти машины были вероятно чрезвычайно просты, но их прославила как чудо невежественная и легковерная толпа. Но я убеждён, что первые семена истины, посаженные природой в человеческих умах, которые мы заглушаем, ежедневно читая и слушая о стольких заблуждениях, имели такую мощь в этой наивной и простой древности, что с помощью того же света ума, который дал им возможность узреть необходимость предпочтения добродетели — удовольствию, чести — пользе, хотя они и не сознавали оснований этого предпочтения, они достигли истинных идей в философии и математике, даже если ещё и не могли постичь эти науки в совершенстве. И мне кажется, что некоторые следы этой истинной математики можно заметить ещё y Паппа и Диофанта, которые, хотя и не относятся к ранним векам, всё же жили задолго до нашего времени. Но я склоняюсь к убеждению, что писатели из пагубной хитрости сами потом утаили её, ибо подобно тому, что известно об обращении художников с их произведениями, они, весьма боясь, как бы лёгкость и простота их открытия не умалили его ценности, сделав его общедоступным, и чтобы заставлять восхищаться собой, предпочли взамен его показывать как произведения их искусства кой-какие бесплодные, хотя и остроумно выведенные истины, вместо того чтобы обучать самому искусству, которое, будучи понятным, не вызывало бы более никакого удивления. Наконец несколько гениальнейших людей нашего времени пытаются воскресить это искусство, ибо не чем иным, как искусством, представляется им наука, обозначаемая иностранным названием «алгебра», если её освободить лишь от множества загромождающих её знаков и непонятных фигур настолько, чтобы y неё не было недостатка в той высшей ясности и простоте, которую мы предполагаем необходимой для истинной математики. Такие размышления, отвлекшие меня от занятий только арифметикой и геометрией к общему исследованию математических наук, сначала натолкнули меня на вопрос, что подразумевается именно под эти последним названием и почему не только вышеупомянутые науки, но также астрономия, музыка, оптика, механика и многие другие считаются как бы частями математики? В данном случае недостаточно рассмотреть лишь происхождение слова, ибо если слово «математика» означает только «наука», то науки, которые я здесь перечисляю, имеют неменьшее право называться математическими, чем геометрия. Впрочем нет такого человека, который, коснувшись лишь порога школы, не сумел бы легко распознать, какие из данных предметов относятся к ведению математических, какие — к ведению других наук. Всякий, кто внимательно обдумает это, поймёт наконец, что к области математики относятся только те науки, в которых рассматривается либо порядок либо мера, и совершенно несущественно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера; таким образом должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем всеобщей математики, ибо она содержит в себе всё то, благодаря чему другие науки называются частями математики. Насколько она превосходит своей лёгкостью и доступностью все эти подчинённые ей науки, видно из того, что она простирается на предметы всех этих наук, так же как и многих других, и если она заключает в себе некоторые трудности, то такие же трудности содержатся и в последних, имеющих ещё сверх того и другие, которые проистекают из частных объектов их и для неё не существуют. Чем же объясняется то, что теперь, когда всем известно название этой науки и все, даже не занимавшиеся ею, знают, в чём состоит её предмет, большинство, не жалея сил, ищет знаний в других науках, зависящих от неё, и никто не пытается обратиться к ней самой? Я удивлялся бы этому наверное, если бы не знал, что все считают её слишком лёгкой, и если бы я давно не заметил, что человеческий ум всегда отстраняет то, что ему кажется легко выполнимым, и прямо стремится к познанию самого нового и важного.
Я же, сознавая свои слабости, решил в поисках познаний упорно придерживаться такого порядка: всегда начинать с самых простых и лёгких вещей и никогда не переходить к другим до тех пор, пока я не увижу, что не могу больше из них ничего извлечь. Поэтому до сего времени я совершенствовал по мере своих сил эту всеобщую математику и полагаю, что могу теперь заняться науками несколько более высокого порядка, не боясь того, что мои силы ещё недостаточно зрелы. Но прежде чем покидать эту область, я попытаюсь собрать в одно место я привести в порядок всё то, что я нашёл достойным внимания в предшествующих исследованиях, как для того, чтобы иметь возможность повторить это в случае надобности по своей книжке, когда с возрастом ослабеет моя память, так и для того, чтобы, облегчив этим мою память, я мог перейти к другим исследованиям с более свободной душой.
ПРАВИЛО V
Весь метод состоит в порядке и размещении того, на что должно быть направлено острие ума в целях открытия какой-либо истины. Мы строго следуем ему если будем постепенно сводить тёмные и смутные положения к более простым и затем пытаться, исходя из интуиции простейших, восходить по тем же ступеням к познанию всех остальных.
В этом одном пункте заключается главнейшая задача всех человеческих усилий, и для того, кто стремится достичь знаний, соблюдение этого правила не менее необходимо, чем нить Тезея для того, кто хочет проникнуть в Лабиринт. Но многие либо не думают о том, что оно предписывает, либо совсем не знают о нём, либо считают его ненужным и часто так беспорядочно исследуют труднейшие вопросы, что кажутся мне похожими на того, кто пытается одним прыжком взобраться с земли на верх здания, пренебрегая ступенями лестницы, предназначенными для этой цели, или не замечая их. Так поступают все астрологи, которые без знания природы звезд и даже без исчерпывающих наблюдений над их движениями надеются определить их влияние. Так поступает большинство тех людей, которые занимаются механикой, пренебрегая физикой, и наугад изготавливают новые двигатели. Так же поступают и те философы, которые, пренебрегая опытом, думают, что истина выйдет из их головы, как Минерва из головы Юпитера.
Именно все они очевидно грешат против этого правила, a так как порядок, предписываемый им, часто может показаться настолько тёмным и сложным, что не все будут в состоянии понять, в чём он заключается, то вряд ли возможно избежать ошибок, если не будет тщательно соблюдено то, что изложено в следующем правиле.
ПРАВИЛО VI
Для того чтобы отделять наиболее простые вещи от трудных и придерживаться при этом порядка, необходимо во всяком ряде вещей, в котором мы непосредственно выводим какие-либо истины из других истин, следить, какие из них являются самыми простыми и как отстоят от них другие: дальше, ближе или одинаково.
Хотя это правило и кажется не поучающим ничему новому, оно тем не менее содержит главный секрет метода, и во всём этом трактате нет правила более полезного: оно указывает именно на то, что все вещи можно разбить по определённым классам, конечно не по отношению к тому или иному роду существ, наподобие того как философы подразделяли вещи на категории, но по зависимости познания одной вещи от познания другой, так что всякий раз, когда y нас возникнет какое-либо затруднение, мы тотчас же можем узнать, не будет ли полезным исследовать сначала что-нибудь другое, что именно и в каком порядке исследовать.
Для того же чтобы правильно производить это действие, нужно, во-первых отметить, что все вещи в отношении полезности их для нашей задачи, если их не рассматривать изолированно одну от другой, но сравнивать, чтобы познать одни через посредство других, можно назвать абсолютными или относительными.
Абсолютным я называю всё, что содержит в себе искомую ясность и простоту, например всё, что рассматривают как независимое, причину, простое, всеобщее, единое, равное, подобное, прямое и т. п. Я считаю, что абсолютное является также самым простым и самым лёгким и что им надлежит пользоваться при решении всех вопросов.
Наоборот, относительным я называю то, что имеет ту же природу или по крайней мере нечто общее с ней, благодаря чему его можно соотнести с абсолютным и вывести из него, следуя известному порядку. Но кроме того оно содержит в своём понятии ещё нечто другое, что я называю отношениями. К последним надлежит причислить всё, что называется зависимым, следствием, сложным, отдельным, множественным, неравным, несходным, косвенным и т. д. Относительное тем более отдалено от абсолютного, чем более содержит в себе подобных соподчинённых отношений. В настоящем правиле мы советуем различать эти отношения, соблюдая их взаимную связь и естественный порядок таким образом, чтобы, идя от последнего из них через все прочие, мы могли достигнуть абсолютнейшего.
Именно в неустанном искании самого абсолютного и заключается весь секрет метода, ибо некоторые вещи кажутся более абсолютными с одной точки зрения, чем другие, рассматриваемые же иначе, они оказываются более относительными. Так например всеобщее, разумеется, более абсолютно, чем частное, потому что оно обладает более простой природой, но его же можно назвать и более относительным ибо оно нуждается для своего существования в единичных вещах, и т. д. Например если мы рассматриваем отдельные предметы, то вид представляет собой нечто абсолютное, если же рассматриваем род, то вид становится относительным; для измеримых вещей абсолютно протяжение, для протяжения — длина и т. д. Наконец, для того чтобы сделать более понятным, что мы рассматриваем здесь группы подлежащих нашему познанию вещей, a не природу каждой из них по отдельности, мы умышленно относим причину и равное к абсолютным вещам, хотя в действительности они по своей природе относительны, ибо для философов причина и следствие — корреляты. Однако же если мы хотим понять действие, то мы должны сначала понять причину, a не наоборот. Равные вещи находятся во взаимном соответствии, но мы узнаем о неравенстве вещей только путём сопоставления их с равными, a не наоборот, и т. д.
Во-вторых, нужно заметить, что, строго говоря, очень мало существует таких ясных и простых вещей, которые можно интуитивно постичь с первого взгляда и через самих себя непосредственно, не через посредство каких-либо других, но с помощью опыта над ними самими или некоего присущего нам света; и я говорю, что их надлежит тщательно подмечать, ибо они являются тем, что мы называем простейшим в каждом ряде. Все же прочие мы можем познать не иначе, как путём выведения их из этих вещей либо непосредственно и прямо, либо через посредство двух-трёх различных заключений, либо многих различных заключений, число которых тоже необходимо отметить, для того чтобы знать, на сколько степеней они отстоят от первого простейшего положения. Такова везде связь следствий, порождающая те ряды искомых вещей, к которым надлежит свести всякую проблему, чтобы исследовать её по правильному методу. Но так как очень трудно обозревать их все одновременно, a кроме того они не столько требуют сохранения в памяти, сколько различения при известном изощрении ума, то нужно найти средство для воспитания последнего таким образом, чтобы всякий раз при первой надобности он тотчас же имел возможность их заметить. Для этого, как я знаю по собственному опыту, конечно нет ничего более полезного, как приучаться обдумывать до тонкости мельчайшие детали того, что мы уже поняли ранее.
В-третьих, отметим наконец, что не нужно с самого начала браться за исследование трудных вещей, но прежде чем приступать к разрешению каких-либо определённых вопросов, нужно сначала собрать все без разбора сами собой пришедшие в голову сведения, затем постепенно просмотреть их, чтобы узнать, нельзя ли вывести из них какие-нибудь другие, из этих последних ещё и т. д. Затем, сделав это, нужно тщательно обдумать все найденные истины, внимательно исследовать, почему одни из них оказалось возможным найти скорее и легче, чем другие, и что они собой представляют, дабы приступая к разрешению какого-либо определённого вопроса, мы отсюда узнали также, с исследования чего лучше начинать прежде всего. Например, заметив, что число 6 есть удвоенное 3, я буду затем искать удвоенное 6, т. е. 12, и далее, если это мне кажется нужным, удвоенное 12, т. е. 24, потом удвоенное 24, т. е. 48, и т. д. и т. д. Из этого я без труда сделаю вывод, что между числами 3 и 6 существует то же отношение, что и между 6 и 12, между 12 и 24 и т. д., и следовательно числа 3, 6, 12, 24, 48 и др. последовательно пропорциональны. Отсюда, хотя бы всё это было настолько просто, что казалось бы детской забавой, тщательно обдумав, я узнаю, в чём заключаются все вопросы, касающиеся связей или соотношений вещей, и в каком порядке их нужно исследовать. Этим и исчерпывается всё содержание чистой математики.
Действительно, я замечаю, во-первых, что найти удвоенное 6 не труднее, чем удвоенное 3, что всюду подобным образом найденное соотношение между какими бы то ни было двумя величинами может быть дано в бесчисленном множестве других величин, находящихся в том же отношении, и что сущность трудности не изменяется, рассматривается ли три, четыре или большее число таких величин, так как нужно отыскивать каждое из соотношений по отдельности, не обращая внимания на все другие. Далее, я замечаю, что хотя для данных величин 3 и 6 я нахожу третью, последовательно пропорциональную им, т. e. 12, но что найти для двух данных крайних величин, a именно 3 и 12, промежуточную, т. е. 6, не является столь же лёгким делом. Обдумав это, можно ясно увидеть, что здесь мы имеем дело с трудностью совсем другого рода, чем предшествующие, ибо для нахождения промежуточной пропорциональной необходимо в одно и то же время мыслить о двух крайних и об отношении между ними, чтобы получить путём их деления некую новую величину; это действие очень отличается от того, когда для двух данных величин отыскивается третья последовательно пропорциональная. Следуя далее, я рассматриваю, одинаково ли легко найти промежуточные пропорциональные величины 6 и 12 для двух данных крайних 3 и 24. Здесь приходится сталкиваться с трудностью иного рода и гораздо более серьёзной, чем предшествовавшие, ибо здесь нужно думать не только об одной или двух величинах одновременно, но о трёх, для того чтобы найти для них четвёртую. Можно пойти ещё дальше и для данных только 3 и 48 узнать, не будет ли ещё труднее найти одно из промежуточных и пропорциональных им чисел 6, 12, 24, как это может показаться с первого взгляда. Но тотчас же обнаружится, что эту трудность можно расчленить и упростить, если найти сначала лишь одно промежуточное пропорциональное число между 3 и 48, именно 12, затем другое промежуточное пропорциональное между 3 и 12, a именно 6, другое между 12 и 48, а именно 24, и таким образом привести её ко второму роду трудности, который мы уже изложили.
Из всего предшествующего мы видим, как можно прийти к познанию одной и той же вещи различными путями, из которых один более труден и более тёмен, чем другой. Например если для отыскания четырёх последовательно пропорциональных чисел — 3, 6, 12, 24 — даются два последовательных числа — 3 и 6, или 6 и 12, или 12 и 24, то для того, чтобы найти посредством их остальные, действие производится очень легко; и в этом случае можно сказать, что искомое соотношение исследуется прямо. Но если даётся по два числа через одно, a именно 3 и 12 или 6 и 24, для того чтобы найти по ним другие, можно сказать, что трудность исследуется косвенно первым способом. Таким же образом, если даются два крайних числа 3 и 24, чтобы найти для них промежуточные 6 и 12, то в этом случае трудность исследуется косвенно вторым способом. Я мог бы следовать таким же образом и дальше и извлечь из одного этого примера множество ещё и других следствий, но тех, которые я уже вывел, будет достаточно, для того чтобы читатель видел, что я подразумеваю под положением, выведенным непосредственно или косвенно, и знал, что простейшие и элементарнейшие вещи, будучи поняты, помогут многое найти в других науках тому, кто внимательно вдумывается и применяет к исследованию всю остроту своего ума.
ПРАВИЛО VII
Для завершения знания надлежит всё, относящееся к нашей задаче, вместе и порознь обозреть последовательным и непрерывным движением мысли и охватить достаточной и методической нумерацией.
Соблюдение настоящего правила является необходимым, для того чтобы считать достоверными те истины, которые, как мы говорили выше, не выводятся непосредственно из первичных и самоочевидных принципов. Действительно, иногда это осуществляется через посредство столь длинного ряда последовательных положений, что, достигнув их, мы с трудом восстанавливаем в памяти всю ту дорогу, которая нас к ним привела. Поэтому мы и говорим, что необходимо оказывать помощь памяти в её слабости своего рода последовательным движением мысли. Так например если я нахожу посредством различных действий отношение сначала между величинами A и В, затем между В и С, между С и Д и наконец между Д и Е, я уже при этом не вижу, какое отношение существует между A и Е, и не могу точно установить его по известным мне отношениям до тех пор, пока не вспомню их все. По этой причине я должен обозревать их путём последовательного движения представления так, чтобы оно представляло одно из них и в то же время переходило бы к другому, до тех пор пока я не научусь переходить от первого к последнему настолько быстро, чтобы почти без участия памяти охватывать их все одновременно. Такой метод, помогая памяти, в то же время устраняет медлительность ума и как бы увеличивает его вместимость.
Однако добавим, что это движение не должно нигде прерываться. Действительно, нередко те люди, которые пытаются весьма быстро и из отдалённых принципов вывести какое-либо следствие, не обозревают всей цепи промежуточных заключений с должной тщательностью и опрометчиво перескакивают через многие из них. Но зато, как только они пропускают одно, хотя бы самое незначительное из всех, цепь их тотчас же прорывается, и вся достоверность заключения колеблется.
Кроме того я говорю, что для завершения знания необходима нумерация, так как если все другие предписания и содействуют разрешению многих вопросов, то только посредством нумерации мы можем создать всегда прочное и достоверное суждение о вещах, с которыми мы имеем дело. Благодаря ей ничто совершенно не ускользает от нас и мы оказываемся осведомлёнными понемногу обо всём.
Следовательно эта нумерация, или индукция, есть столь тщательное и точное исследование всего относящегося к тому или иному вопросу, что с помощью её мы можем с достоверностью и очевидностью утверждать: мы ничего не упустили в ней по нашему недосмотру. Если же, несмотря на её применение, искомая вещь остаётся скрытой от нас, мы будем по крайней мере более опытными, твёрдо убедившись, что ни один из известных нам путей не может привести к познанию этой вещи, a если случайно, как это бывает часто, мы сумели обозреть все доступные человеку ведущие к ней пути, то мы можем смело утверждать, что познание её превышает силы человеческого ума.
Кроме того отметим, что под достаточной нумерацией, или индукцией, мы подразумеваем лишь то, посредством чего истина может быть выведена легче, нежели всякими другими способами доказательства, за исключением простой интуиции, и коль скоро познание той или иной вещи нельзя свести к индукции, надлежит отбросить все узы силлогизмов и вполне довериться интуиции как единственному остающемуся y нас пути, ибо все положения, непосредственно выведенные нами одно из другого, если заключение ясно, уже сводятся к подлинной интуиции. Но когда мы выводим какое-либо положение из многочисленных и разрозненных положений, то объём нашего интеллекта часто оказывается недостаточно большим, для того чтобы охватить их все единым актом интуиции; в данном случае интеллекту надлежит удовольствоваться надёжностью этого действия. Подобным же образом мы не можем различить одним взглядом все кольца слишком длинной цепи, но тем не менее если мы видели соединение каждого кольца с соседним порознь, то этого нам уже будет достаточно, чтобы сказать, что мы видели связь последнего кольца с первым.
Я сказал, что это действие должно быть достаточным, ибо оно часто может иметь погрешность и следовательно вводить в заблуждение. A именно, бывают случаи, когда, обозрев посредством нумерации всю цепь положений совершеннейшей очевидности, мы однако пропускаем одно, хотя бы и самое незначительное из них, то цепь уже порывается и заключение теряет всю свою достоверность. Иногда же мы, правда, охватываем нумерацией все положения, но не различаем каждого положения в отдельности и таким образом получаем обо всём лишь смутное представление.
Далее, иногда эта нумерация должна быть полной, иногда раздельной, a в иных случаях от неё не требуется ни того, ни другого, поэтому я и говорил, что она должна быть достаточной. Действительно, если я хочу посредством нумерации доказать, сколько родов существ являются телесными или каким-либо образом воспринимаются чувствами, я не буду утверждать, что их имеется столько-то, a не более, пока я твёрдо не удостоверюсь в том, что охватил их все своей нумерацией и различил их порознь друг от друга. Но если я тем же способом хочу доказать, что разумная душа бестелесна, то мне незачем прибегать к полной нумерации, а достаточно будет собрать все тела в несколько групп таким образом, чтобы доказать, что разумная душа не относится ни к одной из них. Если наконец я хочу доказать посредством нумерации, что площадь круга больше площадей всех других фигур, описанная которых равна его окружности, то нет необходимости исследовать все фигуры, но достаточно доказать это на нескольких из них, чтобы путём индукции вывести то же самое и для всех других.
Я уже говорил, что нумерация должна быть методической потому, что против уже изложенных выше погрешностей нет лучшего средства, нежели порядок при исследовании всех вещей, a также и потому, что если, как это часто случается, потребуется исследовать всё относящиеся к каждой вещи порознь то на это не хватит никакой человеческой жизни либо оттого, что вещи слишком многочисленны, либо оттого, что при этом неизбежны частые повторения. Но если мы расположим их все в совершенном порядке так, что большая часть их разместится по определённым классам, то будет достаточно исследовать точно либо один из этих классов, либо что—нибудь одно из всех классов, либо один из них прежде, чем какой-нибудь другой, и по крайней мере никогда бесполезно не просматривать одну и ту же вещь дважды. Это выгодно в том отношении, что с помощью правильно избранного метода нередко удаётся в короткое время и без усилий выполнить работу, которая с первого взгляда кажется необъятной.
Однако порядок предметов, подлежащих нумерации, большей частью может меняться сообразно желанию каждого, a для того чтобы он был по возможности лучше, нужно вспомнить сказанное нами в правиле V. Даже в самых лёгких человеческих искусствах есть весьма много вещей, метод нахождения которых всецело заключается в правильном установлении этого порядка. Так, если нужно составить полную анаграмму из перестановки букв какого-либо имени, то нет нужды ни переходить от более простого к более сложному, ни различать абсолютное и относительное — эти приёмы здесь совершенно неуместны; в перестановке рассматриваемых букв достаточно будет установить лишь такой порядок, чтобы одно и то же сочетание никогда не рассматривалось дважды, например разбить их на определённые группы так, чтобы сразу же можно было увидеть, в какой из них можно скорее найти искомое. Таким образом эта работа отнимет очень немного времени и покажется лишь детской забавой. Впрочем не нужно отделять друг от друга эти три последних правила. Большей частью нужно держать их в уме все одновременно, ибо они одинаково способствуют совершенствованию метода. Безразлично, которое из них мы будем заучивать в первую очередь. Мы изложили их здесь в немногих словах потому, что в оставшейся части этого трактата мы не будем заняты ничем иным кроме изложения в частности всего того, что мы обозрели здесь в целом.
ПРАВИЛО VIII
Если в ряде исследуемых вещей встретится какая—либо одна, которую наш ум не может достаточно хорошо понять, то нужно на ней остановиться и не исследовать других, идущих за ней, воздерживаясь от лишнего труда.
Три предшествующих правила предписывают и объясняют порядок; настоящее же указывает, когда он является совершенно необходимым и когда только полезным. Ведь то, что составляет цельную ступень в лестнице, ведущей от относительного к абсолютному или наоборот, необходимо должно быть рассмотрено прежде всего остального. Но если, как это часто имеет место, множество вещей относится к одной и той же ступени, то всегда бывает полезно просмотреть их по порядку. Однако соблюдение этого правила не обязательно должно быть точным и строгим. Большей частью, хотя бы мы ясно поняли не все вещи, a лишь немногие или даже какую-нибудь одну из них, мы можем переходить дальше.
Это правило с необходимостью вытекает из положений, приведённых в правиле II. Однако не нужно думать, что оно не содержит в себе ничего нового, расширяющего наши знания, хотя и кажется лишь удерживающим нас от исследования некоторых вещей и не сообщает никаких истин, кроме того что учит новичков лишь не тратить напрасно силы, исходя почти из тех же соображений, которые приведены в правиле II. Но тому, кто хорошо усвоил семь предыдущих правил, оно указывает, каким образом можно удовлетвориться в любых научных исследованиях настолько, чтобы больше ничего не желать, ибо всякий, кто в разрешении какой-либо трудности строго соблюдал первые правила и при всём том согласно предписанию этого правила остановится на чём-нибудь, тот будет твёрдо убеждён, что знание, к которому он стремится, недостижимо никакими способами не только по причине несовершенства ума, но и потому, что этому противостоит сама природа трудности или человеческое состояние. Такое познание является не менее ценным, чем то, которое вскрывает саму природу вещей, и тот, кто в этом случае будет простирать своё любопытство дальше, может показаться безумцем.
Поясним все это одним или двумя примерами. Если например кто-нибудь, занимавшийся исключительно математикой, отыскивает линию, называемую в диоптрике анакластической, линию, в которой параллельные лучи преломляются таким образом, что после преломления они все пересекаются в одной точке, то он конечно легко заметит по правилам V и VI, что определение этой линии зависит от отношения между углами преломления и падения, но, поскольку этот человек не может произвести такого исследования, так как оно относится к области физики, a не математики, он должен остановиться на его пороге, и в разрешении этой задачи ему не могут оказать никакой помощи ни философы ни опыт, если он вздумает к ним прибегнуть; этим он нарушил бы именно правило III. Кроме того это положение будет до известной степени сложным и относительным, a опыт может дать достоверное знание только в отношении самого простого и абсолютного, как это мы покажем в своём месте. Тщетно будет он также предполагать некоторое соотношение между этими двумя углами, считая его абсолютно верным, ибо тогда он будет искать не анакластическую линию, a только линию, которая могла бы быть ею, по его предположению.
Но если кто-нибудь, сведущий не только в математике и желающий по правилу I достичь знаний обо всём, с чем он встречается, встретится с этой трудностью, то он найдёт далее, что отношение между углом падения и углом преломления зависит от изменения их вследствие различия сред, что это изменение в свою очередь зависит от того, как луч проходит через всё прозрачное тело, что знание свойств проникновения света предполагает уже известной природу света и что наконец для понимания действия света нужно знать, что такое естественная сила вообще — последнее положение абсолютнейшее из всех. После того как посредством интуиции ума он ясно постигнет всё это, он возвратится теми же ступенями по правилу V, и если на второй ступени он тотчас же не будет в состоянии постичь природу действия света, то он перечислит по правилу VII все естественные силы, так что из знания чего-либо другого, по крайней мере по аналогии, позднее он постигнет также и это. Затем он будет узнавать, каким образом луч проникает через всё прозрачное тело, обозревая таким образом по порядку всё до тех пор, пока не дойдёт наконец до анакластической линии. Хотя доныне её тщетно искали многие, но я однако не вижу, что могло бы помешать в её явственном представлении тому, кто в совершенстве использовал бы наш метод.
Но я дам наилучший пример. Если кто-нибудь задаётся целью исследовать все истины, познание которых доступно человеческому разуму (исследование, которое, мне кажется, должен произвести однажды в своей жизни всякий, кто серьёзно стремится к истинной мудрости) то он вероятно поймёт благодаря данным мной правилам, что ничто не может быть познано прежде самого интеллекта, ибо познание всех прочих вещей зависит от интеллекта, a не наоборот. Затем, исследовав всё, непосредственно идущее за познанием чистого интеллекта, он перечислит все другие средства познания, которыми мы обладаем, кроме интеллекта; он увидит, что их только два, a именно: воображение (или фантазия) и чувство. Следовательно он приложит все старания к тому, чтобы различить и исследовать эти три орудия познания, и, видя, что истина и заблуждение могут иметь место только в интеллекте, но часто исходят лишь от воображения и чувств, он усердно займётся исследованием всего того, что способно ввести его в заблуждение, дабы оградиться от последнего и старательно перечислить все пути к истине, открытые для человека, дабы следовать лучшему из них, ибо они не столь многочисленны, чтобы все их нельзя было без труда найти даже посредством достаточной нумерации. И то, что неопытным покажется удивительным и невероятным, тотчас же после того, как он для отдельных объектов отличит знания, лишь заполняющие или украшающие память, от знаний, которые дают право считать их обладателя действительно просвещённым, что даже без труда достигается . . . . . . . . . . . . . , он вполне убедится в том, что никакое знание больше не будет закрыто для него за недостатком y него ума или опытности и что кто-либо другой совсем не может знать ничего, что и он не способен познать, если только он не применит к этому должным образом свой ум. И хотя бы y него часто возникало много таких вопросов, исследование которых запрещается этим правилом, он будет ясно сознавать, что последние превышают все силы человеческого ума, и поэтому более не будет считать себя невеждой, но само достигнутое им знание — что никто не может знать ничего по этому вопросу, вполне удовлетворит его любознательность, если он благоразумен.
Для того же, чтобы не быть всегда неуверенными в способностях нашего ума и чтобы не утруждать себя бесполезно и бесцельно, прежде чем приступать к исследованию каждой вещи по отдельности, необходимо хоть один раз в жизни тщательно исследовать, каких знаний способен достичь человеческий разум. Ради большего успеха в этом деле необходимо из одинаково лёгких вещей выбирать для исследования сначала наиболее полезные.
Этот метод подобен тем техническим искусствам, которые не нуждаются в помощи извне, т. е. сами указывают тому, кто желает ими заняться, способ изготовления инструментов. В самом деле, если кто-либо пожелает заняться каким-нибудь одним из них, например кузнечным ремеслом, и если y него нет для этого никаких инструментов, то он будет вынужден сначала взять в качестве наковальни какой-нибудь твёрдый камень или кусок грубого железа, a в качестве молота — булыжник, приспособить два куска дерева в виде щипцов и по мере надобности обращаться за другими подобными же материалами. Закончив эти приготовления, он не приступит тотчас же к выковыванию копий или шлемов или иных железных предметов, нужных для других, но прежде всего изготовит себе молоты, наковальню, щипцы и прочие инструменты, которые нужны ему самому. Этот пример показывает нам, что, поскольку в этих начальных правилах мы могли сделать лишь самые простые предписания которые кажутся скорее прирождёнными нашим умам, нежели плодом искусства, не следует немедленно же пытаться с помощью их прекратить философские споры или разрешить математические проблемы. Ими скорее надлежит пользоваться для тщательнейшего исследования всего того, что является наиболее необходимым для познания истины, тем более, когда нет никакого основания думать, что это делать труднее, чем разрешать любой из тех вопросов, с которыми обычно приходится встречаться в геометрии, в физике и в других науках.
Но в данном случае не может быть ничего более полезного, нежели исследовать, что такое человеческое познание и как далеко оно простирается. Потому-то мы и соединяем эту двойную задачу в одну и думаем, что следует заняться ею как самой важной из всех согласно изложенным ранее правилам. Это должен сделать однажды в своей жизни каждый человек, как бы мало он ни любил истину, ибо такое исследование заключает в себе все верные средства познания и весь метод. Но ничто не кажется мне более нелепым, чем смелые споры о загадках природы, о влиянии звёзд, о тайнах грядущего и о других подобных вещах, споры, в которые пускаются многие люди, никогда даже не задав себе вопроса, доступно ли всё это человеческому разуму. Нам не должно казаться недоступным или трудным определение границ нашего ума, который находится в нас самих, если мы часто не колеблемся высказывать мнения даже о вещах, которые находятся вне нас и являются для нас совершенно чуждыми. И задача обнять мыслью всё, что существует в мире, уже не будет для нас неизмеримо большой, когда мы будем знать, каким образом каждая вещь подлежит исследованию нашего ума; ведь нет ничего настолько многообразного или разрозненного, чего ум не сумел бы посредством нумерации, о которой мы трактовали, заключить в строгие границы и разместить по соответствующим классам. Чтобы сделать опыт в поставленной нами задаче, сначала разделим на две части всё, что к ней относится, a именно, она должна касаться нас, способных познавать, и самих вещей, которые могут быть познаны. Обе эти части мы обсудим по отдельности.
Прежде всего заметим, что познавательная способность присуща только интеллекту, но что для него могут быть помехой или помощью три другие способности, a именно: воображение, чувства и память. Следовательно нужно по порядку рассмотреть, в чём нам может вредить или помогать каждая из этих способностей, для того чтобы мы остерегались их или пользовались всеми теми благами, которые они нам предоставляют. И таким образом посредством достаточной нумерации мы обсудим эту первую часть, что будет показано в следующем правиле.
Затем нужно перейти к самим вещам и рассматривать их лишь постольку, поскольку они доступны нашему интеллекту. В этом отношении мы разделяем их на простейшие и комплексные, или сложные. Простые могут быть только духовными или телесными или теми и другими вместе; и в заключение: иные сложные вещи интеллект воспринимает таковыми прежде, чем он успеет вынести о них какое—либо определённое суждение, другие же он составляет сам. Всё это будет более пространно изложено в правиле XII, где мы докажем, что заблуждение возможно лишь относительно последних, которые создаются интеллектом, почему мы и разделяем их ещё на два вида: на выводимые из простейших вещей и известные сами собой — о них мы будем говорить в следующей книге,— и на такие, которые согласно нашему опыту предполагают другие, сложные по существу, — этим мы посвятим всю третью книгу.
Во всём же этом трактате мы хотим исследовать с такой тщательностью и сделать настолько доступными все пути, ведущие человека к познанию истины, чтобы всякий, кто проникся этим методом, как бы ни был посредственен его ум, увидел, что нет ничего скрытого от него более, чем от других, и что в дальнейшем от него не будет скрыто ничего вследствие несовершенства его ума или недостатка опытности. Но всякий раз, когда он обратит свой ум к познанию чего-либо, он или вполне этого достигнет или догадается, что успех этого зависит от опыта, который для него невозможен, и поэтому он не будет обвинять свой ум, хотя и был вынужден остановиться; или наконец он докажет, что исследование данной вещи превышает силы всякого человеческого ума, и поэтому уже более не будет считать себя невеждой, ибо такой вывод есть знание не менее ценное, чем всякое другое.
ПРАВИЛО IX
Нужно обращать острие ума па самые незначительные и простые вещи и долго останавливаться на них, пока не привыкнем отчётливо и ясно прозревать в них истину.
Дав изложение двух действий нашего интеллекта, a именно интуиции и дедукции, о которых мы говорили, что только ими надлежит пользоваться в целях достижения знания, продолжим в этом и в следующем правилах объяснение тех способов, посредством которых мы можем научиться лучше производить эти действия, a также и развивать две главные способности нашего ума: его проницательность в отчётливой интуиции отдельных вещей и остроту в искусном выведении одного из другого.
Как нужно пользоваться интуицией ума, мы познаем уже из сравнения её с зрением, ибо тот, кто хочет охватить одним взглядом одновременно большое количество объектов, не различает ясно ни одного из них, равным образом и тот, кто имеет обыкновение обращаться одним актом мысли одновременно ко многим объектам, имеет смутный ум. Однако мастера, которые занимаются тонкими ремёслами и привыкают тщательно рассматривать каждую точку, путём упражнения приобретают способность в совершенстве различать самые незаметные и тонкие вещи; равным образом и всякий, кто никогда не разбрасывается мыслью по различным объектам одновременно, но всецело направляет её на исследование всегда самых простых и лёгких вещей, становится проницательным.
Всеобщий порок смертных — смотреть на мудрёные вещи как на самые лучшие. Большинство людей думает, что они ничего не знают, когда находят очень ясную и простую причину какой-нибудь вещи, и между тем восхищается выспренними (высоко возвышенными) и глубокомысленными рассуждениями философов, чаще всего покоящимися на основаниях, которые никогда достаточно не проверялись. Это восхищение конечно бессмысленно, ибо они предпочитают мрак свету. Но нужно заметить, что тот, кто действительно обладает знанием, с одинаковой лёгкостью познает истину, выводит ли он её относительно трудной вещи или относительно простой. Именно, один раз придя к истине, он улавливает её всегда сходным, единым и одинаковым действием; вся разница заключается только в пути, который конечно должен быть длиннее, если он ведёт к истине более отдалённой от самых простых и абсолютных начал.
Следовательно всякому надлежит привыкнуть одновременно охватывать мыслью столь малое количество объектов и объектов столь простых, чтобы он никогда не считал себя знающим то, что не постигается так же ясно, как и то, что постигается с наибольшей отчётливостью. Конечно одни рождаются гораздо более одарёнными в этом отношении, чем другие, но наука и упражнение могут сделать ум гораздо более искусным. Здесь есть пункт, который, мне кажется, необходимо особенно подчеркнуть, a именно: каждый должен быть твёрдо убеждён, что не из многозначительных, но тёмных, a только из самых простых и наиболее доступных вещей должны выводиться самые сокровенные истины.
Ибо например если я пожелаю узнать, существует ли какая-нибудь естественная сила, которая могла бы моментально перенестись в отдалённое место через всё расстояние, отделяющее её от этого места, то я не обращусь тотчас же к исследованию магнитной силы или влияния звёзд или даже скорости света, чтобы узнать, не являются ли их действия моментальными, ибо доказать это было бы труднее, чем то, что мне нужно; лучше я подумаю о том, как передвигаются с места на место тела, ибо нет ничего во всей этой области более понятного. И я замечу, что камень конечно не может моментально перенестись с одного места на другое, так как он представляет собой тело, но что сила, подобная той, которая движет камень, должна передаваться только моментально, если она одна переходит с одного места на другое. Так например, когда я передвигаю конец палки, то как бы последняя ни была длинна, я легко соображаю, что сила, двигающая её, в один и тот же момент приводит в движение и все другие её части, ибо здесь передаётся только она[5] и не входит в какое-либо тело, как например в камень, который переносит её в себе.
Подобным же образом, если я хочу узнать, как одна и та же причина может одновременно производить различные действия, я не обращусь к лекарствам врачей, изгоняющим одни соки и удерживающим другие, и не буду городить вздор, будто луна согревает своим светом и охлаждает каким-либо другим, скрытым свойством, но я скорее обращу внимание на весы, на которых одни и те же гири поднимают одну чашу и в то же время опускают другую, или на что-нибудь подобное этому.
ПРАВИЛО X
Для того чтобы сделать ум проницательным, необходимо упражнять его в исследовании вещей, уже найденных другими, и методически изучать все даже самые незначительные искусства, но в особенности те, которые объясняют или предполагают порядок.
Признаюсь, я родился с таким умом, что главное удовольствие при научных занятиях для меня заключалось не в том, что я выслушивал чужие мнения, a в том, что я всегда стремился создать свои собственные. Это — единственное, что уже в молодости привлекало меня к наукам, и всякий раз, когда какая-либо книга сулила в своём заглавии новое открытие, я пытался, прежде чем приступить к её чтению, узнать, не могу ли я достичь чего-нибудь подобного с помощью своей природной проницательности, и исправно старался не лишать себя этого невинного удовольствия поспешным чтением. Неизменный успех таких попыток наконец убедил меня в том, что я приходил к истине не неуверенными и слепыми поисками и скорее благодаря счастливой случайности, нежели умению, как это делают обыкновенно другие, но устанавливал путём длительного опыта верные правила, оказывавшие мне в этих занятиях немалую помощь, правила, которыми я пользовался потом для установления и многих других. Тщательно разработав таким образом весь этот метод, я пришёл к убеждению, что с самого начала я пользовался наиболее совершенным методом исследования.
Но так как не все одарены от природы одинаковой способностью производить исследования только своими собственными силами, то настоящее правило учит нас, что не следует с первого раза приступать к изучению трудных и недоступных вещей, но необходимо начинать с самых лёгких и простых и главным образом таких, в которых более всего господствует порядок. Примером последнего может служить искусство ткачей и обойщиков, искусство женщин вязать спицами или переплетать нити тканей в бесконечно разнообразные узоры; таковы все действия над числами и вообще всё, что относятся к арифметике, и т. п. Все эти искусства удивительно хорошо развивают ум, если только мы постигаем их не с помощью других, a самостоятельно. Не заключая в себе ничего тёмного и будучи всецело доступными человеческому уму, они с необыкновенной отчётливостью вскрывают перед нами бесчисленное множество систем, хотя и отличающихся друг от друга, но тем не менее правильных, в надлежащем соблюдении которых заключается почти вся проницательность человеческого ума.
Поэтому мы и напоминали здесь о необходимости методического подхода к изучению их, ибо метод является для этих незначительных искусств не чем иным, как постоянным соблюдением порядка, присущего им самим по себе или введённого в них остроумной изобретательностью. Например, желая прочесть неизвестные нам письмена, мы, несмотря на то, что в них не видно никакого порядка, должны однако представить себе в них некоторый порядок как для проверки всех соображений, могущих возникнуть относительно каждого знака, слова или фразы, так и для размещения последних таким образом, чтобы посредством нумерации мы могли узнать, что можно из них вывести. Более всего нужно остерегаться терять время в бессистемном разгадывании случайных совпадений, ибо хотя оно часто и увенчивается успехом без помощи метода, a в счастливых случаях иногда даже и скорее, чем с его помощью, но благодаря этому ум настолько притупляется, что, привыкнув к ребяческим забавам и безделицам, становится после этого способным лишь поверхностно касаться всех вещей, не будучи в силах проникнуть в них глубже. Со всем тем мы не будем поддаваться заблуждению людей, размышляющих только о серьёзных и возвышенных вещах и приобретающих о последних после долгих трудов лишь смутные представления вместо того глубокого познания, к которому они стремятся. Итак, надлежит начинать с методического исследования самых простых вопросов и открытыми и известными путями всегда приучаться как бы играючи проникать в их сокровенную истину, ибо мы увидим, что таким образом мы можем постепенно, но с быстротой, превосходящей все наши ожидания, и с одинаковой лёгкостью выводить из очевидных принципов множество положений, которые с первого взгляда кажутся весьма трудными и тёмными.
Но некоторые, быть может, удивятся тому, что мы, исследуя здесь способы научиться искусству выводить одни истины из других, умалчиваем о всех тех предписаниях, посредством которых диалектики надеются управлять человеческим разумом, предписывая ему определённые формы рассуждения, с такой неуклонностью приводящие к заключениям, что разум, доверившись им, может, даже если он иной раз и немного отвлекается от строгой и внимательной проверки цепи доводов, делать благодаря одним только этим формам правильные заключения. Но мы замечаем, что истина часто ускользает из этих уз, и пользующиеся ими запутываются в них сами. Это гораздо реже случается с другими, и мы знаем из опыта, что самые остроумные софизмы почти никогда не обманывают того, кто доверяет только своему разуму, a обманывают только самих софистов.
Поэтому, особенно остерегаясь того, чтобы наш разум не бездействовал, исследуя какую-либо истину, отбросим эти формы как препятствующие достижению нашей цели и будем лучше отыскивать все возможные средства для усиления внимательности нашей мысли, как мы это покажем в дальнейшем. Для большей очевидности того, что вышеупомянутые формы рассуждения ни в какой мере не содействуют познанию истин, надлежит заметить, что диалектики не могут составить ни одного силлогизма, дающего правильное заключение, если они для этого не имеют материала, т. е. если они уже не знают выводимой ими таким образом истины. Отсюда следует, что с помощью этих форм рассуждений они сами не познают ничего нового, и обычная диалектика совершенно бесполезна для того, кто хочет достичь знаний, но что иногда она может быть полезна лишь для лучшего изложения другим уже известного, почему её и нужно перенести из области философии в область риторики.
ПРАВИЛО XI
После того как мы усвоим несколько простых положений и выведем из них какое-либо иное, полезно обозреть их путём последовательного и непрерывного движения мысли, обдумать их взаимоотношения и отчётливо представить одновременно наибольшее их количество; благодаря этому наше знание сделается более достоверным и наш ум приобретёт больший кругозор.
Здесь представляется случай яснее изложить то, что нами было сказано в правилах III и VII относительно интуиции ума. В одном мы её противопоставляли дедукции, в другом же — только нумерации, которую мы определили как собирание следствий, выведенных из многочисленных и разрозненных положений, говоря в том же месте, что простая дедукция одного положения из другого совершается посредством интуиции.
В этом различении мы основываемся на том, что предъявляем к интуиции два требования, a именно, рассматриваемые положения должны быть ясными и отчётливыми и постигаться одновременно, a не последовательно одно за другим. Дедукция же, если мы будем рассматривать её так, как это делалось в правиле III, является не одновременным действием, а как бы посредством некоторого движения мысли выводит одно положение из другого; это и давало нам право отличать её от интуиции. Однако же если мы будем рассматривать её уже как завершённую, то, по сказанному нами в правиле VII, она не будет больше представлять собой никакого движения, а будет пределом движения. Поэтому мы и полагаем, что её надлежит рассматривать как интуицию, когда она проста и очевидна, но не тогда, когда она сложна и темна. Мы называли её в этом случае нумерацией, или индукцией, потому что она не может быть целиком охвачена интеллектом и её достоверность в известной мере зависит от памяти, которая должна удерживать суждения, вынесенные о каждом отдельном члене нумерации, для того чтобы из всех этих суждений было возможно вывести нечто единое.
Все эти различения мы приводим здесь именно в качестве пояснения к настоящему правилу, ибо в правиле IX говорилось только об интуиции ума, в правиле X — только об нумерации, между тем как настоящее правило объясняет, каким образом эти два действия способствуют друг другу и взаимно дополняют друг друга так, что кажутся слившимися в одно действие, благодаря известному движению мысли, которая, внимательно вникая в один объект, одновременно переходит к другому.
В этом мы отмечаем для себя двойную выгоду, a именно: более правильно выводим заключения, которых мы добиваемся, и делаем наш ум более искусным в открытиях других истин, ибо, когда память, от которой, по вышесказанному, зависит достоверность заключений, слишком сложных для того, чтобы их можно было обнять одним актом интуиции, оказывается неустойчивой и слабой, её нужно освежать и подкреплять этим непрерывным и повторным движением мысли. Так например, когда посредством многих действий я узнаю отношения сначала между первой и второй величиной, затем между второй и третьей, далее между третьей и четвёртой и наконец между четвёртой и пятой, то при этом я не могу увидеть отношения между первой и пятой величиной и не сумею его вывести из известных уже мне величин, если не вспомню их все, для чего мне необходимо мысленно снова обозревать их до тех пор, пока я не буду в состоянии настолько быстро переходить от первого отношения к последнему, что почти без участия памяти смогу охватывать их все одним актом интуиции.
Всякому ясно, что такой метод избавляет ум от медлительности, a также и расширяет его кругозор. Кроме этого нужно заметить, что огромная польза настоящего правила состоит в том, что мы благодаря обдумыванию взаимной зависимости простых положений приобретаем навык мгновенно различать, какие из этих положений более и какие менее относительны и на сколько ступеней они отстоят от абсолютных. Например, рассматривая несколько последовательно пропорциональных величин, я могу заметить, что только таким, a не более лёгким и не более трудным, путём можно узнать об отношении между первой и второй величиной, второй и третьей, третьей и четвёртой и т. д., тогда как мне не удастся с такой же лёгкостью уловить зависимость второй величины от первой и третьей одновременно и ещё труднее будет уловить зависимость второй от первой и четвёртой величины и т. п. Далее, из этого я пойму, почему я могу легко найти третью и четвёртую величины и т. д., если мне даны первая и вторая, a именно потому, что я достигаю этого путём частных и раздельных представлений. Если же мне даны только первая и третья величины, то я не могу с такой же лёгкостью найти среднюю между ними, потому что это возможно только при помощи представления, обнимающего обе данные величины одновременно. Для данных только первой и четвёртой величин ещё труднее интуитивно уловить две промежуточные между ними, так как при этом нужно охватить мыслью три представления одновременно. Точно так же последовательно должно казаться ещё более трудным для данных первой и пятой величин найти три средние, но есть причина, благодаря которой в этом случае дело будет обстоять иначе. Правда, здесь должны быть соединены вместе четыре представления, но однако их можно разделить, поскольку число четыре делится на другое число. Так, я могу отыскивать сначала третью величину по первой и пятой, затем вторую — по первой и третьей и т. д. Тот, кто привыкнет размышлять об этих и подобных вещах, при исследовании нового вопроса всегда очень быстро сообразит, в чём заключается трудность и без особого труда найдёт один из самых простых способов, что оказывает огромную помощь в постижении истины.
ПРАВИЛО XII
Наконец нужно использовать все вспомогательные средства интеллекта, воображения, чувств и памяти как для отчётливой интуиции простых положений и для верного сравнения искомого с известным, чтобы таким путём открыть его, так ещё и для того, чтобы находить те положения, которые должны быть сравниваемы между собой; словом, не нужно пренебрегать ни одним из средств, находящихся в распоряжении человека.
Это правило является заключением ко всему тому, что было сказано ранее, и даёт общее изложение того, чему надлежало быть изложенным таким способом в отдельности.
Для того чтобы достичь познания вещей, нужно рассмотреть только два рода объектов, a именно, нас, познающих, и сами подлежащие познанию вещи. Мы обладаем лишь четырьмя способностями для этой цели, a именно, интеллектом, воображением, чувствами и памятью. Конечно только один интеллект способен познавать истину, хотя он и должен прибегать к помощи воображения, чувств и памяти, чтобы не оставлять без употребления ни одно из средств, находящихся в нашем распоряжении. Что же касается предметов познания, то достаточно рассмотреть их трояко: a именно, сначала то, что обнаруживается для нас само собой, затем, как познаётся одна вещь через другую, и наконец, какие выводы можно сделать из каждой вещи. Такая нумерация мне кажется полной и не упускающей ничего из того, на что могут простираться способности человеческого ума.
Итак, обращаясь к первой части, я хотел бы объяснить здесь, что такое человеческий дух, что такое тело, как первый сообщается с последним, каковы в целом способности, служащие приобретению познаний, и как они все действуют, но эта глава мне кажется слишком тесной, для того чтобы вместить те предварительные сведения, которые необходимо изложить прежде, чем это станет понятным для всех. Ибо я хотел всегда писать так, чтобы не высказывать по вопросам, вызывающим обычно споры, никаких утверждений, если предварительно я не изложил тех доводов, которые привели меня к моему мнению и могут, мне думается, убедить также и других.
Однако за неимением места я вынужден ограничиться здесь возможно более кратким объяснением того способа понимания всех наших познавательных способностей, который, по моему мнению, является наиболее плодотворным. Вы свободны не верить тому, что дело обстоит так, но что помешает вам принять эти предположения, если они нисколько не умаляют истины и даже придают большую ясность всему? И именно в геометрии вы допускаете известное количество предположений, которые нисколько не ослабляют силы доказательств, хотя в физике вы часто думаете о них иначе.
Итак, во-первых, нужно уяснить себе то, что все внешние чувства, поскольку они составляют части тела, хотя мы и применяем их к объектам посредством действия, т. е. местного движения, ощущают собственно лишь пассивно, подобно тому как воск воспринимает фигуру печати. Не нужно думать, что это сказано только ради аналогии, но именно так и нужно представлять процесс восприятия: внешний вид воспринимающего тела при воздействии на него объекта реально изменяется таким же образом, как поверхность воска изменяется под действием на неё печати. И это имеет место не только тогда, когда мы прикасаемся к какому-либо имеющему форму, шероховатому и твёрдому телу, но и тогда, когда мы посредством прикосновения воспринимаем тепло, холод и т. п. Так же обстоит дело и с другими чувствами, a именно: наружная непрозрачная часть глаза воспринимает фигуру, которую отпечатывает на ней окрашенный в различные цвета луч света; внешняя кожа ушей, ноздрей и языка, непроницаемая для объекта, тоже воспринимает новый образ звука, запаха и вкуса.
Подобные представления обо всех этих вещах весьма полезны, поскольку ничто не является для нас более наглядным, чем фигура, ибо её можно и осязать и видеть. Это предположение способно привести к ложным выводам не более, чем всякое другое, доказательством чего может служить то, что представление фигуры связано с любым объектом чувственного восприятия, настолько оно общо и просто. Мы можем например считать цвет всем, чем угодно, но мы не будем однако отрицать того, что он есть нечто протяжённое, a следовательно и имеющее фигуру. Поэтому чем было бы плохо, если бы мы, остерегаясь бесполезных предположений относительно каких бы то ни было новых естеств и не отрицая того, что иным нравится думать о цвете, стали однако рассматривать его только как нечто, имеющее природу фигуры, и понимать различие между белым, голубым, красным и другими цветами как различие между этими или подобными им фигурами?
To же самое можно сказать и обо всём другом, ибо ясно, что бесконечного множества фигур достаточно для изображения всех различий чувственных объектов.
Во-вторых, нужно себе уяснить, что, после того как внешнее чувство приведено объектом в движение, воспринятая фигура моментально сообщается другой части тела, называемой общим чувствилищем, и притом так, что никакое естество не переходит реально с одного места на другое; совершенно так же теперь, когда я пишу, я понимаю, что в тот момент, когда я вычерчиваю каждую букву на бумаге, не только нижняя часть моего пера находится в движении, но она не может совершить ни малейшего движения, не сообщив его тотчас же всему перу, и верхняя часть пера проделывает в воздухе все те разнообразные движения, которые проделывает нижняя, хотя я и знаю, что нет никакого реального перехода чего бы то ни было с одного конца пера на другой. Кто же может думать, что между частями человеческого тела существует меньшая связь, чем между частями пера, и можно ли придумать более простой пример для выражения этой связи?
В-третьих, нужно себе уяснить, что общее чувствилище действует на фантазию или воображение так же, как печать —на воск, запечатлевая фигуры или идеи, которые приходят к нам от внешних чувств чистыми и бестелесными. Это воображение есть настоящая часть тела, и она настолько велика, что её отдельные области могут облачаться во множество различных фигур, обычно долго их сохраняя. Это — то, что носит название памяти.
В-четвёртых, нужно себе уяснить, что движущая сила или сами нервы имеют своё начало в мозгу, где находится воображение, возбуждающее их разными способами, подобно тому как внешнее чувство возбуждает общее чувствилище или как нижняя часть пера приводит в движение всё перо. Этот же пример также показывает нам, как воображение может быть причиной многих нервных возбуждений даже при отсутствии в нём соответствующих впечатлений, лишь бы только в нём были какие—либо другие образы, из которых могли бы исходить эти возбуждения. Действительно, перо в целом движется не так, как его нижняя часть; мало того, верхняя часть его проделывает словно совсем другие, обратные движения. И именно отсюда становится понятным, как могут производиться другими животными все движения, когда мы не предполагаем у них совсем никакого познания вещей, но допускаем для них лишь чисто телесное воображение, а также, как происходят в нас все те движения, которые мы совершаем без всякого участия разума.
Наконец, в-пятых, нужно себе уяснить, что сила, посредством которой мы собственно познаём вещи является чисто духовной, отличающейся от всего телесного не менее, чем кровь от костей или рука от глаза, единственной в своём роде, хотя она вместе с фантазией то воспринимает фигуры, исходящие от общего чувствилища, то оперирует фигурами сохраняющимися в памяти, то создаёт новые которые так заполняют воображение, что оно часто не успевает воспринимать идеи, преподносимые ему общим чувствилищем, и одновременно переводить и х в двигательную силу по чисто телесным подразделениям. Во всех этих случаях познающая сила является иногда пассивной, иногда активной, то она играет роль печати, то воска. Однако это сравнение следует понимать здесь только как простую аналогию, ибо в телесных вещах нет ничего, что было бы подобно этой способности. Это будет одна и та же сила, когда её действия, обращённые совокупно с воображением к внешнему чувству, обозначаются словами «видеть», «осязать» и т. п.; когда они, направленные на одно только воображение, поскольку последнее облекается в различные фигуры, обозначаются словом «вспоминать»; когда они, направленные на воображение для создания новых фигур, обозначаются словами «воображать», «представлять»; когда наконец эта сила действует одна, её действия обозначаются словом «понимать». Я объясню в своём месте более подробно, как совершается это действие. Будем же называть эту силу сообразно её различным функциям, a именно: чистым интеллектом, воображением, памятью или чувством. Она собственно называется умом когда создаёт в воображении новые идеи или когда она оперирует уже над готовыми. Будем пока считать её способной на эти различные действия, a в дальнейшем мы рассмотрим различие всех этих наименований. Поняв таким образом всё это, — внимательный читатель легко рассудит, какую помощь он может ожидать от каждой из этих способностей и в какой мере прилежание может возместить недостатки человеческого ума.
Ведь если интеллект может быть возбуждаем воображением или, наоборот, воздействовать на последнее, воображение же может воздействовать на чувства посредством двигательной силы, направляя их на объекты, или, наоборот, чувства могут воздействовать на воображение, разумеется, рисуя в нём образы тел, и если вдобавок память, по крайней мере та, которая телесна и подобна памяти животных, ничем не отличается от воображения, то из этого несомненно следует, что, когда интеллект имеет дело с объектами, не имеющими ничего телесного или подобного телесному, он не может опираться на эти способности; напротив, чтобы они не были для него помехой, нужно отстранить чувства и освободить воображение от всяких отчётливых впечатлений, насколько это возможно. Но если интеллект приступает к исследованию какой-либо вещи, которая может быть отнесена к разряду телесных, то только в воображении он может создать её наиболее отчётливую идею. Для того чтобы облегчить это действие, необходимо предъявлять внешним чувствам саму вещь, представляемую этой идеей. Большое количество объектов не может содействовать интеллекту в отчётливой интуиции каждого из них в отдельности, но для извлечения какого-нибудь одного объекта из множества их, что приходится делать нередко, нужно отстранить от идей о вещах всё, что не требует в данный момент внимания, чтобы памяти было легче удерживать остальное. Таким же образом в этом случае не будет надобности предъявлять сами вещи внешним чувствам, для этого можно будет ограничиться упрощёнными фигурами, лишь бы последние могли предохранить нас от погрешностей памяти. Чем проще они будут, тем лучше. Всякий, кто будет следовать этим указаниям, мне кажется, не упустит ничего из того, что относится к этой части нашего вопроса.
Для того чтобы перейти к обсуждению также и его второй части, тщательно отличить понятия простых вещей от понятий тех вещей, которые из них составляются, и рассмотреть, в котором из этих двух видов их мы можем заблуждаться, дабы избегать этого, и каковы те, о которых мы можем иметь достоверные знания, дабы иметь дело только с ними, здесь, как и в предшествовавших исследованиях, необходимо допустить некоторые предположения, с которыми может быть не все согласятся. Но что за беда, если мы будем считать их не более реальными, чем те воображаемые орбиты, в которые астрономы помещают свои феномены, лишь бы с их помощью различать, о каких вещах возможны истинные, о каких ложные познания.
Итак, мы говорим, во-первых, что вещи должны быть рассматриваемы по отношению к нашему интеллекту иначе, чем по отношению к их реальному существованию. Ибо если например мы рассмотрим какое-нибудь тело, обладающее протяжением и фигурой, то мы без труда признаем, что оно само по себе есть нечто единое и простое и в этом смысле его нельзя считать составленным из телесности, протяжения и фигуры, как частей, которые реально никогда не существуют в отдельности. Но по отношению к нашему интеллекту мы считаем данное тело составленным из этих трёх естеств, ибо мы мыслим каждое из них в отдельности прежде, чем будем иметь возможность говорить о том, что они все находятся в одной и той же вещи. Поэтому, говоря здесь о вещах лишь в том виде, как они постигаются интеллектом, мы называем простыми только те, которые мы познаём столь ясно и отчётливо, что ум не может их разделить на некоторое число частей, познаваемых ещё более отчётливо. Такими частями являются фигура, протяжение, движение и т. д. Всё же остальное мы представляем себе как бы составленным из этих частей. Это нужно понимать в столь широком смысле, что мы не исключаем из них даже такие вещи, которые мы иногда абстрагируем от простых вещей, как это бывает например, когда мы говорим, что фигура есть предел протяжения, понимая под пределом нечто более общее, чем фигура, ибо конечно можно говорить о пределе длительности, о пределе движения и пр. Ведь в данном случае, хотя понятие предела и является отвлечённым от понятия фигуры, оно тем не менее не должно казаться более простым, чем последнее, но скорее, поскольку его прилагают и к другим вещам, например к окончанию длительности или движения, (toto genere – коренным образом) отличным от фигуры, оно должно быть отвлечённым также и от этих вещей и следовательно является соединением многих совершенно различных естеств, к которым оно прилагается только в различных значениях.
Во-вторых, мы говорим, что вещи, называемые нами простыми по отношению к нашему интеллекту, являются или чисто интеллектуальными, или чисто материальными, или общими. Чисто интеллектуальны те вещи, которые познаются интеллектом посредством некоторого прирождённого ему света, без всякого участия какого-либо телесного образа. Действительно, интеллекту присуще нечто подобное, ибо мы не можем вообразить ничего телесного, для того чтобы представить, что такое знание, сомнение, незнание, a также и действие воли, которое, если будет позволено, я назвал бы волением, и тому подобное; тем не менее всё это реально познаётся нами с такой лёгкостью, что для этого нам достаточно быть только одарёнными разумом. Чисто материальными являются вещи, познаваемые нами только в телах, такие, как фигура, протяжение, движение и т. п. Наконец общими называются те, которые без различия относятся к материальным и духовным вещам, например существование, единство, длительность и т. п. К этой же группе должны быть отнесены все те общие понятия, которые являются как бы своего рода связками для соединения различных простых естеств; на очевидности их мы основываем все выводы рассуждений. Примером этого может служить положение: две величины, равные третьей, равны между собой: a также: две вещи, которые не находятся в одинаковом отношении к третьей, имеют между собой некоторое различие, и т. д. И именно эти общие понятия могут быть познаны чистым интеллектом или интеллектом же, интуитивно исследующим образы материальных вещей.
Впрочем к числу простых вещей можно отнести также и их отсутствие и отрицание, поскольку они доступны нашему пониманию, ибо знание, дающее мне понять, что такое ничто, мгновение и покой не менее истинно, чем то, которое даёт мне понять, что такое существование, длительность и движение. Этот способ понимания в дальнейшем даст нам основание говорить, что все другие вещи, познаваемые нами, являются составленными из таких простых вещей. Так, если я думаю, что некоторая фигура не находится в движении, то я могу сказать, что моя мысль в известном отношении состоит из фигуры, покоя и т. д
В-третьих, мы говорим, что эти простые вещи известны нам сами по себе и никогда не заключают в себе ничего сложного. Это мы легко обнаружим если отметим различие между способностью нашего интеллекта созерцать и познавать вещи и способностью, посредством которой он выносит утвердительные и отрицательные суждения. Ведь может случиться, что мы будем считать вещи, в действительности познанные нами, непознанными, a именно если предположим, что в них кроме того, что мы созерцаем или постигаем нашим мышлением, есть нечто другое, скрытое от нас. Но мысля таким образом, мы впадаем в заблуждение. Очевидно, что мы будем ошибаться, считая что-либо совершенно непознанным в одной из этих простых вещей, ибо если наш ум имеет о ней хотя бы малейшее понятие, что конечно совершенно необходимо, поскольку мы выносим о ней некое суждение, то из этого самого нужно заключить, что мы познали её полностью В противном случае нельзя говорить об её простоте так как в этом случае она должна была бы состоять из тех свойств, которые нам известны, и из тех, которые мы считаем неизвестными.
В-четвёртых, мы говорим, что соединение этих простых вещей может быть необходимым или случайным. Оно необходимо, когда одна вещь так смешивается с понятием другой, что мы не можем отчётливо представить себе ни ту, ни другую из них, если судим о них как об отдельных вещах. Таким образом связана фигура с протяжением, движение — с длительностью или с временем и т. п., ибо невозможно представить себе фигуру, лишённую всякого протяжения, движение —длительности. Так же точно, если я скажу: четыре и три составляют семь; это составление является совершенно необходимым, ибо мы не можем представить себе ясно число семь, если не будем именно смутно мыслить в нём чисел три и четыре. Таким же образом и всё, что было сказано относительно фигур и чисел, находится в необходимой связи с вещами, о которых высказываются утверждения. Эта необходимость присуща не только чувственным вещам. Если например Сократ говорит, что он во всём сомневается, то из этого необходимо следует вывод, что он по крайней мере знает о своём сомнении, a также и знает, что может быть нечто истинное или ложное и т. д., ибо ведь это находится в необходимой связи с природой сомнения. Но подобное соединение случайно, когда вещи не связаны друг с другом неразрывно, как например, когда мы говорим: тело одушевлено, человек одет и т. п. И есть также множество вещей, находящихся в необходимой связи, которую большинство людей считает случайной, ибо они не замечают между этими вещами связи. Примером этого может служить положение: я есть, следовательно бог есть; или ещё другое: я мыслю, следовательно я имею дух, отличный от моего тела, и т. п. Наконец нужно заметить, что есть большое число таких необходимых положений, которые при обращении становятся случайными, например: хотя я и заключаю из своего существования о достоверности существования бога, однако на основании существования бога я не могу утверждать, что существую также и я.
В-пятых, мы говорим, что мы не можем познавать ничего кроме этих простых вещей и их смешений или соединения; и именно часто бывает даже легче обращаться мыслью к соединению множества их, чем выделить из них какое-нибудь одно, ибо например я могу познавать треугольник, хотя бы я и никогда не мыслил, что познание его содержит в себе познание угла, линии, числа трёх, фигуры протяжения и пр. Последнее однако не мешает мне говорить, что природа треугольника заключается в природе всех этих вещей и что они являются для меня более известными, чем треугольник, ибо они есть то самое, что я в нём подразумеваю. Кроме того в этом же треугольнике может быть скрыто ещё и многое другое, ускользающее от нас, как например величина углов, которая в сумме равна двум прямым, бесчисленное множество отношений между сторонами и углами, величина площади и т. д.
В-шестых, мы говорим, что свойства, называемые нами сложными, известны нам либо потому, что мы познаём их таковыми из опыта, либо потому, что мы составляем их сами. Из опыта мы познаём всё, что воспринимается нами посредством чувств, всё, что мы слышим от других, и вообще всё, что привносится к нашему интеллекту либо извне, либо из созерцания им самого себя. Нужно здесь заметить, что интеллект не может быть введён в заблуждение никаким опытом, если он безусловно ограничивается только интуицией вещи, являющейся его объектом, в том виде, в каком она представляется в нём самом или в воображении, и кроме того если он не считает, что воображение правильно представляет объекты чувств, чувства передают реальные фигуры вещей и наконец внешние объекты суть всегда таковы, каковыми они являются. Всё это может ввести нас в заблуждение лишь в тех случаях, когда нам рассказывают сказку, a мы принимаем её за действительность, или когда мы заболеем желтухой и считаем всё жёлтым, ибо наши глаза окрашены в этот цвет, или наконец принимаем за реальность призраки нашего больного воображения, как это имеет место y меланхоликов. Но подобные вещи не обманут опытный ум, ибо, признавая, что всё получаемое им от воображения было действительным впечатлением, он однако никогда не будет утверждать, что данный образ целиком и без изменения перешёл от внешних объектов к чувствам, a от чувств к воображению, покамест сам не убедится в этом каким—либо иным путём. Но мы сами составляем те вещи которые подразумеваем всякий раз, когда предполагаем, что им присуще нечто, постигаемое нашим умом непосредственно, без всякого опыта. Так например, когда человек, заболевший желтухой, убеждается в том, что видимые им предметы окрашены в желтый цвет, то его представление создаётся из того, что ему преподносит воображение и что он прибавляет от самого себя, a именно: всё кажется ему желтым не из-за недостатка его глаз, но потому, что видимые им вещи являются действительно желтыми. Отсюда следует вывод, что мы можем ошибаться только тогда, когда мы доверяем тем вещам, которые мы составляем тем или иным способом.
В-седьмых, мы говорим, что это составление может производиться тремя способами, a именно внушением, догадками и дедукцией. По внушению составляют свои суждения о вещах те люди, которые побуждают свой ум к вере во что-либо, не имея для этого никаких разумных оснований, определяясь на это либо некоторой высшей силой, либо своей доброй волей, либо склонностью своей фантазии. В первом случае никогда не бывает ошибок, во втором — редко, в третьем — почти всегда. Но первый случай не подлежит здесь рассмотрению, ибо он не входит в область науки. Мы составляем суждение путём догадок например тогда, когда из положения что вода, более удалённая от центра, чем земля, имеет также и более тонкую субстанцию, чем последняя, и что воздух, находящийся выше воды, является более тонким, чем вода, мы делаем заключение: над воздухом нет ничего кроме эфирного вещества, чрезвычайно чистого и несравненно более тонкого, чем сам воздух, и т. д. Но все суждения, которые мы составляем таким образом, если и не вводят нас в заблуждение, поскольку мы считаем их только вероятными, но никогда не утверждаем, что они являются истинными, то не делают нас и более сведущими.
Следовательно остаётся только одна дедукция, посредством которой мы можем составлять вещи так, чтобы быть уверенными в их истинности. Однако и y неё могут быть недостатки. Так, если из того, что в этом пространстве, наполненном воздухом, нет ничего воспринимаемого посредством зрения, осязания и других чувств, мы делаем вывод, что это пространство пусто, то мы неправильно соединяем природу пустоты с его природой. Так бывает и во всех тех случаях, когда из частного и случайного мы рассчитываем вывести нечто общее и необходимое. Но мы имеем возможность избежать такой ошибки, именно если мы никогда не будем соединять друг с другом вещи, не убедившись в том, что их соединение совершенно необходимо; так, исходя из необходимости связи фигуры с протяжением, мы делаем заключение: никакая вещь не может обладать фигурой, если она не протяжённая, и т. д.
Из всего этого следует, во-первых, то, что мы изложили теперь ясно и, я думаю, посредством достаточной нумерации, ранее же показанное смутно и лишь в самых общих чертах, a именно: для человека нет иных путей к достоверному познанию истины кроме отчетливой интуиции и необходимой дедукции; a также объяснили, что представляют собой те простые вещи, о которых мы говорили в правиле VIII. Таким образом ясно, что интуиция ума имеет дело как со всеми этими вещами и необходимыми связями, соединяющими их, так наконец и со всеми прочими объектами, которые интеллект находит исключительно или в самом себе или в воображении. О дедукции же мы будем говорить более подробно в следующих правилах.
Во-вторых, из этого следует, что не нужно прилагать никаких усилий для познания этих простых вещей, ибо они достаточно понятны сами собой, но нужно лишь стараться отличать их друг от друга и пристально рассматривать каждое из них по отдельности, пронизывая их острием ума. Не может быть настолько тупоумного человека, который не понимал бы, что в сидячем положении он чем-то отличается от самого себя, когда он стоит, но не все могут отчётливо различить сущность сидячего положения от всего остального, что при нём мыслится, и утверждать, что в этом случае не изменилось ничего кроме положения. И не напрасно мы делаем это замечание, ибо учёные часто оказываются настолько остроумными, что находят возможным становиться слепыми в таких самоочевидных вещах, которые всегда понятны даже крестьянам. Это случается с ними всякий раз, когда они пытаются с помощью чего-нибудь очевидного объяснить сами по себе ясные вещи. Действительно, либо они объясняют что—нибудь другое, либо совсем ничего не объясняют. Кто не понимает прекрасно все те перемены, которые происходят тогда, когда мы меняем место? И кто поймёт то же самое, когда ему говорят, что место есть поверхность окружающего тела? Ведь в то время как эта поверхность может изменяться, я могу оставаться неподвижным и не менять места или, наоборот, она может двигаться со мной таким образом, что, хотя меня будет окружать та же самая поверхность, я однако более не буду находиться на одном и том же месте. Не кажется ли вам, что учёные произносят магические слова, обладающие таинственным смыслом и выходящие за пределы человеческого разумения, когда они говорят, что движение — вещь понятная всем — есть становление в действие скрытой сущности, поскольку она находится в потенции (ПОТЕНЦИЯ лат. potentia — сила). Действительно, кто поймёт эти слова? Кто не знает, что такое движение? И кто не согласится с тем, что они ищут узлы в тростниковом стволе? Итак, необходимо сказать, что совсем нет нужды давать определения подобных вещей, чтобы не принимать простого за сложное, a нужно лишь тщательно отличать их от всех прочих неизвестных вещей и друг от друга и исследовать их с помощью света своего ума.
В-третьих, из сказанного нами следует, что всё человеческое знание заключается в отчётливом усмотрении того, как все эти простые вещи вместе служат для составления других вещей. Это замечание очень полезно потому, что всякий раз, когда представляется надобность исследовать какую-либо трудность, почти все люди останавливаются на пороге исследования в нерешительности, каким мыслям они должны посвятить свой ум, убеждённые в том, что им нужно отыскивать некоторый новый род ещё неизвестных вещей. Когда например их спрашивают о природе магнита, то они, предполагая, что это трудная и неодолимая вещь, тотчас же отдаляются духом от всего очевидного, для того чтобы обратиться к самому трудному и, блуждая в пустом пространстве множества причин, ждут, не подвернётся ли им под руку случайно что-нибудь новое. Но тот, кто думает, что в магните не может быть открыто ничего, что не состояло бы из некоторых простых и известных самих по себе естеств, и не колеблющийся в том, что ему надлежит делать, сначала заботливо соберёт весь возможный для него опыт относительно этого камня, а затем попытается сделать вывод: каково должно быть необходимое соединение простых естеств, для того чтобы оно могло производить все те действия, которые он обнаружил в магните. Достигнув этого, он может смело утверждать, что вскрыл истинную природу магнита, насколько это доступно человеку в пределах данного опыта.
Наконец, в-четвёртых, из сказанного нами следует, что никакие познания нельзя считать более смутными, чем другие, если они все обладают одной и той же природой и заключаются лишь в соединении известных самих по себе вещей. Этого почти никто не замечает, a убеждённые в обратном и именно наиболее самонадеянные позволяют себе даже выдавать свои собственные догадки как действительные доказательства, и в вещах совершенно им неизвестных они чувствуют, что как бы сквозь тучи прозревают истины, часто тёмные, которые они однако не боятся выставлять напоказ, укутывая свои понятия известными терминами, с помощью которых они имеют обыкновение пространно и последовательно рассуждать и говорить, хотя эти термины непонятны ни им самим, ни их слушателям. Что же касается более скромных, то они часто воздерживаются исследовать множество лёгких и очень важных в житейском отношении вопросов только потому, что считают это дело выше своих сил, и, полагая, что эти вопросы могут быть разрешены более сильными умами, они принимают мнения тех, к авторитету которых они питают наибольшее доверие.
В-пятых, мы говорим, что можно только делать выводы из посылок или выводить причины из следствий, или следствия из причин, или подобное из подобного и части или целое из частей . . . . Впрочем, для того, чтобы никто не упускал из виду этот ряд наших указаний, мы разделяем всё, что может быть нами познаваемо, на простые положения и вопросы. Для простых положений мы не даём никаких других указаний кроме тех, которые подготавливают к наиболее отчётливой интуиции и к наиболее проницательному исследованию тех или иных объектов, так как эти положения должны возникать сами собой и не могут быть искомыми. Это мы сделали в первых двенадцати правилах, где мы показали всё, что, по нашему мнению, может в той или иной степени облегчить деятельность нашего разума. Что касается вопросов, то одни из них оказываются совершенно понятными, хотя бы они и не были разрешены; в ближайших двенадцати правилах мы будем говорить только о них; и наконец другие не постигаются в совершенстве, их мы отложим до двенадцати следующих правил. Такое подразделение мы сделали не без умысла; цель его — как избежать необходимости говорить о вещах, предполагающих знание того, что из них следует, так и усвоить сначала то, что нам кажется способствующим воспитанию ума. Нужно заметить, что к числу вопросов, являющихся постижимыми в совершенстве, мы относим лишь те в которых мы отчетливо обнаруживаем три условия, a именно: по каким признакам может быть замечено искомое и когда оно встретится, из чего именно мы должны его выводить, как доказать ту взаимную зависимость исследуемых вещей, что одна из них никоим образом не может измениться, если не изменяется другая. Таким образом мы имеем все предварительные условия, и нам остаётся лишь изучить, способ делать заключение, который состоит не только в выводе какой-либо одной вещи из другой простой (мы уже говорили, что это действие можно производить и без указаний), но и в столь искусном выделении зависимых вещей из многих других, соединённых вместе, чтобы никогда не нуждаться в способностях больших, чем это нужно для простейшего умозаключения. Так как подобные вопросы большей частью носят отвлечённый характер и встречаются только в арифметике и геометрии, то они могут показаться бесполезными людям, несведущим в этих науках; но тем не менее я напоминаю, что этому искусству должен посвятить побольше времени и упражняться в нём тот, кто пожелает в совершенстве усвоить следующую часть настоящего метода, в которой мы займёмся всеми прочими вопросами.
ПРАВИЛО XIII
Когда мы хорошо понимаем вопрос, нужно освободить его от всех излишних представлений, свести его к простейшим элементам и разбить его на такое же количество возможных частей посредством нумерации.
Мы уподобляемся диалектикам лишь в том отношении, что как они при обучении формам силлогизмов предполагают их термины или материал уже известными, так и мы требуем здесь прежде всего, чтобы вопрос был в совершенстве понят. Но мы не различаем подобно им двух крайних и одного среднего терминов, a рассматриваем всю эту вещь таким образом: во-первых, во всяком вопросе необходимо должно быть налицо некоторое неизвестное, ибо иначе вопрос бесполезен; во-вторых, это неизвестное должно быть чем-нибудь отмечено, иначе ничто не направляло бы нас к исследованию к данной вещи, a не какой-нибудь другой; в-третьих, вопрос должен быть отмечен только чем-нибудь известным. Все эти условия предъявляются также и к неполным вопросам. Например если нас спрашивают, какова природа магнита, то смысл, вкладываемый нами в эти два слова «магнит» и «природа» есть известное, которое и направляет нас к разрешению этого вопроса, a не какого-нибудь другого. Но кроме того для полноты вопроса желательно чтобы он был строго определённым, благодаря чему мы не отыскивали бы ничего сверх того, что может быть выведено из данных понятий; например если кто-нибудь меня спросит, какое заключение можно сделать о природе магнита исключительно на основании тех опытов, которые приписывает себе Гильберт, будь они верными или неверными, или когда мне задаётся вопрос, что я могу сказать о природе звука, лишь исходя из того, что струны A, В и С дают одинаковый звук и из них струна В в два раза толще, чем А, но не длиннее её и натянута гирей в два раза более тяжёлой, струна С не толще, чем А, но только в два раза длиннее и в то же время натянута гирей в четыре раза более тяжелой, и т. д. Из этих примеров легко понять, как все неполные вопросы могут быть приведены к полным, что мы объясним более подробно в своём месте, a кроме того выясняется, как можно соблюдать это правило, для того чтобы отстранить от хорошо понятой трудности все излишние представления и свести её к тому, чтобы заниматься уже обдумыванием не того или иного предмета, а только взаимным сопоставлением величин. Ибо например после того как мы приняли решение исследовать лишь тот или иной опыт над магнитом, для нас уже совсем не будет трудным мысленно отвлечься от всех прочих опытов. Кроме того добавим, что нужно приводить трудность к простейшим положениям именно по правилам V и VI и расчленять её по правилу VII. Исследуя например на основании многих опытов магнит, я должен последовательно продумывать каждый из них по отдельности. Подобным же образом, изучая природу звука, как об этом была уже речь выше, я должен по отдельности сравнивать друг с другом струны А и В , затем A и С и т. д., чтобы таким путём охватить их потом все достаточной нумерацией. Эти три правила являются единственными из тех, которые чистый интеллект должен соблюдать по отношению к терминам тех или иных положений, прежде чем он приведёт нас к последнему решению, если у нас недостаёт умения пользоваться одиннадцатью следующими правилами. Как производятся все эти действия, выяснится в третьей части этого трактата. Впрочем под вопросами мы подразумеваем всё, в чём отыскивается истинное или ложное, и для того чтобы определить, что мы сумеем сделать в каждом из них, нужно перечислить их различные виды.
Мы уже сказали, что только в интуиции вещей, безразлично простых или сложных, нет места заблуждению. В этом смысле последние не могут быть названы вопросами, но они тотчас же принимают это название, как только мы решаем вынести относительно их какое-либо определённое суждение. Конечно мы относим к числу вопросов не только те вопросы, которые нам задают другие, но вопросом является и само название или, вернее, сомнение Сократа, когда, впервые обратившись к нему, он начал исследовать, действительно ли он сомневается во всём, в чём он и убедился.
Исследуем же мы или нечто по посылкам, или причины по следствиям, или следствия по причинам, или по частям целое, а также и другие части, или наконец множество вещей по всем этим вещам вместе.
Мы говорим, что нечто исследуется по словесным посылкам всякий раз, когда трудность заключается в неясности языка. Сюда относятся не только все загадки, такие например, как загадка о сфинксе, в которой сначала говорится, что нечто — четвероногое животное, затем —двуногое и после этого наконец трёхногое, или загадка о рыбаках, которые, стоя на берегу, снабжённые удилищами и крючками для рыбной ловли, говорят, что y них нет больше рыб, которых они изловили, но зато есть те, которых они не могли изловить; кроме этих вопросов большая часть вопросов, являющихся предметом споров учёных, почти всегда относится к числу словесных. Однако не следует придерживаться такого плохого мнения о великих умах, что будто они плохо понимают вещи всякий раз, когда они не могут объяснить их в достаточно ясных терминах. Например когда они называют местом поверхность окружающего тела, то они имеют совсем не ложную идею, а только злоупотребляют словом «место», обозначающим в общеупотребительном смысле ту простую и самоочевидную вещь, благодаря которой говорится, что предмет находится здесь или там, вещь, всецело заключающуюся в известном отношении предмета, о котором говорится, что он находится в некотором месте, к внешним частям пространства, ту вещь, которую иные, видя название «место» заменённым «окружающей поверхностью», неудачно называют внутренним где, и т. п. Эти словесные вопросы встречаются столь часто, что если бы философы всегда соглашались в значении слов, то почти все их споры прекратились бы.
Причины по следствиям отыскиваются всякий раз, когда относительно какой-либо вещи пытаются узнать, действительно ли она существует или какова она . . . . . . . . . .
Впрочем потому, что нам предлагается разрешить тот или иной вопрос и мы часто оказываемся не в силах определить с первого взгляда, к какому роду вопросов он относится: нужно ли исследовать нечто по словесным посылкам или причины по следствиям и т. д., мне кажется излишним в этом отношении входить в большие подробности, ибо будет короче и полезнее рассмотреть по порядку всё, что нужно сделать, для того чтобы прийти к решению любой задачи. Таким образом если задаётся какой-либо вопрос, то прежде всего необходимо стараться отчётливо уяснить себе, что им отыскивается.
В самом деле, иные так спешат в исследовании положений, что занимаются их разгадкой со спутанным умом, прежде чем узнают, по каким признакам они заметят искомую вещь, если она им случайно встретится. Такие исследователи не менее глупы чем тот мальчуган, который, будучи послан куда—либо своим хозяином, так старается угодить, что бросается бежать, прежде чем получит поручение, даже не зная, куда ему прикажут идти.
Но если во всяком вопросе и должно быть на лицо что-нибудь неизвестное, иначе вопрос был бы бесцелен, то тем не менее само это неизвестное должно быть обозначено настолько определёнными условиями, чтобы для нас было совершенно необходимым исследовать именно эту вещь, a не какую-либо другую. Таковыми являются все те условия, о которых мы говорили, что исследованием их нужно заняться в первую очередь. Для этого необходимо, чтобы мы обратили острие ума на отчётливую интуицию их, тщательно исследуя, до какой степени искомое неизвестное определяется каждым из них; ведь человеческий ум обыкновенно подвергается двоякого рода заблуждению: или он захватывает больше, чем дано для определения какого-либо вопроса, или же, наоборот, что-нибудь упускает.
Нужно остерегаться допущений большего и более точного, нежели то, что нам дано, особенно в загадках и других хитроумных вопросах, имеющих целью сбить с толку рассудок, a также иногда и в вопросах другого рода, для решений которых подставляется нечто в качестве достоверного, убеждающее нас не в силу каких-либо истинных оснований, но в силу застарелых мнений. Так например в загадке сфинкса не нужно думать что название «нога» обозначает настоящую ногу животного, a нужно также подумать, не может ли оно прилагаться к какой-либо другой вещи, как это и действительно имеет место в отношении рук ребенка и палки старика, ибо старики пользуются при хождении палкой, а дети руками как бы в качестве ног. Таким же образом и в загадке о рыбаках нужно остерегаться, чтобы представление о рыбах настолько не овладело нашим умом, что помешало бы нам вспомнить о тех животных, которых бедняки часто помимо их желания носят с собой повсюду и, изловивши их, бросают. Аналогичный пример, когда нас спрашивают и об устройстве некогда виденной нами вазы с колонной, возвышающейся посредине её и поднимающей статую Тантала в позе человека, который хочет пить. Вода, налитая в эту вазу, спокойно держится в ней до тех пор, пока не поднимается до такой высоты, что может попасть в рот Тантала, но едва она достигает уст несчастного, как тотчас же вытекает вся. С первого взгляда именно кажется, что сущность всего этого сооружения заключается в постановке фигуры Тантала, которая однако в действительности совершенно не определяет вопроса и является лишь дополнением. Вся же трудность заключается в том, чтобы, понять, как устроена ваза, из которой вся вода тотчас же вытекает, как только она достигает определённой высоты, а никак не раньше. Точно так же, наконец, если на основании всех тех наблюдений, которые мы сделали над звёздами, мы пытаемся что-нибудь узнать об их движениях, то не нужно подобно древним легкомысленно допускать, что земля неподвижна и помещается в центре вселенной, потому что так нам казалось с детства, но здесь необходимо прибегнуть также и к сомнению, для того чтобы рассмотреть потом, какое достоверное суждение мы можем вынести по этому вопросу, и т. д.
Не обдумав какого-либо условия, требующегося для определения вопроса, выражено ли оно в самом вопросе или его можно понять каким-либо иным способом, мы всякий раз делаем упущения, например когда мы отыскиваем вечное движение, но не то, которое встречается в природе, вроде движения звёзд или течения рек, a изобретённое человеком; и иной (это изобретение многие считают возможным, принимая во внимание, что земля вечно вращается вокруг своей оси, a магнит содержит в себе все свойства земли) надеется создать вечное движение, приладив камень так, чтобы он вращался по кругу или сообщал своё движение железу со всеми своими прочими достоинствами. Но если бы даже это ему и удалось, то он всё же не создал бы искусственного вечного движения, а воспользовался бы только тем, что уже существует в природе, подобно тому как если бы он установил на речном потоке колесо таким образом, чтобы оно находилось в постоянном вращении. Следовательно, он упускает условие, необходимое для определения вопроса, и т. д.
Но для того чтобы знать, в чём состоит та трудность, которая в нём заключается, не всегда достаточно только понять сам вопрос. Кроме этого нужно ещё обдумать всё, что составляет его сущность, так, чтобы всякий раз, когда встретится какая-либо вещь, которую можно легко найти, отбросить её в сторону и в освобождённом таким образом предложении оставить только то, что нам неизвестно. Так например в вопросе с вазой, описанном немного выше, нам нетрудно понять, как должна быть устроена ваза с колонной посередине, с нарисованной на ней птицей и т. д. Отстранивши всё это как несущественное для вопроса, мы обнажаем в нём трудность, заключающуюся в исследовании того, каким образом происходит то, что вода тотчас же вытекает вся, как только она достигает определённой высоты.
Итак, мы говорим, что особенно важным действием здесь является рассмотрение по порядку всего содержания данного положения, при котором нужно отстранять всё, что нам не кажется очевидно полезным, удерживать всё необходимое и откладывать для более тщательного исследования всё сомнительное.
ПРАВИЛО XIV
Сказанное следует отнести и к реальному протяжению тел, это протяжение нужно всецело представлять в виде простых фигур: таким образом оно сделается более понятным для интеллекта.
Но для того чтобы пользоваться также и помощью воображения, нужно заметить, что всякий раз, когда выводится что-либо неизвестное из другого уже известного, при этом не отыскивается какой-либо новый род естеств, но это знание даёт нам понять, что искомая вещь тем или иным способом приобщается к свойствам того, что дано в первоначальном положении. Например нельзя надеяться, что y слепого от рождения можно какими бы то ни было доводами вызвать верные представления о цветах, получаемые нами через посредство чувств, но человек, когда-либо видевший основные цвета, хотя бы он и никогда не видел промежуточных и смешанных цветов, может посредством особой дедукции представить последние по их сходству с первыми. Таким же образом если магнит обладает какими—либо свойствами, не имеющими ничего общего с теми, которые в нём доселе познавал наш интеллект, то нельзя надеяться, что мы познаем их путём рассуждения; для этого нам нужно иметь или какие—нибудь новые органы чувств или божественный разум. Но всё, что в этом отношении может сделать человеческий ум, мы считаем для него достижимым только после того, как мы очень отчётливо постигнем некоторое соединение уже известных естеств или свойств, которое производит такое же действие, как и магнит.
И конечно все уже известные вещи, такие, как протяжение, фигура, движение и прочие им подобные, которые здесь нет необходимости перечислять, познаются нами всегда в одной и той же идее при самых разнородных предметах. Мы одинаково представляем себе форму короны независимо от того, серебряная она или золотая. Эта общая идея переносится с одного предмета на другой не иначе, как путём простого сравнения, благодаря чему мы утверждаем, что исследуемый предмет подобен в том или ином отношении, тождественен или равен данному предмету; так что во всяком рассуждении мы приходим к точному познанию истины только путём сравнения. Например в рассуждении: всякое А=В, всякое В=С, следовательно всякое А=С, сравниваются друг с другом искомое и данное, а именно А и С, по тому отношению, в котором они оба находятся к В, и т.д. Но поскольку, как мы уже неоднократно упоминали, формы силлогизмов не оказывают никакой помощи в познании истин, то читателю будет полезно отбросить их совсем и понять, что всякое знание, не получаемое посредством простой и чистой интуиции отдельной вещи, достигается путём сравнения двух или многих вещей друг с другом. И почти всё искусство человеческого разума заключается в умении подготавливать это действие. В самом деле, когда оно очевидно и ясно, то для его выполнения совершенно не требуется никакого искусства, а нужен лишь естественный свет для прозрения истины, которая им вскрывается.
И необходимо отметить, что сравнение может быть названо простым и очевидным только тогда, когда искомая вещь и вещь данная равно причастны к какому-нибудь известному естеству, a все другие сравнения нуждаются в приготовлении лишь потому, что это общее естество не в одинаковой степени находится и в той и в другой, но скрыто от них в известных соотношениях и пропорциях; и главная роль человеческого искусства заключается не в чём ином, как в сведении всех этих соотношений к тому, чтобы равенство между искомым и тем, что известно, сделалось совершенно очевидным.
Отметим далее, что никакие вещи не могут быть приведены к этому равенству кроме тех, которые содержат в себе понятие о большем или меньшем, и что все эти вещи должны быть отнесены к области величин, так что после того как, по предшествующему правилу, мы абстрагируем условия задачи от всякого особенного предмета, мы поймём, что предметом нашего исследования являются только величины вообще.
Но, для того чтобы представлять здесь ещё что-нибудь и пользоваться не только одним чистым интеллектом, а прибегать к помощи образов, рисуемых в воображении, заметим наконец, что мы не можем называть величиной вообще то, что не может быть также отнесено к любой величине в частности.
Отсюда нетрудно сделать вывод, что для нас будет довольно полезно переводить всё, о чём говорится как о величине вообще, на изображения величин которые и легче и яснее всего рисуются в нашем воображении. Также величинами является реальное протяжение тел, отвлечённое от всего кроме того, что относится к их фигуре. Это следует из того, что мы говорили в правиле XII, где мы указали, что сама фантазия вместе с представлениями, заключающимися в ней, должна быть понимаема не иначе, как протяжённое и обладающее формой реальное тело. Это очевидно также и само по себе, поскольку нигде не рисуются так отчётливо различия всевозможных соотношений. Если об одной вещи и можно сказать, что она более или менее бела, чем другая, один звук резче или мягче, чем другой и пр., то всё-таки мы не можем точно определить, будет ли это превышение больше в два или в три раза и т. д., иначе, как по известной аналогии его с протяжением тела, имеющего фигуру. Итак, будем считать достоверным и прочным то положение, что совершенно определённые вопросы не содержат в себе почти никакой трудности кроме того, что они требуют раскрытия соотношений в равенствах и все те вещи, в которых встречается именно такая трудность, могут быть легко отделены от всего остального их содержания, a затем сведены к протяжению и фигурам, о чём мы будем говорить далее вплоть до правила XXV, оставивши все прочие размышления.
Мы хотели бы иметь здесь дело только с такими читателями, которые питают склонность к арифметике и геометрии, хотя для меня было бы и лучше, если бы они совсем не занимались ими, нежели были обучены в этих науках по обычному методу, ибо правила, предлагаемые мной, легче применимы к этим наукам, в изучении которых они вполне удовлетворяют, чем ко всякому другому роду вопросов. Польза же этих правил в приобретении знаний более высокого порядка столь велика, что я не страшусь назвать эту часть нашего метода созданной не для решения математических проблем и говорить, что скорее математические науки надлежит изучать лишь для практического усвоения этого метода. Я не предполагаю в этих науках ничего, что не могло бы быть известно само собой и доступно для всех, но знания в этой области, как это имеет обычно место, если и не содержат в себе очевидных заблуждений, то затемняются большим количеством двусмысленных и дурно установленных принципов, что мы в дальнейшем постараемся кой-где исправить.
Под протяжённым мы подразумеваем всё то, что обладает длиной, шириной и глубиной, не интересуясь, будет ли это какое-либо реальное тело или только пространство. Мне кажется, что здесь нет нужды давать более подробное объяснение, ибо нет ничего легче, как представить это в своём воображении. Так как однако учёные часто пользуются столь тонкими различениями, что утрачивают естественный свет и находят мрак даже в таких вещах, которые понятны крестьянам, то нужно напомнить им, что мы не рассматриваем здесь протяжение как нечто отличное от его субъекта и что мы вообще не признаём такого рода философских естеств, которых реально не может представить наше воображение. Ибо если кто-нибудь и сумеет убедить себя в том что при уничтожении всех протяжённых вещей существующих в природе, нельзя отрицать существования протяжения самого по себе, то для представления последнего он воспользуется не идеей тела, a только ложными суждениями своего интеллекта. С этим он согласится сам, если он внимательно обдумает образ такого протяжения, попытавшись представить его в своём воображении. Действительно, он увидит, что представляет его не освобождённым от всех вещей, а совершенно иначе, чем он думал. Таким образом подобные отвлечённые вещи (каковы бы ни были представления интеллекта об истине вещи) никогда не создаются воображением отдельно от их предмета.
Но поскольку мы отныне не предпринимаем ничего, не прибегая к помощи воображения, то для нас весьма важно тщательно различать, какие идеи даются нашему интеллекту в значении каждого слова. Поэтому мы предлагаем рассмотреть следующие три вида выражений: 1) протяжение занимает место;
2) тело обладает протяжением и;
3 протяжение не есть тело.
1) Первое показывает, как протяжение принимается за то, что имеет протяжение. Действительно, я подразумеваю одно и то же, когда говорю, что протяжение занимает место, и когда говорю: то что обладает протяжением, протяжённое, занимает место. Однако из этого вовсе не следует, что во избежание двусмысленности лучше пользоваться выражением: протяжённое, ибо оно не выражало бы ясно ту идею, которую мы подразумеваем, а именно, идею некоторого предмета, занимающего место потому, что этот предмет обладает протяжением. Может быть даже кто-нибудь поймёт выражение: протяжённое есть предмет, занимающий место, только так, как если бы я говорил, что одушевлённое существо занимает место. Отсюда становится ясным, почему мы говорили, что мы будем здесь иметь дело более с самим протяжением, чем с протяжённым, хотя мы считаем, что протяжение не должно быть понимаемо иначе, чем протяжённое.
2) Перейдём теперь к выражению: тело обладает протяжением. Хотя здесь мы придаём разное значение словам протяжение и тело, однако мы не создаём в нашем воображении двух различных представлений: одно — тела, другое — протяжения, a только одно — именно протяжённого тела. В сущности это то же самое, как если бы я говорил: тело протяжённо или протяжённое протяжённо. Это свойственно тому, что существует только в другом и не может быть понято без его субъекта. Иначе обстоит дело с вещами, реально отличающимися от их субъекта. Например если я говорю, что Пётр обладает богатствами, то представление Петра совершенно отлично от представления богатств. Так же если я говорю, что Павел богат, то я представляю себе нечто совершенно иное, чем если бы я говорил: богатый есть богатый. Не замечая этого, большинство придерживается ложного мнения, что протяжение содержит в себе нечто отличное от того, что обладает протяжением, подобно тому, как богатства Павла — нечто другое, чем сам Павел.
3) Наконец когда говорится, что протяжение не есть тело, то слово «протяжение» имеет здесь совершенно иной смысл, чем выше; в этом последнем значении никакая частная идея не соответствует ему в воображении, но такая форма высказывания всецело исходит из чистого интеллекта, который один обладает способностью различать абстрактные сущности подобного рода. Здесь большинству людей даётся повод для заблуждения, ибо, не замечая того, что протяжение, взятое в этом смысле, не может быть воспринято воображением, они представляют его в виде действительной идеи и, поскольку эта идея необходимо вызывает представление тела, говоря, что протяжение, понимаемое таким образом, не есть тело, они сами не знают о том, что запутываются, утверждая: одна и та же вещь есть тело и не тело. Очень важно различать выражения, в которых слова протяжение, форма, число, поверхность, линия, точка, единица и др. имеют столь строгое значение, что иногда исключают из себя даже то, от чего они реально не отличаются, например, когда говорят, что протяжение или фигура не есть тело, число не есть сочтённая вещь, поверхность есть предел тела, линия есть предел поверхности, точка есть предел линии, единица не есть количество и т. д. Все такие положения и другие, подобные им, должны быть совершенно удалены из воображения, как бы они ни были истинны. Вот почему мы и не будем о них говорить в дальнейшем.
Нужно обратить особое внимание на то, что во всех других положениях, где эти названия хотя и удерживают то же самое значение и таким же образом абстрагируются от предметов, но не исключают однако или не отрицают ничего в той вещи, от которой они реально не отличаются, мы можем и должны прибегать к помощи воображения, ибо если интеллект имеет дело только с тем, что обозначается словом, то воображение должно представлять себе действительную идею вещи, для того чтобы интеллект мог по мере надобности обращаться и к другим свойствам, которые не выражены в названии, и опрометчиво не считал бы их исключёнными. Так например, если речь идёт о числе, мы представляем себе какой—нибудь предмет, измеряемый многими единицами, но хотя наш интеллект мыслит здесь только о множественности этого предмета, мы тем не менее должны остерегаться, чтобы он не сделал вывод, будто измеряемая вещь считается исключённой из нашего представления, как это делают те, кто приписывает числам чудесные свойства, — чистейший вздор, к которому они не питали бы такого доверия, если бы не считали число отличным от исчисляемой вещи. Таким же образом, когда мы имеем дело с фигурой, будем думать, что речь идёт о протяжённом предмете, который мы представляем не иначе, как имеющим фигуру. Если мы имеем дело с телом, будем рассматривать его как длинное, широкое и глубокое; если с поверхностью — как длинное и широкое, упуская глубину, но не исключая её, если с линией — только как длину, с точкой — будем мыслить её как нечто существующее, упуская всё остальное.
Хотя я и развиваю здесь все эти мысли очень пространно, но тем не менее умы смертных настолько преисполнены предубеждениями, что я боюсь, что в этом месте лишь очень немногие будут ограждены от всякого рода заблуждений и что мои объяснения могут показаться слишком краткими, несмотря на пространность моего рассуждения. Действительно, даже достовернейшие из всех наук — арифметика и геометрия — вводят нас в этом случае в заблуждение. Какой счётчик не думает, что числа не только являются абстракциями интеллекта от всех предметов, но также, что их нужно отличать от последних и в воображении? Какой геометр не примешивает к очевидности своего объекта противоречивые принципы, когда он рассуждает, что линии не имеют ширины, поверхности — глубины, составляя однако одни из других и не замечая того, что линия, которую он представляет производящей посредством движения поверхность, есть настоящее тело, a линия, не имеющая ширины, есть не что иное, как предел тела и т. д. Но чтобы не задерживаться слишком долго на этих наблюдениях, мы покороче изложим, каким образом должен быть, по нашему мнению, представляем наш объект, чтобы доказать, по возможности проще, всё, что есть в этом отношении истинного в арифметике и геометрии.
Следовательно мы займёмся здесь протяжённым объектом, не рассматривая в нём ничего кроме одного только протяжения и умышленно воздерживаясь от употребления слова «величина», ибо есть настолько изощрённые философы, что они устанавливают различие также и между величиной и протяжением. Мы предполагаем свести все эти вопросы к единственной задаче — к отысканию некоторого протяжения путём сравнения его с каким-либо другим, уже известным. Действительно, поскольку мы не ожидаем здесь познания каких-либо новых вещей, но желаем только сводить соотношения, как бы они ни были запутаны, к тому, чтобы приравнять неизвестное к какому-либо известному, то все различия отношений и в других вещах могут конечно также отыскиваться между двумя или многими протяжениями. И поэтому нам достаточно для нашей цели рассмотреть в самом протяжении те элементы, которые помогут нам изложить различия соотношений. Таких элементов насчитывается три: измерение, единица измерения и фигура.
Под измерением мы подразумеваем не что иное, как способ и основание, по которым та или иная вещь считается измеримой, поэтому измерениями тела являются не только длина, ширина и глубина, но также и тяжесть, по которой тела взвешиваются, и скорость, измеряющая движение, и тому подобные бесчисленные измерения. Само деление на множество равных частей, будь оно реальным или только мысленным, есть собственно измерение, с помощью которого мы вычисляем вещи. Способ образования чисел является, собственно говоря, особым видом измерения, хотя здесь есть известная разница в значении этого слова. Действительно, если мы рассмотрим части по отношению к целому, то это будет вычисление, если же, наоборот, мы рассмотрим целое как разделённое на части, то мы его измерим. Например мы измеряем века годами, днями, часами и секундами, но если мы будем считать секунды, часы, дни и годы, то мы сочтём века.
Отсюда становится понятным, что в одном и том же предмете может быть бесконечное количество различных измерений и что они совершенно не привносят ничего к вещам, которые измеряются, но их надлежит понимать одинаково, независимо от того, имеют ли они реальное основание в самих объектах или они являются только продуктом нашего ума. Действительно, вес тела, скорость движения, разделение веков на годы и дни являются в известном смысле реальными, но разделение дней на часы и минуты не имеет ничего реального. Между тем все они равноценны, если рассматривать их только как измерения, как это надлежит делать здесь и в математических науках, ибо скорее физикам подобает исследовать, имеют ли эти измерения какое-либо реальное основание.
Рассмотрение этого проливает яркий свет на геометрию, ибо большинство людей ошибочно представляет в этой науке три рода величин: линию, поверхность и тело. В действительности, как уже было сказано раньше, линия и поверхность недоступны представлению как совершенно отличные от тела или одна от другой, но если они рассматриваются просто как абстракции интеллекта, то они представляют собой не более различные виды величин, одушевлённое и живое существо в человеке представляют собой различные виды субстанции. Заметим мимоходом, что три известные нам измерения тел — длина, ширина и глубина — различаются между собой только названиями, в действительности же ничто не мешает нам выбирать в каком-либо геометрическом теле любое его измерение в качестве длины, ширины и т. д. И хотя бы только эти три измерения имели реальное основание во всех протяжённых вещах как просто протяжённых, однако мы имеем их здесь в виду не более, чем бесконечное количество других измерений, являющихся созданиями интеллекта или имеющих в вещах другие основания. Так например для точного измерения треугольника необходимо знать в нём три элемента, a именно: три стороны или две стороны и один угол, или два угла и площадь и т. д., для трапеции нужно знать пять величин, для тетраэдра — шесть и т. д., которые все могут быть названы измерениями. Чтобы выбирать те из них, которые более всего помогают нашему воображению, не будем никогда пытаться захватить одновременно больше одного или двух, хотя бы мы и видели, что в исследуемом нами предложении имеется ещё и много других. Искусство состоит именно в разделении их на возможно большее число, чтобы обращать внимание на очень малое число их одновременно и однако последовательно на все.
Единица измерения есть то всеобщее свойство, к которому, как я уже говорил выше, должны быть приобщены все вещи, сравниваемые между собой. Если нет налицо какой-либо определённой единицы измерения, то мы при решении задачи можем взять взамен её или одну из данных уже величин или любую иную, которая и будет общей мерой для всех остальных. При этом мы должны подразумевать, что в ней заключается столько же измерений, сколько и в тех крайних, которые должны быть сравниваемы между собой, a также представлять её просто как нечто протяжённое, тогда она будет тем же, чем является точка y геометров, составляющих посредством её движения линию, или как линию, или как квадрат.
Что касается фигур, то выше уже было показано, каким образом только посредством их одних можно создавать идеи всех вещей. Нам остаётся здесь лишь обратить внимание на то, что из бесконечного количества их различных видов мы будем употреблять только те, которые наиболее просто выражают различия всех отношений или пропорций.
Всех же родов вещей, сравниваемых между собой, насчитывается только два, a именно: множества и величины. Для их наглядного представления мы имеем также и два вида фигур. Так например точки, которые обозначают число треугольников, или генеалогическое дерево,
объясняющее чью-нибудь родословную, и пр., являются фигурами, представляющими множества; фигуры же непрерывные и неделимые, такие, как треугольник или квадрат и пр., изображают величины.
Для того чтобы говорить теперь, которыми из всех этих фигур мы намерены пользоваться, нужно заметить, что все отношения, какие только могут быть между вещами одного и того же рода, должны сводиться к двум главным, a именно к порядку или к мере.
Кроме того нужно заметить, что требуется немалая ловкость, для того чтобы разгадать порядок, как это можно видеть в любой части настоящего метода, тогда как нет ни малейшей трудности понять его после того, как он найден, и по правилу V наш ум может легко обозреть все соподчинённые части по отдельности, ибо именно в этом роде отношений одни части могут быть соотнесены с другими сами по себе, a не через посредство чего-либо третьего, как это имеет место в мерах, исследованием которых поэтому мы здесь исключительно займёмся. Действительно, я узнаю порядок величин A и В , не рассматривая никаких других величин кроме каждой из двух крайних, но я не могу узнать соотношения величин 2 и 3, если при этом не рассмотрю третий член, a именно единицу, которая является общей мерой каждого из этих двух членов.
Нужно также заметить, что непрерывные величины с помощью принятой единицы иногда могут быть все приведены к множеству и всегда по крайней мере частично, a множество единиц может быть затем расположено в таком порядке, что трудность, заключающаяся в знании меры, будет зависеть лишь от рассмотрения порядка, и успеху этого должно много содействовать искусство.
Нужно наконец заметить, что из всех измерений непрерывных величин нет ни одного, которое представлялось бы столь же ясно, как длина и ширина, и что не следует одновременно обращать внимание на большое количество измерений в одной и той же фигуре, но сравнивать только два из них, различающихся одно от другого, ибо если необходимо сравнить больше двух различных измерений, то искусство требует их последовательного рассмотрения и не более, чем по два одновременно.
Заметив это, нетрудно сделать вывод, что если дело касается фигур, о которых говорят геометры, нужно абстрагировать предложения и от этих фигур не менее, чем от всяких других предметов. Для этой цели нужно оставить лишь прямолинейные и прямоугольные поверхности, или прямые линии, которые мы также называем фигурами потому, что они не менее, чем поверхности, помогают нам представлять реально протяжённые предметы, как я уже говорил выше. Наконец в этих же фигурах нужно представлять и непрерывные величины, a также множества и числа. Человеческое искусство для наглядного выражения всех различий между отношениями не может изобрести ничего более простого.
ПРАВИЛО XV
Большей частью также полезно чертить эти фигуры и преподносить их внешним чувствам, для того чтобы таким образом нам было легче сосредотачивать внимание нашего ума.
Как нужно их чертить, чтобы в тот момент, когда они находятся перед нашими глазами, их образы отчётливее представлялись бы в нашем воображении, очевидно само собой. Так, во-первых, единицу мы будем изображать тремя способами, a именно:
Но как бы мы её ни изображали и ни рассматривали, мы будем всегда мыслить её как нечто, обладающее в полном смысле этого слова протяжением и бесконечным количеством измерений. A для того чтобы наглядно представлять также и термины положения, когда мы имеем в них дело одновременно с двумя различными величинами, мы начертим прямоугольник, две стороны которого будут данными величинами,
не прибавляя ничего, поскольку речь идёт не о множестве единиц. Наконец, если мы рассматриваем только одну из этих величин, мы изобразим её в виде прямоугольника, одна сторона которого будет данной величиной, другая – единицей измерения,
ПРАВИЛО XVI
Что же касается измерений, не требующих в данный момент внимания нашего ума, хотя и необходимых для заключения, то лучше изображать их в виде сокращённых знаков, чем полных фигур. Таким образом именно память не будет нам изменять и вместе с тем мысль не будет разбрасываться, чтобы удержать в себе эти измерения в то время, как она занята выведением других.
Впрочем, как мы уже говорили, если из тех бесчисленных измерений, которые может рисовать наше воображение, нужно рассматривать не более двух одновременно одним взглядом или одним актом интуиции, то важно сохранять в памяти все остальные таким образом, чтобы они легко представлялись всякий раз, когда в них будет нужда. По-видимому для этой цели природа и создала память. Но так как эта способность часто страдает погрешностями, то, для того чтобы мы не были вынуждены отрывать часть нашего внимания для её освежения в то время, как мы заняты другими мыслями, искусство весьма кстати изобрело применение письменности. Благодаря этому изобретению мы ничто не возлагаем на память, но, свободно и целиком посвятив своё воображение идеям настоящего момента, изображаем на бумаге всё, что требуется сохранить, посредством чрезвычайно простых фигур, дабы, рассмотрев каждую вещь в отдельности по правилу IX, мы могли по правилу XI обозреть их все быстрым движением мысли и охватить одновременно наибольшее их число актом интуиции.
Следовательно всё, что для разрешения трудности надлежит рассматривать как единицу, мы будем обозначать одним только знаком, который можно изображать ad libitum (по желанию), но для большего удобства мы воспользуемся строчными буквами a, b, с и т. д., чтобы выражать уже известные величины, и прописными A, В, С для выражения неизвестных величин. Часто мы будем ставить цифры 1, 2, 3, 4 и т . д. либо впереди этих знаков для указания числа величин, либо позади, для того чтобы обозначить количество отношений, которые будут в них мыслиться. Так например если я записываю: 2а3 , то это одно и то же, как если бы я говорил: удвоенная величина, обозначаемая буквой a, содержащая 3 отношения. Таким способом мы не только сократим многие выражения, но, что особенно важно, будем выражать термины предложений в столь чистом и простом виде, что, не упуская ничего полезного, мы в то же время не допустим в них ничего излишнего, что напрасно занимало бы ум в то время, когда ему нужно вмещать одновременно множество объектов.
Для того чтобы всё это было более понятно, обратим, во-первых, внимание на то, что счётчики имеют обыкновение обозначать отдельные величины многими единицами или каким-либо числом; мы же здесь отвлекаемся от чисел не менее, чем несколько ранее от геометрических фигур или от каких-либо других вещей. Мы делаем это не только во избежание скуки от длинных и ненужных вычислений, но в особенности ещё и для того, чтобы те части предмета, которые составляют сущность трудности, были всегда отчётливо видны и не скрывались за бесполезными числами. Так например, если нужно найти основание прямоугольного треугольника, данные катеты которого выражаются в числах 9 и 12, то счетчик скажет, что оно = √225, или 15; мы же, положив вместо 9 и 12 a и b, найдём, что основание = √a2+b2 и эти два члена a и Ь, которые были скрыты в числе, останутся в нашей формуле раздельными. Нужно также обратить внимание на то, что под числом отношений необходимо подразумевать пропорции идущие друг за другом в непрерывном порядке, пропорции, которые в обыкновенной алгебре стараются выражать многими измерениями и многими фигурами. Первую из них называют корнем, вторую — квадратом, третью — кубом, четвёртую — биквадратом и т. д. Эти термины, признаюсь, очень долго вводили меня в заблуждение, ибо мне казалось, что для моего воображения не может быть ничего более ясного, чем линия и квадрат, чем куб и другие фигуры, придуманные наподобие этих. Хотя с помощью их я разрешил немало проблем, но после многих опытов я наконец убедился, что такой способ понимания не помог мне найти ничего, что я не сумел бы понять намного легче и намного яснее и без него, и нужно совершенно отбросить все эти выражения, чтобы они не затемняли наших понятий, ибо та самая величина, которая называется кубом или биквадратом, не может между тем по предшествующему правилу быть представлена в воображении иначе, как в виде линии или в виде поверхности. Поэтому нужно ещё особенно отметить, что корень, квадрат, куб и пр. являются не чем иным, как последовательно пропорциональными величинами, которым всегда предшествует наперёд заданная единица, уже упомянутая нами выше. Первая пропорциональная величина стоит непосредственно и в одном отношении к этой единице, вторая — через посредство первой, a следовательно связана с ней двумя отношениями, третья — через посредство первой и второй и связана с ней тремя отношениями и т. д. Поэтому мы будем теперь называть первой пропорциональной ту величину, которая в алгебре называется корнем, второй пропорциональной — ту, которая называется квадратом, и т. д.
И наконец нужно обратить внимание на то, что хотя мы здесь и абстрагируем термины трудности от чисел, для того чтобы исследовать её природу, но она однако часто оказывается легче разрешимой с помощью данных чисел, чем без них. Это происходит при двойном применении чисел, ибо, как мы видели выше, именно одни и те же числа объясняют то порядок, то меру. Поэтому после того, как мы пытались разрешить трудность, выразив её в общих терминах, нужно снова свести её на эти числа, для того чтобы узнать, не могут ли они дать нам более простого решения. Так например, найдя, что основание прямоугольного треугольника с катетами a и b = √a2+b2, где вместо a2 нужно взять 81 и вместо b2 —144, числа дающие в сумме число 225, корень которого, т. е. средняя пропорциональная между единицей и 225 = 15, мы из этого узнаем, что основание 15 соизмеримо со сторонами 9 и 12, но не потому вообще, что оно является основанием такого треугольника, отношения сторон которого = 3 : 4 . Все это мы различаем потому, что стремимся достичь очевидного и отчётливого познания вещей, счётчики же не делают этого потому, что удовлетворяются отысканием нужного им числа, не замечая зависимости его от данных чисел, между тем как только в этом и заключается наука.
Заметим теперь вообще, что не нужно вверять памяти вещи, не требующие нашего постоянного внимания, если мы можем закреплять их на бумаге, во избежание того, чтобы бесполезный труд их припоминания не отвлекал наше мышление от того объекта, которым оно занято в данный момент. Кроме того нужно составить таблицу, чтобы внести в неё сначала условия задачи в том виде, как они представляются с первого взгляда; затем — способ их абстрагирования и фигуры, посредством которых они обозначаются, чтобы, после того как мы найдём решение в самих знаках, мы могли бы легко и без всякого участия памяти применить его к частному предмету, с которым мы будем иметь дело. Нельзя именно абстрагировать какую-либо вещь иначе, нежели от какой-либо другой, менее общей. Это я запишу следовательно так: в прямоугольном треугольнике ABC нужно найти основание АС.
Нужно заметить, что мы будем пользоваться этими четырьмя правилами в третьей части настоящего трактата, где мы дадим им несколько более широкое применение, нежели это было объяснено здесь, как это будет показано в своём месте.
ПРАВИЛО XVII
Встретившуюся трудность нужно просматривать прямо, не обращая внимания на то, что некоторые из её терминов известны, a некоторые неизвестны, и интуитивно следовать правильным путём по их взаимной зависимости.
Четыре предшествующих правила учили, как нужно абстрагировать от отдельных предметов определённые и в совершенстве осмысленные трудности и сводить их к тому, чтобы после этого нам оставалось отыскивать именно только величины по тем или иным отношениям, связующим их с данными величинами. В следующих же пяти правилах мы объясним, как нужно решать эти трудности, чтобы независимо от количества неизвестных величин, содержащихся в одном положении, эти величины пришли к взаимному подчинению, и тем, чем является первая величина по отношению к единице, вторая была бы по отношению к первой, третья — по отношению ко второй, четвёртая — по отношению к третьей, чтобы они, следуя таким же образом далее, независимо от их количества, в целом составили сумму, равную именно данной величине. Всё это должно производиться путём столь строгого метода, чтобы с помощью его мы твёрдо убедились в невозможности приведения этих величин к более простым терминам никакими способами.
Что же касается настоящего правила, то заметим, что во всяком вопросе, подлежащем разрешению именно дедуктивным путём, есть один открытый и прямой путь, по которому мы можем легче всего переходить от одного термина к другому, тогда как все другие пути являются более трудными и косвенными. Для того чтобы это понять, нам нужно вспомнить сказанное нами в правиле XI, где, объясняя сцепление положений мы указали, что если сравнивать каждое положение с его предшествующим и последующим, то можно без труда заметить, что первое и последнее из них связываются друг с другом, хотя мы и не можем с такой же лёгкостью выводить промежуточные положения из крайних. Следовательно теперь, если мы рассматриваем их взаимную зависимость, нигде не прерывая порядка, чтобы сделать из этого вывод, в какой зависимости находится последнее положение от первого, такое рассмотрение будет прямым. Если же, наоборот, зная, что первое и последнее находятся между собой в некоторой связи, мы пожелаем сделать вывод, каковы промежуточные, соединяющие их положения, то мы будем идти косвенным и превратным (неверным) для порядка путём. Поскольку же нас интересуют здесь только неясные вопросы, в которых нужно именно при известных крайних найти без твёрдого порядка промежуточные, всё искусство здесь должно состоять в том, чтобы, предполагая известным неизвестное, находить себе таким образом лёгкий и прямой путь также и для разрешения самых трудных вопросов. И нет ничего, что могло бы препятствовать неизменному успеху подобного действия, поскольку мы предположили в начале этой части, что нам известна такая зависимость неизвестного в данном вопросе от известного, которая совершенно определяет первое последним. Таким образом, если мы размышляем о тех самых вещах, которые представляются нам прежде всего, после того как мы примем это определение то, хотя бы мы по неведению причисляли их к известным, для того чтобы постепенно выводить из них все остальные, a также и известные правильным путём так, как если бы они были неизвестными, мы исполняем все предписания этого правила. Что касается примеров того, что мы хотим здесь объяснить, a также и многих других вещей, о которых мы должны говорить в дальнейшем, то мы отложим их до правила XXIV, ибо там они будут более уместны.
ПРАВИЛО XVIII
Для этой цели необходимы только четыре действия: сложение, вычитание, умножение и деление. Двумя последними из них часто здесь даже нет надобности пользоваться как во избежание ненужных усложнений, так и потому, что в дальнейшем они могут быть более легко выполнимы.
Большое количество правил часто обусловливается невежеством учёных; вещи, которые можно свести к единому и всеобщему принципу, утрачивают свою ясность, когда их разбивают по многим специальным правилам. Вот почему все те наши действия, которыми надлежит пользоваться при исследовании вопросов, т. е. именно при выведении одних величин из других данных, мы сводим лишь к четырём главным. Что этих действий достаточно, мы увидим из самого их объяснения.
A именно, когда мы узнаём какую-либо величину благодаря тому, что нам даны части, составляющие её, то мы пользуемся сложением. Когда мы узнаем часть благодаря тому, что нам дано целое и превышение целого над этой частью, то такое действие будет вычитанием; и нет иных способов выведения одной величины из других величин, взятых в абсолютном смысле, в которых она содержится как бы то ни было. Но если какая-либо величина находится между другими, от которых она совершенно отлична и которые её совсем не содержат в себе, то её необходимо поставить в какое-либо отношение к последним. Это отношение, или соотношение, если его нужно отыскивать прямо, можно найти путём умножения, a если его нужно отыскивать косвенно, то путём деления.
Для лучшего разъяснения этих двух пунктов нужно понять, что единица, о которой мы уже говорили, является здесь принципом, или основой, всех отношений и что в ряде последовательно пропорциональных величин она занимает первую ступень, данные величины — вторую, искомые — третью, четвёртую и все остальные, если отношение оказывается прямым; если же оно косвенное, то искомая величина занимает вторую ступень и другие промежуточные, a данная величина последнюю.
Ибо когда говорится, что единица относится к a или к данному числу 5 так же, как b или данное число 7 относится к искомому ab или 35, то a и b в этом случае находятся на второй ступени, произведение же их ab — на третьей. To же самое когда добавляют: единица относится к с или 9 так же, как ab или 35 относится к искомому abc или 315, в этом случае abc находятся на четвёртой ступени, будучи произведением двойного умножения ab на с, величин, находящихся на второй ступени, ит. д. Подобно этому: как единица относится к a ˂ или ˃ 5, так же и а ˂ или ˃ 5 относится к а2 или 25; или ещё: как единица относится к a ˂ или ˃ 5, так же и а2 ˂ или ˃ 25 относится к а3 ˂ или ˃ 125; или наконец: как единица относится к a или 5, так же и а3 или 125 относится к а4, т. е. к 625, и т. д. Конечно действие умножения производится одинаково, умножается ли величина на саму себя или на какую-нибудь совсем другую величину.
В случае же если говорится: как единица относится к a или 5, к данному делителю, так же В или 7, искомое число, относится к ab или 35, данному делимому, то здесь порядок смешанный и непрямой, вследствие чего искомое В не может быть найдено иначе, как путём деления данного ab на a — тоже данное. To же самое, когда говорится: как единица относится к A или искомому числу 5, так же и A или 5 искомое относится к a2 или 25 данному. Или ещё: как единица относится к A ˂ или ˃ 5 искомому, так же и А2 или 25 искомое относится к a3 или 125 данному и т. д. Мы объединяем все эти действия под названием деления, хотя и нужно заметить, что два последних вида заключают в себе больше трудностей, чем первые, потому что в них искомая величина встречается чаще и следовательно имеет больше отношений. Смысл этих примеров тот же самый, как если бы говорилось, что нужно извлечь квадратный корень из a2 ˂ или ˃ 25 или кубичный из a3 или 125 и т. д. Такой способ выражения, употребительный среди счётчиков, является равнозначным — пользуясь также термином геометров — выражениям, обозначающим действие отыскания средней пропорциональной между наперёд взятой величиной, называемой нами единицей, и той, которая обозначается a2, или двух средне пропорциональных между единицей и a3 и т. д.
Отсюда нетрудно сделать вывод, почему эти два действия удовлетворяют в отыскании любых величин, которые должны выводиться из других величин по тому или иному отношению. Понимая это, нам остаётся объяснить, как эти действия должны быть представлены рассмотрению воображения и как их нужно сделать наглядными, для того чтобы затем объяснить их употребление или обращение с ними.
Если нам нужно произвести сложение или вычитание, то мы будем представлять предмет в виде линии или величины, обладающей протяжением, в которой нужно рассматривать только длину,
Наконец при делении, где дан делитель, мы будем воображать делимую величину в виде прямоугольника, одна сторона которого делитель, a другая — частное.
Что касается таких делений, в которых делитель не дан, a только обозначен некоторым отношением, как например, когда говорят, что нужно извлечь квадратный корень или кубический корень и т. д., то заметим, что в этих случаях делитель и все остальные члены нужно представлять как линии в ряде последовательных пропорций, из которых первой является единица и последней —делимая величина. Как нужно отыскивать все средние пропорциональные величины между делимым и единицей, будет показано в своём месте. Достаточно уже заметить, что мы ещё не считаем поконченным здесь с этими действиями, так как они могут производиться воображением посредством непрямого и обратного действия, a мы говорим здесь только о вопросах, исследуемых прямо.
Что касается прочих действий, то они очень легко производятся при том способе их понимания, о котором мы говорили. Однако нужно объяснить, как необходимо подготавливать их термины, ибо хотя мы и свободны, впервые исследуя какую-либо трудность, представлять её термины в виде линий или прямоугольников и не применять к ним никаких других фигур, как об этом говорилось уже в правиле XIV, но тем не менее в процессе действия часто бывают случаи, когда какой-либо прямоугольник, после того как он был произведён умножением двух линий, вскоре для другого действия требуется понимать как линию или ещё когда один и тот же прямоугольник либо линию, произведённые сложением либо вычитанием, вскоре оказывается нужным понимать как другой прямоугольник, обозначенный вверху линией, которая должна его разделить.
Следовательно здесь важно объяснить, как всякий прямоугольник может быть преобразован в линию или, наоборот, линия или также прямоугольник — в другой прямоугольник с обозначенной стороной. Это очень легко могут делать геометры, лишь бы они замечали, что всякий раз, когда мы, как здесь, составляем из линий какой-либо прямоугольник, мы всегда подразумеваем прямоугольник, одна сторона которого является длиной, принятой нами за единицу. Таким образом вся эта задача сводится к положению: по данному прямоугольнику построить другой, равный ему, на данной стороне.
Хотя это действие привычно даже для тех, кто только что начинает заниматься геометрией, тем не менее я хочу его объяснить, чтобы меня не упрекали в каких-либо упущениях.
ПРАВИЛО XIX
Путём такого метода вычисления нужно отыскивать столько величин, выраженных двумя различными способами, сколько неизвестных терминов мы предполагаем известными, для того чтобы исследовать трудность прямым путём. Именно таким образом мы получим столько же сравнений между двумя равными величинами.
ПРАВИЛО XX
Составивши уравнения, мы должны совершить отложенные нами действия, никогда не пользуясь умножением, если уместно деление.
ПРАВИЛО XXI
Если имеется много таких уравнений, то нужно их привести все к одному, a именно к тому, термины которого займут наименьшее количество ступеней в ряде последовательно пропорциональных величин, где они и должны быть расставлены в соответствующем порядке.
Конец.
-
(в печатном издании) Intuitus… et inductio. Фраза «посредством которых… и индукция» в H дана в следующем виде: «…ullo deceptionis metu periculo licet pervenire», и написанные другой рукой слова «et inductio» были зачеркнуты.
Логическое умозаключение мне кажется будет более последовательным и понятным для восприятия — , посредством которых мы можем достичь познание вещей, не боясь обмануться хотя и рискуя. Возможны только два таких действия, a именно: интуиция и дедукция. ↑
-
(в печатном издании) 2 Перед словами «mentis operationes» добавлено чужой рукой в скобках (regulae circa) — H.
3 Aliae autem mentis operationes, quas harum priorum auxiliis dirigere contendit Dialectica… Текст испорченный, как это можно видеть по ганноверской копии. Смысл требует: Aliae autem regulae, quarum auxilio mentis operationes dirigere se contendit Dialectica.
Логическое умозаключение мне кажется будет более последовательным и понятным для восприятия — Что же касается иных видов или правил умственной деятельности, которые направляют мысль во главе с диалектикой ↑
-
(в печатном издании) — В Ганноверской рукописи правило IV заканчивается этими словами, но вслед за ними идёт надпись, хотя и зачеркнутая: «Vide paginam notatam littera A in fine». И действительно в конце рукописи находится последняя часть этого правила, соответствующая, за исключением мелких деталей, тексту амстердамского издания. Вероятно эта часть опущена в рукописи, потому что она носит автобиографический характер.) ↑
-
Мой комментарий ↑
-
1 Nuda опущено — H
Логическое умозаключение мне кажется будет более последовательным и понятным для восприятия — передаётся только она ↑