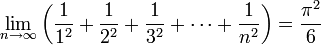Эйлер Леонард
Издатель:
Санкт-Петербург : [тип. Акад. наук]
Дата:
1740
Переводчик:
Адодуров Василий Евдокимович
Описание:
Оригинал хранится в ГПИБ; Пер. кн. Л. Эйлера: Einleitung zur Rechen-Kunst (Петербург, 1738-1740)
Объём:
312 с.
Тематика:
Математика — Учебники и пособия — Дидактические материалы
Код записи:
RU/RGDB/BIBL/0000353513
Целевая аудитория:
для детей среднего возраста, 9-14 лет; для юношества, возраст 14-20 лет
Ограничения:
Открытый доступ
4.4. Учебники математики для академической гимназии
Гимназический курс математики включал преподавание арифметики, геометрии и тригонометрии. Первым учебником математики в гимназии было пособие Хр. Вольфа, » Введение в искусство счета для употребления в гимназии при Императорской Академии наук в С.-Петербурге » (1713), широко распространенное в то время. В нем были реализованы такие методические идеи как приоритетность развития мышления перед формированием практических умений и формализация математического содержания.
Эйлер выдвигает и совершенно иные методические основы гимназического преподавания математики, которые реализуются им прежде всего в учебнике арифметики для академической гимназии.
Учебник арифметики для академической гимназии Л.Эйлера
«Руководство к арифметике для употребления в гимназии при императорской Академии наук» (в двух частях) Эйлера вышло в С.-Петербурге на немецком языке в 1738-40 гг. и в русском переводе в 1740 и 1760 гг. Это учебное пособие положило начало новому направлению в отечественной школьной математической литературе.
Авторская характеристика методических идей. Эйлер в обращении к читателю так характеризует необходимость в отечественном учебнике арифметики: «Число арифметических книг, которые в разных государствах на свет изданы, так велико, что многим сей труд мог бы весьма ненужным казаться… Но русское юношество не может пользоваться иностранными руководствами без больших затруднений и сочинения страдают крупными недостатками».
Под недостатками Эйлер понимает как чисто практический характер учебников математики (например, «Арифметики» Магницкого), так и излишнюю формализацию, ведущую к искусственному усложнению изложения (учебники Хр.Вольфа). Приведем характеристику этих учебников самим Эйлером: «… кои содержат или только одни правила со многими при них положенными примерами, а о основании, на котором те правила утверждаются, не упоминается в них ни одним словом; или хотя праведные основания сея науки в некоторых руководствах и показываются, однако ж так трудным и непонятным образом, что ежели кто к математическому порядку не привык, то не можно почти того и выразуметь». По мнению Эйлера, «если арифметика без оснований и доказательств показываться будет, то оная не довольна ни к разрешению всех случаев, ни к поощрению человеческого разума, о чем наипаче надлежало бы стараться». Эйлер считает, что изучая арифметику, ученики должны приучаться «праведные основания и причину видеть» и через это они » приобыкнут к основательному размышлению».
Таким образом, Эйлер стремился дать обоснованное и вместе с тем понятное изложение числовой арифметики. С современной точки зрения, в своем учебнике он попытался сочетать принципы доступности и научности в изложении математики, что было безусловным шагом вперед в развитии методических идей школьного обучения математике. Будучи первоклассным вычислителем, Эйлер в обращении к читателю делает акцент на необходимости поиска наиболее эффективных способов вычислений: он подчеркивает, что большинство учебников не заботится «о тех способах, чрез которые счисление легче и короче учинить можно, но тем только удовольствуются, чтоб о всем основание в коротких словах показано было».
Итак, Эйлер предъявлял к учебнику арифметики целый ряд прогрессивных методических требований и попытался их реализовать в «Руководстве к арифметике…». Эти требования в обобщенном и осовремененном виде выглядят следующим образом: 1) научность, выражающаяся в необходимости обоснования математических фактов, 2) доступность изложения материала, 3) упрощенная техника арифметических вычислений.
Математическое содержание «Руководства к арифметике…». В предисловии Эйлер раскрывает и свои планы в отношении математического содержания учебника: в первых 2 частях предполагалось изложить действия над целыми и дробными числами, в третьей — правила тройное, ложного положения и др., в четвертой — представить часть курса, «который надлежит до геометрии и до прочих частей математики, и содержит в себе десятичные дроби купно с вычитанием радиксов, а напоследок также и учение о логарифмах и их употреблении толкует». Из-за отъезда Эйлера в Берлин в 1741 г. учебник остался недописанным и вышли только первые 2 его части.
Первая часть называется «О первых арифметических действиях в целых и ломаных числах» и содержит:
— определение понятия числа как множества частей одного рода;
— системы нумераций;
— сложение, вычитание, умножение и деление целых чисел (главы II-V);
— сложение, вычитание, умножение и деление дробей (главы VI-IX).
Вторая часть включает в себя действия над именованными числами, а также таблицы русских и зарубежных мер и весов.
Итак, в «Руководстве к арифметике…» представлено относительно традиционное для того времени математическое содержание, однако четко выделен только арифметический материал, что явилось одним из первых шагов к дифференциации школьной математики и учебных пособий на отдельные предметы.
Особенности изложения материала в «Руководстве к арифметике…»
1. В большинстве современных Эйлеру учебников математики (в том числе и в»Арифметике» Магницкого) нумерация включена в число арифметических действий. В эйлеровском учебнике арифметики нумерация не включается в число арифметических действий, а выделяется в отдельную главу.
2. Эйлер дает определения арифметических действий. Примеры:
«Деление учит данное число на столько равных частей разделить, на сколько кто желает».
«Умножение есть способ как такое число сыскать надлежит, которое бы данного числа вдвое или втрое, или во столько раз было больше, сколько угодно».
Как видно, это не определения умножения и деления, которые вполне строго можно было бы ввести, опираясь на сложение, но и не громоздкие конструкции, которые мы находим, например, в «Арифметике» Магницкого.
3. Все правила действий даются с необходимыми обоснованиями: иногда с полным доказательством (например, признаки делимости), иногда доказательство неполное. Для нахождения наибольшего общего делителя используется алгоритм Евклида. Очень часто рассматриваются не частные приемы выполнения действий, а общий принцип. Так, при сложении и вычитании Эйлер сразу показывает принцип сложения единиц соответствующих разрядов, по которому осуществляется сложение любых чисел.
4. Что касается законов действий (рассматриваются ассоциативность, коммутативность и дистрибутивность), то, несмотря на провозглашенную в обращении к читателю необходимость обоснований, дается удовлетворительное объяснение только коммутативности умножения (при помощи прямоугольника, составленного из рядов точек), причем применяется неполная индукция, не являющаяся методом строгого доказательства.
5. Необычен и характер примеров, иллюстрирующих правила. Если в других руководствах они в основном имели практический характер, то в «Руководстве к арифметике…» Эйлер часто использует примеры из библии или античности, так как теология и история входят в сферу его интересов. Вообще примеры разбираются очень подробно, на них выясняются всевозможные нюансы, частные и особые случаи рассматриваемого вопроса. Кроме того, рассматривается очень много задач естественнонаучного характера, есть и практические задачи.
6. Большое внимание уделено признакам делимости на 2, 4, 8, 5, 3, 6, 9, которые используются для облегчения вычислений.
7. Очень подробно рассматривает Эйлер деление с остатком, естественно переходя от него к дробям. Учение о дробях предшествует разделу об именованных числах, причем Эйлер вводит 2 определения дроби:
Первое — дробь как частное от деления, неосуществляющегося нацело, причем, убеждая в существовании дроби, он рассматривает пример: при делении 17 на 5 частное целым быть не может, «однакож оно есть некоторое количество, или число, потому что можно сказать, что сие частное число больше, нежели 3, а меньше нежели 4».
Второе — дробь как сумма долей единицы: «Всякое ломаное число, когда единица или нечто целое разделится на столько равных частей, сколько показывает нижнее число, содержит в себе столько оных частей, сколько изъявляет верхнее над чертой стоящее число».
На примере Эйлер показывает, что они практически совпадают.
8. Там, где нужно, намечается перспектива, ставятся проблемы, которые будут решаться в дальнейшем. Так, при изучении деления Эйлер специально предлагает задуматься над случаем, когда частное «такими числами, о каких мы теперь рассуждаем, изобразить не можно, но к тому требуются ломаные числа, или доли, которых свойство теперь еще за неизвестное полагается, а истолкование будет в следующем».
9. В конце каждой главы приводятся текстовые задачи, хотя задач и упражнений для самостоятельного решения в учебнике явно недостаточно, а специальных задачников в то время не было.
Итак, Эйлеру удалось написать учебник арифметики, несомненными методическими достоинствами которого можно считать:
1) систематическое изложение материала;
2) достаточно оптимальное сочетание теории и практики;
3) успешные попытки если не обосновать, то хотя бы разъяснить, растолковать каждое правило, что существенно повысило уровень строгости изложения, научности учебника;
4) доступность изложения материала, проявившаяся прежде всего в простом, ясном изложении правил, упрощенной технике вычислений.
Не став стабильным учебником, «Руководство к арифметике» оказало значительное влияние на учебную математическую литературу и стало прецедентом создания выдающимся ученым доступного школьного учебника, не снижая его научного уровня.
Учебники геометрии для академической гимназии
Во времена Эйлера геометрию часто преподавали по «Началам» Евклида, которые в течение XVIII в. трижды переводятся в России . Однако ни один из переводов не был адаптирован для школы, неадаптированный же вариант, безусловно, был мало пригоден для нужд обучения. К тому же к учебникам математики предъявлялись все более серьезные методические требования, поэтому тяжеловесные стиль и структура «Начал» перестают удовлетворять потребностям обучения геометрии. Изданные для математико-навигацкой школы пособия по геометрии, как уже говорилось, носили чисто практический характер, т.е. требовалось создание учебников геометрии нового поколения.
Рукопись, приписываемая Эйлеру. Есть достаточно обоснованные предположения, что Эйлер предпринял попытки создать учебник геометрии: о нем есть упоминания в ряде библиографических источников, найдены рукописные фрагменты учебника геометрии на немецком языке , идентифицированные как принадлежащие Эйлеру. Однако, сама книга, если она все же была издана, по всей видимости, не сохранилась или до сих пор не найдена.
Рассмотрим вкратце содержание сохранившихся фрагментов, так как они уточняют представления о требованиях Эйлера к содержанию школьного учебника геометрии. Особый интерес представляет начало фрагмента, где Эйлер дает определения-описания основных понятий.
«1. Линия, лат. linea, есть длина без ширины и толщины».
«2. Настолько малая часть линии, что она более не имеет длины, называется точкой, punktum»…
«8. И от А к В можно провести только одну-единственную прямую линию; напротив, из А в В может проходить много кривых…»
Далее описываются свойства измерения длин в английских футах и дюймах, русских мерах — саженях, аршинах, верстах, а также немецких милях. После этого определяются простейшие фигуры: угол, его элемнты, равенство углов, окружность и круг и их элементы. Даются без доказательств первые теоремы:
«1. Если в некоторой окружности даны две равные хорды, то и стягиваемые ими дуги будут равны.
2. Поэтому если из концов одинаковых дуг провести радиусы, то и образуемые при этом углы будут также равны между собой».
Затем следуют определения перпендикуляра к прямой, прямого и тупого углов.
Параллельные прямые Эйлер вводит так:
«Две прямые линии ВА и СD сходятся, когда они все более сближаются, в каковом случае они в конце концов встречаются и образуют угол. Поэтому такие линии при продолжении в другие стороны за В и С все больше удаляются одна от другой, что называется расхождением. Если две линии, АВ и СD, не сходятся и не расходятся, то они параллельны, т.е. параллельные линии такие, которые неизменно одинаково удалены одна от другой и, как бы далеко ни продолжались, нигде не сходятся».
После этого следуют теоремы об углах при пересечении двух параллельных прямых третьей и о параллельности и перпендикулярности прямых. Далее помещен небольшой раздел под заголовком «О знаках и их употреблении», в котором вводится современнейшая для того времени символика: знаки =, +, -, <, >.
Следующий раздел называется «О треугольниках» и начинается с определения фигуры как «пространства или места, ограниченного линиями и заключенного внутри них», после чего вводятся понятия трех- , четырех- и пятиугольника. Доказываются теоремы о сумме углов треугольника, о величине угла треугольника и дается классификация треугольников по сторонам и углам. С помощью наложения доказаны первый и второй признаки равенства треугольников. Затем рассматриваются свойства равнобедренного и равностороннего треугольника, довольно оригинально доказывается третий признак равенства треугольников.
После этого Эйлер перечисляет основные задачи на построение:
— треугольников по трем элементам,
— перпендикуляра из заданной точки прямой и из заданной точки на прямую,
— деление угла пополам,
— построение углов в 60o и 30o.
Затем доказана теорема о соотношении сторон и углов треугольника и следствия из нее; теорема о том, что перпендикуляр из данной точки на данную прямую — кратчайшая из всех прямых и как следствие — гипотенуза всегда больше катета. Доказывается также, что сумма 2 сторон треугольника всегда больше третьей.
Заключительный раздел фрагмента назван «О четырехугольниках». Эйлер классифицирует их на параллелограммы и трапеции, параллелограммы в свою очередь на прямоугольники, квадраты, ромбы, обосновывая свойства параллелограммов. Достаточно подробно рассматривается вопрос о равновеликости параллелограммов и треугольников, решаются задачи на построение некоторых равновеликих фигур. Доказываются теоремы о сумме внутренних углов четырех-, пяти-, шестиугольников, произвольного многоугольника. В заключение даются определения правильных многоугольников и приводится таблица величин внутренних углов трех-, двенадцатиугольников и девяностоугольника.
Итак, во фрагментах представлен классический планиметрический материал, изложенный доходчиво и достаточно современно, с обоснованиями важнейших теорем.
Как считает Ю.А.Белый , весьма вероятно, что рукопись предназначалась для преподавания в академической гимназии в первые годы пребывания Эйлера в С.-Петербурге, т. е. в 1727-1730 гг. В эти годы он еще не обнародовал основные педагогические и методические воззрения, но, судя по фрагменту этого учебника, уже руководствовался ими при разработке конкретных пособий.
Продолжим характеристику учебников геометрии, созданных для академической гимназии.
Учебник Г.Крафта. В 1748 г. выходит в свет «Краткое руководство к теоретической геометрии», написанное академиком С.-Петербургской Академии наук Георгом Крафтом специально для академической гимназии . Интересно, что русский вариант этой книги был отредактирован М.В.Ломоносовым, прекрасно знавшим математику, широко использовавшим ее в своих исследованиях и даже внесшим некоторый вклад в развитие математического образования в России . Вопросы, связанные с несоизмеримостью, преимущественно обойдены. Проблемы измерения площадей и объемов решаются с помощью принципа Кавальери и вписания в кривые линии «многоугольников с бесконечно малыми сторонами». Таким образом, несмотря на название курса Г.Крафта, все сколько-нибудь сложные теоретические вопросы обойдены, проблемы же прикладного характера во многом по-прежнему доминируют.
Отказавшись от попыток аксиоматического построения геометрии (аксиомы отсутствуют), автор широко использует движение для преобразования фигур. Кроме теоретического материала книга Крафта содержит многие весьма полезные практические приложения. Она отличается простотой изложения, доступностью материала, однако уровень строгости ее явно недостаточен. Тем не менее, довольно долго ученики академической гимназии пользовались преимущественно ею. «Краткое руководство к теоретической геометрии» было переиздано в 1762 г.
Учебники алгебры для академической гимназии
Точных данных об использовании в академической гимназии тех или иных учебников алгебры не сохранилось. Поэтому ограничимся здесь лишь упоминанием и очень лаконичной характеристикой учебных пособий по алгебре того периода:
1. «Начальное основание математики… Ч. 1, Спб., 1752» военного инженера Н.Е.Муравьева — автора первого русского учебника алгебры. Курс содержал обширный материал, включая бином Ньютона и методы решения уравнений высших степеней. Однако он страдал традиционными для той поры недостатками: несистематичностью изложения, трудностью восприятия материала в силу неясности, нечеткости изложения.
2. «Универсальная арифметика. Спб., 1757» Н.Г.Курганова, которая содержала элементы алгебры.
«Универсальная арифметика» Л.Эйлера
Л.Эйлер создал учебник высшей алгебры, ставший прообразом всех последующих, вплоть до учебников конца XIX — начала ХХ вв. Двухтомное «Полное введение в алгебру» Эйлер подготовил по возвращении в Петербург. Оно издано на немецком языке в 1770 г. Ранее, в 1768-1769 гг. вышел русский перевод этой книги под названием «Универсальная арифметика», который оставил далеко позади все существовавшие тогда в России учебники алгебры. «Универсальная арифметика» Л.Эйлера написана как бы в 2 планах — учебном и исследовательском. Она состоит из 2 томов.
В первом томе разработан основной алгебраический аппарат. Вводный раздел первого тома называется «О разных исчислениях простых количеств» и начинается с общих рассуждений «о математике вообще», определения понятия числа как «отношения одного количества к другому», характеристики предмета алгебры. Эйлер считает, что алгебра, или аналитика, — «основательная часть математики», заключающая «вообще все случаи, какие токмо при учении о числах и исчислении оных место иметь могут». Он характеризует взаимосвязи алгебры с арифметикой как «наукой о числах собственно так называемых», которая «простирается токмо до известных родов исчисления, которые чаще в общежитии случаются». Здесь же излагается алгебраическое знакоположение, рассматриваются действия с положительными и отрицательными числами, а также с дробями. Рассматривается извлечение корней и в связи с этим иррациональные числа. Завершается этот раздел теорией логарифмов.
Во втором разделе, озаглавленном «О разных исчислениях сложных количеств», рассматриваются действия над многочленами, исследуются ряды, получающиеся при делении 1 на (1-а), и бином Ньютона для любого показателя. В третьем разделе первого тома рассматриваются отношения, пропорции, прогрессии, бесконечные десятичные дроби и проценты («исчисление интересов»).
В первом томе Эйлер стремился к возможно более полному обоснованию алгебраических правил. Законам действий отведено немного места: рассматривается лишь переместительный закон умножения. Более подробно рассмотрен случай деления на нуль в духе присущих Эйлеру взглядов на бесконечность. Эти взгляды он частично раскрыл еще в «Руководстве к арифметике». Не обходя трудные места, он достаточно четко и корректно с математической точки зрения их разъясняет. Так, касаясь случая, когда делитель является нулем, Эйлер пишет: «Тогда частное число есть бесконечного количества; но понеже сей случай в обыкновенном делении не приходит, то тем, которые учиться еще начинают, о бесконечных количествах ничего предлагать не надобно».
Не всегда внятно изложена природа отрицательных, иррациональных (по Эйлеру, «неизвлекомых») и мнимых («невозможных») чисел. «Поелику все числа, какие токмо представить себе можно, суть или меньше или больше 0, или суть самый 0, то явствует, что квадратные корни из отрицательных чисел, в число возможных включить не можно, и что следственно оные наименовать должно числами невозможными». Однако Эйлер признает их пользу для алгебры, так как они, по его мнению, служат признаком невозможности решения задачи.
Учение о логарифмах Эйлер изложил заново . Логарифм он определяет как показатель степени выбранного основания. Особенно большое внимание уделил Эйлер процессу логарифмирования и его связям с другими способами вычисления. Общепризнанно, что учение о логарифмах — одна из лучших частей его книги.
Академик В.Я.Буняковский так характеризовал первый том эйлеровской алгебры: «Первая часть «Алгебры» Эйлера послужит драгоценным руководством преподавателю арифметики для собственного образования. Из этого образцового сочинения он научится ясно и отчетливо излагать свои мысли, располагать самым выгодным образом как общие предложения, так и приемы решения частных вопросов и, так сказать, доводить учеников самих к открытию доказываемых истин, что конечно, в высшей степени полезно. С другой стороны, изучавший основательно эту книгу, усилится в теоретической части арифметики, потому что эта часть излагается у Эйлера в самой близкой связи с начальными понятиями об алгебре и, следовательно, получает там более развития и определительности, чем в обыкновенных курсах».
Второй том посвящен уравнениям. В нем излагаются сведения о решении уравнений до 3-й и 4-й степеней включительно, в том числе приближенные методы вычисления действительных корней. Однако общая теория уравнений в нем не рассматривалась.
Кроме того, второй том содержал научные результаты самого Эйлера в области диофантова анализа. В нем он:
— обобщил и систематизировал все, что было известно до него о решении неопределенных уравнений fn(x,V)=0 при n = 2, 3, 4 в рациональных числах;
— впервые четко сформулировал, в чем состоит принципиальное различие между решением неопределенных уравнений второй и третьей степеней; — показал детальное применение «метода секущей» и «метода касательной» для приближенного решения диофантовых уравнений.
Мы специально так подробно охарактеризовали изложение Эйлером теории диофантовых уравнений, чтобы подчеркнуть сугубо исследовательский характер отдельных разделов «Универсальной арифметики». Однако в основной своей части она включает материал, который сейчас принято называть элементарной алгеброй, изложена вполне доступно и в этом отношении превосходит все предыдущие пособия по алгебре. Неудивительно, что «Полное введение в алгебру» Эйлера неоднократно переиздавалось на немецком языке, а также в русском, французском, английском и голландском переводах.
Все же учебник Эйлера включал слишком большой и трудный для гимназического обучения материал, поэтому возникла задача его переработки, которую успешно выполнил ближайший ученик и помощник Эйлера в последние годы его жизни Н.И.Фусс. Он издал книгу «Начальные основания алгебры, выбранные из алгебры Леонарда Эйлера» , неоднократно переиздававшуюся, начиная с 1799 г. Это практически переработанная в учебных целях эйлеровская «Универсальная арифметика» (подробная характеристика учебника дана ниже). Не будет преувеличением сказать, что русские пособия по алгебре до учебника А.П.Киселева включительно продолжали и развивали традицию, «восходящую через Фусса к Эйлеру».
«Сокращения математики» С.Я. Румовского
«Сокращения математики. Часть первая, содержащая начальные основания арифметики, геометрии и тригонометрии, сочиненная Академии наук адъюнктом Степаном Румовским. В Санкт-Петербурге при императорской Академии наук. 1760.» — таково полное название этого учебного пособия. По мнению ряда исследователей , «Сокращения…» написаны под несомненным влиянием трудов видного венгерского ученого первой половины XVIII в., почетного члена Петербургской Академии наук И.А.Сегнера , в нем также прослеживаются методические идеи Хр.Вольфа. Кроме того, при написании «Сокращений…» Румовский широко пользовался тригонометрическими исследованиями Л.Эйлера.
Полное руководство по элементарной математике для учащихся академической гимназии и университета в это время отсутствовало: издание «Универсальной арифметики» Эйлера еще не было закончено, учебника тригонометрии не было вообще, «Краткое руководство к теоретической геометрии» Крафта довольно быстро разошлось. «Сокращения…» Румовского во многом восполнили этот недостаток, став новым руководством для гимназистов по всем разделам элементарной математики, включая алгебру.
Учебное пособие Румовского состоит из «предуведомления» и 4 разделов — начальных оснований арифметики, теоретической геометрии, плоской тригонометрии и практической геометрии. В «Предуведомлении» Румовский в качестве основной цели провозглашает создание математического курса на «российском языке». Вслед за Эйлером Румовский делит учебные пособия на 2 категории: «Издаются математические книги двух родов: одни дают правила без доказательств и снабжают их пояснительными примерами, другие доказывают входящие в них предложения».
Однако вопреки Эйлеру, который предлагает сочетать математическую строгость, доказательность с простотой и ясностью изложения, Румовский признает приоритет доказательности, следуя скорее Хр. Вольфу. «Строгость математическая, которая состоит в том, чтоб ничего кроме известного и ясно доказанного за основание не принимать, нечувствительно приучает рассуждать о вещах твердо и основательно». Поэтому основной метод изложения материала, который провозглашает Румовский в «Предуведомлении», — не ограничиваться только содержанием правил, а приводить «сверх того доказательства и всякого действия причины». Следуя аксиоматическому изложению Евклида, Румовский считает, что «начинающим учиться полезно предлагать математические науки по такой книге, где строгость и порядок математический наблюдается», поэтому изложение материала он считает необходимым начинать «от понятий самых простых и известных» — определений и теорем.
В соответствии с традициями отечественной учебной литературы, он подчеркивает необходимость связи теории и практики, особое значение математики для развития общества: «Почитая за излишнее дело пространно доказывать пользу математики, тем сие заключу, что в общем житии ничего без познания величины и количества в пользу нашу употребить не можем, которое от одной математики заимствовать должно».
В «Предуведомлении» раскрываются и связи математики с другими науками, подчеркивается, что математический метод является самым точным и надежным. Так, о взаимосвязи математики и физики он пишет: «Чем больше в физике открыто будет неоспоримых истин, которые бы могли служить основанием, тем больше математика распространяется». Это говорит о том, заключает автор, «сколь пространно поле математики и сколь нужна арифметика и геометрия к приобретению знания других частей математических». Еще раз, очень настойчиво Румовский подчеркивает в «Предуведомлении», что математика приучает «мысли свои и рассуждения так располагать, чтоб ничего неизвестного, неясного и без доказательства не утверждать», потому что человек «и о других вещах тому же порядку последовать будет», ибо «привычка есть другая природа». Подтверждая свою изумительную эрудицию и интерес к проблемам педагогики, он привлекает в качестве авторитета английского ученого-педагога Дж.Локка: «математические науки весьма способны к приучению разума к твердым и основательным рассуждениям… когда кто, обучаясь математике, получит способность рассуждать порядочно, то тому же порядку последовать будет и в рассуждениях о других вещах». В заключение «Предуведомлений» Румовский предупреждает учащихся, что для овладения математикой необходимы трудолюбие и настойчивость, приводя в качестве аргумента знаменитые слова Евклида о том, что «нет и для государей особливого и способнейшего пути к познанию математики».
Итак, в «Предуведомлении» Румовский излагает свои методические принципы, к которым можно отнести:
— доминирование доказательности, логической составляющей математики как средства в том числе воспитания и развития обучаемого;
— необходимость изложения математики на современном российском языке;
— сочетание теории и практических приложений;
— первоначальное введение аксиом и определений, что можно условно назвать аксиоматическим стилем изложения материала.
Перейдем к характеристике содержания «Сокращений…». Из 4 отделов, перечисленных нами ранее, наиболее интересными по полноте и ясности изложения являются арифметический и тригонометрический. Арифметический отдел Румовский начинает в соответствии со своими методическими принципами с определений. Арифметику он, как и Эйлер, характеризует как науку, которая «показывает свойства чисел и подает правила к решению случающихся в общежитии задач». Целое число, как понимает его Румовский, есть «множество частей одинакового рода, взятых вместе и называемых единицами». При изложении действий над целыми числами Румовский, по его собственным словам, следовал Сегнеру.
Прежде чем вводить понятие дроби, Румовский предлагает учение об отношениях и пропорциях. Действия над дробями он обосновывает свойствами пропорций и использует определения операций. Практическая часть главы о пропорциях и дробях называется «О употреблении пропорций в общежитии», включает тройное правило с его разновидностями и иллюстрируется многочисленными задачами.
Последняя глава арифметического отдела предлагает материал для знакомства с прогрессией как основой логарифмов, которые определяются как члены арифметической прогрессии, соотнесенные с геометрической.
Геометрический отдел «Сокращений…» характеризуется попыткой адаптации Евклида для школьного обучения за счет изменения стиля и структуры евклидовых «Начал», но не касается их фактического содержания. По евклидову образцу определяются основные понятия (точка, прямая, плоскость), перечисляются аксиомы, система которых, естественно, недостаточна. При изложении вопросов метрики случай несоизмеримости обходится, что также вполне естественно (он окончательно решен в математике лишь спустя столетие). Текст отдела богато иллюстрирован рисунками и чертежами.
В третьем отделе «Сокращений…», посвященном плоской тригонометрии, Румовский знакомит читателя с основными тригонометрическими величинами, моделируя их, по примеру Эйлера с помощью единичной окружности. Он рассматривает знаки тригонометрических величин в разных четвертях, устанавливает отношения между основными тригонометрическими величинами, выводит основные тригонометрические формулы. Вторая глава тригонометрического раздела содержит изложение теории синусов и косинусов и решение на этой основе треугольников.
В четвертом отделе, который назван Румовским «Прибавление» и включает начала практической геометрии, излагаются способы проведения прямых и кругов на земной поверхности, приемы измерения углов астролябией, пользования ватерпасом, а также способы приближенного вычисления сегмента с малой высотой и узких круговых секторов. В «Сокращениях…» в соответствии с интересами автора и традициями того времени рассматриваются многие вопросы геодезии и астрономии. Так, в последнем разделе практической геометрии Румовский отмечает, что эта наука имеет прямое отношение к астрономии, механике и оптике и потому особое внимание обращает на характеристику инструментов и способы пользования ими для различных измерений.
Заканчивая краткий разбор «Сокращений математики» Румовского, еще раз подчеркнем, что несмотря на то, что они охватывают широкий круг математических вопросов, раскрывают пути применения математических знаний в других науках, характеризуются тщательным подбором примеров, иллюстрирующих выдвигаемые положения, они все же были трудны для понимания во многом из-за «вольфовского» стиля изложения. Тем не менее, «Сокращения…» были одним из наиболее употребительных в академической гимназии руководств. Заметим, что некоторые авторы объясняют это высоким положением в Академии самого автора.
Источник: Полякова Т.С. История отечественного школьного математического образования. Два века. Кн. I: век восемнадцатый. — Ростов-н/Д: Изд-во Рост. пед.ун-та, 1997. — С.143-156.
См.подробнее:
- Беляев В.И. «Универсальная арифметика» Леонарда Эйлера — прототип учебников элементарной алгебры // Из опыта преподавания математики в VIII-X классах средней школы / под ред. П.В. Стратилатова. -М.: Учпедгиз, 1955. C.130-142.
- Бусев В.М. «Руководство к арифметике» Леонарда Эйлера // Математика, №6, 2007. C.25-30.
- Хармац А.Г. Создание Л.Эйлером учебника арифметики нового типа с повышенной в нем ролью теории // Ученые записки МОПИ. Т.202. Вып.6. -М., 1968. C.373-377.
- Эйлер Л. Руководство к Арифметике для употребления гимназии при Императорской Академии наук. — СПб, 1740.
- Эйлер Л. Универсальная Арифметика. Том первый, содержащий в себе все образы алгебраического вычисления. — СПб, 1768.
libcats.org
Главная →
Руководство к арифметике для употребления гимназии Императорской Академии наук
Руководство к арифметике для употребления гимназии Императорской Академии наук
Эйлер Л.
Скачать книгу бесплатно (djvu, 5.97 Mb)
Читать «Руководство к арифметике для употребления гимназии Императорской Академии наук»
Популярные книги за неделю:
#1
Ф.И.Бурдейный, Н.В.Казанский. Карманный справочник радиолюбителя-коротковолновика (1959, DjVu)
440 Kb
#2
Я.Войцеховский. Радиоэлектронные игрушки (1977, djvu)
13.76 Mb
#3
Подготовка саперов, подразделений специального назначения по разминированию
Категория: Научно-популярная литература (разное)
1.49 Mb
#4
Приспособления для ремонта автомобилей
Росс Твег
Категория: civil, civil, transport
7.37 Mb
#5
Разгаданные загадки третьего рейха. 1933-1941
Безыменский Лев
Категория: society, society, history
5.17 Mb
#6
128 советов начинающему программисту
Очков В.Ф., Пухначев Ю.В.
Категория: computers, computers, prog
8.91 Mb
#7
Английский язык в картинках
I.A. Richards; Christine M. Gibson
Категория: Иностранные языки
5.77 Mb
#8
Ограждение участка. Ограды. Заборы. Калитки. Ворота
В.И.Рыженко
Категория: Строительство
1.23 Mb
#9
Самоделки школьника
Тарасов Б.В.
Категория: science, science, technical, hobby, oddjob
41.91 Mb
#10
Наука и жизнь.Маленькие хитрости
Категория: E_Engineering, EM_Mechanics of elastic materials
3.50 Mb
Только что пользователи скачали эти книги:
#1
Ю.М.Гедзберг. Ремонт черно-белых переносных телевизоров (МРБ-1181, 1992, djvu)
4.38 Mb
#2
Психологическое сопровождение школьников
Александровская Э.М., и др.
Категория: Психология практическая
174 Kb
#3
Применение Ядерного магнитного резонанса в органической химии
Бхакка
Категория: Химия, Физико-химические методы
8.58 Mb
#4
Применение УФ ИК Ядерного магнитного резонанса и масс спектроскопии в органической химии
Казицына
Категория: Химия, Физико-химические методы
7.64 Mb
#5
Курс физической химии
Герасимов Я.И., и др.
Категория: Химия, Физическая химия
5.21 Mb
#6
Хромато-масс-спектрометрия (Методы аналитической химии)
Хмельницкий
Категория: Химия, Хроматография
12.74 Mb
#7
Методы вычислительной математики
Марчук Г.И.
Категория: science, science, exact
2.09 Mb
#8
Английский язык в картинках
I.A. Richards; Christine M. Gibson
Категория: Иностранные языки
5.77 Mb
#9
Домоводство, 1959 г
Категория: info, guide, , hobby, , hobby
16.00 Mb
#10
Сборник самостоятельных работ «Найди ошибку!», 6 класс
Татьяна Васильевна Шклярова
Категория: info, teach, science, human, society, lang
929 Kb
Эйлер, Леонард — Руководство к арифметике : Для употребления Гимназии при Императорской Академии наук
Карточка
Эйлер, Леонард (1707-1783).
Руководство к арифметике : Для употребления Гимназии при Императорской Академии наук / Переведено с немецкаго языка чрез Василья Адодурова Академии наук адъюнкта. — Санктпетербург : [Тип. Акад. наук], [1752]-1760. — 8°.
На тит. л. ч.2: Переведено с немецкаго языка Академии наук студентом Васильем Кузнецовым
На тит. л. ч.1: 1740
Ч.1 напеч. на бумаге фабрики Гончаровых с водяными знаками, относящимися к 1736-1760 гг. Она была издана не в 1740 г., как указано на тит. л., а в 1752 г. В нояб. 1750 г., в ответ на рапорт комиссара Акад. наук С.В. Зборомирского о кн., оставшихся в небольшом количестве для продажи в Акад. кн. лавке, Канцелярия Акад. наук приняла решение о напечатании в числе других кн. двух частей «Руководства к арифметике». В нояб. 1752 г. весь тираж ч.1 передан в Акад. кн. лавку.
4 дек. 1750 г. состоялось распоряжение о напеч. ч.2 тиражом 625 экз. Однако ч.2 в рус. пер. вышла в свет лишь в 1760 г. В марте 1760 г. в Акад. кн. лавку поступил весь тираж ч.2
Тираж ч.1 — 1200 экз., ч.2 — 1233 экз.
Цена каждой из частей 30 к.
Пер. ч.2. «Руководства» был сделан В. Кузнецовым в янв.-апр. 1750 г. и испр. Н.И. Поповым
Описание
| Автор | |
|---|---|
| Заглавие | Руководство к арифметике : Для употребления Гимназии при Императорской Академии наук |
| Дата поступления в ЭК | 01.11.2007 |
| Каталоги | Книги (изданные с 1831 г. по настоящее время) |
| Сведения об ответственности | Переведено с немецкаго языка чрез Василья Адодурова Академии наук адъюнкта |
| Выходные данные | Санктпетербург : [Тип. Акад. наук], [1752]-1760 |
| Физическое описание | 8° |
| Примечание | На тит. л. ч.2: Переведено с немецкаго языка Академии наук студентом Васильем Кузнецовым |
| На тит. л. ч.1: 1740 | |
| Ч.1 напеч. на бумаге фабрики Гончаровых с водяными знаками, относящимися к 1736-1760 гг. Она была издана не в 1740 г., как указано на тит. л., а в 1752 г. В нояб. 1750 г., в ответ на рапорт комиссара Акад. наук С.В. Зборомирского о кн., оставшихся в небольшом количестве для продажи в Акад. кн. лавке, Канцелярия Акад. наук приняла решение о напечатании в числе других кн. двух частей «Руководства к арифметике». В нояб. 1752 г. весь тираж ч.1 передан в Акад. кн. лавку. | |
| 4 дек. 1750 г. состоялось распоряжение о напеч. ч.2 тиражом 625 экз. Однако ч.2 в рус. пер. вышла в свет лишь в 1760 г. В марте 1760 г. в Акад. кн. лавку поступил весь тираж ч.2 | |
| Тираж ч.1 — 1200 экз., ч.2 — 1233 экз. | |
| Цена каждой из частей 30 к. | |
| Пер. ч.2. «Руководства» был сделан В. Кузнецовым в янв.-апр. 1750 г. и испр. Н.И. Поповым | |
| Язык | Русский |
Состав
Эйлер, Леонард (1707-1783).
Руководство к арифметике : Для употребления Гимназии при Императорской Академии наук / Переведено с немецкаго языка чрез Василья Адодурова Академии наук адъюнкта. — Санктпетербург : [Тип. Акад. наук], [1752]-1760. — 8°.
[Ч.1] [Текст]. — 1740. — 312 c.
ещё
Эйлер, Леонард (1707-1783).
Руководство к арифметике : Для употребления Гимназии при Императорской Академии наук / Переведено с немецкаго языка чрез Василья Адодурова Академии наук адъюнкта. — Санктпетербург : [Тип. Акад. наук], [1752]-1760. — 8°.
Ч.2 [Текст]. — 1760. — 312 c.
ещё
Л. Эйлер
| Леонард Эйлер | |
| Leonhard Euler | |
 Портрет 1756 года, выполненный Эмануэлем Хандманном |
|
| Дата рождения: |
4 (15) апреля 1707 |
|---|---|
| Место рождения: |
Базель, Швейцария |
| Дата смерти: |
7 (18) сентября 1783 |
| Место смерти: |
Санкт-Петербург, Россия |
| Гражданство: |
Швейцария |
| Научная сфера: |
Математика, Механика, Физика, Астрономия |
| Альма-матер: |
Базельский университет |
| Научный руководитель: |
Иоганн Бернулли |
Леона́рд Э́йлер (нем. Leonhard Euler; 4 (15) апреля 1707, Базель — 7 (18) сентября 1783, Санкт-Петербург) — выдающийся математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
Эйлер — автор более чем 800 работ[L 1] по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Многие его работы оказали значительное влияние на развитие науки.
Почти полжизни провёл в России, где внёс существенный вклад в становление отечественной науки. В 1726 году он был приглашён работать в Санкт-Петербург. В 1731—1741 и, начиная с 1766 года, был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь почётным членом Петербургской Академии). Хорошо знал русский язык, и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С. К. Котельников), и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.[L 2]
Содержание
- 1 Биография
- 1.1 Швейцария (1707—1727)
- 1.2 Первый приезд в Россию (1727—1741)
- 1.3 Пруссия (1741—1766)
- 1.4 Снова Россия (1766—1783)
- 1.5 Интересные факты
- 1.6 Оценки
- 1.7 Адреса в Санкт-Петербурге
- 2 Вклад в науку
- 2.1 Теория чисел
- 2.2 Математический анализ
- 2.3 Геометрия
- 2.4 Комбинаторика
- 2.5 Другие области математики
- 2.6 Механика и математическая физика
- 2.7 Астрономия
- 2.8 Инженерное дело
- 3 Память
- 3.1 Олимпиады
- 4 Примечания
- 5 Литература
- 6 См. также
- 7 Ссылки
- 7.1 Труды Эйлера в Интернете
Биография
Швейцария (1707—1727)
Леонард Эйлер родился в 1707 году в семье базельского пастора, друга семьи Бернулли. Рано обнаружил математические способности. Начальное обучение получил дома под руководством отца, учившегося некогда математике у Якоба Бернулли. Пастор готовил старшего сына к духовной карьере, однако занимался с ним и математикой — как в качестве развлечения, так и для развития логического мышления. Одновременно с обучением в гимназии мальчик увлечённо занимался математикой под руководством Якоба Бернулли, а в последние гимназические годы посещал университетские лекции младшего брата Якоба, Иоганна Бернулли.
Базельский университет в XVII—XVIII веках
20 октября 1720 года 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета. Но любовь к математике направила Леонарда по иному пути. Вскоре способный мальчик обратил на себя внимание профессора Иоганна Бернулли. Он передал одарённому студенту математические статьи для изучения, а по субботам пригласил приходить к нему домой, чтобы совместно разбирать непонятное. В доме своего учителя Эйлер познакомился и подружился с сыновьями Бернулли — Даниилом и Николаем, также увлечённо занимавшимися математикой.
8 июня 1724 года 17-летний Леонард Эйлер произнёс на латыни речь о сравнении философских воззрений Декарта и Ньютона и был удостоен учёной степени магистра.
Швейцарская банкнота с портретом молодого Эйлера
В последующие два года юный Эйлер написал несколько научных работ. Одна из них, «Диссертация по физике о звуке», получившая благоприятный отзыв, была представлена на конкурс для замещения неожиданно освободившейся в Базельском университете должности профессора физики (1725). Но, несмотря на положительный отзыв, 19-летнего Эйлера сочли слишком юным, чтобы включить в число кандидатов на профессорскую кафедру.
Надо отметить, что число научных вакансий в Швейцарии было совсем невелико. Поэтому братья Даниил и Николай Бернулли уехали в далёкую Россию, где как раз шла организация Академии наук; они обещали похлопотать там и о месте для Эйлера.
В начале зимы 1726 года Эйлеру сообщили из Санкт-Петербурга: по рекомендации братьев Бернулли он приглашён на должность адъюнкта по физиологии с окладом 200 рублей.[L 3] Получение аванса для компенсации проездных расходов растянулось почти на год, и лишь 5 апреля 1727 года Эйлер навсегда покинул родную Швейцарию.
Первый приезд в Россию (1727—1741)
22 января 1724 года Пётр I утвердил проект устройства Петербургской Академии. 28 января вышел указ сената о создании Академии. Из 22 профессоров и адъюнктов, приглашённых в первые годы, оказалось 8 математиков, которые занимались также механикой, физикой, астрономией, картографией, теорией кораблестроения, службой мер и весов.
Одной из важнейших задач Академии стала подготовка отечественных кадров. Позднее при Академии были созданы университет и гимназия. В силу острой нехватки учебников на русском языке Академия обратилась к своим членам с просьбой составить такие руководства. Эйлер, хотя и числился физиологом, составил на немецком языке очень добротное «Руководство к арифметике», которое тут же было переведено на русский и служило не один год в качестве начального учебника. Перевод первой части выполнил в 1740 году первый русский адъюнкт Академии, ученик Эйлера Василий Адодуров. Это было первое систематическое изложение арифметики на русском языке. Ко всеобщему удивлению, Эйлер уже в следующем по приезде году стал бегло говорить по-русски.[L 4]
В 1730 году, когда на русский престол вступила Анна Иоанновна, интерес к Академии упал. За годы своего правления императрица посетила Академию всего лишь один раз.[L 5] Часть приглашённых профессоров стала возвращаться на родину. Освободившееся место профессора физики было предложено Эйлеру (1731), одновременно он получил увеличение оклада до 400 рублей. Ещё через два года Даниил Бернулли вернулся в Швейцарию, и Эйлер занял его кафедру, став академиком и профессором чистой математики с окладом 600 рублей (впрочем, Даниил Бернулли получал вдвое больше). Николай Бернулли, талантливый математик, скоропостижно умер от болезни вскоре после приезда в Россию, в 1726 году.
В один из последних дней 1733 года 26-летний Леонард Эйлер женился на своей ровеснице, дочери живописца (петербургского швейцарца) Катарине Гзель (нем. Katharina Gsell). Молодожёны приобрели дом на набережной Невы, где и поселились. В семье Эйлера родились 13 детей, но выжили 3 сына и 2 дочери.[1]
Эйлер отличался феноменальной работоспособностью. По отзывам современников, для него жить означало заниматься математикой. А работы у молодого профессора было много: картография, всевозможные экспертизы, консультации для кораблестроителей и артиллеристов, составление учебных руководств, проектирование пожарных насосов и т. д. От него даже требуют составления гороскопов, каковой заказ Эйлер со всем возможным тактом переадресовал штатному астроному. Но всё это не мешает ему активно проводить собственные исследования.
За первый период пребывания в России он написал более 90 крупных научных работ. Значительная часть академических «Записок» заполнена трудами Эйлера. Он делал доклады на научных семинарах, читал публичные лекции, участвовал в выполнении различных технических заказов правительственных ведомств.
В 1735 году Академия получила задание выполнить срочное и очень громоздкое астрономическое (по другим данным, картографическое) вычисление. Группа академиков просила на эту работу три месяца, а Эйлер взялся выполнить работу за 3 дня — и справился самостоятельно. Однако перенапряжение не прошло бесследно: он заболел и потерял зрение на правый глаз. Однако учёный отнёсся к несчастью с величайшим спокойствием: «Теперь я меньше буду отвлекаться от занятий математикой», — философски заметил он.
В 1730-е годы Эйлер становится известен и в Европе. Двухтомное сочинение «Механика, или наука о движении, в аналитическом изложении», изданное в 1736 году, принесло ему мировую славу. В этой монографии Эйлер блестяще применил методы математического анализа к решению проблем движения в пустоте и в сопротивляющейся среде. «Тот, кто имеет достаточные навыки в анализе, сможет всё увидеть с необычайной лёгкостью и без всякой помощи прочитает работу полностью», — заканчивает Эйлер своё предисловие к книге. Начиная с этого момента, теоретическая механика становится прикладной частью математики.
Обстоятельства ухудшились, когда в 1740 году умерла императрица Анна Иоанновна, и царём был объявлен малолетний Иоанн VI. «Предвиделось нечто опасное, — писал позднее Эйлер в автобиографии. — После кончины достославной императрицы Анны при последовавшем тогда регентстве… положение начало представляться неуверенным». В самом деле, в регентство Анны Леопольдовны Петербургская Академия окончательно приходит в запустение. Эйлер обдумывает возврат на родину. В конце концов он принимает предложение прусского короля Фридриха, который приглашал его в Берлинскую Академию на весьма выгодных условиях, на должность директора её Математического департамента. Академия создавалась на базе прусского Королевского общества, основанного ещё Лейбницем, но в те годы находившегося в удручающем состоянии.
Пруссия (1741—1766)
Эйлер подал руководству Петербургской Академии прошение об отставке[L 6]:
Того ради нахожусь принужден, как ради слабого здоровья, так и других обстоятельств, искать приятнейшего климата и принять от его Королевского Величества Прусского учиненное мне призывание. Того ради прошу Императорскую Академию наук всеподданнейше меня милостиво уволить и снабдить для моего и домашних моих проезду потребным пашпортом.
Академия не стала возражать. Эйлер был «отпущен от Академии» в 1741 году и утверждён почётным академиком с окладом 200 рублей. Взамен он обещал по мере своих сил помогать Петербургской Академии — и действительно, все проведённые в Пруссии годы добросовестно участвовал в публикациях Академии, редактировал математические отделы русских журналов, приобретал для Петербурга книги и инструменты. На квартире Эйлера, на полном пансионе (оплату которого, кстати, канцелярия Академии присылала с большим опозданием), годами жили молодые русские учёные, командированные на стажировку. Известно об оживлённой переписке Эйлера с Ломоносовым, в творчестве которого он высоко ценил «счастливое сочетание теории с экспериментом». В 1747 году он дал благоприятный отзыв о статьях Ломоносова по физике и химии, утверждая:[2]
Все сии сочинения не токмо хороши, но превосходны, ибо он [Ломоносов] изъясняет физические и химические материи самые нужные и трудные, кои совсем неизвестны и невозможны были к истолкованию самым остроумным ученым людям, с таким основательством, что я совсем уверен в справедливости его изъяснений. При сем я должен отдать справедливость г-ну Ломоносову, что он одарован самым счастливым остроумием для объяснения явлений физических и химических.
Этой высокой оценке не помешало даже то, что Ломоносов математических работ не писал и высшей математикой не владел.[3]
Леонард Эйлер, портрет (1753), выполненный Эмануэлем Хандманном (Kunstmuseum, г. Базель)
В июне 1741 года Леонард Эйлер с женой, двумя сыновьями и четырьмя племянниками прибыл в Берлин. Он провёл тут 25 лет и издал около 260 работ.
Первое время Эйлера встречают в Берлине доброжелательно. Его приглашают даже на придворные балы, хотя вряд ли это мероприятие его особенно привлекало.
Король постоянно в отлучке из-за непрерывных войн, но работы у Эйлера немало. Помимо математики, он занимается многими практическими делами, включая даже лотереи, чеканку монет, прокладку нового водопровода и организацию пенсионного обеспечения.
В 1742 году вышло четырёхтомное собрание сочинений Иоганна Бернулли. Посылая его из Базеля Эйлеру в Берлин, старый учёный писал своему ученику: «Я посвятил себя детству высшей математики. Ты, мой друг, продолжишь её становление в зрелости».
Эйлер оправдал надежды своего учителя. Одна за другой выходят его работы огромной важности для науки: «Введение в анализ бесконечно малых» (1748), «Морская наука» (1749), «Теория движения Луны» (1753), «Наставление по дифференциальному исчислению» (лат. Institutiones calculi differentialis, 1755). Многочисленные статьи по отдельным вопросам печатаются в изданиях Берлинской и Петербургской Академий. В 1744 году Эйлер открывает вариационное исчисление. В его работах используются хорошо продуманная терминология и математическая символика, в значительной степени сохранившиеся до наших дней, изложение доводится до уровня практических алгоритмов. Вскоре Эйлер избирается членом четырёх ведущих Академий наук.
В 1753 году Эйлер купил поместье в Шарлоттенбурге (пригород Берлина) с садом и участком. Мать известила Эйлера о смерти в Швейцарии его отца; вскоре она переехала к Эйлеру.
Огромную популярность приобрели в XVIII веке, а отчасти и в XIX-м, эйлеровские «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе…», которые выдержали свыше 40 изданий на 10 языках (в том числе 4 издания на русском). Это научно-популярная энциклопедия широкого охвата, написанная ярко и общедоступно.
Работоспособность Эйлера до конца жизни оставалась исключительной. Он «выдавал» в среднем 800 страниц «ин-кварто» (страница размером в ¼ от бумажного листа) в год. Это немало даже для сочинителя романов; для математика же такой объём научных трудов можно считать рекордным.
Всемирная слава не вскружила голову Эйлеру. По отзывам современников, он всю жизнь оставался скромным, жизнерадостным, чрезвычайно отзывчивым человеком, всегда готовым помочь другому. Однако отношения с королём не складываются: Фридрих находит нового математика невыносимо скучным, совершенно не светским, и обращается с ним пренебрежительно.
В 1759 году: умер Мопертюи, президент Берлинской Академии наук. Пост президента Академии король Фридрих II предложил Даламберу, но тот отказался. Фридрих, недолюбливавший Эйлера, всё же поручил ему руководство Академией, однако без титула президента.
Во время Семилетней войны русская артиллерия разрушила дом Эйлера; узнав об этом, фельдмаршал Салтыков немедленно возместил потери, а позже императрица Елизавета прислала от себя ещё 4000 рублей.[L 7]
1765: новый шедевр Эйлера, «Теория движения твёрдых тел». В 1766 году опубликованы «Элементы вариационного исчисления». Именно здесь впервые появилось название нового раздела математики, созданного Эйлером и Лагранжем.
С начала 1760-х годов Эйлер, всё более третируемый королём, взвешивал перспективу переезда в Лондон. Однако вскоре его планы изменились. В 1762 году на русский престол вступила Екатерина II, которая осуществляла политику просвещённого абсолютизма. Хорошо понимая значение науки как для прогресса государства, так и для собственного престижа, она провела ряд важных, благоприятных для науки, преобразований в системе народного просвещения и культуры. Императрица предложила Эйлеру управление математическим классом (отделением), звание конференц-секретаря Академии и оклад 1800 рублей в год. «А если не понравится, — говорилось в письме её представителю, — благоволит сообщить свои условия, лишь бы не медлил приездом в Петербург».
Эйлер действительно запросил больше:
- оклад 3000 рублей в год и пост вице-президента Академии;
- ежегодная пенсия 1000 рублей супруге после его смерти;
- оплачиваемые должности для троих его сыновей, в том числе пост секретаря Академии для старшего.
Все эти условия были приняты. В письме от 6 января 1766 года Екатерина пишет канцлеру графу Воронцову[L 8]:
Письмо к Вам г. Эйлера доставило мне большое удовольствие, потому что я узнаю из него о желании его снова вступить в мою службу. Конечно, я нахожу его совершенно достойным желаемого звания вице-президента Академии наук, но для этого следует принять некоторые меры, прежде чем я установлю это звание — говорю установлю, так как доныне его не существовало. При настоящем положении дел там нет денег на жалование в 3000 рублей, но для человека с такими достоинствами, как г. Эйлер, я добавлю к академическому жалованию из государственных доходов, что вместе составит требуемые 3000 рублей… Я уверена, что моя Академия возродится из пепла от такого важного приобретения, и заранее поздравляю себя с тем, что возвратила России великого человека.
Мемориальная доска на доме Эйлера в Берлине
Эйлер подал королю прошение об увольнении со службы, но никакого ответа не получил. Подал повторно — но Фридрих не желал даже обсуждать вопрос о его отъезде. В ответ на это Эйлер прекратил работать для Берлинской Академии.
Решающую поддержку Эйлеру оказали настойчивые ходатайства российского представительства от имени императрицы. 30 апреля 1766 года Фридрих наконец-то разрешил великому учёному покинуть Пруссию, отпустив вдогонку (в письмах того периода) несколько злобных острот. Правда, Кристофа (Christoph), младшего сына Эйлера, служившего подполковником артиллерии (нем. Oberstleutnant), король наотрез отказался отпустить из армии. Позднее благодаря заступничеству Екатерины II он всё же смог присоединиться к отцу; в русской армии он дослужился до генерал-лейтенанта.[L 9]
Эйлер возвращается в Россию, теперь уже навсегда.
Снова Россия (1766—1783)
Здание Петербургской Академии наук во второй половине XVIII века (Кунсткамера)
В июле 1766 года 60-летний Эйлер, его семья и домочадцы (всего 18 человек) прибыли в российскую столицу. Сразу же по прибытии он был принят императрицей. Екатерина, теперь уже Вторая, встретила его как августейшую особу и осыпала милостями: пожаловала 8000 рублей на покупку дома на Васильевском острове и на приобретение обстановки, предоставила на первое время одного из своих поваров и поручила подготовить соображения о реорганизации Академии.
К несчастью, после возвращения в Петербург у Эйлера образовалась катаракта второго, левого глаза — он перестал видеть. Вероятно, по этой причине обещанный пост вице-президента Академии он так и не получил. Однако слепота не отразилась на его работоспособности. Эйлер диктовал свои труды мальчику-портному, который всё записывал по-немецки. Число опубликованных им работ даже возросло; за полтора десятка лет второго пребывания в России он продиктовал более 400 статей и 10 книг.
1767—1770: работа над двухтомной классической монографией «Универсальное арифметика» (издавалась также под названиями «Начала алгебры» и «Полный курс алгебры»). На русском языке этот замечательный труд выходит сразу же (первый том: 1768), на немецком — два года спустя. Книга была переведена на многие языки и переиздавалась около 30 раз (трижды — на русском). Все последующие учебники алгебры создавались под сильнейшим влиянием книги Эйлера.
В эти же годы выходит трёхтомник «Оптика» (лат. Dioptrica, 1769—1771) и фундаментальное «Интегральное исчисление» (лат. Institutiones calculi integralis), тоже в 3 томах.
В 1771 году в жизни Эйлера произошли два серьёзных события. В мае в Петербурге случился большой пожар, уничтоживший сотни зданий, в том числе дом и почти всё имущество Эйлера. Самого учёного с трудом спасли. Все рукописи удалось уберечь от огня; сгорела лишь часть «Новой теории движения луны», но она быстро была восстановлена с помощью самого Эйлера, сохранившего до глубокой старости феноменальную память. Эйлеру пришлось временно переселиться в другой дом.
В сентябре того же года, по особому приглашению императрицы, в Санкт-Петербург прибыл для лечения Эйлера известный немецкий окулист барон Вентцель. После осмотра он согласился сделать Эйлеру операцию и удалил с левого глаза катаракту. Эйлер снова стал видеть. Врач предписал беречь глаз от яркого света, не писать, не читать — лишь постепенно привыкать к новому состоянию. Однако уже через несколько дней после операции Эйлер снял повязку, и вскоре потерял зрение снова. На этот раз — окончательно.
1772: «Новая теория движения Луны». Эйлер наконец завершил свой многолетний труд, приближённо решив задачу трёх тел.
В 1773 году по рекомендации Даниила Бернулли в Петербург приехал из Базеля ученик Бернулли, Никлаус Фусс. Это было большой удачей для Эйлера. Фусс обладал редким сочетанием математического таланта и умения вести практические дела, что и дало ему возможность сразу же после приезда взять на себя заботы о математических трудах Эйлера. Вскоре Фусс женился на внучке Эйлера. В последующие десять лет — до самой своей смерти — Эйлер преимущественно ему диктовал свои труды, хотя иногда пользовался «глазами старшего сына» и других своих учеников.
В 1773 году умерла жена Эйлера, с которой он прожил почти 40 лет; у них было три сына (младший сын Христофор впоследствии был генерал-лейтенантом российской армии и командиром Сестрорецкого оружейного завода). Это было большой потерей для учёного, искренне привязанного к семье. Вскоре Эйлер женился на её сводной сестре Саломее.
1779: выходит «Всеобщая сферическая тригонометрия», первое полное изложение всей системы сферической тригонометрии.
Надгробие Л. Эйлера, гранитный саркофаг, 1837 год
Эйлер активно трудился до последних дней. В сентябре 1783 года 76-летний учёный стал ощущать головные боли и слабость. 7 (18) сентября после обеда, проведённого в кругу семьи, беседуя с астрономом А. И. Лекселем о недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо. Эйлер успел произнести: «Я умираю», — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг.
«Эйлер перестал жить и вычислять», — сказал Кондорсе на траурном заседании Парижской Академии наук (фр. Il cessa de calculer et de vivre).
Его похоронили на Смоленском лютеранском кладбище в Петербурге. Надпись на памятнике гласила: «Здесь покоятся бренные останки мудрого, справедливого, знаменитого Леонарда Эйлера».
В 1955 году прах великого математика был перенесён в «Некрополь XVIII века» на Лазаревском кладбище Александро-Невской лавры. Плохо сохранившийся надгробный памятник при этом заменили.
Интересные факты
А. С. Пушкин приводит романтический рассказ: якобы Эйлер составил гороскоп для новорождённого Иоанна Антоновича (1740), но результат его настолько испугал, что он никому не стал его показывать, и лишь после смерти несчастного царевича рассказал о нём графу К. Г. Разумовскому. Достоверность этого исторического анекдота крайне сомнительна.[L 10]
Маркиз Кондорсе сообщает, что вскоре после переезда в Берлин Эйлера пригласили на придворный бал. На вопрос королевы-матери, отчего он так немногословен, Эйлер ответил: «Прошу меня простить, но я только что из страны, где за лишнее слово могут повесить».[L 11]
Другой рассказ Кондорсе: однажды два студента, выполняя независимо сложные астрономические вычисления, получили немного различающиеся результаты в 50-м знаке, и обратились к Эйлеру за помощью. Эйлер проделал те же вычисления в уме и указал правильный результат.[L 12]
Рассказывают, что Эйлер не любил театра, и если попадал туда, поддавшись уговорам жены, то чтобы не скучать, выполнял в уме сложные вычисления, подобрав их объём так, чтобы хватило как раз до конца представления.
В 1739 году вышла работа Эйлера «Tentamen novae theoriae musicae» по математической теории музыки. По поводу этой работы ходила шутка, что в ней слишком много музыки для математиков и слишком много математики для музыкантов.[L 13]
Оценки
По отзывам современников, по характеру Эйлер был добродушен, незлобив, практически ни с кем не ссорился. К нему неизменно тепло относился даже Иоганн Бернулли, тяжёлый характер которого испытали на себе его брат Якоб и сын Даниил. Ему требовалось для полноты жизни только одно — возможность регулярного математического творчества. В то же время он был жизнерадостен, общителен, любил музыку, философские беседы.[L 14]
Эйлер был заботливым семьянином, охотно помогал коллегам и молодёжи, щедро делился с ними своими идеями. Известен случай, когда Эйлер задержал свои публикации по вариационному исчислению, чтобы молодой и никому тогда не известный Лагранж, независимо пришедший к тем же открытиям, смог опубликовать их первым.[L 15] Лагранж всегда с восхищением относился к Эйлеру и как к математику, и как к человеку; он говорил: «Если вы действительно любите математику, читайте Эйлера».
Академик С. И. Вавилов писал: «Вместе с Петром I и Ломоносовым, Эйлер стал добрым гением нашей Академии, определившим ее славу, ее крепость, ее продуктивность».
«Читайте, читайте Эйлера, он — наш общий учитель», — любил повторять и Лаплас (фр. Lisez Euler, lisez Euler, c’est notre maître à tous.).[L 16] Труды Эйлера с большой пользой для себя изучали и «король математиков» Карл Фридрих Гаусс, и практически все знаменитые учёные XVIII—XIX веков.
Адреса в Санкт-Петербурге
С 1766 года Эйлер проживал в доходном доме по адресу: Николаевская набережная, 15 (с перерывом, вызванным сильным пожаром). В советское время улица была переименована в «Набережную лейтенанта Шмидта». На доме установлена мемориальная доска, сейчас в нём располагается средняя школа.[4]
Вклад в науку
Эйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. С точки зрения математики, XVIII век — это век Эйлера. Если до него достижения в области математики были разрознены и не всегда согласованы, то Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру».
Благодаря Эйлеру в математику вошли общая теория рядов, удивительная по красоте «формула Эйлера», операция сравнения по целому модулю, полная теория непрерывных дробей, аналитический фундамент механики, многочисленные приёмы интегрирования и решения дифференциальных уравнений, число e, обозначение i для мнимой единицы, гамма-функция с её окружением и многое другое.
По существу именно он создал несколько новых математических дисциплин — теорию чисел, вариационное исчисление, теорию комплексных функций, дифференциальную геометрию поверхностей, специальные функции. Другие области его трудов: диофантов анализ, астрономия, оптика, акустика, статистика и т. д. Познания Эйлера были энциклопедичны; кроме математики, он глубоко изучал ботанику, медицину, химию, теорию музыки, множество европейских и древних языков.
Биографы отмечают[L 17], что Эйлер был виртуозным алгоритмистом. Он неизменно старался довести свои открытия до уровня конкретных вычислительных методов.
Эйлер охотно участвовал в научных дискуссиях, из которых наибольшую известность получили[L 18]:
- Спор о струне.
- Спор с Даламбером о свойствах комплексного логарифма.
- Спор с английским оптиком Джоном Доллондом о том, возможно ли создать ахроматическую линзу.
Во всех упомянутых случаях Эйлер отстаивал правильную позицию.
Теория чисел
П. Л. Чебышёв писал: «Эйлером было положено начало всех изысканий, составляющих общую теорию чисел». Большинство математиков XVIII века занимались развитием анализа, но Эйлер пронёс увлечение древней арифметикой через всю свою жизнь. Благодаря его трудам интерес к теории чисел к концу века возродился.
Эйлер продолжил исследования Ферма, ранее высказавшего (под влиянием Диофанта) ряд разрозненных гипотез о натуральных числах. Эйлер строго доказал эти гипотезы, значительно обобщил их и объединил их в содержательную теорию чисел. Он ввёл в математику исключительно важную «функцию Эйлера» и сформулировал с её помощью «теорему Эйлера». Эйлер создал теорию сравнений и квадратичных вычетов, указав для последних критерий Эйлера.
Он опроверг гипотезу Ферма о том, что все числа вида 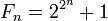
Доказал утверждение Ферма о представлении нечётного простого числа в виде суммы двух квадратов.
Эйлер доказал Великую теорему Ферма для n = 3 и n = 4, создал полную теорию непрерывных дробей, исследовал различные классы диофантовых уравнений, теорию разбиений чисел на слагаемые.
Он открыл, что в теории чисел возможно применение методов математического анализа, положив начало аналитической теории чисел. В основе её лежат тождество Эйлера и общий метод производящих функций.
Эйлер ввёл понятие первообразного корня и выдвинул гипотезу, что для любого простого числа p существует первообразный корень по модулю p; доказать это он не сумел, позднее теорему доказали Лежандр и Гаусс. Большое значение в теории имела другая гипотеза Эйлера — квадратичный закон взаимности, также доказанный Гауссом.
Математический анализ
Одна из главных заслуг Эйлера перед наукой — монография «Введение в анализ бесконечно малых» (1748). В 1755 году выходит дополненное «Дифференциальное исчисление», а в 1768—1770 годах — три тома «Интегрального исчисления». В совокупности это фундаментальный, хорошо иллюстрированный примерами курс, с продуманной терминологией и символикой, откуда многое перешло и в современные учебники.
Основание натуральных логарифмов было известно ещё со времён Непера и Якоба Бернулли, однако Эйлер дал настолько глубокое исследование этой важнейшей константы, что с тех пор она носит его имя. Другая исследованная им константа: постоянная Эйлера — Маскерони.
Первая книга по вариационному исчислению
Он делит с Лагранжем честь открытия вариационного исчисления, выписав уравнения Эйлера — Лагранжа для общей вариационной задачи. В 1744 году Эйлер опубликовал первую книгу по вариационному исчислению («Метод нахождения кривых, обладающих свойствами максимума либо минимума»).
Эйлер значительно продвинул теорию рядов и распространил её на комплексную область, получив при этом знаменитую формулу Эйлера. Большое впечатление на математический мир произвели ряды, впервые просуммированные Эйлером, в том числе не поддававшийся до него никому ряд обратных квадратов:
Современное определение показательной, логарифмической и тригонометрических функций — тоже его заслуга, так же как их символика и обобщение на комплексный случай.[L 19] Формулы, часто именуемые в учебниках «условия Коши — Римана», более правильно было бы назвать «условиями Даламбера — Эйлера».
Он первый дал систематическую теорию интегрирования и используемых там технических приёмов, нашёл важные классы интегрируемых дифференциальных уравнений. Он открыл эйлеровы интегралы — ценные классы специальных функций, возникающие при интегрировании: бета-функция и гамма-функция Эйлера. Одновременно с Клеро вывел условия интегрируемости линейных дифференциальных форм от двух или трёх переменных (1739). Первый ввёл двойные интегралы. Получил серьёзные результаты в теории эллиптических функций, в том числе первые теоремы сложения.
С более поздней точки зрения, действия Эйлера с бесконечными рядами не всегда могут считаться корректными (обоснование анализа было проведено лишь полвека спустя), но феноменальная математическая интуиция практически всегда подсказывала ему правильный результат. Впрочем, дело было не только в интуиции, Эйлер действовал здесь достаточно сознательно, во многих важных отношениях его понимание смысла расходящихся рядов и операций с ними превосходило стандартное понимание XIX века и послужило основой современной теории расходящихся рядов, развитой в конце XIX — начале XX века[L 20].
Геометрия
В элементарной геометрии Эйлер обнаружил несколько фактов, не замеченных Евклидом:
- Три высоты треугольника пересекаются в одной точке (ортоцентре).
- В треугольнике ортоцентр, центр описанной окружности и центр тяжести лежат на одной прямой — «прямой Эйлера».
- Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности (окружности Эйлера).
- Число вершин (В), граней (Г) и рёбер (Р) у любого выпуклого многогранника связаны простой формулой: В + Г = Р + 2.
Второй том «Введения в анализ бесконечно малых» (1748) — это первый в мире учебник по аналитической геометрии и основам дифференциальной геометрии. Термин аффинные преобразования впервые введён в этой книге вместе с теорией таких преобразований.
В 1760 году вышли фундаментальные «Исследования о кривизне поверхностей». Эйлер обнаружил, что в каждой точке гладкой поверхности имеются два нормальных сечения с минимальным и максимальным радиусами кривизны, и плоскости их взаимно перпендикулярны. Вывел формулу связи кривизны сечения поверхности с главными кривизнами.
1771 год: опубликовано сочинение «О телах, поверхность которых можно развернуть на плоскость». В этой работе введено понятие развёртывающейся поверхности, то есть поверхности, которая может быть наложена на плоскость без складок и разрывов. Эйлер, однако, даёт здесь вполне общую теорию метрики, от которой зависит вся внутренняя геометрия поверхности. Позже исследование метрики становится у него основным инструментом теории поверхностей.
Комбинаторика
Магический квадрат Эйлера
Эйлер много внимания уделял представлению натуральных чисел в виде суммы специального вида и сформулировал ряд теорем для подсчёта числа разбиений.
Он исследовал алгоритмы построения магических квадратов методом непрерывного хода шахматного коня.
При решении комбинаторных задач он глубоко изучил свойства сочетаний и перестановок, см.: числа Эйлера I рода.
Другие области математики
- Теория графов началась с решения Эйлером задачи о семи мостах Кёнигсберга.
- Метод ломаных Эйлера, один из простейших методов приближённого решения дифференциальных уравнений, широко применяется до наших дней.
Механика и математическая физика
Множество работ Эйлера посвящены математической физике: механике, гидродинамике, акустике и др. В 1736 году вышел трактат «Механика, или наука о движении, в аналитическом изложении», знаменующий новый этап в развитии этой древней науки. 29-летний Эйлер отказался от традиционного геометрического подхода к механике и подвёл под неё строгий аналитический фундамент. По существу, с этого момента механика становится прикладной математической дисциплиной.
В 1755 году публикуются «Общие принципы движения жидкостей», в которых положено начало теоретической гидродинамике. Выведены основные уравнения гидродинамики (уравнение Эйлера) для жидкости без вязкости. Разобраны решения системы для разных частных случаев.
В 1765 году в книге «Теория движения твёрдых тел» Эйлер математически описал кинематику твёрдого тела конечных размеров (до него исследовалось в основном движение точки). Он ввёл в математику углы Эйлера и теорему вращения. Его имя также носят кинематическая формула распределения скоростей в твёрдом теле, уравнения (Эйлера — Пуассона) динамики твёрдого тела, важный случай интегрируемости в динамике твёрдого тела.
Эйлер обобщил принцип наименьшего действия, довольно путано изложенный Мопертюи, и указал на его основополагающее значение в механике. К сожалению, он не раскрыл вариационный характер этого принципа, но всё же привлёк к нему внимание физиков, которые позднее выяснили его фундаментальную роль в природе.
Астрономия
Эйлер много работал в области небесной механики. Он заложил основу теории возмущений, позднее завершённой Лапласом, и разработал очень точную теорию движения Луны. Эта теория оказалась пригодной для решения насущной задачи определения долготы на море, и английское Адмиралтейство выплатило за неё Эйлеру специальную премию.
Основные труды Эйлера в этой области:
- «Теория движения Луны», 1753.
- «Теория движения планет и комет» (лат. Theoria motus planetarum et cometarum), 1774.
- «Новая теория движения Луны», 1772.
Эйлер исследовал поле тяготения не только сферических, но и эллипсоидальных тел, что представляло собой существенный шаг вперёд.[L 13]
Инженерное дело
В 1757 году Эйлер впервые в истории нашёл формулы для определения критической нагрузки при сжатии упругого стержня. Однако в те годы эти формулы не могли найти практического применения.
Почти сто лет спустя, когда во многих странах — и прежде всего в Англии — стали строить железные дороги, потребовалось рассчитать прочность железнодорожных мостов. Модель Эйлера принесла практическую пользу в проведении экспериментов.
Память
В честь Эйлера названы:
- кратер Euler на Луне.
- астероид 2002 Эйлер.
- Международный математический институт им. Леонарда Эйлера Российской Академии наук, основанный в 1988 году в Петербурге.
- Благотворительный фонд поддержки отечественных учёных.[5]
- Медаль (англ. Euler Medal), с 1993 года ежегодно присуждаемая канадским Институтом комбинаторики и её приложений (англ. Institute of Combinatorics and its Applications) за достижения в этой области математики.
- Множество понятий в математике и других науках, см.: список объектов, названных в честь Леонарда Эйлера.
Полное собрание сочинений Эйлера, издаваемое с 1909 года Швейцарским обществом естествоиспытателей, до сих пор не завершено; планируется выпуск 75 томов, из них вышло 72. 8 дополнительных томов будут посвящены научной переписке Эйлера (свыше 3000 писем[L 21]).
В 1907 году российские и многие другие учёные отметили 200-летие великого математика. В канун его 300-летия (2007) в Петербурге состоялся международный юбилейный форум и был снят кинофильм о жизни Эйлера.[6] Центробанк РФ выпустил памятную монету[7] в ознаменование этого события. Портрет Эйлера помещался на швейцарскую 10-франковую банкноту (6-я серия) и на почтовые марки Швейцарии, России и Германии.
Олимпиады
Очень многие факты в геометрии, алгебре и комбинаторике, доказанные Эйлером, повсеместно используются в олимпиадной математике.
15 апреля 2007 года была проведена интернет-олимпиада для школьников по математике, посвящённая 300-летию со дня рождения Леонарда Эйлера, происходившая при поддержке ряда организаций.[8] В декабре 2008 — марте 2009 года проводится математическая олимпиада имени Леонарда Эйлера для восьмиклассников, призванная отчасти заменить им утрату регионального и заключительного этапов Всероссийской математической олимпиады для 8 классов.[9]
Примечания
- ↑ Nicolas Fuss. Eulogy of Euler by Fuss (англ.). — Read at the Imperial Academy of Sciences of Saint Petersburg 23 October 1783. Проверено 22 октября 2008.
- ↑ Леонард Эйлер. Проверено 22 октября 2008.
- ↑ Владимир Захаров. «Олигархам выгодно, чтобы население России уменьшилось». Известия-Наука (12 сентября 2003). — Ломоносов — это трагическая фигура в науке. Проверено 22 октября 2008.
- ↑ См.: Дом Л. Эйлера (А. Гитшова) (наб. Лейтенанта Шмидта, 15). Энциклопедия Санкт-Петербурга. Проверено 22 октября 2008.
- ↑ См.: Игорь Макаров. Инвестиции в «чистую науку» // Санкт-Петербургский университет : журнал. — 7 марта 2006. — № 4 (3726).
- ↑ См.: Жители Санкт-Петербурга первыми увидели кинокартину «Об Эйлере». Радиостанция «Голос России» (18 апреля 2007). Проверено 22 октября 2008.
- ↑ 300-летие со дня рождения Л. Эйлера. Серия: Выдающиеся личности России. Центральный банк Российской Федерации (2 апреля 2007). Проверено 22 октября 2008.
- ↑ Интернет-олимпиада для школьников, посвящённая 300-летию со дня рождения Леонарда Эйлера.
- ↑ Олимпиада им. Леонарда Эйлера.
- Использованная литература
- ↑ Математика XVIII столетия. Указ. соч. — С. 32.
- ↑ Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — С. 232.
- ↑ Гиндикин С. Г. Рассказы о физиках и математиках. Указ. соч. — С. 220.
- ↑ Яковлев А. Я. Леонард Эйлер. — М.: Просвещение, 1983.
- ↑ Гиндикин С. Г. Рассказы о физиках и математиках. Указ. соч. — С. 218.
- ↑ Гиндикин С. Г. Рассказы о физиках и математиках. Указ. соч. — С. 225.
- ↑ Гиндикин С. Г. Рассказы о физиках и математиках. Указ. соч. — С. 230.
- ↑ Гиндикин С. Г. Рассказы о физиках и математиках. Указ. соч. — С. 231.
- ↑ К 150-летию со дня смерти Эйлера : сборник. — Изд-во АН СССР, 1933.
- ↑ А. С. Пушкин. Анекдоты, XI // Собрание сочинений Т. 6.
- ↑ Marquis de Condorcet. Eulogy of Euler. History of the Royal Academy of Sciences (1783). — Paris: 1786. — P. 37—68.
- ↑ Белл Э. Т. Указ. соч. — С. 123.
- ↑ 1 2 Стройк Д. Я. глава VII // Краткий очерк истории математики / Перевод И. Б. Погребысского. — 3-е изд. — М.: 1984.
- ↑ Литвинова Е. Ф. Эйлер // Коперник, Галилей, Кеплер, Лаплас и Эйлер, Кетле. Биографические повествования. — Челябинск, Урал: 1997 Т. 21. — С. 315. — (Библиотека Ф. Павленкова). — ISBN 5-88294-071-0
- ↑ Белл Э. Т. Указ. соч. — С. 129.
- ↑ Dunham, William. Euler: The Master of Us All. The Mathematical Association of America. — 1999. — P. xiii. — ISBN 0-88385-328-0
- ↑ Белл Э. Т. Указ. соч. — С. 117.
- ↑ Математика XVIII столетия. Указ. соч. — С. 35.
- ↑ Рыбников К. А. Том II // История математики в 2-х томах. — М.: Изд. МГУ, 1963. — С. 26—27.
- ↑ См. например Харди Г. Г. Расходящиеся ряды. Перевод с английского. Изд.2. — URSS, 2006. — С. 504.
- ↑ Рыбников К. А. Указ. соч. — С. 19.
Литература
Сочинения
- Новая теория движения Луны. Л.: Изд. АН СССР, 1934.
- Метод нахождения кривых линий, обладающих свойствами либо максимума, либо минимума. М.–Л.: ГТТИ, 1934.
- Основы динамики точки. М.–Л.: ОНТИ, 1938.
- Дифференциальное исчисление. М.–Л.: 1949.
- Интегральное исчисление. В 3 т. М.: Гостехиздат, 1956–58.
- Избранные картографические статьи. М.–Л.: Геодезиздат, 1959.
- Введение в анализ бесконечных. В 2 т. М.: Физматгиз, 1961.
- Исследования по баллистике. М.: Физматгиз, 1961.
О нём
- Артемьева Т. В. Леонард Эйлер как философ // Философия в Петербургской Академии наук XVIII века. — СПб.: 1999. — 182 с.
- Белл Э. Т. Творцы математики. — М.: Просвещение, 1979.
- Гиндикин С. Г. Рассказы о физиках и математиках. — 3-е изд., расш. — М.: МЦНМО, 2001. — 465 с. — ISBN 5-900916-83-9
- Делоне Б. Н. Леонард Эйлер // Квант. — 1974. — № 5.
- Котек В. В. Леонард Эйлер. — М.: Учпедгиз, 1961.
- К 250-летию со дня рождения Л. Эйлера : сборник. — Изд-во АН СССР, 1958.
- Летопись Российской Академии наук. Том 1. 1724-1802. — М.: Наука, 2000. — ISBN 5-02-024880-0
- Математика XVIII столетия / Под редакцией А. П. Юшкевича. — М.: Наука, 1972. — Т. 3. — (История математики в 3-х томах).
- Полякова Т. С. Леонард Эйлер и математическое образование в России. — КомКнига, 2007. — 184 с. — ISBN 978-5-484-00775-2, ISBN 5-484-00775-5
- Прудников В. Е. Русские педагоги-математики XVIII—XIX веков. — 1956.
- Юшкевич А. П. История математики в России. — М.: Наука, 1968.
См. также
- Список объектов, названных в честь Леонарда Эйлера
- История математических обозначений
Ссылки
- Леонард Эйлер. Интернет-олимпиада для школьников.
- Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Эйлер, Леонард в архиве MacTutor (англ.)
- Проект «Эйлер».
- М. Гордин. Наводя мосты: Эйлер, Кулибин и техническое знание.
Труды Эйлера в Интернете
- Книги Леонарда Эйлера в интернет-библиотеке МЦНМО.
- Книги Леонарда Эйлера в интернет-библиотеке math.ru.
- Статьи Эйлера на arXiv.org
- 830 работ Эйлера в оригинале; из них 115 доступны в англ. переводе.
Источник: Л. Эйлер
We will keep fighting for all libraries — stand with us!
Internet Archive Audio


Featured
- All Audio
- This Just In
- Grateful Dead
- Netlabels
- Old Time Radio
- 78 RPMs and Cylinder Recordings
Top
- Audio Books & Poetry
- Computers, Technology and Science
- Music, Arts & Culture
- News & Public Affairs
- Spirituality & Religion
- Podcasts
- Radio News Archive
Images


Featured
- All Images
- This Just In
- Flickr Commons
- Occupy Wall Street Flickr
- Cover Art
- USGS Maps
Top
- NASA Images
- Solar System Collection
- Ames Research Center
Software


Featured
- All Software
- This Just In
- Old School Emulation
- MS-DOS Games
- Historical Software
- Classic PC Games
- Software Library
Top
- Kodi Archive and Support File
- Vintage Software
- APK
- MS-DOS
- CD-ROM Software
- CD-ROM Software Library
- Software Sites
- Tucows Software Library
- Shareware CD-ROMs
- Software Capsules Compilation
- CD-ROM Images
- ZX Spectrum
- DOOM Level CD
Books


Featured
- All Books
- All Texts
- This Just In
- Smithsonian Libraries
- FEDLINK (US)
- Genealogy
- Lincoln Collection
Top
- American Libraries
- Canadian Libraries
- Universal Library
- Project Gutenberg
- Children’s Library
- Biodiversity Heritage Library
- Books by Language
- Additional Collections
Video


Featured
- All Video
- This Just In
- Prelinger Archives
- Democracy Now!
- Occupy Wall Street
- TV NSA Clip Library
Top
- Animation & Cartoons
- Arts & Music
- Computers & Technology
- Cultural & Academic Films
- Ephemeral Films
- Movies
- News & Public Affairs
- Spirituality & Religion
- Sports Videos
- Television
- Videogame Videos
- Vlogs
- Youth Media
Search the history of over 806 billion
web pages
on the Internet.
Search the Wayback Machine
Search icon
An illustration of a magnifying glass.
Mobile Apps
- Wayback Machine (iOS)
- Wayback Machine (Android)
Browser Extensions
- Chrome
- Firefox
- Safari
- Edge
Archive-It Subscription
- Explore the Collections
- Learn More
- Build Collections
Save Page Now
Capture a web page as it appears now for use as a trusted citation in the future.
Please enter a valid web address
- About
- Blog
- Projects
- Help
- Donate
- Contact
- Jobs
- Volunteer
- People
- About
- Blog
- Projects
- Help
-
Donate
Donate icon
An illustration of a heart shape - Contact
- Jobs
- Volunteer
- People
Универсальная арифметика
Bookreader Item Preview
Flag this item for
-
Graphic Violence
-
Explicit Sexual Content
-
Hate Speech
-
Misinformation/Disinformation
-
Marketing/Phishing/Advertising
-
Misleading/Inaccurate/Missing Metadata
texts
Универсальная арифметика
- by
- Эйлер Л.
- Publication date
-
1768
- Topics
- Математика
- Collection
- librarygenesis_open
- Contributor
- Library Genesis
- Language
- Russian
- Volume
- Т. I.
- Addeddate
- 2013-07-12 10:23:15
- External-identifier
- urn:libgen:126000/e4a68198d7b9e22bbde8ca1e4e975ba9
- Foldoutcount
- 0
- Identifier
- libgen_00126338
- Identifier-ark
- ark:/13960/t0ps05b8b
- Lg_lastmodifieddate
- 2011-06-06 23:01:23
- Ocr
- ABBYY FineReader 11.0 (Extended OCR)
- Pages
- 313
- Ppi
- 300
- Scandate
- 2009-03-30 19:43:34
plus-circle Add Review
plus-circle Add Review
comment
Reviews
There are no reviews yet. Be the first one to
write a review.
211
Views
1
Favorite
DOWNLOAD OPTIONS
download 1 file
ABBYY GZ download
download 1 file
DAISY download
For print-disabled users
download 1 file
DJVU download
download 1 file
EPUB download
download 1 file
FULL TEXT download
download 1 file
JPEG download
download 1 file
KINDLE download
download 1 file
PDF download
download 1 file
SINGLE PAGE PROCESSED JP2 ZIP download
download 1 file
TORRENT download
download 18 Files
download 11 Original
SHOW ALL
IN COLLECTIONS
Library Genesis — Open
Uploaded by
Aaron Ximm
on July 12, 2013
SIMILAR ITEMS (based on metadata)
Terms of Service (last updated 12/31/2014)