Здравствуйте на этой странице я собрала теорию и практику с примерами решения задач по предмету экономика по каждой теме, чтобы вы смогли подготовиться к экзамену или освежить память перед контрольной работой!
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Экономика
Экономика — это наука о том, каким образом люди взаимодействуют друг с другом в процессе производства и распределения того, что они потребляют.
Экономика изучает человеческое общество так же, как физика изучает мир физический. Конечно, человек – это не элементарная частица, но и его поведение подчиняется определенным законам. Законы, по которым люди взаимодействуют друг с другом, объективны и не подвластны нашему желанию, так же как ему не подвластны законы природы. Идти против законов экономики – это все равно что наступать на грабли: неприятные последствия гарантированы.
Производственная программа предприятия
Производственная программа предприятия (ППП) — основной документ, на основе которого осуществляется производственная деятельность, она определяет перечень изделий, их количество, сроки и стоимость изготовления. Основанием для формирования ПП является перспективный план продукции, разрабатываемый по результатам изучения конъюнктуры и емкости рынка, запросов покупателей, качества продукции у потенциальных конкурентов.
Планирование и учет выполнения производственной программы осуществляется в натуральном, условно-натуральном, стоимостном и трудовом выражении.
Объем производства в натуральном выражении характеризуется номенклатурой и ассортиментом выпускаемой продукции в физических единицах, соответствующих их потребительским свойствам (меры веса, длины, объема…).
Для измерения объема производства однородных изделий, различных по материалоемкости или другому признаку, применяют условно-натуральный измеритель.
Трудовой измеритель объема производства, как правило, выражается в нормо-часах, человеко-днях, станко-часах. Используется он для определения численности работников, норм выработки, размера оплаты труда, для планирования ППП различных цехов.
План производства продукции в натуральном выражении служит основой для определения объема продукции в стоимостном выражении. Стоимостные (денежные) измерители являются обобщающими, с их помощью можно определить общий объем производства предприятия. В стоимостном выражении планируются такие важные показатели ППП, как объем товарной, валовой, реализованной продукции.
Товарная продукция (ТП) — изготовленные для реализации на сторону, полностью законченные производством изделия, соответствующие стандартам и техническим условиям.
В состав товарной продукции включаются:
- стоимость готовых изделий и запасных частей к ним;
- стоимость полуфабрикатов своего производства и продукции вспомогательных цехов для реализации на сторону;
- стоимость полуфабрикатов и продукции для поставки своему капитальному строительству и непромышленным хозяйствам своего предприятия;
- стоимость нестандартного оборудования, приспособлений и т.п. общего назначения своего производства, зачисляемых в основные средства предприятия или реализуемых на сторону;
- стоимость услуг и работ промышленного характера по заказам со стороны или для непромышленных хозяйств и организаций своего предприятия, включая работы по капитальному ремонту и модернизации оборудования и транспортных средств своего предприятия.
Валовая продукция (ВП) — включает в себя весь объем работ, намеченный к выполнению или выполненных в данном плановом периоде, не зависимо от места нахождения потребителя и степени готовности продукции. Определяется объем валовой продукции по следующей формуле:
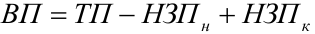
Где 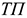
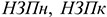
Изменение остатков незавершенного производства учитывается только на предприятиях с длительным (не менее двух месяцев) производственным циклом и на предприятиях, где незавершенное производство велико по объему и может резко изменяться во времени. В машиностроении учитывается также изменение остатков инструментов и приспособлений.
Реализованная продукция (РП) — представляет собой стоимость готовых изделий и полуфабрикатов собственного производства, а также услуг промышленного характера, подлежащих оплате в плановом периоде и предназначенных для реализации на сторону. Включая капитальный ремонт своего оборудования и транспортных средств, выполняемый силами промышленно-производственного персонала, а также стоимость реализации продукции и выполнения работ для своего капитального строительства и других непромышленных хозяйств, находящихся на балансе предприятия.
Денежные поступления, связанные с выбытием основных средств, материальных оборотных и нематериальных активов, продажная стоимость валютных ценностей, ценных бумаг не включается в состав выручки от реализации продукции, а рассматривается как доходы или убытки и учитывается при определении общей (балансовой) прибыли.
Объем реализованной продукции определяется по формуле:
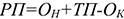
Где 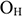
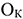
В состав остатков нереализованной продукции на начало года входят:
- готовая продукция на складе, в том числе отгруженные товары, документы по которым не переданы в банк;
- отгруженные товары, срок оплаты которых не наступил;
- отгруженные товары, не оплаченные в срок покупателем;
- товары на ответственном хранении у покупателя.
На конец года остатки нереализованной продукции принимаются в расчет только по готовой продукции на складе и отгруженным товарам, срок оплаты которых не наступил.
Объем реализованной и товарной продукции определяется: в плане — в действующих оптовых ценах предприятия; в отчете — а) в сопоставимых оптовых ценах предприятия на определенную дату; б) в оптовых ценах предприятия, действующих в отчетном периоде.
ТП, РП, и ВП характеризуют и перенесенную и вновь созданную стоимость, т. е. в них воплощены затраты и живого и овеществленного труда.
Существует еще один показатель производственной программы — это показатель чистой продукции (ЧП). ЧП характеризует лишь вновь созданную стоимость, т. е. ту, которая создана работниками данного предприятия.
При определении объема чистой продукции из стоимости товарной продукции предприятия исключают стоимость материальных затрат (сырья и материалов, покупных изделий, топлива, энергии и полуфабрикатов) и суммы амортизации основных фондов.
Для обоснования производственной программы предприятия необходимо иметь расчеты его производственной мощности.
Пример с решением задачи №1:
В отчетном периоде предприятие выпустило изделий А в количестве 200 шт., изделий Б — 300 шт. Цена изделия А 1800 руб., изделия Б — 2 580 руб.
Стоимость услуг промышленного характера, оказанных сторонним предприятиям 37 500 руб. Остаток НЭП на начало года 53 000 руб., на конец года 75 000 руб.
Наряду с основной продукцией произведена тара на сумму 12 000 руб., в том числе для отпуска на сторону на сумму 8 000 руб.
Определить: объем товарной, валовой и реализованной продукции.
Решение:
В объем товарной продукции (ТП) на данном предприятии включается стоимость выпущенных изделий (в оптовых ценах предприятия), стоимость услуг промышленного характера, оказанных сторонним предприятиям и стоимость тары, предназначенной для реализации на сторону.
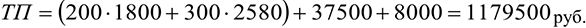
Объем валовой продукции (ВП) отличается от товарной на величину изменения незавершенного производства и стоимости тары, выпущенной для своих нужд.
Объем реализованной продукции (РП) отличается от товарной на сумму изменения остатков нереализованной продукции на складе на начало и конец года. Данной информации в условии задачи не приведено, таким образом, объем реализованной продукции будет равен объему товарной продукции.
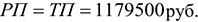
Производственная мощность предприятия
Основанием для расчета производственной программы предприятия является производственная мощность предприятия. Производственная мощность предприятия (ПМ), цеха или производственного участка характеризуется максимальным количеством продукции соответствующего качества и ассортимента, которое может быть произведено в единицу времени при полном использовании основных средств производства в оптимальных условиях эксплуатации. Производственная мощность предприятия определяется по всей номенклатуре выпускаемой им продукции. Она устанавливается в тех же единицах измерения, в каких планируется производство продукции.
Разница между производственной мощностью и производственной программой (ПП) представляет собой резервы предприятия, т.е. ПП показывает степень использования ПМ. Нормативная величина использования производственной мощности 85 %.
Производственная мощность предприятия определяется по мощности производственных единиц: цехов, участков. Производственная мощность цехов и участков определяется по мощности основного технологического оборудования. Метод расчета производственной мощности участка, цеха, предприятия во многом определяется типом производства.
Производственная мощность (ПМ) цеха или участка, оснащенного однотипным предметно-специализированным оборудованием, определяется по формуле:
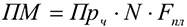
Где 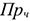
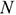
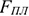
Производственная мощность цехов массового и крупносерийного производства определяется исходя из планового (эффективного) фонда времени, ритма или такта работы конвейеров:
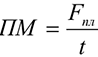
Где 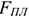
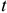
Производственная мощность предприятия или цеха при однородном оборудовании рассчитывается следующим образом:
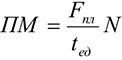
Где 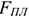
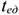
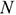
Соответствие пропускной способности ведущих цехов, участков и остальных звеньев предприятия определяется путем расчета коэффициента сопряженности мощностей предприятия 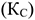
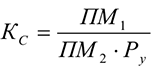
Где 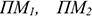
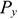
Различают несколько видов производственных мощностей предприятия: входную мощность, выходную, проектную и среднегодовую.
Под входной мощностью 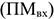
Под выходной мощностью 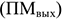
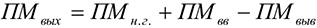
Где 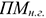
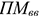
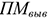
Проектная мощность — это производственная мощность, которая введена в действие но не освоена.
Среднегодовая мощность — это мощность, которой будет располагать предприятие, цех или участок в среднем за расчетный период или за год, она определяется балансовым методом:
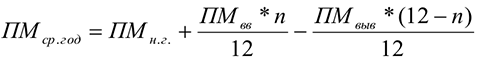
Где 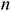
Для анализа загруженности мощности применяется коэффициент использования мощности:
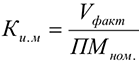
Где 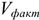
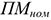
Пример с решением задачи №2:
На 1 января производственная мощность цеха составляла 11 тыс. изделий. По плану реконструкции с 1 апреля производственная мощность должна возрасти на 5 тыс. изделий, а в сентябре еще на 300 изделий. Определить выходную и среднегодовую мощности цеха.
Решение:
Под выходной понимается мощность цеха на конец года с учетом вводимых и выводимых мощностей. В данном цехе вывод мощностей не был предусмотрен, таким образом:
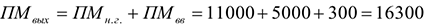
Среднегодовая мощность — это мощность, которой будет располагать предприятие, цех или участок в среднем за расчетный период или за год:
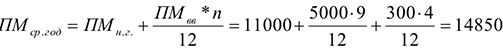
Пример с решением задачи №3:
Количество однотипных станков в цехе 100 единиц, с 1 ноября установлено еще 30 единиц, с 1 мая выбыло 6 единиц, число рабочих дней в году 258, режим работы 2-х сменный, продолжительность смены 8 ч., регламентированный процент простоев оборудования — 6%, производительность одного станка 5 деталей в час, план выпуска за год -1 700 000 деталей.
Определите производственную мощность цеха и коэффициент использования мощности.
Решение:
Производственная мощность цеха или участка, оснащенного однотипным предметно-специализированным оборудованием определяется по формуле:
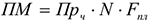
Где 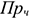
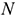
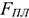
Среднее за год число работающих станков:
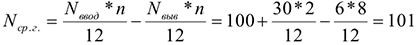
Эффективный годовой фонд времени работы одного станка:
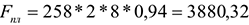
Определим производственную мощность цеха:
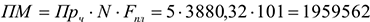
Таким образом, цех может выпустить за год 1 959 562 детали, но запланировано к производству только 1 700 000 деталей.
Коэффициент использования мощности определяем по формуле:
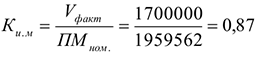
Производственные фонды предприятия
Средства производства, выраженные в стоимостной форме, представляют собой производственные фонды предприятия. Производственные фонды делятся на основные (стоимость средств труда) и оборотные (стоимость предметов труда).
Если средства производства находятся в частной собственности, они представляют основной и оборотный капитал предприятия. В условиях общественной собственности средства производства выступают в форме основных и оборотных производственных фондов.
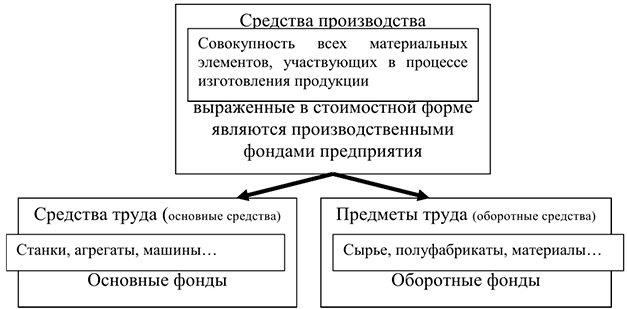
Основные средства предприятия
Основные средства предприятия (ОсС) — это средства труда, которые многократно участвуют в производственном процессе, сохраняя при этом свою натуральную форму, постепенно изнашиваясь, переносят свою стоимость по частям на вновь создаваемую продукцию.
Различают несколько видов стоимостной оценки основных средств предприятия:
- Оценка по первоначальной стоимости, т.е. по фактическим затратам, произведенным в момент создания или приобретения средств труда (включая доставку и монтаж), в ценах того года, в котором они изготовлены или приобретены.
- Оценка по восстановительной стоимости, т.е. по стоимости воспроизводства основных средств на момент переоценки. Эта стоимость показывает, во сколько обошлось бы создание или приобретение в данное время ранее созданных или приобретенных основных фондов.
- Оценка по первоначальной или восстановительной стоимости с учетом износа (остаточной стоимости), т.е. по стоимости, которая еще не перенесена на готовую продукцию. Такая оценка дает реальное представление о величине основных фондов, позволяет определить величину потерь при преждевременном списании основных фондов, при их замене или реконструкции.
Изменение стоимости основных фондов (ОсФ) предприятия непосредственно связано с износом. Орудия производства со временем изнашиваются и становятся непригодными для дальнейшей эксплуатации. Различают физический и моральный износ средств производства.
Физический износ представляет собой утрату первоначальной потребительской стоимости вследствие снашивания, ветхости, устаревания. Уровень физического износа зависит от: первоначального качества основных средств предприятия, степени их эксплуатации, уровня квалификации обслуживающего персонала и т.д.
Моральный износ ОсФ проявляется в потере экономической эффективности и целесообразности их использования до истечения срока полного физического износа.
Постепенный перенос стоимости основных средств предприятия на продукцию называется амортизацией. Различают сумму амортизации и норму амортизации. Сумма амортизационных отчислений за определенный период времени (год, квартал, месяц) представляет собой денежную величину износа основных фондов. Сумма амортизационных отчислений, накопленная к концу срока службы основных фондов, должна быть достаточной для полного их восстановления (приобретения или строительства).
Величина амортизационных отчислений определяется исходя из норм амортизации. Норма амортизации — это установленный размер амортизационных отчислений на полное восстановление, за определенный период времени, по конкретному виду основных средств, выраженный в процентах к их балансовой стоимости.
Амортизация объектов основных средств производится различными способами, различающимися скоростью амортизации.
При линейном способе ежегодная сумма амортизационных отчислений рассчитывается следующим образом:
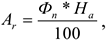
где 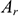
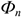
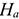
Основным показателем, предопределяющим норму амортизации, является полезный срок службы ОсФ. Норма амортизации определяется по формуле:
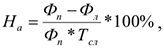
где 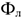
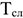
При способе уменьшаемого остатка годовая сумма амортизационных отчислений определяется исходя из остаточной стоимости объекта основных средств на начало отчетного года:
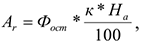
где 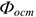
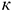
Норма амортизации рассчитывается так же как при линейном методе.
Так как остаточная стоимость ОсФ с увеличением срока их фактического использования уменьшается, то и амортизационные отчисления из года в год уменьшаются. Но при этом способе первоначальная стоимость ОсФ предприятия полностью списана не будет.
При способе списания стоимости по сумме чисел лет срока полезного использования годовую сумму амортизации рассчитывают по формуле:
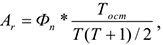
где 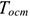
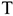
В этом случае, также как и при способе уменьшаемого остатка, в первые годы эксплуатации ОсФ, списывается большая часть их первоначальной стоимости.
При способе списания стоимости пропорционально объему продукции (работ) начисление амортизационных отчислений производится исходя из натурального показателя объема продукции (работ) в отчетном периоде и соотношения первоначальной стоимости объекта основных средств и предполагаемого объема продукции (работ) за весь срок полезного использования объекта основных средств:
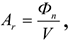
где 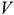
При ускоренном методе амортизации происходит увеличение размера отчислений по линейному способу, но не более чем в два раза.
Для количественной характеристики ОсФ используется их стоимость на начало года и на конец года, стоимость вводимых и ликвидируемых в течение года ОсФ. Стоимость ОсФ на конец года рассчитывается следующим образом:
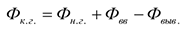
Где 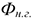
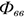
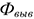
Для более детального анализа процесса воспроизводства ОсФ можно использовать следующие показатели:
1) Коэффициент обновления ОсФ:
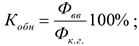
2) Коэффициент выбытия ОсФ:
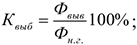
3) Коэффициент прироста ОсФ:
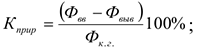
4) Коэффициент износа ОсФ:
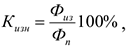
Где 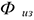
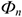
Для оценки использования основных средств предприятия применяются основные (обобщающие) и частные показатели.
Обобщающие показатели отражают конечный результат использования ОсФ. К ним относят фондоотдачу и фондоемкость, фондовооруженность труда и техническую фондовооруженность, рентабельность основных фондов предприятия.
Фондоотдача — показатель выпуска продукции на 1 рубль стоимости ОсФ. Фондоотдача рассчитывается по следующей формуле:
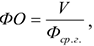
Где 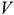
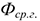
Фондоотдачу можно рассчитывать по объему валовой продукции, по объему собственной продукции и по объему чистой продукции. Последний метод расчета фондоотдачи наиболее точный, так как позволяет исключить влияние изменения стоимости покупных изделий и полуфабрикатов, материальных затрат и суммы амортизации основных фондов на фондоотдачу.
Фондоемкость — величина, обратная фондоотдаче, показывает долю стоимости ОсФ, приходящуюся на каждый рубль выпускаемой продукции:
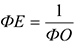
Фондовооруженность труда — показывает сколько ОсФ приходится на одного работающего:
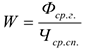
Где 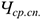
Техническая фондовооруженность показывает сколько активной части ОсФ приходится на одного работающего:
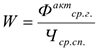
Где 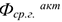
Среднегодовую стоимость ОсФ можно рассчитать следующим способом:
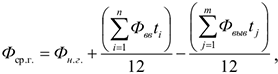
Где 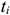
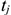
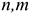
Частные показатели ОсФ характеризуют уровень использования отдельных их групп. К системе взаимосвязанных показателей характеризующих использование непосредственно активной части основных средств и производственных мощностей относятся: коэффициент экстенсивного использования оборудования, коэффициент интенсивного использования оборудования, коэффициент интегрального использования оборудования, коэффициент сменности, коэффициент загрузки оборудования.
Коэффициент экстенсивного использования оборудования, характеризует использование оборудования по времени:
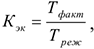
где 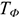
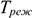
Коэффициент интенсивного использования оборудования, характеризует использование оборудования по мощности:
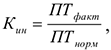
где 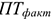
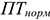
Коэффициент интегрального использования оборудования:
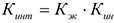
Коэффициент сменности работы оборудования:
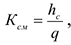
где 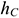
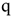
Коэффициент загрузки оборудования (коэффициент внутрисменного использования):
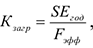
Где 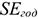
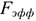
Фактическое время работы оборудования характеризуется станкоемкостью, т.е. временем выпуска всей номенклатуры деталей, обрабатываемых на станке в течении года, т.е.:
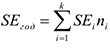
Где 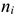
Станкоемкость измеряется в минутах, часах и может быть фактической и нормированной. Если станкоемкость выражается в нормо-часах, вводится коэффициент выполнения норм — 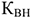
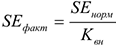
Эффективный (действительный) фонд времени определяется количеством полезно-используемого времени в течение планируемого периода. Он равен режимному фонду (2079ч.) из которого вычитается время необходимое для ремонта, модернизации, профилактики и наладки оборудования. В среднем время простоев принимается 10% от номинального годового фонда времени. Тогда, годовой эффективный фонд времени при работе в 1 смену для единицы оборудования составит 1870 часов [2079(1-0,1)].
Пример с решением задачи №4:
В базисном году объем валовой продукции предприятия составил 400 млн.руб., а материальные затраты составили 120 млн.руб., из которых 40 млн.руб. приходилось на покупные изделия и полуфабрикаты. Стоимость ОсФ предприятия 200 млн. руб.
Определить фондоотдачу по валовой, собственной и условно-чистой продукции.
Решение:
Определим фондоотдачу по валовой продукции:
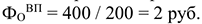
Фондоотдача по собственной продукции:
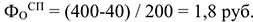
В общем виде расчет фондоотдачи по чистой продукции может быть представлен следующим образом:
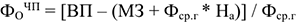
Объем условно-чистой продукции отличается от объема чистой продукции на величину амортизационных отчислений. Фондоотдача по условно-чистой продукции рассчитывается следующим образом:
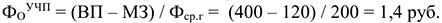
Предположим, что в отчетном году объем валовой продукции увеличился в 1,3 раза, а материальные затраты увеличились до 240 млн. руб., из которых уже 120 млн. руб. пришлись на покупные изделия и полуфабрикаты. Тогда объем валовой и собственной продукции в отчетном году составит:
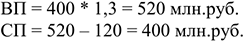
Следовательно при оставшейся на том же уровне среднегодовой стоимости ОсФ:
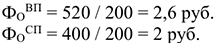
Если же рассчитать фондоотдачу по условно-чистой продукции она не изменится:
в отчетном периоде
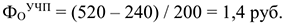
Пример с решением задачи №5:
Определить коэффициенты использования целосменного (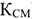
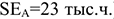
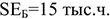
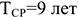
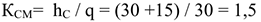
Станкоемкость годовой программы:
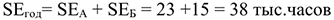
Годовой фонд времени работы единицы оборудования:
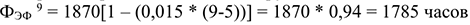
Годовой фонд времени работы парка оборудования в одну смену:
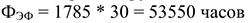
Коэффициент загрузки:
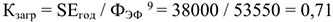
Годовой эффективный фонд времени работы при работе в 1 смену для единицы оборудования составит 1870 часов [2079(1-0,1)]: плановые простои берутся 10% от режимного времени.
Оборотные средства предприятия
Оборотные средства (ОбС) наряду с основными средствами и рабочей силой являются важнейшим элементом производства. Недостаточная обеспеченность предприятия ОбС парализует его деятельность и приводит к ухудшению его финансового положения.
Оборотные средства предприятия — денежные средства, авансированные в средства производства, однократно участвующие в производственном процессе и полностью переносящие свою стоимость на готовый продукт.
Под составом оборотных фондов (ОбФ) понимается совокупность элементов (статей), образующих оборотные средства. Структура ОбФ — это удельный вес стоимости отдельных элементов ОбФ в их общей стоимости.
Все оборотные средства предприятия можно классифицировать по трем основным признакам:
1) По месту и роли в процессе производства:
- оборотные производственные фонды, относятся к сфере производства (производственные запасы и незавершенное производство), на машиностроительных предприятиях составляют большую часть (80%) всех оборотных фондов предприятия;
- фонды обращения, обслуживают сферу обращения, наличие средств в сфере обращения поддерживает непрерывность процесса производства.
2) По источникам формирования: собственные ОбС (средства владельцев предприятия, прибыль…);
- привлеченные средства (краткосрочные кредиты банка, государственный кредит, прочие (остатки фондов, резервов, неиспользуемых по прямому назначению)).
3) По принципам организации:
- нормируемые;
- ненормируемые
Для определения потребности предприятия в ОбС осуществляется их нормирование. Под нормированием ОбС понимается процесс определения экономически обоснованной потребности предприятия в оборотных средствах, обеспечивающих нормальное протекание производственного процесса.
К нормируемым ОбС относятся производственные запасы, незавершенное производство, расходы будущих периодов, готовая продукция на складе.
Нормативы оборотных средств рассчитываются в натуральном выражении (штуки, тонны, метры …), в денежном выражении и в днях запаса. Общий норматив ОбС предприятия рассчитывается только в денежном выражении и определяется путем суммирования нормативов оборотных средств по отдельным элементам:
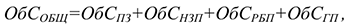
Где 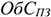
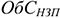
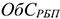
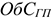
Норматив производственных запасов определяется по формуле
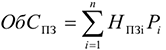
где п — количество различных видов производственных запасов;
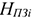
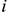
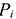
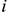
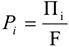
где 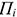
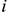
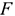
Общая норма запаса (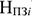
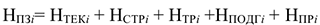
Где 
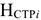
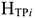
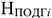
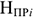
Текущий запас предназначен для обеспечения потребности производства в материальных ценностях между двумя очередными поставками.
Страховой запас, его возникновение обусловлено нарушением в поставках со стороны поставщика.
Транспортный запас определяется как превышение сроков грузооборота (время доставки товара от поставщика покупателю) над сроками документооборота.
Технологический запас — время, необходимое для подготовки материалов к производству. Создается в тех случаях, когда поступающие материальные ценности не удовлетворяют требованиям, предъявляемым технологическим процессом и до запуска в производство проходят соответствующую обработку.
Время приемки.
Норматив ОбС незавершенного производства (НЭП) отражает стоимость продукции, находящейся на разной стадии производственного процесса:
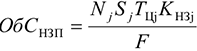
где 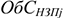
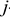
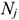
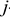
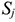
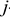
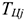
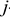
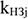
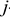
Существенное влияние на размер ОбС в НЗП оказывает коэффициент нарастания затрат на производство продукции. Коэффициент нарастания затрат характеризует степень готовности изделий и определяется отношением средней себестоимости незавершенного производства к производственной себестоимости готовой продукции. Затраты могут осуществляться равномерно и неравномерно, соответственно этому определяется и коэффициент нарастания затрат.
В случае равномерного нарастания затрат на производство коэффициент нарастания затрат рассчитывается по формуле:
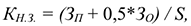
где 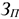
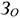
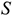
При неравномерном нарастании затрат используют следующую формулу:
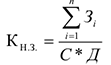
Где 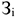
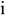
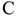
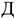
Расходы будущих периодов включают затраты, осуществленные в данном году, а погашенные, т.е. включенные в себестоимость продукции в последующие годы. Норматив оборотных средств расходов будущих периодов включает расходы будущих периодов в предстоящем году, предусмотренные соответствующими сметами за вычетом расходов, которые в планируемом году списываются на себестоимость.
Норматив оборотных средств в запасах готовой продукции на складах предприятия 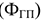
где 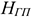
Норма запаса готовой продукции (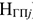
Оборотные средства всегда находятся в движении и проходят три стадии кругооборота, при этом изменяя свою форму (рисунок 1). На 1-й стадии ОбС (или денежный капитал) преобразуются в предметы труда и рабочую силу. На 2-ой стадии предметы труда при участии орудий труда и рабочей силы превращаются в незавершенное производство и по мере завершения производственного процесса в готовую продукцию. На 3-ей стадии предприятие реализует готовую продукцию, и средства, высвобождаясь из товарной формы вновь принимают денежную форму. Кругооборот считается завершенным, когда денежные средства за реализованную продукцию поступят на расчетный счет предприятия.
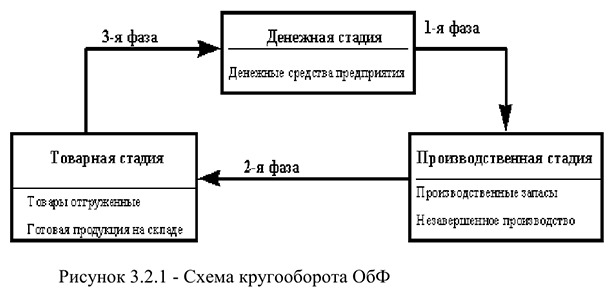
Показателями использования оборотных средств на предприятии являются коэффициент оборачиваемости оборотных средств и длительность одного оборота.
Коэффициент оборачиваемости оборотных средств показывает, сколько оборотов совершили оборотные средства за анализируемый период (квартал, полугодие, год):
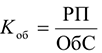
Где РП — объем реализуемой продукции за рассматриваемый период в оптовых ценах, руб.; ОбС — средний остаток всех оборотных средств за рассматриваемый период, руб.
Средний остаток оборотных средств определяется по формуле среднего хронологического.
Длительность одного оборота показывает, за какой срок к предприятию возвращаются его оборотные средства в виде выручки от реализации продукции:
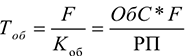
Коэффициент загрузки средств в обороте характеризует величину ОбС, приходящихся на 1 руб. реализованной продукции.
Ускорение оборачиваемости оборотных средств ведет к высвобождению оборотных средств предприятия из оборота. Напротив, замедление оборачиваемости приводит к увеличению потребности предприятия в оборотных средствах.
В результате ускорения оборачиваемости (интенсивности использования ОбС) определенная сумма ОбС высвобождается.
Абсолютное высвобождение происходит, если при постоянном объеме реализации продукции фактические остатки ОбС меньше планируемых.
Относительное высвобождение происходит при ускорении оборачиваемости ОбС с ростом объема производства. В отличие от абсолютного высвобождения высвобожденные при этом средства не могут быть изъяты из оборота без сохранения непрерывности производства.
Абсолютное высвобождение (экономия) оборотных средств определяется следующим образом
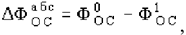
где 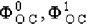
Прирост объема реализации продукции за счет ускорения оборачиваемости оборотных средств определяется по формуле:
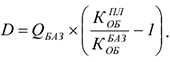
где: 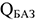
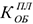
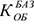
Пример с решением задачи №6:
Сумма всех затрат на производство продукции 50 тыс.руб., первоначальные затраты составили 30 тыс. руб., остальные затраты осуществлялись равномерно, длительность производственного цикла 5 дней. Определить норматив оборотных средств в незавершенном производстве.
Решение:
Если затраты осуществляются равномерно, то коэффициент нарастания затрат рассчитывается по следующей формуле:
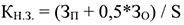
Где 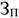
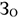
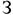
Норматив оборотных средств в незавершенном производстве:
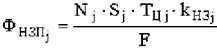
или
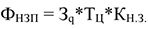
Где 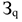
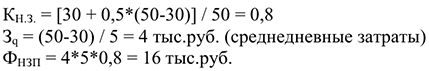
Пример с решением задачи №7:
Себестоимость продукции 1000 рублей. Длительность производственного цикла — 4 дня. Затраты в 1-й день — 300 рублей, во 2-й день — 300 рублей, в 3-ий день — 200 рублей, в 4-й день — 200 рублей. Определить коэффициент нарастания затрат.
При неравномерном нарастании затрат используют следующую формулу:
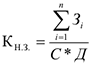
Где 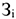
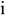
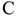
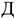
Кадры предприятия, производительность труда, заработная плата
Основными факторами производства на предприятии являются средства труда, предметы труда и человеческий труд, т.е. трудовые кадры предприятия. Именно от состава трудовых кадров предприятия зависит, насколько эффективно используются на предприятии средства производства и насколько успешно работает предприятие в целом.
Кадры предприятия и их изменения имеют определенные характеристики:
1) Количественная характеристика персонала предприятия измеряется такими показателями как:
- списочная численность работников, показатель численности работников на определенную дату с учетом принятых и выбывших за этот день работников;
- явочная численность расчетное количество работников, которые должны явиться на работу для выполнения производственного задания;
- среднесписочная численность.
2) Качественная характеристика персонала определяется степенью профессиональной и квалификационной пригодности ее работников для достижения целей предприятия.
3) Структурная характеристика персонала определяется составом и количественным соотношением отдельных категорий и групп работников предприятия. В зависимости от участия в производственном процессе весь персонал предприятия делится на две категории: промышленно-производственный персонал (ППП) и непромышленный персонал.
Потребность в персонале — это совокупность работников соответствующей структуры и квалификации, объективно необходимых предприятию для реализации стоящих перед ним целей. Плановая численность ППП на действующих предприятиях со стабильным, плавным изменением объема производства может быть определена на основе задания по объему производства и планируемой выработки на одного работника:
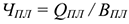
Где 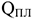
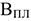
Для вновь создаваемых предприятиях и предприятиях с существенными колебаниями производственной программы наиболее распространенным является метод расчета потребности в рабочих кадрах (явочная численность) по трудоемкости работ:
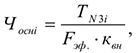
где 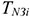
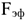
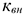
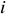
Для расчета среднесписочного числа рабочих можно использовать следующую формулу:
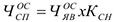
где 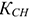
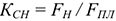
где 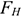
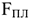
Обеспечение потребности в кадрах действующего предприятия предполагает не только определение численности работников предприятия, но и ее сопоставление с имеющейся рабочей силой, оценкой текучести кадров и определение дополнительной потребности или избытка кадров.
Оборот кадров — это отношение числа всех выбывших (оборот по увольнению) или вновь принятых (оборот по приему) за определенный период времени к среднесписочной численности работающих за этот же период.
Текучесть кадров — это выраженное в процентах отношение числа уволенных работников за определенный период времени к среднесписочной их численности за тот же период.
Показателем эффективности труда является его производительность. Для измерения производительности труда используются два основных показателя: выработка и трудоемкость.
Выработка измеряется количеством продукции, произведенной в единицу рабочего времени или приходящейся на одного среднесписочного работника в год (квартал, месяц).
Это наиболее распространенный и универсальный показатель производительности труда.
Выработка может быть определена на один отработанный человеко-час, на один отработанный человеко-день или на одного среднесписочного работника в год, квартал или месяц. На предприятиях России основным показателем является годовая выработка, в ряде зарубежных стран — часовая.
Трудоемкость — это затраты рабочего времени на производство единицы продукции. В зависимости от состава включаемых в нее трудовых затрат различают технологическую трудоемкость (затраты труда основных рабочих, как сдельщиков, так и повременщиков), производственную трудоемкость (к технологической трудоемкости добавляется трудоемкость обслуживания производства), и полная трудоемкость (к производственной трудоемкости добавляется трудоемкость управления производством).
Политика в области оплаты труда является составной частью управления предприятием, и от нее в значительной мере зависит эффективность его работы, так как заработная плата является одним из важнейших стимулов в рациональном использовании рабочей силы.
Заработная плата — это часть издержек на производство и реализацию продукции, идущая на оплату труда работников предприятия.
В современных условиях на предприятиях применяются различные формы и системы оплаты труда (рис. 2), но наибольшее распространение получили две формы оплаты труда: сдельная и повременная.
Сдельная оплата труда — это оплата труда за количество произведенной продукции.
Повременная оплата труда — это оплата труда за отработанное время, но не календарное, а нормативное, которое предусматривается тарифной системой.
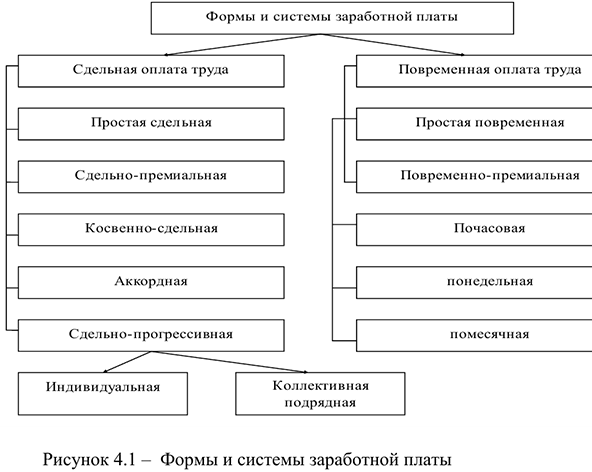
На большинстве предприятий основой для начисления заработной платы является тарифная система, особенно ее такие элементы, как тарифная ставка и тарифные сетки.
Тарифная ставка — абсолютный размер оплаты труда различных групп и категорий рабочих за единицу времени. Исходной является минимальная тарифная ставка или тарифная ставка первого разряда. Она определяет уровень оплаты наиболее простого труда.
Тарифные сетки служат для установления соотношения в оплате труда в зависимости от уровня квалификации. Это совокупность тарифных разрядов и соответствующих им тарифных коэффициентов. Тарифный коэффициент низшего разряда принимается равным единице. Тарифные коэффициенты последующих разрядов показывают, во сколько раз соответствующие тарифные ставки больше тарифной ставки первого разряда.
Фонд заработной платы рабочих включает прямую или тарифную заработную плату и все доплаты к ней. Прямая заработная плата состоит из суммы сдельных расценок, выплачиваемых рабочим-сдельщикам, и заработной платы рабочих-повременщиков, начисляемой по тарифным ставкам.
Фонд заработной платы руководителей, специалистов и служащих определяется по должностным окладам путем умножения месячного оклада каждой группы работников на число месяцев в году и на число работников в группе.
Пример с решением задачи №8:
Выработка продукции в час составила 12 дет. Трудоемкость изготовления продукции после внедрения новой технологии снизилась на 20%. Определить прирост производительности труда после внедрения новой технологии.
Решение:
Прирост производительности труда найдем по выработке. Определим насколько изменилась выработка в текущем периоде.
Выработка измеряется количеством продукции, произведенной в единицу рабочего времени или приходящейся на одного среднесписочного работника. Трудоемкость — это затраты рабочего времени на производство единицы продукции. По выработке можно найти трудоемкость изготовления продукции:
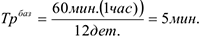
В текущем периоде трудоемкость снизилась на 20%:
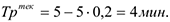
По трудоемкости в текущем периоде найдем часовую выработку в текущем периоде:
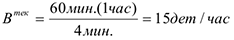
Прирост выработки в текущем периоде:
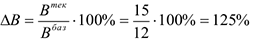
Пример с решением задачи №9:
Производственная трудоемкость работ составила 2 100 тыс. н.-ч., плановый фонд рабочего времени на одного рабочего в год — 1 870 ч., плановое выполнение норм выработки — 110%. Требуется определить численность производственных рабочих-сдельщиков.
Решение:
Численность производственных рабочих (явочная численность) по трудоемкости работ определяется по следующей формуле:
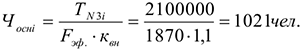
Издержки производства, себестоимость продукции и ценообразование
Издержки производства — это денежное выражение затрат производственных факторов, необходимых для осуществления предприятием своей производственной деятельности.
Существует два подхода к оценке издержек: бухгалтерский и экономический.
Бухгалтерские издержки представляют собой стоимость израсходованных ресурсов, измеренную в фактических ценах их приобретения. Это издержки, представленные в виде платежей за приобретаемые ресурсы (сырье, амортизация, труд…).
Однако для принятия решения о целесообразности продолжения деятельности предприятия владельцы должны учитывать экономические издержки.
Экономические издержки — это стоимость предпринимательской деятельности, от которой следует отказаться.
Для отечественной экономики характерен бухгалтерский подход к оценке издержек, поэтому термины «издержки» и «затраты» можно считать синонимами.
В целях анализа, учета и планирования затраты, входящие в себестоимость продукции, классифицируются по различным признакам (рис.3).
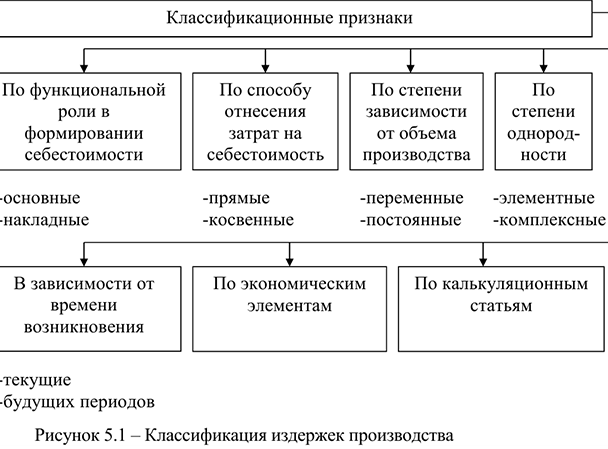
Основными называются затраты, непосредственно связанные с технологическим процессом производства (на сырье и основные материалы, вспомогательные и другие расходы, кроме общепроизводственных и общехозяйственных). Планируются и учитываются по видам продукции.
Накладные расходы образуются в связи с организацией, обслуживанием производства и управлением им (общепроизводственные и общехозяйственные расходы). Они планируются и учитываются по местам их возникновения, т.е. по производственным подразделениям. Это комплексные расходы, косвенно распределяемые между отдельными видами продукции и между законченной продукцией и незавершенным производством.
Планирование этих расходов осуществляется путем разработки на соответствующие цели годовых, квартальных смет с распределением на каждый месяц по каждой производственной единице, цеху в отдельности.
Прямые расходы непосредственно связаны с изготовлением конкретных видов продукции и по установленным нормам относятся на их себестоимость (сырье, материалы, топливо, энергия).
Косвенные расходы обусловлены изготовлением различных видов продукции и включаются в себестоимость пропорционально показателю, установленному на предприятии. К косвенным расходам относятся расходы на содержание и эксплуатацию оборудования (РСЭО), общепроизводственные и общехозяйственные расходы и т.д.
Условно-переменные — затраты, непосредственно зависят от объема производства (3/П производственных рабочих, затраты на сырье и т.д.)
Условно-постоянные затраты при изменении объема производства не изменяются или изменяются незначительно (амортизация зданий, сооружений, топливо для отопления, энергия на освещение, 3/П управленческого персонала…)
Сумма постоянных и переменных издержек составляет валовые издержки предприятия.
К элементным (однородным) относятся затраты, которые нельзя расчленить на составные части (затраты на сырье, основные материалы, амортизации …).
Комплексными называются затраты, состоящие из нескольких однородных затрат (РСЭО, общепроизводственные, общехозяйственные).
К текущим относятся расходы, имеющие частую периодичность осуществления, например расход сырья и материалов.
К расходам будущих периодов относятся затраты, которые производятся на данном отрезке времени, но переносятся на себестоимость продукции в последующем периоде в определенных долях.
Чтобы планировать прибыль от реализации продукции необходимо знать себестоимость выпускаемой продукции. Себестоимость продукции является качественным показателем функционирования предприятия, так как характеризует уровень использования всех ресурсов (переменного и постоянного капитала), находящихся в распоряжении предприятия.
Себестоимость продукции представляет выраженные в денежной форме текущие затраты предприятия на производство и реализацию продукции.
Классификация затрат по экономическим элементам лежит в основе определения общей сметы затрат на производство продукции, служит для определения заданий по снижению себестоимости продукции, расчета потребностей в оборотных средствах, а также для экономического обоснования инвестиций.
Классификация затрат по экономическим элементам содержит однородные по своему экономическому содержанию затраты:
- материальные затраты (за вычетом стоимости возвратных отходов), в том числе сырье и основные материалы, покупные полуфабрикаты и комплектующие изделия; вспомогательные материалы; топливо и энергия; износ малоценных и быстроизнашивающихся предметов и др.;
- затраты на оплату труда;
- отчисления на социальные нужды осуществляются по определенным нормативам от фонда оплаты труда, величина этих нормативов устанавливается в законодательном порядке и может пересматриваться;
- амортизация основных фондов (включаются все амортизационные отчисления по основным средствам за отчетный период);
- прочие затраты (платежи по процентам, износ нематериальных активов, командировочные расходы, представительские расходы, расходы на рекламу, расходы на подготовку кадров и др.).
Группировка затрат по экономическим элементам не позволяет вести учет по отдельным подразделениям предприятия и видам продукции.
Для этого ведется учет затрат по статьям калькуляции:
- Сырье и материалы.
- Возвратные отходы (вычитаются).
- Покупные изделия, полуфабрикаты и услуги производственного характера сторонних предприятий и организаций.
- Топливо и энергия на технологические цели.
- Заработная плата производственных рабочих.
- Отчисления на социальные нужды.
- Расходы на подготовку и освоение производства
- Общепроизводственные расходы.
- Цеховая себестоимость
- Общехозяйственные расходы.
- Потери от брака.
- Прочие производственные расходы.
- Производственная себестоимост ь
- Коммерческие расходы.
Полная себестоимость
Руководство предприятий может вносить изменения в приведенную типовую номенклатуру статей затрат на производство с учетом особенностей в технике, технологии и организации производства.
Под структурой себестоимости понимаются ее состав по элементам или статьям и их доля в полной себестоимости. Структура затрат позволяет выявить основные резервы по их снижению и разработать конкретные мероприятия по их реализации на предприятии.
Для снижения затрат на производство и реализацию продукции на предприятии должна быть разработана комплексная программа. Содержание и сущность такой программы зависят от специфики предприятия, текущего состояния и перспективы его развития.
В общем, в ней должны быть отражены следующие моменты:
- комплекс мероприятий по более рациональному использованию материальных ресурсов;
- мероприятия, связанные с определением и поддержанием оптимального размера предприятия, позволяющие минимизировать затраты в зависимости от объема производства;
- мероприятия, связанные с улучшением использования основных фондов;
- мероприятия, связанные с улучшением использования рабочей силы;
- мероприятия, связанные с совершенствованием организации производства и труда и др.
Цена является одним из важнейших экономических рычагов повышения эффективности производства. От уровня цены зависят: величина прибыли коммерческой организации, конкурентоспособность организации и ее продукции, финансовая устойчивость предприятия.
Цена — денежное выражение стоимости товара, экономическая категория, позволяющая косвенно измерить затраченное на производство товара общественно необходимое рабочее время.
Структура цены и ее формирование представлены на рисунке 4.
Различают три основных вида цен на промышленную продукцию:
- Расчетная цена производителя — цена, которая предусматривает возмещение текущих затрат производства и получение прибыли. На основании этой цены определяются: выручка от реализации продукции как произведение цены на количество, прибыль на единицу продукции как разница между оптовой ценой и ее себестоимостью.
- Цена оптовой организации.
- Розничная цена является конечной ценой, по которой товары народного потребления доходят до потребителя
Следует отметить, что текущие издержки производства являются основополагающими при установлении цен, но на этом процесс ценообразования не завершается. Для раскрытия сущности цены необходимо исследовать взаимосвязь затрат и потребительской стоимости, так как именно потребительская стоимость предопределяет верхнюю границу цены.
К основным методам формирования базовой цены относятся:
- Методы, ориентированные на издержки (основной ориентир -собственные затраты производителя на изготовление товара).
- Методы ценообразования ориентированные на конкуренцию.
- Методы, ориентированные на потребителя (подразумевают точное знание потребностей своего потенциального покупателя).
К основным методам формирования базовой цены, ориентированным на издержки относятся:
1) Метод прямых издержек (или предельной цены), учитывает только те затраты, которые можно непосредственно отнести на производство единицы продукции (используется в основном когда предприятие имеет неиспользованные мощности).
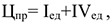
где 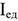
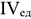
2) Метод расчета цены на основе покрытия полных издержек (техническая цена):
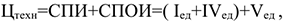
де СПИ — переменные затраты на единицу продукции (средние переменные издержки), руб.; СПОИ — постоянные затраты на единицу продукции (средние постоянные издержки), руб.
3) Метод «средние издержки + прибыль». Учитывает покрытие затрат на производство единицы продукции и некоторую стандартную наценку на эти затраты. Существует два варианта этого метода: с использованием полных и предельных издержек производства:
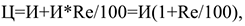
где 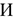
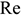
При выборе уровня рентабельности предприятие учитывает свои потребности в уровне прибыльности, среднеотраслевой уровень рентабельности, ограничения на рентабельность, устанавливаемые государственными органами.
4) Метод расчета цены на основе анализа безубыточности и получения целевой прибыли.
Прибыль является индивидуальной величиной каждого конкретного товара. Метод основан на тестировании цен на прибыльность (сопоставлении издержек с ожидаемыми поступлениями при различных уровнях объемов продаж) и определении точки безубыточности. При использовании данного метода предприятие стремится установить цену, которая обеспечит ему желаемый объем прибыли ( в абсолютном выражении):
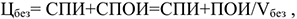
где ПОИ — постоянные затраты на весь объем производства, руб.; 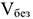
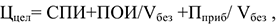
где 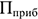
Экономическая эффективность производства
Эффект характеризуется различными стоимостными и натуральными показателями, например, объемами производства, прибылью, экономией по отдельным элементам затрат, общей экономией от снижения себестоимости продукции.
Сопоставление конечного финансового результата хозяйственной деятельности предприятия (эффекта) с затратами на его достижение отражает эффективность производства.
Уровень эффективности производства устанавливается с помощью системы частных и общих показателей.
К частным показателям эффективности производства относятся производительность труда, фондоемкость, материалоемкость продукции и др.
К общим показателям эффективности производства относятся прибыль и рентабельность.
Прибыль — конечный финансовый результат предпринимательской деятельности. Учет прибыли позволяет установить, насколько эффективно ведется хозяйственная деятельность.
Прибыль на предприятии может быть получена за счет различных видов деятельности: от реализации товарной продукции, от сдачи в аренду производственных площадей и оборудования, от посреднических операций и сделок, от долевого участия в деятельности других предприятий и др.
Суммарная величина всех прибылей составляет валовую прибыль предприятия:
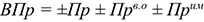
где 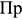
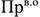
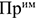
Величина прибыли от реализации продукции определяется как разность отпускной цены и себестоимости продукции:
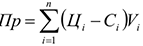
где 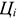
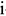
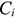
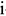
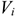
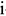
Внереализационная прибыль: доходы от долгосрочных и краткосрочных финансовых вложений, сальдо полученных и уплаченных штрафов, пени, неустоек и др. видов санкций, прибыль прошлых лет, проценты по денежным средствам и т.д.
Прибыль от реализации имущества определяется как разница между его ликвидационной стоимостью 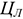
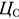
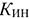
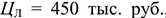
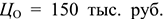
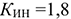
Чистая прибыль — эта часть прибыли, которая остается в распоряжении предприятия после уплаты установленных законом налогов:
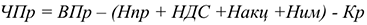
Где 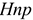
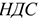
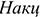
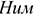
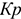
Балансовая прибыль — это валовая прибыль, уменьшенная на сумму льгот по прибыли, отчислений в резервный фонд (дивиденды) и доходов по акциям.
Для оценки эффективности работы предприятия недостаточно использовать только показатель прибыли, необходимо сопоставить прибыль и стоимость производственных фондов, с помощью которых она создана. Это и есть рентабельность.
Рентабельность — это доходность, прибыльность предприятия -показатель экономической эффективности производства, который отражает конечные результаты хозяйственной деятельности.
Различают два вида рентабельности по прибыли: на основе балансовой прибыли и на основе чистой прибыли. Для формирования цен на промышленную продукцию может использоваться рентабельность отдельных изделий, которая рассчитывается как отношение прибыли к себестоимости.
Показатели рентабельности:
1) Рентабельность отдельных видов продукции — характеризует прибыльность различных видов продукции. Используется в качестве базы для расчета прибыли при определении цен и в аналитических целях:
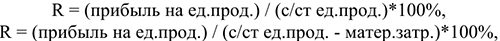
2) Рентабельность реализации оборота показывает, какой % прибыли получают предприятия с каждого рубля реализации:

3) Рентабельность собственных средств:
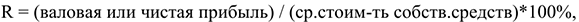
4) Общая рентабельность производственных фондов:
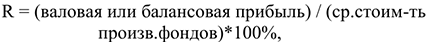
5) Норма балансовой прибыли:
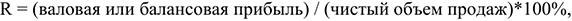
6) Чистая норма прибыли:
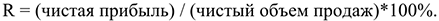
Показатель рентабельности взаимосвязан со всеми показателями эффективности производства, в частности с себестоимостью продукции, фондоемкостью, скоростью оборачиваемости ОбФ.
На величину рентабельности, рассчитанную по балансовой прибыли, влияют три основных фактора: прирост прибыли; уровень использования основных фондов предприятия; уровень использования нормируемых оборотных средств.
Мероприятия, способствующие повышению эффективности производственной деятельности:
Мероприятия, способствующие приросту прибыли:
1) Прирост прибыли в результате увеличения объема производства рассчитывается следующим образом:
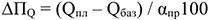
где 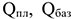
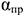
2) При изменении структуры ассортимента в направлении повышения удельного веса изделий с более высокой рентабельностью обеспечивается дополнительный прирост прибыли:
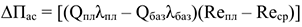
где 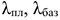
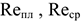
Если в результате структурных сдвигов увеличится удельный вес нескольких высокорентабельных изделий, то общий прирост прибыли определяется как сумма прироста прибыли по каждому изделию.
3) Среди факторов влияющих на прирост прибыли ведущая роль принадлежит снижению себестоимости продукции. Выбор путей сокращения текущих издержек производства основывается на анализе структуры себестоимости. Для материалоемких отраслей наиболее характерным путем является экономия материальных ресурсов, для трудоемких — рост производительности труда, для фондоемких — улучшение использования основных фондов, для энергоемких — экономия топлива и энергии:
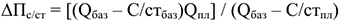
где 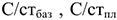
4) При производстве продукции повышенного качества текущие издержки чаще всего возрастают. Однако в результате реализации этой продукции по новым ценам прибыль также может возрасти:
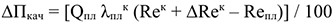
где 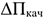
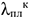
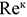
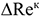
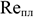
Мероприятия, способствующие эффективному использованию основных фондов предприятия.
Стоимость основных средств предприятия и уровень их использования оказывает большое влияние на рентабельность производства. Уменьшение среднегодовой стоимости основных фондов обеспечивает прирост рентабельности за счет увеличения удельной прибыли, приходящейся на 1 рубль основных фондов, и снижение амортизационных отчислений, приходящихся на единицу продукции.
1) При списании оборудования (лишнего) прирост рентабельности может быть определен по формуле:
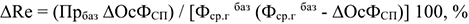
где 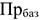
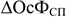
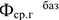
2) В результате сокращения амортизационных отчислений прирост рентабельности определяется следующим образом:
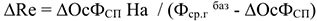
где 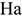
Мероприятия способствующие эффективному использованию оборотных фондов предприятия
Прирост рентабельности производства в результате улучшения использования оборотных средств можно определить по следующей формуле:
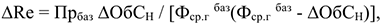
где 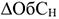
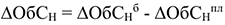
где 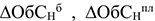
Готовые задачи на продажу и теория из учебников по предмету экономика тут.
Экономическая эффективность капитальных вложений
Инвестиции — денежные средства, ценные бумаги, иное имущество, в том числе имущественные права, иные права, имеющие денежную оценку, вкладываемые в объекты предпринимательской деятельности в целях получения прибыли.
Капитальные вложения (KB) — инвестиции в основные средства предприятия, в том числе затраты на новое строительство, расширение, реконструкцию и техническое перевооружение действующих предприятий, приобретение машин, оборудования, инструмента, инвентаря, проектно-изыскательские работы и др.
По формам воспроизводства основных фондов различают KB на:
- новое строительство;
- реконструкцию и техническое перевооружение действующих предприятий;
- модернизацию оборудования.
Развитие и совершенствование промышленного производства непосредственно связано с осуществлением 
Абсолютная экономическая эффективность характеризует общую величину отдачи инвестиций.
Сравнительная экономическая эффективность характеризует экономическое преимущество одного из вариантов инвестиционных вложений.
Абсолютная эффективность 
а) на народнохозяйственном уровне:
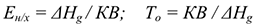
где 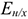
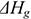
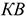
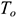
б) на уровне предприятий:
для прибыльных предприятий:

для убыточных предприятий:

где 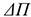
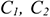
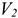
Рассчитанный таким образом показатель абсолютной эффективности 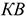
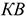
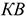
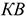
Методика определения сравнительной эффективности 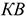
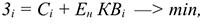
где 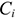
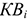
При этом годовой экономический эффект от реализации лучшего варианта определяется по формуле:
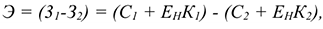
где 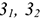
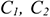
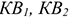
Сравнительный коэффициент эффективности капитальных вложений определяется по формулам:
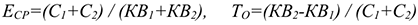
Если 
Наиболее серьезным недостатком при использовании этих методов расчета эффективности 
При оценке эффективности долгосрочных 
Норма дисконтирования рассматривается в общем случае как норма прибыли на вложенный капитал.
Если инициатором проекта выступает само предприятие, норма дисконтирования принимается на уровне средней нормы прибыли для этого предприятия.
При учете интересов другого предприятия, вложившего деньги в проект, норма дисконтирования рассматривается на уровне ставки банковского депозита.
Коэффициент дисконтирования, определяемый для постоянной нормы дисконта:
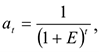
где 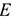
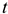
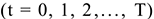
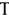
Если же норма дисконта меняется во времени и на 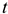
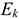
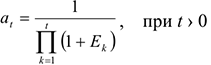
При осуществлении инвестиционных проектов выплаты делятся на капитальные (единовременные) затраты и текущие затраты. Чистый доход от инвестиционного проекта определяется суммарными результатами за срок службы проекта за вычетом расходов от текущей деятельности и единовременных вложений.
Для оценки коммерческой эффективности проектов используются следующие показатели:
- чистый дисконтированный доход (ЧДД), или интегральный доход;
- индекс доходности (ИД);
- внутренняя норма доходности (ВИД);
- срок окупаемости.
Использование в практике оценки долгосрочных KB величины чистого дисконтированного дохода вызвано очевидной неравноценностью для инвестора сегодняшних и будущих доходов. Иными словами, доходы инвестора, полученные в результате реализации проекта, подлежат корректировке на величину упущенной выгоды в связи с «замораживанием» денежных средств, отказом от их использования в других сферах применения капитала.
Чистый дисконтированный доход (ЧДД) представляет собой оценку сегодняшней стоимости потока будущего дохода. Он определяется как сумма текущих эффектов за весь расчетный период, приведенная к начальному шагу, или как превышение интегральных результатов над интегральными затратами:
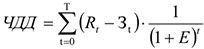
где 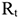
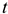
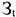
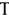
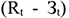
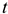
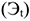
На практике часто пользуются модифицированной формулой для определения ЧДД. Для этого из состава затрат, осуществляемых на 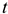
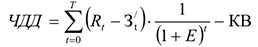
где 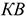
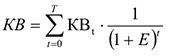
где 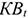
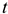
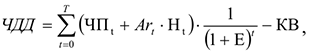
где 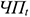
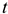
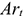
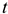
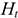
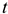
Таким образом, ЧДД — это сумма приведенных величин чистой прибыли и амортизационных отчислений за минусом приведенных капитальных вложений.
Индекс доходности (ИД) представляет собой отношение суммы приведенных эффектов к величине капиталовложений:
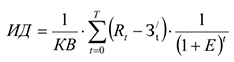
или
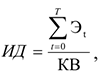
Где 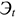
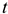
Индекс доходности тесно связан с ЧДД: если ЧДД положителен, то 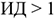
Правило 2. Если 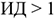
Внутренняя норма доходности (ВИД) представляет собой ту норму дисконта (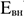
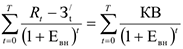
Если расчет ЧДД инвестиционного проекта дает ответ, на вопрос, является он эффективным или нет при некоторой заданной норме дисконта 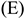
Правило 3. Если внутренняя норма доходности равна или больше требуемой инвестором нормы дохода на капитал, то инвестиции в данный инвестиционный проект оправданы, и может рассматриваться вопрос о его принятии. В противном случае инвестиции в данный проект нецелесообразны.
Срок окупаемости проекта — время, за которое поступления от производственной деятельности предприятия покроют затраты на инвестиции. Измеряется он в годах или месяцах.
Результаты и затраты, связанные с осуществлением проекта, можно вычислять с дисконтированием или без него. Соответственно получатся два различных срока окупаемости. Срок окупаемости рекомендуется определять с использованием дисконтирования.
Пример с решением задачи №10:
Руководство предприятия решило осуществить техническое перевооружение одного из ведущих цехов с целью снижения издержек производства и улучшения качества продукции.
На основе разработки бизнес-плана было установлено, что на осуществление инвестиционного проекта потребуются денежные средства в размере 1,5 млрд. рублей. Предполагаемые доходы по годам составят: 1-ый год — 0,5 млрд.рублей; 2-ой год — 1 млрд.рублей; 3-ий год — 1,7 млрд.рублей; 4-ый год — 2,5 млрд.рублей; 5-ый год — 3,2 млрд.рублей. Ставка дисконта принимается на уровне 12 %.
Требуется определить эффективны ли капитальные вложения.
Решение:
1) Определяем текущую (дисконтированную) стоимость проекта, т.е. приводим все доходы к начальному моменту времени (моменту вложения инвестиций):
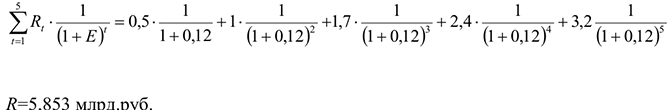
2) Чистый дисконтированный доход:
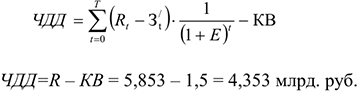
3) Индекс доходности:
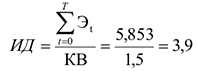
Чистый дисконтированный доход больше нуля, индекс доходности больше единицы, следовательно, проект эффективен.
Задачи на все темы по экономике
Экономика — хозяйственная деятельность общества, а также совокупность отношений, складывающихся в системе производства, распределения, обмена и потребления.
Слово «экономика» впервые появилось в научной работе в IV веке до н.э. у Ксенофонта, который называет его «естествознание». Аристотель противопоставлял экономику прагматизму — отрасли человеческой деятельности, связанной с получением прибыли.
В современной философии экономика рассматривается как система общественных отношений, рассматриваемая с точки зрения ценности и стоимости.
Главная функция экономики — постоянно создавать такие блага, которые необходимы людям для жизни и без которых общество не может развиваться. Экономика помогает удовлетворять потребности людей в мире ограниченных ресурсов.
Экономика общества — это сложный и всеохватывающий организм, который поддерживает каждого человека и общество.
Предельные затраты и предельная выручка
Предельные издержки — дополнительные издержки, связанные с производством дополнительной единицы продукта наиболее дешевым способом.
Производство дополнительной единицы продукции, порождая дополнительные издержки, с другой стороны, приносит и дополнительный доход, выручку от ее продажи. Величина этого дополнительного, или предельного дохода (выручки) представляет собой разность между валовой выручкой от продажи
Задача с решением №1 :
Известны следующие данные об объеме продаж и изменении переменных затрат фирмы:
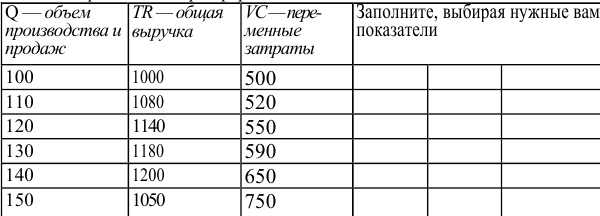
а) Определите объем продаж фирмы, максимизирующий прибыль, и цену, которую она выберет. (5 баллов)
б) Действует ли фирма на рынке совершенной или несовершенной конкуренции (аргументируйте ответ)? (5 баллов)
в) Изобразите графически кривую предложения фирмы в том случае, если бы фирма действовала на рынке совершенной конкуренции. (5 баллов)
Решение;
Для решения задачи необходимо на основе данных таблицы определить значения предельных затрат и предельной выручки для фирмы:
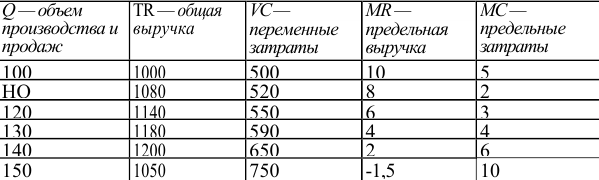
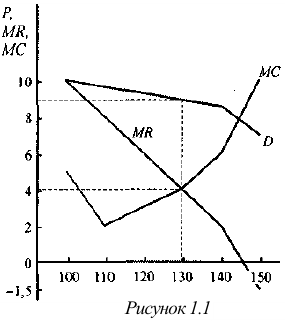
Равенство предельных затрат предельной выручке достигается при объеме выпуска, равном 130. Именно при таком объеме продаж и при цене, равной приблизительно 9, фирма достигает максимальной прибыли.
Фирма действует на рынке несовершенной конкуренции, поскольку зависимость выручки от объема продаж демонстрирует, что фирма в со стоянии влиять на цену товара. Спрос на товар фирмы, зависимость ее предельной выручки и предельных затрат от объема продаж и производства представлены на рисунке 1.1.
Если бы фирма действовала на рынке совершенной конкуренции, ее индивидуальное предложение совпадало бы с кривой предельных затрат при ценах, превышающих минимальное значение средних переменных затрат. Таким образом, для ответа на этот вопрос необходимо определить средние переменные затраты фирмы при соответствующем объеме выпуска:
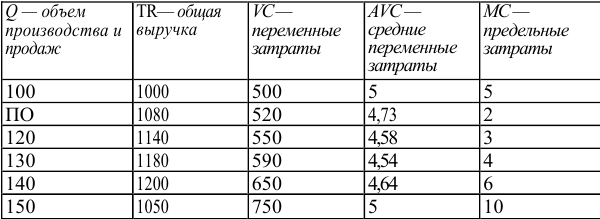
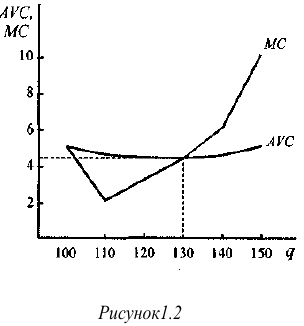
На рисунке 1.2 видно, что кривой предложения фирмы принадлежат только две комбинации цены и объема продаж: цена, равная 6, при объеме Л КС, продаж, равном 140, и цена, равная 10, Л/С при объеме продаж, равном 150.
Задача ставит целью проверить знания:
- основных различий между рынками совершенной конкуренции и несовершенной конкуренции;
- принципа выбора объема продаж и цены на рынке несовершенной конкуренции;
- определения индивидуального предложения фирмы на рынке совершенной конкуренции.
Решение этой задачи может иллюстрировать важное различие между фирмами, действующими на рынках совершенной и несовершенной конкуренции. Видно, что на рынке несовершенной конкуренции (когда продавец обладает рыночной властью) при заданном уровне затрат фирма может выбрать такой объем продаж, который был бы для нее невыгоден, если бы она действовала на рынке совершенной конкуренции. Опираясь на приведенный пример, можно еще раз подчеркнуть, что барьером входа на рынок и причиной образования монополии может быть низкая емкость спроса. При достаточно низком спросе и заданных технологии и ценах ресурсов может случиться, что рынок допускает получение прибыли фирмой-монополистом, но не эффективное функционирование.
Совершенная конкуренция
Совершенная, или чистая, свободная, конкуренция — это структура рынка, описывающая идеализированное состояние рынка, когда отдельные покупатели и продавцы не могут влиять на рыночную цену в одиночку, но формируют её своими суммарными вкладами в рыночный спрос и в рыночное предложение.
Задача с решением №2 :
На рынке совершенной конкуренции действуют идентичные фирмы. Для каждой фирмы зависимость выпуска от объема использования груда выглядит следующим образом:

Ставка заработной платы составляет 1 тыс. руб. в месяц. Для простоты мы считаем, что труд является единственным переменным ресурсом фирмы.
В свою очередь, рыночный спрос описывается следующей зависимостью объема спроса от цены:

а) Определите параметры рыночного равновесия (цену и объем продаж) при условии, что на рынке действуют 100 фирм. (20 баллов)
б) Как изменится ответ на вопрос «а», если на рынок войдут еще 50 фирм? (10 баллов)
Решение;
Для решения задачи необходимо по данным о деятельности одной фирмы определить кривую рыночного предложения.
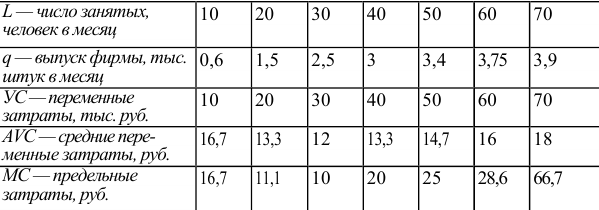
Кривая предложения фирмы совпадает с кривой предельных затрат при ценах, превышающих минимальное значение средних переменных затрат. Следовательно, по приведенным данным зависимость объема предложения фирмы и рынка от цены выглядит следующим образом:

Соотношение между индивидуальным и рыночным предложением выглядит, как показано на рисунке 1.3.
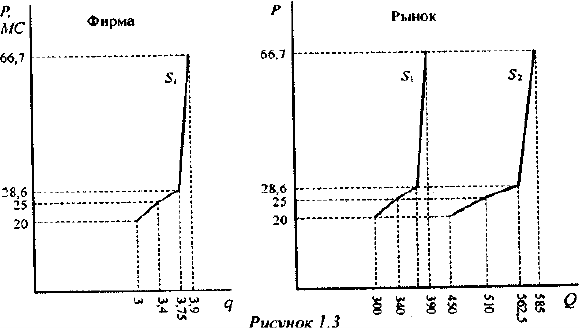
Сопоставив данные шкалы предложения с приведенной в условии задачи шкалой спроса, определим, что при 100 фирмах на рынке равновесие установится при цене 25 руб. за штуку и объеме продаж 340 тыс. штук в месяц; при 150 фирмах на рынке равновесие установится при цене 20 руб. за штуку и объеме продаж 450 штук в месяц.
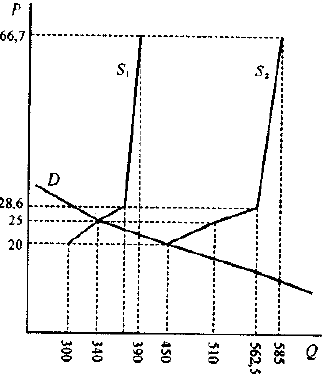
Изменение рыночного равновесия в зависимости от числа фирм-продавцов на рынке иллюстрируется графиком, представленным на рисунке 1.4.
Эта задача позволяет повторить сразу несколько важных концепций:
- связь между показателями производительности труда и показателями затрат на единицу продукции;
- связь между предельными затратами фирмы и индивидуальным предложением фирмы на рынке совершенной конкуренции;
- сумма индивидуальных предложений всех фирм на рынке;
- рыночное равновесие;
- количество продавцов на рынке как важный неценовой фактор предложения, влияющий на рыночную цену.
Выводы этой задачи могут быть успешно использованы впоследствии (в рамках курса следующего уровня сложности) для объяснения связи между краткосрочным и долгосрочным периодами на рынке совершенной конкуренции. Но даже во вводном курсе разбор задания можно использовать для объяснения динамики цен и объема продаж на рынке совершенной конкуренции. Если при цене, равной 25 руб., фирмы будут получать экономическую прибыль, это привлечет в отрасль новых конкурентов. Отсутствие барьеров входа позволит потенциальным конкурентам войти на рынок, число фирм на рынке увеличится, вырастет и рыночное предложение. В результате равновесная цена снизится при увеличении равновесного количества. Следует заметить, что рыночный объем продаж повысится, несмотря на снижение объема продаж каждой из фирм, действующих на рынке.
Рынок совершенной конкуренции
Рынок совершенной конкуренции — это структура рынка, описывающая идеализированное состояние рынка, когда отдельные покупатели и продавцы не могут влиять на рыночную цену в одиночку, но формируют ее своими суммарными вкладами в рыночный спрос и в рыночное предложение.
Задача с решением №3 :
Фирма действует на рынке совершенной конкуренции. Зависимость общих производственных затрат фирмы от ее выпуска представлена в таблице:

а) Какова цена отсечения для фирмы (та минимальная цена, при которой фирма еще будет продавать что-либо на рынке)? (5 баллов)
б) Какое количество продукции будет продавать фирма при цене, равной 18 руб. за штуку? (5 баллов)
в) Постройте функцию индивидуального предложения фирмы — зависимость объема продаж от рыночной цены. (5 баллов)
г) При какой минимальной цене фирма будет получать экономическую прибыль, если в качестве единственного источника средств фирмы выступает акционерный капитал в сумме 500 тыс. руб. и акционеры могут получать 20% годовых, вкладывая деньги в государственные ценные бумаги? (5 баллов)
Решение;
Для определения цены отсечения следует узнать минимальное значение средних переменных затрат. Определив, что постоянные затраты составляют 700 тыс. руб. (так как эти затраты не зависят от объема выпуска, фирма несет их в том числе и при нулевом выпуске), определяем зависимость переменных и средних переменных затрат от выпуска.
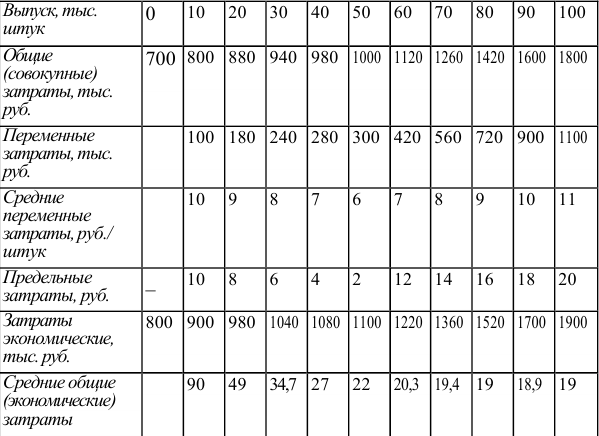
Минимальное значение средних переменных затрат составляет 6 руб. Именно эта цена служит нижней планкой, при которой фирма захочет оставаться на рынке. Действительно, при такой цене, производя 50 тыс. штук, фирма будет терпеть убытки, в точности равные постоянным затратам, т.е. той сумме убытков, которые она понесет, прекратив производство. Выручка фирмы составит 300 тыс. руб. и будет достаточна только для того, чтобы покрыть переменные затраты. При более высокой цене фирма может найти выпуск, при котором се убытки будут ниже, чем сумма постоянных затрат, т.е. стратегия продолжения производства будет предпочтительнее стратегии прекращения производства.
б) Определив предельные затраты, видим, что они равны цене 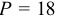
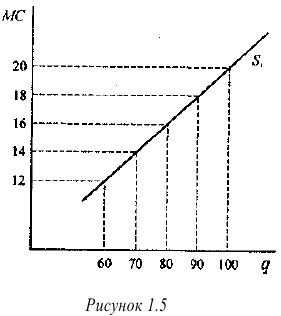
в) Индивидуальное предложение фирмы на рынке совершенной конкуренции совпадает с графиком предельных затрат при ценах, превышающих цену отсечения. По приведенным данным индивидуальное предложение выглядит, как показано на ри- сунке 1.5. -МС
г) Для определения того уровня цены, когда фирма в состоянии получать экономическую прибыль, необходимо найти экономические затраты фирмы в отличие от приведенных в задаче бухгалтерских затрат. Для фирмы — акционерного общества альтернативной ценностью собственного (акционерного) капитала будет служить та сумма, которую в состоянии получить акционеры при ином использовании своих средств. Риском в данной задаче можно пренебречь, учитывая вводный уровень курса. Альтернативная ценность собственного капитала (неявные затраты фирмы) равны 100 тыс. руб. Исходя из этого, определим зависимость средних общих экономических затрат фирмы от выпуска. Минимальное значение средних общих экономических затрат составляет 18,9 руб. Следовательно, это именно тот нижний уровень цены, начиная с которого фирма в состоянии получать экономическую прибыль. Помимо показателя средних экономических затрат, эта задача дает возможность еще раз повторить особенности определения альтернативной ценности собственных ресурсов для фирм различной организационно-правовой формы.
Эта задача служит иллюстрацией сразу нескольких важных в микроэкономической теории концепций:
- различие между постоянными и переменными затратами;
- цена отсечения (цена ухода) для фирмы;
- экономические затраты в сравнении с бухгалтерскими.
Условие максимизации прибыли
Максимизация прибыли – это процесс, целью которого является получение наивысших выгод от коммерческой деятельности. Каждое коммерческое предприятие всегда стремится увеличить собственную прибыль и сделать прибыль максимально высокой.
Задача с решением №4 :
Цена на товар фирмы, действующей на рынке совершенной конкуренции, равна 1 руб. Ставка заработной платы равна 7 руб./час. Зависимость выпуска от объема использования труда показана в таблице:

а) Какое количество труда будет использовать фирма, чтобы получить максимальную прибыль? (5 баллов)
б) Определите зависимость объема спроса на труд фирмы от ставки заработной платы и постройте индивидуальную кривую спроса на труд.(10 баллов)
Решение;
Определим, как предельный продукт труда и предельная выручка от предельного продукта труда зависят от объема использования труда:
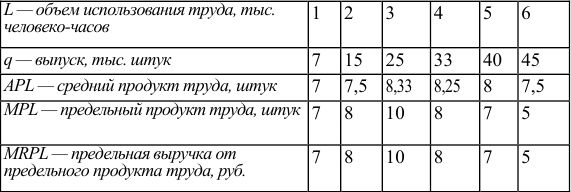
По условию максимизирующего прибыль спроса фирмы на труд она должна использовать такое количество труда, чтобы выполнялось условие 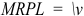
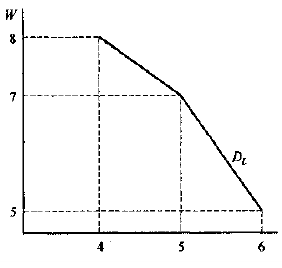
Задача иллюстрирует зависимость спроса на труд фирмы, действующей на конкурентном рынке и ресурсов, и готовой продукции, от изменения предельного продукта труда и цены производимого товара.
Разбор этой задачи позволил бы показать, что условия максимизирующего прибыль объема предложения готовой продукции и максимизирующего _ прибыль объема спроса на труд, 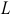
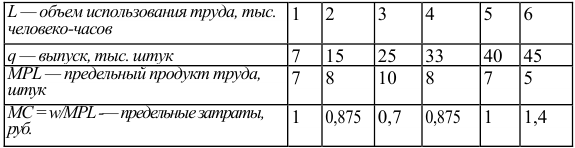
Видно, что условие равенства предельных затрат цене готовой продукции при увеличении предельных затрат с ростом выпуска выполняется при объеме использования труда 5 тыс. человеко-часов и при выпуске, равном 40 тыс. штук. Альтернативный способ решения задачи дает тот же самый ответ.
Концепция альтернативной ценности
Концепция альтернативной стоимости исходит из того, что оценки издержек отражают ценность данных ресурсов при их наилучшем, т. е. альтернативном, использовании. Иными словами, речь идёт о ценности тех вероятных (альтернативных) возможностей, которыми приходится жертвовать, когда данные ресурсы используются для производства конкретного изделия.
Задача с решением №5 :
Господин Сидоров построил дом на 100 квартир для того, чтобы сдавать их внаем. Все 100 квартир — одинаковой площади. Строительство дома в 1994 г. обошлось господину Сидорову в 600 млн. руб. Сегодня господину Сидорову предлагают за его дом 4 млн. руб. (с учетом деноминации). Вложив деньги в безрисковые государственные ценные бумаги, господин Сидоров может получать 40% годовых на вложенную сумму.
а) Можно ли на основании этих данных определить приблизительную величину арендной платы за квартиру? (10 баллов)
б) Как, изменится величина арендной платы, если:
при прочих равных условиях доходность вложения в государственные ценные бумаги снизится до 20%? (10 баллов)
при прочих равных условиях цена, которую предлагают господину Сидорову за дом, вырастет ? (10 баллов)
Объясните ваши ответы, используя концепцию альтернативной ценности.
Решение;
Сумма, уплаченная в качестве арендной платы, должна быть не ниже чем 40% от 4 млн. руб. (1600 тыс. руб.). Таким образом, арендная плата за проживание составит не менее 16 тыс. руб. с каждой квартиры в год. При доходности государственных ценных бумаг 20% годовых минимальная ставка арендной платы составит 8 тыс. руб. с квартиры в год. Рост цены дома приведет к росту альтернативной ценности господина Сидорова и росту арендной платы за жилье.
Условие максимизации выручки
Для максимизации прибыли валовой доход должен превышать валовые издержки. В краткосрочном периоде необходим анализ издержек производства для определения оптимального объема продукции предприятия при условии, что часть издержек постоянна. Для определения объема получаемой прибыли необходимо соединить анализ предельных издержек и предельного дохода с анализом динамики средних издержек.
Задача с решением №6 :
Владелец концертного зала стремится получить максимальную выручку от продажи билетов на концерт популярной рок-группы. Спрос на концерт описывается уравнением 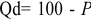
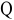
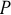
Решение;
Максимальная выручка достигается при комбинации цены и количества: 50 руб. за билет; 50 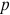
Рыночный спрос
Рыночный спрос — это спрос, предъявляемый на товар всеми потребителями (покупателями) на рынке данного товара.
Задача с решением №7 :
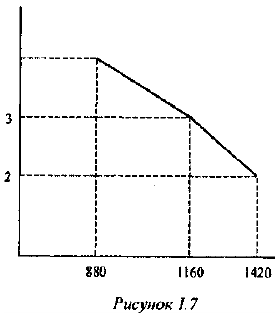
На рынке картофеля пять групп покупателей, численность каждой группы и зависимость объема их спроса на картофель указана в таблице:
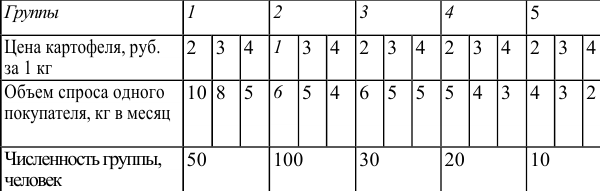
Постройте кривую рыночного спроса на картофель. Определите, как меняется эластичность спроса на картофель по мере роста цены. Является спрос на картофель эластичным или неэластичным?
Решение;
По приведенным данным рыночный спрос на картофель выглядит, как показано на рисунке 1.7.
Показатели дуговой эластичности спроса на картофель, составляют:
Ценовая эластичность спроса
Ценовая эластичность спроса – это чувствительность потребителей к изменению цены продукта. Она отражает зависимость изменения количества покупаемой продукции от изменения её цены. Коэффициент эластичности спроса измеряется в процентах.
Задача с решением №8 :
Фирма посылает своего представителя приобретать лак для волос на оптовом рынке. Ему сказано: «Если цена лака 25 руб. за флакон, бери 10 тыс. штук, если 30 — 8 тыс. штук, если 35 — 5 тыс. штук». Определите показатели ценовой эластичности спроса на лак (считая для простоты, что единицами измерения цены служат рубли, а количества — тыс. штук).
Решение;
При повышении цены с 25 до 30 руб. за флакон 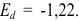
Зависимость спроса от цены
Зависимость между величиной спроса и ценой описывается законом спроса, согласно которому между ценой (Р) и спросом (Qd) существует обратная зависимость: при увеличении цены спрос падает, при снижении – растет.
Задача с решением №9 :
АО «Москович» провело изучение зависимости объема спроса на новую марку своих автомобилей «Князь Владимир» от устанавливаемой им цены, от цены автомобиля «Жигули» десятой модели, от уровня дохода потребителей. Было установлено, что ценовая эластичность спроса на «Князя Владимира» составляет -4, эластичность спроса по доходам покупателей равна 2, эластичность спроса по цене автомобиля «Жигули» равна 3. Аналитики фирмы предупреждают, что в будущем году АО «АвтоВАЗ» собирается снизить цену на десятую модель «Жигулей» на 5%. Одновременно Госкомстат России сообщает, что в будущем году предполагается рост доходов граждан на 4%.
Как должна фирма изменить цену на автомобиль «Князь Владимир», чтобы объем его продаж в будущем году, по крайней мере, не сократился?
Решение;
Если АО «Москвич» сохранит цену автомобиля неизменной, объем спроса на автомобиль снизится на 7%. Для сохранения объема продаж неизменным, т.е. для повышения объема спроса на автомобиль «Князь Владимир» на 7%, необходимо уменьшить цену на 1,75%.
Рынок свободной конкуренции
Под рынком свободной конкуренции следует понимать рынок, функционирующий в условиях чистой (совершенной) конкуренции. Такой рынок, как правило, характеризуется высокой мобильностью факторов производства и свободным доступом к экономической информации.
Задача с решением №10 :
Известны шкала спроса и шкала предложения для рынка молока.
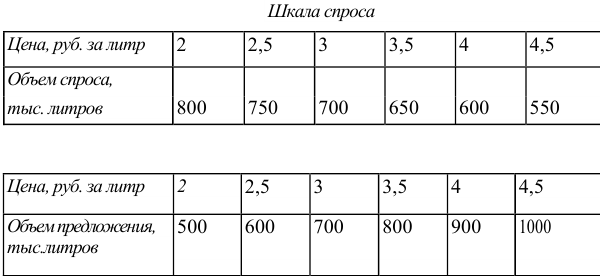
Государство, стремясь поддержать производителей молока, устанавливает минимальную цену товара на уровне 4 руб. за литр. Определите, как изменятся объем продаж молока, расходы покупателей и выручка продавцов по сравнению с рынком свободной конкуренции, если:
а) государство не будет осуществлять закупки молока; (10 баллов)
б) государство будет осуществлять закупки молока так, чтобы все произведенное молоко было продано. (10 баллов)
Решение;
Равновесной ценой будет цена, равная 3, при которой объем продаж составит 700 тыс. литров молока. При равновесной цене выручка продавцов и расходы покупателей на молоко составят 2100 тыс. руб. Если государство установит минимальную цену на молоко на уровне 4 руб. за литр, объем продаж на рынке понизится до 600 тыс. литров в день, возникнет избыточное предложение в размере 300 тыс. литров в день. Общая выручка продавцов молока вырастет до 2400 тыс. руб., даже если государство не будет закупать избыток молока.
Функция полезности потребителя
Функция полезности — функция, с помощью которой можно представить предпочтения потребителя на множестве допустимых альтернатив. Числовые значения функции помогают упорядочить альтернативы по степени предпочтительности для потребителя.
Задача с решением №11 :
Функция полезности потребителя 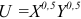
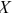
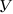
а) Определите объем сбора, уплачиваемого арендатором. (5 баллов)
б) Определите, было ли бы арендатору выгоднее, если бы государство вместо сбора (акцизного налога) ввело аккордный налог на доход (так, что бы налоговые поступления в государственный бюджет при разных налоговых схемах были одинаковыми). (10 баллов)
Решение;
а) Введение сбора со сделок повышает цену 1 кв.м жилья для арендатора до 2,5 долл. Государство получает 0,5 долл. сбора с каждого метра арендованного жилья. Чтобы определить общий размер отчислений потребителя в государственный бюджет, найдем оптимальный объем потребления жилья, воспользовавшись условием максимизации полезности потребителя при данном бюджетном ограничении — равенством предельной нормы замещения товара 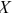
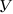
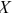
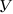
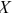
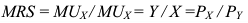
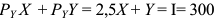
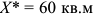
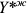
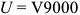
Следовательно, государство получает в качестве сбора 60 • 0,5 = 30 долл.
б) Если бы был введен аккордный налог, бюджет потребителя сократился бы до 270 долл. Оптимальный объем аренды жилья и расходов на все остальные товары удовлетворял бы условиям:
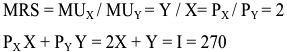
Отсюда 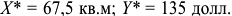
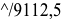
Можно сделать вывод, что аккордный (подоходный) налог предпочтительнее, поскольку при том же объеме налоговых отчислений в пользу государства он позволяет потребителю достичь более высокого уровня полезности.
Представленное решение иллюстрируется на рисунке 1.10.
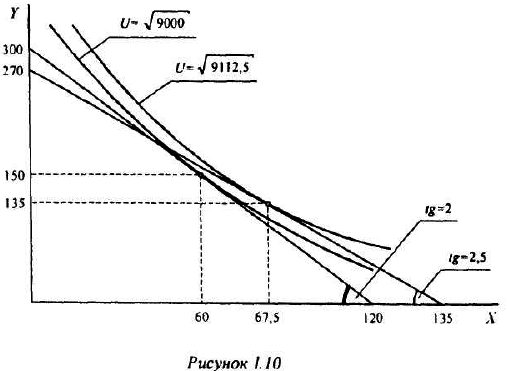
Задача ставит целью как проверить знания принципов и условий максимизации полезности потребителя, так и еще раз вернуться к проблеме эффективности схемы налогообложения. На примере этой задачи можно еще раз указать, что аккордные налоги предпочтительнее поштучных, поскольку они не приводят к искажению ценовых пропорций.
Параметры равновесия
Параметры рыночного равновесия — это цена и объем продукта (PE, QE ), при которых величина спроса и величина предложения равны (QD =QS).
Задача с решением №12 :
В стране 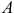
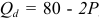
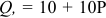
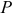

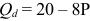
а) Предположим, что до недавнего времени политический конфликт между странами способствовал замыканию их рынков в национальных границах. Каковы были параметры равновесия на рынках сигарет двух стран? (5 баллов)
б) После многих лет отчуждения главы правительств подписывают соглашение о свободной торговле. Это означает, что сигареты можно свободно ввозить и вывозить без уплаты импортного (экспортного) тарифа. Существуют ли у производителей и потребителей этих стран стимулы к международной торговле? Каковы будут параметры равновесия в новой ситуации (считать издержки транспортировки сигарет для простоты равными нулю)? (5 баллов)
Решение;
а) Параметры равновесия на изолированных рынках найдем, приравняв объем спроса к объему предложения. В стране 
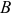
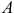
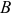
б) В условиях свободной торговли очевидно, что страна 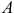
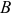
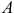
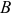
Теперь можно считать, что равновесие формируется на едином рынке двух стран, в результате взаимодействия суммарного спроса и суммарного предложения. Функция суммарного спроса составит 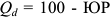
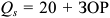
Подставив цену, равную 2 долл., в функции спроса и предложения стран 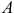
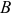
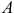
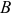
Проверим полученные результаты, сложив объем спроса и объем предложения двух стран. Видим, что суммарный объем спроса и суммарный объем предложения равны друг другу и составляют 80 млн. пачек.
Задача ставит целыо:
- проверить навыки операций с кривыми спроса и предложения (сложение индивидуальных спросов и предложений — в данном случае спрос в каждой конкретной стране можно рассматривать как индивидуальный по отношению к спросу мирового рынка (рынка двух стран), то же самое по отношению к предложению);
- обсудить проблемы выигрышей и потерь в международной торговле, заинтересованности продавцов и покупателей в либеральной и протекционистской внешнеторговой политике.
Разбирая решение задачи, можно показать, что в любой экономике существуют как сторона, заинтересованная во внешней торговле, так и сторона, которой либеральная внешнеторговая политика приносит потери. В любой из приведенных в нашей задаче стран в либеральном режиме внешней торговли заинтересованы либо продавцы, либо покупатели, но не тс и другие одновременно.
Рынок монопольной конкуренции
Монополистическая конкуренция — тип рыночной структуры несовершенной конкуренции, где обладающие рыночной властью продавцы дифференцированного продукта конкурируют за объём продаж. Это распространённый тип рынка, наиболее близкий к совершенной конкуренции.
Задача с решением №13 :
Общие затраты фирмы, действующей на рынке моно политической конкуренции, зависят от объема выпуска как
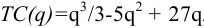
Обратная функция остаточного спроса (зависимость цены, которую готов заплатить покупатель за товар фирмы, от объема ее продаж) выглядит как 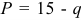
Решение;
На рынке монополистической конкуренции в долгосрочном равновесии фирма не получает экономической прибыли. Найдем объем продаж и цену, при которой фирма достигает максимальной прибыли (по условию равенства предельных издержек предельной выручке), а затем определим объем прибыли (или сравним цену со средними издержками).
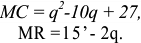
Равенство предельных издержек предельной выручке достигается при двух объемах выпуска и продаж: 2 и 6. Второму условию максимума прибыли удовлетворяет объем выпуска, равный 6.
При объеме продаж, равном 6, цена на товар фирмы равна 9, средние затраты — 9; общая выручка фирмы составляет 54. Общие затраты фирмы также равны 54, экономическая прибыль равна нулю, следовательно, фирма находится в состоянии долгосрочного равновесия (рисунок 1.11).
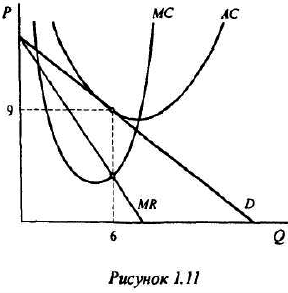
Разбирая задачу, можно еще раз указать, что в долгосрочном равновесии на рынке монополистической конкуренции фирма не получает прибыли, однако и не достигает минимально возможного 6 2 уровня средних затрат. Так, наша фирма производит количество, равное 6, при том, что минимальный уровень средних затрат достигается при выпуске 7,5. Разницу между этими объемами выпуска часто называют избыточной мощностью фирмы на рынке монополистической конкуренции. Наличие избыточной мощности может рассматриваться как аргумент в пользу тезиса о неэффективности монополистической конкуренции как структуры рынка. Однако существует и противоположная точка зрения: избыточная мощность рассматривается как своего рода плата за дифференциацию продукта, которая позволяет максимально удовлетворить спрос покупателей с разными вкусами.
Модель Курно
Курно модель дуополии — [Соurnot duopoly model] простая модель олигополии (на примере ее частного случая дуополии), где фирмы конкурируют друг с другом, производя однородный товар и зная общую кривую рыночного спроса.
Задача с решением №14 :
На рынке работают две фирмы, взаимодействующие по Курно. Средние издержки фирм не зависят от объема выпуска, равны и составляют 10. Рыночный спрос описывается формулой 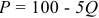
а) Определите параметры рыночного равновесия по Курно. (5 баллов)
б) Как изменятся параметры рыночного равновесия, если в результате введения ресурсосберегающей технологии издержки на единицу продукции одной из фирм снизились до 8? (2 балла)
в) Как изменятся параметры равновесия, если фирма, обладающая преимуществом в издержках, приобретет роль Штакельберговского лидера на рынке? (5 баллов)
г) Как изменятся параметры равновесия, если фирмы заключат кар тельное соглашение (при условии одинаковых средних затрат, равных 10)? (3 балла)
д) Будем считать, что в рамках картельного соглашения фирмы разделили объем продаж поровну. Как изменится прибыль фирмы, если она увеличит объем продаж на единицу по сравнению со своей квотой? Как изменится прибыль картеля, если другая фирма сохранит объем продаж неизменным? (5 баллов)
Решение;
а) Определим функции реакции фирм, взимодействующих по Курно, основываясь на принципе максимизации прибыли. Прибыль каждой фирмы (считая, что их затраты идентичны), зависит от ее выпуска как:
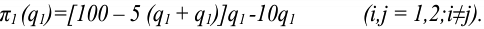
Оптимальный объем продаж 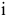
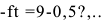
Отсюда оптимальный объем продаж обеих фирм составляет по 6 единиц товара, рыночная цена — 40, прибыль каждой фирмы — 180 единиц.
б) Изменение затрат на единицу продукции приведет к изменению функции реакции одной из фирм (будем считать, что это первая фирма). Ее прибыль и объем продаж «наилучшей реакции» (максимизирующей прибыль) зависит от выпуска второй фирмы как:
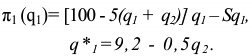
Зная, что функция реакции второй фирмы по сравнению с условием, сформулированным в пункте «а», не изменилась, найдем оптимальный объем продаж обеих фирм. Первая фирма будет продавать приблизительно 6,27, вторая — 5,87 единиц, рыночная цена снизится до 39,3, прибыль первой фирмы увеличится приблизительно до 196, а второй — снизится до 172. Последствия снижения затрат первой фирмы представлены на рисунке 1.12.
в) Если фирма приобретет роль Штакельберговского лидера, т.е. будет выбирать объем выпуска, учитывая реакцию конкурента на свои решения, то для нее зависимость прибыли от объема выпуска будет выглядеть как:
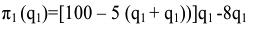
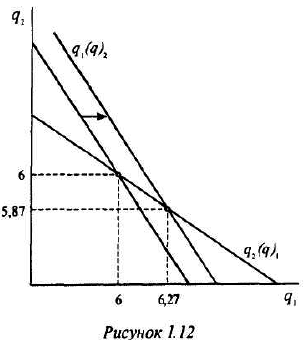
Отсюда оптимальный объем продаж первой фирмы равен 9,4, второй — 4,3, рыночная цена — 31,5, прибыль фирм соответственно составляет 220,9 и 92,45. Видно, что фирма, использующая помимо преимущества в издержках, еще и преимущество «первого хода», добивается увеличения прибыли за счет прибыли второго продавца.
г) Заключив картельное соглашение, фирмы будут вести себя как «кол лективный монополист», продавая количество, равное 8, и назначив цену, равную 60. Прибыль каждой фирмы при условии раздела рынка пополам составит 200.
д) Если каждая фирма в рамках квоты продавала количество, равное 4, «нарушитель соглашения», продав количество, равное 5, что снизит рыночную иену до 55, получит прибыль 225, что на 25 единиц больше, чем если бы он соблюдал заключенное соглашение. Заметим, что суммарная прибыль фирм, входящих в картель, вырастет до 405, однако прибыль соблюдающей соглашение фирмы сократится до 180. Задача ставит целью:
- проверить знания принципов выбора объема продаж и определения рыночной цены на рынке олигополии при условии взаимодействия фирм по Курно и при условии заключения картельного соглашения;
- продемонстрировать различные факторы, влияющие на рыночную долю и прибыль фирм, действующих на рынке олигополии, в том числе преимущество в издержках и преимущество «первого хода» (стратегического поведения, учитывающего реакцию конкурента на собственный выбор);
- показать проблему неустойчивости картельного соглашения.
При разборе задачи следует еще раз подчеркнуть, что существует достаточно большой набор возможных комбинаций цен и объемов продаж на рынке олигополии; какая из этих комбинаций будет выбрана, зависит от поведения фирм по отношению друг к другу.
Эффективность инвестиций
Эффективность инвестиций – это соответствие полученных от реализации инвестиционного проекта результатов произведенным затратам. Каждый инвестор, пытаясь дать объективную оценку собственным вложениям, опирается в своих расчетах на определенные показатели.
Задача с решением №15 :
Фирма располагает четырьмя вариантами осуществления инвестиционного проекта. Выберите наилучший из них, считая цену капитала фирмы положительной:
Решение;
По приведенным данным определим показатели чистой текущей ценности (Net Present Value) для четырех инвестиционных проектов, принимая цену капитала фирмы, которая служит ставкой дисконтирования, за 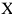
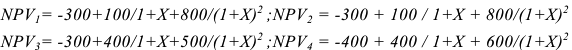
Легко заметить, что первый и второй варианты имеют совершенно одинаковую чистую текущую ценность. В то же время третий вариант предпочтительнее первого и второго, так как:
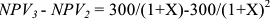
что больше нуля при любом положительном 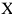
В свою очередь, третий вариант предпочтительнее четвертого, так как
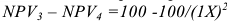
положительно при любом положительном значении цены капитала 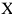
Альтернативным способом решения этой задачи служит определение значения внутренней нормы доходности для каждого из представленных инвестиционных проектов. Известно, что внутренняя норма доходности равна такой величине цены капитала, при которой чистая текущая ценность обращается в ноль. Внутреннюю норму доходности для первого из представленных инвестиционных проектов находим, решая относительно 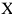
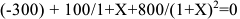
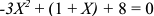
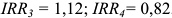
Задача ставит целыо проверить знания показателей эффективности инвестиционных решений — принципов определения спроса фирмы на финансовые ресурсы.
При разборе задачи необходимо подчеркнуть, что использованные нами методы определения эффективности инвестиционных решений в данном случае дают ответ на вопрос о соотношении эффективности предлагаемых инвестиционных проектов. Не зная цену капитала фирмы, который будет использоваться для осуществления инвестиционного проекта, мы не можем сказать, является ли избранный нами наилучший инвестиционный проект действительно эффективным.
Производственная функция
Производственная функция — экономико-математическая количественная зависимость между величинами выпуска (количества продукции) и факторами производства, такими как затраты ресурсов, уровень технологий. Может выражаться как множество изоквант.
Задача с решением №16 :
Капитал в объеме 100 машино-часов и труд в объеме 40 человеко-часов распределяются между производством продуктов 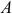
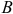
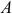
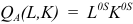
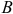
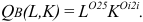
а) Найдите цены капитала и труда, при которых будет достигаться Парето-эффективное размещение ресурсов. (5 баллов)
б) Определите несколько (минимум четыре) точек, принадлежащих кривой производственных контрактов. (5 баллов)
в) Определите приблизительный вид кривой производственных возможностей для продуктов 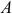
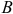
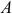
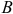
Решение;
Воспользуемся критерием оптимального по Парето распределения ресурсов между производством товаров 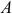
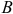
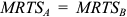
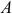
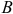
Пусть 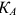
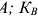
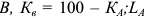
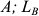
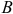
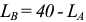
Предельная норма замещения труда капиталом в производстве продукта 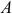
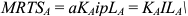
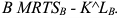
Такое размещение ресурсов будет достигнуто при любых ценах ресурсов, удовлетворяющих условию 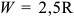
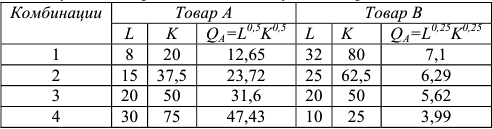
Кривая производственных контрактов и кривая производственных возможностей, соответствующие решению задачи, приведены на рисунках 1.13 и 1.14. Кривая производственных возможностей демонстрирует возрастающую предельную норму трансформации продукта 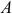
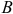
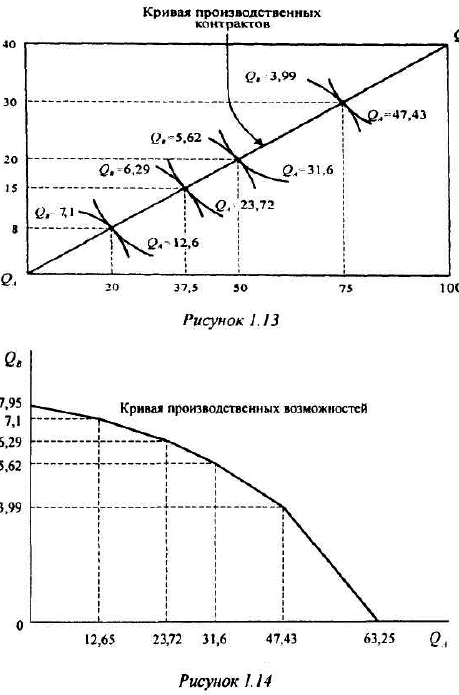
Задача ставит целью проверить знание:
- проблем минимизации затрат производителей;
- принципов определения общего равновесия в размещении ресурсов;
- связи между характеристиками производственных функций для рассматриваемых продуктов и характером кривой производственных возможностей.
Равновесная цена
Равновесная цена — это цена, объём спроса при которой равен объёму предложения, и этот объём, соответственно, является равновесным.
Задача с решением №17 :
Спрос и предложение на рынке сигарет «Ява» описываются следующими уравнениями: 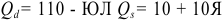
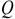
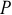
а) Найдите равновесную цену и равновесный объем продаж сигарет. (5 баллов).
б) Как изменятся параметры равновесия, сели правительство введет налог в размере 2 руб. на пачку сигарет? (5 баллов)
в) Рассчитайте, как повлияет введение налога на выигрыш потребителя и выигрыш производителя? От чего зависит распределение налогового брс мени между покупателями и продавцами (ответьте на вопрос, не прибегая к расчетам)? (5 баллов)
Решение;
а) Равновесные цена 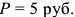
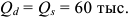
б) Новое равновесие устанавливается при
в) Выигрыши и потребителей, и производителей сокращаются на 55 тыс. руб. Дополнительные доходы государственного бюджета от введс ния количественного налога равны 100 тыс. руб., мертвые (чистые, безвоз вратные) потери благосостояния составляют 10 тыс. руб.
Общая полезность
Общая полезность – это суммарная польза от потребления определенного количества благ (или блага). Предельная полезность – это приращение общей полезности при увеличении потребления блага на одну дополнительную единицу.
Задача с решением №18 :
Федор распределяет между говядиной и сосисками 150 руб. в неделю. Цена 1 кг говядины — 25 руб., цена 1 кг сосисок — 15 руб. Общая полезность от потребления говядины и сосисок зависит от количества приобретенных им и съеденных продуктов так, как это представлено в таблице:
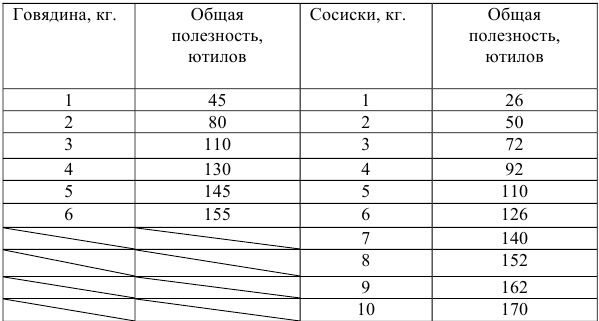
Решение;
Условиям 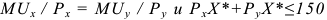
Труд и капитал
Термин «капитал» имеет много значений. Даже по поводу происхождения существуют разные версии. По одной из них, слово происходит от латинского capita — голова скота и появилось в те времена, когда мерилом богатства хозяйства было количество скота. По другой версии, оно происходит от латинского capitalis – главный. В обыденной жизни часто любые деньги называют капиталом. В научном политэкономическом словаре понятия «деньги» и «капитал» не отождествляются, так как они выражают разные производственные отношения.
«Под рабочей силой, или способностью к труду, — пишет Маркс, — мы понимаем совокупность физических и духовных способностей, которыми обладает организм, живая личность человека, и которые пускаются им в ход всякий раз, когда он производит какие-либо потребительные стоимости»
Рабочая сила становится товаром в определенных исторических условиях:
- Владелец рабочей силы лично свободен.
- Владелец рабочей силы не имеет средств существования и средств производства, чтобы стать простым товаропроизводителем.
Задача с решением №19 :
Производственная функция фирмы описывается уравнением 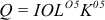
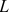
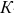
а) Определите объем использования труда и капитала и охарактеризуйте технологию, используемую фирмой, а также необходимую сумму затрат, если ставка заработной платы составляет 10 руб. в час, а арендная плата — 10 руб. за один машино-час. (5 баллов)
б) Как изменится технология, общие и средние затраты фирмы, если ставка заработной платы вырастет втрое и составит 30 руб. в час? (5 баллов)
Решение;
а)Оптимальные объемы использования труда и капитала 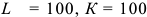
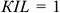
б) 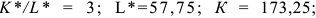
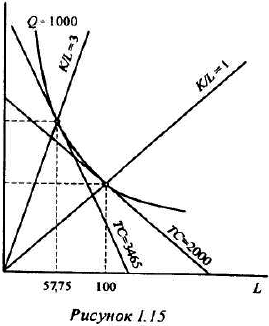
Долгосрочное равновесие
Долгосрочное равновесие (Long-run equilibrium) — это такое состояние экономики, когда уровень совокупного спроса, уровень совокупного предложения, а также уровень долгосрочного совокупного предложения выравниваются в одной точке равновесия.
Задача с решением №20 :
Общие затраты фирмы (с учетом нормальной прибыли) на рынке совершенной конкуренции в долгосрочном периоде зависят от ее выпуска как:
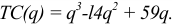
Определите, сколько фирм будет действовать на рынке в долгосрочном равновесии, если объем рыночного спроса зависит от цены как
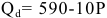
Решение;
На рынке в состоянии долгосрочного равновесия могут действовать 70 фирм (рисунок 1.16)
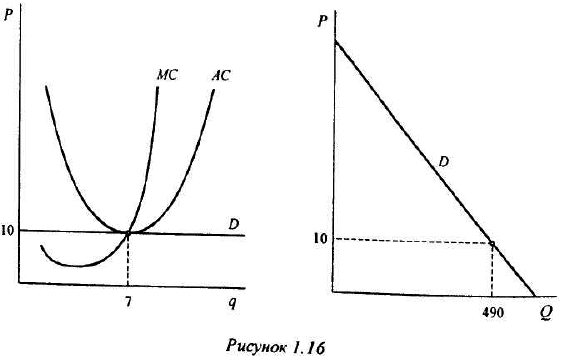
Чистая монополия
Чистая монополия — положение на рынке товаров и услуг, характеризующееся наличием только одного продавца данного вида товара или услуги. Характерными чертами данной ситуации являются: уникальность продукта, владение основными видами сырья, низкие средние затраты.
Задача с решением №21 :
Известно, что функция средних издержек фирмы в краткосрочном периоде описывается уравнением 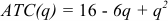
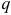
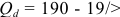
а) на рынке совершенной конкуренции; (10 баллов)
б) на рынке чистой монополии. Найдите величину чистых потерь общества от монополии. (10 баллов)
Решение;
Минимальное значение средних затрат в краткосрочном периоде, равное значению долгосрочных средних затрат, составляет 7 руб. В долгосрочном равновесии на рынке совершенной конкуренции 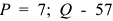
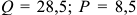
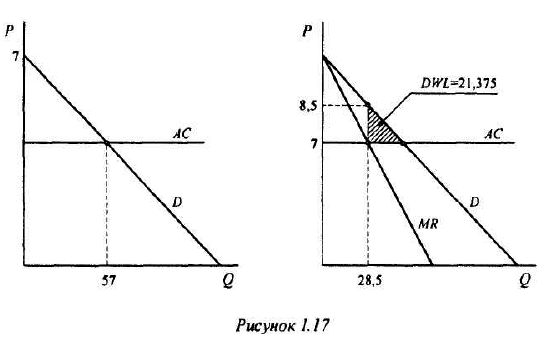
Товары — совершенные заменители
Товары — совершенные заменители — к данной группе товаров относятся все предметы и услуги, которые потребитель готов заменить один на другой в постоянном соотношении, т.е. MRS = const (например, конкурирующие марки практически одинаковых продуктов питания — молока, йогурта, сахара и т.д.).
Задача с решением №22 :
Ирина рассматривает мороженое и пирожное как со вершенные заменители в пропорции 1:1.
а) Определите, какой набор она приобретет, если сумма денег, выделенная на эти продукты, составляет 30 руб. в неделю, цена одного мороженого — 5 руб., а цена одного пирожного — 6 руб.? (10 баллов)
б) Как повлияет на выбор Ирины снижение цены пирожного до 5 руб.? (5 баллов)
Решение;
При цене пирожного, равной 6 руб., 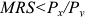
Когда цена пирожного снизится до 5 руб., предельная нормы замещения пирожного мороженым будет равна отношению цен товаров при любой комбинации приобретения пирожного и мороженого.
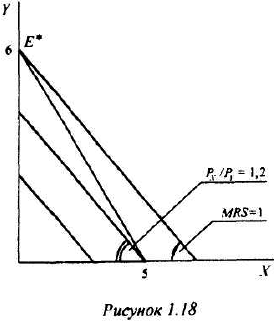
Влияние НДС на производителя
Давайте представим, что вы владелец предприятия по производству стульев. Чтобы их выпускать, вам требуется древесина, которую вы приобретаете у сторонней организации. Итоговый продукт – стулья – вы продаете по более высокой стоимости, чем закупаете древесину. На эту разницу, так называемую добавленную стоимость, государство и начисляет налог – НДС.
Прежде чем говорить о том, какие будут последствия повышения ставки НДС на финансы предприятия, отметим следующее. Сумма налога, которую организация-налогоплательщик получает от клиентов в виде надбавки к отпускной цене, не считается полученным доходом, ее рассматривают в качестве обязательства перед бюджетом в момент отражения выручки.
Формально НДС не принимает участия в расчете финансового результата в бухгалтерском учете, а также не подлежит включению в показатели Отчета о прибылях и убытках. Предлагаем не рассматривать НДС как одну из составляющих количественной оценки налоговой нагрузки на финансовый результат. И, тем не менее, предприятие должно учитывать, каким образом влияет группа налогов с оборота, включая НДС, в следующих случаях:
- Прогнозируя доходы как соотношение рыночной и отпускной цен на продукцию (работы, услуги). Размер реальных доходов будет ниже потенциальной выручки в аналогичных условиях хозяйственной деятельности, в отсутствие НДС.
- Рассчитывая налоговую нагрузку на денежные потоки предприятия. Суммы налоговых платежей с оборота, фактически выплачиваемых предприятием в бюджет, составляют часть его денежных потоков. И в прогнозе бюджетных средств на будущий период они должны быть учтены как операции расхода (оттока) денежных средств, которые должны быть осуществлены в установленный законодателем период.
Задача с решением №23 :
Предположим, вы член Государственной Думы. Правительство предлагает в будущем году увеличить налог на добавленную стоимость (НДС), уплачиваемый производителями водки и шоколада. Что вы можете сказать о влиянии увеличения НДС на положение производите лей в этих двух отраслях (рассматривая НДС для простоты рассуждений как поштучный, количественный, налог)?
Решение;
На рынке водки введение налога приведет к большему сокращению равновесного количества, большему росту цены, налоговое бремя будет в большей степени возлагаться на продавцов (рисунок 1.19):
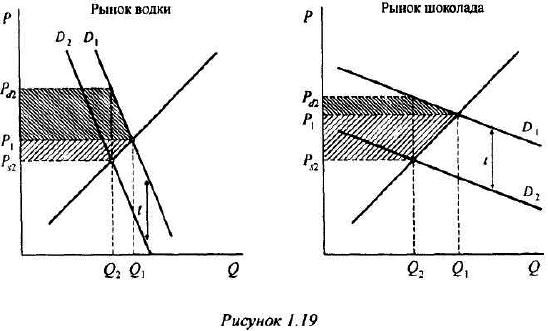
Выбор потребителя
Потребительский выбор (consumer choice) — это выбор, максимизирующий функцию полезности рационального потребителя в условиях ограниченности ресурсов (денежного дохода).
Задача с решением №24 :
Функция полезности домохозяйства описывается формулой 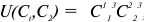
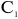
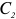
Располагаемый доход домохозяйства в текущем и будущем годах составит 33 тыс. руб. Ставка процента по депозитам (и кредитам) — 10%.
а) Будет ли домохозяйство в текущем году сберегать или пользоваться кредитом и в каком объеме? (5 баллов)
б) Определите реакцию домохозяйства, эффект дохода и эффект замещения по Слуцкому при повышении ставки процента до 20% годовых. (10 баллов)
Решение;
а) Найдем оптимальный объем потребительских расходов в текущем году, воспользовавшись правилом доли дохода:
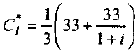
или
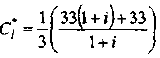
в зависимости от того, приводим ли мы суммы доходов к эквиваленту текущего или будущего года. Отсюда оптимальный объем потребительских расходов в текущем году — 21 тыс. долл. Сумма сбережений в текущем году составляет 12 тыс. долл. Оптимальный объем потребительских расходов в будущем году составит 46,2 тыс. долл.
б) Изменение ставки процента приведет к изменению выбора потребителя так, что оптимальный объем потребительских расходов в текущем году составит 20,17 тыс. долл. Сумма сбережений возрастет до 12,83 тыс. долл. в текущем году, объем потребительских расходов в будущем году — до 48,4 тыс. долл.
Для определения эффекта дохода и эффекта замещения определим, какую комбинацию потребительских расходов в текущем и будущем году выбрал бы потребитель, если бы он располагал в качестве первоначального набора комбинацией, избранной при ставке процента 10% в год — 21 тыс. долл. в первом году, 46,2 тыс. долл. во втором году.
Повышение ставки процента до 20% годовых изменит текущую ценность избранного потребителем набора 21 тыс. долл. в текущем и 46,2 тыс. долл.. потребительских расходов в будущем году. Новый оптимальный объем потребительских расходов в текущем году составит:
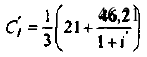
или
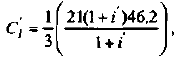
где 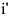
Отсюда оптимальный объем потребительских расходов в текущем периоде равен 19,83.
Следовательно, эффект замещения по Слуцкому составляет: 19,83 — 21 =
= -1,17 тыс. долл., эффект дохода — 20,17 — 19,83 = 0,34 тыс. долл. Мы видим, что эффект дохода в результате повышения ставки процента положителен, поскольку наш потребитель выступал в качестве кредитора: более высокая ставка процента позволила ему расширить границу возможных комбинаций потребительских расходов в текущем и будущем периодах. Решение задачи иллюстрируется на рисунке 1.22.
Задача ставит целью-проверить.знания проблем межвременного, выбора и особенностей эффекта дохода при изменении ставки процента..
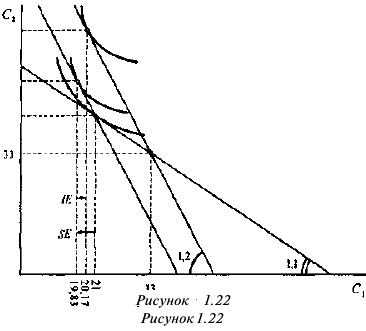
Ценовая дискриминация
Ценовая дискриминация (англ. price discrimination) — ценовая политика, при которой в один и тот же момент один и тот же товар или услуга продается различным покупателям по различным ценам, а эта разница в цене не оправдывается разными издержками производства этого товара или услуги.
Задача с решением №25 :
Фирма, производящая товар с нулевыми издержками, продает товар на двух рынках, спрос на которых описывается формулами: на первом рынке 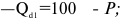
а) Определите цены, объем продаж и прибыль фирмы, осуществляющей ценовую дискриминацию в том случае, если рынки абсолютно изолированы. (5 баллов)
б) Представим себе, что покупатели приобрели возможность арбитража, не сопряженного с дополнительными затратами. Как изменятся объем продаж и прибыль фирмы, а также выигрыш потребителей на рынке, если фирма назначила цены такие, как мы определили в пункте «а»? (5 баллов)
в) Пусть арбитраж возможен, однако сопряжен с трансакционными издержками в размере 10 на единицу продукции. Ответьте на вопрос пункта «а» с учетом изменившихся условий. (5 баллов)
г) Определите зависимость объема продаж на рынках и цены товаров от уровня грансакционных затрат, сопряженных с арбитражем. (5 баллов)
Решение;
а). Из условия максимизирующего прибыль выбора продаж на двух-рынках при ценовой дискриминации третьего типа 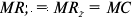
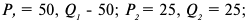
Решение отражается; графиками, представленными- на рисунке 1.23.
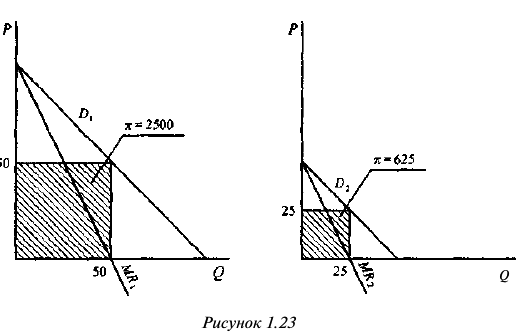
б) В результате использования арбитража, сопряженного с нулевыми затратами, все покупатели приобретают товар на рынке с более низкими ценами: 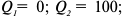
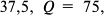
в) Для предотвращения арбитража цена на первом рынке (с большей емкостью) должна превышать цену на втором рынке не более чем на 10 единиц.
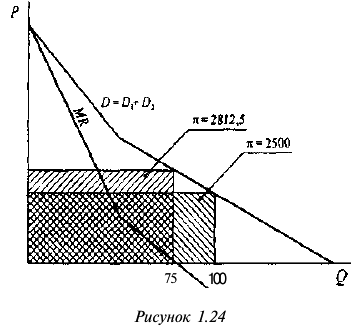
Тогда прибыль монополиста зависит от назначаемых им цен как:
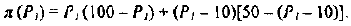
Определяя максимизирующую прибыль цену на первом рынке, получаем:
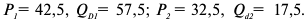
Прибыль монополиста, проводящего ценовую дискриминацию в условиях возможности арбитража, составляет 3012,5.
Обратим внимание, что возможность арбитража понижает цену на рынке с более емким спросом, но повышает цену на рынке с менее емким спросом. Рассчитав выигрыш покупателей, мы придем к тем же результатам: возможность арбитража повышает выигрыш на первом рынке, но понижает его на втором, при увеличении общей суммы выигрыша потребителей.
г) Обозначив трансакционные затраты на единицу продукции как t, получаем зависимость прибыли фирмы-монополиста от цены, устанавливаемой на первом рынке:
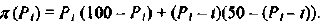
Решая задачу максимизации прибыли, получаем зависимость от трансакционных затрат цены и объема продаж:
на первом рынке
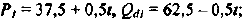
на втором рынке
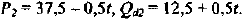
Таким образом, мы видим, что изменение траисакциоиных затрат оказывает разное влияние на цену, объем продаж и благосостояние потребителей на рынках с большей и меньшей емкостью спроса.
Задача ставит целью повторить:
- принципы ценообразования монополиста;
- ценовую дискриминацию третьего типа;
- влияние возможности арбитража и сопряженных с ним затрат на цены, объем продаж, прибыль продавца и выигрыш покупателей.
Потери и выигрыши от государственной политики
Существенной проблемой в государственном регулировании экономики становится возрастающая сложность задач, решаемых в сфере политики. Как правило, правительство должно решить многоцелевую задачу, причем наиболее распространёнными современными экономическими проблемами являются:
- обеспечение экономического роста за счет производства наибольшего объема и наилучшего качества продукции;
- обеспечение полной занятости подразумевает поиск подходящего занятия всем, кто способен и желает трудиться;
- повышение экономической эффективности для получения максимальной отдачи при минимальных издержках и ограниченных ресурсах; поддержание стабильного уровня цен для сокращения рисков инфляции или дефляции;
- обеспечение экономической свободы предпринимателям, рабочим и потребителям; обеспечение справедливости при распределении доходов.
Задача с решением №26 :
Спрос на товар на внутреннем рынке описывается формулой Q= 120 — 2Р, а предложение отечественных производителей — Q = 4Р — 8. На отечественный рынок проникает зарубежная фирма, обладающая преимуществом в издержках (средние издержки производства товара постоянны и равны 3, транспортные издержки считаем равными нулю), и начинает играть доминирующую роль. Определите объем продаж фирмы-импортера и отечественных производителей и уровень благосостояния на внутреннем рынке если:
а) государство проводит либеральную внешнеторговую политику; (5 баллов)
б) государство вводит импортный тариф в размере 2 единиц; (5 баллов)
в) государство вводит импортный тариф в размере 4 единиц. (5 баллов)
Рассчитайте показатели общественного благосостояния в каждом из трех представленных случаев и сделайте вывод о влиянии протекционизма на благосостояние в условиях несовершенной конкуренции. (10 баллов)
Решение;
а) Если государство проводит либеральную внешнеторговую политику, определение параметров равновесия на рынке и уровня благосостояния сводится к решению задачи о ценообразовании доминирующей фирмы в конкурентном окружении.
Остаточный спрос для ценового лидера определяется как:
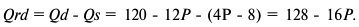
Обратная функция спроса на товар лидера выглядит как:
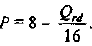
Приравнивая предельную выручку предельным затратам:
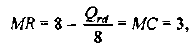
определяем оптимальный объем продаж импортера, равный 40. Из обратной функции спроса на товар лидера определяем рыночную цену, равную 5,5, из функции предложения отечественных продавцов — их объем продаж, равный 14. Осуществляем проверку: объем рыночного спроса по цене, равной 5,5, составляет 54.
б) Алгоритм решения тот же, с единственным различием — введение импортного тарифа оказывает такое же влияние на выбор объема продаж импортера, как оказало бы повышение средних затрат на ту же величину. Введение импортного тарифа приводит к снижению объема продаж импортера — ценового лидера, повышению рыночной цены и повышению объема продаж отечественных фирм.
Анализируя влияние импортного тарифа па благосостояние, мы можем заключить, что его влияние на внутренний рынок противоречиво, и может быть сведено к трем основным эффектам:
- повышение цены (эффект отрицательный);
- повышение выигрыша отечественных производителей (эффект положительный);
- повышение доходов государственного бюджета (эффект положительный).
Эти три эффекта представлены на рисунке 1.25.
Суммарное влияние повышения импортного тарифа зависит от соотношения абсолютной величины трех указанных эффектов.
При небольшом положительном значении импортного тарифа его рост повышает выигрыш производителей и сумму поступлений в государственный бюджет, причем сумма положительного изменения превышает снижение отечественного благосостояния в результате снижения выигрыша потребителей.
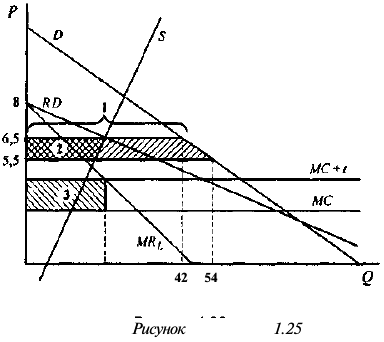
в) Находя новые параметры равновесия внутреннего рынка, определяем, что при повышении импортного тарифа с 2 до 4 сумма выигрыша покупателей, отечественных продавцов и дохода государства от импортного тарифа снижается.
Параметры равновесия при различных вариантах государственной внешнеторговой политики указаны в таблице:
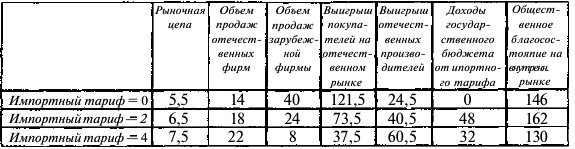
Общий вывод состоит в том, что оптимальный импортный тариф в условиях лидерства импортера на внутреннем рынке оказывается ненулевым. Протекционизм во внешнеторговой политике может иметь положительное влияние на общественное благосостояние.
Задача ставит целью проверить знание:
- принципов ценообразования доминирующей фирмы в конкурентном окружении (в окружении аутсайдеров);
- влияния поштучного (потоварного, косвенного) налога на объем продаж фирмы, обладающей рыночной властью, и рыночную цену;
- принципов определения потерь и выигрышей от осуществления государственной политики регулирования рынков.
Принципы ценообразования в картеле
Картель — это группа фирм, действующих совместно и согласующих решения по поводу объемов выпуска продукции и цен так, как если бы они были единой монополией. Поскольку картель — это группа фирм, а не одна фирма, он сталкивается с трудностями при установлении монопольных цен, которых не существует для чистой монополии. Основная проблема, с которой сталкивается картель, — это проблема согласования решений между фирмами-членами картеля по вопросу установления системы ограничений (квот) для каждой фирмы.
Задача с решением №27 :
Рыночный спрос описывается уравнением 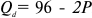
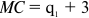
а) Определите оптимальный объем выпуска картеля и некартелиро-ванных фирм и цену, которая складывается на рынке. (7 баллов)
б) Сравните прибыль фирмы, входящей и не входящей в картель. Сделайте выводы об устойчивости картеля. (8 баллов)
Решение;
а) Фирмы, объединенные в картель, играют роль ценового лидера, следовательно, объем их продаж и цена складывается на основе взаимодействия остаточного спроса и предельных затрат.
В свою очередь, фирмы, не объединенные картелем, не имеют возможности назначать цену, но и не заинтересованы в ограничении объема выпуска. Предложение фирмы, не входящей в картель, определяется из условия 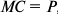
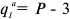
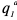
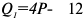
Тогда остаточный спрос на товар картеля, который играет роль ценового лидера на рынке 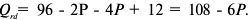
Условием максимизации прибыли фирм, входящих в картель, является равенство предельной выручки предельным затратам каждого члена картеля:
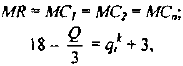
где 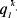
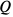
Отсюда оптимальный выпуск каждого члена картеля составляет 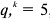
Оптимальный выпуск фирм, не объединенных в картель, находим из их функции предложения 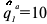
б) Определив общие затраты фирм как 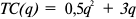

Мы можем еще раз обратить внимание на то, что картельные соглашения неустойчивы потому, что прибыль фирмы-аутсайдера, не ориентированной на максимизацию прибыли всей отрасли, оказывается выше прибыли фирмы, входящей в картель. Обратим внимание на то, что в нашем примере прибыль фирмы-аутсайдера выше, несмотря даже на убывающую отдачу от масштаба производства, действие которой дестимулирует расширение выпуска.
Задача ставит целью проверить знание:
- принципов ценообразования доминирующей фирмы в конкурентном окружении;
- проблемы устойчивости картельных соглашений.
Дилемма заключенного
Дилемма заключённого — фундаментальная проблема в теории игр, согласно которой рациональные игроки не всегда будут сотрудничать друг с другом, даже если это в их интересах. Предполагается, что игрок («заключённый») максимизирует свой собственный выигрыш, не заботясь о выгоде других.
Задача с решением №28 :
На рынке безалкогольных напитков два крупнейших продавца — «Пепси-Кола» и «Кока-Кола». В течение нескольких последних лет цена и объем продаж продукции фирм стабильны, фирмы делят между собой сумму прибыли, составляющую 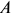
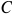
а) Выпишите нормальную (матричную) форму игры. При каких величинах 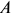
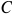
б) Предположим, 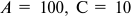
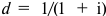
Решение;
а) Нормальная форма игры:
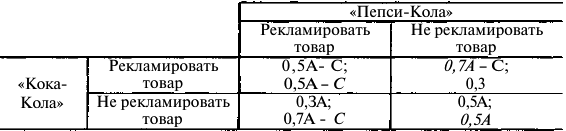
Видно, что если обе фирмы не рекламируют товар, их прибыль больше, нежели в том случае, если обе фирмы рекламируют товар.
«Дилемма заключенного» возникает в том случае, если доминирующей стратегией для обоих продавцов служит стратегия «рекламировать товар». Для этого должны быть выполнены два условия:
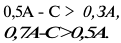
Сумма расходов на рекламу должна быть меньше, чем 20% прибыли рынка.
б) При 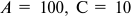
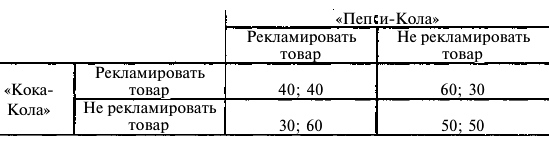
Равновесие по Нэшу в неповторяющейся игре формируют стратегии «рекламировать товар». В игре, повторяющейся конечное число раз, равновесие будет таким же.
При бесконечно повторяющемся взаимодействии фирм выбор между стратегиями «хищничества» (рекламировать товар) и «руки, дрожащей на курке» (не рекламировать товар в период t, если соперник не рекламировал его в период t — 1; рекламировать в другом случае) зависит от соотношения текущей ценности прибыли фирм при выборе двух стратегий.
Максимальный выигрыш при стратегии «хищничества»: 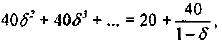
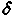
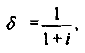
где 
Максимальный выигрыш при стратегии «курка»:
Равновесие по Нэшу в игре обеспечивается при любой стратегии, если выполняется условие:
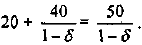
Откуда
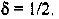
При значении дисконтирующего множителя, меньшем, чем 1/2, доминирующей служит стратегия «хищничества», при большем — стратегия «курка».
Задача ставит целью проверить знание элементов теории игр и их экономического применения.
Дизайн этой задачи очень типичен для заданий, ставящих целью показать проблемы конкуренции фирмы на рынках. Аналогичные проблемы возникают при стратегическом выборе суммы расходов на инновации (типичная задача, посвященная этой проблеме, приведена в варианте 3).
Вариации денежного дохода по Слуцкому и по Хиксу
Положение о разложении общего эффекта изменения цен на эффект замены и эффект дохода впервые выдвинул российский экономист, математик и статистик Евгений Евгеньевич Слуцкий (1880-1948). В 1915 г. он опубликовал в итальянском экономическом журнале статью «К теории сбалансированного бюджета потребителя». Эта статья была «открыта» в 30-х гг. английским экономистом, математиком и статистиком Р. Алленом. О приоритете научного исследования этой проблемы Е. Слуцким говорит английский экономист Дж. Хикс в своей работе «Стоимость и капитал», в которой он указывает, что разработанная им в Соавторстве с Р. Алленом теория поведения потребителя «принадлежит по существу Слуцкому, с той лишь оговоркой, что я совершенно не был знаком с его работой ни во время завершения своего собственного исследования, ни даже некоторое время после опубликования содержания этих глав в журнале «Экономика» Р. Алленом и мной».
Подходы Слуцкого и Хикса к определению реального дохода отличаются. По Хиксу, разные уровни денежного дохода, обеспечивающие один и тот же уровень удовлетворения, представляют одинаковый уровень реального дохода. По Слуцкому, только тот уровень денежного дохода, который достаточен для приобретения одного и того же набора или комбинации товаров, обеспечивает и неизменный уровень реального дохода.
Задача с решением №29 :
Функция полезности домохозяйства описывается формулой 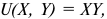
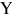
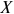
Решение;
Оптимальный объем приобретения товара 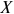
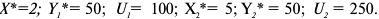
По Слуцкому компенсирующая вариация денежного дохода равна —30, а эквивалентная вариация 75.
Минимизация расходов пр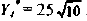
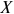
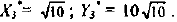
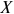
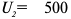
Эквивалентная вариация денежного дохода по Хиксу — 58,11.
Компенсирующая вариация изменения цен
Компенсирующее изменение – это то изменение дохода, которое при изменении цен возвращает потребителя на прежний уровень полезности (т. е. тот уровень, который имел потребитель до изменения цен и при неизменном доходе).
Задача с решением №30 :
Функция полезности потребителя 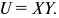
а) Определите эквивалентную и компенсирующую вариацию денежного дохода потребителя (по Слуцкому). (5 баллов)
б) Доход потребителя индексируется исходя из расчета индекса потребительских цен (индекса Ласпейреса). Сколько составит номинальный доход потребителя в 1996 г.? (5 баллов) Как изменится благосостояние потребителя в 1996 г. по сравнению с 1995 г.? (5 баллов)
Решение;
а) Компенсирующая вариация изменения цен (по Слуцкому) — 10,5, эквивалентная- -7,5.
б) Индекс цен Ласпейраса = 1,25. Индексированный денежный доход = 40,5. Полезность в базовом году 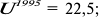
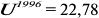
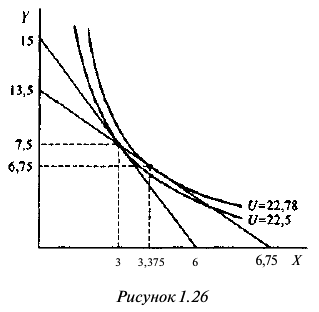
Валовый национальный продукт
Валовой национальный продукт — один из основных макроэкономических показателей системы национальных счетов. Зачастую употребляется совместно с показателем ВВП, или заменяется им, что в общем неверно.
Задача с решением №31 :
Даны следующие макроэкономические показатели:

Определить: ВНП (двумя способами), ВВП, ЧНП, НД, ЛД, РЛД, личные сбережения, сальдо торгового баланса, чистые инвестиции.
Решение;
ВНП (по расходам) = Расходы наличное потребление + Валовые инвестиции + Госзакупки товаров и услуг + Экспорт — Импорт = 325 + 76 + 4- 105 + 57- 10 = 553.
ВНП (по доходам) = Заработная плата + Процентные платежи + Арендная плата + Доходы от собственности + Прибыль корпораций (которая равна: Налог на прибыль корпораций + Дивиденды + Нераспределенная прибыль корпораций) + Косвенные налоги на бизнес + Стоимость потребленного капитала = 382 + 25 + 24 + 63 + 31 (9 + 18 + 4) + 11 + 17= 553.
ВВП = ВНП — Доходы, полученные гражданами страны за рубежом + Доходы, полученные иностранцами в данной стране = 553 — 12 + 8 = 549.
ЧНП = ВНП — Стоимость потребленного капитала = 553 — 17 = 536.
НД = ЧНП — Косвенные налоги на бизнес = 536 — 11 = 525.
Или НД = Заработная плата + Процентные платежи + Арендная плата + Доходы от собственности + Прибыль корпораций = 382 + 25 + 24 + 63 + + 31=525.
ЛД = НД — Взносы на социальное страхование — Налог на прибыль корпораций — Нераспределенная прибыль корпораций + Трансфертные платежи + Проценты по государственным облигациям = 525 — 43-9-4 + 16 + 19 = 504.
РЛД = ЛД — Индивидуальные налоги = 504 — 41 = 463.
Личные сбережения = РЛД — Расходы на личное потребление = 463 —325 = 138.
Сальдо торгового баланса = Экспорт — Импорт = 57 — 10 = 47.
Чистые инвестиции = Валовые инвестиции — Стоимость потребленного капитала = 76 — 17 = 59.
Номинальный и реальный ВНП
Номинальный ВВП – представлен суммой стоимости всего произведенного. Реальный ВВП, по сравнению с номинальным, несет информацию о том, сколько стоят товары на самом деле.
Задача с решением №32 :
В Алабамбии производятся только три товара: ананасы, авоськи и аквариумы. Поданным, приведенным в таблице, рассчитайте номинальный и реальный ВНП 1990 и 1997 гг., дефлятор и ИПЦ, если 1990 г. — базовый:
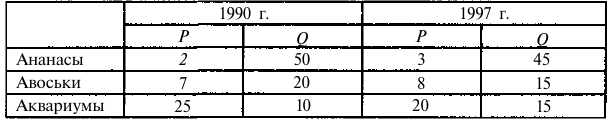
Как изменились за этот период стоимость жизни и уровень цен?
Решение;
Номинальный ВНП 1990 г. = Реальный ВНП 1990 г. (поскольку этот год базовый) = 2 • 50 + 7 • 20 + 25 • 10 = 490.
Номинальный ВНП 1997 г. = 3 • 45 + 8 • 15 + 20 • 15 = 555.
Реальный ВНП 1997 г. =2 • 45 + 7 • 15 + 25 * 15 = 570.
Дефлятор ВНП = (3 • 45 + 8 • 15 + 20 • 15)/(2 • 45 + 7 • 15 + 25 • 15) = 555/570 = 0,97. Следовательно, уровень цен снизился на 3%, т.е. в экономике произошла дефляция.
ИПЦ=[(3 • 50 + 8 • 20 + 20 • 10)/(2 • 50 + 7 • 20 + 25 • 10)] • 100% = = (510/490) • 100%= 104%.
Следовательно, стоимость жизни возросла на 4%.
Сальдо торгового баланса
Сальдо торгового баланса (англ. — tradebalance) – торговое сальдо: разница между поступлениями и расходами по внешнеторговым сделкам страны.
Задача с решением №33 :
Экономика страны характеризуется следующими показателями: инвестиции равны 900 млрд. лир, частные сбережения 400 млрд. лир, излишек государственного бюджета 200 млрд. лир. Определите сальдо торгового баланса.
Решение;
В соответствии с макроэкономическим тождеством совокупные расходы равны совокупному доходу, т.е. = Потребительские расходы 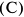
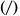
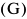
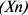
Или Инъекции = Изъятиям, т.е. 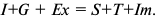
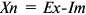
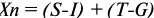
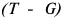
В Экономикс имеет место дефицит торгового баланса, равный 300 млрд. лир.
Темп экономического роста
В самом общем виде под экономическим ростом подразумевается количественное увеличение на душу населения и качественное совершенствование во времени валового национального продукта (или валового внутреннего продукта) как главного источника повышения жизненного уровня населения. Если экономика какой-либо страны в состоянии воспроизвести больше совокупного продукта, чем его было произведено в предыдущий период, то принято говорить о расширенном воспроизводстве. Именно динамика расширенного воспроизводства характеризует экономический рост. Наиболее распространенное определение таково: экономический рост – это скорость изменения объема реального ВВП (или ВНП) за определенный период времени.
Задача с решением №34 :
Реальный ВНП 1993 г. составил 2600 млрд. песо. Дефлятор ВНП в 1994 г. был равен 1,3, а номинальный ВНП 2800. Определите темп экономического роста и фазу цикла.
Решение;
ВНП реальный 1994 г. = ВНП номинальный 1994 г. / Дефлятор ВНП = 2800/1,3 =2154 (млрд. песо).
Темп экономического роста = (Реальный ВНП 1994 г. — Реальный ВНП 1993 г.) / Реальный ВНП 1993 г. = (2154 — 2600)/2600 = -0,17.
Следовательно, реальный объем производства снизился в 1994 г. на 17%, что соответствует фазе экономического спада.
Индекс потребительских цен
Индекс потребительских цен (ИПЦ, индекс инфляции, англ. Consumer Price Index, CPI) — один из видов индексов цен, созданный для измерения среднего уровня изменения цен на товары и услуги (потребительской корзины) за определённый период в экономике.
Задача с решением №35 :
Известно, что индекс потребительских цен в 1991 г. был равен 110%, а в 1992 — 125 %. Считая, что темп инфляции в следующем году не изменится, вы решили предоставить другу заем, предполагая получить со своих денег 5% годовых. Какова будет реальная доходность вашего капитала, если теми инфляции но итогам года составил 15%?
Решение;
Используем определение для нахождения уровня инфляции 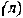
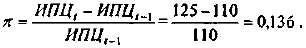
Инфляция за год составила 13,6 %. Используя уравнение Фишера для ставки процента ex ante:
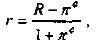
подсчитаем номинальный процент 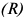
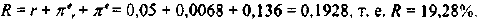
Теперь, используя уравнение Фишера для ставки ex post, подсчитаем реальный процент, который будет получен при фактическом уровне инфляции
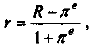
где 
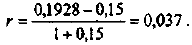
Таким образом, реальная ставка процента будет равна 3,8 %.
Предельная склонность к сбережению
Предельная склонность к сбережению (Marginal propensity to save, MPS) — это часть полученной населением дополнительной денежной единицы, которая увеличивает реальный наличный доход населения и направленная на дополнительное сбережение.
Задача с решением №36 :
Экономика страны характеризуется следующими показателями: предельная склонность к сбережению 
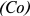
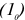
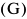
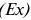
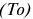
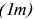
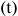
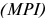
Рассчитайте величину равновесных инвестиций, сбережений, мультипликаторы автономных расходов и налогов, величину налоговых поступлений и сальдо государственного бюджета. При какой величине ВНП сальдо торгового баланса будет равно 0.
Решение;
Запишем условие равновесия товарного рынка:
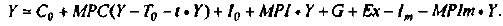
Отсюда получаем равновесный
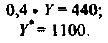
Следовательно, равновесные инвестиции составят:
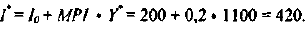
Равновесные сбережения:
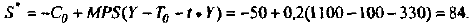
Величина налогов:
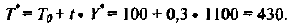
Сальдо государственного бюджета:
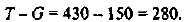
Мультипликатор автономных расходов:
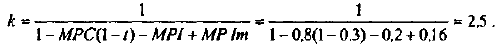
Мультипликатор налоговый:
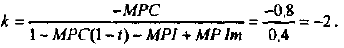
Для подсчета величины ВНП, необходимой для того, чтобы сальдо торгового баланса равнялось 0, надо решить следующее уравнение:
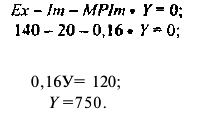
Чувствительность спроса на деньги
В современных условиях представители неоклассического направления также признают, что фактором спроса на деньги является не только уровень дохода, но и ставка процента, причем зависимость между спросом на деньги и ставкой процента обратная. Однако они по-прежнему придерживаются точки зрения, что существует единственный мотив спроса на деньги – трансакционный. И именно трансакционный спрос обратно зависит от ставки процента. Эта идея была предложена и доказана двумя американскими экономистами Уильямом Баумолем (1952 г.) и лауреатом Нобелевской премии Джеймсом Тобином (1956 г.) и получила название модели управления наличностью Баумоля-Тобина.
Задача с решением №37 :
Известно, что при номинальном ВНП 4000 у.е. и уровне цен 2, номинальное предложение денег составило 2000 у.е., а равновесная ставка процента 10%. Когда произошло снижение уровня цен в экономике в 2 раза, а номинальный ВНП составил 25% от прежнего уровня, номинальное предложение денег сократилось до 300 и равновесная ставка процента выросла до 15%. Определить чувствительность спроса на деньги к изменениям дохода и ставки процента, если известно, что реальный спрос на деньги линейно зависит от уровня дохода и от ставки процента.
Решение;
Запишем линейную зависимость реального спроса на деньги от уровня дохода и ставки процента:
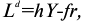
где 
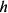
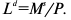
Теперь составим систему, подставив в это уравнение два разных сочетания дохода, ставки процента, реального денежного предложения:
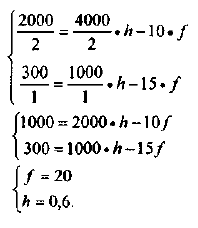
Кейсианское условие равновесия
Кейнсианское равновесие формируется в условиях неполной занятости, при которой величина безработицы обусловлена зависимостью спроса на труд от величины эффективного спроса и жесткой фиксацией номинальной ставки заработной платы.
Задача с решением №38 :
Рассмотрим экономику, описанную следующим образом:
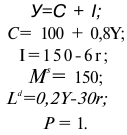
Для данной экономики нужно:
а) найти уравнения 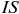
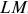
б) найти состояние равновесия в модели 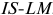
в) определить, изменилось ли и как состояние равновесия в модели 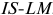
г) определить, как должна изменится чувствительность инвестиций к ставке процента, чтобы равновесный доход принял прежнее значение.
Решение;
а) Из кейнсианского условия равновесия товарного рынка (доходы экономики в точке равновесия равняются се расходам) выводим уравнение 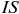
Уравнение 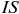
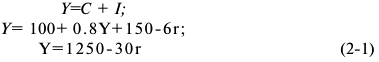
Из кейнсианского условия равновесия денежного рынка (спрос на реальные кассовые остатки в точке равновесия равен реальному денежному предложению) построим для данной экономики уравнение кривой 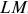
Уравнение 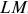

б) По условию требуется найти точку, одновременно удовлетворяющую условию равновесия как товарного, так и денежного рынка. Геометрически такой точкой будет являться точка пересечения кривых 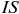
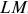
Равновесие товарного и денежного рынка:
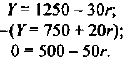
Решая данную систему, получаем равновесные для обоих рынков значения ставки процента и уровня дохода:
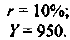
в) Так как условия, задающие равновесие на денежном рынке изменились, требуется построить новую кривую всевозможных состояний равновесия денежного рынка
Уравнение 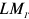
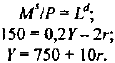
В этом случае точка равновесия модели 
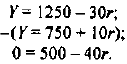
Решая систему, получаем равновесные для обоих рынков значения ставки процента и уровня дохода в новых условиях:
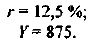
г) В новых условиях опять, как и в предыдущем случае, происходит изменение условий, задающих равновесие в модели 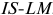
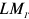
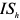
Равновесие 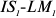
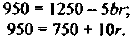
Решая систему, получаем равновесные для обоих рынков значения ставки процента и уровня дохода в новых условиях:
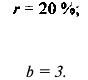
Графически поиск новых точек равновесия при изменении первоначальных условий можно проиллюстрировать на графике, представленном на рисунке 2.1.
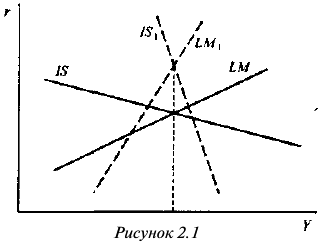
Эффект вытеснения
Эффект вытеснения (англ. crowding out) — эффект стимулирующей фискальной политики государства. Увеличивая размеры государственных расходов, правительство выходит на денежный рынок, чтобы профинансировать бюджетный дефицит.
Задача с решением №39 :
Домашнее хозяйство сберегает 20% прироста своего дохода, а автономное сбережение составляет -40, инвестиции заданы формулой 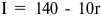
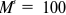
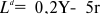
Определить:
а) равновесное значение ставки процента, уровня дохода, потребления и инвестиций;
б) равновесное значение ставки процента, уровня дохода, потребления и инвестиций при условии, что произошел рост государственных расходов за счет продажи государственных ценных бумаг;
в) чему равен в этом случае эффект вытеснения;
г) какую политику должен проводить ЦБ в этом случае, чтобы ликвидировать эффект вытеснения.
Решение;
а) Согласно кейнсианскому условию равновесия товарного рынка (доходы экономики в точке равновесия равняются ее расходам) выводим уравнение 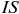
Уравнение 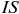
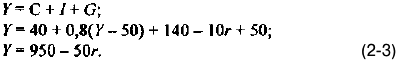
Из кейнсианского условия равновесия денежного рынка (спрос на реальные кассовые остатки в точке равновесия равен реальному денежному предложению) построим для данной экономики уравнение кривой 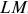
Уравнение 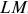

Далее найдем точку, одновременно удовлетворяющую условию равновесия как товарного так и денежного рынка. Геометрически такой точкой будет являться точка пересечения кривых 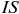
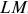
Равновесие 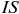
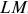
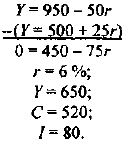
б) Так как условия, задающие равновесие на товарном рынке изменились, то требуется построить новую кривую всевозможных состояний равновесия товарного рынка 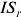
Уравнение 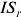
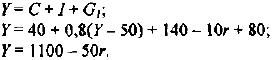
Далее найдем точку, одновременно удовлетворяющую новому условию равновесия товарного рынка и старому условию равновесия денежного рынка, т.е. равновесие 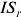
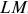
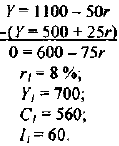
в) Для того чтобы найти эффект вытеснения 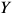

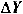
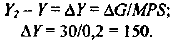
Затем подсчитать мультипликативный эффект воздействия 
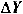
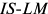
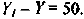
Теперь подсчитаем разницу этих воздействий, т.е. эффект вытеснения:
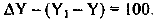
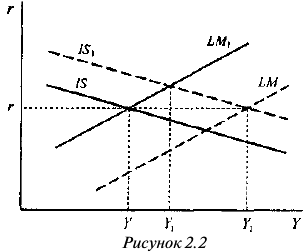
г) Для ликвидации эффекта г вытеснения необходимо, чтобы экономика перешла в новое равновесное состояние, характеризуемое равновесным доходом 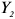
Так как условия, задающие равновесие на денежном рынке в этом случае изменятся, то для экономики изменится кривая всевозможных состояний равновесия денежного рынка.
Подсчитаем новую кривую всевозможных состояний равновесия денежного рынка — 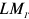
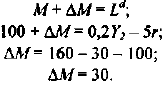
Уравнение IS и уравнение LM
Mодель IS-LM — неокейнсианская макроэкономическая модель, которая описывает общее макроэкономическое равновесие в закрытой экономике как результат одновременного равновесия на товарном (кривая IS) и денежном (кривая LM) рынках. Модель была разработана английским и американским экономистами Джоном Хиксом и Элвином Хансеном и впервые использована в 1937 году.
Модель предназначена для анализа бизнес-циклов и является моделью короткого периода. Название модели происходит от названия кривых: кривая IS и кривая LM, описывающих множества равновесий на рынках инвестиций-сбережений и рынке денег.
Модель является в значительной степени устаревшей, однако иногда используется для анализа и в учебных целях. Современные модели бизнес-циклов построены в рамках новой классической и новой кейнсианской теорий.
Задача с решением №40 :
Номинальное количество денег в обращении равно 200, скорость их оборота равна 10, спекулятивный спрос 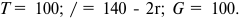
Решение;
а) Из кейнсианского условия равновесия товарного рынка (доходы экономики в точке равновесия равняются ее расходам) выводим уравнение 
Уравнение 
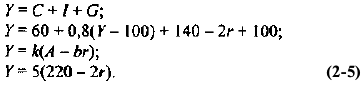
Из кейнсианского условия равновесия денежного рынка (спрос на реальные кассовые остатки в точке равновесия равен реальному денежному предложению) построим для данной экономики уравнение кривой 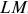
Уравнение 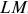

Далее найдем точку, одновременно удовлетворяющую условию равновесия как товарного, так и денежного рынка. При снятии условия постоянства цен точка равновесия в модели 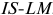
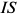
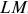
Уравнение 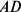
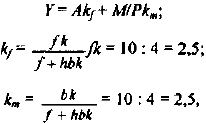
где 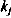
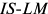
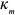
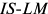
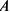
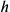
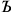
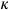
Решив данное уравнения относительно уровня цен, получим искомое значение:
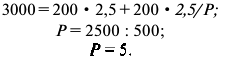
Спрос фирм на труд
Спрос на труд — количество труда, которое работодатели желают нанять в данный период времени заопределенную ставку заработной платы. Спрос на труд определяется: — объемом производства и его отраслевой структурой; — степенью трудоемкости производства; — ценой труда.
Задача с решением №41 :
(Спрос фирм на труд.) Дана производственная функция 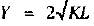
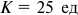
Найдите: реальную и номинальную ставки заработной платы, объем выпуска и количество работников (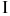
Решение;
Из производственной функции получаем предельный продукт труда, который при условии оптимизации прибыли конкурентной фирмой равен ставке реальной заработной платы одного работника:
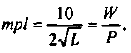
Доход фирмы распадается на доход труда и доход капитала (по теореме Эйлера, так как производственная функция однородна первой степени, т.е. отдача от масштаба — постоянная):
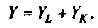
Поскольку все работники являются собственниками и владеют одинаковой долей капитала можно записать доход фирмы как сумму заработков работников и их дивидендов (в реальном выражении, в данном случае — в штуках изделий фирмы):
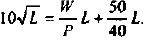
Подставим вместо ставки заработной платы предельный продукт труда:
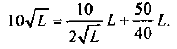
Отсюда, 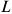
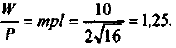
Номинальная ставка заработной платы равна реальной, умноженной на цену изделия:
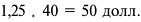
Выпуск фирмы находим из производственной функции, он равен 40. Доход труда равен ставке заработной платы, умноженной на количество работников, т.е. 20.
Бюджетное ограничение потребителя
Бюджетное ограничение представляет собой максимальную сумму денег, которую человек готов израсходовать на приобретение имеющихся в магазинах товаров и услуг по тем ценам, которые запрашивают продавцы.
Задача с решением №42 :
(Предложение сбережений домохозяйствами.) Предположим, что жизненный цикл домохозяйства (потребителя) состоит из двух одинаковых периодов (для простоты — двух лет). Функция полезности потребителя 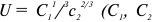
Решение;
Запишем бюджетное ограничение потребителя дня двух периодов:
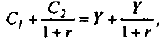
отсюда
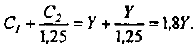
Поскольку жизненный цикл домохозяйства состоит из двух периодов, сбережения составляют разницу между доходом и потреблением первого периода:
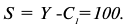
Следовательно:
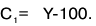
Из условий оптимизации задачи межвременного выбора известно, что в точке оптимального выбора углы наклонов бюджетного ограничения и кривой безразличия, совпадают.
Угол наклона бюджетного ограничения
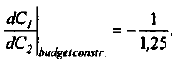
Угол наклона кривой безразличия:
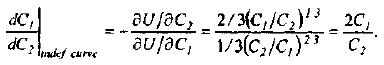
Следовательно:
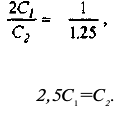
Подставляем в бюджетное ограничение:
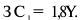
Отсюда:
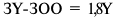
Следовательно:
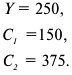
Теория Тобина
Коэффициент Тобина (q) — отношение рыночной стоимости компании к восстановительной стоимости активов компании. Это соотношение было разработано в 1969 году американским экономистом Джеймсом Тобином.
Задача с решением №43 :
(Теория 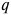
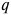
Решение;
Стоимость одной акции фирмы равна дисконтированной стоимости ожидаемых дивидендов и составляет:
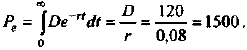
Рыночная стоимость фирмы равна произведению рыночной стоимости акции на число акций: 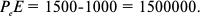
Коэффициент 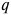
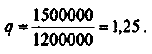
Поскольку коэффициент больше единицы, фирма примет решение осуществлять инвестиции.
Модель Баумоля
Модель Баумоля (Baumol model) — алгоритм, позволяющий оптимизировать размер среднего остатка денежных активов предприятия с учетом объема его платежного оборота.
Задача с решением №44 :
(Модель Баумоля — Тобина.) Предполагается индивидуум, оптимизирующий свой финансовый портфель, получающий доход в начале периода в форме доходных активов и осуществляющий равномерное потребление этого дохода в течение данного периода (года). Оплата потребления возможна только наличными, конвертация активов в наличные влечет аккордные издержки в виде комиссионного сбора.
Сумма трансакционных издержек и издержек недополученных процентов индивидуума при оптимальном финансовом портфеле равна 56 долл., процентная ставка равна 7% годовых. Известно, что интервал между посещениями банка индивидуумом 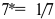
Решение;
Издержки состоят из издержек недополученных процентов (процента на средний кассовый остаток) и комиссионного сбора, умноженного на количество посещений банка (величину, обратную интервалу). Средний кассовый остаток равен среднеарифметической величине обмениваемой суммы, т.е. величине потребления, умноженной па интервал и деленной пополам: 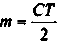
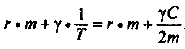
Если выполняется условие оптимизации — формула квадратного корня — 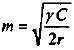
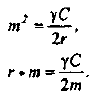
Следовательно, издержки каждого вида равны их полусумме:
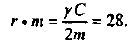
Отсюда:
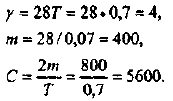
Неоклассическая модель
Неоклассическая экономическая теория возникла в 1870-е годы.
Экономисты неоклассического направления разработали теорию предельной производительности; теорию общего равновесия, согласно которой механизм свободной конкуренции и рыночного ценообразования обеспечивает справедливое распределение доходов и полное использование экономических ресурсов; экономическую теорию благосостояния, принципы которой положены в основу современной теории государственных финансов (П. Сэмуэльсон); теорию рациональных ожиданий и др.
Задача с решением №45 :
(Неоклассическая модель.) Закрытая экономика соответствует следующей модели:

Найдите изменения в равновесном состоянии при временном увеличении государственных расходов на 10 ед. и финансировании их за счет денежной эмиссии. Определите постоянный эффект этой политики. Опишите основные последствия проводимой политики.
Решение;
а) Процентную ставку для неоклассической модели можно найти из равновесия товарного рынка:
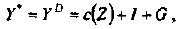
где 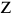
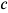
Составим уравнение товарного рынка и определим процентную ставку:
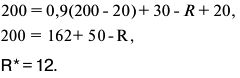
Равновесие рынка денег в неоклассической модели определяет уровень цен:
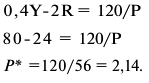
б) Найдем изменения переменных при политике монетизации дефицита государственного бюджета. Следует подчеркнуть, что изменение денежного предложения, необходимое для покрытия дефицита выражено в реальной величине.
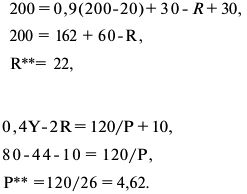
Политика монетизации дефицита государственного бюджета вызвала значительное изменение цен и процентной ставки. Следствием изменения процентной ставки является эффект вытеснения частных инвестиций:
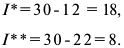
Инвестиции упали в 2,25 раза, что скажется в дальнейшем на темпах роста объема капитала и естественного уровня объема производства Следствием изменения цен в данном случае является пропорциональное изменение всех номинальных величин.
в) Постоянным последствием данной политики является изменение денежного предложения, которое не уменьшится само по себе даже при прекращении се осуществления.
Равновесие товарного рынка восстановится на первоначальном уровне, однако введенный номинальный объем денежного предложения в размере 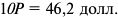
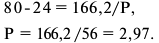
Цены несколько понизятся от возросшего уровня, но к первоначальному уровню не вернутся. Процентная ставка и другие реальные величины не изменятся, эффект вытеснения не возникнет. Все номинальные величины возрастут пропорционально уровню цен. Деньги являются нейтральными.
Гипотеза двойственного решения
Гипотеза двойного решения дает теоретическое обоснование кейнсианской функции потребления посредством понятий и постулатов неоклассической концепции. Домашнее хозяйство формирует план потребления на основе максимизации полезности своей хозяйственной деятельности. Но если при заданных ценах не удается реализовать гипотетическое предложение труда, то доход индивида из эндогенного превращается в экзогенный параметр, определяющий размер текущего потребления.
Гипотеза двойного решения распространяется и на поведение предпринимателей. Они определяют объемы выпуска и спроса на факторы производства из условия максимизации прибыли при заданных ценах. Если в ходе реализации намеченных планов предприниматели встречают ограничения на одном из рынков, то они корректируют свои операции на других рынках.
Задача с решением №46 :
(Гипотеза двойственного решения.) Дано: производственная функция 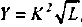
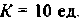

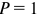
Вследствие недостаточного уровня эффективного спроса безработица составляет 20% от естественного уровня занятости.
Найдите: эффективный и теоретический спрос на рынке труда, соответствующие уровни реальной заработной платы, эффективный спрос на товарном рынке, естественный уровень выпуска.
Решение;
Теоретический спрос на труд определяется исходя из концепции предельной производительности и максимизации прибыли конкурентной фирмой.
Спрос на труд будет оптимален при равенстве предельного продукта труда ставке реальной заработной платы:
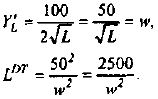
Теперь можно найти теоретическое равновесие:
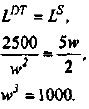
Искомые теоретические величины равны:
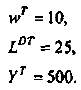
Эффективный спрос по условию составляет 80% от уровня теоретического, следовательно:
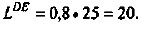
Эффективное равновесие определяется равенством эффективного спроса на труд предложению труда:
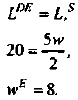
Эффективный спрос на товарном рынке находим подставляя величину эффективного спроса на труд в производственную функцию:

Модель закрытой экономики
Закрытаяэкономика (также известная под определением «автаркия») — это модель государства, в котором все нужды населения удовлетворяются исключительно собственными силами и только за счет имеющихся ресурсов.
Задача с решением №47 :
(Кейнсианская модель с эндогенными ценами.) Возьмем модель закрытой экономики в следующих линейных уравнениях:
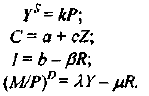
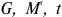
Покажите, как изменения в ставке налога могут воздействовать на выпуск.
Решение;
Запишем уравнения равновесия товарного и денежного рынков — уравнения 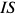
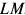

Из уравнения 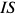
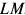
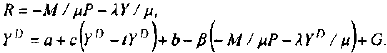
Равновесие модели достигается при равновесии совокупного спроса и совокупного предложения при равновесной цене, поэтому переменную 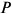
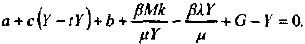
Для того чтобы определить воздействие изменений ставки налога на выпуск, необходимо продифференцировать данное уравнение по переменным 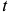
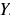
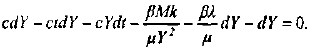
Теперь выразим зависимость между изменениями налоговой ставки и объема выпуска:
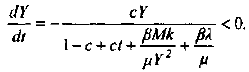
Поскольку все переменные и параметры правой части положительны, знак полученного выражения отрицательный, поэтому зависимость между изменениями ставки налога и выпуском обратная.
Готовые задачи с решениями по экономике
Термин «экономика» имеет два значения:
- Во-первых, так называют способ организации деятельности людей, направленной на создание благ, необходимых им для потребления. Синонимом этого значения является понятие «хозяйство».
- Во-вторых, «экономика» (или «экономике» — как принято писать в англоязычных странах) обозначает науку, которая исследует, как люди используют имеющиеся ограниченные ресурсы для удовлетворения своих неограниченных потребностей в жизненных благах.
Поскольку экономическая наука изучает поведение людей, то она относится к категории общественных (социальных) наук, так же, как история или философия, хотя применяемые в ней методы исследования предполагают более широкое использование математики и разнообразных графиков.
Основы теории спроса и предложения
Механизм рыночной саморегуляции включает следующие элементы: спрос и предложение; цены; конкуренцию.
В основе формирования спроса лежат потребности. Но не всякая потребность учитывается рынком и превращается в спрос. Желание получить тот или иной товар (услугу) должно дополняться возможностями потребителя, т.е. рынок учитывает лишь платежеспособные потребности.
Под спросом понимается количество товара, которое желают и могут приобрести покупатели в единицу времени в конкретной рыночной ситуации. Функция спроса — функция, определяющая зависимость спроса от всех влияющих на него факторов. Обычно она задается алгебраически:
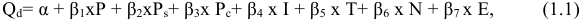
где 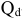
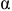
При предположении, что функция спроса носит линейный характер, а основной, определяющей переменной является цена, функция предложения может быть представлена в следующем виде:

где 
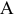
В отличие от спроса предложение отражает поступление товаров на рынок для их продажи или обмена на другие экономические блага. Если спрос формируют покупатели, то предложение — продавцы.
Предложение- это совокупность товаров и услуг, являющихся результатом производства и представленных на рынке с целью продажи (обмена) в единицу времени в конкретной рыночной ситуации. Оно определяется производством, но не всегда совпадает с ним. При одном и том же объеме производства в зависимости от цен на товары и услуги предложение может изменяться.
При предположении, что функция предложения носит линейный характер, а основной, определяющей переменной является цена, функция предложения может быть представлена в следующем виде:

Уравнение отражает прямую зависимость между уровнем цены и количеством продукции, которую производитель готов предложить рынку.
Цены играют роль ориентира для производителей и покупателей: производителям они помогают принимать решения об объемах производства, о выборе технологий с учетом допустимого уровня издержек производства; потребителям — принимать решения о приобретении товаров и услуг при данном уровне дохода.Цена равновесия — это цена, при которой величина спроса равна величине предложения.
Конкуренция (от латинского сопсштеге — сталкиваться) — это соперничество на рынке за лучшие условия производства, купли, продажи.
Способность спроса и предложения адаптироваться к изменяющимся рыночным условиям называется эластичностью. Понятие эластичности не является чисто экономическим. Она может определяться практически для любых процессов (физических, химических и т. д.) Под эластичностью понимается мера (степень) реагирования одной переменной величины на изменение другой переменной величины.
Эластичность — важнейшая характеристика спроса, показывающая зависимость изменения величины спроса от изменения различных факторов (цены, дохода и др.). Это показатель степени чувствительности, реакции потребителей к изменениям цены товара.
Любой покупатель и продавец реагируют на изменение многих социально-экономических условий на рынке. Видов эластичности спроса и предложения может быть столько, сколько факторов влияет на изменение этих переменных. Однако влияние многих из этих факторов крайне трудно оценить и формализовать, поэтому на практике анализируется воздействие лишь наиболее значимых из них.
При анализе спроса наиболее важными факторами, вызывающими его изменение, являются цены анализируемых товаров, цены заменителей, взаимодополняющих товаров, доходы потребителей. Поэтому и исследуются, как правило, три вида эластичности спроса:
- прямая эластичность спроса (эластичность спроса по цене);
- эластичность спроса по доходу;
- перекрестная эластичность спроса, отражающая меру реагирования спроса на изменение цен других товаров.
Оценивается эластичность с помощью коэффициентов эластичности, которые показывают, на сколько процентов изменится одна переменная (в данном случае спрос) при изменении на 1% другой переменной (цены, дохода). Коэффициент эластичности обозначается Е с добавлением соответствующих индексов: верхний индекс показывает, изменение какой переменной анализируется, нижний — под воздействием какой переменной происходит изменение. Например, коэффициент эластичности спроса по цене рассчитывается по формуле

где 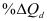
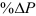
Процентное изменение переменной определяется как отношение ее абсолютного изменения к первоначальному уровню, выраженное в процентах

Так как между ценой товара и объемом спроса на него существует обратная зависимость, определяемая законом спроса, то коэффициент ценовой эластичности спроса имеет отрицательное значение. Экономисты обычно учитывают лишь абсолютную величину коэффициента эластичности спроса, т.е. берут значение коэффициента по модулю 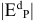
Существуют два подхода к вычислению эластичности:
- метод вычисления эластичности в точке (в конкретной ситуации);
- метод вычисления эластичности по дуге (на основе знаний о состоянии процесса в двух ситуациях).
Эластичностью функции 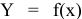
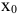
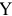
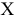
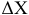
Таким образом, точечная эластичность спроса определяется по формуле

где 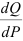
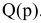
Если же известны цены и соответствующие им объемы спроса для двух ситуаций (двух точек кривой спроса), вычисляется эластичность спроса по дуге (дуговая эластичность). В этом случае формула коэффициента эластичности принимает вид

Задача №1.
Функции спроса и предложения на рынке заданы с помощью формул:
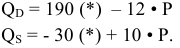
Определите рыночные цену и объем покупок.
(*) Для каждого варианта значение функций спроса и предложения увеличивается на номер варианта, умноженный на 5, то есть, например, для 14 варианта увеличится на 14 * 5 = 70 и составит 190 + 70 = 260.
Решение:
1) Используем условие для определения рыночной цены:
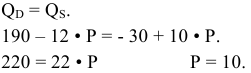
2) Рассчитаем рыночный объем покупок, для этого подставим цену в функцию спроса.
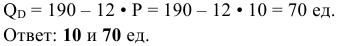
Задача №2.
Для каждого варианта величина спроса уменьшается на номер варианта, умноженный на 100, то есть, например, для 14 варианта уменьшится на 14 * 100 = 1400 и составит 10000 — 1400 = 8600.
Решение:
Линейная функция спроса имеет вид
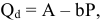
где 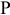
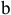
Следовательно
Для определения 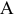
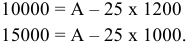
Отсюда следует
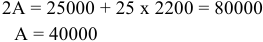
Функция спроса
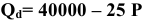
2) Определим выручку продавца по каждой цене по формуле:
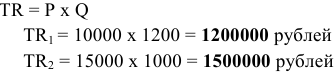
3) Максимальная выручка достигается при единичной эластичности спроса. Ценовая эластичность спроса равна 1 в точке, когда цена товара
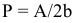
Следовательно 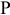
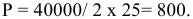
В этом случае выручка составит
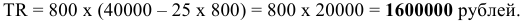
Возможен и другой вариант определения условий получения максимальной выручки. Любая функция достигает максимума при условии, что производная от этой функции равна 0.
- Уравнение рыночной кривой спроса представляет
, а уравнение кривой предложения
. Какой в этом случае будет равновесная рыночная цена?
- На рынке видеокассет следующая ситуация:

- Постройте графики спроса и предложения.
- Определите равновесную цену. Какая ситуация будет на рынке при цене по первому столбцу? При цене по предпоследнему столбцу?
- Если при увеличении доходов, спрос при каждой цепе увеличился на 15 (*) шт., каковы будут новые условия равновесия?
Задача №3.
Для каждого варианта значение цены увеличивается на номер варианта, умноженный на 1, то есть, например, для 14 варианта увеличится на 14 * 1 = 14 и составит 8 + 14 = 22 и т.д по каждому столбцу. Значение спроса при увеличении доходов изменяется по такому же принципу: то есть, например, для 14 варианта увеличится на 14 * 1 = 14 и составит 15 + 14 = 29 шт.
Решение:
График равновесия строим по соответствующим значениям цены, величины спроса и величины предложения.
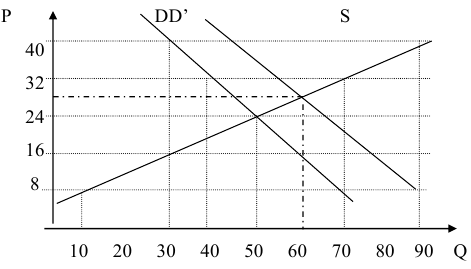
В соответствии с графиком и представленными данными равновесная цена будет равна 24 руб. При этой цене объем спроса равен объему предложения и равны 50 тыс. шт.
Если цена будет равна 8 руб., на рынке возникнет дефицит, при котором объем спроса составит 70 тыс. шт., а объем предложения — 10 тыс. шт. Величина дефицита, таким образом, будет равна 60 тыс. шт.
При цене, равной 32, на рынке будет относительный излишек, так как объем предложения составит 70 тыс. шт., а объем спроса — 40 тыс. шт. Следовательно, величина излишка будет равна 30 тыс. шт.
Если рост дохода увеличит спрос при каждом уровне цены, новые параметры рынка составят:

Кривая спроса сдвинется на 15 тыс. шт. вправо и займет положение 
- Определите денежную выручку, тип эластичности и ее коэффициент, заполнив таблицу:
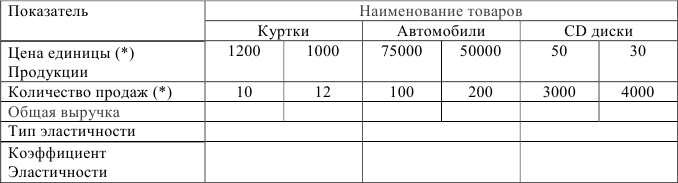
Задача №4.
Для каждого варианта значение цены увеличивается на номер варианта, умноженный на 10, то есть, например, для 14 варианта увеличится на 14 * 10 = 140 и составит 1200 + 140 = 1340 и т.д. по каждому столбцу. Значение количества продаж увеличивается на номер варианта, умноженный на 1, то есть, например, для 14 варианта увеличится на 14 * 1 = 14 и составит 10+14 = 24 шт. и т.д. по каждому столбцу.
Решение:
Определяем общую выручку 
для курток
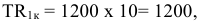
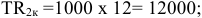
для автомобилей:
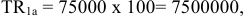
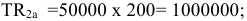
для 
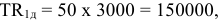
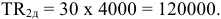
Тип эластичности определяем на основе характеристики зависимости между изменением цены и объемов продаж. На основании влияния снижения цены на изменение объема продаж можно судить об эластичности спроса. Для курток: снижение цены не меняет общую выручку. Поэтому спрос обладает единичной эластичностью. Для автомобилей: снижение цены увеличивает общую выручку. Спрос эластичный. Для 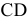
Для подсчета коэффициентов эластичности используем показатель среднего значения (расчет по центральной точке), то есть изменение соответствующих параметров делим не на базовые значения цены и объема, а на их средние значения.
Для курток:
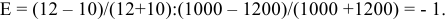
Для автомобилей:
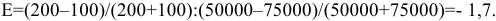
Для 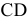
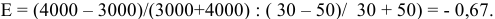
Основы теории потребительского выбора
В данной теме рассматривается формирование одной из двух сторон рыночного механизма — спроса. Поскольку спрос предъявляется потребителями, то предмет изучения составляет рациональное потребительское поведение, или теории потребительского выбора.
Исследованием взаимосвязи потребностей и спроса занимались представители теории предельной полезности, которая возникла как альтернатива трудовой теории стоимости, согласно которой стоимость товара определяется затратами труда на его производство.
Сторонники теории предельной полезности полагают, что стоимость товара нельзя определять затратами живого труда или всех ресурсов (факторов производства). Она определяется полезностью товара, которую оценивают потребители, а именно предельной полезностью.
Если бы домашние хозяйства и отдельные индивиды располагали неограниченными доходами (и временем), то могли бы потреблять столько благ, сколько захочется. Однако в реальной действительности доходы и ресурсы ограниченны. Поэтому люди всегда вынуждены выбирать между различными вариантами действий (покупками, использованием времени, видами труда и многим другим).
Модель рационального экономического поведения подразумевает, что экономический агент имеет множество целей и что ни одна из них не является полностью достижимой, но достижимой лишь до определенного уровня. Предполагается также, что экономический агент совершает обмен и уменьшает уровень потребления одного блага ради увеличения другого, реагируя, таким образом, на изменения своих относительных возможностей. Имеющиеся варианты индивидом системно ранжируются, и делается выбор на основе максимизации индивидуального уровня «удовлетворения» при минимальных затратах.
Закон убывающей предельной полезности не только объясняет причины действия закона снижающегося спроса, но и помогает определить условие потребительского равновесия, при котором потребитель получает максимальное удовлетворение потребностей при имеющемся денежном доходе и сложившихся предпочтениях.
Рациональный потребительский выбор определяют следующие основные факторы:
- Стремление потребителя на свой денежный доход получить максимальную общую полезность, или максимальное удовлетворение потребностей.
- Предпочтения и вкусы.
- Денежный доход потребителя (потребительский бюджет).
- Цены на товары и услуги.
Исходя изкардиналистской теории потребительского поведения, при определении рационального потребительского выбора покупатель должен учитывать предельную полезность и цены товаров. Потребитель с постоянным денежным доходом и сложившимися предпочтениями при выборе покупки товаров с различными ценами может получить максимальную полезность, или максимальное удовлетворение потребностей, только при соблюдении следующего условия потребительского равновесия:

где 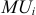
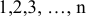
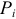
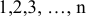
Недостатком кардиналистского подхода является исключительно индивидуальный, субъективный характер оценок полезности: один и тот же товар может представлять большую ценность для одного потребителя и значительно меньшую, а то и никакой — для другого.
Ординалистская (порядковая) теория полезности основывается на том, что предпочтения индивидуума относительно предлагаемых к выбору альтернатив не могут измеряться количественно, а только сравниваться, то есть одна альтернатива хуже или лучше другой.
Кривая безразличия — геометрическое место точек, координаты которых отражают те или иные равноценные для потребителя наборы из двух товаров «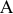
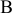
Для любых двух товаров может быть построено множество кривых безразличия, называемое картой безразличия. Кривые безразличия для любой пары доброкачественных товаров обладают рядом свойств:
1) кривая безразличия, лежащая выше и правее других), представляет собой более предпочтительные наборы товаров;
2) для любой пары доброкачественных благ кривые безразличия вогнуты к началу координат;
3) кривые безразличия имеют отрицательный наклон;
4) кривые безразличия не могут пересекаться;
5) кривые безразличия могут быть проведены через любую точку в пространстве.
Кривые безразличия позволяют исследовать способность товаров замещать друг друга при потреблении. Предельная норма замещения 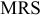
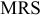

Предельная норма замещения является весьма важной категорией: она измеряет склонность индивида к обмену одного блага на другое.
Построение кривых безразличия является первым этапом изучения состояния потребительского равновесия. На этом этапе не принимается во внимание денежный доход потребителя и цены анализируемых товаров.
На втором этапе определения рационального поведения потребителей анализируются бюджетные ограничения, то есть денежный доход, который может использоваться потребителем с целью покупки рассматриваемых товаров при заданных рынком ценах на эти товары.
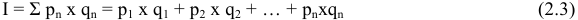
где 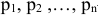
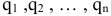
Наклон бюджетной линии определяется отношением цен анализируемых товаров. Это отношение 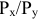
На третьем этапе объединяют анализ потребительских предпочтений и бюджетных ограничений и определяют рациональный потребительский выбор, обеспечивающий потребителю максимальную общую полезность. Графически этому варианту соответствует точка касания бюджетной линии и одной из кривых безразличия. Более высокий уровень потребления при ограниченном бюджете просто недостижим.
Задача №5.
Чему будет равен бюджет потребителя, если он должен купить 40 () единиц товара А по цене 60 руб. за ед., а также 35 штук товара Б по цене 220 () руб. за шт.?
(*) Для каждого варианта значение цены увеличивается на номер варианта, умноженный на 10, то есть, например, для 14 варианта увеличится на 14 * 10 = 140 и составит 220 + 140 = 360. Значение количества товара увеличивается на номер варианта, умноженный на 1, то есть, например, для 14 варианта увеличится на 14 * 1 = 14 и составит 40 + 14 = 54 шт.
Решение:
1) Используем формулу бюджетного ограничения:
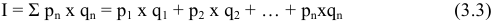
Подставляем данные из условия задачи:
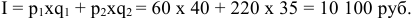
Ответ: 10 100 руб.
Задача №6.
Определите предельную полезность следующих покупок товаров:
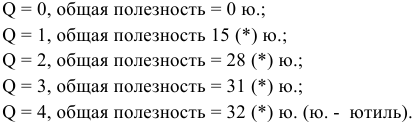
Действует ли для этого случая закон убывающей предельной полезности?
(*) Для каждого варианта общая полезность увеличивается на номер варианта, умноженный на 1, то есть, например, для 14 варианта увеличится на 14 * 1 = 14 и составит 15 + 14 = 29 шт. и т.д.
Решение:
1) Предельная полезность определяется как отношение приращения общей полезности к приращению объема покупок.
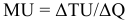
где 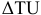
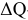
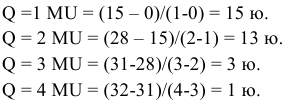
Ответ: Да, для данного случая действует закон убывающей предельной полезности:
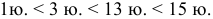
Задача №7.
Владимир Иванович считает, что ему одинаково полезно еженедельно выпивать как 8 () стаканов молока и три стакана кефира, так и 6 () стаканов молока и 4 стакана кефира. Чему в этом случае равна его предельная норма замещения кефира на молоко?
(*) Для каждого варианта количество стаканов молока увеличивается на номер варианта, умноженный на 1, то есть, например, для 14 варианта увеличится на 14 * 1 = 14 и составит 8 + 14 = 22 шт. и т.д.
Решение:
Предельная норма замещения 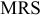
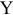
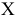
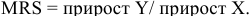
Если сокращение потребления кефира на один стакан (с 4 до 3 стаканов) приведет к увеличению потребления молока на два стакана (с 6 до 8 стаканов), следовательно, 1 стакан молока может заменить 1/ 2 стакана кефира. То есть предельная норма замещения кефира на молоко равна 1 /2.
Задача №8.
Функция полезности для данного потребителя 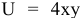
Чему в этом случае равны цены первого и второго благ?
(*) Для каждого варианта значение выделенного для покупок дохода увеличивается на номер варианта, умноженный на 1, то есть, например, для 14 варианта увеличится на 14 * 1 = 14 и составит 24 + 14 = 38.
Решение:
Принимаем 
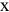
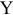
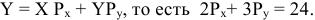
Одновременно должно выполняться условие равновесия потребителя 6 соотношение цен двух товаров равно соотношению их предельных полезностей
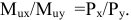
Предельные полезности экономических благ могут определяться как производные от функции общей полезности:
Отсюда,
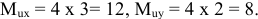
Поэтому
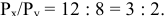
Можно выразить
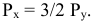
Затем, подставив это выражение в уравнение бюджетного ограничения, получим:
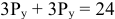
или
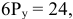
следовательно,
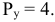
Тогда
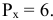
Теория производства. Издержки производства и прибыль
Для осуществления процесса производства фирма использует экономические ресурсы (факторы производства): природные ресурсы, капитал, труд (рабочую силу), предпринимательские способности. С одной стороны, они дополняют друг друга в процессе производства, с другой — их характеризует взаимозаменяемость. Так, реальный капитал, материализованный в машинах, оборудовании и других средствах труда, невозможно использовать без рабочей силы. Вместе с тем техника может вытеснять живой труд из процесса производства, заменяя его.
Производственная функция характеризует взаимосвязь факторов производства с выпуском продукции:

где 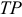
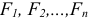
Технически эффективными называют варианты производства, при которых нельзя увеличить производство продукта без увеличения расхода ресурсов, а также сократить затраты какого-либо ресурса без снижения выпуска и без увеличения затрат других ресурсов. Производственная функция учитывает только технически эффективные варианты. Ее значение -это наибольшее количество продукта, которое может произвести предприятие при данных объемах потребления ресурсов.
При заданном уровне технических знаний все факторы, определяющие объем выпуска, обычно представляют в виде двух агрегатов: труд 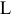
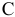

Одно и то же количество продукции можно получить при различных сочетаниях затрат этих ресурсов. Можно использовать небольшое количество машин (т. е. обойтись небольшими затратами капитала), но при этом придется затратить большое количество труда; можно, напротив, механизировать те или иные операции, увеличить количество машин и за счет этого снизить затраты труда. Если при всех таких сочетаниях наибольший возможный объем выпуска остается постоянным, то эти сочетания изображаются точками, лежащими на одной и той же изокванте.
Зафиксировав объем выпуска продукта на другом уровне, мы получим другую изокванту той же самой производственной функции. Выполнив серию горизонтальных разрезов на различных высотах, получим так называемую карту изоквант — наиболее распространенное графическое представление производственной функции от двух аргументов.
Производственная функция во многом похожа на функцию полезности в теории потребления, а изокванты — на кривые безразличия. Свойства и характеристики производственной функции имеют много аналогий в теории потребления. Это объясняется тем, что на рынке экономических ресурсов фирма ведет себя как потребитель, и производственная функция характеризует именно эту сторону производства — производство как потребление. Тот или иной набор ресурсов полезен для производства постольку, поскольку он позволяет получить соответствующий объем выпуска продукта. Можно сказать, что значения производственной функции выражают полезность для производства соответствующего набора ресурсов. В отличие от потребительской полезности эта «полезность» имеет вполне определенную количественную меру — она определяется объемом производимой продукции.
Изменение фирмой объема и издержек производства зависят от возможностей изменения количества и структуры применяемых для изготовления продукции экономических ресурсов, которые во многом определяются типом рыночного периода.
Краткосрочный период — отрезок времени, в течение которого фирма не может изменить общие размеры основного капитала: зданий, сооружений, машин, оборудования, используемых в производстве, т.е. производственные мощности остаются неизменными.
Изменение объема производства и издержек в краткосрочном периоде связано с действием закона убывающей отдачи.
Он действует только в краткосрочном периоде, когда к какому-либо постоянному ресурсу добавляются однородные единицы определенного переменного ресурса.
Согласно закону убывающей отдачи (убывающей предельной производительности) при неизменных производственных мощностях и технологии, начиная с определенного момента, последовательное присоединение одинаковых единиц какого-либо переменного ресурса (например, труда) к постоянному (например, капиталу или земле) дает уменьшающийся предельный продукт в расчете на каждую дополнительную единицу переменного ресурса, т.е. его предельная производительность снижается.
Предельный продукт и предельная производительность обозначаются и определяются одинаково. Предельный продукт (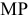
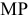
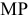

где 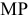
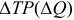
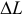
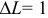

Причина действия закона убывающей отдачи кроется в нарушении сбалансированности в производстве между постоянными и переменными факторами. Низкая эффективность при слабой загрузке оборудования может быть повышена за счет вовлечения в производство дополнительного переменного фактора, но лишь до определенного предела. Максимальная производительность оборудования ограничена его техническими параметрами, то есть неизбежно наступает момент, когда вовлечение в производство дополнительных единиц переменных факторов приведет к существенно большему росту затрат по сравнению с увеличением отдачи от привлечения этого фактора. Интенсивность действия закона обусловлена особенностями технологии и в каждом производстве различна.
Долгосрочным периодом называется такой период, в течение которого к изменяющимся рыночным условиям может приспособиться вся отрасль. Фирмы, ранее функционировавшие в отрасли, могут изменять количество всех ресурсов, включая производственные мощности, технику, технологию. Может измениться также количество фирм в отрасли.
В процессе расширения производственных мощностей фирмы в долгосрочном периоде одновременно увеличиваются и объемы выпускаемой продукции, и валовые издержки производства. Долгосрочные средние валовые издержки 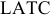
Дугообразную форму кривой долгосрочных издержек 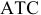
Положительный эффект роста масштабов производства объясняет снижающуюся часть кривой долгосрочных издержек 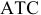
При достижении определенного уровня производственных мощностей дальнейшее расширение фирмы может привести к действию отрицательного эффекта от роста масштабов производства, к увеличению средних общих издержек
Динамика долгосрочных 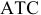
Более того, государству бывает выгодно иметь в ряде отраслей только одну крупную фирму, что ведет к возникновению естественных монополий. Естественная монополия — это такая рыночная структура, при которой минимальные средние издержки достигаются в данной отрасли только при наличии одной фирмы. Если в отрасли будет действовать большее количество фирм, то неизбежно увеличиваются средние издержки, и снижается эффективность производства.
Если на кривой 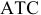
Возможен также вариант с постоянной отдачей от масштабов производства, когда выпуск продукции и валовые издержки растут в равной степени. В таких отраслях возможно сосуществование крупных, средних и мелких фирм. Здесь возможно функционирование таких рыночных структур, как монополистическая конкуренция и мягкая олигополия.
Все виды издержек фирмы в краткосрочном периоде делятся на постоянные и переменные.
Постоянные издержки (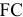
Переменные издержки (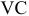
Валовые издержки (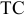
От величины совокупных постоянных, совокупных переменных и валовых издержек зависят средние издержки фирмы. Средние издержки определяются в расчете на единицу выпущенной продукции. Они обычно используются для сравнения с ценой единицы продукции.
В соответствии со структурой совокупных издержек фирмы различают средние постоянные (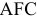
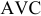
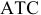

Одним из важных показателей являются предельные издержки. Предельные издержки (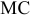

Одна из основных целей любой фирмы, с точки зрения микроэкономики, — получить максимальную валовую прибыль 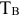

В случае отрицательного значения 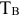
Объем производства, при котором прибыль фирмы максимальна (убытки минимальны), называется равновесным выпуском. Для определения фирмой оптимального, наиболее выгодного объема производства могут быть использованы два метода (подхода):
1) сопоставление валовой выручки с валовыми издержками;
2) метод предельного (маргинального) анализа.
Первый метод предполагает постепенное изменение фирмой объемов выпускаемой продукции и сопоставление для каждого объема общей выручки и общих издержек. Этот метод успешно может применяться на рынке совершенной конкуренции, так как на этом рынке цена каждой единицы продукции одинакова, поскольку не зависит ни от одного субъекта рынка. Для остальных рынков этот метод часто называют методом проб и ошибок. Изменение объемов выпуска может сопровождаться изменением как издержек производства, так и рыночной цены товара, что затрудняет получение достоверных результатов анализа, а проверка всех вариантов на практике может потребовать слишком больших затрат времени, а в некоторых случаях — даже привести к убыткам.
Логика предельного анализа такова: прибыль может быть представлена не только как разница между общей выручкой и общими убытками, но и как сумма прибылей (убытков) от каждой единицы продукции:
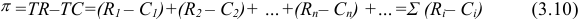
Эта сумма будет увеличиваться до тех пор, пока выручка от реализации дополнительной единицы продукции (предельная выручка) больше, чем издержки на производство этой единицы (предельные издержки). Таким образом, условие максимизации прибыли принимает вид:

Поскольку во многих случаях при всех уровнях производства отсутствует точное равенство предельной выручки и предельных издержек, то фирме следует произвести последнюю единицу продукции, при выпуске которой
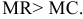
В долгосрочном периоде, когда фирма стремится увеличить производство за счет увеличения всех факторов, она учитывает эффект роста масштабов производства, который, как ни печально, может быть не только положительным (когда производство растет быстрее, чем затраты на ресурсы), но и отрицательным (когда производство отстает от роста затрат на ресурсы).
Задача №9.
Функция общих затрат на предприятии имеет вид:
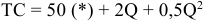
Определить функции: 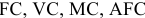
(*) Для каждого варианта указанное в функции значение увеличивается на номер варианта, умноженный на 10, то есть, например, для 14 варианта увеличится на 14 * 10 = 140 и составит 50 + 140 = 190.
Решение:
1) Постоянные издержки не зависят от выпуска продукции. Следовательно,
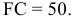
2) 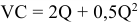
3) Предельные издержки — это издержки на выпуск дополнительной единицы продукции. Их можно определять как производную от функции общих издержек. Тогда 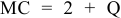
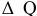
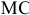
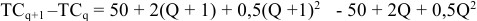
После несложных преобразований получим
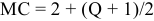
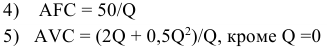
Поведение фирмы в условиях совершенной и несовершенной конкуренции
Чистая (совершенная) конкуренция представляет собой рыночную структуру, при которой большое количество продавцов и покупателей взаимодействуют друг с другом, предлагая и запрашивая однородный продукт. Чистая конкуренция как абстрактная рыночная структура обладает следующими признаками:
- Большое количество производителей и продавцов в отрасли. Это основная черта любого конкурентного рынка. При этом все фирмы действуют независимо друг от друга и не могут оказывать влияния на решения, принимаемые другими участниками.
- Абсолютная однородность одноименных товаров. Этот признак означает, что покупатели воспринимают экономические блага как совершенные заменители.
- Наличие у всех участников полной информации о рыночных условиях.
- Абсолютная мобильность материальных, финансовых, трудовых и прочих факторов производства в долгосрочном периоде.
- Свободное вступление в отрасль новых фирм и выход из нее действующих.
В таких условиях ни одна из множества фирм не в состоянии влиять на уровень цены, график спроса на продукцию чисто конкурентной фирмы является совершенно эластичным.
Любое количество однородной продукции фирма продает по одной и той же рыночной цене, которая сложилась в конкурентной отрасли. Кривая спроса на продукцию конкурентной отрасли, к которой принадлежит данная фирма, имеет снижающийся вид. Отрасль может продать больше продукции при условии снижения ее цены, и наоборот. В этих случаях любой фирме, функционирующей в отрасли, придется продавать свою продукцию по новой цене, сложившейся в изменившихся условиях.
И предельная, и средняя выручка в условиях чистой конкуренции равны равновесной рыночной
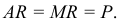
Поэтому условие равновесия конкурентной фирмы состоит в равенстве предельных издержек рыночной цене продукта:
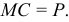
Использование маргинального (предельного) анализа определения фирмой оптимального объема производства, основанного на сравнении предельной выручки с предельными издержками, позволяет выяснить взаимосвязь кривой предельных издержек с предложением конкурентной фирмы при различных рыночных ценах.
Какая бы цена, превышающая минимум средних переменных издержек, ни сложилась на конкурентном отраслевом рынке, оптимальный объем производства всегда определяется точкой на кривой предельных издержек. Это количество продукции и будет определять в краткосрочном периоде предложение рационально действующей конкурентной фирмы, нацеленной на достижение наибольшей выгоды. Таким образом, отрезок кривой предельных издержек фирмы 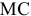
Таким образом, фирма будет продолжать свою деятельность в двух случаях:
1) если она получит валовую экономическую прибыль;
2) если она будет нести валовой убыток, но в меньшем размере, чем величина ее постоянных издержек.
В долгосрочном периоде рыночная цена в результате изменения количества фирм и конкурентной борьбы будет стремиться к уровню, равному минимуму средних валовых издержек. В результате долговременных изменений положение долгосрочного равновесия в отрасли и на отдельных фирмах установится при производстве оптимального количества продукции, соответствующего цене 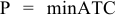
В положении долгосрочного равновесия конкурентной фирмы равны друг другу цена, предельная выручка (предельный доход), предельные издержки и минимальные средние валовые издержки:
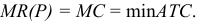
Рынки несовершенной конкуренции — это такие рынки, на которых не действует хотя бы один из признаков совершенной конкуренции. В реальной экономике практически любой рынок является рынком несовершенной конкуренции, где производители имеют хотя бы минимальную возможность воздействовать на цену путем регулирования объема выпуска продукции.
Графически эта возможность отражается убывающей кривой спроса на товар отдельной фирмы.
Чем большей долей отраслевого предложения располагает фирма-производитель, тем более чувствителен рынок к изменению объема выпуска этой фирмой, тем сильнее ее влияние на рыночную цену.
Монопольная (рыночная) власть производителя — это обусловленная особенностями рыночной организации его способность оказывать воздействие на рыночную цену блага посредством регулирования объема его предложения.
В роли монополии не обязательно выступает крупная фирма, главное -удельный вес фирмы (фирм) в производстве и сбыте конкретного вида продукции. Чем более значительной долей отраслевого предложения располагает фирма, тем более чувствителен рынок к изменению ее объема выпуска, и тем сильнее влияние этой фирмы на цену. Иными словами, более важен относительный, а не абсолютный размер фирмы, хотя эти показатели, как правило, взаимосвязаны.
Другим источником рыночной власти может служить эластичность рыночного спроса. Чем менее эластичным является спрос на продукцию фирмы, тем она более свободна в выборе цены, так как может не опасаться отрицательной реакции потребителей на повышение цены. Низкой эластичности спроса на товар конкретной фирмы способствует отсутствие у ее продукции товаров — заменителей (у потребителей просто нет выбора, и они вынуждены приобретать товары конкретного производителя).
Наличие монопольной власти, тем не менее, не означает, что производитель может произвольно устанавливать цену на свою продукцию. Изменить цену на свой товар фирма может, лишь соответственным образом изменив предложение. Изменение общей выручки в этом случае будет зависеть от изменения цены 
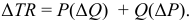
Разделив обе части уравнения на 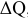
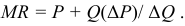
Если и числитель, и знаменатель выражения 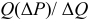
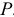
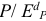
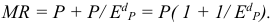
При оценке предельной выручки фирмы нельзя забывать, что 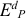
Для оценки степени монополизации рынка может использоваться несколько показателей. Наиболее известными и применяемыми являются индекс Херфиндаля — Хиршмана и индекс Лернера.
Индекс Лернера (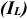
Если для конкурентной фирмы цена равняется предельным издержкам, то фирмы, обладающие монопольной властью, имеют возможность продавать товары по ценам, превышающим предельные издержки. Следовательно, монопольная власть может быть измерена через превышение цены, обеспечивающей максимизацию прибыли, над предельными издержками производства. Индекс Лернера определяется как отношение разности цены (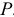
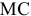
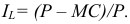
Этот индекс всегда имеет значение в пределах от 0 до 1. Для фирмы, действующей в условиях совершенной конкуренции он равен 0. Чем ближе значение индекса к 1, тем больше степень монопольной власти.
Используя условие максимизации прибыли 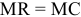
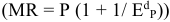

Рыночная власть фирмы находится, таким образом, в обратной зависимости от эластичности спроса на ее продукцию.
Индекс Херфиндаля — Хиршмана 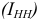
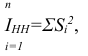
где 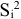
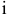
Если в отрасли действует 1000 одинаковых фирм, то 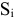
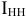
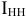
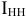
Наличие монопольной власти дает возможность вмешиваться в механизм установления рыночного равновесия, нарушая соответствие интересов производителей и потребителей. В условиях монополизации отрасли потребители получат меньше продукции 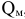
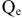
Оптимум Парето при этом не соблюдается, монополия вызывает перераспределение богатства в свою пользу таким образом, что происходит снижение общественного благосостояния.
Одной из форм поведения фирмы, обладающей монопольной властью, является осуществление политики ценовой дискриминации. Под ценовой дискриминацией понимается продажа одного и того же товара по разным ценам разным покупателям или группам покупателей, причем различия в ценах обусловлены не различиями в издержках производства, а различиями в оценке товара покупателями и их платежеспособности.
Смысл проведения такой политики ценообразования состоит в стремлении присвоить себе излишек потребителя и тем самым максимизировать свою прибыль. Ее применение возможно при следующих условиях:
- продавец обладает достаточно высокой степенью монопольной власти, обеспечивающей ему контроль над производством и ценами;
- наличие возможности сегментировать рынок — разбить покупателей на группы, различающиеся степенью эластичности спроса по цене;
- невозможность для покупателя, приобретающего товар дешевле, повлиять на равновесную рыночную цену путем перепродажи;
издержки проведения фирмой дискриминационной политики не должны превышать выгод от данной деятельности.
Цены могут различаться в зависимости от объема потребления, дохода покупателя, времени покупки и т.д. Таким образом, на один и тот же товар существует множество цен.
Экономические последствия применения ценовой дискриминации:
- увеличение прибылей применяющих такую политику фирм;
- расширение объема выпуска и, следовательно, более эффективное использование ресурсов, чем при моноценовой монополии.
Задача №10.
На конкурентном рынке функция общих затрат производителя имеет вид
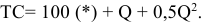
Равновесная цена
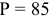
Определить величину максимально возможной прибыли фирмы.
(*) Для каждого варианта значение функции увеличивается на номер варианта, умноженный на 10, то есть, например, для 14 варианта увеличится на 14 * 10 = 140 и составит 100 + 140 = 240. Значение равновесной цены увеличивается на номер варианта, умноженный на 5, то есть, например, для 14 варианта увеличится на 14 * 5 = 70 и составит 85 + 70 = 155.
Решение:
1) Условие максимизации прибыли на данном рынке
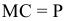
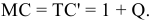
Тогда
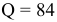
2) Рассчитаем прибыль при этих условиях по формуле:
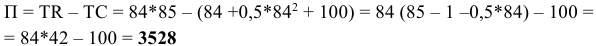
Задача №11.
Издержки конкурентной фирмы равны:
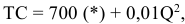
где 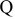
Цена единицы товара равна 6 (*) рублей.
Найти равновесный выпуск и максимальную прибыль фирмы.
(*) Для каждого варианта значение функции увеличивается на номер варианта, умноженный на 10, то есть, например, для 14 варианта увеличится на 14 * 10 = 140 и составит 700 + 140 = 840. Значение цены единицы товара увеличивается на номер варианта, умноженный на 5, то есть, например, для 14 варианта увеличится на 14 * 5 = 70 и составит 6 + 70 = 76.
Решение:
1) Условие равновесия
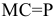
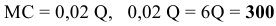
2) При выпуске 300 прибыль равна
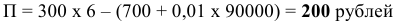
Задача №12.
Фирма монополист определила, что при существующем спросе на ее продукцию функция зависимости средней выручки от объема предложения описывается формулой:
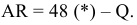
Данная фирма несет средние издержки по производству, которые рассчитываются по формуле:

Какую прибыль или убыток получает фирма, оптимизируя выпуск в краткосрочном периоде?
(*) Для каждого варианта значение функции увеличивается на номер варианта, умноженный на 5, то есть, например, для 14 варианта увеличится на 14 * 5 = 70 и составит 48 + 70 = 118 и т.д.
Решение:
1) Сначала найдем функции общего дохода и общих издержек:
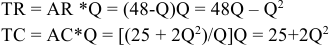
2) Затем, используя производные от полученных формул, определим значения предельных издержек и предельного дохода, для того, чтобы использовать правило оптимизации объема:
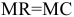
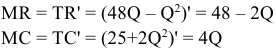
Таким образом,
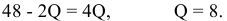
3) Определим, что получит фирма-монополист при оптимальном выпуске в 8 ед. Для этого рассчитаем величину прибыли, используя формулы общего дохода и общих издержек:
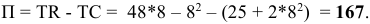
Задача №13.
Функция спроса на продукцию монополиста:
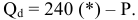
Функция издержек монополии:
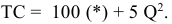
Найти равновесный выпуск и максимальную прибыль в краткосрочном периоде.
(*) Для каждого варианта значение функции увеличивается на номер варианта, умноженный на 5, то есть, например, для 14 варианта увеличится на 14 * 5 = 70 и составит 240 + 70 = 310 и т.д.
Решение:
Условие максимизации прибыли на любом рынке определяется через равенство предельной выручки и предельных издержек. Они в свою очередь определяются как производные от функций общей выручки и общих издержек.
1) Общая выручка
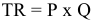
Выразив цену из заданной функции спроса, получаем:
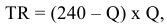
Тогда
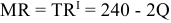
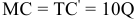
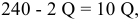
отсюда равновесный выпуск равен 20. Прибыль определяется как разница между общей выручкой и общими издержками производства.
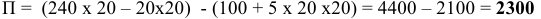
Задача №14.
9. Рассчитать индекс Лернера для фирмы, действующей в условиях рынка несовершенной конкуренции и стремящейся к максимальной прибыли, если спрос описывается функцией
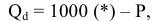
издержки фирмы
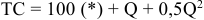
(*) Для каждого варианта значение функции увеличивается на номер варианта, умноженный на 100, то есть, например, для 14 варианта увеличится на 14 * 100 = 1400 и составит 1000 + 1400 = 2400 и т.д.
Решение:
Условие максимизации прибыли — равенство предельной выручки и предельных издержек производства
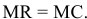
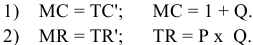
Из функции спроса выражаем
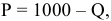
тогда
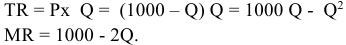
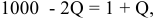
отсюда,
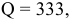
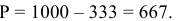
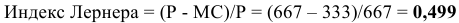
Возможно эти страницы вам будут полезны:
- Предмет экономика
- Контрольная работа по экономике
- Заказать экономику
- Помощь по экономике
- Решение задач по макроэкономике
- Контрольная работа по макроэкономике
- Заказать макроэкономику
- Помощь по макроэкономике
- Решение задач по микроэкономике
- Контрольная работа по микроэкономике
- Заказать микроэкономику
- Помощь по микроэкономике
- Решение задач по экономической теории
- Контрольная работа по экономической теории
- Заказать экономическую теорию
- Помощь по экономической теории
- Деньги кредит банки задачи с решениями
- Помощь по экономике предприятия
- Помощь по экономике организации
Министерство
образования и науки Республики Казахстан
КГКП
Балхашский гуманитарно-технический колледж имени А.Мусина
О.
Ю. Масалова
Методические рекомендации по решению
экономических задач
для
специальностей 0515000 – «Менеджмент» (по областям применения), 0518000 — «Учет
и аудит (по отраслям)»
Балхаш
Издательский
центр методического кабинета
2019 год
УДК
ББК
Рецензент:
Джамбекова
А.К., преподаватель высшей математики
высшей категории,
БГТК им. А.Мусина
Масалова О.Ю., составитель
Методическая
разработка
«Методические
рекомендации
по
решению экономических задач»
по
дисциплинам экономического цикла
среди
студентов БГТК технического отделения
специальностей
0515000 –
«Менеджмент»
(по областям применения)
0518000 —
«Учет и аудит (по отраслям)»
Издательский
центр методического кабинета
Балхашский
гуманитарно-технический колледж
имени
А.Мусина, 2019
Настоящие методические
рекомендации подготовлены с целью оказания помощи студентам в подготовке к
урокам по дисциплинам экономического цикла, а также для формирования навыков
применения готовых инструкций решения задач и поисков собственных алгоритмов
расчета.
Рассмотрено на Утверждено
к использованию
заседании предметно-цикловой методическим
советом
комиссии экономических дисциплин Балхашского
гуманитарно-технического
Балхашского гуманитарно-технического колледжа
им. А.Мусина
колледжа им. А.Мусина Протокол
№ от « » ___________.2019
Протокол № от « » _______.2019 Председатель
МС
Председатель ПЦК ___________________
Махатова К.Д.
_________________Ш.С.Мамырбаева
УДК
ББК
©Масалова О.Ю.
ПОЯСНИТЕЛЬНАЯ
ЗАПИСКА
Экономика изучает базовые основы и прикладные формы деятельности
рыночных структур и механизмов взаимодействия субъектов экономической
деятельности общества.
Показатели методические рекомендации разработаны в
соответствии с Государственным общеобразовательным стандартом среднего
профессионального образования Республики Казахстан.
Методические рекомендации являются частью
учебно-методического комплекта по дисциплине «Экономика отрасли (организации)»
и «Экономика организации (предприятия)».
Цель методической разработки
1. Дидактическая цель:
Предоставление поддержки студентам в выполнении заданий
по решению экономических задач с использованием теоретических знаний.
2. Воспитательная цель:
Способствовать воспитанию ответственности, аккуратности
и воспитание интереса к избранно профессии.
3. Развивающая цель:
-развить, расширить и углубить теоретические и
практические знания, полученные в колледже;
-формирование у студентов новой идеологии
экономического менталитета, стратегии применения знании в практических целях
рыночной экономики;
-закрепление и расширение познавательных способностей
студентов в рамках реализации Стратегия «Казахстан-2050».
Экономическое образование невозможно без решения задач
по экономическим дисциплинам.
Грамотный
специалист в любой сфере деятельности обязан уметь решать практические задачи,
так как без умения применять методы экономической математики невозможно
представить современного специалиста.
Необходимость и важность
методических рекомендаций по решению экономических задач, заключается в подборе
заданий по темам, развивающих профессиональные компетенции их прорешивание и
артикуляция, а так же наработка навыков применения экономических формул.
Пример в виде текста с
экономическим содержанием – это один из самых важных видов задачи для
экономических специальностей.
Алгоритм расчета данного вида
задач связано со знанием некоторых специфических математических моделей из
области экономики, умением аргументировать сформулированные в виде текста условия
в уравнения и неравенства и пониманием того, как интерпретировать показатели
полученных уравнений.
Подготовка к решению экономической
задачи начинается прежде всего, исходя из правил решения текстовых задач вообще,
а именно:
•чтение условия задачи;
-студент должен точно
сформулировать суть описанного в задаче процесса, и исчислить, что необходимо
найти, и какие показатели у него для этого даны в задаче;
•выбор переменных;
-необходимо исчислить факторы,
влияющие на результативный показатель;
-факторы вводятся в таком
количестве, в каком они необходимы для того, чтобы просто и логично составлять
уравнения и неравенства;
•компоновка алгоритма решения, нужна
для того, что бы найти в процессе решения недостающий результирующий показатель;
•затем уравнение необходимо
прорешать;
•анализ полученного результата и
нахождение ответа на проблему, поставленную в задаче.
Необходимо студенту постоянно помнить этапы
решения текстовой задачи в голове.
Базовый алгоритм решения экономических
задач складывается из:
1. Чтения и
анализа условия задачи. Студенту необходимо осознание, о сути проблемы задачи,
понятий используемых в задаче, и о каких явлениях и закономерностях идёт речь.
2. Разложение
данных задачи на общие и частные, то есть понять причинно-следственные связи в
целях получения требуемого результата. Это поможет студенту использовать ранее
изученные готовые формулы, интерпретировать результаты, построить логические
цепочки.
3. Производить
вычисления с описанием действия.
4. Делать
выводы по результатам вычислений задачи.
Тема I.
«Эффективность использования средств в оборотах».
Эффект от использования средств
в оборотах играет большую роль в обеспечении бесперебойной работы организации, а
также в увеличении показателя доходности производства.
Главными показателями эффективности использования средств в
оборотах являются показатель рентабельности; коэффициенты оборачиваемости средств
в оборотах (продолжительность одного оборота); прямой коэффициент
оборачиваемости (количество оборотов); обратный коэффициент оборачиваемости или
коэффициент загрузки (закрепления).
Относительный показатель доходности (рентабельность) характеризует
величину прибыли, получаемой на каждый тенге оборотного капитала, и отражает
финансовую эффективность и устойчивость организации.
Пример 1.
Исчислить коэффициент оборачиваемости
(число оборотов) средств в оборотах, если выручка в организации за отчётный период
составила 750 млн. тенге, а остатки средств в оборотах в среднем по периоду – 150
млн. тенге.
Алгоритм расчета:
Важно! В расчете коэффициентов оборачиваемости в числителе всегда
находится «ВЫРУЧКА», а в знаменателе среднее значение того показателя,
оборачиваемость которого мы находим.
Формула коэффициента оборачиваемости средств в оборотах
определяется:
КОБ = 5
оборотов.
Пример 2.
Используя следующие показатели, приведённые в таблице, исчислить:
1. необходимость (расчетную потребность) средств
в оборотах на создание запасов ТМЗ и ТМЦ в базовом периоде по нормативу расхода
отчётного и базового периодов;
2.показатель высвобождения средств в
оборотах в абсолютном выражении в результате рационального использования товарно-материальных
ценностей.
|
Показатель |
Товар 1 |
Товар 2 |
Товар 3 |
Товар 4 |
Товар 5 |
|
Годовой |
30 |
60 |
50 |
90 |
70 |
|
Расход |
120 |
140 |
110 |
180 |
160 |
Норматив запаса ТМЗ и ТМЦ- 25 суток. В базовом
периоде предполагается снизить нормы расхода: по Товару «1» на 5%, «2» – на
10%, «3» – на 8%, «4» – на 6%.
Годовой объём производства возрастает в
среднем на 10%. Цены принять неизменными.
Алгоритм решения задачи
1.
Необходимость средств в оборотах на создание запасов в базовом
периоде:
— по нормативу
расхода отчётного периода:
|
30 |
60 |
50 |
90 |
70 |
|
х |
х |
х |
х |
х |
|
120 |
140 |
110 |
180 |
160 |
|
3600 |
8400 |
5500 |
16200 |
11200 |
|
суммируем |
3600 |
|||
|
+ |
||||
|
8400 |
||||
|
+ |
||||
|
5500 |
||||
|
+ |
||||
|
16200 |
||||
|
= |
||||
|
44900 |
||||
|
44900 |
/ |
365 |
= |
123,0137 |
|
123,013699 |
х |
25 |
= |
3075,342 |
—
по нормативу расхода базового периода:
|
30 |
60 |
50 |
90 |
70 |
|
х |
х |
х |
х |
х |
|
10% |
10% |
10% |
10% |
10% |
|
33 |
66 |
55 |
99 |
77 |
|
х |
х |
х |
х |
х |
|
120 |
140 |
110 |
180 |
160 |
|
х |
х |
х |
х |
х |
|
0,95 |
0,91 |
0,9 |
0,92 |
0,94 |
|
114 |
127,4 |
99 |
165,6 |
150,4 |
|
3762 |
8408,4 |
5445 |
16394,4 |
11580,8 |
|
суммируем |
3762 |
|||
|
+ |
||||
|
8408,4 |
||||
|
+ |
||||
|
5445 |
||||
|
+ |
||||
|
16394,4 |
||||
|
= |
||||
|
45590,6 |
||||
|
45590,6 |
/ |
365 |
= |
124,9058 |
|
124,905753 |
х |
25 |
= |
3122,644 |
2.
Размер высвобождения средств в оборота:
ОС =3075,342+ 3122,644= 6197,986
тыс. тенге
Пример 3.
Объем реализованной продукции в организации
2017 периоде составил 6000 тыс. тенге, в 2018 периоде – 6120 тыс. тенге
Среднегодовые остатки средств в оборотах
соответственно 1200 тыс. тенге и 1105 тыс. тенге. Исчислить коэффициент
оборачиваемости средств в оборотах, коэффициент загрузки и Продолжительность
одного оборота, абсолютное и относительное высвобождение средств в оборотах
Алгоритм решения задачи.
1.Коэффициент оборачиваемости средств в оборотах:
обор./год
обор./год
2.Коэффициент загрузки:
тенге/тенге
тенге/тенге
3.Продолжительность оборота:
дня
суток
3. Абсолютное высвобождение средств в оборотах:
тыс.
тенге
4.Необходимость в средств в оборотах в 2017 периоде:
тыс.
тенге
5. Высвобождение средств в оборотах в относительном выражении:
тыс.
тенге
Пример 4.
На основе отчетных данных за год и
планируемых вариантов улучшения использования средств в оборотах в организации.
Исчислить показатели (заполнить таблицу).
|
Показатели |
Отчетный |
Вариативность |
||
|
первый |
второй |
третий |
||
|
Объем |
14400 |
1800 |
14400 |
15264 |
|
Средний |
400 |
400 |
320 |
508,8 |
|
Продолжительность |
10 |
8 |
8 |
12 |
Алгоритм решения задачи
1.Объем реализованной продукции по первому варианту:
тыс.
тенге
2.Средний остаток средств в оборотах:
— по второму варианту:
тыс.
тенге
— по третьему варианту:
тыс.
тенге
Пример 5
План реализации продукции в год установлен
в сумме 17100 тыс. тенге База средств в оборотах запланирована в сумме 380 тыс.
тенге. В итоге проведения мероприятий скорость оборота повысилась на 2 дня. Исчислить
базовую и текущую продолжительность одного оборота и высвобожденную суму средств
в оборотах в результате ускорения.
Алгоритм решения задачи
1.Базовая Продолжительность одного оборота:
суток
2.Фактическая продолжительность одного оборота:
суток
3.Сумма средств в оборотах, высвобождаемая в результате усиления
их оборачиваемости:
тыс.
тенге
Примеры для самостоятельного решения
Пример 1В
В текущем периоде слесарное предприятие
выполнило объем работ на сумму 3,0 млн. тенге при среднегодовом остатке средств
в оборотах 600 тыс. тенге.
Исчислить дополнительный объем работ,
который выполнит предприятие в базовом периоде при тех же размерах средств в
оборотах, если число оборотов будет увеличено на один.
Пример 2В
Расчетная стоимость производства
(себестоимость) базового выпуска товарной продукции в год – 11 млн. тенге, в
том числе затраты на материалы – 5 млн. тенге.
Норматив запаса ТМЗ и ТМЦ —
15 суток, норматив запаса готовой продукции – 10 суток.
Затраты на тенге товарной продукции 0,7
тенге/тенге.
Продолжительность цикла производства – 30 суток.
Коэффициент нарастания затрат 0,73.
Исчислить общую сумму нормируемых средств
в оборотах (товарно-материальных ценностей, готовой продукции и в незавершенном
производстве), коэффициент оборачиваемости средств в оборотах.
Пример 3В
В текущем периоде оборотные средства организации
составили 1400 тыс. тенге. Доля ТМЗ и ТМЦ в общем итоге средств в оборотах –
25%.
В базовом периоде предполагается снизить издержки
ТМЗ и ТМЦ на одно изделие на 15%.
Исчислить объем средств в оборотах в базовом
периоде с учетом сокращения норм расхода материала.
Пример 4В
В текущем периоде сумма нормируемых средств
в оборотах в организации составила 100 тыс. тенге.
Продолжительность одного оборота средств в
оборотах в – 35 суток.
В базовом периоде объем реализуемой
продукции увеличится на 5%.
Исчислить сокращение времени оборота средств
в оборотах при той же величине нормируемых средств в оборотах.
Пример 5В
В текущем периоде в организации оборотные
средства составили 50 тыс. тенге.
Объем реализованной продукции – 1000 тыс.
тенге в базовом периоде ожидается увеличение планируемого объема продукции до
1100 тыс. тенге в результате плановых организационно — технических мероприятий
предполагается сократить скорость оборота средств в расчетах на 1 день.
Исчислить абсолютную и относительную экономию
средств в оборотах при увеличении оборачиваемости средств в оборотах.
Тема II. «Средства в обороте»
Средства в обороте — это те
средства, организации которые она использует для своего функционирования,
оборотные средства включают в себя материальные запасы организации,
незавершенное производство, запасы готовой и отгруженной продукции, дебиторскую
задолженность, кроме того денежные средства в кассе и денежные средства на
счетах в банке.
Совокупность денежных средств, необходимая
для создания оборотных производственных фондов и фондов обращения,
обеспечивающих непрерывный кругооборот денежных средств, и возвращающаяся в исходную
денежную форму после завершения каждого цикла – это оборотные средства, но не
стоит путать их с денежными средствами, вложенными в основные фонды.
Пример 1.
Материальные издержки в организации за три
месяца составляют 650 тыс. тенге, План запасов ТМЗ и ТМЦ– 36 суток. Исчислить
норму запаса ТМЗ и ТМЦ на три месяца.
Алгоритм расчета
650 х 36 / 90= 260 тыс.
тенге
Пример 2.
Исчислить План средств в оборотах в по
инструментарию, находящемуся в эксплуатации, если Норматив средств в оборотах в
на одного работника составляет 250 тенге, численность рабочих в организации–
750 человек. Расход исчисляется в размере 45% при выдаче инструментария в
эксплуатацию и 65% после окончания их срока службы.
Срок службы равен 2 годам.
Алгоритм расчета
250 х 750 х 0,45 = 84,375 тыс.
тенге
Пример 3.
Исчислить норму незавершенного
производства, пи следующих данных,- количество монтажных работ составляет 2500
тыс. тенге в год.
План незавершенного производства принять в
размере 30%.
Алгоритм расчета
25000 х 0,3 = 750 тыс. тенге
Пример 4.
Исчислить План средств в оборотах по
элементам: производственные запасы товарно-материальных ценностей,
незавершенное производство, готовая продукция, общая сумма нормируемых средств
в оборотах.
Обязательна определенная сумма средств в
оборотах, для бесперебойной работы бесперебойного производства и процесса
реализации продукции.
Базовый объем выпуска– 1700 изделий в год.
Расчетная стоимость производства
(себестоимость) одного изделия -2500 тенге.
В незавершенном производстве используется
следующий коэффициент нарастания затрат – 0,88. Расход ТМЗ и ТМЦ на одно
изделие – 15500 тенге при норме запаса – 30 суток.
Норматив запаса готовой продукции – 15
суток.
Продолжительность производственного цикла
– 22 дня.
Алгоритм расчета
1.
План запаса товарно-материальных ценностей:
(1700х2500х30)/360
= 354 166, 67 тенге
2. План незавершенного производства:
1700
х 15500 / 360 х 22 х 0,88 = 1 417 044,44 тенге
План готовой продукции:
1700х
15500 / 360 х 15 = 1 097 916, 67 тенге
Общая сумма нормируемых средств в
оборотах:
354 166,67+1 417 044,44+1 097 916,67 =2 869 127,78 тенге
Пример 5.
Исчислить норму средств в оборотах в
незавершенном производстве. Годовой выпуск продукции– 50 000 изделий.
Производственная стоимость изделия – 888
тенге затрат в незавершенном производстве, коэффициент нарастания принять за–
0,75.
Цикл производства 16 суток.
Алгоритм расчета
888 х 50 000 х 16 х 0,75 = 53 280 000 тенге
Примеры для самостоятельного решения
Пример 1А
Исчислить объем производственного запаса
ТМЗ и ТМЦ для бесперебойной работы организации в объеме 2500 изделий в
год. Поставки ТМЗ и ТМЦ производятся 1 раз в
квартал.
Норматив расхода ТМЗ и ТМЦ –
65 кг.
Пример 2А
Для бесперебойной работы и ритмичного
выпуска изделий и реализации выпущенной продукции, обязательна определенная
сумма средств в оборотах в товарно-материальных запасах производства
материальных ресурсов.
План организации рассчитан на выпуск
изделия «1» -500 единиц изделий, «2» — 300 единиц изделий. Показатели о расходе
ТМЗ и ТМЦ приведены в таблице.
|
Виды |
Норматив |
Цена |
Норматив |
Норматив |
|
|
1 |
2 |
||||
|
Бронзовое |
0,2 |
0,3 |
1200 |
30 |
15 |
|
Сталь |
0,5 |
0,7 |
2000 |
60 |
25 |
|
Жаропрочный |
0,08 |
0,04 |
9000 |
90 |
45 |
Пример 3А
Базовый объем выпуска составляет 888
изделий, объем продаж – 959 тыс. тенге, расчетная стоимость производства
(себестоимость) одного изделия 2500 тенге.
Издержки распределяются равномерно в
течение одного производственного цикла (цикла производства – от момента покупки
материалов до момента выхода готовой продукции).
Продолжительность цикла производственного
процесса – 42 дня.
Норматив расхода материала на одно изделие
680 тенге, при норме запаса 30 суток.
Норматив расхода вспомогательных товарно-материальных
ценностей (ТМЦ) на годовой выпуск – 84 тыс. тенге при норме запаса 35 суток, горюче-смазочные
вещества (ГСМ) соответственно 32 тыс. тенге и 32 дня, прочих производственных
запасов – 94 тыс. тенге и 56 дня.
Исчислить базовое количество средств в
оборотах по элементам:
·
запасы в производстве
·
незавершенное производство
·
суммарный запас нормируемых средств производства.
Пример 4А
Исчислить общий базовый объем средств в
оборотах, если расчетная стоимость производства (себестоимость) годового
выпуска продукции составляет 2200 тыс. тенге, затраты на материалы – 650 тыс.
тенге, норматив запасов производства – 14 суток. Норматив запаса готовой
продукции – 12 суток, продолжительность цикла производства – 30 суток.
Пример 5А
Норматив средств в оборотах в
производственных запасах – 2800 тыс. тенге, норматив расходов будущих периодов
– 220 тыс. тенге. Плановый объём выпуска продукции – 2500 единиц изделий, продолжительность
цикла производства 45 суток. Расчетная стоимость производства (себестоимость) единицы
изделия 19,5 тыс. тенге.
Показатель нарастания затрат – 0,4.
Норматив запаса готовой продукции на
складе – 5 суток.
Рентабельность выпущенной продукции 30%.
Тема III. «Основные средства».
Материальные
активы (средства производства), которые предназначены для использования в
процессе производства, реализации товаров и оказания услуг, передачи в аренду,
предполагаются к использованию в течение более чем одного отчетного периода
называются — основные средства.
Основные средства организации (ОС) – это
имущество это организации, которое она использует более 12 месяцев в целях
производства продукции, оказания услуг или выполнения тех или иных работ.
Виды стоимости основных средств предприятия,-
·
первоначальная;
·
амортизируемая;
·
остаточная;
·
ликвидационная;
·
восстановительная;
·
рыночная;
·
балансовая;
·
текущая;
·
среднегодовая;
·
входящая и выходящая.
Пример 1.
Исчислить среднегодовую стоимость основных
средств (СГСОС) организации, если на 01.01 стоимость основных средств
составляет 500 млн. тенге, в марте приобретено оборудование на сумму 120 млн.
тенге, в октябре списано оборудование на сумму 40 млн. тенге.
Алгоритм решения задачи
Среднегодовая стоимость:
млн.
тенге
Пример 2
Исчислить первоначальную стоимость
оборудования «А» и «С», исходя из следующих данных.
Цена приобретения оборудования: «А» 410 .
тенге, «С» — 820 тыс. тенге Общая сумма транспортных расходов – 220 тыс. тенге,
погрузо-разгрузочных работ – 50 тыс. тенге.
На долю оборудования «Х» приходится 25%
затрат на транспортировку и монтажные работы. Расходы на доставку и установку оборудования
«А» — 60 тыс. тенге, «С »- 80 тыс. тенге.
Алгоритм решения задачи
1.
Первоначальная стоимость оборудования «А»:
410 + (220
+ 50) * 0,25 + 60 = 537,5 тыс. тенге
2.
Первоначальная стоимость оборудования «С»:
820 + (220 + 50) * 0,75 + 80 = 1102,5 тыс.
тенге
Пример 3.
Исчислить стоимость основных фондов на
конец отчетного периода.
|
Агрегация |
На |
Изменение |
|
1.Здания |
341510 |
|
|
2.Сооружения |
64610 |
|
|
3.Передаточные |
36920 |
+440 |
|
4.Рабочие |
378430 |
+23500 |
|
5.Силовые |
18460 |
-530 |
|
6.Инструменты |
23998 |
-810 |
|
7.Инвентарь |
21229 |
+750 |
|
8.Транспортные |
22152 |
-910 |
|
9.прочие |
15691 |
-230 |
|
Всего |
923000 |
Алгоритм решения задачи
Стоимость основных фондов на конец года:
923000 + (440+23500+750) –
(530+810+910+230) = 945210 тыс. тенге
Примеры для самостоятельного
решения
Пример 1С
Основные производственные фонды организации
на 01.01 составили 2825 млн. тенге. Ввод и выбытие основных фондов в течение
года отражены в таблице.
|
Наличие |
Основные |
|
|
Февраль |
40 |
6 |
|
Май |
50 |
4 |
|
Август |
70 |
8 |
|
Ноябрь |
10 |
5 |
Исчислить среднегодовую и выходящую
стоимость основных производственных фондов.
Пример 2С
Исчислить входящую стоимость оборудования
исходя из следующих данных: оптовая цена оборудования
— 720 тыс. тенге.
Общая сумма расходов по транспортировке на
доставку оборудования – 220 тыс. тенге, стоимость
погрузо-разгрузочных работ – 50 тыс. тенге.
Расходы на установку — 40 тыс. тенге, на
монтаж оборудования — 60 тыс.
тенге.
Пример 3С
Исчислить остаточную стоимость оборудования
первоначальная стоимость составляла 568 тыс. тенге. За срок эксплуатации сумма
начисленного износа составила 76% от первоначальной стоимости. Затраты на
демонтаж составили – 34 тыс. тенге
Тема IV.
«Износ и амортизация основных фондов».
Износ, как понятие, в бухгалтерском учете
есть не что иное, как отражение уменьшения потребительских свойств объекта при
эксплуатации или хранении, в процессе которых объект теряет свои функциональные
свойства и, следовательно, уменьшается в цене.
Амортизация — это процесс переноса затрат,
связанных с приобретением долгосрочных материальных активов, на отчетные
периоды, в течение которых ожидается получение текущих доходов от использования
этих активов.
Способы исчисления амортизации:
·
линейным способом (метод равномерного начисления амортизации);
·
способом уменьшаемого остатка (метод исчисления амортизации от
остаточно стоимости);
·
способом списания стоимости по сумме чисел лет срока полезного
использования (кумулятивный метод начисления амортизации);
·
способом списания стоимости пропорционально объему продукции
(производственный метод начисления амортизации).
Пример 1.
Исчислить сумму амортизационных
отчислений, если стоимость зданий составила 5 млн. тенге, автотранспортных
средств-10 млн. тенге, станков -4 млн. тенге.
Средний норматив амортизационных
отчислений по видам основных средств составила соответственно 5, 10 и 12 %.
Алгоритм решения задачи
Амортизационные отчисления составят:
5 * 0,05 + 10 * 0,1 + 4 * 0,12
= 1,73 млн. тенге
Пример 2.
Исчислить сумму амортизационных отчислений
за фактический срок службы оборудования, используя метод начисления амортизации
по методу уменьшаемого остатка при следующих исходных данных.
Стоимость оборудования – 150 млн. тенге, базовый
срок службы оборудования – 8 лет. Предполагаемый срок эксплуатации оборудования
3 года. Коэффициент ускорения – 2.
Алгоритм решения задачи
Годовой норматив амортизации:
1 : 8 = 0,125 или 100 / 8=25%
Амортизация за первый год эксплуатации:
2
* 0,125 *150 = 37,5 млн. тенге
Амортизация за первый год эксплуатации:
2 * 0,125 * (150 – 37,5) =
28,13 млн. тенге
Амортизация за первый год эксплуатации:
2 * 0,125 * (150 – 37,5 –
28,13) = 21,1 млн. тенге
Сумма амортизации за фактический срок эксплуатации:
37,5 + 28,13 + 21,1 = 86,73 млн.
тенге
Пример 3.
Исчислить сумму амортизационных отчислений
за 3 года работы станков и оборудования при использовании способа начисления
амортизации по сумме чисел лет срока полезного использования.
Стоимость оборудования 354 тыс. тенге.
Полезный срок службы – 10 лет.
Алгоритм решения задачи
1. Сумма чисел лет срока службы:
(1 +2+3+4+5+6+7+8+9+10) = 55
(кумулятивное число)
2. Амортизационные отчисления за первый год эксплуатации:
3. Амортизационные отчисления за первый год эксплуатации:
4. Амортизационные отчисления за первый год эксплуатации:
5.Сумма амортизации за фактический срок эксплуатации:
64,36 + 57,93 + 51,49 = 173,78
тыс.тенге
Пример 4.
Исчислить годовую сумму амортизационных
отчислений от стоимости автомобиля грузоподъемностью 5 тонн с предполагаемым
пробегом – 400 тыс. км.
В текущем периоде пробег по факту составит
– 5 тыс. км. Стоимость автомобиля 1230 тыс. тенге.
Алгоритм решения задачи
Сумма амортизационных отчислений за год:
1230 / 400 * 5 = 15,38 тыс. тенге
Пример 5.
На основании имеющихся данных Исчислить
показатели, приведенные в таблице (заполнить таблицу).
|
№ |
Наименование ОС |
Первоначальная |
Плановый |
Норматив |
Время |
Остаточная стоимость, |
Начислено за срок эксплуатации, млн. тенге |
|
1 |
Станок |
10 |
8 |
12,5 |
3 |
6,25 |
3,75 |
|
2 |
Здание |
60 |
20 |
5 |
12 |
24 |
36 |
Алгоритм решения задачи
1. Станок
а) Норматив амортизации: На =100/8=12,5% или 0,125
б) остаточная стоимость: млн.
тенге
в) расчетное начисление за фактический срок эксплуатации: млн.
тенге
2.Здание
а) первоначальная стоимость:
млн.
тенге
б) расчетное начисление за фактический срок эксплуатации: млн.
тенге
Примеры для самостоятельного решения
Пример 1D
Исчислить норму амортизации производственного
оборудования, если его первоначальная стоимость – 90 млн. тенге.
На модернизацию и ликвидацию изношенного
оборудования было израсходовано 20 тыс. тенге.
Стоимость изношенного оборудования при
ликвидации станков – 10 тыс. тенге.
Срок службы оборудования – 5 лет.
Пример 2D
Первоначальная стоимость основных
производственных фондов организации на начало года составила 300 млн. тенге.
В течение года в эксплуатацию введено оборудования
на сумму 30 млн. тенге.
Выбыло оборудования на сумму – 20 млн. тенге.
Износ основных фондов на начало года
составил 30%.
Плановый норматив амортизации за год –
10%.
Исчислить среднегодовую норму амортизации
и сумму амортизационных отчислений в текущем периоде.
Пример 3D
Первоначальная стоимость станка 87 млн. тенге.
Базовый срок службы 12 лет.
Выручка от реализации отдельных узлов и
деталей станка, стоимость лома после износа – 260 000 тенге
Исчислить амортизацию равномерным методом.
Пример 4D
Приобретен актив основного средства
стоимостью 45 млн. тенге.
Срок полезного использования определен – 5
лет.
Исчислить по годам объем амортизационных
отчислений, используя метод «по сумме чисел лет срока полезного использования».
Пример 5D
Исчислить степень различного вида износа «физического
и морального» износа станка, если, первоначальная стоимость станка – 12 млн.
тенге;
Базовый срок службы 10 лет.
Фактический срок эксплуатации 3 года.
Сумма начисленного износа 3900 тыс. тенге.
производительность станка 16 тыс. деталей в год.
В результате повышения эффективности
производства затраты на изготовление станка снижены до 8 млн. тенге.
Производительность нового оборудования 20
тыс. деталей в год.
Тема V.
«Оценка состояния, движения и использования основных фондов»
Уровень
физического износа основных средств зависит от:
·
первоначального
качества основных фондов; степени их эксплуатации;
·
уровня
агрессивности среды, в которой функционируют основные фонды;
·
уровня
квалификации обслуживающего производственного состава работников предприятия;
·
своевременности
соблюдения и проведения (ППР) планово предупредительных ремонтов и др.
Учет этих
факторов в работе предприятий может в значительной мере повлиять на физическое состояние
основных фондов.
Подвергаясь
в процессе производства физическому износу, основные средства, ежегодно теряют
часть своей потребительской стоимости, равную той части показателя, которая
перенесена на изготовленную в течение этого года продукцию.
Величина рассчитывается
следующей формулой:
УИ = Сф / Ап *
100,
(1.1)
Где,
УИ – процентный износ основных
средств;
Сф — срок фактической эксплуатации
основных фондов (лет);
А — нормативный срок службы
(амортизационный период) фондов (лет).
Качественные характеристики уровня
физического износа основных фондов раскрываются в ряде показателей.
Пример
1.
В цехе организации установлено 100
станков.
Режим работы – 2 смены. Продолжительность
смены 8 часов.
Годовой объем выпуска продукции – 280 тыс.
изделий.
Производственная мощность организации –
310 тыс. изделий. Количество рабочих суток в периоде – 260. время фактической
работы одного станка – 4000 час.
Исчислить коэффициенты экстенсивной и
интенсивной загрузки и интегральный коэффициент
Алгоритм
решения задачи
1.
Номинальный фонд рабочего времени:
2.
Коэффициент экстенсивной загрузки:
3. Коэффициент
интенсивной загрузки:
4.
Коэффициент интегральной загрузки:
Пример 2.
Исчислить фондоотдачу основных средств и
фондоёмкости продукции, если их стоимость составила 2 млн. тенге, объем выпуска
продукции – 25 тыс. единиц изделий по цене 500 тенге за единицу.
Алгоритм решения задачи
1.Фондоотдача основных фондов:
2.Фондоемкость продукции:
Пример 3.
Стоимость основных фондов промышленного организации
по сравнению с прошлым годом возросла с 2500 до 2600 тыс. тенге. При этом
фондоотдача снизилась с 4,8 до 4,7 тенге на тенге основных фондов.
Исчислить объем выпуска продукции, который
недополучило предприятие за счет снижения фондоотдачи.
Алгоритм решения задачи
1.
Плановый выпуск продукции при плане фондоотдачи:
тыс.
тенге
2.
Выпуск продукции в текущем периоде:
тыс.
тенге
3. Недостаток получения продукции в текущем
периоде в результате уменьшения фондоотдачи:
тыс.
тенге
Пример 4.
Исчислить фондовооруженность труда и
фондоотдачу в натуральном выражении в организации, если среднегодовая стоимость
основных фондов 20 млн. тенге
Штатное количество работников 1200
человек, производительность труда – 1460 тыс. тонн/ чел.
Алгоритм решения задачи
1.
Фондовооруженность труда на предприятии:
тыс.
тенге
2.
Фондоотдача основных фондов:
Пример 5.
На 1.01 текущего года стоимость основных производственных
фондов составила 145 млн. тенге. С 1. 03 введено новое оборудование стоимостью
25 млн. тенге, с 1. 12 ликвидировано морально устаревшее оборудование на сумму
8 млн. тенге.
Годовой объем выпуска продукции – 300 млн.
тенге.
Исчислить среднегодовую стоимость основных
производственных фондов, фондоотдачу и фондоёмкость.
Алгоритм решения задачи
1.
Среднегодовая стоимость основных фондов:
млн.
тенге
2.
Фондоотдача основных фондов:
тенге/
тенге
3.
Фондоёмкость продукции:
тенге/тенге
Примеры для самостоятельного решения
Пример 1Е
В текущем периоде предприятие за счет
организационно-технических мероприятий сократило потери рабочего времени на
проведение планово-предупредительных ремонтов оборудования.
Продолжительность времени работы
организации – 256 дня.
Режим работы – 2 смены.
Исчислить коэффициенты экстенсивной и
интенсивной загрузки оборудования, коэффициент интегральной загрузки,
фондоотдачу в предыдущем и текущем периодах.
Исходные показатели приведены в таблице.
|
Показатели |
Ед. |
Базисный |
Отчетный |
|
1.Объем |
Тыс. |
2240 |
2670 |
|
2.Среднегодовая |
Тыс. |
2700 |
2780 |
|
3.Среднегодовая |
Тыс. |
1244 |
1271 |
|
4.Фактически |
час |
3340 |
3649 |
|
5.Плановые |
% |
7 |
4 |
Пример 2Е
Объем реализованной продукции в прошлогоднем
периоде составил 2015 млн. тенге.
Среднегодовая стоимость основных производственных
фондов – 485 млн. тенге.
В текущем периоде ( факт текущего года) объем
выпуска и реализации увеличился на 19%, а среднегодовая стоимость – на 8%.
Исчислить, как изменится фондоотдача.
Пример 3Е
Стоимость основных фондов промышленного организации
в текущем периоде составила 4850 тыс. тенге.
При этом фондоотдача снизилась с 5,8 до
5,3 тенге на тенге основных фондов.
Исчислить объем выпуска продукции, который
недополучило предприятие за счет снижения фондоотдачи.
Пример 4Е
Предприятие за год выпустило 4180 тыс.
изделий по цене 1200 тенге.
Среднегодовая стоимость основных
производственных фондов на 1 число текущего года
составила 2125 млн. тенге за год было приобретено новое оборудование, которое
введено в действие в августе.
Стоимость нового оборудования – 45 млн.
тенге.
Исчислить фондоотдачу на начало следующего
года.
Пример 5Е
В прошлом периоде предприятие изготовило
изделий на сумму 980 млн. тенге, среднегодовая стоимость основных
производственных фондов составила 400 млн. тенге.
В текущем периоде выпущено продукции на
сумму 1070 млн. тенге, среднегодовая стоимость основных производственных фондов
увеличилась на 7%.
Исчислить, насколько
изменилась фондоотдача основных фондов и фондоёмкость продукции.
Пример 6Е
На основании имеющихся данных заполнить
таблицу.
|
№ |
Стоимость |
Стоимость |
Общая |
Объем |
Фондоёмкость |
|
1 |
46 |
58 |
102 |
146 |
|
|
2 |
20 |
37 |
0,71 |
||
|
3 |
94 |
125 |
1,31 |
||
|
4 |
84 |
200 |
0,8 |
Тема VI. «Кадровый состав предприятия».
Кадровый
состав предприятия – это один из самых важных факторов производственного
процесса.
Потому
что, именно человек, с его умственными и физическими способностями, является
основой производства: человек управляет машинами и оборудованием, руководит
производством и планирует его.
Трудовые ресурсы — это часть населения, обладающая необходимым
физическим развитием, знаниями и практическим опытом для работы в народном
хозяйстве.
В списочном составе – должны быть учтены как фактически
работающие, так и отсутствующие на работе по каким-либо причинам, но не
прервавшие договорных отношений с предприятием.
Среднесписочная численность – это численность работников в среднем
за (месяц, квартал, с начала года, за год) определенный период.
Среднесписочная численность работников за месяц определяется путем
суммирования численности работников списочного состава за каждый календарный
день месяца, включая праздничные и выходные дни, и деления полученной суммы на
число календарных суток месяца.
Трудоемкость
– характеризует затраты рабочего времени на производство добавленной стоимости
или на выполнение конкретной производственной задачи.
1. Коэффициент оборота по приему = численность работников,
принятых за период / среднесписочную численность за этот период.
2. Коэффициент оборота по
выбытию = численность работников, выбывших за период / среднесписочную
численность за этот период.
3. Коэффициент текучести = (Число принятых – Число выбывших) /
среднесписочную численность
Производительность
труда – эффект от деятельности персонала предприятия.
Пример 1.
Исчислить потребную списочную численность
работников для выполнения 100 тыс. единиц изделий, если норматив выработки на 1
работника составляет 20 изделий в месяц.
Коэффициент замещения – 1,15.
Алгоритм решения задачи
1.Явочная численность работников:
чел.
2.Списочная численность работников:
чел.
Пример 2.
Базовая трудоемкость выполнения плана
организации652 тыс. нормо-часов, полезный фонд рабочего времени 1865 час.
Планируемое среднее выполнение норм
выработки — 110%.
Исчислить базовую явочную численность
сдельщиков.
Алгоритм решения задачи
чел.
Пример 3.
Исчислить среднесписочную численность
работников на основе следующих данных.
Количество обслуживаемых станков – 120. Норматив
обслуживания на одного наладчика – 6 станков в смену, режим работы – 2 смены.
Коэффициент использования номинального
фонда рабочего времени – 0,9.
Алгоритм решения задачи
чел.
Пример 4.
Исчислить среднесписочную численность
работников на основе следующих данных. Сменное производственное задание – 60 единиц
изделий. Норматив времени на изготовление одного изделия – 3 часа.
Базовый коэффициент выполнения базового
задания – 1.2, режим работы – двусменный. Продолжительность рабочей смены – 8
часов. Коэффициент использования номинального фонда времени – 0,95. Коэффициент
замещения – 1,17.
Алгоритм решения задачи
Явочная численность работников:
чел.
Списочная численность работников:
чел.
Пример 5.
Численность производственного кадрового
состава в организации в текущем периоде составила 300 человек.
В результате внедрения мероприятий по
совершенствованию организации труда и повышения норм обслуживания необходимость
в рабочих повременщиках уменьшится на 15 человек.
Одновременно планируется повысить нормы
выработки для рабочих сдельщиков на 10%.
Доля рабочих сдельщиков в текущем периоде
составляла 35%, рабочих повременщиков — 50% общей численности.
Исчислить численность производственного состава
работников предприятия в базовом периоде.
Алгоритм решения задачи
1.
Численность рабочих в текущем периоде:
— сдельщиков: чел.
— повременщиков: чел.
2. Численность производственного кадрового
состава в базовом периоде:
-сдельщиков:
чел.
— повременщиков:
чел.
— служащих:
чел.
— всего численность производственного кадрового состава:
чел.
Примеры для самостоятельного решения
Пример 1Ж
Исчислить численность рабочих-сдельщиков
на основе следующих данных.
Технологическая трудоемкость выполнения
плана организации составляет по плану 3560 тыс. нормо-часов.
Реальный фонд рабочего времени в базовом
периоде 225 суток.
Реальная продолжительность рабочего дня
7,78 часа, планируемый коэффициент выполнения норм выработки 1,2.
Пример 2Ж
Исчислить среднесписочный состав бригады
на основе следующих данных. Общий годовой объем работы бригады – 800 тыс. тонн.
Суточный норматив выработки – 120 тонн.
Коэффициент выполнения норм – 1,2.
Коэффициент использования номинального
фонда рабочего времени 0,95. работа производится круглосуточно 365 суток.
Пример 3Ж
Исчислить возможное уменьшение численности
работников, если известно, что в текущем периоде в организации изготовлено 2780
изделий нескольких видов стоимостью 9760 тыс. тенге
Затраты живого труда (трудоемкость)
производства в текущем периоде составила 3370 тыс. нормо-часов. В базовом
периоде планируется увеличить объем выпуска для 3000 изделий стоимостью 10700
тыс. тенге.
По нормативу отчетного года суммарная
трудоемкость составит 3570 тыс. нормо-часов. Планируется увеличить выполнение
норматива выработки на 10%. Фонд полезного времени одного работающего – 1800
часов
Пример 4Ж
Исчислить численность работников в базовом
периоде, если известны следующие показатели.
Численность работников в текущем периоде
составляла 265 чел., из них рабочих 64%.
Планируется увеличить объем производства
продукции на 5,8%, а производительность труда — на 5%
Пример 5Ж
В текущем периоде цех выпустил валовой
продукции на 240 млн. тенге, при списочном составе работающих 156 человек.
В базовом периоде задание по выпуску
продукции составляет 750 изделий по цене 450 тыс. тенге предусматривается
увеличение незавершенного производства на 18 млн. тенге.
Задание по росту производительности труда
составляет 8%.
Исчислить, как изменится списочный состав
работников в базовом периоде на предприятии.
Тема
VII. «Эффективность использования трудовых
ресурсов».
Эффективность использования трудовых
ресурсов измеряется показателями производительности труда.
Прямой показатель производительности
(показатель отдачи) труда называется — выработкой
Пример 1.
Исчислить производительность труда в
организации в стоимостном выражении, если объем выпуска продукции составил 2500
изделий по цене 700 тенге за единицу, явочная численность 100 чел, коэффициент
замещения – 1,15.
Для увязки движения рабочей силы с ситуацией
на рынке труда необходим коэффициент замещения рабочей силы, который
определяется по формуле:
Алгоритм решения задачи
2500*700/100*1,15=15217,4
тенге/чел.
Пример
2.
Исчислить выработку продукции на одного
работающего в натуральном и денежном выражении на основе данных/
Годовой объем выпуска продукции – 200 тыс.
шт.; годовой объем валовой продукции — 3 млн. тенге; среднесписочное число
работающих в организации– 500 чел.
Алгоритм
решения задачи
1.Выработка
в натуральном выражении:
2.Выработка в стоимостном выражении:
3
млн.тенге/500=6000 тенге/чел.
Пример
3.
Исчислить технологическую трудоемкость
годовой программы в целом по предприятию и по видам работ.
За отчетный период нормированные затраты
труда рабочих сдельщиков составили:
по продукции «А» — 65 тыс. нормо-часов;
по продукции «Б» – 20 тыс. нормо-часов;
по продукции «С» — 35 тыс. нормо-часов.
Средний уровень выполнения нормы выработки
в организации составил соответственно 112%, 105%, 90%.
Затраты труда рабочих, занятых на
повременных работах, по указанным видам работ составили соответственно: 8,5
тыс. чел-часов, 2 тыс. чел-часов и 4,2 тыс. чел-часов.
Коэффициент не учтенных работ составил
1,004.
Алгоритм
решения задачи
1.Технологическая
трудоемкость производства продукции «А»:
тыс.
нормо-часов
2.Технологическая
трудоемкость производства продукции «Б»:
тыс.
нормо-часов
3.Технологическая
трудоемкость производства продукции «С»:
тыс.
нормо-часов
4.Технологическая
трудоемкость производства продукции на предприятии:
66,5 + 21,1 + 43,1 = 130,7 тыс.
нормо-часов
Пример
4.
В третьем квартале производством выпущено
продукции на 150 тыс. тенге, выработка продукции на одного работника составила
5000 тенге/чел.
В четвертом квартале производство
планирует выпустить больше на 15% единиц изделий и одновременно снизить
численность персонала на 8 чел.
Исчислить выработку на одного работника в четвертом
квартале и нормативный прирост производительности труда в процентах.
Алгоритм решения задачи
1.Численность работников в 3 квартале:
чел.
2.Выработка продукции на одного работника в 4 квартале:
тенге/чел.
2.
Прирост производительности труда:
Пример 5.
Исчислить текущую технологическую
трудоемкость сборки изделий I, B,
C в человеко-часах на основании следующих данных.
Годовая программа выпуска изделий
составляет: изделий
«I» — 120 шт., изделий «B»
— 140 шт., изделий «C» – 25 шт.
Нормированная трудоемкость сборки одного
изделия составляет: «I» 1900 нормо-час., изделия «B»-
1800 нормо-час., изделия «C» -5000 нормо-час.
Средний процент выполнения норм выработки
по цеху составляет 110%
Алгоритм решения задачи
тыс.
человеко-часов.
Примеры
для самостоятельного решения
Пример
1З
Исчислить трудоемкость единицы продукции
по плану и фактически, а также рост производительности труда на основе данных.
Трудоемкость товарной продукции по плану –
30 тыс. нормо-часов;
Базовый объем выпуска продукции – 200 шт.;
Фактическая трудоемкость товарной
продукции – 26 тыс. нормо-часов;
Фактический объем
выпуска продукции – 220 шт.
Пример
2З
Объем производства продукции в базовом
периоде увеличился на 8%. Численность работников уменьшилась на 2 %.
Исчислить рост
производительности труда в базовом периоде.
Пример 3З
Исчислить рост производительности труда за
счет совершенствования технического уровня, если известно, что среднесписочная
численность работников составляет 150 человек, рабочий парк оборудования – 50
единиц, производительность действующего оборудования 1300 изделий за месяц.
С первого марта списано устаревшего
оборудования — 20 единиц и введено в действие 15 единиц нового оборудования.
Производительность вновь преобретенного
(вновь введенного) на 40% выше действующего.
Пример 4З
Исчислить рост производительности труда в
организации в базовом периоде и количество высвобождаемых рабочих, если
известно, что с первого января в организации будет дополнительно установлено 12
станков, производительность которых на 20% выше, чем у действующих.
Кроме того, в результате модернизации 30
станков их производительность увеличится на 10%.
Парк станочного оборудования организации в
текущем периоде составлял 50 станков.
У действующего парка станков
производительность составляет 250 изделий за смену.
Норматив обслуживания на одного рабочего 2
станка.
Режим работы организации односменный.
Количество рабочих суток за год — 252 дня.
Пример 5З.
Технологическая трудоемкость продукции
составила в текущем периоде 2,2 тыс. нормо-часов.
В результате проведения различных текущих
и оперативных мероприятий по совершенствованию организации производства
планируется снижение трудоемкости на 12%.
А также, в результате усиления ритмичности
производственного процесса, технологии оснащения основных и вспомогательных
работ, планируется сокращение численности вспомогательных рабочих на 13
человек.
Общее число рабочих в организации120
человек.
Исчислить снижение производственной
трудоемкости и увеличение производительности работы (процесса изготовления
продукции предприятия) в результате планируемых мероприятий.
Тема VIII. «Нормирование труда в
организации».
Нормирование
труда в организации – область производственного менеджмента
организации, включающая менеджмент и совершенствование процесса установления
научно-обоснованных норм затрат труда на выполнение работ.
Норматив времени – это количество
рабочего времени, необходимое для выполнения определенной работы (операции) в
наиболее рациональных для данного предприятия организационных, технических,
хозяйственных условиях.
Норматив времени устанавливается в
часах, минутах, секундах, человеко-часах.
Норматив выработки – это объем
работы в единиц изделий, метрах, тоннах (других натуральных единицах), который
должен быть выполнен в единицу времени (час, смену, месяц).
Норматив выработки рассчитывается
как результат деления фонда времени на норму времени.
Норматив обслуживания – это
установленное количество единиц оборудования (число рабочих мест, квадратные
метры площади), обслуживаемых одним рабочим или группой рабочих в течение
смены.
Норматив численности работающих –
это численность работников определенного профессионально-квалификационного
состава, обязательная для выполнения конкретного объема работ как
производственного, так и управленческого характера.
Норматив
управляемости определяет количество работников, которое должно быть
непосредственно подчинено одному руководителю.
Нормированное задание –
установленный состав и объем работ, который должен быть выполнен одним или
группой работников за определенный период времени.
Пример 1.
Исчислить
норму времени и норму выработки за смену:
норматив
оперативного времени – 15 мин; время обслуживания рабочего места — 5%
оперативного времени, время на отдых и личные надобности – 2% оперативного
времени; продолжительность смены – 8 часов.
Алгоритм решения задачи
1.
Норматив времени на производство единицы изделия:
мин.
2. Норматив выработки за смену:
изделий
Пример 2.
Исчислить норму обслуживания аппаратчика агрегата
сушильной установки периодического действия на основе следующих данных.
Продолжительность смены – 480 мин.
Планы времени обслуживания 1 сушилки за
цикл – 37 мин. Подготовительно-заключительное время – 20 мин.
Время на отдых и личные надобности – 25
мин.
Алгоритм решения задачи
1.Время обслуживания сушилки за смену:
мин.
2. Норматив обслуживания устанавливается на
основе нормы времени обслуживания:
циклов
обслуживания
Пример 3.
Исчислить норму выработки станочника на
изготовление детали на основе приведенных данных.
Время автоматизированной машинной обработки
составляет 12 мин.
Время ручной обработки – 4 мин.
Затраты на обслуживания рабочего места —
2,5%. на отдых и личные надобности – 4% оперативного времени.
Продолжительность рабочей смены 480 мин.
Алгоритм решения задачи
1.Норматив времени:
мин.
2. Норматив выработки:
деталей
/ смену.
Пример 4.
Исчислить коэффициент использования
рабочего времени и возможное повышение производительности труда на основе
приведенных данных.
|
№ |
Наименование |
Продолжительность, |
|
1 |
Подготовительно-заключительное |
20 |
|
2 |
Оперативное |
360 |
|
3 |
Обслуживание |
40 |
|
4 |
Перерывы |
25 |
|
5 |
Перерывы, В |
35 20 |
|
6 |
Продолжительность |
480 |
Алгоритм решения задачи
1.Коэффициент использования рабочего времени:
2.Коэффициент возможного повышения производительности труда:
Пример 5.
Исчислить на основе данных хронометража
норму оперативного времени, норму штучного времени и норму выработки за смену.
Карта учета времени работы — карта
операции «обточка детали на токарном станке» приведена в таблице.
|
№ |
Наименование |
Порядковый наблюдения |
Сумма |
Число |
Среднее значение |
|||
|
1 |
2 |
3 |
4 |
|||||
|
Наблюдаемое |
||||||||
|
1 |
Установить |
7 |
8 |
10 |
20 |
45 |
4 |
11,25 |
|
2 |
Включить станок |
3 |
4 |
4 |
4 |
15 |
4 |
3,75 |
|
3 |
Обточить |
700 |
730 |
710 |
715 |
2855 |
4 |
713,75 |
|
4 |
Отвести суппорт |
3 |
3 |
10 |
4 |
20 |
4 |
5 |
|
5 |
Снять |
5 |
6 |
6 |
5 |
22 |
4 |
5,5 |
|
Норматив |
739,25 |
Длительность рабочей смены 8 часов.
Временные затраты на обслуживание рабочего
места 5%, время на отдых и личные надобности – 2,55 оперативного времени.
Алгоритм решения задачи
1.Норматив оперативного времени:
739, 25сек. (см. таблицу)
2.Норматив штучного времени:
сек.
3. Норматив выработки:
деталей
за смену.
Примеры для самостоятельного решения
Пример 1И
Исчислить
норму времени и норму выработки за смену:
Норматив
оперативного времени – 35 мин;
время
обслуживания рабочего места — 5% оперативного времени,
время
на отдых и личные надобности – 3% оперативного времени;
продолжительность
смены – 8 часов.
Пример 2И
Исчислить коэффициент использования
рабочего времени, коэффициент потерь рабочего времени и возможное повышение
производительности труда на основе приведенных данных.
|
№ |
Наименование |
Продолжительность, |
|
1 |
Подготовительно-заключительное |
25 |
|
2 |
Оперативное |
350 |
|
3 |
Обслуживание |
42 |
|
4 |
Перерывы |
20 |
|
5 |
Перерывы, В |
Исчислить 20 |
|
6 |
Продолжительность |
480 |
Пример 3И
Исчислить коэффициент использования
рабочего времени, коэффициент потерь рабочего времени и возможное повышение
производительности труда на основе приведенных данных.
Результаты фотографии рабочего дня за
смену приведены в таблице
|
№ |
Наименование |
Вид |
Время, |
|
1 |
Получение |
8 |
|
|
2 |
Инструктаж |
12 |
|
|
3 |
Выполнение |
380 |
|
|
4 |
Ожидание |
15 |
|
|
5 |
Ожидание |
15 |
|
|
6 |
Исправление |
3 |
|
|
7 |
Хождение |
4 |
|
|
8 |
Перерывы |
22 |
|
|
9 |
Подготовка |
17 |
|
|
10 |
Позднее |
4 |
Пример 4И
Исчислить норму обслуживания на основе
следующих данных. Продолжительность смены – 480 мин.
Планы времени обслуживания оборудования –
37 мин.
Подготовительно-заключительное время – 30
мин. Время на отдых и личные надобности – 40 мин.
Норматив времени на техническое, и
организационное обслуживание рабочего места составляет 2% от нормы времени
обслуживания.
Пример 5И
Исчислить норму оперативного времени на
осмотр и ремонт электродвигателя.
|
№ |
Содержание |
Результаты |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
1 |
Винты |
2,51 |
1,92 |
2,64 |
1,99 |
2,48 |
|
2 |
Замок |
0,26 |
0,38 |
0,21 |
0,35 |
0,33 |
|
3 |
Состояние |
2,11 |
2,84 |
3,06 |
2,06 |
2,71 |
|
4 |
Состояние |
2,15 |
2,72 |
3,02 |
2,54 |
2,62 |
|
5 |
Крышку |
0,54 |
0,72 |
0,48 |
0,55 |
0,64 |
|
6 |
Крышку |
3,82 |
3,64 |
4,02 |
3,54 |
3,68 |
Тема IX.
«Организация заработной платы».
Заработная плата – это вознаграждение за
труд.
На предприятиях организованы
отделы по организации заработной платы, в этих отделах рассчитываются
показатели взаимосвязи количества и качества труда с размерами его оплаты,
путем использования нормирования, тарифной системы, премии, доплат и надбавок.
Главная задача оплаты труда
состоит в том, чтобы поставить заработную плату в зависимость от времени,
качества и объема выполненной работы.
Отделы по организации заработной платы
ставят своими задачами:
— определение систем, видов и форм оплаты
труда работников предприятия;
— наработку критериальных признаков и
определение размеров доплат за различные достижения, и прочие условия работы;
— применение должностных окладов инженерно-техническим
работникам, руководителям и служащим;
— положение о премировании работников
предприятия.
Пример 1.
Расценка сдельная в текущем периоде
составила 500 тенге за единицу изделия. Исчислить прямую сдельную заработную
плату рабочего, если в базовом периоде предполагается снизить норму времени на
5 процентов при одновременном росте заработной платы на 7 процентов.
Объем выпуска в базовом периоде составит 240 тыс. изделий в год.
Алгоритм решения задачи
500*1,07*0,95*240
000=121 980 000
Пример 2
Рабочий 6 разряда укладывает за час 1,5 м2
площади.
Часовая тарифная ставка – 116,82 тенге. Исчислить
сдельную расценку за м2 площади.
Алгоритм решения задачи
1. Норматив выработки рабочего за час – 1,5 м2
площади
2. Расценка сдельная за единицу продукции (1 м2
площади).
116,82/1,5 = 77,9 тенге/м2
Пример 3
Бригада из шести человек выполняет
ремонтные работы на путях движения трамваев. За смену они сделали протяженность
8 километров.
Расценка сдельная для бригады 712,2 тенге
за метр погонный. Исчислить сдельный заработок бригады и каждого работника при
условии, что все рабочие бригады имеют одинаковый разряд.
Алгоритм решения задачи
1. Бригадная расценка сдельная –712,2 тенге/п.м.
2. Бригадный средний заработок:
тенге /смену
3. Заработок рабочего в среднем:
тенге смену.
Пример 4
Провести распределение заработанных
средств между рабочими бригады на основе ниже приведенных значений.
Бригада, состоящая из четырех человек,
заработала по сдельным расценкам 80 537,76
тенге.
За выполнение плана по выпуску продукции
бригаде начислена премия в размере 30% сдельного заработка.
Индивидуально каждый проработал количество
времени, приведенное в таблице.
|
Разряд |
Часовая |
Отработанное |
|||
|
всего |
В |
В |
В |
||
|
5 |
32,86 |
184 |
8 |
64 |
64 |
|
4 |
28,39 |
184 |
64 |
64 |
|
|
3 |
25,52 |
184 |
64 |
64 |
|
|
3 |
25,52 |
184 |
64 |
64 |
Доплатные коэффициенты за работу в
праздничные дни – 0,0435 к заработной плате за отработанное время, доплата за
работу в ночное время – 40%, за работу в вечернее время 20% к часовой тарифной
ставке.
Алгоритм решения задачи
1.Тарифный заработок бригады:
2.Коэффициент сдельного приработка:
80537,76:61982,24=1,299
3.Расчет месячной заработной платы рабочих приведен в таблице
|
Разряд рабочего |
Тарифный заработок (тарифной ставке* |
Сдельный заработок (тарифный заработок* *1,299) |
Премия (сдельный заработок * 0,3) |
Доплаты |
Месячный |
||
|
праздничные |
вечернее |
ночное время |
|||||
|
5 |
6046,24 |
7854,07 |
2356,22 |
341,65 |
1209,25 |
2418,50 |
14179,69 |
|
4 |
5223,76 |
6785,66 |
2035,70 |
1044,75 |
2089,50 |
11955,61 |
|
|
3 |
4695,68 |
6099,69 |
1829,91 |
939,14 |
1878,27 |
10747,01 |
|
|
3 |
4695,68 |
6099,69 |
1829,91 |
939,14 |
1878,27 |
10747,01 |
Пример 5
Исчислить заработок рабочего за месяц.
Рабочий сдельщик 6 разряда выполнил норму
выработки на 120%.
Его заработок по сдельным расценкам
составил 8765 тенге. По положению сдельные расценки за продукцию сверх 110%
нормы увеличиваются на 20%.
Алгоритм решения задачи
1.
Сдельный заработок за выполнение производственного задания на 110%
составит:
тенге
2. Сдельная заработная плата за исполнение
производственного задания по повышенной сдельной расценке:
тенге,
Где
0,1 – перевыполнение производственного задания сверх установленной нормы;
1,2
– коэффициент увеличения сдельной расценки при выполнения задания сверх
установленной нормы
3.Заработок рабочего за месяц
тенге
Примеры для самостоятельного решения
Пример 1К
Исчислить заработную плату рабочего по прямой
сдельной форме оплаты труда, если ЧТС — часовая тарифная ставка составляет 1570
тенге, Норматив времени составляет 1,5 часа на единицу продукции.
Объем выпуска продукции составил 180 единиц
изделий.
Пример 2К
Штатная численность работников организации
— 540 человек, из них 140 человек, за вредные условия труда получают доплаты в
размере 12%, 103 человека – в размере 9,5%.
Тарифный фонд заработной платы за год в
организации составляет 735 000 000 тенге.
Исчислить средний уровень доплат за
вредные условия труда в организации, и исчислить ФЗП (фонд заработной платы) с
учетом всех видов доплат.
Пример 3К
Исчислить оплату труда работника
организации при сдельно-премиальной системе, если Норматив времени – 0,65 часа,
расценка сдельщика 3060 тенге за месяц изготовлено 32 единиц изделий.
По факту отработано за месяц 20 дня при 6-часовой
продолжительности рабочего дня.
При выполнении плана установлена премия в
размере 24% заработной платы сдельщика, за каждый процент перевыполнения – 2%
от сдельно оплаты.
Пример 4К
Исчислить, как изменится размер фонда оплаты
труда в организации, если ее среднесписочный состав производственных рабочих
уменьшился на 0,5%, а средняя оплата труда увеличилась на 14%.
Пример 5К
Исчислить причитающуюся заработную плату
бригадному коллективу за месяц, если оплата стоимости работы выполняется по
простой бригадной системе. Коллектив состоит из — один человек — 5 разряд; один
человек — 4 разряд; и 3 разряд два человека.
По монтажу задание бригадой было выполнено,
его стоимость составила 235 678 тенге.
Рабочие 3 разряда проработали по 162 часа,
рабочие 4 и 5 разрядов по 174 часа.
Источники информации:
1.https://mylektsii.ru/
2.http://urist7.ru/nalog/buxgalterskij-uchet/koefficient-oborachivaemosti-oborotnyx-sredstv-raschet-formula-po-balansu.html
3.https://megalektsii.ru/s31164t3.html
Экономический анализ, Задания, ситуации, руководство по решению, Герасимова Е.Б., Игнатова Е.А., 2011.
В учебном пособии представлен сборник практических и ситуационных задач, подготовленных для изучения курса Экономический анализ. Задания охватывают несколько разделов курса. Предложенная логика изложения материала позволяет выполнять задания как последовательно, так и выборочно, с целью более детального изучения отдельных тем курса.
Введение.
В последнее время в профессиональном сообществе преподавателей высшей школы все чаще обсуждаются проблемы поиска наиболее современных методик обучения студентов решению задач в области микроэкономического анализа. Эти методики должны базироваться на синтезе достижений ряда наук: философии, логики, экономики, юриспруденции и методики обучения экономическому анализу. Между тем ощущается недостаток специальных руководств по решению задач, что ограничивает возможности применения задачи как одного из способов формирования профессиональной компетенции.
Практические учебные и ситуационные задания в области экономического анализа во многом определяют компетентность будущего экономиста. Если на лекциях студент приобретает знания, то в процессе выполнения практических заданий он работает над остальными компонентами компетенции:
- осваивает умения решения профессиональных задач;
- формирует отношение к объекту анализа (предприятию, организации) и предмету анализа (системе показателей, факторов и резервов);
- накапливает опыт применения инструментария экономического анализа, составления методики анализа и разработки рекомендаций.
- Несформированность описанных выше компонент компетенции является, как правило, следствием следующих причин:
- решая задачу, студенты не осознают должным образом свою собственную деятельность, т. е. не понимают сущности задач и хода их решения;
- студенты нс всегда анализируют содержание задачи, проводят ее осмысление и обоснование;
- не вырабатывают общие подходы к решению и не определяют последовательность действий;
- часто неправильно используют экономические категории, термины и определения, а также математические действия.
Содержание:
Общее руководство к решению заданий по экономическому анализу
Раздел 1 ОСНОВЫ ТЕОРИИ ЭКОНОМИЧЕСКОГО АНАЛИЗА
Ситуационные задания по разделу I
Руководство по решению заданий раздела I
Вопросы для самоконтроля
Задания для самоконтроля по разделу I
Раздел 2 АНАЛИЗ ВЗАИМОСВЯЗИ ОБЪЕМА ПРОДАЖ, ЗАТРАТ И ПРИБЫЛИ
Ситуационные задания по разделу 2
Руководство по решению заданий раздела 2
Вопросы для самоконтроля
Задания для самоконтроля по разделу 2
Раздел 3 РОЛЬ АНАЛИЗА В РАЗРАБОТКЕ И МОНИТОРИНГЕ ПЛАНОВЫХ ПОКАЗАТЕЛЕЙ
Ситуационные задания по разделу 3
Руководство по решению заданий радели 3
Вопросы для самоконтроля
Задания для самоконтроля по разделу 3
Раздел 4 КОМПЛЕКСНЫЙ АНАЛИЗ ФИНАНСОВО-ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ ОРГАНИЗАЦИИ
Руководство по решению заданий раздела 4
Ситуационные задания по разделу 4
A Анализ объемов производства и реализации продукции
Вопросы для самоконтроля (часть А)
Задания для самоконтроля (часть А)
Б Анализ производственных ресурсов
Вопросы для самоконтроля (часть Б)
Задания для самоконтроля (часть Б)
B Анализ затрат и финансовых результатов
Вопросы для самоконтроля (часть В)
Задания для самоконтроля (часть В)
Г Анализ финансового состояния организации
Вопросы для самоконтроля (часть Г)
Задания для самоконтроля (часть Г)
Приложение 1 Бухгалтерский баланс ОАО «Свет»
Приложение 2 Отчет о прибылях и убытках ОАО «Свет»
Приложение 3, Отчет о движении денежных средств ОАО «Свет»
Приложение 4 Ответы на задания для самоконтроля
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Экономический анализ, Задания, ситуации, руководство по решению, Герасимова Е.Б., Игнатова Е.А., 2011 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу — Экономический анализ, Задания, ситуации, руководство по решению, Герасимова Е.Б., Игнатова Е.А., 2011.
— Яндекс Народ Диск.
Скачать книгу — Экономический анализ, Задания, ситуации, руководство по решению, Герасимова Е.Б., Игнатова Е.А., 2011. — depositfiles.
Дата публикации: 26.03.2012 07:18 UTC
Теги:
книга по экономике :: руководство по решению :: Герасимова :: Игнатова :: 2001
Следующие учебники и книги:
- Экономика организаций (предприятий), Сергеев И.В., Веретенникова И.И., 2005
- Управленческий учет, Кукукина И.Г., 2004
- Экономика строительства, Степанова И.С., 2007
- Банковское дело, Лаврушин О.И., 2009
Предыдущие статьи:
- Экономика, анализ и планирование на предприятии торговли, Соломатин А.Н., 2009
- Теория экономического анализа, Шеремет А.Д., 2011
- Макроэкономика, Абель Э., Бернанке Б., 2010
- Анализ финансово-хозяйственной деятельности, Практикум, Губина О.В., Губин В.Е., 2012
Экономика — это система хозяйствования включает отрасли материального производства и нематериальные сферы, которые обеспечивают общество материальными и нематериальными благами. На этой странице собрано много решений задач по экономике на разные темы.
Содержание:
- Что такое экономика
- Примеры решения типовых задач по экономике на разные темы
- Ответы на вопросы по заказу заданий по экономике
- Решение задач с примерами
- Использование матричного вычисления при решении экономических задач
- Задачи балансового анализа
- Задачи экономического содержания
- Экономические задачи, связанные с последовательностью и ее границей (элементы математики финансов)
- Понятие процента
- Три основные задачи на проценты
- Формула простого процента
- Формула сложного процента
- Формула, когда проценты начисляются непрерывно
- Дисконтирование
- Использование матрицы затрат
- Формула простых процентов
- Модель «спрос-предложение»
- Определение результатов деятельности предприятия
- Определение простых и сложных процентов
- Задача о производительности труда
- Предельный анализ
- Эластичность функции
- Свойства эластичности функции
- Применение производной в экономической теории
- Расчёт производительности ресурса
- Применение функций нескольких переменных в исследованиях экономических процессов
- Понятие о эмпирических формулах и метод наименьших квадратов
- Взаимосвязь между производительностью и основными средствами
- Применение интегралов в некоторых экономических задачах
- Нахождение производственной функции
- Кривая Лоренца
- Кривая обучения
- Закон спроса и предложения
- Задача дисконтирования
- Определение предельного дохода
- Использование дифференциальных и разностных уравнений в экономических задачах
- Воспроизведение общих издержек производства по предельным характеристикам
- Нахождение функций затрат, спроса, цены товара с их эластичностью
- Модель естественного роста
- Модель естественного роста выпуска продукции
- Модель естественного роста при насыщенности рынка
- Динамика рыночных цен
- Использование разностных уравнений в экономике
- Паутинная модель рынка
- Модель развития Самуэльсона-Хикса
- Определение издержек производства
- Расчёт текущей стоимости ценных бумаг
- Задача межотраслевого баланса
- Нахождения расходов сырья, топлива и трудовых ресурсов
- Оптимизация с экономическим содержанием
- Рост инвестиций
Если у вас нет времени на выполнение задачи и заданий по экономике, вы всегда можете попросить меня, пришлите задания мне в 
 Ответы на вопросы по заказу задачи и заданий по экономике:
Ответы на вопросы по заказу задачи и заданий по экономике:

- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

- Доработка бесплатна. Срок выполнения от 1 до 2 дней.

- Оценка стоимости бесплатна.

- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

- Присылайте в любое время! Я стараюсь быть всегда онлайн.

Слово «экономика» греческого происхождения (oikonomike— «искусство домохозяйства»), оно означает «законы хозяйствования». В целом под термином «экономика» понимают хозяйство, в широком смысле этого слова — науку о хозяйстве и хозяйствовании, а также отношениях между людьми в процессе хозяйствования. Экономика, как и любая учебная дисциплина, имеет свой предмет изучения.
- Во-первых, экономика — это хозяйственная система, обеспечивающая удовлетворение потребностей людей и общества в целом созданием необходимых благ (экономика отрасли, региональная экономика (района, края, области, страны), мировая экономика).
- Во-вторых, экономика — это совокупность экономических (производственных) отношений между людьми, складывающихся в процессе производства, распределения, обмена и потребления материальных благ и услуг.
- В-третьих, экономика — это наука о выборе наиболее эффективных (рациональных) способов удовлетворения безграничных потребностей людей ограниченными экономическими ресурсами.
Существуют и другие определения предмета экономики, но общепризнанным в последние годы считается следующее. Экономика—это наука об оптимальном, эффективном использовании редких, ограниченных экономических ресурсов с целью удовлетворения безграничных и постоянно меняющихся потребностей людей, фирмы и общества в целом.
Экономика выполняет методологическую, научно-познавательную, критическую и практическую функции.
Экономика анализирует хозяйственную деятельность в основном на двух различных уровнях: микроэкономическом и макроэкономическом.
Решение задач с примерами
Задача З6
На рынке некоторого качественного товара кривая спроса задана следующей функцией: 



a) значение коэффициента прямой эластичности спроса
b) значение коэффициента перекрестной эластичности спроса при
c) значение эластичности спроса по доходу при 
d) до какого значения изменилось значение коэффициента прямой эластичности спроса при
e) до какого значения изменилось значение коэффициента перекрестной эластичности спроса при
Решение:
а)
б)
c) 
При
d) После увеличения дохода уравнение кривой спроса принимает вид
e) Рассчитаем 

Ответы:
Задача 40.
Линейная кривая предложения сдвинулась параллельно вверх вдоль оси цен на 5 единиц, где одна единица равна одному рублю, если цены измеряются в рублях. Ценовая эластичность первоначальной кривой предложения в точке, где цена была равна 8, составляла 3. Определите ценовую эластичность кривой предложения, полученной в результате вышеописанного сдвига, в точке, где цена равна 11.
Решение:
Если
Если
Ответ:
Задача 46
Точечная эластичность линейной кривой спроса в точке 

Решение:
Используя решение задачи № 20, получаем, что
Пусть 







Задача 10.
Производственная функция в краткосрочном периоде имеет вид 
Решение:
Данная производственная функция показывает зависимость объема выпуска продукции от количества нанятых работников
Ответ:
Задача 22.
Информация о деятельности фирмы, кроме представленной в таблице, оказалась в очередной раз утраченной. Восстановите недостающую информацию. Какой объем выпуска следует выбрать фирме?
Решение:

Приведем другие необходимые при расчетах формулы и в качестве примера рассчитаем значения остальных показателей пятой строки.
В пятой строке:
Для расчета по известному значению предельной прибыли необходимо знать величину общей прибыли из 4-й строки. Пусть 

Значения остальных неизвестных параметров из таблицы рассчитываются аналогично. См. также задачу N2 2.
Цель фирмы — получение максимальной прибыли, следовательно, оптимальный выпуск:
Ответ:
Задача 30.
Кривая спроса на билеты в театре задана обратным уравнением спроса: 
a) какую цену на билеты должна установить администрация, чтобы получить максимальную выручку;
b) изменится ли ваш ответ, если дополнительно известно, что число посадочных мест в театре равно 50.
Решение:
b) В данном случае функция выручки — парабола, с ветвями вниз, выходящая из начала координат. Координаты вершины: 



Данную задачу также можно решать исходя из взаимосвязи эластичности линейной функции и выручки. Выручка максимальна в точке единичной эластичности линейной функции спроса (середина графика, т. е. при 


Ответы:
Задача 36
А Фирма, имевшая положительную экономическую прибыль, увеличила производство продукции с 100 до 200 единиц в год. В результате средние затраты уменьшились на 50 р. и цена снизилась на 20 р.
- a) Как в результате данных событий изменилась прибыль фирмы?
- b) Как изменится ответ на вопрос задачи, если предположить, что вначале фирма получала нормальную прибыль?
- c) Как изменится ответ на вопрос задачи, если предположить, что вначале фирма получала убытки?
Б Фирма, имевшая положительную экономическую прибыль, увеличила производство продукции с 100 до 200 единиц в год. В результате средние затраты уменьшились на 10 р. и цена снизилась на 20 р.
- a) Как в результате данных событий изменилась прибыль фирмы?
- b) Как изменится ответ на вопрос задачи, если предположить, что вначале фирма получала нормальную прибыль?
- c) Как изменится ответ на вопрос задачи, если предположить, что вначале фирма получала убытки?
Решение .1.
а) Обозначим цену и средние затраты при 




а прибыль соответственно составит
так как 

b) В п. а) получили выражение для изменения прибыли:

Тот факт, что фирма до описанных изменений получала нормальную прибыль, означает, что ее экономическая прибыль была нулевой (нормальная прибыль включается в издержки)

c) Допустим, что вначале фирма получала убытки, т. е. 
следует, что изменение прибыли 

т. е. прибыль увеличилась в том случае, если первоначальные убытки были менее 6000;
т. е. прибыль не изменилась, если первоначальные убытки были равны 6000;
т. е. прибыль упала, если первоначально убытки превышали 6000.
Ответы: а) прибыль выросла; Ь) прибыль выросла; с) если убытки были меньше 6000, то прибыль выросла; если убытки были равны 6000, то прибыль не изменилась; если убытки были больше 6000, то прибыль упала.
Решение .2.
а) Обозначим цену и средние затраты при 




а прибыль соответственно составит
Так как 

если 
если 
если 
b) Воспользуемся соотношением между 


c) Допустим, что вначале фирма получала убытки, т. е. 

Ответы: а) если прибыль была больше 2000, то прибыль выросла; если прибыль была равна 2000, то прибыль не изменилась; если прибыль была меньше 2000, то прибыль упала; Ь) прибыль упала; с) прибыль упала.
Задача 40.
Кривая спроса на поездки в маршрутном такси от станции метро «Коньково» до станции «Юго-Западная» задается уравнением 

a) Если цена одной поездки равна 20 р., то какова ежедневная выручка транспортной компании на этом маршруте? Какова ценовая эластичность спроса на поездки в маршрутном такси при данной цене? Если данная компания хочет увеличить выручку, что ей следует сделать: увеличить или понизить цену?
b) Каковы будут ваши ответы, если бы изначальная цена составляла не 20, а 22,5 р. за поездку?
c) Каковы будут ваши ответы, если бы изначальная цена составляла не 20, а 25 р. за поездку?
Решение:
а) Если


b) Из решения п. а) получили, что 
цену и объем выпуска менять не следует.
c) 


Ответы: a) 


Задача 42.
Кривая рыночного спроса для поездок на пригородном автобусе задается функцией
где 

a) Если цена равна 50 р. за поездку, какую ежедневную выручку будет иметь автостанция? Какова ценовая эластичность спроса на автобусные поездки? Если автостанция хочет повысить выручку, что ей следует сделать: увеличить или понизить цену?
b) Как изменятся ваши ответы, если начальная цена составляет не 50, а 80 р. за поездку?
Решение:
а) При
Выручка максимальна при единичном значении по модулю ценовой эластичности спроса. При данном значении цены (при 
Ь) При
Рассуждение аналогично п. а), следовательно, и в данном случае фирме необходимо уменьшать цену.
Ответы: 

Задача 44.
Во сколько раз изменятся общая и предельная выручка фирмы со снижением объема продаж вдвое при функции спроса с постоянной эластичностью:
Решение:
а) Выручка максимальна в точке единичной эластичности. Соответственно для функции спроса с постоянной ценовой эластичностью 
Ь) Восстановим общий вид функции спроса:
с) Восстановим общий вид функции спроса:





Возможно, вас также заинтересует:
- Заказать работу по экономике помощь в учёбе
- Контрольная работа по экономике заказать
- Помощь по экономике онлайн
- Курсовая работа по экономике заказать готовую онлайн
- РГР по экономике расчетно графическая работа
- Задачи по экономике с решением
- Решение задач
Использование матричного вычисления при решении экономических задач
Решение примеров:
Пример 1.107
Два железобетонных завода выпускают изделия 
Какой общий выпуск изделий по определениям качества?
Решение. Количество изделий, выпущенных первым заводом, можно рассмотреть как элементы матрицы 
Сложив их, получим матрицу 
Пример 1.108.
При изготовлении деталей четырех видов материалов, рабочей силы и электроэнергии задаются следующей таблицей (в условных единицах):
Вычислить общую потребность в материалах 


Решение. Общая потребность в материалах, рабочей силы и электроэнергии для изготовления количества 




При 

то есть для изготовления заданного количества деталей каждого вида необходимо 28 единиц материалов, 47 единиц рабочей силы, 32 единицы электроэнергии.
Пример 1.109
В следующей таблице в выбранных единицах приведен состав витаминов в пищевых продуктах
1. Сколько витаминов каждого вида содержится в рационе, что включает 5 единиц продукта 

2. Учитывая только стоимость витаминов каждого продукта с расчета соответственно 10, 20, 25 и 50 рублей за единицу каждого продукта.
3. Рассчитать стоимость рациона, состав которого приведен в п. 1.
Решение. Введем такие определения: 









1. Обозначим 


что содержатся в рационе. Тогда,
2. Обозначим 



3. Обозначим через 
Тогда,
Пример 1.110.
Из некоторого материала необходимо выкроить 200 заготовок типа 

При этом можно использовать три способа раскроя. Количество заготовок, полученных из каждого листа при каждом способе раскройки, приведена в таблице. Записать в математической формы условия выполнения задания. Установить, сколько листов нужно для выкройки определенного количества раскроек.
Решение. Обозначим через 







Аналогично получим уравнения:
которым должны удовлетворять неизвестные 

Система линейных уравнений
выражается в математической формы условия выполнения всего задания по заготовкам
Для решения системы используем метод Гаусса. Перепишем полученную систему в виде
Преобразуем расширенную матрицу системы
Запишем упрощенную систему в соответствие расширенной матрицы
Следует,
Пример 1.111
Пусть функция, которая характеризирует валовый доход предприятия, имеет вид 




1. Выходя из матричной формы задания функции валовой прибыли
где 

2. Обозначить всю совокупность функции валовой прибыли, что удовлетворяет указанной в п. 1 системе уравнений.
Решение. Запишем функцию валовой прибыли в виде:
Подставим заданные значения из таблицы:
Получим систему:
Решим ее методом Гаусса:
Ранг матрицы системы и ранг расширенной матрицы совпадают и равны 2. Система совместима. Так как 
2. Вся совокупность валовой прибыли
Задачи балансового анализа
К экономическим задачам, что приводятся к системам линейных уравнений, относятся задачи балансового анализа. Цели балансового анализа — ответить на вопросы, что возникают в макроэкономики и связаны с эффективностью ведения многоотраслевого государства: каким может быть объем производства каждого из 
Связь между отраслями, как правило получается в таблицах межотраслевого баланса, а математическая модель, что позволяет их анализировать, разработана в 1936 году американским экономистом В. Леонтьевым. Рассмотрим досконально модель Леонтьева многоотраслевой экономики.
Предположим, что рассматриваются 
Рассмотрим процесс производства, например, за год.
Введем такие понятия: 








Поскольку валовый объем продукции любой 

Это соотношение баланса. Будем рассматривать стоимость межотраслевого баланса, когда все величины, что входят в уравнение баланса, имеют стоимость выражения.
Введем коэффициенты прямых затрат:
что показывают затраты продукции 


Так построенная модель межотраслевого баланса получила название линейной.
Запишем соотношение баланса в виде
Введем обозначения:
где 


Тогда соотношение баланса в матричном виде является
Основная задача международного баланса заключается в поиске такого вектора валового выпуска 
Перепишем соотношения баланса в виде
Эта система линейных уравнений относительно 
Если матрица 

Матрица 
Чтобы выяснить экономическое содержание элементов матрицы 








Соответственно к экономическому содержанию задачи значения 
Матрица 


В этом случае и модель Леонтьева называется продуктивной.
Примеры решения задач балансового анализа:
Пример 1.112.
В таблице приведены данные для вычисления баланса за отчетный период.
Вычислить необходимый объем валового выпуска в каждой отрасли, если конечное потребление энергетической отрасли увеличивается вдвое, а машиностроение остается в прежнем количестве.
Решение. По условию 
Находим коэффициенты прямых затрат по формуле
Матрица прямых затрат
Она не имеет отрицательных элементов и удовлетворяет критерию продуктивности
Потому для любого вектора конечного продукта 

Находим матрицу полный трат
Поскольку 
По условию вектор конечного продукта 

Следует, валовый выпуск в энергетической области нужно увеличить к 179, 28 условных единиц, а в машиностроении — к 111, 28 условных единиц.
Задачи экономического содержания
Рассмотрим некоторые примеры использования линейной зависимости в экономике.
- Если через
обозначить тариф перевозки груза за единицу расстояния,
— затраты при перевозке груза, что не зависит от расстояния
то общая стоимость
перевозки груза на расстояние
можно вычислить с помощью формулы
- Если обозначить через
затраты производства в течении месяца при выпуске
единиц однородной продукции, то может быть обозначенной по формуле
где величина
будет обозначать переменные траты, что зависят от объема выпуска. Величина
обозначает постоянные затраты предприятия. которые не зависят от объема продукции, что выпускается.
Примеры решения задач:
Задача 2.76
Валовая продукция на 1 га сельскохозяйственных пастбищ за 4 года увеличилась на 24%. Сложить уравнение прямой, которая отображает изменение валовой продукции на 1 га на протяжении четырех лет по условию, что валовая продукция в процентах изменяется пропорционально времени. Исследовать влияние расширения тракторного парка к возрастанию урожая зерновых.
Решение. Валовую продукцию, выпущенную в первый год, примем за 100% и будем искать уравнение прямой в виде
следует, 

Задача 2.77
В 1980 году страна имела 108,5 тысяч тракторов и получила из одного гектара 8,5 ц зерновых. В 1995 году страна имела 510 тысяч тракторов и получила из одного гектара 21 ц зерновых.
Решение. обозначим время — 


По условию задачи имеют четыре точки:
найдем уравнение прямых — графиков возрастания тракторного парка и урожайности зерновых из одного гектара за 1980 — 1995 годы в виде 
Используя уравнение прямой, что проходит через две заданные точки, получим:
таким образом. угловой коэффициент прямой возрастания тракторного парка будет:
Используя точки 

Следует ее угловой коэффициент будет:
Из условий задачи можно сделать вывод, что при возрастании траекторного парка урожайности зерновых из 1 га возрастает. Но угловой коэффициент 

Задача 2.78
Транспортные затраты перевозки единицы груза 


где 
Решение. Построим графики графики транспортных затрат перевозки (см. рис. 2.19). Графики прямых пересекаются в точке 

Графики затрат позволяют сделать вывод:
а) когда 

б) когда 

Приведем примеры задач, связанные с использованием уравнений второго порядка.
Задача 2.79.
Исследованием выявлено, что затраты топлива судном на подводных поршнях возрастают пропорционально квадрату скорости судна. Нужно найти аналитическую зависимость между затратами топлива 



Решение. Согласно с условием задачи искомую зависимость записать в виде:
где 
Уравнение этой формулы с уравнением параболы 




Таким образом, аналитическая зависимость между затратами топлива и скоростью судна будет:
График этой зависимости изображен на рис. 2.20. Из последней формулы получается, что при скорости 60 км/час затраты топлива (в литрах) за время должны быть равны:

Задача 2.80
Два однотипных предприятия 





Решения. Обозначим через 



Найдем множество точек, для которых 
Это круг. Таким образом, для потребителя посередине угла выгоднее покупать в пункте 

Задача 2.81
Компания производит изделия 



Обозначить еженедельное количество изготовления и продажи изделий 
Решение. Доходы от продажи 

Для равновесия дохода и затрат нужно чтобы выполнялось равенство:
Следует, эта задача имеет две точки равновесия. Компания может выполнять 


Рассмотрим на этом примере возможности компании. обозначим еженедельную прибыль 
Из полученного равенства получается, что при 



Когда 





Экономические задачи, связанные с последовательностью и ее границей (элементы математики финансов)
Рассмотрим общепринятые в рыночной экономике алгоритмы расчета процента в зависимости от термина ссуды, типа процентов, схемы их расчета.
Понятие процента
Процентом от числа 

Например, 

Для того чтобы найти процентное выражение заданного числа, достаточно умножить это число на 100.
Пример 3.123
Процентное выражение числа 5 является 


Пример 3.124
Три основные задачи на проценты
1 задача. Найти полный процент заданного числа. Заданное число 
Пример 3.125
Полное процентное произведение угля на шахте должно составлять 3000 т. Шахта выполняет процентный план на 120%. Сколько тонн угля она произвела?
2 задача. Найти число по известному значению его процента. Заданное значение процента искомого числа делим на число, что выражает этот процент, а результат умножим на 100.
Пример 3.126
Масса сахара — 12,5% массы переработанных свеклы. Сколько нужно свеклы для получения 5000 т сахара?
3 задача. Найти выражение данного числа в дробях другого. Делим одно число на другое и результат умножим на 100.
Пример 3.125
Плановое добывание нефти должно составлять 160 млн т, фактическое добывание достигает 164 млн т. На сколько процентов был выполнен план добычи нефти?
Формула простого процента
Отношение данного процента определенного числа к тому же числу называется процентной ставкой и обозначается
Удельной процентной суммой (нормой процента) называется соотношение:
Если определенный процент некоторой денежной суммы складывается к этой сумме, то говорят про накопление денег.
Если процент не начисляется на первый процент, что складывается к начальному числу, говорят про простой процент.
Обозначим через 


после второго года:
Следует
Пример 3.128
Если 

Если процент начального числа складывается к этому числу, а далее процент начисляется на полученную сумму, то есть на большее число, то говорят про сложные проценты.
Формула сложного процента
Пусть на начальное число 

после 1-го года:
после 2-го года:
после 
остаточная (конечная) сумма 

Основная формула сложного процента начисляется на протяжении 
Выражение 
Пример 3.129
Пусть определенный вклад 
Решение. Обозначим 




Сложим таблицу:
Формула, когда проценты начисляются непрерывно
Пусть проценты начисляются равномерно 

Пусть проценты теперь начисляются непрерывно, то есть 
Следует,
Эту формулу можно использовать для любых вычислений, связанных с сложными процентами.
Пример 3.130
Сумма 2000 ден. ед положена в банк по схеме непрерывного начисления процентов по ставке 10% за год. Найти увеличенную на протяжении года сумму 
Решение
Результаты вычислений приведем в таблице:
Дисконтирование
Приведенные выше формулы связывают переменные величины 

Например, из основной формуле для начисления сложенных процентов 
Разницей 


Если денежные средства 


Следует, дисконтированные денежные средства станут:
в случае сложных процентов получим: 
Коэффициенты 
Пример 3.131
Нужно найти суммарное значение долга, полная сумма через 3 года получится 7 млн ден. ед. Проценты начисляются со следующей ставкой 20% в конце каждого года.
Решение


Примеры решения задач:
Пример 3.132
Пусть 2 млн ден. ед. выдано в кредит на 6 месяцев под простые проценты по ставке 10% за месяц. Найти увеличенное значение долга на конец каждого месяца.
Решение. Обозначим 





Увидим, что последовательность 

Пример 3.133
Сумма 800 тыс. ден. ед. инвестируется на 3 года под сложные проценты по ставке 80% годовых. Найти увеличенную функцию за этот период.
Решение. Воспользуемся формулой 


Использование матрицы затрат
Пример 1.1. Три мебельных комбината — Харьковский, Днепропетровский и Ужгородский — производят 5 типов продукции: кухни, передние, гостиные, спальни, уголки с мягкой мебелью. В бухгалтерии этих комбинатов поступают сведения об объемах производства, которые заносятся в учетную документацию и там накапливаются. Эти данные представляются в виде матрицы. На 1 июня матрица продукции имела вид:
где

На конец июня аналогичная матрица имела вид:
Найти объем каждого типа продукции, произведенной в июне.
Решение. Объем продукции которая была произведена в июне, определяется матрицей 
Пример 1.2. Строительная фирма «Надежная крыша» производит металлочерепицу трех видов: цветная, устойчивая, экологическая. При этом применяются различные технологические операции, соответствующие рабочим местам № 1-5.
Сделать расчет заработной платы, приходящейся на каждый заказ при изготовлении изделий каждого типа, если известно
а) затраты времени (в часах) на каждом рабочем месте на изготовление единицы продукции соответствующего вида, приведены в таблице:
б) количество изделий (в единицах) в каждом заказе:
в) заработная плата за один час (в рублях) на каждом рабочем месте:
Решение. Затраты времени на каждом рабочем месте, количество изделий и заработную плату за один час можно рассматривать как элементы матриц 

Поскольку матрица 


Следовательно,
Поскольку матрица 

Таким образом,
то есть на выполнение заказа Иванова И. И. начисления заработной платы составляет 99,60 грн, заказ Петрова П. В. — 81,90 грн, заказ Сидорова С. И. — 102,55 грн.
Пример 1.3. Машиностроительный завод «Дормаш» выпускает тракторы трех видов: ДМТ-100, ДМТ-300 и ДМТ-500. При этом используется сталь трех марок: Ст4пс, Ст2кп и Ст20кп. Нормы расходов каждой марки стали (в тоннах) на один трактор, а также запасы стали приведены в таблице:
Сколько тракторов каждого вида может выпустить завод при условии использования всего запаса стали.
Решение. Обозначим количество тракторов каждого вида через 


Решим эту систему тремя способами: по формулам Крамера, с помощью обратной матрицы и методом Жордана-Гаусса.
1. Правило Крамера. Вычислим определитель системы 
Поскольку 

По формулам Крамера имеем:
то есть
2. Матричный способ. Для решения системы с помощью обратной матрицы обозначим
В матричном виде система записывается так: 



где 

а именно:
Тогда
Получено то же решение:
3. Метод Жордана-Гаусса. Решение системы уравнений подаем в таблице (схема Жордана-Гаусса).
Таким образом, получаем:
Итак, машиностроительный завод, используя все запасы стали, выпускает один трактор вида ДМТ-100, один трактор вида ДМТ-300 и два трактора вида ДМТ-500.
Пример 1.4. Семейная фирма производит напитки «Лето» и «Водограй». Для производства 1 л напитка «Лето» нужно 0,02 часов работы оборудования, а для 1 л напитка «Водограй» — 0,04 часов. Расходы основных веществ напитков равны 0,01 кг и 0,04 кг на 1 л напитков «Лето» и «Водограй» соответственно. В день фирма располагает 16 кг основных составляющих веществ и 24 часа работы оборудования. Прибыль фирмы от продажи 1 л напитков
«Лето» и «Водограй» составляет 0,1 и 0,4 грн соответственно. Прибыль за один рабочий день составляет 160 грн.
Определить, сколько напитков каждого типа производит фирма ежедневно, если известно, что все ресурсы используются полностью.
Решение. Запишем условие задачи в виде таблицы:
Обозначим через 


Составим математическую модель задачи. Это система линейных уравнений:
Решим систему методом Жордана — Гаусса. проведем эквивалентные преобразования расширенной матрицы системы:
Рангах матрицы системы и расширенной матрицы равны 2, а количество переменных — 3. Это означает, что система имеет множество решений.
По преобразованной матрицей запишем систему уравнений в виде:
где 


Определим базисные неизвестные через свободные
и запишем решение системы в матричной форме
Система имеет множество решений в зависимости от того, каких значений приобретает свободная неизвестна 


то есть 


Проанализируем полученный результат. Пусть фирма будет производить 800 л напитка «Лето» 











Пример 1.5. В таблице приведено межотраслевой баланс за отчетный период в условных денежных единицах:
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли необходимо увеличить вдвое, а машиностроения — оставить на прежнем уровне.
Решение. Обозначим через 







Модель Леонтьева «затраты-выпуск» имеет вид:
По условиям задачи имеем: 
Отсюда найдем коэффициенты прямых затрат. Имеем:
Запишем матрицу прямых затрат в виде:
Все элементы матрицы являются неотъемлемыми. Проверим, является ли эта матрица продуктивной. Найдем собственные значения матрицы с характеристическим уравнением:
то есть:
Характеристический многочлен матрицы имеет вид:
или
Отсюда находим:
Следовательно, 





Рассмотрим случай, когда конечное потребление энергетической отрасли увеличилось вдвое, а в машиностроении — осталось на прежнем уровне. В этом случае имеем:
Вычислим определитель матрицы:
Следовательно, существует обратная матрица
Тогда:
то есть валовой выпуск продукции в энергетической отрасли нужно увеличить до 177,2 условной единицы, а в машиностроении — до 99,1 условной единицы.
Пример 1.6. Найти соотношение национальных доходов Казахстана, Украина и Беларусь для сбалансированной торговли, если структурная матрица имеет вид:
Решение. Составляем матричное уравнение:
где 
Имеем:
Это матричное уравнение можно представить в виде системы алгебраических уравнений:
После эквивалентных преобразований система принимает вид:
отсюда имеем общее решение:
Пусть 
Итак, сбалансированность торговли Казахстана, Украины и Беларуси достигается, если их национальные доходы определяются соответственно по соотношению
Формула простых процентов
Пусть осуществляется вклад сбережений в банк под простые проценты — проценты, начисляемые только на первоначальную сумму вклада. Какая сумма подлежит выплате вкладчику через несколько лет?
Введем обозначения величин, указанных в условии задачи:





По условию задачи за один год вклад увеличится на сумму 


Следовательно,
где множитель 
Формула простых процентов содержит две переменные величины 

Модель «спрос-предложение»
Следующая задача требует знаний некоторых экономических понятий, связанных с товарным рынком:
спрос — потребность в товарах рынка со стороны покупателей, а предложение — представлена на рынке возможность приобрести товар;
закон спроса — закон, согласно которому снижение цены приводит соответствующий рост величины спроса, и наоборот;
закон спроса и предложения — цена любого товара изменяется, чтобы уравновесить спрос (объема 

равновесие товарного рынка — состояние рынка, когда для продажи предлагается такое количество товара, которое потребитель готов купить;
равновесная цена 
равновесный объем 
Экономическую модель, описывающую процесс ценообразования на рынке, называют моделью «спрос-предложение».
Простейший случай математической модели получаем в случае линейной зависимости объемов спроса и предложения от цены товара и наоборот. На рис. 7.14 схематично воспроизведено прямую спроса 


Рис. 7.14
Рассмотрим конкретный пример задачи о спросе и предложении.
По данным таблицы 7.2 найти точку равновесия товарного рынка.
Исходные данные для построения модели «спрос-предложение» Таблица 7.2
Зависимость спроса и предложения от цены товара линейная (приросты одинаковы).
Решение задачи сводится к нахождению точки пересечения прямых, описывающих спрос и предложение.
Для записи уравнений прямых спроса и предложения воспользуемся уравнением прямой, проходящей через две точки (7.12).
Уравнение прямой спроса имеет вид:
а уравнение прямой предложения —
Решаем систему двух уравнений с двумя неизвестными при условии, что имеет место равенство
Получено значение равновесной цены 

При 


Определение результатов деятельности предприятия
Пример 2.1. За плановый период предприятие изготовило 200 единиц продукции первого вида, 150 единиц второго и 100 единиц третьего вида. Прибыль от реализации единицы каждого вида составляет соответственно 3, 5 и 10 грн.
Вычислить прибыль от реализации всей продукции.
Решение. Доходы от реализации каждой единицы продукции можно считать координатами вектора 


Пример 2.2. Расходы предприятия на изготовление 10 единиц продукции составляет 1000 грн, а на 50 единиц этой же продукции — 2000 грн. Определить затраты предприятия на изготовление 30 единиц продукции при условии, что общие затраты на производство продукции является линейной функцией от объема.
Решение. По условию задачи затраты на производство являются линейной функцией от объема. Уравнение соответствующей линии будем искать как уравнение прямой, проходящей через две точки:
Используя условие задачи, имеем:
Отсюда:
Следовательно, мы получили функцию, характеризующий зависимость издержек производства от объема. Теперь найдем значение этой функции при 
Ответ: на производство 30 единиц товара расходуется 1500 грн.
Пример 2.3. Через пункты 






Решение. Сначала найдем уравнение прямой, по которой на плане местности проходит шоссейная дорога. Для этого запишем уравнение прямой 

Итак:
Короткая прямая, которая пройдет через точку 







Теперь найдем точку пересечения прямых 

Таким образом, точка 

Ответ:
Пример 2.4. В прошлом году цена единицы некоторого товара составила 50 грн, а в текущем — увеличилось до 60 грн. Найти зависимость цены товара от номера года, если предположить, что цена ежегодно будет увеличиваться на ту же величину. Составить прогноз цены на 3 и на 5 лет вперед.
Решение. Обозначим номер предыдущего года через 1, тогда текущем году будет отвечать номер 2.
Составим уравнение прямой, проходящей через две точки, а именно через точки 

Через три года, то есть для года, номер которого равен 



Пример 2.5. Предложение и спрос на сахар в некоторый период на рынке описывались функциями:
где 


Найти рыночную цену на сахар в этот период.
Решение. Рыночная цена определяется условием 
отсюда
Пример 2.6. Предприятие тратит на производство единицы продукции 20 грн. Расходы, которые не зависят от объема продукции, например, зарплата, амортизационные отчисления и т.п. равны 200 грн в неделю. Найти себестоимость единицы продукции.
Решение. Пусть 



Таким образом, затраты на производство единицы продукции обратно пропорционально зависят от объема производства, а именно: при росте 

Пример 2.7. Зависимость объема производства от затрат ресурсов двух видов 

Определить затраты ресурсов на изготовление 23 единиц продукции.
Решение. По условию задачи 


Сведем это уравнение линии 2-го порядка к каноническому виду:
Следовательно, мы получили уравнение, которое определяет эллипс с центром в точке 
Для каждого значения объема расходов ресурса первого вида, описываются значением 



Пример 2.8. Расстояние между двумя торговыми организациями равно 8 км. Найти множество возможных мест расположения базы таким образом, чтобы сумма расстояний от базы к этим организациям была постоянной величиной и равна 10 км.
Решение. Выберем оси координат следующим образом: торговые организации обозначим точками 







Определим 

Тогда:
или
Возносим обе части данного соотношения в квадрат и получаем:
Поднимем еще раз обе части соотношения в квадрат:
Поделив обе части данного соотношения на 225, получим уравнение эллипса в канонической форме:
Ответ: если база расположена на линии, которая является эллипсом: 
Определение простых и сложных процентов
Пример 3.1. Клиент положил 10000 грн в банк по ставке 7%. Найти накопления через 5 лет в случае: а) простых процентов; б) сложных процентов. Результаты сравнить.
Решение. В случае простых процентов накопленная сумма вычисляется по формуле
Следовательно,
Если предполагается капитализация процентов, то есть начисление процентов на проценты, то накопленная сумма вычисляется по формуле
Тогда
Сравнивая результаты, видим, что более выгодным является вложение денег под сложные проценты.
Пример 3.2. 150000 грн положено в банк по ставке 18% на 5 лет. Построить числовую последовательность для характеристики денежных накоплений с учетом сложных процентов.
Решение. Для построения числовой последовательности применяем формулу
где
Результаты вычислений приведены в таблице
Пример 3.3. Спрос на бумагу в канцелярии университета в течение определенного месяца составил 20 пачек и от того ежемесячно растет на 5%. Определите, за какое время спрос увеличится вдвое, если эта тенденция сохранится.
Решение. Применяя формулу 
Прологарифмируем обе части:
отсюда
Итак, через 14 месяцев спрос на бумагу в канцелярии увеличится вдвое.
Пример 3.4. Предприниматель решил инвестировать в проект по строительству нового отеля 10 млн грн, рассчитывая получить через 3 года 20 млн грн. Определите, какой должна быть для этого процентная ставка.
Решение. По формуле сложных процентов
необходимо найти 
Далее имеем:
отсюда
Следовательно, для того чтобы через три года получить 20 млн грн, процентная ставка должна быть 26%.
Пример 3.5. Универмаг продает за день 150 пар обуви. После открытия еще одного отдела было решено довести ежедневный продажу в 750 пар. Сколько для этого нужно времени, если ежедневно увеличение продаж составит 25%?
Решение. По формуле
имеем:
Отсюда
Значит, надо 7 дней, чтобы увеличить ежедневный продажа обуви до 750 пар.
Пример 3.6. Клиент положил деньги в банк под сложные проценты по ставке 8%. Через пять лет он получил 29 386,6 грн. Какую сумму было положено в банк?
Решение. По формуле сложных процентов имеем:
откуда
Таким образом, было положено в банк 20 000 грн.
Пример 3.7. Численность населения Украины в 2010 году составляла 47 млн. Найти численность населения Украины через 5 лет, если она будет расти ежегодно: а) на 0,5%; б) на 1,5%.
Решение. Если 

а именно:
Следовательно, при росте численности населения на 0,5%, через 5 лет она составит 48190000, а при росте на 1,5% — 50660000.
Пример 3.8. Студент, получивший на конкурсе премию 10 000 грн, положил ее на 3 года в банк по схеме непрерывного начисления процентов по ставке 10%. Построить числовую последовательность накоплений при 
Решение. Для построения числовой последовательности применяем формулу
а именно:
Результаты вычислений представим в виде таблицы.
Задача о производительности труда
Пусть функция 












Следовательно, производная объема произведенной продукции по времени 

Максимизация прибыли:
Максимизация прибыли является одним из основных критериев оценки деятельности производственной или коммерческой структуры. Прибыль 
Исследования, проведенные фирмой, показали еженедельную продажу 



Найдем все стационарные точки из условия равенства нулю производной функции прибыли
С целью идентификации этой точки находим
Значит, точка 
Таким образом, для максимизации своей прибыли фирма должна еженедельно реализовывать 2000 единиц продукции. При этом ее доход будет максимальным и составит 1500 гривен.
Предельный анализ
В практике экономических исследований широко применяются производственные функции, которые используют для установления зависимостей, например, выпуска продукции от затрат ресурсов, издержек производства от объема дохода от продажи товара и т. д. В предположении дифференцированности производственных функций важное значение приобретают их дифференциальные характеристики, связанные с понятием производной. Анализ, основанный на использовании предельных величин (относительных приростов) для исследования экономических процессов, называется предельным, или маржинальным анализом.
Рассмотрим производные для указанных типов производственных функций.
1. Пусть производственная функция 
Предположим, что количество продукции увеличилось на 



Средний прирост совокупных издержек производства определяется как
Это прирост совокупных издержек производства на единицу прироста количества продукции.
Предельными издержками производства (marginal cost) называются дополнительные затраты на производство единицы дополнительной продукции. Они определяются как предел отношения изменения совокупных расходов количеству дополнительной продукции, которая была изготовлена
Предельные издержки производства совпадают со скоростью изменения издержек производства. Величина 
2. Обозначим 

Предельным доходом (marginal revenue) называется дополнительный доход, полученный от реализации дополнительной единицы продукции. Он определяется как предел отношения изменения совокупного дохода количеству реализованной продукции его обусловила
3. Пусть производственная функция 
Предельным продуктом (marginal product) называется дополнительный продукт, произведенный при использовании дополнительной единицы ресурса. Он определяется как предел отношения изменения количества продукта с количеством используемого ресурса, его обусловила
Эластичность функции
Понятие эластичности было введено Альфредом Маршаллом, лидером кембриджской школы маржинализма, в конце XIX века в связи с анализом функции спроса. Сейчас это понятие широко используется для характеристики и других экономических функций.
Сначала введем некоторые понятия. В экономике часто используется понятие относительных изменений определенной величины. Пусть функция 








Относительное изменение величины часто выражают в процентах
Рассмотрим отношение
которое показывает относительное изменение функции 


Отношение 



В том случае, когда единицы измерения аргумента 

Пусть точка 



Тогда величина
будет определять относительное изменение функции, приходящейся на единицу относительного изменение аргумента.
Пусть задана функция 
Эластичностью функции 


Ее обозначают 
Величину 


Свойства эластичности функции
1. Эластичность произведения двух функций равна сумме эластичности этих функций:
2. Эластичность доли двух функций равна разности эластичности этих функций:
3. Если 
Эластичность функции применяется для анализа спроса и потребления. Например, эластичность спроса в отношении цены 





Цена за единицу продукции представлена функцией
где 

Имеем
Далее,
Значит, если цена одного холодильника уменьшить на 0,2%, то спрос на холодильники увеличится на 1% (с 2000 штук увеличится до 2020 штук).
На этом примере мы видим, что можно рассматривать и обратную зависимость:
Тогда для нашего примера имеем:
Это значит, что увеличение цены на один холодильник на 1% приводит к уменьшению спроса на холодильники на 5% (с 2000 штук уменьшится до 1900 штук).
Пусть совокупные издержки производства в зависимости от количества 


1. Предельные издержки производства определяются как производная от функции издержек
При соответствующих объемах продукции:
Таким образом, увеличение количества производимой продукции, приводит к замедлению роста затрат на ее выпуск.
2. Эластичность функции
В данном примере
Следовательно, если при объеме производства 100 единиц увеличить выпуск продукции на 1%, то есть на одну единицу, то относительные издержки производства увеличатся примерно на 0,67%; при объеме 20 единиц увеличение выпуска продукции на 1% приведет к увеличению относительных затрат примерно на 0,95%.
Применение производной в экономической теории
Рассмотрим экономическую интерпретацию теоремы Ферма (теорема 16.1).
Сначала сформулируем один из базовых законов теории производства: оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода.
То есть уровень выпуска 



Обозначим функцию прибыли 









Второе важное понятие теории производства — это уровень наиболее экономичного производства, которому соответствуют минимальные средние издержки (average cost) на производство товара. Соответствующий экономический закон гласит: уровень наиболее экономичного производства определяется равенством средних и предельных издержек.
Получим это условие как следствие теоремы Ферма. Средние расходы 


Отсюда получаем 


Понятие выпуклости функции также находит свою интерпретацию в экономической теории.
Одним из самых известных экономических законов является закон убывающей доходности, по отношению к которому с увеличением производства объем дополнительной продукции, полученной на каждую новую единицу ресурса (трудового, технологическому и т. д.), с некоторого момента возрастает более медленно, чем растет фактор производства .
Другими словами, величина 




Другим базовым понятием экономической теории является функция полезности 


Закон убывающей полезности формулируется так: с ростом количества товара дополнительная полезность от каждой новой его единицы с некоторого момента спадает. Очевидно, что на языке математики этот закон можно представить следующим образом: функция полезности является выпуклой вверх. В такой постановке закон убывающей предельной полезности является исходным пунктом для математического исследования в теории спроса и предложения.
Предприятие производит 

Найти оптимальный для предприятия объем выпуска продукции и соответствующий ему максимальный выпуск.
Пусть 



где 
Для решения задачи следует исследовать функцию 



Проведем это исследование.
1. Формируем 


получаем
или
Следовательно, 
2. Находим 
Следовательно, 

3. Находим максимальную прибыль производства, то есть
При объеме производства 

Издержки производства равны
следовательно, имеем максимальную прибыль от продажи 

Расчёт производительности ресурса
Пример 4.1. Функция выпуска продукции имеет вид
Найти предельную производительность ресурса (скорость изменения выпуска), если расходы ресурса составляют 2 условные единицы.
Решение. Скорость изменения выпуска найдем по производной
Следовательно, если расходы составляют 2 усл. ед., то скорость изменения выпуска составляет 8 усл. ед.
Пример 4.2. Объем продукции, произведенной бригадой рабочих в течение одной рабочей смены, определяется уравнением
где 
Решение. Производительность труда в любой момент времени — это производная от объема продукции, следовательно,
Скорость — это производная от производительности труда, то есть производная второго порядка от объема
Темп изменения производительности труда есть производная от логарифма производительности или отношение скорости к производительности
При 
При 
Следовательно, производительность труда в конце рабочего дня уменьшается.
Пример 4.3. Вычислить эластичность функции расходов y от объема 
а также определить средние и предельные издержки по объему продукции, который составляет 5 единиц.
Решение. Для вычисления эластичности функции применяем формулу
Находим 
Тогда
Следовательно,
То есть при производстве продукции объемом 5 единиц увеличение выпуска на 1% приведет к увеличению расходов на 0,33%.
Функция средних затрат определяется как отношение функции расходов y к объему продукции
Если объем продукции составляет 5 единиц, то
Для нахождения предельных издержек находим производную от функции затрат:
и вычисляем ее при 
Следовательно, в случае выпуска 5 единиц продукции средние и предельные издержки составляют соответственно 150 и 50 условных единиц.
Пример 4.4. Опытным путем было установлено функцию спроса
и функцию предложения 



Решение.
Равновесная цена определяется при
или
отсюда 
Следовательно, цена равновесия единицы товара равна 2 условных единицы.
Найдем эластичности спроса и предложения по формуле
Поскольку цена равновесия 
Следовательно, спрос и предложение данного товара при цене равновесия 
Пример 4.5. Предприятие производит x единиц продукции еженедельно и реализует ее по цене
Суммарные издержки производства составляют
При каком объеме производства прибыль предприятия будет наибольшей?
Решение. Определяем прибыль
следовательно,
Исследуем функцию 
Находим ее производную:
Дальше необходимым условием экстремума получаем значение критической точки:
Теперь определяем вторую производную


Пример 4.6. Пусть функция издержек имеет вид:
Вычислить предельные издержки производства, если объем производства составляет 

Решение. Для вычисления предельных издержек находим производную от функции издержек
и вычисляем ее в соответствующих точках: 
Следовательно, если объем производства растет, предельные издержки падают.
Область определения функции: 


Найдем производную второго порядка:
Следовательно, функция затрат растет медленнее, потому что 

Пример 4.7. Фирма планирует выпускать пластиковые окна. Опытным путем установлена зависимость спроса 




Определить максимальную прибыль.
Решение. Валовая прибыль равна 

Из уравнения 
Тогда
или
Находим производные
За необходимым условием экстремума:
отсюда 


Вычисляем:
Пример 4.8. Функция спроса на товар имеет вид
где 
1) будет самым наибольшим; 2) исчезнет. Найти темп изменения спроса.
Решение. Предельный спрос — это производная от функции спроса, а именно:
За необходимым условием экстремума имеем
Следовательно, по цене 

Спрос равен 
откуда 

Темп изменения спроса находим по производной второго порядка от функции спроса, а именно:
Если цена возрастает до 







Предельный спрос определяется формулой 


Пример 4.9. Зависимость издержек производства от объема задана функцией
При каком объеме продукции издержки производства начнут спадать?
Решение. Найдем производную:
Расходы падают, когда 
отсюда
Учитывая, что 
Следовательно, расходы начнут спадать, если объем производства
Пример 4.10. Пусть функция 

Решение. Прибыль фирмы составляет
где 


Из уравнения q
Тогда
или
Следовательно, надо исследовать эту функцию на экстремум.
По необходимым условием экстремума:
Тогда 

Соответствующая цена 
Сравниваем оптимальную цену с предельными издержками:
Следовательно, максимальный объем продукции фирмы составляет 15 единиц, соответствующая цена — 12,5 грн, наиболее выгодная цена для фирмы в 2,5 раза больше предельных издержек.
Применение функций нескольких переменных в исследованиях экономических процессов
Функции нескольких переменных широко применяются в различных областях знаний, в том числе и в экономике для описания различных процессов и явлений. Обратим внимание на то, что методы нахождения локальных или глобальных экстремумов функции нескольких переменных положены в основу методов построения экономических моделей и определение стратегии управления экономическими процессами с целью оптимизации работы экономических систем. Остановимся на некоторых важных примерах.
Понятие о эмпирических формулах и метод наименьших квадратов
Пусть при исследовании какого-либо явления или процесса (в частности, экономического) ведется наблюдение за двумя переменными величинами 



Результаты наблюдений Таблица 20.1
Необходимо по данным эксперимента найти функциональную зависимость 

Эмпирическими формулами называются функциональные зависимости, построенные по результатам эксперимента. Поскольку значения зависимой переменной (функции) 



Построение эмпирической формулы осуществляется в два этапа.
Первый этап предусматривает определение множества возможных функций, к которой может, согласно теоретическим предположениям, принадлежать искомая зависимость. Выбор функции, которую целесообразно использовать для приближенного описания (аппроксимации) результатов исследований, осуществляется на основе теоретических предположений относительно природы явления, которое исследуется, или по результатам визуального анализа расположения точек на плоскости.
Каждый класс функций характеризуется несколькими числовыми параметрами 





На втором этапе вычисляют значения числовых параметров, определяющих каждую из выбранных функций 
Одним из самых распространенных методов, применяемых для нахождения параметров эмпирических формул, является метод наименьших квадратов (МНК). Его базовый принцип заключается в том, что функция считается лучшей для аппроксимации эмпирических данных, если сумма квадратов разностей между эмпирическими значениями зависимой переменной 


Рис. 20.1
Разница между значениями 
то есть отклонения эмпирических значений функциональной переменной от теоретических, является погрешностями модели. Эти погрешности обозначают через
Следовательно,
Согласно принципу МНК неизвестные параметры функции, с помощью которой осуществляется аппроксимация, выбирают так, чтобы сумма квадратов ошибок была минимальной:
Функция (20.1) называется функцией ошибок. Понятно, что она зависит от параметров модели 



Нахождение параметров эмпирических формул осуществляется по следующему алгоритму:
1) составляют сумму квадратов отклонений эмпирических значений зависимой переменной от ее теоретических значений, то есть по формуле (20.1) образуют функцию погрешностей
2) записывают необходимое условие локального экстремума функции 
3) решают систему, полученную в пункте 2), и находят числа 
Доказано, что соответствующая стационарная точка является точкой минимума функции
Рассмотрим построение эмпирической формулы в случае, когда аппроксимирующей есть линейная функция 
За необходимым условием экстремума находим ее частные производные первого порядка и приравниваем их к нулю. Получаем систему уравнений:
Для всех сумм, которые содержит полученная система, существуют специальные обозначения, принятые в математической статистике:
С использованием этих обозначений необходимое условие экстремума можно записать в виде системы уравнений
или в матричной форме:
Эта система называется системой нормальных уравнений для нахождения параметров эмпирической формулы. Отсюда определяем, что
Решение системы (20.2) дает наилучшие значения искомых параметров, при которых для выбранного вида функции сумма квадратов погрешностей будет наименьшей.
В случае, когда зависимость между переменными 

Например, если зависимость переменной 



Если зависимость является степенной, то есть 
Введем новые переменные: 


Пусть приближением функции является квадратный трехчлен, то есть имеем:
Тогда функция ошибок, которую нужно минимизировать, имеет вид:
Определим ее частные производные по неизвестным 

Преобразуем эту систему с целью сведения к системе нормальных уравнений:
Поделив обе части каждого уравнения на 
Следует отметить, что значения параметров определенной функции, вычисления которых проводилось по методу наименьших квадратов, обеспечивают наименьшую сумму квадратов ошибок по сравнению с другими параметрами этой функции. Однако, если для аппроксимации применить другую функцию, то можно получить меньшее значение суммы квадратов погрешностей.
Покажем это на примере. В таблице 20.2 приведены данные по численности населения Харьковской области за последние 10 лет.
Численность населения харьковской области Таблица 20.2
Определим функцию, по которой целесообразно осуществлять аппроксимацию эмпирических данных с целью последующей сборки краткосрочного прогноза. Для этого по исходным данным построим график (рис. 20.2), что позволит визуально оценить вид аппроксимирующей функции.
Рассмотрим сначала простейшую модель — линейную. То есть по виду графика предположим, что население с годами уменьшается по линейной функцией. Для упрощения вычислений вместо года в модели будем использовать его номер. Следовательно, будем искать параметры эмпирической формулы
где 
Приведем вычисления в виде таблицы.
Расчет параметров линейной модели Таблица 20.3
Подставляя средние значения из последней строки таблицы в формулы (20.3), получаем параметры линейной модели:
Следовательно, аппроксимирующая функцию найдена в виде:
Рис. 20.2
Вычислим за этим приближением теоретические значения функции и определим сумму квадратов ошибок (последние два столбца табл. 20.3). Оказалось, что сумма квадратов погрешностей в этом случае равна 0,00032. Это наименьшая величина по сравнению с тем, которую мы получили с помощью других линейных функций. Если эту формулу использовать для прогноза, то в 2012 году можно ожидать, что количество населения составит:
Рассмотрим аппроксимацию с помощью квадратного трехчлена, что тоже можно предположить, исходя из вида графика (рис. 20.2):
Определив все коэффициенты системы нормальных уравнений (20.4) и решив эту систему (предлагаем сделать это самостоятельно), получаем соответствующую аппроксимирующую функцию:
Применив эту модель, также вычислим значения 
Предположим, что количество населения в зависимости от года определяется гиперболой, то есть
Тогда получим следующую формулу для определения
Соответственно сумма квадратов отклонений при применении этой функции равен 0,0078, то есть в 20 раз больше, чем при применении линейной модели.
Следовательно, лучшей моделью данной задачи можно считать квадратичную модель (сумма квадратов отклонений эмпирических данных от теоретической линии — наименьшая).
Взаимосвязь между производительностью и основными средствами
Пример 5.1. Найти эмпирическую формулу, описывающую зависимость между стоимостью основных средств и выработкой на одного рабочего, которые заданы таблицей.
Решение. По 




Рис. к задаче 5.1
Чтобы составить эту систему, надо найти
Результаты расчетов размещаем в таблице:
Используя суммы (последняя строка таблицы), записываем систему нормальных уравнений:
Обе части первого уравнения разделим на 6, а второго — на 21.
В результате получаем систему:
Решив систему уравнений, получим:
Следовательно, эмпирическая формула имеет вид:
Сравним значения 




Отметим, что сумма, полученная по уравнению, и эмпирическая (3-й столбец) с точностью до десятых совпали (39,5).
На графике приведена линия, уравнением которой является 
Кстати, из этого уравнения следует, что выработка продукции на одного рабочего увеличится на 1,13 тыс. грн, если стоимость основных средств увеличится на 1 млн грн.
Пример 5.2. Найти эмпирическую формулу, описывающую зависимость между стоимостью основных средств и себестоимости единицы продукции, которые заданы таблицей.
Решение. По 

По содержанию задачи и видом графика можно сделать вывод, что «лучшей» линией для определения зависимости является гипербола. Поэтому эмпирическую формулу будем искать в виде:
Сначала линеаризуемо эту зависимость.
Обозначим 
Параметры 

Результаты вспомогательных расчетов для определения коэффициентов системы нормальных уравнений представим в виде таблицы:
Используя суммы последней строки таблицы, имеем:
С этой системы получаем:
Следовательно, эмпирическая формула относительно переменной 
Теперь вернемся к исходной переменной
Для оценки адекватности эмпирической формулы вычислим 


Пример 5.3. Зависимость между стоимостью основных средств и месячным выпуском продукции задана таблицей:
Найти эмпирическую формулу, описывающую зависимость между стоимостью основных средств 
Решение. Эмпирическую формулу будем искать в виде:
Применяя метод наименьших квадратов, параметры 
Для того чтобы составить систему нормальных уравнений, необходимо вычислить 

Система нормальных уравнений принимает вид:
Эту систему линейных уравнений можно решить, например, по методу Жордана-Гаусса. Для этого удобно проводить преобразования не с самыми уравнениями, а с расширенной матрицей системы, а именно:
Следовательно, решением системы являются: 
Вычислим значение 



Пример 5.4. Пусть выпуск некоторого товара характеризуется производственной функцией: 



Решение. Скорость любого процесса характеризует производная функции. Чтобы определить изменение производственной функции в зависимости от фактора 


Для определения изменения производственной функции в зависимости от фактора 

Вычисляем эластичности 
Тогда
При 
Ответ: с ростом фактора 



Пример 5.5. Фирма производит два вида продукции, которые продает по ценам 500 и 600 грн за единицу. Объемы выпуска продукции составляют 


Решение. Прибыль от продажи продукции обоих видов составит 
Проведем исследование этой функции на экстремум. находим стационарные точки, для чего определяем частные производные:
За необходимым условием существования экстремума: 
откуда
Проверим, что при таком объеме продукции прибыль будет максимальной. Для этого построим матрицу Гессе (матрицу производных второго порядка) и вычислим ее определитель в точке (200. 50).
Тогда 

Ответ: прибыль в размере 65 000 грн фирма получит, если производить 200 единиц продукции по цене 500 грн и 50 единиц продукции по цене 600 грн.
Пример 5.6. Фирма реализует часть товара на внутреннем рынке, где цена единицы товара составляет 






Решение. По уравнению 
а из уравнения 
Прибыль от реализации товаров составляет:
С учетом затрат фирма имеет прибыль:
или
Находим частные производные первого порядка функции 
По необходимым условием существования экстремума имеем:
откуда 

При достаточным условием экстремума проверим, что при 


Поскольку 
функция имеет экстремум. Кроме того, 

Ответ: фирма будет иметь максимальную прибыль, если на внутреннем рынке реализовывать 90 единиц, а на внешнем — 120 единиц товара, при этом 
Пример 5.7. Стоимость строительства 



где 



Решение. Найдем частные производные первого порядка от функции стоимости строительства:
По необходимым условием экстремума составим систему уравнений относительно координат стационарной точки:
Из второго уравнения найдем 
Теперь из первого уравнения последней системы имеем:
Тогда
Проверим, имеет функция 

Находим частные производные второго порядка этой функции:
Для проверки достаточного условия экстремума вычисляем 


Имеем: 


Ответ: стоимость будет минимальной при таких размерах дома:
Пример 5.8. На предприятии используют два вида ресурсов в количествах 


Решение. Надо найти такие значения 



Решим уравнение 



Мы получили функцию одной переменной. Найдем ее производную:
За необходимым условием экстремума:
откуда 
Проверяем, есть ли найденная стационарная точка точкой максимума функции. Для этого определяем в ней знак второй производной:
Следовательно, действительно, в стационарной точке функция 
Ответ: на выделенные средства необходимо приобрести 9994 единицы первого ресурса и 3 единицы второго. Прибыль при этом составит
Пример 5.9. Функция общих затрат предприятия имеет вид:
где 



Общее количество произведенной продукции должен составлять 1000 единиц. Определить количества единиц товаров 

Решение. Надо найти такие значения 

имеет минимум при
Для исследования этой функции на условный экстремум составим функцию Лагранжа:
Находим ее частные производные первого порядка:
При необходимым условием экстремума имеем:
Отсюда: 
Для проверки достаточного условия экстремума определяем частные производные второго порядка
Составляем второй дифференциал функции Лагранжа при фиксированном
С учетом условия 
Следовательно, 


Ответ: минимальные затраты составят 821 000 (ум. ед.), Если предприятие изготовит 600 единиц продукции 
Пример 5.10. Годовые расходы предприятия (амортизация, ремонт, вклады на восстановление и т.п.) в зависимости от объема двух видов продукции 

где 
Определить условия хозяйствования предприятия.
Решение. Исследуем на экстремум функцию
Находим частные производные первого порядка этой функции:
При необходимом условии экстремума составляем систему уравнений:
Вычитаем из первого уравнения второе и получаем:
откуда
Подставляем 
получаем:
Отсюда, объем продукции второго вида равна:
Теперь в соотношение 

Проверим, имеет функция минимум при этих значениях 
Найдем частные производные второго порядка:
Определим знак 


Каждое слагаемое является положительным, так 


Ответ: расходы предприятия будут минимальными, если оно будет производить продукцию в таких объемах:
Применение интегралов в некоторых экономических задачах
Интегрирование в экономике имеет широкий спектр использования. Например, для нахождения функций затрат, прибыли, потребления, если известны соответствующие функции предельных издержек, предельного дохода, предельного потребления и тому подобное. Для определения произвольной постоянной интегрирования необходимо дополнительное условие. При нахождении функции затрат используется условие: при количестве продукции 

Рассмотрим ряд экономических задач, для решения которых используется понятие неопределенного и определенного интегралов.
Нахождение производственной функции
Для данного предприятия определены функции предельного дохода в зависимости от объема 
Найдем функцию прибыли этого предприятия как первоначальную для функции предельного дохода:
Эта функция должна удовлетворять определенные условия. Так, при 


Пусть функция предельных издержек предприятия при производстве 
Необходимо:
1) найти функцию затрат, если расходы на 100 единиц продукции составляют 7 тыс. Грн;
2) найти фиксированные расходы;
3) определить, какими будут затраты на производство 250 единиц продукции;
4) найти максимальное значение прибыли, если цена составляет 65,5 грн за единицу продукции.
Решение этой задачи, как и предыдущей, сводится к неопределенному интегрированию функции предельных издержек с последующим исследованием восстановленной функции издержек.
1) Найдем функцию затрат как первоначальную для функции предельных издержек предприятия:
Вычислим произвольную постоянную 

Таким образом, функция издержек имеет вид:
2) Для нахождения фиксированных расходов вычислим функцию затрат при
3) Затраты на производство 250 ед. продукции составляют:
4) Прибыль предприятия определяем по формуле:


следовательно,
Для определения максимального значения прибыли проведем исследование функции прибыли на экстремум. Сначала находим критические точки функции прибыли
(но объем производства не может быть отрицательным).
Определим знак второй производной в критической точке:
При 



Известно, что издержки производства 

Объем производства меняется от 100 до 200 единиц. Определить средние издержки производства.
Для того чтобы определить средние издержки производства, используем теорему о среднем (23.16):
По известной подынтегральной функции 

Следовательно, средние издержки производства составляют 2233 гр. ед.
Кривая Лоренца
Рассмотрим известную в экономике задачу об определении коэффициента Джини, характеризующий степень неравенства в распределении доходов населения страны. Пусть функция 

На рис. 24.20 приведен график функции 
Рис. 24.20
Если распределение доходов равномерное (в идеале), то функцией, которая характеризует такое распределение, является прямая линия 



Обозначим его через 




Пусть для одной из стран кривая Лоренца задается уравнением


Вычислим коэффициент Джини: 
Следовательно,
Таким образом, существенное по сравнению с нулем значение 
Кривая обучения
Рассмотрим некоторые вопросы, возникающие при освоении производства новой продукции. Пусть функция 







Рис. 24.21
Действительно, функция 
Время, которое будет потрачено на производство единицы продукции с номерами от 

Пусть после производства 100 часов оказалось, что время, нужное для производства следующих изделий, приходит в соответствии с формулой: 
Согласно формуле 
Закон спроса и предложения
Пусть кривая спроса на некоторый товар описывается функцией 

Вдоль оси 



Рис. 24.22
Традиционно кривая спроса обозначается буквой 


Найдем выигрыш потребителей от установленной цены 


На каждом частичном промежутке 


Тогда средний выигрыш на промежутке 
Если функция спроса непрерывная и 

Таким образом, выигрыш потребителей равен:
Аналогично находим выигрыш поставщиков:
Очевидно, что выигрыш потребителей равен площади между кривой спроса 


Найдем выигрыше потребителей и поставщиков, если функция спроса имеет вид 
Сначала определим точку рыночного равновесия:
или
Корни квадратного уравнения 

По формуле (24.19) определяем выигрыш поставщика:
Задача дисконтирования
Еще одной реальной экономической задачей, к решению которой применяется интегральное исчисление, является задача дисконтирования. Определение первоначальной суммы капиталовложений за ее конечной стоимости, полученная в течение времени 

Пусть вычисления прибыли происходит в течение периода 




Таким образом, сумма в конце 
Отсюда определим начальную сумму:
Если поступления осуществляются ежегодно в течение определенного промежутка времени, то дисконтированная стоимость определяется как сумма по всем периодам поступления денег:
где 
По формуле (24.20) предполагается, что стала процентная ставка действует в течение всего промежутка времени. Если ежегодный доход меняется со временем, то будущие поступления целесообразно рассматривать как непрерывный денежный поток, характеризующийся определенной интенсивностью — прибылью за единицу времени.
Разобьем весь период времени 








Формула (24.21) описывает интегральную сумму. Если перейти к границе этой суммы при условии, что 
Если вместо ставки дисконта применить другую характеристику — силу роста, которая определяется формулой 
Предположим, что фирма предполагает выпуск продукции в течение года и за этот период планирует получить прибыль 100 млн грн.
Продажа продукции осуществляется равномерно в течение года.
Ставка дисконта составляет 15%.
Текущую стоимость будущих поступлений можно приближенно оценить, если рассматривать дискретный денежный поток с периодом, составляет 1 год. Так, по формуле (24.20) при 
Однако такой расчет является приближенным, так как денежный поток является непрерывным. По условию задачи средства от реализации продукции поступают регулярно в течение года, поэтому будем считать интенсивность потока постоянной величиной, равной 100 млн грн / год. Определяем, что сила роста составляет 
Значение 
Определение предельного дохода
Пример 6.1. Пусть задана функция предельного дохода в зависимости от объема: 
Решение. Поскольку 
Доход равен нулю, если не реализовано ни одного изделия, поэтому имеем: 

Если 


6.2. Найти объем продукции, которую будет производить малое предприятие за первые три часа работы, если функция производительности труда имеет вид:
Решение. Объем продукции исчисляется по формуле
Следовательно,
Пример 6.3. Найти объем продукции, произведенной за два часа, если известна функция производительности
Решение. Для нахождения объема продукции вычислим определенный интеграл:
Пример 6.4. На изготовление 100 почтовых конвертов (1 единица продукции) было потрачено 50 минут. В дальнейшем при изготовлении менялся по формуле: 
Решение. Вычисляем интеграл:
Пример 6.5. Найти среднее значение затрат, если объем производства изменяется от 3 до 5 условных единиц, когда известно, что расходы в зависимости от объема производства можно описать функцией: 
Решение. Используем теорему о среднем значении функции:
в результате чего получим:
Следовательно, средние издержки производства равны 
Теперь найдем объем производства продукции, при котором расходы приобретают значение 



Следовательно, при 
Пример 6.6. Функция предельных издержек имеет вид: 
Решение. По условию задачи известно, что 

Фиксированные расходы составляют 1200 гр. ед., поэтому имеем:
Вычислим расходы на производство 200 изделий:
Прибыль в зависимости от объема составляет:

Для определения максимальной прибыли находим производную:
Дальше необходимым условием существования экстремума имеем: 




Следующим образом: функция издержек 
Пример 6.7. Пусть известны законы спроса и предложения:
Найти выигрыш потребителя и выигрыш поставщика.
Решение. Найдем точку рыночного равновесия 
откуда 
Если количество товара составляет 8 усл. ед., то рыночная цена составляет: 
Тогда цена всего товара равна 
Некоторые потребители могут заплатить за товар больше рыночной цены.
Тогда выигрыш потребителя (24.18) составит:
Выигрыш поставщика (24.19) составит:
Следовательно, выигрыш потребителя приближенно составляет 341,3 (гр. ед.), а выигрыш поставщика — 21,3 (гр. ед.).
Пример 6.8. Функция совокупных затрат предприятия и уравнение спроса на товар задаются следующими функциями: 

Решение. Выигрыш потребителя определяется формулой:
где 

Прибыль предприятия составляет:
Находим производную и критические точки функции
откуда 


Тогда
Таким образом, потребитель имеет выигрыш:
Следовательно, если объем производства составляет 6 единиц, то предприятие имеет максимальную прибыль, а потребитель — выигрыш 198 денежных единиц.
Пример 6.9. Определить дисконтированную (начальную) прибыль за 5 лет, если процентная ставка равна 8%, а годовой доход является функцией времени:
Решение. На промежутке времени 
По условию задачи имеем:
Для вычисления интеграла применим формулу интегрирования по частям:
Таким образом, дисконтированный доход за 5 лет, если процентная ставка равна 8%, составит 
Пример 6.10. Распределение дохода в некоторой стране определяется кривой Лоренца: 

Решение. Найдем долю дохода, которую получают 10% наиболее незащищенного населения:
Итак, 10% наиболее незащищенного населения получают 2,89% совокупного дохода.
Вычислим коэффициент неравномерного распределения совокупного дохода, равный отношению площади 




Определяем соответствующие площади, а именно:
Тогда
Таким образом, коэффициент неравномерного распределения совокупного дохода (коэффициент Джини) составляет 0,2634.
Пример 6.11. Пусть после изготовления 50 мобильных телефонов оказалось, что время на изготовление следующих телефонов уменьшается по формуле 
Решение. Время, необходимое на производство единицы продукции с номерами от

Для данной задачи:
Следовательно, на изготовление дополнительно 10 телефонов необходимо потратить 49,47 единицы времени.
Использование дифференциальных и разностных уравнений в экономических задачах
Рассмотрим ряд традиционных задач, математическими моделями которых являются дифференциальные и разностные уравнения.
Воспроизведение общих издержек производства по предельным характеристикам
Среди основных видов издержек производства экономическая теория рассматривает в частности такие:
валовые расходы (общие расходы) как сумму постоянных и переменных издержек для каждого конкретного объема производства;
предельные издержки — расходы, необходимые для выпуска дополнительной единицы продукции.
Нахождение за предельными издержками общих расходов сводится к решению простого дифференциального уравнения:
то есть к обретению первоначальной для заданной функции 
и определения значения произвольной постоянной
Пусть функция предельных издержек 

Найдем функцию общих издержек производства. Для этого интегрируем дифференциальное уравнение и получим множество функций общих расходов:
Найдем одну из них по заданной начальным условием — постоянными затратами при нулевом объеме производства:
функция общих затрат.
Пусть функция предельного дохода в зависимости от объема производства x имеет вид:
Найдем функцию прибыли 

Множество первобытных находим интегрированием по частям:
По начальным условием 
Итак, функцией прибыли в зависимости от объема производства является функция
Нахождение функций затрат, спроса, цены товара с их эластичностью
Напомним, что эластичностью функции одной переменной 


Если эластичность функции задано, то тем самым задано дифференциальное уравнение с разделяющимися переменными относительно функции
Найдем функцию затрат в зависимости от объема производства 
Согласно условию задачи и по формуле (31.3) имеем уравнение:

Решаем его:
Итак, общим решением уравнения является функция
Найдем функцию спроса 




Согласно определению (31.3) по условию задачи имеем дифференциальное уравнение:
которое является уравнением с разделяющимися переменными. Надо найти его частное решение, удовлетворяющее заданную начальную условие
Определяем общее решение:
Таким образом, имеем:
Значение постоянной 
Окончательно функция спроса в зависимости от цены товара имеет вид:
Найдем цену 


Согласно определению (31.3) по условию задачи имеем дифференциальное уравнение:
Находим его общее решение:
Следовательно,
По начальном условии 
Цена товара в зависимости от объема товара описывается функцией:
Модель естественного роста
Предположим, что функция 

где 
Функция 
или в явном виде
Впервые это уравнение получил Якоб Бернулли. оно называется уравнением естественного роста и описывает много различных процессов в природе и обществе. В экономике этим уравнением описывают: процессы кредитования, выпуск продукции, рост денежного взноса в банке, рост населения.
Задача Бернулли о кредитовании. Пусть заемщик за пользование кредитом ежегодно выплачивает кредитору проценты 

По условию задачи проценты растут непрерывно, следовательно скорость уменьшения суммы долга 

Отсюда имеем уравнение:
Общим решением этого уравнения является функция 


Таким образом, за каждую единицу занятой суммы заемщик обязан платить сумму
а за год эта сумма составит: 
Модель естественного роста выпуска продукции
Найдем закон роста выпуска продукции при условии, что рынок не насыщается.
Предположим, что некоторый товар продается по цене 




Пусть на инвестиции 

Благодаря расширению производства растет прибыль, и его 


В результате получили дифференциальное уравнение вида (31.4), где 

Модель естественного роста при насыщенности рынка
В приведенных выше примерах решением дифференциального уравнения естественного роста является функция 

Противоречие между моделью (31.4) — (31.5) и реальностью, возникает на достаточно длительном промежутке времени, учитывается в модели роста, в которой коэффициент пропорциональности 




То есть в отличие от уравнения (31.4) коэффициент 
Уравнение (31.7) является дифференциальным уравнением первого порядка. Отделив в нем переменные, находим:
Интегрируя обе части последнего равенства, получим общий интеграл уравнения:
Отсюда находим общее решение — функцию
описывающей процесс роста населения в условиях насыщенности рынка.
Аналогичную модель можно также использовать для роста выпуска продукции в условиях конкуренции.
В частном случае, если в (31.8) положить 


которая называется логистической функцией, а ее график — логистической кривой (рис. 31.1).
Рис. 31.1
Прямая 
Логистическая функция используется в статистических моделях для прогнозирования того, состоится или нет определенное событие. В терминах математической статистики, изучается позже, функцию (31.9) называют функцией распределения вероятностей логистического распределения случайной величины.
Рассмотрим пример применения модели (31.7).
Пусть население некоторого региона в зависимости от времени
В начальный момент времени 
Определить, через сколько лет она увеличится в четыре раза.
На основании (31.7) по условию задачи 
Определяем постоянную 
Итак, частным решением дифференциального уравнения является функция
По условию задачи необходимо определить, при каком значении аргумента 

С последнего равенства имеем:
Следовательно, население региона вырастет в 4 раза примерно через 9 лет.
Динамика рыночных цен
Спрос и предложение являются основными экономическими категориями рыночных отношений. Обозначим через 


Рассмотрим простейшую модель, в которой спрос и предложение являются линейными функциями цены единицы товара, а именно:
Уравнения отражают динамику рынка: спрос в зависимости от цены товара должен падать с ростом 




Найдем равновесную цену из условия
По формулам (31.10) имеем:
откуда
При равновесной цене рынок на определенном промежутке времени является сбалансированным, и цена на товар остается постоянной. В действительности спрос далеко не всегда соответствует предложению, то есть 


Определим функцию

С учетом (31.10) получим равенство:
Запишем равенство (31.12) несколько иначе:
Таким образом, динамическая модель описывается линейным неоднородным дифференциальным уравнением первого порядка.
Время (31.13) является уравнением с разделяющимися переменными.
Отделим их, учитывая (31.11):
Интегрируя левую и правую части уравнения (31.14), получим его общий интеграл:
Таким образом, общее решение уравнения (31.13) имеет вид:
Найдем постоянную 

Итак,
При неограниченном времени реализации товара 
в таких случаях говорят, что рынок динамично стабильный.
Заключение (с (31.17)): необходимым и достаточным условием динамической стабилизации рынка является выполнение неравенства
В зависимости от соотношения между ценой 


Рис. 31.2
1) 
2) 

3) 


Рассмотрим задачу спроса и предложения в несколько иной постановке. Как отмечалось ранее, спрос 


Если функция 

При условии равенства 
или
Общим интегралом этого уравнения является равенство:
Окончательно:
где 
Функции спроса и предложения имеют вид:
Найти зависимость равновесной цены от времени, если 
Определим равновесную цену при условии, что 
Отсюда находим:
Определяем постоянную 

Отметим, что при 


Функции спроса и предложения на некоторый товар имеют вид:
1. Найти зависимость равновесной цены 
2. Найти 
Для нахождения равновесной цены приравниваем спрос и предложение и получаем уравнение:
Отсюда,
Итак,
По начальным условием
Итак,
Найдем 
Пусть спрос и предложение на товар определяются соотношениями:
где 


Исходя из требования соответствия спроса предложения, найти зависимость цены от времени.
Из условия равновесия спроса и предложения:
которое является неоднородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами:
Соответствующее однородное уравнение:
Характеристическое уравнение
Общее решение однородного уравнения запишется следующим образом:
Частное решение неоднородного уравнения будем искать в виде:
тогда:
Подставив эти значения в дифференциальное уравнение, получим:
Итак, общее решение неоднородного уравнения таков:
Учтем начальные условия и определим
Тогда
Находим производные при
Учитывая, что по условию задачи 

Итак, зависимость цены от времени описывается функцией:
Использование разностных уравнений в экономике
Рассмотрим некоторые экономические задачи, математическими моделями которых разностные уравнения. Отметим, что в задачах, которые сводятся к дифференциальным уравнениям, рассматривается функция 



Традиционными моделями задач такого типа является паутинная модель рынка и экономическая модель развития Самуэльсона-Хикса.
Паутинная модель рынка
Рассмотрим задачу по спросу и предложению в такой постановке. Предположим, что цена товара на рынке является функцией времени 




где 
Исходя из условий соответствия спроса (в момент времени 


или
При стабильности рынка на данный момент времени: 

Общее решение разностного уравнения 1-го порядка является суммой общего решения соответствующего однородного уравнения и частные решения данного неоднородного уравнения:
Найдем общее решение однородного уравнения:
Ему соответствует характеристическое уравнение 


Если 






Рис. 31.3
В действительности бесконечно растущие колебания невозможны, поэтому при больших отклонениях от равновесия линейные модели зависимости спроса и предложения от цены на практике не реализуются.
Модель развития Самуэльсона-Хикса
Пусть функция 



где 

Предположим также, что предприниматели вкладывают инвестиции 
То есть
где 
Условие равновесия спроса и предложения имеет вид:
или
Уравнение (31.24) называется уравнением Хикса. Если величины 

Характеристическое уравнение соответствующего однородного уравнения имеет вид:
Самым интересным для исследований является случай комплексно-сопряженных корней характеристического уравнения (в этом случае решение имеет колебательный характер). Это имеет место, когда дискриминант уравнения (31.25) отрицательный:
и корнями характеристического уравнения является комплексно-сопряженные числа:
Таким образом, общим решением однородного разностного уравнения является последовательность:
где
Частное решение разностного уравнения (31.24) искать в виде 


Общим решением разностного уравнения Хикса является последовательность:
В реальных задачах экономики 



Решим уравнение Хикса, если
При таких условиях уравнение (31.24) принимает вид:
Найдем общее решение соответствующего однородного уравнения, для чего составляем и решаем его характеристическое уравнение:
Тогда общее решение однородного уравнения таков:
Итак,
Найдем частное решение данного уравнения. По виду правой части имеем: 


Подставим 
Таким образом, общим решением неоднородного разностного уравнения является последовательность с общим членом
Определение издержек производства
Пример 7.1. Пусть функция предельных издержек имеет вид: 
Решение. Данное уравнение перепишем так:
Поскольку дифференциалы уровне, то интегралы от них тоже равны с точностью до константы. Итак,
То есть функция издержек имеет вид:
Значение произвольной постоянной 
Пример 7.2. Пусть функция предельного дохода имеет вид: 
Решение. Преобразуем исходное уравнение:
отсюда
Понятно, что при 
Следовательно, функция прибыли имеет вид:
Пример 7.3. Найти цену товара как функцию объема x, если цена единицы товара 
Решение. Используя формулу
имеем:

Интегрируем:
Отсюда
С учетом начального условия 
Следовательно, цена товара как функции объема такова:
Пример 7.4. Найти функцию спроса 



Решение. По определению эластичности имеем:
Итак, дифференциальное уравнение имеет вид:
Далее интегрируем:
и получаем
Постоянную 
Следовательно, функция спроса имеет вид:
Пример 7.5. Найти производственную функцию 



Решение. Известно, что по определению эластичность производственной функции определяется как
Итак, имеем дифференциальное уравнение:
которое является однородным уравнением.
Сделаем замену переменной: 


Таким образом, мы получили уравнение с обособленными переменными. Далее интегрируем
и отсюда получаем:
или
Поскольку 
Найдем значение постоянной 



Тогда
Итак, имеем производственную функцию:
Пример 7.6. Полные издержки производства 
продукции x. Известно, что предельные и полные затраты для всех значений 

Решение. Для нахождения функции полных затрат y надо решить дифференциальное уравнение:
которое является линейным неоднородным дифференциальным уравнением первого порядка. Его решение будем искать в виде: 



Далее рассматриваем систему дифференциальных уравнений:
Из первого уравнения этой системы находим функцию 
Выражение для функции 
Переменные отделены, следовательно, можно осуществлять интегрирование:
Применив интегрирование по частям, имеем:
Тогда получаем общее решение уравнения:
По начальным условием 
Теперь определяем частное решение:
Следовательно, функция полных издержек, удовлетворяет начальное условие 
Пример 7.7. Функции спроса x и предложения y в зависимости от равновесной цены 


Решение. Если спрос и предложение совпадают, то
Откуда
Итак, получили дифференциальное уравнение первого порядка с разделяющимися переменными:
Тогда
или
По заданной начальным условием 
Итак, 
Таким образом, зависимость равновесной цены 

Пример 7.8. Пусть спрос и предложение на определенный товар определяются в соответствии соотношениями: 


Решение. Исходя из условия, что 
Мы получили дифференциальное уравнение с разделяющимися переменными:
откуда
или
По начальным условием 
Теперь 
Итак, для равновесия спроса и предложения необходимо, чтобы цена в зависимости от времени менялась по закону:
Пример 7.9. Численность населения 


Решение. Найдем решение уравнения:
откуда
Интегрируем:
Дробь 
Отсюда имеем уравнение для определения коэффициентов 
с которого, если 
Тогда:
Итак,

Найдем 
Тогда имеем:
Теперь определим, через сколько лет численность населения возрастет в 10 раз:
Таким образом, в данном регионе население возрастет в 10 раз примерно через 48 лет.
Пример 7.10. Пусть скорость роста общих потребностей населения 


Решение. По условию задачи ее математической моделью является дифференциальное уравнение:
Это уравнение второго порядка, в котором отсутствуют функция 

Интегрируем обе части уравнения, в результате чего слева получим производную первого порядка от функции
Интегрируя второй раз, получим:
Итак, мы определили общее решение уравнения.
Поскольку без получения доходов потребления невозможно, то есть начальное условие: 



Подставляем найдены 

Итак, зависимость общих потребностей населения от процента прибыли описывается функцией:
Пример 7.11. Пусть спрос и предложение на товар определяются в соответствии соотношениями: 



Решение. По условию 
откуда
Находим решение этого линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами: 


Запишем соответствующее однородное уравнение: 


Далее будем искать некоторое частное решение 
неоднородного уравнения в виде:
Определяем производные и подставляем их и саму функцию 
Следовательно,
Находим 

1)
2) поскольку 
Следовательно, зависимость цены от времени, учитывая начальные условия, описывается функцией:
Пример 7.12. Пусть спрос и предложение некоторого товара на рынке описывается соответственно уравнениями: 
Решение. Исходя из условий соответствия спроса и предложения, имеем разностное уравнение для нахождения равновесной цены в момент времени
или
При начальном условии 

Однородной уравнению 


Частное решение неоднородного уравнения уже было найдено:
Следовательно, имеем общее решение разностного уравнения Хикса:
Поскольку 
Пример 7.13. Найти решение разностного уравнения Хикса:
Решение. Общее решение ищем как сумму общего решения соответствующего однородного уравнения и любого частных решений данного неоднородного уравнения:
Частное решение уравнения берем в виде:
Подставляем 
Находим общее решение однородного уравнения:
Ему соответствует характеристическое уравнение: 
Следовательно,
где
Таким образом,
Расчёт текущей стоимости ценных бумаг
Пример 8.1. Определить текущую стоимость ценных бумаг, срок погашения которых составляет 5 лет, если процентная ставка по ним составляет 7%, ежегодные расходы достигают 5 усл. ед., а стоимость на момент погашения равна 200 усл. Ед.
Решение. По исходным данным задачи текущая стоимость ценных бумаг составит:
Первые пять слагаемых образуют частичную сумму 
Использовав формулу
имеем:
Тогда
Итак, текущая стоимость ценных бумаг составляет примерно 163,1 усл. ед.
Пример 8.2. Вычислить количество производимой продукции в течение первого часа работы, если известно, что производительность труда в течение дня меняется как 
Решение. Количество производимой продукции за промежуток времени 
По условию задачи 
Поскольку первоначальную от подынтегральной функции могут быть в виде конечного числа элементарных функций, то вычислим этот интеграл приближенно с помощью рядов. Используем расписание функции 
Для функции производительности получаем соотношение:
Тогда
Вычислим, например, сумму первых четырех членов ряда:
Погрешность не превышает по абсолютному значению первого из отброшенных членов ряда
Следовательно, количество производимой продукции в течение часа, составляет примерно 0,37 усл. ед.
Задача межотраслевого баланса
В некоторых задачах макроэкономики ставится вопрос об эффективное ведение многоотраслевого хозяйства. Здесь каждая отрасль является и производителем, и потребителем некоторой продукции (как своей, так и продукции, произведенной другими отраслями).
Однако, с экономической точки зрения, межотраслевой баланс является более
эффективным в стоимостном выражении. При этом объединение отдельных отраслей в подгруппы облегчает составление балансов продукции.
Введем следующие обозначения:
xi — общая стоимость продукции, произведенной в i-й отрасли (план валового выпуска продукции) (i = 1, 2, …, n);
xij — стоимость продукции i-й отрасли, необходимой для выпуска продукции j-го подразделения (j = 1,2, …, n);
yi — стоимость продукции i-ой отрасли, предназначенной для реализации (конечный продукт).
Прямые расходы единиц i-й отрасли, используемые для выпуска единицы изделия продукции j-й отрасли, а также конечный продукт заданы таблицей:
Связь между этими величинами запишем в виде системы уравнений:
Уравнения этой системы называются балансовыми.
Обозначим aij — стоимость продукции i-й отрасли, необходимой для выпуска единицы продукции j-й отрасли:
Матрица, составленная из величин aij
A = 
а ее элементы — коэффициентами прямых затрат.
Учитывая, что xij = aij xj, исходная система запишется так:

Обозначим через


Предыдущая система запишется в виде матричного уравнения X – AX = Y, или EX – AX = Y, отсюда (E – A) X = Y, где E — единичная матрица.
Обозначим E – A = B, тогда система линейных алгебраических уравнений запишется так BX = Y.
Умножим слева обе части уравнения на B-1: B-1BX = B-1Y. Отсюда X = B-1Y.
То есть вектор-план X можно найти, умножив B-1 на вектор конечных продуктов.
Матрица B-1 называется матрицей полных затрат. Элементы этой матрицы включают прямые и косвенные затраты.
Задача 1. Прямые затраты трех отраслей производства, а также объемы конечных продуктов (в денежных единицах) заданы в таблице:
Нужно найти:
1) матрицу полных затрат;
2) план каждой отрасли;
3) производственную программу отраслей;
4) коэффициенты косвенных затрат.
Решение. Из таблицы видно, что матрица прямых затрат будет:
A = 
Обозначим через Х — вектор–план отраслей производства, Y — вектор конечных продуктов:
Связь между величинами, записанными в таблице, представим в виде системы линейных уравнений:
В матричной форме имеем: Х – AХ = Y, или (E – A) X = Y.
Обозначим E – A = B. Система линейных алгебраических уравнений запишется в матричной форме: BX = Y. Отсюда X = B-1Y.
В нашей задаче
Для нахождения обратной В-1 к матрице В, вычислим определитель:
Поэтому для матрицы В существует обратная В1. Найдем алгебраические дополнения к элементам матрицы В:
Матрица из этих алгебраических дополнений будет:
а присоединенная.
Обратная матрица имеет вид:
Элементы этой матрицы B-1 — это коэффициенты полных затрат, а сама матрица является матрицей коэффициентов полных затрат.
2) Для нахождения плана каждой отрасли, умножим B-1 на вектор конечных продуктов Y:
Значит: x1 = 821; x2 = 1402; x3 = 1577.
Итак, если известен объем конечной продукции (в денежных единицах) y1 = 50; y2 = 80; y3 = 100, то нужно запланировать такие объемы производства для первой отрасли — 821, для второй — 1402 и для третьей — 1577.
3) Для нахождения производственной программы каждой отрасли, найдем произведение коэффициентов прямых затрат и валового выпуска продукции:
Разность между матрицей полных затрат B-1 и матрицей прямых расходов A определяет матрицу косвенных (посреднических) расходов C:
Таким образом, элементы сij матрицы C и являются коэффициентами косвенных (посреднических) расходов.
Нахождения расходов сырья, топлива и трудовых ресурсов
Задача 2. (задача нахождения расходов сырья, топлива и трудовых ресурсов.) Используя исходные данные и результаты вычислений предыдущей задачи 1, нужно найти:
1. Суммарные затраты сырья, топлива и трудовых ресурсов для выполнение программы производства.
2. Коэффициенты прямых затрат сырья, топлива и труда на единицу продукции каждой отрасли.
3. Полные затраты сырья, топлива и труда отдельными отраслями и хозяйством в целом.
4. Внутрипроизводственные расходы отраслей.
5. Внутрипроизводственные затраты на каждую единицу товарной продукции.
При этом известны расходные нормы сырья и топлива на производство единицы продукции каждой отрасли, трудоемкость в человеко-часах на единицу продукции, их стоимость, и представлены таблицей:
Решение. Запишем матрицу D, составленную из норм расходования сырья, топлива и труда, а также матрицу-строку P стоимости этих показателей
Запишем также результаты вычислений предыдущей задачи:
где X — матрица-столбец плана валового выпуска продукции; B-1 — матрица коэффициентов полных затрат.
1) Умножив матрицу D норм расходования сырья, топлива и труда и матрицу-столбец плана валового выпуска продукции X, получим матрицу-столбец суммарных затрат сырья, топлива и трудовых ресурсов:
Итак, для выполнения программы производства нужно израсходовать 3951 единиц сырья, 7720 единиц топлива и 21463 рабочих человеко-часов.
2) Произведение матрицы D норм расходования сырья, топлива и труда и матрицы коэффициентов полных затрат B-1 определяет матрицу коэффициентов прямых затрат сырья, топлива и труда на единицу продукции каждой отрасли:
Здесь элементы первого столбца означают количество расходов сырья, второго — топлива и третьего — рабочих человеко-часов, которые нужны для изготовления единицы продукции 1-й, 2-й и 3-й отраслей.
3) Произведения матриц-столбцов норм расходования сырья, топлива и труда и планового выпуска продукции выражают расхода сырья, топлива и труда каждого из трех отраслей:
Таким образом, матрица полных затрат сырья, топлива и труда по трем отраслям имеет вид:
4) Умножив матрицу-строку стоимости сырья, топлива и труда на матрицу полных затрат этих показателей, получим матрицу-строку стоимости расходов каждой из трех отраслей:
Это означает, что стоимость расходов первой отрасли составляет 14778 единиц, второй — 27339 и третьей — 35797,9.
5) Произведение матрицы-строки стоимости P на матрицу прямых затрат V сырья, топлива и труда дает внутрипроизводственные затраты на каждую единицу товарной продукции:
Задача 3. Для изготовления детских игрушек используются отходы полотняных материалов (М1, М2, М3) различных размеров. Вычислить количество материала, который расходуется при раскрое тремя способами, если количество заготовок, полученных с каждого материала, а также количество необходимых заготовок представлены в таблице:
Решение. Если x1, x2, x3 — количество исходного материала (М1, М2, М3), который используется для раскроя соответственно первым, вторым и третьим способами, то для выполнения поставленной задачи, нужно решить систему линейных уравнений:
Решим ее методом Гаусса. Исключим неизвестную величину x1 из второго и третьего уравнений. Для этого умножим первое уравнение на «–2», «–4» и прибавим соответственно ко второму и третьему уравнениям:
Исключим неизвестную x2 из третьего уравнения. При этом умножим второе уравнение на «5» и добавим к третьему уравнению:
Отсюда, решение системы линейных уравнений будет х1 = 15; х2 = 18; х3 = 25. Следовательно, при определенных методах раскроя материала, нужно иметь 15 шт. материала М1, 18 шт. материала М2 и 25 шт. материала М3 .
Задача 4. Для изготовления четырех видов продукции P1 , P2 , P3 , P4 используются три вида сырья S1, S2, S3. Нормы расхода и запасы сырья приведены в таблице:
Определить количество продукции P1 , P2 , P3 , P4 , если ресурсы полностью исчерпаны.
Решение. Обозначим через x1 , x2 , x3 , x4 количество единиц продукции P1 , P2 , P3 , P4 . Условие нашей задачи можно записать в виде системы линейных уравнений:
Решим ее методом Жордана-Гаусса в табличной форме. В качестве первой таблицы запишем коэффициенты, стоящие при неизвестных, и столбец из свободных членов. Столбец (Σ) является контрольным, представляющий сумму чисел соответствующей строки.
Таблица 1. В качестве ключевого элемента взято число «1» в третьей строке и первом столбце. Для образования нулей в ключевом столбце на месте цифр «2», «3», умножим элементы ключевого строки на «–2» и «–3», и прибавим к соответствующим элементам второй и первой строк. Этим исключим неизвестное x1 в первом и втором уравнениях.
Таблица 2. В качестве ключевого элемента возьмем число «1» (вторая строка и второй столбец). Умножим элементы второй строки на числа «4» и «–2» и добавим к элементам первой и третьей строк. При этом произошел процесс исключения неизвестного x2 в
первом и третьем уравнениях.
Таблица 3. За ключевой элемент возьмем число «–12». Поделим на него все элементы первой строки. Запишем полученные числа элементами первой строки следующей таблицы.
Таблица 4. Умножим элементы первой строки на «–6» и «2» и добавим к элементам третьей и второй строки таблицы 3.
Результаты вычислений запишем второй и третьей строками этой таблицы. Полученные нули третьего столбца выражают исключения неизвестного x3 из второго и третьего уравнений.
Последней таблице соответствует система линейных уравнений
Она совместима по теореме Кронекера-Капелли, поскольку ранг основной и расширенной матриц равен 3. Так как это число (3) меньше, чем количество неизвестных (4), то система линейных уравнений имеет множество решений. Неизвестные x1 , x2 , x3 являются базисными, поскольку определитель, составленный из коэффициентов, стоящих при неизвестных, отличный от нуля.
Поэтому
Поскольку x1 , x2 , x3 выражают количество реализованной продукции, поэтому xi ≥0. Значит

Из последней системы следует, что
Итак, произвольному значению 
Задача 1. Бюро экономического анализа предприятия установило, что при производстве x комплектов мебели ежеквартальные расходы V (x) выражаются формулой V (x) = 2050 + 15x (рублей), а доход D (x), полученный от продажи x комплектов мебели, определяется по формуле D (x) = 25 x — 0,1x2 (рублей).
Каждый квартал предприятие производит 80 комплектов, но стремится увеличить выпуск мебели до 110 единиц. Вычислить приращение расходов, доходов и прибыли. Найти среднюю величину приращения прибыли на единицу приращения продукции.
Решение. Планируемое приращение продукции будет
Приращение расходов:

Приращение дохода:

Обозначим прибыль через Р (x). Тогда прибыль будет:
(x) = D (x) – V (x) = 25 x – 0,1x2 – 2050 – 15 x = –2050 + 10x –0,1x2.
Приращение прибыли будет таким:

то есть уменьшится на 270 рублей. Средняя величина прибыли на единицу приращения продукции будет:
Задача 2. В одном из областных центров во всех высших учебных заведениях учится 35 тыс. студентов. Ежегодно количество студентов увеличивается на 3%. Какое количество студентов будет в указанном областном центре через восемь лет?
Решение. Используем формулу возрастания по сложным процентам:
где 


На основании формулы возрастания по сложным процентам имеем:

Задача 3. Вкладчик предоставляет банку 2000 рублей под сложные проценты с условием их непрерывного роста на 12 % годовых. Вычислить накопления капитала за 4 года.
Решение. Используем формулу непрерывного возрастания по сложным процентам
Если 

На основании формулы непрерывного возрастания по сложным процентам, получаем такой ответ:

Оптимизация с экономическим содержанием
Задача 1. На предприятии отходов жестяных листов прямоугольной формы размерами 8 дм × 5 дм решили изготавливать открытые сверху ящики наибольшего объема, вырезав по углам равные квадратики и загнув жесть, чтобы получить боковые стенки. Какой длины
должны быть стороны вырезанных квадратов?
Рис. 11.
Решение. Пусть x — стороны вырезанных квадратов (рис.11). Тогда размеры ящика будут 8 –2x, 5 – 2x и x. Объем ящика V = x (5 – 2x) (8 – 2x). Найдем наибольшее значение этой функции при условии, что 

Приравняв ее к нулю, найдем критические точки первого рода:
Поскольку точка 
Найдем вторую производную V »:
Итак, в точке x = 1 функция V достигает максимума. При x = 0 и x = 2,5, V = 0.
Ответ: 
Задача 2. Надо изготовить открытый цилиндрический бак объема V. Материал, из которого изготавливают дно бака, стоит 

Решение. Пусть r — радиус основания, а h — высота бака. Тогда объем бака 

Выразим из формулы объема 

Находим критические точки:
вторая точка r = 0 не входит в область определения функции.
Найдем
Итак, в точке 
Находим
Найдем соотношение
Итак, радиус дна к высоте бака должен относиться как цена материала дна к цене материала боковой поверхности.
Задача 3. Фирма решила выпускать новые радиоприемники. Экономическим подразделением фирмы установлено, что при выпуске x приемников ежеквартально затраты будут V (x) = 90000 + 30 x (рублей), а количество проданных приемников в зависимости от цены 

Решение. Найдем цену р:

Найдем маржинальный доход и, приравняв его к нулю, найдем критические точки:
Поскольку 

Достигается это значение дохода при цене на приемник

Прибыль 
Находим маржинальную прибыль и, приравняв его к нулю, критические точки:

Поскольку 


Из формулы прибыли видно, что максимальная прибыль достигается, если D’ (x) = V’ (x), то есть когда маржинальные затраты равны маржинальному доходу.
Максимальная прибыль достигается при выпуске и продаже 4050 приемников по цене 
Следовательно, максимальная выручка (доход) 675 000 руб. достигается при выпуске и реализации 4500 радиоприемников по цене 150 руб. за приемник, а максимальная прибыль в 456 219 руб. — при выпуске и реализации 4050 радиоприемников по цене 165 руб. за приемник.
Задача 1. Полные затраты К — функция объема производства x. Найти функцию К затрат, если известно, что скорость роста затрат для всех значений x равна средним затратам.
Решение. Скорость роста затрат является производной 


Итак, 
Отсюда, 
Задача 2. Количество населения y является функцией времени t, то есть со временем количество населения меняется. Скорость изменения приращения населения пропорциональна количеству населения. Надо найти формулу для определения количества населения в любой момент времени t.
Решение. По условию задачи скорость изменения приращения населения пропорциональна численности населения. Это можно записать так:

В полученном дифференциальном уравнении разделим переменные:

Далее будем получим:

Получена формула для определения количества населения как функции времени. Она содержит произвольную постоянную, которая может принимать любые числовые значения.
Покажем на примере как по формуле (7.19) можно прогнозировать рост населения. Для удобства возьмем приблизительные данные.
Пусть по переписи 1980 населения на Земле было, например, 5 млрд. Начнем отсюда отсчет, то есть t0 = 0. А в 1990 году населения на Земле стало 6 млрд., то есть t = 10 (лет). Тогда, использовав эти начальные условия, получим: 5 = С · еk·0; C = 5.
Подставим найденное C = 5 в формулу y = Cekt, имеем:
Мы нашли коэффициент пропорциональности.
Учитывая, что 


Формула (7.20) дает возможность найти численность населения в любой момент времени t, например, найдем количество населения в 2010 году (t = 30):
Задача 3. Пусть в момент времени t величина вклада в банк g = g (t). Очевидно, что увеличение (изменение) вклада пропорционально его величине:

Пусть при t = 0 первоначальный взнос в банк был g0, тогда g0 = Ce0 и формула (7.21) запишется:

Пусть величина вклада меняется непрерывно со временем и за месяц возрастает на N %:

Подставим k в (7.22):
Последняя формула дает возможность определить величину вклада в банк в любой момент времени t.
Рост инвестиций
Задача 4. Экономисты установили, что скорость роста инвестированного капитала в любой момент времени t пропорциональна величине капитала с коэффициентом пропорциональности, равным согласованному проценту R непрерывного роста капитала. Надо найти закон возрастания инвестированного капитала, учитывая величину начальной (при t = 0) инвестиции K0.
Решение. Обозначим K (t) — величина инвестированного капитала в момент времени t (искомая функция).
Тогда 
По условию задачи имеем:
Получили задачу Коши для дифференциального уравнения первого порядка. Общим решением дифференциального уравнения будет функция
Согласно начальным условием при t = 0 имеем 
Итак, решением задачи будет функция 
Задача 5. Известно, что эластичность спроса η определяется по формуле

Решение. По условию задачи:
Нашли зависимость между количеством товара и его стоимостью, то есть функцию спроса.
Что такое экономика
1. Государство оказывает двоякое воздействие на экономику:
2. Государство, становясь субъектом рынка, осуществляет государственные закупки, что меняет функцию совокупных плановых расходов следующим образом:
3. Влияние изменения государственных закупок аналогично влиянию изменения автономных плановых инвестиций, а мультипликатор государственных закупок считается по такой же формуле:
4. В случае введения автономных налогов функция плановых расходов примет следующий вид:
5. Увеличение автономных налогов сдвигает функцию плановых расходов параллельно вниз на величину изменения потребительских расходов 
6. Мультипликатор автономных налогов рассчитывается по следующей формуле:
7. Сравнивая мультипликатор расходов (в том числе и государственных закупок) и мультипликатор налогов, можно сказать, что, во-первых, мультипликатор налогов действует в противоположном направлении, о чем свидетельствует минус перед дробью, а, во- вторых, налоговый мультипликатор меньше мультипликатора расходов, так как налоги действуют не прямо, а косвенно, через располагаемый доход. Это приводит к тому, что изменение в потреблении меньше, чем изменение налогов, так как изменение в располагаемом доходе распределяется на изменение в потреблении и изменение в сбережении.
8. Норвежским экономистом Т. Хаавельмо выведена теорема сбалансированного бюджета, согласно которой, независимо от того, каково исходное состояние государственного бюджета, при одновременном и одинаковом росте государственных закупок и налоговых поступлений и неизменных инвестициях, национальный доход возрастает на величину роста государственных закупок, а сам мультипликатор сбалансированного бюджета равен 1
9. В случае введения в анализ пропорционального налогообложения налоги можно выразить в виде налоговой функции:




10. При сохранении прежней склонности к потреблению уже по отношению не ко всему, а только к располагаемому доходу, склонность к потреблению по отношению ко всему доходу превращается в 


Графически это означает, что меняется наклон функции плановых расходов, он становится меньше, потому что населению теперь приходится отдавать какую-то часть каждого полученного рубля в виде налогов, так что в его распоряжении остается только 
11. В экономике с системой подоходного налогообложения мультипликатор расходов рассчитывается по следующей формуле:
а мультипликатор автономных налогов — по формуле:
Фискальная политика — это политика государства в определении государственных расходов и налогов. Ее цель — воздействие на совокупный спрос (совокупные плановые расходы) с тем, чтобы приблизить экономику к уровню полной занятости при неинфляционном развитии.
Фискальную политику, в зависимости от механизмов ее реагирования на изменение экономической ситуации, подразделяют на дискреционную и автоматическую фискальную политику.
Дискреционная фискальная политика — это сознательное манипулирование государственными закупками и налогами. Ее цель — в максимальном приближении равновесного дохода к уровню дохода при полной занятости.
Необходимое изменение плановых расходов можно рассчитать по следующей формуле:
Фискальная политика, которая приводит к расширению совокупного спроса, называется экспансионистской, или стимулирующей фискальной политикой.
Добиться увеличения совокупного спроса (совокупных плановых расходов) можно двумя путями:
1. Увеличить государственные закупки;
2. Уменьшить налоги.
Фискальная политика, которая приводит к уменьшению совокупного спроса, называется рестриктивной, или сдерживающей фискальной политикой.
Добиться сокращения совокупного спроса (совокупных плановых расходов) можно либо за счет уменьшения государственных закупок, либо за счет роста налогов.
В своей простейшей форме дискреционная фискальная политика должна приводить к дефициту государственного бюджета в период экономического спада и к активному сальдо бюджета в период быстрого роста цен.
Примеры решения типовых задач по экономике на разные темы
Задача 1
Функция потребления 
100 ед., автономные инвестиции и автономные государственные закупки — по 50 ед.
A) запишите вид функции плановых расходов и определите равновесный уровень дохода;
B) как изменится уровень дохода, если государственные закупки возрастут на 20 ед.?
C) как изменится уровень дохода, если автономные налоги уменьшатся на 20 ед.?
Д) что произойдет, если государство одновременно увеличит налоги и государственные закупки на 20 ед.?
Решение:
1. По условию задачи в экономике действуют только автономные налоги, поэтому функция плановых расходов может быть представлена следующим образом:
В равновесии
2. Увеличение государственных закупок приводит к мультипликативному увеличению национального дохода. Помним, что
Соответственно, увеличение государственных закупок на 20 ед. приводит к увеличению равновесного выпуска на 100 ед.
На графике кейнсианского креста функция плановых расходов сдвигается параллельно вверх на величину государственных закупок (20 ед.), что приводит к увеличению равновесного уровня дохода на 100 ед.
3. Уменьшение автономных налогов увеличивает располагаемый доход и, соответственно потребительские расходы на величину
Графически произойдет сдвиг функции плановых расходов вверх на величину 
Это приводит к тому, что изменение в потреблении меньше, чем изменение налогов, так как изменение в располагаемом доходе распределяется на изменение в потреблении и изменение в сбережении.
Изменение в равновесном уровне национального дохода можно рассчитать двояко: либо умножив величину 
Мультипликатор автономных налогов рассчитывается по следующей
формуле: 
Видим, что налоги — менее эффективный инструмент, чем государственные закупки.
4. При одновременном увеличении государственных закупок и автономных налогов на 20 ед. срабатывает теорема сбалансированного бюджета, согласно которой национальный доход возрастет на величину
Графически это можно проиллюстрировать следующим образом: увеличение государственных закупок сдвигает функцию плановых расходов вверх на 20 ед., но одновременно, в результате увеличения автономных налогов, она сдвигается параллельно вниз на 16 ед. В результате функция плано-
вых расходов сдвигается вверх на 4 ед., что, с учетом мультипликатора расходов, приводит к увеличению равновесного выпуска на 20 ед.
Задача 2
Известны следующие данные: автономное потребление составляет 1000 млрд. долл., государственные закупки — 1000 млрд. долл., 
A) определите равновесный уровень дохода;
B) насколько возрастет равновесный доход, если государственные закупки вырастут на 250 млрд. долл.?
C) покажите, что рост государственных закупок на 250 млрд. долл. сдвигает уровень равновесного дохода в большей степени, нежели уменьшение на туже величину автономных чистых налогов. Объясните это обстоятельство.
Решение:
1. В экономике с системой пропорционального налогообложения и отсутствием автономных налогов функция плановых расходов принимает следующий вид:
В равновесии 
2. Если государственные закупки возрастут на 250, то равновесный уровень дохода вырастет в соответствии с эффектом мультипликатора расходов на величину
В экономике с системой подоходного налогообложения мультипликатор расходов рассчитывается по следующей формуле:

3. В экономике с системой подоходного налогообложения мультипликатор автономных налогов рассчитывается по формуле:
Следовательно, при уменьшении автономных налогов на 250, равновесный уровень дохода вырастет в соответствии с эффектом мультипликатора автономных налогов на величину
Задача 3
Функция потребления задана как 

A) каков равновесный уровень дохода в экономике?
B) какова величина мультипликатора расходов в этой экономике?
C) чему равен бюджетный избыток 
Д) чему равен бюджетный избыток, когда инвестиции возрастают до 100? За счет чего произошли изменения в бюджетном избытке?
E) в предположении, что уровень дохода при полной занятости равен 1200, рассчитайте бюджетный избыток при полной занятости при
F) чему равен 


Решение:
1. В лекции было введено понятие чистых налогов: 

Тогда функция плановых расходов может быть представлена следующим образом:
В равновесии 
2. В экономике с системой подоходного налогообложения мультипликатор расходов рассчитывается по следующей формуле:
3. Из лекции помним, что
Запишем для нашей задачи формулу бюджетного избытка:

4. Если в экономике выросли инвестиции на 50 ед., то соответственно, мультипликативно растет национальный доход:
Новый равновесный уровень дохода равняется 1125 ед. В результате роста дохода растут и налоговые поступления в бюджет, что ведет к изменению бюджетного избытка: 
5. Бюджетный избыток при полной занятости рассчитывается по той же формуле, только фактический доход заменяется на потенциальный:
Обратите внимание, что бюджетный избыток при полной занятости не зависит от величины инвестиций в экономике. От них зависит фактический уровень дохода, по величине которого мы рассчитываем налоговые поступления в бюджет. При расчете же бюджетного избытка при полной занятости мы в качестве основы для расчета величины налоговых поступлений берем потенциальный уровень дохода, а он не зависит от величины инвестиций.
6. В исходной ситуации (см. пп. 1-3) экономика находится в рецессион-ном разрыве, следовательно, правительство решается на проведение стимулирующей фискальной политики. Увеличение государственных закупок до 250 ед. приводит к тому, что бюджетный избыток при полной занятости становится отрицательным:
Для оценки направленности фискальной политики используется 


Задача 4
Предполагается, что станок будет служить 3 года, принося ежегодный доход в 2000 долл. Его остаточная стоимость к концу третьего года составит 6000 долл. Определите цену станка, полностью направляемую на покрытие издержек, если:
A) ставка процента составляет 8%;
B) ставка процента составляет 10%;
С) ставка процента равна 8%, но предполагаемая инфляция составит 7%
в год.
Решение:
Чтобы определить цену станка, целиком направляемую на покрытие издержек, следует суммировать текущие дисконтированные стоимости, приведенные в таблице 1.

Ответы:
Задача 5
Экономика страны характеризуется следующими данными: функция потребления дана в виде 

A) начертите кривую 

B) предположим, что госрасходы возрастают со 100 до 150. Насколько сдвинется кривая
Решение:
А) Для того, чтобы начертить кривую 
Используем условие равновесия:

Далее чертим график полученной линейной функции:
В) Для определения величины сдвига кривой 


Соответственно, меняется и уравнение кривой:
Задача 6
В экономике без участия государства и заграницы функции сбережений и инвестиций имели соответственно следующий вид; С появлением государства была введена постоянная ставка подоходного налога 10%, и все собранные налоги расходовались на покупку благ. Функция сбережений тогда приобретает вид:
Определить линию 
Решение:
Для выведения кривой 


С появлением государства меняется функция сбережений, теперь национальный доход не совпадает с располагаемым:



При построении графиков следует обратить внимание не только на сдвиг кривой 
Услуги:
- Заказать экономику помощь в учёбе
- Контрольная работа по экономике заказать
- Помощь по экономике онлайн
- Курсовая работа по экономике заказать готовую онлайн
- РГР по экономике расчетно графическая работа



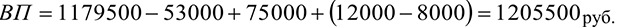
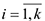
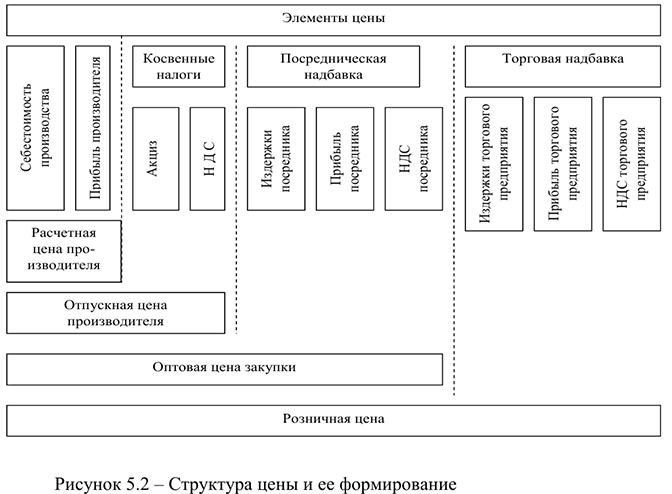
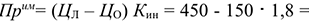
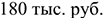
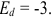
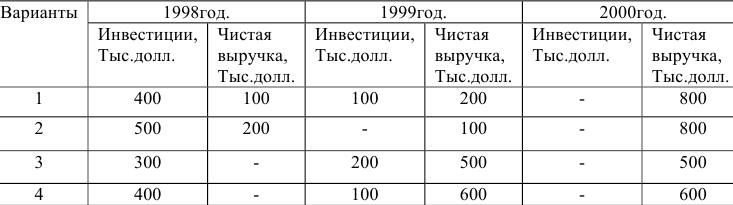
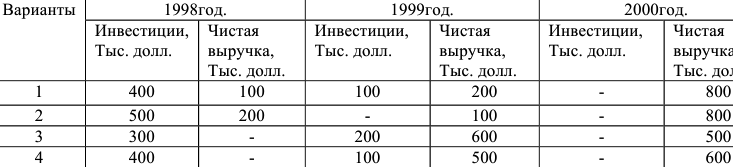
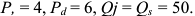
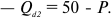
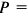
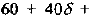
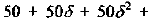
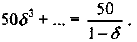
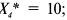
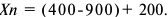
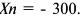
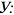
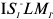
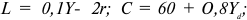
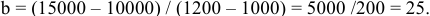
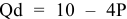 , а уравнение кривой предложения
, а уравнение кривой предложения 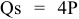 . Какой в этом случае будет равновесная рыночная цена?
. Какой в этом случае будет равновесная рыночная цена?



 Ответы на вопросы по заказу задачи и заданий по экономике:
Ответы на вопросы по заказу задачи и заданий по экономике:



























































































































 обозначить тариф перевозки груза за единицу расстояния,
обозначить тариф перевозки груза за единицу расстояния,  — затраты при перевозке груза, что не зависит от расстояния
— затраты при перевозке груза, что не зависит от расстояния  то общая стоимость
то общая стоимость  перевозки груза на расстояние
перевозки груза на расстояние  можно вычислить с помощью формулы
можно вычислить с помощью формулы 
 где величина
где величина  будет обозначать переменные траты, что зависят от объема выпуска. Величина
будет обозначать переменные траты, что зависят от объема выпуска. Величина  обозначает постоянные затраты предприятия. которые не зависят от объема продукции, что выпускается.
обозначает постоянные затраты предприятия. которые не зависят от объема продукции, что выпускается. 











































































































































































































































































































































































































































































































































































































































































































































































































































































































