Руководство некоторой компании решает создавать ли для выпуска новой продукции крупное производство - RukovodstvoRus.ru

Анализ и решение задач с помощью дерева решений

Процесс принятия
решений с помощью дерева решений в общем
случае предполагает выполнение следующих
пяти этапов.

Этап
1. Формулирование
задачи. Прежде
всего, отбросить не относящиеся к
проблеме факторы, а среди множества
оставшихся выделить существенные и
несущественные. Это позволит привести
описание задачи принятия решения к
поддающейся анализу форме. Должны быть
выполнены следующие основные процедуры:
определение возможностей сбора информации
для экспериментирования и реальных
действий; составление перечня событий,
которые с определенной вероятностью
могут произойти; установление временного
порядка расположения событий, в исходах
которых содержится полезная и доступная
информация, и тех последовательных
действий, которые можно предпринять.

Этап
2. Построение дерева решений.

Этап 3. Оценка
вероятностей состояния среды,
т.е сопоставление шансов возникновения
каждого конкретного события. Следует
отметить, что указанные вероятности
определяются либо на основании имеющейся
статистики, либо экспертным путем.

Этап
4. Установление выигрышей
(или проигрышей
как выигрышей со знаком минус) для каждой
возможной комбинации альтернатив
(действий) и состояний среды.

Этап
5. Решение задачи.

Пример.
Руководство
некоторой компании решает, создавать
ли для выпуска новой продукции крупное
производство, малое предприятие или
продать патент другой фирме. Размер
выигрыша, который компания может
получить, зависит от благоприятного
или неблагоприятного состояния рынка.

Номер стратегии	Действия компании	Выигрыш, дол., при состоянии экономической среды
благоприятном	неблагоприятном
1	Строительство крупного предприятия	200 000	— 180 000
2	Строительство малого предприятия	100 000	— 20 000
3	Продажа патента	10 000	10 000

Вероятность
благоприятного и неблагоприятного
состояний экономической среды равна
0,5.

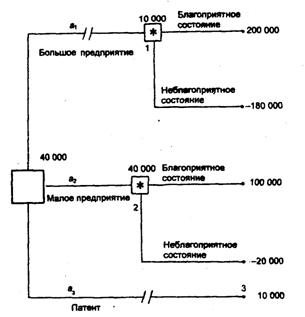
На основе таблицы
выигрышей можно построить дерево
решений.

На
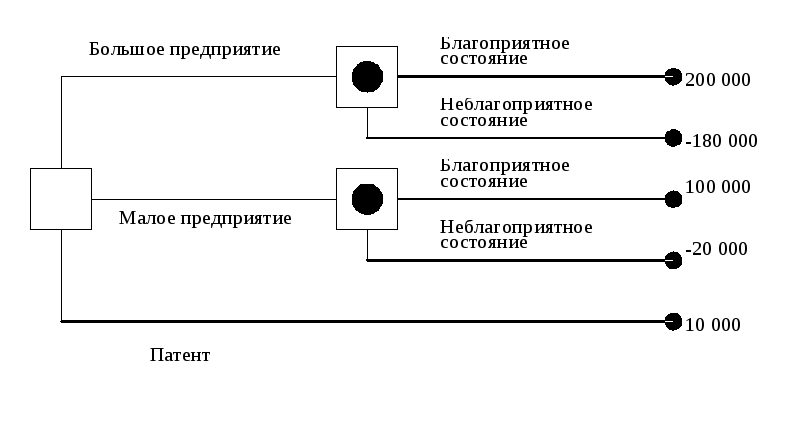
дереве решений: пустой квадрат – решение,
принимаемое игроком; заполненный квадрат
– случай, решение зависит от «случая».

Процедура принятия
решения заключается в вычислении для
каждой вершины дерева (при движении
справа налево) ожидаемых денежных
оценок, отбрасывании неперспективных
ветвей и выборе ветвей с максимальной
ожидаемой денежной оценкой.

Средний ожидаемый
выигрыш для вершины – «случая»
определяется как математическое
ожидание.

По данному дереву
крайние ветви отбрасывают как
неперспективные, таким образом, ожидаемая
денежная оценка наилучшего решения
равна 40 000.

Необходимо
отметить, что наличие состояния с
вероятностями 50% неудачи и удачи на
практике часто означает, что истинные
вероятности игроку, скорее всего,
неизвестны и он всего лишь принимает
такую гипотезу.

Пример.

В условиях
предыдущей задачи: пусть теперь перед
тем как принимать решение о строительстве,
руководство компании должно определить,
заказывать ли дополнительное исследование
состояния рынка или нет, причем
предоставляемая услуга обойдется
компании в 10 000. Руководство понимает,
что дополнительное исследование
по-прежнему не способно дать точной
информации, но оно поможет уточнить
ожидаемые оценки конъюнктуры рынка,
изменив тем самым значения вероятностей.

Относительно
фирмы, которой можно заказать прогноз,
известно, что она способна уточнить
значения вероятностей благоприятного
и неблагоприятного исхода. Возможности
фирмы в виде условных вероятностей
благоприятности и неблагоприятности
рынка сбыта представлены в таблице.

Прогноз фирмы	Фактически
благоприятный	Неблагоприятный
Благоприятный	0,78	0,22
Неблагоприятный	0,27	0,73

Предположим, что
фирма, которой заказали прогноз состояния
рынка, утверждает:

ситуация будет
благоприятной с вероятностью 0,45;
ситуация будет
неблагоприятной с вероятностью 0,55.

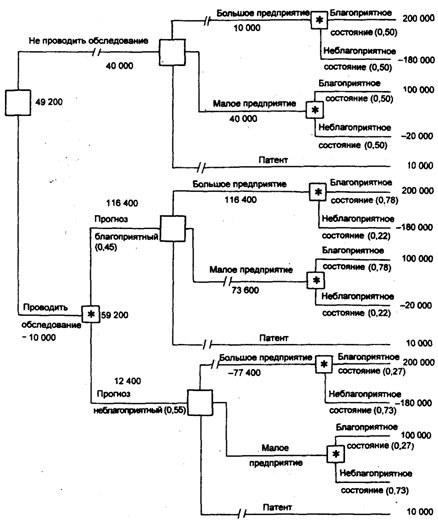
На основании
дополнительных сведений можно построить
новое дерево решений.

Из анализа дерева
решений следует:

необходимо
проводить дополнительное исследование
конъюнктуры рынка, поскольку это
позволяет существенно уточнить
принимаемое решение;
если фирма
прогнозирует благоприятную ситуацию
на рынке, то целесообразно строить
большое предприятие (ожидаемая
максимальная прибыль 116 400 дол.), если
прогноз неблагоприятный – малое
(ожидаемая максимальная прибыль – 12
400 дол.)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

4.4. выбор решений с помощью дерева решений (позиционные игры)

Рассмотрим более сложные (позиционные, или многоэтапные) решения в условиях риска. Одноэтапные игры с природой, таблицы решений (см. разд. 3.3), удобно использовать в задачах, имеющих одно множество альтернативных решений и одно множество состояний среды. Многие задачи, однако, требуют анализа последовательности решений и состояний среды, когда одна совокупность стратегий игрока и состояний природы порождает другое состояние подобного типа. Если имеют место два или более

последовательных множества решений, причем последующие решения основываются на результатах предыдущих, и/или два или более множества состояний среды (т.е. появляется целая цепочка решений, вытекающих одно из другого, которые соответствуют событиям, происходящим с некоторой вероятностью), используется дерево решений.

Дерево решений это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды.

4.4.1. Принятие решений с применением дерева решений

В постановочном плане рассмотрим несколько задач, которые могут быть решены с помощью данного метода.

Задача 1. Разведывательное бурение скважин. Некоторая нефтяная разведывательная партия должна решить, стоит ли бурить скважины на данном участке до того, как истечет срок контракта. Для руководителей партии не ясны многие обстоятельства:

в какую сумму обойдется стоимость бурения, зависящая от качества грунта, глубины залегания нефти и т.д.;

на какие запасы нефти в этом месте можно рассчитывать;

сколько будет стоить эксплуатация скважины.

В распоряжении руководства имеются объективные данные об аналогичных и не вполне похожих скважинах этого типа. При помощи сейсмической разведки можно получить дополнительную информацию, которая, однако, не дает исчерпывающих сведений о геофизической структуре разведываемого участка. Кроме того, получение сейсмической информации стоит недешево, поэтому еще до того, как будет принято окончательное решение (бурить или нет), следует определить, есть ли необходимость собирать эти сведения.

Задача 2. Выпуск нового товара. Большая химическая компания успешно завершила исследования по усовершенствованию строительной краски. Руководство компании должно решить, производить эту краску самим (и если да, то какой мощности строить завод) либо продать патент или лицензию, а также технологию независимой фирме, которая имеет дело исключительно с производством и сбытом строительной краски.

Основные источники неопределенности:

рынок сбыта, который фирма может обеспечить при продаже новой краски по данной цене;

расходы на рекламу, если компания будет сама производить и продавать краску;

время, которое потребуется конкурентам, чтобы выпустить на рынок подобный товар (успеет ли компания за этот срок окупить затраты, понесенные для того, чтобы стать лидером в данной сфере производства).

Компания может получить некоторые дополнительные сведения, имеющие косвенное отношение к проблемам проникновения конкурентов на рынок сбыта, опросив часть поставщиков краски. Но к материалам опросов следует относиться с осторожностью, ибо поставщики в действительности могут поступать не так, как они первоначально предполагают. В качестве подтверждения последнего суждения можно привести исследования, проведенные американскими автомобильными корпорациями для того, чтобы определить спрос на большие легковые автомобили. Несмотря на надвигающийся энергетический кризис 1971 — 1973 гг., результаты анкетирования показали, что американские покупатели по-прежнему предпочитают многоместные легковые автомобили. Однако на деле все произошло с точностью до наоборот, и на рынке стали пользоваться спросом небольшие, экономичные машины. Такие результаты опроса могут быть частично объяснены скрытностью человеческого характера, и это должно учитываться при принятии решений.

4.4.2. Анализ и решение задач с помощью дерева решений

Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов.

Этап 1. Формулирование задачи. Прежде всего необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволит привести описание задачи принятия решения к поддающейся анализу форме. Должны быть выполнены следующие основные процедуры: определение возможностей сбора информаци для экспериментирования и реальных действий; составление перечня событий, которые с определенной вероятностью могут произойти; установление временного порядка расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, которые можно предпринять.

Этап 2. Построение дерева решений.

Этап 3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события. Следует отметить, что указанные вероятности определяются либо на основании имеющейся статистики, либо экспертным путем.

Этап 4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды.

Этап 5. Решение задачи.

Прежде чем продемонстрировать процедуру применения дерева решений, введем ряд определений. В зависимости от отношения к риску решение задачи может выполняться с позиций так называемых «объективистов» и «субъективистов». Поясним эти понятия на следующем примере. Пусть предлагается лотерея: за 10 дол. (стоимость лотерейного билета) игрок c равной вероятностью p = 0,5 может ничего не выиграть или выиграть 100 дол. Один индивид пожалеет и 10 дол. за право участия в такой лотерее, т.е. просто не купит лотерейный билет, другой готов заплатить за лотерейный билет 50 дол., а третий заплатит даже 60 дол. за возможность получить 100 дол. (например, когда ситуация складывается так, что, только имея 100 дол., игрок может достичь своей цели, поэтому возможная потеря последних денежных средств, а у него их ровно 60 дол., не меняет для него ситуации).

Безусловным денежным эквивалентом (БДЭ) игры называется максимальная сумма денег, которую ЛПР готов заплатить за участие в игре (лотерее), или, что то же, та минимальная сумма денег, за которую он готов отказаться г Л от игры. Каждый индивид имеет свой БДЭ.

Определение

Индивида, для которого БДЭ совпадает с ожидаемой денежной оценкой (ОДО) игры, т. е. со средним выигрышем в игре (лотерее), условно называют объективистом, индивида, для которого БДЭ Ф ОДО, субъективистом. Ожидаемая денежная оценка рассчитывается как сумма произведений размеров выигрышей на вероятности этих выигрышей. Например, для нашей лотереи ОДО = 0,5 х 0 + 0,5 х 100 = 50 дол. Если субъективист склонен к риску, то его БДЭ > ОДО. Если не склонен, то БДЭ < ОДО. Вопрос об отношении к риску более строго рассматривается в теме 4.

Предположим, что решения принимаются с позиции объективиста.

Рассмотрим процедуру принятия решения на примере следующей задачи.

Задача 3. Руководство некоторой компании решает, создавать ли для выпуска новой продукции крупное производство, малое предприятие или продать патент другой фирме. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка (табл. 4).

На основе данной таблицы выигрышей (потерь) можно построить дерево решений (рис. 3).

Таблица 4

10 000 Благоприятное состояние

200 000

Большое предприятие

Неблагоприятное состояние

-•-180000

40000

40 ООО Благоприятное состояние

100 000

Малое предприятие

Неблагоприятное состояние

-20 000

10 000

Патент

Рис. 3. Дерево решений без дополнительного обследования конъюнктуры рынка

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО.

Определим средний ожидаемый выигрыш (ОДО):

для вершины 1 ОДО1 = 0,5 х 200 000 + 0,5(-180 000) = 10 000 дол.;

для вершины 2 ОДО2 = 0,5 х 100 000 + 0Д-20 000) = 40 000 дол.;

для вершины 3 ОДО3 = 10 000 дол.

Вывод. Наиболее целесообразно выбрать стратегию а2, т.е. строить малое предприятие, а ветви (стратегии) а1 и а3 дерева решений можно отбросить. ОДО наилучшего решения равна 40 000 дол. Следует отметить, что наличие состояния с вероятностями 50% неудачи и 50% удачи на практике часто означает, что истинные вероятности игроку скорее всего неизвестны и он всего лишь принимает такую гипотезу (так называемое предположение «fifty-fifty» пятьдесят на пятьдесят). Усложним рассмотренную выше задачу.

Пусть перед тем, как принимать решение о строительстве, руководство компании должно определить, заказывать ли дополнительное исследование состояния рынка или нет, причем предоставляемая услуга обойдется компании в 10 000 дол. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей.

Относительно фирмы, которой можно заказать прогноз, известно, что она способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Возможности фирмы в виде условных вероятностей благоприятности и неблагоприятности рынка сбыта представлены в табл. 5. Например, когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,73.

Таблица 5

Прогноз фирмы	Фактически
Благоприятный	Неблагоприятный
Благоприятный	0,78	0,22
Неблагоприятный	0,27	0,73

Предположим, что фирма, которой заказали прогноз состояния рынка, утверждает:

ситуация будет благоприятной с вероятностью 0,45;

ситуация будет неблагоприятной с вероятностью 0,55.

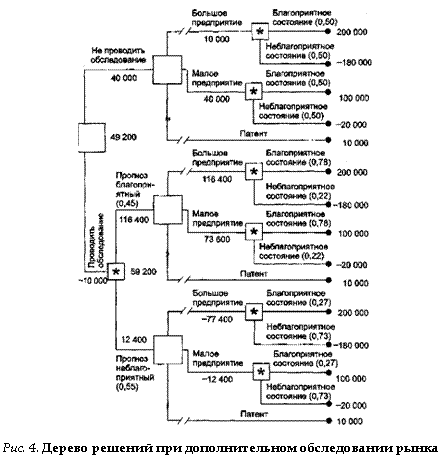На основании дополнительных сведений можно построить новое дерево решений (рис. 4), где развитие событий происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным.

4.4.3. Ожидаемая ценность точной информации

Предположим, что консультационная фирма за определенную плату готова предоставить информацию о фактической ситуации на рынке в тот момент, когда руководству компании надлежит принять решение о масштабе производства. Принятие предложения зависит от соотношения между ожидаемой ценностью (результативностью) точной информации и величиной запрошенной платы за дополнительную (истинную) информацию, благодаря которой может быть откорректировано принятие решения, т.е. первоначальное действие может быть изменено.

Ожидаемая ценность точной информации о фактическом состоянии рынка равна разности между ожидаемой денежной оценкой (ОДО) при наличии точной информации и максимальной ожидаемой денежной оценкой при отсутствии точной информации.

Рассчитаем ожидаемую ценность точной информации для примера, в котором дополнительное обследование конъюнктуры рынка не проводится. При отсутствии точной информации, как уже было показано выше, максимальная ожидаемая денежная оценка равна:

ОДО = 0,5 х 100 000 0,5 х 20 000 = 40 000 дол.

Если точная информация об истинном состоянии рынка будет благоприятной (ОДО = 200 000 дол., см. табл. 4), принимается решение строить крупное производство, если неблагоприятной, то наиболее целесообразное решение продажа патента (ОДО=10 000 дол.). Учитывая, что вероятности благоприятной и неблагоприятной ситуаций равны 0,5, значение ОДОт.и (ОДО точной информации) определяется выражением:

ОДОт.и= 0,5 х 200 000 + 0,5 х 10 000 = 105 000 дол.

Тогда ожидаемая ценность точной информации равна:

ОЦт.и = ОДОт.и ОДО = 105 000 40 000 = 65 000 дол.

Значение ОЦт.и показывает, какую максимальную цену должна быть готова заплатить компания за точную информацию об истинном состоянии рынка в тот момент, когда ей это необходимо.

Задачи

Примеры решения

Задача 1. Компания «Российский сыр» небольшой производитель различных продуктов из сыра на экспорт. Один из продуктов сырная паста поставляется в страны ближнего зарубежья. Генеральный директор должен решить, сколько ящиков сырной пасты следует производить в течение месяца. Вероятности того, что спрос на сырную пасту в течение месяца будет 6, 7, 8 или 9 ящиков, равны соответственно 0,1; 0,3; 0,5; 0,1.

Затраты на производство одного ящика равны 45 дол. Компания продает каждый ящик по цене 95 дол. Если ящик с сырной пастой не продается в течение месяца, то она портится и компания не получает дохода. Сколько ящиков следует производить в течение месяца?

Решение. Пользуясь исходными данными, строим матрицу игры. Стратегиями игрока 1 (компания «Российский сыр») являются различные показатели числа ящиков с сырной пастой, которые ему, возможно, следует производить. Состояниями природы выступают величины спроса на аналогичное число ящиков. Вычислим, например, показатель прибыли, которую получит производитель, если он произведет 8 ящиков, а спрос будет только на 7.

Каждый ящик продается по 95 дол. Компания продала 7, а произвела 8 ящиков. Следовательно, выручка будет 7 х 95, а издержки производства 8 ящиков 8 х 45. Итого, прибыль от указанного сочетания спроса и предложения будет равна 7 х 95 8 х 45 = 305 дол. Аналогично производятся расчеты при других сочетаниях спроса и предложения.

В итоге получим следующую платежную матрицу в игре с природой (табл. 6). Как видим, наибольшая средняя ожидаемая прибыль равна 352,5 дол. Она отвечает производству 8 ящиков.

Таблица 6

На практике чаще всего в подобных случаях решения принимаются исходя из критерия максимизации средней ожидаемой прибыли или минимизации ожидаемых издержек. Следуя такому подходу, можно остановиться на рекомендации производить 8 ящиков, и для большинства ЛПР рекомендация была бы обоснованной.

Однако, привлекая дополнительную информацию в форме расчета среднего квадратичного отклонения как индекса риска, мы можем уточнить принятое на основе максимума прибыли или минимума издержек решение. Это в полной мере согласуется с характеристиками вариантов, представленных на рис. 1. Дополнительные рекомендации могут оказаться неоднозначными, зависимыми от склонности к риску ЛПР.

Вспомним необходимые для наших исследований формулы теории вероятностей

[5. С. 109, 119]:

дисперсия случайной величины Е равна DS, = M(<Е,2 )-(МЕ)2; среднее квадратичное отклонение а£, = -у/ DS,, где D и М соответственно символы дисперсии и математического ожидания.

Проводя соответствующие вычисления для случаев производства 6, 7, 8 и 9 ящиков, получаем:

ящиков

M (^2 ) = 3002 (0,1 + 0,3 + 0,5 + 0,1) = 90 000;

(M^)2 = 3002 = 90 000; D^ = 90 000 90 000 = 0; а^ = 0.

ящиков

M ) = 0,1 х 2552 + 0,9 х 3502 = 116 752,5;

(M^)2 = 340,52 = 115 940; = 116 752,5 -115 940 = 812,5;

= V812,5 = 28,5 .

ящиков

M ) = 0,1 х 2102 + 0,3 х 3052 + 0,6 х 4002 = 128 317,5;

(M^)2 = 352,52 = 124 256,25; = 128 317,5 -124 256,25 = 4 061,25;

= V4 061,25 = 63,73.

ящиков

M (;2) = 0,1 х 1652 + 0,3 х 2602 + 0,5 х 3552 + 0,1 х 4502 = 106 265; (M^)2 = 3172 = 100 489; = 106 265 -100 489 = 5 776; = V5 776 = 76.

Вывод. Из представленных результатов расчетов с учетом полученных показателей рисков средних квадратичных отклонений очевидно, что производить 9 ящиков при любых обстоятельствах нецелесообразно, ибо средняя ожидаемая прибыль, равная 317, меньше, чем для 8 ящиков (352,5), а среднее квадратичное отклонение (76) для 9 ящиков больше аналогичного показателя для 8 ящиков (63,73). А вот целесообразно ли производство 8 ящиков по сравнению с 7 или 6 неочевидно, так как риск при производстве 8 ящиков (= 63,73) больший, чем при производстве 7 ящиков (= 28,5) и тем более 6 ящиков, где = 0 . Вся информация с учетом ожидаемых прибылей и рисков налицо. Решение должен принимать генеральный директор компании «Российский сыр» с учетом его опыта, склонности к риску и степени достоверности показателей вероятностей спроса: 0,1; 0,3; 0,5; 0,1. Авторы, учитывая все приведенные числовые характеристики случайной величины прибыли, склоняются к рекомендации производить 7 ящиков (не 8, что вытекает из максимизации прибыли без учета риска!). Читателю предлагается обосновать свой выбор.

Задача 2. Рассмотрим упомянутую выше проблему закупки угля для обогрева дома. Имеются следующие данные о количестве и ценах угля, необходимого зимой для отопления дома (табл. 7). Вероятности зим: мягкой —0,35; обычной 0,5; холодной 0,15.

Таблица 7

Зима	Количество угля, т	Средняя цена за 1 т в ф. ст.
Мягкая	4	7
Обычная	5	7,5
Холодная	6	8

Эти цены относятся к покупкам угля зимой. Летом цена угля 6 ф. ст. за 1 т, у вас есть место для хранения запаса угля до 6 т, заготавливаемого летом. Если потребуется зимой докупить недостающее количество угля, докупка будет по зимним ценам. Предполагается, что весь уголь, который сохранится до конца зимы, в лето пропадет. Сколько угля летом покупать на зиму?

Решение. Построим платежную матрицу (табл. 8).

Таблица 8

‘ ~~—■—^^^Вероятность Зима —	0,35 0,5 0,15
Мягкая Обычная Холодная
Мягкая (4 т)	-(4 х 6) -(4 х 6 + 1 х 7,5) -(4 х 6 + 2 х8)
Обычная (5 т)	-(5 х 6) -(5 х 6 + 0 х 7,5) -(5 х 6 + 1 х
Холодная (6 т)	-(6 х 6) -(6 х 6 + 0 х 7,5) -(6 х 6 + 0 х

Произведем расчет ожидаемой средней платы за уголь (табл. 9).

Таблица 9

Зима	Средняя ожидаемая плата
Мягкая	-(24 х 0,35 + 31,5 х 0,5 + 40 х 0,15) = -30,15
Обычная	-(30 х 0,35 + 30 х 0,5 + 38 х 0,15) = -31,2
Холодная	-(36 х 0,35 + 36 х 0,5 + 36 х 0,15) = -36

Из табл. 9 видно, что, наименьшая ожидаемая средняя плата приходится на случай мягкой зимы (30, 15 ф. ст.). Соответственно, если не учитывать степени риска, то представляется целесообразным летом закупить 4 т угля, а зимой, если потребуется, докупить уголь по более высоким зимним ценам.

Если продолжить исследование процесса принятия решения и аналогично задаче 1 вычислить средние квадратичные отклонения платы за уголь для мягкой, обычной и холодной зимы, то соответственно получим:

для мягкой зимы о£, = 5,357;

для обычной зимы о£, = 2,856;

для холодной зимы о£, = 0.

Минимальный риск, естественно, будет для холодной зимы, однако при этом ожидаемая средняя плата за уголь оказывается максимальной 36 ф. ст.

Вывод. Мы склоняемся к варианту покупки угля для обычной зимы, так как, согласно табл. 9, ожидаемая средняя плата за уголь по сравнению с вариантом для мягкой зимы возрастает на 3,5%, а степень риска при этом оказывается почти в 2 раза меньшей (= 2,856 против 5,357).

Отношение среднего квадратичного отклонения к математическому ожиданию

(средний риск на затрачиваемый 1 ф. ст.) для обычной зимы составляет 2^856 = 0,0915

5,357

против аналогичного показателя для мягкой зимы, равного — = 0,1777, т.е. вновь раз30,15

личие почти в 2 раза.

Эти соотношения и позволяют нам рекомендовать покупку угля, ориентируясь не на мягкую, а на обычную зиму.

Задача 3. АО «Фото и цвет» небольшой производитель химических реактивов и оборудования, которые используются некоторыми фотостудиями при изготовлении 35мм фильмов. Один из продуктов, который предлагает «Фото и цвет» ВС-6. Президент АО продает в течение недели 11, 12 или 13 ящиков ВС-6. От продажи каждого ящика АО получает 35 дол. прибыли. Как и многие фотографические реактивы, ВС-6 имеет очень малый срок годности. Поэтому, если ящик не продан к концу недели, он должен быть уничтожен. Каждый ящик обходится предприятию в 56 дол. Вероятности продать 11, 12 и 13 ящиков в течение недели равны соответственно 0,45; 0,35; 0,2. Как вы советуете поступить? Как вы порекомендуете поступить, если бы «Фото и цвет» мог сделать ВС-6 с добавкой, значительно продлевающей срок его годности?

Решение. Матрицу игры с природой (здесь АО «Фото и цвет» игрок с природой, а природа торговая конъюнктура) строим по аналогии с рассмотренными выше задачами (табл. 10).

Расчет средней ожидаемой прибыли производится с использованием вероятностей состояний природы, как и в задачах 1 и 2.

Вывод. Наибольшая из средних ожидаемых прибылей (385 дол.) отвечает при заданных возможностях спроса производству 11 ящиков ВС-6.

Производство 11 ящиков в неделю и следует рекомендовать АО «Фото и цвет», ибо показатель риска среднее квадратичное отклонение, как нетрудно убедиться, о£, =0 -минимален при максимальной средней ожидаемой прибыли.

Если срок службы химического реактива будет удлинен, то его производство даже при прежнем спросе можно увеличить, частично производя на склад для последующей реализации.

Задачи для самостоятельного решения

Задача 1. Компания, производящая стиральный порошок, работает в условиях свободной конкуренции. Порошок выпускается блоками, причем цена одного блока в будущем месяце является неопределенной: 10 руб. с вероятностью 0,3; 15 руб. с вероятностью 0,5; 20 руб. с вероятностью 0,3. Полные затраты (ПЗ) на производство Q блоков стирального порошка определяются зависимостью ПЗ = 1000 + 5Q + 0,0025Q2.

Постройте таблицу решений и определите суточный выпуск продукции компании (в блоках), при котором среднесуточная прибыль будет максимальной.

Задача 2. Спрос на некоторый товар, производимый монополистом, определяется зависимостью Q = 100 5р + 5j, где j достоверно неизвестный уровень дохода потребителей, р цена товара. По оценкам экспертов,

[2 с вероятностью 0,6; j [4 с вероятностью 0,4.

Полные затраты на производство товара определяются зависимостью ПЗ = 5 + 4Q + 0,05Q2. Сколько товара должен выпускать монополист и по какой цене продавать, чтобы максимизировать свою ожидаемую прибыль?

Задача 3. Молодой российский бизнесмен предполагает построить ночную дискотеку неподалеку от университета. По одному из допустимых проектов предприниматель может в дневное время открыть в здании дискотеки столовую для студентов и преподавателей. Другой вариант не связан с дневным обслуживанием клиентов. Представленные бизнес-планы показывают, что план, связанный со столовой, может принести доход в 250 тыс. руб. Без открытия столовой бизнесмен может заработать 175 тыс. руб. Потери в случае открытия дискотеки со столовой составят 55 тыс. руб., а без столовой— 20 тыс. руб. Определите наиболее эффективную альтернативу на основе средней стоимостной ценности в качестве критерия.

Задача 4. Небольшая частная фирма производит косметическую продукцию для подростков. В течение месяца реализуется 15, 16 или 17 упаковок товара. От продажи каждой упаковки фирма получает 75 руб. прибыли. Косметика имеет малый срок годности, поэтому, если упаковка не продана в месячный срок, она должна быть уничтожена. Поскольку производство одной упаковки обходится в 115 руб., потери фирмы составляют 115 руб., если упаковка не продана к концу месяца. Вероятности продать 15, 16 или 17 упаковок за месяц составляют соответственно 0,55; 0,1 и 0,35. Сколько упаковок косметики следует производить фирме ежемесячно? Какова ожидаемая стоимостная ценность этого решения? Сколько упаковок можно было бы производить при значительном продлении срока хранения косметической продукции?

Задача 5. Магазин «Молоко» продает в розницу молочные продукты. Директор магазина должен определить, сколько бидонов сметаны следует закупить у производителя для торговли в течение недели. Вероятности того, что спрос на сметану в течение недели будет 7, 8, 9 или 10 бидонов, равны соответственно 0,2; 0,2; 0,5 и 0,1. Покупка одного бидона сметаны обходится магазину в 70 руб., а продается сметана по цене 110 руб. за бидон. Если сметана не продается в течение недели, она портится, и магазин несет убытки. Сколько бидонов сметаны желательно приобретать для продажи? Какова ожидаемая стоимостная ценность этого решения?

Задача 6. Найти наилучшие стратегии по критериям: максимакса, Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимизма равен 0,4) для следующей платежной матрицы игры с природой (элементы матрицы выигрыши):

(5 3 6 87 4 ^ 7 5 5 4 8 1 13 -1 10 0 2 к9 9 7 1 3 6У .

Задача 7. Директор лицея, обучение в котором осуществляется на платной основе, решает, следует ли расширять здание лицея на 250 мест, на 50 мест или не проводить строительных работ вообще. Если население небольшого города, в котором организован платный лицей, будет расти, то большая реконструкция могла бы принести прибыль 250 тыс. руб. в год, незначительное расширение учебных помещений могло бы приносить 90 тыс. руб. прибыли. Если население города увеличиваться не будет, то крупное расширение обойдется лицею в 120 тыс. руб. убытка, а малое 45 тыс. руб. Однако информация о том, как будет изменяться население города, отсутствует. Постройте дерево решений и определите лучшую альтернативу, используя критерий Вальда. Чему равно значение ОДО для наилучшей альтернативы в отсутствие необходимой информации?

Пусть при тех же исходных данных государственная статистическая служба предоставила информацию об изменении численности населения: вероятность роста численности населения составляет 0,7; вероятность того, что численность населения останется неизменной или будет уменьшаться, равна 0,3. Определите наилучшее решение, используя критерий максимизации ожидаемой денежной оценки. Чему равно значение ОДО для наилучшей альтернативы при получении дополнительной информации? Какова ожидаемая ценность дополнительной информации?

Задача 8. При крупном автомобильном магазине планируется открыть мастерскую по предпродажному обслуживанию и гарантийному ремонту автомобилей. Консультационная фирма готова предоставить дополнительную информацию о том, будет ли рынок благоприятным или нет. Эти сведения обойдутся магазину в 13 тыс. руб. Администрация магазина считает, что эта информация гарантирует благоприятный рынок с вероятностью 0,5. Если рынок будет благоприятным, то большая мастерская принесет прибыль в 60 тыс. руб., а маленькая 30 тыс. руб. При неблагоприятном рынке магазин потеяет 65 тыс. руб., если будет открыта большая мастерская, и 30 тыс. руб.— если откроется маленькая. Не имея дополнительной информации, директор оценивает вероятность благоприятного рынка как 0,6. Положительный результат обследования гарантирует благоприятный рынок с вероятностью 0,8. При отрицательном результате рынок может оказаться благоприятным с вероятностью 0,3. Постройте дерево решений и определите:

Следует ли заказать консультационной фирме дополнительную информацию, уточняющую конъюнктуру рынка?

Какую мастерскую следует открыть при магазине: большую или маленькую?

Какова ожидаемая денежная оценка наилучшего решения?

Какова ожидаемая ценность дополнительной информации?

Задача 9. Фирма, производящая вычислительную технику, провела анализ рынка нового высокопроизводительного персонального компьютера. Если будет выпущена крупная партия компьютеров, то при благоприятном рынке прибыль составит 250 тыс.

руб., а при неблагоприятных условиях фирма понесет убытки в 185 тыс. руб. Небольшая партия техники в случае ее успешной реализации принесет фирме 50 тыс. руб. прибыли и 10 тыс. руб. убытков при неблагоприятных внешних условиях. Возможность благоприятного и неблагоприятного исходов фирма оценивает одинаково. Исследование рынка, которое может провести эксперт, обошлось фирме в 15 тыс. руб. Эксперт считает, что с вероятностью 0,6 рынок окажется благоприятным. В то же время при положительном заключении благоприятные условия ожидаются лишь с вероятностью 0,8. При отрицательном заключении с вероятностью 0,15 рынок также может оказаться благоприятным. Используйте дерево решений для того, чтобы помочь фирме выбрать правильную технико-экономическую стратегию. Ответьте на следующие вопросы:

Следует ли заказывать эксперту дополнительное обследование рынка?

Какую максимальную сумму фирма может выплатить эксперту за проделанную работу?

Какова ожидаемая денежная оценка наилучшего решения?

Задача 10. Автомобильный завод получает реле поворота от двух поставщиков: А и В. Качество этих изделий характеризуется данными в табл.11.

Таблица 11

Процент	Вероятность для поставщика
брака	А В
1	0,7 0,4
2	0,1 0,3
3	0,09 0,15
4	0,07 0,1
5	0,04 0,05

Полные затраты, связанные с ремонтом одного бракованного реле, составляют 5 руб.

Реле поступают партиями по 20 000 шт. Поскольку качество изделий у поставщика В хуже, он уступает всю партию на 500 руб. дешевле. Постройте дерево решений. Какого поставщика следует выбрать?

Источник

Дерево решений задачи

1. Группа медиков собирается открыть
частную медицинскую фирму. Если рынок будет благоприятным, они
будут иметь прибыль $ 100 000. Если рынок неблагоприятный, они понесут потери
$ 40 000. Они также могут осуществить маркетинговое исследование, которое стоит
$5000. Результаты исследования могут быть благоприятными или неблагоприятными:

Медики хотят построить дерево решений и
отразить на нем свою денежную отдачу.

2 Женщина-предприниматель собирается
открывать ресторан недалеко от университетского городка. По
одному плану проект включает бар с продажей пива, другой план не
включает бар. В том и другом случае ее шансы на успех будут 0.6 (и на
провал 0.4). Ежегодный доход, включая бар, равен $325 000. Без бара
доход составит только $250000. Провал при наличии бара был бы оценен
$70 000, а без бара — $20 000. Выберите вариант для предпринимателя,
используя показатель денежной отдачи как критерий решения Должен ли
бизнес-план включать бар?

3. Промышленное предприятие
получает выключатели от двух поставщиков.
Качество выключателей от этих
поставщиков показано ниже.

Процент дефектов

Вероятность для поставщика А

Вероятность для поставщика В

0.70

0.20

0.10

0.30

0.40

0.30

Объем поставки 10000
выключателей. Неисправный выключатель может быть отремонтирован за 15 руб. Хотя
качество у поставщика В ниже, но он просит за 10000 выключателей на 1100 руб
меньше, чем поставщик А. Нарисуйте дерево решений.

Какой поставщик будет
использоваться?

Какая цена должна быть у
худшего поставщика, чтобы выровнять ситуацию?

4 Предприниматель собирается
открыть велосипедный магазин. Он может открыть маленький магазин, большой
магазин или ничего не открывать. Возможна пятилетняя аренда здания под магазин,
и предприниматель хочет сделать корректное решение. Он также собирается
пригласить своего профессора по курсу маркетинга для маркетингового
исследования, которое покажет состояние рынка для его сервиса. Из исследования
видно, будут ли результаты сервиса благоприятными или неблагоприятными.
Постройте дерево решений для предпринимателя.

6.Отдел исследований и
развития маленькой парфюмерной компании проводит исследования по средству,
улучшающему рост волос. Он имеет три возможности. Первая: продать новшество
большой медицинской компании — это принесет $10 миллионов; вторая: начать
экспериментальное лабораторное исследование и затем принимать решение; третье:
провести финансирование агрессивной маркетинговой программы в надежде, что
тестирование нового средства будет идти хорошо. Реальная цель этих трех решений
— двигаться так быстро, чтобы конкуренты имели минимальный шанс их настигнуть.
Программа экспериментального лабораторного исследования будет стоить $5 миллионов
и имеется шанс 50:50, что будут получены благоприятные результаты. При
неблагоприятных результатах тестирования с шансом 1:10 доход составит только $1
миллион. С другой стороны, если благоприятная формула косметического средства
будет найдена, будут получены $20 миллионов. Но так как компания маленькая, с
ограниченными ресурсами и рыночными возможностями, даже с благоприятными
результатами лабораторного исследования успех товара на рынке составит только
40%. При благоприятном результате лабораторного исследования затраты будут
включать на только $5 миллионов на тестирования, но и также $3 миллиона на
маркетинг.

При третьей возможности
компания проводит агрессивную маркетинговую стратегию. Президент компании
считает, что существует только один шанс к пяти, что это надо делать. Однако
выигрыш при успехе агрессивного маркетинга $100 миллионов (эта цифра в 5 раз
больше, чем $ 20 миллионов, отражающих передачу рынка реальному конкуренту
путем заключения с ним соглашения). В третьем случае маркетинговые затраты
равны $3 миллиона и тестирование будет стоить $5 миллионов.

7. Придумать и дать решения
для 4 задач на деревья в области изготовления и продажи косметики на примере
Андрея Трубникова (статьи в журналах Эксперт за 2006 и 2013гг)

Шпаргалка

Процесс принятия решений с
помощью дерева решений в общем случае предполагает выполнение следующих пяти
этапов.

Этап 1. Формулирование задачи.
Прежде всего необходимо отбросить не относящиеся к проблеме факторы, а среди
множества оставшихся выделить существенные и несущественные. Это позволит
привести описание задачи принятия решения к поддающейся анализу форме. Должны
быть выполнены следующие основные процедуры: определение возможностей сбора
информаций для экспериментирования и реальных действии; составление перечня
событии, которые с определенной вероятностью могут произойти; установление
временного порядка расположения событий, в исходах которых содержится полезная
и доступная информация, и тех последовательных действий, которые можно
предпринять.

Этап 2. Построение дерева
решений.

Этап 3. Оценка вероятностей
состояний среды, т.е. сопоставление шансов возникновения каждого конкретного
события. Следует отметить, что указанные вероятности определяются либо на
основании имеющейся статистики, либо экспертным путем.

Этап 4. Установление выигрышей
(или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации
альтернатив (действий) и состояний среды.

Этап 5. Решение задачи.

Прежде чем продемонстрировать
процедуру применения дерева решений, введем ряд определений.

В зависимости от отношения к
риску решение задачи может выполняться с позиций так называемых «объективистов»
и «субъективистов». Поясним эти понятия на следующем примере. Пусть предлагается
лотерея: за 10 дол. (стоимость лотерейного билета) игрок с равной вероятностью
р = 0,5 может ничего не выиграть или выиграть 100 дол. Один индивид пожалеет и
10 дол. за право участия в такой лотерее, т.е. просто не купит лотерейный
билет, другой готов заплатить за лотерейный билет 50 дол., а третий заплатит
даже 60 дол. за возможность получить 100 дол. (например, когда ситуация
складывается так, что, только имея 100 дол., игрок может достичь своей цели,
поэтому возможная потеря последних денежных средств, а у него их ровно 60 дол.,
не меняет для него ситуации).

Безусловным денежным
эквивалентом (БДЭ) игры называется максимальная сумма денег, которую ЛПР готов
заплатить за участие в игре (лотерее), или, что то же, та минимальная сумма
денег, за которую он готов отказаться от игры. Каждый индивид имеет свой БДЭ.

Индивида, для которого БДЭ
совпадает с ожидаемой денежной оценкой (ОДО) игры, т.е. со средним выигрышем в
игре (лотерее), условно называют объективистом, индивида, для которого БДЭ ^
ОДО, — субъективистом. Ожидаемая денежная оценка рассчитывается как сумма
произведений размеров выигрышей на вероятности этих выигрышей. Например, для
нашей лотереи ОДО = 0,5*0 + 0,5*100 = 50 дол. Если субъективист склонен к
риску, то его БДЭ > ОДО. Если не склонен, то БДЭ < ОДО. Вопрос об
отношении к риску более строго рассматривается в гл. 4i

Предположим, что решения
принимаются с позиции объективиста.

Рассмотрим процедуру принятия
решения на примере следующей задачи.

Задача 3.4. Руководство
некоторой компании решает, создавать ли для выпуска новой продукции крупное
производство, малое предприятие или продать патент другой фирме. Размер
выигрыша, который компания может получить, зависит от благоприятного или
неблагоприятного состояния рынка (табл. 3.1).

На основе данной таблицы
выигрышей (потерь) можно построить дерево решений (рис. 3.1).

Таблица 3.1

Номер стратегии	Действия компании	Выигрыш, дол., при состоянии экономической среды*
благоприятном	неблагоприятном
1	Строительство крупного предприятия (а1)	200 000	-180 000
2	Строительство малого предприятия (a2)	100 000	-20 000
3	Продажа патента (a3)	10 000	-10 000

• Вероятность благоприятного и
неблагоприятного состояний экономической среды равна 0,5.

Процедура принятия решения
заключается в вычислении для каждой вершины дерева (при движении справа налево)
ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей,
которым соответствует максимальное значение ОДО.

• для вершины 1 ОДО1 = 0,5*200
000 + 0,5(-180 000) = 10 000 дол.;

• для вершины 2 ОДО2 = 0,5*100
000 + 0,5(-20 000) = 40 000 дол.;

• для вершины 3 ОДО3 = 10 000
дол.

Вывод. Наиболее целесообразно
выбрать стратегию а2, т.е. строить малое предприятие, а ветви (стратегии) а1 и
а3 дерева решений можно отбросить. ОДО наилучшего решения равна 40 000 дол.
Следует отметить, что наличие состояния с вероятностями 50 % неудачи и 50 %
удачи на практике часто означает, что истинные вероятности игроку скорее всего
неизвестны и он всего лишь принимает такую гипотезу (так называемое
предположение «fifty — fifty» — пятьдесят на пятьдесят).

Усложним рассмотренную выше
задачу.

Пусть перед тем, как принимать
решение о строительстве, руководство компании должно определить, заказывать ли
дополнительное исследование состояния рынка или нет, причем предоставляемая
услуга обойдется компании в 10 000 дол. Руководство понимает, что
дополнительное исследование по-прежнему не способно дать точной информации, но
оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым
значения вероятностей.

Относительно фирмы, которой
можно заказать прогноз, известно, что она способна уточнить значения
вероятностей благоприятного или неблагоприятного исхода. Возможности фирмы в
виде условных вероятностей благоприятности и неблагоприятности рынка сбыта
представлены в табл. 3.2. Например, когда фирма утверждает, что рынок
благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью
0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности
рынка оправдывается с вероятностью 0,73.

Таблица 3.2

Прогноз фирмы	Фактически
Благоприятный	Неблагоприятный
Благоприятный	0,78	0,22
Неблагоприятный	0,27	0,73

Предположим, что фирма,
которой заказали прогноз состояния рынка, утверждает:

• ситуация будет благоприятной
с вероятностью 0,45;

На основании дополнительных
сведений можно построить новое дерево решений (рис. 3.2), где развитие событий
происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных
состояний к начальным.

Рис. 3.2. Дерево решений при
дополнительном обследовании рынка (см. условные обозначения к рис. 3.1)

Анализируя дерево решений,
можно сделать следующие выводы:

• необходимо проводить
дополнительное исследование конъюнктуры рынка, поскольку это позволяет
существенно уточнить принимаемое решение;

• если фирма прогнозирует
благоприятную ситуацию на рынке, то целесообразно строить большое предприятие
(ожидаемая максимальная прибыль 116 400 дол.), если прогноз неблагоприятный — малое
(ожидаемая максимальная прибыль 12 400 дол.).

Источник

2.2.2. Критерий математического ожидания – дисперсии. Выбор стратегии по математическому ожиданию, оказывается, связан с большим риском. Одним из способов оценки риска служит математическое ожидание отклонения случайной величины выигрыша от своего математического ожидания, т. е. дисперсия случайной величины выигрыша. Действительно, из неравенства Чебышева (при конечной дисперсии) имеем
(14)
где
,
,
дисперсия выигрыша ОС при его стратегии х в случае непрерывной и дискретной случайной величине z соответственно. Таким образом. s2(f(x, ּ)) оценивает вероятность отклонения от математического ожидания выигрыша W(х) при той же стратегии.
С целью уменьшить «риск» сильного отклонения случайной величины выигрыша от математического ожидания используют критерий математического ожидания – дисперсии. В этом критерии отражено стремление увеличить математическое ожидание выигрыша и уменьшить вероятность отклонения от него случайной величины выигрыша. Критерий имеет вид
W8(x)=W7(x) – Ks (f(x, ּ)). (15)
Здесь К 0 — коэффициент не склонности к риску. В случае минимизации проигрыша ОС соответственно
W9(x)=W7(x) + Ks(f(x, ּ)). (16)
При значении К = 0 ОС ориентируется только на математическое ожидание выигрыша и не интересуется риском отклонения величины выигрыша от математического ожидания W7(х). Если К>0, то максимизируя W8, ОС стремиться к максимизации W7 и минимизации среднеквадратичного отклонения s. Чем больше К, тем большее значение для ОС имеет минимизация s и меньшее значение имеет максимизация W7. Из (15) следует, что при росте величины К ОС все больше стремиться уменьшить вероятность отклонения выигрыша от величины математического ожидания. Тем самым ОС становится все менее склонной к риску. Величина коэффициента К определяется ОС субъективно в зависимости от сложившейся ситуации, т. е. нет четких правил определения величины К. В рассмотренном примере можно отметить, что при малых значениях К (K<k1, k1 0.15) оптимальной остается вторая стратегия, при k1<K< оптимальной станет первая стратегия, а при К> оптимальной по критерию W9 – третья стратегия. Однако при использовании третьей стратегии в случае любой реализации z ОС получит выигрыш не больший, чем при применении первой стратегии. Таким образом, необоснованное увеличение коэффициента К в (15) может привести к неправильным выводам.
Пример 5. Ежедневный спрос на булочки в продовольственном магазине может принимать одно из следующих значений: {100; 150; 200; 250; 300}. Булочки обходятся магазину по 25 ден. ед. Свежие булочки продаются по цене 49 ден. ед., а не проданные в тот же день, продаются в конце дня по 15 ден. ед. Какое число булочек нужно заказывать с тем, чтобы ежедневная валовая прибыль (выручка от продажи минус затраты на закупку) была максимальной. При этом нужно учитывать следующие условия:
а) булочки продаются поддонами по 50 шт. на одном поддоне;
б) по цене 15 ден. ед. продаются все булочки;
в) известны вероятности каждой величины спроса: P(100)=0.2;
P(150)=0.25; P(200)=0.3; P(250)=0.15; P(300)=0.1.
Решение. Контролируемым фактором х является количество заказываемых магазином булочек. Величина х может принимать одно из следующих значений х{0; 50; 100; 150; 200; 250; 300;…}.
Неконтролируемым фактором является спрос на булочки. По условию задачи спрос является случайной величиной, принимающей конечное число значений Z={100;150;200:250; 300}. Неопределенных факторов нет (Y=).
Критерием операции является количество денег, полученных от продажи булочек за вычетом суммы, которую магазин заплатил за них. Если магазин закупил х булочек, а спрос в этот день составил z булочек, то магазин продает будочки по цене 49 ден. ед. в количестве min{x,z}. Действительно, нельзя продать больше, чем имеется, и нельзя продать больше, чем спрашивают покупатели. По цене 15 ден. ед. будет продано (x — min{x,z}) булочек. Если количество х закупленных магазином булочек превосходит спрос z (x — z>0), то z булочек будет продано по цене 49 ден. ед. и (x — z) булочек – по цене 15 ден. ед. Если же спрос z превышает х, то х булочек будет продано по цене 49 ден. ед., а по цене 15 ден. ед. булочки продаваться не будут. Итак, критерий операции имеет вид
F(x, z)= 49(min{x, z}) + 15(x – min{x, z}) – 25x =
= 24(min{x, z})-10(x – min{x, z}).
Таким образом, математическая модель операции { Х, (Z,), f } определена. Исходя из вида целевой функции, можно сократить множество X, на котором следует искать максимум целевой функции по x. Действительно, следует закупать не менее 100 булочек, так как спрашиваться будет не менее 100 булочек и каждая такая булочка приносит прибыль в 24 ден. ед. Каждая булочка сверх 300 не будет продана днем и принесет убытки в 10 ден. ед., следовательно, закупать булочки в количестве более 300 не выгодно. Итак, множество X следует уменьшить до X={100; 150; 200; 250; 300}.Так как множества X и Z конечны, целевую функцию удобно представить в виде таблицы
Таблица значений целевой функции F(x, z)

	Значения z
x	z = 100	z = 150	z = 200	z = 250	z = 300
100	2400	2400	2400	2400	2400
150	1900	3600	3600	3600	3600
200	1400	3100	4800	4800	4800
250	900	2600	4300	6000	6000
300	400	2100	3800	5500	7200

Здесь строка соответствует значению x, а столбец – значению z. Так значение F(200;150) находится на пересечении третьей строки (x=200) и второго столбца (z=150). При этом
F(200, 150)=24´min{200;150} – 10´(200 – min{200;150})=3600 – 500=3100.
Oценим эффективность произвольной стратегии х. Оценивать будем по критериям «ожидаемое значение» и «ожидаемое значение – дисперсия».

По критерию «ожидаемое значение» (13) имеем

=;
=1900
+;
=(
;
Аналогично получаем
=3495; =3040.
Итак, по критерию «ожидаемое значение» лучшей является стратегия х*= 200.
Найдем теперь решение по критерию (см.(15)) при K=1
W9(100)=W7(100) – ;
W9(150)=W7(150) – =
=3260-680=2580;
W9(200)= W7(200) –
–
»3695 – 1447 = 2348;
Аналогично получаем
W9(250) » 2023; W9(300)»1437.
Итак, в этом случае лучшей оказалась более осторожная стратегия закупки – 150 булочек ежедневно.
2.2.3. Критерий предельного уровня. Этот критерий соответствует не понятию оптимальности, а приемлемому способу действия. Данный критерий применяется, когда трудно оценить выигрыш (проигрыш) при той или иной стратегии ОС. Рассмотрим пример.
Пример 6. Предположим, что величина спроса z в единицу времени на товар является случайной величиной с непрерывной функцией плотности распределения (z), т. е. d((z)) = (z)dz или (z) = ‘(z). Если запасы товара в начальный момент невелики, то в некоторый момент возможен дефицит товара. Если запасы очень велики, то к концу рассматриваемого периода (день, неделя, месяц и т. д.) может оказаться большой запас нереализованного товара. В случае дефицита товара появляются потери в связи с уменьшением потенциальной прибыли и потери клиентов, не купивших нужный товар. В случае излишков товара появляются потери, связанные с его закупкой и хранением. Затраты на хранение можно трактовать как плату за то, что денежные средства «лежат» на складе, а не приносят прибыль другим способом.
Определить потери от дефицита товара в полном объеме очень трудно, поэтому ОС может принять решение исходя из критерия предельного уровня, добиваясь, чтобы величина ожидаемого дефицита не превышала А1 единиц, а величина ожидаемых излишков не превышала А2 единиц. Математически это можно записать в данном примере следующим образом. Пусть I — определяемый уровень запасов, тогда
,
При произвольном выборе А1 и А2 указанные условия могут оказаться противоречивыми. В этом случае необходимо увеличить одно или оба ограничения, чтобы обеспечить существование решения.
Приведенный пример не единственная ситуация, когда используется этот критерий. Критерий предельного уровня имеет смысл применять, когда в момент решения нет полного представления о множестве возможных альтернатив либо трудности для ОС по определению всего множества альтернатив и вычислению на этом множестве значений критерия операции превосходят потери от неточного решения.
Пусть, например, владелец предприятия сферы услуг, которое может работать с различной скоростью обслуживания (прачечная, ресторан, парикмахерская), рассматривает вопрос о скорости обслуживания. Быстрое обслуживание, удовлетворяя интересы клиентов, может оказаться невыгодным для владельца, т. к. требует дополнительных затрат на новое оборудование и количество обслуживающего персонала. Медленное обслуживание требует меньших затрат, но может привести к потере клиентов, не желающих долго ждать.
Пусть в данной ситуации можно задать или определить из эксперимента распределение вероятностей потока клиентов и времени их обслуживания. В силу многократного проведения операции по оказанию услуг представляется приемлемым определение оптимального уровня скорости обслуживания исходя из минимизации общих ожидаемых потерь в единицу времени. Общие потери складываются из затрат на оказание услуг и потери ожидаемой прибыли в случае отказа клиента дожидаться обслуживания. Обе составляющие потерь зависят от уровня скорости обслуживания, при этом, чем больше значение первой, тем меньше значение второй и наоборот. Однако рассматриваемый критерий практически неприменим из-за трудности оценивания приемлемого времени ожидания для различных клиентов.
2.3. Оценка эффективности в условиях риска и неопределенности
В случае, когда Z¹Æ и Y¹Æ, для оценки эффективности стратегии ОС xÎX обычно применяется суперпозиция оценок из пунктов 2.1, 2.2. Например, оценка эффективности

является суперпозицией критерия наилучшего гарантированного результата по неопределенным факторам и критерия ожидаемого значения по случайным факторам.
Пример 7. Пусть руководство фабрики решает, какой объем x продукции нужно производить, если известно:
максимальный объем не может превосходить величину V;
цена единицы продукции – случайная величина z, функция распределения вероятностей которой w(z) установлена на основе статистических исследований;
себестоимость единицы продукции зависит от величины объема выпускаемой продукции s(x);
величина налога y (в процентах) может быть изменена правительством перед началом анализируемого года в пределах от Nmin до Nmax.
Цель операции максимизировать сумму, оставшуюся после продажи и уплаты налогов. Предполагается, что реализуется вся продукция.
В рассматриваемом примере контролируемым фактором является величина объема производства продукции xÎX, где X=[0;V]. Неконтролируемые факторы: y – налог, и z – цена. При этом Y=[Nmin; Nmax], Z=[0; ∞).
Валовая прибыль от продажи равна x(z—s(x)), а после уплаты налогов останется сумма равная
(1 – y/100)(z – s(x))x.
Если руководство фабрики будет оценивать свою стратегию исходя из суперпозиции критериев Лапласа и ожидаемого значения, то произвольная стратегия х будет оцениваться величиной
x(z – s(x))d(z)dy
В случае использования суперпозиции критериев гарантированного результата и ожидаемого значения соответствующая оценка будет иметь вид
W(x) = min x(z – s(x))d(z)
2.4. Пример использования «дерева решений»
Пусть операция имеет несколько этапов, на каждом из которых, множество возможных действий ОС зависит от того, какое действие было использовано на предыдущем этапе. В этом случае для поиска решения часто используют так называемое «дерево решений». «Дерево решений» представляет собой граф, в вершинах которого либо происходит выбор одного из возможных действий ОС, либо реализуется одно из возможных значений неконтролируемого фактора. Возможные действия ОС или возможные реализации неконтролируемого фактора изображаются дугами этого графа.
Рассмотрим процедуру принятия решения на следующем примере [1].
В научном центре некоторой компании была разработана технология выпуска новой продукции. Руководство компании (далее ОС) решает, создавать ли для выпуска новой продукции крупное производство, малое предприятие или продать патент другой фирме.
Размер дохода, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка (таблица 1).
Руководство кампании оценивает вероятность благоприятного состояния рынка величиной 0.55, а и неблагоприятного – 0.45
На основе данной таблицы выигрышей (потерь) можно построить дерево решений (рисунок 1).

Таблица 1

Номер стратегии	Действия компании	Выигрыш, дол., при состоянии рынка
благоприятном	неблагоприятном
1	Строительство крупного предприятия	200000	-180000
2	Строительство малого предприятия	100000	-20000
3	Продажа патента	10000	10000

Процедура принятия решения заключается в вычислении для каждого из возможных действий ОС математического ожидания выигрыша, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальная величина ожидаемого значения выигрыша.

Рис1. Дерево решений без дополнительного обследования конъюнктуры рынка: ÿ — решение принимает ОС, § — случай, || — отвергнутое решение.

Определим средний ожидаемый выигрыш (ОВ):
• для вершины 1 ОВ = 0.55´200000 + 0.45´( –180000) = 29000 долл.;
• для вершины 2 ОВ = 0.55´100000 + 0.45´( –20000) = 46000 долл.;
• для вершины 3 ОВ = 10000 долл.
Вывод. Наиболее целесообразно выбрать стратегию строительства малого предприятия, а остальные стратегии дерева решений можно отбросить. ОВ наилучшего решения равен 46000 долл.
Усложним рассмотренную выше задачу.
Пусть перед принятием решения о строительстве руководство компании должно определить, заказывать ли дополнительное исследование состояния рынка или нет, причем предоставляемая услуга обойдется компании в 10 000 дол. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей.
Фирма, которой заказывается прогноз, способна уточнить значения вероятностей благоприятного или неблагоприятного состояния рынка. При этом известно:
– если фирма делает прогноз, что рынок будет благоприятным, то он будет благоприятным с вероятностью 0.78, а неблагоприятным – 0.22;
– если фирма делает прогноз, что рынок будет неблагоприятным, то он будет неблагоприятным с вероятностью 0.73, а благоприятным – 0.27.
На основании дополнительных сведений можно построить новое дерево решений (рис. 2), где развитие событий происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным. Определим ожидаемый выигрыш в этом случае. Если прогноз конъюнктуры рынка не заказывается, результат уже был получен: нужно строить малое предприятие, ожидаемый выигрыш – 46 000 долл. В случае, когда прогноз заказывается, действия ОС и, соответственно результаты, зависят от прогноза. Если будет получен прогноз о благоприятной конъюнктуре рынка, то вероятность благоприятной конъюнктуры рынка будет 0.78, а неблагоприятной – 0.22. Тогда:
При строительстве большого предприятия ОВ = 200000´0.78 + +(–180000´0.22)= 116 400 долл.;
При строительстве малого предприятия ОВ = 100000´0.78 +
+(–20000´0.22)= 73 600 долл.;
при продаже патента ОВ = 10 000 долл.
Следовательно, при благоприятном прогнозе нужно строить большое предприятие, при этом ОВ = 116 400 долл.
Если будет получен прогноз о неблагоприятной конъюнктуре рынка, то вероятность благоприятной конъюнктуры рынка будет 0.27, а неблагоприятной – 0.73. Тогда:
при строительстве большого предприятия ОВ=200000´0.27 +
+(–180000´0.73)= -77 400 долл.;
при строительстве малого предприятия ОВ = 100000´0.27 +
+(-20000´0.73)= 12 400 долл.;
при продаже патента ОВ = 10 000 долл.
В случае неблагоприятного прогноза необходимо строить малое предприятие, при этом ОВ = 12 400 долл.
Так как руководство компании принимает решение заказывать,
или не заказывать прогноз до того как прогноз будет получен, то для оценки возможного результата оно может воспользоваться своими предварительными данными о вероятности благоприятной и неблагоприятной конъюнктуре рынка. Таким образом, если прогноз будет заказан, ожидаемый выигрыш составит ОВ = 116400´0.55 + 12400´0.45 = =59200долл. После уплаты за прогноз 10000долл. остается 49200 долл., что больше, чем в случае, когда прогноз не заказывается.

Анализируя дерево решений, можно сделать следующие выводы:
• необходимо проводить дополнительное исследование конъюнктуры рынка, поскольку это позволяет существенно уточнить принимаемое решение и увеличить ожидаемую прибыль;
• если фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно строить большое предприятие (ожидаемая максимальная прибыль 116 400 долл.), если прогноз неблагоприятный — малое (ожидаемая максимальная прибыль 12 400 долл.).
Руководство компании может определить для себя ожидаемую ценность информации. Это величина равна разности между ожидаемым выигрышем в случае, когда прогноз будет заказываться и ожидаемым выигрышем без прогноза. В примере эта величина равна 59200 – 46000 = 13200, что больше платы за информацию. Если бы плата была больше ожидаемой ценности информации, то по такой цене эту информацию не имело бы смысла покупать.
3. Примеры решения задач
Здесь будут рассмотрены задачи на составление модели операции и оценку эффективности стратегии.
Составление модели операции состоит в определении множества Х— стратегий ОС, множества Y— неопределенных факторов, множества Z и функции распределения (z) случайных факторов z и в определении критерия операции f(x, у, z) исходя из цели операции.

Задача 1

Скорость движения машин в автомобильном туннеле не превышает 50 км/ч и связана с плотностью потока ( количеством машин на километр дороги ) Р следующим эмпирическим соотношением

Р = , где v0 = 60 км/ч, a z— случайная величина, которая в любой момент определяется отношением грузовых и легковых машин, проходящих через туннель. Известно, что величина z распределена равномерно на отрезке [0.5;1]. Регулировка движения в туннеле производится выбором скорости движения v. За проезд по туннелю с легковой машины взимается плата денежных единиц, а с грузовой — (0<<). Цель операции состоит в получении максимальной платы за 1 час работы туннеля. Требуется составить математическую модель операции и определить оценку эффективности произвольной стратегии ОС.
Решение. Контролируемым фактором х является скорость движения v по туннелю. Множество X контролируемых факторов по условию задачи определяется соотношением
X={x: 0x50}.
Неконтролируемым фактором является случайная величина zZ =[0.5;1] с равномерным законом распределения:

Неопределенных неконтролируемых факторов нет (Y= ).
Критерием операции является количество денег, полученных в течение часа. Так как плата взимается при въезде в туннель, то для определения этой величины найдем количество С(x,z) машин, въезжающих в туннель за один час, при заданных величинах (х, z).
С(x, z)=xP=
Найдем, сколько среди них грузовых и легковых. Так как
z=,
где — количество грузовых машин, a g — количество легковых машин, то
g= ; =
Следовательно:
f(x, z): .
Итак, все компоненты математической модели {X, Y, (Z,(z)), f} определены.
Оценим эффективность произвольной стратегии х. Рассмотрим только два критерия эффективности:
1) критерий ожидаемого значения, т. е. ОС допускает осреднение;

Источник