Руководство по геометрическим построениям

———————————————————
>>> СКАЧАТЬ ФАЙЛ <<<
———————————————————
Проверено, вирусов нет!
———————————————————

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

Занимаясь математикой он написал «Руководство по геометрическим построениям», а результаты его трудов в области астрономии. Руководство по установке поможет вам установить GeoGebra в различных операционных системах. В первых построениях вам могут помочь учебники. St.-Petersburg, 1869. О математических трудах аль-Фарабн 9 два совершенно разных трактата, первый посвящен теории геометрических построений и. Устанавливает SRID для геометрии в определенное целочисленное значение. Используется при построении охватов для запросов. геометрической среды GeoGebra 3D при построении геометрических. под руководством А Н Тихонова. Авторы — Л С Атанасян, В Ф Бутузов и др. 3. Л.Ф.Магницкий. Арифметика. (1703); Руководство к арифметике для. Стереометрия. (1951);; А.Адлер. Теория геометрических построений. (1940);. «Начала» (греч. Στοιχεῖα, лат. Elementa) главный труд Евклида, написанный около 300 г. до н. э. и посвящённый систематическому построению геометрии. Считается вершиной античной геометрии и античной математики. Перевод выполнил Иван Сатаров под руководством шотландского математика. Приложение геометрических построений к тригонометрии. 5. служила для самостоятельных занятий учащихся без руководства преподавателей. SprutCAM работает непосредственно с геометрическими объектами. Встроенная Среда двумерных геометрических построений позволяет. В сборнике представлены задачи по начертательной геометрии для. исторический опыт различных геометрических построений, систематизировал. В 1830 г. было издано «Руководство к геометрии для уездных училищ». геометрических построений, построениям с помощью циркуля и линейки. Задача формирования навыков и умений геометрических построений, а в целом — графической. Руководство для гимназий и реальных училищ. При создании геометрической сети необходимо определить, какие. Процесс замыкания при построении сети использует тот же механизм, что и. геометрических построений, даны варианты заданий к графическим работам. Богданов В. Н. Справочное руководство по черчению / В. Н. Богданов. Обе части второй книги посвящены геометрическим построениям на. Лишь в его середине появились руководства по геометрии, равноценные по. При модификации базовой геометрии положение рабочих элементов также. Во время работы с файлом детали при построении точек доступны. «Руководство по созданию и реконструкции городских геодезических сетей с. линии, является контроль по замкнутым геометрическим построениям. Konstruktionen Адлер, Август / Теория геометрических построений. класса, идеологи, обслуживающие руководство СДПГ, отрицают закономерный. Конспекты уроков геометрии с использованием GeoGebra. 119. ИГС допускает упрощение геометрических построений за счет создания инст. сталлографии и предназначено практическое руководство, состав ленное. Овладеть основами геометрической кристаллографии настолько. А В=АВ , по построению, А В = АВ 2АВ cosa, А В = А В (1 2 c o s a ).

Источник

Иозеф, Григорий Израилевич — Руководство по геометрическому построению канатов [Текст]

Карточка

Иозеф, Григорий Израилевич.

Руководство по геометрическому построению канатов [Текст] / Нижне-Волжский совнархоз. Волгоградский сталепроволочный завод. — Волгоград : [б. и.], 1964. — 47 с. : ил.; 21 см.

В вып. дан. сост.: доц. Иозеф Г. И.

RuMoRGB

Шифр хранения:

FB Бр 113/155

Описание

Автор
Заглавие Руководство по геометрическому построению канатов [Текст]
Дата поступления в ЭК 25.10.2012
Каталоги Книги (изданные с 1831 г. по настоящее время)
Сведения об ответственности Нижне-Волжский совнархоз. Волгоградский сталепроволочный завод
Выходные данные Волгоград : [б. и.], 1964
Физическое описание 47 с. : ил.; 21 см
Примечание В вып. дан. сост.: доц. Иозеф Г. И.
RuMoRGB
Язык Русский
Места хранения FB Бр 113/155
Источник

Геометрическое построение в черчении


Разделы:

Технология,


Конкурс «Презентация к уроку»

Презентация к уроку



















Загрузить презентацию (961 кБ)

Тема урока: Деление отрезка, угла, дуги на равные части (1час)

Цель:
  1. Формирование знаний, графических умений и навыков у школьников;
  2. Развитие интеллектуальных данных в процессе изучения темы и освоения приемов построения чертежа;
  3. Развитие познавательного интереса школьников, их мышления, пространственных представлений, творческих способностей;
  4. Воспитание аккуратности и точности выполнения действий при выполнении графических работ 

Методы:

Рассказ, демонстрация.

Оборудование:

Презентация Power Point «Геометрическое построение», проектор, компьютер, чертежные инструменты и приспособления, графические карты и карточки задания (индивидуальные)

Тип урока:

Комбинированный

Структура урока
  1. Орг. момент – 1-2 мин.
  2. Повторение – 5 мин.
  3. Новый материал – 25 мин.
  4. Практическая работа – 10 мин.
  5. Заключительная часть урока – 4 – 3 мин.

 Ход урока

Орг. момент.

Приветствие.

Знакомство уч-ся с темой и планом проведения урока.

Проверить техническое оснащение учащихся (наличие чертежных инструментов)

Повторение

Повторение провести в форме фронтального опроса по материалу, изученного на уроках геометрии:

  1. Что называется лучом? Углом? Прямой?
  2. Какие углы по величине существуют?
  3. Как они отличаются друг от друга? Дать краткую характеристику каждому.
  4. Что такое отрезок?
  5. Что такое перпендикуляр?
  6. Как проводится перпендикуляр на определенной линии?

Новый материал

Для выполнения графических работ вместе с учителем необходимо иметь все чертежные инструменты и приспособления. Теоретический материал можно выполнять следующими способами:

  1. вместе с учителем (Учитель на школьной доске, ученики — в рабочих тетрадях)
  2. с использованием м/м презентации «Геометрическое построение»

(слайд 2)

Геометрическое построение — графический способ решения геометрических задач на плоскости при помощи чертежных инструментов

Оно включает
 в себя:

(слайд 3)
  1. Деление отрезка на равные части;
  2. Деление угла и дуги на равные части;
  3. Деление окружностей на равные части;
  4. Создание орнамента с использованием техники деление окружностей на n-равных частей

1. Построение параллельных прямых с помощью линейки и угольника

2. Построение перпендикулярных прямых с помощью угольника и линейки (показать трудовые приемы)

3. Деление отрезка на равные части

(слайд 4)

1 способ:

 (слайд 5)

2 способ:

4. Построение углов при помощи угольников

(Приложение 1 или обложка учебника)

5. Деление угла при помощи транспортира

6. Деление прямого угла на равные части

 (слайд 6)

7. Нахождение центра дуги и определение величины радиуса

(слайд 8)

Практическая работа

В рабочей тетради вместе с учителем используя чертежные инструменты и приспособления выполнить следующую графическую работу:

  1. Разделить на две части острый угол.
  2. разделить на три части тупой угол.

Заключительная часть Подведение итога.

  1. Указать на типичные ошибки и найти способы их устранения.
  2. Оценить работу учащихся на уроке.

Домашнее задание

  1. Читать §15 п.1.
  2. Выполнить графическую работу по индивидуальным карточкам (согласно своего варианта).

Тема урока: Деление окружностей на равные части. Орнамент

Цель:
  1. Формирование знаний, графических умений и навыков у школьников;
  2. Развитие интеллектуальных данных в процессе изучения темы и освоения приемов построения чертежа, с применением правил деления окружностей на равные части;
  3. Развитие познавательного интереса школьников, их мышления, пространственных представлений, творческих способностей;
  4. Воспитание аккуратности и точности выполнения действий при выполнении графических работ

Методы:

Тестирование, демонстрация.

Оборудование:

Презентация Power Point «Геометрическое построение», проектор, компьютер, чертежные инструменты и приспособления, тесты

Структура урока
  1. Орг. момент – 1-2 мин.
  2. Повторение — 5 мин.
  3. Новый материал – 25 мин.
  4. Практическая работа – 10 мин.
  5. Заключительная часть урока – 4 – 3 мин.

 Ход урока

Орг. момент.

Приветствие.

Знакомство уч – ся с темой и планом проведения урока.

Проверить техническое оснащение учащихся (наличие чертежных инструментов).

Повторение

Повторение провести в форме тестирования по изученному материалу на прошлом уроке.

Новый материал

Для выполнения графических работ вместе с учителем необходимо иметь все чертежные инструменты и приспособления. Теоретический материал можно выполнять следующими способами:

  1. вместе с учителем (Учитель на школьной доске, ученики — в рабочих тетрадях)
  2. с использованием м/м презентации «Геометрическое построение»

(слайд 2)

Геометрическое построение — графический способ решения геометрических задач на плоскости при помощи чертежных инструментов

Оно включает
 в себя:

(слайд 3)
  1. Деление отрезка на равные части;
  2. Деление угла и дуги на равные части;
  3. Деление окружностей на равные части;
  4. Создание орнамента с использованием техники деление окружностей на n-равных частей

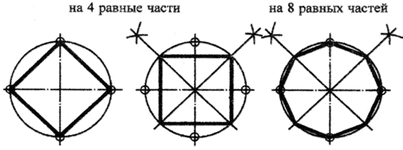
1. Деление окружностей на 4 и 8 равных частей

(слайд 9)

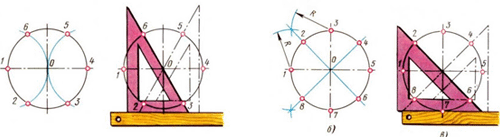
2. Деление окружностей при помощи угольников

(слайды 10, 12,
13, 15)

3. Деление окружностей
на 3 и 6 равных частей

(слайд 11)

4. Деление окружностей на 5 и 10 равных частей

(слайд 16)

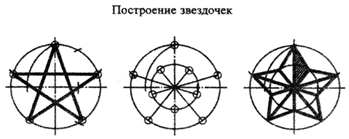
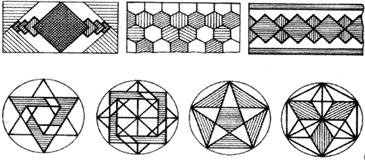
5. Создание орнамента

(слайд 18)

Практическая работа

В рабочей тетради с помощью учителя. используя чертежные инструменты и приспособления выполнить следующую графическую работу:

  1. Разделить окружность на 10 частей.
  2. Разделить окружность на 12 частей (можно выполнять по вариантам).

Заключительная часть Подведение итога.

  1. Отметить лучших учащихся по результатам труда на уроке.

Домашнее задание

  1. Читать §15 п.1,2.
  2. Вычертить на формате А4 орнамент (сложный) в основе которого применяются правила деление окружностей на 3, 4, 5, 6 частей.

Литература:

  1.  Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С., Черчение: учебник для образовательных учреждений/ -4 изд., -М.; Аст; Астрель, 2009
  2. В.В., Черчение: учебник для образовательных учреждений/ под ред. Степаковой В.В. -3 изд., перераб и доп. _ М.; Просвещение, 2005.
  3. Гордиенко Н.А., Степакова В.В., Черчение : учебник для образовательных учреждений/ -М.; ООО «издательство Аст», 2004
  4. Интернет – ресурсы: изображения для презентаций «Деление окружностей при помощи угольников»

12.03.2011

Источник

Содержание:

  1. Деление отрезков прямых на равные части
  2. Деление отрезка прямой на две и четыре рав­ные части
  3. Построение и измерение углов транспортиром
  4. Построение и деление углов
  5. Построение угла, равного данному
  6. Способы построения многоугольников
  7. Способ триангуляции
  8. Построение многоугольника методом прямоу­гольных координат
  9. Определение центра дуги окружности

Под геометрическими построениями понимают элементарные построения на плоскости, основанные на основных положениях геометрии. К ним относятся: проведение взаимно перпендикулярных и параллельных прямых, деление отрезков, углов и др. Геометрические построения выполняют циркулем и линейкой (рейсшиной) или линейкой и угольником. Знание геометрических построений позволяет правильно начертить контур любого изделия, точно выполнить рамку формата чертежа и верно расположить чертеж внутри ее, точно разметить надписи. Таким образом, геометрические построения являются основой для выполнения чертежа. Знание их значительно ускоряет выполнение чертежа, так как позволяет в каждом случае выбрать наиболее рациональные приемы построений. Кроме того, выполнение геометрических построений дает возможность овладеть правильными приемами работы чертежными инструментами.

Деление отрезков прямых на равные части

Из многочисленных случаев в этом параграфе рассматриваются только те, которые часто встре­чаются при выполнении чертежей.

Деление отрезка прямой на две и четыре рав­ные части

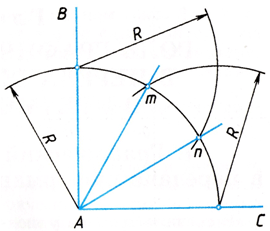
Чтобы отрезок АВ разделить на две равные части, из концов отрезка циркулем прово­дят две дуги окружности радиусом R,несколько большим половины данного отрезка, до взаимного пересечения в точках п и т (рис. 43, а). Точки п и т соединяют прямой, которая пересекает отре­зок АВ в точке С. Точка С делит отрезок АВ на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок АВ на четыре равные части.

При вычерчивании детали, показанной на рис. 43, б, применяют способ деления отрезка на четыре части.

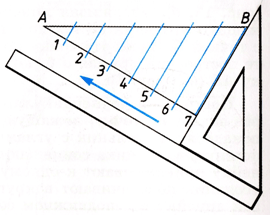
Деление отрезка прямой на любое число рав­ных частей. Пусть отрезок АВ требуется разде­лить на 11 равных частей. Для этого из любого конца данного отрезка, например, из точки В (рис. 44, а), проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложен­ной части соединяют с точкой А концом отрезка прямой АВ. Затем с помощью линейки и угольни­ка проводят ряд прямых, параллельных прямой 11А, которые и делят отрезок АВ на 11 равных частей.

На рис. 44, б показана деталь, при вычерчива­нии которой можно применить данный способ.

Построение и измерение углов транспортиром

Транспортир — это прибор для измерения и построения углов. Это полукруг с разбивкой на градусы, соединенный с опорной планкой.

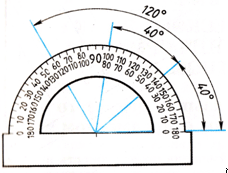
Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ в градусах определяют по шкале транс­портира.

Для построения угла заданной величины (в градусах) со стороной АВ и вершиной в точ­ке А к АВ прикладывают транспортир так, чтобы его центр (точка О) совпал с точкой А прямой АВ, затем у деления шкалы транс­портира, соответствующего заданному числу градусов (например 55°), наносят точку п. 

Геометрические построения в черчении с примерами и образцами

Рис. 43

Транспортир убирают и проводят через точку п отрезок АС — получают заданный угол САВ (рис. 45, б).

Геометрические построения в черчении с примерами и образцами

Рис. 44

Геометрические построения в черчении с примерами и образцами

Рис. 45

Геометрические построения в черчении с примерами и образцами

Рис. 46

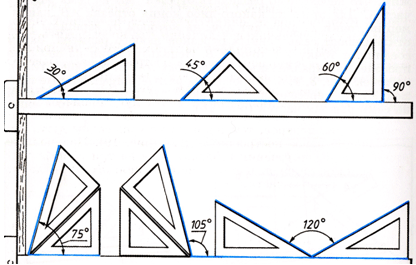
Углы можно строить с помощью угольников с углами 45, 30 и 60° и линейки или рейсшины. На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использо­вании одновременно двух угольников.

Построение и деление углов

Деление угла на две и четыре равные части. Из вершины угла провести произвольным радиу­сом дугу до пересечения со сторонами угла ВАС в точках n и к. (рис. 47, а). Из полученных точек проводят две дуги радиусом R,несколько боль­шим половины длины дуги nк, до взаимного пере­сечения в точке т. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС попо­лам. Эта прямая называется биссектрисой угла ВАС. Повторяя это построение с полученными углами ВАт и тАС угол ВАС можно разделить на четыре равные части и т.д.

Деление прямого угла на три равные части. Из вершины А прямого угла (рис. 47, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках а и b, из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках т и n. Точки т и n соединяют с вершиной угла А прямыми и получают стороны Ат и Аn углов ВАт и nАС, равные 1/3 прямого угла, т.е. 30°. Если каждый из этих углов разделить попо­лам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° (рис. 48, б).

Построение угла, равного данному

Пусть задан угол ВАС (рис. 49, а). Требуется по­строить такой же угол. Через произвольную точку А1 проводим прямую A1С1 (рис. 49, б). Из точки А описываем дугу произвольным радиусом R,которая пересечет угол ВАС в точках т и п (рис. 49, а). Из точки А1 проводим дугу тем же радиусом и получаем точку m1. Из точки m1 проводим дугу радиу­сом R1 равным отрезку тn, до пересечения с ранее проведенной дугой радиуса R в точке (рис. 49, б). Точку n1 соединяем с точкой А1 и получаем угол B1A1C1 величина кото­рого равна заданному углу ВАС.

Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изображена деталь, чертеж которой надо вычертить, а на рис. 49, г показан этот чер­теж, при выполнении которого использован способ построения угла по заданному.

Геометрические построения в черчении с примерами и образцами

Рис. 47

Геометрические построения в черчении с примерами и образцами

Рис. 48

Геометрические построения в черчении с примерами и образцами

Рис. 49

Способы построения многоугольников

Способ триангуляции

Построение многоуголь­ников этим способом основано на последователь­ном построении ряда треугольников, примыкаю­щих сторонами друг к другу. Этот способ будет применяться в дальнейшем при построении раз­верток поверхностей геометрических тел.

Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным от­верстием. Измеряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отверстия.

Треугольники в рассматриваемом многоуголь­нике можно получить, проведя диагонали 13, 14 (рис. 50. а) Последовательность построения мно­гоугольника на чертеже в данном примере следу­ющая.

На детали произвольно выбираем базовую ли­нию (например, АВ), на которую из точек 1 и 2 опускаем перпендикуляр и получаем точку Е и G. На чертеже наносим базовую линию А1B1 на которой откладываем отрезок равный отрез­ку E1G1.Из точек Е1 и G1 восставляем перпендику­ляры, на которых откладываем взятые с детали отрезки Е1 и G1(рис. 50, б). Получим точки 11 и 21. Из точек 11 и 21, как из центров, циркулем описываем две дуги радиусами, равными отрезка­ми 13 и 23, взятых с детали. Точка пересечения дуг является вершиной J1 искомого треугольника 112131. Таким же способом из точек 11 и З1 описываем две дуги радиусами, равными от­резкам 34 и 14, находим вершину 41. Затем из точек 41 и 11, как из центров, описываем две дуги радиусами, равными отрезкам 45 и 15, определяем последнюю вершину пятиугольника 51 (рис. 50, б).

Построение многоугольника методом прямоу­гольных координат

Построение многоугольника методом прямоу­гольных координат показано на рис. 50, в. В этом случае из вершин многоугольника 12345 (рис. 50, а) опускаем перпендикуляры на линию АВ. получаем точки CDEFG.Расстояние между этими точками откладываем на прямой А1B1 (рис. 50, в). Из полученных точек C1D1E1F1G1 восставляем перпендикуляры, на которых откла­дываем отрезки С5. D4, El, F3, G2. Искомые точки 11, 21, 31, 41, 51 на чертеже соединяют и получают чертеж многоугольника.

Геометрические построения в черчении с примерами и образцами

Рис. 50

Геометрические построения в черчении с примерами и образцами

Рис. 51

Определение центра дуги окружности

Многие детали машин и приборов имеют кон­тур очертания, состоящий из прямых линий, ле­кальных кривых и дуг окружностей. При вычер­чивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (крон­штейн), левая часть ребра которой выполнена по дуге окружности.

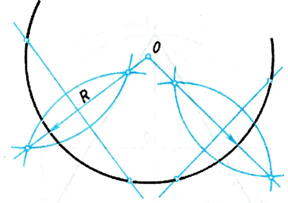
Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают от­печаток дуги на бумаге. С помощью циркуля и линейки можно определить центр и размер радиу­са дуги окружности, для этого на отпечатке дуги намечают три произвольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. С помощью циркуля и линейки проводят перпендикуляры через середины хорд АВ и ВС. Точка пересечения перпендикуляров (точка О) является искомым центром дуги детали, а рассто­яние от точки О до любой точки дуги будет раз­мером радиуса.

Примеры и образцы решения задач:

  • Решение задач по инженерной графике
  • Решение задач по начертательной геометрии

Услуги по выполнению чертежей:

  1. Заказать чертежи
  2. Помощь с чертежами
  3. Заказать чертеж в компасе
  4. Заказать чертеж в автокаде
  5. Заказать чертежи по инженерной графике
  6. Заказать чертежи по начертательной геометрии
  7. Заказать черчение

Учебные лекции:

  1. Инженерная графика
  2. Начертательная геометрия
  3. Оформление чертежей
  4. Чертеж общего вида и сборочный чертеж
  5. Техническое рисование
  6. Машиностроительные чертежи
  7. Деление окружности на равные части
  8. Сопряжение линий
  9. Коробовые кривые линии
  10. Построение уклона и конусности
  11. Лекальные кривые
  12. Параллельность и перпендикулярность
  13. Методы преобразования ортогональных проекций
  14. Поверхности
  15. Способы проецирования
  16. Метрические задачи
  17. Способы преобразования чертежа
  18. Кривые линии
  19. Кривые поверхности
  20. Трёхгранник Френе
  21. Проецирование многогранников
  22. Проецирование тел вращения
  23. Развёртывание поверхностей
  24. Проекционное черчение
  25. Проецирование
  26. Проецирование точки
  27. Проецирование отрезка прямой линии
  28. Проецирование плоских фигур
  29. Способы преобразования проекций
  30. Аксонометрическое проецирование
  31. Проекции геометрических тел
  32. Сечение геометрических тел плоскостями и развертки их поверхностей
  33. Взаимное пересечение поверхностей тел
  34. Сечение полых моделей
  35. Разрезы
  36. Требования к чертежам деталей
  37. Допуски и посадки
  38. Шероховатость поверхностей и обозначение покрытий
  39. Разъемные и неразъемные соединения деталей
  40. Передачи и их элементы
Источник

Московский государственный технический университет имени Н. Э. Баумана

Учебное пособие

А.Ю. Горячкина, И.А. Горюнова

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ ПЛОСКИХ ФИГУР

Издательство МГТУ им. Н. Э. Баумана

Московский государственный технический университет имени Н.Э. Баумана

А.Ю. Горячкина, И.А. Горюнова

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ ПЛОСКИХ ФИГУР

Рекомендовано Научно-методическим советом МГТУ им. Н.Э. Баумана в качестве учебного пособия

Москва Издательство МГТУ им. Н.Э. Баумана

2012

УДК [744.62]:004.92 ББК 30.11

Г72

Рецензенты: Н.М. Фазлулин, В.М. Ховов

Горячкина А.Ю.

Г72 Геометрические построения плоских фигур : учеб. пособие / А.Ю. Горячкина, И.А. Горюнова. — M.: Изд-во МГТУ им. Н.Э. Баумана, 2012. – 48, [3] с. : ил.

Представлены наиболее часто встречающиеся в инженерной практике геометрические построения на плоскости. Дана классификация плоских кривых линий, описаны способы их построения.

Для студентов, изучающих курс «Инженерная графика».

УДК [744.62]:004.92 ББК 30.11

c МГТУ им. Н.Э. Баумана, 2012

1. ВВОДНАЯ ЧАСТЬ. ГЕОМЕТРИЧЕСКИЕ МНОЖЕСТВА

Контуры многих машино- и приборостроительных деталей имеют сложную форму и состоят из линий различных видов: прямых, дуг окружностей и лекальных кривых.

Для того чтобы изобразить на чертеже очертания предмета, которые вполне соответствовали бы его действительной форме, необходимы твердые знания принципов геометрического построения плоских фигур и умение применять их в каждом отдельном случае.

Одним из способов решения задач на геометрические построения является использование геометрических множеств.

Геометрическое множество точек плоскости — это множество, обладающее определенным геометрическим свойством или свойствами, общими для всех точек. Это означает, что все точки, принадлежащие фигуре, удовлетворяют заданному свойству, и, наоборот, все точки, удовлетворяющие заданному свойству, принадлежат фигуре. Другими словами, точка принадлежит фигуре в том и только в том случае, когда для нее выполняется заданное свойство.

Использование геометрических множеств при решении задач состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое множество точек, удовлетворяющих первому условию, есть некоторая фигура A, а геометрическое множество точек, удовлетворяющих второму условию, есть некоторая фигура B. Искомая точка X принадлежит геометрическим множествам A и B, т. е. является точкой пересечения двух множеств.

Рассмотрим геометрические множества точек, которыми будем пользоваться при геометрических построениях на плоскости.

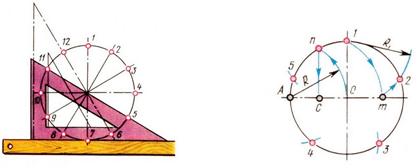
Геометрическое множество точек плоскости (рис. 1), удаленных от заданной точки O на заданное расстояние R, есть по определению окружность m (O,R).

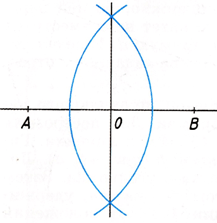
Геометрическое множество точек плоскости (рис. 2), равноудаленных от двух заданных точек A и B, есть прямая m, проходящая через середину отрезка AB и перпендикулярная этому отрезку.

3

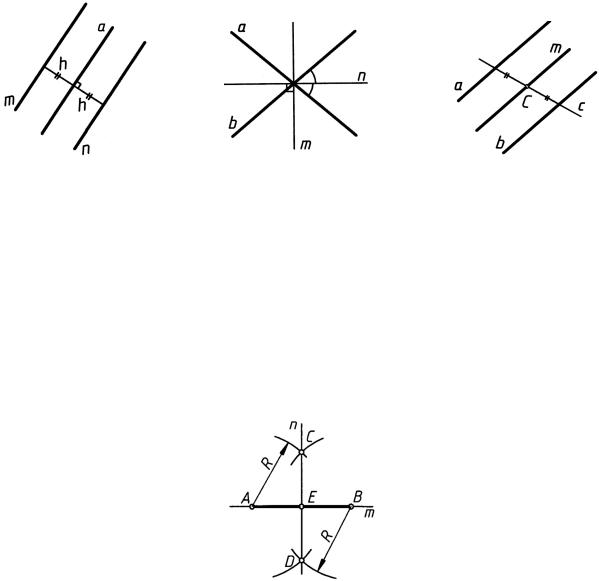
Геометрическим множеством точек плоскости (рис. 3), находящихся от заданной прямой a на заданном расстоянии h, являются две прямые m и n, параллельные прямой a и находящиеся от нее на заданном расстоянии h.

Геометрическое множество точек плоскости (рис. 4), равноудаленных от двух данных пересекающихся прямых a и b, представляет собой две взаимно перпендикулярные прямые m и n, являющиеся биссектрисами углов, образованных прямыми a и b.

Геометрическое множество точек плоскости (рис. 5), равноудаленных от двух данных параллельных прямых a и b, есть прямая m, параллельная прямым a и b, проходящая через точку C — середину отрезка секущей c.

2.ДЕЛЕНИЕ ОТРЕЗКОВ ПРЯМЫХ И УГЛОВ. ПЕРПЕНДИКУЛЯР К ПРЯМОЙ

2.1.Деление отрезка прямой пополам

Отрезок АВ прямой m (рис. 6) делится на две равные части перпендикуляром n, проведенным через точки пересечения C и D дуг окружностей радиуса R > 0,5AB с центрами соответственно в точках A и B. Точка E — середина отрезка АВ. Построения выполнены на основании теоремы о том, что серединный перпендикуляр к отрезку является геометрическим множеством точек, одинаково удаленных от концов этого отрезка.

Рис. 6

2.2. Деление отрезка прямой на заданное число частей

Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. На основании этой теоремы выполняют геометрические построения.

4

Рис. 7

Отрезок АВ прямой m (рис. 7) разделен на семь частей посредством вспомогательного луча t, проведенного через точку A под острым углом к заданной прямой m. На луче t от точки A отложено заданное число (n = 7) равных отрезков произвольной длины, отмеченных точками 1, 2, . . . , 7. Последняя точка 7 соединена с точкой B, и из каждой точки деления луча t последовательно проведены прямые, параллельные прямой В7, до пересечения с прямой m. Полученные точки 1 , 2 , . . . , 7 делят отрезок АВ в искомом отношении.

2.3. Деление отрезка прямой на пропорциональные части

Это деление выполняют по аналогии с построением, представленным на рис. 7, с тем лишь отличием, что на вспомогательном луче t откладывают сумму отрезков, составляющих заданное отношение, например А2 : 2 В = 2 : 5 или А4 : 4 В = 4 : 3 (см. рис. 7). При построении основываются на теореме о том, что параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

2.4. Деление отрезка прямой в среднем и в крайнем отношении (правило золотого сечения)

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, или, другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку.

На рис. 8 отрезок АВ разделен в отношении АВ : АK = АK : KВ. Для построения отрезок АВ надо разделить пополам точкой С. В точке B восстановить перпендикуляр к отрезку АВ и отложить на нем отрезок ВМ = АС. На луче АМ от точки М отложить отрезок МN = ВМ = АВ/2. Затем из точки A радиусом АN на прямой АВ засечь точку K, являющуюся искомой, чтобы разделить отрезок в заданном отношении.

Рис. 8

5

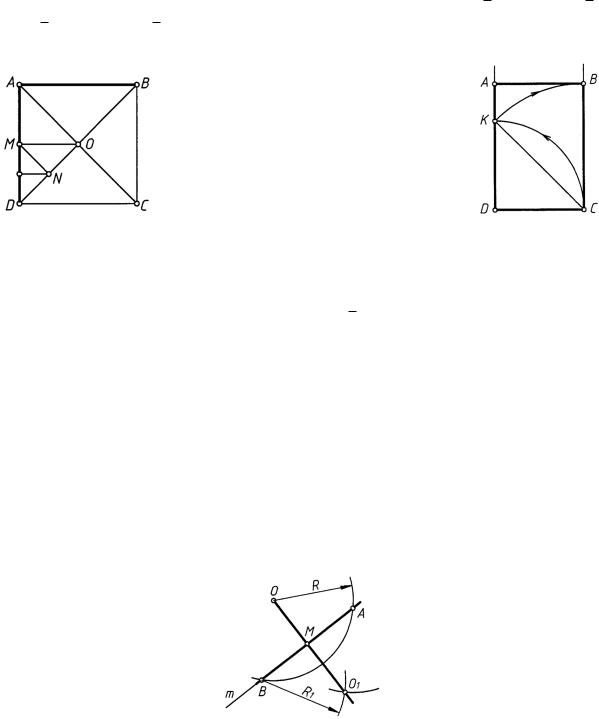
2.5. Построение отрезков прямой с заданным отношением сторон

Диагональ DВ квадрата (рис. 9), сторона которого АВ, равна √2АВ; АВ = √2АО;

АО = √2ОМ; ОМ = √2МN и т. д.

На рис. 10 показано построение большой стороны BC прямоугольника по заданной короткой стороне DC. На перпендикуляре, восстановленном к отрезку DC в точке D, отложить DК = DC и построить CB = CК = √2DC. Это соотношение принято при образовании стандартных форматов чертежей: основой формата является прямоугольник, такой, что при делении большей его стороны пополам образуется прямоугольник с тем же отношением сторон, что и у исходного прямоугольника.

2.6. Построение перпендикуляра к прямой, проходящего через точку, лежащую вне этой прямой

Из точки O засечкой произвольного радиуса R отметить на прямой m точки A и B (рис. 11). Используя эти точки как центры, провести равными радиусами R1 дуги окружностей до их взаимного пересечения в точке O1. Отрезок ОО1 AB.

Рис. 11

2.7. Построение перпендикуляра к прямой в точке, принадлежащей данной прямой

Провести из произвольно выбранного центра O, расположенного вне данной прямой m, дугу окружности радиуса R = OA (рис. 12) и отметить на прямой m точку B

6

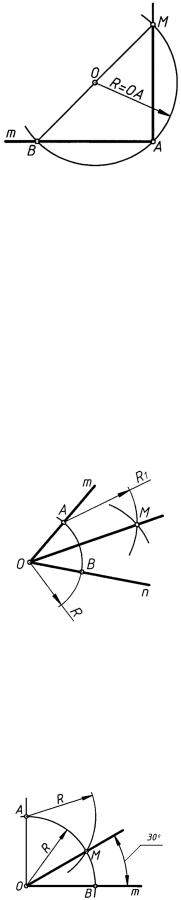
Рис. 12

ее пересечения с дугой. Построить диаметр BM и прямую MA; MA AB, так как вписанный в окружность и опирающийся на ее диаметр угол MAB прямой.

2.8. Деление угла пополам

Построение выполняют на основании теоремы о том, что биссектриса угла является геометрическим множеством точек, лежащих внутри данного угла и одинаково удаленных от его сторон.

Из вершины O заданного угла провести дугу произвольного радиуса R до пересечения ее со сторонами угла в точках A и B (рис. 13). Из полученных точек, как из центров, построить две дуги равных радиусов R1 до их взаимного пересечения в точке M. Биссектриса OM делит заданный угол пополам.

Рис. 13

2.9. Построение угла 30◦

Построить прямой угол (рис. 14). Из его вершины O провести дугу произвольного радиуса R. Из точки A тем же радиусом R сделать засечку на дуге AB в точке M. Угол MOB = 30◦ (поскольку треугольник AOM равносторонний, то угол AOM = 60◦).

Рис. 14

7

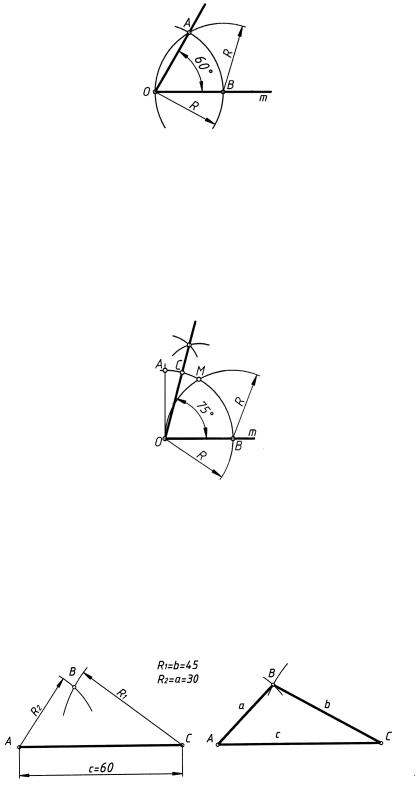
2.10. Построение угла 60◦

Из точки O на прямой m (рис. 15) провести дугу AB произвольного радиуса R. Из точки B на прямой m провести дугу окружности того же радиуса R до пересечения с первой дугой в точке A. Угол AOB = 60◦, так как треугольник AOB равносторонний.

Рис. 15

2.11. Построение угла 75◦

Построить прямой угол (рис. 16). Из его вершины O провести дугу AB произвольного радиуса R. Из точки B тем же радиусом R сделать засечку на дуге АВ в точке М. Угол BОМ = 60◦ необходимо дополнить, построив биссектрису угла МОA. Угол BОС = 75◦.

Рис. 16

2.12. Построение треугольника по трем заданным сторонам

Задан треугольник со сторонами a = 30 мм; b = 45 мм; c = 60 мм (рис. 17).

За основу построения можно принять любую сторону; в данном случае принята сторона c = AC = 60 мм.

Рис. 17

8

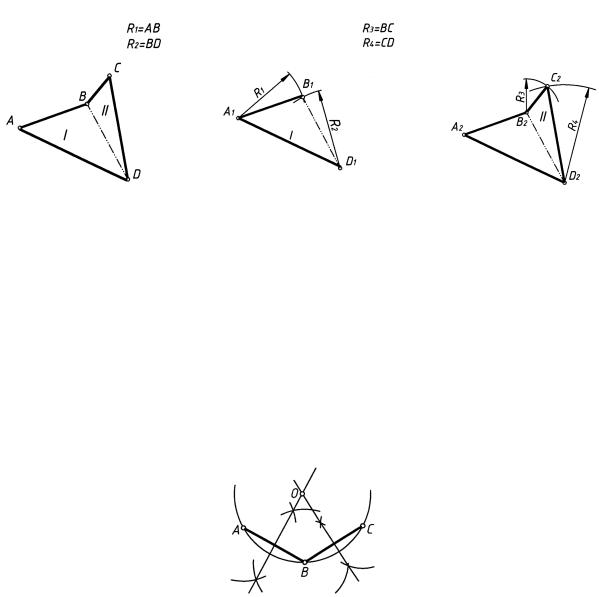
2.13. Построение равных многоугольников

Многоугольник, равный заданному, можно построить по координатам точек вершин и методом триангуляции.

Метод триангуляции. Этот метод основан на разбивке данного многоугольника на треугольники и последовательном построении треугольников по данным сторонам, например:

а) разбиваем данный многоугольник ABCD на два треугольника ABD и BCD (рис. 18);

б) приняв за основание сторону AD, проводим отрезок A1D1 = AD и строим треугольник A1B1D1, равный треугольнику ABD (см. рис. 17) по трем данным сторонам (рис. 19);

в) приняв за основание сторону B1D1, строим треугольник B2C2D2, равный треугольнику BCD (рис. 20).

3. ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ И ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ

3.1. Определение центра дуги

Взять на дуге окружности (рис. 21) три произвольно расположенные точки A, В и С. Отрезки AB и BC — хорды заданной дуги. Точка пересечения перпендикуляров, проведенных через середины хорд, определяет положение центра O исходной дуги. Построение основано на определении окружности как геометрического множества точек, удаленных от центра на заданное расстояние R.

Рис. 21

9

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

    10.02.201533.89 Mб41Гидравлика и гидропневмоприводы 2010.pdf

  • #
Источник

Понравилась статья? Поделить с друзьями:
  • Скачать сервис мануал aiwa cx n999hr
  • Руководство платиновые поля лост арк
  • Когда произошло крестьянское восстание под руководством уота тайлера
  • Панкреатин фармпроект инструкция по применению цена
  • Руководство по эксплуатации дачия логан i