Методы оптимальных решений
В этом разделе вы найдете он-лайн учебник по методам оптимальных решений, в котором приведены краткие теоретические сведения, а также подробнейшим образом разобраны решения типовых задач.
Почему методы оптимальных решений для чайников? Потому что разобраны основные разделы, которые изучают студенты в курсе МОР: постановка задачи линейного программирования (в данном случае в форме задачи планирования и оптимизации производства), а также методы ее решения: симплексный, графический, программный с помощью Excel разных версий, а также решение методом Гомори.
Внимательно следите за расчетами и чертежами, повторяйте их для учебной задачи, а потом для своей, и вы научитесь решать задачи. Ниже вы найдете полезные ссылки на решенные примеры и контрольные по различным разделам оптимизации и математическому программированию, статьи. Удачи в учебе!
Мини-учебник по МОР
Глава 1. Задачи оптимизации
- 1.1. Обзор и типизация задач математического программирования
Глава 2. Производственная задача
- 2.1. Постановка производственной задачи
- 2.1.1. Производственная задача. Графический способ решения
- 2.1.2. Производственная задача. Симплексный способ решения
- 2.1.3. Решение производственной задачи в Excel 2007 и выше
- 2.1.4. Решение производственной задачи в Excel 2003 и ниже
- 2.1.5. Решение целочисленной производственной задачи методом Гомори
Примеры с решением по МОР
- Примеры решений по линейному программированию
- Примеры решений по математическим методам и моделям в экономике
- Контрольные по методам оптимальных решений
- Контрольные по линейному программированию
- Контрольные по экономико-математическим методам
- Контрольные по теории игр
- Контрольные по системному анализу
- Контрольные по теории принятия решений
- Методы оптимальных решений: тест с ответами
Где заказать решение задач по МОР? В МатБюро!
Полезные статьи по методам оптимизации
- Дерево решений в теории игр
- Обзор методов решения задач линейного программирования
- Симплексный метод решения задач линейного программирования
- Транспортная задача: постановка и решение
624.131.2
Р851
Руководство по лабораторному определению оптимальных значений влажности и объемного весаскелета связанных грунтов применительно к уплотнению катками [Текст]. — Л. : ВНИИТ, 1975. — 41 с. — 0р.27к.
| УДК |
624.131.2 |
Рубрики: ТЕХНИКА
СТРОИТЕЛЬСТВО
ЗЕМЛЯНЫЕ РАБОТЫ
Кл.слова (ненормированные):
земляные работы — исследования — грунты — уплотнение
Экземпляры всего: 1
6-5 (1)
Свободны: 6-5 (1)
3. РЕКОМЕНДАЦИИ ПО ОПРЕДЕЛЕНИЮ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ ОЗП
3.1. Для достижения максимальных значений условного коэффициента звукопоглощения ОЗП в заданном диапазоне частот необходимо:
определить расчетную частоту Fр, на которой должен находиться максимум условного КЗП объемного звукопоглотителя;
определить оптимальный характерный размер r объемного звукопоглотителя;
выбрать звукопоглощающий материал и защитное покрытие ОЗП с оптимальными акустическими характеристиками;
рассчитать частотную характеристику условного КЗП и величину эквивалентной площади звукопоглощения Aшт в нормируемом диапазоне частот;
определить величину радиуса зоны влияния h ОЗП.
3.2. По заданному спектру шума определяется диапазон частот, где уровни звукового давления превышают допустимые значения; выбирается расчетная частота Fр, на которой превышение допустимых уровней звукового давления наибольшее.
3.3. Радиус сферы rсф, для которого приведенные значения параметра kr лежат в максимальном диапазоне частот, где уровни звукового давления превышают допустимые значения (согласно п. 3.2) определяются по табл. 1.
Примечание. Значения параметра kr, приведенные в табл. 1 для данного значения rсф удовлетворяют условию максимума в пределах границ указанного диапазона частот (согласно условию

ОЗП приближается к
эквивалентной плоской конструкции.
Таблица 1
|
Радиус сферы rсф, см |
Значения параметра kr на среднегеометрической частоте октавных полос Fр, Гц |
|||||||
|
125 |
160 |
200 |
250 |
315 |
400 |
500 |
630 |
|
|
15 |
0,343 |
0,439 |
0,549 |
0,686 |
0,864 |
1,098 |
1,372 |
1,729 |
|
20 |
0,457 |
0,585 |
0,732 |
0,915 |
1,153 |
1,464 |
1,83 |
2,3 |
|
25 |
0,572 |
0,732 |
0,915 |
1,143 |
1,44 |
1,830 |
2,287 |
2,88 |
|
30 |
0,686 |
0,878 |
1,098 |
1,372 |
1,729 |
2,196 |
2,745 |
3,458 |
|
40 |
0,915 |
1,17 |
1,464 |
1,83 |
2,3 |
2,928 |
3,660 |
4,611 |
Продолжение табл. 1
|
Радиус сферы rсф, см |
Значения параметра kr на среднегеометрической частоте октавных полос Fр, Гц |
|||||||
|
800 |
1000 |
1250 |
1600 |
2000 |
2500 |
3150 |
4000 |
|
|
15 |
2,196 |
2,745 |
3,431 |
4,392 |
5,49 |
6,862 |
8,646 |
10,98 |
|
20 |
2,928 |
3,66 |
4,557 |
5,856 |
7,32 |
9,15 |
11,53 |
— |
|
25 |
3,66 |
4,575 |
5,718 |
7,320 |
9,15 |
11,43 |
— |
— |
|
30 |
4,392 |
5,49 |
6,862 |
8,784 |
10,98 |
— |
— |
— |
|
40 |
5,856 |
7,32 |
9,150 |
11,71 |
— |
— |
— |
— |
3.4. По выбранному радиусу rсф на частоте Fр из табл. 1 определяется значение параметра kr.
3.5. Для данного параметра kr по табл. 2 определяются оптимальные значения составляющих импеданса (,
) ОЗП.
Таблица 2
|
Параметр kr |
Составляющие импеданса |
Параметр kr |
Составляющие импеданса |
||
|
|
|
|
|
||
|
0,35 |
0,19 |
-0,2 |
2,9 |
0,8 |
-0,6 |
|
0,45 |
0,2 |
-0,24 |
3,45 |
0,86 |
-0,64 |
|
0,55 |
0,26 |
-0,25 |
3,65 |
0,93 |
-0,65 |
|
0,65 |
0,33 |
-0,26 |
4,4 |
0,96 |
-0,66 |
|
0,7 |
0,38 |
-0,28 |
4,55 |
1 |
-0,65 |
|
0,75 |
0,39 |
-0,3 |
4,6 |
1 |
-0,65 |
|
0,85 |
0,4 |
-0,31 |
5,5 |
1,05 |
-0,65 |
|
0,9 |
0,42 |
-0,32 |
5,7 |
1,09 |
-0,65 |
|
1,1 |
0,44 |
-0,33 |
5,85 |
1,3 |
-0,66 |
|
1,15 |
0,46 |
-0,35 |
6,85 |
2,3 |
-0,66 |
|
1,35 |
0,57 |
-0,39 |
7,3 |
1,13 |
-0,66 |
|
1,4 |
0,6 |
-0,4 |
8,65 |
1,2 |
-0,66 |
|
1,45 |
0,62 |
-0,41 |
8,75 |
1,22 |
-0,66 |
|
1,7 |
0,72 |
-0,45 |
8,8 |
1,14 |
-0,66 |
|
1,75 |
0,74 |
-0,49 |
9,15 |
1,19 |
-0,65 |
|
1,85 |
0,77 |
-0,48 |
11 |
1,10 |
-0,65 |
|
2,2 |
0,78 |
-0,5 |
11,45 |
1,21 |
-0,66 |
|
2,3 |
0,82 |
-0,54 |
11,55 |
1,2 |
-0,65 |
|
2,75 |
0,83 |
-0,56 |
11,7 |
1,23 |
-0,66 |
|
2,85 |
0,84 |
-0,6 |
— |
— |
— |
Примечание. Значения и
получены путем усреднения оптимальных величин
и
, вычисленных по формуле (6) из условия максимума КЗП (при коэффициенте отражения, равном нулю) для различных мод колебаний n.
3.6. По справочной литературе подбираются акустические материалы заполнения ОЗП и защитного покрытия с такими характеристиками, чтобы суммарные значения составляющих импеданса ,
этих материалов (импеданс ОЗП) на расчетной частоте Fр были близки к оптимальным
,
.
3.7. Значения составляющих импеданса акустических материалов и звукопоглощающих конструкций определяются согласно «Рекомендациям по расчету и проектированию звукопоглощающих облицовок».
3.8. Экспериментальные значения составляющих импеданса и волнового сопротивления некоторых акустических материалов приведены в табл. 1, 2 прил. 2.
Если ОЗП имеет слой звукопоглощающего материала толщиной 50 мм, то составляющие импеданса ,
могут выбираться по табл. 1 прил. 2, если ОЗП заполняется звукопоглощающим материалом полностью, то согласно п. 1.9, составляющие волнового сопротивления этого материала Wr, Wi могут выбираться по табл. 2 прил. 2.
3.9. Характерным размером сферического ОЗП является радиус сферы rсф. Для ОЗП другой формы характерным размером является эквивалентный радиус rэкв, который определяется из условия равенства объемов сферического ОЗП Vсф и ОЗП данной формы V.
Например, для ОЗП, имеющего форму куба, характерный размер — сторона куба , определяется из равенства объемов Vсф = Vк, где
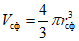


3.10. Расчет частотных характеристик , Aшт и радиуса зоны влияния (h) ОЗП производится на ЭВМ по программе, приведенной в прил. 1.
Скачать документ целиком в формате PDF
Методические указания Методические указания по проектированию земляного полотна (выемок) в легковыветривающихся скальных породах
ВСЕСОЮЗНЫЙ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
УТВЕРЖДАЮ:
Зам. Директора института
/Г. ХАСХАЧИХ/
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ПРОЕКТИРОВАНИЮ ЗЕМЛЯНОГО ПОЛОТНА (ВЫЕМОК) В ЛЕГКОВЫВЕТРИВАЮЩИХСЯ СКАЛЬНЫХ
ПОРОДАХ
Москва 1974
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ
1.
ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИЕ СВОЙСТВА ЛЕГКОВЫВЕТРИВАЮЩИХСЯ СКАЛЬНЫХ ПОРОД И
ОСОБЕННОСТИ ИРОЕКТИРОВАНИЯ откосов В
них
2.
РАСЧЕТ ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ВЫЕМОК
3.
ОЦЕНКА МЕСТНОЙ УСТОЙЧИВОСТИ
4.
ПРОЧНОСТНЫЕ ПАРАМЕТРЫ СКАЛЬНЫХ ПОРОД И МЕТОДЫ ИХ ОПРЕДЕЛЕНИЯ
5.
ВОЗМОЖНЫЕ ТИПОВЫЕ И ИНДИВИДУАЛЬНЫЕ РЕШЕНИЯ
6.
ХАРАКТЕР И ОБЪЕМ ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ
ПРИЛОЖЕНИЕ
1 МЕТОДИКА КЛАССИФИКАЦИИ ПОРОД ПО СТЕПЕНИ УСТОЙЧИВОСТИ К ВЫВЕТРИВАНИЮ
ПРИЛОЖЕНИЕ
2 МЕТОДИКА НАХОЖДЕНИЯ ОПТИМАЛЬНОГО ОЧЕРТАНИЯ ОТКОСОВ ВЫЕМОК
ПРИЛОЖЕНИЕ
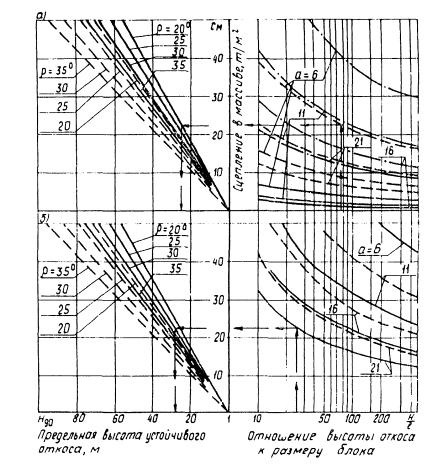
3 НОМОГРАММЫ ДЛЯ ОЦЕНКИ ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ВЫЕМОК
ПРИЛОЖЕНИЕ
4 ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАСЧЕТОВ ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ПО СХEME
IХ х
Приложение 5 ПОСЛЕДОВАТЕЛЬНОСТЬ
ВЫПОЛНЕНИЯ РАСЧЕТОВ ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ПО СХЕМЕ X 1
ПРИЛОЖЕНИЕ
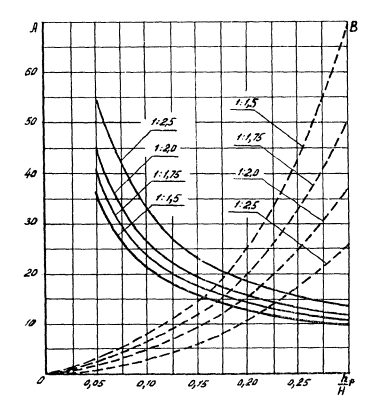
6 График для определения коэффициентов
А и В при расчете местной устойчивости
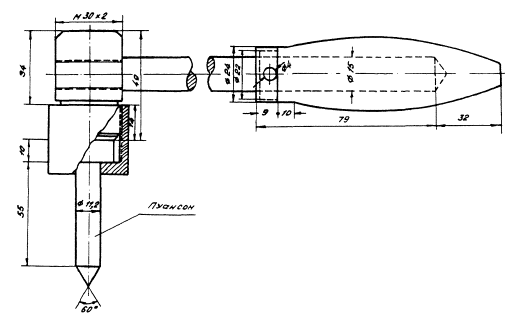
ПрИЛоженИе 7 Использование динамического
пробника для получения расчетных параметров ускоренным методом
Приложение 8 Значения ρТР при отсутствии
заполнителя по контактам поверхностей ослабления 1
ПРИЛОЖЕНИЕ 9 Значения СТР, при отсутствии
заполнителя по контактам поверхностей ослабления [2, 9]
Приложение 10 Примеры расчета общей
устойчивости откосов выемок
ЛИТЕРАТУРА
ПРЕДИСЛОВИЕ
Настоящие Методические указания разработаны в
развитие «Предложений по совершенствованию норм проектирования скальных
выемок» (ЦНИИС, 1968). Они освещают вопросы прогнозирования общей и
местной устойчивости откосов выемок в легковыветривающихся породах, получения
расчетных параметров, типового и индивидуального проектирования и др.
Приводимые количественные показатели расчетных параметров и значений
интенсивности выветривания являются ориентировочными и подлежат дальнейшему
уточнению по мере накопления опыта проектирования.
Методические указания
предназначены дня использования при проектировании выемок вновь строящихся дорог
и при разработке оздоровительных мероприятий на эксплуатируемых объектах.
Основные вопросы,
освещенные в методических указаниях, предварительно рассматривались в
Ленгипротрансе, Мосгипротрансе, Киевгипротрансе, Харгипротрансе и
Томгипротрансе, были одобрены и рекомендованы к изданию Главтранспроектом.
Методические указания
составлены в лаборатории конструкций земляного полотна кандидатами техн. наук
Ф.И. ЦЕЛИКОВЫМ, Е.А. ЯКОВЛЕВОЙ, А.И. ПЕСОВЫМ и инженерами А.М. ВОЛОДИНЫМ, Г.И.
КОКОВАШИНОЙ, Л.М. БИРЮКОВОЙ, Л.И. КУЗНЕЦОВОЙ.
ЗАМ. ДИРЕКТОРА
ИНСТИТУТА
/Г. ХАСХАЧИХ/
РУКОВОДИТЕЛЬ ОТДЕЛЕНИЯ
ЗЕМЛЯНОГО ПОЛОТНА И
ВЕРХНЕГО СТРОЕНИЯ ПУТИ
/Б. ЦВЕЛОДУБ/
1. ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИЕ СВОЙСТВА
ЛЕГКОВЫВЕТРИВАЮЩИХСЯ СКАЛЬНЫХ ПОРОД И ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ откосов В них
Характеристика
легковыветривающихся пород
1.1. Легковыветривающиеся породы (аргиллиты, алевролиты, глинистые
мергели и др.) обычно встречаются в различных сочетаниях между собой, а также
переслаиваются с более стойкими по отношению к выветриванию породами (песчаниками,
известняками, доломитами и др.).
1.2. Рассматриваемые породы, даже если они имеют первоначально
относительно высокую прочность, после обнажения в откосах начинают в
большинстве случаев быстро разрушаться (в пределах зоны активного воздействия
выветривания). При этом в поверхностных частях вскрытого массива образуется
преимущественно щебенисто-дресвяный или дресвяно-песчаио-пылевато-глинистый
материал.
1.3. С увеличением степени выветрелости пород прочность их и объемный вес
уменьшаются, а пористость и влажность возрастают.
1.4. Породы одного наименования могут иметь различную степень
устойчивости по отношению к выветриванию. Это объясняется комплексным влиянием
на степень устойчивости к выветриванию легковыветривающихся пород большого
числа, трудно поддающихся количественному учету различно воздействующих
факторов: состава и типа цемента, степени метаморфизма, химического и
минералогического составов и т.п.
Классификация пород
1.5. Основным показателем состояния пород в откосе следует считать их
отношение к переменному высушиванию и увлажнению. Методика определения этого
показателя приведена в приложении
1.
Поведение породы в
условиях переменного высушивания и увлажнения дает возможность прогнозировать
состояние откосов во времени,1 так как оно отражает совокупное
влияние на трудно поддающихся количественному учету факторов, определяющих
выветриваемосгь пород.
1. Имеющиеся общие инженерно-геологические
классификации предусматривающих регистрацию состояния пород на момент
обследования, но не увязаны с состоянием их (интенсивность выветривания) на
ближайшую перспективу [ 1,
2,
3,
4].
Разделение пород на слабо- и легковыветривающиеся в проектно-изыскательской
практике обычно не предусматривает четких количественных критериев для
отнесения пород к той или иной группе [ 5,
6,
7,
8].
1.6.
Разделение легковыветривающихся пород по степени устойчивости их к выветривания
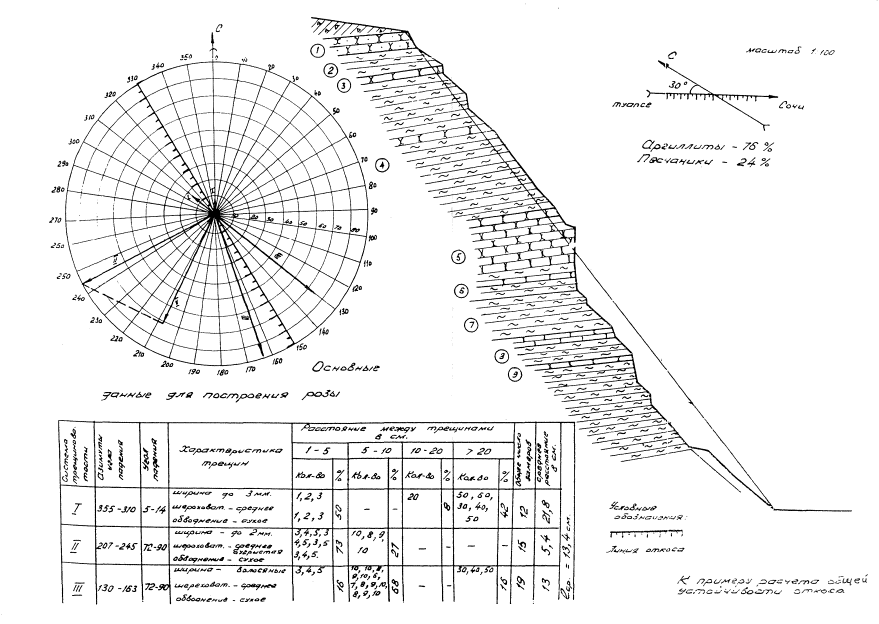
на группы представлено на рис, 1.
Рис. 1 . Зависимости потери образцов в весе (за счет фракций менее 10 мм) от
количества циклов высушивания — водонасыщения для различных по степени
устойчивости групп пород: QI , QII , QIII , QI V , QV — средние
значения потерь в весе пород соответствующих групп;
— границы
между группами
A) I группа — породы относительной
устойчивости
Б) II группа — породы средней устойчивости
B) III группа —
порода слабой устойчивости
Г) IV группа — породи неустойчивые
Д) V группа — породы
весьма неустойчивые
Методика
использования графика приведена в приложении 1 и в разделах 2
и 3.
1.7. Для каждой
выделенной группы пород по устойчивости их к выветриванию прогнозируется
вероятная мощность образования в них зоны выветривания во времени ( рис. 2) и
интенсивность осыпания продуктов выветривания с 1 м2 поверхности
откоса в зависимости от крутизны и литологии пород ( рис. 3).
Виды деформаций откосов выемок
1.8. Основными видами
деформаций откосов выемок и полувыемок в легковыветривающихся скальных породах
являются:
осыпи интенсивно
выветривающихся пород;
выпадение из откосов отдельных
глыб (обломков) пород более стойких к выветриванию (песчаников, известняков и др.), чем переслаивающие их
легковыветривающиеся породы;
обвалы из-за нарушения
общей устойчивости откосов;
оползни и сплывы сильно
выветрившегося поверхностного слоя коренных пород и делювиального покрова;
размывы откосов,
сложенных выветрившимися породами.
Особенности проектирования откосов в легковыветривающихся скальных
породах
1.9. В процессе
проектирования необходимо осуществлять прогнозирование (расчет) общей и местной
устойчивости откосов.
На основании полученных
результатов оценки общей и местной устойчивости можно установить оптимальную в
технико-экономическом отношении конфигурацию откосов по методике, приведенной в приложении
2.
1.10. Расчет общей
устойчивости необходим для оценки вероятности возникновения обвалов и оползней.
Определение местной устойчивости
требуется для прогнозирования интенсивности осыпания продуктов выветривания с
откосов в процессе эксплуатации и возможности появления сплывов, а также для
осуществления технико- экономического
сравнения вариантов и выбора оптимального очертания откосов.
|
|
Рис. 2. Зависимости изменения А) I группа — породы относительно Б) II группа — породы средней В) III группа — Г) IV группа — породы неустойчивые ( amax = 1,405 м/год) Д) V группа — породы |
|
|
Рис. 3 . Зависимости А) I группа — Б) II группа — породы средней В) III группа — Г) IV группа — породы неустойчивые |
1.11. Особенности проектирования откосов в
легковыветривающихся скальных породах связаны с тем, что массивы, в которых они
устраиваются, являются структурной анизотропной (неоднородной) средой, поэтому
к ним, как правило, не применимы основные расчетные методы, разработанные для
оценки устойчивости рыхлых грунтов.
Учет структурной анизотропии исключает (или весьма затрудняет)
возможность использования какого-либо универсального способа оценки общей
устойчивости откосов, вызывает появление множества расчетных схем, а также
необходимость определения большого количества различных параметров и требует
тщательной регистрация инженерно-геологических особенностей массива.
2. РАСЧЕТ
ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ВЫЕМОК
Расчетные схемы
2.1. Общую устойчивость откосов (при индивидуальном проектировании)
следует оценивать в зависимости от их очертания, характера и расположения
поверхностей ослабления (трещиноватости, слоистости) по отношению к
проектируемому откосу, группы пород по устойчивости к выветриванию (см. рис. 1) и
прочностных параметров.
2.2. При оценке общей устойчивости следует руководствоваться расчетными
схемами 1, представленными в табл. 1 и на рис. 4, где отражены
наиболее характерные условия, встречающиеся в практике. Расчет общей
устойчивости сводится к определению предельной высоты устойчивого откоса
заданной крутизны при принятом коэффициенте запаса.
1 В
основу предлагаемых схем положены рекомендации Фисенко Г.Л. [ 2,
9,
10]
и Савкова Л.В. [ 11,
12],
учтены при этом результаты обобщения и анализа других расчетных методов, а
также исследований, проведенных в ЦНИИСе.
Рис. 4 . Расчетные схемы общей
устойчивости:
1 — контур
поверхности сооружения
Таблица 1
|
№ расчетных схем |
Характеристика расчетных условий для определения |
Последовательность расчетов (расчетные формулы) |
Необходимые расчетные параметры |
Примечания |
|
I |
Откос вертикальный, расположение поверхностей ослабления |
|
С , ρ, γ0, |
Рис. Рис. 4 |
|
II |
Откос вертикальный, расположение поверхностей ослабления |
|
СТР , ρТР, γ0 |
Рис. Рис. 4 |
|
III |
Откос различной крутизны (α), |
|
СТР , ρТР, γ0 |
Рис. Рис. 4 |
|
IV |
Поверхность откоса совпадает с направлением поверхностей ослабления. |
|
СТР , ρТР, СМ, |
Рис. Рис. 4 |
|
V |
Откос более пологий, чем поверхности |
|
СТР , ρТР, СМ, |
Рис. Рис. 4 |
|
V I |
Наличие двух (или более) систем |
|
γ0 , ρТР, |
Рис. Рис. 4 |
|
V II |
Наличие двух (или более) поверхностей ослабления, падающих в сторону |
|
γ0 , ρстр (для двух систем поверхностей ослабления) |
Рис. Рис. 4 |
|
V III |
Наличие двух (или более) систем поверхностей ослабления, одна из |
|
СТР , ρТР, γ0, |
Рис. Рис. 4 |
|
I Х |
Откос различной крутизны (α) |
Последовательность расчетов приведена в Приложении Для ускоренных определений можно использовать график на рис. 5 (по имеющимся значениям H 90 , ρ и α определяется |
С , ρ, СМ, |
Рис. Рис. 4 |
|
Х |
Откос различной крутизны (α) |
Последовательность расчетов приведена в Приложении |
С , ρ, СМ, |
Рисунок Рис. 4 |
|
XI |
Откос различной крутизны (α) |
|
СТР , γ0, ρТР, |
Рис. β — угол наклона косогора Рис. 4 |
|
Х II |
Откос различной крутизны (α) |
Последовательность расчетов в этом случае такая же, как и в расчетной |
С , ρ, СМ, СТР, |
Рис. 4 |
|
Х III |
Откос различной крутизны (α) |
Последовательность расчетов в этом случае аналогична расчетам в схеме |
СМ = С, ρ, γ |
Рис. 4 |
Примечания.
1. Сдвиговые параметры по контактам более пологих
поверхностей ослабления обозначены в номограммах для этих расчетных схем через С1 и ρ .
2. ρ
— угол внутреннего трения в образце, град.;
ρТР — угол внутреннего трения
по контактам поверхностей ослабления, град;
С — сцепление образца, т/м2;
СМ — сцепление в массиве, т/м2,
СТР — сцепление по контактам
поверхностей ослабления, т/м2;
γ0 — объемный вес, т/м3;
σР — сопротивление отрыву по
системе трещин, наклоненных в сторону массива.
Высота проектируемого откоса не должна превышать ее значения, полученного
расчетом.
2.3. Для расчетных схем I — V III и Х I (см. рис. 4) в ЦНИИСе по специально
разработанным программам на ЭВМ произведены вычисления для различных сочетаний
практически встречающихся в природе значений расчетных параметров. Некоторые из
полученных результатов, оформленные в виде номограмм, представлены в приложении
3.
Характеристика расположения
поверхностей ослабления
2.4. В расчетных схемах, приведенных в табл.
1, под благоприятным понимается следующее расположение поверхностей ослабления:
горизонтальное;
наклонное в сторону массива (запрокинутое);
вертикальное;
наклонное в сторону откоса под углом, меньшим ρТР ;
расположение вкрест простирания с поверхностью откоса, за исключением
случаев, когда поверхности ослабления пересекают поверхность откоса под углом,
меньшим 30о, и одновременно имеют угол падения в направлении откоса,
превышающий ρТР.
2.5. Под неблагоприятным залеганием поверхностей ослабления понимается
наклонное расположение их в сторону откоса под углом, превышающим ρТР, а также
расположение вкрест простирания с поверхностью откоса, когда поверхности
ослабления пересекают поверхность откоса под углом, меньшим 30° и одновременно
имеют угол падения в направлении откоса, превышающий ρТР.
Учет обводнения
2.6. Гидростатическое и гидродинамическое давление при расчетах общей
устойчивости откосов в легковыветривающихся скальных породах в большинстве
случаев не учитывается, поскольку указанные породы, как правило, разбиты системами
трещин и поэтому имеют пологую депрессионную кривую подпора [ 2,
9].
2.7. Учет
гидростатического и гидродинамического давления рекомендуется осуществлять при
наличии возможности повышения пьезометрического уровня вода вследствие
частичной и полной закупорки трещин во внешней зоне откосов (например, из-за
забивки водоносных трещин льдом и т.п.).
2.8. Учет обводнения при
расчете общей устойчивости откосов сводится к тому, что в уравнении равновесия
призм возможного обрушения учитывается уменьшение нормальной составляющей Ni веса блоков (которыми эта призма условно разбивается при
расчете) на величину Δ Ni, равную
где
li
— длина поверхности обрушения на участке подтопленного блока;
Di — величина гидростатического давления в середине основания
каждого подтопленного блока 1.
1 По исследованиям Г.Л. Фисенко [2], суммарное
влияние фильтрационного потока (гидростатическое взвешивание и
гидродинамическое давление) на призму возможного обрушения проявляется как гидростатическое
давление, распределенное по поверхности скольжения (в зоне обводнения),
нормальное к ней и изменяющее только нормальную составляющую. На касательную
составляющую водное давление существенного влияния не оказывает.
Последовательность выполнения расчетов общей устойчивости откосов
2.9. Общая
последовательность расчетов при оценке устойчивости откосов выемок принимается
следующей:
на основании имеющихся
инженерно-геологических материалов, полученных и результате обследования
массива, в котором проектируется откос, строят розу устойчивости, которая
характеризует ориентацию поверхностей ослабления по отношению к проектируемому
откосу и дает возможность выявить наиболее опасные их системы. В зависимости от
сложности инженерно-геологических условий строят одну или несколько роз
устойчивости откоса. Образец ее построения приведен в приложении
10.
В зависимости от
характера расположения поверхностей ослабления по отношению к проектируемому
откосу, выявленному после построения роз устойчивости, устанавливают наиболее
опасный (с точки зрения устойчивости) участок по длине проектируемого откоса и
наиболее опасные системы поверхностей ослабления, располагающиеся
неблагоприятно по отношению к откосу, которые должны быть учтены при выборе
расчетной схемы;
с учетом расположения
поверхностей ослабления выбирают расчетную схему в соответствие с указаниями
табл. 1 и рис. 4;
определяют значения
расчетных параметров в соответствии с указаниями, изложенными в разделе
4. Принятие значения прочностных параметров С, ρ, СТР, ρТР, С M уменьшают на величину
коэффициента запаса устойчивости К,
который рекомендуется брать равным не менее 1,3, т.е.
для принятой крутизны
откоса, применительно к выбранной расчетной схеме, определяется предельная
высота устойчивого откоса (по формулам, приведенным в табл. 1 или в приложениях
4 и 5,
а также по номограммам в приложении
3 и на рис.
5 и 6 );
если полученная расчетом
высота устойчивого откоса НР
оказывается меньше проектной Нп,
то производят перепроектировку (изменение конфигурации) откоса и расчет
повторяют до тех пор, пока не будет обеспечиваться условие, при котором Нп < Н P.
2.10. В случаях, когда
инженерно-геологические условия удовлетворяют одновременно нескольким расчетным
схемам, определение общей устойчивости осуществляется по каждой из них и за
окончательный результат принимается тот, который дает наиневыгоднейшее
очертание откоса.
2.11. При наличии в
откосе слабых прослоек, расположенных выше его подошвы, необходимо осуществлять
дополнительную проверку общей устойчивости, ориентируясь на возможность
прохождения линии обрушения через указанные прослойки (применительно к одной из
схем, указанных в табл. 1).
Рис. 5 . Зависимость Н/Н90
от угла наклона откоса (α) при
разных значениях ρ.
Рис. 6. Предельная высота
устойчивого откоса при расчете no схеме Х (для некоторых
частных случаев);
1 — при β = -30°; 2 — при β =
-20°;
3 — при β = -10°; 4
— при β = 0°
5 — при β = +10° 6
— при β = +20°
3.
ОЦЕНКА МЕСТНОЙ УСТОЙЧИВОСТИ
Общие положения
3.1. Расчеты местной устойчивости производят для прогнозирования
возможности возникновения деформаций (осыпей, сплывов, промоин) и интенсивности
их проявления.
3.2 . Для осуществления расчетов местной устойчивости легковыветривающихся
скальных пород необходимо прежде всего классифицировать их по устойчивости к
выветриванию.
По графику на рис.
1 определяется группа пород, слагающих откос, в соответствии с
указаниями приложения
1. Для этого на графике фиксируется положение экспериментально
полученных значений отношения к переменному высушиванию и увлажнению
рассматриваемой породы и устанавливается осредненное расположение
экспериментальной кривой по отношению к линии средних значений указанного
отношения в группе, к которой она отнесена.
С этой целью вычисляется соотношение
|
|
(2) |
где
пФ.К — количество циклов высушивания и
увлажнения, при котором зафиксирован определенный процент потерь в весе
исследуемых образцов;
— количество циклов высушивания и увлажнения,
соответствующее тому же проценту потерь в весе для линии средних значений
отношения к переменному высушиванию и увлажнению в группе i ;
— количество циклов высушивания и увлажнения,
соответствующее 100 % потерь в весе для линии средних значений выделенной
группы;
К — количество сравниваемых значений процентов
потерь в весе.
Пример практического использования формулы (2) для вычисления соотношения
приведен в приложении
1.
3.3 . Расчет местной устойчивости для пород I — III и IV — V групп проводится по двум принципиально
различным методам, что обусловлено разной степенью раздробления пород этих
групп в процессе выветривания. В то время как породы I — III груш выветриваются преимущественно до состояния
каменисто-щебенисто-дресвяных фракций, породы IV — V групп — до состояния глинисто-пылевато-песчано-дресвяных фракций.
Помимо этого породы IV —
V групп характеризуются повышенной интенсивностью выветривания во времени и
отличаются значительной мощностью выветрелой зоны, в пределах которой в
перспективе их можно считать рыхлыми грунтами. Поэтому на эти породы при
расчетах устойчивости (как общей, так и местной) можно распространять те же рекомендации,
которые приняты для рыхлых грунтов.
Расчет местной устойчивости для пород I — III групп
3.4. Расчет местной
устойчивости для пород I
— III групп сводятся к
определению интенсивности поступления продуктов выветривания (объема осыпи) с
единицы поверхности откоса и величины отступления бровки откоса во времени. При
этом предполагается или периодически убирать продукты выветривания, или
оставлять их у подошвы откоса, что влияет на методику расчета.
3.5. Последовательность
расчетов при условии периодической уборки продуктов выветривания следующая:
по графику, приведенному
на рис. 3, для полученной по испытаниям на
переменное высушивание и увлажнение группы пород, вычисленной по формуле ( 2) величина соотношения и исходной (заданной)
крутизны откоса определяется величина интенсивности осыпания рассматриваемых
пород JαФ по выражению
|
|
(3) |
где
— среднее
значение интенсивности осыпания пород выделенной группы при заданной крутизне
откоса α, м3 /м 2 год;
по выражению (3) для
рассматриваемых пород и на основании рис. 3 строится зависимость интенсивности
осыпания от крутизны откоса
J αФ = f(α)
по полученному графику J αФ = f( α) определяют значения интенсивности осыпания по мере
уположения откоса и прежде всего — возможную интенсивность осыпания в первый
год после сооружения откоса заданной крутизны J αФ1 условно принимая
крутизну откоса в течение года неизменной, равной запроектированной или
фактически полученной после разработки;
вычисляют полную длину Z 1 образующей откоса в первый год его существования по выражению
|
|
(4) |
где
Н1 и α1
— первоначальные (проектные или фактически полученные) значения высоты и
крутизны откоса соответственно;
определяют объем осыпи с 1 пог. м длины откоса (вдоль подошвы) за первый
год его существования по выражению
|
|
(5) |
Объем осыпи, накопившейся в течение первого года с 1 пог. м откоса,
приводится к объему породы в плотном состоянии по выражению
|
|
(6) |
где
КР — коэффициент разрыхления, который может
быть принят равным 1,5;
вычисляют размер отступления бровки откоса выемки l α1 н а
первый год по выражению
|
|
(7) |
определяют новый (более пологий) угол наклона откоса
после его годичного существования по выражению (рис. 7)
|
|
(8) |
где
ε1 — величина уплотнения откоса за первый год
его существования.
Рис. 7. Схема в расчету уположения откоса во времени
(за счет осыпания продуктов выветривания)
Затем (для второго года эксплуатации) вычисления повторяют в той же
последовательности при принятии в качестве исходного угла α1 — ε1
и т.д.
3.6. При оставлении осыпи у подошвы откоса выемки последовательность
расчета поступления продуктов выветривания и величины отступания бровки откоса
во времени принципиально остается такой же, какой она указана в п. 3.5. Однако
расчетная высота откоса, с которой возможно в последующем поступление продуктов
выветривания, уменьшается на высоту осыпи, ежегодное возрастание которой Δh делается по формуле (13).
|
|
(9) |
где
h — высота осыпи в предшествующем году (см.
рис. 7);
α — крутизна откоса в предшествующем году;
lα — величина
отступания бровки откоса в рассматриваемом году;
Н — расчетная высота откоса;
КР — коэффициент разрыхления;
αос — угол наклона откоса осыпи (ориентировочно 35
— 40°);
ε — величина уположения откоса в рассматриваемом году.
При наличии в пределах
проектируемого откоса толщи переслаивающихся пород, имеющих различную
устойчивость по отношению к выветриванию, целесообразно осуществлять построение
графика J αФ = f( α) по описанному
в п. 3.5. методу для каждой литологической разности, а в качестве расчетного
для всего откоса приникать выражение J αФ = f( α),
осредненное (взвешенное) по мощности переслаивающихся пород.
Расчет местной устойчивости для пород IV — V групп
3.7. Проверка местной
устойчивости откосов в породах IV
— V групп заключается в определении вероятности образования на них
поверхностных сплывов выветрелого до состояния мелкозема грунта, что
оценивается величиной коэффициента местной устойчивости.
3.8. Последовательность
расчетов местной устойчивости в этом случае принимается следующей;
для полученной по
испытаниям на переменное высушивание и увлажнение группы пород, по величине
соотношения и расчетного срока
существования относа t вычисляется
мощность прогнозируемой зоны выветривания mtФ
по выражению
|
|
(10) |
где
— среднее
значение мощности зоны выветривания выделенной группы i на расчетный срок существования откоса, и определяемое по
графику на рис. 2;
оценивается
местная устойчивость выветрелого слоя путем определения величины Кместн,
в условиях избыточного
увлажнения (возникающего, например, весной при оттаивании грунта, осенью и летом после затяжных или ливневых дождей) по формуле (14).
|
|
(11) |
где
n = ctg α —
заложение относа;
γ0
— обменный вес выветрелого грунта, т/м3;
α — крутизна откоса, град;
ρ — угол
внутреннего трения выветрелого слоя грунта, град;
С — сцепление
этого же грунта, т/м2;
Н — высота откоса, м;
А и В — безразмерные
коэффициенты, определяемые в зависимости от отношения по специальный
графикам в приложении
6;
hP — глубина зоны возможного сплывообразования, принимается
равной 0,4 — 0,8 м [14].*
* Расчет производится в той же
последовательности, как и для откосов в обычных (рыхлых) грунтах в связи с
указаниями п. 3.3,
a также с учетом, что при индивидуальном проектировании очертание
откосов в пределах I — V групп не следует делать круче 1:1,5 (см. раздел 5)
4.
ПРОЧНОСТНЫЕ ПАРАМЕТРЫ СКАЛЬНЫХ ПОРОД И МЕТОДЫ ИХ ОПРЕДЕЛЕНИЯ
Перечень параметров
4.1. Основными
параметрами при расчетах общей устойчивости откосов являются: ρ , ρтр, С; СМ,
СТР (значения параметров см. в табл. 1).
4.2. Основными
(дополнительно к указанным выше) параметрами при расчетах местной устойчивости
легковыветривающихся скальных откосов являются:
J — интенсивность осыпания с 1 м2 поверхности откоса
различной крутизны, ;
КР — коэффициент разрыхления, принятый в среднем равный
1,50.
Численные значения ρ и С
4.3. Для получения численных значений сцепления С и угла внутреннего трения ρ
легковыветривающихся скальных пород необходимо произвести соответствующие
испытания образцов пород.
Эти испытания в основном сводятся или к сдвигу со сжатием в наклонных
матрицах по методике ВНИМИ [15],
или же к раскалыванию пластин и раздавливанию образцов полуправильной формы,
широко используемому в ИГД им. Скочинского
[16].
По результатам проведенных испытаний строится так называемый паспорт
прочности породы — зависимость напряжения сдвига от напряжения сжатия ( рис. 8). При
использовании методики ВНИМИ паспорт
прочности получается графоаналитическим путем [ 9,
15]. При раскалывании пластин и раздавливания образцов полуправильной формы
применяют расчетный прием построения огибающей к предельным кругам напряжений
Мора, разработанные М.М. Протодьяконовым [16,
1 7].
4.4. Значения С и ρ при наличии паспорта прочности
обычно определяют графически следующим построением [ 1 7]:
из начала координат проводят два луча под углами 30 и 50°к оси τ (см. рис. 8);
через точки пересечения лучей с огибающей проводят секущую;
отрезок, отсекаемый секущей на оси τ,
считая от начала координат, дает величину С,
а угол, образуемый ею с горизонталью, —ρ,
Для получения достаточно надежных расчетных значений указанных параметров
такие определения целесообразно выполнять с необходимой повторностью (не менее
чем с трехкратной) и осуществлять статистическую обработку полученных
результатов.
4.5. Ориентировочные значения расчетных величин угла внутреннего трения в
образцах, отобранных в массиве для некоторых легковыветривающихся пород и
переслаивающих их литологических разностей, составляют, град.:
Аргиллиты 29
— 32
Алевролиты 31
— 33
Мергели глинистые 30
Мергеля известковые 32
Песчаники 34
— 38.
4.6. Приблизительное
значение расчетных величин сцепления в образце можно определить двумя
способами:
1) по выражению
|
|
(12) |
где
σсж — сопротивление образцов на одноосное сжатие (с
соотношением высоты к ширине, равным 1,5 ÷ 2:1);
2) по графику на рис. 9, на
котором значение С берется в
зависимости от относительной механической прочности, определяемой по
динамическому пробнику, краткое описание и способ пользования которым приведены
в Приложении
7.
Определение ρТР
и СТР
4.7. Значения ρТР
при отсутствии заполнителя по контактам поверхностей ослабления назначаются по
таблице приложения
8 в зависимости от характера поверхностей ослабления. При возможности
обводнения поверхностей контактов указанные в этой таблице значения ρТР
уменьшается на 2-4°.
4.8. При наличии
заполнителя трещин расчетные значения ρТР
принимаются по графику на рис. 10 в зависимости от влажности заполнителя и
шероховатости стенок поверхностей ослабления.
4.9. Расчетные значения СТР при отсутствии заполнителя назначаются по
таблице приложения
9. При наличии заполнителя расчетные значения СТР определяется по графику на рис. 11 в зависимости от влажности и
характера заполнителя.
Рис. 8. Пример построения для получения значений С и ρ в образце;
1 — паспорт прочности
(огибающая к кругам Мора);
2 — луч под углом 80° к ocи τ;
3 — луч под углам 50° к
оси τ
4 —
секущая, проведенная через точки пересечения лучей с огибающей
Рис. 9. Корреляционная зависимость R ОТН от С (по данным ЦНИИСа)
Рис. 10 . Зависимость угла внутреннего
трения по контактам
поверхностей ослабления ρТР от влажности заполнителя:
1 — поверхности ослабления шероховатые
2 — поверхности ослабления гладкие
Рис. 11 . Зависимость сцепления по
контактам поверхностей ослабления СТР
при наличии заполнителя трещин от влажности заполнителя
4.10. При отсутствии
сведений о заполнителя трещин, его влажности и шероховатости стенок
поверхностей ослабления принимается наиболее неблагоприятное из реально
возможных сочетаний расчетных параметров ρТР
и СТР, (т.е. поверхности
считаются гладкими, допускается наличие заполнителя, учитывается возможность
его увлажнения).
Угол внутреннего трения и сцепление в массиве
4.11. Значения угла внутреннего
трения в массиве (при направлении поверхностей обрушения поперек к поверхностям
ослабления) принимается равными значениям угла внутреннего трения в образце,
т.е. ρМ = ρ.
4.12.
Сцепление в массиве СМ
рекомендуется определять по формуле 1
|
|
(13) |
где
С — сцепление в образце, т/м2;
Н — проектная высота откоса, м;
а — коэффициент,
определяемый по графику на рис. 12 в зависимости от Сх;
СТР — сцепление по контактам поверхностей ослабления,
т/м2;
l —
осредненная блочность пород в массиве, м
|
|
(14) |
где
|
|
(15) |
l1 , l2 ….. ln — средние расстояния между трещинами первой, второй и п-й систем, м.
1 . С целесообразно определять посредством опытных
сдвигов в натурных условиях по имеющимся методикам [ 18,
19].
х График зависимости α = f (с) построен по материалам полевых
исследований ЦНИИСа и соответствует последним данным ВНИМИ.
Рис. 12 . Зависимость коэффициента a от величины сцепления в
образце (по данным ЦНИИСа)
Размер и форма
элементарных структурных блоков определяются обычно тремя наиболее характерными
системами трения.
Некоторые особенности выбора расчетных параметров скальных пород
4.13. Обычно различные литологические равности
легковыветривающихся пород встречаются во всевозможных сочетаниях между собой и с переслаивающими их более прочными
и устойчивыми к выветриванию породами. В связи с этим при расчетах по схемам I, IV, V, IХ, X, Х III,
в которых поверхность обрушения на каком-либо участке пересекает вкрест
поверхности ослабления, параметры принимаются или по наиболее слабым
разновидностям пересекаемых пород (в запас безопасности), или средневзвешенными
по мощности пересекаемых литологических равностей (что более правильно, но
требует тщательных инженерно-геологических исследований).
4.14. При определении
величины сдвиговых параметров для расчетов по схеме Х III (использующейся для пород IV —
V групп) необходимо учитывать возможность избыточного увлажнения грунта выветрелой
зоны, мощность которой определяется в соответствии с указаниями п. 3.9. При
выборе расчетных значений ρ и С следует использовать
результаты сдвиговых испытаний паст, приготовленных из рассматриваемых пород. В
этом случае ρ = φ — углу внутреннего трения рыхлых
грунтов.
4.15. При расчетах по
схеме V III сопротивление на разрыв по трещинам δР обычно
принимается равным нулю (в запас устойчивости).
4.16. Объемный вес пород γ0 определяют
по справочникам [20]
или по данным лабораторных определений согласно выражению
,
где
Р — вес образца, г;
W — объем
образца, см3.
При этом объем образцов
неправильной формы может быть определен измерением объема вытесненной воды при
погружении в нее образца. Перед погружением в воду образцы неводостойких пород
следует покрывать тонкой водонепроницаемой пленкой (например, клеем БФ и т.п.).
5.
ВОЗМОЖНЫЕ ТИПОВЫЕ И ИНДИВИДУАЛЬНЫЕ РЕШЕНИЯ
Общие принципы проектирования откосов
5.1. При установления
рациональных очертаний откосов выемок можно исходить из двух основных
принципов:
1) обеспечения общей и
местной устойчивости;
2) обеспечения общей
устойчивости с одновременным, частичным допущением осыпей, вызванных нарушением
местной устойчивости (при соответствующем технико-экономическом обосновании
целесообразности такого решения, методика осуществления которого приведена в приложении
2).
5.2. Возможны следующие
конструктивные решения, применительно к типовому и индивидуальному
проектированию:
пологие откосы крутизной,
равной углу естественного откоса образующихся на них продуктов выветривания
(1:1,25 — 1:1,5) с кюветом, закюветней полкой или кювет-траншеей.
крутые откосы (в пределах
1:0,5 — 1:1) с кювет-траншеей для сбора продуктов выветривания, поступающих с
откоса, или с улавливающей стеной, выполняющей те же функции;
крутые откосы с кюветом
или лотком при защите откосов при выветривания какими-либо покрытиями;
крутые откосы (вплоть до
вертикальных) с широкими полками, рассчитанными на размещение продуктов
выветривания в процессе всего периода существования откоса до его
самоуположения на всю высоту,
комбинированные
конструктивные решения:
откосы ломаного очертания
(выпуклого или вогнутого — в зависимости от состава пород и их расположения по
высоте откоса);
защищенные от выветривания
участки по высоте и длине откосов, чередующиеся с неукрепленными, и др.
5.3. Выбор конструкции
откоса определяемся степенью общей и местной устойчивости слагающих его пород,
высотой проектируемого откоса и технико-экономическими показателями.
Типовое проектирование
5.4. Сферы типового
проектирования для различных групп пород, с указанием конструктивных
особенностей типовых решений, приведены в табл. 2.
Таблица 2
|
Группа пород по степени устойчивости к |
Условия применения типового проектирования |
Конструктивные особенности типовых решений |
|
V — I V |
Благоприятное расположение поверхностей ослабления. Высота Н не свыше 12 м |
Крутизна откоса 1:1,5. Откосы укрепляются травосеянием по слою |
|
III — II |
Благоприятное расположение поверхностей ослабления. Высота откоса Н не свыше 16 м |
Крутизна откоса 1:1,25. При высоте откоса Н ≤ 6 м у подошвы его устраивается кювет и закюветная полка |
|
I |
Такие же, как для пород I — II |
Крутизна откоса 1:0,5-1:1. У подошвы откоса устраивается |
Примечание . В элювиально-делювиальном
слое заложение откосов во всех типовых конструкциях принимается не круче 1:1,5.
ИНДИВИДУАЛЬНОЕ ПРОЕКТИРОВАНИЕ
5.5. Область
индивидуального проектирования охватывает все сочетания инженерно-геологических
и проектных условий, выходящие за рамки типового проектирования
(неблагоприятное расположение поверхностей ослабления, высота откосов более 12
— 16 м, наличие обводнения и др.).
5.6. При индивидуальном
проектировании очертания откосов определяют, исходя из необходимости
обеспечения их общей устойчивости, и уточняют на основании оценки местной
устойчивости — для возможности выбора оптимальной в технико-экономическом
отношении конфигурации их (в соответствии с Приложением 2). Для пород V — IV очертания откосов не
следует назначать круче 1:1,5.
5.7. при индивидуальном
проектировании выемок следует учитывать, что по технико-экономическим
показателям предпочтительнее других конструктивных решений могут быть:
крутые откосы (вплоть до
вертикальных) с уширенными полками, рассчитанными на размещение продуктов
выветривания при самоуположении откосов, — для выемок высотой 6 — 8 м и
полувыемок на косогорах не круче 1:2;
крутые откосы с траншеями
у подошвы — для прорезных выемок большой глубины и полувыемок на крутых
косогорах;
крутые откосы,
укрепленными защитными покрытиями, — для полувыемок на косогорах при
значительной стоимости разработки скальных пород.
6. ХАРАКТЕР И ОБЪЕМ ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИХ ИССЛЕДОВАНИЙ
6.1. Полный комплекс
инженерно-геологических обследований, необходимых для оценки общей и местной
устойчивости откосов выемок в легковыветривающихся скальных породах, включает в
себя определение следующих показателей:
наименование пород, их
размещения и процентного содержания в пределах проектируемого откоса;
ориентация поверхностей
ослабления;
генезиса поверхностей
ослабления;
качественной
характеристики трещиноватости (характера заполнения трещин, степени
шероховатости стенок, обводнения, изменчивости трещин в зависимости от
пересечения различных литологических разностей, протяженности и выдержанности
направлений трещин);
количественной оценки
трещиноватости (числа трещин каждой системы, приходящихся на 1 пог. м в
направлении, перпендикулярном плоскости трещин, определение блочности по формуле (15);
объемного веса γ0 ;
сопротивления одноосному
сжатию δс ж;
сцепления и угла
внутреннего трения в монолите (образце) С
и ρ;
оцепления с учетом
структурного ослабления в массиве СМ;
сцепления и угла
внутреннего трения по контактам поверхностей ослабления СТР и ρТР;
отношения к переменному
высушивания и увлажнения.
Методы осуществления
различиях видов инженерно-геологических обследований приведена в соответствующих
пособиях и методических указаниях [ 21,
22,
23].
Сведения о способах
определения механических характеристик даны также в разделе
4 настоящей работы.
6.2. Объем
инженерно-геологических обследований применительно к конкретным расчетным схемам
может быть значительно сокращен по сравнению с полным комплексом, приведенным в
п. 6.1.
Перечень необходимых
определений из указанного комплекса при различных расчетных схемах общей
устойчивости (с учетом необходимости оценки местной устойчивости} приведен в
табл. 3.
6.3. Некоторые
инженерно-геологические характеристики можно уточнять в процессе разработки
выемок. Если при этом выявится несоответствие первоначально принятым условиям,
то необходима дополнительная проверка устойчивости откосов и корректировка
проектных решений.
Таблица 3
|
Расчетные схемы и |
Перечень необходимых определений |
||||||||||
|
Наименование пород и их содержание в откосе, % |
γ0 |
σж |
Ориентация трещин в |
количественная оценка |
С |
ρ |
СМ |
СТР |
ρТР |
Отношение к переменному |
|
|
Схема I |
|||||||||||
|
σсж ≥ 400 кг/см2 |
+ |
— |
+ |
+ |
— |
— |
— |
— |
— |
— |
+ |
|
σсж < 400 кг/см2 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
— |
+ |
|
Схема II |
+ |
+ |
— |
+ |
+ |
— |
— |
— |
+ |
+ |
+ |
|
Схема III |
+ |
+ |
— |
+ |
+ |
— |
— |
— |
+ |
+ |
+ |
|
Схема I V |
|||||||||||
|
σсж ≥ 400 кг/см2 |
+ |
— |
+ |
+ |
— |
— |
— |
— |
— |
— |
— |
|
σсж < 400 кг/см2 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Схема V |
|||||||||||
|
σсж ≥ 400 кг/см2 |
+ |
— |
+ |
+ |
— |
— |
— |
— |
— |
— |
+ |
|
σсж < 400 кг/см2 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Схема V I |
+ |
+ |
— |
+ |
+ |
— |
— |
— |
+ |
+ |
+ |
|
Схема V II |
+ |
+ |
— |
+ |
+ |
— |
— |
— |
+ |
+ |
+ |
|
Схема V III |
+ |
+ |
— |
+ |
+ |
— |
— |
— |
+ |
+ |
+ |
|
Схема I Х |
|||||||||||
|
σсж ≥ 400 кг/см2 |
+ |
— |
+ |
+ |
— |
— |
— |
— |
— |
— |
+ |
|
σсж < 400 кг/см2 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Схема Х |
|||||||||||
|
σсж ≥ 400 кг/см2 |
+ |
— |
+ |
+ |
— |
— |
— |
— |
— |
— |
+ |
|
σсж < 400 кг/см2 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Схема Х I |
+ |
+ |
— |
+ |
+ |
— |
— |
— |
+ |
+ |
+ |
|
Схема Х II |
+ |
+ |
+ |
— |
— |
+ |
+ |
+ |
+ |
+ |
+ |
|
Схема Х III |
+ |
+ |
— |
— |
— |
+ |
+ |
— |
— |
— |
+ |
Примечание.
1. знак «+» показывает необходимость
выполнений определений, а знак «минус» -отсутствие такой
необходимости.
2. При σсж ≥ 400 кг/см2 (что
соответствует примерно С ≥ 100 кг/см2) при
благоприятном расположении поверхностей ослаблений откосы устойчивы при Н ≤ 60 м
ПРИЛОЖЕНИЕ
1
МЕТОДИКА КЛАССИФИКАЦИИ ПОРОД ПО СТЕПЕНИ УСТОЙЧИВОСТИ К ВЫВЕТРИВАНИЮ
Отбор образцов
Из участков массива,
прорезаемого откосам выемки (проектируемой или существующей), отбирают образцы
пород произвольной формы весом от 100 до 300 г каждый.
Образцы отбирают из
подошвенной, средней и верхней частей откоса в количестве не менее трех по
каждому из поперечников (при наличия однородного сложения толщи). Расстояние
между поперечниками, в случае выдержанности элементов залегания пород,
принимается равным 150 — 200 м. При изменчивости и невыдержанности элементов
залегания расстояние между поперечниками уменьшается до 25 — 50 м.
В случае переслаивания
различных пород по высоте проектируемого откоса образцы отбирают из каждой
литологической разности.
Отбор образцов
осуществляется из кернов или из обнажения пород.
Испытание образцов
При испытании отобранных
образцов на высушивание-увлажнение их ставят в фарфоровых или стеклянных чашках
в сушильный шкаф и выдерживают при температуре 105°С примерно 7 — 8 ч. Затем их
вынимают из шкафа, взвешивают и заливают водой, в которой выдерживают не менее
7 — 8 ч.
После слива воды через
фильтр (чтобы задержать мелкие частицы) образцы вновь ставят в сушильный шкаф 1.
Далее процесс (цикл) повторяется.
1 При отсутствии сушильного шкафа процесс
высушивания при испытании можно осуществлять в лабораторных условиях (при
комнатной температуре). При этом целесообразно увлажненную породу рассыпать на
бумагу или металлический лист и т.п.), что ускоряет просушивание. Длительность
процесса высушивания в этом случае составляет не менее 15 ч.
После определенного числа
циклов (3 — 5) следует производить просев образцов через сито с ячейками 10 мм
(с водой ила в сухом состоянии). Прошедшие через сито частица высушиваются (в
случае просеивания с водой) и взвешивают с точностью до 0,01 г,
Затем вычисляют потерю в
весе исследуемого образца, которая равняется отношению веса частиц, прошедших
через сито с ячейками 10 мм, к первоначальному весу образца (в процентах).
Общее количество циклов испытаний определяется степенью устойчивости
исследуемой порода к высушиванию-увлажнению. При неустойчивых породах
достаточно ограничиться несколькими циклами, чтобы получить потери образцов в
весе, достигающие 100 %. В устойчивых породах потери в весе, равной 100 %,
может вообще не наступить, поэтому в этих случаях испытания можно ограничить 30
— 40 циклами.
Обработка результатов
По потере образцов в
весе, в зависимости от количества циклов высушивания-увлажнения, строится
график в координатах Q = f(п),
где Q.- потеря образцов в весе, %;
п — количество
циклов высушивания и увлажнения.
Полученная зависимость
сопоставляется (совмещается) с графиком, приведенном на рис. 1 настоящих
Методических указаний; определяется группа пород по степени устойчивости к
выветриванию. При этом необходимо определять также положение полученной
зависимости по отношению к линии средних значений потерь в весе рассматриваемой
группы по соотношению
|
|
(1) |
где — количество циклов,
соответствующе 100 % потерь для линии средних значений группы. Применительно к I и II группам пород
по рис. 1 в разделе 1 вместо принимается
количество циклов, соответствующее наибольшему значению потерь, показанному на
графике;
пфк — количество циклов высушивания и
увлажнения, при котором зафиксирован определенный процент потерь в весе
исследуемого образца;
— количество циклов высушивания и
увлажнения, соответствующее тому же проценту похерь в весе для линии средних
значений в группе l (см. рис.
1 в разделе 1);
К — количество сравниваешь значений
процентов потерь в веса образца ( Qin).
Пример
В
результате проведения опытов на высушивание и увлажнение с какой-либо породой
получена следующая зависимость: Q = f ( n)
|
пфк |
4 |
8 |
12 |
16 |
20 |
24 |
|
Qin |
5 |
10 |
40 |
60 |
70 |
80 |
После сопоставления этой
зависимости с графиком на рис. 1 можно заключить, что исследуемая порода
относится к III группе.
Полученным из опыта значениям процентов потерь в весе соответствует следующее
количество циклов по линии
средних значений QIII К.
|
|
3 |
6 |
13,5 |
16,3 |
17,6 |
19,2 |
|
QIII К |
5 |
10 |
40 |
60 |
70 |
80 |
По указанной
выше формуле (1) находим отношение . В рассматриваемом примере % = 6 (шесть сравниваемых величин
процентов потерь породы в весе при просеивании через сито 10 мм: 5, 10, 40, 60,
70, 80 %; = 22 цикла.
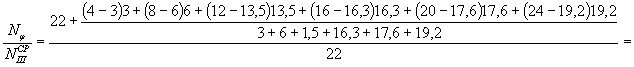
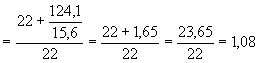
Второй член числителя в
формуле для определения (в нашем примере он
равен +1,65) показывает, на сколько сместится экспериментальная зависимость Q = f ( n ) от линии средних значений. В рассматриваемом случае она сместится правее линии средних
значений QIII. При этом сдвиг
вправо составит в среднем 1,65 цикла (т.е. 1,65 n) в каждой
сравниваемой точке, что можно использовать при нанесении осредненного очертания
полученной опытным путем зависимости а
= f( n). Если бы этот член получился
отрицательным, то осредненное очертание экспериментальной зависимости
сместилось бы левее линии средних значений QIII на соответствующую величину циклов. Таким образом, если > 1 — то
экспериментальная зависимость пройдет правее от линии средних значений, если < 1 — то левее;
при = 1 экспериментальная
зависимость совпадает с линией средних значений.
Для определения
интенсивности осыпания следует JIII (см. рис. 2)
разделить на полученное соотношение, т.е. умножить на отношение = 0,925.
Аналогичным образом это
соотношение используется при определении мощности коры выветривания (применительно
к та на рис. 3).
ПРИЛОЖЕНИЕ
2
МЕТОДИКА НАХОЖДЕНИЯ ОПТИМАЛЬНОГО ОЧЕРТАНИЯ ОТКОСОВ ВЫЕМОК
При назначении
оптимальных в технико-экономическом отношении очертаний откосов следует
исходить из условий обеспечения их общей устойчивости и такого сочетания
строительных и эксплуатационных расходов, которые бы ( с учетом отдаленности затрат) были минимальными.
Чем круче запроектированы
откосы (при обязательности сохранения их общей устойчивости), тем меньше
строительная стоимость разработки выемки, но тем больше затраты, связанные с
необходимостью уборки осыпающихся продуктов выветривания в процессе
эксплуатации.
Для возможности
сопоставления суммарных строительных и эксплуатационных затрат в
рассматриваемых вариантах с учетом отдаленности во времени рекомендуется
сравнивай так называемые приведенные расходы, определяемые по формуле [24].
|
|
(1) |
где Σ np — приведенные суммарные
строительные и эксплуатационные расходы;
Kt u Э t — соответственно
капиталовложения и эксплуатационные расходы в соответствующем году t;
—
коэффициент приведения (отдаленности), учитывающий уменьшение значимости
затрат, совершаемых через t лет;
tc — год, ограничивающий период суммирования расходов по
рассматриваемым вариантам;
Енп — норматив для приведения разновременных затрат, установленный
в размере 0,08 [25].
В общую сумму затрат по
указанной формуле включаются и первоначальные капиталовложения (как затраты
первого этапа), условно относимые к
нулевому году эксплуатация, т.е. принимаемые с коэффициентом приведения, равным
1.
При рассмотрении приведенных расходов применительно к скальным выемкам
под капитальными затратами понимается строительная стоимость сооружения 1 пог.
м продольной длины выемки, а эксплуатационные расходы складываются из стоимости
уборки осыпающихся продуктов выветривания с 1 пог. м длины откосов (вдоль
выемки).
Период суммирования приведенных затрат ограничивается двадцатью годами.
При этом интенсивность осыпания продуктов выветривания с откосов заданной
крутизны и интенсивность отступания бровки откосов выемки (степень уположення
откосов во времени) подсчитывают при сравнении вариантов в соответствии с
рекомендациями, изложенными в разделе 3.
По указанной методике производится сравнение различных конструктивных
вариантов (в том числе откосов, защищенных от выветривания различными
покрытиями, откосов с уширенными полками, рассчитанными на самоуположение их и
размещение продуктов выветривания в процессе эксплуатации и др.).
ПРИЛОЖЕНИЕ
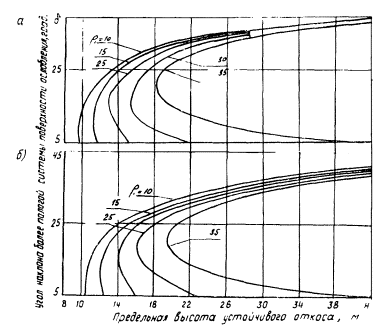
3
НОМОГРАММЫ ДЛЯ ОЦЕНКИ ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ВЫЕМОК
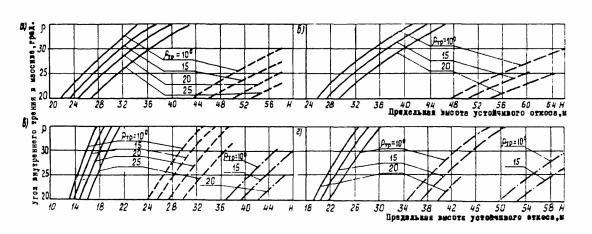
Рис. 1 . Номограммы для определения
предельной высоты устойчивого вертикального откоса при благоприятной
расположении поверхностей ослабления (расчетная схема I ):
а С =
100 т/м2; С =
600 т/м2;
С = 1100 т/м2;
б — — С
= 1600 т/м2; —— — С =
2100 т/м2;
— γ0δ
= 2,5 т/м3; —— — γ0δ
= 2,0 т/м3
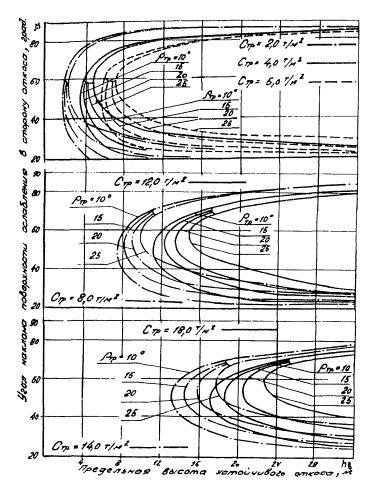
Рис. 2. Номограммы для определения
предельной высоты устойчивого вертикального откоса при неблагоприятном
расположении поверхностей ослабления (расчетная схема II )
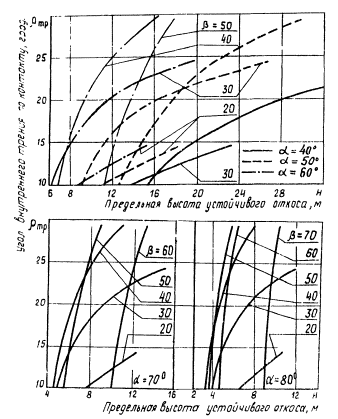
Рис. 3 . Номограммы для определения
предельной высоты устойчивого откоса различной крутизны при неблагоприятной
расположении поверхностей ослабления (расчетная схема III ):
СТР = 2 т/м2; γ0 = 2,5 т/м3
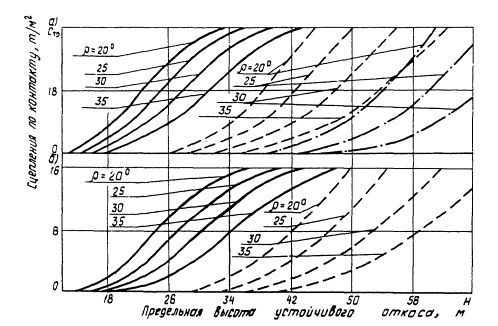
Рис 4. Номограммы для определения
предельной высоты устойчивого откоса
при неблагоприятном расположении поверхностей ослабления и совпадении их с
откосом (для некоторых расчетных сочетания)
(расчетная
схема I V):
— СМ
= 10 т/м2; — СМ
= 20 т/м2; — • — — СМ
= 30 т/м2;
а — β
= 50°; ρТР = 10°; γ0 = 2,5 т/м3;
б — β
= 50°; ρТР = 15°; γ0 = 2,5 т/м3;
Рис. 5. Номограммы для определения предельной
высоты устойчивого откоса при неблагоприятном расположении поверхностей
ослабления и при откосе более пологом, чем плоскости ослабления (для некоторых
расчетных сочетаний) (расчетная схема V):
— См
= 10 т/м2;
СМ
= 20 т/м2; — • — — СМ = 30 т/м2;
а — β
= 60°; СТР
= 0; α = 50°; γ0
= 2,5 т/м2;
б — β
= 60°; CСР
= 4 т/м2; α = 50°; γ0
= 2,5 т/м2;
в — β
= 60°; СТР = 0; α = 60°; γ0
= 2,5 т/м2;?
г — β
= 60°; СТР = 4 т/м 2; α = 60°; γ0
= 2,5 т/м2;?
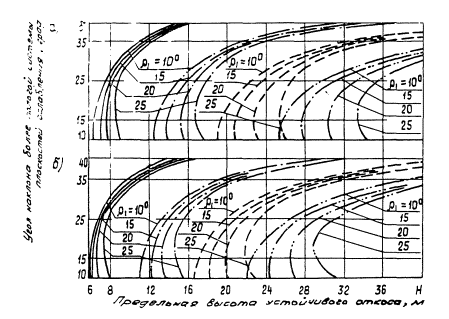
Рис, 6 . Номограммы для определения
предельной высоты устойчивого откоса при наличии двух или более систем
поверхностей ослабления, падающих в сторону откоса под различными углами, одна
из которых совпадает с откосом (для некоторых расчетных сочетаний) (расчетная
схема V I ):
а — β
= 50°; ρТР
= 10°; СТР = 0; γ0
= 2,5 т/м3;
б — β
= 50°; ρТР = 15°; СТР = 0; γ0
= 2,5 т/м3;
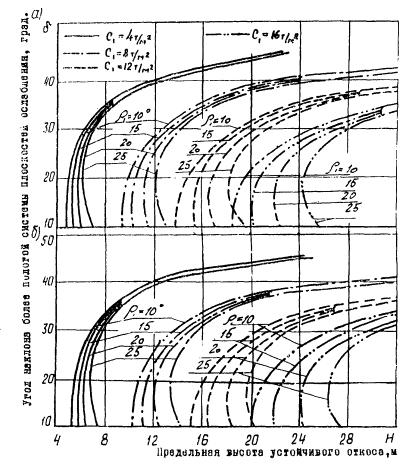
Рис. 7. Номограммы для определения
предельной высоты устойчивого откоса при наличии двух или более систем
поверхностей ослаблений, падающих в сторону откоса под различными углами, одна
из которых совпадает с откосом (для некоторых расчетных сочетаний) (расчетная
схема I ):
а — β
= 50°; ρТР
= 25°; СТР = 0; γ0
= 2,5 т/м3;
б — β
= 50°; ρТР = 20°; СТР = 0; γ0
= 2,5 т/м3;
— С1
= 4 т/м2; — • — — С1
= 8 т/м2; — — — — С1
= 12 т/м2;
С1
= 16 т/м2
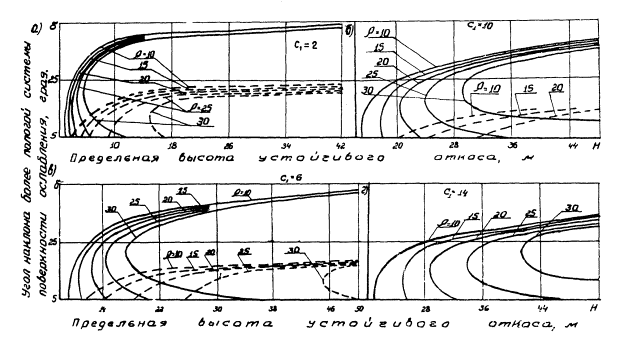
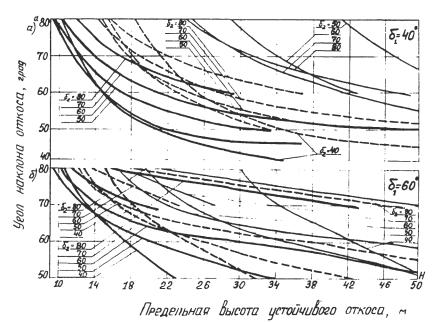
Рис. 8 . Номограммы для определения
предельной высоты устойчивого откоса (для некоторых расчетных сочетаний) при
наличии двух или более систем поверхностей ослабления, падающих в сторону
откоса под различными углами β и
δ и несовпадающих с углом откоса
α; β > α
> δ (расчетная схема V II ):
β = 60°; СТР = 0; ρТР
= 10°; а — С1 = 2; б — С1 = 2; в — С1 = 10; г — С1
= 14 т/м2;
— а
= 50°; — — — — а = 30°;
Рис. 9 . Номограммы для определения
предельной высоты устойчивого откоса (для некоторых расчетных сочетаний) при
наличии двух или более систем поверхностей ослабления, падающих в сторону
откоса под углами различными β и δ и
несовпадающих с углом откоса α β > α > δ.
(расчетная схема V II ):
а — β
= 60°; СТР
= 0; ρТР = 15°;
б — β
= 60°; СТР = 0; ρТР = 20°;
С1 = 6 т/м2; α = 50°
Рис. 10. Номограммы для
определения предельной высоты устойчивого откоса с углом наклона α при наличии двух или белее систем
поверхностей ослабления, одна из которых имеет падение в сторону выемки под
углом δ (δ < α), а другая — в сторону массива
под углом φ (для некоторых
расчетных сочетаний) (расчетная схема V III )
ρТР = 10°; СТР
= 1 т/м2; γ0
= 2,5 т/м3
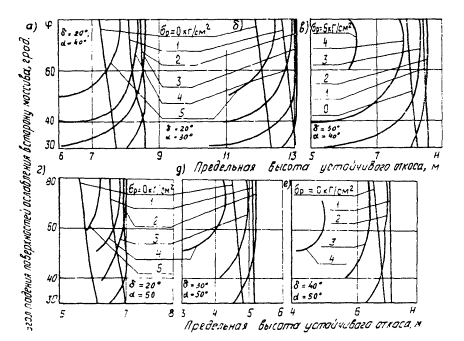
а) δ = 20°; α =
40°; б) δ = 20°; α = 30°; в) δ = 30°; α =
40°; г) δ = 20°; α = 50°; д) δ = 30°; α =
50°; е) δ = 40°; α = 50°;
Рис. 11. Номограммы для определения предельной
высоты устойчивого откоса, при расчетной схеме, учитывающей объемное
расположение поверхностей ослабления (для некоторых расчетных сочетаний)
(расчетная схема Х I ):
а — СТР = 2 т/м2; γ0
= 2,5 т/м3; β = 0°; А0
= 90°; А1 = 130°; А2 = 50°
б — СТР = 2 т/м2; γ0
= 2,5 т/м3; β = 15°; А0 =
90°; А1 = 130°; А2 = 50°
в — СТР
= 2 т/м2; γ0 = 2,5 т/м3; _____ β
= 30°; А0 = 90°; А1 = 130°; А2
= 50°
ПРИЛОЖЕНИЕ
4
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАСЧЕТОВ ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ПО СХEME IХ х
В данной расчетной схеме
массив принимается макрооднородным (квазиизотропным), а расчетная поверхность обрушения
— круглоцилиндрической с вертикальным верхним участком высотой H90, в пределах которого считается, что порода
работает на разрыв. Сопротивление разрыву скальной породы в массиве в запас
безопасности принимается равным нулю.
х Изложенные в настоящем приложении методики
основываются на разработках Г.Л. Фисенко [ 2,
9,
10]
и уточнены по результатам исследований некоторых других авторов (10 , 26,
27,
28).
Положение
наиболее опасной поверхности обрушения для заданной конфигурации откоса, т.е.
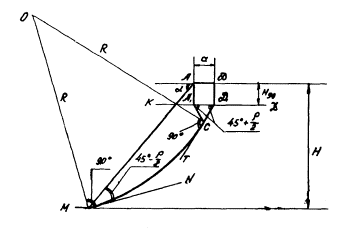
для конкретных значений крутизны α и высоты его Н, определяют в следующей последовательности (рис. 1);
Рис. 1 . Построение поверхности
обрушения в расчетной схеме IX
определяют высоту
вертикального участка поверхности обрушения Н90
— вертикальной трещины отрыва — по формуле для расчетной схемы 1 (см. табл. 1 раздела 2);
проводят на уровне проектируемого
откоса горизонтальную линию АД, на глубине Н90 от нее проводят
пряную К Z, параллельную
АД;
определяет ширину призм
обрушения α (см. рис. 1) по
формуле [10, 26 ]
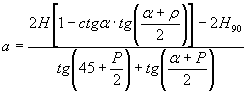
где
Н — высота рассматриваемого откоса, м;
Р — угол внутреннего трения массива
вкрест по направлению к поверхностям ослабления, град;
Откладываю т ширину
призмы обрушения «а» от бровки откоса (участок АД на рис. 1);
проводят прямую под углом (45 — ) к линии поверхности проектируемого откоса через подошву
откоса (точку М);
опускают из точек Д и А
перпендикуляра ДД l и АА1 на линию К Z . Из точки Д1
проводят прямые Д1Т под углом (45 + ) к линии К Z
(в сторону откоса); из точки А1
проводят прямую под углом (45 + ) к линии К Z
(в сторону, противоположную откосу) до пересечения с Д1Т в узловой
точке С;
восстанавливают
перпендикуляры к линиям М N
из точки М и Д1Т — из точки С. Пересечешь этих перпендикуляров дает
точку О, являющуюся центром окружности, из которой радиусом R проводят криволинейный участок MC поверхности обрушения.
Дальнейший расчет общей
устойчивости участка массива, ограниченного полученной поверхностью обрушения и
поверхностью откоса, проводят по общепринятому способу:
разбивают вертикальными поверхностями этот массив на отсеки;
определяют вес каждого отсека Bi , приходящийся на 1 пог. м длины выемки;
вычисляют коэффициент устойчивости Ky . по выражению
где
Ni = Qi·cos αi; Ti = Qi
sin αi;
αi — осредненный угол
наклона к горизонту поверхности обрушения в пределах каждого выделенного
отсека, град;
Z — длина поверхности обрушения в пределах
участка;
— средняя высота отсека, м;
— средняя ширина отсека, м;
γ0 — объемный вес пород, т/м3:
СМ — сцепление в массиве, т/м2;
ρ — угол внутреннего трения в массиве, град.
При выполнении расчета величины параметров ρ и СМ, в соответствии с указаниями раздела
4, уменьшается на величину коэффициента запаса, равного 1,3.
Получение в результате расчета Ку
= 1 свидетельствует о том, что рассматриваемый откос устойчив при коэффициенте
запаса, равном 1,3. Если Ку
> 1, то предельная высота откоса при той же крутизне (при коэффициенте
запаса 1,3) может быть увеличена; при Ку
< 1 — высота должна быть уменьшена или откос соответственно уположен.
Для определения предельно допустимой высоты откоса при данной его крутизне
и коэффициенте запаса 1,3 достаточно выполнить два расчета, изменяя Н во втором расчете в большую или
меньшую сторону в зависимости от результатов первого.
По результатам двух таких вычислений строят график изменения коэффициента
К от высоты откоса. Для этого в
точках, являющиеся основанием откоса в двух выполненных расчетах,
восстанавливают перпендикуляры к линии откоса в соответствии с рис. 2 и
откладывают в одинаковых масштабах отрезки, превышающие 1 в величине Ку или недостающие до 1.
Рис. 2 . Определение высоты
предельного устойчивого откоса по двум расчетам
Концы этих перпендикуляров соединяют прямой, точка пересечения которой с
линией откоса и укажет подошву искомого откоса (см. рис. 2).
Для ускоренных определений предельной высоты устойчивого откоса можно
использовать график, приведенный на рис. 5 раздела 2 [2, 9, 10]. На этом
графике приведены величины предельной высоты Н в долях от Н90,
определяемой по схеме I табл.
1 раздела 2 в зависимости от значений Р, величина которого снижается на
коэффициент запаса (1,3).
Приложение 5
ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАСЧЕТОВ ОБЩЕЙ УСТОЙЧИВОСТИ ОТКОСОВ ПО
СХЕМЕ X 1
Настоящая расчетная схема, как и схема IX , (см. приложение
4) отражает размещение поверхности обрушения в верхней части
массива, как в квазиизотропной среде; в нижней части поверхности обрушения
предполагается ее прохождение по контактам плоскостей ослабления (см. рисунок).
В этом случае рекомендуется следующая последовательность расчета:
1 .
Данная методика разработана во ВНИМИ [ 10,
27,
28,
29].
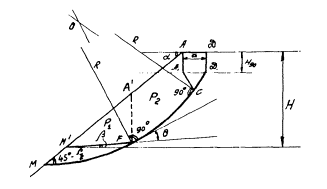
Построение поверхности обрушения в расчетной схеме X
ориентировочно для заданной крутизны откоса и сдвиговых параметров ρ
и СМ (уменьшенных на коэффициент
запаса устойчивости) по графику, приведенному на рис. 5 раздела 2, определяют предельную
высоту устойчивого откоса, как для квазиизотропного массива;
по способу, изложенному для расчетной схемы IX , осуществляется построение поверхности
обрушения для найденной (в соответствии с указанием предшествующего абзаца)
высоты откоса;
на произвольно выбранном от подошвы откоса расстоянии проводят линию,
совмещенную с поверхностью ослабления год углом β к горизонту (см. рисунок), что определяет очертание призмы
возможного обрушения;
в призме возможного
обрушения M1АДД1 F выделяют призму упора (1)
М’А’ F и
призму активного давления (2) A’ AДД1 F;
призму активного давленая
разбивают на отдельные отсеки. Вес каждого из них составляет
,
где
— осредненная
высота отсека, м;
а i — ширина отсека, м;
γ0 — объемный вес массива пород, т/м3;
определяют
нормальные и сдвигающие составляющие для каждого отсека. После алгебраического
сложения удерживающих и сдвигающих сил, действующих по поверхности обрушения в
пределах участка призмы активного давления ( FCD1) их проектируют на направление поверхности
ослабления ( m ‘ f).
В результате определяются:
Σ Ti cos θ — сдвигающая сила, возникающая на
поверхности под действием призмы активного давленая;
( tg ρΣNi + CMZa)
cos θ + (Σ Ti — Σ Ni tg ρ — CMZa ) sin θ tg ρ TP — удерживающая сила на поверхности M1 F, возникающая под
влиянием призмы активного давления.
В этих выражениях:
Ni = P2i·cosαi;
Ti = P2i·sinαi;
αi — осредненный угол наклона к горизонту поверхности обрушения
в пределах каждого выделенного отсека, град.;
Zа — длина поверхности
обрушения на участке призмы активного давления, м;
θ — угол, град., между направлением
поверхности ослабления (М1 F) и перпендикуляром, опущенным из точки F к радиусу поверхности обрушения на
участке FC (см.
рисунок);
определяют силы, возникающие на поверхности m ‘ f под действием призм упора:
Р1 , c os β tg ρtp + CTPZy — удерживающая сила;
Pi sin β — сдвигающая сила, при падении слоев в сторону
массива эта сила становится удерживающей).
В приведенных выражениях:
Р1 — вес призмы упора, т;
Zy — длина поверхности обрушения на участке призмы
упора, м;
устанавливают величину коэффициента устойчивости
рассматриваемого откоса, которую вычисляют в случае падения поверхностей
ослабления в сторону откоса по выражению
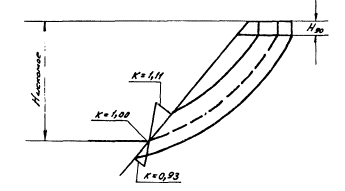
а при падении поверхностей ослабления в сторону массива —
изменяют положение нижнего участка поверхности обрушения, совмещаемого с
плоскостью ослабления, и расчет повторяют;
определяют высоту откоса заданной крутизны, при которой К = 1. Способ ее отыскания остается
таким же, как и для расчетной схемы IX (см. рис.2 приложения 4).
По большому количеству подобных расчетов во ВНИМИ [28]
составлены таблицы, с помощью которых можно ускоренно определить искомую
предельную высоту устойчивого откоса (по заданным характеристикам сопротивления
сдвигу на различных участках поверхности обрушения и углам наклона откоса).
При этом последовательность расчетов принимается следующей;
по графику на рис. 5 раздела 2, по
принятым значениям α и ρ (уменьшенным на коэффициент запаса устойчивости) определяют предельную
высоту Н квазиизотропного откоса;
для получения искомой предельной высоты устойчивого откоса по принятой
расчетной схема (см. рис. 4 раздела 2)
полученная в соответствии с рекомендациями предшествующего пункта высота откоса
Н уменьшается на поправочный
коэффициент в, т.е.
Н1 = Н·в.
Для определения коэффициента в необходимо предварительно
вычислить коэффициент С по выражению
,
где
σТР — средняя интенсивность нормального напряжения
по поверхности скольжения, т/м2
σСР = 0,3γ0·Н· cos β
После этого вычисляют коэффициент в
по выражению
в = в0
— Сδ
в котором вспомогательные коэффициенты в и δ принимают по
таблице, приведенной в настоящем приложении.
По указанной методике ускоренного определения
в ЦНИИСе вычислены искомые значения Н
для некоторых значений крутизны откоса, величины и направления угла β и величины Н90 (см. рис. 6,
раздел 2).
|
Угол откоса град. |
Значения коэффициентов в и δ при угле |
|||||||||||||
|
+30° |
+20° |
+10° |
0° |
-10° |
-20° |
-30° |
||||||||
|
в0 |
δ |
в0 |
δ |
в0 |
δ |
в0 |
δ |
в0 |
δ |
в0 |
δ |
в0 |
δ |
|
|
40 |
1,000 |
0,045 |
0,920 |
0,079 |
0,850 |
0,118 |
0,795 |
0,160 |
0,740 |
0,300 |
0,532 |
0,400 |
0,470 |
0,440 |
|
50 |
1,000 |
0,063 |
0,910 |
0,110 |
0,815 |
0,150 |
0,785 |
0,250 |
0,687 |
0,340 |
0,550 |
0,380 |
||
|
60 |
1,000 |
0,100 |
0,880 |
0,140 |
0,800 |
0,220 |
0,660 |
0,295 |
0,590 |
0,340 |
||||
|
70 |
1,000 |
0,135 |
0,880 |
0,205 |
0,720 |
0,265 |
0,620 |
0,305 |
||||||
|
80 |
1,000 |
0,195 |
0,800 |
0,245 |
0,690 |
0,280 |
Примечание . Углы
падения β в сторону пассива
обозначены со знаком » + «, а в сторону откоса — со знаком » —
«.
ПРИЛОЖЕНИЕ
6
График для определения коэффициентов А и В при
расчете местной устойчивости
ПрИЛоженИе 7
Использование динамического пробника для
получения расчетных параметров ускоренным методом
Принцип использования динамического пробника конструкции Ю.Д. Белова [ 30,
31,
32]
основан на оценке относительной механической прочности породы по количеству
работы, затраченной на погружение в нее металлического штыря (пуансона)
сечением S = 1 см2, забиваемого молотком
весом 1 кг. Общий вид динамического пробника представлен на рисунке.
Относительная механическая прочность вычисляется по выражению,
где R отн — относительная механическая прочность, кг/см2;
п — число ударов;
l — глубина погружения (внедрения) пуансона,
см;
А — работа одного плечевого удара молотка
весом 1 кг, принимаемая в среднем равной 160 кг/см [30, 31].
Преимуществом использования динамического пробника является возможность
осуществления по очень простой методике массовых определений прочности
непосредственно в натурных условиях, т.е. возможность учета естественного
состояния и сложения исследуемых пород в имеющихся обнажениях.
Несмотря на то, что точность отдельных определений невелика, но за счет
массовости испытаний надежность получаемых результатов (при их статистической
обработке) достаточна для практических целей.
Полученная относительная механическая прочность может быть корреляционно
связана с различными прочностными параметрами, определяемыми по более точной
методике (например, по типу зависимости, изображенной на рис. 9 раздела 4.
Динамический
пробник
Приложение 8
Значения ρ ТР при отсутствии заполнителя по контактам поверхностей
ослабления 1
|
Характеристика пород |
ρТР , град, при поверхностях |
|||
|
неровных шероховатых |
ровных шероховатых |
неровных гладких |
ровных гладких |
|
|
Крепкие песчаники |
28 — 31 |
24 — 28 |
22 — 27 |
20 — 26 |
|
Известняки |
24 — 27 |
28 — 25 |
20 — 22 |
16 — 19 |
|
Аргиллиты, глинистые сланцы |
28 — 26 |
21 — 28 |
18 — 20 |
15 — 18 |
|
Контакт песчаника с известняком |
— |
— |
— |
88 |
|
Мергели |
— |
— |
— |
16 |
|
Глинистые сланцы |
— |
— |
— |
18 |
|
Аргиллиты с зеркалами скольжения на |
— |
— |
— |
14 |
|
Алевролиты |
— |
27 — 28 |
— |
22 — 28 |
|
Алевролиты с очень гладкими (местами |
— |
— |
18 — 16 |
|
|
Мелкозернистый песчаник на глинистом |
88 |
— |
— |
— |
Примечание :
при возможности обводнения указанные в таблице значения ρТР следует уменьшать на 2 — 4о.
1
Таблица составлена на основании данных Г.Л. Фисенко [ 2,
9],
Н.Н. Куваева, изложенных в его диссертационной работа «Влияние
трещиноватости на устойчивость бортов скальных разрезов», ВНИИ, 1958.
ПРИЛОЖЕНИЕ
9
Значения СТР,
при отсутствии заполнителя по контактам поверхностей ослабления [2, 9]
|
Характеристика поверхностей ослабления |
Характеристика толщи |
СТР , т/м2 |
|
Поверхность скольжения по контактам слоев |
Дислоцированная осадочная толща |
2-5 |
|
Контакты слоев |
Неуплотненная недислоцированная слаборассланцованная осадочная порода |
50 % от сцепления под углом к наслоению |
|
Контакты слоев |
Уплотненная слаборассланцованная осадочная толща |
10 — 18 |
|
Контакты слоев |
Метаморфизованная осадочная толща |
5-10 |
|
Сплошные неровные трещины и тектонические нарушения |
Массивы изверженных и метаморфических пород |
5-10 |
Приложение 10
Примеры расчета общей устойчивости откосов выемок
Пример 1
Исходные данные Проверить расчетом общую устойчивость
откоса, изображенного на рисунке. Высота откоса Н = 22 м, осредненная крутизна α = 55°.
Литология: аргиллиты — 76, песчаники — 24 %. На рисунке показано
расположение слоистости и сочетание слоев, дана роза устойчивости, построенная
по методу В.Н. Славянова, и основные данные для ее построения [33].
Выделены три системы трещин: I и III имеют благоприятное по
отношению к откосу падение; II система характеризуется
неблагоприятным падением, но угол ее наклона круче угла откоса (72 — 90° против
55 — 60°).
Таким образом, из имеющихся расчетных схем можно использовать схему IX , рассматривающую откос в качестве
квазиизотропного массива. Из таблицы, характеризующей трещиноватость
рассматриваемого массива, следует, что средний размер элементарного
структурного блока lCP ≈ 18,0 см. При Н = 22 м .
При таком соотношения массив считается
квазиизотропным [34].
Последовательности расчета
1. Определяем необходимые расчетные параметры для схемы IX ,
Требуется знать С, ρ, γ0, ρТР,
СМ, .
2. Согласно указаниям, изложенным в разделе
4, принимаем для аргиллитов ρ = 82°, для песчаников ρ
= 84°.
Величина сцепления в куске 1 для аргиллитов САРГ = 60 т/м2;
для песчаников C ПЕСЧ = 1420 т/м2.
1 В
рассматриваемом примере приняты фактические значения прочностных параметров,
полученные в результате испытаний образцов с рассматриваемого объекта в
лабораторных условиях.
3. Определяем значения ρ и С в куске, взвешенные по мощности литологических разностей:
т/м2
;
т /м3 (взвешенное по мощности
значение).
4. Вычисляем окончательные расчетные значения С и ρ с учетом уменьшения их величин на коэффициент
запаса
; ρРАСЧ
= 26о;
≈ 30
кг/см2.
5. Находим значение СМ
по формуле (13) (см. раздел 4)
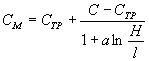
Так как обводнения не отмечено, шероховатость
стенок поверхностей ослабления (трещин) средняя, а заполнитель отсутствует, то
согласно рекомендациям, изложенным в разделе 4, по таблице в приложении
9 находим:
СТР = 8,5 т/м2 (для аргиллитов и
песчаников принимаем среднее минимальное значение);
расчетное значение 2,7 т/м2;
по рис. 12 раздела 4 при С = 30
кг/см2, а = 22
т/м2.
6. Согласно табл. 1 раздела 2 м
7. По графику,
приведенному в разделе 2 на рис. 5, при α
=55° и ρ = 26° получаем ; т. e,
Таким образом,
рассматриваемый откос вполне устойчив, коэффициент запаса превышает 1,3.
Пример 2
Исходные денные. Оценить общую устойчивость обводненного откоса из
выветрелого до состояния мелкозема аргиллита, Мощность выветрелого слоя до 5 м.
Крутизна откоса 83° (1:1,5), высота его 16 м.
В данном случае применима
расчетная схема Х III. Полученные при испытаниях на пастах
для влажности до 88 % расчетные
параметры выветрелого до мелкозема аргиллита оказались равными:
С = 3,5 т/м2;
ρ = 12°;
γ = 2,0 т/м2,
Последовательность расчета
Мелкозем можно
рассматривать как изотропный материал, т.е. СМ
= С и ρТР = ρ.
Для получения расчетных
значений исходные параметры прочности уменьшаем на коэффициент запаса К = 1,3
ρРАСЧ = 9°15′;
СРАСЧ = = 2,7 т/м2.
По графику на рис. 5 в
разделе II для α = 38° (крутизна откосов) и ρ
= 9°15′ получаем: ;
Н = Н’· H90 = 4,8·3,2 = 15 м < 16 м.
Таким образом, откос
заданной крутизны (33°) имеет коэффициент запаса устойчивости менее 1,3.
Для обеспечения
надлежащей устойчивости необходимо запроектировать более пологий откос.
Принимаем заложение откоса 1:2 (26°24′). Тогда по графику на рис. 5 получим:
Н = Н’·Н90
= 5,6·3,2 = 18 м > 16 м
Следовательно, при
заложении откоса 1:2 устойчивость его достаточна.
ЛИТЕРАТУРА
1.
Локтадзе В.Д. Инженерная геология. Инженерная петрология, Л.,
«Недра», I970.
2. Фисенко
Г.Л. Устойчивость сортов карьеров и отвалов. М., «Недра», 1965.
3. Сергеев
Е.М., Голодковская Г.А., Зиангиров Р.С., Осипов В.И., Трофимов В.Г.,
Грунтоведение, М., Изд-во МГУ, 1971.
4.
Строительные нормы и правила. СНиП II-Б 1-62. Основания зданий и сооружений. Нормы проектирования.
М., Госстройиздат, 1962.
5.
Указания по проектированию земляного полотна железных и автомобильных дорог
(СН-449-72). М., Оргтрансстрой, 1973.
6.
Строительные нормы и правила, часть II, раздел Д, глава I, Железные дороги, нормы проектирования (СНиП II-Д I-62). М., Изд-во литературы по строительству, 1964.
7.
Технические условия сооружения железнодорожного земляного полотна (СН 61-59). M., Изд-во литературы по
строительству, архитектуре и строительным материалам, 1960.
8. Альбом
типовых поперечных профилей земляного полотна вновь строящихся железных дорог.
М., Главтранспроект, 1964.
9.
Руководство по определению оптимальных углов наклона бортов карьеров и отвалов,
Л., изд. вними, 1962.
10.
Методические указания по определению углов наклона бортов, откосов уступов и
отвалов строящихся и эксплуатируемых карьеров. Л, изд. ВНИМИ, 1972.
11.
Савков Л.В. Расчет устойчивости откосов в скальных трещиноватых породах.
«Физико-механические проблемы разработки полезных ископаемых», № 6,
Новосибирск, «Наука», 1965.
12.
Савков Л.В. К вопросу учета трещиноватости при расчетах устойчивости откосов в
скальных породах. «Физико-технические проблемы разработки полезных
ископаемых», № 1 Новосибирск, «Наука», 1967.
13.
Звонарев Н.К., Кагермазова С.В. Предварительный расчет параметров осыпания
откосов на карьерах в результате выветривания. Известия высших учебных
заведений. Геология и разведка, № 12, М., изд. МГРИ, 1969.
14.
Методические указания по оценке местной устойчивости откосов и выбору способов
их укрепления в различных природных условиях. М., изд. ЦНИИСа, 1970.
15.
Матвеев Б.В. Методика лабораторного определения свойств горных пород на сдвиг
(срез). Л., изд. ВНИМИ, 1961.
16.
Протодьяконов М.М., Койфман М.И., Чирков С.Е., Кунтыш М.Ф., Тедер Р.И. Паспорта
прочности горных пород и методы их определения. М., «Наука», 1964.
17.
Чирков С.Е. Влияние масштабного фактора на прочность углей. М.,
«Наука», 1969.
18.
Методические указания по производству натурных испытаний сопротивления сдвигу
неоднородных слоистых и трещиноватых пород. Л., изд. ВНИМИ, 1965.
19.
Методическое пособие по натурным методам механических испытаний горных пород.
Л., изд. ВНИМИ, 1969.
20. Барон
Л.И., Логунцов Б.М., Позин Е.В. Определение свойств горных пород.
Госгортехиздат, 1962.
21.
Методические указания по исследованию скальных массивов при изысканиях дорог.
М., изд. ЦНИИСа, 1967.
22.
Предложения по совершенствованию норм проектирования скальных выемок. М., изд.
ЦНИИСа, 1968.
23.
Методика инженерно-геологического обследования оползней на железных дорогах.
«Вопросы геотехники», № 14. Днепропетровск, 1969.
24.
Методические указания по сравнению вариантов проектных решений железнодорожных
линий, узлов и станций. М., Оргтрансстрой, 1973.
25.
Типовая методика определения экономической эффективности капитальных вложений,
М., «Экономика», 1969.
26. Мочалов A . M . Определенна ширины призмы обрушения
плоского откоса, «Физико-технические проблемы разработки полезных
ископаемых», № 4, Новосибирск, «Наука», 1968.
27. Мочалов A . M . Расчет устойчивости слоистых откосов. Труды
ВНИМИ, сб. 83, Л., изд. ВНИМИ, 1971.
28. Козленко П.Д. Расчет устойчивости слоистых откосов. Труды ВНИМИ, сб. 58,
Л., изд. ВНИМИ, 1966.
29. Козленко П.Д. Расчет углов наклона бортов карьеров в условиях
анизотропных пород. Труды ВНИМИ, сб. 38, Л., изд. ВНИМИ, 1960.
30 . Белов Ю.Д. Определение прочности горных пород динамическими пробниками.
Труды ВНИМИ, сб. 60. Л., изд. ВНИМИ, 1966.
31 . Кагермазова С.В. Некоторые результаты изучения выветривания горных
пород на карьерах. Труды ВНИМИ, сб. 64. Л., изд. ВНИМИ, 1968.
32. Инструкция по наблюдению за деформациями бортов, откосов уступов и
отвалов на карьерах и разработке мероприятий по обеспечению их устойчивости.
Л., изд. ВНИМИ, 1971.
33 . Славянов В.Н. Инженерно-геологические прогнозы устойчивости откосов.
М., Изд-во литературы по строительству, 1964
34 . Куваев Н.Н. Влияние трещиноватости на устойчивость бортов карьеров.
«Научные записка УкрНИИпроекта», вып. 10, Киев, 1963.
Как определить оптимальный размер заказа
- Оптимальный размер заказа, график поставок, уровень товарных запасов
- Причины выбора системы ABM Inventory для определения оптимального размера заказа
- Оптимальный размер заказа, уменьшение уровня упущенных продаж и другие результаты проекта
Если ваша торговая компания относится к среднему и крупному бизнесу, то вручную определить оптимальный размер заказа — непростая задача. Ппо мере роста бизнеса, вам следует рассмотреть вопрос об инвестировании в систему управления запасами, чтобы управлять запасами более эффективно.
Есть много причин, почему бизнес должен инвестировать в систему для расчета оптимального заказа, и все они выходят за рамки простого отслеживания уровня наличия. С основными предпосылками и причинами инвестировать в автоматизированную систему управления запасами совсем недавно столкнулась крупная розничная сеть восточного региона Украины.
О компании
Компания в сфере ритейла в Восточном регионе, насчитывающая около 20 магазинов. У компании есть собственное производство: кондитерский цех, пекарня. Имеется собственный распределительный центр и оптовая база.
- Общая торговая площадь – более 6,5 тыс м2
- Общее количество активных SKU – больше 11 000
- Количество пользователей системы – больше 30
- Более 500 акционных предложений ежедневно
Оптимальный размер заказа, график поставок, уровень товарных запасов и прочие предпосылки
Часто в компаниях оптимальный размер заказа определяют по разным интерпретациям формулы Уилсона вручную:
где
S — годовое потребление,
C0C0 — затраты на выполнение заказа,
C1C1 — цена единицы продукции,
i — затраты на содержание запасов (%).
Оптимальный объем заказа (формула Уилсона, EOQ-модель) — модель оптимального размера заказа, определяющая оптимальный объём заказываемого товара, который позволяет минимизировать общие переменные издержки, связанные с заказом и хранением запасов.
На момент предпроектного обследования сети в модель оптимального размера заказа была заложена формула, которая опиралась на прогноз продаж. Все заказы сети формировались в полуавтоматическом режиме с помощью товарно-учетной системы 1С 8.2 по методу «мин-макс», что увеличивало трудозатраты и снижало качество заказов, в сети возникали излишки по одним товарам и нехватки других. Графики поставок велись менеджерами в Excel, поэтому при формировании заказов менеджеры в ручном режиме учитывали эту информацию. Также в учетной системе практически отсутствовала возможность оценки излишних товарных запасов и причин их возникновения.
Для эффективной деятельности торговой компании, которой является клиент, необходимо выполнить два условия: с одной стороны, обеспечить прибыль, путем снижения товарных запасов, не продавая товар со скидками, поставляя более дорогим и быстрым видом транспорта, а с другой стороны – увеличивать продажи, для этого держать больше товарных запасов, продавать со скидками, поставлять более дорогим и быстрым видом транспорта. Чтобы удовлетворить оба условия сети необходимо определить оптимальную партию заказа обеспечить постоянное наличие нужного товара в нужном месте в нужное время, при этом не иметь товарных излишков.
Для оптимизации работы сети и улучшения финансовых показателей, ТОП-менеджмент принял решение внедрить специализированное решение по управлению товарными запасами.
Узнайте сроки и стоимость внедрения
Критерии выбора системы для определения оптимального размера заказа
Для выбора программы для управления запасами и автоматического определения оптимального размера заказа был проведен анализ рынка, компания привлекала внешнего консультанта для оценки возможностей системы и после детального изучения основных характеристик продукта выбор остановили на решении от АВМ Cloud.
Решение ABM Inventory для дистрибуции и ритейла базируется на двух установках:
- Поставлять для обеспечения наличия;
- Создать и поддерживать надежную систему дистрибуции, направленную на обеспечение наличия товара.
В отличие от классической модели пополнения запасов по прогнозу продаж, система использует понятие «буфер запаса», характеризующий необходимый и достаточный уровень запаса на каждой точке хранения для каждой управляемой единицы, а также динамическое изменение этого запаса в зависимости от зоны нахождения остатка.
Система ABM Inventory обеспечивает:
- Поддержание объемов товарных запасов на установленном уровне, который обеспечивает постоянное наличие товара при оптимальных запасах в системе. Это достигается путем автоматического выполнения процессов:
1.1. Планирование заказа
1.2. Формирование заказа
1.3. Расчет оптимального размера заказа
1.4. Оптимизация заказа
1.5. Отправка заказа
1.6. Периодическая корректировка необходимого уровня хранения
1.7. Экономическое обоснование поддерживаемого уровня
1.8. Контроль за состоянием запасов - Управление ассортиментом (путем определения наименее востребованных потребителями позиций; а также определение позиций заказного ассортимента, пользующихся постоянным спросом для ввода их в регулярную ассортиментную матрицу)
- Развернутую аналитику о состоянии запасов и их влиянии на финансовые показатели бизнеса.
Кроме методологической составляющей, важным аргументом для принятия решения в пользу системы АВМ Inventory стала возможность использования программы, как услуги, модель SaaS. Облачная модель продукта не предполагает покупки системы и установки на компьютеры пользователей, оплата производится ежемесячно, по факту использования системы. Это позволяет существенно экономить: не требуются капитальные инвестиции в продукт, нет доп.расходов на дорогостоящее оборудование и поддержание системы в рабочем состоянии. Компания получает доступ к системе, установленной на защищенных серверах в дата-центре, где и происходят все расчеты и процессы работы с запасами и заказами.
Описание проекта
Проект проходил в 2 этапа: подключение внешних поставщиков и подключение распределительного центра.
Перед началом проекта были сформулированы цели, которых предстояло достичь:
- Определить оптимальную партию заказа
- Уменьшить излишки товарных запасов и оптимизировать ассортимент;
- Улучшить показатели оборачиваемости предприятия;
- Автоматизировать заказы;
- Оптимизировать рабочее время персонала за счет автоматизации процессов работы с запасами и заказами.
В ходе проекта к системе управления товарными запасами ABM были подключены все основные категории товаров, кроме группы товаров Фреш-сегмента. В настоящий момент под управлением системы 332 поставщика, около 108 тыс. позиций товаров.
Система ежедневно автоматически формирует от 150 до 200 заказов центральному складу в зависимости от согласованного графика заказов, а также от 500 до 1000 заказов на внешних поставщиков, причем около трети этих заказов (28%) отправляются на поставщиков без участия менеджера, остальные заказы корректируются меньше чем на 20%.
По каждому SKU на каждой точке хранения при подключении устанавливается свой уровень запаса (буфер), который рассчитывается, исходя из потребления из данного звена и графика поставок. По прошествии нескольких циклов система автоматически (либо после подтверждения менеджером) изменяет буферы, исходя из реального потребления (не прогнозного). Этот механизм называется Dynamic Buffer Managemen (DBM, Динамическое управлением буфером) и является одним из основных инструментов в управлении запасами по методологии ТОС. Оптимальный уровень заказа виден на графике.
В процессе подключения системы по управлению запасами менеджеры провели работу по корректному заполнению параметров товаров в товаро-учетной системе 1С, прорисовыванию планограмм (т.к. эту информацию есть возможность автоматически учитывать при формировании заказа). Используя данные системы, были выявлены и скорректированы несоответствия полковыкладки продажам. Это позволило улучшить показатели оборачиваемости запаса: оборачиваемость самой полки была ускорена с 32 до 20 дней, а данные по ее оборачиваемости использовались в проведении переговоров с поставщиками для обоснования маркетинговых платежей.
Около 30% всего ассортимента поставляется на полки без хранения на РЦ, в системе это реализовано с помощью функционала Кросс-Докинг. Данный функционал позволяет более рационально использовать площадь склада, при том, что для поставщика процедура поставки не усложняется путем развоза товаров по торговым точкам – то есть система обоюдно выгодна как поставщику, так и покупателю. Кроме того, снижается нагрузка на склад, уменьшаются логистические издержки, более оптимально используется складская площадь.
Для фокусировки внимания специалистов, основные показатели эффективности управления товарными запасами — излишки, упущенные продажи и оборачиваемость — представлены на главном экране системы. Упущенные продажи –показатель, который довольно сложно посчитать, хотя проще всего выявить визуально – так как упущенная продажа – это неосуществленная продажа по причине отсутствия товара на полке, и который больше всего влияет на впечатление от магазина.
Отслеживать динамику излишков и упущенных продаж и причины их возникновения, особенно по TOP-mover (товары, генерирующие 80 и более % оборота компании), новым товарам, товарам в акции, – одна из ключевых функций менеджера, ведь только определив причину возникновения проблемы можно найти оптимальное решение. Из главного экрана есть возможность перейти в список проблемных позиций и фокусироваться именно на них.
Компания проводит активную маркетинговую политику, что включает в себя акции и распродажи с целью привлечения клиентов. Также продажи некоторых товаров имеют ярко выраженные сезонные колебания. Для управления такими товарными позициями в системе ABM предусмотрена процедура планирования всплесков, которая широко используется менеджерами в ежедневной работе.
Оптимальный экономичный размер заказа, графики поставок и данные минимального заказываемого количества указываются напрямую в системе, что позволяет изменять их сразу же при получении новой информации от поставщика и тут же формировать заказ согласно обновленной информации.
Система ABM, помимо непосредственной функции – автозаказа, еще и позволяет контролировать эффективность управления запасами с помощью системы отчетности. Система генерирует около 30 отчетов по различным процессам управления запасами: коррекция отправленных заказов менеджерами, оптимальный размер заказа, исполнение заказов поставщиками, товары с излишним уровнем запасов, упущенные продажи, список ТОР-товаров (обеспечивающих 80% оборота), остатки товаров, выводимых из ассортимента и др.
Специалисты компании-клиента используют отчет о динамике запасов, как по всему предприятию, так и в разрезе складов и поставщиков для оценки работы. График содержит информацию о всех основных ключевых показателях эффективности управления запасами – излишки, упущенные продажи, уровень остатков и продаж, а также оборачиваемость и ROI. К концу года запасы сети несколько увеличились, что связано с открытием нового магазина, а также предварительным увеличением запаса менеджерами накануне Нового года.
Еженедельная динамика показателей управления запасами.
Активно используется ежедневный отчет по недостаткам ТОР-товаров, который предупреждает о риске возникновения нехватки товара еще до момента его возникновения и дает возможность сделать внеплановый заказ у поставщика.
С помощью отчета по NON-movers (товары, генерирующие меньше 2% прибыли предприятия) принимается решение по выведению товара из ассортимента.
В переговорной деятельности используются данные отчета о надежности поставщика, где просчитана его дисциплина по выполнению договорных обязательств.
Оптимальный размер заказа, уменьшение уровня упущенных продаж и другие результаты проекта
За период с января 2016 года по ноябрь 2016 были достигнуты следующие результаты:
- Заказы автоматизированы, процесс заказа, как и управления запасами в целом, стал прозрачным. Автоматически определяется оптимальная партия заказа запаса.
- По основным показателям управления запасами:
- Оборачиваемость сократилась в 1,5 раза.
- Упущенные продажи уменьшились на 39 %.
- Излишки сократились на 21%.
- Оптимизирован ассортимент магазинов. Выявлены и выведены из ассортимента низкооборачиваемые товары, ассортимент сокращен на 6%. Как результат, улучшились показатели оборачиваемости, снижен уровень устаревших запасов, высвобождены замороженные денежные средства.
- Оптимизирована модель оптимального заказа акционных товаров.
Благодарим команды проекта за профессионализм и плодотворную работу над достижением поставленных целей. Особая благодарность ТОР-менеджменту компании за активную позицию в вопросах внедрения, а также за постоянный поиск возможностей улучшения текущих показателей управления запасами.
Хотите внедрить систему для расчета оптимального запаса?
Обращайтесь!
Запросить презентацию
Блог по теме:
- Грузинская сеть Daily выбрала ABM Inventory для управления запасами
- Проблемы управления запасами в магазинах дрогери
- Запуск программы лояльности для «КОЛО»
Узнайте про возможности системы ABM Inventory для вашего бизнеса.
..и давайте вместе делать Ваш бизнес еще прибыльнее!
Запросить презентацию
Регулятор,
включенный в АСР, может иметь несколько
настроек, каждая из которых может
изменяться в достаточно широких пределах.
При этом при определенных значениях
настроек система будет управлять
объектом в соответствии с технологическими
требованиями, при других может привести
к неустойчивому состоянию.
Поэтому
стоит задача, во-первых, определить
настройки, соответствующие устойчивой
системе, и, во-вторых, выбрать из них
оптимальные.
Оптимальными
настройками регулятора называются
настройки, которые соответствуют
минимуму (или максимуму) какого-либо
показателя качества. Требования к
показателям качества устанавливаются
непосредственно, исходя из технологических.
Чаще всего накладываются требования
на время регулирования (минимум) и
степень затухания ( зад).
Однако,
изменяя настройки таким образом, чтобы
увеличить степень затухания, мы можем
прийти к слишком большому времени
регулирования, что нецелесообразно. И
наоборот, стремясь уменьшить время
регулирования, мы получаем более
колебательные процессы с большим
значением .
Зависимость
от tp
в общем случае имеет вид, изображенный
на графике (см. рисунок 1.61).
Поэтому
для определения оптимальных настроек
разработан ряд математических методов,
среди которых можно выделить:
— метод сканирования
плоскости настроек,
— формульный метод,
— метод D-разбиения.
Метод
сканирования
заключается в разбиении области
допустимых настроек выбранного регулятора
с равным шагом и определении показателей
качества для каждого набора настроек
в узлах получившейся сетки. После
просмотра всех узлов выбираются наборы
настроек, соответствующие наилучшим
показателям качества. Настройки могут
быть уточнены далее также путем
сканирования окрестности выбранного
узла с более мелким шагом.
Формульный
метод
определения настроек регуляторов
используется для быстрой и приближенной
оценки значений настроек регуляторов.
Если
объект управления представляет собой
инерционное звено с запаздыванием, т.е.
описывается передаточной функцией
,
где
K
– коэффициент усиления, Т — постоянная
времени,
— запаздывание (см. п. 2.6.5), то настройки
П-, И-, ПИ- и ПИД-регуляторов могут быть
определены по приведенным в таблице 1.5
формулам в зависимости от того, какой
вид переходного процесса требуется
получить. Во второй колонке таблицы
приведены формулы для апериодического
процесса без перерегулирования, в
третьей – с перерегулированием 20 %, в
четвертой – для процесса с максимальным
быстродействием (процесс может быть
сильно колебательным).
Метод
D-разбиения
заключается в определении области
настроек в пространстве допустимых
значений настроек выбранного регулятора,
соответствующих области устойчивости
или заданному показателю качества.
Кривая D-разбиения
представляет собой границу устойчивости
в пространстве настроек и поэтому
строится с использованием какого-либо
критерия устойчивости.
Построение
кривой D-разбиения
по методу Гурвица сводится к решению
системы неравенств вида i
0, определяющих условие устойчивости.
Пример.
Определение области устойчивости АСР
по методу Гурвица.
Структура
АСР представлена на рисунке 1.30 (см. п.
2.6.4). Параметры K2
= 1, K4
= 2, K5
= 0,5. Параметры K0
и K1
являются переменными. Требуется записать
условие устойчивости относительно K0
и K1.
Для
записи условия устойчивости в данном
примере наиболее удобно воспользоваться
критерием Гурвица.
Характеристическое
уравнение замкнутой системы имеет вид
(пример определения характеристического
уравнения см. в п. 2.6.4):
D(s)
= 2.s3
+ 4.s2
+ (K1
+ 1).s
+ K0.
Таблица 1.5
|
Регулятор |
Апериодический |
Процесс с |
Процесс с |
|
П |
|
|
|
|
И |
|
|
|
|
ПИ |
|
, |
|
|
ПИД |
|
|
|
Матрица
имеет размер 3х3, так как степень D(s)
равна 3:
.
Диагональные
миноры матрицы:
1
= 4 >
0,
,
.
Согласно
критерию Гурвица система устойчива,
если все i
> 0. Тогда получаем систему неравенств
(1
= 4 уже удовлетворяет этому условию,
поэтому далее не учитывается):
2
= 4.K1
+ 4 – 2.K0
> 0 K0
< 2.K1
+ 2
3
= K0.
2
> 0 K0
> 0
То есть условие
устойчивости можно записать как 0 < K0
< 2.K1
+ 2. Графически она изображена на рисунке
1.62.
Кривая
D-разбиения
в данном примере представляет собой
прямую
K0
= 2K1
+ 2,
выше
которой настройки соответствуют
неустойчивой системе. Система с
настройками, взятыми из области
устойчивости, будет устойчива.
Для
систем с запаздыванием при определении
границы устойчивости можно воспользоваться
критериями Михайлова или Найквиста.
Методика
определения границы устойчивости по
критерию Михайлова сводится к решению
системы уравнений
R
eD()
= 0,
ImD
()
= 0.
Это
условие границы устойчивости вытекает
из требования прохождения годографа
Михайлова (для системы, находящейся на
границе устойчивости) через начало
координат, т.е. точку с координатами (Re
= 0, Im
= 0).
Пример.
Определение
области устойчивости АСР по критерию
Михайлова.
Рассмотрим
одноконтурную АСР (см. рисунок 1.27),
состоящую из ПИ-регулятора с передаточной
функцией Wp(s),
объекта с передаточной функцией Wоу(s)
и отрицательной обратной связи.
Передаточные функции имеют вид
,
.
Последовательность
расчета соответствует порядку применения
критерия (см. п. 3.1.5).
Характеристическое
выражение
замкнутой системы:
D(s) =
(K1.s
+ K0).2.e-s
+ s.(3.s
+ 1) = 3.s2
+ s + 2.(K1.s
+ K0).e-s.
Подстановка
s =
j.
дает:
D(j.)
= -3.2
+ j.
+
2.(
j.K1.
+ K0).(cos
— j.sin
)
= -3.2
+ j.
+
+
j.2.K1..cos
+ 2.K1..sin
+ 2.K0.cos
— j.2.K0.sin
= ReD
+ j.ImD,
где
ReD
= -3.2
+ 2.K1..sin
+ 2.K0.cos
,
ImD
=
+ 2.K1..cos
— 2.K0.sin
.
Приравнивание
полученных выражений к нулю дает систему
из двух уравнений с тремя неизвестными:
K0,
K1
и :
ReD
= -3.2
+ 2.K1..sin
+ 2.K0.cos
= 0,
ImD
=
+ 2.K1..cos
— 2.K0.sin
= 0.
Решение системы
относительно K0
и K1:
K0
= 0,5..sin
+ 1,5.2.cos
,
K1
= 1,5..sin
— 0,5.cos
.
Далее,
варьируя
от 0 до бесконечности, по последним
выражениям в пространстве K0
и K1
строится
кривая D-разбиения
(см. рисунок 1.63), которая ограничивает
область устойчивости.
Знание области
устойчивости для рассматриваемой АСР
позволяет ограничить область поиска
оптимальных настроек. Поиск может
производится путем сканирования (в т.ч.
с переменным шагом) только области
устойчивости.
Часто
ставится задача поиска настроек,
соответствующих оптимальным (максимальным
или минимальным) значениям показателей
качества Ci:
,
которые
могут образовывать векторный критерий
С = {Ci}.
Поиск
оптимальных параметров в смысле
векторного критерия достаточно сложен.
Для упрощения он может быть сведен к
достаточно хорошо изученной задаче
минимизации некоторой скалярной функции,
которая является интегральным критерием
I.
Функция I
определяется путем сворачивания
векторного критерия в скалярный одним
из методов:
1)
аддитивный
критерий
,
где αi
– веса (весовые коэффициенты) показателей.
Если показатели
имеют разные шкалы или размерности, то
для облегчения выбора весов иногда эти
показатели нормируют:
,
где
—
минимально (максимально) возможное
значение показателя или диапазон его
шкалы. Веса также нормированы, т.е.
.
2)
линейно-квадратичный
критерий
.
Минимизация по
такому критерию эквивалентна нахождению
точки, ближайшей к началу координат (с
учетом весов).
3)
Минимаксный
(Чебышёвский) критерий
.
Смысл
– минимизация самой большой потери.
4)
Модель
справедливого компромисса.
.
Для
случая n
= 2 имеем α = α1
= α2
= 0,5 и решение
.
То есть относительные
потери по одному критерию приводят к
относительному преобразованию другого.
К
критериям Ci
предъявляются требования:
1) Ci
> 0,
2) для оптимальных
настроек Ci
min
(если изначально Ci
max,
то вместо него вводится в рассмотрение
критерий
,
который стремится к минимуму при Ci
max).
После
определения интегрального критерия
производится его минимизация в области
устойчивости (методом сканирования,
градиентным методом и т.д.).
Поиск
оптимальных настроек может вестись при
заранее введенных ограничениях на
какие-либо показатели качества:
или
,
где
Ci.зад.
– заданное значение показателя.
Достигнутое при поиске значение должно
быть не хуже заданного. Для решения
такой задачи поиска строятся т.н. кривые
D-разбиения
равного значения показателя качества
одним из перечисленных ниже методов в
зависимости от вида показателя.
При
ограничении на степень устойчивости
зад.
Кривая
D-разбиения
изначально являлась границей устойчивости,
поэтому, чтобы можно было применить те
же методы построения кривой (т.е. применять
критерии устойчивости), производят
смещение осей координат Этим смещением
вынуждают систему оказаться на границе
устойчивости.
В
отношении степени устойчивости достаточно
сместить мнимую ось Im
влево на величину зад
(ось Im
z
на рисунке 1.64) путем подстановки
s = z +
зад
в
характеристическое выражение D(s).
Выражение D(z
+ зад)
называется смещенным
характеристическим выражением.
Далее
производится построение кривой D-
разбиения известными
методами. Каждая точка кривой будет
соответствовать заданной степени
устойчивости.
При ограничении
зад.
В
этом случае для вывода системы на границу
устойчивости необходимо повернуть оси
Re
и Im
на угол зад
(см. рисунок
1.65) путем
подстановки
s = z.e
j
.
При
ограничении на степень колебательности
m
mзад.
Поскольку
показатели m
и
связаны однозначно отношением m
= tg
,
то для вывода системы на границу
устойчивости также используется поворот
осей на угол .
Подстановка имеет вид
s = j.
— m..
Далее
строится кривая D-разбиения
по критерию Михайлова.
При
ограничении на степень затухания
зад.
Имеется
формула, связывающая со
степенью колебательности m:
,
откуда
.
Далее строится
кривая D-разбиения
равной степени колебательности m.
При ограничении
на показатель колебательности М
Мзад
.
Применяется
методика Ротача, согласно которой
необходимо определить выражение для
АЧХ замкнутой системы по заданию
А
з()
= |Фз(j.
)|.
П
оказатель
колебательности М определяется как
максимум функции Аз()
(см. рисунок 1.66). Условие максимума
записывается в виде системы:
Аз()
= М
при
.
Поскольку в общем
случае выражение для Аз()
является функцией не только частоты ,
но и настроек регулятора, то система
уравнений (при М = Мзад)
решается относительно них. Далее,
варьируя ,
в пространстве настроек строится кривая
D‑разбиения,
каждая точка которой соответствует
Мзад.
При ограничении
на показатель колебательности МЕ
МЕ зад.
Построение кривой
D-разбиения
строится аналогично как решение системы:
АЕ()
= МЕ зад
при
,
где АЕ()
= |ФЕ(j.
)|
— АЧХ замкнутой системы по ошибке.
Количество
настроек, в пространстве которых строятся
кривые D-разбиения,
как показано в п. 4.1, для разных регуляторов
различно. Так, ПИ-регулятор имеет две
настройки K0
и K1,
поэтому кривая D-разбиения
для него имеет вид кривой на плоскости.
Для ПИД-регулятора с настройками K0,
K1
и K2
кривая D-разбиения
представляет собой поверхность в
трехмерном пространстве. Для ограничения
области поиска настройку K2
рассматривают как зависимую от K0
и K1:
,
где
— коэффициент, оптимальные значения
которого соответствуют диапазону
0,15
0,6.
Тогда поверхность
вырождается в кривую на плоскости K0
и K1.
Доказано, что
оптимальные настройки ПИ- и ПИД-регуляторов
в смысле минимума интегрального
квадратичного критерия
,
где eп(t)
= e(t)
– eуст
– переходная составляющая ошибки,
соответствуют максимуму
K0
на кривой равного значения.
Задача поиска
оптимальных настроек регуляторов
относится к задачам параметрической
оптимизации. В целом при синтезе АСР
различают три уровня оптимизации
(начиная с нижнего):
1) параметрический
– заключается в настройке параметров
– для данного уровня существуют наиболее
разработанные и формализованные
методики;
2) структурный
– подбираются оптимальные структуры
регуляторов, различных корректирующих
звеньев – достаточно хорошо разработаны
методики для одноконтурных систем;
3) топологический
– оптимизация некоторого критерия
путем подбора структуры всей АСР (выбор
количества и мест включения обратных
связей, регуляторов, дополнительных
звеньев) – существуют лишь частные
методики, которые могут давать физически
нереализуемые решения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


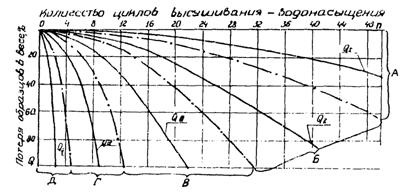
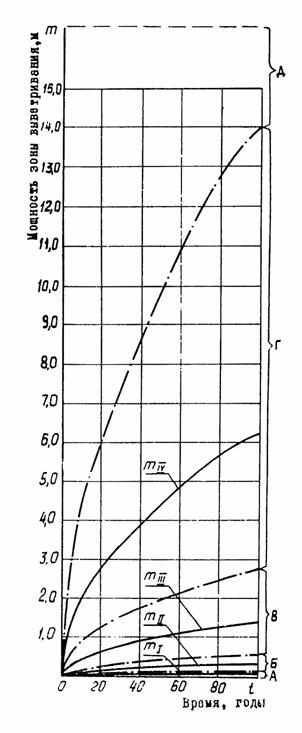
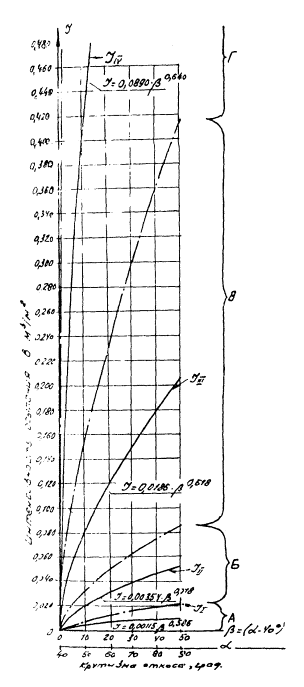
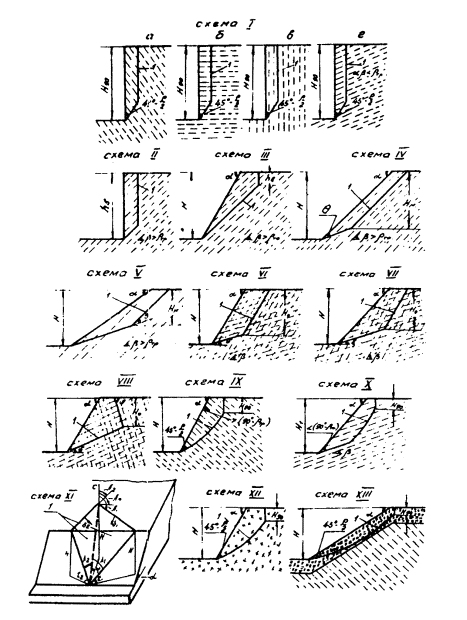
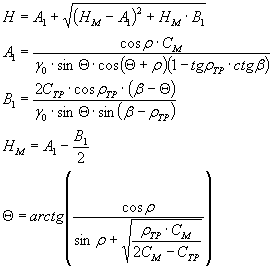
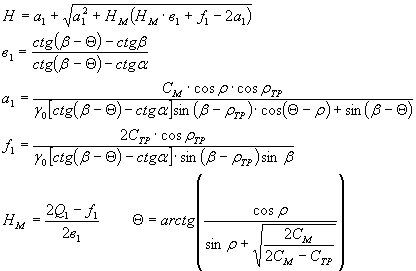
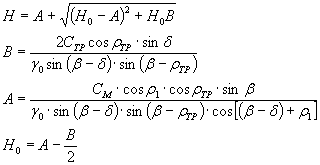
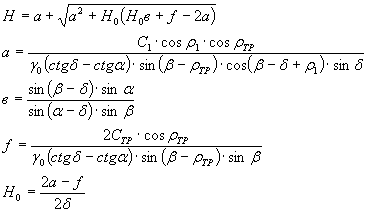
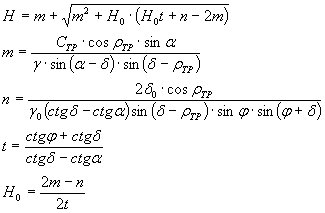
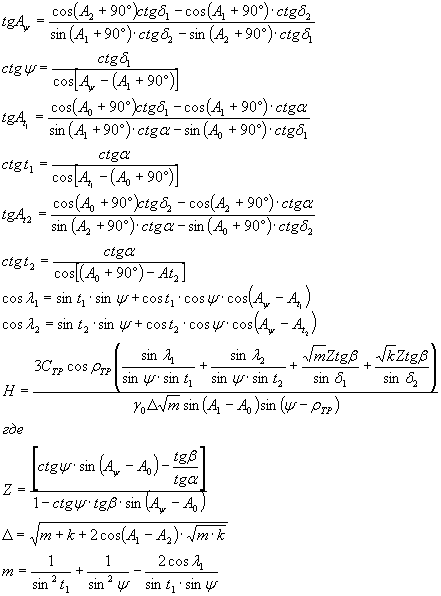
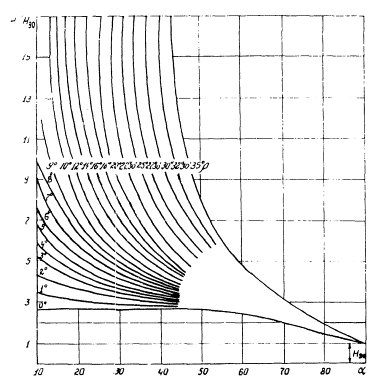
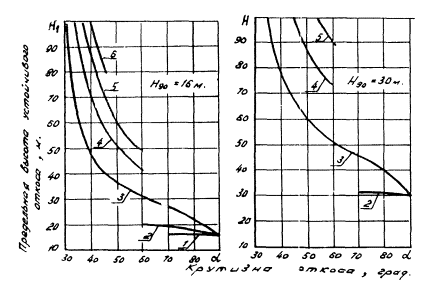
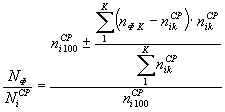
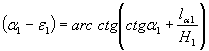 ,
,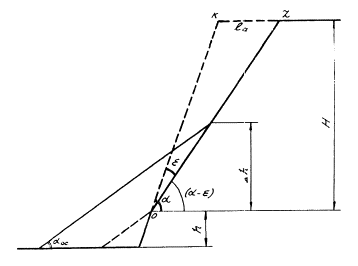
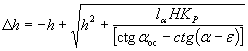 ,
,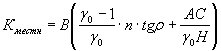 ,
,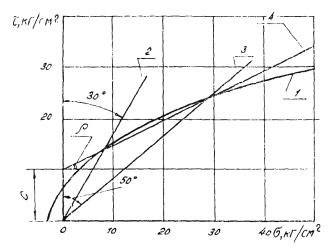
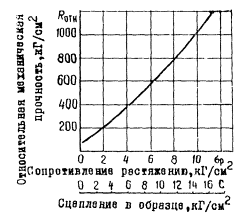
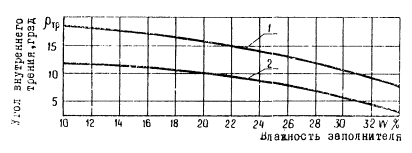
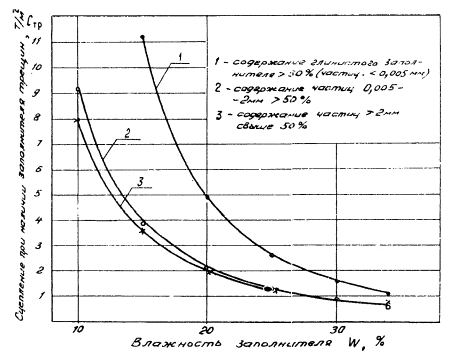
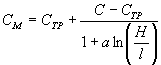 ,
,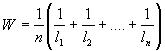 ,
,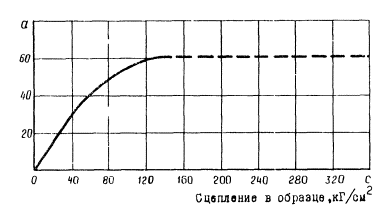
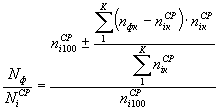 ,
,