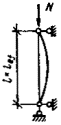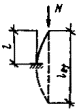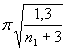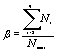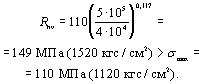ЦНИИСК им. Кучеренко Госстроя СССР
ПОСОБИЕ
по проектированию стальных конструкций
(к СНиП II-23-81*)
Москва 1989
ОРДЕНА ТРУДОВОГО КРАСНОГО
ЗНАМЕНИ ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ И ПРОЕКТНО-ЭКСПЕРИМЕНТАЛЬНЫЙ
ИНСТИТУТ КОМПЛЕКСНЫХ ПРОБЛЕМ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ И СООРУЖЕНИЙ им. В. А.
КУЧЕРЕНКО (ЦНИИСК им. КУЧЕРЕНКО) ГОССТРОЯ СССР
ПОСОБИЕ
по проектированию стальных конструкций
(к СНиП II-23-81*)
Утверждено
приказом ЦНИИСК им. Кучеренко Госстроя СССР
от 15 августа 1985 г. № 243/л
Москва
Центральный
институт типового проектирования
1989
Рекомендовано к изданию
секцией металлических конструкций научно-технического совета ЦНИИСК им.
Кучеренко Госстроя СССР.
Пособие по проектированию
стальных конструкций (к СНиП II-23-81* “Стальные
конструкции” ЦНИИСК им. Кучеренко Госстроя СССР. — М.: ЦИТП Госстроя СССР,
1989. -148 с.
Содержит разъяснения к СНиП II-23-81* “Стальные конструкции”.
Приведены материалы по проектированию новых конструктивных форм, подбору
сечений элементов, расчету технико-экономических показателей конструкций, а
также по новым методам расчета стальных конструкций.
Приведены примеры расчета и конструирования.
Для инженерно-технических
работников проектных организаций, а также для инженеров, научных работников,
специализирующихся в области строительных металлических конструкций, и
студентов строительных факультетов.
Табл. 106, ил. 69.
При пользовании Пособием
следует учитывать утвержденные изменения строительных норм и правил и
государственных стандартов, публикуемые в журнале “Бюллетень строительной
техники”, “Сборнике изменений к строительным нормам и правилам” Госстроя СССР и
информационном указателе “Государственные стандарты СССР” Госстандарте СССР.
Содержание
ПРЕДИСЛОВИЕ
Пособие разработано к СНиП II-23-81* “Стальные конструкции”.
Основополагающими
документами при разработке Пособия наряду со СНиП II-23-81* явились СТ
СЭВ 3972-83 “Надежность строительных конструкций и оснований. Конструкции
стальные. Основные положения по расчету” и СТ СЭВ 384-87 “Надежность
строительных конструкций и оснований. Основные положения по расчету”.
Разд. 1-11 Пособия повторяют
структуру СНиП II-23-81*. В них даются разъяснения
к разделам и пунктам СНиП II-23-81*; такой же
характер имеют разд. 12, 13 и частично разд. 21 и 22, остальные содержат
материалы по проектированию новых конструктивных форм, подбору сечений
элементов, определению технико-экономических показателей, новому подходу к
расчету конструкций.
В Пособии номера пунктов СНиП II-23-81* приведены в скобках.
Пособие разработано ЦНИИСКом
им. Кучеренко Госстроя СССР (кандидаты техн. наук Г.Е. Бельский — разд. 1, 4, пп. 3.1-33, 5.1-5.14, 5.16-5.20, 5.23,
5.24, 5.26, 5.31-5.37, 5.40, 5.41, 5.45, 6.1-6.4, В.Н. Потапов — разд. 2, 10, пп. 3.4-3.7, 5.46, 12.2; М.И. Егоров — пп. 2.1-2.7, 3.4-3.7,
12.2; Е.Р. Мацелинский — пп.
2.8-2.13, 3.12, 3.13, 11.2, 11.3; А.А.
Фадеев — пп. 3.4-3.7, 5.46; В.М.
Барышев — пп. 3.8-3.11, 11.1, 12.1; д-р техн. наук Б.М. Броуде — разд. 8, пп. 5.15, 5.21, 5.22, 5.25, 530, 5.38, 5.39,
5.42-5.44; 21.1-21.6; канд. техн. наук М.И.
Гукова — пп. 6.5-6.15; д-р техн. наук В.М.
Горпинченко, канд. техн. наук Е.М.
Кондрахов — разд. 22, пп. 9.1-9.5; инж. Б.И.
Беляев — разд. 13; кандидаты техн. наук Б.Н.
Решетников — разд. 14, 18; Б.С Цетлин — разд. 18, пп. 15.9-15.17,
16.5-16.19, И.Л. Пименов — разд. 19;
д-р техн. наук, проф. В.И. Трофимов —
разд. 20, 24; инж. Ю.А. Чернов,
кандидаты техн. наук А.М. Ларионов —
разд. 20; Ю.Н. Симаков — пп.
21.7-21.12; д-р техн. наук Н.С. Москалев
— разд. 23; кандидаты техн. наук П.Г.
Еремеев — разд. 24; А.Я. Дривинг — прил.
1; Б.Н. Кузнецов — прил. 2) при
участии ЦНИИпроектстальконструкции им. Н.П. Мельникова Госстроя СССР (д-р техн.
наук проф. Н.Н. Стрелецкий — пп.
11.2-11.9, 21.13-21.15, 21.19-21.21, инж. М.М.
Кравцов — пп. 3.14-3.16; д-р техн. наук проф. В.В. Ларионов — пп. 9.6-9.8; инж. ВМ. Бабушкин — разд. 13, пп. 11.2, 11.4, 11.7, 11.9; канд. техн.
наук И.В. Левитанский — разд. 26, 27,
пп. 16.1-16.5, 16.18-16.24; инженеры В.В.
Севрюгин — пп. 15.1-15.5, 15.14, 15.16-15.19, 15.21-15.26; Б.Н. Емельянов — пп. 15.6-15.8;
кандидаты техн. наук В.В. Березин, Л.А.
Сорокин — разд. 17; Ю.Я. Леус —
пп. 21.18, 21.19; Э.Л. Айрумян —разд.
25, прил. 3; В.Ф. Беляев — разд. 25; М.И. Беккерман — разд. 26; д-р техн.
наук И.С. Ковнер — разд. 29) и МИСИ
им. В.В. Куйбышева Гособразования СССР (канд. техн. наук Ю.В. Соболев — разд. 28, п. 15.20). В разработке Пособия
участвовали: филиал МИСиС Гособразования СССР, г. Электросталь (канд. техн.
наук В.И. Моисеев — разд. 7, пп.
5.27-5.29; 21.20-21.24), Одесский инженерно-строительный институт
Гособразования СССР (д-р. техн. наук Н.Л.
Чернов — пп. 5.31-5.33, 21.14-21.17), ВНИКТИстальконструкция
Минмонтажспецстроя СССР (инж. З.П. Абрам
— пп. 15.16-15.18); Белгородский технологический институт строительных
материалов Гособразования СССР (инж. Ф.Ф.
Куклин — пп. 16.1-16.5, 16.14, 16.16, 16.18-16.24),
ВНИПИпромстальконструкция Минмонтажспецстроя СССР (канд. техн. наук В.В. Каленов — разд. 27, прил. 3;
инженеры В.Д. Мартынчук — разд. 27; Е.С. Марков, Л.М. Сахаров — прил. 3).
Пособие рецензировалось в
ЦНИИСКе им. Кучеренко Госстроя СССР, ЦНИИпроектстальконструкции им. Н.П.
Мельникова Госстроя СССР, МИСИ им. В.В. Куйбышева Гособразования СССР,
ЦНИИпромзданий Госстроя СССР, ВНИКТИстальконструкции Минмонтажспецстроя СССР,
УкрНИИпроектстальконструкции Госстроя СССР, Энергосетьпроекте Минэнерго СССР.
Пособие подготовлено под
общей редакцией докторов техн. наук профессоров В.А. Балдина, В.И. Трофимова, кандидатов техн. наук Г.Е. Бельского, Е.М. Кондрахова, Б.С.
Цетлина, инж. Б.М. Беляева.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА
ОБЩИЕ ПОЛОЖЕНИЯ
1.1.
Расчет стальных конструкций следует выполнять по методу предельных состояний
[1, 2].
Предельные состояния конструкций — такие состояния, при которых конструкции
перестают удовлетворять заданным эксплуатационным требованиям или требованиям
производства работ. При этом нормальная эксплуатация зданий и сооружений
становится невозможной.
1.2. Нормальная эксплуатация — это эксплуатация, которая
осуществляется без ограничений в соответствии с технологическими и бытовыми
условиями, предусмотренными в нормах и заданиях на проектирование и
учитывающими безопасную работу людей, оборудования и сохранность ограждающих
конструкций.
1.3.
В соответствии с требованиями [2] при расчетах стальных конструкций на действие
соответствующих нагрузок необходимо учитывать их предельные состояния,
приведенные в табл. 1.
Таблица
1
|
Группа состояний |
Предельное состояние |
|
|
вид |
характеристика |
|
|
Первая |
Несущая способность |
Пластическое, хрупкое и |
|
Потеря устойчивости формы или |
||
|
Переход в изменяемую систему |
||
|
Полная непригодность к |
Текучесть материала |
|
|
Неупругий сдвиг в соединениях |
||
|
Качественное изменение |
||
|
Вторая |
Пригодность к нормальной |
Перемещения (прогиб, поворот |
|
Колебания |
||
|
Изменение положения |
||
|
Сдвиг в соединениях |
1.4.
Нормативные значения нагрузок, коэффициенты надежности по нагрузке gf и коэффициенты сочетаний
нагрузок для определения их расчетных значений следует принимать согласно [3].
При проверке конструкций по предельным состояниям первой группы необходимо
принимать, как правило, gf > 1,0 (за исключением усталостного разрушения и
тех случаев расчета, когда уменьшение постоянной нагрузки ухудшает условия
работы конструкций). При проверке усталостного разрушения (выносливости) и
предельных состояний второй группы gf £ 1,0.
Согласно [2] расчетные
нагрузки, применяемые в расчетах по первой группе предельных состояний, могут
быть названы предельными, а в расчетах по второй группе и на выносливость —
эксплуатационными.
Поскольку при gf >
1,0 расчетные предельные нагрузки повторяются редко (например, по литературным
данным, от одного крана — один раз в 20 лет; ветровая — один раз в 10-15 лет;
снеговая — в среднем один раз в 10-12 лет; на перекрытия — один раз в 15-20
лет), стальные конструкции при проверке по предельным состояниям первой группы
(за исключением усталостного разрушения) следует рассчитывать на однократное
действие этих нагрузок.
1.5.
Цель расчета — не допустить с определенной обеспеченностью наступления
предельных состояний первой группы или перехода за предельные состояния второй
группы в течение всего срока эксплуатации зданий и сооружений, а также в
процессе их возведения при минимальном расходе материалов и наименьшей
трудоемкости изготовления, транспортирования и монтажа конструкций.
1.6.
При расчете несущей способности сечения или элемента конструкции наибольшее
возможное за время эксплуатации (или возведения) усилие F в элементе от расчетных
предельных нагрузок и воздействий не должно превышать соответствующей
наименьшей предельной несущей способности S сечения или элемента с учетом начальных несовершенств
F £ S. (1)
Усилие F (продольная и поперечная силы; изгибающий, крутящий моменты)
следует определять по формуле
F = gnSaiFnigfi, (2)
где gn — коэффициент надежности по назначению [4];
ai — коэффициент перехода от нормативной нагрузки к
усилию;
Fni —
нормативная нагрузка;
gfi — коэффициент надежности по нагрузке.
Предельную несущую
способность S, соответствующую виду
усилия (сжатию, растяжению, сдвигу, изгибу, кручению и т.д.), необходимо
определять по формуле
, (3)
где b —
коэффициент, учитывающий вид усилия, предельное состояние и работу стали за
пределом упругости (j; jе; jb; с и
т.д.);
Ф —
геометрическая характеристика сечения (A, W);
Rn — нормативное сопротивление
материала;
gс — коэффициент условий работы;
gт — коэффициент надежности по
материалу.
Начальными несовершенствами
стальных конструкций являются совокупность геометрических отклонений формы и
размеров, факторов, влияющих на свойства стали, и отступлений от принятой
расчетной схемы, возникающих при изготовлении, транспортировании и монтаже
конструкций.
Основное неравенство метода
предельных состояний (1) может быть представлено в форме сравнения учитываемых
в расчетах напряжений с их предельными значениями, устанавливаемыми СНиП II-23-81*.
1.7.
При расчете конструкций по предельным состояниям полной непригодности к
эксплуатации перемещения (деформации), соответствующие расчетным значениям
предельных нагрузок и воздействий, не должны превышать предельных значений
перемещений (деформаций), устанавливаемых в нормативных документах по условиям
необходимости прекращения эксплуатации в связи с качественным нарушением
геометрической формы.
Условия расчета по предельным
состояниям полной непригодности к эксплуатации допускается [1] представлять в
форме проверки усилий или напряжений (как при расчетах несущей способности),
определяемых с учетом неупругих деформаций; эта форма принята в СНиП II-23-81*.
1.8.
При расчете конструкций по предельным состояниям второй группы перемещения,
параметры колебаний и изменения положения от расчетных эксплуатационных
нагрузок не должны превышать предельно допустимых значений этих перемещений или
указанных параметров, установленных в СНиП II-23-81* и в других нормативных документах, т.е.
, (4)
где f — перемещения или параметры
колебаний и изменения положения, возникающие в конструкциях от действия
расчетных эксплуатационных нагрузок;
fu — предельно допустимые
значения этих перемещений или параметров, регламентируемые нормами на основе
требований нормальной эксплуатации.
При установлении нормативных
значений fu учитываются нормальные
условия для пребывания людей, работа технологического оборудования, сохранность
ограждающих конструкций.
_________
1 Поскольку в
большинстве случаев gf = 1,0, эти нагрузки в п. 13.1
СНиП II-23-81* названы “нормативными”.
1.9 (1.7). Выбор расчетных схем, исходных предпосылок и допущений необходимо
определять на основе применяемого метода расчета. При использовании, например,
вычислительной техники необходимо наиболее полно учитывать действительные
условия работы конструкций и рассчитывать их как единые пространственные
системы с учетом неупругих деформаций стали, деформированной схемы и, в случае
необходимости, геометрической нелинейности.
Существует значительное
число программ расчета стальных конструкций на ЭВМ. Одной из них, позволяющей
решать широкий класс задач, является диалоговая система расчета (ДИАРАМА),
разработанная ЦНИИпроектстальконструкцией им. Н.П. Мельникова [5].
ЦНИИСКом им. Кучеренко
разработана программа расчета на ЭВМ структурных конструкций, учитывающая
особенности их работы. Программа обеспечивает расчет структурных плит вплоть до
разрушающих нагрузок и стержневых оболочек, включая потерю устойчивости с
учетом характера деформирования элементов при упругой и упругопластической
работе материала.
Допускается применять
приближенные методы расчета и более простые расчетные схемы, основанные на
разделении единых пространственных систем на плоские конструкции и отдельные
элементы. При этом следует учитывать особенности взаимодействия элементов
стальных конструкций между собой и с основанием. Вместе с тем, в общем случае
предпочтение следует отдавать методам расчета стальных конструкций как единых
пространственных систем.
1.10 (1.8). Для статически неопределимых стержневых конструкций расчетные усилия
допускается определять по недеформированной схеме в предположении упругих
деформаций стали. Расчет на устойчивость отдельных стержней при действии этих
усилий следует выполнять по деформированной схеме с учетом неупругих деформаций.
1.11.
Расчеты элементов стержневых и балочных конструкций, а также пластинок,
образующих сечение, необходимо выполнять с учетом неупругих деформаций стали и,
как правило, в предположении малости перемещений с использованием приближенного
выражения для кривизны (т.е. на основе геометрически линейной теории). При этом
рекомендуется применять теорию малых упругопластических деформаций при простом
нагружении; в ряде случаев допускается использовать модель жесткопластического
тела.
1.12.
По своей физической природе строительные стали являются упругопластическим
материалом с различными зависимостями между деформациями и напряжениями при
нагрузке и разгрузке.
Однако при
проверке конструкций по предельным состояниям первой группы на однократное
действие расчетных предельных нагрузок применяемые стали рекомендуется
рассматривать как нелинейно упругий материал, характеризующийся одной и той же
нелинейной или кусочно линейной зависимостью между деформациями и напряжениями
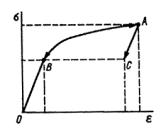
при нагрузке и разгрузке (рис. 1, кривая ОВАВ).
Рис. 1. Зависимость
между напряжениями и деформациями при нагружении ОА и разгрузке для упругопластического материала АС, для нелинейно упругого материала АВ
Если в процессе деформирования конструкции в
некоторых ее частях появится частичная разгрузка, то жесткость системы в целом
должна увеличиться. В связи с этим принятое допущение приводит, как правило, к
некоторому запасу несущей способности, что позволяет в практических расчетах в
большинстве случаев надежно пользоваться моделью нелинейно упругого материала.
1.13.
При возможном убывании нагрузок, а также при повторно-переменной нагрузке
анализ поведения стальных конструкций за пределом упругости должен основываться
на использовании модели упругопластического материала с различными
зависимостями между деформациями и напряжениями при нагрузке и разгрузке (рис.
1, кривая ОВАС).
1.14.
Расчет стальных, конструкций и их элементов на усилия от действия внешних
нагрузок, как правило, необходимо
выполнять с использованием геометрических гипотез: плоских сечений,
секторальных площадей и прямых нормалей.
1.15.
При необходимости расчета стальных конструкций и их элементов с учетом влияния
собственных остаточных напряжений sr (от сварки, прокатки, холодной правки и т.д.)
допускается применять гипотезу об алгебраическом суммировании условных
деформаций er = sr/Е с деформациями от внешней нагрузки (Е — модуль упругости).
1.16.
Надежность и экономичность стальных конструкций должны быть обеспечены
одновременным выполнением требований к выбору материалов, расчетам и конструированию
(а также изготовлению и монтажу).
В случаях, когда наступление
предельных состояний конструкций сопряжено только с экономическими
последствиями, их расчет допускается выполнять вероятностно-экономическим
методом, обеспечивающим оптимальное соотношение между надежностью и
материалоемкостью сооружений [6].
1.17 (1.9). При проектировании стальных конструкций следует принимать минимальные
сечения элементов, удовлетворяющие требованиям СНиП II-23-81*. Подбор сечений необходимо выполнять с учетом
технико-экономического обоснования принимаемого проектного решения,
действующего сортамента, применения эффективных марок сталей, профилей,
унифицированных типовых или стандартных конструкций, а также других требований СНиП II-23-81*.
ПРЕДЕЛЬНЫЕ СОСТОЯНИЯ СТАЛЬНЫХ КОНСТРУКЦИЙ
1.18.
Изложенные в СНиП II-23-81* методы проверки
стальных конструкций по предельным состояниям, классификация которых приведена
в табл. 1, разработаны с учетом свойств сталей, назначения и условий
эксплуатации конструкций, вида их работы, характера внешних нагрузок и
воздействий, а также технологии изготовления и монтажа.
1.19.
Пластическое разрушение элементов и конструкций сопровождается значительным
развитием пластических деформаций и в ряде случаев предполагает работу стали в
области самоупрочнения.
При соответствующем
обосновании допускается не учитывать область самоупрочнения стали и расчеты
конструкций выполнять на основе идеализированной упругопластической (Прандтля)
или жесткопластической диаграмм.
В соответствии со СНиП II-23-81* проверку пластического
разрушения необходимо выполнять при расчете на прочность следующих элементов из
пластических сталей с отношением su/sy > 1,3 (где sи —
временное сопротивление, обозначаемое sb, по государственным стандартам и техническим
условиям на сталь; sу —
предел текучести, обозначаемый sт, по государственным
стандартам и техническим условиям на сталь), несущих статическую нагрузку:
а) растянутых, нормальная
эксплуатация которых возможна и после достижения металлом предела текучести
(некоторые типы листовых конструкций, в основном, с равномерным распределением
растягивающих напряжений: листовые настилы, отдельные виды трубопроводов и
резервуаров с учетом опыта их эксплуатации);
б) сечений, ослабленных
отверстиями для болтов, в болтовых конструкциях, а также в местах стыков,
выполненных на болтах (кроме конструкций на высокопрочных болтах);
в) растянутых одиночных
уголков, прикрепляемых одой полкой болтами;
г) стенок перфорированных
балок.
Пластическое разрушение
учитывается согласно СНиП II-23-81* также при
установлении расчетных сопротивлений сварных и болтовых соединений.
К пластическому разрушению
следует относить предельные состояния конструкций при повторяющихся нагрузках
по условиям переменной текучести и прогрессивного разрушения.
1.20.
Хрупкое разрушение сопровождается малой деформацией, как правило, при
концентрации напряжений, низких температурах или ударных воздействиях, в
большинстве случаев при одновременном действии указанных факторов.
В соответствии со СНиП II-23-81* способность стальных
конструкций противостоять хрупкому разрушению следует обеспечивать главным
образом выполнением требований к выбору сталей, применению соответствующих
конструктивных решений, технологии обработки деталей и образования отверстий.
Согласно СНиП II-23-81* рекомендуется также проверка расчетом на прочность
с учетом хрупкого разрушения, в первую очередь, центрально- и
внецентренно-растянутых элементов и зон растяжений изгибаемых элементов в
предположении упругих деформаций стали при действии расчетных предельных
нагрузок.
1.21.
Усталостное разрушение сопровождается образованием и развитием трещин в
результате многократно повторяющихся силовых воздействий от подвижных,
вибрационных и других переменных нагрузок, приложенных непосредственно к
конструкциям.
Проверка этого предельного
состояния согласно СНиП II-23-81* выполняется
расчетом элементов конструкций на выносливость в пределах упругих деформаций
стали при действии расчетных эксплуатационных нагрузок с учетом характеристик
сталей, вида напряженного состояния, конструктивной схемы узла или соединения,
технологии обработки детали, вида нагрузки и числа циклов нагружений.
1.22.
Потеря устойчивости формы или положения характеризуется тем, что конструкция
или элемент утрачивают способность сохранять свое равновесное состояние,
соответствующее действующим при этом внешним нагрузкам и воздействиям.
Проверку устойчивости формы
или положения следует выполнять для системы в целом и для ее отдельных
элементов.
В соответствии со СНиП II-23-81* проверка потери
устойчивости формы заключается в установлении максимального значения нагрузки,
которая может быть воспринята элементом, имеющим, как правило, начальные
несовершенства, при расчете его по деформированной схеме с учетом неупругих
деформаций стали.
При соответствующем
обосновании допускается рассчитывать на устойчивость идеальные системы или
элементы в пределах упругих деформаций. Этот метод, в частности, использован в СНиП II-23-81* при определении расчетных
длин сжатых стержней, установлении приведенной гибкости сжатых сквозных
стержней, проверке балок на общую устойчивость и т.д.
1.23.
Переход конструкции в изменяемую систему характеризуется превращением ее в
кинематический механизм, у которого возможность изменения формы в направлении
действия нагрузки не ограничена никакими связями.
1.24.
Предельное состояние в результате текучести материала, неупругих сдвигов в
соединениях, качественного изменения конфигурации означает переход конструкций
в такое состояние, когда при сохранении общей несущей способности необходимо
прекратить эксплуатацию конструкций в связи с существенным нарушением
геометрической формы и выполнить ремонтные работы по замене или восстановлению
конструкций. Указанное предельное состояние, как и потеря несущей способности,
относится к первой группе и проверяется на действие тех же расчетных предельных
нагрузок.
В отличие от несущей
способности, когда критериями предельных состояний являются силовые факторы
(или нагрузки) и выполняется проверка усилий или напряжений, для полной
непригодности к эксплуатации предельные состояния конструкций при сохранении их
несущей способности по существу должны оцениваться на основе деформационных
критериев — ограничений перемещений или деформаций конструкций, работающих за
пределом упругости.
Вместе с тем проверка
рассматриваемого предельного состояния в ряде случаев может выполняться в
традиционной форме сравнения напряжений (усилий).
1.25.
Предельные состояния по ограничению перемещений, сдвигов в соединениях,
колебаний и изменения положения конструкций и элементов (вторая группа)
характеризуются тем, что нарушаются условия нормальной эксплуатации, связанные
с пребыванием людей, работой технологического оборудования и сохранностью
ограждающих конструкций.
Значения указанных
деформационных величин, определяемые расчетом, как правило, в пределах упругих
деформаций стали не должны превышать предельно допустимых значений,
установленных СНиП II-23-81*.
В отличие от предельных
состояний первой группы, возможность наступления которых, в принципе, не
допускается системой частных коэффициентов метода предельных состояний,
установленные СНиП II-23-81* для второй
группы предельно допустимые значения перемещений или параметров колебаний и
изменения положения конструкций могут быть достигнуты (но не превзойдены) в
процессе работы конструкций при действии расчетных эксплуатационных нагрузок.
2. МАТЕРИАЛЫ ДЛЯ КОНСТРУКЦИЙ И СОЕДИНЕНИЙ
В СНиП II-23-81* приведены новые положения, направленные на снижение
расхода черных металлов в стальных конструкциях. К ним относятся:
упразднение системы
разделения различных марок сталей для металлических конструкций на классы
прочности;
отказ от унификации
расчетных сопротивлений по минимальным значениям нормативных сопротивлений
марок стали, отнесенных к различным классам;
назначение нормативных
сопротивлений по пределу текучести и временному сопротивлению по величинам,
установленным государственными общесоюзными стандартами и техническими
условиями на поставку проката;
установление коэффициентов
надежности по материалу gm, с учетом обеспеченности
нормативных сопротивлений и принятых методов контроля качества стального
проката при поставке;
введение в перечень
материалов для стальных конструкций эффективных сталей, поставляемых по ГОСТ
23570-79 и ТУ 14-1-3023-80, с указанием предпочтительности их применения по
сравнению со сталями, поставляемыми по ГОСТ 380-71*, ГОСТ
19281-73* и ГОСТ
19282-73*;
дифференцирование назначения сталей и их расчетных
характеристик по видам проката (лист, фасон, труба).
В СНиП II-23-81* включены также положения, направленные на
унификацию требований, предъявляемых к материалам при проектировании:
сокращение числа групп
конструкций до четырех;
районирование территории
СССР в соответствии с ГОСТ
16350-80.
Новые требования к применению сталей в конструкциях
зданий и сооружений позволяют снизить их расход более чем на 7 %.
ОСНОВНЫЕ ТРЕБОВАНИЯ К ПРОКАТУ
2.1.
Прокат, применяемый в конструкциях, должен отвечать требованиям соответствующих
государственных общесоюзных стандартов или технических условий на его поставку.
2.2 (2.1*). При выборе марок прокатной стали следует учитывать степень
ответственности конструкций зданий и сооружений, а также условия их
изготовления и эксплуатации в соответствии с табл. 50* СНиП II-23-81*.
Примерный перечень отдельных
групп конструкций и их элементов приведен в [7, табл. 1].
При проектировании
металлоконструкций промышленных зданий и сооружений необходимо стремиться к
максимальному сокращению марок применяемых сталей и типоразмеров проката,
используя при этом “Сокращенный сортамент металлопроката для применения в
строительных стальных конструкциях”, утвержденный Госстроем СССР.
2.3 (2.1*). По хладостойкости металл проката должен отвечать требованиям,
указанным в табл. 2.
2.4.
Марки стали дня элементов стальных конструкций и сооружений, воспринимающих
растягивающие нагрузки в направлении толщины проката, следует принимать по
табл. 50* СНиП II-23-81*, при этом прокат толщиной
свыше 60 мм без проведения дополнительных испытаний применять не рекомендуется.
Для изготовления элементов,
в которых в направлении по толщине проката возникают высокие растягивающие
напряжения от внешней нагрузки, приближающиеся к 0,5 Ru, и высокие растягивающие
реактивные напряжения, рекомендуется применять марки стали, используемые для
конструкций группы 1.
Фланцы и подобные им
элементы тяжело нагруженных ферм, балок и т.п. при толщине элементов свыше 40
мм рекомендуется выполнять из
листового проката с пониженным содержанием серы, выплавляемого по техническим
условиям (например, по ТУ 14-1-3765-84 S не более 0,015 или по ТУ 14-105-465-82 S не более 0,020).
Таблица 2
|
Гарантированные |
Требования к сталям по |
||||||||||
|
1 |
2 |
3 |
4 |
||||||||
|
Климатический район |
|||||||||||
|
I1 |
I1, II2, II3 |
II4, II5 и др. |
I1 |
I1, II2, II3 |
II4, II5 и др. |
I1 |
I2, II2, II3 |
II4, II5 и др. |
I1, I2, II2, |
II4, II5 и др. |
|
|
sТ < |
Не применять |
KCU-50; КСА |
KCU-20; КСА |
Не применять |
KCU-40; КСА |
KCU-20; КСА |
Не применять |
KCU-40 |
КСА** |
KCU-20; |
Не предъявляются |
|
295 (30) £ |
KCU-70; КСА |
KCU-50; |
KCU-40; КСА |
KCU-70; КСА |
KCU-50; КСА |
KCU-40 |
KCU-50 |
KCU-40 |
KCU-40 |
— |
— |
|
390 (40) £ |
KCU-70; КСА |
KCU-50; |
KCU-40; КСА |
KCU-70; КСА |
KCU-50; |
KCU-40 |
KCU-70 |
KCU-50* |
KCU-40 |
— |
— |
Обозначения, принятые в табл. 2:
KCU — ударная вязкость, определенная на образце с
концентратором вида U (при соответствующей температуре)
по ГОСТ
9454-78*.
КСА — ударная вязкость после
механического старения по ГОСТ
7268-82*.
__________
* Допускаются
также стали, удовлетворяющие требованиям KCU-40
и КСА.
** Только для
района 114.
Для изготовления элементов
ответственных конструкций, в которых заведомо ожидается большой уровень
реактивных напряжений, например, вследствие приварки защемленных элементов при
наличии зазоров между ними, также рекомендуется использовать
конструктивно-технологические решения, исключающие возникновение высоких
растягивающих реактивных напряжений в направлении толщины проката.
Материал элементов конструкций,
воспринимающих растягивающие напряжения по толщине листа, в зонах, прилегающих
к местам наложения сварных швов, рекомендуется на заводах металлоконструкций
дополнительно (до сварки) подвергать ультразвуковому дефектоскопическому
контролю на наличие внутренних несплошностей типа расслоев, грубых шлаковых
включений и т.п. Площадь максимально допустимого дефекта не должна превышать 1
см2, а допустимая частота дефектов — 10 м-2. Расстояние
между дефектами не должно быть меньше величины наибольшего из них.
2.5. (2.9). Физические характеристики стального проката следует принимать с учетом
их изменения в диапазоне климатических температур, как указано в табл. 3.
Таблица 3
|
Характеристика |
Значения |
|
|
при t = 20 °С |
при климатической ti |
|
|
Плотность, кг/м3 |
r |
|
|
Коэффициент линейного |
a = 0,12 × 10-4 |
ai = a [1 + 0,02(ti — t)]* |
|
Модуль упругости, МПа (кгс/см2) |
Е = 2,06 × |
Ei = E[1 + 0,27 × 10-3 (ti — t)]* |
|
Модуль сдвига, МПа (кгс/см2) |
G = 0,78 × 105 (0,8 × 106) |
|
|
Коэффициент поперечной |
v = 0,3 |
__________
* Получено
обобщением данных, приведенных в статье И. Г. Кожевникова и Л. А. Новицкого
“Теплофизические свойства материалов при низких температурах” (М.:
Машиностроение, 1982. — С. 7-27).
** Получено с учетом данных книги Я. Б. Фридмана. “Механические
свойства металлов”. Т. 1 (М.: Машиностроение, 1974. — С. 238, 239).
2.6.
При выборе марок стали следует руководствоваться результатами
технико-экономических расчетов с учетом получения максимальной экономии металла
при минимальном использовании дефицитных легирующих элементов за счет
расширенного применения термической обработки и с учетом обеспечения надежности
конструкций в условиях климатических воздействий.
2.7.
Для конструкций из листового проката толщиной менее 4 мм можно применять марки
углеродистой стали по ГОСТ 380-71* с
физическими характеристиками (плотностью, коэффициентом линейного расширения, модулем
упругости, модулем сдвига, коэффициентом поперечной деформации) в соответствии
с табл. 50* СНиП II-23-81*. Расчетные
сопротивления следует устанавливать делением нормативных значений предела
текучести и временного сопротивления, указанных в ГОСТ 380-71* для
проката толщиной до 20 мм, на коэффициент надежности по материалу, равный 1,05
в соответствии с табл. 2 СНиП II-23-81*.
БОЛТЫ И ГАЙКИ ДЛЯ СОЕДИНЕНИЙ
2.8 (2.4*). Выбор болтов следует производить по табл. 57* СНиП II-23-81* с учетом условий их применения — климатического района,
характера действующих нагрузок, условий работы в соединениях (растяжение или
срез).
Для конструкций, возводимых
в климатических районах I1, I2, II2 и II3, но эксплуатируемых в
отапливаемых помещениях, болты следует назначать по табл. 4.
2.9.
Для болтовых соединений следует, как правило, использовать крепежные изделия из
“Сокращенного сортамента крепежных изделий для строительных металлических
конструкций”, утвержденного Госстроем СССР. Применение, в случае необходимости,
крепежных изделий, не включенных в указанный сортамент, должно быть согласовано
проектной организацией с изготовителем проектируемого объекта и утверждено
Госстроем СССР.
Таблица 4
|
Условия работы болтов |
Технологические |
||
|
класс прочности (табл. |
дополнительные виды |
марка стали |
|
|
В конструкциях, не |
|||
|
Растяжение или срез |
4.6; 5.6 |
Поз. 1 |
По табл. 1 |
|
4.8; 5.8 |
Тоже |
Тоже |
|
|
6.6 |
“ |
35 |
|
|
В конструкциях, |
|||
|
Растяжение или срез |
4.6; 5.6 |
Поз. 1 и 4 |
По табл. 1 |
|
6.6 |
То же |
35 |
|
|
Срез |
4.8; 5.8 |
Поз. 1 |
По табл. 1 |
2.10.
Крепежные изделия применяют обычно без покрытия. Применение, в случае
необходимости, крепежных изделий с покрытием по ГОСТ 1759-70** должно быть
согласовано проектной организацией с изготовителем проектируемого объекта.
2.11.
Запрещается использовать болты без клейма и маркировки. Клеймение и маркировка
должны соответствовать ГОСТ 1759-70**.
2.12.
Запрещается использовать крепежные изделия с отклонениями от соответствующих
стандартов, в том числе крепежные детали 2-го сорта и болты, изготовленные из
автоматных сталей.
2.13.
Запись условных обозначений крепежных изделий на всех стадиях разработки и
производства стальных конструкций следует выполнять только по форме,
приведенной в ГОСТ 1759-70**. Запрещается при записи условных обозначений
крепежных изделий делать пропуск каких-либо характеристик, предусмотренных
соответствующими стандартами, в том числе дополнительных требований, за
исключением длины болтов в чертежах КМ.
ФУНДАМЕНТНЫЕ БОЛТЫ
2.14.
По условиям эксплуатации болты подразделяются на расчетные и конструктивные.
К расчетным болтам относятся болты, воспринимающие нагрузки, возникающие при эксплуатации
строительных конструкций.
К конструктивным болтам относятся болты, предусматриваемые для крепления
строительных конструкций, устойчивость которых против опрокидывания или сдвига
обеспечивается собственным весом конструкций.
Конструктивные болты
предназначаются для рихтовки строительных конструкций во время их монтажа,
обеспечения стабильной работы во время эксплуатации конструкций, а также для
предотвращения случайных смещений конструкций.
2.15.
Выбор марки стали шпилек расчетных болтов, предназначенных для крепления
строительных конструкций, следует производить по табл. 5 с учетом климатических
районов.
Шпильки болтов допускается
изготовлять из сталей других марок, механические свойства которых не ниже
свойств сталей марок, указанных в табл. 5.
Таблица 5
|
Климатический район |
II4 (-30 > t ³ -40); II5 и др. (t ³ -30) |
I2, II2 и II3 (-40 > t ³ -50) |
I1 (-50 > t ³-65) |
|
Марка стали шпилек |
ВСт3кп2 (по ГОСТ |
09Г2С-6 и 10Г2С1-6 |
09Г2С-8 и 10Г2С1-8 |
Для климатических районов строительства
II4, II5 и других (t ³ -40 °С) допускается изготовлять шпильки расчетных
болтов с резьбой диаметром 56 мм и более из низколегированной стали марок
09Г2С-2 и 10Г2С1-2 по ГОСТ
19281-73*.
2.16.
Шпильки конструктивных болтов для всех климатических районов следует
изготовлять из стали марки ВСт3кп2 по ГОСТ 380-71*.
Марки стали шпилек
конструктивных болтов, если последние подлежат проверке на сейсмические
воздействия, следует назначать как для шпилек расчетных болтов.
2.17.
Гайки и муфты фундаментных болтов следует изготовлять из сталей тех же марок,
что и шпильки.
3. РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И СОЕДИНЕНИЙ
ОБЩИЕ ПОЛОЖЕНИЯ
3.1.
Основной интегральной характеристикой сопротивления стали деформированию при
действии нагрузки является экспериментально получаемая зависимость между
напряжением s = N/A и относительным удлинением e = Dl/l — диаграмма работы
(деформирования) стали при одноосном растяжении (где N — растягивающая сила; А — площадь сечения образца; l — расчетная длина образца).
Значение напряжения,
соответствующего наибольшей нагрузке, предшествующей разрушению образца, называется
временным сопротивлением su. При значениях напряжений,
равных физическому (для сталей с явно выраженной площадкой текучести) или
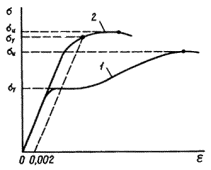
условному пределу текучести (рис. 2), работа стали сопровождается
соответственно текучестью или развитием значительных упругопластических
деформаций без ее разрушения.
Рис. 2. Диаграммы работы стали
1 — при наличии явно выраженной площадки
текучести; 2 — при отсутствии
площадки текучести
Таким образом, основными
параметрами для оценки работы стали при действии нагрузки являются значения
временного сопротивления su и предела текучести sу, устанавливаемые в
государственных общесоюзных стандартах и технических условиях на поставку
металлопроката.
3.2 (3.1). Значения временного сопротивления su и предела текучести sу для металлопроката,
выпускаемого металлургической промышленностью, имеют некоторый разброс. С
учетом случайной изменчивости этих характеристик в СНиП II-23-81* установлены значения нормативных сопротивлений соответственно
по временному сопротивлению Run = su (sb) и по
пределу текучести Ryn = sу (sТ), обеспеченность которых при поставке
металлопроката по государственным общесоюзным стандартам и техническим условиям
составляет, как правило, не менее 0,95, что соответствует требованиям [2].
3.3 (3.2). Возможные отклонения сопротивлений сталей в неблагоприятную сторону от
их нормативных значений согласно [2] учтены с помощью коэффициентов надежности
по материалу gm,
которые установлены в СНиП II-23-81* в зависимости
от обеспеченности нормативных сопротивлений, гарантируемой методами контроля
качества металлопроката на металлургических предприятиях.
Чем выше обеспеченность
нормативных сопротивлений поставляемого проката, тем более низкими приняты
коэффициенты надежности по материалу (см. табл. 2 СНиП II-23-81*).
РАСЧЕТНЫЕ СОПРОТИВЛЕНИЯ СТАЛЬНОГО ПРОКАТА
3.4 (3.1). Значения основных расчетных сопротивлений определены делением значений
Run и Rуn на коэффициент надежности по материалу —gm > 1,0:
Ru = Run/gm; Ry = Ryn/gm, (5)
где Ru — расчетное сопротивление по
временному сопротивлению;
Ry —
расчетное сопротивление по пределу текучести.
Значения коэффициента
надежности по материалу gm в формулах (5) приняты одинаковыми при определении Run и Rуn.
3.5.
Расчетные сопротивления проката для различных видов напряженных состояний
приведены в табл. 1* СНиП II-23-81* в соответствии
с государственными общесоюзными стандартами с использованием коэффициентов
перехода от основных расчетных сопротивлений. Хотя механические свойства
проката вдоль и поперек направления прокатки несколько отличаются, расчетные
сопротивления в СНиП II-23-81* приняты
одинаковыми независимо от направления прокатки.
3.6.
Расчетные сопротивления проката Rth при растяжении в направлении толщины следует определять по формуле
Rth = 0,5 Run/gm. (6)
Развернутая формула для определения
величины Rth будет иметь вид
. (7)
Значение коэффициента
снижения прочности проката на растяжение в направлении толщины листа gth практически не зависит от марки стали и толщины
листа в пределах до 60 мм и равно 0,72. При этом обеспеченность нормативного
сопротивления на растяжение в направлении толщины gth Run на основании статистических данных принята 0,95.
Неоднородность прочностных
свойств проката по толщине существенно выше, чем в плоскости листа. С учетом
этого коэффициент надежности по материалу при растяжении в направлении толщины
листа принят gmth = 1,1 gm.
Формула (7) предусматривает
расчет на прочность по временному сопротивлению, т.е. предельным состоянием
является разрушение. Для предотвращения разрушения в формулу (7) введен
коэффициент надежности gu = 1,3.
После подстановки числовых
значений коэффициентов gth, gmth, gu в формулу (7) расчетное
сопротивление Rth приводится к виду (6).
При расчете проката по Rth коэффициент надежности gu,
определяемый в соответствии с разд. 4* СНиП II-23-81*, учитывать не следует.
3.7. В изгибаемых элементах
конструкций (типа пластин, плит, фланцев) малой высоты сопротивление проката
переходу в упругопластическое состояние из-за наличия больших градиентов
напряжений существенно превышает расчетные сопротивления Ry, приведенные в СНиП II-23-81*.
В связи с этим в СНиП II-23-81* предусмотрена возможность
учета повышенных значений сопротивления металла при определении высоты сечения
(толщины) элементов конструкций типа опорных плит введением для них
коэффициентов условий работы gс >
1 (см. п. 5.46).
РАСЧЕТНЫЕ СОПРОТИВЛЕНИЯ СВАРНЫХ СОЕДИНЕНИЙ
3.8 (3.4). Формулы для определения расчетных сопротивлений сварных соединений,
приведенные в СНиП II-23-81*, предполагают
следующие условия:
подготовка материалов, сборка конструкций, сварка и
контроль качества осуществляется в соответствии с требованиями [8] и других
нормативных документов;
сварочные материалы для
стыковых соединений соответствуют прочности свариваемой стали и условиям
эксплуатации конструкций и применяются в соответствии с табл. 55* СНиП II-23-81*;
сварочные материалы для
расчетных угловых швов применяются в соответствии с табл. 56 СНиП II-23-81* с учетом условий эксплуатации конструкций,
указанных в табл. 55* СНиП II-23-81*.
3.9.
Расчетные сопротивления стыковых соединений, выполняемых всеми видами дуговой
сварки, принимаются равными расчетным сопротивлениям стального проката при
условии соблюдения требований п. 13.4 СНиП II-23-81* о полном проваре соединяемых элементов,
обеспечиваемом сварками: двусторонней, односторонней с подваркой корня шва, на
подкладках, а также при физическом контроле качества швов.
В случаях, когда в стыковых
соединениях невозможно обеспечить полный провар элементов, рекомендуется
принимать Rwy = 0,7.
3.10.
Несущая способность сварных соединений с угловыми швами зависит от ориентации
шва относительно направления усилия, действующего на соединение. Однако
расчетные сопротивления соединений с угловыми швами в СНиП II-23-81* упрощенно приняты для наименее благоприятной
ориентации — флангового шва и независимыми от угла между продольной осью шва и
направлением -силы, действующей на него.
3.11.
Предельным состоянием для сварных соединений с угловыми швами является
разрушение. В связи с этим их расчетные сопротивления в СНиП II-23-81* установлены по временному сопротивлению металла:
для металла шва в зависимости от его нормативного сопротивления Rwf = f(Rwun); для металла границы сплавления — в зависимости от
нормативного сопротивления основного металла Rwz
= f(Run).
Числовые значения расчетных
сопротивлений сварных соединений с угловыми швами приведены в табл. 56 СНиП II-23-81* и в табл. 3 [9].
РАСЧЕТНЫЕ СОПРОТИВЛЕНИЯ ОДНОБОЛТОВЫХ СОЕДИНЕНИЙ
3.12 (3.5). Расчетные сопротивления болтов в табл. 5* и 58* СНиП II-23-81* назначены в зависимости от классов прочности по
ГОСТ 1759-70**.
Класс прочности зависит от
марки стали и способа изготовления болтов и обозначен двумя числами. Первое
число, умноженное на 10, означает величину минимального временного
сопротивления в кгс/мм2, второе — умноженное на 10, — отношение
предела текучести к временному сопротивлению в процентах; произведение чисел —
величину предела текучести в кгс/мм2.
3.13.
Расчетные сопротивления растяжению болтов классов прочности 4.8 и 5.8 по
сравнению с болтами других классов для обеспечения надежности работы приняты в СНиП II-23-81* пониженными ввиду того,
что они изготовляются методом холодной высадки без последующей термообработки,
вследствие чего стержень болта характеризуется пониженными пластическими
свойствами из-за сильного наклепа материала1.
_________
1 Потапов
В. Н, Мищик Б. С. Оценка работоспособности болтов, работающих на растяжение
в стальных конструкциях. //Промышленное стр-во. — 1982. — № 5. -С. 23-25.
ХАРАКТЕРИСТИКИ СТАЛЬНЫХ КАНАТОВ
3.14.
Для стальных канатов (витых заводского изготовления и из параллельных проволок)
с временным сопротивлением проволок — Runj до 1800 МПа (180 кгс/мм2) при
антикоррозионной защите согласно СНиП 2.03.11-85 (для
сооружений на открытом воздухе) или другими методами, соответствующими сроку
службы и условиям работы сооружения, при диаметрах проволок не менее 2,4 мм в
витых канатах и 3 мм — при параллельных проволоках расчетное усилие растяжения
каната в расчетах на прочность должно удовлетворять неравенству [10]:
, но не более 0,7 Run, (8)
где A —
суммарная номинальная площадь сечения всех проволок каната;
Run — нормативное сопротивление
каната по временному сопротивлению, определяемое в соответствии с п. 3 [10];
gи = 1,3 — коэффициент
надежности для элементов конструкций, рассчитываемых по временному
сопротивлению разрыву, учитывающий особую опасность предельного состояния
(вязкое разрушение) по сравнению с предельным состоянием — чрезмерным развитием
пластических деформаций;
gm = 1,2 — коэффициент
надежности стальных канатов по материалу, учитывающий наряду со статистическим
разбросом временного сопротивления также допуски на размер проволок, наличие
большего числа проволок в поперечном сечении каната, большую длину канатных
элементов, специфические условия Приемки отбраковки проволоки и канатов;
gn — коэффициент надежности по
назначению, учитывающий степень надежности и капитальности сооружения и
принимаемый по табл. 6; для стальных канатов gn отражает срок службы сооружения в большей степени,
чем для других элементов, а также то, что специальный коэффициент длительной
прочности из формулы прочности стальных канатов исключен;
gс — коэффициент условий работы канатного элемента,
принимаемый по табл. 7 и учитывающий неравномерное распределение усилий между
несколькими канатами, входящими в состав одного элемента, разные степени
опасности случайных механических повреждений канатов, перераспределение усилий
перед достижением предельного состояния в пространственных и предварительно
напряженных конструкциях, а также опасность усталостных разрушений от ветровых
воздействий для канатов, не рассчитываемых на выносливость;
gk — коэффициент условий
работы, учитывающий влияние на прочность каната местных концентраторов
напряжений и принимаемый по табл. 8.
Таблица 6
|
Категория зданий и |
Коэффициент gn |
|
1. Трубопроводные мосты |
1,1 |
|
2. Здания и сооружения, имеющие |
1,0 |
|
3. Здания и сооружения, имеющие |
0,95 |
|
4. Здания и сооружения, имеющие |
0,90 |
|
5. Временные здания и сооружения |
0,85 |
Таблица 7
|
Элементы конструкций |
Коэффициент gс |
|
1. Кабели, ванты, шпренгели и другие канатные элементы |
0,85 |
|
2. Канатные элементы |
0,95 |
|
3. Ветровые пояса, затяжки, оттяжки, обратные кабели и |
1,0 |
|
4. Оттяжки мачт и несущие элементы канат них полотен |
0,80-0,95 |
Таблица
8
|
Узлы и детали канатных |
Коэффициент gk |
|
Концевые крепления с заливкой |
|
|
а) закрытых |
0,95 |
|
б) |
1,0 |
|
Концевые крепления с холодной |
1,0 |
|
Концевые крепления со стальными |
1,0 |
|
Перегибы каната вокруг жесткого |
|
|
а) при |
1,0 |
|
б) при |
0,90 |
|
Узлы с поперечным обжатием |
|
|
|
|
|
где N — |
|
|
SNb |
|
|
l — длина контакта каната с основанием |
0,90 |
|
Концевые крепления |
0,90 |
Примечания: 1. Указанные в таблице
коэффициенты gk
(в том числе и для других типов анкеров при меньших r и больших интенсивностях q)
допускается корректировать по статистически обоснованным результатам испытаний
образцов узлов и канатных элементов.
2. Запрещается
применять в постоянных сооружениях конструктивные решения, требующие введения gk < 0,85, кроме
отдельных узлов антенных сооружений связи, конструкция которых определяется
технологическими требованиями.
3.15. Нормативное
сопротивление Run следует определять одним из
способов:
а) если в государственных
общесоюзных стандартах или технических условиях для данного типа каната
приведены значения разрывного усилия каната в целом Run или Nun определяется статистически обоснованным способом с обработкой
экспериментальных данных:
; (9)
б) если в государственных
общесоюзных стандартах или технических условиях значение разрывного усилия
каната в целом не приведено, но указано суммарное разрывное усилие всех
проволок в канате Nt:
, (10)
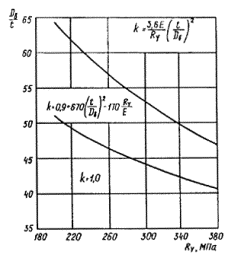
где k —
коэффициент агрегатной прочности каната, определяемый в зависимости от
конструкции каната по табл. 9;
Таблица 9
|
Тип каната (пучка) |
Коэффициент k |
|
Из параллельных проволок |
1,00 |
|
Спиральный закрытый |
0,90 |
|
Спиральный из круглых проволок |
0,85 |
|
Многопрядный |
0,80 |
в) если в технических
условиях указано только временное сопротивление Runj проволоки:
Run = kRunj, (11)
г) если в технических
условиях указано только временное сопротивление проволоки, а канат составлен из
проволок с разными временными сопротивлениями Runj и в каждой группе
номинальная площадь одной проволоки Aj и число одинаковых проволок сj:
. (12)
3.16.
Модули упругости витых стальных канатов и пучков параллельных проволок Е рекомендуется принимать по табл. 10.
Для витых стальных канатов значения Е
даны после предварительной вытяжки.
Таблица
10
|
Конструкция стальных |
Е, МПа (кгс/см2), при расчете нагрузки |
|
|
временные |
постоянные |
|
|
Пучки параллельных проволок |
2×105 |
2×105 |
|
Витые канаты: |
||
|
спиральные |
||
|
а) 7-10 |
1,5×105(1,47×106) |
1,2×105(1,18×106) |
|
б) 12-14 |
1,7×105(1,67×106) |
1,4×105(1,37×106) |
|
многопрядные |
||
|
а) прядей и |
1,3×105(1,27×106) |
1,0×105 |
|
б) прядей |
1,5×105(1,47×106) |
1,2×105(1,18×106) |
|
с |
1,1×105(1,08×106) |
1,0×105 |
4. УЧЕТ УСЛОВИЙ РАБОТЫ И НАЗНАЧЕНИЯ КОНСТРУКЦИЙ
КОЭФФИЦИЕНТЫ НАДЕЖНОСТИ И УСЛОВИЙ РАБОТЫ
4.1 (разд. 4*). Достижение временного сопротивления означает полное разрушение
материала со всеми недопустимыми последствиями. Поэтому ненаступление этого
состояния должно иметь относительно большую обеспеченность, что достигается в СНиП II-23-81* введением коэффициента
надежности gu = 1,3. Этот коэффициент
имеется в расчетных формулах для проверки элементов конструкций, рассчитываемых
на прочность с использованием расчетных сопротивлений Ru, а также учтен при
назначении расчетных сопротивлений для сварных и болтовых соединений.
Принятое значение
коэффициента gu обеспечивает возможность надежно использовать в
расчетах диаграммы работы сталей в зонах больших деформаций. Например, для
наиболее массовых малоуглеродистых пластичных сталей диаграмма работы при этом
используется до значений относительных удлинении е = 4-5 %, что хорошо согласуется с экспериментальными данными.
4.2 (разд. 4*). В целях снижения стоимости и материалоемкости строительства введены в
действие Правила [4]. При этом степень ответственности учитывается
коэффициентом надежности по назначению gn.
На коэффициент надежности по
назначению gn следует умножать расчетные
значения нагрузок, усилий или иных воздействий [см. формулу (2)] и делить предельные значения
перемещений и параметров колебаний и изменения положения конструкций [см.
формулу (4)].
Примечание. Правилами допускается делить на коэффициент gn предельные
значения несущей способности S, определяемой по
формуле (3).
4.3 (разд. 4*). Согласно требованиям [2] особенности действительной работы стали,
элементов конструкций и их соединений, имеющие систематический характер, но не
отражаемые непосредственно в расчетах, учитываются коэффициентами условий
работы.
Установленные в табл. 6* СНиП II-23-81* коэффициенты условий
работы gс для элементов конструкций введены с целью учета:
а) упрощения расчетных схем
при расчетах на общую устойчивость сплошных балок, которые рассчитываются как
идеально упругие системы (поз. 4 табл. 6* СНиП II-23-81*), а также сжатых элементов из одиночных уголков,
прикрепляемых одной полкой и рассчитываемых как центрально-сжатые, хотя схема
их работы соответствует внецентренному сжатию (поз. 9 и 10 табл. 6* СНиП II-23-81*);
б) фактических значений
начальных искривлений сжатых составных элементов таврового сечения из уголков,
в которых в связи с несимметричным расположением швов при приварке прокладок
между уголками начальные искривления превышают учитываемые в расчетах (поз. 3
табл. 6* СНиП II-23-81*);
в) воздействия на
конструкции больших постоянных и длительно действующих временных нагрузок,
приводящих в процессе эксплуатации к высокому уровню напряжений, незначительное
превышение которого может вызвать опасность наступления предельных состояний
первой группы (поз. 1,2 и 5 табл. 6* СНиП II-23-81*);
г) локального повышения
прочностных свойств стали возле отверстий при расчете на прочность сечений,
ослабленных отверстиями для болтов (поз. 6-8 табл. 6* СНиП II-23-81*). Подробные разъяснения этих требований приведены в
разд. 5
настоящего Пособия.
4.4 (11.7*). При расчетах болтовых соединений коэффициенты условий работы gb по табл. 35* СНиП II-23-81* введены для:
а) учета неравномерности
работы болтов в многоболтовых соединениях на болтах классов точности В и С (gb = 0,9);
б) исключения возможности
разрушения соединяемых элементов при уменьшенных расстояниях между болтами и от
края элемента до ближайшего отверстия (gb = 0,80; gb = 0,75).
Коэффициенты условий работы gс, установленные для элементов конструкций согласно
поз. 1 и 2 табл. 6* СНиП II-23-81*, следует
учитывать и при расчетах болтовых соединений (включая одноболтовые).
4.5.
Коэффициенты условий работы gс (gb) < 1, приведенные в табл. 6* и СНиП II-23-81*, в расчетах одновременно
учитывать, как правило, не следует.
ОСОБЕННОСТИ РАСЧЕТА СТАЛЬНЫХ КОНСТРУКЦИЙ С УЧЕТОМ НЕУПРУГИХ ДЕФОРМАЦИЙ
4.6.
Учет неупругих деформаций за счет использования двух видов расчетных
сопротивлений стали Ry, Ru и условия ограничения
пластических деформаций в сечениях имеет свои особенности по сравнению с ранее
применявшимися методами расчета стальных конструкций.
4.7. Введение в расчеты
коэффициента надежности gu = 1,3 в значительной мере ограничивает область
использования диаграмм работы сталей.
Для малоуглеродистых
пластичных сталей [sу = 220 — 240 МПа (2450
кгс/см2)] с отношением su/sу = 1,5-1,7 при расчете
растянутых элементов оказывается возможным в ряде случаев учитывать
значительное развитие неупругих деформаций и даже переход в стадию
самоупрочнения до значений e = 4-5 % (см. п. 1.19).
Для сталей высокой прочности
[sу > 600
МПа (6100 кгс/см2)] с отношением su/sу =
1,15-1,20 введение коэффициента gu = 1,3 приводит к тому, что в связи с близостью
значений su и sу расчет, как правило, будет выполняться в пределах
упругости. При этом учет неупругих деформаций при расчетах растянутых элементов
не допускается.
4.8. Временное сопротивление при
растяжении характеризует полное разрушение стали. При осевом сжатии сталь
разрушить труднее, поэтому в исключительных случаях работы стали на сжатие в
расчетах допускаются высокие напряжения, близкие к временному сопротивлению
(например, при смятии торцевой поверхности при наличии пригонки).
В остальных случаях осевого
сжатия расчет на прочность элементов из сталей с отношением su/sу =
1,5-1,7 следует выполнять так же, как при растяжении.
В то же время для сжатых
элементов из сталей с отношением su/sу =
1,15-1,20 в отличие от растяжения расчет можно выполнять с учетом неупругих
деформаций, что обеспечит более полное использование прочностных свойств
сталей.
4.9.
Исчерпание несущей способности большинства сжатых (с учетом начальных
несовершенств) и сжато-изгибаемых элементов происходит из-за потери
устойчивости формы, которая определяется главным образом параметрами длины и
жесткости сечения. Поскольку жесткость изменяется с развитием пластических
деформаций, проверку потери устойчивости формы необходимо выполнять на основе
расчетного сопротивления Ry
для всех марок строительных сталей, что реализовано в СНиП II-23-81* (в отличие от требований отмененной главы СНиП II-В.3-72).
4.10.
Особенности учета неупругих деформаций при простом растяжении и сжатии,
изложенные в пп. 1.19 и 4.7, могут быть распространены на случай изгибаемых
элементов соответственно для растянутой и сжатой областей сечения. При этом для
сталей с отношением su/sу =
1,5-1,7 в расчетах на прочность при изгибе в ряде случаев можно учитывать
значительное развитие неупругих деформаций и переход в зону самоупрочнения.
Для изгибаемых элементов из
высокопрочных сталей (su/sу = 1,15-1,20) неупругие
деформации могут учитываться только в сжатой области сечения; в растянутой —
расчет, как правило, следует выполнять в пределах упругости. Согласно пп. 5.12
и 5.18 СНиП II-23-81* расчет таких элементов
следует выполнять без учета развития пластических деформаций.
4.11.
Применение условия ограничения пластических деформаций в сечениях при расчете
изгибаемых элементов имеет цель обеспечить более полное использование
прочностных свойств стали для элемента в целом по сравнению с требованиями
отмененной главы СНиП II-В.3-72. При этом необходимо
иметь в виду, что с увеличением пластических деформаций силовые факторы в
сечении возрастают. Однако при этом снижается эффективность компоновки сечений
по условиям общей и местной устойчивости, а также жесткости элементов в целом,
что необходимо учитывать при подборе сечений минимальной площади. В связи с
этим в ряде случаев более эффективным может оказаться расчет с учетом меньших
значений пластических деформаций, определяемых назначением конструкций,
условиями их эксплуатации, а также применяемыми сталями и профилями поперечных
сечений.
4.12.
При выполнении расчетов стальных конструкций с учетом изложенных особенностей
расчет на прочность по условию пластического разрушения следует выполнять с
использованием расчетного сопротивления Ru и характеристик сечения “нетто”.
При расчете конструкций на
прочность по условию ограничения пластических деформаций необходимо
использовать расчетное сопротивление Ry и, как правило, геометрические характеристики сечения “брутто” (более
подробные разъяснения этого метода расчета приведены в разд. 5).
4.13.
Изложенный подход к расчету стальных конструкций в целом характеризуется тем,
что при расчете на основе Ru большинства конструкций из сталей с отношением su/sу >
1,3 значительное развитие пластических деформаций (для пластичных
малоуглеродистых сталей даже переход в стадию самоупрочнения) предполагается
лишь на небольшой длине (например, в пределах отверстий), что не будет
сопровождаться ростом общих перемещений системы.
При расчетах конструкций из
сталей с отношением su/sу <
1,3 развитие пластических деформаций в растянутых элементах или зонах
растяжения изгибаемых элементов обычно не допускается; ограниченные
пластические деформации предполагаются в сжатых элементах или в зонах сжатия
изгибаемых элементов при условии обеспечения местной и общей устойчивости.
4.14.
При существующих кривых распределения фактических значений предела текучести sу обеспеченность установленных СНиП II-23-81* расчетных сопротивлений Ry, как правило, выше 0,98, в связи с чем фактические
перемещения и деформации в конструкциях при расчетных предельных (gf > 1,0) нагрузках в целом
будут меньше определяемых по расчету, а часть конструкции при этом будет работать
в пределах упругих деформаций.
5. РАСЧЕТ ЭЛЕМЕНТОВ НА ОСЕВЫЕ СИЛЫ И ИЗГИБ
ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ И ЦЕНТРАЛЬНО-СЖАТЫЕ ЭЛЕМЕНТЫ
5.1 (5.1). Согласно требованиям [1] в расчетах стальных конструкций разрешается
использовать два вида расчетных сопротивлений — по пределу текучести Ry и по временному
сопротивлению Рu. При
этом в расчетах необходимо учитывать значения отношений Ru/Ry, которые изменяются в
пределах от 1,17 до 1,70. Кроме того, следует также различать элементы, не
ослабленные и ослабленные отверстиями для болтов. Эти особенности работы стали
отражены в [1] и были учтены при формулировке требований СНиП II-23-81* по расчету на прочность, разъяснение которых
приводится в пп. 5.2-5.4 настоящего Пособия.
5.2 (5.1). При проверке прочности центрально растянутых элементов с ослаблением
сечений отверстиями для болтов не более 15 % в общем случае должны быть
выполнены следующие условия
; (13)
, (14)
где gи —
коэффициент, принимаемый согласно СНиП
II-23-81*;
b — коэффициент, принимаемый
свыше 1,0 [11];
An —
площадь сечения “нетто”;
Ru и Ry —
расчетные сопротивления, принимаемые согласно СНиП II-23-81*;
А —
площадь сечения „брутто».
Условие равнопрочности по
формулам (13) и (14) для центрально-растянутых элементов получит вид
, (15)
где a = An/A.
Из формулы (15) следует:
если Ru/Ry > gu/(ab), решающей является
проверка по формуле (14); в противном случае — по формуле (13).
При a = 0,85 и b =
1,1 [11] следует, что при Ru/Ry >
1,39 достаточно выполнить проверку по формуле (14), если Ru/Ry < 1,39, то необходима проверка по
двум формулам (13) и (14).
5.3 (5.1). При ослаблении сечений отверстиями для болтов свыше 15 % формула (13) остается без изменения, а формула
(14) получит вид
, (16)
где 1,18 aА —
условная площадь, вводимая в расчет при ослаблении сечения свыше 15 % (см. СНиП II-23-81*).
Из условия равнопрочности
при проверках по формулам (13) и
(16) имеем
. (17)
5.4 (5.1). Для упрощения практических расчетов в СНиП II-23-81* расчетные формулы (13), (14) и
(16) приведены к одной формуле с
введением соответствующего коэффициента условий работы gс:
. (18)
Коэффициент условий работы gс определен из сопоставления формул (13), (14) и (16)
с формулой (18).
Для большинства наиболее
широко применяемых углеродистых сталей с отношением Ru/Ry
> 1,39 находим:
при a ³ 0,85 gс = 1/a;
” 0,75 £ a < 0,85 gс = 1,18.
Для сталей с отношением Ru/Ry < 1,39
.
При наиболее вероятном
ослаблении сечения отверстиями для болтов от 8 до 25 % (a = 0,92-0,75) и Ru/Ry > 1,39 gс = 1,09-1,18. При Ru/Ry < 1,39 gс = 0,99-1,18; при этом меньшее значение gс соответствует Ru/Ry = 1,17, что выполняется
для двух марок сталей 12Г2СМФ и 12ГН2МФАЮ, приведенных в СНиП II-23-81*.
С учетом изложенного в СНиП II-23-81* приняты gс = 1,1 для
сталей с пределом текучести sу £ 440 МПа (4500 кгс/см2);
gс = 1,0 — для сталей с пределом текучести sу > 440 МПа (4500 кгс/см2).
С целью упрощения расчетов
на прочность сечений, ослабленных отверстиями для болтов, указанные значения
коэффициентов gс приняты и для других видов
напряженно-деформированных состояний элементов конструкций (сжатие, изгиб,
сжатие или растяжение с изгибом; см. поз. 6-8 табл. 6* СНиП II-23-81*).
5.5.
При расчете на прочность центрально-сжатых элементов необходимо учитывать
особенности работы стали на сжатие (см. п. 4.8).
В частности, расчет на прочность центрально-сжатых элементов с соединениями на
болтах класса точности А допускается выполнять как для неослабленных элементов
[1].
5.6 (5.2). Работа растянутых элементов стальных конструкций после достижения
металлом предела текучести при Ru/Ry > gи =
1,3 допускается в ограниченных случаях, когда при значительных деформациях
конструкций не нарушается их нормальная эксплуатация. К таким конструкциям
относятся, как правило, отдельные листовые конструкции, в основном, с
равномерным распределением напряжении (например, листовые настилы, некоторые
виды трубопроводов и резервуаров и т.п.). Учитывать работу стали после
достижения предела текучести в каждом конкретном случае необходимо на основе
опыта проектирования и эксплуатации соответствующего типа конструкций.
5.7. Требования по проверке
устойчивости центрально-сжатых стержней установлены в СНиП II-23-81* на основе расчета внецентренно-сжатых стержней с
учетом влияния формы сечения, начального искривления оси, случайного
эксцентриситета сжимающей силы, а также соединительных элементов (для сквозных
стержней).
Начальные искривления или
случайные эксцентриситеты приняты в соответствии с допускаемыми отклонениями,
установленными в нормах на изготовление стальных конструкций [8].
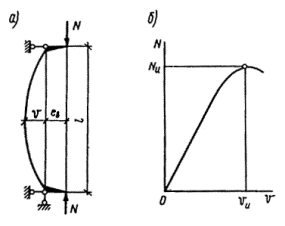
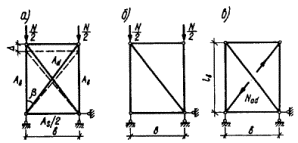
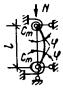
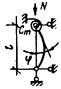
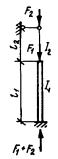
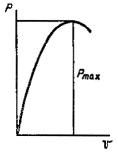
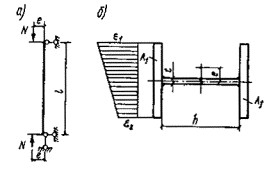
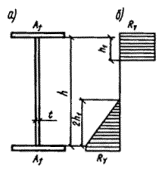
При решении поставленной
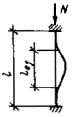
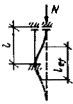
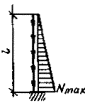
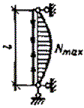
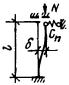
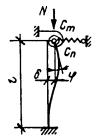
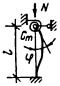
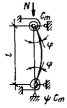
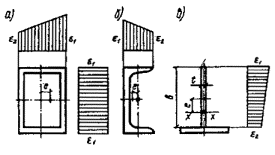
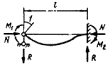
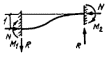
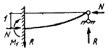
задачи был рассмотрен внецентренно-сжатый стержень, схема которого приведена на
рис. 3, а. При этом решение
выполнялось в предположении малости перемещений по деформированной схеме с
учетом пластических деформаций, а значение расчетной несущей способности
принято равным предельному значению сжимающей силы Nu, которая может быть воспринята элементом (рис. 3, б). Форма изогнутой оси принималась по
полуволне синусоиды.
Рис.
3. К расчету сжатых стержней
а — расчетная схема; б — кривая состояния равновесия
5.8 (5.3). В СНиП II-23-81* методика
практических расчетов центрально-сжатых элементов приведена с использованием
коэффициентов устойчивости при центральном сжатии j (коэффициентов продольного изгиба), которые
вычислены с учетом рекомендаций п. 5.7
настоящего Пособия в зависимости от условной гибкости и приняты равными j = Nu/(a Ry).
При вычислении значений
коэффициентов j типы поперечных сечений
сжатых элементов принимались в соответствии с табл. 73 СНиП II-23-81*, а начальные несовершенства еb — по формуле
, (19)
где i —
радиус инерции сечения;
l — расчетная длина элемента.
При нормировании
коэффициентов j определялась также критическая сила упругих
идеальных стержней по методу Эйлера. Окончательные значения коэффициентов j принимались наименьшими из
двух: вычисленных с учетом начальных несовершенств или по методу Эйлера с
введением коэффициента надежности gе = 1,3 . Это было сделано для ограничения прогибов сжатых стержней
при относительно больших гибкостях, когда влияние начальных несовершенств,
определяемых по формуле (19), становилось несущественным.
Полученные таким образом
значения коэффициентов j для различных форм
поперечных сечений были осреднены и аппроксимированы с помощью формул (8)-(10) СНиП II-23-81*, на основании которых для
различных значений расчетных сопротивлений Ry
была составлена табл. 72 СНиП II-23-81*.
Анализ значений
коэффициентов j позволяет использовать в
расчетах и более простые приближенные зависимости (с точностью до 1,5 %)
следующего вида:
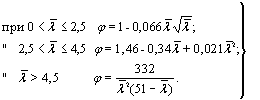
Значения j, полученные по формулам
(20), приведены в табл. 11.
Таблица 11
|
Условная гибкость |
Значения j×1000 |
|||||||||||
|
до 390(4000) |
св. 390(4000) |
|||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0 |
0,5 |
|
|
0 |
1000 |
998 |
995 |
989 |
983 |
977 |
969 |
961 |
953 |
944 |
1000 |
978 |
|
1 |
934 |
924 |
913 |
902 |
891 |
879 |
866 |
854 |
841 |
827 |
939 |
887 |
|
2 |
813 |
799 |
785 |
770 |
755 |
739 |
718 |
695 |
673 |
651 |
826 |
757 |
|
3 |
628 |
608 |
587 |
567 |
547 |
527′ |
508 |
489 |
471 |
453 |
645 |
539 |
|
4 |
436 |
419 |
402 |
386 |
370 |
355 |
340 |
326 |
312 |
298 |
442 |
353 |
|
5 |
289 |
278 |
268 |
259 |
250 |
241 |
233 |
226 |
218 |
211 |
289 |
241 |
|
6 |
205 |
199 |
193 |
187 |
182 |
177 |
172 |
167 |
162 |
158 |
205 |
177 |
|
7 |
154 |
150 |
146 |
143 |
139 |
136 |
132 |
129 |
126 |
123 |
154 |
136 |
|
8 |
121 |
118 |
115 |
113 |
110 |
108 |
106 |
104 |
102 |
100 |
121 |
108 |
|
9 |
098 |
096 |
094 |
092 |
090 |
089 |
087 |
085 |
084 |
082 |
098 |
089 |
|
10 |
081 |
079 |
078 |
077 |
076 |
074 |
073 |
072 |
071 |
070 |
081 |
074 |
Примечание. Указанные значения коэффициентов j
для элементов из стали с пределом текучести до 390 МПа (4000 кгс/см2)
определены по формулам (20), свыше 390 МПа (4000 кгс/см2) — по разд.
5 СНиП II-23-81* при sу
= 430 МПа (4400 кгс/см2).
5.9 (5.5). В основу проверки
изгибно-крутильной формы потери устойчивости тонкостенных стержней принята
теория В. З. Власова.
В
общем случае условие потери устойчивости шарнирно опертого центрально-сжатого
упругого тонкостенного стержня имеет вид
, (21)
где ;
;
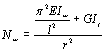
,
здесь aх и ау — координаты центра изгиба относительно осей
соответственно х-х и у-у.
Для стержня с одной осью
симметрии у-у (см. рис. 1 СНиП II-23-81*) аy
= 0, при этом из формулы (21) получим
. (22)
Разделив на Ny Nw r2 все члены уравнения (22),
получим
. (23)
Введем обозначения с =
N/Ny; d = Ny/Nw [12]. С учетом этих обозначений из формулы (23)
получим
(1 — с)(1 — сd) — с2b2 = 0, (24)
где .
Из уравнения (24) находим
. (25)
После простых преобразований
зависимости (25) получим
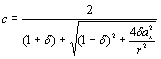
В практических расчетах по
формуле (26) учитывается частичное стеснение депланации опорных сечений
введением коэффициента 2 в первый член числителя формулы для Nw [см. формулу (21)], чем приближенно оцениваются
фактические условия в узлах стержневых конструкций. В окончательном виде с
использованием безразмерных величия эта формула приведена в СНиП II-23-81* под номером (12).
Формула (11) СНиП II-23-81* основана на предположении,
что соотношение критических сил при работе элемента за пределом упругости
принято таким же, как при работе его в пределах упругости.
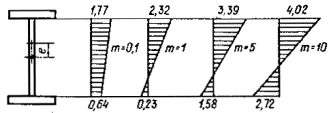
5.10 (5.5). Пример расчета центрально-сжатого тонкостенного стержня П-образного
сечения (см. рис. 1, а СНиП II-23-81*) с параметрами b = b/h = 0,5 и h/t = 15.
Площадь А и моменты инерции сечения Ix и Iу равны:
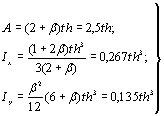
Величины, входящие в формулу
(12) СНиП II-23-81*, равны:
;
;
;
Значения коэффициентов с для
различных гибкостей lу приведены в табл. 12, в
которой обозначения приняты в соответствии с формулой (12) СНиП II-23-81*.
Таблица 12
|
lу |
m |
16а2/m |
d |
с |
lх |
|
40 |
7,945 |
1,496 |
0,455 |
0,716 |
28,4 |
|
60 |
8,407 |
1,414 |
0,430 |
0,728 |
42,7 |
|
80 |
9,054 |
1,313 |
0,399 |
0,743 |
56,8 |
|
100 |
9,885 |
1,203 |
0,367 |
0,759 |
71,1 |
|
120 |
10,901 |
1,091 |
0,332 |
0,778 |
85,3 |
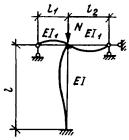
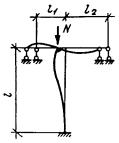
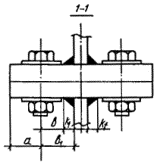
5.11 (5.6). Влияние податливости соединительных элементов на снижение жесткости
сквозного сжатого стержня в расчетах приближенно учитывается введением
приведенной гибкости lef, превышающей гибкость стержня lу = Iy/iy, вычисленную по
геометрической длине и радиусу инерции (где Iy — момент инерции сечения
сквозного стержня относительно свободной оси у-у, см. табл. 7, тип сечения 1,
СНиП II-23-81*).
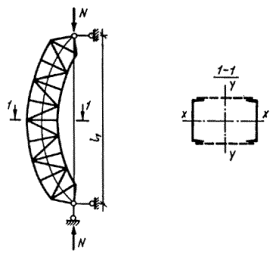
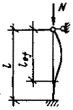
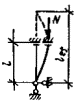
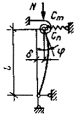
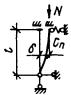
При достаточно большом числе
панелей (свыше 
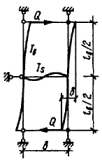
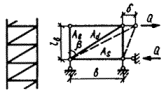
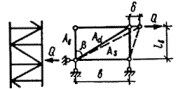
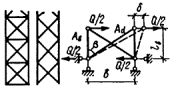
упругого сквозного стержня (рис. 4) коэффициент приведенной длины получен в
следующем виде [13]:
, (28)
где g1 = d/lb —
угол сдвига, зависящий от типа соединительных элементов.
Рис. 4. Шарнирно опертый сквозной стержень
Формулы для определения g1 и m при различных схемах
соединительных элементов, полученные по правилам определения перемещений в
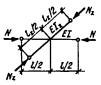
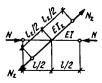
рамных и стержневых системах [13], приведены в табл. 13. Для схем решеток типа 3-5 в соответствии с рис. 2 СНиП II-23-81* имеем
. (29)
Для схемы решетки типа 2 получим
. (30)
При подстановке значений a в формулы табл. 13 получим
формулы, приведенные в табл. 7 СНиП
II-23-81*. Следует
отметить, что формулы табл. 13 в ряде случаев являются более строгими, чем
приближенные формулы СНиП II-23-81*, применение
которых, однако, существенно не влияет на конечные результаты.
5.12 (5.6). Формулы табл. 13 могут быть использованы при определении lеf для четырехгранного сквозного стержня с
подстановкой в них соответствующих геометрических характеристик всего стержня и
его отдельных ветвей. Однако результаты экспериментальных исследований
четырехгранных стержней с гибкостями g = 20-40 из стали с пределом
текучести sу = 250-278 МПа (2550-2830 кгс/см2)
показывают, что такой расчет в связи с наличием начальных несовершенств
приводит к завышенным значениям вычисленных предельных нагрузок. В связи с этим
в СНиП II-23-81* предлагаются условные
формулы (15), (18) и (21), в которые одновременно входят геометрические характеристики
элементов стержня для обеих плоскостей потери устойчивости. Сравнение
теоретических и экспериментальных данных показывает в этом случае достаточно
удовлетворительное соответствие результатов.
5.13 (5.6). Формулы табл. 7 СНиП II-23-81* (тип сечения 3) для определения lef для трехгранных сквозных стержней основаны на
рассмотрении их потери устойчивости в плоскостях х-х и у-у в предположении
неизменности расстояний между ветвями стержня при изгибе.
5.14 (5.6). Формулы табл. 13 настоящего Пособия получены
без учета влияния начальных несовершенств и продольных сил в ветвях на значение
угла сдвига g1. В связи с этим в СНиП II-23-81* введены ограничения на
значения гибкостей отдельных ветвей.
Для стержней с планками
гибкость lb отдельной ветви, при которой влияние указанных
факторов несущественно, составляет 40.
При большем значении lb формулы для g1 и m необходимо
уточнять заменой выражений (1 + 2n) и
(1 + п) соответственно на (1/b + 2n) и (1/b + n), где (здесь j — коэффициент, вычисляемый
для стержня по приведенной гибкости lef).
Таблица
13
|
№ п.п. |
Схема соединительных |
Формулы для |
|
|
одной |
двух |
||
|
1 |
|
При n £
|
При n £ |
|
здесь
Ib — момент инерции сечения пояса; Is — момент инерции сечения одной планки. |
|||
|
2 |
|
|
|
|
здесь и в поз. 3-5 A = 2Ab; Ad — площадь сечения одного раскоса; А — площадь сечения всего стержня. |
|||
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
5.15 (5.6). При расчете сквозных
решетчатых стержней начальные несовершенства обычно учитываются коэффициентом j в формуле (7) СНиП II-23-81* на стадии подбора сечения всего стержня и проверки
устойчивости его отдельных ветвей. В то же время имеются работы 1; 2,
в которых показано, что на несущую способность сквозного стержня с решетками
существенное влияние оказывают увеличение гибкости панели, а также начальные
искривления стержня и отдельных панелей. В связи с этим в п. 5.6 СНиП II-23-81* введены ограничения на
значения гибкостей отдельных ветвей между узлами.
______________
1 Корчак М. Д. О влиянии
начальных искривлений пояса на устойчивость решетчатого стержня //
Совершенствование и развитие норм проектирования стальных строительных
конструкций: Сб. науч. тр. ЦНИИСКа им. Кучеренко. — М., 1981.-С. 119-127.
2 Горев В. В., Путилин В. М.
О несущей способности и деформативности сжатых сквозных стержней // Строит.
механика и расчет сооружений. — 1976. — № 3. — С. 34-37.
В ряде случаев при lb £ 120 эти ограничения
согласно СНиП II-23-81* могут быть сняты. При этом
требуется выполнить расчет сквозного стержня по деформированной схеме, которую
можно учесть приближенным практическим способом расчета, существо которого
сводится к следующему:
если гибкость отдельной
ветви на участке между узлами ³ 3,2, то расчетное
сопротивление при проверке сквозного стержня с решетками по формулам (7) или
(51) СНиП II-23-81* может быть принято равным jbRy (правые части этих формул
будут равны jbRygc), здесь jb — коэффициент продольного
изгиба для отдельной ветви, расчетную гибкость которой можно принять 0,7lb; коэффициенты j и jе в формулах (7) и (51) СНиП II-23-81* необходимо принимать соответственно по табл. 72 и
75 СНиП II-23-81* при указанном расчетном
сопротивлении jbRy в зависимости от lef и ;
при £ 2,5 значение j принимается
равным 1,0, а в интервале 2,5 < < 3,2 — по линейной интерполяции между
1,0 и значением jb при = 3,2.
Коэффициент расчетной длины mb =
0,7 при lb приближенно учитывает
взаимодействие ветви колонны с элементами решетки, а также вероятность
одновременного совпадения расчетных значений начальных несовершенств для всего
стержня и отдельной панели ветви.
5.16 (5.7). Соединение составных стержней вплотную или через прокладки
обеспечивает совместную работу составляющих его элементов и равномерное
распределение между ними продольной силы.
Для сжатых стержней длина
участка между соединениями равна 40i, что соответствует гибкости
lb =
40 в сквозных стержнях с планками. При этом влияние продольной силы на
деформирование элементов, составляющих стержень, несущественно (см. п. 5.14 настоящего Пособия).
5.17 (5.8*). Условная поперечная сила Qfic определяется как проекция продольной сжимающей силы N на ось, перпендикулярную
изогнутой оси шарнирно опертого внецентренно-сжатого с эксцентриситетом еb стержня сквозного сечения, имеющего начальное
искривление vb, в его предельном состоянии
(рис. 5) и вычисляется по формуле
Qfic = Nu sin a » Nu a. (31)
Рис. 5. К определению условной поперечной силы
а — изогнутая ось стержня; б — идеализированное сечение
Для синусоидальной формы
начального искривления и изогнутой оси стержня получим
(32)
Для вычисления Nu и vu были определены предельные
параметры внецентренно-сжатого стержня идеализированного сечения, состоящего из
двух одинаковых полок, связанных между собой жесткой связью (см. рис. 5, б). Влияние решетки на предельное
значение Nu учитывалось
введением приведенной гибкости lef по формуле (17) СНиП II-23-81*.
Полученные значения Qfic для различных Ry и l аппроксимированы в СНиП II-23-81* приближенной зависимостью
, (33)
которая учитывает возможность недонапряжения
сквозного стержня в плоскости соединительных элементов; здесь k =
7,15 × 10-6.
Значения множителя k при N/j в правой части формулы (33) для различных значений
расчетных сопротивлений Ry
и Е = 2,06 — 105 МПа
приведены в табл. 14.
Таблица
14
|
Ry, |
k |
Ry, |
k |
|
210(2150) |
0,0097 |
330(3350) |
0,0122 |
|
230(2350) |
0,0103 |
350(3550) |
0,0125 |
|
250(2550) |
0,0108 |
370(3750) |
0,0127 |
|
270(2750) |
0,0112 |
400(4100) |
0,0130 |
|
300(3050) |
0,0118 |
500(5100) |
0,0137 |
5.18 (5.10). Для определения дополнительных усилий в раскосах перекрестной решетки
с целью учета влияния обжатия поясов в сквозных стержнях рассматривается один
раз статически неопределимая система, схема которой приведена на рис. 6, а. Разрез одного из раскосов дает
основную систему, схемы нагружения которой показаны на рис. 6, б,
в.
Рис.
6. К расчету перекрестной решетки
а — расчетная схема; б — основная система; в — дополнительное усилие в раскосе
Из решения рассматриваемой задачи получено
дополнительное усилие, возникающее в раскосах

Принимая Ad/As » 1 и Ad cos3 b/Ab » 0, можно получить формулу (26) СНиП II-23-81*.
Принимая обозначения sаd = Nad/Ad и sn = Nb/Ab = N/A, получим
, (35)
где d = lb/b.
Значения отношения sad/sn для различных d приведены в табл. 15.
Таблица 15
|
d |
0,5 |
0,6 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
|
sad/sn |
0,082 |
0,117 |
0,200 |
0,293 |
0,396 |
0,475 |
0,554 |
0,620 |
Получаемое таким образом
дополнительное усилие в раскосах от обжатия поясов стержня сжимающей силой
необходимо прибавить к усилию в раскосах от условной (или фактической)
поперечной силы Q.
5.19 (5.11). Расчет стержней,
предназначенных для уменьшения расчетной длины сжатых элементов, необходимо
выполнять на усилие, равное Qfic и определяемое с использованием данных табл. 14 и формулы (33) в зависимости от продольной силы N и коэффициента продольного изгиба j для основного подкрепляемого
элемента.
Расчет распорок,
предназначенных для уменьшения расчетной длины колонн в направлении вдоль
здания (из плоскости рам), при наличии нагрузок от мостовых кранов допускается
выполнять на усилие, определяемое по формуле (33), в которой значение N принимается равным сумме продольных сил в двух соседних колоннах.
ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ
5.20 (5.14*). В балках, рассчитываемых в пределах упругих деформаций, необходимо
проверять прочность стенки при сложном напряженном состоянии путем определения
обобщенного напряжения (интенсивности напряжений) на основе энергетической
теории прочности по формуле (33) СНиП
II-23-81*.
Обобщенное напряжение, вычисляемое по этой формуле, сравнивается с расчетным
сопротивлением, увеличенным на 15 %, что предполагает развитие локальных
неупругих деформаций в стенке.
Указанный расчет необходимо
выполнять в первую очередь для проверки стенок двутавровых балок в месте
соединения стенки с верхним поясом. При этом в стенках разрезных балок
напряжения sx и sу обычно имеют одинаковые знаки, в то время как в
сечениях у опор неразрезных балок эти напряжения могут иметь разные знаки, что
необходимо учитывать при пользовании формулой (33) СНиП II-23-81*.
5.21 (5.15). Для определения критических напряжений jbRy при потере устойчивости
балок двутаврового сечения с двумя осями симметрии, изгибаемых в плоскости
стенки, были использованы результаты работ С. П. Тимошенко [13], которые для
практических расчетов представлены в СНиП II-23-81* в виде формул (34) и (174). Необходимо подчеркнуть,
что в работе [13] исследовались идеальные упругие балки. Для расчета реальных
стальных балок в формуле (34) СНиП
II-23-81* влияние
начальных несовершенств (в частности, начального искривления оси балки в
плоскости наименьшей жесткости) учтено при выводе формул для коэффициента Y, а также введением
коэффициента условий работы gс (см. поз. 4 табл. 6* СНиП II-23-81*).
Коэффициенты в табл. 77 СНиП II-23-81* приведены для случая
шарнирного опирания в плоскости наименьшей жесткости и свободной депланации
концов расчетного участка балки.
Значения Y вычислены в предположении,
что Iу/Iх £ 1. Если отношение Iу/Iх не очень мало, то значения Y следует умножать на .
Для балок двутаврового
сечения с одной осью симметрии коэффициенты j1 и j2, определяемые по формулам (177) и (178) СНиП II-23-81*, были получены в работе
[14] на основе использования уравнений В. З. Власова при указанных граничных
условиях.
5.22 (5.15). Для случая, когда
критические напряжения при потере устойчивости балок превышают предел
пропорциональности, методика расчета разработана на основе исследования
соотношения между критическим напряжением неограниченно упругого
центрально-сжатого стержня scr и действительным напряжением s следующего вида:
(36)
В формуле (36) предел
пропорциональности принят равным 0,85sy, а отношение s/sу =
1 при scr/sy = 2,42, что эквивалентно
отношению sy/scr = Еr/Е = 0,412 (где Еr — приведенный модуль).
Для балок двутаврового
сечения с двумя осями симметрии критические напряжения примерно пропорциональны
значению , где G = const.
На этом основании принято scr/sy = » 1,55 при s/sу =
1. В интервале 0,85 £ scr/sy £ 1,55 значение s/sу изменяется
линейно, в связи с чем рекомендуется формула (см. п. 1* прил. 7* СНиП II-23-81*):
jb =
0,68 +0,21j1 при j1 > 0,85. (37)
Балки двутаврового сечения с
одной осью симметрии исследованы в [14]. При этом была принята та же методика,
что и для сечений с двумя осями симметрии, но значения отношения Еr/Е
принимались различными для верхнего и нижнего поясов балки. На основе этих
исследований для практических расчетов рекомендуется табл. 81 СНиП II-23-81*.
5.23 (5.16*). Требование надежной связи сжатого пояса балки со сплошным жестким
настилом, когда не нужна проверка устойчивости балок, должно быть предусмотрено
в проектах строительных конструкций и производства работ.
При устройстве закреплений
сжатого пояса в отдельных точках (узлы продольных или поперечных связей, точки
крепления жесткого настила) такие закрепления следует рассчитывать на
фактическую или условную поперечную силу в горизонтальной плоскости. При этом
каждая точка закреплений предназначена для уменьшения расчетной длины сжатого
пояса балки (см. п. 5.19 настоящего
Пособия).
При непрерывном прикреплении
сжатого пояса балки к жесткому настилу это прикрепление следует рассчитывать на
максимальное значение эквивалентной поперечной нагрузки, действующей на пояс в
горизонтальной плоскости [13]:
, (38)
где N — продольная сжимающая сила;
vb —
начальное искривление пояса;
vu —
искривление пояса при действии сжимающей силы N;
l —
пролет балки.
С учетом формул (32) и (38) получим
. (39)
При плоском и
профилированном металлических настилах или волнистой стали надежной связью
является соединение их со сжатым поясом балки сваркой на болтах или дюбелях.
Сплошной просечно-вытяжной
настил следует приваривать к сжатому поясу балки в соответствии с требованием
ГОСТ 8706-78* о защемлении настила. При этом листы настила необходимо
располагать просечкой поперек пролета (перпендикулярно оси балки).
Для сборных железобетонных
плит из различных бетонов под надежной связью следует понимать крепление
закладных деталей плит к сжатому поясу балки сваркой или на болтах.
При монолитных
железобетонных плитах надежной связью может служить приварка арматуры или
специальных закладных деталей к сжатому поясу балки либо замоноличивание этого
пояса в слое бетона толщиной не менее 20 мм.
При устройстве прикреплений
необходимо учитывать конструктивные требования для применяемого вида соединений
(минимальные размеры швов, расстояния между болтами и от края элемента и т.д.).
5.24 (5.16*). Наибольшие значения условной гибкости верхнего пояса балки , при которых не требуется выполнять расчет на устойчивость
балок, определяются по формулам табл. 8* СНиП II-23-81*, которые получены на основе методики, изложенной в п. 5.22 настоящего Пособия, при выполнении
условия jb = 1. Значения для различных значений b/t и h/b приведены в табл. 16.
Таблица
16
|
Место приложения |
b/t |
Наибольшие значения |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
К верхнему поясу |
15 |
0,858 |
0,628 |
0,551 |
0,513 |
0,490 |
0,475 |
|
20 |
0,774 |
0,594 |
0,534 |
0,504 |
0,486 |
0,474 |
|
|
25 |
0,690 |
0,560 |
0,517 |
0,495 |
0,482 |
0,473 |
|
|
30 |
0,606 |
0,526 |
0,499 |
0,486 |
0,478 |
0,473 |
|
|
35 |
0,522 |
0,492 |
0,482 |
0,477 |
0,474 |
0,472 |
|
|
К нижнему поясу |
15 |
1,238 |
0,928 |
0,825 |
0,773 |
0,742 |
0,721 |
|
20 |
1,154 |
0,894 |
0,807 |
0,764 |
0,738 |
0,720 |
|
|
25 |
1,070 |
0,860 |
0,790 |
0,755 |
0,734 |
0,720 |
|
|
30 |
0,986 |
0,826 |
0,773 |
0,746 |
0,730 |
0,719 |
|
|
35 |
0,902 |
0,792 |
0,755 |
0,737 |
0,726 |
0,718 |
|
|
Независимо от уровня приложения нагрузки при расчете |
15 |
0,948 |
0,703 |
0,621 |
0,580 |
0,556 |
0,540 |
|
20 |
0,884 |
0,679 |
0,611 |
0,576 |
0,556 |
0,542 |
|
|
25 |
0,820 |
0,655 |
0,600 |
0,572 |
0,556 |
0,545 |
|
|
30 |
0,756 |
0,631 |
0,589 |
0,568 |
0,556 |
0,547 |
|
|
35 |
0,692 |
0,607 |
0,579 |
0,564 |
0,556 |
0,550 |
Для получения значений lef/b значения , приведенные в таблице, следует умножить на
.
5.25 (5.17, 5.18). При изгибе балки в двух главных плоскостях потеря устойчивости
выражается достижением предельной нагрузки (максимума на кривой состояний
равновесия). В этом случае изгиб в обеих плоскостях и кручение возникают с
самого начала нагружения и, постепенно возрастая, приводят к развитию
пластических деформаций и исчерпанию несущей способности.
Для двутавровых балок,
рассчитываемых по формуле (38) СНиП
II-23-81*, проверку
устойчивости при двухосном изгибе можно выполнять согласно рекомендациям ЕКМК
[15], полученным как частный случай из уравнения взаимодействия для стержня,
сжатого с двухосным эксцентриситетом, по формуле
. (40)
При приложении нагрузки,
действующей в плоскости, параллельной плоскости х-х, только к одному (верхнему) поясу балки во втором члене формулы
(40) следует принимать изгибающий момент My,f и момент сопротивления Wy,f соответственно для этого (верхнего) пояса балки. В
этом случае расчет следует выполнять по формуле
. (41)
5.26 (5.18). Расчет статически
определимых изгибаемых элементов, несущих статическую нагрузку, может
выполняться по ограниченным пластическим деформациям в соответствии с
предложением, выдвинутым Н. С. Стрелецким. В СНиП II-23-81* это предложение реализовано в виде коэффициентов сi > 1, вводимых к упругим моментам сопротивления
сечений. При определении коэффициентов сi, (табл. 66 СНиП II-23-81*) в качестве количественного критерия было принято
достаточно большое ограничение пластических деформаций с (где
; er — остаточная деформация в сечении после полной
упругой разгрузки). В общем случае при таком подходе уменьшение предельных
моментов по сравнению с моментами, соответствующими полным пластическим
шарнирам, составляет не более 3-5 %, а для двутавровых сечений — 1 %.
При одновременном действии в
сечении момента М и поперечной силы Q учитывается кривая
взаимодействия их предельных значений [16], в связи с чем вводимое в расчет
отношение c1/c для двутавровых сечений при
0,5Rs < t £ 0,9Rs, [формула (43) СНиП II-23-81*] не должно превышать
значений, приведенных в табл. 17 и вычисленных по формулам (43) и (44) СНиП II-23-81*.
Таблица
17
|
t/rs |
£ |
0,55 |
0,60 |
0,65 |
0,70 |
0,75 |
0,80 |
0,85 |
0,90 |
|
с1/c |
1,00 |
0,987 |
0,97 |
0,950 |
0,925 |
0,892 |
0,848 |
0,787 |
0,695 |
При этом значение
коэффициента с1 не должно
быть меньше единицы; в противном случае расчет необходимо выполнять в пределах
упругой работы стали по формулам (28) и (29) СНиП II-23-81*.
При наличии в балке протяженной
зоны чистого изгиба, когда развитие пластических деформаций предполагается не в
одном сечении, а на определенном участке ее длины, с целью ограничения общих
перемещений значение предельного момента уменьшается и принимается равным
полусумме предельных моментов при работе сечения в пределах и за пределом
упругости.
Методика расчета балок с
учетом ограниченных пластических деформаций открывает новые возможности для их
дальнейшей оптимизации. Для этого в п. 5.18 СНиП II-23-81* указано, что допускается принимать меньшие значения
коэффициентов сi, соответствующие меньшим
значениям пластических деформаций. Это позволяет рассчитывать балки при
различных значениях ограниченных деформаций, что практически важно для
получения оптимальных сечений с учетом назначения элемента, условий
эксплуатации, конструктивного решения, формы сечения и соотношений его размеров
и т.д. При этом проверку прочности сечения, местной устойчивости пластинок
этого сечения, общей устойчивости балки и ее жесткости следует выполнять в
зависимости от значения принимаемой деформации, правильный выбор которой
обеспечит минимум площади сечения. Таким образом, основной задачей расчета с
учетом ограниченных деформаций является проектирование балок минимальной массы 1.
__________
1 Бельский Г. Е. Оптимизация изгибаемых
элементов на основе деформационного критерия // Строит. механика и расчет
сооружений. — 1986. — № 2.- С. 8-11.
5.27 (7.5). Методика расчета стенок балок на устойчивость с учетом пластических
деформаций основана на результатах решения задачи об устойчивости пластинки при
совместном действии нормальных и касательных напряжений. Проверка устойчивости
стенки заключается в сравнении изгибающего момента М для расчетного отсека, вычисленного в соответствии с указаниями
п. 7.2* СНиП II-23-81*, с критическим Мcr при известных касательных напряжениях [17]. В
качестве критического принимается момент, соответствующий потере устойчивости
стенки при определенном напряженно-деформированном состоянии и условии, что
устойчивость поясных листов обеспечена. При этом предполагалось, что с
увеличением пластических деформаций степень защемления стенки в поясах
уменьшается. При значительном развитии пластических деформаций, соответствующих
критической гибкости стенки = 2,2, эффект
защемления стенки в поясах не учитывается. Закрепление поперечных сторон
расчетного отсека стенки принимается шарнирным независимо от степени развития
пластических деформаций.
Расчет на устойчивость
стенок балок двутаврового поперечного сечения с двумя осями симметрии,
укрепленных только поперечными ребрами жесткости, следует выполнять по формуле
(78) СНиП II-23-81*, которая устанавливает
значение критического момента Мcr для всей балки. При этом в
формуле (78) СНиП II-23-81* первое
слагаемое выражает часть критического момента, воспринимаемого поясами балки Mf,cr = RyAfhefgc, а второе — часть
критического момента, воспринимаемого стенкой Mw,cr = Ryh2eftagc. При
отсутствии касательных напряжений (t = 0) максимальное значение Mw,cr = 0,24Ryh2eftagc при = 2,2.
В табл. 18 приведены значения коэффициента a, вычисленные для различных
значений и t/Rs.
Для балок двухстенчатого
сечения с двумя осями симметрии значение критического момента, получаемого по
формуле (78) СНиП II-23-81*, необходимо
умножать на коэффициент 2,0 и принять в этой формуле Аw
= 2heft.
5.28 (7.5). Стенки балок асимметричного сечения (с более развитым сжатым поясом),
укрепленные только поперечными ребрами жесткости, работают в условиях
совместного действия внецентренного растяжения и сдвига. Исследование работы
таких стенок за пределом упругости [17] показали, что при проверке их
устойчивости расчетную высоту можно принимать равной удвоенной высоте сжатой
зоны, так как влияние остальной растянутой зоны стенки на ее устойчивость
незначительно. Если в сжатой зоне стенки не возникает пластических деформаций
[выполняются условия (28), (29), (31) СНиП II-23-81*], то ее устойчивость можно проверять по формуле
(74) СНиП II-23-81*, принимая hef = 2h1 (где h1 —
высота сжатой зоны). Необходимо отметить, что появление пластических деформаций
в растянутой зоне (s = M/Wmin > Ry) нарушает линейный закон
распределения напряжений в сечении. С учетом этого фактора высоту сжатой зоны h1 и напряжения на кромке стенки следует определять из
уравнений, соответствующих напряженно-деформированному состоянию в расчетном
отсеке. Если напряжения в поясах балки асимметричного сечения равны Ry, то устойчивость ее стенки
при ограничениях, указанных в п. 7.5 СНиП II-23-81*, можно проверить по формуле
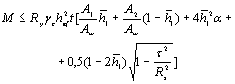
где A1 и A2 — соответственно площади
сжатого и растянутого поясов;
— принимается по формуле
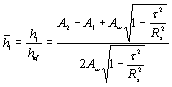
a —
коэффициент, определяемый по формуле (78) СНиП II-23-81* или принимаемый по табл. 18 настоящего Пособия.
Для балок двухстенчатого
сечения значение критического момента, получаемое в правой части формулы (42),
необходимо умножать на коэффициент 2,0 и принять в этой формуле Аw = 2heft.
5.29 (7.24). Расчет на устойчивость поясных листов (полок) балок с учетом развития
пластических деформаций рекомендуется выполнять в предположении их шарнирного
опирания по линии соединения поясов со стенкой при условии, что длина полуволны
пластинки равна 3bef (где bef — расчетная ширина свеса).
Наибольшие значения отношения bef/t, приведенные в табл. 30 СНиП II-23-81*, получены из условия
равноустойчивости стенки и сжатого пояса балки при чистом изгибе, так как в
этом случае деформации сжатого пояса достигают максимальных значений.
При действии касательных
напряжений в расчетном отсеке балки отношения bef/t
могут быть увеличены и приняты по табл.
19 настоящего Пособия, в которой учитывается уменьшение деформаций в поясе
за счет касательных напряжений в стенке.
Минимальные значения
условной гибкости для свесов при чистом изгибе соответствуют
значительному развитию пластических деформаций; максимальные — с некоторым запасом
соответствуют такому уровню нагрузки, при котором в поясах балки сжимающие
напряжения достигают значения Ry.
Таблица
18
|
t/Rs |
Значения a при |
|||||||||||
|
2,2 |
2,5 |
2,7 |
3,0 |
3,2 |
3,5 |
3,7 |
4,0 |
4,2 |
4,5 |
4,7 |
5,0 |
|
|
0,0 |
0,240 |
0,239 |
0,237 |
0,234 |
0,231 |
0,225 |
0,221 |
0,213 |
0,206 |
0,195 |
0,187 |
0,174 |
|
0,1 |
0,239 |
0,238 |
0,237 |
0,234 |
0,231 |
0,225 |
0,220 |
0,212 |
0,205 |
0,194 |
0,186 |
0,173 |
|
0,2 |
0,234 |
0,233 |
0,232 |
0,229 |
0,226 |
0,220 |
0,215 |
0,206 |
0,200 |
0,189 |
0,181 |
0,167 |
|
0,3 |
0,227 |
0,226 |
0,225 |
0,222 |
0,219 |
0,213 |
0,208 |
0,199 |
0,193 |
0,182 |
0,174 |
0,160 |
|
0,4 |
0,216 |
0,215 |
0,214 |
0,211 |
0,208 |
0,202 |
0,197 |
0,188 |
0,182 |
0,171 |
0,163 |
0,149 |
|
0,5 |
0,203 |
0,202 |
0,200 |
0,198 |
0,195 |
0,189 |
0,184 |
0,175 |
0,169 |
0,158 |
0,150 |
0,136 |
|
0,6 |
0,186 |
0,185 |
0,184 |
0,181 |
0,178 |
0,172 |
0,167 |
0,158 |
0,152 |
0,141 |
0,133 |
0,119 |
|
0,7 |
0,167 |
0,166 |
0,165 |
0,162 |
0,159 |
0,153 |
0,148 |
0,140 |
0,133 |
0,122 |
0,114 |
0,100 |
|
0,8 |
0,144 |
0,136 |
0,142 |
0,139 |
0,136 |
0,130 |
0,125 |
0,116 |
0,110 |
0,099 |
0,091 |
0,077 |
|
0,9 |
0,119 |
0,118 |
0,117 |
0,114 |
0,111 |
0,105 |
0,100 |
0,091 |
0,085 |
0,074 |
0,066 |
0,052 |
Таблица
19
|
Сечение |
tIRs |
Значения |
||||||
|
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
||
|
Двутавровое |
0,0 |
0,30 |
0,30 |
0,33 |
0,38 |
0,44 |
0,50 |
0,55 |
|
0,1 |
0,30 |
0,30 |
0,33 |
0,40 |
0,45 |
0,52 |
0,57 |
|
|
0,2 |
0,30 |
0,30 |
0,33 |
0,41 |
0,46 |
0,52 |
0,59 |
|
|
0,3 |
0,30 |
0,30 |
0,34 |
0,42 |
0,47 |
0,53 |
0,60 |
|
|
0,4 |
0,30 |
0,30 |
0,34 |
0,43 |
0,48 |
0,55 |
0,60 |
|
|
0,5 |
0,30 |
0,31 |
0,36 |
0,44 |
0,50 |
0,57 |
0,60 |
|
|
0,6 |
0,30 |
0,32 |
0,38 |
0,46 |
0,52 |
0,60 |
0,60 |
|
|
0,7 |
0,30 |
0,34 |
0,40 |
0,50 |
0,56 |
0,60 |
0,60 |
|
|
0,8 |
0,30 |
0,36 |
0,44 |
0,55 |
0,58 |
0,60 |
0,60 |
|
|
0,9 |
0,32 |
0,40 |
0,52 |
0,60 |
0,60 |
0,60 |
0,60 |
|
|
Коробчатое |
0,0 |
0,75 |
0,92 |
1,10 |
1,25 |
1,40 |
1,55 |
1,70 |
|
0,1 |
0,75 |
0,92 |
1,10 |
1,26 |
1,42 |
1,58 |
1,72 |
|
|
0,2 |
0,75 |
0,93 |
1,11 |
1,28 |
1,44 |
1,61 |
1,75 |
|
|
0,3 |
0,76 |
0,95 |
1,13 |
1,30 |
1,47 |
1,65 |
1,80 |
|
|
0,4 |
0,77 |
0,97 |
1,15 |
1,33 |
1,50 |
1,69 |
1,85 |
|
|
0,5 |
0,78 |
1,00 |
1,18 |
1,37 |
1,55 |
1,75 |
1,95 |
|
|
0,6 |
0,80 |
1,03 |
1,21 |
1,42 |
1,62 |
1,82 |
2,05 |
|
|
0,7 |
0,85 |
1,10 |
1,28 |
1,50 |
1,70 |
1,95 |
2,10 |
|
|
0,8 |
0,90 |
1,20 |
1,40 |
1,65 |
1,90 |
2,15 |
2,20 |
|
|
0,9 |
1,00 |
1,30 |
1,60 |
1,90 |
2,20 |
2,30 |
2,30 |
5.30 (5.20). Для балок, изгибаемых в плоскости наибольшей жесткости и
рассчитываемых с учетом развития пластических деформаций, необходимо обеспечить
их общую устойчивость из плоскости изгиба. При этом более высокий уровень
развития пластических деформаций в балках (что связано с увеличением
коэффициентов сi), требует более частой
развязки сжатого пояса в горизонтальной плоскости вплоть до непрерывного его
закрепления жестким настилом. При максимальных значениях коэффициентов сi равных значениям с по табл. 66 СНиП II-23-81*, следует
уменьшать значения отношений lef/b по табл. 16 умножением на коэффициент d = 0,3 или применять
непрерывное закрепление пояса; при сi = 1,0, что соответствует
работе балки в пределах упругости, значения отношений lef/b следует принимать по табл. 16. Для промежуточных случаев в
СНиП II-23-81* допускается линейная
интерполяция.
Указанные в п. 5.20 СНиП II-23-81* требования относятся к
случаю чистого изгиба и соответствуют принятому значению ограничения
пластических деформаций в сечении.
При действии, например,
сосредоточенной силы в середине балки значения отношений lef/b могут быть увеличены на 25
% по сравнению с их значениями при чистом изгибе.
5.31 (5.22). При условиях, указанных в п. 5.22 СНиП II-23-81*, расчет неразрезных и защемленных балок может
выполняться с одновременным учетом работы сечений за пределом упругости и
соответствующего перераспределения опорных и пролетных изгибающих моментов.
Практическая методика расчета сводится к определению коэффициента
перераспределения моментов а, вводимого к наибольшему изгибающему моменту в
пролете или на опоре 1.
_________
1 Чернов Н. П. Расчет стальных
неразрезных балок по ограниченным пластическим деформациям // Строит. механика
и расчет сооружений. — 1980. — № 2. — С. 68-71.
Формула (46) СНиП II-23-81* для определения
коэффициента а получена из условия ограничения максимальных остаточных
деформаций в сечении значением (где
= er,тах Е/Rу).
В соответствии с
требованиями п. 5.22 СНиП II-23-81* допускается
принимать значения коэффициента a, соответствующие меньшему
ограничению пластических деформаций < 3. В этом случае
коэффициент a необходимо определять по
формуле
. (44)
Проверку прочности в
характерных сечениях неразрезных балок необходимо выполнять согласно
требованиям п. 5.22 СНиП II-23-81* с учетом
одновременного действия в сечении изгибающего момента M и поперечной силы Q.
5.32 (5.23). При изгибе неразрезных балок в двух главных плоскостях коэффициенты
перераспределения изгибающих моментов a необходимо определять в
каждой плоскости отдельно с учетом условий и требований, относящихся к балкам,
изгибаемым в одной плоскости.
5.33 (5.22). Рассмотрим примеры расчета неразрезных балок за пределом упругости.
Пример 1. Определить значение коэффициента a для четырехпролетной балки,
нагруженной сосредоточенными силами в третях каждого пролета (рис. 7, а).
Рис. 7. Перераспределение изгибающих моментов в неразрезной балке
а — схема нагружения и эпюры моментов; б — эпюры моментов для свободно опертых
балок
Наибольший изгибающий
момент, определяемый из расчета неразрезной балки в предположении упругой
работы материала, действует на опоре 1
и его значение равно Мmах = 0,2856Рl.
Найдем наибольшее значение
изгибающего момента Mef. Изгибающий момент в крайнем
пролете, вычисляемый как в свободно опертой балке (рис. 7, б), при а = 0,3333l равен M1 = 0,3333Pl.
По формуле (47) СНиП II-23-81* находим
.
Для второй силы в этом
пролете при а = 0,6667l получим
.
Для промежуточного пролета
имеем M2 = 0,3333Pl;
по формуле (48) СНиП II-23-81* находим
Мef = 0,5M2 = 0,3333Pl/2 =
0,1667Pl.
Наибольшее значение Mef = 0,25Рl.
По формуле (46) СНиП II-23-81* находим a — значение
коэффициента перераспределения моментов
Расчетное значение
изгибающего момента М равно
М = aМmах =
0,9376 × 0,2856Pl = 0,2678Pl.
Уменьшение изгибающего
момента за счет перераспределения моментов составляет 6,24 %. Эпюра расчетных
моментов показана на рис. 7, а
сплошной линией.
Пример
2. Определить значение коэффициента a для
однопролетной статически неопределимой балки (рис. 8).
Рис.
8. Эпюры моментов в однопролетной статически неопределимой балке
Пластические деформации
ограничены значением .
Наибольший изгибающий момент
в заданной балке при упругой работе материала действует в заделке и его
значение равно Мтах =
0,125ql2. Наибольший изгибающий момент в пролете на
расстоянии а = 0,375l от левой опоры равен М = 0,07031ql2. Изгибающий момент M1 на расстоянии а
= 0,375l от левой опоры, вычисленный
как в однопролетной свободно опертой балке, равен M1 = 0,1172ql2.
По формуле (47) СНиП II-23-81* находим
.
Значение коэффициента a определяем по формуле (44)
.
Расчетное значение
изгибающего момента М равно
М = 0,894 × 0,125ql2 = 0,112ql2.
Уменьшение расчетного
момента за счет перераспределения моментов составляет 10,6 %. Эпюра расчетных
моментов М показана на рис. 8 сплошной линией.
Пример 3. Определить значение коэффициента a для однопролетной балки с
обоими защемленными концами (рис. 9).
Рис. 9. Эпюры
моментов в однопролетной балке с обоими защемленными концами
Наибольший изгибающий момент
в заданной балке при упругой работе материала достигается одновременно на
опорах и в пролете; его значение равно Мтах
= 0,125Pl. Изгибающий момент в
середине пролета, вычисленный как в однопролетной свободно опертой балке, равен
М3 = 0,25Pl. Согласно п. 5.22 б СНиП II-23-81* имеем a = 1.
В рассматриваемой балке
перераспределения изгибающих моментов при работе материала за пределом
упругости не происходит.
ЭЛЕМЕНТЫ, ПОДВЕРЖЕННЫЕ ДЕЙСТВИЮ ОСЕВОЙ СИЛЫ С ИЗГИБОМ
5.34 (5.24*, 5.25). Согласно требованиям СНиП
II-23-81* расчет на
устойчивость элементов при действии осевой силы с изгибом обычно выполняется с
учетом развития пластических деформаций. При этом приближенную формулу (49) СНиП II-23-81* для проверки прочности
сечения можно считать предельным условием расчета на устойчивость при l = 0, поэтому при указанных в п. 5.24* СНиП II-23-81* условиях достаточно
ограничиться только проверкой устойчивости по формуле (51) СНиП II-23-81* В этом случае условия формулы (49) СНиП II-23-81* в принципе, должны быть удовлетворены автоматически
(рис. 10).
Что касается формулы (50) СНиП II-23-81*, то проверка прочности
сечения в пределах упругих деформаций может привести к меньшим значениям
предельных нагрузок, чем проверка устойчивости по формуле (51) СНиП II-23-81* особенно для коротких стержней. Поэтому проверку
прочности сечения по формуле (50) СНиП
II-23-81*
необходимо выполнять помимо проверки устойчивости с учетом указанных в СНиП II-23-81* условий применения этой
формулы (см. рис. 10).
Коэффициенты сi в формуле (49) СНиП II-23-81* установлены с учетом разъяснений, изложенных в п. 5.26 настоящего Пособия; коэффициент п характеризует “полноту” поверхностей
кривых взаимодействия для различных типов сечений (рис. 11).
Рис. 10. К расчету внецентренно сжатых элементов
1 — на прочность по формуле (49) СНиП II-23-81*, 2 — на прочность по формуле (50) СНиП II-23-81*, 3—4 — области возможных значений N и М при проверке
устойчивости
Рис. 11. Зависимость “полноты” кривых
взаимодействия от значений коэффициента n
При установлении значений
коэффициентов с(сх) в табл. 66 СНиП II-23-81* предполагалось, что изгиб элементов происходит в
плоскости у-у, а нагрузки во всех
случаях действуют сверху вниз. При установлении значений коэффициентов су принималось, что изгиб
элементов происходит в плоскости х-х.
Коэффициенты п (при My = 0) необходимо принимать с учетом того, что
эксцентриситеты приложения нагрузки во всех случаях расположены сверху схем
сечения, т.е. так же, как это показано в табл. 73 СНиП II-23-81*. Это важно при расчете несимметричных сечений
относительно оси х-х.
При небольших значениях
осевой силы N/(AnRy) £ 0,1 рассматриваемые
элементы приближаются к изгибаемым, в связи с чем при их расчете необходимо
учитывать соответствующие условия и требования.
5.35 (5.27*). Расчеты на устойчивость внецентренно-сжатых и сжато-изгибаемых
элементов в плоскости действия момента, совпадающей с плоскостью симметрии
сечения, выполняются согласно общим рекомендациям, изложенным в п. 5.7 настоящего Пособия. При этом начальные несовершенства
в связи с малой вероятностью совпадения их максимальных значений с расчетным
значением эксцентриситета е = M/N в расчетах не учитываются.
Расчеты выполняются с
использованием коэффициентов jе устойчивости при внецентренном сжатии, которые
получены в соответствии с расчетной схемой, приведенной на рис. 3, в зависимости от относительного эксцентриситета mеf и условной гибкости :
. (45)
При этом на рис. 3 вместо начального
эксцентриситета еb следует принимать расчетный
эксцентриситет е. Если еb > е,
то вместо коэффициентов jе необходимо принимать
коэффициенты j.
Вычисленные по результатам
исследований внецентренно-сжатых стержней коэффициенты, необходимые для
расчета, сведены в табл. 73-75 СНиП
II-23-81*.
Табл. 74 СНиП II-23-81* составлена для стержней сплошного прямоугольного
сечения, а табл. 75 СНиП II-23-81* — для сквозных
стержней идеализированного сечения из двух полос, соединенных жесткой связью в
плоскости, параллельной плоскости изгиба (см. рис. 5, б). В
табл. 73 СНиП II-23-81* приведены коэффициенты
влияния формы сечения h, с помощью которых
учитывается развитие пластических деформаций и таким образом стержни различных
типов сечений по значению предельных сил Nu приводятся к стержню прямоугольного сечения (для
которого h =
1) при одной и той же гибкости l.
5.36 (5.29). Расчетные значения изгибающего момента и продольной силы в элементе
для вычисления эксцентриситета е
определяются из расчета упругой системы по недеформированной схеме и
принимаются при одном и том же сочетании нагрузок с учетом изменения
изгибающего момента по длине элемента и условий закрепления концов элемента.
Увеличение прогибов v
внецентренно-сжатых элементов при изгибе учтено в расчете отдельного стержня по
деформированной схеме при определении предельной силы Nu (см. рис. 3) и, следовательно, коэффициентов jе.
5.37 (5.28). При расчете внецентренно-сжатых стержней, имеющих резко несимметричные
типы сечений (10 и 11 по табл. 73 СНиП
II-23-81*),
возникает опасность появления значительных деформаций со стороны растянутого
волокна. Этого нельзя допустить для стержней из сталей с пределом текучести
свыше 580 МПа (5900 кгс/см2), поскольку отношение su/sу для таких сталей сравнительно
невелико (1,17 и менее). В связи с этим для таких стержней, наряду с проверкой
их устойчивости предусмотрена проверка прочности растянутого волокна по формуле
(54) СНиП II-23-81*, в которой изгибающий
момент приближенно определяется с учетом деформированной схемы.
5.38 (5.30). При изгибе внецентренно-сжатых элементов в плоскости наибольшей
жесткости х-х (Ix > Iу), совпадающей с плоскостью симметрии, становится
возможной потеря устойчивости из плоскости действия момента при
изгибно-крутильных деформациях раньше достижения предельной силы N, принимаемой в качестве
критерия при плоской форме потери устойчивости (см. рис. 3).
В этом случае проверку
устойчивости следует выполнять в плоскости наименьшей жесткости у-у как центрально-cжатого
элемента с введением коэффициента с,
учитывающего влияние изгибающего момента Мх
на пространственную потерю устойчивости стержня. В табл. 10 СНиП II-23-81* для различных типов сечений установлены
коэффициенты a и b для определения
коэффициентов с на основе результатов
теоретических и экспериментальных исследований [12].
При больших изгибающих
моментах Мx(тx ³ 10) требования СНиП II-23-81* обеспечивают переход к
случаю потери устойчивости изгибаемых элементов. При этом формула (56) СНиП II-23-81* с учетом формулы (58) СНиП II-23-81* может быть записана в
следующем виде:
. (46)
5.39 (5.31). При гибкости ly >
lc = 3,14 потеря устойчивости внецентренно-сжатых стержней при
изгибно-крутильных деформациях происходит обычно в пределах упругих деформаций.
В этом случае для определения коэффициента с
использована теория устойчивости тонкостенных стержней В. З. Власова.
Для внецентренно-сжатого
шарнирно опертого стержня двутаврового сечения с двумя осями симметрии,
изгибаемого в плоскости стенки, условие потери устойчивости имеет вид [12]:
, (47)
где еx — эксцентриситет приложения сжимающей силы
относительно оси х—х;
.
Остальные обозначения
соответствуют принятым в формуле (21)
настоящего Пособия. Необходимо отметить, что для рассматриваемого сечения аx = ay = 0.
Из решения квадратного
уравнения (47) с использованием безразмерных параметров получена формула (60) СНиП II-23-81* для определения
коэффициента с = N/Ny.
Таким же образом получена
формула (173) СНиП II-23-81* для вычисления
коэффициентов с для двутавровых и
тавровых сечений с одной осью симметрии.
Для приближенной оценки
фактических условий закрепления концов стержней в формулах (60) и (173) СНиП II-23-81* учитывалось частичное
стеснение депланации опорных сечений введением коэффициента 2 в первый член
формул для определения коэффициента m (см. также п. 5.9 настоящего Пособия).
5.40 (5.31). Пример определения коэффициентов с
для внецентренно-сжатого тонкостенного стержня двоякосимметричного двутаврового
сечения, имеющего соотношения размеров: h = 60t, b = 0,5h, t1 = 2t
(рис. 12).
Рис. 12. Двутавровое
сечение
Вычисляем геометрические характеристики сечения:
A = 60t × t + 30t × 2t × 2 = 180t2;
;
It = 0,433 [2 × 30t(2t)3 + 60t × t3] = 234t4.
Значения r и m,
входящие в формулу (60) СНиП II-23-81* равны:
m =
2 + 0,564 × 10-4ly2.
Значения коэффициентов с для различных гибкостей и
эксцентриситетов приведены в табл. 20.
5.41 (5.33). При расчете сквозных внецентренно-сжатых стержней необходимо выполнять
проверку устойчивости всего стержня согласно п. 5.27* СНиП II-23-81* с учетом рекомендаций п. 5.15 настоящего Пособия, а также отдельных ветвей как в
плоскости изгиба в пределах панели, так и из плоскости изгиба всей ветви с
учетом ее раскрепления в направлении, перпендикулярном плоскости соединительных
элементов.
Таблица 20
|
ly |
m |
d |
Значения с при отношении Mx/(Nh), равном |
||||||
|
0,15 |
0,30 |
0,45 |
0,60 |
0,75 |
0,90 |
1,05 |
|||
|
60 |
2,203 |
0,378 |
0,943 |
0,834 |
0,730 |
0,644 |
0,573 |
0,516 |
0,468 |
|
80 |
2,361 |
0,352 |
0,948 |
0,845 |
0,743 |
0,657 |
0,587 |
0,529 |
0,481 |
|
100 |
2,564 |
0,325 |
0,954 |
0,857 |
0,759 |
0,674 |
0,603 |
0,545 |
0,496 |
|
120 |
2,811 |
0,296 |
0,959 |
0,870 |
0,776 |
0,692 |
0,622 |
0,563 |
0,514 |
Проверка устойчивости
отдельных ветвей должна обеспечивать сквозной стержень от преждевременного
исчерпания несущей способности, при этом допускается учитывать взаимодействие
элементов решетки и диафрагм жесткости с ветвями колонны.
При определении расчетной
длины ветвей в обеих плоскостях допускается учитывать переменность продольной
силы по длине ветви за счет изменения изгибающего момента (см. разд. 6
настоящего Пособия).
5.42 (5.34). Задача устойчивости стержня, сжатого с изгибом в двух главных
плоскостях, сводится к определению предельной точки на кривой состояний
равновесия с учетом работы стали за пределом упругости. В связи со сложностью
решения задачи результаты, пригодные для практического использования, получены
лишь для определенных типов сечений с одинаковыми эксцентриситетами на концах.
Важное значение для оценки надежности теоретических результатов имеют
экспериментальные исследования [12].
5.43 (5.34). В связи с тем, что для случая сжатия с изгибом в одной из главных
плоскостей в СНиП II-23-81* приведены
достаточно точные способы расчета с помощью табл. 74, 73 и 10 коэффициентов
соответственно je и с, оказалось целесообразным расчет таких же стержней, но сжатых с
двухосным эксцентриситетом, выполнять с использованием указанных таблиц.
Для двутавровых сечений с
одной осью симметрии этот подход реализован использованием формулы (62) СНиП II-23-81* в которой при hту < тx
предусмотрено ограничение jеху £ cjy, что приводит в частных
случаях при тx = 0 и ту = 0 к указанным точным решениям.
5.44 (5.34). Для стержней замкнутого или сплошного сечения с двумя осями симметрии
(трубы, брусья прямоугольного сечения) влияние кручения на предельную нагрузку
несущественно. В связи с этим проверку устойчивости таких стержней, сжатых с
изгибом в двух главных плоскостях, при можно выполнять по
формулам:
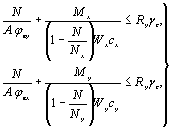
где
5.45 (5.35). При определении расчетной длины отдельных ветвей, рассчитываемых как
внецентренно-сжатые элементы по формулам (51) и (56) СНиП II-23-81* допускается учитывать переменность продольной силы
по длине ветви за счет изменения изгибающего момента Мх (см. разд. 6 настоящего
Пособия).
5.46. При
расчете изгибаемых элементов из углеродистой стали с сечениями малой высоты
(см. п. 3.7 настоящего Пособия) требуемая
толщина плиты с учетом влияния градиента напряжений определяется по формуле
, (49)
где М —
изгибающий момент на единицу ширины плиты;
gс — коэффициент условий
работы опорных плит, принимаемый по поз. II табл. 6* СНиП II-23-81*
6. РАСЧЕТНЫЕ ДЛИНЫ И ПРЕДЕЛЬНЫЕ ГИБКОСТИ
ОБЩИЕ ПОЛОЖЕНИЯ
6.1.
Расчетную (эффективную) длину рекомендуется принимать для расчета, главным
образом, стержневых конструкций при проверке несущей способности их отдельных
стержней.
Использование
понятия расчетной длины предполагает разделение стержневых систем на отдельные
элементы, при этом необходимо учитывать взаимодействие рассматриваемого
элемента с основанием и другими элементами (в первую очередь, примыкающими к
нему в узлах).
Расчетные
длины сжатых, внецентренно-сжатых и сжато-изгибаемых элементов стержневых и
рамных систем необходимо устанавливать в случаях, когда выполнить расчет
конструкций как единых систем по деформированной схеме с учетом пластических
деформаций не представляется возможным.
6.2 (6.8). Под расчетной длиной стержня обычно понимают условную длину
однопролетного стержня, критическая сила которого при шарнирном закреплении его
концов такая же, как для заданного стержня [18].
По физическому смыслу
расчетная длина стержня с произвольными закреплениями концов является
наибольшим расстоянием между двумя точками перегиба изогнутой оси, определяемым
из расчета этого стержня на устойчивость по методу Эйлера.
Согласно этому определению
для установления расчетной длины необходимо применять метод расчета на
устойчивость систем с прямыми стержнями при приложении нагрузок в узлах в
предположении упругих деформаций [19]. При этом следует учитывать продольные
усилия в стержнях и, как правило, исключать из рассмотрения поперечные нагрузки
и эксцентриситеты, вызывающие изгиб стержней.
При проектировании расчетную
длину стержня lef обычно определяют по
формуле
lef = mI, (50)
где m — коэффициент расчетной
длины, зависящий от условий закрепления концов стержня и вида нагрузки;
l — геометрическая длина
рассматриваемого стержня.
Для плоских стержневых систем расчетную длину сжатых стержней следует
определять как в плоскости, так и из плоскости системы (перпендикулярной ей).
6.3.
При подборе сечений стержней обычно выполняется поэлементный расчет, требующий
определения расчетной длины для каждого стержня. При этом необходимо принимать
такие расчетные схемы, которые отражают действительные условия нагружения
стержней и закрепления их концов с учетом неравномерности распределения
нагрузок между стержнями и различия их жесткостей, наличие конструктивных
элементов, обеспечивающих ту или иную форму потери устойчивости здания или
сооружения.
В частности, при
практическом определении расчетной длины стоек многоэтажных рам в нормах, как
правило, используется приближенная расчетная схема в виде простейшей ячейки
независимо от числа этажей и соотношения продольных сил в стойках.
Следует отметить, что
применение такой расчетной схемы не предполагает пропорционального возрастания
нагрузок на систему в целом.
6.4.
В СНиП II-23-81* значения расчетной длины
стержней для различных систем приведены, как правило, для наиболее
неблагоприятных случаев нагружения и работы системы, т.е. зачастую с некоторым
запасом. Поэтому в дальнейшем, наряду с разъяснением требований норм, будут
приведены также и более строгие расчетные схемы для определения и уточнения
значений расчетной длины на основе учета действительной работы системы и схемы
загружения.
Расчетная длина стержней
одной и той же системы различна при разных сочетаниях нагрузок, хотя в п. 6.11*
СНиП II-23-81* по этому поводу имеется
упрощающее разрешение. В связи с этим при проектировании возможно уточнение
значений расчетной длины в соответствии с тем сочетанием нагрузок, при котором
выполняется подбор сечений некоторых стержней.
ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ДЛИН ЭЛЕМЕНТОВ
6.5 (6.9*). Коэффициенты m для определения расчетной
длины элементов постоянного сечения в зависимости от условий закрепления концов
и характера нагружения следует принимать по табл. 21 и 22.
Таблица
21
|
№ п.п. |
Расчетная схема |
Коэффициент m |
№ п.п. |
Расчетная схема |
Коэффициент m |
|
1 |
|
1,0 |
4 |
|
2,0 |
|
2 |
|
0,7 |
5 |
|
2,0 |
|
3 |
|
0,5 |
6 |
|
1,0 |
Таблица 22
|
№ п.п. |
Расчетная схема |
Коэффициент m |
№ п.п. |
Расчетная схема |
Коэффициент m |
|
1 |
|
1,12 |
3 |
|
0,69 |
|
2 |
|
0,73 |
4 |
|
0,56 |
6.6.
Коэффициенты m для установления
расчетной длины элементов постоянного сечения с упругими закреплениями концов
следует определять по формулам табл. 23.
Таблица
23
|
Обобщенная расчетная |
Формулы для |
Частные случаи |
Расчетные схемы |
Формулы для |
|
|
|
0,5 £ m |
0 £ n1 |
n = 0 |
|
2,0 ³ |
|
n = |
|
1,0 ³ m |
|||
|
0 £ n £ |
n1 = 0 |
|
2,0 ³ |
||
|
n1 = |
|
0,5 £ m £ |
|||
|
|
0,5 £ m |
n1 = 0 £ n £ |
Y = |
||
|
Y = 1 |
|
1,0 ³ m |
|||
|
Y = 0 |
|
1,0 ³ m |
|||
|
|
m ³ 1,0 |
0 £ n £ |
n1 = |
||
|
0 < n1 |
n = |
|
2,0 ³ m |
||
|
n = 0 |
|
|
|||
|
n1 > p2 |
1,0 |
Обозначения, принятые в табл. 23:
;
;
Cm — коэффициент жесткости упругого
защемления, равный значению реактивного момента, возникающего в опорном сечении
при повороте его на угол, равный 1,0;
Сn
— коэффициент жесткости упругой опоры, равный значению реактивной силы,
возникающей в опорном сечении при смещении его на 1,0.
В табл. 24 приведены примеры
определения коэффициентов Сm и Сn.
6.7 (6.3*). Коэффициенты m и mz;
для установления расчетной длины lef = ml(lef,z — mzlz) пересекающихся элементов
постоянного сечения в зависимости от конструктивной схемы узла пересечения
следует определять по формулам табл. 25.
Приведенные в табл. 25 расчетные схемы
соответствуют следующим случаям загружения и конструкции пересечения элементов
в узле:
1) оба элемента не
прерываются, поддерживающий элемент сжат;
2) оба элемента не
прерываются, поддерживающий элемент растянут;
Таблица 24
|
№ пп |
Расчетная схема |
Определение m |
|
1 |
|
(VI) при |
|
2 |
|
(VI) при |
|
3 |
|
(V) при |
|
4 |
|
(I) при |
|
5 |
|
(IV) при |
|
6 |
|
(IV) при |
|
7 |
|
(IV) при |
|
8 |
|
(III) при |
3) рассматриваемый элемент
не прерывается, поддерживающий элемент сжат, прерывается и перекрывается
фасонкой;
4) рассматриваемый элемент
не прерывается, поддерживающий элемент растянут, прерывается и перекрывается
фасонкой;
5) рассматриваемый элемент
прерывается и перекрывается фасонкой, поддерживающий элемент растянут и не
прерывается.
На рис. 13 приведено сопоставление
значений коэффициентов m и mz
пересекающихся стержней, определенных по формулам табл. 25 и по табл. 12 СНиП II-23-81*. Как следует из рис. 13,
коэффициенты, согласно СНиП II-23-81*, не зависят от
соотношения усилий в стержнях и совпадают с точными значениями только при
неработающем поддерживающем стержне.
Таблица
25
|
№ п.п |
Расчетная схема |
m при az = Nz/N |
|
1 |
|
|
|
|
||
|
2 |
|
az > 0 |
|
3 |
|
|
|
mz = 0,5 |
||
|
4 |
|
az > 0 |
|
5 |
|
m = 0,5 при
|
Условные обозначения:
— по СНиП II-23-81*
— по схемам 1
и 2 табл. 25
— по схемам 3
и 4 табл. 25
Рис. 13. График для
определения значений коэффициентов расчетных длин пересекающихся стержней (при
равных длинах и жесткостях) при различных усилиях в них
6.8.
Расчетные длины lef(lef,1) неразрезных стержней
постоянного сечения с различными сжимающими или растягивающими усилиями в
пролетах как в плоскости, так и из плоскости конструкции можно определять по
формулам табл. 26. Граничные
условия, приведенные в поз. 1 и 2 табл.
26 соответствуют расчетной схеме верхнего пояса фермы, а в поз. 3 и 4 —
подкрановой ветви решетчатой колонны. При вычислении параметра D по поз. 2 и 4 табл. 26 растягивающие усилия в
стержнях необходимо принимать со знаком “минус”.
6.9 (6.10*). Коэффициенты расчетной
длины m колонн постоянного сечения
свободных рам в плоскости рамы при жестком креплении ригелей к колоннам и при
одинаковом нагружении верхних узлов следует определять по формулам табл. 17, а СНиП II-23-81*. При этом вместо формул (70, а) и (70, б) при
предельных значениях параметров р и п допускается пользоваться формулами табл. 27.
6.10.
Коэффициенты расчетной длины m колонн постоянного сечения
несвободных рам (рис. 14) в плоскости рамы при жестком креплении ригелей к
колоннам и при одинаковом нагружении верхних узлов следует определять по
формуле 70, в СНиП II-23-81*. При этом в частных случаях эта формула может быть
упрощена:
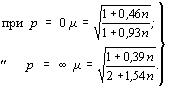
Таблица
26
|
№ пп |
Расчетная схема |
Отношение усилий |
Расчетная длина lef(lef1) |
|
1 |
В плоскости |
1 ³ a |
l(0,17a3 + 0,83) ³ 0,8l |
|
2 |
Из плоскости |
(q – 1) ³ b ³ -0,5 |
|
|
3 |
В плоскости |
1 ³ a |
|
|
4 |
Из плоскости |
(q – 1) ³ b ³ 0 |
|
Таблица
27
|
p |
n |
Формулы для определения |
|
|
От 0,03 до 0,2 |
|
|
Св. 0,2 |
|
|
|
0 |
От 0,03 до 0,2 |
|
|
Св. 0,2 |
2,0 |
|
|
0,03 £ р |
|
|
Рис.
14. Схемы деформаций несвободных рам
а — одноэтажных; б — многоэтажных; в —
многопролетных
6.11.
При наличии жесткого диска покрытия или продольных связей по верху колонн в
расчетный блок допускается включать по две рамы с каждой стороны, перпендикулярной
плоскости рассматриваемой рамы. При этом коэффициент mmax расчетной длины наиболее
нагруженной колонны постоянного сечения в производственном здании с кранами
(мостовыми или подвесными) при неравномерном распределении нагрузок от крана
следует определять по формуле
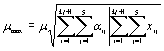
(но не менее 0,7m),
где m — коэффициент расчетной длины рассматриваемой
колонны одно- и многопролетного здания при равномерном нагружении узлов,
определенный согласно пп. 6.9 и 6.10;
;
здесь Nтах — усилие в наиболее нагруженной колонне
рассматриваемой плоской рамы;
Nij — усилия во всех колоннах
(в том числе в рассматриваемой) расчетного блока;
;
Ic,max — момент инерции наиболее нагруженной колонны
рассматриваемой плоской рамы;
Icij — моменты инерции всех
колонн расчетного блока;
i = 1, 2, …, kl + 1 — номер колонны в плоскости рамы (kl — число пролетов);
j = 1, 2, 3, 4, 5 — номер рамы.
6.12 (6.11*). Коэффициенты m1 расчетной длины нижнего
участка одноступенчатых колонн при различном креплении их верхних концов
следует определять в зависимости от соотношения нагрузок, длины и жесткостей
верхнего и нижнего участков по формулам табл.
28, в которой приведены конструктивные схемы производственных зданий,
соответствующие различным расчетным схемам колонн, и табл. 29.
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ РАСЧЕТНЫХ ДЛИН СТОЕК РАМ
Пример 1. Рассмотрим случаи определения коэффициентов m расчетной длины стоек при предельных значениях п и р.
При п и р, стремящихся к
бесконечности, по формулам табл. 27
находим:
а) при р = и n = 0,2
;
б) при р = и n = 5,0
.
При р = 50 и п = 0,2 и п = 5,0 согласно п.
6.10* СНиП II-23-81* получим соответственно m = 1,49 и m = 1,03.
В случае шарнирного
закрепления в фундаменте стойки одного яруса рамы рекомендуется пользоваться
формулами табл. 27 при р = 0 и n > 0,2. Откуда находим:
а) при р = 0 и n = 1,0 ;
б) при р = 0 и n =
.
Таблица
28
|
№ п.п. |
Конструктивная схема |
Расчетная схема |
Формулы для |
Границы изменения |
|
1 |
|
|
|
При a1
при a1 n £ 1,35 – 0,35 |
|
2 |
|
|
При a1 £ 1,2
при a1 > 1,2 |
0,1 £ m £ |
|
3 |
|
|
|
|
|
4 |
|
|
|
0,1 £ m £ 2,0 |
Обозначения, принятые в табл. 28:
;
;
;
.
Таблица
29
|
№ п.п. |
Расчетная схема |
Условие нагружения |
Формулы для |
|
1 |
|
F2 = 0 |
m11 |
|
2 |
F1 = 0 |
|
|
|
3 |
|
F2 = 0 |
|
|
4 |
F1 = 0 |
При при |
|
|
5 |
|
F2 = 0 |
|
|
6 |
F1 = 0 |
|
|
|
7 |
|
F2 = 0 |
|
|
8 |
F1 = 0 |
|
Обозначения, принятые в табл. 29:
Пример
2. Требуется определить значения коэффициентов расчетной длины m средних колонн многопролетных и многоэтажных
зданий.
1. Исходные данные. Двухпролетная одноэтажная рама с жестким закреплением
колонн в фундаментах и жестким креплением ригелей к колоннам постоянного
сечения. Здесь и далее в примерах принимаем lr1 = lr2 = lr; Ir1 = Ir2 = Ir; (одинаковые пролеты и
сечения ригелей); Ir/Ic = 3; lc/lr = 0,2;
а) здание, нагруженное
силами N во всех узлах по верху
колонн.
При k = 2 и
вычислим ;
по табл. 17, a СНиП II-23-81*
б) здание при неравномерном
нагружении узлов в плоскости рамы (одной колонны силой N, а двух других — силами 0,5N).
По формуле (52) при Sai = 1 + 0,5 + 0,5 = 2 и SХi
= 3
в) здание при наличии
продольных связей в конструкции и нагружении в расчетном блоке (из пяти рам)
одной колонны в средней раме силой N
и двух других колонн в средней раме силами 0,5N, а остальных колонн в четырех рамах — силами 0,3N.
Тогда Sai = 12 × 0,3 + 2 × 0,5 + 1 = 5,6, и SХi
= 15.
По формуле (52) ;
г) здание при нагружении
одной колонны в средней раме силой N,
двух других колонн силами 0,3N и всех колонн в оставшихся
четырех рамах расчетного блока силами 0,1 N.
При Sai = 12 × 0,1 + 2 × 0,3 + 1 = 2,8 и SХi
= 15 по формуле (52) .
Так как вычисленное m < 0,7, следует принять m = 0,7 (см. поз. 2 табл. 21);
д) конструкция обеспечена от
возможности боковой потери устойчивости системы в целом и ее можно отнести к
категории несвободной рамы.
При п = 0,8 по формуле (51)
2. Исходные данные. Десятипролетная одноэтажная рама с жестким
закреплением колонн в фундаментах и жестким креплением ригелей равных пролетов
и сечений к колоннам постоянного сечения нагружена силой N во всех узлах:
а) Ir/Ic = 3; lc/lr
= 0,2.
При k = 10 и ;
по табл. 17, a СНиП II-23-81*
б) Ir/Ic = 3; lc/lr = 2.
При k = 10 и
;
по табл. 17, a СНиП II-23-81*
Пример
3. Требуется определить значения коэффициентов m1 расчетной длины нижнего
участка одноступенчатых колонн при различных значениях параметров, приведенных
в табл. 28 и 29:
1) для схемы 1 при r = 0,2, m =
2,0, I2/I1 = 0,5, n = 0,25 вычислим = 1,6; при 1,35 –
0,35a1 = 0,91 > n по формуле поз. 1 табл. 28 m1 = 3,28;
2) для схемы 1 при F1 = 0 и m = 2,0, I2/I1 = 0,5, n = 0,25 вычислим = 8,0; при 1,35 —
0,35a1 = 0,36 > n по формуле поз. 1 табл. 28 m1 = 7,15;
3) для схемы 2 при r = 0,2, m = 2,0, I2/I1 = 0,5, n = 0,25 вычислим = 1,6; при 1,35 –
0,35a1 = 0,91 > n по формуле поз. 2 табл. 28 m1 = 2,12;
4) для схемы 2 при r = 0,8, m =
2,0, I2/I1 = 1,2 > 1, n = 0,6 вычислим = 2,7; при 1,35 —
0,35a1 = 0,78 > n по формуле поз. 2 табл. 28 m1 = 2,59;
5) для схемы 3 при F2 = 0 и r = 0, т =
2,0; I2/I1 = 0,04, п = 0,02 по формуле поз. 5 табл. 29 m1 = 1,86;
6) для схемы 3 при F1
= 0 и r = 1,0, т = 0,1, I2/I1 = 1,0, п = 10,0 по формуле поз. 6 табл.
29 m1 = 0,77;
7) для схемы 4 при F2 = 0 и r = 0, т =
2,0, I2/I1 = 0,04, п = 0,02 по формуле поз. 7 табл. 29 m1 = 1,83;

= 0 и r = 1,0, т = 0,1, I2/I1 = 1,0, n = 10,0 по формуле поз. 8 табл. 29 m1 = 0,55.
6.13 (6.15*). Ограничения гибкостей сжатых стержней вводятся с целью повышения
экономичности и надежности стальных конструкций. В определенной мере это
реализуется за счет более полного использования прочностных свойств стали как
материала, поскольку с увеличением гибкости стержней уровень использования
прочности стали уменьшается. Отсюда следует, что применять высокопрочные стали
при больших гибкостях экономически нецелесообразно. Ограничения гибкостей
способствуют также уменьшению искривлений стержней при изготовлении,
транспортировании и Монтаже. Для стержней, сечения которых назначаются по
предельным гибкостям, допускается увеличить предельную гибкость в соответствии
со СНиП II-23-81*.
7. ПРОВЕРКА УСТОЙЧИВОСТИ СТЕНОК И ПОЯСНЫХ ЛИСТОВ ИЗГИБАЕМЫХ И СЖАТЫХ
ЭЛЕМЕНТОВ
ОБЩИЕ ПОЛОЖЕНИЯ
7.1.
При решении вопросов устойчивости пластинок, образующих сечения элементов
стальных конструкций, обычно рассматриваются прямоугольные пластинки под
действием внешней нагрузки в срединной плоскости пластинки. В докритическом
состоянии пластинки считаются идеально плоскими (рис. 15).
За критическое состояние
пластинки принимается момент бифуркации (разветвления) форм ее равновесия,
когда одновременно с плоской формой равновесия может существовать форма,
возникающая при выпучивании пластинки.
Рис. 15. Схема
загружения пластинки
7.2.
Решение задачи устойчивости пластинки состоит из двух этапов. На первом этапе вычисляются компоненты
напряженно-деформированного докритического состояния в пределах упругости или с
применением одной из теорий пластичности. При этом обычно рассматривается
изолированная пластинка, загруженная по контуру нагрузкой, и для любой точки с
координатами х, у вычисляются компоненты напряжений и деформаций. Однако,
целесообразнее на этом этапе исследовать работу стержня, в состав которого
входит пластинка, и определить для нее компоненты напряженно-деформированного
состояния.
На втором этапе решается задача определения критического состояния пластинки, которая
может быть сформулирована в различной постановке. При прямом ходе решения
задачи для заданной гибкости пластинки и вычисленных компонентов
напряженно-деформированного состояния определяется внешняя нагрузка,
соответствующая критическому состоянию. При обратном ходе решения для заданной
внешней нагрузки вычисляется гибкость пластинки, соответствующая ее
критическому состоянию. В упругопластических задачах чаще применяется обратный
ход решения, так как за пределом упругости связь между параметром нагрузки и
деформациями пластинки становится неоднозначной, что значительно усложняет
процесс определения критической нагрузки для пластинки заданной гибкости.
Особенно трудоемким становится этот процесс при наличии нескольких компонентов
напряжений.
7.3.
Компоненты напряжений и деформаций, как правило, вычисляются с использованием
зависимостей теории малых упругопластических деформаций, разработанной А. А.
Ильюшиным [20], и с учетом концепции Шенли о продолжающемся нагружении в момент
бифуркации. Справедливость этой концепции доказана в ряде работ. В работе 121]
показано, что результаты расчета, полученные с учетом концепции Шенли, наиболее
близки к экспериментальным данным. Кроме того, активность всех пластических
деформаций в процессе потери устойчивости уменьшает сопротивление пластинки
выпучиванию, что идет в запас устойчивости, а также существенно упрощает
исследования.
7.4.
При решении задачи устойчивости для изолированных пластинок внешняя нагрузка
принимается в виде эпюр компонентов деформаций или напряжений, удовлетворяющих
уравнениям равновесия в интегральной форме (например, внецентренное сжатие и
чистый сдвиг). В этом случае не рассматривается первый этап решения задачи, что
ограничивает область применения полученных результатов, так как действительное
распределение компонентов напряжений и деформаций в сечениях элементов не
всегда соответствует принятой схеме расчета пластинки.
Более обоснованной является
постановка, включающая оба этапа решения задачи. В этом случае на первом этапе
определяется нагрузка, соответствующая принимаемому предельному состоянию
стержня. Это может быть точка максимума на кривой равновесных состояний (рис.
16) или другая точка, соответствующая предельному состоянию стержня. Из решения
задачи для предельного состояния всего стержня вычисляются компоненты
напряженно-деформированного состояния, которые являются исходными данными для
определения критической гибкости пластинок, составляющих поперечное сечение
стержня. Такой подход позволяет реализовать принцип равноустойчивости, сущность
которого заключается в том, что предельное состояние всего стержня и элементов
сечения (пластинок) соответствует одному значению внешней нагрузки. Описанная
схема реализована в расчетах устойчивости стенок и поясов центрально- и
внецентренно-сжатых стержней, когда напряженно-деформированное состояние в
опасном сечении определялось из решения соответствующей задачи для всего
стержня.
Рис. 16. Кривая равновесных состояний стержня
Р — параметр нагрузки; v — характерное перемещение стержня
7.5.
Анализ результатов решения задач для элементов сечений стержней позволил
получить достаточно общую зависимость критической гибкости пластинки от
величины деформаций и закона их распределения. В общем случае условная гибкость
пластинки может быть вычислена
из формулы
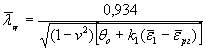
где v — коэффициент Пуассона;
qо, k1 — коэффициенты, приведенные в табл. 30 для
диаграммы Прандтля в зависимости от параметра , характеризующего распределение деформаций по ширине
пластинки;
— деформации на продольных
кромках пластинки ();
— деформация, соответствующая
пределу пропорциональности.
Здесь ;
,
.
Таблица
30
|
Условная гибкость |
Коэффициенты |
Значения qо |
||||
|
0 |
0,5 |
1,0 |
1,5 |
2,0 |
||
|
|
qо |
0,167 |
0,127 |
0,0896 |
0,0523 |
0,030 |
|
k1 |
0,361 |
0,249 |
0,1600 |
0,0898 |
0,0498 |
|
|
|
qо |
0,250 |
0,187 |
0,1290 |
0,0750 |
0,0419 |
|
k1 |
0,345 |
0,239 |
0,1520 |
0,0855 |
0,0475 |
|
|
|
qо |
2,320 |
1,730 |
1,1700 |
0,8900 |
0,8650 |
|
k1 |
3,540 |
2,500 |
1,3300 |
1,1100 |
0,9280 |
|
|
|
qо |
2,320 |
1,450 |
0,5770 |
0,0800 |
0,0422 |
|
k1 |
3,540 |
3,320 |
1,0800 |
0,1280 |
0,0690 |
|
|
|
qо |
2,320 |
2,100 |
1,7400 |
1,4400 |
1,1600 |
|
k1 |
3,540 |
2,640 |
2,6200 |
1,3200 |
1,1700 |
Обозначения, принятые в табл. 30:
— условная
гибкость стенки двутавра или прямоугольного коробчатого сечения с учетом
частичного защемления в поясах;
— условная
гибкость стенки швеллера или квадратного трубчатого сечения при шарнирном
закреплении продольных сторон;
— условная
гибкость полки двутавра или крестового сечения;
— условная
гибкость одиночного свеса, наиболее напряженного по закрепленной кромке;
— условная
гибкость одиночного свеса, наиболее напряженного по свободной кромке.
В табл. 31 приведены
значения условной гибкости в зависимости от
максимальной пластической деформации и параметра a. При этом учитывалось изменение коэффициента
Пуассона, влияние начальных несовершенств пластинки [22] и уменьшение эффекта
защемления при развитии пластических деформаций. В упругой области коэффициент
упругого защемления определялся по данным работы [22].
Таблица
31
|
a |
|
Значения |
|||||||
|
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
6,0 |
||
|
0,0 |
|
1,822 |
1,471 |
1,162 |
1,155 |
1,040 |
0,891 |
0,805 |
0,746 |
|
|
1,644 |
1,356 |
1,204 |
1,109 |
0,938 |
0,882 |
0,800 |
0,745 |
|
|
|
0,523 |
0,433 |
0,379 |
0,343 |
0,317 |
0,278 |
0,252 |
0,233 |
|
|
|
0,523 |
0,433 |
0,379 |
0,343 |
0,317 |
0,278 |
0,252 |
0,233 |
|
|
|
0,523 |
0,433 |
0,379 |
0,343 |
0,317 |
0,278 |
0,252 |
0,233 |
|
|
0,5 |
|
2,297 |
1,775 |
1,515 |
1,371 |
1,240 |
1,069 |
0,964 |
0,894 |
|
|
1,976 |
1,625 |
1,436 |
1,316 |
1,117 |
1,051 |
0,955 |
0,891 |
|
|
|
0,639 |
0,519 |
0,451 |
0,408 |
0,378 |
0,329 |
0,299 |
0,278 |
|
|
|
0,694 |
0,508 |
0,425 |
0,375 |
0,345 |
0,296 |
0,266 |
0,246 |
|
|
|
0,576 |
0,484 |
0,426 |
0,387 |
0,361 |
0,316 |
0,287 |
0,252 |
|
|
1,0 |
|
2,900 |
2,223 |
1,889 |
1,698 |
1,536 |
1,327 |
1,198 |
1,112 |
|
|
2,467 |
2,029 |
1,785 |
1,627 |
1,387 |
1,306 |
1,189 |
1,110 |
|
|
|
0,808 |
0,683 |
0,601 |
0,569 |
0,509 |
0,451 |
0,411 |
0,384 |
|
|
|
1,151 |
0,866 |
0,730 |
0,647 |
0,594 |
0,511 |
0,462 |
0,428 |
|
|
|
0,662 |
0,524 |
0,448 |
0,402 |
0,369 |
0,323 |
0,292 |
0,267 |
|
|
1,5 |
|
3,366 |
2,996 |
2,527 |
2,248 |
2,036 |
1,762 |
1,592 |
1,179 |
|
|
3,353 |
2,733 |
2,385 |
2,256 |
1,841 |
1,735 |
1,881 |
1,477 |
|
|
|
0,967 |
0,790 |
0,689 |
0,624 |
0,572 |
0,502 |
0,457 |
0,427 |
|
|
|
3,326 |
2,467 |
2,118 |
1,864 |
1,691 |
1,467 |
1,327 |
1,234 |
|
|
|
0,760 |
0,646 |
0,584 |
0,526 |
0,485 |
0,430 |
0,394 |
0,361 |
|
|
2,0 |
|
5,489 |
4,085 |
3,414 |
3,004 |
2,723 |
2,359 |
2,133 |
1,983 |
|
|
4,644 |
3,735 |
3,225 |
2,890 |
2,468 |
2,327 |
2,121 |
1,981 |
|
|
|
1,002 |
0,842 |
0,736 |
0,664 |
0,612 |
0,540 |
0,494 |
0,463 |
|
|
|
4,628 |
3,456 |
2,892 |
2,547 |
2,310 |
2.002 |
1,811 |
1,683 |
|
|
|
0,883 |
0,725 |
0,632 |
0,569 |
0,524 |
0,462 |
0,423 |
0,382 |
Применение в расчетах данных
табл. 31 позволяет вычислять
наибольшую гибкость элементов сечения (стенок и поясов) в зависимости от вида
напряженно-деформированного состояния и уровня напряжений. Применение такой
методики целесообразно, когда внешние нагрузки меньше предельных для всего
стержня, так как в этом случае расчет по формулам СНиП II-23-81* приводит к излишним ужесточениям. Однако для
пользования данными табл. 31 необходимо выполнить расчет всего стержня для
определения деформаций в наиболее опасном сечении с учетом требований СНиП II-23-81*.
СТЕНКИ И ПОЯСНЫЕ ЛИСТЫ ЦЕНТРАЛЬНО-, ВНЕЦЕНТРЕННО-СЖАТЫХ,
СЖАТО-ИЗГИБАЕМЫХ И ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ
7.6 (7.1; 7.2*). Проверка устойчивости стенок и поясных листов изгибаемых и сжатых
элементов выполняется на основе теории устойчивости прямоугольных пластинок,
работающих в упругой стадии или за пределом упругости и имеющих соответствующие
граничные условия. Остаточные напряжения, закритическая стадия работы и
начальные несовершенства пластинок, за исключением стенок тонкостенных балок,
учтены косвенным путем — корректировкой результатов, полученных без учета этих
факторов.
Стенки балок, в которых
действуют все компоненты напряженного состояния (s, t и sloc), рассчитываются в
предположении упругой работы материала. В стенках балок, в которых отсутствуют
местные напряжения (sloc = 0), допускается учет
развития пластических деформаций при выполнении условий, указанных в п. 7.5 СНиП II-23-81*.
7.7 (7.3). Установленные ограничения условной гибкости стенок приведены для
балок, работающих в пределах упругих деформаций. При этом наиболее опасным
напряженным состоянием для устойчивости стенки является чистый сдвиг, когда
касательные напряжения в стенке равны Rs. Принимая в этом случае в
формуле (76) СНиП II-23-81* tcr = Rs m = 2 (усредненное значение), получим = 3,5. Для сечений
балок, находящихся под действием изгиба, эти ограничения могут быть несколько
увеличены в соответствии с формулой (75) СНиП II-23-81* при scr = Ry.
Для балок с односторонними
поясными швами указанное значение снижено на 10 % в
связи с уменьшением степени защемления стенки балки в поясах.
7.8 (7.4*; 7.6*-7.9). При одновременном действии в сечении балок,
работающих в упругой области, нормальных s,
касательных t и местных sloc напряжений проверка устойчивости стенок выполняется на основе
зависимости для предельных поверхностей взаимодействия между указанными
напряжениями, принципы построения которых приведены в [23]. Для практических
расчетов эти зависимости представлены в СНиП II-23-81* в виде формул (74), (79), (82) и (87).
Устойчивость стенок балок
проверяется с учетом их частичного защемления в поясах, степень которого при
упругой работе балки зависит от соотношения жесткостей пояса и стенки. Эффект
защемления стенки поперечными ребрами жесткости не учитывается, и в местах их
постановки принимается шарнирное опирание кромок.
Формула (75) СНиП II-23-81* дает минимальное значение
критических напряжений при чистом изгибе стенки, которые соответствуют
отношению длины отсека к его высоте a/hef = 0,667. Если отношение a/hef не кратно 0,667, то
критические напряжения будут выше. Коэффициент, учитывающий упругое защемление
стенки в поясах, изменяется в пределах от 1,39 при d =
0,8 до 1,65 при d = 30, где d — определяется по формуле (77) СНиП II-23-81*. Эти значения подтверждаются результатами,
приведенными в [22].
Значение критических
касательных напряжений зависит от отношения сторон расчетного отсека, гибкости
стенки и условия закрепления ее продольных сторон. Влияние этих параметров для
упругой пластинки подробно рассмотрено в [22], где получены значения коэффициента,
характеризующего влияние упругого защемления продольных сторон пластинки.
Формула (76) СНиП II-23-81* дает значения
критических касательных напряжений с некоторым запасом, который соответствует
минимальным значениям коэффициента d, характеризующего
соотношение жесткостей пояса и стенки.
7.9 (7.6*). Значения критического локального напряжения sloc,cr, вычисляемые по формуле
(80) с учетом данных табл. 23 СНиП
II-23-81*,
принимаются независимыми от длины распределения давления колеса крана lef.
Изменение lef влияет на величину
коэффициента r = (3,4/c)(lef/hef), где с =
3,25 — для сварных балок; с = 4,5 — для балок на высокопрочных болтах.
Табл. 23 СНиП II-23-81* получена для постоянного
значения р = 0,38. Более точно
значение sloc,cr c учетом длины распределения
давления колеса допускается определять по формуле
, (54)
где ;
значения aij, приведены в табл. 32.
Таблица 32
|
i |
Значения aij при j, равном |
||
|
1 |
2 |
3 |
|
|
0 |
—0,815 |
4,577 |
—1,02 |
|
1 |
9,467 |
—25,50 |
16,93 |
|
2 |
1,011 |
22,84 |
—19,70 |
Значения Х при вычисляются по
формуле
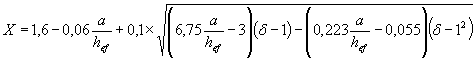
При d > (7a/hef + 0,5) значения X принимаются постоянными,
равными значению Х, вычисленному при d = 7a/hef + 0,5. При 0 £ d £ 1 значения Х вычисляются линейной интерполяцией
между значениями Х = 1 и Х = 1,6 — 0,067a/hef.
Пример. Расчет sloc,cr по предлагаемой методике и СНиП II-23-81*.
Исходные данные: а = 150 см, hef = 156 см, tf = 2 см, t = 1,4 см, bf = 60 см, I1f = 1587 см*.
Вычисляем
необходимые параметры:
см; a/hef = 0,962;
.
Из табл. 23 СНиП II-23-81* находим с1
= 19,7; .
По формуле (55) вычисляем Х = 1,74; .
Вычисляем коэффициенты,
входящие в формулу (54):
ао = —0,815 + 4,577 × 0,962 — 1,02 × 0,9622 = 2,644;
а1 = 9,467 — 25,5 × 0,962 + 16,93 × 0,962 = -0,606;
а2 = 1,011 + 22,84 × 0,962 — 19,70 × 0,962 = 4,753.
Тогда .
Применение формул (54) и (55) дает возможность учитывать изменение параметра r и приводит к увеличению sloc,cr.
7.10 (7.5). При расчете стенок балок, работающих за пределом упругости,
распределение напряжений в стенке вычисляется с применением зависимостей теории
пластичности. Величина напряжения на кромках не является основной
характеристикой их взаимодействия как в упругой области, поэтому в дальнейших
расчетах при проверке устойчивости стенки используется величина изгибающего
момента, а не краевого напряжения.
Подробный
анализ расчета устойчивости стенок и поясов изгибаемых элементов, работающих за
пределом упругости, приведен в разд. 5.
7.11.
Размеры стенок и поясов центрально-сжатых элементов установлены из условия
равноустойчивости стержня и элементов его сечения. Предельное состояние стержня
и деформации в расчетном сечении определены с учетом случайных эксцентриситетов
внешней нагрузки и начальных несовершенств стержня. Случайные эксцентриситеты
принимались относительно оси, перпендикулярной поясам сечения (рис. 17).
Рис.
17. К расчету на устойчивость стенки сжатого стержня
а — схема стержня; б — схема сечения и эпюры деформаций
При вычислении критической
гибкости стенки в расчетные формулы необходимо подставлять значение гибкости
стержня l, которое использовалось при
проверке общей устойчивости стержня. В сквозных стержнях устойчивость стенки
каждой ветви проверяется на устойчивость в пределах участка между узлами
решетки с учетом расчетного значения гибкости ветви на этом участке.
7.12 (7.14*). Формулы табл. 27* СНиП II-23-81* получены из расчета
устойчивости пластинки, которая является стенкой центрально-сжатого стержня и
работает по схеме (см. рис. 17). При этом учитывается частичное защемление
стенки в поясах, которое зависит от уровня сжимающих деформаций и от
соотношения жесткостей стенки и поясов в упругой области. В [23] показано, что
увеличение площади поясов несколько улучшает условия работы стенки, однако это
влияние незначительно и в СНиП II-23-81* не учитывается.
Для стержней швеллерного и
коробчатого сечений при одинаковой гибкости стержня необходимы более толстые
стенки, чем для двутавра. Это объясняется тем, что в стенках таких стержней
возникают значительно большие деформации сжатия, чем в стенке двутавра (рис.
18), а эффект защемления стенки в полках таких сечений практически отсутствует.
Рис.
18. Эпюры деформаций сжатых стержней
а —
трубчатое сечение; б — швеллер; в — тавр
Анализ зарубежных норм и
исследований работы стержней с гибкой стенкой показывает, что нижний предел
критической гибкости стенки двутавра можно повысить до , так как условия работы стенки благоприятнее, чем пластинки,
шарнирно опертой по контуру, которая принята в качестве расчетной в СНиП II-23-81*. В то же время необходимо
снизить верхнюю границу критической гибкости стенки, принятую в СНиП II-23-81* равной, так как в таких пластинках могут быть значительные
несовершенства, а также усиливается отрицательное влияние на устойчивость
остаточных напряжений. Целесообразно объединить трубчатые прямоугольное и
квадратное сечения, так как нет принципиальной разницы в работе их стенок при
центральном сжатии.
Условие устойчивости стенок
центрально- и внецентренно-сжатых стержней может быть представлено неравенством
, (56)
где ;
— предельные (наибольшие)
значения гибкости устойчивой стенки, приведенные в табл. 33.
Значения
, являются функцией расчетной гибкости стержня и зависят от
уровня напряжений в сечении стержня. При их возрастании уровень напряжений в
стержне снижается, что позволяет принимать большие значения . Если условие (56) не выполняется, то стенка неустойчива и в
расчет вводится часть ее высоты hred, которая вычисляется в соответствии с требованиями п.7.20* СНиП II-23-81*.
Таблица
33
|
Относительный |
Сечение элемента |
Значения |
Формулы для |
|
m = 0 |
Двутавровое |
|
но не более 2,3 |
|
Коробчатое, швеллерное прокатное |
|
но не более 1,6 |
|
|
Швеллерное, кроме прокатного |
|
но не более 1,6 |
|
|
m ³ |
Двутавровое, коробчатое |
|
но не более 3,1 |
Обозначения, принятые в табл. 33:
— условная
гибкость элемента, принимаемая в расчете на устойчивость при центральном
сжатии;
— условная гибкость элемента,
принимаемая в расчете на устойчивость в плоскости действия момента.
Примечания: 1. К коробчатым относятся
замкнутые прямоугольные профили (составные, гнутые прямоугольные и квадратные).
2. В
коробчатом сечении при m > 0 значение определяется для
стенки, параллельной плоскости изгибающего момента.
3. При
значениях 0 < m < 1,0 значите для двутаврового и
коробчатого сечений следует определять линейной интерполяцией между значениями,
вычисленными при m = 0 и m = 1,0.
7.13 (7.14*). Стенки внецентренно-сжатых стержней работают в условиях сжатия с
изгибом и их гибкость определяется видом напряженно-деформированного состояния
в зависимости от значений изгибающего момента и продольной силы в предельном
состоянии стержня (см. рис. 16).
Независимость гибкости стенки таких стержней от
значения относительного эксцентриситета m (формулы табл. 33)
объясняется тем, что возрастание m приводит
к увеличению максимальных деформаций на кромке стенки, однако при этом
возрастает неравномерность их распределения по высоте (рис. 19). Увеличение приводит к уменьшению
, а возрастание градиента деформаций — к ее увеличению.
Взаимное влияние этих факторов, зависящих от значений m, и Аf/Aw, приводит к тому, что
гибкость стенки практически не
изменяется с возрастанием m. На рис. 19 показано
изменение деформаций для двутаврового сечения при Аf/Aw = 0,5, 1 = 1,5 в зависимости от возрастания m от 0,1 до 10, при этом
значение изменяется в
незначительных пределах от 1,77 до 1,86.
Рис. 19. Эпюры
деформаций в стенке двутаврового сечения при возрастании эксцентриситета
При т < следует определять
линейной интерполяцией между значениями, вычисленными по формулам табл. 33 для центрально-сжатого и
внецентренно-сжатого стержня при т =
1 и =
х.
7.14 (7.16*). Расчет устойчивости стенки при сжатии с изгибом по формуле (90) СНиП II-23-81* выполняется в том случае,
если стержень теряет общую устойчивость по изгибно-крутильной форме в пределах
упругих деформаций. Эта формула получена на основании результатов [23], где
рассматривалась устойчивость изолированной упругой пластинки при совместном
действии изгиба, сжатия и сдвига. При этом не учитывались дополнительные
нормальные напряжения, возникающие при деформировании элемента.
Расчет устойчивости стенки
при 0,5 < a < 1 является
приближенным, позволяющим определять hef/t с некоторым запасом, так
как формулы п. 7.12 предполагают наличие
пластических деформаций в сечении.
7.15 (7.17*). Снижение гибкости стенки для других форм поперечного сечения учитывает
уменьшение упругого защемления стенки поясами в этих сечениях.
7.16 (7.18*). Определение размеров элементов таврового сечения выполнено на
основании результатов решения задачи, учитывающей совместную работу стержня и
пластинок, образующих сечение. При вычислении критической гибкости стенки тавра
hef/t принято предположение, что
эксцентриситет e направлен в сторону
свободной кромки (см. рис. 18).
Стенка тавра рассматривалась как пластинка, имеющая свободный край и частичное
защемление другой продольной стороны. Принятая схема загружения является
наиболее невыгодной для устойчивости стенки тавра. Полученные результаты без
учета защемления кромки применимы для определения размеров свесов равнобоких
уголков, которые теряют устойчивость по изгибно-крутильной форме, что приводит
к некоторому запасу устойчивости, так как деформации в наиболее напряженной
полке уголка меньше, чем в стенке тавра.
7.17.
При проектировании центрально- и внецентренно-сжатых стержней расчет стенок
допускается выполнять таким образом, что при действии расчетной нагрузки они либо
сохраняют устойчивое состояние, либо частично выпучиваются.
Частичное выпучивание стенки
не означает полное исчерпание несущей способности стержня. В этом случае при
определении несущей способности стержня в поперечное сечение (рис. 20)
включается так называемая редуцированная высота стенки hred [21].
Рис. 20. Расчетные
сечения стержней с гибкими стенками
В зависимости от состояния
стенки (устойчивое или неустойчивое) проверка выполняется в два этапа. На
первом этапе, который необходимо выполнять во всех случаях, действительная
гибкость стенки сравнивается с
наибольшим допустимым значением , которое соответствует критическому состоянию и вычисляется
по табл. 33.
Если <
, стенка устойчива и проверка на этом заканчивается. Если
>
, необходимо определить несущую способность стержня с учетом
редуцированной высоты стенки, когда расчетная площадь сечения меньше
геометрической.
При проектировании сжатых
стержней с гибкими стенками необходимо, чтобы редуцированная высота hred составляла не менее
половины полной высоты (hred ³ 0,5hef). В противном случае в связи с уменьшением расчетной площади сечения
несущая способность стержней может снижаться на 25 % и более, что экономически
нецелесообразно.
7.18 (7.20*). Расчетные формулы табл. 33
определяют критическую гибкость устойчивых стенок, т.е. без учета закритической
стадии работы. Если >
, расчет выполняется в соответствии с требованиями п. 7.20* СНиП II-23-81*. Когда фактическое
значение hef/t превышает значение, определяемое по п. 7.14* (для центрально-сжатых
элементов не более чем в два раза), в расчетных формулах за значение А следует принимать значение Ared, вычисленное с высотой
стенки hred (в коробчатом сечении
определяются hred и hred1, см. черт. 20, для пластинок, образующих сечение и
расположенных соответственно параллельно и перпендикулярно плоскости изгиба):
для двутаврового и
швеллерного сечения Ared = А — (hef — hred)t;
для коробчатого сечения:
при центральном сжатии Ared = А — 2(hef — hred)t — 2(hef1 — hred1)t1;
при внецентренном сжатии и
сжатии с изгибом Ared = А — 2(hef — hred)t.
Значения hred следует определять:
для центрально-сжатых
элементов двутаврового и коробчатого сечения
, (57)
для швеллерного сечения ,
где — условная гибкость стенки соответствующего сечения по табл. 33 при т = 0;
— условная гибкость стенки, при
вычислении hred1 принимаемая равной
;
k — коэффициент, принимаемый
равным для двутаврового сечения k = 1,2 + 0,15 (при
> 3,5 следует
принимать = 3,5) и для
коробчатого сечения k = 2,9 + 0,2 — 0,7
(при
> 2,3 следует
принимать = 2,3); здесь
— условная гибкость
элемента, принятая в табл. 33;
для внецентренно-сжатых и
сжато-изгибаемых элементов по формуле (57),
где значение следуют вычислять по табл. 33, а значение k при
=
1.
Проверка общей устойчивости
стержня с редуцированной стенкой выполняется по формулам СНиП II-23-81*, в которых вместо площади сечения А подставляется редуцированная площадь Ared = k1А. Коэффициент k1 учитывает уменьшение площади сечения при
редуцировании стенки; его значения приведены в табл. 34-39.
Применение данных таблиц позволяет выполнить расчет центрально-сжатых стержней
двутаврового сечения без вычисления редуцированной высоты стенки по формуле (57).
Для внецентренно-сжатых
стержней редуцированная высота стенки является функцией гибкости стержня,
относительного эксцентриситета, соотношения площадей элементов сечения, а также
степени развития пластических деформаций, которые влияют на степень защемления
стенки в поясах. Если гибкость стенки превышает критическое значение, то
редуцированная высота стенки определяется из формулы (57). При этом , определяется в соответствии с табл. 33, а в коробчатом сечении редуцируются обе
стенки, параллельные плоскости действия момента.
Если при центральном сжатии
и при т = 1 стенка коробчатого
сечения неустойчива, то расчетная площадь Ared при т
< 1 вычисляется линейной интерполяцией между значениями, полученными при
центральном сжатии (редуцируются четыре стенки) и т = 1 (редуцируются две стенки в плоскости действия момента); при
этом должна быть обеспечена устойчивость поясов внецентренно-сжатого стержня в
соответствии с требованиями п. 7.26* СНиП II-23-81*.
Пример. Проверить устойчивость стенки двутаврового стержня гибкостью = 1 и определить его
несущую способность.
Размеры сечения: стенка 800´12 мм, пояса 400´20 мм, материал ВСт3кп2-1
(ТУ 14-1-3023-80), Ry = 210 МПа (2150 кгс/см2).
По формулам табл. 33 вычисляем
;
Таблица
34
|
|
Значения k1 при Af/Aw = 0,25 и |
|||||||||
|
0 |
0,8 |
1,0 |
1,2 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
|
|
1,3 |
1,00 |
Зона устойчивой |
||||||||
|
1,5 |
0,904 |
0,950 |
0,998 |
|||||||
|
2,0 |
0,748 |
0,783 |
0,804 |
0,816 |
0,833 |
0,891 |
0,957 |
0,983 |
0,983 |
0,983 |
|
2,5 |
0,655 |
0,690 |
0,701 |
0,701 |
0,727 |
0,763 |
0,788 |
0,832 |
0,836 |
0,836 |
|
3,0 |
0,652 |
0,678 |
0,714 |
0,732 |
0,737 |
0,737 |
||||
|
3,5 |
|
0,616 |
0,646 |
0,661 |
0,661 |
|||||
|
4,0 |
0,602 |
0,631 |
0,646 |
0,646 |
||||||
|
4,6 |
0,583 |
0,583 |
Таблица
35
|
|
Значения k1 при Af/Aw = 0,5 и |
|||||||||
|
0 |
0,8 |
1,0 |
1,2 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
|
|
1,3 |
1,00 |
Зона устойчивой |
||||||||
|
1,5 |
0,928 |
0,963 |
0,982 |
|||||||
|
2,0 |
0,812 |
0,841 |
0,853 |
0,868 |
0,898 |
0,970 |
||||
|
2,5 |
0,742 |
0,767 |
0,775 |
0,785 |
0,805 |
0,855 |
0,932 |
0,949 |
0,950 |
0,950 |
|
3,0 |
0,730 |
0,743 |
0,778 |
0,835 |
0,850 |
0,853 |
0,853 |
|||
|
3,5 |
0,723 |
0,766 |
0,780 |
0,784 |
0,784 |
|||||
|
4,0 |
|
0,714 |
0,728 |
0,732 |
0,732 |
|||||
|
4,6 |
0,679 |
0,685 |
0,685 |
Таблица
36
|
|
Значения k1 при Af/Aw = 0,75 и |
|||||||||
|
0 |
0,8 |
1,0 |
1,2 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
|
|
1,3 |
1,00 |
Зона устойчивой |
||||||||
|
1,5 |
0,943 |
0,971 |
0,986 |
|||||||
|
2,0 |
0,849 |
0,873 |
0,882 |
0,894 |
0,921 |
0,976 |
||||
|
2,5 |
0,793 |
0,814 |
0,820 |
0,828 |
0,844 |
0,884 |
0,945 |
0,959 |
0,960 |
0,959 |
|
3,0 |
0,784 |
0,795 |
0,822 |
0,868 |
0,880 |
0,882 |
0,882 |
|||
|
3,5 |
0,778 |
0,813 |
0,824 |
0,827 |
0,827 |
|||||
|
4,0 |
|
0,771 |
0,782 |
0,786 |
0,786 |
|||||
|
4,6 |
0,744 |
0,748 |
0,748 |
Таблица
37
|
|
Значения k1 при Af/Aw = 1,0 и |
|||||||||
|
0 |
0,8 |
1,0 |
10 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
|
|
1,3 |
1,00 |
Зона устойчивой |
||||||||
|
1,5 |
0,952 |
0,976 |
0,988 |
|||||||
|
2,0 |
0,874 |
0,893 |
0,902 |
0,912 |
0,932 |
0,980 |
||||
|
2,5 |
0,828 |
0,845 |
0,850 |
0,857 |
0,870 |
0,903 |
0,954 |
0,966 |
0,966 |
0,966 |
|
3,0 |
0,820 |
0,829 |
0,852 |
0,890 |
0,900 |
0,901 |
0,902 |
|||
|
3,5 |
0,815 |
0,844 |
0,853 |
0,856 |
0,856 |
|||||
|
4,0 |
|
0,809 |
0,818 |
0,821 |
0,821 |
|||||
|
4,6 |
0,786 |
0,790 |
0,790 |
Таблица
38
|
|
Значения k1 при Af/Aw = 1,5 и |
|||||||||
|
0 |
0,8 |
1,0 |
1,2 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
|
|
1,3 |
1,00 |
Зона устойчивой |
||||||||
|
1,5 |
0,964 |
0,982 |
0,991 |
|||||||
|
2,0 |
0,906 |
0,920 |
0,926 |
0,934 |
0,949 |
0,985 |
||||
|
2,5 |
0,871 |
0,884 |
0,898 |
0,893 |
0,903 |
0,927 |
0,966 |
0,974 |
0,975 |
0,975 |
|
3,0 |
0,863 |
0,872 |
0,889 |
0,845 |
0,925 |
0,926 |
0,927 |
|||
|
3,5 |
0,862 |
0,883 |
0,890 |
0,891 |
0,892 |
|||||
|
4,0 |
|
0,857 |
0,863 |
0,866 |
0,866 |
|||||
|
4,6 |
0,839 |
0,842 |
0,842 |
Таблица
39
|
|
Значения k1 при Af/Aw = 2,0 и |
|||||||||
|
0 |
0,8 |
1,0 |
1,2 |
1,5 |
2,0 |
2,5 |
3,0 |
4,0 |
5,0 |
|
|
1,3 |
1,00 |
Зона устойчивой |
||||||||
|
1,5 |
0,971 |
0,985 |
0,993 |
|||||||
|
2,0 |
0,925 |
0,936 |
0,941 |
0,947 |
0,959 |
0,988 |
||||
|
2,5 |
0,897 |
0,907 |
0,910 |
0,914 |
0,922 |
0,942 |
0,973 |
0,979 |
0,980 |
0,980 |
|
3,0 |
0,892 |
0,897 |
0,911 |
0,934 |
0,940 |
0,941 |
0,980 |
|||
|
3,5 |
0,889 |
0,906 |
0,912 |
0,913 |
0,913 |
|||||
|
4,0 |
|
0,886 |
0,891 |
0,893 |
0,893 |
|||||
|
4,6 |
0,872 |
0,874 |
0,874 |
Так как , то необходимо вычислить редуцированную высоту стенки по
формуле (57):
В соответствии с данными п.
7.20* СНиП II-23-81* вычисляем редуцированную
площадь Ared:
Ared = A —(hef — hred)t = 256 — (80 — 53,28)´1,2 = 223,7 см2.
Несущая способность стержня N равна:
N = jA1Rуgc = 0,933 ×
223,7Rуgc = 209 Rуgc;
При применении данных табл. 34-39 вычисления упрощаются, так как, получив условие , интерполяцией данных табл. 36, 37
находим для Af/Aw = 0,83 k1 = 0,874 и определяем
несущую способность стержня N.
N = k1jARygc = 0,874 × 256 × 0,9337Rygc = 209Rygc.
8. РАСЧЕТ ЛИСТОВЫХ КОНСТРУКЦИЙ РАСЧЕТ НА УСТОЙЧИВОСТЬ
РАСЧЕТ НА УСТОЙЧИВОСТЬ
8.1 (8.5). Известная в [21] формула для критического напряжения упругой круговой
цилиндрической оболочки при осевом сжатии
scr = 0,605Et/r, (58)
полученная на основе линейной теории, дает
завышенные значения scr по сравнению с экспериментальными данными. Это
объясняется большой чувствительностью таких оболочек к начальным
несовершенствам и остаточным (сварочным) напряжениям.
Поскольку амплитуда и форма
начальных искривлений являются случайными величинами (функциями), практический
расчет упругих тонких оболочек базируется на результатах экспериментальных
исследований. В этом случае критическое напряжение определяется по формуле
(58), в которую вместо 0,605 вводится коэффициент с, являющийся убывающей функцией параметра r/t (табл. 31 СНиП II-23-81*).
8.2 (8.5). В строительных конструкциях часто применяются оболочки, напряжения в
которых близки к расчетному сопротивлению. Такие оболочки рассчитываются с
учетом влияния начальных несовершенств и развития пластических деформаций. Как
показали исследования, невыгоднейшей формой начального искривления является
осесимметричная форма, подобная первой собственной функции идеальной оболочки.
В работе1 учет
осесимметричного начального искривления и развития пластических деформаций
сведен к расчету за пределом упругости внецентренно-сжатого стержня, лежащего
на упругом основании. При этом показано, что для оболочек малой и средней
гибкости учет неупругой работы материала оказывает существенное влияние на
предельную нагрузку при потере устойчивости. С использованием некоторых
допущений получена расчетная формула (100) в СНиП II-23-81* для практических расчетов оболочек при достаточно
малых значениях r/t.
В случае комбинации осевого
сжатия круговой цилиндрической оболочки с внутренним равномерным давлением
критическое значение осевых напряжений повышается. Для практических расчетов
можно пользоваться рекомендациями Фына и Зехлера2, применимыми к
оболочкам, теряющим устойчивость в пределах упругости. Осевое критическое
напряжение scr определяется по формуле
scr = scr1 +0,19 , (59)
но принимается не более чем scr1 + 0,23Et/r,
где scr1 = cEt/r — осевое критическое
напряжение при отсутствии внутреннего давления;
= qr/t — окружное напряжение от внутреннего давления.
Формулой (59) можно
пользоваться при комбинации внецентренного сжатия с внутренним давлением. В
этом случае под scr1 понимается соответствующее
значение, принимаемое согласно п. 8.5 СНиП II-23-81*. Следует подчеркнуть, что указанный способ применим
лишь в пределах упругости, т.е. при scr £ 0,8Rу.
___________
1
Броуде Б. М. Особенности расчета на
устойчивость металлических оболочек // Строит, механика и расчет сооружений. —
1977.-№ 4.- С. 35.
2 Броуде Б. М. Практические методы
расчета на устойчивость тонких оболочек. — В кн.: Исследования по стальным
конструкциям. Вып. 13. — М.: Госстройиздат. — 1962.- С. 57, 58.
8.3 (8.6). Формула (101) СНиП II-23-81* относится к
случаю, когда на сжатый или сжато-изгибаемый трубчатый стержень действует расчетная
нагрузка, определяемая в соответствии с требованиями разд. 5 СНиП II-23-81*. Если проверка по этим требованиям дает запас
несущей способности, превышающий 20 %, то ограничение по формуле (101) СНиП II-23-81* можно снять и оболочку в
этом случае необходимо рассчитывать на устойчивость при сжатии с изгибом
согласно требованиям п. 8.5 СНиП
II-23-81*, а расчетное
напряжение s1 определять по формуле
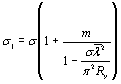
где s = N/A — расчетное осевое напряжение;
т = 2e/r — относительный
эксцентриситет [е = M/N; М — расчетный момент; в случае осевого сжатия значение е следует принимать по формуле (19)];
— условная гибкость трубчатого
сечения ().
8.4 (8.8). Требование проверки устойчивости кольцевых ребер в своей плоскости как
сжатых стержней и получаемые при этом их размеры исходят из того, что ребра
являются жесткими элементами, обеспечивающими образование узловой линии по
окружности оболочки.
В ряде случаев
рассматриваемые конструкции могут рассчитываться как оболочки, подкрепленные
гибкими шпангоутами [21], при этом указанные требования для кольцевых ребер
жесткости могут быть несколько смягчены.
9. РАСЧЕТ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ НА ВЫНОСЛИВОСТЬ
9.1 (9.1). Выносливость стальных конструкций зависит от ряда факторов. Главными
из них являются:
величина максимального
напряжения в рассчитываемом элементе smax (или амплитуда напряжений sа);
концентрация напряжений,
зависящая от конструкции элемента и типа соединений (группа элементов);
характер циклической
нагрузки (стационарная, нестационарная);
число циклов нагружений за
период эксплуатации конструкций;
температура эксплуатации конструкции и т.п.
9.2 (9.2*). Методика расчета на выносливость СНиП II-23-81* исходит из того, что явления усталости в элементе
возникают под воздействием максимальных напряжений smax. Существует и другой подход, согласно которому
основное влияние на усталостное разрушение оказывает амплитуда напряжений цикла
sа = (smax — smin)/2. Поскольку обе методики опираются на одни и те
же экспериментальные данные и являются их аппроксимацией, конечные результаты,
получаемые при их использовании, мало отличаются друг от друга.
9.3 (9.2*). Применение сталей повышенной и высокой прочности в конструкциях,
подверженных циклическим воздействиям, является оправданным только при
отсутствии в них существенных концентраторов напряжений (1- и 2-я группы
элементов табл. 83* СНиП II-23-81*). В остальных
случаях (3 — 8-я группы элементов табл. 83*СНиП II-23-81*) применение сталей с повышенными прочностными
показателями к повышению выносливости не ведет и потому их применение должно
иметь соответствующее инженерное и экономическое обоснование.
9.4 (9.2*). Подавляющее большинство строительных конструкций, работающих на
переменные воздействия, находится в условиях изменчивости напряжений во времени
(амплитуда напряжений во времени не является постоянной), т.е. режим нагрузок
(и напряжений) не является стационарным.
Учет нестационарности
нагрузок позволяет на 10-20 % повысить расчетную выносливость [правая часть
формулы (115) СНиП II-23-81*] для всех групп
элементов [влияние нестационарности приближенно учтено при назначении числовых
коэффициентов в формулах (116) и (117) СНиП II-23-81*].
9.5.
Эксплуатация конструкций при температуре до минус 40° С не снижает выносливости стальных
конструкций.
При более низких
температурах эксплуатации требуются специальные мероприятия по повышению
выносливости конструкций: применение сталей, удовлетворяющих требованиям по
ударной вязкости; исключение соединений с наиболее острыми концентраторами
напряжений (7 и 8-й групп элементов); применение технологических мероприятий по
повышению выносливости сварных соединений (механическая обработка швов,
сплавление их в струе аргона и т.п.).
РАСЧЕТ НА МАЛОЦИКЛОВУЮ ПРОЧНОСТЬ
9.6 (9.3). Расчет металлических конструкций на малоцикловую прочность ведется на
переменные усилия при наличии спектра эксплуатационных нагрузок и
распространяется на металлические конструкции, эксплуатирующиеся при пониженных
(до минус 40 °С), нормальных и повышенных
(до 250 °С) температурах.
9.7 (9.3). Срок эксплуатации металлических конструкций и спектр действующих
эксплуатационных нагрузок должны быть заданы при их проектировании. Примеры
спектра переменных нагрузок приведены в табл. 40 (газгольдеры аэродинамических
труб) при коэффициенте асимметрии = 0.
Таблица
40
|
Дамские, % от |
Число нагружений |
Частота нагружений, % |
|
100 |
2 |
0,01 |
|
85 |
21 |
0,1 |
|
70 |
299 |
1,5 |
|
54 |
881 |
4,4 |
|
37 |
897 |
4,5 |
|
28 |
17930 |
89,5 |
|
Итого: |
N = 2×104 |
100,0 |
Для воздухонагревателей
доменных печей цикл изменения внутреннего давления от 0 до остается постоянным и
за 20 лет эксплуатации составляет 5×104.
Магистральные газо- и
нефтепроводы за 20 лет эксплуатации испытывают 7×103 циклов с
изменением давления от 0 до .
9.8 (93). Проверка малоцикловой прочности основного металла элементов или
соединений на сварке, болтах или штырях для 5×105 циклов
производится по формуле
, (61)
где Nb = 5×105 — базовое число циклов нагружения при
расчете на малоцикловую прочность;
N —
малоцикловая долговечность элемента металлической конструкции (при N = Nb, данный расчет и расчет на выносливость по СНиП II-23-81* совпадают);
т, то — параметры,
характеризующие угол наклона кривой малоцикловой усталости; т = тос;
то — принимается по табл.
41;
с —
коэффициент, принимаемый по табл. 42.
Таблица
41
|
Нормативное временное |
До 390 |
Св. 390 (4000) |
Св. 450 (4600) |
Св. 490 (5000) |
Св. 540 (5500) |
Св. 590 |
|
(4000) |
до 450 (4600) |
до 490 (5000) |
до 540 (5500) |
до 590 (6000) |
(6000) |
|
|
Параметр то |
0,16 |
0,18 |
0,20 |
0,22 |
0,24 |
0,26 |
Таблица
42
|
Группа элементов по СНиП II-23-81* |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Коэффициент с |
1,0 |
0,90 |
0,80 |
0,75 |
0,72 |
0,68 |
0,65 |
0,62 |
Остальные обозначения
принимаются по п. 9.2* СНиП II-23-81*.
При N = Nb = 5×105 для 1- и 2-й
групп элементов a = 1,52, для 3-8-й групп
элементов a = 1,85.
При расчетах на малоцикловую
прочность по формуле (61) значение
произведения не должно превышать
.
Пример расчета. Необходимо рассчитать на малоцикловую прочность горизонтальный
газгольдер вместимостью 178 м3, наружным диаметром d = 3250 мм, длиной 23 м.
Газгольдер изготовлен из листовой стали Ст3 [sb = 450 МПа (4600 кгс/см2)]
толщиной стенки в цилиндрической части t = 16 мм, сферических днищ — 10 мм. Газгольдер нагружается пульсирующим
давлением до 11 ати с эксплуатационным числом циклов 4×104. Эксплуатация
газгольдера производится при нормальной температуре.
Для проверочного расчета
выбраны два вида сварного соединения:
первый вид — основной металл
над шпангоутом (7-я группа соединений по СНиП II-23-81*). При рабочем давлении 11 ати нормальное напряжение
в основном металле smax = 110 МПа (в направлении, перпендикулярном
шпангоуту).
По СНиП II-23-81* определяется сопротивление усталости Rnv при N = Nb = 5×105 циклов. Для
этого вычисляются коэффициенты a и:
;
;
Rv = 3,6 МПа (370 кгс/см2), табл. 32 СНиП II-23-81*.
Таким образом, при N = Nb = 5×105 циклов Rnv = Rv a = 36 × 1,85 × 1,67 = 111 МПа(1130 кгс/см2).
Далее определяется параметр т:
т = тос.
Параметр то для данной стали равен
0,18, а коэффициент с для 7-й группы
соединений соответствует 0,65, т.е. т
= тос = 0,117.
Определяется сопротивление
усталости при эксплуатационном числе циклов нагружений N = 4 × 104:
Следовательно,
сопротивляемость малоцикловому разрушению обеспечена: 110 < 149;
второй вид — кольцевой
сварной шов на сферической поверхности (5-я группа соединений). В
рассчитываемом элементе при внутреннем давлении, равном 11 ати, нормальные
напряжения smax =
110 МПа (1120 кгс/см2).
В этом случае Rv = 60 МПа (610 кгс/см2)
— табл. 32 СНиП II-23-81*.
Таким образом, при N = Nb = 5×105 циклов
параметр т = тос с учетом коэффициента с = 0,72 для 5-й группы соединений (см. табл. 42) будет равен 0,13.
Сопротивление усталости при
эксплуатационном числе циклов нагружений N
= 4 × 104 равно:
Сопротивляемость малоцикловому разрушению
обеспечена: 110 < 256.
10. РАСЧЕТ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ С УЧЕТОМ
ХРУПКОГО разрушения
10.1.
Основными факторами, влияющими на склонность стальных конструкций к хрупкому
разрушению, являются:
температура и характер ее
изменения в процессе эксплуатации;
концентрация напряжений,
зависящая от конструктивной формы элемента или узла;
толщина элементов, с
увеличением которой возрастает степень объемности напряженного состояния, а
также другие геометрические размеры узлов и конструкций в целом (масштабный
фактор, определяющий запас упругой энергии, накапливаемой в системе);
характер нагружения (наличие
ударных или циклических нагрузок, создающих условия дня постепенного и скрытого
накопления повреждений в металле);
уровень растягивающих
напряжений и степень неоднородности эпюры напряжений (например, изгиб,
внецентренное растяжение);
качество стали (степень
раскисления, размер зерна, количество вредных элементов: фосфор, сера, азот,
кислород, водород).
Ввиду значительного числа
факторов, способствующих переходу стали в хрупкое состояние, разрушение
конструкций имеет вероятностный характер. Поэтому основные мероприятия по
предупреждению хрупкого разрушения (рекомендации по выбору марок стали,
указания по конструированию) дополнены поверочным расчетом для ряда
конструктивных форм пониженной хладостойкости с целью снизить вероятность их
разрушения.
10.2.
В основу методики расчета на прочность с учетом хрупкого разрушения положены
данные о прочности конструктивных форм пониженной хладостойкости. Снижение
прочности в области климатических температур характеризуется коэффициентом b. Величина коэффициента b меняется в зависимости от толщины элемента в
расчетном сечении, уровня прочности стали и расчетной температуры района
строительства. Температура эксплуатации конструкций учитывается дополнительно в
соответствии с п. 2.1* СНиП II-23-81*.
10.3.
При расчете на прочность с учетом хрупкого разрушения максимальные
растягивающие напряжения, действующие в расчетном сечении по площади “нетто”,
принимаются без учета коэффициента динамичности, поскольку динамический характер
импульса, не учитываемого в расчетах, учтен принятой величиной коэффициента b, установленной в табл. 84 СНиП II-23-81*
10.4.
Расчет на прочность с учетом хрупкого разрушения не распространяется на конструкции,
содержащие дефекты, превышающие нормы [8].
11. РАСЧЕТ СОЕДИНЕНИЙ
СВАРНЫЕ СОЕДИНЕНИЯ
11.1.
Положения для расчета сварных соединений изложены в [9], в котором приведены:
обоснование назначения
расчетных сопротивлений;
обоснование необходимости
применения сварочных материалов, обеспечивающих высокую прочность металла шва;
таблицы расчетных сечений,
по которым производится проверка прочности соединений с угловыми швами в
зависимости от соотношения прочностных свойств металла шва и основного металла;
таблицы предельных усилий на
сварные соединения с угловыми швами;
данные для расчета тавровых
соединений с угловыми швами;
примеры расчета сварных
соединений.
БОЛТОВЫЕ СОЕДИНЕНИЯ
Болтовые соединения без контролируемого натяжения
11.2.
Для болтов класса прочности 10.9 и высокопрочных расчетные сопротивления срезу
и растяжению следует определять по тем же формулам табл. 5* СНиП II-23-81*, что и для болтов класса прочности 8.8.
Расчетные сопротивления
срезу Rbs и растяжению Rbt болтов класса прочности
10.9 и высокопрочных приведены в табл. 43.
Таблица
43
|
Напряженное состояние |
Условное обозначение |
Расчетное |
|
|
класса прочности 10.9 |
высокопрочных с Rbun = 1100 МПа (110 кгс/мм2) |
||
|
Срез |
Rbs |
400 (4000) |
440 (4400) |
|
Растяжение |
Rbt |
500 (5000) |
550 (5500) |
Предельные
усилия болтов на растяжение, срез и смятие элементов приведены в табл. 44.
11.3.
При расчете многоболтовых соединений без контролируемого натяжения по формулам
(127), (128) СНиП II-23-81* следует
учитывать коэффициенты условий работы соединений
gb = gb1gb2. (62)
При определении расчетного
усилия, которое может быть воспринято одним болтом многоболтового соединения
при расчете на срез и смятие, для болтов класса точности A gb1 = 1, для болтов классов точности В и С gb1 = 0,9. В расчете на смятие
соединяемых, элементов конструкций из стали с пределом текучести до 380 МПа
(3900 кгс/см2) при расстояниях: а
(вдоль усилия от края элемента до центра ближайшего отверстия), равном или
больше 2d, и b (между центрами отверстий),
равном или больше 2,5d (d — диаметр отверстия),
коэффициент gb2 = 1. При а
= 1,5d, а в многоболтовом
соединении при а = 1,5d и b = 2d gb2 = 0,85.
Таблица
44
|
Класс прочности болта |
Напряженное состояние |
Временное |
Предельное усилие, кН, |
||||||||
|
16 |
20 |
22 |
24 |
27 |
30 |
36 |
42 |
48 |
|||
|
5.6 |
Растяжение |
— |
33,0 |
51,4 |
— |
73,9 |
— |
— |
— |
— |
— |
|
Срез |
— |
34,4 |
53,7 |
— |
77,3 |
— |
— |
— |
— |
— |
|
|
5.8 |
Растяжение |
— |
31,4 |
49,0 |
— |
70,4 |
— |
— |
— |
— |
— |
|
Срез |
— |
36,2 |
56,5 |
— |
81,3 |
— |
— |
— |
— |
— |
|
|
8.8 |
Растяжение |
— |
62,8 |
98,0 |
— |
141 |
— |
— |
— |
— |
— |
|
Срез |
— |
57,9 |
90,4 |
— |
130 |
— |
— |
— |
— |
— |
|
|
10.9 |
Растяжение |
— |
78,5 |
122 |
151 |
176 |
— |
— |
— |
— |
— |
|
Срез |
— |
72,4 |
113 |
137 |
163 |
— |
— |
— |
— |
— |
|
|
110 (по ГОСТ |
Растяжение |
— |
— |
135 |
167 |
194 |
252 |
308 |
454 |
616 |
809 |
|
Срез |
— |
— |
124 |
150 |
179 |
226 |
280 |
402 |
548 |
717 |
|
|
110 (по ТУ |
Растяжение |
— |
— |
135 |
167 |
194 |
252 |
308 |
454 |
616 |
809 |
|
Срез |
— |
— |
97,0 |
117 |
141 |
180 |
224 |
321 |
441 |
582 |
|
|
Все классы |
Смятие с учетом gb = 0,9, |
345 (35) |
58,3 |
72,9 |
80,2 |
87,5 |
98,4 |
110 |
131 |
153 |
175 |
|
355 (36) |
60,5 |
75,6 |
83,2 |
90,7 |
102 |
113 |
136 |
159 |
181 |
||
|
365 (37) |
63,4 |
79,2 |
87,1 |
95,0 |
107 |
119 |
143 |
166 |
190 |
||
|
370 (38) |
64,8 |
81,0 |
89,1 |
97,2 |
109 |
122 |
146 |
170 |
194 |
||
|
380 (39) |
67,7 |
84,6 |
93,1 |
102 |
114 |
127 |
152 |
178 |
203 |
||
|
390 (40) |
69,8 |
87,3 |
96,0 |
105 |
118 |
131 |
157 |
183 |
210 |
||
|
400 (41) |
73,9 |
90,9 |
100 |
109 |
123 |
136 |
164 |
191 |
218 |
||
|
410 (42) |
75,6 |
94,5 |
104 |
113 |
128 |
142 |
170 |
198 |
227 |
||
|
420 (43) |
78,3 |
97,9 |
108 |
118 |
132 |
147 |
176 |
206 |
235 |
||
|
430 (44) |
81,4 |
102 |
112 |
122 |
137 |
153 |
183 |
214 |
244 |
||
|
440 (45) |
84,4 |
105 |
116 |
127 |
142 |
158 |
190 |
222 |
253 |
||
|
450 (46) |
87,3 |
109 |
120 |
131 |
147 |
164 |
196 |
229 |
262 |
||
|
460 (47) |
90,2 |
113 |
124 |
135 |
152 |
169 |
203 |
237 |
271 |
||
|
470 (48) |
93,4 |
117 |
129 |
140 |
158 |
175 |
210 |
245 |
280 |
||
|
480 (49) |
96,5 |
121 |
133 |
145 |
163 |
181 |
214 |
253 |
289 |
||
|
490 (50) |
99,5 |
124 |
137 |
149 |
168 |
187 |
224 |
261 |
295 |
||
|
500 (51) |
103 |
127 |
142 |
154 |
174 |
193 |
232 |
270 |
302 |
||
|
510 (52) |
106 |
133 |
146 |
159 |
179 |
199 |
239 |
279 |
319 |
||
|
520 (53) |
110 |
137 |
151 |
164 |
185 |
205 |
247 |
288 |
329 |
||
|
530 (54) |
113 |
141 |
155 |
169 |
191 |
212 |
254 |
296 |
339 |
||
|
540 (55) |
116 |
145 |
160 |
175 |
196 |
218 |
262 |
305 |
349 |
||
|
550 (56) |
120 |
150 |
165 |
180 |
202 |
225 |
270 |
314 |
359 |
||
|
560 (57) |
123 |
154 |
170 |
185 |
208 |
231 |
278 |
324 |
370 |
||
|
570 (58) |
127 |
159 |
174 |
190 |
214 |
238 |
285 |
333 |
381 |
||
|
580 (59) |
130 |
163 |
179 |
196 |
220 |
245 |
294 |
342 |
391 |
При значениях а, промежуточных между 1,5d и 2d; и b — между 2d и 2,5d gb2 следует определять линейной
интерполяцией. При этом в случае одновременного уменьшения а и b следует принимать меньшее
значение gb2.
Пример. Соединение с болтами класса точности В — gb1 = 0,9; а
= 1,8d, gb2 = 0,94; b = 2,1d; gb2 = 0,88.
Принимаем gb2 = 0,88; gb = gb1 gb2 = 0,9 ´ 0,88 = 0,792.
Болтовые соединения с контролируемым натяжением
Фрикционные
соединения на высокопрочных болтах
11.4. Проверку прочности
фрикционного соединения на высокопрочных болтах следует выполнять исходя из
условия
T £ Qbh = Rbh Abn mgb/gh, (63)
где Т — сдвигающее усилие от учитываемых
расчетных нагрузок, приходящееся на один болтоконтакт, определяемое в
предположении равномерного распределения полной сдвигающей силы между болтами.
Момент, действующий в плоскости соединения, уравновешивается парами сдвигающих
усилий, одинаковых по величине и приходящихся на один болт (в предположении
прямоугольных эпюр распределения усилий между болтами). Между элементами стыка
или узла усилия распределяются без учета податливости фрикционных соединений и
в предположении упругой работы стали;
Qbh — расчетное сдвигающее
усилие, которое может быть воспринято каждой контактной поверхностью
соединяемых элементов, стянутых одним болтом;
Rbh — расчетное сопротивление высокопрочного
болта растяжению при предварительном напряжении с обжатием пакета, принимаемое
в соответствии с п. 3.7 СНиП II-23-81*. Расчетное
сопротивление увеличено и назначено с учетом экономически оправданного числа
болтов (1-2 болта из 1000), разрушающихся при натяжении с контролируемым
усилием Р = 0,7RbunАbп.
При этом среднестатистическое значение усилия натяжения болтов на 8-10 %
превышает контролируемое;
Аbп — площадь сечения болта
“нетто”, принимаемая по табл. 62* СНиП
II-23-81*. Значения
контролируемого усилия натяжения Р
для высокопрочных болтов из стали 40Х “селект” приведены в табл. 45;
m — коэффициент трения,
принимаемый, по табл. 36* СНиП II-23-81* и зависящий от
способа обработки (очистки) соединяемых поверхностей. Нормы регламентируют
средние статистические (наиболее вероятные) коэффициенты трения. Согласно
результатам доследовании установлено, что коэффициенты трения не зависят от
прочности стали соединяемых элементов. В фрикционных соединениях с числом
болтов в узле до четырех, выполненных из стали с временным сопротивлением не
более 370 МПа (3750 кгс/см2), разрешается вместо газопламенной
обработки использовать внедряемый проволочный элемент в виде звезды,
изготовленный из высокопрочной проволоки по ГОСТ
9389-75*, ГОСТ 7372-79*, ГОСТ
14963-78* в соответствии с табл.
46.
Таблица
45
|
Номинальный диаметр db, мм |
16 |
20 |
22 |
24 |
27 |
|
Р, кН (тс) |
121 (12,1) |
189 (18,9) |
233 (23,3) |
271 (27,1) |
353 (35,3) |
Таблица
46
|
Номинальный диаметр |
Усилие натяжения |
Диаметр проволоки, мм |
Длина проволоки, мм |
Внутренний диаметр |
Высота волны, мм |
Число волн |
|
22 |
233 (23,3) |
0,7 |
141 |
32 |
5 |
7 |
|
24 |
271 (27,1) |
0,8 |
142 |
34 |
5 |
7 |
Для фрикционных соединений
допускается обработка контактных поверхностей ротационным способом стальными
шариками [24] с коэффициентом трения m = 0,50, а также
пескоструйным, дробеметным или дробеструйным способом одной поверхности,
стальными щетками — другой поверхности с коэффициентом трения m = 0,42;
gb — коэффициент условий
работы, определяемый в соответствии с п. 11.13* СНиП II-23-81* и учитывающий уменьшение сдвигающего усилия,
приходящегося на один болт, из-за уменьшения числа болтов в соединении. С
уменьшением числа болтов в результате неблагоприятного влияния статистического
разброса усилий натяжения болтов и коэффициентов трения в зоне плотного
контакта увеличивается вероятность снижения сопротивления сдвигу, приходящегося
на один болт;
gh — коэффициент надежности,
принимаемый по табл. 36* СНиП II-23-81* и учитывающий
требуемую степень сдвигоустойчивости соединения, а также изменчивость
коэффициентов трения и усилий натяжения болтов (в многоболтовых соединениях).
11.5.
Предусматривается две степени сдвигоустойчивости соединения — повышенная и
нормальная. Требуемая степень сдвигоустойчивости зависит от разности
номинальных диаметров отверстий и болтов d и от характера нагрузок —
динамической (если наряду со статическими воспринимаются также учитываемые в
расчете подвижные, вибрационные, ударные или другие динамические нагрузки) или
только статической. Повышенная сдвигоустойчивость требуется для d ³ 2 мм при динамической и d ³ 5 мм при статической
нагрузках, а нормальная сдвигоустойчивость для d £ 1 мм при динамической и d £ 4 мм при статической
нагрузках.
Разность диаметров отверстий
и болтов в значительной степени определяет величину смещений в центрах
соединений после преодоления сил трения и общих перемещений в конструкции, а
также перераспределение усилий в статически неопределимых конструкциях.
Небольшие сдвиги могут нарушать геометрию конструкции и строительный подъем, и
их следует рассматривать как предельное состояние II группы, характеризуемое
затруднениями для нормальной эксплуатации. Значительный сдвиг устанавливает
предел эксплуатационной пригодности конструкции и является критерием
предельного состояния I группы. Величины предельных
смещений при динамической нагрузке меньше, чем при статической.
Повышенная сдвигоустойчивость
соединения гарантирует от появления предельного состояния I группы
и соответствующий коэффициент gh создает обеспеченность в
три стандарта от наступления предельного состояния. Нормальная
сдвигоустойчивость соединения гарантирует от предельного состояния II
группы, а коэффициент gh создает обеспеченность в два
стандарта от наступления предельного состояния.
Коэффициенты надежности gh зависят от способа регулирования усилия натяжения
болтов. При регулировании по углу поворота гайки усилие натяжения болта
получается в среднем на 20 % больше усилия Р,
соответствующего расчетному, т.е. примерно на 10 % больше, чем при
регулировании по моменту закручивания. Обрывы болтов при этом исключаются
вследствие эффекта саморегулирования. Соответственно при регулировании по углу
поворота гайки коэффициент gh примерно на 10 % меньше,
чем при регулировании по моменту закручивания.
В случае невозможности
обеспечения натяжения болтов по углу поворота регулирование усилий допускается
производить по моменту закручивания. При этом расчетный момент закручивания
должен быть увеличен на 10 %.
Предельные усилия Qbh фрикционных соединений на
высокопрочных болтах М24 приведены в табл. 47.
Таблица 47
|
Способ |
Усилие, кН (тс), на |
||||||
|
обработки (очистки) |
регулирования |
n £ 4 |
n = 5-9 |
n ³ 10 |
|||
|
Qbh1 |
Qbh2 |
Qbh1 |
Qbh2 |
Qbh1 |
Qbh2 |
||
|
Пескоструйный, дробеструйный или дробеметный двух |
По моменту закручивания М |
93 |
112 |
104 |
126 |
116 |
140 |
|
(9,3) |
(11,2) |
(10,4) |
(12,6) |
(11,6) |
(14,0) |
||
|
По углу поворота a |
105 |
123 |
118 |
139 |
131 |
154 |
|
|
(10,5) |
(12,3) |
(11,8) |
(13,9) |
(13,1) |
(15,4) |
||
|
То же, с консервацией, металлизацией распылением цинка или |
По моменту закручивания М |
80 |
97 |
90 |
109 |
100) |
121 |
|
(8,0) |
(9,7) |
(9,0) |
(10,9) |
(10,0 |
(12,1) |
||
|
По углу поворота a |
90 |
106 |
102 |
120 |
113 |
133 |
|
|
(9,0) |
(10,6) |
(10,2) |
(12,0) |
(11,3) |
(13,3) |
||
|
Кварцевым песком или дробью одной поверхности с |
По моменту закручивания М |
80 |
97 |
90 |
109 |
100 |
121 |
|
(8,0) |
(9,7) |
(9,0) |
(10,9) |
(10,0) |
(12,1) |
||
|
По углу поворота a |
90 |
106 |
102 |
120 |
113 |
133 |
|
|
(9,0) |
(10,6) |
(10,2) |
(12,0) |
(11,3) |
(13,3) |
||
|
Газопламенный двух поверхностей без консервации |
По моменту закручивания М |
67 |
82 |
76 |
92) |
84 |
102 |
|
(6,7) |
(8,2) |
(7,6) |
(9,2 |
(8,4) |
(10,2) |
||
|
По углу поворота a |
76 |
90 |
86 |
101 |
95 |
112 |
|
|
(7,6) |
(9,0) |
(8,6) |
(10,1) |
(9,5) |
(11,2) |
||
|
Стальными щетками двух поверхностей без консервации |
По моменту закручивания М |
56 |
65 |
63 |
73 |
70 |
81 |
|
(5,6) |
(6,5) |
(6,3) |
(7,3) |
(7,0) |
(8,1) |
||
|
По углу поворота а |
61 |
72 |
68 |
81) |
76 |
90 |
|
|
(6,1) |
(7,2) |
(6,8) |
(8,1 |
(7,6) |
(9,0) |
||
|
Без обработки |
По моменту закручивания |
32 |
42 |
36 |
47 |
40 |
52 |
|
(3,2) |
(4,2) |
(3,6) |
(4,7) |
(4,0) |
(5,2) |
||
|
По углу поворота a |
36 |
45 |
41 |
50 |
45 |
56 |
|
|
(3,6) |
(4,5) |
(4,1) |
(5,0) |
(4,5) |
(5,6) |
Обозначения, принятые в табл. 47:
Qbh1 — усилие
на один болтоконтакт при действии динамических нагрузок и d = 3-6 мм, статических нагрузок и d = 5-6 мм;
Qbh2 — усилие на
один болтоконтакт при действии динамических нагрузок и d
= 1 мм, статических нагрузок и d
= 1-4 мм;
d
— разность номинальных диаметров отверстий и болтов.
Фрикционно-срезные соединения на высокопрочных болтах
11.6. Проверку прочности по
условию предупреждения среза болтов для фрикционно-срезных соединений на
высокопрочных болтах выполняют, как и для соединений на болтах без
контролируемого натяжения, по формуле (127) СНиП II-23-81*. При попадании резьбы в плоскость среза в расчете
следует учитывать площадь сечения болта “нетто”.
Проверку прочности по
условию предупреждения чрезмерных перемещении сдвига и деформаций смятия в
соединении выполняют исходя из условия
, (64)
Первый член этого условия отвечает трению, второй —
смятию.
Расчет основан на
использовании деформационных критериев предельного состояния. Способ обработки
(очистки) контактных поверхностей принимается, как правило, стальными щетками
без консервации, когда коэффициент трения m = 0,35.
В формуле (64):
Т — сдвигающее усилие от учитываемых расчетных
нагрузок, приходящееся на один болт, воспринимаемое трением и одновременно
смятием соединяемых элементов. Между элементами стыка или узла усилия
распределяют в предположении упругой работы стали, но с учетом податливости
соединений в предельном состоянии;
Qbn — расчетное сдвигающее
усилие, воспринимаемое одним болтоконтактом;
Qbh — см. п. 11.4;
mp — коэффициент, учитывающий
уменьшение начального натяжения болтов после общего сдвига в соединении и
принимаемый по табл. 48;
Таблица
48
|
Расчетное |
Значения тр при нагрузке |
|
|
динамической |
статической |
|
|
До 260 (27) |
0,90 |
0,90 |
|
Св. 260 (27) |
0,85 |
0,80 |
a — коэффициент использования
нормативного усилия смятия при условии ограничения деформации смятия. Для
соединений с предварительной выборкой зазоров a = 1, без предварительной выборки a принимается по табл. 49;
gр —
коэффициент условий работы, учитывающий изменение разности номинальных
диаметров отверстий и болтов, неравномерность распределения усилий между
болтами и принимаемый по табл. 49;
Таблица
49
|
Коэффициент |
Нагрузка |
Разность номинальных |
Число болтов в |
||
|
1-4 |
5-9 |
10 и более |
|||
|
a |
Динамическая |
1 |
1,00 |
1,00 |
1,00 |
|
3 |
0,45 |
0,55 |
0,60 |
||
|
Статическая |
1 |
1,00 |
1,00 |
1,00 |
|
|
3 |
0,60 |
0,65 |
0,70 |
||
|
gр |
Любая |
1 |
0,85 |
0,95 |
1,00 |
|
3 |
0,75 |
0,90 |
1,00 |
Nbn — нормативное усилие смятия
для рассматриваемого среза болта (болтоконтакта), вызывающее деформацию смятия
сдвигаемых элементов, равную нормативной деформации смятия Dр, принимаемой равной 1 мм
при динамических и 1,5 мм — при статических нагрузках, Nbn определяется по табл. 50 в
зависимости от толщин t1 и t2 соединяемых элементов.
В односрезном соединении t1 и t2 равны действительной
толщине соединяемых элементов; в двухсрезном соединении t1 — толщина накладки, t2 — половина толщины
стыкуемого листа.
11.7.
Фрикционно-срезные соединения на высокопрочных болтах (с контролируемым натяжением),
применяемые в конструкциях, в которых перемещения сдвига в соединениях не
ограничены, допускается рассчитывать на смятие как соединение на высокопрочных
болтах без контролируемого натяжения, если воспринимаемое сдвигающее усилие nb при
таком расчете получается больше, чем при расчете по деформационному критерий
(см. п. 11.6).
При расчетной оценке влияния
перемещений сдвигав соединениях на распределение усилий в статически
неопределимых системах расчетную величину перемещения (сдвига) Ds в каждом соединении допускается принимать равной:
для одноболтового соединения
Ds = (d + 0,5Dр)a; 65)
для соединения с числом
болтов 10 и более
Ds = 0,5(d + 0,5Dр)a. 66)
При числе болтов свыше 1 до
10 допускается линейная интерполяция.
Предельные усилия
фрикционно-срезных соединений на высокопрочных болтах М24 с Rbun = 1100 МПа (110 кгс/мм2)
при очистке контактных поверхностей стальными щетками, регулировании натяжения
болтов по углу поворота гайки и отсутствии предварительной выборки зазоров
приведены в табл. 51.
Таблица
50
|
t2, мм |
Значения Nbn, кН, для элементов из стали |
|||||||||
|
углеродистой |
низколегированной |
|||||||||
|
при t1, равной, мм |
||||||||||
|
5 |
10 |
15 |
20 |
25 |
5 |
10 |
15 |
20 |
25 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
25 и более |
|
|
|
|
|
|
|
|
|
|
Примечание. Значения над чертой — при
динамической (Dр = 1 мм), под чертой — при
статической (Dр = 1,5 мм) нагрузках. При
промежуточных значениях (t1 и t2 nbn определяют линейной
интерполяцией.
Таблица
51
|
Расчетная толщина |
Предельные усилия Qbn, кН, на один болт М24 при одной плоскости |
|||||||||||||||
|
статической |
динамической |
|||||||||||||||
|
для элементов из |
||||||||||||||||
|
углеродистой |
низколегированной |
углеродистой |
низколегированной |
|||||||||||||
|
при d, мм |
||||||||||||||||
|
3 |
1 |
3 |
1 |
3 |
1 |
3 |
1 |
|||||||||
|
с числом болтов в |
||||||||||||||||
|
n £ 4 |
n ³ 10 |
n £ 4 |
n ³ 10 |
n £ 4 |
n ³ 10 |
n £ 4 |
n ³ 10 |
n £ 4 |
n ³ 10 |
n £ 4 |
n ³ 10 |
n £ 4 |
n ³ 10 |
n £ 4 |
n ³ |
|
|
5 |
84 |
112 |
112 |
125 |
86 |
116 |
107 |
131 |
65 |
87 |
90 |
112 |
67 |
91 |
95 |
118 |
|
10 |
98 |
134 |
128 |
156 |
104 |
143 |
139 |
169 |
74 |
103 |
113 |
139 |
77 |
108 |
120 |
147 |
|
15 |
108 |
149 |
146 |
178 |
114 |
159 |
159 |
179 |
80 |
112 |
126 |
154 |
85 |
121 |
139 |
169 |
|
20 |
114 |
159 |
159 |
179 |
125 |
175 |
178 |
179 |
83 |
118 |
134 |
163 |
90 |
131 |
152 |
179 |
|
25 и более |
117 |
163 |
164 |
179 |
127 |
179 |
179 |
179 |
85 |
121 |
139 |
169 |
91 |
133 |
156 |
179 |
Расчет на выносливость
11.8.
Расчет на выносливость соединений на высокопрочных болтах с контролируемым
натяжением следует выполнять в соответствии с п. 9.2* СНиП II-23-81* относя фрикционные соединения к 1-й,
фрикционно-срезные соединения на высокопрочных болтах из низколегированной
стали — ко 2-й, из углеродистой стали — к 3-й группе элементов.
Учет ослаблений
11.9.
Прочность соединяемых элементов, ослабленных отверстиями под высокопрочные
болты в фрикционных соединениях, проверяют в предположении, что 50 % усилия,
приходящегося на каждый болт в рассматриваемом сечении, уже передано силами
трения:
, (67)
где N —
расчетное усилие в элементе;
An — расчетная площадь сечения
элемента, принимаемая в соответствии с п. 11.14 СНиП II-23-81*;
ni — число рабочих
болтоконтактов в проверяемом сечении;
п — число рабочих болтоконтактов в соединении, равное
числу болтов, умноженному на число поверхностей трения;
Ry — расчетное сопротивление
стали.
Прочность элементов,
ослабленных отверстиями во фрикционно-срезных соединениях на высокопрочных
болтах, и в соединениях без контролируемого натяжения болтов, проверяют с
учетом полного ослабления сечений болтовыми отверстиями.
Для соединений на болтах
класса прочности 10.9 и высокопрочных без контролируемого натяжения необходима
проверка крайней зоны на вырыв материала по формуле
, (68)
где а — расстояние вдоль усилия от края
элемента до центра ближайшего отверстия.
12. ПРОЕКТИРОВАНИЕ СВАРНЫХ СОЕДИНЕНИЙ
12.1.
Рекомендации по проектированию сварных соединений приведены в Пособии [9], в
котором даны иллюстративный материал, раскрывающий содержание рекомендаций, и
примеры применения односторонних угловых швов в стальных конструкциях.
12.2.
При проектировании сварных узлов, один из элементов которых испытывает
растягивающие напряжения по толщине листа, следует принимать конструктивные
решения тавровых и угловых соединений с уменьшенным риском возникновения
слоистых трещин, для этого необходимо:
отказаться от применения
одностороннего углового шва и перейти к двустороннему со сведением к минимуму
концентрации деформаций в вершине сварного шва (рис 21, а);
Рис. 21. Тавровые и
угловые соединения, в которых возможно возникновение слоистых трещин в основном
металле
Слева от стрелок
а — с односторонними швами без скоса
кромок; б, в—с двусторонними швами с
двумя скосами одной кромки; г—е — с односторонними швами со скосом
одной кромки; ж — с двумя
прикрепляемыми через лист-прокладку элементами
Справа от стрелок показаны предпочтительные типы соединений
в тех случаях, когда это
возможно, применять соединения без разделки кромок с минимально возможным
объемом наплавленного металла взамен соединений с полным проплавлением (рис. 21,
б);
применять при статических
нагрузках соединения с разделкой кромок (h £ t/3) и неполным проплавлением, которые предпочтительнее соединений с
полным проплавлением (рис. 21, в);
по возможности избегать
применения V-образной разделки, применяя К-образную разделку (рис.21, г);
во всех случаях, когда это
возможно, применять тавровые соединения вместо угловых (рис. 21, д);
для снижения растягивающих
напряжений по толщине листа применять нетиповые решения разделки кромок в
угловых соединениях (рис. 21, е);
в угловом соединении с двумя
прикрепляемыми элементами лист-прокладку перекрывать сварным швом до половины
толщины прикрепляемых элементов (черт. 21, ж).
13. ПРОЕКТИРОВАНИЕ БОЛТОВЫХ СОЕДИНЕНИЙ
ВИДЫ БОЛТОВЫХ СОЕДИНЕНИЙ И УСЛОВИЯ ИХ ПРИМЕНЕНИЯ
13.1.
В строительных стальных конструкциях применяются расчетные соединения на болтах
как с контролируемым, так и без контролируемого натяжения болтов. К соединениям
с контролируемым натяжением болтов относятся:
фрикционно-срезные на
высокопрочных болтах, при расчете которых учитывается вся совокупность
сопротивлений трению, смятию и срезу;
фланцевые, при расчете
которых учитываются сопротивления растяжению болтов (в необходимых случаях и
другие сопротивления).
Фланцевые соединения на
высокопрочных болтах применительно к стыкам ферм рассмотрены в разд.
27.
В соединениях без
контролируемого натяжения могут использоваться болты различных классов
прочности, в том числе и высокопрочные. В расчетах таких соединений учитываются
сопротивления растяжению, смятию и срезу без учета сил трения.
13.2.
Области применения соединений на болтах приведены в табл. 52. В расчетных
соединениях, как правило, следует применять болты классов прочности 5.8, 8.8,
10.9 по ГОСТ
7798-70* и высокопрочные по ГОСТ
22353-77* и ТУ 14-4-1345-85. В соединениях, рассчитываемых на срез и
смятие, диаметр гладкой части стержня применяемых болтов должен быть равен, как
правило, номинальному диаметру резьбы, в связи с чем применение так называемых
облегченных болтов (диаметр гладкой части стержня равен среднему диаметру
резьбы) по ГОСТ
7798-70* и высокопрочных по ТУ 14-4-1345-85 не рекомендуется. Болты классов
прочности 4.6, 4.8, 5.6, 6.6 имеют те же области применения, что и болты класса
прочности 5.8. В качестве сборочных для сварных соединений могут применяться
болты классов прочности не ниже 4.6 и не выше 8.8.
Таблица
52
|
Условия работы |
Область применения работающих |
||||||
|
с контролируемым |
без контролируемого |
||||||
|
фрикционные на |
фрикционно-срезные |
||||||
|
Класс прочности болтов |
|||||||
|
110; 110ХЛ (ГОСТ |
110; 110ХЛ (ГОСТ |
110; 110ХЛ (ГОСТ |
5.8 (ГОСТ |
||||
|
Разность |
|||||||
|
1-6 |
1 |
3 |
1 |
2-3 |
1 |
2-3 |
|
|
В конструкциях, непосредственно воспринимающих |
+ |
+ |
— |
+ |
— |
+ |
— |
|
В многоболтовых соединениях конструкций из стали с |
+ |
+ |
— |
+ |
— |
— |
— |
|
В соединениях, требующих расчета на выносливость |
+ |
+ |
— |
— |
— |
— |
— |
|
В конструкциях, для которых перемещения сдвига в центрах |
+ |
— |
— |
— |
— |
— |
— |
|
В конструкциях, в которых перемещения сдвига в соединениях |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
При r > 0 |
При r > 0 |
При r > 0 |
При r > 0 |
||||
|
В слабо нагруженных соединениях (связей, фахверка, |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
При r < 0 |
При r > 0 |
При r < 0 |
При r > 0 |
____________
1 При r
< 0 усилие, меньшее по абсолютной величине, должно восприниматься трением,
где r = Tmin/Tmax (значения
Т принимаются в соответствии с п. 11.6).
2
Отклонение диаметра и овальность отверстий + 1,0 мм.
13.3.
Для высокопрочных болтов, изготовленных по ГОСТ
22353-77* допускается установка одной шайбы только под вращаемым элементом
(головкой болта или гайкой) при разности номинальных диаметров отверстия и
болта, не превышающей 4 мм, в конструкциях, изготовленных из стали с временным
сопротивлением не ниже 440 МПа (4500 кгс/см2).
13.4.
Резьба болта должна, как правило, располагаться вне плоскостей среза и отстоять
от ближайшей из них не менее чем на 5 мм. Головки болтов следует располагать со
стороны более тонкого элемента.
13.5.
При размещении болтов, прикрепляющих одиночный уголок, в шахматном порядке
отверстия, наиболее удаленные от конца уголка, следует располагать на риске,
ближайшей к обушку.
14. ФЕРМЫ ИЗ ОДИНОЧНЫХ УГОЛКОВ
ОБЩИЕ ПОЛОЖЕНИЯ
14.1.
Рекомендации настоящего раздела распространяются на проектирование плоских ферм
с поясами и решеткой из одиночных уголков, прикрепляемых в узлах
преимущественно одной полкой (внахлестку), с соединениями, выполняемыми сваркой
угловыми швами, дуговой точечной сваркой (в том числе проплавлением) или на
болтах (в том числе высокопрочных).
14.2.
Плоские фермы из одиночных уголков целесообразно применять в покрытиях зданий
вместо традиционных ферм из парных уголков, тавров и т.п. как более
технологичные.
Характерной особенностью
одноуголковых ферм является асимметрия сечений и прикреплений элементов
относительно плоскости фермы, вызывающая смещение продольных сил с осей уголков
в сторону полок, параллельных плоскости фермы (в сторону обушков)1.
Величина этого смещения зависит от ряда факторов: жесткости сечения поясного
уголка на кручение, степени защемления его от скручивания, изгибной жесткости
его полок, типа узла (наличия и размеров фасонки, наличия прикреплений по
второй полке, числа сходящихся в узле элементов решетки, знака и величины
усилий в них, углов примыкания к поясу) и других.
______________
1 Решетников Б. Н.
Особенности действительной работы и расчета элементов из одиночных уголков в
составе решетчатых конструкций. — В кн.: Исследование прочности элементов
строительных металлических конструкций/ЦНИИСК им. Кучеренко. — М., 1982. — С.
35-44.
Возникающие при этом в
уголках изгибающие моменты могут быть названы моментами от неоднородной
жесткости прикреплений. Установленные экспериментально для элементов решетки
бесфасоночных ферм расчетные значения эксцентриситетов продольных сил из
плоскости фермы (“эксцентриситетов прикрепления”) еу, отнесенных к геометрической характеристике сечения z, приведены в табл. 53
(значения eу).
Теоретически и
экспериментально1 установлено, что при жестких прикреплениях
одиночных уголков по одной полке (сваркой или более чем одним болтом) в них
возникают добавочные (помимо моментов от внеузловой нагрузки, расцентровки
узлов и жесткости узлов) изгибающие моменты также и в плоскости фермы. По знаку
эти моменты такие, что вызывают смещение продольных сил в сторону перьев
уголков, а по абсолютной величине составляют около 60 % соответствующих
моментов из плоскости фермы. Отнесенные к z эмпирические значения “эксцентриситетов прикрепления в плоскости
фермы” еха
(соответствующих указанным добавочным моментам) также приведены в табл. 53
(значения eха).
_____________
1 Балдин В. А., Решетников Б.
Н., Гукова М. И., Мелкумян Б. С. Испытания ферм покрытий из одиночных
уголков с соединениями дуговой точечной сварной в составе пространственных
блоков. — В кн.: Новые конструктивные решения строительных металлических
конструкций/ ЦНИИСК им. Кучеренко. — М., 1983. — С. 32-47.
Таблица
53
|
Элементы решетки ферм |
Относительные |
|
|
в плоскости фермы eха |
из плоскости фермы eу |
|
|
Прикрепляемые по одной полке: |
||
|
растянутые |
0,36 |
—0,6 |
|
сжатые |
0,48 |
—0,8 |
|
растянутые и |
|
—1,0 |
|
Прикрепляемые по двум полкам: |
||
|
растянутые |
0,12 |
—0,2 |
|
сжатые |
0,24 |
—0,4 |
Обозначения, принятые в табл. 53:
а — расстояние от обушка уголка до оси
болта (риска уголка);
zo,
z —
см. п. 14.4.
14.3.
В отличие от пространственных решетчатых конструкций из одиночных уголков типа
опор ЛЭП плоские фермы покрытий характеризуются: более высокими соотношениями
усилий в элементах решетки и поясов и, соответственно, меньшей разницей сечений
этих элементов; наличием растянутых и, при беспрогонных решениях, изгибаемых
поясов; закреплением сжатых поясов (прогонами в узлах или настилом по всей
длине) от скручивания. Указанные особенности определили использование для
плоских ферм особой методики расчета, основанной на прямом учете
внецентренности усилий в стержнях ферм.
расчет
14.4. Расчет элементов ферм из
одиночных уголков следует выполнять с учетом изгибающих моментов в плоскости
фермы Мх и из плоскости
фермы My, определяемых по формулам:
Мх = Mp
+ eхаNz, My = eyNz, (69)
где Мр
= Mq + Ме + Mf,
Mq, Ме, Mf — изгибающие моменты
соответственно от внеузловой нагрузки, от расцентровки стержней в узлах и от
перемещений системы (от жесткости узлов);
N — продольная сила,
принимаемая со знаком, соответствующим знаку усилия (“плюс” — при растяжении,
“минус” — при сжатии);
z = zo — 0,5d — расстояние от центральной
оси до середины толщины полки уголка;
zo — расстояние от центральной
оси до наружной грани полки уголка;
eха, ey — относительные эксцентриситеты прикрепления,
определяемые по табл. 53 (для
поясов ферм eха = ey = 0).
Изгибающие моменты Mq, Ме, Mf, Мр следует
принимать положительными, если они вызывают растяжение на пере уголка, и
отрицательными — в обратном случае.
Моменты от жесткости узлов Mf при расчете растянутых
элементов, а также при отсутствии моментов Mq и Mе допускается не учитывать.
14.5.
Расчет на прочность внецентренно-сжатых, сжато-изгибаемых,
внецентренно-растянутых и растянуто-изгибаемых элементов из одиночных уголков,
не подвергающихся непосредственному воздействию динамических нагрузок, следует
выполнять по формуле
, (70)
где v — коэффициент, определяемый
по табл. 54 в зависимости от условных относительных эксцентриситетов eх и ey;
gс — коэффициент условий работы, определяемый по поз.
6 табл. 6* СНиП II-23-81*.
Таблица
54
|
Условный относительный |
Коэффициент v при условном относительном эксцентриситете из плоскости |
|||||
|
0 |
—0,2 |
—0,4 |
—0,6 |
—0,8 |
—1,0 |
|
|
—1,0 |
0,60 |
0,56 |
0,52 |
0,48 |
0,44 |
0,41 |
|
—0,8 |
0,67 |
0,62 |
0,57 |
0,52 |
0,48 |
0,44 |
|
—0,6 |
0,74 |
0,68 |
0,62 |
0,57 |
0,52 |
0,48 |
|
—0,4 |
0,82 |
0,75 |
0,68 |
0,62 |
0,57 |
0,52 |
|
—0,2 |
0,90 |
0,82 |
0,75 |
0,68 |
0,62 |
0,56 |
|
0 |
1,00 |
0,90 |
0,82 |
0,74 |
0,67 |
0,60 |
|
0,05 |
0,93 |
0,93 |
0,84 |
0,76 |
0,68 |
0,61 |
|
0,10 |
0,90 |
0,90 |
0,85 |
0,77 |
0,70 |
0,62 |
|
0,15 |
0,87 |
0,87 |
0,87 |
0,78 |
0,71 |
0,63 |
|
0,20 |
0,83 |
0,83 |
0,83 |
0,80 |
0,72 |
0,65 |
|
0,25 |
0,81 |
0,81 |
0,81 |
0,81 |
0,74 |
0,66 |
|
0,30 |
0,77 |
0.77 |
0,77 |
0,77 |
0,76 |
0,67 |
|
0,4 |
0,71 |
0,71 |
0,71 |
0,71 |
0,71 |
0,70 |
|
0,6 |
0,63 |
|||||
|
0,8 |
0,55 |
|||||
|
1,0 |
0,50 |
|||||
|
1,2 |
0,45 |
|||||
|
1,4 |
0,41 |
Значения eх следует определять по формуле
, (71)
где ех — эксцентриситет
продольной силы в плоскости фермы (ех
= Mx/N), вычисляемый с учетом знаков изгибающих моментов и продольной силы
(положительному эксцентриситету соответствует направление к перу, а
отрицательному — к обушку уголка).
Эксцентриситет продольной
силы из плоскости фермы совпадает с эксцентриситетом прикрепления (еу = Mу/N = eyz; ey — см. п. 14.4).
В остальных случаях расчет
следует выполнять по формуле
, (72)
где хо и уо —
координаты рассматриваемой точки сечения уголка относительно его главных осей
(рис. 22).
Изгибающие моменты и
следует определять по
формулам:
= Мх cosa — My sin a; (73)
= Мх sin a + My cosa, (74)
где a — угол наклона главных осей
сечения уголка к полкам, отсчитываемый от горизонтальной оси (см. рис. 22).
Рис. 22. Сечения элементов из одиночных уголков
а — равнополочного; б —
неравнополочного
Изгибающие моменты Мх и My следует подставлять в
формулы (73) и (74) со своими знаками (см. п.
14.4).
Моменты инерции сечения и
для равнополочных
уголков следует определять по сортаменту ГОСТ 8509-86.
Для неравнополочных уголков следует определять по
сортаменту ГОСТ 8510-86
(обозначению Iу в нем соответствует обозначение Iumin), а — по формуле
= Ix + Iy —
. (75)
14.6.
Расчет на прочность внецентренно-сжатых и сжато-изгибаемых верхних поясов ферм
из одиночных уголков, непрерывно раскрепленных из плоскости фермы жестким
настилом и не подвергающихся непосредственному воздействию динамических
нагрузок, следует проверять по формуле (49) СНиП II-23-81* рассматривая сечение пояса как тавровое, при этом коэффициент n при эксцентриситете в сторону полки (обушка) следует принимать равным
3,0, а при эксцентриситете в сторону стенки (пера) — равным 1,0.
14.7.
Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых элементов из
одиночных уголков, не имеющих промежуточных закреплений в одном направлении,
следует выполнять по формуле (51) СНиП
II-23-81*, в
которой коэффициент jе рекомендуется определять по
формуле
. (76)
Для равнополочных уголков
при ey = —0,8 (т.е. для сжатых
элементов решетки, прикрепляемых по одной полке сваркой или одним болтом и
более) значения jе рекомендуется определять по
табл. 55.
Таблица
55
|
Условный относительный |
Коэффициент |
||||||
|
0 |
0,5 |
1,0 |
2.0 |
3,0 |
4,0 |
5,0 |
|
|
—1,0 |
0,44 |
0,43 |
0,42 |
0,40 |
0,32 |
0,26 |
0,22 |
|
—0,8 |
0,48 |
0,46 |
0,44 |
0,40 |
0,32 |
0,26 |
0,22 |
|
—0,6 |
0,52 |
0,49 |
0,46 |
0,40 |
0,32 |
0,26 |
0,22 |
|
—0,4 |
0,57 |
0,51 |
0,47 |
0,40 |
0,32 |
0,26 |
0,22 |
|
—0,2 |
0,62 |
0,54 |
0,49 |
0,41 |
0,33 |
0,27 |
0,22 |
|
0 |
0,67 |
0,57 |
0,51 |
0,42 |
0,34 |
0,28 |
0,22 |
|
0,2 |
0,72 |
0,59 |
0,52 |
0,43 |
0,36 |
0,29 |
0,23 |
|
0,3 |
0,76 |
0,60 |
0,52 |
0,44 |
0,37 |
0,30 |
0,23 |
|
0,4 |
0,71 |
0,61 |
0,53 |
0,45 |
0,38 |
0,31 |
0,23 |
|
0,6 |
0,63 |
0,58 |
0,53 |
0,46 |
0,39 |
0,32 |
0,24 |
|
0,8 |
0,55 |
0,53 |
0,51 |
0,45 |
0,38 |
0,31 |
0,23 |
|
1,0 |
0,50 |
0,48 |
0,46 |
0,42 |
0,36 |
0,30 |
0,22 |
|
1,2 |
0,45 |
0,43 |
0,41 |
0,38 |
0,33 |
0,27 |
0,21 |
|
1,4 |
0,41 |
0,39 |
0,37 |
0,34 |
0,30 |
0,25 |
0,20 |
В формуле (76) коэффициенты и
следует определять в
соответствии с п. 5.27* СНиП II-23-81* в зависимости
от условной гибкости и
(вычисляемой
соответственно относительно осей хо-хо
и уо-уо) и
приведенного относительного эксцентриситета и
для равнополочных
уголков определяемого по формулам:
; (77)
, (78)
где
; (79)
. (80)
Значения изгибающих моментов
и
, необходимые для вычисления условных относительных
эксцентриситетов и
при расчете на
устойчивость, следует принимать для сечений с наибольшим и наименьшим
значениями Мх в пределах
средней трети длины стержня.
Коэффициент следует определять в
соответствии с п. 5.3 СНиП II-23-81* для наименьшей
гибкости стержня (относительно оси хо-хо).
14.8.
Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых верхних поясов
ферм из одиночных уголков, непрерывно раскрепленных из плоскости фермы жестким
настилом, а также устойчивость других элементов, имеющих между узлами
промежуточное закрепление в одном направлении, следует выполнять в соответствии
с п. 5.27* СНиП II-23-81* принимая в
качестве , е и W соответствующие
характеристики в плоскости, перпендикулярной к плоскости закрепления.
14.9.
Расчетные длины lef элементов ферм из одиночных
уголков следует принимать по табл. 56.
Таблица
56
|
Элементы ферм |
Расчетная длина lef |
|
Сжатые и растянутые пояса, |
0,9l |
|
Сжато-изгибаемые пояса (в |
0,8l |
|
Раскосы и основные стойки |
0,8l1 |
|
Дополнительные стойки |
0,9l1 |
Обозначения, принятые в табл. 56:
l — геометрическая длина элемента (расстояние между центрами
узлов; при нецентрированных узлах — расстояние между точками пересечения
геометрических осей элементов) в плоскости фермы;
l1 — расстояние между ближайшими узлами по длине
элемента.
14.10.
При бесфасоночных узлах следует производить расчет поясных элементов в узлах на
участках между прикреплениями элементов решетки на сдвиг по формуле (29) СНиП II-23-81* принимая в качестве Q разность перпендикулярных к
оси пояса составляющих усилий в элементах решетки, а в качестве I, S и t — геометрические
характеристики сечения уголка относительно оси х—х.
14.11.
Расчет сварных точечных соединений в прикреплениях элементов из одиночных
уголков (рис. 23), на действие
продольной силы и момента в плоскости расположения точек следует производить по
формулам:
на срез точек
, (81)
где
;
на сложное разрушение (срез и разрыв или сжатие)
основного металла, окружающего точки:
а) в прикрепляемом элементе:
при g ³ 0,58 (f + l)
; (82)
при g < 0,58 (f + l)
; (83)
б) в поясном элементе:
при tg q ³ 0,58 (q ³ 30°)
; (84)
при tg q < 0,58 (q < 30°)
. (85)
Рис.
23. Схема сварного точечного соединения двух элементов из одиночных
уголков
КОНСТРУИРОВАНИЕ
14.12.
При проектировании ферм из одиночных уголков следует стремиться к выполнению
узлов без фасонок, для чего рекомендуется принимать размеры полок уголков в
плоскости фермы возможно большими для поясов и возможно меньшими — для
элементов решетки.
14.13.
Толщина прикрепляемых элементов решетки, как правило, не должна превышать
толщины поясов. Суммарная толщина пакета деталей, соединяемых дуговой точечной
сваркой со сквозным проплавлением, не должна превышать 26 мм.
14.14.
Расстояния между краями смежных элементов решетки в узлах следует принимать не
менее 5 мм, а расстояния между краями элементов решетки и внутренней стороной
выступающей полки уголка пояса — не менее радиуса закругления между полками
этого уголка.
14.15.
Для обеспечения размещения сварных швов или болтов в пределах полок поясных
уголков без их уширения в узлах (без фасонок), а также для обеспечения резки
уголков решетки без скоса полок допускается смещать точки пересечения осей
элементов решетки в узлах с осей поясов в сторону обушков (с соответствующим
учетом возникающих при этом изгибающих моментов в стержнях Ме, см. п. 14.4).
14.16.
В случае недостаточного размера полок поясных уголков для прикрепления к ним элементов
решетки в отдельных узлах ферм следует предусматривать уширение этих полок
приваркой к ним фасонок встык с зачисткой шва с внутренней стороны поясного
уголка заподлицо с поверхностью полки.
14.17.
Сварные точки в прикреплениях элементов из одиночных уголков следует размещать
в соответствии с возможностями имеющегося оборудования для сварки. Точки
следует располагать на максимальных расстояниях друг от друга в один или два
ряда параллельно оси уголка. Каждый конец элемента следует прикреплять не менее
чем двумя точками. Расстояния между центрами точек в любом направлении следует
принимать не менее 1,5d, а
расстояния от центра точки до краев элемента (пера или торца уголка) — не менее
1,2 d, где d — номинальный диаметр точки
в плоскости среза.
14.18.
За осевую плоскость фермы (совмещаемую с разбивочной осью в плане и с центром
опорного ребра) следует принимать плоскость, удаленную от обушка уголка
верхнего пояса на расстояние, равное расстоянию до центра тяжести сечения
верхнего пояса с округлением до 5 мм в меньшую сторону.
14.19.
Сжатые опорные раскосы и стойки и другие сильно нагруженные элементы решетки из
одиночных уголков рекомендуется выполнять с прикреплением их в узлах по двум
полкам, т.е. с прикреплением полки, перпендикулярной плоскости фермы, к
соответствующим полкам поясных уголков или к опорному ребру фермы
(непосредственной приваркой впритык либо с помощью приваренной планки или
прокладки).
15. ФЕРМЫ И СВЯЗИ ИЗ ГНУТОСВАРНЫХ ПРОФИЛЕЙ
МАТЕРИАЛЫ
15.1.
Для элементов ферм и связей применяются гнутосварные профили по ТУ 36-2287-80.
Материал профилей
назначается в соответствии с требованиями СНиП II-23-81*. Профили изготовляются из листовой горячекатаной
стали, поставляемой в рулонах по ГОСТ 19903-74*):
углеродистой общего назначения толщиной 4 мм и более — по ГОСТ
14637-79, толщиной 3 мм — по ГОСТ
16523-70*; низколегированной толщиной 4 мм и более — по ГОСТ
19282-73* толщиной 3 мм — по ГОСТ
17066-80*.
15.2.
Для монтажных фланцевых узлов растянутых поясов применяются высокопрочные болты
из стали 40Х “селект” по ГОСТ
22353-77* или ту 14-4-1345-85
с характеристикой 6g110ХЛ1
или 8g110ХЛ1, гайки по ГОСТ
22354-77* с характеристикой 6h
110 или 7h 110.
15.3.
Для фланцев растянутых поясов применяется толстолистовая горячекатаная
термообработанная сталь марки 14Г2АФ по ТУ 14-105-465-82, расчетное
сопротивление которой в направлении толщины проката принимается равным Rth = 275 МПа (2800 кгс/см2).
Допускается изготовление фланцев из других марок низколегированных сталей, применяемых
для строительства с проверкой механических свойств стали в направлении толщины
проката по специальной методике, изложенной в [25].
15.4. Расчетные сопротивления
гнутосварных профилей следует принимать по СНиП II-23-81*
Рекомендуется учитывать
повышение предела текучести материала за счет упрочнения зон изгиба в
соответствии с методикой, приведенной в п. 2.3.1 [26].
15.5.
Профилированный настил рекомендуется прикреплять к поясам самонарезающими болтами
М6-8g ´ 20.56.099 по ОСТ
34-13-016-77, точечной сваркой в соответствии с [27] или дюбелями в
соответствии с [28] и ОСТ 36-122-85.
РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
15.6.
Расчет элементов на прочность следует производить в соответствии с разд. 5 СНиП II-23-81* и п. 15.4 настоящего Пособия.
Проверку устойчивости
элементов необходимо осуществлять в соответствии с разд. 5 СНиП II-23-81* стенок и полок — в соответствии с пп. 7.14*, 7.20*,
7.26* СНиП II-23-81* и п. 2.2.2 [26] [для
элементов, рассчитываемых по формуле (56) СНиП II-23-81*].
МЕСТНАЯ УСТОЙЧИВОСТЬ СТЕНОК ПРИ СОСРЕДОТОЧЕННЫХ НАГРУЗКАХ
15.7.
При совпадении плоскости действия нагрузки с плоскостью стенки (опирание по
типу, указанному на рис. 24, б)
наибольшую величину сосредоточенной нагрузки или реакции в опорном сечении,
действующей на каждую стенку, следует определять:
а) реакцию крайней опоры,
нагрузку на конце консоли и на участках 1,5h¢ (где h¢ = Н — 2t, см. рис. 24, а), прилегающих к опорам, по формуле
; (86)
б) реакцию промежуточной
опоры и опоры консоли, нагрузку на участках, расположенных на расстоянии более
1,5h¢ от опор, по формуле
. (87)
Рис.
24. К расчету местной устойчивости стенок элементов из гнутосварных профилей
а — схема нагрузок и реакций; б — опирание через прокладку; в — непосредственное опирание
15.8.
При несовпадении плоскости действия нагрузки с плоскостью стенки (опирание по
типу, указанному на рис. 24, в):
; (88)
(89)
здесь
; (90)
. (91)
В формулах (86) — (91):
t — толщина стенки профиля;
z — условная длина
распределения сосредоточенного груза, не повышающая высоту стенки h’;
r — внутренний радиус
закругления, не превышающий 4t;
Ry — в МПа;
P1 и Р2 — в кН.
БЕСФАСОНОЧНЫЕ УЗЛЫ ФЕРМ
15.9.
Бесфасоночные узлы ферм (рис. 25), состоящие из пояса и примыкающих к нему
элементов решетки, следует проверять на:
продавливание (вырывание)
участка стенки пояса, контактирующей с элементом решетки;
несущую способность участка
боковой стенки пояса (параллельной плоскости узла) в месте примыкания сжатого
элемента решетки;
несущую способность элемента
решетки в зоне примыкания к поясу;
прочность
сварных швов прикрепления элемента решетки к поясу.
Рис. 25. Бесфасоночные узлы ферм
а — К-образный; б — раскосный; в —
опорный; г — Х-образный; д — Т-образный
15.10. В
случае одностороннего примыкания к поясу двух элементов решетки или более с
усилиями разных знаков (см. рис. 25, а,
б), а также одного элемента в опорных
узлах (см. рис. 25, в) при d/D £ 0,9 и c/b £ 0,25 несущую способность
пояса на продавливание (вырывание) следует проверять для каждого примыкающего
элемента по формуле
, (92)
где N —
усилие в примыкающем элементе;
М — изгибающий момент от основного воздействия в
примыкающем элементе в плоскости узла в сечении, совпадающем с примыкающей
полкой пояса (момент от жесткости узлов допускается не учитывать);
gс — коэффициент условий работы, принимаемый по поз. 1
и 2 табл. 6* СНиП II-23-81*;
gd — коэффициент влияния знака
усилия в примыкающем элементе, принимаемый равным 1,2 при растяжении и 1,0 — в
остальных случаях;
gD — коэффициент влияния
продольной силы в поясе, определяемый при сжатии в поясе, если / (ARy) > 0,5, по формуле
gD = 1,5 — / (ARy), (93)
в остальных случаях gD = 1,0;
F — продольная сила в поясе
со стороны растянутого элемента решетки;
А —
площадь поперечного сечения пояса;
Ry — расчетное сопротивление
стали пояса;
t — толщина стенки пояса;
b — длина участка линии
пересечения примыкающего элемента с поясом в направлении оси пояса, равная db/sina;
с — половина расстояния между смежными стенками
соседних элементов решетки или поперечной стенкой раскоса и опорным ребром;
f = (D — d)/2,
a — угол примыкания элемента решетки к поясу.
Формула (92) относится к узлам К-образного
типа, т.е. антисимметричным по усилиям в примыкающих элементах, при не слишком
больших отношениях поперечных размеров элемента решетки и пояса и малой
раздвижке раскосов. При выводе формулы использованы опытные данные и теория
предельного равновесия в кинематическом варианте. Формула (93) получена с
учетом опытных данных.
15.11. Несущую
способность пояса на продавливание в крестообразных, Т-образных узлах (см. рис. 25, г, д), а также в узлах,
указанных в п. 15.10 при с/b > 0,25 следует проверять
по формуле
. (94)
Формула (94), полученная
аналитически, относится к Т-, У- и Х-образным узлам, а также при достаточно
большой раздвижке раскосов — к узлам К-образного типа. В последнем случае
условной границей областей применения формул (92) и (94) является значение с/b = 0,25 (на самом деле это значение зависит от параметров d/D и b/D).
15.12. Несущую способность стенки
пояса в плоскости узла в месте примыкания сжатого элемента решетки при d/D > 0,85 следует проверять по
формуле
, (95)
где gt — коэффициент влияния
тонкостенности пояса, для отношений Db/t ³25 принимаемый равным 0,8, в
остальных случаях — 1,0;
k — коэффициент, принимаемый
в зависимости от тонкостенности пояса Db/t и расчетного сопротивления стали Ry по формулам, соответствующим трем областям,
приведенным на графике 26.
Рис. 26. График для определения значений коэффициента k в зависимости от тонкостенности пояса
Формулой (95) учтена возможность исчерпания
несущей способности узла от выпучивания боковой стенки пояса при достаточно
больших отношениях d/D (когда продавливание
затруднено). Коэффициент k учитывает
возможное снижение несущей способности участка стенки пояса как сжатой
пластинки, работающей в упругой или упруго-пластической стадии (k = scr/Ry; scr — критическое напряжение). Для сталей с Ry £ 400 МПа (4100 кгс/см2)
при отношениях Db/t £ 40 k = 1,0.
15.13.
Несущую способность элемента решетки в зоне примыкания к поясу следует
проверять:
а) в узлах, указанных в п. 15.10, при углах примыкания a = 40 — 50° — по формуле
, (96)
где k — определяется, как и в п. 15.12, но с заменой характеристик пояса
на характеристики элемента решетки (Db — на большее из значений d и db; t на td; Ry на Ryd);
Ryd — расчетное сопротивление
стали элемента решетки;
Ad — площадь поперечного
сечения элемента решетки;
td — толщина стенки элемента
решетки;
для элемента решетки
неквадратного сечения в правую часть формулы (96) следует вводить множитель ;
б) в узлах, указанных в п. 15.11, — по формуле
. (97)
Выражение в
круглых скобках формулы (97) не должно быть менее 0. Для элементов решетки
неквадратного сечения в правую часть формулы (97) следует вводить множитель
.
15.14.
Несущую способность сварных швов, прикрепляющих элементы решетки к поясу,
следует проверять:
а) в узлах, указанных в п. 15.10, при углах примыкания a = 40 — 50° -по формуле
, (98)
где bf, kf, gwf, Rwf следует принимать согласно указаниям разд. 11 и п. 12.8 СНиП II-23-81*,
б) в узлах, указанных в п. 15.11, — по формуле

в) сварные швы, выполненные
при наличии установочного зазора, равного 0,5-0,7 толщины стенки примыкающего
элемента, с полным проплавлением стенки профиля, следует рассчитывать как
стыковые.
15.15.
Формулы (96) — (99) учитывают
неравномерное распределение напряжений по периметру торца элемента решетки и
при относительно высокой несущей способности пояса могут лимитировать расчетную
прочность узла. Они получены на основе анализа и обработки экспериментальных
данных. Коэффициент k в
формулах (96) и (97) имеет тот же смысл, что в формуле
(95).
УЗЛЫ СВЯЗЕЙ
15.16.
Узлы связей из гнутосварных профилей (рис. 27) проверяют:
а) на прочность и
устойчивость элементов узла и примыкающей к узлу зоны профиля;
б) на прочность сварных
соединений.
Рис. 27. Узлы связей из гнутосварных профилей
а — типы хвостовиков; б — соединение с фасонкой; 1 — линия центра тяжести сечения фасонки
связи с ребром; 2 — ось фасонки
фермы; 3 — ось профиля
15.17.
Несущую способность при растяжении элемента связи проверяют:
а) для узлов типа Ф(см. рис.
27, а) — по формуле
, (100)
где N —
усилие в элементе связи;
Ryf — расчетное сопротивление
стали фланца;
Df — длина фланца вдоль
фасонки связи;
Ryd — расчетное сопротивление
стали элемента связи;
формула (100) получена на
основе допущения образования в пластине фланца вдоль фасонки связи линейных
пластических шарниров;
б) для узлов типа Фн
(см. рис. 27, а) — по формуле (100), но с заменой td на td + 0,6th, где th — толщина накладки;
в) для узлов типа В (см. рис. 27, а) — по условию
, (101)
где А —
площадь поперечного сечения элемента связи;
gf — коэффициент влияния
глубины врезки, принимаемый:
при 0,8 £ l1/db, < 1,6
gf = 0,51 l1/db + 0,18;
” l1/db ³ 1,6
gf = 1,0.
15.18.
Несущую способность при сжатии элементов связей следует проверять:
а) для узлов типа Ф (см. рис. 27, а) — по формуле (100) и по формулам:
; (102)
; (103)
б) для узлов типов Фр
и Вр — по формуле (103) и по формуле
. (104)
В формулах (102) — (104):
е, e1 — расстояния соответственно
от оси фасонки закрепляемой конструкции до оси элемента связи и до центра
тяжести таврового сечения фасонки связи с ребром (см. рис. 27, б);
A, W — соответственно площадь
сечения и момент сопротивления профиля относительно оси фасонки связи;
Afc, Wfс — соответственно площадь и момент сопротивления
фасонки связи с учетом ребра (при его наличии);
gf — коэффициент условий
работы, принимаемый в зависимости от наибольшей условной гибкости профиля:
при gf = 0,6;
” gf = 0,54 + 0,15
,
но не более
1,0.
Формулы справедливы при
соотношении размеров поперечного сечения элемента связи и отношении большего
размера профиля к толщине не более 45.
15.19.
Расчет сварных соединений профиля и фасонки связи с фланцем узлов типов Ф, Фн,
Фр следует производить в соответствии с п. 11.2* СНиП II-23-81* с учетом коэффициента условий работы gсf = 0,8, учитывающего
неравномерность передачи усилий, и по металлу границы сплавления с фланцем в
направлении толщины проката по формуле
. (105)
ПРОЕКТИРОВАНИЕ
15.20.
Расчетная длина панелей верхних поясов ферм беспрогонных покрытий lef определяется по формуле
lef = ml, (106)
где l —
длина панели;
m — коэффициент расчетной
длины, принимаемый:
— для панели пояса, не
граничащей с шарнирным узлом (например, фланцевое соединение на болтах), и при
наличии равномерно распределенной нагрузки на соседних панелях;
— для панели пояса, граничащей
с шарнирным узлом или с панелью, не загруженной распределенной нагрузкой;
здесь — параметр
распределенной нагрузки ;
q — распределенная нагрузка
на пояс;
N — продольная сила;
Н —
высота сечения пояса;
Нt
— высота фермы по осям поясов;
L — пролет фермы.
15.21.
Отношение высоты поясов к толщине стенки следует принимать не более 45,
элементов решетки — не более 60.
15.22.
Размеры элементов решетки по ширине (из плоскости конструкции) не следует
принимать свыше D — 2 (t + td) для удобства наложения
сварных швов.
15.23.
Для элементов решетки размер d
рекомендуется принимать не менее 0,6 поперечного размера пояса D.
15.24.
Расстояние между смежными стенками (носками) раскосов должно быть минимальным
из условия наложения двух сварных швов.
15.25.
Заводские стыки элементов рекомендуется выполнять сваркой встык на остающейся
подкладке. Размещение этих стыков в растянутых элементах с напряжениями свыше
0,9 Ry не рекомендуется.
15.26.
Монтажные стыки рекомендуется выполнять фланцевыми на высокопрочных
предварительно напряженных болтах с учетом положений [25].
16. ФЕРМЫ С ПОЯСАМИ ИЗ ШИРОКОПОЛОЧНЫХ ДВУТАВРОВ
ОБЩИЕ ПОЛОЖЕНИЯ
16.1.
Рекомендации настоящего раздела распространяются на проектирование ферм
покрытий из двутавров с параллельными гранями полок (широкополочных) типа К или
Ш с решеткой из замкнутых гнутосварных профилей и широкополочных двутавров,
непосредственно примыкающих к полкам поясов, для районов с расчетной
температурой минус 40 °С и выше.
Для указанных ферм следует
использовать сталь с Ryn £ 380 МПа (3850 кгс/см2)
и сварочные материалы с Rwun = 490 МПа (5000 кгс/см2).
16.2.
Расчет ферм следует производить в соответствии с п. 13.8 СНиП II-23-81*. Узловые эксцентриситеты (рис. 28, 29)
допускается не учитывать при e/Db £ 1/10 (где Db — высота сечения пояса; е — расстояние от точки пересечения осей
элементов решетки до оси пояса).
16.3.
Изгибающие моменты от узловых эксцентриситетов и жесткости узлов в элементах
ферм с постоянным знаком нормального усилия (при отсутствии поперечной нагрузки
на стержень) допускается учитывать по формуле
, (107)
где N и М — соответственно расчетные нормальное
усилие и момент;
А и W —
соответственно площадь поперечного сечения и момент сопротивления стержня.
При этом значения моментов
от узловых эксцентриситетов Me
должны удовлетворять условию1
Me £ W(Ry — N/A), (108)
где W, А, Ry —
соответственно момент сопротивления, площадь сечения и расчетное сопротивление
стали одной из панелей пояса расцентрованного узла.
___________
1 Левитанский И. В., Куклин Ф.Ф.
Разработка и экспериментальные исследования новых типов строительных ферм из
широкополочных и гнутосварных профилей. — В кн.: Экспериментальные исследования
конструкций производственных зданий /Сб. науч. тр. ЦНИИпроектстальконструкции
им. Мельникова. — М.: Стройиздат, 1984. — С. 52-61.
Формула (107) учитывает
допустимость пластических деформаций металла в концевых сечениях стержней.
16.4. Для растянутых элементов решетки, рассчитываемых
без учета изгибающих моментов, следует принимать коэффициент условий работы gс = 0,85.
Рис. 28. Типы сопряжений двутавров с
прямоугольными гнутосварными профилями
а — К-образное; б — Т-образное; в —
опорное
Рис. 29. Типы сопряжении двутавров
а — К-образное; б — опорное
16.5.
Расчет устойчивости сжатых стержней при отсутствии на них поперечной нагрузки
выполняется без учета изгибающих моментов. Расчетные длины принимаются по табл.
11 СНиП II-23-81*.
Для ферм, при расчете которых учитываются изгибающие
моменты, допускается уменьшать расчетные длины элементов решетки в плоскости
фермы с учетом их упругого защемления в обоих поясах.
При отсутствии в узлах
сжатого пояса элементов усиления (см. п. 16.19)
в расчете его на устойчивость следует применять коэффициент условий работы gс = 0,85.
Элементы, раскрепляющие
сжатый пояс из плоскости фермы, и их крепления должны быть рассчитаны в
соответствии с п. 5.11 СНиП II-23-81*.
РАСЧЕТ УЗЛОВ
16.6.
Неподкрепленные узлы ферм (см. рис. 28,
29), состоящие из двутаврового
пояса и примыкающих к нему элементов решетки, следует проверять:
на отгиб участка полки
пояса, контактирующей с элементом решетки;
на несущую способность
участка стенки пояса, соответствующего сжатому элементу решетки;
на несущую способность
поперечного сечения пояса;
на несущую способность
элемента решетки в зоне примыкания к поясу;
на прочность сварных швов
прикрепления элемента решетки к поясу.
16.7.
В неподкрепленных примыканиях к поясу прямоугольного гнутосварного профиля в
К-образных и опорных узлах (см. рис.
28, а, в) при с £ 15 мм (с — половина расстояния между носками элементов решетки) несущую
способность пояса на отгиб полки следует проверять для каждого примыкания в
отдельности по формуле
, (109)
где N —
усилие в элементе решетки;
М — изгибающий момент в примыкающем элементе в
плоскости узла в сечении, совпадающем с примыкающей полкой пояса;
gс — коэффициент условий работы, принимаемый по табл.
6* СНиП II-23-81*;
gD — коэффициент, равный 1,5 —
s/Ry, если пояс сжат при s/Ry > 0,5, и 1 — в остальных случаях;
s — продольное напряжение в панели пояса со стороны растянутого
раскоса;
Ry —
расчетное сопротивление стали пояса;
Ryd — расчетное сопротивление
стали элемента решетки.
16.8.
В неподкрепленных примыканиях к поясу прямоугольного гнутосварного профиля в
узлах Т-образного типа (см. рис. 28,
б), а также в К-образных и опорных
узлах при с > 15 мм несущую
способность пояса на отгиб полки следует проверять по формуле
. (110)
При db = d можно пользоваться формулой
. (111)
16.9.
В неподкрепленных примыканиях к поясу широкополочного двутавра в К-образных и
опорных узлах при с < 15 мм (см. рис. 29) несущую способность пояса на
отгиб полки следует проверять по формуле
, (112)
где Ad — площадь поперечного сечения раскоса.
16.10.
Несущую способность стенки неподкрепленного двутаврового пояса под воздействием
сжатого элемента решетки из прямоугольного гнуто-сварного профиля следует
проверять по формуле
N £ 10gcgDRуtw(t + td)/sina. (113)
16.11.
Несущую способность стенки неподкрепленного двутаврового пояса под воздействием
сжатого элемента решетки из широкополочного двутавра следует проверять по
формуле
N £ 1,5gcgDRуdbtw/sin2a. (114)
16.12.
Несущую способность поперечного сечения неподкрепленного двутаврового пояса под
воздействием поперечной силы в узле следует проверять по формуле
, (115)
где Q — поперечная сила в узле,
равная в узлах К-образного типа меньшему из произведений Nsina;
— коэффициент, равный 1,3 — s/Ry, но не более 1,0;
Rs
— расчетное сопротивление стали пояса срезу;
А —
площадь поперечного сечения пояса;
;
r —
радиус закругления профиля пояса.
16.13.
Несущую способность элемента решетки в зоне примыкания к неподкрепленному
двутавровому поясу следует проверять по формуле
, (116)
где gd — коэффициент влияния знака усилия в примыкающем
элементе, принимаемый равным 1,2 при растяжении и 1,0 — при сжатии;
Ryd — расчетное сопротивление
стали элемента решетки;
x — коэффициент, равный для
элементов прямоугольного гнутосварного профиля в узлах:
а) К-образного типа — 0,14;
б) опорных — 0,06;
в) Т-образного типа — 0,10.
Для элементов из
широкополочного двутавра в К-образных и опорных узлах x = 0,05.
16.14.
Сварные швы, прикрепляющие элементы решетки (в неподкрепленных и усиленных
узлах), следует рассчитывать по прочности участков (стенок, полок) элемента
решетки.
16.15.
В узлах ферм, усиленных наклонными планками (рис. 30), следует проверять
несущую способность участка стенки двутаврового пояса, соответствующего
элементу решетки, по формуле
. (117)
Рис.
30. Узел фермы, усиленный наклонными планками
16.16.
В узлах, указанных в п. 16.15, рекомендуется проверять также несущую
способность наклонных планок, определяя действующую на них силу как разность
между усилием в элементе решетки N и
несущей способностью элемента, вычисленной в соответствии с рекомендациями п. 16.13.
16.17.
Формулы (109)-(112) построены на допущении одновременного развития пластичности
в полке пояса и контактирующем с ней участке стенки полки элемента решетки1.
Формулы (113), (114), (117), а также (115)2 основаны на упрощенных
представлениях о работе поясной стенки в зоне узла. Расчет по основанной на
опытных данных формуле (116) примыканий элементов решетки из гнутосварных
профилей лимитирует несущую способность неподкрепленных узлов в довольно
широком диапазоне параметров, значительно снижая коэффициент использования
сечения этих элементов решетки и требуя, тем самым, подкрепления полок поясных
двутавров.
___________
Цетлин Б. С.
Практический способ расчета узлов ферм с поясами из двутавров. //Строит.
механика и расчет сооружений. — 1983. -№ 1.- С. 71-73.
Wardenier J. Hollow Section Joints.
Delft University Press, 1982. — 544 с.
КОНСТРУИРОВАНИЕ
16.18.
Примыкания элементов решетки к поясам следует проектировать бесфасоночными
сварными.
16.19. Для
обеспечения несущей способности узлов рекомендуется полки двутавров в месте
примыкания к ним элементов решетки подкреплять продольными наклонными планками
(см. рис. 30). В местах примыкания
элементов решетки из двутавров, а также в Т-образных узлах со стойками при
наличии вертикальных фасонок для крепления связей допускается установка парных
ребер жесткости.
16.20.
Укрупнительные стыки ферм рекомендуется проектировать болтовыми фланцевыми: в
уровне сжатого пояса — на обычных, в уровне растянутого пояса — на
высокопрочных болтах (см. разд.
27).
16.21.
Горизонтальные связи по фермам допускается крепить к наружным полкам поясов.
16.22.
В соединении с колоннами (надколонниками) необходимо исключать вертикальные
перемещения конца верхнего пояса и обеспечивать его горизонтальную подвижность
на величину смещения относительно опорного узла.
16.23. Угловые швы на носках элементов решетки из
гнутосварных профилей при td > 5 мм рекомендуется выполнять с предварительной подготовкой кромок
(рис. 31).
|
|
a, град |
b, град |
S, мм |
|
35-45 |
90 |
2-3 |
|
|
46-60 |
75 |
3-4 |
|
|
61-90 |
55 |
3-5 |
Рис. 31. Деталь
приварки носков гнутосварных профилей
16.24.
Расстояние между поперечными швами на полках поясов (у носков элементов
решетки) следует принимать:
в опорных узлах и стыковых
узлах сжатого пояса — не менее 5 мм;
в остальных случаях (см. например, g на рис. 30) — не менее 20 мм.
17. ФЕРМЫ С ПОЯСАМИ ИЗ ШИРОКОПОЛОЧНЫХ ТАВРОВ И ПЕРЕКРЕСТНОЙ РЕШЕТКОЙ ИЗ
ОДИНОЧНЫХ УГОЛКОВ
ОБЩИЕ ПОЛОЖЕНИЯ
17.1.
Рекомендации настоящего раздела распространяются на фермы с поясами из
широкополочных тавров и перекрестной решеткой из одиночных равнополочных
уголков для покрытий производственных зданий (рис. 32).
Рис. 32. Схема и узел
фермы
17.2.
В разделе приведена подтвержденная результатами испытаний методика расчета
раскосов перекрестной решетки из одиночных уголков для ферм с поясами из
широкополочных тавров.
Особенность методики заключается в том, что
расчетная длина сжатого раскоса из плоскости фермы определяется как для центрально-сжатого
стержня с промежуточной упругой опорой с учетом внецентренности передачи усилия
в поддерживающем раскосе. Поскольку при работе в перекрестной решетке сжатого
раскоса с растянутым (основной случай) собственный прогиб растянутого раскоса
из плоскости фермы (без учета совместной работы раскосов) направлен в ту же
сторону, что и сжатого, влияние растянутого раскоса как поддерживающего стержня
уменьшается. Это проявляется в увеличении расчетной длины сжатого раскоса
перекрестной решетки. Предусматривается, что раскосы имеют равные длины, а узел
пересечения делит их пополам.
РАСЧЕТ ЭЛЕМЕНТОВ РЕШЕТКИ
17.3.
Расчет сжатых раскосов производится по формуле (7) СНиП II-23-81*с учетом коэффициента gс = 0,75.
Расчетная длина lef сжатого раскоса в плоскости
фермы принимается равной половине геометрической длины ld раскоса.
Расчетная длина lef сжатого раскоса из
плоскости фермы определяется по формуле
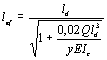
где Q — поперечная сила в узле пересечения
раскосов, определяемая в зависимости от характера усилия в поддерживающем
раскосе по формулам:
при растяжении
; (119)
при нулевом усилии
; (120)
при сжатии
; (121)
у — прогиб узла пересечения
раскосов из плоскости фермы, определяемый по формуле
; (122)
Ic, Ih — моменты инерции сечения
уголков относительно оси х—х соответственно сжатого и
поддерживающего раскосов;
Мс, Мh — изгибающие моменты
соответственно в сжатом и поддерживающем раскосах, определяемые как
произведение усилия Nc и Nh соответственно в сжатом и
растянутом раскосе на значение zo уголков раскосов;
nh, nc — безразмерные параметры
соответственно для поддерживающего и сжатого раскосов, определяемые по
формулам:
; (123)
. (124)
Радиус инерции i сечения уголка сжатого
раскоса принимается:
при расчетной длине в
плоскости фермы — минимальный (i = iyo min),
при расчетной длине из
плоскости фермы — относительно оси х—х (i
= ix).
17.4.
Расчет растянутого поддерживающего раскоса выполняется на прочность по формуле
, (125)
где Ah — площадь сечения уголка раскоса;
k — коэффициент, равный для
раскосов: опорного 0,9, рядового 1,0.
18. КОНСТРУКЦИИ ИЗ КРУГЛЫХ ТРУБ
ОБЩИЕ ПОЛОЖЕНИЯ
18.1.
Решетчатые конструкции из труб следует проектировать, как правило, с
непосредственными (без фасонок) сварными соединениями стержней в узлах,
предусматривая выполнение фигурной резки и разделки кромок труб для таких соединений
на специальных газорезательных машинах.
18.2.
Для трубчатых элементов конструкций следует применять преимущественно
электросварные трубы по ГОСТ 10704-76*.
При соответствующем обосновании допускается применять и другие виды стальных
труб.
18.3.
В решетчатых конструкциях, особенно при эксплуатации в агрессивной среде,
рекомендуется выполнять из труб как сжатые, так и растянутые стержни, при этом
наиболее нагруженные (сжатые — при гибкости не более 60) выполнять из стали с
пределом текучести 440 МПа (4500 кгс/см2) и более.
РАСЧЕТ
18.4. При
расчете сварных стыковых соединений трубчатых элементов при сварке без
подкладного кольца следует вводить коэффициент условий работы gwc = 0,75, а соединений
впритык (тавровых) с углом раскрытия шва более 30° (рассчитываемых как
стыковые) при сварке без подварки корня — gwc = 0,85.
18.5.
Расчетные длины lef элементов решетчатых
конструкций из труб с бесфасоночными узлами, за исключением элементов
перекрестной решетки, следует принимать по табл. 57.
Таблица
57
|
Направление |
Расчетная длина lef |
|||
|
поясов, опорных |
прочих элементов |
|||
|
без сплющивания концов |
со сплющиванием концов |
|||
|
одного или двух в |
двух в одной плоскости |
|||
|
В плоскости решетки |
l |
0,85 l |
0,9l |
0,95l |
|
В направлении, перпендикулярном плоскости решетки (из |
l1 |
0,85l1 |
0,9l1 |
0,95 l1 |
Обозначения, принятые в табл. 57:
l — геометрическая длина элемента (расстояние между центрами
узлов);
l1 — расстояние между
узлами, закрепленными от смещения из плоскости решетки.
18.6.
Расчет на прочность элементов из труб диаметром D и толщиной t со
сплющенными концами, подверженных центральному сжатию, следует выполнять по
формуле (5) СНиП II-23-81* с учетом
коэффициента gct, определяемого:
а) при свободном
формировании переходного участка от круглого сечения к сплющенному (с неплавным
переходом) по формуле
, (126)
но не более 0,7 и не менее 0,3;
б) при принудительном
формировании переходного участка [с плавным переходом на длине (2,5-3) D] по формуле
, (127)
но не более 1,0
и не менее 0,4.
18.7.
Расчет сварных стыковых соединений элементов из труб на центральное растяжение
или сжатие следует производить по формуле
, (128)
где Dm — средний (равный полусумме
наружного и внутреннего) диаметр трубы с меньшей толщиной стенки;
t —
наименьшая толщина стенки соединяемых труб;
Rwy и gwc — соответственно расчетное сопротивление и
коэффициент условий работы сварного стыкового соединения, принимаемый в
соответствии с п. 18.4.
Расчет сварных стыковых
соединений не требуется выполнять в случае сварки на подкладных кольцах с
применением сварочных материалов согласно прил. 2 СНиП II-23-81* и физического контроля качества растянутых швов.
18.8.
Расчет сварных соединений в прикреплениях элементов из труб впритык к другим
деталям (рис. 33) с цилиндрической
или плоской поверхностью (головным деталям) при действии продольной силы N следует выполнять по
формулам:
N £ 0,85 (Swh + Swt); (129)
N £ 2Swh; (130)
N £ 2Swt; (131)
где Swh и Swt —
несущая способность соответственно пяточной и носковой частей сварного шва
(частей шва, относящихся к половине сечения раскоса со стороны соответственно
острого и тупого углов пересечения оси трубы с поверхностью головной детали),
определяемая по формулам:
Swh = (tdlwahRwygwc + kflwfhRwd)gс; (132)
Swt = (tdlwatRwygwc + kflwftRwd)gс, (133)
здесь Rwy — расчетное сопротивление
сварного стыкового соединения растяжению или сжатию, принимаемое в соответствии
с п. 3.4 СНиП II-23-81*;
Rwd — меньшее из двух значений:
0,7Rwf или Rwz;
Rwf и Rwz — расчетные сопротивления
углового шва срезу (условному) соответственно по металлу шва и по металлу
границы сплавления;
td — толщина стенки
прикрепляемой трубы;
kf — катет (высота) углового
шва;
lwah и lwat — суммарные длины участков
шва, рассматриваемых как стыковые швы, соответственно в пяточной и носковой
частях шва;
lwfh и lwft — суммарные длины участков
шва, рассматриваемых как угловые швы, соответственно в
пяточной и носковой частях шва;
gwc — коэффициент условий работы сварного соединения
впритык, принимаемый в соответствии с п. 18.4.
В качестве угловых швов
следует рассматривать:
а) при резке конца
прикрепляемой трубы без скоса кромки (см. рис. 33, в)
участки шва, для которых угол раскрытия шва q, определяемый по формуле (134), составляет менее 30 или более
60°;
б) при резке конца
прикрепляемой трубы со скосом кромки под постоянным или переменным углом w (см. рис. 33, г и д) — участки, для которых значение q, вычисленное по формуле (134), составляет менее 15 или более
60°;
в) при резке конца
прикрепляемой трубы фрезой (см. рис.
33, е), а также в соединениях с
пропуском прикрепляемой трубы через отверстие в головной детали — всю длину
шва;
г) при пересечении раскосов
между собой, если рассматривается прикрепление “пропущенного” (не прерванного
на линии пересечения) раскоса к другому (“прерванному”), — всю длину участка
взаимного пересечения раскосов.
Остальные участки шва
следует рассматривать как стыковые швы.
Угол q следует определять по
формуле
, (134)
где bin = din/D — отношение внутреннего
диаметра прикрепляемой трубы к наружному диаметру головной детали (при
прикреплении к плоской поверхности bin = 0);
jd — угловая координата
прикрепляемой трубы для рассматриваемой точки шва, отсчитываемая от носковой
образующей.
Полную длину соответственно
пяточной и носковой частей шва lwh и lwt можно определять по графику
рис. 34, а относительную длину
участков углового шва lwfh/lwh и lwft/lwt — по графикам рис. 35. Длины участков стыкового шва
равны
lwah = lwh — lwfh; lwat = lwt — lwft.
Рис. 33. Схемы сечений сварного шва в узловом
соединении двух труб
а — развертка прикрепляемой трубы (А — носок; В — борт; С — пятка); б — эпюра q угла раскрытия сварного шва при резке без скоса
кромки; в — сечения шва при резке без
скоса кромки; г — то же, со скосом
кромки под постоянным углом w;
д — то же, со скосом кромки под
переменным углом w; е — то же, фрезой
Рис. 34. Графики для определения полной длины пяточного lwh и носкового lwt участков сварного шва
в соединении двух труб
18.9.
Расчет узла решетчатой трубчатой конструкции (плоской или пространственной
фермы), состоящего из одного не прерывающегося в узле трубчатого элемента
(пояса с тонкостенностью d не менее 20 и не более 60)
и п примыкающих элементов (рис. 36), на местный изгиб (промятие)
стенки пояса следует производить для примыкания каждого (j-го) элемента (dj ³ 0,2D) при всех расчетных
сочетаниях усилий в элементах узла по формулам:
(135)
. (136)
В формулах (135), (136):
i — номер примыкающего
элемента;
j — номер рассматриваемого
примыкающего элемента;
Ni или Nj — продольная сила в
примыкающем элементе, принимаемая с учетом знака “плюс” — при растяжении,
“минус” — при сжатии;
mi — коэффициент, при i = j определяемый по формуле
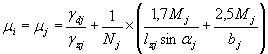
при i ¹ j mi = 1,
Рис. 35. Графики для определения коэффициентов lwfh/lwh и lwft/lvt при резке труб
а — без скоса кромки; б —
со скосом кромки
здесь gdj — коэффициент влияния знака усилия в рассматриваемом
примыкающем элементе, принимаемый равным 0,8 при растяжении и 1 — в остальных
случаях;
lzj — длина участка примыкания
(от носка до пятки) рассматриваемого элемента (для трубчатых элементов lzj = dj/sinaj);
gzj — коэффициент влияния длины
примыкания рассматриваемого элемента, для нецилиндрических примыканий
определяемый по формуле
,
для цилиндрических
примыканий (труб) gzj = 1;
Рис. 36. Узел пространственной решетчатой конструкции из труб
А — пятка, В — борт, С — носок
bi или bj — ширина примыкающего
элемента (для трубчатого элемента bi = di или bj = dj),
Мj,
— изгибающие моменты от основного воздействия в рассматриваемом
элементе в сечении, проходящем через точку пересечения оси этого элемента с образующей
пояса, соответственно в плоскости и из плоскости узла (момент от жесткости
узлов допускается не учитывать);
S — характеристика несущей способности пояса,
определяемая по формуле
S = 13 (1 +0,02d)t2Rygc; (137)
здесь Ry — расчетное сопротивление стали пояса;
d = D/t — тонкостенность пояса;
gс — коэффициент условий работы, принимаемый равным
0,9 при Ry ³ 375 МПа (3800 кгс/см2)
и 1 — в остальных случаях;
gDj — коэффициент влияния
продольной силы в поясе, при сжатии в поясе определяемый по формуле
, (138)
в остальных случаях gDj = 1;
Fj — наибольшее значение
продольной силы в поясе от носка до пятки рассматриваемого примыкающего
элемента;
А —
площадь сечения пояса;
gij — коэффициент влияния
подкрепления стенки пояса в узле поперечными пластинами (диафрагмами и т.п.),
принимаемый равным 1,25 при расположении подкрепляющей пластины в пределах
участка рассматриваемого примыкания (от носка до пятки) и 1 — в остальных
случаях;
eij — коэффициент влияния
расположения каждого из смежных (i-х)
примыкающих элементов по отношению к рассматриваемому (j-му), определяемый по табл. 58; при i = j
eij = 1;
yi = arcsinbwi,
bwi = bwi/D;
bwi — ширина охвата пояса
примыкающим элементом между кромками сварного шва (при bi £ 0,7 допускается принимать bwi = bw; при bi > 0,7 bwi = bw — tdi);
при bi £ 0,7 допускается принимать yi = 1,05bi (bi см. табл. 58);
при bi > 0,7 допускается принимать yi = 1,05bi(1 + 0,15bi).
Формула расчета несущей
способности пространственных узлов (135),
как и предложенные ранее для плоских узлов формулы (10) и (11) в [29], может
быть интерпретирована как уравнение некоторой предельной поверхности
(поверхности взаимодействия) в n-мерном
пространстве, координатами которого служат отношения несущей способности
отдельных примыканий (У-образных узлов) к несущей способности тех же примыканий
в составе сложных узлов. Уравнения, описывающие поверхность взаимодействия,
характеризуют соотношения между совокупно действующими усилиями в элементах
узла в его предельном состоянии.
18.10.
Прочность трубчатых элементов решетки в поперечном сечении, проходящем через
пятку, следует проверять по формуле
, (139)
где N — продольная сила в элементе
решетки;
c — коэффициент, принимаемый
равным: 0,008 — для раскосов в К-образных узлах, при расчете примыканий которых
значение коэффициента x,
определяемого по табл. 58,
составляет менее 0,85; 0,015 — в остальных случаях;
Ad — площадь поперечного
сечения элемента решетки;
gcd — коэффициент условий
работы, принимаемый равным: 0,85 — для элементов, пересекающихся в узле с двумя
другими элементами, имеющими разные знаки усилий; 1 — в остальных случаях;
Ryd — расчетное сопротивление
стали элемента решетки.
Таблица
58
|
Расположение оси |
Тип узла |
gij |
eij |
|
В той же плоскости и с той же стороны пояса (Фij = 0) |
К |
— |
|
|
В той же плоскости, но с противоположной стороны пояса (Фij = p) |
Х |
0 £ |
|
|
³ D |
0 |
||
|
В перпендикулярной плоскости (Фij = p/2) |
L |
0 £ gij < D/2 |
|
|
³ D/2 |
0 |
При
0 < eij
< p/2
или p/2 < Фij
< p следует eij принимать
интерполяцией между соответствующими значениями для Фij
= 0 и Фij = p/2
или для Фij = p/2
и Фij = p.
Значения xij следует принимать равными:
при
cij £
0 xij = 0,6;
”
0 < cij < D xij = 1 — 0,4(1 — cij/D)4;
” cij ³ D, xij = 0
Обозначения, принятые в табл.58 (см. рис. 36):
Фij — угол между плоскостями
примыкания смежного и рассматриваемого примыкающих элементов, рад (плоскость
примыкания проходит через ось примыкающего элемента параллельно оси пояса);
cij — наименьшее
расстояние вдоль оси пояса между сварными швами, прикрепляющими к поясу
рассматриваемый и смежный элементы решетки (продольный просвет): ;
gij — расстояние вдоль
пояса между бортами рассматриваемого и смежного примыкающих элементов:
;
bi
= bi/D — отношение ширины
примыкания смежного элемента к диаметру пояса (для трубчатых элементов (bi = di/D).
18.11.
При подкреплении стенки пояса в узле (в местах примыкания рассматриваемого
примыкающего элемента) прилегающей и приваренной к поясу накладкой толщиной td в формуле (137) вместо Ry следует принимать расчетное
сопротивление материала накладки Rya, а вместо t —
приведенную толщину tef, принимаемую равной: для растянутых примыкающих элементов ta, но не более l,5t; для сжатых — tmax + 0,25 tmin, где tmax — большая, a tmin — меньшая из толщин t и ta.
18.12.
В случае, если рассматриваемый элемент решетки пересекается в зоне узла с т смежными элементами (рис. 37),
расположенными в той же плоскости примыкания (Ф = 0), вместо Nisinai = Njsinaj = Рj
в формуле (135) следует
принимать приведенное усилие Рefj, определяемое по формуле
, (140)
где Pki — значения Pi для каждого из смежных
элементов, пересекающихся с рассматриваемым (j-м);
xkj — доля периметра сечения
смежного элемента, соответствующая участку его пересечения с рассматриваемым
(для трубчатых элементов );
здесь lkj, dk — соответственно длина
участка периметра сечения смежного элемента, соответствующая пересечению с
рассматриваемым, и наружный диаметр смежного элемента.
Если сварной шов не
охватывает всего периметра смежного элемента (см., например, рис. 37, б), то xkj следует принимать равным , где
— сумма участков
периметра смежного элемента, соответствующих участкам наложения сварных швов.
Если у
элемента решетки, пересекающегося с другими в зоне узла, приварка к поясу
отсутствует или мала (xD < 0,25, где xD — доля периметра сечения элемента, соответствующая
участку его приварки к поясу), то действие такого элемента на пояс не следует
учитывать, т.е. значение pj или рi для
него в формулу (135) не
подставлять, а полностью распределять добавлением xkjPki между смежными элементами.
Рис. 37. Бесфасоночные узлы с пересечением элементов решетки между собой
а — с двумя элементами решетки (I — развертка трубы 1; II —
развертка трубы 2); б — с тремя
элементами решетки (со сплющиванием стойки); 1 — “прерванный” элемент решетки; 2 — “пропущенный” элемент решетки; 3 — участок взаимного пересечения элементов решетки
18.13.
Для каждого элемента решетки, пересекающегося в узле с другими элементами,
следует проверять совокупную прочность стенок всех элементов (пояса и решетки),
с которыми пересекается рассматриваемый элемент, по формуле
, (141)
где Nj — усилие в рассматриваемом элементе;
Sp — характеристика несущей
способности каждого из головных (играющих роль пояса) элементов (пояса и
смежных элементов решетки, пересекающихся с рассматриваемым), определяемая по
формуле (137), в которой в
качестве d, t и Ry принимаются соответствующие
характеристики головного элемента;
gDp — коэффициент влияния
продольной силы в каждом головном элементе, определяемый по формуле (138), в которой в качестве F, А и Ry
принимаются соответствующие характеристики головного элемента;
xрj — доля периметра сечения рассматриваемого элемента,
соответствующая линии его пересечения с каждым головным элементом, определяемая
по формуле
xрj = lpj/(pdj);
здесь lpj — длина участка периметра
сечения рассматриваемого элемента, соответствующая линии пересечения с головным
элементом;
ypj — угол полуохвата каждого
головного элемента примыканием рассматриваемого элемента, определяемый по
формуле
ypj = arc sin(bwj/Dp);
здесь Dp — наружный диаметр головного элемента;
apj — угол примыкания
рассматриваемого элемента к каждому головному элементу.
КОНСТРУИРОВАНИЕ
18.14.
Толщину стенок труб, применяемых для основных несущих элементов конструкций
(поясов и опорных раскосов, ветвей колонн и т.п.) следует принимать не менее 3
мм, для прочих — не менее 2,5 мм.
18.15.
При непосредственных (бесфасоночных) соединениях в узлах тонкостенность 5
поясов рекомендуется принимать не более значений, приведенных в табл. 59, тонкостенность примыкающих
элементов — по возможности максимальной, но не более значений, приведенных в табл. 59. Толщину стенок примыкающих
элементов следует принимать не больше толщины стенок поясов.
Таблица
59
|
Предел текучести стали |
Тонкостенность |
||
|
поясов d |
примыкающих элементов dd = d/td |
||
|
сжатых |
растянутых |
||
|
До 295 (3000) |
30 |
90 |
90 |
|
Св. 295 (3000) до 390 (4000) |
35 |
80 |
90 |
|
Св. 390 (4000) |
40 |
70 |
90 |
Примечания: 1. Указанные в табл. 59
значения d для поясов являются
ориентировочными и не исключают необходимости проверки прочности узлов.
2. Для сжатых
примыкающих элементов при указанных в табл.
59 значениях dd не требуется проверки их стенок на местную
устойчивость.
18.16.
При бесфасоночных узлах диаметры труб решетки рекомендуется принимать равными
не менее 0 диаметра поясов и не более диаметра поясов.
19. ПОКРЫТИЯ ИЗ ПЕРЕКРЕСТНЫХ ЭЛЕМЕНТОВ
ОБЩИЕ ПОЛОЖЕНИЯ
19.1.
Покрытия из перекрестных элементов (далее для краткости — “покрытия”) относятся
к пространственным конструкциям, которые образованы из линейных в плане несущих
элементов, ориентированных по двум направлениям и более. Элементы соединены
между собой в местах пересечения и под внешними воздействиями работают
совместно. При прямоугольной или квадратной форме покрытия внутренние элементы
обычно располагаются параллельно сторонам плана на равных расстояниях между
собой и при пересечении образуют регулярную сетчатую систему с прямоугольными
или квадратными ячейками (рис. 38).
Рис. 38. Покрытие из перекрестных элементов
По
форме покрытия могут быть плоскими или вспарушенными относительно
горизонтальной поверхности. Внутренние элементы покрытия могут опираться на
колонны, расположенные по периметру покрытия, или на контурные элементы,
которые в свою очередь могут располагаться на сплошных стенах, на рядах
отдельных колонн или на колоннах по углам покрытия.
19.2.
Покрытия могут применяться для общественных зданий и производственных зданий
промышленности и сельского хозяйства. При опирании по углам покрытия эффективно
используются при квадратной или прямоугольной разреженной сетке колонн с шагом
не менее 12 м и имеют размеры: 12´18, 18´18, 18´24, 24´24, 30´30 м и более. При этом
покрытия обычно делятся на отдельные блоки, соответствующие сетке колонн. Для
монтажа покрытия блоками рационально используется конвейерная сборка и
крупноблочный монтаж.
КОНСТРУКЦИИ ПОКРЫТИЙ
19.3.
Несущие элементы покрытия (см. рис. 38)
разделяются на контурные 3 и
внутренние — основные 1, 2 и дополнительные 5. В состав покрытия входят также элементы ограждения 4, которые вместе с дополнительными
элементами могут совмещать в себе функцию несущих элементов. Контурные и
внутренние несущие элементы выполняются в виде балок или ферм. Покрытие с
элементами из балок будет однослойным, а с элементами из ферм — двухпоясным.
Дополнительные элементы выполняют функцию прогонов, распорок, шпренгелей и пр.
Основным видом ограждающих элементов является стальной профилированный настил.
Могут также применяться стальные или алюминиевые плоские листы — мембраны. При
теплых кровлях по настилу или мембранам укладывается эффективный утеплитель с
пароизоляцией и рулонным ковром. Материалы для конструкций покрытия и
соединений выбираются в соответствии с требованиями СНиП II-23-81*.
19.4.
Отдельные элементы или покрытие в целом могут быть предварительно напряжены.
При нестесненных по высоте габаритах и опирании по углам может быть
использовано покрытие, у которого основные несущие элементы направлены по
диагоналям плана и вспарушены в центре. Жесткие или гибкие дополнительные
несущие элементы располагаются между диагональными основными и ориентированы в
каждом из четырех секторов параллельно соответствующим сторонам покрытия.
19.5.
Главной конструктивной особенностью покрытий является пересечение несущих
элементов. Обычно оно осуществляется в одном или в двух уровнях как поэтажное.
В случае форменных покрытий понятия “в одном уровне” или “поэтажное” относятся
к пересечению поясов ферм противоположных направлений. Пересечения внутренних
элементов между собой, а также соединение их с контурными элементами должны
обеспечивать совместную деформацию элементов в узле. При проектировании чаще
предусматривается жесткая работа узла пересечения без дополнительной
податливости.
19.6.
Покрытия за счет своей пространственности эффективно работают на восприятие
неравномерных или сосредоточенных нагрузок. Условная эквивалентная нагрузка на
покрытие от подвесных кранов при квадратных планах в 1,5-2 раза меньше, чем на
аналогичные покрытия из плоских ферм или балок.
19.7.
Жесткость и неизменяемость покрытия обеспечиваются системой перекрещивающихся
элементов и связей, а также за счет крепления к верхним поясам покрытия
прогонов, профилированного настила или мембран. Элементы ограждения участвуют в
восприятии сдвигающих усилий, действующих на покрытие в горизонтальной
плоскости, и их крепление к несущим элементам должно обеспечивать передачу этих
усилий. Крепление настила или мембраны осуществляется на самонарезающих болтах
или дюбелях, устанавливаемых в каждой волне настила с шагом не менее 300 мм.
РАСЧЕТ
19.8.
Покрытия при изгибе от внешней нагрузки в своей плоскости или из плоскости
являются статически неопределимыми системами. Расчет их следует производить на
ЭВМ как упругой стержневой системы с использованием стандартных программ.
Соединения в узлах следует принимать шарнирными и, как правило,
недеформируемыми. Возможную податливость соединений следует учитывать в
расчете.
Нормативные требования к
покрытиям и отдельным элементам в части предельных прогибов, деформаций,
гибкостей и пр. устанавливаются в соответствии с требованиями СНиП II-23-81*
19.9.
При невозможности использовать для расчета ЭВМ расчет покрытия рекомендуется
выполнять приближенными способами; например, как системы, состоящей из
неразрезных балок на упруго оседающих опорах, основываясь на следующих
предпосылках:
1) покрытие условно
разбивается на две системы перпендикулярных главных и второстепенных балок
(рис. 39). При этом если элементы одного из направлений обладают большей
жесткостью, то они считаются главными, например, элементы большей длины при
прямоугольной форме плана (см. рис. 39). Тогда элементы перпендикулярного
направления считаются второстепенными. В покрытиях с элементами равной
жесткости главными могут быть приняты элементы любого направления;
Рис. 39. Разбивка покрытия на главные и второстепенные балки
2) в основной расчетной
системе, в местах пересечения второстепенных балок с главными, предполагаются
условные шарниры; главные балки (неразрезные) являются упругими опорами для второстепенных
(см. рис. 39). Влияние кручения на работу балок не учитывается;
3) коэффициенты податливости
упругих опор определяются в зависимости от геометрических параметров главных
балок и места их пересечения с второстепенными балками;
4) изгибающие моменты в
месте условных шарниров определяются исходя из равенства нулю углов поворота на
концах второстепенных балок.
19.10.
Для квадратных покрытий, у которых внутренние элементы одинаковой жесткости при
пересечении образуют регулярную квадратную сетку с числом ячеек на стороне от 4
до 6, нагруженных равномерно распределенной нагрузкой и имеющих сплошное
опирание по контуру (рис. 40), усилия во внутренних балках рекомендуется
определять по формулам:
максимальный изгибающий
момент
М =
aраl2, (142)
нагрузка на 1 м длины балки
q = bра, (143)
где a, b — коэффициенты,
определяемые по табл. 60;
р —
интенсивность нагрузки на 1 м2 покрытия;
l — сторона покрытия, м;
— размер ячейки, м;
n — число ячеек на стороне
покрытия.
Рис. 40. Квадратное покрытие из перекрестных элементов с регулярной квадратной
сеткой
Таблица 60
|
Число ячеек на стороне |
Коэффициенты |
Значения коэффициентов |
||
|
а |
2a |
3а |
||
|
4 |
a |
520 |
703 |
520 |
|
b |
4150 |
5620 |
4150 |
|
|
5 |
a |
395 |
686 |
686 |
|
b |
3160 |
5550 |
5550 |
|
|
6 |
a |
366 |
654 |
794 |
|
b |
2930 |
5230 |
6350 |
19.11.
При равномерной нагрузке на покрытие внутренние основные элементы, расположенные
ближе к середине покрытия, значительно перегружены по сравнению с элементами,
близкими к контуру. Для выравнивания усилий с целью последующей унификации
сечений внутренних элементов для квадратных или близких к квадратным покрытий,
опертых по углам под действием равномерной нагрузки (см. рис. 40), установлено, что отношение площадей сечений
контурных элементов Ae и внутренних элементов Ai должно подчиниться зависимости:
Ae/Ai = 0,5n ¸ 0,5(n + 2). (144)
КОНСТРУИРОВАНИЕ
19.12.
Покрытия образуются из конструктивных элементов-балок, ферм, прогонов и
элементов, аналогичных входящим в состав покрытий из плоских элементов.
Расчет и проектирование
элементов покрытий и соединений производятся в соответствии с требованиями СНиП II-23-81*.
19.13.
Балочные покрытия рационально используются при пролетах в двух направлениях
18-24 м и нагрузках на покрытие до 4 кН/м2 (400 кгс/м2).
Внутренние элементы у них принимаются длиной на пролет покрытия и не делятся на
основные и дополнительные. В ферменных покрытиях, как правило, различают
основные форменные элементы и дополнительные типа прогонов.
19.14.
В балочных покрытиях внутренние элементы принимаются, как правило, в виде двутавров:
прокатных обычных и широкополочных, сварных с обычными и тонкими стенками,
составных бистальных, с перфорированными стенками и других. Контурные элементы
при пролетах до 18 м также принимаются балочными, а при больших пролетах — в
виде шпренгельных систем или ферм.
19.15.
В ферменных покрытиях плоскости внутренних и контурных ферм ориентированы
перпендикулярно плоскости покрытия. Фермы принимаются трапециевидного очертания
или с параллельными поясами, а сечения поясов и решетки принимаются открытого
либо замкнутого профиля. Замкнутый профиль чаще применяется из тонкостенных
гнутых профилей.
19.16.
Крепление контурных ферм к колоннам, а также внутренних ферм к контурным
осуществляется чаще с использованием нисходящего раскоса. Пересечение
внутренних ферм между собой, а также примыкание к контуру осуществляется в
узлах. Внеузловое сопряжение ферм не рекомендуется.
19.17.
Дополнительные прогоны в ферменных покрытиях принимаются сплошного сечения или
со шпренгелем. Членение крупных ячеек прогонами увязывается с ориентацией
гофров профилированного настила. При перпендикулярной ориентации прогонов и
гофров настила (см. рис. 38)
достигается наилучшее их использование для придания покрытию жесткости в
горизонтальной плоскости, развязки верхних поясов внутренних ферм и обеспечения
работы профилированного настила на длине ячейки по двухпролетной схеме.
19.18.
В местах пересечения внутренних элементов и в местах примыкания их к контуру
осуществляется их совместная работа, выражающаяся в совместности деформаций, а
также в передаче вертикальных и горизонтальных усилий с элемента на элемент.
Соединение элементов выполняется болтами нормальной точности, высокопрочными
(фрикционными), сваркой или различными замковыми сочленениями.
19.19.
Узлы пересечения могут быть заводскими или монтажными. Конструкция определяется
принятой технологией сборки и монтажа покрытия. Податливость узлов зависит от
деформативности деталей и соединений. Соединения на высокопрочных болтах или
сваркой, практически недеформируемы, а на болтах нормальной точности их
деформативность определяется неупругими подвижками за счет разности диаметров
болтов и отверстий.
19.20.
Для балочных покрытий узлы соединения аналогичны соединениям в балочных
клетках. При поэтажном сопряжении совместность работы обеспечивается
соединением соприкасающихся поясов балок на высокопрочных болтах. Соединения в
одном уровне чаще выполняются за счет передачи вертикальных усилий через
столики, а горизонтальных — через ребра свариваемые или на болтах.
19.21.
В покрытиях с фермами чаще используются пересечения в одном уровне. При этом
монтажные стыки располагаются непосредственно в местах пересечения либо в
других местах. При квадратных ячейках и расположении монтажных стыков в узлах
пересечения отправочные марки внутренних ферм принимаются одинаковой длины,
равной размеру ячеек.
19.22.
В покрытиях с фермами из парных уголков узлы пересечения и примыкание к контуру
решаются по типу примыкания плоских стропильных ферм к подстропильным. Они
выполняются на фасонках или фланцах. При больших усилиях в поясах, а также при
замкнутых и Н-образных профилях в сжатые стыки верхних поясов вводятся
дополнительные замковые элементы на болтах типа жестких тумб, а растянутые
пояса при этом соединяются между собой через плоские узловые крестовины,
объединяющие пояса по трем-четырем направлениям.
19.23.
Для ферм из прямоугольных и квадратных замкнутых тонкостенных профилей при
поэтажном пересечении поясов может быть использовано решение (рис. 41), при котором
фермы одного направления 1 имеют
полную заводскую готовность, а фермы другого направления 2 поступают на монтаж с отсоединенными нижними поясами. При сборке
блоков покрытия отсоединенный пояс ферм второго направления пропускается через
решетку ферм первого направления и присоединяется к узлам верхней части ферм
своего направления на болтах, работающих в основном на сдвиг (рис. 42).
Рис. 41. Узел пересечения ферм из прямоугольных замкнутых профилей
Рис. 42. Узел фермы с отсоединяющимся нижним поясом
20. СТРУКТУРНЫЕ КОНСТРУКЦИИ ПОКРЫТИЙ ИЗ ПРОкатных профилей
ОБЩИЕ ПОЛОЖЕНИЯ
20.1.
Рекомендации настоящего раздела распространяются на проектирование структурных
конструкций из прокатных профилей, предназначенных для покрытий одноэтажных
производственных зданий массового применения, а также зданий и сооружений
гражданского и сельского строительства [30].
Структурные конструкции из
прокатных профилей представляют собой двухпоясную пространственную стержневую
систему с ограждающими конструкциями покрытия, опирающимися на верхние пояса,
которые выполняются неразрезными из двутавров или других профилей, эффективно
работающих на сжатие с поперечным изгибом. Остальные элементы системы
выполняются из одиночных уголков, прикрепляемых в узлах одной полкой непосредственно
или через фасонку, с соединениями на болтах нормальной точности или сваркой. В
некоторых случаях допускается применение в элементах парных уголков.
Конструкция может иметь
регулярную (каждая ячейка заполнена раскосами) или нерегулярную решетку (в ряде
ячеек раскосы отсутствуют), рис. 43.
20.2.
Расчет структурной конструкции рекомендуется производить по недеформированной
схеме без учета физической нелинейности работы стали.
20.3.
В качестве расчетной модели конструкции принимается пространственный стержневой
блок, опирающийся на четыре колонны, воспринимающий вертикальные нагрузки, а
также горизонтальные воздействия от примыкающих элементов здания или
оборудования с учетом особенностей их приложения и конструктивного решения
узлов (рис. 44). Расчетная модель
включает неразрезные поясные элементы, в том числе продольные изгибно-жесткие
элементы верхнего пояса, загруженные по своей длине поперечной нагрузкой.
Условные обозначения:
___________ верхние пояса ————
раскосы _________ нижние пояса
Рис. 43. Схемы структурных конструкций из прокатных профилей
1 — балочные элементы верхнего пояса; 2 — верхние пояса торцевых ферм; 3 — распорки верхнего пояса; 4 — сжатые раскосы приопорной зоны
20.4.
Для конструкций с регулярной решеткой допускается принимать шарнирно-стержневую
расчетную модель с узловой передачей нагрузки.
Изгибающие моменты М в продольных сжато-изогнутых поясах
определяются сложением эпюр:
для внутренних поясов
M = Mq + Mf,
где Mq, Mf — соответственно моменты
для многопролетной неразрезной балки на жестких опорах и моменты в балке от
прогиба всей системы;
для контурных (крайних)
поясов
M = Mq + Mf
+ Me + Mh,
где Me, Mh — соответственно момент от
эксцентрического крепления верхнего пояса (см. рис. 44, а, б) и момент от горизонтальной нагрузки,
передаваемой колонной на опору блока.
Рис.
44. Узловые соединения элементов из прокатных профилей
а-в — верхних поясов; г-к
— нижних поясов; л—м — распорок
РАСЧЕТ ЭЛЕМЕНТОВ
20.5.
Верхний пояс при устройстве кровли по стальному профилированному настилу
следует рассчитывать на устойчивость как сжато-изогнутую неразрезную балку
только в плоскости действия момента. Конструкция крепления настила к поясу
должна обеспечивать его устойчивость из плоскости действия момента, о чем
следует указать в проекте. При недостаточном креплении профилированного настила
к поясам или при ограждающих конструкциях покрытия без профилированного настила
(например, асбестоцементные плиты, деревянные щиты и т.д.) верхние пояса
следует рассчитывать на устойчивость как в плоскости, так и из плоскости
действия момента.
Расчет на устойчивость
сжато-изгибаемых элементов поясов постоянного сечения в плоскости действия
момента, совпадающей с плоскостью симметрии, следует производить в соответствии
с п. 5.27* с учетом требований пп. 5.28 и 5.33 СНиП II-23-81*.
Величину изгибающего момента
М при определении эксцентриситета e = M/N следует принимать равной наибольшему значению в пределах средней трети
длины панели.
20.6.
Контурные верхние сжато-изогнутые пояса кроме расчета на устойчивость в
центральных панелях с наибольшей продольной силой следует проверять на
устойчивость в первой и второй панелях от опоры. Величину изгибающего момента
следует принимать равной наибольшему значению в пределах ближайшей к опоре
трети длины панели.
20.7.
Контурные двутавровые пояса в крайней и во второй от опоры панелях и их
крепление в опорном узле следует проверять также на прочность в соответствии с
п. 5.25 СНиП II-23-81*. При этом в формуле (49) СНиП II-23-81* величины изгибающих
моментов Mx и My следует принимать с учетом
всех нагрузок и условий закрепления пояса: для крайней панели — в сечении у
опоры, для второй панели — у первого узла от опоры блока.
При расчете пояса во второй
панели влияние изгибающего момента My допускается не учитывать.
20.8.
Расчетную длину lef сжато-изогнутых двутавровых
поясов следует принимать равной 0,85l
(где l — геометрическая длина
панели).
20.9.
Расчет на устойчивость верхних контурных поясов из одиночных уголков при
действии узловой нагрузки следует выполнять как центрально-сжатых элементов в
соответствии с п. 5.3 СНиП II-23-81*.
В приопорной панели следует
производить расчет поясов на устойчивость в плоскости наименьшей жесткости при
действии продольной силы N и
изгибающего момента М от внецентренно
передаваемой на опору структуры горизонтальной нагрузки. Расчет следует
выполнять в соответствии с п. 5.27* СНиП II-23-81*. При этом величину M следует принимать равной наибольшему значению в пределах длины панели,
а расчетную длину lef —
равной 0,85l при радиусе инерции i = imin.
Устойчивость пояса из
плоскости действия момента при отсутствии внеузловой нагрузки проверять не
следует.
20.10.
Расчет на прочность элементов нижнего пояса необходимо производить в
ослабленных сечениях стыков и узлов.
Расчет на прочность
элементов, присоединенных в узлах двумя полками на болтах с симметричным
расположением отверстий на полках на расстоянии от обушка, равном 2zo, следует выполнять как
центрально-растянутых в соответствии с п. 5.1, а в остальных случаях — в
соответствии с п. 5.2 СНиП II-23-81*, при этом
значения коэффициента gс в формуле (6) СНиП II-23-81* следует принимать по табл.
61 настоящего Пособия, а площадь сечения элемента Аn
в формулах (5) и (6) СНиП II-23-81* при
невыполнении условий п. 12.19* СНиП
II-23-81* —
определять с учетом ослабления его отверстиями, расположенными в
зигзагообразном сечении поперек усилия.
Таблица
61
|
Элементы конструкций |
Коэффициент условий |
|
1. Неразрезные сжато-изогнутые (элементы 1, см. рис. 43) и |
1,00 |
|
2. Сжатые контурные пояса из одиночных уголков (элементы 2, см. рис. 43), соединенные болтами или сваркой в расчетах |
0,95 |
|
3. Разрезные сжатые пояса (элементы 3, см. рис. 43) из одиночных уголков, |
|
|
одним (см. рис. 44, и-м), |
0,75 |
|
двумя болтами и более или |
0,85 |
|
4. Сжатые раскосы из одиночных уголков, прикрепляемые одной |
|
|
сваркой или двумя болтами и |
1,00 |
|
сваркой или двумя болтами и |
0,85 |
|
одним болтом на обоих концах |
0,75 |
|
сваркой |
0,90 |
|
5. Растянутые нижние пояса из одиночных равнополочных |
|
|
при b/t = 12-13; d/b = 0,21-0,24: |
|
|
c/b = 0,3 |
0,75 |
|
c/b = 0,4; c/b = 0,7 |
0,80 |
|
c/b = 0,5; c/b = 0,6 |
0,90 |
|
” b/t = 15-16; d/b |
|
|
c/b = 0,3; c/b = 0,7 |
0,85 |
|
c/b = 0,4 |
0,90 |
|
c/b = 0,5 |
0,95 |
|
” b/t = 15-16; d/b |
|
|
c/b = 0,3; c/d = 0,4 |
0,90 |
|
c/b = 0,5; c/b = 0,6; c/b |
0,95 |
Обозначения, принятые в табл. 61 (см. рис. 43 и 44).
b, t — соответственно ширина и толщина
полки уголка;
d — диаметр отверстия;
с — расстояние от обушка до центра
отверстия.
Примечание. При промежуточных значениях с/b коэффициент gc определяется линейной
интерполяцией.
При ослаблении сечения менее
чем на 5 % в формулах следует принимать площадь сечения А и коэффициент условий работы gс = 1,0.
20.11.
Расчет стыковых накладок нижних поясов при размещении средних отверстий на продольной
оси следует производить на центральное растяжение по формуле (5) СНиП II-23-81*, а при смещении с оси — на
внецентренное растяжение по формуле (50) СНиП II-23-81*.
20.12.
Расчет на прочность растянутых элементов из одиночных уголков, присоединяемых в
узлах двумя полками сваркой, а также нижних поясов в сварных торцевых фермах,
следует выполнять как центрально-растянутых в соответствии со СНиП II-23-81*. Коэффициент условий работы для опорного раскоса,
прикрепляемого сваркой, следует принимать равным 0,9, в остальных случаях — по
табл. 6*СНиП II-23-81*.
20.13.
Растянутые элементы и пояса из одиночных уголков, прикрепленных одной полкой на
сварке, следует рассчитывать на прочность как внецентренно- растянутые в
соответствии с п. 5.25* СНиП II-23-81*. При этом
значения коэффициентов Сх,
Су в формуле (49) СНиП II-23-81*, учитывающие развитие
пластических деформаций, следует принимать равными 1,25, а коэффициента п — равным 1,5.
Значение изгибающего момента
при отсутствии на элементе поперечной нагрузки следует принимать в плоскостях:
перпендикулярной прикрепленной полке My = eхN, параллельной Mх = eyN (еx
= zo; eу = zo — a ; где а — расстояние от обушка уголка до центра тяжести сварных швов).
Обозначения и ориентацию сечения см. на рис.
22.
При распределении сварных
швов на обушке и пере уголка в соотношении от 0,5:0,5 до 0,65:0,35 влиянием
момента, действующего в плоскости, параллельной прикрепленной полке, допускается
пренебрегать. Элементы с таким креплением допускается также рассчитывать на
прочность как центрально-растянутые по формуле (5) СНиП II-23-81* с коэффициентом условий работы gс = 0,75.
20.14.
Расчетная несущая способность элементов из одиночных уголков, прикрепленных
одной полкой на болтах, определяется по прочности, устойчивости, смятию металла
элемента и по срезу болтов.
20.15.
Растянутые элементы из одиночных уголков, прикрепленные одной полкой на болтах,
рассчитываются как центрально-растянутые в соответствии с п. 5.2 СНиП II-23-81*. При этом коэффициент gс условий работы в формуле (6) СНиП II-23-81* следует принимать по прил. 4* СНиП II-23-81*
20.16.
Сжатые элементы из одиночных уголков, прикрепленные в узле одной полкой
сварными швами с центром тяжести швов или болтами с риской на расстоянии 0,45-
0,55b от обушка (где b — ширина полки уголка),
следует рассчитывать на устойчивость как центрально-сжатые в соответствии с п.
5.3 СНиП II-23-81*. При определении гибкости
этих элементов радиус инерции i
сечения уголка принимается равным imin, а расчетная длина lef = ml, где m определяется по рис. 45
настоящего Пособия в зависимости от lо = l/imin.
Коэффициенты условий работы gс принимаются для блоков: с регулярной решеткой — по табл. 61 настоящего Пособия, с
разреженной — независимо от места установки элемента в конструкции и условий
закрепления в узлах gс = 0,75.
20.17.
Сжатые элементы из одиночных уголков в случаях, не оговоренных в пп. 20.9 и
20.16, следует рассчитывать на устойчивость в соответствии с п. 5.34 СНиП II-23-81*.
При вычислении приведенного
относительного эксцентриситета mef,y = hmy для сечений из одиночных уголков коэффициент h следует определять как для
сечений типа 11 по табл. 73 СНиП
II-23-81*/
В расчетах следует принимать
значения изгибающего момента М и
радиуса инерции сечения i
относительно главных осей сечения.
При определении гибкости
верхних контурных поясов в обеих плоскостях расчетная длина lef = 0,85l.
Расчетная величина изгибающих моментов в каждой плоскости принимается равной
наибольшей в пределах панели пояса.
Рис. 45. График для определения значений m для раскосов и
разрезных поясов, прикрепленных в узлах одной полкой
1 — одним болтом; 2 — двумя болтами и более (вдоль элементов) или сваркой
20.18.
Расчетную несущую способность болтового соединения следует определять в
соответствии с пп. 11.7* и 11.8 СНиП
II-23-81*;
коэффициент условий работы gc принимается равным 1,0, а коэффициент условий
работы gb для соединений прокатных
элементов из стали с пределом текучести до 380 МПа (3900 кгс/см2),
осуществляемых на болтах нормальной точности, — по табл. 62 настоящего Пособия.
Таблица
62
|
Вид расчета и |
Коэффициент условий |
|
|
одноболтового |
многоболтового |
|
|
На срез |
1,00 |
0,90 |
|
На смятие при расстояниях: |
||
|
a ³ 2d; b ³ |
1,00 |
0,90 |
|
а = 1,63d; b ³ |
0,90 |
0,80 |
|
а = 1,5d; b > 2d; и a > 1,5d; b = 2d |
0,85 |
0,75 |
|
а ³ 2d; b = 2,32d |
1,00 |
0,85 |
|
а = l,35d; a1 = l,35d при |
0,65 |
0,60 |
|
На смятие элементов, работающих только на сжатие (раскосы |
||
|
b = 2,5d |
1,00 |
0,90 |
|
b = 2,3d |
1,00 |
0,85 |
|
b = 2d |
1,00 |
0,75 |
Обозначения, принятые в табл. 62:
а — расстояние от края
элемента до центра ближайшего отверстия вдоль усилия;
а1 — расстояние от края скоса
до центра ближайшего отверстия;
b — расстояние между центрами отверстий;
d — диаметр отверстия.
Примечания: 1. Значения коэффициентов gb, относятся к элементам из уголков без cкоса полки с отверстием (рис. 46, в).
2. Скос полки
с отверстием в растянутых элементах следует выполнять по рис. 46, б — г, при этом a1
³
1,35d при толщине полки, равной или меньше 6 мм, и а1 ³1,25 — при толщине
полки свыше 6 мм. В сжатых элементах скос допускается выполнять по рис. 46, д при а ³
1,25d. Скосы при изготовлении выполняются без допуска в сторону
уменьшения, о чем должны быть даны указания в проекте.
3. При
промежуточных значениях а и b коэффициент gb определяется линейной
интерполяцией. При одновременном изменении а
и b в соединении следует принимать значение коэффициента,
полученного интерполяцией для а при b = 2,5d и для b при а = 2d.
Рис.
46. Расположение отверстий для болтов в уголках структурных
конструкций
а — без скоса полки; б—д — со скосом полки; е—и
— развертки соответственно для а—в и г,
д; 1—1, 2—2, 2-2¢,
2-2¢¢ — расчетные сечения
КОНСТРУИРОВАНИЕ
20.19.
При проектировании структурных конструкций из прокатных профилей кроме
требований разд. 12 СНиП II-23-81* следует
соблюдать дополнительные требования, приведенные в настоящем разделе.
20.20.
Элементы структурных конструкций и узловых соединений следует конструировать с
максимальной унификацией элементов, деталей и технологических операций с учетом
изготовления их на автоматизированных поточных технологических линиях. Для
каждого номера профиля следует принимать одну толщину и одну марку стали.
Деление конструкции на
сборочные элементы следует производить с учетом исключения для большинства
элементов операций сборки и сварки, сосредоточивая их на минимальном числе
транспортабельных стержневых и плоскостных элементов.
Конструкция заводских,
монтажных или комбинированных узловых соединений определяется их назначением и
принятой технологией изготовления, сборки и монтажа покрытия. Заводские
соединения следует выполнять сварными, монтажные — на болтах.
20.21.
Узловые соединения уголковых элементов следует конструировать без фасонок. При
конструктивной невозможности размещения большого числа болтов в узле
допускается применять накладные (или пристыкованные к перу поясного уголка
сваркой) фасонки при условии заведения уголков решетки на полку поясного
уголка.
Для обеспечения размещения
сварных швов или болтов в пределах полок поясных уголков допускается смещать
точки пересечения осей элементов решетки в узлах с осей поясов до обушков
уголка.
20.22.
Для соединения элементов следует принимать болты нормальной точности, а диаметр
отверстия назначать больше диаметра болта на 1,5 мм. Соединение элементов, в
которых возникают знакопеременные усилия, следует проектировать сварными или на
высокопрочных болтах.
Болты следует принимать
одного диаметра и не более чем трех размеров по длине.
20.23.
Сдвиговые деформации в соединениях из-за разности в диаметрах отверстия и болта
следует учитывать при назначении строительного подъема и конструировании
соединений структурной конструкции с неподатливыми элементами зданий и
оборудования (фахверком, стенами, перегородками, трубами и т. п.). Соединения
всех элементов конструкции должны иметь одинаковые конечные сдвиговые
деформации. При разной податливости элементов следует учитывать в расчете
перераспределение усилий, которое определяется при расчетной нагрузке.
Для компенсации сдвиговых
деформаций в двухскатных конструкциях структурных покрытий пролетом 18 и 24 м
при разработке деталировочных чертежей следует увеличивать принятый в проекте
уклон поясов на 1 %.
20.24.
Отверстия под болты в стыках нижних поясов следует размещать в один ряд или в
шахматном порядке, при этом риску или центр группы болтов следует размещать на
расстоянии 2z0 от обушка с округлением до 5 мм в меньшую сторону.
При одно- и многорядном
расположении болтов в каждом ряду их не должно быть свыше 5. При расположении
болтов в шахматном порядке наиболее удаленный от узла болт следует располагать
на наименьшей риске.
В элементах решетки из
одиночных уголков, прикрепленных одной полкой и подверженных растяжению,
отверстия под болты при однорядном и центр группы при многорядном расположении
следует размещать на расстоянии от обушка, равном 0,35-0,45b, а в элементах,
подверженных сжатию, 0,45-0,55b (b — ширина полки уголка). При
креплении таких элементов сваркой швы следует распределять между обушком и
пером в соотношении от 0,5:0,5 до 0,65:0,35. В элементах из парных уголков,
составленных в тавровое сечение, отверстия под болты и центр тяжести сварных
швов следует размещать на расстоянии от обушка соответственно 0,35-0,45b и 0,3-0,4b.
Минимальное расстояние от
края элемента до центра ближайшего отверстия вдоль усилия в растянутых
элементах следует назначать не менее 1,5d и не менее 1,35d по
нормали до скоса полки без допуска в сторону уменьшения при изготовлении (где d — диаметр отверстия). При
этом линия скоса должна пересекаться с осями отверстия за пределами полки (см. рис. 46, б—г). В элементах,
подверженных только сжатию, расстояние от центра ближайшего отверстия до скоса
по нормали следует назначать не менее l,25d без допуска в сторону
уменьшения при изготовлении. Несущая способность соединения в этом случае не
снижается. Пересечение линии скоса с краями элемента допускается в пределах
полки (см. рис. 46, д).
20.25.
Верхние пояса из двутавров при передаче нагрузки от кровли через стальной
профилированный настил следует раскреплять в плоскости наименьшей жесткости
постановкой самонарезающих болтов, дюбелей или электрозаклепок в каждой волне.
При креплении дюбелями и электрозаклепками усилия в элементах конструкции
следует определять с учетом включения настила в работу системы.
21. БАЛКИ
РАСЧЕТ БАЛОК С ГИБКОЙ СТЕНКОЙ И РЕБРАМИ
21.1 (18.2*). Расчетные формулы приведены для балок со стенками, подкрепленными
поперечными ребрами жесткости, несущих статическую нагрузку, с относительной
гибкостью стенки , находящейся в пределах от 6 до 13. Ограничение сверху
сделано для предотвращения выпучивания в плоскости стенки сжатых поясов балки,
выполняемых из листовой стали. Ограничение снизу указано ориентировочно, в
связи с чем этим методом расчета можно пользоваться и при < 6, если проверка
выполняется в соответствии с пп. 7.1, 7.2*, 7,3, 7.4* СНиП II-23-81*. Сущность применяемого метода состоит в учете
закритической стадии работы стенки.
21.2 (18.2*). Наиболее полное решение для балки симметричного двутаврового сечения
при чистом изгибе получено в работе [31]. Придельное значение момента Ми найдено из выражения,
аппроксимирующего точное решение:
Ми/(WRy) = (y + 0,224c)/(y + 0,224), (145)
где y = Af/Aw; c = 0,259 + 1,945/( — 1,1).
В табл. 63 приведены значения
предельных моментов, вычисленные по формуле (145).
Таблица
63
|
Значение y |
Значения Ми/(WRy) |
|||
|
8 |
10 |
12 |
14 |
|
|
0,5 |
0,858 |
0,838 |
0,826 |
0,817 |
|
1,0 |
0,916 |
0,904 |
0,897 |
0,892 |
|
2,0 |
0,954 |
0,947 |
0,943 |
0,940 |
Эпюры предельных мембранных
напряжений sх [31] показывают, что в зоне растяжения эпюра близка
к линейной, но краевое напряжение не достигает предела текучести. Для
практических расчетов в СНиП II-23-81* принята
упрощенная схема предельного состояния, в которой сжатая зона стенки
представляет собой прямоугольник высотой h1 с напряжением, равным
расчетному сопротивлению Ry (рис. 47). Краевое растягивающее напряжение также принято равным по
абсолютной величине Ry.
При малой толщине поясов по сравнению с высотой стенки и получена формула
(159) СНиП II-23-81*, которая дает несколько
преувеличенные (от 1 до 3,6 %) значения Ми,
поскольку в действительной эпюре напряжений в растянутом поясе расчетное
сопротивление не достигается.
Рис.
47. Схема предельного состояния сечения балки при изгибе
а — сечение балки; б — эпюра напряжений
21.3 (18.2*). Поперечная сила Qu, воспринимаемая стенкой, слагается из двух частей: силы Qcr = tсрht, отвечающей критической нагрузке, и дополнительной силы DQ,
возникающей в закритической стадии вследствие образования диагональной или
близкой к ней растянутой полосы. Различные модели отличаются углом наклона и
шириной этой полосы, а также значением предельного растягивающего напряжения
(распределение напряжений обычно считается равномерным). В работе [32] принято,
что ось полосы совпадает с диагональю (рис. 48), а ширина полосы определяется
положением пластического шарнира, возникающего вследствие изгиба пояса. В
сечение пояса включается полоса стенки шириной от 0 до 30t в зависимости от tср/Ry. Предельное напряжение растяжения в диагональной полосе находится из
условия, чти интенсивность напряжений равна пределу текучести.
Рис. 48. Схема отсека
стенки балки при сдвиге
Метод Рокки-Шкалоуда [32]
можно существенно упростить посредством допущений, ведущих к некоторому
уменьшению предельной нагрузки. Этот вариант реализован в СНиП II-23-81*.
Предельное касательное
напряжение в стенке tu определяется из выражения
, (146)
где m = a/h;
tcr — критическое касательное напряжение;
co/a — определяется из формул:
(147)
;
Wp — пластический момент
сопротивления сечения пояса, в который включается полоса стенки шириной ; при вычислениях по формуле (162) СНиП II-23-81* для упругого тавра вместо Wp подставляется 2Wmin.
Если в практических расчетах
получается, что co/a > 0,4, то необходимо принимать co/a =
0,4. Значение tcr следует вычислять с учетом упругого защемления
стенки в поясах, например, по формуле (76) СНиП II-23-81*. Из формулы (146) настоящего Пособия получена
формула (160) СНиП II-23-81*.
21.4 (18.3). В описанной модели предельного состояния закритическая работа стенки
обусловлена появлением диагональной растянутой полосы, следовательно, ребро
должно выполнять роль сжатой стойки и воспринимать усилие DQ = (tu — tcr)ht.
В сечение ребра можно
включить часть стенки по 0,65t с каждой стороны. При проверке прочности и устойчивости одностороннего
ребра следует учитывать эксцентриситет сжимающей силы, равный расстоянию от
срединной плоскости стенки до центра тяжести сечения ребра. Этот способ расчета
приведен в СНиП II-23-81*.
21.5 (18.2*). Комбинация изгиба со сдвигом теоретически рассмотрена с использованием
обычных допущений (упругая пластинка, условные критерии предельного состояния).
Кривая взаимодействия момента и поперечной силы близка к известной кривой для
критических нагрузок. Истинная кривая должна быть более выпуклой, так как формы
выпучивания от предельного момента и предельной поперечной силы, действующих
порознь, различаются больше, чем соответствующие собственные функции линейных
краевых задач.
Экспериментальная проверка
выполнена на малом числе образцов, поэтому для практических расчетов обычно
рекомендуются эмпирические кривые взаимодействия в координатах Q/Qu и М/Ми (символы без индексов
относятся к комбинированному нагружению), в частности, формула (158) СНиП II-23-81*, дающая небольшой запас
несущей способности.
21.6 (18.7*). Предельное значение сосредоточенной силы, приложенной к поясу (bftf) двутавровой тонкостенной
балки, находится из условия, что наибольшее напряжение в стенке под грузом
равно расчетному сопротивлению:
Fu =
3,26tRy,
где .
Тогда 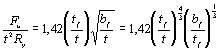
При передаче давления через
полку двутавра, лежащего на балке, или через прокладку значение Fu можно увеличить на 10 %.
РАСЧЕТ БАЛОК С ГИБКОЙ НЕПОДКРЕПЛЕННОЙ СТЕНКОЙ (18.9*)
21.7.
Рекомендации настоящего подраздела распространяются на расчет и проектирование
сварных двутавровых балок из стали с пределом текучести до 430 МПа (4400 кгс/см2)
со стенками, не укрепленными поперечными ребрами жесткости, за исключением
опорных участков, и имеющими гибкость .
21.8.
Расчет разрезных балок, нагруженных равномерно распределенной нагрузкой,
следует выполнять в соответствии с требованиями разд. 18 СНиП II-23-81*.
Для получения равнопрочного
поперечного сечения в пролетной и опорных зонах балки значения следует назначать в
пределах 22 £ y £ 26.
21.9.
Прочность сечений балок, нагруженных неравномерной нагрузкой, следует проверять
по формулам:
при М/Мu £ 0,5 Q/Qu £ 1;
” 0,5 < М/Ми
< 1 (Q/Qu — 0,5)2 + (М/Ми — 0,5)2 £ 0,25;
” М/Ми = 1 Q/Qu £ 0,5,
где М и Q — соответственно момент и
поперечная сила в рассматриваемом сечении балки;
Мu
— предельный момент, вычисляемый по формуле
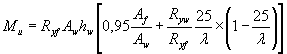
Qu — предельная поперечная
сила, H, вычисляемая по формуле
, Ryw в МПа.
21.10.
При передаче нагрузки на верхний пояс следует предусматривать конструктивные
мероприятия, исключающие появление эксцентриситета, превышающего половину
толщины стенки.
21.11.
Начальные прогибы стенки балок относительно вертикальной плоскости не должны
превышать величины , см.
21.12.
Заводской сварной стык стенки следует располагать на расстоянии не менее 3hw от опорного ребра.
РАСЧЕТ БИСТАЛЬНЫХ БАЛОК
21.13.
В расчетах прочности бистальных балок, в которых стенка выполнена из менее
прочной стали, чем пояса (или один пояс), применяются следующие главные
критерии:
а) предельных (ограниченных)
пластических деформаций, выражающийся в ограничении наибольшей интенсивности
пластических деформаций в стенке нормой
предельной интенсивности пластических деформаций , при этом в расчетах учитываются пластические деформации не
только в стенке, но и в поясах;
б) предельных напряжений
(расчетных сопротивлений) в поясе балки при упругой его работе, при этом в
расчетах учитываются пластические деформации только в стенке.
21.14.
Для расчета на прочность устанавливаются следующие группы бистальных балок,
отличающиеся критерием прочности и нормой предельных интенсивностей
пластических деформаций :
1 — для которой расчеты
прочности выполняются по критерию предельных напряжений в поясе — балки при
расчетном сопротивлении стали поясов Rf = Ru/g, меньшем расчетного
сопротивления по пределу текучести; подкрановые балки под краны с режимами
работы 1К-5К согласно ГОСТ 25546-82;
2-4 — для которых расчеты прочности выполняются по
критерию ограниченных пластических деформаций, в частности:
2 — для которой = 0,1 % — балки,
непосредственно воспринимающие подвижные и вибрационные нагрузки (балки рабочих
площадок, бункерных и разгрузочных эстакад, транспортерных галерей, под краны
гидротехнических сооружений и т.п.);
3 — для которой = 0,2 % — балки,
работающие на статические нагрузки (балки перекрытий и покрытий; ригели рам,
фахверка; балки, поддерживающие технологическое оборудование; ригели эстакад и
другие изгибаемые, растянуто-изгибаемые и сжато-изгибаемые балочные элементы);
4 — для которой = 0,4 % — балки
работающие на статическую нагрузку, но не имеющие продольных ребер жесткости,
не воспринимающие местных нагрузок и отличающиеся повышенной общей
устойчивостью и устойчивостью стенок и свесов поясов аналогично балкам,
рассчитываемым на прочность в соответствии с п. 5.18 СНиП II-23-81*.
21.15.
Расчет на прочность бистальных балок всех групп следует выполнять по формулам:
при изгибе в одной из
главных плоскостей
; (149)
при изгибе в двух главных
плоскостях
; (150)
при осевой силе с изгибом
. (151)
21.16.
Коэффициенты сх и су определяются по табл. 64 и 65 в зависимости от группы конструкций, принятых величин
расчетных сопротивлений поясов Rf и стенки Rw, а также от отношений площадей элементов сечения.
21.17.
Коэффициент сNx определяется по формуле
сNx = Rw/Rf + h(cx — Rw/Rf), (152)
где
h = h1 + 1235h2(Rf — Rw)/E, (153)
h1 и h2 — коэффициенты, принимаемые
по табл. 66.
Для сечения № h1 принимается независимо от величины действительной
асимметрии (считая, что оба пояса имеют площадь большего пояса Af).
Коэффициент cNy определяется по формуле
cNy = 1 + h1(сy — 1). (154)
При наличии зоны чистого
изгиба коэффициенты cх и cу определяются по формулам:
; (155)
, (156)
где l и v —
длины соответственно пролета балок и зоны чистого изгиба;
и
— коэффициенты соответственно сx и су, принимаемые по табл. 64 и 65 в
зависимости от и расчетных
сопротивлений Rf и Rw.
21.18.
Расчет на выносливость бистальных балок следует выполнять на эксплуатационные
нагрузки с учетом общих указаний СНиП
II-23-81* как
моностальных из материала пояса, расположенного у проверяемой фибры.
21.19.
Жесткость бистальной балки (под нормативными нагрузками) допускается проверять
в предположении упругой работы балки, включая случаи, в которых вычисленные в
этом предположении от нормативных нагрузок напряжения в стенке превышают Ry.
21.20.
Общую устойчивость бистальной балки допускается проверять как для моностальной,
выполненной из стали, примененной в сжатом поясе бистальной балки.
21.21.
Устойчивость полок поясов в бистальных балках 1-й группы проверяется и
обеспечивается согласно требованиям СНиП II-23-81* в предположении упругой работы стали.
21.22.
В бистальных балках 2-4-й групп двутаврового сечения отношение расчетной ширины
свеса сжатой полки пояса к ее толщине tt при sloc = 0 не должно превышать 0,35.
21.23. В бистальных балках
двутаврового сечения, укрепленного только поперечными ребрами жесткости, при sloc = 0 устойчивость стенки
проверяется по формулам:
для симметричных сечений
; (157)
для асимметричных сечений с
более развитым сжатым поясом
. (158)
В формулах (157), (158):
, но не менее 0,25;
;
— относительная гибкость
стенки;
t — среднее касательное
напряжение (не более 0,5Rsw);
s1 и s3 — напряжения соответственно
в сжатом и растянутом поясах; если s1 ³ Rf, принимают s1 = Rf,
если s3 ³ Rf , принимают
s3 = Rf;
А1, А3
— площади сечения соответственно большего и меньшего пояса бистальной балки;
h1 — высота сжатой зоны стенки, определяемая из
условий равновесия.
21.24.
Проверка устойчивости стенки выполняется по формулам разд. 7 СНиП II-23-81*, если компоненты напряжений, вычисленные для
расчетного отсека стенки, удовлетворяют требованиям пп. 5.12-5.14* СНиП II-23-81*.
Пример расчета. Рассчитать бистальную
балку, относящуюся к 3-й группе, на изгиб моментами Мх = 1250 кН×м; My = 46 кН×м и сжатие осевой силой N = 620 кН; расчетные
сопротивления поясов Rf =
370 МПа, стенки R = 260 МПа.
Принимаем сечение,
показанное на рис. 49. Отношение
площадей элементов сечения Af/Aw = 44,8/99 = 0,453; площадь
нижнего пояса 0,5Af. По табл. 64 для сечения №
2 при = 0,2 % коэффициент сх
= 1,06, по табл. 65 коэффициент су = 1,39. По табл. 66 для одинаковых знаков sх от Мх
и N в верхнем поясе при N/Af(1,5Rf + Rw) = 620/44,8(1,5×37 + 26) = 0,170h1 =
0,579; h2 = 0,687.
По формуле (153) h = 0,579 + 1235×0,687(370 — 260)/206000 = 1,032.
По формуле (152) cNx = 260/370 + 1,032(1,06 — 260/370) =
1,09.
По табл. 66 при N/(2AfRf + AwRw) = 0,106 h1 = 1,68.
По формуле (154) сNy = 1 +1,68(1,39 — 1) = 1,66.
Таблица
64
|
Номер сечения |
Сечение |
Rw |
Rf |
Коэффициенты с для |
|||||||||||
|
МПа (кгс/см2) |
1 |
2 |
4 |
||||||||||||
|
при Af/Aw, равных |
|||||||||||||||
|
0,25 |
0,5 |
1 |
2 |
0,25 |
0,5 |
1 |
2 |
0,25 |
0,5 |
1 |
2 |
||||
|
1 |
|
230 (2350) |
300 |
0,97 |
0,98 |
0,99 |
0,99 |
1,02 |
1,01 |
1,01 |
1,00 |
1,05 |
1,03 |
1,02 |
1,01 |
|
(3050) |
|||||||||||||||
|
330 |
0,95 |
0,97 |
0,98 |
0,99 |
0,98 |
0,99 |
0,99 |
1,00 |
1,01 |
1,01 |
1,01 |
1,00 |
|||
|
(3350) |
|||||||||||||||
|
370 |
0,93 |
0,98 |
0,97 |
0,99 |
0,94 |
0,96 |
0,98 |
0,99 |
0,97 |
0,98 |
0,99 |
0,99 |
|||
|
(3750) |
|||||||||||||||
|
400 |
0,91 |
0,94 |
0,97 |
0,98 |
0,91 |
0,94 |
0,97 |
0,98 |
0,94 |
0,96 |
0,98 |
0,99 |
|||
|
(4100) |
|||||||||||||||
|
455 |
0,88 |
0,92 |
0,96 |
0,98 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
|||||||||||||||
|
260 (2650) |
330 |
0,98 |
0,98 |
0,99 |
1,00 |
1,02 |
1,02 |
1,01 |
1,00 |
1,06 |
1,04 |
1,02 |
1,01 |
||
|
(3350) |
|||||||||||||||
|
370 |
0,95 |
0,97 |
0,98 |
0,99 |
0,98 |
0,99 |
0,99 |
0,99 |
1,01 |
1,01 |
1,00 |
1,00 |
|||
|
(3750) |
|||||||||||||||
|
400 |
0,93 |
0,96 |
0,98 |
0,99 |
0,95 |
0,97 |
0,98 |
0,99 |
0,98 |
0,99 |
0,99 |
1,00 |
|||
|
(4100) |
|||||||||||||||
|
455 |
0,90 |
0,94 |
0,97 |
0,98 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
|||||||||||||||
|
300 (3050) |
370 |
0,98 |
0,99 |
0,99 |
1,00 |
1,03 |
1,02 |
1,01 |
1,00 |
1,07 |
1,05 |
1,03 |
1,01 |
||
|
(3750) |
|||||||||||||||
|
400 |
0,96 |
0,98 |
0,99 |
0,99 |
0,99 |
0,99 |
1,00 |
1,00 |
1,03 |
1,02 |
1,01 |
1,01 |
|||
|
(4100) |
|||||||||||||||
|
455 |
0,94 |
0,96 |
0,98 |
0,99 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
|||||||||||||||
|
330 (3350) |
400 |
0,98 |
0,99 |
0,99 |
1,00 |
1,03 |
1,02 |
1,01 |
1,00 |
1,08 |
1,06 |
1,03 |
1,01 |
||
|
(4100) |
|||||||||||||||
|
455 |
0,96 |
0,97 |
0,98 |
0,99 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
|||||||||||||||
|
2 |
|
230 (2350) |
300 |
0,97 |
0,97 |
0,97 |
0,98 |
1,10 |
1,09 |
1,05 |
1,03 |
1,16 |
1,18 |
1,17 |
1,10 |
|
(3050) |
|||||||||||||||
|
330 |
0,94 |
0,96 |
0,96 |
0,97 |
1,03 |
1,03 |
1,02 |
1,01 |
1,11 |
1,14 |
1,12 |
1,07 |
|||
|
(3350) |
|||||||||||||||
|
370 |
0,91 |
0,93 |
0,95 |
0,96 |
0,96 |
0,97 |
0,98 |
0,98 |
1,04 |
1,09 |
1,07 |
1,04 |
|||
|
(3750) |
|||||||||||||||
|
400 |
0,88 |
0,91 |
0,94 |
0,96 |
0,90 |
0,93 |
0,95 |
0,97 |
1,00 |
1,06 |
1,04 |
1,00 |
|||
|
(4100) |
|||||||||||||||
|
455 |
0,84 |
0,88 |
0,82 |
0,96 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
|||||||||||||||
|
260 (2650) |
330 |
0,97 |
0,97 |
0,97 |
0,98 |
1,10 |
1,09 |
1,05 |
1,03 |
1,17 |
1,19 |
1,17 |
1,20 |
||
|
(3350) |
|||||||||||||||
|
370 |
0,94 |
0,96 |
0,96 |
0,98 |
1,02 |
1,02 |
1,00 |
1,00 |
1,11 |
1,14 |
1,12 |
1,07 |
|||
|
(3750) |
|||||||||||||||
|
400 |
0,92 |
0,94 |
0,95 |
0,97 |
0,96 |
0,97 |
0,98 |
0,98 |
1,06 |
1,10 |
1,08 |
1,04 |
|||
|
(4100) |
|||||||||||||||
|
455 |
0,88 |
0,91 |
0,94 |
0,96 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
|||||||||||||||
|
300 (3050) |
370 |
0,98 |
0,98 |
0,98 |
0,99 |
1,11 |
1,09 |
1,05 |
1,03 |
1,19 |
1,20 |
1,18 |
1,10 |
||
|
(3750) |
|||||||||||||||
|
400 |
0,96 |
0,95 |
0,97 |
0,98 |
1,04 |
1,03 |
1,01 |
1,01 |
1,16 |
1,16 |
1,13 |
1,07 |
|||
|
(4100) |
|||||||||||||||
|
455 |
0,92 |
0,94 |
0,95 |
0,97 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
|||||||||||||||
|
330 (3350) |
400 |
0,98 |
0,98 |
0,98 |
0,98 |
1,10 |
1,08 |
1,04 |
1,03 |
1,18 |
1,20 |
1,17 |
1,10 |
||
|
(4100) |
|||||||||||||||
|
455 |
0,95 |
0,96 |
3,96 |
0,98 |
— |
— |
— |
— |
— |
— |
— |
— |
|||
|
(4640) |
Примечания: 1. Коэффициенты сx определяются
линейной интерполяцией по Af/Аw и по соотношению
площадей поясов при принятая ближайших значений Rw
и Rf.
2. Для 3-й
группы балок коэффициенты сх
определяются линейной интерполяцией в соответствии с примеч. 1 и, кроме того,
по .
Таблица
65
|
Группа балок |
Коэффициенты су при расчетных |
||||
|
300 |
330 |
370 |
400 |
455 |
|
|
(3050) |
(3350) |
(3750) |
(4100) |
(4640) |
|
|
1 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
2 |
1,33 |
1,31 |
1,30 |
1,28 |
1,00 |
|
3 |
1,41 |
1,40 |
1,39 |
1,38 |
1,00 |
|
4 |
1,47 |
1,46 |
1,45 |
1,44 |
1,00 |
Таблица
66
|
Номер сечения |
Сечение |
|
h1 |
h2 |
Номер сечения |
Сечение |
|
h1 |
h2 |
||
|
+ |
— |
+ |
— |
||||||||
|
1 |
|
0 |
1 |
1 |
2 |
|
0 |
1 |
1 |
1 |
1 |
|
0,1 |
1,63 |
—0,57 |
0,1 |
0,67 |
1,13 |
0,33 |
—0,13 |
||||
|
0,2 |
2,47 |
—1,35 |
0,2 |
0,54 |
1,25 |
0,84 |
—0,39 |
||||
|
0,3 |
3,20 |
—2,08 |
0,3 |
0,74 |
1,32 |
0,51 |
—0,38 |
||||
|
0,4 |
3,49 |
—2,39 |
0,4 |
1,07 |
1,34 |
0,12 |
—0,43 |
||||
|
0,5 |
3,57 |
—2,54 |
0,5 |
1,35 |
1,31 |
—0,14 |
—0,52 |
||||
|
0,7 |
3,05 |
—2,17 |
0,7 |
1,66 |
1,17 |
—0,42 |
—0,82 |
Примечание. При одинаковых знаках напряжений
sx в большем поясе от усилий М и N
следует принимать графу, обозначенную знаком “+”, а при разных знаках — графу,
обозначенную знаком “-”.
Рис.
49. Сечение бистальной балки
Проверяем условные
напряжения в точке а (см. рис. 49)
верхнего пояса по формуле (151):
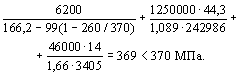
22. ПОДКРАНОВЫЕ БАЛКИ
22.1 (13.33). Стенки сварных подкрановых балок, находящихся в особо тяжелых условиях
работы, следует рассчитывать на выносливость согласно п. 13.35* СНиП II-23-81*. Примерный перечень
производственных зданий, в которых подкрановые балки должны рассчитываться на
выносливость, приведен в табл. 67.
Расчет на выносливость
выполняется на воздействие от нормативных нагрузок одного крана.
22.2 (13.35). Расчетными сечениями при расчете подкрановых балок на выносливость
являются:
для разрезных балок —
сечение, отстоящее на расстояние 0,2 а
+ 0,35lef от ближайшего к середине пролета поперечного ребра
жесткости (в направлении к середине пролета);
для неразрезных балок —
сечение, отстоящее от опорного ребра жесткости на расстояние 0,2 а + 0,35lef, где а —
шаг ребер; lef — условная длина, на
которую распределяется давление колеса крана (см. п. 13.34*СНиП II-23-81*).
Таблица 67
|
Здания |
Заводы |
|
Дворы изложниц |
Металлургические |
|
Шихтовые дворы |
” |
|
Отделения раздевания слитков |
” |
|
Скрапо-разделочные базы; |
” |
|
Склады чугуна и слитков |
” |
|
Здания очистки и смазки |
” |
|
Пролеты складов заготовок; |
” |
|
Здания нагревательных колодцев |
” |
|
Здания (пролеты или производства), в которых |
Любые |
22.3 (13.35*). Расчет на выносливость выполняется для верхней зоны стенки в месте
примыкания ее к верхнему поясу балки. В этом месте стенка находится в условиях
сложного напряженного состояния, определяемого воздействием косого изгиба,
стесненного кручения и местными воздействиями сосредоточенных сил и моментов
[33].
Причиной усталостных
повреждений верхних зон подкрановых балок являются многократные сдвиги,
обусловливаемые максимальными касательными напряжениями от совместного действия
поперечного изгиба, местного смятия и кручения .
22.4 (13.35*). Величина с достаточной степенью точности определяется суммированием
максимальных касательных напряжений поперечного изгиба , местного смятия 0,4 sloc,y и кручения 0,5 sfy. В двух последних случаях
для упрощения расчета значения максимальных касательных напряжений определены
через нормальные напряжения, которые вычисляются по известным формулам Б. М.
Броуде и А. А. Апалько (см. п. 13.34* СНиП II-23-81*).
Суммированием приведенных
величин при k = 0,3 (k учитывает
плавность изменения эпюры касательных напряжений в расчетном сечении [33])
получена формула (148) СНиП II-23-81*.
Пример расчета на
выносливость
Исходные данные. Проверить расчетом сопротивляемость усталостным разрушениям сварной
балки пролетом 12 м под краны грузоподъемностью 30 т (рис. 50); нормативное
давление на пояс Р = 35,5 тс = 355
кН. Кран с гибким подвесом груза; число подъемов груза за срок службы равно 2×106. Расчет
прочности и устойчивости элементов двутаврового сечения выполнен по расчетным
усилиям от двух кранов: М = 289 тс×м = 2890 кН×м; Q = 115 тс = 1150 кН; F = 46,9 тс = 469 кН. На
основании этих расчетов было выбрано поперечное сечение балки (верхний и нижний
пояса из листов соответственно размерами 450´25 мм и 450´18 мм, стенка размером 1390´12 мм). Шаг поперечных ребер
жесткости 1,5 м; рельс КР 120.
Рис. 50. Схема
подкрановой балки и крановой нагрузки
Геометрические
характеристики сечения, необходимые для расчета на усталость: момент инерции
сечения Ix = 1219068 см4,
момент сопротивления верхней кромки стенки Wx = 19278 см3, момент сопротивления
верхней кромки стенки Ws = 7420 см3; условная длина распределения местных напряжений
смятия lef = 52,2 см; моменты инерции
кручения: рельса It = 1310 см4,
верхнего пояса — If = 234 см4.
Для рассматриваемого примера
расчетное сечение размещается на расстоянии (0,2×150 — 0,35×52,2 = 48 см) от ближайшего
к середине балки поперечного ребра. Нагрузка от крана размещается на балке так,
чтобы определить в расчетном сечении максимальную поперечную силу и соответствующий
ей изгибающий момент. В рассматриваемом случае: М = 104 тс×м = 1040кН×м; Q = 21 тс = 210 кН.
Нормативные величины
вертикальной F и горизонтальной Qt нагрузок дня расчета на
усталость равны: F = 0,8´35,5 = 28,4 тc = 284
кН; Qt = 0,1´35,5 = 3,55 тc = 35,5
кН. Величина местного крутящего момента Мt = 28,4´0,015 + 0,75´3,55´0,17 = 0,88 тс×м = 8,8 кН×м.
Сопротивление усталостным
разрушениям материала зоны стенки, примыкающей к верхнему поясному шву,
проверяется по формуле
,
где
;
;
;
Rv = 75 МПа (как для разрезной
балки согласно п. 13.35*СНиП II-23-81*).
Напряжения sx, txу, sloc,y и sfy вычислены согласно п.
13.34*СНиП II-23-81*.
Сопротивляемость усталостным
разрушениям обеспечена.
ОБЩИЕ ПОЛОЖЕНИЯ
23.1.
Висячими называются покрытия, в которых пролетные конструкции, непосредственно
несущие нагрузку, представляют собой нити, т.е. гибкие криволинейные растянутые
стержни, закрепленные за опоры. Нити могут обладать изгибной жесткостью, в этом
случае их называют жесткими нитями. Если начальная длина нити равна или меньше
расстояния между опорами, то такую нить называют струной или предварительно
напряженной струной. Если струна не несет поперечной нагрузки, ее называют
вантой или оттяжкой.
23.2.
Поверхности покрытия рационально придавать ту форму, которая соответствует
равновесию образующих ее нитей под полной нагрузкой. Например, если нити
расположены в плане параллельно друг другу, то покрытие будет опираться на них
лентами постоянной ширины, полную нагрузку можно принять постоянной по пролету,
кривизна нитей тогда будет постоянной, а очертание — параболическим. Если нити
расходятся радиально из какого-либо узла, то интенсивность нагрузки и,
следовательно, кривизна нити будет расти пропорционально расстоянию от узла, и
естественной формой их кривой будет кубическая парабола. Поэтому форма
поверхности не может быть любой, а будет зависеть от формы кривых нитей, ее
образующих. Возможно форму самой кровли несколько видоизменить по желанию,
введя между кровлей и нитями специальную надстроенную конструкцию.
23.3. Пролетная конструкция может быть выполнена в виде:
а) сеток из нитей,
расположенных параллельно друг другу, ортогонально, гексагонально, косоугольно,
радиально и т.д.;
б) систем плоских или
пространственных (рис. 51,52);
в) ванто-балочных систем;
г) оболочек железобетонных
висячих;
д) систем комбинированных;
возможны двухпоясные покрытия (рис. 53).
Рис. 51. Виды систем и опорных контуров
а — радиальная система на контуре,
круглом в плане; б — система
параллельных нитей на плоском прямоугольном контуре; в, г — седловидные сетки
на криволинейных контурах; д-ж —
висячие системы и контуры зданий, квадратных в плане; з — висячая система на двух диагональных арках
23.4.
Неотъемлемой частью висячего покрытия является опорная конструкция,
воспринимающая усилия прикрепленных к ней нитей. В качестве опор желательно
назначать те элементы здания, которые уже имеются в его конструктивном решении.
Например, несущие стены, перекрытия, рамные конструкции пристроек, “ноги”
трибун и т.д. Кроме того, это могут быть специальные конструкции: опорные
балки, опорные контуры, рамы, оттяжки, закрепленные за анкерные фундаменты,
пилоны.
Рис. 52. Покрытия
а — ванто-балочное; б — радиально-кольцевое шатровое; в — ячеистое
Рис. 53. Двухпоясные покрытия
а — виды систем; б — примеры радиальных покрытий
23.5.
Форму контура в пространстве следует выбирать таким образом, чтобы изгибающие
моменты в нем, вызванные воздействием нитей, были минимальными. В овальных
зданиях это достигается за счет подбора кривой оси, соответствующей кривой давления.
В прямоугольных зданиях выгоднее нити направлять в углы контура. Возможно
применение диагональных арок, поддерживающих нити покрытия. Сами контуры могут
покоиться на стенах или частых опорах, но могут передавать нагрузку на
отдельные пилоны.
23.6.
Сети, образованные из провисающих нитей (чаши), обладают наибольшей несущей
способностью. Для повышения стабильности в чашеобразных и цилиндрических
покрытиях не рекомендуется превращать их в предварительно напряженные
железобетонные оболочки, что сильно увеличивает массу и усложняет возведение.
Желательно применять сетки, состоящие из жестких нитей. Это решение позволит
значительно снизить массу покрытая, применить легкий сборный настил и упростить
возведение. Положительной особенностью гексагональных сетей, кроме того,
является равенство распоров в стержнях при нагрузках произвольного вида, что
делает опорный контур практически безмоментным. Жесткие нити проще всего
изготовлять из проката, желательно из стали повышенной прочности.
23.7.
Рационально применять совместно два вида нитей — систему жестких нитей и
натянутую на них сетку из высокопрочных стальных канатов. Седловидные покрытия
обладают меньшей несущей способностью, чем чашеобразные, зато они более
стабильны. Эти свойства позволяют использовать в качестве нитей седловидных
систем высокопрочные тросы и применять эластичные кровли, например тентовые.
Рекомендуется применять металлические или деревянные настилы.
Чем меньше разница между
начальной длиной нити и расстоянием между опорами, тем меньше возможные
кинематические перемещения нити под нагрузкой. Но упругие прогибы при этом
могут расти. Используя эти свойства, можно применять струнные конструкции,
причем для протяженных многопролетных зданий струны рационально направлять в
продольном направлении и стабилизировать поперечными балками. Для квадратных и
овальных в плане однопролетных покрытий зданий из струн рационально
образовывать сетку, позволяющую пространственное перераспределение нагрузки
между струнами.
23.8.
Деформативность висячего покрытия под действием временных нагрузок не должна
превышать пределов, допустимых для данной принятой конструкции кровли, из
условия сохранения ее герметичности. Особенно важно ограничить изменение
кривизны покрытия как вдоль, так и поперек пролета от действия местной
нагрузки. Чем хрупче материал и конструкция кровли, тем жестче или натянутой
должны быть несущие нити. Гибкие, эластичные настилы предпочтительнее. Применяя
жесткие плиты и панели, надлежит обеспечивать герметичность стыков, которая
достигается применением жестких нитей, укладкой на. них настилов, плит или
панелей по неразрезной схеме, применением нащельников, предварительным
напряжением.
РАСЧЕТ
23.9.
Расчет отдельной нити на прочность рекомендуется производить, задаваясь
пролетом нити l, шагом и стрелкой провеса f под расчетной нагрузкой.
Для заданной нагрузки q расчетное усилие распора
определяется по формуле
, (159)
где h —
разница уровней опор;
f — угол наклона касательной
нити у нижней опоры (рис. 54).
Рис. 54. К расчету
нити на прочность
Если опоры расположены на
одном уровне, формула (159) приобретет вид
, (160)
где М — изгибающий момент от расчетной
нагрузки q в свободно опертой балке
пролетом l.
Расчетное усилие Т определяется по формуле
, (161)
где Q —
поперечная сила (реакция) у более нагруженной опоры.
Требуемое сечение нити А определяется по формуле
,
где gc — коэффициент условий
работы;
Ry — расчетное сопротивление
металла нити.
Расчет по недеформированной
схеме позволяет получить не только расчетное усилие и требуемое сечение нити,
но, при известном модуле упругости Е
определить растяжимую жесткость ЕА и,
следовательно, начальную длину нити (заготовки) и рассчитать монтажную
(начальную) геометрию нити, исходя из которой при расчетной нагрузке она займет
принятое расчетное положение.
23.10.
При расчете на прочность системы или сетки сопряженных нитей можно, как и для
отдельной нити, задаться стрелкой и определить усилие в нити от полной
нагрузки. Но это усилие будет максимальным (расчетным) только для тех сеток,
несущие нити которых не пересекаются, например, в цилиндрических или
седловидных покрытиях. В чашеобразных покрытиях все нити будут несущими, и если
они пересекаются, то максимальное усилие в нити вызывает не полная нагрузка на
покрытие, а та, которая расположена вдоль нити. Остальные нити при этом должны
быть нагружены минимально — только весом покрытия. Расчет систем обычно
производится на ЭВМ.
23.11.
Расчет висячего покрытия на деформации и перемещения производится для проверки
системы покрытия на пригодность к эксплуатации.
Для гибких конструкций сетей
свойственны перемещения по трем осям координат: и — вдоль данной нити; v —
поперек данной нити; w —
в вертикальном направлении.
Эти перемещения могут быть
большими из-за большой растяжимости и кинематичности нитей. Висячие конструкции
следует проверять по первым и вторым производным перемещений:
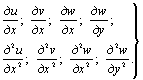
Полученные величины от местных нагрузок необходимо
сравнивать с допустимыми для данной конструкции кровли с точки зрения ее
герметичности. Если к кровле подвешивается оборудование, трубопроводы, кабели,
то необходимо проверить их целостность. Повышение стабильности достигается за
счет введения предварительного напряжения системы, применения жестких нитей,
включения в работу настилов. Для небольших пролетов допускается применять
висячие железобетонные оболочки.
Расчет сложных висячих
систем следует производить с учетом податливости контура и нелинейности. Как
правило, расчет производится на ЭВМ. В простейших случаях для расчета
перемещений отдельной нити можно воспользоваться следующими формулами для
вертикальных перемещений нити и их производных от действия произвольной
вертикальной нагрузки qi:
;
;
,
где Mi, Qi — соответственно изгибающий
момент и поперечная сила в данной точке пролета х;
Мо, Qo, qo — соответственно изгибающий
момент, поперечная сила и интенсивность нагрузки исходного состояния,
относительно которого определяются перемещения;
Нi,
Но — соответственно
распоры для нагружений qi и qо; если Нi неизвестен, то его
определяют по формуле
,
здесь Di — характеристика нагрузки, равная ;
a — коэффициент
температурного расширения;
t° —
изменение температуры, град;
S, l — соответственно длина и
пролет нити;
— поправка на кривизну;
DS, Dl — соответственно удлинение
нити и уменьшение пролета, вызвавшие изменение распора (Нi
— Нo),
h — разница уровней опор.
Упругий провес нити (рис.
55) определяется следующим образом.
Рис. 55. К расчету
нити на упругий провес
Если к начальной нагрузке
постоянной интенсивности g
прибавить нагрузку постоянной интенсивности р,
то начальная стрелка нити получит приращение Df, определяемое по формуле
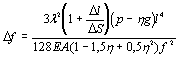
где
.
При загружении нагрузкой
постоянной интенсивности половины пролета (рис. 56) прогиб нити w в четвертях пролета будет равен
;
где Df — упругий провес;
.
Горизонтальные перемещения
нити и в точке х определяются как разность длины нити на данном участке Ох до и после загружения:
u = (Sxo — Sxi + DSx)cosj,
где DSx — удлинение нити на участке
Ох;
j — угол наклона касательной в точке х (рис. 57).
Рис. 56. К расчету
нити на загружение полупролета
Рис. 57. К расчету
нити на горизонтальные перемещения
24. МЕМБРАННЫЕ КОНСТРУКЦИИ
ОБЩИЕ ПОЛОЖЕНИЯ
24.1.
Основными элементами мембранных систем являются тонколистовая пролетная
конструкция, совмещающая несущие и ограждающие функции, а также опорный контур,
воспринимающий цепные усилия с мембраны. Пролетная конструкция может быть
подкреплена системой элементов, используемых для монтажа оболочки, ее
стабилизации, устройства подвесного потолка, технологического этажа и т.п.
24.2.
При проектировании зданий и сооружений с применением мембранных систем должны
быть комплексно решены:
очертание конструкции в
плане;
форма поверхности мембраны;
способ стабилизации
пролетной конструкции;
рациональное восприятие распора
с мембраны;
гидро- и теплоизоляция
ограждений;
водоотвод с покрытия;
устройство различных
проходок, фонарных и других проемов и отверстий.
24.3.
Мембранные (тонколистовые) системы подразделяются по конструктивным
особенностям на:
мембранные сплошные оболочки;
ленточные покрытия;
предварительно наряженные
блоки с мембранными обшивками;
тонколистовые сплошные
обшивки стержневых конструкций;
мембранные каркасные панели
ограждения;
ленточные ограждающие
конструкции;
мембранные конструкции
специальных сооружений.
24.4.
Мембранные оболочки выполняются из отдельных тонколистовых полотнищ,
объединяемых на монтаже в сплошную пространственную систему.
Ими можно перекрывать здания
с разнообразным очертанием плана — треугольник, квадрат, прямоугольник,
многоугольник, круг, овал, эллипс, а также с более сложным комбинированным
очертанием. Мембранные оболочки могут иметь различную форму поверхности:
нулевой гауссовой кривизны
(цилиндрические и конические);
положительной гауссовой
кривизны (сферические, в виде эллиптического параболоида, очерченные по
поверхностям вращения с вертикальной осью);
отрицательной гауссовой
кривизны (седловидные, в том числе в виде гиперболического параболоида,
шатровые);
составную — в виде
комбинации оболочек с одинаковой или различной геометрией поверхности.
24.5.
Ленточные покрытия (из переплетенных лент и двухслойные седловидные)
монтируются из отдельных, не соединяемых друг с другом лент. По статической
схеме ленточные покрытия приближаются к работающим дискретно вантовым системам.
Покрытия из переплетенных
лент имеют провисающую поверхность положительной гауссовой кривизны и
предназначены для зданий с круговым или овальным очертанием плана.
Покрытия из переплетенных
лент с подкрепляющей системой имеют провисающую составную поверхность и
предназначены для зданий с многоугольным очертанием плана (треугольник,
прямоугольник и т.д.).
Двухслойные ленточные
покрытия имеют седловидную форму поверхности и предназначены для зданий с
прямоугольным, овальным или более сложным (составным) очертанием плана.
24.6.
Предварительно напряженные прямоугольные в плане блоки покрытий с мембранными
обшивками длиной, равной перекрываемому пролету, имеют пространственный каркас,
состоящий из двух продольных полигональных ферм, объединенных системой прогонов
и вертикальных связей, а также верхнюю и нижнюю тонколистовую обшивку [34].
Мембранная обшивка по
верхним поясам ферм (кровля) предварительно напрягается. Обшивка по нижним
поясам (подвесной потолок) может быть и без предварительного напряжения. Обе
обшивки включаются в работу основного каркаса.
24.7.
Тонколистовые обшивки из объединяемых на монтаже в сплошную мембрану рулонных
полотнищ располагаются по нижним поясам стержневых систем (структур,
перекрестных и параллельных ферм) и включаются в их работу, выполняя
одновременно роль подвесных потолков [34].
24.8.
Прямоугольные мембранные панели включают продольно-поперечный каркас, обшитый с
одной или двух сторон тонким листом, предварительно напряженным или без
предварительного напряжения, и используются в качестве конструкций стенового и
кровельного ограждения [34].
24.9.
Ограждающие ленточные мембранные конструкции подвесных потолков, кровель и стен
выполняются из отдельных рулонных лент, не объединяемых на монтаже между собой
(полистовая сборка). Цепные усилия с лент от поперечной нагрузки, температурных
деформаций, предварительного напряжения передаются на основной каркас здания
[34].
24.10.
Тонколистовые конструкции рекомендуется применять в специальных сооружениях
различного назначения: градирнях, зернохранилищах, складчатых оболочках, в том
числе трансформируемых, водонапорных башнях и др. Используя основной принцип
пространственной работы тонкого листа на растяжение, мембрана в этих системах
включается в работу основных конструкций и используется в качестве ограждающих
конструкций [34].
24.11.
Мембранные системы на прямоугольном плане рекомендуется применять при замене
устаревших конструкций покрытий реконструируемых промышленных зданий без
остановки производства [35].
МАТЕРИАЛЫ ДЛЯ КОНСТРУКЦИЙ ПОКРЫТИЙ
24.12.
Для изготовления пролетной конструкции мембранных систем применяются
углеродистые, низколегированные, в особых случаях нержавеющие стали,
выпускаемые в виде листов или рулонов. Выбор материала определяется конкретными
условиями эксплуатации мембранных конструкций, их изготовления, монтажа,
экономической целесообразностью.
Поверхности металлических
мембран должны быть защищены от атмосферной и контактной коррозии, при этом
особое внимание следует обращать на антикоррозионную защиту поверхности мембран
со стороны кровли.
24.13.
Для пролетной конструкции мембранных систем используются полотнища,
сворачиваемые в рулоны. Длина полотнища принимается равной всему пролету, а для
оболочек с круглым и овальным планом и имеющих центральное кольцо — половине
пролета. Ширина полотнища принимается не более 12 м и ограничивается габаритом
и весом рулона, а также производственными возможностями завода-изготовителя.
При назначении ширины полотнища для мембранных покрытий необходимо учитывать
кривизну поверхности покрытия.
Рулонные полотнища толщиной
от 3 мм и более изготовляются из отдельных листов размером 1,5´6 м, свариваемых друг с
другом встык на специальных высокомеханизированных установках. Стыковые сварные
швы должны обладать той же прочностью, что и основной металл.
Изготовление полотнищ
толщиной менее 3 мм следует предусматривать из рулонных лент, поставляемых
металлургической промышленностью.
24.14.
Ленточные покрытия и ограждающие конструкции (подвесные потолки, стены)
выполняются из рулонных лент, поставляемых металлургической промышленностью, с
обрезными кромками без какого-либо заводского передела.
24.15.
Опорный контур мембранных покрытий рекомендуется проектировать из сборного,
сборно-монолитного или монолитного железобетона (в соответствии со СНиП 2.03.01-84),
в том числе из трубобетона.
В отдельных случаях (сложная
геометрия опорного контура, сжатые сроки воздействия и т.п.), при
соответствующем обосновании, в качестве материала опорного контура мембранных
покрытий допускается применять металл.
Контур мембранных панелей,
обрамляющие элементы ограждающих мембранных конструкций, каркас специальных
сооружений с применением мембран рекомендуется выполнять из металла.
24.16.
Стальные мембраны допускаются к эксплуатации без выполнения специальных
мероприятий по огнезащите.
КОНСТРУИРОВАНИЕ
Пролетная конструкция
24.17.
По способу формообразования мембранные оболочки подразделяются на покрытия с
первоначально заданной стрелой провиса и первоначально плоские.
24.18.
Покрытия с заданной стрелой провиса монтируются путем укладки на монтажные
элементы (“постель”) отдельных полотнищ, соединяемых в пространственную
мембрану. Геометрия элементов “постели” определяет начальную форму поверхности
мембранной оболочки и должна соответствовать проектной, что достигается
регулировкой длины элементов “постели”.
24.19.
Первоначально плоские мембранные покрытия, собираемые на спланированной
площадке или подмостях, после подъема или раскружаливания провисают под
действием собственного веса. Форма образующейся при этом поверхности и стрела
провиса покрытия зависят от следующих факторов:
“рыхлости” мембраны,
возникающей из-за сварочных деформаций; начальных погибей, оставшихся после
правки листа или рулона; остаточных деформаций, появляющихся в результате
сворачивания и разворачивания рулона и т.д.;
податливости опорного
контура;
упругих деформаций мембраны.
Рекомендуется начальную
стрелу провиса принимать равной не менее 1/60 меньшей стороны или диаметра
покрытия.
24.20.
Пролетную конструкцию мембранных покрытий следует выполнять из полотнищ
максимальной площади (с учетом условий изготовления, перевозки и монтажа),
поставляемых на монтажную площадку в рулонах. Полотнища рекомендуется
располагать в направлении действия максимальных усилий в покрытии.
24.21.
При существенной неравномерности распределения цепных усилий в пролетной
конструкции для снижения расхода материала и обеспечения равнопрочности
мембраны разрешается применять листы разной толщины (с учетом технологии
изготовления и монтажа тонколистовых полотнищ) или усиливать мембрану в
наиболее напряженных участках дополнительными листами, крепящимися к основному
полотнищу.
24.22.
В пролетную конструкцию мембранных покрытий в большинстве случаев включаются
элементы подкрепления, служащие в период монтажа “постелью”, на которую
укладываются полотнища мембраны. Элементы “постели” состоят из направляющих и
поперечных связей.
Направляющие располагаются
вдоль мембранных полотнищ шагом, равным их ширине. При ширине полотнища свыше 6
м направляющие рекомендуется устанавливать шагом, равным половине ширины
мембранного полотнища. Шаг направляющих необходимо увязывать с шагом основных
колонн и с размером сборных элементов опорного контура.
Поперечные элементы
“постели”, объединяющие отдельные направляющие в пространственную систему,
рекомендуется устанавливать с шагом 3-6 м. При монтаже покрытия на подмостях
или внизу на спланированной площадке элементы “постели” применять не требуется.
24.23.
Направляющие рекомендуется выполнять металлическими длиной на пролет из полосы,
гнутых, прокатных или сварных элементов (тавр, двутавр, два швеллера), легких
висячих ферм с верхней горизонтальной полкой шириной 300 — 500 мм.
Поперечные элементы
рекомендуется выполнять из гнутых или прокатных профилей, подбираемых расчетом
на нагрузку, приходящуюся на них от веса полотнища мембраны. При этом
максимальный прогиб поперечного элемента не должен превышать 1/200 его пролета.
Рекомендуется крепление поперечных элементов к направляющим конструировать
таким образом, чтобы обеспечить их работу по неразрезной схеме. Допускается
поперечные элементы с мембраной не соединять.
24.24.
Площадь сечения направляющих рекомендуется включать в работу пролетной
конструкции при расчетах на эксплуатационную нагрузку. Для этого необходимо
обеспечить совместность работы мембраны и направляющих за счет надлежащего их
соединения между собой и с опорным контуром.
24.25.
Мембранные полотнища рекомендуется соединять между собой и с опорным контуром
внахлестку сваркой (непрерывным угловым швом, точечной сваркой проплавлением
[27]) или высокопрочными болтами. При выполнении стыков односторонним сварным
угловым швом необходима постановка сварных точек проплавлением или
высокопрочных болтов (рис. 58).
Рис.
58. Монтажный стык полотнищ мембраны
а — без “постели”; б — с “постелью”, внахлестку полотнищ мембраны; в — с “постелью”, внахлестку на
направляющих элементах; 1 — мембрана;
2 — направляющие элементы “постели”; 3 — болты или сварные точки; 4 — сварка
При наличии монтажной
“постели” соединение отдельных полотнищ рекомендуется осуществлять на
направляющих с нахлесткой кромок полотнищ.
24.26.
Конструктивное решение узла присоединения мембраны к бортовому элементу (см. п. 24.40) должно обеспечивать надежную
передачу значительных цепных (нормальных и касательных) усилий с пролетной
конструкции на опорный контур. Присоединение мембраны к бортовому элементу
контура рекомендуется выполнять сплошным с использованием опорного столика.
24.27.
В связи с незначительной изгибной жесткостью мембранных оболочек необходима их
стабилизация, предотвращающая потерю общей устойчивости покрытия (его “выхлоп”
в сторону, противоположную провису), уменьшающая повышенную деформативность
мембранных систем от неравномерных нагрузок и обеспечивающая нормальную работу
покрытия на динамические воздействия, в частности, ветровые. В некоторых
случаях стабилизация необходима для предотвращения местной потери устойчивости
тонкого листа, которая может привести к расстройству кровли.
Стабилизация тонколистовых
ограждающих конструкций позволяет максимально использовать их в совместной
работе с обрамляющими элементами основного каркаса, повышает их жесткость и
улучшает эксплуатационные качества.
Стабилизация тонколистовых
покрытий осуществляется увеличением собственного веса покрытия, введением в
конструкцию элементов, обладающих изгибной жесткостью и предварительным
напряжением (растяжением).
24.28.
Стабилизация покрытия за счет увеличения собственного веса достигается
применением утеплителей с повышенным удельным весом, укладкой цементной или
бетонной стяжки, использованием специальных балластных пригрузов, подвеской
постоянного технологического оборудования (рис. 59, а). Такой способ обеспечивает растягивающие напряжения в мембране
даже при ветровом отсосе и уменьшает долю неравномерных временных нагрузок.
Указанный способ является наименее эффективным, так как приводит к увеличению
нагрузок на покрытие и на нижележащие конструкции, поэтому его применение
требует дополнительного обоснования.
Однако, в большинстве
случаев оказывается, что применяемые в настоящее время традиционные конструкции
кровель совместно с мембраной обеспечивают требуемый для стабилизации вес
покрытия.
24.29.
Стабилизирующие изгибно-жесткие элементы следует располагать вдоль линий
главных кривизн поверхности оболочек и выполнять металлическими из сплошных
прокатных или сварных элементов или в виде висячих ферм (рис. 59, б). Стабилизирующие элементы следует
использовать в качестве монтажной “постели”.
Рис.
59. Стабилизация покрытий
а — пригрузом; б — с использованием изгибно-жестких элементов; 1 — мембрана; 2 — пригруз; 3 —
кольцевой кран; 4 — основные
(продольные или радиальные) ребра; 5
— вспомогательные (поперечные или радиальные) ребра
24.30.
Предварительное напряжение мембран осуществляется различными способами в
зависимости от формы поверхности покрытия (рис. 60):
притягиванием мембраны к
контуру натяжными устройствами или изменением положения опорного контура (для
оболочек отрицательной гауссовой кривизны, плоских обшивок);
натяжением нижнего пояса,
элементов решетки или оттяжек вантовых ферм, включенных в пролетную конструкцию
(для оболочек нулевой и положительной гауссовой кривизны);
притягиванием концов
поперечных подкрепляющих элементов к основанию (для цилиндрических оболочек).
Рис.
60. Стабилизация покрытий предварительным напряжением
а — притягиванием мембраны к контуру; б, з
— изменением геометрии покрытия; в, г, д,
ж — натяжением вантовых ферм; е — притягиванием поперечных балок к
основанию: 1 — мембрана; 2 — стабилизирующие ванты; 3 — центральный пригруз; 4 — оттяжки
24.31.
Необходимый для стабилизации вес покрытия, изгибная жесткость ребер, величина
предварительного напряжения определяются расчетом на нормативные временные
нагрузки в зависимости от назначения стабилизации, а также пролета, геометрии
поверхности покрытия и нагрузок. Выбор способа стабилизации следует производить
на основе технико-экономических обоснований с учетом
архитектурно-технологических требований и возможности упрощения изготовления и
монтажа.
24.32.
В пролетной конструкции мембранных систем разрешается предусматривать проемы в
пределах расстояния между элементами подкрепления (если они имеются) для
установки зенитных фонарей, пропуска коммуникаций и т.п. Проемы следует
размещать в местах, удаленных от опорных контуров. Проемы необходимо обрамлять
листом, расположенным в плоскости мембраны и имеющим площадь поперечного
сечения не менее половины площади ослабления мембраны.
Проемы следует проектировать
круглыми, овальными или многоугольными с закруглениями углов радиусом не менее
200 мм.
24.33.
Крепление технологического оборудования к мембранному покрытию рекомендуется
осуществлять на гибких подвесках. При наличии элементов “постели” подвески
рекомендуется крепить к этим элементам. Возможно крепление подвесок
непосредственно к мембране с использованием распределительных шайб.
Опорный контур
24.34.
Опорный контур воспринимает цепные усилия, передающиеся с пролетной части
покрытия. Различают замкнутый контур, который все горизонтальные составляющие
цепных усилий воспринимает в уровне покрытия и на нижележащие конструкции
передает в основном вертикальные усилия, и разомкнутый опорный контур, при
котором усилия с пролетной части покрытия передаются на нижележащие конструкции
(колонны, рамы, пилоны, конструкции трибун, боковых пристроек). Цепные усилия с
покрытия при разомкнутом опорном контуре могут также восприниматься оттяжками.
Ввиду пологости пролетной
конструкции величина распора весьма значительна, поэтому большое значение имеет
рациональное конструирование опорного контура, воспринимающего эти силы,
трудоемкость изготовления и материалоемкость которого занимают значительный
удельный вес в общих показателях, влияющих на экономичность покрытия.
Рекомендуется применять
замкнутый опорный контур. Применение разомкнутого контура может быть оправдано
лишь при наличии конструкций трибун, боковых пристроек и т.п., способных
воспринимать распоры без существенных дополнительных затрат.
Если опорный контур выполнен
в виде нескольких наклонных плоских арок или ломаных балок, не лежащих в одной
плоскости, он оказывается внешне распорным. Для восприятия распора
рекомендуется предусматривать затяжки. Применение контрфорсов менее
рационально.
24.35.
Форма опорного контура определяется линией пересечения поверхности покрытия с
поверхностью стенового ограждения. Его ось может быть очерчена плоской или
пространственной кривой или состоять из отрезков прямых, плоских и
пространственных кривых. Криволинейный опорный контур может быть заменен
полигональным для упрощения изготовления его элементов.
Наружный опорный контур
может лежать на сплошном основании, образованном стенами, или на отдельных
колоннах, в том числе расположенных только по углам покрытия.
24.36.
В общем случае опорный контур воспринимает сжатие с изгибом в одной или двух
плоскостях в зависимости от условий его опирания. Кроме того, в опорном контуре
могут возникать крутящие моменты. При проектировании необходимо стремиться к
тому, чтобы опорный контур был внешне безраспорным и малоизгибным.
Напряженно-деформированное
состояние неплоского (депланированного) опорного контура, опертого на стены или
часто расположенные колонны и обычно имеющего небольшое отклонение от
плоскости, можно принимать эквивалентным работе плоского опорного контура.
24.37.
Поперечное сечение контура определяется расчетом покрытия с учетом его
податливости. Уменьшение изгибной жесткости контура приводит к снижению в нем
величин изгибающих моментов.
Высота сечения опорного
контура принимается при опирании на сплошное основание по конструктивным
соображениям, а на отдельно стоящие опоры — по расчету. В последнем случае
следует учитывать, что кручение контура вызывает в нем дополнительные
изгибающие моменты в вертикальной плоскости.
24.38.
Мембранная пролетная конструкция, прикрепленная по всему периметру к замкнутому
выпуклому опорному контуру, обеспечивает его устойчивость в плоскости мембраны,
за исключением покрытий на прямоугольном и треугольном плане, для которых
необходимо проверять устойчивость опорного контура в этой плоскости.
Устойчивость контура из плоскости покрытия проверяется расчетом с учетом
условий его опирания и нагружения.
24.39.
Металлический опорный контур мембранных покрытий малых и средних пролетов
рекомендуется выполнять в виде балок из прокатных или сварных профилей. Для
покрытий больших пролетов металлический опорный контур рекомендуется выполнять
коробчатого сечения из листов, усиленных поперечными и продольными ребрами и
диафрагмами, обеспечивающими местную устойчивость стенок, неизменяемость
поперечного сечения и передачу усилий с мембраны на все сечение опорного
контура.
При больших размерах
покрытия и существенной разнице в величинах усилий вдоль опорного контура
металлические коробчатые элементы заводского изготовления рекомендуется
принимать с двумя типами поперечного сечения (приопорным и пролетным),
отличающимися толщиной листов стенки при сохранении габаритных размеров.
24.40.
Опорный столик, необходимый для соединения мембраны с бортовым элементом
контура, рекомендуется крепить сваркой к закладным деталям, стальной опалубке
железобетонного контура или к стальному опорному контуру (рис. 61). При
проектировании необходимо обращать особое внимание на анкеровку закладных
деталей и усиление стенки стального короба в местах установки столика.
Рекомендуется плоскость
опорного столика выполнять с наклоном, равным наклону касательной к поверхности
мембранной оболочки в месте примыкания к контуру под максимальной нагрузкой.
Опорный столик необходимо подкреплять вертикальными ребрами не реже чем через
300 мм. Толщину листа опорного столика рекомендуется назначать не менее 1,3
толщины мембраны; ширину — не менее 300-400 мм.
Рис.
61. Узел присоединения мембраны к контуру
а — внахлестку; б — с использованием подкладного листа; 1 — мембрана; 2 — опорный
контур; 3 — опорный столик; 4 — подкладка
24.41.
Опорный контур обычно жестко соединяется с вертикальными конструкциями здания,
на которые он опирается (колонны, стены). При этом деформация опорного контура
от его обжатия и температурных воздействий вызывает в нижележащих конструкциях
изгибающие моменты, а при опирании на колонны в самом контуре возникает
дополнительное кручение.
РАСЧЕТ
24.42.
В основу расчета мембранных конструкций может быть положена теория безмоментных
пластинок или оболочек, так как их напряженное состояние определяется в
основном цепными напряжениями, ввиду весьма малой жесткости мембраны на изгиб.
Однако в месте примыкания мембраны к контуру возможно возникновение быстро
затухающего моментного напряженного состояния.
В большинстве случаев расчет
следует производить с учетом геометрической нелинейности системы. При
относительно большой начальной стреле провиса мембранных оболочек и равновесных
нагрузках их можно рассчитывать по линейной теории.
24.43.
Следует различать два вида расчетов мембранных конструкций:
а) предварительные — для
обоснования технических решений и вариантов конструкций;
б) рабочие — для обоснования
рабочих чертежей.
Методы решения задач расчета
мембранных конструкций разделяются на аналитические и численные. Аналитические
методы в большинстве случаев применимы для предварительных расчетов. Мембранные
системы с большим числом конструктивных особенностей на стадии рабочего
проектирования рекомендуется рассчитывать численными методами на ЭВМ.
24.44.
При расчете мембранных конструкций за основные искомые величины принимаются
напряжения и перемещения пролетной конструкции, изгибающие и крутящие моменты,
продольные усилия, поперечные силы и перемещения опорного контура от силовых и
температурных воздействий, определяемые методами теории упругости на основе
уравнений равновесия и совместности деформаций, геометрических и физических
уравнений с учетом граничных условий.
24.45.
Усилия и перемещения на стадии рабочего проектирования следует определять
расчетом мембранной конструкции как единой пространственной системы с учетом
продольной, изгибной и крутильной жесткостей опорного контура; элементов
подкрепления пролетной части конструкции (в случае их наличия); связи опорного
контура с поддерживающими конструкциями; эксцентриситетов между линией
крепления мембраны к опорному контуру и его нейтральной осью по вертикали и по
горизонтали; отверстий в мембране при их размерах свыше 1/10 меньшего размера
плана оболочки.
24.46.
Расчет мембранных покрытий рекомендуется выполнять с учетом неупругих
деформаций железобетонного или стального опорного контура. При железобетонном
опорном контуре рекомендуется учитывать деформации усадки и ползучести бетона.
При расчете пролетной части
мембранных конструкций по первой группе предельных состояний рекомендуется
ограничиваться упругой стадией работы материала.
25. ПРОФИЛИРОВАННЫЙ НАСТИЛ
ОБЩИЕ ПОЛОЖЕНИЯ
25.1.
Рекомендации настоящего раздела распространяются на профилированные настилы из
оцинкованной стали, включенные в ГОСТ
24045-86 для применения в утепленных покрытиях производственных зданий
различного назначения.
Рекомендации не
распространяются на профилированный настил покрытий, находящихся в особых
условиях эксплуатации (в зданиях, подвергающихся сейсмическим, интенсивным
температурным воздействиям или воздействиям агрессивных сред), покрытий
уникальных зданий, а также в покрытиях специальной конструкции (предварительно
напряженных, пространственных, висячих).
25.2.
Перечень профилеразмеров настила по ГОСТ
24045-86 и ширины заготовок для их изготовления приведен в табл. 68.
Таблица 68
|
Марка настила |
Размеры заготовки, мм |
Поперечное сечение |
Масса m 1 м2, кг |
Удельная |
|
|
ширина |
толщина t |
||||
|
НС40-800 |
1100 |
0,6 |
|
7,1 |
3,8 |
|
0,7 |
8,1 |
3,2 |
|||
|
ПС44-1000 |
1400 |
0,7 |
|
8,3 |
3,3 |
|
Н57-750 |
1100 |
0,7 |
|
8,7 |
3,3 |
|
0,8 |
9,8 |
2,7 |
|||
|
Н60-845 |
1250 |
0,7 |
|
8,8 |
3,8 |
|
0,8 |
9,9 |
3,1 |
|||
|
0,9 |
11,1 |
2,6 |
|||
|
Н75-750 |
1250 |
0,8 |
|
11,2 |
2,1 |
|
0,9 |
12,5 |
2,0 |
|||
|
H114-750 |
1400 |
0,8 |
|
12,5 |
2,1 |
|
0,9 |
14,0 |
2,1 |
|||
|
1,0 |
15,4 |
2,1 |
|||
|
H114-600 |
1250 |
0,8 |
|
14,0 |
2,3 |
|
09 |
15,6 |
2,3 |
|||
|
1,0 |
17,2 |
2,3 |
Примечание. Удельная металлоемкость
настилов определялась как отношение их массы т к расчетной предельной нагрузке q на 1 м2
площади настила. Нагрузка q в данном случае
рассчитывалась для неразрезного двухпролетного настила с пролетами по 3 м при
высоте гофров не более 75 мм или с пролетами 4 м при высоте гофров 114.
Применение профилей одной
марки, но разной толщины в настиле покрытия одного здания не допускается.
25.3.
Конструкция и уклон кровли по профилированному настилу принимаются в соответствии
со СНиП II-26-76 [36]. В типовых конструкциях покрытий с применением
профилированного настила принят уклон кровли не более 1,5 %.
25.4.
Профили настила следует изготовлять из рулонной оцинкованной стали марки БСтЗ любой
степени раскисления по ГОСТ 380-71*,
групп ХП и ПК с цинковым покрытием первого класса с двух сторон по ГОСТ
14918-80*.
По заказу потребителя
допускается изготовлять профили из оцинкованной рулонной стали с лакокрасочным
покрытием по ТУ 67-443-86.
Механические характеристики
материала профилей определяются заводом-изготовителем по результатам
стандартных испытаний и должны быть указаны в сертификатах на готовые профили.
25.5.
При расчете настилов расчетное сопротивление стали при растяжении, сжатии и
изгибе принимается не менее Ry = 220 МПа (2250 кгс/см2), расчетное сопротивление срезу Rs = 130 МПа (1330 кгс/см2).
ХАРАКТЕРИСТИКИ НАСТИЛОВ
25.6.
Основные характеристики поперечного сечения профилей по ГОСТ
24045-86 приведены в табл. 69.
25.7.
Расчетная ширина плоских участков сжатых полок профилей принимается равной 40t при определении моментов
сопротивления и 60t —
при определении моментов инерции, приведенных в табл. 69.
Криволинейные участки,
стенки гофров и растянутые полки настила включены в расчетную площадь сечения
полностью.
расчет
25.8.
Прочность и жесткость (прогиб) профилированных настилов при поперечном изгибе
проверяются по приведенным в пп. 25.9 и 25.10 рекомендациям, составленным с
использованием [37].
Устойчивость гладких стенок
гофров над средними опорами при неразрезных схемах раскладки настилов
проверяется по методике, приведенной в п.
25.11. Устойчивость стенок ступенчатого поперечного сечения в неразрезных
настилах из профилей Н75-750-0.8 (0,9), H114-600-0,8 (0,9) и
Н114-750-0,8 (0,9) проверяется над средними опорами в соответствии с пп. 25.12
и 25.13 с учетом требований СНиП
II-23-81* к стенке
сжато-изогнутого элемента, укрепленной продольным ребром жесткости.
25.9.
Прочность изгибаемого настила следует проверять по формуле
, (163)
где М — расчетное значение изгибающего
момента в рассматриваемом сечении;
Wmin — минимальный расчетный
момент сопротивления в рассматриваемом сечении, принимаемый по табл. 69;
Ry — расчетное сопротивление изгибу;
gn — коэффициент надежности по назначению [37].
25.10.
Прогиб настила fp от нормативной нагрузки,
определяемый как для балки с моментом инерции Ix, по табл.
69, следует проверять по формуле
, (164)
где l —
расчетный пролет настила.
Таблица
69
|
Обозначение профиля |
Размеры сечения, мм |
Площадь сечения А, см2 |
Масса 1 м длины |
Справочные данные на 1 |
||||||
|
узких |
широких |
|||||||||
|
t |
h |
момент инерции Iх, см4 |
момент сопротивления, |
момент инерции Iх, см4 |
момент сопротивления, |
|||||
|
Wx1 |
Wx2 |
Wx1 |
Wx2 |
|||||||
|
НС40-800-0,6 |
0,6 |
40 |
6,6 |
5,6 |
23,3 |
10,5 |
13,0 |
22,3 |
9,8 |
9,4 |
|
НС40-800-0,7 |
0,7 |
40 |
7,7 |
6,5 |
27,1 |
12,2 |
15,1 |
27,1 |
11,8 |
12,1 |
|
НС44-1000-0,7 |
0,7 |
44 |
9,8 |
8,3 |
32,9 |
13,4 |
16,8 |
32,9 |
13,0 |
13,6 |
|
Н57-750-0,7 |
0,7 |
57 |
7,7 |
6,5 |
53,8 |
14,8 |
21,1 |
53,8 |
16,4 |
19,7 |
|
Н57-750-0,8 |
0,8 |
57 |
8,8 |
7,4 |
6l,2 |
17,9 |
24,4 |
61,2 |
18,9 |
24,0 |
|
Н60-845-0,7 |
0,7 |
60 |
8,8 |
7,4 |
62,1 |
14,6 |
24,4 |
59,1 |
16,5 |
18,7 |
|
Н60-845-0,8 |
0,8 |
60 |
10,0 |
8,4 |
70,6 |
17,7 |
28,1 |
69,9 |
19,0 |
22,7 |
|
Н60-845-0,9 |
0,9 |
60 |
11,3 |
9,3 |
79,0 |
20,9 |
31,8 |
78,7 |
21,5 |
27,0 |
|
Н75-750-0,8 |
0,8 |
75 |
10,0 |
8,4 |
114,9 |
25,8 |
32,2 |
114,9 |
28,5 |
33,1 |
|
Н75-750-0,9 |
0,9 |
75 |
11,3 |
9,3 |
129,6 |
30,2 |
37,6 |
119,6 |
31,6 |
38,0 |
|
H114-750-0,8 |
0,8 |
114 |
11,2 |
9,4 |
307,9 |
51,2 |
57,1 |
307,9 |
51,2 |
57,1 |
|
H114-750-0,9 |
0,9 |
114 |
12,6 |
10,5 |
345,2 |
57,4 |
64,0 |
345,2 |
57,4 |
64,0 |
|
H114-750-1,0 |
1,0 |
114 |
14,0 |
11,7 |
383,6 |
63,8 |
71,1 |
383,6 |
63,8 |
71,1 |
|
H114-600-0,8 |
0,8 |
114 |
10,0 |
8,4 |
320,9 |
53,3 |
59,7 |
320,9 |
52,4 |
55,8 |
|
H114-600-0,9 |
0,9 |
114 |
11,3 |
9,3 |
361,0 |
60,0 |
67,2 |
361,0 |
59,6 |
65,9 |
|
H114-600-1,0 |
1,0 |
114 |
12,5 |
10,3 |
405,4 |
67,6 |
75,0 |
405,4 |
67,6 |
75,0 |
25.11. Устойчивость стенок гофров
над средними опорами неразрезного настила высотой не более 60 мм проверяется
согласно [37] по формуле
, (165)
где s — нормальное напряжение от
изгиба, определяемое по формуле (163);
sloс — местное напряжение от реакции средней опоры,
определяемое по формуле (166);
so — нормальное критическое
напряжение, определяемое по формуле (167);
scr — местное критическое
напряжение, определяемое по формуле (168);
т = 1 — при опирании настила на прогон из двутавра,
двух швеллеров или гнутосварного замкнутого профиля;
т = 0,9 — при опирании
настила на прогон из одиночного швеллера;
, (166)
где Вo — опорная реакция на одну
стенку гофра;
z — ширина расчетного участка
стенки гофра, равная b +
2r, но не более 1,5 h;
b — ширина полки прогона или
другого элемента несущих конструкций покрытия, на который опирается настил;
r — радиус сопряжения стенок
гофров с полками профиля;
, МПа, (167)
где ko — коэффициент, зависящий от
характера напряжений в участке и принимаемый по табл. 70;
ko1 — коэффициент, определяемый по формуле (169);
ho = h — 2 (r + t) — расчетная высота гофра;
Таблица 70
|
Марка настила |
А |
ko |
|
НС40-800-0,6 |
21,6 |
3,57 |
|
НС40-800-0,7 |
25,3 |
3,55 |
|
НС44-1000-0,7 |
24,8 |
3,66 |
|
Н57-750-0,7 |
23,2 |
3,09 |
|
Н57-750-0,8 |
26,6 |
3,19 |
|
Н60-845-0,7 |
22,9 |
2,94 |
|
Н60-845-0,8 |
26,2 |
2,91 |
|
Н60-845-0,9 |
29,6 |
2,97 |
, (168)
где Ry — в МПа;
А — коэффициент, зависящий от размеров сечения стенки
и определяемый по табл. 70;
k — коэффициент, определяемый
по табл. 71 в зависимости от ширины опоры настила при условии, что b £ (1,5 h — 2r),
. (169)
Таблица 71
|
b, мм |
40 |
60 |
80 |
120 |
160 |
200 |
|
k |
0,192 |
0,161 |
0,141 |
0,118 |
0,104 |
0,094 |
Примечание. В интервале между значениями, приведенными в таблице,
коэффициент k определяется линейной
интерполяцией.
Если или
, то принимается ko1 = 1,0.
25.12.
При проверке устойчивости стенок ступенчатого поперечного сечения в гофрах
неразрезного профилированного настила уступ на стенке рассматривается как
продольное ребро эквивалентной жесткости (рис. 62).
Рис. 62. Участок стенки а,
рассматриваемый как ребро жесткости, и его расчетное сечение б
25.13.
Продольное ребро жесткости в виде уступа делит стенку гофра на два расчетных
отсека, высоты которых hо1 и ho2 равны расстояниям от выкружек уступа соответственно
до нижней и верхней полок настила (рис.
63).
Устойчивость каждого из
отсеков стенки в надопорных зонах настила считается обеспеченной, если
выполняются условия:
hо1 £ ho; ho2 £ ho,
где ho — наибольшая по условиям
устойчивости ширина сжато-изогнутой пластины, зависящая от значения
коэффициента a, определяемого по формулам:
(для отсека 1);
(для отсека 2),
здесь
— наибольшее сжимающее
напряжение в отсеке 1, принимаемое со
знаком “плюс”;
— напряжение, соответствующее sс, у противоположной расчетной границы отсека;
у — расстояние от опорной полки гофра до
горизонтальной оси уступа на стенке, принимаемое по ГОСТ
24045-86;
Wx1 и Wх2 -моменты сопротивления сечения настила,
принимаемые по табл. 69;
st — наибольшее
растягивающее напряжение в надопорном сечении настила, принимаемое со знаком
“минус”.
|
|
|
Рис. 63. Расчетная схема для проверки устойчивости
ступенчатой стенки
1, 2
— расчетные отсеки пластинок
При a £ 0,5 значение ho определяется по формуле (здесь sс — в МПа).
При a ³ 1,0 значение ho
определяется по формуле 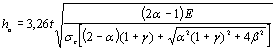
где g — коэффициент, учитывающий
местное смятие согласно [38] и определяемый по формуле
g = 0,42 (2a — 1) sloc/sc;
b — коэффициент, зависящий от
характера напряжений в надопорном сечении стенки и определяемый по формуле
;
здесь tо = t1 — среднее касательное напряжение в отсеке 1, определяемое по формуле
;
tо = t2 — среднее касательное
напряжение в отсеке 2, определяемое
по формуле
.
В интервале 0,5 < a < 1,0 значение ho определяется линейной
интерполяцией между значениями ho при a = 0,5 и a = 1,0.
Если ho1 > ho или ho2 > ho, устойчивость стенок гофров считается необеспеченной и расчетную
нагрузку на настил следует уменьшить.
КРЕПЛЕНИЕ НАСТИЛОВ
25.14.
К прогонам и другим несущим элементам покрытия настил прикрепляется
самонарезающими болтами по ОСТ 34-13-016-77 Куйбышевского завода “Электрощит”
или винтами по ТУ 67-269-79 Челябинского завода профилированного стального
настила (ЧЗПСН) с уплотнительными шайбами.
25.15.
Настил допускается крепить к поддерживающим стальным элементам сварными
электрозаклепками согласно [27].
25.16.
К несущим стальным элементам толщиной от 5 до 12 мм настил допускается крепить
пристрелкой дюбелями согласно ОСТ 36-122-85.
25.17.
Во всех случаях, кроме указанных в пп. 25.18 и 25.19, настил на крайних опорах
и в стыках следует крепить в каждом гофре, на промежуточных опорах неразрезных
настилов — через гофр.
25.18. Крепления и соединения
настила, выполняющего функцию горизонтальных связей в покрытиях зданий или
учитываемого в расчете как диск, рекомендуется выполнять согласно [38].
25.19.
В углах здания и по внешнему контуру покрытия на участках шириной 1,5 м, а
также при расчетном отрицательном давлении ветра свыше 1,5 кН/м2
(153кгс/м2) настил необходимо крепить к несущим конструкциям в
каждом гофре на всех опорах.
25.20.
Профили настила следует соединять между собой продольными крайними полками
внахлест комбинированными заклепками по ОСТ 34-13-017-78 Куйбышевского завода
„Электрощит», ТУ 67-730-86 ЧЗПСН или ТУ 36-2088-85 Минмонтажспецстроя
СССР.
При укрупнении профилей
настила в монтажные карты до их установки в проектное положение допускается
использовать вместо комбинированных заклепок точечную сварку, выполняемую согласно
[27].
Шаг комбинированных заклепок
или сварных точек в продольных стыках настила следует принимать равным 500 мм,
кроме случаев, предусмотренных п. 25.18.
25.21.
Стыки настила по длине следует осуществлять над прогонами или другими несущими
элементами покрытия.
Ширину опирания настила
рекомендуется принимать не менее 40 мм на крайних и 60 мм — на промежуточных
опорах.
26. КОЛОННЫ С ВЕТВЯМИ ИЗ СВАРНЫХ ДВУТАВРОВ С ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ
СТЕНКОЙ
26.1.
Применение стержней с растянутыми стенками основано на использовании
предварительного напряжения для повышения местной устойчивости сжатых элементов
конструкций.
Предварительное
напряжение стенок стержневых элементов металлоконструкций, работающих на
сжимающие эксплуатационные силовые воздействия, уменьшает толщину стенок и
снижает площадь сечения и металлоемкость стержневых элементов. Применение
предварительного напряжения стенок особенно эффективно в ветвях решетчатых
колонн.
26.2.
Элементы конструкций с предварительным напряжением стенок, создаваемым в
процессе их изготовления, имеют традиционное двутавровое сечение и
изготовляются известными методами, из которых наиболее желательно изготовление
на механизированных и поточных линиях, при этом включение в технологические
процессы операций по предварительному напряжению стенок (например, термическим
способом) не нарушает взаимосвязи этих процессов и не снижает
производительности линий.
26.3.
Предварительное напряжение стенок и увеличение концентрации материала в поясах
позволяет использовать для стержневых элементов в качестве материала стали
различной прочности (менее прочные для стенок и более прочные для полок) и тем
самым повысить эффективность применения сталей повышенной и высокой прочности в
сжатых элементах строительных металлоконструкций.
26.4.
Рациональными областями применения конструкций с предварительно напряженными
стенками являются центрально сжатые сварные стержни решетчатых систем, в том
числе сварные подкрановые ветви решетчатых колонн.
Целесообразность
изготовления сварных сжатых стержней с предварительно напряженными стенками
определяется наличием на заводе-изготовителе соответствующих механизированных
(поточных) линий или установок и степенью снижения приведенных затрат по
сравнению с традиционными аналогами (прокатные и обычные сварные профили).
26.5.
Область рационального применения сварных двутавров с предварительно напряженной
стенкой в качестве подкрановой ветви решетчатых колонн охватывает колонны
промышленных зданий с мостовыми кранами высотой от 10,8 до 18 м, пролетами от
18 до 36 м, с шагом колонн 12 м, грузоподъемностью мостовых кранов 50 т включ.
Расчетное сопротивление материала поясов Ryf ³ 345 МПа (3500 кгс/см2).
26.6.
Расчет решетчатых колонн с ветвями из сварных двутавров с предварительно
напряженной стенкой включает: определение оптимальных размеров сечения;
проверку несущей способности ветви по общей и местной устойчивости, а также
проверку несущей способности решетчатой колонны относительно свободной оси.
26.7.
Вначале определяется комплексный параметр стержня Cх по формуле
, (170)
где
;
(для двутавра),
здесь Р = Aw/A; ;
kw = 2,8—4 для бистальных колонн; kw = 4-6 — для моностальных
колонн (уточняется в процессе расчета).
26.8.
Коэффициент площади сечения yx определяется для бистальных колонн по табл. 72, для
моностальных — по табл. 73.
Для бистальных колонн
параметр определяется по табл.
72, для моностальных — принимается = 1.
Для бистальных колонн
определяется параметр sp = Ryf и назначается расчетное сопротивлений материала стенки Ryw:
Ryw ³ (1 — b)sр.
Таблица 72
|
Хх |
yх |
|
Хх |
yх |
|
|
15 |
1,550 |
0,80 |
75 |
2,325 |
0,55 |
|
25 |
1,725 |
0,70 |
100 |
2,600 |
0,45 |
|
50 |
2,050 |
0,60 |
Таблица
73
|
Xx |
1 |
5 |
7,5 |
10 |
15 |
20 |
|
yх |
1,111 |
1,333 |
1,428 |
1,515 |
1,639 |
1,754 |
26.9.
Допускаемая гибкость стенки без учета предварительного напряжения определяется по
формуле
, (171)
где — условная гибкость
колонны относительно оси х-х,
определяемая по табл. 74 в зависимости от параметров и jхp.
. (172)
Требуемая гибкость () предварительно напряженной стенки определяется по формуле
. (173)
Таблица 74
|
Ry, |
|
|
||||||
|
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
0,3 |
||
|
450 |
0,0 |
1,21 |
1,96 |
2,55 |
3,12 |
3,74 |
4,40 |
5,25 |
|
0,2 |
1,15 |
1,93 |
2,48 |
3,05 |
3,67 |
4,33 |
5,16 |
|
|
0,4 |
1,09 |
1,80 |
2,36 |
2,94 |
3,55 |
4,24 |
5,10 |
|
|
(4600) |
0,6 |
0,99 |
1,66 |
2,23 |
2,83 |
3,42 |
4,15 |
5,03 |
|
0,8 |
0,93 |
1,54 |
2,08 |
2,68 |
3,31 |
4,06 |
4,96 |
|
|
1,0 |
0,87 |
1,43 |
1,93 |
2,53 |
3,20 |
3,97 |
4,89 |
|
|
540 |
0,0 |
1,24 |
2,00 |
2,60 |
3,15 |
3,78 |
4,46 |
5,28 |
|
0,2 |
1,18 |
1,95 |
2,51 |
3,08 |
3,72 |
4,38 |
5,22 |
|
|
0,4 |
1,12 |
1,82 |
2,39 |
2,97 |
3,59 |
4,28 |
5,17 |
|
|
(5500) |
0,6 |
1,01 |
1,68 |
2,26 |
2,87 |
3,46 |
4,20 |
5,11 |
|
0,8 |
0,95 |
1,56 |
2,10 |
2,72 |
335 |
4,11 |
5,03 |
|
|
1,0 |
0,89 |
1,44 |
1,94 |
2,57 |
3,24 |
4,02 |
4,95 |
26.10.
Допускаемая гибкость свеса полки без учета предварительного напряжения в соответствии с п.
7.23* СНиП II-23-81* определяется по формуле
. (174)
Требуемая гибкость свеса
полок с учетом предварительного напряжения определяется по
формуле
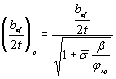
26. 11. Оптимальные размеры сечения определяются по формулам:
площадь сечения ; (176)
” стенки Аw
= bA; (177)
” полки Af
= 0,5(1 — b) × A; (178)
ширина стенки ; (179)
толщина ” ; (180)
ширина полки ; (181)
толщина ” . (182)
26.12. Расчетное сопротивление материала стенки Ryw
определяется по формуле
Ryw ³ (1 — b)sp.
26.13.
Наиболее близкие к оптимальным размеры сечения назначаются с учетом сортамента
и выполняется проверка общей и местной устойчивости колонн в соответствии с пп.
26.14-26.16.
26.14.
Для бистальных колонн параметр kw уточняется по формуле
, (183)
где — определяется по формуле (171).
Затем по табл. 73 линейной интерполяцией
определяется параметр в зависимости от
параметра Xх определяемого по формуле (170). Для моностальных колонн принимается = 1.
26.15.
Расчет на устойчивость центрально-сжатой ветви колонны относительно оси х-х выполняется по формуле
, (184)
где F —
расчетное продольное усилие;
А —
площадь сечения брутто;
jxp — коэффициент продольного
изгиба, принимаемый по табл. 75 в функции от и условной гибкости
:
,
здесь lx — расчетная длина относительно оси х-х,
i — радиус инерции сечения
относительно оси х-х.
При ³ 1,5 jxp определяется линейной интерполяцией;
< 1,5 jxp определяется линейной экстраполяцией.
Таблица
75
|
Ry, |
s |
jxр при |
||||||
|
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
||
|
450 |
0,0 |
0,861 |
0,795 |
0,708 |
0,621 |
0,538 |
0,460 |
0,388 |
|
0,2 |
0,855 |
0,787 |
0,697 |
0,609 |
0,527 |
0,449 |
0,379 |
|
|
0,4 |
0,842 |
0,764 |
0,676 |
0,590 |
0,508 |
0,434 |
0,370 |
|
|
(4600) |
0,6 |
0,8 |
0,740 |
0,655 |
0,574 |
0,489 |
0,420 |
0,360 |
|
0,8 |
0,808 |
0,715 |
0,630 |
0,550 |
0,475 |
0,408 |
0,351 |
|
|
1,0 |
0,790 |
0,693 |
0,608 |
0,530 |
0,463 |
0,398 |
0,341 |
|
|
540 |
0,0 |
0,865 |
0,800 |
0,716 |
0,620 |
0,542 |
0:467 |
0,394 |
|
0,2 |
0,853 |
0,789 |
0,702 |
0,614 |
0,534 |
0,458 |
0,386 |
|
|
0,4 |
0,843 |
0,768 |
0,682 |
0,595 |
0,514 |
0,440 |
0,367 |
|
|
(5500) |
0,6 |
0,828 |
0,745 |
0,663 |
0,578 |
0,494 |
0,427: |
0,362 |
|
0,8 |
0,811 |
0,719 |
0,635 |
0,555 |
0,480 |
0,414 |
0,357 |
|
|
1,0 |
0,797 |
0,697 |
0,615 |
0,535 |
0,468 |
0,403 |
0,346 |
26.16.
Расчет на устойчивость сжатой ветви колонны относительно оси у-у выполняется по формуле
, (185)
где jyp — коэффициент продольного изгиба, принимаемый по
табл. 76 в функции от и условий гибкости
,
здесь lу — расчетная длина
относительно оси у-у;
iy — радиус инерции сечения
относительно оси у-у.
При ³ 1,5 jyp определяется линейной интерполяцией;
< 1,5 jyp определяется линейной экстраполяцией.
Таблица
76
|
Ry, |
|
jyр при |
||||||
|
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
||
|
450 |
0,0 |
0,921 |
0,854 |
0,774 |
0,680 |
0,582 |
0,492 |
0,413 |
|
0,2 |
0,909 |
0,827 |
0,730 |
0,632 |
0,542 |
0,463 |
0,394 |
|
|
0,4 |
0,897 |
0,793 |
0,679 |
0,581 |
0,502 |
0,433 |
0,372 |
|
|
(4600) |
0,6 |
0,884 |
0,763 |
0,631 |
0,534 |
0,460 |
0,395 |
0,344 |
|
0,8 |
0,879 |
0,739 |
0,591 |
0,484 |
0,418 |
0,363 |
0,312 |
|
|
1,0 |
0,858 |
0,707 |
0,553 |
0,444 |
0,373 |
0,321 |
0,280 |
|
|
540 |
0,0 |
0,923 |
0,857 |
0,777 |
0,684 |
0,588 |
0,498 |
0,419 |
|
0,2 |
0,910 |
0,830 |
0,734 |
0,636 |
0,533 |
0,468 |
0,399 |
|
|
0,4 |
0,898 |
0,795 |
0,684 |
0,586 |
0,506 |
0,438 |
0,376 |
|
|
(5500) |
0,6 |
0,886 |
0,765 |
0,633 |
0,538 |
0,464 |
0,398 |
0,348 |
|
0,8 |
0,890 |
0,742 |
0,593 |
0,486 |
0,422 |
0,367 |
0,316 |
|
|
1,0 |
0,859 |
0,710 |
0,558 |
0,446 |
0,375 |
0,324 |
0,282 |
26.17.
Расчет на устойчивость предварительно напряженной стенки выполняется с учетом:
собственных растягивающих
напряжений spw определяемых по формуле
Rpw ³ (1 — b)sp. (186)
критических напряжений
стенки scr,w, определяемых по
формуле
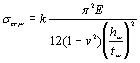
где k — определяется по табл. 77
в зависимости от параметра aw; при промежуточных значениях awk определяется линейной
интерполяцией.
Таблица
77
|
aw |
0,00 |
0,80 |
2,10 |
5,70 |
10,00 |
|
k |
7,00 |
6,08 |
5,26 |
4,61 |
4,00 |
Параметр aw определяется по формуле
. (188)
Устойчивость стенки
считается обеспеченной, если выполняется условие
spw + scr,w — 0,1Ryw £ jpRyf, (189)
где jp — принимается равным
минимальному из коэффициентов jxp и jур.
26.18.
Устойчивость свеса полки считается обеспеченной, если выполняется условие
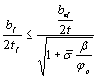
где — определяется по
формуле (174) в зависимости от
наибольшей условной гибкости стержня.
26.19.
Расчет на устойчивость решетчатой колонны относительно свободной оси
выполняется по формуле
, (191)
здесь jе — коэффициент, определяемый в соответствии с п.
5.27* СНиП II-23-81*.
26.20.
Конструктивное оформление сварных колонн с ветвями двутаврового сечения с
предварительно напряженными стенками следует производить с применением новых
эффективных решений и так, чтобы не вызывать существенного снижения
предварительного напряжения, полученного при изготовлении стержней.
26.21.
При проектировании колонн с предварительно напряженными стенками рекомендуется:
для максимального снижения
тепловложений от сварки применять только расчетные сварные швы, завариваемые
механизированными методами, в том числе швы с уменьшенными катетами;
вспомогательные элементы
колонн, рассчитываемые по прочности, изготавливать из сталей повышенной и
высокой прочности.
Если концевые участки
стержней, где возможна потеря предварительного напряжения при изготовлении,
являются расчетными, то снижение предварительного напряжения слезет
предотвратить или компенсировать за счет включения в работу концевых деталей —
опорных и подкрановых траверс, башмаков, плит, утолщений стенок, стыковых и
соединительных деталей, создающих жесткие торцевые окаймления стержней.
27. ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ НА ВЫСОКОПРОЧНЫХ БОЛТАХ, РАБОТАЮЩИЕ НА
РАСТЯЖЕНИЕ
27.1.
Рекомендации настоящего раздела следует соблюдать при проектировании,
изготовлении и монтажной сборке фланцевых соединений элементов открытого
профиля (двутавров, тавров, швеллеров и т.п.) стальных конструкций
производственных зданий, подверженных растяжению, растяжению с изгибом при
однозначной эпюре растягивающих напряжений (smin/smax ³ 0,5), а также действию
местных поперечных усилий.
Рекомендации не распространяются
на фланцевые соединения:
воспринимающие
знакопеременные нагрузки, а также многократно действующие подвижные,
вибрационные или другого вида нагрузки с числом циклов свыше 105 при
коэффициенте асимметрии напряжений в соединяемых элементах r = smin/smax ³ 0,8;
эксплуатируемые в
сильноагрессивной среде.
27.2.
Фланцевые соединения следует выполнять только с предварительно напряженными
высокопрочными болтами. Величину предварительного натяжения болтов Во для расчетов следует
принимать равной
Во = 0,9Вр = 0,9RbhAbn,
где Вр
— расчетное усилие растяжения болта.
27.3.
Для фланцевых соединений следует применять высокопрочные болты М24 и М27 из
стали 40Х “селект” исполнения ХЛ с временным сопротивлением не менее 1100 МПа
(110 кгс/мм2), а также гайки высокопрочные и шайбы к ним по ГОСТ
22353-77* — ГОСТ
22356-77*.
27.4.
Для фланцев следует применять листовую сталь по ГОСТ 19903-74* марок
09Г2С-15 по ГОСТ
19282-73* и 14Г2АФ-15 по ТУ 14-105465-82 с гарантированными механическими
свойствами в направлении толщины проката.
27.5.
Фланцы могут быть выполнены из других марок низколегированных сталей по ГОСТ
19282-73*, предназначенных для строительных стальных конструкций, при этом:
сталь должна быть 12-й
категории;
временное сопротивление и
относительное сужение стали в направлении толщины проката должны быть sbz ³ 0,8sb, yz ³ 20 % (где sb — нормативное значение временного сопротивления для
основного металла, принимаемое по государственным общесоюзным стандартам или
техническим условиям).
Проверку механических
свойств стали в направлении толщины проката осуществляет завод-изготовитель
металлоконструкций по методике, изложенной в [25].
27.6.
Дефекты стали для фланцев (внутренние расслои, грубые шлаковые включения и
т.п.) должны удовлетворять требованиям, указанным в табл. 78. Контроль качества
стали методами ультразвуковой дефектоскопии осуществляет завод-изготовитель
металлоконструкций.
Таблица
78
|
Зона дефектоскопии |
Характеристика дефекта |
||||
|
площадь, см2 |
частота допустимая |
длина максимально |
Расстояние между |
||
|
минимально учитываемая |
максимально допустимая |
||||
|
Листы фланцев |
0,5 |
1,0 |
10 м-2 |
4 |
10 |
|
Прикромочная |
0,5 |
1,0 |
3 м-1 |
4 |
10 |
Примечания: 1. Дефекты, расстояния между
краями которых меньше протяженности минимального из них, оцениваются как один дефект.
2. По усмотрению завода-изготовителя металлоконструкций разрешается
дефектоскопический контроль материала фланцев выполнять после приварки их к
элементам конструкций.
27.7.
Фасонки, ужесточающие фланцы (ребра жесткости), следует выполнять из стали тех
же марок, что и основные профили.
27.8.
Для механизированной сварки фланцевых соединений следует применять сплошную
сварочную проволоку по ГОСТ 2246-70* или
порошковую проволоку ПП-АН8 по ТУ 144-1059-80.
27.9. При
конструировании фланцевых соединений болты следует располагать безмоментно
относительно центра тяжести сечения соединяемого элемента с учетом
неравномерности распределения внешних усилий между болтами наружной и внутренней
зон (рис. 64) в соответствии с табл. 79. Предельное усилие на один болт
внутренней зоны следует принимать Ni = 0,9Bp.
Таблица
79
|
Диаметр болта |
Толщина фланца, мм |
Отношение внешнего |
|
М24 |
20 |
2,6 |
|
25 |
1,8 |
|
|
30 |
1,5 |
|
|
40 |
1,1 |
|
|
М27 |
25 |
2,1 |
|
30 |
1,7 |
|
|
40 |
1,2 |
Болты
следует располагать как можно ближе к элементам присоединяемого профиля, при
этом (см. рис. 64):
kf + ds/2 + 2 £ b1 £ 3,5d, мм;
a ³ 0,8 ds;
w £ 4b,
где ds — наружный диаметр шайбы, мм;
d — наружный диаметр стержня
болта, мм.
27.10.
Число болтов внутренней зоны определяет конструктивная форма соединения, а
наружной зоны — предварительно назначается из условия
,
где ne, ni — число болтов
соответственно наружной и внутренней зон;
N —
внешнее усилие на фланцевое соединение.
27.11. Фланцевые соединения
растянутых элементов конструкций проверяют расчетом на прочность:
болтов;
фланцев на изгиб;
соединения при воздействии
поперечных усилий;
сварного соединения фланца с
профилем.
27.12.
Прочность фланца и болтов, относящихся к внутренней зоне, следует считать
обеспеченной, если толщина фланца находится в пределах от 20 до 40 мм, болты
расположены в соответствии с п. 27.9, а
нагрузка на болт от действия внешних усилий не превышает величины, равной 0,9Вр.
Рис. 64. Схема фланцевых соединений стропильных
ферм с поясами
а — из широкополочных тавров; б — из парных равнополочных уголков
27.13.
При расчете на прочность болтов и фланца, относящихся к наружной зоне, выделяют
участки фланца, которые рассматривают как Т-образные фланцевые соединения
шириной w (см. рис. 64).
Прочность соединения следует
считать обеспеченной, если
,
где Nj — расчетное усилие на j-й
болт наружной зоны, равное
Nj = min(Nbj,
Nfj),
здесь Nbj — расчетное усилие на j-й болт, определяемое из
условия прочности соединения по болтам
Nbj = (a — blgXj) Вр,
a, b — коэффициенты, принимаемые
по табл. 80;
Xj — параметр жесткости болта,
определяемый по формуле
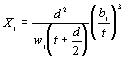
bj — расстояние от оси j-го болта до края сварного
шва;
wj — ширина j-го участка фланца (см. рис. 64);
t — толщина фланца;
Таблица 80
|
Отношение толщины |
Коэффициенты |
|
|
a |
b |
|
|
0,83 |
0,336 |
0,207 |
|
1,04 |
0,388 |
0,257 |
|
1,25 |
0,425 |
0,278 |
|
1,46 |
0,470 |
0,270 |
|
1,67 |
0,527 |
0,239 |
Nfj — расчетное усилие на j-й болт, определяемое из
условия прочности фланца на изгиб
,
mi — параметр, определяемый по
формуле
,
gj — параметр, определяемый по
табл. .81 или из уравнения
1,4Xj(gj — 1)3 — g2j + mjgj(gj — 1) = 0.
Ry — расчетное сопротивление
стали фланца.
Таблица
81
|
Параметр жесткости |
Значения g при m, |
|||||||||
|
1,4 |
1,6 |
1,8 |
2,0 |
2,2 |
2,4 |
2,7 |
3,0 |
4,0 |
5,0 |
|
|
0,02 |
3,252 |
2,593 |
2,221 |
1,986 |
1,826 |
1,710 |
1,586 |
1,499 |
1,333 |
1,250 |
|
0,06 |
2,960 |
2,481 |
2,171 |
1,962 |
1,812 |
1,702 |
1,582 |
1,497. |
1,333 |
1,250 |
|
0,1 |
2,782 |
2,398 |
2,130 |
1,939 |
1,799 |
1,694 |
1,578 |
1,494 |
1,332 |
1,249 |
|
0,5 |
2,186 |
2,036 |
1,908 |
1,776 |
1,711 |
1,636 |
1,545 |
1,475 |
1,327 |
1,248 |
|
1,0 |
1,949 |
1,860 |
1,780 |
1,707 |
1,643 |
1,586 |
1,514 |
1,454 |
1,321 |
1,246 |
|
2,0 |
1,757 |
1,704 |
1,653 |
1,607 |
1,564 |
1,524 |
1,470 |
1,424 |
1,312 |
1,242 |
|
3,0 |
1,660 |
1,621 |
1,584 |
1,548 |
1,515 |
1,483 |
1,440 |
1,402 |
1,303 |
1,238 |
|
4,0 |
1,599 |
1,568 |
1,537 |
1,508 |
1,480 |
1,454 |
1,417 |
1,384 |
1,296 |
1,235 |
|
5,0 |
1,555 |
1,529 |
1,503 |
1,478 |
1,454 |
1,431 |
1,399 |
1,370 |
1,289 |
1,232 |
|
6,0 |
1,522 |
1,498 |
1,476 |
1,454 |
1,433 |
1,413 |
1,384 |
1,357 |
1,283 |
1,230 |
|
8,0 |
1,473 |
1,454 |
1,436 |
1,418 |
1,401 |
1,384 |
1,360 |
1,337 |
1,273 |
1,224 |
|
10 |
1,438 |
1,422 |
1,406 |
1,391 |
1,377 |
1,362 |
1,341 |
1,322 |
1,264 |
1,219 |
|
15 |
1,381 |
1,369 |
1,358 |
1,346 |
1,335 |
1,324 |
1,308 |
1,293 |
1,247 |
1,210 |
27.14.
Прочность фланцевого соединения на действие местной поперечной силы следует
проверять по формуле
,
где п — число болтов наружной зоны для
фланцевых соединений элементов открытого профиля или общее число болтов для
соединений элементов замкнутого профиля;
Rj — контактные усилия,
принимаемые равными 0,1Bo для фланцевых соединений элементов замкнутого профиля, а для элементов
открытого профиля, определяемые по формуле
Rj = Bp — 1,2Nbj;
m — коэффициент трения
соединяемых поверхностей фланцев, принимаемый в соответствии с указаниями п.
11.13 СНиП II-23-81*.
При отсутствии местной
поперечной силы в расчет вводится условное значение Qloc = 0,1mN.
27.15.
Расчет сварного соединения фланца с профилем следует производить в соответствии
с п. 4.10 [25].
27.16.
При изготовлении конструкций с фланцевыми соединениями сборку элементов следует
осуществлять только в кондукторах.
Сварку фланца и
присоединяемого элемента следует выполнять механизированным способом, при этом
технология сварки должна обеспечивать минимальные сварочные деформации фланцев.
После выполнения сварки внешние поверхности фланцев должны быть отфрезерованы.
Толщина фланцев после фрезеровки должна быть не менее указанной в чертежах КМ
или КМД.
Точность изготовления отправочных
элементов конструкций с фланцевыми соединениями должна соответствовать
следующим требованиям:
тангенс угла отклонения
фрезерованной
поверхности фланцев не
должен превышать……………………… 0,0007;
предельные отклонения не
должны
превышать следующих
значений, мм:
зазор между внешней
плоскостью
фланца и ребром стальной
линейки. ………………………………… 0,3;
смещение фланца от
проектного
положения относительно осей
сечения
присоединяемого элемента.
…………………………………………. ± 1,5;
допускаемое отклонение длины
элемента
с фланцевым соединением при
проектной
длине элемента, м:
св. 4,5 до
9……………………………………………………………… ± 2;
” 9 ” 15
…………………………………………………………………..
±2,5.
Калибр диаметром, равным
номинальному диаметру болта, должен при контрольной сборке проходить во все
отверстия соединения.
27.17.
Предварительное натяжение высокопрочных болтов при монтажной сборке фланцевых
соединений следует производить закручиванием гаек до значения момента
закручивания Mt, определяемого по формуле
Mt = nkBod,
где п — коэффициент, принимаемый равным: при
натяжении высокопрочных болтов 1,06; при контроле усилия натяжения болтов 1,0;
k —
среднее значение коэффициента закручивания для каждой партии болтов по
сертификату или принимаемое равным 0,18 при отсутствии таких значений в
сертификате;
Во — усилие предварительного натяжения болтов,
определяемое в соответствии с п. 27.2,
тс;
d — номинальный диаметр
болта, м.
27.18.
Контроль усилия натяжения следует осуществлять во всех установленных
высокопрочных болтах тарированными динамометрическими ключами. Контроль усилия
натяжения следует производить не ранее чем через 8 ч после выполнения натяжения
всех болтов в соединении.
Контроль следует
осуществлять по моменту закручивания, определяемому в соответствии с п. 27.17.
Отклонение фактического
момента закручивания от расчетного должно быть от 0 до + 10 %. Если при
контроле обнаружатся болты, не отвечающие этому условию, то усилие натяжения
таких болтов должно быть доведено до требуемой величины с последующим контролем
через 6 ч.
27.19.
После выполнения монтажной сборки конструкции отклонения от проектных линейных
размеров и геометрической формы фланцевых соединений не должны превышать
следующих значений, мм:
просвет между фланцами или
фланцем и
полкой колонны после
предварительного
натяжения высокопрочных
болтов по линии
стенок и полок профиля.
………………………………………. 0,2;
то же, по краям фланцев при
толщине
фланцев, мм:
до 25
………………………………………………………………. 0,6;
св. 25
……………………………………………………………… 1,0;
щуп толщиной 0,1 мм не должен проникать в зону
радиусом 40 мм от оси болта.
28. ПОДБОР СЕЧЕНИЙ ЦЕНТРАЛЬНО-СЖАТЫХ, СЖАТО-ИЗГИБАЕМЫХ И ИЗГИБАЕМЫХ
ЭЛЕМЕНТОВ
ОБЩИЕ ПОЛОЖЕНИЯ
28.1.
Подбор поперечных сечений стальных элементов обычно выполняется в три этапа:
первый
— предварительный расчет, выявляющий ориентировочные параметры элементов
сечения;
второй
— компоновка сечения и вычисление его геометрических характеристик;
третий
— поверочный расчет сечения элемента и уточнение его параметров.
28.2.
Основным этапом, определяющим
качество всего расчета, является первый.
От него зависит, насколько эффективным будет окончательно принятое сечение
элемента и какова трудоемкость расчета. Значение первого этапа подбора сечения
возросло в связи со строгими требованиями к качеству расчета, предъявляемыми СНиП II-23-81*. Предварительный расчет
должен позволять производить за один раз компоновку сечения при обеспечении
всех нормативных требований. Его можно выполнять при двух условиях,
предъявляемых к габаритам сечения:
первом — габариты могут быть
заданы или приняты из конструктивных соображений;
втором — габариты должны
быть определены из критериев оптимальности.
При первом условии расчет
выполняется обычным порядком исходя из ориентировочных зависимостей расчетных
параметров от размеров сечения; при втором — с использованием прямого метода
подбора сечения, позволяющего наиболее просто получить оптимальное решение, под
которым обычно понимают достижение минимума массы или стоимости элемента.
28.3.
Второй этап подбора выполняется с
целью увязки расчетных параметров с действительными размерами элементов
составного сечения в соответствии с требованиями конструирования и фактическими
размерами элементов, указанными в сортаменте. Этот этап является, как правило,
вспомогательным, не определяющим размеры поперечного сечения, а лишь вносящим
некоторую корректировку, учитывающую реальное проектирование.
28.4.
Третий этап — завершение подбора
сечения поверочным расчетом в соответствии с требованиями СНиП II-23-81*. При необходимости на этом этапе производится
несущественное уточнение параметров и характеристик сечения, не вызывающих
необходимость перерасчета.
ЦЕНТРАЛЬНО-СЖАТЫЕ ЭЛЕМЕНТЫ
28.5.
Требуемая площадь поперечного сечения А
при заданных габаритах определяется по формуле (7) СНиП II-23-81*:
. (192)
Коэффициент продольного
изгиба j при рекомендуется
определять из выражения j = k(0,95 — 0,035), где коэффициент k принимается
по табл. 82. Для предварительного расчета при k может быть принят равным единице.
Таблица 82
|
Ry, |
Значения k при |
|||||||
|
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
|
|
210 |
1,037 |
1,019 |
1,006 |
1,000 |
1,003 |
0,982 |
1,004 |
1,112 |
|
290 |
1,038 |
1,021 |
1,010 |
1,006 |
1,014 |
0,994 |
1,015 |
1,120 |
|
380 |
1,039 |
1,024 |
1,015 |
1,015 |
1,027 |
1,006 |
1,027 |
1,128 |
|
530 |
1,040 |
1,028 |
1,023 |
1,028 |
1,048 |
1,028 |
1,047 |
1,142 |
При > 4,0
, т.е. для предварительных расчетов допускается расширить
диапазон использования выражения (10) СНиП II-23-81* с погрешностью до 1 % при = 4,0 — 4,5.
Условная гибкость стержня (где
) может быть определена с использованием приближенных
значений радиусов инерции сечений относительно главных осей ix, iy, принимаемых по табл. 83 (х — горизонтальная, у — вертикальная оси).
Таблица
83
|
Радиус инерции |
Приближенные значения |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ix |
0,35d |
0,29h |
0,43h |
0,30h |
0,20h |
0,20h |
0,32h |
0,32h |
0,32h |
|
iy |
0,35d |
0,29h |
0,24b |
0,20b |
0,20b |
0,40h |
0,49b |
0,58b |
0,40b |
Продолжение табл. 83
|
Радиус инерции |
Приближенные значения |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ix |
0,30h |
0,32h |
0,28h |
0,40h |
0,40h |
0,40h |
0,43h |
0,21h |
0,41b |
|
iy |
0,22b |
0,20b |
0,24b |
0,51b |
0,44b |
0,60b |
0,43b |
0,21b |
0,41b |
Для сквозных стержней при
вычислении относительно
свободной оси вместо l принимается lef, определяемая по табл. 7 СНиП II-23-81*. Для составных стержней сквозного сечения с
планками при (где hb — ширина планки; b — расстояние в осях ветвей)
следует считать Isl/(Ibb) ³ 5.
28.6.
Оптимальное сечение стержня заданной формы должно удовлетворять двум условиям:
равноустойчивости, т.е. lx = lу;
предельной тонкостенности
элементов сечения (стенки и полки) в соответствии с табл. 27* и 29* и пп.
7.14*; 7.18*-7.20* СНиП II-23-81*.
Верхняя граница рациональной
области применения стали повышенной и высокой прочности определяется из условия
снижения массы стержня (площади поперечного сечения А) с ростом величины расчетного сопротивления, т.е. dA/dRy £ 0, которое выполняется при £ 3,9. Поэтому стержни с
условной гибкостью > 3,9 должны
выполняться из малоуглеродистой стали, так как при l > 120 применение стали с
расчетным сопротивлением Ry > 210 МПа (2150 кгс/см2) является нерентабельным.
Применение стали повышенной
и высокой прочности экономически эффективно (наблюдается не только снижение
массы, но и стоимости конструкции) при £ 2,5.
28.7. Прямой метод подбора
поперечного сечения стержня позволяет получить значение требуемой условной
гибкости за один раз. Для
этого формула (7) СНиП II-23-81* преобразована в
формулу
, (193)
где
D = ВС;
— параметр исходных данных;
—
квадрат удельного радиуса инерции поперечного сечения относительно одной из
главных осей.
Для наиболее
распространенных сплошностенчатых сечений значения параметра С могут быть определены по данным табл.
84.
Таблица
84
|
Параметр |
Поперечное сечение |
||||||
|
|
|
|
|
|
|
|
|
|
Сx |
|
|
|
|
|
|
|
|
Cy |
|
|
|
|
|
|
|
Обозначения, принятые в табл. 84:
— соотношение площадей вертикальных (стенок) и
горизонтальных (полок) элементов сечения;
nw и nf
— соответствующее число элементов в составе сечения;
—
соответственно гибкость стенки и полки;
= — соотношение размеров (габаритов) сечения — высоты к
ширине.
В табл. 84 указан также
размер от ближайшего края до центра тяжести сечения, несимметричного
относительно оси х- х:
Для двутаврового сечения с
неустойчивой (работающей в закритическом состоянии) стенкой формулы для
определения параметра С приведены в
табл. 85.
Таблица 85
|
Сечение |
Формулы для |
|
|
Cx |
Су |
|
|
|
|
|
Обозначения, принятые в табл. 85:
;
.
При центральном сжатии в
соответствии с п. 7.20* СНиП II-23-81* допускается
принимать . Тогда для двутаврового сечения получим значения 2/3 £ uef/u £ 1, при которых
. Итак, при расчете двутаврового сечения с неустойчивой
стенкой в качестве исходного значения следует принять uef = 2u/3. Полная площадь сечения, включая неустойчивую часть стенки, равна
.
Для составных сечений из
прокатных наиболее тонкостенных профилей значения параметра С приведены в табл. 86.
При гибкости широких полок
уголков значения С должны быть уменьшены в lf/15 раз; нижние и верхние
значения С для двутавров и швеллеров
соответствуют малым и большим номерам профилей ГОСТ 8239-72* и ГОСТ 8240-72*.
Для сквозного трехгранного симметричного сечения Сx
= Су = b/6А (где b —
расстояние между осями ветвей).
28.8. С
учетом выражения из формулы (193) при
условную гибкость
стержня можно представить в виде , где m =
1; k = 0,045 — 3,4 Ry/E; п = —0,028 + 2,13Ry/E
при 0 < < 2,5, т.е. при D ³ 0,115 + 3,5 Ry/E. Принятое выражение j отличается от нормативного
(8), но ошибка в величине не превосходит 1 %.
m =
1,47 — 13Ry/E; k = 0,371 — 27,3Rу/Е; п = 0,0275 — 5,53Ry/E
при 2,5 < £ 4,5, т.е. при 0,115 +3,5 Ry/E > D > 0,0175. Здесь принято
нормативное выражение j по формуле (9).
Поскольку влияние Ry на величину j мало (см. табл. 82), то при
£ 3,9 можно использовать
следующее приближенное выражение (с ошибкой до 3 %):
при D ³ 0,03. (194)
Заметим, что при 0,07 > D ³ 0,03 более точное решение
можно получить, заменив в формуле (194) коэффициент 0,04 на 0,033 + 0,1 Д.
При 3,9 < < 6,5, приняв
приближенное выражение j = 7,2/2, из формулы (193) получим
при 0,03 > D > 0,0036. (195)
С учетом выражения j = D2 из формулы (193) по основной формуле (192) определяются требуемые (расчетные) площади
поперечного сечения:
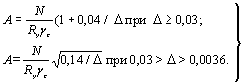
28.9.
Оптимальные соотношения основных размеров (габаритов) поперечных сечений сжатых
элементов при обеспечении их равноустойчивости определяются из выражения
, (197)
где определяется по
данным табл. 87.
Таблица 86
|
Параметр |
Сечение |
|||
|
|
|
|
|
|
|
Сx |
0,36 |
0,50 |
0,16 |
1,3-2,0 |
|
Cy |
0,75 |
0,35 |
1,2 |
b2/4A |
Таблица 87
Примечание. , где l1
£
0,6lef,x £ 40 в случае
соединения ветвей сквозной колонны планками, имеющими ширину hb ³
20b/l1,
в этом случае они считаются абсолютно жесткими, e
= 14A/Adl2ef,x в случае
соединения ветвей треугольной решеткой с диагональю, наклоненной к ветви под
углом 45°, площадью поперечного сечения Ad.
При невозможности
удовлетворить соотношение по конструктивным
соображениям расчет на устойчивость выполняется только в одном направлении.
Так, для двутавра при = 1 расчет на
устойчивость производится только в плоскости полок (относительно оси у-у) при
СЖАТО-ИЗГИБАЕМЫЕ И ВНЕЦЕНТРЕННО-СЖАТЫЕ ЭЛЕМЕНТЫ
28.10. При
заданных габаритах сечения требуемая (расчетная) площадь стержня А определяется из формулы (51) СНиП II-23-81*.
, (198)
где je — коэффициент, определяемый
по табл. 74 или 75 СНиП II-23-81* в зависимости
от и mef = hm;
здесь h — коэффициент, принимаемый по табл. 78* СНиП II-23-81* (для сквозных стержней h = 1);
т — относительный эксцентриситет, значение которого
определяется по формуле
, (199)
— параметр исходных данных,
являющийся безразмерной величиной, зависящей от отношений эксцентриситета е = M/N к расчетной длине стержня lef и а/i, а
также от характеристики материала Е и
Ry.
а — расстояние от центра тяжести сечения до его
расчетного сжатого волокна. Для симметричного в грузовой плоскости сплошного
сечения а = h/2; для несимметричного
сечения некоторые значения а
приведены в табл. 84 настоящего
Пособия.
Значения радиуса инерции i принимаются по табл. 83 настоящего Пособия.
28.11.
Для сжато-изгибаемых элементов с сечением, несимметричным в грузовой плоскости,
условием качественного выполнения предварительного расчета является правильное
назначение (с допуском не более 2 % высоты сечения) положения центра тяжести.
Для двутаврового обобщенного сечения (рис.
65) положение его центра тяжести и радиусы инерции определяются по
следующим формулам:
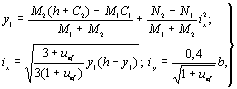
где N1, M1; N2, M2 — расчетные комбинации
соответственно продольной силы и изгибающего момента для первой и второй ветвей
или полок сжатого элемента.
При устойчивой стенке
;
При неустойчивой стенке
.
Требуемые площади поясов
(полок) определяются по формулам:
, (201)
где A = A1 + A2 + heft — расчетная площадь
поперечного сечения.
При полная площадь
поперечного сечения элемента равна .
Для частных случаев:
а) при сквозном сечении (C1 = С2
= uef = 0);
i =
0,45h,
Рис.
65. Схема двутаврового обобщенного сечения с неустойчивой стенкой
б) при сплошном сечении с
первой ветвью из листа (С1
= 0; h + С2 » 1,1 h)
;
.
28.12.
Двутавровое сечение целесообразно проектировать с неустойчивой (работающей в
закритическом состоянии) стенкой или со стенкой, укрепленной продольным ребром
с включением его в состав сечения.
Требуемые размеры ребра,
обеспечивающего устойчивость стенки, определяются из условий:
+ 50 мм — ширина ребра,
поставленного с одной стороны стенки;
+ 40 мм — ширина (с каждой
стороны стенки) двустороннего ребра,
где — условная гибкость
стенки;
Ry — расчетное сопротивление
стали ребра;
— толщина ребра, принимаемая не
более толщины стенки tw.
При указанных размерах ребра
заведомо выполняется требование п. 7.19* СНиП II-23-81*.
28.13.
Оптимальное сечение заданной формы должно удовлетворять двум условиям:
равноустойчивости стержня,
т. е. jе = Cjy в соответствии с пп. 5.27*
5.30 и 5.31 СНиП II-23-81*;
предельной тонкостенности
элементов сечения (стенки и полок) в соответствии с пп. 7.14*-7.20* и
7.23*-7.27* СНиП II-23-81*.
Из условия равноустойчивости
определяется оптимальное соотношение размеров (габаритов) поперечного сечения:
, (202)
где y — параметр для наиболее
часто встречающихся сечений, приведенный в табл. 87 настоящего Пособия.
Значения отношений гибкостей
могут быть определены по формулам:
при тx £ 5
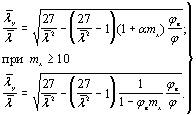
При 5 < mx < 10 отношение определяется линейной
интерполяцией между граничными значениями отношений при тx
= 5 и тx = 10.
В формулах (203):
и
— условная гибкость
стержня соответственно в грузовой плоскости (относительно оси х-х) и в перпендикулярном направлении;
— коэффициент продольного
изгиба;
a — коэффициент, принимаемый по табл. 10 СНиП II-23-81*.
Выражение [] является оптимальным условием лишь при
(где
принимается в
соответствии с п. 28.7); в противном
случае компоновку оптимального сечения следует выполнять с учетом
конструктивных соображений (при > 3 и т > 5).
28.14.
Прямой метод подбора оптимального сечения сжато-изгибаемого и внецентренно-сжатого
стержней с использованием двучленной формулы Ясинского можно свести к расчету
центрально-сжатого стержня на условную продольную силу . Тогда
при De ³ 0,03
;
, (204)
где
при 0,03 > De > 0,0036
, (205)
где
Здесь можно определить
последовательным приближением с исходным значением De = D = ВС. Процесс сходимости
очень быстрый, так что достаточно 3-4 итерации. Приближенное значение 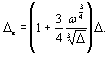
Указанный метод дает
достаточно точный результат для и, как правило,
завышает до 5-15 % величину расчетной площади поперечного сечения.
28.15.
Строгий метод прямого подбора сечения стержня основывается на определении
требуемой условной гибкости , выражение которой получено преобразованием формулы (51) СНиП II-23-81*:
.
Для получения решения можно
воспользоваться следующими аппроксимирующими зависимостями для je:
при D ³ 0,03
при D < 0,03
,
где (см. п. 28.10).
Значения коэффициентов k и п определяются по табл. 88.
Таблица 88
|
Тип сечения |
Значения k при |
п |
||
|
D |
0,1 ³ |
D |
||
|
Сплошное |
|
0,84 |
0,51 + 11D |
0,8 |
|
Сквозное |
|
1,25 |
0,65 + 20D |
0,75 |
С учетом требуемые (расчетные)
площади поперечного сечения стержня определяются по формуле (198), в которой при определении je необходимо принимать:
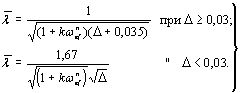
Отсюда при = 1,03 — 1,05 ( что соответствует
) придем вновь к
для Центрально-сжатых
стержней (см. п. 28.8).
28.16.
Для сжато-изгибаемых элементов верхняя граница области рационального применения
стали повышенной и высокой прочности должна снижаться по мере возрастания
относительного эксцентриситета т во
избежание больших поперечных перемещений оси. Установлено, что при действии
эксцентрично приложенной по концам шарнирно опертого стержня продольной силы с
нормативной величиной , где коэффициент перегрузки п = 1,2, относительный прогиб f/l при аппроксимации диаграммы
работы стали диаграммой Прандтля будет иметь значения, указанные в табл. 89.
Таблица
89
|
|
Значения 100 |
||||||
|
0,5 |
1,0 |
2,0 |
4,0 |
6,0 |
10,0 |
20,0 |
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
Примечание. Над чертой приведены результаты для сквозного, под
чертой — для сплошного прямоугольного сечения.
Исходя из условия £ 0,01, получены следующие
ограничения для основных сжатых элементов:
(207)
или
В случае соблюдения
указанных неравенств целесообразно применять сталь повышенной и высокой
прочности, в противном случае необходимо переходить к малоуглеродистой стали с
расчетным сопротивлением Ry
= 210 МПа (2150 кгс/см2). Таким образом, все сжато-изгибаемые
элементы с гибкостью l > 120 должны, как
правило, выполняться из малоуглеродистой стали.
ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ
28.17.
Высота стенки балки hw » 0,96h, где h — высота балки симметричного сечения, назначаемая из конструктивных
соображений (строительная высота) , должна, как правило, располагаться в
интервале значений между минимальной и оптимальной высотами hmin £ hw £ hopt.
Минимальная высота балки hmin определяется по формуле
, (208)
где — норма прогиба для
балки;
W — площадь эпюры изгибающего момента на длине
балки l от нормативной величины
поперечной нагрузки;
— принимается в соответствии со
СНиП II-23-81*
Оптимальную высоту можно
определять из единого выражения для любых случаев (балка постоянного и
переменного селений, бистальная балка и балка, рассчитываемая с учетом
ограниченной пластичности), так как некоторое ее изменение практически не
влияет на оценку минимума массы или стоимости конструкции. Поэтому в дальнейшем
используется выражение оптимальной высоты для упругой балки переменного сечения
(см. п. 28.21):
. (209)
При hopt £ hmin £ 1,25hopt допускается принимать hw = hmin.
Из последнего условия
определяется максимально возможное значение расчетного сопротивления материала
балки (поясов бистальной балки) Ry.
28.18.
Гибкость стенки — может быть
определена из условия ее прочности на срез:
(k = 1,0 при учете пластических деформаций в опорном сечении балки; k = 1,2 при расчете по
упругой стадии). При hw = hopt получается неравенство , к которому можно прийти формальным путем, приняв
. В частности, при
действии на балку равномерно распределенной нагрузки с интенсивностью р и
. Так как обычно
, условие прочности, как правило, не будет лимитировать
гибкость стенки балки с оптимальной высотой, особенно при учете
упруго-пластической стадии работы опорного сечения, и в случае применения стали
повышенной и высокой прочности.
28.19.
Гибкость упругой стенки lw лимитируется сверху условием ее местной
устойчивости. При укреплении стенки только поперечными ребрами максимальная
гибкость стенки определяется из формулы
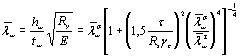
где — максимальные
условные гибкости стенки соответственно при действии только нормальных (в том
числе и sloc) и только касательных
напряжений в расчетном сечении при среднем их значении , вычисляемые в соответствии с пп. 7.4*, 7.5, 7.6* СНиП II-23-81*:
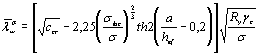
;
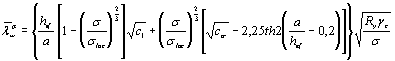
;
при
;
при
.
Наибольшие значения для устойчивой стенки
балки с поперечными ребрами жесткости в зависимости от напряженного состояния
отсеков и соотношения размеров их сторон приведены в статье1.
___________
1 Соболев Ю. В. О проектировании стальных составных
балок рационального сечения // Изв. вузов. Стр-во и архитектура. — 1985. № 1. —
С. 18-24.
Для стенки балки,
укрепленной кроме поперечных основных ребер одним продольным ребром на
расстоянии от сжатого пояса , ее условная гибкость
может быть
ориентировочно увеличена до раз по сравнению с
для стенки балки с
поперечными ребрами.
28.20.
Условная гибкость стенки упруго-пластической балки при обеспечении ее проверки
на устойчивость в соответствии с п. 7.5 СНиП II-23-81*: должна находиться в интервале значений:
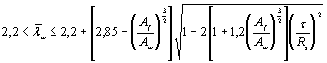
В частности, для распространенного
соотношения площадей сечения полки и стенки (балки переменного сечения) Af/Aw = 0,67 окажется, 2,2 < < 2,2 + 2,3
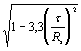
£ 4,5 и
.
Соответственно для
бистальной балки установлено, что упруго-пластическая устойчивая стенка должна
иметь условную гибкость в ориентировочных пределах:
2,2 < £ 2,2 + 3,2
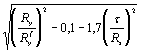
. (212)
Тогда (например, при ) окажется, что
£ 4,1 и
.
28.21.
Средняя по длине (для балки переменного сечения) площадь поперечного сечения А симметричной балки определяется из
выражения
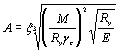
где
;
af и aw — конструктивные
коэффициенты для полки и стенки;
— оптимальная высота балки с
условной гибкостью стенки = 5,8;
c1 — коэффициент, определяемый по формулам (42) и (43)
СНиП II-23-81*.
При этом значения
коэффициента будут следующими:
для упругой балки
переменного сечения (af = 0,85; aw = 1,10) и оптимальной высотой
;
для оптимальной упругой
балки постоянного сечения (af = 1; aw = 1,10) .
При учете ограниченной
пластичности (с1 > 1)
значения для балки переменного
сечения, при которых обеспечивается выполнение проверки местной устойчивости
стенки согласно п. 7.5 СНиП II-23-81* при t = 0, приведены в табл. 90.
Таблица 90
|
|
Значения |
||||
|
1,04 |
1,06 |
1,08 |
1,10 |
1,12 |
|
|
3,0 |
1,77 |
1,69 |
1,67 |
1,67 |
1,69 |
|
3,5 |
1,66 |
1,60 |
1,54 |
1,60 |
1,63 |
|
4,0 |
1,56 |
1,54 |
1,55 |
1,59 |
1,64 |
|
4,5 |
1,50 |
1,54 |
1,60 |
1,67 |
1,76 |
Минимальным значениям соответствует с1 = 1,22-0,04
.
Сопоставление минимальных
значений для упругой и
упруго-пластической балок показывает, что при:
> 4,5 минимальной по массе
будет упругая балка;
= 4,5-4,0 учет ограниченной
пластичности приводит к снижению массы балки на 2-3 %;
= 3,5-3,0 эффект от учета
пластических деформаций составляет 3-5 %;
< 3,0 эффект в среднем равен
5-10 % и может достигать 15 % при < 2,2.
Так как коэффициент уменьшается с ростом
, то оказывается, что упругая балка является обычно наиболее
эффективной (здесь не принимается в сравнение бистальная балка). Экономический
эффект от учета пластических деформаций может быть получен при < 4,0, т.е. когда
исключена возможность компоновки оптимального сечения упругой балки (например,
из-за снижения строительной высоты) или когда толщина стенки определяется из
условия прочности на срез и принимается больше требуемой толщины из
конструктивных соображений.
28.22.
Соотношение площадей сечения полки и стенки в общем случае определяется по формуле
. (214)
Требуемая
площадь сечения полки определяется по формуле:
,
где
.
Толщину неокаймленной сжатой
полки балки для обеспечения ее устойчивости согласно табл. 30 СНиП II-23-81* следует принимать равной:
— для упругой (и для бистальной
с заменой Ry на ) балки;
— для балки с ограниченной
пластичностью при 2,7 £ < 4,5.
Толщину полки следует
принимать по возможности минимальной (желательно не более 20 мм), так как при
этом возрастает расчетное сопротивление стали Ry, за счет чего может быть получен дополнительный
экономический эффект.
ПРЕДВАРИТЕЛЬНЫЙ РАСЧЕТ
28.23.
Метод прямого подбора оптимального сечения центрально-сжатого элемента состоит
в следующем.
При расчет на
устойчивость двутаврового сечения всегда следует выполнять относительно оси у—у,
т.е. принимать:
D = ByCy; ;
(
, где
и при учете
закритической работы стенки); или с учетом
получим
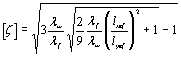
Рассмотрим два расчетных
случая.
Первый
(D <
0,027). и
;
;
(
— при неустойчивой стенке согласно табл. 27* и 29* и п.
7.20* СНиП II-23-81*).
Второй
(D ³ 0,027). By ³ 0,017(1 + 0,26)2, при этом
и А определяются соответственно по
формулам (194) и (196); ;
при 0,8 £
£ 4,0 (см. табл. 27*и 29* СНиП II-23-81*).
При вычислении и
необходимо принять в
первом приближении значения , исходя из следующего:
= 1 при
;
= 2 при
³ By ³
;
= 3 при
³ By (где
),
затем последовательно вычислить параметры:
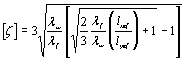
при
— из конструктивных
соображений; ;
и
(где D = ByCy).
При учете закритической
работы стенки принимается ;
при
. Остальные выражения остаются прежними.
При вычислении может оказаться, что
»
. В этом случае
расчетные параметры будут соответствовать оптимальному сечению.
Если >
, что означает избыток местной устойчивости листов (полок и
стенки), то необходимо выполнить оптимизацию сечения, для чего следует принять
откорректированное значение и повторить расчет.
28.24.
В том случае, когда задача подбора оптимальных сечений сжато-изгибаемых
элементов не усложняется требованием получения равноустойчивого сечения
элемента и особенно когда по конструктивным соображениям задается
тонкостенность сечения, решение достигается достаточно просто. Предварительный
расчет целесообразно выполнять в два этапа:
первый — по рекомендациям п. 28.14 определить расчетные параметры;
второй — по рекомендациям п. 28.15 проверить и при необходимости
откорректировать расчетные параметры.
28.25.
Проиллюстрируем метод прямого подбора оптимального сечения сжато-изгибаемого
(внецентренно-сжатого) элемента на примерах двутаврового составного сечения.
Расчет выполняется в
грузовой плоскости с обеспечением условия равноустойчивости . Для соблюдения местной устойчивости листов составного
сечения учитываются требования пп. 7.16* и 7.23* СНиП II-23-81* с соблюдением гарантии, что исходное значение не превысит
расчетного значения , на каждом шаге итерации, подобно тому, как это выполнялось
при расчете центрально-сжатых элементов.
На первом этапе расчета
следует воспользоваться методом п. 28.14
и завершить корректировку предварительного расчета, применив рекомендации п. 28.15.
На первом шаге итерации
следует принять =
, исходя из следующего:
= 1 при
;
= 2 при
;
= 3 при
,
где
;
;
.
Гибкость листов двутаврового
сечения при обеспечении их местной устойчивости в соответствии с требованиями
пп. 7.14* и 7.23* СНиП II-23-81* определяется из
выражений:
;
при
2,0;
при
.
В случае проектирования
сечения с неустойчивой стенкой значение lw принимается больше
величины, указанной выше. При этом ;
.
Из выражения (197) с учетом и
получим
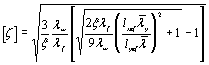
определяется в
соответствии с п. 28.13 (на первом шаге
или 1,5 при
проектировании сечения с неустойчивой стенкой).
Заметим, что = 1 для сечения с устойчивой стенкой.
Далее определим ; D = BxCx где
;
(для сечений с
устойчивой стенкой );
;
,
где ;
;
.
При несовпадении вычисленного
значения , с первоначально принятым значением расчет следует
повторить, принимая исходные данные предшествующего этапа. При этом ;
;
;
;
.
ПРИМЕРЫ
Пример 1. Требуется определить оптимальное составное двутавровое сечение колонны
при следующих исходных данных: N =
2000 кН; lyef = 400 см; lxef = 3lyef. Листы из стали марки 18 кп
по ГОСТ 23570-79 (Ry = 220
МПа при толщине проката 4-20 мм); = 936;
; gс = 1.
Первый этап — предварительный расчет
Вычислим величину параметра
исходных данных By:
.
Так как при этом , где
, за исходное значение примем
= 1.
Данные расчета по прямому
подбору оптимального сечения центрально-сжатого элемента приведены в табл. 91.
Таблица 91
|
Шаг итерации |
|
lw |
lf |
|
u |
Cy |
D |
|
А, см2 |
|
Первый |
1,0 |
35,5 |
28,2 |
1,52 |
0,92 |
0,315 |
0,169 |
2,14 |
113 |
|
Второй |
1,8 |
55,1 |
33,1 |
1,56 |
0,73 |
0,460 |
0,245 |
1,87 |
106 |
В результате проведения
второго (оптимизационного) шага итерации . При этом условная
гибкость снизилась с 2,14 до
1,87, что привело к уменьшению площади поперечного сечения на » 7 %.
Второй этап — компоновка сечения
см,
тогда b =
4,56 × 7,0 = 31,9 см; h = b[] = 319 × 1,56 = 49,8 см.
Примем b =
32,0 см; h = 50,0 см, тогда
см;
см;
принимаем tf = 1,0 см.
Итак, получили составное двутавровое сечение:
2(—320 × 10) + (—500 × 9) : A = 2 × 32 × 1 +
50 × 0,9
= 109 см2; ;
см;
см.
Третий этап — проверка решения
;
.
Коэффициент продольного
изгиба определяем с использованием данных табл. 82: j = 1,002×(0,95 — 0,035 × 1,852) = 0,832. При этом МПа = Ry.
Пример 2. Требуется рассчитать верхний пояс большепролетной трубчатой фермы при
следующих исходных данных: N =
1050 кН; е = 30 см; lxef = 600 см; lyef = 1200 см; материал трубы — сталь марки 16Г2АФ по ТУ 14-3-567-76 с
расчетным сопротивлением Ry = 400 МПа (при толщине стенки 6-9 мм); ;
; gc =
1.
Первый этап — предварительный расчет
Вычислим необходимые расчетные параметры:
;
.
При конструктивном
ограничении гибкости стенки трубы вычислим параметр
при
; D = BC = 0,0376 × 1,6 = 0,060.
Определим значение , при этом
кН. Тогда уточненное
значение . Следовательно,
см2.
Уточним значения и А:
m = = 1,62 × 1,96 = 3,18. По табл. 73 СНиП II-23-81* определим коэффициент h = 1,35 — 0,05 × 3,18 — 0,01(5 — 3,18) — 1,96 = 1,155, при этом
= 1,155 × 1,62 = 1,87.
Из табл. 89 настоящего Пособия при 0,1 ³ D ³ 0,03 (в нашем случае D = 0,06) получим k = 0,84; п = 0,8,
тогда
см2.
Так как , при этом
, применение высокопрочной стали с Ry =
400 МПа является оправданным.
Второй этап — компоновка сечения
Примем стальную трубу по ГОСТ
10704-76* Æ377´9 (А = 104 см2; i =
13,01 см; W = 935 см3).
Третий этап — проверка решения
;
;
h = 1,35 — 0,05 × 3,34 — 0,01 × (5 — 3,34)× 2,03 = 1,15; mef = 1,15 × 3,34 = 3,84;
jе = 0,266 (по табл. 74 СНиП II-23-81*)
МПа < Ry.
(ly = 92 < 120); j = 0,43 > je, т.е. устойчивость элемента
из плоскости фермы обеспечена.
Пример 3. Требуется подобрать сечение надкрановой части ступенчатой колонны в
виде симметричного составного двутавра при следующих исходных данных: N = 930 кН; М = 319 кН×м ; расчетный момент при проверке устойчивости элемента из
плоскости изгиба ; lxef = 1560 см; lyef = 360 см. Листы из стали марки ВСт3кп2-1 по ТУ 14-1-3023-80 с
расчетным сопротивлением Ry = 210 МПа (при толщине проката 11-20 мм); ;
= 31,3; gс = 1.
Первый этап — предварительный расчет
(приближенный метод)
Вычислим необходимые
расчетные параметры:
;
,
где ;
.
Предположим, что стенка
устойчива и примем в качестве исходных значений . Данные расчетов
по прямому подбору сечения приведены в табл.
92.
Как видно из этой таблицы,
уже второй шаг итерации дает практически точное решение задачи не только в
отношении А и , но и
.
Первый этап — предварительный расчет
(уточненный метод)
Определим m = 0,93 × 1,9 = 1,77; ;
h = 1,45 — 0,05 × 1,77 — 0,01(5 — 1,77)× 1,9 = 1,30; wef = 1,30×— 0,93 = 1,21;
;
je = 0,096 × 1,952 = 0,366;
см2.
Второй этап — компоновка сечения
;
см,
тогда h = 2,71 × 25,5 = 69,0 см; см;
см, примем tw =
1,2 см; см, примем tf = 0,8 см.
Итак, скомпоновано
оптимальное составное двутавровое сечение 2 (—260 × 0,8) + (—684 × 12).
Третий этап — проверка решения
А =
2 × 26 × 0,8 + 68,4 × 1,2 = 123,6 см2,
см;
см3;
см;
см;
;
;
;
;
Таблица
92
|
Шаг итерации |
|
|
lf |
lw |
|
u |
Cy |
D |
w |
Dе |
|
А, см2 |
|
Первый |
1,0 |
1,0 |
28,8 |
53,2 |
2,12 |
1,22 |
4,63 |
0,083 |
0,87 |
0,204 |
2,03 |
131 |
|
Второй |
1,7 |
2,38 |
33,2 |
54,8 |
2,67 |
2,16 |
5,09 |
0,091 |
0,93 |
0,239 |
1,92 |
131 |
|
Третий |
1,9 |
2,68 |
34,4 |
58,0 |
2,71 |
2,17 |
5,40 |
0,096 |
0,93 |
0,242 |
1,89 |
130 |
h = 1,45 — 0,05 × 1,81 — 0,01(5 — 1,81)× 1,93 = 1,30; mef = 1,3 × 1,81 = 2,36; je = 0,367, при этом в плоскости изгиба МПа < Ry,
; a = 0,65 + 0,05 × 1,21 = 0,71;
; jy = 0,998(0,95 — 0,035 × 2,632) = 0,707, при этом из
плоскости изгиба МПа < Ry.
Пример 4. Требуется подобрать оптимальное сечение однопролетной балки в виде
составного симметричного двутавра при следующих исходных данных: пролет балки l = 1200 см; шаг балок настила
(расчетная длина между точками закрепления) lef =100 см; расчетные усилия в балке от действия
равномерно распределенной нагрузки: изгибающий момент в середине пролета М = 2800 кН×м и опорная реакция Q = 930 кН; материал
конструкции — сталь 18Гпс по ГОСТ 23570-79 с расчетным сопротивлением Ry = 230 МПа при толщине
проката 4-20 мм; ; gс = 1.
Первый этап — предварительный расчет
Требуемая величина упругого
момента сопротивления сечения балки см3.
Предполагаем, что ребро
жесткости поставлено под каждую балку настила ( = 0), принимаем ориентировочное значение
= 5,5, тогда гибкость
стенки .
Согласно формуле (209) оптимальная высота стенки
упругой балки равна см, т.е. толщина
стенки см.
Принимаем tw = 0,8 см; hw = 125 см; = 5,2.
Проверим из условия на срез
при k = 1,0 (см. п. 28.18), что
Убедимся, что hmin в формуле (208) не превышает hw, где nо = 400; W = = 18700 кН×м2; 1,2 —
коэффициент перегрузки.
Тогда см. Требуемая площадь
поясного листа см2;
толщина листа пояса см, примем tf = 1,8 см;
см.
Убедимся, что при шаге ребер
а = 100 см стенка балки является
устойчивой при = 5,2. Предварительно
определим параметр и, следовательно, при
для отсека стенки в
месте изменения сечения балки (на расстоянии l/6 от опоры) = 5,30. Это значение
будет минимальным среди остальных. Такой же результат получим из формулы (210).
Таким образом, стенка
устойчива.
Второй этап — компоновка сечения
Примем составной двутавр 2 × (—450 × 18) + (—1250 × 8);
A= 2,45 × 1,8
+ 125 × 0,8 = 262 см2;
Ix =
780000 см4;
Wx = 12150см3.
Третий этап — проверка решения
Выполняется в соответствии с
требованиями СНиП II-23-81*. Результаты
подтверждают, что принятое сечение балки обладает требуемой прочностью и
местной устойчивостью без излишних резервов.
29. ТЕХНИКО-ЭКОНОМИЧЕСКИЕ ПОКАЗАТЕЛИ
ОБЩИЕ ПОЛОЖЕНИЯ
29.1.
Строительство и эксплуатация металлической конструкции в составе здания или
сооружения осуществляются разными организациями (проектным институтом, заводом,
монтажным управлением и т.д.). Соответственно, имеется совокупность
технико-экономических показателей, характеризующих различные этапы
строительства и эксплуатации, соответствующих интересам каждой из организаций и
удобных для использования в их работе. В настоящем Пособии внимание уделяется
технико-экономическим показателям, необходимым при проектировании.
Технико-экономические
показатели при проектировании нужны для оценки качества проектного решения,
совершенства конструктивной формы, выявления затрат, связанных с изготовлением,
транспортированием и монтажом (в отдельных случаях и с эксплуатацией)
конструкции и оценки технологичности.
Технико-экономические
показатели, используемые при оценке качества, подразделяются на абсолютные и относительные (безразмерные
и размерные, построенные на основе абсолютных). В настоящем Пособии
рассматриваются только абсолютные
показатели.
29.2.
При проектировании в первую очередь следует рассматривать технико-экономические
показатели, характеризующие качество проектного решения и технологичность
конструкции с точки зрения затрат в отрасли строительства. Такими показателями
являются:
масса металла;
затраты на основные
материалы;
трудоемкость изготовления;
технологическая
себестоимость изготовления;
себестоимость изготовления;
затраты на железнодорожный
транспорт;
трудоемкость монтажа;
технологическая
себестоимость монтажа;
себестоимость в деле.
Затраты на основные
материалы включают затраты на прокат, сварочные и лакокрасочные материалы,
рассчитанные на основе действующих прейскурантов.
Трудоемкость изготовления или монтажа есть суммарное количество рабочего времени,
затраченного по всем операциям технологического процесса изготовления или
монтажа.
Себестоимость изготовления в данном случае есть сумма затрат на изготовление в
условиях заводского производства.
Технологическая себестоимость изготовления или монтажа есть сумма затрат на
изготовление или монтаж без учета затрат на основные материалы.
Себестоимость в деле есть сумма технологической себестоимости
изготовления, технологической себестоимости монтажа, транспортных затрат и
затрат на основные материалы.
Наиболее полным показателем,
характеризующим всю совокупность затрат в отрасли строительства, является
себестоимость в деле. Из этого не следует, что сравнение вариантов проектных
решений всегда необходимо проводить по этому показателю. Если различия в
сравниваемых конструкциях проявляются лишь на отдельных этапах строительства,
то сравнение нужно вести по частным показателям, характеризующим этапы
строительства, различия в которых существенны. Частные показатели позволяют
также выявить структуру затрат, что важно при определении направления работы по
совершенствованию конструкции.
Далее перечисляются еще
несколько технико-экономических показателей, использование которых при
проектировании в ряде случаев является полезным.
Стоимость в деле включает те же затраты, что и себестоимость в деле, но к себестоимости
изготовления и к затратам при монтаже добавляется расчетная прибыль
завода-изготовителя и расчетная прибыль монтажной организации. Стоимость в деле
не несет в себе новой информации по сравнению с себестоимостью в деле. Она
удобнее для расчета затрат, которые будет нести организация-заказчик объекта
строительства.
Приведенная стоимость. Под этим показателем понимается себестоимость или
стоимость конструкции в деле с добавлением слагаемых, характеризующих
отнесенные к конструкции затраты смежных отраслей, связанные с изготовлением
или эксплуатацией конструкции, и слагаемых, характеризующих капитальные
вложения в строительство.
При проектировании учет
эксплуатационных затрат нужен в случаях, когда сравниваются варианты проектных
решений, существенно различающихся с точки зрения эксплуатационных свойств
объекта строительства. Учет капитальных вложений в отрасли строительства или в
смежных отраслях нужен тогда, когда изготовление или монтаж проектируемой
конструкции требуют специальных дополнительных капитальных вложений.
В состав проекта объекта
строительства обязательно должна входить сметная документация, в которой
приводятся результаты расчета сметной стоимости. Сметная стоимость вычисляется
на основе оптовых цен. Оптовая цена не отражает непосредственно преимуществ и
недостатков конкретного проектного решения. Например, какое-либо
усовершенствование конструкции может обеспечить снижение ее трудоемкости
себестоимости, но оптовая цена может остаться прежней; усовершенствование все
равно даст экономический эффект, и он реализуется, поскольку увеличится прибыль
завода-изготовителя.
Таким образом, оптовая цена
и сметная стоимость не могут использоваться как основные показатели при
проектировании.
НОРМАТИВНАЯ БАЗА РАСЧЕТА
29.3.
Расчеты технико-экономических показателей разных вариантов конструкций
независимо от применяемого метода расчета должны вестись для одинаковых условий
изготовления, транспортирования и монтажа. Поэтому должны быть установлены
определенные условия — расчетные условия, применительно к которым должны
вестись все расчеты и исходя из которых должны определяться коэффициенты
приближенных формул. Расчетные условия могут периодически установленным
порядком изменяться с учетом прогресса конструктивной формы, материалов и
технологии.
В случае, если для
рассматриваемой конструкции на каком-либо этапе строительства имеются
существенные отличия от расчетных условий, результаты расчета по
соответствующим статьям затрат необходимо корректировать по индивидуальной
методике.
29.4. Расчетные условия
изготовления и монтажа задаются в виде информационных моделей, включающих
следующие составные части:
а) комплект описаний типовых
технологических процессов изготовления и монтажа, в том числе перечень
технологических операций и соответствующих рабочих мест; перечень оборудования
применительно к каждому рабочему месту;
б) нормы трудоемкости и
штучно-калькуляционного времени;
в) нормативы затрат по
статьям себестоимости, отнесенные к каждому из рабочих мест;
г) прейскуранты на прокат,
сварочные и лакокрасочные материалы (в части проката и материалов, используемых
в строительстве).
29.5.
При неизвестных при проектировании месте строительства или месте изготовления
затраты на железнодорожный транспорт определяются для установленных расчетных
расстояний перевозки.
29.6.
Информационная модель, отвечающая требованиям п.
29.4, разработана применительно к металлоконструкциям каркаса промышленного
здания [40]. На основе модели создана нормативная база данных, используемая
автоматизированной системой расчета технико-экономических показателей.
За основу технологии
изготовления принят комплект типовых технологических процессов [39],
разработанных с ориентацией на технологию передовых заводов отрасли.
Технологический процесс в
модели разбит на 65 операций. Некоторые операции разделены на переходы.
Перечень операций и переходов приведен в [40].
Затраты по статьям
себестоимости, отнесенные к основному оборудованию рабочих мест, приняты по
данным специального исследования, основные результаты которого опубликованы в
[41].
Применительно к монтажу
конструкций принята традиционная технология поэлементного монтажа. Основной
процесс разбит на четыре укрупненные операции: монтаж, сварка, окраска, работа
крана. Учитываются также работы, связанные с доставкой конструкций: разгрузка,
транспортирование, работы на складе.
База данных для
автоматизированного расчета технико-экономических показателей включает 173
таблицы, наименования которых приведены в [40].
МЕТОДЫ РАСЧЕТА
29.7.
Для расчета технико-экономических показателей строительных металлических
конструкций могут быть использованы два метода: калькуляционный и укрупненный
(аналитический).
29.8. Калькуляционный метод включает:
подетальный расчет
потребного проката;
расчет затрат на основные
материалы непосредственно по прейскурантам;
пооперационный или
попереходный расчет трудоемкости изготовления и монтажа;
пооперационный расчет затрат
по статьям себестоимости.
Калькуляционный метод,
опирающийся на статистические данные, относящиеся к отдельным операциям или
даже переходам, дает возможность проектировщику конкретно учитывать влияние
особенностей проектного решения на трудоемкость, себестоимость и другие
технико-экономические показатели, а также выявляет структуру затрат, что
является ценной информацией для дальнейшего совершенствования конструкции.
Метод пригоден для расчета технико-экономических показателей новых
конструктивных форм, опыт изготовления которых отсутствует. Любая реализация
калькуляционного метода допускает замену нормативной базы.
Для калькуляционного метода
необходимы исходные данные, характеризующие конструкцию в целом, и данные,
характеризующие входящие в конструкцию сборочные единицы и детали. Поскольку
необходимо, чтобы расчет технико-экономических показателей мог производиться
как на основе данных чертежей КМД, так и КМ, калькуляционный метод должен
включать приближенное доопределение неоговоренных на чертежах КМ габаритов и
числа мелких фасонных деталей.
Расчет калькуляционным
методом, требующим большого объема вычислений и использования обширной
справочно-нормативной информации, следует выполнять на ЭВМ.
29.9.
Укрупненный (аналитический) метод
сводит определение технико-экономических показателей к некоторой
последовательности формул. Нормативные данные непосредственно в расчете не
используются. Исходные данные для расчета ограничиваются небольшим числом
параметров, характеризующих конструкцию в целом. Основой, на которой
составляются аналитические методы, являются зависимости между основными
параметрами конструктивной формы и параметрами процессов изготовления и
монтажа, полученные путем обработки статистических данных, относящихся к
конструкции в целом. Каждая конкретная методика укрупненного расчета
ориентирована на определенный вид конструкций, определенные основные проектные
решения, уровень развития конструктивной формы и нормативную базу. Замена
нормативной базы, переход на новые конструктивные формы, появление новых
технологических процессов требуют, как правило, коренной переработки методики.
Укрупненные (аналитические)
методы ориентированы на ручной счет [42] — [45].
Калькуляционный метод расчета на ЭВМ технико-экономических показателей
металлических конструкций каркаса промышленного здания
29.10.
Калькуляционный метод расчета на ЭВМ технико-экономических показателей
металлических конструкций каркаса промышленного здания реализован в составе
подсистемы расчета технико-экономических показателей металлических конструкций
Системы автоматизации проектирования (САПР) ЦНИИпроектстальконструкции им. Н.
П. Мельникова. Подробное описание подсистемы приведено в документации САПР,
основные положения изложены в трудах1, 2.
____________
1 Геммерлинг Г. А. Система
автоматизированного проектирования строительных конструкций. — М.: Стройиздат,
1987-216 с.
2 Ковнер И. С., Зеленков В. И.
Подсистема технико-экономических расчетов строительных металлоконструкций// Тр.
ЦНИИпроектстальконструкции им. Н. П. Мельникова — Исследование систем
автоматизированного проектирования стальных конструкций. — М. 1983, — С. 20-23.
Программа расчета
технико-экономических показателей, входящая в состав подсистемы и оформленная в
соответствии с требованиями Единой системы программной документации (ЕСПД),
имеется в Межотраслевом фонде алгоритмов и программ автоматизированных систем в
строительстве [40]. Программу можно использовать изолированно (вне системы).
Программу можно
эксплуатировать на ЭВМ Единой системы.
Время работы на ЭВМ ЕС-1060
для расчета одной конструкции в среднем равно 4 мин общего монопольного
времени, в том числе 1 мин процессорного времени.
29.11.
Результаты автоматизированного расчета технико-экономических показателей
приведены в табл. 93-96 на примере расчета несложной
конструкции — подкрановой балки, изображенной на рис. 66. В табл. 93 приведены результаты расчета
трудоемкости изготовления балки с учетом 30 операций заводского изготовления, в
табл. 94 — результаты расчета
себестоимости заводского изготовления балки, в табл. 95 — показатели затрат при монтаже и себестоимость
в деле. Показатели, приведенные в табл. 93-95, рассчитаны для партии, состоящей
из 5 конструкций. Основные показатели сведены в табл. 96.
Рис. 66. Рабочий
чертеж подкрановой балки БК4
Таблица
93
(Форма)
Трудоемкость
изготовления конструкции
Чертеж № 3-Ф1086-5КМ
Марка по чертежу 6К4
|
Операция |
Время на выполнение |
Раздел УНВ, на основе |
|
Подготовительные и транспортные операции (нормы ЗМК) |
||
|
1.Подготовка металла |
3,421 |
— |
|
2. Предварительная стыковка, сварка и роспуск листа |
6,526 |
— |
|
3. Комплектование |
1,909 |
— |
|
4. Транспортирование в цехе |
7,240 |
— |
|
5. Транспортирование в цехе |
3,421 |
— |
|
6. Прием и транспортирование полуфабрикатов в цехе |
1,591 |
— |
|
Обработка и изготовление деталей (УНВ) |
||
|
7. Правка |
3,509 |
— |
|
8. Изготовление шаблонов |
0,144 |
— |
|
9. Разметка и наметка |
2,321 |
— |
|
10. Газовая резка |
2,783 |
— |
|
11.Резка на ножницах и прессах |
3,633 |
— |
|
12.Зачистка деталей от грата |
0,793 |
— |
|
13. Строгание |
0,555 |
— |
|
14.Фрезерование |
0,160 |
— |
|
15.0бразоваиие отверстий |
2,302 |
— |
|
16. Гибка |
— |
— |
|
17. Нанесение номера плавки |
— |
— |
|
18.Токарные работы |
— |
— |
|
Сборка (УНВ) |
||
|
19.Установка базовых деталей на место сборки конструкции |
0,088 |
Сб. 5, вып. 1, карта№ |
|
20. Сборка двутавров в |
2,280 |
Сб. 5, вып. 1, |
|
21. Сборка копиров для ферм |
— |
— |
|
22. Сборка конструкции в целом (оформление базовых |
9,672 |
Сб. 5, вып. 1, |
|
Сварка (УНВ) |
||
|
23. Сварка поясных швов |
3,759 |
Сб. 3, вып. 2, |
|
24. Сварка конструкции после полной сборки |
10,902 |
— |
|
25. Зачистка швов |
1,890 |
— |
|
26. Подача, установка, кантовка и уборка конструкции на |
1,870 |
— |
|
Отделка, окраска, погрузка (нормы ЗМК) |
||
|
27. Правка пейнеров |
0,900 |
— |
|
28. Отделка |
9,547 |
— |
|
29. Очистка и окраска |
3,638 |
— |
|
30. Погрузка |
7,956 |
— |
|
Итого: |
92,81 |
— |
Таблица 94
(Форма)
Расчет себестоимости изготовления конструкции
Чертеж № 3-Ф1086-5КМ
Марка по чертежу 5К4
|
Состав затрат |
Сумма, руб. |
|
1. Затраты на основные материалы |
1558 |
|
В том числе |
1385 |
|
2. Технологическая |
267 |
|
Полная |
1825 |
|
Себестоимость |
231 |
|
Расчетная |
1962 |
Таблица 95
(Форма)
Основные технико-экономические показатели монтажа конструкции
Чертеж № 3-Ф1086-5КМ
Марка по чертежу 6К4
|
Показатель |
Значение (единица |
|
1. Расчетная цена |
2104 руб. |
|
2. Основная заработная плата |
43 руб. |
|
3. Затраты на материалы |
2191 руб. |
|
В том числе |
2165 руб. |
|
4. Затраты на эксплуатацию |
53 руб. |
|
5. Прямые затраты на монтаж без стоимости конструкции |
236 руб. |
|
6. Трудоемкость монтажа |
57,2 чел.-ч |
|
7. Расчетная себестоимость |
2608 руб. |
Таблица 96
(Форма)
Основные
технико-экономические показатели конструкции 5К4 при изготовлении партиями по 5
шт.
(Чертеж № 3-Ф1086-5КМ,
подкрановая балка БК4)
|
Показатель |
Единица измерения |
Значения показателей |
|
|
на 1 конструкцию |
на 1 серию (из 5 шт.) |
||
|
1. Массе конструкции (с учетом |
т |
7,955 |
39,77 |
|
2 Затраты на материалы при изготовлении |
руб. |
1558 |
7790 |
|
3. Число деталей |
шт. |
35 |
175 |
|
4. Трудоемкость изготовления |
чел.-ч |
92,8 |
464,0 |
|
5. Удельная трудоемкость |
чел.-ч |
11,7 |
11,70 |
|
6. Технологическая |
руб. |
267 |
1335 |
|
7. Себестоимость изготовления |
руб. |
1825 |
9125 |
|
8. Расчетная цена |
руб. |
2104 |
10520 |
|
9. Трудоемкость монтажа |
чел.-ч |
57,2 |
286,0 |
|
10. Прямые затраты на монтаж без стоимости конструкции |
руб. |
236 |
1180 |
|
11. Себестоимость в деле |
руб. |
2499 |
12495 |
|
12. Расчетная себестоимость |
руб. |
2608 |
13040 |
|
13. Расчетная стоимость в деле |
руб. |
2817 |
14085 |
По желанию пользователя
кроме данных табл. 94-96 может быть выдана на печать
дополнительная информация:
а) входная информация и
диагностические сообщения, если входная информация содержит синтаксические
ошибки;
б) сводка массы конструкции
по стержням и деталям;
в) сводка массы конструкции
по видам проката;
г) результаты расчета углов,
длины примыкания деталей, длины и катетов сварных швов, не указанных на
чертеже;
д) результаты расчета числа
деталей и заготовок, результаты определения состава операций (и переходов)
изготовления на каждую деталь и расчета трудоемкости изготовления каждой
детали;
е) для конструкций ферм из
труб и широкополочных двутавров: число и масса деталей в сборочных единицах
разного уровня, суммарная длина швов каждого вида соединения.
29.12.
Расчет технико-экономических показателей разделен на этапы:
кодирование;
трудоемкость;
себестоимость;
дело.
Этапы выполняются
последовательно, в указанном порядке. Последующие этапы используют результаты
предыдущих. Имеется возможность ограничить расчет выполнением части этапов.
На этапе “Кодирование”
выполняется ввод данных в ЭВМ, логический контроль данных и формирование
внутримашинного описания конструкции. Выполняется также расчет масс деталей,
стержней и отправочных марок.
На этапе “Трудоемкость”
выполняется расчет трудоемкости заводского изготовления. По выбору пользователя
расчет в его различных частях может производиться с разным уровнем подробности.
Расчет трудоемкости изготовления деталей может производиться по укрупненным
нормативам времени, относящимся к целой конструкции, или по нормативам,
относящимся к каждой детали. Расчет сварки может производиться по нормативам на
конструкцию или на единицу длины шва. Более подробный расчет возможен только
при условии подробного кодирования описания конструкции на входных бланках (см.
п. 29.13).
При сокращенном кодировании
на основе чертежей КМ в ходе выполнения данного этапа программа дорабатывает
информацию чертежей до уровня, обеспечивающего привязку к нормативным таблицам.
На этапе “Себестоимость”
выполняется расчет затрат на прокат и на основные материалы, а также расчет
себестоимости изготовления.
На этапе “Дело” выполняется
расчет затрат на монтаж и расчет себестоимости в деле.
В составе одного задания для
одной конструкции можно произвести расчет для нескольких значений серийности
изготовления.
Для каждого значения будут
произведены все расчеты и выданы все результаты.
В составе одного задания
можно выполнить расчет не только одной конструкции, но и группы конструкций.
Помимо печати выходных
документов программа формирует записи в памяти на дисках, содержащие значения
основных показателей в каждой конструкции при каждом показателе серийности. Эти
записи могут быть использованы при оптимизационных расчетах.
29.13.
Исходные данные для расчета представляют собой упрощенное описание конструкции,
содержащее только информацию, необходимую для данного расчета и составленное
непосредственно по чертежам КМ или КМД.
Подготовка исходных данных
заключается в занесении сведений о конструкции на бланки анкетной формы
установленного типа [40]. Операция подготовки данных на бланках далее
называется “кодированием”. Выполнение кодирования не требует от исполнителя
каких-либо знаний, кроме умения разбираться в чертежах КМ и КМД. Бланки и программы
переработки данных предусматривают возможность подробного описания самых
сложных конструкций и содержат для этого необходимое число граф и строк. Бланки
ориентированы на занесение информации, достаточной для выполнения любых видов
технико-экономических расчетов, а также автоматизированных работ по технической
подготовке производства. Поэтому при кодировании информации о конкретной
металлической конструкции заполняется только часть (часто малая) полей бланков,
а иногда только часть бланков. Состав данных, заносимых на бланки, существенно
уменьшается также в случае расчета технико-экономических показателей только по
укрупненным нормативам времени.
29.14.
Полные возможности системы описания, учет подробностей конструктивной формы
необходимы только при описании новых, нетрадиционных конструктивных форм, для
.которых не набрана статистика изготовления и отсутствуют укрупненные нормативы
времени.
При кодировании традиционных
конструкций следует использовать сокращенное кодирование: описывать не
полностью или вообще не описывать узлы и стержни, опустить описание
дополнительных элементов фермы и сварных швов, не описывать мелкие детали, а
вводить строительные коэффициенты массы и числа деталей.
29.15.
Данные, необходимые для расчета, включают, кроме описания металлических
конструкций, директивы о режиме работы программы и о требуемой печати. Запись
директив весьма проста, она изложена в [40].
ПРИЛОЖЕНИЕ 1
РАСЧЕТ СТАЛЬНЫХ КОНСТРУКЦИЙ
ВЕРОЯТНОСТНО-ЭКОНОМИЧЕСКИМ МЕТОДОМ
В основе
вероятностно-экономического метода лежит принцип чисто экономической
ответственности. Под этим подразумевается, что отказ элемента или конструкции
не влечет за собой опасности травматизма и тем более человеческих жертв.
Следовательно, оптимальный уровень надежности может быть определен из чисто
экономических соображений.
Поскольку нагрузки и
свойства материалов носят изменчивый, случайный характер, решение задачи
возможно только в вероятностной постановке.
Первую апробацию
вероятностно-экономический метод получил в нашей стране в области тепличного
строительства [6] и привел к снижению материалоемкости несущих конструкций
теплиц.
При расчете
вероятностно-экономическим методом в расчет вводятся не нормативные (расчетные)
значения нагрузок и прочностных свойств материала, а статистические характеристики
их распределений — средние значения и коэффициенты вариации.
ОБЩИЕ ПОЛОЖЕНИЯ
1.
Настоящий метод может быть применен при расчете несущих стальных конструкций
зданий и сооружений, в которых по условиям технологии производства и
эксплуатации нет постоянных рабочих мест (для работающих).
Примечание. Условия технологии производства и эксплуатации зданий
и сооружений, в которых нет постоянных рабочих мест (для работающих),
устанавливаются в заданиях на проектирование, в утвержденных типовых проектах, а
также в соответствующих документах по эксплуатации.
2.
Проектирование зданий и сооружений, несущие конструкции которых рассчитываются
по настоящему методу, в остальном должно осуществляться в соответствии со СНиП II-23-81*.
3.
При расчете конструкции по настоящему методу не должны применяться коэффициенты
надежности по назначению,
установленные [4].
4.
Средние значения и коэффициенты вариации давления ветра следует принимать по
табл. 1.
Таблица 1
Статистические
характеристики давления ветра
|
Ветровой район по [3] |
Среднее значение |
Коэффициент вариации vf |
|
I |
196 (20) |
0,44 |
|
II |
265 (27) |
0,37 |
|
III |
353 (36) |
0,32 |
|
IV |
471 (48) |
0,30 |
5.
Среднее значение ветровой нагрузки следует определять по
формуле
= kc
o, (1)
где o —
среднее значение давления ветра, принимаемое по табл. 1;
k — коэффициент, учитывающий
изменение скоростного давления ветра по высоте и принимаемый в соответствии с
[3];
с —
аэродинамический коэффициент, принимаемый согласно [3].
6.
Средние значения и коэффициенты вариации веса снегового покрова следует
принимать по табл. 2.
Таблица 2
Статистические
характеристики веса снегового покрова
|
Снеговой район по [3] |
Среднее значение веса |
Коэффициент вариации vf |
|
I |
485 (50) |
0,45 |
|
II |
685 (70) |
0,40 |
|
III |
980 (100) |
0,35 |
|
IV |
1470 (150) |
0,30 |
|
V |
1960 (200) |
0,30 |
7.
Среднее значение снеговой нагрузки на 1 м2
горизонтальной проекции кровли следует определять по формуле
, (2)
где — среднее значение
веса снегового покрова;
m — коэффициент перехода от
веса снегового покрова земли к снеговой нагрузке на покрытие, принимаемый
согласно [3].
8. Средние
значения веса конструкций и оборудования следует принимать равными нормативным
значениям, определенным в соответствии с [3]. Коэффициенты вариации веса
конструкций и оборудования следует принимать по табл. 3.
Таблица 3
Коэффициенты
вариации веса конструкций, оборудования
|
Конструкции, |
Коэффициент вариации vf |
|
Стальные конструкции |
0,025 |
|
Асбестоцементные листы, |
0,05 |
|
Деревянные конструкции |
0,05 |
|
Стяжки, засыпки, выполняемые на |
0,15 |
|
Стационарное оборудование |
0,10 |
9.
При расчете конструкций на основные сочетания, включающие одну кратковременную
нагрузку, ее величину следует учитывать без снижений, а при расчете на основные
сочетания, включающие две кратковременные нагрузки или более, средние значения
этих нагрузок или соответствующие им усилия необходимо умножать на коэффициент
сочетаний y, определяемый по формуле
y = 1 — kgf × 0,1, (3)
где k — коэффициент, равный
отношению нормативного значения нагрузки к ее среднему значению. Для всех
нагрузок, кроме ветровой, следует принимать k
= 1. Значения k для ветровой нагрузки
приведены в табл. 4;
gf — коэффициент надежности по
нагрузке, определяемый для каждой нагрузки согласно [3].
Таблица 4
Коэффициенты k для ветровой нагрузки
|
Ветровой район по [3] |
I |
II |
III |
IV |
|
Значения k |
1,35 |
1,30 |
1,25 |
1,15 |
МАТЕРИАЛЫ
10.
Средние значения и коэффициенты вариации предела текучести стали следует
принимать по табл. 5 и 6.
Таблица 5
Статистические
характеристики стали, поставляемой по ГОСТ 380-71*
|
Профили, марки стали |
Среднее значение |
Коэффициент вариации vm |
|
1. Гнутые, толщина листа св. 3 мм, марки стали: |
||
|
ВСт3пс3, |
305 (31) |
0,08 |
|
ВСт3кп3, |
285 (29) |
0,08 |
|
ВС2пс3, |
295 (30) |
0,08 |
|
ВСт2кп3, |
275 (28) |
0,09 |
|
2. Прокатные, толщина полки до 5 мм, марки стали: |
||
|
ВСт3Гсп2 |
315 (32) |
0,07 |
|
ВСт3пс2 |
295 (30) |
0,08 |
|
ВСт3кп2 |
275 (28) |
0,09 |
|
3. То же, св. 5 мм, марки стали, указанные в поз. 2 |
270 (28) |
0,08 |
Таблица 6
Статистические
характеристики стали, поставляемой по ТУ 14-1-3023-80
|
Марка стали и вид проката |
Толщина листа или |
Сталь группы I |
Сталь группы II |
||
|
Среднее значение |
Коэффициент вариации vm |
Среднее значение |
Коэффициент вариации vm |
||
|
ВСт3сп, лист |
4-6 |
285 (29,0) |
0,049 |
321 (32,7) |
0,064 |
|
8-10 |
283 (28,8) |
0,050 |
315 (32,1) |
0,060 |
|
|
12-16 |
273 (27,8) |
0,052 |
303 (30,9) |
0060 |
|
|
ВСт3пс, лист |
4-6 |
280 (28,5) |
0,055 |
313 (31,9) |
0,058 |
|
8-10 |
277 (28,3) |
0,056 |
309 (31,5) |
0,055 |
|
|
12-16 |
270 (27,5) |
0,053 |
298 (30,4) |
0,055 |
|
|
ВСт3сп, фасон |
4-6 |
293 (29,9) |
0,080 |
330 (33,6) |
0,062 |
|
8-10 |
292 (29,8) |
0,080 |
325 (33,1) |
0,058 |
|
|
12-16 |
282 (28,7) |
0,051 |
311 (31,7) |
0,056 |
|
|
ВСт3пс, фасон |
4-6 |
284 (28,9) |
0,050 |
318 (32,4) |
0,062 |
|
8-10 |
282 (28,7) |
0,050 |
313 (31,9) |
0,053 |
|
|
12-16 |
280 (28,5) |
0,051 |
308 (31,4) |
0,053 |
РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
11.
Расчет элементов конструкций вероятностно-экономическим методом производится в
соответствии со СНиП II-23-81* с заменой во
всех формулах расчетного сопротивления Ry на среднее значение предела текучести , определяемого по
табл. 5, 6 настоящего приложения;
расчетной продольной силы N на
значение продольной силы от средних значений
нагрузок; расчетного момента М — на
значение момента от средних значений
нагрузок; коэффициента условий работы gс — на приведенный коэффициент условий работы , определяемый в соответствии с п. 13 настоящего приложения.
Примечание. Значения ,
от средних значений
нагрузок определяются теми же способами, что значения М, N от расчетных
значений нагрузок.
12.
Напряжения (условные напряжения) от средних значений ,
стоящие в левых
частях основных проверочных неравенств, следует умножать на коэффициент
надежности gd, определяемый в
соответствии с п. 15 настоящего приложения.
13.
Приведенный коэффициент условий работы определяется по
формулам:
для сжатых элементов = 1 — 0,5 (1 — gс); (4)
” прочих ” » = 1 — 0,75 (1 — gс); (5)
где gс — коэффициент условий
работы, определяемый в соответствии со СНиП II-23-81*.
14.
Коэффициент продольного изгиба сжатых элементов при расчете их на устойчивость
следует определять по формулам:
при
< 4,20; (6)
»
³ 4,20, (7)
где ;
l — гибкость элемента;
— среднее значение предела
текучести, принимаемое в зависимости от марки стали по табл. 5 и 6 настоящего приложения.
Примечание. Формулы (6), (7) применяются вместо формул (8) — (10)
СНиП II-23-81*.
15.
Коэффициент надежности gd определяется по формуле
, (8)
где vd — расчетный коэффициент
вариации, определяемый в соответствии с п. 16 настоящего приложения;
v — коэффициент, определяемый
в соответствии с п. 20
настоящего приложения;
— коэффициент экономической
ответственности, определяемый в соответствии с п. 19 настоящего приложения;
b = Ен.п — норматив для приведения разновременных затрат,
принимаемый согласно Инструкции по определению экономической эффективности
капитальных вложений в строительстве; b = 0,08.
16.
Расчетный коэффициент вариации определяется по формуле
, (9)
— коэффициент, определяемый в
соответствии с п. 17 настоящего приложения;
где vm -коэффициент вариации
предела текучести стали, принимаемый в соответствии с табл. 5 настоящего
приложения;
vs — коэффициент вариации
усилий, определяемый в соответствии с п. 18 настоящего приложения.
17.
Коэффициент при проверке
устойчивости сжатых элементов, а также плоской формы изгибаемых и
внецентренно-сжатых в одной плоскости элементов, определяется по формуле
. (10)
Во всех остальных случаях
коэффициент принимается равным 1.
18.
Коэффициент vs определяется по формуле
, (11)
где Vfi — коэффициенты вариации
нагрузок, определяемые в соответствии с п.
8 настоящего приложения;
Vi — долевой коэффициент,
определяемый по формуле
, (12)
— напряжение в элементе от
среднего значения i-й нагрузки.
19.
Коэффициент экономической ответственности определяется по
формуле
, (13)
где — средняя стоимость
устранения ущерба, вызванного отказом конструкции;
cо — ожидаемая стоимость несущей конструкции в деле;
— ожидаемое значение
коэффициента надежности.
Примечание. Значение следует принимать
равным: для металлических конструкций теплиц — 8; для металлических конструкций
комплексов послеуборочной обработки зерна — 2,5.
20. Коэффициент v
показывает, какую часть стоимость ремонта несущей конструкции после отказа
составляет от полной ее стоимости. Допускается принимать v = 0,5.
21.
Расчет соединений элементов конструкций производится на усилия от расчетных
значений нагрузок в соответствии со СНиП II-23-81*. Усилия от расчетных значений нагрузок определяются
умножением усилий от средних значений нагрузок на соответствующие коэффициенты
надежности по нагрузке, определяемые согласно [3]. Усилия от ветровой нагрузки
дополнительно умножаются на коэффициент, определяемый по табл. 4 настоящего
приложения.
22.
Перемещения элементов конструкций от средних значений нагрузок не должны
превышать величин, приведенных в СНиП
II-23-81*, а для
теплиц — в [6].
Пример. Проверка сжатого элемента ферм покрытия на устойчивость.
Исходные
данные
Элементы таврового сечения 2
L75´5; А = 14,78 см2; ix = 2,31 см; iy = 35 см; lef = 185 см. Материал — сталь марки ВСт3кп, ГОСТ 380-71*.
Кровля двухскатная, a = 15 °, покрытие
бесфонарное; IV снеговой район.
Нормативные значения
нагрузок: снеговой So = 150 кг/см2; от собственного веса стальных конструкций
покрытия — 50 кг/м2; от собственного веса конструкций кровли
(деревянные прогоны, обрешетка, асбестоцементные плиты) — 100 кг/м2.
Усилия в элементе от нормативных значений нагрузок: снеговой — 8,0 т; от веса
стальных конструкций — 2,67 т; от веса конструкций покрытий — 5,25 т;
коэффициент надежности по назначению gn = 0,95; коэффициент экономической ответственности = 2,5; v = 0,5.
Расчет по СНиП II-23-81*
Нормативный собственный вес
покрытия qn =
150 кг; qn/so = 1; gf = 1,4 (п. 5.7 [3]). Коэффициент надежности по
нагрузке для собственного веса покрытия gf = 1,1 (п. 2.2 [3]). Расчетное усилие в элементе N = 8,0 × 1,4 + 8,0 × 1,1 = 20,0 т. Гибкость
элемента = 80. Коэффициент
продольного изгиба j = 0,686 (табл. 72).
Коэффициент условий работы gc = 0,8 (поз. 4 табл. 6*). По табл. 51* Ry = 2300 кг/см2.
Проверяем устойчивость элемента (п. 5.3): gnN/jA £ Rygc; кг/см2
> 0,8 × 2300 = = 1840 кг/см2.
Неравенство не выполняется. Устойчивость элемента не обеспечена.
Расчет по настоящему
Пособию
Определяем напряжение от
средней снеговой нагрузки = 540 кг/см2;
от собственного веса стальных конструкций = 180 кг/см2,
от веса кровли = 360 кг/см2.
По формуле (12)
определяем: v1 = 0,5; v2 = 0,166; v3 = 0,334. По табл. 2 и 3
находим: v1 = 0,3; v2 = 0,025; v3 = 0,05. По формуле (11) определяем: 0,151. По табл. 5 находим vm = 0,08.
Определяем условную гибкость:
. По формуле (10) определяем: d = 0,57. По формуле (9) определяем:
= 0,158. По формуле (8) определяем:
. По формуле (6) определяем:
;
= 8,0 + 5,23 + 2,67 =
16 т. По формуле (4)
определяем: gc = 1 — 0,5(1 — 0,8) = 0,9. По табл. 5 находим: = 2900 кг/см2.
Проверяем устойчивость элемента: ;
кг/см2
< 2900 × 0,9 кг/см2 = 2610 кг/см2.
Неравенство соблюдается.
Устойчивость элемента обеспечена.
ПРИЛОЖЕНИЕ 2
РАСЧЕТ СТАЛЬНЫХ РАМ КАК ЕДИНЫХ НЕЛИНЕЙНЫХ СИСТЕМ
1.
Настоящие рекомендации распространяются на проектирование стальных рам со
сплошностенчатыми колоннами, воспринимающих произвольную статическую нагрузку,
за исключением нагрузок от кранов VI—VIII режимов работы, при
выполнении одного из следующих условий:
(1)
или
, (2)
где Pd — параметр расчетной
нагрузки, с точностью до которого заданы расчетные значения нагрузок;
Pe — параметр критической
нагрузки Эйлера, определяемый согласно п. 4 настоящего приложения.
При пользовании настоящими
рекомендациями не требуется проверять:
изгибаемые элементы на
прочность — по формуле (28) СНиП
II-23-81*;
внецентренно-сжатые и
сжато-изогнутые стержни, удовлетворяющие условию (1), на устойчивость — по
формуле (51) СНиП II-23-81*.
2. Проверка
несущей способности рамы производится по формуле
Pd.£ Pu, (3)
где Pu — параметр предельной нагрузки, принимаемый равным
, (4)
но не более Pa;
Рs —
параметр предельной пластической (приспособляющей) нагрузки, определяемый
согласно п. 7 настоящего
приложения;
Рa
— параметр нагрузки пластической усталости, определяемый согласно п. 6 настоящего приложения;
; (5)
, (6)
; (7)
. (8)
В формулах (5) — (8):
Py — параметр нагрузки краевой
текучести, при котором впервые появляется текучесть материала, определяемый
согласно п. 5 настоящего
приложения;
b — коэффициент, учитывающий
соответствие форм деформирования и потери устойчивости рамы, определяемый
согласно п. 7 настоящего
приложения.
3.
В зависимости от числа опасных сочетаний и вида нагрузок расчет рамы
выполняется одним из следующих способов:
при большом числе опасных
сочетаний нагрузок, когда расчет рамы на каждое сочетание поочередно требует
больших затрат машинного времени, параметры Ру,
Рs и b
определяются из расчета рамы на приспособляемость, а параметр Pe — из расчета на
устойчивость при максимально возможной вертикальной нагрузке на раму согласно
п. 4 настоящего приложения;
при небольшом числе опасных
сочетаний нагрузок расчет рамы выполняется на каждое сочетание поочередно, а в
качестве параметра предельной нагрузки Рu принимается наименьшее из
полученных значений.
4.
Параметр первой критической нагрузки Pe определяется из расчета на устойчивость упругой рамы. Рекомендуется
использовать метод перемещений, для которого единичные реакции сжатых стержней
принимаются согласно следующей таблице и табулированы в [19]:
5. Параметр
нагрузки краевой текучести Ру
принимается равным
, (9)
где знак “плюс” перед радикалом относится к случаю с1 < 0, а знак “минус” — к
случаю с1 > 0.
Коэффициенты с1 и с2 вычисляются для
поперечного сечения, содержащего наиболее напряженное волокно, по формулам:
;
, (10)
где ;
W — момент сопротивления
поперечного сечения для наиболее напряженного волокна;
и
— нормальная сила и
изгибающий момент, определяемые из линейного расчета рамы при Р = 1 [их значения, приведенные в
формулах (10), принимаются положительными];
— изгибающий момент в основной
системе рамы, определяемый из линейного расчета при Р = 1.
Если , то параметр Ру
принимается равным
. (11)
|
Схема стержня |
Выражения единичных |
||
|
М1 |
М2 |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
Основная
система рамы образуется из заданной рамы постановкой фиктивных опор против
линейных смещений. Для свободных рам основной системой будет соответствующая
несвободная рама с фиктивными опорами в уровне ригелей. Для несвободных рам
фиктивные опоры ставятся таким образом, чтобы они препятствовали потере
устойчивости рамы по низшим и, по возможности, не препятствовали по высшим
формам.
6.
Параметр нагрузки пластической усталости Ра
определяется от нормативных значений нагрузок при повторно-переменном нагружении
рамы по формулам, идентичным формулам (9)-(11) настоящего приложения для Ру с заменой на 0,35 D
;
на 0,35 D
, и
на 0,35 D
. Диапазоны изменения усилий D
,
D и D
определяются для расчетного поперечного сечения, в котором
имеется наибольший размах краевых напряжений.
7.
Параметры Рs и b определяются путем
аппроксимации зависимости Рр =
Рр (h) степенной функцией
Рр = Рs h—b (b ³ 0,1), (12)
где Рр — параметр предельной
пластической (приспособляющей) нагрузки, определяемый по деформированной схеме;
h — условное безразмерное перемещение рамы.
Построение кривой
предельного равновесия (приспособляемости) “в большом” Рр = Рр
(h) производится статическим,
кинематическим или другими известными методами.
8.
Статический метод предельного равновесия сводится к нахождению тах h (или тах Рр) при выполнении следующих ограничений:
(Рр) (13)
записанных для всех расчетных поперечных сечений,
где Mri — остаточные изгибаемые
моменты в i-том расчетном сечении,
определяемые по недеформированной схеме;
;
Мрli — предельные значения
изгибающих моментов, воспринимаемые i-тым
расчетным сечением, определяемые с учетом действия нормальных сил в колоннах и
поперечных сил в ригелях по формулам (39), (42) — (44) СНиП II-23-81*. Допускается определять нормальные и поперечные
силы из линейного расчета рамы.
Кинематический метод
предельного равновесия сводится к нахождению тах h (или тах Рр)
при выполнении следующих ограничений:
, (14)
записанных для каждого j-го кинематически возможного механизма пластического разрушения
конструкции,
где и
— соответственно работа поперечных (активных) нагрузок при Р = 1 и диссипация энергии, определяемые
на рассматриваемом механизме пластического разрушения, равные:
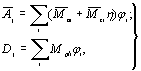
здесь i — номер поперечного
сечения, в котором образуется пластический шарнир;
ji —
угол поворота i-того пластического шарнира; знак суммы распространяется на все
пластические шарниры.
Оба метода сводятся к
задачам математического программирования, линейным относительно параметра h, для решения которых
рекомендуется использовать симплекс-метод.
9.
Расчет на местную устойчивость внецентренно-сжатых и сжато-изогнутых элементов
производится в соответствии со СНиП
II-23-81* с заменой
условной гибкости на приведенную гибкость
Приведенная гибкость
принимается по табл. 74
СНиП II-23-81* по соответствующим
значениям коэффициентов mеf и jе.
Приведенный относительный эксцентриситет mеf определяется в соответствии
со СНиП II-23-81*, а коэффициент снижения
расчетных сопротивлений jе — по формуле
. (16)
Устойчивость из плоскости
действия момента должна быть обеспечена постановкой связей в тех поперечных
сечениях, где образуются пластические шарниры при расчете рамы методом
предельного равновесия по жесткопластической схеме.
10.
Расчет рамы производится в следующем порядке:
а) предварительные размеры
элементов рамы определяются по СНиП
II-23-81*;
б) проверяется область
применения настоящих рекомендаций согласно п. 1 настоящего приложения;
в) вычисляется параметр
критической нагрузки Эйлера Pе согласно п. 4 настоящего приложения;
г) вычисляется параметр
нагрузки краевой текучести материала Ру
согласно п. 5 настоящего
приложения;
д) вычисляется параметр
нагрузки пластической усталости Ра
согласно п. 6 настоящего
приложения;
е) строится кривая
предельного равновесия (приспособляемости) „в большом» согласно п. 8 настоящего приложения;
ж) вычисляются параметры Ps и b
кривой предельного равновесия “в большом” согласно п. 7 настоящего приложения;
з) вычисляется параметр
предельной нагрузки Ри и
проверяется несущая способность рамы согласно п. 2 настоящего приложения;
и) проверяется местная
устойчивость элементов согласно п. 9
настоящего приложения;
к) производится уточненный
подбор сечений элементов рамы, если параметр предельной нагрузки Ри превышает расчетный
параметр Pd более чем на 5 %.
ПРИМЕР
Рассмотрим замкнутую
прямоугольную раму, нагруженную вертикальными q [0,5P, Р], V [0,5P, Р]
и горизонтальными Т[-Р, Р]
нагрузками, рис. 1 настоящего приложения (в квадратных скобках указаны пределы
изменения каждой из действующих нагрузок во времени независимо друг от друга; Р — параметр нагрузки).
Рама является упрощенной
моделью ячейки многоярусного каркаса, а при бесконечно жестком нижнем ригеле —
одноэтажной рамы. Она подробно исследована Н.В. Корноуховым [19] для оценки
устойчивости сложных стержневых систем и использована в п. 6.10* СНиП II-23-81* для определения свободных
длин стоек многоэтажных рам. Таким образом, принятая расчетная схема отражает
основные особенности целого класса сооружений.
Рис. 1. Расчетная
схема рамы
Исходные данные. Рама выполнена из стали марки 18пс с расчетным сопротивлением Ry = 240 МПа.
Стойка из широкополочного
двутавра № 20 Б3 имеет следующие геометрические характеристики: h = 202 мм; b = 100,4 мм; d = 5,6 мм; t = 9,6 мм; Н = 4 м; А = 3,06×10-3 м2,
Ix = 2,15 × 10-6 м4;
Wx = 2,13×10-4 м3;
rx = 8,39×10-2 м.
Ригель из широкополочного
двутавра № 20 Б* имеет следующие геометрические характеристики: h = 194 мм; b =
99,3 мм; d = 4,5 мм; t = 5,5 мм; L = 4 м; Ix = 1,3×10-5 м4;
Wx = 1,34×100-4 м3;
Sx = 7,58×10-5 м3.
Нагрузки: q = l8,355P, кН/м; T = 3,234Р, кН; V = 204,93Р, кН.
а) Расчет по
СНиП П-23-81*
Отношение жесткостей на 1 м
длины ригеля и стойки n
равно:
Изгибающие моменты в угловых
сечениях 1 и 7 будут следующими:
от вертикальной нагрузки q (рис. 2, а настоящего приложения):
, кН×м;
от горизонтальной нагрузки Т (рис. 2, б настоящего приложения):
кН×м.
Рис. 2. Эпюры изгибающих моментов
а — от вертикальной нагрузки; б — от горизонтальной нагрузки Т; в
-от лишней неизвестной Х
Коэффициенты расчетной длины
m стойки определим по формуле
(70, б) СНиП II-23-81* при р = п= 0,624:
.
В соответствии с п. 5.27* СНиП II-23-81* определяем:
относительный эксцентриситет
;
отношение площади полки к
площади стенки: Af/Aw = 0,948;
коэффициент влияния формы
сечения h = 1,51;
приведенный относительный
эксцентриситет mef = mh = 2,40;
гибкость стойки l = 71,5;
условную гибкость .
По табл. 74 СНиП II-23-81* принимаем коэффициент снижения расчетных
сопротивлений jе = 0,329.
Из формулы (51) СНиП II-23-81* находим расчетное значение
параметра нагрузки Pd:
.
б) Проверка
области применения настоящих рекомендаций
Проверим условие (1):
.
Условие (1) выполнено,
следовательно, раму можно рассчитывать на основе настоящего Пособия.
в) Вычисление
параметра критической нагрузки Pе
Условие потери устойчивости
рамы по антисимметричной форме имеет вид трансцендентного уравнения [19] относительно
параметра устойчивости v,
равного
,
где — нормальная сила в
стойке при Р = 1, равная
.
Первый (низший) корень
трансцендентного уравнения при п =
0,624 равен v = 2,1. Соответствующее
ему значение параметра критической нагрузки Pe будет равно
г) Определение
параметра нагрузки краевой текучести материала Ру
Согласно п. 5 настоящего приложения основной
системой заданной свободной рамы будет соответствующая несвободная рама с
фиктивной опорой от горизонтального смещения в уровне ригеля, которая полностью
воспринимает горизонтальную нагрузку Т и не воспринимает вертикальную нагрузку q. Поэтому
эпюра изгибающих моментов в основной системе рамы будет равна Mo = Мq (см. рис. 2, а настоящего
приложения), а эпюра изгибающих моментов от лишней неизвестной z (горизонтального смещения
рамы) будет равна Мz = Мr
(см. рис. 2, б настоящего приложения).
Наиболее напряженным
поперечным сечением, в котором возникает первый пластический шарнир, является
правое опорное сечение ригеля. По формулам (10) и (9) настоящего приложения находим:
д) Определение
параметра нагрузки пластической усталости Pa
Наибольший размах напряжений
Ds имеет место в крайнем
внутреннем волокне концевого сечения правой стойки. В этом волокне наибольшее
сжимающее напряжение sтах имеет место при сочетании
нагрузок q(P), V(P) и Т(Р), а наименьшее сжимающее (или наибольшее растягивающее)
напряжение smin — при сочетании нагрузок q(0,5P), V(0,5P) и Т(—Р).
По формулам пп. 5 и 6 вычисляем:
кН×м;
кН×м;
кН×м;
кН×м;
м.
Согласно п. 6 настоящего приложения параметр
нагрузки пластической усталости Рa вычисляется при нормативных
значениях нагрузок. Примем среднее значение коэффициента перегрузки k = 1,2.
.
е) Построение
кривой предельного равновесия “в большом” Рр
= Рр (h)
Для иллюстрации применим оба
метода предельного равновесия: статический
и кинематический. В силу симметрии рамы и нагрузки будем рассматривать
только верхнюю половину рамы. В соответствии с эпюрами моментов Mq (рис. 2, а) и Мr (рис. 2, б) примем безразмерные координаты расчетных поперечных
сечений i такими:
0;
0,1;
0,2;
0,3;
0,4;
0,5;
1,0.
СТАТИЧЕСКИЙ МЕТОД
Согласно п. 8 настоящего приложения задача
формулируется следующим образом. Найти maxh (или max Рр) при выполнении ограничений:
Составляющие изгибающего
момента в ригеле равны:
;
.
Эпюра остаточных моментов Мri в ригеле постоянна (рис. 2, в) и равна
Мri = Mr.
Максимальное значение
поперечной силы Qi имеет место у правой опоры
ригеля в расчетном сечении i =
7 и равно
, кН.
Отношение среднего
касательного напряжения к расчетному
сопротивлению стали сдвигу Rs (Rs = 0,58Ry согласно табл. 1* СНиП II-23-81*), равно:
Согласно п. 5.18 СНиП II-23-81* при значениях , чему соответствует
, предельные изгибающие моменты Мpli(Рр) во всех
расчетных поперечных сечениях можно определять без учета поперечных сил по
формулам (39) и (42) СНиП II-23-81*.
Мpli = WpliRy = 2SRy = 2 × 0,758 × 104 × 2,4 × 105 = 36,38 кН × м.
С учетом полученных
выражений для моментов ограничения-неравенства для семи расчетных поперечных
сечений будут такими:
1) Мr
+ 6,468 Ррh £ 36,38 + 20,254Pp;
2) Мr + 5,174 Ррh £ 36,38 + 7,042Pp;
3) Мr + 3,880 Ррh £ 36,38 — 3,253Pp;
4) Мr + 2,587 Ррh £ 36,38 — 10,575Pp;
5) Мr + 1,294 Ррh £ 36,38 — 14,979Pp;
6)
Мr £ 36,38 — 16,446Pp;
7) Мr — 6,468 Ррh ³ -36,38 + 20,254 Pp.
Для примера определим
координаты двух точек на кривой предельного равновесия “в большом” Рp = Pp(h), приняв Pp = Pd = 1. Тогда система
ограничений-неравенств становится линейной относительно двух варьируемых
параметров Mr и h. В общем случае
поставленная задача решается методами линейного программирования, например,
симплекс-методом. В данном простом примере решение maxh = 4,631 получено “ручным”
счетом. При этом четвертое и седьмое из ограничений переходят в строгие
равенства, что соответствует образованию пластических шарниров в расчетных
сечениях с координатами и
.
Вторую точку на кривой
предельного равновесия “в большом” найдем, приняв h = 1, тогда система
ограничений-неравенств становится линейной относительно двух варьируемых
параметров Мr и Pp. Максимальное значение
параметра Pp,
удовлетворяющее полученной системе ограничений-неравенств, будет равно тахРр = 1,686. При этом
шестое и седьмое из ограничений переходят в строгие равенства, что
соответствует образованию пластических шарниров в расчетных поперечных сечениях
с координатами и
. Аналогичным путем можно определить координаты любой точки
на кривой предельного равновесия “в большом”.
КИНЕМАТИЧЕСКИЙ МЕТОД
Согласно п. 8 настоящего приложения задача
ставится следующим образом. Найти minP
(или minh) при выполнении условий совместности для всех j кинематически возможных
механизмов пластического разрушения рамы:
.
Рама один раз статически
неопределима, поэтому для превращения ее в механизм достаточно образования двух
пластических шарниров. Первый пластический шарнир образуется в наиболее
напряженном расчетном поперечном сечении i = 7 на правом опорном конце ригеля, второй — в одном из расчетных
сечений i = 1—6.
Удельная работа внешних сил и диссипация энергии Dj на рассматриваемых
механизмах пластического разрушения рамы (рис. 3 настоящего приложения)
соответственно равны:
Рис. 3. Схема механизма пластического разрушения рамы
С учетом указанных последних
выражений ограничения-неравенства (14) настоящего приложения для каждого из
шести возможных механизмов пластического разрушения будут такими:
12,936 hPp ³ 72,76;
(14,68 + 12,936 h) Pp ³ 80,844;
(29,36 + 12,936 h) Pp ³ 90,95;
(44,04 + 12,936 h) Pp ³ 103,943;
(58,72 + 12,936 h) Pp ³ 121,267;
(73,4 + 12,936 h) Pp ³ 145,52.
Для наглядности определим
две точки на кривой предельного равновесия “в большом” Рp
= Pp(h),. Первую точку найдем,
приняв Pp = Pd = 1. Минимальное значение
параметра h, удовлетворяющее полученной
системе линейных ограничений-неравенств, будет minh = 4,631. При этом четвертое
из ограничений переходит в строгое равенство, что соответствует образованию
второго пластического шарнира в расчетном поперечном сечении с координатой. Вторую точку на кривой предельного равновесия “в большом”
найдем, приняв h = 1. Минимальное значение
параметра Pp,
удовлетворяющее полученной системе линейных ограничений-неравенств, будет minPp = 1,686. При этом шестое из
ограничений переходит в строгое равенство, что соответствует образованию
второго пластического шарнира в расчетном поперечном сечении с координатой . Аналогичным путем можно определить координаты любой точки
на кривой предельного равновесия “в большом”.
Как и следовало ожидать,
результаты расчета рамы статическим и кинематическим методами совпали.
ж) Определение
параметров Рs и b кривой предельного
равновесия “в большом”
Подставляя координаты второй
точки h = 1 и Рр = 1,686 в формулу (12) настоящего приложения, найдем Рs
= 1,686. Подставляя координаты первой точки h = 4,631 и Рр = 1 в это же выражение,
получим:
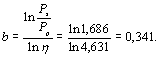
з) Проверка несущей способности рамы
По формулам (4)-(8) настоящего приложения
вычислим:
a — b = 7,565 — 0,341 =
7,224;
что превосходит параметр расчетной нагрузки Pd = 1 на 23,9 %.
Следовательно, имеется
существенный резерв несущей способности рамы.
и) Проверка
местной устойчивости элементов
Поскольку стержни рамы
выполнены из прокатных профилей, местная устойчивость считается обеспеченной.
к) Уточненный
подбор сечений элементов
Задаемся новыми,
уменьшенными сечениями элементов стоек и весь расчет повторяем заново до тех
пор, пока не будет выполнено условие
0,95 Pu £ Pd £ Pu.
ПРИЛОЖЕНИЕ 3
ДЮБЕЛЬНЫЕ СОЕДИНЕНИЯ
1.
Настоящее приложение рекомендуется применять при проектировании дюбельных
соединений стальных конструкций, работающих в условиях статического нагружения,
изготовленных из стали с нормативным временным сопротивлением от 355 до 590 МПа
(от 36 до 60 кгс/мм2), эксплуатируемых в районах с расчетной
температурой до минус 65 °С.
Применение конструкций на
дюбельных соединениях не допускается:
при толщине опорных
элементов to до 4 и свыше 20 мм;
в районах с сейсмичностью
свыше 6 баллов;
в сильноагрессивных средах.
2.
Для дюбельных соединений следует применять дюбели по ТУ 14-4-1434-87,
механические свойства которых приведены в табл. 1.
Таблица 1
Механические
характеристики дюбелей
|
Номинальный диаметр |
Марка стали |
Технические условия |
Нормативное временное |
|
70К-ПВ |
ТУ 14-1-3747-86 |
||
|
4,5 |
70ПВ |
ТУ 14-1-3746-86 |
2000 (205) |
|
70 |
ТУ 14-1-1881-76 |
3.
Суммарная толщина присоединяемых элементов t в зависимости от толщины опорного элемента to и нормативного временного сопротивления стали Roun опорного элемента не должна превышать
значений, приведенных в табл. 2. Минимальная толщина отдельного присоединяемого
элемента равна 0,5 мм.
Таблица 2
Толщина
элементов, соединяемых дюбелями
|
Толщина опорного |
Суммарная толщина |
||||
|
до 370 (38) |
св. 370 (38) |
св. 430 (44) |
св. 450 (46) |
св.510 (52) |
|
|
до 430 (44) |
до 450 (46) |
до 510 (52) |
до 590 (60) |
||
|
От 4 до 6 |
4 |
4 |
4 |
4 |
4 |
|
Св. 6 ” 8 |
6 |
6 |
4 |
4 |
4 |
|
” 8 ” 10 |
6 |
4 |
4 |
4 |
4 |
|
” 10 ” 12 |
4 |
4 |
4 |
4 |
— |
|
” 12 ” 16 |
4 |
4 |
4 |
4 |
— |
|
” 16 ” 20 |
4 |
4 |
4 |
— |
— |
4.
Расчетные сопротивления однодюбельных соединений следует принимать по табл. 3.
Таблица 3
Расчетные
сопротивления элементов, соединяемых одним дюбелем
|
Напряженное состояние |
Ограничение значения |
Условное обозначение |
Расчетное |
|
|
Срез стержня дюбеля |
t ³ 1,5 |
Rds |
0,5Rdun |
|
|
Смятие присоединяемых элементов |
0,5 £ t < 1,5 |
Rdp |
2,0Run |
|
|
Растяжение |
Отрыв присоединяемых элементов |
Нет |
Rdt1 |
0,3Run |
|
Выдергивание дюбеля из опорного элемента |
Нет |
Rdt2 |
0,3Roun |
5.
В дюбельных соединениях при действии продольной силы N, проходящей через центр
тяжести соединения, распределение ее между дюбелями следует принимать
равномерным.
6.
Расчетные усилия Nd, которые могут быть
восприняты одним дюбелем, следует определять по формулам:
на срез Nd = RdsAdnsgigt; (1)
на смятие Nd = Rdpdtgi; (2)
на отрыв Nd = Rdt1A1; (3)
на выдергивание Nd = Rdt2A2 (4)
В формулах (1)-(4):
— расчетная площадь сечения
дюбеля;
пs
— число расчетных срезов одного дюбеля;
A1 = pDt — расчетная площадь отрыва
присоединяемых элементов;
D —
диаметр шайбы;
A2 = pDtoe —
расчетная площадь при выдергивании дюбеля;
toe — эффективная толщина
опорного элемента, определяемая по формулам.
(5)
gt — коэффициент, учитывающий вероятность
потери несущей способности соединения по смятию, определяемый по формулам:
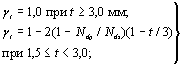
gi — коэффициент, учитывающий
тип соединения, определяемый по табл. 4.
Таблица 4
Коэффициент,
учитывающий тип соединения
|
Тип соединения |
|
|
|
Коэффициент gi |
1,0 |
0,8 |
Продолжение
табл. 4
|
Тип соединения |
|
|
|
Коэффициент gi |
0,7 |
0,6 |
7.
Число дюбелей пd в соединении при действии
силы N следует определять из
условия
пd ³ N/Nmin, (7)
где Nmin — минимальное значение расчетного усилия для одного дюбеля, вычисленное
в соответствии с п. 6 настоящего приложения.
8.
При действии на соединение момента, вызывающего сдвиг соединяемых элементов,
распределение усилий на дюбели следует принимать пропорционально расстояниям от
центра тяжести соединения до рассматриваемого дюбеля.
9.
Дюбели, работающие одновременно на сдвиг и растяжение, следует проверять на
равнодействующее усилие.
10.
Расчетные сечения элементов при соединении их дюбелями следует определять без
учета отверстий, образуемых дюбелями.
11.
Минимальные расстояния от центра дюбеля до края элемента и между центрами
дюбелей независимо от направления усилий следует принимать равными 2d.
СПИСОК ЛИТЕРАТУРЫ
1. СТ
СЭВ 3972-83. Надежность
строительных конструкций и оснований. Конструкции стальные. Основные положения
по расчету.
2. СТ СЭВ 384-87. Надежность строительных
конструкций и оснований. Основные положения по расчету.
3. СНиП 2.01.07-85. Нагрузки и воздействия.
4. Правила учета степени ответственности
зданий и сооружений при проектировании конструкций. — Приведены в СНиП 2.01.07-85. Нагрузки и воздействия.
5. Техническая документация САПР-ЦНИИПСК.
Подсистема расчета несущих конструкций (Ф1). Задача “Диалоговый расчет
металлоконструкций с архивом суперэлементов” (ДИАРАМА). Руководство по
применению. Общая часть. Режим “Статика”. Вып.
ОММИС-205-1/ЦНИИпроектстальконструкция им. Н.П. Мельникова. — М., 1983. — 88 с.
6. Дривинг А.Я. Вероятностно-экономический
метод в нормах расчета строительных конструкций//Строит. механика и расчет
сооружений. — 1982. -№3.-С. 7-11.
7. Рекомендации по применению стали для
стальных строительных конструкций зданий и
сооружений/ЦНИИпроектстальконструкция им. Н.П. Мельникова. — М., 1983. — 42 с.
8. СНиП III-18-75. Металлические конструкции.
9. Пособие по расчету и конструированию
сварных конструкций (к главе СНиП
II-23-81)/ЦНИИСК
им. Кучеренко. — М.: Стройиздат, 1984. — 40 с.
10. Рекомендации по расчету прочности
стальных канатов, применяемых в строительных металлических
конструкциях/ЦНИИпроектстальконструкция. — М., 1982. — 28 с.
11. Балдин В.А. Об учете пластических
деформаций при неравномерном распределении напряжений по сечению//Строит.
механика и расчет сооружений. — 1977. — №1.- С. 29-31.
12. Чувикин Г.М. Об устойчивости за
пределом упругости внецентренно сжатых тонкостенных стержней открытого профиля.
— В кн.: Исследования по стальным конструкциям. Вып. 13. — М.: Госстройиздат,
1962. — С. 70-159.
13. Тимошенко С.П. Устойчивость упругих
систем. — М.: Гостехтеоретиздат, 1955. — 567 с.
14. Чувикин Г.М. Устойчивость двутавровых балок моносимметричного сечения//Строит.
механика и расчет сооружений. — 1968. — № 2. — С. 34-38.
15. Eurocode № 3: Common unified Rules for steel
Structures/ Commission of the Europian Communities Industrial processes
Building and civil Engineering. Eur. 8849. 1984.
16. Мразик А., Шкалоуд М., Тохачек М.
Расчет и проектирование стальных конструкций с учетом пластических деформаций.
— М.: Стройиздат, 1986. — 456 с.
17. Моисеев В.И. Расчет местной
устойчивости стальных балок за пределом упругости//Строит. механика и расчет
сооружений. — 1982. — № 6. — С. 43-46.
18. Ясинский Ф.С. Избранные работы по
устойчивости сжатых стержней. — М. — Л.: Гостехтеоретиздат, 1952. — 427 с.
19. Корноухой Н.В. Прочность и
устойчивость стержневых систем. — М.: Госстройиздат, 1949. — 376 с.
20. Ильюшин А.А. Пластичность. — М.:
Гостехиздат, 1948. — 376 с.
21. Вольмир А.С. Устойчивость
деформируемых систем. — М.: Наука, 1967. — 984 с.
22. Броуде Б.М., Моисеев В.И. Устойчивость
прямоугольных пластинок с упругим защемлением продольных сторон//Строит.
механика и расчет сооружений. — 1982. — № 1. — С. 39-42.
23. Броуде Б.М. Устойчивость пластинок в
элементах стальных конструкций. — М.: Машстройиздат, 1949. — 240 с.
24. Рекомендации по применению в
строительстве ротационного способа подготовки контактных поверхностей при
проектировании и выполнении фрикционных соединений стальных строительных
конструкций/ ЦНИИпроектстальконструкция им. Н.П. Мельникова. -М., 1983. — 8 с.
25. Руководство по проектированию,
изготовлению и сборке монтажных фланцевых соединений стропильных ферм с поясами
из широкополочных двутавров/ЦНИИпроектстальконструкция. М., 1982. — 60 с.
26. Руководство по проектированию стальных
конструкций из гнутосварных замкнутых профилей/ЦНИИпроектстальконструкция. —
М., 1978. — 42 с.
27. Рекомендации по точечной дуговой
примерке профилированного настила стальным элементом каркаса/ЦНИИСК им.
Кучеренко. — М., 1979. — 43 с.
28. Руководство по применению нагелей для
крепления профилированного стального настила в покрытиях производственных зданий/ЦНИИпроектстальконструкция,
ВНИПИпромстальконструкция. — М., 1982. — 24 с.
29. Рекомендации по проектированию стальных
конструкций с применением круглых труб/ЦНИИСК им. Кучеренко. — М., 1974. — 93
с.
30. Рекомендации по проектированию
структурных конструкций/ЦНИИСК им. Кучеренко. — М.: Стройиздат, 1984. — 298 с.
31. Евстратов А.А. О предельном состоянии
пластинок при чистом изгибе//Известия Северо-Кавказского научного центра, сер.
Технические науки, — 1975. — № 3. — С. 99-102.
32. Rockey К.
Skaloud. The ultimate load behaviour of plate girders
loaded in shear. IABSE CoUoq. „Design of plate and box girders for ultimate
strength.» — London, 1971. -P. 111-148.
33. Балдин B.A, Горпинченко В.М., Лазарян А.С. Расчет на выносливость верхней зоны стенки подкрановой
балки//Строит. механика и расчет сооружений. 1976, № 4. — С. 34-38.
34. Трофимов В.И. Ограждения сооружений из
растянутых алюминиевых поверхностей. — М.: Стройиздат, 1975. — 159 с.
35. Рекомендации по проектированию
мембранных покрытий на прямоугольном плане для реконструируемых зданий и
сооружений/ЦНИИСК им. Кучеренко. — М., 1986. — 90 с.
36. СНиП II-26-76. Кровли.
37. Рекомендации по применению стальных
профилированных настилов нового сортамента в утепленных покрытиях
производственных зданий/ ЦНИИпроектстальконструкция им. Н.П. Мельникова. — М.,
1985. — 30 с.
38. Рекомендации по учету жесткости
диафрагм из стального профилированного настила в покрытиях одноэтажных
производственных зданий при горизонтальных
нагрузках/ЦНИИпроектстальконструкция. — М., 1980. — 32 с.
39. Васылев В.Н., Гампель В.И., Клыков В.М.,
Ковнер И.С., Хорошавина З.В.
Разработка типовых технологических процессов изготовления металлических
конструкций для САПР-ЦНИИПСК//Тр. ЦНИИпроектстальконструкции. 1978. — Вып. 25.
— С. 87-95.
40. Программа расчета технико-экономических
показателей стальных каркасов промышленных зданий. Руководство
программиста/ЦНИИпроект. — М., 1984. — 110 с. (Межотраслевой фонд алгоритмов и
программ автоматизированных систем в строительстве. Вып. II-48).
41. Пихтарников Я.М., Ладыженский Д.В.,
Яковенко О.В., Клещевников В.В.
Исследование технико-экономических показателей технологического оборудования
для изготовления металлических конструкций//Тр. ЦНИИпроектстальконструкции. —
Исследование процессов заводского производства строительных металлических
конструкций. — М., 1981. — С. 78-90.
42. Кузнецов А.Ф. Строительные конструкции
из сталей повышенной и высокой прочности. — М.: Стройиздат, 1975. — 80 с.
43. Лихтарников Я.М. Вариантное
проектирование и оптимизация стальных конструкций. — М.: Стройиздат, 1979. —
319 с.
44. Металлические конструкции. Справочник
проектировщика. Под ред. Н.П. Мельникова, 2-е изд. — М.: Стройиздат, 1980. —
776 с.
45. Руководство по количественной оценке
технологичности металлических конструкций промышленных зданий на стадии
проектирования/ЦНИИпроектстальконструкция. — М., 1982. — 83 с.
Данное Пособие отсканировано по причине того, что в Word-овских вариантах формулы распознаны небрежно и зачастую содержат ошибки, а нашей профессии — это не есть гуд.
Спасибо моему коллеге Володе К., проделавшему труд по сканированию документа.
Комментарии
Комментарии могут оставлять только зарегистрированные
участники
Авторизоваться
Комментарии 1-10 из 13
@LEXx
, 13 января 2009 в 08:31
#1
Спасибо, хороший скан.
Sid Barret
, 13 января 2009 в 09:33
#2
и мне спасибо за оригинал )))))))))))
ФАХВЕРК
, 13 января 2009 в 10:45
#3
Спасибо ОГРОМНЕЙШЕЕ, Коллеги!!!
Romka
, 13 января 2009 в 12:26
#4
Sid Barret
Тебе также ОГРОМНОЕ спасибо.
Haos
, 13 января 2009 в 19:31
#5
Пасиба!
, 14 сентября 2009 в 20:09
#6
Спасибо за пособие!!!
, 15 марта 2010 в 21:00
#7
Спасиьо большое за Пособие!
911
, 20 мая 2011 в 08:42
#8
посмотрите ф92. Там опечатка:-(
byman12
, 12 октября 2011 в 16:15
#9
Спасибо огромное!!!
CpL
, 13 марта 2012 в 10:22
#10
Спасибо!
- empty
- empty
- empty
6 июня 2023
Круглый стол «Строительно-монтажные компании: как выбрать и не ошибиться»
Подробнее
6 июня 2023
Круглый стол «Развитие нормативно-технической базы в области металлоконструкций. Реализация Дорожных карт Минстроя России»
Подробнее
7 июня 2023
Ежегодная конференция участников
Ассоциации развития стального строительства
Подробнее
6 июня 2023
Круглый стол «Строительно-монтажные компании: как выбрать и не ошибиться»
Подробнее
6 июня 2023
Круглый стол «Развитие нормативно-технической базы в области металлоконструкций. Реализация Дорожных карт Минстроя России»
Подробнее
7 июня 2023
Ежегодная конференция участников
Ассоциации развития стального строительства
Подробнее
СТО АРСС
Конструирование металлоконструкций
| Самохвалов Я. А. Справочник техника-конструктора — Скачать 8.2 mb В справочнике приведены данные по сопротивлению материалов, справочные данные по допускам и посадкам, а также по конструкционным материалам, рекомендации по их выбору. Кратко изложены сведения о резьбовых и сварных соединениях, винтовых механизмах, валах, муфтах, подшипниках, шпоночных и шлицевых соединениях, ременных, ценных, зубчатых и червячных передачах, пружинах и покрытиях. |
|
| Васильченко В.Т. Справочник конструктора металлических конструкций — Скачать 4.4 mb
В справочнике систематизированы данные, необходимые для разработки чертежей строительных металлоконструкций на стадии КМ и КМД: сортамент прокатных и гнутых профилей стали, указания по конструированию основных конструктивных элементов промышленных зданий и сооружений, расчету соединений и др. Особое внимание уделено вопросам упрощения конструирования. Нормативные материалы приведены по состоянию на 01.08.80. |
|
| Абаринов А. А. Составление деталировочных чертежей металлических конструкций — Скачать 4.5 mb
Рассмотрены основные вопросы выполнения рабочих деталировочных чертежей стальных конструкций. Приведены рекомендации по оформлению чертежей, способствующие быстрому и правильному их чтению. Даны примеры рабочих чертежей строительных конструкций. См. также html-версию книги. |
Проектирование металлоконструкций
| Бирюлев В. В. Проектирование металлических конструкций — Скачать 32.5 mb
Содержатся материалы по проектированию легких металлических конструкций, облегченных балок и ферм, рам и пространственных конструкций. Уделено внимание проектированию конструкций, эксплуатируемых при низких температурах. Изложены способы защиты металлических конструкций от коррозии, усиления конструкций, в том числе предварительным напряжением. Для студентов строительных вузов. Год издания — 1990. |
|
| Лихтарников Я.М. Расчет стальных конструкций — Скачать 3,9 mb
Изложены основные расчетные положения, примеры расчета, рекомендации по конструированию стальных строительных конструкций. Второе издание дополнено прогрессивными конструкциями из сталей повышенной и высокой прочности, из гнутых и гнутосварных профилей и др., переработано в соответствии с новыми нормативами. 1975 г. |
|
| Мельников Н.П. Металлические конструкции. Справочник проектировщика — Скачать 18.5 mb
Обобщение опыта исследования и проектирования металлических конструкций в СССР. Приведены сведения о материалах и полуфабрикатах для строительных металлических конструкций, общие положения по их расчету и конструированию, методы расчета и оптимизации конструкций с помощью ЭВМ. Даны сведения о способах изготовления, транспортирования и монтажа металлических конструкций, технологичности проектируемых конструкций и их экономике. Освещены вопросы их унификации, типизации и стандартизации. |
|
| Мельников Н.П. Справочник проектировщика. Металлические конструкции промышленных зданий и сооружений — Скачать 52,6 mb
В справочнике «Металлические конструкции промышленных зданий и сооружений» изложены сведения и рекомендации, необходимые при проектировании строительных конструкций из стали и алюминиевых сплавов для промышленных зданий и сооружений. Год выпуска: 1962. |
|
| Михайлов А.М. Металлические конструкции в примерах — Скачать 28,9 mb
В книгу включены примеры двух типов: 1) примеры, иллюстрирующие расчеты металлических конструкций и их элементов, наиболее часто встречающиеся при курсовом и дипломном проектировании; 2) примеры, которые служат связующим звеном между теорией сопротивления материалов и теорией расчета металлических конструкций. Книга предназначена для учащихся техникумов при изучении курса «Металлические конструкции», а также при курсовом и дипломном проектировании. |
|
| Муханов К.К. Металлические конструкции — Скачать 7,3 mb
Изложены основы проектирования и расчета металлических конструкций (стальных и алюминиевых), применяемых в промышленном и гражданском строительстве. Учебник для вузов. Изд. 3-е, испр. и доп. M. Стройиздат, 1978. 572 с. |
|
| Файбишенко В.К. Металлические конструкции — Скачать 5,1 mb
Методическими особенностями настоящего издания являются сжатая, концентрированная форма изложения материала, сопровождаемая большим количеством иллюстраций, что в значительной мере облегчает его усвоение с учетом требований преподавания инженерных дисциплин для архитектурных специальностей. Год издания — 1984. |