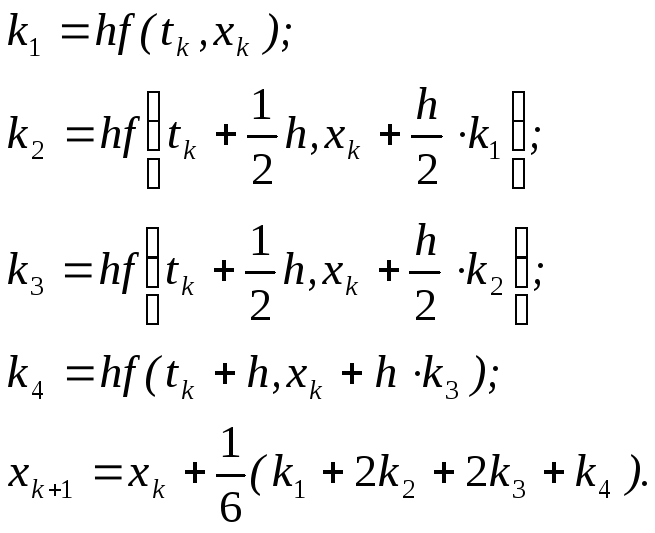Оглавление 1-й книги
| Предисловие | |||
| Основные обозначения | |||
| Введение | |||
| Глава I.Дифференциальные уравнения первого порядка | |||
| 1. | Обыкновенные дифференциальные уравнения и их решения | ||
| 2. | О составлении дифференциальных уравнений | ||
| 2.1. | Некоторые задачи математического моделирования | ||
| 2.2. | Обратная задача теории дифференциальных уравнений | ||
| 3. | Уравнения в полных дифференциалах | ||
| 4. | Интегрирующий множитель | ||
| 5. | Уравнения с разделяющимися переменными и приводящиеся к ним | ||
| 6. | Однородные и приводящиеся к ним уравнения | ||
| 7. | Линейные дифференциальные уравнения первого порядка | ||
| 7.1 | Уравнения, приводящиеся к линейным | ||
| 8. | Нелинейные уравнения специального вида (Бернулли, Риккати, Миндинга-Дарбу) | ||
| 9. | Теоремы существования и единственности задачи Коши | ||
| 9.1. | Теорема Пикара | ||
| 9.2. | Продолжение решения | ||
| 10. | Уравнения, не разрешенные относительно производной | ||
| 11. | Особые решения уравнений первого порядка | ||
| 11.1. | Особые решения уравнения, разрешенного относительно производной | ||
| 11.2. | Особые решения уравнения, не разрешенного относительно производной | ||
| 12. | Геометрический подход к исследованию дифференциальных уравнений первого порядка | ||
| 13. | Приближенные методы решения задачи Коши для уравнений первого порядка | ||
| 13.1. | Приближенные аналитические методы | ||
| 13.2. | Численные методы решения | ||
| Глава II. Нелинейные дифференциальные уравнения высших порядков и системы дифференциальных уравнений | |||
| 14. | Виды нелинейных уравнений, интегрируемых в квадратурах | ||
| 14.1. | Обратная задача для уравнений высших порядков | ||
| 14.2. | Уравнения, интегрируемые в квадратурах | ||
| 15. | Уравнения, допускающие понижение порядка | ||
| 16. | Нормальные системы уравнений. Метод исключения | ||
| 17. | Системы симметричного вида. Подбор интегрируемых комбинаций | ||
| Приложение 1 | |||
| Основные типы дифференциальных уравнений первого порядка | |||
| Приложение 2 | |||
| Неопределенный интеграл и его свойства | |||
| Приложение 3 | |||
| Гиперболические функции | |||
| Ответы к задачам | |||
| Список рекомендуемой литературы |
Оглавление 2-й книги
| Глава 3. Линейные дифференциальные уравнения высших порядков | |||
| 18. | Линейно зависимые и линейно независимые функции | ||
| 19. | Структура общего решения линейных уравнений п-то порядка | ||
| 19.1. | Восстановление дифференциальных уравнений по заданным частным решениям | ||
| 20. | Линейные однородные дифференциальные уравнения с постоянными коэффициентами | ||
| 21. | Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами | ||
| 21.1. | Уравнение со специальной правой частью | ||
| 22. | Метод вариаций произвольных постоянных | ||
| 23. | Уравнение Эйлера и приводящиеся к нему | ||
| 24. | Линейные дифференциальные уравнения с переменными коэффициентами общего вида | ||
| 25. | Интегрирование дифференциальных уравнений методом степенных рядов | ||
| 26. | Специальные формы линейных дифференциальных уравнений 2-го порядка | ||
| Глава 4. Граничные задачи для обыкновенных дифференциальных уравнений | |||
| 27. | Граничные задачи для линейных дифференциальных уравнений 2-го порядка | ||
| 28. | Сопряженные уравнения | ||
| 29. | Функция Грина граничной задачи | ||
| 30. | Задача Штурма-Лиувилля | ||
| Глава 5. Понятие о системах линейных дифференциальных уравнений | |||
| 31. | Нормальные системы дифференциальных уравнений | ||
| 32. | Метод Эйлера интегрирования систем линейных однородных уравнений с постоянными коэффициентами | ||
| 33. | Исследование на устойчивость по первому приближению | ||
| 33.1. | Устойчивость по Ляпунову | ||
| 33.2. | Устойчивость по линейному приближению | ||
| 34. | Подходы Ляпунова к исследованию устойчивости | ||
| 34.1. | Метод линеаризации Ляпунова | ||
| 34.2. | Исследование на устойчивость с помощью функции Ляпунова | ||
| Глава 6. Уравнения в частных производных первого порядка | |||
| 35. | Уравнения первого порядка от двух независимых переменных | ||
| 35.1. | Восстановление уравнения в частных производных по заданному решению | ||
| 36. | Линейные дифференциальные уравнения. Уравнения характеристик | ||
| 36.1. | Линейные неоднородные уравнения | ||
| 37. | Квазилинейные дифференциальные уравнения | ||
| 37.1. | Задача Коши для квазилинейных уравнений | ||
| Глава 7. Основы математического моделирования | |||
| 38. | Методика математического моделирования | ||
| 39. | Фундаментальные законы природы, вариационные принципы, иерархический подход. Элементарные математические модели | ||
| 40. | Форма равновесия канатов висячих мостов | ||
| 41. | Уравнение сплошности (закон сохранения материи) | ||
| 42. | Прямолинейное движение материальной точки | ||
| 43. | Вертикальное падение тяжелых тел | ||
| 43.1. | Свободное падение тела (упрощенная модель) | ||
| 43.2. | Падение тела в среде с сопротивлением (усложненные модели) | ||
| 44. | Поступательное движение тела вдоль прямой | ||
| 45. | Движение тела по криволинейной траектории | ||
| 45.1. | Упрощенная модель | ||
| 45.2. | Усложненные модели, учитывающие сопротивление среды | ||
| 46. | Механика тел переменной массы | ||
| 46.1. | Уравнение Мещерского | ||
| 46.2. | Реактивное движение. Формулы Циолковского | ||
| Ответы к задачам | |||
| Приложение. Единицы физических величин | |||
| Список рекомендуемой литературы |
Предисловие
Примеры учат лучше, чем теория
Исаак Ньютон
Счастлив тот, кто имеет вкус к умственным занятиям
Великий французский философ
Жюльен Офре де Ламетри
Дифференциальные уравнения – один из курсов, составляющих
основу фундаментального математического образования студентов
технических и классических университетов. Его можно
рассматривать как часть математического анализа и весьма важный
раздел математики в части приложения к проблемам естествознания
и техники. В настоящее время трудно представить себе прогресс в
получении качественных и количественных оценок процессов,
протекающих в экономике и социологии, без использования теории
дифференциальных уравнений.
Материал каждого параграфа представляет практическое задание по
одной соответствующей теме, поэтому пособие удобно использовать
как руководство для преподавателя, ведущего занятие, и для
студентов, изучающих курс. Пособие построено как сопровождение к
проведению практических занятий по материалу, изложенному в
учебниках [15-16].
При подборе задач большое внимание обращалось на те из них,
которые можно решать разными методами с целью выработки навыков
предварительного анализа сформулированных задач (примеров) и
выбора наиболее оптимальной стратегии нахождения решения. И,
конечно же, возможности проверки правильности результата.
В цели авторов входило не только желание дать студентам образцы
ре-шения и исследования важнейших классов обыкновенных
дифференциаль-ных уравнений, но и желание приобщить их к
необходимости проведения изначальной классификации видов и типов
уравнений, а также выработки стратегии построения решения. При
составлении пособия были использованы задачники и руководства по
дифференциальным уравнениям А.Ф. Филиппова, В.В. Амелькина, А.К.
Боярчука – Г.П. Головача; А.А. Есипова – Л.И. Сазонова – В.И.
Юдовича; Н.М. Матвеева, М.А. Перестюка – М.Р. Свищука; А.А.
Самарского – А.П. Михайлова; К.К. Пономарева, А.М. Самойленко
– С.А. Кривошеи – М.А. Перестюка; Ю.С. Сикорского и др.
Авторы выражают благодарность А.В. Безусу, Г.В. Ержакову,
А.В. Литвиненко и к. ф.-м. н. Т.А. Васильеву за помощь в
подготовке и оформлении рукописи книги. Кроме того, особая
благодарность доцентам С.Н. Кудряшову и В.Н. Тышлеку за полезные
обсуждения и замечания, высказанные по тексту рукописи и
способствовавшие улучшению изложения материала.
Об авторах
Валерий Анатольевич ШАЛДЫРВАН (род. в 1941 г.)
Доктор физико-математических наук, профессор. В 1964 г. окончил механико-математический факультет
Ростовского государственного университета. Научная карьера началась в январе 1966 г. в отделе
математического моделирования Института прикладной математики и механики АН УССР. С марта 1971 г. – доцент, с мая 1982 г. – профессор кафедры теории упругости и вычислительной математики Донецкого
государственного университета, с 1987 г. – заведующий кафедрой математической физики физического факультета ДонГУ,
а с 2002 г. – профессор этой же кафедры. Автор и соавтор более 150 научных работ (в том числе монографий
«Толстые многосвязные пластины», «Технология решения на ЭВМ пространственных задач теории упругости»),
8 учебных пособий («Методы математической физики», «Дифференциальные уравнения» и др.).
Имеет авторское свидетельство «Листовая рессора», зарегистрировал в фонде алгоритмов и программ АН УССР
два программных комплекса для расчета газотранспортной сети и диспетчерского управления режимом работы сети
высокого давления (Надым, «Газпром»). С 2004 г. – заслуженный профессор Донецкого национального университета.
Кирилл Владимирович МЕДВЕДЕВ (род. в 1983 г.)
Кандидат физико-математических наук, старший
преподаватель кафедры информатики социальных
процессов социологического факультета МГУ им.яМ.В.Ломоносова.
В 2005 г. окончил механико-математический факультет МГУ им.М.В.Ломоносова.
Стипендиат Правительства РФ, участник международных программ РФФИ,
DFG, INTAS, лауреат всероссийских конкурсов учителей физики и математики
в 2008–2011 гг.
2023. 496 с. Твердый переплет. 659 р.
«Русская трагедия» (2002) – последний социологический роман классика русской литературы, всемирно известного писателя Александра Александровича Зиновьева (1922–2006). В книге рассматривается один из самых трагических периодов новейшей отечественной истории, когда «поголовное предательство правящего… (Подробнее)
2023. 160 с. Твердый переплет. 869 р.
Эта книга — трогательная история для взрослых о поиске себя. Большая Панда и Маленький Дракон отправляются в путешествие по временам года. Они часто теряются, как и многие из нас. Но, заблудившись, делают для себя множество прекрасных открытий. (Подробнее)
URSS. 2023. 272 с. Мягкая обложка. 799 р.
В 2001 г. за разработку новой технологии производства посадочного материала методом зеленого черенкования Михаилу Трофимовичу Тарасенко была присуждена Государственная премия Российской Федерации в области науки и техники.
В настоящей книге обобщены результаты полувековых исследований автора… (Подробнее)
URSS. 2023. 312 с. Мягкая обложка. 879 р.
Вниманию читателей предлагается книга одного из наиболее выдающихся экономистов XX века Йозефа Шумпетера, в которую вошли биографические и одновременно теоретико-экономические статьи о жизни и творчестве ученых, ставших классиками экономической науки. Автор обобщает колоссальный объем знаний… (Подробнее)
URSS. 2023. 448 с. Мягкая обложка. 969 р.
Вниманию читателей предлагается книга, в которой собраны наиболее значительные произведения Фридриха Энгельса по военным вопросам. В книге содержатся статьи и извлечения из работ Энгельса, посвященные общетеоретическим проблемам военного дела, оперативно-стратегическим и военно-техническим… (Подробнее)
2023. 672 с. Твердый переплет. 999 р.
Примерно половина населения мира разговаривает на языках, ведущих свое происхождение от общего предка — праиндоевропейского языка. Но кем были носители этого древнего наречия и как им удалось расселиться по земному шару? До недавнего времени их идентичность оставалась загадкой для лингвистов и археологов…. (Подробнее)
2023. 476 с. Интегральный переплет. 539 р.
Книга выпущена в рамках издательской программы Института системно-стратегических исследований (рук. А.И. Фурсов). 2022 год во всех смыслах стал переломным. Военная фаза длительного украинского конфликта стала продолжением деструкции политического, социально-экономического и культурного (в самом… (Подробнее)
URSS. 2023. 208 с. Мягкая обложка. 539 р.
Вниманию читателей предлагается книга советского историка и публициста М.П.Павловича. цель которой — облегчить читателям изучение некоторых вопросов, затронутых В.И.Лениным в работах, статьях или речах, посвященных этим вопросам. С этой точки зрения рассматриваются ленинская критика воззрений… (Подробнее)
URSS. 2023. 512 с. Мягкая обложка. 1139 р.
Широкое внедрение алгебраических методов в теоретическую физику не является новостью. Калибровочные поля и их интерпретация на языке расслоенных пространств, суперсимметричные расширения полевых теорий, возникновение теорий Великого объединения, струнных моделей, квантовой петлевой гравитации —… (Подробнее)
2023. 1896 с. Твердый переплет. 3499 р.
Стивен Коткин, всемирно известный историк, профессор Принстонского университета (США), предпринял успешную попытку написать тотальную историю сталинского режима и его воздействия на Евразию и остальной мир. В первом томе — «Парадоксы власти» — изучается история жизни и деятельности Сталина от рождения… (Подробнее)
Методические рекомендации Решение обыкновенных дифференциальных уравнений.
Задача
Коши.
Пусть
дано обыкновенное дифференциальное
уравнение первого порядка, разрешенное
относительно производной функции
:
при
начальном условии
.
Численно
решить уравнение – это значит в некоторых
точках (t1,
t2,
… , tN)
найти приближения x1,
x2,
. . . , xN
для значений точного решения x(t1),
x(t2),
. . . , x(tN).
Метод
Эйлера
Метод
Эйлера – простейший метод численного
интегрирования обыкновенных
дифференциальных уравнений. Получается
путем замены производной функции ее
численной аппроксимацией:
.
Приближённые
значения определяются по формуле:
.
Погрешность
метода Rk
имеет
порядок h2.
Метод
Рунге-Кутты IV
порядка
Порядок
точность можно повысить за счет усложнения
расчетной схемы. В частности во всех
расчетных методах Рунге – Кутты точность
повышается за счет включения в расчетную
схему ряда значений функции правой
части дифференциального уравнения в
промежуточных точках расчетного шага
.
Для
метода Рунге – Кутты четвёртого порядка
получаются следующие расчетные формулы:
При
вычислениях по приведённым формулам
сначала последовательно находятся k1,
k2,
k3,
k4,
а затем определяется xk+1.
Формулы
Рунге – Кутты m-го
порядка (m> 2) имеют
погрешность порядкаhm+1.
Явный
многошаговый метод Адамса
В
методах Рунге-Кутта значение зависело
только от информации в предыдущей
точке.
Кажется вполне очевидным, что можно
добиться большей точности, если
использовать информацию о нескольких
предыдущих точках. Именно так работают
многошаговые методы.
Большой
и важный класс многошаговых методов
возникает на основе следующего подхода.
Если подставить в исходное дифференциальное
уравнение точное решение и проинтегрировать это уравнение на
отрезке,
то получится следующий результат:
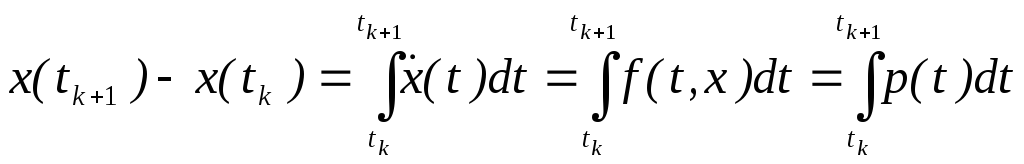
где
в последнем члене предполагаем,
что p(t)-полином,
аппроксимирующийf(x,t).
Чтобы построить этот полином, предположим,
чтоxk , xk-1 ,
… , xk-n – приближения к решению в точкахtk , tk-1 ,
… , tk-n.Gо-прежнему считаем, что
узлы расположены равномерно с шагомh.
Тогда(i
= k, k-1, …, k-n) есть
приближения к
в
точкахtk , tk-1 ,
… , tk-n,
и мы в качестве полиномаpвозьмём
полином для набора данных(i = k, k-1, …, k-n) .
Таким образом,p-полином
степениn,
удовлетворяющий условиям,
(i = k, k-1, …, k-n) .
В принципе, можно проинтегрировать этот
полином явно, что ведёт к следующему
методу:

В
простейшем случае, когда n=0,
полиномpесть константа,
равнаяfk,
и мы получаем обычный метод Эйлера.
Еслиn=1,
тоpесть линейная функция, и
интегрируя этот полином на,
получаем следующий метод:
, (1)
который
является двухшаговым, поскольку
использует информацию в двух
точках tk , tk-1.
Аналогично, еслиn=2,
тоpесть квадратичный полином,
а соответствующий метод имеет вид:
. (2)
Если n=3,
то интерполяционный полином является
кубическим, а соответствующий метод
определяется формулой:
(3)
Отметим,
что метод (2) является трёхшаговым, а (3)
-четырёхшаговым. Формулы (1)-(3) известны
как явные методы Адамса (Адамса-
Башфорта) , т.к. они для нахождения xk+1 не
требуют решения никаких уравнений.
Метод (1) имеет второй порядок точности,
поэтому его называют методом второго
порядка. Аналогично, методы (2) и (3)
называют соответственно методами
Адамса- Башфорта третьего и четвёртого
порядков.
Правило
Рунге
Правило
Рунге — правило оценки погрешности численных
методов, было предложено К. Рунге в
начале 20 века.
Основная
идея (для методов Рунге-Кутты решения обыкновенных
дифференциальных уравнений) состоит в
вычислении приближения выбранным
методом с шагом h, а затем с шагомh/2, и дальнейшем рассмотрении
разностей погрешностей для этих двух
вычислений.
Для
оценки погрешности численного
решений обыкновенных дифференциальных
уравнений на регулярных сетках
требуется решить задачу на 2 сетках,
один раз с шагом h()
и второй — с шагомh/2().
Формула:
дает
погрешность решения .
Подпонимается
порядок точности использованного
численного метода. Например, для
численного метода, имеющего четвёртый
порядок точности (метод Рунге-КуттыIV), формула принимает вид:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Код товара: 3368405
Наличие:
товар закончился
Цена интернет-магазина:
Настоящее пособие посвящено методам решения и качественного исследования задач курса «Обыкновенные дифференциальные уравнения». Цель книги — помочь студентам-прикладникам в формировании их математического мышления, в выработке практических навыков решения и исследования дифференциальных уравнений, описывающих эволюционные процессы в различных областях знаний.
Цена в интернет-магазине может отличаться от цены в магазинах сети.
- Вид товара:Книги
- Рубрика:Математический анализ. Функциональный, комбинаторный анализ. Теория графов
- Целевое назначение:Учебники и учеб. пособ.д/ высшей школы(ВУЗы)
- ISBN:978-5-397-06506-1
- Серия:Несерийное издание
- Издательство:
КД Либроком - Год издания:2019
- Количество страниц:242
- Формат:60х90/16
- Штрихкод:9785397065061
- Переплет:мягкая обложка
- Сведения об ответственности:В. А. Шалдырван, К. В. Медведев
- Код товара:3368405