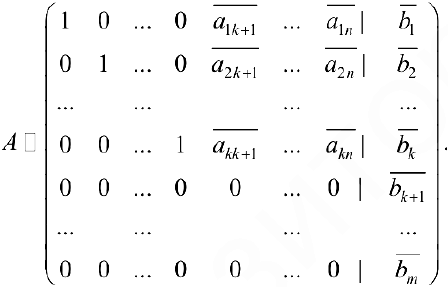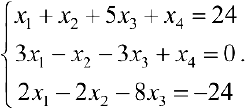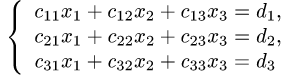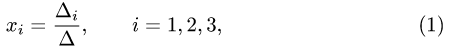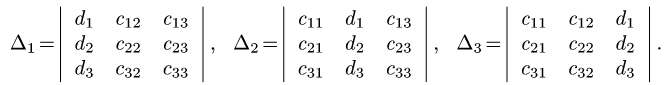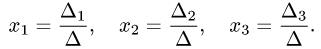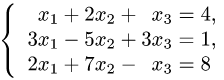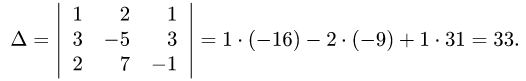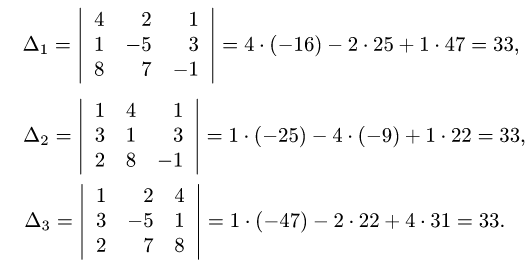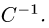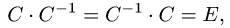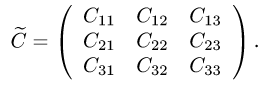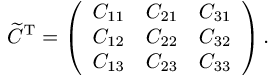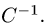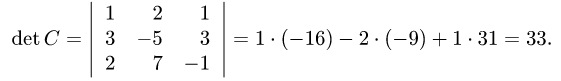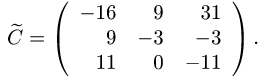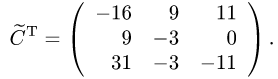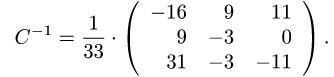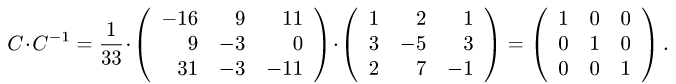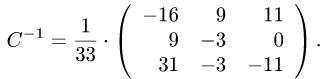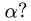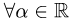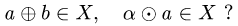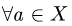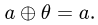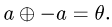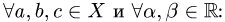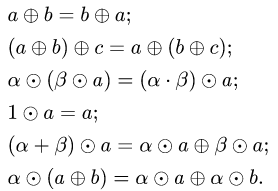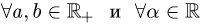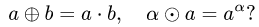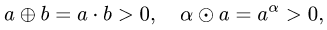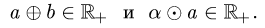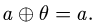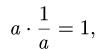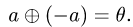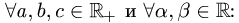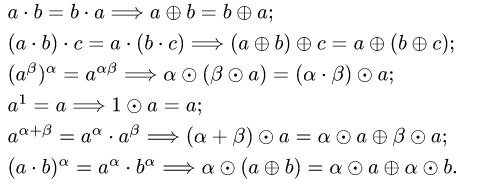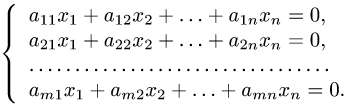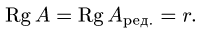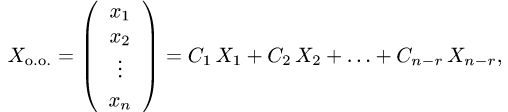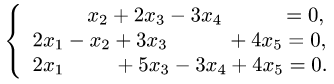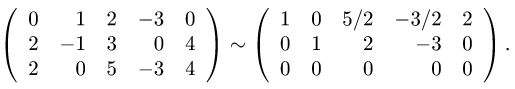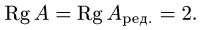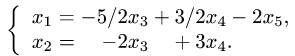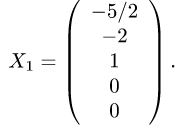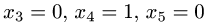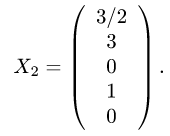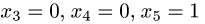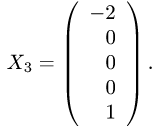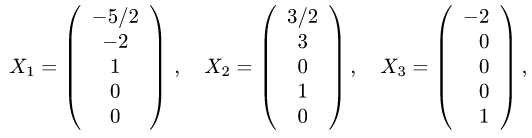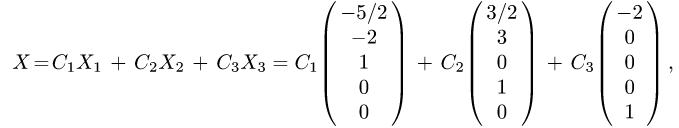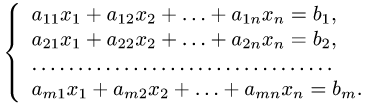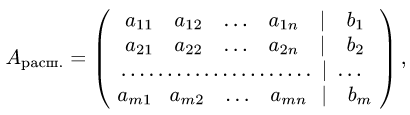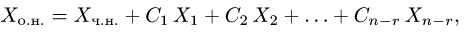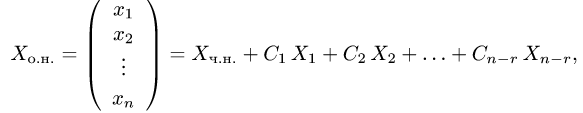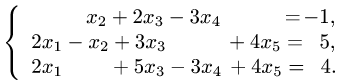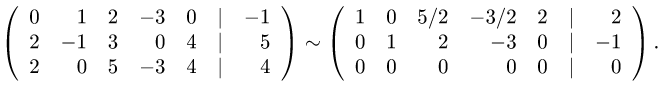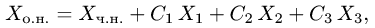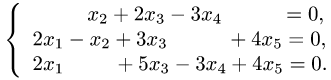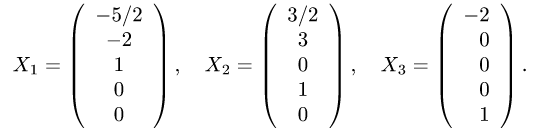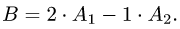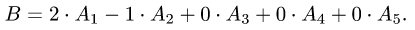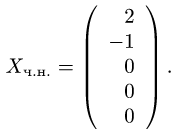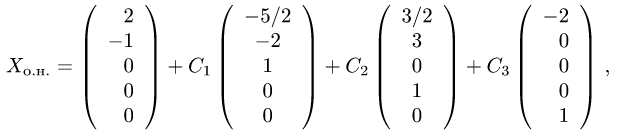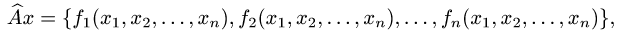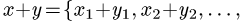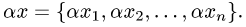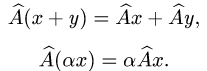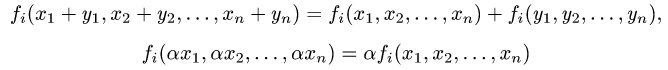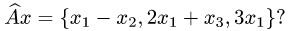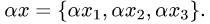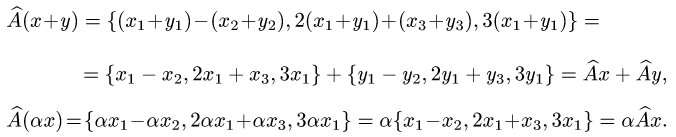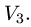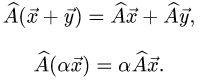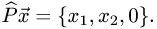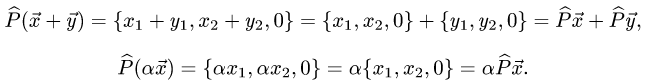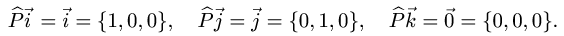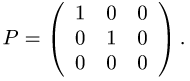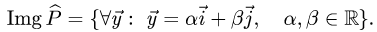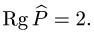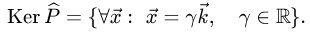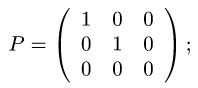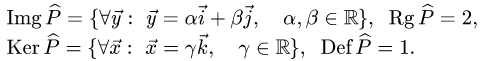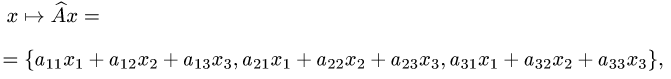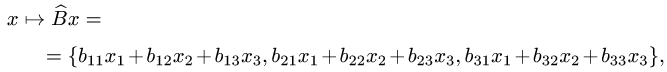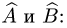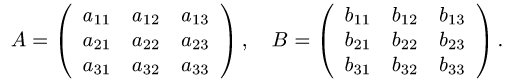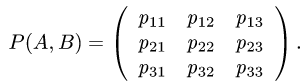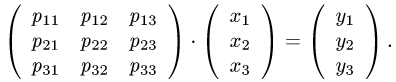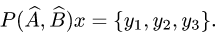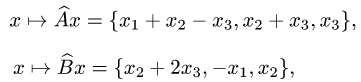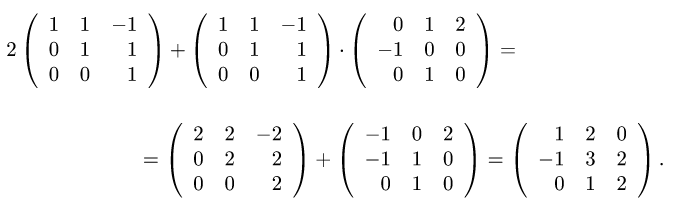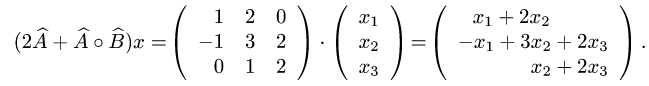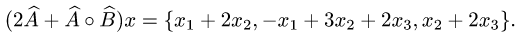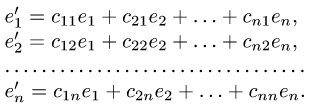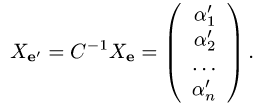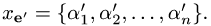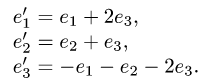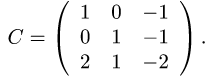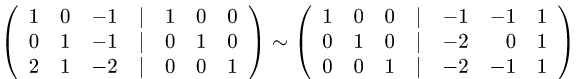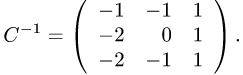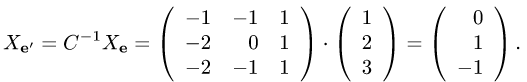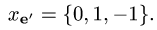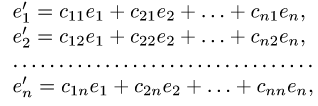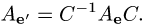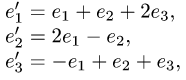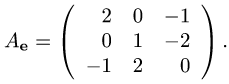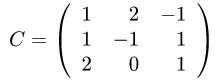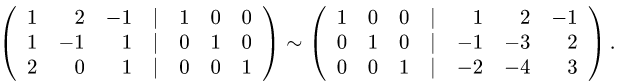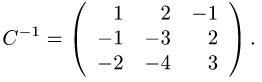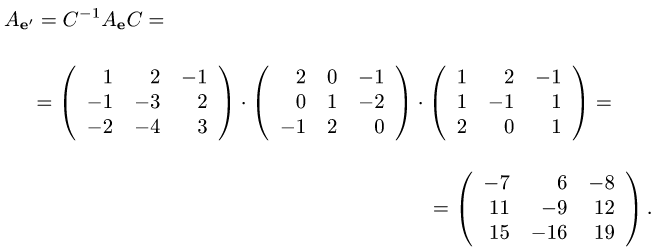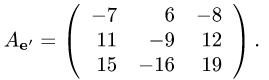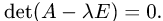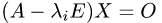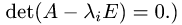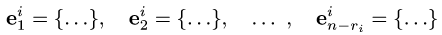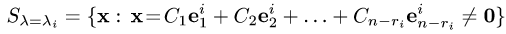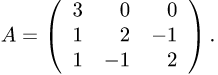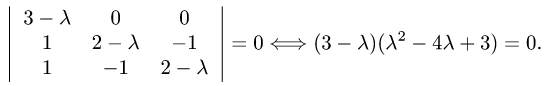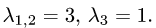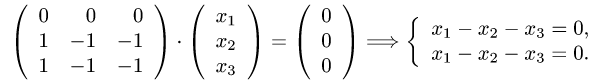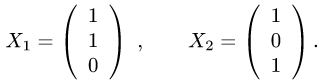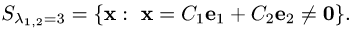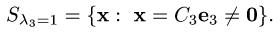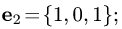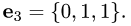Прежде чем изучать готовые решения задач, нужно знать теорию, поэтому для вас я подготовила очень краткую теорию по предмету «линейная алгебра», после которого, чуть ниже размещены подробные решения задач.
Эта страница подготовлена для школьников и студентов любых специальностей и охватывает полный курс предмета «линейная алгебра».
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейная алгебра
Линейная алгебра — это раздел математики, касающийся линейных уравнений. Линейная алгебра занимает центральное место почти во всех областях математики. Например, линейная алгебра является фундаментальной в современных представлениях геометрии, в том числе для определения основных объектов, таких как линии, плоскости и вращения.
Кроме того, функциональный анализ, раздел математического анализа, можно рассматривать как в основном применение линейной алгебры к пространствам функций.
Линейная алгебра также используется в большинстве наук и областей техники , поскольку она позволяет моделировать многие природные явления и эффективно проводить вычисления с такими моделями. Для нелинейных систем, которые не могут быть смоделированы с линейной алгеброй, он часто используются для борьбы с аппроксимациями первого порядка, используя тот факт, что дифференциал из многомерной функции в точке является линейным отображением , что лучше аппроксимирует функцию вблизи этой точки.
Матрицы
Прямоугольная таблица из чисел вида
состоящая из 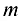
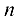
Матрица 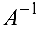
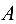
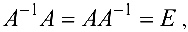
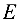
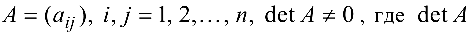
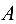
где 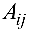
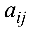
Задача №4.1.
Найти матрицу 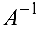
Так как 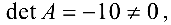
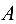
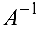
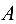
Следовательно,
Возможно эта страница вам будет полезна:
Системы линейных уравнений. Матричный метод. Правило Крамера. Метод Гаусса
Пусть задана система 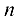
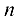
или, в матричной форме
где
Рассмотрим некоторые методы решения системы (4.1).
Формулы Крамера. Если система (4.1) невырождена, то она имеет единственное решение, определяемое формулами Крамера:
где 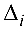

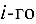
Матричный метод
Решение невырожденной системы (4.1) можно найти по формуле
Метод последовательного исключения неизвестных (метод Гаусса).
С помощью элементарных преобразований над строками система 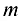
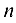
где
Система (4.2) эквивалентна исходной системе. Если хотя бы одно из чисел 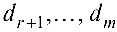
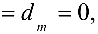
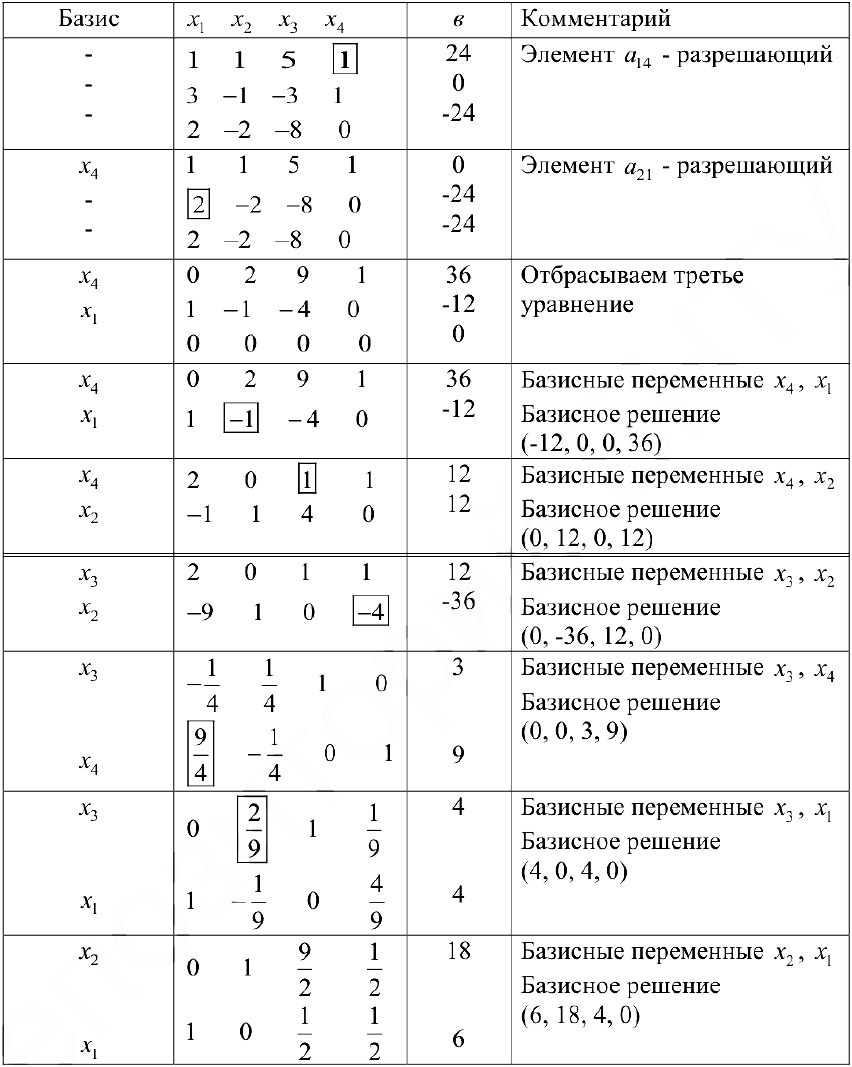
Задача №4.2.
Методом Гаусса решить систему
Решение:
Расширенная матрица системы имеет вид
Производя элементарные преобразования над строками расширенной матрицы, получаем
где цифрами [1] , [2] , [3] обозначены следующие операции:
[1] — первую и вторую строки поменяли местами; [2] — ко второй строке прибавили первую, умноженную на (-2): к третьей прибавили первую, умноженную на (-3); [3] — к третьей строке прибавили вторую, умноженную на (-1).
Этой матрице соответствует система
Отсюда последовательно находим
Ответ:
Задача №4.3.
Решить систему уравнений
используя формулы Крамера.
Решение:
Так как определитель данной системы
то матрица 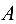
По формулам Крамера находим решение системы:
Возможно эта страница вам будет полезна:
Скалярное произведение векторов в R3
Скалярным произведением векторов 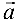
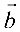
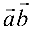
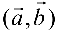
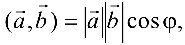
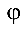
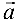
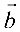
Свойства скалярного произведения:
Свойство 4 выражает условие ортогональности векторов.
Если векторы 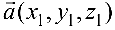
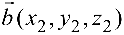
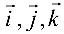
Из этой формулы и определения скалярного произведения следует:
Учитывая, что 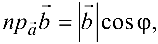
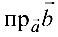
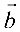
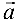
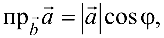
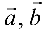
Задача №4.4.
Даны векторы
Найти 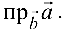
Решение:
Поскольку
а векторы 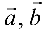
Поэтому
Механический смысл скалярного произведения: работал 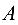
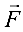
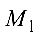
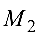
Возможно эта страница вам будет полезна:
Векторное произведение векторов
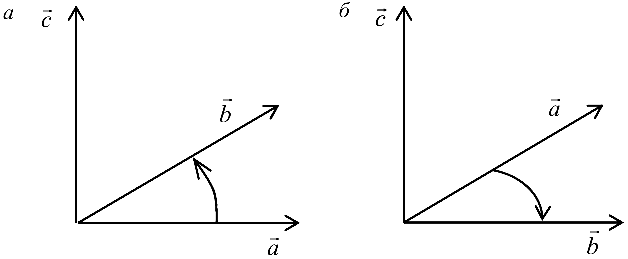
Упорядоченная тройка некомпланарных векторов 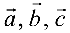
Рис. 4.1: а — тройка 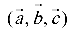
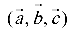
Векторным произведением вектора 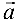
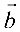
1) 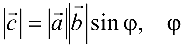
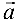
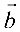
2)
3) Упорядоченная тройка 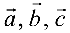
Обозначение:
Свойства векторного произведения
4) 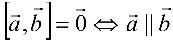
Если векторы 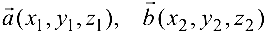
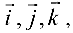
Площадь параллелограмма, построенного на векторах 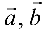
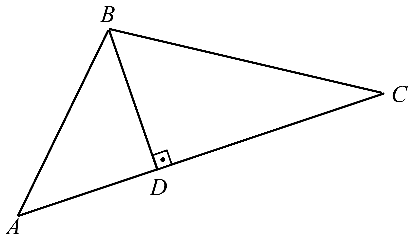
Задача №4.5.
Найти площадь и длину высоты 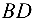
Решение:
Поскольку площадь 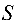
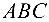
- Находим координаты векторов
и длину
вектора
2. Находим 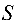
3.
Механический смысл векторного произведения. Пусть точка 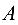
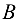
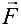
Тогда возникает вращательный момент 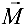
Возможно эта страница вам будет полезна:
Смешанное произведение векторов
Смешанным произведением трех векторов 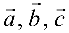
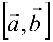
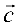
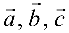
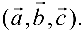
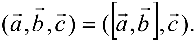
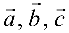
Объем параллелепипеда 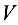
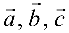
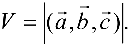
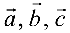
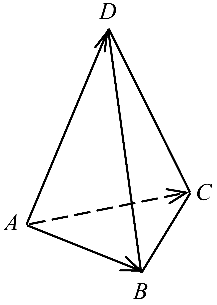
Задача №4.6.
Вычислить объем треугольной пирамиды с вершинами
Решение:
Рассмотрим три вектора
(рис. 4.3).
Можно показать, что объем пирамиды 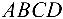
Тогда 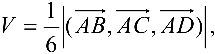
Возможно эта страница вам будет полезна:
Прямая на плоскости
1. Прямая на плоскости
В декартовой прямоугольной системе координат 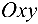
- общее уравнение прямой
(4.3)
- параметрические уравнения прямой
- уравнение прямой в отрезках
Здесь 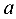
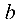
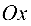
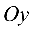
Расстояние 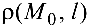
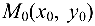
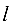
Две прямые, заданные уравнениями 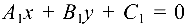
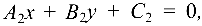
и перпендикулярны, если
Задача №4.7.
Составить уравнение прямой на плоскости, проходящей через точку 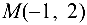
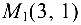
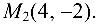
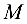
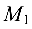
Решение:
Уравнение прямой запишем в виде:
где 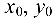
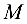
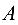
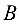
Так как 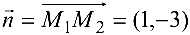
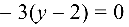
Для нахождения расстояния от точки 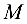
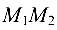
или
Подставляя в формулу (4.4) координаты 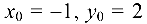
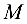
получаем
2. Плоскость
Плоскость в прямоугольной системе координат может быть задана уравнениями:
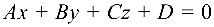
Если в уравнении (4.5) отсутствует свободный член 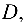
Если в уравнении (4.5) отсутствует одна из переменных, то плоскость параллельна той оси, название которой не входит в это уравнение.
уравнение плоскости, проходящей через точку 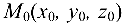
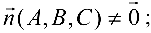
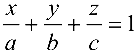
где 
- уравнение плоскости, проходящей через три данные точки
Величина угла 
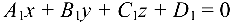
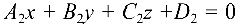
Условие перпендикулярности данных плоскостей запишется в виде
Условие параллельности рассматриваемых плоскостей имеет вид
Расстояние 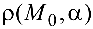
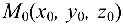
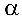
Задача №4.8.
Составить уравнение плоскости, проходящей через точки 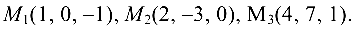
Решение:
Воспользуемся формулой (4.6):
Раскрыв определитель, получаем искомое уравнение плоскости:
Линии второго порядка
Линией второго порядка называется множество точек плоскости, координаты 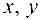
Уравнение (4.7) называется общим уравнением линии второго порядка (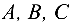
При помощи преобразования прямоугольной системы координат (параллельного переноса и поворота) всегда можно найти такую новую прямоугольную систему координат, в которой уравнение (4.7) имеет один из следующих трех видов (каноническое уравнение):
где 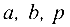
При этом линия, приводимая к виду (4.8), (4.9), (4.10), называется соответственно эллипсом, гиперболой или параболой.
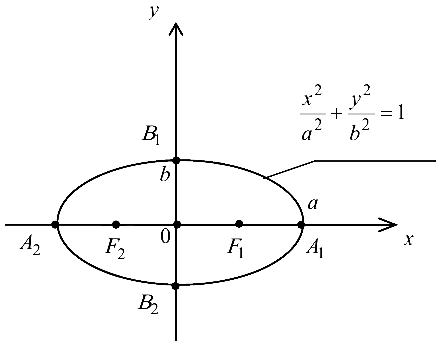
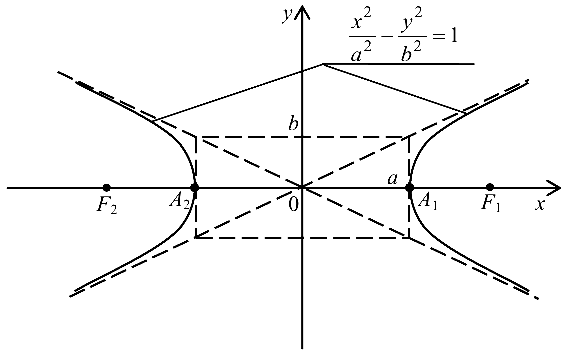
Эллипс с каноническим уравнением
имеет форму, изображенную на рис. 4.4.
Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках 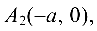
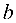
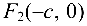
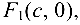
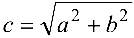
Парабола с каноническим уравнением 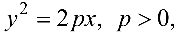
Число 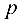
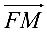
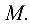
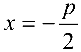
Задача №4.9.
Упростить уравнение 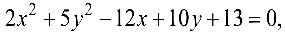
Решение:
Выделим полные квадраты по переменным 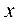
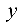
Обозначая 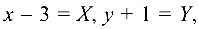
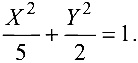
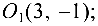
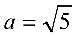
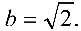
Поверхности второго порядка
Поверхностью второго порядка называется множество точек пространства, координаты 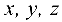
Уравнение (4.11) называется общим уравнением поверхности второго порядка (коэффициенты 
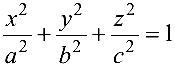
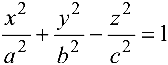
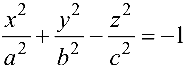
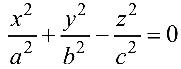
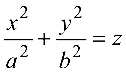
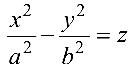
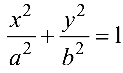
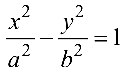
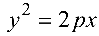
В уравнениях (4.12)-(4.20) 
Задача №4.10.
Построить тело, ограниченное поверхностями
Решение:
Тело ограничено снизу поверхностью параболоида: 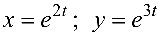
Тело изображено на рис. 4.8.
Задача №4.11.
Построить тело, ограниченное поверхностями.
Решение:
Поверхность 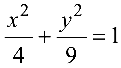
Он пересечен плоскостями 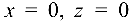
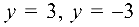
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Дополнительный материал по линейной алгебре
Линейная алгебра — это раздел математики, касающийся линейных уравнений. Линейная алгебра занимает центральное место почти во всех областях математики. Например, линейная алгебра является фундаментальной в современных представлениях геометрии, в том числе для определения основных объектов, таких как линии, плоскости и вращения.
Кроме того, функциональный анализ, раздел математического анализа, можно рассматривать как в основном применение линейной алгебры к пространствам функций.
Линейная алгебра также используется в большинстве наук и областей техники , поскольку она позволяет моделировать многие природные явления и эффективно проводить вычисления с такими моделями. Для нелинейных систем, которые не могут быть смоделированы с линейной алгеброй, он часто используются для борьбы с аппроксимациями первого порядка, используя тот факт, что дифференциал из многомерной функции в точке является линейным отображением , что лучше аппроксимирует функцию вблизи этой точки.
Матрицы. Операции над матрицами
Определение 1. Матрицей размерности 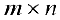
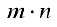
Если 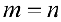
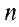
Замечание. Первый индекс в обозначении элемента — номер строки, второй — номер столбца.
Определение 2. Пусть 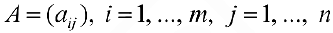
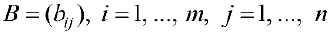
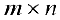
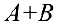
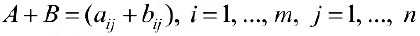
Произведением матрицы 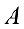
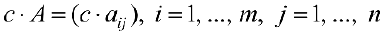
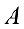
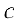
Пример задачи №1.
Найти
Решение:
Определение 3. Пусть 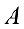
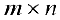
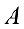
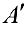
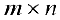
Пример задачи №2.
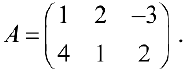
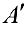
Решение:
Свойства операций сложения матриц и умножения матрицы на число
Для любых матриц 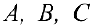
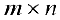
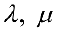
— коммутативность сложения.
2. 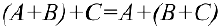
3. Существование нулевого элемента 0, обладающего свойством: 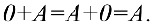
4. Существование противоположного элемента: 
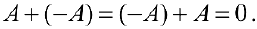
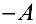
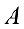
Определение 4. Пусть 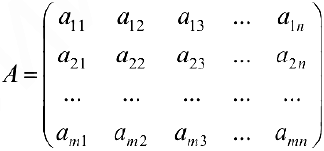
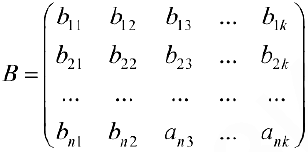
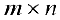
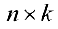
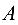
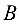
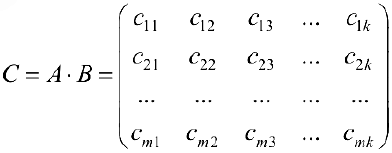
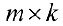
элементы которой находятся по формуле
Пример задачи №3.
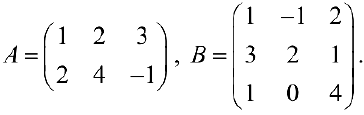
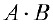
Решение:
По формуле (3):
Замечание. 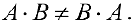
Определители матриц
Определение 5. Пусть 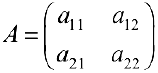
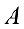
Пусть 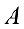
Определителем (детерминантом) матрицы 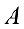
Пример задачи №4.
Свойства определителей
- Если какую-либо строку (столбец) матрицы
умножить на число
то и определитель умножится на число
то есть определитель полученной матрицы
будет равен:
- Если переставить местами любые две строки (столбца) матрицы, то определитель поменяет знак, то есть определитель полученной матрицы
будет равен:
- Если к какой-нибудь строке (столбцу) матрицы А прибавить любую другую строку (столбец) матрицы
умноженной на любое число
то определитель не изменится, то есть определитель полученной матрицы
будет равен:
- Определитель единичной матрицы
равен 1. (единичная матрица — это матрица, у которой на главной диагонали стоят 1, а все остальные элементы равны 0).
- Определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
Замечание. Из свойств 1-5 следуют другие полезные свойства.
Следствие 1. Если строка (столбец) матрицы равны 0, то ее определитель равен 0.
Следствие 2. Если у матрицы две одинаковые строки (столбца), то ее определитель равен 0.
Пример задачи №5.
Найдем определитель из примера 4, предварительно преобразовав матрицу
- Ко второй строке матрицы прибавим первую, и к третьей строке матрицы прибавим первую, умноженную на -2, получим:
2. Переставим местами вторую и третью строки, затем к третьей прибавим вторую, умноженную на -5, получим:
Определение 6. Пусть 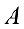
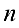
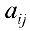
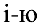
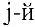
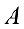
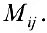
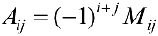
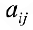
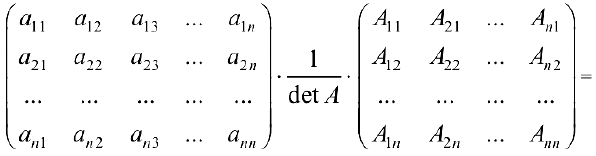
Теорема 1. Пусть 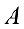
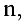
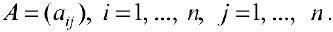
Формула (6) называется формулой разложения определителя по элементам 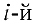
Замечание. Аналогичная формула верна для любого столбца.
Формула (6) сводит вычисления определителя 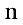
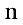
Пример задачи №6.
Вычислим определитель из примера 4. разложенного по элементам первой строки.
Разложим определитель по элементам 2-ого столбца.
Методы вычисления определителя n — ого порядка
- Разложение по элементам строки (столбца).
В этом случае используют теорему 1 и сводят вычисление определителя порядкак вычислению определителя порядка
(см. пример 6).
- Приведение определителя к треугольному виду.
С помощью свойств определителя приводят матрицу к треугольному виду. Определитель полученной матрицы равен произведению элементов, стоящих на диагонали (следует из теоремы 1).
Пример задачи №7.
Вычислить определитель порядка 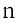
- Прибавим к 1-ой строке все остальные строки, получим:
2. Вычтем 1 -ую строку из всех остальных строк, получим:
Упражнение 1.1. Найти матрицу 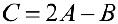
Упражнение 1.2. Даны следующие матрицы:
Обратная матрица
Определение 1. Пусть 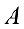

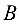
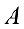
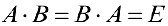
где 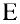
При этом матрица 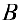
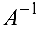
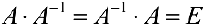
Теорема 1. Если обратная матрица существует. То она единственна.
Доказательство. От противного. Предположим, что для матрицы 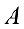
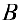
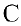
Тогда рассмотрим равенства
Так как левые части равенств равны, то равны и правые, то есть 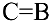
Теорема 2. Для матрицы 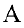
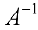
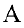
Доказательство.
- Необходимость. Докажем, что если для матрицы
существует обратная матрица
, то
. По свойству (2):
. Тогда
поэтому
, ч.т.д.
- Достаточность. Пусть определитель
не равен 0. Докажем, что для матрицы
существует обратная.
Рассмотрим матрицу из алгебраических дополнений к элементам матрицы, составленную так, что алгебраические дополнения к строкам пишутся в соответствующие столбцы:
Непосредственно проверяем, что для этой матрицы выполняется равенство (2):
Действительно, по формуле (3) элемент 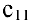
элемент 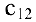
и т.д. Теорема доказана.
Пример задачи №8.
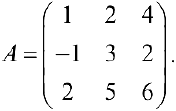
Решение:
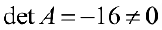
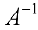
Тогда по формуле (3):
Определение 2. Система уравнений вида
называется системой 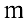
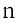
Матрица 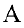
называется матрицей системы, столбец 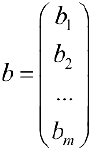
Совокупность чисел 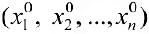
Если система (4) имеет хотя бы одно решение, она называется совместной, в противном случае — несовместной.
Теорема 3. Рассмотрим систему 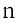
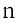
где 
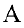
Доказательство. Умножим обе части равенства (6) на 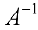
поэтому 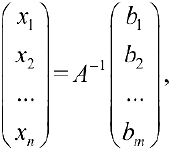
Замечание. Решение системы по формуле (7) называется матричным методом решения системы. Из формул (7) и (3) следует:
тогда
где через 
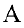
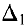
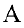
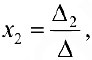
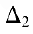
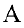
Полученные формулы называются формулами Крамера.
Пример задачи №9.
Решить систему уравнений
1) матричным способом; 2) по формулам Крамера.
Решение:
1) Матричный способ. Перепишем систему в матричном виде:
(см. пример 4), поэтому обратная матрица существует и решение системы единственно.
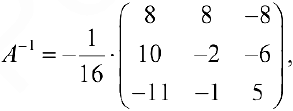
то есть
2) Формулы Крамера.
Замечание. Если рассмотреть матричное уравнение 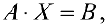
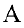
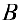
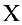
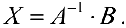
Аналогично, для матричного уравнения
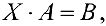
получим формулу:
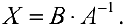
Пример задачи №10.
Решить матричное уравнение
Решение:
(см. пример 1), тогда по формуле (9):
Упражнение 2.1. Найдите обратные матрицы для заданных матриц:
Упражнение 2.2. Выяснить при каких значениях 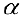
Ранг матрицы
Определение 1. Пусть 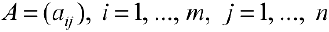
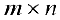
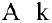
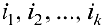
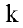
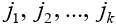
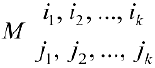
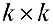
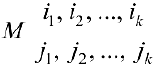
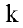
Пример задачи №11.
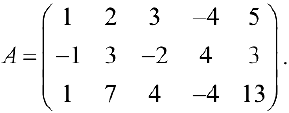
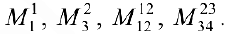
Решение:
Определение 2. Рангом матрицы называется наибольший из порядков миноров, отличных от нуля. Ранг будем обозначать через 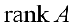
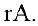
Замечание. Не обязательно перебирать все миноры матрицы, чтобы найти ее ранг.
Оказывается, для этого достаточно рассматривать вложенные друг в друга миноры. На этом основывается, так называемый, метод окаймляющих миноров.
Для нахождения ранга матрицы проводят настолько долго, насколько это возможно следующие операции.
- Рассматривают миноры 1-ого порядка. Если все они равны 0, то
и конец алгоритма.
Если хотя бы одни из них не равен 0, тои переходят на п.2.
- Рассматривают все миноры 2-ого порядка, окаймляющие фиксированный ненулевой минор 1-ого порядка. Если все они равны 0, то
и конец алгоритма.
Если хотя бы один из них не равен 0, тои переходят па рассмотрение миноров 3-ого порядка, окаймляющих фиксированный ненулевой минор 2-ого порядка, и т.д., пока есть что окаймлять.
Пример задачи №12.
Найти ранг 
поэтому
. Рассмотрим минор
, окаймляющий
.
поэтому
- Минор
окаймляют два минора третьего порядка
и
.
поэтому 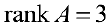
Определение 3. Элементарными преобразованиями матрицы называются:
1) перестановка любых 2-х строк (столбцов) матрицы;
2) умножение любой строки (столбца) матрицы на отличное от нуля число;
3) прибавление к любой строке (столбцу) матрицы любой другой строки (столбца) матрицы, умноженных на произвольное число.
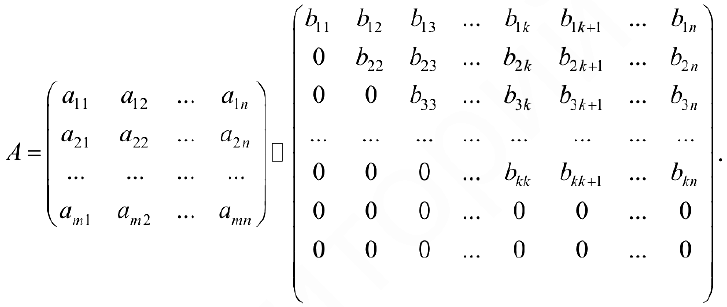
Теорема 1. Элементарные преобразования матрицы не изменяют ее ранга. С помощью элементарных преобразований любую матрицу 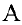
Где все строки, начиная с 
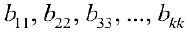
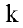
Пример задачи №13.
С помощью элементарных преобразований найти ранг матрицы 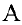
Решение:
1- й шаг. Меняем местами 1-й и 4-й столбцы.
2- й шаг. Ко второй, третьей и четвертой строкам прибавляем первую, умноженную соответственно на -4, -2, -6.
3- й шаг. К третьей и четвертой строкам прибавляем вторую, умноженную соответственно на -1,-2.
4- й шаг. Меняем местами 3-й и 4-й столбцы.
5- й шаг. К четвертому столбцу прибавляем третий, умноженный на -1.
В результате получаем матрицу трапециевидного вида из теоремы 1. Тогда 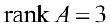
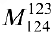
Упражнение 3.1. Найти миноры 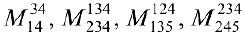
Ответы:
Упражнение 3.2. Найти ранг матрицы методом окаймляющих миноров:
Ответы: а) 3; в) 3; с) 2.
Упражнение 3.3. Найти ранг матрицы с помощью элементарных преобразований:
Ответы: а) 4; в) 4; с) 4; d) 3.
Упражнение 3.4. Найти ранг матрицы в зависимости от значений параметра 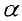
При каких значениях 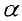
Решение произвольных систем линейных уравнений
Рассмотрим систему 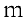
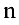
или в матричном виде
где 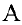
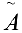
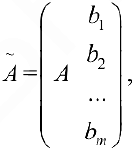
Теорема (Кронекера-Капелли)
Для того, чтобы система уравнений (1) имела решение необходимо и
достаточно, чтобы
Докажем необходимость. Дано: система имеет решение. Докажем, что 
Рассмотрим матрицу 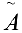
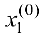

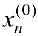
Поэтому
Замечание. Теорема 1 дает конкретный алгоритм решения произвольных систем:
- Находят
Если они не равны, то система не имеет решений.
- Если они равны, рассматриваем базисный минор матрицы
. Все уравнения, нс входящие в базисный минор отбрасывают. Неизвестные в оставшихся уравнениях, не входящие в базисный минор, переносят направо и полученную систему решают по правилам Крамера или матричным методом.
При этомможно находить одновременно методом элементарных преобразований, если последний столбец матрицы
не прибавлять к другим столбцам и не переставлять его с другими.
Пример задачи №14.
Решить систему:
Решение:
Найдем 
1 — й шаг. Переставляем местами 1-й и 2-й столбцы матрицы.
2 — й шаг. Ко второй и третьей строке прибавляем первую, умноженную на -2 и -4 соответственно.
3 — й шаг. От третьей строки отнимаем вторую, 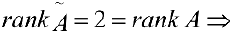
Базисный минор находится в 1, 2 столбце и 1, 2 строке. Отбрасываем 3-е уравнение. Переменные 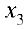
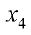
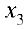
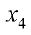
В результате получим систему:
Решим ее по Правилу Крамера:
Таким образом: 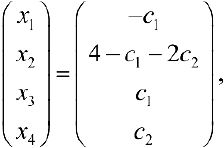
Метод Гаусса
Если при нахождении ранга матриц 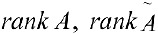
Алгоритм метода Гаусса
- Прямой ход метода Гаусса. Элементарными преобразованиями матрица
приводится к виду:
где 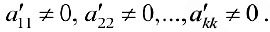
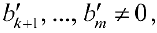
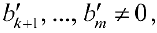
Обратный ход метода Гаусса
Рассмотрим последнее 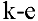
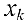
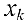
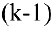
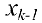
Пример задачи №15.
Решить систему по методу Гаусса.
Решение:
Прямой ход метода Гаусса:
система совместна. Обратный ход метода Гаусса:
Из первого уравнения
Пусть 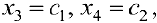
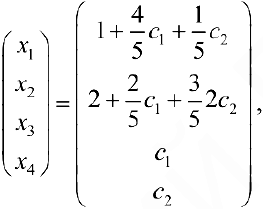
Упражнение 4.1. Исследовать данную систему и в случае совместности решить её.
Ответы:
Линейные векторные пространства
Определение 1. Произвольное множество 
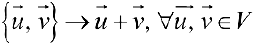
вектора на действительное число 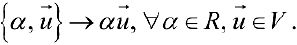
коммутативность сложения векторов.
— ассоциативность сложения векторов.
- Существование нулевого элемента
:
.
- Существование противоположного элемента:
.
.
.
.
.
Пример задачи 1. Множество действительных чисел 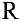
Пример задачи 2. Множество 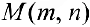
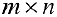
Пример задачи 3. Множество матриц вида:
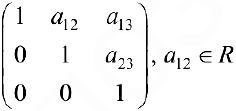
Пример задачи 4. Множество матриц вида
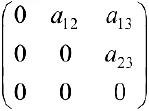
Пример задачи 5. Арифметическое пространство 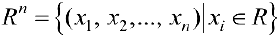
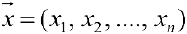
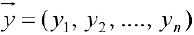
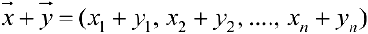
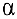
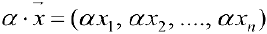
Определение 2. Векторы 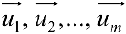
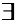
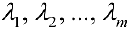
Если же равенство (1) выполняется только при нулевых значениях 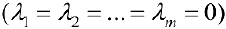
Базисом пространства 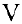
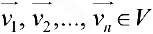
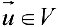
При этом числа 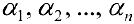
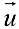
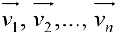
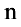
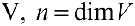
Пример задачи 6. Для линейного пространства 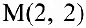
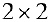
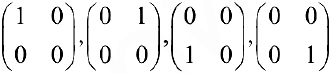
Для линейного пространства 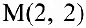
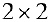
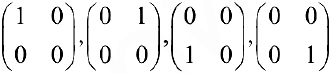
то есть координатами 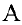
Теорема 1. Координаты вектора в данном базисе определены однозначно.
Доказательство. От противного. Предположим, что 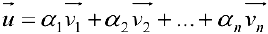
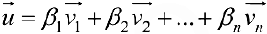
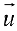
Векторы образующие базис, линейно-независимы, поэтому из (3) следует: 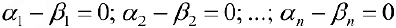
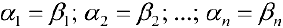
Теорема 2. Система векторов
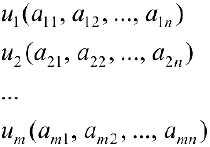
Доказательство. Достаточность. Дано: ранг матрицы равен 
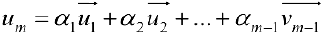
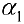
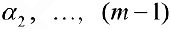
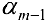
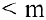
Пример задачи №16.
Даны векторы 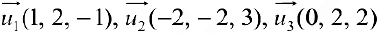
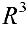
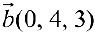
Решение:
Применим теорему 2. Найдем ранг матрицы 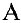
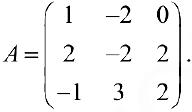
1- й шаг. Ко второй строке прибавляем первую, умноженную третьей строке прибавляем первую.
2- й шаг. Переставляем местами 2-ю и 3-ю строки.
3- й шаг. К третьей строке прибавляем вторую, умноженную на -2. 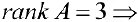
Три линейно-независимых вектора трехмерного пространства образуют базис. Найдем координаты вектора 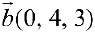
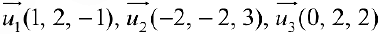
Решая систему, получим 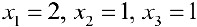
Рассмотрим однородную систему линейных уравнений:
или в матричном виде 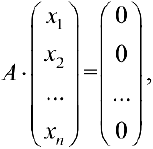
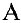
Теорема 3. Система (4) всегда совместна. Множество решений системы (4) образует линейное пространство.
Доказательство. 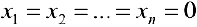
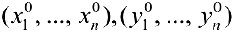
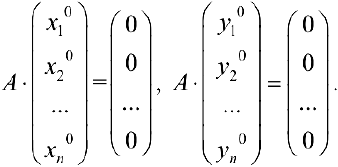
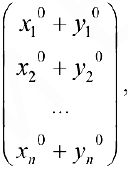
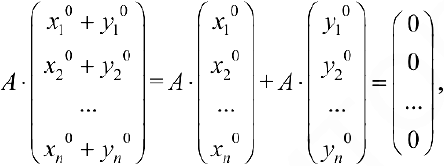
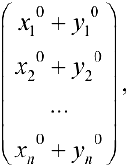
Аналогично доказывается, что
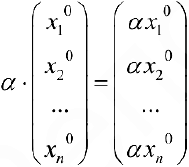
Определение . Базис пространства всех решений системы (4) называется фундаментальной системой решений.
Пример задачи №17.
Найти фундаментальную систему решений:
Решение:
Решим систему по методу Гаусса.
1- й шаг. Ко второй и третьей строкам прибавляем первую умноженную соответственно на -1 и -2.
2- й шаг. К третьей строке прибавляем вторую, умноженную на -1. Вторую строку сокращаем на 2.
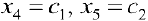
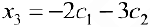
Из второго уравнения 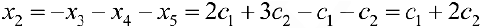
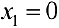
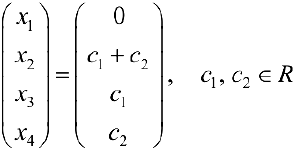
Для того, чтобы получить фундаментальную систему решений, одно из свободных неизвестных приравнивают к 1 остальные берут равными 0.
И так поступают со всеми свободными неизвестными по очереди.
В результате получают векторы фундаментальной системы решений.
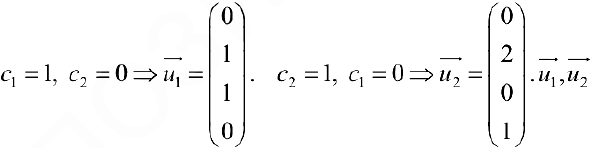
Упражнение 5.1. Даны векторы 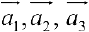
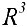
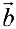
Метод Жордана — Гаусса
Рассмотрим систему уравнений. Решение систем по методу Жордана-Гаусса аналогично решению системы по методу Гаусса. При решении систем проводят элементарные преобразования строк в расширенной матрице системы. При этом, выбрав разрешающий элемент 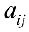
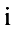
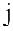
Алгоритм метода Жордана-Гаусса.
- Выписываем расширенную матрицу
системы и в первой строке среди первых
элементов находим ненулевой элемент ( например
). Делим 1-ю строку на
. Проведя элементарные преобразования строк, обнуляем остальные элементы
-ого столбца.
- Во второй строке полученной матрицы находим среди первых
элементов ненулевой элемент
. Проводя элементарные преобразования строк, обнуляем все остальные элементы
— ого столбца и т. д.
Если по ходу алгоритма получаем строки содержащие нули в первых 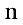
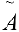
Если хотя бы одно из чисел 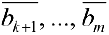
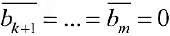
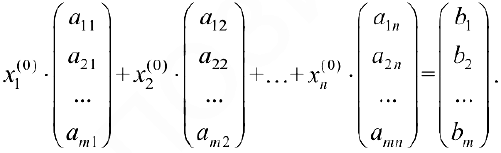
В результате получают частное (базисное решение) 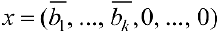
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Пример задачи №18.
Найти все базисные решения системы
Решение:
Линейная алгебра — задания и задачи с примерами решения
При изучении линейной алгебры вы познакомитесь на
примерах с понятиями линейного (векторного) пространства, линейного оператора, его матрицы, образа, ядра, ранга, дефекта, собственных векторов и собственных значений. Вы научитесь выполнять различные операции с операторами и матрицами, исследовать и решать системы линейных уравнений, получать всю информацию об операторе (матрицу, образ, ядро, ранг и дефект, собственные векторы и собственные значения) по его матрице, преобразовывать векторы и матрицы при изменениях базисов.
Правило Крамера
Постановка задачи. Решить систему трех линейных уравнений с тремя неизвестными
по правилу Крамера.
План решения. Если определитель матрицы системы
отличен от нуля, то система имеет решение и притом только одно.
Это решение определяется формулами
где 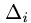
заменой i-ого столбца столбцом свободных членов.
1.Вычисляем определитель матрицы системы
и убеждаемся, что он не равен нулю. Следовательно система уравнений имеет единственное решение.
2.Вычисляем определители
3.По формулам Крамера (1) находим решение системы уравнений
Пример. Решить систему уравнений
по правилу Крамера.
Решение.
1. Вычисляем определитель матрицы системы, разлагая его по
первой строке:
Так как он не равен нулю, то система уравнений имеет единственное
решение.
2.Вычисляем определители
3.По формулам Крамера (1) находим решение системы уравнений
Ответ. 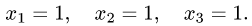
Обратная матрица
Постановка задачи. Задана квадратная матрица третьего
порядка
Установить существование и найти обратную матрицу
План решения. Матрица 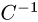
матрице С, если
где Е — единичная матрица.
Если 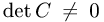
имеет обратную, если det С = 0, то матрица С не имеет обратной.
1.Вычисляем определитель матрицы det С. Если 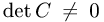
матрица С имеет обратную.
2.Составляем матрицу из алгебраических дополнений
3.Транспонируем матрицу
4.Разделив матрицу 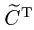
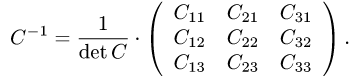
5.Проверяем, что 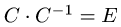
Пример. Задана квадратная матрица третьего порядка
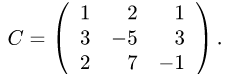
Установить существование и найти обратную матрицу
Решение.
1.Вычисляем определитель матрицы detC:
Так как 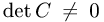
2.Составляем матрицу из алгебраических дополнений
3.Транспонируем матрицу 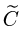
4.Разделив матрицу 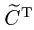
5.Проверяем
Ответ. Матрица, обратная матрице С, есть
Понятие линейного пространства
Постановка задачи. Образует ли линейное пространство заданное множество X, в котором определены «сумма» а 
двух элементов а и b и «произведение» 
любое число
План решения. Исходя из определения линейного пространства,
проверяем следующие условия.
1.Являются ли введенные операции сложения и умножения на
число замкнутыми в X, т.е. верно ли, что 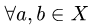
Если нет, то множество X не является линейным пространством, если
да, то продолжаем проверку.
2.Находим нулевой элемент 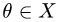
Если такого элемента не существует, то множество X не является
линейным пространством, если существует, то продолжаем проверку.
3.Для каждого элемента 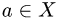
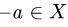
Если такого элемента не существует, то множество X не является
линейным пространством, если существует, то продолжаем проверку.
4.Проверяем выполнение остальных аксиом линейного пространства, т.е.
Если хотя бы одна из аксиом нарушается, то множество X не
является линейным пространством. Если выполнены все аксиомы, то
множество X — линейное пространство.
Пример. Образует ли линейное пространство множество положительных чисел 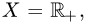
Решение.
1.Введенные таким образом операции являются замкнутыми в
данном множестве, так как если 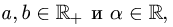
т.е.
2.В качестве нулевого элемента нужно взять единицу 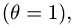
как
а • 1 = а,
иными словами,
3.В качестве элемента —а, противоположного элементу а, нужно
взять 1/а, так как
иными словами,
4.Проверяем выполнение остальных аксиом линейного пространства, т.е.
Все аксиомы выполнены.
Системы линейных уравнений
Задача 1. Однородные системы уравнений
Постановка задачи. Найти размерность d пространства решений, его базис (фундаментальную систему решении) и общее решение однородной системы линейных уравнений
План решения.
1.Записываем матрицу системы:
и с помощью элементарных преобразований строк преобразуем матрицу А так, чтобы в максимальном числе столбцов оказалось по одной единице (в разных строках у разных столбцов), а остальные элементы столбцов были нулями. Очевидно, что такие столбцы линейно независимы. Они называются базисными.
Полученную матрицу будем называть редуцированной и обозначать 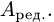
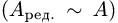
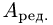
2. Так как 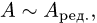
базисных столбцов матрицы 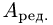
Следовательно, размерность пространства решений есть d = n — r.
Если n = r, то однородная система имеет единственное (нулевое)
решение, если n > r, то фундаментальная система состоит из n — r
линейно независимых решений.
3.Неизвестные, соответствующие базисным столбцам, называются базисными, остальные — свободными (или параметрическими).
Запишем систему уравнений с матрицей 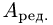
свободных неизвестных в правые части уравнений системы. Придавая свободным неизвестным n — r наборов значений (по одной единице, остальные — нули), для каждого такого набора решаем систему уравнений и находим соответствующие значения базисных
неизвестных. Убедимся, что полученные решения 

Записываем фундаментальную систему решений 
где 

Пример 1. Найти размерность d пространства решений, его базис
(фундаментальную систему решений) и общее решение однородной
системы линейных уравнений
Решение.
1.Записываем матрицу системы и с помощью элементарных преобразований строк преобразуем ее к редуцированному виду:
Очевидно, что первый и второй столбцы матрицы 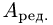
матрицы А) линейно независимы, а остальные столбцы являются их
линейными комбинациями. Поэтому первый и второй столбцы —
базисные.
2.Так как количество линейно независимых столбцов матрицы
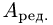
Следовательно, размерность пространства решений
d=n-r=5-2=3
и фундаментальная система решений состоит из трех линейно
независимых решений.
3. Неизвестные 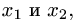
являются базисными, неизвестные 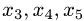
Запишем систему уравнений с матрицей 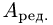
эквивалентна исходной) и перенесем свободные неизвестные в правые части уравнений системы:
Для первого набора свободных неизвестных 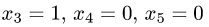
получаем 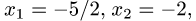
Для второго набора свободных неизвестных
получаем 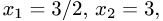
Для третьего набора свободных неизвестных
получаем 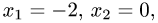
Сделаем проверку, подставив эти решения в исходную систему
уравнений, а также убедимся, что решения линейно независимы (ранг матрицы, составленной из столбцов 
Следовательно, решения 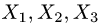
Ответ. Размерность пространства решений есть d = 3. Фундаментальная система решений есть
и общее решение однородной системы имеет вид
где 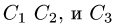
Задача 2. Неоднородные системы уравнений
Постановка задачи. Найти общее решение неоднородной системы линейных уравнений
План решения.
1.Записываем расширенную матрицу системы
и с помощью элементарных преобразований строк преобразуем матрицу 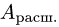
2.Вычисляем ранги основной матрицы системы А и расширенной
матрицы 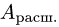
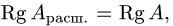
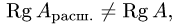
3.Пусть 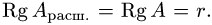
где 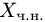
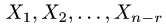

Чтобы найти фундаментальную систему решений однородной сис-
системы уравнений 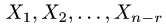
4.Столбец свободных членов В расширенной матрицы есть линейная комбинация базисных столбцов матрицы А. Добавляя к этому выражению остальные столбцы с нулевыми коэффициентами, получаем разложение столбца свободных членов по всем столбцам матрицы А. Коэффициенты этого разложения образуют частное решение неоднородной системы 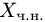
5.Записываем общее решение неоднородной системы линейных
уравнений:
где 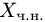
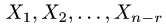

Пример 2. Найти общее решение неоднородной системы линейных уравнений
Решение.
1.Записываем расширенную матрицу системы и с помощью элементарных преобразований строк преобразуем матрицу 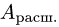
редуцированному виду:
2.Так как 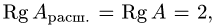
n — r = 5 — 2 = 3, то общее решение неоднородной системы линейных
уравнений определяется формулой
где 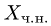
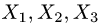
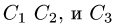
3.Запишем соответствующую однородную систему уравнений
Она совпадает с системой, приведенной в примере 1. (Если однородная система уравнений не совпадает с системой, приведенной в примере 1, то для нахождения фундаментальной системы решений повторим операции, использованные при решении примера 1.)
При решении примера 1 была найдена фундаментальная система
решений однородной системы уравнений:
4.Найдем какое-нибудь частное решение неоднородной системы.
Столбец свободных членов В расширенной матрицы есть линейная
комбинация базисных столбцов матрицы А, т.е. столбцов 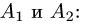
Добавляя к этому выражению остальные столбцы с нулевыми коэффициентами, получим
Коэффициенты в этом разложении образуют частное решение неоднородной системы
Сделаем проверку, подставив 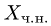
Ответ. Общее решение системы имеет вид
где 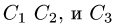
Линейные операторы
Постановка задачи. Пусть в некотором базисе линейного пространства 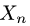
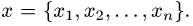
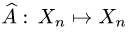
где 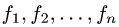
План решения. Если 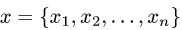
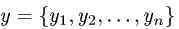
произвольные векторы пространства 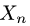
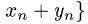
Проверяем условия линейности оператора:
Если условия линейности выполнены, т.е.
при i = 1, 2,…, n, то оператор 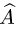
оператор 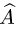
Пример. Пусть в некотором базисе линейного пространства 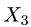
задан произвольный вектор 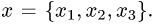
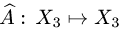
Решение. Пусть 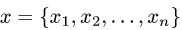
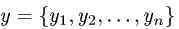
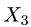
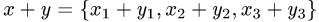
Проверяем условия линейности оператора:
Условия линейности выполнены. Следовательно, оператор 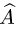
Ответ. Оператор 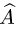
Матрица, образ, ядро, ранг и дефект оператора
Постановка задачи. Задан оператор 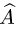
Доказать линейность, найти матрицу (в базисе 
ранг и дефект оператора 
План решения.
1.По определению доказываем линейность оператора 
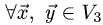
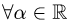
2.Строим по определению матрицу оператора 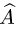
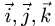
в базисе 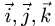
образов базисных векторов.
3.Находим образ, ранг, ядро и дефект оператора 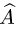
определений.
Пример. Доказать линейность, найти матрицу (в базисе 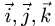
образ, ядро, ранг и дефект оператора проецирования пространства
геометрических векторов 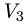
Решение.
1.Докажем по определению линейность оператора проецирования. Пусть в базисе 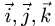
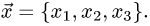
Тогда его образ (проекция) есть
По правилам операций с геометрическими векторами в координатной форме 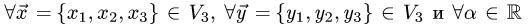
2.Так как по определению матрицы оператора ее столбцы —
это столбцы координат образов базисных векторов, найдем образы
базисных векторов 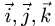
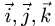
Таким образом, матрица оператора проецирования 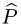
3.Находим образ, ранг, ядро и дефект оператора 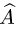
определений.
Образ оператора проецирования 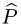
лежащих в плоскости XOY, следовательно, в базисе 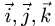
Отсюда
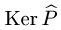
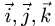
Отсюда
Заметим, что
Ответ. Оператор 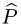
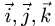
Действия с операторами и их матрицами
Постановка задачи. В некотором базисе трехмерного линейного пространства 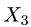
где 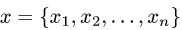
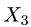
Найти координаты вектора 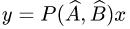
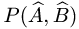
План решения. Так как при сложении операторов их матрицы
складываются, при умножении на число — умножаются на это число,
а матрица композиции операторов равна произведению их матриц,
то нужно найти матрицу Р(А, В), где А и В — матрицы операторов
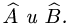
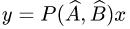
1.Построим матрицы операторов
2.По правилам сложения матриц, умножения матрицы на число и
умножения матриц находим матрицу Р(А,В):
3.Находим столбец координат образа вектора х:
Записываем ответ в виде
Пример. В некотором базисе трехмерного линейного пространства 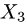
где 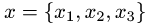
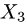
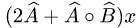
Решение.
1.Построим матрицы операторов
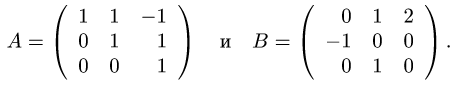
2.По правилам сложения матриц, умножения матрицы на число и
умножения матриц вычисляем матрицу 2А + А • В:
3.Находим столбец координат образа вектора х:
Ответ.
Преобразование координат вектора
Постановка задачи. Вектор х в базисе 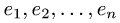
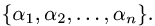
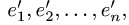
План решения. Координаты вектора при переходе от базиса
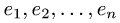
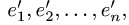
где 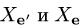
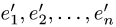
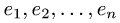
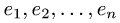
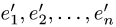
1.Находим матрицу перехода С. Так как столбцы матрицы перехода от базиса 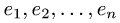
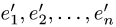
координат векторов 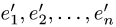
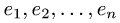
2.Находим обратную матрицу 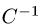
3.По формуле (1) находим столбец координат вектора х в базисе
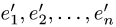
Записываем ответ в виде
Пример. Вектор х в базисе 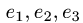
Найти координаты вектора х в базисе 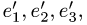
Решение.
1.Находим матрицу перехода
2.Находим обратную матрицу 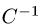
Таким образом,
Проверяем, что 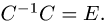
3.По формуле (1) находим столбец координат вектора х в базисе
Ответ.
Преобразование матрицы оператора
Постановка задачи. Найти матрицу некоторого оператора 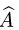
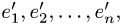
если в базисе 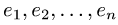
План решения. При переходе от базиса 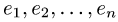
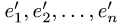
где С — матрица перехода от базиса 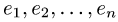
1.Находим матрицу перехода С. Так как столбцы матрицы пе-
перехода от базиса 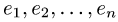
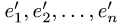
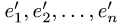
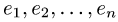
2.Находим обратную матрицу 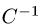
3.Находим матрицу оператора 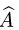
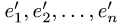
Пример. Найти матрицу оператора 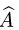
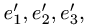
если в базисе 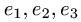
Решение.
1.Находим матрицу перехода
2.Находим обратную матрицу 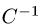
Таким образом,
Убеждаемся, что
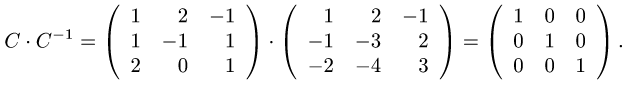
3.Находим матрицу оператора 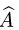
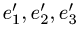
Ответ.
Собственные значения и собственные векторы оператора
Постановка задачи. Найти собственные значения и собственные векторы оператора 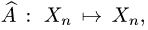
базисе матрицей
План решения. Собственные значения оператора 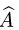
корнями его характеристического уравнения
1.Составляем характеристическое уравнение и находим все его
вещественные корни (среди них могут быть и кратные).
2.Для каждого собственного значения 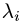
и находим фундаментальную систему решений 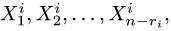
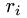
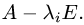
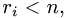
3.Столбцы 
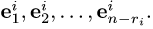
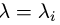
Замечание. Множество собственных векторов, соответствующих собственному значению 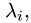
Пример. Найти собственные значения и собственные векторы оператора 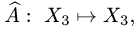
Решение.
1.Составляем характеристическое уравнение:
Поэтому
2.Для собственного значения 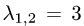
Очевидно, ранг матрицы этой системы равен 1 (n — r = 2 — размерность пространства решений), следовательно, система нетривиально совместна и ее фундаментальная система решений имеет вид
Итак, двукратному собственному значению 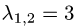
два линейно независимых собственных вектора 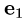
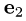
= {1,0,1}. Множество всех собственных векторов 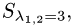
соответствующих собственному значению 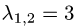
Аналогично находим собственный вектор, соответствующий
собственному значению 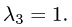
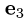
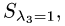
собственному значению 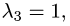
Ответ.
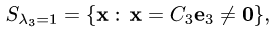
Дополнительные лекции:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Линейная алгебра с приложениями, Руководство к решению задач, Зенков А.В., 2010.
Пособие содержит примеры решения задач по линейной алгебре, тензорному исчислению, системам дифференциальных уравнений и теории устойчивости. Оно рассчитано на использование совместно с учебниками «Линейная алгебра и тензорное исчисление» и «Системы дифференциальных уравнений и элементы теории устойчивости», подготовленными автором, и следует принятым там очерёдности изложения, терминологии и системе обозначений. Вопросы, достаточно подкреплённые примерами в названных книгах, как правило, заново не рассматриваются.
В пособии учтён методический опыт каф. «Вычислительные методы и уравнения математической физики» УГТУ-УПИ, на которой автор работал много лет.
Каждая глава пособия завершается индивидуальными заданиями или подборкой задач (частично с ответами и указаниями к решению) для самостоятельной работы студентов.
В конце приведён список изданий, повлиявших на содержание данного пособия и/или рекомендуемых автором для желающих приобрести лучшие навыки в решении задач.
В данном (втором) издании исправлены замеченные опечатки и местами улучшено изложение.
Примеры.
Псевдотензор Т веса М в базисе е представлен массивом чисел Т. Найти соответствующий массив чисел в новом базисе e’, связанном со старым матрицей перехода Аε → ε’ = А.
Показать справедливость формулы
([a х b], [с х d]) = (а, с) (b, d) — (a, d) (b. с).
Для базиса е1 = 2i + j, e2 = i-j в пространстве Е2 найти взаимный базис, матрицы метрических тензоров, ко- и контравариантные координаты вектора х = i + j.
Оглавление
Глава I. ЛИНЕЙНАЯ АЛГЕБРА
1. Линейная зависимость векторов. I
2. Линейная зависимость векторов. II
3. Ранг системы векторов. I
4. Ранг системы векторов. II
5. Сумма и пересечение нодн|юстраиств
6. Матрица перехода. I
7. Матрица перехода. II
8. Матрица оператора. I
9. Матрица оператора. II
10. Произведение операторов
11. Ортогонализация по Граму-Шмидту
12. Матрица сопряжённою оператора
13. Линейная форма
14. Билинейная форма
15. Кривая второго порядка
16. Задания по линейной алгебре
Глава II. ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ
1. Линейная комбинация тензоров
2. Тензорное произведение. I
3. Тензорное произведение. II
4. Скалярное произведение
5. Симметрия тензоров
6. Симметрирование и альтернирование. I
7. Симметрирование и альтернирование. II
8. Симметрирование и альтернирование. III
9. Тензоры в евклидовом пространстве. I
10. Тензоры в евклидовом пространстве. II
11. Шаровой тензор и девиатор
12. Тензорная поверхность
13. Инварианты тензора
14. Псевдотензоры
15. Тензор Леви-Чивиты
16. Дуальный вектор
17. Упражнения по тензорному исчислению
18. Ответы
Глава III. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1. Общее решение системы
2. Метод исключения
3. Метод интегрируемых комбинаций
4. Линейная однородная система с постоянными коэффициентами
5. Линейная неоднородная система с постоянными коэффициентами
6. Упражнения по системам дифференциальных уравнений
7. Ответы
Глава IV. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
1. Определение устойчивости по Ляпунову
2. Простейшие типы точек покоя. Узел
3. Простейшие типы точек покоя. Седло
4. Простейшие типы точек покоя. Фокус
5. Простейшие типы точек покоя. Центр
6. Простейшие типы точек покоя. Вырожденный узел
7. Исследование на устойчивость по первому приближению. Фазовый портрет системы
8. Метод функций Ляпунова
9. Упражнения по теории устойчивости
10. Ответы
Библиографический список.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Линейная алгебра с приложениями, Руководство к решению задач, Зенков А.В., 2010 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 07.09.2015 08:08 UTC
Теги:
учебник по алгебре :: алгебра :: Зенков
Следующие учебники и книги:
- Уравнения с частными производными, Теория и практика, Короткий А.И., 2004
- Функциональный анализ, Лекции и упражнения, Дерр В.Я., 2013
- Теория функций действительной переменной, Лекции и упражнения, Дерр В.Я., 2008
- Контрпримеры в теории вероятностей, Стоянов Й., 2014
Предыдущие статьи:
- Линейная алгебра и тензорное исчисление, Зенков А.В., 2010
- Руководство к решению задач и упражнений по теории вероятностей и математической статистке, Булдык Г.М., 2009
- Формулы по статистике с описанием
- Практикум по введению в математическую логику, Воротников С.М., Егоров В.А., Матюшенко Л.Н., 1998
Примеры решений по линейной алгебре
Линейная алгебра для чайников
В этом разделе вы найдете бесплатные примеры по линейной алгебре (линалу): по основным темам, которые студенты изучают на 1 курсе:
матрицы и векторы, их характеристики, линейные пространства и подпространства и нахождение базиса, системы линейных уравнений, линейные отображения и операторы, квадратичные формы.
Не складывается с решением задач? Поможем подробно и быстро. После консультации вы сможете выполнить и оформить задачи в Word, с формулами, чертежами и пояснениями. Узнайте подробнее о решении алгебры для студентов.
Проконсультируем по решению алгебраических задач
Разделы и темы
- Векторы и действия с ними (17)
- Матрицы и определители (9)
- Многочлены и уравнения (8)
- Системы линейных алгебраических уравнений (8)
- Линейные пространства (7)
- Линейные операторы (6)
- Квадратичные формы (6)
Полезное на сайте
|
|



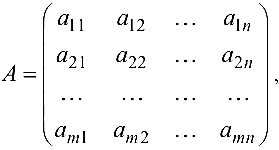
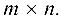
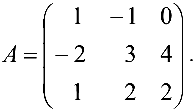
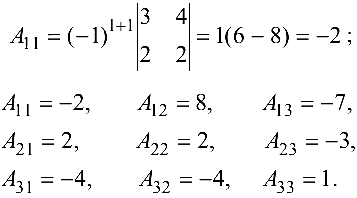
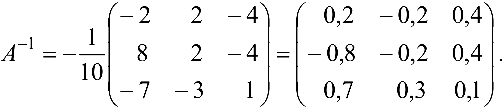
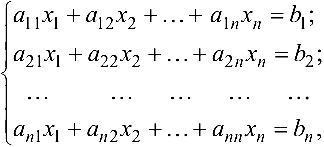
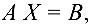
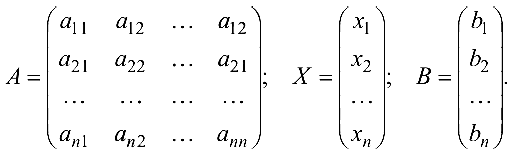
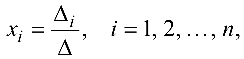
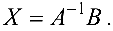
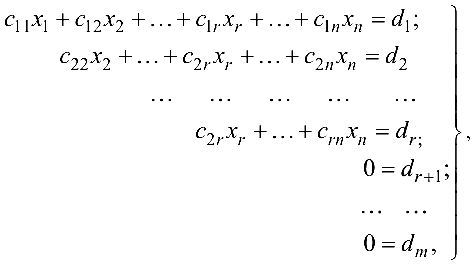
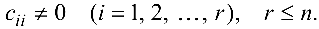
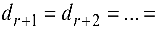
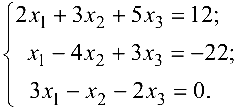
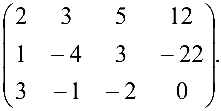
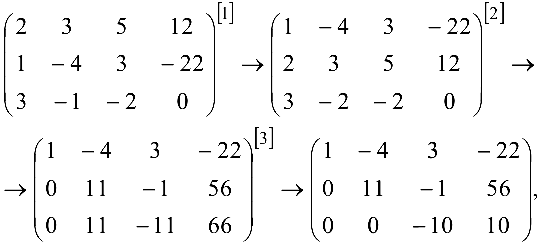
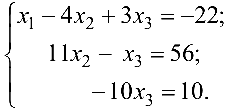
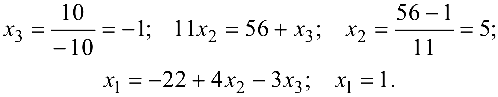
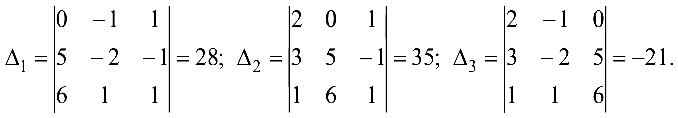
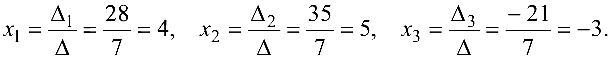
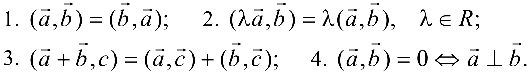
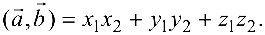
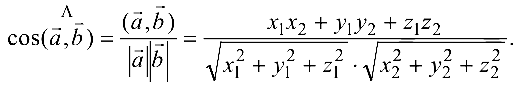
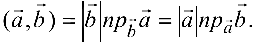
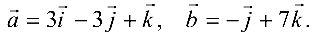
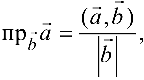
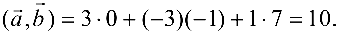
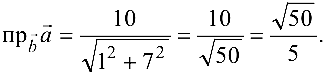
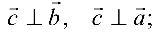
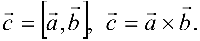
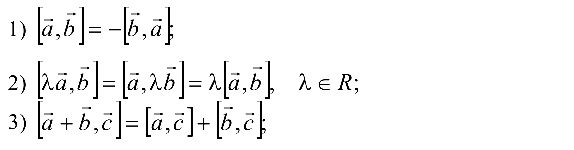
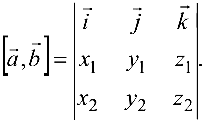
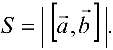
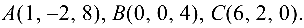
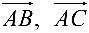 и длину
и длину  вектора
вектора 
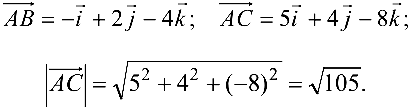
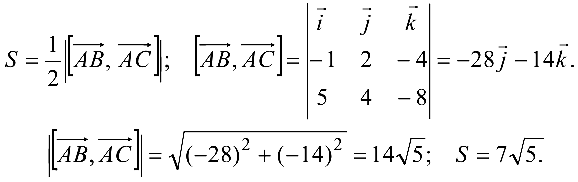
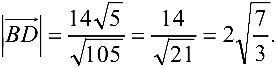
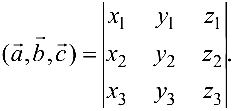
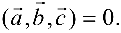
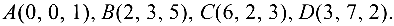
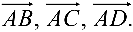
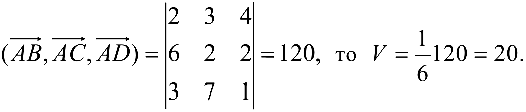
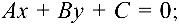 (4.3)
(4.3)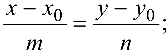
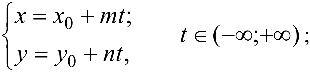
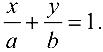
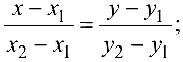
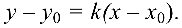
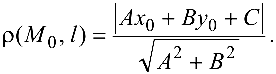
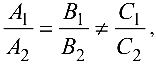
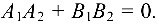
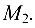
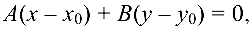
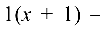
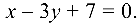
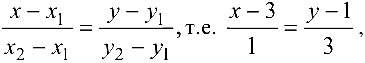
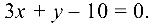
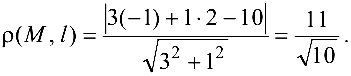
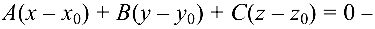
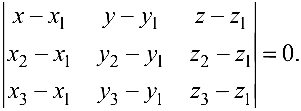
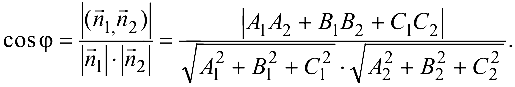
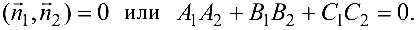
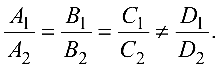
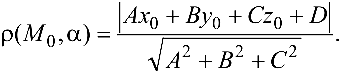
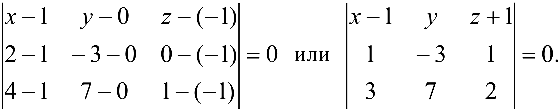
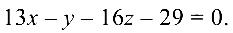
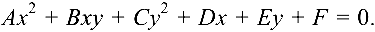
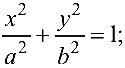
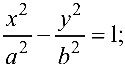
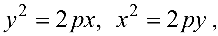
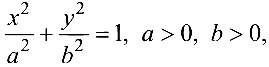
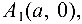
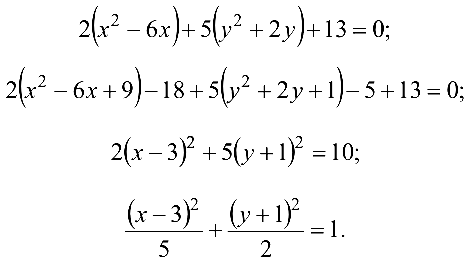
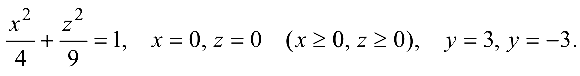
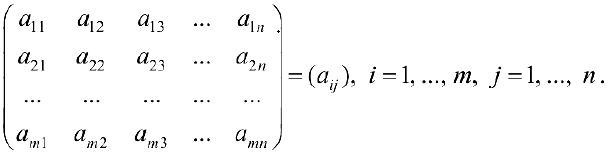
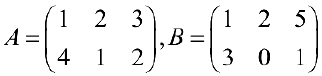
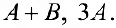
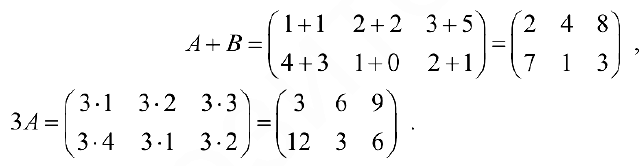
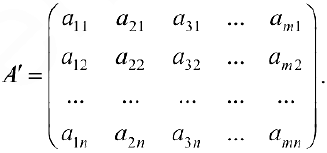

 — коммутативность сложения.
— коммутативность сложения.
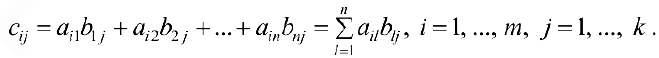
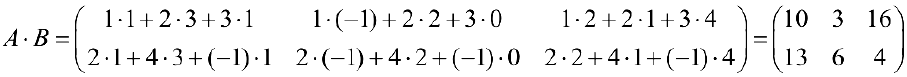
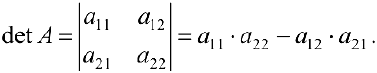
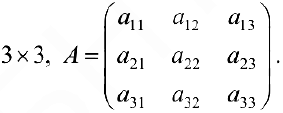
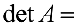
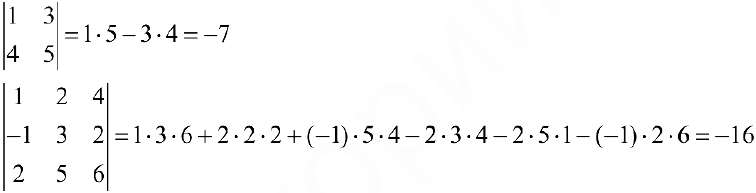
 то и определитель умножится на число
то и определитель умножится на число  будет равен:
будет равен: 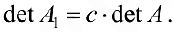
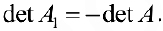
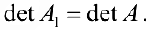
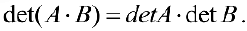
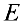 равен 1. (единичная матрица — это матрица, у которой на главной диагонали стоят 1, а все остальные элементы равны 0).
равен 1. (единичная матрица — это матрица, у которой на главной диагонали стоят 1, а все остальные элементы равны 0).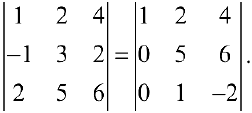
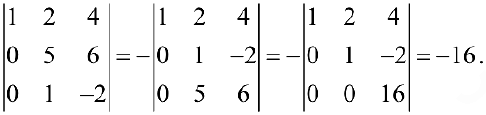
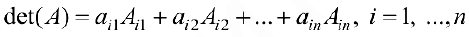
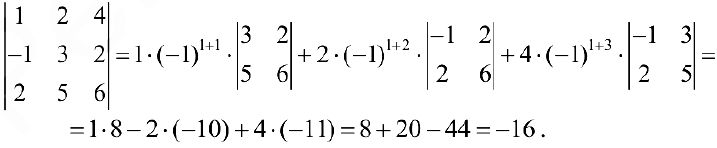
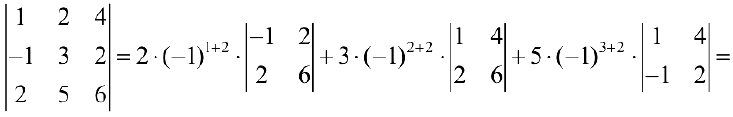
 (см. пример 6).
(см. пример 6).


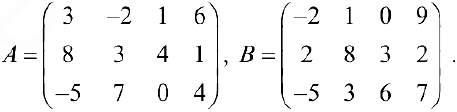
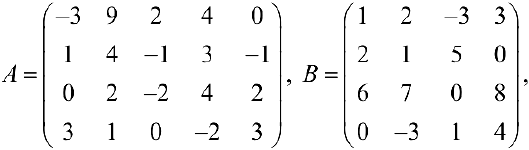
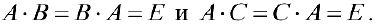
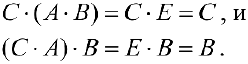
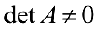 . По свойству (2):
. По свойству (2): 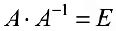 . Тогда
. Тогда 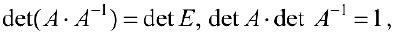 поэтому
поэтому 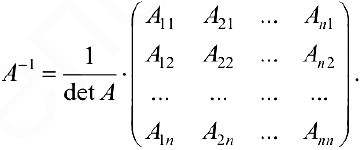

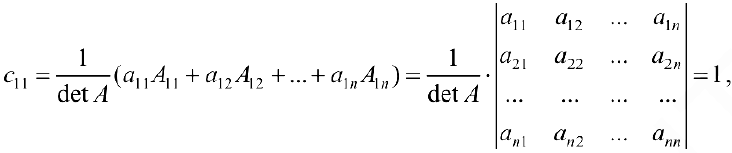
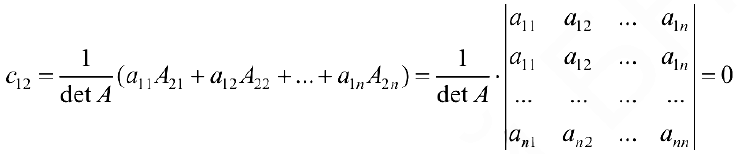
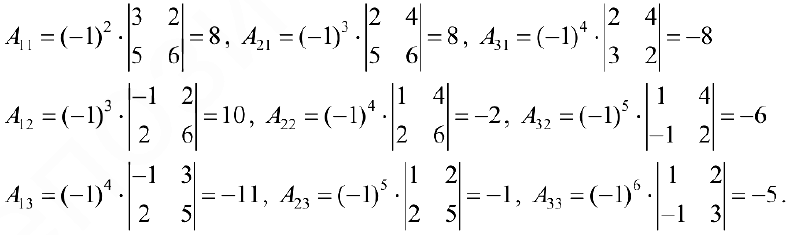
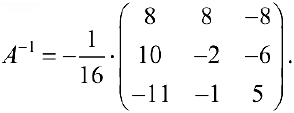
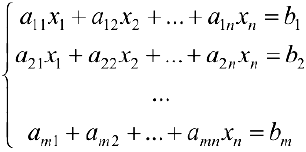
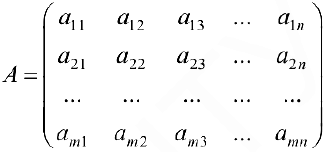

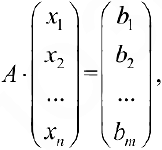
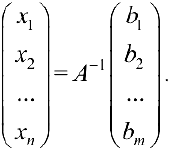
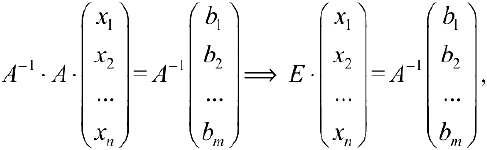
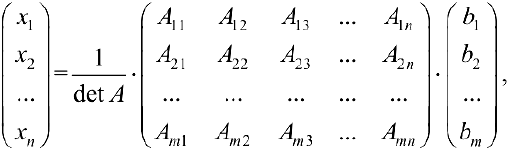
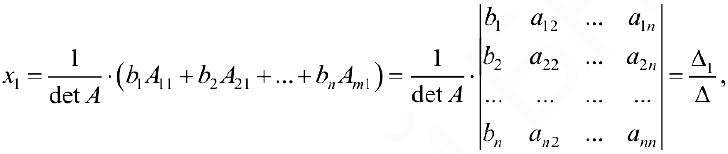
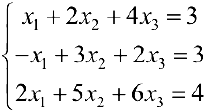
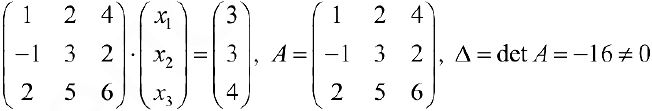
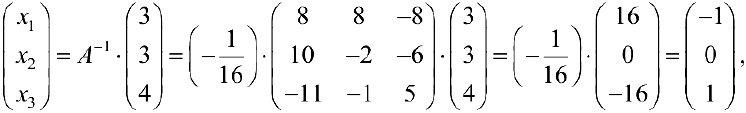
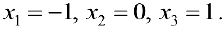
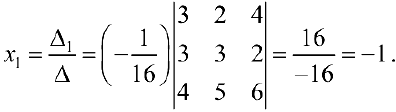
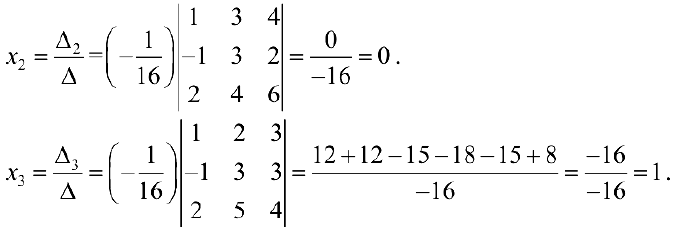
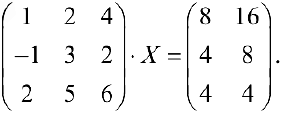
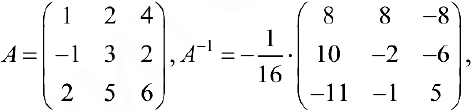
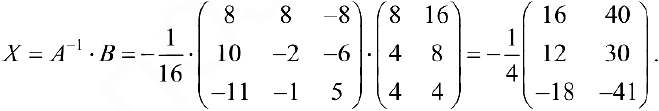
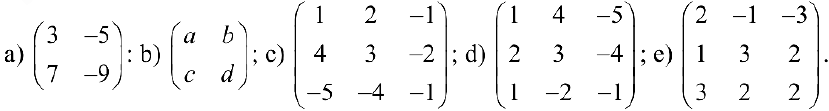
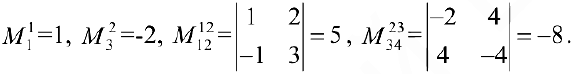
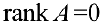 и конец алгоритма.
и конец алгоритма.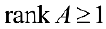 и переходят на п.2.
и переходят на п.2.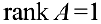 и конец алгоритма.
и конец алгоритма.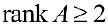 и переходят па рассмотрение миноров 3-ого порядка, окаймляющих фиксированный ненулевой минор 2-ого порядка, и т.д., пока есть что окаймлять.
и переходят па рассмотрение миноров 3-ого порядка, окаймляющих фиксированный ненулевой минор 2-ого порядка, и т.д., пока есть что окаймлять.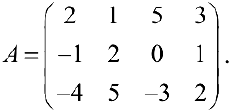
 поэтому
поэтому  . Рассмотрим минор
. Рассмотрим минор 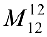 , окаймляющий
, окаймляющий 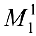 .
.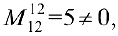 поэтому
поэтому 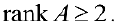
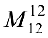 окаймляют два минора третьего порядка
окаймляют два минора третьего порядка 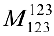 и
и 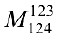 .
.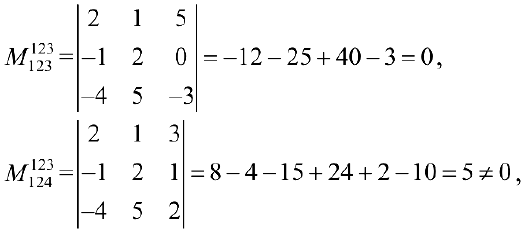
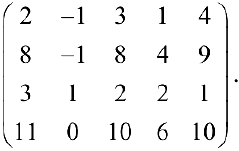
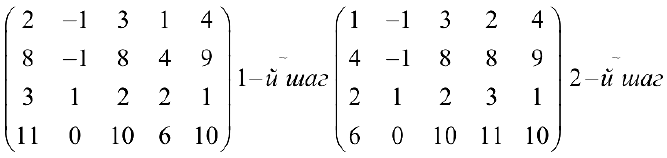
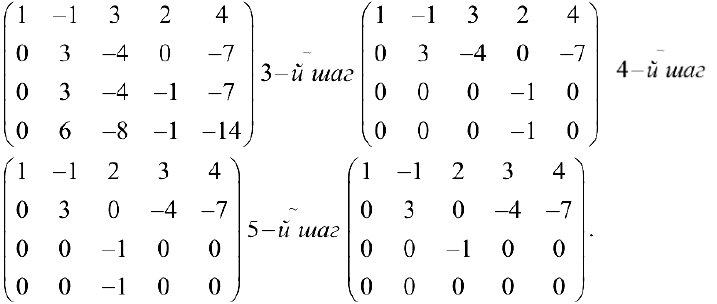
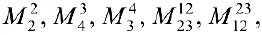
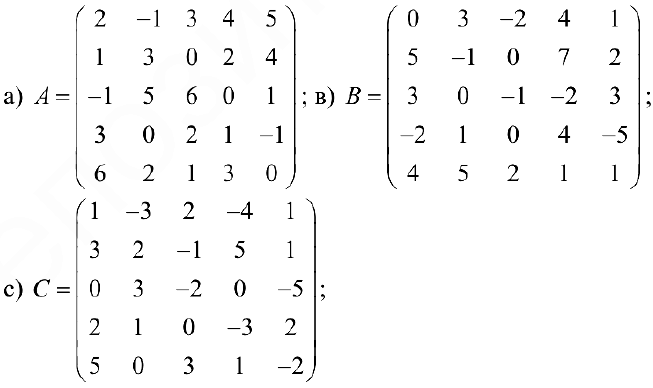
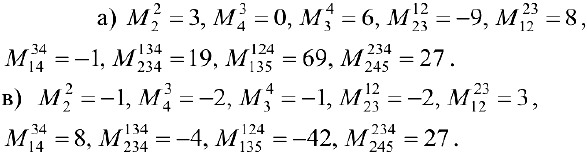
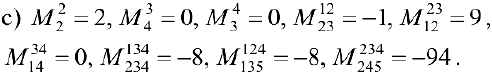


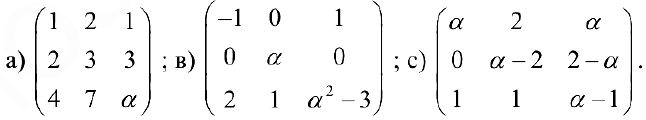
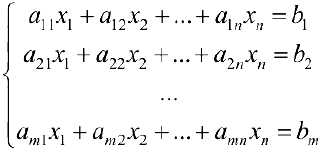
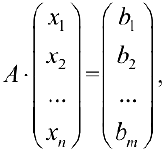
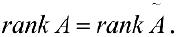
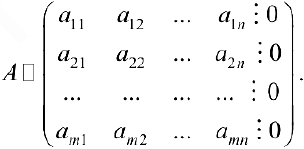
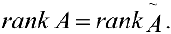
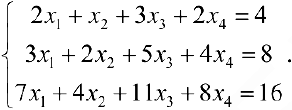

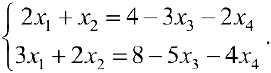
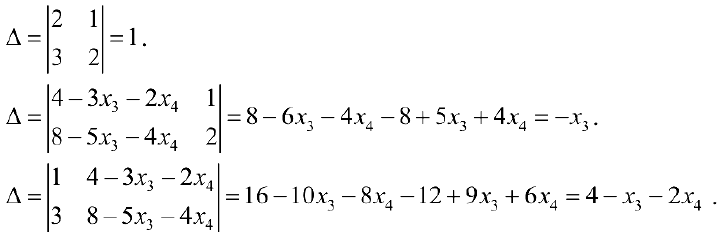
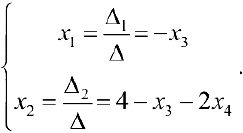
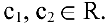
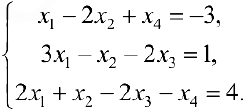
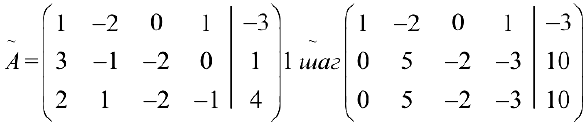
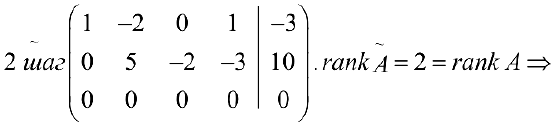
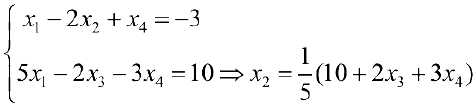
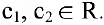
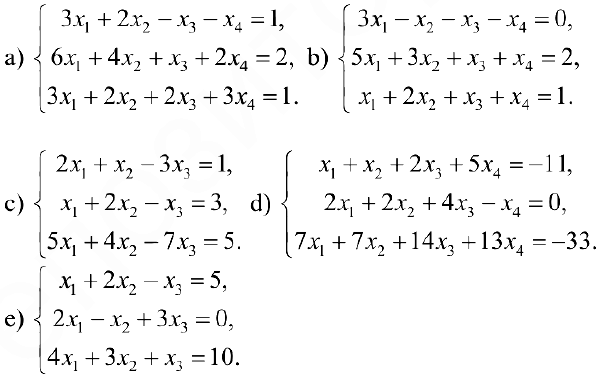
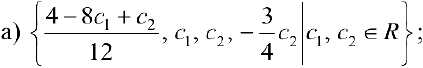
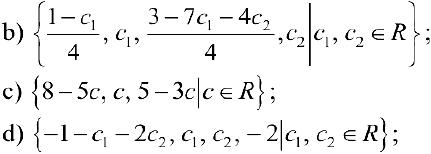
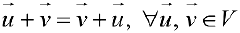 коммутативность сложения векторов.
коммутативность сложения векторов.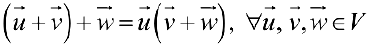 — ассоциативность сложения векторов.
— ассоциативность сложения векторов.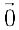 :
: 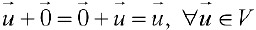 .
.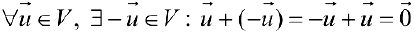 .
.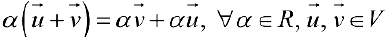 .
.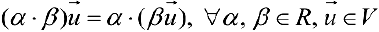 .
.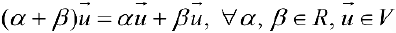 .
.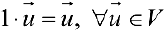 .
.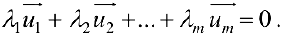
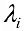
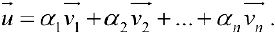
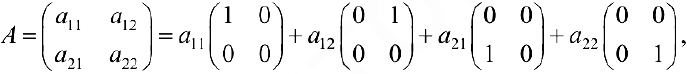
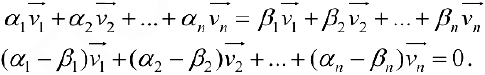
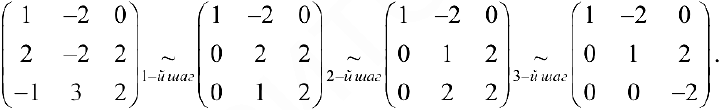
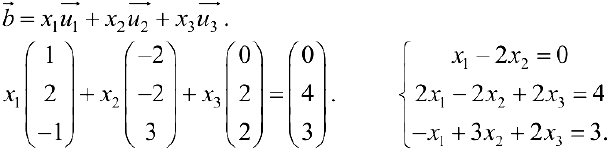
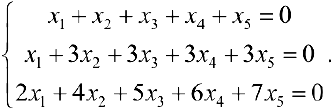
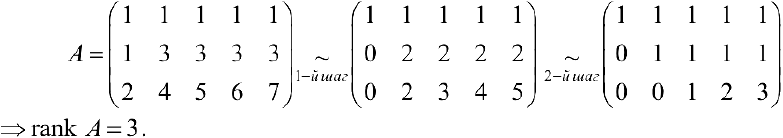
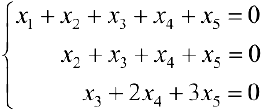
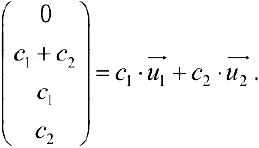
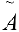 системы и в первой строке среди первых
системы и в первой строке среди первых 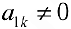 ). Делим 1-ю строку на
). Делим 1-ю строку на 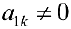 . Проведя элементарные преобразования строк, обнуляем остальные элементы
. Проведя элементарные преобразования строк, обнуляем остальные элементы 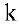 -ого столбца.
-ого столбца.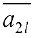 . Проводя элементарные преобразования строк, обнуляем все остальные элементы
. Проводя элементарные преобразования строк, обнуляем все остальные элементы 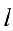 — ого столбца и т. д.
— ого столбца и т. д.