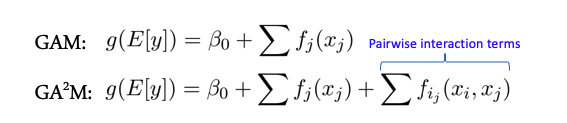Мы рассмотрим
- Принципы выбора лучшей линейной модели
- Сравнение линейных моделей разными способами:
- частный F-критерий
- тесты отношения правдоподобий
- информационные критерии AIC и BIC
Принципы выбора лучшей линейной модели
“Essentially, all models are wrong,
but some are useful”
Georg E. P. Box
Важно не только тестирование гипотез, но и построение моделей
- Проверка соответствия наблюдаемых данных предполагаемой функциональной связи между зависимой перменной и предикторами:
- оценки параметров,
- тестирование гипотез,
- оценка объясненной изменчивости ((R^2)),
- анализ остатков
- Построение моделей для предсказания значений в новых условиях:
- Выбор оптимальной модели
- Оценка предсказательной способности модели
Какую модель можно подобрать для описания этой закономерности?
Начнем с линейной модели
Все ли хорошо с подобранной моделью?
Для этих данных можно подобрать несколько моделей
Какая из этих моделей лучше описывает данные?
Для этих данных можно подобрать несколько моделей
В недообученной (underfitted) модели слишком мало параметров, ее предсказания неточны.
В переобученной (overfitted) модели слишком много параметров, она предсказывает еще и случайный шум.
Последствия переобучения модели
Переобучение происходит, когда модель из-за избыточного усложнения описывает уже не только отношения между переменными, но и случайный шум
При увеличении числа предикторов в модели:
- более точное описание данных, по которым подобрана модель
- низкая точность предсказаний на новых данных из-за переобучения.
При постоении моделей важно помнить о трех типах дисперсии
При постоении моделей важно помнить о трех типах дисперсии
| Объясненная дисперсия | Остаточная дисперсия | Полная дисперсия |
|---|---|---|
| (SS_{Regression}=sum{(hat{y}-bar{y})^2}) | (SS_{Residual}=sum{(hat{y}-y_i)^2}) | (SS_{Total}=sum{(bar{y}-y_i)^2}) |
| (df_{Regression} = 1) | (df_{Residual} = n-2) | (df_{Total} = n-1) |
| (MS_{Regression} =frac{SS_{Regression}}{df}) | (MS_{Residual} =frac{SS_{Residual}}{df_{Residual}}) | (MS_{Total} =frac{SS_{Total}}{df_{Total}}) |
Компромисс при подборе оптимальной модели:
точность vs. описание шума
Хорошее описание существующих данных
Полный набор переменных:
- большая объясненная изменчивость ((R^2)),
- маленькая остаточная изменчивость ((MS_{Residual}))
- большие стандартные ошибки
- сложная интерпретация
Принцип парсимонии
Entia non sunt multiplicanda praeter necessitatem
Минимальный набор переменных, который может объяснить существующие данные:
- объясненная изменчивость меньше ((R^2)),
- остаточная изменчивость больше ((MS_{Residual}))
- стандартные ошибки меньше
- интерпретация проще
Критерии и методы выбора моделей зависят от задачи
Объяснение закономерностей
- Нужны точные тесты влияния предикторов: F-тесты или тесты отношения правдоподобий (likelihood-ratio tests)
Описание функциональной зависимости
- Нужна точность оценки параметров
Предсказание значений зависимой переменной
- Парсимония: “информационные” критерии (АIC, BIC, AICc, QAIC, и т.д.)
- Нужна оценка качества модели на данных, которые не использовались для ее первоначальной подгонки: методы ресамплинга (кросс-валидация, бутстреп)
Дополнительные критерии для сравнения моделей:
Не позволяйте компьютеру думать за вас!
-
Хорошая модель должна соответствовать условиям применимости
-
Другие соображения: разумность, целесообразность модели, простота, ценность выводов, важность предикторов.
Знакомство с данными для множественной линейной регрессии
Пример: рак предстательной железы
От каких характеристик зависит концентрация простат-специфического антигена? (Stamey et al. 1989)
Переменных много, мы хотим из них выбрать оптимальный небольшой набор
97 пациентов:
lcavol— логарифм объема опухолиlweight— логарифм весаage— возраст пациентаlbph— логарифм степени доброкачественной гиперплазииsvi— поражение семенных пузырьковlcp— логарифм меры поражения капсулыgleason— оценка по шкале Глисонаpgg45— доля оценок 4 и 5 по шкале Глисонаlpsa— логарифм концентрации простат-специфичного антигена
Модель из прошлой лекции
prost <- read_excel("data/Prostate.xlsx")
mod3 <- lm(lpsa ~ lcavol + lweight + age + lbph + svi + gleason, data = prost)
Влияют ли предикторы?
summary(mod3)
## ## Call: ## lm(formula = lpsa ~ lcavol + lweight + age + lbph + svi + gleason, ## data = prost) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.8084 -0.4056 0.0057 0.4410 1.5954 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.2709 1.0957 0.25 0.8053 ## lcavol 0.5421 0.0786 6.90 7e-10 *** ## lweight 0.4533 0.1698 2.67 0.0090 ** ## age -0.0170 0.0110 -1.55 0.1247 ## lbph 0.1069 0.0583 1.83 0.0702 . ## svi 0.6943 0.2110 3.29 0.0014 ** ## gleason 0.1106 0.1159 0.95 0.3425 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.708 on 90 degrees of freedom ## Multiple R-squared: 0.648, Adjusted R-squared: 0.624 ## F-statistic: 27.6 on 6 and 90 DF, p-value: <2e-16
Не все предикторы влияют, возможно эту модель можно оптимизировать…
Сравнение линейных моделей
Вложенные модели (nested models)
Вложенные модели (nested models)
Две модели являются вложенными, если одну из них можно получить из другой путем удаления некоторых предикторов.
Удаление предиктора — коэффициент при данном предикторе равен нулю.
Полная модель (full model)
М1: (y _i = beta _0 + beta _1 x _1 + beta _2 x _2 + epsilon _i)
Неполные модели (reduced models)
М2: (y _i = beta _0 + beta _1 x _1 + epsilon _i)
М3: (y _i = beta _0 + beta _2 x _2 + epsilon _i)
M2 вложена в M1
M3 вложена в M1
M2 и M3 не вложены друг в друга
Нулевая модель (null model), вложена в полную (M1) и в неполные (M2, M3)
(y _i = beta _0 + epsilon _i)
Задание
Для тренировки запишем вложенные модели для данной полной модели
(1)(y _i = beta _0 + beta _1 x _1 + beta _2 x _2 + beta _3 x _3 + epsilon _i)
Решение
Для тренировки запишем вложенные модели для данной полной модели
(1)(y _i = beta _0 + beta _1 x _1 + beta _2 x _2 + beta _3 x _3 + epsilon _i)
Модели:
- (2)(y _i = beta _0 + beta _1 x _1 + beta _2 x _2 + epsilon _i)
- (3)(y _i = beta _0 + beta _1 x _1 + beta _3 x _3 + epsilon _i)
- (4)(y _i = beta _0 + beta _2 x _2 + beta _3 x _3 + epsilon _i)
- (5)(y _i = beta _0 + beta _1 x _1 + epsilon _i)
- (6)(y _i = beta _0 + beta _2 x _2 + epsilon _i)
- (7)(y _i = beta _0 + beta _3 x _3 + epsilon _i)
- (8)(y _i = beta _0 + epsilon _i)
Вложенность:
- (2)-(4)- вложены в (1)
- (5)-(7)- вложены в (1), при этом
- (5)вложена в (1), (2), (3);
- (6)вложена в (1), (2), (4);
- (7)вложена в (1), (3), (4)
- (8)- нулевая модель — вложена во все
Частный F-критерий
Сравнение вложенных линейных моделей при помощи F-критерия
Полная модель
(y _i = beta _0 + beta _1 x _{1 i} + … + beta _k x _{k i} + beta _{l} x _{l i} + epsilon _i)
(p = l + 1) – число параметров (df _{reduced, full} = p — 1)
(df _{error, full} = n — p)
Уменьшеная модель (без (beta _l x _{l i}))
(y _i = beta _0 + beta _1 x _{1 i} + … + beta _k x _{k i} + epsilon _i)
(p = k + 1 = l) – число параметров (df _{reduced, reduced} = (p — 1) — 1)
(df _{error, reduced} = n — (p — 1))
Как оценить насколько больше изменчивости объясняет полная модель, чем уменьшенная модель?
- Разница объясненной изменчивости — (SS _{error,reduced} — SS _{error,full})
- С чем, по аналогии с обычным F-критерием, можно сравнить эту разницу объясненной изменчивости?
- Можно сравнить с остаточной изменчивостью полной модели — (SS _{error, full})
Сравнение вложенных линейных моделей при помощи F-критерия
Полная модель
(y _i = beta _0 + beta _1 x _{1 i} + … + beta _k x _{k i} + beta _{l} x _{l i} + epsilon _i)
(p = l + 1) – число параметров (df _{reduced, full} = p — 1)
(df _{error, full} = n — p)
Уменьшеная модель (без (beta _l x _{l i}))
(y _i = beta _0 + beta _1 x _{1 i} + … + beta _k x _{k i} + epsilon _i)
(p = k + 1 = l) – число параметров (df _{reduced, reduced} = (p — 1) — 1)
(df _{error, reduced} = n — (p — 1))
Частный F-критерий — оценивает выигрыш объясненной дисперсии от включения фактора в модель
[F = frac {(SS _{error,reduced} — SS _{error,full}) / (df _{reduced, full} — df _{reduced, reduced})} {(SS _{error, full})/ df _{error, full}}]
Сравнение линейных моделей при помощи частного F-критерия
Постепенно удаляем предикторы. Модели обязательно должны быть вложенными! *
Обратный пошаговый алгоритм (backward selection)
-
- 1.Подбираем полную модель
- Повторяем 2-3 для каждого из предикторов:
- 2.Удаляем один предиктор (строим уменьшенную модель)
- 3.Тестируем отличие уменьшенной модели от полной
- 4.Выбираем предиктор для окончательного удаления: это предиктор, удаление которого минимально ухудшает модель. Модель без него будет “полной” для следующего раунда выбора оптимальной модели.
- Повторяем 1-4 до тех пор, пока что-то можно удалить.
- — Важно! Начинать упрощать модель нужно со взаимодействий между предикторами. Если взаимодействие из модели удалить нельзя, то нельзя удалять и отдельно стоящие предикторы, из которых оно состоит. Но мы поговорим о взаимодействиях позже
Частный F-критерий в R
Влияют ли предикторы?
- Незначимо влияние age, lbph, gleason. Можем попробовать оптимизировать модель
summary(mod3)
## ## Call: ## lm(formula = lpsa ~ lcavol + lweight + age + lbph + svi + gleason, ## data = prost) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.8084 -0.4056 0.0057 0.4410 1.5954 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.2709 1.0957 0.25 0.8053 ## lcavol 0.5421 0.0786 6.90 7e-10 *** ## lweight 0.4533 0.1698 2.67 0.0090 ** ## age -0.0170 0.0110 -1.55 0.1247 ## lbph 0.1069 0.0583 1.83 0.0702 . ## svi 0.6943 0.2110 3.29 0.0014 ** ## gleason 0.1106 0.1159 0.95 0.3425 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.708 on 90 degrees of freedom ## Multiple R-squared: 0.648, Adjusted R-squared: 0.624 ## F-statistic: 27.6 on 6 and 90 DF, p-value: <2e-16
Частный F-критерий, 1 способ: anova(модель_1, модель_2)
Вручную выполняем все действия и выбираем, что можно выкинуть, и так много раз.
mod4 <- update(mod3, . ~ . - age) anova(mod3, mod4) mod5 <- update(mod4, . ~ . - lbph) anova(mod3, mod5) mod6 <- update(mod3, . ~ . - gleason) anova(mod3, mod6) # Удаляем gleason, и потом повторяем все снова...
Но мы пойдем другим путем
Частный F-критерий, 2 способ: drop1()
Вручную тестировать каждый предиктор с помощью anova() слишком долго. Можно протестировать все за один раз при помощи drop1()
drop1(mod3, test = "F")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + age + lbph + svi + gleason ## Df Sum of Sq RSS AIC F value Pr(>F) ## <none> 45.1 -60.4 ## lcavol 1 23.84 68.9 -21.2 47.61 7e-10 *** ## lweight 1 3.57 48.6 -55.0 7.13 0.0090 ** ## age 1 1.20 46.3 -59.8 2.40 0.1247 ## lbph 1 1.68 46.8 -58.8 3.36 0.0702 . ## svi 1 5.42 50.5 -51.3 10.83 0.0014 ** ## gleason 1 0.46 45.5 -61.4 0.91 0.3425 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Нужно убрать gleason
Тестируем предикторы (шаг 2)
# Убрали gleason mod4 <- update(mod3, . ~ . - gleason) drop1(mod4, test = "F")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + age + lbph + svi ## Df Sum of Sq RSS AIC F value Pr(>F) ## <none> 45.5 -61.4 ## lcavol 1 28.77 74.3 -15.9 57.50 2.8e-11 *** ## lweight 1 3.23 48.8 -56.7 6.45 0.01282 * ## age 1 0.96 46.5 -61.4 1.92 0.16953 ## lbph 1 1.86 47.4 -59.5 3.71 0.05716 . ## svi 1 5.95 51.5 -51.5 11.90 0.00085 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Нужно убрать age
Тестируем предикторы (шаг 3)
# Убрали age mod5 <- update(mod4, . ~ . - age ) drop1(mod5, test = "F")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + lbph + svi ## Df Sum of Sq RSS AIC F value Pr(>F) ## <none> 46.5 -61.4 ## lcavol 1 27.83 74.3 -17.8 55.08 5.6e-11 *** ## lweight 1 2.80 49.3 -57.7 5.54 0.021 * ## lbph 1 1.30 47.8 -60.7 2.57 0.112 ## svi 1 5.81 52.3 -51.9 11.49 0.001 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Нужно убрать lbph
Тестируем предикторы (шаг 4)
# Убрали lbph mod6 <- update(mod5, . ~ . - lbph) drop1(mod6, test = "F")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + svi ## Df Sum of Sq RSS AIC F value Pr(>F) ## <none> 47.8 -60.7 ## lcavol 1 28.04 75.8 -17.9 54.6 6.3e-11 *** ## lweight 1 5.89 53.7 -51.4 11.5 0.001 ** ## svi 1 5.18 53.0 -52.7 10.1 0.002 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Больше ничего не убрать
Итоговая модель
summary(mod6)
## ## Call: ## lm(formula = lpsa ~ lcavol + lweight + svi, data = prost) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.7297 -0.4577 0.0281 0.4640 1.5701 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.2681 0.5435 -0.49 0.623 ## lcavol 0.5516 0.0747 7.39 6.3e-11 *** ## lweight 0.5085 0.1502 3.39 0.001 ** ## svi 0.6662 0.2098 3.18 0.002 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.717 on 93 degrees of freedom ## Multiple R-squared: 0.626, Adjusted R-squared: 0.614 ## F-statistic: 52 on 3 and 93 DF, p-value: <2e-16
Задание
Проверьте финальную модель на выполнение условий применимости
Решение
1) График расстояния Кука
- Выбросов нет
mod6_diag <- fortify(mod6)
mod6_diag_full <- data.frame(
mod6_diag,
prost[, c("lcp", "pgg45", "age", "lbph", "gleason")])
ggplot(mod6_diag_full, aes(x = 1:nrow(mod6_diag_full), y = .cooksd)) +
geom_bar(stat = "identity")
Решение
2) График остатков от предсказанных значений
- Выбросов нет
- Гетерогенность дисперсии не выявляется
- Есть намек на нелинейность связей
gg_resid <- ggplot(data = mod6_diag_full, aes(x = .fitted, y = .stdresid)) + geom_point() + geom_hline(yintercept = 0) gg_resid
Решение
3) Графики остатков от предикторов в модели и нет
Решение
3) Код для графиков остатков от предикторов в модели и нет
res_1 <- gg_resid + aes(x = lcavol)
res_2 <- gg_resid + aes(x = lweight)
res_3 <- gg_resid + aes(x = age)
res_4 <- gg_resid + aes(x = lbph)
res_5 <- gg_resid + aes(x = svi)
res_6 <- gg_resid + aes(x = lcp)
res_7 <- gg_resid + aes(x = gleason)
res_8 <- gg_resid + aes(x = pgg45)
library(gridExtra)
grid.arrange(res_1, res_2, res_3, res_4,
res_5, res_6, res_7, res_8, nrow = 2)
Решение
4) Квантильный график остатков
- Отклонения от нормального распределения остатков не выявляются
library(car) qqPlot(mod6)
## [1] 39 96
Описываем финальную модель
summary(mod6)
## ## Call: ## lm(formula = lpsa ~ lcavol + lweight + svi, data = prost) ## ## Residuals: ## Min 1Q Median 3Q Max ## -1.7297 -0.4577 0.0281 0.4640 1.5701 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.2681 0.5435 -0.49 0.623 ## lcavol 0.5516 0.0747 7.39 6.3e-11 *** ## lweight 0.5085 0.1502 3.39 0.001 ** ## svi 0.6662 0.2098 3.18 0.002 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.717 on 93 degrees of freedom ## Multiple R-squared: 0.626, Adjusted R-squared: 0.614 ## F-statistic: 52 on 3 and 93 DF, p-value: <2e-16
Тесты отношения правдоподобий
Вероятность и правдоподобие
Правдоподобие (likelihood) — способ измерить соответствие имеющихся данных тому, что можно получить при определенных значениях параметров модели.
Мы оцениваем это как произведение вероятностей получения каждой из точек данных
[L(theta| data) = Pi^n _{i = 1}f(x| theta)]
где (f(data| theta)) — функция плотности распределения с параметрами (theta)
Выводим формулу правдоподобия для линейной модели с нормальным распределением ошибок
(y_i = beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i} + epsilon_i)
Выводим формулу правдоподобия для линейной модели с нормальным распределением ошибок
(y_i = beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i} + epsilon_i)
Пусть в нашей модели остатки нормально распределены ((epsilon_i sim N(0, sigma^2))) и их значения независимы друг от друга:
(N(epsilon_i; 0, sigma^2) = frac {1} { sqrt {2pisigma^2} } exp (-frac {1} {2 sigma^2} epsilon_i^2))
Выводим формулу правдоподобия для линейной модели с нормальным распределением ошибок
(y_i = beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i} + epsilon_i)
Пусть в нашей модели остатки нормально распределены ((epsilon_i sim N(0, sigma^2))) и их значения независимы друг от друга:
(N(epsilon_i; 0, sigma^2) = frac {1} { sqrt {2pisigma^2} } exp (-frac {1} {2 sigma^2} epsilon_i^2))
Функцию правдоподобия (likelihood, вероятность получения нашего набора данных) можно записать как произведение вероятностей:
(L(epsilon_i|mathbf{y}, mathbf{x}) = Pi^n _{n = 1} N(epsilon_i, sigma^2) = frac {1} {sqrt{(2pisigma^2)^n}} exp(- frac {1} {2sigma^2} sum {epsilon_i}^2))
Выводим формулу правдоподобия для линейной модели с нормальным распределением ошибок
(y_i = beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i} + epsilon_i)
Пусть в нашей модели остатки нормально распределены ((epsilon_i sim N(0, sigma^2))) и их значения независимы друг от друга:
(N(epsilon_i; 0, sigma^2) = frac {1} { sqrt {2pisigma^2} } exp (-frac {1} {2 sigma^2} epsilon_i^2))
Функцию правдоподобия (likelihood, вероятность получения нашего набора данных) можно записать как произведение вероятностей:
(L(epsilon_i|mathbf{y}, mathbf{x}) = Pi^n _{n = 1} N(epsilon_i, sigma^2) = frac {1} {sqrt{(2pisigma^2)^n}} exp(- frac {1} {2sigma^2} sum {epsilon_i}^2))
Поскольку (epsilon_i = y_i — (beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i}))
то функцию правдоподобия можно переписать так:
(L(beta_1…beta_{p — 1}, sigma^2| mathbf{y}, mathbf{x}) = frac {1} {sqrt{(2pisigma^2)^n}}exp(- frac {1} {2sigma^2} sum (y_i — (beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i}))^2))
Подбор параметров модели методом максимального правдоподобия
Чтобы найти параметры модели
(y_i = beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i} + epsilon_i)
нужно найти такое сочетание параметров (beta_0), (beta_1), … (beta_{p — 1}), и (sigma^2), при котором функция правдоподобия будет иметь максимум:
(begin{array}{l} L(beta_1…beta_{p — 1}, sigma^2| mathbf{y}, mathbf{x}) &= frac {1} {sqrt{(2pisigma^2)^n}} exp(- frac {1} {2sigma^2} sum {epsilon_i}^2) = \ &= frac {1} {sqrt{(2pisigma^2)^n}}exp(- frac {1} {2sigma^2} sum (y_i — (beta_0 + beta_1x_{1i} + … …beta_{p — 1}x_{p — 1 i}))^2) end{array})
Логарифм правдоподобия (loglikelihood)
Вычислительно проще работать с логарифмами правдоподобий (loglikelihood)
Если функция правдоподобия
(begin{array}{l} L(beta_1…beta_{p — 1}, sigma^2| mathbf{y}, mathbf{x}) &= frac {1} {sqrt{(2pisigma^2)^n}} exp(- frac {1} {2sigma^2} sum {epsilon_i}^2) = \ &= frac {1} {sqrt{(2pisigma^2)^n}}exp(- frac {1} {2sigma^2} sum (y_i — (beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i}))^2) end{array})
то логарифм правдоподобия
(begin{array}{l} logLik(beta_1…beta_{p — 1}, sigma^2| mathbf{y}, mathbf{x}) &= & \ ln L(beta_1…beta_{p — 1}, sigma^2| mathbf{y}, mathbf{x}) &= &- frac{n}{2} (ln2pi + lnsigma^2) — frac{1}{2sigma^2}(sum epsilon^2_i) = \ &= &- frac{n}{2} (ln2pi + lnsigma^2) — \ & &- frac{1}{2sigma^2}(sum (y_i — (beta_0 + beta_1x_{1i} + … + beta_{p — 1}x_{p — 1 i}))^2) end{array})
Чем больше логарифм правдоподобия тем лучше модель
Подбор параметров модели методом максимального правдоподобия
Для подбора параметров методом максимального правдоподобия используют функцию glm()
# Симулированные данные set.seed(9328) dat <- data.frame(X = runif(n = 50, min = 0, max = 10)) dat$Y <- 3 + 15 * dat$X + rnorm(n = 50, mean = 0, sd = 1) # Подбор модели двумя способами Mod <- lm(Y ~ X, data = dat) # МНК Mod_glm <- glm(Y ~ X, data = dat) # МЛ # Одинаковые оценки коэффициентов coefficients(Mod)
## (Intercept) X ## 2.95 15.02
coefficients(Mod_glm)
## (Intercept) X ## 2.95 15.02
Логарифм правдоподобия
(LogLik) для модели можно найти с помощью функции logLik()
logLik(Mod_glm)
## 'log Lik.' -65.5 (df=3)
Логарифм правдоподобия вручную
# Предсказанные значения dat$predicted <- predict(Mod) # Оценка дисперсии SD <- summary(Mod)$sigma # Вероятности для каждой точки dat$Prob <- dnorm(dat$Y, mean = dat$predicted, sd = SD) # Логарифм вероятностей dat$LogProb <- log(dat$Prob) # Логарифм произведения, равный сумме логарифмов sum(dat$LogProb)
## [1] -65.5
Тест отношения правдоподобий (Likelihood Ratio Test)
Тест отношения правдоподобий позволяет определить какая модель более правдоподобна с учетом данных.
[LRT = 2lnBig(frac{L_1}{L_2}Big) = 2(lnL_1 — lnL_2)]
- (L_1), (L_2) — правдоподобия полной и уменьшенной модели
- (lnL_1), (lnL_2) — логарифмы правдоподобий
Разница логарифмов правдоподобий имеет распределение, которое можно апроксимировать (chi^2), с числом степеней свободы (df = df_2 — df_1) (Wilks, 1938)
Тест отношения правдоподобий в R
Задание
Для этой полной модели
GLM1 <- glm(lpsa ~ lcavol + lweight + age + lbph + svi + gleason, data = prost)
Подберите оптимальную модель при помощи тестов отношения правдоподобий
Тест отношения правдоподобий можно сделать с помощью тех же функций, что и частный F-критерий:
- по-одному
anova(mod3, mod2, test = "Chisq") - все сразу
drop1(mod3, test = "Chisq")
Решение (шаг 1)
drop1(GLM1, test = "Chisq")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + age + lbph + svi + gleason ## Df Deviance AIC scaled dev. Pr(>Chi) ## <none> 45.1 217 ## lcavol 1 68.9 256 41.2 0.00000000014 *** ## lweight 1 48.6 222 7.4 0.0066 ** ## age 1 46.3 218 2.6 0.1100 ## lbph 1 46.8 218 3.6 0.0594 . ## svi 1 50.5 226 11.0 0.0009 *** ## gleason 1 45.5 216 1.0 0.3231 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Нужно убрать gleason
Решение (шаг 2)
# Убираем gleason GLM2 <- update(GLM1, . ~ . - gleason) drop1(GLM2, test = "Chisq")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + age + lbph + svi ## Df Deviance AIC scaled dev. Pr(>Chi) ## <none> 45.5 216 ## lcavol 1 74.3 261 47.5 5.5e-12 *** ## lweight 1 48.8 220 6.6 0.00998 ** ## age 1 46.5 216 2.0 0.15497 ## lbph 1 47.4 218 3.9 0.04893 * ## svi 1 51.5 226 11.9 0.00056 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Нужно убрать age
Решение (шаг 3)
# Убираем lbph GLM3 <- update(GLM2, . ~ . - age) drop1(GLM3, test = "Chisq")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + lbph + svi ## Df Deviance AIC scaled dev. Pr(>Chi) ## <none> 46.5 216 ## lcavol 1 74.3 259 45.5 1.5e-11 *** ## lweight 1 49.3 220 5.7 0.01720 * ## lbph 1 47.8 217 2.7 0.10190 ## svi 1 52.3 225 11.4 0.00073 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Нужно убрать lbph
Решение (шаг 4)
# Убираем lbph GLM4 <- update(GLM3, . ~ . - lbph) drop1(GLM4, test = "Chisq")
## Single term deletions ## ## Model: ## lpsa ~ lcavol + lweight + svi ## Df Deviance AIC scaled dev. Pr(>Chi) ## <none> 47.8 217 ## lcavol 1 75.8 259 44.8 2.2e-11 *** ## lweight 1 53.7 226 11.3 0.00078 *** ## svi 1 53.0 225 10.0 0.00158 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Больше ничего убрать не получается
Решение (шаг 5)
summary(GLM4)
## ## Call: ## glm(formula = lpsa ~ lcavol + lweight + svi, data = prost) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.7297 -0.4577 0.0281 0.4640 1.5701 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -0.2681 0.5435 -0.49 0.623 ## lcavol 0.5516 0.0747 7.39 6.3e-11 *** ## lweight 0.5085 0.1502 3.39 0.001 ** ## svi 0.6662 0.2098 3.18 0.002 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for gaussian family taken to be 0.514) ## ## Null deviance: 127.918 on 96 degrees of freedom ## Residual deviance: 47.785 on 93 degrees of freedom ## AIC: 216.6 ## ## Number of Fisher Scoring iterations: 2
Финальную модель снова нужно проверить на выполнение условий применимости
Информационные критерии
AIC — Информационный критерий Акаике (Akaike Information Criterion)
(AIC = -2 logLik + 2p)
- (logLik) — логарифм правдоподобия для модели
- (2p) — штраф за введение в модель (p) параметров
Чем меньше AIC — тем лучше модель
Важно! Информационные критерии можно использовать для сравнения даже для невложенных моделей. Но модели должны быть подобраны с помощью ML и на одинаковых данных!
Некоторые другие информационные критерии
| Критерий | Название | Формула |
|---|---|---|
| AIC | Информационный критерий Акаике | (AIC = -2 logLik + 2p) |
| BIC | Баесовский информационный критерий | (BIC = -2 logLik + p cdot ln(n)) |
| AICc | Информационный критерий Акаике с коррекцией для малых выборок (малых относительно числа параметров: (n/p < 40), Burnham, Anderson, 2004) | (AIC_c = -2 logLik + 2p + frac{2p(p + 1)}{n — p — 1}) |
- (logLik) — логарифм правдоподобия для модели
- (p) — число параметров
- (n) — число наблюдений
Информационные критерии в R
Рассчитаем AIC для наших моделей
AIC(GLM1, GLM2, GLM3, GLM4)
## df AIC ## GLM1 8 217 ## GLM2 7 216 ## GLM3 6 216 ## GLM4 5 217
- Судя по AIC, лучшая модель GLM2 или GLM3. Но если значения AIC различаются всего на 1-2 единицу — такими различиями можно пренебречь и выбрать более простую модель (GLM3).
Уравнение модели:
(lpsa = 0.15 + 0.55lcavol + 0.39lweight + 0.09lbph + 0.71svi)
Рассчитаем BIC для наших моделей
BIC(GLM1, GLM2, GLM3, GLM4)
## df BIC ## GLM1 8 238 ## GLM2 7 234 ## GLM3 6 231 ## GLM4 5 229
- Судя по BIC, нужно выбрать модель GLM4
Уравнение модели:
(lpsa = — 0.27 + 0.55lcavol + 0.51lweight + 0.67svi)
Как выбрать способ подбора оптимальной модели?
Вы видели, что разные способы подбора оптимальной модели могут приводить к разным результатам.
Не важно, какой из способов выбрать, но важно сделать это заранее, до анализа, чтобы не поддаваться соблазну подгонять результаты.
Take-home messages
- Модели, которые качественно описывают существующие данные включают много параметров, но предсказания с их помощью менее точны из-за переобучения
- Для выбора оптимальной модели используются разные критерии в зависимости от задачи
- Сравнивая модели можно отбраковать переменные, включение которых в модель не улучшает ее
- Метод сравнения моделей нужно выбрать заранее, еще до анализа
Что почитать
-
Must read paper! Zuur, A.F. and Ieno, E.N., 2016. A protocol for conducting and presenting results of regression‐type analyses. Methods in Ecology and Evolution, 7(6), pp.636-645. - Кабаков Р.И. R в действии. Анализ и визуализация данных на языке R. М.: ДМК Пресс, 2014
- Zuur, A., Ieno, E.N. and Smith, G.M., 2007. Analyzing ecological data. Springer Science & Business Media.
- Quinn G.P., Keough M.J. 2002. Experimental design and data analysis for biologists
-
Logan M. 2010. Biostatistical Design and Analysis Using R. A Practical Guide
Время на прочтение
7 мин
Количество просмотров 11K
Мы снова в эфире и продолжаем цикл заметок Дата Сайентиста и сегодня представляю мой абсолютно субъективный чек-лист по выбору модели машинного обучения.
Это топ-10 свойств задачи и просто пунктов (без порядка в них), с точки зрения которых я начинаю выбор модели и вообще моделирование задачи по анализу данных.
Совсем не обязательно, что у вас он будет таким же — здесь все субъективно, но делюсь опытом из жизни.
А какая у нас вообще цель? Интерпретируемость и точность — спектр
Источник
Пожалуй самый важный вопрос, который стоит перед дата сайентист перед тем, как начать моделирование это:
В чем, собственно, состоит бизнес задача?
Или исследовательская, если речь об академии, etc.
Например, нам нужна аналитика на основе модели данных или наоборот нас только интересуют качественные предсказания вероятности того, что письмо — это спам.
Классический баланс, который я видел, это как раз спектр между интерпретируемостью метода и его точностью (как на графике выше).
Но по сути нужно не просто прогнать Catboost / Xgboost / Random Forest и выбрать модельку, а понять, что хочет бизнес, какие у нас есть данные и как это будет применяться.
На моей практике — это сразу будет задавать точку на спектре интерпретируемости и точности (чтобы это не значило здесь). А исходя из этого уже можно думать о методах моделирования задачи.
Тип самой задачи
Дальше, после того как мы поняли, что хочет бизнес — нам нужно понять к какому математическому типу задач машинного обучения относится наша, например
- Exploratory analysis — чистая аналитика имеющихся данных и тыканье палочкой
- Clustering — собрать данные в группы по какой-тому общему признаку(ам)
- Regression — нужно вернуть целочисленный результат или там вероятность события
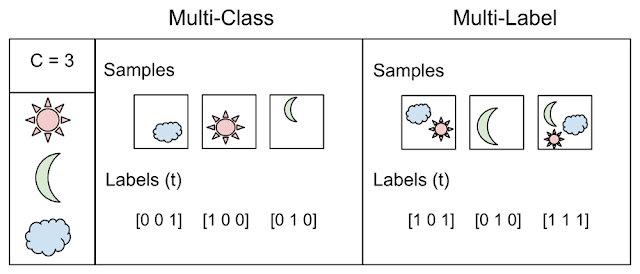
- Classification — нужно вернуть одну метку класса
- Multi-label — нужно вернуть одну или более меток класса для каждой записи
Примеры
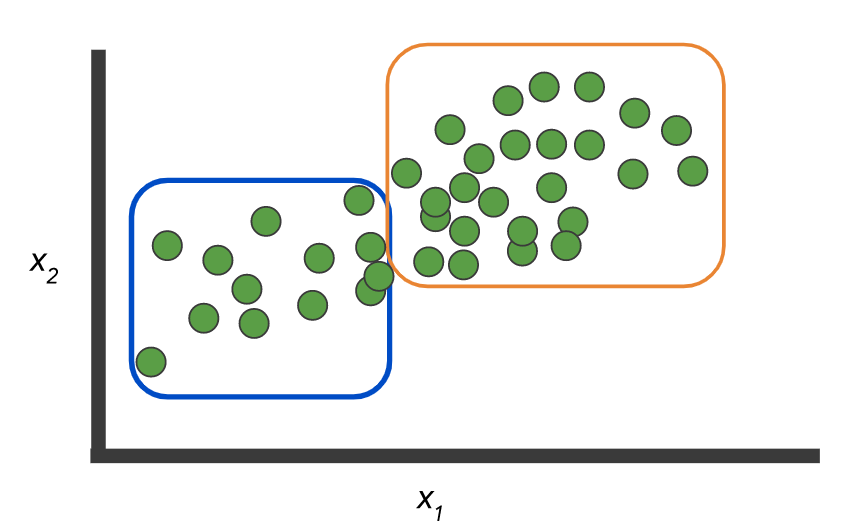
Данные: имеются два класса и набор записей без меток:
И нужно построить модель, которая разметит эти самые данные:
Или как вариант никаких меток нет и нужно выделить группы:
Как например вот здесь:
Картинки отсюда.
А вот собственно пример иллюстрирует разницу между двумя понятиями: классификация, когда N > 2 классов — multi class vs. multi label
Взято отсюда
Вы удивитесь, но очень часто этот пункт тоже стоит напрямую проговорить с бизнесом — это может сэкономить вам действительно много сил и времени. Не стесняйтесь рисовать картинки и давать простые примеры (но не слишком упрощенные).
Точность и как она определена
Начну с простого примера, если вы банк и выдаете кредит, то на неудачном кредите мы теряем в пять раз больше, чем получаем на удачном.
Поэтому вопрос об измерении качества работы первичен! Или представьте, что у вас присутствует существенный дисбаланс в данных, класс А = 10%, а class B = 90%, тогда классификатор, который просто возвращает B всегда умеет 90% точность! Скорее всего это не то, чтобы хотели увидеть, обучая модель.
Поэтому критично определить метрику оценки модели включая:
- weight class — как в примере выше, вес плохого кредита 5, а хорошего 1
- cost matrix — возможно перепутать low и medium risk — это не беда, а вот low risk и high risk — уже проблема
- Должна ли метрика отражать баланс? как например ROC AUC
- А мы вообще считаем вероятности или прям метки классов?
- А может быть класс вообще «один» и у нас precision/recall и другие правила игры?
В целом выбор метрики обусловлен задачей и ее формулировкой — и именно у тех, кто ставит эту задачу (обычно бизнес-люди) и надо выяснять и уточнять все эти детали, иначе на выходе будет швах.
Model post analysis
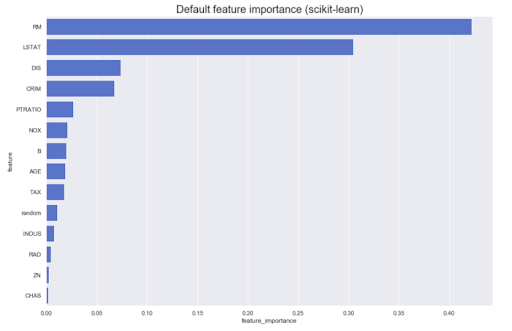
Часто приходится проводить аналитику на основе самой модели. Например, какой вклад имеют разные признаки в исходный результат: как правило, большинство методов могут выдать что-то похожее на вот это:
Однако, что если нам нужно знать направление — большие значения признака A увеличивают принадлежность классу Z или наоборот? Назовем их направленные feature importance — их можно получить у некоторых моделей, например, линейных (через коэффициенты на нормированных данных)
Для ряда моделей, основанных на деревьях и бустинге — например, подходит метод SHapley Additive exPlanations.
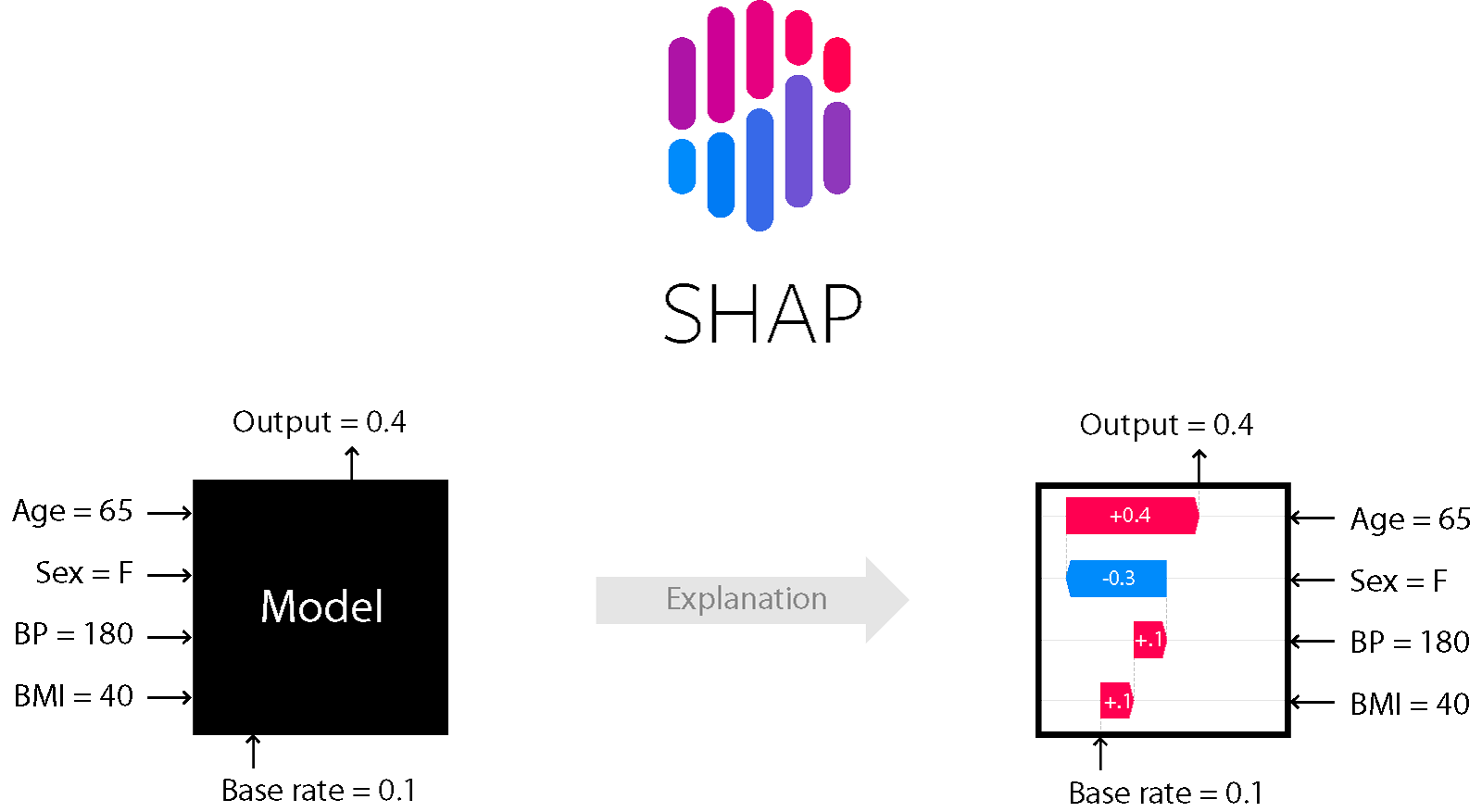
SHAP
Это один из методов анализа модели, который позволяет заглянуть «под капот» модели.
Он позволяет оценить направление эффекта:
Причем для деревьев (и методах на них основанных) он точный. Подробнее об этом тут.
Noise level — устойчивость, линейная зависимость, outlier detection и тд
Устойчивость к шуму и все эти радости жизни — это отдельная тема и нужно крайне внимательно анализировать уровень шума, а также подбирать соответствующие методы. Если вы уверены, что в данных будут выбросы — нужно их обязательно качественно чистить и применять методы устойчивые к шуму (высокий bias, регуляризация и тд).
Также признаки могут быть коллинеарны и присутствовать бессмысленные признаки — разные модели по-разному на это реагируют. Приведем пример на классическом датасете German Credit Data (UCI) и трех простых (относительно) моделях обучения:
- Ridge regression classifier: классическая регрессия с регуляризатором Тихонова
- Decition trees
- CatBoost от Яндекса
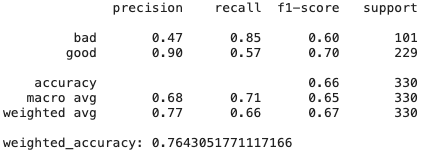
Ridge regression
# Create Ridge regression classifier
ridge_clf = RidgeClassifier(class_weight=class_weight, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(pd.get_dummies(X), y, test_size=0.33, random_state=42)
# Train model
ridge_model = ridge_clf.fit(X_train, y_train)
y_pred = ridge_model.predict(X_test)
print(classification_report(y_test,y_pred))
print("weighted_accuracy:",weighted_accuracy(y_test,y_pred))
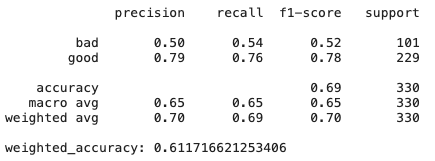
Decision Trees
# Create Ridge regression classifier
dt_clf = DecisionTreeClassifier(class_weight=class_weight, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(pd.get_dummies(X), y, test_size=0.33, random_state=42)
# Train model
dt_model = dt_clf.fit(X_train, y_train)
y_pred = dt_model.predict(X_test)
print(classification_report(y_test,y_pred))
print("weighted_accuracy:", weighted_accuracy(y_test,y_pred))
CatBoost
# Create boosting classifier
catboost_clf = CatBoostClassifier(class_weights=class_weight, random_state=42, cat_features = X.select_dtypes(include=['category', object]).columns)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# Train model
catboost_model = catboost_clf.fit(X_train, y_train, verbose=False)
y_pred = catboost_model.predict(X_test)
print(classification_report(y_test,y_pred))
print("weighted_accuracy:",weighted_accuracy(y_test,y_pred))

Как мы видим просто модель гребневой регрессии, которая имеет высокий bias и регуляризацию, показывает результаты даже лучше, чем CatBoost — тут много признаков не слишком полезных и коллинеарных, поэтому методы, которые к ним устойчивы показывают хорошие результаты.
Еще про DT — а если чуть чуть поменять датасет? Feature importance может поменяться, так как decision trees вообще чувствительные методы, даже к перемешиванию данных.
Вывод: иногда проще — лучше и эффективнее.
Масштабируемость
Действительно ли вам нужен Spark или нейросети с миллиардами параметров?
Во-первых, нужно здраво оценивать объем данных, уже неоднократно доводилось наблюдать массовое использование спарка на задачах, которые легко умещаются в память одной машины.
Спарк усложняет отладку, добавляет overhead и усложняет разработку — не стоит его применять там, где не нужно. Классика.
Во-вторых, нужно конечно же оценивать сложность модели и соотносить ее с задачей. Если ваши конкуренты показывают отличные результаты и у них бегает RandomForest, возможно стоит дважды подумать нужна ли вам нейросеть на миллиарды параметров.
И конечно же необходимо учитывать, что если у вас и правда крупные данные, то модель должна быть способной работать на них — как обучаться по батчам, либо иметь какие-то механизмы распределенного обучения (и тд). А там же не слишком терять в скорости при увеличении объема данных. Например, мы знаем, что kernel methods требуют квадрата памяти для вычислений в dual space — если вы ожидаете увеличение размера данных в 10 раз, то стоит дважды подумать, а умещаетесь ли вы в имеющиеся ресурсы.
Наличие готовых моделей
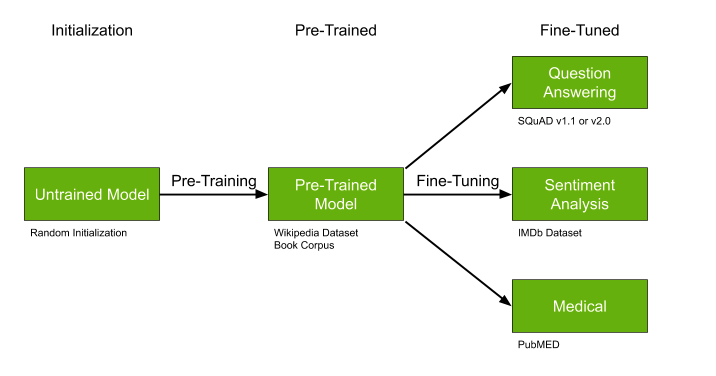
Еще одна важнейшая деталь — это поиск уже натренированных моделей, которые можно до-обучить, идеально подходит, если:
- Данных не очень много, но они очень специфичны для нашей задачи — например, медицинские тексты.
- Тема в целом относительно популярна — например, выделением тем текста — много работ в NLP.
- Ваш подход допускает в принципе до-обучение — как например с некоторым типом нейросетей.
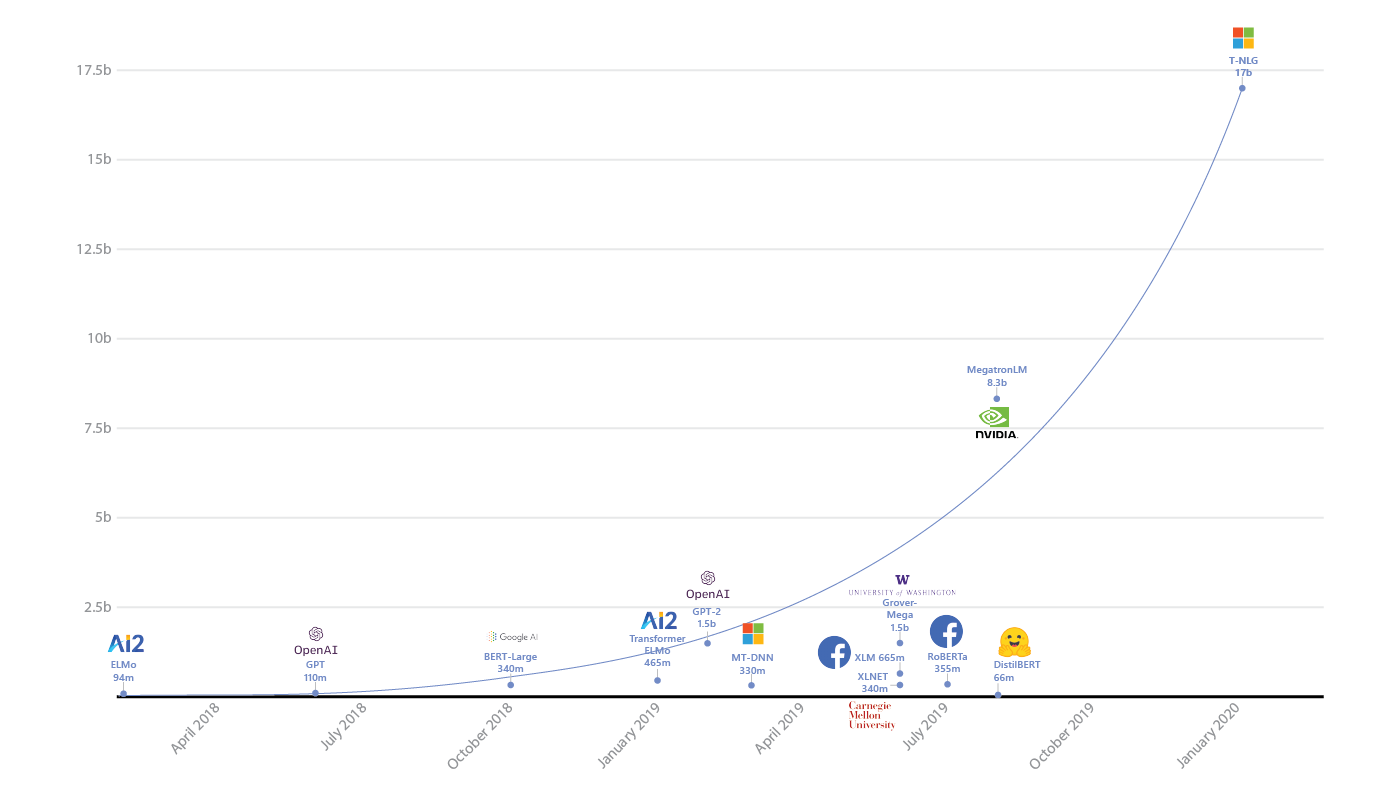
Pre-trained модели как GPT-2 и BERT могут существенно упростить решение вашей задачи и если уже натренированные модели существуют — крайне рекомендую не проходит мимо и использовать этот шанс.
Feature interactions и линейные модели
Некоторые модели лучше работают, когда между признаками (features) нет сложных взаимодействий — например весь класс линейных моделей — Generalized Additive Models. Есть расширение этих моделей на случай взаимодействия двух признаков под название GA2M — Generalized Additive Models with Pairwise Interactions.
Как правило такие модели показывают хорошие результаты на таких данных, отлично регуляризируются, интерпретируемые и устойчивы к шуму. Поэтому однозначно стоит обратить на них внимание.
Однако, если признаки активно взаимодействуют группами больше 2, то данные методы уже не показывают таких хороших результатов.
Package and model support
Многие крутые алгоритмы и модели из статей бывают оформлены в виде модуля или пакета для python, R и тд. Стоит реально дважды подумать, прежде чем использовать и в долгосрочной перспективе полагаться на такое решение (это я говорю, как человек написавший немало статей по ML с таким кодом). Вероятность того, что через год будет нулевая поддержка — очень высок, ибо автору скорее всего сейчас необходимо заниматься другими проектами нет времени, и никаких incentives вкладываться в развитие модуля или репозитория.
В этом плане библиотеки а-ля scikit learn хороши именно тем, что у них фактически есть гарантированная группа энтузиастов вокруг и если что-то будет серьезно поломано — это рано или поздно пофиксят.
Biases and Fairness
Вместе с автоматическими принятиями решений к нам в жизнь приходят люди недовольные такими решениями — представьте, что у нас есть какая-то система ранжирования заявок на стипендию или грант исследователя в универе. Универ у нас будет необычный — в нем только две группы студентов: историки и математики. Если вдруг система на основе своих данных и логики вдруг раздала все гранты историкам и ни одному математику их не присудила — это может неслабо так обидеть математиков. Они назовут такую систему предвзятой. Сейчас об это только ленивый не говорит, а компании и люди судятся между собой.
Условно, представьте упрощенную модель, которая просто считает цитирования статей и пусть историки друг друга цитируют активно — среднее 100 цитат, а математики нет, у них среднее 20 — и пишут вообще мало, тогда система распознает всех историков, как «хороших» ибо цитируемость высокая 100 > 60 (среднее), а математиков, как «плохих» потому что у них у всех цитируемость куда ниже среднего 20 < 60. Такая система вряд ли может показаться кому-то адекватной.
Классика сейчас предъявить логику принятия решения и тренировки моделей, которые борются с таким предвзятым подходом. Таким образом, для каждого решения у вас есть объяснение (условно) почему оно было принято и как вы собственно приложили усилия к тому, чтобы модель не сделала фигню (ELI5 GDPR).
Подробнее у гугла тут, или вот в статье тут.
В целом многие компании начали подобную деятельность особенно в свете выхода GDPR — подобные меры и проверки могут позволить избежать проблем в дальнейшем.
Если какая-то тема заинтересовала больше остальных — пишите в комментарии, будем идти в глубину. (DFS)!
Пошаговое руководство по выбору оптимальной видеокарты
Выбор оптимальной видеокарты может быть сложным процессом, но следуя нескольким простым шагам, вы будете более уверены в своем выборе.
Шаг 1: Определите свой бюджет
Первым шагом при выборе видеокарты должно быть определение вашего бюджета. Видеокарты могут варьироваться в цене от нескольких тысяч до десятков тысяч рублей. Поэтому заранее определите, сколько вы готовы потратить на новую видеокарту, чтобы не переплачивать или не получить более дешевую, чем вам нужно.
Шаг 2: Определите свои потребности
Определите, зачем вам нужна видеокарта. Если вы играете в игры, вам может потребоваться более мощная карта, чем если вы работаете с графикой или просматриваете видео. Определите, какие задачи вы хотите, чтобы ваша новая видеокарта выполняла, чтобы выбрать оптимальную модель.
Шаг 3: Исследуйте рынок
Исследуйте возможности рынка видеокарт. Просмотрите разные модели и их характеристики. Узнайте, какие карты поддерживаются вашей операционной системой или какие совместимы с вашей материнской платой. Изучите тесты производительности разных моделей, чтобы понять, насколько быстро карта может обрабатывать графику.
Шаг 4: Сравните модели
После того, как вы изучили рынок, сравните модели видеокарт на основе их характеристик и стоимости. Обратите внимание на различия в производительности, референсном дизайне или охлаждении моделей, опции разгона и т.д. Более дорогие модели обычно имеют лучше характеристики, но не всегда они дают существенное увеличение в производительности.
Шаг 5: Прочтите отзывы
Прочтите отзывы других пользователей о моделях, которые вы рассматриваете. Это может помочь вам понять, насколько надежна карта, какие у нее проблемы и достоинства.
Шаг 6: Сделайте свой выбор
После того, как вы проанализировали все возможные факторы, сделайте свой выбор. Определитесь с оптимальной моделью видеокарты, которая отвечает вашим требованиям и бюджету.
Вывод
Выбор оптимальной видеокарты может занять время, но если следовать приведенным выше шагам, вы сможете выбрать качественную видеокарту, которая удовлетворит ваши потребности.
Перед потенциальным оператором мотобура обязательно встает проблема выбора этого агрегата. Как выбрать мотобур? Какими критериями руководствоваться чтобы сделать правильный выбор? Чем отличаются модели одна от другой? Какие аксессуары к мотобуру не забыть купить?
Для правильного выбора оптимальной модели мотобура вам нужно ответить себе на три самых простых вопроса:
- Для достижения каких именно целей Вам требуется мотобур? Мотобур может быть нужен вам для бурения отверстий для последующей установки столбов, для бурения льда и даже скважинного бурения. Таким образом, для установки столбов на вашем дачном участке и вокруг него, Вас скорее всего вполне устроит лёгкий мотобур для одного управления одним оператором (то есть, подобным мотобуром может осуществлять работы один человек), для бурения льда следует применять всё тот же лёгкий мотобур со шнеком (специальным сверлом для буров) для бурения отверстий во льду. Для осуществления более сложной и трудоёмкой работы и бурения отверстий больших диаметров Вам следует приобрести мотобур для двух операторов.
- В комплектацию мотобуров не входят шнеки. В зависимости от поставленных задач, глубины бурения, диаметра нужного вам отверстия следует подбирать подходящий мотобур и шнек (шнеки) для него.
- Как правило, обычная длина шнека (сверла мотобура) составляет — 1 м. Для увеличения глубины бурения вам обязательно понадобится удлинитель для шнека (удлинители бывают двух видов).
Мотобур является винтообразным буром (шнеком) с приводом от двигателя, как правило, это двухтактный бензиновый двигатель. Преимуществами шнекового бурения являются: довольно высокая скорость и практически полное отсутствие в необходимости выполнения вспомогательных работ в процессе бурения и после его завершения. Кроме того, не появляются проблемы с извлечением «выработанного» грунта, так, как в процессе углубления скважины он автоматически выбрасывается наверх, также как по ленте транспортёра. Мотобур выполнит аккуратные и ровные лунки нужной вам определенной ширины и глубины и даже в тяжелых для бурения почвах и при этом сэкономит ваше время и силы.
Обычно, для работы с мотобурами достаточно сил одного, порой даже не очень опытного оператора плюс шнек. К тому, же многие модели мотобуров оснащаются особыми системами безопасности, которые блокируют двигатель в случаях застревания шнека либо потери управления агрегатом, а также предупреждают случайный запуск мотобура. Мотобур обладает полной независимостью от наличия электросети и электрического кабеля. Такие параметры, конечно же по достоинству оценят владельцы небольших земельных участков, но тем не менее периодической заправки мотобура все-таки не избежать. Выбирая мотобур следует помнить, что в его техническом описании указан вес с пустым топливным баком, а заправленный горючим мотобур будет весить несколько больше.
Спектр задач, которые может решить тот или иной мотоинструмент (в том числе и мотобур), прежде всего зависит от мощности его двигателя. В компетенцию самых «младших» мотобуров входят рыхлый, посадочный грунт, а вот для для уплотненной либо глинистой почвы требуется выбрать мотобур помощнее. В тех критических случаях, когда потребуется сравнить почву с хорошо схватившимся бетоном, вас могут выручить профессиональные модели мотобуров. Ресурс двигателя таких агрегатов рассчитан на довольно продолжительное бурение в особо суровых условиях, а их конструкция предусматривает управление инструментом двумя операторами, так, как одному человеку это не под силу.
Полезные рекомендации
- Особого внимания заслуживают вопросы безопасности при работе мотобуром. Несмотря на предусмотрительность и скрупулёзность производителей и наличие различных предохраняющих систем, вам не стоит пренебрегать и защитными аксессуарами, такими как: шлем, очки, перчатки и наушники (беруши). Кстати, по в вполне понятным причинам, нужно обязательно отказаться от длиннополой свисающей одежды.
- Для того, чтобы мотобур (бензиновый) служил вам верой и правдой долгие годы, нужно заправлять его смесью бензина не ниже марки Аи-92 (отдельные специалисты настоятельно советуют не использовать 95-й) и масла для 2-тактных двигателей, хранить мотобур разобранным и тщательно смазанном, своевременно проводить его техобслуживание – одним словом, нужно соблюдать традиционные «правила хорошего тона» в отношении инструмента.
Задачами мотобура (ямобура) являются: эффективное и качественное бурение ям для установки столбов, опор заборов, небольших свай. Кроме того, мотобуром производится бурение скважин.
Пробурить отверстия мотобуром под столбы, значительно выгоднее, нежели заказывать целую буровую машину. Бурение отверстий для столбов или свайных фундаментов осуществляется весьма быстро, эффективно и качественно и при этом не нарушается существующий ландшафт.
Приобретя мотобур, вы сможете быстро и без лишней грязи установить опору, забор, сделать свайный фундамент. И всё это благодаря оборудованию для производства бурения.
В сети магазинов «Удачная техника» вы сможете приобрести надежные мотобуры ведущих брендов:
Stihl — это немецкий бренд высочайшего класса, основанный в 1926 году в Германии, в городе Штутгарде. Главными конкурентными преимуществами которого является высокое качество, надежность, долговечность, эргономичность и доступная цена.
Echo – американский бренд, основанный в 1963 году, одно из лидирующих предприятий мира по производству качественной садовой техники, инвентаря и оборудования, сельскохозяйственных и лесоводческих машин. Главными конкурентными преимуществами этого бренда являются высокое качество, эргономичность и удобство в эксплуатации.
HITACHI — японский бренд, основанный в 1910 г. Продукция этого бренда отличается следующими преимуществами: надежность и качество инструментов, экологичность, использование инновационных технологий, доступная цена.
Выбор модели машинного обучения
Перевод
Ссылка на автора
Часть искусства, часть науки выбора идеальной модели машинного обучения.
Количество блестящих моделей может быть огромным, что означает, что люди часто обращаются к тем, кому доверяют больше всего, и используют их для решения всех новых задач. Это может привести к неоптимальным результатам.
Сегодня мы узнаем, как быстро и эффективно сузить пространство доступных моделей, чтобы найти те из них, которые с наибольшей вероятностью будут наиболее эффективны для вашего типа проблемы. Мы также увидим, как мы можем отслеживать производительность наших моделей с использованием весов и уклонов и сравнивать их.
Вы можете найти сопроводительный код Вот,
Что мы покроем
- Выбор модели в конкурентной науке о данных против реального мира
- Королевский гул моделей
- Сравнение моделей
Давайте начнем!
В отличие от Властелина колец, в машинном обучении нет ни одного кольца (модели), чтобы управлять ими всеми. Различные классы моделей хороши для моделирования базовых шаблонов различных типов наборов данных. Например, деревья решений хорошо работают в тех случаях, когда ваши данные имеют сложную форму:
В то время как линейные модели работают лучше всего, когда набор данных линейно разделим:
Прежде чем мы начнем, давайте немного углубимся в несоответствие между выбором моделей в реальном мире и конкурентной наукой о данных.
Выбор модели в конкурентной науке о данных против реального мира
Как сказал Вильям Форхиес в своем Сообщение блога «Соревнования Kaggle подобны гонкам формулы для науки о данных. Победители вытесняют конкурентов с четвертого знака после запятой и, как и гоночные машины Формулы 1, не многие из нас приняли бы их за ежедневных гонщиков. Количество выделенного времени и иногда экстремальные методы не подходят для среды производства данных ».
Модели Kaggle действительно похожи на гоночные автомобили, они не созданы для повседневного использования. Реальные модели производства больше похожи на Lexus — надежные, но не кричащие.
Соревнования Kaggle и реальный мир оптимизируются под самые разные вещи, с некоторыми ключевыми отличиями:
Определение проблемы
Реальный мир позволяет вам определить вашу проблему и выбрать показатель, который определяет успех вашей модели. Это позволяет оптимизировать более сложную функцию полезности, чем просто единичную метрику, где соревнования Kaggle идут с одной заранее определенной метрикой и не позволяют эффективно определять проблему.
метрика
В реальном мире мы заботимся о выводах и скоростях обучения, ограничениях ресурсов и развертывания и других показателях производительности, тогда как в соревнованиях Kaggle единственное, что нас волнует, — это один показатель оценки. Представьте, что у нас есть модель с точностью 0,98, которая требует очень много ресурсов и времени, а другая — с точностью 0,95, которая намного быстрее и требует меньше вычислительных ресурсов. В реальном мире для многих доменов мы могли бы предпочесть модель точности 0,95, потому что, возможно, мы больше заботимся о времени вывода. В соревнованиях Kaggle не имеет значения, сколько времени потребуется для обучения модели или сколько графических процессоров ей требуется, чем выше точность, тем лучше.
Интерпретируемость
Точно так же в реальном мире мы предпочитаем более простые модели, которые легче объяснить заинтересованным сторонам, тогда как в Kaggle мы не обращаем внимания на сложность модели. Интерпретируемость модели важна, потому что она позволяет нам предпринимать конкретные действия для решения основной проблемы. Например, в реальном мире, глядя на нашу модель и видя корреляцию между особенностью (например, выбоины на улице) и проблемой (например, вероятность автомобильной аварии на улице), более полезна, чем повышение прогноза точность на 0,005%.
Качество данных
Наконец, в соревнованиях Kaggle наш набор данных собирается и спорется за нас. Любой, кто занимался наукой о данных, знает, что в реальной жизни это почти никогда не происходит. Но способность собирать и структурировать наши данные также дает нам больший контроль над процессом обработки данных.
стимулы
Все это стимулирует огромное количество времени, затрачиваемое на настройку наших гиперпараметров для извлечения последних падений производительности из нашей модели и, иногда, изощренных методологий инженера функций. Несмотря на то, что соревнования Kaggle являются отличным способом обучения науке данных и проектированию функций, они не учитывают реальные проблемы, такие как объяснение модели, определение проблемы или ограничения развертывания.
Королевский гул моделей
Пришло время начать выбор моделей!
Выбирая наш начальный набор моделей для тестирования, мы хотим помнить о нескольких вещах:
Выберите разнообразный набор начальных моделей
Различные классы моделей хороши для моделирования различных типов базовых шаблонов в данных Поэтому хорошим первым шагом является быстрое тестирование нескольких различных классов моделей, чтобы узнать, какие из них наиболее эффективно отражают базовую структуру вашего набора данных! В рамках нашего типа проблемы (регрессия, классификация, кластеризация) мы хотим попробовать сочетание моделей на основе дерева, экземпляра и ядра. Выберите модель из каждого класса, чтобы проверить. Мы расскажем больше о различных типах моделей в разделе «модели для тестирования» ниже.
Попробуйте несколько разных параметров для каждой модели
Хотя мы не хотим тратить слишком много времени на поиск оптимального набора гиперпараметров, мы хотим попробовать несколько различных комбинаций гиперпараметров, чтобы у каждого класса моделей была возможность работать хорошо.
Выберите сильнейших соперников
Мы можем использовать самые эффективные модели этого этапа, чтобы дать нам представление о том, в какой класс моделей мы хотим углубиться. Панель инструментов «Веса и уклоны» покажет вам класс моделей, которые лучше всего подходят для вашей задачи.
Погрузитесь глубже в модели в лучших классах моделей.
Затем мы выбираем больше моделей, относящихся к лучшим классам моделей, которые мы включили в шорт-лист выше! Например, если кажется, что линейная регрессия работает лучше всего, было бы неплохо также попробовать регрессию лассо или гребня.
Исследуйте гиперпараметрическое пространство более подробно.
На этом этапе я бы посоветовал вам потратить некоторое время на настройку гиперпараметров для ваших моделей-кандидатов. (В следующем посте этой серии мы углубимся в интуицию о выборе лучших гиперпараметров для ваших моделей.) В конце этого этапа у вас должны быть самые эффективные версии всех ваших самых сильных моделей.
Делая окончательный выбор — Kaggle
Выберите окончательные представления от разных моделей.В идеале мы хотим выбрать лучшие модели из более чем одного класса моделей. Это потому, что если вы сделаете свой выбор только из одного класса моделей, а он окажется неправильным, все ваши представления будут работать плохо. Соревнования Kaggle обычно позволяют вам выбрать более одной заявки для финального представления. Я бы порекомендовал выбирать прогнозы, сделанные вашими самыми сильными моделями из разных классов, чтобы добавить некоторую избыточность в ваши представления.
Таблица лидеров — это не ваш друг, ваши результаты перекрестной проверки.Самое важное, что нужно помнить, это то, что публичный список лидеров не ваш друг. Выбор моделей исключительно на основе ваших общедоступных рейтинговых таблиц приведет к переобучению набора данных обучения. И когда личный список лидеров раскрывается после окончания соревнования, иногда вы можете увидеть, что ваш рейтинг сильно падает. Вы можете избежать этой маленькой ловушки, используя перекрестную проверку при обучении ваших моделей. Затем выберите модели с лучшими показателями перекрестной проверки вместо лучших результатов в таблице лидеров. Делая это, вы противодействуете переобучению, измеряя производительность своей модели по нескольким наборам проверки, а не только по одному подмножеству тестовых данных, используемых публичной таблицей лидеров.
Делая окончательный выбор — Реальный мир
Ресурсные ограничения.Разные модели используют разные типы ресурсов, и знание правильности развертывания моделей на IoT / мобильном устройстве с небольшим жестким диском и процессором или в облаке может иметь решающее значение.
Время тренировки против времени прогноза против точности.Знание того, какие показатели вы оптимизируете, также важно для выбора правильной модели. Например, автомобили с самостоятельным вождением нуждаются в молниеносном прогнозировании, а системы обнаружения мошенничества должны быстро обновлять свои модели, чтобы быть в курсе последних фишинговых атак. Для других случаев, таких как медицинская диагностика, мы заботимся о точности (или площади под кривой ROC) гораздо больше, чем время обучения.
Сложность против объяснимости Компромисс.Более сложные модели могут использовать на порядок больше функций для обучения, а для прогнозирования требуется больше вычислений, но при правильном обучении можно получить действительно интересные шаблоны в наборе данных. Это также делает их запутанными и труднее объяснить, хотя. Знание того, как важно легко объяснить модель заинтересованным сторонам, а не просто захватить некоторые действительно интересные тенденции, в то время как отказ от объяснения является ключом к выбору модели.
Масштабируемость.Знание того, насколько быстро и насколько велика ваша модель для масштабирования, может помочь вам сузить выбор.
Размер обучающих данных.Для действительно больших наборов данных или тех, которые имеют много функций, нейронные сети или расширенные деревья могут быть отличным выбором. Принимая во внимание, что меньшие наборы данных могут лучше обслуживаться логистической регрессией, наивным байесовским или KNN.
Количество параметров.Модели с большим количеством параметров дают вам большую гибкость для получения действительно высокой производительности. Однако могут быть случаи, когда у вас нет времени, необходимого, например, для обучения параметров нейронной сети с нуля. Модель, которая хорошо работает из коробки, была бы подходящим вариантом в этом случае!
Сравнение моделей
Веса и уклоны позволяет отслеживать и сравнивать производительность ваших моделей с одной строкой кода.
После того, как вы выбрали модели, которые хотели бы попробовать, обучите их и просто добавьтеwandb.log ({‘Score’: cv_score})для регистрации вашего модельного состояния. После того, как вы закончили обучение, вы можете сравнить свои модели в одной простой панели!
Вы можете найти код, чтобы сделать это эффективно Вот, Я призываю вас раскошелиться это ядро и играть с кодом!
Вот и все, теперь у вас есть все инструменты, необходимые для выбора подходящих моделей для вашей задачи!
Выбор модели может быть очень сложным, но я надеюсь, что это руководство проливает свет и дает вам хорошую основу для выбора моделей.
Во второй части, «Вихревой тур по моделям машинного обучения», мы углубимся в модели ML, когда вы должны их использовать!
Если у вас есть какие-либо вопросы или пожелания, не стесняйтесь чирикать мне!