Лекция 7. КРУЧЕНИЕ
Крутящие моменты (внутренний силовой фактор) в поперечных сечениях
стержня. Кручение стержней круглого поперечного сечения: допущения,
деформации, напряжения, углы закручивания. Условия прочности, жёсткости.
Построение эпюр крутящих моментов.
Кручение имеет место в случае действия на вал момента (пары сил)
относительно его продольной оси, и в поперечных сечениях бруса возникает
только один силовой фактор – крутящий момент. Брус, работающей на
кручение называется валом. При кручении вала его поперечные сечения
поворачиваются друг относительно друга, вращаясь вокруг оси бруса.
Напряжения и деформации при кручении бруса. Под действием внешнего
скручивающего момента, приложенного на правом конце бруса, левый конец
которого жестко закреплен, брус будет закручиваться. Выделим из бруса
элементарный цилиндр длиной dx (рис. 19). Будем считать, что левое
сечение бруса жестко закреплено. Под действием крутящего момента T
правое сечение повернется на некоторый угол dφ.Так как ds = γ•dx = ρ•dφ,
то получаем 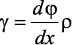
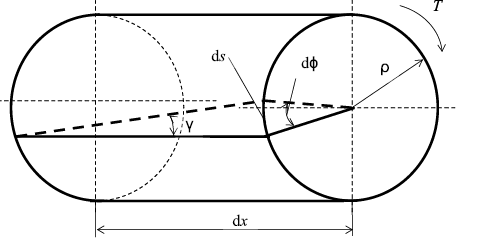
Рис. 19. Расчетная схема при кручении
Деформация бруса при кручении характеризуется относительным углом закручивания 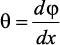
При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:
1. Поперечные сечения, плоские и перпендикулярные к его оси до
деформации, остаются плоскими (не коробятся) и перпендикулярными к оси
вала и после деформации (гипотеза Бернулли).
2. Радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины.
3. Длина вала в результате закручивания не изменяется.
Поперечное сечение вала ведет себя при кручении, как жесткий диск,
и деформацию кручения можно рассматривать, как результатсдвига одного
поперечного сечения относительно другого. В этом случае в точках
поперечного сечения вала возникают только касательные напряжения.
Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными.
Согласно закону Гука при сдвиге, имеем 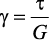
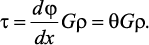
Из полученной зависимости следует, что касательные напряжения изменяются по радиусу по линейному закону.
При кручении все внутренние силы, распределенные по поперечному
сечению, приводятся к одной составляющей – к крутящему моменту.
Касательные напряжения перпендикулярны радиусам, проведенные через точки
их действия (рис. 20). Крутящий момент T в сечении бруса определяется
по формуле
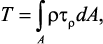
где ρ – плечо элементарной силы.
Подставляя значение касательного ускорения, получим
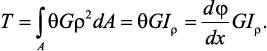
Элементарный угол закручивания бруса: 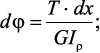
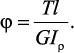
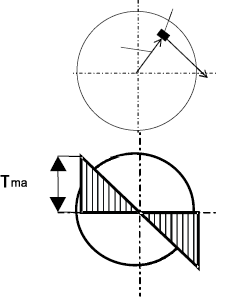
Рис. 20. Эпюра
Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости:
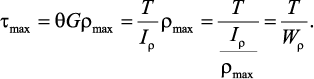
Прочность и жесткость при кручении. Условие прочности при кручении имеет вид
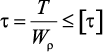
Условие жесткости:
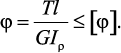
Для бруса круглого сечения эти условия принимают вид:
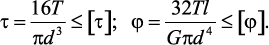
Построение эпюр крутящих моментов. Крутящий момент, возникающий
в поперечном сечении стержня, определяется методом сечений. Крутящий
момент равен алгебраической сумме скручивающих моментов, приложенных
к любой из частей стержня. Эпюра крутящих моментов – это график,
показывающий изменения крутящего момента по длине вала. Правило знаков
для эпюры крутящих моментов
При построении эпюры крутящих моментов используется правило
знаков: скручивающий момент, вращающий рассматриваемую часть стержня
против хода часовой стрелки при взгляде на поперечное сечение, вызывает
в этом сечении положительный крутящий момент.
Брус разбивается на участке, на каждом участке проводится сечение
и определяется крутящий момент. Затем строится эпюра крутящих моментов.
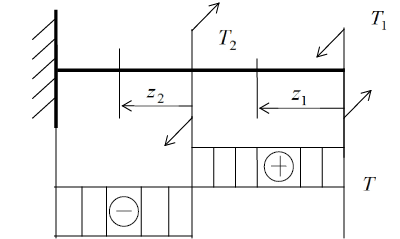
Рис. 21. Эпюра крутящих моментов
Кручение стержней с круглым поперечным сечением. Внутренние усилия при кручении, напряжения и деформации. Напряженное состояние и разрушение при кручении. Расчет на прочность и жесткость вала круглого поперечного сечения.
9. ПРОСТЫЕ ВИДЫ СОПРОТИВЛЕНИЯ. КРУЧЕНИЕ
9.1. Определение внутренних усилий при кручении
Кручение – простой вид сопротивления (нагружения), при котором на стержень действуют моменты в плоскостях, перпендикулярных к продольной оси стержня.
Стержень, работающий на кручение, в дальнейшем будем называть валом.
Используя метод мысленных сечений (см. рисунок), находим величину внутренних усилий, действующих в сечении вала при кручении. Очевидно, что в данном случае нагружения из шести уравнений равновесия, составленных для отсеченной части стержня относительно внешних сил и внутренних усилий, лишь одно не обращается тождественно в ноль:
∑Mx =0 Mx = Mкр .
Таким образом, при кручении в произвольном поперечном сечении вала из шести внутренних силовых факторов возникает только один – внутренний крутящий момент (Мx).
9.2. Определение напряжений и деформаций при кручении
Выведем формулу для определения касательных напряжений τ и найдем зависимость между углом закручивания ϕ и внутренним крутящим моментом Мx. Данная задача применительно к валам круглого сечения может быть решена с помощью элементарного математического аппарата, если ввести соответствующие гипотезы, которые достаточно хорошо подтверждаются экспериментами.
Гипотезы, принимаемые при расчете на кручение:
1)сечения, плоские до деформации, остаются плоскими и после деформации (гипотеза Бернулли, гипотеза плоских сечений);
2)все радиусы данного сечения остаются прямыми (не искривляются) и поворачиваются на один и
тот же угол ϕ, то есть каждое сечение поворачивается относительно оси x как жесткий тонкий диск;
57
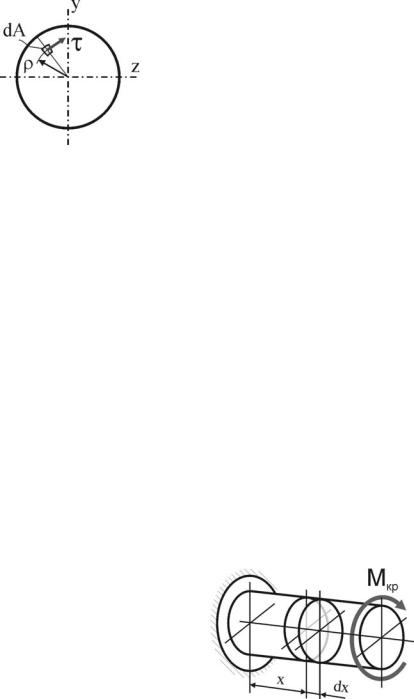
3) расстояния между сечениями при деформации не изменяются.
Статическая сторона задачи
Чтобы определить напряжения в поперечных сечениях стержня, рассмотрим, прежде всего, статическую сторону задачи.
Поскольку крутящий момент Мx – единственный внутренний силовой фактор в поперечном сечении, действующий при этом в плоскости данного сечения, можно предположить, что при кручении в поперечных сечениях вала возникают только касательные напряжения.
В сечении вала выделим элементарную площадку dA на расстоянии ρ от продольной оси (ось x) стержня. При кручении на площадке dA, будут действовать касательные напряжения τ, которые создадут элементарный крутящий
момент dMx относительно оси x: dMx =τdAρ.
Тогда полный момент, возникающий во всем сечении, найдем как
где τ – касательное напряжение, действующее на элементарной площадке dA, расположенной на произвольном расстоянии (радиусе) ρ от центра сечения.
Перпендикулярность вектора касательных напряжений радиусу объясняется отсутствием на поверхности вала касательных напряжений, параллельных его оси, и, соответственно (по закону парности касательных напряжений), отсутствием касательных напряжений вдоль радиуса.
Как видим, задача является внутренне статически неопределимой (см. лекцию № 4), так как неизвестен характер распределения касательных напряжений по сечению – τ(ρ)=?. В соответствии с общим планом решения статически неопределимых задач, рассмотрим геометрическую картину деформаций.
Геометрическая сторона задачи
Рассмотрим деформацию элемента стержня (вала) длиной dx, выделенного из закручиваемого стержня в произвольной точке с координатой x.
Условно примем, что левое сечение элемента dx остается неподвижным, а правое поворачивается на угол dϕ, создаваемый за счет закручивания вала на
58

длине dx. Один из радиусов OB, оставаясь прямым, поворачивается вместе с сечением на угол dϕ, при этом точка B переходит в положение B1, а образующая CB – в положение CB1, поворачиваясь на угол γ – угол сдвига в этой точке вала.
Длину дуги BB1 найдем из рассмотрения треугольников OBB1 и CBB1:
BB1 =ρdϕ=γdx
|
γ =ρ |
dϕ |
. |
(9.2) |
|
dx |
Физическая сторона задачи
Запишем закон Гука, связывающий касательные напряжения с углом сдвига (см. лекцию № 9)
Математическая сторона задачи
Подставим выражение (9.2) в формулу (9.3):
τ=ρ G ddxϕ,
а полученное выражение (9.4) – в формулу (9.1):
M x = ∫ρ2 G dϕ dA.
A dx
Так как в выражении (9.5) величины G и dϕ/dx, в соответствии с принятыми гипотезами, остаются постоянными по данному сечению, то их можно вынести за знак интеграла:
M x =G ddxϕ ∫A ρ2 dA.
Величина
Jρ = ∫ρ2 dA
A
называется полярным моментом инерции и является геометрической характеристикой данного сечения (см. лекцию № 2).
Таким образом, окончательно можем записать
|
M x =G |
dϕ |
Jρ , |
(9.6) |
|
|
dx |
||||
59
или, подставляя (9.4) в (9.6),
M x = ρτ Jρ .
Величина касательных напряжений при кручении определяется следующим образом:
τ= M x ρ .
Jρ
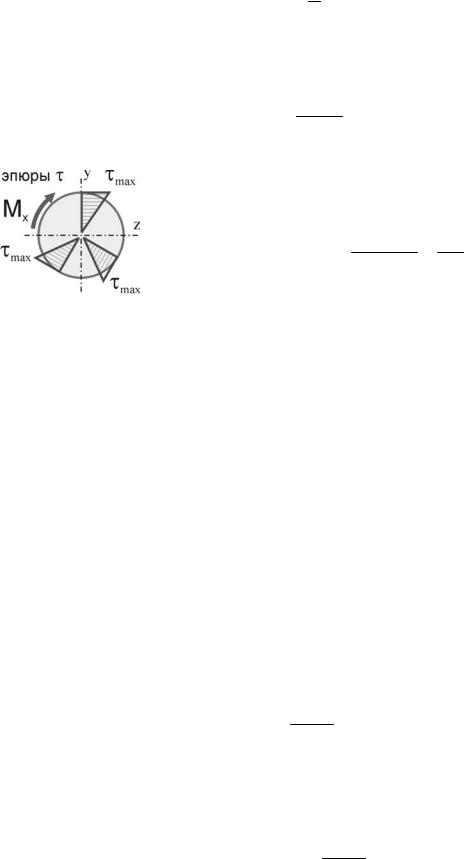
Как видим, касательные напряжения распределены по сечению вала по линейному закону и достигают максимальной величины на поверхности вала (при ρ=ρmax):
τmax = M x ρmax = Mx ,
Jρ Wρ
где Wρ=Jρ/ρmax – полярный момент сопротивления.
Из формулы (9.6) легко найти и другие величины, характеризующие деформацию вала при кручении.
Величина |
|||
|
θ= |
dϕ |
(9.7) |
|
|
dx |
|||
называется относительным (погонным) углом закручивания и имеет размер-
ность рад/м.
Используя выражение (9.6), найдем формулу для определения относительного угла закручивания:
|
θ= |
M x |
. |
(9.8) |
|
G Jρ |
Зная формулы (9.7) и (9.8) для определения относительного угла закручивания, можно записать формулу для определения взаимного угла поворота двух сечений, расположенных на расстоянии l друг от друга:
ϕ= ∫l M x dx . 0 G Jρ
Если в пределах участка длиной l крутящий момент и геометрические характеристики сечения вала остаются постоянными, то угол закручивания можно определить как
ϕ=θ l = Mx l G Jρ
60
Соседние файлы в папке Лекции по сопромату
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье начнем говорить о кручении. Это одна из базисных тем в сопромате, как и растяжение-сжатие. Знания этой темы помогут тебе при изучении более сложных тем курса «сопротивление материалов».
Кручение – это такой вид деформации, при котором в сечениях стержня возникают крутящие моменты (T).
На кручение, как правило, работают детали, которые называются валами. Детали, которые широко используются в машиностроении.
Что такое крутящий момент?
Крутящий момент – это внутренний силовой фактор, возникающий в сечениях стержней испытывающих деформацию кручения.
На практике же стержни не работают исключительно на кручение, они могут и растягиваться, и изгибаться. Но это уже более продвинутые темы – сложное сопротивление. В этом же разделе будем рассматривать чистое кручение.
В чем измеряется крутящий момент и как обозначается?
Крутящие моменты обозначаются буквой – T (сокращённое с английского: Torque – крутящий момент), однако, часто в другой литературе ты можешь встретить обозначение — Мкр. Ты можешь использовать любое обозначение, какое больше нравиться, либо которое использует твой преподаватель.
В задачах тебе будут даны крутящие моменты, скорее всего, в Н·м либо кН·м.
Построение эпюры крутящих моментов
В этой статье расскажу, как строить эпюры при кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов).
На самом деле, многие рассматриваемые здесь принципы сильно похожи на те, что мы изучали ранее в уроке про построение эпюр при растяжении (сжатии). Здесь фактически будем делать всё то же самое, только оперировать другими обозначениями и названиями. После изучения того урока, с кручением у тебя точно не возникнет никаких трудностей.
В качестве примера, возьмём следующую расчётную схему:

Будем считать, что стержень изготовлен из стали (G = 8 · 1010 Па), а диаметры ступеней равны: d1=150 мм, d2=200 мм, d3=300 мм.
Под действием внешних моментов (M), их еще часто называют вращающими или скручивающими моментами, в поперечных сечениях стержня возникают внутренние моменты – крутящие (T).

Правило знаков для крутящих моментов
Чтобы построить эпюру крутящих моментов, необходимо задаться каким-то правилом знаков для крутящих моментов. В этой статье я буду использовать следующее правило:
- Если внешний момент (M), в плоскости сечения, поворачивает ПРОТИВ часовой стрелки, то крутящий момент (T) – положительный.

- Если внешний момент (M), в плоскости сечения, поворачивает ПО часовой стрелке, то крутящий момент (T) – отрицательный.

Можно учитывать знак крутящего момента ровно наоборот. Главное, придерживаться этого правила при расчёте всех участков и ориентироваться по полученным эпюрам: в какую сторону у тебя будут направлены внешние моменты, внутренние – крутящие моменты, куда будут поворачиваться сечения. Как видишь, знаки здесь нам нужны, чтобы задать определённые правила игры, а правило знаков – условное и не имеет физического смысла.
Расчёт крутящих моментов
Что же, давай, наконец, приступим к расчёту крутящих моментов. Пронумеруем расчётные участки:

Используя правило знаков, описанное выше, рассчитаем крутящие моменты на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры касательных напряжений при кручении
Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.
Расчёт максимальных касательных напряжений
Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.
Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи диаметры участков известны. Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры углов закручивания (поворотов)
Под действием внешних – скручивающих моментов, поперечные сечения стержня будут поворачиваться на определенный угол (φ). В этом разделе будем учиться определять эти углы закручивания (поворотов) поперечных сечений и строить эпюру.
Обозначим точки в характерных сечениях стержня:

Расчёт начинаем от жёсткой заделки и сразу можем записать, что в точке A, угол поворота равен нулю, т. к. здесь заделка ограничивает любые повороты сечения:
Чтобы рассчитать поворот сечения B, нужно учесть поворот предыдущего сечения:
А также, угол закручивания участка между расчётными сечениями:
Угол закручивания участка можно посчитать по формуле:

где l – длина участка; Ip – полярный момент инерции; G – модуль сдвига.
G – модуль сдвига (модуль упругости 2 рода) – определяется при испытании образцов на кручение, тем самым зависит от материала образца.
Модуль сдвига (G) известен, по условию задачи.
Формула для определения полярного момента инерции для круглого сечения следующая:

Зная диаметры, сразу вычислим полярные моменты инерции для каждого участка:

Определим угол закручивания сечения B, с учётом вышеуказанных формул:

Также можно перевести это значение в привычные градусы:

Для двух других сечений расчёт производится аналогичным образом.
Угол поворота сечения С

Угол поворота сечения D

По рассчитанным значениям, построим эпюру углов закручивания поперечных сечений:

Таким образом, свободный торец стержня, повернётся на 0.58 градуса, относительно неподвижного сечения A.
Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям.
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
Условие прочности
За допустимое касательное напряжение [τ], часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ]:

Максимальные касательные напряжения (τmax) в сечениях можно найти по формуле:

где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления можно посчитать этим формулам.
8.3. ИЗГИБ С КРУЧЕНИЕМ
Изгиб с кручением – вид сложного сопротивления, при котором в поперечном сечении бруса возникают изгибающие и крутящий моменты. Рассмотрим случай, при котором внешние силы располагаются в плоскости поперечного сечения, но не пересекают геометрическую ось х (рис. 8.12, а). Силу F разложим на ее составляющие Fz, Fy. Методом сечений определим внутренние усилия в произвольном сечении х (рис. 8.12, б). Спроецировав все силы на координатные оси и составив уравнения моментов относительно координатных осей, найдем внутренние усилия. Из шести внутренних усилий не равно нулю пять. На выделенном элементе В (рис. 8.12, б) показаны действующие по его граням напряжения (рис. 8.13, а). От поперечных сил и крутящего момента возникают касательные напряжения τQy, τQz, τT. От изгибающих мо- ментов – нормальные напряжения σ′ и σ″. Для длинных валов и балок (ℓ > 10 d) влиянием поперечных сил часто пренебрегают. Таким образом, учитывают только три момента: крутящий и два изгибающих. От них возникают три напряжения: одно касательное и два нормальных (рис. 8.13, б). Расчет на прочность при изгибе с кручением Из рисунка 8.13, б следует, что в произвольном сечении возникает плоское напряженное состояние Рис. 8.12. Определение внутренних усилий при изгибе с кручением Рис. 8.13. Анализ напряженного состояния Как при изгибе, так и при кручении круглого сечения опасными являются точки на периферии. Для круга и кольца Условие прочности для пластичных материалов по III теории прочности (наибольших касательных напряжений): σэкв = σ1 − σ3 ≤ [σ] Поскольку для круглого и кольцевого сечений не существует точки, одинаково удаленной от обеих осей инерции z, y, то используют результирующий момент – геометрическую сумму векторов изгибающих моментов относительно осей z, y: Условие прочности при совместном действии изгиба и кручения: σ=≤[σ] Мприв – приведенный момент, действие которого эквивалентно совместному действию My, Mz, T в соответствии с используемыми теориями прочности. По III теории прочности (наибольших касательных напряжений) Приведенного момента в действительности не существует, изобразить его нельзя, вектора он не имеет. Величина приведенного момента зависит от используемой теории прочности. Результаты расчетов по III и IV теориям прочности близки, отличаются примерно на 5–10 %. Пример 8.9. (Вольмир А. С. Сборник задач … 6.52). Вал с кривошипом подвергается действию силы F = 3,5 кН. Определить диаметр вала по третьей теории прочности при [σ] = 160 МПа; ℓ = 50 см, а = 10 см. Решение. Внутренние усилия определяем методом сечений. Рассекаем вал на две части в произвольном сечении х, Отбрасываем одну из частей (поз. б рисунка), Заменяем действие отброшенной части внутренними усилиями и в координатной системе xyz составляем У равнения статики: Строим эпюры изгибающего и крутящего моментов, действующих в поперечных сечениях вала (поз. в и г рисунка). Находим приведенный момент в опасном сечении – в защемлении: Из условия прочности при изгибе с кручением σ [σ] Округлив до большего значения, принимаем диаметр вала d = 50 мм.
7.4 Кручение с изгибом. Определение внутренних усилий и напряжений
Ранее нами был рассмотрен расчет на прочность валов при чистом кручении. Однако круглые валы редко работают на чистое кручение. Как правило, при работе вал изгибается собственным весом, весом шкивов, давлением на зубья шестерен, натяжением ремней и т. д. В таком случае вал будет находиться в условиях сложного сопротивления и испытывать совместное действие кручения и изгиба.
Кручение с изгибом – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.
Определение внутренних усилий и напряжений при кручении с изгибом. Для определения внут-ренних усилий воспользуемся методом мысленных сечений:

Обычно две составляющие попе-речной силы (Qy, Qz) и изгибающего момента (My, Mz) приводят к их полным результирующим

Заметим, что часто поперечной силой пренебрегают (для достаточно длинных валов) и рассматривают кручение с изгибом как совместное действие крутящего (Mx, Mкр, T) и изгибающего (Mи) моментов.
Рекомендуемые материалы
Опасное сечение вала будем искать, как и прежде, по эпюрам внутренних усилий. При построении эпюр внутренних усилий при кручении с изгибом необходимо иметь ввиду следующие правила:
— эпюры крутящего момента Mx, а также эпюры составляющих поперечной силы Qy, Qz и изгибающего момента My, Mz строятся по той же процедуре, что и ранее;
— результирующая поперечная сила Q может не лежать в плоскости действия результирующего изгибающего момента Mи, а потому между ними уже не будет соблюдаться зависимость Журавского (dM/dx=Q), а, следовательно, и правила проверки эпюр, введенные для плоского изгиба;
— эпюра полного изгибающего момента будет прямой только на тех участках, где My и Mz ограничены прямыми с общей нулевой точкой, на участках, где такая общая точка отсутствует эпюра Mи будет описываться вогнутой кривой и строится по точкам (связано с тем, что вектор Mи в разных сечениях имеет различное направление).
Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего Mx и полного изгибающего Mи моментов. Опасным будет считаться то сечение, где оба момента достигают своей максимальной величины. Если моменты достигают максимума в разных сечениях, необходимо проверить все сечения, в которых эти внутренние усилия достаточно велики.
Рис.53. Напряжения
Для определения максимальных напря-жений используем принцип независимости дей-ствия сил и найдем напряжения отдельно от кручения и отдельно от изгиба:
напряжения при кручении


напряжения при изгибе

или

где Jос – осевой момент инерции для круглого сечения (Jос = Jz = Jy).
Вводя обозначение 
Родителям отвечает психолог — лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

при этом

где Wос – осевой момент сопро-тивления для круглого сечения (Wос=Jос/

Опасными точками в сечении будут являться точки наиболее удаленные от нейтральной оси (для круглого сечения – линии, перпендикулярной плоскости действия результирующего изгибающего момента). При этом в токах сечения будет возникать плоское напряженное состояние, а потому расчет на прочность необходимо проводить с привлечением известных теорий прочности.






